图1 单导线自由扭转覆冰示意图
Fig.1 Schematic diagram of free torsional on wire by icing
摘要 输电线路冰灾长期威胁电网安全稳定运行，结合输电线路实际覆冰情况，建立准确的输电线路覆冰增长模型对电网冰灾防御具有重要意义。但现有的输电线路覆冰增长模型多忽略了输电线路自由扭转覆冰过程。该文基于野外自然环境下输电线路单导线自由扭转覆冰的观测结果，建立了反映导线自由扭转覆冰动态过程的仿真分析模型。在重庆大学雪峰山能源装备安全国家野外科学观测研究站开展GJ50导线自由扭转覆冰实验，将实验结果与数值仿真结果进行对比分析。结果表明：导线扭转角度和单位覆冰质量沿单导线中心点对称分布；仿真获得的导线覆冰形状与实际情况吻合；导线扭转角度和单位覆冰质量仿真值与测量值误差平均值均在10%以内。
关键词：单导线 扭转覆冰 数值仿真 野外实验验证
冬季，输电线路覆冰是严重威胁电网安全运行的重要原因之一。轻则引发闪络跳闸等故障，重则造成断线倒塔等严重事故，迫使大面积地区长期断电[1-3]。2008年后，我国在输电线路覆冰形成机理、输电线路覆冰致灾机制、输电线路防冰和除冰技术方面取得了一定的进展，防止了大面积、长时间电网冰灾的发生[4-8]。但近年来，极端天气频发，易覆冰的“微地形小气候”区域数量大幅增加。此外，随着我国电网建设的不断完善，输电线路不可避免地经过低温高湿的易覆冰区，输电线路依然长期面临冰灾风险，输电线路冰灾仍时有发生[9]。
长期以来，建立准确、方便、具有实际应用价值的输电线路覆冰模型是国内外电网冰灾研究学者的一致追求。早在1953年，I. Imai便提出针对雨凇覆冰，以温度、风速为主要变量的输电线路覆冰模型[10]。R. W. Jr. Lenhard和K. F. Jones分别于1955年和1998年提出了以降水量为核心影响因素的输电线路覆冰模型[11-12]。1998年，重庆大学蒋兴良等对三峡地区输电线路覆冰进行了仿真分析[13]。2000年，L. Makkonen提出考虑导线覆冰物理过程的输电线路覆冰模型，很好地提升了模型的准确度[14]。但彼时数值仿真技术发展有限，输电线路覆冰模型求解困难。覆冰环境下，大气覆冰环境参数难以准确获取，也使模型缺乏有效输入参量。随着计算机技术的进步，输电线路覆冰模型的求解问题得以缓解。重庆大学蒋兴良课题组研究开发的积冰装置实现了大气覆冰环境参数的实时获取[15-17]。基于此，文献[18-19]采用计算流体动力学（Computational Fluid Dynamics, CFD）或有限元法实现了输电线路覆冰的动态模拟。
但输电线路实际运行条件下的覆冰情况多与上述模型的数值仿真结果不同。其原因在于输电线路实际覆冰时导线将绕其中心自由扭转形成圆形冰。而上述输电线路覆冰模型大多忽略了这一过程，获取的仿真结果仅为沿导线迎风侧逐步生长的单侧覆冰。输电线路自由扭转覆冰难以在实验室内通过人工覆冰实现，相关实验需要在野外自然环境下开展。文献[20-21]对导线扭转刚度进行实验与仿真计算，发现输电线路覆冰厚度的增加会影响输电线路自由扭转覆冰。文献[22]的研究结果表明，导线扭转是分裂导线发生翻转的重要原因，并通过有限元计算进行了仿真分析。胡琴等[23]的野外观测表明，在覆冰环境相同的情况下，单导线的扭转角度比分裂导线大。蒋兴良等[24]开展了导线覆冰扭转特性仿真研究，并进行了实验验证，但没有对导线冰形进行对照分析。韩兴波等[25]分析了输电线路覆冰与扭转的相互影响机制，提出导线扭转是输电线路覆冰的重要影响因素。
综上所述，通过数值仿真实现输电线路覆冰的动态模拟具有重要意义，但输电线路自由扭转覆冰过程尚未被很好地考虑进去。因此，本文在重庆大学雪峰山能源装备安全国家野外科学观测研究站（后文简称“雪峰山国家野外站”）观测单导线自由扭转覆冰。由观测结果并基于流体力学与力学平衡原理，建立输电线路单导线自由扭转覆冰仿真模型，实现单导线自由扭转覆冰的动态模拟。进而在雪峰山国家野外站开展单导线野外自然覆冰实验，将实验结果与仿真结果进行对比分析。本文的研究成果将为输电线路覆冰仿真分析与覆冰扭转研究提供参考。
受实验条件及场地限制，输电线路自由扭转覆冰难以在实验室内通过人工覆冰实验实现。因此，本文在雪峰山国家野外站观测野外自然环境下的单导线自由扭转覆冰。单导线以两侧等高方式悬挂于雪峰山国家野外站内的两座雨凇塔之间，长度均为100 m，保持弧垂一致。
输电线路单导线自由扭转覆冰示意图如图1所示。其可分为三个主要阶段。第一阶段是水滴在导线迎风侧累积形成单导线翼形冰。覆冰首先在导线迎风面发生，随着导线表面过冷却水滴冻结质量的增加，覆冰在导线表面逐步累积，呈现如图2所示的飞机机翼一般的形状，即翼形冰。此后，若覆冰环境变化导致导线覆冰终止或覆冰速度大幅降低，则导线持续保持翼形冰形态不发生扭转。
图1 单导线自由扭转覆冰示意图
Fig.1 Schematic diagram of free torsional on wire by icing
图2 野外自然环境下单导线表面的翼形冰
Fig.2 Wing ice of wire on natural environment
与之相反，若覆冰持续保持或加强，则进入输电线路单导线自由扭转覆冰的第二阶段——冰层带动导线自由扭转。在该阶段，单导线跟随冰层自由扭转一定角度，促使一部分原本位于背风侧的导线转向迎风侧；同时，冰层位于导线迎风侧的部分经过扭转后由翼形冰前沿转变为翼形冰上表面区域。单导线自由扭转覆冰的第三阶段为相持阶段，该阶段紧随第二阶段产生。在此阶段，单导线保持上一阶段自由扭转后的角度不变，覆冰持续在迎风侧导线及冰层上累积。当单导线在相持阶段生成足够厚的冰层后，则会再次进入冰层带动导线自由扭转阶段，并随之进入下一个新的相持阶段，且会在整个覆冰期间反复经历这一过程，最终在导线表面形成如图3所示的圆形冰。根据相持阶段的特征可以发现，自由扭转覆冰的第一阶段本质上为导线扭转角度为零的相持阶段。因此，可以认为单导线自由扭转覆冰是第二和第三阶段交替出现的过程。
图3 野外自然环境下单导线表面的圆形冰
Fig.3 Circular ice of wire on natural environment
冰层带动单导线自由扭转物理过程示意图如图4所示。导线截面中心点为O，当导线迎风侧生成翼形冰后，随之产生促使导线发生扭转的冰扭力矩Ti，该力矩由导线自身具备的反扭力矩Tc相平衡，翼形冰的重心为O′。随着翼形冰的逐步累积，覆冰所产生的重力增大，重心O′位置也发生变化，从而增大冰扭力矩。当冰扭力矩大于导线产生的反扭力矩时，导线发生第一次扭转，自由扭转角度为β0。扭转后，冰层力矩的力臂减小，冰扭力矩再次回到小于导线自身反扭力矩的状态，覆冰持续在导线表面发展。随着新的冰层生成，导线覆冰质量持续增加，冰层重心再次发生改变，由O′变化为O″，直至再次达到冰扭力矩大于导线自身反扭力矩时，导线再度自由扭转一定角度，扭转后，冰层在原来的扭转位置上增加了β1角度。此后循环往复冰扭力矩与导线自身反扭力矩动态平衡的过程。导线最终的扭转角度为历次扭转产生的导线扭转角度增量之和。
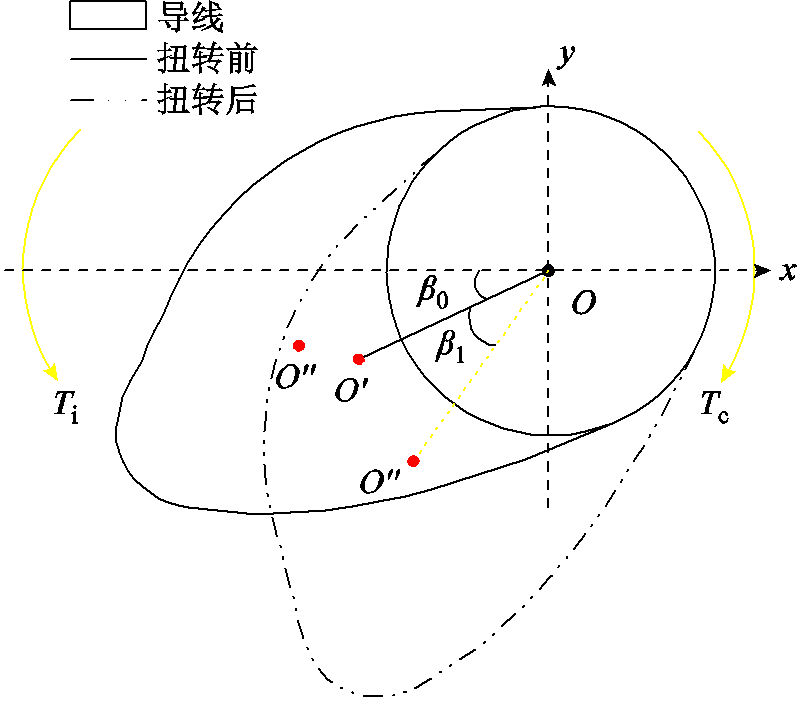
图4 冰层带动单导线自由扭转物理过程示意图
Fig.4 Sketch of free torsional on single conductor by icing
由野外自然环境下的单导线自由扭转覆冰观测可知，单导线自由扭转覆冰是冰层产生的冰扭力矩与导线自身反扭力矩的动态平衡过程。本文根据此过程建立单导线自由扭转覆冰数值仿真模型。
本文依据L. Makkonen输电线路覆冰模型基本思想[14]，将单导线外部流场简化为二维平面，通过求解单导线外部流场确定过冷却水滴碰撞过程。在简化的二维平面内，将空气中所含过冷却水滴的运动过程表示为离散项，其随气流运动的方程为
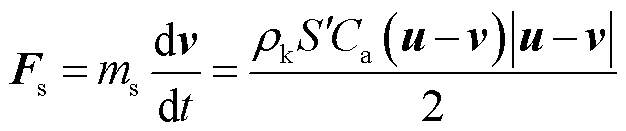（1）
式中，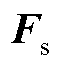
为气流对过冷却水滴的曳力，N；ms为过冷却水滴质量，kg；ρk为空气密度，kg/m3；S'为过冷却水滴横截面积的最大值，m2；Ca为空气阻尼系数；u为二维平面内空气的速度向量，m/s，；v为二维平面内过冷却水滴的速度向量，m/s。
覆冰环境中，气流的运动过程在简化的二维平面内，可视作低速不可压缩的粘性流动。采用式（2）所示的N-S（Navier-Stokes）方程表示其动量方程和连续性方程。
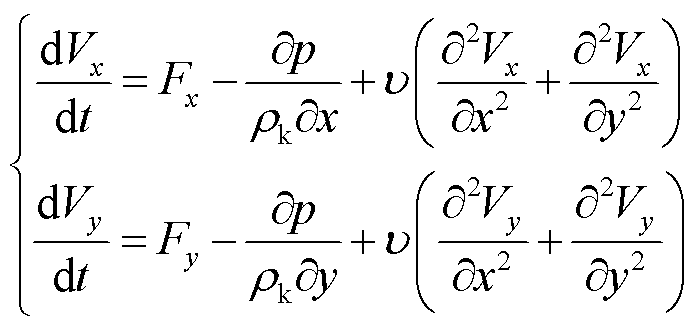（2）
其中
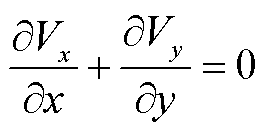（3）
式中，Vx为气流沿着x轴方向的速度，m/s；Vy为气流沿着y轴方向的速度，m/s；Fx为气流场沿x轴方向的分力，N；Fy为气流场沿y轴方向的分力，N；p为压强，Pa；∂p/∂x与气流密度的比值表示二维平面内气流场的压差力；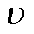
为空气运动粘度，m2/s，其与(∂2Vx/∂x2+∂2Vx/∂y2)、(∂2Vy/∂x2+∂2Vy/∂y2)的乘积表示气流场的粘性力。
为简化方程式（2）和式（3）的计算过程，提高计算效率，采用边界元法[26]对输电线路外部流场进行求解，由求解结果结合式（1）计算过冷却水滴运动轨迹及其与导线碰撞的坐标点。
单导线覆冰质量M的动态增长计算采用式（4）所示的三参数模型。
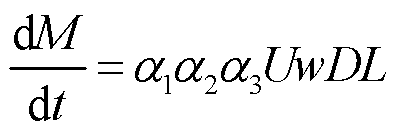（4）
式中，α1、α2和α3分别为碰撞系数、捕获系数和冻结系数，分别表示覆冰环境中，过冷却水滴随气流运动遭遇导线后与导线的碰撞过程、过冷却水滴与导线碰撞后被导线捕获依附于导线表面的捕获过程和过冷却水滴在导线表面凝固为冰的冻结过程；U为风速，m/s；w为空气中液态水含量，g/m3，D为导线直径，m；L为导线长度，m。
过冷却水滴与导线表面的碰撞系数α1由2.1节中导线外部流场的求解结合文献[27]所提的经验公式获取。本文认为所有与导线碰撞的过冷却水滴均不会离开导线表面，且不考虑导线出现冰棱的过冷却水滴未冻结的情况，因此，表示导线捕获过冷却水滴的捕获系数α2取值为1。冻结系数α3的取值为
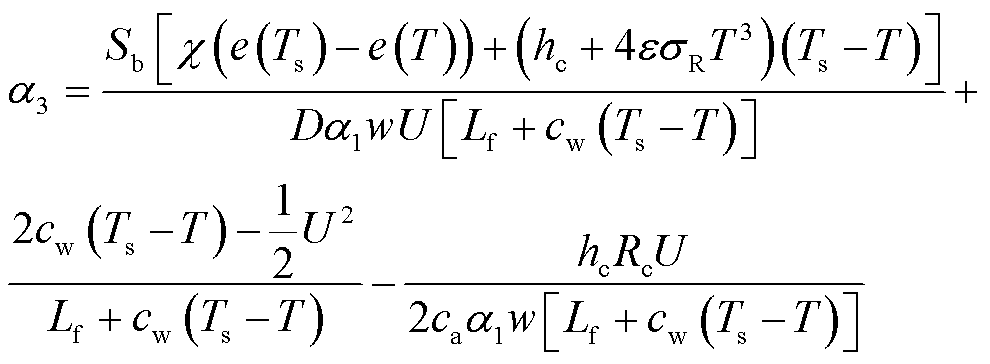（5）
式中，Sb为导线表面积，m2；χ为蒸发或升华系数，J/(m2·kPa)；e(T)为温度T下输电线路冰面的饱和水汽压，kPa；Ts和T分别为导线冰层表面温度和环境温度，K；hc为表面传热系数，J/(m2·K)；ε为发射率，ε=0.95；σR为斯忒藩-玻耳兹曼常量；Lf为冰的融化潜热，Lf =3.35×105 J/kg；cw为冰的比热容，cw= 4.2×103 J/(kg·℃)；ca为空气的比热容，ca= 1 030 J/(kg·℃)；Rc为覆冰导线表面的局部恢复系数，Rc=0.79。
单导线自由扭转覆冰过程中，在冰扭力矩作用下，冰层带动导线绕中心轴转动，在导线表面形成不规则覆冰。将冰层形状分割为n个三角形，面积为Ai的三角形重心坐标为(xi, yi)，i = 1, 2,…, n，则冰层的重心O坐标(Ox, Oy)为
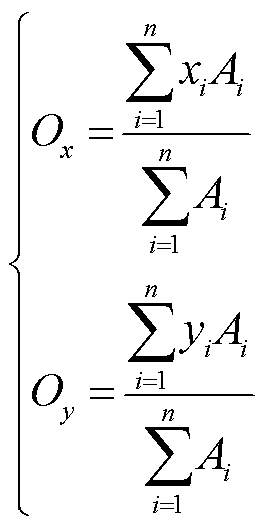（6）
根据文献[23,28]，输电线路在冰层带动下扭转角度β后，其状态可表示为
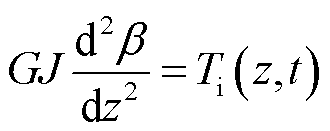（7）
式中，G为导线的切变模量，Pa；J为导线截面极惯性矩，m4；GJ为导线扭转刚度，N·m2；z表示沿导线方向；t为时间，s；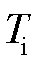
为冰扭力矩，N·m。导线扭转刚度沿其长度分布不一，导线上j处的扭转刚度可等效为长度为lj的导线与长度为L-lj的导线并联的扭转刚度[28]，即
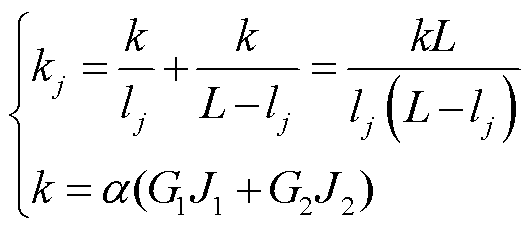（8）
式中，kj为导线上j处的等效刚度，N·m2；lj为导线上j处距离导线端点的距离，m；α为绕拧系数；G1、G2分别为钢和铝的切变模量，Pa；J1、J2分别为导线钢芯和铝绞线截面极惯性矩，m4。
冰扭力矩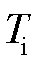可表示为
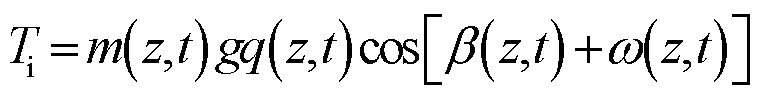（9）
式中，m(z,t)为沿导线方向t时刻的单位覆冰质量，kg/m；g为重力加速度，m2/s；q(z,t)为沿导线方向t时刻导线冰层重心与原点的距离，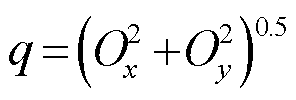
，m；β(z,t)为沿导线方向t时刻导线在冰层作用下的扭转角度，rad；ω(z,t)为沿导线方向t时刻冰层的重心坐标角度，rad。
由式（7）～式（9）可得，在导线j处有
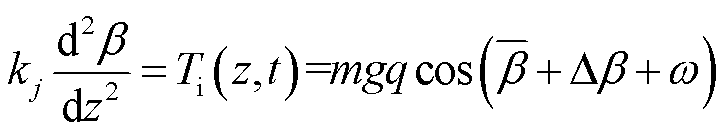（10）
式中，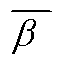
为冰层带动导线扭转的平均扭转角；Δβ为冰层带动导线扭转角度的增量，且
。
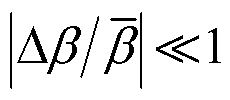将式（10）展开化简可得
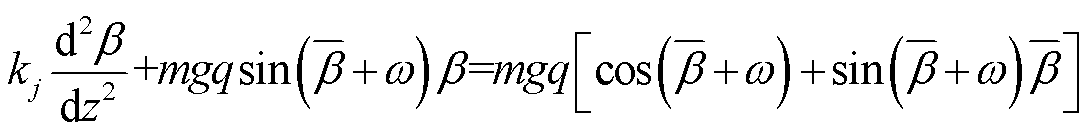（11）
将式（11）离散，通过标准中心差分方程得到导线各点覆冰扭转角ψj（j =1, 2,…, N）的矩阵方程为
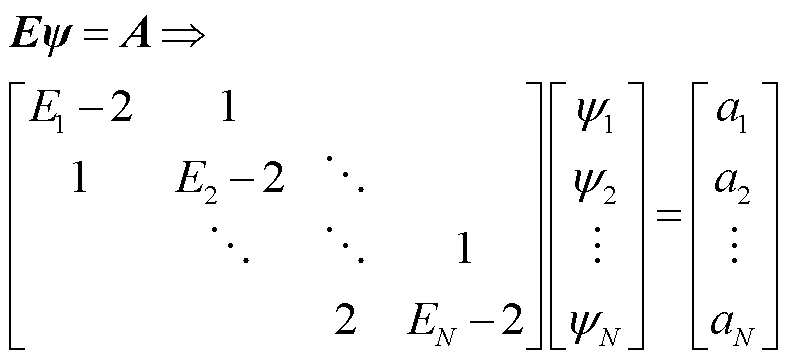（12）
其中
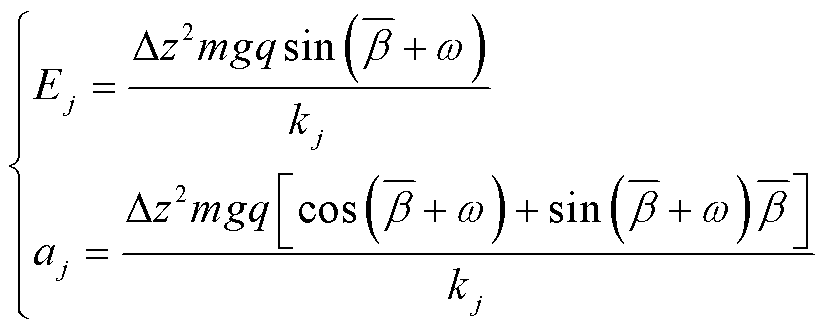（13）
式中，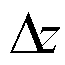
为从导线悬挂点到中点，导线各点位置变化沿导线方向长度增加的数值。
由前文可知，根据导线外部流场及导线过冷却水滴冻结系数的计算，由式（4）可得单导线未发生扭转时的覆冰形状及质量。再将单导线覆冰质量代入式（12）可得当前冰扭力矩下单导线的扭转角度，并根据该扭转角度更正导线覆冰形状，从而实现单导线自由扭转覆冰的动态模拟。由此建立如图5所示的单导线自由扭转覆冰数值仿真流程。为便于求解，降低计算复杂度，本文将导线分为长度相等的线段，对其中一段用N个点将其分割为N-1个单元，在每个单元内，导线自由扭转覆冰的质量及角度均相同。
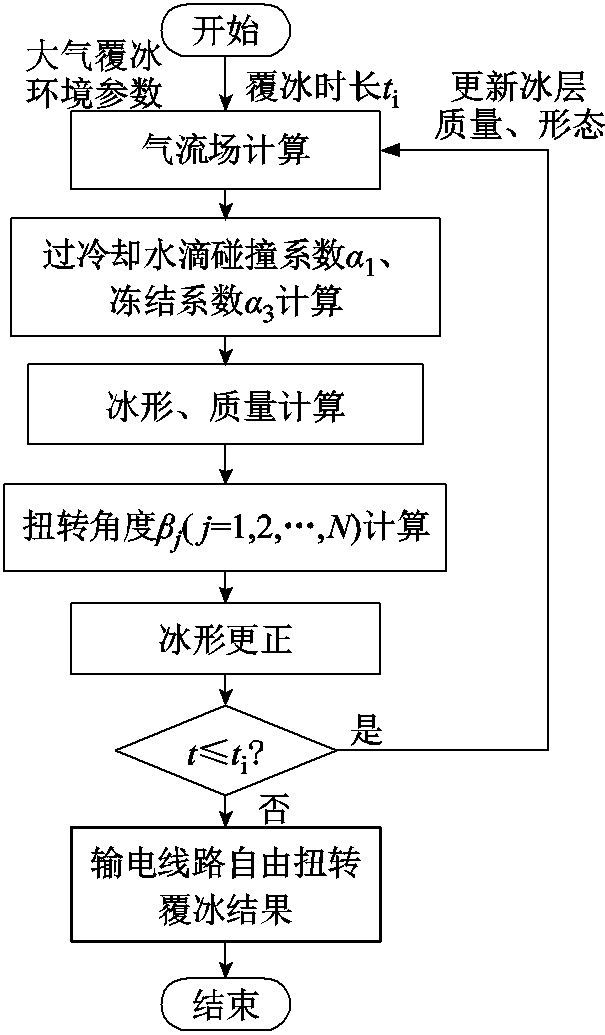
图5 单导线自由扭转覆冰数值仿真流程
Fig.5 Calculation for free torsion of wire by icing
计算时，由外部输入大气覆冰环境参数（环境温度T、风速U，空气中液态水含量w、过冷却水滴中值直径（Mean Volume Diameter, MVD））和覆冰持续时间。根据输入的大气覆冰环境参数计算导线各个点的外部流场情况。通过外部流场计算和式（4）、式（5）获取导线各点覆冰形状及质量。根据覆冰质量获取输电线路各点的扭转角度并据此对覆冰形状加以更正。反复迭代上述过程直到覆冰时间达到要求，实现导线自由扭转覆冰的动态数值仿真。
本文的野外自然覆冰实验在图6所示的雪峰山国家野外站开展。其处于东南暖湿气流与西北寒流交汇的昆明准静止锋线尾端，天然的微地形小气候特征提供了形成多类型典型覆冰的条件，每年10月至次年3月均存在覆冰可能，年最大覆冰厚度达到500 mm，最大风速达35 m/s，是研究自然覆冰的理想场所。
图6 重庆大学雪峰山国家野外站
Fig.6 Xuefeng Mountain National Observation and Research Station of Chongqing University
如图7所示，在雪峰山国家野外站的两座雨凇塔之间等高布置GJ50型号的导线进行实验，雨凇塔之间的距离为80 m，导线长度为100 m。导线自由扭转覆冰过程中的扭转角度由BWT901CL数字姿态传感器获取。该传感器内置充电模块，工作时无需外接电源，数据信息通过蓝牙模式无线传输，工作温度为-45～80℃，适用于覆冰导线扭转角度观测。传感器内置高精度陀螺仪模块并自带适配计算机端及手机端的数据采集系统，通过卡尔曼滤波融合算法排除环境中其他因素干扰，数据输出稳定，测量范围为-180°～180°，测量精度为±0.2°。导线扭转角观测布置示意图如图8所示，传感器紧固于导线表面，覆冰过程中跟随导线一同扭转，实时记录导线扭转角度。在导线上均匀布置9个数字姿态传感器，按雨凇塔Ⅰ至雨凇塔Ⅱ的方向，依次记为1～9号观测点。
图7 野外现场实验导线布置
Fig.7 Wire layout of natural test
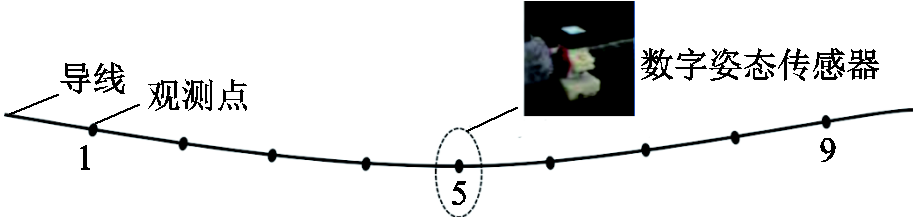
图8 导线扭转角观测布置示意图
Fig.8 Ice density measurement process
大气覆冰环境参数采用如图9所示的自主研发的四圆柱旋转多导体积冰器采集。其采用基于四圆柱体覆冰增量反演大气覆冰参数的方法，不仅能获取环境温度和风速，同时还能采集常规仪器设备难以获取的空气中液态水含量和过冷却水滴中值直径两大关键参数[15-17]。
图9 四圆柱旋转多导体积冰器
Fig.9 Four rotation ice accretor
自然覆冰发生前，布置好传感器及四圆柱旋转多导体积冰器，并测试两者的信息传递是否完整准确。自然覆冰过程中，导线扭转角度及覆冰环境参数的观测自动进行。每隔0.5 h对观测点进行巡查，确定是否有不利于实验的情况发生，并检查扭转角度及环境参数采集是否正常。覆冰结束后在各观测点采集冰块，测量各观测点导线的单位覆冰质量，并用相机记录观测点的覆冰形状。
按照图5所示的数值仿真流程，将获取的大气覆冰环境参数代入建立的单导线自由扭转覆冰模型，通过Matlab编程计算获得数值仿真结果，并将其与实验结果进行对比分析。
GJ50导线1～9号观测点在5个自然覆冰期扭转角度的测量值与仿真值如图10所示。从图中可以看出，不同冰期下9个观测点扭转角度的测量值与仿真值的变化趋势保持一致。按照式（14）计算冰期1～5中导线在各观测点测量值与仿真值误差的平均值。
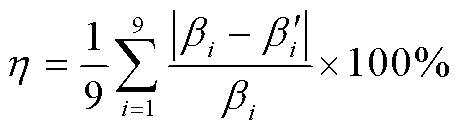（14）
式中，βi为导线扭转角度在观测点i处的测量值；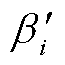
为导线扭转角度在观测点之处的仿真值。由此获得冰期1～5下，导线在9个观测点测量值与仿真值误差的平均值分别为8.55%、7.61%、7.67%、9.11%和8.51%。
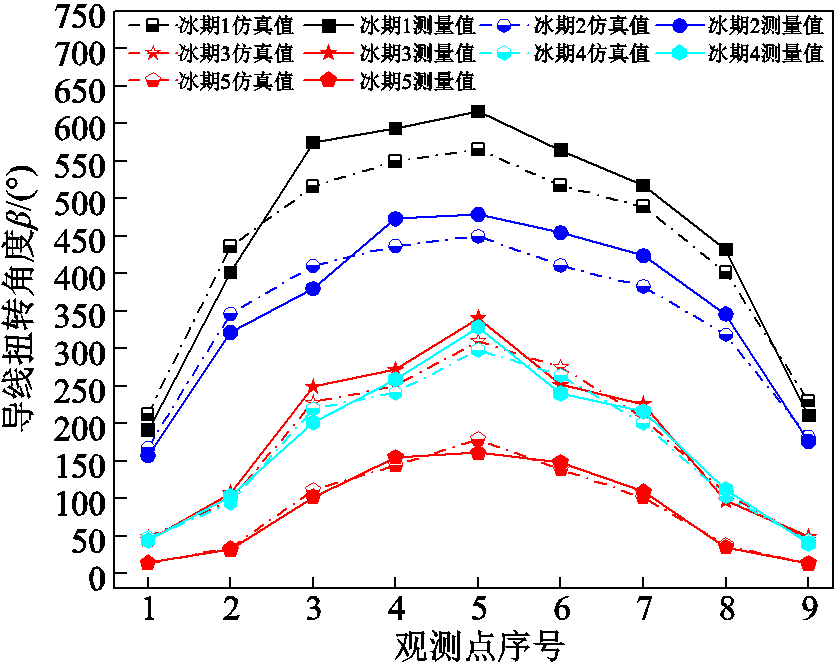
图10 不同冰期各观测点扭转角度仿真值与测量值
Fig.10 Calculated value and measured value of twisting angle on different points in different situations
从图10可看出，不同冰期下导线扭转角度基本沿导线中点对称分布，最大值出现在观测点5，最小值出现在观测点1或观测点9。从观测点1至观测点5，导线扭转角度逐渐增大；从观测点5至观测点9，导线扭转角度逐步减小。定义导线两端与观测点5距离相同的一对观测点为对称观测点，则对称观测点之间扭转角度的误差可表示为
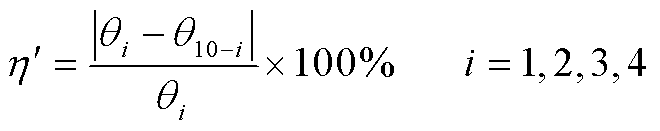（15）
式中，θi为导线扭转角度在观测点i处的测量值或仿真值。按照式（15）分别计算导线对称观测点之间扭转角度测量值与仿真值的误差，计算结果如图11所示。由图11可知，GJ50导线对称观测点扭转角度测量值误差在4.24%～11.75%之间，其平均值为8.35%；仿真值对称观测点误差在4.10%～9.80%之间，其平均值为7.92%。
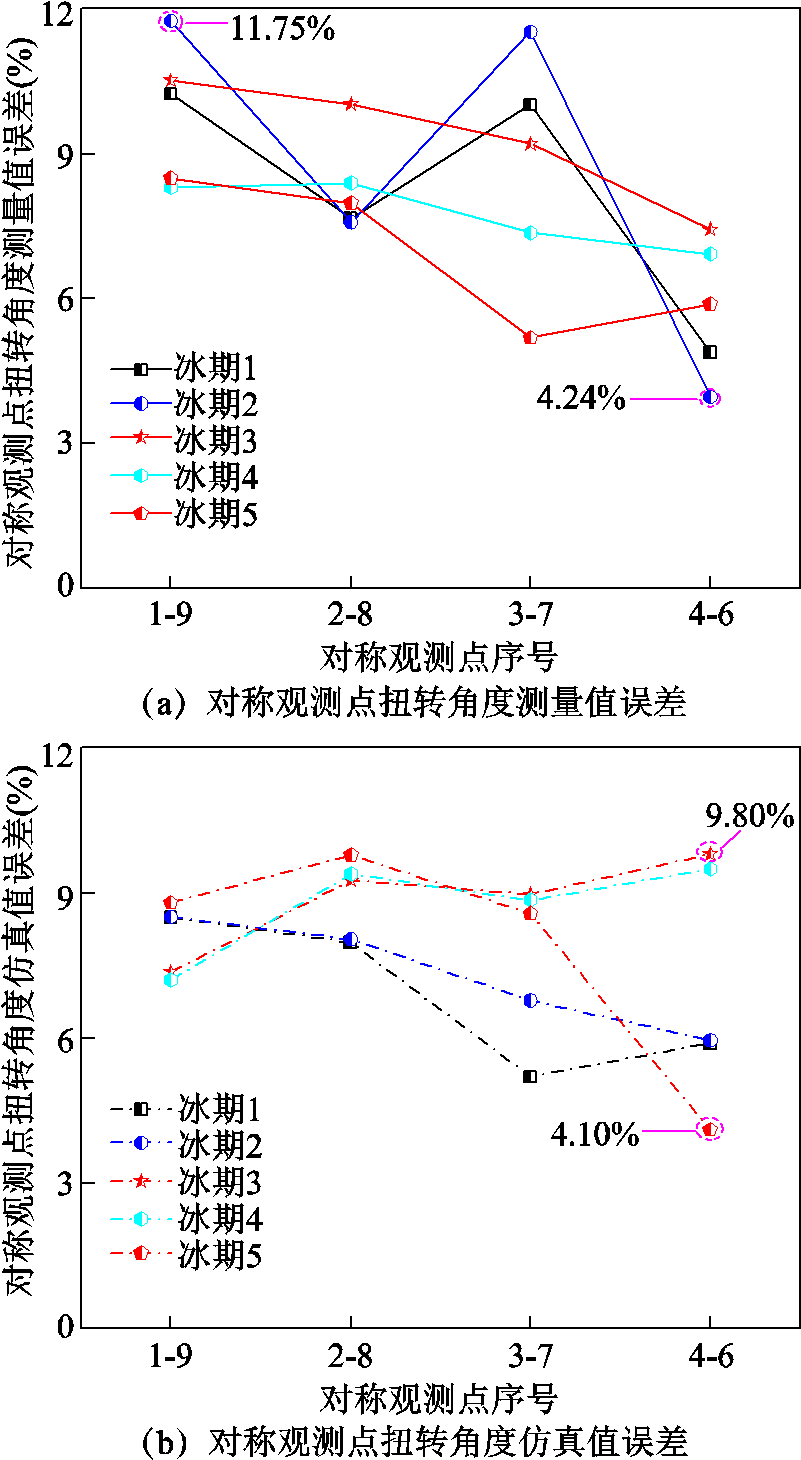
图11 不同冰期对称观测点扭转角度误差值
Fig.11 Error values for torsion angles at symmetrical measuring points in in different situations
从图10可以看出，不同冰期下，沿导线一侧出发距离导线中心点越近导线扭转角度越大，由此说明越靠近导线中心位置，导线越容易发生自由扭转覆冰。结合式（8）分析，离导线中点越近，导线等效扭转刚度越小，抗扭转能力越低，越容易发生扭转。但不同冰期下，导线自由覆冰扭转角度沿导线轴向变化情况不同。以冰期1和冰期5导线自由扭转覆冰情况为例进行说明。冰期1时，GJ50导线扭转角度测量结果的平均值为435.24°，而在冰期5，其扭转角度测量结果的平均值为85.6°，前者为后者的5.08倍。在观测点1，冰期1时GJ50导线扭转角度的测量结果为191.1°，当观测点变为5后，其扭转角度的测量结果为615.97°，后者比前者增加了424.87°；而在冰期5时，GJ50导线在观测点1扭转角度的测量值为14.51°，观测点5的测量值为160.78°，相较于前者增加了146.27°。
观测点1、3、5在冰期1下的扭转角度随时间增长的情况如图12所示。从图12中可以看出，在冰期1内，三个观测点测量值与仿真值的变化趋势一致。观测点1、3、5测量值与仿真值的误差平均值分别为7.62%、5.33%和6.73%。在三个观测点，GJ50导线扭转角度随覆冰时间增长均呈先快后慢，最后趋于平缓的增长趋势。观测点离导线中心越近，扭转角度保持增长趋势的时间越短，最终保持平稳的扭转角度值越大。
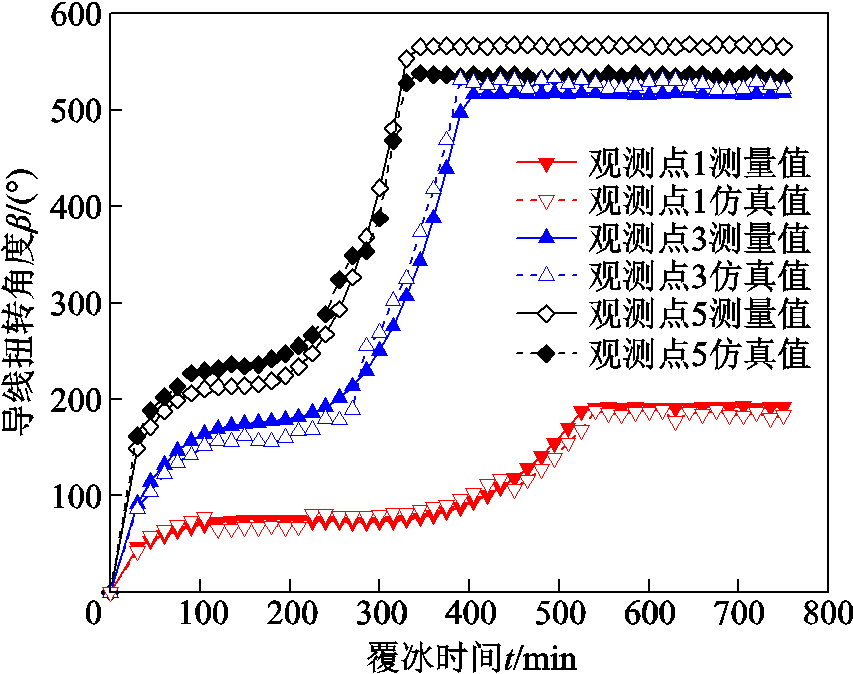
图12 冰期1不同观测点导线扭转角度计算值与测量值
Fig.12 Calculated value and measured value of twisting angle on different points in icing term 1
不同冰期下1～9号观测点的单位覆冰质量如图13所示。由图13可知，不同冰期下，各观测点单位覆冰质量的仿真值与测量值的变化趋势保持一致。
冰期1～5各观测点单位覆冰质量仿真值与测量值误差平均值为
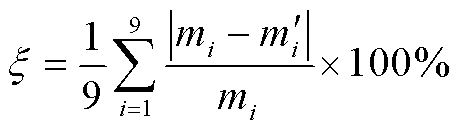（16）
式中，mi为导线单位覆冰质量在观测点i处的测量值；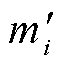
为导线扭转角度的仿真值。由此可获得冰期1～5下，导线各观测点单位覆冰质量仿真值与测量值误差平均值分别为8.60%、9.32%、9.60%、9.18%和8.40%。
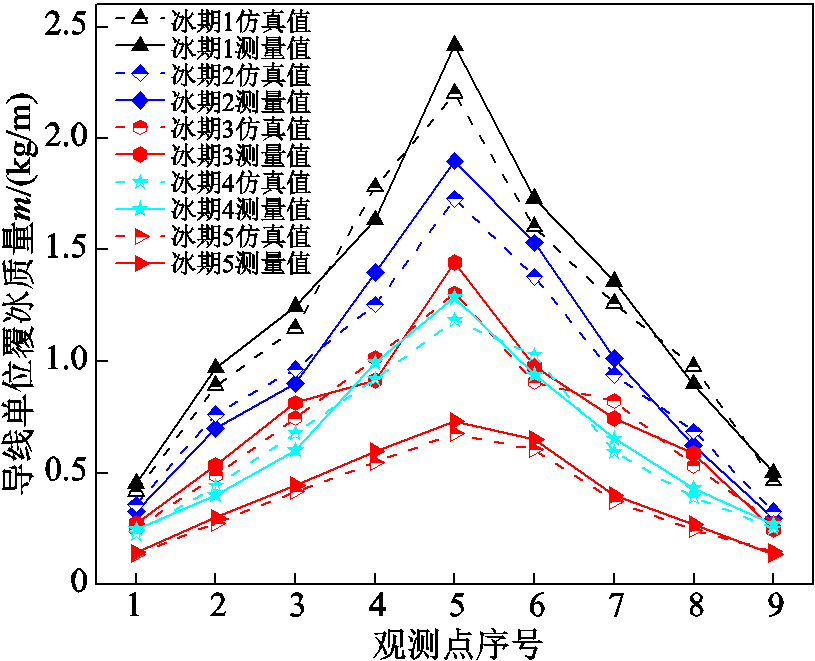
图13 不同冰期各观测点单位覆冰质量计算值与实测值
Fig.13 Calculated value and measured value of unit ice mass on different points in different situations
与导线扭转角度相同，GJ50导线单位覆冰质量同样呈对称分布，则导线对称观测点单位覆冰质量的误差值为
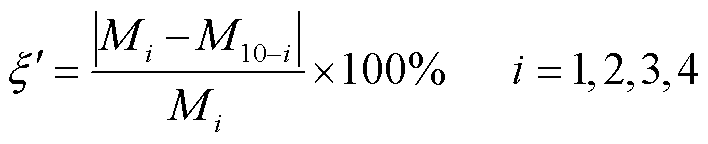（17）
式中，Mi为在观测点i处导线单位覆冰质量的测量值或仿真值。计算结果表明，GJ50导线不同冰期下对称观测点单位覆冰质量仿真结果误差在2.51%～10.22%之间，其平均值为8.04%；对称观测点测量结果误差在9.07%～12.27%之间，其平均值为10.79%。可以看到，无论是仿真值还是测量值，导线对称观测点单位覆冰质量误差均出现了超过10%的情况。由导线覆冰形成机理结合实验情况进行分析，风速、温度、空气中液态水含量等环境参数直接影响导线覆冰。将实验场地以导线中心点为界分为两个区域，这两个区域的场地情况并非完全一致，加之雪峰山处于典型的微地形小气候区域，因此在这两个区域中任意环境参数的不同均可能加大对称观测点之间的误差。而仿真结果与测量结果之间的差别，除了两个区域覆冰情况不一致外，覆冰质量的测量误差也扩大了两者的差异。
由于观测点4、5的现场测试操作困难，通过仿真分析了冰期5下观测点5处的导线覆冰增长规律，如图14所示；观测点1～3的冰形如图15所示。图14中黑线表示导线，红线为仿真冰形。图15中左侧为仿真分析得到的导线覆冰形状，其中黑线表示导线，红线为仿真冰形；右侧为自然覆冰结束后，在观测点1～3拍摄的导线实际覆冰形状。观测点4距离观测点5较近，其仿真结果类似。从图14中可以看出，空气中的过冷却水滴在导线迎风侧累积，结合实际情况，冰层增长的位置方向与水滴碰撞位置相对应。在接近导线中心点的位置，覆冰形状呈现椭圆形；而距离观测点5越远，导线覆冰不对称性越严重，会出现如图15左侧所示导线覆冰形状。
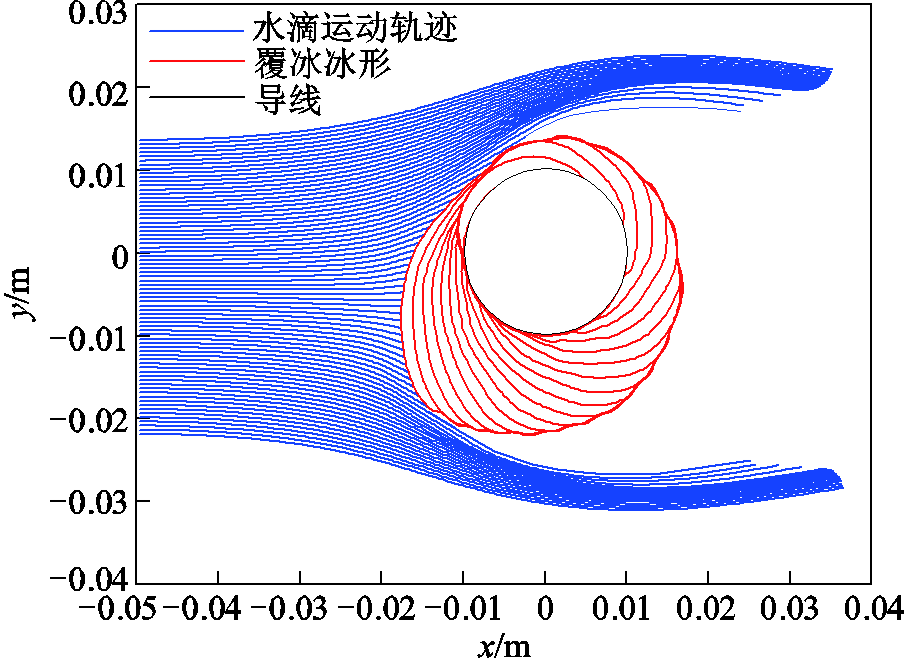
图14 冰期5下观测点5处导线的覆冰增长情况
Fig.14 The icing of conductor on point 5 in icing term 5
图15 不同观测点冰形
Fig.15 Ice shape of measurement point
对比图15中仿真和实测两种覆冰形状可知，数值仿真获得的GJ50导线最终覆冰形状与实际情况下的覆冰形状相吻合。在三个观测点，覆冰形状均随导线自由扭转而发生明显变化，观测点位置不同，导线覆冰形状存在明显差别。在观测点1，导线发生扭转，但其覆冰形状更接近于翼形冰；观测点2处覆冰形状相较于观测点1更接近于圆形冰；而观测点3覆冰形状则出现了椭圆形轮廓。由此可以发现，离导线中心点越近，导线覆冰越接近于圆形冰。
同时可以发现，尽管此次覆冰类型为雨凇，但无论是仿真结果还是实验结果，导线冰层表面粗糙不平的现象均较为明显。这一现象的产生是由于覆冰过程中，随着冰层质量的增加，导线发生扭转，导致空气中过冷却水滴与既有冰层或未覆冰的导线表面各碰撞点的碰撞情况产生较大差异。因此，在各碰撞点冻结的过冷却水滴数量不一，从而引起覆冰形状变化，使冰层表面呈现参差不齐的粗糙状。
1）在雪峰山国家野外站观测单导线自由扭转覆冰现象，分析了单导线自由扭转覆冰过程。单导线自由扭转覆冰以在导线表面形成翼形冰为起点，随着覆冰环境的保持或覆冰强度的增加，反复经历冰扭力矩小于导线反扭力矩的相持过程与冰扭力矩大于导线反扭力矩时冰层带动导线自由扭转的过程，逐步形成圆形冰。
2）根据单导线自由扭转覆冰过程中冰扭力矩与反扭力矩的动态平衡过程，基于流体力学及力学平衡原理建立了单导线自由扭转覆冰仿真分析模型。首先计算导线未扭转时的覆冰形状及质量，然后通过求解力矩平衡方程，获取该质量下导线绕其中心自由扭转的角度并对冰层形状进行更正。循环上述过程，最终实现单导线自由扭转覆冰动态模拟。
3）开展GJ50导线自由扭转覆冰野外自然实验和数值仿真研究，将实验结果与仿真结果进行对比分析。结果表明，不同冰期下仿真值与测量值扭转角度与单位覆冰质量误差平均值均在10%以内，仿真获取的导线覆冰形状与实际覆冰形状相吻合。
4）仿真和实验结果表明，单导线自由扭转覆冰时，导线扭转角度和单位覆冰质量均沿导线中心点对称分布。相同冰期内，距离导线中心点越近，导线自由扭转覆冰的扭转角度与单位覆冰质量越大，覆冰形状也越接近于圆形。
参考文献
[1] 蒋兴良, 易辉. 输电线路覆冰及防护[M]. 北京: 中国电力出版社, 2002.
[2] 吴海涛, 韩兴波, 蒋兴良, 等. 基于水滴碰冻效率的扩径导线防冰特性分析[J]. 电工技术学报, 2023, 38(11): 3033-3040, 3051.
Wu Haitao, Han Xingbo, Jiang Xingliang, et al. Analysis of anti-icing characteristics of expanded diameter conductor based on water droplet collision and freezing efficiency[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 3033-3040, 3051.
[3] 于周, 舒立春, 胡琴, 等. 覆冰厚度对气动脉冲除冰效果影响的数值仿真与试验验证[J]. 电工技术学报, 2024, 39(3): 844-851.
Yu Zhou, ShuLichun, Hu Qin, et al. Numerical simulation and experimental verification of the influences of icing thicknesses on pneumatic impulse de-icing effects[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 844-851.
[4] 韩兴波, 吴海涛, 郭思华, 等. 用于覆冰环境测量的旋转多导体直径选择方法研究[J]. 电工技术学报, 2022, 37(15): 3973-3980.
Han Xingbo, Wu Haitao, Guo Sihua, et al. Research on diameter selection method of rotating multi-conductor for measurement of icing environmental parameters[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3973-3980.
[5] 黄亚飞, 蒋兴良, 任晓东, 等. 采用涡流自热环防止输电线路冰雪灾害的方法研究[J]. 电工技术学报, 2021, 36(10): 2169-2177.
Huang Yafei, Jiang Xingliang, Ren Xiaodong, et al. Study on preventing icing disasters of transmission lines by use of eddy self-heating ring[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2169-2177.
[6] 胡琴, 朱茂林, 舒立春, 等. 风力发电机叶片防除冰涂层(二): 温升数值计算及防除冰性能[J]. 电工技术学报, 2024, 39(1): 246-256.
Hu Qin, Zhu Maolin, Shu Lichun, et al. Anti-deicing coatings for wind turbine blades part 2: numerical calculation of temperature rise and anti-deicing performance[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 246-256.
[7] 毕聪来, 蒋兴良, 韩兴波, 等. 采用扩径导线替代分裂导线的防冰方法[J]. 电工技术学报, 2020, 35(11): 2469-2477.
Bi Conglai, Jiang Xingliang, Han Xingbo, et al. Anti-icing method of using expanded diameter conductor to replace bundle conductor[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2469-2477.
[8] 蒋兴良, 毕聪来, 王涵, 等. 倒T型布置对绝缘子串覆冰及其交流闪络特性的影响[J]. 电工技术学报, 2019, 34(17): 3713-3720.
Jiang Xingliang, Bi Conglai, Wang Han, et al. Effect of inverted T arrangement on icing and AC flashover characteristics of insulator string[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3713-3720.
[9] 蒋兴良, 张志劲, 胡琴, 等. 再次面临电网冰雪灾害的反思与思考[J]. 高电压技术, 2018, 44(2): 463-469.
Jiang Xingliang, Zhang Zhijin, Hu Qin, et al. Thinkings on the restrike of ice and snow disaster to the power grid[J]. High Voltage Engineering, 2018, 44(2): 463-469.
[10] Imai I. Studies on ice accretion[J]. Researches on Snow and Ice, 1954, 3(1): 35-44.
[11] Lenhard R W Jr. An indirect method for estimating the weight of glaze on wires[J]. Bulletin of the American Meteorological Society, 1955, 36(1): 1-5.
[12] Jones K F. A simple model for freezing rain ice loads[J]. Atmospheric Research, 1998, 46(1-2): 87-97.
[13] 蒋兴良, 孙才新, 顾乐观, 等. 三峡地区导线覆冰的特性及雾凇覆冰模型[J]. 重庆大学学报(自然科学版), 1998, 21(2): 16-19.
Jiang Xingliang, Sun Caixin, Gu Leguan, et al. Power lines icing characteristics of the Three Gorges district and a model of the accumulation of ice on electric on electric power lines[J]. Journal of Chongqing University (Natural Science Edition), 1998, 21(2): 16-19.
[14] Makkonen L. Models for the growth of rime, glaze, icicles and wet snow on structures[J]. Philosophical Transactions of the Royal Society A, 2000, 358(1776): 2913-2939.
[15] 韩兴波, 蒋兴良, 毕聪来, 等. 基于分散型旋转圆导体的覆冰参数预测[J]. 电工技术学报, 2019, 34(5): 1096-1105.
Han Xingbo, Jiang Xingliang, Bi Conglai, et al. Prediction of icing environment parameters based on decentralized rotating conductors[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1096-1105.
[16] 蒋兴良, 申强, 舒立春, 等. 利用旋转多圆柱导体覆冰质量预测湿增长过程覆冰参数[J]. 高电压技术, 2009, 35(12): 3071-3076.
Jiang Xingliang, Shen Qiang, Shu Lichun, et al. Prediction of wet growth icing parameters by icing quantity of rotating multi-cylindrical conductors[J]. High Voltage Engineering, 2009, 35(12): 3071-3076.
[17] Yang Guolin, Liao Yi, Jiang Xingliang, et al. Research on value-seeking calculation method of icing environmental parameters based on four rotating cylinders array[J]. Energies, 2022, 15(19): 7242.
[18] He Qing, Zhang Jian, Deng Mengyan, et al. Rime icing on bundled conductors[J]. Cold Regions Science and Technology, 2019, 158: 230-236.
[19] 梁曦东, 李雨佳, 张轶博, 等. 输电导线的覆冰时变仿真模型[J]. 高电压技术, 2014, 40(2): 336-343.
Liang Xidong, Li Yujia, Zhang Yibo, et al. Time-dependent simulation model of ice accretion on transmission line[J]. High Voltage Engineering, 2014, 40(2): 336-343.
[20] 李清, 马伦, 解健, 等. 大档距多分裂输电导线扭转刚度计算分析[J]. 高压电器, 2020, 56(2): 158-162.
Li Qing, Ma Lun, Xie Jian, et al. Calculation and analysis on torsional stiffness of large-span multi-conductor bundle[J]. High Voltage Apparatus, 2020, 56(2): 158-162.
[21] 樊社新, 何国金, 廖小平, 等. 结冰导线扭转刚度实验[J]. 中国电力, 2005, 38(10): 45-47.
Fan Shexin, He Guojin, Liao Xiaoping, et al. Tests on tensional stiffness of iced conductor[J]. Electric Power, 2005, 38(10): 45-47.
[22] 解健. 大档距多分裂导线扭转及翻转特性研究[D]. 杭州: 浙江大学, 2019.
Xie Jian. Study on torsional and turnover characteristics of large span multi-bundle conductor[D]. Hangzhou: Zhejiang University, 2019.
[23] 胡琴, 于洪杰, 徐勋建, 等. 分裂导线覆冰扭转特性分析及等值覆冰厚度计算[J]. 电网技术, 2016, 40(11): 3615-3620.
Hu Qin, Yu Hongjie, Xu Xunjian, et al. Study on torsion characteristic and equivalent ice thickness of bundle conductors[J]. Power System Technology, 2016, 40(11): 3615-3620.
[24] 蒋兴良, 侯乐东, 韩兴波, 等. 输电线路导线覆冰扭转特性的数值模拟[J]. 电工技术学报, 2020, 35(8): 1818-1826.
Jiang Xingliang, Hou Ledong, Han Xingbo, et al. Numerical simulation of torsion characteristics of transmission line conductor[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1818-1826.
[25] 韩兴波, 吴海涛, 郭思华, 等. 输电线路单导线覆冰和扭转的相互影响机制分析[J]. 电工技术学报, 2022, 37(17): 4508-4516.
Han Xingbo, Wu Haitao, Guo Sihua, et al. Analysis of interaction mechanism between icing and torsion of single transmission lines[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4508-4516.
[26] Fu Ping, Bouchard G, Farzaneh M. Simulation of ice accumulation on transmission line cables based on time-dependent airflow and water droplet trajectory calculations[C]//23rd International Conference on Offshore Mechanics and Arctic Engineering, Vancouver, British Columbia, Canada, 2004, 3: 971-977.
[27] 陈凌, 蒋兴良, 胡琴, 等. 自然条件下基于旋转多圆柱体覆冰厚度的绝缘子覆冰质量估算[J]. 高电压技术, 2011, 37(6): 1371-1376.
Chen Ling, Jiang Xingliang, Hu Qin, et al. Evaluation of ice mass on insulator under natural icing condition based on the ice thickness accumulated on rotating multi-cylinder[J]. High Voltage Engineering, 2011, 37(6): 1371-1376.
[28] Nigol O, Buchan P G. Conductor galloping-part Ⅱtorsional mechanism[J]. IEEE Transactions on Power Apparatus and Systems, 1981, PAS-100(2): 708-720.
Abstract Power grid security has been threatened by transmission line ice disaster for a long time. Considering the actual icing process of transmission line, it is of great significance to establish an accurate icing model for power grid ice disaster prevention. However, the process of free torsional icing on transmission lines has not yet been well taken into account. Based on the observation results of free torsional icing on single conductors in natural environment, a mathematical simulation for the dynamic process of free torsional icing on single conductors is established in this paper. A natural site experiment of free torsional icing of GJ50 wire was carried out in Xuefeng Mountain Energy Equipment Safety National Observation and Research Station of Chongqing University, and the experimental results were compared with the simulation results.
The findings of this paper are as follows: (1) The single conductor free torsional icing phenomenon was observed at the XuefengMountainNational Observation and Research Station and the single conductor free torsional icing process was analysed. Single conductor free twisting icing to the formation of wing-shaped ice on the surface of the conductor as a starting point, with the maintenance of the ice environment or the increase in the strength of the ice cover, repeatedly through the ice torsion torque less than the conductor counter-torsion torque holding process and ice torsion torque greater than the conductor counter-torsion torque ice driven by the conductor free twisting process, gradually forming round ice. (2) Based on the dynamic equilibrium process of ice torsional moment and counter-torsional moment during the free twisting of a single conductor over ice, a simulation model of free twisting of a single conductor over ice is established based on the principles of hydrodynamics and mechanical equilibrium. Firstly, the ice shape and mass of the wire is calculated when the wire is not twisted, and then the moment balance equation is solved to obtain the angle of free twisting of the wire around its central at this mass and to correct the ice shape. This process is repeated to achieve a dynamic simulation of a single conductor free to twist. (3) The GJ50 conductor free torsional icing field experiments and numerical simulations were carried out, and the experimental results were compared with the simulation results. The results show that under different ice periods, the simulation and experimental values of torsion angle and unit ice quality error are within 10% of the average value, the simulation of the wire ice shape and the actual shape of the ice cover match. (4) Simulation and experimental results show that when a single conductor is free to twist the ice, the angle of twist and the unit ice mass are symmetrically distributed along the centre of the conductor. During the same ice period, the closer to the centre of the conductor, the greater the torsion angle and unit ice mass of the conductor, and the closer the ice shape is to a circle. The research results of this paper will provide a reference for transmission line ice-cover simulation analysis and ice-cover reversal research.
Keywords: Single conductors, free torsional icing, numerical simulation, field experiment validation
DOI: 10.19595/j.cnki.1000-6753.tces.230244
中图分类号：TM85
国家自然科学基金资助项目（51637002）。
收稿日期 2023-03-03
改稿日期 2023-03-20
杨国林 男，1994年生，博士研究生，研究方向为电网高压绝缘与冰灾防护。E-mail：GL_Yang@cqu.edu.cn（通信作者）
蒋兴良 男，1961年生，教授，博士生导师，研究方向为高电压与绝缘技术、能源装备安全与灾害防御。E-mail：xljiang@cqu.edu.cn
（编辑 李 冰）