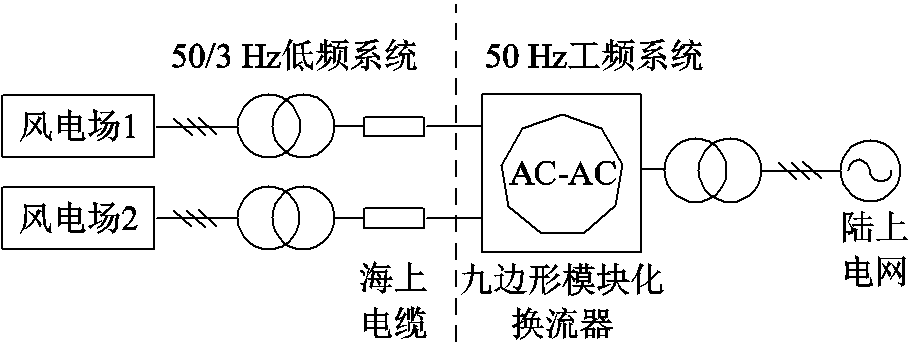
图1 基于九边形MMC的分频输电汇集系统
Fig.1 Fractional frequency transmission collection system based on nonagonal-MMC
摘要 九边形模块化多电平变换器(N-MMC)是一种具备多端口、低频性、高可靠性等特点的AC-AC变换器,在海上风电领域应用前景广阔。但是,九边形变换器存在不同频率的电气分量强耦合的问题。为此,该文提出了一种九边形变换器的解耦方法。首先,根据九边形变换器的拓扑结构,分析了其桥臂电压、电流的关系,建立了九边形变换器的解耦模型;然后,在此基础上推导了PI控制策略和非线性的无源控制(PBC)策略;最后,在Matlab仿真平台和RT-Lab半物理平台上进行了多种工况的仿真和实验验证,对比了解耦后采用PBC控制、PI控制、未解耦直接采用准比例谐振(QPR)控制的效果,验证了所提解耦模型与PBC控制的可行性与优越性。
关键词:海上风电 九边形模块化多电平变换器 多端口变换器 解耦模型 无源控制
近年来,环境恶化以及资源滥用导致气候变暖、能源紧缺,是当今社会面临的最大公共危机。这对人类社会的生产制造和经济发展产生了巨大冲击,造成了一系列威胁。因此,推进全球能源变革转型势在必行[1-2]。在发掘新型可再生能源的进程中,海上风电因其稳定性强、年利用小时数高、受地形地貌影响小、适合大规模开发等特点,正成为国内外新能源领域的研究重点[3-4]。
在远距离海上风电场的输电与并网中,低频交流输电是应用最为广泛的一种输电方式,它能够降低输电频率以减小电抗,在提高输电容量和距离等方面极具优势[5-7]。此外,低频交流输电系统只需一个AC-AC换流站,能够节省大量的设备投资成本,经济性十分可观。工频与低频间的交-交(即AC-AC)变换是低频输电系统的核心环节,一种方法是采用2个背靠背模块化多电平变换器(Modular Multilevel Converter, MMC或M2C),但该系统需进行交-直-交变换,成本耗费高且设备体积巨大[8-10]。另一种方法是采用模块化多电平矩阵变换器(Modular Multilevel Matrix Converter, MMMC或M3C),它省掉了直流环节,可以实现直接的AC-AC变换,并且具备高电压、大容量的优点[11-13],在大功率低频交流系统中占据优势地位,但其内部耦合复杂,环流抑制难度较大。在M3C拓扑的基础上,德国L. Baruschka等提出了一种新型六边形模块化多电平交-交变换器,仅用6条桥臂实现直接变压变频控制,也适用于高电压大功率场合[14]。文献[15]研究了六边形变换器(Hexagonal Converter, Hexverter)在海上风电场景中的应用,提出了包括环流抑制、内环电流控制、并网/无源工况下的外环电压控制在内的整体控制方案。文献[16]提出了一种六边形MMC的荷电状态(State of Charge, SOC)平衡控制方法,探究了各桥臂间子模块的平衡策略。文献[17]通过在六边形MMC中增添无源前端,拓展得到了一种三端口六边形变换器,虽然它能实现3个系统间的直接AC-AC变换,但其需要附加移相变压器,系统复杂且设备体积大。文献[18]提出的三端口六边形采用了有源前端,但仍需移相变压器来连接外部交流系统,成本问题依然存在。文献[19]将六边形MMC的桥臂数量增加到9条桥臂,扩展为九边形MMC,不仅保留了六边形MMC的低频特性和直接AC-AC变换的能力,而且构建了3个交流端口,能够用于海上风电汇集系统中,十分具有发展潜力,但其采用的内模控制在模型失配时,控制效果会变差,甚至导致系统不稳。文献[20-21]研究了九边形MMC的控制策略,但其电流跟踪控制采用了传统的准比例谐振(Quasi Proportional Resonance, QPR)控制,QPR控制对参数变化的自适应能力较差,并不能达到令人满意的控制效果。目前,国内外学者对九边形MMC的研究处于起步阶段,鲜有文献深入推导九边形内部电气量的数学关系,针对其控制策略的研究也很少。然而,对于九边形MMC这种多对象的复杂系统而言,深究其内部关系,建立解耦模型,能够将复杂系统分解成若干相互独立的子系统,并将耦合效应降低到最小,进而降低控制设计的复杂度,简化控制器的设计过程,有助于系统的优化和参数调节,以便于在复杂变化工况下运用先进控制方法来弥补传统控制方法的不足。
因此,本文提出了九边形MMC的解耦模型,建立了桥臂电压电流关系,并提出了PI控制与无源控制(Passivity-Based Control, PBC)两种策略。首先对九边形MMC的拓扑结构和工作原理进行了介绍,推导了解耦数学模型,设计了三端口的PI控制器;然后分析了九边形MMC的无源性和稳定性,提出了无源控制策略;最后在Matlab平台上搭建了九边形MMC的QPR控制、PI控制与PBC系统仿真,模拟了多种工况;并在RT-Lab实验平台进行了半物理仿真,验证了本文所提解耦模型与控制策略的可行性与优越性。
基于九边形MMC的分频输电汇集系统结构如图1所示。在海上风电系统中,常见的换流器如M3C、六边形等只能实现一条低频线路的并网,在线路复杂的情况下会耗费较高的成本。因此在AC-AC环节考虑采用三端口的九边形MMC,实现两条低频线路的并网,同时能够减少开关器件,提高系统集成度。
九边形MMC的拓扑结构如图2所示。九边形MMC由9条桥臂构成,每条桥臂由N个级联H桥子模块(Sub Module, SM)与一个电感L及负载R串联而成,9条桥臂依次首尾相接组成九边环形。

图1 基于九边形MMC的分频输电汇集系统
Fig.1 Fractional frequency transmission collection system based on nonagonal-MMC
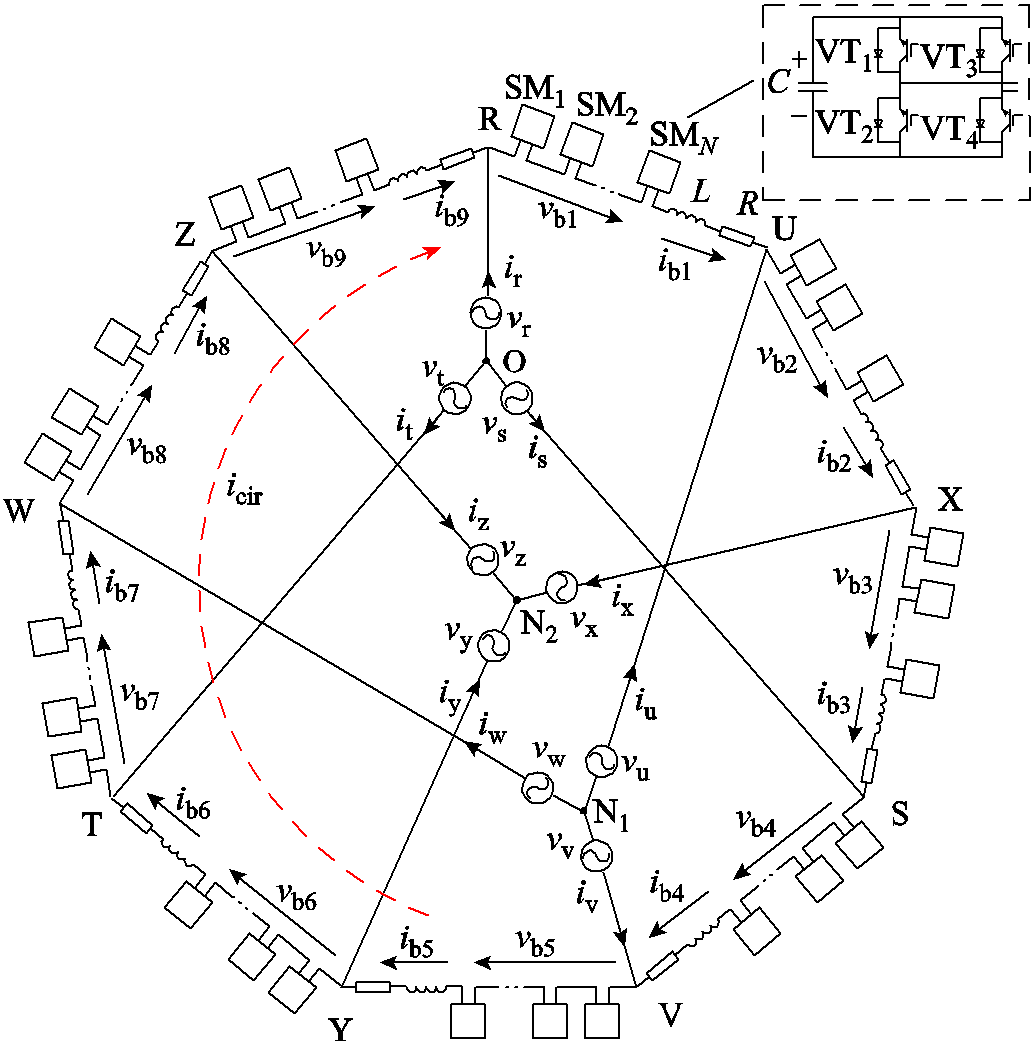
图2 九边形MMC的拓扑结构
Fig.2 Topology of nonagonal-MMC
九边形MMC的9个节点可以连接3个交流系统,其端口1、2、3的三相电压为vr/vs/vt、vu/vv/vw、vx/vy/vz,端口1、2、3的相应电流分别为ir/is/it、iu/iv/iw、ix/iy/iz。由图1或2可见,在分频输电汇集系统中,端口1和端口2可以分别连接两个低频的风电场,端口3用于连接工频的陆上电网。
为简化分析,可将各桥臂的子模块等效为一个电压源,桥臂电压以vbk表示,桥臂电流以ibk表示,其中k=1, 2, 3, ···, 9,循环电流以icir表示。以点O、N1、N2分别代表3个端口的中性点,以vN1、vN2代表N1、N2相对O点的中性点偏移电压差。
结合电路Kirchhoff定律分析图2,可将端口电压与桥臂电流表示为
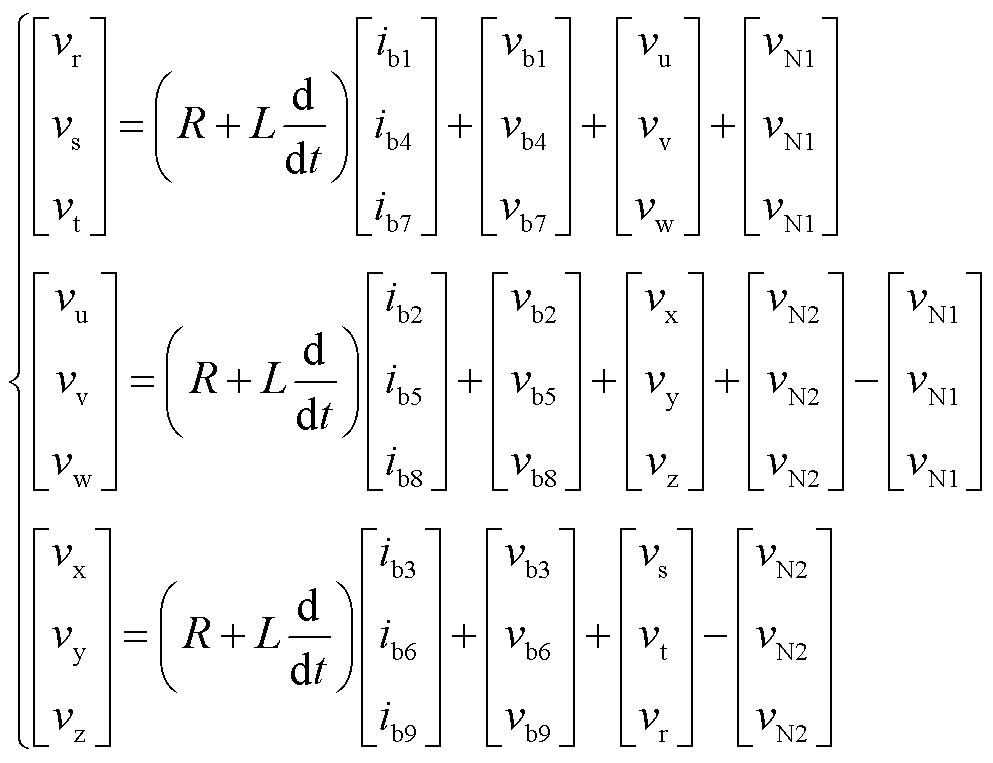 (1)
(1)
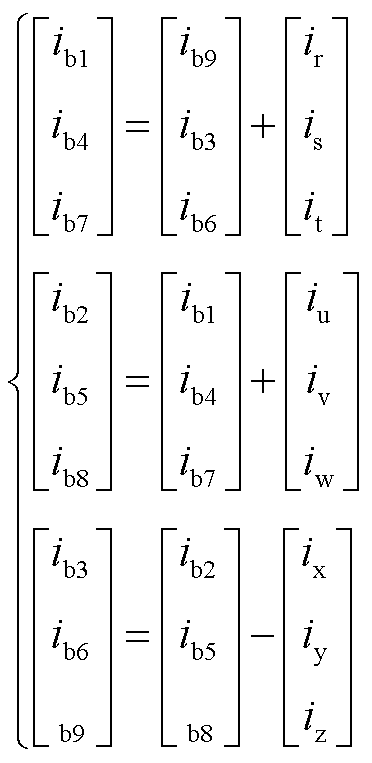 (2)
(2)
由上述分析可知,9条桥臂的电压与电流相互耦合,难以针对一条桥臂建立解耦模型。因此,结合式(1)将不同的交流系统所涉及的桥臂分为一组,相应地将九条桥臂分为3组:第1组为桥臂1、4、7;第2组为桥臂2、5、8;第3组为桥臂3、6、9。对3组分别进行αβ0变换,可得
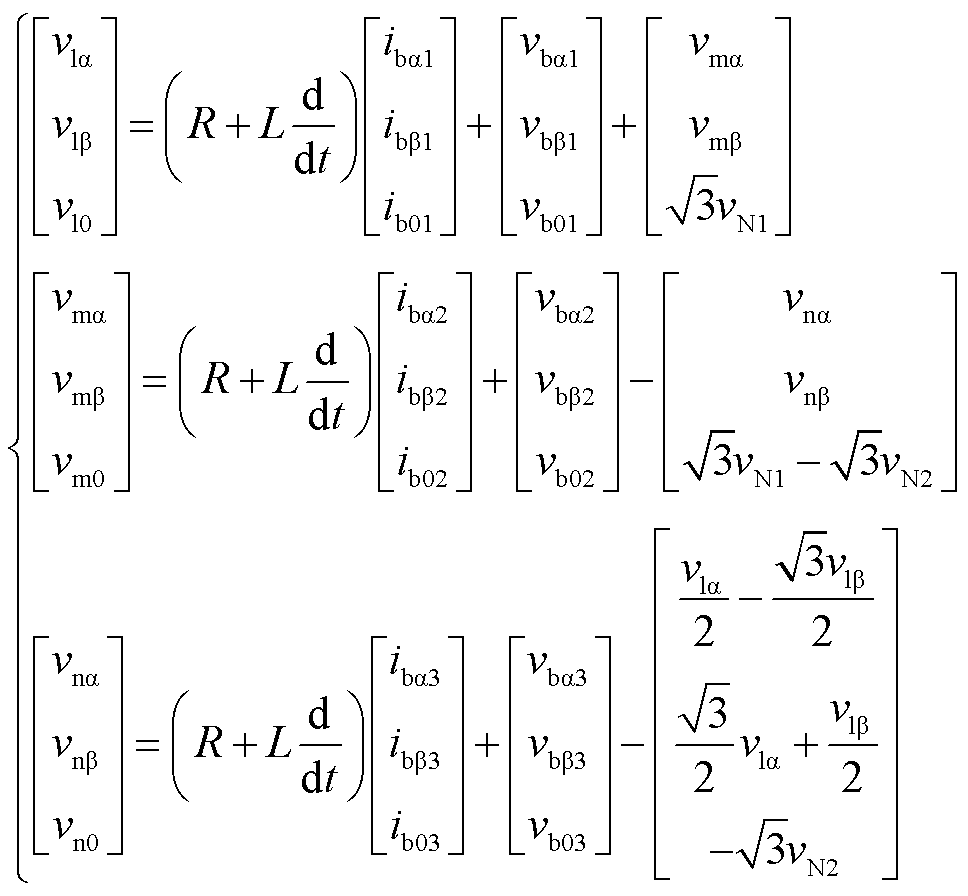 (3)
(3)
式中,vij、ibjp、vbjp分别为端口电压vλ、桥臂电流ibk、桥臂电流vbk在αβ0坐标下的量。i=l, m, n,代表三个交流系统的频率;j=α, β, 0,代表α、β、0坐标轴;p=1, 2, 3,代表组别;λ=r, s, t, ···, z,代表各端口。
将式(1)中各式相加,可将环流表示为
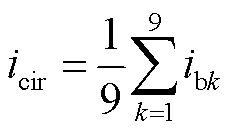 (4)
(4)
将式(1)中的各组关系式两两相减,可得
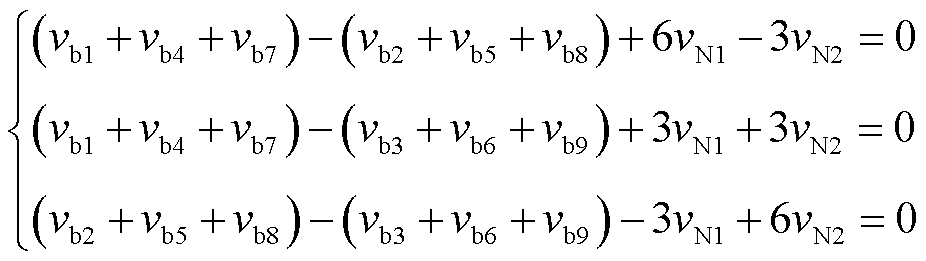 (5)
(5)
对式(4)、式(5)进行αβ0变换,可得桥臂电压、电流的零序分量间的关系为
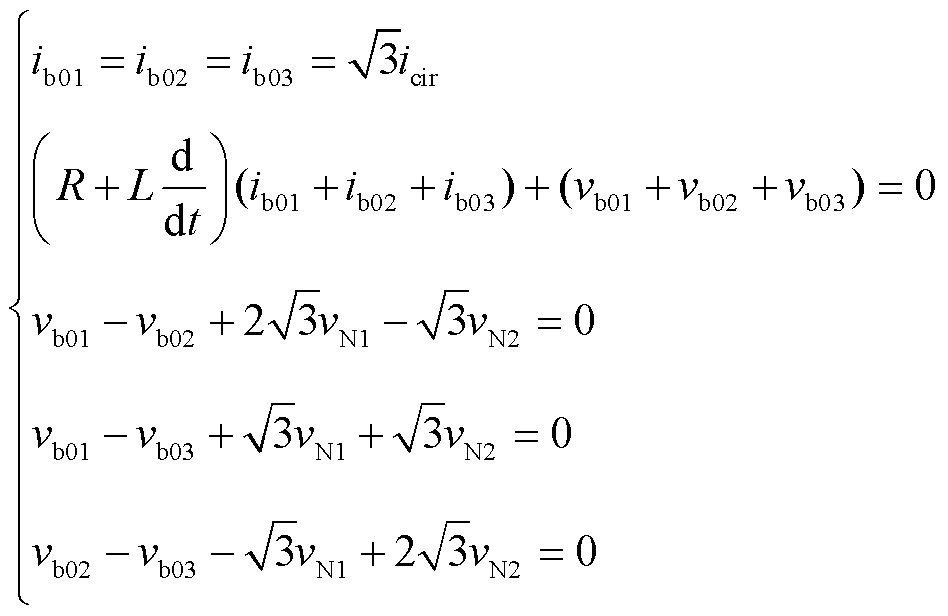 (6)
(6)
结合式(3)和式(6),可将桥臂电流的αβ分量表示为
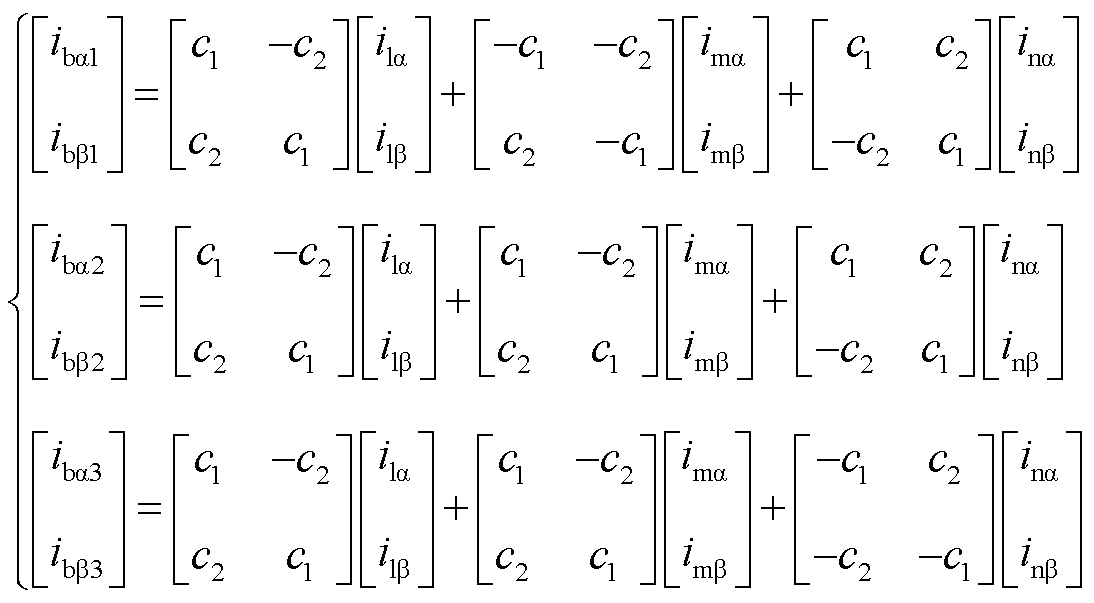 (7)
(7)
式中,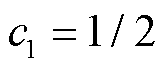 ,
,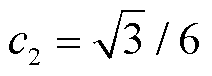 ;iij为端口电流iλ在交流系统频率为i时,αβ0坐标下的量。
;iij为端口电流iλ在交流系统频率为i时,αβ0坐标下的量。
将式(7)代入式(3),可得桥臂电压的αβ分量表达式为
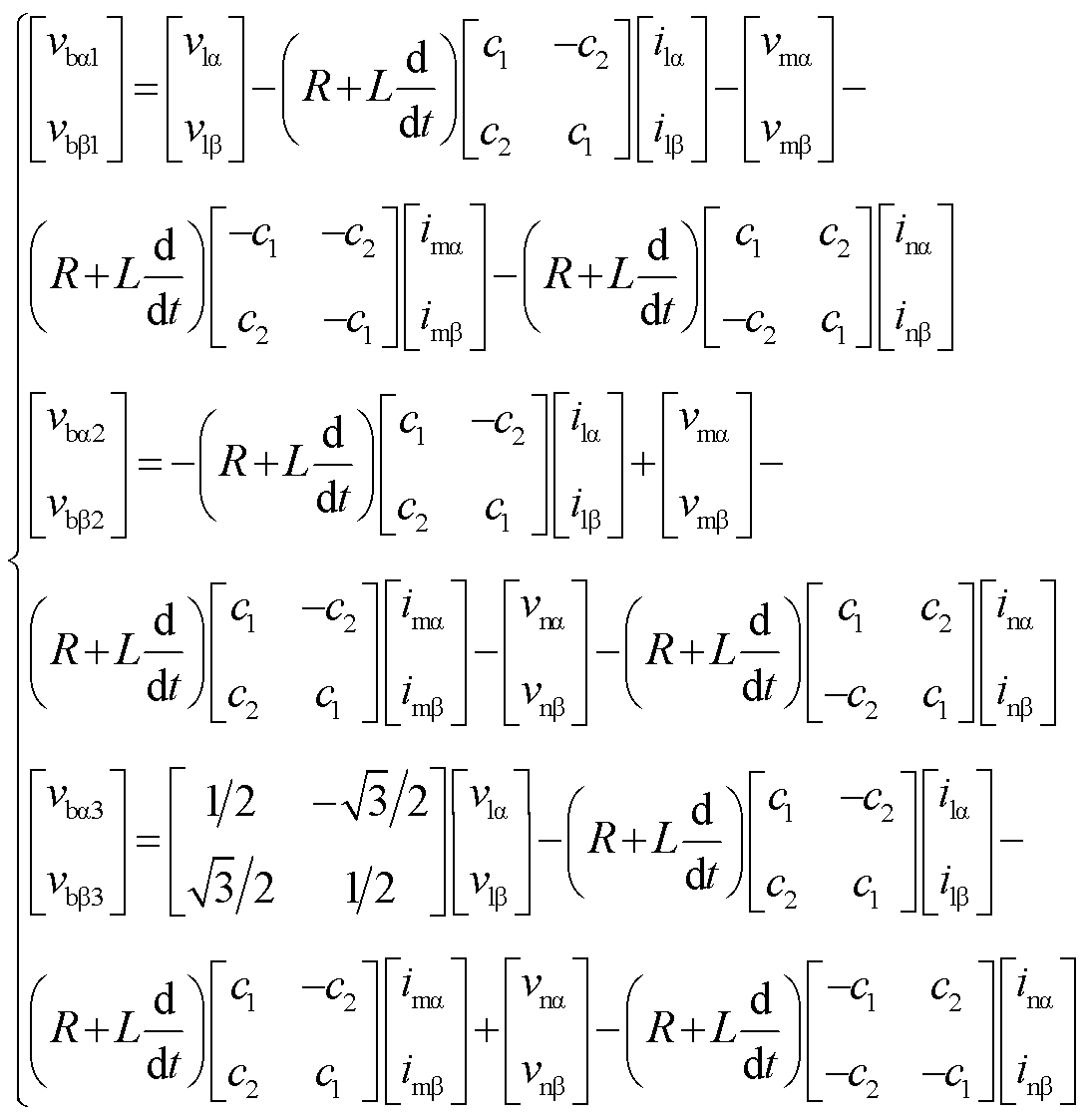 (8)
(8)
由式(8)可知,各支路的桥臂电压均包含频率l、m、n的分量。为将其解耦,对式(8)的三组桥臂电压表达式分别进行频率为l、m、n的dq变换,可将各频率分量变换到对应的dq坐标中,也即
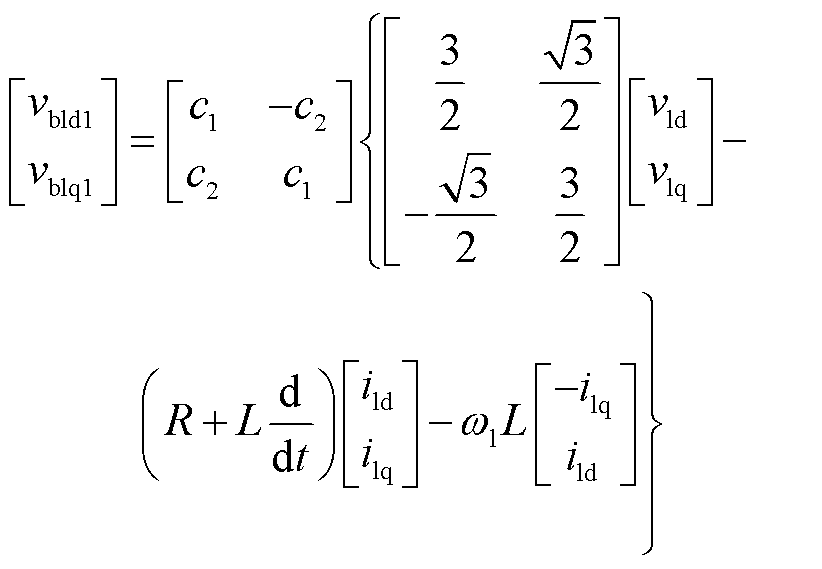 (9)
(9)
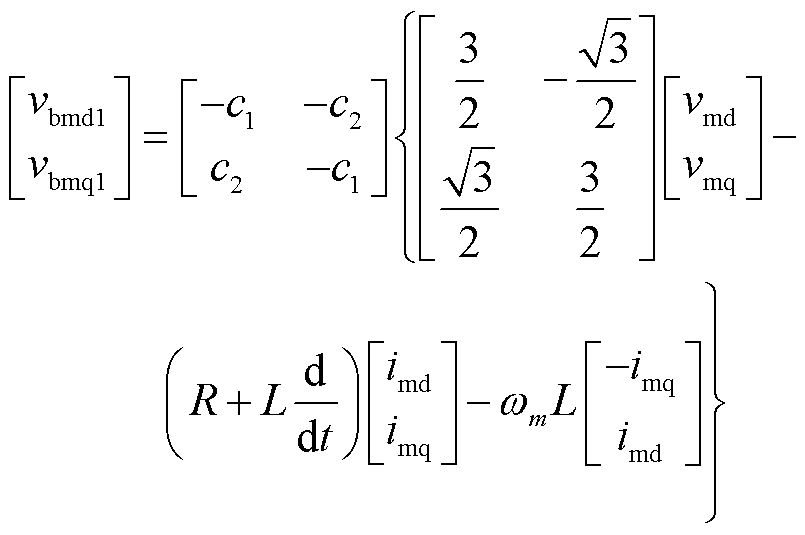 (10)
(10)
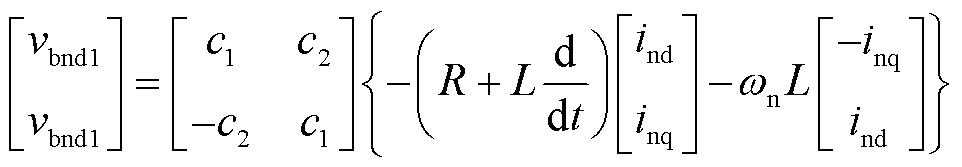 (11)
(11)
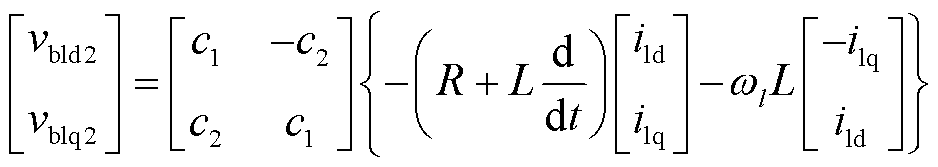 (12)
(12)
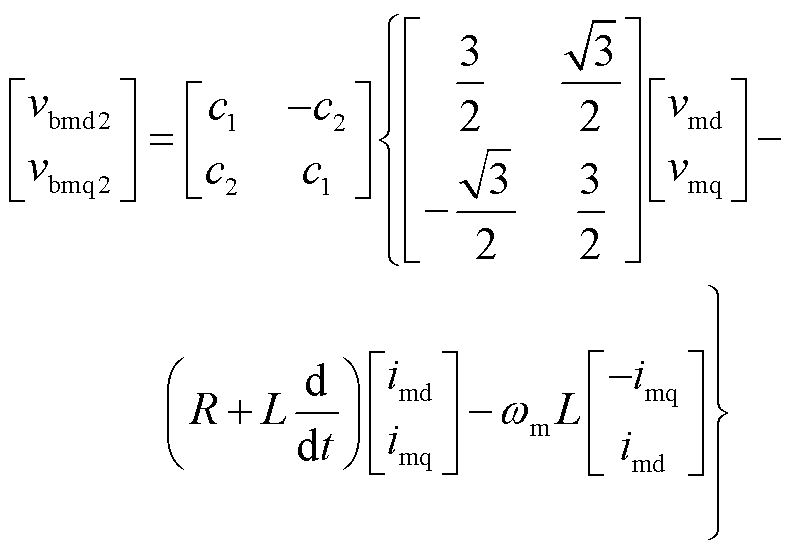 (13)
(13)
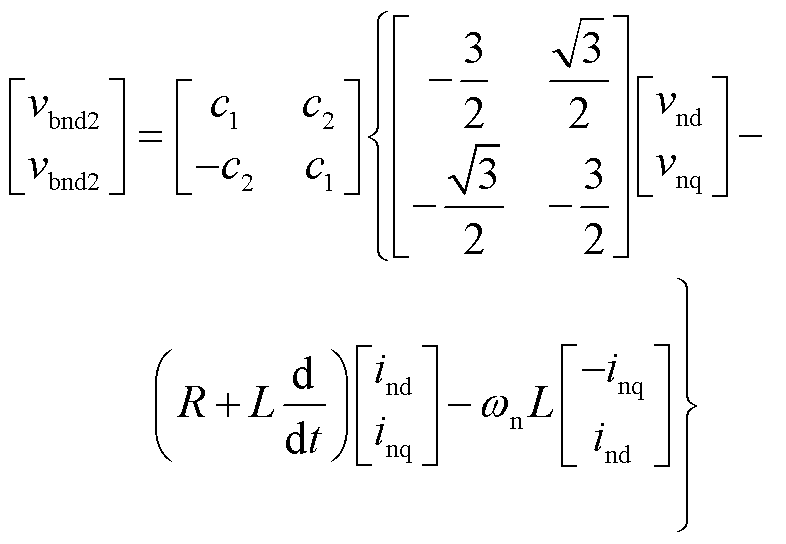 (14)
(14)
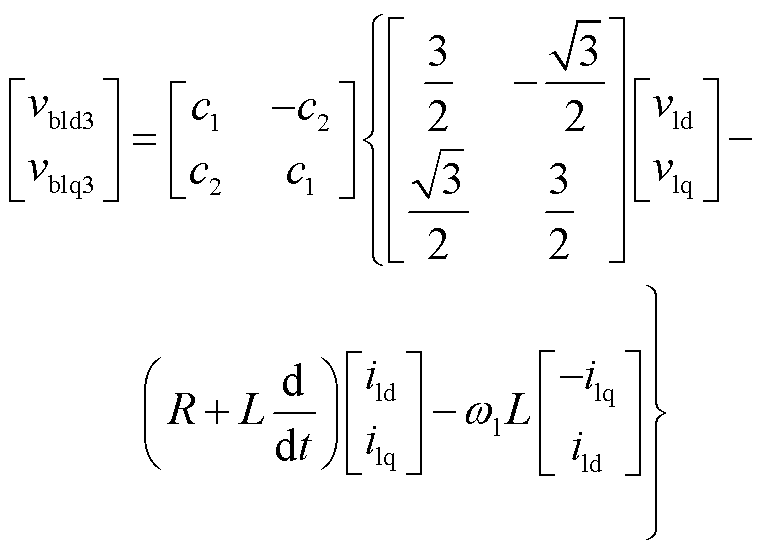 (15)
(15)
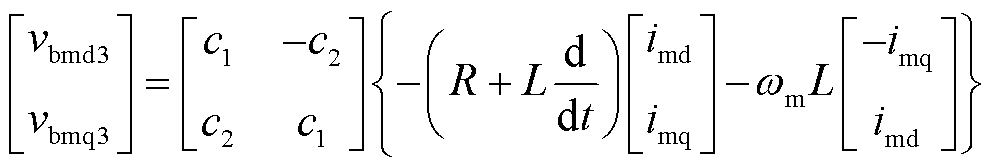 (16)
(16)
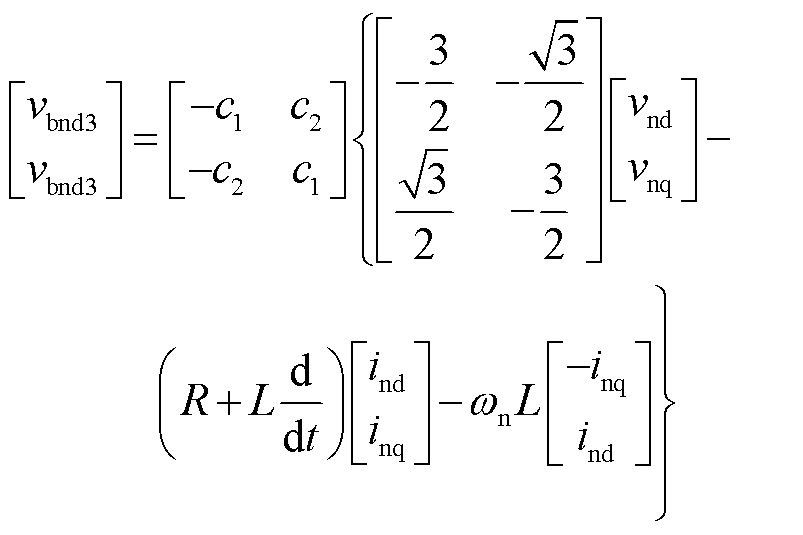 (17)
(17)
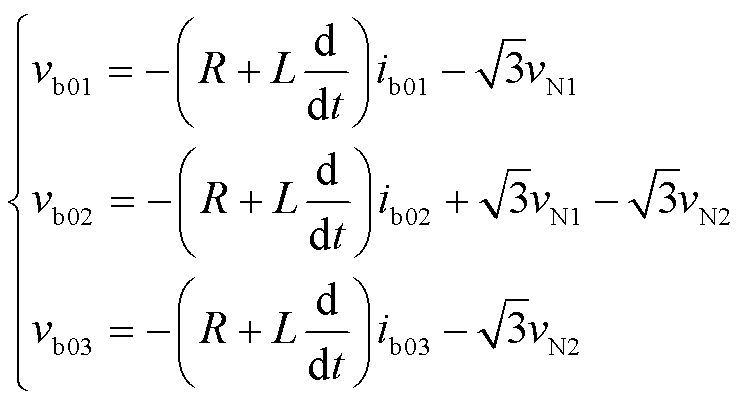 (18)
(18)
式中,vid、viq、iid、iiq分别为端口电压、端口电流在频率i上的dq分量;vbidp、vbiqp分别为p组桥臂电压在相应频率i上的dq分量;vb0p为p组桥臂电压的零序分量。
式(9)~式(18)即为九边形MMC各桥臂的解耦模型。其中式(18)为桥臂电压的零序分量,在三相对称系统中可忽略,故后续的控制策略中不再分析零序分量。
根据九边形MMC桥臂的解耦模型,可以推导出桥臂电压的PI控制策略,以第1组桥臂为例,所设计的PI控制器为
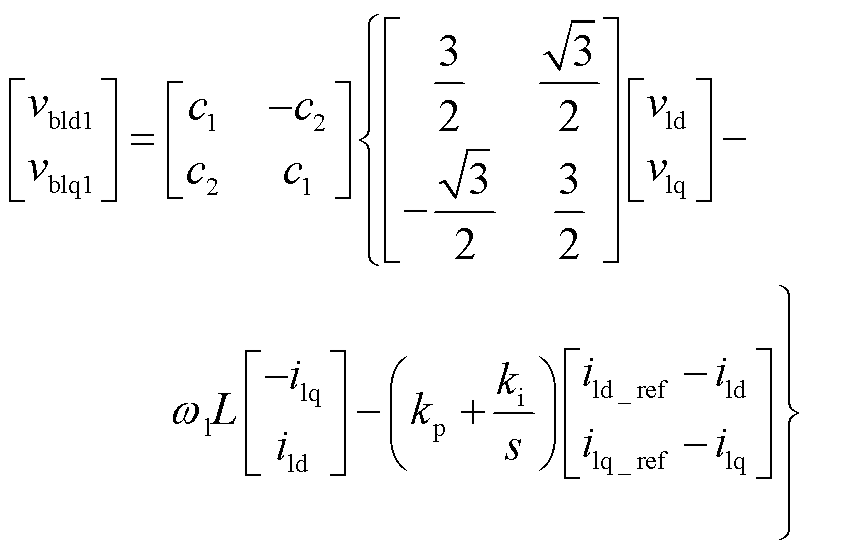 (19)
(19)
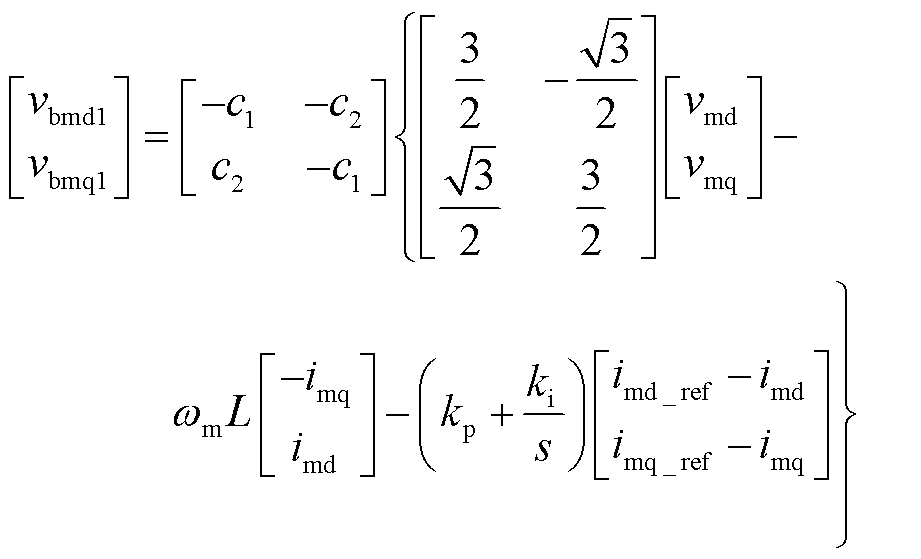 (20)
(20)
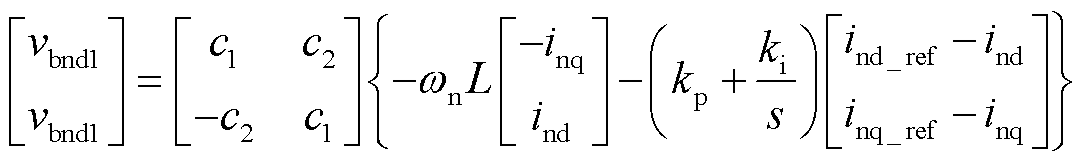 (21)
(21)
式中,ild_ref、ilq_ref分别为电流ild、ilq的参考值;kp、ki分别为PI控制的比例、积分参数。
然而,PI控制的适用范围有限,仅在线性系统中能表现出较好的控制效果。在应对复杂的非线性九边形MMC系统时,因其具有非线性的动态特性、不确定性和强耦合性,PI控制器的性能会受到限制。通常情况下PI控制器的参数设计是系统稳态运行下的最优性能参数,但工况变化如系统发生大范围功率突变时,PI控制器的参数未做调整,此时可能并非为最优设计参数,无法完全适应九边形MMC的非线性特性,导致控制性能下降,如内环电流的跟踪速度和精度也会降低。因此,对于复杂非线性的九边形MMC,仅通过参数调节来克服PI控制的缺点是有限的,需要考虑非线性控制方法,以实现更好的控制性能,从而本文提出将非线性的无源控制(PBC)用于九边形MMC系统控制中。
无源控制(PBC)是一种基于全局稳定的非线性控制,具有物理意义清晰、鲁棒性强、跟踪速度更快的优点。其核心思想是系统的能量增长总和总是小于或等于外部注入的能量总和,通过利用能量函数收敛到期望能量函数,从而实现系统的渐近稳定。
2.2.1 九边形MMC的无源性及稳定性分析
以九边形MMC的第1组桥臂(1、4、7)为例,由式(9)可得Euler-Lagrange模型为
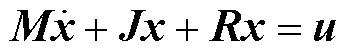 (22)
(22)
其中
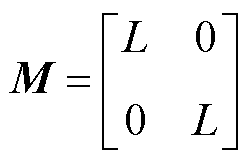
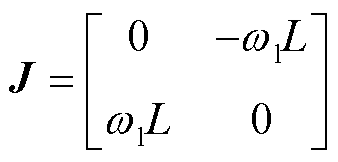
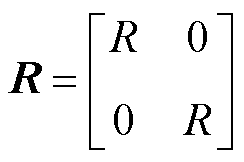
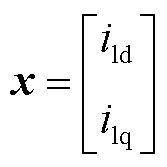
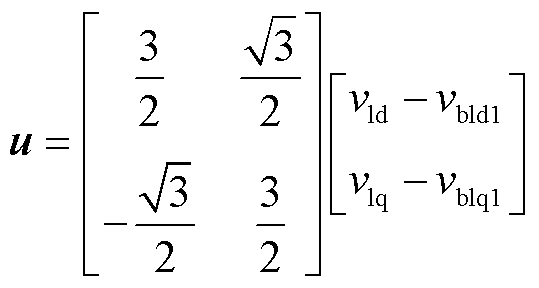
式中,M为系统的正定矩阵;J为系统的反正定矩阵;R为系统的对称正定矩阵;u为系统的输入向量;x为状态变量。
考虑m输入m输出的系统为
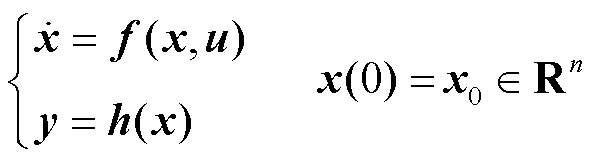 (23)
(23)
式中,x∈Rn为状态向量;u∈Rm为输入向量;y∈Rm为输出向量;f为关于(x,u)局部Lipschitz的函数。
对于式(9),如果存在半正定的储存函数H(x)和正定函数Q(x)满足关系
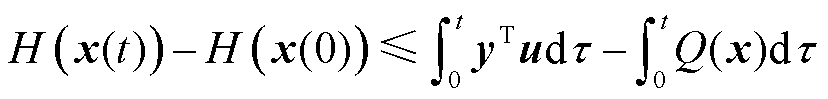 (24)
(24)
或
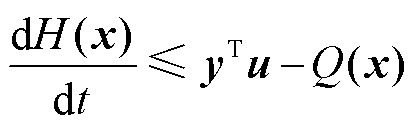 (25)
(25)
则系统是严格无源的。
本文的能量存储函数配置为
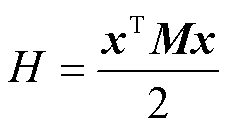 (26)
(26)
求导后可得
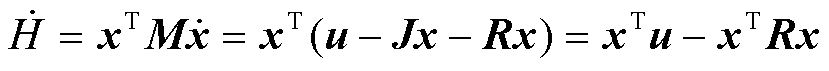 (27)
(27)
令y=x,Q(x)=xTR x,可得式(25),类似可将式(10)~式(17)推导为式(25),因此九边形MMC是严格无源的。根据无源控制的理论,严格无源的系统一定可以采用无源控制且控制系统是稳定的[22]。
2.2.2 无源控制器的设计
无源控制系统期望的稳定平衡点为
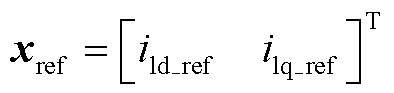 (28)
(28)
令系统的状态变量误差为xe=x-xref,可得
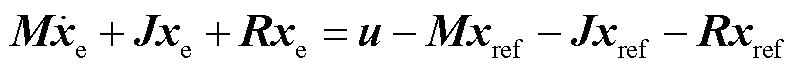 (29)
(29)
取无源系统的能量误差函数为
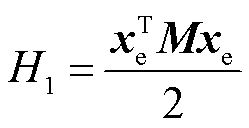 (30)
(30)
为使H1收敛至0,可以注入阻尼加快无源系统的能量耗散,提升系统响应速度,使系统迅速收敛,达到期望的稳定平衡点。
注入阻尼耗散项为
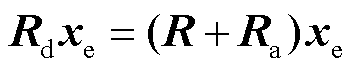 (31)
(31)
式中,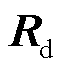 为耗散项系数;
为耗散项系数;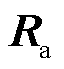 为注入阻尼系数。
为注入阻尼系数。
将式(31)代入式(30),可得
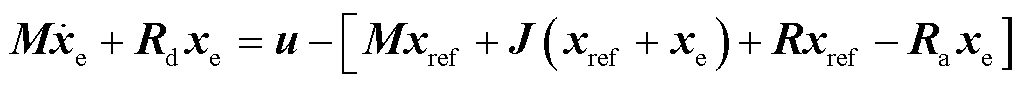 (32)
(32)
由此可将九边形MMC第1组桥臂的内环电流无源控制器设计为
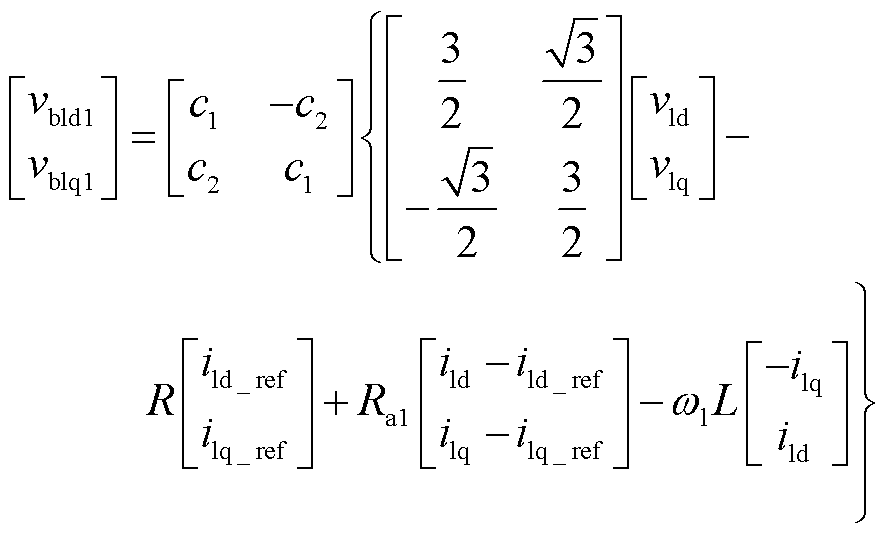 (33)
(33)
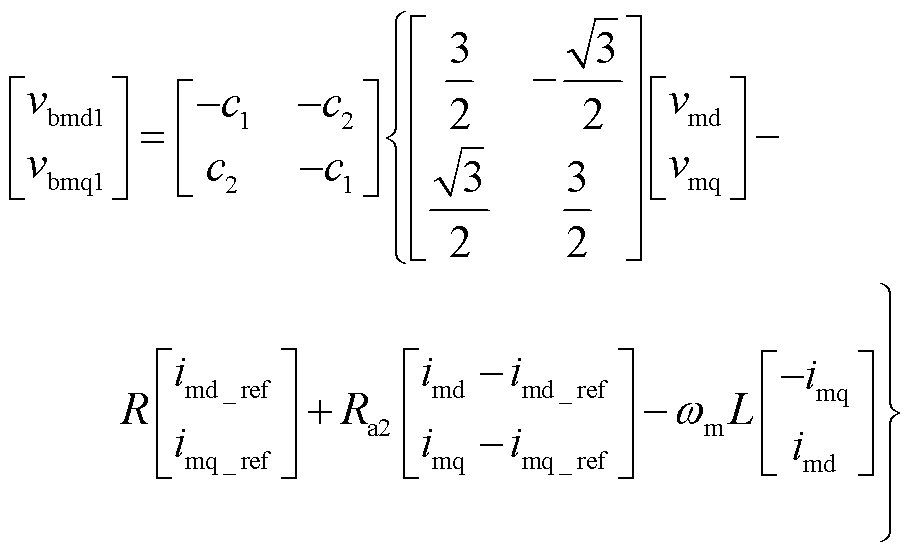 (34)
(34)
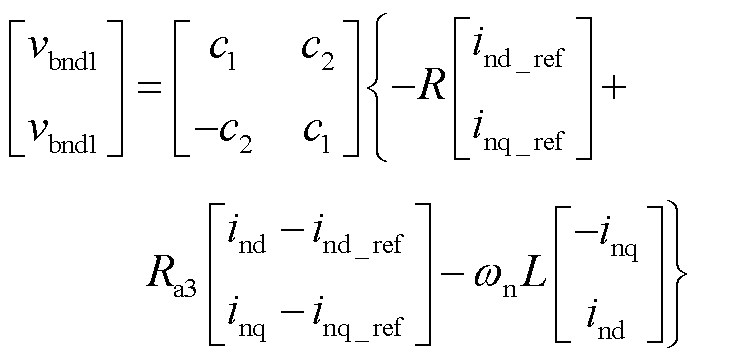 (35)
(35)
由式(33)~式(35)可得第1组桥臂的无源控制框图,如图3所示。

图3 九边形MMC第1组桥臂的无源控制框图
Fig.3 PBC control block diagram of the first group of bridge arms in nonagonal-MMC
类似地,可以推导出第2、3组桥臂的无源控制器为
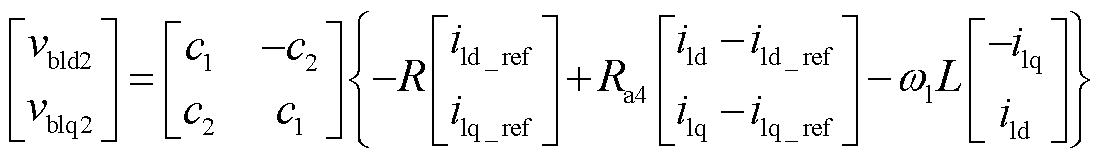 (36)
(36)
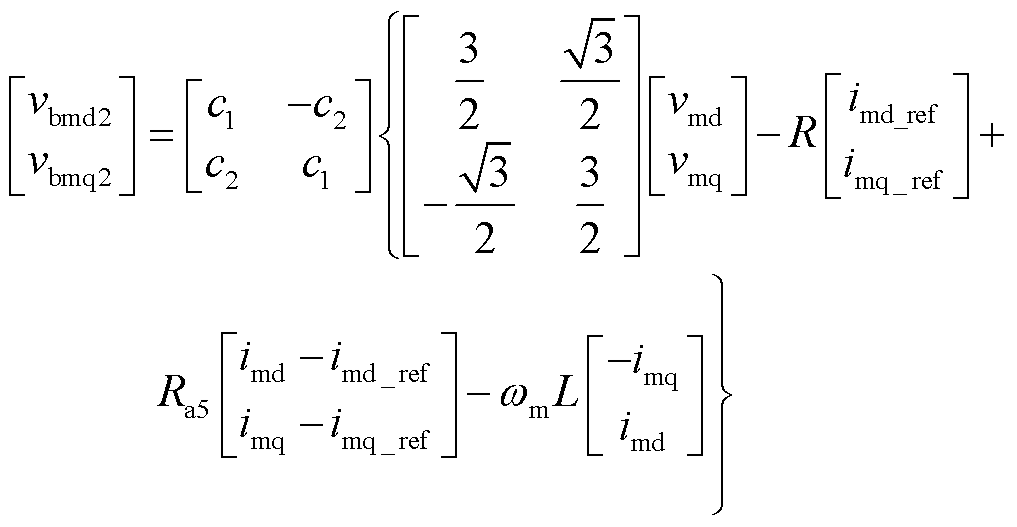 (37)
(37)
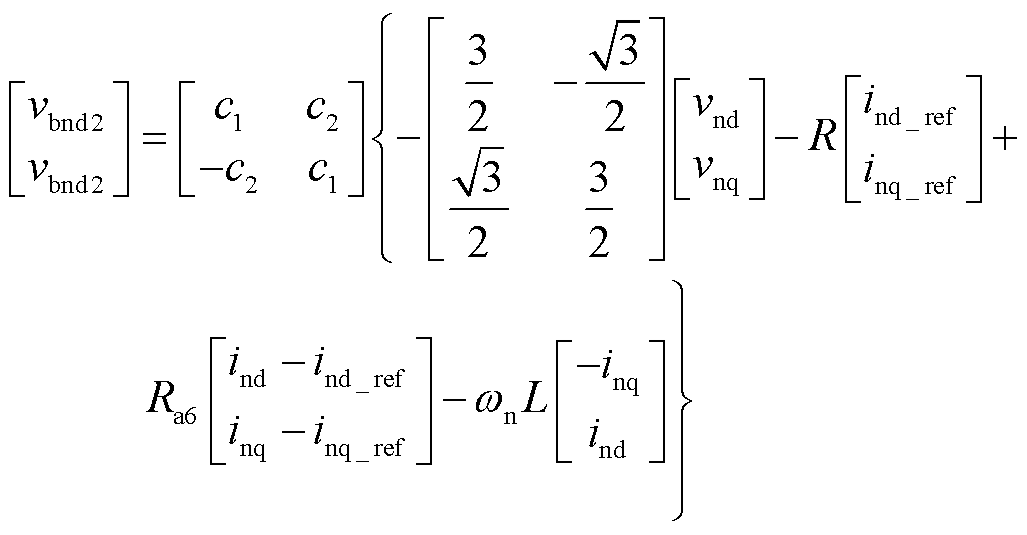 (38)
(38)
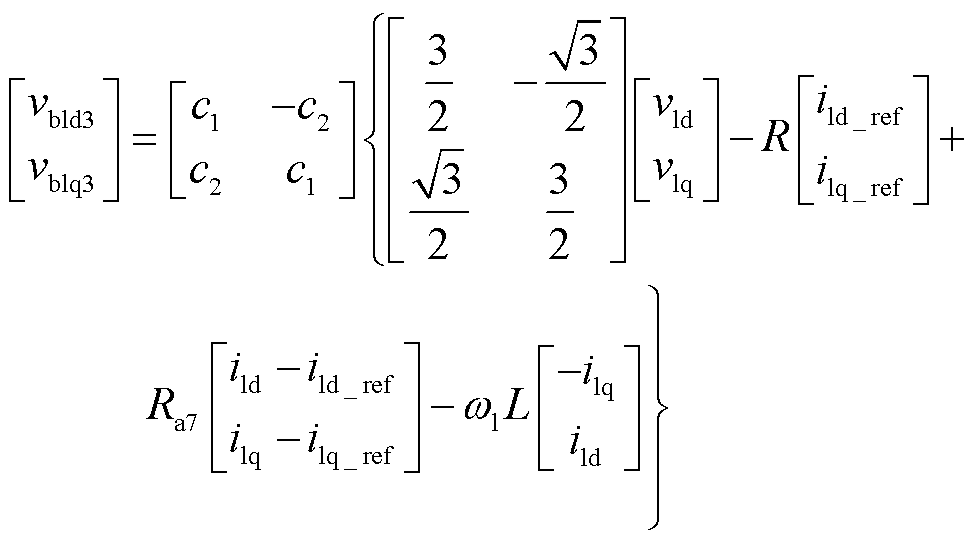 (39)
(39)
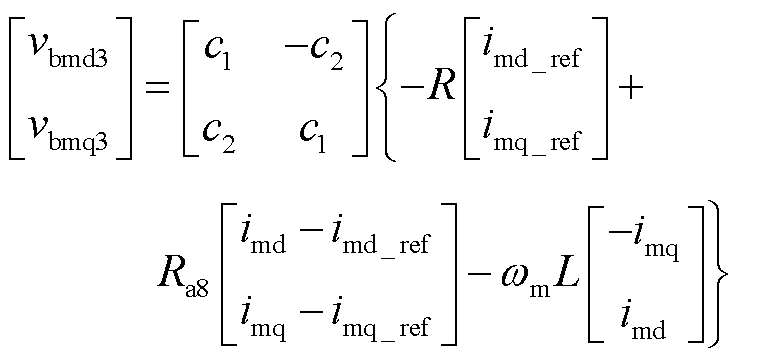 (40)
(40)
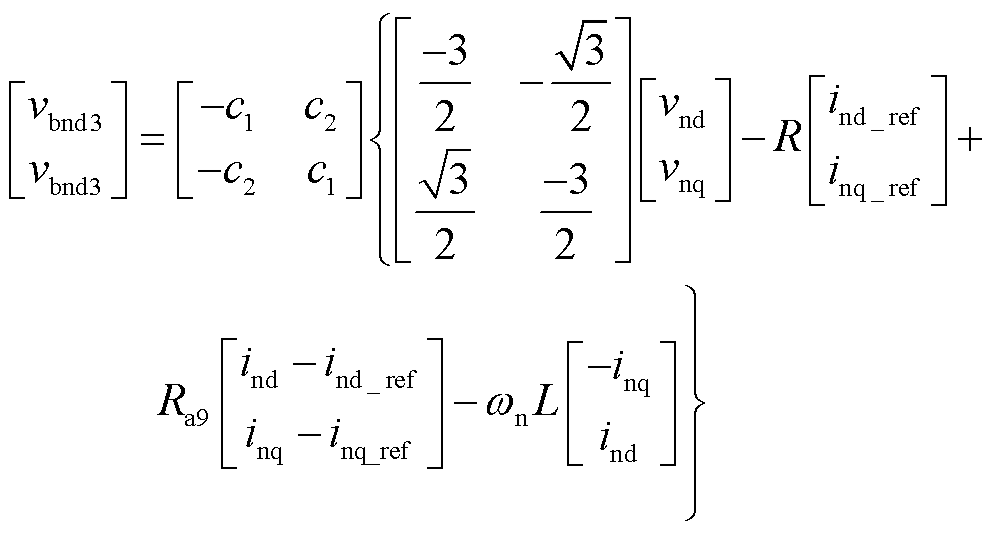 (41)
(41)
在分频输电汇集系统中,两个不同的风电场通过九边形MMC向电网输送电能,为保证整个系统的稳定运行,需分析九边形MMC的三个端口的能量分布,根据能量流动规律设计功率平衡控制策略。
若九边形MMC能够稳定运行,其3个端口必须满足条件
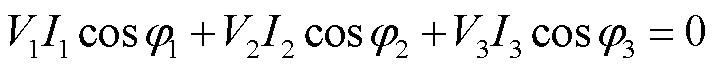 (42)
(42)
即3个端口的有功功率应保持平衡状态,由式(42)可进一步推导出外环功率平衡控制,以第1组桥臂为例,表达式为
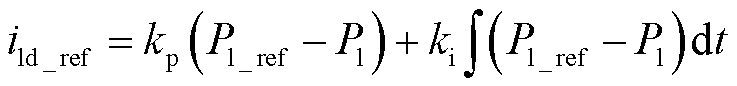 (43)
(43)
式中,V1~V3、I1~I3分别为三个端口的线电压、线电流有效值;Pl为端口1的实际功率;Pl_ref为其设定值。
同时,电流q轴分量应满足关系
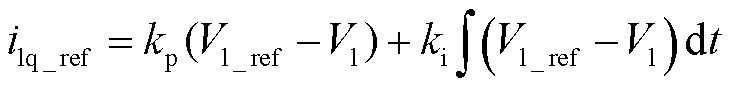 (44)
(44)
式中,Vl_ref为Vl的设定值。
本文采用子模块独立均压控制使各子模块的电容电压达到稳定、均衡,其具体原理为
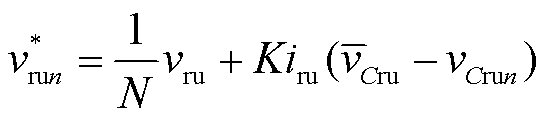 (45)
(45)
式中,N为子模块个数;vru为ru桥臂的调制信号,K为增益;iru为ru桥臂上的电流;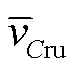 为ru桥臂子模块的平均电容电压;vCrun为ru桥臂中第n个子模块的电压;
为ru桥臂子模块的平均电容电压;vCrun为ru桥臂中第n个子模块的电压;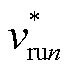 为均压控制后该子模块的调制信号。
为均压控制后该子模块的调制信号。
综上所述,本文所设计的九边形MMC系统总体控制框图如图4所示。
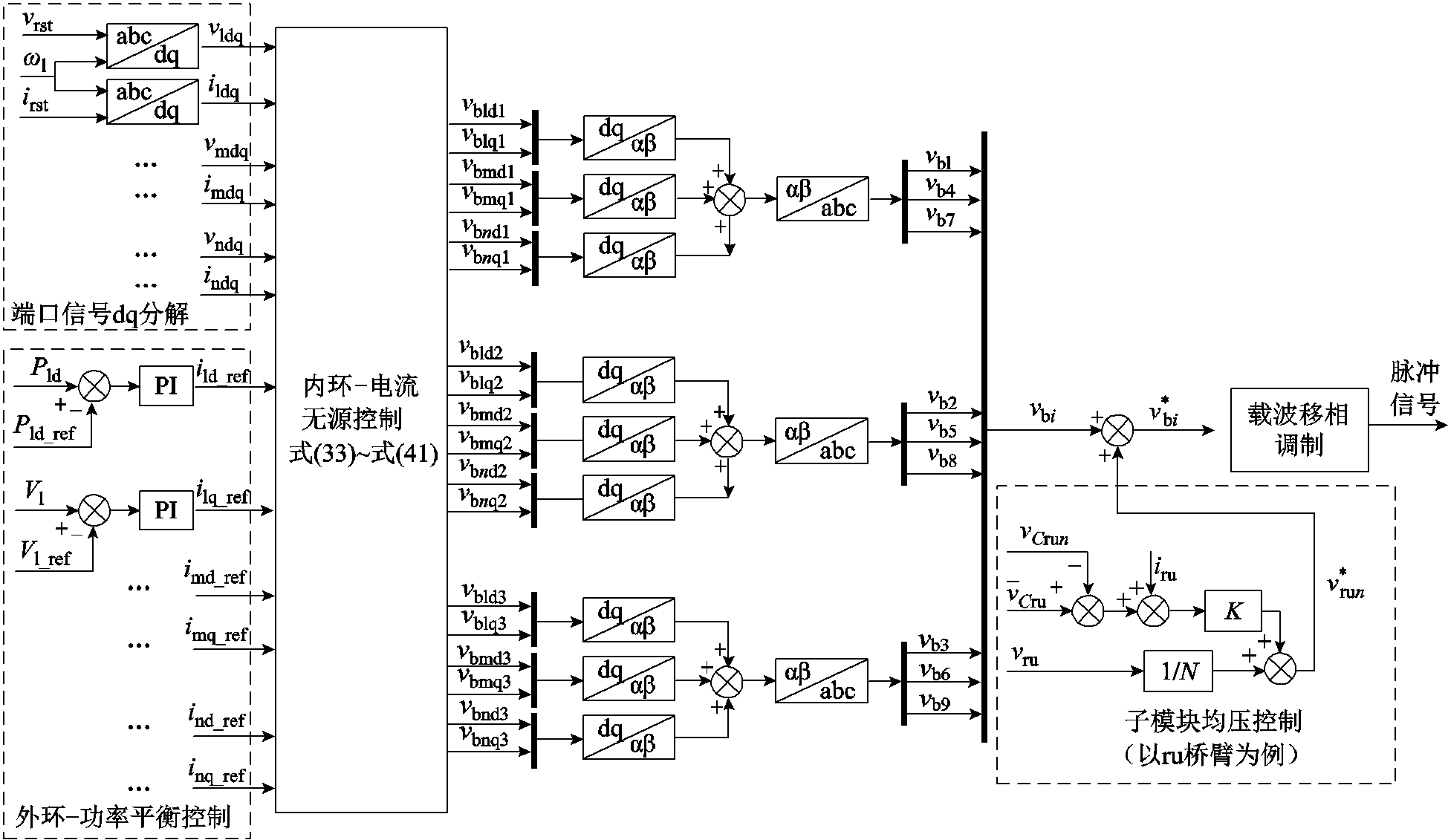
图4 九边形MMC系统总体控制框图
Fig.4 General control block diagram of nonagonal-MMC
为验证本文所提出的九边形MMC的解耦模型及控制策略的正确性与优越性,在Matlab仿真平台上搭建了九边形MMC控制系统,从系统的稳态性能与动态性能出发,模拟了正常运行、功率变化、电压等级变化、系统频率变化以及单端口故障五种不同工况。分析了动态工况下的三端口电压和电流、桥臂电压和电流、电流谐波畸变率等参数的变化情况,并对比了未解耦直接采用QPR控制、解耦后采用PI控制与无源控制的实验效果,说明本文所提解耦模型与无源控制的有效性。系统的仿真参数见表1。
表1 系统仿真参数
Tab.1 Simulation parameters of system

参数数值 端口1电压vrst/kV10 端口2电压vuvw/kV10 端口3电压vxyz/kV10 端口1频率fl/Hz50/3 端口2频率fm/Hz50/3 端口3频率fn/Hz50 端口1额定功率Pl /MW6.125 端口2额定功率Pm /MW6.125 端口3额定功率Pn /MW12.25 桥臂电阻R/Ω0.01 桥臂电感L/mH20 桥臂子模块数目N 7 子模块电容电压vC /V3 000 子模块电容C/mF10
在九边形MMC正常运行工况下,端口1和端口2连接风电场,频率为50/3Hz,端口3连接陆上电网,频率为50Hz,承担AC-AC变换的作用。仿真实验波形如图5所示,其中,图5a~图5l分别为九边形MMC的端口1的电压vrst和电流irst、端口2的电压vuvw和电流iuvw、端口3的电压vxyz和电流ixyz、低频侧(端口1)电流d轴分量ild、三端口有功功率Plmn、桥臂环流icir、桥臂电压vux、桥臂电流iux以及ux桥臂上的各子模块电容电压。
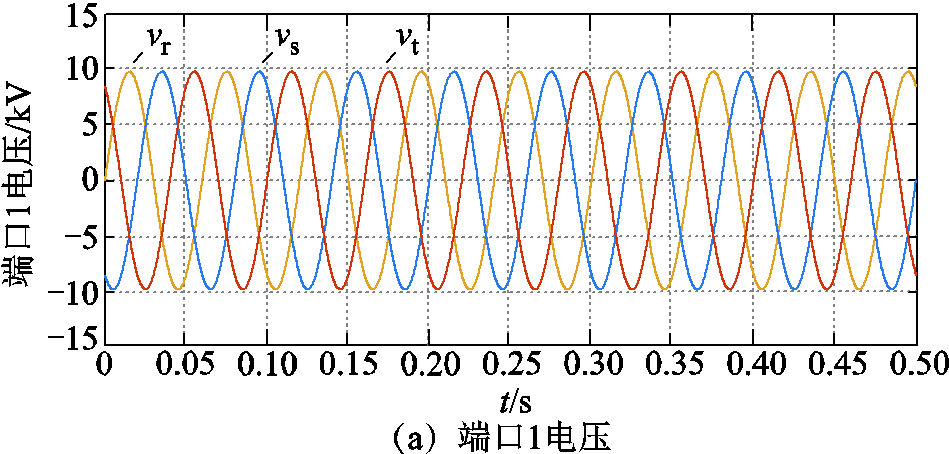
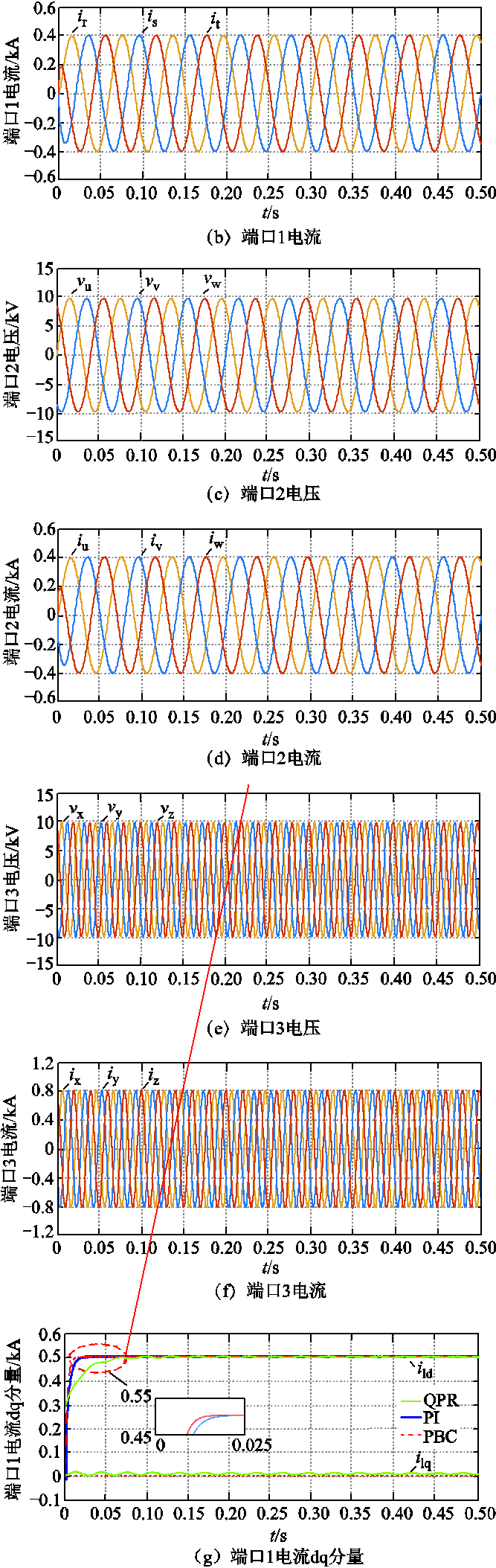
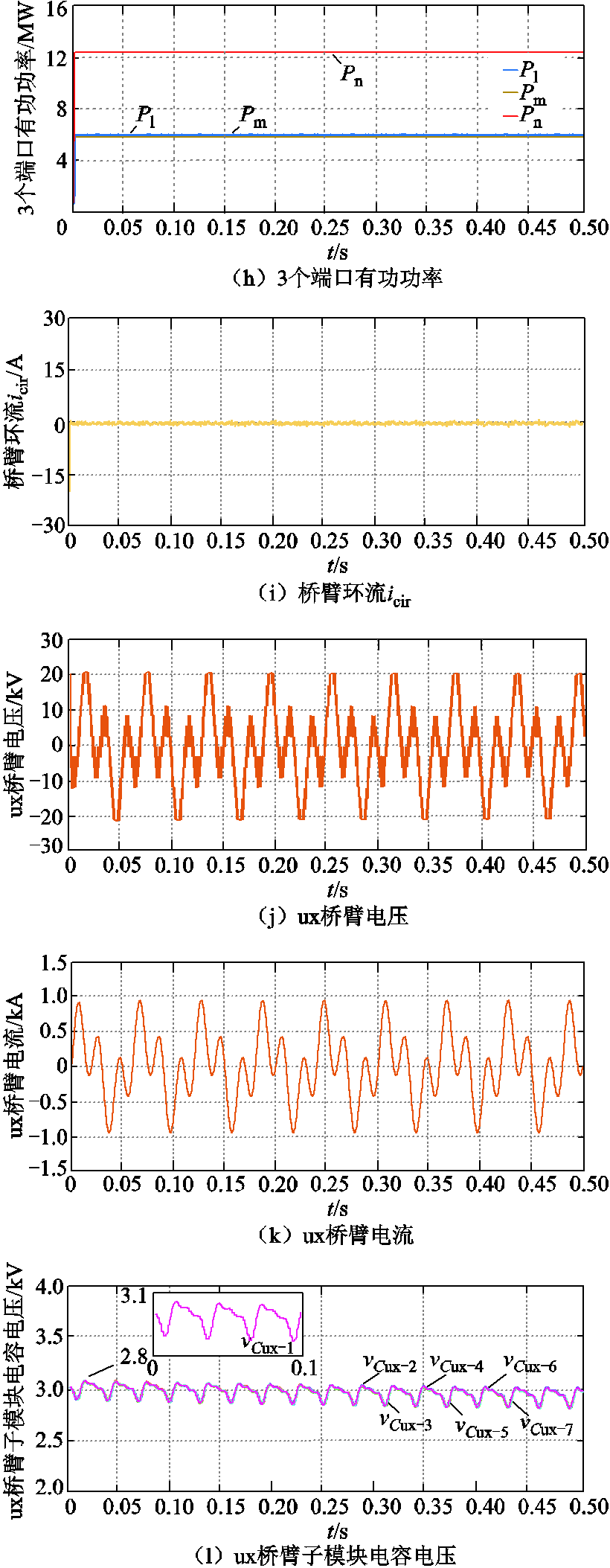
图5 正常运行时九边形MMC的仿真波形
Fig.5 Simulation waveforms of nonagonal-MMC under normal operating condition
由图5a~图5f可知,九边形MMC的3个端口均呈现三相对称交流特性,端口电流幅值和频率也符合预设值,具有AC-AC变换能力。由图5g可知,不进行内部电气量解耦而直接采用QPR控制,虽能使系统稳定,但其电流响应速度缓慢,且其dq电流分量均会在参考值附近波动,与PI、PBC相比有明显差距;详细分析局部放大部分中PI与PBC的控制效果可知,两者的控制曲线平滑,均可使电流稳定于参考值,波动极小,但PBC策略下的电流的响应速度更高,控制效果更优,表明了解耦后采用非线性的PBC方法能够使系统的性能更加优越。由图5h可知,系统的3个端口功率符合功率平衡原理,且均能保持稳定,表明了本文所提功率平衡控制的有效性。由图5i~图5l可知,桥臂电流、电压波形良好,环流波动很小,子模块电容电压能够稳定在3 000V左右,表明了本文所提子模块均压控制的效果较好。综上所述,九边形MMC具有AC-AC变换能力,作为连接低频与工频系统的变频器能够使系统稳定运行,也进一步证明了本文提出的解耦模型与控制策略的正确性与有效性。
3.2.1 功率变化工况
为模拟九边形MMC系统的功率变化工况,设定在0.1 s时,端口3的功率由12.25MW突增为17.25MW,在0.2s时,端口3的功率由17.25MW突降为7.25MW,其他参数不变,分析仿真波形变化。仿真波形如图6所示。
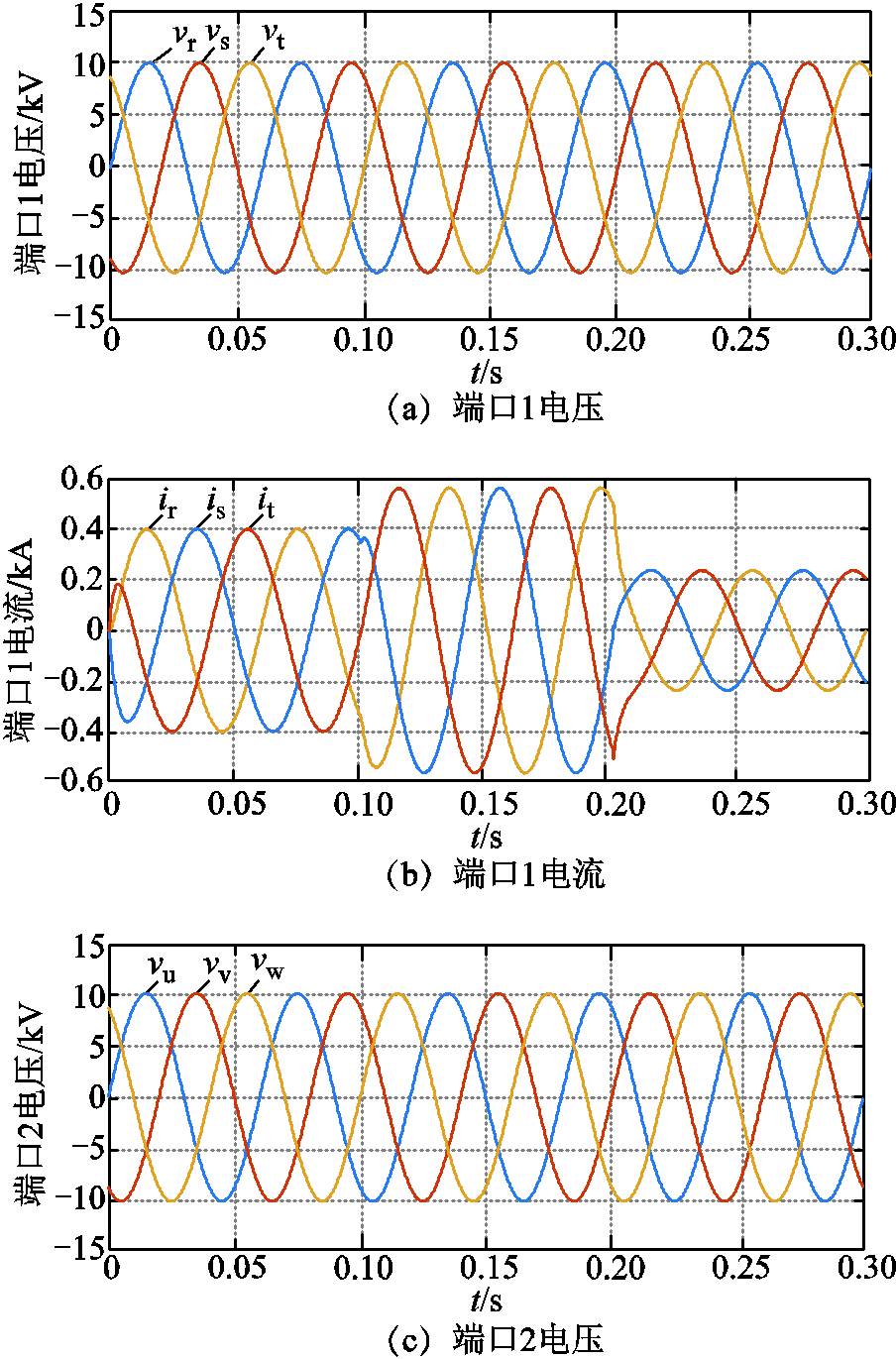
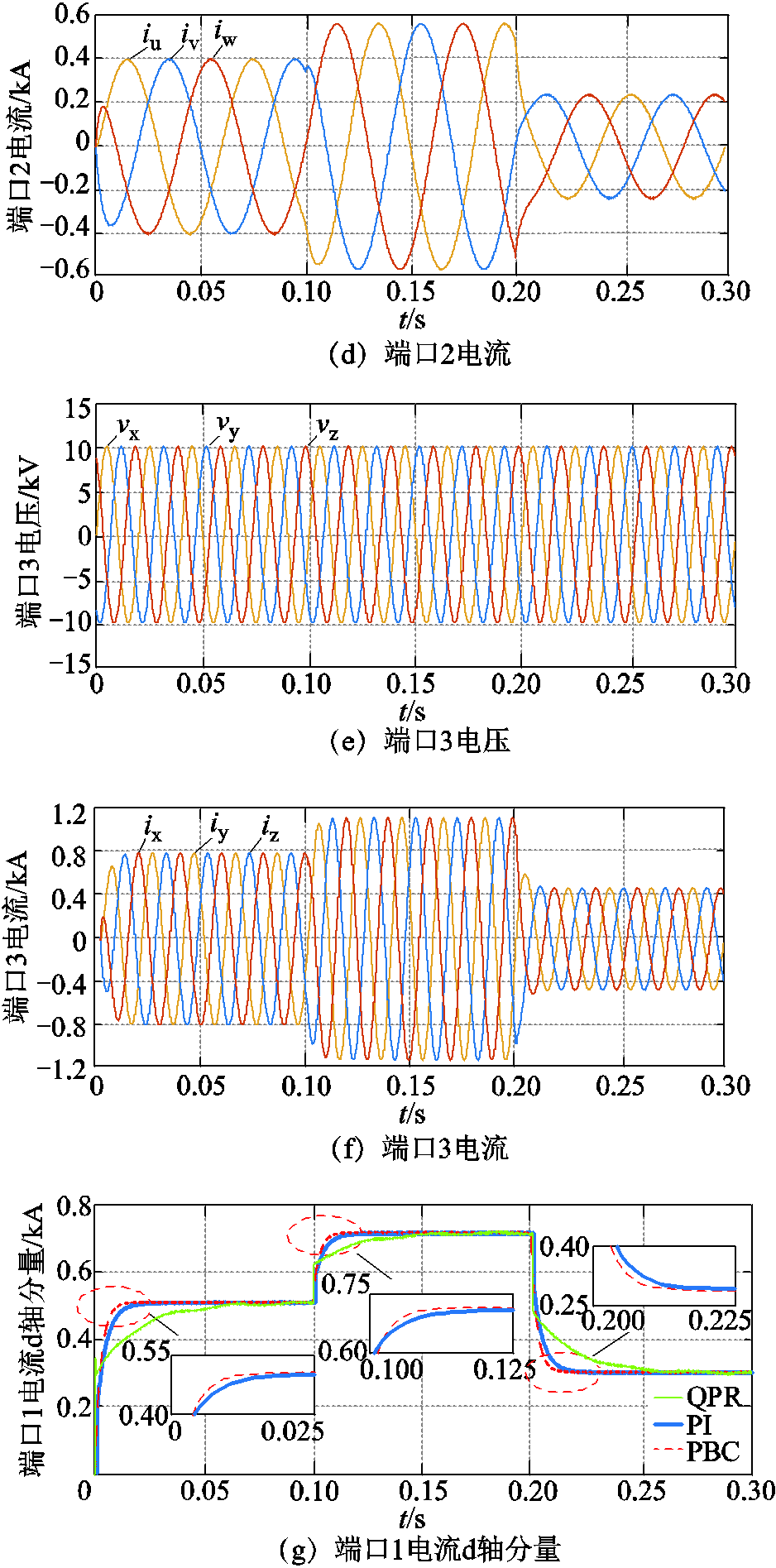
图6 功率变化工况下九边形MMC的仿真波形
Fig.6 Simulation waveforms of nonagonal-MMC under power variation condition
由图6a~图6f验证了本文提出的解耦模型与控制策略的正确性与有效性。分析可知,在端口3功率变化工况下,各端口的电压和电流仍能保持良好的三相对称性。图6g呈现了QPR、PI、PBC三种控制策略下电流直流量的变化情况,表2列出了电流性能指标。分析可知,当系统功率出现变化时,三种控制下的系统均能趋于稳定。在0~0.1s起始阶段、0.1~0.2s功率突增阶段、0.2~0.3s功率突降阶段,PBC控制下的系统相较QPR、PI控制下的系统更具快速性、动态稳定性,且PBC下THD值更低,谐波污染更小,电能质量更高,表明PBC下的控制效果优于QPR、PI控制,验证了所提解耦模型与控制策略的有效性。
表2 功率变化工况下电流性能指标分析
Tab.2 Current performance index under the condition of power variation
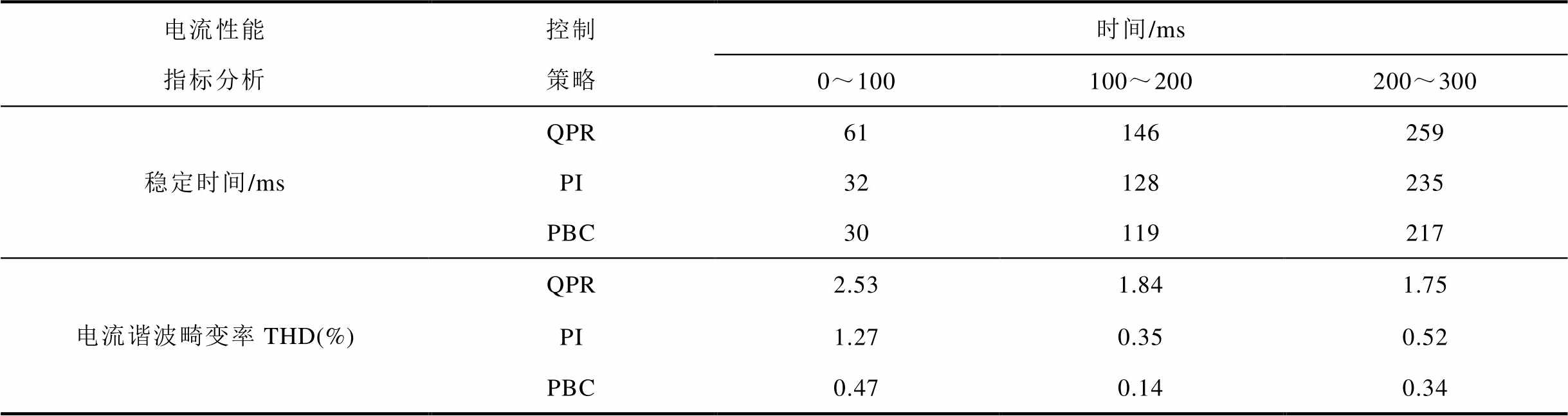
电流性能指标分析控制策略时间/ms 0~100100~200200~300 稳定时间/msQPRPI6132146128259235 PBC30119217 电流谐波畸变率THD(%)QPR2.531.841.75 PI1.270.350.52 PBC0.470.140.34
3.2.2 电压等级变化工况
为模拟九边形MMC电压等级变化工况,设定在0.1s时,端口1的电压幅值暂升10%,在0.2s时暂降10%,其他参数不变,分析仿真波形变化。仿真波形如图7所示。
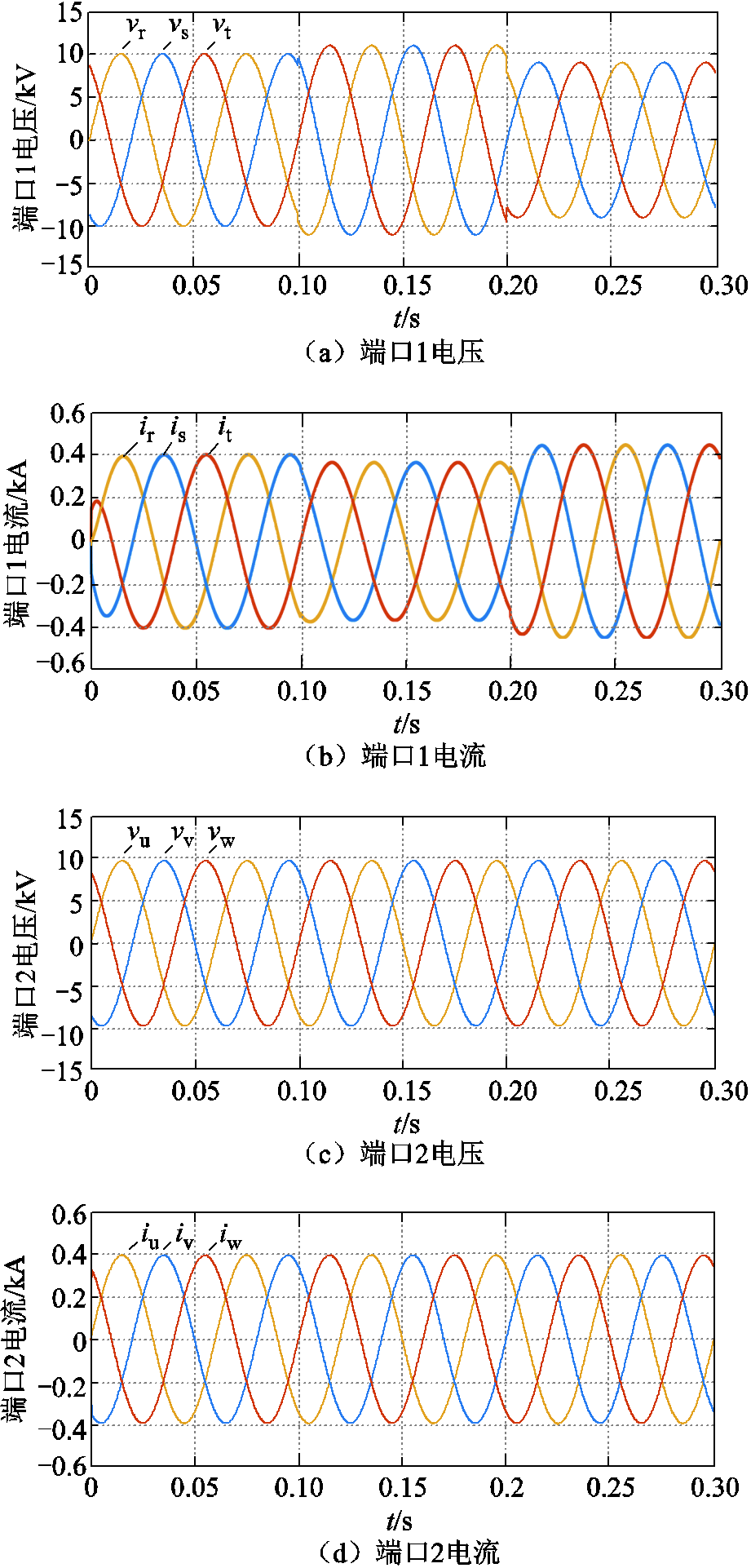
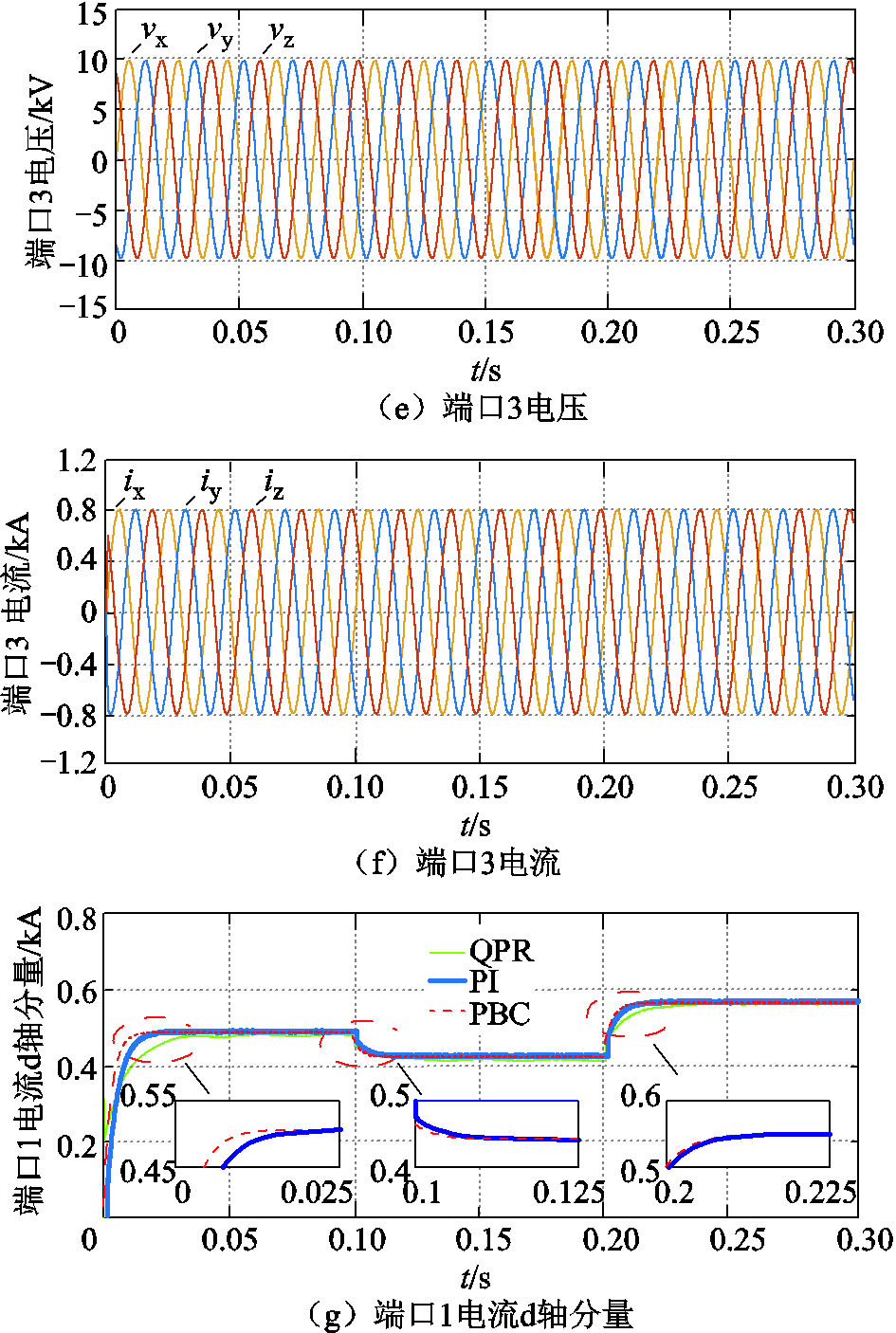
图7 电压等级变化工况下九边形MMC的仿真波形
Fig. 7 Simulation waveforms of nonagonal-MMC when voltage level changes
由图7a~图7f可知,在端口1电压等级变化工况下,各端口的电压和电流仍能保持良好的三相对称性,在0.1s电压暂升后,根据功率平衡原理,电流也出现了相应幅度的降低,0.2s功率暂降后,电流出现相应幅度的升高,验证了功率外环控制的有效性。图7g对比了QPR、PI和PBC控制下端口1电流d轴分量的稳定速度,表3列出了各控制策略下的电流性能指标。分析可知,三种控制方法下的电流均能快速、平稳地达到新的工作值,且PBC下电流的响应速度最快,THD值较低。相比于QPR、PI控制,PBC无论是在稳态还是动态工况下,都更具优势,动态稳定性与快速性更好,电能质量更高。
表3 电压等级变化工况下电流性能指标分析
Tab.3 Current performance index under the condition of voltage level change
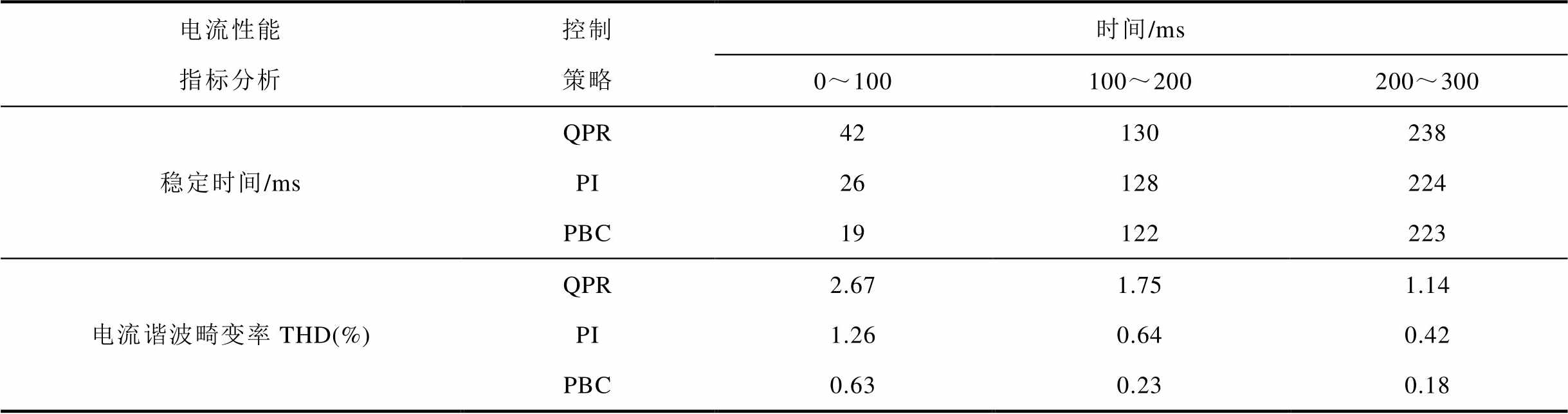
电流性能指标分析控制策略时间/ms 0~100100~200200~300 稳定时间/msQPRPI4226130128238224 PBC19122223 电流谐波畸变率THD(%)QPRPI2.671.261.750.641.140.42 PBC0.630.230.18
为验证九边形MMC的高可靠性,模拟了单端口断路故障的工况,设定低频端口1和工频端口3正常运行,分别连接海上风电场和陆上电网,端口2处于断路故障,系统功率为12.25MW,其他参数不变。仿真结果如图8所示。
分析图8a~图8d可知,端口1和端口3的电压、电流的三相对称性良好,在端口2发生断路故障后,端口3的能量仅由端口1提供,系统等效为双端口的六边形MMC,仍能进行稳定的AC-AC变换。由图8e可见,端口1电流的dq分量能够迅速且平稳地跟踪各自的参考值,反映了系统的响应速度较好。由图8f可见,系统的有功功率能够稳定于额定值12.25MW,无功功率也能够稳定于理论值0var,实现了功率的平衡与稳定。由图8g和图8h可知,子模块电容电压能够稳定于设定值3 000V,环流也能够控制在0附近。仿真结果说明了在单端口断路故障下,九边形MMC依然能够实现从低频到工频的AC-AC变换,证明了系统的高可靠性与稳定性。
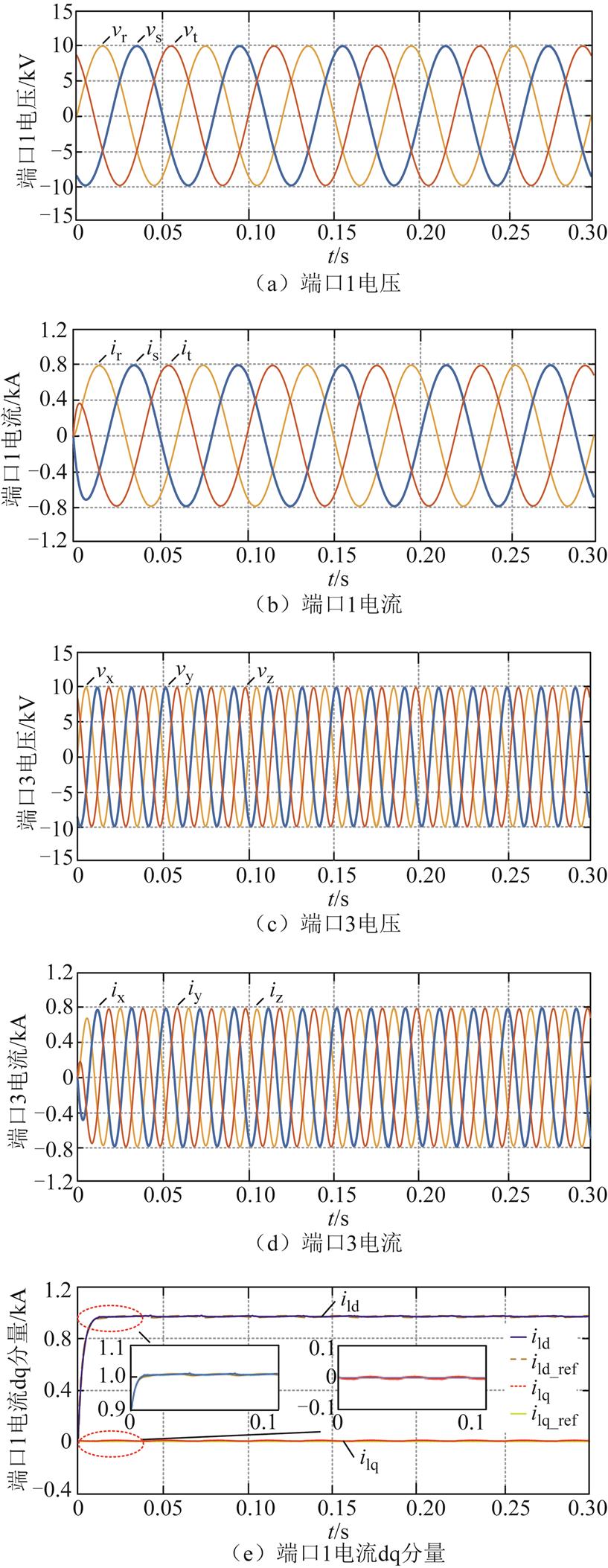
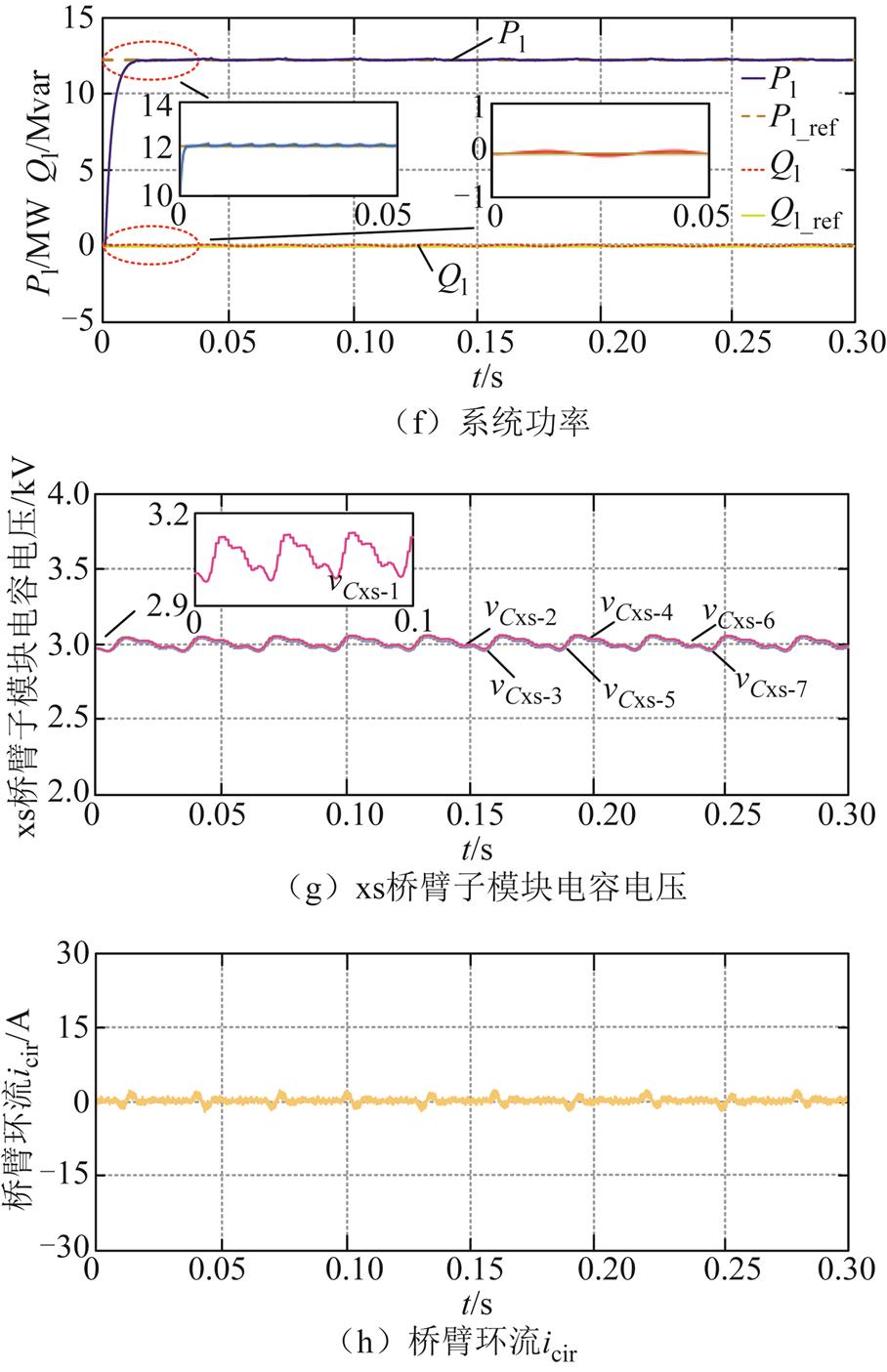
图8 单端口断路故障下九边形MMC的仿真波形
Fig.8 Simulation waveforms of nonagonal-MMC under single-port open circuit fault
由上述不同工况的仿真结果可以看出,本文所提解耦模型与控制策略可行、有效;PBC下的电流与系统功率的跟踪效果相较PI控制更好;系统内部子模块电容电压与桥臂环流的波动范围较小;系统能够在单端口断路故障下等效六边形MMC,具备良好的低频性与可靠性。
为验证本文所提出的九边形MMC解耦模型的可行性,在RT-Lab仿真平台上进行了半物理实验,仿真平台示意图如图9所示。所搭建的RT-Lab实时系统包括九边形MMC、低频和工频交流端口,dSPACE控制器用于实现控制与调制策略,其中DS1103控制板用于连接硬件和Matlab/Simulink仿真环境,编译算法并写入dSPACE处理器中。最终RT-Lab驱动系统可将九边形MMC模型加载到实时仿真平台上,通过配置所需的I/O接口进行实时仿真。
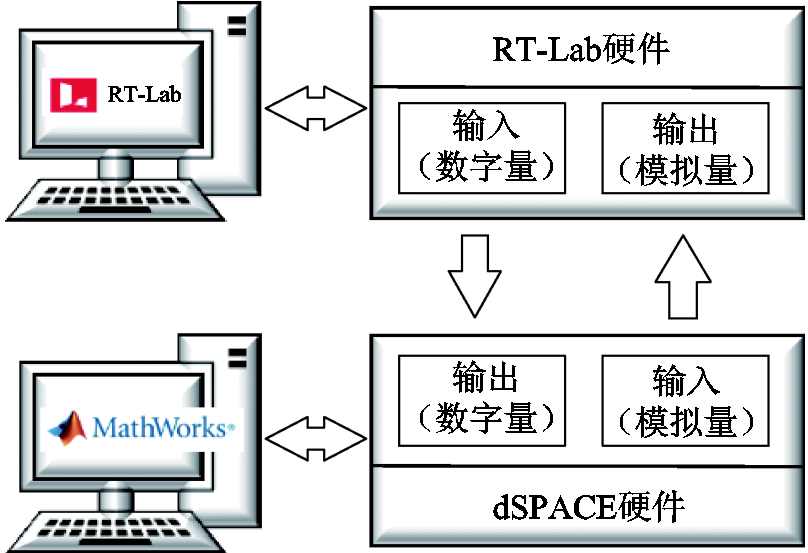
图9 RT-Lab仿真平台示意图
Fig.9 Diagram of RT-Lab simulation platform
对功率变化工况进行实验验证,所得低频端口1三相电流如图10a所示,低频端口1与工频端口3的电流对比如图10b所示,端口1电流d轴分量如图10c所示。
由图10a、图10b可知,端口电流三相对称,且能实现从低频到工频的变换;由图10c可知,在功率变化工况下,端口1的d轴电流仍能快速达到稳定,系统能够稳定运行。综上所述,RT-Lab实验结果与Simulink仿真波形一致,验证了本文提出的九边形MMC解耦方法正确、可行。
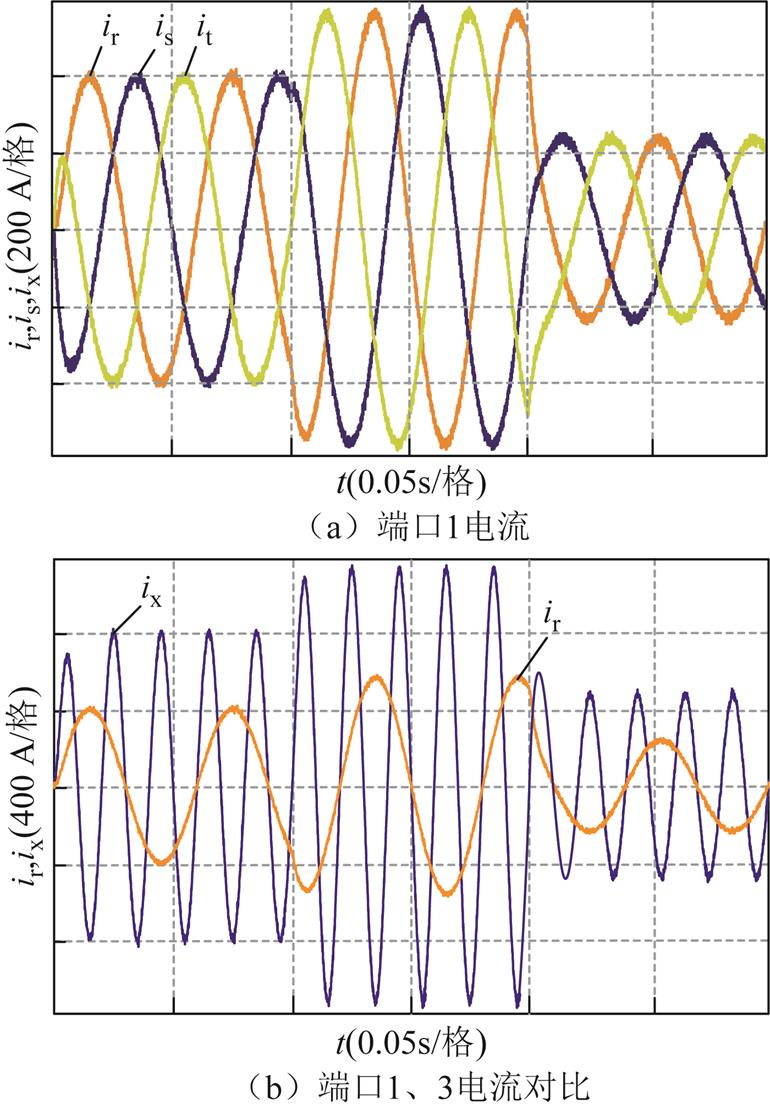
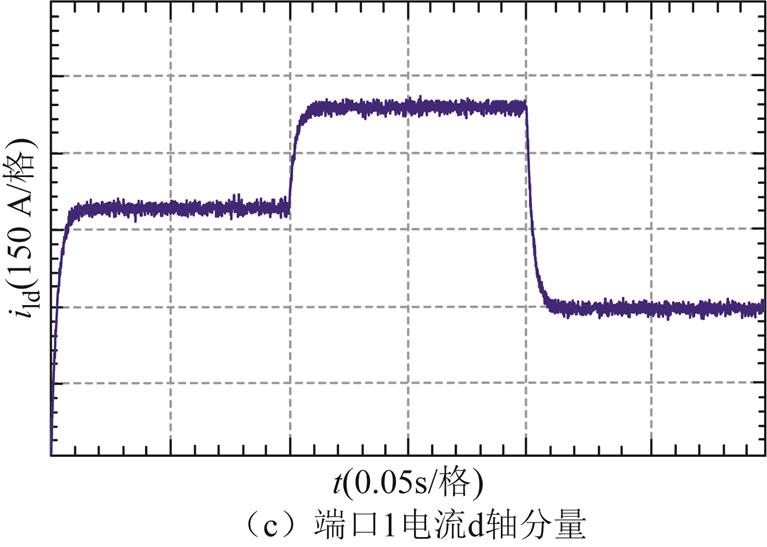
图10 基于RT-Lab平台的实验波形
Fig.10 The experimental waveforms on RT-Lab
本文提出了分频海上风电送出方案中九边形变换器的解耦方法及控制策略,通过理论分析和实验验证可归纳结论如下:
1)本文所提解耦模型能够实现九边形变换器的桥臂电压、桥臂电流各频率分量的解耦,在此基础上设计的PI和PBC控制策略均能使系统稳定运行,且在稳态、动态、单端口开路故障等多种工况下,系统均表现出了良好的控制特性。
2)与未解耦直接采用QPR控制相比,解耦后采用PBC的跟踪速度能够提高一倍左右,PI控制的跟踪速度能够提高50%左右;且PBC下谐波含量能够控制在0.63%以下,而PI控制、QPR控制下谐波含量分别在0.35%~1.27%和1.14%~2.67%内,表明了解耦模型的可行性与优越性,验证了PBC下的跟踪速度更快,动态稳定性与快速性更好,谐波污染更低。
3)与M3C、六边形变换器的方案相比,九边形变换器不仅保留了良好的低频特性和直接AC-AC变换的特点,而且能够实现多端口的高效互联,提高了系统集成度,其在分频输电汇集系统及海上风电领域十分具有发展潜力。
参考文献
[1] Rifikin J. The Third Industrial Revolution: How Lateral Power is Transforming Energy, the Economy, and the World[M]. New York: Palgrave Macmillan Trade, 2011.
[2] You Shutang, Zhao Jiecheng, Yao Wenxuan, et al. FNET/GridEye for future high renewable power grids-aplications overview[C]//2018 IEEE PES Transmission & Distribution Conference and Exhibition-Latin America (T&D-LA), Lima, Peru, 2018: 1-5.
[3] Yaramasu V, Wu Bin, Sen P C, et al. High-power wind energy conversion systems: state-of-the-art and emerging technologies[J]. Proceedings of the IEEE, 2015, 103(5): 740-788.
[4] Wu Jiahui, Wang Haiyun, Wang Weiqing, et al. Performance evaluation for sustainability of wind energy project using improved multi-criteria decision-making method[J]. Journal of Modern Power Systems and Clean Energy, 2019, 7(5): 1165-1176.
[5] Luo Jiajie, Zhang XiaoPing, Xue Ying, et al. Harmonic analysis of modular multilevel matrix converter for fractional frequency transmission system[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1209-1219.
[6] Ruddy J, Meere R, Donnell T O. Low frequency AC transmission for offshore wind power: A review[J]. Renewable and Sustainable Energy Reviews, 2016, 56: 75-86.
[7] Al-Tameemi M, Miura Y, Liu J, et al. A novel control scheme for multi-terminal low-frequency AC electrical energy transmission systems using modular multilevel matrix converters and virtual synchronous generator concept[J]. Energies, 2020, 13(3): 747-765.
[8] 武鸿, 王跃, 刘熠, 等. 基于广义电容电压不平衡度的MMC子模块开路故障诊断策略[J]. 电工技术学报, 2023, 38(14): 3909-3922.
Wu Hong, Wang Yue, Liu Yi, et al. Open circuit fault diagnosis strategy of mmc sub-module based on generalized capacitor voltage unbalance[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3909-3922.
[9] 刘座辰, 林磊, 殷天翔, 等. 一种模块化多电平换流器子模块开路故障的快速检测与诊断方法[J]. 电工技术学报, 2022, 37(19): 4883-4894.
Liu Zuochen, Lin lei, Yin Tianxiang, et al. A fast open-circuit fault detection and diagnosis method for sub-modules of modular multilevel converters[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4883-4894.
[10] 樊强, 俞永杰, 夏嘉航, 等. 低容值半桥型模块化多电平变换器直流故障辅助清除策略[J]. 电工技术学报, 2022, 37(14): 3713-3722.
Fan Qiang, Yu Yongjie, Xia Jiahang, et al. Auxiliary strategy for DC fault clearing of low capacitance half-bridge modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3713-3722.
[11] Kawamura W, Hagiwara M, Akagi H. Control and experiment of a modular multilevel cascade converter based on triple-star cells[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3536-3548.
[12] 李遥, 许烈, 李永东. 模块化多电平矩阵变换器开关次数最优的拓扑连接策略[J]. 电工技术学报, 2018, 33(2): 342-352.
Li Yao, Xu Lie, Li Yongdong. Topology connecting strategy of the modular multilevel matrix converter for optimal switching times[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 342-352.
[[13] 唐英杰, 张哲任, 徐政. 基于有源型M3C矩阵变换器的海上风电低频送出方案[J]. 电力系统自动化, 2022, 46(8): 113-122.
Tang Yingjie, Zhang Zheren, Xu Zheng. Low-frequency transmission scheme for offshore wind power based on active modular multilevel matrix converter[J]. Automation of Electric Power Systems, 2022, 46(8):113-122.
[14] Baruschka L, Mertens A. A new three-phase AC/AC modular multilevel converter with six branches in hexagonal configuration[J]. IEEE Transactions on Industry Applications, 2013, 49(3): 1400-1410.
[15] Meng Yongqing, Liu Bo, Luo Huiyong, et al. Control scheme of hexagonal modular multilevel direct converter for offshore wind power integration via fractional frequency transmission system[J]. Journal of Modern Power Systems and Clean Energy, 2018, 6(1): 168-180.
[16] Zhang Chong, Jiang Daozhuo, Zhang Xuan, et al. The study of a battery energy storage system based on the hexagonal modular multilevel direct AC/AC converter (hexverter)[J]. IEEE Access, 2018, 6: 43343-43355.
[17] Wang Pa, Liu Fei, Zha Xiaoming, et al. A regenerative hexagonal-cascaded multilevel converter for two-motor asynchronous drive[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(4): 1687-1699.
[18] 刘飞, 高海祐, 刘文君, 等. 部分能量输入的三端口六边形 MMC功率分析及环流控制[J]. 中国电机工程学报, 2019, 39(20): 6056-6064, 6186.
Liu Fei, Gao Haiyou, Liu Wenjun, et al. Power analysis and circulating current control of a partial energy input based three-port hexagonal MMC[J]. Proceedings of the CSEE, 2019, 39(20): 6056-6064, 6186.
[19] Liu Wenjun, Liu Fei, Gao Haiyou, et al. A transformerless three-port nonagonal MMC for the grid connection and local consumption of distributed generation[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(01): 108-117.
[20] Zhou Shijia, Rong Fei, Sun Wenlong, et al. AC/AC grid connection of six-phase wind power generator based on enneagon MMC converter[J]. International Journal of Electrical Power & Energy Systems, 2020, 118: 105810-105817.
[21] 刘飞, 沈煜, 黄文慧, 等. 分频风电汇集系统的九边形变换器及三端口功率控制研究[J]. 中国电机工程学报,2020, 40(15): 4977-4987.
Liu Fei, Shen Yu, Huang Wenhui, et al. A nonagonal modular multilevel converter with three-port power control applied in offshore wind power collection of fractional frequency transmission system[J]. Pro-ceedings of the CSEE, 2020, 40(15): 4977-4987.
[22] 程启明, 赖宇生, 李剑辉, 等. 基于六边形变换器的无源滑模控制策略[J]. 电网技术, 2023, 47(10): 4323-4330.
Chen Qiming, Lai Yusheng, Li Jianhui, et al. Research on passivity-based sliding-mode control strategy based on hexagonal converter[J]. Power System Technology, 2023, 47(10): 4323-4330.
Abstract In the process of exploring new renewable energy, offshore wind power is becoming the focus of research in the field of new energy at home and abroad because of its strong stability, high annual utilization hours, small impact on topography, suitable for large-scale development and other characteristics. And thefractional frequency transmission is the most widely used transmission mode,nonagonal modular multilevel converter has attracted much attention because of its multi-port, direct AC-AC conversion capability, good low frequency performance and high reliability. However, nonagonal converter has the problem of strong coupling of electrical components with different frequencies, current research usually does not decouple the internal electric quantity but directly controls it, and the control effect needs to be improved. To address these issues, this paper proposes a decoupling method of the nine-sided converter. On this basis, the advanced control method is used to make up for the deficiency of the traditional control method, so as to improve the control performance of the system.
Firstly, according to the topological structure of nonagon converter, the relationship between voltages and currents of the bridge arms is deduced in detail, and the decoupling mathematical model of nonagonal converter is derived. In this way, the complex system can be decomposed into several independent subsystems, and the coupling effect is reduced to a minimum, thus reducing the complexity of control design, simplifying the controller design process, and contributing to the adoption of advanced control methods, so as to optimize the system and adjust parameters. Then, PI control of N-MMC is proposed in this paper. However, when dealing with complex nonlinear nonagonal MMC system, the performance of PI controller will be limited due to its nonlinear dynamic characteristics, uncertainty and strong coupling. For example, the tracking speed and accuracy of the inner loop current will also be reduced. Therefore, for complex nonlinear nonagonal MMC, it is limited to overcome the shortcomings of PI control only through parameter adjustment, and it is necessary to consider nonlinear control methods to achieve better control performance. Then, nonlinear passive control (PBC) is proposed for the control of nonagonal MMC. Finally, the PI control and PBC control system simulation of the nonagonal MMC is built on the MATLAB platform, and a variety of working conditions including dynamic working conditions and fault working conditions are simulated. By comparing the effects of PBC control, PI control, and quasi proportional resonance (QPR) control without decoupling, semi-physical simulation is carried out on RT-LAB experiment platform to verify the feasibility and superiority of the decoupling model and control strategy proposed in this paper.
The following conclusions can be drawn from the simulation analysis: (1) The decoupling model proposed in this paper can realize the decoupling of the frequency components of the bridge arm voltage and the bridge arm current of the nine-sided converter, and the PI and PBC control strategies designed on this basis can make the system run stably, and the system shows good control characteristics under various working conditions such as steady state, dynamic and single-port open fault. (2) By comparing QPR control, PI control and PBC control, it can be seen that the tracking speed under PBC control is faster, the dynamic stability and rapidity are better, and the harmonic pollution is lower. (3) Compared with M3C and hexagonal converter schemes, the nonagonal converter not only retains good low-frequency characteristics and the characteristics of direct AC-AC conversion, but also can realize the efficient interconnection of multi-ports and improve the integration of the system, which has great development potential in the field of fractional frequency transmission collection system and offshore wind power.
keywords:offshore wind power, nonagonal modular multilevel converter, multi-port converter, decoupling mathematical model, passivity-based control
DOI: 10.19595/j.cnki.1000-6753.tces.230724
中图分类号:TM762
国家自然科学基金项目(61905139)和上海市电站自动化技术重点实验室项目(13Z2273800)资助。
收稿日期 2023-05-22
改稿日期 2023-10-18
程启明 男,1965年生,教授,硕士生导师,研究方向为电力系统自动化、发电过程控制、先进控制及应用等。E-mail:chengqiming@sina.com
杜婷伟 女,2000年生,硕士研究生,研究方向为新能源发电控制、海上风力发电控制等。E-mail:dutingwei_2000@163.com(通信作者)
(编辑 郭丽军)