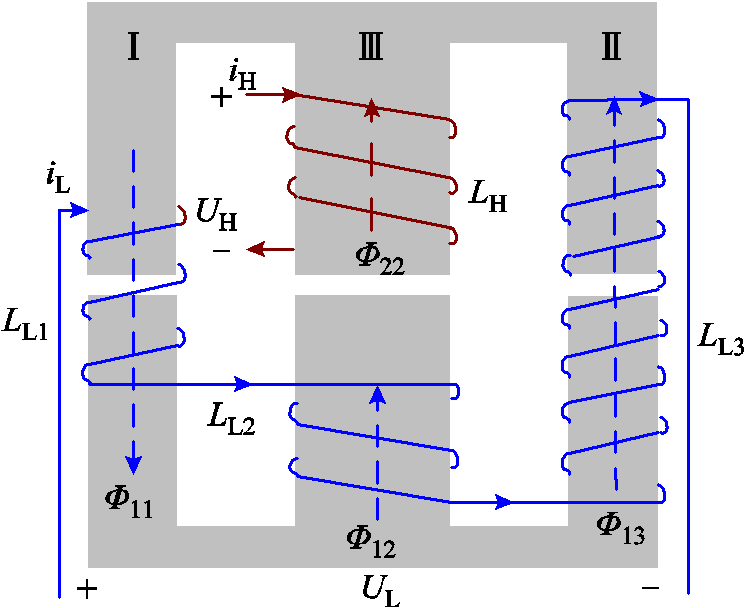
图1 TSWIM结构
Fig.1 TSWIM Structure
摘要 双频 Buck 变换器由两个降压单元级联构成,具有动态响应快,开关损耗小等优势。然而不足的是磁件占据了整个系统的大部分体积与重量,降低了系统的功率密度。针对这一问题,提出一种三段式绕制磁集成技术,将磁件以解耦的方式集成在一副磁心中。该文首先建立集成磁件的磁路等效模型,通过抵消各绕组之间的耦合作用推导出解耦条件,并详细阐述了磁心的选取、匝数以及气隙的设计原则。其次,利用有限元仿真平台对所提集成磁件进行建模分析,与现有的集成方法相比,磁通密度分布更为均匀,磁心的利用率得到了有效提升。最后,搭建一台48 V/12 V、108 W 的实验样机,体积和重量同分离磁件相比降低了 31.2%和25.3%,提高了系统的功率密度,验证了该集成方法理论分析的正确性和可行性。
关键词:双频Buck变换器 解耦集成 有限元仿真 磁通密度 功率密度
随着电力电子技术的发展,对高频化、小型化和高功率密度的追求已然成为趋势,但高频化势必会引起变换器开关损耗的增加,从而降低了变换器的效率并加剧了电磁干扰问题,在一定程度上限制了变换器性能的改善[1-4]。文献[5]提出了一种双频Buck(Double Frequency Buck, DF Buck)变换器拓扑结构,相比于传统Buck变换器,DF Buck变换器通过引入低频单元来分取高频开关上的电流,从而降低高频开关损耗,同时又能保持变换器良好的动态响应速度。文献[6-11]主要阐述了DF Buck变换器的参数设计原则、功率传输路径,并通过建立小信号模型,证明了DF Buck变换器输出特性主要取决于高频参数,而与低频参数无关。虽然DF Buck变换器改善了单个高频化和输出效率的矛盾关系,但却因为拓扑中增加了一个低频大电感而使得变换器的体积和质量都有所增加,增加了成本,使其使用环境受限。为了解决这一问题,需要对DF Buck变换器的磁件进行研究,引入磁集成技术[12-13]来降低磁件的体积和质量。文献[14]利用耦合集成将输入电感器、两个功率传输电感器和一个辅助电感器集成在一个磁心中,呈现出“零”输出电流纹波,使其具有更好的动态性能。文献[15]中提出了一种高增益耦合集成电感方法,通过改变耦合电感的匝数比来改变电压增益,与集成前相比提高了变换器的电压增益且降低了输出电流纹波。文献[16]提出了DF Buck变换器的解耦磁集成方法,虽然减小了磁件的体积和质量,但这种集成结构存在可能会引起侧柱饱和、磁通密度分布不均等问题,而且低频电感绕制在磁心侧柱,绕组匝数分布密集,不易于散热。文献[17]针对LLC谐振变换器将谐振电感与变压器集成在同一磁心中,降低了集成磁件的磁饱和问题。
为解决DF Buck变换器中磁件的体积、质量以及文献[16]中的磁心磁通密度分布不均等问题,本文在文献[16-18]的基础上提出了一种三段式绕制集成磁件(Three-Section Winding Integrated Magnetic, TSWIM)技术,将变换器中的磁件解耦集成在一副磁心中,通过对低频大电感的分段绕制,使其分布疏散,在一定程度上解决了集成磁件由于多层绕制而导致热点集中的问题,并对比分离磁件(Segregation Magnetic, SM)和现有的集成磁件(Integrated Magnetic, IM),该方法能有效减小磁件体积,使磁心磁通密度分布更为均匀,提高了变换器的功率密度。
TSWIM的结构如图1所示,为了确保整个TSWIM的磁心有更均匀的磁通密度分布,按以下方式绕制和整合磁性部件。首先,低频大电感LL被分成三部分,分别绕制在磁心的两个边柱和中柱的下半部分;另外,高频小电感LH绕制在中柱的上半部分。第一段的低频电感LL1绕制在磁柱Ⅰ上,匝数为N11;第二段的低频电感LL2和第三段的低频电感LL3分别绕在磁柱Ⅲ和磁柱Ⅱ上,匝数为N12和N13,且低频电感器LL = LL1 + LL2 + LL3。绕制在磁柱Ⅲ上半部分的高频小电感LH的匝数为N22。LH产生的磁通用Ф22表示,Ф11、Ф12和Ф13分别为低频电感LL1、LL2和LL3产生的磁通。最后,UH和UL分别为高频和低频电感上的电压,iH和iL代表相应高频电感和低频电感电流。为使后文的比较更为明确,现将文献[16]中所述的IM结构给出,其中IM低频电感绕制在磁柱Ⅰ和磁柱Ⅱ,匝数分别为NL1和NL2;IM高频电感绕制在磁柱Ⅲ,匝数为NH。如图2所示,IM具体分析过程不再赘述。

图1 TSWIM结构
Fig.1 TSWIM Structure
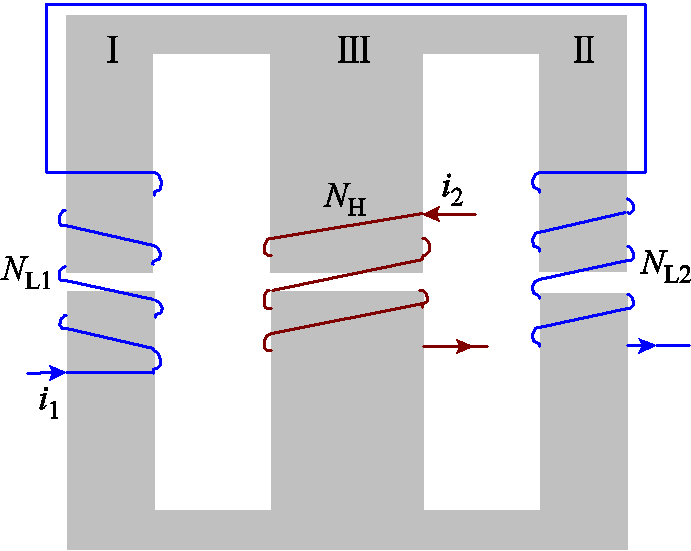
图2 IM结构
Fig.2 IM Structure
根据图1的TSWIM结构可以得出其等效磁路模型,如图3所示,其中R1、R2、R3分别代表磁柱Ⅰ、磁柱Ⅱ、磁柱Ⅲ上的等效电阻;低频电感LL1、LL2、LL3产生的磁动势分别用N11iL、N12iL、N13iL表示;高频电感LH产生的磁动势用N22iH表示;Ф1、Ф2、Ф3为对应磁柱上各个绕组相互作用下的叠加磁通。
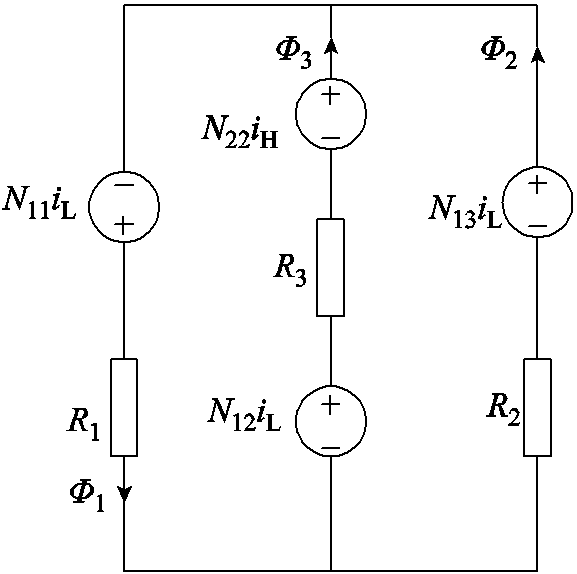
图3 TSWIM的等效磁路模型
Fig.3 Equivalent magnetic circuit model of TSWIM
根据磁路的欧姆定律,可得
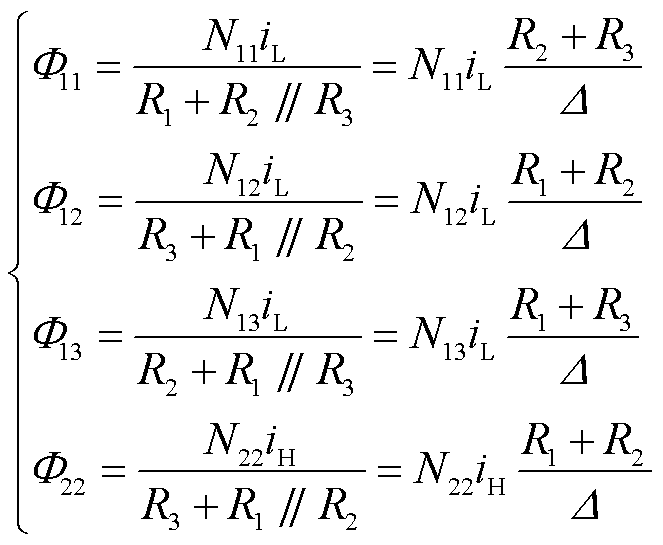 (1)
(1)
式中,Δ=R1R2+R2R3+R1R3。
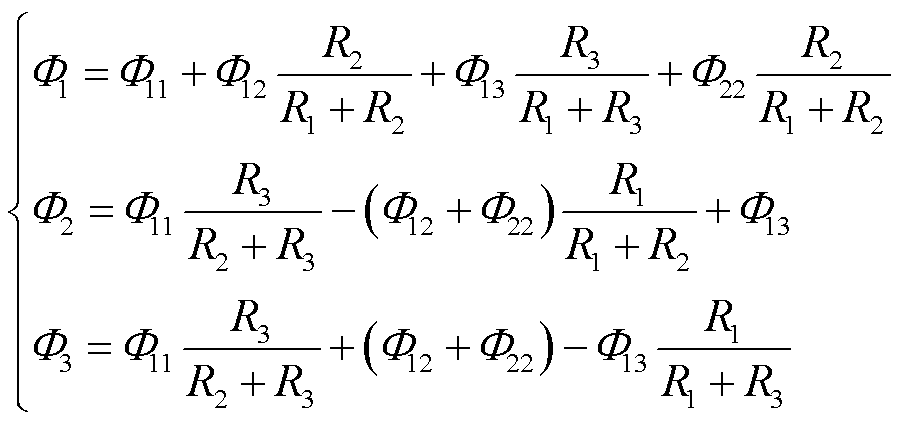 (2)
(2)
将式(1)代入式(2),可得
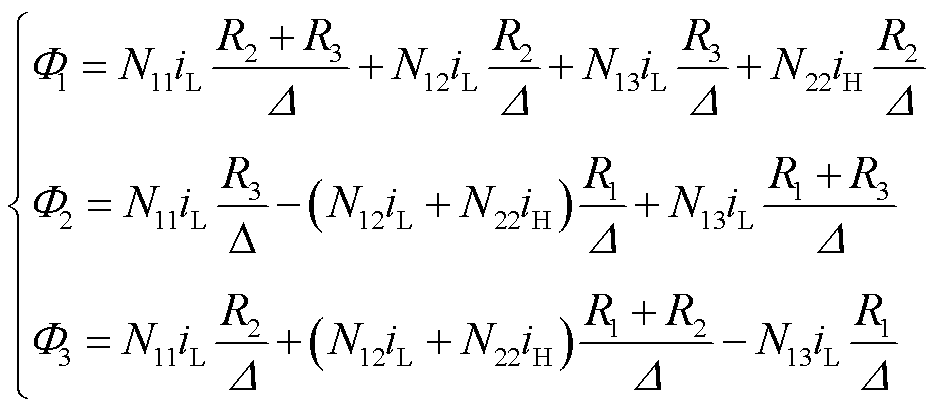 (3)
(3)
高低频电感两端电压由法拉第电磁感应定律可得
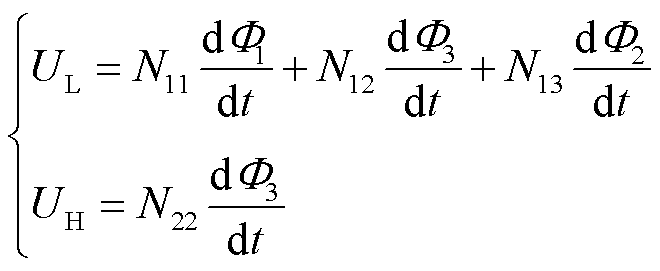 (4)
(4)
将式(3)代入式(4)可得
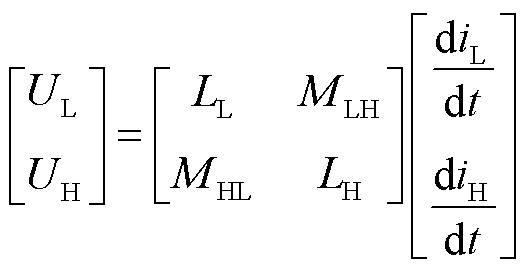 (5)
(5)
式中,MLH为低频电感器对高频电感器的互感;MHL为高频电感器对低频电感器的互感。具体参数为
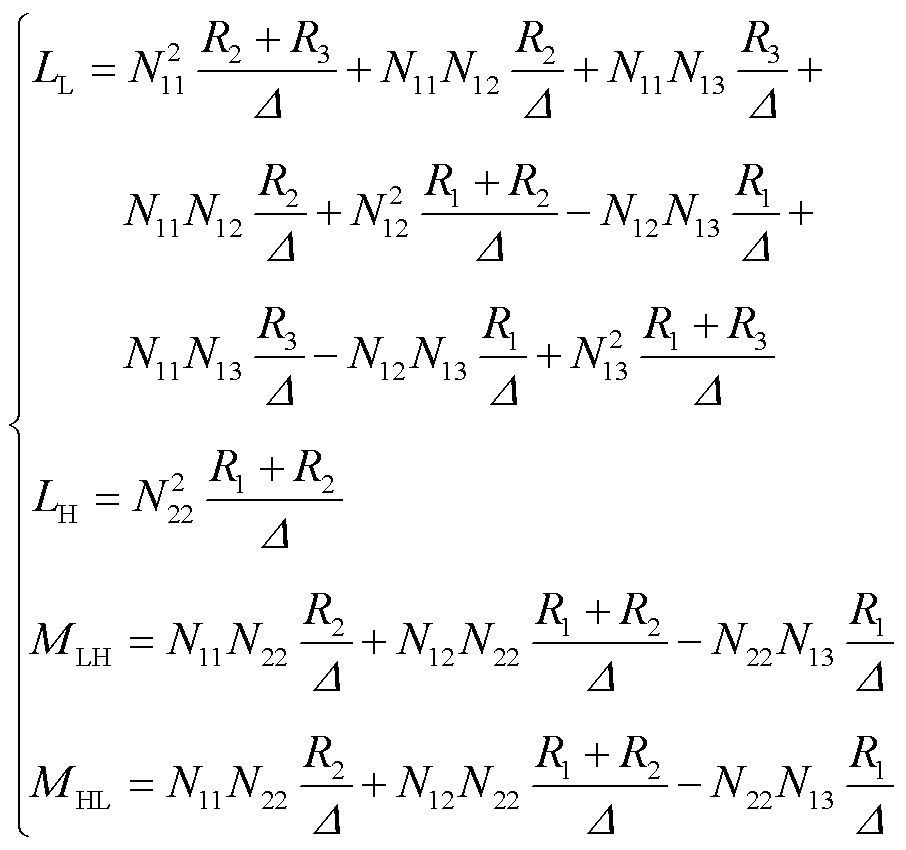 (6)
(6)
可以得出,当MLH=MHL=0时,此时的高频和低频电感可满足解耦,有
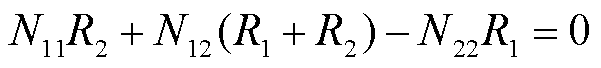 (7)
(7)
为了计算方便,取EE磁心的中柱截面积近似为侧柱截面积的2倍[16],所以有
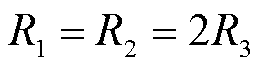 (8)
(8)
将式(8)代入式(7)中,可得解耦条件为
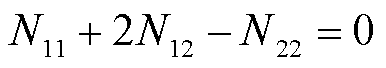 (9)
(9)
当TSWIM的低频电感满足式(9)时,高低频电感即可满足解耦集成。
对于磁心来说,必须考虑磁柱饱和问题,这就需要在选定一个磁心之前,第一是计算出每个磁柱可能经过的最大磁通来判断磁柱是否在饱和状态或者饱和边界;第二是有合适的窗口面积来容纳绕组。根据磁路的欧姆定律,各个磁柱上产生的最大磁通密度为
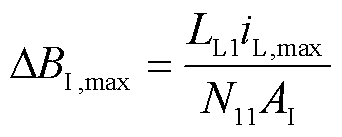 (10)
(10)
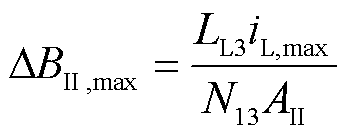 (11)
(11)
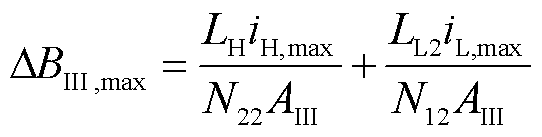 (12)
(12)
各个磁柱上产生的最小磁通密度为
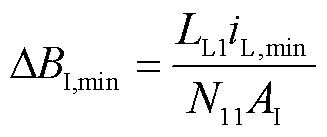 (13)
(13)
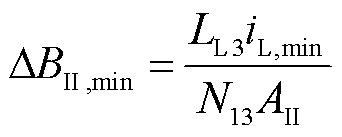 (14)
(14)
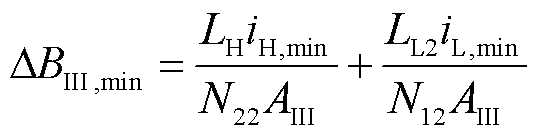 (15)
(15)
式中,ΔBI,max/ΔBI,min、ΔBⅡ,max/ΔBⅡ,min和ΔBⅢ,max/ΔBⅢ,min分别为磁柱Ⅰ、Ⅱ和Ⅲ上的最大/最小磁通密度;iH,max/iH,min和iL,max/iL,min分别为高频和低频电感电流的峰值/谷值。
根据叠加定理,各个磁柱上的最大磁通密度绝对值可以表示为
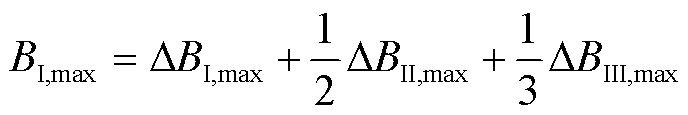 (16)
(16)
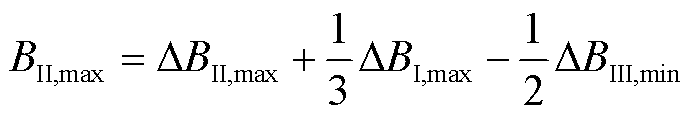 (17)
(17)
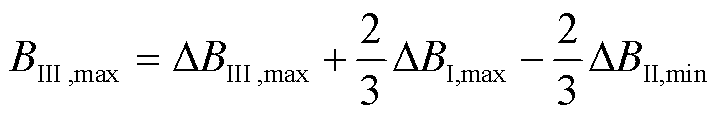 (18)
(18)
通过上述各式可以判断磁心是否会发生局部饱和。
对于SM而言,磁心通常以面积乘积(Area Product, AP)法[19]进行选取,即
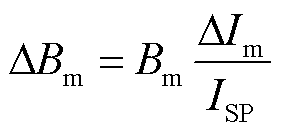 (19)
(19)
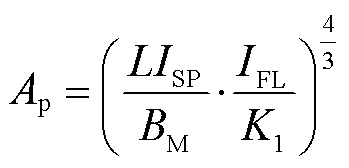 (20)
(20)
确定绕组匝数为
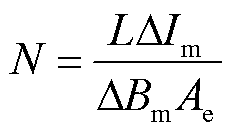 (21)
(21)
确定磁心气隙为
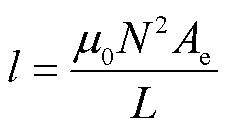 (22)
(22)
式中,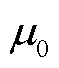 为空气磁导率;ΔBm为最大磁通密度摆幅;ΔIm为电感电流纹波值;L为电感值大小;ISP为最大短路电流;IFL为满负荷时电感电流的有效值;K1为单线圈电感系数;Ae为磁心的有效截面积。
为空气磁导率;ΔBm为最大磁通密度摆幅;ΔIm为电感电流纹波值;L为电感值大小;ISP为最大短路电流;IFL为满负荷时电感电流的有效值;K1为单线圈电感系数;Ae为磁心的有效截面积。
而对于TSWIM能否集成在一副EE磁心中,绕组共用的最大窗口面积应为
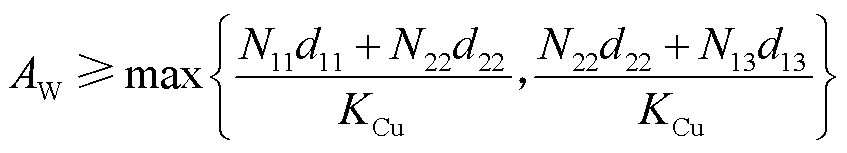 (23)
(23)
式中,AW为窗口面积;d11、d22、d13为对应绕组直径;KCu为铜的填充系数。
EE磁心截面积和气隙大小如图4所示,三个磁柱开相同气隙,AⅠ、AⅡ、AⅢ为磁柱Ⅰ、Ⅱ、Ⅲ的截面积,CⅠ、CⅡ、CⅢ为磁柱Ⅰ、Ⅱ、Ⅲ的等效磁导。
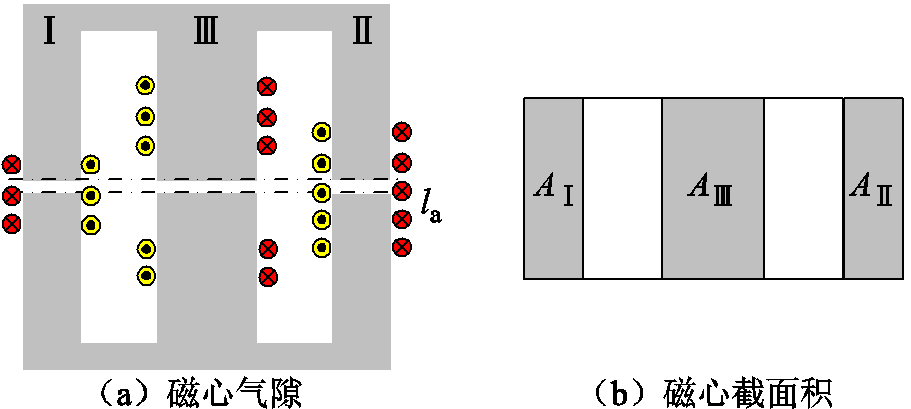
图4 磁心气隙与截面积
Fig.4 Core air gap and cross-sectional area
根据文献[19],可得每个磁柱上的等效磁导
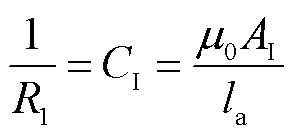 (24)
(24)
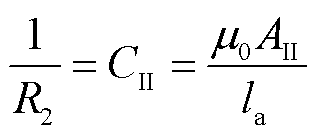 (25)
(25)
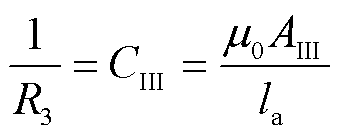 (26)
(26)
式中,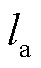 为气隙长度。
为气隙长度。
将式(24)~式(26)代入式(6)可得
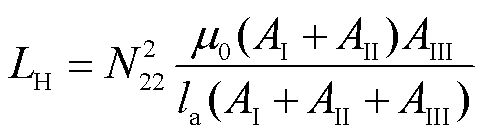 (27)
(27)
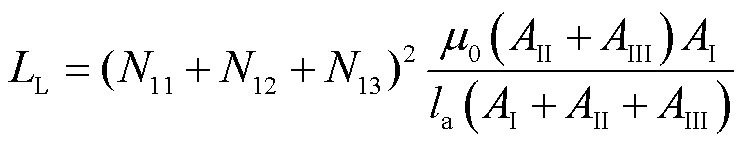 (28)
(28)
由上述公式可以求得TSWIM的匝数和气隙长度。
TSWIM结构下的DF Buck变换器如图5所示,Q1~Q4为开关管。其中,Q1和Q4是高频开关,而Q2和Q3是低频开关。据文献[10],开关状态可分为四种,见表1。图6为相应的模态转换,表2为不同模态下高低频电感电流波形的变化率,表3为不同模态下绕组磁通的变化率。图7为TSWIM类型下DF Buck变换器的理论输出波形。
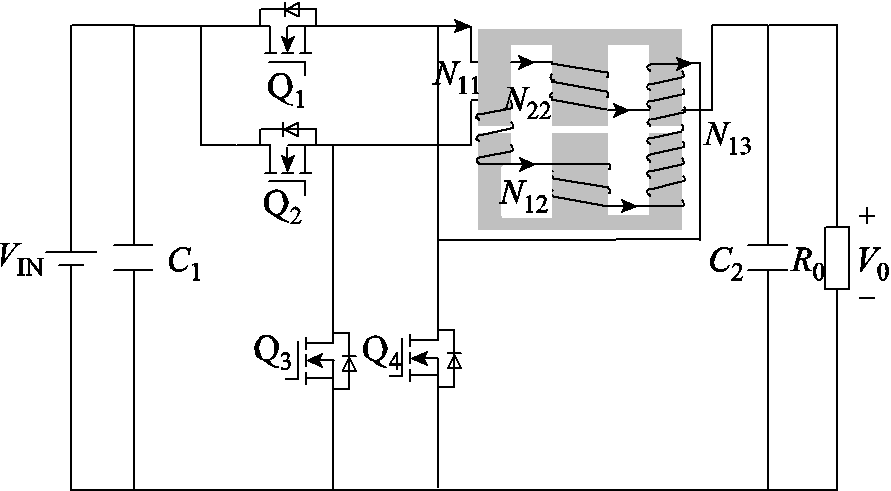
图5 TSWIM下的DF Buck变换器
Fig.5 DF Buck converter under TSWIM
表1 四种开关状态
Tab.1 Four switching states
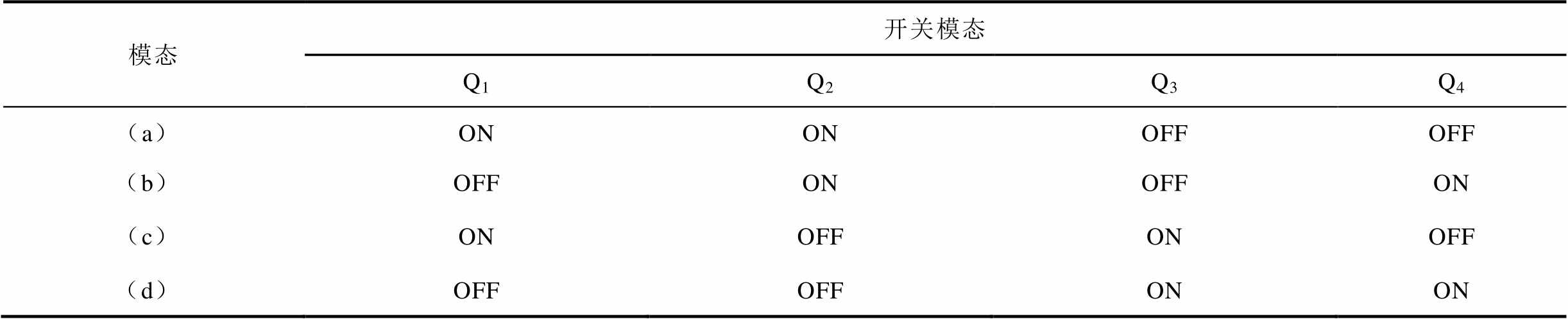
模态开关模态 Q1Q2Q3Q4 (a)ONONOFFOFF (b)OFFONOFFON (c)ONOFFONOFF (d)OFFOFFONON
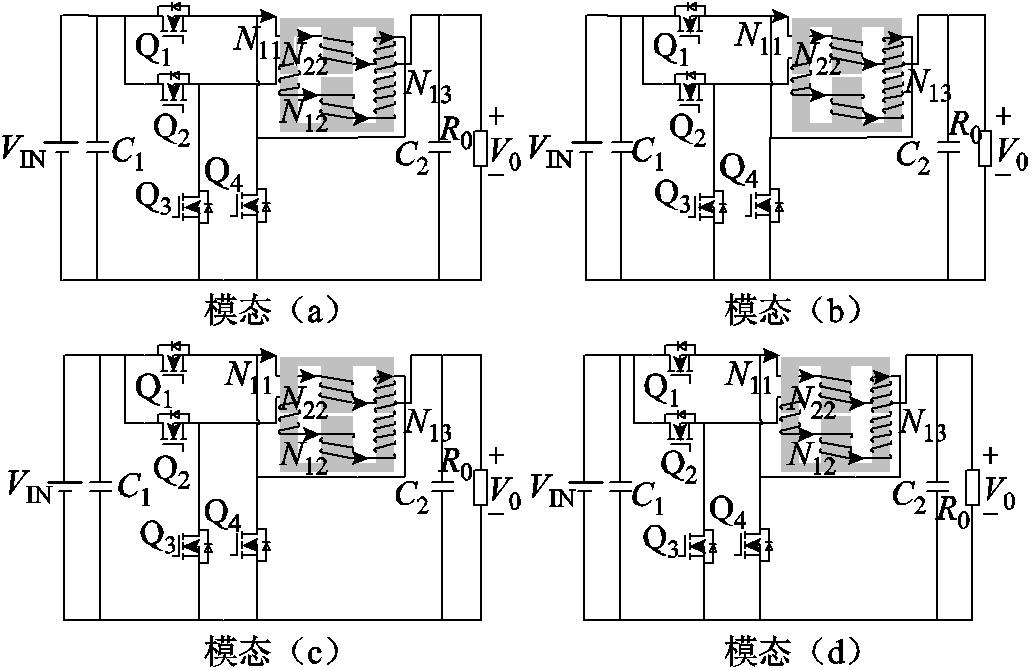
图6 模态切换
Fig.6 Modal switching
表2 电感电流波形变化率
Tab.2 Rate of change of inductor current waveform

模态UHdiH/dtULdiL/dt (a)VIN-V0(VIN-V0)/LH00 (b)-V0-V0/LHVINVIN/LH (c)VIN-V0(VIN-V0)/LH-VIN-VIN/LH (d)-V0-V0/LH00
变换器处于模态(a)时,状态方程可表示为
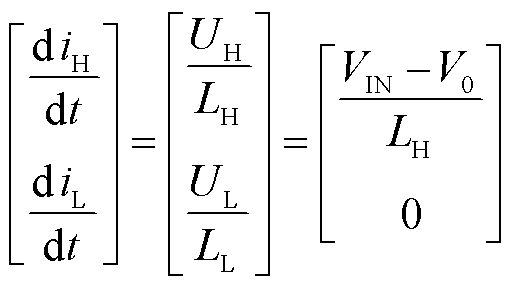 (29)
(29)
在该模态下,LH两端电压为正,LL两端电压为零。电流iH线性上升,低频电感电流iL不发生变化。
表3 绕组磁通变化率
Tab.3 Winding flux rate of change

模态Ф11Ф12Ф13Ф22 (a)000 (b) (c) (d)000
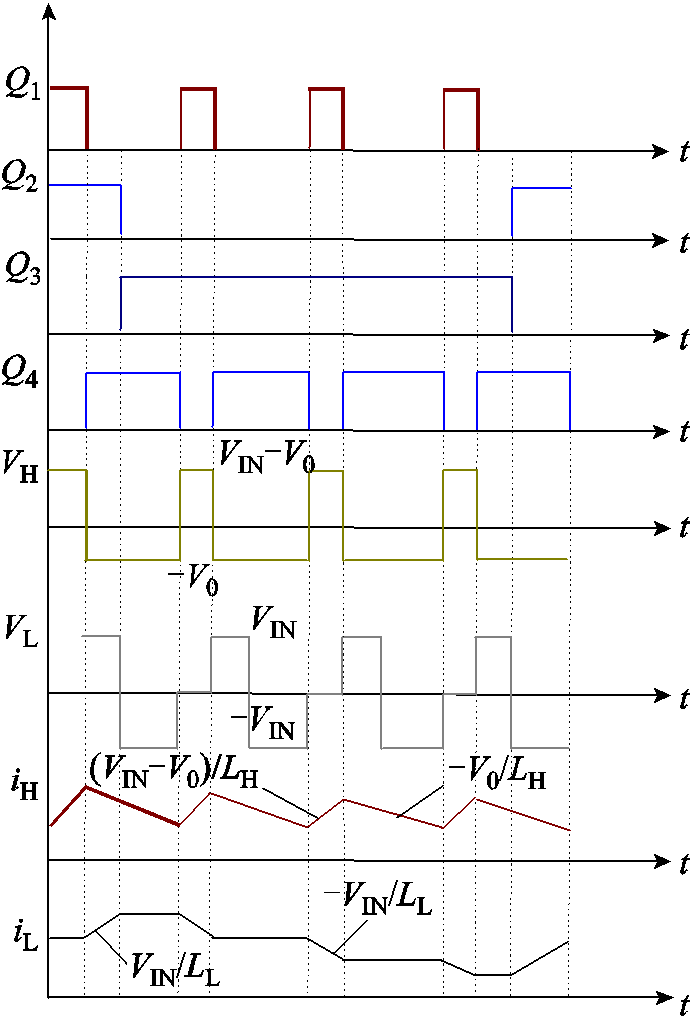
图7 TSWIM DF Buck输出波形
Fig.7 TSWIM DF buck output waveforms
当变换器处于模态(b)时,状态方程可表示为
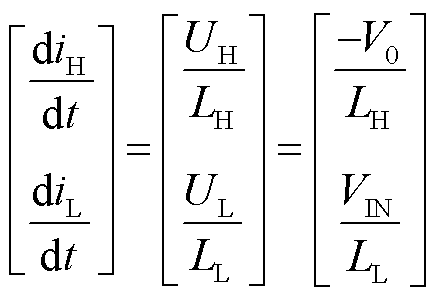 (30)
(30)
在该模态下,LH两端电压为负,电流iH减小;LL两端电压为正,iL逐渐上升。
当变换器处于模态(c)时,状态方程可表示为
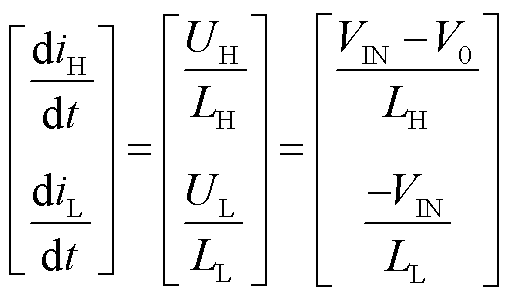 (31)
(31)
在该模态下,LH两端电压为正,iH上升;LL两端电压为负,iL减小。
当变换器处于模态(d)时,状态方程可表示为
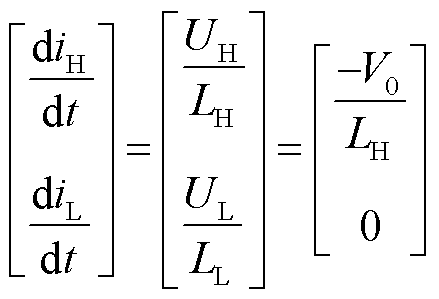 (32)
(32)
在该模态下,LH两端电压为负,iH开始下降;LL两端电压为零,流过的电流iL维持不变。
回转器-电容模型[17,20]可以建立起电与磁在仿真中的联系,因此多用于电路和磁路仿真中。为验证所提出的TSWIM结构能否正常工作在DF Buck变换器中,利用Pspice中对拓扑及器件仿真的优越性,构建出TSWIM的回转器-电容模型,如图8所示。并通过Matlab/Simulink对电路进行闭环控制,Pspice和Matlab/Simulink联合仿真的参数见表4,联合仿真电路模型如图9所示。
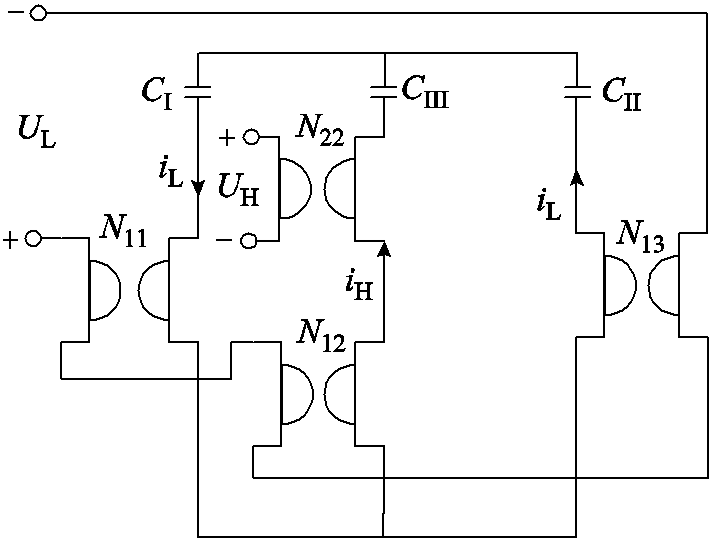
图8 TSWIM的回转器-电容模型
Fig.8 Gyrator-capacitor model of TSWIM
表4 仿真参数
Tab.4 Simulation parameters

参数数值 输入电压VIN/V48 输出电压V0/V12 电容C1,C2/μF330 高频电感LH/μH50 低频电感LL/μH200 电阻R0/Ω1.33 高频开关频率f/kHz200 低频开关频率f/kHz50

图9 DF Buck变换器的联合仿真电路结构
Fig.9 Co-simulation circuit structure of DF Buck converter
在DF Buck变换器中加入利用回转器-电容器模型构建的等效集成磁性部件TSWIM后,仿真波形如图10~图12所示。图10是稳态波形,显示输出电压稳定在12 V,电压纹波幅度为4 mV,高频电感电流纹波和低频电感电流纹波约为1 A,与理论计算值相符。为了测试DF Buck变换器的动态响应速度,对其进行了负载跳变测试,从图11可以看出,当负载从R0变为0.5 R0时,输出电压有约3 V的过冲,2 ms后恢复到稳定状态。图12为变换器中各个开关器件的电流流向,可以看出流向高频开关Q1和Q4的电流非常小,而流向低频开关Q2和Q3的电流非常大,这是由于低频单元分取高频单元的电流,以此用来降低高频开关损耗,这是DF Buck变换器的一大特点。
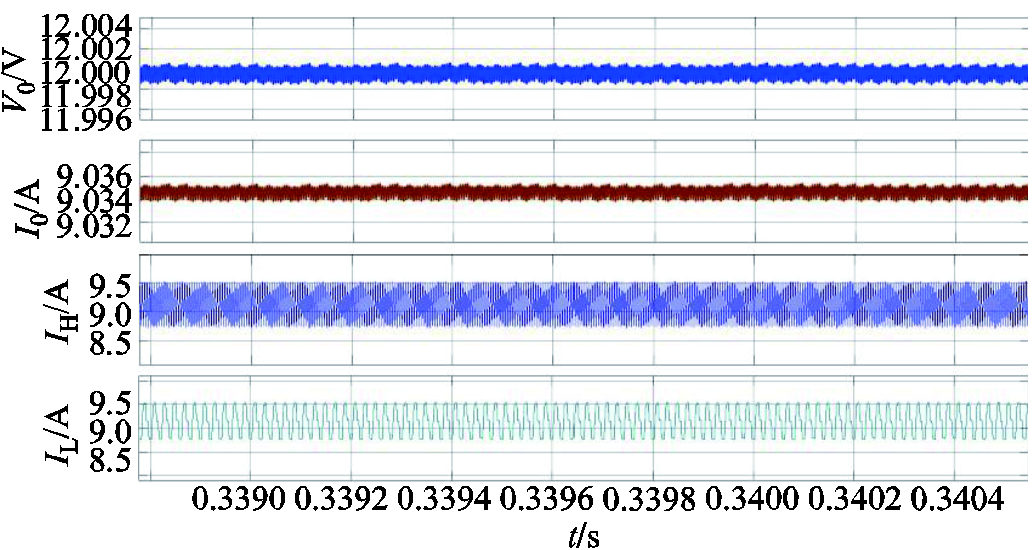
图10 TSWIM下DF Buck变换器稳态波形
Fig.10 Steady-state waveforms of DF Buck converter under TSWIM
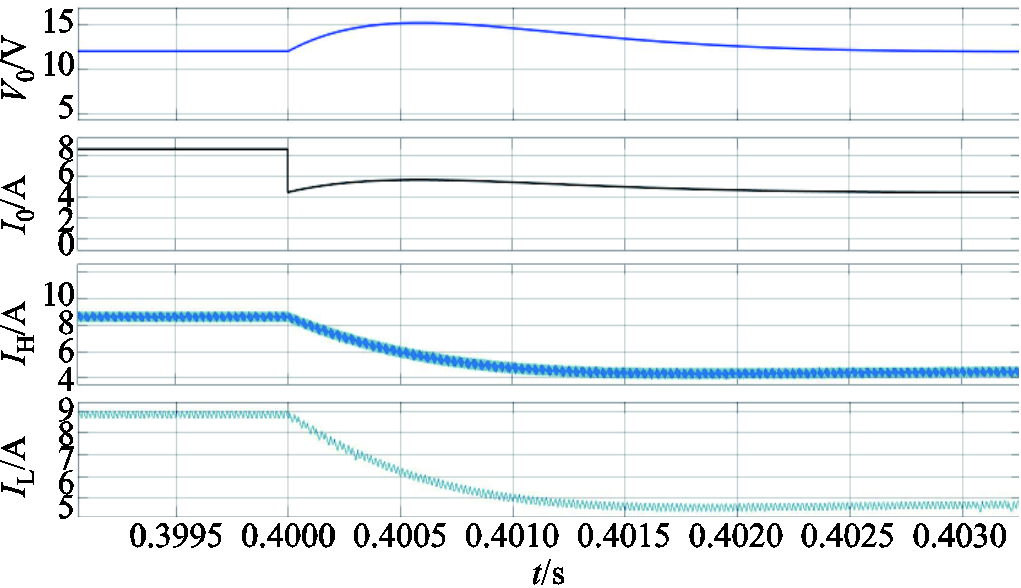
图11 TSWIM下DF Buck变换器负载跳变波形
Fig.11 DF Buck converter load hopping waveforms under TSWIM
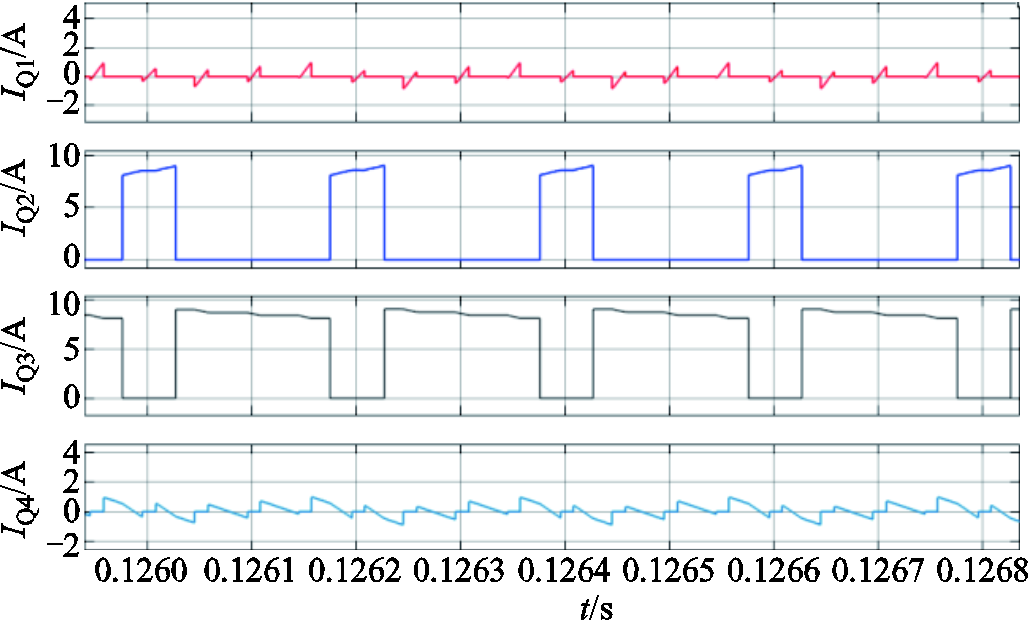
图12 Q1~Q4的电流大小
Fig.12 Amount of current in Q1~Q4
通过前文的分析,代入相关设计参数,可以得出SM、IM及TSWIM的磁心类型、匝数以及气隙大小,三者所选磁心材料均为TDK公司PC95型,为留有一定裕度,饱和磁通密度取为0.35 T,具体参数见表5~表7。
表5 SM参数
Tab.5 Parameters of the SM

磁心类型电感类型绕组匝数气隙/mm EE33高频电感140.6 EE42低频电感341.2
表6 IM参数
Tab.6 Parameters of the IM

磁心类型电感类型绕组匝数气隙/mm EE42高频电感241.2 低频电感34
表7 TSWIM参数
Tab.7 Parameters of the TSWIM

磁心类型电感类型绕组匝数气隙/mm EE42高频电感N22171.2 低频电感N1112 低频电感N1212 低频电感N1336
通过表6、表7的IM和TSWIM磁件参数,建立有限元仿真。图13为IM的有限元仿真结果,磁柱Ⅰ的工作平均磁通密度相对较低,只有0.05 T左右;磁柱Ⅱ的工作平均磁通密度为0.21 T,但有少部分已经到达了0.3 T;磁柱Ⅲ的工作磁通密度为0.15T,少部分已经达到了0.3 T,可以看出IM的三个磁柱磁通密度相差较大,尤其磁柱Ⅰ的利用率很低。图14为TSWIM的有限元仿真,磁柱Ⅰ的工作平均磁通密度为0.15 T,最大为0.21 T;磁柱Ⅱ工作的平均磁通密度为0.17 T,最大为0.23 T;磁柱Ⅲ的工作平均磁通密度为0.1 T,最大为0.2 T。可以看出TSWIM的磁通密度分布更为均匀,磁心利用率相比于IM更高。同时,工作磁通密度与磁心损耗息息相关,随着磁通密度的增大,磁心损耗也会增加[17,21-23]。图15为IM的磁力线分布情况,可以看出磁通主要集中在侧柱Ⅱ和侧柱Ⅲ上,侧柱Ⅰ上分布极少,这就导致同时磁心利用率大幅降低,也增加了成本。图16为TSWIM的磁力线分布,能够看出三个磁柱的磁通分布较IM而言更为均匀。图17为两种磁心结构各个磁柱上的平均磁通密度对比图,对于选取磁心而言,为了防止磁心磁通出现饱和情况,通常以最大磁通密度来选择,这就意味着在保证磁心不饱和的条件下,IM选择的磁心型号要比TSWIM更大,而且IM磁心的Ⅱ柱更容易达到饱和。
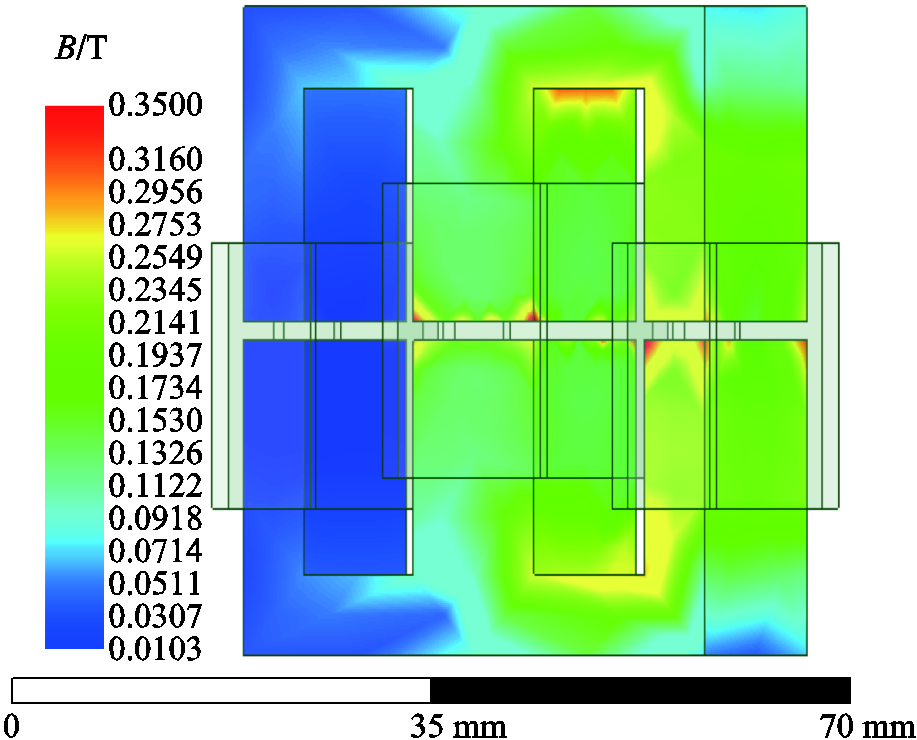
图13 IM满载有限元仿真
Fig.13 IM full load finite element simulation
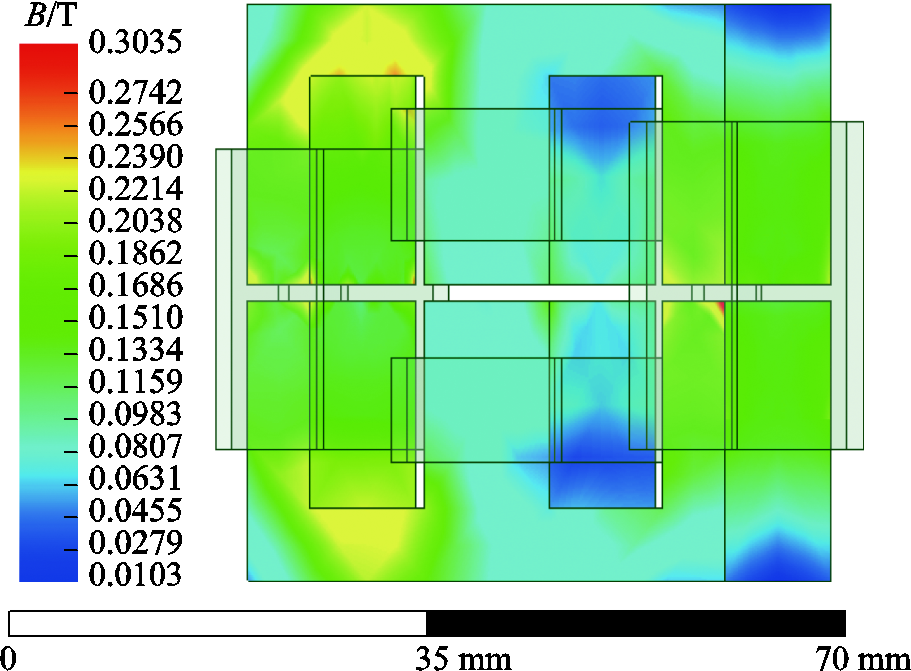
图14 TSWIM满载有限元仿真
Fig.14 TSWIM full load finite element simulation
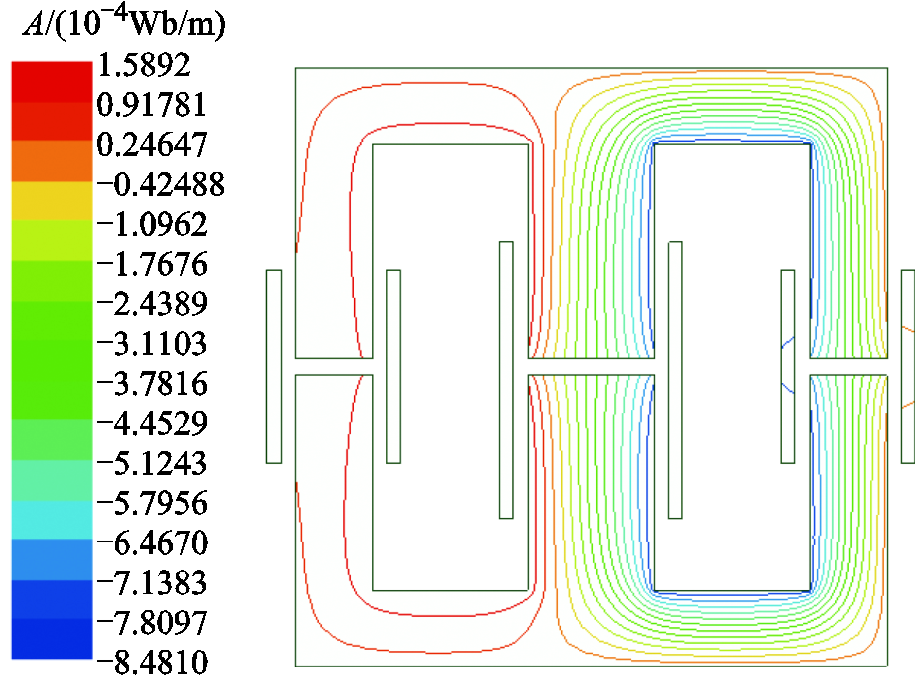
图15 IM磁力线分布
Fig.15 IM magnetic line distribution
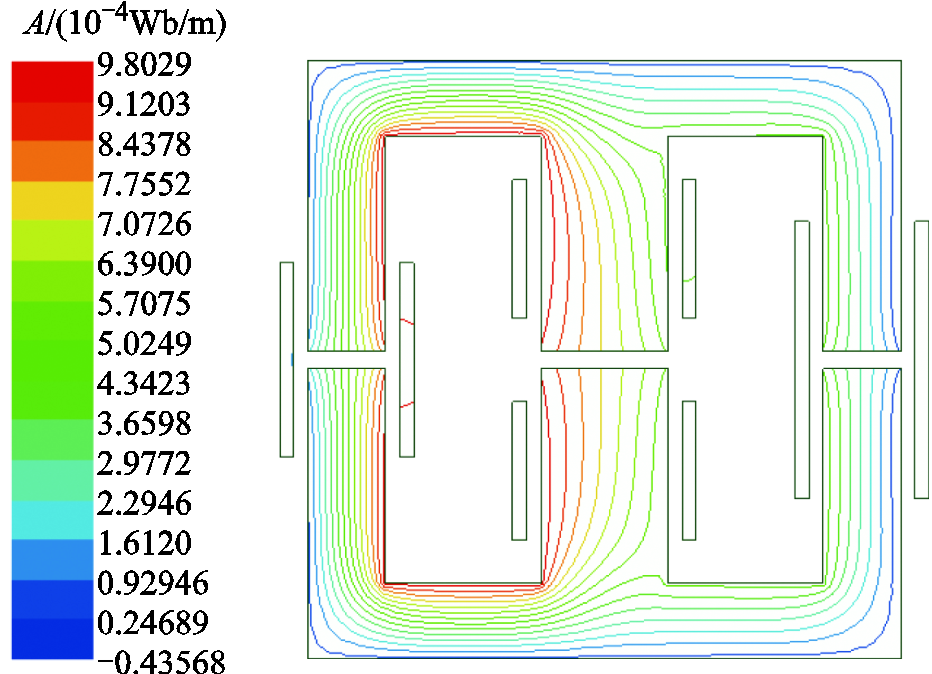
图16 TSWIM磁力线分布
Fig.16 TSWIM magnetic line distribution
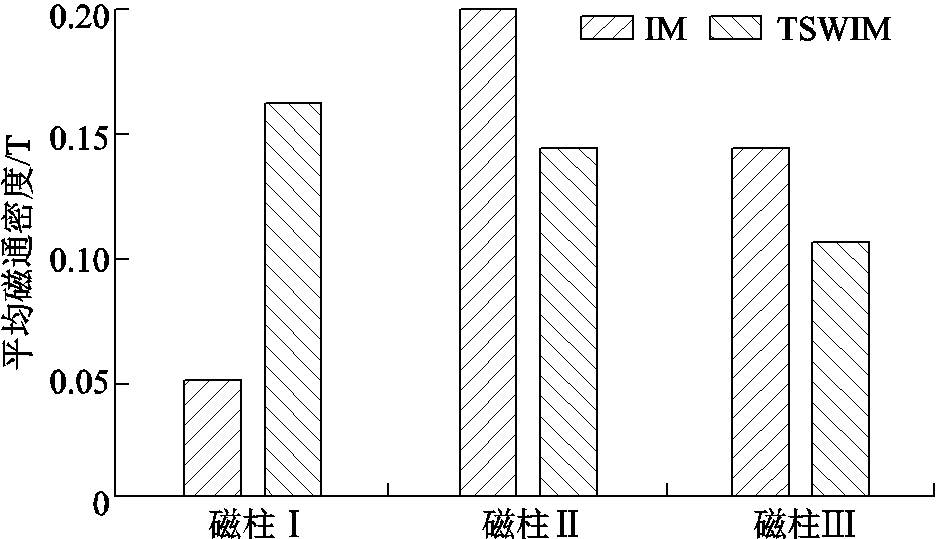
图17 集成磁件各个磁柱的平均磁通密度
Fig.17 Average magnetic flux density of each column of the integrated magnetic part
磁件损耗主要包括铁损和铜损,铁损一般指磁滞损耗、涡流损耗;铜损一般指绕组的等效电阻损耗。在集成磁件IM和TSWIM中,由于线圈匝数以及流经的电流大小相近,为了便于估算磁件损耗,将二者的铜损大小视为相等,着重计算磁心损耗。磁心损耗与磁性材料特性和工作频率等密切相关。在高频下,磁性元件损耗占整机损耗的比重不可忽略。在文献[18]中,磁心损耗用一个Steinmetz经验公式来表示,但公式只适用在正弦激励下,而开关电源领域是以脉冲激励为主。文献[19]针对Steinmetz经验公式加以改进,得出了一个适用在非正弦激励下的磁心损耗公式为
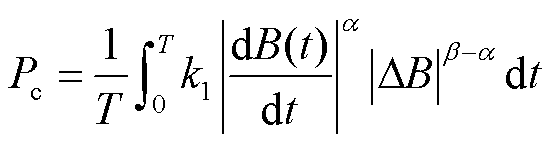 (33)
(33)
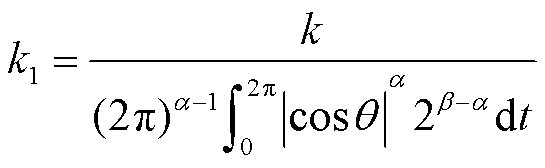 (34)
(34)
根据法拉第电磁感应定律有
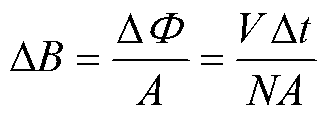 (35)
(35)
式中,Pc为磁心损耗,W;N为变压器绕组匝数;ΔB为磁通密度峰-峰值,T;k、α、β为损耗系数,主要与磁心材料有关。由式(33)可知,磁心损耗与磁通密度密切相关,根据图17所仿真得到的IM和TSWIM的平均磁通密度中得出IM最大平均磁通密度为0.21 T,而TSWIM为0.17 T,因此通过对绕组的合理设计以降低集成磁件中磁通大小是提高变换器效率的途径之一。
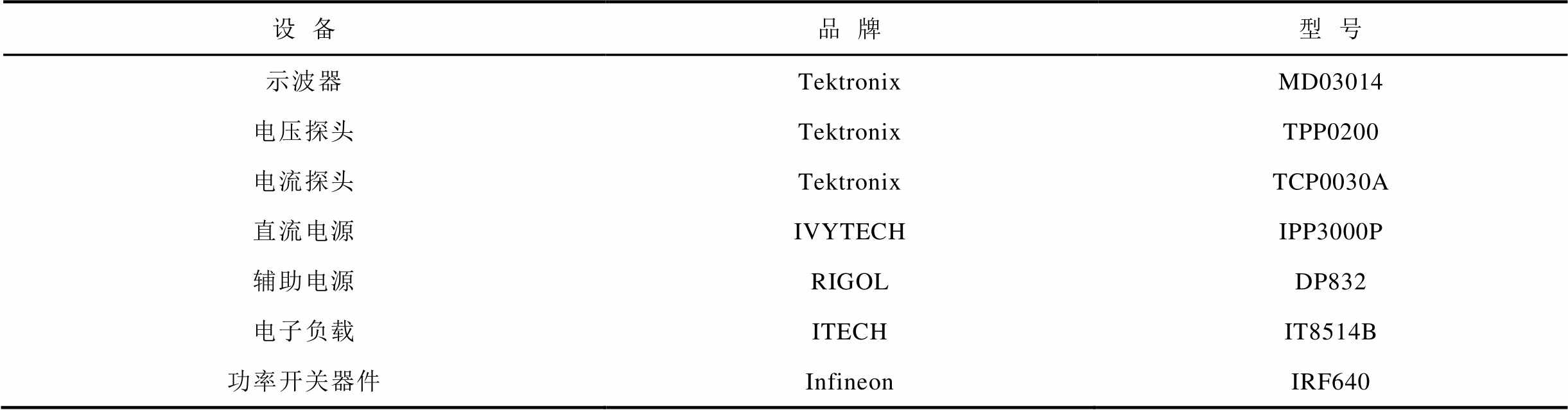
为对比分析TSWIM与SM、IM的性能,现搭建了108 W的DF Buck变换器的实验样机,实验平台利用该平台如图18所示。分别对SM、IM、TSWIM进行暂稳态实验验证,控制方法采用对输出电压以及电感电流进行双闭环控制,表8为实验所用设备名称及型号。实验过程除了更换变换器磁件外,其他参数均与仿真参数保持一致。

图18 实验平台
Fig.18 Experimental platform
表8 实验设备及器件
Tab.8 Experimental equipment and devices
设备品牌型号 示波器TektronixMD03014 电压探头TektronixTPP0200 电流探头TektronixTCP0030A 直流电源IVYTECHIPP3000P 辅助电源RIGOLDP832 电子负载ITECHIT8514B 功率开关器件InfineonIRF640
图19~图21分别是DF Buck变换器用SM、IM、TSWIM的稳态波形。从图中可以看出,在稳态时三种磁件都可以使变换器稳定地运行,输出电压纹波幅度为0.1 V。为了验证三种磁件下变换器的动态响应速度情况,现对变换器用三种不同磁件做了满载到半载的切载实验,图22为负载跳变波形,为了便于观察,图23~图25对各个磁件跳变波形做了局部放大处理,从三者波形对比中可以发现:在输出电压和高频电感电流动态响应速度上,IM和TSWIM都比较接近SM,响应速度大约为2.85 ms;而对于低频电感电流来说,TSWIM和SM紧跟高频电感电流的变化而变化,二者响应速度大约为 3.2 ms,几乎保持同步,而IM的动态响应速度最慢,分流效果不能及时跟踪高频电感电流的变化,此时低频开关为了调节占空比大小,导致一部分低频电感电流会反向流经高频开关Q1,造成损耗的增加。由此可以发现,在保证变换器稳定运行的同时,TSWIM保持了和SM同样的动态性能。图26为实验样机的根据不同输出电流的效率,从效率对比上容易看出,TSWIM的效率更接近于SM,验证了理论分析的正确性。
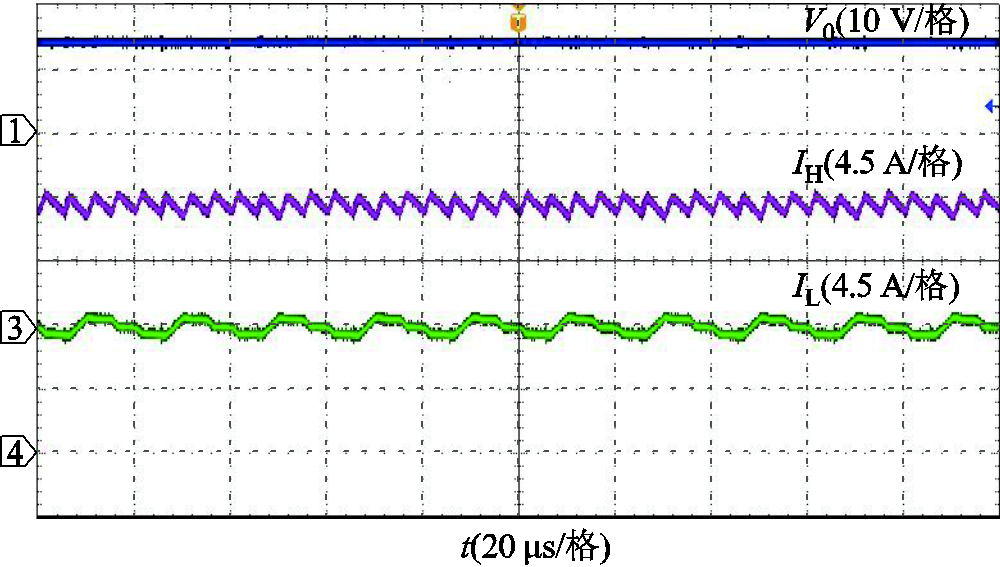
图19 SM下的DF Buck变换器稳态波形
Fig.19 Steady-state waveforms of DF Buck converter under SM
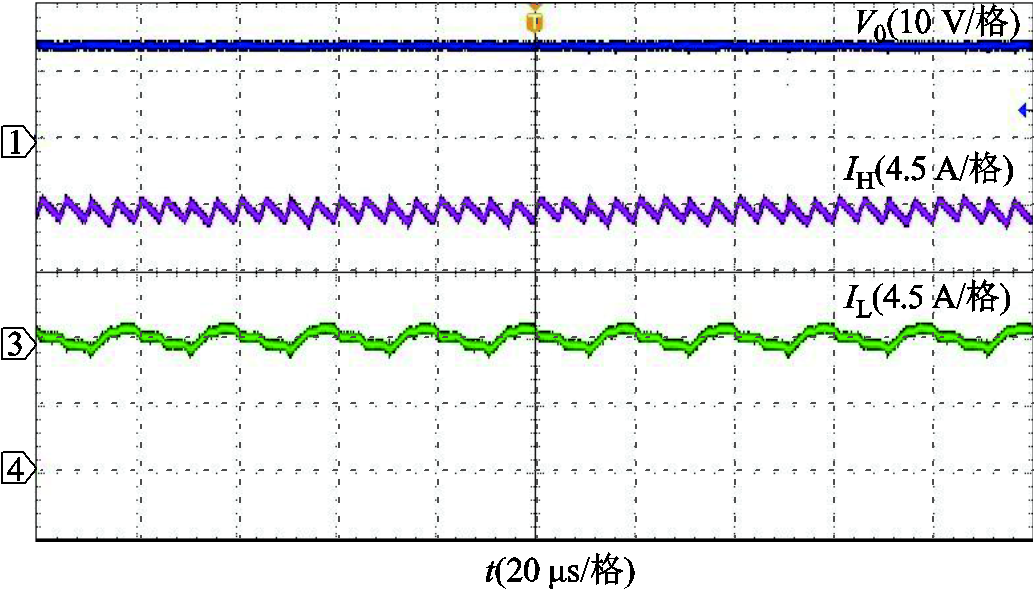
图20 IM下的DF Buck变换器稳态波形
Fig.20 Steady-state waveforms of DF Buck converter under IM
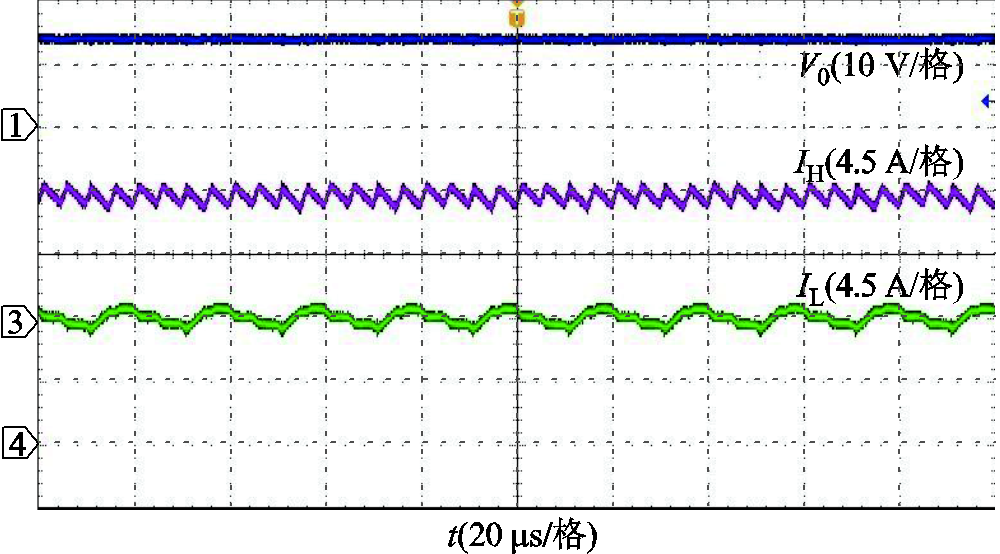
图21 TSWIM下的DF Buck变换器稳态波形
Fig.21 Steady-state waveforms of DF Buck converter under TSWIM
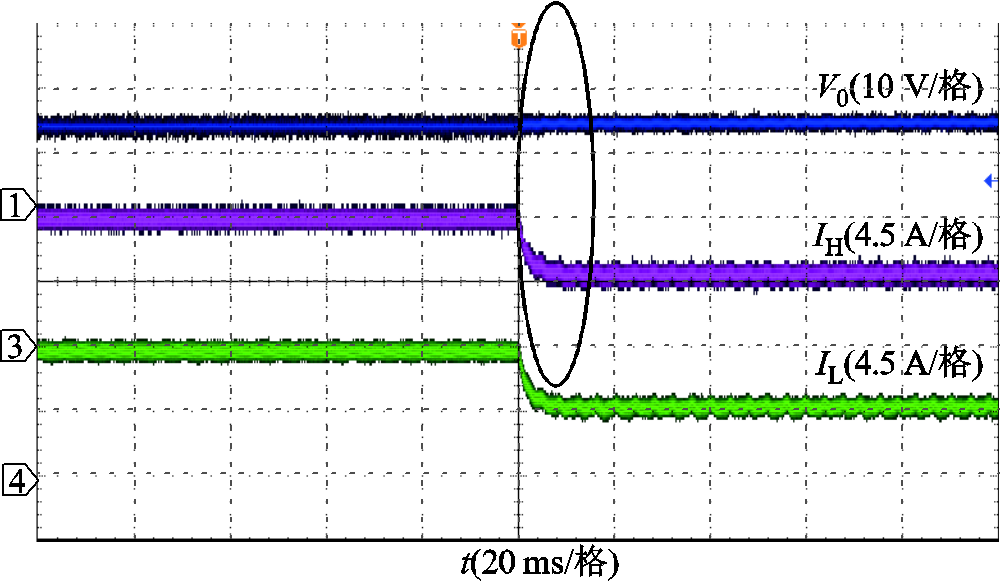
图22 DF Buck变换器切载波形
Fig.22 Cut load waveforms of DF Buck converter
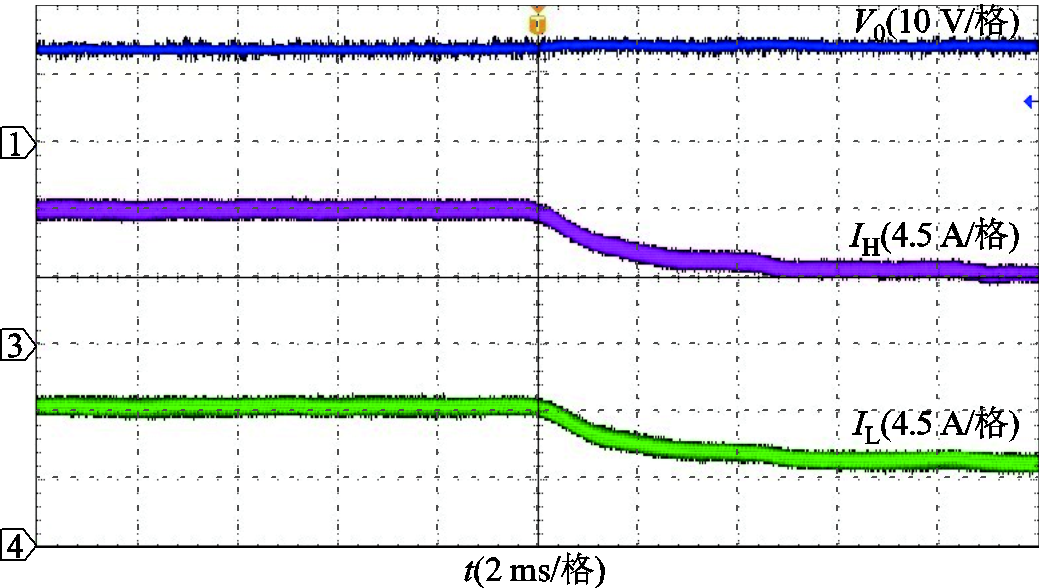
图23 SM下DF Buck变换器切载波形
Fig.23 Cut load waveforms of DF Buck converter under SM
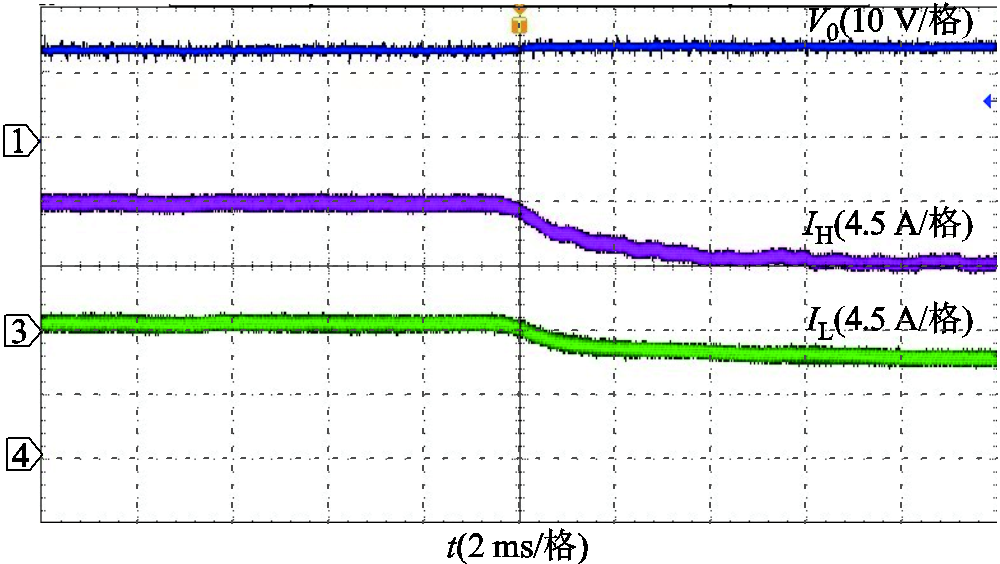
图24 IM下DF Buck变换器切载波形
Fig.24 Cut load waveforms of DF Buck converter under IM
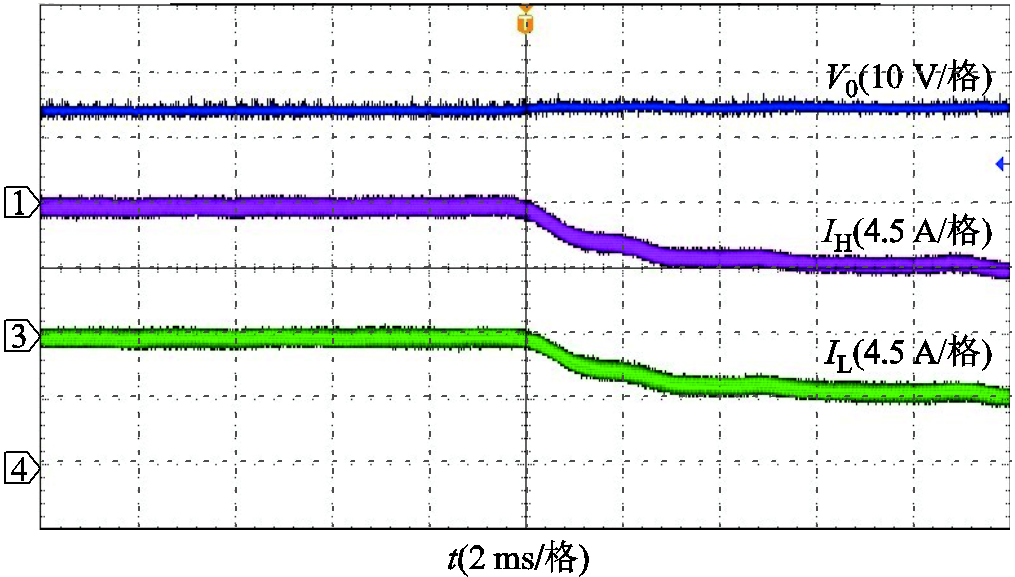
图25 TSWIM下DF Buck变换器切载波形
Fig.25 Cut load waveforms of DF Buck converter under TSWIM
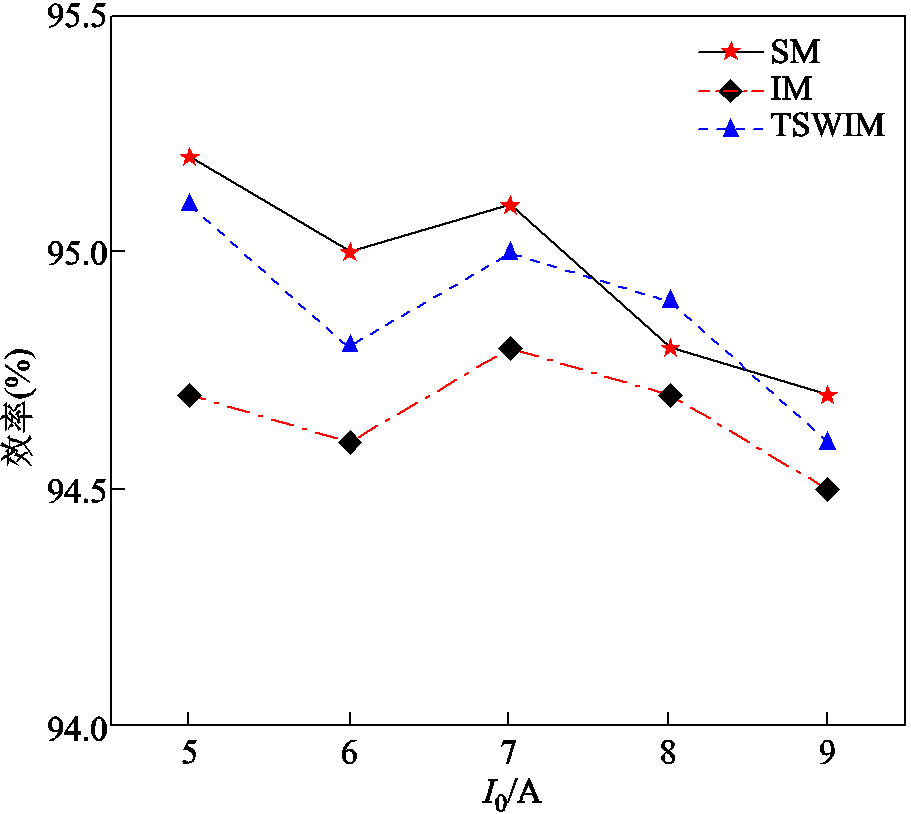
图26 效率对比
Fig.26 Efficiency comparison
本文针对双频Buck变换器存在磁件多、功率密度低等问题,提出了一种三段式绕制磁集成结构。该集成结构将低频大电感与高频小电感集成在一个磁心中,充分有效地降低了变换器中磁件体积和质量的占比,进而满足变换器小型化、轻量化和高功率密度的要求。通过对所提集成结构进行理论分析、仿真和实验验证,证明了该集成方法的有效性。在同等工作条件下,根据仿真和实验结果,能够得到以下结论:
1)与现有的集成方法相比,该集成磁件的磁通密度分布更为均匀,低频单元分流能力更好,磁心利用率更高。
2)与分离磁件相比,该集成磁件可替换传统的分离磁件,并使变换器磁件的体积和重量分别减少31.2%和25.3%,有效提高了系统的功率密度。
参考文献
[1] 王哲, 李驰, 郑泽东, 等. 一种基于耦合电感的高增益软开关谐振变换器[J]. 电工技术学报, 2024, 39(1): 194-205.
Wang Zhe, Li Chi, Zheng Zedong, et al. A high-gain soft-switching resonant converter based on coupled inductors[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 194-205.
[2] 杨晓光, 王德鑫, 贾哲, 等. 负载和输入电压自适应零电压软开关全桥变换器[J]. 电工技术学报, 2022, 37(12): 3061-3072.
Yang Xiaoguang, Wang Dein, Jia Zhe, et al. A load and input voltage adaptive zero-voltage-switching full bridge converter[J]. Transactions of China Electrote-chnical Society, 2022, 37(12): 3061-3072.
[3] Sadeq A li Qasem Mohammed, Jin Woo Jung. A state of the art review on soft-switching techniques for DC-DC, DC-AC, AC-DC and AC-AC power converters[J]. IEEETransactions on Industria Electronics, 2021, 17(10): 6569-6582.
[4] 倪硕, 吴红飞, 陈君雨, 等. 交错并联临界导通模式Buck电感高密度集成与优化[J]. 电工技术学报, 2022, 37(18): 4688-4696.
Ni Shuo, WuHongfei, Chen Junyu, et al. Integration and optimization of a high power density inductor for an interleaved critical conduction mode Buck converter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4688-4696.
[5] 周雒维, 杜雄, 付志红, 等. 双频Buck变换器[J].中国电机工程学报, 2006, 26(6): 68-72.
Zhou Luowei, Du Xiong, Fu Zhihong, et al. The Buck converter with double frequency[J]. Proceedings of the CSEE, 2006, 26(6): 68-72.
[6] 杜雄, 周雒维, 罗全明, 等. 双频Buck变换器参数对系统性能的影响[J]. 电工技术学报, 2005, 20(11): 49-55.
Du Xiong, Zhou Luowei, Luo Quanming, et al. Relationship between circuit parameter and system performance of Buck converter with double fre-quency[J]. Transactions of China Electrotechnical Society, 2005, 20(11): 49-55.
[7] 罗全明, 周雒维, 卢伟国, 等. 双频Buck变换器的性能分析及设计[J]. 电工技术学报, 2008, 23(5): 56-61.
Luo Quanming, Zhou Luowei, Lu Weiguo, et al. Performance analysis and design of double frequency Buck converter[J]. Transactions of China Electrote-chnical Society, 2008, 23(5): 56-61.
[8] 罗全明, 杜雄, 周雒维, 等. 双频Buck变换器工作模式[J]. 电工技术学报, 2008, 23(11): 72-78.
Luo Quanming, Du Xiong, Zhou Luowei, et al. The operation mode of double frequency Buck converter[J]. Transactions of China Electrotechnical Society, 2008, 23(11): 72-78.
[9] 罗全明, 杜雄, 周雒维, 等. 复合双频Buck变换器[J]. 中国电机工程学报, 2008, 28(9): 1-6.
Luo Quanming, Du Xiong, Zhou Luowei, et al. Hybrid double frequency Buck converter[J]. Proceedings of the CSEE, 2008, 28(9):1-6.
[10] Du Xiong, Zhou Luowei, Tai Heng Ming. Double frequency Buck converter[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5): 1690-1698.
[11] 方堃, 周林, 刘强, 等. 变换器中双频变换理论研究综述[J]. 电网技术, 2010, 34(11): 135-139.
Fang Kun, Zhou Lin, Liu Qiang, et al. A survey on double-frequency conversion theory for converters[J]. Power System Technology, 2010, 34(11): 135-139.
[12] 陈乾宏, 阮新波, 严仰光. 开关电源中磁集成技术及其应用[J]. 电工技术学报, 2004, 19(3): 1-8.
Chen Qianhong, RuanXinbo, YanYangguang. The application of the magnetic-integration techniques in switching power supply[J]. Transactions of China Electrotechnical Society, 2004, 19(3): 1-8.
[13] 廖志贤, 李彬彬, 索之闻, 等. 磁集成三端口电力电子变压器的改进控制方法[J]. 电力系统自动化, 2023, 47(11): 133-143.
Liao Zhixian, Li Binbin, Suo Zhiwen, et al. lmproved control method for three-port power electronic transformer based on magnetic integration[J]. Auto-mation of Electric Power Systems, 2023, 47(11): 133-143.
[14] Zhu Hongyu, Zhang Donglai, Zhou Yilong, et al. Integrated magnetic Buck-Boost converter with “Zero” output current ripple[J]. IEEE Transactions on Industrial Electronics, 2021, 68(7): 5281-5832.
[15] 李洪珠, 刘飞扬, 刘艳, 等. 一种新型磁集成高增益耦合电感倍压Boost变换器[J]. 电工技术学报, 2020, 35(20): 450-460.
Li Hongzhu, Liu Feiyang, Liu Yan, et al. A new magnetically integrated high gain coupled inductance voltage-doubled Boost converter[J]. Transactions of China ElectrotechnicalSociety, 2020, 35(S2): 450-460.
[16] 张晓峰, 周雒维, 罗全明, 等. 磁集成双频DC-DC变器[J]. 电工技术学报, 2010, 25(1): 77-83, 89.
Zhang Xiaofeng, Zhou Luowei, Luo Quanming, et al. Double frequency DC-DC converter with magnetic integration[J]. Transactions of China Electrotechnical Society, 2010, 25(1): 77-83, 89.
[17] Gao Shengwei, Zhao Ziyi. Magnetic integrated LLC resonant converter based on independent inductance winding[J]. IEEE Transactions on Industrial Electro-nics, 2021, 9: 660-672.
[18] 高圣伟, 王浩, 刘晓明, 等. 新型磁集成双频DC/DC变换器[J]. 中国电机工程学报, 2020, 40(24): 8131-8144.
Gao Shengwei, Wang Hao, Liu Xiaoming, et al. A novel double frequency DC/DC converter with magnetic integration[J]. Proceedings of the CSEE, 2020, 40(24): 8131-8144.
[19] 周洁敏, 赵修科. 开关电源磁性元件理论及设计[M]. 北京: 北京航空航天大学出版社, 2014.
[20] Liang Y, Lehman B. A capacitor modeling method for integrated magnetic components in DC/DC converters[J]. IEEE Transactions on Power Electronics, 2005, 20(5): 987-996.
[21] Reinert J, Brockmeyer A, De Doncke RWAA. Calculation of losses in ferro- and ferrimagnetic materials based on the modified Steinmetz equatio[J]. IEEE Transactions on Industry Applications, 2001, 37(4): 1005-1060.
[22] Venkatachalam K, Sullivan C R, Abdallah T, et al. Accurate prediction of ferrite core loss with nonsinusoidal waveforms using only Steinmetz parameters[C]//2002 IEEE Workshop on Computers in Power Electronics, Mayaguez, PR, USA, 2002: 36-41.
[23] 管乐诗, 温兆亮, 许晓志, 等. 适用于宽增益范围的可重构单级DC-DC变换器及其磁元件设计[J]. 电工技术学报, 2023, 38(6): 1571-1583.
Guan Leshi, Wen Zhaoliang, Xu Xiaozhi, et al. A modular reconfigurable single-stage DC-DC converter suitable for wide gain range and its magnetic design[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1571- 1583.
Abstract Miniaturization and high power density are the development trends in modern power electronic converters. However, the increase in high frequency inevitably leads to intensified switching losses, reduced converter efficiency, and increased electromagnetic interference. These factors, to some extent, limit the improvement of converter performance. In response to these challenges, various methods have been proposed to address the conflicting relationship between high frequency and efficiency. Soft switching technology, converter parallel technology, and double frequency converters have been utilized in power electronic converters to enhance system performance. Although these methods contribute to improvement, most of them involve the converter's magnetic components, leading to larger converter sizes and related environmental issues. To address these issues, this paper proposes a three-section winding integrated magnetic (TSWIM) technique based on a double frequency DC-DC converter. This technique decouples and integrates the magnetic components within one core of the converter. Through theoretical analysis, simulation, and experimental validation, it is demonstrated that this integration method achieves a uniformly distributed magnetic flux density within the magnetic core. Consequently, it reduces the volume and weight of the converter, while improving the power density of the system.
Firstly, this paper establishes an equivalent magnetic circuit model for the TSWIM and deduces the decoupling condition by mitigating the coupling effect between each winding. To select a suitable core model, careful consideration is given to the magnetic saturation problem and window area dimensions. Mathematically deriving the maximum magnetic flux density generated by each magnetic column of the core from the TSWIM helps determine if the core's saturation magnetic flux density is reached. Finally, the number of turns in the integrated winding and the calculation method of the air gap are elaborated upon.
Secondly, the working principle of the double frequency DC-DC converter under the integration is analyzed, and by constructing the gyrator-capacitor model of the TSWIM, the co-simulation method is utilized to verify that the integration method can enable the converter to operate normally. Then, the TSWIM is subjected to finite element simulation with the existing integration method (IM), and the results show that the TSWIM has a more uniform flux density distribution, smaller flux density, and smaller magnetic loss by comparing the flux density and magnetic core loss of the two.
Finally, a 48 V/12 V, 108 W experimental prototype was constructed to validate the TSWIM and compare it with the separated magnetic part (SM) as well as the IM. Based on the experimental findings, it can be concluded that both the IM and the TSWIM demonstrate a relatively similar response speed, approximately 2.85 ms, with respect to output voltage and dynamic response of high-frequency inductor current. In terms of low-frequency inductor current, the TSWIM and the SM mirror the fluctuations in high-frequency inductor current, exhibiting a response speed of around 3.2 ms. Consequently, the TSWIM and the SM remain nearly synchronized. Conversely, the IM exhibit a comparatively slower dynamic response speed. From the efficiency comparison, the efficiency of the TSWIM is closer to that of the SM, and the volume and weight are reduced by 31.2% and 25.3% compared with the SM, which improves the power density of the system, and the experiments and simulations verify the correctness of the theoretical analysis.
Keywords:Double frequency Buck converter, decoupling integration, finite element simulation, magnetic flux density, power density
DOI: 10.19595/j.cnki.1000-6753.tces.230720
中图分类号:TM46
国家自然科学基金(51807139)和天津科技规划项目(20YDTPJC01520)资助。
收稿日期 2023-05-19
改稿日期 2023-08-11
高圣伟 男,1978年生,教授,硕士生导师,研究方向为电力电子变换器及应用。E-mail:gaoshengwei@tiangong.edu.cn
李永宵 男,1997年生,硕士研究生,研究方向为电力电子变换器及磁集成技术。E-mail:799917922@qq.com(通信作者)
(编辑 郭丽军)