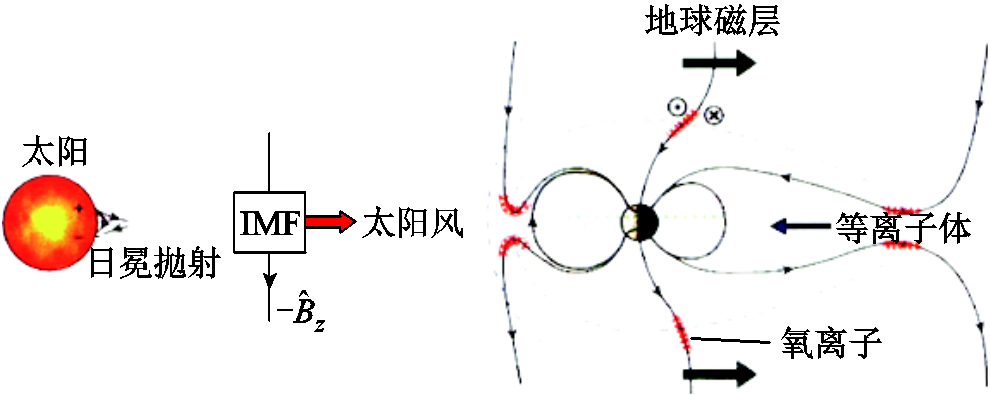
图1 太阳风与地球磁场耦合示意图[14]
Fig.1 Schematic diagram of coupling between solar wind and earth's magnetosphere[14]
摘要 地磁暴期间,电网中的变压器受到地磁感应电流(GIC)影响而导致无功损耗会显著增大,这种不确定的、突发群发的无功扰动会引发电网电压波动。超高压、特高压电网由于其特殊的电气特性更容易受到地磁暴的侵害,造成电压跌落至不合格区间甚至引发电压崩溃而导致大规模停电。该文以地球三维磁流体力学(MHD)模型预测的地磁扰动(GMD)为基础,采用模型预测控制(MPC)方法修正MHD模型计算的无功扰动并调整可控主导节点的注入功率进行优化调度,平抑地磁暴期间超高压、特高压电网电压波动。该文还以华东超高压、特高压电网为算例,仿真对比了特大地磁暴发生期间电网实施优化调度前后的电压波动,并提出了波动率指标验证了所提方法的有效性,为保证地磁暴期间的电压稳定性和合格率提供了指导。
关键词:地磁暴 地磁感应电流 电压波动 磁流体力学 无功扰动
地磁暴对于电网是一种“低概率、高风险”的自然灾害,其来源于太阳剧烈活动时随日冕抛射(Coronal Mass Ejection, CME)出的高速等离子体云对地球磁场全球性的剧烈扰动,即地磁扰动(Geomagnetic Disturbance, GMD)。GMD作用于电网时,会感生出地磁感应电流(Geomagnetically Induced Current, GIC)。GIC流经变压器会导致铁心偏磁饱和,并造成变压器温升[1-2]、振动增加[3]和无功功率损耗[4]增大。由于太阳活动引起的地磁暴在全球范围内几乎于同一时间发生,地磁暴引发的无功扰动具有全网突发、群发的特点,它会造成整个电网电压波动甚至引发电压崩溃而导致大规模停电的灾害性后果[5-6]。
超高压、特高压线路采用八分裂导线,其单位长度的电阻比普通电压等级线路电阻小得多,相同地磁暴强度下产生的GIC更大[7]。此外,超、特高压变电站一般采用由三台单相变压器组成的变压器组设计,单相四柱式或单相五柱式变压器被广泛应用于超高压、特高压变电站。这种结构的变压器对GIC的耐受能力比三相三柱式或三相五柱式变压器更差,GIC通过变压器时产生的无功损耗更大。这种电气特性使得超、特高压电网更容易受到地磁暴的侵害。文献[8-9]分别模拟了我国甘肃和华东新建超、特高压电网对强地磁暴的响应过程,计算结果表明,地磁暴期间变压器的无功增量会造成电网电压出现较大的波动。以华东特高压电网为例,最大电压偏移达到-7.13%,超过了运行电压偏移不超过额定电压±5%的规程规定。
目前工程上一般采用抑制或减小地磁感应电流进入变压器的思路防止地磁暴侵害电网,比如在变压器中性点串联电阻[10]或电容[11]的方法。串联电阻法结构简单可靠,但地磁暴强度较大时不能有效地阻隔GIC进入变压器,此外这种方法改变了电网零序阻抗分布,可能会影响继电保护装置正常动作;串联电容法可以有效地抑制GIC通过中性点进入变压器,但这种方法不仅成本高,而且安全性较差,同时这种方法改变了GIC在电网中的流通路径,有可能导致其他节点通过的GIC更大[9],反而有可能增大电网电压的波动幅值和增加电网电压崩溃的风险。近年来,随着地球物理和空间天气领域相关理论的发展,模拟太阳活动对地球磁层-电离层的耦合作用模型日趋成熟,磁流体力学(Magnetohydro-dymanics, MHD)模型通过太阳风信息已能较为准确地预测地磁暴发生时的GMD。由CME形成到太阳风到达地球诱发地磁暴间隔数天,可由预测的GMD评估地磁暴期间电网流通的GIC水平[12-13],并采取相应灾害预防措施。
基于上述原因,本文提出一种基于MHD模型预测控制(Model Predictive Control, MPC)的方法平抑地磁暴期间超、特高压电网电压波动。首先基于MHD模型预测地磁暴期间目标电网GMD并计算电网各节点的无功扰动;然后由模型预测控制方法中反馈校正和滚动优化思想对无功扰动预测值进行修正;最后再对电网进行优化调度,通过对可控主导节点的注入功率进行调整,有效平抑地磁暴期间电网的电压波动,避免地磁暴造成电压崩溃等次生灾害。
CME发生时,太阳风能压迫改变地球磁场,形成一个名为磁层的空腔。磁层的形状由太阳风与其携带的行星际磁场(Interplanetary Magnetic Field, IMF)所决定,在日侧磁层被挤压,而夜侧磁层有一个长长的磁尾,如图1所示。

图1 太阳风与地球磁场耦合示意图[14]
Fig.1 Schematic diagram of coupling between solar wind and earth's magnetosphere[14]
太阳风-地球磁场耦合是一个极其复杂的过程,MHD模型是把太阳风等离子体当成导电流体介质并基于流体力学和电动力学理论建立的模型,用来描述导电流体的运动,可通过计算机设置数值和处理条件来模拟太阳风-电磁层-电离层相互作用耦合过程[15]。
目前已有多个MHD模型在地球物理和空间天气领域得到应用,如美国密西根大学空间环境建模中心(Center for Space Environment Modeling,CSEM)牵头开发的BATS-R-US模型。通过将卫星观测的太阳风等离子体的密度、温度、速度、磁感应强度参数转换到地心太阳磁层坐标系(Geocentric Solar Magnetospheric Coordinate System, GSM)下作为输入,利用该模型可预测地表目标区域的GMD。
下面以2015年6月22日—23日发生的急始型特大磁暴事件为例,对MHD模型及本文所述方法进行说明,由于该磁暴事件是发生在第24个太阳周的第14次大磁暴事件[16],以下简称D14。D14发生期间卫星记录的太阳风参数如图2所示。

图2 世界时2015-06-22 17:00至2015-06-23 5:00太阳风参数
Fig.2 Solar wind parameters between 2015 June 22 UT 17:00 and June 22 UT 5:00
将太阳风参数输入BATS-R-US模型后得到地理坐标(30°N, 120°E)处预测的地磁扰动北向分量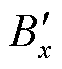 和东向分量
和东向分量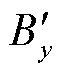 ,如图3所示。该坐标点邻近杭州市,将预测的地磁扰动数据与杭州地磁台(30°15′36″N, 120°9′36″E)磁通门磁力仪实测的地磁扰动秒采数据Bx、By进行比较可以看出,预测的地磁扰动数据与实测数据的发生时间和扰动特征相似程度很高。基于这种高精度的预测GMD计算地磁暴发生期间电网各节点的GIC-Q无功扰动并进行优化调度是平抑地磁暴期间电压波动的前提条件,为后续利用MPC方法修正地磁暴期间的无功扰动预测值以及进行电压波动平抑优化调度奠定了基础。
,如图3所示。该坐标点邻近杭州市,将预测的地磁扰动数据与杭州地磁台(30°15′36″N, 120°9′36″E)磁通门磁力仪实测的地磁扰动秒采数据Bx、By进行比较可以看出,预测的地磁扰动数据与实测数据的发生时间和扰动特征相似程度很高。基于这种高精度的预测GMD计算地磁暴发生期间电网各节点的GIC-Q无功扰动并进行优化调度是平抑地磁暴期间电压波动的前提条件,为后续利用MPC方法修正地磁暴期间的无功扰动预测值以及进行电压波动平抑优化调度奠定了基础。
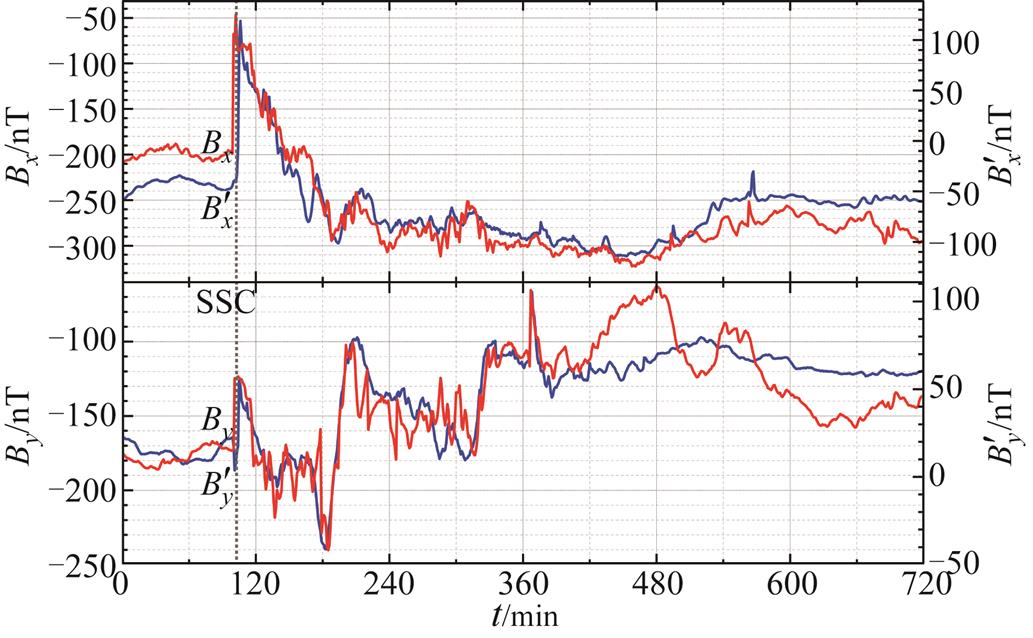
图3 D14期间实测和预测的杭州附近地磁扰动
Fig.3 Forecasted and calculated value of geomagnetic disturbance at Hangzhou during geomagnetic storm D14
地磁暴造成的剧烈的GMD会在地球表面感生出电场,其时变的北向分量、东向分量分别为
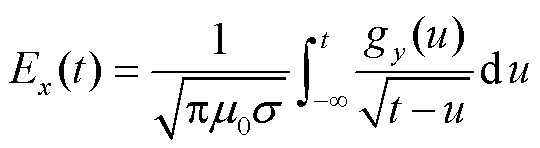 (1)
(1)
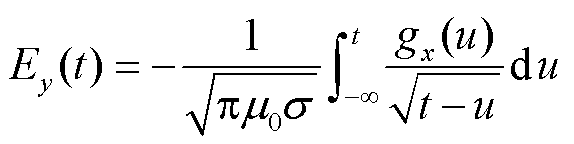 (2)
(2)
式中,gy(u)=dBy/dt和gx(u)=dBx/dt分别为磁场磁感应强度相应方向的分量随时间的变化率;σ为大地等效电导率系数,与大地电性结构相关,由大地不同深度电导率综合作用确定[7];μ0为真空磁导率。
地面感应电场使电网接地点之间存在电位差,作用相当于在电网接地点之间施加电压源U,在其作用下GIC从大地由接地的变压器中性点流入电网,经过输电线路,最后通过其余接地的变压器流回大地构成通路。设i、j分别表示给定输电线路的两端点,地磁暴等效直流电压Uij的大小相当于地面感应电场各分量沿该线路走向的乘积,即
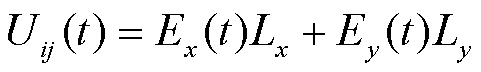 (3)
(3)
式中,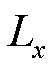 、
、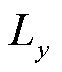 为线路沿正北和正东方向的投影长度。
为线路沿正北和正东方向的投影长度。
利用Lehtinen-Pirjola算法[17],引入系统导纳矩阵Y和网络接地阻抗矩阵Z,计算出超、特高压电网中流通的地磁感应电流IGIC,具体方法可以参考文献[7],在此不再赘述。
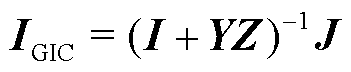 (4)
(4)
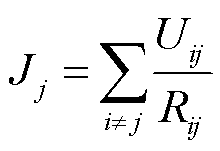 (5)
(5)
式中,I为n×n单位矩阵;J为理想条件下的n×1接地电流矩阵;Rij为节点i至节点j之间线路的等效电阻。
需要注意的是,计算GIC时电网电气参数的设定值与实际值之间存在的误差可能会导致后续预测各节点无功扰动出现误差,需要通过MPC方法对预测值进行修正,以保证优化调度的准确性和电压平抑的效果。
由于超高压、特高压两个不同电压等级通过特高压变电站的自耦变压器相互电气连接,地磁暴期间,除了特高压系统的GIC经串联绕组流向自耦变中性点外,超高压系统的GIC也会经公共绕组流向自耦变中性点,若用nT表示自耦变压器高压侧对中压侧的实际电压比,则自耦变压器GIC有效值为
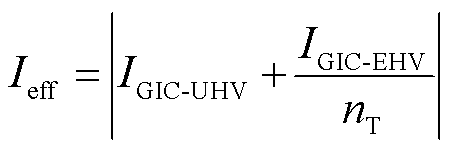 (6)
(6)
式中,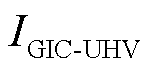 、
、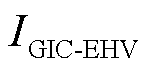 分别为从超高压、特高压电网流入自耦变压器的GIC。
分别为从超高压、特高压电网流入自耦变压器的GIC。
地磁暴期间,变压器增发的无功损耗与通过变压器的GIC成线性关系,工程上一般采用k值法计算。
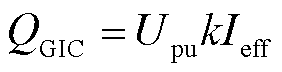 (7)
(7)
式中,QGIC为GIC流经变压器时增发的无功损耗(以下称为GIC-Q);Upu为变压器端电压标幺值;k为变压器无功损耗系数,单位为Mvar/A,其量值与变压器的铁心结构有关,对于超高压变压器,k值取1.18,对于特高压变压器,k值取2.44[18]。
将预测的地表感应电场时间序列代入式(3)~式(7)即可算出各变电站的无功扰动序列,将其作为无功负荷代入潮流计算,即可预测地磁暴期间电网各节点的电压波动。
特高压线路电压等级高,输电距离远,线路的电容特性使得特高压交流输电线路的充电功率很大,其值约为超高压线路的4~5倍。同时,特高压线路输送功率可达每回4 000~6 000 MW,当特高压输送功率较大时,线路电抗消耗的无功功率很大。目前,特高压变电站采用“固定高抗”与“分组低容低抗”结合的无功补偿模式[19],在特高压层面只装设固定容量的高压电抗器来平衡线路轻载或空载时的充电功率。此外,在特高压变电站的主变低压侧连接分组投切的并联电容器和并联电抗器,辅助补偿由于线路电抗、变电站高抗及变压器产生的无功损耗。这种无功配置方式以及特高压变压器缺乏有载调压能力导致特高压层面的电压调节能力不足。
大型发电厂由特高压变电站的超高压母线接入超、特高压电网,这使得超高压母线电压可控性强,能够控制附近区域的电压水平,这类节点一般称之为可控主导节点[20-21]。超高压、特高压电网无功补偿与电压控制示意图如图4所示。
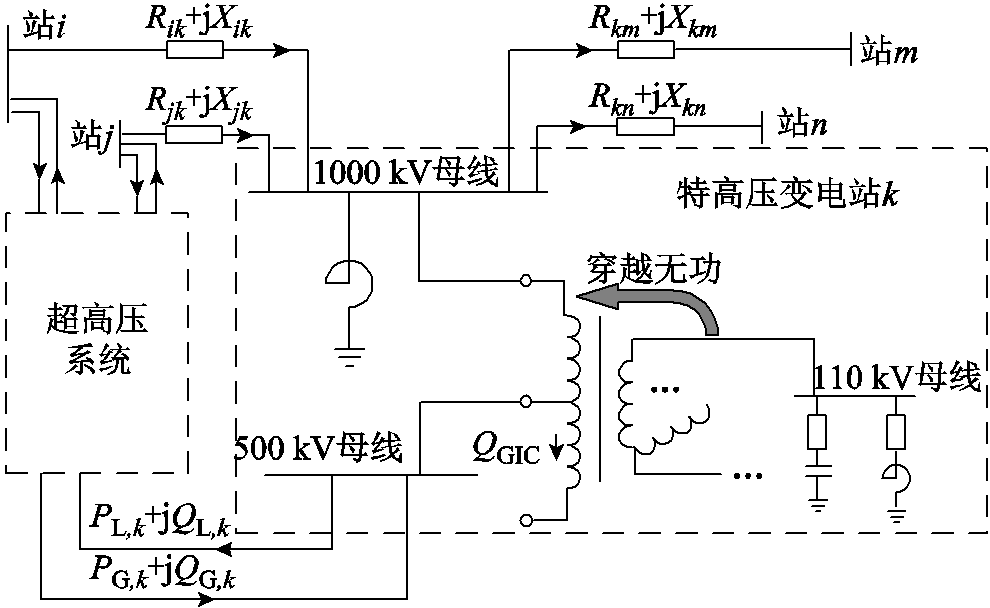
图4 超、特高压电网无功补偿与电压控制示意图
Fig.4 Schematic diagram of reactive power configuration and voltage control for EHV&UHV grid
如图4所示超、特高压电网中,节点i、j、k、m、n为特高压变电站,各个站点之间在特高压、超高压层面分别通过线路连接,当地磁暴衍生的GIC-Q未达到站点的无功功率裕度上限时可视其为可控主导节点。采用调整机组出力、投入无功补偿装置、优化负荷分配等方式改变可控主导节点的注入功率,即可实现控制超、特高压电网电压的目的。
设图4中潮流流向如箭头所示,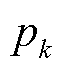 、
、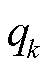 为超高压系统向k站的注入功率,则根据潮流平衡,满足
为超高压系统向k站的注入功率,则根据潮流平衡,满足
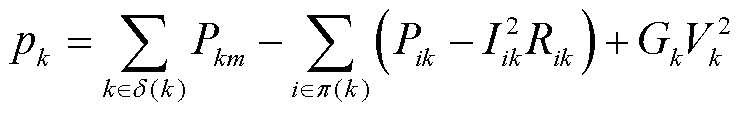 (8)
(8)
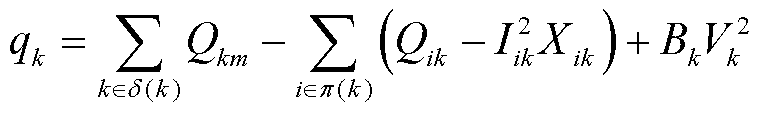 (9)
(9)
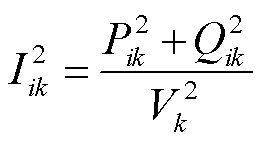 (10)
(10)
式中,δ(k)为以k站为首端节点的线路集合;π(k)为以k站为末端节点的线路集合;Rij、Xij分别为节点i到节点j之间线路的等效电阻、电抗;Gk、Bk分别为与k站相连的线路及高抗的等效电导、电纳。
式(9)中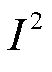 X项代表线路电抗消耗的无功,由于线路输送功率P∝I,线路消耗的无功功率与线路负载的二次方成正比,如果此时叠加地磁暴衍生的突发性、群发性GIC-Q,会造成电网电压波动并易发生系统性无功失衡,引发电压崩溃。此外,GIC流过变压器引起变压器直流偏磁,不仅导致变压器无功损耗增大,还会使得变压器铁心饱和,影响变压器低压侧的电容器向高、中压侧补偿的“穿越无功”流动,致使超、特高压电网无功功率更加不平衡。
X项代表线路电抗消耗的无功,由于线路输送功率P∝I,线路消耗的无功功率与线路负载的二次方成正比,如果此时叠加地磁暴衍生的突发性、群发性GIC-Q,会造成电网电压波动并易发生系统性无功失衡,引发电压崩溃。此外,GIC流过变压器引起变压器直流偏磁,不仅导致变压器无功损耗增大,还会使得变压器铁心饱和,影响变压器低压侧的电容器向高、中压侧补偿的“穿越无功”流动,致使超、特高压电网无功功率更加不平衡。
基于以上原因,本文提出优化调度方法,对预测的GIC-Q进行修正并建立优化问题,对电网可控主导节点的注入功率进行求解,平抑地磁暴期间的电压波动,并维持电网的无功平衡,避免电压崩溃导致大范围停电。
对电网进行优化调度以平抑地磁暴期间的电压波动时,首先应通过相量测量单元(Phasor Measurement Unit, PMU)量测地磁暴期间电网的运行状态,并通过量测的历史数据对基于MHD模型预测的无功扰动进行修正。再根据电网当前运行状态,得到电网各节点的注入功率-电压波动关系,并建立约束方程,以满足电压平抑指标和注入功率变动最小作为控制目标,求解超、特高压电网中各可控主导节点注入功率的最优序列。将注入功率序列用于电网的实际控制,平抑电网电压波动,保持系统无功平衡。为应对预测误差带来的不利影响,地磁暴过程中采用时域滚动方式重复上述过程形成反馈机制,直至地磁暴预警解除。
2.2.1 无功扰动修正方法
MPC是一种过程控制方法[22-24]。由于MHD模型的固有预测能力限制和太阳风-地球磁场耦合过程中一些不可知扰动的影响,预测的GMD在幅值和时序上不可避免地存在一定的误差,增加了优化调度中的不确定性和风险。由历史量测值对MHD模型的预测值进行修正,并通过MPC方法中的滚动优化和反馈校正过程形成反馈机制,提高优化调度在时空尺度上的有效性,构建MHD模型预测控制优化调度模型架构如图5所示。
将地磁暴发生之前通过MHD模型计算得到的各节点GIC-Q序列称为MHD预测值,将从电网量测的电气量称为测量值,对比历史数据中MHD预测值和测量值的误差,组成“近期误差序列”,并延拓出当前优化时段内预期误差对模型预测的GIC-Q进行修正。在地磁暴预警未解除前采用时域滚动的方式进行反馈校正以形成反馈机制。
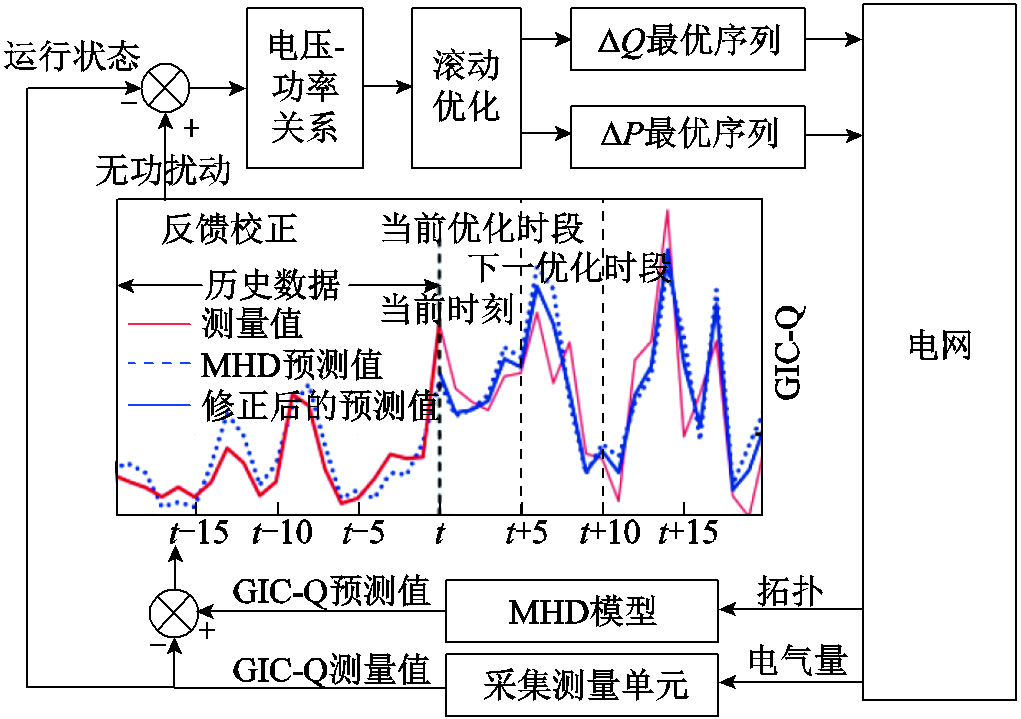
图5 MHD模型预测控制优化调度架构
Fig.5 Architecture of optimal dispatch based on magnetohydrodynamics model
2.2.2 注入功率-电压波动关系
在电网当前运行状态的基础上,获得优化时段内各可控主导节点的注入功率变化序列,需要求解注入功率-电压波动关系。基于潮流计算的雅可比方程,在稳态解处将非线性的潮流方程式线性化,得到矩阵表达式[25]为
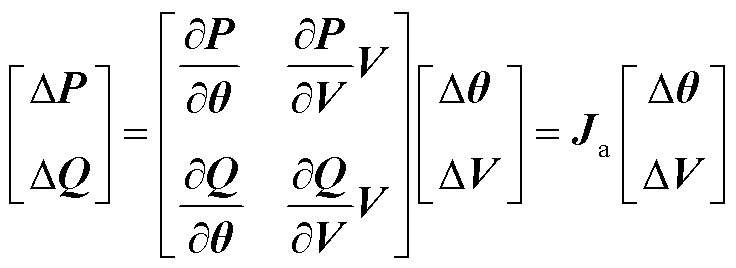 (11)
(11)
式中,Δθ、ΔV分别为各节点电压相角、幅值的变化量矩阵;ΔP、ΔQ分别为各节点注入系统的有功、无功功率的变化量矩阵; 为潮流计算的雅克比矩阵。
为潮流计算的雅克比矩阵。
对式(11)求逆可得
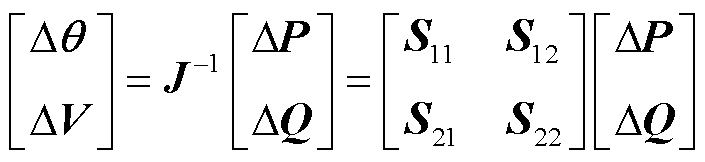 (12)
(12)
电压变化量与有功、无功功率的关系可表示为
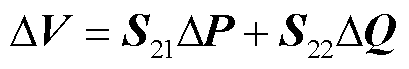 (13)
(13)
式中,S21、S22分别为电压-有功功率、电压-无功功率的灵敏度因子。
设共有N个可控主导节点,ΔPj(t+1)、ΔQj(t+1)表示下一时刻t+1可控主导节点j的注入功率相对当前时刻t的变化量,则可控主导节点i的电压幅值变化量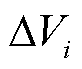 (t+1)可表示为
(t+1)可表示为
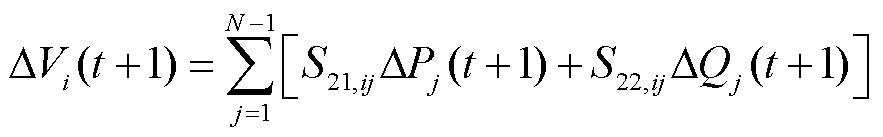 (14)
(14)
2.2.3 控制指令序列求解
地磁暴衍生的大量GIC-Q使得系统无功失衡是影响电网电压稳定性的根本原因和最大的威胁,特别是在地磁暴开始的急始阶段(Storm Sudden Commencement, SSC),大地水平磁场的变化短而急促,会产生大且突然的GIC,突发群发的无功增量可能超过可控主导节点可调度的无功功率上限,造成电压跌落并严重威胁系统运行安全。
为了防止这一状况的发生,对超高压、特高压电网的优化调度应首先满足系统各节点的无功平衡需求,根据式(9)可知,当节点无功容量不足时,应及时对可控主导节点的注入有功功率进行调节,减小相邻特高压线路上的无功损耗,使节点无功功率能够满足电压稳定需求。设当前时刻特高压变电站k的无功负载、最大无功容量、模型预测的无功增量分别为QL,k、Qmax,k、QGIC,k,由式(8)和式(9)可得,节点k注入功率变化量应满足
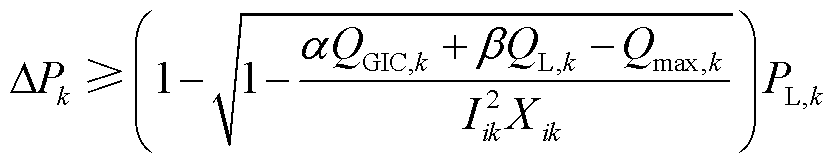 (15)
(15)
式中,α为优化时段内MHD模型的最大幅值误差倍数,视选用的MHD模型精度确定;β为优化时段内可能的最大负荷波动倍数,结合负荷波动的剧烈程度与优化时段的长短确定。
在每个优化调度时段,选取当前时刻之前的d个数据点,以PMU量测的变压器无功增量和MHD预测的GIC-Q之间差值作为预测误差,组成近期误差序列e,并利用最小二乘法拟合成一条直线。对直线进行延拓作为当前优化时段的预期误差,并以此对MHD模型的预测的GIC-Q进行修正。修正后的GIC-Q为
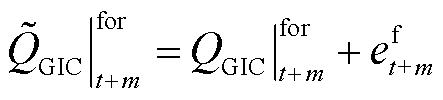 (16)
(16)
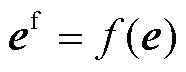 (17)
(17)
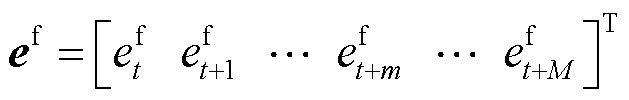 (18)
(18)
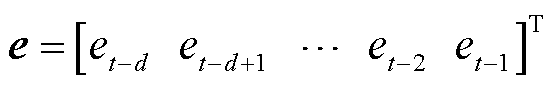 (19)
(19)
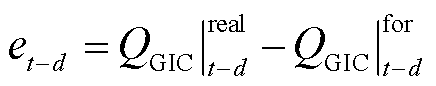 (20)
(20)
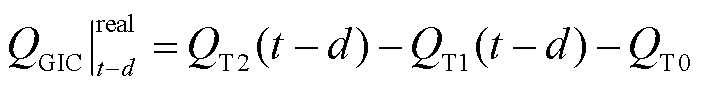 (21)
(21)
式中,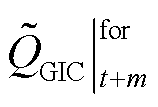 、
、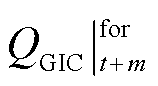 分别为预测时段内t+m时刻MHD模型修正前和修正后的预测无功增量;
分别为预测时段内t+m时刻MHD模型修正前和修正后的预测无功增量;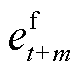 为t+m时刻预测误差;M为优化时段总的时间长度;
为t+m时刻预测误差;M为优化时段总的时间长度;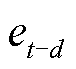 为t-d时刻历史预测误差;函数f(e)为由历史预测误差序列e拟合生成的直线;
为t-d时刻历史预测误差;函数f(e)为由历史预测误差序列e拟合生成的直线;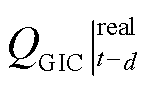 为过去历史数据中t-d时刻从电网量测的GIC-Q;QT2为变压器超高压侧流入的无功功率;QT1为变压器特高压侧流出的无功功率;QT0为正常情况下变压器本体消耗的无功功率。
为过去历史数据中t-d时刻从电网量测的GIC-Q;QT2为变压器超高压侧流入的无功功率;QT1为变压器特高压侧流出的无功功率;QT0为正常情况下变压器本体消耗的无功功率。
利用修正过的GIC-Q,将超、特高压电网电压波动平抑优化调度转换为一个优化问题。将优化时段内各可控主导节点总的电压波动和总的无功注入功率最小作为目标函数,可得
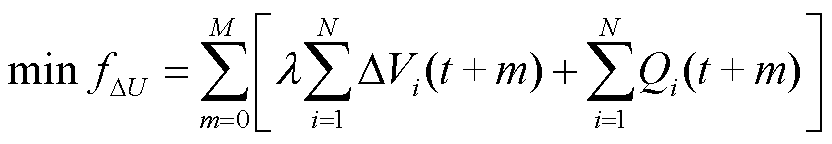 (22)
(22)
式中,λ为电压偏差惩罚系数;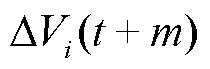 为可控主导节点i所在变电站特高压母线在t+m时刻的偏差值,kV;
为可控主导节点i所在变电站特高压母线在t+m时刻的偏差值,kV;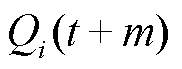 为可控主导节点i在t+m时刻的无功注入功率,Mvar。
为可控主导节点i在t+m时刻的无功注入功率,Mvar。
该优化问题考虑的运行约束除了节点功率平衡和电压稳定,即式(8)~式(10)和式(15)外,还包括以下条件。
1)电源出力上、下限约束为
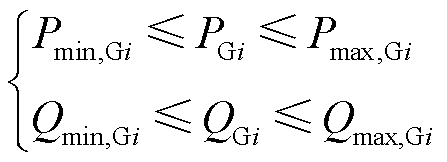 (23)
(23)
式中,PGi、QGi分别为发电机节点i的有功、无功功率。
2)节点电源出力爬坡约束
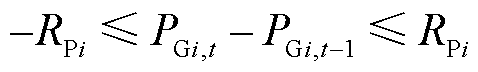 (24)
(24)
式中,PGi,t为节点i在t时刻的注入有功功率;RPi为受限于节点i连接的电厂爬坡速率限制。
从太阳风形成到到达地球引起地球磁场剧烈反应大概需要五六天时间。目前通过将卫星观测的太阳风信息代入MHD模型已经可以实现至少提前24 h获得比较精确的地磁扰动的预测数据。
地磁暴是一个持续几小时到几十个小时的动态过程,当空间天气预报发出地磁暴预警时,可基于MHD模型和MPC方法进行上文所述优化调度方法,平抑地磁暴期间的超、特高压电网的电压波动,其主要流程如图6所示。
具体步骤包括:
(1)当空间天气预警地磁暴即将发生时,将太阳风数据输入MHD模型获得目标电网所在区域地磁扰动预测数据,并由所在区域大地电导率模型得到目标电网所在区域地表感应电场预测数据。
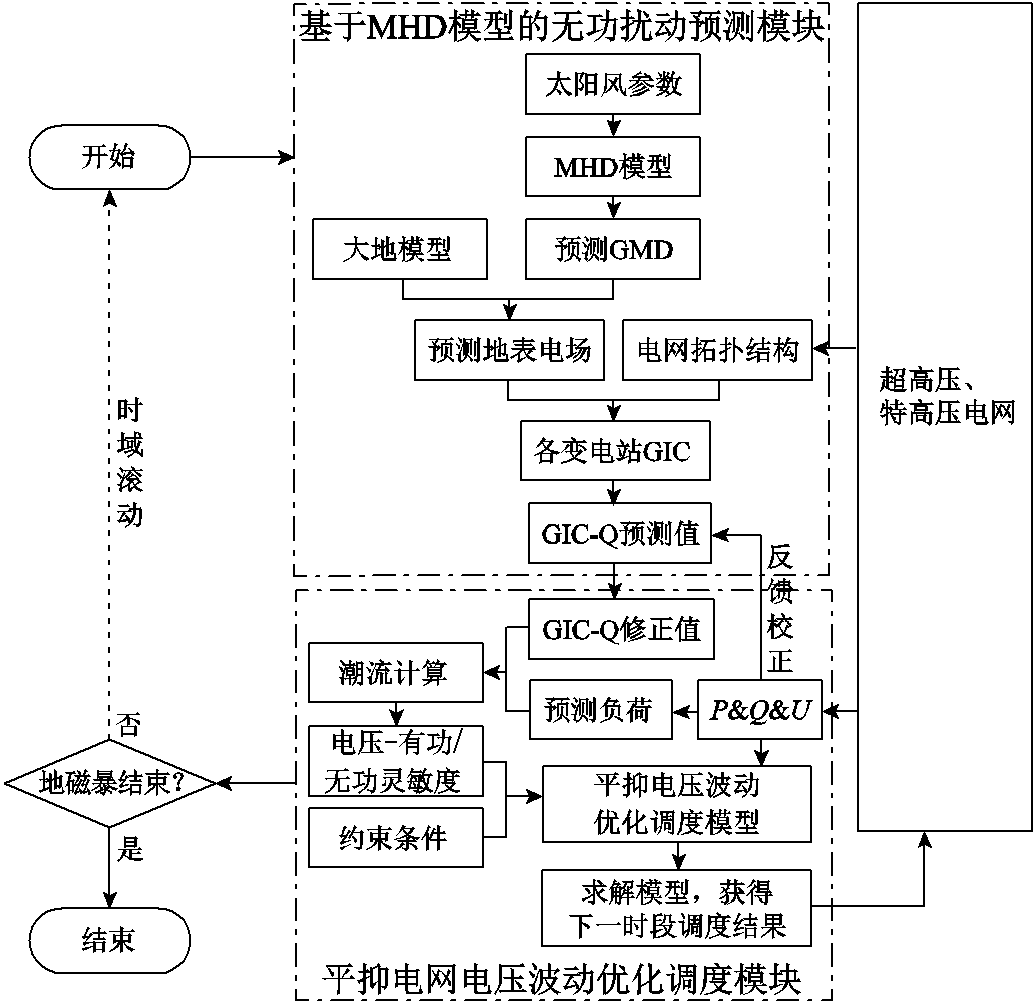
图6 基于MHD模型的地磁暴期间平抑超、特高压电网电压波动优化调度流程
Fig.6 MHD model-based optimized scheduling process for smoothing voltage fluctuations in EHV &UHV grids during geomagnetic storms
(2)通过电网拓扑结构与电网参数计算各变电站的GIC,并利用k值法生成GIC-Q预测序列。
(3)根据负荷波动的剧烈程度,确定优化时长M,负荷波动加剧时缩短优化时长M以减小负荷波动对电压波动造成的误差。
(4)量测电网当前运行状态的电气量并由负荷曲线预测负荷增量,生成各可控主导节点的电压-功率灵敏度因子。
(5)运用MPC方法中的反馈校正思想,根据当前优化时段较近的一段PMU量测的无功扰动历史数据对MHD模型预测的无功扰动进行修正,再基于约束条件建立以电网总电压偏差和无功注入最小为目标函数的优化调度模型。
(6)运用商业软件或算法包,如CPLEX、GUROBI求解最优化问题,获得优化调度时段内各可控主导节点的有功功率与无功功率增量序列作为控制指令,将其作用于电网。
(7)若地磁暴预警解除,则结束;否则,自动执行下一时段的优化调度。
华东地区是我国经济最发达、电力消费最集中,也是电力供需矛盾最为激烈的地区。华东特高压电力网络目前已基本建成,由淮苏沪、皖电东送、浙福特高压工程一起构成华东特高压交流环网和受端网架,将华东四省一市电网紧密联接。图7所示为华东超、特高压电网拓扑。
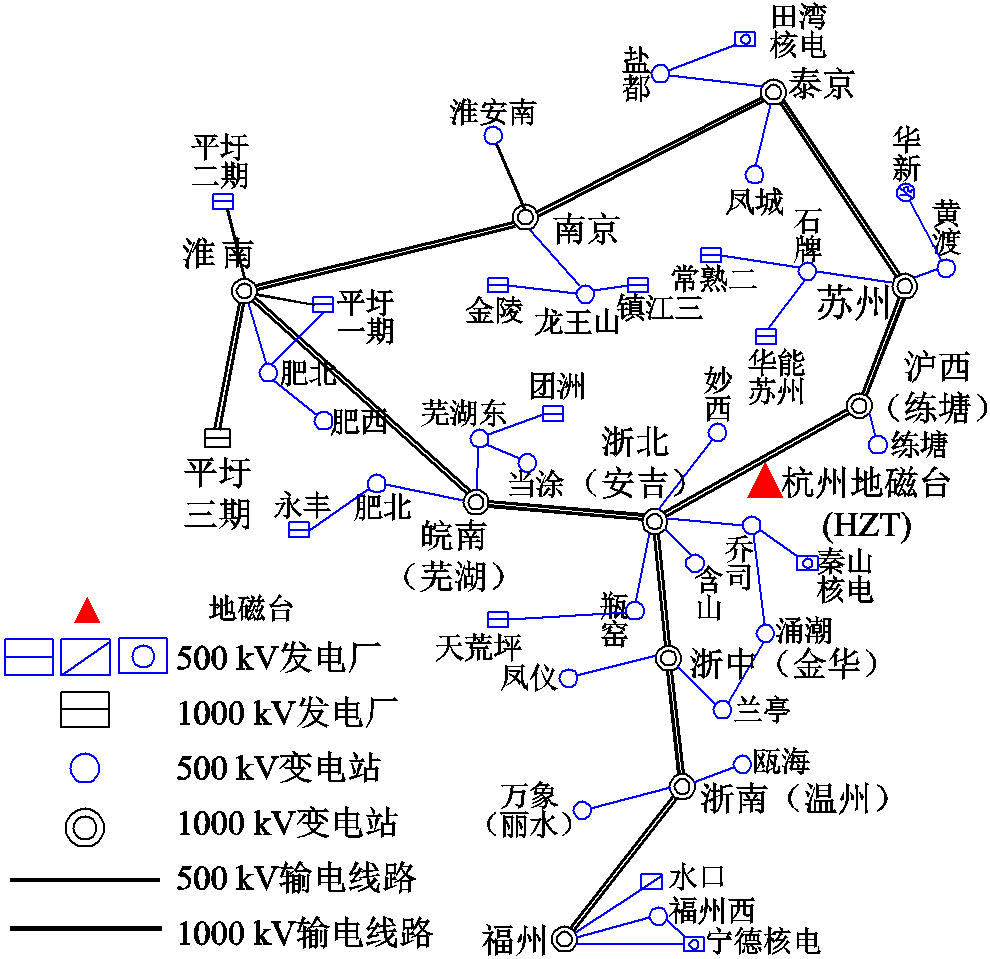
图7 华东超高压、特高压电网示意图
Fig.7 Schematic diagram of Eastern China EHV & UHV power grid
根据对华东地区大地电性结构的勘测[26],设置华东地区的大地电导率分层结构见表1。
表1 华东地区大地电导率
Tab.1 Ground conductivity of Eastern China

深度/km大地电导率/(S/m) 0~300.005 30~900.013 90~1500.04 >1500.3
当特高压变电站的超高压母线所连接的大型发电厂具有无功调节裕度时,可将其视为可控主导节点。根据华东超高压、特高压电网的结构,设置各节点的无功功率裕度见表2。当一个站点为可控主导节点时,在潮流计算中视为PV节点;为非可控主导节点时,视为PQ节点。此外,设华东特高压电网特高压输电线路单位长度电阻r=0.01 Ω/km,单位长度电抗x=0.29 Ω/km,单位长度电纳b=4.56× 10-6 S/km。各可控主导节点的有功爬坡速率Rpi均设为3.5 MW/min。
表2 华东超、特高压电网可控主导节点无功功率裕度
Tab.2 Reactive power margin of controllable pilot node in Eastern China EHV&UHV power grid

变电站ΔQmax/Mvar变电站ΔQmax/Mvar 淮南400皖南420 南京320浙北350 泰州380浙中350 苏州280浙南320 沪西250福州420
以华东超、特高压电网作为对象,基于D14事件评估上文所述优化调度方法对地磁暴引起的电压波动的平抑效果。
首先计算大地电导率分层结构的地表波阻抗,再假设各层电导率均为σ(相当于大地模型电导率为σ的均匀模型),然后进行等效变换使之满足地表波阻抗与分层大地模型的地表波阻抗相等,求解其等效σ值。将σ值和实测、预测的GMD数据代入式(1)和式(2)计算得到D14期间华东地区地表感应电场,结果如图8所示。
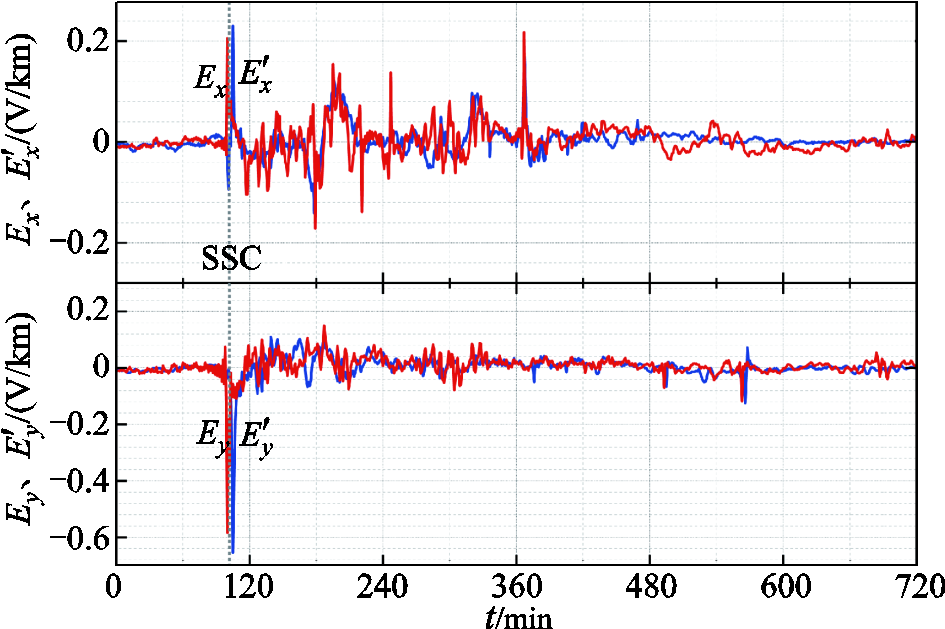
图8 D14期间实测和预测的华东地区地表感应电场
Fig.8 Forecasted and calculated value of electric field induced on earth surface of Eastern China during geomagnetic storm D14
为便于分析和比较本文方法实施前后电压波动的变化,以2021年华东超高压、特高压电网最大运行方式的数据为基础进行仿真。为了验证本文所提方法的有效性并排除负荷波动对电压波动的影响,假设电网负荷在地磁暴期间保持不变。
综合地表感应电场序列和电网拓扑与参数计算各节点的无功增量,并利用杭州地磁台实测的GMD得出的GIC-Q模拟电网量测结果作为测量值,对MHD模型预测的GIC-Q进行修正,反馈校正数据为每个采样时刻前的100个秒采数据。根据华东超、特高压电网运行电压的具体要求,取电压偏差惩罚系数λ=30,确定优化时段内的目标函数,再以5 min为滚动优化步长求解满足平抑电压波动的最优化控制指令序列。BATS-R-US模型在置信水平0.95上的最大相对误差值为1.2,取该值作为优化时段内MHD模型的最大幅值误差倍数α。取优化时段内可能的最大负荷波动倍数β=1.05。
计算D14期间各节点的无功扰动,并利用测量值对MHD预测值进行修正。图10给出了淮南变电站MHD预测无功、测量无功及修正后的预测无功之间的比较。可以看出,经反馈校正和滚动优化环节后获得的修正后预测值与测量值之间误差更小。
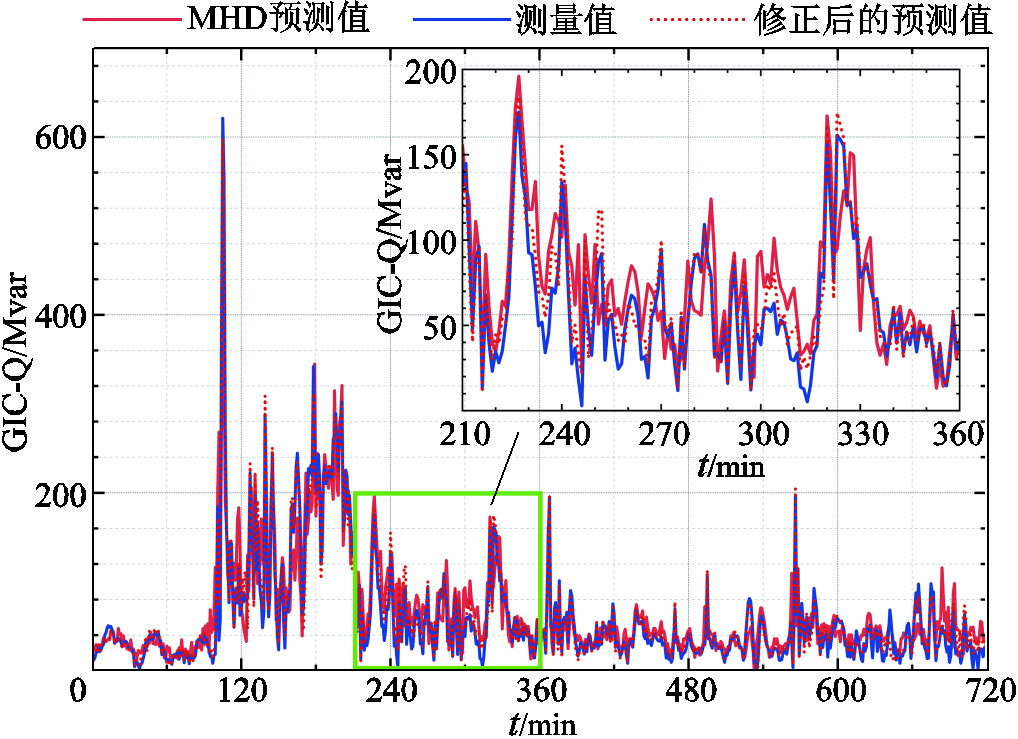
图9 D14期间淮南变电站无功扰动
Fig.9 Reactive power disturbance of Huainan substation during geomagnetic storm D14
算出各节点的预测无功扰动修正值后将其代入注入功率-电压波动敏感度关系式,求解各可控主导节点的控制指令。图10为淮南变电站控制指令的计算结果,可以看出,其无功注入功率序列与地磁暴期间地面感应电场幅值大致呈正相关关系,这是因为无功功率不适合远距离输送,该变电站的电压-无功注入功率灵敏度因子S22ii要比其他站电压-无功注入功率灵敏度因子S22ij高得多,所以其他变电站的注入无功对淮南站电压影响较小。
此外,淮南变电站无功注入功率与东西方向的地面感应电场Ey关系更为密切,这是由于其连接的东北方向的淮南—南京和东南方向淮南—皖南线路可抵消一部分南北向地面感应电场Ex影响,但这两条线路东西方向累积电势形成的GIC却全部流向淮南站。由于Ey在SSC时刻的幅值很大,MHD模型预测的GIC-Q甚至超过淮南变无功功率裕度,需根据MHD模型时序和幅值上的最大预测误差减小可控主导节点的有功注入功率,以保证SSC时刻系统的电压稳定与无功平衡。
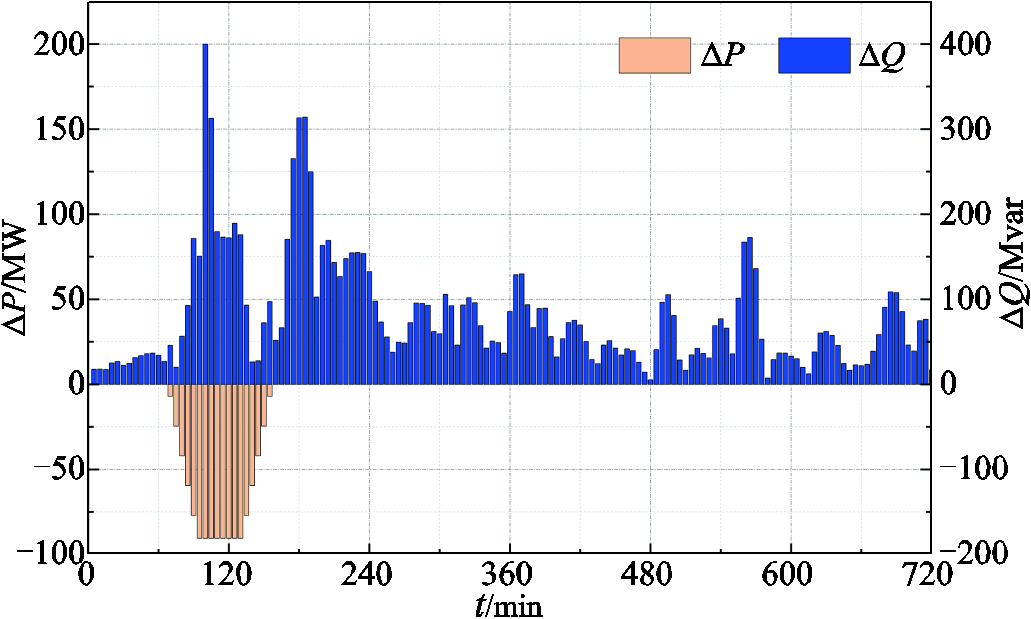
图10 D14期间淮南变电站可控主导节点控制指令序列
Fig.10 Control command sequence of controllable pilot node in Huainan substation during geomagnetic storm D14
图11对比了优化调度前后淮南变电站特高压母线电压波动,可以看出,在未进行优化调度的情况下淮南变电站在地磁暴期间电压波动幅值很大,会出现电压突然下降、突然上升的剧烈波动,即电压波动时间序列上出现的“毛刺”。
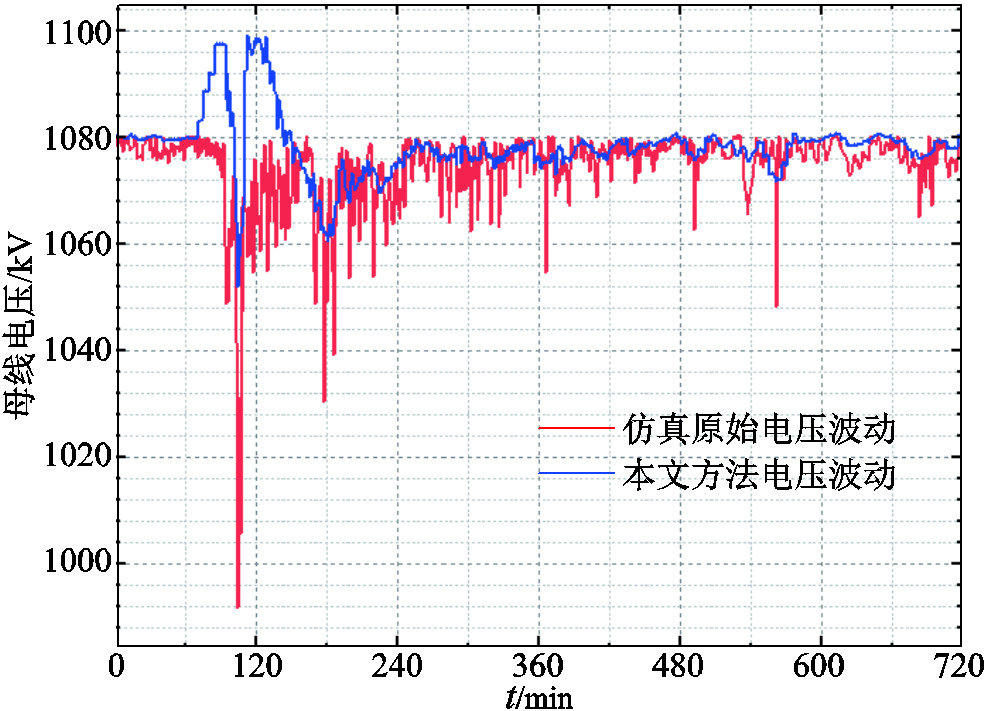
图11 优化调度前后淮南变电站特高压母线电压波动
Fig.11 Voltage fluctuation of UHV bus of Huainan substation before and after optimal dispatch
在SSC时刻,电压波动最为剧烈,电压偏移大大超过了规程规定,甚至低于电压合格区间。运用本文所述优化调度后,电网内增发的GIC-Q大部分被主导节点注入功率抵偿,电压波动明显趋于平缓,“毛刺”基本消失。在SSC时刻,通过减小注入有功功率,减少了特高压线路上的无功功率损耗,短暂地提高了淮南站母线运行电压,即使突发、群发的GIC-Q造成母线电压跌落,仍可保证系统无功功率的平衡和母线电压运行在合格区间。
为了定量刻画和直观比较本文所述优化调度方法平抑地磁暴期间电压波动的效果,定义用于衡量电压波动程度的指标——波动率r,并将其分为两部分,一部分为描述电压波动剧烈程度的指标r1,另一部分描述电压波动趋势的指标r2,它们的表达式为
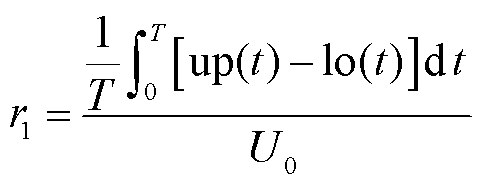 (25)
(25)
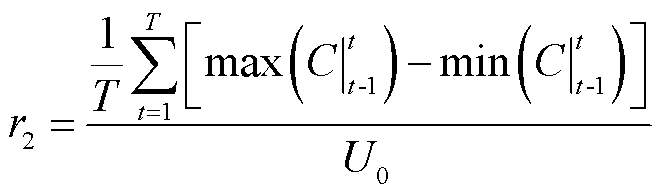 (26)
(26)
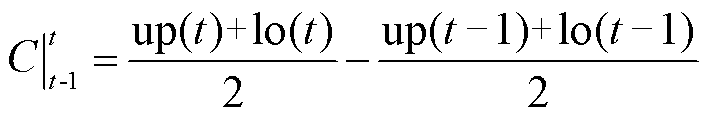 (27)
(27)
式中,up、lo分别为变电站母线电压的上、下峰值包络线;U0为母线基准电压;T为优化调度总时长。
综合以上两个指标,定义电压波动率r为
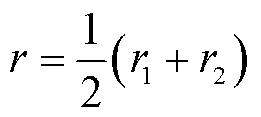 (28)
(28)
图12给出了优化调度前后华东超、特高压电网在D14期间各变电站的最大电压偏移范围和电压波动率变化情况。图中r1-原、r1-优分别表示优化调度前后各站电压波动剧烈程度指标,r2-原、r2-优分别表示优化调度前后各站电压波动趋势指标。
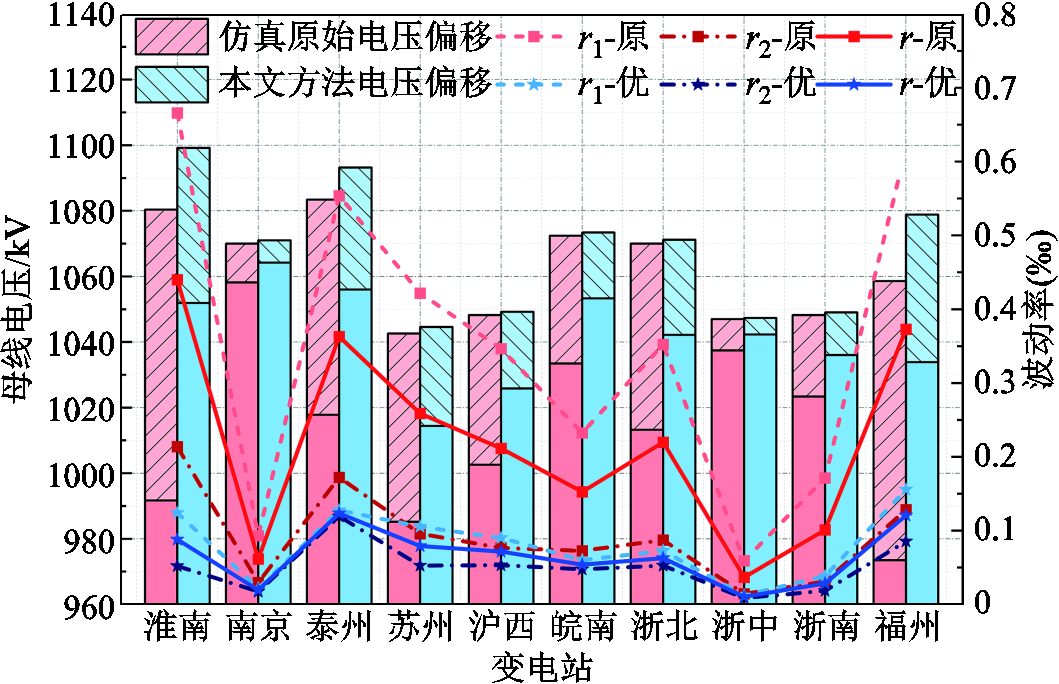
图12 优化调度前后华东超、特高压电网电压波动平抑效果
Fig.12 Voltage fluctuation smoothing of Eastern China EHV&UHV power grid before and after optimal dispatch
由图12结果可知,优化调度前除南京、浙中站外各站电压波动均较大。经优化调度后,各节点的电压偏移幅值大幅缩小,最大电压波动偏移由0.887%下降到0.473%,各节点最大电压波动幅值平均下降53.03%。但值得注意的是,淮南站、泰州站、福州站最高运行电压相较优化调度前要高不少,这是由于这三个变电站处于电网拓扑的拐角处或末端,由于“拐角效应”[27],这些节点会产生的更大的GIC-Q,超过了变电站无功功率裕度,只能通过减小注入有功功率的方式,提高运行电压保证系统的电压稳定性。
此外经分析可得,优化调度后华东超、特高压电网各变电站的电压波动剧烈程度和波动趋势均显著下降,各站电压波动剧烈程度指标r1平均下降77.01%,电压波动剧烈程度指标r2平均下降44.91%,电压波动率r平均下降70.34%。本文所述优化调度方法平抑地磁暴引起的电压波动效果明显,可以有效增强地磁暴期间电网的电压稳定性。
为了应对地磁暴的威胁,本文提出一种基于MHD模型预测控制的优化调度方法,平抑地磁暴期间超、特高压电网的电压波动。相较传统方法,该方法无需新增设备,更加安全经济。通过对华东超、特高压电网的仿真分析与验证,证明了该方法的有效性,得到如下结论:
1)通过优化调度统筹协调超、特高压电网内的有功无功资源,能有效平抑地磁暴期间的电压波动,减小电压波动的剧烈程度和平缓电压波动趋势。
2)在地磁暴SSC时刻,突发、群发的无功扰动易超过变电站无功裕度造成无功失衡和电压跌落,通过减小有功注入功率的方式,可以提高系统电压稳定性,防止发生电压崩溃等地磁暴次生灾害。
3)电网拓扑拐角或末端的节点是无功失衡的“薄弱点”,在电网规划设计阶段应适当提高这些站点的无功储备,以增强电网抵御地磁暴的能力。
致谢:本文中太阳风数据来自于NASA OMNI(https://omniweb.gsfc.nasa.gov/),地磁数据来自于国家重大科技基础设施子午工程科学数据中心(https://data.meridianproject.ac.cn/),BATS-R-US模型运算由Community Coordinated Modeling Center(https://ccmc.gsfc.nasa.gov/)提供。
参考文献
[1] 黄天超, 王泽忠, 李宇妍. 换流变压器直流偏磁对油箱涡流损耗的影响[J]. 电工技术学报, 2023, 38(8): 2004-2014.
Huang Tianchao, Wang Zezhong, Li Yuyan. The influence of converter transformer DC bias on eddy current loss of tank[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2004-2014.
[2] 张长庚, 田亚坤, 李永建, 等. 谐波及直流偏磁下变压器叠片式磁屏蔽杂散损耗模拟与验证[J]. 电工技术学报, 2022, 37(15): 3733-3742.
Zhang Changgeng, Tian Yakun, Li Yongjian, et al. Modeling and validation of stray-field loss in laminated magnetic shield of transformer under harmonics and DC bias[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3733-3742.
[3] 潘超, 安景革, 刘闯, 等. 变压器偏磁效应噪声特性的多场耦合分析与抑制[J]. 电工技术学报, 2023, 38(18): 5077-5088.
Pan Chao, An Jingge, Liu Chuang, et al. Multi-field coupling analysis and suppression for biased magnetic noise in transformer[J]. Transactions of China Elec-trotechnical Society, 2023, 38(18): 5077-5088.
[4] 王泽忠, 司远, 刘连光. 地磁暴对电力系统稳定性的影响[J]. 电工技术学报, 2022, 37(7): 1780-1788.
Wang Zezhong, Si Yuan, Liu Lianguang. Influence of geomagnetic storms on the stability of power system[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1780-1788.
[5] Kappenman J G. Geomagnetic storms and their impact on power systems[J]. IEEE Power Engineering Review, 1996, 16(5): 5.
[6] Wik M, Viljanen A, Pirjola R, et al. Calculation of geomagnetically induced currents in the 400 kV power grid in southern Sweden[J]. Space Weather, 2008, 6(7): 07005.
[7] 郑宽. 大电网地磁感应电流影响因素及建模方法研究[D]. 北京: 华北电力大学, 2014.
Zheng Kuan. Research on influence factors and modelling methods of geomagnetically induced currents in large power grid[D]. Beijing: North China Electric Power University, 2014.
[8] 刘连光, 钱晨, 朱溪, 等. 应用K值算法的甘肃电网GIC-Q扰动计算[J]. 电网技术, 2016, 40(8): 2370-2375.
Liu Lianguang, Qian Chen, Zhu Xi, et al. Calculation of geomagnetically induced currents reactive power loss disturbance in Gansu grid with parameter K[J]. Power System Technology, 2016, 40(8): 2370-2375.
[9] 刘连光, 钱晨, 秦晓培. 考虑500kV影响的特高压电网GIC-Q扰动计算[J]. 中国科学: 技术科学, 2016, 46(11): 1146-1156.
Liu Lianguang, Qian Chen, Qin Xiaopei. Calculation of geomagnetically induced currents reactive power loss disturbance in China’s UHV power grid considering the influence of 500 kV power grid[J]. Scientia Sinica (Technologica), 2016, 46(11): 1146-1156.
[10] 杨培宏, 郑许朋, 刘连光, 等. 变压器中性点配置小电阻器对治理电网GIC的效果分析[J]. 电网技术, 2017, 41(4): 1324-1331.
Yang Peihong, Zheng Xupeng, Liu Lianguang, et al. Effects of transformer neutral grounding via small resistor on mitigating geomagnetically induced currents in power grid[J]. Power System Technology, 2017, 41(4): 1324-1331.
[11] 刘春明, 黄彩臣, 林晨翔. 抑制变压器地磁应电流的电容隔直装置安装位置优化[J]. 电力系统自动化, 2016, 40(16): 132-137.
Liu Chunming, Huang Caichen, Lin Chenxiang. Installation position optimization of capacitor DC blocking devices for suppressing geomagnetically induced currents in transformers[J]. Automation of Electric Power Systems, 2016, 40(16): 132-137.
[12] 王开让, 刘连光, 魏恺, 等. 基于行星际太阳风信息和三维磁流体力学模型预测电网GIC的计算方法[J]. 中国电机工程学报, 2015, 35(24): 6341-6350.
Wang Kairang, Liu Lianguang, Wei Kai, et al. A GIC forecasting algorithm for power grid based on interplanetary solar wind information and three dimensional magnetohydrodynamics model[J]. Pro-ceedings of the CSEE, 2015, 35(24): 6341-6350.
[13] Zhang J J, Yu Y Q, Chen W Q, et al. Simulation of geomagnetically induced currents in a low-latitude 500 kV power network during a solar superstorm[J]. Space Weather, 2022, 20(4): e2021SW003005.
[14] Gonzalez W D, Joselyn J A, Kamide Y, et al. What is a geomagnetic storm?[J]. Journal of Geophysical Research: Space Physics, 1994, 99(A4): 5771-5792.
[15] Powell K G, Roe P L, Linde T J, et al. A solution-adaptive upwind scheme for ideal magneto hydro-dynamics[J]. Journal of Computational Physics, 1999, 154(2): 284-309.
[16] 刘春明, 王红梅, 王璇. 多次磁暴下特高压电网GIC统计规律研究[J]. 中国电机工程学报, 2019, 39(15): 4606-4614.
Liu Chunming, Wang Hongmei, Wang Xuan. Statistical analysis of geomagnetically induced currents in UHV power grids under multiple geomagnetic storms[J]. Proceedings of the CSEE, 2019, 39(15): 4606-4614.
[17] Pirjola R. Calculation of geomagnetically induced currents (GIC) in a high-voltage electric power transmission system and estimation of effects of overhead shield wires on GIC modelling[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2007, 69(12): 1305-1311.
[18] 刘连光, 朱溪, 王泽忠, 等. 基于K值法的单相四柱式特高压主体变的GIC-Q损耗计算[J]. 高电压技术, 2017, 43(7): 2340-2348.
Liu Lianguang, Zhu Xi, Wang Zezhong, et al. Calculation for reactive power loss of single-phase four limbs UHV main transformer due to geomag-netically induced currents with parameter K[J]. High Voltage Engineering, 2017, 43(7): 2340-2348.
[19] 陈锐, 郭庆来, 孙宏斌, 等. 自动电压控制中的中枢母线选择方法[J]. 电力自动化设备, 2012, 32(9): 111-116.
Chen Rui, Guo Qinglai, Sun Hongbin, et al. Pilot bus selection in automatic voltage control[J]. Electric Power Automation Equipment, 2012, 32(9): 111-116.
[20] 龙启峰, 丁晓群, 刘小波, 等. 基于可控主导节点的电压分区及电压校正研究[J]. 电网技术, 2005, 29(24): 59-62.
Long Qifeng, Ding Xiaoqun, Liu Xiaobo, et al. Study of voltage partition based on controllable pilot nodes and voltage correction[J]. Power System Technology, 2005, 29(24): 59-62.
[21] 熊虎, 向铁元, 詹昕, 等. 特高压交流输电系统无功与电压的最优控制策略[J]. 电网技术, 2012, 36(3): 34-39.
Xiong Hu, Xiang Tieyuan, Zhan Xin, et al. An optimal control strategy of reactive power and voltage for UHVAC power transmission system[J]. Power System Technology, 2012, 36(3): 34-39.
[22] 孔令国, 王嘉祺, 韩子娇, 等. 基于权重调节模型预测控制的风-光-储-氢耦合系统在线功率调控[J]. 电工技术学报, 2023, 38(15): 4192-4207.
Kong Lingguo, Wang Jiaqi, Han Zijiao, et al. On-line power regulation of wind-photovoltaic-storage-hydrogen coupling system based on weight adjustment model predictive control[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4192-4207.
[23] 唐早, 刘佳, 刘一奎, 等. 基于随机模型预测控制的火电-储能两阶段协同调频控制模型[J]. 电力系统自动化, 2023, 47(3): 86-95.
Tang Zao, Liu Jia, Liu Yikui, et al. Two-stage coordinated frequency regulation control model for thermal power and energy storage based on stochastic model predictive control[J]. Automation of Electric Power Systems, 2023, 47(3): 86-95.
[24] 王磊, 周建平, 朱刘柱, 等. 基于分布式模型预测控制的综合能源系统多时间尺度优化调度[J]. 电力系统自动化, 2021, 45(13): 57-65.
Wang Lei, Zhou Jianping, Zhu Liuzhu, et al. Multi-time-scale optimization scheduling of integrated energy system based on distributed model predictive control[J]. Automation of Electric Power Systems, 2021, 45(13): 57-65.
[25] 王景亮, 张焰, 王承民, 等. 基于灵敏度分析与最优潮流的电网无功/电压考核方法[J]. 电网技术, 2005, 29(10): 65-69.
Wang Jingliang, Zhang Yan, Wang Chengmin, et al. Power system reactive power/voltage assessment based on sensitivity analysis and optimal power flow[J]. Power System Technology, 2005, 29(10): 65-69.
[26] 袁学诚. 中国地球物理图集[M]. 北京: 地质出版社, 1996.
[27] Boteler D H, Bui-Van Q, Lemay J. Directional sensitivity to geomagnetically induced currents of the Hydro-Quebec 735 kV power system[J]. IEEE Transactions on Power Delivery, 1994, 9(4): 1963-1971.
Abstract Geomagnetic storms originate from the geomagnetic disturbances (GMD) caused by the intense solar activity, and the GMD will induce geomagnetic induction currents (GIC) when it is applied to the grid. As the geomagnetic storms caused by solar activity occur almost at the same time around the world, the reactive power disturbance caused by geomagnetic storms has the characteristics of sudden and mass occurrence in the whole grid. The extra-high voltage (EHV) and the ultra-high voltage (UHV) power grids are more vulnerable to geomagnetic storms due to their special electrical characteristics, which can cause voltage fluctuations in the whole grid and even lead to voltage collapse and catastrophic consequences of large-scale power outages.
The traditional methods generally use the method of connecting resistors or capacitors in series at the neutral point of the transformer, but these methods are not fully adapted to smoothing the voltage fluctuations of the grid. In recent years, with the development of theories related to geophysics and space weather, the three-dimensional magnetohydrodynamics (MHD) model has been able to predict the GMD of geomagnetic storms more accurately. This paper proposes an optimal dispatch based on the MHD model to smooth out voltage fluctuations in EHV and UHV grids during geomagnetic storms. The EHV and UHV grids achieve voltage control by adjusting the injected power from the EHV grids to the UHV grids. In this paper, the sequence of injected power change amount of controllable pilot nodes is calculated from the voltage-power sensitivity factor. To cope with the adverse effects caused by forecast errors, rolling optimization is performed in certain steps, and only control commands for the current optimization period are sent each time, instead of all periods. And comparing the difference between the phasor measurement unit (PMU) measured reactive power increment and the historical predicted value, and correcting the predicted value of the MHD model in the current optimization period. By this way, a feedback mechanism is formed through rolling optimization and feedback correction to improve the effectiveness of optimal dispatch. Compared with traditional methods, the proposed method is safer and more economical as no new equipment is required.
Through the simulation analysis and verification of the Eastern China EHV and UHV power grids, the following conclusions are obtained: (1)The proposed optimal dispatch scheduling coordinates the active and reactive resources in the EHV and UHV grids, effectively suppressing voltage fluctuations during geomagnetic storms, reducing the severity of voltage fluctuations and smoothing the trend of voltage fluctuations. (2)At the time of geomagnetic storm sudden commencement (SSC), the sudden and mass reactive disturbances tend to exceed the substation reactive power margin causing reactive power imbalance and voltage dip. By reducing active power injection, the system voltage stability can be improved and secondary disasters of geomagnetic storm such as voltage collapse can be prevented. (3)The nodes at the corners or ends of the grid topology are the "weak points" of reactive power imbalance, and the reactive power reserves at these substations should be increased appropriately in the planning and design stage to improve the grid's ability to cope with geomagnetic storms.
keywords:Geomagnetic storm, geomagnetic induced current(GIC), voltage fluctuation, magneto- hydrodynamics (MHD), reactive disturbance
DOI: 10.19595/j.cnki.1000-6753.tces.230804
中图分类号:TM712
国家自然科学基金资助项目(52177081)。
收稿日期 2023-05-31
改稿日期 2023-09-18
辛文凯 男,1990年生,博士研究生,研究方向为电网灾害评估,电力系统电压稳定分析与控制。E-mail:392527396@qq.com
刘春明 男,1972年生,教授,博士生导师,研究方向为电网安全运行与灾变控制。E-mail:liuchunming@ncepu.edu.cn(通信作者)
(编辑 郭丽军)