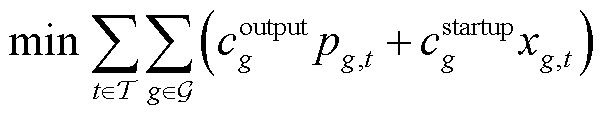 (1)
(1)
摘要 电-气互联系统调度决策问题旨在实现天然气系统和电力系统中可调节资源的最佳配置,其精准性与高效性直接影响电-气互联系统运行的安全性与经济性。为描述可调节资源离散状态、非线性运行特性等物理性质,电-气互联系统调度决策问题中含有规模庞大的离散决策变量,模型复杂度高,使得现有依赖于商业混合整数线性规划(MILP)求解器的电力系统运筹优化技术面临“组合爆炸”的计算负担。为此,该文提出一种分支定界搜索信息深度引导的电-气互联系统调度决策加速求解方法。所提方法利用分支定界初始搜索阶段的信息构建小规模辅助MILP模型,并内嵌于分支定界搜索过程,引导剪除更多冗余搜索空间,在不损失最优性的前提下加速收敛。基于RTS-GMLC电力系统和天然气系统不同负荷水平及线性分段数下的30个算例仿真结果说明,相比于直接使用商业MILP求解器,所提方法在不损失最优性的前提下可实现平均4.20倍的加速,验证了所提方法的有效性。
关键词:电-气互联 调度决策 混合整数线性规划 加速算法
电-气互联系统可实现电力能源和天然气能源之间的灵活互补支撑,是一种提高能源利用效率、助力能源结构转型的重要手段[1-3]。电-气互联系统调度决策问题的数学本质是考虑天然气系统和电力系统物理约束的运筹优化,在确保电-气互联系统可有效应对负荷需求及清洁能源出力等运行工况变化的前提下,实现可调节资源的最佳配置,其精准性与高效性直接影响电-气互联系统的安全性与经济性[4-6]。
由于模型中的离散变量和计算中的收敛性、鲁棒性要求,电-气互联系统调度决策问题通常被构建为混合整数线性规划(Mixed Integer Linear Programming, MILP)形式,即考虑线性或经线性化处理后的电-气互联系统物理运行约束(如线性化后的电力系统交流潮流方程[7]、线性化后的天然气系统Weymouth方程[8]等),在由连续决策变量(如可调节资源出力)和离散决策变量(如机组开停机方案、分段线性辅助变量等)共同构成的离散空间中寻找最优解。
作为一种NP难(Non-deterministic Polynomial-time Hardness)问题,MILP的可行解数目随着离散变量的规模呈指数增长,无法在多项式时间内通过穷举得到最优解。电力工业领域求解MILP问题的方法主要包括分支定界法、Benders分解法[9]、拉格朗日松弛法[10]、锥松弛法[11]、智能算法[3]等。随着近年来以分支定界为核心算法的开源和商用MILP求解器的快速发展,MILP问题的求解效率、稳定性和通用性都得到了极大提升[12],MILP求解器已成为求解这类问题的主流运筹优化技术。目前,我国各电网调度运行机构普遍采用CPLEX、GUROBI等商用MILP求解器求解日前机组组合等大规模电力系统调度决策问题[13-14],当前的电-气互联系统调度决策求解也通常采用建模后交由商用MILP求解器的计算方式[15]。而电-气互联系统调度决策问题在传统电力系统的基础上需进一步考虑天然气系统的物理运行规律,通过分段线性(Piecewise Linear Formulation)形式引入大量辅助离散变量及其相应约束,以便能高精度地描述原有的非线性特征[16-18],这使得调度决策模型规模更大、复杂度更高,面临“组合爆炸”的求解瓶颈,对当前运筹优化技术提出了更严峻的挑战[19]。
现有针对电-气互联系统调度决策问题求解的加速研究往往集中于外围模型处理,即在调用MILP求解器之前利用电力系统专家经验或领域知识对MILP模型的变量、约束和建模方式进行削减和重构,旨在尽可能降低后续求解器处理的复杂度。建模方式方面,采用不同的线性化方式[20-21]或约束凸包构建[22-23]实现紧密性建模(Tightening Formulation),旨在降低原模型和松弛模型之间的间隙,不损失最优性,但通常难以获得在所有场景下均表现最佳的建模方式;约束削减方面,在起作用约束辨识领域已有大量研究,研究对象以线路潮流约束为主,通过数据驱动在内的方法辨识起作用约束,并通过迭代或惰性约束的形式保证最优性[24-25];变量削减方面,往往采用启发式的方法削减运筹优化寻优空间,例如通过离散变量聚合[26-27]或固定[28]的方式大幅削减离散变量规模,通过粗颗粒度分段估计最优解所在邻域,确保每次迭代的离散变量规模有限[20]等,能够大幅提高计算效率,但通常无法保证最优性甚至可行性。工程应用中需要保证最终决策的质量,即确定运筹优化技术的误差边界,而现有集中在外围模型处理的电-气互联系统运筹优化技术难以兼顾高决策效率和低决策误差边界的需求。
调用MILP求解器后,求解器使用以分支定界为核心的一系列运筹优化算法搜索MILP模型的最优解。当前电-气互联系统调度领域还罕有涉及求解器内部流程的算法研究,往往只基于最优解等有限的外围信息,对求解器内部大量与求解进程有关信息的收集和利用程度较低。已有部分前沿工作将电力系统领域知识与分支定界搜索信息相结合,设计电力系统领域知识驱动的定制化高效求解策略,取得了初步成效。文献[29]将离散变量的物理意义与分支定界的分支信息相结合,按照资源、时段等特征划分离散变量,分别对各个分组构建单独的预测器用于拟合分支定界的分支决策过程;文献[14]同样基于电力系统领域知识与分支定界搜索信息相结合的基本思想,将电力系统线路阻塞这一特征与分支定界的可行解、松弛解信息相结合,实现上界更新。而对于电-气互联系统调度决策问题,尚未有相关文献针对其特殊结构和特殊性质提出类似的定制化高效求解策略。
本文提出了一种分支定界搜索信息深度引导的电-气互联系统调度决策加速求解方法。所提方法的基本思想在于充分收集和利用大量MILP求解器内部搜索信息,并应用于电-气互联系统调度决策问题中分段线性化处理这一特殊结构,从而引导分支定界算法更快收敛,实现电-气互联系统调度决策的无损加速。首先,所提方法在分支定界初始搜索阶段收集大量松弛解信息,构建搜索信息数据集;其次,所提方法使用机器学习方法分析所得数据集,评估分段辅助离散决策变量在最优解中可能的取值范围;再次,所提方法基于取值评估结果构建削减大量分段辅助离散决策变量的小规模辅助MILP模型,通过高效求解获得电-气互联系统调度决策问题的高质量可行解;最后,所提方法将高质量可行解用于辅助分支定界算法剪除冗余搜索空间,在保证最优性的前提下加速收敛。基于RTS-GMLC电力系统和天然气系统不同负荷水平及线性分段数下的30个算例仿真结果说明,相比于直接使用商业MILP求解器,所提方法在不损失最优性的前提下可实现平均4.20倍的加速,验证了所提方法的有效性。
1)目标函数
电力系统侧的调度决策成本主要由机组出力成本和机组起动成本两部分构成,有
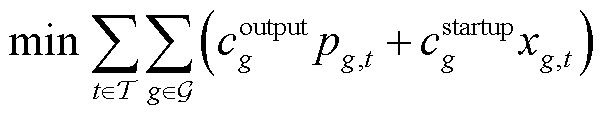 (1)
(1)
式中,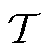 、
、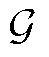 分别为调度时段集合和调度机组集合;常数
分别为调度时段集合和调度机组集合;常数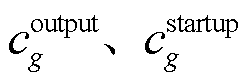 分别为机组g的出力成本系数和起动成本系数;连续决策变量
分别为机组g的出力成本系数和起动成本系数;连续决策变量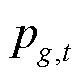 为机组g在时段t的出力;离散决策变量
为机组g在时段t的出力;离散决策变量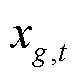 为机组g在时段t是否起动的标志(即从关机到开机)。
为机组g在时段t是否起动的标志(即从关机到开机)。
2)系统侧约束
系统侧约束包括负荷平衡约束和线路潮流约束。负荷平衡约束要求各个时段下机组出力之和与系统负荷相等,即
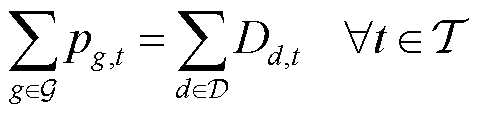 (2)
(2)
式中,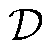 为系统负荷集合;
为系统负荷集合;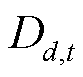 为负荷节点d在时段t的负荷。线路潮流约束通常采用直流潮流形式取代非线性交流潮流,要求各个时段下各条线路的支路潮流功率不大于线路容量,即
为负荷节点d在时段t的负荷。线路潮流约束通常采用直流潮流形式取代非线性交流潮流,要求各个时段下各条线路的支路潮流功率不大于线路容量,即
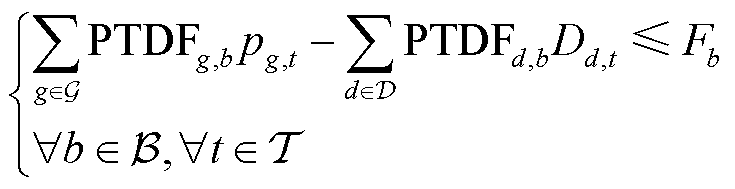 (3)
(3)
式中,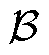 为网络线路集合;常数
为网络线路集合;常数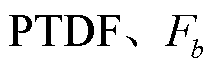 分别为功率转移分布因子(Power Transfer Distribution Factor, PTDF)和线路b的最大容量。
分别为功率转移分布因子(Power Transfer Distribution Factor, PTDF)和线路b的最大容量。
3)机组侧约束
各个机组需要满足的约束包括离散决策变量之间的逻辑约束、容量约束、爬坡约束。逻辑约束通过最小启停时间等联系离散决策变量(均为0-1变量),有
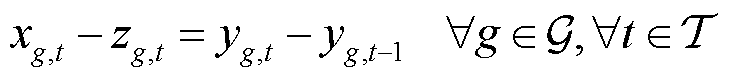 (4)
(4)
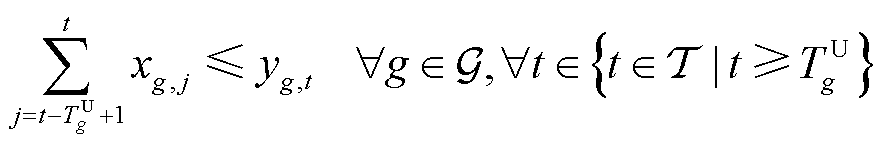 (5)
(5)
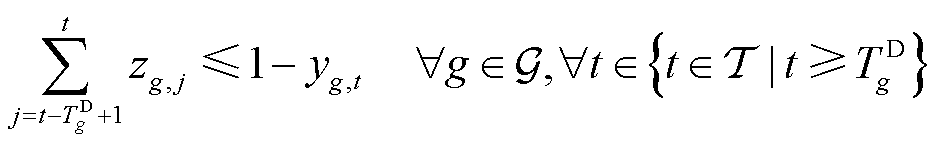 (6)
(6)
式中,离散决策变量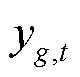 、
、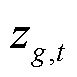 分别为机组g在时段t的运行状态(开/关)和是否关停的标志(即从开机到关机);常数
分别为机组g在时段t的运行状态(开/关)和是否关停的标志(即从开机到关机);常数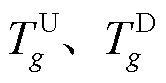 分别为机组g最小起、停时间。容量约束限制机组出力上、下限,有
分别为机组g最小起、停时间。容量约束限制机组出力上、下限,有
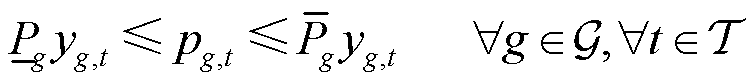 (7)
(7)
式中,常数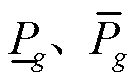 分别为机组g的最小出力和最大出力。爬坡约束限制了机组出力在相邻时段之间的变化速率,即
分别为机组g的最小出力和最大出力。爬坡约束限制了机组出力在相邻时段之间的变化速率,即
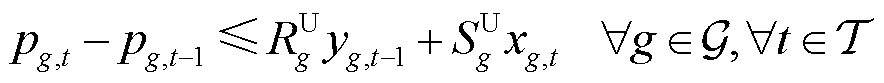 (8)
(8)
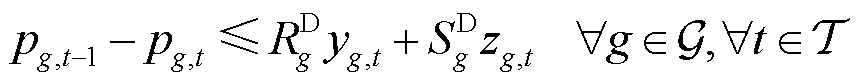 (9)
(9)
式中,常数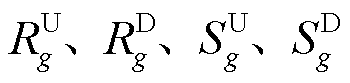 分别为机组g的上/下爬坡速率和起动/关停速率。
分别为机组g的上/下爬坡速率和起动/关停速率。
天然气系统包括气源、管道、压缩机、燃气机等设备,需满足各自的物理运行约束。
1)目标函数
天然气系统侧的调度决策成本主要由气源成本构成,即
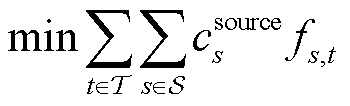 (10)
(10)
式中,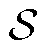 为气源集合;
为气源集合;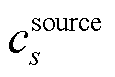 为气源s成本系数;连续决策变量
为气源s成本系数;连续决策变量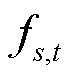 为时段t下气源s的流出流量。
为时段t下气源s的流出流量。
2)气源约束
气源出气需满足上、下限约束,即
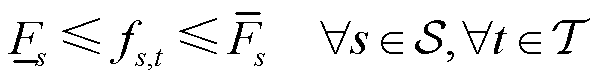 (11)
(11)
式中,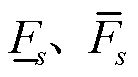 分别为气源s的最小出气和最大出气。
分别为气源s的最小出气和最大出气。
3)压缩机约束
各个压缩机需要满足的约束包括流量上限约束和始末端压强约束。流量上限约束限制了流经压缩机的气流量,有
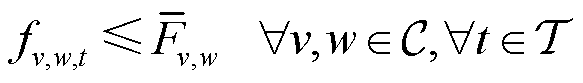 (12)
(12)
式中,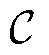 为压缩机集合;
为压缩机集合;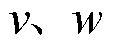 分别为压缩机的始端和末端;
分别为压缩机的始端和末端;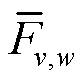 为压缩机容量上限;连续决策变量
为压缩机容量上限;连续决策变量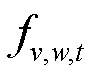 为时段t下流经压缩机的气流量。始末端压强约束限制了压缩机始末端的气网节点压强,有
为时段t下流经压缩机的气流量。始末端压强约束限制了压缩机始末端的气网节点压强,有
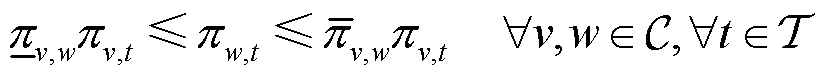 (13)
(13)
式中,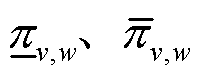 分别为各个压缩机的压缩系数下限和上限;连续决策变量
分别为各个压缩机的压缩系数下限和上限;连续决策变量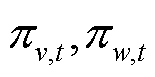 分别为时段t下压缩机始末端压强。
分别为时段t下压缩机始末端压强。
4)气网节点约束
气节点约束包括节点压强约束和节点气流平衡约束。节点压强约束限制了各个气节点的压强,有
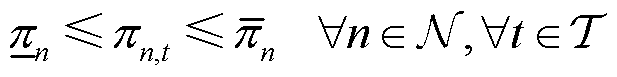 (14)
(14)
式中,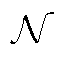 为气网节点集合;
为气网节点集合;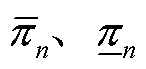 分别为节点n的压强上、下限;连续决策变量
分别为节点n的压强上、下限;连续决策变量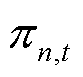 为时段t下节点n的压强。节点气流平衡约束要求各个时段下各个气节点流入和流出的气流总量相等,其中流入节点的气流包括气源出气、管道末端流出气流和压缩机末端流出气流,流出节点或消耗的气流包括燃气机组耗气、气负荷、管道始端流入气流、压缩机始端流入气流和压缩机耗气,有
为时段t下节点n的压强。节点气流平衡约束要求各个时段下各个气节点流入和流出的气流总量相等,其中流入节点的气流包括气源出气、管道末端流出气流和压缩机末端流出气流,流出节点或消耗的气流包括燃气机组耗气、气负荷、管道始端流入气流、压缩机始端流入气流和压缩机耗气,有
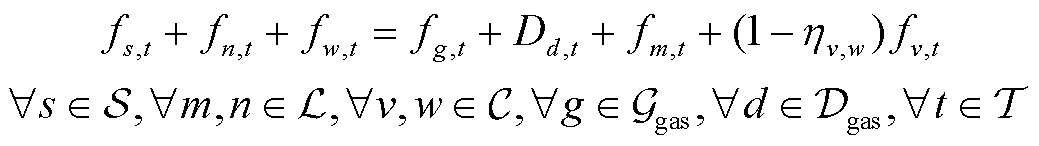 (15)
(15)
式中,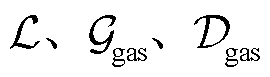 分别为管道、燃气机组和气负荷集合;
分别为管道、燃气机组和气负荷集合;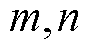 分别为管道的始端和末端;
分别为管道的始端和末端;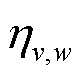 为压缩机耗气系数;连续决策变量
为压缩机耗气系数;连续决策变量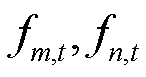 分别为管道始端和末端流入流出气流;
分别为管道始端和末端流入流出气流;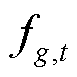 为燃气机组耗气。
为燃气机组耗气。
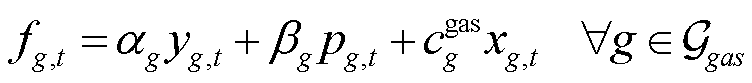 (16)
(16)
式中,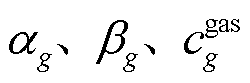 为燃气机组耗气系数。
为燃气机组耗气系数。
5)气网管道约束
各个管道需要满足的约束包括管道容量约束、管存约束和Weymouth方程。管道容量约束限制了管道流量,即
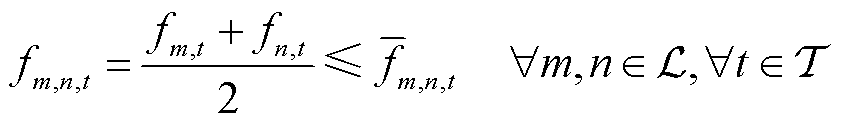 (17)
(17)
式中,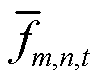 为各个管道的最大容量。管存约束限制了管道始末端压强和随时段变化的管存量,即
为各个管道的最大容量。管存约束限制了管道始末端压强和随时段变化的管存量,即
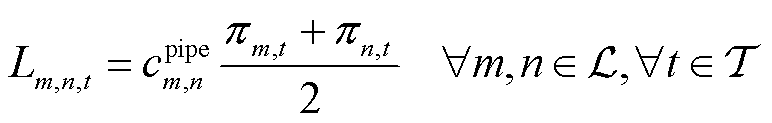 (18)
(18)
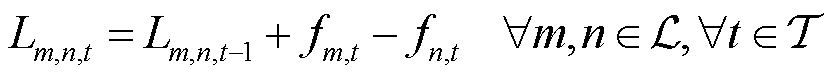 (19)
(19)
式中,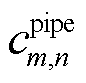 为各个管道的管存系数;连续决策变量
为各个管道的管存系数;连续决策变量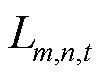 为各个时段下各个管道的管存。Weymouth方程使用二次函数的形式建立管道流量和管道始末端节点压强的关系,有
为各个时段下各个管道的管存。Weymouth方程使用二次函数的形式建立管道流量和管道始末端节点压强的关系,有
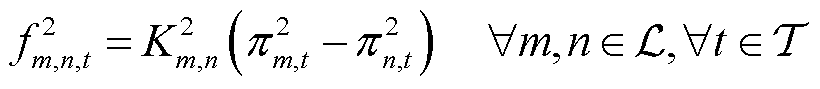 (20)
(20)
式中,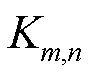 为管道流量模型系数。
为管道流量模型系数。
由于Weymouth方程含有二次函数,往往通过分段线性化的形式将其转换为含辅助离散决策变量的线性化形式。对于自变量取值范围为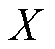 的非线性函数
的非线性函数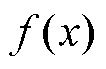 ,引入辅助连续决策变量
,引入辅助连续决策变量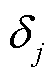 表示线性化后的自变量取值;辅助离散决策变量(均为0-1变量)
表示线性化后的自变量取值;辅助离散决策变量(均为0-1变量)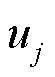 表示自变量位于的分段,
表示自变量位于的分段,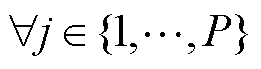 ,将
,将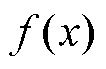 通过分段为
通过分段为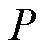 的线性函数
的线性函数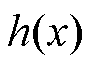 替代。
替代。
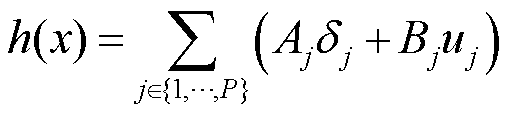 (21)
(21)
式中,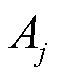 、
、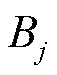 为每个分段内由两者构成的一次线性函数,且满足
为每个分段内由两者构成的一次线性函数,且满足
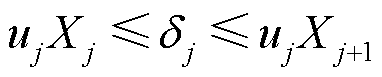 (22)
(22)
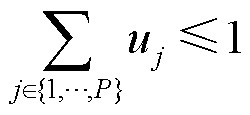 (23)
(23)
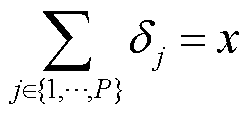 (24)
(24)
分别对管道流量和节点压强应用分段线性化处理,即可线性化Weymouth方程,使得电-气互联系统调度决策问题转变为MILP形式。
值得注意的是,管道流量和节点压强的取值范围较广,因此分段总数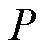 与线性化精度密切相关,分段总数较少时难以精准近似。然而根据上述分段线性化处理过程可知,分段总数越多,需要引入的离散决策变量以及相应约束就更多,极大地增加了电-气互联系统调度决策问题的模型复杂度,带来了显著的计算负担。
与线性化精度密切相关,分段总数较少时难以精准近似。然而根据上述分段线性化处理过程可知,分段总数越多,需要引入的离散决策变量以及相应约束就更多,极大地增加了电-气互联系统调度决策问题的模型复杂度,带来了显著的计算负担。
针对Weymouth方程分段线性化引入大量离散决策变量、增加电-气互联系统调度决策问题求解负担的问题,本文基于分支定界算法的基本原理提出了一种搜索信息深度引导的思路,并构建了电-气互联系统调度决策加速求解的基本框架。
电-气互联系统调度决策问题构建为MILP形式后,调用MILP求解器即可开始求解。MILP求解器由多种算法模块组成,包括预处理[30]、割平面[31]、分支定界、启发式[32]。其中分支定界算法是MILP求解器的核心,通过构建分支定界搜索树对具有最优解可能性的可行解进行策略性穷举。
搜索树的数学本质是依次求解一系列可行域被切割的线性规划(Linear Programming, LP)模型(表示为搜索树节点),从而动态评估最优解的上下界,实现对冗余搜索空间的剪除(Prune)。当上界和下界之间的距离小于阈值(即MILP gap)时,分支定界算法收敛,结束求解。因此,分支定界算法的搜索耗时与搜索树规模呈正相关,剪除更多搜索树节点有利于在不损失最优性的前提下加速分支定界算法收敛。
搜索树节点所表示的LP模型在原MILP模型的基础上将离散决策变量视为连续决策变量(又称为松弛),并随着分支的深入而依次约束这些变量在各个LP模型中的取值。求解当前LP模型得到的解,如果其中所有离散决策变量的取值都恰好为整数(0或1),那么LP模型的解也是原MILP模型的可行解(Feasible Solution),不再往下分支;否则为松弛解(Relaxation Solution),需继续分支生成两个新的子节点。因此搜索树规模随离散决策变量数目呈指数型增长,造成了显著的计算负担。
为避免对冗余搜索空间的过度计算,分支定界算法动态评估最优解的上下界。所有可行解中取值最小的目标函数即为当前搜索树的上界(Upper Bound),最优解的目标函数取值必定不大于当前上界。由于子节点通过约束下一个离散决策变量进一步削减可行域,因此后续节点求解得到的目标函数不小于当前节点的松弛解;所有仍需分支节点的松弛解中取值最小的目标函数即为当前搜索树的下界(Lower Bound),最优解的目标函数取值必定不小于当前下界。处于上界和下界之外的搜索树节点即被剪除,同时不影响求解最优性。随着搜索深入,上界不断下降,下界不断提高,直到两者收敛。
由上述原理可知,只要存在一个目标函数更低的可行解,则上界更新;但只有完全探索当前节点的子节点后才能更新下界。因此,本文所提方法的基本思想在于尽快获得高质量可行解,从而在分支定界搜索的初始阶段大幅剪除冗余搜索空间。
在通用运筹优化领域,已有多种启发式技术研究致力于尽快获得高质量可行解,加速分支定界算法收敛,并已应用于MILP求解器中。这类启发式技术的基本思想在于利用当前阶段分支定界搜索树中获得的数学信息,如可行解、松弛解、起作用约束等,构建相比MILP模型更容易求解的辅助LP模型[33]或离散决策变量规模更小的辅助MILP模型[32]。其中辅助MILP模型求解耗时更长,但往往能获得质量更高的可行解[14]。
启发式技术的关键问题在于利用哪些分支定界搜索信息,以及如何基于搜索信息辨识辅助MILP模型中需要被着重优化的离散决策变量集合。当前运筹决策技术往往针对通用MILP问题,而缺乏对特定问题结构(如电-气互联系统调度决策问题中的分段线性化处理)的考虑。
令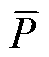 、
、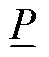 分别为分段辅助离散决策变量
分别为分段辅助离散决策变量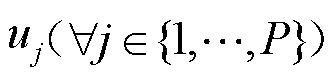 有效取值(即取值为1)的上、下界,即
有效取值(即取值为1)的上、下界,即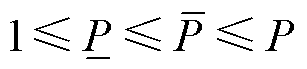 ,修改分段线性约束式(23)为
,修改分段线性约束式(23)为
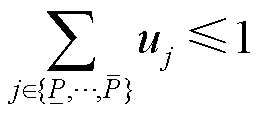 (25)
(25)
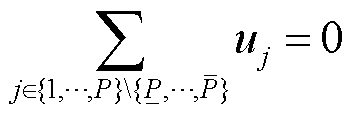 (26)
(26)
当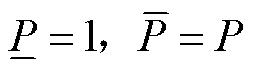 时,式(25)、式(26)和原始分段线性约束式(23)等价;否则,式(25)、式(26)表示将分段数目从
时,式(25)、式(26)和原始分段线性约束式(23)等价;否则,式(25)、式(26)表示将分段数目从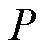 减少到
减少到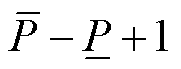 。因此,基于分支定界搜索信息估计
。因此,基于分支定界搜索信息估计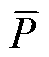 、
、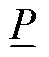 ,可以构建离散决策变量规模削减的辅助MILP模型。
,可以构建离散决策变量规模削减的辅助MILP模型。
本文基于分支定界初期搜索过程中的松弛解,评估与分段线性化处理相关的辅助离散决策变量在最优解中可能的取值范围,构建分段数目减少的小规模辅助MILP模型,从而获得高质量可行解引导分支定界加速收敛。所提方法的基本框架如图1所示,由主进程和子进程通过并行交互实现。其中主进程即为MILP求解器求解过程,将分支定界算法搜索过程中获得的信息提供给子进程,并接收子进程提供的可行解用于加速搜索;子进程收集主进程搜索信息用于评估分段辅助离散决策变量的有效取值范围,从而构建分段数目削减后的小规模辅助MILP模型,最后基于可行性修复方法求解该模型获得高质量可行解。由于该辅助MILP模型没有改变其他物理运行约束,因此获得的可行解也是原始MILP模型的可行解,可以用于改进主进程中的上界。
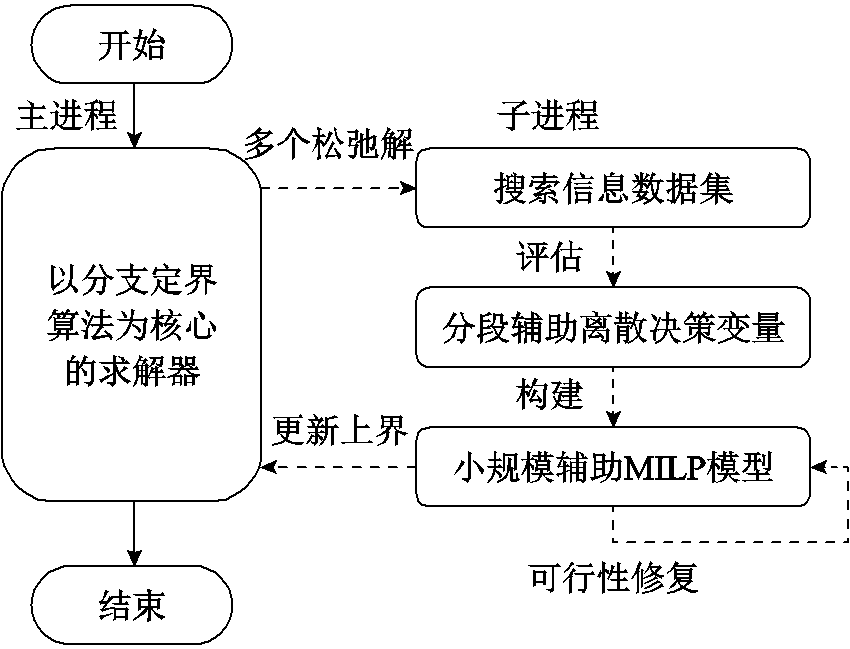
图1 所提方法基本框架
Fig.1 Framework of the proposed method
利用所提方法收集分支定界初始搜索阶段的松弛解信息。一方面,相比于可行解,更容易在分支定界搜索初期获得大量松弛解信息,其数目与当前已搜索节点相关;另一方面,尽管无法满足原始MILP模型的可行性,松弛解信息仍从最优性(即最优解的下界评估)的角度表明分支定界搜索树后续的收敛方向,有助于评估分段辅助离散决策变量在最优解中的取值。例如,如果被分段线性化的非线性函数在已有的松弛解中都位于相似分段,那么大概率在后续的搜索过程乃至最优解中都遵从相同规律。
每个松弛解都表示搜索信息数据集中的一个样本,令分支定界初始搜索阶段收集的样本总数为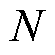 。每个样本由输入和标签构成。样本输入表示该松弛解区别于其他松弛解的信息,因此所提方法采用松弛解的目标函数取值
。每个样本由输入和标签构成。样本输入表示该松弛解区别于其他松弛解的信息,因此所提方法采用松弛解的目标函数取值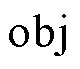 作为输入。样本标签表示该松弛解提供的分段辅助离散决策变量有效取值范围信息。该信息的原始形式有三种可能:
作为输入。样本标签表示该松弛解提供的分段辅助离散决策变量有效取值范围信息。该信息的原始形式有三种可能: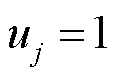 、
、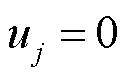 或
或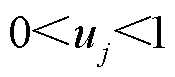 。由于分析目标是估计
。由于分析目标是估计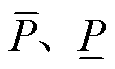 ,即确定最优解中
,即确定最优解中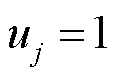 可能的分段集合,为充分利用信息,所提方法采用
可能的分段集合,为充分利用信息,所提方法采用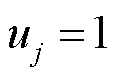 和
和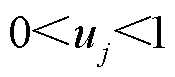 中
中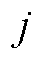 的平均值作为标签,即
的平均值作为标签,即
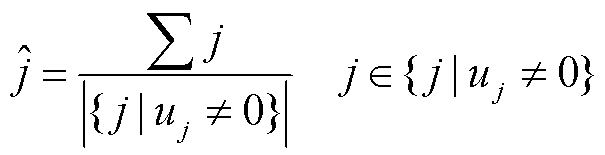 (27)
(27)
对所有需要分段线性化处理的非线性函数成立。因此,搜索信息数据集构建了输入和标签之间的映射关系: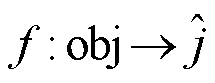 。
。
有多种机器学习方法可作为概率分析工具拟合上述映射关系。本文使用k近邻回归算法(k-Nearest Neighbours regression, KNN)。KNN结构简单,基本原理是计算相邻k个邻域标签的平均值。通常采用欧式距离计算测试样本和每个训练样本之间的距离,有
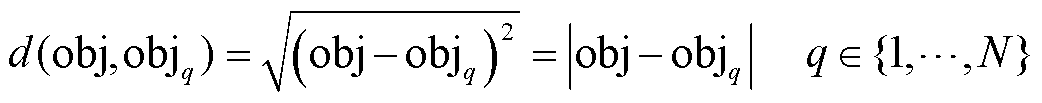 (28)
(28)
式中,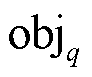 为训练样本q的目标函数取值。由于搜索信息数据集中的样本输入只有一维,因此该距离也等同于目标函数取值之间的绝对差值。KNN对测试样本的输出结果为
为训练样本q的目标函数取值。由于搜索信息数据集中的样本输入只有一维,因此该距离也等同于目标函数取值之间的绝对差值。KNN对测试样本的输出结果为
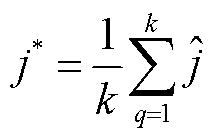 (29)
(29)
式中,q属于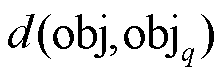 最小的k个样本集合。因此,KNN的输出结果可以被邻域数目k直接调整。通常来说,k设置得越大,考虑的松弛解信息就越多,评估得到的分段辅助离散决策变量有效取值范围也就越大。
最小的k个样本集合。因此,KNN的输出结果可以被邻域数目k直接调整。通常来说,k设置得越大,考虑的松弛解信息就越多,评估得到的分段辅助离散决策变量有效取值范围也就越大。
需确定测试样本的输入(即目标函数取值)作为KNN邻域中心。由于最优解的目标函数取值未知,无法直接作为测试样本,因此选取的测试样本应尽可能接近最优解。搜索信息数据集中的松弛解位于搜索树的不同位置,例如,靠近树起点的松弛解由于取值非整数的离散决策变量较多,目标函数取值较小;而位置过度深入的松弛解目标函数取值较大,有可能远离最优解所在子树。其本质在于部分松弛解位于已经或即将被剪除的冗余搜索空间。因此,为尽可能近似最优解邻域,所提方法以当前下界为中心构建k近邻,即:式(28)使用当前下界目标函数取值作为KNN的输入,式(29)输出下界附近的分段辅助离散决策变量评估结果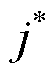 。
。
考虑到简便性,假设辅助离散决策变量的有效取值范围关于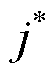 对称,并分别对
对称,并分别对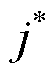 向上、向下取整后得到分段辅助离散决策变量的有效取值范围
向上、向下取整后得到分段辅助离散决策变量的有效取值范围 和
和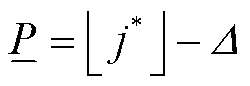 ,其中
,其中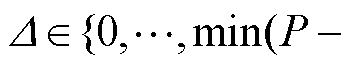
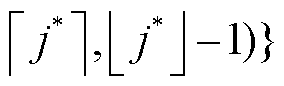 ,可知,
,可知,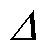 设置得越大,分段辅助离散决策变量的有效取值范围也就越大。
设置得越大,分段辅助离散决策变量的有效取值范围也就越大。
最后,将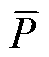 、
、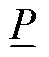 代入式(25)、式(26)中即可构建小规模辅助MILP模型。通过子进程求解时,及时将小规模辅助MILP模型获得的可行解提供给主进程,从而更早地与主进程交互,无需等待小规模辅助MILP模型求解完毕。由于主进程和子进程采取并行模式,求解辅助MILP模型不会增加主进程的计算耗时,也不影响分支定界算法求解原MILP模型的最优性。
代入式(25)、式(26)中即可构建小规模辅助MILP模型。通过子进程求解时,及时将小规模辅助MILP模型获得的可行解提供给主进程,从而更早地与主进程交互,无需等待小规模辅助MILP模型求解完毕。由于主进程和子进程采取并行模式,求解辅助MILP模型不会增加主进程的计算耗时,也不影响分支定界算法求解原MILP模型的最优性。
由于在辅助MILP模型中大幅削减了分段数目,因此如果分段辅助离散变量的有效取值范围评估过窄,则辅助MILP模型有可能不可行,从而对主进程中的分支定界搜索加速不起作用;另一方面,如果该范围评估过宽,则辅助MILP模型的求解耗时较长,对主进程中的分支定界搜索效率提升有限。
为平衡辅助MILP模型的可行性和求解效率,提出基于试探的可行性修复方法。从上述分析可知,参数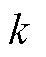 、
、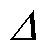 可联合确定分段取值范围,且
可联合确定分段取值范围,且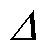 的影响更大。因此,可设置一组逐次递进的
的影响更大。因此,可设置一组逐次递进的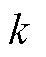 、
、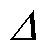 参数,有
参数,有
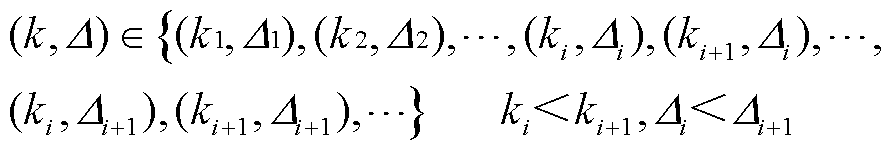 (30)
(30)
式(30)控制辅助MILP模型的离散决策变量规模从小到大。由于可行性的判别速度较快,上述可行性修复策略可在有限耗时内迅速找到一组参数使得辅助MILP模型可行,同时不过度损失求解效率。该参数设置见算例分析部分。
综上所述,本文提出了一种分支定界搜索信息深度诱导的电-气互联系统调度决策加速方法,其伪代码流程见表1。所提方法首先收集N个原始MILP模型分支定界初始搜索阶段中的松弛解及其目标函数取值信息用于构建搜索信息数据集;然后估计分段辅助离散变量的有效取值范围;最后构建并求解相应的小规模辅助MILP模型,将高质量可行解用于引导分支定界算法剪除更多冗余搜索空间,加速收敛。
表1 所提方法伪代码流程
Tab.1 Pseudocode of proposed method

所提方法 主进程,当gap>设定误差时 1 if 已收集松弛解的数目<N 2 收集松弛解及其目标函数取值 3 else 4 停止收集,开启子进程 5 end if 6 if 子进程返回更好的可行解 7 更新当前上界 8 end if 9 (分支定界的剩余部分) 子进程 1 通过目标函数取值和式(27)构建搜索信息数据集 2 通过式(28)、式(29)(即KNN)和给定参数k预测 3 通过给定参数计算 4 通过式(25)、式(26)构建小规模辅助MILP模型 5 求解该小规模辅助MILP模型 6 if 该小规模辅助MILP模型不可行 7 更新参数k和,返回行2 8 else if 获得新的可行解 9 将可行解返回主进程 10 end if 11 (分支定界的剩余部分)
测试算例由RTS-GMLC电力系统和天然气系统联合构成。其中电力系统有73个节点,158台机组(含2台燃气机组),120条线路;天然气系统有10个节点,2个气源,3条管道,3个压缩机;调度时段为日前24 h。测试设备为Intel i5-9300H CPU,RAM 32G。使用的MILP求解器为通过Python接口调用的CPLEX 12.9,求解终止条件为MILP gap达到0.01%或求解时间达到104 s。
算法有效性的对比基准是使用默认参数设置和16线程并行的CPLEX直接求解;所提方法设置主进程和子进程分别调用单线程计算,其中分支定界松弛解的收集阈值设置为总数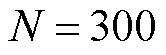 ,可行性修复参数依次取
,可行性修复参数依次取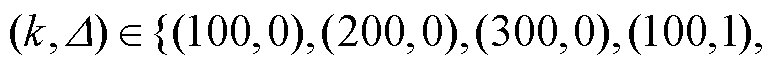
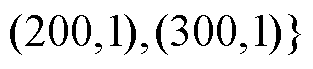 。
。
在同一电-气互联系统中,考虑分段线性数目不同构建相应的MILP模型,对比CPLEX和所提方法的求解效率,其结果如图2所示。数值结果显示,所提方法在分段数目取值15~20的范围内的求解耗时均低于CPLEX,验证了所提方法在不同分段数目下的有效性。其中,CPLEX求解耗时范围为 1 245.69~10 000 s(分段数目19的算例被终止条件截止),所提方法求解耗时为270.98~1 188.97 s,加速比(CPLEX求解耗时/所提方法求解耗时)为1.60~36.90倍以上(分段数目19的算例加速比大于36.90倍),平均加速11.28倍。
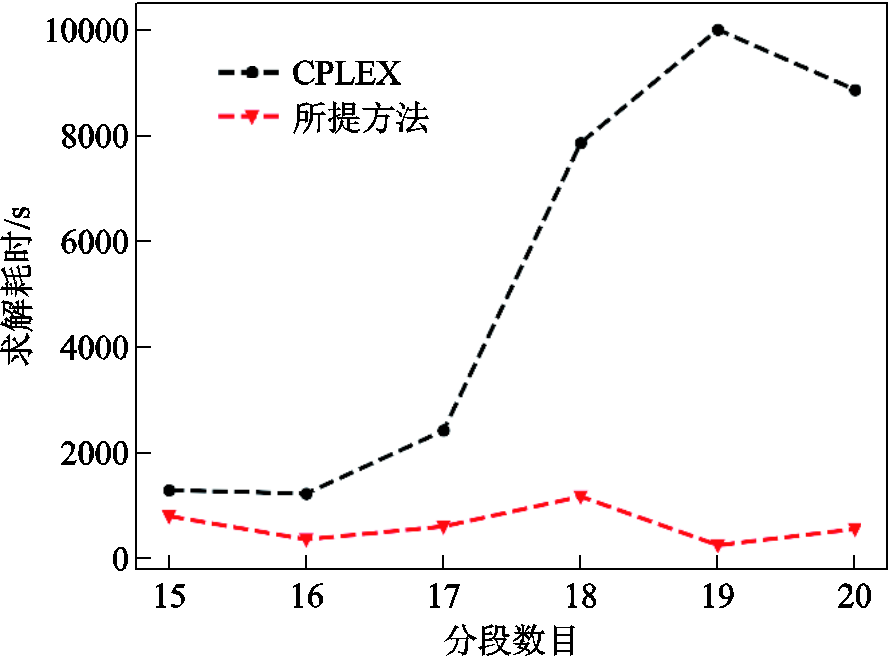
图2 不同分段数目的有效性验证
Fig.2 Effectiveness for different pieces
此外,图2显示,随着分段数目的增加,直接调用CPLEX求解将带来计算负担陡增,而所提方法能够显著缓解这一瓶颈,从而在提高分段线性化建模精度的同时,也提高了电-气互联系统的调度决策效率。
为验证所提方法在不同负荷条件电-气互联系统调度决策问题中的有效性,基于4.1节基础负荷随机生成10条负荷曲线如图3所示,以不同的分段数目(范围为10~20)构建电-气互联系统调度决策模型共计30个。其中,负荷曲线峰值服从±7.5%的标准分布,各个时段斜率服从标准差为0.01的正态分布。最终,10条负荷曲线峰谷差范围为34.08%~45.04%,最大爬坡范围为7.60%~13.15%,体现了爬坡快、峰谷差大的时段强耦合特性。
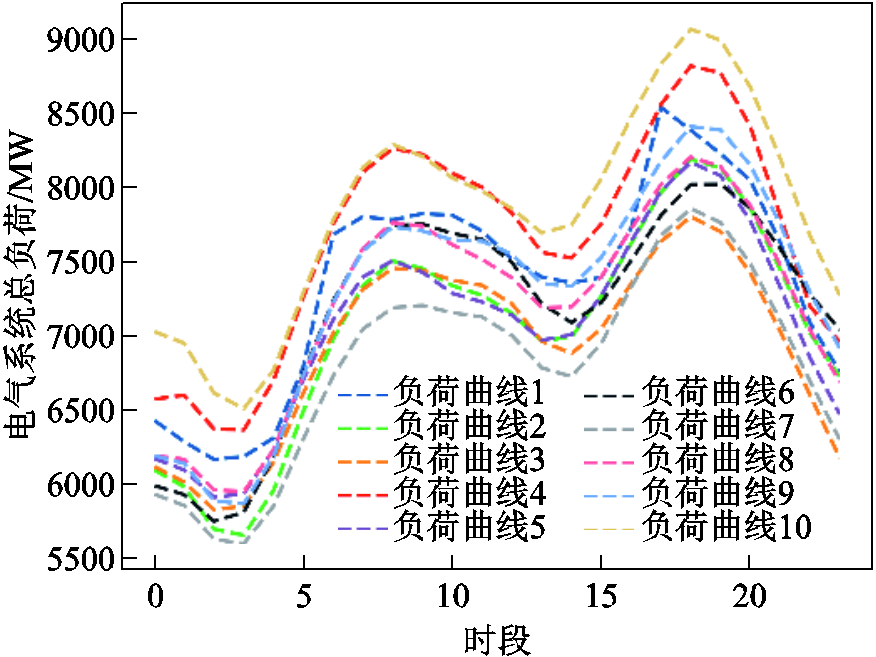
图3 测试算例负荷曲线
Fig.3 Load curves in test cases
CPLEX和所提方法的求解效率对比如图4所示,其中纵坐标为指数坐标。数值结果显示,所提方法在不同算例的求解耗时均低于CPLEX,验证了所提方法在不同负荷条件下的有效性。其中,CPLEX求解耗时范围为216.38~5 671.70 s,所提方法求解耗时范围为72.33~734.36 s,加速比为1.64~13.52倍,平均加速4.20倍。
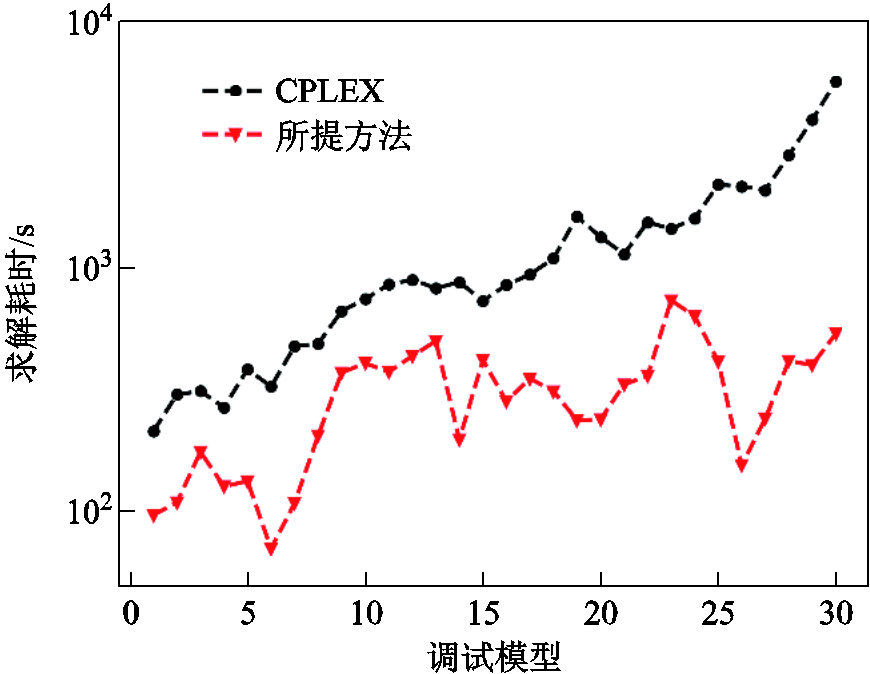
图4 不同方法的求解效率
Fig.4 Solving efficiency for different method
1)可行性修复参数
所提方法收集分支定界初始信息后构建小规模辅助MILP模型,图5展示了30个测试算例中所提方法的可行性修复参数选择情况。其中,83.33%的测试算例在(300,0)、(100,1)、(200,1)三组参数范围内得到了可行的辅助MILP模型,其他算例则在其他参数下得到了可行模型。辅助MILP模型相比于原始电-气互联系统调度决策模型,将问题规模平均削减了76.15%,即所提方法平均只需优化23.85%与分段线性处理相关的离散变量,从而减轻了辅助MILP模型的计算负担。因此,所提可行性修复方法实现了不同测试算例中辅助MILP模型的可行性和求解效率平衡,表明了有效性。
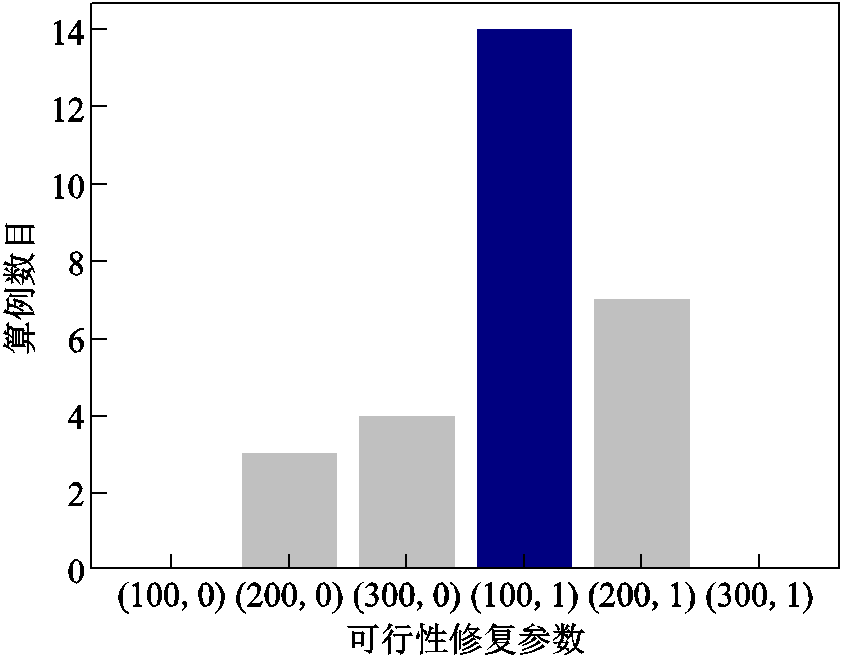
图5 测试算例的可行性修复参数选择
Fig.5 Feasibility repair parameters in test cases
2)KNN拟合精度
本文所提方法使用KNN作为一种概率分析工具挖掘搜索信息数据集中表征的模式,即分段辅助离散决策变量可能的取值范围,从而构建小规模辅助MILP模型用以获得原始模型的高质量可行解。由于所提方法以更新上界的方式与原始求解过程交互,引导搜索树剪除冗余搜索空间实现加速,并未改变原始模型的约束和变量,因此能够保证最优性,KNN拟合精度不会影响所提方法的准确性。另一方面,KNN拟合精度决定了所获得高质量可行解与实际最优解之间的误差,倘若误差较大,则所提方法提供的可行解对原始求解过程作用较小,乃至无法提供可行解(需可行性修复),将影响计算效率的提升。30个测试算例经可行性修复后,KNN拟合精度范围为98.49%~99.97%,平均精度99.43%,表明所获得可行解与实际最优解之间的误差较小。
3)上界收敛与搜索树规模
通过子进程对辅助MILP模型的求解,所提方法能够在早期为主进程中的分支定界算法提供更好的上界,从而辅助搜索树剪除更多冗余搜索空间。图6展示了部分测试算例中的上界收敛情况,可见相比于使用CPLEX直接求解,所提方法能够更快地提供初始可行解。图7对比了CPLEX和所提方法分别构建的分支定界搜索树规模(纵坐标为对数坐标),其中CPLEX搜索节点规模为7 844~1 759 217个,所提方法搜索节点规模为800~5 898个,削减倍数(CPLEX搜索节点数目/所提方法搜索节点数目)为5.34~565.85倍,平均削减76.09倍,表明了所提方法在剪除冗余搜索空间方面的有效性。
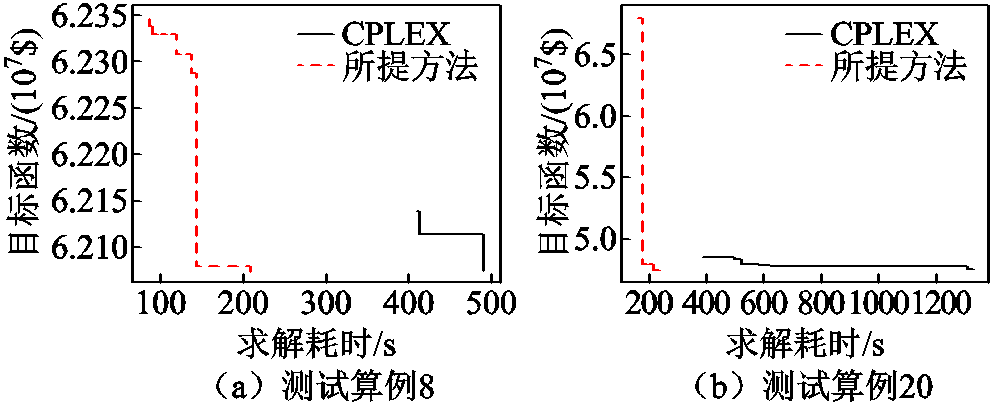
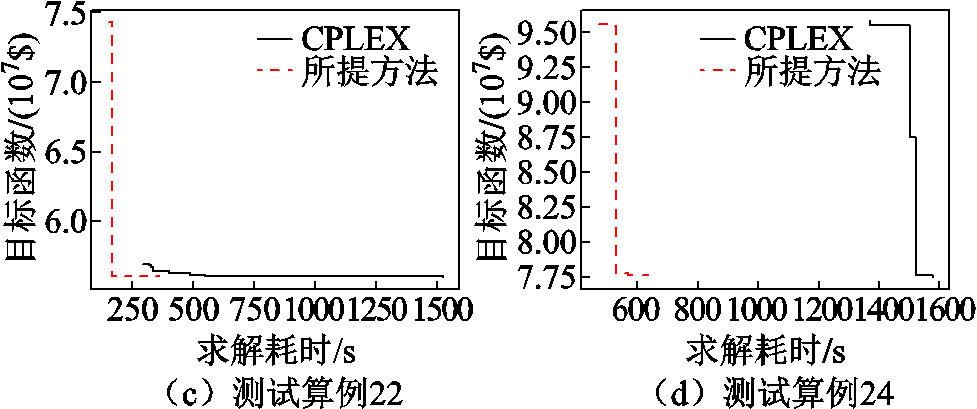
图6 部分测试算例分支定界上界收敛对比
Fig.6 Convergence of upper bounds in several cases
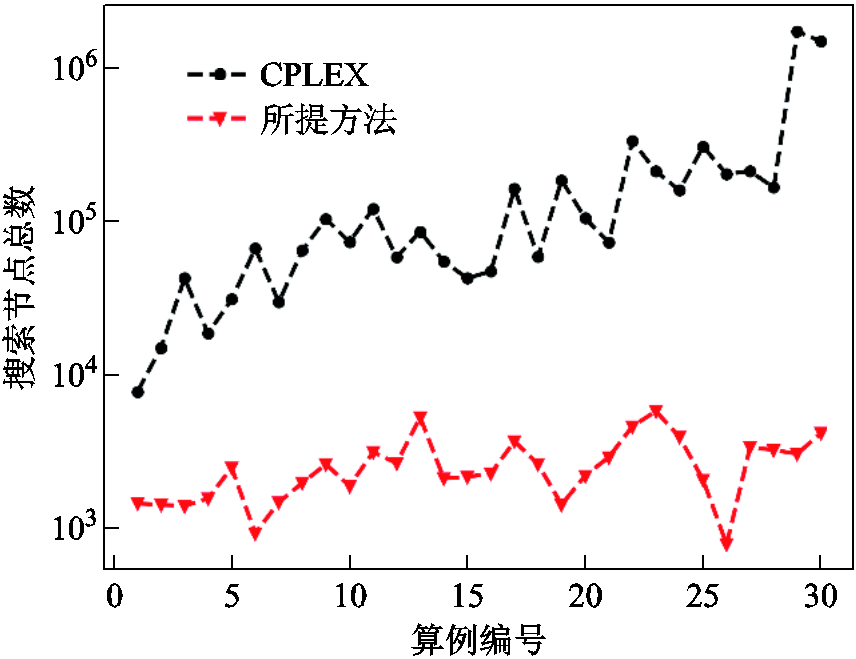
图7 分支定界搜索树规模对比
Fig.7 Comparison on the scale of search tree
4)各步骤耗时
以算例18为例,所提方法各步骤耗时情况见表2。其中,单次KNN拟合与单次可行性判别表示使用可行性修复方法时每次调用的平均耗时。算例18选择(100, 1)作为参数,因此经历了4次KNN拟合与3次可行性判别。由表2可知,所提方法能够在有限耗时内起作用。
表2 算例18中的所提方法各步骤耗时
Tab.2 Time consumption for each step in Case 18

步骤耗时/s 搜索信息数据集构建51.04 单次KNN拟合0.18 单次可行性判别0.58 小规模辅助MILP模型求解285.11 其余2.25 总计340.86
本节采用比利时20节点天然气系统联合构成电-气互联系统,分析所提方法的计算效果。其中,该天然气系统具有20个节点,3个气源,16条管道,3台压缩机。由于系统规模较大,设置收敛gap为0.25%。在计算效率方面,数值结果表示,CPLEX达到预设收敛要求耗时3 420.61 s,所提方法耗时 1 198.42 s,加速比为2.85倍,验证了所提方法在大规模系统中的计算效率。对比CPLEX和所提方法在10 000 s内的收敛曲线如图8所示,可以看出,所提方法得到的优化结果在求解进程中持续优于CPLEX。此外,求解终止时(计算时间达到10 000 s)CPLEX搜索树规模为246 969节点,而所提方法搜索树规模为51 480节点,削减了79%,验证了所提方法剪除冗余搜索空间的有效性。与此同时,所提方法可保证计算结果的最优性。这是由于所提方法以更新上界的方式与原始求解过程交互,通过在分支定界早期阶段提供高质量可行解引导搜索树剪除冗余搜索空间从而实现加速,并未改变原始模型的约束和变量,因此能够保证最优性。
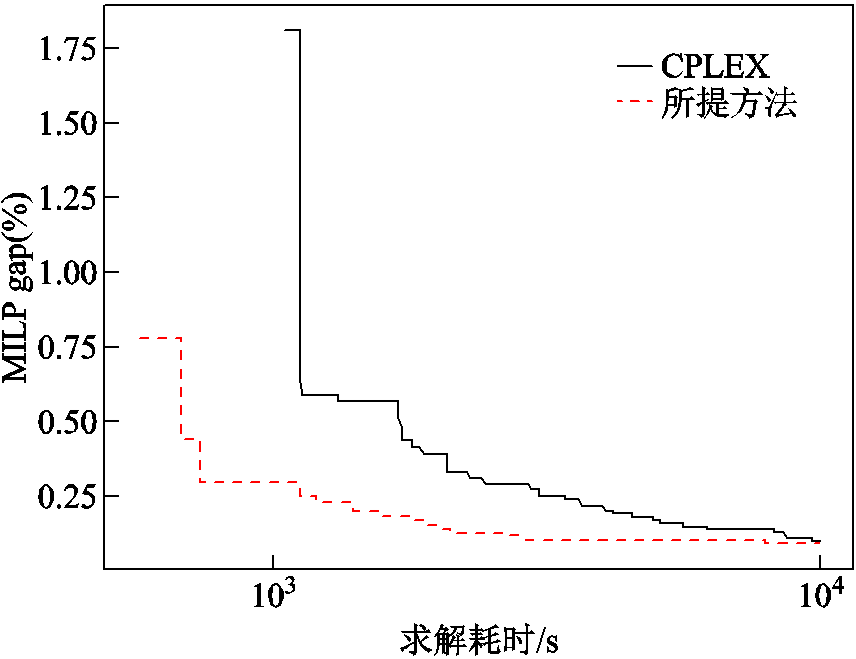
图8 大规模系统分支定界上界收敛对比
Fig.8 Convergence of upper bounds in a large-scale system
针对电-气互联系统调度决策问题中含有规模庞大的离散决策变量、模型复杂度高、面临“组合爆炸”计算负担的难题,本文提出了一种分支定界搜索信息深度诱导的电-气互联系统调度决策加速求解方法。所提方法的基本思想在于结合分支定界初始阶段搜索信息和分段线性化处理的特殊结构,构建更快获得高质量可行解的小规模辅助混合整数线性规划模型。从而,所获得的高质量可行解能够引导分支定界算法剪除更多冗余搜索空间,在保证最优性的前提下加速收敛。算例仿真结果验证了所提方法相比于直接使用商业求解器可实现平均4.20倍的无损加速,为电力系统运筹优化技术提供了新的研究思路。
本文方法在理论上适用于包括电-气互联系统调度决策在内,具有分段线性化特殊结构的MILP问题;更进一步地,本文思想也可扩展到与分段线性化原理类似,仅有少量离散变量有效的组合优化结构中。需要注意的是,本文方法的实施前提是分支定界初期搜索信息能够在一定程度上用于评估未知的最优解情况,从而构建能够得到高质量可行解的小规模MILP模型。然而,电-气互联系统等综合能源系统组合优化问题性质复杂,不同问题中分支定界初期搜索信息和最优解之间的关联机理尚未明晰,因此难以保障实践中本文方法在其他MILP问题中的有效性,需要更深入的分析与研究。另一方面,本文方法作为一种加速算法,并无法完全解决大规模离散优化的组合爆炸瓶颈,电-气互联系统等综合能源系统组合优化问题尚具有更多特殊的物理性质,需要结合求解器底层算法进一步研究紧密贴合组合优化问题物理特征的定制化加速方法。
参考文献
[1] 国家能源局关于“互联网+”智慧能源(能源互联网)示范项目评审办法的公示—国家能源局[EB/OL]. [2023-04-05]. http://www.nea.gov.cn/2016-12/09/c_ 135893950.htm.
[2] Tang Yi, Zhao Yuan, Li Wenyuan, et al. Reliability evaluation of EGIES with highly nonlinear modeling of gas system components[J]. Electric Power Systems Research, 2021, 195: 107119.
[3] 刘雨佳, 樊艳芳, 白雪岩, 等. 基于优化计算型区块链系统的虚拟电厂模型与调度策略[J]. 电工技术学报, 2023, 38(15): 4178-4191.
Liu Yujia, Fan Yanfang, Bai Xueyan, et al. Virtual power plant model and scheduling strategy based on optimized computing block-chain system[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4178-4191.
[4] 陈明昊, 孙毅, 谢志远. 基于双层深度强化学习的园区综合能源系统多时间尺度优化管理[J]. 电工技术学报, 2023, 38(7): 1864-1881.
Chen Minghao, Sun Yi, Xie Zhiyuan. The multi-time-scale management optimization method for park integrated energy system based on the Bi-layer deep reinforcement learning[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1864-1881.
[5] 潘超, 范宫博, 王锦鹏, 等. 灵活性资源参与的电热综合能源系统低碳优化[J]. 电工技术学报, 2023, 38(6): 1633-1647.
Pan Chao, Fan Gongbo, Wang Jinpeng, et al. Low-carbon optimization of electric and heating integrated energy system with flexible resource participation[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1633-1647.
[6] 刘小慧, 王小君, 张义志, 等. 考虑生物质储运模式的多区域综合能源系统协同规划[J]. 电工技术学报, 2023, 38(6): 1648-1661.
Liu Xiaohui, Wang Xiaojun, Zhang Yizhi, et al. Multi-regional integrated energy system collaborative planning considering biomass storage and transportation mode[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1648-1661.
[7] Yang Zhifang, Xie Kaigui, Yu Juan, et al. A general formulation of linear power flow models: basic theory and error analysis[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1315-1324.
[8] Correa-Posada C M. Gas network optimization: a comparison of piecewise linear models[J/OL]. Optimization online, 2014: 1-24. https://optimization-online.org/wp-content/uploads/2014/10/4580.pdf.
[9] Constante-Flores G E, Conejo A J, Qiu Feng. AC network-constrained unit commitment via relaxation and decomposition[J]. IEEE Transactions on Power Systems, 2022, 37(3): 2187-2196.
[10] Wu Jianghua, Luh P B, Chen Yonghong, et al. A novel optimization approach for sub-hourly unit commitment with large numbers of units and virtual transactions[J]. IEEE Transactions on Power Systems, 2022, 37(5): 3716-3725.
[11] Quarm E, Madani R. Scalable security-constrained unit commitment under uncertainty via cone programming relaxation[J]. IEEE Transactions on Power Systems, 2021, 36(5): 4733-4744.
[12] Mittelmann H. Decison Tree for Optimization Software[EB/OL]. [2023-04-05]. http://plato.asu.edu/ bench.html.
[13] Chen Yonghong, Pan Feng, Holzer J, et al. A high performance computing based market economics driven neighborhood search and polishing algorithm for security constrained unit commitment[J]. IEEE Transactions on Power Systems, 2021, 36(1): 292-302.
[14] Gao Qian, Yang Zhifang, Yin Wotao, et al. Internally induced branch-and-cut acceleration for unit commitment based on improvement of upper bound[J]. IEEE Transactions on Power Systems, 2022, 37(3): 2455-2458.
[15] 王晗, 侯恺, 刘晓楠, 等. 基于全局灵敏度分析的电气互联系统韧性提升方法[J]. 电力系统自动化, 2023, 47(3): 59-67.
Wang Han, Hou Kai, Liu Xiaonan, et al. Resilience enhancement method for electricity-gas interconnection system based on global sensitivity analysis[J]. Automation of Electric Power Systems, 2023, 47(3): 59-67.
[16] Shao Chengcheng, Wang Xifan, Shahidehpour M, et al. An MILP-based optimal power flow in multicarrier energy systems[J]. IEEE Transactions on Sustainable Energy, 2017, 8(1): 239-248.
[17] Wang Xu, Bie Zhaohong, Liu Fan, et al. Co-optimization planning of integrated electricity and district heating systems based on improved quadratic convex relaxation[J]. Applied Energy, 2021, 285: 116439.
[18] 徐玉琴, 方楠. 基于分段线性化与改进二阶锥松弛的电-气互联系统多目标优化调度[J]. 电工技术学报, 2022, 37(11): 2800-2812.
Xu Yuqin, Fang Nan. Multi objective optimal schedulingof integrated electricity-gas system based on piecewise linearization and improved second order cone relaxation[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2800-2812.
[19] Li Xuan, Zhai Qiaozhu, Zhou Jingxuan, et al. A variable reduction method for large-scale unit commitment[J]. IEEE Transactions on Power Systems, 2020, 35(1): 261-272.
[20] Chen Sheng, Wei Zhinong, Sun Guoqiang, et al. Optimal power and gas flow with a limited number of control actions[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5371-5380.
[21] Luo Songlin, Yang Lun, Zhang Xin, et al. A fully linear-constrained optimal electricity-gas flow in an integrated energy system[C]//2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 2018: 1-6.
[22] Tejada-Arango D A, Lumbreras S, Sánchez-Martín P, et al. Which unit-commitment formulation is best? A comparison framework[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2926-2936.
[23] Knueven B, Ostrowski J, Watson J P. On mixed-integer programming formulations for the unit commitment problem[J]. Informs Journal on Computing, 2020: ijoc.2019.0944.
[24] Ma Ziming, Zhong Haiwang, Cheng Tong, et al. Redundant and nonbinding transmission constraints identification method combining physical and economic insights of unit commitment[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3487-3495.
[25] 朱正春, 杨知方, 余娟, 等. 面向小样本场景的数据驱动安全约束经济调度快速计算方法[J]. 中国电机工程学报, 2022, 42(12): 4430-4440.
Zhu Zhengchun, Yang Zhifang, Yu Juan, et al. A data-driven fast calculation method for security-constrained economic dispatch with small sample requirements[J]. Proceedings of the CSEE, 2022, 42(12): 4430-4440.
[26] Du Ershun, Zhang Ning, Kang Chongqing, et al. A high-efficiency network-constrained clustered unit commitment model for power system planning studies[J]. IEEE Transactions on Power Systems, 2019, 34(4): 2498-2508.
[27] Zhang Menghan, Yang Zhifang, Lin Wei, et al. Enhancing economics of power systems through fast unit commitment with high time resolution[J]. Applied Energy, 2021, 281: 116051.
[28] Xavier Álinson S, Feng Qiu, Shabbir A. Learning to solve large-scale security-constrained unit commitment problems[J]. Informs Journal on Computing, 2020, 33(2): 739-756.
[29] Gu Xiaoyi, Dey S S, Xavier S, et al. Exploiting instance and variable similarity to improve learning-enhanced branching[J]. arXiv, 2022. https://doi.org/ 10.48550/arXiv.2208.10028
[30] Achterberg T, Bixby R E, Gu Zonghao, et al. Presolve reductions in mixed integer programming[J]. Informs Journal on Computing, 2020, 32(2): 473-506.
[31] CPLEX. What are cuts? - IBM Documentation[EB/OL]. [2023-04-05]. https://www.ibm.com/docs/en/icos/22. 1.0?topic=cuts-what-are.
[32] Danna E, Rothberg E, Le Pape C. Exploring relaxation induced neighborhoods to improve MIP solutions[J]. Mathematical Programming, 2005, 102(1): 71-90.
[33] Berthold T, Lodi A, Salvagnin D. Ten years of feasibility pump, and counting[J]. EURO Journal on Computational Optimization, 2019, 7(1): 1-14.
Abstract The dispatch problem in integrated electricity and gas system is formulated as the mixed-integer linear programming (MILP) form to describe the discrete feature of resources (such as the unit statuses) and nonlinear operation rules (such as the power flow equation, the Weymouth equation, etc.). The optimal solution achieves the best allocation of resources and indicates the security and economic of the integrated electricity and gas system. However, the large-scale integer variables bring the “combinatorial explosion” challenge, even for the state-of-the-art commercial solvers. To address this problem, existing research focuses on the external algorithms, such as reformulating, reducing the scale of constraints/integer variables, etc. However, it is hard to balance the solution efficiency and the error bound guarantees in practice.
Therefore, this paper proposes an internal algorithm that is highly combined with the search information in the branch-and-bound process. The distinct advantage of the proposed method is that the unique structure of integrated electricity and gas system is considered along with the abundant information during the solution process. As a result, the proposed method can achieve an acceleration with optimality guaranteed. This paper reviews the MILP formulation of the dispatch problem in integrated electricity and gas system, and focuses on the computational bottleneck, i.e., the large-scale integer variables introduced by the piecewise linearization structure of the Weymouth equation. Because most of integer variables in the piecewise linearization structure remains zero, this paper proposes to evaluate the potential effective range of integer variables in the optimal solution, based on the branch-and-bound search information.
First, the proposed method collects the relaxation solutions during the initial stage of the branch-and-bound process, to build a search information dataset that implies the optimal value of the piecewise linearization structure. The relaxation solutions are easy to obtain, and they provide lower bounds to the current search tree. Therefore, the idea is that if an integer variable of the piecewise linearization always lies in a similar range across the abundant relaxation solutions, it is likely to remain the same pattern in the optimal solution. Second, the k-nearest neighbors regression algorithm is used to estimate the potential effective range of the piecewise linearization structure. Third, the proposed method builds a small-scale MILP model and solves it in parallel to produce a better solution than the main branch-and-bound process. As a result, the redundant search space in the search tree is pruned by the better solution with no accuracy loss and the optimality is guaranteed.
In the case study, the effectiveness of the proposed method has been demonstrated in several aspects based on test cases of RTS-GMLC and gas system. First, for different scales of piecewise linearization structures, compared with the commercial solver, the proposed method accelerates the dispatch problem from 1.60 times to 36.90 times (11.28 times on average). The result also shows that with the improvement of the piecewise linearization scale, the computational burden suddenly increases and can be significantly mitigated by the proposed method, which provides a balance between the formulation precision and the computational efficiency. Second, for 30 test cases using different power demands, the proposed method accelerates the dispatch problem from 1.64 times to 13.52 times (4.20 times on average). It shows that the proposed method behaves well in complicated operation conditions. Third, the case study discusses some details of the proposed method, including the feasibility repair, the prediction accuracy, the upper bound convergence, the search tree scale, and time cost of each step, which provides a thoroughly analysis for the proposed method. Finally, a test case is used to demonstrate the effectiveness in the large-scale system.
In conclusion, this paper proposes an acceleration algorithm for the dispatch problem in integrated electricity and gas system. The proposed method improves the solution efficiency without the loss of the optimality guarantees, which is promising in practical and provides a novel view on the optimization in power systems.
keywords:Integrated electricity and gas system, dispatch, mixed-integer linear programming, acceleration algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.230714
中图分类号:TM73
国家电网有限公司科技项目资助(5700-202255193A-1-1-ZN)。
收稿日期 2023-05-22
改稿日期 2023-10-14
高 倩 女,1997年生,博士研究生,研究方向为电力系统优化、混合整数线性规划、机器学习。E-mail:gaoqianmail@cqu.edu.cn
杨知方 男,1992年生,博士,教授,博士生导师,研究方向为电力系统优化、电力市场。E-mail:zfyang@cqu.edu.cn(通信作者)
(编辑 赫 蕾)