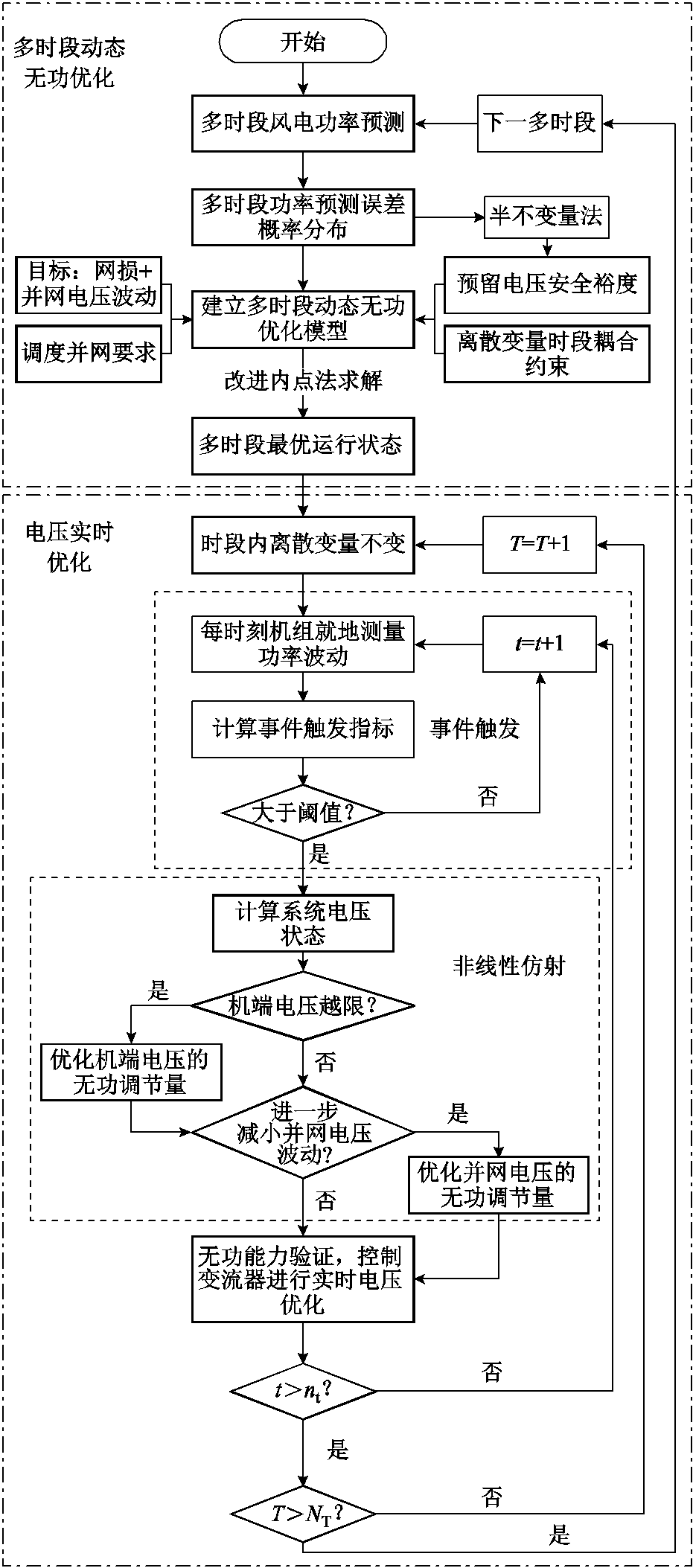
图1 风电场电压实时计算和优化方法流程
Fig.1 The solving procedure of real-time voltage calculation and optimization method for wind farm
摘要 该文提出一种基于非线性仿射的风电场电压实时计算和优化方法。首先,以网损和并网电压波动综合最小为目标,建立风电场多时段动态无功优化模型,利用半不变量法分析风电功率不确定性对机端电压的影响,采用改进内点法实现模型的高效求解;其次,提出一种非线性仿射方法,快速准确地获得计及风电功率波动后的系统电压状态,并通过计算风机无功调节量来实现系统电压实时优化;再次,设计考虑风电功率对机端电压和并网电压综合影响的事件触发算法,降低风电功率波动平缓时风机的无功控制频率;最后,在我国某实际风电场的仿真试验表明,非线性仿射法能够快速获得系统实时电压状态,电压实时优化方法能够有效地防止机端电压越限并减小并网电压波动。
关键词:多时段动态无功优化 非线性仿射变换 实时计算和优化 事件触发
近年来,为满足“双碳”目标和构建新型电力系统的需要,风力发电获得快速发展[1]。风电的大力开发利用在节约资源、治理环境污染和改善能源结构方面发挥着重要作用[2],但是,风力资源的不确定性也给风电场的运行控制带来一些挑战[3]。
风速的不确定性使风电出力发生波动[4-5],进而引起机端电压波动,加上集电线路电压存在不均衡性,容易引发机端电压越限现象[6-7]。特别是机端电压高于允许值时可能导致风机脱网,不仅降低发电效率,还会冲击主网安全稳定运行[8]。文献[9]提出有功无功联合控制策略,通过控制转子动能和分频段无功来抑制机端电压波动。文献[10]提出一种风电场多目标无功优化方法,通过调节机组和补偿装置无功,防止机组因机端电压越限而发生脱网事故。文献[11]提出一种分散式无功电压优化策略,来降低风电场内部损耗、均衡机组端电压和线路电压。并网电压是否平稳影响上级系统的电压质量[12]。由于所有风机功率都经并网点汇入电力系统,同区域风机功率具有强相关性和类似变化规律,风电功率变化容易导致并网点电压明显波动。为此,国内外学者对风电电压主动支撑技术进行大量研究[13],相关标准也对风电场并网技术进行严格规定[14]。文献[15]提出一种无功电压分层协调控制策略,来实现在网侧支撑较弱情况下风电场并网电压的平稳运行。文献[16]提出一种基于网络分析-智能粒子群算法的风电场多目标无功优化策略,来提高风电并网电压的稳定性,并降低机组机端电压偏差。保持机端电压安全和并网电压平稳对风电场正常运行具有重要意义,但现有文献难以直接揭示风电功率不确定性对机端电压和并网电压的非线性影响及其内在关联。
为在线评估风电功率波动对风电场运行状态(包括机端电压和并网电压)的影响,需要频繁执行潮流计算来获得系统电压,或者基于线性仿射方法,利用灵敏度信息快速计算考虑功率波动后的电压状态[17],但在风电功率波动较大时,线性仿射方法的计算结果存在较大误差[18]。传统风电场通常运行于恒电压、恒无功功率或恒功率因数等方式[9],而忽略场站内部优化[19]。随着风电场规模和单机容量的增大,风电场内部的无功功率和电压优化分布越来越被关注[20]。周期性优化方法被用来实现风电场的优化控制[21],但其控制精度随控制周期的增大而降低[22]。为适应风电功率波动,集中式优化方法需要频繁求解最优潮流,导致出现较大的计算量和通信负担[23],而分布式优化方法通过局部协调来实现系统调控,收敛性难以保证,且对通信配置要求较高[24]。目前,在有限风电场计算和通信资源下,如何高效地计算考虑风电功率波动后的系统电压状态并优化机端和并网电压,仍是亟须解决的问题。
本文提出一种基于非线性仿射的风电场电压实时计算和优化方法。以网损和并网电压波动综合最小为目标,建立风电场多时段动态无功优化模型,利用半不变量法分析风电功率不确定性对机端电压的影响,采用一种改进内点法实现模型的快速求解。提出一种非线性仿射法来快速准确地计算考虑风电功率波动后的系统电压状态,并计算风机的实时无功调节量,用来消除风电功率波动可能导致的机端电压越限和进一步减小并网电压波动。同时,设计一种事件触发算法来降低功率波动平缓时机组的无功控制频率。最后,通过我国某实际风电场的仿真案例,验证了所提方法的有效性。
本文提出一种基于非线性仿射的风电场电压实时计算和优化方法,由多时段动态无功优化和电压实时优化两部分组成,其流程如图1所示。在多时段动态无功优化模型中,首先,风电场总控制器基于历史数据,对机组进行多时段功率预测,考虑上级调度并网要求和离散变量时段耦合约束条件,以网损和并网电压波动加权最小为目标,建立多时段动态无功优化模型;然后,利用计及相关性的半不变量法分析风电功率不确定性引起的机端电压不确定性,在约束条件中预留电压安全裕度,来防止可能出现的机端电压越限;最后,利用基于解析化梯度矩阵和海森矩阵的改进内点法快速求解模型,将所得结果作为时段内电压实时计算和优化的基准运行点。
电压实时优化控制中,各风机通过微调无功来应对风电有功功率的瞬时波动。首先,机组在每个时刻就地测量有功功率波动量,并基于事件触发算法计算机组有功功率波动对机端电压和并网电压的综合影响指标,判断是否执行电压实时计算和优化。然后,利用非线性仿射法快速计算考虑机组有功功率波动后的系统电压状态,并判断机端电压是否会发生越限。如果是,则计算防止机端电压越限的无功功率调节量,并在保证机端电压安全下进一步计算减小并网电压波动的无功功率调节量。最后,验证风电机组的无功功率调节能力,通过控制变流器快速地调节机组无功功率,实现系统电压实时优化。由于在电压实时优化控制中,各机组只根据非线性灵敏度信息进行计算,不需要进行潮流计算或最优潮流计算,同时设计事件触发算法降低风电功率波动平缓时的无功功率控制频率,因而,所提方法能够以较少的计算时间成本实现风电场电压实时计算和优化。

图1 风电场电压实时计算和优化方法流程
Fig.1 The solving procedure of real-time voltage calculation and optimization method for wind farm
以网损和并网电压波动综合最小为目标函数,建立多时段动态无功功率优化模型,如式(1)~式(3)所示。通过合理设置加权系数(使k1f1≈k2f2),在多时段优化中兼顾提高运行经济性和减小并网电压波动。
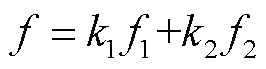 (1)
(1)
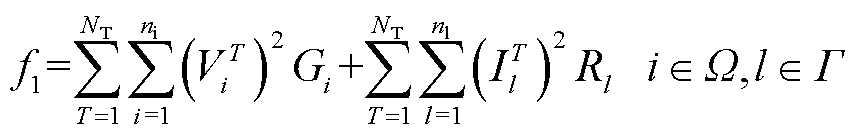 (2)
(2)
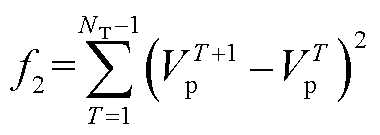 (3)
(3)
式中,f1为网损;f2表征多时段内并网点电压波动程度;k1和k2为加权系数;NT为多时段动态无功功率优化模型总时段数;VT i为T时段节点i的电压幅值;Gi为节点i的接地电导;IT l为T时段支路l的电流;Rl为支路l的电阻;ni和nl分别为系统节点总数和支路总数;Ω和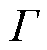 分别为所有节点集合和支路集合;VT p为T时段并网点电压。
分别为所有节点集合和支路集合;VT p为T时段并网点电压。
2.2.1 等式约束
多时段内系统各节点应满足有功功率平衡方程和无功功率平衡方程,即
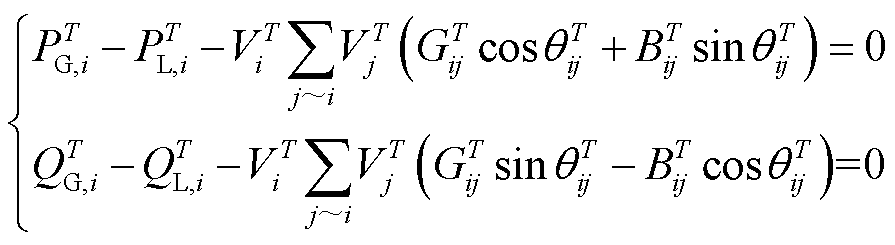 (4)
(4)
式中,PT G,i和QT G,i分别为T时段注入节点i的有功功率和无功功率,包括风机出力、电容器和静止无功补偿器(Static Var Generator, SVG)出力等;PT L,i和QT L,i分别为T时段节点i的有功和无功负荷,包括升压站站用电负荷、电缆电容无功负荷等;GT ij和BT ij分别为T时段系统节点导纳矩阵中关联节点i和j的电导和电纳,由于电容器投入组数和变压器电压比等为离散变量,系统节点导纳矩阵随时段T而变化;θT ij为节点i与j的相位差;j~i表示节点j和节点i相连。
2.2.2 不等式约束
计及不确定性的各节点电压幅值和相位应在可行范围内,系统各支路潮流均应小于线路的最大传输容量,风电机组的有功功率和无功功率应在其能力范围内。
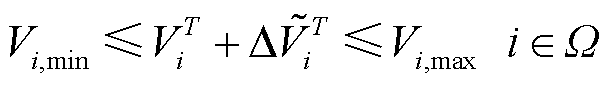 (5)
(5)
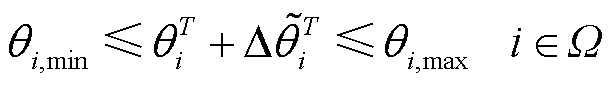 (6)
(6)
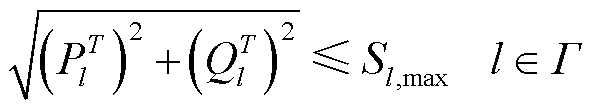 (7)
(7)
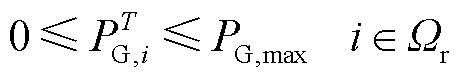 (8)
(8)
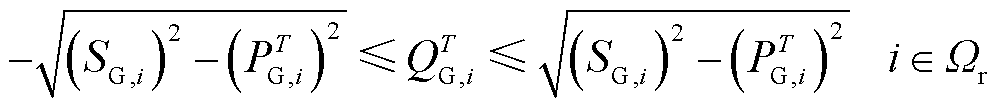 (9)
(9)
式中,Vi,max和Vi,min分别为节点i电压幅值上、下限;θT i、θi,max和θi,min分别为T时段节点i电压相位及其上、下限;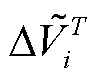 和
和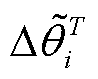 分别为T时段节点i电压幅值和相位的波动量;PT l、QT l和Sl,max分别为T时段支路l有功功率、无功功率及其最大传输容量;PG,max为机组最大有功功率;SG,i为节点i机组变流器的容量,其值大于PG,max;Ωr为含风电机组节点集合。
分别为T时段节点i电压幅值和相位的波动量;PT l、QT l和Sl,max分别为T时段支路l有功功率、无功功率及其最大传输容量;PG,max为机组最大有功功率;SG,i为节点i机组变流器的容量,其值大于PG,max;Ωr为含风电机组节点集合。
电容器组数和变压器电压比为离散变量,应在允许范围内,如式(10)、式(11)所示。为防止电容器和变压器过度切换而降低其使用寿命,多时段间其切换次数不应超过规定的总次数,如式(12)、式(13)所示。变压器在相邻时段的电压比切换速度不应超过限定值,如式(14)所示。需要注意的是,离散变量在各时段内部保持不变。
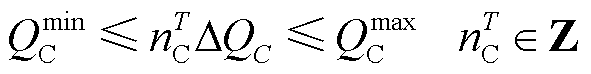 (10)
(10)
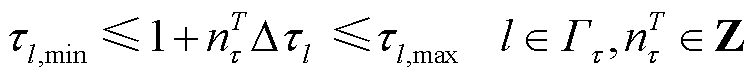 (11)
(11)
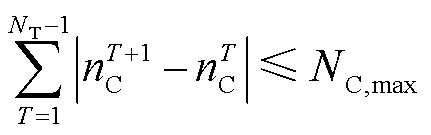 (12)
(12)
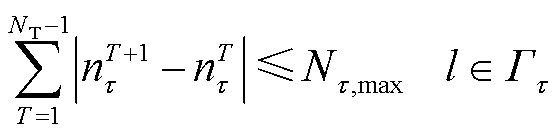 (13)
(13)
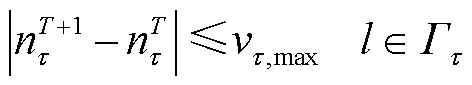 (14)
(14)
式中,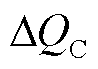 为单组电容器无功功率容量;nT C为T时段电容器投入运行组数;Qmax C和Qmin C分别为电容器总无功出力上、下限;
为单组电容器无功功率容量;nT C为T时段电容器投入运行组数;Qmax C和Qmin C分别为电容器总无功出力上、下限;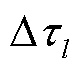 为支路l变压器相邻挡位电压比差值;nT τ为T时段变压器电压比挡位;τl,max和τl,min分别为支路l变压器电压比上、下限;NC,max为多时段内电容器组允许投切总组次;Nτ,max为多时段内变压器允许切换总挡数;vτ,max为变压器电压比切换速度;
为支路l变压器相邻挡位电压比差值;nT τ为T时段变压器电压比挡位;τl,max和τl,min分别为支路l变压器电压比上、下限;NC,max为多时段内电容器组允许投切总组次;Nτ,max为多时段内变压器允许切换总挡数;vτ,max为变压器电压比切换速度;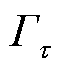 为含变压器支路集合。
为含变压器支路集合。
2.3.1 电压概率分布
风力发电的不确定性会导致系统节点电压发生波动。假设多时段内风电有功功率预测误差服从某一概率分布,利用计及相关性的半不变量法,可得到系统电压的概率分布。一般风电场系统相关系数矩阵CW为正定矩阵,对该矩阵进行Cholesky分解[25-26],可得式(15)。又由于相关系数矩阵CW为对称矩阵,则存在一正交矩阵B,可将具有相关性的输入变量W转换成不相关的输入变量X,如式(16)所示。由于构建的不相关变量X的相关系数矩阵CY为单位矩阵I,可通过式(17)推导出G为B的逆矩阵,进一步可将具有相关性的变量W表示成不相关的变量X的组合,如式(18)所示。
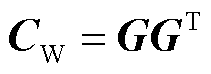 (15)
(15)
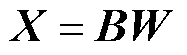 (16)
(16)
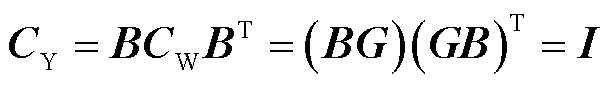 (17)
(17)
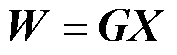 (18)
(18)
式中,变量X为互相独立的变量。
接着按照输入变量不存在相关性的情形,采用传统半不变量法求取目标变量的概率分布。已知输入变量的概率分布时,通过式(19)可求得输入变量的特征函数ψ(t)。由式(20)可得输入变量的各阶原点矩,进一步由式(21)得到输入变量的各阶半不变量。根据半不变量的可叠加性,可计算系统各节点电压幅值和相位波动量的各阶半不变量,如式(22)所示。最后,将电压及其半不变量归一化,并利用Gram-Charlier级数得到电压幅值和相位的概率分布,如式(23)、式(24)所示。
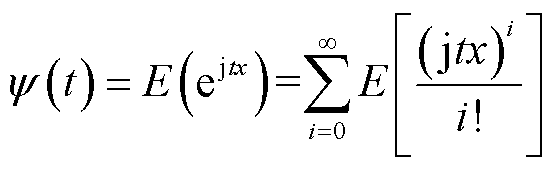 (19)
(19)
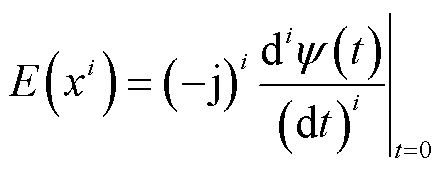 (20)
(20)
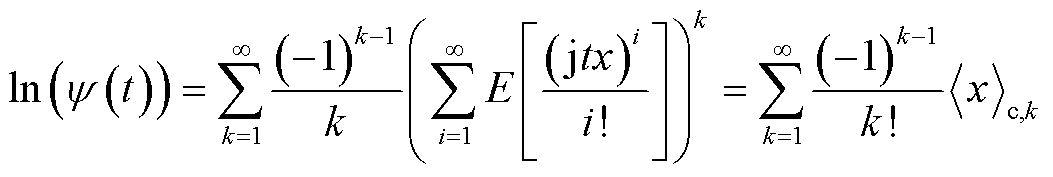 (21)
(21)
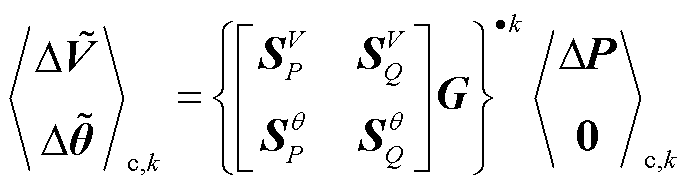 (22)
(22)
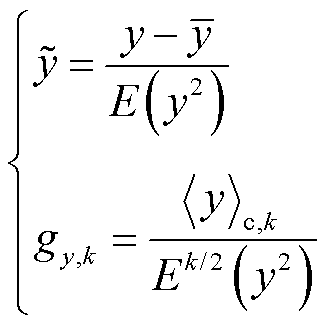 (23)
(23)
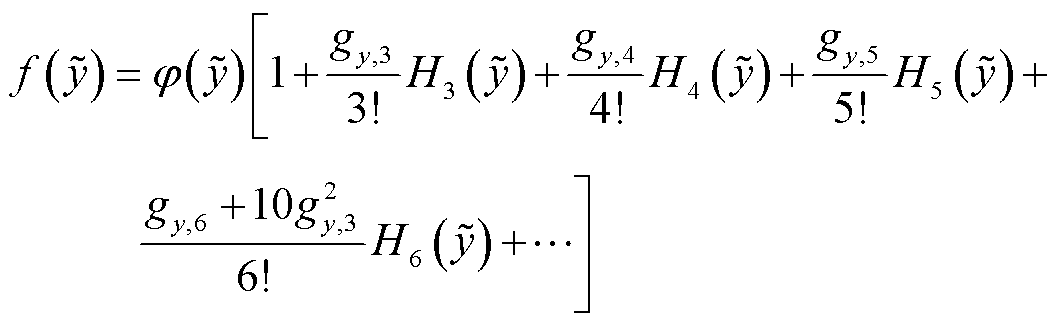 (23)
(23)
式中,x为输入变量,由风电功率预测误差经式(16)转换所得;E(xi)为变量x的i阶原点矩;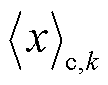 为变量x的k阶半不变量;SV P、SV Q、Sθ P和Sθ Q分别为T时段系统电压幅值和相位对节点有功功率和无功功率的灵敏度矩阵,由雅克比矩阵求逆得到[18];
为变量x的k阶半不变量;SV P、SV Q、Sθ P和Sθ Q分别为T时段系统电压幅值和相位对节点有功功率和无功功率的灵敏度矩阵,由雅克比矩阵求逆得到[18];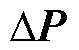 、
、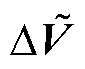 和
和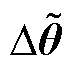 分别为有功功率波动向量、节点电压幅值和相位波动向量;y为输出随机变量,即节点电压幅值和相位波动量;
分别为有功功率波动向量、节点电压幅值和相位波动向量;y为输出随机变量,即节点电压幅值和相位波动量;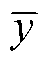 为变量y的均值;
为变量y的均值;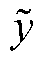 为归一化后变量;
为归一化后变量;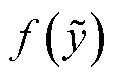 为
为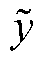 的概率分布函数;
的概率分布函数;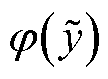 为标准正态分布函数;gy,k为归一化后半不变量;
为标准正态分布函数;gy,k为归一化后半不变量;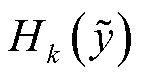 为Hermite多项式。
为Hermite多项式。
2.3.2 电压安全裕度
为提高系统电压的安全性,利用机会约束规划思想在约束条件中预留电压安全裕度,来防止风电波动可能导致的机端电压越限。分别取机端电压波动量不超过一定置信度的分位值作为该机端电压安全裕度,如式(25)所示,并将其代入式(5)、式(6)中,得到预留安全裕度后的电压幅值和相位约束条件,如式(26)、式(27)所示。
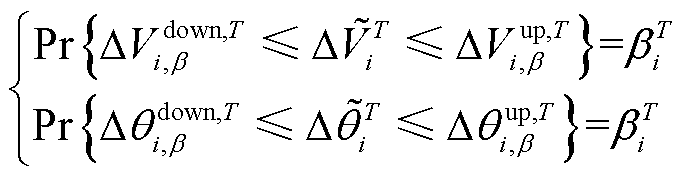 (25)
(25)
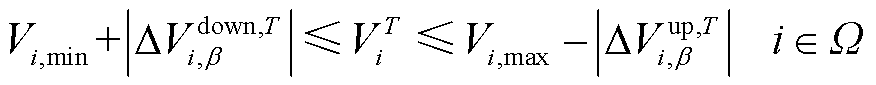 (26)
(26)
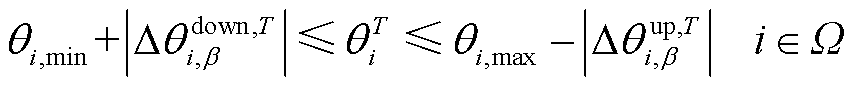 (27)
(27)
式中,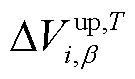 和
和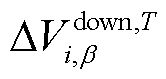 分别为T时段节点i电压β置信度下的上、下分位值,同理于
分别为T时段节点i电压β置信度下的上、下分位值,同理于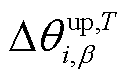 和
和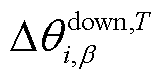 ;βT i为置信度;Pr{x}为事件x成立的概率。
;βT i为置信度;Pr{x}为事件x成立的概率。
式(1)~式(4)、式(7)~式(14)、式(26)、式(27)构成多时段动态无功功率优化模型,由于混合整数非线性规划问题难以快速求解,本文通过在目标函数中增加惩罚项的方法,将原问题转换为非线性规划问题。惩罚项为
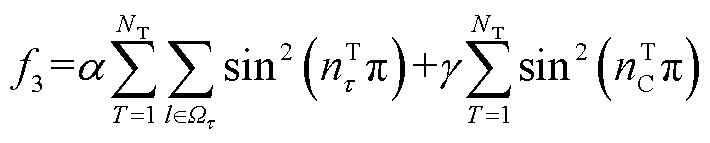 (28)
(28)
式中,α和γ为惩罚系数,α和γ满足随迭代而逐渐增大,迭代收敛时,惩罚项趋于0。这种处理方法所得结果是系统次优运行点,但能同时兼顾模型求解速度和优化结果,满足工程实际应用要求。
在文献[27-28]的内点法基础上,本文所提改进内点法通过加入解析化梯度矩阵和海森矩阵来提高算法的求解效率,其中目标函数和约束条件对系统变量的梯度矩阵和海森矩阵的解析化表达式可参照文献[18]求得。在Matlab软件中编程求解经转换后的非线性规划模型,所得多时段优化结果将作为时段内电压实时计算和优化的基准。
经过多时段动态无功功率优化后,系统实现以时段为时间尺度的优化运行,但时段内风电功率的瞬时波动导致系统运行状态发生偏移,可能导致机端电压越限或并网电压波动。为此,本文提出基于非线性仿射的电压实时优化方法,通过实时调节风机无功功率来响应其瞬时有功功率波动。首先,在时段内的每个时刻,基于非线性仿射法快速获取考虑风电功率波动后的系统电压状态;其次,判断瞬时功率波动是否会导致机组机端电压越限,如果是,进行消除机端电压越限的无功功率调节;再次,判断能否进一步减小并网电压波动,如果能,进行进一步减小并网电压波动的无功功率调节;最后,各机组快速调节变流器无功功率实现电压实时优化控制。由于电压实时优化是各机组在时段运行点处利用非线性灵敏度系数,就地微调风机无功功率完成的,不需要进行全局性的优化和协调,因此,其计算速度较快。
为评估风电功率波动对系统状态的影响,传统方法采用频繁的潮流计算或线性仿射法来在线计算系统电压,这会导致较大的计算负担或计算误差。本文提出一种非线性仿射法来解决这一问题。首先,将有功功率和无功功率平衡方程在多时段优化运行点处泰勒展开,以三阶展开项为例进行说明,可得系统功率波动关于系统电压波动的非线性函数,有
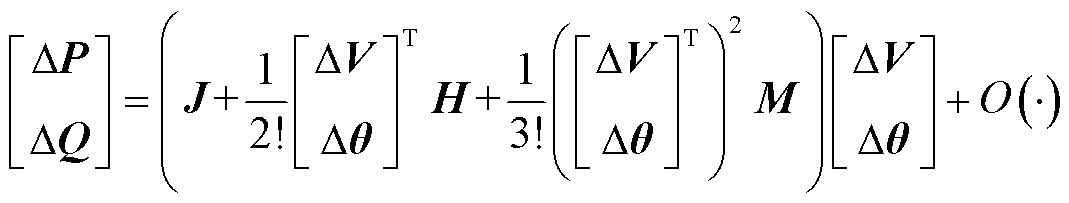 (29)
(29)
式中,J为系统雅克比矩阵;H为系统海森矩阵;M为功率平衡方程的三阶偏导数矩阵;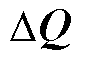 为系统无功功率波动向量;
为系统无功功率波动向量;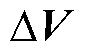 和
和 分别为系统电压幅值和相位波动向量;
分别为系统电压幅值和相位波动向量;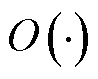 为余项。
为余项。
接着,采用类比方法来求解系统电压波动关于系统功率波动的解析化函数。对形如式(30)的三次函数进行近似求解,取有实际工程意义的根对其进行泰勒展开,并保留三阶展开项,可以得到如式(31)所示的近似解。
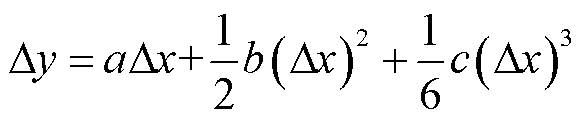 (30)
(30)
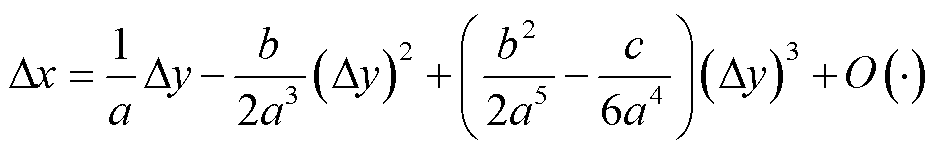 (31)
(31)
式中,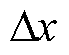 和
和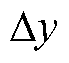 分别为三次函数的自变量和因变量。
分别为三次函数的自变量和因变量。
最后,将式(31)类比到电力系统,可得系统电压波动对系统功率波动的三阶非线性函数,有
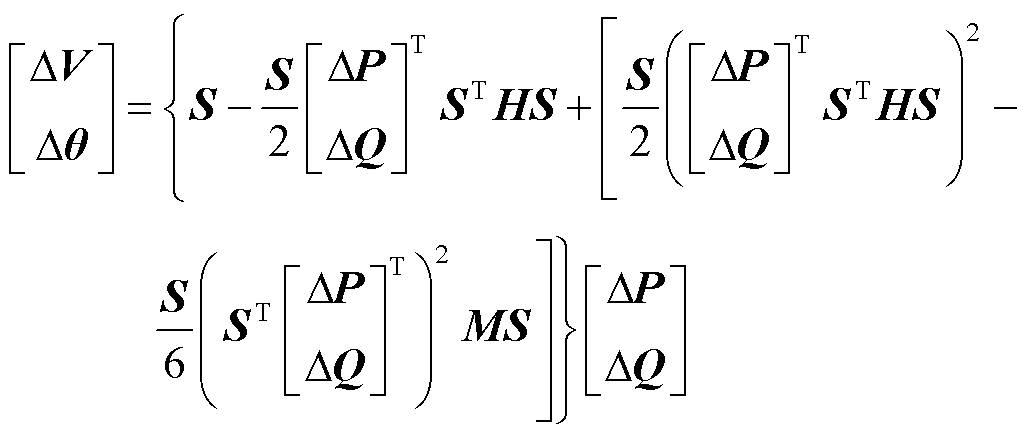 (32)
(32)
式中,S为线性灵敏度矩阵,由雅克比矩阵求逆获得。
式(32)给出了电力系统电压波动对系统功率波动的三阶非线性仿射变换的解析化表达式。采用类似方法可得到更高阶的非线性灵敏度信息,随着阶数的提高,系统电压计算结果更加准确,但计算时间也相应增加。为兼顾系统计算速度和结果的准确性,本文采用二阶非线性灵敏度来设计事件触发算法的评估指标及进行电压实时计算和优化控制,所用二阶非线性灵敏度为
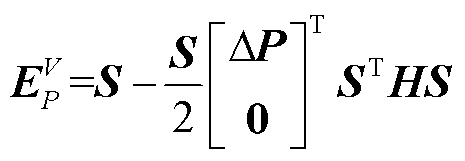 (33)
(33)
式中,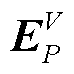 为二阶非线性灵敏度矩阵。
为二阶非线性灵敏度矩阵。
针对某一运行点附近的功率波动,所提方法根据基准点状态、灵敏度矩阵和海森矩阵快速得到计及功率波动后的系统电压状态。和线性仿射函数相比,该方法考虑了系统二阶非线性特征,结果更接近于实际;和潮流计算相比,所提方法不需要进行迭代计算,降低了计算量。
当风机功率波动平缓时,通过设计事件触发算法来降低风机无功功率控制频率。对于电压灵敏度大的机组,即使功率波动较小,但可能对电压影响较大;对于电压灵敏度小的机组,即使功率波动较大,但可能对电压影响较小。此外,机组功率波动对并网电压和机端电压影响程度不同。为此,本文基于非线性仿射综合考虑功率波动对机端电压和并网电压影响,构建如式(34)所示的评估指标,用于判断是否执行电压实时优化控制。
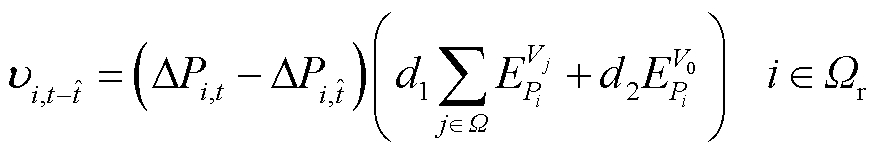 (34)
(34)
式中,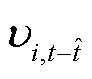 为事件触发算法的评估指标;
为事件触发算法的评估指标;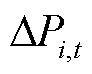 为机组i在时刻t的功率波动值;时刻
为机组i在时刻t的功率波动值;时刻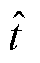 为上一次执行电压实时优化控制的参考时刻;d1=1/80,d2=1;
为上一次执行电压实时优化控制的参考时刻;d1=1/80,d2=1;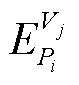 为机组j机端电压对机组i有功功率的二阶非线性灵敏度,同理,
为机组j机端电压对机组i有功功率的二阶非线性灵敏度,同理,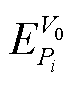 为并网点电压对机组i有功功率的二阶非线性灵敏度,由式(33)获得。
为并网点电压对机组i有功功率的二阶非线性灵敏度,由式(33)获得。
事件触发算法的示意图如图2所示,当评估指标大于阀值γ时,在时刻t机组执行电压实时优化控制;当评估指标小于阀值γ,时刻t机组无功功率将保持不变。红色实箭头代表由于风机功率波动导致综合指标的变化,绿色虚箭头代表电压实时优化控制的无功功率调节。
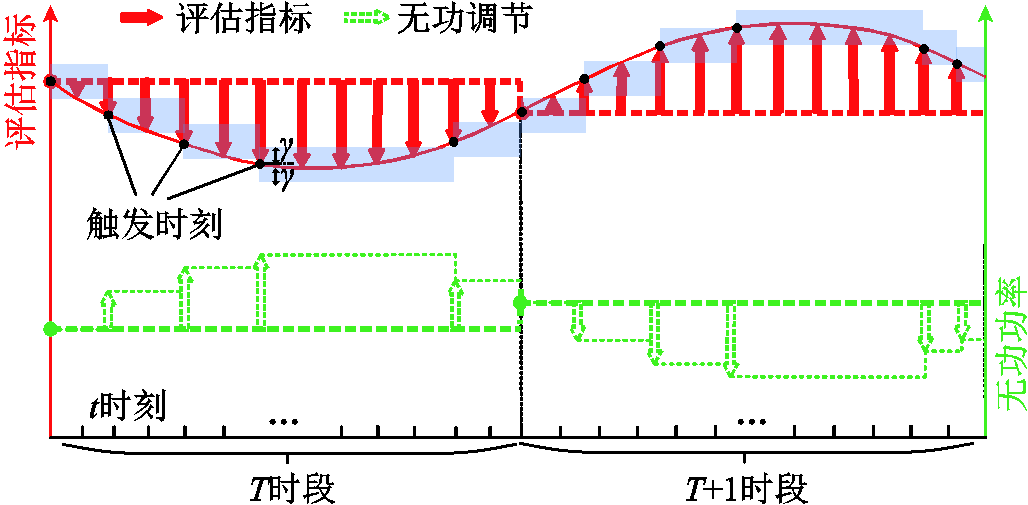
图2 事件触发算法示意图
Fig.2 The schematic of event-triggered algorithm
风电场经多时段无功功率优化后,系统电压将靠近上限值,而距离电压下限值较远,这是因为提高电压水平有利于降低系统网损。因此,本文以防止节点电压越上限为例研究电压实时优化方法。根据3.2节,当风机功率波动的评估指标大于阈值γ时,机组将进行电压实时优化控制。机组控制器根据非线性仿射法快速获得考虑风机功率波动后的系统状态,并判断是否会导致机端电压越限,如果是,首先调节机组无功功率以防止机端电压越限,然后再考虑进一步降低并网点电压波动。
1)消除机端电压越限
由于机端电压越限可能导致机组脱网,因而,优先处理机组功率波动可能导致的机端电压越限问题。利用式(33)二阶非线性灵敏度快速计算功率波动导致的系统电压波动,叠加至系统基准电压,可得计及功率波动后的系统实时电压状态,用来判断是否会发生机端电压越限。如果发生电压越限,利用式(35)计算消除所有可能机端电压越限所需要的无功功率调节量。
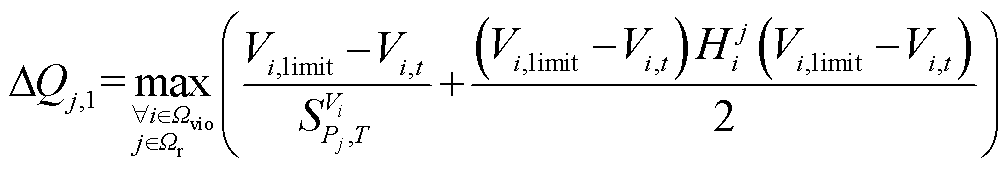 (35)
(35)
式中,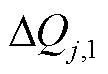 为消除所有机端电压越限所需要的机组无功功率调节量;Vi,limit为节点i的电压上限值;Vi,t为计及节点j功率波动后的节点i电压;
为消除所有机端电压越限所需要的机组无功功率调节量;Vi,limit为节点i的电压上限值;Vi,t为计及节点j功率波动后的节点i电压;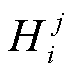 为海森矩阵中第j节点功率平衡方程与节点i相关的元素;
为海森矩阵中第j节点功率平衡方程与节点i相关的元素;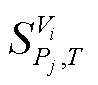 为时段T节点i电压对节点j有功功率的线性灵敏度;Ωvio为存在机端电压越限的机组集合。
为时段T节点i电压对节点j有功功率的线性灵敏度;Ωvio为存在机端电压越限的机组集合。
2)进一步降低并网电压波动
并网电压平稳性是风电场接入系统的重要考核指标。当机端电压不发生越限时,进一步考虑通过实时调节机组无功功率来减小并网电压波动。通过式(36)获得为完全消除并网点电压波动的无功功率调节量,但是该无功功率调节量不应使机组发生新的电压越限,即不能超过由式(37)计算得到的不发生机端电压越限的最大允许无功功率调节量。
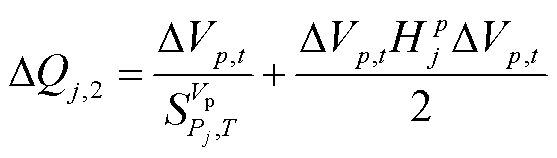 (36)
(36)
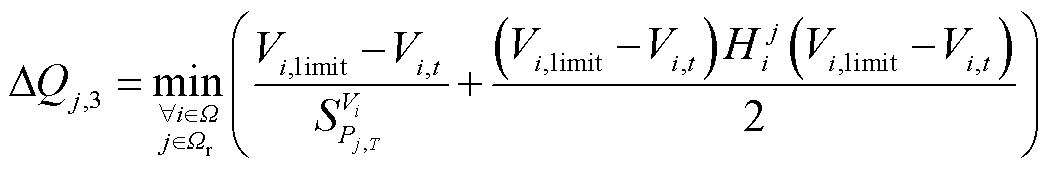 (37)
(37)
式中,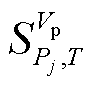 为T时段并网点电压对节点j功率的线性灵敏度;
为T时段并网点电压对节点j功率的线性灵敏度;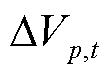 为机组有功功率波动引起并网点电压波动的大小;
为机组有功功率波动引起并网点电压波动的大小;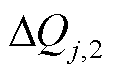 为完全消除并网点电压波动所需的无功功率调节量;
为完全消除并网点电压波动所需的无功功率调节量;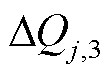 为在不导致机端电压越限的前提下机组最大允许的无功功率调节量;
为在不导致机端电压越限的前提下机组最大允许的无功功率调节量;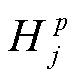 为海森矩阵中并网点p的功率平衡方程与节点j相关的元素。
为海森矩阵中并网点p的功率平衡方程与节点j相关的元素。
3)确定无功功率调节量
由于机端电压和并网点电压对风机有功功率和无功功率灵敏度大小和方向存在差异,根据“优先防止机端电压越限,再降低并网电压波动”的原则,风机j的无功功率调节量计算可分为以下四种,如式(38)所示。
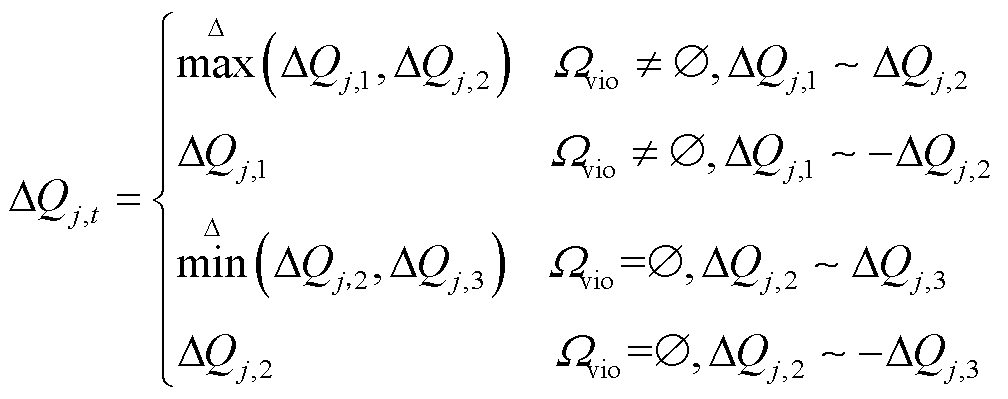 (38)
(38)
式中,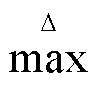 和
和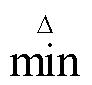 分别为取绝对值最大函数和取绝对值最小函数;
分别为取绝对值最大函数和取绝对值最小函数;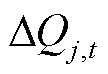 为节点j机组的最终无功功率调节量;~表示数值同号。
为节点j机组的最终无功功率调节量;~表示数值同号。
(1)机端电压发生越限,且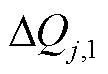 和
和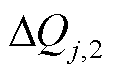 数值同号,则节点j的无功功率调节量为
数值同号,则节点j的无功功率调节量为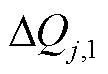 和
和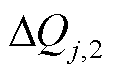 的绝对值中较大者。其过程为调节无功功率(
的绝对值中较大者。其过程为调节无功功率(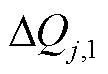 )先满足消除机端电压越限;再考虑能否进一步减小并网点电压波动。如果
)先满足消除机端电压越限;再考虑能否进一步减小并网点电压波动。如果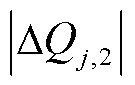 >
>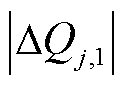 ,进行无功功率(
,进行无功功率(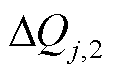 -
-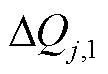 )调节;如果
)调节;如果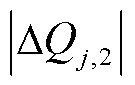 ≤
≤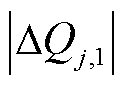 ,则不再进行调节。
,则不再进行调节。
(2)机端电压发生越限,且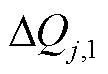 和
和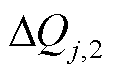 数值异号,则节点j的无功功率调节量为
数值异号,则节点j的无功功率调节量为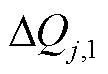 。数值异号表示无功功率调节不能同时满足消除机端电压越限和减小并网点电压波动,那么应优先满足消除机端电压越限。
。数值异号表示无功功率调节不能同时满足消除机端电压越限和减小并网点电压波动,那么应优先满足消除机端电压越限。
(3)机端电压未发生越限,且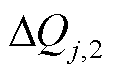 和
和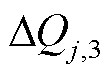 数值同号,则节点j的无功功率调节量为
数值同号,则节点j的无功功率调节量为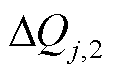 和
和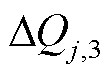 的绝对值较小值。数值同号表示无功功率调节在减小并网点电压波动的同时可能会引起新的机端电压越限。应在保证电压安全的前提下进行消除或减小并网电压波动的无功功率调节,故应选绝对值较小者作为无功功率调节量。
的绝对值较小值。数值同号表示无功功率调节在减小并网点电压波动的同时可能会引起新的机端电压越限。应在保证电压安全的前提下进行消除或减小并网电压波动的无功功率调节,故应选绝对值较小者作为无功功率调节量。
(4)机端电压未发生越限,且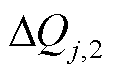 和
和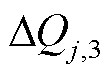 数值异号,则节点j最终的无功功率调节量为
数值异号,则节点j最终的无功功率调节量为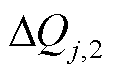 。数值异号表示无功功率调节在减小并网点电压波动的同时不会引起新的机端电压越限,故选
。数值异号表示无功功率调节在减小并网点电压波动的同时不会引起新的机端电压越限,故选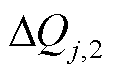 为无功功率调节量。
为无功功率调节量。
式(35)~式(38)揭示了风电场机端电压优化和并网电压优化控制的内在联系。总体上,如果消除电压越限和减小并网点电压波动相矛盾,应优先满足前者;否则,在满足机端电压不越限的条件下,考虑进一步减小并网点电压波动。由于电压实时优化控制是通过利用机组剩余发电容量来实现的,最终的机组无功出力须在机组无功能力范围内,有
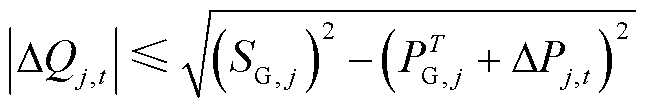 (39)
(39)
总之,本文所提风电场电压实时优化策略,在多时段动态无功功率优化基础上,利用非线性仿射法进行电压实时优化控制,来消除风电功率波动可能导致的机端电压越限并减小并网点电压波动,从而提高系统电压质量。
为验证所提基于非线性仿射的风电场电压实时计算和优化方法的可行性,以我国某实际风电场为例进行仿真试验。如图3所示,风电场共有40台金风科技公司的额定容量为5.6 MW的直驱永磁风机,风机变流器输出交流低压为900 V,经额定容量为6.3 MV·A的风机变压器接入35 kV集电线路,再经2台120 MV·A升压变压器并入220 kV电网。35 kV母线为风电场的并网点,装有5组10 Mvar电容器组和1组5 Mvar静止无功发生器,风机变压器的电压比为1±(2×1.25%)。考虑到风电出力具有明显的波动性以及兼顾模型求解速度,风电场总控制器以4×1 min为周期进行多时段动态无功功率优化,风机每1 s就地测量一次有功功率波动量并判断是否执行电压实时优化。多时段优化中电容器组最大允许投切次数设为1次,变压器分接头最大允许投切次数设为2次,而在电压实时优化时电容器组和变压器分接头保持不变。系统电压可行范围为0.9(pu)~1.1(pu)。为便于分析,设同一集电线路风机功率相同,各风机第一时段功率预测误差服从均值为0 MW,标准差为0.2 MW的正态分布,集电线路之间的相关系数矩阵如式(40)所示。目标函数的权重系数取k1=0.7和k2=0.3。
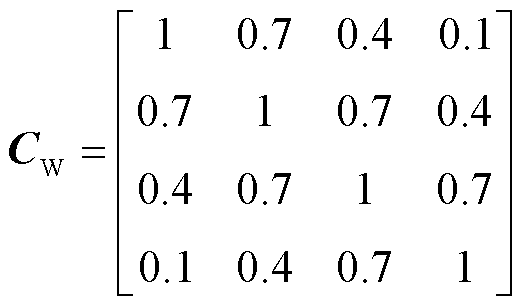 (40)
(40)
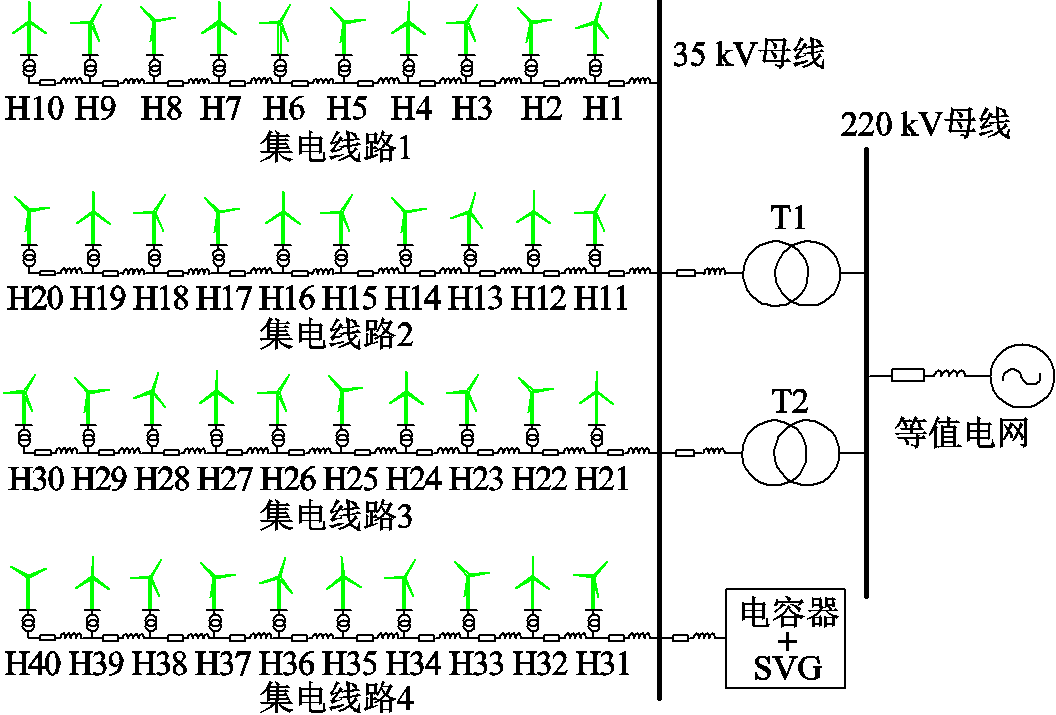
图3 风电场拓扑
Fig.3 Topology of a wind farm
随机选取三组不同开机组合及不同风机出力工况研究风电场无功功率优化。设风电场随机有6台风电机组因风电出力过低而停机,剩余各风机处于开机状态,如图4a所示。按照2~5 MW的随机分布选取各风机功率,如图4b所示。对以上三组不同开机组合及风机出力的工况进行无功功率优化,所得风机无功出力曲线和优化后机端电压如图4c和图4d所示。由于风电场起停组合及各风机出力不同,经风电场系统无功功率优化后,风电场机端电压曲线呈明显折线形,且整体电压靠近上限值。
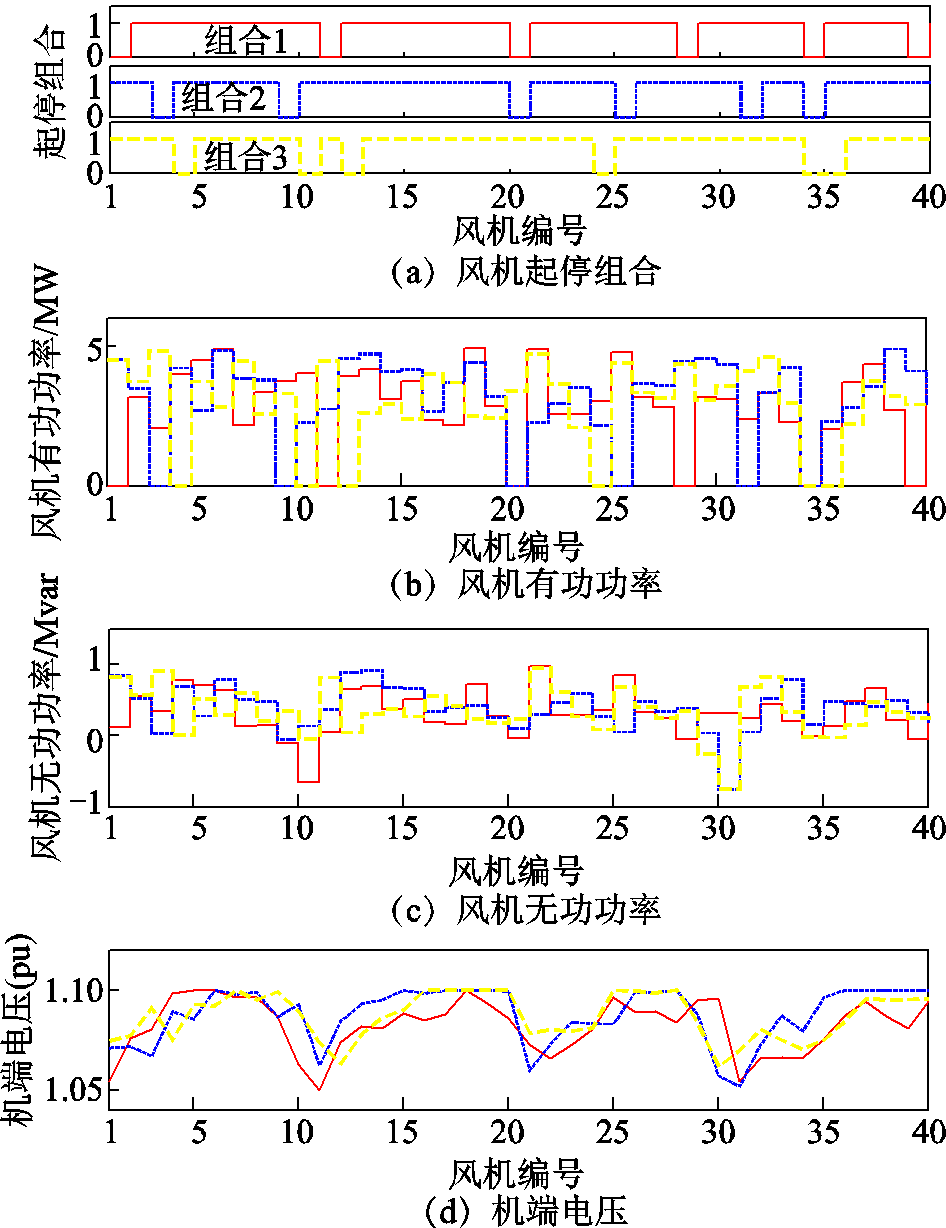
图4 不同风机开机组合及不同风电出力的优化结果
Fig.4 Optimization results for different unit commitment and outputs of wind generators
假设本案例中风电场各风机均开机且有功出力如图5所示,图中,空心圆点为多时段风电预测功率,实线为风电实测功率。案例共包含三个4时段动态无功功率优化,采用不同求解方法对优化模型进行求解,所得结果见表1。采用CPLEX求解器直接求解所建混合整数非线性规划模型,所得的优化结果是理论上的最优解,但是其计算时间成本高达2~3 min,当应用于风电场优化场景中时,难以满足实时性要求。本文方法通过在目标函数中增加惩罚项将所建模型转换为非线性规划模型,并采用基于解析化梯度和海森矩阵的改进内点法求解模型,虽然所得优化结果比最优解高0.04%,但其时间成本仅为3~4 s,约为CPLEX方法的2.14%。因而,本文所提多时段动态无功功率优化模型求解方法在获得次优解的同时,大大减小计算时间成本,提高求解效率,为电压实时优化提供基础。
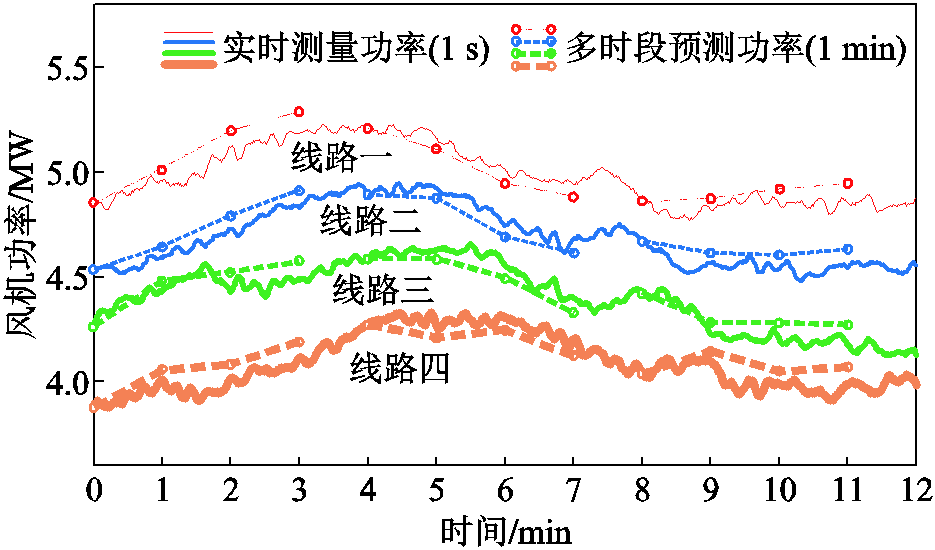
图5 风机有功功率曲线
Fig.5 The active power output of wind generators
表1 多时段动态无功功率优化模型求解
Tab.1 Solving of multi-period reactive power optimization model

不同方法多时段/min目标函数时间成本/s CPLEX方法1~450.66155 5~854.55163 9~1251.74160 本文方法(改进内点法)1~450.673.8 5~854.583.1 9~1251.763.3 比值(本文方法/CPLEX方法)1.000 40.021 4
经多时段优化后的风机变压器电压比k如图6所示,集电线路首端风机变压器电压比大于末端风机,从而使各机端电压更加均衡。由于35 kV母线节点的无功出力变化较小,电容器组的投入组数始终为1组(即5 Mvar),剩余无功功率(红色虚线和蓝色实线的差值)由SVG承担,如图7所示。所得风机变压器电压比和电容器组在时段内的电压实时优化中保持不变。
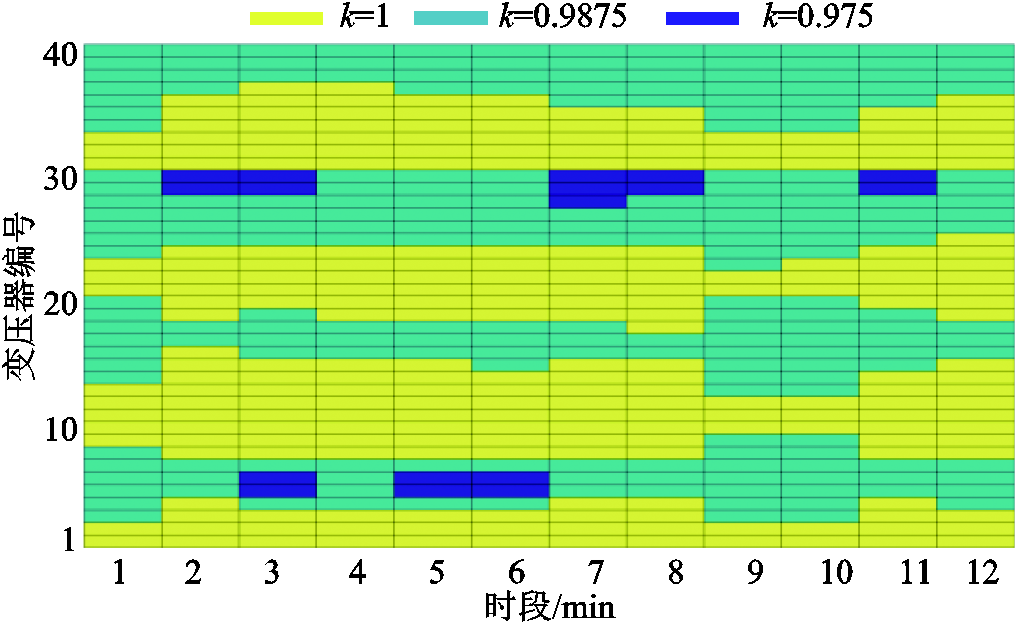
图6 变压器电压比切换
Fig.6 Tap changes of transformers
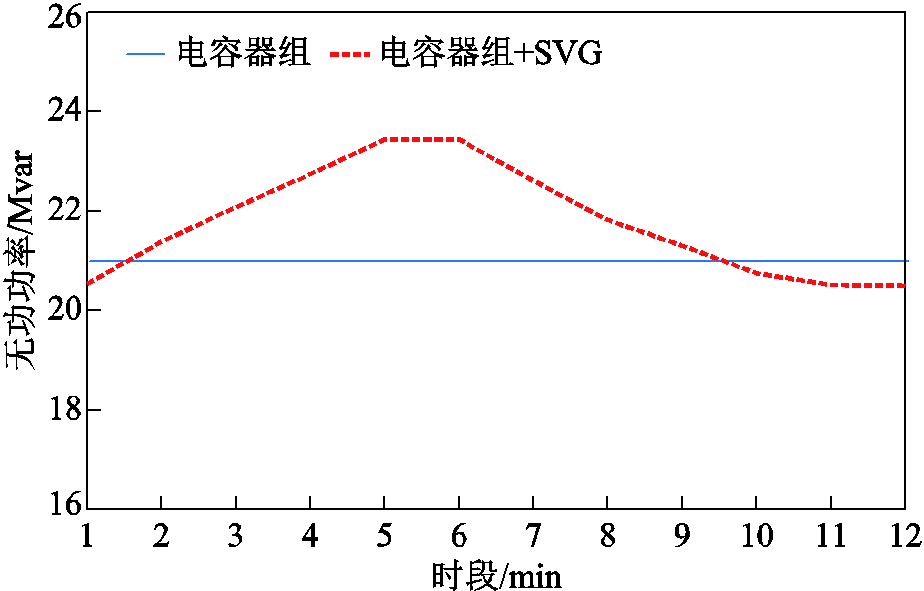
图7 电容器组投切
Fig.7 Capacitor bank switching
第一个多时段优化后的系统电压对风机功率的线性灵敏度矩阵和海森矩阵信息,分别如图8a和图8b所示。节点电压对风机有功功率的灵敏度为负值,对风机无功功率的灵敏度为正值,说明风机有功功率的增加使系统电压下降,无功功率的增加使系统电压上升。同时,各风机机端电压对自身功率变化的灵敏度远大于其他节点。灵敏度为评估风机功率波动对系统电压状态影响提供媒介。图8c和图8d为并网点有功功率和无功功率平衡方程的海森矩阵信息。由式(33)可知,线性灵敏度矩阵和海森矩阵共同决定二阶非线性灵敏度随机组有功功率波动而变化的趋势。
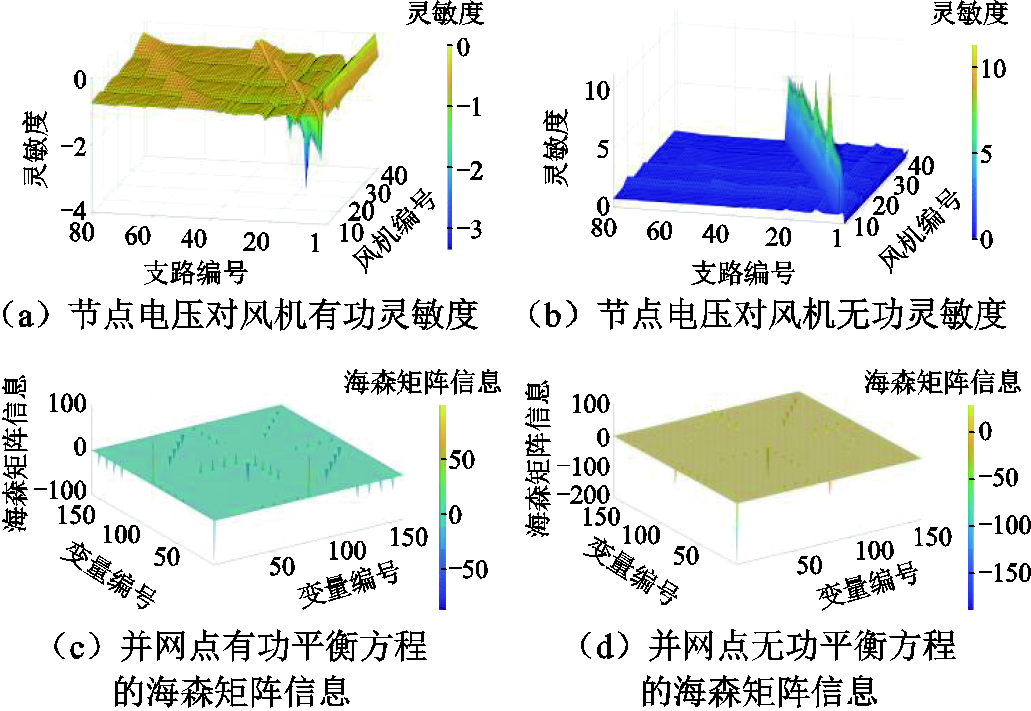
图8 线性灵敏度和海森矩阵信息
Fig.8 Linear sensitivity and Hessian matrix information
设某一集电线路风机瞬时功率(MW)波动分别为{-1.5, -1, -0.5, 0.5, 1, 1.5},采用不同方法计算系统电压状态,所得结果如图9所示。红色粗实线表示未发生功率波动的基准电压状态,可由未预留电压安全裕度的多时段优化得到;紫色细实线表示计及瞬时功率波动后的实际系统电压状态,可由潮流计算得到;蓝色点画线表示线性仿射法所得系统电压状态,线性仿射法是利用线性灵敏度来获得计及风机有功功率波动后的系统电压状态;绿色虚线表示本文非线性仿射法所得的系统电压状态。由图8可知,当功率波动较小时(-0.5 MW, 0.5 MW),线性仿射法和非线性仿射法都能有效跟踪实际系统电压状态。当功率波动较大(-1.5 MW, 1.5 MW),线性仿射法存在较大误差,而非线性仿射法所得结果接近于实际系统电压状态。和潮流计算相比,非线性仿射法不需要进行迭代计算,其计算速度远高于潮流计算。不同方法计算时间成本见表2,非线性仿射法求系统电压状态的计算时间成本为ms级,是线性仿射法的39.20倍,仅为潮流计算的0.58%,满足实时性要求。因而,非线性仿射法能够在计及瞬时功率波动下快速而准确地计算系统电压状态。
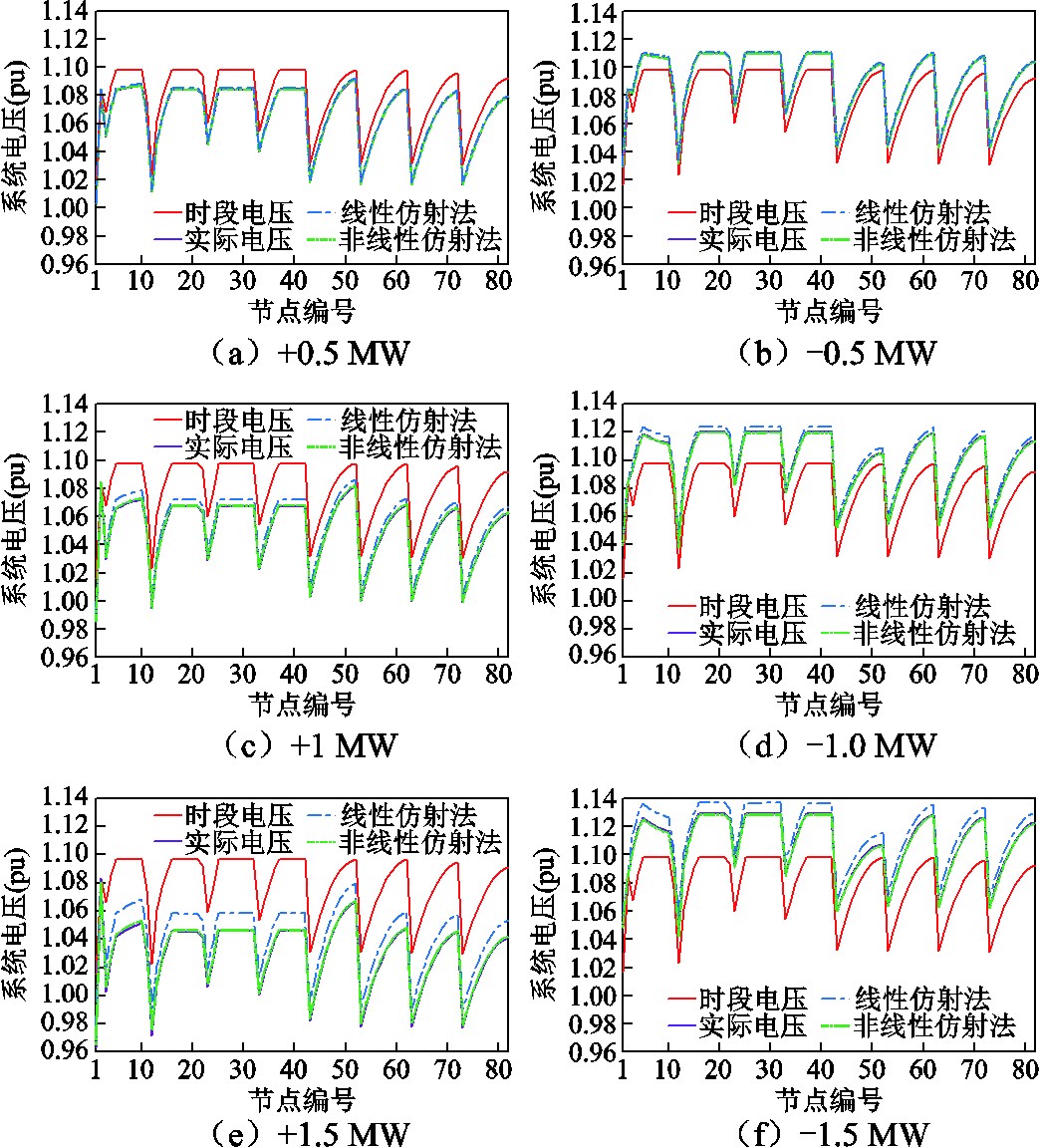
图9 计及风电功率波动的系统电压曲线
Fig.9 System voltage profiles considering wind power fluctuations
表2 不同方法计算时间成本
Tab.2 The time cost for different methods

方法平均计算时间成本/ms 潮流计算法1 350 线性仿射法0.20 非线性仿射法7.84
4.4.1 单时间断面系统电压和无功功率分析
以时刻{50 s, 530 s}系统电压为例来分析所提方法的优化效果。在第50 s,不同方法的系统电压曲线如图10所示。红色虚线为多时段动态无功功率优化所得时段电压状态,通过预留较小的电压安全裕度,使系统整体电压靠近1.1(pu),从而获得更低的目标值。蓝色实线是采用无功功率指令控制法获得的系统电压(无功功率指令控制法指经多时段无功功率优化后将无功功率指令下发给各风机,在时段内风机无功功率保持不变),此时,并网点的电压明显低于时段并网电压。采用本文所提基于非线性仿射电压实时优化方法所得电压曲线如(绿色)点画线所示,机端电压未发生越限,且并网电压波动比无功功率指令控制法更小,但并网电压波动无法被完全消除,因为进一步调节无功功率来消除并网电压波动会引起新的发机端电压越限。在第530 s的系统电压曲线如图11所示,采用无功功率指令控制法的机端电压发生越限现象,且并网电压向上偏移。采用本文所提方法的机端电压未发生越限,且并网点电压波动近乎被完全消除。因而所提方法能够有效防止机端电压越限,同时减小并网电压波动。由于和时段优化相比实时电压优化的时间尺度更小,其风电不确定性可被忽略,即使实时优化后系统电压接近1.1(pu),仍能保证系统电压安全性。
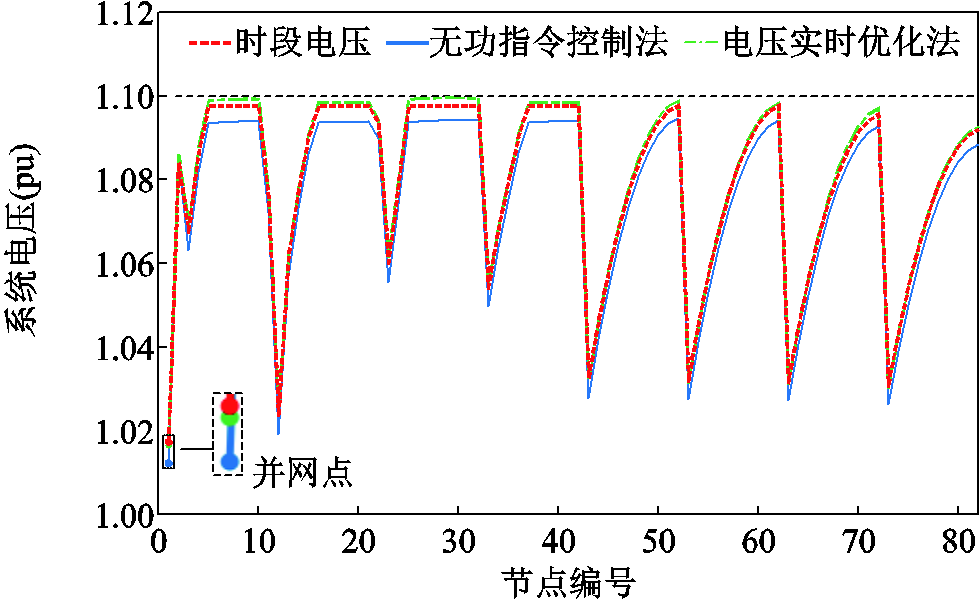
图10 第50 s系统电压曲线
Fig.10 System voltage profile at 50 s
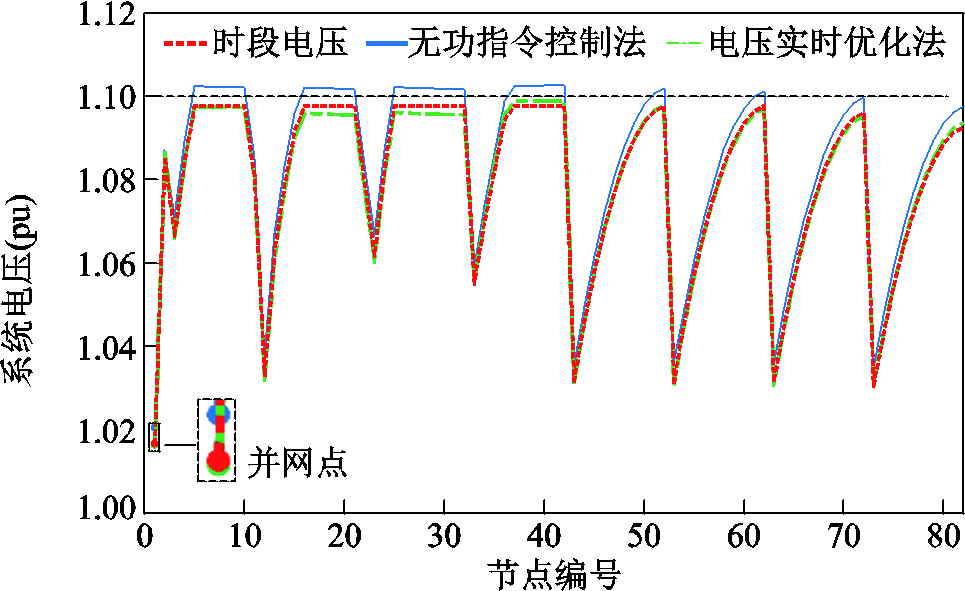
图11 第530 s系统电压曲线
Fig.11 System voltage profile at 530 s
无功功率指令控制法的风机无功出力如图12和图13的蓝色实线所示,本文所提电压实时优化法的风机无功出力如(红色)虚线所示。结合图3、图10和图12分析,在第50 s时,风电功率正向波动导致系统整体电压下降,所提方法和无功功率指令控制法相比,通过增加机组无功出力抬高系统电压,在不引起新的机端电压越限下,减小并网点电压波动。结合图3、图11和图13分析,在第530 s时,风电功率负向波动导致系统发生电压越限,所提方法通过减小风机无功出力,来降低系统电压,在消除系统机端电压越限的同时,减小并网电压波动。
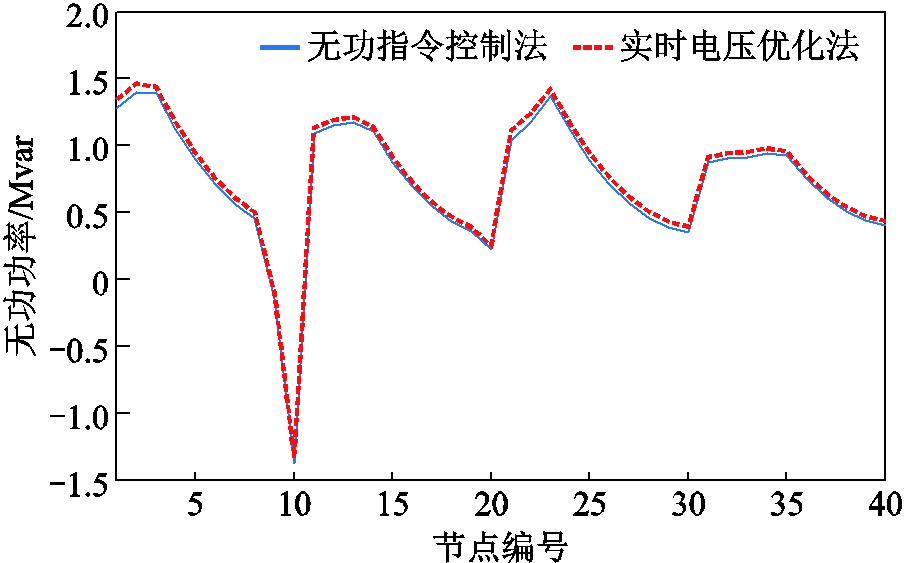
图12 第50 s机组无功功率曲线
Fig.12 Reactive power output of wind generators at 50 s
4.4.2 事件触发算法分析
本文所提综合考虑风机功率波动对机端电压和并网电压影响的事件触发算法的阀值取0.002(pu),风电场40台风机的触发状态如图14所示。因为案例中同一集电线路的风机功率变化相同,所以其触发状态规律类似。对同一集电线路而言,由于并网点电压对集电线路首端风机的灵敏度较高(因为电气距离更近),首端风机触发的次数大于末端风机。在时序仿真中,如果未采用事件触发算法,每台风机每个时刻(1 s)都要进行无功功率控制,而采用所提事件触发算法,各风机的触发概率将大大减小。各风机触发概率如图15所示,经过统计,风电场无功功率控制频率平均降低为原来的38.11%。
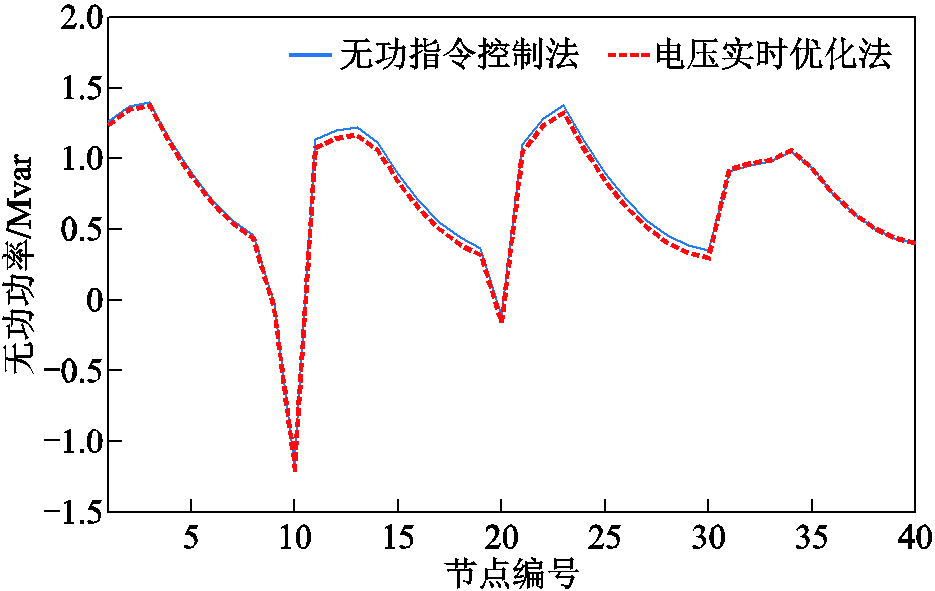
图13 第530 s机组无功功率曲线
Fig.13 Reactive power output of wind generators at 530 s
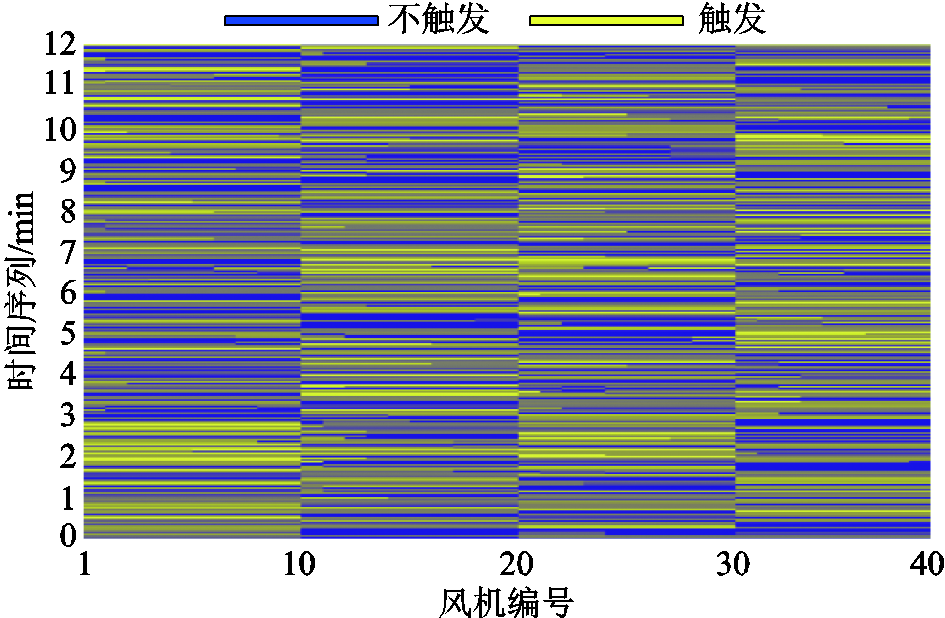
图14 各风机触发状态
Fig.14 Event-triggered state of wind generators
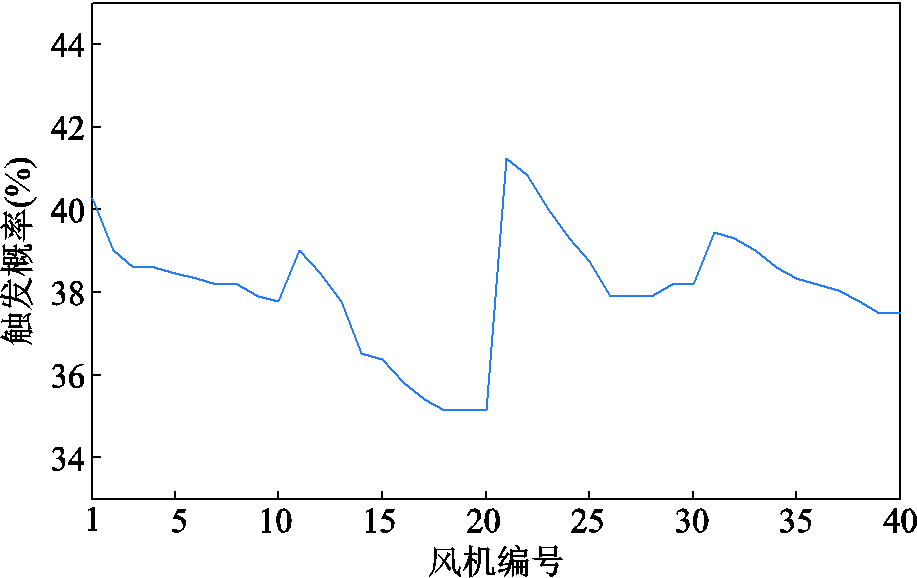
图15 各风机触发概率
Fig.15 Event-triggered probability of wind generators
4.4.3 系统时序电压分析
当采用无功功率指令控制法时,时序仿真系统电压曲面如图16a所示,风电功率波动导致系统出现不同程度电压越限现象,特别是机端电压(节点3~42)越限明显。当采用电压实时优化法,不论是否基于事件触发机制,所得系统电压始终在安全范围内,所有的风机均未出现电压越限现象,如图16b和图16c所示,但引入事件触发机制能够大大减小无功功率控制频率。因而,本文所提基于事件触发的电压实时优化法能够有效防止系统机端电压越限,并减小无功功率调节频率。
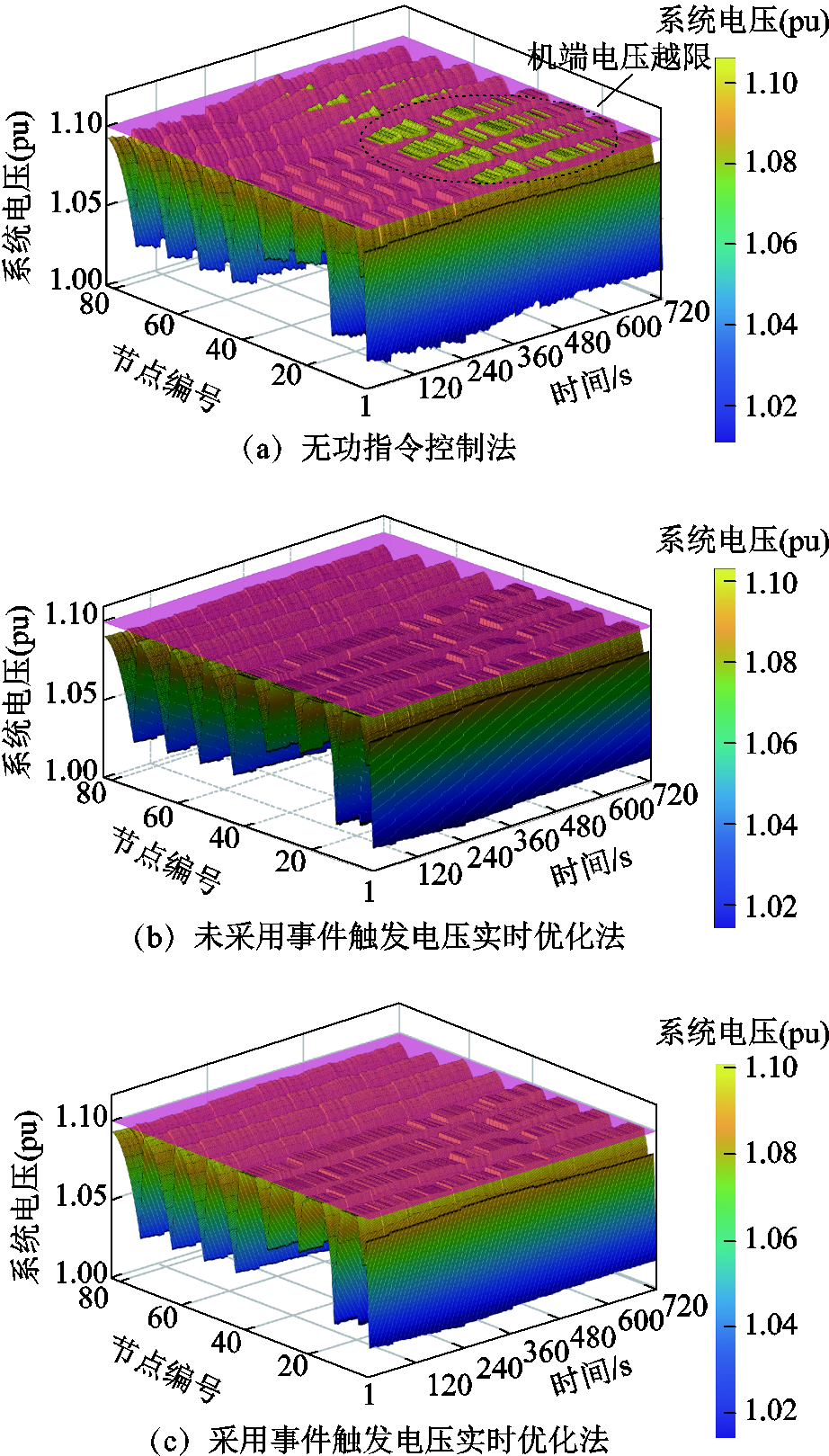
图16 不同优化方法系统电压曲面
Fig.16 System voltage surfaces for different optimization methods
在时序仿真中,经多时段动态无功功率优化所得并网电压如图17(红色)点画线所示,将其作为基准电压来评价本文所提方法减小并网电压波动的效果。无功功率指令控制法的并网点电压如(蓝色)粗实线所示,在某些时刻系统并网电压出现较大的波动(如232 s和414 s)。当采用本文所提基于事件触发的电压实时优化方法,所得的并网点电压如(绿色)虚线所示,和无功功率指令控制法相比,并网电压波动大幅降低,特别是在风电功率负向波动时(5~12 min)。虽然引入事件触发机制后,并网点电压波动有所增大,但无功功率控制频率大幅降低。经表3统计,在时序仿真中,本文所提基于事件触发的电压实时优化法的并网电压波动平均值约为无功功率指令控制法的35.12%,仅比无事件触发的电压实时优化法高约为1.22%,证明了所提方法能够有效减小风电场并网电压波动。
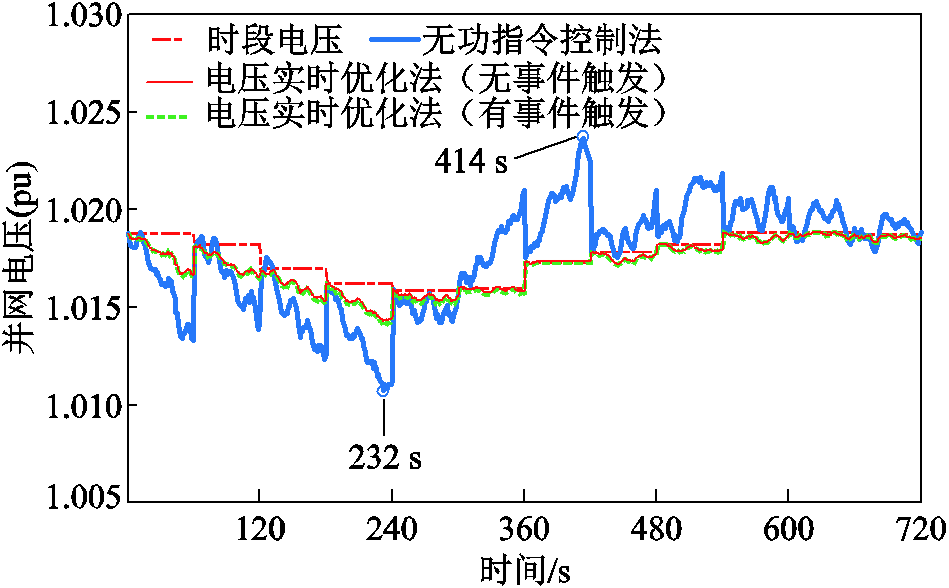
图17 风电场并网点电压曲线
Fig.17 The voltage curves of grid-connected point
表3 并网电压波动统计
Tab.3 The statistics of voltage fluctuations at grid-connected point (10-3pu)
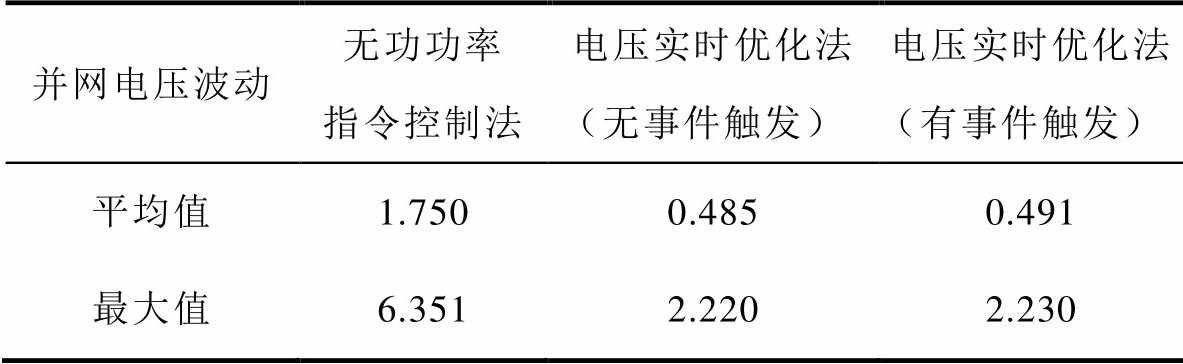
并网电压波动无功功率指令控制法电压实时优化法(无事件触发)电压实时优化法(有事件触发) 平均值1.7500.4850.491 最大值6.3512.2202.230
本文提出一种基于非线性仿射的风电场电压实时计算和优化方法,快速获取计及风电功率不确定性的系统电压状态,并实时优化风电场电压。经过理论分析与算例验证,得出以下结论:
1)本文提出在目标函数中增加惩罚项和基于解析化梯度及海森矩阵的改进内点法,求解多时段动态无功功率优化模型,能够兼顾模型求解速度和优化效果。该方法的目标函数比最优解高约0.04%,计算时间仅为传统方法的2.14%,满足风电场优化实时性要求。
2)本文给出了电力系统中电压关于功率的三阶非线性仿射变换的解析化表达式,为分析风电不确定性对系统电压状态影响提供有力工具。所提非线性仿射法能够快速且准确地获取系统电压状态,计算成本约为潮流计算的0.58%,其计算结果比线性仿射法更加准确。此外,设计综合考虑功率波动对机端电压和并网电压影响的事件触发算法,风机无功功率控制频率降低至原来的38.11%。
3)所提基于非线性仿射的电压实时优化方法能够有效防止风电功率波动可能导致的机端电压越限,并进一步减小并网电压波动,提高风电场电压质量。和传统无功功率指令控制法相比,机端电压越限完全被消除,并网电压波动降低至原来的35.12%。
所提方法通过微调无功功率实现系统电压状态优化,提高了系统运行的安全性,但需要机组预留一定无功功率调节容量,在风机满负荷运行时,可能导致发电机有功出力减小而出现“弃风”现象,降低了部分经济性。未来,将进一步对多个风电场间的时空相关性进行建模,同时将所提方法扩展应用至风电场群、主动配电网和微电网优化中,研究源网荷储多重不确定性下的系统电压实时优化问题。
参考文献
[1] 李晖, 刘栋, 姚丹阳. 面向碳达峰碳中和目标的我国电力系统发展研判[J]. 中国电机工程学报, 2021, 41(18): 6245-6259.
Li Hui, Liu Dong, Yao Danyang. Analysis and reflection on the development of power system towards the goal of carbon emission peak and carbon neutrality[J]. Proceedings of the CSEE, 2021, 41(18): 6245-6259.
[2] 秦世耀, 齐琛, 李少林, 等. 电压源型构网风电机组研究现状及展望[J]. 中国电机工程学报, 2023, 43(4): 1314-1334.
Qin Shiyao, Qi Chen, Li Shaolin, et al. Review of the voltage-source grid forming wind turbine[J]. Proceedings of the CSEE, 2023, 43(4): 1314-1334.
[3] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477.
Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two stage robust optimization method for the whole-process power system restoration considering wind power uncertainty[J]. Transactions of China Electro-technical Society, 2022, 37(21): 5462-5477.
[4] 王晨, 寇鹏, 王若谷, 等. 利用多空间尺度下时空相关性的点云分布多风机风速预测[J]. 电力系统自动化, 2021, 45(22): 65-73.
Wang Chen, Kou Peng, Wang Ruogu, et al. Wind speed forecasting for multiple wind turbines with point cloud distribution using spatio-temporal correlation on multiple spatial scale[J]. Automation of Electric Power Systems, 2021, 45(22): 65-73.
[5] 王耀翔, 戴朝波, 杨志昌, 等. 考虑风电机组无功潜力的风电场无功电压控制策略[J]. 电力系统保护与控制, 2022, 50(24): 83-90.
Wang Yaoxiang, Dai Chaobo, Yang Zhichang, et al. Voltage control strategy for a wind farm considering the reactive capability of DFIGs[J]. Power System Protection and Control, 2022, 50(24): 83-90.
[6] Li Shenghu, Zhang Yifan, Yu Xinyu, et al. Reactive power dispatch of DFIGs in wind farm based on multi-object optimization[J]. International Transactions on Electrical Energy Systems, 2020, 30(3): 1-16.
[7] 刘其辉, 逄思敏, 吴林林, 等. 大规模风电汇集系统电压不平衡机理、因素及影响规律[J]. 电工技术学报, 2022, 37(21): 5435-5450.
Liu Qihui, Pang Simin, Wu Linlin, et al. The mechanism, factors and influence rules of voltage imbalance in wind power integration areas[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5435-5450.
[8] 王德胜, 颜湘武, 刘辉, 等. 基于动态无功支撑的全功率变流风电机组高电压穿越改进控制[J]. 中国电机工程学报, 2022, 42(3): 957-968.
Wang Desheng, Yan Xiangwu, Liu Hui, et al. High voltage ride through improved control of full power converter wind turbines based on dynamic reactive power support[J]. Proceedings of the CSEE, 2022, 42(3): 957-968.
[9] 符杨, 魏钰柠, 贾锋, 等. 分布式风电机组电压波动特性分析及平抑控制策略[J]. 中国电机工程学报, 2020, 40(14): 4496-4505, 4729.
Fu Yang, Wei Yuning, Jia Feng, et al. The voltage fluctuation characteristic of distributed wind generators and its smoothing control strategy[J]. Proceedings of the CSEE, 2020, 40(14): 4496-4505, 4729.
[10] 蔡游明, 李征, 蔡旭. 以并网点电压和机端电压平稳性为目标的风电场无功电压协调控制[J]. 电力自动化设备, 2018, 38(8): 166-173.
Cai Youming, Li Zheng, Cai Xu. Coordinated control of reactive power and voltage for wind farm aiming at voltage stability of PCC and generator terminal[J]. Electric Power Automation Equipment, 2018, 38(8): 166-173.
[11] 王渝红, 廖逸犇, 宋雨妍, 等. 风电场内部分散式无功电压优化控制策略[J]. 高电压技术, 2022, 48(12): 5047-5056.
Wang Yuhong, Liao Yiben, Song Yuyan, et al. Distributed optimal control strategy of reactive power and voltage in wind farm[J]. High Voltage Engineering, 2022, 48(12): 5047-5056.
[12] 朱星阳, 张建华, 刘文霞, 等. 风电并网引起电网电压波动的评价方法及应用[J]. 电工技术学报, 2013, 28(5): 88-98.
Zhu Xingyang, Zhang Jianhua, Liu Wenxia, et al. Evaluation methodology and its application of voltage fluctuation in power network caused by inter-connected wind power[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 88-98.
[13] 王渝红, 宋雨妍, 廖建权, 等. 风电电压主动支撑技术现状与发展趋势[J]. 电网技术, 2023, 47(8): 3193-3205.
Wang Yuhong, Song Yuyan, Liao Jianquan, et al. Review and development trends of DFIG-based wind power voltage active support technology[J]. Power System Technology, 2023, 47(8): 3193-3205.
[14] 国家市场监督管理总局, 国家标准化管理委员会. 风电场接入电力系统技术规定第1部分:陆上风电: GB/T 19963.1—2021[S]. 北京: 中国标准出版社, 2021.
[15] 张哲, 王成福, 董晓明, 等. 基于分层模型预测控制的风电场电压协调控制策略[J]. 电力系统自动化, 2019, 43(11): 34-42, 94.
Zhang Zhe, Wang Chengfu, Dong Xiaoming, et al. Coordinated voltage control strategy of wind farms based on hierarchical model predictive control[J]. Automation of Electric Power Systems, 2019, 43(11): 34-42, 94.
[16] 张建委, 蔺红. 考虑风电机组电压均衡性的风电场无功优化策略[J]. 水力发电, 2020, 46(9): 115-119.
Zhang Jianwei, Lin Hong. Reactive power optimi-zation strategy of wind farm considering voltage balance of wind turbine[J]. Water Power, 2020, 46(9): 115-119.
[17] 刘承锡, 张兆毅, 赖秋频. 考虑风电功率短期波动的风电场无功快速跟踪优化[J]. 中国电机工程学报, 2023, 43(15): 5850-5863.
Liu Chengxi, Zhang Zhaoyi, Lai Qiupin. Fast-tracking optimization of reactive power for wind farm considering short-term fluctuations of wind generations[J]. Proceedings of the CSEE, 2023, 43(15): 5850-5863.
[18] 胡畔, 冀肖彤, 王易, 等. 基于置信度机会约束规划的风电场无功优化技术[J]. 科学技术与工程, 2022, 22(17): 7002-7012.
Hu Pan, Ji Xiaotong, Wang Yi, et al. Reactive power optimization technology of wind farm based on confidence chance-constrained programming[J]. Science Technology and Engineering, 2022, 22(17): 7002-7012.
[19] 张晋华, 吴文静, 王卓然, 等. 基于降低风电场损耗的风电场优化调度研究[J]. 太阳能学报, 2018, 39(4): 1085-1096.
Zhang Jinhua, Wu Wenjing, Wang Zhuoran, et al. Research of wind farm optimal scheduling based on reducing wind farm losses[J]. Acta Energiae Solaris Sinica, 2018, 39(4): 1085-1096.
[20] 朱建华, 何卓林, 闫伟军, 等. 风电场自动电压控制中风机和静止无功发生器的无功分配研究[J]. 电气技术, 2022, 23(4): 31-36.
Zhu Jianhua, He Zhuolin, Yan Weijun, et al. Research on reactive power distribution of wind turbine and static var generator in automatic voltage control of wind farm[J]. Electrical Engineering, 2022, 23(4): 31-36.
[21] 徐询, 谢丽蓉, 梁武星, 等. 考虑风电预测误差时序性及风电可信度的双层优化模型[J]. 电工技术学报, 2023, 38(6): 1620-1632, 1661.
Xu Xun, Xie Lirong, Liang Wuxing, et al. Bi-level optimization model considering time series characteristic of wind power forecast error and wind power reliability[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1620-1632, 1661.
[22] Wang Licheng, Yan Ruifeng, Saha T K. Voltage management for large scale PV integration into weak distribution systems[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 4128-4139.
[23] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049.
Yang Jun, Hou Junhao, Liu Yawei, et al. Distributed cooperative control method and application in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4035-4049.
[24] 薛帅, 高厚磊, 郭一飞, 等. 大规模海上风电场的双层分布式有功控制[J]. 电力系统保护与控制, 2021, 49(3): 1-9.
Xue Shuai, Gao Houlei, Guo Yifei, et al. Bi-level distributed active power control for a large-scale wind farm[J]. Power System Protection and Control, 2021, 49(3): 1-9.
[25] 石东源, 蔡德福, 陈金富, 等. 计及输入变量相关性的半不变量法概率潮流计算[J]. 中国电机工程学报, 2012, 32(28): 104-113, 12.
Shi Dongyuan, Cai Defu, Chen Jinfu, et al. Probabilistic load flow calculation based on cumulant method considering correlation between input variables[J]. Proceedings of the CSEE, 2012, 32(28): 104-113, 12.
[26] 卫鹏, 刘建坤, 周前, 等. 基于半不变量和Gram-Charlier级数展开法的随机潮流算法[J]. 电力工程技术, 2017, 36(1): 34-38.
Wei Peng, Liu Jiankun, Zhou Qian, et al. A probabilistic power flow algorithm based on semi-variable and gram-charlier series expansion[J]. Electric Power Engineering Technology, 2017, 36(1): 34-38.
[27] Waltz R A, Morales J L, Nocedal J, et al. An interior algorithm for nonlinear optimization that combines line search and trust region steps[J]. Mathematical Programming, 2006, 107(3): 391-408.
[28] Byrd R H, Gilbert J C, Nocedal J. A trust region method based on interior point techniques for nonlinear programming[J]. Mathematical Programming, 2000, 89(1): 149-185.
Abstract The uncertainty of wind speed leads to fluctuations in wind power, resulting in voltage fluctuations at the sending end and grid-connected point. Traditional methods for evaluating the impact of wind power fluctuations on the system state online either entail frequent power flow calculations to obtain real-time system voltages, which creates a substantial computational burden, or employ linear affine methods that yield significant errors when wind power fluctuations are large. To optimize the sending-end voltage and grid-connected point voltage considering the wind power fluctuations, centralized optimization methods require frequent optimal power flow calculations, leading to heavy computational burdens. On the other hand, distributed algorithms require advanced communication facilities, which many wind farms may struggle to meet. Therefore, this paper proposes a real-time voltage calculation and optimization method based on nonlinear affine transformation to rapidly calculate the voltage state and optimize the system voltage considering wind power fluctuations, with limited computation and communication resources.
Firstly, the method establishes a multi-period dynamic reactive power optimization model to minimize the power loss and the voltage fluctuations of the grid-connected point. The cumulant method is used to analyze the sending-end voltage influenced by uncertain wind generation. Secondly, an improved interior point method, based on the analytic gradient matrix and Hessian matrix, is utilized to solve the established model, with the obtained results serving as a reference for real-time voltage optimization. Thirdly, at each moment the wind generator measures the local active power fluctuation and uses the designed event-triggered algorithm to determine whether real-time voltage optimization is necessary. Then, the nonlinear affine method is used to rapidly calculate the real-time system voltage state, and obtain the reactive power adjustment to prevent potential voltage violations at the sending end, while also reducing voltage fluctuations at the grid-connected point. Finally, the reactive power of each wind generator is regulated simultaneously by controlling the converter to achieve real-time voltage optimization of the whole wind farm. Overall, the proposed real-time voltage optimization method can improve the voltage quality of wind farms in real time.
The following conclusions can be drawn from the simulation analysis: (1) The solution speed is greatly improved by adding a penalty term to the objective function of the multi-period dynamic reactive power optimization model. The improved interior point method based on analytic gradient and Hessian matrix can solve the model efficiently. (2) Based on the third-order nonlinear affine transformation of system voltage w.r.t. active/reactive power derived in this paper, the proposed method could rapidly and accurately obtain the system voltage state considering the wind power fluctuations. The computational time cost is about 0.58% of the power flow calculation, and the calculation results are more accurate compared with the linear affine method. (3) The proposed real-time voltage optimization method based on nonlinear affine transformation could effectively prevent sending-end voltage violations and further reduce the grid-connected point voltage fluctuations, thus improving the voltage quality of wind farms. Statistically, the sending-end voltage violations are eliminated throughout the simulation, and the voltage fluctuation of the grid-connected point is reduced to 35.12% of the conventional method.
Keywords: Multi-period dynamic reactive power optimization, nonlinear affine transformation, real-time calculation and optimization, event-triggered
DOI: 10.19595/j.cnki.1000-6753.tces.230788
中图分类号:TM614
国家重点研发计划资助项目(2022YFF0610600)。
收稿日期 2023-05-29
改稿日期 2023-08-17
张兆毅 男,1992年生,博士研究生,研究方向为含新能源电力系统优化运行与控制,新型电力系统标准研制。E-mail:zhangzhaoyi@whu.edu.cn
樊友平 男,1970年生,教授,博士生导师,研究方向为电力系统优化运行与控制,复杂电网/输变电设备安全稳定运行的参数测试、信息处理、融合与控制决策,新型电力系统标准研制等。E-mail:ypfan@whu.edu.cn(通信作者)
(编辑 赫 蕾)