 (1)
(1)
摘要 暂态稳定实时性判别是响应式稳定控制的核心,新能源和直流输电并网下电网的结构、运行和响应特征复杂程度骤增,现有实时性判别方法的准确性和泛化性面临挑战。该文针对含新能源和直流输电的复杂电网暂态稳定性,提出了一种基于可量测暂态能量特征的自适应逻辑推理判稳方法,实现无电网模型依赖且具有可解释性的实时性稳定性判别。首先,基于发电机转子运动的能量关系,结合特勒根定理构建了面向复杂电网响应信息的能量函数并论证了其守恒性;然后,根据系统动能-势能能量转换特征定义了稳定预判因数,并结合最大功角差构成了判稳关键特征量,提出了基于自适应模糊推理神经网络(ANFIS)的关键特征量与稳定状态之间的映射模型,实现了暂态稳定性实时推理评估;最后,在简单系统中量化分析了关键特征量与系统稳定性间的关系,并在修改后含新能源与直流输电的IEEE 10机39节点系统中验证了该文所提方法的有效性与泛化性。
关键词:暂态稳定性 响应驱动 特勒根定理 能量函数 复杂电网 自适应逻辑推理
在国家能源“碳达峰、碳中和”目标发展驱动下,风电、光伏并网规模实现跨越式增长,高压直流输电广泛应用,深刻改变了电力系统的电源与网络结构[1-3]。该电网结构运行工况多变,不确定性增加,典型方式难以刻画,且新能源电源与直流输电响应特性显著区别于传统同步电源和交流输电特性,导致受扰后电网设备间电气量耦合作用复杂,暂态稳定演化过程非线性程度加深,响应信息与系统稳定性之间的映射关系难以准确表达[4-5]。在此背景下,如何进行暂态稳定性实时准确判别,为紧急响应控制提供可靠动作依据,成为目前关注的重要问题。
暂态稳定性实时判别同时追求判稳的准确性和快速性。传统的暂态稳定分析方法主要包括时域仿真法[6]、暂态能量函数(Transient Energy Function, TEF)法[7-11]和扩展等面积(Extended Equal Area Criterion, EEAC)法[12-13]。时域仿真基于电力系统微分-代数方程(Differential Algebraic Equations, DAE)模型,依赖于电网准确的模型及其参数,采用数值积分计算功角轨迹进行判稳,求解速度无法满足实时性要求;传统TEF方法的主导不稳定平衡点(Controlling Unstable Equilibrium Point, CUEP)法[7], 势能边界面(Potential Energy Boundary Surface, PEBS)法[8-9]和基于稳定域边界的主导不稳定平衡点(Boundary of stability region based CUEP, BCU)法[10-11],均通过故障切除时总能量与临界能量大小判别稳定,同样依赖电网模型与参数,且临界能量无法实时准确获取;EEAC法需结合各同步发电机轨迹信息进行超前与滞后机群分群,将两机群映射为单机无穷大系统,并采用等面积准则判稳,然而,分群的准确性与快速性要求制约了其在稳定性实时判别中的应用。
近年来,广域量测系统部署日臻成熟,为获取受扰后电网实时响应数据提供了技术手段,基于响应信息的暂态稳定实时判别得到了发展。文献[14-15]提出了基于量测数据计算的最大李雅普诺夫指数(Maximum Lyapunov Exponent, MLE)实时稳定性判别方法,MLE本质适用于监测非线性系统的混沌行为,量测计算窗口难以确定,判稳的准确性和时效性均难以保障。文献[16-17]提出了基于多机等值的单机无穷大系统的相轨迹凹凸性进行暂态稳定判别,方法中分群准确性和判稳指标微分形式均会影响判稳可靠性。文献[18-19]采用支路两端电压和相位信息提出了基于简化支路输电能力指数(simplified Branch Transient Transmission Capability, sBTTC)的暂态判稳指标,但其稳定性判定阈值需人为经验设置。文献[20-21]针对传统恒功率负荷的交流电网,基于暂态过程中能量在支路中的演化特征,提出了基于支路势能的暂态稳定判别方法,但判稳指标构成中所需的故障后系统稳定平衡点难以准确实时获取。文献[18-21]判稳方法需要基于每条支路的电压、相位和功率信息构建指标,并排序找到关键支路,收集所有支路信息进行计算增加了通信代价和数据要求,判稳时效性存在不足。
当获取电网海量数据成为现实,以数据驱动为核心的人工智能(Artificial Intelligence, AI)技术在暂态稳定实时评估方面得到快速发展,其通过离线对大量稳定/失稳样本进行学习以得到判稳评估模型,并应用于在线实时稳定判别,具有快速响应特性。基于AI暂态稳定实时评估的准确性关键在于选取合适的数据集特征以及构建可靠的AI判稳模型。文献[22]采用故障清除后第3和6个周波时发电机的功角与电压作为数据特征量,使用人工神经网络(Artificial Neuron Network, ANN)建立了判稳模型。文献[23]基于故障发生时刻和清除后第6和9个周波的发电机功角及角速度作为特征量,建立了基于极限学习机(Extreme Learning Machine, ELM)的稳定判别方法。文献[24-25]选取线路功率、节点电压、发电机出力、机端电压和转子角速度等电气量作为特征量,提出了基于支持向量机(Support Vector Machine, SVM)的判稳模型。文献[26]基于发电机出力、支路潮流、节点电压和负荷水平等稳态信息作为原始特征,采用遗传算法进行特征选择和削减,构建了基于最邻近节点算法(K-Nearest Neighbor, KNN)的稳定判别方法。文献[27]基于节点注入功率和节点电压数据构造特征量,采用了长短期记忆(Long Short-Term Memory, LSTM)网络进行暂态稳定的在线预测。文献[28]以故障前、故障中和故障后的发电机电压、功率和功角信息构造特征集,构建了基于自注意力编码器的稳定预判方法。文献[29]同样提取故障前中后三个时间断面下的节点电压、相位和注入功率作为特征量,利用图卷积神经网络(Graph Convolutional Network, GCN)建立了稳定评估模型。以上文献,特征量均基于可直接量测的电气量选取,但缺乏特征量对暂态稳定/失稳机理过程的可靠表征,导致其与系统稳定性间的映射关系弱,对稳定判别结果缺乏相应的可解释性;此外,文献中的人工智能判稳模型缺乏对输入特征与输出结果间的可解释性推理,使得输入-输出间因果关系不明,判稳模型的泛化能力较弱,难以有效适用于复杂电力系统。
针对上述人工智能判稳方法中存在的问题,本文对含新能源的交直流混联复杂电网的实时稳定进行判别,一方面,构建了面向复杂电网响应信息的精细化暂态能量函数,通过分析系统稳定/失稳时动能-势能转换特征,定义了稳定预判因数,并结合最大功角差构成了可充分表征稳定/失稳演化过程的关键特征量;另一方面,为建立输入特征与稳定/失稳结果之间可解释推理的映射关系,提出了基于自适应神经模糊推理系统(Adaptive Network based Fuzzy Inference System, ANFIS)的稳定判别模型,实现暂态稳定性实时判别。通过以上两方面,提升对复杂电网暂态稳定实时判别的可解释性与泛化性,增强判稳结果的可靠性。
同步发电机转子方程刻画了电网中发电机的运行特性,蕴含了以受力-速度为核心的牛顿运动学能量关系。对于集合为G的同步发电机,在系统同步发电机惯量中心(Center Of Inertia, COI)坐标系下,第i台发电机的转子运动方程表达式为
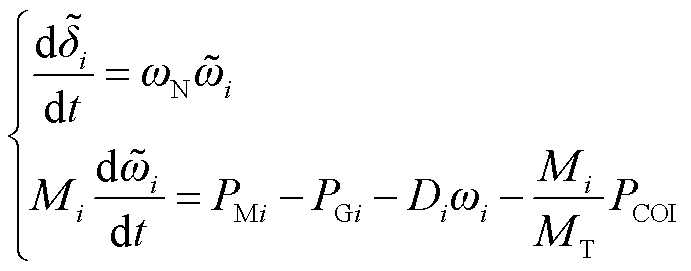 (1)
(1)
其中
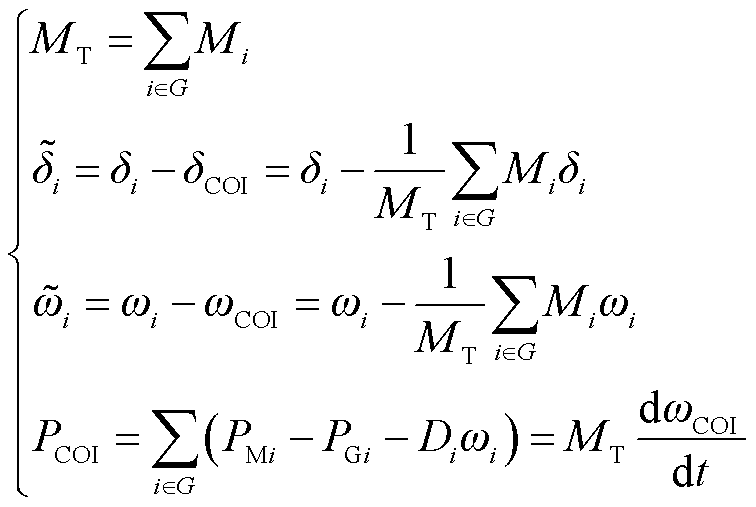 (2)
(2)
式中,![]() 和
和![]() 分别为同步坐标系下发电机转速、发电机额定转速和惯量中心系下发电机转速;δi和
分别为同步坐标系下发电机转速、发电机额定转速和惯量中心系下发电机转速;δi和![]() 分别为同步坐标系下和惯量中心系下发电机功角;
分别为同步坐标系下和惯量中心系下发电机功角;![]() 和
和![]() 分别为系统同步发电机系下的惯量中心转速和功角;PMi、PGi、Di和Mi分别为发电机的机械功率、电磁功率、阻尼系数和转动惯量;MT为系统同步发电机转动惯量总和;PCOI为惯量中心功率。
分别为系统同步发电机系下的惯量中心转速和功角;PMi、PGi、Di和Mi分别为发电机的机械功率、电磁功率、阻尼系数和转动惯量;MT为系统同步发电机转动惯量总和;PCOI为惯量中心功率。
为构造基于运动方程的系统能量函数,对式(1)中方程进行交叉相乘并加和后,可得到
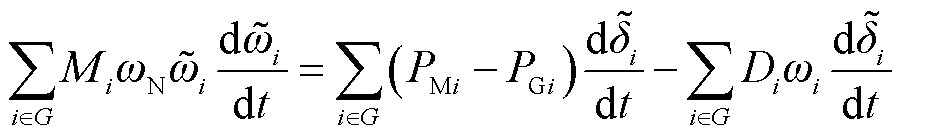 (3)
(3)
式(3)推导过程包括了为零的表达式(4)。
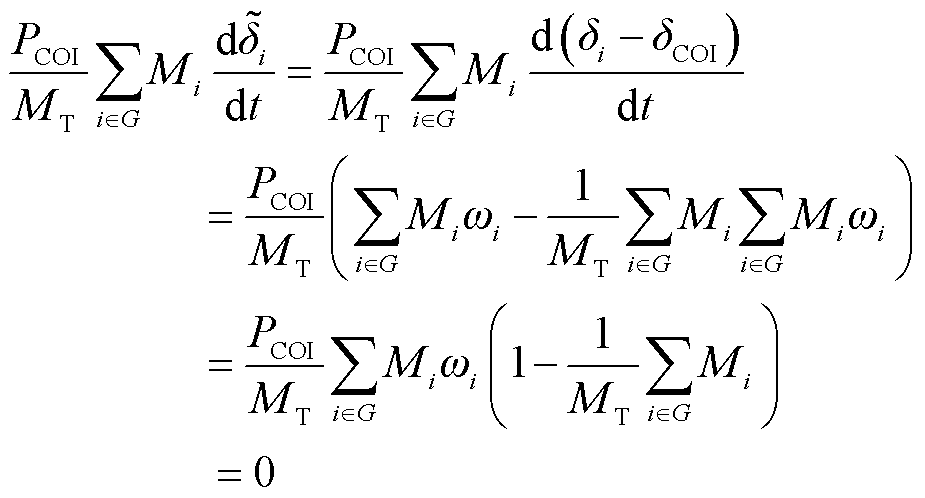 (4)
(4)
进一步,将式(3)对时间积分运算,整理后得到表达系统运动过程的暂态能量函数式(5)。
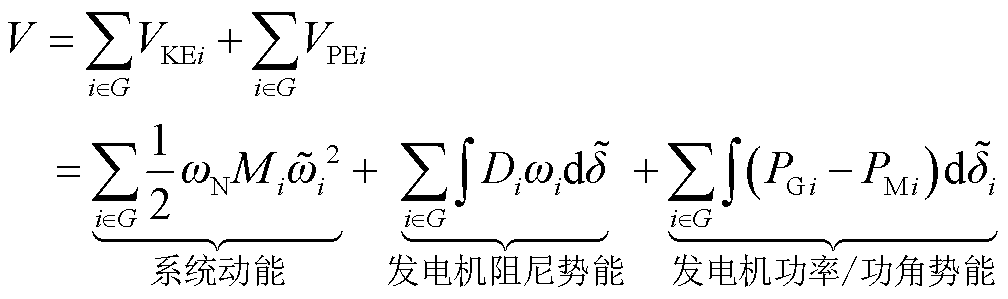 (5)
(5)
式中,VKEi和VPEi分别为发电机的动能和势能。
式(5)描述了基于发电机运动方程的暂态能量函数,包含系统动能、发电机阻尼势能和发电机功率/功角势能。其中,功率/功角势能通过发电机电磁功率与机械功率的不平衡量作用在功角上来表达,而其中电磁功率会因功率平衡要求与电网中不同元件产生联系,各元件能量将在势能上得以体现。
短路故障时系统会被注入大量暂态能量而导致发电机动能增加,动能与势能相互转化,当势能能够完全消纳动能时,则根据能量守恒特性,系统渐近稳定。基于结构保持能量函数理论,暂态能量将在网络元件中广域分布,元件稳定薄弱性源于动态过程中吸纳能量的多少,积聚能量越多的元件环节可视为关键环节。为剖析网络中不同类型元件对暂态能量的消纳水平,需精细化表征出各元件能量。
基于基尔霍夫定律的特勒根第一定理描述了网络中在任何时刻,各支路对应电流与电压乘积之和恒为零。电网中功率满足基尔霍夫电流定律,即节点注入功率等于输出功率;节点角频率满足基尔霍夫电压定律,即闭合回路中从一点出发各段角频率代数和恒等于零。复杂电力系统结构如图1所示。针对图1所示复杂电网,在动态过程中的任意时刻,应用特勒根第一定律,有
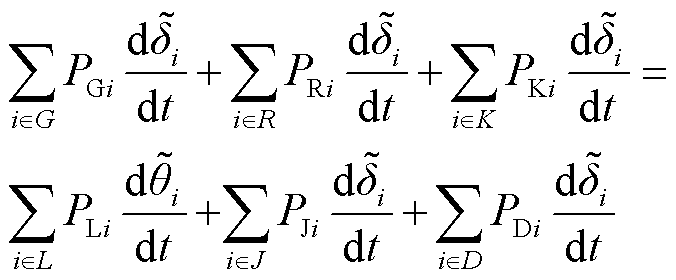 (6)
(6)
式中,R、K、L、J和D分别为新能源节点、直流输电逆变侧节点、增广网络支路、直流输电整流侧节点和负荷节点的集合;PRi和PKi分别为新能源和直流输电逆变侧注入的功率;PJi和PDi分别为直流输电整流侧和负荷吸收的功率;PLi和![]() i分别为增广网络支路(含发电机等效内阻抗增广)的支路功率和支路两侧相位差。
i分别为增广网络支路(含发电机等效内阻抗增广)的支路功率和支路两侧相位差。
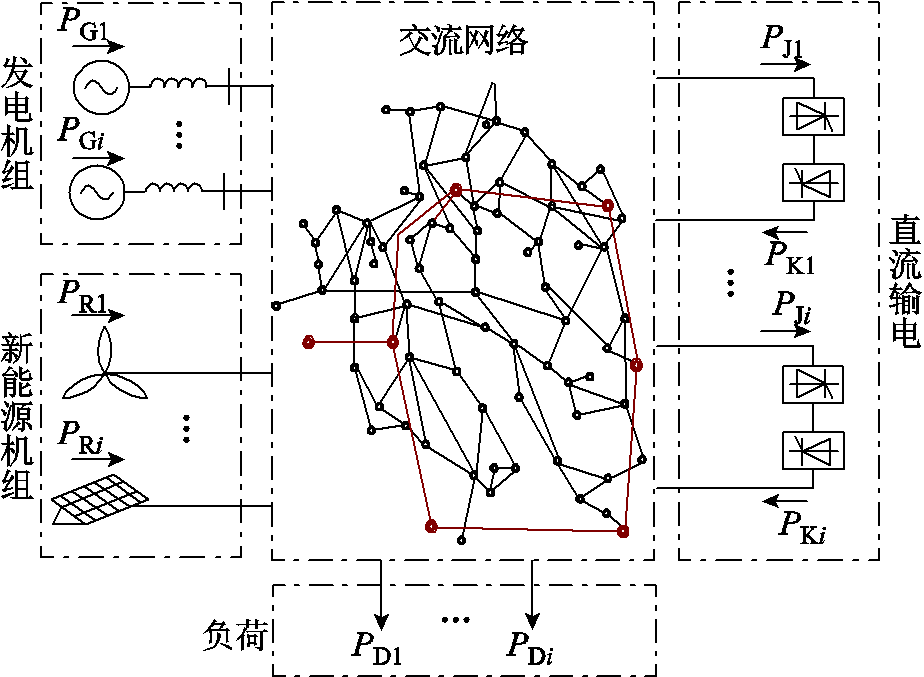
图1 复杂电力系统结构
Fig.1 Structure of a complex power system
故障后保护动作切除故障线路,为使得满足拓扑一致性要求的特勒根定理成立,可视故障后被切除线路为无穷大虚拟阻抗支路,故障前后网络拓扑等效一致。由此,根据特勒根第二定理,基于故障前稳态功率和故障后动态过程角频率,可得
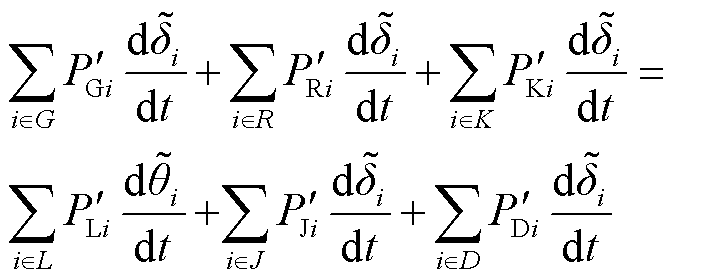 (7)
(7)
式中,带上标“′”的量表示故障前元件稳态功率。
考虑暂态时间尺度下机械功率变化不大,故障后稳态电网发电机电磁功率与机械功率相等,式(7)中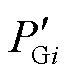 可替换为PMi,对式(6)和式(7)进行时间积分后相减,可将暂态能量函数式(5)中发电机功率/功角势能解构为包括网络中各元件(含开断的无穷大虚拟阻抗支路)能量的代数和形式,复杂电网暂态能量函数的精细化模型可表示为
可替换为PMi,对式(6)和式(7)进行时间积分后相减,可将暂态能量函数式(5)中发电机功率/功角势能解构为包括网络中各元件(含开断的无穷大虚拟阻抗支路)能量的代数和形式,复杂电网暂态能量函数的精细化模型可表示为
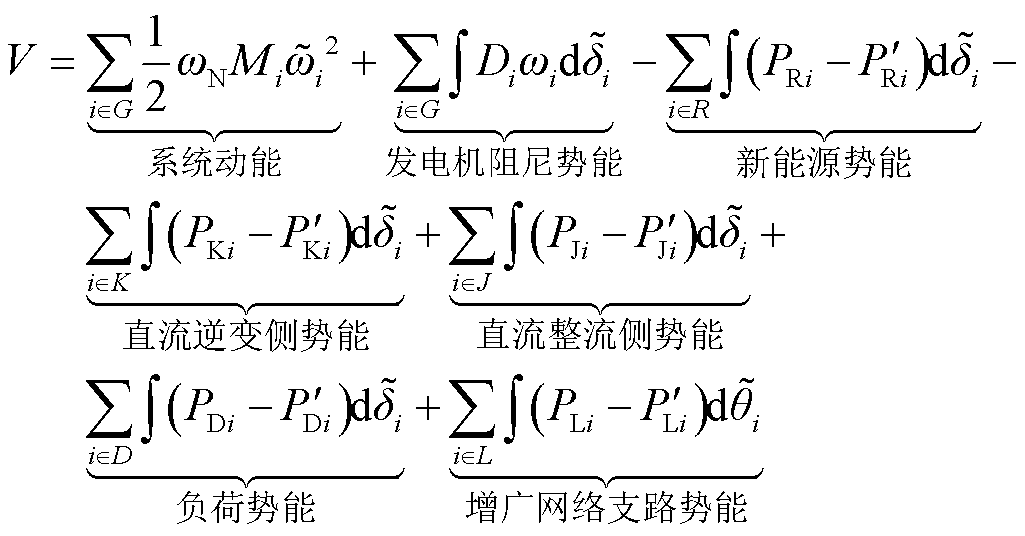 (8)
(8)
式(8)针对复杂电力系统构建了精细化的全网能量函数,充分表达出了各电网环节/元件的暂态能量,为分析暂态过程中不同元件动态的能量响应特性奠定了基础。
故障持续期间电网被注入能量,在故障清除后能量摄入源被阻断,故障后电网动态过程中将发生动能与势能的相互转化,系统总能量保持守恒。为说明所构建能量函数的准确性,对其能量守恒性进行证明。
由式(8)整理可得式(9),式(9)对时间求导运算得到式(10)。
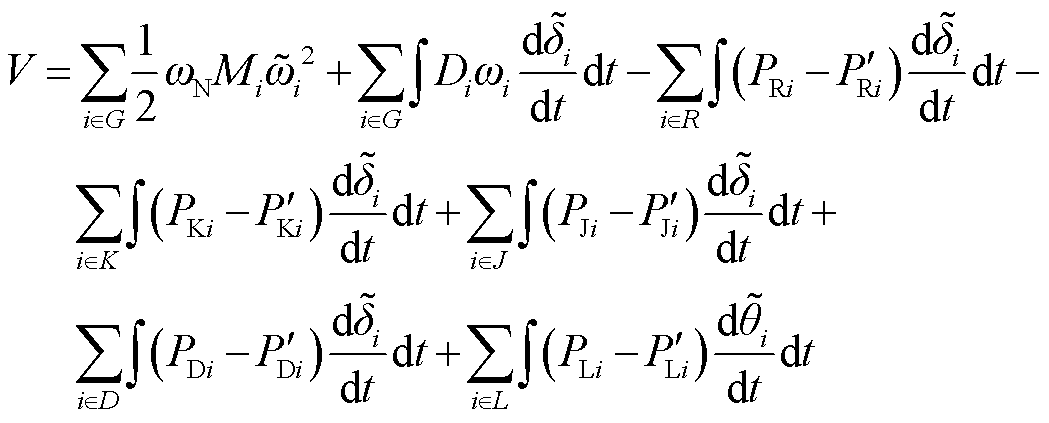 (9)
(9)
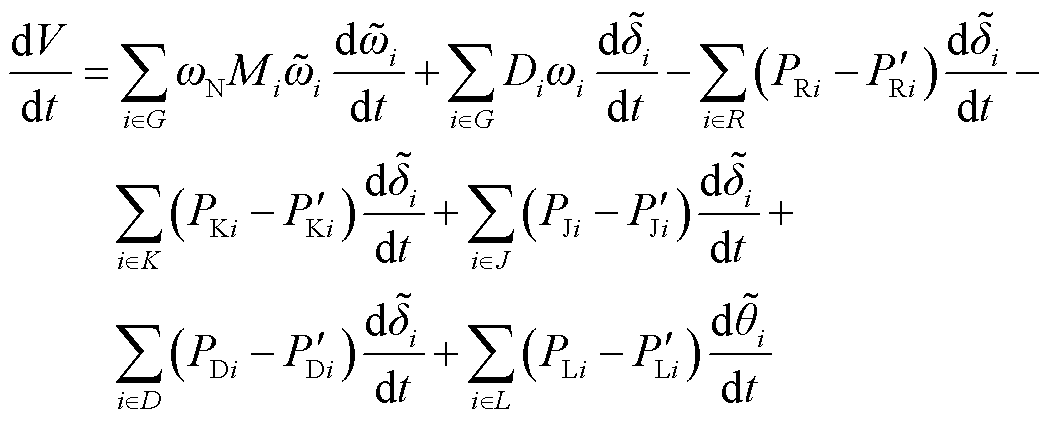 (10)
(10)
式(10)中等号右侧除前两项外,其余项为式(6)和式(7)整理获得,即为其各自等号左侧第一项之差的形式,进而得到式(11),结合式(3)可知式(11)恒为零。
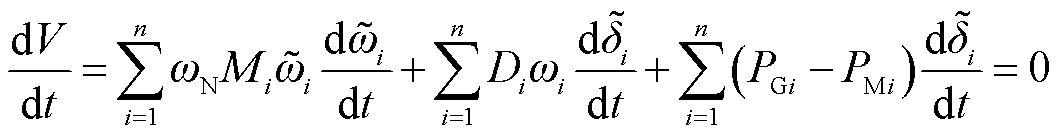 (11)
(11)
式中,n为系统内同步发电机的总数。式(11)表明了本文所构建能量函数的守恒特性。
本文所构建的能量函数面向电网动态响应功率轨迹,而不依赖于具体的元件数学模型及其参数(例如,发电机六阶模型、电动机三阶模型等),相较于现有能量函数构建方法[30-32],可有效地减少电网模型及参数不准确对能量函数建模的影响,便于在线实时计算,对复杂电网具有更强的适应性和鲁棒性。
能量函数刻画下的暂态过程中动能和势能的相互转化关系与系统稳定性直接相关,结合系统稳定/失稳过程中动势能演化特征,提取反映系统稳定状态的特征量作为关键特征量。
1)简单系统稳定/失稳过程的能量特征。在单机对无穷大母线构成的简单系统中,其稳定情况可由功角特性曲线中加速面积与减速面积的大小关系判断。如图2所示,当系统稳定时,对应的加速面积Sabcd等于减速面积Sdefg,此时在加速过程中系统动能的增加量将在减速过程中到达f点时消减为零,对应势能达到极大值,功角摆开至δm,映射滚球模型中,滚球在移动至势能极大值的高度hm(对应功角δm)处时速度减小为零,此时动能完全转化为势能,小球将最终回摆到稳定运行点(Stable Equilibrium Point, SEP);当系统失稳时,对应加速面积Sabkh大于减速面积Shij,此时加速过程中累积的动能在减速过程到达j点时未完全转化为势能,对应总势能极大值时刻仍保留了部分动能,功角将在到达δu的基础上进一步增大,在滚球模型中体现为功角摆开至δu时,滚球到达势能极大值的高度hu处(不稳定平衡点(Unstable Equilibrium Point, UEP))时速度不为零,滚球将越过UEP而无法回到SEP,对应功角持续增大。以上针对简单系统表明,若动能在势能极大值时为零,动能完全转化为极大值时的势能,系统可保持稳定;若动能在势能极大值时不为零,则系统将失去稳定。
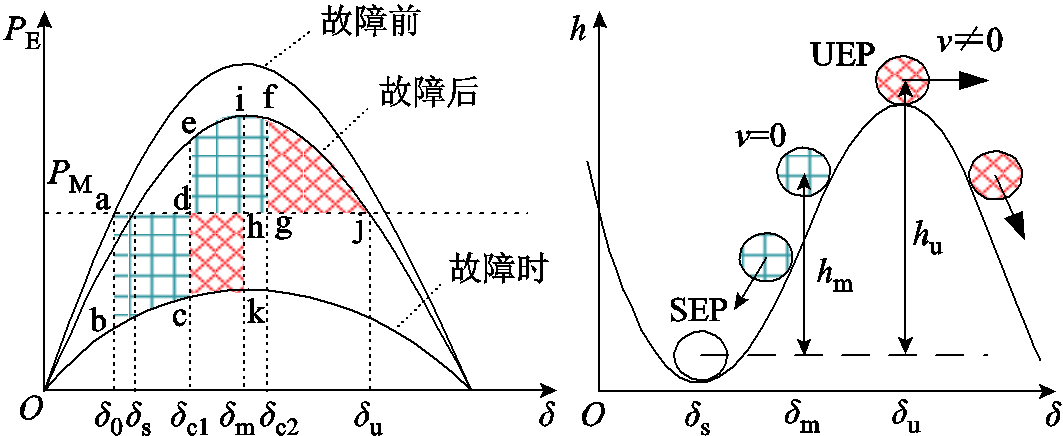
图2 暂态稳定/失稳过程分析
Fig.2 Transient stability/instability process analysis
2)复杂系统稳定/失稳的关键特征提取。针对复杂系统,新能源和直流输电等新型电气元件的接入,其对应的势能部分更改了原系统的能量分布,但复杂系统暂态过程总体动势能转化过程仍与简单系统类似,当势能能够完全消纳动能时,系统渐近稳定。
以IEEE 10机39节点系统为例,图3和图4分别描述了稳定与失稳情况下发电机转速、总动能和总势能的轨迹。稳定状态下,在势能极大值时刻(绿色虚线所示时刻)各发电机转速轨迹聚焦于COI转速轨迹上,系统同步性得以保持,式(5)中系统总动能趋近零,如图3中蓝色的动能轨迹所示;失稳情况下,在势能极大值时刻各发电机转速与COI转速呈现较大差异性,此时总动能较大,系统失步性得以体现。基于上述,为表征复杂系统暂态稳定程度,结合动态过程中总势能极大值时刻的动能特征,定义系统稳定预判因数(Stability Prediction Factor, SPF),表达式为
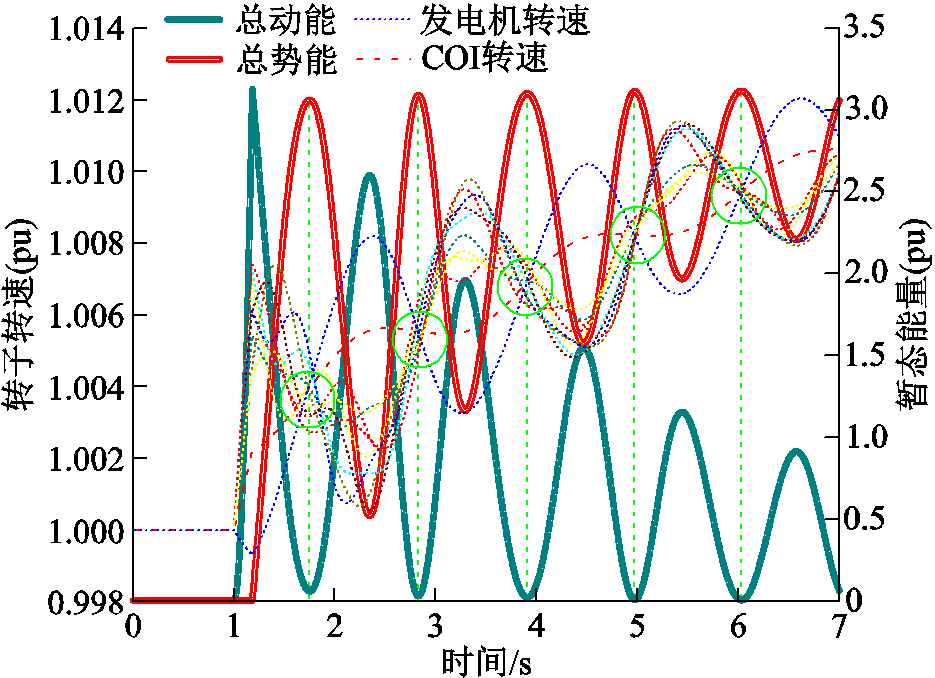
图3 稳定情况下转子转速与暂态能量
Fig.3 Rotor speed and transient energy under stable status
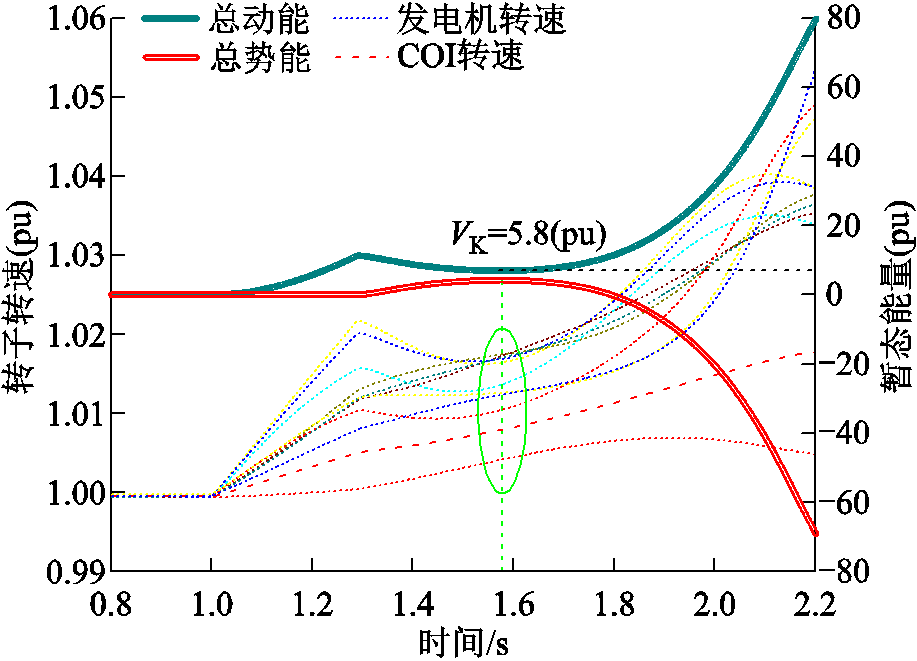
图4 失稳情况下转子转速与暂态能量
Fig.4 Rotor speed and transient energy under unstable status
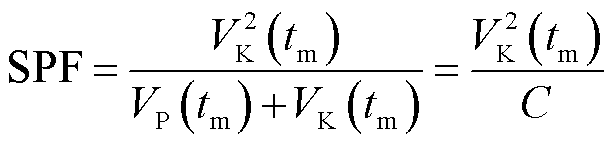 (12)
(12)
式中,tm为系统总势能极大值对应时刻;VK、VP分别为系统总动能与总势能;C为故障后系统暂态总能量,为常数。
上述SPF作为表征系统稳定/失稳的关键特征量,其计算仅需各发电机的转速ω量测信息,便于实时计算。SPF数值越大表明系统在势能极大值时动能越大,系统易于失稳;SPF数值趋于零时表明在势能极大值时动能亦趋近零,同步性保持,系统易于稳定。同时,引入总势能极大值时刻对应的发电机最大功角差(Maximum Angle Deviation, MAD)作为另一关键特征量以提高判稳可靠性,当SPF数值大、MAD数值大,表征系统呈现失稳状态;SPF数值小,MAD数值小,系统呈现稳定状态。
上述所构建的关键特征量与系统稳定/失稳状态具有直接的逻辑推理关系,然而具体特征量与稳定/失稳状态的映射关系难以直接建模。为此,本文提出一种基于数据驱动ANFIS逻辑推理的暂态稳定判别模型,实现关键特征量与稳定/失稳状态间的量化映射,用于实时暂态稳定判别,所构成的判稳结构如图5所示。ANFIS融合了神经网络和模糊逻辑,针对样本数据结合反向传播算法和最小二乘法的混合算法自适应构建出if-then形式的逻辑推理系统,对推理结果具备相应的可解释性。ANFIS共包含模糊化层、规则层、归一化层、解模糊层、输出层五个层次[33-34]。
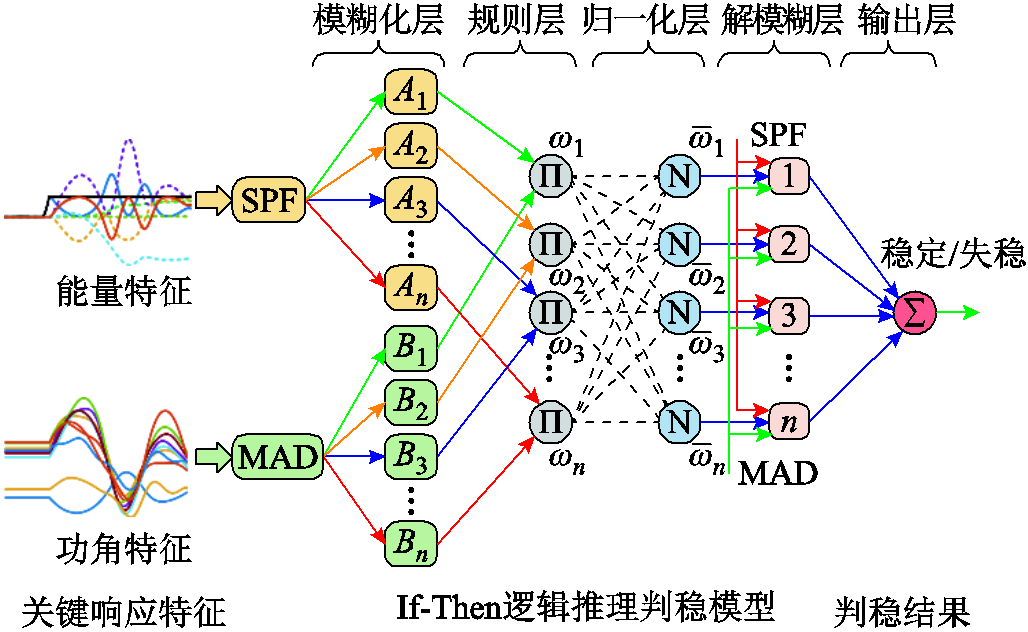
图5 基于ANFIS逻辑推理判稳结构
Fig.5 Transient stability assessment structure based on ANFIS logical reasoning
模糊化层:通过隶属度函数对输入特征量(SPF和MAD)进行模糊处理得到隶属度,有
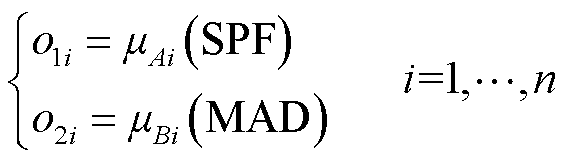 (13)
(13)
式中,n为模糊集数;o1i、o2i分别为输入特征对应的隶属度;Ai、Bi为模糊集;μAi和μBi为各特征的隶属度函数,其隶属度函数中的参数(条件参数)通过样本数据由反向传播算法优化调整。
规则层:将每个特征的隶属度进行代数积得到推理规则,确定各条规则的触发强度ωi。
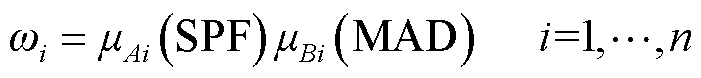 (14)
(14)
归一化层:将上层规则触发强度进行归一化,表征出各规则在整个规则库中的触发比重![]() i。
i。
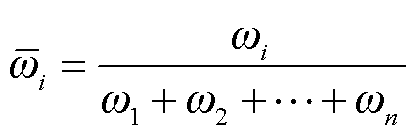 (15)
(15)
解模糊层:确定模糊规则的输出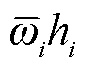 。
。
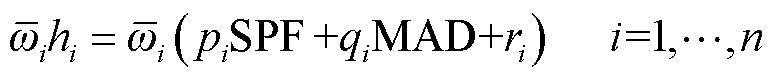 (16)
(16)
式中,pi、qi和ri为规则后件参数,通过样本数据由最小二乘法计算得出。
输出层:通过将解模糊层结果加权求和,得到最终输出结果h。
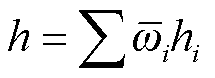 (17)
(17)
综合上述ANFIS各层表达,其输入-输出可总结归纳为if-then的推理结构,推理表达形式为
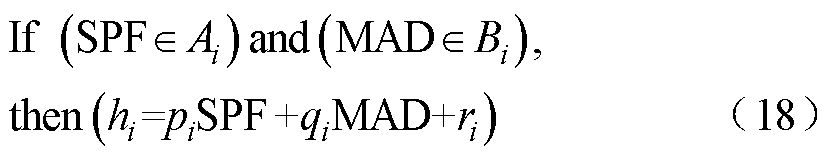
此结构能直观地体现出SPF和MAD与系统稳定/失稳状态间的映射关系,具有相应的可解释性。
ANFIS基于样本数据学习确定其条件参数和后件参数,以得到ANFIS稳定推理模型,进而应用于在线实时稳定判别。样本数据包括SPF、MAD特征量和稳定与否状态量的数据集,数据集针对不同故障场景和运行方式,通过收集发电机转速与功角信息,在势能极大值时刻计算SPF和MAD特征量,稳定状态的0-1标签量则通过式(19)得到。
 (19)
(19)
式中,∆δmax为仿真时间内任意两发电机间的功角差最大值。SLab<0时,为失稳样本,对应标签为1;反之,对应标签为0。
基于学习得到的ANFIS判稳模型,在线应用时针对故障后量测的发电机转速和功角信息,计算特征量SPF和MAD以实时推断稳定/失稳状态,为紧急响应控制提供动作依据。
基于IEEE 9节点测试系统[35]的简单算例系统如图6所示。稳态时发电机G1和G2出力分别为85 MW和163 MW,节点1为无限大功率母线。考虑节点8处发生三相短路故障,分别针对不含风电接入和有风电接入情况下的SPF和MAD与系统稳定性状态间的关系进行分析。
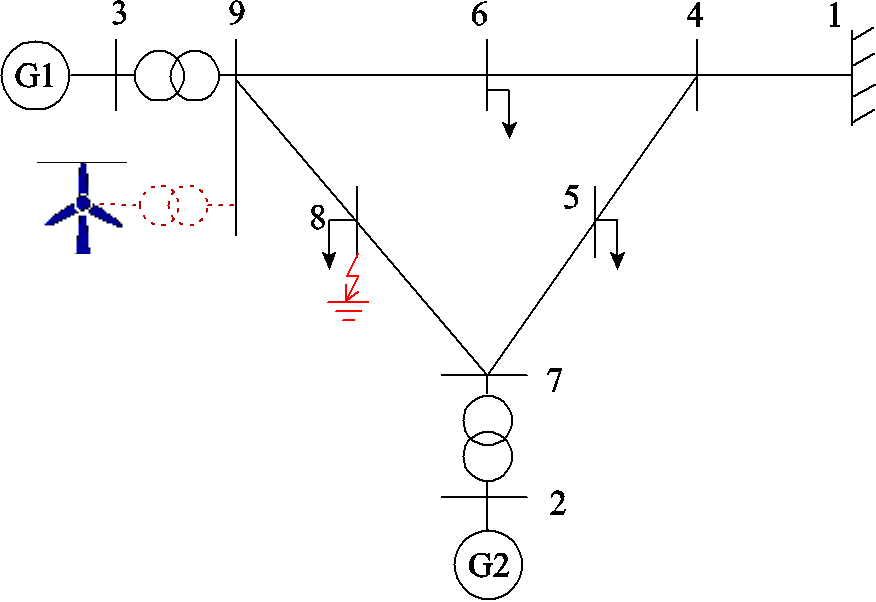
图6 简单算例系统
Fig.6 Simple test system
不含风电接入时,故障持续9~14周波下对应的SPF和MAD与系统稳定状态关系如图7所示。故障持续时间增加,系统逐渐由稳定转变为失稳状态,在稳定状态时,SPF和MAD数值小,尤其SPF数值较小,当系统为临界稳定状态时,SPF和MAD数值分别为0.004和2.73;当系统失稳时,对应的SPF和MAD数值均大于稳定状态时数值,在临界失稳时,SPF和MAD数值为0.012和2.91。根据稳定与失稳状态时SPF和MAD的数值差异可判别系统是否失稳。
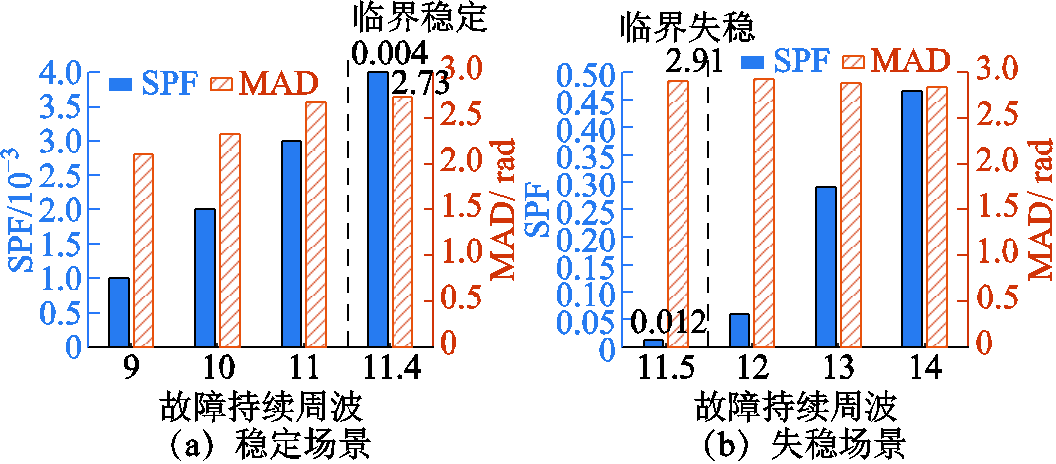
图7 稳定/失稳情况下关键特征量化范围
Fig.7 Range of key features values for stable/unstable status
考虑节点9处接入双馈风电机组,其稳态时出力为发电机G1出力的50%,故障持续9~14周波时对应的SPF和MAD与系统稳定状态关系如图8所示。同样地,在稳定状态时SPF和MAD相较于失稳状态时的数值小,临界稳定时SPF和MAD分别为0.071和2.66,临界失稳时SPF和MAD分别为0.08和2.68。双馈风机的接入影响了系统暂态稳定的响应过程,改变了能量分布,在稳定和失稳状态时SPF和MAD数值发生了变化,但SPF和MAD数值较大时系统表征为失稳状态,SPF和MAD数值较小时系统呈现稳定状态的性质不变。
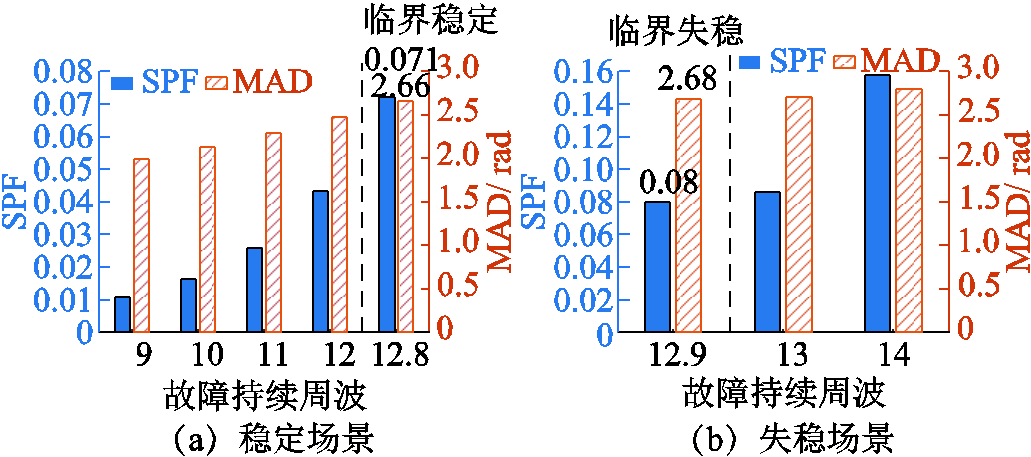
图8 含风机时系统稳定/失稳情况下关键特征量化范围
Fig.8 Range of key features values for stable/unstable status in system with wind turbine
随着系统规模增大,含有新能源等新型元件接入时,系统动态复杂程度增加,难以直接利用经验解析出SPF和MAD数值大小与系统稳定性间的关系。为此,本文引入具有逻辑推理性质的数据驱动ANFIS算法建立SPF和MAD与系统稳定性间的映射模型。
标准IEEE 10机39节点系统包含10台同步发电机、在12台变压器和46条交流线路[36]。本文在标准系统的基础上,在26节点和28节点接入双馈风电机组,稳态时出力分别为220 MW和250 MW,3-18和4-14交流线路替换为直流输电线路,23节点和24节点负荷为感应电动机负载,其余节点负荷为恒阻抗负荷,系统的整体结构如图9所示。
3.2.1 稳定/失稳场景下功角/能量轨迹
以5节点处发生三相短路故障,故障清除同时切除线路的场景为例,故障持续时间分别为190 ms和220 ms,能量积分从故障清除时开始计算,得到稳定和失稳情况下的功角及能量轨迹如图10和图11所示。
从系统总能量角度分析,故障期间能量持续注入,而故障切除后系统总能量保持守恒。由图10所示,稳定状态下总势能与总动能均具有边界性,在每个总势能极大值时动能占比极小,在首个总势能波峰处对应SPF和MAD数值分别为0.021和2.71,其后波峰处的SPF和MAD数值均减少,系统表现为同步性;由图11所示,失稳状态下,在总势能极大值时(1.90 s),SPF为0.26、MAD为3.23,此后系统总动能持续增大,系统失去同步稳定性。SPF和MAD特征能够有效反映出系统稳定/失稳状态,可用于后续的稳定推理评估。此外,针对不同元件的暂态能量轨迹,稳定时各元件能量均为有界演化而失稳时部分元件的能量逐渐趋于无界(负荷势能、风机势能、支路势能),直流输电的整流侧和逆变侧势能具有抵消性,二者之和的势能变化不大,失稳过程中能量分摊较多的元件受影响最为严重,视为电网薄弱性环节,可用于指导稳定紧急控制,1.2节所构建的精细化能量函数将在后续研究中进一步用于关键环节定位与紧急控制。
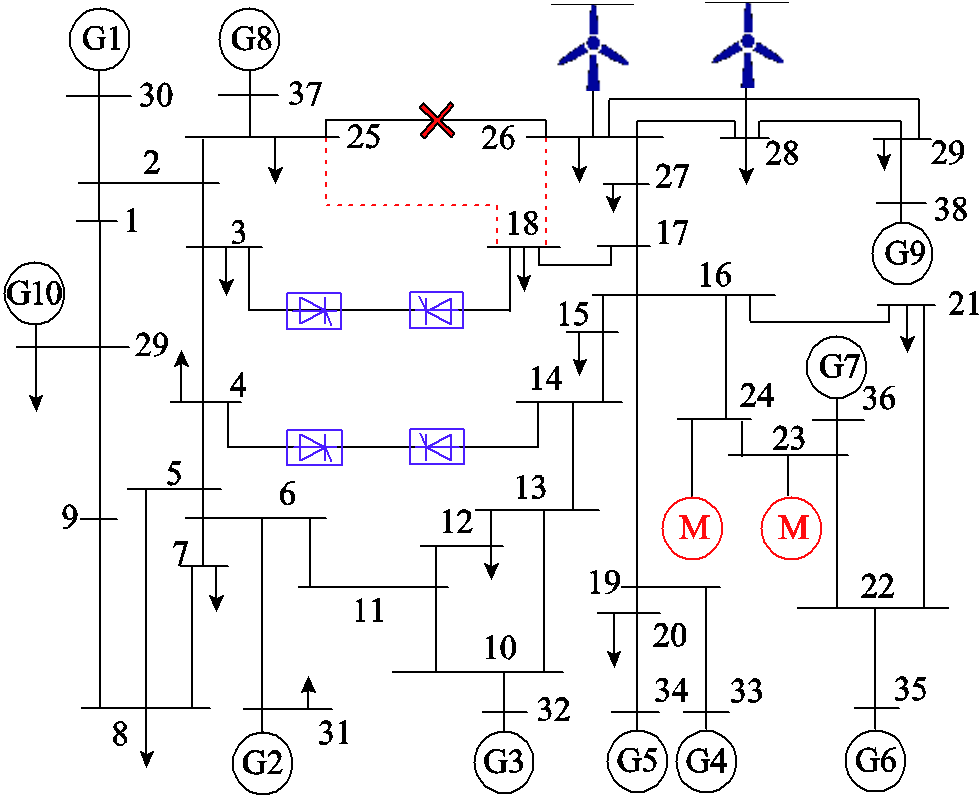
图9 修改后的10机39节点系统
Fig.9 Modified 10-machine 39-bus system
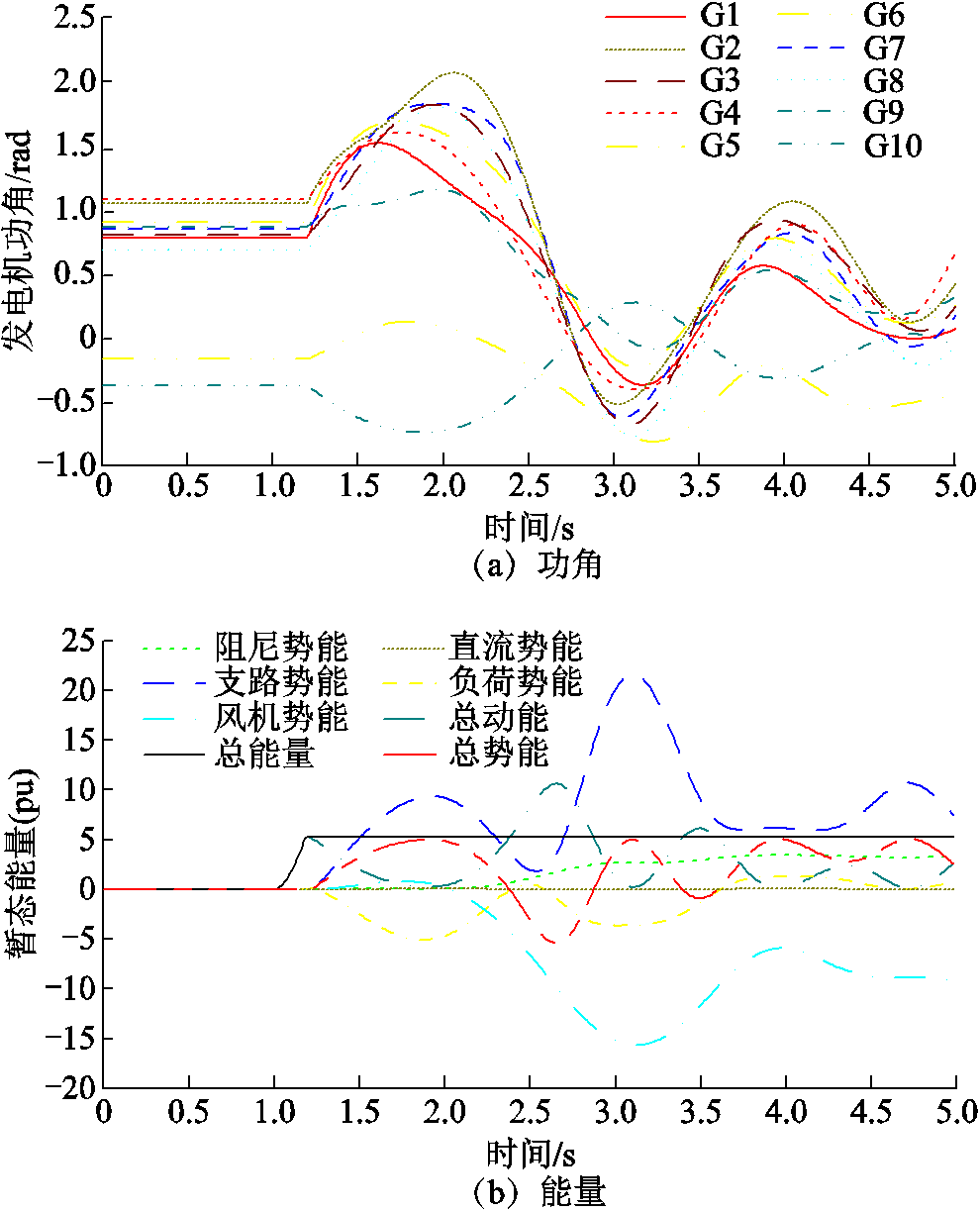
图10 稳定场景下功角与能量轨迹
Fig.10 Trajectory of angle and transient energy under stability
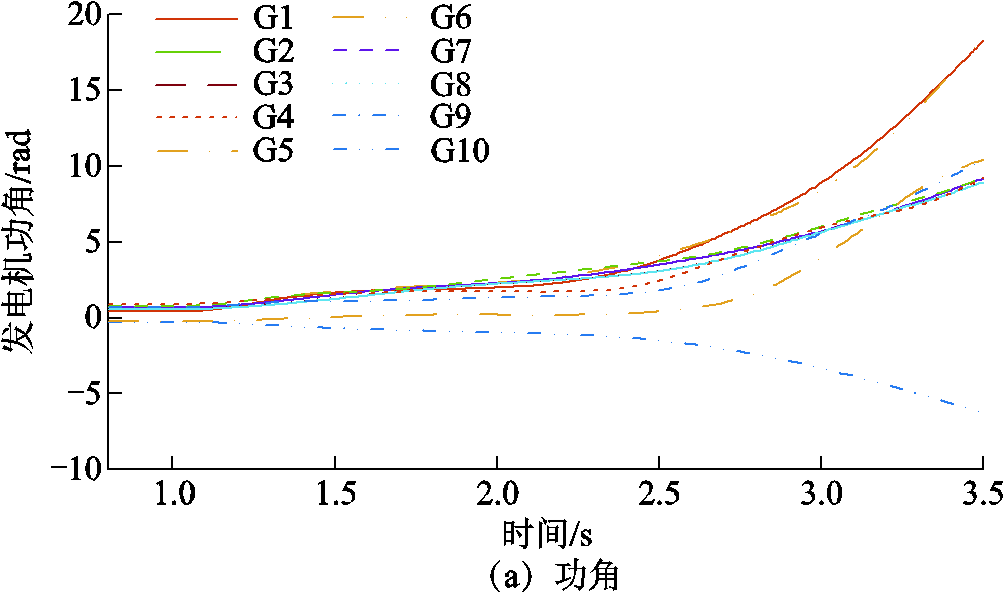
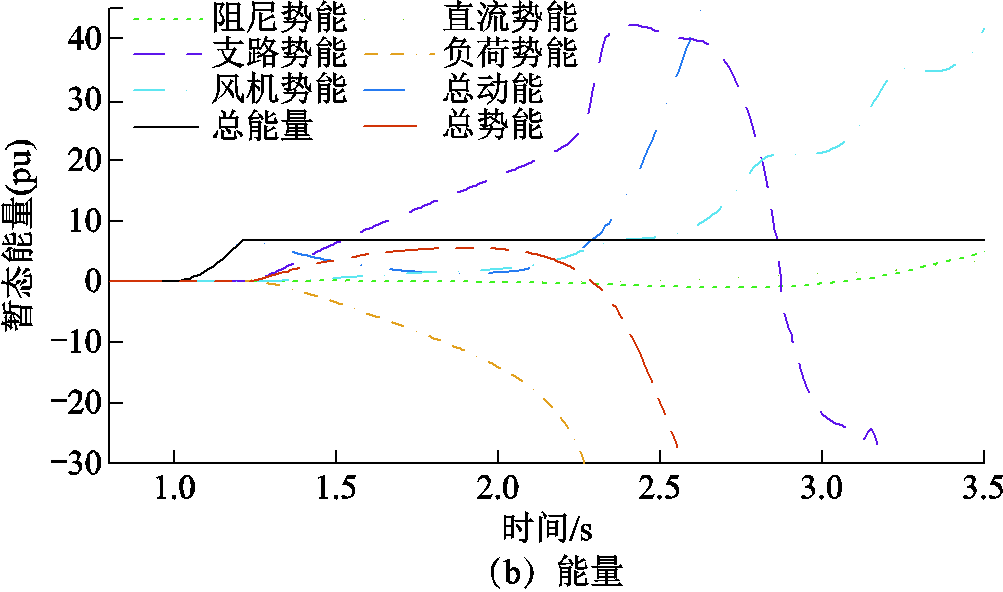
图11 失稳场景下功角与能量轨迹
Fig.11 Trajectory of angle and energy under unstable status
3.2.2 自适应逻辑推理判稳效果
以系统中各节点处发生持续时间为6、7、8,9和10个周波三相短路故障作为故障集,其中,故障的处理方式包括直接清除故障和在清除故障同时切除对应线路。在不同发电机出力与节点负荷大小情况下共生成算例样本2 700组,其中稳定样本与失稳样本比例为3:1(2 025:675),训练集与测试集的比例为5:1(2 250:450)。
为说明本文所提稳定性判别方法的准确性,将测试集的判稳效果展示于表1中。其中,错判表示将稳定场景判定为失稳;漏判表示将失稳场景判定为稳定;超前时间表示判稳时刻较系统最大功角差摆开至![]() 时刻所提前的时间。由表1所示,不同故障持续时间下,本文所提稳定判别方法在保持较快判定时间的同时兼具较高的准确程度。
时刻所提前的时间。由表1所示,不同故障持续时间下,本文所提稳定判别方法在保持较快判定时间的同时兼具较高的准确程度。
表1 逻辑推理判稳效果
Tab.1 Performance of the proposed method

周波平均超前时间/ms错判率(%)漏判率(%)准确率(%) 6544.31.111.1197.78 7631.401.1198.89 8657.102.2297.78 9518.21.111.1197.78 10483.71.112.2296.67
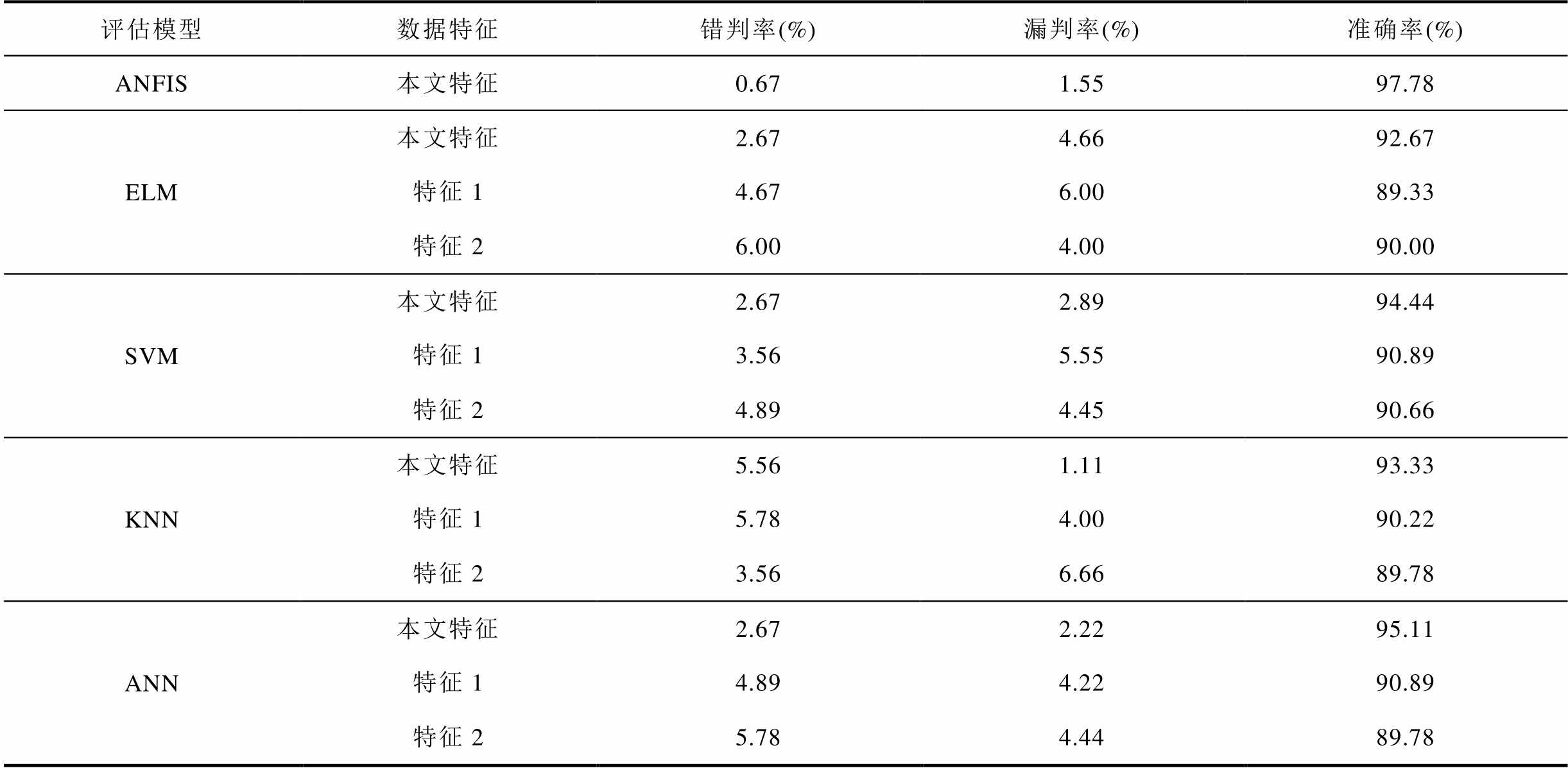
为展现本文方法的优势,选取多种人工智能算法分别使用包含本文所提关键特征在内的不同稳定判定特征进行对比。所对比的人工智能算法包括极限学习机(ELM)、支持向量机(SVM)、临近算法(KNN)、人工神经网络(ANN)。其中,ELM隐层神经元数为20,激活函数选择Sigmoid;SVM选择高斯核函数,正则化参数为1 000;KNN临点个数设置为3,距离量度选择Euclidean,等距离权重;ANN层数为4层,每层神经元个数为10,激活函数选择ReLU。同时,为说明本文特征量选取的有效性,对比了特征1:文献[37]中所采用的故障清除时刻、清除后第6个周波和9个周波时的7维电气量信息;特征2:文献[38]中所采用的故障前、故障发生时刻和故障清除后第2个周波的4维电气量信息。针对上述450个测试集,对比结果见表2。相比其他人工智能算法,本文结合所选取的特征量及逻辑推理判稳方法能够更准确地判别稳定状态,判稳准确率达97.78%,相较于其他方法对复杂电网的判稳准确率更高。同时,相较其他输入特征,本文所提的稳定特征更能够反映系统的稳定状态,具备与稳定状态关联的强物理属性,采用本文特征亦能够提高其他人工智能方法的判稳准确性。
表2 判稳效果对比
Tab.2 Comparison of different stability assessment methods
评估模型数据特征错判率(%) 漏判率(%)准确率(%) ANFIS本文特征0.671.5597.78 ELM本文特征2.674.6692.67 特征14.676.0089.33 特征26.004.0090.00 SVM本文特征2.672.8994.44 特征13.565.5590.89 特征24.894.4590.66 KNN本文特征5.561.1193.33 特征15.784.0090.22 特征23.566.6689.78 ANN本文特征2.672.2295.11 特征14.894.2290.89 特征25.784.4489.78
3.2.3 泛化性能分析
泛化能力描述了基于既有样本场景下习得的稳定判别模型对新场景下的适用能力。为展现本文所提判稳方法的泛化性能,进一步考虑了线路25-26断开,线路25-18和26-18投运的新拓扑结构,考虑三相故障持续6~10个周波,每个故障周波生成750个样本,具体判稳效果见表3。
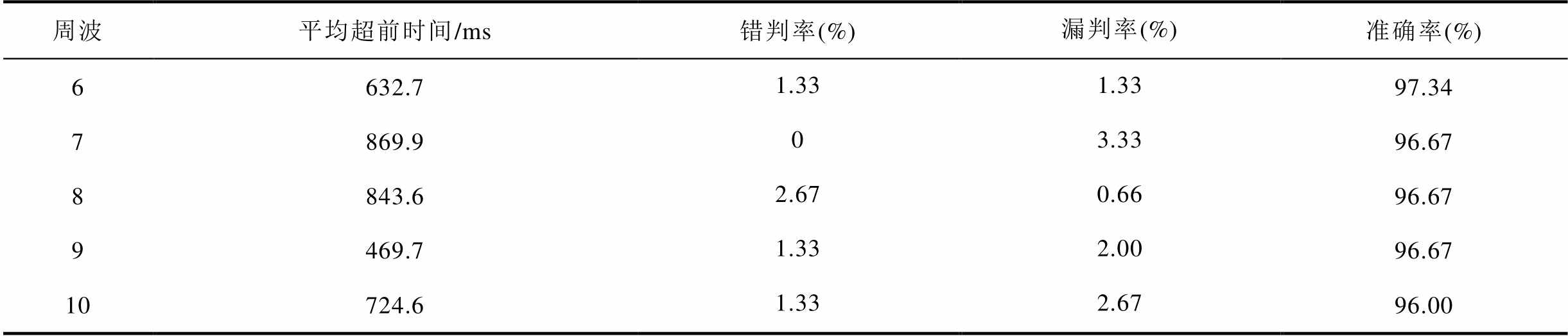
表3 新拓扑场景下本文方法判稳效果
Tab.3 Performance of the proposed method with a new topology scenario
周波平均超前时间/ms错判率(%) 漏判率(%)准确率(%) 6632.71.331.3397.34 7869.903.3396.67 8843.62.670.6696.67 9469.71.332.0096.67 10724.61.332.6796.00
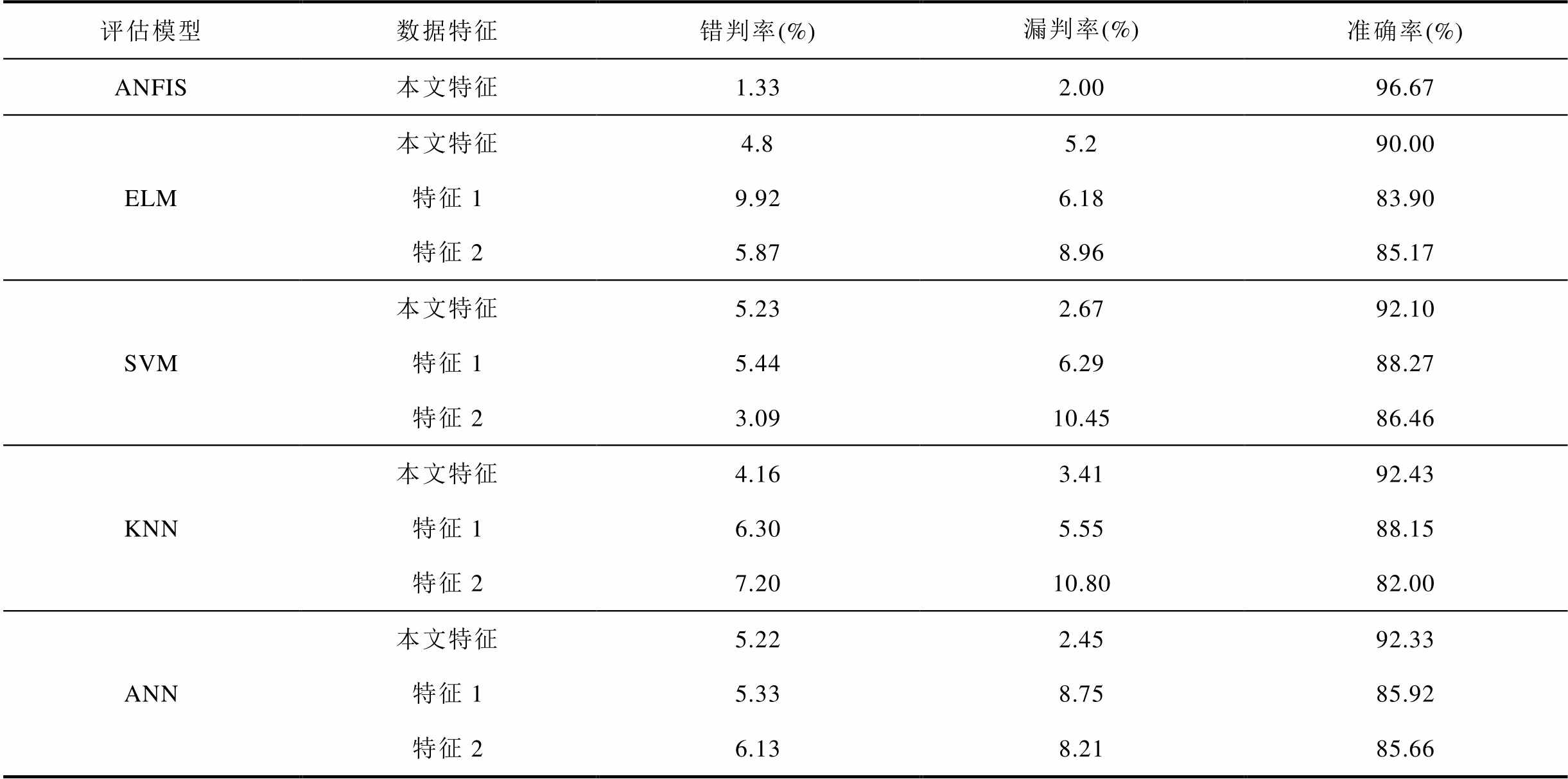
与表1相比,本文所提方法面向拓扑结构更改后系统的稳定性判别仍保持较高的准确率,这说明通过原始样本集构建的稳定/失稳映射关系对于系统拓扑结构的改变具有适应性。表4给出了不同人工智能算法在新拓扑结构下的判稳效果,相较本文方法,其他方法的稳定判别准确率下降明显。应用本文所提取的特征量SPF和MAD判别稳定性时的准确度相对较高,判稳准确率为96.67%,而基于SPF和MAD的ELM、SVM、KNN和ANN方法的准确率分别为90.00%、92.10%、92.43%和92.33%。基于其他文献特征的判稳准确率下降更大,准确率均不超过90.00%。本文所提出的基于ANFIS逻辑推理的稳定判别方法在系统拓扑结构变化时仍具有较好的判稳适应性。
表4 新拓扑场景下不同判稳方法效果对比
Tab.4 Comparison of different stability assessment methods with a new topology scenario
评估模型数据特征错判率(%) 漏判率(%)准确率(%) ANFIS本文特征1.332.0096.67 ELM本文特征4.85.290.00 特征19.926.1883.90 特征25.878.9685.17 SVM本文特征5.232.6792.10 特征15.446.2988.27 特征23.0910.4586.46 KNN本文特征4.163.4192.43 特征16.305.5588.15 特征27.2010.8082.00 ANN本文特征5.222.4592.33 特征15.338.7585.92 特征26.138.2185.66
为提高含新能源的交直流混联复杂电网的实时稳定性判别水平,实现具有逻辑推理性的实时稳定判别。本文结合转子运动方程与特勒根定理构建了面向电网响应信息的可精细化解构能量函数,提取了与系统稳定情况强相关的关键特征量SPF和MAD,提出了基于ANFIS的自适应逻辑推理的稳定/失稳映射模型。最终,在简单系统中量化分析了SPF和MAD与系统稳定性之间的关系,在含新能源和直流输电的IEEE 10机39节点系统中验证了本文方法的有效性和泛化性。研究过程中所得结论如下:
1)利用系统各元件动态响应信息构建了适用于复杂电力系统暂态能量函数模型,所提取的关键特征量SPF和MAD与系统稳定/失稳状态具有强关联特性,相较于其他响应特征量可更直接地表征系统稳定状态。
2)所建立的基于数据驱动ANFIS的if-then逻辑推理稳定性判别模型,输入特征量SPF和MAD与稳定性状态间的映射过程更具有可解释性,面向复杂系统暂态稳定性判别准确率更高,判稳准确率高达97.78%。
3)所提出的判稳方法在电网拓扑变化情况下仍保持较高判稳准确率,在电网拓扑变化后基于原有ANFIS判稳模型和响应特征量SPF和MAD的判稳准确率为96.67%,仍具有较好的泛化性能。
参考文献
[1] 陈国平, 李明节, 许涛, 等. 关于新能源发展的技术瓶颈研究[J]. 中国电机工程学报, 2017, 37(1): 20-27.
Chen Guoping, Li Mingjie, Xu Tao, et al. Study on technical bottleneck of new energy development[J]. Proceedings of the CSEE, 2017, 37(1): 20-27.
[2] 肖湘宁. 新一代电网中多源多变换复杂交直流系统的基础问题[J]. 电工技术学报, 2015, 30(15): 1-14.
Xiao Xiangning. Basic problems of the new complex AC-DC power grid with multiple energy resources and multiple conversions[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 1-14.
[3] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822.
Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4808-4822.
[4] 叶瑞丽, 刘瑞叶, 刘建楠, 等. 直驱风电机组风电场接入后的电力系统暂态稳定计算[J]. 电工技术学报, 2014, 29(6): 211-218.
Ye Ruili, Liu Ruiye, Liu Jiannan, et al. Transient stability calculation of power system integrated with direct-drive wind farm with permanent magnet synchronous generators[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 211-218.
[5] 郑超, 孙华东, 牛振波. 暂态功角多群失稳机制及基于广域支路响应的阻断控制[J]. 电网技术, 2023, 47(2): 722-731.
Zheng Chao, Sun Huadong, Niu Zhenbo. Transient rotor angle multi-group instability mechanism and fast blocking control based on wide area branches’ response[J]. Power System Technology, 2023, 47(2): 722-731.
[6] 吴政球, 荆勇. 基于时域仿真的暂态稳定裕度灵敏度分析[J]. 中国电机工程学报, 2001, 21(6): 19-24.
Wu Zhengqiu, Jing Yong. Transient stability sensitivity based on time domain simulation[J]. Proceedings of the CSEE, 2001, 21(6): 19-24.
[7] Lee J, Chiang H D. A singular fixed-point homotopy method to locate the closest unstable equilibrium point for transient stability region estimate[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2004, 51(4): 185-189.
[8] 林玉章, 蔡泽祥. 基于PEBS法的交直流输电系统暂态稳定分析[J]. 电力自动化设备, 2009, 29(1): 24-28.
Lin Yuzhang, Cai Zexiang. Transient stability analysis of AC/DC power system based on PEBS method[J]. Electric Power Automation Equipment, 2009, 29(1): 24-28.
[9] Chiang H D, Wu F F, Varaiya P P. Foundations of the potential energy boundary surface method for power system transient stability analysis[J]. IEEE Transactions on Circuits and Systems, 1988, 35(6): 712-728.
[10] 李锡林, 查晓明, 田震, 等. 考虑频率突变影响的孤岛微电网系统建模和基于Lyapunov第二法的暂态稳定性分析[J]. 电工技术学报, 2023, 38(增刊1): 18-31.
Li Xilin, Zha Xiaoming, Tian Zhen, et al. Modeling of island microgrid considering frequency mutation and transient stability analysis based on lyapunov second method[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 18-31.
[11] Chiang H D, Wu F, Varaiya P. Foundations of direct methods for power system transient stability analysis[J]. IEEE Transactions on Circuits and Systems, 1987, 34(2): 160-173.
[12] 黄通, 王杰. 基于改进EEAC法的随机复杂多机系统的暂态稳定性分析[J]. 电网技术, 2017, 41(4): 1174-1182.
Huang Tong, Wang Jie. Transient stability analysis of stochastic complex multi-machine system based on improved extended equal-area criteria[J]. Power System Technology, 2017, 41(4): 1174-1182.
[13] Paudyal S, Ramakrishna G, Sachdev M S. Application of equal area criterion conditions in the time domain for out-of-step protection[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 600-609.
[14] 魏少攀, 杨明, 韩学山, 等. 基于相轨迹MLE指标的暂态功角稳定在线辨识[J]. 电力系统自动化, 2017, 41(16): 71-79.
Wei Shaopan, Yang Ming, Han Xueshan, et al. Online identification for transient angle stability based on MLE index of phase trajectory[J]. Automation of Electric Power Systems, 2017, 41(16): 71-79.
[15] Wei Shaopan, Yang Ming, Qi Junjian, et al. Model-free MLE estimation for online rotor angle stability assessment with PMU data[J]. IEEE Transactions on Power Systems, 2018, 33(3): 2463-2476.
[16] 谢欢, 张保会, 于广亮, 等. 基于相轨迹凹凸性的电力系统暂态稳定性识别[J]. 中国电机工程学报, 2006, 26(5): 38-42.
Xie Huan, Zhang Baohui, Yu Guangliang, et al. Power system transient stability detection theory based on characteristic concave or convex of trajectory[J]. Proceedings of the CSEE, 2006, 26(5): 38-42.
[17] 范新凯, 杨松浩, 赵一铭, 等. 基于相轨迹凹凸性的暂态失稳判据准确性验证[J]. 电力自动化设备, 2021, 41(1): 159-165, 171.
Fan Xinkai, Yang Songhao, Zhao Yiming, et al. Accuracy verification of transient instability criterion based on concavity and convexity of phase trajectory[J]. Electric Power Automation Equipment, 2021, 41(1): 159-165, 171.
[18] 郑超, 孙华东, 赵兵. 基于关键支路sBTTC指数幅相相关性的主导稳定形态判别与多级主动控制[J]. 中国电机工程学报, 2022, 42(7): 2474-2486.
Zheng Chao, Sun Huadong, Zhao Bing. Dominant stability mode discrimination and multilevel stability control based on amplitude-phase correlation of critical branch’s sBTTC index[J]. Proceedings of the CSEE, 2022, 42(7): 2474-2486.
[19] 郑超, 孙华东, 张爱军, 等. 基于广域支路响应的功角与电压主导稳定模式判别及紧急控制[J]. 中国电机工程学报, 2021, 41(18): 6148-6160.
Zheng Chao, Sun Huadong, Zhang Aijun, et al. Discrimination of rotor angle stability and voltage stability based on wide-area branch response and emergency control[J]. Proceedings of the CSEE, 2021, 41(18): 6148-6160.
[20] 蔡国伟, 穆钢, Chan K W, 等. 基于网络信息的暂态稳定性定量分析: 支路势能法[J]. 中国电机工程学报, 2004, 24(5): 1-6.
Cai Guowei, Mu Gang, Chan K W, et al. Branch potential energy method for power system transient stability assessment based on network dynamic variables[J]. Proceedings of the CSEE, 2004, 24(5): 1-6.
[21] Padiyar K R, Krishna S. Online detection of loss of synchronism using energy function criterion[J]. IEEE Transactions on Power Delivery, 2006, 21(1): 46-55.
[22] Amjady N, Majedi S F. Transient stability prediction by a hybrid intelligent system[J]. IEEE Transactions on Power Systems, 2007, 22(3): 1275-1283.
[23] 李扬, 李国庆, 顾雪平, 等. 基于集成OS-ELM的暂态稳定评估方法[J]. 电工技术学报, 2015, 30(14): 412-418.
Li Yang, Li Guoqing, Gu Xueping, et al. Transient stability assessment of power systems based on ensemble OS-ELM[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 412-418.
[24] 周艳真, 吴俊勇, 冀鲁豫, 等. 基于两阶段支持向量机的电力系统暂态稳定预测及预防控制[J]. 中国电机工程学报, 2018, 38(1): 137-147, 350.
Zhou Yanzhen, Wu Junyong, Ji Luyu, et al. Two-stage support vector machines for transient stability prediction and preventive control of power systems[J]. Proceedings of the CSEE, 2018, 38(1): 137-147, 350.
[25] You Dahai, Wang Ke, Ye Lei, et al. Transient stability assessment of power system using support vector machine with generator combinatorial trajectories inputs[J]. International Journal of Electrical Power & Energy Systems, 2013, 44(1): 318-325.
[26] 王同文, 管霖, 章小强, 等. 基于扩展k阶近邻法的电力系统稳定评估新算法[J]. 电力系统自动化, 2008, 32(3): 18-21, 75.
Wang Tongwen, Guan Lin, Zhang Xiaoqiang, et al. A new method for power system stability assessment based on extended k-nearest neighbor classifier[J]. Automation of Electric Power Systems, 2008, 32(3): 18-21, 75.
[27] 王步华, 朱劭璇, 熊浩清, 等. 基于长短期记忆神经网络的检修态电网暂态稳定评估方法[J]. 电气技术, 2023, 24(1): 29-35, 43.
Wang Buhua, Zhu Shaoxuan, Xiong Haoqing, et al. Assessment method of transient stability for maintenance power system based on long short term memory neural network[J]. Electrical Engineering, 2023, 24(1): 29-35, 43.
[28] 房佳姝, 刘崇茹, 苏晨博, 等. 基于自注意力Transformer编码器的多阶段电力系统暂态稳定评估方法[J]. 中国电机工程学报, 2023, 43(15): 5745-5759.
Fang Jiashu, Liu Chongru, Su Chenbo, et al. Multi-stage transient stability assessment of power system based on self-attention transformer encoder[J]. Proceedings of the CSEE, 2023, 43(15): 5745-5759.
[29] 陈灏颖, 管霖. 基于主动迁移学习的电力系统拓扑自适应暂态稳定评估[J]. 中国电机工程学报, 2023, 43(19): 7409-7423.
Chen Haoying, Guan Lin. Anactive transfer learning scheme for power system transient stability assessment adaptive to the topological variability[J]. Proceedings of the CSEE, 2023, 43(19): 7409-7423.
[30] 汪小明, 刘涤尘, 吴军, 等. 基于能量函数法的电网暂态稳定性分析[J]. 电网技术, 2011, 35(8): 114-118.
Wang Xiaoming, Liu Dichen, Wu Jun, et al. Energy function-based power system transient stability analysis[J]. Power System Technology, 2011, 35(8): 114-118.
[31] 王科, 秦文萍, 张宇, 等. 双馈风机等效惯量控制比例系数对系统功角首摆稳定的影响机理分析[J]. 电工技术学报, 2023, 38(3): 741-753.
Wang Ke, Qin Wenping, Zhang Yu, et al. Mechanism analysis of effect of equivalent proportional coefficient of inertia control of DFIG on stability of first swing of power angle[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 741-753.
[32] 贾天下, 孙华东, 赵兵, 等. 基于结构保持能量函数的电力系统暂态稳定分析方法研究[J]. 中国电机工程学报, 2020, 40(9): 2819-2826.
Jia Tianxia, Sun Huadong, Zhao Bing, et al. Research on transient stability analysis method of power system based on network structure preserving energy function[J]. Proceedings of the CSEE, 2020, 40(9): 2819-2826.
[33] 梁得亮, 丁文, 鱼振民. 基于自适应网络模糊推理系统的开关磁阻电机建模方法[J]. 中国电机工程学报, 2008, 28(9): 86-92.
Liang Deliang, Ding Wen, Yu Zhenmin. Modeling for switched reluctance motor based on adaptive network-based fuzzy inference system[J]. Proceedings of the CSEE, 2008, 28(9): 86-92.
[34] 于希宁, 程锋章, 朱丽玲, 等. 基于T-S模型的自适应神经模糊推理系统及其在热工过程建模中的应用[J]. 中国电机工程学报, 2006, 26(15): 78-82.
Yu Xining, Cheng Fengzhang, Zhu Liling, et al. ANFIS modeling based on T-S model and its application for thermal process[J]. Proceedings of the CSEE, 2006, 26(15): 78-82.
[35] Sauer P W, Pai M. Power System Dynamics and Stability[M]. Upper Saddle River: Prentice Hall, 1998.
[36] 卢锦玲, 郭鲁豫. 基于改进深度残差收缩网络的电力系统暂态稳定评估[J]. 电工技术学报, 2021, 36(11): 2233-2244.
Lu Jinling, Guo Luyu. Power system transient stability assessment based on improved deep residual shrinkage network[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2233-2244.
[37] 李扬, 顾雪平. 基于改进最大相关最小冗余判据的暂态稳定评估特征选择[J]. 中国电机工程学报, 2013, 33(34): 179-186, 27.
Li Yang, Gu Xueping. Feature selection for transient stability assessment based on improved maximal relevance and minimal redundancy criterion[J]. Proceedings of the CSEE, 2013, 33(34): 179-186, 27.
[38] 王怀远, 陈启凡. 基于代价敏感堆叠变分自动编码器的暂态稳定评估方法[J]. 中国电机工程学报, 2020, 40(7): 2213-2220, 2400.
Wang Huaiyuan, Chen Qifan. A transient stability assessment method based on cost-sensitive stacked variational auto-encoder[J]. Proceedings of the CSEE, 2020, 40(7): 2213-2220, 2400.
Abstract Real-time transient stability assessment is the core of response-driven stability control. With renewable energy and DC transmissions connecting to power systems, the complexity of grid’s structure, operation and characteristics increases significantly, which have challenged the effectiveness and accuracy of existing stability assessment methods. For real-time stability assessment in the complex power system including renewable energy and DC transmissions, an adaptive network based fuzzy inference system (ANFIS) based model-free and interpretable stability assessment method was proposed by using measurable transient energy features. First, based on the energy relation of generator motion equation and the Tellegen’s theorem, the transient energy function using the response information of the complex grid was constructed and its energy conservation was also validated. Then, according to the conversion characteristic between kinetic energy and potential energy, the stability prediction factor was defined, which was combined with maximum angle deviation to obtain the key features of the stability judgment. A mapping model between the key features and stability status based on ANFIS adaptive logic reasoning was proposed to realize real-time prediction of transient stability. Finally, the quantitative analysis of the relationship between the key features and system stability status was illustrated in a simple system, and the effectiveness and generalization of the proposed method were verified in the modified IEEE 10-machine 39-bus system with new energies and DC transmissions.
Firstly, based on the energy relation of the generator rotor movement and the Tellegen’s theorem, a refined energy function model was developed by using the response information of a complex grid, and the energy conservation property of the model was proven. The energy function model can depict the energy response characteristics of various components in the system. By introducing the virtual impedance branch, the potential energy of each component can be conveniently calculated using the pre-fault equilibrium point of power system, which does not depend on the component model and its parameters, showing good generality. Secondly, the conversion characteristics between kinetic energy and potential energy were analyzed under stable and unstable conditions, and then a stability prediction factor (SPF) were defined at the maximum potential energy point. Together with the maximum angle deviation (MAD) at the same point, the critical features SPF and MAD for stability assessment were obtained, which have strong representational ability to indicate the stable/unstable status of the system. Finally, a response-driven stability discrimination model was constructed with the key features SPF and MAD. The stability discrimination model was established based on logical reasoning ANFIS, which can obtain an interpretable mapping model between the key features and the stable/unstable status of the system. This model enables real-time transient stability assessment with interpretability.
This paper quantitatively analyzed the relationship between the key features (SPF and MAD) and system stability status in a modified simple IEEE 9-bus system , and evaluated the effectiveness and generalization of the proposed stability discrimination model in a modified IEEE 10-machine 39-bus system with new energy sources and DC transmissions. The simulation results demonstrated that the proposed key features SPF and MAD, showing strong physical attributes associated with the system stability, can effectively reflect the system stability status. Compared to other AI stability discrimination models, the proposed data-driven ANFIS stability discrimination model had a higher accuracy of stability discrimination in a complex power grid. Thus, it can be effectively applied in subsequent emergency response-driven stability control.
The conclusions of this paper are given as follows: (1) The key features SPF and MAD, extracted from the constructed energy function model, have a strong correlation with the system stable/unstable status. They can directly characterize the system stability condition compared to other response features. (2) The data-driven ANFIS based stability discrimination model establishes the if-then logical inference process between the input features (SPF and MAD) and the system stable/unstable status. It can detect the unstable condition in real-time and show higher accuracy of stability discrimination in a complex power grid compared to other AI stability discrimination methods. (3) The proposed stability analysis method maintains high accuracy even in the presence of changes in the power grid topology, showing good generalization performance.
keywords:Transient stability, response-driven, Tellegen’s theorem, transient energy function, complex power system, adaptive logical reasoning
DOI: 10.19595/j.cnki.1000-6753.tces.230857
中图分类号:TM712
国家重点研发计划资助项目(2021YFB2400800)。
收稿日期 2023-06-06
改稿日期 2023-08-10
杨 浩 男,1988年生,博士,硕士生导师,研究方向为电力系统安全稳定分析与控制,人工智能技术在电力系统中的应用。E-mail:hao_yang@neepu.edu.cn
刘 铖 男,1985年生,博士,硕士生导师,研究方向为电力系统稳定分析与控制。E-mail:05dylc@163.com(通信作者)
(编辑 赫 蕾)