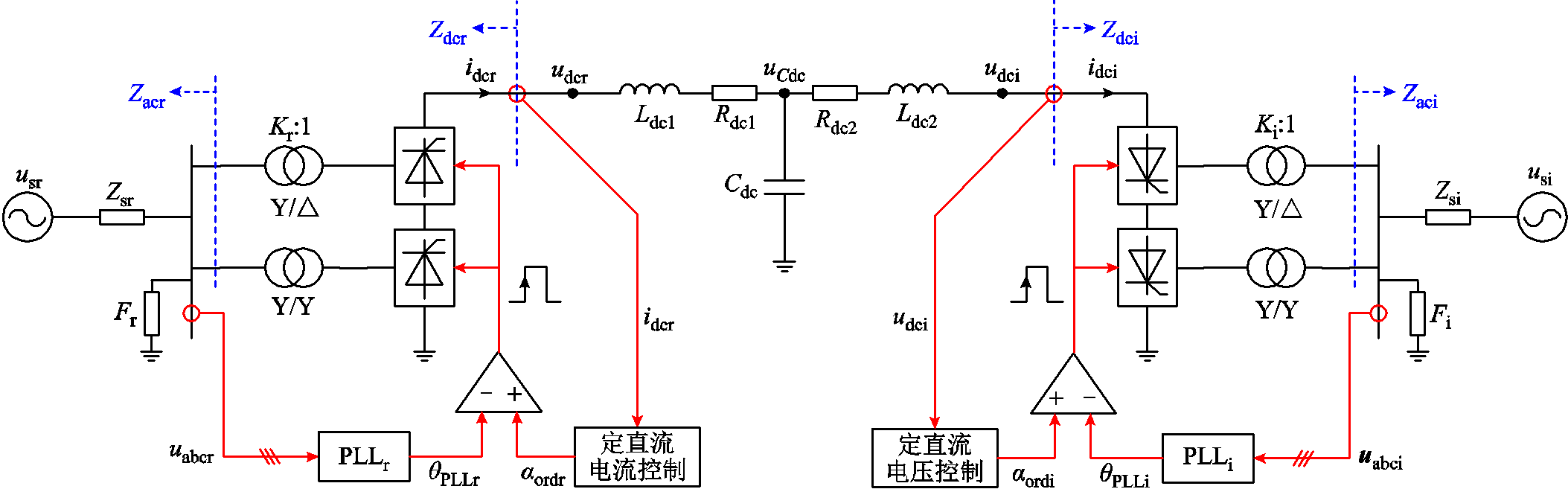
图1 LCC-HVDC单线框图
Fig.1 LCC-HVDC single line block diagram
摘要 阻抗模型是电网换相换流器型高压直流输电系统小信号稳定性分析的重要基础，阻抗模型的准确程度直接影响系统小扰动稳定性分析。该文首先从同步触发原理出发，引入基于单边调制产生的映射函数，该函数蕴含控制及换相信息，可以准确建立换相/非换相期间交直流侧的映射关系；其次，考虑换相动态并通过谐波线性化和傅里叶变换建立完整的直流侧电压和交流侧电流的频域小信号动态模型；再次，考虑控制和换流阀阻尼回路，建立整流侧和逆变侧直流阻抗解析模型；最后，以CIGRE高压直流标准测试模型为例，基于PSCAD/EMTDC平台验证了直流侧阻抗模型的准确性及其用于小扰动稳定性分析的有效性。
关键词：电网换相换流器 单边调制 映射函数 换相动态 换流阀阻尼回路 直流侧阻抗
我国能源资源蕴藏量颇为丰富，但其地域分布极不均衡，用于发电的煤炭、风力、太阳能等能源资源广泛蕴含于西北和华北地区，然而负荷中心主要集中于东部及南部沿海地区。为缓解东南沿海地区能源紧张问题，并充分发挥西北和华北地区的能源资源优势，适合大规模电能跨地区调配的高压直流输电技术得到广泛应用。与柔性直流输电相比，电网换相换流器型高压直流输电系统（Line Commutated Converter based High Voltage Direct Current, LCC-HVDC）凭借输送容量大和线路损耗小等优势已经得了到快速发展[1-2]。随着输送容量的不断增大，交流电网强度逐渐减弱，LCC-HVDC系统的谐振[3-5]问题日渐凸显。由于物理概念清晰，阻抗分析法[6-7]在LCC-HVDC系统的谐振分析方面得到广泛应用，该方法的关键在于阻抗模型的准确程度。
目前已有部分国内外学者对LCC-HVDC系统的阻抗建模展开了相关研究。基于LCC-HVDC系统状态空间模型[8-11]的阻抗建模是目前直流侧阻抗建模的一种常用方法，但该方法存在天然缺陷：①不能清晰地描述谐波传递过程；②拓展性差，状态空间模型随着系统结构变化需重新建立；③运算量大，复杂的控制结构使得状态空间模型的阶数急剧增加。谐波线性化[12]方法是LCC-HVDC阻抗建模的另一种常用方法，该方法的关键在于建立交直流量之间的转换关系，即开关函数[13]。文献[14-16]在不考虑换相的前提下，用3D傅里叶级数法对开关函数进行分解，而后通过谐波线性化思路建立计及频率耦合的LCC-HVDC交流侧和直流侧阻抗模型，然而在实际的LCC-HVDC中换相过程始终存在。进一步，文献[17]提出基于开关函数理论的LCC-HVDC直流侧阻抗计算方法，该方法计及了换相过程的影响，但未考虑阀电流在换相期间的非线性变化以及控制系统的影响。文献[18]分析了稳态工况阀电流在换相过程中的变化规律，并给出相应电流开关函数表达式。在此基础上，文献[19]提出了基于改进开关函数的直流阻抗建模方法，但在建模过程中无法考虑详细的换相动态。除此之外，开关函数因本身存在固有的缺陷，所以在小扰动工况下无法非常精确地刻画交直流侧映射。为解决上述建模过程中换相动态描述不准确的问题，文献[20]提出一种新思路，基于无限个六脉动换流器假设，采用平均法在dq坐标系下对换相过程的换相电压、电流及换相重叠角进行了准确描述。基于同样的无限个六脉动换流器假设，文献[21]首次明确提出换流阀阻尼回路（RC回路）对交流侧导纳高频段产生影响，至于该回路对直流侧阻抗的影响该文并没有阐述。文献[22]考虑准确的换相动态并提出了一种ab坐标系下的LCC-HVDC精确阻抗模型，但仅涉及交流侧阻抗且未考虑换流阀阻尼回路带来的影响。综上所述，目前关于LCC系统直流侧阻抗存在两个问题，首先交直流侧映射关系不够精准，其次建模的影响因素考虑尚不全面，这些问题在一定程度上影响阻抗模型的精确程度，进而影响基于阻抗模型的稳定性分析。因此，建立准确的交直流映射关系并综合考虑详尽换相动态、控制回路及换流阀阻尼回路等影响因素建立精准阻抗模型具有重要意义。
本文在上述研究的基础上，首先根据六脉动换流器换流阀的导通状态和同步触发原理，通过单边调制，精准地推导出六脉动换流器在换相/非换相期间反映交直流映射关系的映射函数；其次，拓展至十二脉动换流器，考虑换相动态并通过谐波线性化和傅里叶变换建立完整的直流侧电压和交流侧电流的频域小信号动态模型；接着，考虑控制和换流阀阻尼回路，建立直流侧阻抗频域模型；最后，以CIGRE高压直流标准测试模型为例，分析换相动态和RC回路对直流侧阻抗频响特性的影响，并对本文所建直流侧阻抗模型的准确性和该阻抗模型用于小扰动稳定性分析的有效性进行了仿真验证。
CIGRE高压直流标准测试模型主电路及控制框图如图1所示。其中，下标“r”和“i”分别表示整流侧和逆变侧的相关变量；us为交流电网电压；Zs为交流电网阻抗；F为交流系统滤波器组，K为换流变压器匝比；uabc为公共耦合点（Point of Common Coupling, PCC）三相电压；qPLL为锁相环的输出相位；aord为触发角指令值；udc为直流电压；idc为直流电流；Rdc1、Rdc2、Ldc1、Ldc2和Cdc分别为T型直流输电线路的等值电阻、等值电感和等值电容；Zdc为直流侧阻抗，由换流站出口看向换流器；Zac为交流侧阻抗，由PCC看向交流电网。
图1 LCC-HVDC单线框图
Fig.1 LCC-HVDC single line block diagram
本文所涉及的变量，需提前说明：变量前缀“D”表示扰动变量，时域和频域通用；变量下标“0”表示该变量的稳态值，例如，aordr0为稳态工况下定直流电流控制器输出的触发角指令值；时域变量x(t)对应的频域表达式为X(f)，f为频率，例如稳态工况下PCC处a相电压ua(t)的频域表达式为Ua(f)；s为复频率；a(t)、m(t)、q(t)和d(t)对应的频域表达式分别为a(f)、m(f)、q(f)和d(f)，例如锁相环输出qPLL(t)的频域表达式为qPLL(f)；频域矩阵变量用斜粗体表示，例如X。
映射函数是LCC系统建模的核心部分，体现换流器的工作原理，反映交直流侧映射关系。映射函数的本质是取值为“1”或“0”的矩形脉冲序列函数，该函数与换流器导通状态密切相关。为精准地建立映射函数模型，本节对六脉动换流器的换流阀导通状态展开分析，考虑换相动态过程并通过单边调制原理推导映射函数时域表达式，进而建立映射函数频域模型。
以图1所示LCC-HVDC整流侧与Y/Y联结变压器相连的六脉动换流器为例，忽略下标“r”，换流器拓扑如图2所示。ua、ub和uc为换流变压器网侧相电压；ia、ib和ic为换流变压器阀侧相电流；Lc为归算至换流变压器阀侧的漏感；u+为换流阀共阴极点的电位；u-为换流阀共阳极点的电位；udc_Y为换流器两端的电压；VT1～VT6为换流阀编号，其中VT1、VT3和VT5为共阴极换流阀，VT4、VT6和VT2为共阳极换流阀。
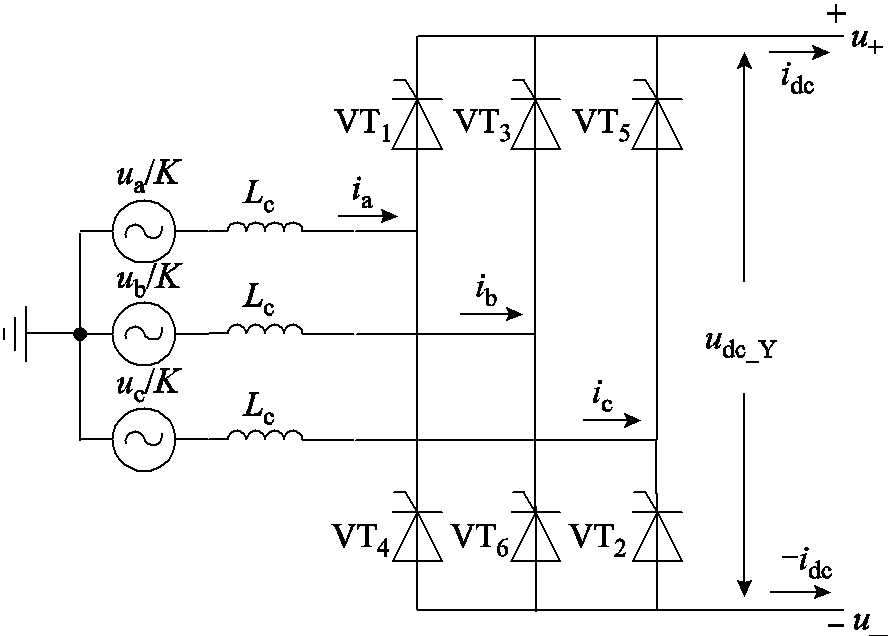
图2 六脉动换流器拓扑
Fig.2 Topology diagram of six pulse converter
非换相期间（Non-Commutation Period, NCP）上下半桥臂同时各有1个换流阀导通；换相期间（Commutation Period, CP），3个换流阀同时导通，即换相半桥2个换流阀同时导通，非换相桥1个换流阀导通。用映射函数描述六脉动换流器工作原理，该函数反映交直流侧映射关系。对单个周期内不同时段的换流阀导通情况、直流电压、换流变压器阀侧电流（考虑到三相对称性，本文以a相电流为例）和相应的映射函数进行定义，六脉动换流器导通状态见表1。
表1 六脉动换流器导通状态
Tab.1 Conduction state of six pulsating converter
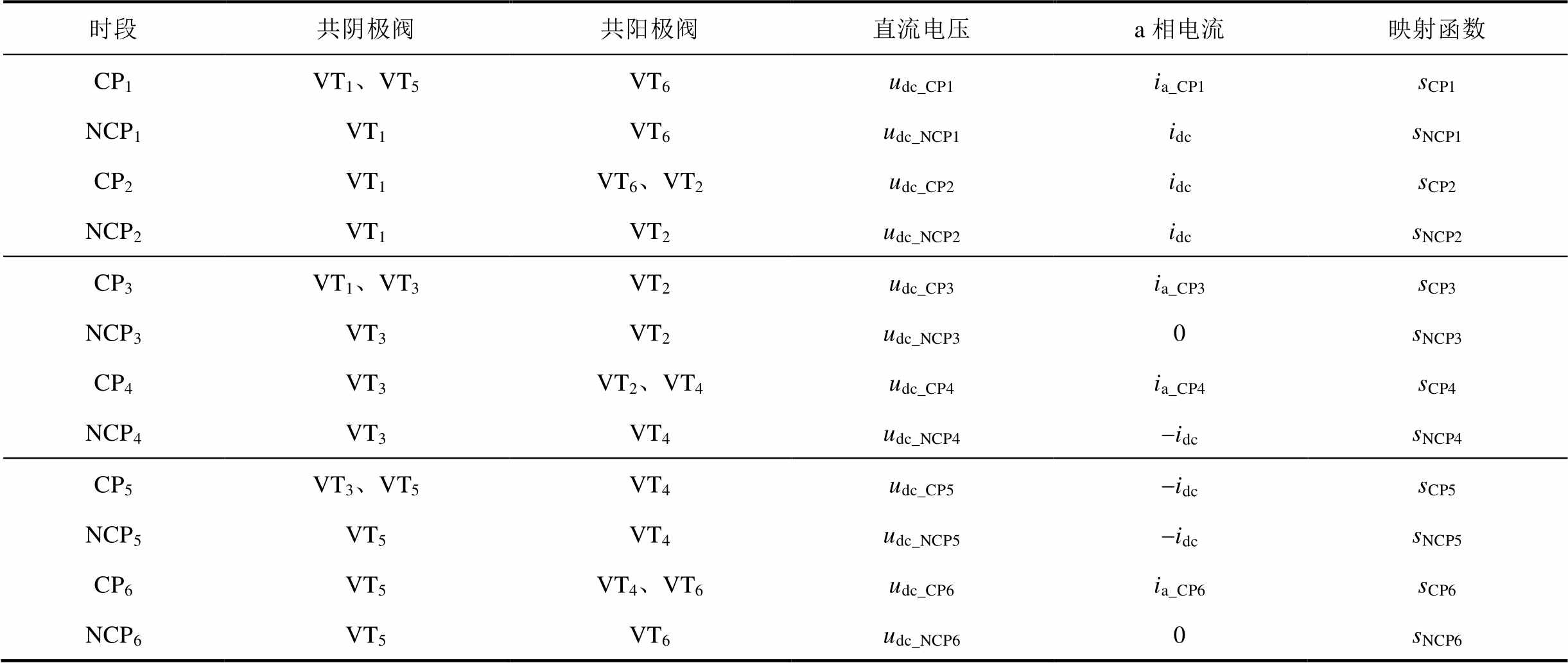
时段共阴极阀共阳极阀直流电压a相电流映射函数 CP1VT1、VT5VT6udc_CP1ia_CP1sCP1 NCP1VT1VT6udc_NCP1idcsNCP1 CP2VT1VT6、VT2udc_CP2idcsCP2 NCP2VT1VT2udc_NCP2idcsNCP2 CP3VT1、VT3VT2udc_CP3ia_CP3sCP3 NCP3VT3VT2udc_NCP30sNCP3 CP4VT3VT2、VT4udc_CP4ia_CP4sCP4 NCP4VT3VT4udc_NCP4-idcsNCP4 CP5VT3、VT5VT4udc_CP5-idcsCP5 NCP5VT5VT4udc_NCP5-idcsNCP5 CP6VT5VT4、VT6udc_CP6ia_CP6sCP6 NCP6VT5VT6udc_NCP60sNCP6
表1中，i=1,2,3,4,5,6；CPi表示以tfi/tei为起始/结束时刻的换相期间；NCPi表示以tei/tf(i+1)为起始/结束时刻的非换相期间；udc_CPi/udc_NCPi、ia_CPi/ia_NCPi和sCPi/sNCPi分别表示CPi/NCPi的直流电压、换流变压器阀侧a相电流和映射函数。映射函数在作用时段取值为“1”，其余时段取值为“0”，例如，在[tf1, te1]时段内sCP1=1，其他时段sCP1=0。考虑到换流阀的实际导通状态，部分ia_CPi/ia_NCPi已用idc/-idc/0进行等值替换。例如，在NCP1，换流阀VT1和VT6导通，其他换流阀关断，流过a相的电流为直流电流idc，即ia_NCP1=idc；在NCP3，换流阀VT2和VT3导通，其他换流阀关断，a相没有电流流过，即ia_NCP3=0。
令图2所示六脉动换流器a相电压达到峰值的瞬间为起点0时刻，j(t)为t时刻所对应的电角度。换流阀VT5至换流阀VT1换相期间（CP1）的六脉动换流器直流电压和a相电流波形示意图如图3所示。
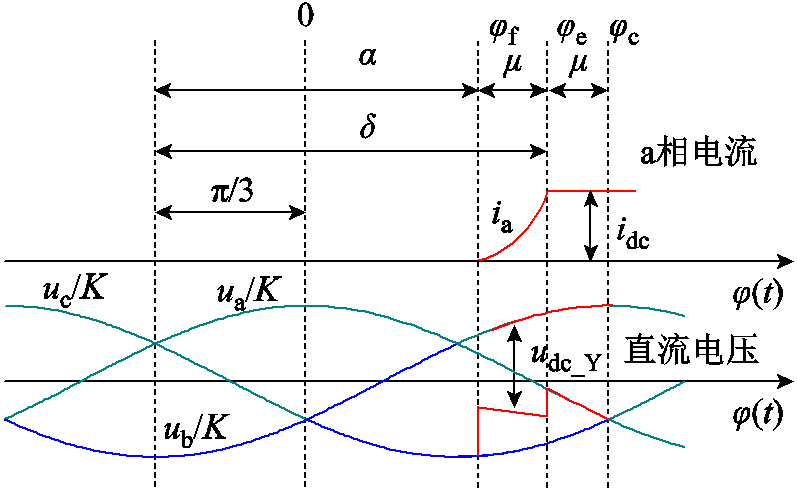
图3 直流电压和a相电流波形示意图
Fig.3 Schematic diagram of DC voltage and phase a current waveform
图3中，jf、je和jc分别为tf、te和tc时刻对应的电角度；a为实际触发角；m为换相重叠角；g为关断角；d为a与m之和，即d(t)=a(t)+m(t)。换相过程是一个复杂的非线性动态过程，参考文献[20]，直接写出小扰动工况下换相角的频域表达式为
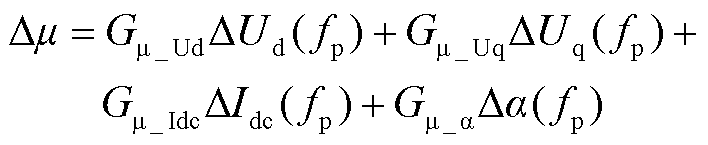(1)
式中，fp为LCC系统直流侧小扰动频率；Ud和Uq分别为PCC处dq轴电压ud和uq的频域形式；Gm_Ud、Gm_Uq、Gm_Idc和Gm_a分别为DUd、DUq、DIdc和Da到Dm的传递函数。
由d(t)=a(t)+m(t)，求得Dd的频域表达式为
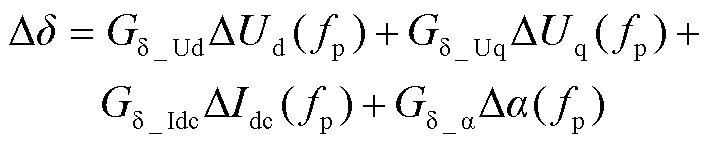(2)
式中，Gd_Ud、Gd_Uq、Gd_Idc和Gd_a分别为DUd、DUq、DIdc和Da到Dd的传递函数。
本文所提映射函数可由锯齿载波与调制波通过单边调制[23]产生的脉冲序列进一步导出。
锯齿载波为稳态工况换流阀VTi的同步相位qi,0(t)，其生成规律可由式（3）表示。
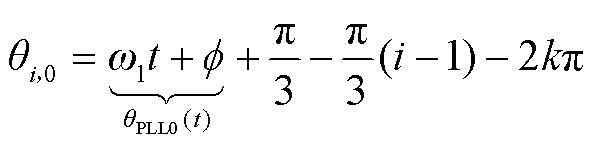（3）
式中，qPLL0(t)为稳态工况下三相同步参考坐标系锁相环（Synchronous Reference Frame Phase-Locked Loop, SRF-PLL）输出的相位；w1为基频角频率；f为a相基频正序电压初相位；引入2kπ是为限制qi,0在[0,2p]范围内，其中k为整数。
调制波为a(t)、d(t)和a(t)+p/3。其中，a(t)满足a(t)=aord(t)-DqPLL(t)，DqPLL(t)为SRF锁相环输出的扰动相位。
单边调制特指占空比为100%的锯齿载波（例如qi,0(t)）与调制波相交生成幅值为“1”或“0”的脉冲序列，即锯齿载波与调制波相交时刻脉冲序列下降沿到来，锯齿载波过零点对应的时刻脉冲序列上升沿到来。图4给出了以锯齿载波qi,0(t)和调制波a(t)为例的单边调制原理示意图。
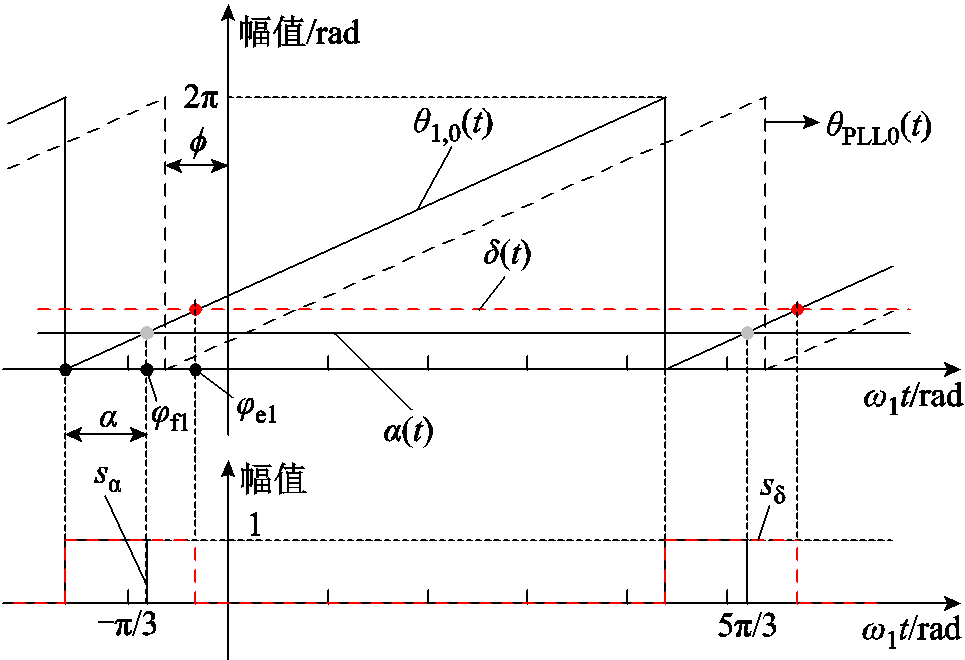
图4 闭环触发方式的单边调制原理
Fig.4 Schematic diagram of single-sided modulation in closed-loop trigger mode
图4中，φf1为换流阀VT1导通时刻tf1（q1,0(t)与a(t)相交时刻）对应的电角度；φe1为换相结束时刻te1（q1,0(t)与d(t)相交时刻）对应的电角度；qi,0(t)过零点对应的时刻，脉冲序列sa和sd的取值由“0”阶跃至“1”，tf1时刻sa的取值阶跃至“0”，te1时刻sd的取值阶跃至“0”。同理，脉冲序列sa+p/3由锯齿载波q1,0(t)与调制波a(t)+p/3通过单边调制生成。sa、sd和sa+p/3的具体推导过程详见附录。
映射函数sCP1和sNCP1由相应的脉冲序列之差决定，具体为
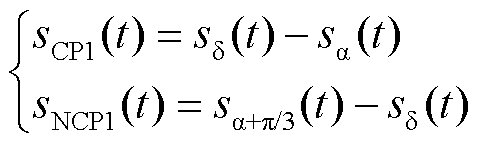（4）
将附录中sa、sd和sa+p/3的详细表达式代入式（4）中，sCP1和sNCP1可化简为
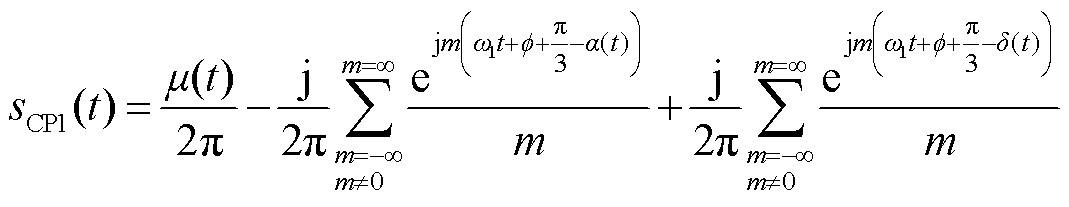（5）
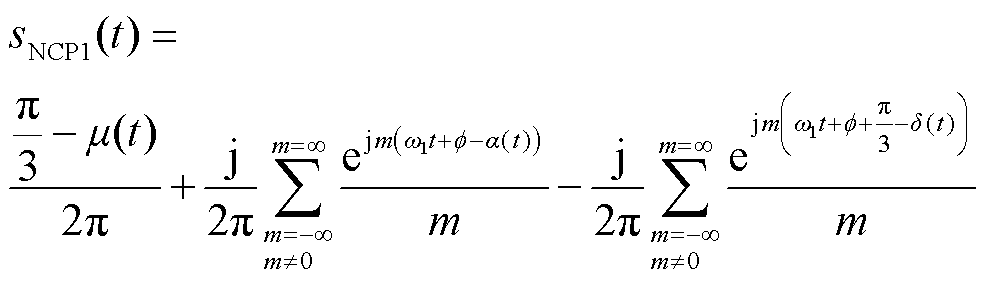（6）
式中，m为非0整数。表1所示CPi/NCPi的映射函数表达式可根据换流器导通状态通过单边调制导出，由于篇幅有限不再一一给出。
为简化分析，本文的建模暂不考虑高次稳态谐波分量。在直流系统中注入频率为fp的扰动，a(t)、m(t)和d(t)具体时域表达式为
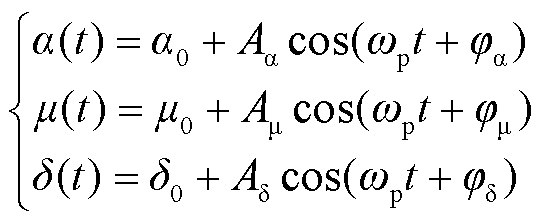（7）
式中，wp为扰动角频率；Ax和jx分别为扰动幅值和扰动初相位（x=a, m, d）。将式（7）代入式（5），并应用Jacobi-Anger定理可得
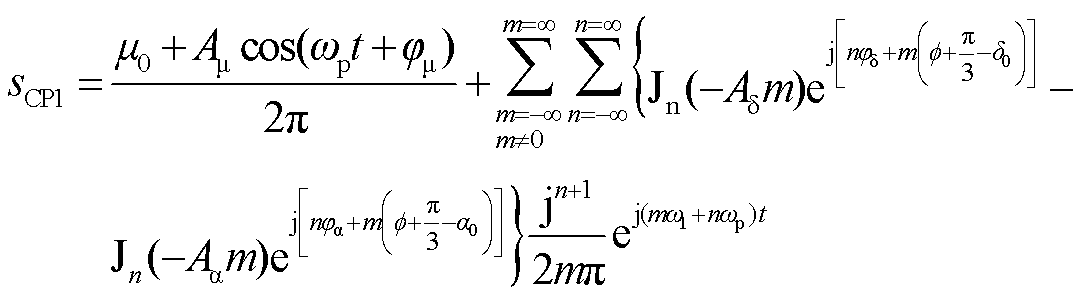（8）
式中，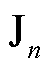
(x)为第一类Bessel函数；n为函数阶数，n取“0”和“1”。
通过傅里叶变换，将式（8）转换至频域，有
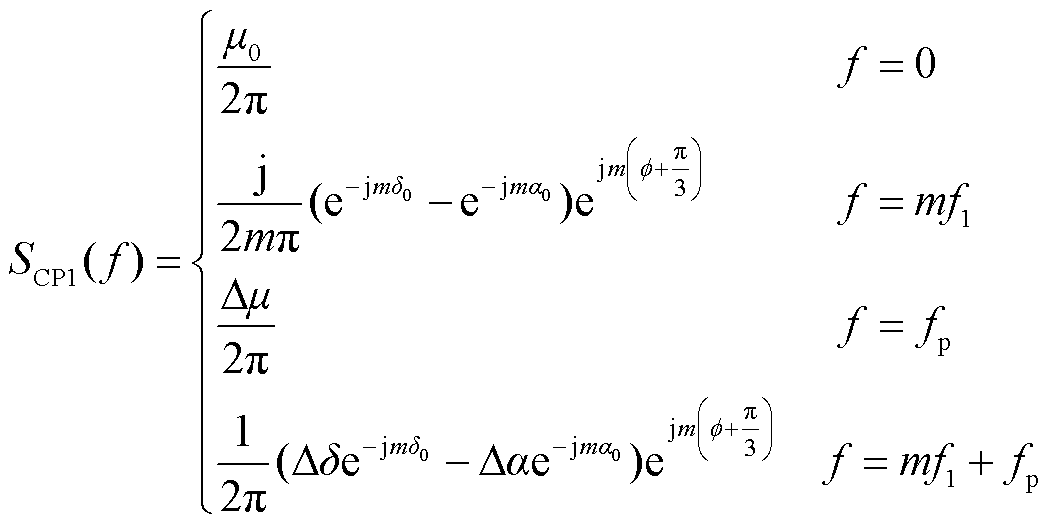（9）
式中，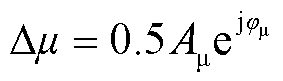
；
；
。
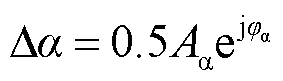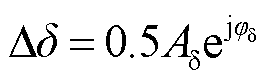以SCP1为例，当m取“±1, ±2”时（不做特别说明m均取“±1,±2”，后文不再赘述）将映射函数SCP1的稳态分量写成Toeplitz矩阵SCP1，扰动分量写成列向量DSCP1，SCP1和DSCP1分别如式（10）和式（11）所示。
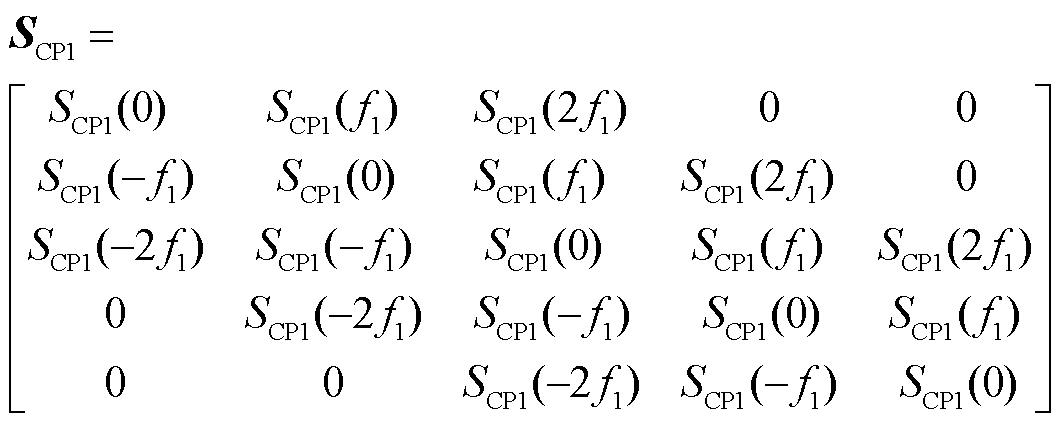（10）
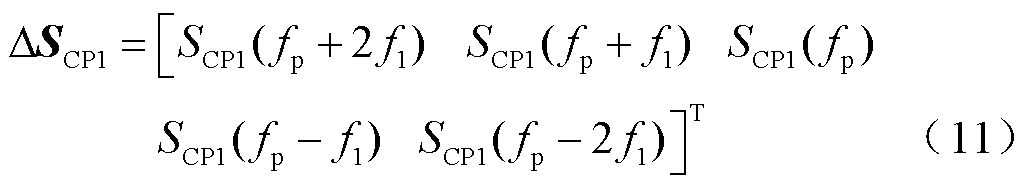
显然，SCP1为5阶复数方阵，DSCP1为随着扰动频率fp变化而变化的5阶扰动列向量，按照同样的思路可求得SNCP1的稳态Toeplitz矩阵SNCP1和扰动列向量DSNCP1。其他映射函数的Toeplitz矩阵和扰动列向量可根据频域表达式写出。不失一般性，本文所涉及的其他Toeplitz矩阵均为5阶复数方阵，扰动列向量均为关于fp的5阶扰动列向量。将2.2节所示Dm和Dd（式（1）和式（2））代入映射函数的扰动列向量中，可得映射函数扰动列向量DSCPi和DSNCPi均为关于DUd、DUq、DIdc和Da的扰动列向量。
图1所示LCC-HVDC换流器由2个六脉动换流器串联组成，结合三相对称性质可求得LCC-HVDC完整的直流电压udc和“Y/Y”型变压器阀侧a相电流ia的时域表达式，分别为
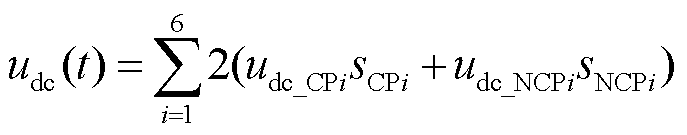（12）
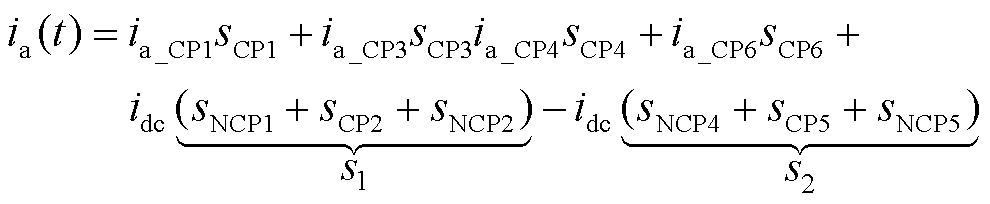（13）
式中，s1为sNCP1、sCP2和sNCP2之和；s2为sNCP4、sCP5和sNCP5之和。
接下来，对式（12）和式（13）中相关变量的频域表达式进行求解，并通过谐波线性化得到完整的直流侧电压和阀侧a相电流小信号动态模型。
结合表1、图2及文献[20]可推算出CP1/NCP1的直流电压的时域表达式udc_CP1、udc_NCP1为
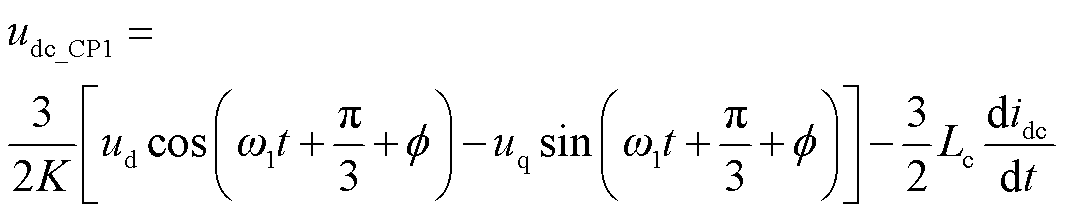（14）
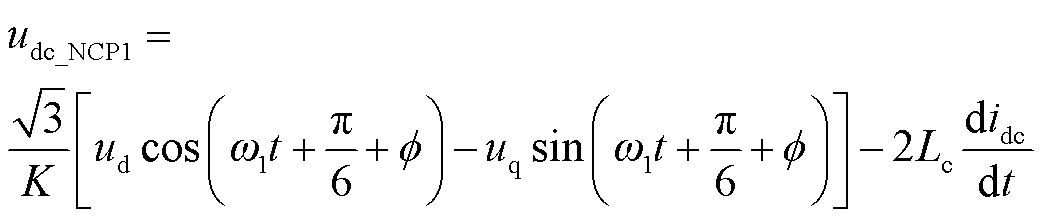（15）
通过拉氏变换将式（14）转换至频域，可得
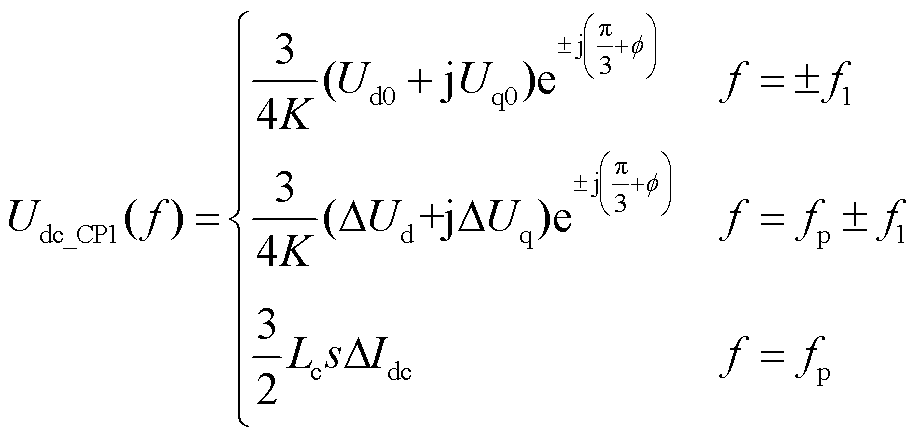（16）
udc_NCP1与udc_CP1形式一致，可写出udc_NCP1(t)的频域表达式Udc_NCP1( f )。将Udc_CP1和Udc_NCP1的稳态分量写成Toeplitz矩阵Udc_CP1和Udc_NCP1，扰动分量写成列向量DUdc_CP1和DUdc_NCP1。显然，直流侧电压扰动列向量DUdc_CP1和DUdc_NCP1为关于DUd、DUq和DIdc的扰动列向量。
将式（12）所示完整的直流侧电压udc(t)在稳态工作点线性化并转换至频域，LCC-HVDC换流站直流扰动电压列向量DUdc为
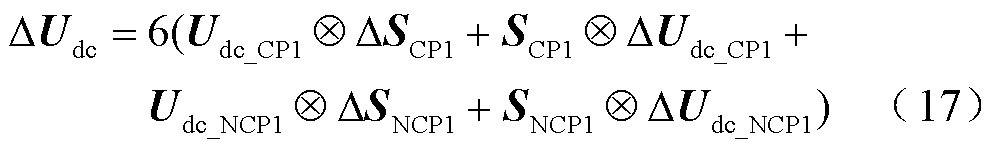
式中，“Ä”表示频域卷积；DUdc为5阶列向量。DUdc中第3个元素为直流扰动电压DUdc(fp)，即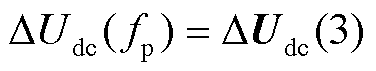
。代入相关变量的频域表达式，进一步解得LCC-HVDC换流站直流侧扰动电压DUdc(fp)为
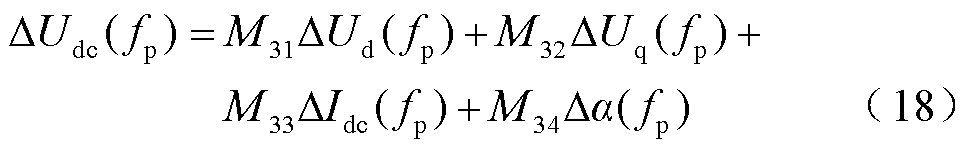
式中，M31～M34分别为DUd、DUq、DIdc和Da到DUdc的传递函数。式（18）为直流侧电压Udc小信号模型。
结合表1、图2及文献[20]可推算出CP1/NCP1的换流变压器阀侧a相电流的时域表达式ia_CP1、ia_NCP1为
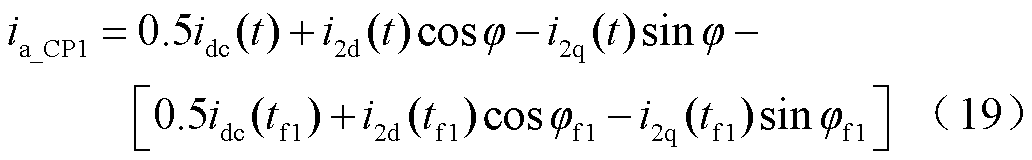
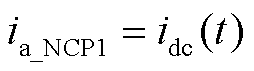（20）
式中，i2d和i2q为i2a、i2b和i2c（i2a、i2b和i2c为仅与交流电压相关的阀电流分量[20]）通过派克变换所得的dq轴电流。
以idc和ia_CP1时域表达式为例，说明在小扰动工况下它们的频域表达式推导过程。当系统受到小扰动时，φf1满足：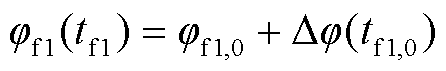
，其中，φf1,0为稳态工况换流阀VT1导通时刻tf1,0对应的电角度；Dj为扰动电角度。在小扰动工况下，将
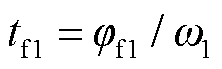代入idc(tf1)并忽略高阶小量，可用tf1,0时刻直流电流扰动量Didc(tf1,0)替代tf1时刻直流侧电流扰动量Didc(tf1)，具体为
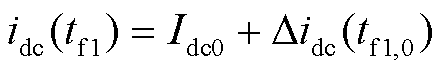（21）
由图4可知，Dj(tf1,0)=Da(tf1,0)。将式tf1代入i2d(tf1)和i2q(tf1)，并忽略高阶小量，得
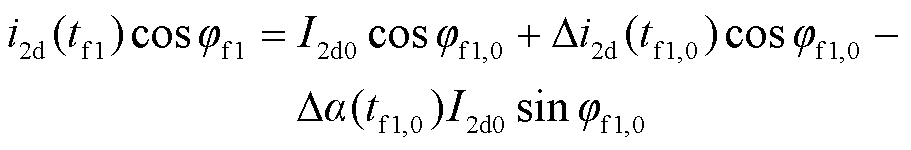（22）
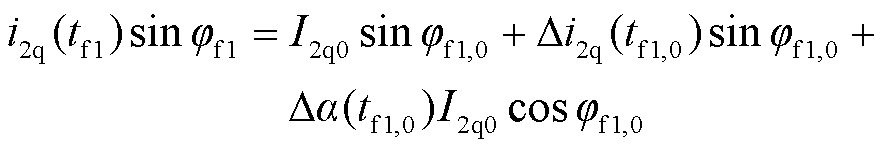（23）
将式（21）～式（23）代入式（19），解得
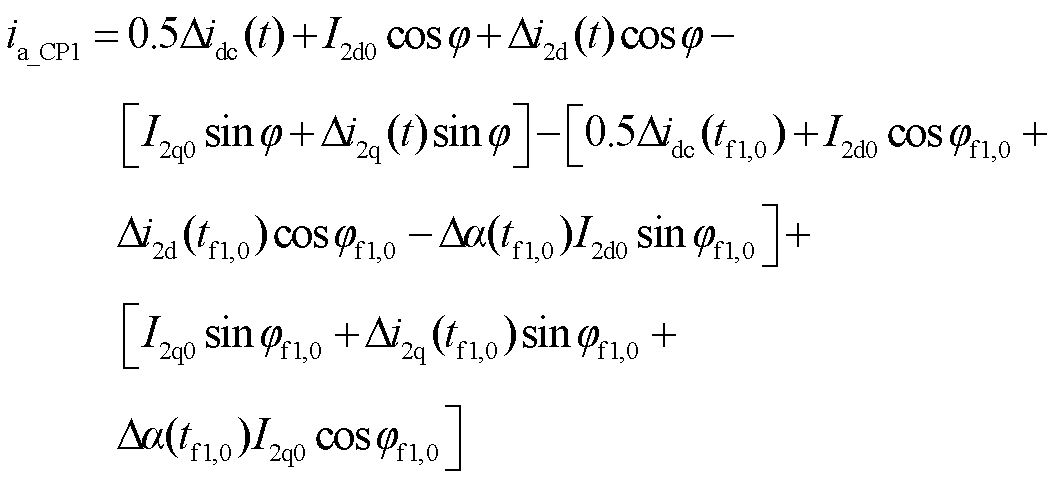（24）
式中，Didc(tf1,0)、Di2d(tf1,0)、Di2q(tf1,0)和Da(tf1,0)均为扰动变量在tf1,0时刻取值大小。
以Didc为例，说明Didc(tf1,0)的取值原理。Didc的采样保持示意图如图5所示，图中，Didch(t)为Didc的采样保持函数。由于六脉动换流器的每个换流阀在一个周期内只导通一次，故采样周期Ts为20 ms，tf1,0时刻Didch(t)的值为Didc(tf1,0)，下一采样时刻，即0.02+tf1,0时刻，Didch(t)的值更新为Didc(0.02+tf1,0)。Didc(tf1,0)的频域表达式如式（25）所示，具体推导过程详见附录。
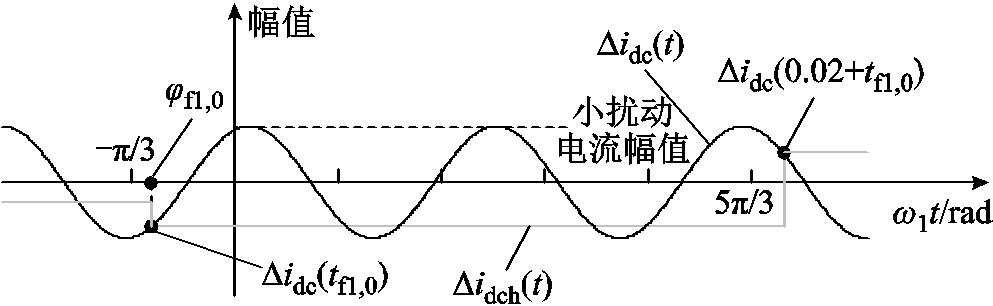
图5 Didc的采样保持示意图
Fig.5 Sketch map of Didc sampling and holding
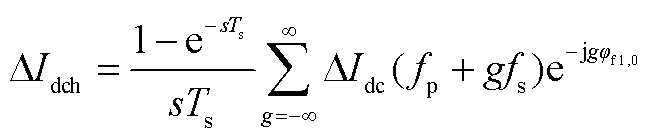（25）
式中，fs为零阶保持器采样频率，fs=f1；g为任意整数。同理，可求得Di2d(tf1,0)、Di2q(tf1,0)和Da(tf1,0)的频域形式DI2dh、DI2qh和Dah。
将式（24）转换至频域并代入DIdch、DI2dh、DI2qh和Dah的解析式，易得
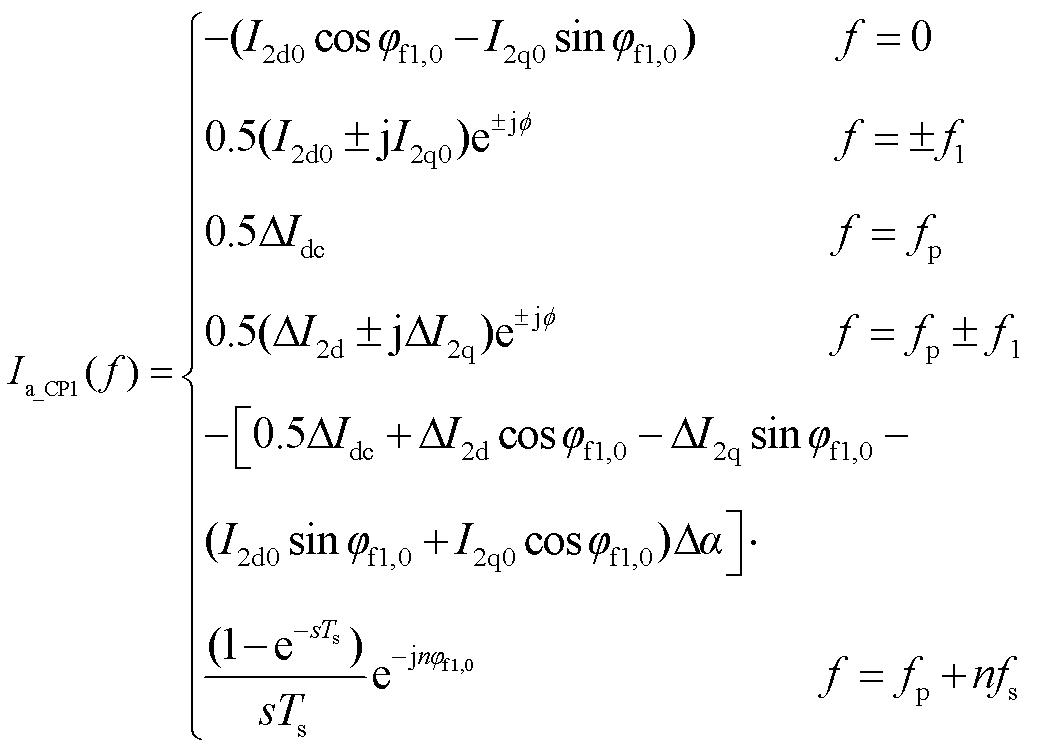（26）
ia_CP3、ia_CP4和ia_CP6的频域表达式可按照同样的思路推导。
将Ia_CP1、Ia_CP3、Ia_CP4、Ia_CP6和Idc的稳态分量写成Toeplitz矩阵Ia_CP1、Ia_CP3、Ia_CP4、Ia_CP6和Idc，扰动分量写成列向量DIa_CP1、DIa_CP3、DIa_CP4、DIa_CP6和DIdc。显然，DIa_CP1、DIa_CP3、DIa_CP4和DIa_CP6均为关于DUd、DUq、DIdc和Da的扰动列向量；DIdc为关于DIdc的扰动列向量。将映射函数SCP3、SCP4、SCP6、S1和S2的稳态分量写成Toeplitz矩阵SCP3、SCP4、SCP6、S1和S2，扰动分量写成列向量DSCP3、DSCP4、DSCP6、DS1和DS2。
基于上述Toeplitz矩阵和扰动列向量，将式（13）所示完整的a相电流ia(t)在稳态工作点线性化并转换至频域，易得LCC-HVDC换流变压器阀侧a相电流扰动列向量DIa为
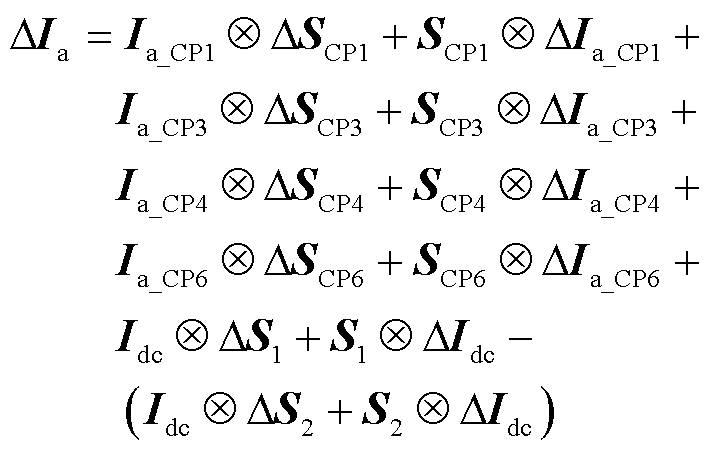（27）
在直流侧注入频率为fp的小扰动激励，交流侧产生频率为fp+f1和fp-f1的响应，分别对应DIa的第2个元素DIa(2)和第4个元素DIa(4)。将相关变量的解析式代入式（27）中，最终解得LCC-HVDC频率为(fp±f1)的a相电流为
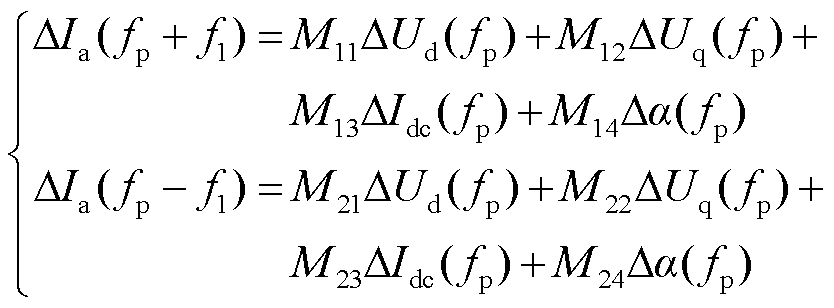（28）
式中，M11～M24为相应的传递函数。式（28）即为Y/Y联结变压器阀侧a相电流ia小信号模型。
经第3节的推导分析，可定义LCC换流站输入为dq轴电压ud和uq、直流电流idc和触发角a，输出为换流变压器阀侧电流ia和换流站出口直流电压udc。在稳态运行点线性化并通过拉氏变换，得到矩阵方程为
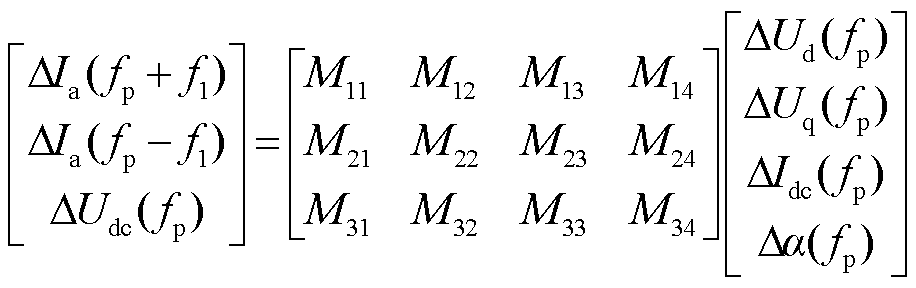（29）
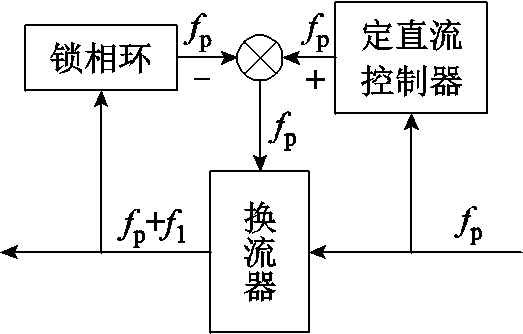
以整流站为例，代入控制回路，则式（29）所示小信号矩阵方程可用图6所示框图表示，其中，Ga_Idc为定直流电流控制器传递函数；GPLL为整流站和锁相环传递函数。
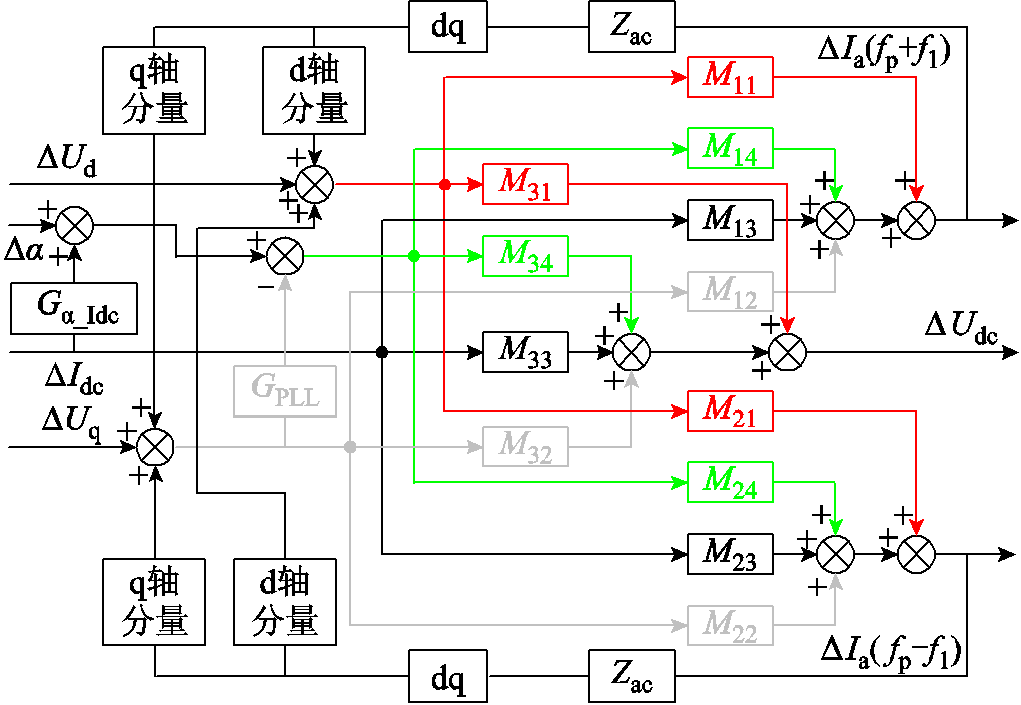
图6 附带控制回路的LCC小信号框图
Fig.6 LCC small signal block diagram with control circuit
向直流系统注入频率为fp的小扰动量，系统直流侧出现频率为fp的谐波分量，该分量通过换流器的调制使得交流侧产生谐波频率为fp±f1的分量，交流侧谐波分量又再次通过换流器影响直流侧，谐波的调制与传递过程如附图1所示。由此可见扰动谐波的传递与调制是一个非常复杂的过程。直流侧小扰动电压DUdc与直流侧小扰动电流DIdc的比值即为LCC系统直流侧阻抗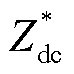
，具体推导过程如下。
由欧姆定律可知，换流变压器网侧a相扰动电压为
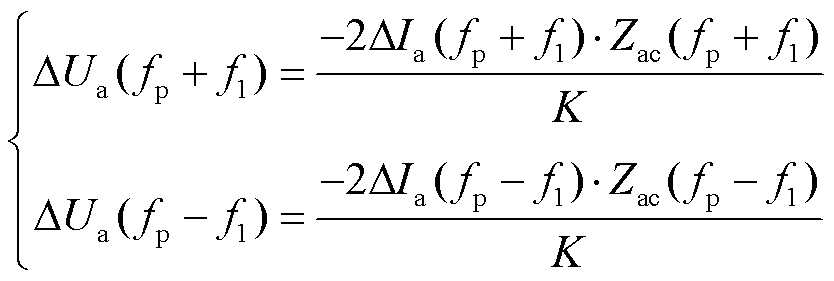（30）
整流站采用定直流电流控制，逆变站采用定直流电压控制，实际扰动触发角Dar和Dai分别为
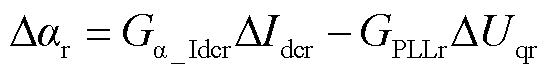（31）
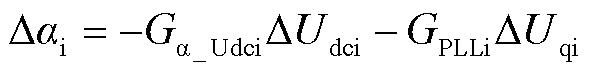（32）
式中，Ga_Idcr和Ga_Udci分别为定直流电流控制器和定直流电压控制的传递函数；GPLLr和GPLLi分别为整流站和逆变站的锁相环传递函数。
将式（30）和实际扰动触发角计算公式代入式（29）中，解得
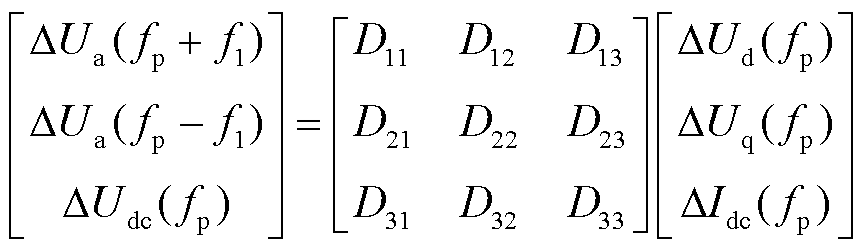（33）
式中，D11～D33为相应传递函数。
通过派克变换，扰动电压可表示为
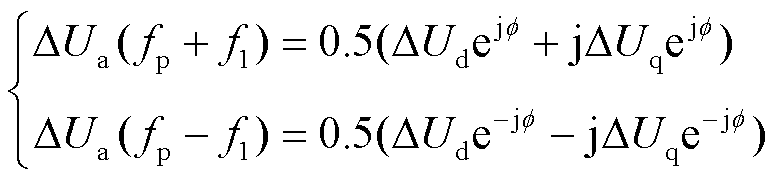（34）
联立式（33）和式（34），可求得
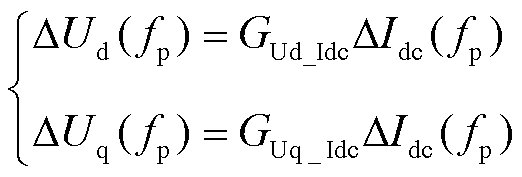（35）
式中，GUd_Idc为DIdc到DUd的传递函数；GUq_Idc为DIdc到DUq的传递函数。
将式（35）代入式（33）的DUdc的表达式中，解得LCC直流侧阻抗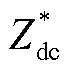
为
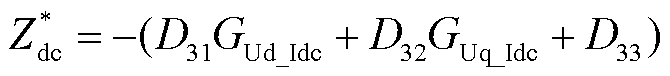（36）
然而，实际的换流器中换流阀阻尼回路（RC回路）会影响LCC系统阻抗特性[21]，因此在阻抗模型中有必要考虑RC回路。
考虑RC回路的六脉动换流器结构如图7所示。图7中，R和C分别为阻尼回路的电阻和电容。
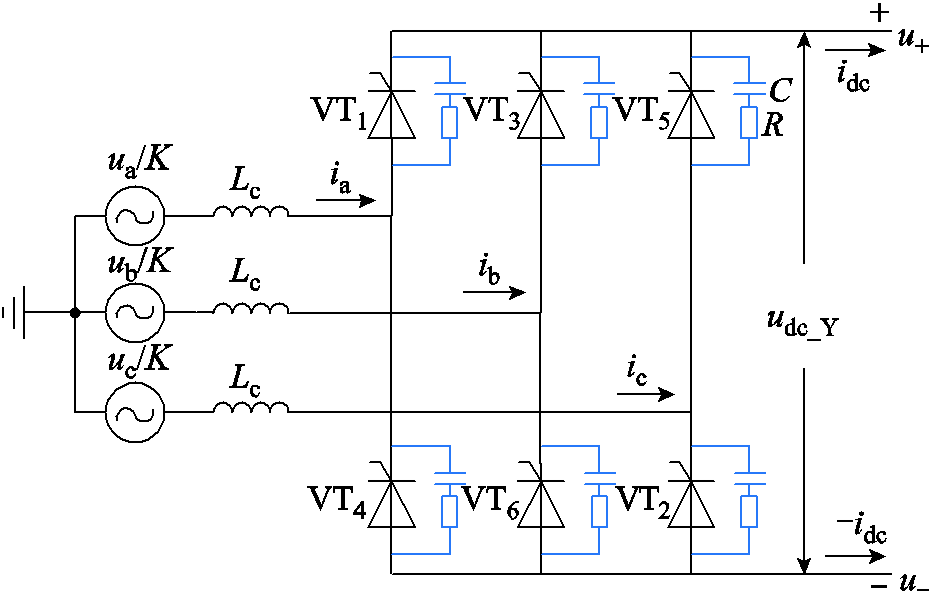
图7 计及RC回路的六脉动换流器示意图
Fig.7 Schematic diagram of 6-pulse converter with RC Loop
令换流阀VTi及其并联的RC回路为支路li。VTi导通时，支路li正向电压降为0，即支路li被短路；阀VTi关断时，流过阀VTi的电流为0，即支路li为RC回路。
CP1期间，换流阀VT1、VT5和VT6同时导通，其余换流阀关断，即支路l1、l5和l6为短路支路，l2、l3和l4为RC回路，3条RC回路并联。NCP1期间，VT1和VT6同时导通，其余换流阀关断，即l1和l6为短路支路，l2、l3、l4和l5为RC回路。考虑到此时c相电流ic在换流阀VT1和VT6关断或者导通瞬间均为0，且换相电感的存在使得相电流不能突变，故在NCP1期间l2和l5串联，再与l3和l4并联。将RC回路等效到直流侧，有
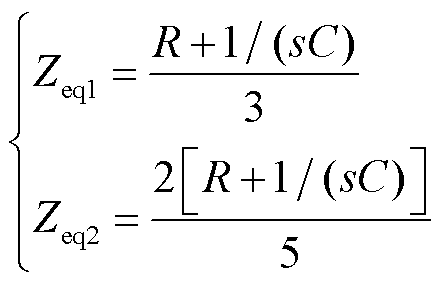（37）
不失一般性，Zeq1/Zeq2为换相/非换相期间的等效阻抗。
图1所示系统的十二脉动换流器由2个六脉动换流器串联组成，一个周期内换流器所处阶段存在以下三种情况：①上六脉动换流器处于换相阶段，下六脉动换流器处于非换相阶段；②上六脉动换流器处于非换相阶段，下六脉动换流器处于非换相阶段；③上六脉动换流器处于非换相阶段，下六脉动换流器处于换相阶段。将RC回路等效至直流侧，等效阻抗为
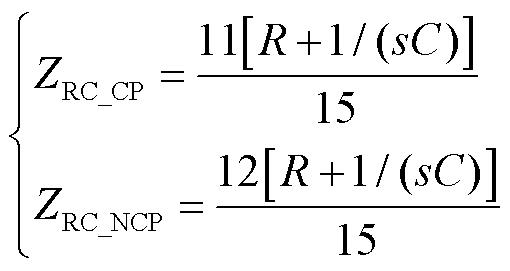（38）
式中，ZRC_CP为情况①和情况③所述的RC回路等效阻抗；ZRC_NCP为情况②所述的等效阻抗。
类似于文献[17]对换相电感的处理，本文采用平均的思想对ZRC_CP和ZRC_NCP进行进一步的等效处理，如图8a所示。最终的RC回路等效阻抗表达式Zeq如式（39）所示。
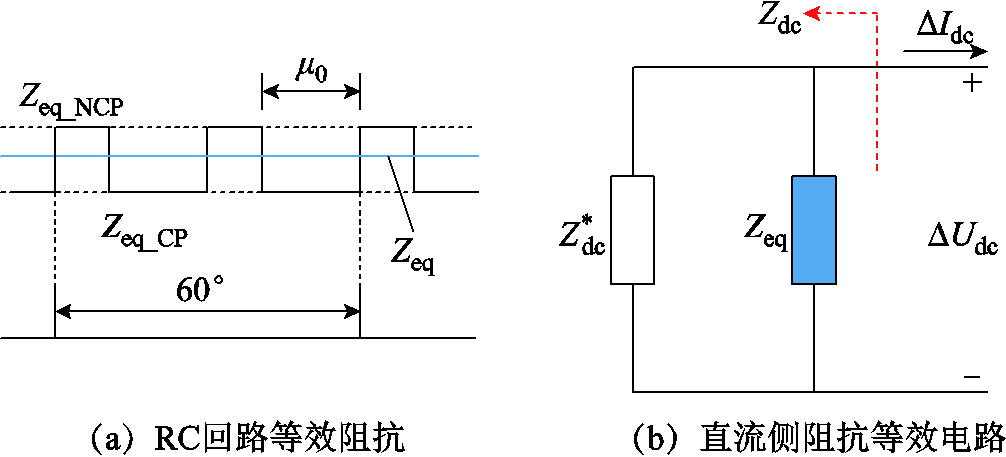
图8 等效电路及等效阻抗
Fig.8 Equivalent circuit and equivalent impedance
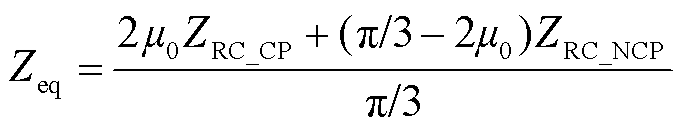（39）
本节首先根据换流阀导通状态，将换流阀RC回路等效至直流侧，并给出换相/非换相期间的等效阻抗；然后，考虑LCC换流器之间的配合，采用平均化思路对RC回路进一步处理，式（39）即为最终的RC回路等效阻抗。
考虑RC回路，只需将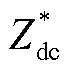与Zeq并联，其等效结构如图8b所示，最终的直流侧阻抗为
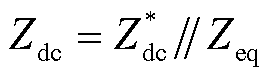（40）
式（40）即为考虑换相过程和换流阀阻尼电路的LCC-HVDC直流侧阻抗。
CIGRE HVDC标准测试模型运行参数和控制系统参数详见附表1和附表2。基于PSCAD/ EMTDC平台，对整流侧和逆变侧直流阻抗进行仿真验证。
定义平均相对误差（Average Relative Error, ARE）用以定量衡量直流侧阻抗解析值的精度，ARE计算公式为
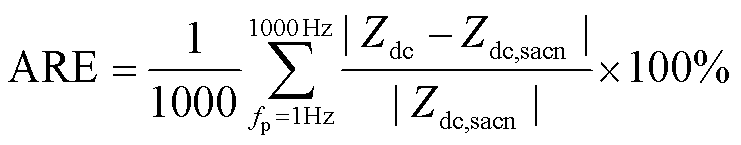（41）
式中，Zdc为直流侧阻抗解析值；Zdc,sacn为直流侧阻抗扫描值，扫频区间为1～1 000Hz。
4.3.1 换相动态及RC回路对直流侧阻抗的影响
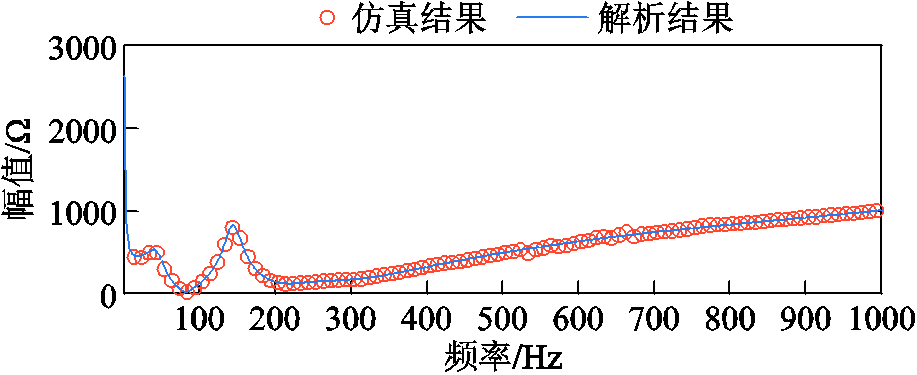
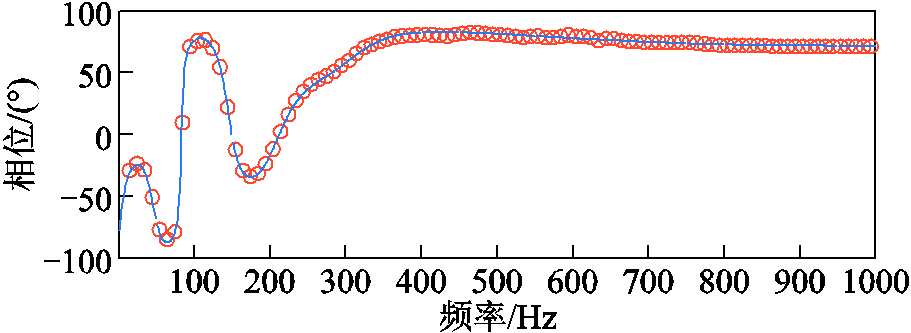
给定运行参数以及控制参数，换相动态及RC回路对直流侧阻抗频响特性的影响如图9和图10所示。图中，橙色圆圈为电磁暂态仿真结果；蓝色实线为本文所求直流侧阻抗，即式（40）给出的解析值；绿色虚线为不考虑换相动态的直流侧阻抗解析值；黑色虚线为不考虑RC回路的直流侧阻抗解析值。显而易见，换相动态对直流侧阻抗的影响主要体现在较低频段，而RC回路对直流侧阻抗的影响主要体现在较高频段。对上述曲线精度进行评估，直流侧阻抗平均相对误差如图11所示。
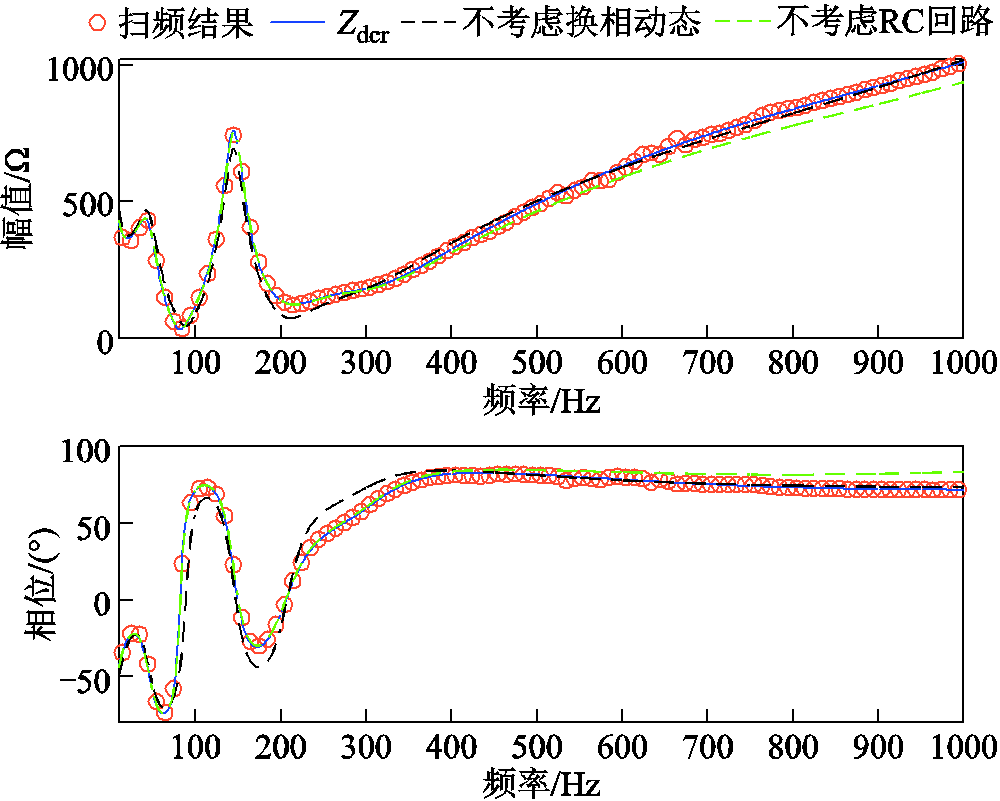
图9 整流侧直流阻抗
Fig.9 DC impedance of rectifier side
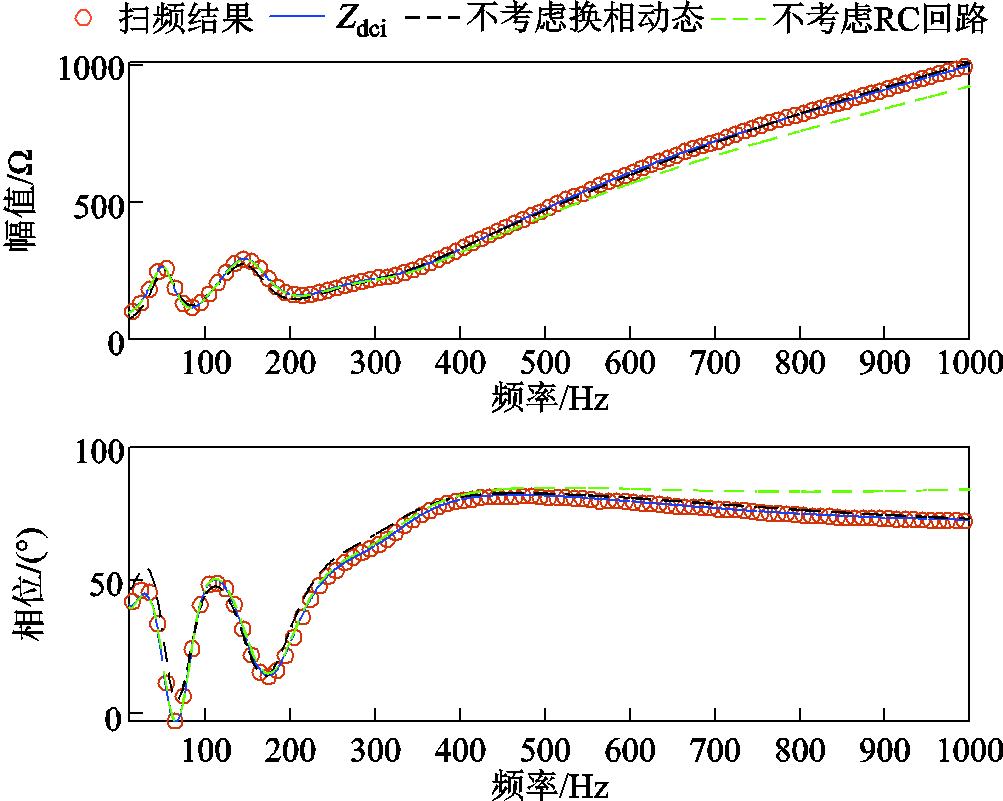
图10 逆变侧直流阻抗
Fig.10 DC impedance of inverter side
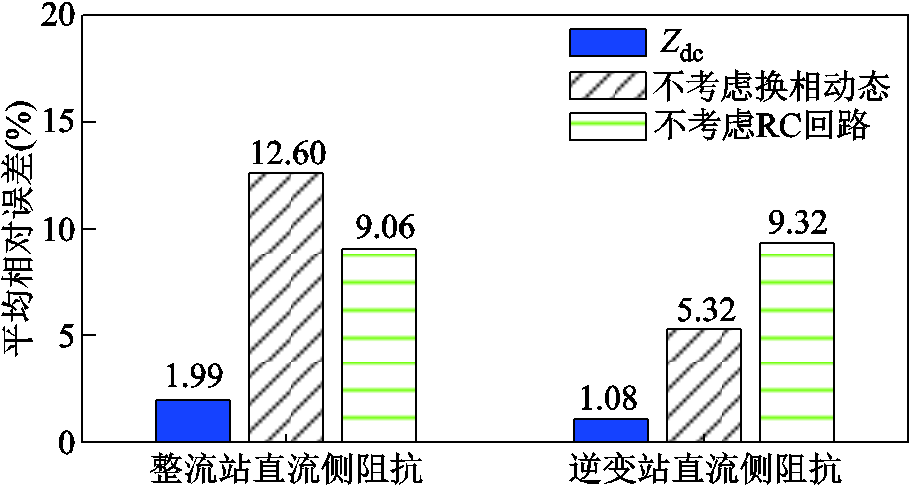
图11 直流侧阻抗平均相对误差
Fig.11 Average relative error of DC side impedance
由图11可知，对整流站直流侧阻抗而言，换相动态的整体影响大于RC回路。对逆变站直流侧阻抗而言，换相动态的整体影响小于RC回路。
更进一步，验证本文建立直流侧阻抗模型的准确性，在不同控制参数条件下，对整流站和逆变站的直流侧阻抗分别进行对比验证。考虑到文章篇幅，不同控制参数下理论结果与仿真结果的对比如附图2～附图5所示。
4.3.2 与其他方法的对比分析
将本文推导的直流侧阻抗解析值与开关函数方法推导的直流侧阻抗解析值进行对比。整流侧和逆变侧的对比结果分别如图12和图13所示。
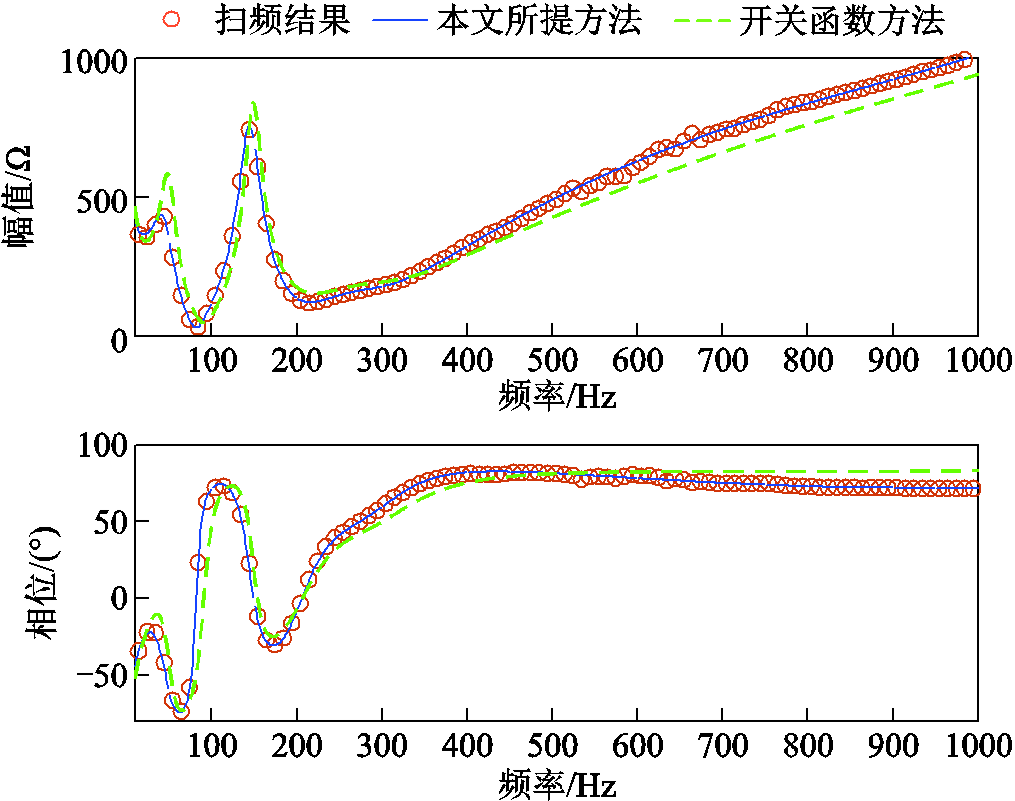
图12 整流侧直流阻抗对比
Fig.12 Comparison diagram of DC impedance at rectifier side
图12和图13中，橙色圆圈为电磁暂态仿真结果；蓝色实线和绿色虚线分别为本文所提方法和开关函数方法推导的直流侧阻抗解析值。对上述曲线精度进行评估，对于整流站直流侧阻抗，基于开关函数方法所得直流侧阻抗解析值平均相对误差高达20.36%，而本文所用方法的误差仅为1.99%；同理，对逆变侧直流侧而言，本文所建直流侧阻抗解析值误差仅为1.08%，远小于开关函数方法的12.58%。综上所述，与开关函数方法相比，本文所提出关于直流侧阻抗建模方法具有更高的精度。
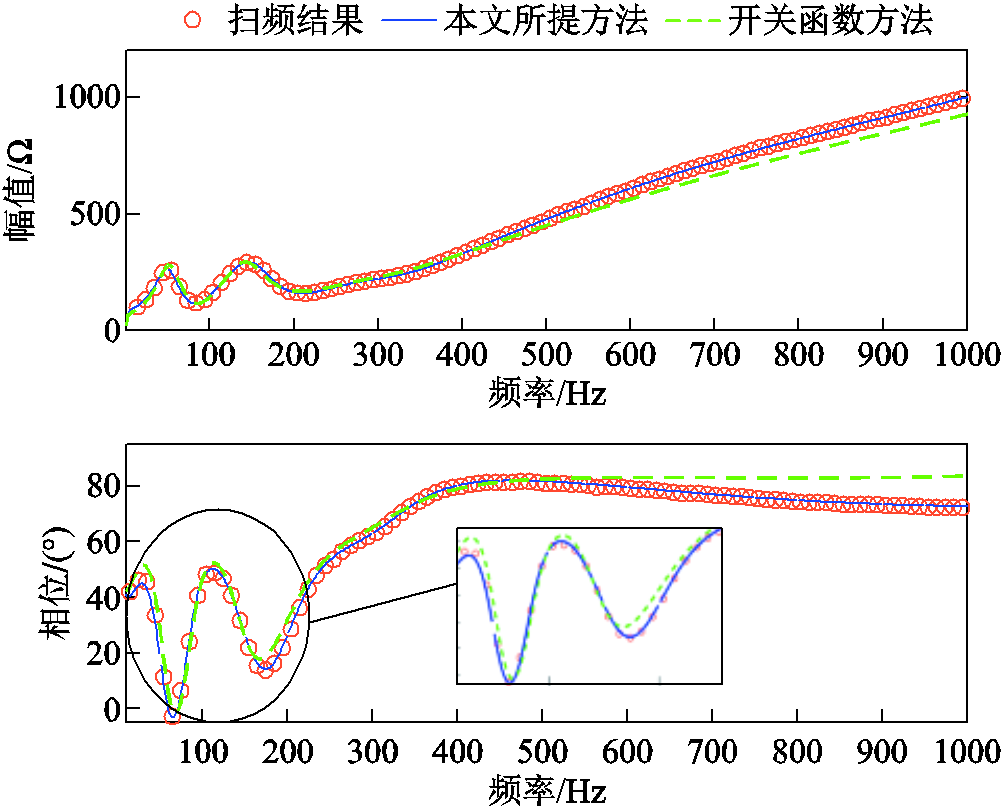
图13 逆变侧直流阻抗对比
Fig.13 Comparison diagram of DC impedance at inverter side
本文所研究的LCC-HVDC小信号电路图如图14a所示，整流站用小扰动电流源Dis并联整流侧直流阻抗Zdcr等效表示，逆变站用小扰动电压源Dus串联逆变侧直流阻抗Zdci等效表示。将直流输电线路阻抗等效至整流侧，Zr（如式（42）所示）为诺顿等效直流侧阻抗，Dir为诺顿等效小扰动电流源，等效电路如图14b所示。
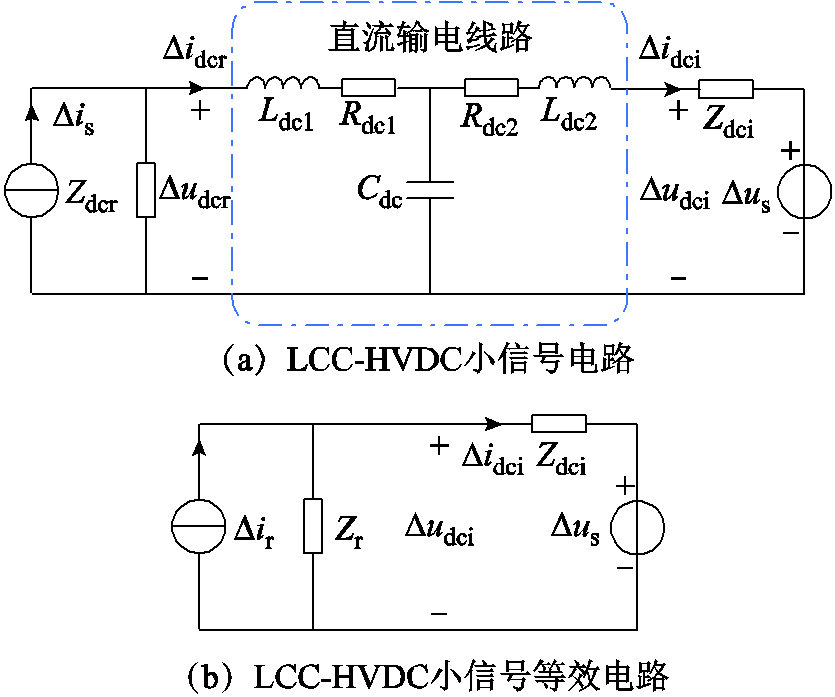
图14 LCC-HVDC小信号电路
Fig.14 LCC-HVDC small signal circuit
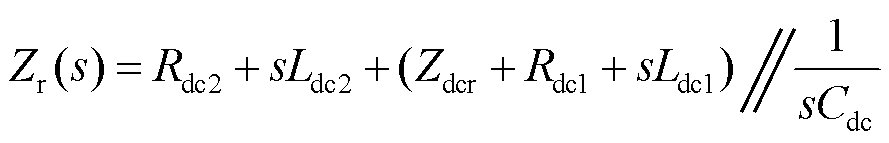（42）
根据阻抗分析法[24]，LCC-HVDC的小扰动稳定性可由阻抗Zr(s)与Zdci(s)的频响特性确定。当Zr和Zdci幅频特性曲线不存在交点，系统保持稳定；当Zr和Zdci的幅频特性曲线存在交点（该交点对应频率为截止频率fc），截止频率fc处Zr和Zdci的相位差的绝对值小于180°，系统稳定，否则系统不稳定。
通过改变定电压控制器时间常数Tii，分析其对系统小扰动稳定性的影响，以进一步验证所建直流侧阻抗模型的准确性及用于小扰动稳定性分析的有效性。当Tii取0.028Tii0时，Zr和Zdci的Bode图如图15所示。
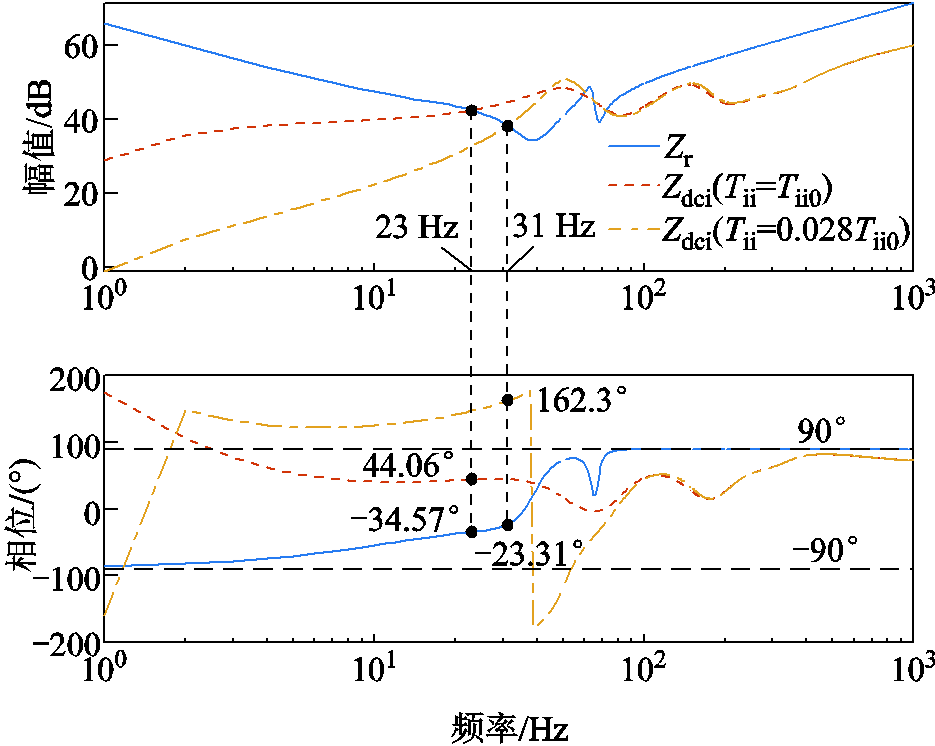
图15 改变Tii的直流侧阻抗Bode图
Fig.15 Bode diagram of DC side impedance by changing Tii
由图15相频特性曲线可知，当Tii取Tii0时，Zdci的相位介于[-90°, 90°]之间，表现为正阻尼特性；当Tii取0.028Tii0时，Zdci的相位在1～54 Hz频段内超出[-90°, 90°]，表现为负阻尼特性，此时系统存在不稳定的可能性。Tii=0.028Tii0时，Zr与Zdci的幅值曲线相交于31 Hz处（即fc=31 Hz），对应的相位分别为-23.31°和162.3°，相位差绝对值为185.61°，由此可判定系统不稳定，且系统振荡频率为31 Hz。
基于PSCAD/EMTDC仿真平台，令Tii在t=3 s时由Tii0阶跃至0.028Tii0，触发角指令值aordi（aordi由逆变站直流侧电压udci经定直流电压控制器所得，两者谐波特性保持一致）时域仿真结果及其快速傅里叶变换（Fast Fourier Transform, FFT）如图16所示。
由图16可知，Tii由Tii0阶跃至0.028Tii0，aordi开始振荡，振荡频率为31 Hz，该频率与理论分析的截止频率31 Hz保持一致。由上述理论分析与仿真结果可知，当Tii超过某特定值，Zdci由正阻尼特性变为负阻尼特性，系统稳定性减弱。直流侧阻抗模型用于小扰动稳定性分析的有效性得到验证。
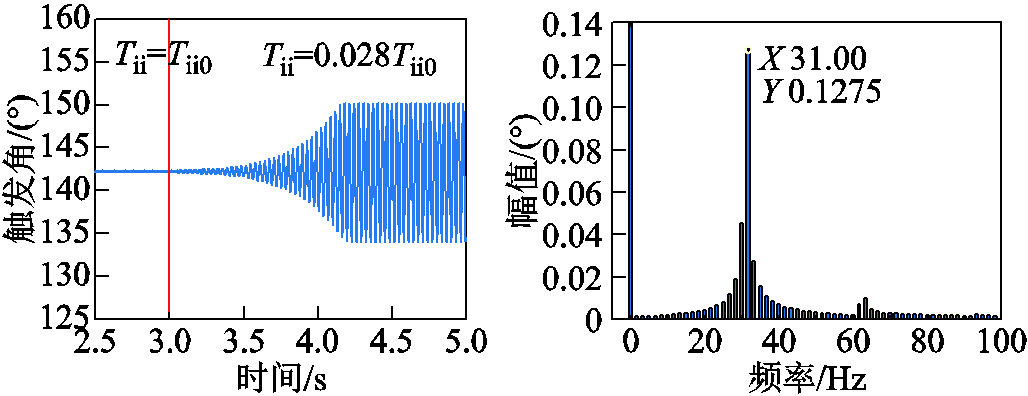
图16 改变Tii的仿真验证
Fig.16 Simulation verification of changing Tii
本文首先从系统同步触发和单边调制的原理出发，推导了映射函数解析表达式，该表达式精准地反映了LCC换流器在换相/非换相期间的交直流调制关系；其次，结合映射函数与换流阀导通状态下的直流电压和换流变压器阀侧电流时域表达式，考虑换相动态并通过谐波线性化及傅里叶变换得到直流电压和交流电流的频域小信号动态模型；再次，考虑控制回路和RC回路，建立直流侧阻抗模型；最后，代入CIGRE高压直流标准测试模型相关参数，对直流侧阻抗的解析结果和其用于小扰动稳定性分析的有效性进行了仿真验证。将本文的贡献总结如下：
1）考虑同步触发及准确的换相动态，提出了基于单边调制的映射函数，该函数能精准地反映LCC换流器换相/非换相期间的交直流调制关系。
2）分析了换相动态及RC回路对直流侧阻抗的影响，换相动态对直流侧阻抗的影响主要体现在较低频段，而RC回路对其影响主要体现在较高频段。
3）建立精确的直流侧阻抗模型。该模型考虑了详尽换相动态、控制环节和换流阀RC回路等影响因素，与现有基于开关函数建模方法相比，本文建模方法准确性更高。
附 录
1. 单边调制推导
将正文图3锯齿载波q1,0(t)展开为傅里叶级数，有
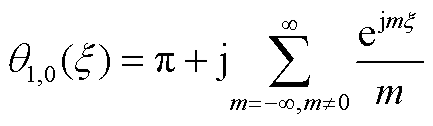（A1）
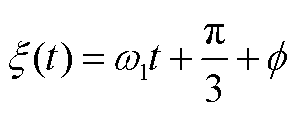（A2）
由文献[23]可知，正文图4所示脉冲序列Sa公式为
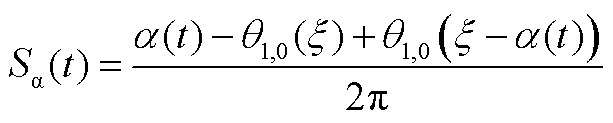（A3）
代入相关数据可得
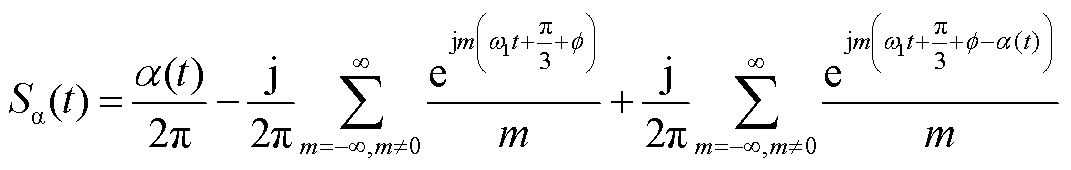（A4）
将式（A4）中a(t)用d(t)替换可得
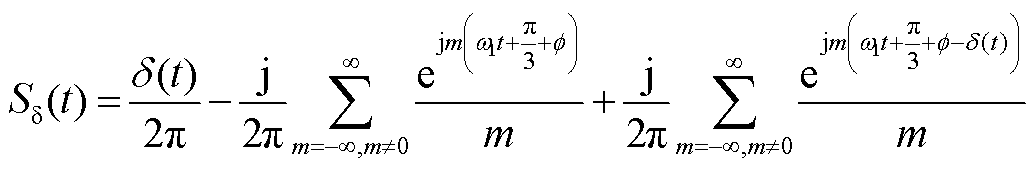（A5）
将式（A4）中a(t)用a(t)+p/3替换可得
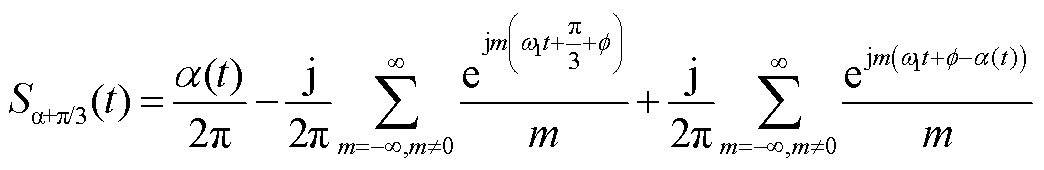（A6）
2. 采样保持频域推导
令正文图5蓝色实线为Didch(t)，其时域表达式为
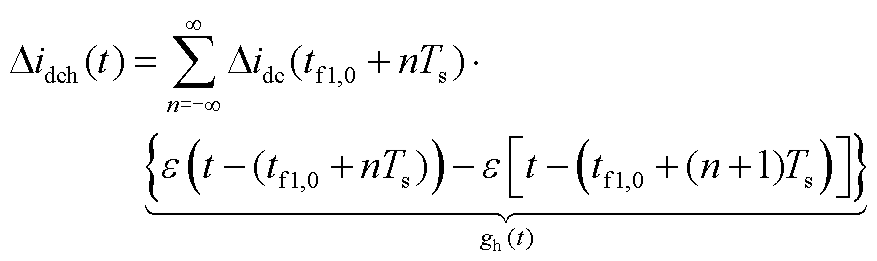（A7）
式中，ε(t)为单位阶跃函数；Didc(tf1,0+nTs)为(tf1,0+nTs)时刻的直流侧电流采样数值；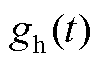
为零阶保持器时域表达式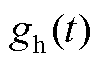，通过拉氏变换后可表示为
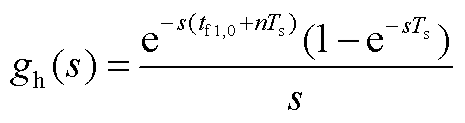（A8）
将式（A7）转换至频域，频域表达式为
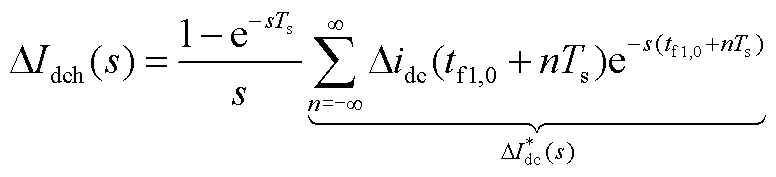（A9）
式中，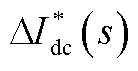
为扰动直流电流采样信号
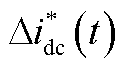经拉氏变换所得的频域表达式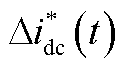，表达式为
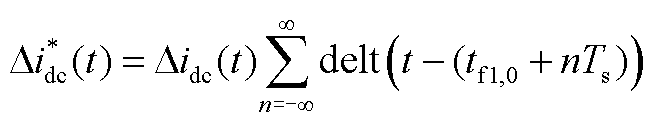（A10）
式中，
(t)为单位冲击函数，(t-(tf1,0+nTs))表示只有在
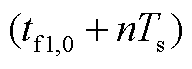时刻取值为1，其他时刻取值均为0。
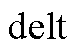对(t)进行傅里叶级数展开后，直接写出(t-(tf1,0+nTs))为
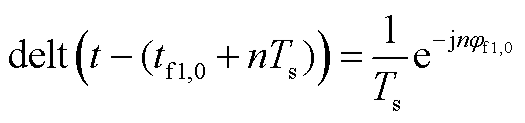（A11）
将式（A11）代入式（A10），可得
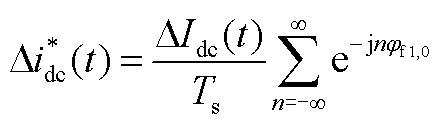（A12）
将式（A12）转换至频域后代入式（A9），解得
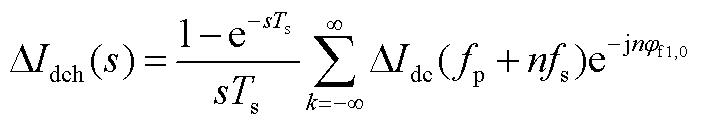（A13）
3. CIGRE HVDC标准测试模型参数
附表1 CIGRE HVDC标准测试模型运行参数
App.Tab.1 CIGRE HVDC standard test model operating parameters
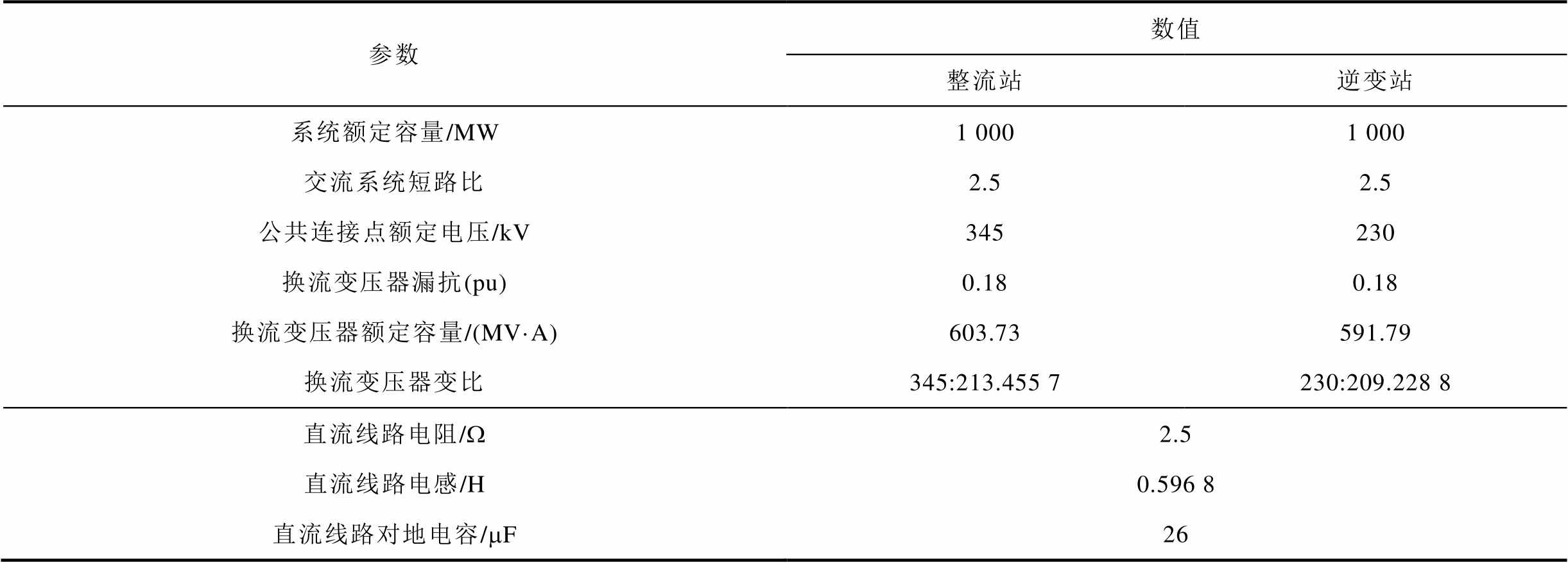
参数数值 整流站逆变站 系统额定容量/MW1 0001 000 交流系统短路比2.52.5 公共连接点额定电压/kV345230 换流变压器漏抗(pu)0.180.18 换流变压器额定容量/(MV·A)603.73591.79 换流变压器变比345:213.455 7230:209.228 8 直流线路电阻/W2.5 直流线路电感/H0.596 8 直流线路对地电容/mF26
附表2 CIGRE HVDC标准测试模型控制参数
App.Tab.2 CIGRE HVDC standard test model control parameters
控制器参数 定直流电流控制器Kpr0=1.098 9，Trr0=0.010 92 s Gr0=1/2，Tr0=0.005 s 定直流电压控制器Kpi0=0.750 6，Tii0=0.054 4 s Gi0=1/490，Ti0=0.005 s 整流侧锁相环KpPLL1=10，KiPLL1=50，wPLLr=2.316 Hz 逆变侧锁相环KpPLL2=10，KiPLL2=50，wPLLi=2.316 Hz
附图1 谐波传递与调制过程示意图
App.Fig.1 Schematic diagram of harmonic transmission and modulation process
4. 理论与仿真结果对比
LCC-HVDC直流侧阻抗在不同控制参数下的理论结果与仿真结果的对比分析，具体如附图2～附图5所示。图题中的括号内容表示只改变该参数，其他参数保持不变。
附图2 整流站直流侧阻抗（Kpr=1.5）
App.Fig.2 DC side impedance of rectifier station (Kpr=1.5)
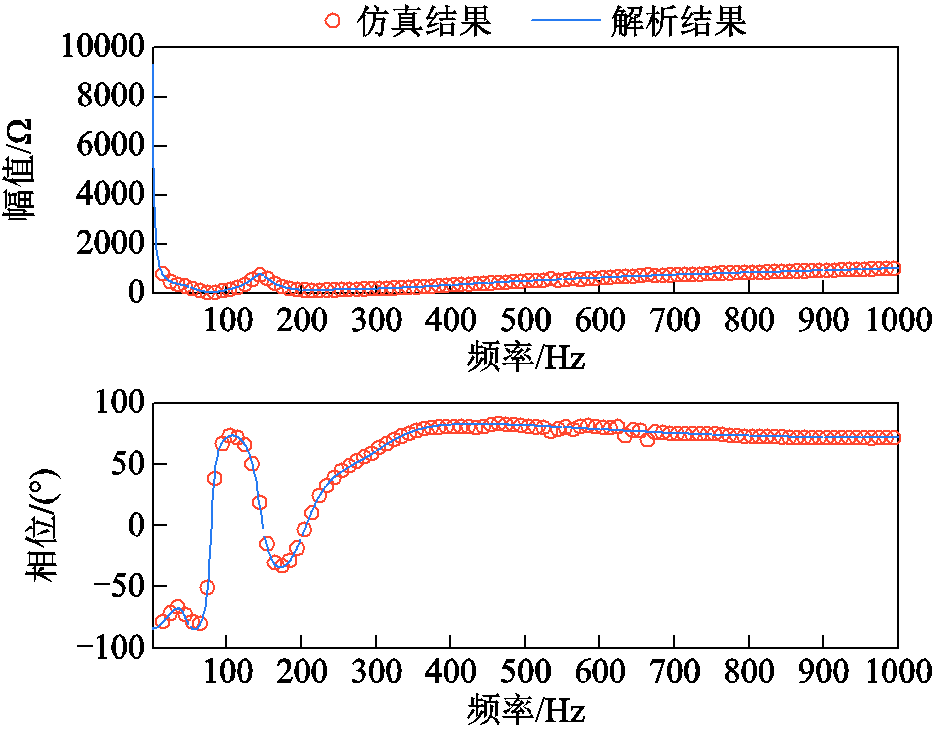
附图3 整流站直流侧阻抗（Trr=0.003 s）
App.Fig.3 DC side impedance of rectifier station (Trr=0.003 s)
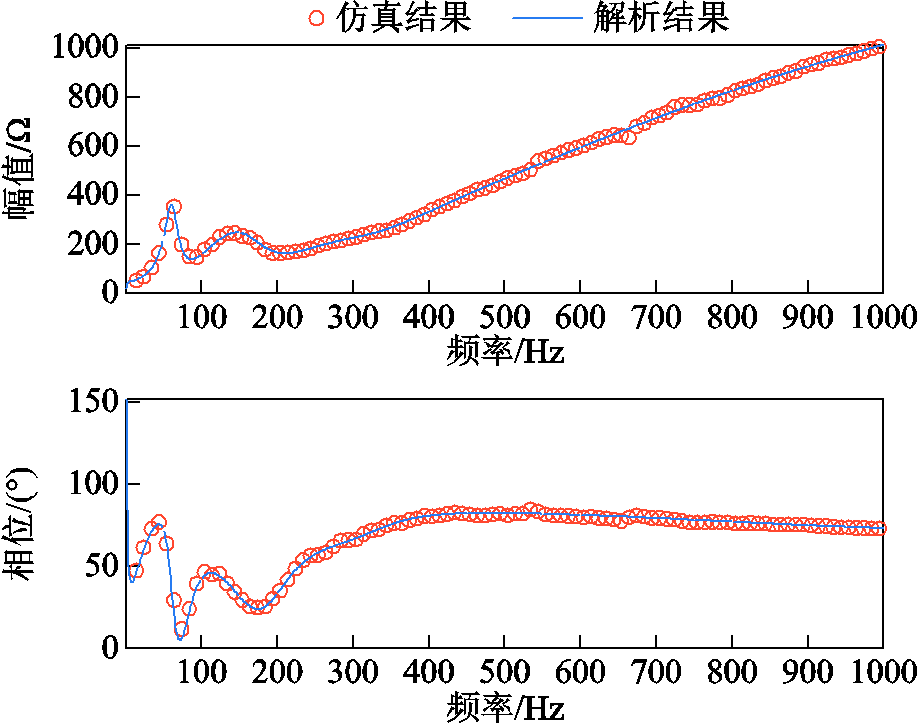
附图4 逆变站直流侧阻抗（Kpi=2）
App.Fig.4 DC side impedance of inverter station (Kpi=2)
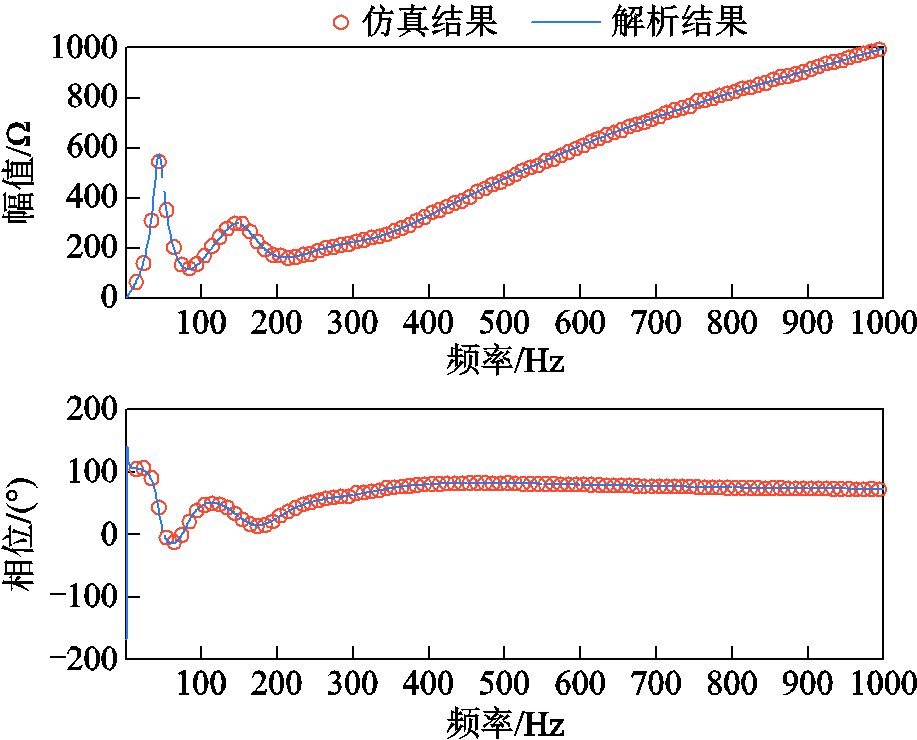
附图5 逆变站直流侧阻抗（Tii=0.002 s）
App.Fig.5 DC side impedance of inverter station (Tii=0.002 s)
参考文献
[1] 汤广福, 庞辉, 贺之渊. 先进交直流输电技术在中国的发展与应用[J]. 中国电机工程学报, 2016, 36(7): 1760-1771.
Tang Guangfu, Pang Hui, He Zhiyuan. R & D and application of advanced power transmission technology in China[J]. Proceedings of the CSEE, 2016, 36(7): 1760-1771.
[2] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822.
Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4808-4822.
[3] 丁扬, 种芝艺, 黄杰, 等. 高压直流输电工程谐振研究[J]. 电网技术, 2012, 36(12): 189-194.
Ding Yang, Chong Zhiyi, Huang Jie, et al. Study on DC resonance in HVDC power transmission projects[J]. Power System Technology, 2012, 36(12): 189-194.
[4] 甄自竞, 杜文娟, 王海风. 近似强模式谐振下高压直流输电系统引起的次同步振荡仿真研究[J]. 中国电机工程学报, 2019, 39(7): 1976-1985.
Zhen Zijing, Du Wenjuan, Wang Haifeng. The simulation study on SSOs caused by the HVDC under the condition of near strong modal resonance[J]. Proceedings of the CSEE, 2019, 39(7): 1976-1985.
[5] 郭春义, 吕乃航, 张加卿. 提高LCC-HVDC在弱交流系统下的稳定性和动态性能的控制参数优化方法[J]. 电工技术学报, 2023, 38(7): 1751-1764, 1779.
Guo Chunyi, Lü Naihang, Zhang Jiaqing. Optimization of control parameters to enhance stability and dynamic performance of LCC-HVDC under weak AC condition[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1751-1764, 1779.
[6] Cespedes M, Sun Jian. Impedance modeling and analysis of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1254-1261.
[7] 赵书强, 李忍, 高本锋. 基于状态空间的阻抗分析法在次同步振荡中的应用[J]. 电力系统自动化, 2018, 42(18): 25-32, 113.
Zhao Shuqiang, Li Ren, Gao Benfeng. Application of state space based impedance analysis method in sub-synchronous oscillation[J]. Automation of Electric Power Systems, 2018, 42(18): 25-32, 113.
[8] 贺永杰, 向往, 周家培, 等. LCC-MMC串联型混合直流输电系统小信号建模[J]. 电工技术学报, 2021, 36(7): 1492-1506.
He Yongjie, Xiang Wang, Zhou Jiapei, et al. Small-signal modelling of LCC-MMC series hybrid HVDC transmission system[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1492-1506.
[9] 郑安然, 郭春义, 殷子寒, 等. 提高弱交流系统下混合多端直流输电系统小干扰稳定性的控制参数优化调节方法[J]. 电工技术学报, 2020, 35(6): 1336-1345.
Zheng Anran, Guo Chunyi, Yin Zihan, et al. Optimal adjustment method of control parameters for improving small-signal stability of hybrid multi-terminal HVDC system under weak AC condition[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1336-1345.
[10] 叶运铭, 汪娟娟, 陈威, 等. LCC-HVDC系统直流控制回路小干扰稳定性分析[J]. 电力系统自动化, 2021, 45(16): 178-188.
Ye Yunming, Wang Juanjuan, Chen Wei, et al. Small-signal stability analysis of DC control loop for LCC-HVDC system[J]. Automation of Electric Power Systems, 2021, 45(16): 178-188.
[11] 陈威, 叶运铭, 周保荣, 等. 定电压与预测型定关断角控制对HVDC小干扰稳定性的影响[J]. 电力系统自动化, 2020, 44(18): 98-106.
Chen Wei, Ye Yunming, Zhou Baorong, et al. Influence of constant voltage control and predictive constant extinction angle control on small-signal stability of HVDC[J]. Automation of Electric Power Systems, 2020, 44(18): 98-106.
[12] Sun Jian, Bing Zhonghui, Karimi K J. Small-signal modeling of multipulse rectifiers for more-electric aircraft applications[C]//2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 2008: 302-308.
[13] Hu L, Yacamini R. Harmonic transfer through converters and HVDC links[J]. IEEE Transactions on Power Electronics, 1992, 7(3): 514-525.
[14] Liu Hanchao, Sun Jian. DC terminal impedance modeling of LCC-based HVDC converters[C]//2013 IEEE 14th Workshop on Control and Modeling for Power Electronics (COMPEL), Salt Lake City, UT, USA, 2013: 1-8.
[15] Wang Xi, Shi Peng, Liu Yiming, et al. Impedance-based stability analysis of LCC-HVDC connected to weak grid considering frequency coupling characteristic [C]//2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nanjing, China, 2022: 153-157.
[16] Nian Heng, Liu Yiming, Li Haipan, et al. Commutation overlap characteristic modeling and stability analysis of LCC-HVDC in sending AC grid[J]. IEEE Transactions on Sustainable Energy, 2022, 13(3): 1594-1606.
[17] 马玉龙, 肖湘宁, 姜旭, 等. HVDC换流器的阻抗频率特性[J]. 电力系统自动化, 2006, 30(12): 66-69, 91.
Ma Yulong, Xiao Xiangning, Jiang Xu, et al. Study on impedance-frequency characteristic of HVDC conver-ter[J]. Automation of Electric Power Systems, 2006, 30(12): 66-69, 91.
[18] 贺永杰, 向往, 赵静波, 等. 一种用于LCC-HVDC系统小干扰稳定性分析的改进动态相量模型[J]. 电网技术, 2021, 45(4): 1417-1428.
He Yongjie, Xiang Wang, Zhao Jingbo, et al. Modified dynamic phasor model for small-signal stability analysis of LCC-HVDC system[J]. Power System Technology, 2021, 45(4): 1417-1428.
[19] 莫泽, 汪娟娟, 丁天皓, 等. 基于改进开关函数的LCC-HVDC直流阻抗建模及小扰动稳定性分析[J]. 电网技术, 2022, 46(11): 4491-4505.
Mo Ze, Wang Juanjuan, Ding Tianhao, et al. LCC-HVDC impedance modeling and small disturbance stability analysis based on improved switching function[J]. Power System Technology, 2022, 46(11): 4491-4505.
[20] Qi Yi, Zhao Huanfeng, Fan Shengtao, et al. Small signal frequency-domain model of a LCC-HVDC converter based on an infinite series-converter approach[C]//2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2020: 1.
[21] 周盛宇, 汪娟娟, 刘岳坤, 等. 考虑换流阀阻尼电路的LCC-HVDC系统小信号精准建模[J]. 电网技术, 2022, 46(10): 3730-3744.
Zhou Shengyu, Wang Juanjuan, Liu Yuekun, et al. Small signal accurate modeling of LCC-HVDC system considering converter valve damping circuit[J]. Power System Technology, 2022, 46(10): 3730-3744.
[22] Chen Xiang, Ma Junpeng, Wang Shunliang, et al. An accurate impedance model of line commutated converter with variable commutation overlap[J]. IEEE Transactions on Power Delivery, 2022, 37(1): 562-572.
[23] Mouton H, Putzeys B. Understanding the PWM nonlinearity: single-sided modulation[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 2116-2128.
[24] 丁天皓. 考虑谐波扰动的高压直流换流器开关函数建模及应用[D]. 广州: 华南理工大学, 2021.
Abstract With the continuous increase of the transmission capacity of the line commutated converter based high voltage direct current (LCC-HVDC) system in the power grid, the coupling strength of AC and DC continues to deepen, and the strength of the AC system continues to weaken. The problems of small disturbance oscillation instability in the LCC-HVDC system are becoming increasingly prominent. Due to the clear physical concepts, impedance analysis method has been widely applied in the resonance analysis of LCC-HVDC systems, and the key to this method is to establish an impedance model. The accuracy of the impedance model directly affects the small disturbance stability analysis of the system. To improve the impedance modeling accuracy of LCC-HVDC, this article proposes a DC side impedance modeling method based on single-side modulated mapping function, which significantly improves the accuracy of the DC side impedance model.
Firstly, starting from the principle of synchronous triggering, a mapping function based on single-side modulation is introduced, which contains control and commutation information, and thus accurately establishes the mapping relationship between the AC and DC sides during commutation/non commutation.
Then, by combining the mapping function with the DC side voltage and converter transformer valve side current under different conduction states of the converter valve, the detailed commutation dynamics are considered and the complete frequency domain small signal dynamic models of DC side voltage and AC side current are obtained through harmonic linearization and Fourier transform.
Furthermore, considering the damping circuit of the control and converter valve, establish analytical models for the DC impedance of the rectifier and inverter sides.
Finally, taking the CIGRE high-voltage DC standard test model as an example, the accuracy of the DC side impedance model and its effectiveness in small disturbance stability analysis were verified based on the PSCAD/EMTDC platform.
The following conclusions can be drawn from the simulation analysis: (1) Considering synchronous triggering and accurate commutation dynamics, a mapping function based on single-side modulation is proposed, which can accurately reflect the AC/DC modulation relationship during commutation/non commutation of LCC converters. (2) Analyzed the influence of commutation dynamics and RC circuit on the DC side impedance. The influence of commutation dynamics on the DC side impedance is mainly reflected in the lower frequency range, while the influence of RC circuit on it is mainly reflected in the higher frequency range. (3) Establish an accurate DC side impedance model that takes into account factors such as detailed commutation dynamics, control links, and RC circuit of the converter valve. Compared with existing switch function based modeling methods, this modeling method has higher accuracy.
Keywords：Line commutated converter, single-sided modulation, mapping function, converter valve damping circuit, commutation dynamics, DC side impedance
DOI: 10.19595/j.cnki.1000-6753.tces.230682
中图分类号：TM712
国家自然科学基金资助项目（52277102）。
收稿日期 2023-05-16
改稿日期 2023-07-21
汪娟娟 女，1974年生，教授，研究方向为电力系统稳定与控制、高压直流输电等。E-mail：epjjwang@scut.edu.cn
莫 泽 男，1997年生，硕士，研究方向为高压直流输电。E-mail：1286963144@qq.com（通信作者）
（编辑 赫 蕾）