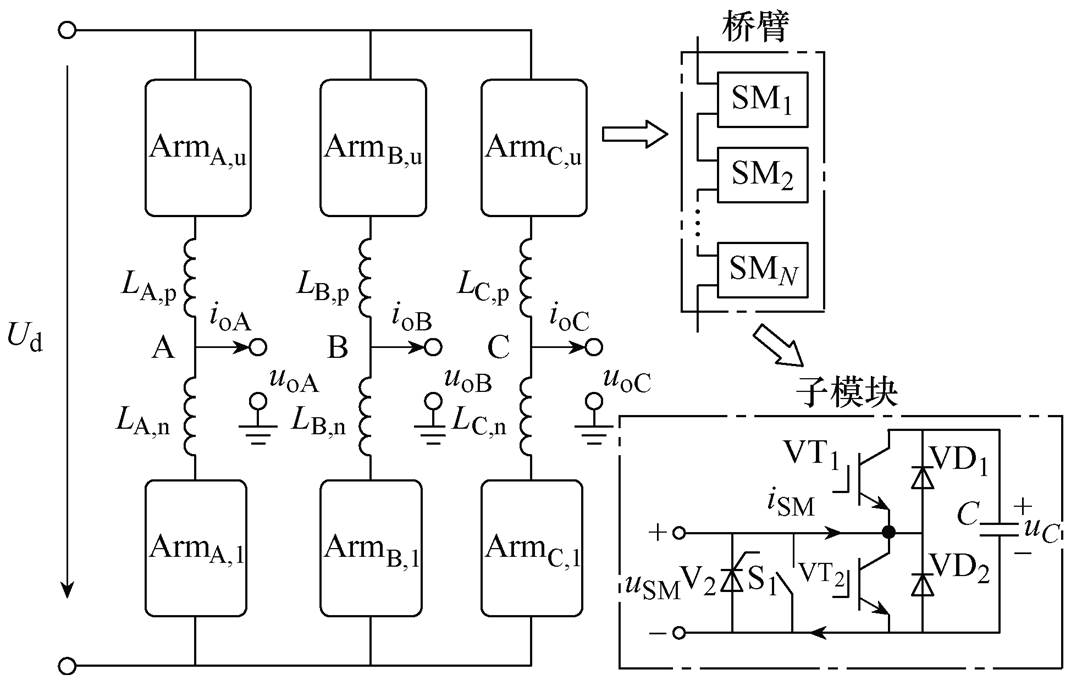
图1 MMC主电路及其子模块结构
Fig.1 The topology structure of MMC and sub-module
摘要 针对现有模块化多电平换流器(MMC)子模块故障诊断过程中所需传感器较多、测量干扰较大等问题,提出一种基于深度学习的MMC子模块IGBT开路故障诊断方法。在对MMC子模块开路故障特征进行分析的基础上,利用短时傅里叶变换(STFT)提取桥臂电压信号的谐波分量信息作为故障诊断所需的特征参数。将所得到的特征参数进行处理后构建故障诊断样本,在通过深度置信网络实现故障类型快速检测的基础上,依据不同故障类型,构建多个基于卷积神经网络的故障定位网络,进而实现开路故障的检测与定位。通过129电平的MMC系统仿真模型和降功率的MMC实验系统搭建,对该文所提方法进行了验证。仿真和实验结果表明,所提故障诊断方法可以在减少传感器数量的基础上实现子模块开路故障的诊断,提高系统的可靠性。
关键词:模块化多电平换流器 开路故障诊断 短时傅里叶变换 卷积神经网络
模块化多电平换流器(Modular Multilevel Converter, MMC)凭借其开关频率低、输出波形质量高、对电力电子器件开关一致性要求低等显著优势,已在电力电子传动、轨道交通牵引控制及高压柔性直流输电等领域得到广泛应用[1-8]。然而,MMC通常包含数目较多的子模块(Sub-Module, SM),而每个子模块内部的开关器件都是潜在的故障点。研究资料表明,换流器故障主要集中于功率开关器件IGBT上[9]。常见的IGBT故障有短路故障与开路故障两类。IGBT短路故障破坏性较强,因此现有驱动电路均包含短路保护措施对短路模块进行及时切除[10];而IGBT开路故障特征较为微弱,不易被检测到,但处理不当可能造成连锁故障,继而威胁到系统的正常运行[11]。
现有的MMC故障诊断方法主要分为基于硬件电路和基于软件算法两类。基于软件算法无需增设硬件电路,实现较为简易方便。根据具体的实现方式,又可进一步分为基于数学模型、基于信号分析以及基于机器学习三类[12-13]。近年来,随着人工智能、深度学习等计算机技术的不断发展,基于机器学习的诊断算法得到了越来越广泛的关注。此种方法通过智能算法对现有的大量样本数据进行深层次的特征分析,继而实现子模块的故障诊断。常见的算法有反向传播(Back Propagation, BP)神经网络[14]、深度置信网络(Deep Belief Network, DBN)[15-16]、长短时记忆(Long-Short Term Memory, LSTM)网络[17-18]、卷积神经网络(Convolutional Neural Network, CNN)[19]等。其中,BP神经网络结构简单、训练时间短,但由于下层与上层神经元完全连接,导致模型深度增加时梯度消失等问题越发严重。DBN通过简化的二值神经元提高网络深度,且对于含噪信号具有较好的鲁棒性,但全连接的网络结构仍使其无法自主提取故障特征,难以对不同子模块故障间的微弱特征进行辨析[20-21]。鉴于实际应用中电气量均为时间序列,因此部分文献采用LSTM进行故障诊断,虽然该网络在序列学习和时间预测方面有着较为优异的表现,但此方法实现复杂度较高,且运行所需时间较长[22]。而基于CNN的MMC子模块开路故障诊断方法直接将时间、子模块电容电压、桥臂环流和输出相电流等系统参数作为卷积网络的输入,将具体的故障类型标签作为网络的输出,利用CNN局部感知、权值共享以及空间下采样的特点,在加深网络层数的同时有效地减少了参数量,提高了训练速度和诊断速度。此外CNN还可以通过不同的滤波器对输入中的不同特征进行提取,如边缘信息及突变点信息等,使得CNN对单个子模块及多个子模块的故障诊断均有较高的准确率[23-24]。
因此,本文针对MMC子模块开路故障,提出了一种基于短时傅里叶变换(Short-Time Fourier Transform, STFT)和深度网络的诊断方法。所提方法仅需采集桥臂电压数据,通过短时傅里叶变换对桥臂电压进行预处理,不仅能够提取得到数据的深层次特征,同时也能利用较少的原始数据生成大量数据样本,避免训练样本不足时网络的过拟合现象。将数据样本代入预先训练好的深度网络中,通过DBN实现快速的故障类型检测,在此基础上利用CNN提取输入样本中的细微差别,进而实现故障定位。最后通过仿真和降功率MMC实验系统的测试,验证了所提故障诊断方法的有效性与可行性。
图1为MMC主电路及其子模块的拓扑结构。图1中,Ud为直流侧电压,直流侧中性点接地以提供参考电平;uoJ、ioJ分别为J相的输出电压及电流,J=A, B, C;uC为子模块电容电压基准值,iSM为流过子模块的电流。MMC三相之间相互独立,每相由上、下两个桥臂构成,每个桥臂由N个子模块串联组成,两桥臂间串联两个规格相同的电抗器LJ,p=LJ,n,以达到在系统启动时抑制充电电流、运行时抑制内部环流及故障时减小电流上升率的作用。每个子模块均由上、下两个IGBT开关管VT1、VT2和电容C并联构成,此外端口处安装有机械开关S1和高速晶闸管V2,分别实现VT2故障时子模块的可靠旁路以及子模块闭锁时为并联二极管VD2分流的功能。MMC的模块化结构使其可通过增减SM的数量来满足不同电压和功率等级的需求。

图1 MMC主电路及其子模块结构
Fig.1 The topology structure of MMC and sub-module
子模块的电容电压均衡是MMC正常稳定运行的基础。本文MMC系统采用载波移相调制方式,该方式下各SM驱动信号的开关频率相近,但由于载波相位差异,其充放电能力并不完全一致[25],需要采用电压均衡策略使各SM电容电压尽可能一致。目前常用策略依靠SM内部电压传感器对各模块电压进行排序,随后依据电压大小分别优先放电和充电[26-27],该方法显然不适用于本文所提仅使用桥臂电压传感器的诊断策略。本文利用桥臂电流对SM电容电压进行预测,并通过实际测量的桥臂电压对预测电压进行校正[28-29]。在获得各模块电容电压的校正值后,可通过改变对应模块调制波幅值对驱动信号的充放电能力进行调整[30],进而实现子模块电容电压均衡。
由于MMC三相结构对称,因此以a相为例,针对子模块VT1开路进行具体分析,当发生VT2开路时分析过程与之类似。
子模块上管VT1开路故障示意图如图2所示。当子模块处于切除状态时,VT1开路故障对系统没有影响;而当子模块处于投入状态时,由图2中故障通路可得:当子模块电流iSM>0,即电流流入子模块时,VT1开路仍然对系统没有影响;但若电流iSM<0时那本应流经开关管VT1的电流只能经过反并联二极管VD2流出模块,使得子模块的端口输出电压uSM为零,同时本应处于放电状态的电容C被旁路,电容电压维持不变,无法正常放电导致子模块电容电压持续上升。
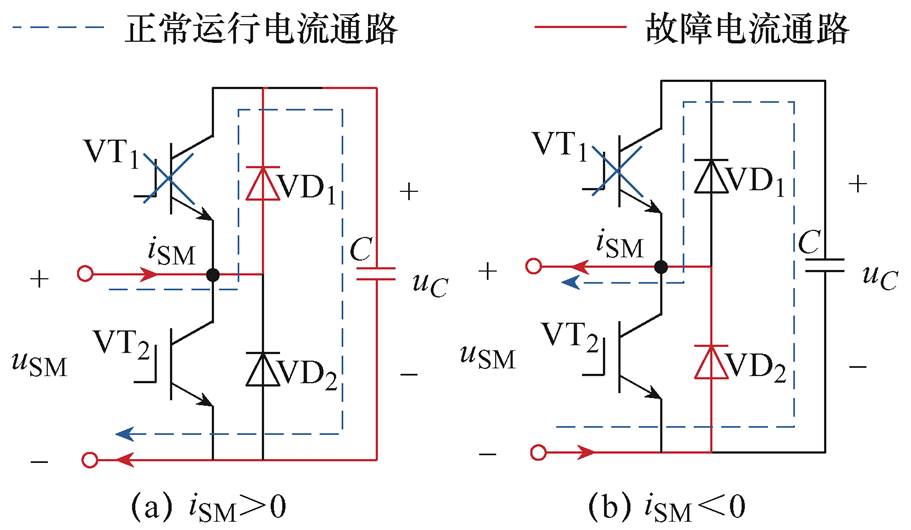
图2 子模块上管VT1开路故障示意图
Fig.2 The diagram under VT1 open-circuit fault on sub-module
MMC子模块在不同运行状态下的端口输出电压特性归纳见表1。根据表1中数据对比分析可知,故障前后子模块的端口电压会出现较大差异。然而对子模块电压进行逐个测量成本较高,鉴于桥臂电压为各个子模块端口电压的线性组合,因此本文选取桥臂电压作为故障变量,通过短时傅里叶变换的方法对其进行时频域分析,提取深层的子模块故障特征参数,并利用深度学习网络实现故障诊断。
表1 MMC不同状态下子模块输出电压
Tab.1 Sub-module output voltage in different states of MMC
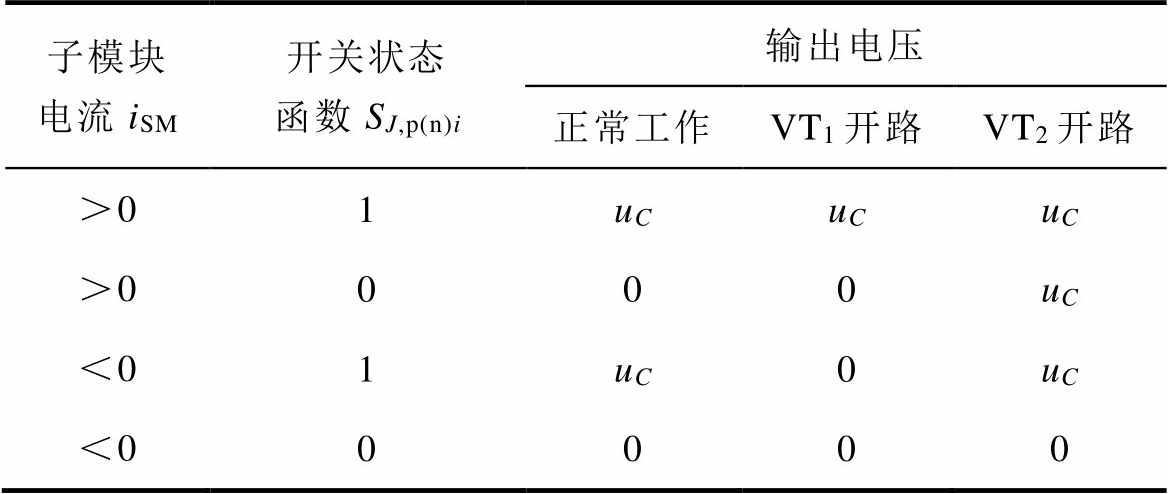
子模块电流iSM开关状态函数SJ,p(n)i输出电压 正常工作VT1开路VT2开路 >01uCuCuC >0000uC <01uC0uC <00000
有效提取故障信号的深层特征是故障诊断算法的基础和关键,而传统信号分析方法往往只包含时域或频域的单一信息,无法对故障特征进行准确提取,因此本文选用短时傅里叶变换实现故障特征参数提取。
短时傅里叶变换引入“局部频谱”的概念,通过选取固定长度的窗函数截取原信号,将其分割为多个相互独立的时域信号。随后分别对每段独立信号进行傅里叶变换,并将所得频谱信息按时间顺序排列,最终得到表征原始信号不同频率分量随时间变化规律的时频谱信息。
对于给定输入电压信号u(t),可对其进行短时傅里叶变换得
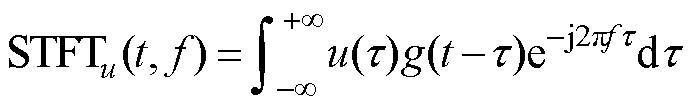 (1)
(1)
式中,STFTu(t, f)为短时傅里叶变换的输出;f为变换单位频率;g(t)为窗函数。常用的窗函数包括矩形窗、三角窗和汉宁窗等。其中,矩形窗函数具有最短的主瓣宽度,能量更为集中,因此本文选取矩形窗函数进行变换,表达式为
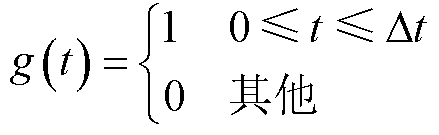 (2)
(2)
单次STFT与傅里叶变换类似,可将窗函数范围内原始信号从时域转换至频域,而通过窗函数的滑动则可以产生对应不同时域节点的频域信息。
为减少计算量及存储需求,采用累计贡献率法对不同频率谐波分量对整体信号波形的影响程度进行分析,计算式为
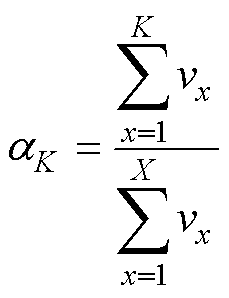 (3)
(3)
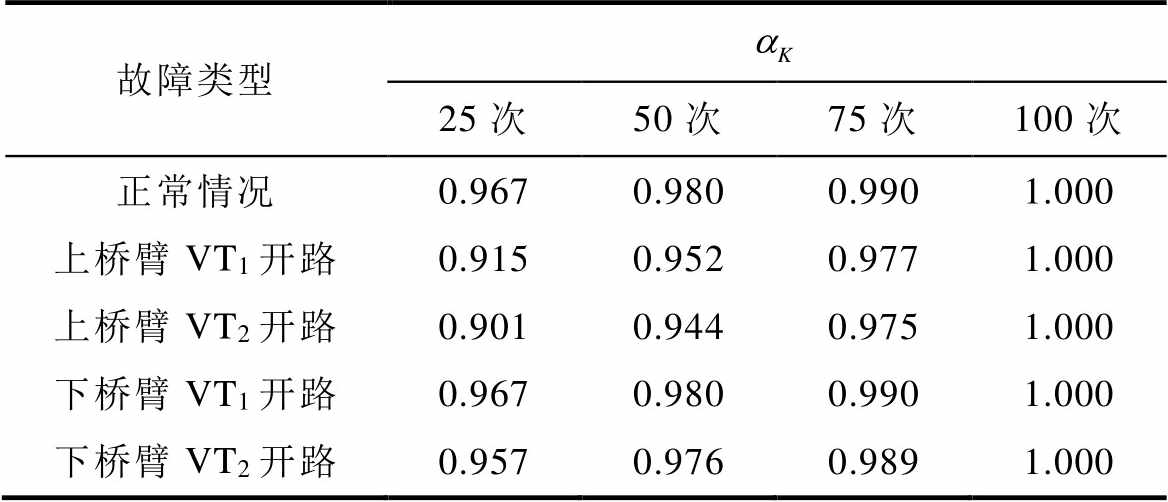
式中,X为总谐波分量的个数,此处取X=100;vx为桥臂电压第x次谐波的幅值;aK为前K次谐波的累计贡献率。以上桥臂电压为例,不同故障类型下各谐波贡献率见表2。
表2 谐波累计贡献率
Tab.2 Harmonic cumulative contribution ratio
故障类型 25次50次75次100次 正常情况0.9670.9800.9901.000 上桥臂VT1开路0.9150.9520.9771.000 上桥臂VT2开路0.9010.9440.9751.000 下桥臂VT1开路0.9670.9800.9901.000 下桥臂VT2开路0.9570.9760.9891.000
本文中设定累计贡献率阈值为95%,即选取50倍频以内的谐波数据进行训练。所选故障信号的长度及窗函数的宽度均为一个基本工频周期,窗函数的滑动步长为0.02个工频周期,不同样本间相差0.1个工频周期,此时单个样本包含5个滑动窗函数范围内的频域信息。上述方法使不同样本间存在约0.9个工频周期的重叠采样部分。重叠采样可利用较少波形生成大量样本,也可使故障特征参数的变化更为平滑,具体构建方式如图3所示。
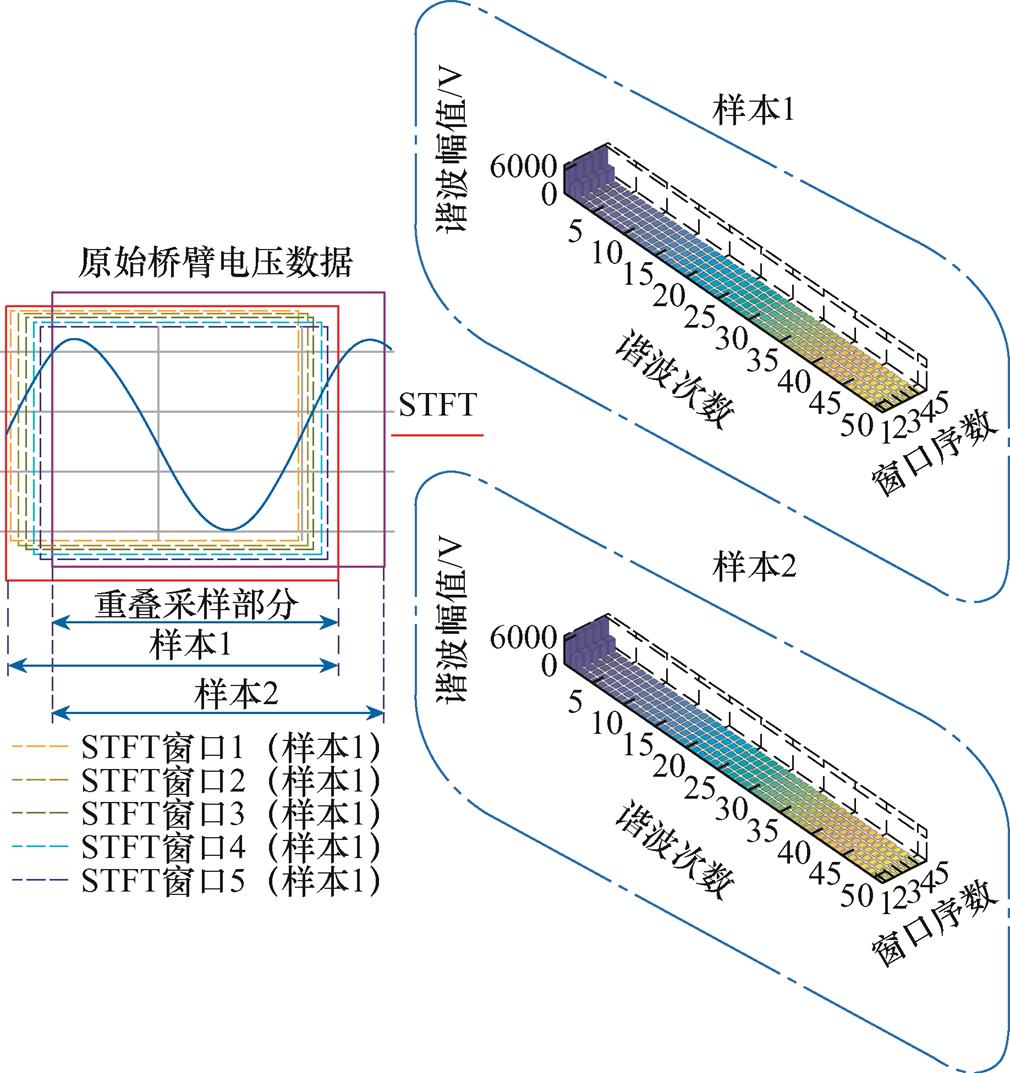
图3 故障特征样本构建原理
Fig.3 The construction principle of fault feature samples
另外,考虑到故障诊断时需要分别采集上、下桥臂电压信息,故单个训练样本的故障特征参数如图4所示。

图4 输入样本故障特征参数组成
Fig.4 The composition of input sample fault characteristic parameters
1.4.1 深度置信网络
深度置信网络由多个受限玻耳兹曼机(Restricted Boltzmann Machine, RBM)堆叠而成,各隐藏层可以进行相对独立的预训练,并且网络节点多为二元变量,训练、检测用时相对较短,能够较好地满足故障诊断的时间要求,因而本文利用DBN实现故障桥臂及故障类型的初步检测。
DBN模型结构及训练过程如图5所示,典型DBN包含可见层和多个隐藏层,其中输出层一般采用BP神经网络,其余各层一般采用RBM结构。
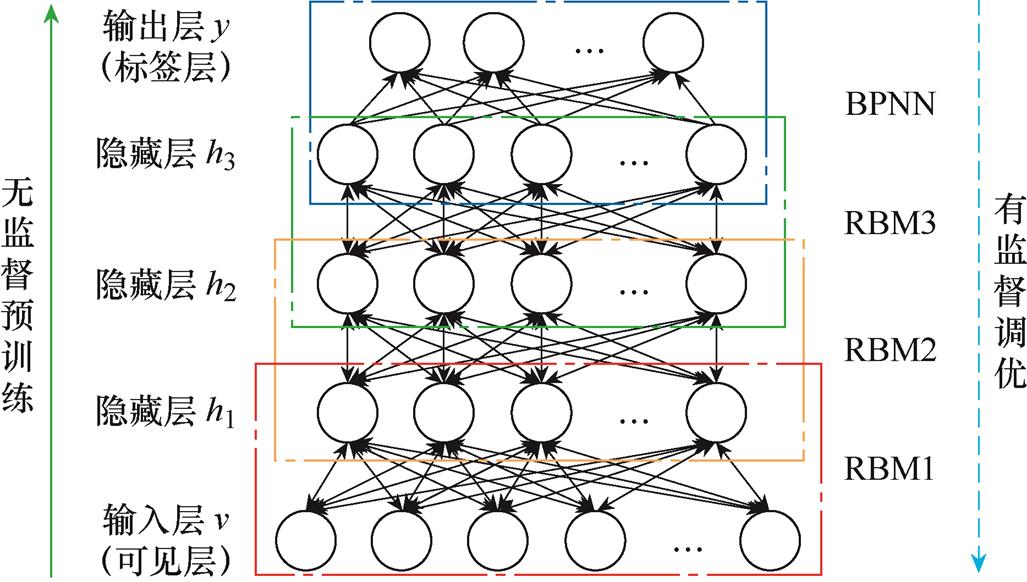
图5 DBN结构及训练过程
Fig.5 The structure and training process of DBN
单个RBM可以表述为一个由可见层及隐藏层组成的两层递归神经网络,分别用v和h代表可见层的输入变量和隐藏层的隐藏变量。对于任意给定状态(v, h),其联合能量函数E及联合概率分布P分别为
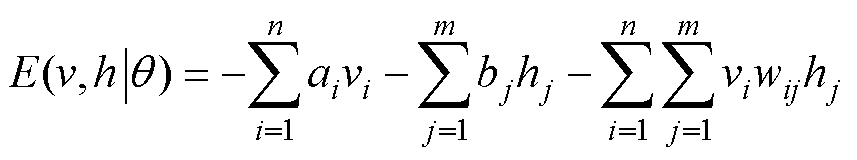 (4)
(4)
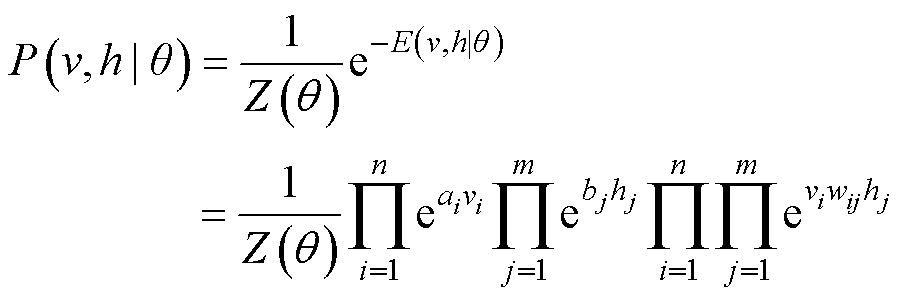 (5)
(5)
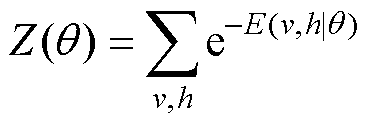 (6)
(6)
式中,θ={w, a, b}为RBM基本参数;n、m分别为v和h的维数;vi、ai分别为可见层内部第i节点的激活状态和偏置量;hj、bj分别为隐藏层内部第j节点的激活状态和偏置量;wij为第i、j节点间的连接权重。如果已经确定可见层各节点的状态分布,则可计算隐藏层第j个节点的激活概率为
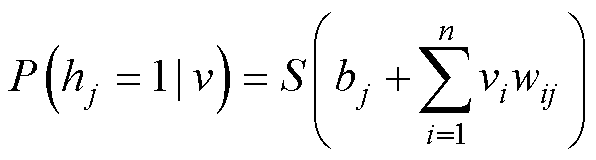 (7)
(7)
式中,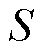 为Sigmoid激活函数。相应地,可得在确定隐藏层节点状态情况下,可见层节点激活概率为
为Sigmoid激活函数。相应地,可得在确定隐藏层节点状态情况下,可见层节点激活概率为
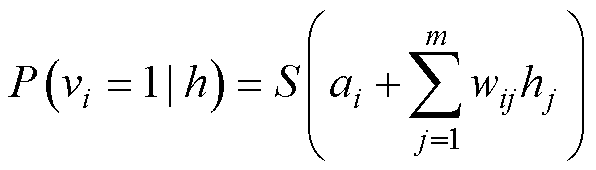 (8)
(8)
由于DBN为多个RBM的叠加,因而具有L个隐藏层的DBN可定义为
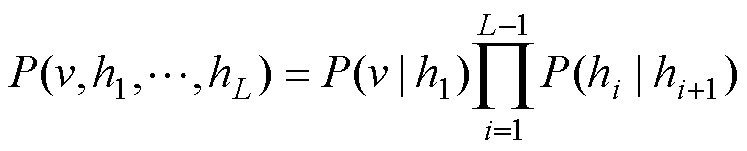 (9)
(9)
由式(9)可知,求解DBN需要计算隐藏层节点中的多个RBM,为避免计算所有节点的边缘密度函数,G. E. Hinton教授等提出了逐层贪婪算法(Layer-wise Greedy Algorichm, LWGA)[31],将DBN的训练分解为无监督预训练阶段和有监督调优阶段两部分。该方法首先利用贪婪算法逐层训练隐藏层参数,所得参数仅针对本层最优,随后利用传统全局寻优方法(如BP算法)对节点参数进行微调,从而实现模型参数的全局优化。
1.4.2 卷积神经网络
DBN的结构和训练过程都相对简明,可较好地满足故障检测的时间要求,但是当判断具体故障模块位置时,不同模块的故障特征差异占整体波形比例极小,而DBN会将所有输入同等处理,导致定位效果较差,此时可以使用CNN对故障特征差异进行特征化提取,提升故障诊断的整体性能。
卷积神经网络是一种具有强大特征提取能力的前馈神经网络,其通过构建多个卷积核将输入数据中的信息逐层提取出来,并通过卷积层和池化层实现空间降采样,进而减少输入维度。典型CNN由提取特征的卷积层、池化层及实现样本分类的全连接层构成。
卷积层实现了上一层数据的特征提取,每个卷积层具有复数个卷积核,每个卷积核包含一个权重系数和一个偏移系数,对一卷积层数为M的网络而言,l~l+1层的卷积为
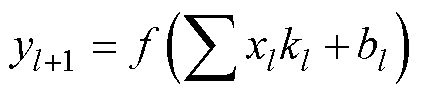 (10)
(10)
式中,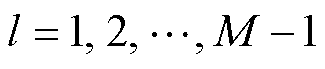 ;
;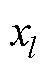 为l层输入特征图集合;kl为l层核函数集合;bl为偏置项;f(x)为激活函数;yl+1为l层的输出特征图集合。
为l层输入特征图集合;kl为l层核函数集合;bl为偏置项;f(x)为激活函数;yl+1为l层的输出特征图集合。
池化本质上是一种下采样操作,CNN经由池化后可以有效地减少卷积后的特征空间和网络参数,进而可有效减少模型参数并降低过拟合。常用池化操作有平均值池化和最大值池化两类。本文采用最大值池化卷积后的特征图进行处理,窗口宽度及步幅均为2,公式为
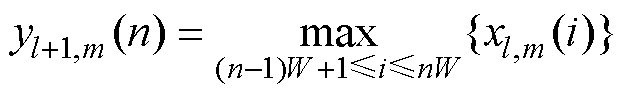 (11)
(11)
式中,xl,m(i)为第l层第m帧中第i个元素的值,i∈[(n-1)W+1, nW];W为池化窗口的宽度;yl+1,m为池化后该帧所对应的值。
本文所提出的基于DBN的开路故障检测流程如下:
(1)采集系统不同状态下的桥臂电压。
(2)依照图3过程对桥臂电压进行变换,并将变换得到的特征参数按照周期的先后以及上、下桥臂各倍频分量的顺序依次排列,并展平为一维张量,即
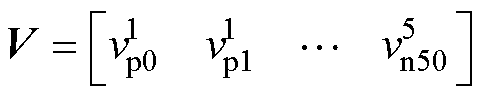 (12)
(12)
式中,V为输入网络的样本;下标字母p表示上桥臂电压;下标字母n表示下桥臂电压;下标数字表示桥臂电压谐波分量倍频次数;上标数字表示滑动周期。
(3)将输入样本按照6∶2∶2的比例划分为训练集、验证集与测试集,并采用0-1规范化进行数据预处理,具体计算公式为
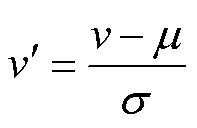 (13)
(13)
式中,v为处理前数据;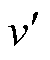 为处理后数据;μ为数据的均值;s 为数据的标准差。
为处理后数据;μ为数据的均值;s 为数据的标准差。
(4)将处理后的样本输入DBN中进行训练及测试,从而实现子模块开路故障类型的检测。按照故障子模块所在桥臂以及故障开关管的类型可将故障分为16类,系统故障类型及故障编码对应关系见表3。
由于共有16类系统故障状态(包括正常情况),则DBN输出层节点数即为16,依次对应表3中的每一种故障类型为
表3 系统故障类型及故障编码对应关系
Tab.3 The correspondence between system fault types and fault codes

系统故障类型故障编码 无故障正常运行0 单子模块故障上桥臂单子模块VT1管开路1 上桥臂单子模块VT2管开路2 下桥臂单子模块VT1管开路3 下桥臂单子模块VT2管开路4 双子模块故障上桥臂双子模块VT1管开路5 上桥臂双子模块VT2管开路6 上桥臂双子模块VT2管开路伴下桥臂双子模块VT1管开路14 多子模块故障上、下桥臂子模块VT1、VT2管均开路15
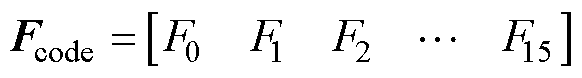 (14)
(14)
式中,Fcode为网络最终输出的故障检测结果;Fi(i=0, 1,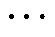 , 15)为输出层第i个节点的数值。对输出 层数据加以约束,使之满足关系
, 15)为输出层第i个节点的数值。对输出 层数据加以约束,使之满足关系
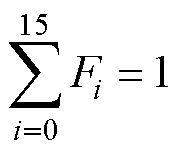 (15)
(15)
由于DBN每一个隐藏层节点值均为二元变量,任意时刻检测网络输出始终满足
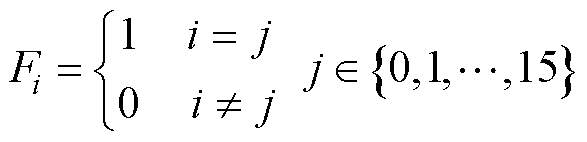 (16)
(16)
上述故障检测流程如图6所示。
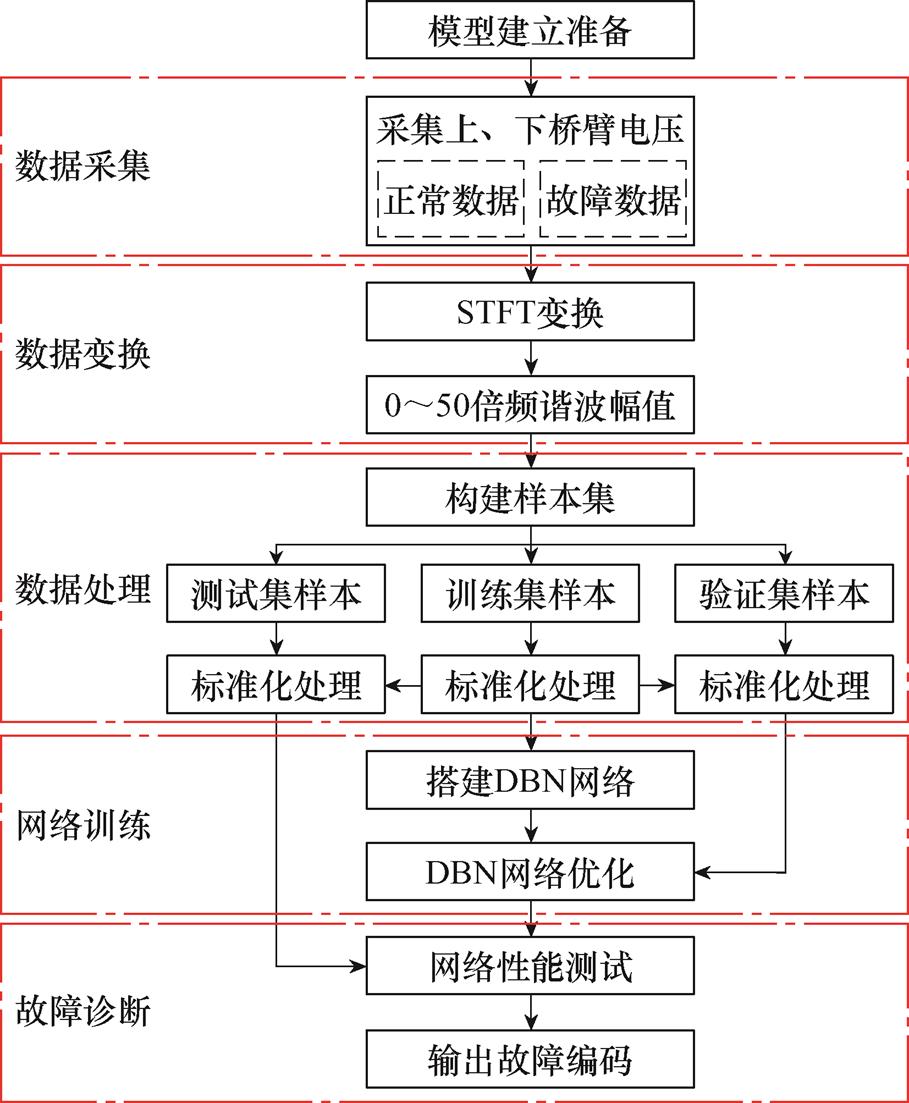
图6 基于DBN的故障检测流程
Fig.6 The flow chart of fault detection based on DBN
基于CNN的故障定位流程为:
(1)选取故障桥臂电压的特征参数作为输入,以上桥臂为例,网络输入为上桥臂电压的255个特征参数,构建样本结构为
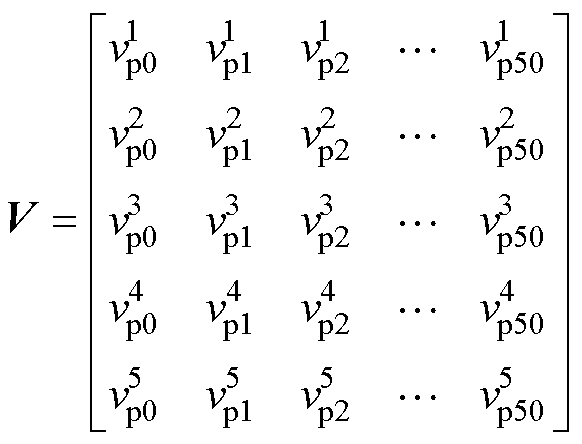 (17)
(17)
(2)通过交替的卷积层和池化层提取故障特征,对不同故障类型的定位网络逐一进行有监督的预训练。
(3)当DBN检测到故障发生后,根据检测结果选择对应定位网络并构建相应输入样本。以上桥臂双子模块VT1管开路为例,此时输入数据为上桥臂电压谐波分量幅值,定位网络为上桥臂双子模块定位网络。
(4)将处理后的样本输入CNN网络中进行测试,得到故障标签,从而实现故障开路子模块的具体定位。
利用CNN进行故障定位时,合理的参数设置可避免模型陷入欠拟合或者过拟合。本文所建网络输入样本尺寸较小,但不同数据间相似度较高,因此在标准LeNet-5网络的基础上,通过增加卷积层以及池化层的数量,同时减小卷积核和过滤器的尺寸,以实现更为细致的特征识别与分类。建立改进LeNet-5网络的结构参数见表4。
表4 改进LeNet-5网络结构及参数
Tab.4 The structure and parameters of improved LeNet-5 network
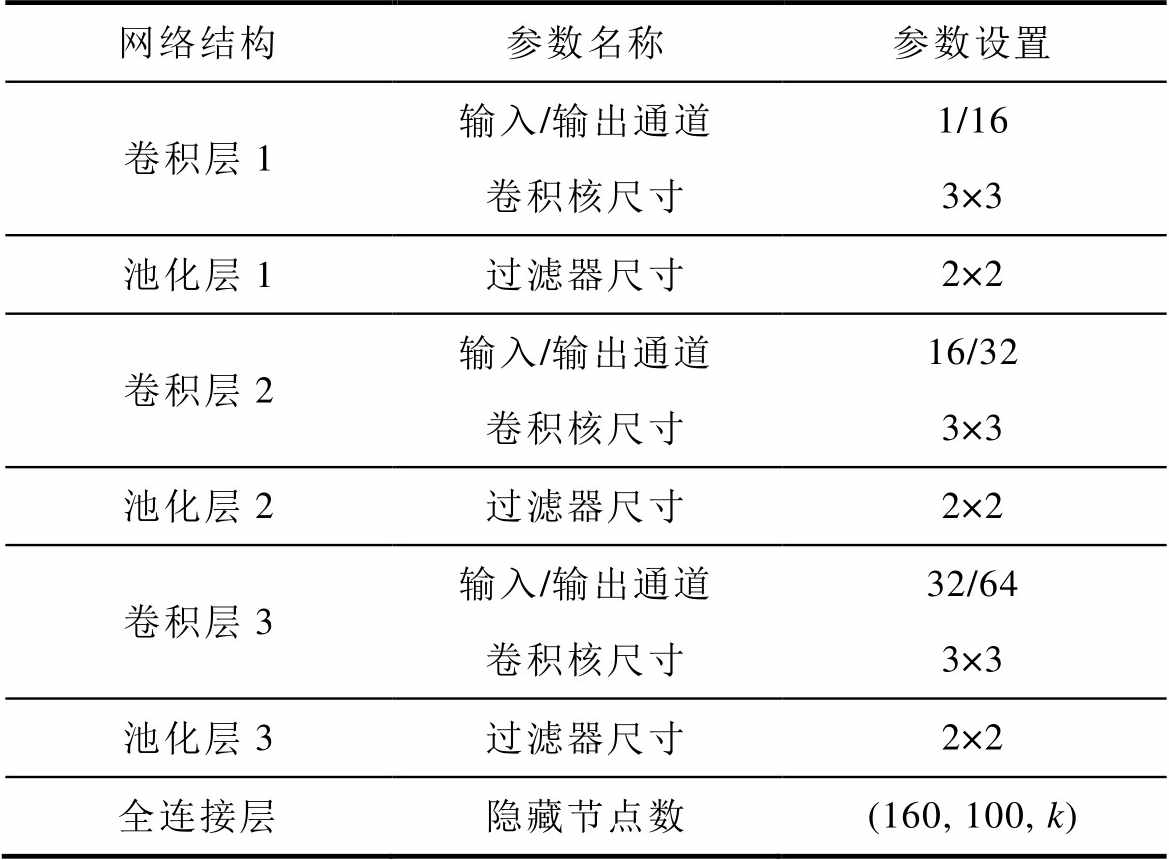
网络结构参数名称参数设置 卷积层1输入/输出通道1/16 卷积核尺寸3×3 池化层1过滤器尺寸2×2 卷积层2输入/输出通道16/32 卷积核尺寸3×3 池化层2过滤器尺寸2×2 卷积层3输入/输出通道32/64 卷积核尺寸3×3 池化层3过滤器尺寸2×2 全连接层隐藏节点数(160, 100, k)
表4中,k为输出层节点数目,以129电平MMC单子模块定位为例,上桥臂模块定位结果有128种,因此网络的输出层节点数即为128。此时,网络输出的定位结果可用向量P表示为
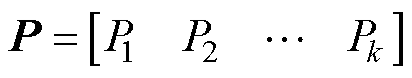 (18)
(18)
式中,Pi(i=1, 2,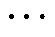 , 128)为故障侧第i个子模块发生故障的概率。为更直观地体现故障定位的结果,在网络的输出层设置Softmax分类器,将网络输出转化为唯一确定的数值Plabel,即为故障子模块的序号。具体计算为
, 128)为故障侧第i个子模块发生故障的概率。为更直观地体现故障定位的结果,在网络的输出层设置Softmax分类器,将网络输出转化为唯一确定的数值Plabel,即为故障子模块的序号。具体计算为
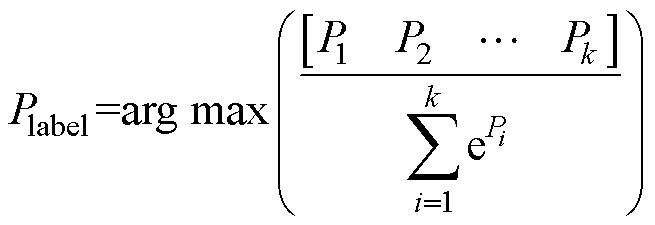 (19)
(19)
考虑到卷积操作其本质上仍是一种线性运算,因此需要引入非线性的激活函数提升模型的表达能力,常用函数包括Sigmod函数和ReLU函数等。就本文的研究背景而言,输入数据变化幅度较大,即便经过规范化处理后的数据在网络的迭代过程中也可能会出现较大的正负偏差,此时ReLU函数缺陷显著,故本文最终选取Sigmod函数作为网络的激活函数。又考虑到Sigmod函数的饱和现象,利用批量标准化(Batch Normalization, BN)算法对其进行优化。上述故障定位流程如图7所示。
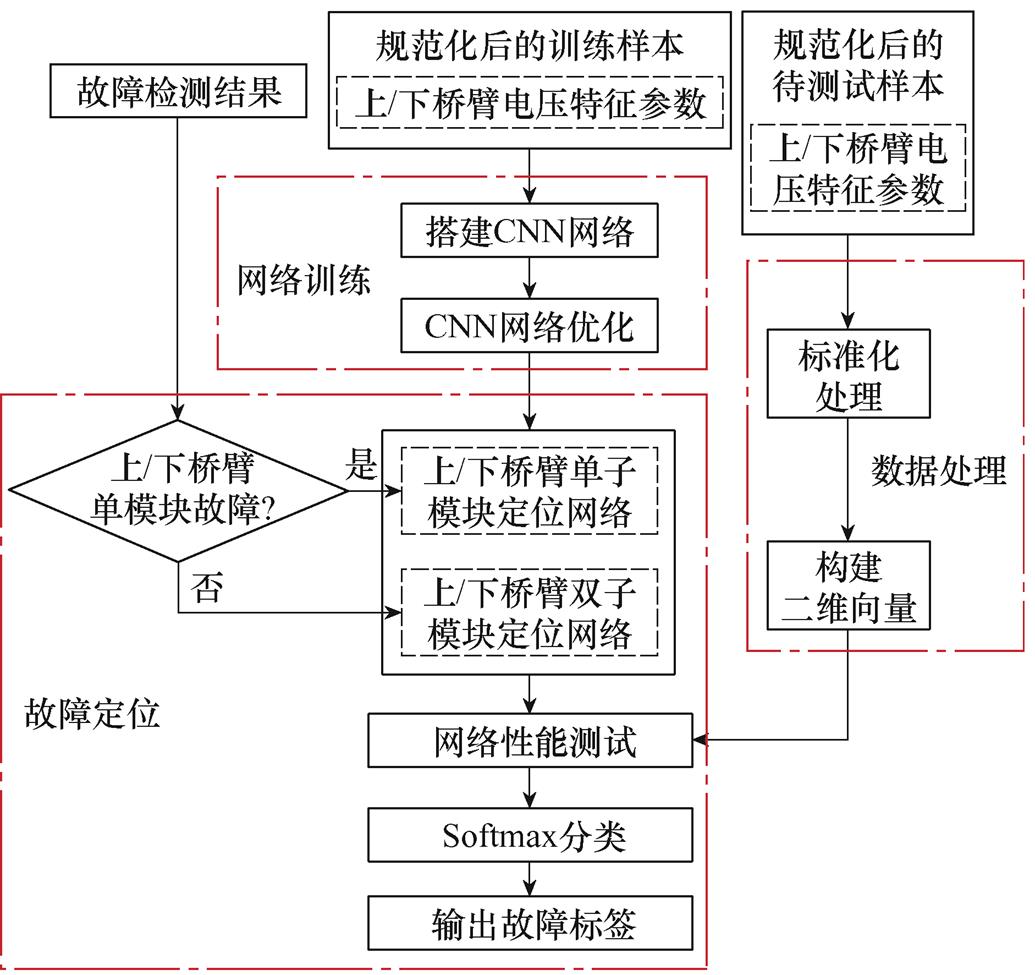
图7 基于CNN的故障定位流程
Fig.7 The flow chart of fault location based on CNN
本文故障诊断算法的实现在一台CPU为Intel Core i5-6400,GPU为NVIDIA GeForce GTX 750、运行内存为8 G的计算机上完成,深度学习网络的构建平台为PyCharm,编程语言为Python。首先,基于Matlab/Simulink搭建了129电平MMC模型,仿真模型参数见表5。
表5 仿真模型参数
Tab.5 The parameters of simulation model
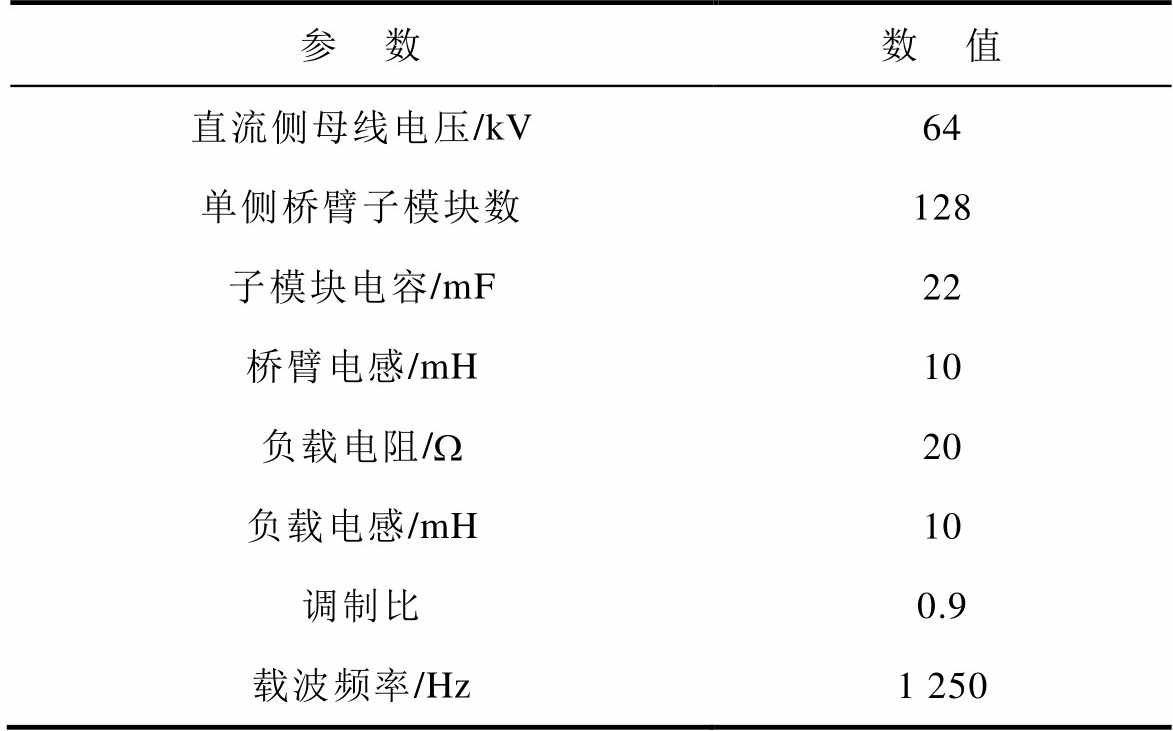
参 数数 值 直流侧母线电压/kV64 单侧桥臂子模块数128 子模块电容/mF22 桥臂电感/mH10 负载电阻/W20 负载电感/mH10 调制比0.9 载波频率/Hz1 250
在载波移相调制策略下,各SM电容电压在500 V附近波动。未采用均压策略时,电压值会逐渐偏离目标值,而采用均压策略后,各SM电容电压一致性明显提高,与前述分析一致。相应上桥臂各SM电容电压输出波形如图8所示。
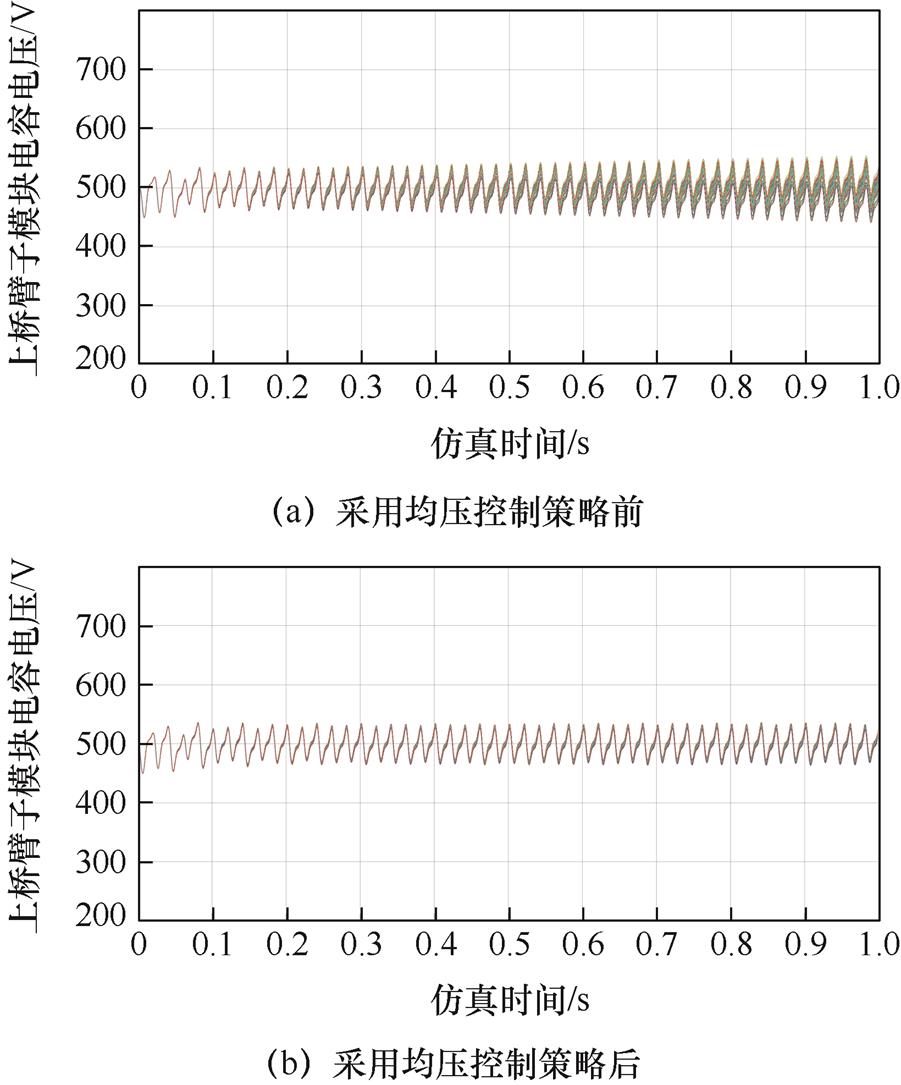
图8 采用均压策略前后上桥臂各SM电容电压
Fig.8 The SM capacitor voltage before and after voltage balancing strategy
对于故障情况,以0.4 s时分别发生四种单子模块故障为例(故障1:SMp1VT1开路;故障2:SMp1VT2开路;故障3:SMn1VT1开路;故障4:SMn1VT2开路),故障前后桥臂电压波形分别如图9所示。
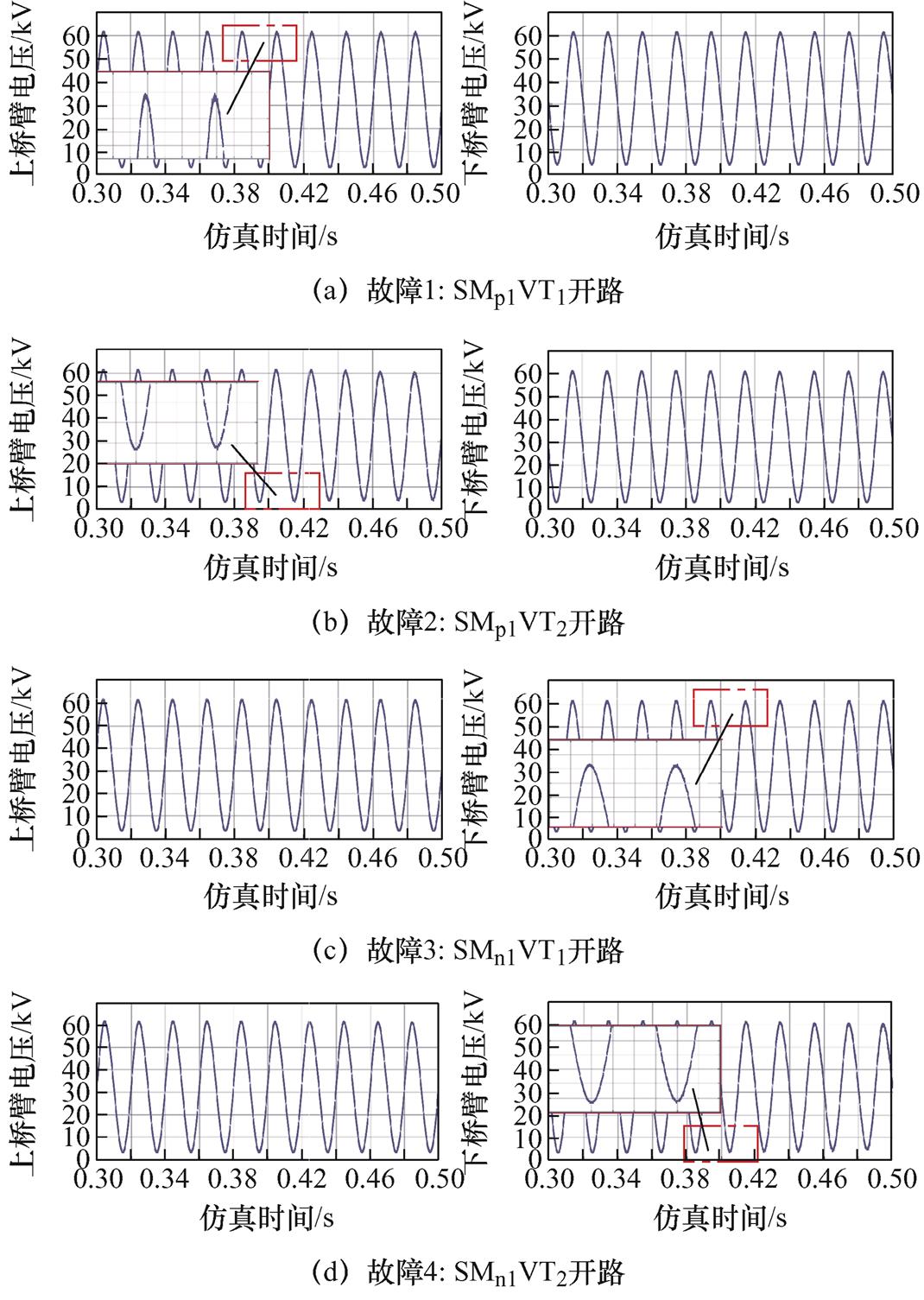
图9 单子模块开路故障时桥臂电压
Fig.9 The arm voltage under open-circuit fault in single SM
图9波形表明,子模块IGBT发生开路后,故障子模块所在桥臂的电压会直接受到影响,且当不同子模块发生相同类型IGBT开路时对故障桥臂电压的影响较为类似。在子模块VT1管发生开路故障的初期,故障特征主要体现在桥臂电压的正半周,而VT2管开路故障的特征则主要体现在桥臂电压的负半周。以上桥臂为例,对上述四种故障波形进行相似性分析,结果见表6。
表6 不同类型故障下的上桥臂电压相似度
Tab.6 The similarity of upper arm voltage under various types of faults

故障类型正常故障1故障2故障3故障4 相似度(%)—99.9999.9999.9999.98
相似计算使用皮尔逊相关系数法,相似度越接近于1,则表明两组数据相似度越高。表6表明,系统故障前后桥臂电压在时域上的相似度极高,系统开路故障对于桥臂电压波形的影响程度较为微弱,因而直接从时域角度进行分析以实现精确的故障诊断较为困难。
仍以上桥臂电压为例,将时域数据通过快速傅里叶变换(Fast Fourier Transform, FFT)至频域进行分析,故障数据均以正常数据为基准进行归一化,结果见表7。表7中,虚线内数据为故障前后变化幅度最大的谐波分量。表7中数据表明,子模块IGBT开路后故障侧桥臂电压谐波幅值在1 250 Hz(载波频率)附近显著增加,且在VT2管开路时增加更为明显。
表7 不同类型故障下的上桥臂电压谐波幅值
Tab.7 The amplitude of upper bridge arm voltage harmonics under various types of faults
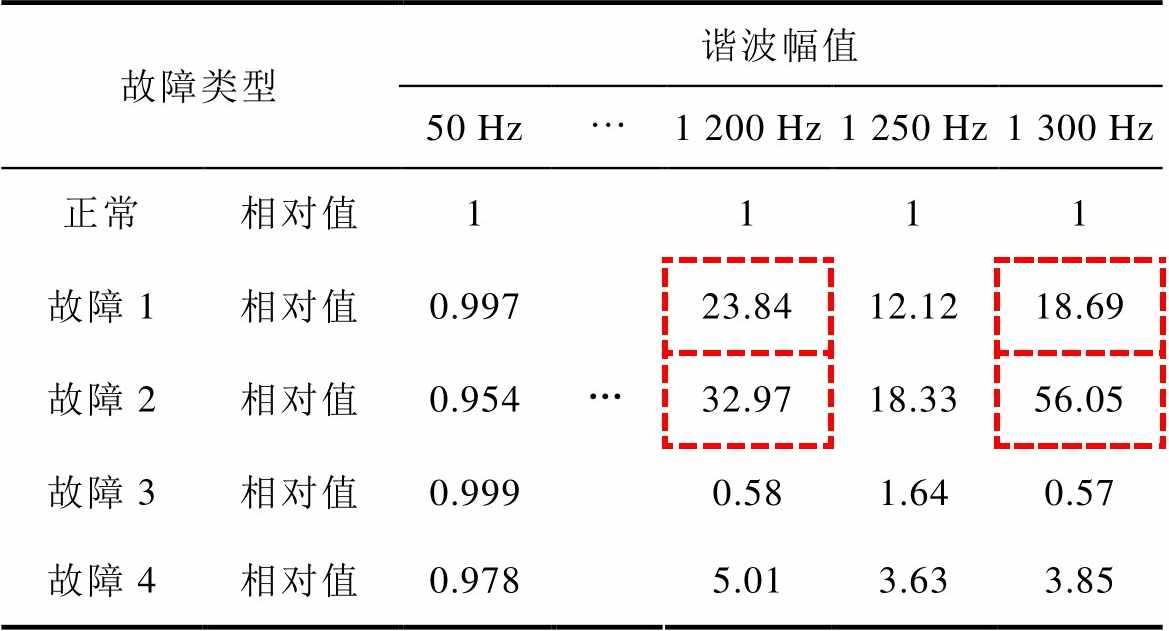
故障类型谐波幅值 50 Hz1 200 Hz1 250 Hz1 300 Hz 正常相对值1…111 故障1相对值0.99723.8412.1218.69 故障2相对值0.95432.9718.3356.05 故障3相对值0.9990.581.640.57 故障4相对值0.9785.013.633.85
以载波频率为例,对桥臂电压数据进行STFT,结果见表8。与表6相比较易得,同单一时域或频域特征相比,对于不同类型的故障,经过STFT变换的时频谱信息间差异更为显著,能更好地表征故障前后的桥臂电压变化,有利于提高故障诊断的准确率。
表8 不同类型故障上桥臂电压载波频率谐波幅值
Tab.8 The amplitude of carrier frequency harmonics on arm voltage under various types of faults (单位: V)
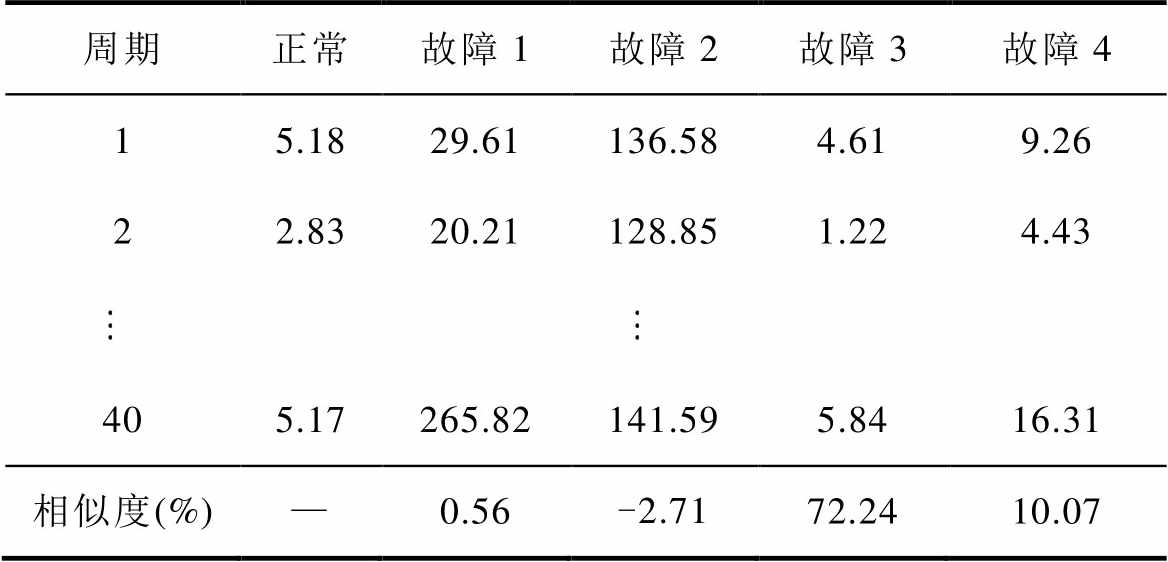
周期正常故障1故障2故障3故障4 15.1829.61136.584.619.26 22.8320.21128.851.224.43 405.17265.82141.595.8416.31 相似度(%)—0.56-2.7172.2410.07
采集不同故障状态下的桥臂电压数据,并按照图6中数据采集及变换流程构建输入样本并进行规范化处理,其中包括正常样本1类,单子模块故障256类(上、下桥臂子模块VT1开路故障或VT2开路故障)及部分双子模块故障和多子模块故障,故障编码参照表3,将样本按照6 2
2 2的比例划分训练集、测试集和验证集。随后对DBN网络结构进行设计,为减少模型复杂度、提高故障检测速度,对各隐藏层采用相同节点数,主要对隐藏层数及单个隐藏层节点数进行调试,所得结果如图10所示。此时准确率和检测用时均随着隐藏层数和节点数的增加而增加,综合考虑指标后设置DBN隐藏层结构为三层,单层隐藏节点数为300。
2的比例划分训练集、测试集和验证集。随后对DBN网络结构进行设计,为减少模型复杂度、提高故障检测速度,对各隐藏层采用相同节点数,主要对隐藏层数及单个隐藏层节点数进行调试,所得结果如图10所示。此时准确率和检测用时均随着隐藏层数和节点数的增加而增加,综合考虑指标后设置DBN隐藏层结构为三层,单层隐藏节点数为300。
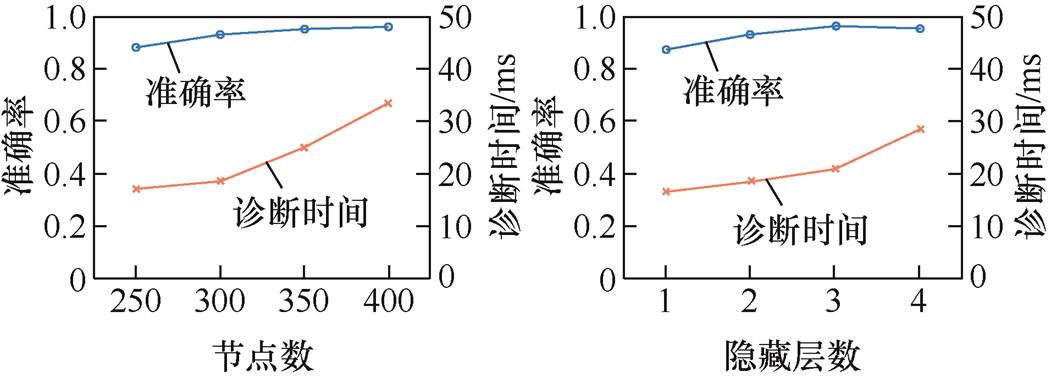
图10 基于DBN的故障检测网络参数调节过程
Fig.10 Parameter adjustment process of fault detection network based on DBN
将上述桥臂电压数据分别使用FFT及所提STFT方法进行变换。构建如式(12)所示故障样本后,依次输入预训练完毕的DBN故障检测网络进行测试,所得检测结果见表9,所用时间为信号处理时间与故障发生至波形可被检测时间之和。
表9 不同处理方法下故障检测网络效果对比
Tab.9 The comparison of fault detection network performance under different processing method
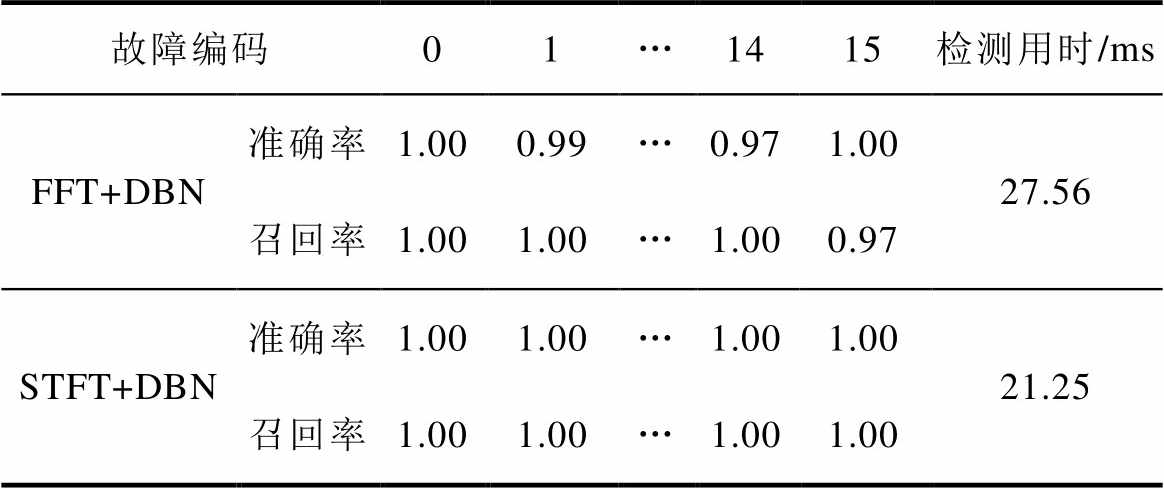
故障编码01…1415检测用时/ms FFT+DBN准确率1.000.99…0.971.0027.56 召回率1.001.00…1.000.97 STFT+DBN准确率1.001.00…1.001.0021.25 召回率1.001.00…1.001.00
表9结果表明,本文所提STFT+DBN的故障检测方法,在保证较高的检测准确率的前提下,能够有效降低检测用时。
在检测到故障发生后,还需进一步确定故障子模块的具体位置。以上桥臂单子模块VT2管开路故障为例,此时故障位置共有128种可能,因此故障定位网络全连接层输出节点k=128,具体故障标签见表10。
表10 上桥臂单子模块发生VT2开路时故障标签
Tab.10 The fault labels under VT2 open-circuit fault on single sub-module of the upper bridge arm

系统故障类型故障标签 SMp1VT2开路1 SMp2VT2开路2 SMp128VT2开路128
自仿真数据中采集表10所示故障类型的桥臂电压数据,利用2.2节所示方法构建二维输入样本,同样按照6 2
2 2比例划分样本,并通过样本数据对网络进行训练及调校,对网络在不同激活函数、批量大小、学习率及迭代次数下的性能进行了测试,所得结果如图11所示。
2比例划分样本,并通过样本数据对网络进行训练及调校,对网络在不同激活函数、批量大小、学习率及迭代次数下的性能进行了测试,所得结果如图11所示。
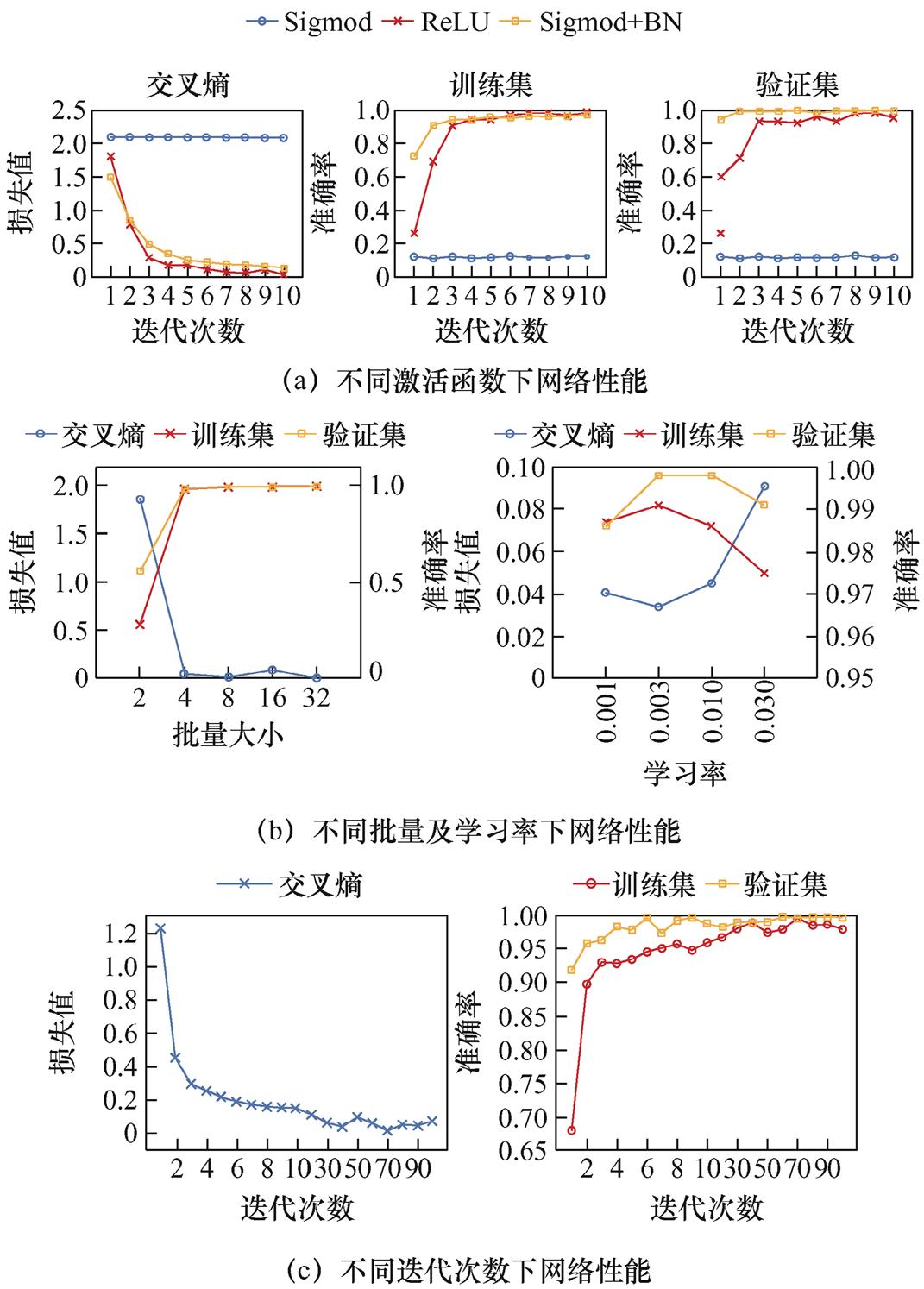
图11 基于CNN的故障定位网络参数调节过程
Fig.11 Parameter adjustment process of fault location network based on CNN
综合训练时间及验证集准确率,设置激活函数为添加Batch Normalization层的Sigmoid函数,batch size为8,学习率为0.003,训练迭代次数为40。针对单子模块故障和双子模块故障两种情况分别构建定位网络,其中单子模块故障选取前述上桥臂子模块VT2故障,而由于双子模块故障组合类型较多,故选取上桥臂1号、20号、40号子模块的不同故障情形进行测试,共12类故障类型。多子模块情形的部分故障标签设置见表11。
表11 上桥臂双子模块开路时部分故障标签
Tab.11 The partial fault labels under open-circuit fault on dual sub-module of the upper bridge arm

系统故障类型故障标签 SMp1VT2及SMp20VT1开路1 SMp1VT1及SMp40VT1开路2 SMp20VT1及SMp40VT1开路3 SMp20VT2及SMp40VT1开路12
利用预设网络结构分别对单子模块故障及双子模块故障样本进行故障定位,同时将结果与基于DBN网络的定位结果进行比较,所得结果见表12。结果表明,相较于DBN网络,CNN网络的定位准确率和用时均有显著提高;对于复合故障的定位,CNN网络的准确率较单一故障时略有下降,但依旧在0.95以上。
表12 不同故障定位网络性能对比
Tab.12 The performance comparison of different fault location networks
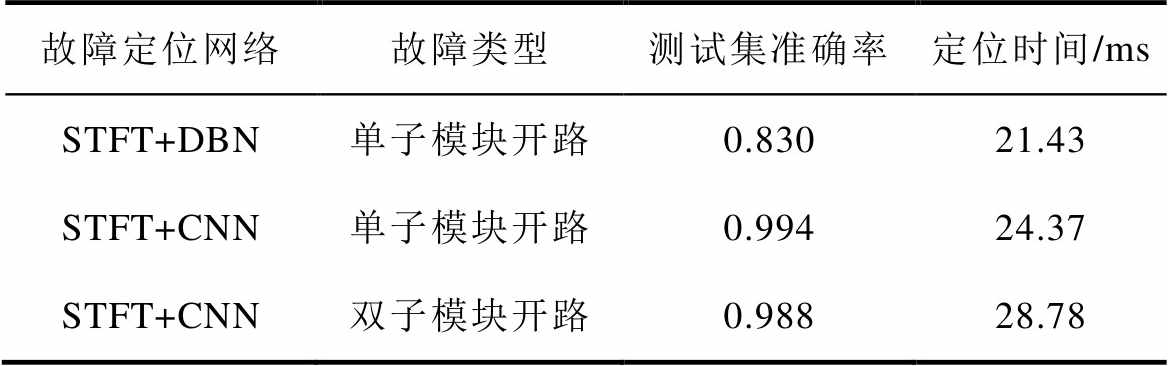
故障定位网络故障类型测试集准确率定位时间/ms STFT+DBN单子模块开路0.83021.43 STFT+CNN单子模块开路0.99424.37 STFT+CNN双子模块开路0.98828.78
综上所述,无论是单模块故障或是双模块故障,所建DBN故障检测网络均能够快速检测出故障类型;所建CNN故障定位网络能够在确定故障类型基础上,短时间内准确地完成故障子模块的具体定位,基本满足故障诊断的相关要求。
为验证本文所提出的故障诊断策略的有效性,在实验室环境下设计并搭建了降功率等级的单相MMC实验系统,相关参数见表13。控制采用DSP/FPGA联合控制板,其中DSP28335控制主电路的预充电及正常与故障态间的切换,FPGA核心为Spartan6,负责输出PWM及继电器的控制信号;IGBT采用英飞凌公司的FF50R12RT4,系统整体结构如图12所示。
表13 实验系统参数
Tab.13 The parameters of experimental system
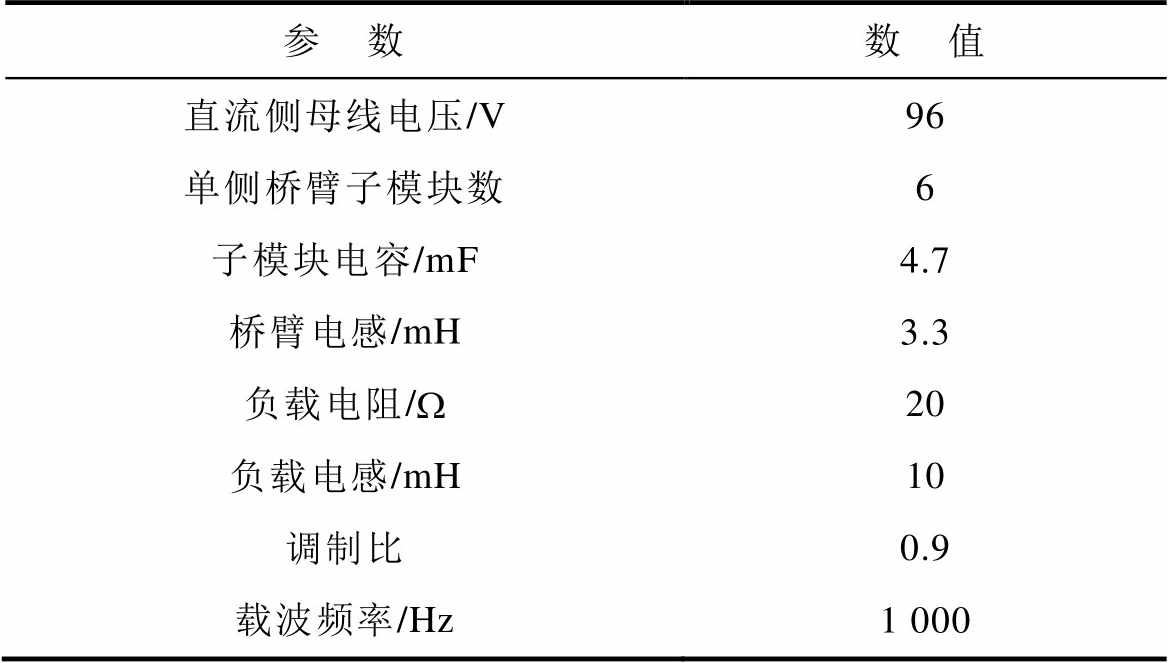
参 数数 值 直流侧母线电压/V96 单侧桥臂子模块数6 子模块电容/mF4.7 桥臂电感/mH3.3 负载电阻/W20 负载电感/mH10 调制比0.9 载波频率/Hz1 000

图12 单相MMC实验系统
Fig.12 Single phase MMC experimental system
系统正常运行时桥臂电压及部分子模块电容电压分别如图13、图14所示。此时上、下桥臂电压幅值相同、相位相反,运行期间保持稳定;子模块电压维持稳定,在目标值上下波动。
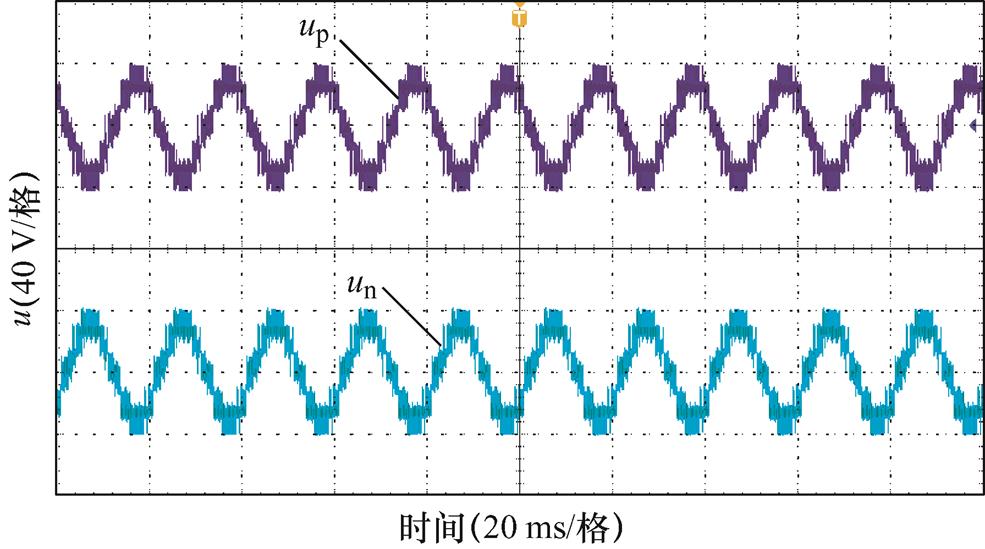
图13 系统稳态时桥臂电压实验波形
Fig.13 The experimental waveforms of arm voltage under steady state
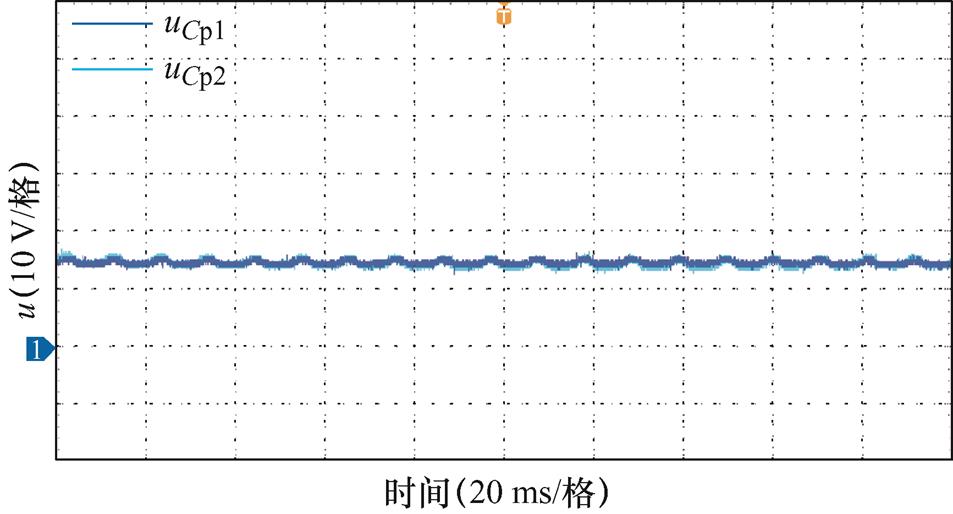
图14 系统稳态时子模块电容电压实验波形
Fig.14 The experimental waveforms of SM capacitor voltage under steady state
对于单子模块故障,以SMp1VT1开路为例,故障后桥臂电压波形如图15所示,图中t1、t2分别为故障发生和故障诊断时刻。
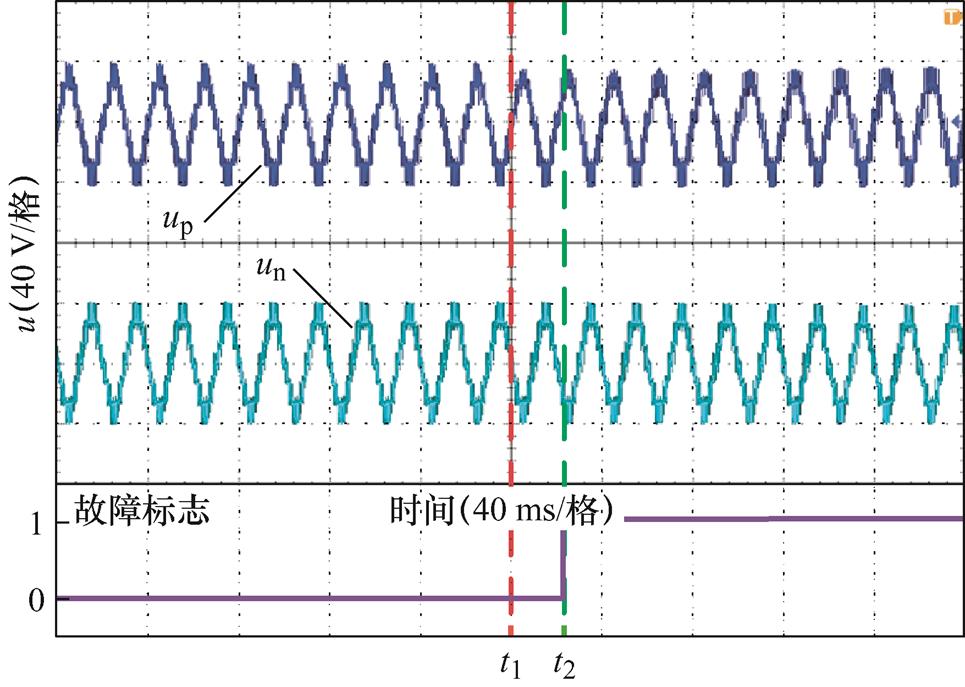
图15 单子模块开路故障下桥臂电压实验波形
Fig.15 The experimental waveforms under open-circuit fault on single sub-module
实验过程中,采集不同情形下桥臂电压数据并离线上传至上位机,随后利用Pycham构建并划分样本集,通过训练集及验证集样本对故障诊断网络进行训练,利用测试集样本对网络性能进行评估,后文结果中的准确率均指验证集准确率。
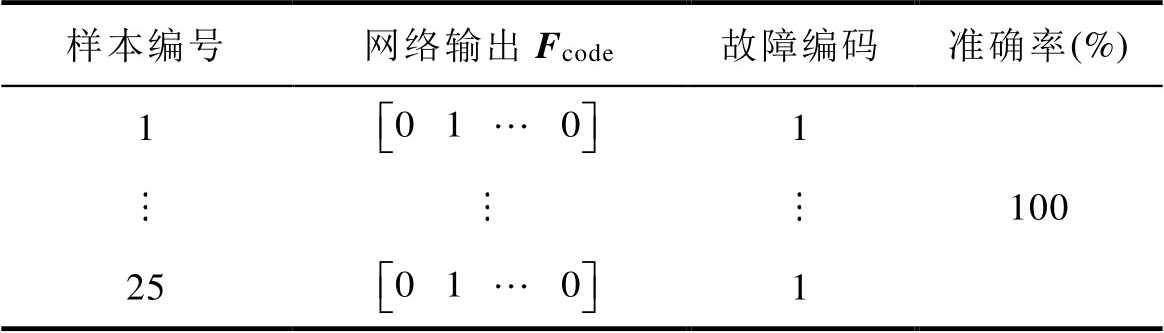
实验波形检测及定位结果分别见表14和表15。由表14和表15可得,所搭建的网络均能够对故障样本实现正确诊断,平均用时约为0.1 s,诊断正确率可达到100%。
对于多子模块故障,以单桥臂双子模块故障为例,采集SMp1VT1和SMp4VT1同时开路、SMp1VT2和SMp4VT2同时开路以及SMp1VT1和SMp4VT2同时开路三种故障情形的数据,其桥臂电压波形如图16所示。
表14 实验样本下单子模块开路故障检测结果
Tab.14 Detection results of single-module open-circuit fault under experimental data
样本编号网络输出Fcode故障编码准确率(%) 11100 251
表15 实验样本下单子模块开路故障定位结果
Tab.15 Location results of single-module open-circuit fault under experimental data
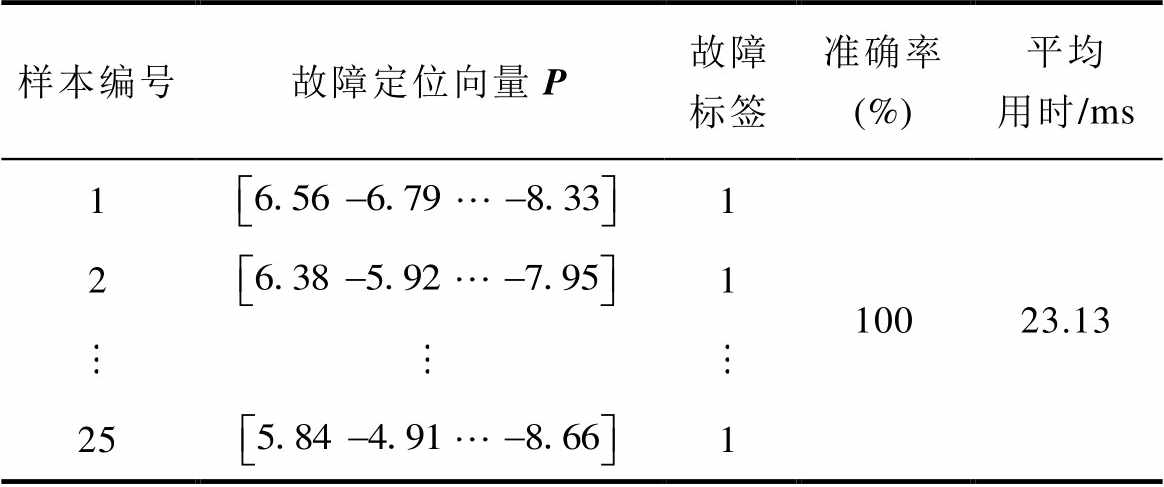
样本编号故障定位向量P故障标签准确率(%)平均用时/ms 1110023.13 21 251
图16表明,同桥臂多子模块的单一类型故障与单子模块同类型故障特征相似,但变化幅度更高;而当同一桥臂同时出现VT1开路及VT2开路两类故障时,时域波形近似两类故障单独出现时的叠加。
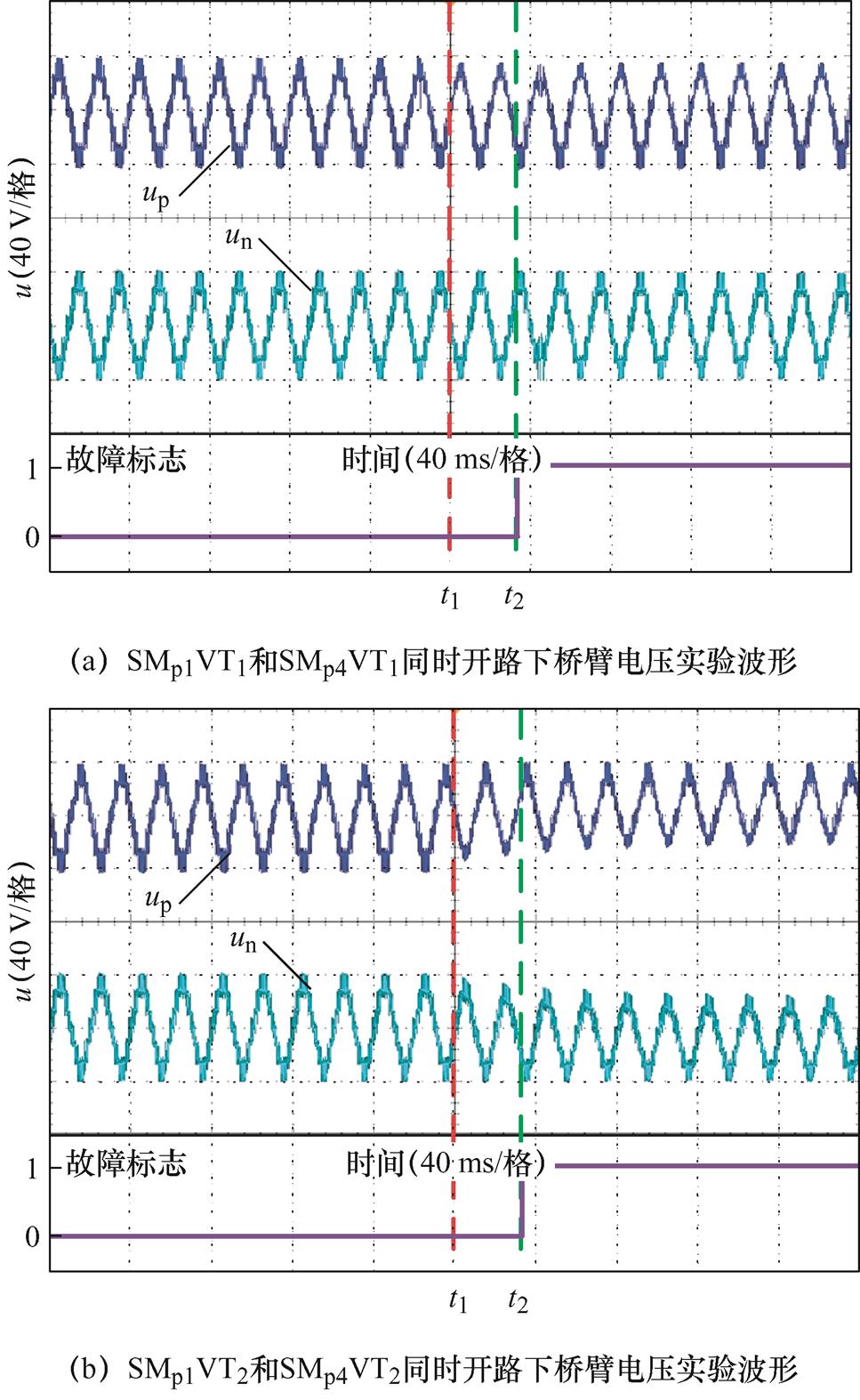
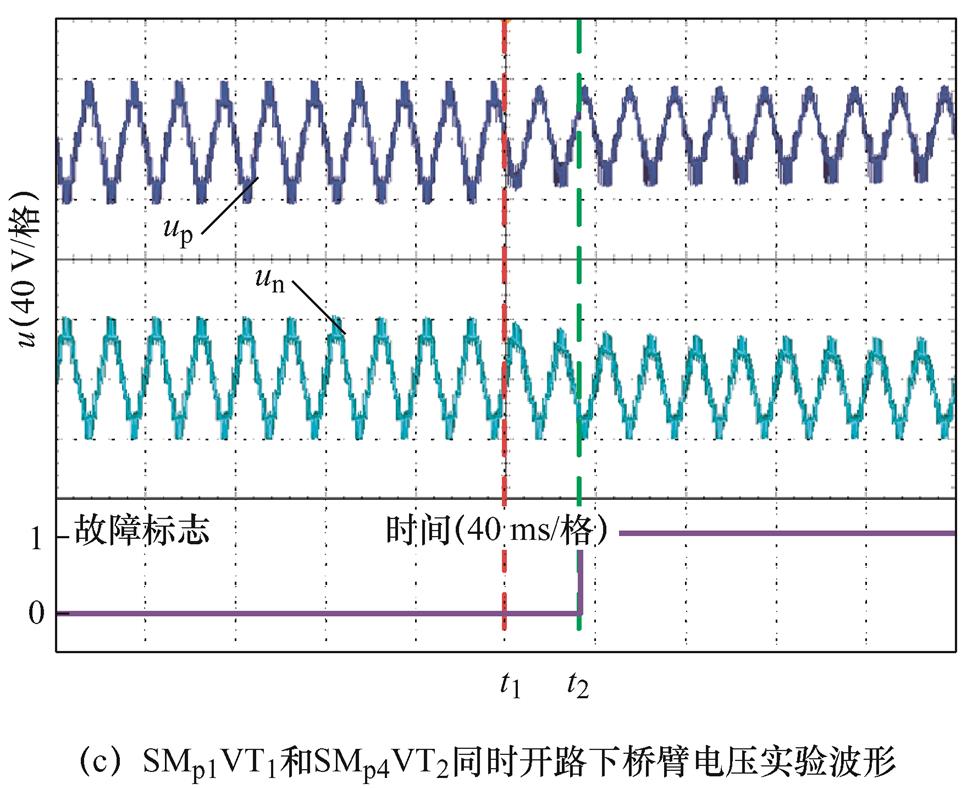
图16 双子模块开路故障下桥臂电压实验波形
Fig.16 The experimental waveforms under open-circuit fault on dual sub-module
对表3中单、双子模块故障类型依次进行实验,并采集实验数据对故障诊断网络进行整体性能测试。共构建测试集样本15类,总数约3 000个。利用所提方法对样本进行故障类型检测及相应故障类型下的定位,整体故障检测及定位结果见表16、表17。
表16 实验样本下子模块开路故障整体检测结果
Tab.16 The overall detection results of sub-module open-circuit faults under experimental data
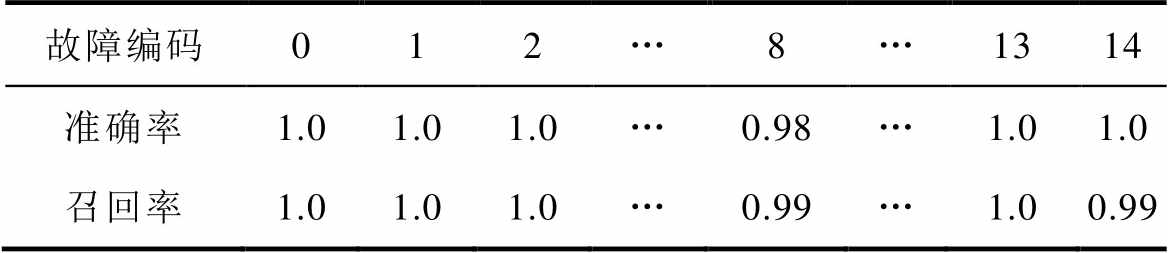
故障编码012…8…1314 准确率1.01.01.0…0.98…1.01.0 召回率1.01.01.0…0.99…1.00.99
表17 实验样本下子模块开路故障整体定位结果
Tab.17 The overall location results of sub-module open-circuit faults under experimental data

故障类型训练集准确率测试集准确率定位时间/ms 单子模块故障0.9940.98524.14 双子模块故障0.9960.97629.78
上述实验结果表明,所提STFT-DBN故障检测方法整体准确率超过0.98,具备较好的故障检测能力。在故障检测的基础上,所提STFT-CNN故障定位方法对于单子模块IGBT开路故障,准确率约0.98,对于双子模块故障,定位准确率约0.97。
综上所述,本文所搭建的故障诊断网络能够较好地完成MMC子模块IGBT开路故障的诊断。
本文以模块化多电平换流器为研究对象,提出了一种有效的MMC子模块IGBT开路故障诊断策略。通过短时傅里叶变换提取桥臂电压信号中潜在的故障特征,避免了额外传感器的使用,降低了系统成本。所提STFT-DBN方法相较于FFT-DBN,在不损害检测准确率的前提下,降低了故障检测用时。在确定故障类型的基础上,提出了基于STFT-CNN的故障定位方法,进一步提高了故障定位的准确率。最后,通过仿真和降功率等级的MMC实验系统进行测试,测试结果验证了所提故障诊断策略的有效性和可行性,所提方法为减少MMC子模块IGBT故障诊断过程中传感器的使用提供了新思路。
参考文献
[1] 盛景, 陈聪, 向鑫, 等. 模块化多电平谐振变换器多自由度调压控制及子模块电容均压方法[J]. 电工技术学报, 2022, 37(24): 6216-6229. Sheng Jing, Chen Cong, Xiang Xin, et al. Multiple- degree-of-freedom control and capacitor voltage balancing method of modular multilevel resonant converter[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6216-6229.
[2] 罗丹, 陈民铀, 赖伟, 等.基于Haar小波变换重构开关序列的MMC子模块电容值在线监测方法[J]. 电工技术学报, 2022, 37(20): 5278-5289. Luo Dan, Chen Minyou, Lai Wei, et al. Online monitoring method for sub-module capacitance in modular multilevel converter based on Haar wavelet transform reconstruction switch sequence[J]. Tran- sactions of China Electrotechnical Society, 2022, 37(20): 5278-5289.
[3] 刘座辰, 林磊, 殷天翔, 等. 一种模块化多电平换流器子模块开路故障的快速检测与诊断方法[J]. 电工技术学报, 2022, 37(19): 4883-4894. Liu Zuochen, Lin Lei, Yin Tianxiang, et al. A fast open-circuit fault detection and diagnosis method for sub-modules of modular multilevel converters[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4883-4894.
[4] 和敬涵, 张佳宝, 李猛, 等. 基于孪生模型的模块化多电平换流器保护[J]. 电力系统自动化, 2023, 47(21): 119-126. He Jinghan, Zhang Jiabao, Li Meng, et al. Protection for modular multilevel converter based on twin model[J]. Automation of Electric Power Systems, 2023, 47(21): 119-126.
[5] 杨贺雅, 邢纹硕, 向鑫, 等. 基于多元高斯分布异常检测模型的MMC子模块开路故障诊断方法[J]. 电工技术学报, 2023, 38(10): 2744-2756. Yang Heya, Xing Wenshuo, Xiang Xin, et al. A sub- module open-circuit fault detection and location strategy for modular multilevel converters based on multivariate gaussian distribution[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2744- 2756.
[6] 武鸿, 王跃, 刘熠, 等. 基于广义电容电压不平衡度的MMC子模块开路故障诊断策略[J]. 电工技术学报, 2023, 38(14): 3909-3922. Wu Hong, Wang Yue, Liu Yi, et al. Open circuit fault diagnosis strategy of MMC sub-module based on generalized capacitor voltage unbalance[J]. Transac- tions of China Electrotechnical Society, 2023, 38(14): 3909-3922.
[7] 孙冠群, 尹项根, 赖锦木, 等. 模块化多电平直流变压器容错控制策略[J]. 电工技术学报, 2022, 37(增刊1): 246-256, 287. Sun Guanqun, Yin Xianggen, Lai Jinmu, et al. Fault-tolerant control strategy of modular multilevel DC transformer[J]. Transactions of China Electro- technical Society, 2022, 37(S1): 246-256, 287.
[8] Ronanki D, Williamson S S. Modular multilevel converters for transportation electrification: challenges and opportunities[J]. IEEE Transactions on Transpor- tation Electrification, 2018, 4(2): 399-407.
[9] Liu Zhijie, Li Kejun, WangJinyu, et al. General model of modular multilevel converter for analyzing the steady-state performance optimization[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 925-937.
[10] Zhou Dehong, Yang Shunfeng, Tang Yi. A voltage- based open-circuit fault detection and isolation approach for modular multilevel converters with model-predictive control[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9866-9874.
[11] Wang Jun, Ma Hao, Bai Zhihong. A submodule fault ride-through strategy for modular multilevel converters with nearest level modulation[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1597-1608.
[12] Yang Shunfeng, Tang Yi, Wang Peng. Seamless fault-tolerant operation of a modular multilevel converter with switch open-circuit fault diagnosis in a distributed control architecture[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 7058-7070.
[13] Zhang Jianzhong, Hu Xing, Xu Shuai, et al. Fault diagnosis and monitoring of modular multilevel converter with fast response of voltage sensors[J]. IEEE Transactions on Industrial Electronics, 2020, 67(6): 5071-5080.
[14] Wang Songda, Dragicevic T, Gao Yuan, et al. Neural network-based model predictive controllers for modular multilevel converters[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 1562-1571.
[15] 李宝琴, 吴俊勇, 李栌苏, 等. 基于主动迁移学习的电力系统暂态稳定自适应评估[J]. 电力系统自动化, 2023, 47(4): 121-132. Li Baoqin, Wu Junyong, Li Lusu, et al. Adaptive assessment of power system transient stability based on active transfer learning[J]. Automation of Electric Power Systems, 2023, 47(4): 121-132.
[16] 叶鑫杰, 兰生, 肖思捷, 等. 基于小波包能量熵和DBN的MMC-HVDC输电线路单极接地故障定位方法[J]. 南方电网技术, 2021, 15(2): 82-91. Ye Xinjie, Lan Sheng, Xiao Sijie, et al. Single pole grounding fault location method of MMC-HVDC transmissionline based on wavelet packet energy entropy and DBN[J]. Southern Power System Tech- nology, 2021,15(2): 82-91.
[17] 杨彦杰, 董哲, 姚芳, 等. 基于1D-CNN-LSTM混合神经网络模型的双桥并联励磁功率单元故障诊断[J]. 电网技术, 2021, 45(5): 2025-2032. Yang Yanjie, Dong Zhe, Yao Fang, et al. Fault diagnosis of double bridge parallel excitation power unit based on 1D-CNN-LSTM hybrid neural network model[J]. Power System Technology, 2021, 45(5): 2025-2032.
[18] Xue Z Y, Xiahou K S, Li M S, et al. Diagnosis of multiple open-circuit switch faults based on long short-term memory network for DFIG-based wind turbine systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2600-2610.
[19] Kiranyaz S, Gastli A, Ben-Brahim L , et al. Real-time fault detection and identification for MMC using 1-D convolutional neural networks[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8760-8771.
[20] Gong Wenfeng, Chen Hui, Zhang Zehui, et al. A data-driven-based fault diagnosis approach for electrical power DC-DC inverter by using modified convolutional neural network with global average pooling and 2-D feature image[J]. IEEE Access, 2020,8: 73677-73697.
[21] Sun Quan, Wang Youren, Jiang Yuanyuan. A novel fault diagnostic approach for DC-DC converters based on CSA-DBN[J]. IEEE Access, 2017, 6: 6273-6285.
[22] Song Qiang, Wang Mingsheng, Lai Wuxuan, et al. On Bayesian optimization-based residual CNN for estimation of inter-turn short circuit fault in PMSM[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 2456-2468.
[23] Kim S H, Yoo D Y, An S W, et al. Fault detection method using a convolution neural network for hybrid active neutral-point clamped inverters[J]. IEEE Access, 2020, 8: 140632-140642.
[24] Gong Wenfeng, Chen Hui, Zhang Zehui, et al. A novel deep learning method for intelligent fault diagnosis of rotating machinery based on improved CNN-SVM and multichannel data fusion[J]. Sensors, 2019, 19(7): 1693.
[25] 金林. 高频载波移相调制下模块化多电平变换器子模块故障检测技术研究[D]. 杭州: 浙江大学, 2021. Jin Lin. Research on submodule failure diagnosis methods of MMC with high frequency carrier phase: shifting modulation[D]. Hangzhou: Zhejiang University, 2021.
[26] Chu Zunfang, Li Yaohua, Wang Ping, et al. A novel voltage balancing method of modular multilevel converter based on phase shifted carrier pulse width modulation[C]//2014 9th IEEE Conference on Indu- strial Electronics and Applications, Hangzhou, China, 2014: 364-367.
[27] Moranchel M, Bueno E J, Rodriguez F J, et al. Implementation of nearest level modulation for modular multilevel converter[C]//2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 2015: 1-5.
[28] Yue Yufei, Xu Qianming, Guo Peng, et al. Capacitor voltage predictor-corrector balancing approach with single sensor for single-phase modular multilevel converter[J]. International Journal of Electrical Power & Energy Systems, 2021, 129: 106729.
[29] D'Arco S, Suul J A. Estimation of sub-module capacitor voltages in modular multilevel con- verters[C]//2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2013: 1-10.
[30] 韩雪, 贺荣栋, 凌志斌. 部分接入电池储能系统的模块化多电平换流器控制方法[J]. 电力系统自动化, 2024, 48(1): 100-108. Han Xue, He Rongdong, Ling Zhibin. Control method of modular multilevel converter with partly integrated battery energy storage system[J]. Automation of Electric Power Systems, 2024, 48(1): 100-108.
[31] Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554.
Abstract The modular multilevel converter (MMC) is a new type of multilevel converter that features low switch frequency, high output waveform quality, and low consistency requirements for power electronic device switching. Therefore, it has been widely applied in various fields such as flexible DC transmission, power electronic transmission, and rail transit traction control. However, the increase in the number of sub-modules also means an increase in potential failure points. To meet the growing demands for system safety and reliability, timely and effective diagnosis needs to be carried out after system failures. Existing MMC fault diagnosis methods mainly fall into two categories: additional hardware circuit-based and software algorithm-based. Among them, the hardware-based method exhibits excellent diagnostic accuracy and short diagnostic time but may incur additional hardware costs and wiring complexity, while the software-based method does not require additional hardware circuitry and is relatively simple and convenient to implement. However, existing software-based method often heavily depends on the capacitance voltage information of sub-modules during the diagnosis process. The excessive number of voltage sensors not only increases the complexity of system wiring but also adds to the potential failure points of the system.
To this end, a deep learning-based IGBT open-circuit fault diagnosis method for MMC sub-modules using a minimum number of voltage sensors is proposed, which only requires two arm voltage sensors for each phase. Based on the analysis of open-circuit fault characteristics of MMC sub-module IGBTs, the bridge arm voltage is selected as the required electrical parameter for fault diagnosis. The short-time Fourier transform (STFT) is utilized to extract harmonic component information from the bridge arm voltage signal. By arranging frequency domain information at different sampling times, the matrix containing time-frequency domain information is constructed as the diagnostic sample. By combining with the deep belief network (DBN), an IGBT open-circuit fault detection method based on STFT-DBN is proposed, which realizes the rapid diagnosis of the fault type. Meanwhile, to address the problem of relatively low location accuracy of the DBN, a convolutional neural network (CNN) based faulty sub-module location network is established for each fault type after the fault type is identified by the fault detection network. Combining these two methods allows for rapid fault type detection and high-accuracy faulty sub-module location.
A 129-level MMC simulation model was established using Matlab/Simulink, and arm voltage information was collected under normal operation and various fault conditions. By applying the proposed method for data preprocessing, input samples were constructed, and the dataset was divided. Then the fault diagnosis networks were trained and tested separately, and the effectiveness of the proposed method was verified based on simulation data. Finally, the hardware and software of an MMC experimental system were designed in the laboratory environment, and an experimental system with reduced power levels was constructed. The control unit was implemented by a combination of DSP TMS320F28335 and FPGA, and various fault conditions were simulated by changing the drive signals. Arm voltage sensors were used to collect data from the experimental system under different fault conditions. The experimental results show that the proposed method can achieve high-precision and short-time fault diagnosis by using only arm voltage information.
keywords:Modular multilevel converter(MMC), open-circuit fault diagnosis, short-time Fourier transform, convolutional neural networks
DOI:10.19595/j.cnki.1000-6753.tces.230689
中图分类号:TM46
国家自然科学基金资助项目(51777141)。
收稿日期 2023-05-18
改稿日期 2023-12-25
朱琴跃 女,1970年生,教授,博士生导师,研究方向为电气智能诊断和电力电子变流控制。E-mail:zqymelisa@tongji.edu.cn(通信作者)
于逸尘 男,1998年生,硕士研究生,研究方向为模块化多电平换流器的故障诊断。E-mail:2130679@tongji.edu.cn
(编辑 陈 诚)