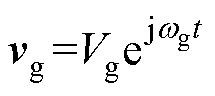 ,正常情况下电网角频率wg等于额定角频率wn;PCC电压矢量
,正常情况下电网角频率wg等于额定角频率wn;PCC电压矢量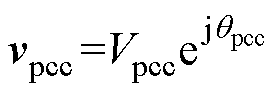 ;vc为VSC输出电压矢量;ip为PCC流入电网的电流矢量;ic为VSC流向PCC的电流矢量。Pout、Qout分别为从PCC流入电网的有功功率和无功功率;Rg和Lg分别为PCC和交流系统之间的等值电阻和等值电感。
;vc为VSC输出电压矢量;ip为PCC流入电网的电流矢量;ic为VSC流向PCC的电流矢量。Pout、Qout分别为从PCC流入电网的有功功率和无功功率;Rg和Lg分别为PCC和交流系统之间的等值电阻和等值电感。摘要 随着电力系统中新能源占比的增加,传统电网的强度越来越弱,短路比降低,导致基于电压定向的跟网型电压源型换流器(VSC)的稳定性变弱。为了解决跟网型VSC连接弱网时的稳定性问题和功率传输极限问题,基于功率定向的构网型VSC得到广泛关注,尤其是采用功率同步控制(PSC)和虚拟同步机(VSG)控制的并网VSC,因结构简单而迅速发展。然而,考虑电网和线路等值电感动态时,构网型换流器在感性网络的等效电阻较小时易发生一种同步频率谐振(SFR),导致系统失稳。该文主要以PSC-VSC为研究对象,通过建立小信号模型分析其发生SFR的机理,发现除了线路电阻小之外,非最小相位效应是引发SFR的另一个原因。为了抑制这种同步频率谐振,该文提出采用陷波器的谐振抑制方法,与采用低通滤波器方法(等效VSG控制)相比,该文所提方法对控制参数更具有鲁棒性,同时能提高系统的带宽。最后,建立实验平台,通过物理实验验证该文所提出控制策略的有效性。
关键词:构网型换流器 同步频率谐振 陷波器 稳定性
随着我国能源结构逐渐转向清洁化发展,风能、太阳能等清洁化一次能源正被大量开发,其装机容量持续升高[1-2]。电压源型换流器(Voltage Source Converter, VSC)作为新能源发电与电网间的重要接口,已被广泛应用于以新能源发电为主导的新型电力系统[3-4]。根据VSC控制方式的不同,可以分为跟网(grid-following)型VSC和构网(grid-forming)型VSC两种[5-7]。目前,在工程中广泛应用的主要是跟网型VSC,即采用矢量电流控制来调节换流器的输出电流,进而控制有功/无功功率[8]。另外,为了实现换流器与电网之间的同步,跟网型VSC需要采样公共连接点(Point of Common Coupling, PCC)的电压,同时依赖锁相环(Phase Locked Loop, PLL)准确地检测其频率和相位。然而,随着电网中新能源渗透率的升高以及电力电子设备的不断接入,电网强度逐渐减弱[9-10],导致PLL的负阻效应愈发明显[11-12]。同时,由于电网阻抗的存在,注入电网电流的变化会引发PCC电压剧烈变化,进而严重影响并网VSC的稳定性。此外,跟网型VSC本质上被控制为电流源,无法直接为电网的电压和频率提供支撑,而且在孤岛运行时,系统本身不存在交流电压源,因此跟网型VSC不能正常稳定运行,往往需要增加额外的控制或者切换控制策略[5, 13],这些问题都限制了跟网型VSC的进一步应用。
为了提高VSC在连接弱电网时的稳定性,同时方便给孤岛供电,提出了构网型VSC的概念[14],不同于跟网型VSC,其同步过程基于功率定向,不需要依赖PLL。目前,构网型VSC有多种控制方案,其中功率同步控制(Power Synchronization Control, PSC)[15-16]和虚拟同步机(Virtual Synchronous Generator, VSG)控制[17]作为最简单的构网型控制方法,得到广泛关注。它们模拟了传统电网有功-频率、无功-电压的下垂特性。除此之外,VSG控制为了缓解大规模新能源并网带来的电网惯性减少问题,配合额外的储能或者加大电容等,模拟了传统同步电机的摇摆方程和惯性响应,使VSC具备对系统频率和惯性支撑[18-19]。在不考虑储能影响时,VSG控制与引入一阶低通滤波器的PSC可以相互等效变换。在忽略电网电感动态时,VSG功率环可被视为二阶系统,当其阻尼系数较小时可能引发系统低频振荡,现有的研究中已提出多种提高阻尼的方法抑制这种低频振荡。然而,考虑电网和线路等值电感动态,采用PSC或VSG控制的VSC,在连接到等效电阻较小的感性网络时均会发生一种特殊的振荡,振荡频率在50 Hz左右。这种现象在文献[16]中被称为同步频率谐振(Synchronous Frequency Resonance, SFR),会给电力系统的稳定运行带来巨大威胁[16, 20]。
为了分析SFR发生的原因,文献[21]建立的VSG小信号模型能够反映出系统二倍频以内的频率特性,然而,并未分析有功功率控制环(Active Power Control Loop, APCL)和无功功率控制环(Reactive Power Control Loop, RPCL)的耦合对系统的影响。文献[22]根据复功率的定义,建立了VSG的功率控制模型,指出VSG功角较小时,即系统轻载时发生SFR的主要原因是PCC与电网之间的等效电阻太小,但缺乏详细的数学模型和物理解释。文献[23]建立了VSG的宽频动态模型,指出APCL和RPCL的动态耦合存在负阻尼效应会加剧SFR。
在抑制并网VSC的SFR时,常采用加入虚拟电阻的方法以提高系统的等效阻尼[9, 23]。文献[23]验证了引入虚拟电阻,可以有效抑制VSG中的SFR,并且文献[24]进一步提出在VSG系统的电压电流双环控制中引入虚拟复阻抗,重塑系统输出阻抗使其呈阻性以提高系统的稳定性。然而,虚拟电阻会增加系统的等效电阻,导致系统等效阻感比Rg/Xg增加,进而加强了APCL和RPCL之间的耦合效应[25],使系统的独立控制更加困难。另外,文献[25]指出虚拟电阻会改变系统的功率传输特性,降低VSC的稳定有功传输能力,因此,构网型VSC的SFR抑制策略仍有待进一步研究。为解决上述问题,本文建立了并网PSC-VSC的小信号模型,推导了APCL和RPCL相互耦合的等效数学模型,验证了感性网络的等效电阻较小可能引发VSC发生SFR。同时发现造成SFR的另外一个原因,即非最小相位效应。为了抑制并网PSC-VSC的SFR现象,确保系统的稳定运行,本文提出了一种基于陷波器的构网型换流器SFR抑制策略。此方法相比使用一阶低通滤波器(或VSG控制)时系统稳定裕度更高,对控制参数的鲁棒性更高,同时系统带宽较高,响应速度较快。最后在实验室建立了三相并网换流器的实验平台以进行实验验证,实验结果验证了本文所提抑制策略的有效性。
并网PSC-VSC主电路及控制框图如图1所示,Lf和Cf分别为VSC输出端滤波电感和滤波电容,电网电压矢量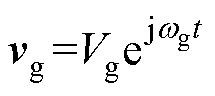 ,正常情况下电网角频率wg等于额定角频率wn;PCC电压矢量
,正常情况下电网角频率wg等于额定角频率wn;PCC电压矢量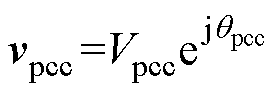 ;vc为VSC输出电压矢量;ip为PCC流入电网的电流矢量;ic为VSC流向PCC的电流矢量。Pout、Qout分别为从PCC流入电网的有功功率和无功功率;Rg和Lg分别为PCC和交流系统之间的等值电阻和等值电感。
;vc为VSC输出电压矢量;ip为PCC流入电网的电流矢量;ic为VSC流向PCC的电流矢量。Pout、Qout分别为从PCC流入电网的有功功率和无功功率;Rg和Lg分别为PCC和交流系统之间的等值电阻和等值电感。
PSC功率控制模块中Dp为频率-有功下垂系数,Dq为电压-无功下垂系数,正常运行时取值范围由并网导则确定;Pref和Qref分别为有功和无功功率参考值;Vref为额定电压幅值;qr为PCC输出电压的相位参考,Vpr为PCC输出电压的幅值参考。电压和电流内环采用PI控制器使vpcc跟踪PSC控制回路输出的参考电压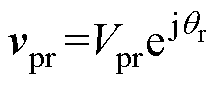 。为了实现快速跟踪,本文设计电压和电流内环的带宽远高于PSC功率外环。
。为了实现快速跟踪,本文设计电压和电流内环的带宽远高于PSC功率外环。
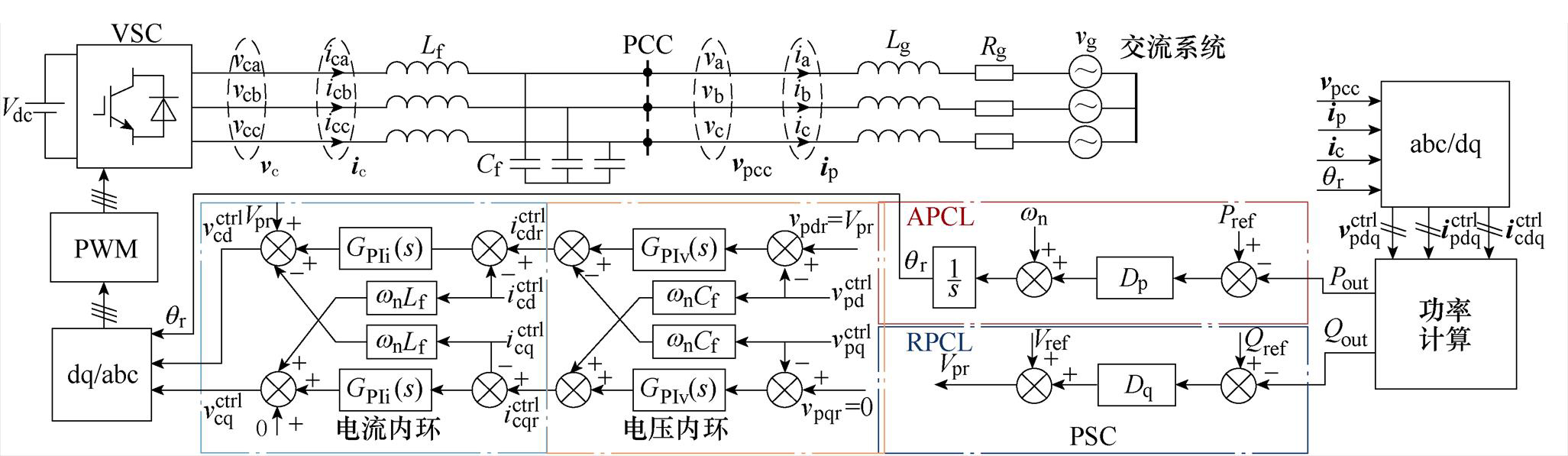
图1 并网PSC-VSC主电路与控制结构图
Fig.1 Main circuit and control structure of grid-connected PSC-VSC
根据图1可得滤波电感Lf、滤波电容Cf及线路等值电感Lg在abc坐标系中的动态方程,将其进行Park变换转换至同步旋转坐标系下,故可描述为
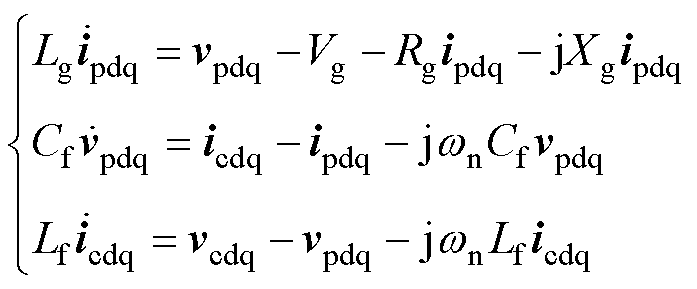 (1)
(1)
式中,d轴以vg的a相为参考。电压矢量vg、vpcc、vc和电流矢量ip、ic经Park变换后分别表示为旋转坐标系中的电压矢量vgdq=Vg、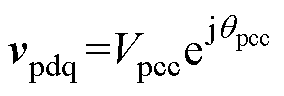 、vcdq和电流矢量ipdq、icdq,其中dpcc=qpcc-wgt为虚拟功角。
、vcdq和电流矢量ipdq、icdq,其中dpcc=qpcc-wgt为虚拟功角。
根据式(1)可计算出PCC稳态功率Pe和Qe分别表示为
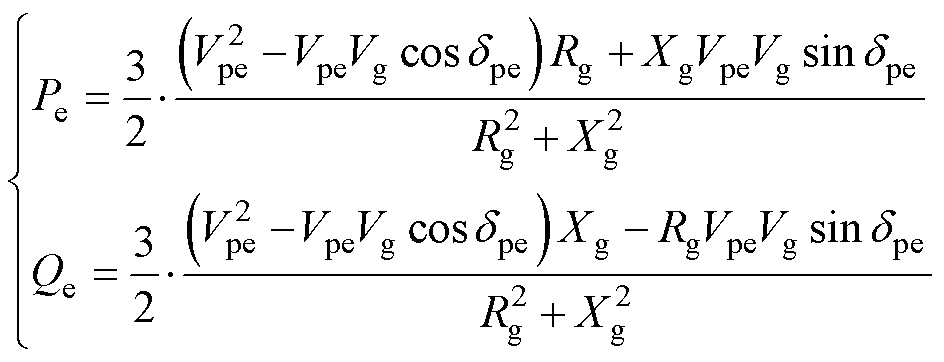 (2)
(2)
式中,Xg=wnLg为坐标变换引入的同步电抗;Vpe和dpe分别为Vpcc和dpcc的稳态值。
将Pout和Qout在平衡点处小信号化,经拉氏变换可得到频域小信号模型为
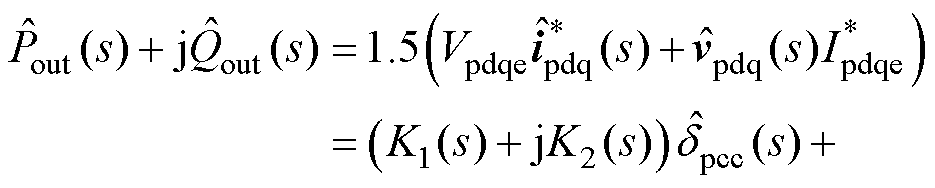
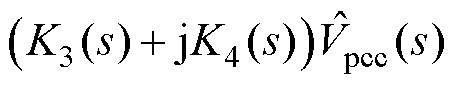 (3)
(3)
其中
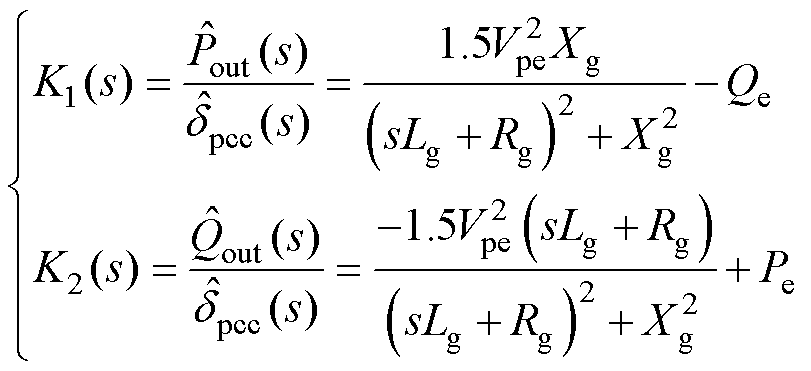 (4)
(4)
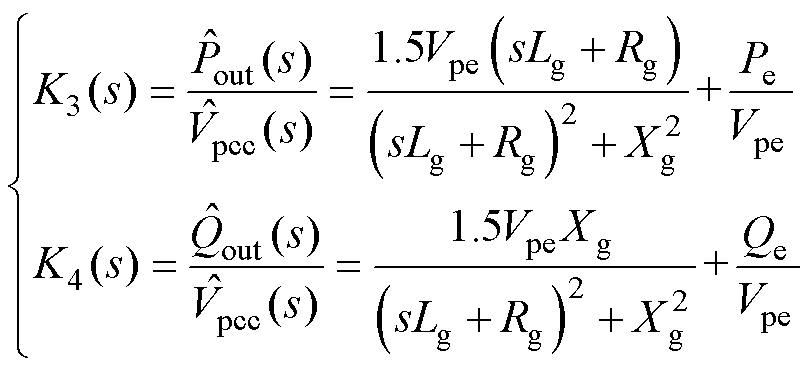 (5)
(5)
式(4)、式(5)表征的是考虑等值电感动态后,Vpcc和qpcc与该点输出功率之间的固有关系,当功率环采用PSC或VSG控制时均成立。
依据图1中APCL和RPCL的控制框图,可得PCC电压相位和幅值的基准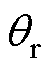 和Vpr分别为
和Vpr分别为
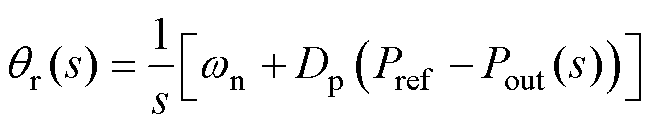 (6)
(6)
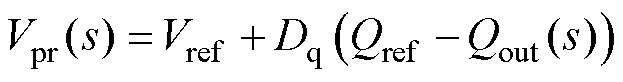 (7)
(7)
在VSG控制中,APCL和RPCL的控制方程为
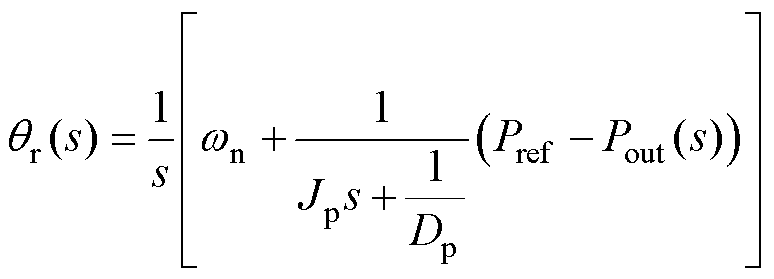 (8)
(8)
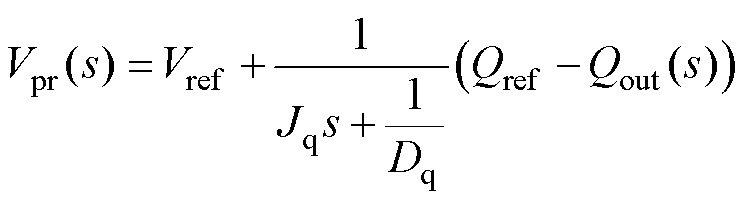 (9)
(9)
式中,Jp、Jq分别为有功和无功惯性系数。
从式(6)~式(9)中不难看出,参数满足Dp(q)wcp(q)=1/Jp(q)时,VSG控制与在下垂系数前引入一个一阶低通滤波器GLPF_p(q)(s)=wcp(q)/(s+wcp(q))的PSC结构等效,wcp(q)为APCL或RPCL中滤波器带宽。
考虑到PSC中功率环输出相位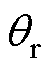 的影响,因此区别于式(1)中的系统坐标系,存在控制坐标系,在上标中加入“ctrl”以示区别。根据图1中电压电流内环控制框图,可得其小信号数学模型为
的影响,因此区别于式(1)中的系统坐标系,存在控制坐标系,在上标中加入“ctrl”以示区别。根据图1中电压电流内环控制框图,可得其小信号数学模型为
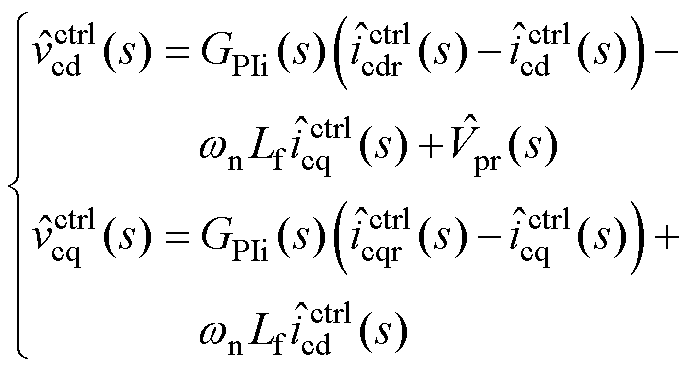 (10)
(10)
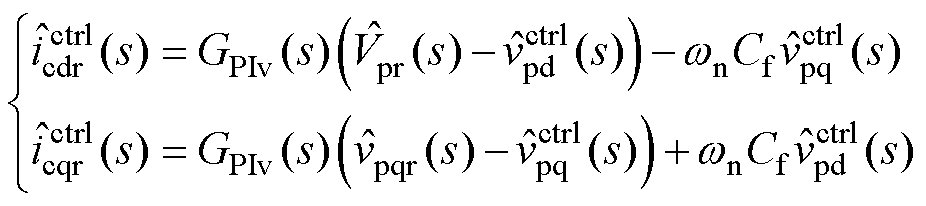 (11)
(11)
式中,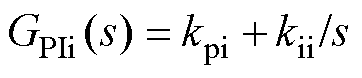 为电流控制环PI调节器;
为电流控制环PI调节器;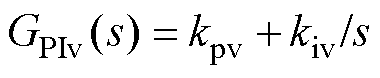 为电压控制环PI调节器。
为电压控制环PI调节器。
将式(11)代入式(10),联立式(1)的小信号数学模型,并代入系统坐标系与控制坐标系中dq分量间的关系(见附录式(A1)~式(A4)),可得
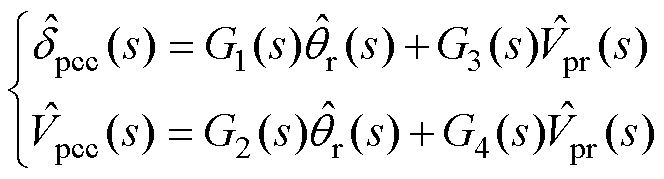 (12)
(12)
式中,G1(s)~G4(s)表征了电压电流内环以及VSC输出端滤波器的动态,其具体表达式见附录式(A5)、式(A6)。
基于式(3)~式(12),即可得到系统小信号模型,如图2所示。
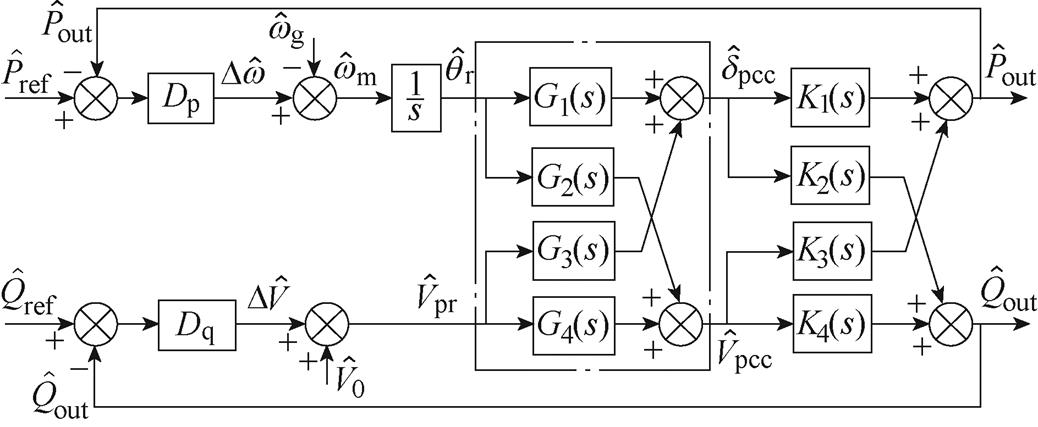
图2 系统的小信号模型
Fig.2 Small-signal model of the system
根据图2可推得计及内环影响的APCL和RPCL的开环增益为
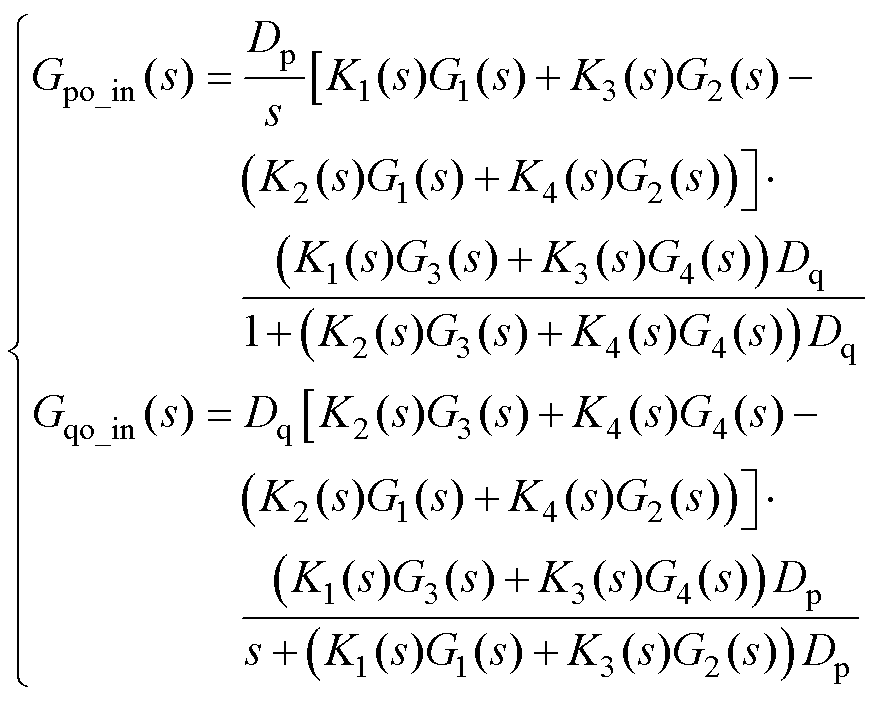 (13)
(13)
其伯德图如图3中实线所示。
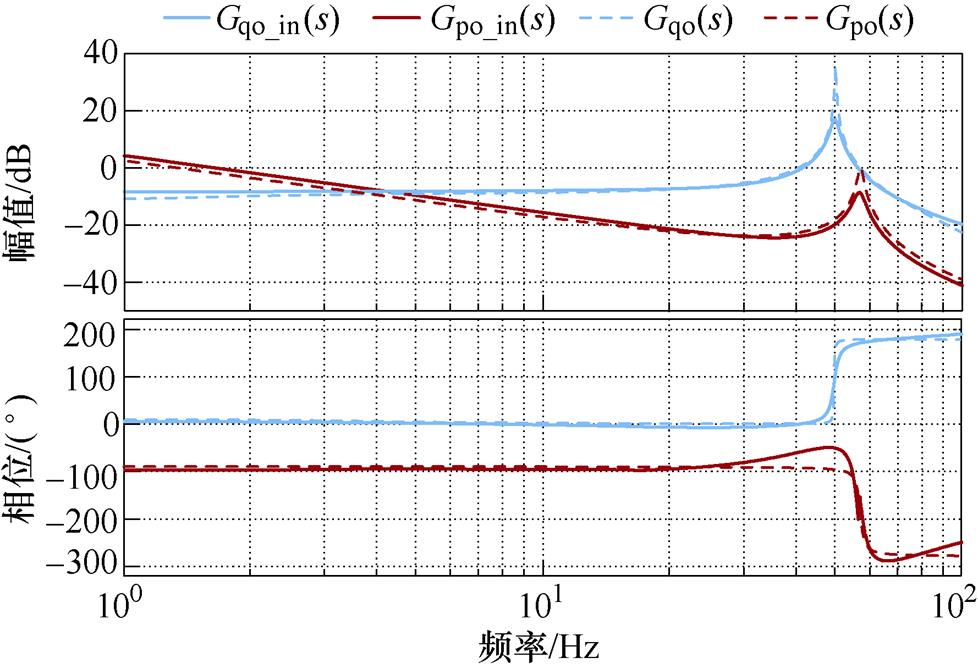
图3 Gpo_in(s)、Gqo_in(s)、Gpo(s)和Gqo(s)的伯德图
Fig.3 Bode plot of Gpo_in(s)、Gqo_in(s)、Gpo(s) and Gqo(s)
若将内环和滤波器的动态(见图2中点画线框出部分)等效为单位增益的比例环节,可推得此时APCL和RPCL的开环增益分别为
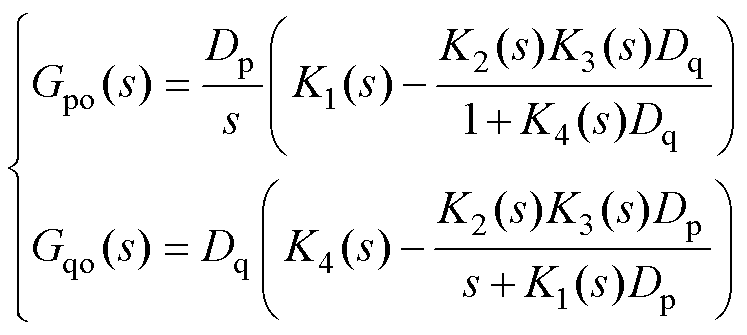 (14)
(14)
其伯德图如图3中虚线所示,可见考虑内环动态前后,系统开环增益在1~100 Hz这一频段内的伯德图基本重合。因此,为了简化分析SFR产生的原因,本文在后续分析中认为内环足够快,能够实现理想的电压跟踪,使Vpcc=Vpr、qpcc=qr。
为了进一步研究并网PSC-VSC的同步频率谐振机理,根据式(14)可得APCL和RPCL的闭环传递函数为
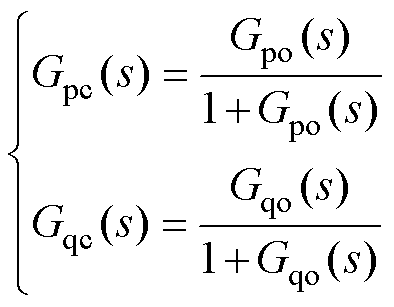 (15)
(15)
线路阻抗参数一般可以根据典型线路阻抗比和短路比(Short Circuit Ratio, SCR)确定,而在高压系统中,Rg相较于Xg通常较小,若取Xg=0.5(pu),令Rg在[0.002, 0.02](pu)范围内变化,可得闭环系统的特征根变化如图4所示。从图4中可以看出,当Rg减小时,系统的一对共轭特征根逐渐从复平面的左半平面向虚轴方向运动并最终进入右半平面,且其振荡频率均在50 Hz附近。因此,线路等效电阻较小时,易引发SFR,系统失稳。不同于并网换流器中可通过阻尼设计改善的低频振荡问题,这种振荡的频率范围主要在40~60 Hz附近。因此,本文提出了一种基于陷波器的并网换流器SFR抑制策略。
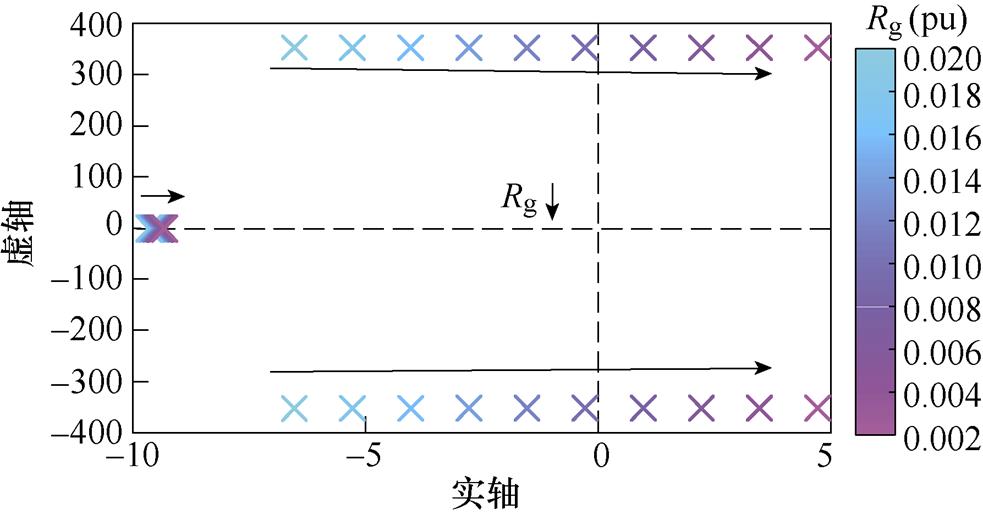
图4 Rg变化时系统的特征根分布
Fig.4 Eigenvalues of the system when Rgvaries
功率控制环的参数同样会影响系统的稳定性,引发SFR。通常,PSC控制中的下垂系数由并网导则确定[26],如Dp=0.02(pu),Dq=0.17(pu)。根据奈奎斯特稳定性判据,可以通过Gpo(s)与Gqo(s)的伯德图和奈奎斯特曲线判断系统的稳定性如图5所示。 Gpo(s)的奈奎斯特曲线包围(-1, j0)点的圈数R=2,且此时Gpo(s)的右半平面极点数P=0,即P≠R,因此判定系统不稳定。同时,从Gpo(s)的伯德图中可以看出系统的振荡频率在同步频率附近。
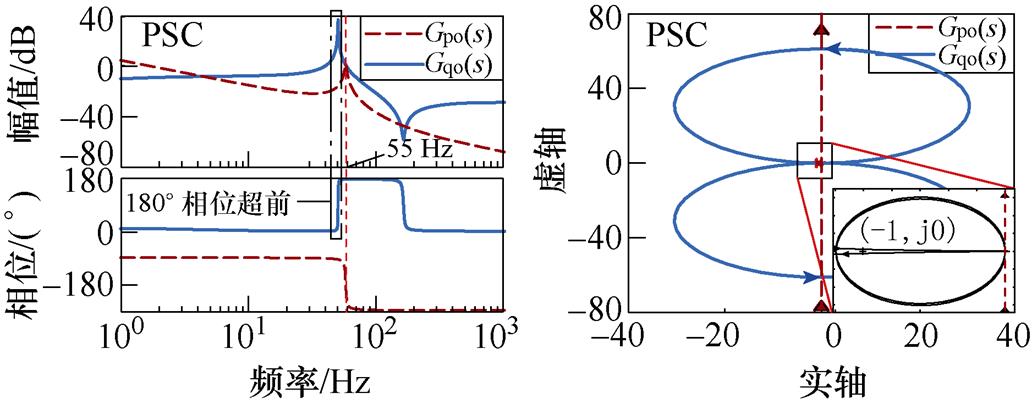
图5 Gpo(s)和Gqo(s)的伯德图和奈奎斯特曲线
Fig.5 Bode plot and Nyquist Plot of Gpo(s) and Gqo(s)
根据控制理论,将在复平面右半平面上有极点或零点的系统定义为非最小相位系统,其中开环极点对系统的稳定性影响较大。通过分析伯德图中的幅频特性曲线和相频特性曲线,易判断系统中是否存在开环极点的非最小相位环节。一组最小相位二阶振荡环节Gm(s)和非最小相位二阶振荡环节Gn(s)的伯德图如图6所示。从图6可以看出,二者幅频曲线一致,根据谐振峰所在频率处的相频曲线存在180°相位滞后或是超前易区分二者。
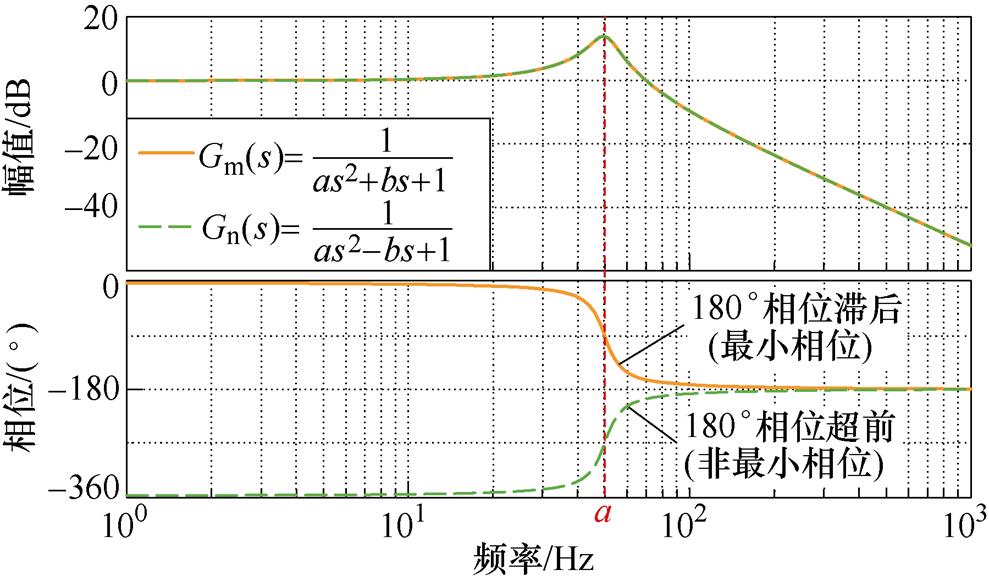
图6 Gm(s)和Gn(s)的伯德图
Fig.6 Bode plot of Gm(s) and Gn(s)
图5中的Gqo(s)在50 Hz附近存在180°相位超前,可知Gqo(s)中存在非最小相位振荡环节,此时RPCL有右半平面极点(P=2),代入具体参数也可验证此结论。又因为R=0,所以无功控制环会因为非最小相位效应引发系统不稳定。
为了验证上述理论分析,在Simulink仿真系统中令PSC并网换流器启动于Dp=0.01(pu),Dq= 0.01(pu),系统能够稳定运行,在5 s时切换至Dp= 0.02(pu),Dq=0.17(pu),Pout和Qout波形如图7所示。从图7中可以看出,系统在5 s后发生了振荡,处于不稳定状态。对其5 s后的Pout振荡波形进行快速傅里叶变换(Fast Fourier Transform, FFT)分析,其频率与图5中的理论分析基本吻合。
在图1所示的系统中,改变Dp和Dq的取值时,系统的不稳定因素如图8所示。即Dq取值不变时令Dp逐渐增大,开始时,P=R=0,系统稳定(见图8中区域Ⅰ);Dp略微增大后P=0,但因APCL和RPCL奈奎斯特曲线包围点(-1, j0)导致系统失稳,即 R≠0(见图8中区域Ⅱ);Dp逐渐增大时,APCL不稳定的因素相同,但RPCL出现非最小相位环节导致系统失稳,即P=2,R=0(见图8中区域Ⅲ)。
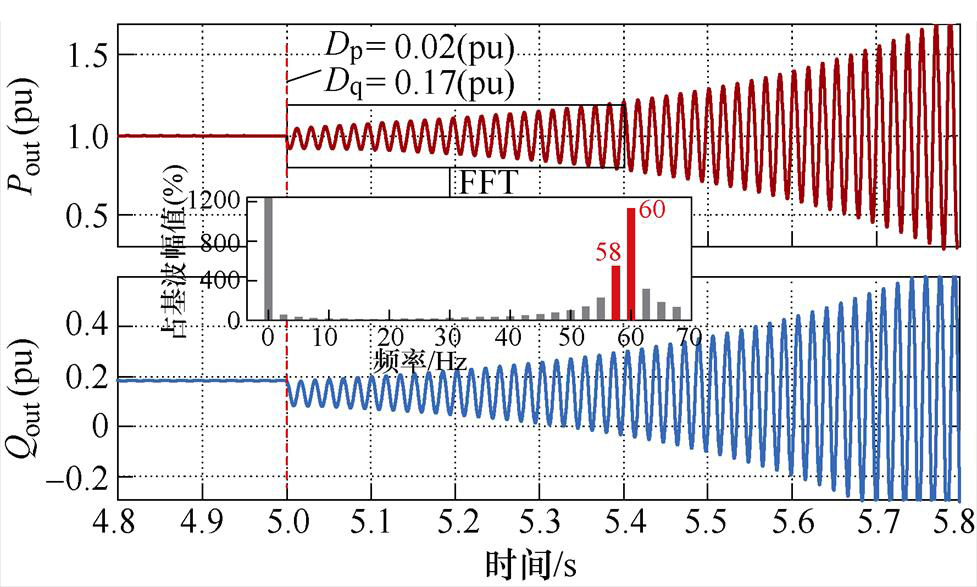
图7 功率仿真波形和FFT分析
Fig.7 Simulation waveforms and FFT analysis result
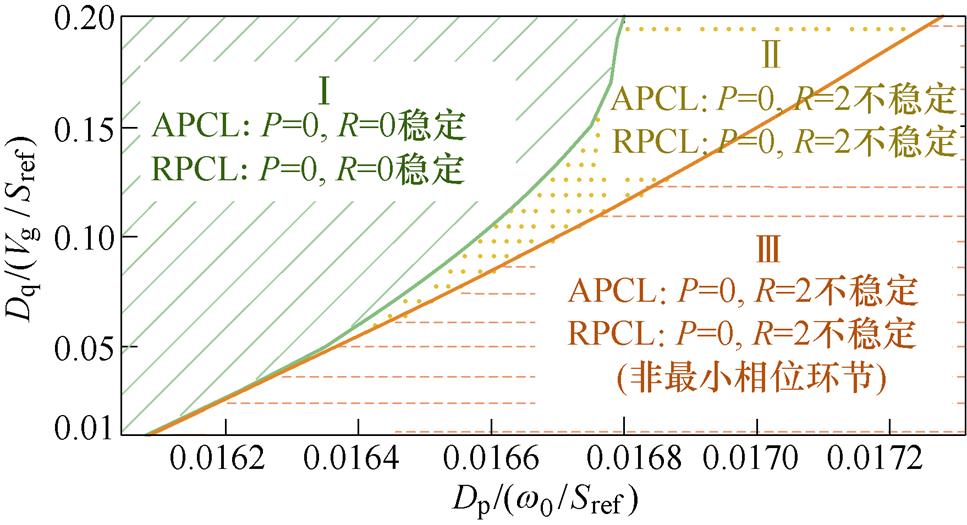
图8 功率环不稳定因素与下垂系数的关系
Fig.8 Relationship between unstable factors of power loop and droop coefficient
通常,相比PSC,VSG控制能提供虚拟惯量,抑制谐振峰。引入一阶低通滤波器的PSC与VSG控制等效,也能抑制并网PSC-VSC发生SFR。实际上,一阶低通滤波器主要通过抑制和削弱所设定带宽以上的信号在功率环中传播以消除SFR。考虑到SFR发生在同步频率附近,本节进一步提出引入陷波器滤除功率环中同步频率附近的信号,并比较两种滤波器的SFR抑制效果。加入低通滤波器或陷波器后的功率控制环如图9所示。
图9中,在APCL或RPCL引入的陷波器传递函数为
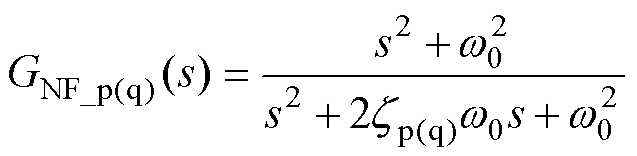 (16)
(16)
式中,w0为陷波器的中心频率;zp(q)为阻尼系数。
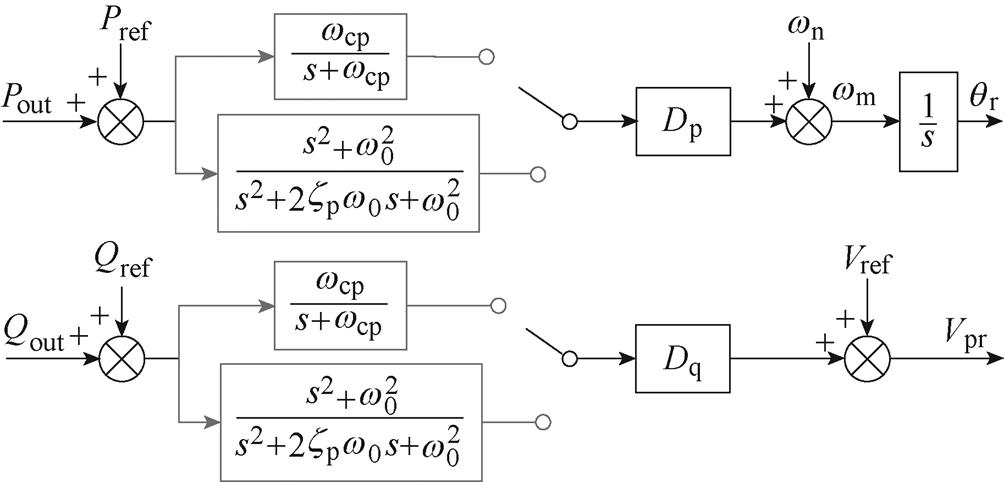
图9 引入一阶低通滤波器或陷波器后的PSC功率控制
Fig.9 PSC power control loop with first-order low-pass filters or notch filters
采用陷波器后,APCL和RPCL的开环传递函数变为
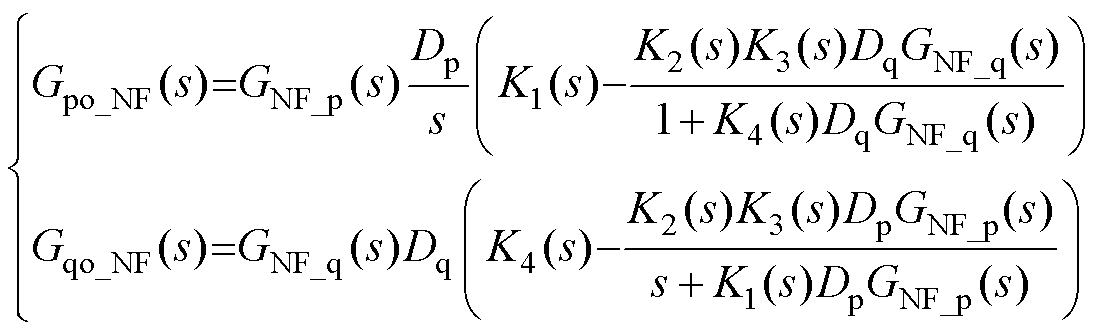 (17)
(17)
同理,结合GLPF_p(q)(s)易得到投入一阶低通滤波器时APCL和RPCL的开环传递函数Gpo_LPF(s)和Gqo_LPF(s)。当网络等效电阻较小时,分别取滤波器带宽wcp=wcq为0.2p, p, 2p, 6p, 12p rad/s,对应于采用VSG控制时有功惯性系数Jp分别取25, 5, 2.5, 0.83, 0.42(pu),而无功惯性系数Jq分别取0.94, 0.19, 0.09, 0.03, 0.02(pu)的情形,此时Gpo_LPF(s)和Gqo_LPF(s)的伯德图和奈奎斯特曲线如图10所示。
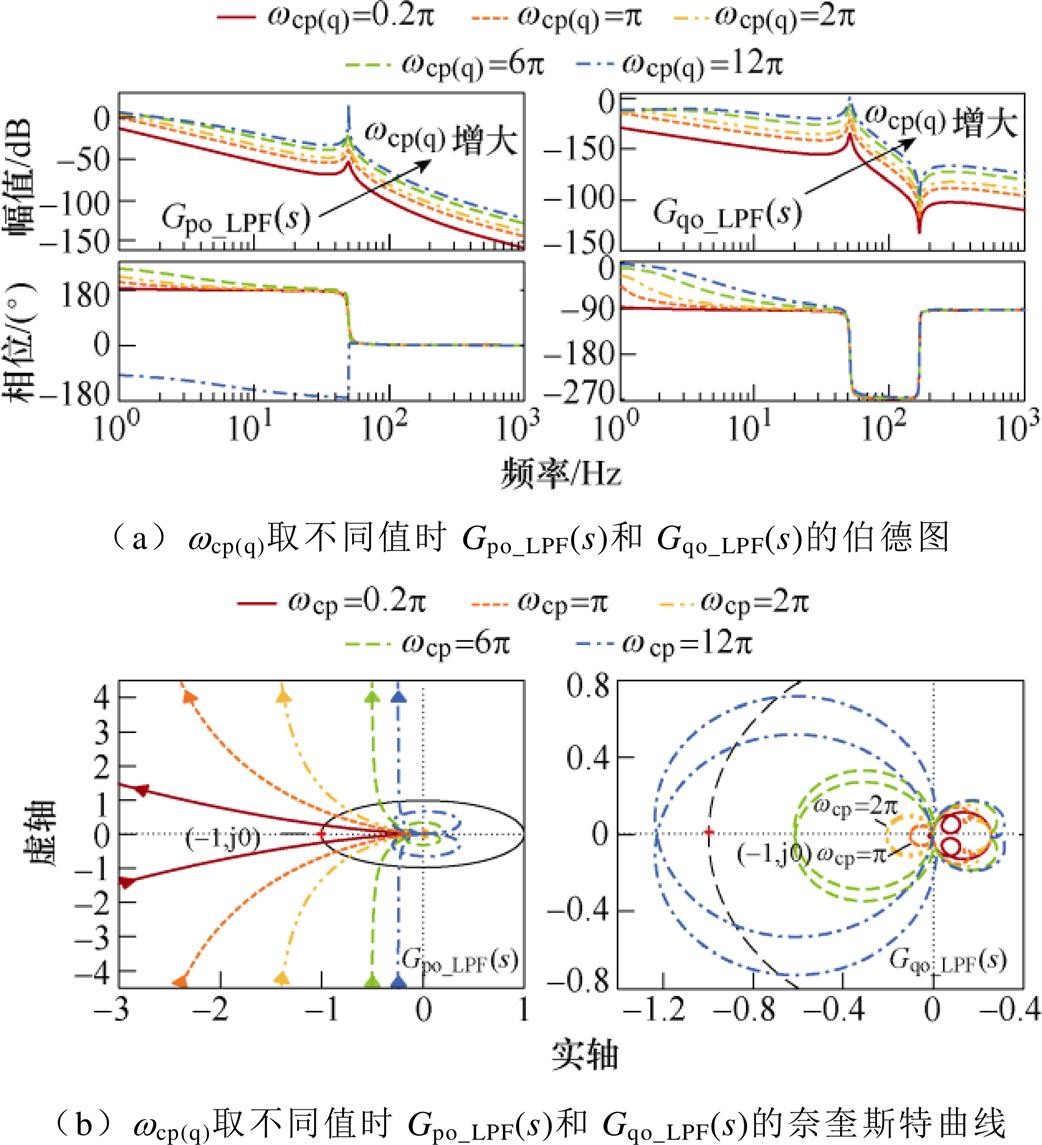
图10 Gpo_LPF(s)和Gqo_LPF(s)的伯德图和奈奎斯特曲线
Fig.10 Bode and Nyquist plot of Gpo_LPF(s) and Gqo_LPF(s)
显然,wcp(q)取值在[0.2p, 6p]rad/s之间,图10a中,Gpo_LPF(s)和Gqo_LPF(s)的谐振峰虽然存在但其幅值被抑制;图10b中,相应的奈奎斯特曲线均未包围点(-1, j0),系统稳定。而当wcp(q)取值过大,如wcp(q)=12p rad/s时,Gqo_LPF(s)的奈奎斯特曲线包围了点(-1, j0),此时系统不稳定,这与VSG控制中惯性系数Jq取值较小导致系统惯性不足从而引发SFR的机理相一致。此外wcp(q)=0.2p rad/s,图10b中Gpo_LPF(s)的奈奎斯特曲线靠近(-1, j0)点,其与单位圆交点处频率约为0.4 Hz。因此,wcp(q)取值过小可能在系统中引发更低频的振荡。
当wcp≠wcq时,进一步分析发现,系统的稳定性主要受wcq的影响,如图11a中令wcq=2p rad/s,取wcp∈[0.2p, 6p] rad/s,系统能保持稳定;而如图11b中令wcq=12p rad/s,取wcp∈[0.2p, 12p] rad/s,Gqo_LPF(s)的奈奎斯特曲线始终包围点(-1, j0)(P= 0, R=2),系统不稳定。因此,在PSC中采用一阶低通滤波器可以起到抑制SFR的作用,但是其带宽wcp(q)过大或过小均可能造成系统不稳定。
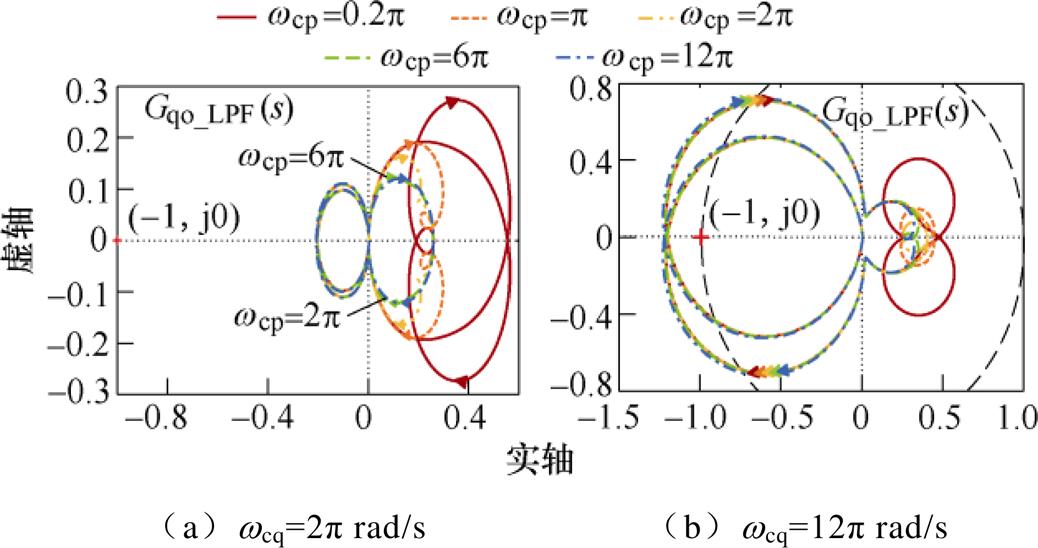
图11 wcp≠wcq时Gqo_LPF(s)的奈奎斯特曲线
Fig.11 Nyquist plot of Gqo_LPF(s) with wcp≠wcq
投入陷波器以抑制SFR时,根据同步频率谐振选定中心频率为w0=100π rad/s,令zp=zq在[0.1, 5]范围内取不同值,对应的Gpo_NF(s)和Gqo_NF(s)伯德图和奈奎斯特曲线如图12所示。从图12a的伯德图幅频特性曲线中可以看出,Gpo_NF(s)和Gqo_NF(s)在50 Hz附近的谐振峰由于陷波器的作用被抑制,且图12b的奈奎斯特曲线均未包围点(-1, j0)。因此,选用陷波器,能够有效抑制由网络等效电阻较小引发的SFR。此外,将系统的具体参数代入式(17),其中非最小相位环节也被消去,因此采用陷波器也能抑制由非最小相位环节引发的SFR。同时,zp和zq在[0.1, 5]范围内取值不等时,系统均能保持稳定运行,因此为了便于实际应用,令二者取值保持一致。
进一步分析发现,采用陷波器时对系统参数更具适应性,保持较大稳定裕度的同时可以增大系统带宽。Dp增至0.1(pu),引入不同参数的一阶低通滤波器或陷波器,系统相位裕度和带宽见表1。
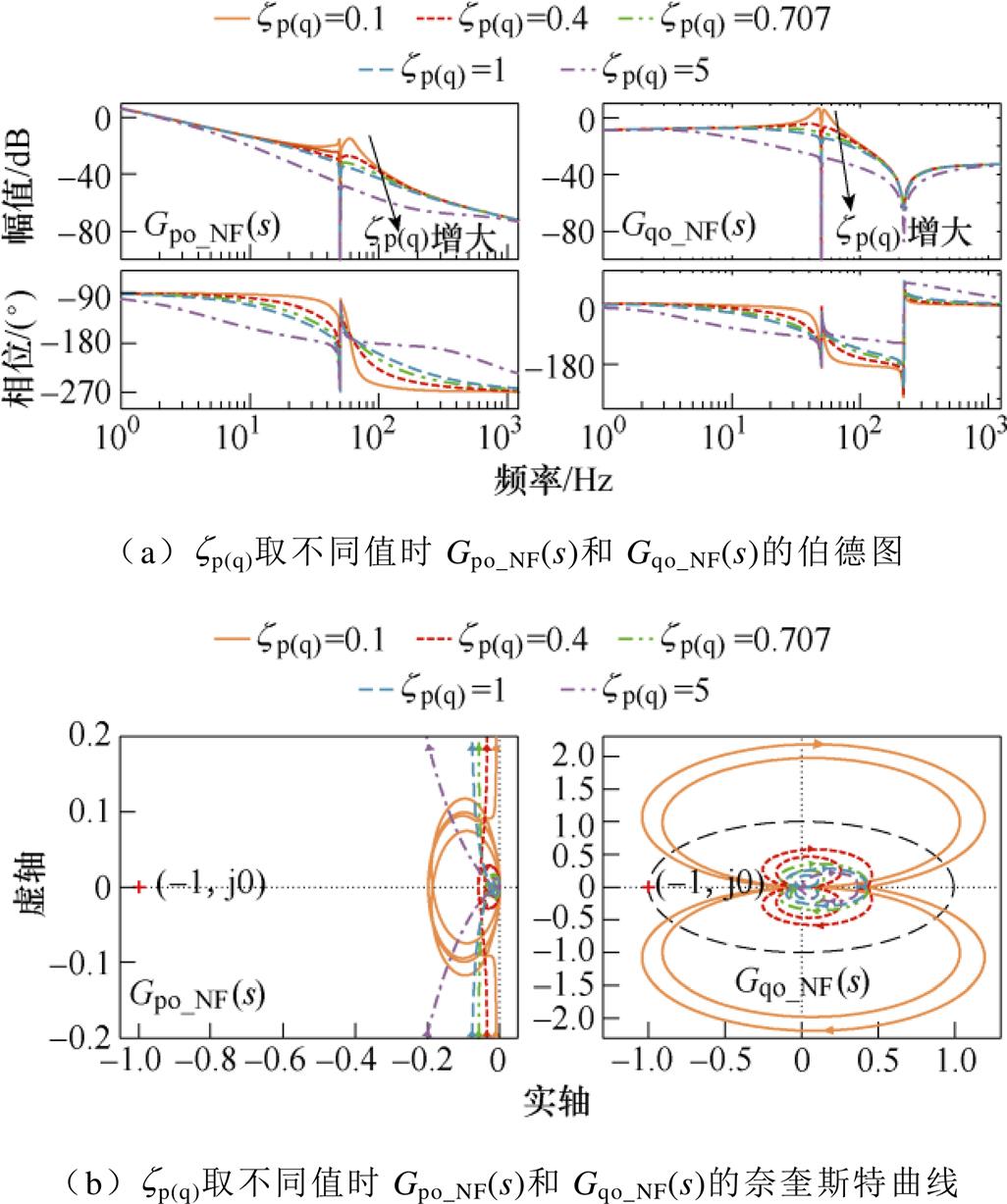
图12 Gpo_NF(s)和Gqo_NF(s)的伯德图和奈奎斯特曲线
Fig.12 Bode and Nyquist plot of Gpo_NF(s) and Gqo_NF(s)
表1 Dp=0.1(pu)时系统采用低通滤波器或陷波器后的相位裕度和带宽
Tab.1 Phase margin and bandwidth of the system using low-pass filter or notch filter when Dp=0.1(pu)
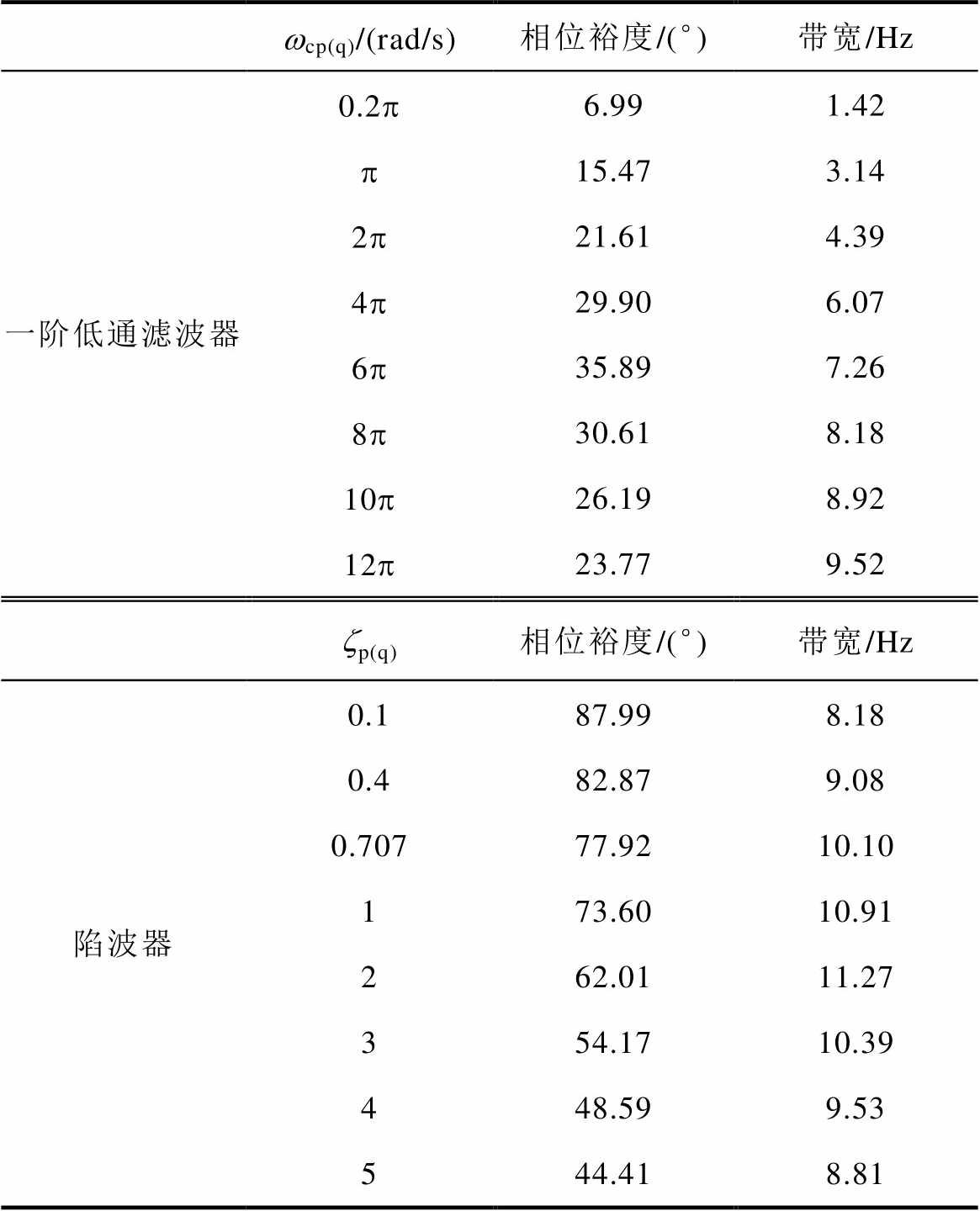
wcp(q)/(rad/s)相位裕度/(°)带宽/Hz 一阶低通滤波器0.2p6.991.42 p15.473.14 2p21.614.39 4p29.906.07 6p35.897.26 8p30.618.18 10p26.198.92 12p23.779.52 zp(q)相位裕度/(°)带宽/Hz 陷波器0.187.998.18 0.482.879.08 0.70777.9210.10 173.6010.91 262.0111.27 354.1710.39 448.599.53 544.418.81
从表1可以看出,引入一阶低通滤波器,wcp(q)取值过小(wcp(q)≤2p rad/s)或过大(wcp(q)=12π rad/s)时相位裕度均小于25°,即系统的稳定裕度较小,这与图10中分析相符。而引入陷波器时,系统的相位裕度均高于40°,这表明在不同阻尼比zp(q)下,系统均有较为充足的稳定裕度。同时,引入陷波器的系统控制带宽均在8 Hz以上,普遍高于绝大多数引入一阶低通滤波器的系统。
定义引入一阶低通滤波器或者陷波器后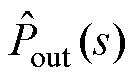 与
与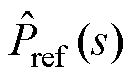 之间的闭环传递函数分别为Gppc_LPF(s)、Gppc_NF(s),其伯德图如图13所示。
之间的闭环传递函数分别为Gppc_LPF(s)、Gppc_NF(s),其伯德图如图13所示。
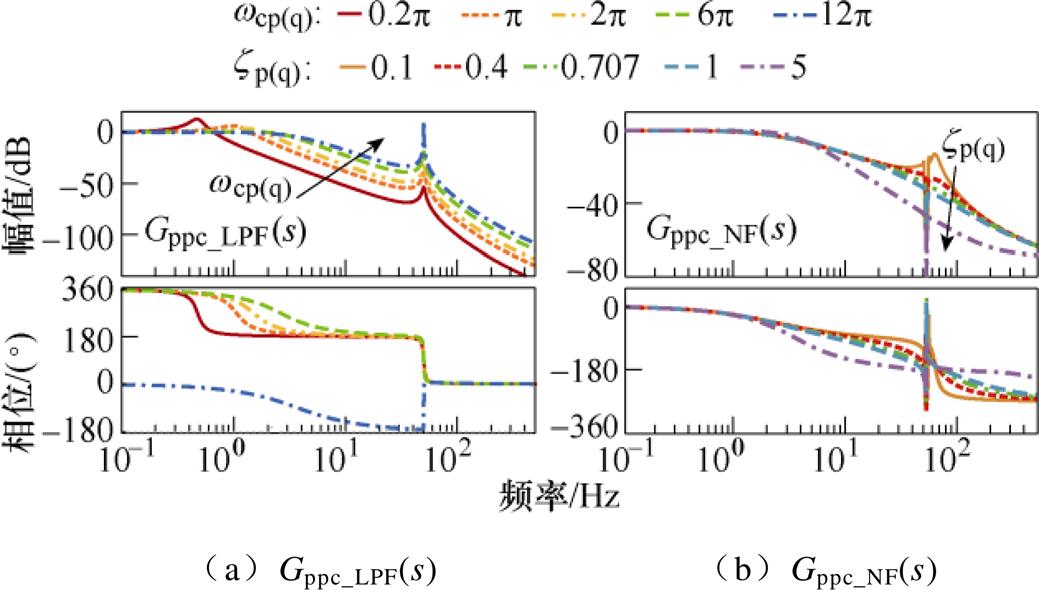
图13 Gppc_LPF(s)和Gppc_NF(s)的伯德图
Fig.13 Bode plot of Gppc_LPF(s) and Gppc_NF(s)
从图13a Gppc_LPF(s)的幅频曲线可以看出,wcp(q)增大时,低频段的谐振峰逐渐减小,控制带宽逐渐增大,响应速度逐渐加快。而从图13b不难看出,陷波器的zp(q)取不同值时控制带宽均较高,系统的响应速度均较快。
为了验证上述理论分析的正确性,在实验室中建立了三相并网换流器实验平台,如图14所示。主电路和控制回路的参数见表2。
首先验证第2节中一阶低通滤波器和陷波器的同步频率谐振抑制能力。令原系统启动时的下垂系数为Dp=0.01(pu),Dq=0.01(pu)(对应图8的区域Ⅰ),在t1时刻切换至Dp=0.02(pu),Dq=0.17(pu)(对应图8的区域Ⅲ),并在t2时刻分别投入如图9所示的低通滤波器或陷波器,实验结果如图15和图16所示。
图15和图16中的实验波形从上至下依次为PCC的有功功率Pout、无功功率Qout、a相电压va和a相电流ia,最下方为局部放大的Pout波形。
根据实验波形,系统在t1时刻切换至Dp= 0.02(pu),Dq=0.17(pu)后会发生同步频率谐振。其中图15在0.2 s后投入一阶低通滤波器,当wcp(q)= 6π rad/s时振荡现象得到抑制;当wcp(q)=0.2π rad/s时,系统发生更低频的振荡;当wcp(q)=12π rad/s时同步频率谐振仍然存在。实验结果与前述理论分析相符,验证了投入低通滤波器抑制并网PSC-VSC中的SFR时,低通滤波器的参数取值范围有限,鲁棒性较差。

图14 三相并网换流器实验平台
Fig.14 Three-phase grid-connected PSC-VSC experimental platform
表2 并网PSC-VSC的主要参数
Tab.2 Main parameters of the grid-connected PSC-VSC
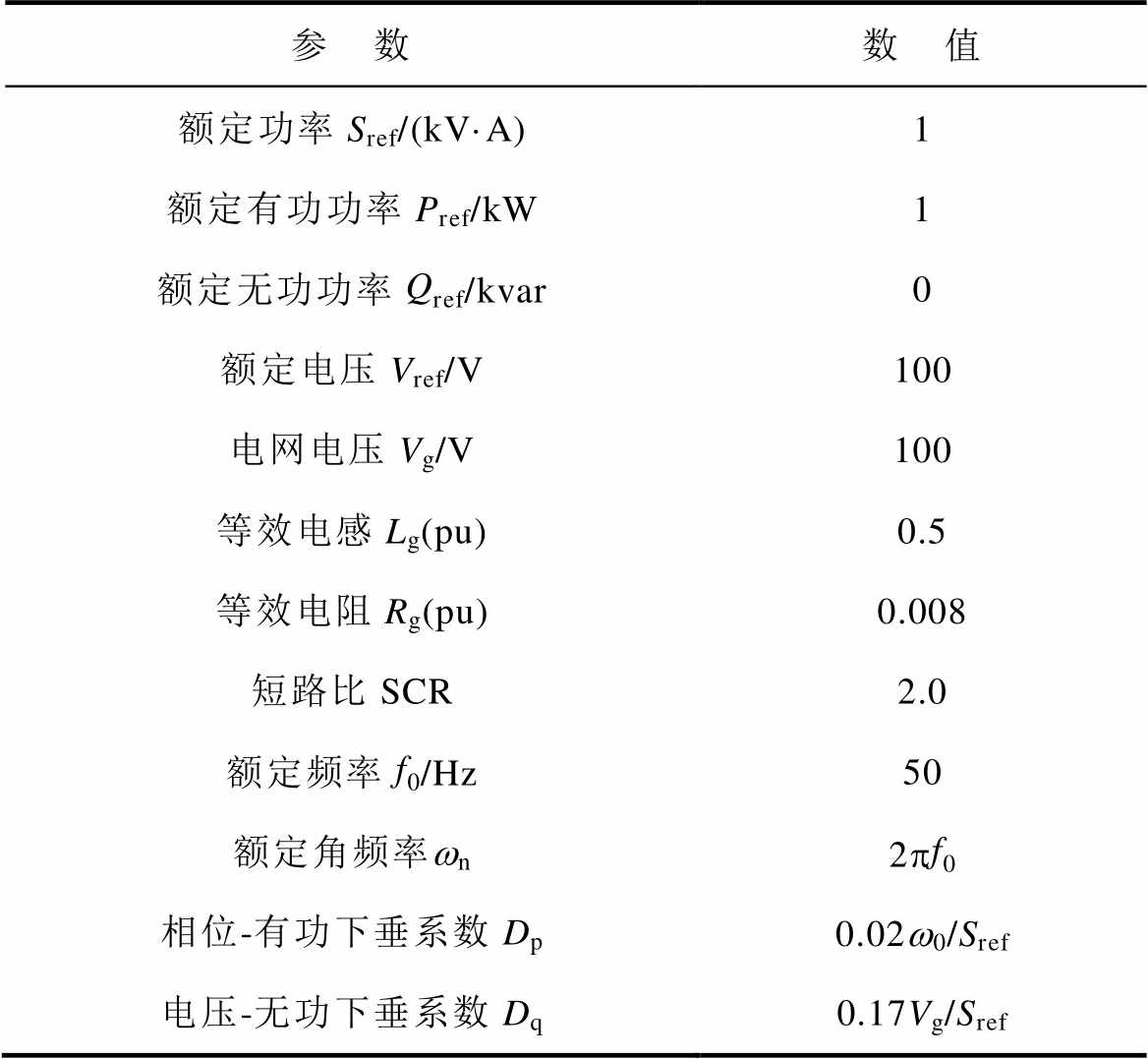
参 数数 值 额定功率Sref/(kV·A)1 额定有功功率Pref/kW1 额定无功功率Qref/kvar0 额定电压Vref/V100 电网电压Vg/V100 等效电感Lg(pu)0.5 等效电阻Rg(pu)0.008 短路比SCR2.0 额定频率f0/Hz50 额定角频率wn2pf0 相位-有功下垂系数Dp0.02w0/Sref 电压-无功下垂系数Dq0.17Vg/Sref
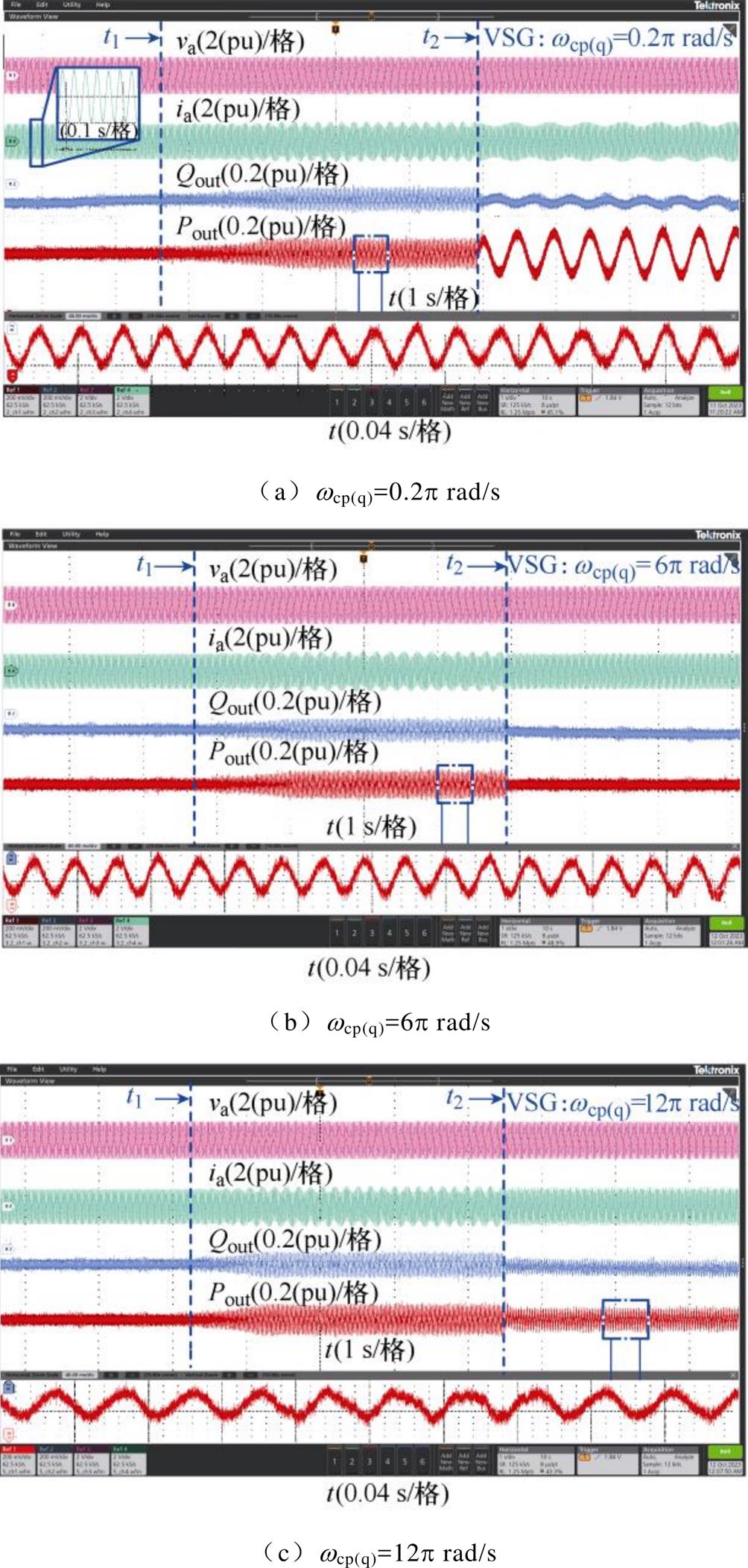
图15 投入不同带宽的低通滤波器时的实验波形
Fig.15 Experimental waveforms with low pass filter of different bandwidth
而图16中改为在系统发生SFR后分别投入阻尼系数为zp(q)=1或zp(q)=5的陷波器,SFR均在1.5 s内被抑制,验证了zp(q)设计值处于[0.1, 5]范围内,系统稳定性均较好。实际上,只要zp(q)设计值超过0.001,陷波器均能有效抑制SFR。因此,在保证系统稳定运行的前提下,陷波器控制参数选取范围远超一阶低通滤波器的带宽取值范围,即系统对zp(q)的设计精度要求更低。

图16 投入不同阻尼系数的陷波器时的实验波形
Fig.16 Experimental waveforms with notch filter of different damping coefficient
为了验证本文所提抑制策略对系统参数的适应性更强,增大Dp时的实验波形如图17所示,系统初始时刻投入了带宽wcp(q)=6p rad/s的一阶低通滤波器,在t3时刻提高Dp,此时功率波形中出现明显振荡,在t4时刻改为投入zp(q)=1的陷波器,振荡在2 s内被抑制。这表明引入一阶低通滤波器的并网PSC-VSC系统在控制参数改变时,可能引发失稳,而引入陷波器的系统仍能保持正常稳定运行。因此,采用陷波器的系统相比于采用一阶低通滤波器的系统对控制参数改变的适应性更强,系统的带宽更高,与表1中引入陷波器时系统相位裕度普遍更高的理论分析相符。
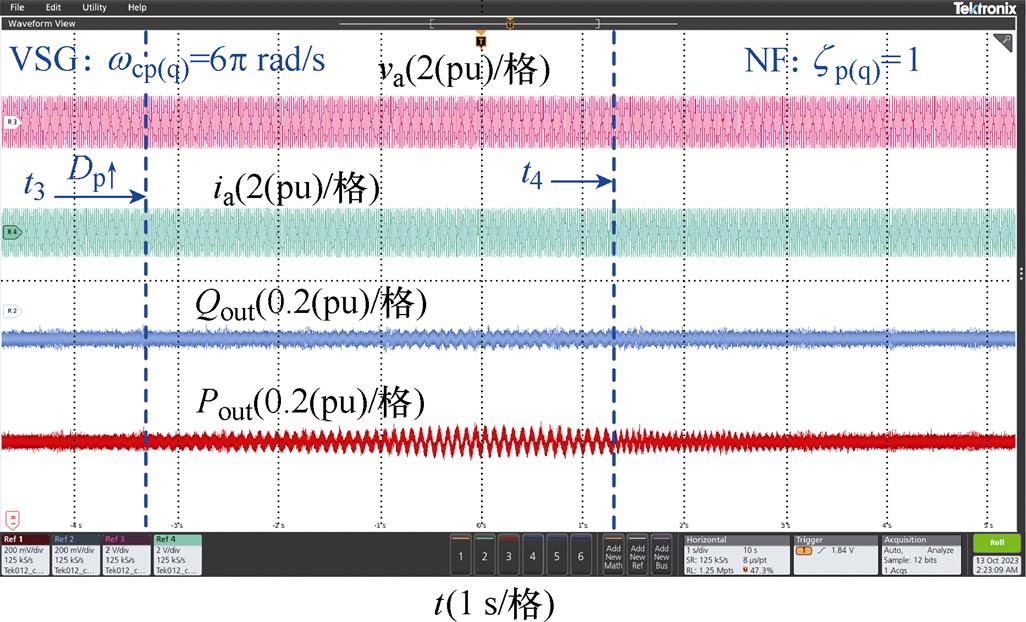
图17 增大Dp时的实验波形
Fig.17 Experimental waveforms with increased Dp
本文以功率同步控制的构网换流器为研究对象,建立了PSC-VSC的小信号数学模型,分析了其SFR现象发生的机理,并提出了一种基于陷波器的构网型换流器SFR抑制策略,最后通过实验验证了所提方法的有效性。得到的结论如下:
1)建立了APCL和RPCL相互耦合的并网PSC- VSC频域小信号模型,并根据闭环系统根轨迹验证了感性网络的等效电阻较小会引发SFR。通过奈奎斯特判据分析非最小相位效应是引发SFR的另一个原因。
2)提出一种采用陷波器的并网PSC-VSC同步频率谐振抑制方法。该方法相比于引入一阶低通滤波器(等效VSG控制),不仅能够有效抑制谐振峰,还对参数设计的精度要求更低,控制参数鲁棒性更强,其系统的稳定裕度也更充足。
3)基于建立的三相并网换流器实验平台验证了理论分析的正确性,证明了所提方法相比于采用一阶低通滤波器更具优越性。
附 录
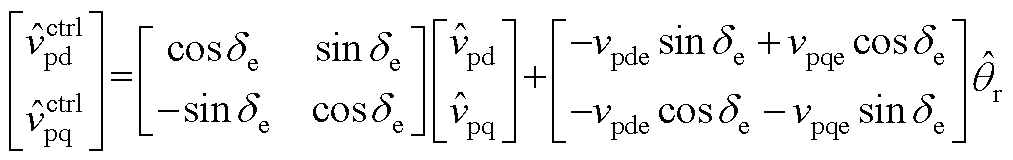 (A1)
(A1)
 (A2)
(A2)
 (A3)
(A3)
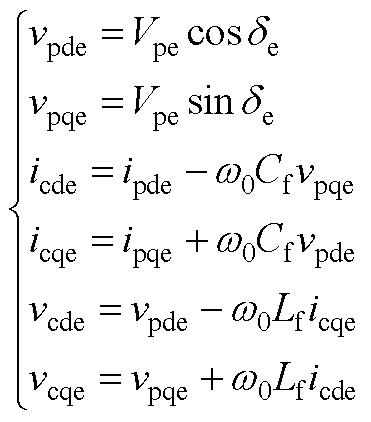 (A4)
(A4)
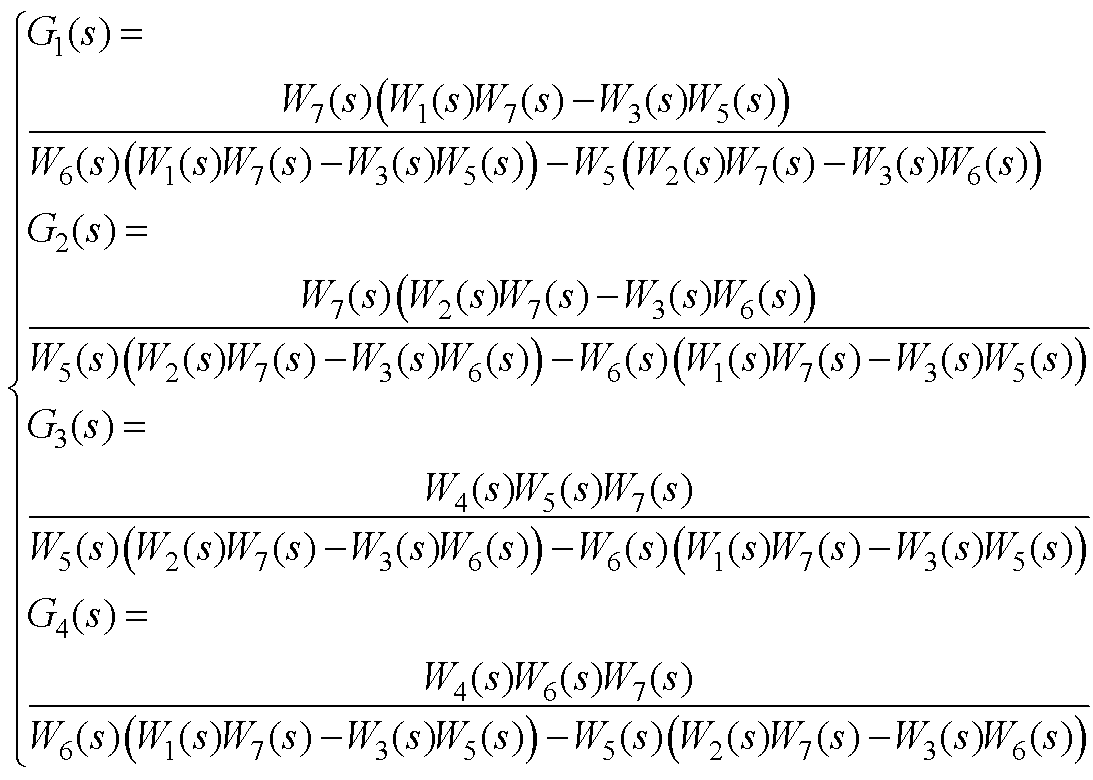 (A5)
(A5)
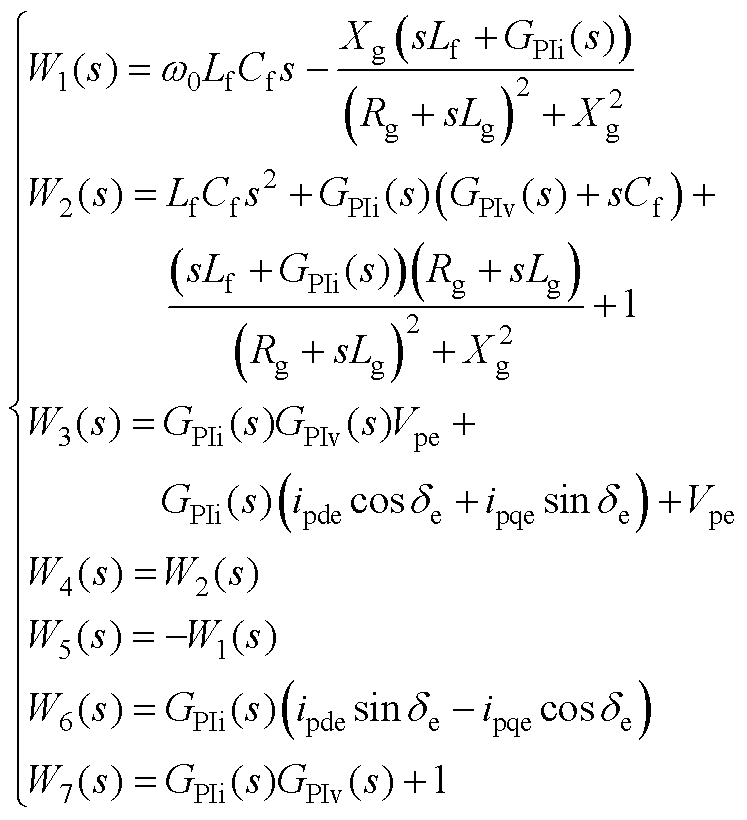 (A6)
(A6)
参考文献
[1] 马宁宁, 谢小荣, 贺静波, 等. 高比例新能源和电力电子设备电力系统的宽频振荡研究综述[J]. 中国电机工程学报, 2020, 40(15): 4720-4732.
Ma Ningning, Xie Xiaorong, He Jingbo, et al. Review of wide-band oscillation in renewable and power electronics highly integrated power systems[J]. Pro- ceedings of the CSEE, 2020, 40(15): 4720-4732.
[2] 张尧翔, 刘文颖, 庞清仑, 等. 高比例风电接入系统光热发电-火电旋转备用优化方法[J]. 电工技术学报, 2022, 37(21): 5478-5489.
Zhang Yaoxiang, Liu Wenying, Pang Qinglun, et al. Optimal power spinning reserve method of con- centrating solar power and thermal power for high- proportion wind power system[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5478- 5489.
[3] 杨铭, 曹武, 赵剑锋, 等. 受控电压/电流源型变流器混合多机暂态电压支撑策略[J]. 电工技术学报, 2023, 38(19): 5207-5223, 5240.
Yang Ming, Cao Wu, Zhao Jianfeng, et al. Transient voltage support strategy for hybrid multi-converter of controlled voltage/current source converter[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(19): 5207-5223, 5240.
[4] 杜步阳, 邵德军, 朱建行, 等. 电压源型变流器并网系统多时间尺度间相互作用[J]. 电工技术学报, 2023, 38(20): 5547-5559.
Du Buyang, Shao Dejun, Zhu Jianhang, et al. The interaction between multiple timescales of the grid-tied voltage source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5547- 5559.
[5] 胡宇飞, 田震, 查晓明, 等. 构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略[J]. 电力系统自动化, 2022, 46(24): 121-131.
Hu Yufei, Tian Zhen, Zha Xiaoming, et al. Impedance stability analysis and promotion strategy of islanded microgrid dominated by grid-connected and grid- following converters[J]. Automation of Electric Power Systems, 2022, 46(24): 121-131.
[6] 温春雪, 黄耀智, 胡长斌, 等. 虚拟同步发电机接口变换器并联运行虚拟阻抗自适应控制[J]. 电工技术学报, 2020, 35(增刊2): 494-502.
Wen Chunxue, Huang Yaozhi, Hu Changbin, et al. Adaptive control of virtual impedance in parallel operation of virtual synchronous generator interface converter[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 494-502.
[7] 颜湘武, 张伟超, 崔森, 等. 基于虚拟同步机的电压源逆变器频率响应时域特性和自适应参数设计[J]. 电工技术学报, 2021, 36(增刊1): 241-254.
Yan Xiangwu, Zhang Weichao, Cui Sen, et al. Frequency response characteristics and adaptive parameter tuning of voltage-sourced converters under VSG control[J]. Transactions of China Electro- technical Society, 2021, 36(S1): 241-254.
[8] 涂春鸣, 邹凯星, 高家元, 等. 基于不对称正负反馈效应的PQ功率控制并网逆变器稳定性分析[J]. 电工技术学报, 2023, 38(2): 496-509.
Tu Chunming, Zou Kaixing, Gao Jiayuan, et al. Stability analysis of grid-connected inverter under PQ power control based on asymmetric positive-negative- feedback effects[J]. Transactions of China Electro- technical Society, 2023, 38(2): 496-509.
[9] 涂春鸣, 高家元, 赵晋斌, 等. 弱电网下具有定稳定裕度的并网逆变器阻抗重塑分析与设计[J]. 电工技术学报, 2020, 35(6): 1327-1335.
Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.
[10] 于彦雪, 马慧敏, 陈晓光, 等. 弱电网下基于准静态模型的混合控制微电网逆变器同步稳定性研究[J]. 电工技术学报, 2022, 37(1): 152-164.
Yu Yanxue, Ma Huimin, Chen Xiaoguang, et al. Synchronous stability research of inverters in hybrid microgrid based on the quasi-static models under weak grid[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 152-164.
[11] Wen Bo, Dong Dong, Boroyevich D, et al. Impedance-based analysis of grid-synchronization stability for three-phase paralleled converters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 26-38.
[12] Wu Heng, Ruan Xinbo, Yang Dongsheng, et al. Small-signal modeling and parameters design for virtual synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4292-4303.
[13] 刘津铭, 陈燕东, 伍文华, 等. 孤岛微电网序阻抗建模与高频振荡抑制[J]. 电工技术学报, 2020, 35(7): 1538-1552.
Liu Jinming, Chen Yandong, Wu Wenhua, et al. Sequence impedance modeling and high-frequency oscillation suppression method for island microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1538-1552.
[14] 王志洁, 李书江, 胡红阳, 等. 构网型光伏发电系统振荡模态分析及抑制策略[J]. 电力电子技术, 2022, 56(12): 82-86.
Wang Zhijie, Li Shujiang, Hu Hongyang, et al. Oscillation mode analysis and suppression strategy of grid-forming photovoltaic power generation system[J]. Power Electronics, 2022, 56(12): 82-86.
[15] 李梦杰, 谢震, 高翔, 等. 弱电网下双馈风电机组混合功率同步控制策略及稳定性分析[J]. 中国电机工程学报, 2023, 43(21): 8388-8400.
Li Mengjie, Xie Zhen, Gao Xiang, et al. Hybrid power synchronization control strategy of DFIG-based wind turbines and its stability analysis under weak grid[J]. Proceedings of the CSEE, 2023, 43(21): 8388-8400.
[16] Zhang Lidong, Harnefors L, Nee H P. Power- synchronization control of grid-connected voltage- source converters[J]. IEEE Transactions on Power Systems, 2010, 25(2): 809-820.
[17] 潘子迅, 杨晓峰, 赵锐, 等. 不平衡电网下虚拟同步机的多模式协调策略[J]. 电工技术学报, 2023, 38(16): 4274-4285.
Pan Zixun, Yang Xiaofeng, Zhao Rui, et al. Multi- mode coordination control of virtual synchronous generator under unbalanced power grid[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(16): 4274-4285.
[18] 徐健, 曹鑫, 郝振洋, 等. 基于电网谐波电压前馈的虚拟同步整流器电流谐波抑制方法[J]. 电工技术学报, 2022, 37(8): 2018-2029.
Xu Jian, Cao Xin, Hao Zhenyang, et al. A harmonic- current suppression method for virtual synchronous rectifier based on feedforward of grid harmonic voltage[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2018-2029.
[19] Xiong Xiaoling, Wu Chao, Blaabjerg F. An improved synchronization stability method of virtual syn- chronous generators based on frequency feedforward on reactive power control loop[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 9136-9148.
[20] 于彦雪, 关万琳, 陈晓光, 等. 基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报, 2022, 37(10): 2584-2595.
Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual syn- chronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[21] 吴恒, 阮新波, 杨东升, 等. 虚拟同步发电机功率环的建模与参数设计[J]. 中国电机工程学报, 2015, 35(24): 6508-6518.
Wu Heng, Ruan Xinbo, Yang Dongsheng, et al. Modeling of the power loop and parameter design of virtual synchronous generators[J]. Proceedings of the CSEE, 2015, 35(24): 6508-6518.
[22] Yang Dongsheng, Wu Heng, Wang Xiongfei, et al. Suppression of synchronous resonance for VSGs[J]. The Journal of Engineering, 2017, 2017(13): 2574- 2579.
[23] 李武华, 王金华, 杨贺雅, 等. 虚拟同步发电机的功率动态耦合机理及同步频率谐振抑制策略[J]. 中国电机工程学报, 2017, 37(2): 381-391.
Li Wuhua, Wang Jinhua, Yang Heya, et al. Power dynamic coupling mechanism and resonance supper- ssion of synchronous frequency for virtual syn- chronous generators[J]. Proceedings of the CSEE, 2017, 37(2): 381-391.
[24] 马也, 史丽萍, 李衡, 等. 基于VSG控制的微网逆变器工频振荡现象研究[J]. 电力系统保护与控制, 2022, 50(1): 107-115.
Ma Ye, Shi Liping, Li Heng, et al. Power frequency oscillation of a microgrid inverter based on VSG control[J]. Power System Protection and Control, 2022, 50(1): 107-115.
[25] Xiong Xiaoling, Wu Chao, Blaabjerg F. Effects of virtual resistance on transient stability of virtual synchronous generators under grid voltage sag[J]. IEEE Transactions on Industrial Electronics, 2022, 69(5): 4754-4764.
[26] European Committee for Electrotechnical Standardi- zation. EN 50438 Requirements for the connection of micro generators in parallel with public low-voltage distribution networks[S]. 2008.
Abstract As an important interface between new energy power generation and the grid, the Voltage Source Converter (VSC) has been widely used in new power systems. At present, the grid following VSC based on current vector control has extensive application in engineering practice. However, with the increasing integration of new energy sources and the continuous addition of power electronic equipment, power grid stability weakens, leading to challenges in the stability of grid-following VSCs. The concept of grid-forming VSC is proposed to improve the stability, especially in weak grid scenarios and for power supply to isolated islands. Power Synchronization Control (PSC) and Virtual Synchronous Generator (VSG) control have gained significant attention due to their simplicity. It is found that PSC control with a first-order low-pass filter can be equivalent to VSG control when the influence of energy storage is ignored. However, an issue known as Synchronous Frequency Resonance (SFR) arises when VSCs controlled by PSC or VSG are connected to inductive grids with small equivalent resistances.
Based on the control equation, VSG control and PSC control with a first-order low-pass filter can be equivalent to each other. The coupling effect between the active power control loop (APCL) and reactive power control loop (RPCL) is explored, and an equivalent mathematical model for their mutual coupling is deduced. Secondly, the influence of the voltage and current inner loop dynamics of the system is analyzed, demonstrating that the inner loop does not change the system characteristics near the synchronization frequency. Therefore, to simplify the analysis of the synchronous frequency resonance mechanism, the inner loop is considered fast enough to achieve ideal voltage tracking. Thirdly, based on the small signal model in the frequency domain, it is verified that a small equivalent resistance in an inductive grid may cause SFR, and power control loop parameters can affect system stability. The Nyquist criterion analysis indicates that the presence of a non-minimum phase system is a cause of SFR.
Finally, the mechanism of the SFR phenomenon of the grid-forming converter is analyzed, and an SFR suppression strategy is proposed. The effectiveness of the proposed method is verified. The following conclusions can be drawn from the analysis: (1) A small signal model in the frequency domain of grid-forming PSC-VSC coupled with APCL and RPCL is established. According to the closed-loop system eigenvalue loci, it is verified that a small equivalent resistance of the inductive grid can cause SFR. The non-minimum phase effect is another reason for SFR. (2) Compared with the first-order low-pass filter (equivalent to VSG control), the proposed SFR suppression method can effectively suppress the resonance peak and require lower precision of parameter design. Meanwhile, it also has strong robustness in control parameters and a more substantial stability margin for the system. (3) The theoretical analysis is verified based on the established three-phase grid-connected converter experiment platform.
keywords:Grid-forming converter, synchronous frequency resonance (SFR), notch filter, stability
DOI: 10.19595/j.cnki.1000-6753.tces.230526
中图分类号:TM721.1
国家自然科学基金(52277176)、中央高校基本科研业务费专项资金(2022MS004)和《台达电力电子科教发展计划》资助项目。
收稿日期 2023-04-24
改稿日期 2023-09-26
熊小玲 女,1984年生,博士,副教授,博士生导师,研究方向为高压直流输电系统的控制和稳定性分析,电力电子系统建模、分析和设计。E-mail: xiongxl1102@ncepu.edu.cn (通信作者)
李昕悦 女,2000年生,硕士研究生,研究方向为构网型换流器的建模、分析和设计。E-mail: lixinyue2022@ncepu.edu.cn
(编辑 陈 诚)