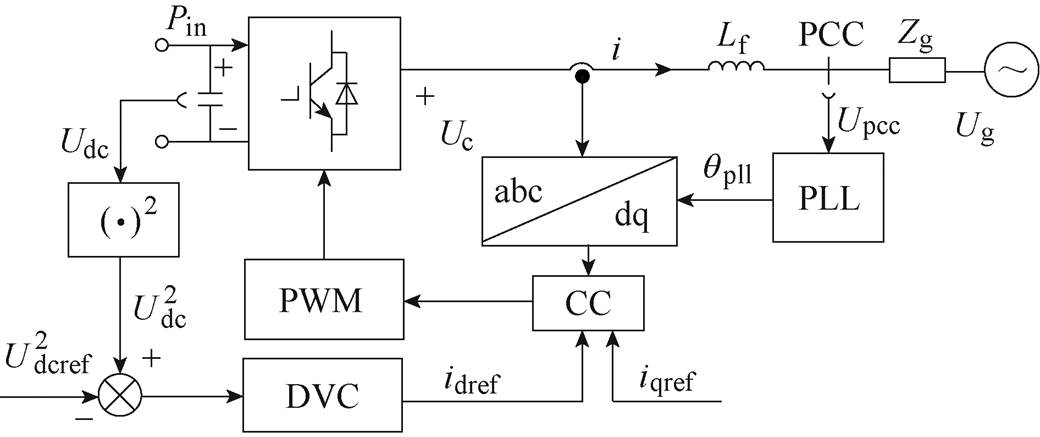
图1 跟网型变换器的电路拓扑与控制框图
Fig.1 VSC circuit and control-system block diagram
摘要 弱电网下，跟网型变换器易出现因阻尼不足导致的小扰动同步失稳问题。为此，该文借鉴复转矩分析理论，计及复杂控制耦合，建立跟网型变换器的复转矩模型。量化多环控制耦合、线路阻抗、控制参数等因素对系统阻尼转矩的影响，从阻尼的角度揭示跟网型变换器的小扰动同步失稳机理。根据理论分析，提出一种基于相位补偿的锁相环阻尼重塑控制策略，通过补偿多环控制耦合引入的负阻尼，增强变换器的小扰动同步稳定性。最后，开展相应的仿真与实验，验证理论分析的正确性与改进控制策略的有效性。
关键词：跟网型变换器 小扰动同步稳定 多环控制耦合 复转矩分析法 阻尼重塑
由于电力系统惯量的下降，公共耦合点（Point of Common Coupling, PCC）电压的波动性、不确定性随之加剧[1]，因而对跟网型变换器的同步稳定性提出更高的要求[2]。
对于跟网型变换器，控制参数选取不当时，锁相环（Phase Locked Loop, PLL）会呈现负阻尼[3]。文献[4-5]指出PLL的阻尼在扰动的作用下可能会急剧减小，引发系统失稳，但该文献忽略了其他控制环的动态。在实际工程中，变换器一般采用多环控制结构，多环控制中存在频带重叠效应[6-7]。因此，在研究跟网型变换器的同步稳定性时，要注意同时考虑PLL、控制环等动态[8]。文献[9]计及电流控制（Current Control, CC）环动态，揭示了电流环引入负阻尼导致变换器小扰动同步失稳的机理。文献[10]建立阻抗模型，分析了CC和PLL对系统同步振荡的影响，但均忽略了直流母线电压控制（DC-link Voltage Control, DVC）环的影响。直流母线作为变换器系统的重要环节之一，其动态特性直接影响系统的稳定运行[11]。文献[12]基于阻抗模型，分析了直流母线对交流网络同步稳定性的影响，但忽略了其他控制环的动态。文献[13-14]基于幅相运动方程，分析了DVC、PLL等控制环节对系统稳定性的影响规律，然而该文献未考虑CC环的动态。综上所述，在机理研究方面，现有研究大多基于简化模型，简化多环控制的影响，可能会为稳定性分析带来一定的不确定性。因此，综合考虑各控制环节的动态，基于精细化建模，开展同步稳定性的分析，可进一步量化跟网型变换器的小扰动同步失稳机理。
在增强变换器同步稳定性方面，文献[15]研究了一种基于相位补偿的改进控制策略，用于补偿PLL的负阻尼，提高变换器的同步稳定性，然而，该文献没有考虑电流环与PLL之间的耦合。文献[16]提出了一种基于自动虚拟变阻器的改进PLL架构，使系统能够补偿线路阻抗的压降，增强静态小干扰同步稳定性。文献[17]研究了一种自动电压调节控制策略，通过自动调整锁相环的输入，改善跟网型变换器的同步运行性能。文献[18]提出了一种自适应PLL，当瞬态扰动发生时，锁相环的阻尼比自动增大，增强了系统的小扰动同步稳定性。然而，上述文献的改进控制策略均基于简化模型，由于简化分析的保守性，在极端工况下可能存在改进控制策略失效的风险。
在实际工况中，复杂多环控制结构的解耦条件可能得不到保证，PLL、DVC、CC等环节相互耦合，共同影响系统的动力学特征[19]。为此，文中计及DVC、CC复杂控制耦合引入的附加阻尼分量，建立考虑复杂多环控制耦合的跟网型变换器复转矩模型，量化分析电网阻抗、控制器参数等因素对小扰动同步稳定性的影响。在机理分析的基础上，提出一种基于相位补偿的阻尼重塑控制策略，所提控制策略可有效地补偿DVC、CC控制耦合引入的负阻尼，改善PLL的阻尼特性，从而提高系统的小扰动稳定性。最后，基于搭建的实验样机，验证理论分析的准确性与所提控制策略的有效性。
典型跟网型变换器的电路拓扑与控制框图如图1所示。图中，Udc、Udcref分别为直流母线电压及其参考值；Lf为滤波器电感，此处忽略滤波电感的寄生电阻；Ug为电网电压；Zg为等效线路阻抗，一般为阻感性，即Zg=Rg+jwLg；逆变器的输出电流和输出电压分别为i和Uc；qpll为锁相环输出相位。
图1 跟网型变换器的电路拓扑与控制框图
Fig.1 VSC circuit and control-system block diagram
由图1可知，PLL、CC、DVC之间存在耦合，因此在讨论系统的同步稳定时，需要综合考虑各控制环的动态。
由图1，根据基尔霍夫电压定律，同时在平衡点处进行线性化处理，得到Upcc的d、q轴小扰动分量为
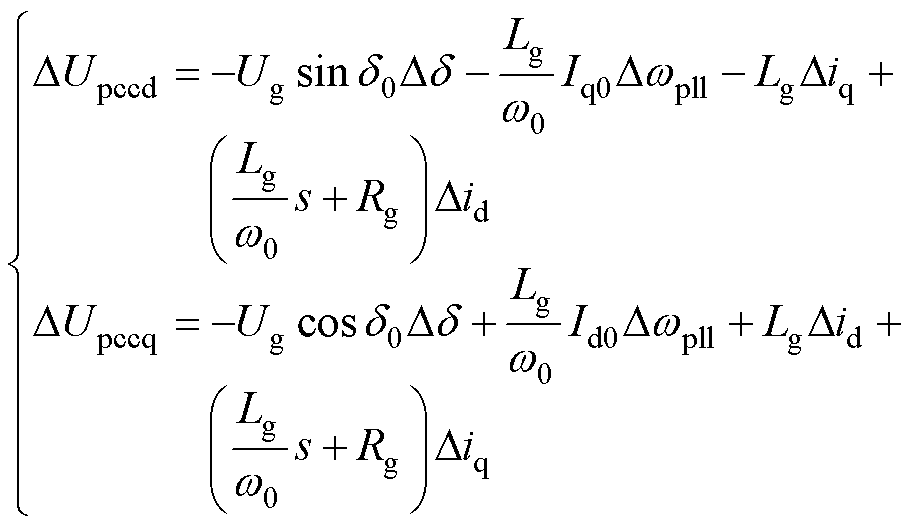（1）
式中，s为微分算子；1/w0为标幺化引入因子；Id0和Iq0分别为并网电流d、q轴稳态值；Did和Diq分别为并网电流d轴和q轴增量；Dwpll为角速度增量；d 为广义功角，是PLL输出相位与电网电压相位差；Dd 为功角增量；d0为功角的稳态值。
根据式（1），计及线路阻抗的影响，弱电网下锁相环的小信号动态模型如图2所示。
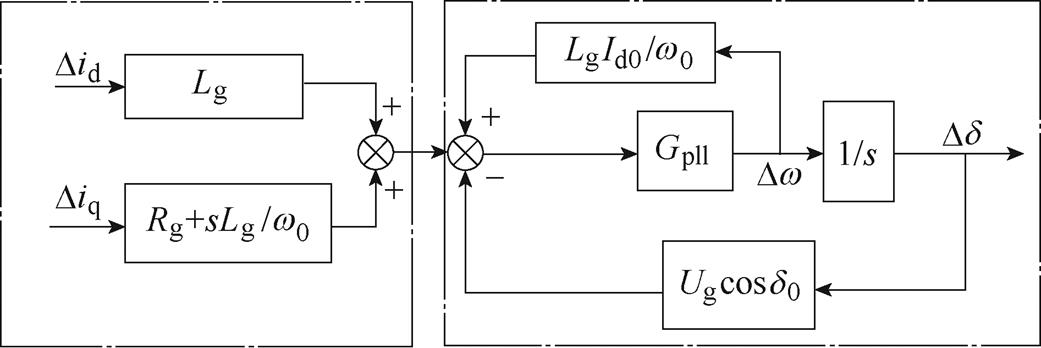
图2 PLL小信号动态模型
Fig.2 The small signal dynamic analysis model of PLL
图2表明，线路阻抗为控制环与PLL之间的耦合桥梁。电流动态经线路阻抗影响PLL的输入，进而直接影响PLL的动态行为；CC与DVC存在耦合，DVC通过CC、线路阻抗间接参与PLL的动态。因此，在分析以PLL为主导的小扰动同步稳定时，需要系统地考虑多环控制耦合、线路阻抗、控制参数等因素。
根据图1的电路拓扑，得到变换器输出电压d、q轴分量的小扰动动态特性表示为
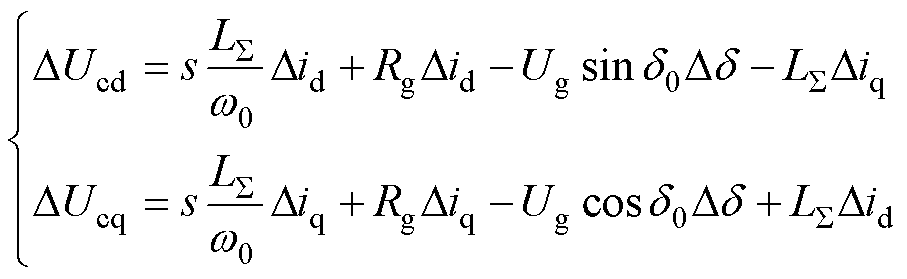（2）
式中，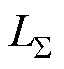
=Lf +Lg。
考虑DVC、CC的多环控制结构框图如图3所示。图中，Gcc和Gdvc分别为CC与DVC的控制器，此处均使用比例积分（Proportional-Integral, PI）控制器。
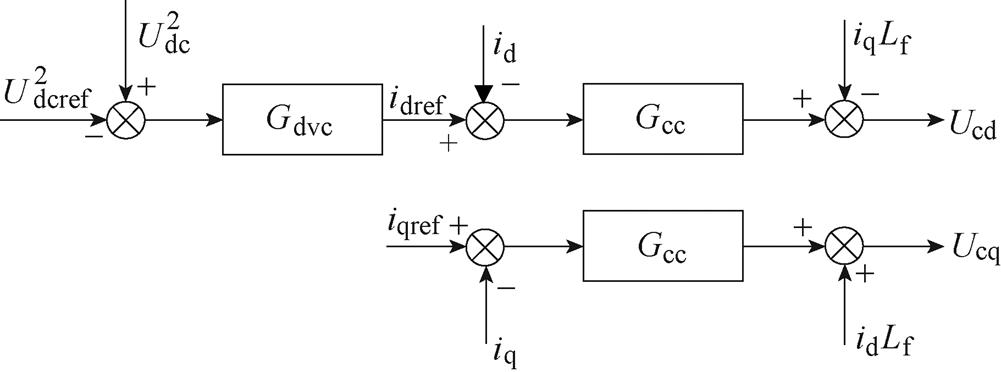
图3 DVC外环与CC内环的结构框图
Fig.3 The structure of DVC and CC
图3表明，DVC与CC为串联结构，CC的输入参考值idref为DVC的输出，两者存在直接的耦合。
进一步地，结合图3，同时联立式（2），得到Did、Diq的表达式分别为
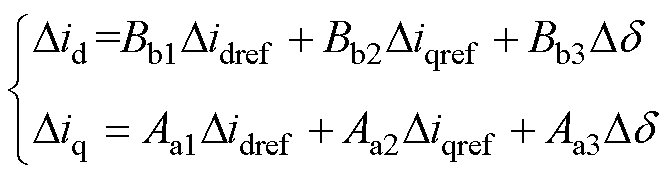（3）
式中，Aa1～Bb3的表达式如附录式（A1）所示。
将式（3）代入式（1），有
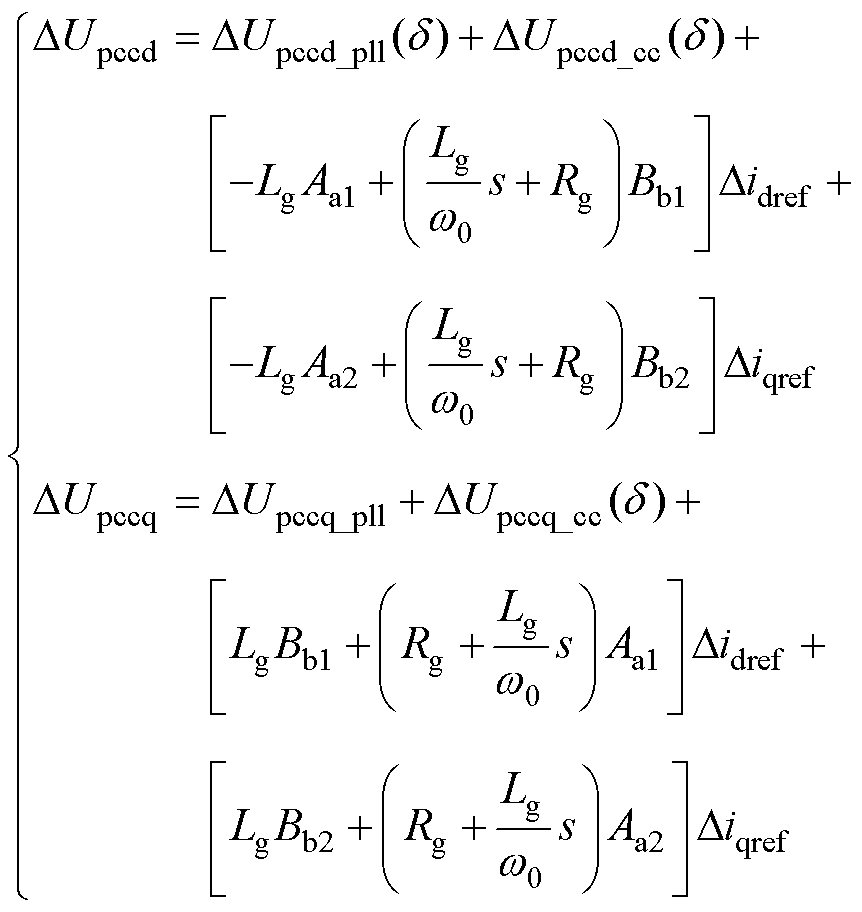（4）
式中，DUpccd,q_pll和DUpccd,q_cc分别为PLL自身动态相关的电压分量和CC环引入的耦合电压分量。其表达式如附录式（A2）所示。
对图3中DVC进行小扰动建模，同时结合能量守恒定律，联立式（4），得到Didref与Dd 之间的关 系为
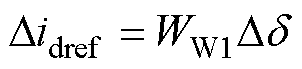（5）
其中
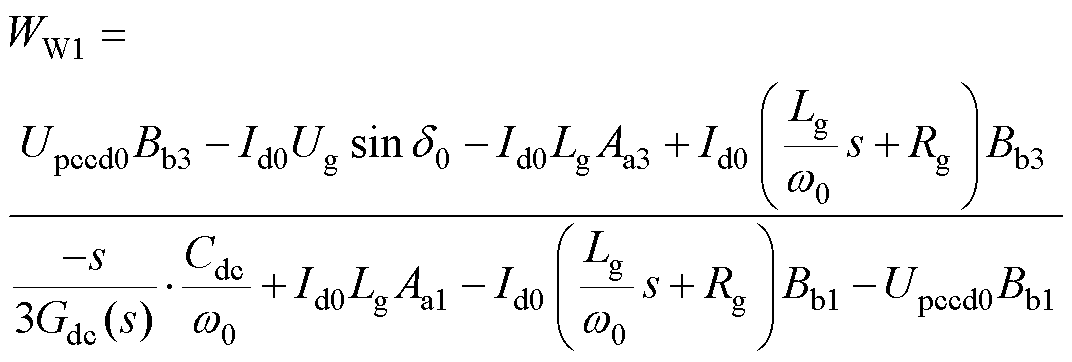（6）
综上所述，电流环通过影响PCC电压与PLL直接耦合，DVC动态通过影响电流环间接影响PLL的输出相位，系统中存在“外环控制（DVC）-电流环（CC）-线路阻抗-PLL”的耦合路径。因此，研究PLL的动力学特性时，简化多环控制耦合可能会对稳定性分析带来一定的不确定性。
计及CC内环和DVC外环的动态时，Didref≠0，Diqref=0，联立式（3）、式（5），进一步得到Did、Diq与Dd 之间的关系为
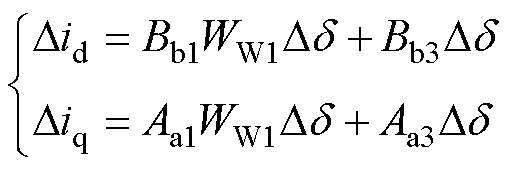（7）
因此，综合考虑CC、PLL和DVC动态时，PCC电压q轴分量的动态模型为
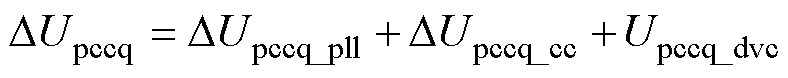（8）
式中，DUpccq_dvc为DVC引入的电压分量，即
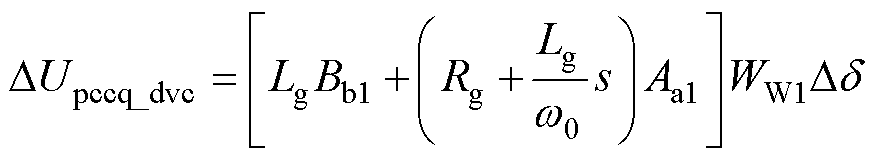（9）
结合图3与式（8），得到综合CC和DVC动态交互的PLL动态模型，如图4所示。
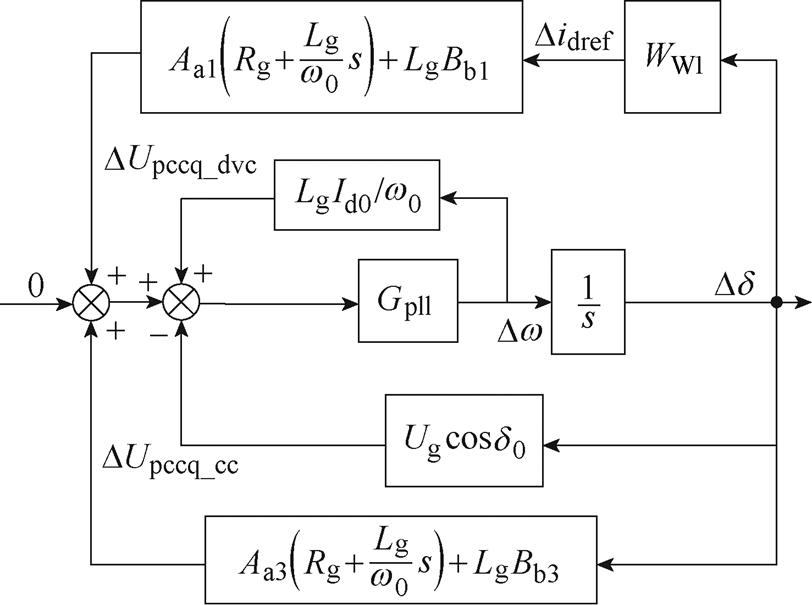
图4 弱电网下考虑CC和DVC影响的 PLL动态分析模型
Fig.4 The PLL dynamic analysis model considering CC and DVC in weak grid
由图4所示的PLL动态模型可明显看出，该模型和同步机的Philips-Heffron模型[20]类似。文中采用类比研究法，使用复转矩法研究跟网型变换器因阻尼不足带来的小扰动同步稳定问题。PLL回路的复转矩分析模型如图5所示。图中，G1_pll、G2_cc和G3_dvc分别与PLL、CC和DVC相关，Gx为框图变换过程中所推算的传递函数，表达式如附录式（A3）所示。其中，CC和DVC对PLL的影响主要体现在引入的电压动态DUcc和DUdvc上；DUpll与锁相环自身动态相关。
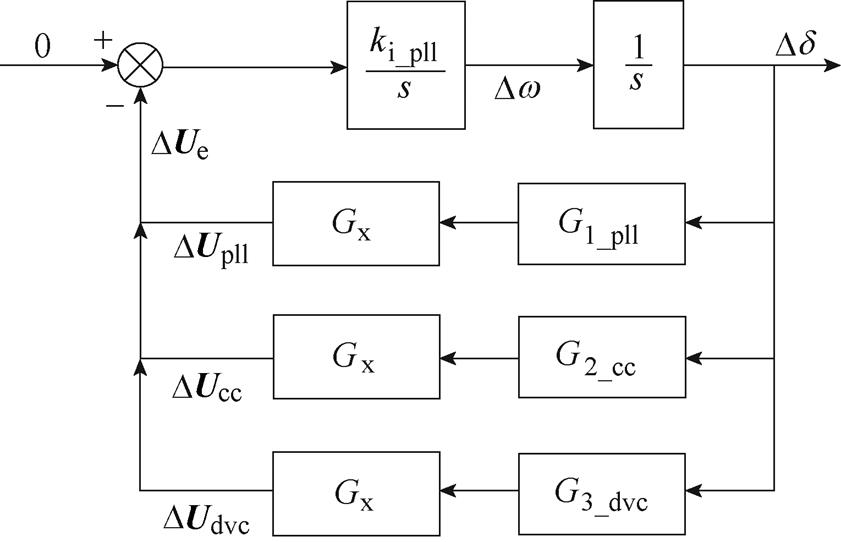
图5 PLL回路复转矩分析模型
Fig.5 The complex torque analysis model of PLL
图5表明，控制耦合会为PLL带来附加阻尼，该阻尼项与线路阻抗、控制参数有关，具有时变性、非线性和不确定性等复杂特性。在特定工况下，耦合项引入的附加阻尼可能表现为负阻尼，严重时甚至会抵消PLL本身的正阻尼，使得PLL整体阻尼为负，进而导致PLL输出相位振荡或发散，引发跟网型变换器的同步失稳。进一步地，通过量化DUcc和DUdvc引入的附加阻尼分量，厘清不同环路对系统同步回路的影响机理，为控制系统的设计提供理论指导。
根据图5，在弱电网下，对PLL、CC环和DVC环引入的阻尼进行定性分析如图6所示。分别画出G1_pllGx、G2_ccGx和G3_dvcGx的伯德图，如图6a所示。
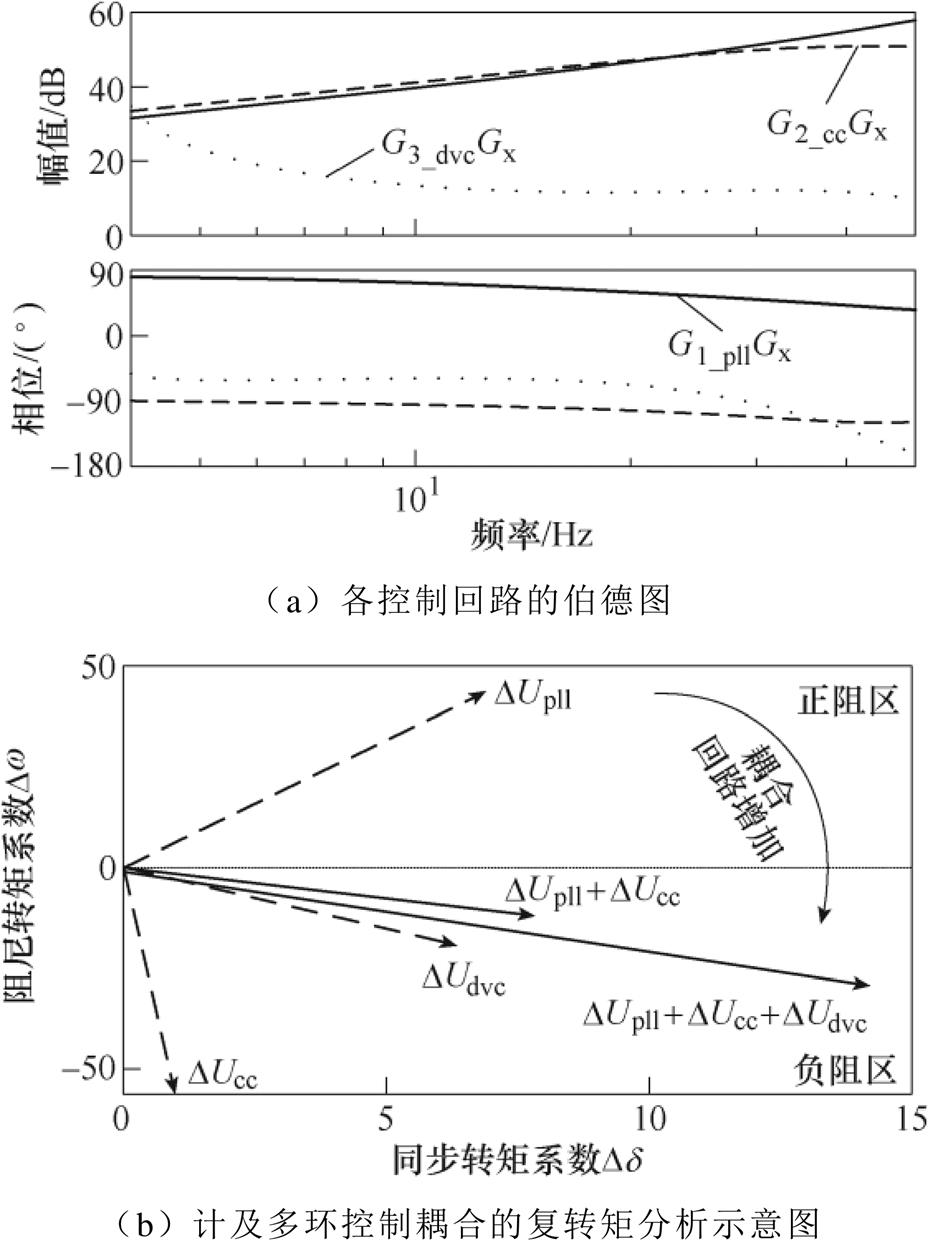
图6 各控制回路伯德图及相应的复转矩分析
Fig.6 Bode diagram and the complex torque analysis
图6a表明：①PLL自身引入的DUpll，其幅值和相位均大于0，负反馈成立，根据复转矩分析理论，其阻尼系数大于0；②受CC环影响的DUcc，幅值大于0 dB，且相频曲线位于第三、四象限，CC环动态引入的附加阻尼为负；③由DVC环引入的DUdvc，幅值大于0 dB，相频率曲线位于第四象限，引入的附加阻尼为负。
本文研究的跟网型变换器控制系统主要包括PLL、DVC环和CC环，不同控制带宽的三个控制回路之间的交互作用将会导致系统特性在频域中呈现宽频带分布；系统不同频带之间或同一频带内的特性受多个控制回路共同作用，图6b为根据图6a在8 Hz下的幅值和相位得到的复转矩分析，表明在某一确定的频率下，系统的转矩系数同时受PLL、DVC环和CC环的影响。忽略某一环路，系统的同步稳定性分析可能会存在一定的保守性，导致稳定性结果误判。因此，本节重点分析DVC、CC与PLL三者之间的耦合作用对系统同步振荡模式中阻尼的影响情况。
为进行定量分析，基于图5，推导输出功角的特征方程为
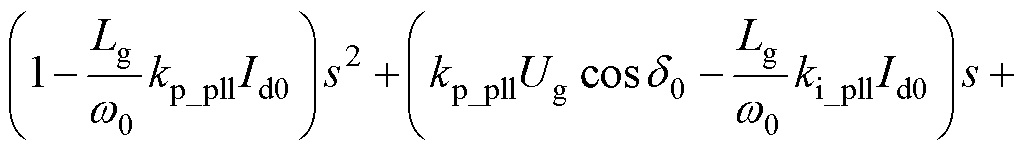
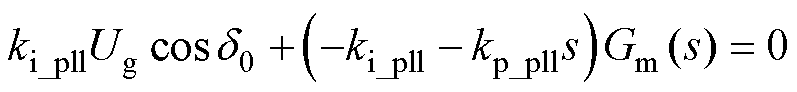（10）
式中，Gm=-G2_cc-G3_dvc。
相较于只考虑PLL回路的情况，系统特征方程式（10）中增加了(-kp_plls-ki_pll)Gm(s)项。由于该项的存在，同步回路的阻尼受到CC、DVC的影响。在弱阻尼los的情况下，用jwos代替式（10）中的s，同时对其进行求解，得到表征系统振荡行为阻尼的实部和表征振荡行为频率的虚部分别为
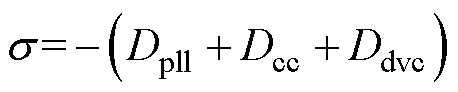（11）
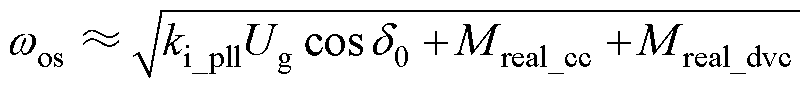（12）
式中，Dpll、Dcc和Ddvc分别为PLL自身的固有阻尼、CC环动态和DVC环动态引入的附加阻尼，具体的表达式如附录式（A4）所示；Mreal_cc,dvc和Mimag_cc,dvc分别为CC和DVC引入特征根的实部和虚部，其表达式如附录式（A5）所示。
选取短路比、PLL控制参数、外环控制参数作为变量，从理论上分析上述参数对系统阻尼特性的影响机理，从而得到变换器同步失稳的规律。
2.2.1 并网点短路比对阻尼的影响机理分析
通常使用短路比（Short Circuit Ratio, SCR）来评估电网强度，电网阻抗越大，SCR越小，电网强度越弱。一般情况下，线路阻抗以感性为主，因此文中使用不同Lg表征SCR的变化。
本文主要研究变换器的小扰动稳定性，该稳定性问题由系统阻尼特性主导。根据复转矩分析理论，分析系统的阻尼特性时，需求解系统的振荡频率；将式（12）改写成等式的形式为
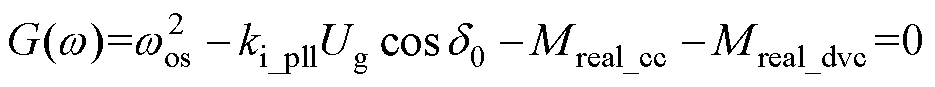（13）
对式（13）进行求解，可得到振荡频率如图7a所示，曲线与直线G(w)=0的交点所对应的频率，即为该振荡模式所对应的振荡频率，此处分别记为f1_lg、f2_lg和f3_lg。图中表明，电网阻抗增大，同步回路的振荡频率变小，且振荡频率均在10 Hz以内。分别将f1_lg、f2_lg和f3_lg代入Dpll、Dcc、Ddvc及总阻尼Dall（Dall=Dpll+Dcc+Ddvc）的表达式中，得到在该Lg下的阻尼大小，如图7b～图7e所示。表明，电网阻抗增大，Dpll变小，Ddvc和Dcc的负阻尼效应加剧，当电网强度下降至某一临界情况时，导致PLL自身的正阻尼小于CC、DVC环引入的负阻尼时，PLL整体阻尼为负，系统存在同步失稳的风险。
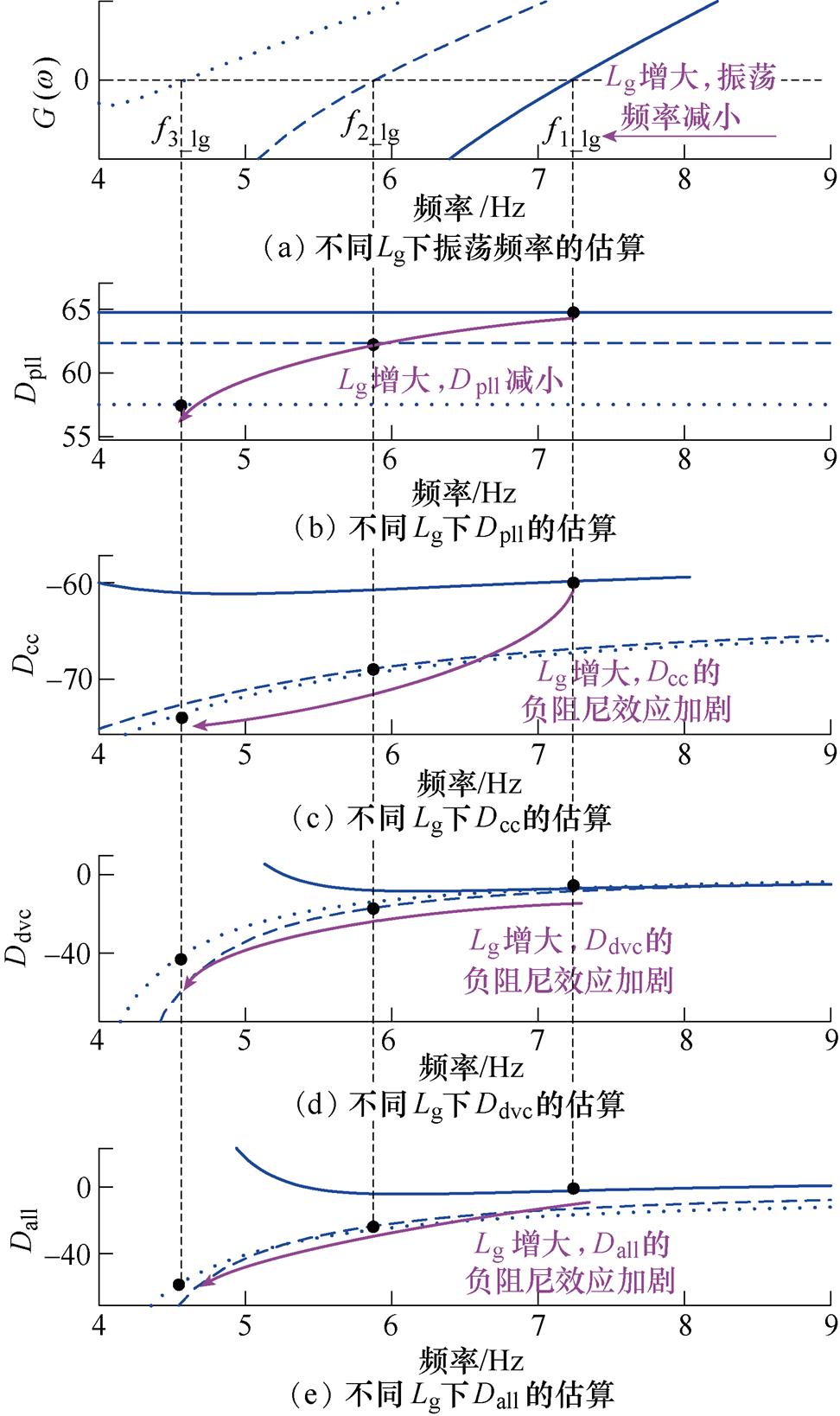
图7 同步振荡模式随Lg变化的曲线
Fig.7 The analysis of oscillation mode varying with Lg
2.2.2 锁相环参数对阻尼的影响机理分析
结合式（12）和式（A4）可知，PLL控制器参数不仅影响振荡频率，同时也和阻尼大小密切相关。图8和图9分别为不同kp_pll和ki_pll下系统同步振荡模式的变化情况。
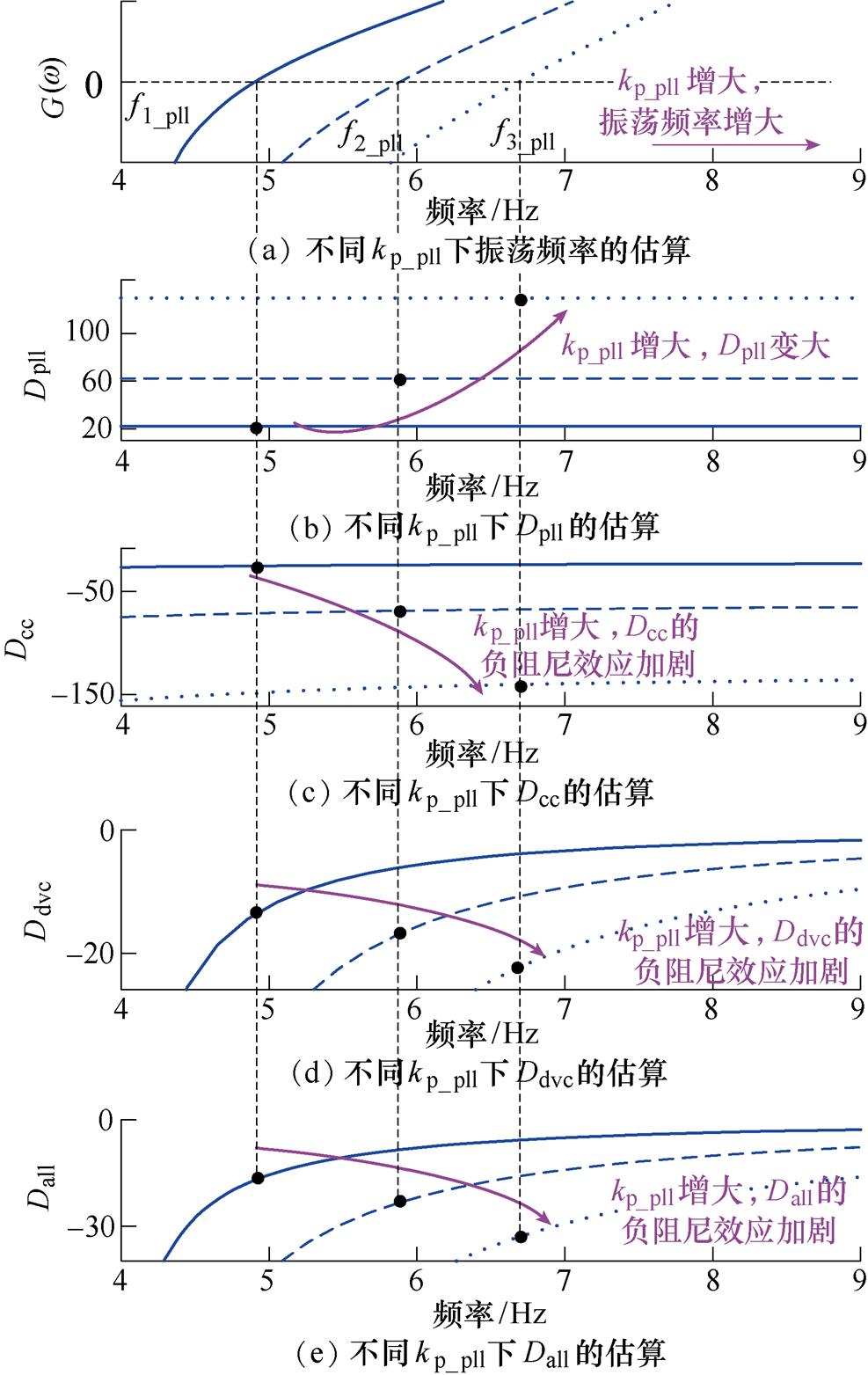
图8 同步振荡模式随kp_pll变化的曲线
Fig.8 The analysis of oscillation mode varying with kp_pll
图8表明，随着kp_pll的增大，振荡频率变大，图中记为f1_pll、f2_pll和f3_pll；将其分别代入阻尼的计算公式，得到不同kp_pll下的阻尼，如图8b～图8e所示，表明kp_pll增大，有助于增大PLL的固有阻尼，然而CC与DVC环节引入的负阻尼效应加剧。图9表明，ki_pll的变化，不影响振荡频率和阻尼。
2.2.3 CC与DVC控制参数对阻尼的影响机理分析
根据附录式（A4）中Dpll、Dcc和Ddvc的表达式可知，kp_dvc和ki_dvc对Dpll和Dcc曲线的变化没有影响，主要通过影响振荡频率和Ddvc来影响系统同步振荡模式及总阻尼的大小，参数kp_dvc对系统振荡频率及阻尼的影响规律如图10所示。
图9 同步振荡模式随ki_pll变化的曲线
Fig.9 The analysis of oscillation mode varying with ki_pll
图10表明，随着kp_dvc增大，同步振荡频率变大，Dpll保持不变，Dcc和Ddvc的负阻尼效应随之减弱，有助于增强变换器的小扰动稳定性。
DVC中积分参数ki_dvc和CC的控制参数（kp_cc、ki_cc）对系统同步振荡模式影响的分析方法与上述分析类似，受限于篇幅，此处不再赘述，直接给出分析结果：①ki_dvc变大，系统振荡频率基本不变，PLL固有阻尼Dpll及附加阻尼Dcc恒定，Ddvc的负阻尼效应加剧，变换器的小扰动同步稳定性减弱；②kp_cc增大，Dcc和Ddvc的负阻尼效应减弱，PLL总阻尼变大，系统同步稳定性增强；③ki_cc增大，同步振荡频率变大，PLL的固有阻尼Dpll基本维持不变，Dcc和Ddvc负阻尼效应加剧，系统同步稳定性减弱。
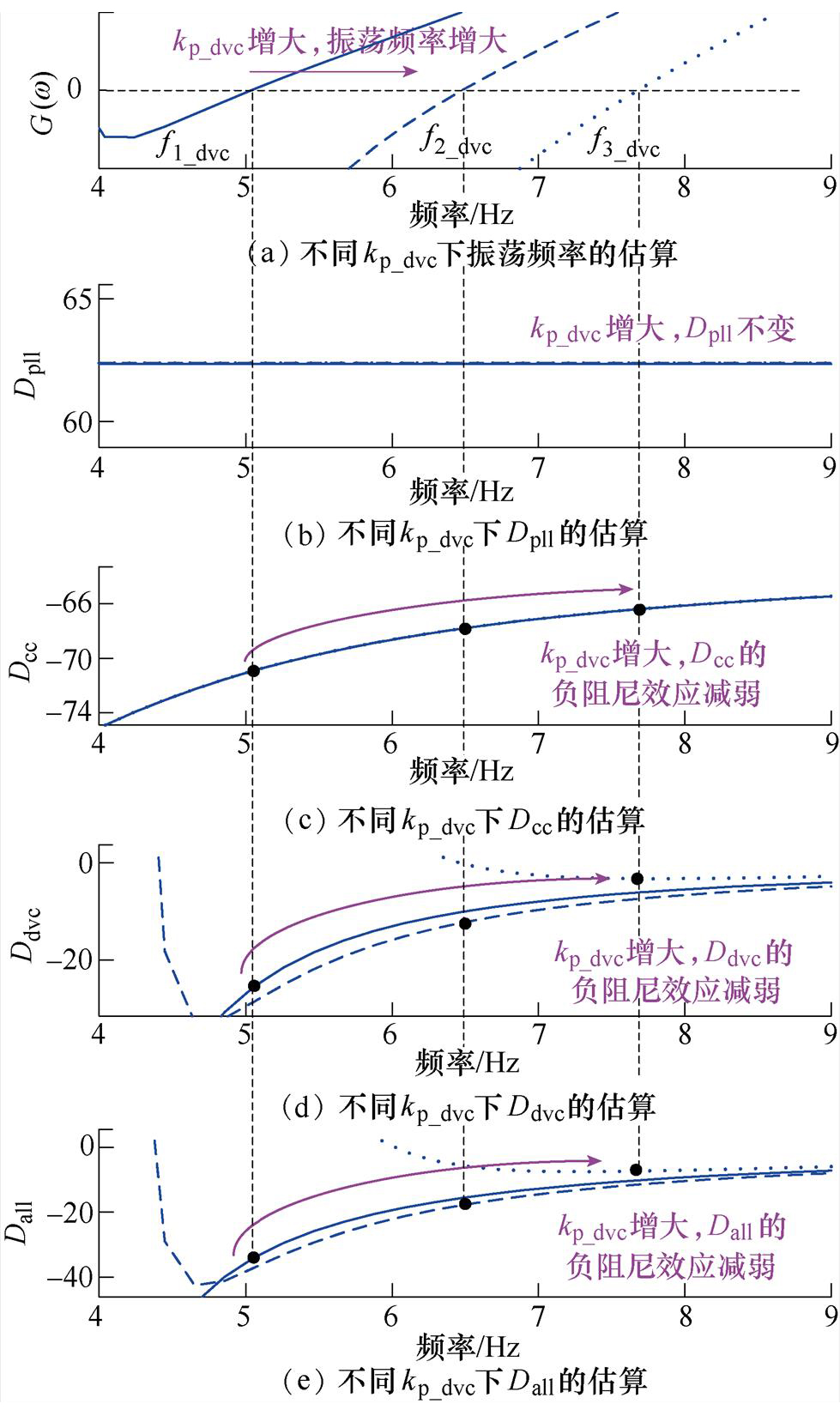
图10 同步振荡模式随kp_dvc变化的曲线
Fig.10 The analysis of oscillation mode varying with kp_dvc
基于上述理论分析可知，控制耦合会引入相应的电压矢量，附加电压矢量DUdvc、DUcc与PLL的电压矢量DUpll相互作用，导致等效电压矢量DUe在不同象限中运动，使得PLL呈现出不同的阻尼特性，影响系统同步稳定性。以并网点SCR小扰动为例，不同电网阻抗下，相应的电压矢量变化情况如图11所示。
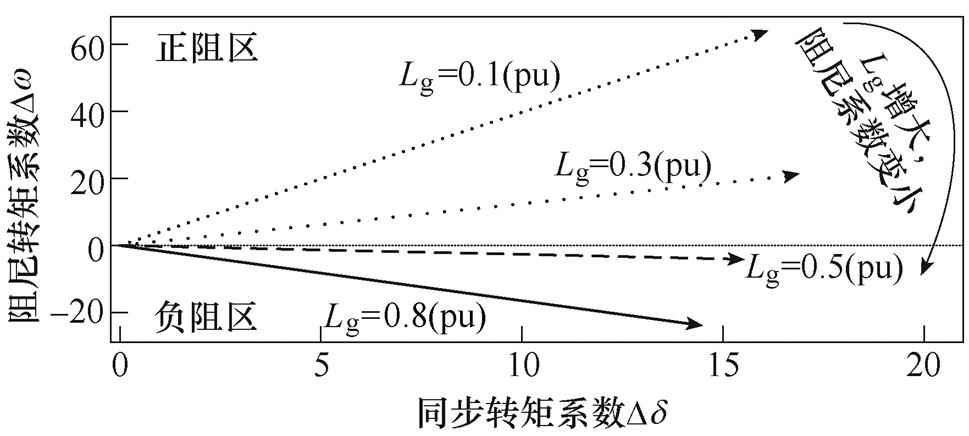
图11 DUe的复转矩分析
Fig.11 The complex torque analysis of DUe
图11中，由于控制耦合附加电压矢量DUdvc、DUcc的影响，PLL的等效输入电压矢量DUe随Lg的变化在不同象限之间运动。当Lg=0.5(pu)（SCR=2）和Lg=0.8(pu)（SCR=1.25）时，线路等效阻抗较大，PLL与多环控制之间的耦合效应增强，CC环、DVC环引入的等效输入电压DUcc和DUdvc之和滞后于Dd，电压矢量DUe落在第四象限（负阻系数区），此时PLL整体阻尼系数为负，PLL的输出功角易发生振荡，导致跟网型变换器同步失稳，根据式（12），计算得到振荡频率分别为6.9 Hz和4.7 Hz。
为了改善系统在弱电网下的小扰动同步稳定性，提出一种基于相位补偿器的改进PLL控制策略；如图12a所示。图中，Giq_d为并网电流q轴分量Diq与PLL输出功角增量Dd 之间的传递函数，Gcom为补偿器。基于并网电流的q轴分量iq设计合适的反馈回路，在原有PLL的输入电压中叠加一个与Dw 同相位的电压分量DUcom，如图12b所示。当DUcom落在第二象限时，则会产生一个正的阻尼转矩，将原本落在第四象限的DUe拉回至第一象限。
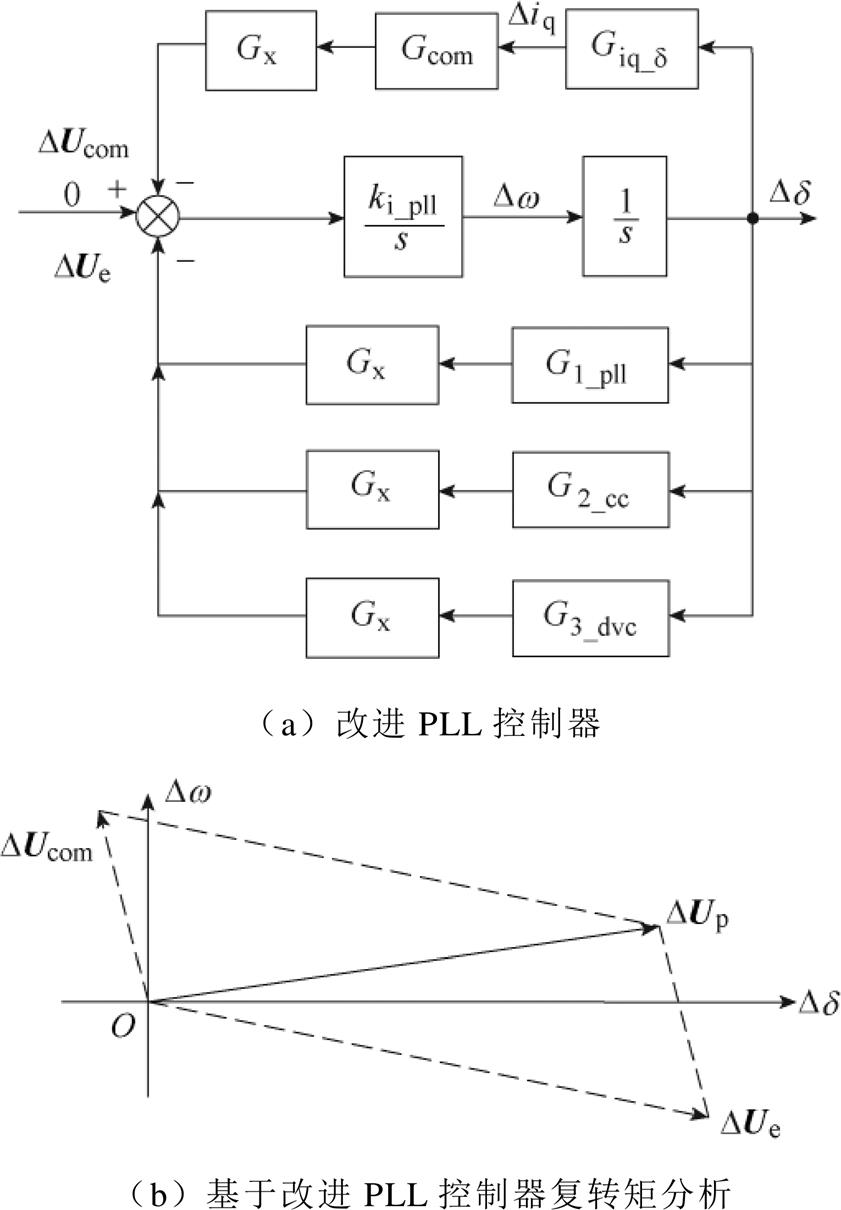
图12 基于阻尼补偿器的PLL示意图
Fig.12 Diagram of damping compensator of PLL
为了控制DUcom精准落入第二象限，基于相位补偿器的原理，选取超前网络作为补偿器，其传递函数为
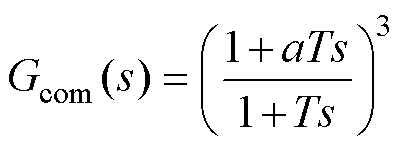（14）
式中，a为分度系数；T为时间常数。
值得注意的是，为了减小改进控制对PLL稳态性能的影响，需要对相应的补偿器进行改进。因此，对式（14）进行改进，得
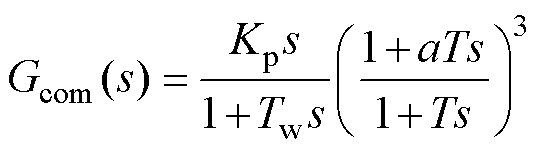（15）
式中，串联了一个隔离环节，其中Tw为隔离环节的时间常数，参考文献[15]，取Tw=3，Kp为参数，主要用来调节幅值。
以Lg=0.8(pu)的极弱电网工况为例，相位补偿器的设计步骤如下：
（1）由图7a结合式（13），确定补偿前该工况下系统的振荡角频率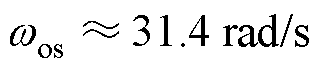
。
（2）由式（7）知，Diq与Dd 的传递函数Giq_d为
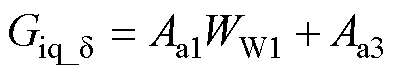（16）
图13为传递函数Giq_dGx的伯德图，从图中可以看出，在振荡频率处，相位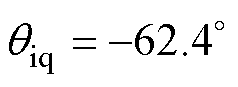
。
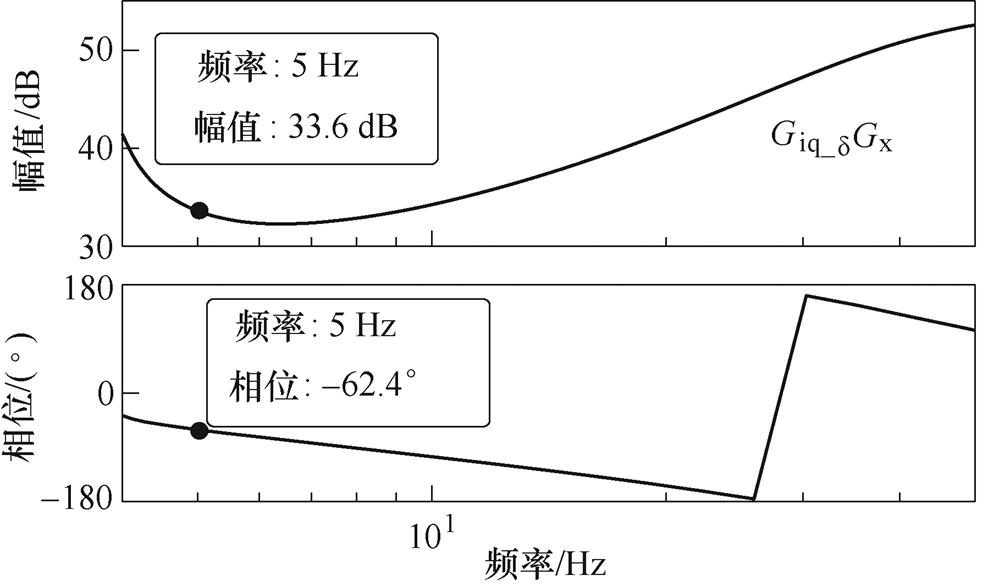
图13 Giq_dGx的伯德图
Fig.13 Bode diagram of Giq_dGx
假设补偿后PLL的输入电压落入如图12b的第一象限，本文选择第二象限中DUcom的相位qcom= 100°，这样可得到补偿器Gcom需要补偿的相位qp为
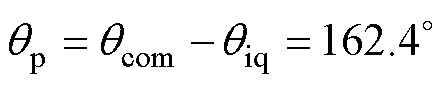（17）
（3）设计补偿器参数。本文选择的是三级超前补偿器，采取逐级补偿的思路，则每级补偿的相位为
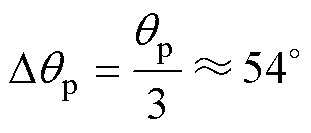（18）
由超前环节可得其参数为
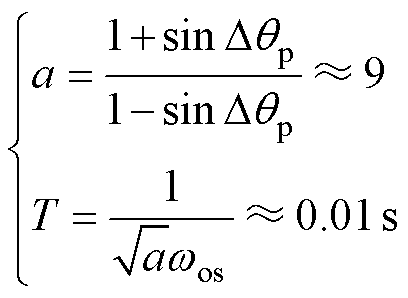（19）
因此，得到补偿器的传递函数为
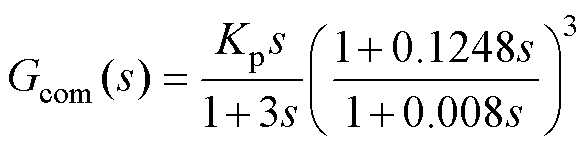（20）
图14为补偿回路中传递函数Giq_d、Gcom、Gx在不同Kp下的伯德图。由图可知，Kp不影响补偿回路的相位；在相同的振荡频率下，Kp越大，相应的幅值变大，并且相位始终保持为98.4°。
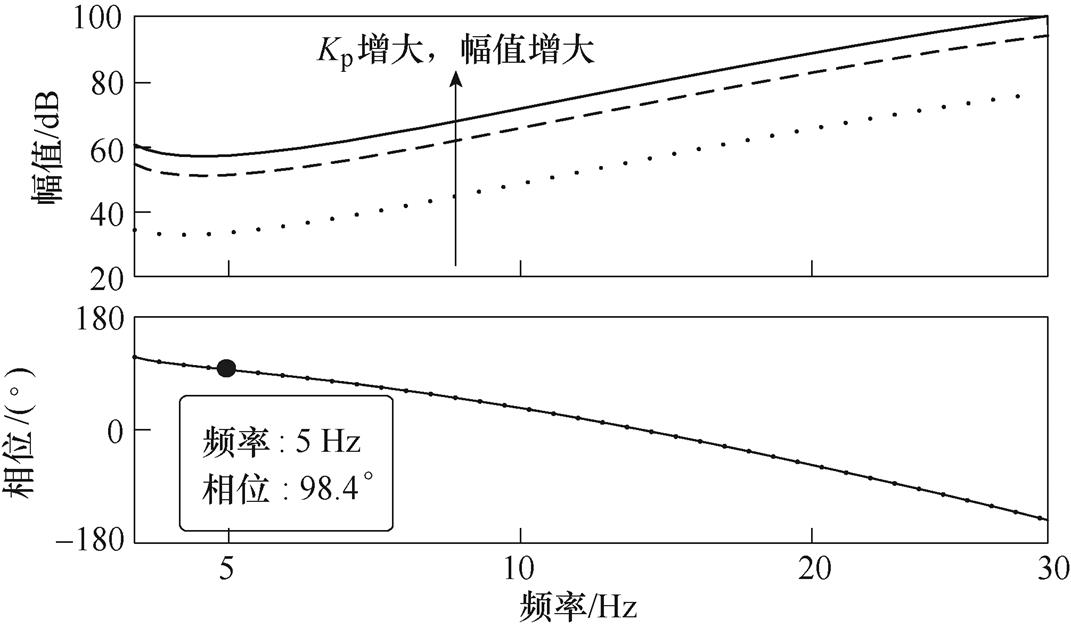
图14 不同Kp下Giq_dGcomGx的伯德图
Fig.14 Bode diagram of Giq_dGcomGx with different Kp
不同参数Kp下，补偿后系统PLL输入电压DUp的复转矩分析如图15所示。由图15可知，当Kp过小时（Kp=0.01），DUp落入第四象限（负阻区），此时阻尼转矩系数为负，根据式（13），可计算得到振荡频率约为5.3 Hz；而Kp过大时（Kp=0.3），DUe落入第二象限，此时同步转矩系数为负，为避免发生失步性失稳，同时综合考虑小扰动同步稳定性与暂态同步稳定，选取Kp=0.2。
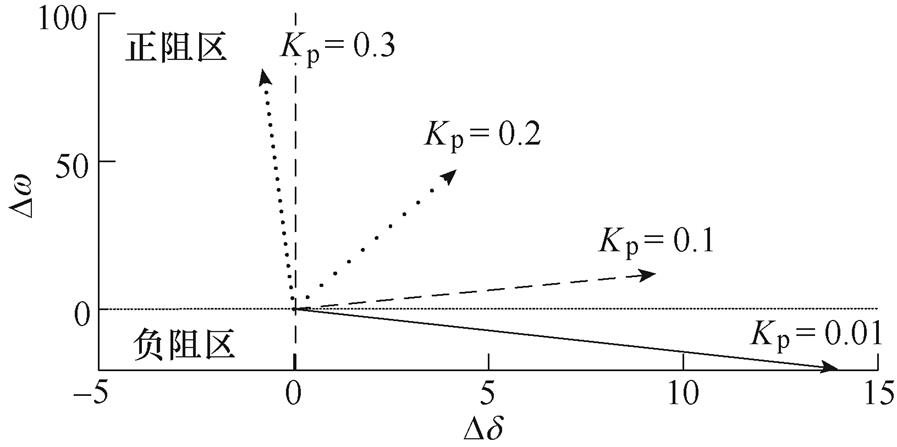
图15 不同Kp下DUp的复转矩分析
Fig.15 The complex torque analysis of DUp with different Kp
综上所述，最终得到补偿器的表达式为
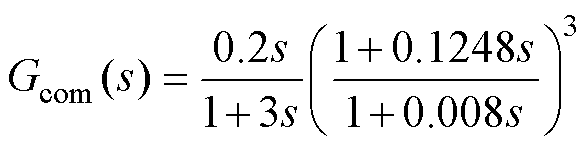（21）
结合图12a及式（21），给出了在不同SCR下基于改进PLL的DUp复转矩分析，如图16所示。
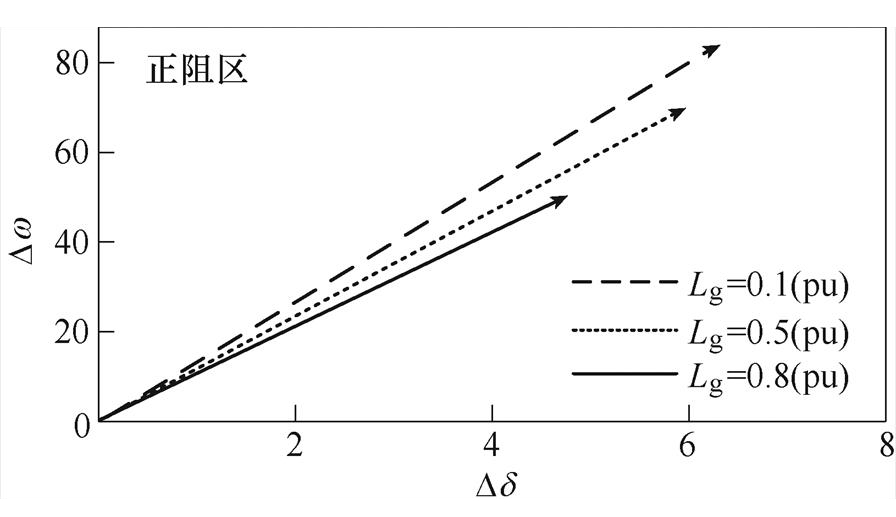
图16 不同Lg下DUp的复转矩分析
Fig.16 The complex torque analysis of DUp with different Lg
图16表明，电网由强到弱变化（Lg在0.1～0.8(pu)之间变化）时，DUp始终落在复平面的第一象限，系统的同步转矩和阻尼转矩系数均为正，系统小干扰稳定性得到改善。
为了验证基于阻尼补偿器改进PLL控制策略的可行性，基于Matlab/Simulink仿真软件，搭建了相应的控制模型，其主要参数见表1。
表1 并网逆变器主要参数
Tab.1 Main parameters of the simulation model
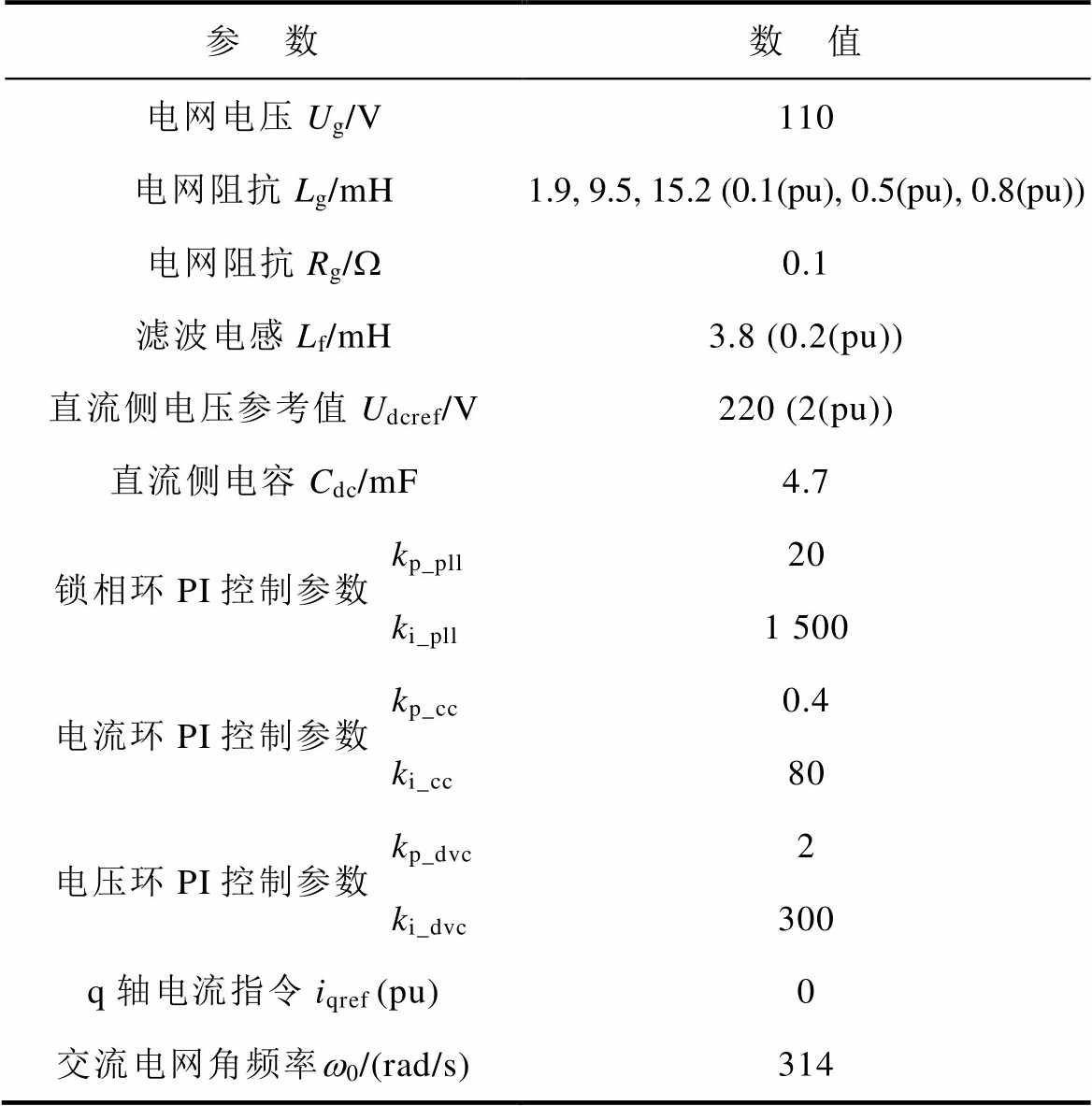
参 数数 值 电网电压Ug/V110 电网阻抗Lg/mH1.9, 9.5, 15.2 (0.1(pu), 0.5(pu), 0.8(pu)) 电网阻抗Rg/W0.1 滤波电感Lf/mH3.8 (0.2(pu)) 直流侧电压参考值Udcref/V220 (2(pu)) 直流侧电容Cdc/mF4.7 锁相环PI控制参数kp_pll20 ki_pll1 500 电流环PI控制参数kp_cc0.4 ki_cc80 电压环PI控制参数kp_dvc2 ki_dvc300 q轴电流指令iqref (pu)0 交流电网角频率w0/(rad/s)314
采用传统PLL控制结构时，在不同电网阻抗下，a相的并网电流和PCC电压波形如图17所示，可知，强电网（Lg=0.1(pu)）下，系统是稳定的。
以SCR作为小扰动，即在t=3 s时电网感抗分别从0.1(pu)（SCR=10）增大至0.5(pu)（SCR=2）和0.8(pu)（SCR=1.25）。由于控制耦合的影响，随着线路阻抗的增大，电流环和电压环给系统带来的附加负阻尼增大，当负阻尼大于PLL自身的正阻尼，系统总阻尼小于0时，系统电流和电压发生振荡。不同SCR工况下，其振荡频率不同，Lg=0.5(pu)时，振荡频率为6.9 Hz；Lg=0.8(pu)时，振荡频率为4.7 Hz；振荡频率在10 Hz以内。仿真结果与上述理论分析结论基本吻合。
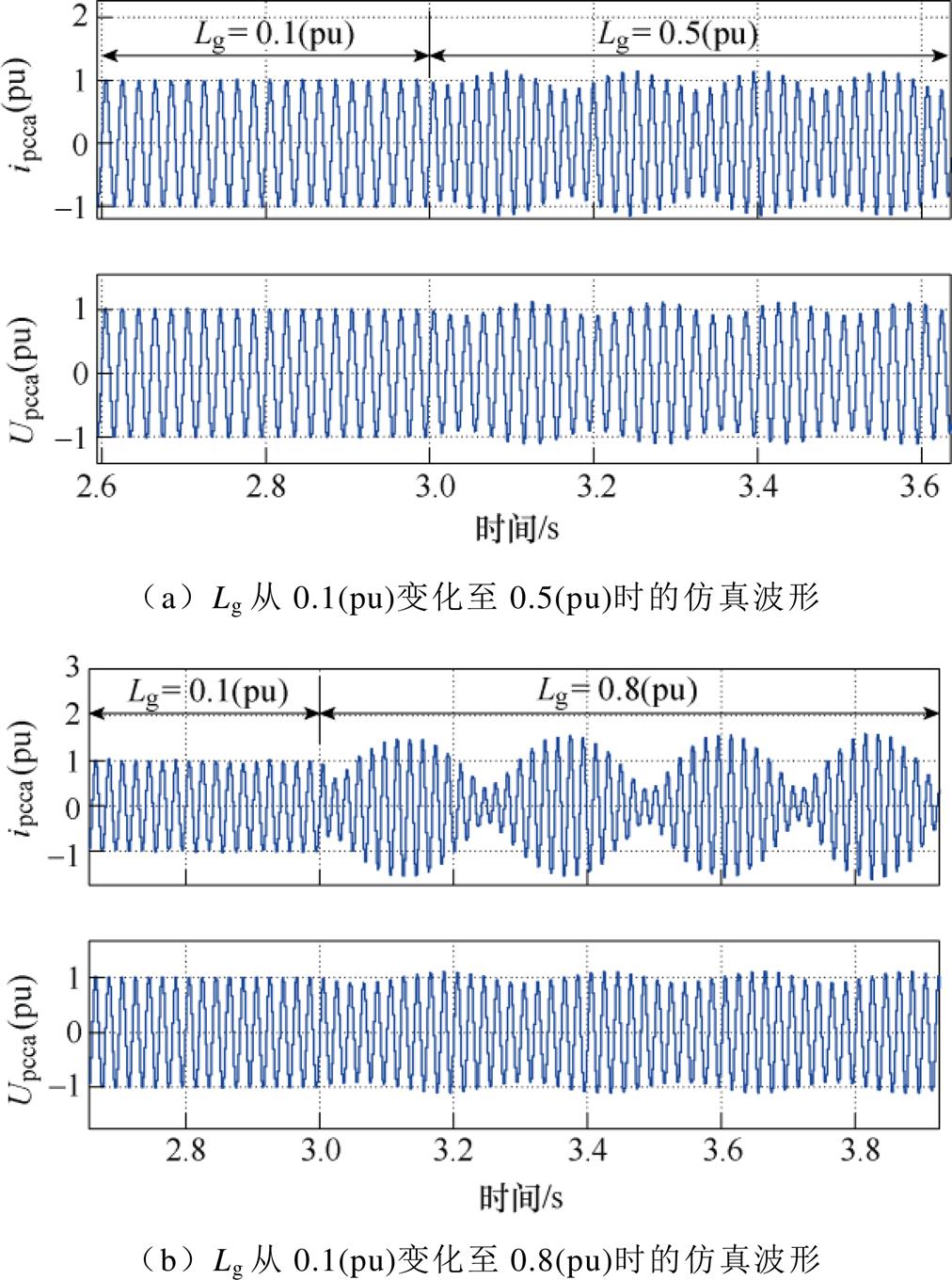
图17 传统PLL控制下不同SCR的仿真波形
Fig.17 Simulation waveforms based on traditional PLL with different SCR
采用本文所提的改进控制策略，进行相应的仿真验证，其仿真波形如图18所示。图18a和图18b中，电网阻抗分别为0.5(pu)和0.8(pu)，此时系统振荡。在t=4 s时投切所提的改进控制，由于补偿器补偿了控制耦合引入的负阻尼，系统由振荡状态回到稳定运行的状态，此时并网电流和PCC电压同相，并网电流能无差地跟踪其参考量，稳态性能良好。仿真结果表明：基于所提的改进控制策略，跟网型变换器在弱电网工况下仍然能稳定运行，系统的小扰动同步稳定性得到提升。
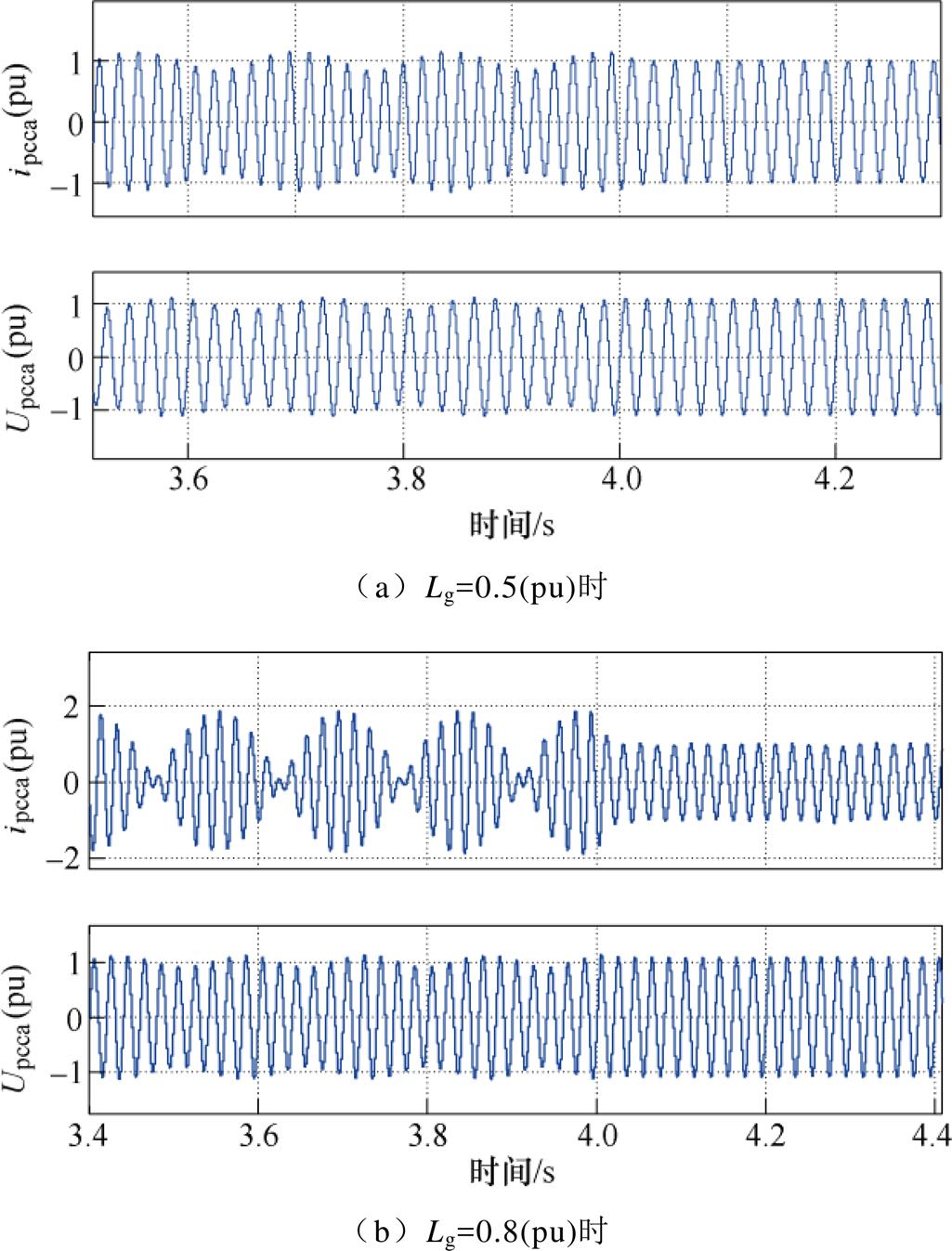
图18 不同Lg下投切改进PLL控制下的仿真波形
Fig.18 Simulation waveforms under improved PLL controller with different Lg
本文根据搭建的仿真模型，研制了额定功率为6 kW的三相并网逆变器实验样机，验证所提方法的有效性。实验平台如图19所示。
图19 并网逆变器的实验平台
Fig.19 Test platform of grid-connected inverter
图19中，控制芯片选择TI公司的TMS320F28335，开关器件IGBT选用英飞凌FF100R12KS4模块；电网阻抗Lg由串联电感模拟；实验平台的相关参数见表1。
采用经典PLL控制方案的并网电流实验波形如图20所示。图中，电网阻抗Lg=0.1(pu)（SCR=10）时，并网变换器系统稳定运行，并网电流能较好地跟踪参考值，此时并网电流的总谐波畸变率（Total Harmonic Distortion, THD）为3.1%。在t=3 s时，Lg分别增大至Lg=0.5(pu)（SCR=2）和Lg=0.8(pu)（SCR=1.25），系统由于阻尼不足，并网电流出现与功角振荡频率一致的振荡波形。同时，在不同的电网阻抗下，并网电流的振荡频率不同，分别为6.6 Hz（Lg=0.5(pu)）与5 Hz（Lg=0.8(pu)），与图17所示的仿真结果基本一致。类似地，通过同样的实验方法，可以验证CC与DVC控制参数对同步振荡模态的影响规律，受限于篇幅，此处不再赘述。
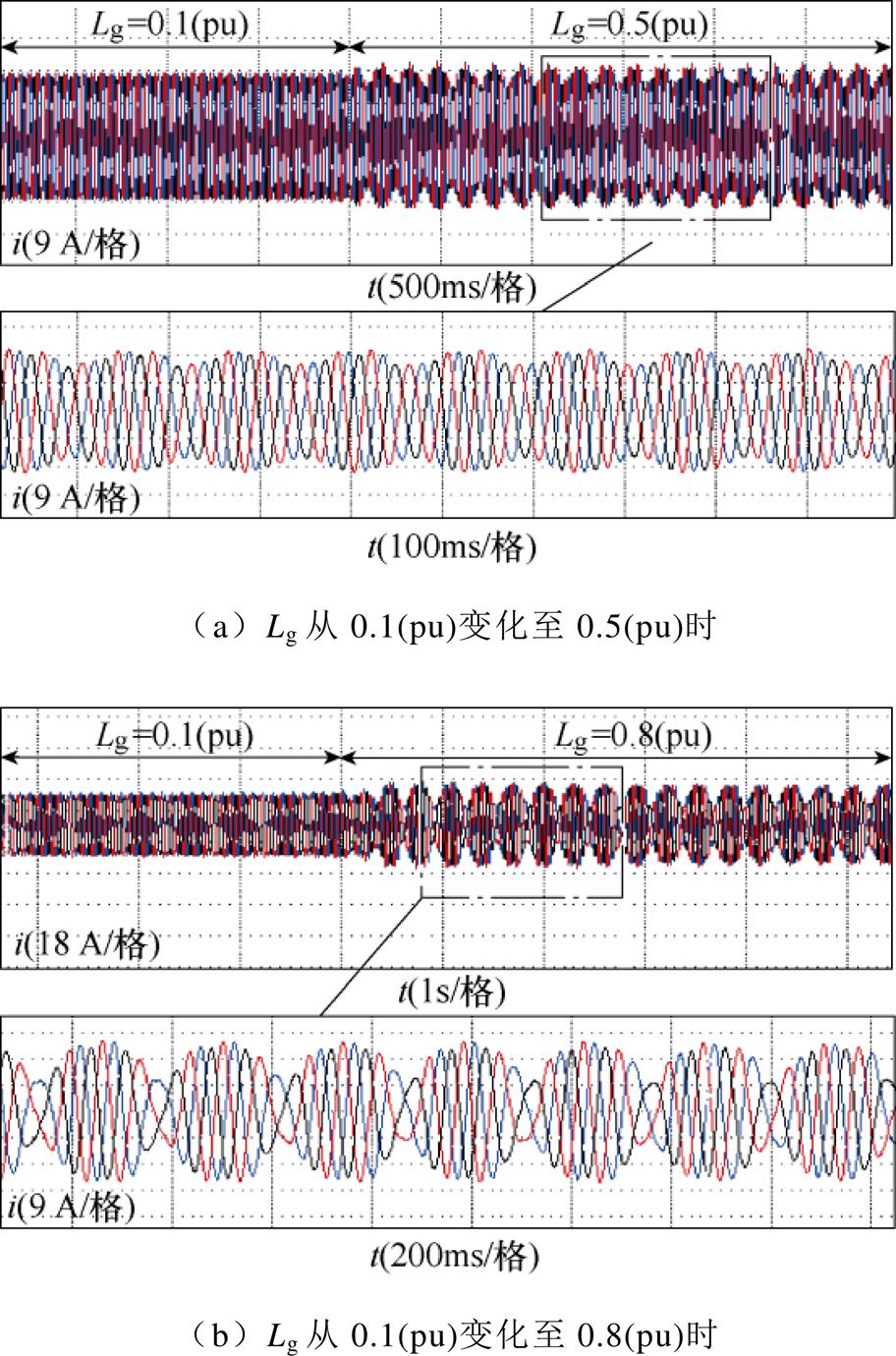
图20 不同Lg下基于经典PLL控制的并网电流实验波形
Fig.20 Experimental waveforms of grid-connected current based on classical PLL control for Lg varies
采用本文所提出的改进PLL控制策略的实验波形如图21所示。为验证所提控制策略的有效性，将电网阻抗Lg分别增大至Lg=0.5(pu)（SCR=2）和Lg=0.8(pu)（SCR=1.25），此时系统振荡。在t=3 s时，投切基于相位补偿器的改进控制策略，由于控制耦合引入的负阻尼得到补偿，系统总阻尼由负变正，系统由振荡状态重新回到稳定平衡点，此时并网电流的THD分别为3.5%和3.7%，满足相应的并网标准。
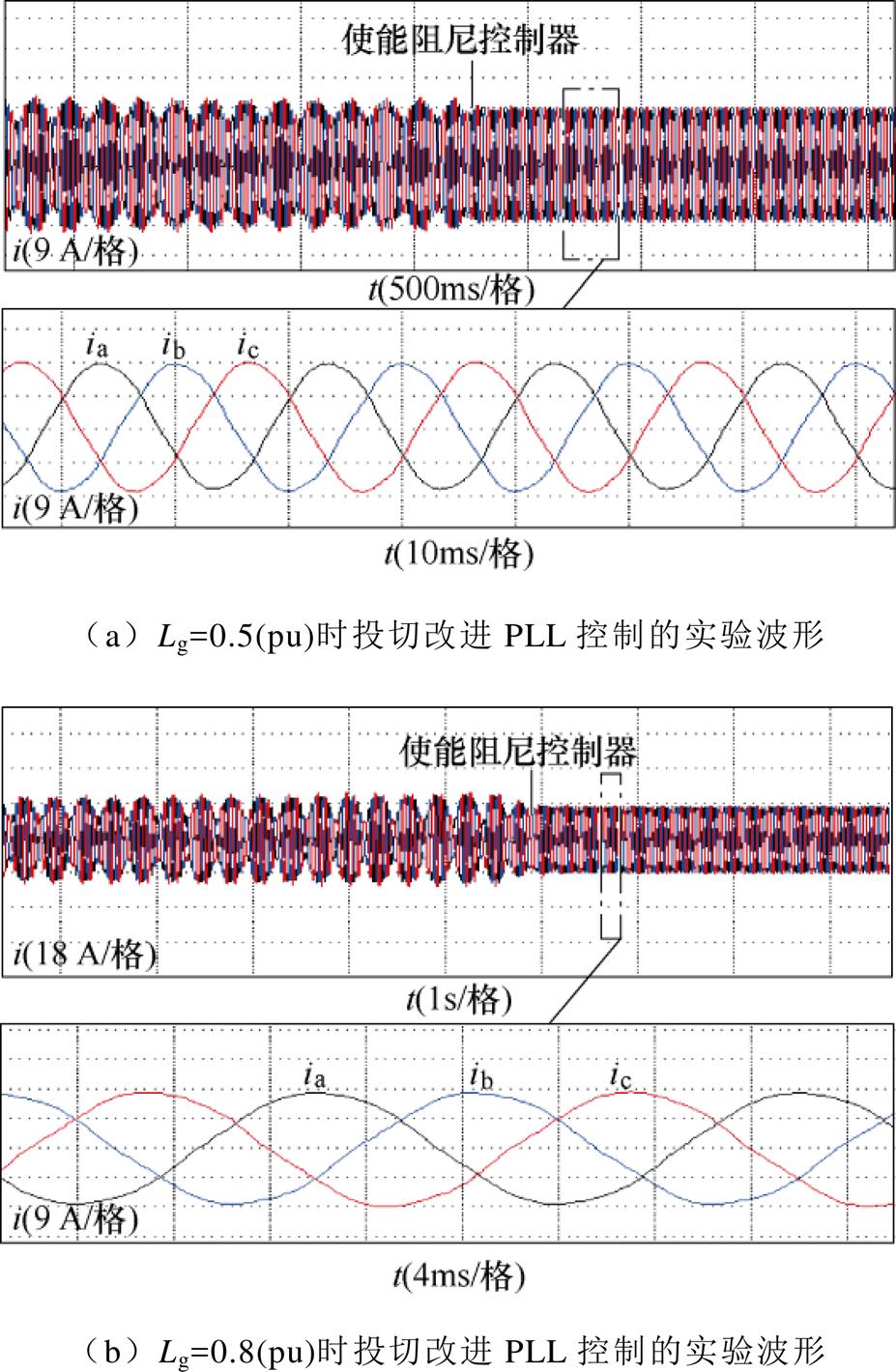
图21 不同Lg下投切改进PLL控制的并网电流实验波形
Fig.21 Experimental waveforms of grid-connected current with improved PLL control for Lg varies
上述实验表明，本文提出的基于相位补偿器的PLL改进控制策略可提高变换器在弱电网下的小扰动同步稳定性。
弱电网情况下，CC环和DVC环与PLL的耦合会给系统带来负附加阻尼，电网强度越弱，耦合程度越大，负阻尼效应越大，恶化系统的小干扰同步稳定性。为此，该文提出了基于PLL固有阻尼重塑的改进控制策略，解决了由于环路耦合引起的小干扰同步稳定性问题。相关工作总结如下：
1）建立了考虑CC环、DVC环影响的PLL复转矩分析模型，揭示了“PLL-控制环-线路阻抗-PCC电压-PLL”的闭环耦合路径，从阻尼的角度直观地解释了系统小扰动失稳机理。
2）量化分析了电网阻抗及各控制参数对系统阻尼情况的影响机理：增大CC环和DVC环中的比例参数均可减弱控制耦合对PLL动态引入的负阻尼效应，增强稳定性；增大电网阻抗、PLL中比例增益、CC环和DVC环的积分参数，会加剧系统的负阻尼效应，不利于增强系统的同步稳定性。
3）基于相位补偿器，所提的改进PLL控制结构，重塑了PLL等效阻尼，使系统在小扰动下，阻尼始终维持为正阻尼特性，增强了系统的小干扰稳定性。
附 录
系统传递函数模型
式（3）中，Aa1～Bb3的表达式为
（A1）
式（4）中的传递函数具体表达式为
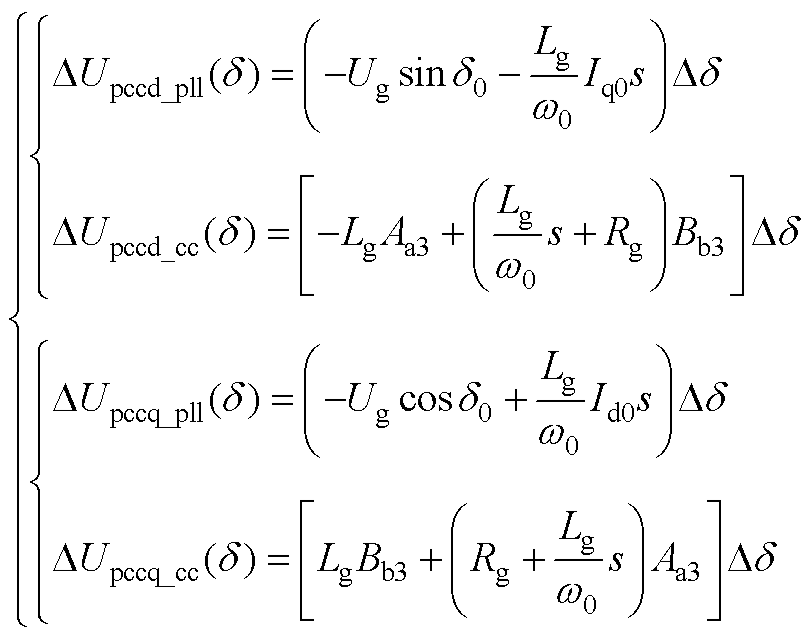（A2）
图5中，相关传递函数的具体表达式为
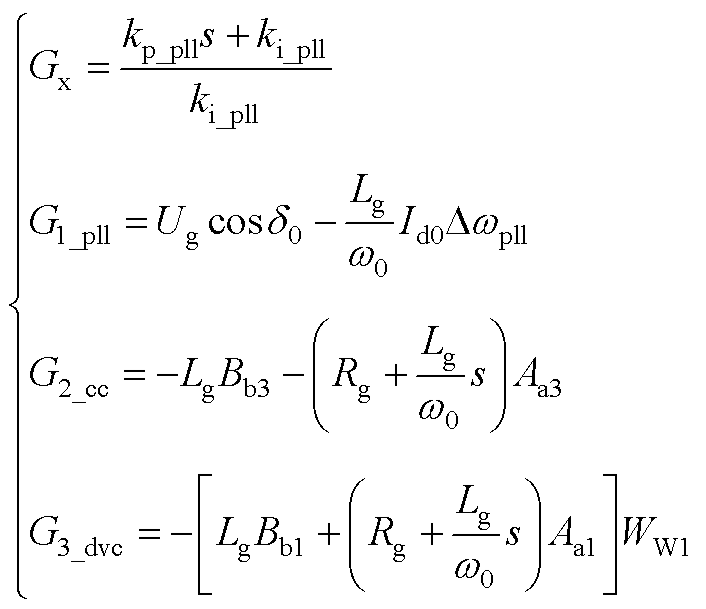（A3）
式（11）中阻尼的具体表达式为
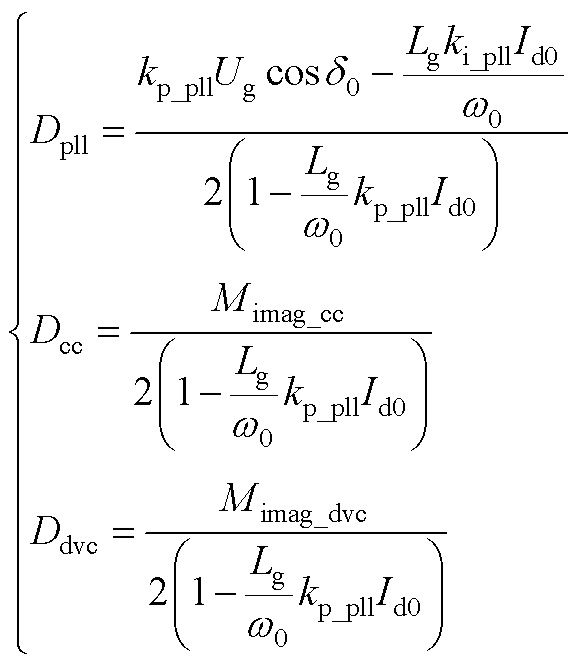（A4）
式（A4）中的部分参数表达式为
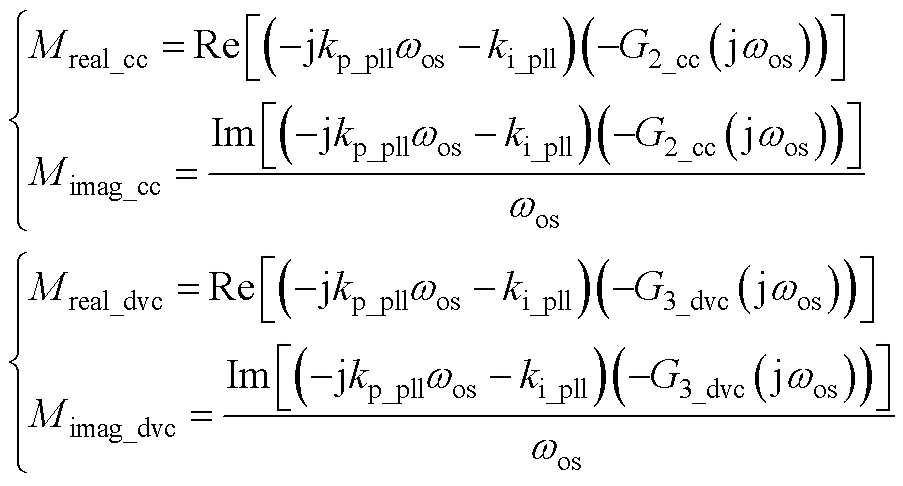（A5）
参考文献
[1] 沈姝衡, 方天治, 章益凡. 高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究[J]. 电工技术学报, 2022, 37(21): 5548- 5561.
Shen Shuheng, Fang Tianzhi, Zhang Yifan. A high- bandwidth digital-control LCL-type grid-tied inverter and resonance-suppressing technique for improving the robustness of grid-connected system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(21): 5548-5561.
[2] 胡宇飞, 田震, 查晓明, 等. 构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略[J]. 电力系统自动化, 2022, 46(24): 121-131.
Hu Yufei, Tian Zhen, Zha Xiaoming, et al. Impedance stability analysis and promotion strategy of islanded microgrid dominated by grid-connected and grid- following converters[J]. Automation of Electric Power Systems, 2022, 46(24): 121-131.
[3] Zhao Jiantao, Huang Meng, Zha Xiaoming. Nonlinear analysis of PLL damping characteristics in weak- grid-tied inverters[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2020, 67(11): 2752- 2756.
[4] Geng Hua, Liu Lu, Li Ruiqi. Synchronization and reactive current support of PMSG-based wind farm during severe grid fault[J]. IEEE Transactions on Sustainable Energy, 2018, 9(4): 1596-1604.
[5] Zhao Jiantao, Huang Meng, Yan Han, et al. Nonlinear and transient stability analysis of phase-locked loops in grid-connected converters[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 1018-1029.
[6] 李光辉, 王伟胜, 刘纯, 等. 直驱风电场接入弱电网宽频带振荡机理与抑制方法(一): 宽频带阻抗特性与振荡机理分析[J]. 中国电机工程学报, 2019, 39(22): 6547-6562.
Li Guanghui, Wang Weisheng, Liu Chun, et al. Mechanism analysis and suppression method of wideband oscillation of PMSG wind farms connected to weak grid (part Ⅰ): analysis of wideband impe- dance characteristics and oscillation mechanism[J]. Proceedings of the CSEE, 2019, 39(22): 6547-6562.
[7] 杜步阳, 邵德军, 朱建行, 等. 电压源型变流器并网系统多时间尺度间相互作用[J]. 电工技术学报, 2023, 38(20): 5547-5559.
Du Buyang, Shao Dejun, Zhu Jianhang, et al. Research on the interaction between multiple times- cales of the grid tied voltage source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5547-5559.
[8] 颜湘武, 常文斐, 崔森, 等. 基于线性自抗扰控制的静止无功补偿器抑制弱交流风电系统次同步振荡策略[J]. 电工技术学报, 2022, 37(11): 2825-2836.
Yan Xiangwu, Chang Wenfei, Cui Sen, et al. Sub- synchronous oscillation suppression strategy of weak AC wind power system with static var compensator based on linear active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2825-2836.
[9] 胡祺, 付立军, 马凡, 等. 弱电网下基于锁相控制并网变换器小扰动同步稳定分析[J]. 中国电机工程学报, 2021, 41(1): 98-108, 401.
Hu Qi, Fu Lijun, Ma Fan, et al. Small signal synchronizing stability analysis of PLL-based VSC connected to weak AC grid[J]. Proceedings of the CSEE, 2021, 41(1): 98-108, 401.
[10] 刘其辉, 洪晨威, 逄思敏, 等. 基于弹性系数的双馈风电机组控制参数对次同步振荡作用分析及调整方法[J]. 电工技术学报, 2022, 37(14): 3528-3541.
Liu Qihui, Hong Chenwei, Pang Simin, et al. Analysis and adjustment method of doubly-fed fan control parameters on subsynchronous oscillation based on impedance elastic sensitivity[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3528- 3541.
[11] 黄云辉, 宋泽凡, 唐金锐, 等. 连接弱电网的并网变换器直流电压时间尺度稳定器的设计与分析[J]. 电工技术学报, 2018, 33(增刊1): 185-192.
Huang Yunhui, Song Zefan, Tang Jinrui, et al. Design and analysis of DC-link voltage stabilizer for voltage source converter as connected to weak grid[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 185-192.
[12] 舒展, 熊华强, 蔡霞, 等. 直驱风机直流母线电压控制对系统功率振荡的影响分析及改进方法[J]. 电网技术, 2020, 44(9): 3441-3449.
Shu Zhan, Xiong Huaqiang, Cai Xia, et al. Influence of DC bus voltage control of direct-drive PMSG on power oscillation and its improvement[J]. Power System Technology, 2020, 44(9): 3441-3449.
[13] Yuan Hao, Yuan Xiaoming, Hu Jiabing. Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-link voltage control time- scale[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3981-3991.
[14] Huang Yunhui, Yuan Xiaoming, Hu Jiabing, et al. DC-bus voltage control stability affected by AC-bus voltage control in VSCs connected to weak AC grids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 445-458.
[15] 刘巨, 姚伟, 文劲宇. 考虑PLL和接入电网强度影响的双馈风机小干扰稳定性分析与控制[J]. 中国电机工程学报, 2017, 37(11): 3162-3173, 3371.
Liu Ju, Yao Wei, Wen Jinyu. Small signal stability analysis and control of double-fed induction generator considering influence of PLL and power grid strength[J]. Proceedings of the CSEE, 2017, 37(11): 3162-3173, 3371.
[16] 裴金鑫, 姚骏, 黄森, 等. 电网短路故障下新能源并网变换器的暂态同步机制及其自适应稳定控制策略[J]. 中国电机工程学报, 2022, 42(16): 5922- 5934, 6167.
Pei Jinxin, Yao Jun, Huang Sen, et al. Transient synchronization mechanism and adaptive stability control strategy for renewable energy grid-connected converter under grid faults[J]. Proceedings of the CSEE, 2022, 42(16): 5922-5934, 6167.
[17] Huang Sen, Yao Jun, Pei Jinxin, et al. Transient syn- chronization stability improvement control strategy for grid-connected VSC under symmetrical grid fault[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 4957-4961.
[18] Wu Heng, Wang Xiongfei. An adaptive phase-locked loop for the transient stability enhancement of grid-connected voltage source converters[C]//2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 2018: 5892-5898.
[19] Cecati F, Zhu Rongwu, Pugliese S, et al. State feed- back reshaping control of voltage source converter[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14280-14293.
[20] 刘取. 电力系统稳定性及发电机励磁控制[M]. 北京: 中国电力出版社, 2007.
Abstract With the increasing integration of renewable energy and power electronic equipment, the power system is characterized by low inertia and weak damping. Consequently, grid-following converters employing a phase-locked loop (PLL) for synchronization face the risk of oscillation instability, especially in complex control coupling. This paper proposes a complex torque analysis model that examines the damping mechanism for small disturbance synchronous instability. To reveal the small disturbance synchronization instability mechanism of grid-following converters, a PLL complex torque analysis mode is built considering the current control (CC) loop and DC-link voltage control (DVC) loop. Accordingly, the accurate damping characteristics and oscillation risk of the low-frequency mode can be assessed. The effects of typical multi-loop control coupling, line impedance, and control parameters on the damping torque of the system are quantified.
Firstly, a typical grid-following topology and control strategy is introduced, including the PLL, current inner current loop, and DC-link voltage outer loop. Secondly, a synchronous dynamic analysis model is established, considering both CC and DVC, resembling in the Phillips-Heffron model used in low-frequency oscillation analysis for synchronous machines. Based on the equivalent block diagram transformation, the complex torque model of the synchronous loop is derived, enabling the examination of equivalent second-order motion driven by unbalanced voltage, as shown in Fig.A1. It indicates that by introducing equivalent voltage components by CC and DVC, control coupling has an uncertain damping effect on the PLL. Thirdly, the intrinsic damping of PLL and additional damping from CC and DVC are extracted using the developed model, facilitating an investigation into the influence of control interaction on the PLL’s equivalent motion. Moreover, the study analyzes the impacts of multi-loop control coupling, line impedance, and various control parameters on the low-frequency oscillation characteristics of grid-following systems. Finally, a damping compensator, utilizing d-axis current feedback, is proposed to improve the low-frequency damping characteristics of grid-following and enhance the small perturbation synchronization stability of the converter.
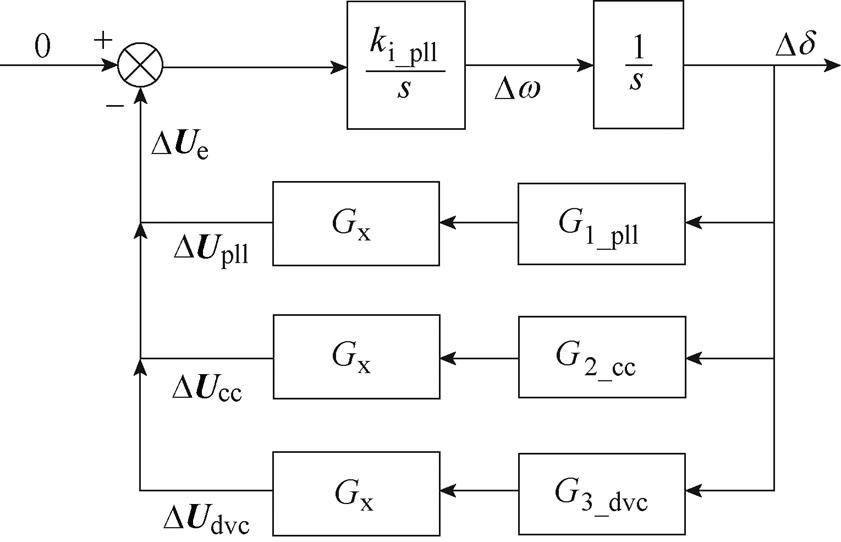
Fig.A1 The complex torque analysis of PLL
The results show that incorrect controller parameters can lead to synchronization instability with oscillation frequencies below 10 Hz, particularly in weak grids. The influence of key parameters on the system’s oscillation mode is summarized as follows:
(1) Increasing the proportional coefficient of PLL and the integration parameter of CC can lead to a higher oscillation frequency and exacerbate the negative damping effect.
(2) Amplifying the proportional gain in the CC loop and DVC enhances the system’s oscillation frequency but weakens the negative damping effect.
(3) The increase in the grid impedance reduces the oscillation frequency and intensifies the negative damping effect of the system.
Furthermore, leveraging the enhanced PLL, the system exhibits positive damping and remains stable as the grid transitions from strong to weak. As the grid impedance increases from 0.1(pu) to 0.8(pu), the positive damping persists, signifying an improved dynamic characteristic of the grid-following system.
keywords：Grid following converter, small signal synchronization stability, multi-loop control coupling, complex torque analysis, damping reshaping
DOI: 10.19595/j.cnki.1000-6753.tces.230493
中图分类号：TM464
国家自然科学基金（62141103）和广东省基础与应用基础研究基金（粤桂联合基金-重点项目）（2021B1515420006）资助项目。
收稿日期 2023-04-18
改稿日期 2023-07-13
李 红 女，1993年生，博士研究生，研究方向为新能源并网系统的控制与稳定性分析。E-mail: lihong.me@foxmail.com
陈延明 男，1966年生，教授，博士生导师，研究方向为新能源发电技术。E-mail: yanmingchen@126.com（通信作者）
（编辑 陈 诚）