图1 MD-EPS控制原理
Fig.1 Control principle of MD-EPS control
摘要 该文提出一种双有源桥（DAB）DC-DC变换器的多级离散扩展移相（MD-EPS）控制，旨在提升DAB DC-DC变换器系统的动态响应性能。同时，考虑效率优化，兼顾额定功率范围、输出电压纹波等性能指标，研究MD-EPS控制的离散参数分布方式对控制性能的影响及参数设计方法。通过搭建160 W小功率实验样机对MD-EPS的控制性能进行了验证。实验结果表明，与传统扩展移相控制相比，DAB DC-DC变换器的MD-EPS控制能够大幅提升变换器系统的动态响应速度（响应时间缩短99.95%），最高效率为94.54%。
关键词：双有源桥变换器 离散移相 动态性能 效率
在储能系统中，DC-DC变换器是连接直流母线与储能装置的重要环节。它需要根据可再生能源的输出功率与负载需求，快速调节输出功率的大小和流向，以防止负载波动、电压下跌和其他外界干扰所引起的直流母线波动对系统造成大的影响，从而保证输出电能的品质和系统可靠性[1-2]。双有源桥（Dual Active Bridge, DAB）DC-DC变换器具有高功率密度、能量双向流动、易于实现软开关等优点，被广泛应用于电动汽车、微电网储能系统[3]。其中，扩展移相（Extended-Phase-Shift, EPS）调制是DAB DC-DC变换器常用的调制方式之一。它通过优化算法调节外/内移相比D1/D2，可以实现对变换器回流功率、电流应力或者软开关的优化[4-5]。然而，传统的基于比例-积分（PI）算法的EPS控制，需要根据变换器的输入、输出电压和电流值以及PI调节器的输出结果，实时计算优化的D1/D2值，导致较大的运算量，限制了控制性能的进一步提升。此外，由于控制环路带宽受限，传统基于PI调节器EPS控制系统难以实现快速的动态响应[6-8]。当储能系统直流母线或负载发生扰动时，较慢的动态响应速度将造成直流母线电压振荡，会影响变换器的性能及稳定性。
目前，提升DAB DC-DC变换器动态性能的控制方法主要包括两类：一类是通过增加负载电流或输入电压反馈控制环路提高负载或输入电压突变时变换器的动态响应速度[9-11]。但是，这些方法需要引入额外的控制环路，增加了控制器的复杂度，同时，动态控制效果仍然受限于控制器带宽。另一类是采用非线性控制，如模型预测控制在每一个开关周期内求解有限时域开环最优解控制问题得到当前开关周期的移相比[12]；模糊控制将复杂系统进行模糊化，基于模糊规则得到控制参数，进而实现对DAB DC-DC变换器的控制[13]；滑模控制根据变换器系统所期望的动态特性，设计切换超平面，通过滑动模态控制器使系统状态从超平面之外向切换超平面收束，实现对变换器输出功率的精确控制[14-15]。这些非线性控制方法虽然能够有效提高DAB DC- DC变换器的动态性能，但采样信号多、计算量大，增加了控制系统的复杂度。
脉冲序列调制（Pulse-Train Modulation, PTM）是一种非线性离散的调制方法[16-17]。基于PTM的开关变换器控制技术具有控制原理简单和动态响应速度快等优点[18-20]。文献[21]将PTM应用于DAB DC-DC变换器，预设两组外/内移相比离散分布的高功率控制脉冲组PH和低功率控制脉冲组PL，根据输出电压与参考电压的关系，选择并输出控制脉冲组PH或PL，实现对输出电压的快速调节。但是，文献[21]所提出的方法未考虑宽负载范围、效率优化等问题，也未对离散移相控制DAB DC-DC变换器的输出电压纹波、离散控制脉冲分布方式等问题进行分析。
为此，本文将PTM与EPS调制方法结合，同时考虑电感电流峰峰值优化，提出DAB DC-DC变换器的多级离散扩展移相（Multilevel Discrete Extended-Phase-Shift, MD-EPS）控制方法，旨在同时提升DAB DC-DC变换器系统的效率、稳态及动态性能。本文所提方法的创新点和主要贡献在于：
（1）提出了MD-EPS控制的控制规则，并研究了MD-EPS控制DAB DC-DC变换器系统离散的功率传输特性，进而说明了MD-EPS控制的实现原理与控制效果。
（2）以四级离散扩展移相（4-Level Discrete Extended-Phase-Shift, 4LD-EPS）控制为例，研究并明确了MD-EPS控制的离散控制参数与DAB DC-DC变换器系统输出功率、输出电压纹波和电感电流峰峰值之间的关系，以指导离散外/内移相比D1/D2设计。
（3）对所提出的4LD-EPS控制DAB DC-DC变换器系统稳定性和稳态性能进行了定量分析，说明了该离散控制方法的特点。
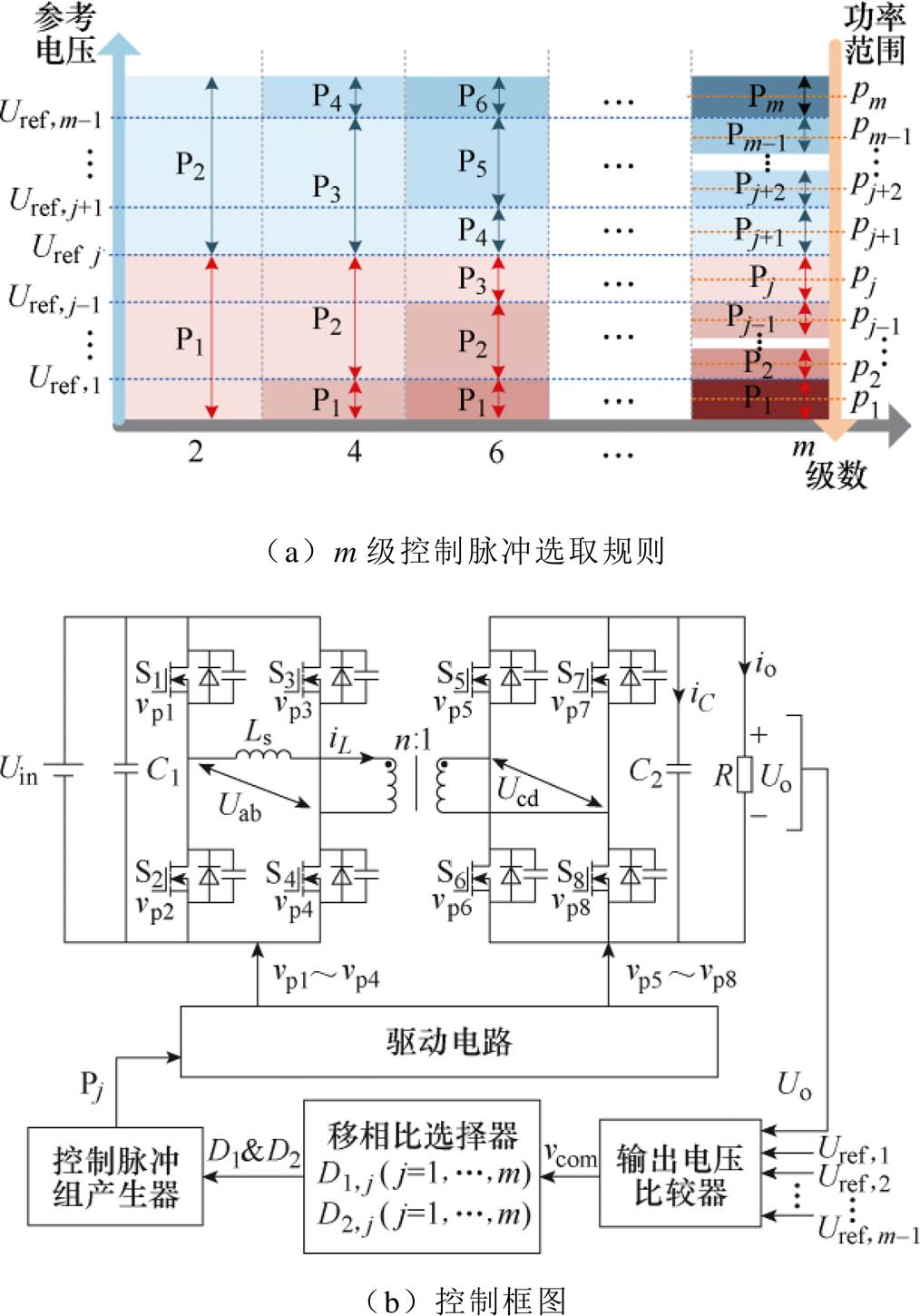
如图1所示为DAB DC-DC变换器的MD-EPS控制原理。图中，Uin和Uo分别为输入和输出电压，Uab和Ucd分别为一次侧和二次侧H桥交流电压，Ls为变压器辅助电感，C1和C2分别为输入和输出电容，R为负载电阻，iL、iC和io分别为电感电流、电容电流和输出电流。所提出的MD-EPS控制有一系列预设的离散控制参数，包括：
（1）m-1级预设的输出电压参考值Uref, j（j=1,···, m-1，m为偶数），满足Uref,1＜…＜Uref, j-1＜Uref, j＜Uref, j+1＜…＜Uref,m-1，且相邻的输出电压参考值构成一个输出电压区间[Uref, j-1, Uref, j]，如图1a所示。
（2）每个输出电压区间[Uref, j-1, Uref, j]对应预设的外/内移相比信号D1, j和D2, j，其中，D1, j和D2, j是根据变换器性能要求而预先设定的。
图1 MD-EPS控制原理
Fig.1 Control principle of MD-EPS control
（3）D1, j和D2, j对应控制脉冲组Pj和传输功率标幺值pj，Pj包含8个控制信号vp1～vp8，分别用于控制DAB DC-DC变换器的8个开关管S1～S8。
如图1b所示，MD-EPS控制器在每个开关周期开始时刻采样输出电压Uo，并与m-1级Uref, j进行比较。产生的比较信号vcom输入移相比选择器，用以在预设的m组离散移相比信号中，选择出有效的移相比信号。当Uo∈[Uref, j-1,Uref, j]时，MD-EPS控制器将D1, j和D2, j赋值于D1和D2，即D1=D1, j和D2=D2, j。信号D1和D2作为控制脉冲产生器的输入，产生控制脉冲组Pj，用于驱动开关管S1～S8。
根据DAB DC-DC变换器的工作原理可得，在Pj作用的开关周期内，DAB DC-DC变换器的输出功率标幺值pj可以表示[22]为
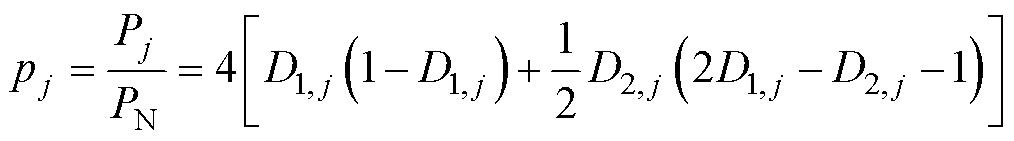（1）
式中，PN=nUinUo/(8 fsLs)为DAB DC-DC变换器的最大输出功率，n为变压器电压比，fs为开关频率。
根据式（1）可知，pj只与D1, j和D2, j有关，而与输出电压Uo的值无关。结合1.1节中MD-EPS控制原理，一旦确定了各级控制脉冲组的离散控制参数D1, j和D2, j，pj也随之确定。因此，为了实现MD-EPS控制对DAB DC-DC变换器输出电压的有效调节，各级pj的设计需要满足
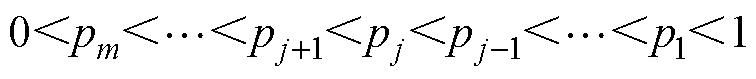（2）
根据式（2），MD-EPS控制的输出功率标幺值与输出电压的变化存在如下关系：当Uo∈[Uref, j-1, Uref, j]时，控制器选择控制脉冲组Pj为当前开关周期的有效控制信号。若从输入传递到负载的功率pj大于此时负载所需要的输出功率po，输出电压上升；反之，输出电压下降。
根据1.2节中输出功率标幺值与输出电压变化的关系可知，当负载所需输出功率满足po∈[pj+1, pj]时，根据式（2），MD-EPS控制器对输出电压的调节存在两种情况：
（1）当Uo＜Uref, j时，根据MD-EPS控制原理，控制器可能输出的控制脉冲组包括Pj, Pj-1,…, P1。由于po＜pj＜pj-1＜…＜p1，此时的控制效果为输出电压上升。
（2）当Uo≥Uref, j时，根据MD-EPS控制原理，控制器可能输出的控制脉冲组包括Pj+1, Pj+2,…, Pm。由于po＞pj+1＞pj+2＞…＞pm，此时的控制效果为输出电压下降。
因此，MD-EPS控制DAB DC-DC变换器（假设输出功率为po∈[pj+1, pj]）的实际控制效果为：稳态时，MD-EPS控制器产生控制脉冲组Pj和Pj+1组成一个控制脉冲组循环周期，当Uo＜Uref, j时，控制器通过产生控制脉冲组Pj使DAB DC-DC变换器的输出电压上升；当Uo≥Uref, j时，控制器通过产生控制脉冲组Pj+1使DAB DC-DC变换器的输出电压下降。最终作用效果为DAB DC-DC变换器的输出电压在Uref, j附近上下波动。瞬态时，MD-EPS控制器可以根据输出电压的变化，直接选取合适的控制脉冲组，实现对输出电压的快速调节。由于无需误差放大器和相应的补偿网络，MD-EPS控制具有非常快速的动态性能。
根据第1节所述的MD-EPS控制原理可知，MD-EPS控制根据控制规则，在预先设置的移相比中选择并输出合适的移相比，实现对DAB DC-DC变换器输出电压的调节。因此，预先设置的离散移相比参数直接影响MD-EPS控制DAB DC-DC变换器的稳态及动态性能。为此，本节将以四级离散扩展移相控制（4LD-EPS）为例，考虑DAB DC-DC变换器的功率范围和电感电流峰峰值优化，对MD- EPS控制的输出电压参考值和离散移相比的参数分布方式进行研究和设计。
根据图1a所示的MD-EPS控制原理可得4LD- EPS控制包括3级输出电压参考值Uref,1、Uref,2和Uref,3。三个输出电压参考值将输出电压分为四个电压区间[0, Uref,1
、[Uref,1, Uref,2、[Uref,2, Uref,3和[Uref,3, +∞。4LD-EPS控制的控制原理波形如图2所示，4个电压区间分别对应四组预设的离散移相比（D1,1, D2,1）、（D1,2, D2,2）、（D1,3, D2,3）和（D1,4, D2,4）。4组移相比分别对应4级控制脉冲的输出功率标幺值p1、p2、p3和p4。Ts为开关周期，Ths=0.5Ts为半个开关周期，ipp, j（j=1, 2, 3, 4）为控制脉冲组所对应的电感电流峰峰值。
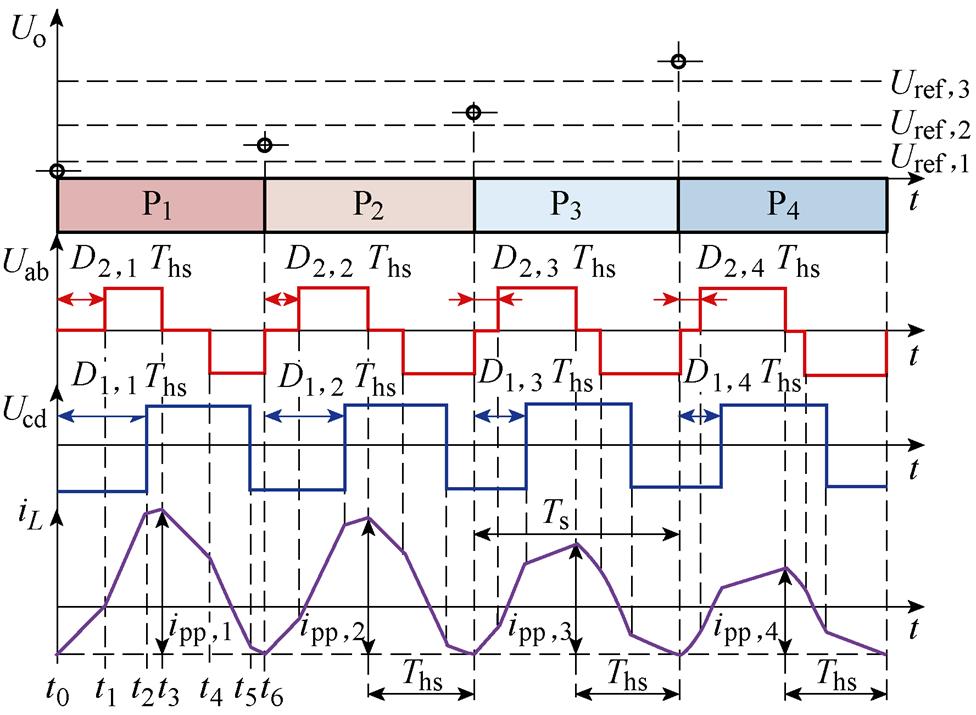
图2 4LD-EPS控制的控制原理波形
Fig.2 Control principle waveforms of 4LD-EPS control
4LD-EPS控制DAB DC-DC变换器存在以下四种控制脉冲组选择情况：
（1）当Uo∈[0, Uref,1时，4LD-EPS控制器选择控制脉冲组P1为当前开关周期的有效控制信号。此时，根据输出功率情况，输出电压的变化存在两种可能的情况：当0＜po＜p1时，变换器的输出电压上升；当p1＜po＜1时，变换器的输出电压下降。
（2）当Uo∈[Uref,1, Uref,2时，4LD-EPS控制器通过产生控制脉冲组P2为当前开关周期的有效控制信号。当0＜po＜p2时，变换器的输出电压上升；当p2＜po＜1时，变换器的输出电压下降。
（3）当Uo∈[Uref,2, Uref,3时，4LD-EPS控制器通过产生控制脉冲组P3为当前开关周期的有效控制信号。当0＜po＜p3时，变换器的输出电压上升；当p3＜po＜1时，变换器的输出电压下降。
（4）当Uo∈[Uref,3, +∞时，4LD-EPS控制器通过产生控制脉冲组P4为当前开关周期的有效控制信号。当0＜po＜p4时，变换器的输出电压上升；当p4＜po＜1时，变换器的输出电压下降。
综上所述，4LD-EPS控制DAB DC-DC变换器的控制效果为：当po∈[p2, p1]时，控制器将选择控制脉冲组P1和P2使输出电压在Uref,1附近上下波动；当po∈[p3, p2]时，控制器将选择控制脉冲组P2和P3使输出电压在Uref,2附近上下波动；当po∈[p4, p3]时，控制器将选择控制脉冲组P3和P4使输出电压在Uref,3附近上下波动。可见，4LD-EPS控制的效果与控制脉冲组的组合情况有关，而控制脉冲组合情况直接与功率相关。因此，在进行4LD-EPS的参数设计时，首先考虑额定功率和功率范围，对4LD-EPS的各控制脉冲组所对应的功率范围进行设计。
4LD-EPS控制DAB DC-DC变换器的4级控制脉冲组P1～P4所对应的一个开关周期内的输出功率标幺值p1～p4满足：0＜p4＜p3＜p2＜p1＜1。当Uo＜Uref,1时，如果输出功率标幺值p1＜po，则即使4LD-EPS控制器持续选择控制脉冲组P1作为有效控制信号，仍无法使DAB DC-DC变换器的输出电压升高到参考电压Uref,1。此时，4LD-EPS控制器失控。与此类似，当Uo＞Uref,3时，如果po＜p4，则即使4LD-EPS控制器持续选择控制脉冲组P4，仍无法使DAB DC-DC变换器的输出电压降低到参考电压Uref,3。此时，4LD-EPS控制器失控。可见，4LD-EPS控制DAB DC-DC变换器的输出功率范围为[p4, p1]。即控制脉冲组P1和P4的外/内移相比（D1,1和D2,1）和（D1,4和D2,4）决定了4LD-EPS控制DAB DC-DC变换器的功率范围。本文中，根据额定功率范围，设计p1=0.95，p4=0.4。
如图2所示，4LD-EPS控制DAB DC-DC变换器的电感电流iL为
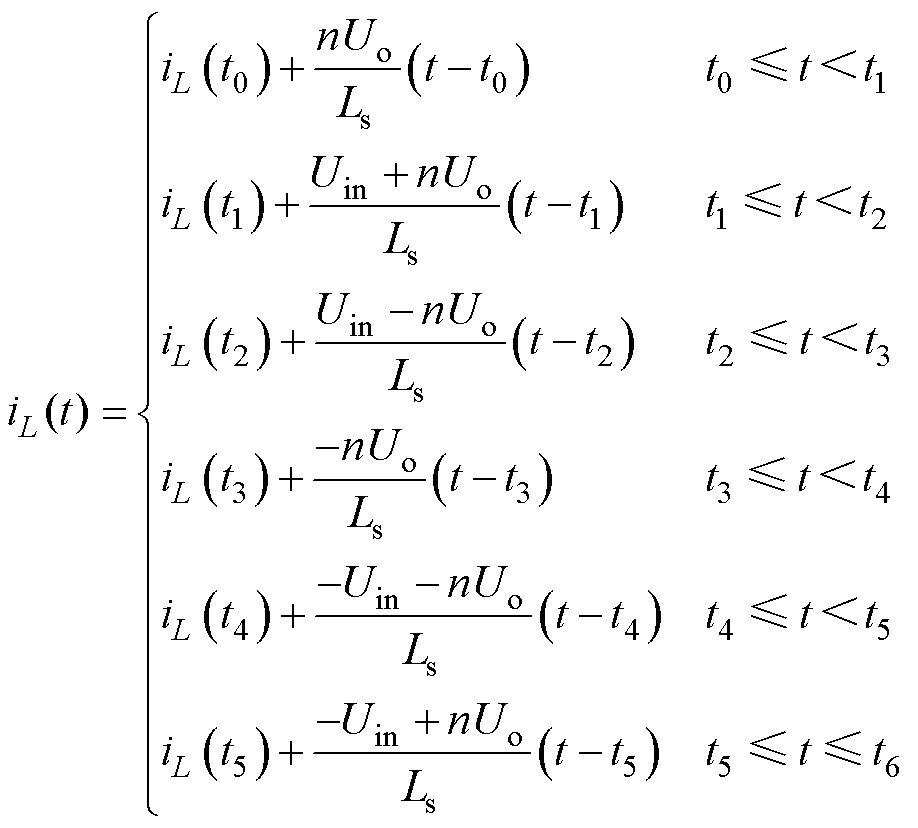（3）
由图1b得DAB DC-DC变换器的电容电流iC为
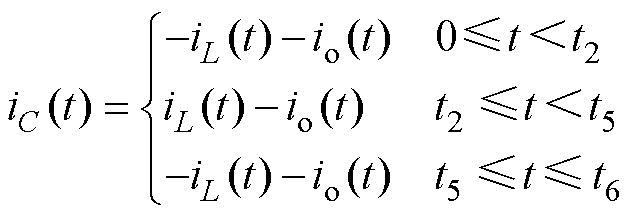（4）
结合式（3）、式（4），对输出滤波电容电流iC进行积分，可得各级控制脉冲组Pj作用的开关周期内的输出电压变化量DUo,j（j=1, 2, 3, 4）为
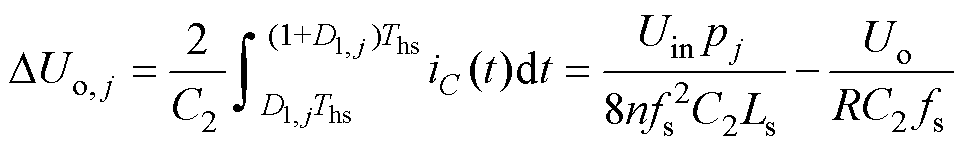（5）
4LD-EPS控制中间两级功率p2和p3的设计则需要综合考虑DAB DC-DC变换器的输出电压纹波和控制精度问题。由式（5）可知，4LD-EPS控制DAB DC-DC变换器的输出电压变化量DUo,j与输出功率标幺值pj呈正相关。结合式（1）可知，当所设计的p2和p3的差值较小时，可以获得更小的输出电压纹波，但对应的功率范围较小。此时，变换器更多的工作在[p2, p1]和[p4, p3]区间内，由于对应的参考电压分别为Uref,1和Uref,3，将造成一定的静态误差。
因此，设计p2和p3时，应在保证输出电压纹波满足要求的同时，尽量扩大功率范围，使输出电压围绕额定参考电压Uref,2上下波动。本文考虑额定输出功率Po=100 W、输出电压参考值Uref,2=36 V时。根据式（1）计算可得po=0.617 28，考虑变换器死区时间、电路寄生参数等引起的功率损耗，设计p2= 0.82和p3=0.5。结合式（6）与表1电路参数可得，输出电压变化量绝对值|DUo,j|和输出功率标幺值的关系曲线如图3所示，此时控制脉冲组P2和P3对应的最大输出电压变化量绝对值|DUo,2|max=|DUo,3|max= 0.061 3 V。
表1 DAB DC-DC变换器电路主参数
Tab.1 Parameters of DAB DC-DC converter
参 数数 值 输入电压Uin/V72 输出电压Uo/V36 开关频率fs/kHz50 辅助电感Ls/μH40 输入电容C1/μF100 输出电容C2/μF470 变压器电压比n1
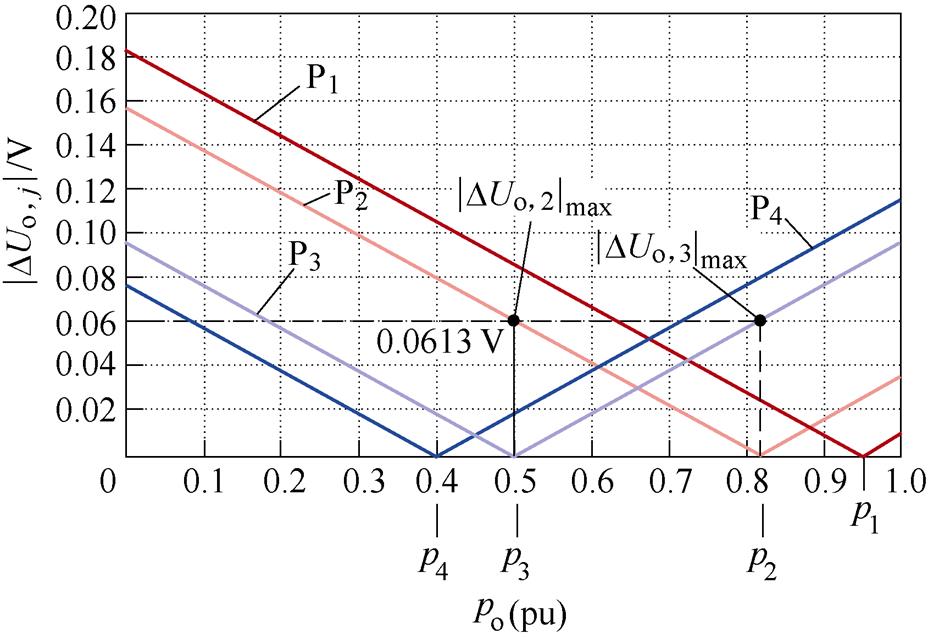
图3 输出电压变化量绝对值|DUo, j|与输出功率标幺值po的关系曲线
Fig.3 The relation curves between absolute value |DUo, j| of output voltage variation and normalized output power po
定义4LD-EPS控制相邻两级输出电压参考值之差分别为eref,1=Uref,2-Uref,1和eref,2=Uref,3-Uref,2。当eref,1和eref,2过大时，如图4a所示，4LD-EPS控制器需要连续选择同一组控制脉冲组，才能使得输出电压达到参考电压，导致较大的变换器输出电压纹波和较慢的动态响应速度。但是，较小的eref,1和eref,2将造成4LD-EPS控制器对输入电压和负载扰动敏感，导致控制器“跨级选取”控制脉冲组，输出电压纹波增大，如图4b所示。
因此，在设计参考电压时，需要考虑相应的控制脉冲周期内DAB DC-DC变换器的输出电压变化量DUo,j。通过设计eref,j值略大于对应控制脉冲组Pj在一个开关周期内的最大输出电压变化量绝对值|DUo,j|max，实现最佳的控制效果。
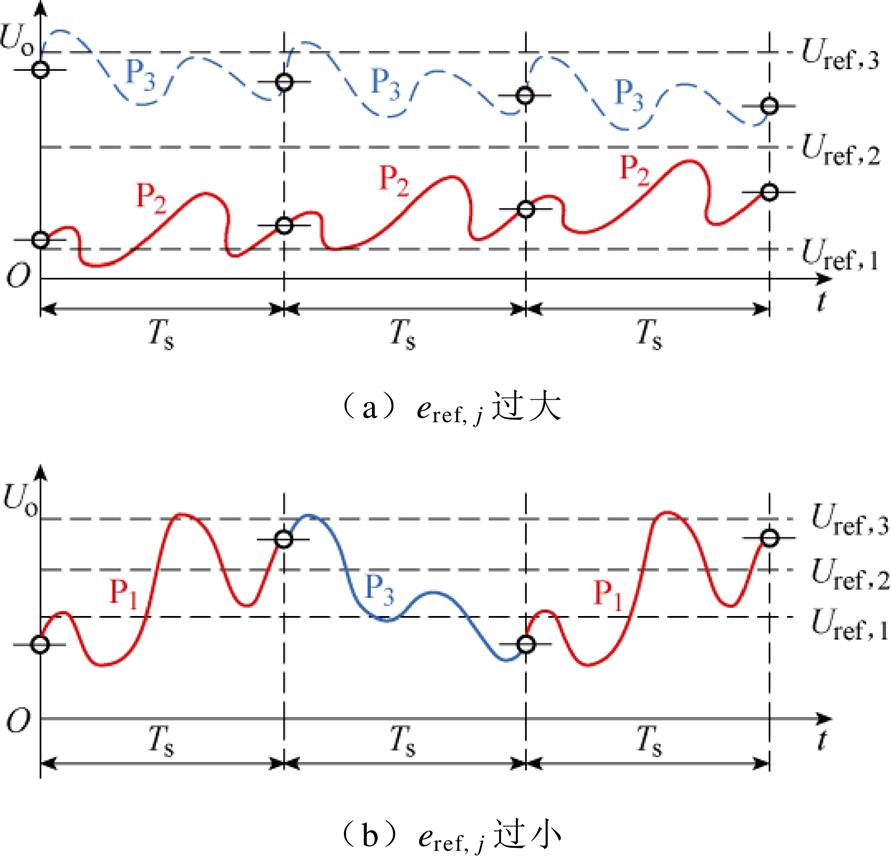
图4 eref, j取值影响
Fig.4 The influence of eref, j
考虑eref,j值应略大于一个Pj开关周期内的最大输出电压变化量绝对值|DUo,j|max。如图3所示，由于[p3, p2]内控制脉冲组P2和P3的最大输出电压变化量绝对值为0.061 3 V，则eref,1和eref,2需要满足：①eref,1＞|DUo,2|max=0.061 3V；②eref,2＞|DUo,3|max= 0.061 3V。
同时，考虑变换器系统的非理想情况，设置一定的控制裕度，将eref,1和eref,2的值设置为0.1 V。由此可得，4LD-EPS控制DAB DC-DC变换器的三级输出电压参考值分别为：Uref,1=(36-0.1) V=35.9 V、Uref,2=36 V（额定输出电压）、Uref,3=(36+0.1) V=36.1 V。
4LD-EPS控制DAB DC-DC变换器离散移相比的设计考虑电感电流峰峰值最小化原则，旨在提高动态响应速度的同时，获得较高的效率。由式（3）可得，各级控制脉冲组所对应的电感电流峰峰值ipp, j（j=1, 2, 3, 4）为
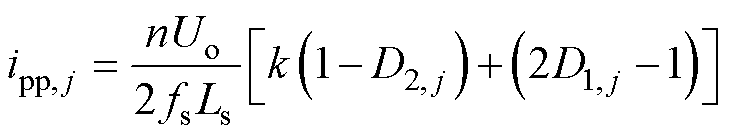（6）
式中，k=Uin/(nUo)为DAB DC-DC变换器的输入、输出电压转换比。
根据式（6）可得考虑约束条件0≤D2, j≤D1, j≤1时的最小电感电流峰峰值ippmn, j为
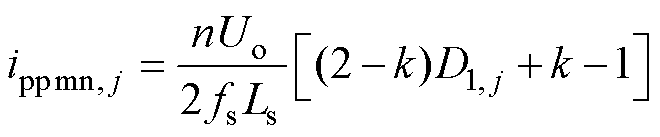（7）
结合式（1）可知，当0≤D1, j=D2, j≤1时，DAB DC-DC变换器的输出功率标幺值表达式为
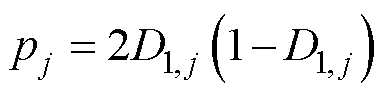（8）
由式（8）可知，当0≤D1, j=D2, j≤1时，pj范围为[0, 0.5]。因此，当0≤pj≤0.5时，令D1, j=D2, j，可得最小电感电流峰峰值，根据式（8）可得此时的外/内移相比为
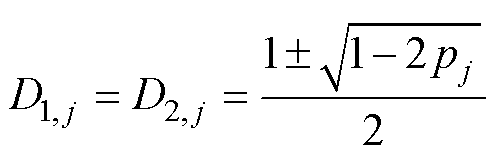（9）
当0.5≤pj≤1时，以电感电流峰峰值ipp,j最小化为原则，构造拉格朗日函数为
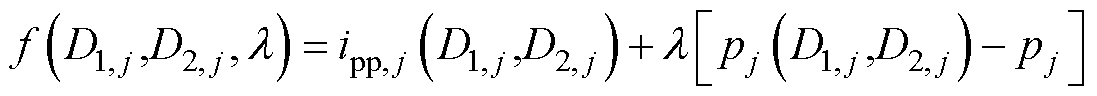（10）
根据式（1）、式（6）和式（10）可得电感电流峰峰值最小化移相比组合为
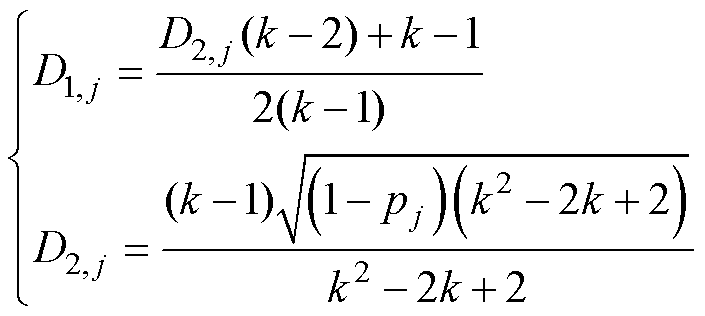（11）
综上所述，基于电感电流峰峰值优化的4LD- EPS控制离散移相比设计规则为
（1）当0≤pj≤0.5时，则根据式（9）计算外/内移相比D1, j与D2, j。
（2）当0.5＜pj≤1时，则根据式（11）计算外/内移相比D1, j与D2, j。
根据上述设计原则，在表1电路参数的基础上考虑k=2的情况，可得ippmn, j与pj的关系曲线如图5所示。图5中，当0≤pj≤0.5时，ippmn, j=9 A。当0.5＜pj≤1时，ippmn, j随pj的增大而增大。根据2.2节中设计的输出功率标幺值（p1=0.95(pu)、p2= 0.82(pu)、p3=0.5(pu)、p4=0.4(pu)）。p1、p2均大于0.5(pu)，因此，P1和P2所对应的外/内移相比需要根据式（11）进行设计，分别设为：（D1,1=0.5，D2,1=0.158）和（D1,2=0.5，D2,2=0.3）。而p3和p4均小于等于0.5(pu)，因此，P3和P4所对应的外/内移相比可以根据式（9）设计为：D1,3=D2,3=0.5和D1,4= D2,4=0.276。综上所述，将本文所采用的4LD-EPS控制器参数列于表2。后续将基于该组参数对4LD- EPS控制DAB DC-DC变换器的控制性能进行分析和验证。
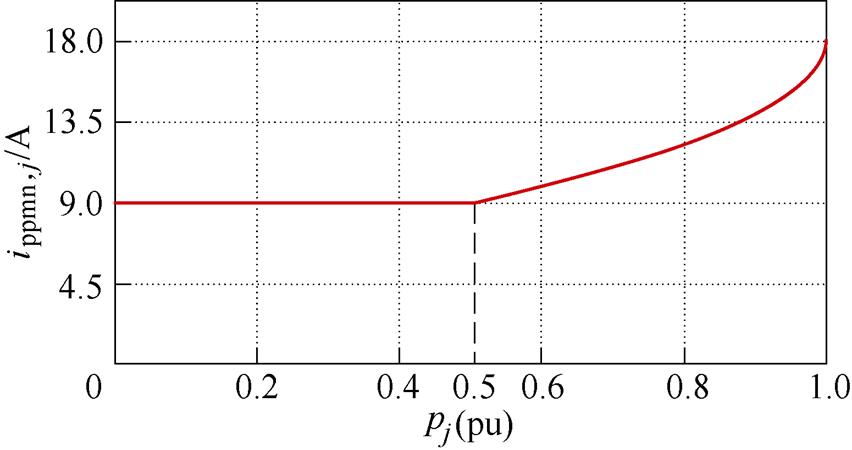
图5 k=2时最小电感电流峰峰值ippmn, j与输出功率标幺值pj的关系曲线
Fig.5 When k=2, the relation curves between minimum peak-to-peak current value ippmn, j and normalized output power pj
表2 4LD-EPS控制DAB DC-DC变换器控制参数
Tab.2 Control parameters of 4LD-EPS controlled DAB DC-DC converter
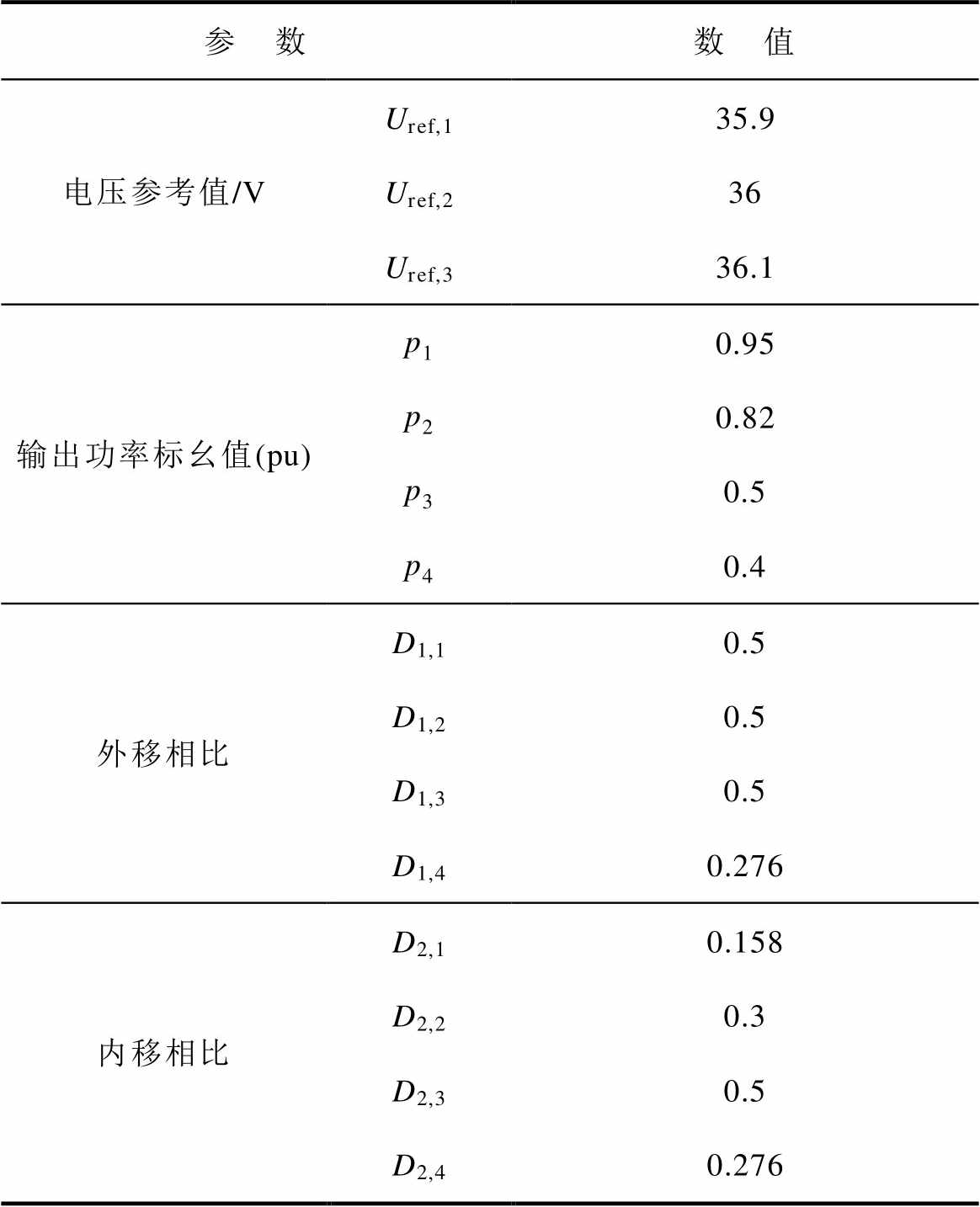
参 数数 值 电压参考值/VUref,135.9 Uref,236 Uref,336.1 输出功率标幺值(pu)p10.95 p20.82 p30.5 p40.4 外移相比D1,10.5 D1,20.5 D1,30.5 D1,40.276 内移相比D2,10.158 D2,20.3 D2,30.5 D2,40.276
根据4LD-EPS控制原理可知，与传统的基于线性控制理论的PWM移相控制方法不同，在连续的开关周期内，4LD-EPS控制器产生的外/内移相比并非连续变化，而是离散分布的。因此，传统的小信号建模分析方法不适用于本文所提出的4LD-EPS控制DAB DC-DC变换器系统。因此，本节通过建立4LD-EPS控制DAB DC-DC变换器的输出电压一维迭代模型对变换器系统的稳定性和稳态性能进行研究。
设Uo,n和Uo,n+1分别为4LD-EPS控制DAB DC-DC变换器第n个开关周期起、止时刻的输出电压值，根据式（5）可得4LD-EPS控制DAB DC-DC变换器的输出电压一维迭代模型为Uo,n+1=Uo,n+ DUo,j，其中j=1, 2, 3, 4，即
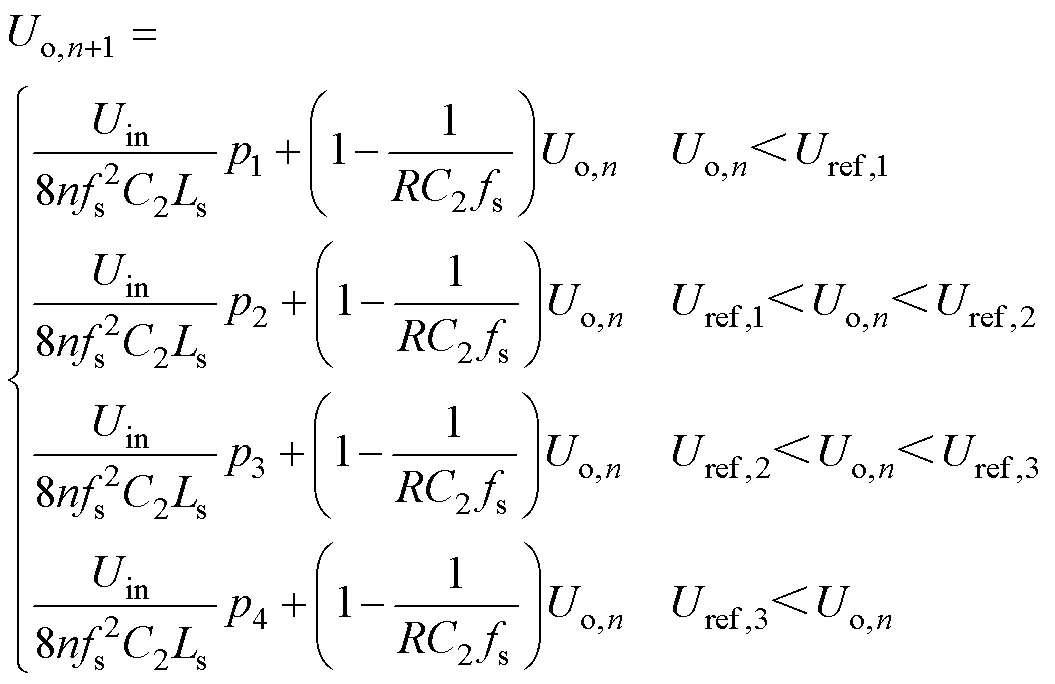（12）
对式（12）求导可得4LD-EPS控制DAB DC-DC变换器的特征值l 为
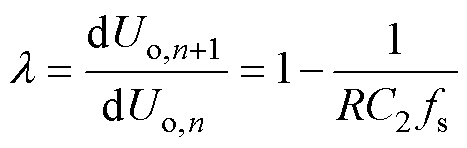（13）
由式（13）可得，4LD-EPS控制DAB DC-DC变换器随负载电阻变化时的李雅普诺夫指数如图6所示。图6中，李雅普诺夫指数恒小于零，表明4LD- EPS控制DAB DC-DC变换器在负载范围[R1, R4]内，均处于稳定的工作状态。其中，R1～R4分别为控制脉冲组P1～P4对应的输出电压变化量等于0时的负载电阻。
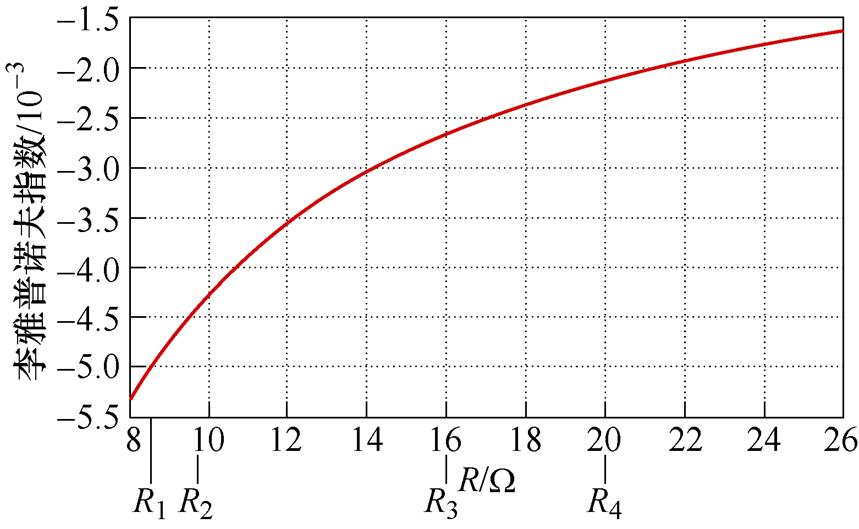
图6 李雅普诺夫指数
Fig.6 Lyaponuv exponent diagram
4LD-EPS控制器通过选择合适的控制脉冲实现对DAB DC-DC变换器输出电压的控制。因此，稳态时，4LD-EPS控制的控制脉冲将组成一个控制脉冲组循环周期，表示为mjPj-mj+1Pj+1，其中，mj和mj+1分别表示一个控制脉冲组循环周期中控制脉冲组Pj和Pj+1的数量，其值满足
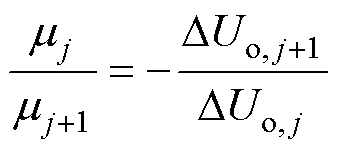（14）
由式（5）和式（14）可得，4LD-EPS控制DAB DC-DC变换器在一个控制脉冲组循环周期中控制脉冲组的数量之比与负载的关系如图7所示。当R∈[R1, R2]时（即po∈[p2, p1]），控制器通过产生控制脉冲组P1和P2实现对DAB DC-DC变换器输出电压的调节。随着R的增大，由于需要更少的输出功率，控制脉冲组P1在循环周期中所占的比重逐渐减小。直到R=R2时，结合图3可知，控制脉冲组P2作用的开关周期已无法使DAB DC-DC变换器的输出电压降低。因此，当R∈[R2, R3]时，控制器开始产生控制脉冲组P2和P3，对DAB DC-DC变换器输出电压进行调节。R∈[R2, R3]和R∈[R3, R4]时的控制脉冲组合规律变化情况与此类似，不再赘述。
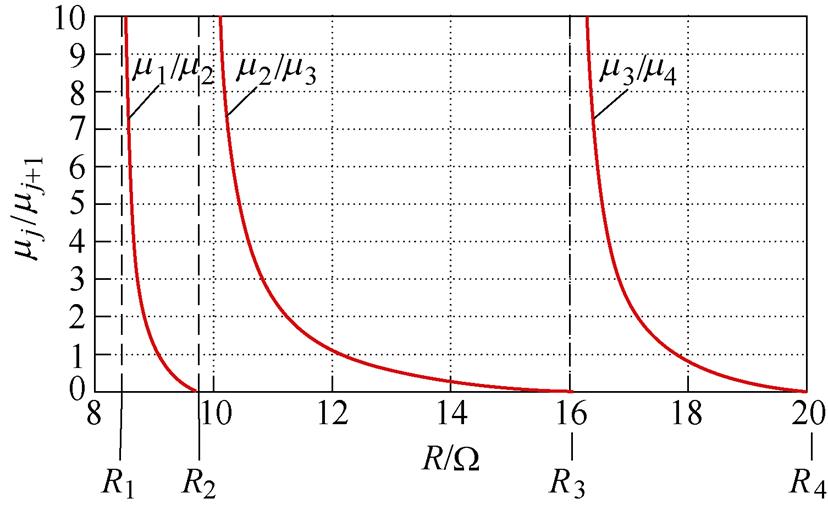
图7 控制脉冲组数量之比mj/mj+1与负载电阻R的关系曲线
Fig.7 The relation curves between the ratio mj/mj+1 of control pulse group and load resistance R
根据4LD-EPS控制的控制脉冲组循环周期的组合情况，可以对4LD-EPS控制DAB DC-DC变换器的输出电压纹波进行估算。输出电压Uo的波形如图8所示。如图8a、图8b所示，控制脉冲组循环周期Pj-mj+1Pj+1和mjPj-Pj+1的输出电压纹波DUrip,1和DUrip,2可以分别表示为
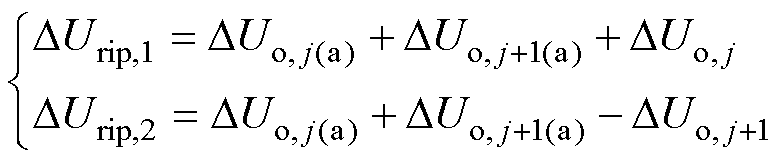（15）
式中，DUo,j(a)和DUo,j+1(a)分别为Pj和Pj+1作用的开关周期开始时刻到输出电压第一个波谷的输出电压变化量。
如图9所示为基于表1电路参数仿真实测的DUo,j(a)和DUo,j+1(a)随负载电阻R的变化曲线。由式（15）可知，控制脉冲组循环周期的输出电压纹波主要由输出电压变化量较大的控制脉冲组决定，通过分析控制脉冲组输出电压变化量的变化趋势，可以得到输出电压纹波的整体变化趋势。当1＜mj/mj+1时，控制脉冲组循环周期中的控制脉冲组Pj+1对应的输出电压变化量更大，输出电压纹波的变化趋势与控制脉冲组Pj+1对应的输出电压变化量的变化趋势相同；当mj/mj+1＜1时，控制脉冲组循环周期中的控制脉冲组Pj对应的输出电压变化量更大，输出电压纹波的变化趋势与控制脉冲组Pj对应的输出电压变化量的变化趋势相同。
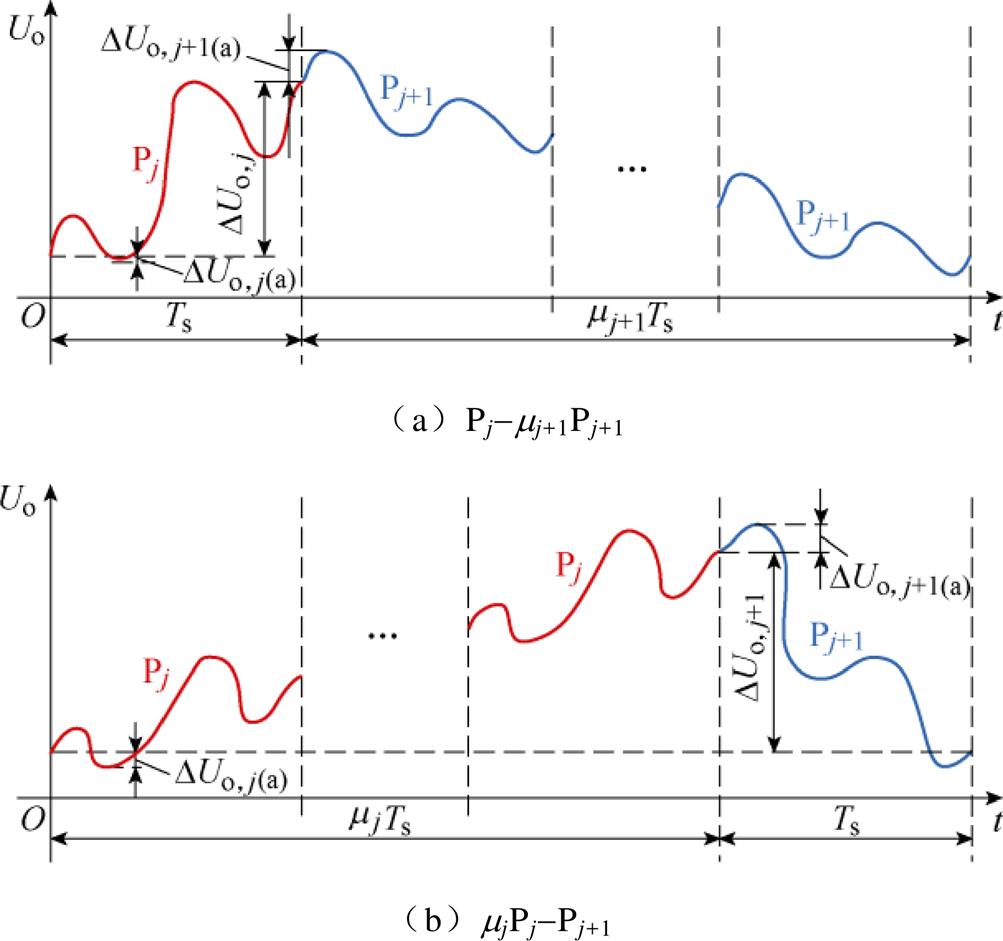
图8 输出电压Uo的波形
Fig.8 Waveforms of output voltage Uo
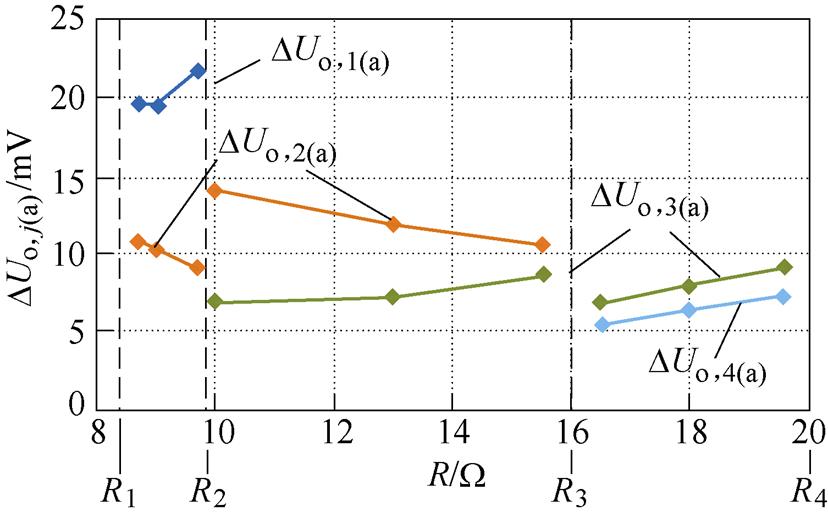
图9 DUo,j(a)与DUo,j+1(a)随负载电阻R的变化曲线
Fig.9 The variation curves of DUo,j(a) and DUo,j+1(a) with load resistance R
结合图3可知，控制脉冲组Pj在对应工作区间内的输出电压变化量绝对值|DUo,j|随着负载电阻的增大而增大；控制脉冲组Pj+1在对应工作区间内的输出电压变化量绝对值|DUo,j|随着负载电阻的增大而减小。当1＜mj/mj+1时，输出电压纹波随着负载电阻的增大而减小；当mj/mj+1＜1时，输出电压纹波随着负载电阻的增大而增大。因此当mj/mj+1=1时，输出电压纹波最小。如图10所示为理论分析和仿真实测的输出电压纹波DUrip与负载电阻R的关系曲线。由图10可知，仿真实测结果与上述理论分析结果一致。
根据4LD-EPS控制原理可知，输出电压采样精度可能对4LD-EPS控制器的控制效果产生影响。而在实际应用中，采样信号误差难以避免。为此，本节通过向理想的输出电压采样信号中，注入幅值为0.025 V、频率为32、38、44、50 kHz的混合正弦信号DUo，模拟输出电压采样值Usam存在误差的情况，仿真分析采样误差对4LD-EPS控制DAB DC-DC变换器稳态及动态性能的影响，如图11和图12所示。
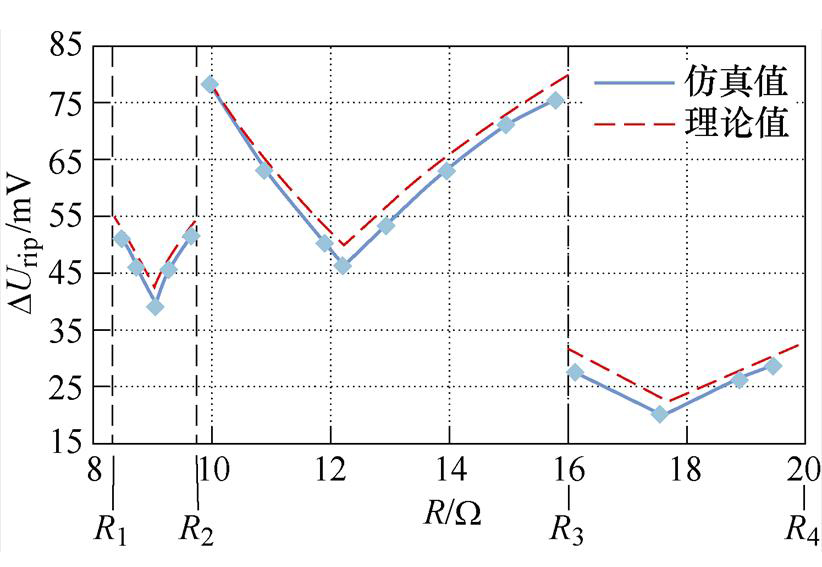
图10 输出电压纹波DUrip与负载电阻R的关系曲线
Fig.10 The relation curves between output voltage ripple DUrip and load resistance R
图11a所示为理想状态下4LD-EPS控制的稳态波形。此时，输出电压采样值的变化范围为[35.96, 36.04] V，控制器根据输出电压采样值，选取控制脉冲组P2和P3对变换器的输出电压进行调节，输出电压纹波约为80 mV。如图11b所示，当输出电压采样存在误差时，输出电压采样值的变化范围变为[35.9, 36.15] V。因此，控制器选择控制脉冲组P2、P3和P4对DAB DC-DC变换器进行控制。此时，控制器仍可以实现对输出电压的有效调节，但与图11a相比，输出电压的采样误差会引起输出电压纹波的增大（增大为120 mV）。
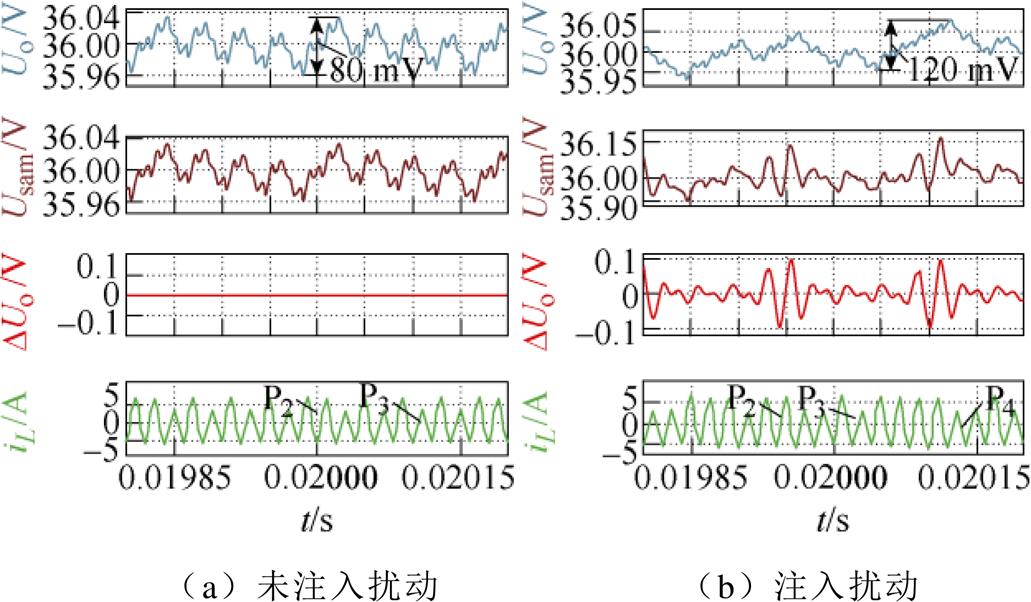
图11 输出电压采样误差对4LD-EPS控制DAB DC-DC变换器稳态性能的影响
Fig.11 Effect of output voltage sampling error on steady-state performance of 4LD-EPS controlled DAB DC-DC converter
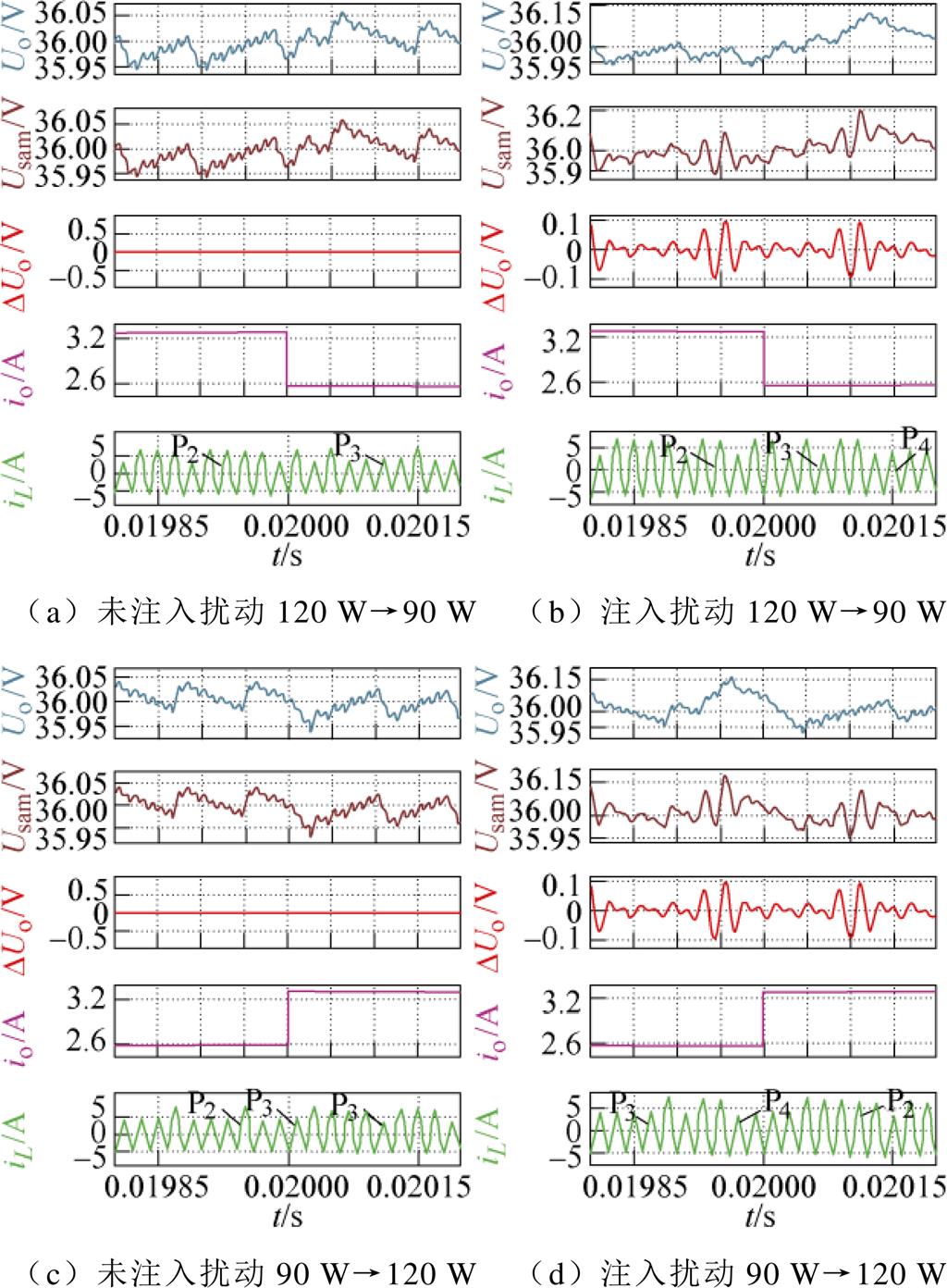
图12 输出电压采样误差对4LD-EPS控制DAB DC-DC变换器动态性能的影响
Fig.12 Effect of output voltage sampling error on transient performance of 4LD-EPS controlled DAB DC-DC converter
如图12所示分别为理想情况和存在输出电压采样误差情况时4LD-EPS控制DAB DC-DC变换器的动态仿真波形。由图12可知，当变换器的负载在90 W和120 W之间跳变时，4LD-EPS控制器均可以在几个开关周期内控制DAB DC-DC变换器达到新的稳态。因此，输出电压采样误差的存在，对动态性能的影响较小。
为了验证所提出的MD-EPS控制的稳态性能和动态性能，本文以TMS320F28335为核心控制芯片搭建了160 W的DAB DC-DC变换器小功率实验样机，实验平台主要参数和控制参数见表1和表2。
如图13所示为不同负载情况下4LD-EPS控制以及电感电流峰峰值优化4LD-EPS控制的实验波形。图13中，当DAB DC-DC变换器处于稳态时，控制器主要产生控制脉冲组P2和P3，负载从100 W增加到130 W时，分别对比图13a、图13c与图13b、图13d。可知在重载时，控制脉冲组循环周期中控制脉冲组P2的数量更多；在轻载时，控制脉冲组循环周期中控制脉冲组P3的数量更多，符合四级离散扩展移相（4LD-EPS）控制DAB DC-DC变换器的控制原理。
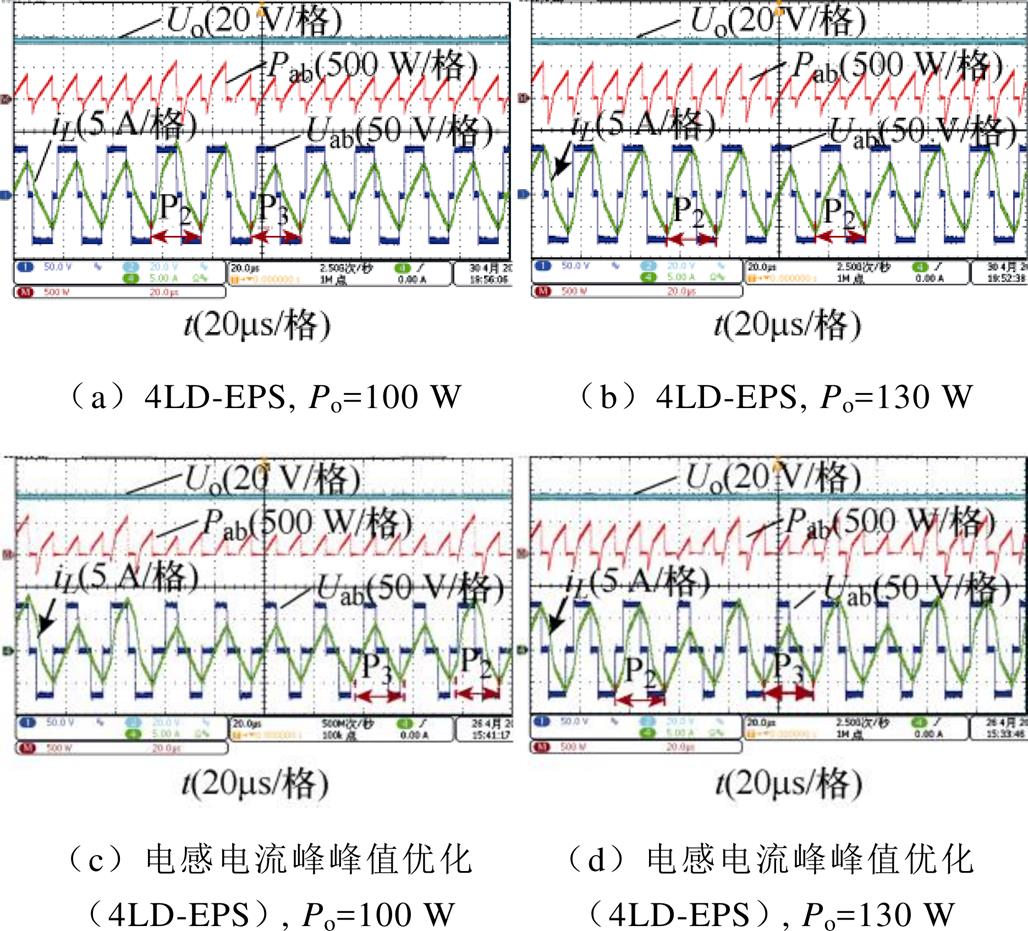
图13 4LD-EPS控制DAB DC-DC变换器的实验波形
Fig.13 The experimental waveforms of 4LD-EPS controlled DAB DC-DC converter
图14为不同控制方法下DAB DC-DC变换器的电感电流峰峰值随输出功率标幺值变化的曲线和效率柱状图。由图14可知，传统4LD-EPS控制DAB DC-DC变换器的电感电流峰峰值高于所提出的电感电流峰峰值优化4LD-EPS控制DAB DC-DC变换器的电感电流峰峰值。相应地，与传统4LD-EPS控制方法相比，电感电流峰峰值优化4LD-EPS控制DAB DC-DC变换器具有更高的效率。
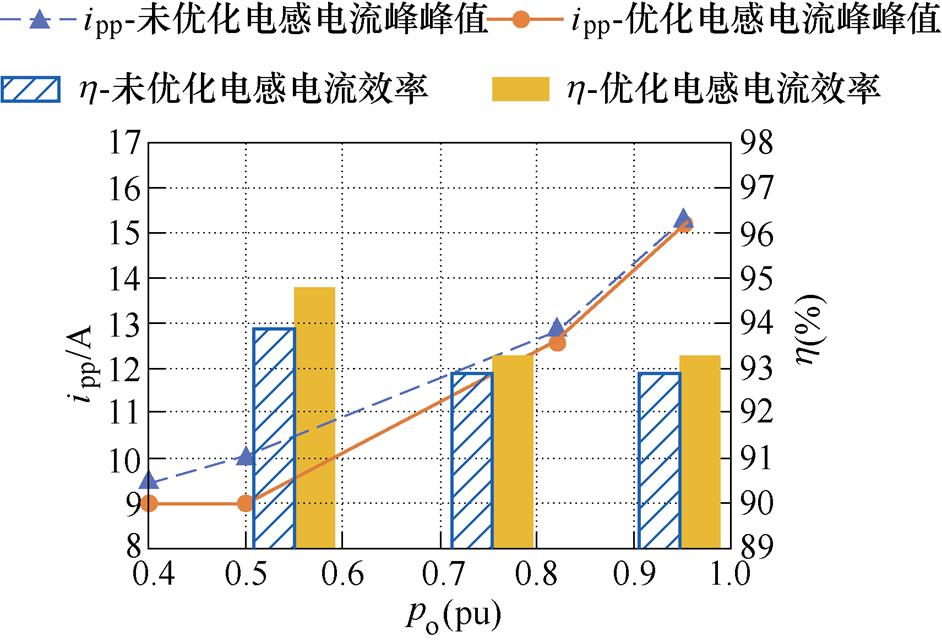
图14 4LD-EPS控制DAB DC-DC变换器的电感电流峰峰值曲线和效率柱状图
Fig.14 The current peak-to-peak value curves and efficiency histograms of 4LD-EPS controlled DAB DC-DC converter
如图15所示为DAB DC-DC变换器在电感电流峰峰值优化的4LD-EPS控制与传统PWM-EPS控制负载由100 W切换到130 W时的实验波形。由图15a可知，传统PWM-EPS控制DAB DC-DC变换器在负载突增时动态响应速度慢，动态响应时间大约为35 ms。如图15b所示，电感电流峰峰值优化的4LD-EPS控制在负载突增时的动态响应时间约为20 ms，且没有输出电压超调量。在负载突增后，电感电流峰峰值优化的4LD-EPS控制采用功率较低的控制脉冲组P3来减小输出电压，使得DAB DC-DC变换器快速进入稳态。
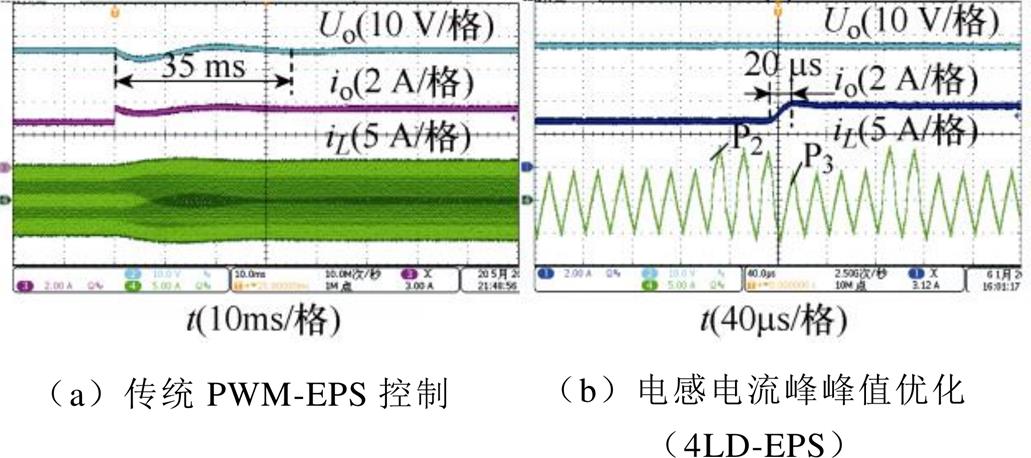
图15 负载突增实验波形
Fig.15 Experimental waveforms when the load steps up
如图16所示为所提出的电感电流峰峰值优化的4LD-EPS控制与传统PWM-EPS控制DAB DC-DC变换器在负载突减时的实验波形。由图16a可知，传统PWM-EPS控制DAB DC-DC变换器在负载突减时动态响应速度慢，动态响应时间大约为40 ms；如图16b所示，电感电流峰峰值优化的4LD- EPS控制在负载突减时动态响应时间大约为20 ms且没有超调量，动态响应速度快。在负载突减后，电感电流峰峰值优化的4LD-EPS控制采用功率较高的控制脉冲组P2来增加输出电压，使得DAB DC-DC变换器快速进入稳态。
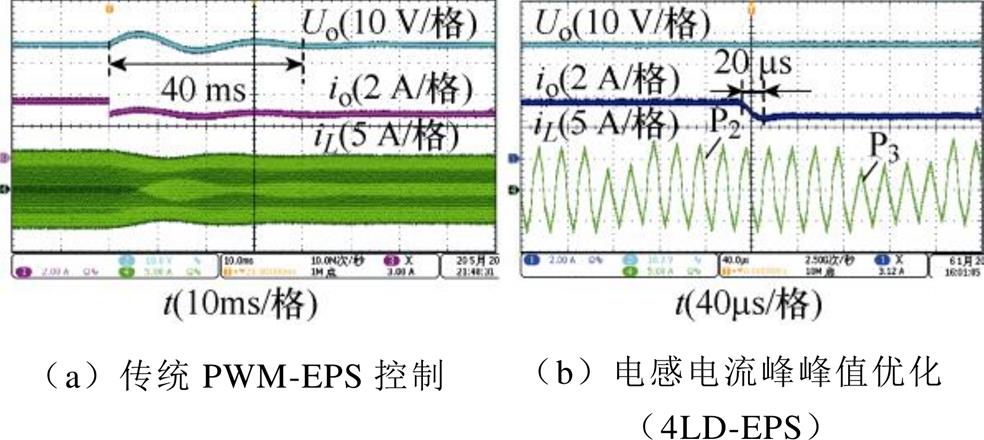
图16 负载突减实验波形
Fig.16 Experimental waveforms when the load steps down
当负载电阻为R=10 Ω时，如图17和图18所示为DAB DC-DC变换器在两种控制方法下输入电压在67 V与72 V之间切换时的实验波形。将电感电流峰峰值优化的4LD-EPS控制与传统PWM-EPS控制进行对比，由图17可知，传统PWM-EPS控制DAB DC-DC变换器在输入电压突增时动态响应速度慢，动态响应时间大约为20 ms；4LD-EPS控制在输入电压突增时动态响应时间大约为1 ms且没有超调量，动态响应速度快。结合图18可知，传统PWM-EPS控制DAB DC-DC变换器在输入电压突增时动态响应速度慢，动态响应时间大约为24 ms；可以看出4LD-EPS控制DAB DC-DC变换器在输入电压突变时具有优异的动态性能。
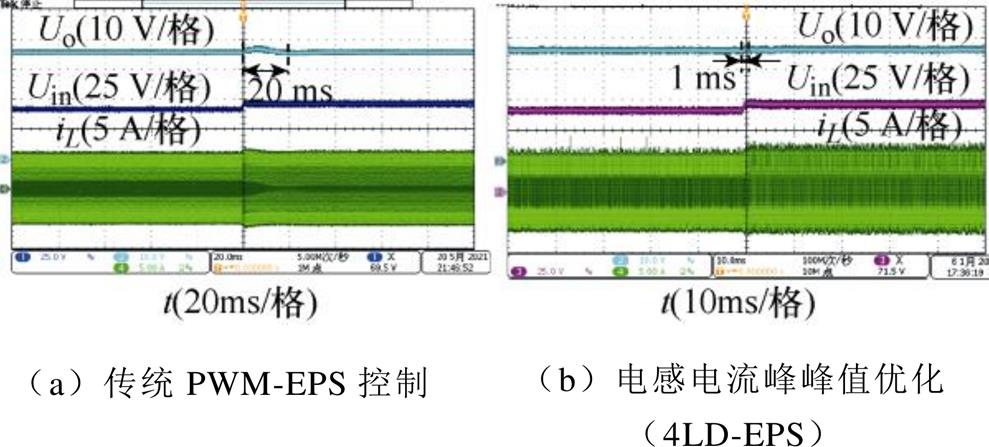
图17 输入电压突增实验波形
Fig.17 Experimental waveforms when the input voltage steps up
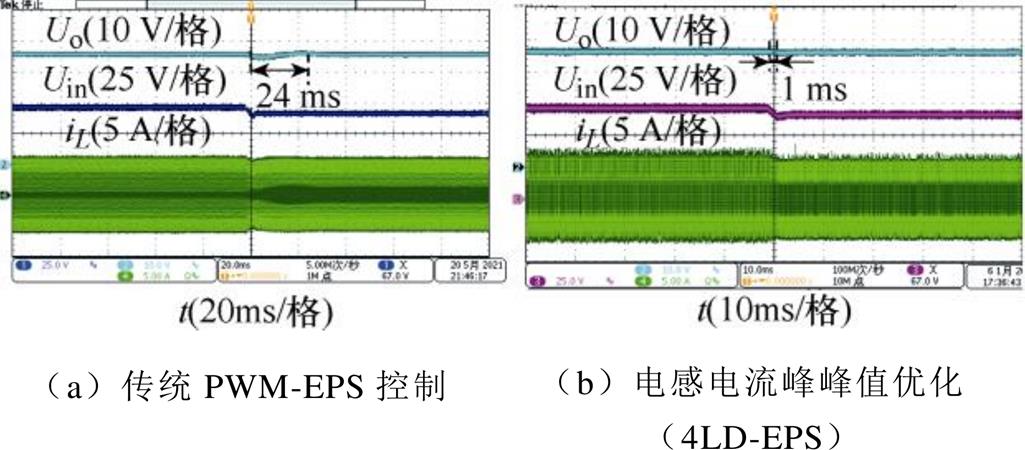
图18 输入电压突减实验波形
Fig.18 Experimental waveforms when the input voltage steps down
本文针对传统移相控制DAB DC-DC变换器动态响应慢的问题，提出了MD-EPS控制。为了提高DAB DC-DC变换器的效率，基于MD-EPS控制，本文提出了针对电感电流峰峰值的优化算法，并与传统PWM-EPS控制方法进行了对比分析。理论分析与实验结果可以证明以下结论：
1）本文的实验结果表明，所提出的MD-EPS控制方法根据输出电压所在的电压区间，经过简单的逻辑运算，即可在较宽负载范围内实现对输出电压的高效、快速调节，且控制方法具有计算量小、控制成本低等优点。
2）相对于传统PWM-EPS控制，MD-EPS控制不需要误差放大器及其相应的补偿网络，其控制原理及结构简单，具有优异的动态性能和高可靠性。
3）对于MD-EPS控制DAB DC-DC变换器的电感电流峰峰值优化算法，实现了电感电流峰峰值最小化。与未经优化的MD-EPS控制相比，采用电感电流峰峰值优化控制算法的MD-EPS控制可以得到最高的效率。
参考文献
[1] 郭慧, 汪飞, 顾永文, 等. 基于电压分层控制的直流微电网及其储能扩容单元功率协调控制策略[J]. 电工技术学报, 2022, 37(12): 3117-3131.
Guo Hui, Wang Fei, Gu Yongwen, et al. Coordinated power control strategy for DC microgrid and storage expansion unit based on voltage hierarchical control[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3117-3131.
[2] 倪萌, 王蓓蓓, 朱红, 等. 能源互联背景下面向高弹性的多元融合配电网双层分布式优化调度方法研究[J]. 电工技术学报, 2022, 37(1): 208-219.
Ni Meng, Wang Beibei, Zhu Hong, et al. Study of two-layer distributed optimal scheduling strategy for highly elastic multi-resource fusion distribution network in energy interconnection environment[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 208-219.
[3] Iyer V M, Gulur S, Bhattacharya S. Small-signal stability assessment and active stabilization of a bidirectional battery charger[J]. IEEE Transactions on Industry Applications, 2019, 55(1): 563-574.
[4] Xu Guo, Li Liting, Chen Xiaoying, et al. Optimized EPS control to achieve full load range ZVS with seamless transition for dual active bridge con- verters[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(9): 8379-8390.
[5] Zhou Bingkai, Yang Xiaofeng, Zhang Zhi, et al. Backflow power optimization of DAB with gradient descent algorithm based extended-phase-shift control in EER application[C]//2019 IEEE 3rd International Electrical and Energy Conference (CIEEC), Beijing, China, 2020: 1737-1742.
[6] Hou Nie, Ding Li, Gunawardena P, et al. A com- prehensive comparison of two fast-dynamic control structures for the DAB DC-DC converter[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 6488-6500.
[7] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720-4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A hybrid optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720-4731.
[8] 王仁龙, 杨庆新, 操孙鹏, 等. 一种优化电流应力的双有源桥式DC-DC变换器双重移相调制策略[J]. 电工技术学报, 2021, 36(增刊1): 274-282.
Wang Renlong, Yang Qingxin, Cao Sunpeng, et al. An optimized dual phase shift modulation strategy for dual active bridge DC-DC converter[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 274-282.
[9] 侯聂, 宋文胜, 武明义. 全桥隔离DC/DC变换器的直接功率控制方法[J]. 电力系统自动化, 2016, 40(17): 204-209.
Hou Nie, Song Wensheng, Wu Mingyi. Direct power control scheme of full-bridge isolated DC/DC converters[J]. Automation of Electric Power Systems, 2016, 40(17): 204-209.
[10] 侯聂, 宋文胜, 武明义. 双向全桥DC-DC变换器的负载电流前馈控制方法[J]. 中国电机工程学报, 2016, 36(9): 2478-2485.
Hou Nie, Song Wensheng, Wu Mingyi. A load current feedforward control scheme of dual active bridge DC/DC converters[J]. Proceedings of the CSEE, 2016, 36(9): 2478-2485.
[11] Song Wensheng, Hou Nie, Wu Mingyi. Virtual direct power control scheme of dual active bridge DC-DC converters for fast dynamic response[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(2): 1750-1759.
[12] An Feng, Song Wensheng, Yang Kexin, et al. Improved dynamic performance of dual active bridge DC-DC converters using MPC scheme[J]. IET Power Electronics, 2018, 11(11): 1756-1765
[13] Liu Baolong, Zha Yabing, Zhang Tao, et al. Fuzzy logic control of dual active bridge in solid state transformer applications[C]//2016 Tsinghua University- IET Electrical Engineering Academic Forum, Beijing, China, 2016: 1-4.
[14] Jeung Y C, Lee D C. Voltage and current regulations of bidirectional isolated dual-active-bridge DC-DC converters based on a double-integral sliding mode control[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6937-6946.
[15] Ruiz I, Vidal-Idiarte E, Calvente J. Direct digital design of a proportional robust control based on sliding for dual active bridge converters[C]//IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 2019: 1696- 1701.
[16] Telefus M, Shteynberg A, Ferdowsi M, et al. Pulse train control technique for flyback converter[J]. IEEE Transactions on Power Electronics, 2004, 19(3): 757-764.
[17] Wang Jinping, Xu Jianping, Zhou Guohua, et al. Pulse-train-controlled CCM Buck converter with small ESR output-capacitor[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5875-5881.
[18] Sha Jin, Xu Jianping, Zhong Shu, et al. Control pulse combination-based analysis of pulse train controlled DCM switching DC-DC converters[J]. IEEE Transa- ctions on Industrial Electronics, 2015, 62(1): 246- 255.
[19] Sha Jin, Xu Duo, Chen Yiming, et al. A peak- capacitor-current pulse-train-controlled Buck con- verter with fast transient response and a wide load range[J]. IEEE Transactions on Industrial Electronics, 2016, 63(3): 1528-1538.
[20] Sha Jin, Xu Jianping, Bao Bocheng, et al. Effects of circuit parameters on dynamics of current-mode- pulse-train-controlled Buck converter[J]. IEEE Transa- ctions on Industrial Electronics, 2014, 61(3): 1562- 1573.
[21] Sha Jin, Chen Lirong, Zhou Guohua. Discrete extended- phase-shift control for dual-active-bridge DC-DC converter with fast dynamic response[J]. IEEE Transactions on Industrial Electronics, 2023, 70(6): 5662-5673.
[22] Shi Haochen, Wen Huiqing, Chen Jie, et al. Minimum-backflow-power scheme of DAB-based solid-state transformer with extended-phase-shift control[J]. IEEE Transactions on Industry Appli- cations, 2018, 54(4): 3483-3496.
Abstract The DC-DC converter plays a pivotal role in renewable energy systems by serving as an interface converter connecting the DC bus and energy storage devices. The application demands a fast dynamic response to accommodate load fluctuations, voltage drops, or other external disturbances. Therefore, a multi-stage discrete extended-phase-shift (MD-EPS) control method is proposed for DAB DC-DC converters, considering peak-to-peak value current optimization during the control design. Thus, the proposed MD-EPS control can achieve both a fast dynamic response and high efficiency across a wide load range.
Firstly, this paper provides a comprehensive introduction to the principle of MD-EPS control. Different from conventional linear control methods, the proposed MD-EPS controller has (m-1) level output voltage references Uref, j (j=1,···, m-1, and m is an even number), dividing the output voltage into m output voltage intervals [Uref, j–1,Uref, j]. Each interval corresponds to preset fixed inner/outer phase-shift duty ratio signals D1, j and D2, j. At the beginning of each switching cycle, the output voltage Uo is sampled and compared with m-1 level Uref, j to determine the instantaneous output voltage’s corresponding interval when Uo∈[Uref, j–1,Uref, j], D1 (D1=D1, j) and D2 (D2=D2, j) are selected as the active phase-shift duty ratio signals for the current switching cycle. Secondly, the control parameter design method is presented using the 4-level discrete extended-phase-shift (4LD-EPS) controlled DAB DC-DC converter as an example. The rated power range, output voltage ripple, and peak current optimization are considered during the parameter design. Thirdly, the steady-state performance, dynamic performance, and interference immunity of the 4LD-EPS controlled DAB DC-DC converter are explored by theoretical analysis and simulation verification. Finally, the control performance of the proposed converter is verified by a 160W low-power test prototype. The experimental results highlight a remarkable improvement in the dynamic response of the converter system, with a 99.95% reduction in recovery time and a maximum efficiency of 94.54%.
The following conclusions can be drawn through the theoretical and experimental analysis: (1) The proposed MD-EPS control offers a simple control principle, ease of implementation, fast dynamic performance, and high reliability. Moreover, compared with conventional PWM-EPS control, the proposed MD-EPS control eliminates the need for an error amplifier and corresponding compensation circuits. (2) The proposed MD-EPS controlled DAB DC-DC converter effectively minimizes current peak values, thereby achieving high efficiency.
keywords：Dual active bridge converter, discrete phase-shift, dynamic performance, efficiency
DOI: 10.19595/j.cnki.1000-6753.tces.230676
中图分类号：TM46
国家自然科学基金资助项目（52277200）。
收稿日期 2023-05-15
改稿日期 2023-09-01
刘 赞 男，2000年生，硕士研究生，研究方向为电力电子与电力传动。E-mail: liuzangege@my.swjtu.edu.cn
沙 金 女，1987年生，副研究员，硕士生导师，研究方向为新能源接口变换器技术、开关变换器控制技术、开关变换器动力学建模与分析。E-mail: j.sha@swjtu.edu.cn（通信作者）
（编辑 陈 诚）