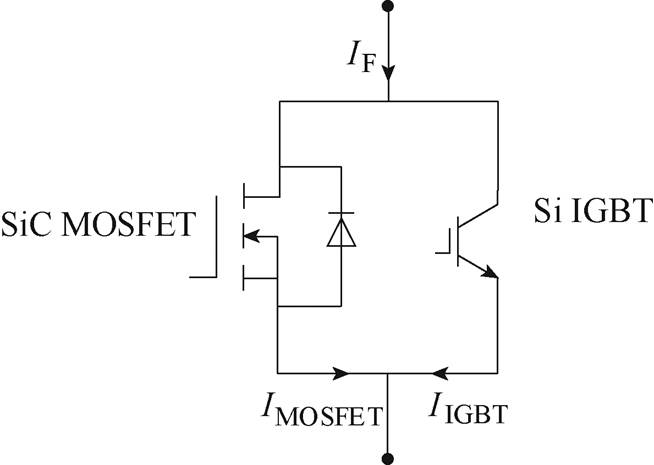
图1 Si/SiC混合器件结构
Fig.1 Structure of Si/SiC hybrid switches
摘要 由硅(Si)绝缘栅双极型晶体管(IGBT)与碳化硅(SiC)金属氧化物半导体场效应晶体管(MOSFET)并联构成的混合器件可打破单一Si基器件和SiC基器件的局限性,实现损耗和成本间的有效均衡。结温估计对于Si/SiC混合器件的可靠运行至关重要,然而,目前针对热监测的研究往往需满足热稳态平衡和功率损耗可测两大条件,在实际变流器中实用性较低。基于此,该文以零输入响应法为切入点,首先,对Si/SiC混合器件热结构特性进行分析,详细阐述零输入响应法直接应用于混合器件时所带来的高阶热约束条件难以表征的问题;其次,通过对Si IGBT与SiC MOSFET进行热网络分区处理实现模型的降阶,构建出壳温降温曲线时间常数与热参数之间的约束关系,提出了基于热网络分区等效思想的混合器件耦合热参数辨识方法,所提方法简化了功率损耗测量步骤与热平衡态条件,在并联器件耦合热参数辨识研究中具有简单、通用、流程化高的应用优势;最后,通过实验验证了该文所提方法的准确性和有效性。
关键词:耦合热参数辨识 Si/SiC混合器件 热网络分区 热时间常数 热约束
Si IGBT/SiC MOSFET混合器件有效结合了Si IGBT的大载流能力和SiC MOSFET的低开关损耗优点,混合后整体开关损耗接近SiC基器件,其成本更接近Si基器件。Si/SiC混合器件的应用对突破单一Si IGBT与SiC MOSFET功率器件技术瓶颈,满足电力电子变换器对于高效率、高功率密度和低成本的迫切需求具有重要意义[1-4]。
在Si/SiC混合器件中,一般通过调节门级延时时间实现SiC MOSFET先于Si IGBT开通,后于Si IGBT关断,以此降低混合器件的总损耗[5-7]。然而,在门级延时时间内,高热阻的SiC MOSFET会承担全部负载电流,使得重载下的SiC MOSFET易出现过热现象[8-10]。由电力电子系统可靠性调研报告可知,温度是诱发功率器件失效的主要成因[11-12]。因此,实时结温监测对于提高整个混合器件的可靠性非常关键。
现有学者针对结温测量提出了光学测量法、物理接触法、温敏电参数法和热网络模型法四类方 法[13-14]。其中,光学测量法和物理接触法需要破坏模块封装,不符合结温在线测量的要求,温敏电参数法需要设计复杂的电路测量电气参数,而热网络模型法具有非侵入式、对硬件条件要求低的优势,是极具潜力的结温在线估计方法[15-17]。混合器件的热网络本质上而言是多器件并联构成的热结构,其耦合热网络参数的获取对混合器件结温监测准确度以及难度起着至关重要的作用。
目前,针对类似混合器件的多芯片并联结构,已提出了多种耦合热网络参数辨识方法。第一种是通过计算热路交叠单元数值求解出芯片间耦合热阻抗[18-19];第二种是通过有限元仿真获取瞬态热阻抗响应曲线[20-21]。以上两种方法依赖于精确的几何尺寸以及材料参数,可以准确辨识出初始完全健康状态下器件的热参数,但难以有效计及器件内部材料发生的疲劳损伤,反映器件当前健康状态。为解决以上问题,有学者提出根据实验测量得到的数据信息来反馈器件实时健康状态下的热阻和热容参数[22-23]。文献[24]通过在两个芯片的壳温节点间添加耦合热阻,基于稳态温度数据计算出各个热阻参数,但未获取热容值。文献[25]以壳温为参考点,将IGBT模块自身和外部冷却条件的热耦合阻抗进行解耦,通过测量所有芯片和节点的瞬态热响应来表征热阻热容参数。然而,这些实验测量法须得满足IEC标准的测试要求[26-27]:①芯片的功率损耗可测;②器件必须被加热到热平衡态。由于功率器件一般运行在开关模式,其内部的结温通常处于波动状态,即在实际变流器中混合器件难以满足热平衡条件,且由于电压电流的快速变化,如何准确捕捉功率损耗至今仍是一个难题。这两大测试条件增加了混合器件热参数监测的成本和复杂度,在实际变流器中应用局限性较大。
现有研究表明,零输入响应法可以有效简化功率测量步骤和热稳态平衡条件。文献[28-29]和文献[30-32]分别利用IGBT单芯片工作下结温和壳温降温曲线热时间常数与热参数之间的关系,辨识出IGBT模块的RC参数,实现了IGBT健康状态的准确监测。但该方法忽略了其他芯片侧向热传递带来的热耦合影响,目前仅应用于单芯片热网络结构中。通过本文研究发现,在并联器件中简单套用零输入响应法将会使得热约束条件难以有效表征,导致耦合热参数辨识难度大增。
为克服以上问题和挑战,本文对零输入响应法在混合器件耦合热参数辨识中的应用规律进行了深入挖掘和探索,提出了一种基于热网络分区等效思想的Si/SiC混合器件耦合热参数辨识新方法。通过对Si IGBT与SiC MOSFET的热网络进行分区处理构造出低阶等效热网络,最后基于耦合热参数与壳温降温曲线时间常数的热约束关系开展热参数辨识。
本文所使用的混合器件由Si IGBT和SiC MOSFET并联构成,混合器件的结构如图1所示。
当两个器件同时工作时,热量横向传导会使得芯片间的热流路径相互交叉,形成热耦合效应。由于IGBT和MOSFET为安装在同一散热器上的独立器件,因此芯片之间无直接热耦合,而是通过散热器进行两个器件间热量的横向传递。
本文定义器件间热量横向传递路径上的热阻为耦合热阻,而Si IGBT和SiC MOSFET不一样的芯片面积会影响芯片下方的热扩散面积,导致器件间的相互热耦合作用有所差异,所以耦合热阻的设置必须考虑热传递方向。为简化模型,单个器件的结到壳、壳到散热器基板的热阻均可视为一阶热阻,Si IGBT/SiC MOSFET混合器件的Cauer型耦合热网络模型如图2所示。

图1 Si/SiC混合器件结构
Fig.1 Structure of Si/SiC hybrid switches
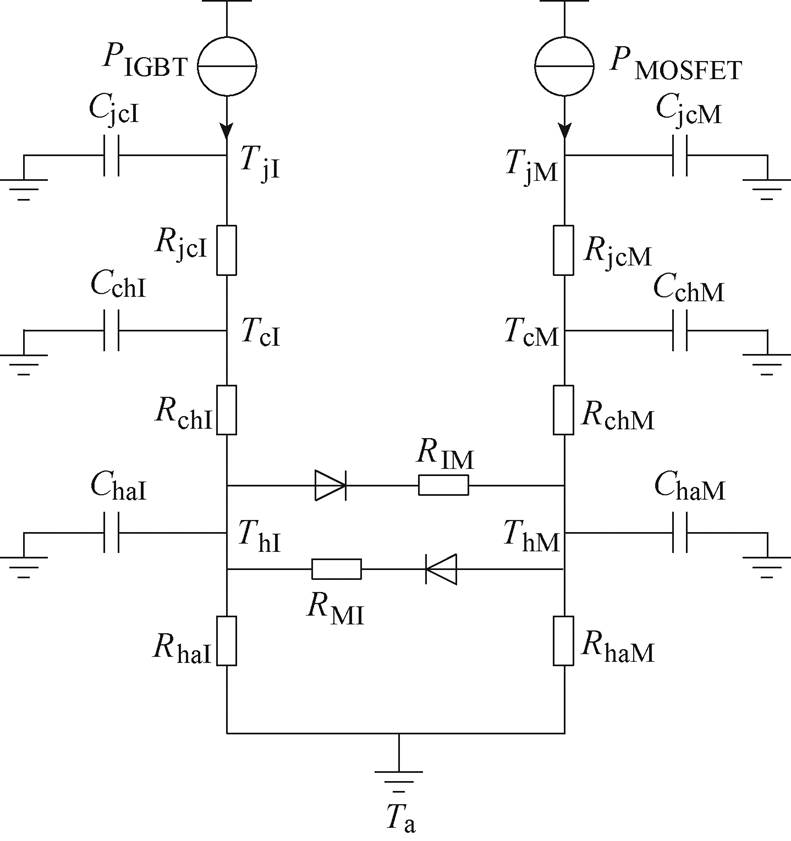
图2 混合器件耦合热网络模型
Fig.2 Hybrid switch coupled thermal network model
图2中,TjI和TcI分别为IGBT的结温和壳温;TjM和TcM分别为MOSFET的结温和壳温;ThI和ThM分别为IGBT和MOSFET正下方的散热器温度;Ta为环境温度;RjcI和CjcI分别为IGBT结到壳的热阻和热容;RjcM和CjcM分别为MOSFET结到壳的热阻和热容;RchI和CchI分别为IGBT壳到散热器基板的热阻和热容;RchM和CchM分别为MOSFET壳到散热器基板的热阻和热容;RhaI和ChaI分别为IGBT正下方散热器的热阻和热容;RhaM和ChaM分别为MOSFET正下方散热器的热阻和热容;RIM为从IGBT向MOSFET传热的横向热阻,RMI为从MOSFET向IGBT传热的横向热阻,即定义RIM和RMI为IGBT和MOSFET间的耦合热阻。
1.2.1 零输入响应法
零输入响应法指的是在不需要考虑激励信号的前提下,在时域中根据热网络时间常数对热参数进行辨识的方法[30]。首先,根据热结构分析RC网络参数与零输入响应条件下时间常数之间的关系;然后,通过改变散热条件,得到待辨识热网络参数的约束方程组;最后,根据多组热约束方程组进行RC参数辨识。
目前,常用的时间常数获取方法是基于器件冷却阶段的结温降温曲线或壳温降温曲线进行数据拟合而成,由于结温获取难度较大,本文以基于壳温降温曲线的热参数辨识方法为例进行分析。
1.2.2 零输入响应法在混合器件中的应用挑战
热电比拟理论是热网络模型的基础,其基本原理是通过将热参数转化为电参数,将热学相关问题转化为电学问题予以求解。如热阻和热容对应的是电阻和电容,温度和热流对应的是电压和电流。因此,在已知热网络模型各个热参数的前提下,通过求解电路方程便可轻松得到两类器件的结温信息和壳温信息。
针对图2所示的混合器件耦合热网络模型,当混合器件进入冷却阶段时,根据电热比拟理论,器件的降温过程可以等效为电路中的零输入响应。为了简化分析过程,将热网络转换到拉氏域,降温过程中混合器件等效热网络模型如图3所示。图3中,电压源UjI/s、UjM/s、UcI/s、UcM/s、UhI/s和UhM/s分别为混合器件运行一段时间后每个热容的初始电压。
针对图3所示混合器件等效热网络模型,列写拉氏域节点电压方程为
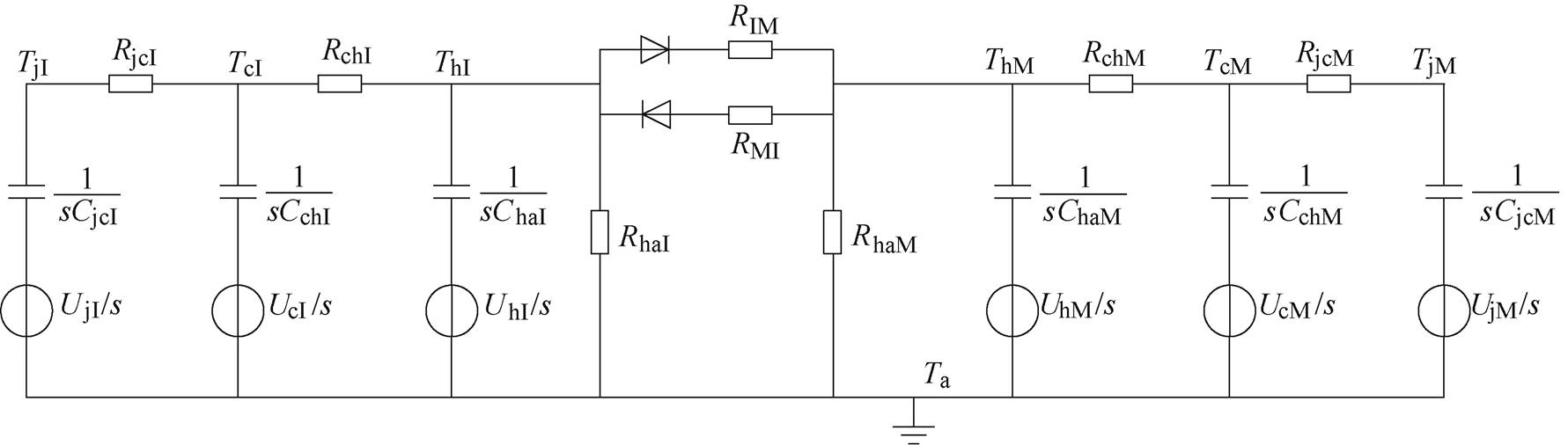
图3 降温过程中混合器件等效热网络模型
Fig.3 Equivalent thermal network model of hybrid switch during cooling process
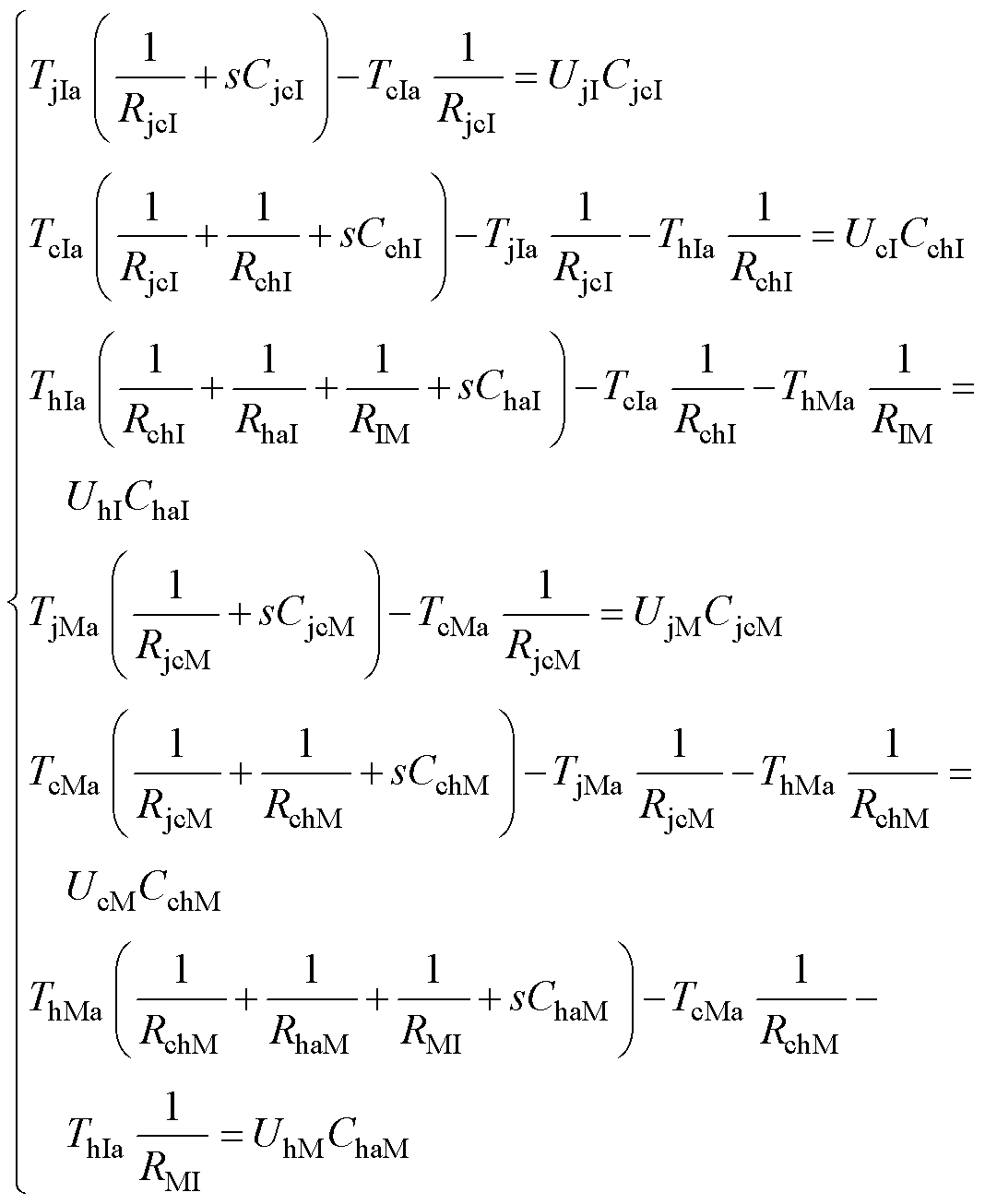 (1)
(1)
通过求解式(1)所示方程组可以得到节点电压TcIa=TcI-Ta或TcMa=TcM-Ta响应的拉氏表达式为
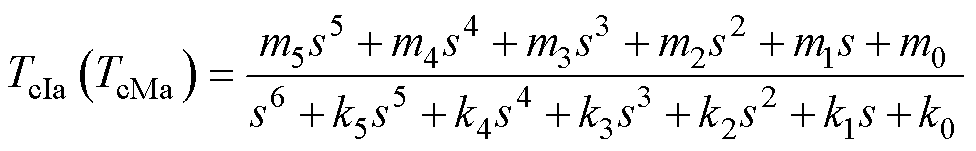 (2)
(2)
式中,系数m0~m5与RC参数以及热容初始电压相关;系数k0~k5仅与RC参数有关。由于式(2)的分母为Cauer型网络的特征方程,若已知特征方程的根,便可以根据根与系数的关系对所有RC参数进行求解。然而由于图3所示等效热网络模型的节点电压表达式(2)为6阶方程,根据满秩求解原则,特征方程的6个根必须全部已知方可辨识出所有RC参数。而根的求解往往是通过对混合器件的壳温降温曲线按照式(2)对应的时域方程式(3)拟合而成。
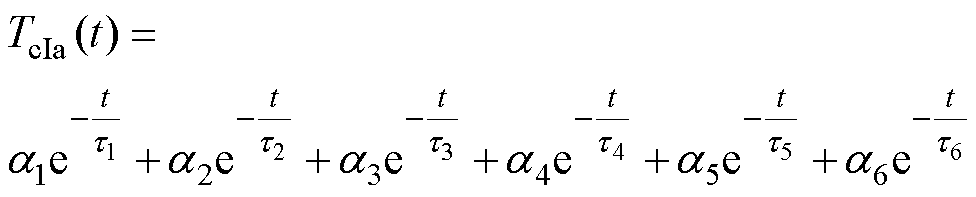 (3)
(3)
由式(3)可知,在混合器件中直接使用零输入响应法的前提是拟合出壳温降温曲线的6个热时间常数。然而,由于冷却过程中壳温的变化幅度不大,6阶拟合难度系数较高,进而导致热参数求解方程无法构建。综合分析可知,零输入响应法直接应用于混合器件时带来的挑战如下:
(1)混合器件耦合热网络阶数过高导致RC参数存在无法辨识的风险。
(2)高阶时间常数拟合困难,导致热约束条件无法构建。
因此,现有零输入响应法难以适用于高阶混合器件耦合热网络开展热参数辨识。
考虑到混合器件热网络中Si IGBT和SiC MOSFET仅在散热器上存在热耦合部分,结-壳热阻以及壳-散热器热阻为两套独立的级联系统。本文通过加热单一芯片对耦合热网络进行分区,将高阶热网络划分成2个低阶的等效热网络模型,降低零输入响应法的热参数辨识难度。
本文的应用对象为Si IGBT与SiC MOSFET并联构成的混合器件,由于功率器件多以热传导为主,垂直方向上的热量仅会由上往下传递。当Si IGBT与SiC MOSFET中只有单一芯片工作时,混合器件的热量传递路径如图4所示。
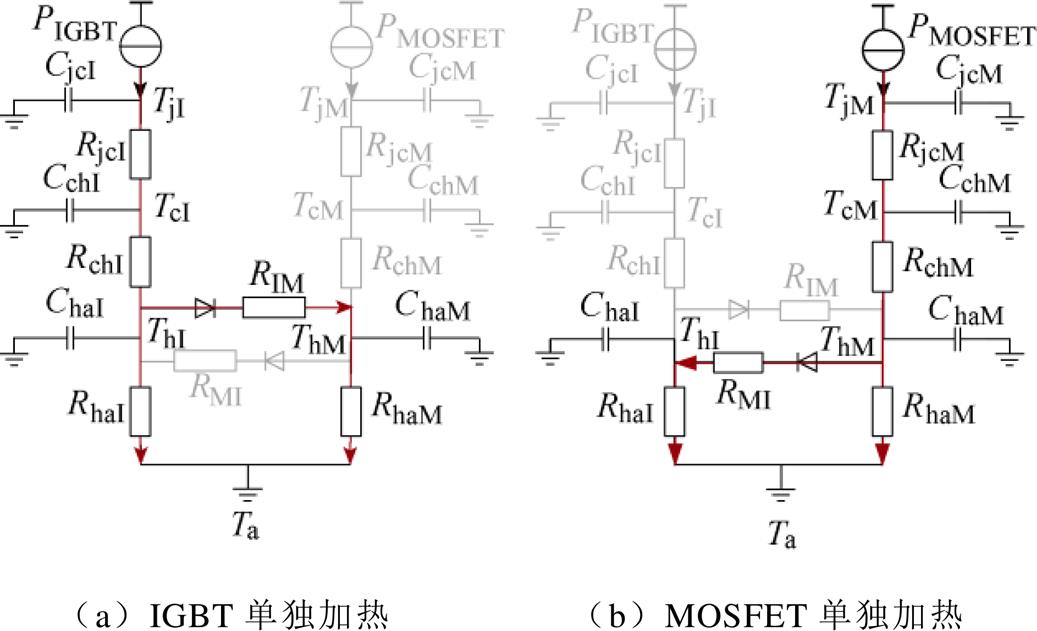
图4 热网络分区处理下的热量传递路径
Fig.4 Heat transfer path under partition processing of hybrid switch
由图4的热量传递路径可知,当混合器件中Si IGBT或SiC MOSFET单独工作时,耦合热网络模型会被划分成包含共同散热器热阻的两大块区域,这两块区域分别对应两个4阶的等效热网络模型。由于混合器件内芯片间的热耦合影响仅通过散热器耦合热阻进行传递,因此,通过分区处理可以在体现热耦合效应的基础上实现热网络模型的降阶,为零输入响应法的应用提供架构。实施过程如下。
首先分别独立给IGBT和MOSFET施加功率损耗PIGBT和PMOSFET,当器件加热一段时间后,关闭加热源,分别获取IGBT和MOSFET的壳温降温曲线。转换到拉氏域进行的具体热网络模型如图5所示,图5中,电压源UjI1/s、UcI1/s、UhI1/s和UhM1/s分别为单独加热IGBT后每个热容的初始电压,电压源UjM2/s、UcM2/s、UhM2/s和UhI2/s分别为单独加热MOSFET后每个热容的初始电压。
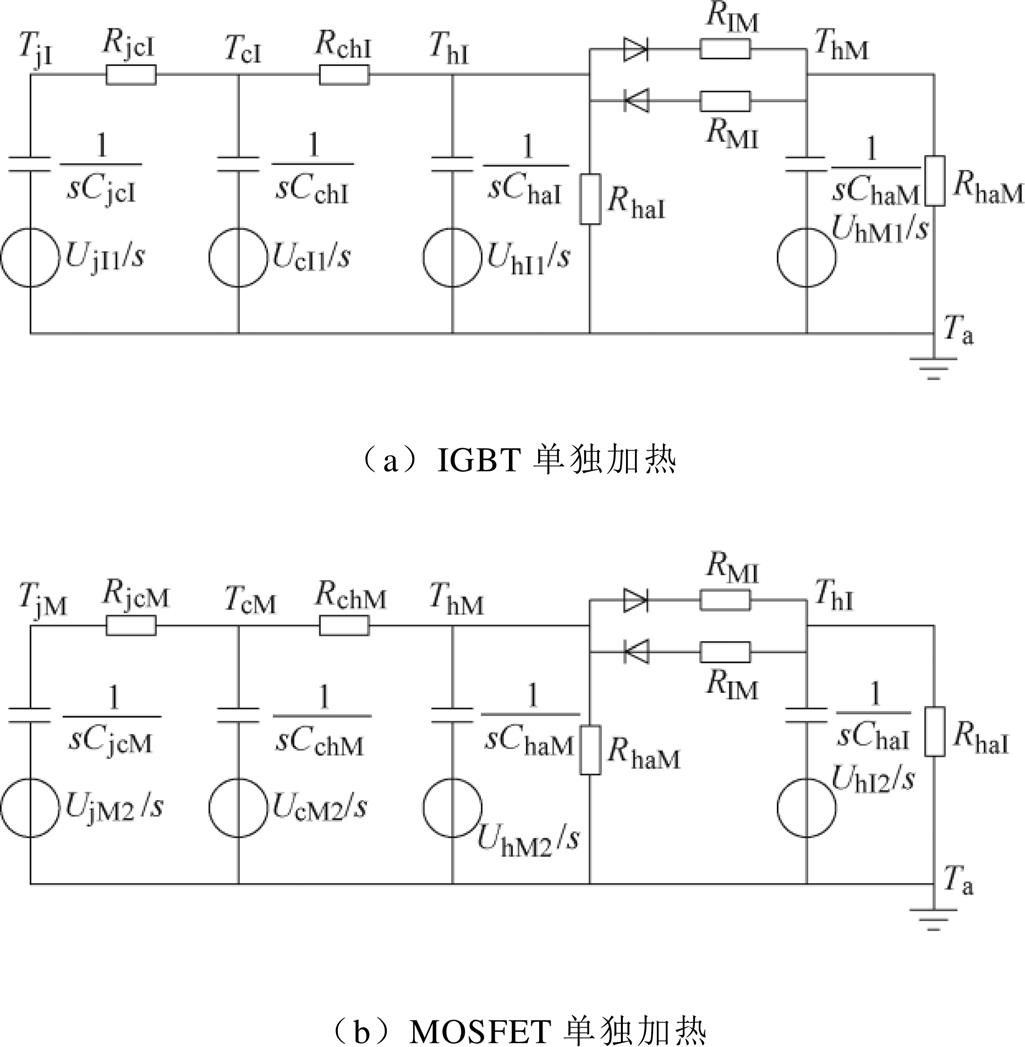
图5 分区处理后混合器件等效热网络模型
Fig.5 Equivalent thermal network model of hybrid switch after partition processing
根据基尔霍夫定律及节点电压方程,可以推导得到
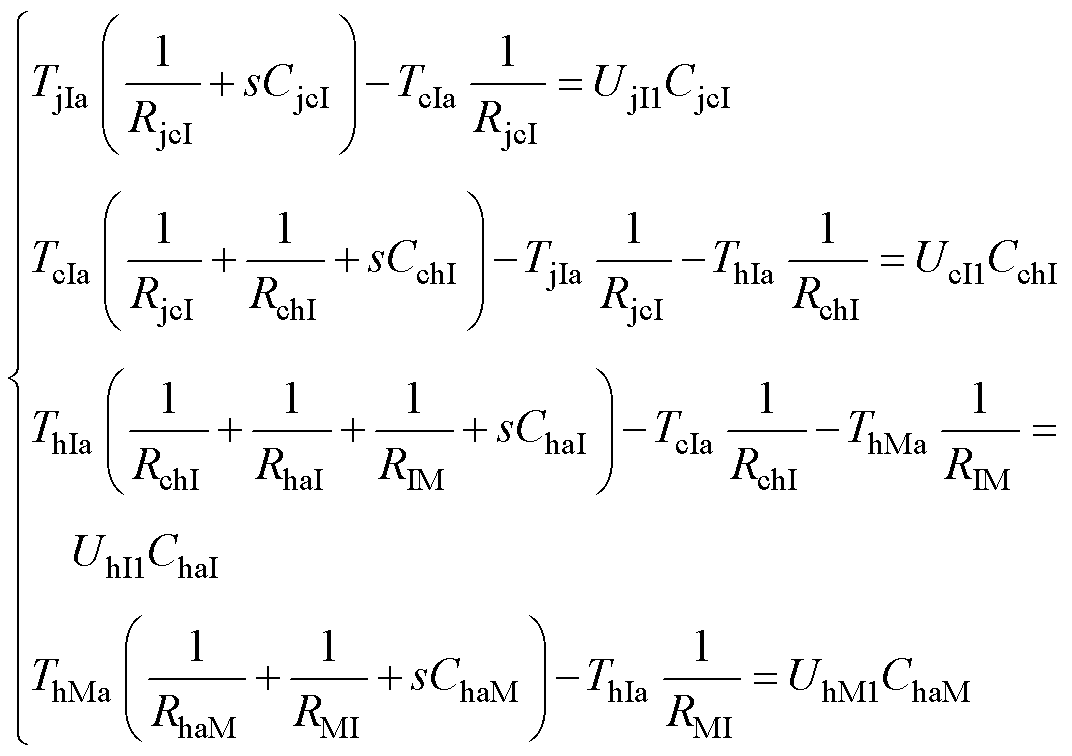 (4)
(4)
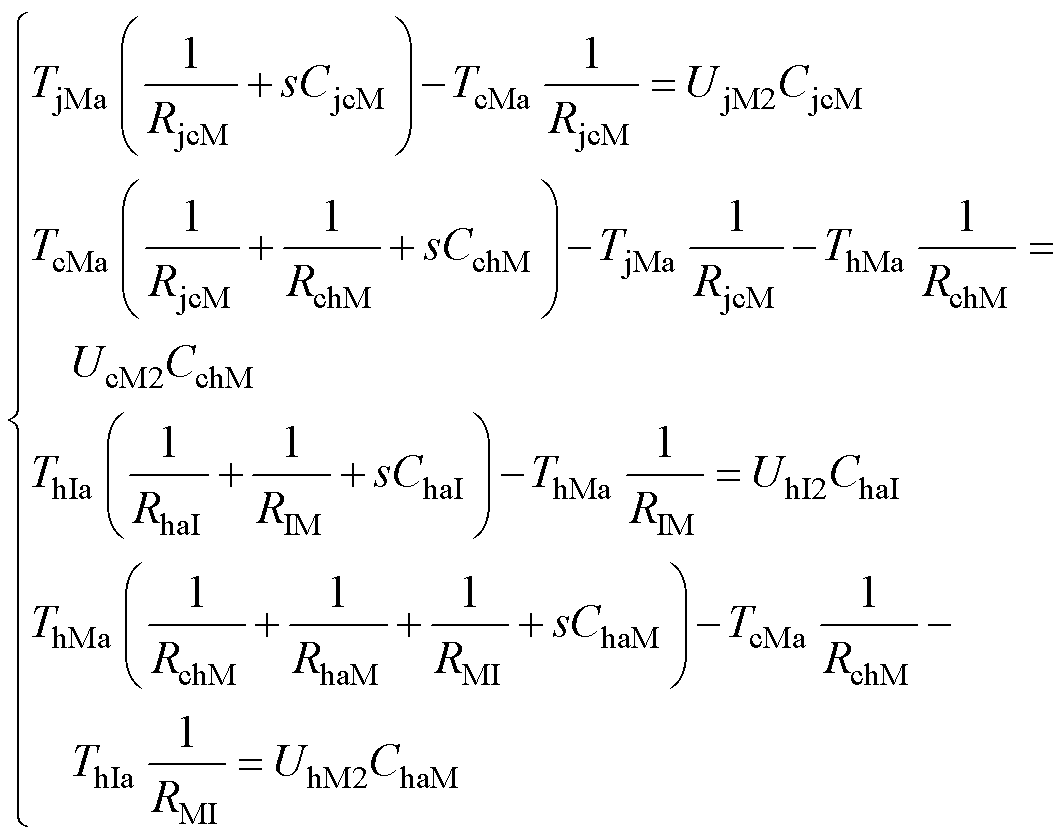 (5)
(5)
求解方程组式(4)、式(5),可得节点电压TcIa=TcI-Ta和TcMa=TcM-Ta响应的拉氏表达式为
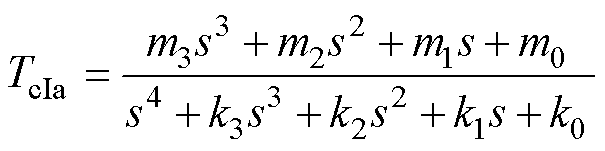 (6)
(6)
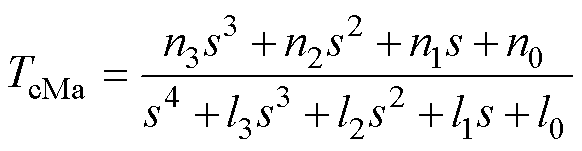 (7)
(7)
式中,系数m0~m3、n0~n3和RC参数以及热容初始电压相关;系数k0~k3、l0~l3仅和RC参数有关,如式(A1)和式(A2)所示。
由于式(6)、式(7)的分母为Cauer型网络的特征方程,并且该方程的解都是位于负实轴的单阶解,因此式(6)、式(7)可以通过部分分式展开成
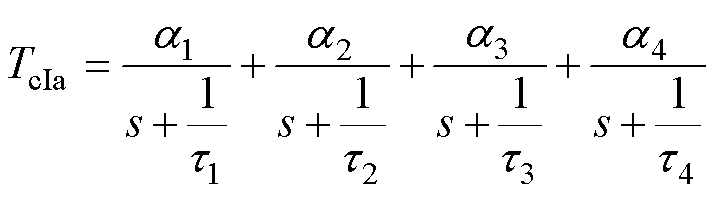 (8)
(8)
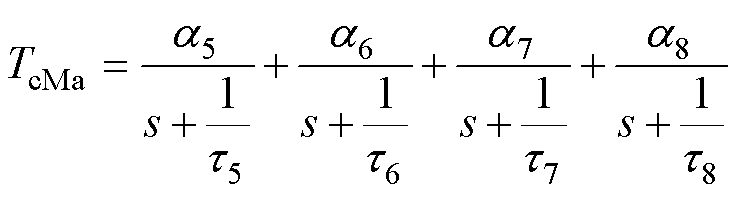 (9)
(9)
式中,a1~a4为与极点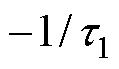 、
、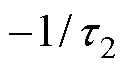 、
、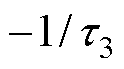 、
、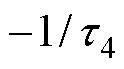 相关的系数;a5~a8为与极点
相关的系数;a5~a8为与极点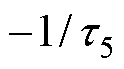 、
、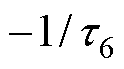 、
、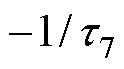 、
、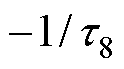 相关的系数。
相关的系数。
对式(8)、式(9)进行拉氏反变换,IGBT和MOSFET壳温降温曲线的时域表达式分别为
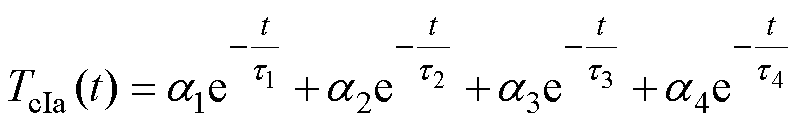 (10)
(10)
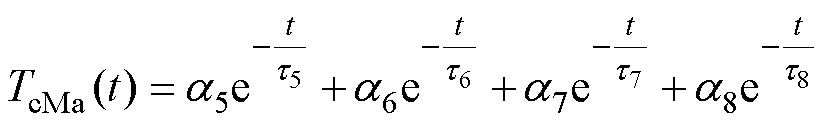 (11)
(11)
由式(10)、式(11)可知,基于热网络分区等效思想得到的TcIa和TcMa对应的时间常数仅为4个,相比于式(3)而言数量减少2个,通过对TcIa和TcMa进行曲线拟合便可以轻松获取时间常数t1~t8。根据零输入响应法的求解原则,下一步需要构建时间常数与RC参数之间的约束方程组。
由式(8)、式(9)可知,极点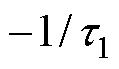 、
、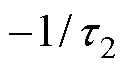 、
、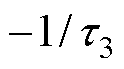 、
、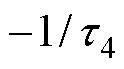 是特征方程
是特征方程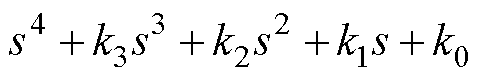 的根,极点
的根,极点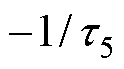 、
、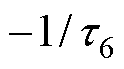 、
、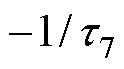 、
、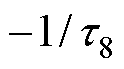 是特征方程
是特征方程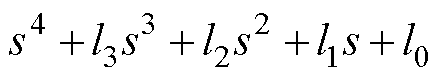 的根。根据一元四次方程根与系数的关系,可以得到时间常数与热参数之间的约束方程为
的根。根据一元四次方程根与系数的关系,可以得到时间常数与热参数之间的约束方程为
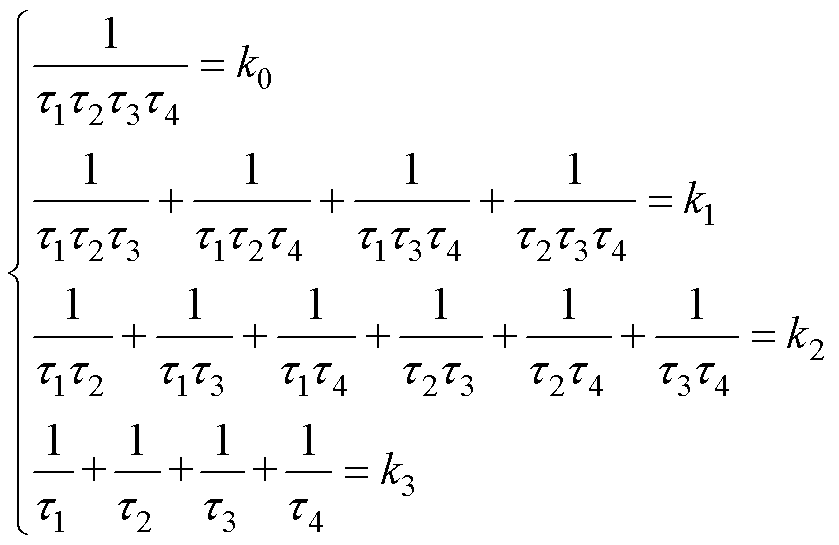 (12)
(12)
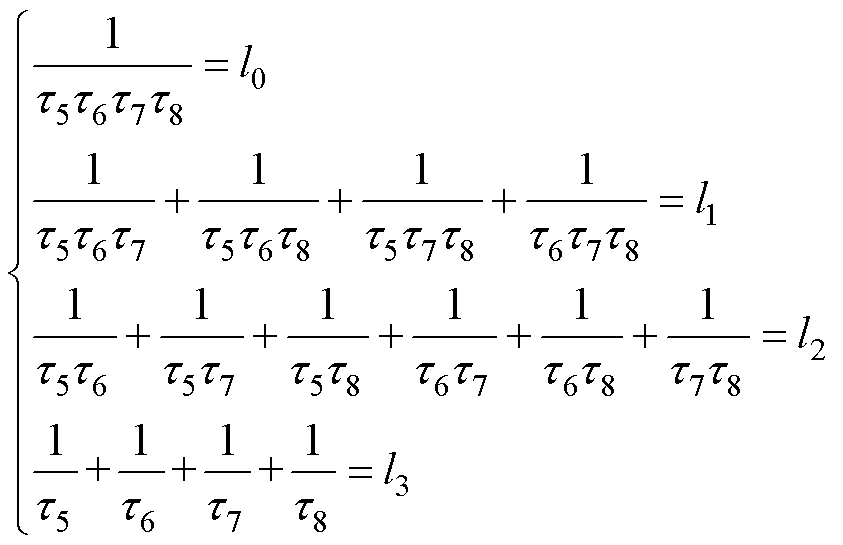 (13)
(13)
实际测试中,通过数据采集器可记录IGBT和MOSFET的壳温降温曲线,然后根据式(10)、式(11)进行数据拟合获取时间常数t1~t8,即t1~t8可视为已知量。由式(12)、式(13)可知,目前方程数量为8个,但未知量为14个:RjcI、RchI、RhaI、RjcM、RchM、RhaM、RIM、RMI、CjcI、CchI、ChaI、CjcM、CchM、ChaM。当未知量的数量大于方程数量时,方程的解不唯一。因此,仅通过一种工况下的降温曲线热时间常数不足以求解出所有热参数,需要增加新的约束条件方可辨识出所有热网络参数。
改变外部散热条件是实用性相对较高的一种解决方案,当外部散热条件发生变化时,只有RhaI、RhaM、RIM、RMI、ChaI、ChaM这6个值受到影响,通过增加一组散热工况便可以导出一组新的约束方程。由于改变散热工况对IGBT和MOSFET的结壳热阻抗以及导热硅脂热阻抗并无影响,因此,IGBT和MOSFET的热约束方程任意选用一组即可,表示为
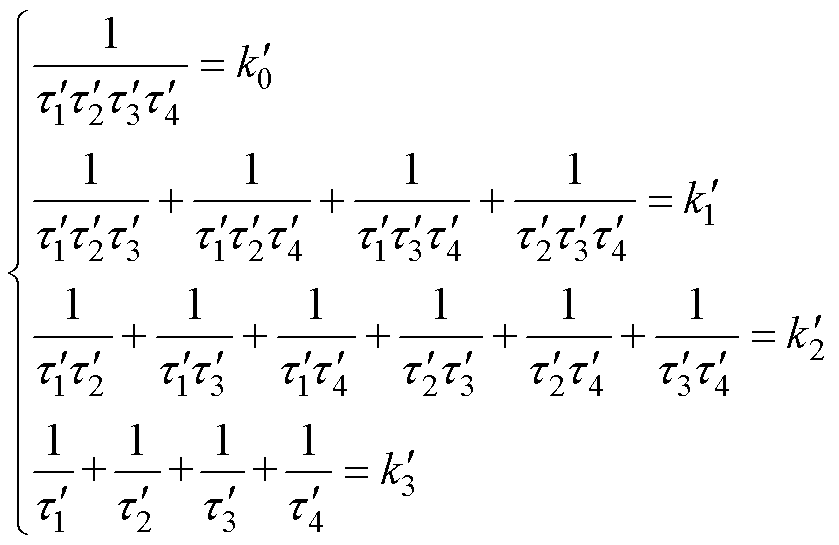 (14)
(14)
式中,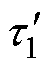 ~
~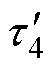 为第二组散热工况下IGBT单独加热时壳温降温曲线的时间常数;
为第二组散热工况下IGBT单独加热时壳温降温曲线的时间常数;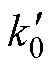 ~
~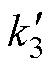 的表达式如式(A3)所示。由于RhaI、RhaM、RIM、RMI、
的表达式如式(A3)所示。由于RhaI、RhaM、RIM、RMI、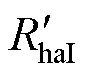 、
、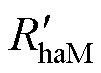 、
、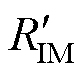 、
、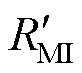 可以较为容易测量得到,其可视为热约束方程组求解的已知量和前提条件。由式(12)~式(14)可知,共12个方程包含12个未知数:RjcI、RchI、RjcM、RchM、CjcI、CchI、ChaI、CjcM、CchM、ChaM、C'haI、C'haM,因此,通过联立求解热网络分区等效下的方程组式(12)~式(14)便可以辨识出剩余所有的热参数。
可以较为容易测量得到,其可视为热约束方程组求解的已知量和前提条件。由式(12)~式(14)可知,共12个方程包含12个未知数:RjcI、RchI、RjcM、RchM、CjcI、CchI、ChaI、CjcM、CchM、ChaM、C'haI、C'haM,因此,通过联立求解热网络分区等效下的方程组式(12)~式(14)便可以辨识出剩余所有的热参数。
本文针对Si IGBT/SiC MOSFET混合器件提出了热网络分区等效思想,并结合壳温降温曲线详细介绍了其热参数辨识方法,图6给出了所提方法的具体实施步骤。
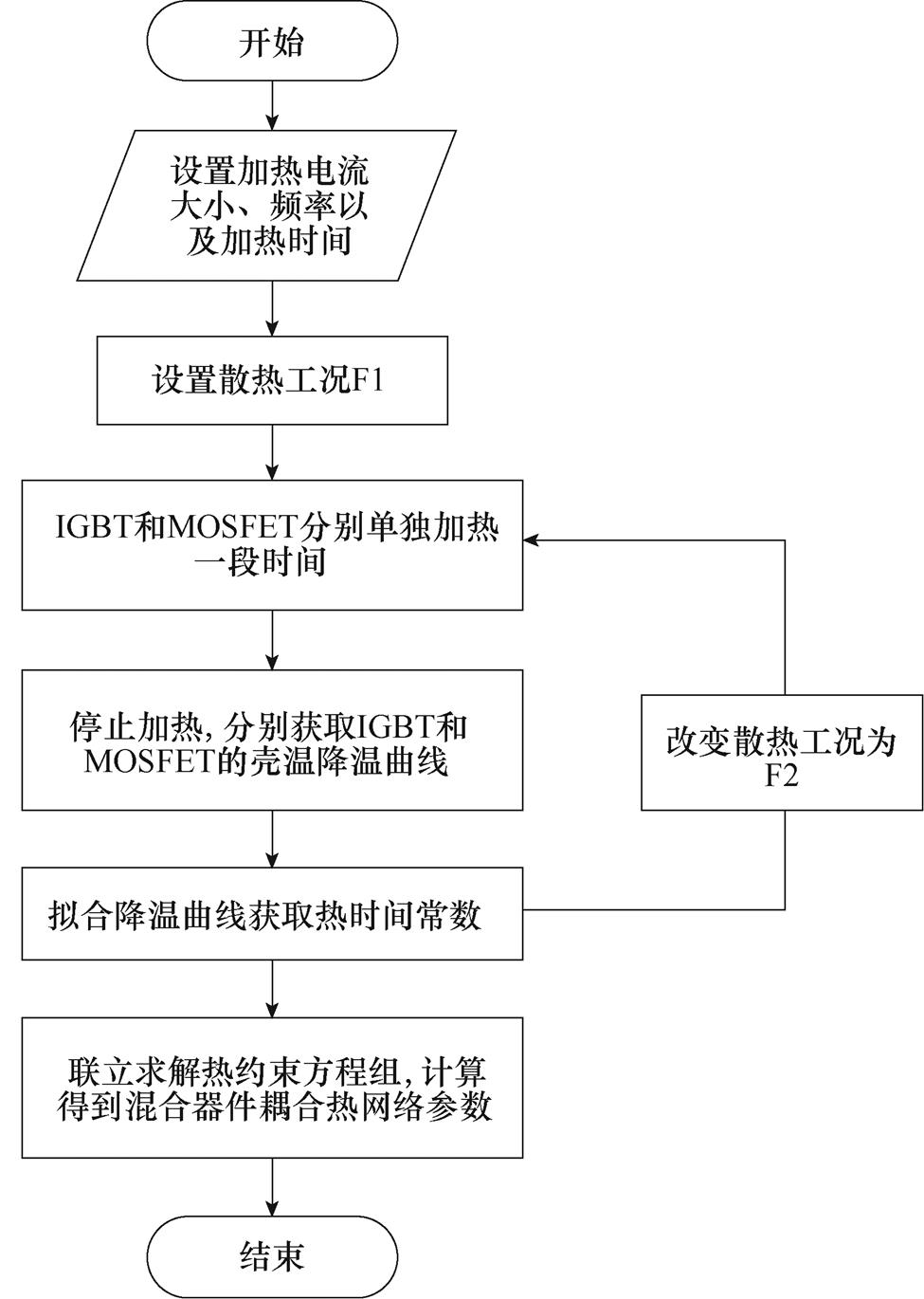
图6 热参数辨识流程
Fig.6 Thermal parameter identification process
首先,将散热工况设定为F1,分别独立给IGBT和MOSFET施加功率损耗;其次,当器件运行一段时间后,停止加热,分别获取IGBT和MOSFET的壳温降温曲线,通过对TcIa和TcMa进行数据拟合得到时间常数t1~t8;然后,将散热工况调整为F2,按照同样的方式获取F2下的时间常数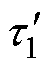 ~
~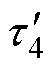 ;最后,通过求解时间常数与热参数之间的约束方程组式(12)~式(14),便可以辨识出所有RC参数。综上所述,混合器件的耦合热网络参数已全部求解得到。
;最后,通过求解时间常数与热参数之间的约束方程组式(12)~式(14),便可以辨识出所有RC参数。综上所述,混合器件的耦合热网络参数已全部求解得到。
为验证所提方法,本文搭建了如图7所示的实验平台,该平台主要由直流加热电源、DSP控制板、主功率板、数据采集器以及配套上位机构成。测试所用器件为英飞凌公司的Si IGBT(IGW25N120H3)和CREE公司的SiC MOSFET(C2M0160120D)并联构成的混合器件。

图7 实验平台
Fig.7 Experimental platform
待测混合器件安装于同一风冷散热器上,IGBT和MOSFET底部芯片正下方均用胶水粘有K型热电偶用来检测器件壳温;用导热硅脂填补器件底部和散热器之间的空隙部分;通过在芯片正下方散热器上进行平行挖槽,埋放K型热电偶用来检测散热器温度。针对IGBT壳温TC_IGBT、MOSFET壳温TC_MOSFET和对应散热器温度检测TH_IGBT、TH_MOSFET的K型热电偶安装示意图如图8所示。
散热工况可以通过改变散热风扇的调速进行调整,由于散热风扇的风速与驱动电压成正比,本文设定第一种散热工况对应的驱动电压为24 V,命名为F1,第二种散热工况对应的驱动电压为10 V,命名为F2。测试电路的原理如图9所示。
测试流程为:
(1)IGBT单独加热工况模拟。首先,使回路中的S1和待测混合器件中的IGBT处于常通状态,在S2的驱动口施加一个方波信号用来控制混合器件支路电流的切换。当S2导通时,待测器件IGBT和S2共同分担回路电流;当S2关断时,待测器件IGBT单独承担所有电流。如此设置可以让IGBT内部产生一定的温度波动,处于一个非热平衡状态。
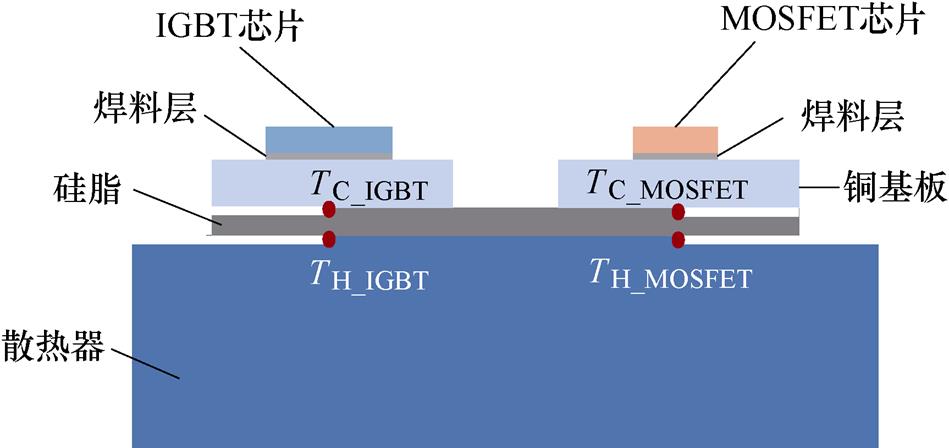
图8 热电偶安装示意图
Fig.8 Thermocouple installation diagram
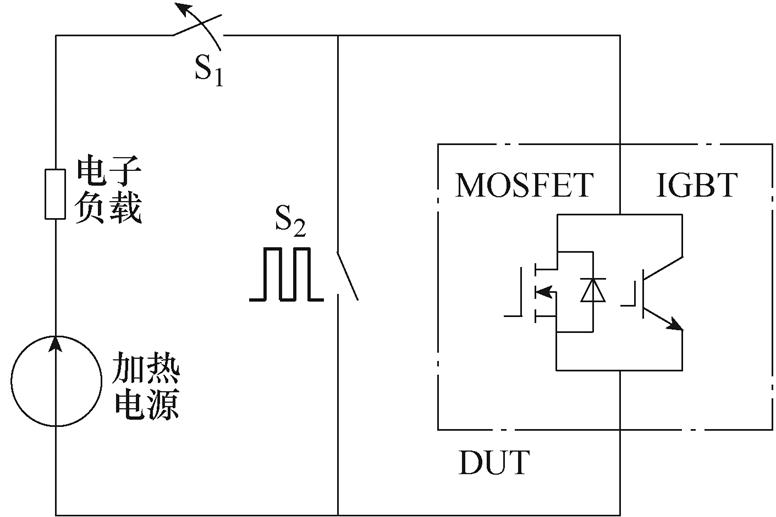
图9 实验测试电路原理
Fig.9 Schematic diagram of experimental testing circuit
(2) MOSFET单独加热工况模拟。按照步骤(1)所述,参考IGBT运行模式仅使MOSFET处于温度波动状态。
(3)壳温降温曲线获取。在散热工况F1下,对应步骤(1)和步骤(2)所述两种加热工况,当IGBT或MOSFET单独加热一段时间后,断开S1,利用温度测量系统对冷却过程中的IGBT或MOSFET壳温以及环境温度进行采集,直至壳温降至环境温度。然后,将散热工况调整为F2,重复以上步骤,获取第二组壳温降温曲线。
当回路电流为10 A时,两种加热工况下IGBT和MOSFET的测试电流IF波形如图10所示。
两种散热工况下,IGBT和MOSFET降温过程中分别对应的壳温以及环境温度波形如图11所示。
F1和F2下IGBT和MOSFET的Tca(t)=Tc(t)-Ta(t)的波形如图12所示。
使用Matlab的数学拟合工具箱按照式(10)、式(11),对两种散热工况下的降温曲线进行时间常数拟合,拟合结果见表1。
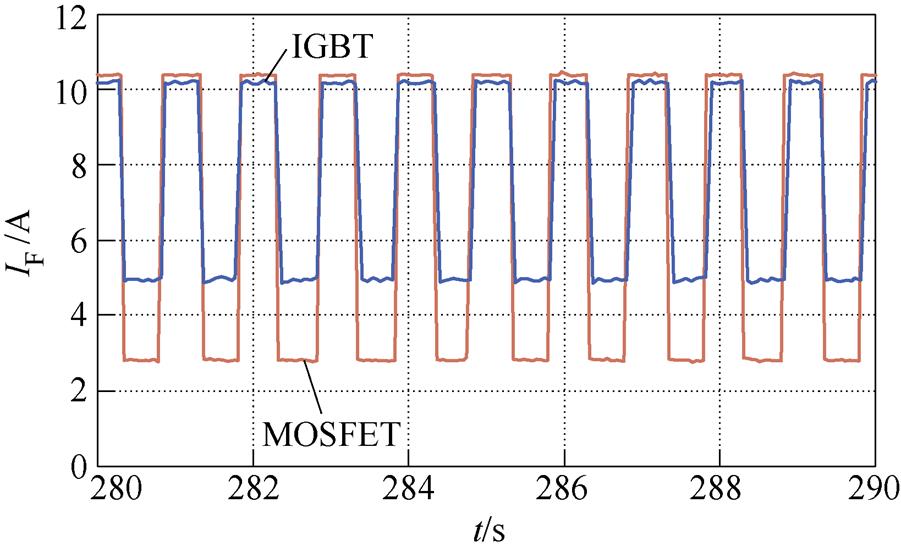
图10 IGBT和MOSFET单独加热时的测试电流
Fig.10 Test current when IGBT and MOSFET are heated separately
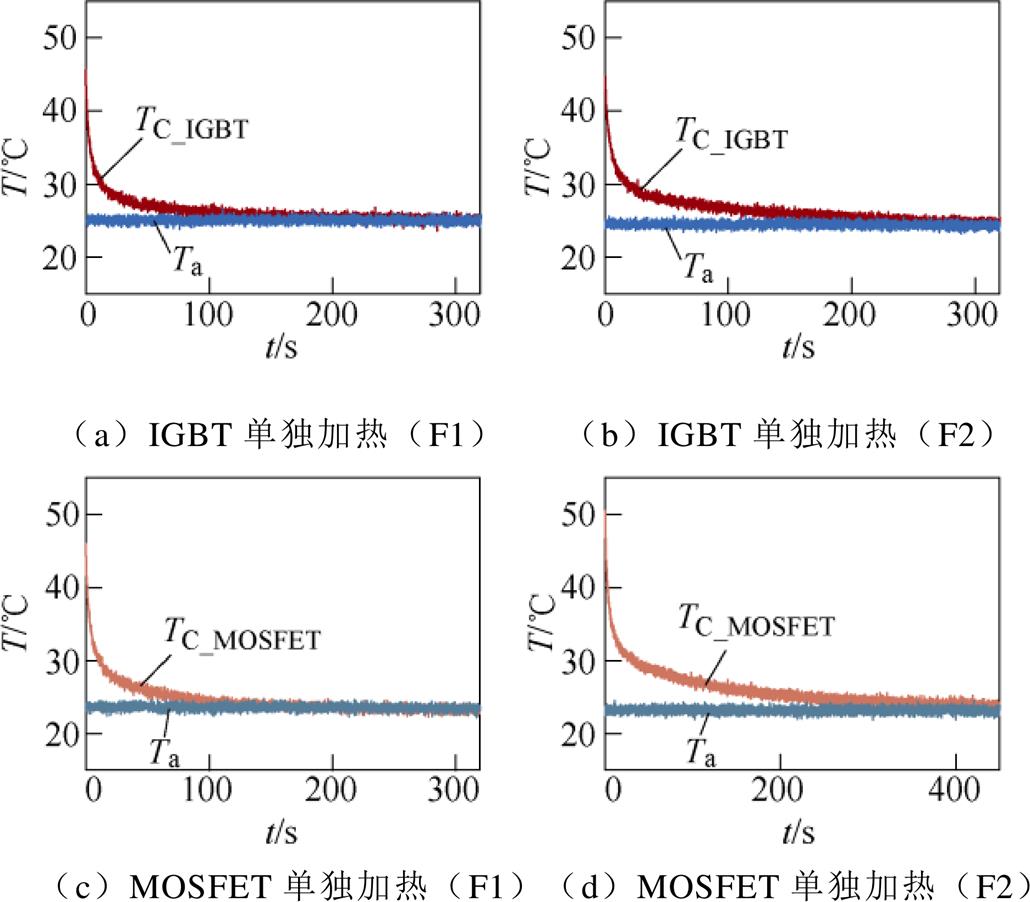
图11 两种散热工况下的壳温、环境温度曲线
Fig.11 Case temperature and ambient temperature curves under two heat dissipation conditions
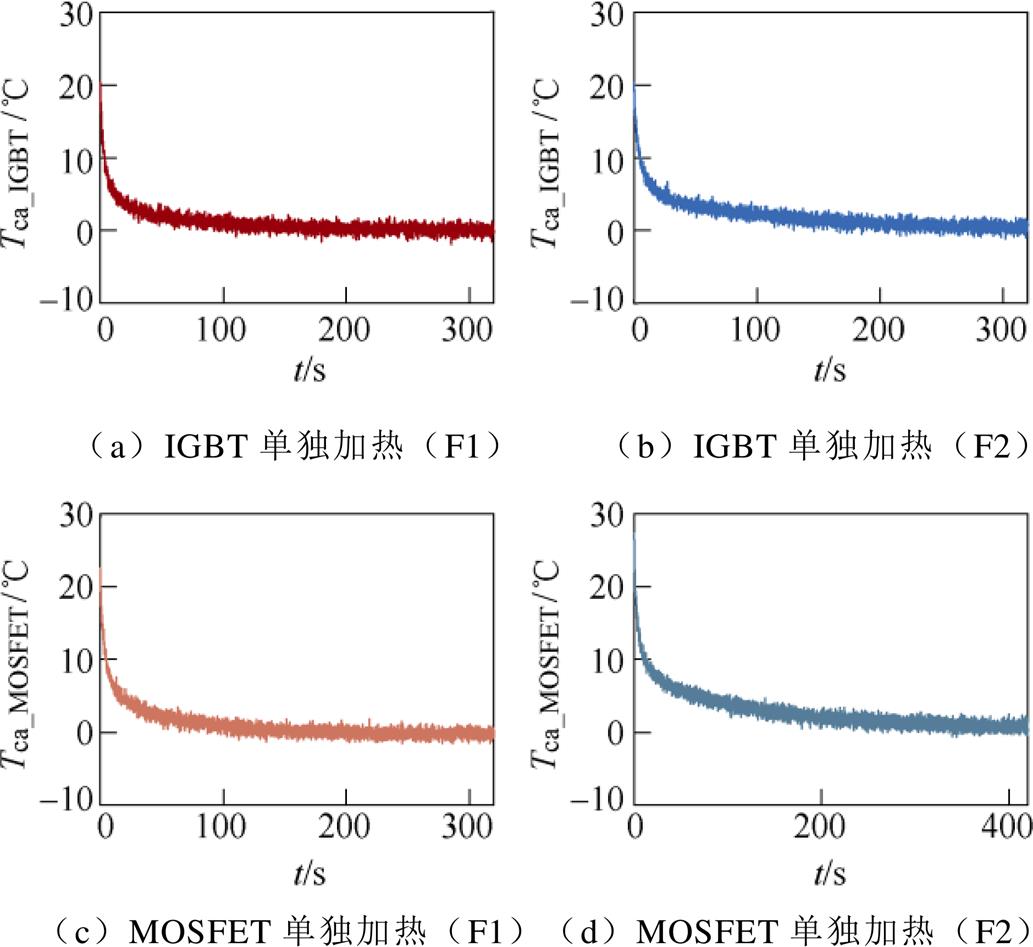
图12 两种散热工况下混合器件的Tca降温曲线
Fig.12 Tca cooling curves of hybrid switch under two heat dissipation conditions
表1 不同散热工况下的时间常数
Tab.1 Time constant under different heat dissipation conditions
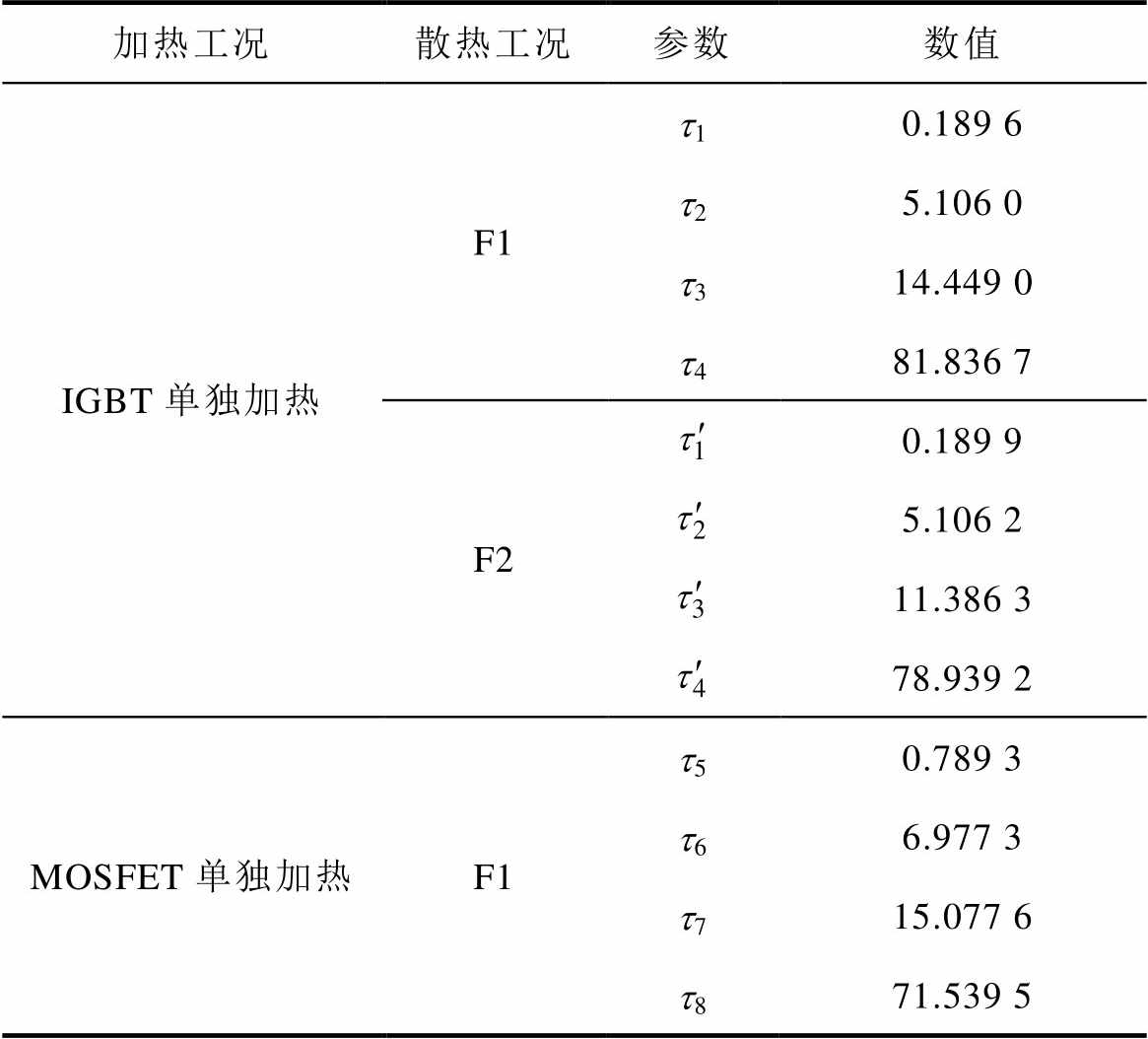
加热工况散热工况参数数值 IGBT单独加热F1t10.189 6 t25.106 0 t314.449 0 t481.836 7 F20.189 9 5.106 2 11.386 3 78.939 2 MOSFET单独加热F1t50.789 3 t66.977 3 t715.077 6 t871.539 5
将提前测量得到的RhaI、RhaM、RIM、RMI、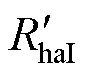 、
、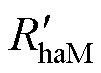 、
、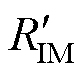 、
、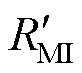 以及表1所示的时间常数代入式(12)~式(14),使用Matlab中的非线性最小二乘函数lsqnonlin以及trust-region-reflective算法求解方程组,辨识得到的混合器件耦合热网络参数见表2。
以及表1所示的时间常数代入式(12)~式(14),使用Matlab中的非线性最小二乘函数lsqnonlin以及trust-region-reflective算法求解方程组,辨识得到的混合器件耦合热网络参数见表2。
表2 混合器件耦合热网络参数辨识结果
Tab.2 Parameter identification results of hybrid switch coupled thermal network
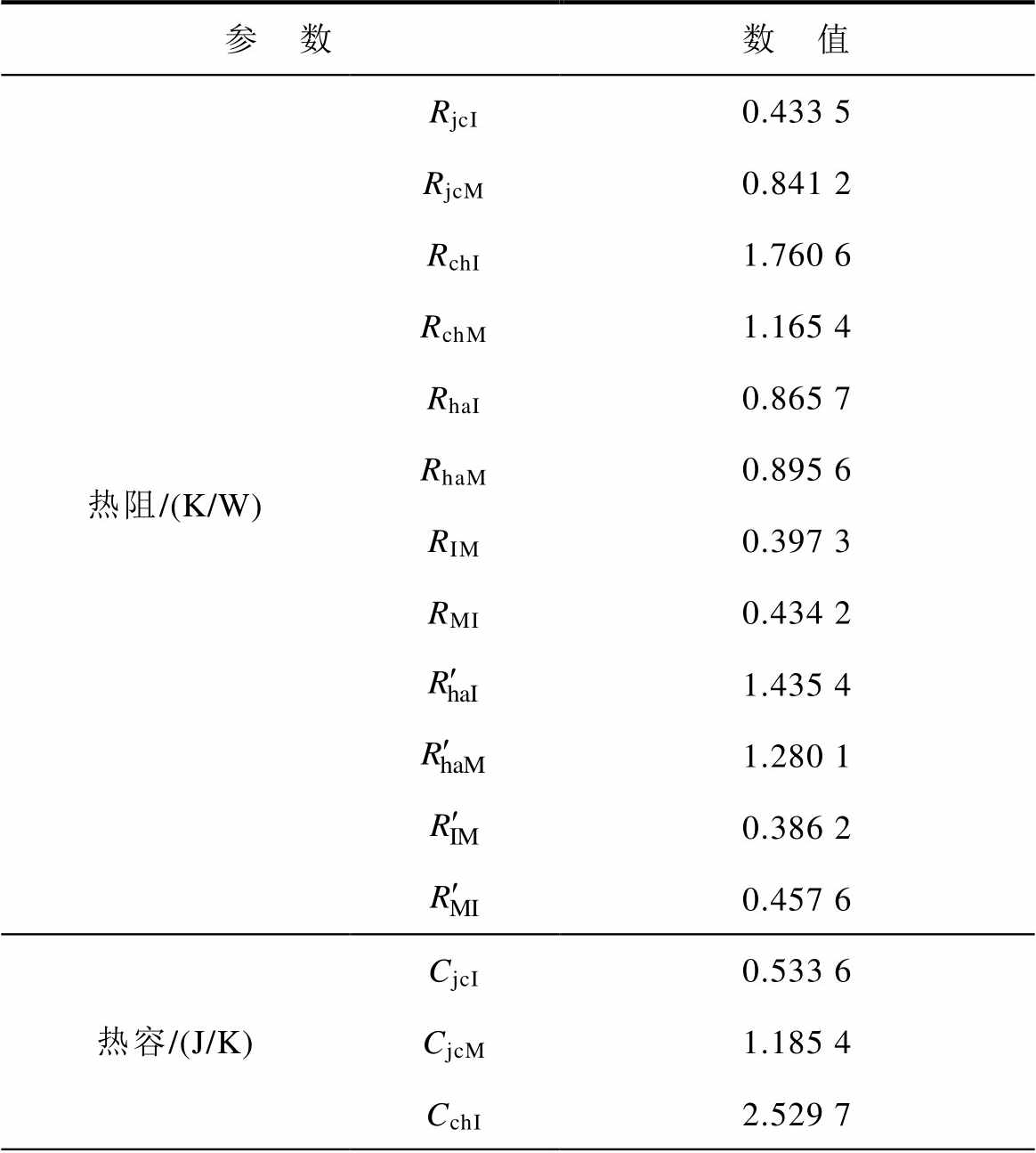
参 数数 值 热阻/(K/W)RjcI0.433 5 RjcM0.841 2 RchI1.760 6 RchM1.165 4 RhaI0.865 7 RhaM0.895 6 RIM0.397 3 RMI0.434 2 1.435 4 1.280 1 0.386 2 0.457 6 热容/(J/K)CjcI0.533 6 CjcM1.185 4 CchI2.529 7
(续)
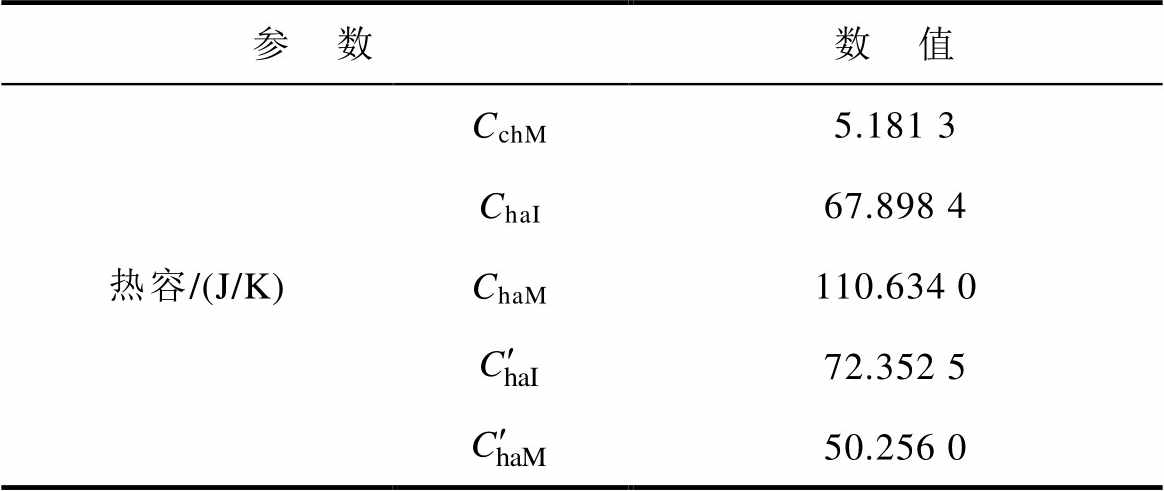
参 数数 值 热容/(J/K)CchM5.181 3 ChaI67.898 4 ChaM110.634 0 72.352 5 50.256 0
本文通过IEC标准测试和结温对比实验来验证耦合热网络参数辨识结果的准确性。
3.3.1 IEC标准测试
根据IEC标准的测试要求,首先需测量器件加热至热稳态时的功率损耗P以及结温Tj和壳温Tc之间的温度差,然后计算器件的稳态结壳热阻Rth(j-c)为
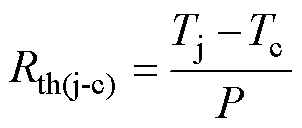 (15)
(15)
将本文的热参数辨识结果与通过IEC标准测试得到的稳态结壳热阻对比见表3。由表3中数据可知,本文所提方法与IEC标准测试下IGBT和MOSFET的结壳热阻误差均在2%以内,说明两种方法测量得到的结壳热阻基本相同。
表3 结壳热阻对比
Tab.3 Comparison of junction to case thermal resistance
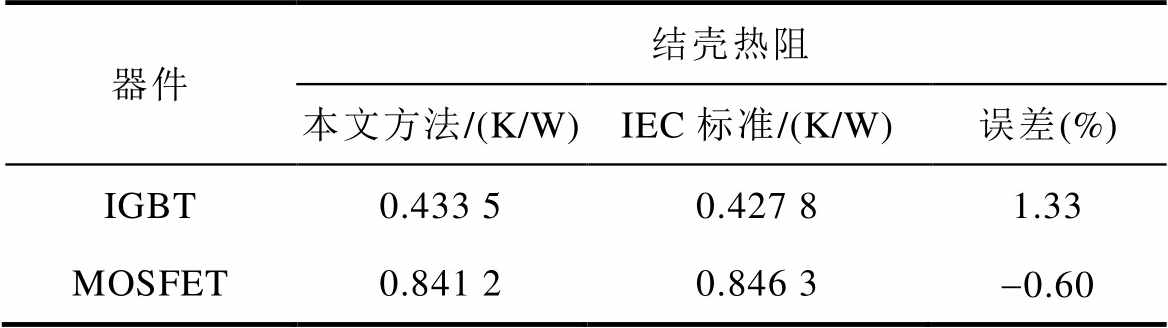
器件结壳热阻 本文方法/(K/W)IEC标准/(K/W)误差(%) IGBT0.433 50.427 81.33 MOSFET0.841 20.846 3-0.60
3.3.2 结温对比实验
由于红外热成像仪扫描频率较低,其难以准确捕捉瞬态结温值,为实现结温实时提取,本文采用大电流注入法来测量结温。
首先,将器件放置于干燥箱中一段时间,使其达到恒温状态;然后,在不同电流下测取温度和器件通态压降之间的关系,为防止器件导通时间过长引起芯片结温的改变,单次采样测量时间被控制在ms级。IGBT和MOSFET在不同电流等级下的结温和通态压降实验数据如图13所示。
由图13可知,大电流注入下IGBT结温和通态压降间的三维数据库可提前测得,其中电流等级覆盖了IGBT和MOSFET的额定工作区间。若已知器件电流和压降,便可通过查表提取出芯片结温。基于此,本文采用大电流注入法来获取器件运行过程中的瞬态结温。
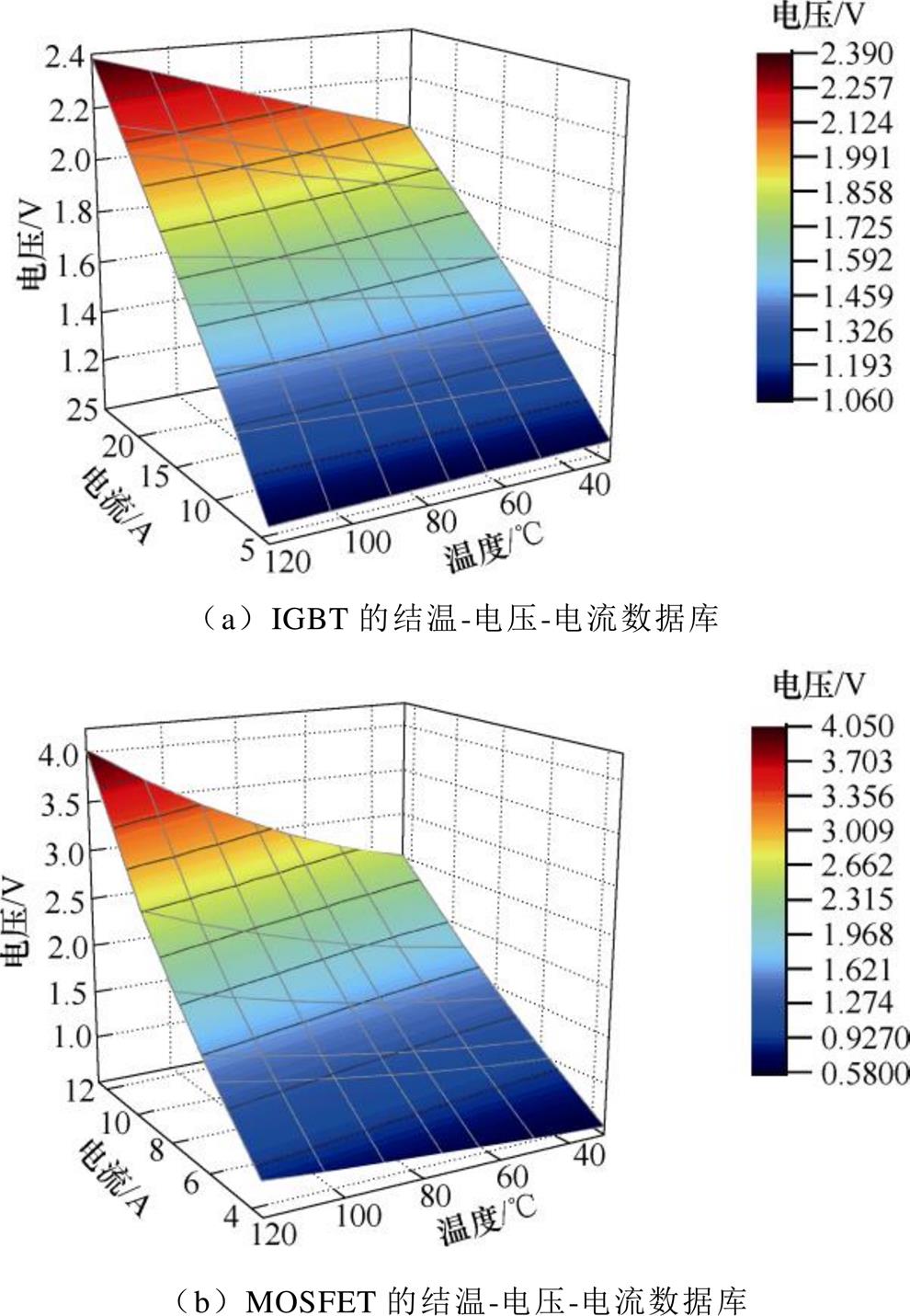
图13 基于大电流注入法的器件结温-电压-电流数据库
Fig.13 Device junction temperature-voltage-current database based on high current injection method
为验证混合器件的热耦合准确性,本文选取IGBT和MOSFET同时工作的工况开展瞬态结温对比实验。当回路电流为30 A,加热时间分别为0.5 s和5 s时,IGBT和MOSFET的采用本文所提方法的估算结温和基于大电流注入法得到的实测结温对比如图14和图15所示。
由图14和图15所示的瞬态结温对比情况可知,尽管热参数结果由IGBT和MOSFET单独加热下的壳温降温曲线拟合求解得到,二者同时工作时的结温实验波形和本文所提方法结温估算波形基本保持一致,证明了基于热网络分区等效思想辨识得到的耦合热参数结果的准确性。
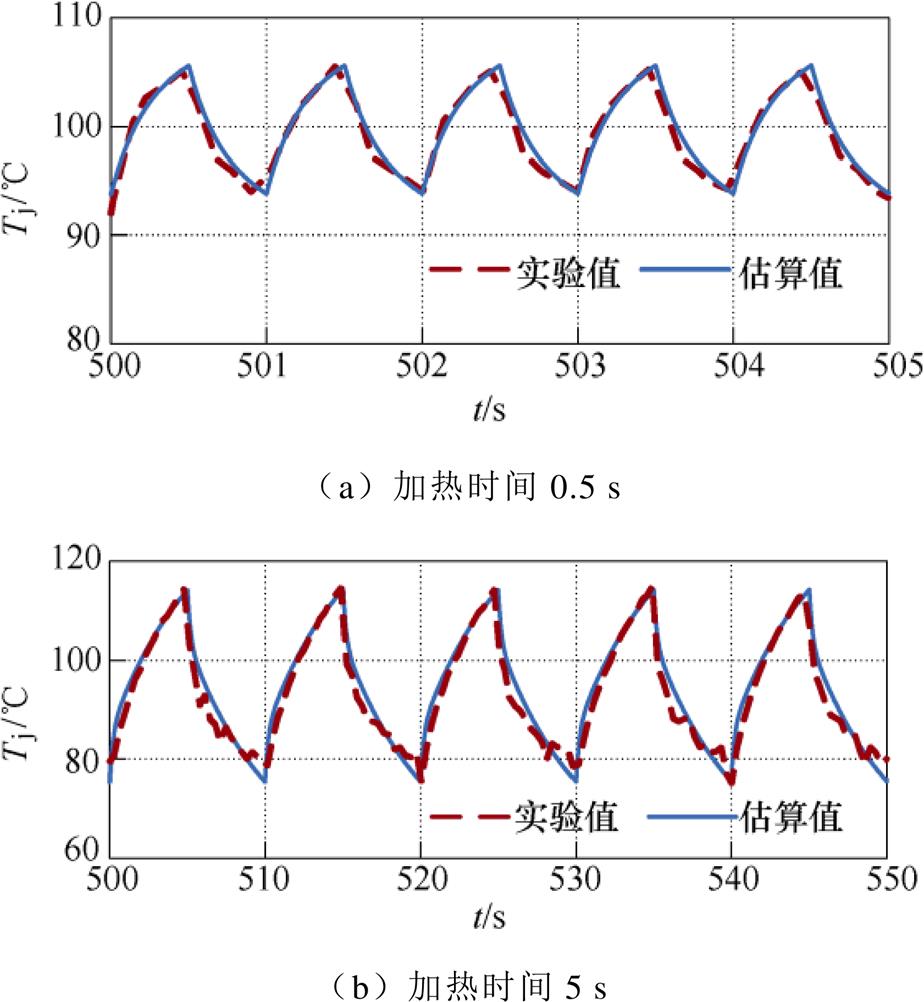
图14 IGBT瞬态估算结温和实测结温对比
Fig.14 Comparison between transient estimated junction temperature and measured junction temperature of IGBT
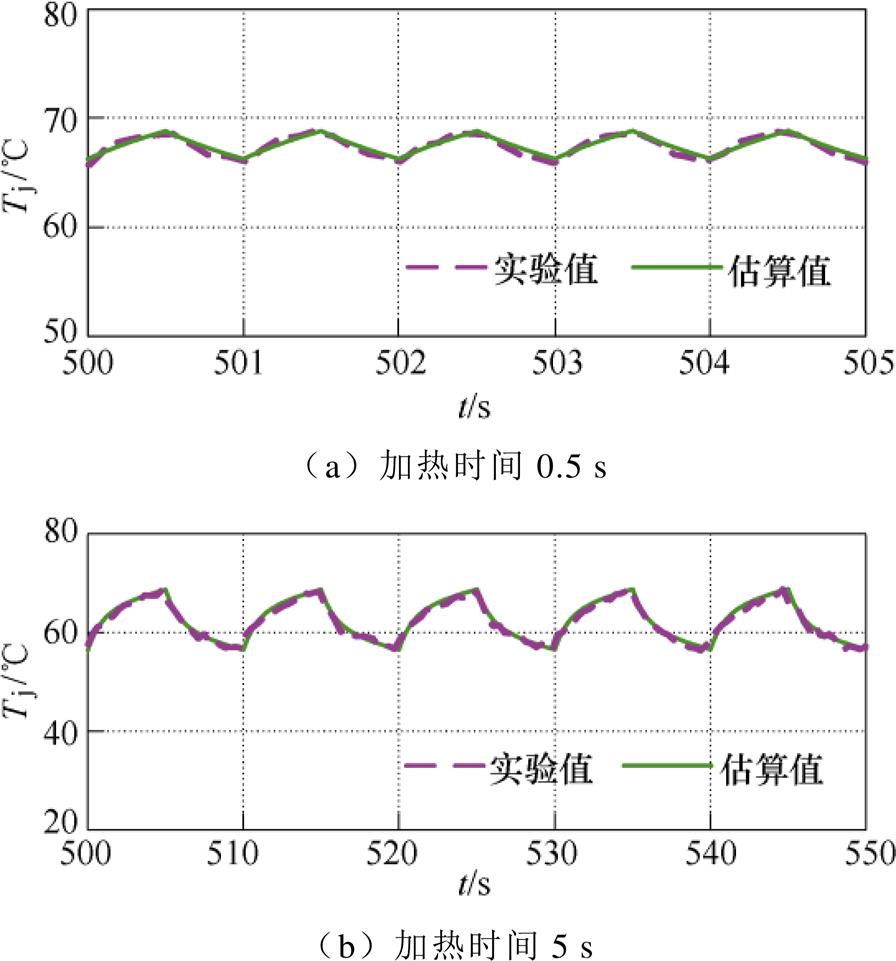
图15 MOSFET瞬态估算结温和实测结温对比
Fig.15 Comparison between transient estimated junction temperature and measured junction temperature of MOSFET
基于上述实验结果可知,采用本文方法得到的混合器件耦合热网络估算结温和实测结温在多种时间尺度下都吻合良好,且稳态结壳热阻和已得到广泛认可的IEC标准测量结果相近,证明了本文方法的可行性和准确性。
本文在传统零输入响应法基础上,针对由Si IGBT和SiC MOSFET并联构成的混合器件,提出了一种基于热网络分区等效思想的耦合热参数辨识方法。该方法利用热网络分区处理减少热时间常数的阶数,进而拟合求解热时间常数与RC参数之间的约束方程,来辨识得到混合器件的耦合热网络参数。本文方法不需要将器件加热至稳态和测量功率损耗,克服了现有并联器件热参数提取的不足,有效地拓宽了零输入响应法在混合器件等并联结构中的应用范围。另外,热网络分区等效思想可以进一步推广至3个及以上器件并联结构,大幅提升了零输入响应法的复杂场景适用性。
本文设计了混合器件热参数测试实验平台,对所提方法进行了验证。实验结果表明,该方法辨识得到的热阻与IEC标准测量结果相近,且热网络估算结温与大电流注入法测得的结温误差较小,证明了该方法的准确性和有效性。
附 录
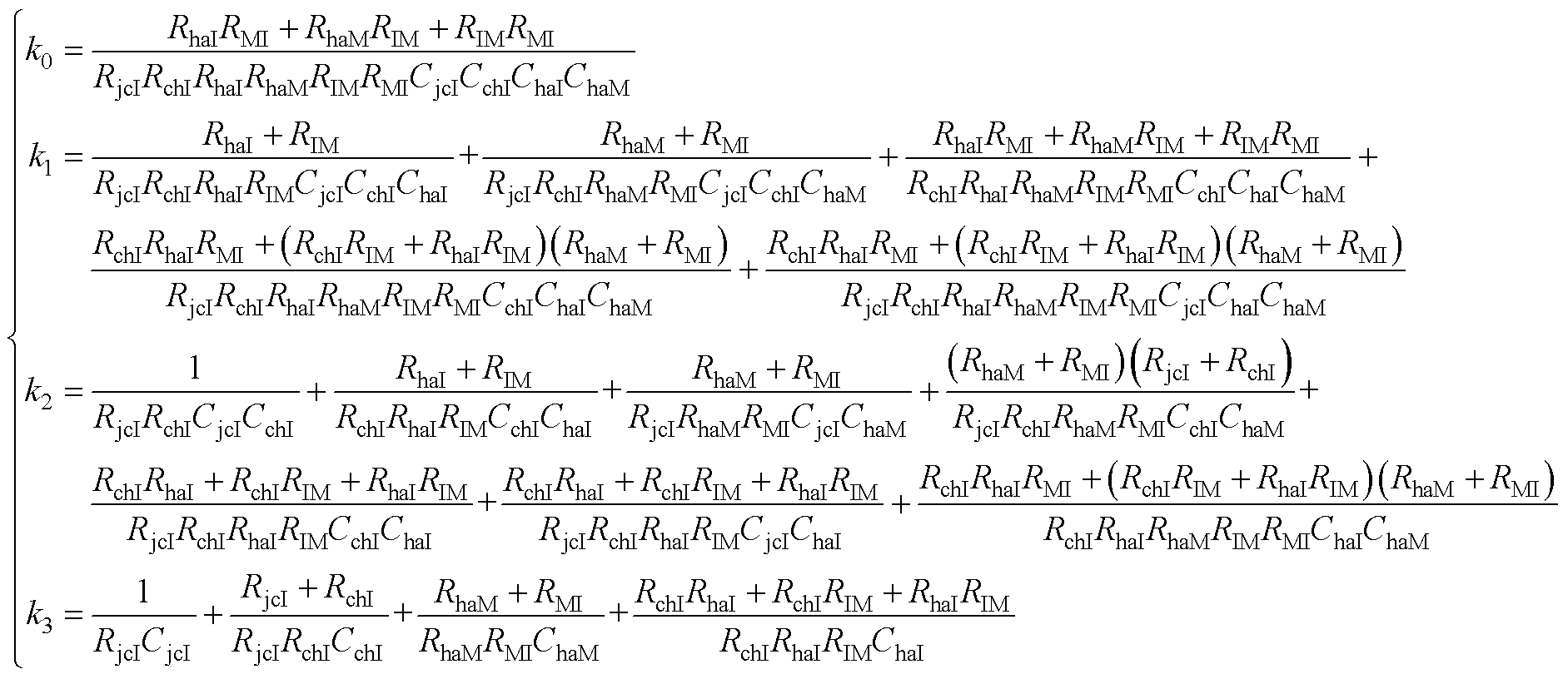 (A1)
(A1)
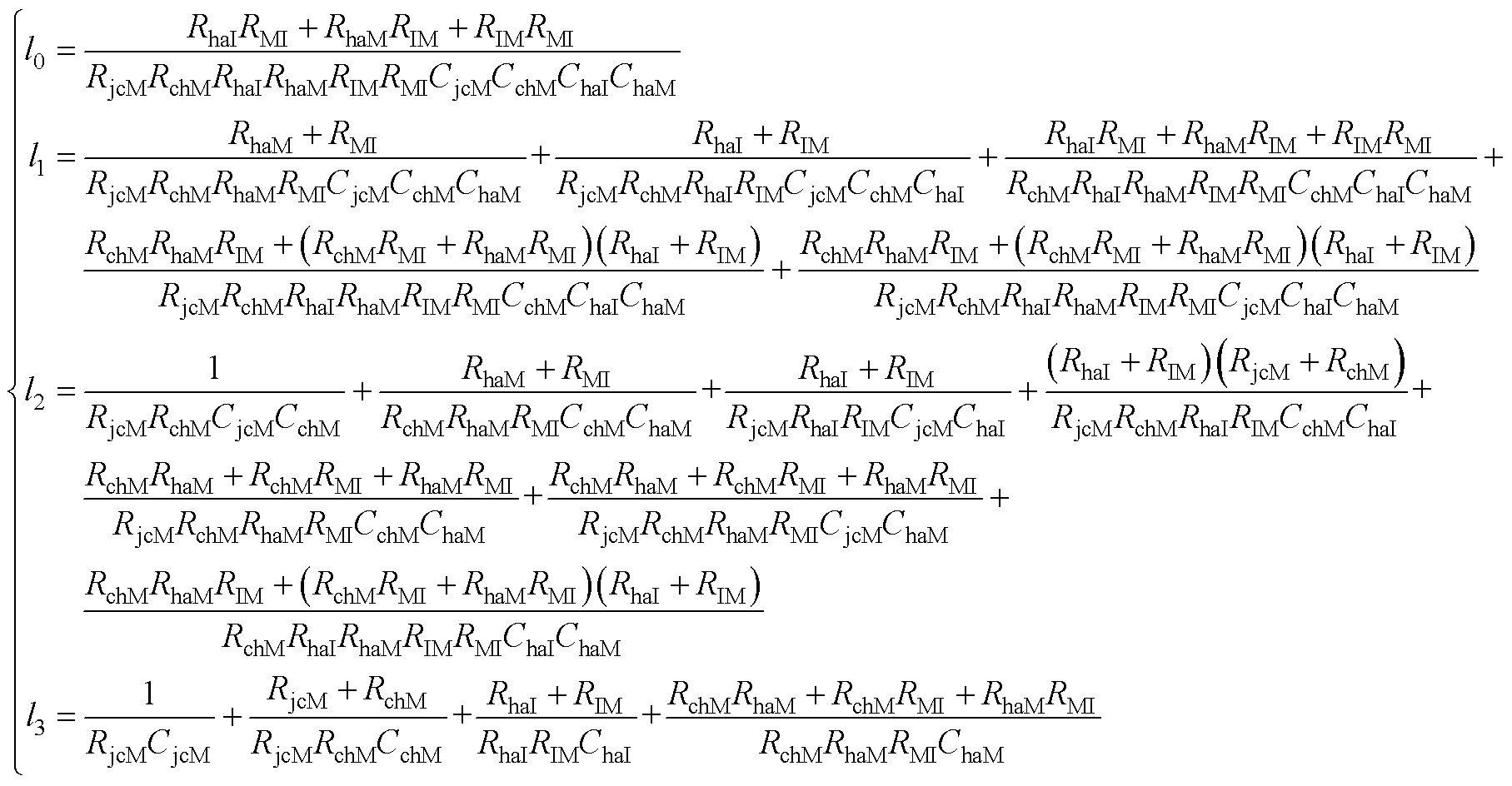 (A2)
(A2)
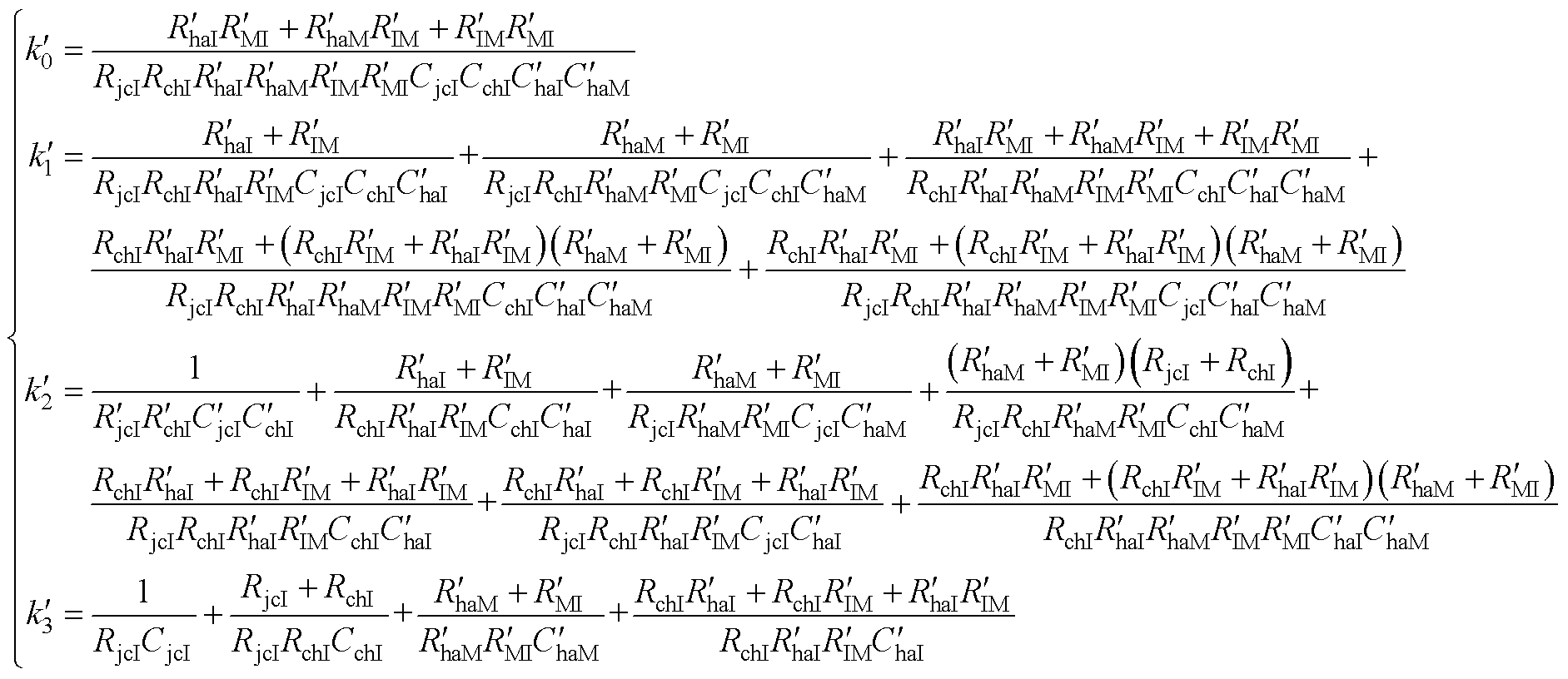 (A3)
(A3)
参考文献
[1] 宁圃奇, 李磊, 曹瀚, 等. 基于Si IGBT/SiC MOSFET的混合开关器件综述[J]. 电工电能新技术, 2018, 37(10): 1-9.
Ning Puqi, Li Lei, Cao Han, et al. Summary of Si IGBT/SiC MOSFET based hybrid switching device[J]. Advanced Technology of Electrical Engineering and Energy, 2018, 37(10): 1-9.
[2] 李锦, 党恩帅, 范雨顺, 等. 一种碳化硅与硅器件混合型三电平有源中点钳位零电压转换软开关变流器[J]. 电工技术学报, 2024, 39(8): 2485-2495.
Li Jin, Dang Enshuai, Fan Yushun, et al. A hybrid three-level active-neutral-point-clamped zero-voltage transition soft-switching converter with silicon car- bide and silicon devices[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2485-2495.
[3] Woldegiorgis D, Hossain M M, Saadatizadeh Z, et al. Hybrid Si/SiC switches: a review of control objectives, gate driving approaches and packaging solutions[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(2): 1737-1753.
[4] 任鹏, 涂春鸣, 侯玉超, 等. 基于Si和SiC器件的混合型级联多电平变换器及其调控优化方法[J]. 电工技术学报, 2023, 38(18): 5017-5028.
Ren Peng, Tu Chunming, Hou Yuchao, et al. Research on a hybrid cascaded multilevel converter based on Si and SiC device and its control optimization method[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5017-5028.
[5] Li Zongjian, Zhang Chao, Yu Jiajun, et al. Dynamic gate delay time control of Si/SiC hybrid switch for loss minimization in voltage source inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(4): 4160-4170.
[6] Peng Zishun, Wang Jun, Liu Zeng, et al. Adaptive gate delay-time control of Si/SiC hybrid switch for efficiency improvement in inverters[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(3): 3437- 3449.
[7] Peng Zishun, Wang Jun, Liu Zeng, et al. Fault- tolerant inverter operation based on Si/SiC hybrid switches[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 545-556.
[8] Peng Zishun, Wang Jun, Liu Zeng, et al. A variable- frequency current-dependent switching strategy to improve tradeoff between efficiency and SiC MOSFET overcurrent stress in Si/SiC-hybrid-switch- based inverters[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 4877-4886.
[9] Li Zongjian, Wang Jun, Deng Linfeng, et al. Active gate delay time control of Si/SiC hybrid switch for junction temperature balance over a wide power range[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5354-5365.
[10] Stecca M, Tan Changyu, Xu Junzhong, et al. Hybrid Si/SiC switch modulation with minimum SiC MOSFET conduction in grid connected voltage source converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(4): 4275- 4289.
[11] 魏云海, 陈民铀, 赖伟, 等. 基于IGBT结温波动平滑控制的主动热管理方法综述[J]. 电工技术学报, 2022, 37(6): 1415-1430.
Wei Yunhai, Chen Minyou, Lai Wei, et al. Review on active thermal control methods based on junction temperature swing smooth control of IGBTs[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1415-1430.
[12] 丁红旗, 马伏军, 徐千鸣, 等. 模块化多电平换流器子模块IGBT损耗优化控制策略[J]. 电力系统自动化, 2021, 45(17): 143-152.
Ding Hongqi, Ma Fujun, Xu Qianming, et al. Loss optimization control strategy for IGBT in sub-module of modular multilevel converter[J]. Automation of Electric Power Systems, 2021, 45(17): 143-152.
[13] 郑丹, 宁圃奇, 仇志杰, 等. 基于老化补偿的功率模块全生命周期在线结温监测方法[J/OL]. 电工技术学报, 2023: 1-14. https://doi.org/10.19595/j.cnki. 1000-6753.tces.230589.
Zheng Dan, Ning Puqi, Chou Zhijie, et al. Full life-cycle online junction temperature monitoring of power module based on aging compensation[J]. Transactions of China Electrotechnical Society, 2023: 1-14. https://doi.org/10.19595/j.cnki.1000-6753.tces. 230589.
[14] 杨舒萌, 孙鹏菊, 王凯宏, 等. 恒流驱动下基于VeE_max的IGBT模块解耦老化影响的结温测量方法[J]. 电工技术学报, 2022, 37(12): 3038-3047, 3072.
Yang Shumeng, Sun Pengju, Wang Kaihong, et al. Junction temperature measurement method of IGBT modules based on VeE_max under constant-current source drive which decouples fatigue effect[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3038-3047, 3072.
[15] 姜鑫, 应展烽, 万萌, 等. 计及环境对流随机性的功率器件结-环境热网络模型[J]. 电工技术学报, 2021, 36(14): 3090-3100.
Jiang Xin, Ying Zhanfeng, Wan Meng, et al. Junction- to-ambient thermal network model of power devices considering randomness of thermal convective environment[J]. Transactions of China Electrotech- nical Society, 2021, 36(14): 3090-3100.
[16] 刘平, 李海鹏, 苗轶如, 等. 基于内置温度传感器的碳化硅功率模块结温在线提取方法[J]. 电工技术学报, 2021, 36(12): 2522-2534.
Liu Ping, Li Haipeng, Miao Yiru, et al. Online junction temperature extraction for SiC module based on built-in temperature sensor[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2522- 2534.
[17] Yang Xin, Heng Ke, Dai Xingyu, et al. A temperature-dependent cauer model simulation of IGBT module with analytical thermal impedance characterization[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 3055-3065.
[18] 陈宇, 吴强, 周宇, 等. 基于傅里叶级数解析热扩散角的功率模块热阻抗物理模型[J]. 中国电机工程学报, 2022, 42(2): 715-728.
Chen Yu, Wu Qiang, Zhou Yu, et al. Physics-based thermal impedance model for power module by analytic Fourier series based heat spreading angle[J]. Proceedings of the CSEE, 2022, 42(2): 715-728.
[19] 何怡刚, 张钟韬, 刘嘉诚, 等. 一种考虑热扩散和热耦合的IGBT模块热阻抗模型[J]. 电工电能新技术, 2020, 39(5): 17-24.
He Yigang, Zhang Zhongtao, Liu Jiacheng, et al. Thermal impedance model for IGBT modules considering heat spreading and thermal coupling[J]. Advanced Technology of Electrical Engineering and Energy, 2020, 39(5): 17-24.
[20] Li Jianfeng, Castellazzi A, Eleffendi M A, et al. A physical RC network model for electrothermal analysis of a multichip SiC power module[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2494-2508.
[21] 许智亮, 葛兴来, 李金, 等. 计及流-热耦合热网络模型的IGBT结温计算[J]. 电气工程学报, 2022, 17(2): 19-26.
Xu Zhiliang, Ge Xinglai, Li Jin, et al. Calculation of IGBT junction temperature with thermal network model considering flow-thermal coupling[J]. Journal of Electrical Engineering, 2022, 17(2): 19-26.
[22] Gao Shan, Ngo K D T, Lu Guoquan. Two- dimensional mapping of interface thermal resistance by transient thermal measurement[J]. IEEE Transa- ctions on Industrial Electronics, 2021, 68(5): 4448- 4456.
[23] Cai Jie, Zhou Luowei, Sun Pengju, et al. Effect of TIM deterioration on monitoring of IGBT module thermal resistance and its compensation strategy[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2022, 12(5): 789-797.
[24] Wei Kaixin, Lu D D C, Zhang Chengning, et al. Modeling and analysis of thermal resistances and thermal coupling between power devices[J]. IEEE Transactions on Electron Devices, 2019, 66(10): 4302-4308.
[25] Xu Mengqi, Ma Ke, Cai Xu, et al. Lumped thermal coupling model of multichip power module enabling case temperature as reference node[J]. IEEE Transa- ctions on Power Electronics, 2022, 37(10): 11502- 11506.
[26] 郑帅, 杜雄, 张军, 等. 采用降温曲线的SiC MOSFET模块热参数的测量[J]. 中国电机工程学报, 2020, 40(6): 1759-1769.
Zheng Shuai, Du Xiong, Zhang Jun, et al. Measurement of thermal parameters of SiC MOSFET modules with cooling curves[J]. Proceedings of the CSEE, 2020, 40(6): 1759-1769.
[27] IEC. Semiconductor devices-discrete devices-part 9: insulated-gate bipolar transistors (IGBTs): IEC 60747-9-2007[S]. Switzerland: IEC, 2007.
[28] 余瑶怡, 杜雄, 张军. 基于热时间常数的IGBT模块热疲劳老化监测方法[J]. 电源学报, 2020, 18(1): 18-27.
Yu Yaoyi, Du Xiong, Zhang Jun. Thermal fatigue monitoring method for IGBT module based on thermal time constants[J]. Journal of Power Supply, 2020, 18(1): 18-27.
[29] Zhang Jun, Du Xiong, Yu Yaoyi, et al. Thermal parameter monitoring of IGBT module using junction temperature cooling curves[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 8148-8160.
[30] Zhang Jun, Du Xiong, Wu Yu, et al. Thermal parameter monitoring of IGBT module using case temperature[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(8): 7942-7956.
[31] Zheng Shuai, Du Xiong, Zhang Jun, et al. Measure- ment of thermal parameters of SiC MOSFET module by case temperature[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 311-322.
[32] 杜雄, 李腾飞, 夏俊, 等. 基于零输入响应的Cauer型RC网络参数辨识方法[J]. 电工技术学报, 2017, 32(1): 222-230.
Du Xiong, Li Tengfei, Xia Jun, et al. Identification method for Cauer type RC network parameter based on the zero-input response[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 222-230.
Abstract The hybrid switch with paralleled Si IGBT and SiC MOSFET can break the limitations of single Si-based and SiC-based devices and effectively balance loss and cost. Junction temperature estimation is crucial for the reliable operation of Si/SiC hybrid switches. However, research on thermal monitoring often needs to meet two major conditions: thermal steady-state balance and measurable power loss. This paper proposes a coupling thermal parameter identification method for hybrid switches utilizing the thermal network partition equivalence concept. The accurate identification of the coupled thermal network parameters can be realized by only three case temperature cooling curves.
Firstly, the thermal structure characteristics of Si/SiC hybrid switches are analyzed, and the challenge of high-order thermal constraints when the zero-input response method is directly applied to a hybrid switch is elaborated. Secondly, the thermal network partition of Si IGBT and SiC MOSFET is carried out to reduce the order of the model. According to Kirchhoff's law and node voltage equation, the Laplace expressions of Si IGBT and SiC MOSFET case temperatures are obtained. Thirdly, based on the mathematical relationship between the root and the coefficient, the constraint equations between the time constant of the case temperature cooling curve and the thermal parameters are constructed. By simultaneously solving the equations under the thermal network partition equivalence, all the remaining thermal parameters can be identified. Finally, the hybrid switch’s coupling thermal parameter identification process is designed. In this process, the experimental steps of thermal time constant extraction are simple, greatly reducing the difficulty of solving the thermal constraint equations.
Based on the experimental platform, the time constants of the cooling curves under two heat dissipation conditions are fitted, and all RC parameters can be solved by substituting the fitted time constants into the thermal constraint equations. Compared with the junction-to-case thermal resistance value tested by the IEC standard, the identification error of Si IGBT and SiC MOSFET in the proposed method is within 2%. In the transient junction temperature experiment, the experimental waveform is consistent with the junction temperature estimation waveform of the proposed method. The estimated and the measured junction temperatures are in good agreement on various time scales. The accuracy of the identified coupled thermal parameters relying on the thermal network partition equivalence is proved.
The following conclusions can be drawn: (1) By heating a single chip to partition the coupled thermal network, the high-order thermal network is divided into two low-order equivalent thermal network models. The difficulty of thermal parameter identification with the zero-input response method is reduced. (2) The proposed method simplifies the power loss measurement steps and thermal equilibrium conditions. It has the advantages of simplicity, universality, and high process ability in coupled thermal parameter identification of parallel devices. (3) The idea of thermal network partition equivalence can be further extended to the parallel structure of three or more devices, which greatly improves the applicability of the zero-input response method in complex scenarios.
keywords:Coupling thermal parameter identification, Si/SiC hybrid switches, thermal network partitioning, thermal time constant, thermal constraints
DOI: 10.19595/j.cnki.1000-6753.tces.230497
中图分类号:TM46
国家自然科学基金重点资助项目(52130704)。
收稿日期 2023-04-19
改稿日期 2023-06-27
龙 柳 女,1996年生,博士研究生,研究方向为功率半导体器件热可靠性分析与综合热管理。E-mail: liu_l@hnu.edu.cn
肖 凡 男,1988年生,讲师,研究方向为电力电子在电力系统中的应用。E-mail: woliaokk123@126.com(通信作者)
(编辑 陈 诚)