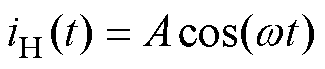 (1)
(1)
摘要 针对电机电流信号特征分析进行转子断条故障诊断时,在低负载工况或早期,转子断条故障存在故障特征微弱以及难以分离等问题,同时需借助速度传感器获取转速信息,增加了硬件成本,该文提出了融合Teager-Kaiser能量算子(TKEO)和Goertzel算法的感应电机转子断条故障诊断方法。首先,采用Teager-Kaiser能量算子对定子电流进行解调处理,将基频分量转化为直流分量并去除,实现边带故障特征分量到转子断条故障特征分量以及固有偏心谐波分量到转子速度谐波分量的转变,抑制基频频谱泄露对故障诊断和转速估计造成的干扰;其次,利用Goertzel算法对归一化解调信号进行频谱分析,完成转子断条故障特征分量和转子速度谐波分量的快速提取,进而实现不同负载和不同严重程度工况下转子断条的故障诊断。此外,与归一化频域能量算子进行比较,分析其计算效率和稳定性。实验结果表明,所提方法在不同负载和不同严重程度工况下均能够有效地识别转子断条故障特征分量,并且计算量少、可靠性高、实时性强以及硬件成本低。
关键词:转子断条 Goertzel算法 固有偏心 Teager-Kaiser能量算子 归一化频域能量算子
感应电机广泛应用于汽车、医疗设备、航空等领域,需要对其可能出现的故障进行即时检测与诊断,否则会导致生产线中断、生产效率降低、甚至电机本身彻底损坏[1]。电机故障主要包括定子、转子、轴承等类型,其中转子断条故障约占10%[2-3]。但是,转子断条故障在初期难以发现,若继续使用,会使电机产生较大噪声和振动,进一步扩大故障[4]。因此,对早期转子断条故障检测具有重要意义。
利用定子电流、电压、振动、声发射等信号均可对转子断条故障进行检测,而定子电流具有易采集、非侵入式等优点,故被广泛应用于故障检测中。作为目前常用的转子断条故障检测技术之一,电机电流信号特征分析(Motor Current Signature Analysis, MCSA)方法使用快速傅里叶变换(Fast Fourier Transform, FFT)进行频谱分析,进而提取转子断条故障特征分量。但电机在轻载工况下运行或者早期故障时,MCSA方法诊断转子断条效果极易受到基频频谱泄露影响[5]。为此,文献[5]对定子电流信号进行平方解调制,将基频分量变成直流分量,从而解决基频频谱泄露现象,但平方项会引起频谱复杂化。文献[6]则利用Hilbert变换对定子电流信号进行包络线提取,提高了故障诊断准确率,但计算量较大。文献[7]采用了经验模态分解方法对转子断条故障进行检测,同时估计故障的严重程度,但为了提高检测精度,需要将频率分解成多个固有模态函数,计算时间较长。文献[8]利用小波变换对电流信号进行滤波,再采用傅里叶变换进行分析,能够有效地对转子断条故障进行检测,但需要依赖母小波,有一定的局限性。
文献[9]提出了采用Teager-Kaiser能量算子(Teager-Kaiser Energy Operator, TKEO)的故障诊断方法,只需使用连续的三个电流信号采样点,减小了计算时间和成本,提高了频谱信噪比。文献[10]则针对TKEO在时域采用差分求导误差较大的问题,提出采用归一化频域能量算子(Frequency Domain Energy Operator, FDEO)的方法,即利用傅里叶变换微分性质和Hilbert变换计算能量算子,该方法虽然具有较好的物理意义,但同时也增加了计算量。然而,文献[9-10]均需利用FFT算法得到所有谱线,来了解信号的整个频域信息。但电机转差率通常小于5%,且供电频率为60 Hz,转子断条故障特征频率通常小于6 Hz,即只需关心低频段的谱线信息。此外,文献[9-10]中的转速信息均需要通过转速传感器进行检测。
针对上述问题,本文首先提出一种利用TKEO和Goertzel算法相结合的感应电机转子断条故障诊断方法。由于低负载工况和转子断条早期故障的特征微弱,加之基频干扰,导致故障特征识别困难,该方法引入TKEO解调定子电流信号,将基频分量转化为直流分量并去除,有效抑制了基频频谱泄露对故障诊断和转速估计的干扰。为进一步灵活获取低频段故障信息,降低计算复杂度,采用Goertzel算法估计解调信号相应频段,提取转子断条故障特征分量和转子速度谐波分量。然后,基于转子速度谐波分量计算转子断条故障特征分量,并与检测到的转子断条故障特征分量对比分析,判断电机是否发生转子断条故障。该方法无需计算所有谱线,可快速地在解调信号中提取所需频谱信息。最后,利用西巴拉那州立大学提供的实验数据集进行实验验证,结果表明,利用TKEO进行转子断条故障检测比FDEO更稳定,有利于提高转子断条故障检测的稳定性和快速性。
当电机在理想情况下正常稳定运行时,定子电流信号中只存在基波分量,若忽略初始相位,则定子电流信号为
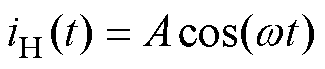 (1)
(1)
式中,iH(t)为无故障电机定子电流;A为电流基频分量幅值;w 为基频分量,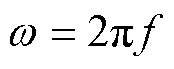 ,f为电源基波频率。
,f为电源基波频率。
当电机出现转子断条故障时,会导致转子磁场出现不对称现象,引起定子电流信号产生分布在基频f两侧的边带故障特征频率分量(1±2s) f。若忽略初始相位,转子断条故障电机电流信号iF(t)为
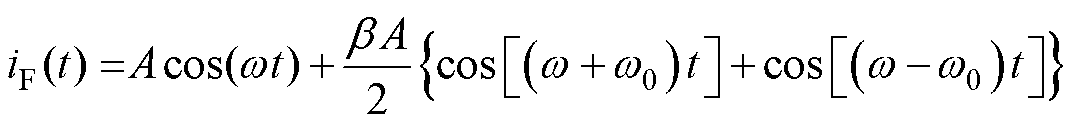 (2)
(2)
式中,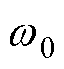 为转子断条故障特征角频率,
为转子断条故障特征角频率,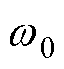 =
=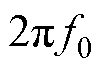 =
= 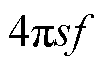 ,
,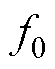 为转子断条故障特征频率,s为电机转差率;
为转子断条故障特征频率,s为电机转差率;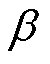 为调制指数,与转子断条故障严重程度有关。
为调制指数,与转子断条故障严重程度有关。
在文献[11]中,F. Filippetti等定义了转子断条数目nF、电机转子条数目Nb、基频幅值Is(Is=A)以及转子断条边带故障特征分量幅值之间的关系为
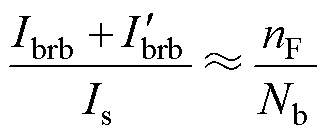 (3)
(3)
式中,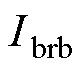 和
和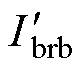 分别为(1+2s) f和(1-2s) f分量幅值。
分别为(1+2s) f和(1-2s) f分量幅值。
结合式(2)和式(3),得b≈nF/Nb。一般nF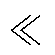 Nb,所以b
Nb,所以b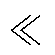 1。因此,转子断条边带故障特征频率分量(1±2s) f幅值远小于基频f幅值,导致直接对定子电流进行FFT频谱分析不易检测出故障。
1。因此,转子断条边带故障特征频率分量(1±2s) f幅值远小于基频f幅值,导致直接对定子电流进行FFT频谱分析不易检测出故障。
Teager-Kaiser能量算子最初是由Teager和Kaiser提出并应用于语音领域。对于连续信号x(t),TKEO表达形式为
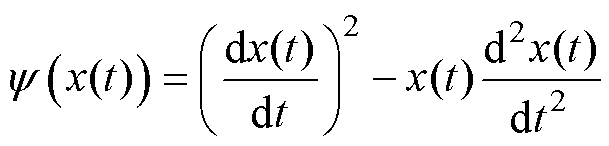 (4)
(4)
对于采样频率为Fs的离散信号x[n],可表示为
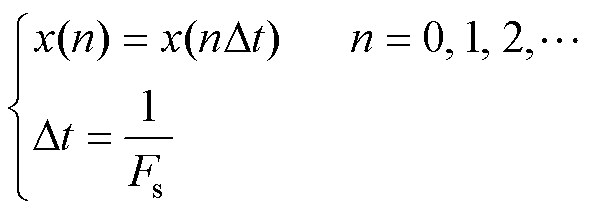 (5)
(5)
利用后向差分表示信号x(t)的导数,即
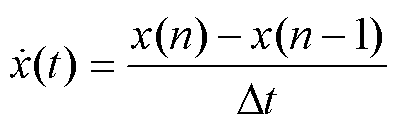 (6)
(6)
结合式(4)~式(6)可得,离散信号的TKEO表达式为
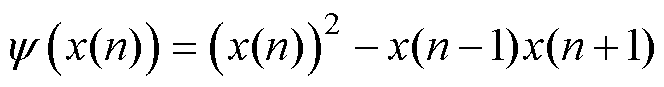 (7)
(7)
由式(7)可以看出,TKEO只需使用连续的三个电流信号采样点。将TKEO应用于式(1)所示的无故障电机定子电流信号,可得无故障电机定子电流TKEO解调信号表达式为
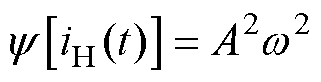 (8)
(8)
观察式(8)可以看出,无故障电机定子电流TKEO解调信号为一项常数。
结合式(2)和式(4),可得转子断条故障电机定子电流TKEO解调信号表达式为
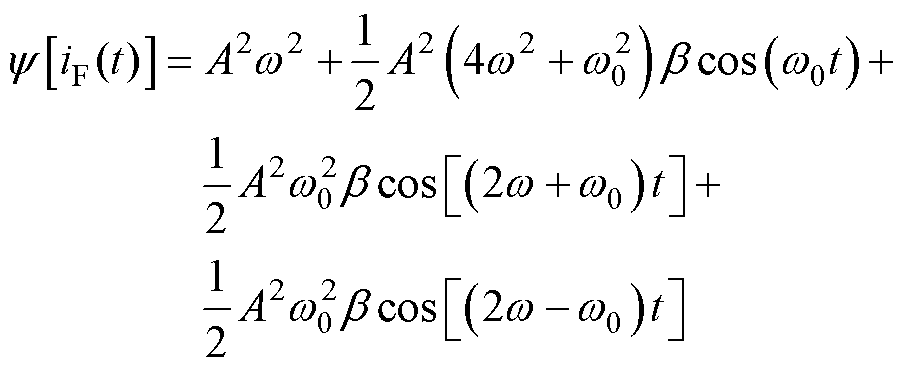 (9)
(9)
式中,由于b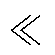 1,故忽略b2项。
1,故忽略b2项。
为了便于诊断转子断条故障,对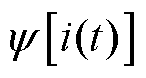 进行归一化处理,可得
进行归一化处理,可得
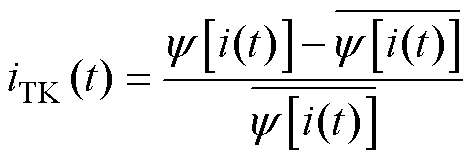 (10)
(10)
式中,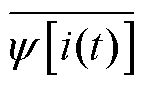 为
为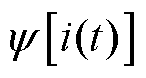 的平均值。
的平均值。
对于无故障电机,结合式(8)和式(10),可得定子电流TKEO归一化解调信号iTK,H(t)=0。同时,结合式(9)和式(10),转子断条故障电机定子电流TKEO归一化解调信号为
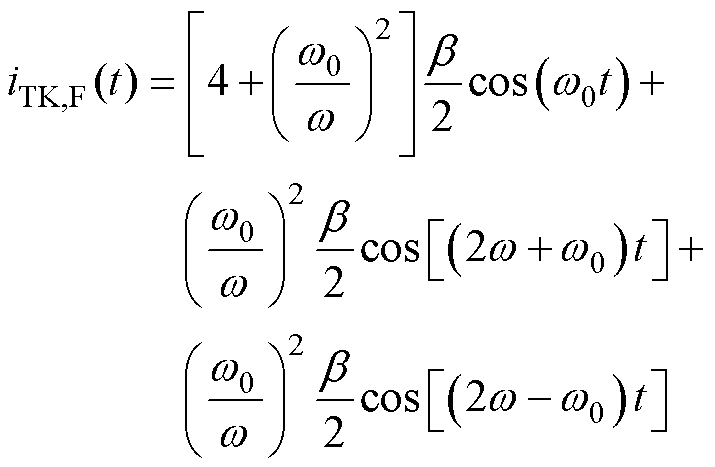 (11)
(11)
观察式(11)可以发现,转子断条故障电机定子电流TKEO归一化解调信号iTK,F(t)含有两项2倍频边带故障特征分量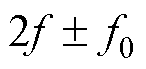 以及一项转子断条故障特征分量f0。对比式(2)和式(11)可以看出,利用TKEO对定子电流信号进行解调,可以将基频分量变为直流分量并去除,实现转子断条边带故障特征分量
以及一项转子断条故障特征分量f0。对比式(2)和式(11)可以看出,利用TKEO对定子电流信号进行解调,可以将基频分量变为直流分量并去除,实现转子断条边带故障特征分量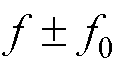 到转子断条故障特征分量f0的转变,进而消除基频频谱泄露对故障诊断造成干扰的影响,有利于电机在轻载工况下运行或者故障严重程度较轻微时的故障特征分量提取。
到转子断条故障特征分量f0的转变,进而消除基频频谱泄露对故障诊断造成干扰的影响,有利于电机在轻载工况下运行或者故障严重程度较轻微时的故障特征分量提取。
在TKEO基础上,文献[10]提出了利用FDEO诊断转子断条故障。该方法利用傅里叶变换的微分特性,求取信号x(t)导数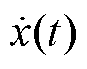 ,然后通过Hilbert变换计算
,然后通过Hilbert变换计算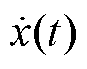 平方包络线获取能量算子。
平方包络线获取能量算子。
对于连续信号x(t),FDEO表达式为
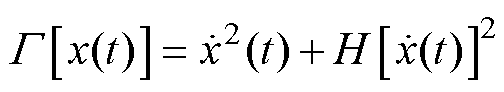 (12)
(12)
式中,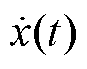 为x(t)的一阶导数,即
为x(t)的一阶导数,即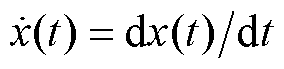 ;
;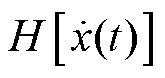 为
为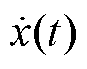 的Hilbert变换。
的Hilbert变换。
利用傅里叶变换导数性质求取信号x(t)导数为
 (13)
(13)
式中,F( · )为傅里叶变换;F-1( · )为傅里叶逆变换。
将FDEO应用于式(1)所示的无故障电机定子电流信号,可得无故障电机定子电流FDEO解调信号的表达式为
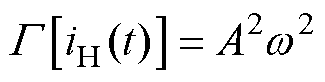 (14)
(14)
结合式(2)和式(12),且忽略b2项,可得转子断条故障电机定子电流FDEO解调信号表达式为
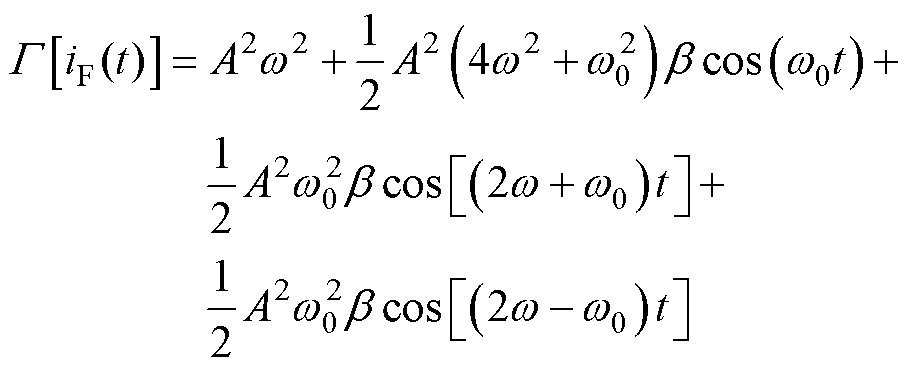 (15)
(15)
为了消除常数项,同样根据式(15)对FDEO解调信号进行归一化处理,得到归一化解调信号数据序列iFD(t)为
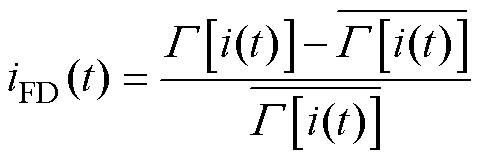 (16)
(16)
式中,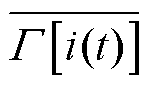 为
为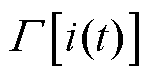 的平均值。
的平均值。
对于无故障电机,结合式(14)和式(16),可得定子电流FDEO归一化解调信号iFD,H(t)=0。同时,结合式(15)和式(16),得到转子断条故障电机定子电流FDEO归一化解调信号为
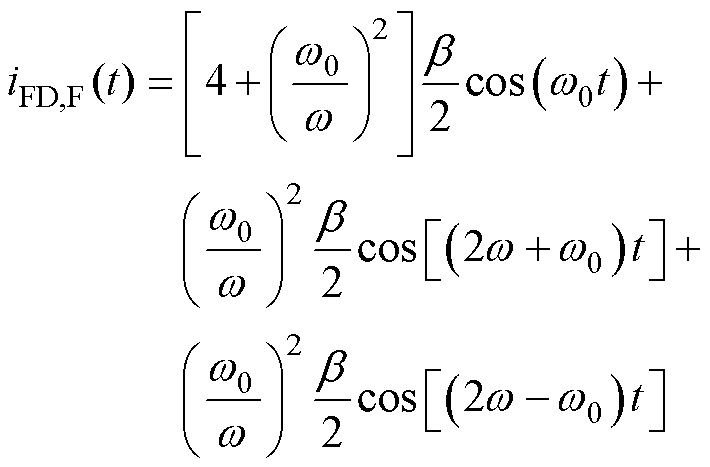 (17)
(17)
对比式(11)和式(17)可以发现,转子断条故障电机定子电流在TKEO和FDEO中的解调信号形式相同,归一化后的解调信号均包含一项转子断条故障特征分量f0。因此,利用TKEO和FDEO均可实现将转子断条故障特征频率由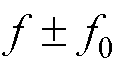 转化成f0,有效抑制基频频谱泄露对故障诊断造成干扰的影响,有助于提高转子断条故障诊断准确性。但是,TKEO仅需使用三个连续的采样点,其计算效率比FDEO更具优势。
转化成f0,有效抑制基频频谱泄露对故障诊断造成干扰的影响,有助于提高转子断条故障诊断准确性。但是,TKEO仅需使用三个连续的采样点,其计算效率比FDEO更具优势。
为了验证TKEO和FDEO两种不同解调方法性能,即TKEO使用差分求导和FDEO使用傅里叶变换微分特征求导。利用式(2)对转子断条故障电机定子电流信号进行仿真分析,仿真分析中设置电流基频分量幅值A=0.2 A,调制指数b=0.01,电源基波频率f=50 Hz,转差率s=0.005,加入噪声大小为10-8 dB。
在未加入噪声和加入噪声两种情况下,采用差分求导和傅里叶微分特性求导结果如图1所示。利用FFT对转子断条故障电机定子电流TKEO归一化解调信号和FDEO归一化解调信号进行频谱分析,结果如图2所示。观察图1a和图2a可以看出,当未加入噪声时,相比于差分估计值,频谱估计值与真实值存在的误差较小,但此时TKEO和FDEO两种解调方法均可以检测出转子断条故障特征分量f0=0.5 Hz。观察图1b和图2b可以看出,当加入噪声后,差分估计值和频谱估计值与真实值存在的误差均较大,但此时TKEO解调方法依然可以识别出故障特征频率f0=0.5 Hz,FDEO解调方法却无法识别出故障特征频率。因此,利用TKEO进行转子断条故障检测比FDEO更稳定。
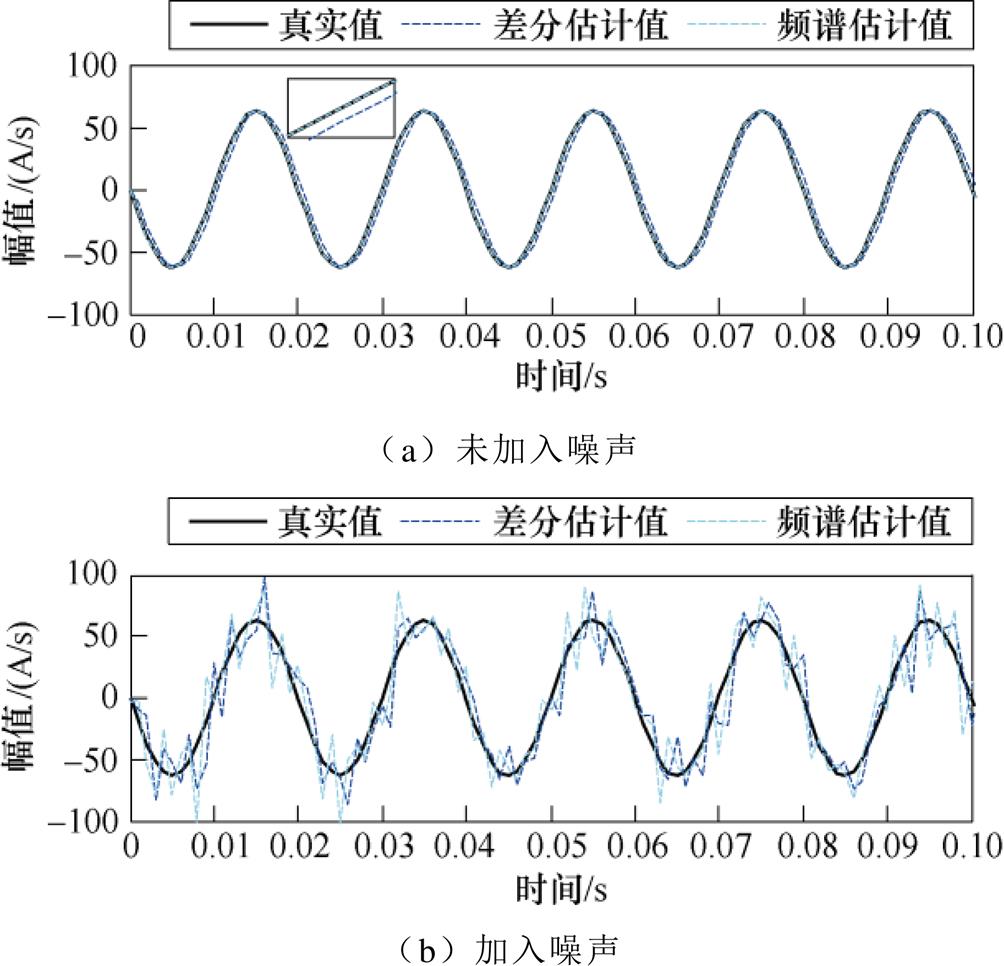
图1 定子电流信号仿真结果
Fig.1 The simulation results of stator current signal
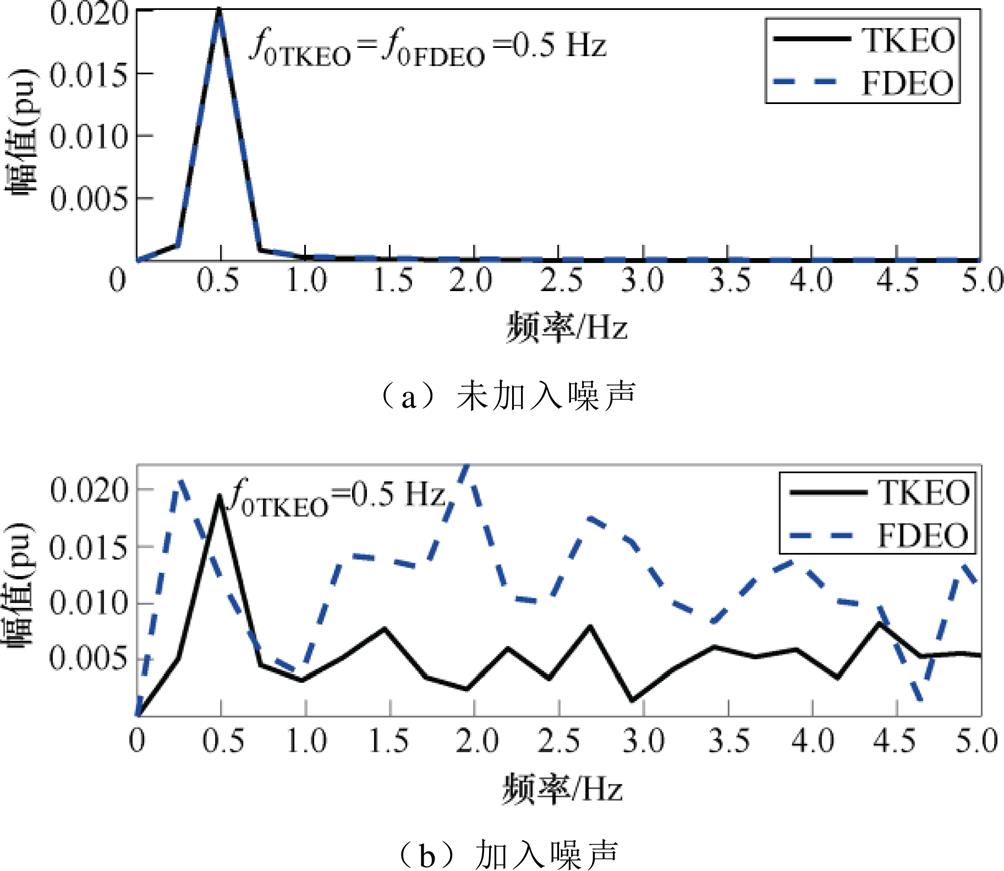
图2 转子断条故障电机定子电流TKEO和 FDEO归一化解调信号FFT频谱
Fig.2 The FFT spectrum of stator current normalized demodulated signals using TKEO and FDEO for broken rotor bar faulty motor
作为一种改进的离散傅里叶变换(Discrete Fourier Transform, DFT)算法,Goertzel算法能够将DFT表示成迭代的线性滤波运算,计算效率高[12]。
Goertzel算法的本质是二阶滤波器,表达式为
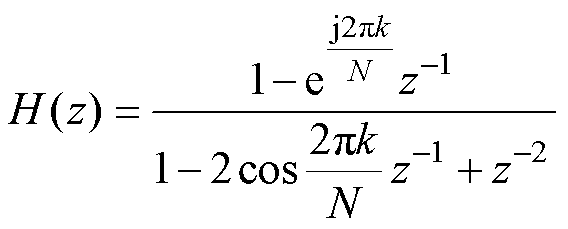 k =0, 1, 2,…, N-1(18)
k =0, 1, 2,…, N-1(18)
式中,H(z)为滤波器的传递函数。
此二阶系统的递推方程为
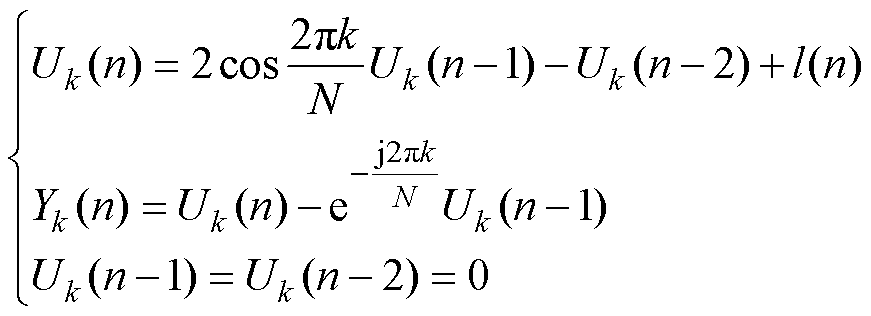 (19)
(19)
式中,l(n)为长度N的信号;Uk(n)为脉冲函数u(n)的离散形式;Yk(n)为l(n)和脉冲响应hk(n)的卷积,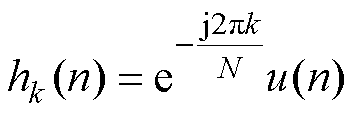 。
。
由式(19)可知,Yk(n)的计算只需要2(N+2)次实数乘法和4(N+1)次实数加法,并且只用了一次复数乘法运算,降低了计算量,有效提高了计算效率。
此外,Goertzel算法的采样点数可以根据实际需要任意选取,相比而言,FFT算法更适合对信号全频段进行频谱分析。由于电机转子断条故障特征频率通常小于6 Hz,分析低频段频谱信息即可实现对转子断条故障分量的检测。因此,本文利用Goertzel算法灵活选取采样点,计算归一化解调信号低频段频谱以识别转子断条故障特征分量,可以减小运算复杂程度,提高计算效率。
为了获取转速信息,除了通过传感器或者观测器进行检测,还可以利用定子电流齿谐波分量或固有偏心谐波分量进行估计[13-15]。由于齿谐波的存在与电机转子槽数和极对数的组合相关,在某些电机转子槽数和极对数的特殊组合下,齿谐波不会出现,从而导致无法通过齿谐波估计电机转速。但是,由于制造误差和装配误差原因,电机始终存在一定程度的固有偏心。因此,本文利用固有偏心谐波分量实现电机转速估计。
电机固有偏心谐波分量fecc为电机固有偏心在定子电流基频分量周围感应出的与转速相关的频率成分[13],即
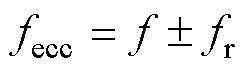 (20)
(20)
考虑电机固有偏心时,无故障电机定子电流iH,ecc(t)表达式为
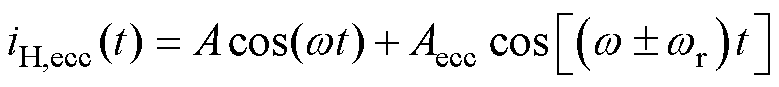 (21)
(21)
式中,Aecc为固有偏心谐波分量幅值;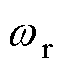 为转子旋转角频率,
为转子旋转角频率,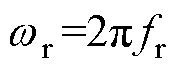 ;fr为转子旋转频率,fr=n/60,n为电机转速。
;fr为转子旋转频率,fr=n/60,n为电机转速。
考虑电机固有偏心和转子断条故障同时存在的情况下,定子电流iF,ecc(t)可以表示为
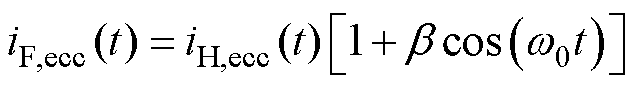 (22)
(22)
将TKEO应用于式(22),且忽略b2项,并将其归一化,可得考虑电机固有偏心时转子断条故障电机定子电流TKEO归一化解调信号为
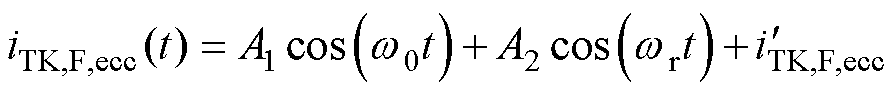 (23)
(23)
式中,A1为转子断条故障特征角频率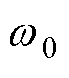 分量幅值;A2为转子旋转角频率
分量幅值;A2为转子旋转角频率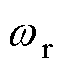 分量幅值;
分量幅值;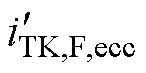 为其余次要分量总和。
为其余次要分量总和。
观察式(23)可知,利用TKEO方法得到的归一化解调信号包含转子速度频率分量fr、转子断条故障特征分量f0以及其余次要分量,同时实现了将转子断条边带故障特征分量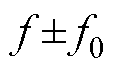 转化为转子断条故障特征分量f0以及固有偏心谐波分量特征频率
转化为转子断条故障特征分量f0以及固有偏心谐波分量特征频率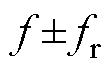 转化成fr,从而可以提取出转子断条故障特征分量f0和转子速度fr。
转化成fr,从而可以提取出转子断条故障特征分量f0和转子速度fr。
根据电机转速估计值、转差率公式以及转子断条故障特征分量表达式,计算转子断条故障特征频率理论值为
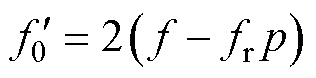 (24)
(24)
式中,p为电机极对数。
本文利用解调策略和Goertzel算法,提出了一种采用TKEO和Goertzel算法相结合的感应电机转子断条故障诊断方法,故障诊断框图如图3所示。图中,ImH为无故障电机转子断条特征分量幅值,ImF为故障电机转子断条特征分量幅值。
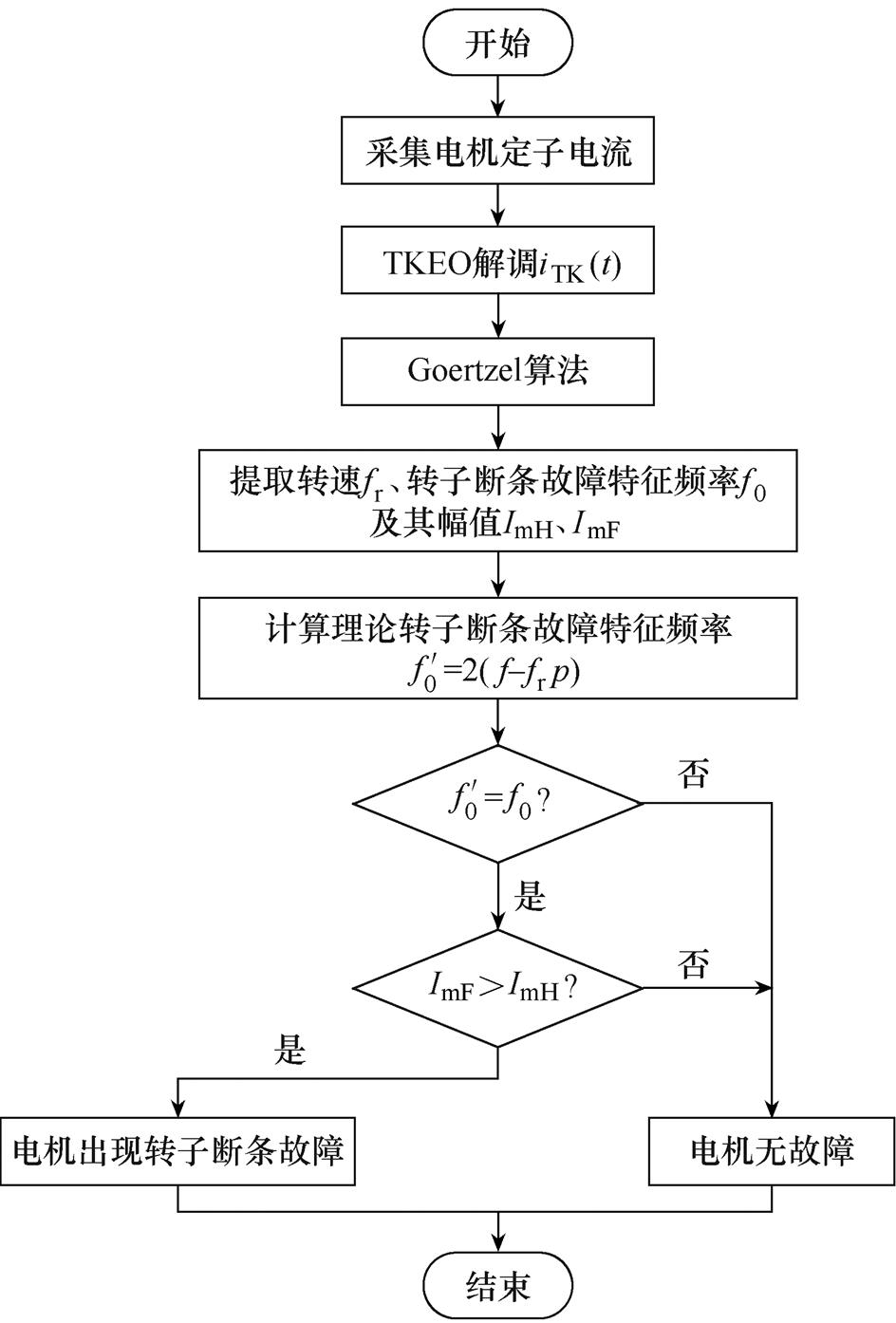
图3 转子断条故障诊断框图
Fig.3 The block diagram of the broken rotor bar fault diagnosis method
主要步骤如下:
(1)采集无故障和故障电机定子电流信号。
(2)利用TKEO对电流信号进行解调并归一化处理,将转子断条故障特征频率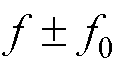 转化成f0=2sf以及固有偏心谐波分量频率
转化成f0=2sf以及固有偏心谐波分量频率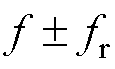 转化成fr。
转化成fr。
(3)利用Goertzel算法对归一化解调信号进行分析,估计相应频段频谱信息。
(4)提取电机转速分量fr,并依据式(24)求取转子断条故障特征分量理论值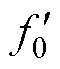 。
。
(5)提取转子断条故障特征分量f0,并确定其幅值信息。
(6)将转子断条故障特征分量理论计算值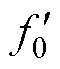 与频谱中提取的转子断条故障特征频率f0以及无故障转子断条特征分量幅值ImH与故障电机转子断条特征分量幅值ImF相比较,若
与频谱中提取的转子断条故障特征频率f0以及无故障转子断条特征分量幅值ImH与故障电机转子断条特征分量幅值ImF相比较,若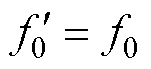 且ImF>ImH,则电机存在转子断条故障;否则,电机工作在无故障状态。
且ImF>ImH,则电机存在转子断条故障;否则,电机工作在无故障状态。
实验数据为西巴拉那州立大学公开数据集[16],该数据集提供振动信号和电流信号,本次实验选用电流信号。实验装置由三相感应电机、直流电机、电流传感器以及数据采集系统等组成,驱动电机为三相感应电机,直流电机模拟负载转矩,实验平台如图4所示。三相感应电机参数为220 V/380 V、3.02 A/1.75 A、4极、60 Hz,额定转矩为4.1 N·m,额定转速为1 715 r/min,转子条数34。通过使用滤波全桥整流器来改变直流电机的磁场绕组电压,从而改变负载转矩大小。电流通过Yokogawa 96033电流钳进行测量,采样频率为50 kHz,采样时间为20 s。

图4 实验平台装置示意图
Fig.4 Diagram of the experimental setup
实验中,在转子一根和两根断条情况下的负载转矩分别为0.5、1.0、2.0、3.0、4.0 N·m。由于转子断条根数为三根和四根时转子断条故障较严重,故只在负载转矩为0.5 N·m下进行了实验。
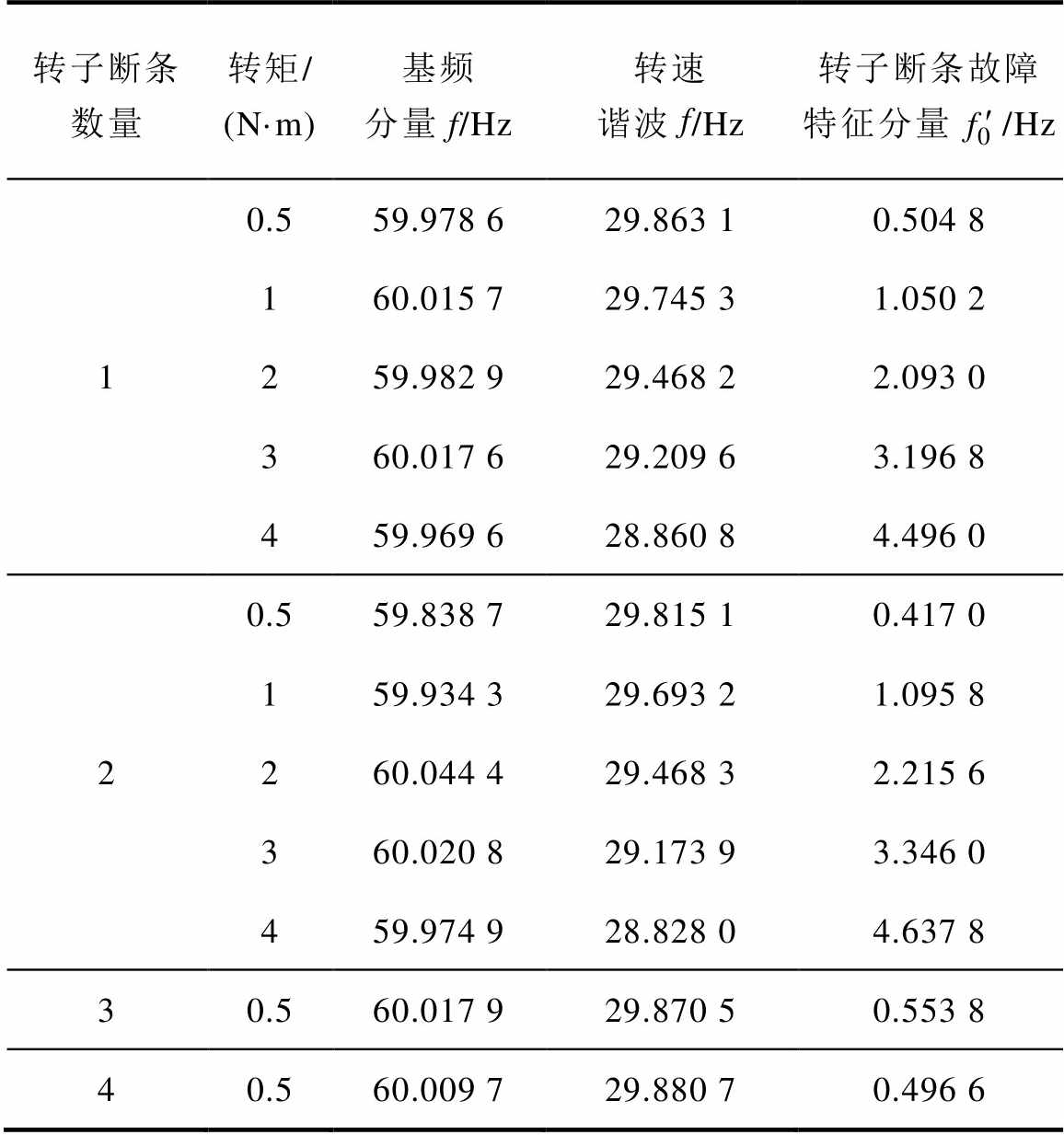
为验证本文所提方法的有效性,对不同转子断条根数以及不同电机转矩情况下的电流信号进行分析。表1为利用Goertzel算法估计电机转速fr后,求取的转子断条故障特征分量理论值。
图5所示为转子带有不同断条根数的故障电机在不同负载情况下,定子电流信号FFT频谱分析。观察图5a~图5e可以看出,对于转子带有一根断条的故障电机,负载转矩为4.0 N·m工况下,在定子电流频谱图形中可以识别出转子断条边带故障特征分量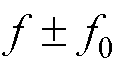 ,但在其他负载情况下,受基频频谱泄露影响以及转子断条故障较轻微,无法识别出转子断条边带故障特征频率分量。通过对比图5f~图5j可以看出,对于转子带有两根断条的故障电机,负载转矩为4.0 N·m和3.0 N·m工况下,在定子电流频谱图形中可以清晰识别转子断条边带故障特征分量
,但在其他负载情况下,受基频频谱泄露影响以及转子断条故障较轻微,无法识别出转子断条边带故障特征频率分量。通过对比图5f~图5j可以看出,对于转子带有两根断条的故障电机,负载转矩为4.0 N·m和3.0 N·m工况下,在定子电流频谱图形中可以清晰识别转子断条边带故障特征分量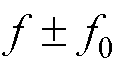 ,但随着负载的降低,转子断条边带故障特征分量
,但随着负载的降低,转子断条边带故障特征分量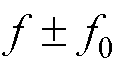 逐渐靠近基频,并且幅值逐渐变小。在负载转矩为0.5 N·m和1.0 N·m工况下,转子断条边带故障特征分量
逐渐靠近基频,并且幅值逐渐变小。在负载转矩为0.5 N·m和1.0 N·m工况下,转子断条边带故障特征分量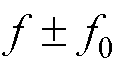 已经完全被基频分量频谱泄露所淹没。观察图5k和图5l可以看出,对于转子分别带有三根和四根断条的故障电机,即使故障严重程度较高,由于基频分量频谱泄露,在轻载工况下也无法有效检测转子断条故障。
已经完全被基频分量频谱泄露所淹没。观察图5k和图5l可以看出,对于转子分别带有三根和四根断条的故障电机,即使故障严重程度较高,由于基频分量频谱泄露,在轻载工况下也无法有效检测转子断条故障。
表1 转子断条故障特征分量理论值
Tab.1 Theoretical value of the characteristic component of broken rotor bar fault
转子断条数量转矩/ (N·m)基频分量f/Hz转速谐波f/Hz转子断条故障特征分量/Hz 10.559.978 629.863 10.504 8 160.015 729.745 31.050 2 259.982 929.468 22.093 0 360.017 629.209 63.196 8 459.969 628.860 84.496 0 20.559.838 729.815 10.417 0 159.934 329.693 21.095 8 260.044 429.468 32.215 6 360.020 829.173 93.346 0 459.974 928.828 04.637 8 30.560.017 929.870 50.553 8 40.560.009 729.880 70.496 6
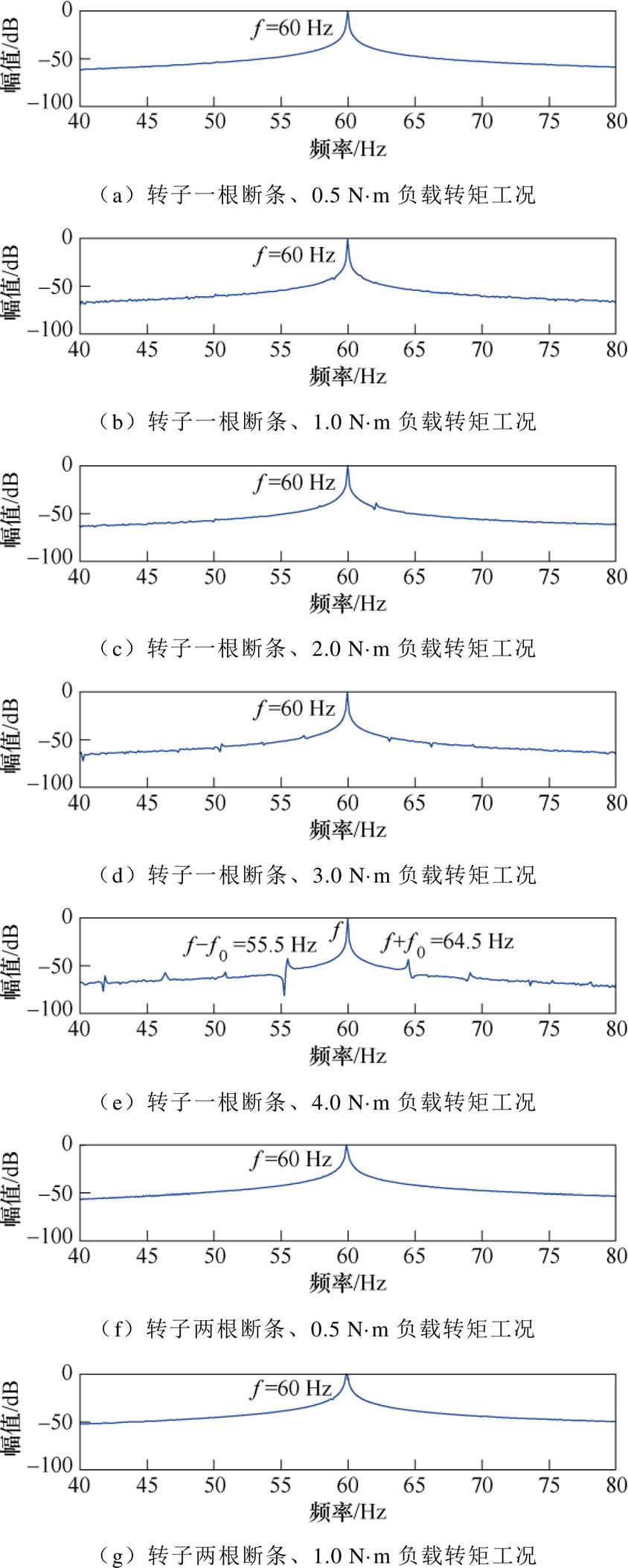
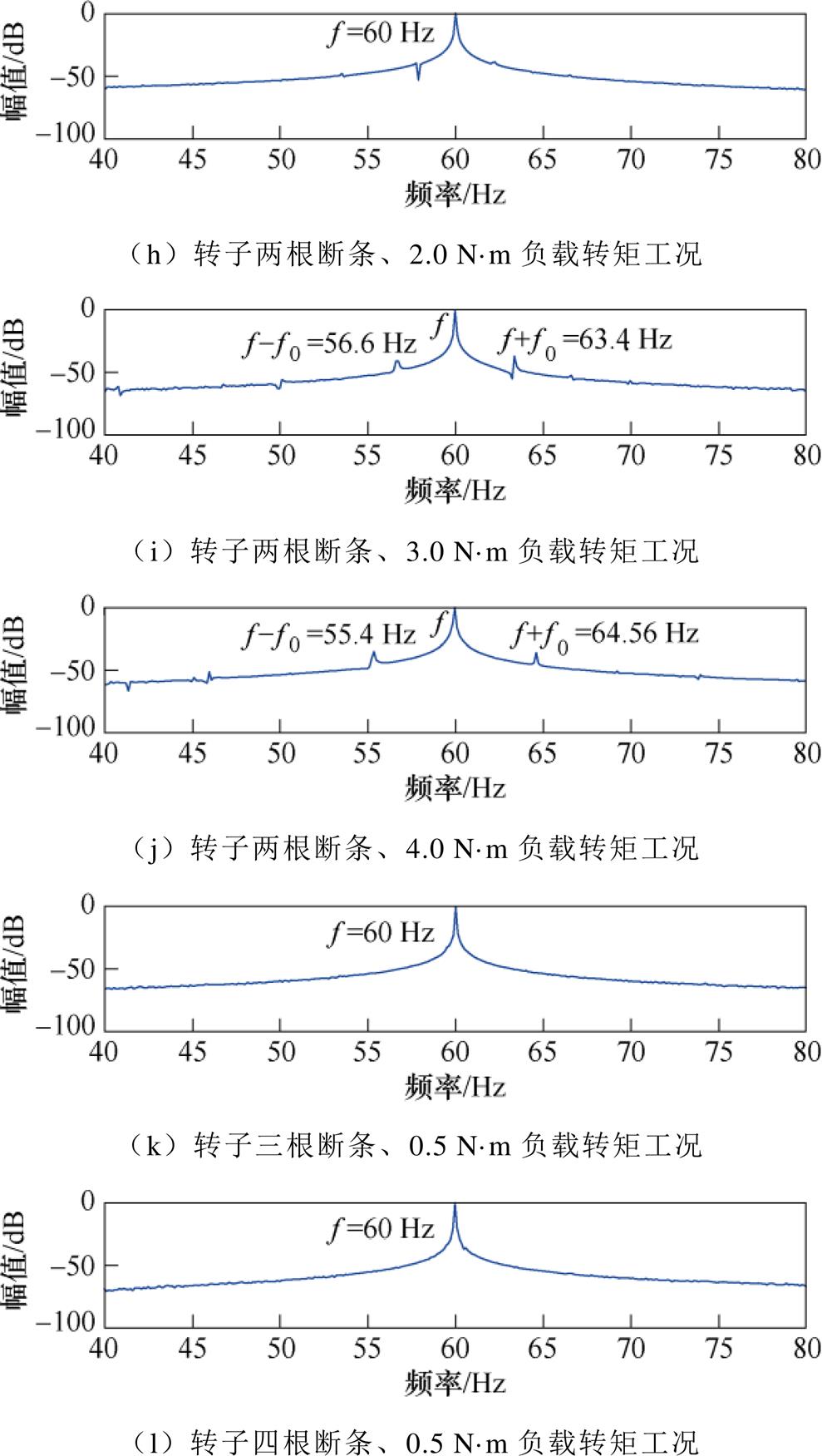
图5 故障电机定子电流信号FFT频谱
Fig.5 The FFT spectrum of faulty motor stator current signal
考虑本文所用电机即使没有出现转子断条故障,其归一化解调信号中也会存在f0分量,为了便于后续幅值对比分析,故对无故障电机TKEO归一化解调信号进行Goertzel算法分析。利用TKEO对无故障电机定子电流信号进行解调,然后采用Goertzel算法对归一化解调信号进行低频段频谱分析,频谱如图6所示。通过图6发现,无故障电机定子电流信号TKEO归一化解调信号频谱中确实存在特征分量f0,但其幅值均较小。
考虑带有不同转子断条根数的故障电机,利用TKEO对其在不同负载工况下的定子电流信号进行解调并归一化处理,然后采用Goertzel算法对归一化解调信号进行低频段频谱分析,如图7所示。对比图7a~图7l可以看出,定子电流进行TKEO解调后,可以将对转子断条边带故障特征分量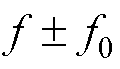 的检测转变为对转子断条故障特征分量f0的直接检测,有效消除了基频频谱泄露的影响。而且在不同转子断条根数和负载工况下,定子电流TKEO归一化解调信号均能够检测出转子断条故障特征分量f0,且与表1所示的理论值相近,体现了转子断条故障检测的准确性和稳定性。此外,相比于FFT频谱分析,采用Goertzel算法仅需估计定子电流TKEO归一化解调信号低频段,可快速地提取转子断条故障特征分量f0,提高转子断条故障诊断实时性。
的检测转变为对转子断条故障特征分量f0的直接检测,有效消除了基频频谱泄露的影响。而且在不同转子断条根数和负载工况下,定子电流TKEO归一化解调信号均能够检测出转子断条故障特征分量f0,且与表1所示的理论值相近,体现了转子断条故障检测的准确性和稳定性。此外,相比于FFT频谱分析,采用Goertzel算法仅需估计定子电流TKEO归一化解调信号低频段,可快速地提取转子断条故障特征分量f0,提高转子断条故障诊断实时性。
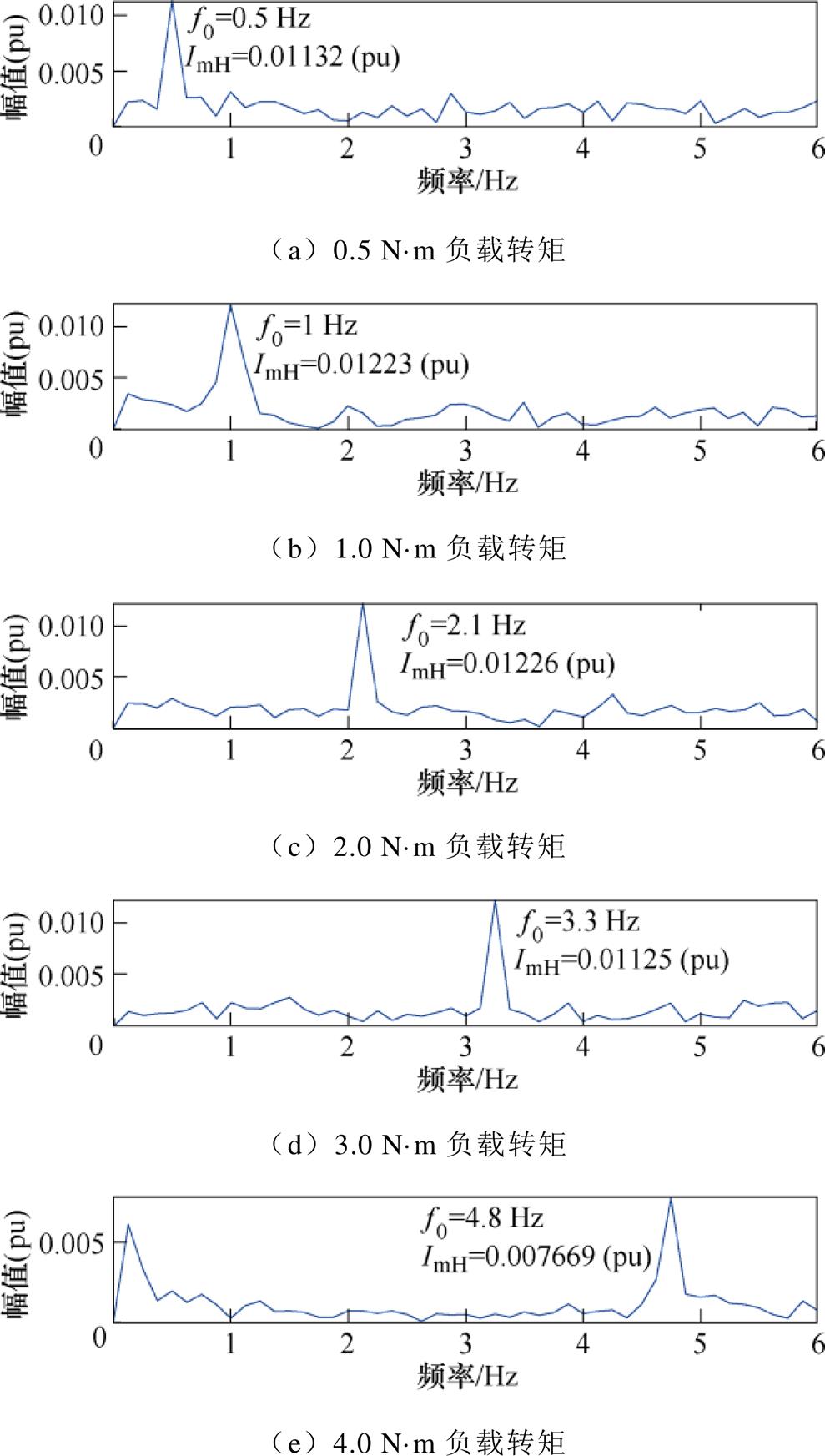
图6 无故障电机TKEO归一化解调信号 Goertzel算法频谱
Fig.6 The Goertzel algorithm spectrum of normalized demodulation signal using TKEO for healthy motor
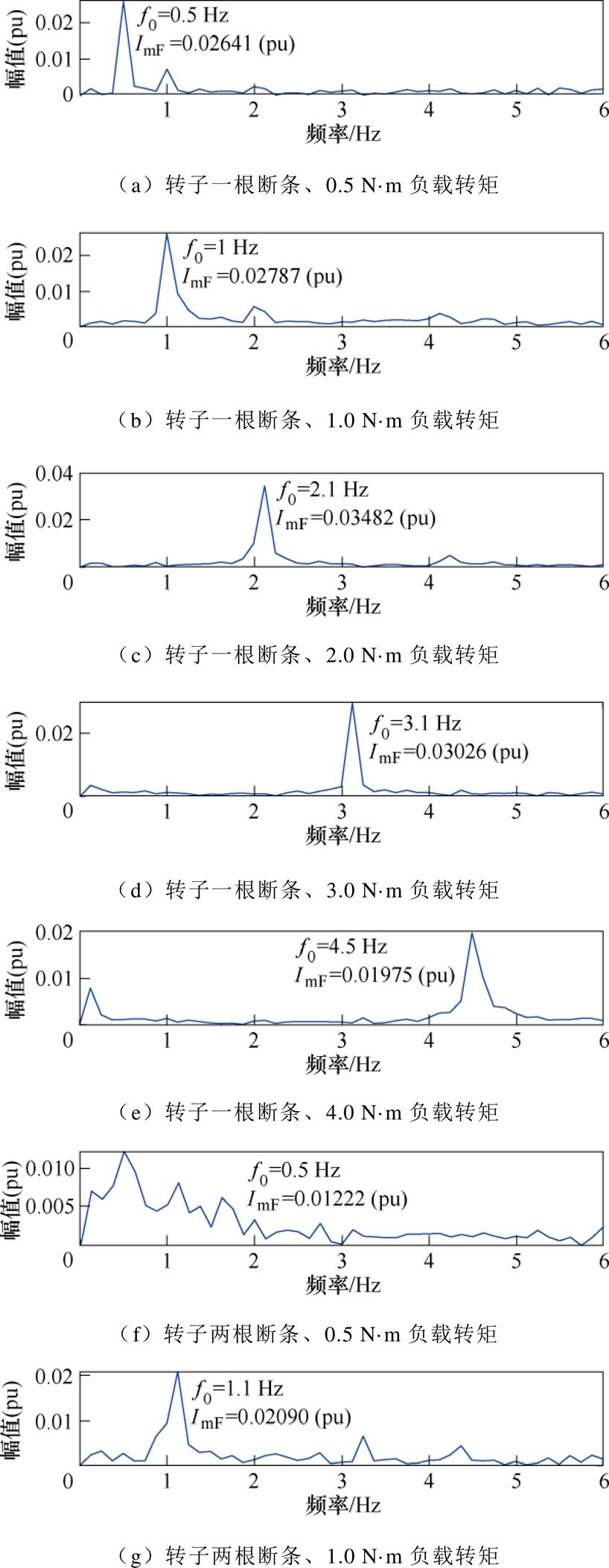
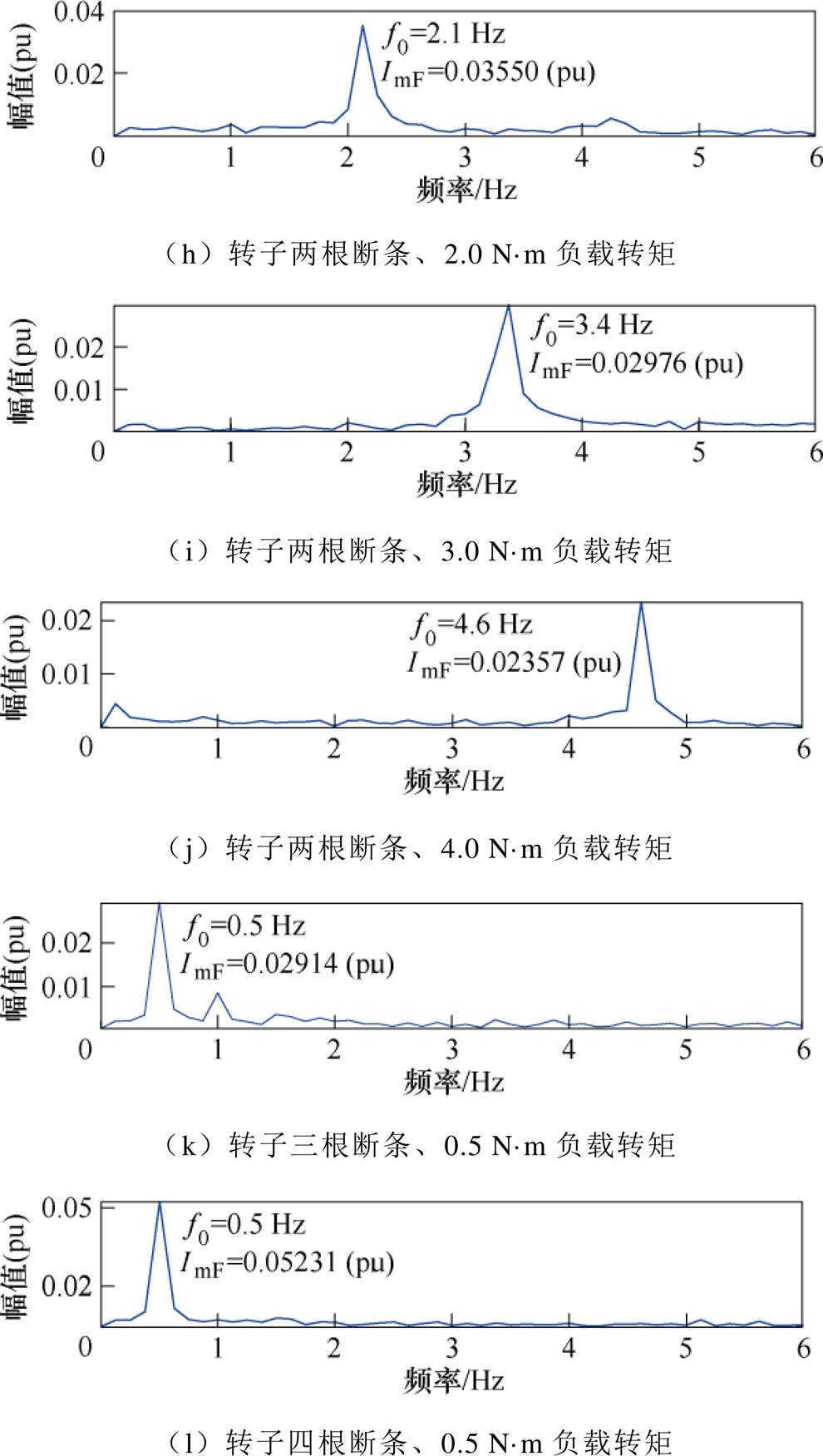
图7 故障电机TKEO归一化解调信号 Goertzel算法频谱
Fig.7 The Goertzel algorithm spectrum of normalized demodulation signal using TKEO for the faulty motor
图8所示为无故障和转子断条故障电机在不同负载工况下,定子电流TKEO归一化解调信号频谱图中f0分量幅值检测结果。通过观察图8可以发现,无故障电机定子电流TKEO归一化解调信号频谱图中f0分量在负载为4.0 N·m时保持在0.008(pu)左右,其他不同负载情况下保持在0.01(pu)左右。当电机发生转子断条故障时,f0分量幅值明显增大,几乎都位于0.02(pu)以上。对于带有转子两根断条故障电机在0.5 N·m工况下,虽然f0分量幅值较小,但与无故障电机相比,其幅值同样稍微增大,依然可准确地检测转子断条故障。
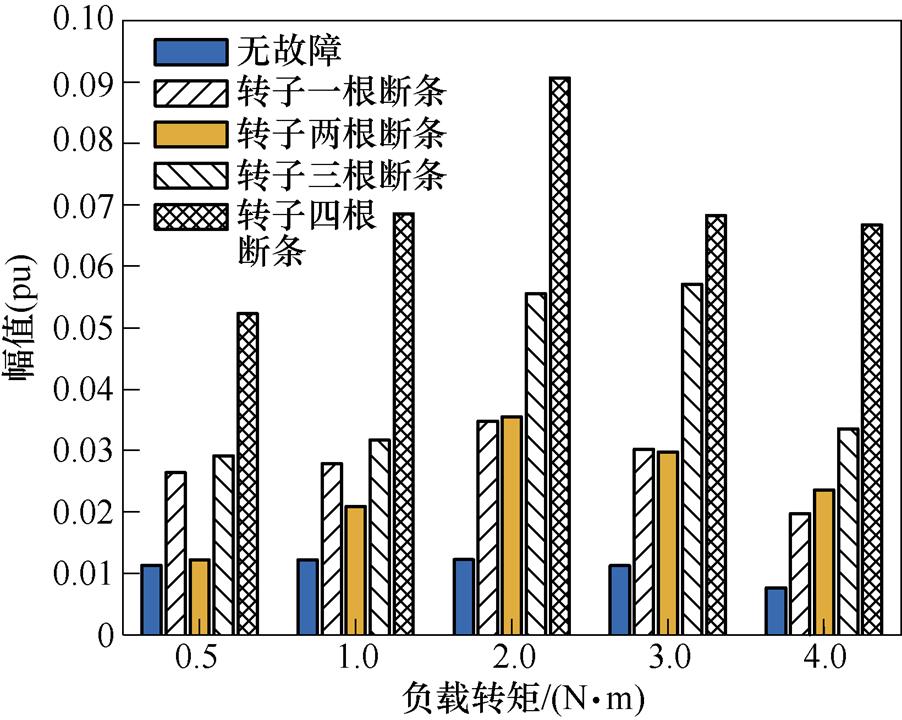
图8 无故障和故障电机定子电流TKEO归一化解调信号故障特征分量幅值
Fig.8 The amplitude of broken rotor bar fault characteristic components for stator current TKEO normalized signal under health and faulty motor
考虑转子带有不同断条根数的故障电机,进一步利用FDEO对其在不同负载工况下的定子电流信号进行解调并归一化处理,然后采用Goertzel算法对归一化解调信号进行低频段频谱分析,如图9所示。对比图9a~图9l可以看出,利用FDEO归一化解调信号同样可将定子电流信号中的边带故障特征分量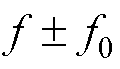 转换为转子断条故障特征分量f0,有效抑制了基频频谱泄露的影响。但是,利用FDEO归一化解调信号进行Goertzel算法频谱分析时,个别负载工况情况下虽然能够准确识别出转子断条故障特征分量f0,大多数负载情况下却无法有效识别。这是因为,采用FDEO进行转子断条故障诊断时,利用傅里叶变换微分特性获取导数过程中,可能由于噪声信号影响,导致此方法稳定性较差,影响故障检测的可靠性。
转换为转子断条故障特征分量f0,有效抑制了基频频谱泄露的影响。但是,利用FDEO归一化解调信号进行Goertzel算法频谱分析时,个别负载工况情况下虽然能够准确识别出转子断条故障特征分量f0,大多数负载情况下却无法有效识别。这是因为,采用FDEO进行转子断条故障诊断时,利用傅里叶变换微分特性获取导数过程中,可能由于噪声信号影响,导致此方法稳定性较差,影响故障检测的可靠性。
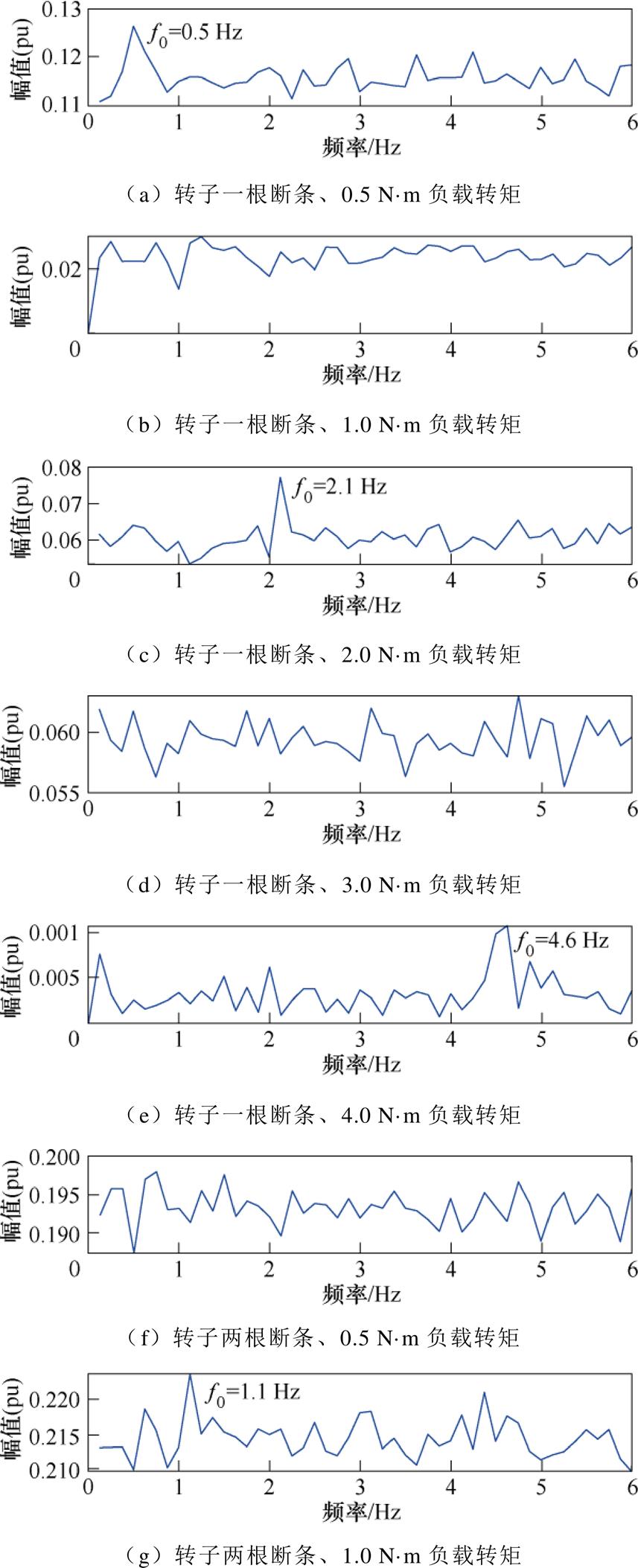
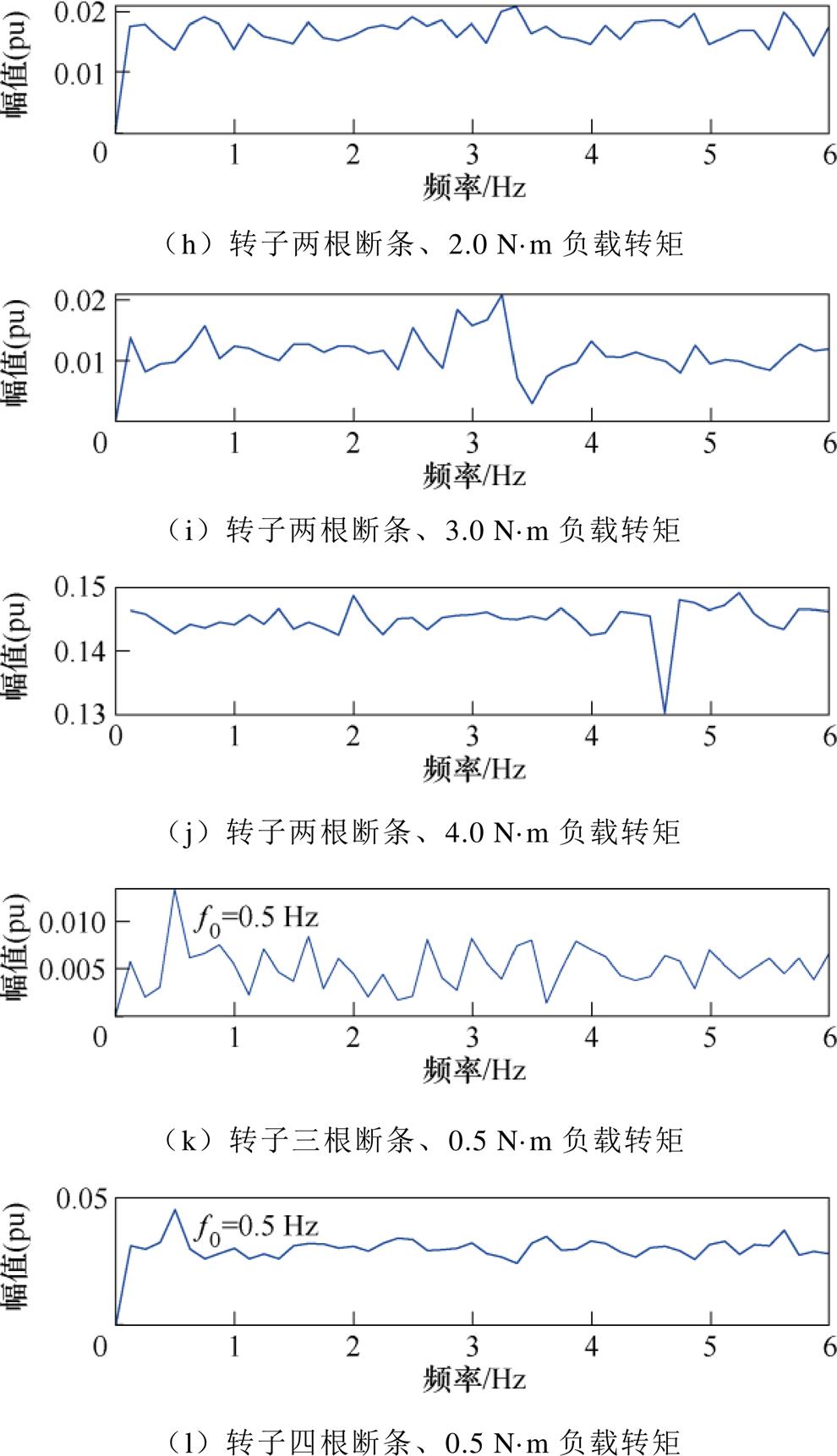
图9 故障电机FDEO归一化解调信号 Goertzel算法频谱
Fig.9 The Goertzel algorithm spectrum of normalized demodulation signal using FDEO for the faulty motor
不同类型感应电机定子电流谐波分量存在差异,无故障电机电流信号中也可能存在相似的转子断条故障特性相关分量。为实现对转子断条故障的有效诊断,除了判断转子断条故障特征相关分量是否存在以外,还需对其转子断条故障特征相关分量幅值进行分析。本文提出一种TKEO解调策略和Goertzel算法相融合的感应电机转子断条故障诊断方法,具有计算量少、可靠性高、实时性强以及硬件成本低的优点,更有助于工业现场实际应用。所提方法采用TKEO解调策略对考虑固有偏心谐波的电机定子电流信号进行处理,实现转子断条边带故障特征分量到转子断条故障特征分量以及固有偏心谐波分量到转子速度谐波分量的转变,有效抑制基频频谱泄露对故障诊断和转速估计造成的干扰。同时,利用Goertzel算法对归一化解调信号进行频谱分析,从而快速提取转子断条故障特征分量和转子速度分量。最后,将TKEO与FDEO解调方法进行性能比较分析。仿真数据和实验数据分析结果表明,利用TKEO解调策略可实现不同负载和不同严重程度故障工况下的转子断条故障检测,而FDEO解调策略则容易受到噪声影响,仅在个别工况下可以检测出转子断条故障特征分量。
参考文献
[1] 陈鹏, 谢颖, 李道璐. 感应电机定子匝间短路故障温升特性研究[J]. 电工技术学报, 2023, 38(18): 4875-4888.
Chen Peng, Xie Ying, Li Daolu. Research on the temperature rise characteristics of induction motors with stator inter-turn fault[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4875-4888.
[2] 王万丁, 宋向金, 陈前, 等. 采用整流技术的变频供电感应电机转子断条故障诊断方法[J]. 电工技术学报, 2022, 37(16): 4074-4083.
Wang Wanding, Song Xiangjin, Chen Qian, et al. Broken rotor bar fault diagnosis in inverter-fed induction motors using the rectification technology[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4074-4083.
[3] 李睿彧, 刘飞, 梁霖, 等. 基于参数优化变分模态分解的交流变频电机转子断条故障识别方法[J]. 电工技术学报, 2021, 36(18): 3922-3933.
Li Ruiyu, Liu Fei, Liang Lin, et al. Fault identification of broken rotor bars for the variable frequency AC motor based on parameter optimized variational mode decomposition[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3922- 3933.
[4] 夏志凌, 胡凯波, 刘心悦, 等. 基于变模态分解的异步电机转子断条故障诊断[J]. 电工技术学报, 2023, 38(8): 2048-2059.
Xia Zhiling, Hu Kaibo, Liu Xinyue, et al. Fault diagnosis of rotor broken bar in induction motor based on variable mode decomposition[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(8): 2048-2059.
[5] 贾朱植, 徐建英, 宋向金, 等. 鼠笼电机转子断条故障的定子电流信号平方解调分析诊断方法[J]. 仪器仪表学报, 2015, 36(9): 2097-2103.
Jia Zhuzhi, Xu Jianying, Song Xiangjin, et al. Square stator current demodulation analysis diagnosis method for broken rotor bar fault of squirrel cage motor[J]. Chinese Journal of Scientific Instrument, 2015, 36(9): 2097-2103.
[6] Abd-el-Malek M, Abdelsalam A K, Hassan O E. Induction motor broken rotor bar fault location detection through envelope analysis of start-up current using Hilbert transform[J]. Mechanical Systems and Signal Processing, 2017, 93: 332-350.
[7] Valles-Novo R, de Jesus Rangel-Magdaleno J, Ramirez-Cortes J M, et al. Empirical mode decom- position analysis for broken-bar detection on squirrel cage induction motors[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(5): 1118- 1128.
[8] Pineda-Sanchez M, Riera-Guasp M, Antonino-Daviu J A, et al. Diagnosis of induction motor faults in the fractional Fourier domain[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(8): 2065- 2075.
[9] Pineda-Sanchez M, Puche-Panadero R, Riera-Guasp M, et al. Application of the Teager-Kaiser energy operator to the fault diagnosis of induction motors[J]. IEEE Transactions on Energy Conversion, 2013, 28(4): 1036-1044.
[10] Li Haiyang, Feng Guojin, Zhen Dong, et al. A normalized frequency-domain energy operator for broken rotor bar fault diagnosis[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 3500110.
[11] Filippetti F, Franceschini G, Tassoni C, et al. AI techniques in induction machines diagnosis including the speed ripple effect[J]. IEEE Transactions on Industry Applications, 1998, 34(1): 98-108.
[12] 李唐安, 李世阳, 张家明, 等. 基于Goertzel算法的红外气体检测方法[J]. 红外与激光工程, 2019, 48(3): 76-81.
Li Tang’an, Li Shiyang, Zhang Jiaming, et al. Infrared detection method of gas based on Goertzel algorithm[J]. Infrared and Laser Engineering, 2019, 48(3): 76-81.
[13] Shi Dongfeng, Unsworth P J, Gao R X. Sensorless speed measurement of induction motor using Hilbert transform and interpolated fast Fourier transform[J]. IEEE Transactions on Instrumentation and Measure- ment, 2006, 55(1): 290-299.
[14] 杨凯, 李孺涵, 罗成, 等. 负载变化下无传感器感应电机主动零频穿越及脉动抑制策略[J]. 电工技术学报, 2023, 38(18): 4910-4920.
Yang Kai, Li Ruhan, Luo Cheng, et al. Proactive low-frequency ride-through method and its ripple reduction for sensorless induction motor drives under load variations[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4910-4920.
[15] Chirindo M, Khan M A, Barendse P. Analysis of non-intrusive rotor speed estimation techniques for inverter-fed induction motors[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 338-347.
[16] Aline E T, Rogério A F, Marcelo S, et al. Experi- mental database for detecting and diagnosing rotor broken bar in a three-phase induction motor[DB/OL]. IEEE Dataport, 2020, https://dx.doi.org/10.21227/ fmnm-bn95.
Abstract As an important energy conversion device, induction motors (IM) are widely used in electric vehicles, industrial machinery, and aerospace appliances. Although broken rotor bar (BRB) faults only account for about 10% of total IM failures, fault-related features are often submerged with strong background noise, which makes it difficult to detect at an early stage.
Compared to other signals that indicate the condition of the IM, such as voltage, vibration, airgap flux, and acoustic emission, the current signal is low-cost, non-invasive, and simple to acquire. However, extracting fault components at low-load operating conditions is challenging for BRB detection using motor current signature analysis (MCSA). Furthermore, conventional approaches of MCSA fail to estimate the rotor speed and compute a small number of selected frequency components. This paper proposes a BRB fault diagnosis method for an IM based on Teager-Kaiser Energy Operator (TKEO) demodulation and the Goertzel algorithm.
Firstly, based on the sideband frequency components caused by the BRB fault and the inherent eccentric harmonic component in the current signal, the demodulation performance of TKEO and frequency domain energy operator (FDEO) are analyzed. With the two demodulation methods, the supply frequency component is converted into a DC component and removed. Meanwhile, the modulation sideband components and the inherent eccentric harmonic components are transformed into the BRB fault characteristic and the rotor speed harmonic components. Therefore, the interference caused by the spectrum leakage of supply frequency components to the fault diagnosis and the speed estimation is suppressed. Then, to reduce the computational complexity, the Goertzel algorithm is used to compute a small number of selected frequency components of the normalized demodulated signal. The fast extraction of the BRB fault characteristic component and rotor speed harmonic component is realized. Finally, the theoretical value of the BRB fault characteristic component is calculated using the estimated rotor speed harmonic component. By comparing the frequencies and amplitudes of the detection and theoretical BRB fault characteristic components, the conclusion can be determined whether the BRB fault occurs.
The effectiveness of the theoretical analysis and the proposed method is validated on the experimental database of Western Parana State University. Even if the severity of the BRB fault is relatively high, due to the spectrum leakage of the supply frequency component, the motor current signal cannot detect the BRB fault characteristic component under light load conditions. The performance of the proposed method and the FDEO under different loads and severity conditions are presented in terms of their efficiency and stability. Although both methods can suppress the spectrum leakage, comparative experiments demonstrate that the FDEO method can only identify the BRB fault characteristic components under several load cases, which is susceptible to noise interference. The proposed method can effectively recognize the BRB fault characteristic components under different loads and severity conditions with less calculation, high reliability, solid real-time performance, and low hardware cost.
keywords:Broken rotor bar, Goertzel algorithm, inherent eccentricity, Teager-Kaiser energy operator, frequency domain energy operator
DOI: 10.19595/j.cnki.1000-6753.tces.230517
中图分类号:TM307
国家自然科学基金(52007078, 62002140)和江苏省双创博士计划资助项目。
收稿日期 2023-04-24
改稿日期 2023-11-10
王照伟 男,1991年生,博士,讲师,硕士生导师,研究方向为工业设备状态监测与智能诊断。E-mail: wangzhaowei@ujs.edu.cn
宋向金 女,1989年生,博士,讲师,硕士生导师,研究方向为交流电机状态监测与故障诊断。E-mail: songxiangjin@ujs.edu.cn(通信作者)
(编辑 崔文静)