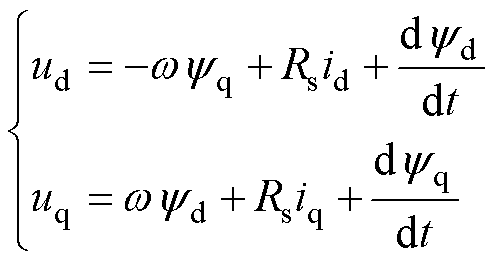 (1)
(1)
摘要 同步磁阻电机因为其成本低、可靠性高,发展前景可观。在低速域无传感器控制方面,因同步磁阻电机转子具有凸极性,使用高频方波信号注入方法进行转子角度估计最为合适。但是,电机在低速运行中伴随着交直轴电感交叉饱和问题,该问题影响着电机的动稳态性能。为此,对传统高频方波注入控制方法进行改进,提出基于静止轴系的双高频方波注入无传感器控制方法,降低高频幅值带来的高频转矩脉动,抑制因交叉饱和效应导致的角度估计误差,提高电机动稳态性能。在1.5 kW同步磁阻电机实验平台上进行实验验证。结果表明,与传统高频注入法相比,改进高频注入法消除了交叉饱合引起的角度估计误差,并降低高频信号带来的转矩脉动问题,提高了电机的动稳态性能。
关键词:同步磁阻电机 双高频方波注入 离线参数辨识 高频转矩脉动 交叉饱和
同步磁阻电机(Synchronous Reluctance Motor, SynRM)于1923年被首次提出。随着电力电子和现控理论的快速发展及微处理器技术的广泛应用,SynRM克服并解决了同步控制问题,使其能够应用于电气驱动[1]。针对电机模型建立,文献[2]提出了一种SynRM的空间矢量动力学模型,包括自饱和、交叉饱和效应和铁损。电机参数的准确辨识有利于提高SynRM的无传感器控制性能。SynRM的参数识别[3-5]方法和无传感器控制策略[6-9]是提高SynRM工业竞争力的两项关键技术应用。
在电感参数辨识中,有限元分析是在设计过程中根据电机结构获取参数的基本方法。文献[10]建立铁氧体辅助同步磁阻电机二维磁场和电路耦合的瞬态有限元模型,重点阐述了其几何建模、网格划分、磁路耦合以及后处理可视化等环节的执行逻辑。然而,详细的设计数据只能由电机设计师和生产商访问,这是受保护的商业秘密[11],因而阻碍了基于有限元分析方法的工业应用。
电力电子变换器在SynRM参数辨识方面与上述方法相比更具竞争力和实用性。文献[12]使用磁滞电压注入方法获得了静止时的磁通饱和数据。并且使用线性最小二乘法(Linear least-Squares Method, LSM)来估计与交叉饱和度相关的参数。因此,所提出的参数估计方法易于实现,可以应用于通用逆变器产品。文献[13]讨论了同步电机在速度或负载瞬态过程中的磁链估计,非线性磁模型是通过径向基函数神经网络获得的,该网络产生了一个可微函数作为电流和磁链之间的联系。文献[14]使用电力电子变换装置生成不同的信号模式,并应用于SynRM。与永磁同步电机的识别程序不同,电流或电压矢量可沿两个轴注入,而无需锁定转子,因为电机没有永磁体,所以不会产生额外转矩。由于SynRM的交叉耦合效应相对严重,因此必须同时注入dq轴电流,在实验过程中可以将转子位置锁死,以保证转子的稳定性。应通过整个dq轴电流平面对测试的SynRM进行函数表达,以覆盖交叉耦合区域。文献[15]采用递推离散傅里叶变换算法计算静止轴系中的电流正负序分量幅值,进而计算电机的参数,该方法具有计算量小、快速准确等优势,在电机基础控制策略中,文献[16]将电压空间矢量调制技术引入传统直接转矩控制,优化了电机的动态性能,降低了损耗。文献[17]开发并提出了一种新的基于递归神经网络的SynRM无模型预测电流控制。该方法依赖于SynRM电流的识别,而不考虑任何参数,避免了电机交叉饱和问题。
在无传感器控制策略中,文献[18]证明了扩展卡尔曼滤波器的位置估计器应用在同步磁阻电机上的可行性并且作出相关算法,验证其有效性。在磁链观测器无感控制中,文献[19]考虑了文献中不常见但专门研究用于支持估计的替代解决方案,即恒定直轴电流和恒定直轴磁链控制。但是,在无感控制过程中会因交叉饱和出现位置估计误差问题,文献[20]提出一种考虑磁场交叉饱和效应补偿的变角度方波电压注入永磁同步电机无位置传感器控制策略,由于注入位置角的改变,可以有效抑制交叉耦合导致的转子位置估计误差。文献[21]在观测器中注入虚拟电压。虚拟电压注入能同时解决系统状态变量能观性、极点分布稳定性和电机参数鲁棒性问题,最终实现系统在低同步转速区域的稳定运行。文献[22]通过注入一些低频电流信号并通过梯度下降算法调整估计的转子角位置,直到最小化在估计的转速上产生的纹波,来检测估计转子位置的误差。文献[23]采用最先进的基于反电动势的无传感器方案,同步电机的磁场定向控制需要实时的转子位置来实现转矩和磁通的解耦控制。文献[24]提出了一种有限控制集模型预测控制技术,利用开关电流纹波进行位置估计,并考虑了交叉饱和引起的位置误差。该方案通过简单的融合结构与自适应投影向量相结合,用于高速区域的位置误差估计,以实现平稳过渡。文献[25]提出了一种新的基于谐振卡尔曼滤波器的SynRM无速度传感器控制方案,解决相位延迟问题。依赖SynRM模型的估计方法无法在较低速度下估计位置。由于SynRM固有的凸极性,即使在静止状态下,基于凸极性的估计位置的方法也很容易适用。这些方法大致可分为信号注入法、改进的基于脉冲宽度调制(Pulse Width Modulation, PWM)法和基于无额外信号的定子电流变化法。基于信号注入的无传感器控制方法依据跟踪SynRM凸极性的原理,该方法在无传感器控制操作的零速度和低速区域有效。基于信号注入的无传感器控制方法可根据注入模式分为旋转信号注入和脉动信号注入。脉动信号可以是正弦或方波信号。
此外,对于低速应用如拉丝机、切割机和矿车跟踪机所需SynRM无传感器低速驱动器要进一步抑制由传统高频信号注入引起的高频转矩脉动和噪声。文献[26]在电机结构上提出齿槽转矩会影响电机的噪声和振动,应尽可能降低齿槽转矩来降低噪声和振动。文献[27]针对双三相绕组永磁同步电机,推导了产生载波谐波振动的载波谐波电磁激振力,并计算了空间载波相位差与时间相位差之间的关系,以抵消激振力。文献[28-29]分别针对永磁电机的噪声和同步磁阻电机的转矩脉动进行了有效分析和处理,对高频信号噪声抑制和转矩脉动抑制起到良好的效果。文献[30]利用改进的伪随机方波注入法,对同步磁阻电机的噪声进行有效抑制。
同步磁阻电机控制的主要困难在于其电机自身的交叉饱和效应,交叉饱和效应会导致位置估计不够准确、控制效率下降等问题。通过不断迭代提升,利用信号注入进行测试的方法较为简洁可靠。该方法可以快速有效地对电机参数进行辨识,抑制交叉耦合效应。另外,在同步磁阻电机的无传感器控制中,其低速下的控制方法与其他同步电机类似,使用高频方波信号注入方法较好。为进一步解决在高频方波注入控制中的转矩脉动问题,可以使用双高频方波注入法对高频转矩脉动进行抑制,提高电机在低速控制中的动稳态性能。
本文主要研究考虑交叉饱和效应的改进高频注入无速度控制策略,理论分析传统高频注入无速度传感器控制策略中,当电机运行在突加突减负载场合时,由于负载变化导致的电流波动引起的转子位置估计误差偏大问题;在此基础上对传统同步磁阻电机无速度控制进行改进,设计相关实验采用磁通图对转子位置偏差进行计算,对高频信号解耦过程中出现的转子误差项进行补偿,最终使得电机在电流变化较大时依然能保持较好的角度跟随。
同步磁阻电机在dq同步旋转坐标系下的数学模型为
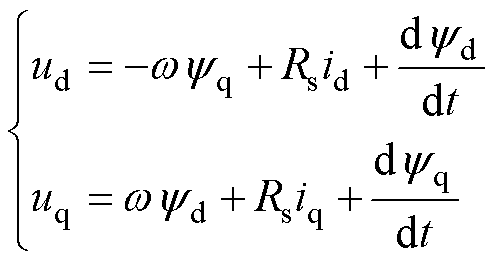 (1)
(1)
式中,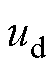 、
、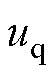 分别为定子电压矢量在d、q轴的电压;
分别为定子电压矢量在d、q轴的电压;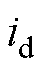 、
、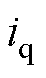 分别为定子电流矢量在d、q轴的电流;
分别为定子电流矢量在d、q轴的电流;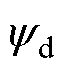 、
、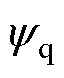 分别为d、q轴磁链;w 为转子角速度;Rs为定子电阻。
分别为d、q轴磁链;w 为转子角速度;Rs为定子电阻。
由于位置估计误差来自于SynRM本身的耦合效应,所以SynRM转子位置估计问题需从电机本身的高频注入原理侧分析,下述分析均是基于忽略交叉耦合的基础上存在的,由于d、q轴系对于误差来源的解释更加清楚,因此建立d、q轴下高频注入后模型为
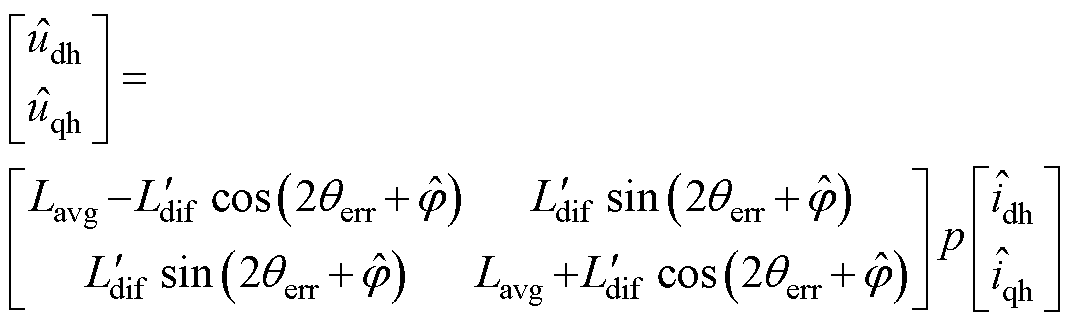 (2)
(2)
式中,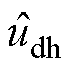 、
、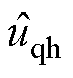 分别为d、q轴系变换至估计轴系下SynRM定子电压高频分量;
分别为d、q轴系变换至估计轴系下SynRM定子电压高频分量;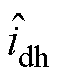 、
、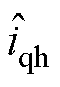 分别为实际d、q轴系变换至估计d、q轴系下SynRM定子电流高频分量;Lavg为均值电感;
分别为实际d、q轴系变换至估计d、q轴系下SynRM定子电流高频分量;Lavg为均值电感;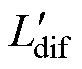 为含交叉耦合信息的电感;qerr为位置估计误差;j 为交叉耦合估计误差;p为微分算子。
为含交叉耦合信息的电感;qerr为位置估计误差;j 为交叉耦合估计误差;p为微分算子。
经式(2)可获得的角度误差信息,其中存在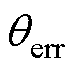 和
和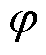 两项误差,这两个误差分别为
两项误差,这两个误差分别为
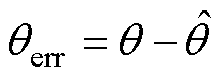 (3)
(3)
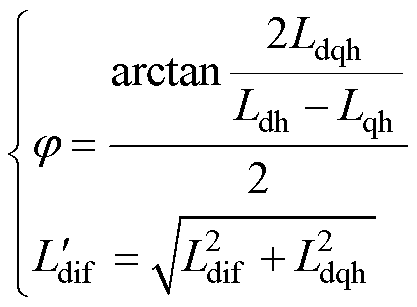 (4)
(4)
式中,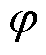 为同步磁阻电机交叉耦合效应所产生的固有角度误差,该误差会影响电机控制的效率和稳定性,为保证电机可靠运行,需对该误差进行抑制;
为同步磁阻电机交叉耦合效应所产生的固有角度误差,该误差会影响电机控制的效率和稳定性,为保证电机可靠运行,需对该误差进行抑制;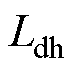 、
、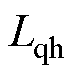 为增量电感;Ldqh为dq轴互感;Ldif为差值电感。
为增量电感;Ldqh为dq轴互感;Ldif为差值电感。
再将高频信号方程注入至坐标变换后的电机模型中,进而计算出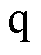 轴的电流变化量为
轴的电流变化量为
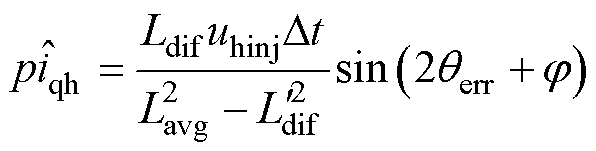 (5)
(5)
式中,uhinj为高频注入信号;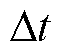 为采样时间间隔。
为采样时间间隔。
SynRM在不同工作条件下存在不同的电磁饱和及交叉耦合程度,导致电机参数变化的同时,会产生角度估计误差。dq轴电流的增大无疑会加重电机的饱和情况,而当dq轴电流同时存在时将导致电机轭部磁场的畸变,进而导致dq轴电感交叉耦合现象以及互感的存在。而角度估计误差的大小由耦合现象以及互感值决定。
根据SynRM的自感及互感表达式分别为
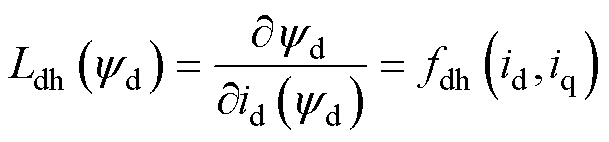 (6)
(6)
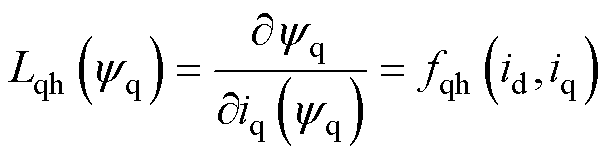 (7)
(7)
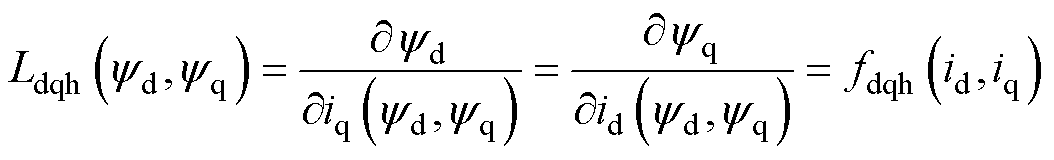 (8)
(8)
式中,fdh、fqh分别为d、q轴自感;fdqh为dq轴定子电流同dq轴互感。
利用Matlab获得的模型再进行偏导运算,通过运算后获得d轴增量电感、q轴增量电感、dq轴增量互感,以上三个函数自变量均为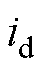 和
和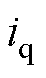 ,作为二元函数可以绘制其三维曲面图,通过控制变量方法对d、q轴的增量电感进行交叉耦合分析获得如图1所示的磁通(增量电感、电流关系)。可以看出,一方面,当q轴电流为0时,随着d轴电流增大,d轴的增量电感前半部分平稳,后半部分迅速降落,且远大于q轴增量电感。而当分别注入1 A和5 A的q轴电流时,会使得迅速降落的部分得到扩大,并且小于q轴增量电感,凸极性能改变。另一方面,当d轴电流为0,q轴电流增大时,对应的q轴电感会稳定地逐渐减小,而当分别注入1 A、5 A的d轴电流时,其电感参数被整体提升一小部分,并且与d轴电流的大小呈正相关,削弱了其凸极效果。
,作为二元函数可以绘制其三维曲面图,通过控制变量方法对d、q轴的增量电感进行交叉耦合分析获得如图1所示的磁通(增量电感、电流关系)。可以看出,一方面,当q轴电流为0时,随着d轴电流增大,d轴的增量电感前半部分平稳,后半部分迅速降落,且远大于q轴增量电感。而当分别注入1 A和5 A的q轴电流时,会使得迅速降落的部分得到扩大,并且小于q轴增量电感,凸极性能改变。另一方面,当d轴电流为0,q轴电流增大时,对应的q轴电感会稳定地逐渐减小,而当分别注入1 A、5 A的d轴电流时,其电感参数被整体提升一小部分,并且与d轴电流的大小呈正相关,削弱了其凸极效果。
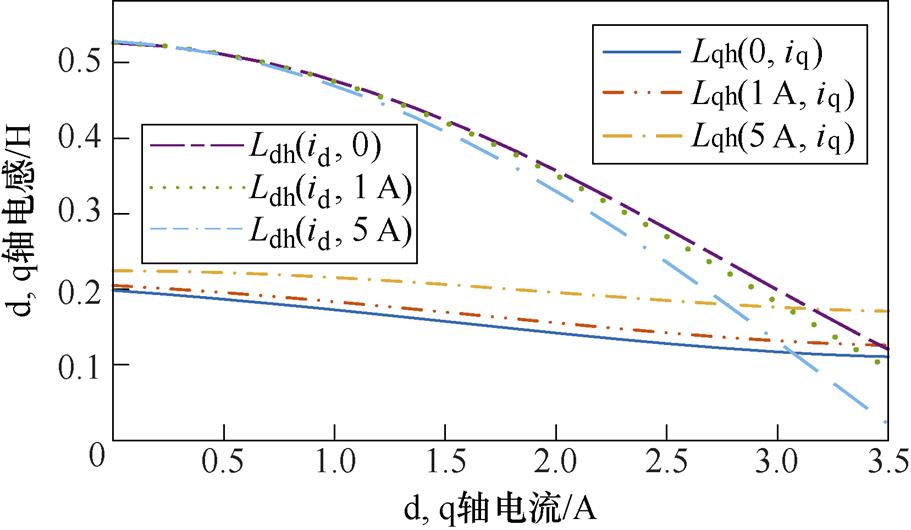
图1 增量电感-电流关系
Fig.1 Incremental inductance current relationship
为直观地可以观察到dq轴电流对电感的影响,分别对上述三个二元函数使用Matlab来对所获得d轴增量电感、q轴增量电感、dq轴增量电感进行三维曲面图绘制,分析其电感变化特点。图2~图4分别绘制了d轴电感、q轴电感、dq轴互感的三维曲面图,可以看出,dq轴自感随电流增加幅值降低,同时受交叉耦合效应影响,dq轴电感值随另一轴电流幅值变化发生改变。交叉耦合效应引起的互感随dq轴电流幅值的增加而增大。
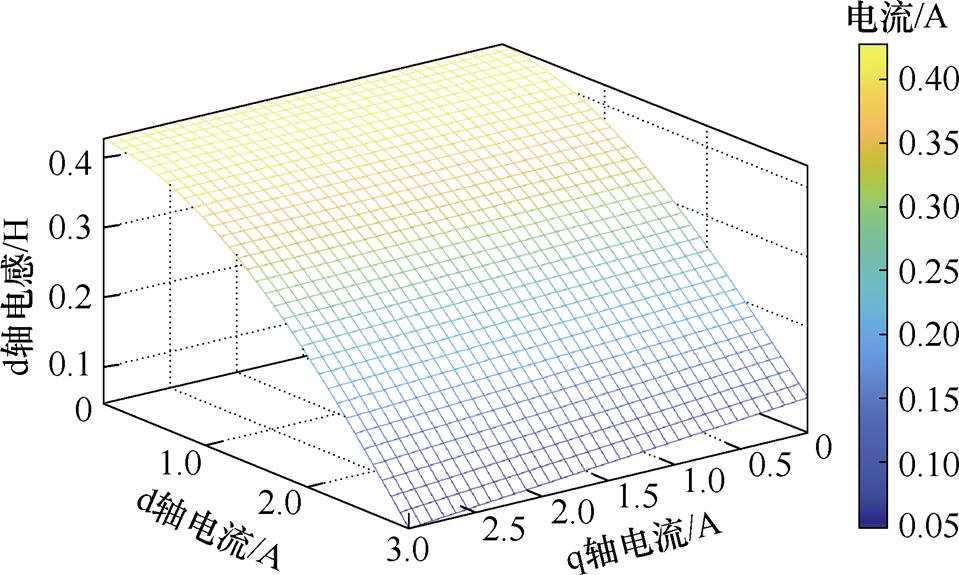
图2 d轴电感-电流关系
Fig.2 d-axis inductance current relationship
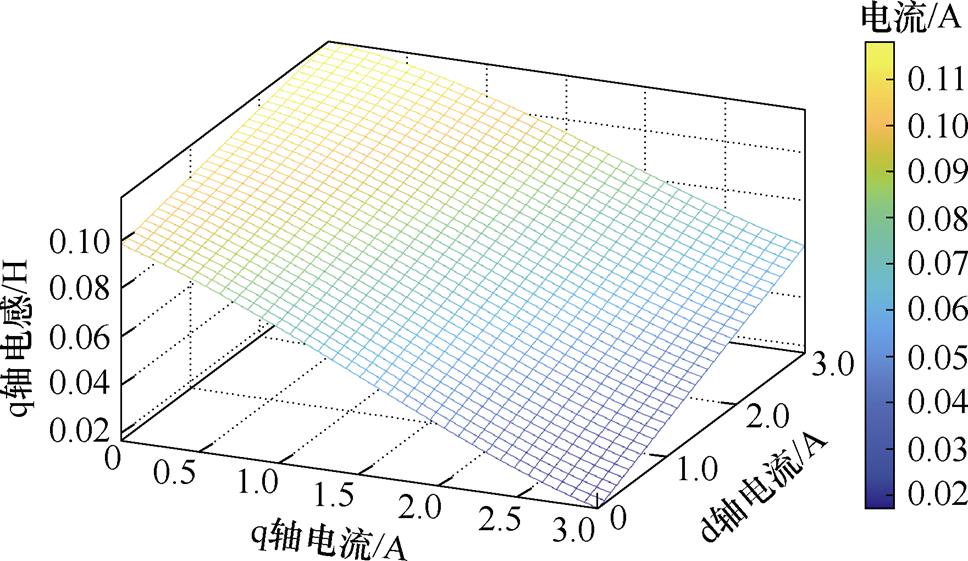
图3 q轴电感-电流关系
Fig.3 q-axis inductance current relationship
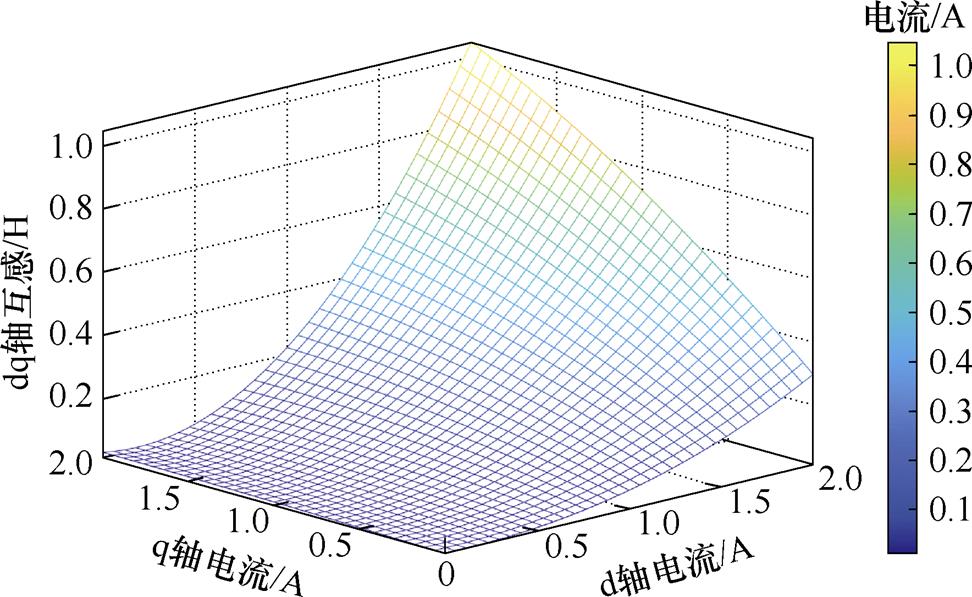
图4 dq轴互感-电流关系
Fig.4 dq-axis mutual inductance current relationship
在获得d轴电感、q轴电感、dq轴互感的函数表达式后,利用转子误差式(4),将d轴增量电感、q轴增量电感和dq互感的函数关系式代入,计算得到转子误差结果如图5所示。从图5中可以看到,在负载较小时,SynRM的dq电流较小,所以其转子位置误差也相对较小,在0附近,而当SynRM负载较大时,dq轴电流较大,由交叉耦合效应导致的转子位置估计误差qe可达44°,因此,若要提高同步磁阻电机的实用性和可靠性,忽略交叉耦合效应将会导致转子位置估计精度受到很大影响,因此需要对交叉耦合效应进行进一步分析。
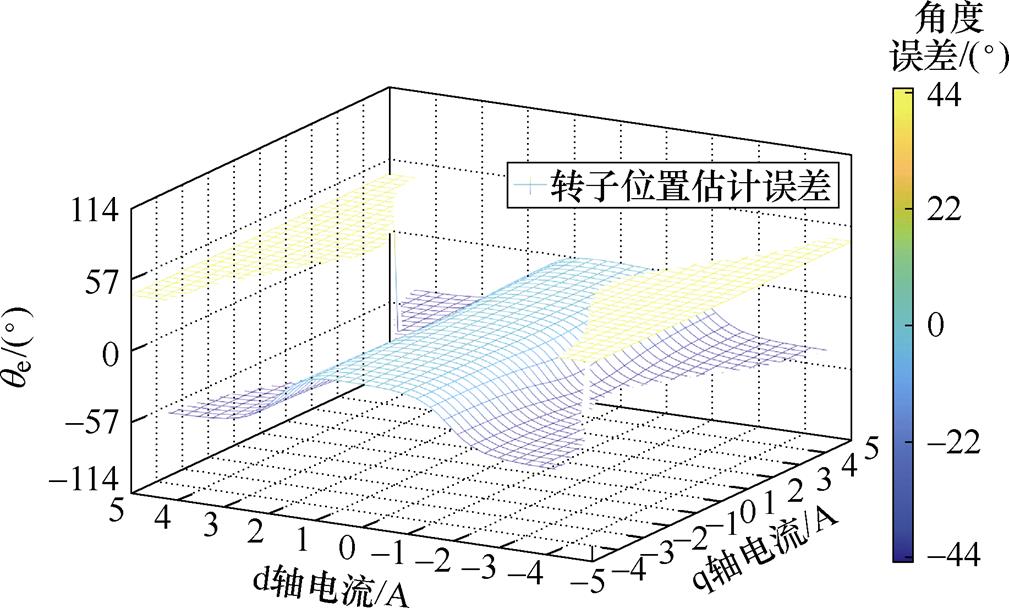
图5 转子误差波形
Fig.5 Rotor error waveforms
本节分别针对信号解耦和信号注入方法对传统的高频信号注入方法进行改进,在信号解耦过程中,将传统的未考虑交叉耦合效应的方法进行优化,提出将交叉耦合误差补偿至信号解耦的过程中去,在信号解耦过程中分别出现的估计误差和因交叉饱和效应导致的固有误差均可以被抑制和补偿。在信号注入过程中,针对传统单轴信号注入方法的高频转矩脉动问题,在静止轴系下使用双轴注入可以有效地对其进行抑制消除,提高电机在低速运行下的性能。
改进高频方波注入法控制框图如图6所示。一方面,在信号解耦过程中添加角度补偿以保证角度估计精度;另一方面,将单d轴注入改为双高频方波注入以降低高频电流幅值波动带来的高频转矩脉动,减小角度估计误差,提高电机动稳态性能。
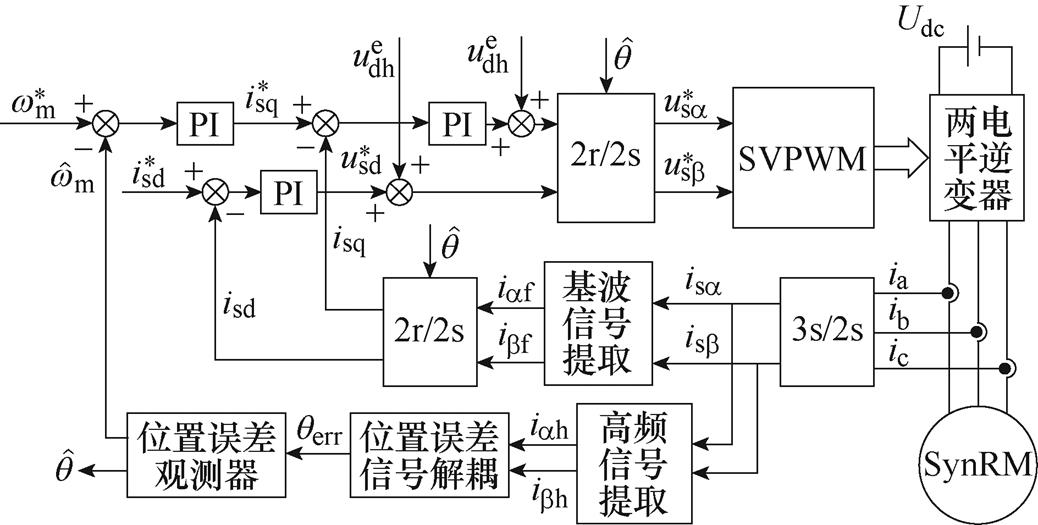
图6 改进高频方波注入法控制框图
Fig.6 Control block diagram of traditional high-frequency square wave injection method
在考虑交叉耦合条件下,通过坐标变换到静止轴系可得
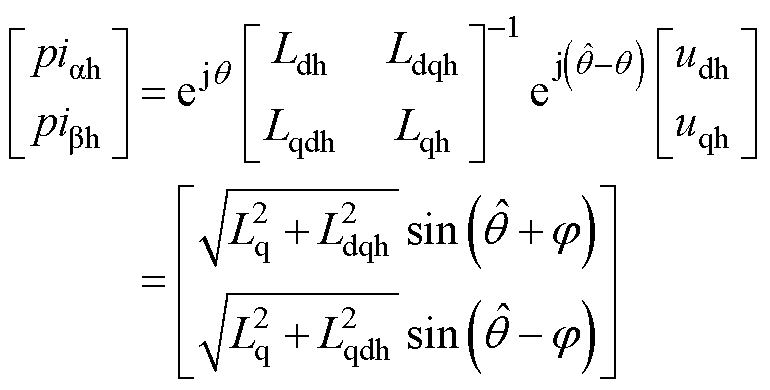 (9)
(9)
式中,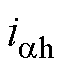 、
、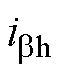 分别为a、b 轴高频电流响应分量;
分别为a、b 轴高频电流响应分量;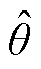 为转子估计位置;q 为坐标变换角。
为转子估计位置;q 为坐标变换角。
根据图6所示进行逐步分析,先对高频注入信号使用带通滤波器(Band-Pass Filte, BPF)进行滤波,滤除高频信号中的IGBT开关信号和基波频率,对应的公式为
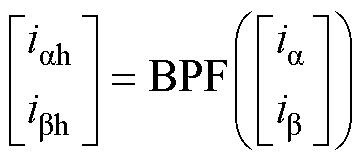 (10)
(10)
式中,ia、ib 分别为定子电流矢量在a、b 轴电流。
在式(10)基础上,对其进行差分计算,有
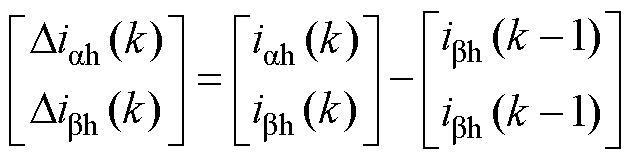 (11)
(11)
因为注入方波电压有正有负,所以要对式(11)的电流信号进行峰值检测计算,即乘以当前高频注入信号的正负符号,可得
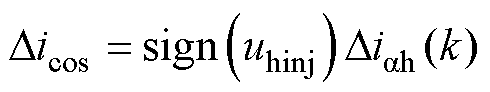 (12)
(12)
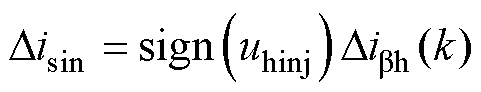 (13)
(13)
矢量叉乘中正余弦参数不再是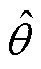 而是
而是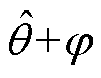 ,其中
,其中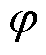 为需要补偿的误差角。
为需要补偿的误差角。
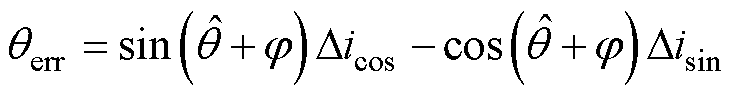 (14)
(14)
式中,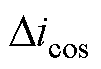 、
、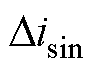 为含有位置信息的标幺化电流。
为含有位置信息的标幺化电流。
根据2.1节中所提出的,利用静止法实验获取电机交叉饱和特性并拟合为多项式函数,利用此函数可以有效对电机转子位置估计进行角度误差补偿。补偿原理如图7所示,实时采样dq轴电流,将dq轴电流通过多项式函数组成的磁通图模型进行计算,进而得到当前的交、直轴电感以及交叉耦合电感。最后代入误差角公式中实时计算得到误差值,直接补偿至矢量叉乘模块中,以此来保证无速度算法输出的角度估计值误差降到合理范围内,从而提高电机的带载能力。
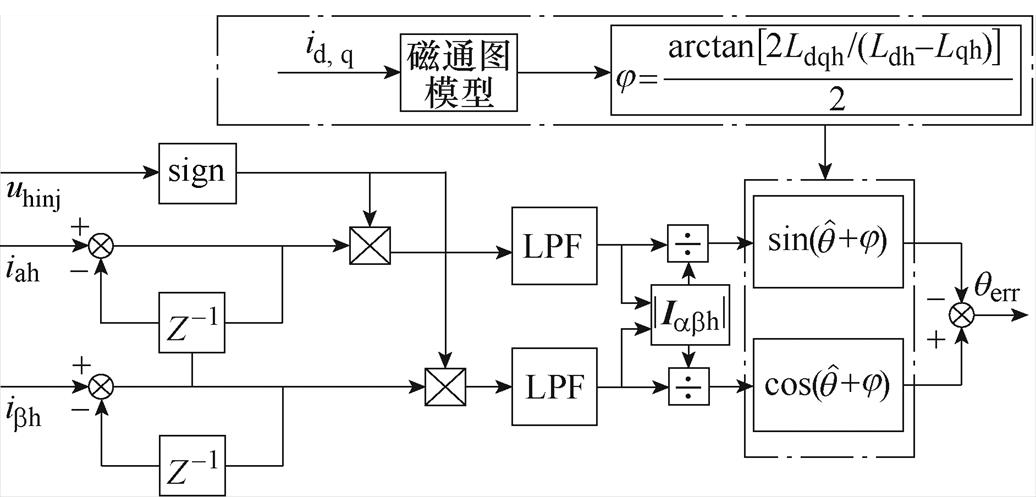
图7 改进的位置信息提取方法
Fig.7 Improved method for extracting position information
由此便获得了静止轴系下的改进位置误差提取方法,在获得误差值后需要对误差进行闭环消除。
单轴注入方式会导致在高频信号注入时产生高频的转矩脉动,影响电机在低速运行时的动态性能,采用双轴注入方式会对高频转矩脉动有效抑制。
高频转矩脉动DTeh为
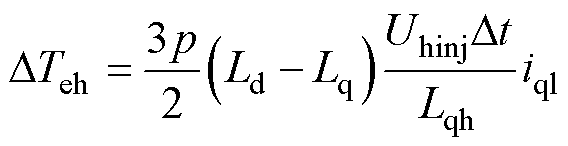 (15)
(15)
式中,p为SynRM极对数;Ld、Lq分别为d、q轴电感;iql为q轴电流分量;Uhinj为高频电压幅值。
高频转矩脉动是因为在同一周期下,不同的高频信号导致的高频响应电流波动变换,最终作用在电磁转矩上,一般情况下该参数因为电机的大惯性环节可以忽略,但是因为同步磁阻电机的参数敏感性,以及为保证更加稳定的低速运行,本文拟采用dq轴同时注入高频信号的方法来抑制其转矩脉动,理论推导为
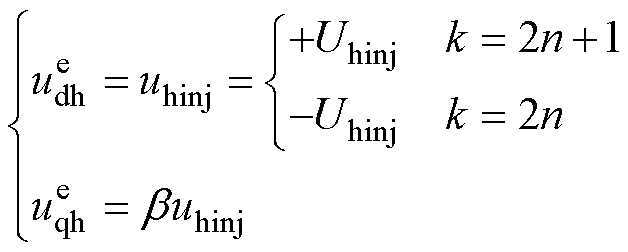 (16)
(16)
其中
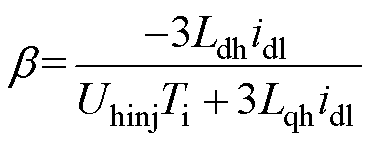
式中,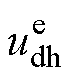 、
、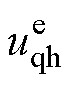 分别为定子电压矢量在d、q估计轴系下电压;n为含零自然数;b 为电感自适应参数,根据电压信号和电流电感参数计算;
分别为定子电压矢量在d、q估计轴系下电压;n为含零自然数;b 为电感自适应参数,根据电压信号和电流电感参数计算;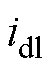 为d轴高频响应电流;
为d轴高频响应电流;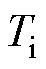 为开关周期。
为开关周期。
利用给出的注入方法,推导得一周期内的转矩波动可以变为0,有
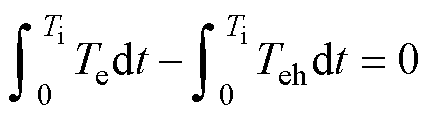 (17)
(17)
式中,Te为无高频信号注入的输出电磁转矩;Teh为注入高频信号的输出电磁转矩。
从式(17)可以看到高频转矩脉动被有效抑制。
同步磁阻电机实验参数见表1,在1.5 kW同步磁阻电机实验平台上进行实验验证。图8给出实验装置,其中图8a为两电平实验平台的硬件实物,通过对控制器进行程序烧写,在主功率板上输出调制的三相交流电与图8b的被测电机连接,进而驱动器运行,图8b右侧加载电机用来配合被测电机进行不同工况的实验。
表1 同步磁阻电机实验参数
Tab.1 Simulation of SynRM parameters
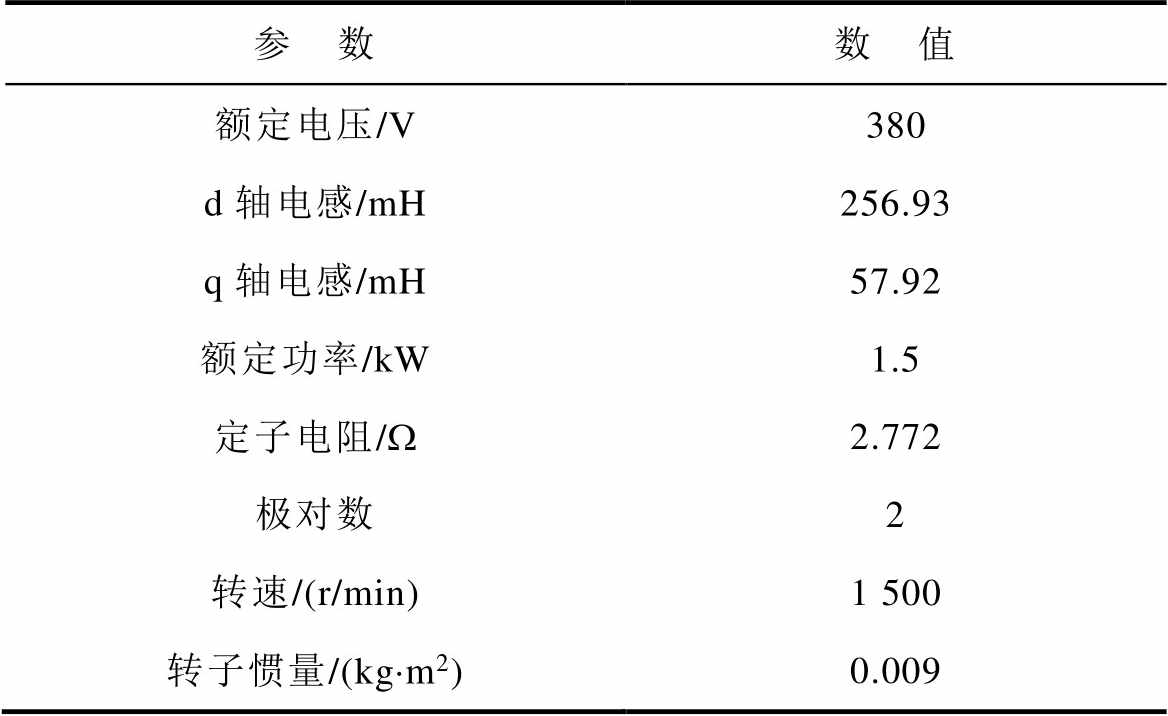
参 数数 值 额定电压/V380 d轴电感/mH256.93 q轴电感/mH57.92 额定功率/kW1.5 定子电阻/W2.772 极对数2 转速/(r/min)1 500 转子惯量/(kg×m2)0.009

图8 实验平台
Fig.8 The experiment platform
分别采用传统高频方波电压注入法和改进高频方波注入法时,SynRM在额定负载的情况下,转速阶跃(0—100—200—300 r/min)下的转速估计误差波形如图9所示,每张图中的波形共有三条,从上而下分别为实际转速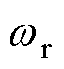 、估计转速误差
、估计转速误差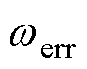 以及A相电流
以及A相电流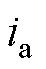 ,中间的放大图为当电机稳定运行时,估计转速与实际转速的差值放大图。由放大波形图可以得出,改进高频方波注入法的转速估计误差峰峰值可以从约10 r/min显著降低至约2 r/min。
,中间的放大图为当电机稳定运行时,估计转速与实际转速的差值放大图。由放大波形图可以得出,改进高频方波注入法的转速估计误差峰峰值可以从约10 r/min显著降低至约2 r/min。
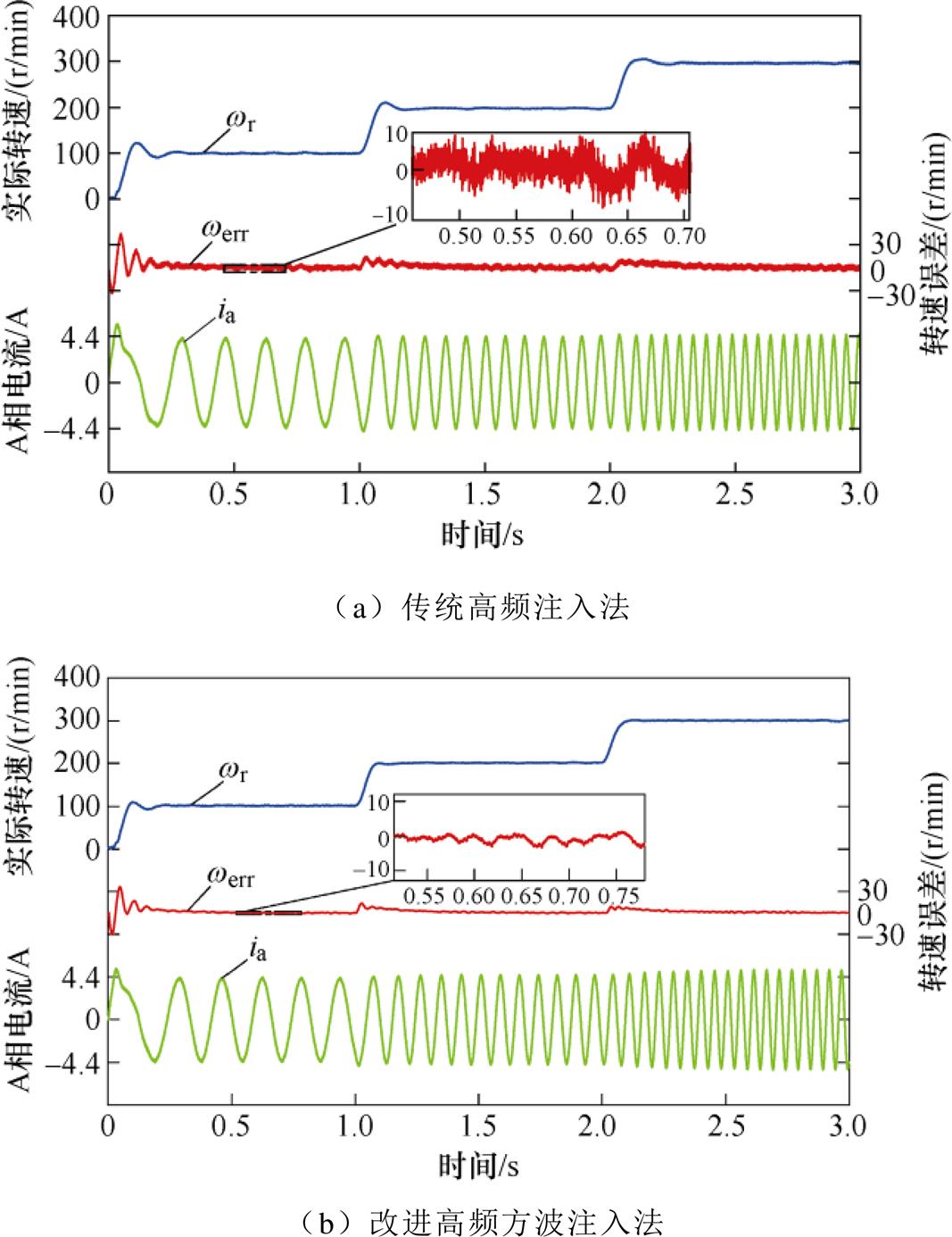
图9 满载下不同转速下转速估计误差波形
Fig.9 Speed estimation error waveforms at different speeds under full load
SynRM运行在100 r/min(6.7%额定转速),突加额定转矩。突加负载后转子角度估计误差波形如图10所示。图中均有三条曲线,从上到下依次分别为转矩Te、转子估计误差qerr以及A相电流ia。中间放大部分为在稳态时转子位置误差的放大图。传统高频方波电压注入法控制下的实验波形如图10a所示,从实验波形的放大部分图分析得到,转子角度估计误差最大达到3.43°。并且一直存在1.7°的位置误差。而改进高频方波注入法如图10b所示,可以将估计误差降低至1°以内,显著提高了估计准确度。因此,从稳态性能方面分析结果表明,改进高频方波注入法优于传统高频注入法,并且在实际应用中也具有更高的实用价值,在转子角度估计方面具有更优异的表现。
表2给出稳态波形结果汇总,表中详细说明了稳态性能中的恒载变速和恒速变载实验。其中,在恒载变速实验转速误差对比中,改进高频注入法比传统高频注入法的转速误差下降了10 r/min;在恒速变载实验转子位置误差对比中,改进高频注入法比传统高频注入法误差减小0.7°。以上为传统高频注入法和改进高频注入法进行稳态性能对比的实验结论。从结论中可以分析得出,改进的高频注入法在稳态性能中优于传统高频注入法。
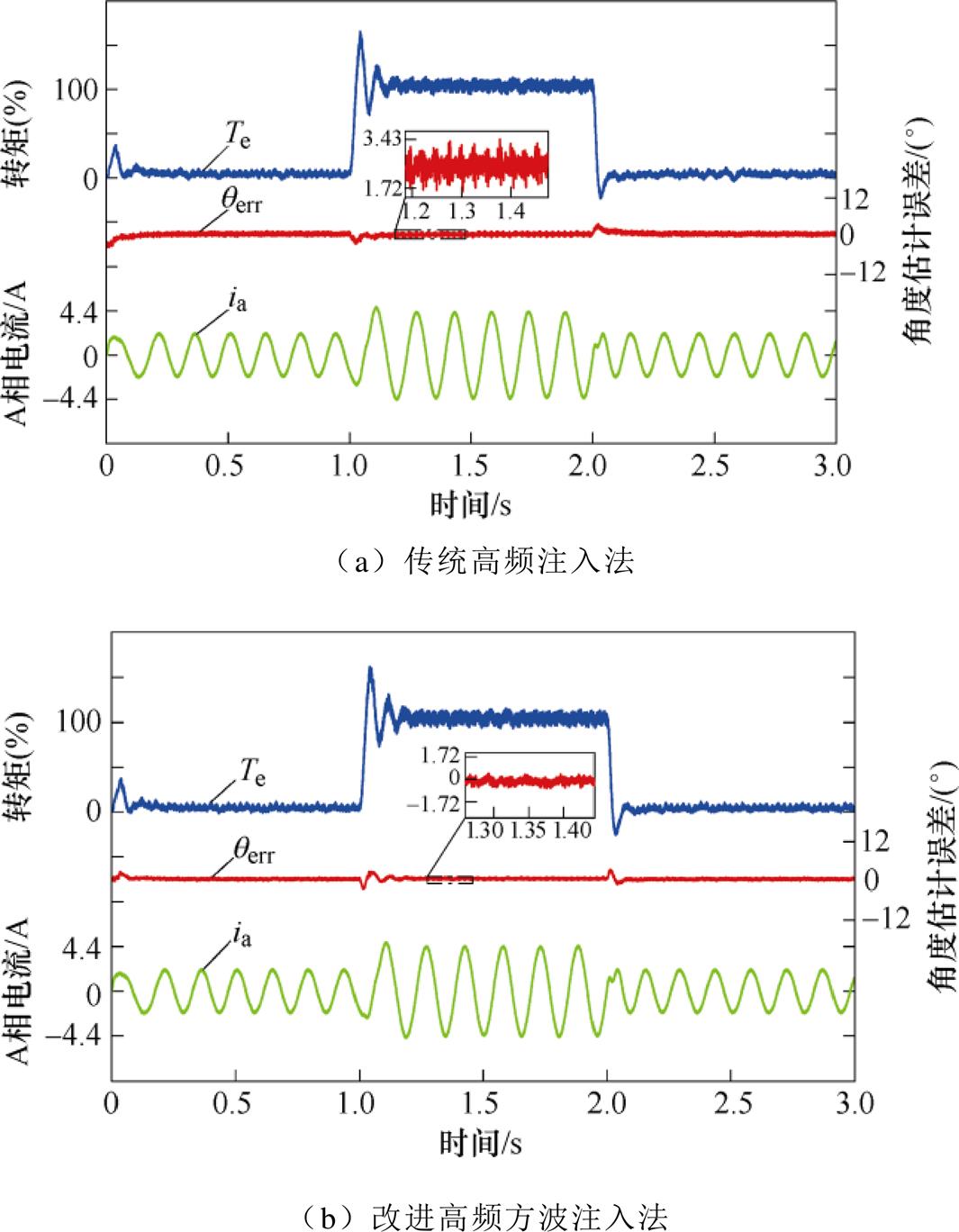
图10 突加负载后转子角度估计误差波形
Fig.10 Error waveforms of rotor angle estimation after sudden load application
表2 稳态性能对比实验汇总
Tab.2 Summary of steady-state performance comparison experiments
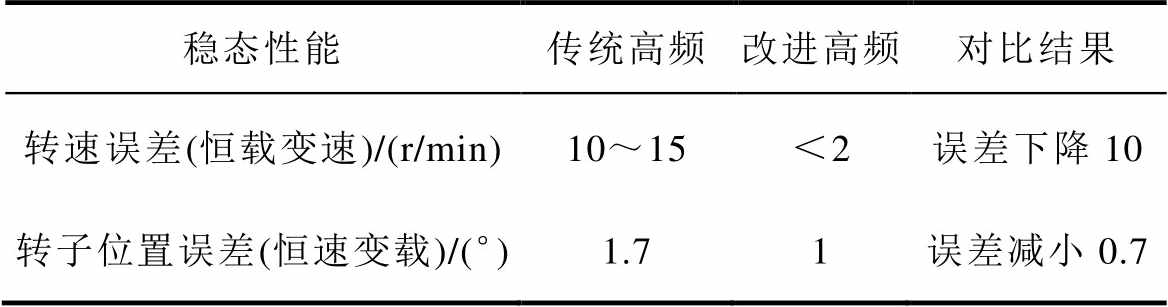
稳态性能传统高频改进高频对比结果 转速误差(恒载变速)/(r/min)10~15<2误差下降10 转子位置误差(恒速变载)/(°)1.71误差减小0.7
SynRM无传感器控制系统分别运行在半载和额定负载时,给定转速阶跃0—100—200—300 r/min。满载时的转子转速估计误差动态对比如图11所示,在突加转速时,传统高频注入方法的转速动态估计误差约为20 r/min,稳态静差约为10 r/min。改进高频方波注入法的转速动态估计误差为20 r/min,稳态静差为3 r/min。从结果来看,所提出的方法在转速估计上优于传统控制方法。
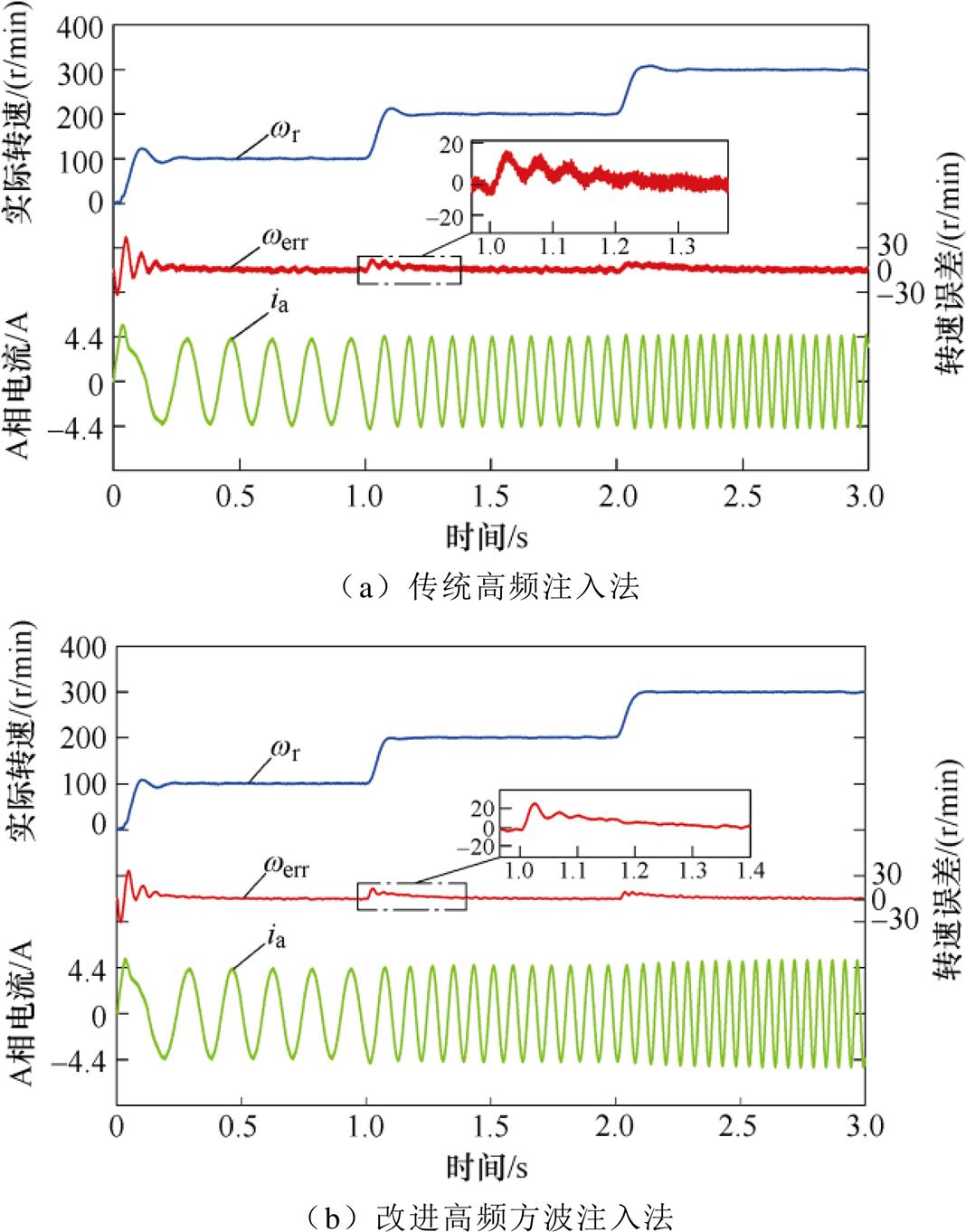
图11 额定负载情况下转速阶跃变化动态对比
Fig.11 Dynamic comparison of speed step change under rated load
当电机运行在100 r/min时,突加额定负载转矩,转子角度估计误差的动态波形如图12所示,由图中的波形可以看到,在负载转矩变化时,传统高频注入方法的最大转子角度估计误差约为3.4°,存在1.7°的稳态静差。改进高频方波注入法的最大转子误差为3.4°,稳态静差几乎为0。从结果来看,所提出的方法优于传统控制方法。如图13所示为满载时转子角度估计误差的动态情况,当转速发生变化时,传统高频注入方法的最大转子位置估计误差约为4.1°,并且根据转速上升误差逐渐增大,在300 r/min时误差增大至10.5°。同条件下改进高频方波注入法最大转子误差为3.4°,稳态静差为1.7°。
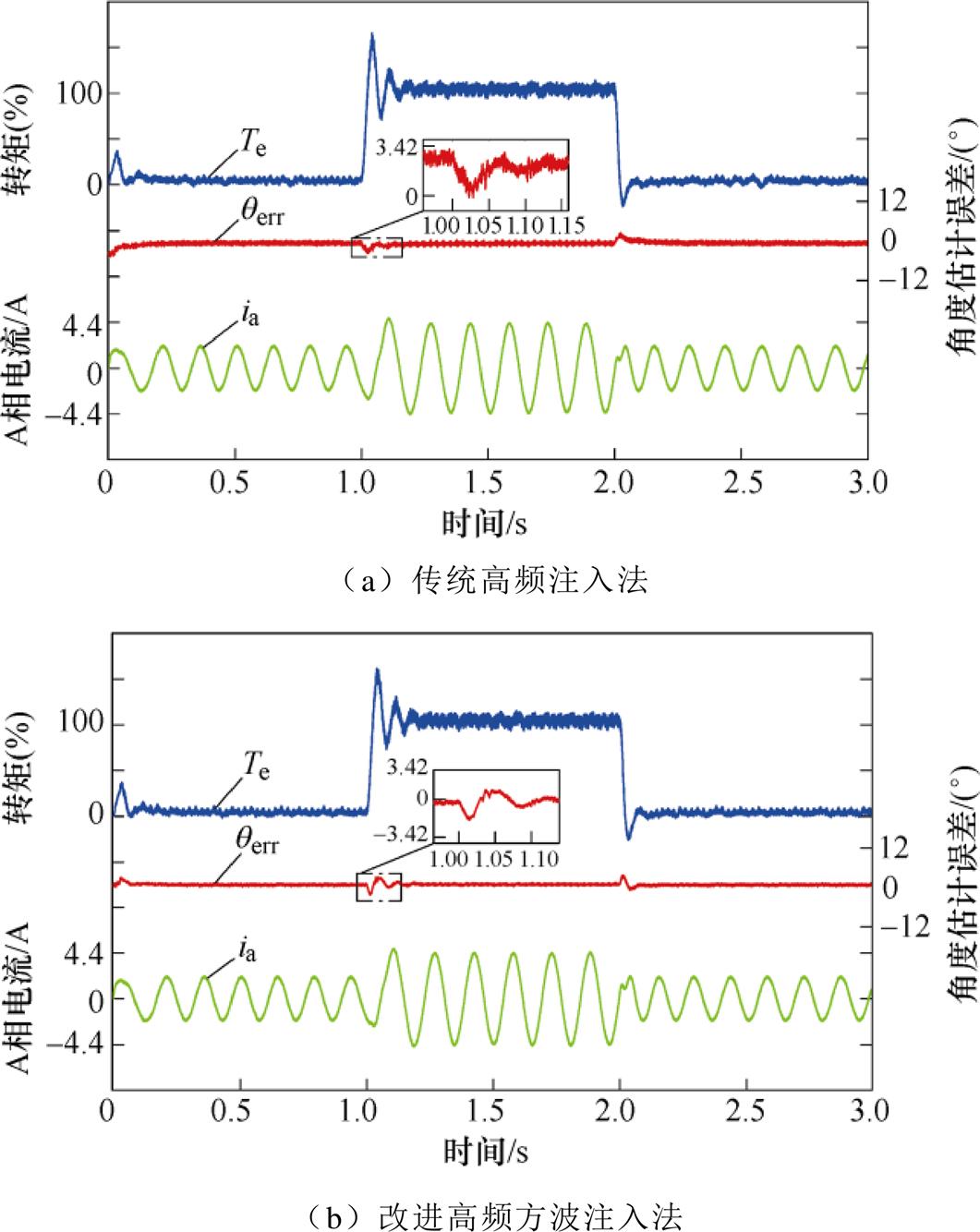
图12 阶跃负载情况时转子估计误差动态波形
Fig.12 Dynamic waveforms of rotor estimation error under step load condition
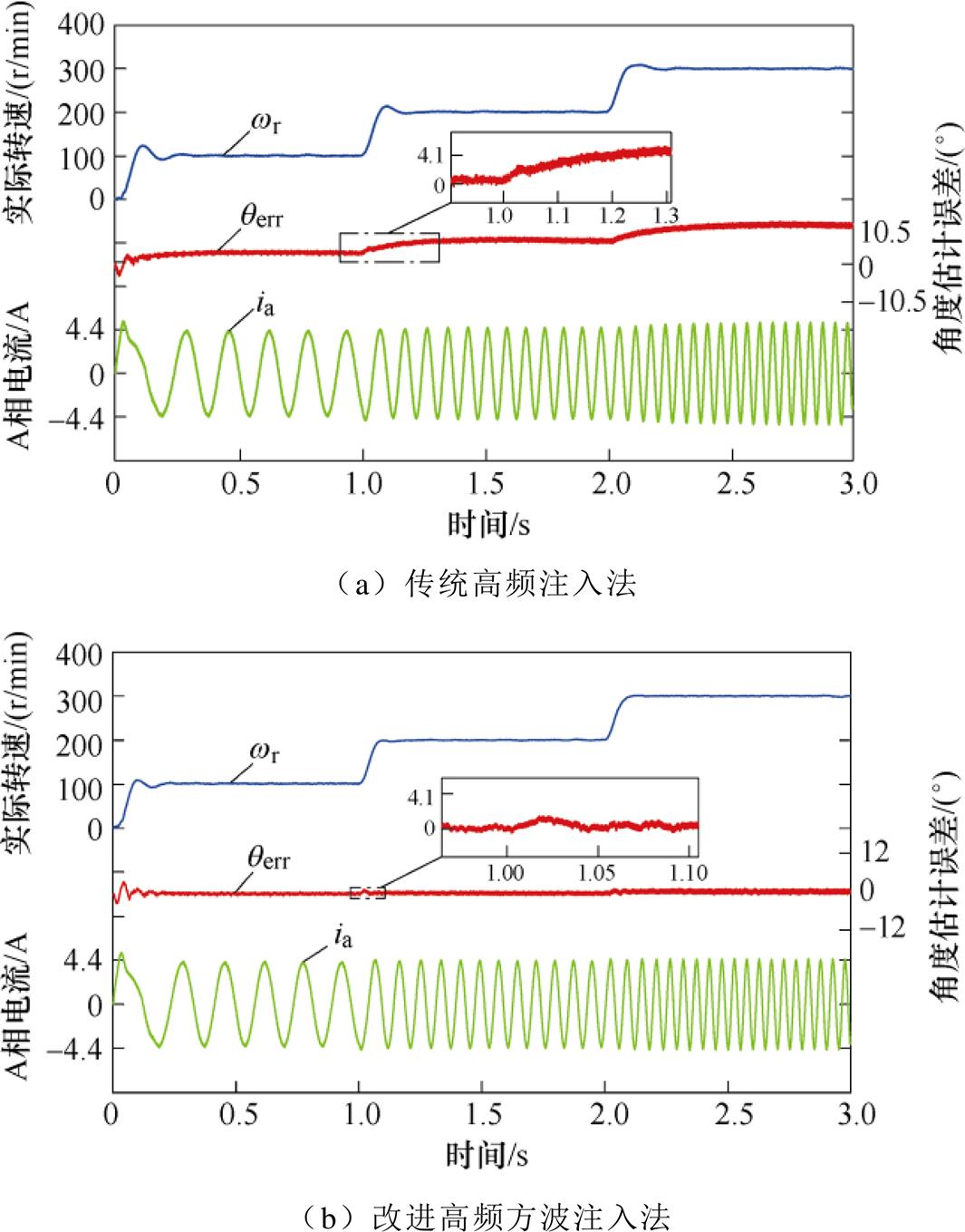
图13 满载情况下角度恢复波形
Fig.13 Angle recovery waveforms under full load
SynRM在零速状态下施加额定负载转矩扰动时的动态表现如图14所示,在静止状态下突加负载时,电机转子的角度变化量较大,转速发生明显变化,且A相电流同时出现较大的波动,产生了不稳定的情况。改进高频方波注入法下,在静止状态下进行突加阶跃负载,电机转子的位置变化量较小,转速无明显变化,且A相电流波动较小,符合零速工作的要求。SynRM在100 r/min空载恒速运行状态下,其A相电流的总谐波畸变率(Total Harmonic Distortion, THD)如图15所示,图15a为传统高频注入下,A相电流的THD分布;图15b为改进高频方波注入下,A相电流的THD分布,可以看到THD总体下降了约1%,提高了电流质量。
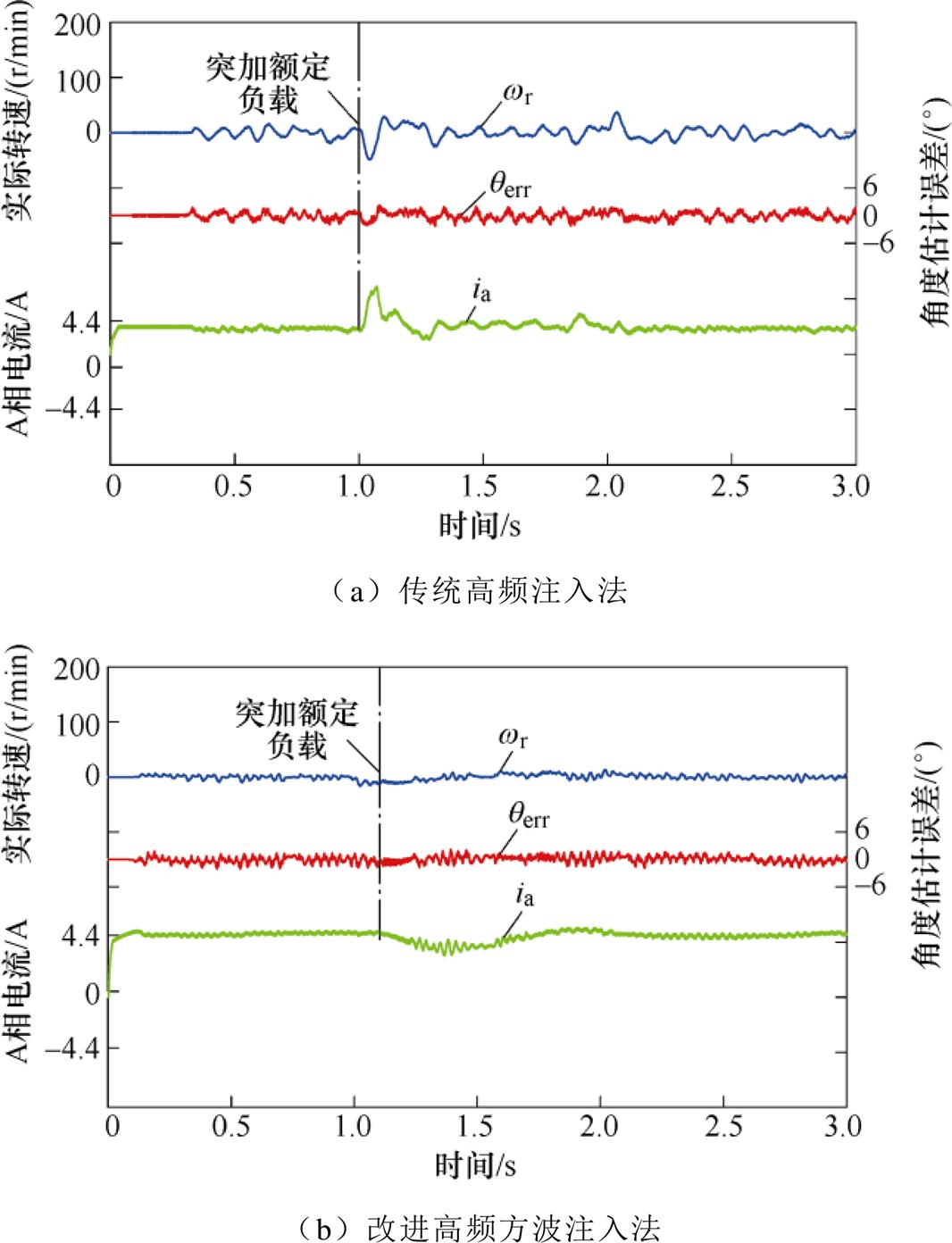
图14 零速下突加额定负载的角度误差波形
Fig.14 Angle error waveforms of sudden rated load at zero speed
表3给出动态性能下传统高频注入与改进高频注入法的对比结果。在恒载变速实验转子位置跟随对比结果中,改进高频注入法比传统高频注入法的最大误差减小7.1°;零速下转子位置跟随情况的对比下,改进高频注入法比传统高频注入法的误差减小了2.4°;恒速变载实验中转子位置跟随情况对比中,改进高频注入法与传统高频注入法相同。综上所述,从结果上看,改进高频注入法的动态性能优于传统高频注入法。
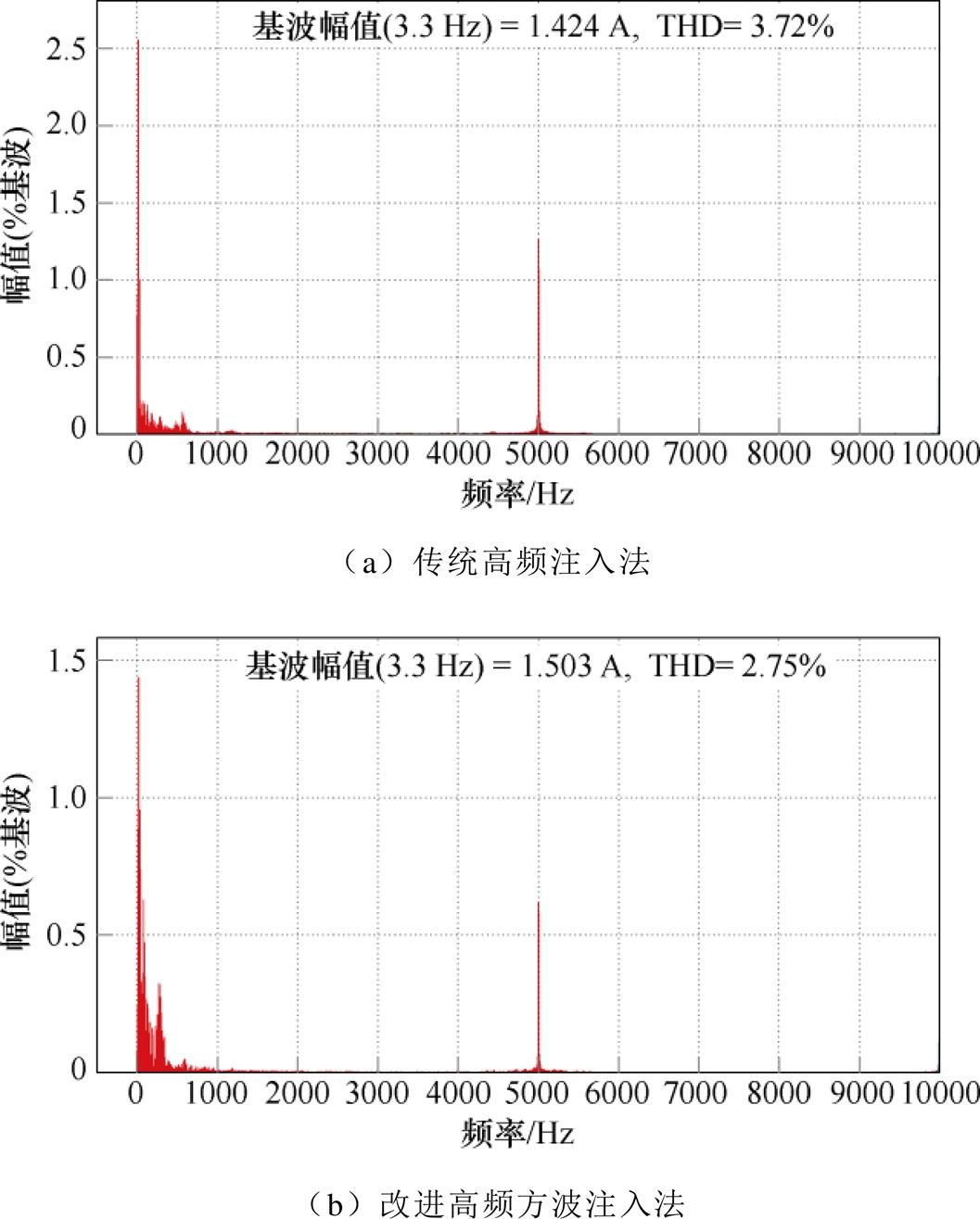
图15 THD波形对比
Fig.15 THD waveforms comparison
表3 动态性能对比实验汇总
Tab.3 Summary of dynamic performance comparison experiments
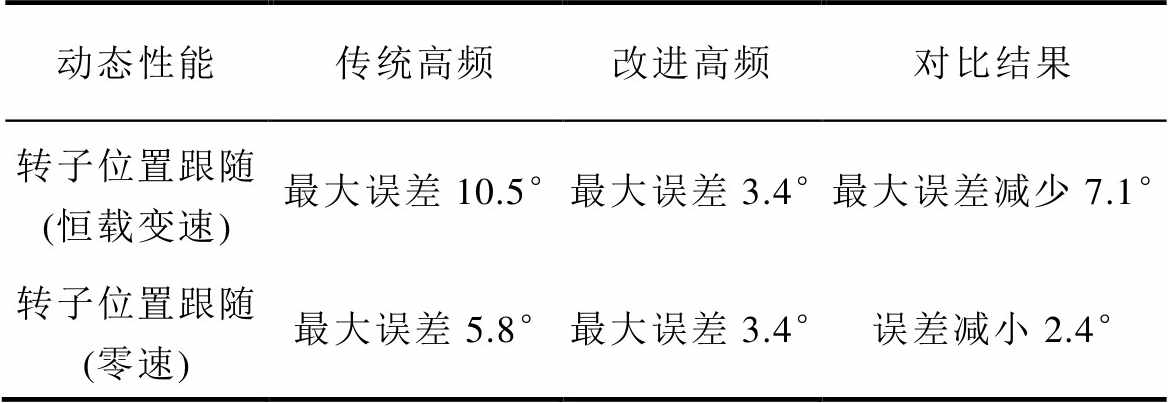
动态性能传统高频改进高频对比结果 转子位置跟随 (恒载变速)最大误差10.5°最大误差3.4°最大误差减少7.1° 转子位置跟随 (零速)最大误差5.8°最大误差3.4°误差减小2.4°
本文以同步磁阻电机为研究对象,提出一种改进的高频注入方法来解决电机在低速运行中伴随的交直轴电感交叉饱和问题。并与传统高频注入法无速度控制进行了对比实验。其研究结论如下:
1)当电机参数变化时,其增量电感参数变化具有规律性。利用离线参数辨识方法对电机的电感参数进行辨识,辨识后的电机参数呈现随电流变化而变化的连续函数特点,利用此特性可以对电机的电感模型进行拟合最终获得增量电感的二元模型,在此基础上计算出角度误差,可以有效解决同步磁阻电机在突加突减负载时,转子位置估计误差变化导致的电机失控问题。
2)高频信号的幅值和频率是决定和影响电机运行的重要参数,而其高频注入时会随之产生高频转矩脉动,在单d轴注入高频信号的基础上,添加q轴高频注入,双高频注入法会对高频转矩脉动有一定的抑制作用。
同时,在研究过程中还有部分问题需要进一步讨论,如电机的参数辨识功能的精确性可以进一步提高,可以使用不同工具获取电机参数,最后使用加权方式提高电机的参数精度;在低速运行时考虑加载至额定负载以上时,控制方法的适用性。
参考文献
[1] 张晓虎, 赵吉文, 王立俊, 等. 基于自适应互联扩展卡尔曼观测器的永磁同步直线电机高精度抗干扰在线多参数辨识[J]. 中国电机工程学报, 2022, 42(12): 4571-4581.
Zhang Xiaohu, Zhao Jiwen, Wang Lijun, et al. High precision anti-interference online multiparameter estimation of PMSLM with adaptive interconnected extend Kalman observer[J]. Proceedings of the CSEE, 2022, 42(12): 4571-4581.
[2] Accetta A, Cirrincione M, Pucci M, et al. Space- vector state dynamic model of the SynRM considering self, cross-saturation and iron losses and related identification technique[J]. IEEE Transactions on Industry Applications, 2023, 59(3): 3320-3331.
[3] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online parameter identification of permanent magnet synchronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
[4] 吴春, 赵宇纬, 孙明轩. 采用测量电压的永磁同步电机多参数在线辨识[J]. 中国电机工程学报, 2020, 40(13): 4329-4340.
Wu Chun, Zhao Yuwei, Sun Mingxuan. Multi- parameter online identification for permanent magnet synchronous machines using voltage measurements[J]. Proceedings of the CSEE, 2020, 40(13): 4329-4340.
[5] 徐伟, 董定昊, 葛健, 等. 基于在线参数辨识补偿的直线感应电机低开关频率模型预测控制策略[J]. 电工技术学报, 2022, 37(16): 4116-4133.
Xu Wei, Dong Dinghao, Ge Jian, et al. Low switching frequency model predictive control strategy based on online parameter identification compensation of linear induction motor for urban rail application[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(16): 4116-4133.
[6] 张国强, 项润华, 王高林, 等. 基于静止轴系脉冲信号注入的永磁同步电机无传感器控制策略[J]. 中国电机工程学报, 2021, 41(12): 4297-4306.
Zhang Guoqiang, Xiang Runhua, Wang Gaolin, et al. Pulse signal injection in stationary reference frame for sensorless PMSM drives[J]. Proceedings of the CSEE, 2021, 41(12): 4297-4306.
[7] Hinkkanen M, Saarakkala S E, Ali Awan H A, et al. Observers for sensorless synchronous motor drives: framework for design and analysis[J]. IEEE Transa- ctions on Industry Applications, 2018, 54(6): 6090- 6100.
[8] Varatharajan A, Pescetto P, Pellegrino G. Injection- less sensorless control of synchronous reluctance machine for zero to low speeds region[C]//2018 IEEE 9th International Symposium on Sensorless Control for Electrical Drives (SLED), Helsinki, Finland, 2018: 72-77.
[9] Liu Tianhua, Haslim H S, Tseng S K. Predictive controller design for a high-frequency injection sensorless synchronous reluctance drive system[J]. IET Electric Power Applications, 2017, 11(5): 902- 910.
[10] 狄冲, 鲍晓华, 潘晋, 等. 基于Elmer开源有限元平台的铁氧体辅助同步磁阻电机的建模和分析[J]. 电工技术学报, 2022, 37(5): 1136-1144.
Di Chong, Bao Xiaohua, Pan Jin, et al. Modelling and analysis of a ferrite assisted synchronous reluctance machine based on the open-source platform Elmer[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1136-1144.
[11] Li Chengrui, Wang Gaolin, Zhang Guoqiang, et al. Review of parameter identification and sensorless control methods for synchronous reluctance machines[J]. Chinese Journal of Electrical Engineering, 2020, 6(2): 7-18.
[12] Woo T G, Park S W, Choi S C, et al. Flux saturation model including cross saturation for synchronous reluctance machines and its identification method at standstill[J]. IEEE Transactions on Industrial Elec- tronics, 2023, 70(3): 2318-2328.
[13] Ortombina L, Pasqualotto D, Tinazzi F, et al. Magnetic model identification of synchronous motors considering speed and load transients[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 4945-4954.
[14] Li Chengrui, Wang Gaolin, Zhang Guoqiang, et al. Adaptive pseudorandom high-frequency square-wave voltage injection based sensorless control for SynRM drives[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3200-3210.
[15] 杨淑英, 刘威, 李浩源, 等. 基于旋转注入的同步磁阻电机电感辨识方案[J]. 电工技术学报, 2019, 34(增刊1): 97-104.
Yang Shuying, Liu Wei, Li Haoyuan, et al. Inductance identification scheme of synchronous reluctance motor based on rotary injection[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 97-104.
[16] 徐心愿, 王云冲, 沈建新. 基于最大转矩电流比的同步磁阻电机DTC-SVM控制策略[J]. 电工技术学报, 2020, 35(2): 246-254.
Xu Xinyuan, Wang Yunchong, Shen Jianxin. Direct torque control-space vector modulation control strategy of synchronous reluctance motor based on maximum torque per-ampere[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 246- 254.
[17] Mesai Ahmed H, Jlassi I, Marques Cardoso A J, et al. Model-free predictive current control of synchronous reluctance motors based on a recurrent neural net- work[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 10984-10992.
[18] Pasqualotto D, Rigon S, Zigliotto M. Sensorless speed control of synchronous reluctance motor drives based on extended Kalman filter and neural magnetic model[J]. IEEE Transactions on Industrial Electronics, 2023, 70(2): 1321-1330.
[19] Credo A, Di Leonardo L, Collazzo F P, et al. The impact of the control strategy in flux observer based sensorless control of synchronous reluctance motors[J]. IEEE Access, 2021, 9: 156380-156391.
[20] 吴春, 陈科, 南余荣, 等. 考虑交叉饱和效应的变角度方波电压注入永磁同步电机无位置传感器控制[J]. 电工技术学报, 2020, 35(22): 4678-4687.
Wu Chun, Chen Ke, Nan Yurong, et al. Variable angle square-wave voltage injection for sensorless control of PMSM considering cross-saturation effect[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4678-4687.
[21] 王震宇, 孙伟, 蒋栋. 基于虚拟电压注入的闭环磁链观测器的感应电机无速度传感器矢量控制系统[J]. 电工技术学报, 2022, 37(2): 332-343.
Wang Zhenyu, Sun Wei, Jiang Dong. Induction motor speed sensorless vector control system based on closed-loop flux observer with virtual voltage injection[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 332-343.
[22] Foti S, De Caro S, Scimone T, et al. Rotor position error compensation in sensorless synchronous reluctance motor drives[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4442-4452.
[23] Zhang Zhendong. Sensorless back EMF based control of synchronous PM and reluctance motor drives-a review[J]. IEEE Transactions on Power Electronics, 2022, 37(9): 10290-10305.
[24] Varatharajan A, Pescetto P, Pellegrino G. Sensorless synchronous reluctance motor drives: a full-speed scheme using finite-control-set MPC in a projection vector framework[J]. IEEE Transactions on Industry Applications, 2020, 56(4): 3809-3818.
[25] Gao Fengtao, Yin Zhonggang, Bai Cong, et al. Speed sensorless control method of synchronous reluctance motor based on resonant Kalman filter[J]. IEEE Transactions on Industrial Electronics, 2023, 70(8): 7627-7641.
[26] Jo I H, Lee H W, Jeong G, et al. A study on the reduction of cogging torque for the skew of a magnetic geared synchronous motor[J]. IEEE Transa- ctions on Magnetics, 2019, 55(2): 8100505.
[27] Miyama Y, Ishizuka M, Kometani H, et al. Vibration reduction by applying carrier phase-shift PWM on dual three-phase winding permanent magnet syn- chronous motor[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5998-6004.
[28] Li Chengrui, Wang Gaolin, Zhang Guoqiang, et al. High frequency torque ripple suppression for high frequency signal injection based sensorless control of SynRMs[C]//2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 2544-2548.
[29] Zhang Yanping, Yin Zhonggang, Du Chao, et al. Noise spectrum shaping of random high-frequency- voltage injection based on Markov chain for IPMSM sensorless control[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(4): 3682-3699.
[30] Zhang Guoqiang, Xiang Runhua, Wang Gaolin, et al. Hybrid pseudorandom signal injection for position sensorless SynRM drives with acoustic noise reduction[J]. IEEE Transactions on Transportation Electrification, 2022, 8(1): 1313-1325.
Abstract Due to their cost advantages and stable structure, synchronous reluctance motors have become increasingly popular for low-cost AC speed regulation. To estimate the rotor angle without sensors in the low-speed domain, the high-frequency square wave signal injection method is most appropriate due to the synchronous reluctance motor's distinct saliency. However, because of the nonlinear characteristics of the d and q-axis inductors, the parameter variation caused by the cross-coupling effect during low-speed operation and loading affects the dynamic and steady-state performance of the motor. Therefore, this paper explores the sensorless control of high-frequency square wave injection in the low-speed domain and accounts for cross-coupling.
Firstly, based on static shafting, the mathematical model of synchronous reluctance motors is established using coordinate transformation theory. The motor experiment is carried out using the traditional speed-free control method of high-frequency square wave injection. The results show that ignoring the effect of cross-saturation on angle estimation also cause additional torque ripples from high-frequency excitation current fluctuations, adversely affecting dynamic and steady-state performance of the motor.
Furthermore, a static method is adopted to determine the offline parameters of the synchronous reluctance motor and fit the inductance flux relationship. Based on the fitted model, the influence of the inductance nonlinearity and its cross-coupling effect on the rotor position estimation is analyzed, and the angle estimation error caused by the cross-coupling effect is calculated. The traditional high-frequency square wave injection control method is enhanced in two ways. Firstly, the cross-coupling effect is considered in the decoupling process of rotor position estimation signals, and angle compensation is added to ensure angle estimation accuracy. Secondly, the double high-frequency square wave injection is used instead of the traditional single D-axis injection to reduce high-frequency excitation current fluctuations and torque ripples caused by high-frequency amplitude.
Finally, a simulation platform is built in Matlab, and comparative tests of speed step, sudden loading, and zero speed loading are conducted on a 1.5 kW synchronous reluctance motor test bed, which verifies the feasibility and effectiveness of the improved control method. Simulation and experimental results show that the motor parameters changing with the current can be obtained by off-line parameter identification of the motor. The rotor position error can solve the motor being out of control, which is caused by changes in the rotor position estimation error when the load of the synchronous reluctance motor is suddenly added or reduced. At the same time, the shaft high-frequency injection is added according to the single shaft high-frequency injection signal, which has an inhibition effect on high-frequency torque ripples and improves the dynamic and steady-state performance of the motor.
keywords:Synchronous reluctance motor, double high-frequency square wave injection, offline parameter identification, high frequency torque ripple, cross saturation
DOI: 10.19595/j.cnki.1000-6753.tces.230966
中图分类号:TM352
国家自然科学基金项目(52177194)、中国博士后科学基金面上项目(2022M722559)和陕西省自然科学基础研究计划一般项目(2022JQ-538)资助。
收稿日期 2023-06-23
改稿日期 2023-07-20
王建渊 男,1979年生,副教授,硕士生导师,研究方向为同步电机控制、能源互联变换器等。E-mail: wangjianyuan2003@163.com
李英杰 男,1998年生,硕士研究生,研究方向为电力电子与电力传动。E-mail: 17791079463@163.com(通信作者)
(编辑 崔文静)