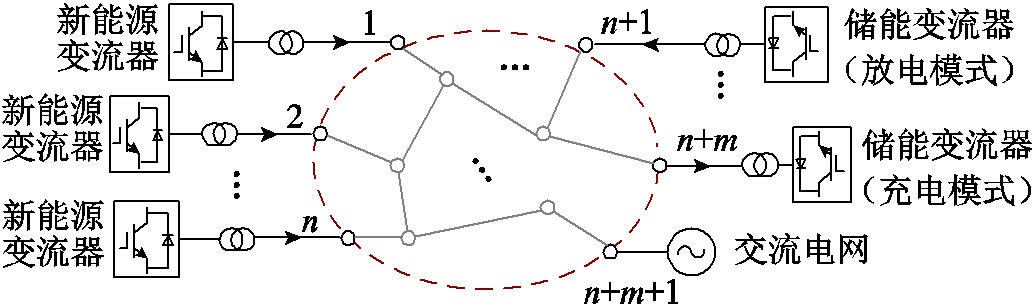
图1 含储能多馈入系统示意图
Fig.1 Schematic diagram of multi-infeed system with energy storage
摘要 储能正常工作时包含充电和放电两种运行模式，导致多储能变流器和多新能源变流器构成的多馈入系统工作点多变，加剧了系统小扰动同步稳定性分析的困难程度。为此，该文聚焦锁相环主导的小扰动同步稳定问题，首先，推导了兼顾储能充/放电运行模式的电网强度评估指标广义短路比，并提出了基于广义短路比及设备临界短路比的系统电压支撑强度分析方法，进而实现了系统小扰动同步稳定裕度的快速评估；然后，探究了跟网型储能变流器的充/放电运行模式对系统小扰动同步稳定裕度的影响规律，并根据矩阵联锁特征值定理论证了跟网型储能变流器工作在充电模式时，系统的小扰动同步稳定裕度高于放电模式；最后，基于仿真算例验证了所提系统小扰动同步稳定性分析方法的有效性。
关键词：系统强度 广义短路比 储能变流器 运行模式 小扰动同步稳定
在“双碳”目标下，为促进电力行业的能源转型和绿色发展，以风电、光伏为代表的新能源渗透率不断增加[1]，然而新能源本身的强随机性和高波动性导致源荷间功率能量平衡的难度激增[2]。储能因其功率双向灵活调节的特点[3]，为高比例新能源电力系统的功率能量平衡难题提供了新的解决方案，近年来受到广泛关注[4-5]。
新能源和储能系统大多由基于锁相环控制的跟网型变流器[6]等电力电子设备（Power Electronic Devices, PEDs）实现并网[7]（不特殊说明，本文所研究的变流器特指跟网型变流器）。此时，多储能变流器和多新能源变流器共同构成电力电子多馈入系统（后文简称“含储能多馈入系统”）。含储能多馈入系统新能源渗透率高、支撑电网的同步机占比低，交流电网相对较弱，导致由锁相环主导的系统小扰动同步失稳问题频发[8-9]。此外，储能变流器正常工作时包含充电和放电两种运行模式，其运行模式的变化会大幅改变系统的稳态工作点，而稳态工作点的变化会进一步通过锁相环影响系统的小扰动同步稳定性（后文简称“小扰动稳定性”）[10]。
目前，国内外关于新能源和储能变流器并网系统的小扰动稳定性分析方法主要包含时域特征值分析法[11]和频域阻抗分析法[10,12]。文献[11]通过时域特征值法研究了新能源和储能联合并网系统的小扰动稳定性，并在此基础上提出小扰动稳定约束下的储能设备优化调度方法；文献[10,12]通过频域阻抗分析和奈奎斯特判据研究了不同运行模式对单一变流器并网系统稳定性的影响规律，研究表明变流器工作在充电模式时，可以有效改善单馈入系统的小扰动稳定性。然而，时域特征值分析法需要依靠系统的详细模型且计算复杂，可能存在“维数灾”问题；阻抗分析法则主要针对电力电子单馈入系统，而在多馈入系统中使用受限，并且上述两种方法均未能提供简单直观的工程实用化指标。
短路比与设备临界短路比的相对差值常用来定量化表征单馈入系统的电压支撑强度（后文简称“系统强度”），进而快速评估系统的小扰动稳定裕度[13]。在此基础上，文献[14-16]将短路比概念拓展至由新能源变流器构成的多馈入系统，揭示了基于广义短路比（generalized Short-Circuit Ratio, gSCR）的电网强度指标以及设备临界短路比指标（反映设备对电网耐受能力）的系统强度评估原理，厘清了常规新能源多馈入系统小扰动稳定性与gSCR之间的内在联系。然而，目前gSCR理论并未考虑储能充/放电运行模式对多馈入系统强度的影响，故无法准确地量化含储能多馈入系统的小扰动稳定裕度。
为应对上述挑战，本文提出计及储能运行模式的含储能多馈入系统电网强度指标构建方法与基于该指标的系统小扰动稳定裕度量化方法。首先，基于含储能多馈入系统的频域模型，探究了该场景下电网强度指标gSCR的具体定义形式，并从小扰动稳定角度提出了含储能多馈入系统强度的源-网协同分析方法，进而实现了系统小扰动稳定裕度的快速评估；然后，探究了储能变流器的充电和放电两种运行模式对系统小扰动稳定裕度的影响规律；最后，基于Matlab/Simulink平台的单馈入系统和五馈入系统模型验证了所提系统强度分析方法的适用性和有效性。
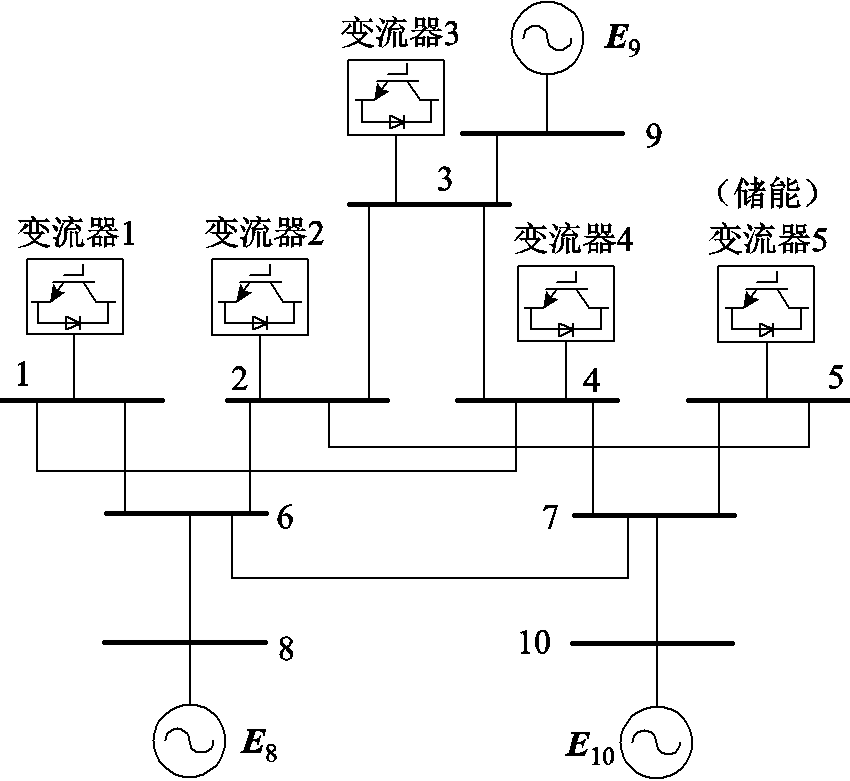
考虑图1所示的含储能多馈入系统，其中的n台新能源变流器和m台储能变流器均采用基于锁相环的双环矢量控制策略（具体的控制框图如附图1所示）。图1中节点1～n连接新能源变流器；节点n+1～n+m连接储能变流器，其中k台储能变流器工作在放电模式（k≤m），其余储能变流器工作在充电模式；节点n+m+1连接外部交流电网，其余a个节点为内部无源节点。
图1 含储能多馈入系统示意图
Fig.1 Schematic diagram of multi-infeed system with energy storage
针对含储能多馈入系统，本文聚焦系统正常运行状态下锁相环主导的小扰动稳定问题，拟研究问题可归纳如下。
1）如何将短路比概念拓展至含储能多馈入系统，以定量化表征系统的小扰动稳定性，此时系统强度应如何评估？
2）当储能变流器分别工作在充电和放电两种运行模式时，该系统的小扰动稳定裕度存在怎样的差异？
为了更好地阐述和论证上述问题，考虑实际高比例新能源送端电网中一类常见的标称多馈入系统——同一类型且运行工况相似的多新能源变流器/场站馈入系统，基于这一类多馈入系统的特点可进行以下合理简化：①交流等效网络为感性占优[17]，网络中电容动态对所研究的锁相环主导的小扰动稳定问题影响较小[18]；②交流网络中所有线路的阻感比均相同[19]；③新能源变流器的动态特性相似，且场站内各变流器端口间（或场站公共连接点（Point of Common Coupling, PCC）间）的电压相位差较小[20]。对于含风电、光伏等不同类型新能源变流器的复杂场景，可借鉴文献[15]中的分析思路将后文所提方法进行拓展，限于篇幅本文不再详细展开讨论。
全局xy坐标系下，含储能多馈入系统的交流电网动态模型（以电流流出变流器为正方向）[21]为
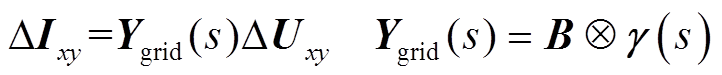（1）
其中
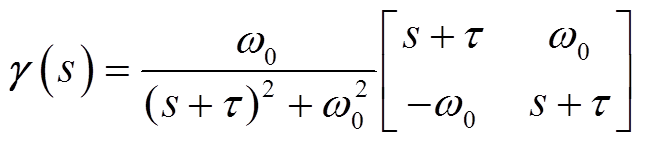（2）
式中，Δ表示变量的微增量；Uxy=[Ux1 Uy1 Ux2 Uy2 … Ux(n+m) Uy(n+m)]T，Ixy=[Ix1 Iy1 Ix2 Iy2 … Ix(n+m) Iy(n+m)]T，Uxi、Uyi分别为节点i的电压x轴和y轴分量，Ixi、Iyi分别为注入节点i的电流x轴和y轴分量；Ygrid(s)为交流电网的导纳传递函数矩阵；
表示Kronecker积；s为拉普拉斯算子；ω0=2πf0为工频角速度；τ为线路电阻与电感的比值，τ=Rij/Lij, i、j为节点；B为消去内部无源节点的工频导纳矩阵，其具体形式可参考文献[21]。
值得一提的是，式（1）、式（2）的推导考虑了交流线路电感和电阻的动态特性，且交流线路阻感比相同，线路电阻的变化仅影响阻感比τ和γ(s)的数值，并不影响后文的分析方法与模态解耦过程[19]。
本文侧重于分析由锁相环与弱电网相互作用导致的次/超同步振荡问题，其中功率外环的动态较慢，可认为还未响应系统变化从而保持静止，故为简化分析，储能变流器和新能源变流器均以锁相环和电流内环为主导环节进行建模，忽略功率外环等其他环节的动态[22-23]。此时两类变流器间动态特性是相似的，差别在于储能变流器可工作于充电和放电两种模式，而新能源变流器仅工作于放电模式。在此基础上，新能源变流器/放电模式下储能变流器的动态模型可以表示（以电流流出变流器为正方向）[24]为
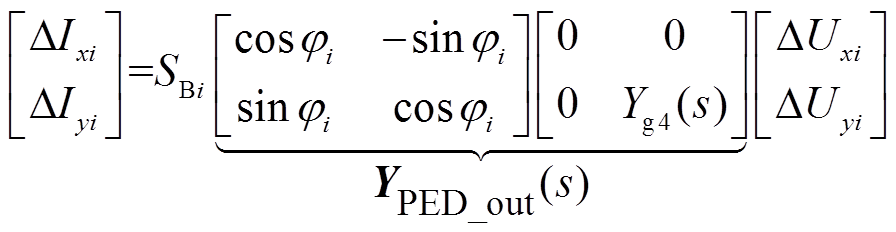（3）
式中，SBi为节点i接入变流器的额定容量，i=1, 2,…, n+k；φi为节点i接入变流器的功率因数角（输出电流超前于端电压的角度）；YPED_out(s)为变流器在放电模式下的导纳传递函数矩阵；Yg4(s)的具体形式为
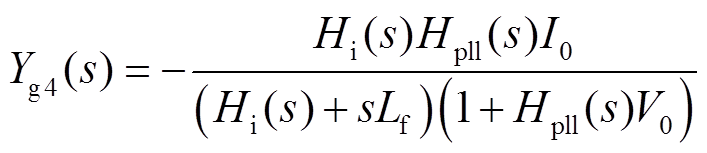（4）
式中，Hpll(s)为锁相环的传递函数，Hpll(s)= (Kppll+ Kipll/s)/s，Kppll和Kipll分别为锁相环的比例和积分参数；Hi(s)=Kpc+Kic/s，Kpc和Kic分别为电流内环的比例和积分参数；V0和I0分别为稳态时的电压和电流幅值，V0=1(pu)，I0=1(pu)。具体推导可参考文献[24]。
而充电模式下储能变流器电流方向与规定正方向相反，因此其动态模型可简化表示为
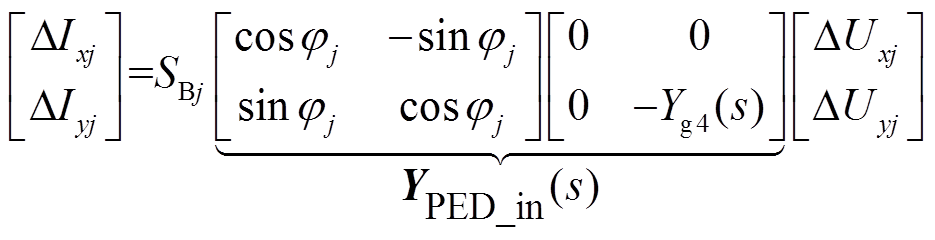（5）
式中，SBj为第j个变流器的额定容量，j=n+k+1,…, n+m；φj为第j个变流器的功率因数角；YPED_in(s)为变流器在充电模式下的导纳传递函数矩阵。
为了便于揭示稳定机理并有助于后文的理论推导，建模时认为各变流器的动态外特性相似。在此基础上，含储能多馈入系统的多变流器动态模型可表示为
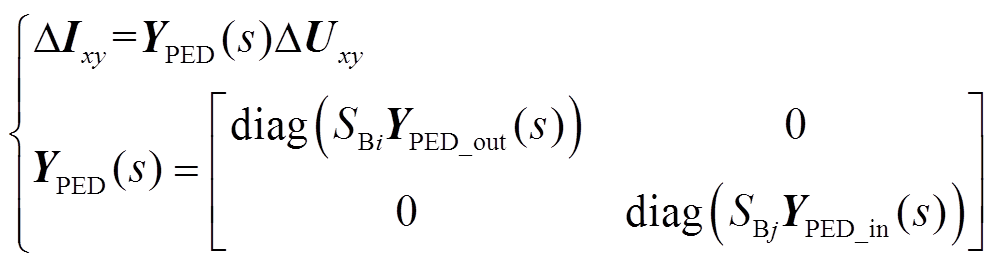（6）
式中，YPED(s)为含储能多馈入系统的多变流器导纳传递函数矩阵；diag(·)表示块对角矩阵。
进一步地，结合式（3）、式（5）和式（6），含储能多馈入系统的多变流器动态模型可简化为
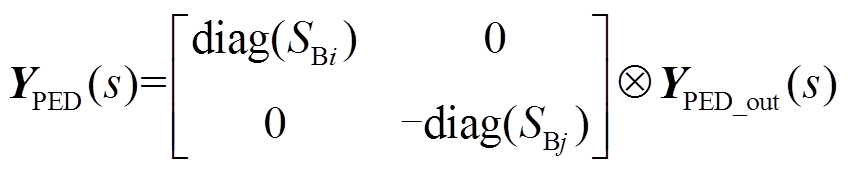（7）
根据多变量反馈控制理论[25]建立含储能多馈入系统的闭环特征方程，该方程由变流器和交流电网两部分的动态模型组成，即
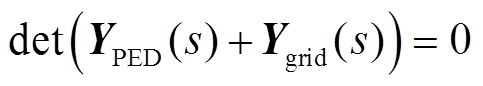（8）
式中，det(·)表示求矩阵的行列式。
结合式（1）、式（7）和式（8），将YPED(s)和Ygrid(s)的具体形式代入可得系统闭环特征方程为
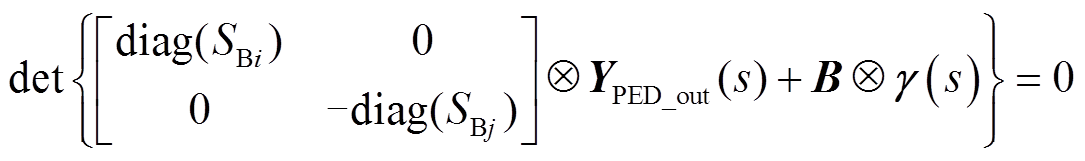（9）
考虑到含储能多馈入系统的闭环特征方程式（9）阶数高，导致该系统小扰动稳定性分析困难，下面通过矩阵相似对角变换将式（9）所示的含储能多馈入系统解耦为n+m个相互独立的等效单馈入系统。
用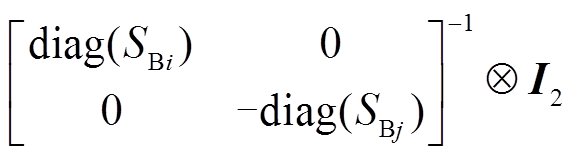
左乘式（9）中的矩阵（I2为2维单位矩阵），系统的特征方程可以等价变换为
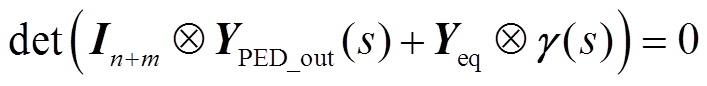（10）
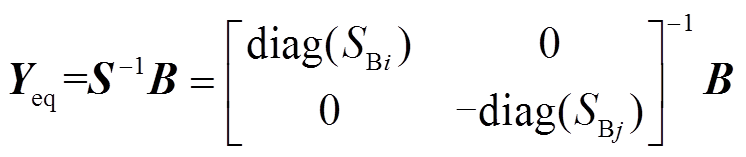（11）
式中，Yeq为拓展导纳矩阵；S为等效设备容量矩阵；In+m为n+m维单位矩阵。
对于拓展导纳矩阵Yeq，其满足以下结论。
结论1：①矩阵Yeq可以对角化，且Yeq的特征值均为实数；②矩阵Yeq的正/负特征值个数与运行在放电/充电模式下的变流器的数量一致。
证明：见附录。
根据结论1，存在可逆矩阵T可将矩阵Yeq相似变换为对角矩阵Λ，即
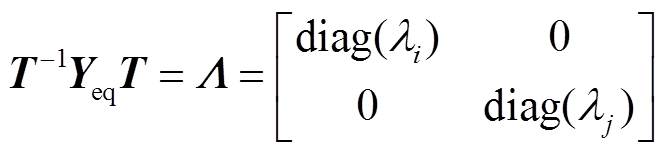（12）
式中，λi为正特征值（i=1, 2, …, n+k）；λj为负特征值（j=n+k+1,…, n+m）。
用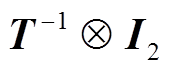
和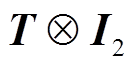
分别左乘和右乘式（10）中的矩阵，可得
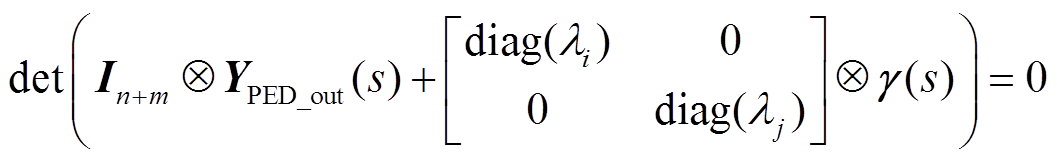（13）
此时，式（13）中各项均为块对角矩阵，因此系统的闭环特征方程可等价变换为
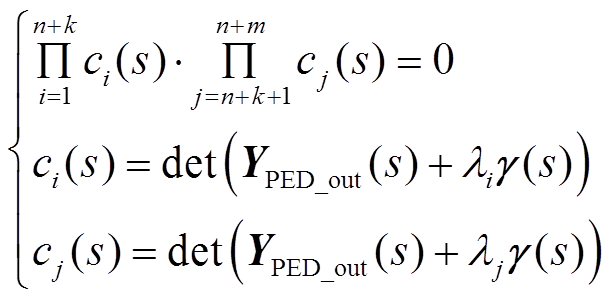（14）
根据式（14）可知，含储能多馈入系统闭环特征方程可以看作n+m个等效单馈入系统闭环特征方程的乘积，即原系统的小扰动稳定性问题可解耦为n+m个等效单馈入系统的小扰动稳定性问题。
由2.1节的分析可知，含储能多馈入系统可以解耦为n+m个相互独立的等效单馈入系统，其中λi（i=1,2, …, n+k）为正特征值，对应n+k个变流器放电模式下的单馈入系统；λj（j=n+k+1,…, n+m）为负特征值，对应m-k个变流器充电模式下的单馈入系统。
一方面，负特征值λj对应锁相环型变流器工作在充电模式下的单馈入系统，其小扰动稳定裕度较大，一般不是稳定主导因素（具体讨论见4.1节算例1）；另一方面，对于锁相环型变流器工作在放电模式下的单馈入系统，其短路比（对应正特征值λi）越小，系统小扰动稳定性越差[26]。根据上述分析可知，含储能多馈入系统小扰动稳定性取决于变流器工作在放电模式下且短路比最小的等效单馈入系统，即最小正特征值所对应的单馈入系统。本文将该最小正特征值定义为含储能多馈入系统场景下的广义短路比。
含储能多馈入系统的电网强度指标gSCR为系统拓展导纳矩阵Yeq的最小正特征值，具体表达式为
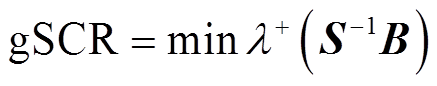（15）
式中，λ+(·)为求解矩阵的正特征值。
需要说明的是，常规新能源多馈入系统中新能源变流器均处于放电模式，矩阵Yeq的特征值均为正实数，故文献[14]针对该系统提出的广义短路比指标为系统拓展导纳矩阵Yeq的最小特征值；与文献[14]不同，本文针对含储能多馈入系统，并计及储能变流器的运行模式差异，此时矩阵Yeq的特征值有正有负，广义短路比指标应为矩阵Yeq的最小正特征值。其中常规新能源多馈入系统可以看作含储能多馈入系统在储能变流器均工作在放电模式时的特例。
系统强度是描述系统受到扰动后的电压响应性能的定性概念，常用于反映系统的安全稳定水平。本节将从小扰动稳定性的角度探讨含储能多馈入系统强度的量化原理。
根据2.1节和2.2节分析可知，含储能多馈入系统的主导特征根sd（对应系统小扰动稳定性）与gSCR存在如式（16）、式（17）所示的函数解析关系，即当设备动态一定时，含储能多馈入系统的小扰动稳定性可以通过静态的电网强度指标gSCR准确量化。
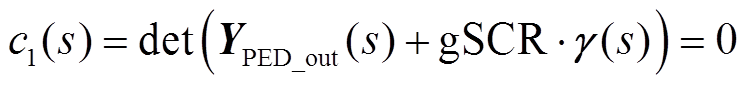（16）
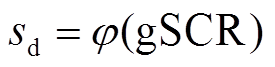（17）
式中，φ(·)为式（16）的反函数。
由式（16）、式（17）可知φ(·)与设备动态特性相关，而gSCR与电网强度特性相关，因此系统的小扰动稳定性由电网强度和设备动态共同决定。进一步地，考虑到单馈入系统短路比越小时小扰动稳定性越弱的单调特性，系统存在保持其小扰动稳定所需的最小短路比（后文简称为“设备临界短路比”，表征了设备对交流电网的耐受能力），即设备临界短路比（Critical Short Circuit Ratio, CSCR）可以反映设备固有的动态特性。CSCR很容易通过单馈入系统的解析计算或仿真实验等方法获得，其中解析计算表达式为
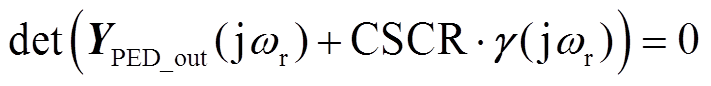（18）
式中，ωr为系统临界稳定时的主导模态。
值得一提的是，含储能多馈入系统小扰动稳定性取决于短路比为gSCR的最弱等效单馈入系统，故含储能多馈入系统临界稳定时对应的gSCR值（即临界广义短路比（Critical generalized Short Circuit Ratio, CgSCR））恰好等于设备临界短路比CSCR。且单馈入系统短路比越小时小扰动稳定性越弱的单调特性可推广至含储能多馈入系统，gSCR与CSCR（CgSCR）之间的差值即反映了系统当前稳态运行点与小扰动稳定边界的距离大小。
综上所述，含储能多馈入系统的小扰动稳定性由电网强度指标gSCR和反映设备耐受能力的CSCR两者共同决定，gSCR与CSCR的相对差值可从小扰动稳定性的维度表征系统强度，差值越大时系统强度越高。因此，基于电网强度指标gSCR以及设备临界短路比CSCR的源-网协同分析方法揭示了含储能多馈入系统强度的量化原理，为1.1节中的问题1提供了解决方法。
基于含储能多馈入系统强度的源-网协同分析方法可实现系统小扰动稳定裕度的准确评估，因此系统稳定裕度评估方法可总结为两个相对简单的子问题：电网强度指标gSCR的计算问题和描述设备耐受能力的CSCR计算问题，具体评估流程如图2所示。
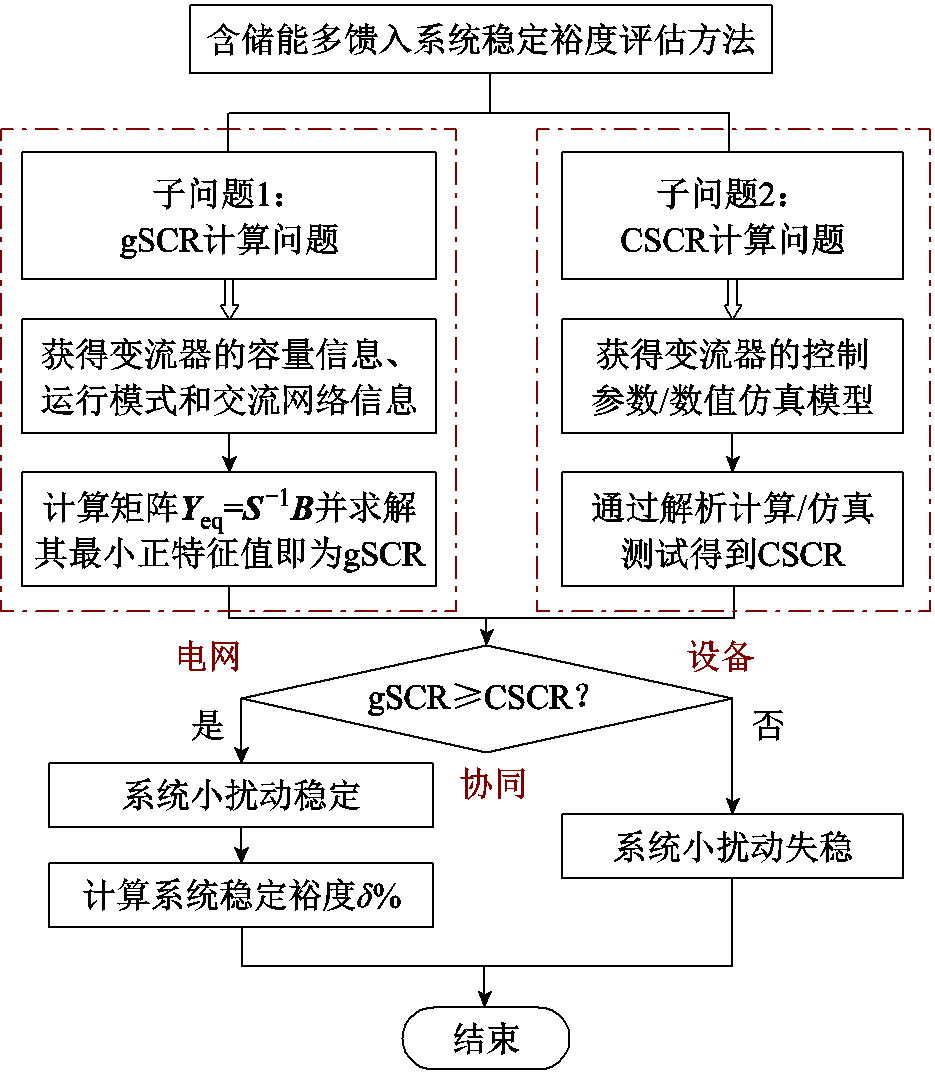
图2 含储能多馈入系统稳定裕度评估流程
Fig.2 Flow chart of stability margin evaluation of multi-infeed system with energy storage
主要步骤包括：
1）根据新能源和储能变流器容量标幺值、储能变流器运行模式和交流网络信息得到等效设备容量矩阵S和工频节点导纳矩阵B，进而计算拓展导纳矩阵Yeq=S-1B，并求解其最小正特征值，得到电网强度指标gSCR。
2）在变流器的控制参数已知的情况下，可通过解析计算式（18）得到CSCR；而在变流器的数值仿真模型已知的情况下，可通过构造变流器放电模式下的单馈入系统进行仿真实验得到SCR，具体过程为：改变单馈入系统的连接阻抗直至系统达到小扰动临界稳定状态，此时系统短路比值即为CSCR。
3）判断gSCR与CSCR的相对大小，当gSCR＜CSCR时，含储能多馈入系统小扰动失稳；当gSCR≥CSCR时，系统小扰动稳定。在实际工程中，为保证系统运行在较为安全的水平，通常要求gSCR不仅大于CSCR，还需要根据工程实践经验保留一定裕度。为此，定义gSCR与CSCR的相对差值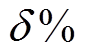
为小扰动稳定裕度评估指标，如需要保留
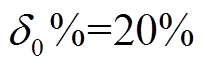的裕度，即满足
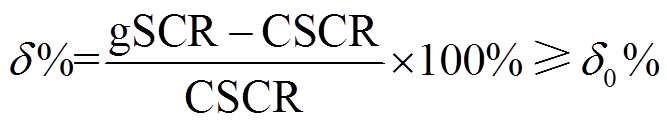（19）
本节基于2.4节所提的含储能多馈入系统小扰动稳定裕度量化方法，分析储能变流器的充/放电运行模式对于锁相环主导的系统小扰动稳定裕度的影响规律。为了便于分析，假设系统中储能变流器的数量为1，即m=1。而对于系统中含多个储能变流器的情况，可基于m=1的分析迭代得知[19]。
假设所接入储能变流器工作在放电和充电两种模式时的含储能多馈入系统gSCR分别为：
1）储能变流器处于放电模式时，系统拓展导纳矩阵Yeq0=S0-1B，其中S0=diag[SB1 SB2 … SB(n+1)]，Yeq0的特征值为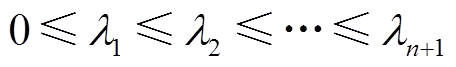
（根据结论1可知，Yeq0的特征值均为正实数），系统gSCR=
。
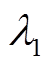2）储能变流器处于充电模式时，系统拓展导纳矩阵Yeq1=S1-1B，其中S1=diag[SB1 SB2 … -SB(n+1)]，Yeq1的特征值为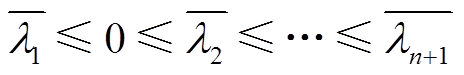
（根据结论1可知，Yeq1具有n个正特征值和1个负特征值），系统gSCR=
。
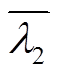根据第2节的分析可知，含储能多馈入系统的小扰动稳定裕度由电网强度指标gSCR和反映设备耐受能力的CSCR两者共同决定。其中储能变流器的功率方向被等价变换至网络侧，设备侧动态不包含功率方向信息，故储能变流器的运行模式仅影响gSCR而不会影响系统CSCR的计算结果。因此，通过比较储能变流器充电和放电模式下的系统gSCR即可揭示由储能变流器的运行模式不同所引起的系统小扰动稳定裕度差异，结论如下。
结论2：所接入储能变流器工作在充电模式时含储能多馈入系统gSCR大于放电模式时，即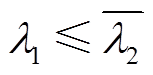
。
证明：
为便于分析储能变流器的运行模式对系统gSCR的影响规律，定义实对称矩阵M为
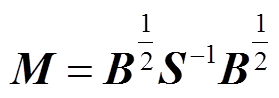（20）
在含储能多馈入系统中，B为对角元均为正实数的实对称矩阵，即实对称正定矩阵，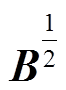
也为实对称正定矩阵，
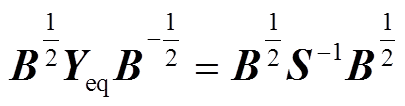，因此矩阵M与Yeq=S-1B为相似矩阵。根据矩阵M与Yeq的相似性，若储能变流器处于放电模式，此时定义矩阵
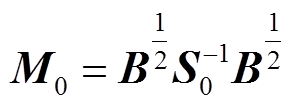（与矩阵Yeq0相似）；若储能变流器处于充电模式，定义矩阵
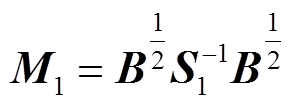（与矩阵Yeq1相似）。
由附录中的推导可知，M1=M0+σxxT，其中 σ=-2/SB(n+1)＜0，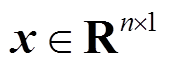
且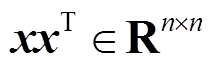
的秩为1，x的具体形式见附录。因此，根据附录中联锁特征值定理[27]可得矩阵M1与M0的特征值（即Yeq1与Yeq0的特征值）存在大小关系，有
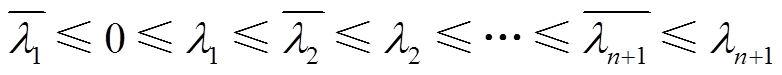（21）
由式（21）可知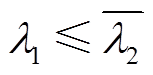，至此结论2证毕。根据上述分析可知，相较于储能变流器工作在放电模式，充电模式时系统gSCR更大且CSCR相等，此时系统gSCR与CSCR的相对差值较大，即论证了：当储能变流器工作在不同运行模式时含储能多馈入系统存在稳定性差异，且储能变流器工作在充电模式时该多馈入系统的小扰动稳定裕度高于放电模式，解答了1.1节问题2。此外，上述结论对于含储能多馈入系统中各储能设备的有功功率如何优化分配和调度，以实现系统稳定裕度的最大化提升等问题具有一定的理论指导意义，具体将在未来的研究中进一步探索。
为验证上述理论分析的有效性，基于Matlab/ Simulink平台搭建附图1所示的单馈入系统模型和附图2所示的五馈入系统电磁暂态仿真模型，其中锁相环型变流器的控制框图如附图1所示，对应控制参数详见附表1。
本节基于典型控制参数下（见附表1）单馈入系统开环传递函数的Nyquist曲线验证了以下结论：当锁相环型变流器处于充电模式时，单馈入系统的小扰动稳定裕度较大。已知在锁相环主导的小扰动稳定问题中，单馈入系统的闭环特征方程可表示[22]为
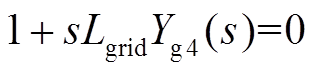（22）
式中，sLgridYg4(s) =Gol(s)为单馈入系统的开环传递函数；Lgrid为单馈入系统的并网电感。
图3分别给出了并网电感Lgrid为0.5(pu)和0.85(pu)，且变流器工作在充电和放电两种模式下Gol(s)的Nyquist曲线。由图3可知，变流器放电模式下，随着并网电感的增大，系统Nyquist曲线与实轴的左侧交点逐渐向左移动，Nyquist曲线从未包围(-1, j0)点至包围(-1, j0)点，对应系统稳定裕度逐渐减小直至失稳。而变流器放电和充电模式下系统Nyquist曲线关于原点对称，因此充电模式下系统Nyquist曲线主要位于右半平面，不包围(-1, j0)点，即说明了相较于变流器放电模式，充电模式下系统的小扰动稳定裕度较大，不是稳定主导因素。
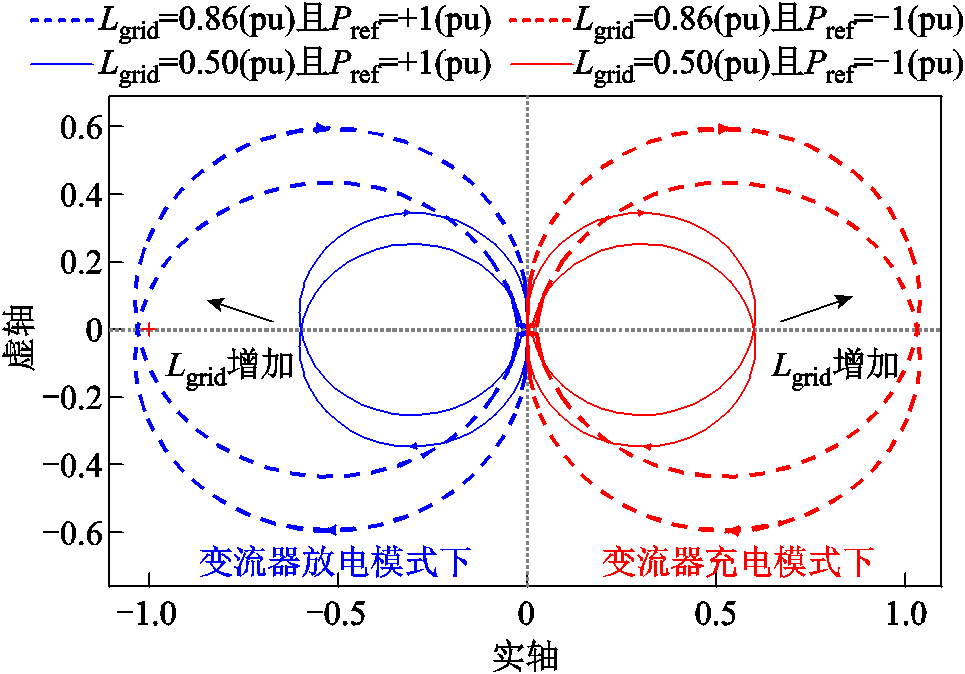
图3 Lgrid增加时Gol(s)的Nyquist曲线对比
Fig.3 Nyquist plot of Gol(s) with varying Lgrid
本节基于五馈入系统的电磁暂态仿真模型，验证了基于gSCR和CSCR的相对差值量化含储能多馈入系统小扰动稳定裕度的有效性。五馈入系统电磁暂态仿真模型如附图2所示，其中节点1～4连接新能源变流器，节点5连接储能变流器，以储能变流器工作在充电模式为例，各设备容量标幺值及网络拓扑参数分别见附表2和附表3。
4.2.1 基于gSCR和CSCR的稳定裕度分析
首先从模态分析的角度验证了基于gSCR和CSCR的稳定判据在评估含储能多馈入系统小扰动稳定性和稳定裕度时的有效性。
图4a和图4b分别给出了线路3-9的电感L39由0.010(pu)增加至0.600(pu)时原始五馈入系统和最弱等效单馈入系统的主导特征根和阻尼比。可以看出，随着电网强度的变化，原始五馈入系统和最弱等效单馈入系统的特征根和阻尼比基本保持一致，因此验证了利用最弱等效单馈入系统来表征原始五馈入系统的小扰动稳定性的有效性。
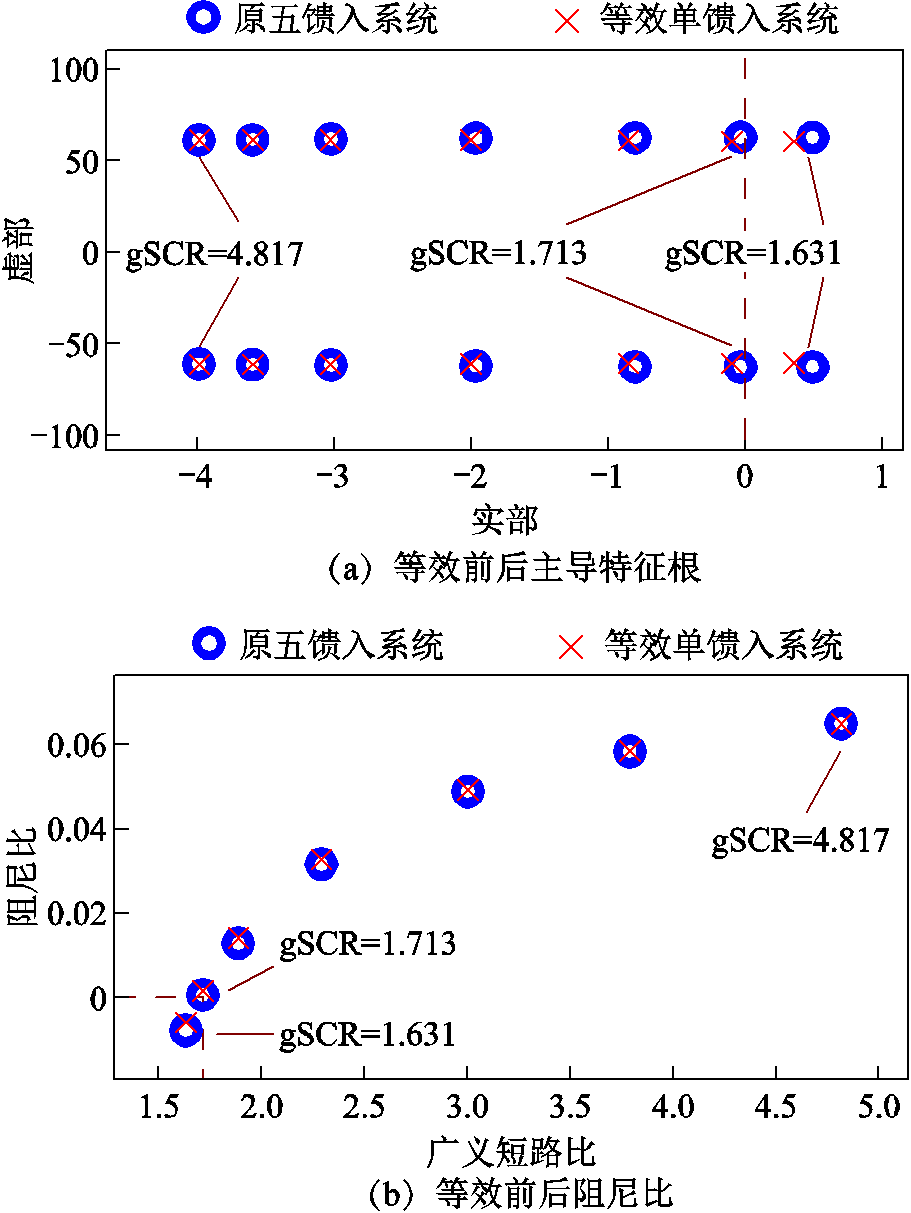
图4 五馈入系统等效前后主导特征根和阻尼比对比
Fig.4 Comparison of dominant roots and damping ratios before and after equivalence of 5-infeed system
进一步地，由图4a和图4b可知，基于gSCR和CSCR可以评估系统小扰动稳定性和稳定裕度。根据式（18）可得CSCR=1.696、gSCR=1.713≈CSCR时，五馈入系统的主导特征根近似位于虚轴，且阻尼比约为0，系统达到临界稳定状态；gSCR＞CSCR时，系统主导特征根均位于左半平面，阻尼比均大于0，系统小扰动稳定，且gSCR越大，主导特征根远离虚轴，稳定裕度越大；gSCR＜CSCR时，主导特征根位于右半平面，阻尼比小于0，系统小扰动失稳。以上分析表明gSCR和CSCR的相对差值对于系统稳定裕度的量化结果与模态分析结果一致。
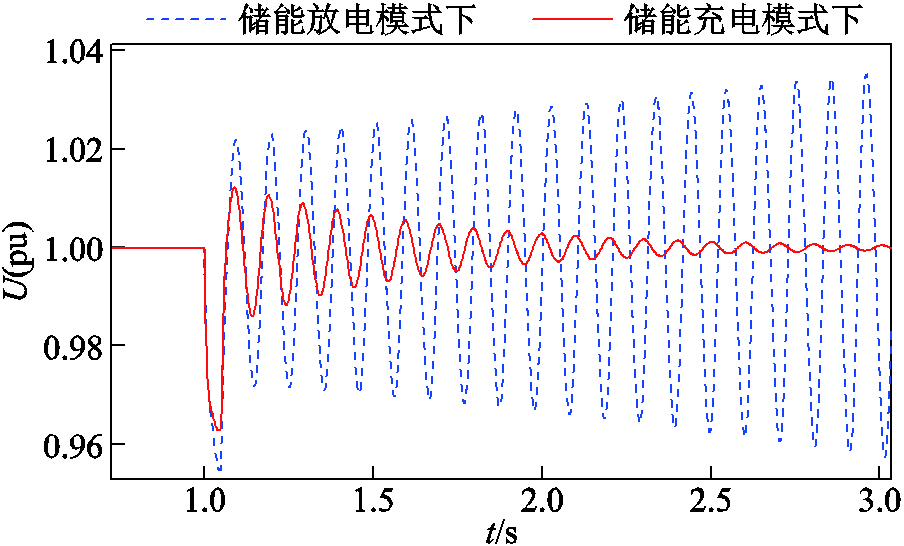
此外，从时域仿真的角度验证基于gSCR和CSCR的小扰动稳定性分析方法在含储能多馈入系统中的正确性。当线路3-9的电感L39设置为0.200(pu)、0.490(pu)和0.600(pu)时，对应的gSCR分别为2.290、1.713和1.631。对系统施加扰动： t=1 s时，附图2中节点8的电压由1(pu)跌落至0.95(pu)，t=1.05 s时电压恢复。此时不同gSCR下设备1端电压的振荡曲线如图5所示，gSCR=2.290＞CSCR时，设备1的端电压曲线振荡收敛，系统小扰动稳定；gSCR=1.713≈CSCR时，端电压曲线近似等幅振荡，系统临界稳定；gSCR=1.631＜CSCR时，端电压曲线发散振荡，系统失稳。
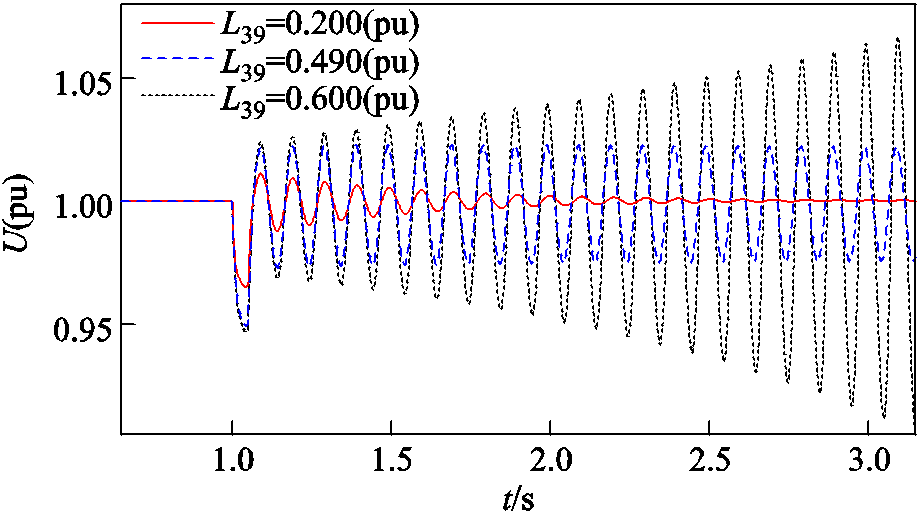
图5 L39改变时五馈入系统的设备端电压
Fig.5 Voltage trajectories of 5-infeed system with different L39
综上所述，本节从模态分析和时域仿真结果两方面验证了基于gSCR和CSCR的稳定判据在含储能多馈入系统中的有效性。
4.2.2 不同运行模式下系统稳定性差异
本节利用模态分析及时域仿真方法验证了储能变流器的充电和放电两种运行模式对于系统小扰动稳定裕度的影响差异。
表1和表2分别给出了在相同的线路电感参数下，储能变流器工作在放电和充电模式下五馈入系统的gSCR、主导特征根和阻尼比。在相同交流网络参数条件下，储能变流器充电模式下系统的gSCR数值均大于放电模式下系统的gSCR数值；而以上两个场景CSCR数值是相等的，由此说明：所接入储能变流器工作在充电模式时五馈入系统的稳定裕度更大。此外，由五馈入系统仿真模型线性化所得的主导特征根和阻尼比结果可知：相较于储能变流器工作在放电模式，充电模式下系统主导特征根更远离虚轴，其阻尼比更大，由此论证了在弱电网下储能变流器工作在充电模式时，含储能多馈入系统的小扰动稳定裕度是高于放电模式的。此外，附图3给出了储能变流器工作在放电和充电两种模式时设备1端电压曲线的对比，进一步从时域波形方面验证了上述结论。
表1 储能放电模式下系统gSCR、主导特征根和阻尼比
Tab.1 gSCR, dominant roots and damping ratio under discharging mode of energy storage
L39(pu)gSCR主导特征根阻尼比 0.1002.189-1.775±61.1940.029 0 0.2301.6550.217±60.658i-0.003 6 0.6001.2773.521±59.173i-0.059 4
表2 储能充电模式下系统gSCR、主导特征根和阻尼比
Tab.2 gSCR, dominant roots and damping ratio under charging mode of energy storage
L39(pu)gSCR主导特征根阻尼比 0.1003.001-3.027±61.845i0.048 9 0.2302.174-1.694±62.306i0.027 2 0.6001.6310.493±62.763i-0.007 9
1）针对含储能多馈入系统，阐述了电网强度指标与该系统小扰动同步稳定性之间的解析关系，探究了储能充/放电运行模式下电网强度指标广义短路比的定义形式，并提出了基于电网广义短路比与反映设备对电网耐受能力的设备临界短路比的系统电压支撑强度分析方法，且所提方法可同时适用于多储能变流器工作在充电和放电两种模式的系统稳定裕度评估。
2）对比分析了跟网型储能变流器的充电和放电两种运行模式对系统小扰动稳定裕度的影响规律。储能两种运行模式对应系统不同的稳态工作点，而工作点进一步通过锁相环影响系统的小扰动稳定性。本文根据矩阵联锁特征值定理，严格论证了跟网型储能变流器工作在充电模式时，系统的小扰动稳定裕度是高于放电模式的。该结论对含储能多馈入系统的优化调度与安全稳定运行等研究具有一定的理论指导意义，将在未来的工作中深入探索。
附 录
1. 结论1证明：
1）在含储能多馈入系统中，B为对角元均为正实数的实对称矩阵，即实对称正定矩阵，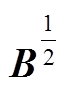
也为实对称正定矩阵，
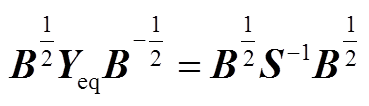，因此矩阵
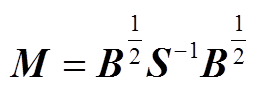与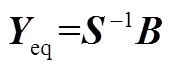
为相似矩阵，具有相同的特征值。又因为矩阵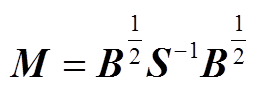为实对称矩阵，其特征值均为实数[28]，因此矩阵Yeq可以对角化且特征值均为实数。第一个子结论成立。
2）矩阵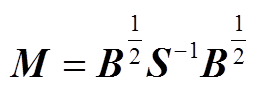与S-1为相合矩阵，具有相同的惯性指数[28]，又矩阵M与Yeq为相似矩阵，因此矩阵Yeq与S-1的惯性指数一致，即矩阵Yeq的正/负特征值个数与运行在放电/充电模式下的变流器的数量一致。第二个子结论成立。至此，结论1证毕。
2. 结论2证明
1）为便于分析矩阵特征值的变化规律，介绍以下引理。
引理1 （联锁特征值定理[27]）：设A为n×n实对称矩阵，其特征值为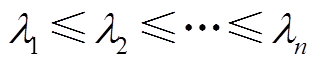
（均为实数），又设
，
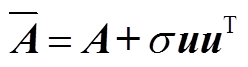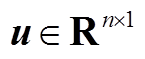是任意向量且
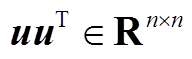的秩为1，其特征值为
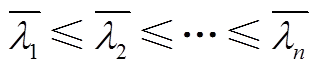，那么：
（1）若σ＞0，则
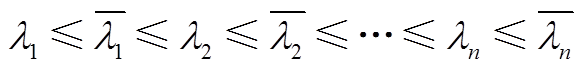（A1）
（2）若σ＜0，则
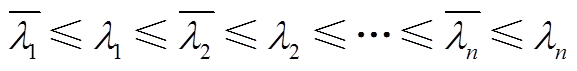（A2）
2）矩阵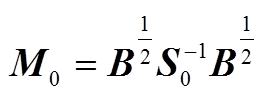
（S0=diag[SB1 SB2 … SB(n+1)]）与矩阵
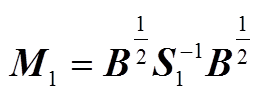（S1=diag[SB1 SB2 … -SB(n+1)]）的特征值大小关系推导（矩阵M1与M0均为实对称矩阵，其特征值均为实数）。
考虑到矩阵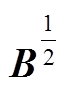为实对称正定矩阵，假设
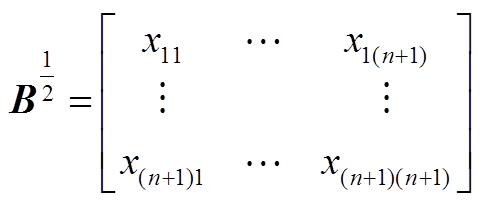（A3）
因此矩阵M1与矩阵M0的数学关系为
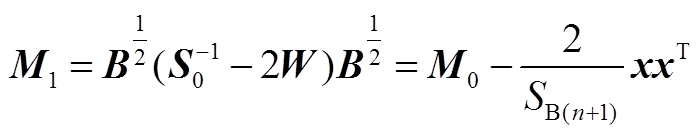（A4）
其中
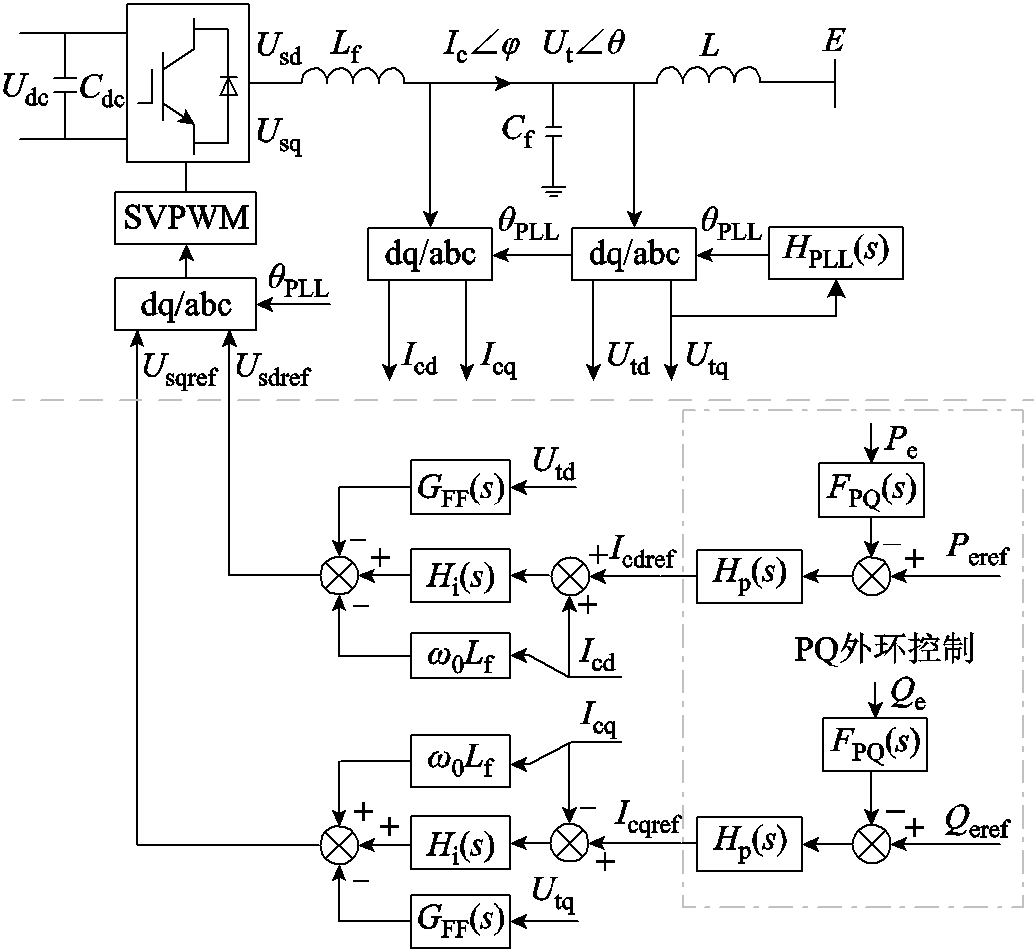
附图1 变流器控制结构
App.Fig.1 The control structure of PED
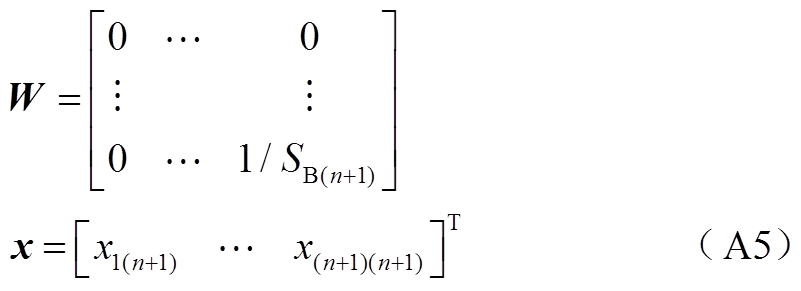
由式（A4）可知矩阵M1与M0存在数学关系为：M1=M0+σxxT，σ=-2/SB(n+1)＜0，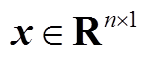
且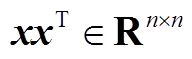
的秩为1。因此，根据引理1（联锁特征值定理[27]）可知矩阵M1与M0的特征值存在大小关系为
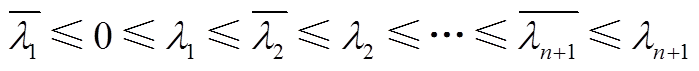（A6）
附图2 五馈入系统结构
App.Fig.2 Structure of 5-infeed power electronic system
附图3 不同运行模式下的设备端电压
App.Fig.3 Voltage trajectories under different operating modes
附表1 并网变流器控制参数
App.Tab.1 Control parameters of grid-connected converters
参数数 值 系统基准容量SB/(kV·A)1 500 交流额定电压UB/V690 滤波电感Lf(pu)0.05 滤波电容C(pu)0.05 直流侧电容Cdc(pu)0.038
（续）
参数数 值 锁相环比例参数kppll10 锁相环积分参数kipll3 750 电流内环比例参数kpc1 电流内环积分参数kic20 功率外环比例参数kpp0.5 功率外环积分参数kip5 电压前馈滤波时间常数TFF0.005 有功功率参考值Pref(pu)±1 无功功率参考值Qref(pu)0
附表2 五馈入系统设备基准容量
App.Tab.2 Rated capacity of PEDs in 5-infeed system（pu）
设备设备基准容量/系统基准容量 11 22 32 41 51.2
附表3 五馈入系统交流网络参数
App.Tab.3 Network parameters of 5-infeed system（pu）
线路电感数值线路电感数值线路电感数值 L140.1L160.2L230.2 L250.1L260.1L340.15 L470.16L570.08L670.3 L680.2L390.2L7,100.2
参考文献
[1] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191. Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[2] 陈泽西, 孙玉树, 张妍, 等. 考虑风光互补的储能优化配置研究[J]. 电工技术学报, 2021, 36(增刊1): 145-153. Chen Zexi, Sun Yushu, Zhang Yan, et al. Research on energy storage optimal allocation considering complementarity of wind power and PV[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 145-153.
[3] 赵彪, 于庆广, 王立雯, 等. 用于电池储能系统并网的双向可拓展变流器及其分布式控制策略[J]. 中国电机工程学报, 2011, 31(增刊1): 244-251. Zhao Biao, Yu Qingguang, Wang Liwen, et al. Bi-directional extensible converter and its distributed control strategy for battery energy storage grid-connected system[J]. Proceedings of the CSEE, 2011, 31(S1): 244-251.
[4] 陆秋瑜, 马千里, 魏韡, 等. 基于置信容量的风场配套储能容量优化配置[J]. 电工技术学报, 2022, 37(23): 5901-5910. Lu Qiuyu, Ma Qianli, Wei Wei, et al. Optimal configuration of energy storage parameters based on confidence capacity of wind farms[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5901-5910.
[5] Yang Li, Hu Zhijian. Coordination of generators and energy storage to smooth power fluctuations for multi-area microgrid clusters: a robust decentralized approach[J]. IEEE Access, 2021, 9: 12506-12520.
[6] 张学广, 夏丹妮, 陈文佳, 等. 三相并网变流器弱电网下频率耦合抑制控制方法[J]. 电工技术学报, 2019, 34(21): 4559-4571. Zhang Xueguang, Xia Danni, Chen Wenjia, et al. Frequency coupling suppression control method for three-phase grid-connected converter under weak grid[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4559-4571.
[7] Wang Xiongfei, Harnefors L, Blaabjerg F. Unified impedance model of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2017, 33(2): 1775-1787.
[8] Fan Lingling, Miao Zhixin. An explanation of oscillations due to wind power plants weak grid interconnection[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 488-490.
[9] 杨明, 杨倬, 李玉龙, 等. 弱电网下基于电网电压前馈的并网逆变器阻抗重塑控制策略[J/OL]. 电工技术学报, 2023: 1-13. DOI:10.1959/j.cnki.1000-6753.tces.230236. Yang Ming, Yang Zhuo, Li Yulong, et al. Impedance Remodeling Control Strategy of Grid-Connected Inverter Based on Feedforward Voltage under Weak Grid[J/OL]. Transactions of China Electrotechnical Society, 2023: 1-13. DOI: 10.1959/j.cnki.1000-6753. tces.230236.
[10] Li Qi, Qiu Yibin, Yang Hanqing, et al. Stability-constrained two-stage robust optimization for integrated hydrogen hybrid energy system[J]. CSEE Journal of Power and Energy Systems, 2020, 7(1): 162-171.
[11] Amin M, Molinas M, Lü Jing, et al. Impact of power flow direction on the stability of VSC-HVDC seen from the impedance nyquist plot[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 8204-8217.
[12] 王凯, 吕敬, 林鸿飞, 等.考虑用电和馈电模式的变流器电驱系统建模与稳定性分析[J/OL]. 电力自动化设备, 2023: 1-13[2023-02-25]. DOI:10.16081/ j.epae.202301024. Wang Kai, Lü Jing, Lin Hongfei, et al. Modeling and stability analysis of converter-based electric drive systemconsidering power consumption and feed modes[J/OL]. Electric Power Automation Equipment, 2023: 1-13 [2023-02-25]. DOI:10.16081/j.epae. 202301024.
[13] 于琳, 孙华东, 赵兵, 等. 新能源并网系统短路比指标分析及临界短路比计算方法[J]. 中国电机工程学报, 2022, 42(3): 919-929. Yu Lin, Sun Huadong, Zhao Bing, et al. Short circuit ratio index analysis and critical short circuit ratio calculation of renewable energy grid-connected system[J]. Proceedings of the CSEE, 2022, 42(3): 919-929.
[14] 辛焕海, 董炜, 袁小明, 等. 电力电子多馈入电力系统的广义短路比[J]. 中国电机工程学报, 2016, 36(22): 6013-6027. Xin Huanhai, Dong Wei, Yuan Xiaoming, et al. Generalized short circuit ratio for multi power electronic based devices infeed to power systems[J]. Proceedings of the CSEE, 2016, 36(22): 6013-6027.
[15] 辛焕海, 甘德强, 鞠平. 多馈入电力系统广义短路比: 多样化新能源场景[J]. 中国电机工程学报, 2020, 40(17): 5516-5527. Xin Huanhai, Gan Deqiang, Ju Ping. Generalized short circuit ratio of power systems with multiple power electronic devices: analysis for various renewable power generations[J]. Proceedings of the CSEE, 2020, 40(17): 5516-5527.
[16] 周瑀涵, 辛焕海, 鞠平. 基于广义短路比的多馈入系统强度量化原理与方法：回顾、探讨与展望[J]. 中国电机工程学报, 2023, 43(10): 3794-3811. Zhou Yuhan, Xin Huanhai, Ju Ping. System strength quantification principle and method of multi-infeed systems based on generalized short-circuit ratio: reviews, discussions and outlooks[J]. Proceedings of the CSEE, 2023, 43(10): 3794-3811.
[17] 董文凯, 杜文娟, 王海风. 用于风电场小干扰稳定性检验的降阶模式计算方法[J]. 电工技术学报, 2021, 36(7): 1468-1479. Dong Wenkai, Du Wenjuan, Wang Haifeng. Reduced-order modal computation method for small-signal stability examination of a wind farm[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1468-1479.
[18] 张冲, 王伟胜, 何国庆, 等. 基于序阻抗的直驱风电场次同步振荡分析与锁相环参数优化设计[J]. 中国电机工程学报, 2017, 37(23): 6757-6767, 7067. Zhang Chong, Wang Weisheng, He Guoqing, et al. Analysis of sub-synchronous oscillation of full-converter wind farm based on sequence impedance and an optimized design method for PLL parameters[J]. Proceedings of the CSEE, 2017, 37(23): 6757-6767, 7067.
[19] Yang Chaoran, Huang Linbin, Xin Huanhai, et al. Placing grid-forming converters to enhance small signal stability of PLL-integrated power systems[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3563-3573.
[20] 周瑀涵, 王冠中, 王康, 等. 用于风电场小干扰稳定性分析的结构保持等值方法[J]. 电力系统自动化, 2021, 45(19): 133-140. Zhou Yuhan, Wang Guanzhong, Wang Kang, et al. Structure-retained equivalent method for small signal stability analysis of wind farm[J]. Automation of Electric Power Systems, 2021, 45(19): 133-140.
[21] Dong Wei, Xin Huanhai, Wu Di, et al. Small signal stability analysis of multi-infeed power electronic systems based on grid strength assessment[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1393-1403.
[22] Xu Luyao, Xin Huanhai, Huang Linbin, et al. Symmetric admittance modeling for stability analysis of grid-connected converters[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 434-444.
[23] Kevorkian J, Cole J D. Multiple Scale and Singular Perturbation Methods[M]. New York: Springer New York, 1996.
[24] 辛焕海, 李子恒, 董炜, 等. 三相变流器并网系统的广义阻抗及稳定判据[J]. 中国电机工程学报, 2017, 37(5): 1277-1293. Xin Huanhai, Li Ziheng, Dong Wei, et al. Generalized-impedance and stability criterion for grid-connected converters[J]. Proceedings of the CSEE, 2017, 37(5): 1277-1293.
[25] 高黛陵, 吴麒. 多变量频率域控制理论[M]. 北京: 清华大学出版社, 1998.
[26] Zhang Lidong. Modeling and control of VSC-HVDC links connected to weak AC systems[D]. Stockholm, Sweden: Royal Institute of Technology, 2010.
[27] 袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 1997.
[28] Horn R A, Johnson C R. Matrix Analysis[M]. Cambridge: Cambridge University Press, 2012.
Abstract With the integration of large-scale renewable energy resources and energy storage into the power grid through power electronic converters, power electronic multi-infeed system is becoming a typical form of modern power system. In particular, the growing penetration of grid-following converters through phase-lock loop under weak grid strength has resulted in frequent oscillation instability risks. Therefore, it is increasingly important to accurately quantify the system voltage support strength (referred to as system strength) and evaluate the stability margin of the system. The relative difference between the short-circuit ratio and device critical short-circuit ratio is commonly used to quantify the system strength and the small-disturbance synchronous stability margin. However, there are two operating modes of charging and discharging when the energy storage system works normally, which leads to the change of the steady-state operating point of the power electronic multi-infeed system composed of multiple energy storage converter and multiple renewable energy converter, and further aggravates the difficulty of small-disturbance synchronous stability analysis. In order to solve the above problems, this paper proposes the generalized short-circuit ratio (gSCR) as the grid strength index of multi-infeed system with energy storage and then presents a fast evaluation method of system strength source-network collaboration based on this index.
Firstly, the frequency-domain model and the closed-loop characteristic equation of multi-infeed system with energy storage are established based on linearization analysis. Secondly, it is theoretically proved that the multi-infeed system with energy storage can be equivalently decoupled into a set of single-infeed subsystems based on the modal decoupling theory. On this foundation, the definition of the gSCR is extended from conventional renewable energy multi-infeed system to multi-infeed system with energy storage considering the charging/ discharging operation mode. The system voltage support strength analysis method based on gSCR and the device critical short-circuit ratio (CSCR) is proposed, and then the fast evaluation of the small-disturbance synchronous stability margin is realized. Furthermore, the influence of the charging/discharging operation mode of the grid-following energy storage converter on the small-disturbance synchronization stability margin of the system is explored through the matrix interlocking eigenvalue theorem. Finally, the effectiveness of the proposed small-disturbance synchronization stability analysis method is verified by simulation example of the 5-infeed power system.
The following conclusions can be drawn: (1) The gSCR (which is related to the grid strength) and CSCR (which is related to the apparatuses’ tolerance towards AC grid) can reflect the system strength and the small-disturbance synchronization stability margin of the multi-infeed system with energy storage, which thus significantly reduces the complexity of small-disturbance synchronization stability analysis of the original multi-infeed system. This proposed method can be applied to different scenarios where multiple energy storage converters work in charging or discharging modes. (2) The two operating modes of grid-following energy storage correspond to different steady-state operating points of the multi-infeed power system, and the steady-state operating points further affect the small-disturbance stability of the system through the phase-locked loop. According to the matrix interlocking eigenvalue theorem, it is demonstrated that the small-disturbance synchronization stability margin of the multi-infeed system when the grid-following energy storage converter works in the charging mode is higher than that of the discharging mode.
keywords：System strength, generalized short-circuit ratio, energy storage converter, operation modes, small-disturbance synchronization stability
DOI: 10.19595/j.cnki.1000-6753.tces.230412
中图分类号：TM712
云南电网有限责任公司电力规划专题研究“提升云南新型电力系统稳定性的新能源与储能协调配置规划研究”资助项目。
收稿日期 2023-04-03
改稿日期 2023-06-21
郝 艺 女，1999年生，硕士研究生，研究方向为高比例新能源电力系统稳定性分析和控制。Email：haoy@zju.edu.cn
辛焕海 男，1981年生，教授，博士生导师，研究方向为高比例新能源电力系统稳定性分析和控制。Email：xinhh@zju.edu.cn（通信作者）
（编辑 赫 蕾）