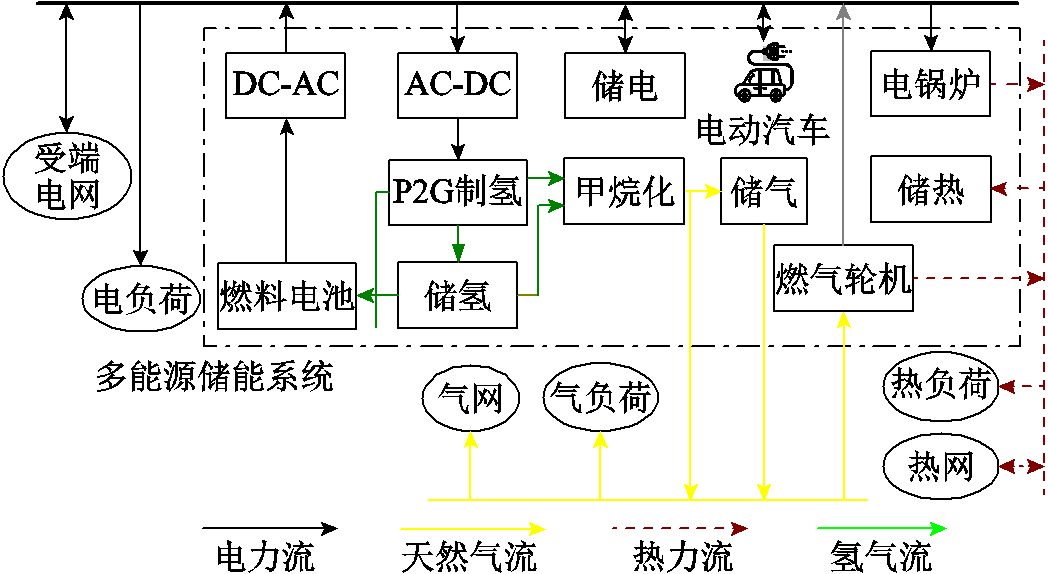
图1 多能源储能系统拓扑结构
Fig.1 Multi-energy storage system topology
摘要 针对大规模可再生能源的接入,导致受端电网的等效惯量和调频能力不断降低,严重影响受端系统频率稳定的问题,该文提出考虑储能支撑的受端电网频率稳定优化控制方法。首先,分析受端电网下多源储能频率响应特性;其次,分析基于多源储能的多能源能量协调与频率变化的关系,建立考虑多能源储能支撑的频率支撑特性模型,并对基于多能源协调对受端电网频率响应等值模型进行修正;再次,建立以受端电网频率变化速度指标和频率跌落指标两方面作为频率稳定指标,并提出基于多源储能支撑的受端电网频率稳定优化控制方法;最后,以某实际受端电网为算例建立仿真模型,算例结果验证了该模型的有效性,基于多能源储能支撑可提高受端电网的频率稳定性能。
关键词:储能 受端电网 频率稳定 优化控制
随着“双碳”目标建设要求的提出[1],我国电力系统进一步加快了由西部大规模可再生能源发电中心向东部能源负荷中心送电的建设规模[2]。一方面,在满足东部地区用电需求的同时,起到了促进新能源发电的大规模消纳、减少电力系统中发电机组带来的碳排放的作用[3];另一方面,大容量、波动性可再生能源的馈入,也给东部地区受端电网的安全稳定运行带来了严重的影响[4]。大容量、波动性可再生能源的馈入替换了东部地区受端电网中部分原有发电机组的配置,当受端电网中发生联锁故障时,电网发生较大的功率缺额,导致系统稳定运行频率易受到波动,使东部地区受端电网的等效惯量、动态调频能力大幅度降低[5-6],严重时可能造成受端电网中部分地区发生解列,发生严重的电网事故[7-9]。
为了保证大容量、波动性可再生能源馈入的受端电网能够维持系统频率稳定、运行稳定,亟须研究可用于解决受端电网受到扰动、故障后保持系统频率稳定的控制方法和优化策略。对于此,国内外部分学者开展了一些研究。文献[10-11]针对华东大受端电网频率稳定性问题,分析了大受端电网各阶段运行特征,并对受端电网中易造成频率扰动等问题的原因进行分析,研究并提出了针对大受端电网的频率稳定控制方法,以保证受端电网能够安全稳定运行。文献[12-14]主要针对含特高压交、直流的受端电网频率稳定问题,研究了受端电网中发生交、直流联锁故障后受端电网的频率特性,以及考虑电压稳定、断面功率极限约束等多约束的受端电网频率紧急协调控制策略,实现了含特高压交、直流的受端电网频率的快速、精确、经济控制。文献[15-17]则主要针对大容量直流电源接入的受端电网频率稳定控制问题,研究并提出了受端电网频率、电压稳定性指标,通过利用调相机、频率控制、发电控制等多种控制手段,制定了受端电网联锁故障下的系统频率紧急控制策略,提高了含直流电源接入的受端电网运行稳定性。
储能技术、多能源互补技术等的出现和发展,为大规模受端电网频率稳定运行控制提供了新的途径。文献[18]通过分析储能设备加入受端电网后的系统惯量与频率变化特性,建立了含风电、光伏、储能的系统虚拟惯量与频率调节模型,从而提高了受端电网运行稳定水平。文献[19-20]基于抽水蓄能机组的优势,研究了考虑抽水蓄能机组参与的受端电网频率稳定控制模型,但对于华东地区来说,单一的抽水蓄能机组应用场景局限性较小,无法完全满足华东地区电网频率响应支撑和调节的需求。文献[21]通过利用电、气、热等多种能源间的互补调节特性,建立了基于多种能源互补协调的受端电网多区域频率协调控制模型,降低了受端电网的运行风险。文献[22-23]通过利用储能装置的快速功率调节特性,建立了含储能系统的电力系统频率响应控制模型,并通过仿真验证了控制模型的可行性。上述基于储能协调的电网频率控制研究,大多针对受端电网自身进行频率响应控制策略与控制方法的研究,较少考虑外部区域频率响应。另一方面,大规模可再生能源与储能联合[24]进行频率稳定优化控制对华东地区受端电网频率响应控制也具有较大的局限性。因此,须结合华东受端电网结构和运行实际情况,研究利用储电、储热、储气的多种能源储能装置与电、热、气等多种能源转换设备相结合的受端电网频率稳定优化控制方法,在满足受端电网电、热、气等多种能源负荷需求的同时,为受端电网提供一定的频率响应支撑能力,以提升受端电网频率稳定的水平。
基于此,本文考虑多能源转换与存储特性,提出了考虑储能支撑与多能源协同调节的受端电网频率稳定控制方法。本文的创新点如下:
1)本文构建了由多种类多能源转换与存储设备构成的多能源储能系统,包含电动汽车、电制氢(Power to Hydrogen, P2H)设备、电制气(Power to Gas, P2G)设备、燃气轮机和储能设备等。分析了多源储能的能量协调特性,并分析了多源储能中惯量对于频率的控制响应特性。
2)分析了受端电网内部频率响应、外部频率响应、多源储能频率响应特性。内部响应考虑有功调节时的原动机和调速器的响应,外部响应利用参数辨识方法进行等值,并对是否考虑外部响应进行了仿真对比分析。
本文构建了由多种类多能源转换与存储设备构成的多能源储能系统,包含电动汽车、P2H、P2G、燃气轮机和储能等设备,通过设备间的能量协调,能够实现为受端电网提供频率支撑的供能,多能源储能系统的拓扑结构如图1所示。

图1 多能源储能系统拓扑结构
Fig.1 Multi-energy storage system topology
多能源储能协调模型中多种类型设备之间的能量转换可以采用耦合矩阵进行描述。本文通过矩阵描述多种能源耦合的输入输出特性,构建的电、热、气多能源协调矩阵可表示为
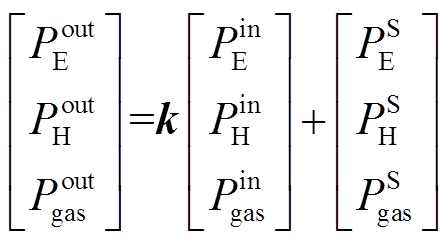 (1)
(1)
其中
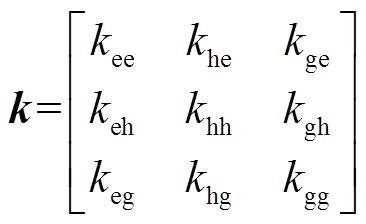
式中,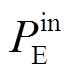 、
、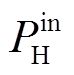 、
、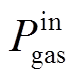 、
、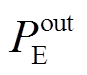 、
、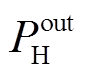 、
、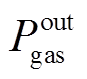 分别为多能源储能系统输入、输出电能、热能、天然气的功率;
分别为多能源储能系统输入、输出电能、热能、天然气的功率;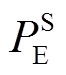 、
、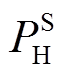 、
、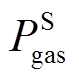 分别为多能源储能系统内储电和电动汽车设备、储热设备、储气设备的输出功率;矩阵k为多能源转换系数,具体可描述为
分别为多能源储能系统内储电和电动汽车设备、储热设备、储气设备的输出功率;矩阵k为多能源转换系数,具体可描述为
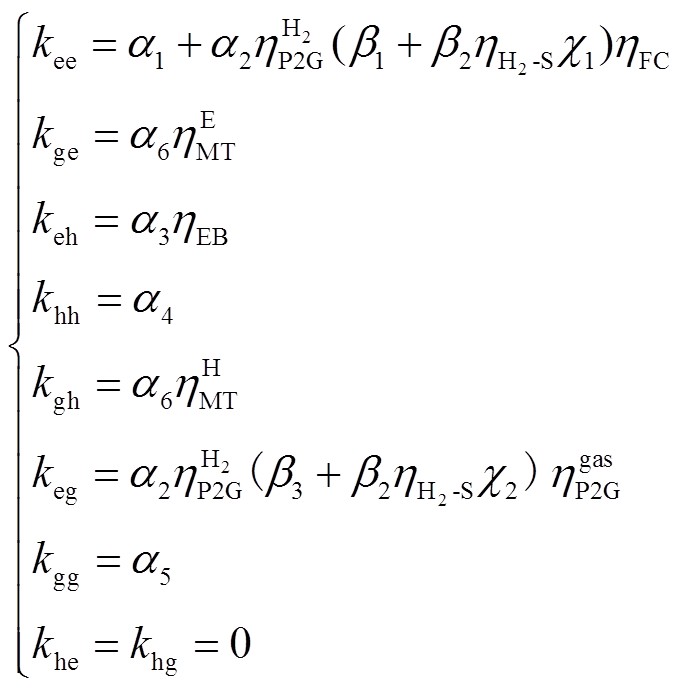 (2)
(2)
式中,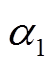 、
、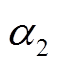 、
、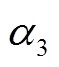 分为电能输入到电能供应、P2G设备、电锅炉的分配系数;
分为电能输入到电能供应、P2G设备、电锅炉的分配系数;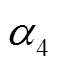 为热能输入到热能供应的分配系数;
为热能输入到热能供应的分配系数;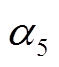 、
、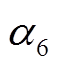 分别为天然气输入到天然气供应、燃气轮机的分配系数;
分别为天然气输入到天然气供应、燃气轮机的分配系数;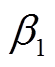 、
、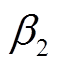 、
、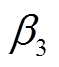 分别为电制氢的氢气输出到燃料电池、储氢、甲烷化的分配系数;
分别为电制氢的氢气输出到燃料电池、储氢、甲烷化的分配系数;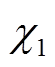 、
、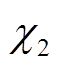 分别为储氢设备氢气输出到燃料电池、甲烷化的分配系数;
分别为储氢设备氢气输出到燃料电池、甲烷化的分配系数;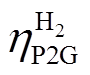 、
、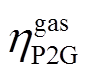 分别为P2G设备电转氢、甲烷化的运行效率;
分别为P2G设备电转氢、甲烷化的运行效率;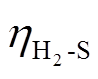 为储氢设备的放能效率;
为储氢设备的放能效率;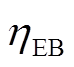 为电锅炉的电热转换效率;
为电锅炉的电热转换效率;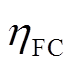 为燃料电池的运行效率;
为燃料电池的运行效率;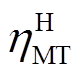 、
、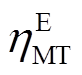 分别为燃气轮机的气转电和气转热效率。
分别为燃气轮机的气转电和气转热效率。
1)P2G模型
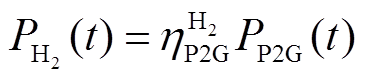 (3)
(3)
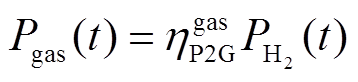 (4)
(4)
式中,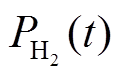 、
、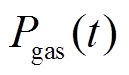 分别为t时刻的P2G输出氢气、天然气的功率;
分别为t时刻的P2G输出氢气、天然气的功率;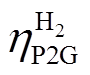 、
、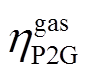 分别为电转氢、甲烷化的效率;
分别为电转氢、甲烷化的效率;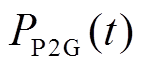 为P2G在t时刻的电能输入功率。
为P2G在t时刻的电能输入功率。
2)储氢、储气模型
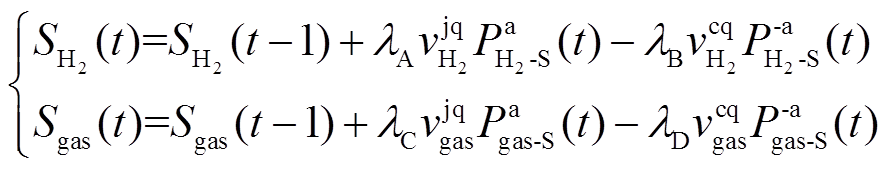 (5)
(5)
式中,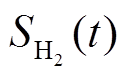 、
、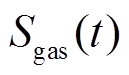 、
、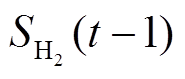 、
、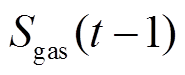 分别为t、
分别为t、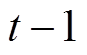 时刻储气设备中氢气、天然气体积;
时刻储气设备中氢气、天然气体积;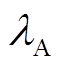 (
(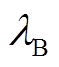 )、
)、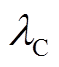 (
(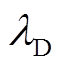 )分别为储氢、储气设备的存储(释放)效率;
)分别为储氢、储气设备的存储(释放)效率;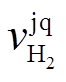 、
、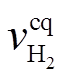 和
和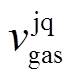 、
、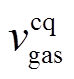 分别为储氢和储气设备的进气、消耗速率
分别为储氢和储气设备的进气、消耗速率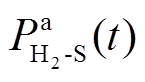 、
、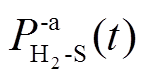 、
、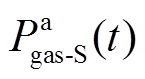 、
、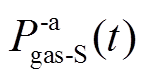 分别为t时刻储氢、储气设备的充、放能功率。
分别为t时刻储氢、储气设备的充、放能功率。
3)燃料电池模型
燃料电池电压输出模型可表示为
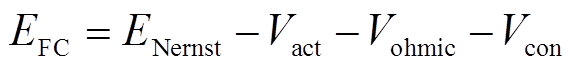 (6)
(6)
式中,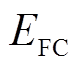 、
、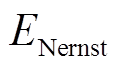 分别为燃料电池的输出电压、可逆电动势;
分别为燃料电池的输出电压、可逆电动势;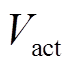 、
、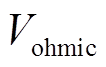 、
、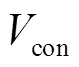 分别为激活过电位、欧姆过电位、浓度过电位。
分别为激活过电位、欧姆过电位、浓度过电位。
4)电锅炉模型
电锅炉是电热能量转换的主要设备,电转热模型为
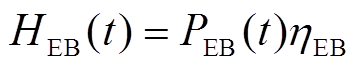 (7)
(7)
式中,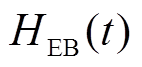 、
、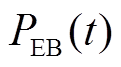 分别为t时刻的产热量、电功率消耗量;
分别为t时刻的产热量、电功率消耗量;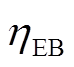 为电热转换效率。
为电热转换效率。
5)储热模型
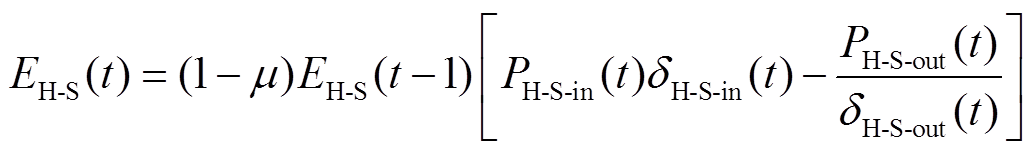 (8)
(8)
式中,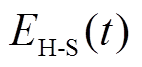 、
、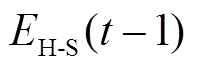 分别为t、
分别为t、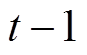 时刻的可用储热容量;
时刻的可用储热容量;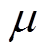 为散热损失率;
为散热损失率;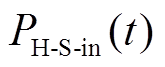 、
、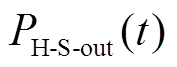 和
和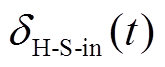 、
、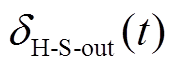 分别为t时刻的吸、放热功率和效率。
分别为t时刻的吸、放热功率和效率。
6)燃气轮机模型
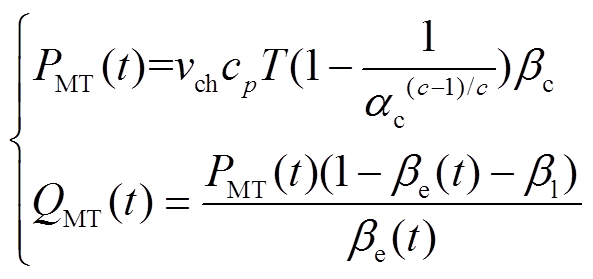 (9)
(9)
式中,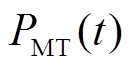 、
、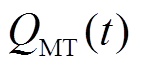 分别为燃气轮机t时刻输出电、热功率;
分别为燃气轮机t时刻输出电、热功率;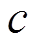 、
、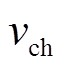 、
、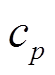 、
、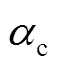 分别为天然气比热容、流量、比定压热容、涡轮膨胀比;
分别为天然气比热容、流量、比定压热容、涡轮膨胀比;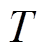 、
、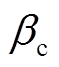 分别为天然气排放温度、有效系数;
分别为天然气排放温度、有效系数;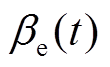 、
、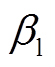 分别为t时刻燃机效率和损失比。
分别为t时刻燃机效率和损失比。
7)电动汽车模型
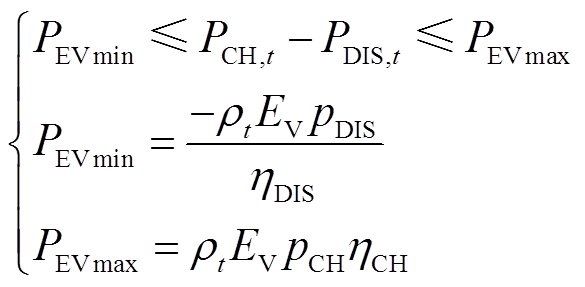 (10)
(10)
式中,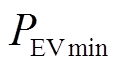 、
、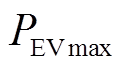 分别为电动汽车在t时段总充放电功率的下限和上限;
分别为电动汽车在t时段总充放电功率的下限和上限;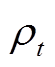 和
和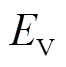 分别为t时段电动汽车驶停概率和电动汽车总数量;
分别为t时段电动汽车驶停概率和电动汽车总数量;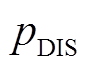 、
、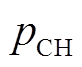 分别为电动汽车的放电功率和充电功率;
分别为电动汽车的放电功率和充电功率;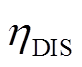 和
和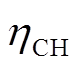 分别为电动汽车的放电效率和充电效率。
分别为电动汽车的放电效率和充电效率。
由于电动汽车在同一时刻只能进行充电或放电,因此同一时刻进行充电或放电的电动汽车数量之和不能超过电动汽车总数量。
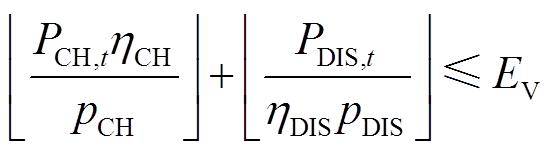 (11)
(11)
式中,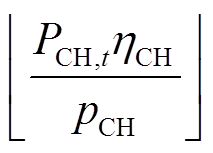 、
、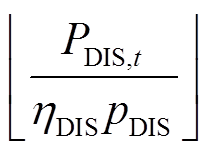 分别为进行充电和放电的汽车数量;
分别为进行充电和放电的汽车数量;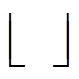 表示向下取整。
表示向下取整。
本文构建了由多种类多能源转换与存储设备构成的多能源储能系统,即采用电动汽车、P2H设备、P2G设备、燃气轮机、储能设备共同参与受端系统的频率调节控制,分析电动汽车、P2H、P2G设备及电动汽车的惯量支撑控制特性,能够实现为受端电网提供频率支撑。
虚拟惯量控制基本思路是将系统的测量频率反馈至变流器有功控制环节以改变有功功率参考值,使并网运行的储能单元表现出和同步机相似的外特性,能够响应电网频率的变化而改变自身的功率输出,为电网提供必要的惯量支撑能力。所以本文利用多能源储能虚拟惯量控制来满足系统的频率调节需求。
1)电动汽车频率控制模型
在所研究的电动汽车进行频率控制的电网中,将电动汽车、电动汽车充电站等视为频率控制响应资源。电动汽车频率控制响应模型如图2所示。
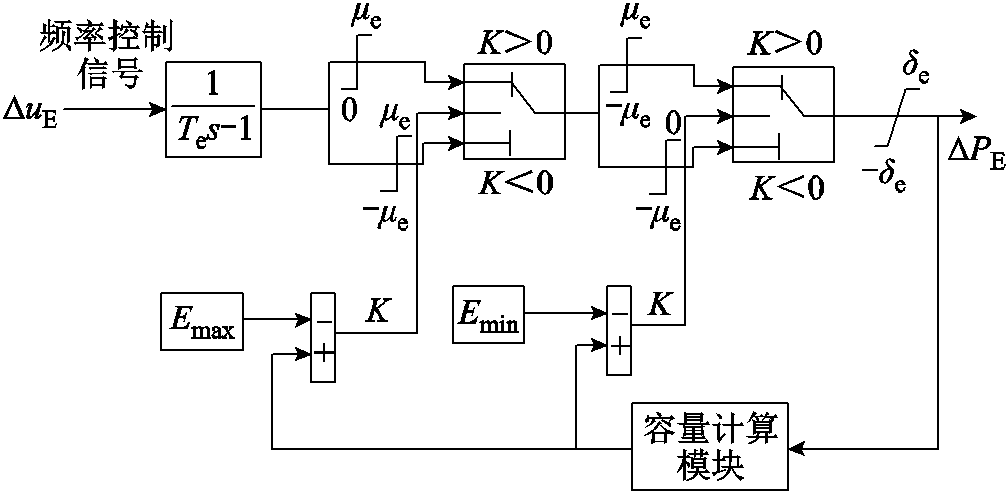
图2 电动汽车频率响应模型
Fig.2 Frequency response model of electric vehicle
图2中,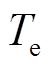 、
、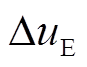 分别为电动汽车的惯性时间常数和电网发出的频率控制信号;
分别为电动汽车的惯性时间常数和电网发出的频率控制信号;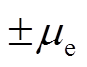 、
、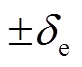 分别为电动汽车逆变器容量上、下限和功率的爬坡上、下限,
分别为电动汽车逆变器容量上、下限和功率的爬坡上、下限,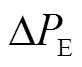 和
和 、
、 分别为电动汽车充放能的变化量和调节容量上、下限。
分别为电动汽车充放能的变化量和调节容量上、下限。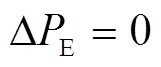 、
、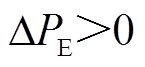 或
或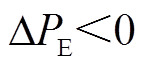 时电动汽车分别为不工作、放电和充电状态。
时电动汽车分别为不工作、放电和充电状态。
受到逆变器容量的限制,电动汽车的充放电功率范围限制在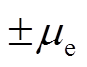 内。当电动汽车的当前容量高于容量最大值
内。当电动汽车的当前容量高于容量最大值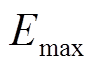 时,电动汽车只能放电,不能进行充电,放电功率范围为
时,电动汽车只能放电,不能进行充电,放电功率范围为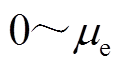 。同样,如果电动汽车当前容量低于容量最小值
。同样,如果电动汽车当前容量低于容量最小值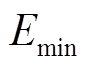 时,电动汽车只能充电,无法进行放电,充电功率范围为
时,电动汽车只能充电,无法进行放电,充电功率范围为 。
。
2)燃气轮机频率控制模型
由于燃气轮机具有可控、输出稳定等特性,可以作为频率控制资源。燃气轮机的频率控制响应模型如图3所示,从图3中可看出燃气轮机输出功率与频率控制信号相关联,同时,燃气轮机输出与调速器相关。
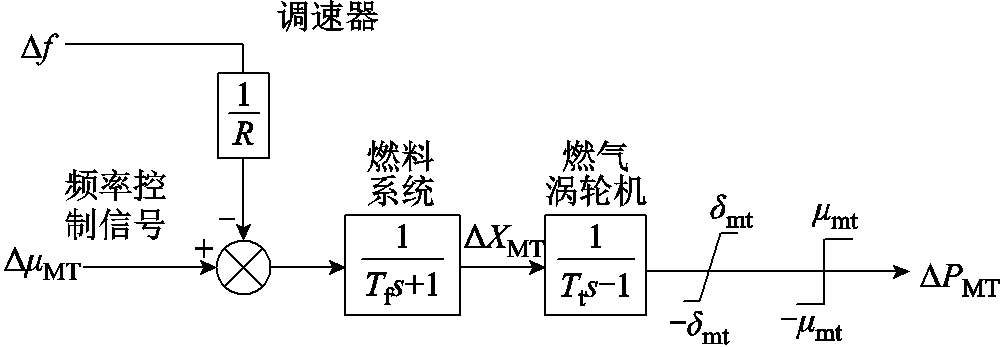
图3 燃气轮机的频率响应模型
Fig.3 Frequency response model of gas turbine
图3中,Tf为燃气涡轮机的时间常数,Tt为燃料系统的时间常数,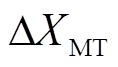 为燃料系统的信号,
为燃料系统的信号,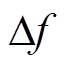 为系统的频率变化,
为系统的频率变化,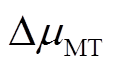 和
和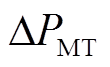 分别为系统发给燃气轮机的频率控制信号和功率输出的变化量。
分别为系统发给燃气轮机的频率控制信号和功率输出的变化量。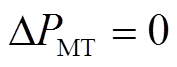 、
、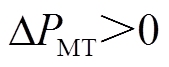 和
和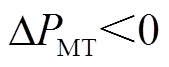 时分别为燃气轮机出力等于、大于和小于额定值。
时分别为燃气轮机出力等于、大于和小于额定值。
3)P2H、P2G设备频率控制模型
P2H、P2G作为可控设备调节性能较优,可以视为虚拟储能。利用Buck电路可调整P2H、P2G的电解槽的电压,进而改变其电解电流,从而实现功率调节。对于气网来说,P2G参与调频时间短,且P2G提供的天然气相对较少,可忽略P2G对于天然气网络的调节。P2G设备的频率控制响应模型如图4所示。
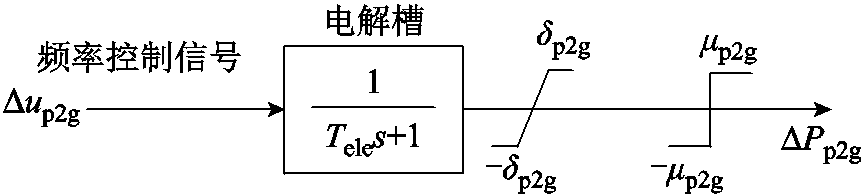
图4 P2G设备频率响应模型
Fig.4 P2G equipment frequency response model
图4中,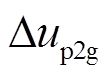 、
、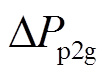 分别为系统发给P2G设备的频率控制信号和功率变化量,
分别为系统发给P2G设备的频率控制信号和功率变化量,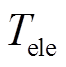 为P2G设备的时间常数,
为P2G设备的时间常数,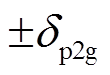 、
、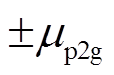 分别为功率变化率和功率变化量的上、下限。
分别为功率变化率和功率变化量的上、下限。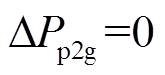 表示P2G设备功率为额定功率;
表示P2G设备功率为额定功率;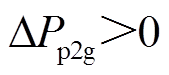 表示P2G设备消耗的功率小于额定功率,相当于储能设备进行放电;
表示P2G设备消耗的功率小于额定功率,相当于储能设备进行放电;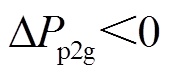 表示P2G设备消耗的功率大于额定功率,相当于储能设备进行充电。P2H的设备频率响应模型与此相同,不再赘述。
表示P2G设备消耗的功率大于额定功率,相当于储能设备进行充电。P2H的设备频率响应模型与此相同,不再赘述。
4)储能频率控制模型
储能频率控制的基本原理是将电网的频率信号发送至变流器有功控制环节,以调整储能功率输出值[25]。
利用拉普拉斯变换法可得储能惯量控制下功率变化与电网频率变化的关系为
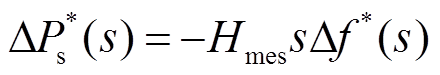 (12)
(12)
式中,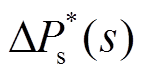 、
、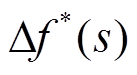 分别为储能惯量控制的功率变化和电网频率变化;
分别为储能惯量控制的功率变化和电网频率变化;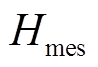 为储能惯量系数。
为储能惯量系数。
受端电网的频率响应过程主要包括内部响应和外部响应两个部分,对于受端电网内部的频率响应主要考虑进行有功调节时的原动机和调速器的响应。则受端电网非再热式汽轮机、再热式汽轮机和水轮机传递函数分别为
 (13)
(13)
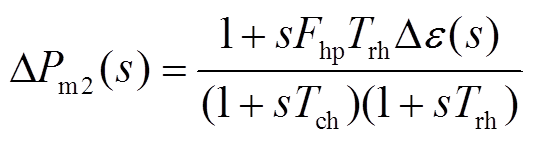 (14)
(14)
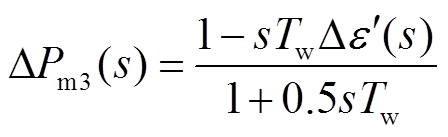 (15)
(15)
式中,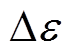 为气门的变化量的标幺值;
为气门的变化量的标幺值;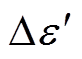 为导水叶开度变化量的标幺值;
为导水叶开度变化量的标幺值;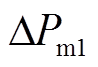 、
、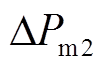 、
、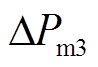 分别为非再热式汽轮机、再热式汽轮机和水轮机传递功率输出变化量的标幺值;
分别为非再热式汽轮机、再热式汽轮机和水轮机传递功率输出变化量的标幺值;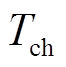 为蒸汽机容积时间常数;
为蒸汽机容积时间常数;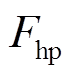 为高压缸的做功比;
为高压缸的做功比;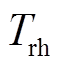 为再加热时间常数;
为再加热时间常数;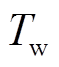 为水锤时间常数。
为水锤时间常数。
将受端电网中的多个发电机组进行聚合等效,得到受端电网的等效惯性时间常数为
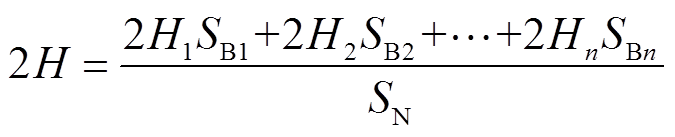 (16)
(16)
式中,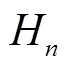 和
和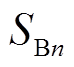 分别为受端电网中
分别为受端电网中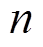 台同步机组的惯性时间常数和额定容量;
台同步机组的惯性时间常数和额定容量;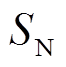 为机组的总容量。
为机组的总容量。
调速器的等效调差系数为
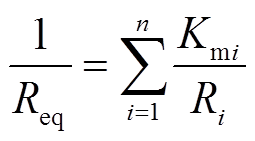 (17)
(17)
式中,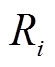 为机组
为机组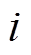 的调差系数;
的调差系数;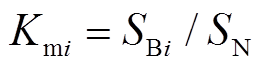 。则同步机的参数
。则同步机的参数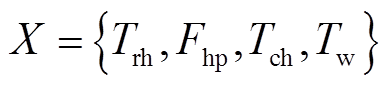 的计算模型为
的计算模型为
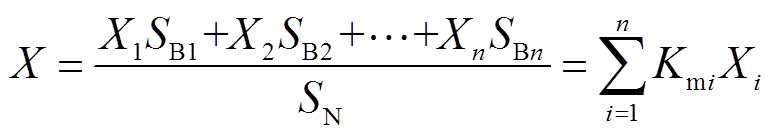 (18)
(18)
受端电网仍会受到外部对其频率的影响,则受端电网外部的频率响应传递函数为
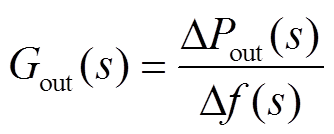 (19)
(19)
式中,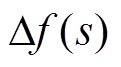 为频率偏差;
为频率偏差;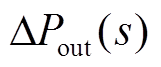 为外部电网的功率。
为外部电网的功率。
在模型等值过程中,外部电网对受端电网的频率响应难以准确量化。为提高辨识精度与效率,并且能够准确描述受端电网外部的频率响应,本文将外部电网频率响应等值为三阶传递函数[26],有
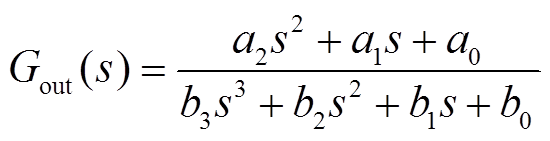 (20)
(20)
采用粒子群算法对传递函数进行参数辨识,得到频率响应模型输出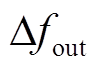 与实际时域仿真输出
与实际时域仿真输出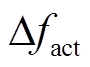 之间误差的二次方和为
之间误差的二次方和为
 (21)
(21)
式中,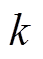 为采样点;
为采样点;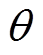 为待辨识参数,
为待辨识参数,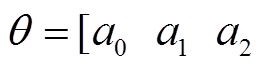
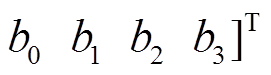 。
。
为提高受端电网的频率响应能力和多能源综合利用效率,基于受端电网频率响应特性分析,本文利用多源储能对受端电网的频率响应进行支撑,研究多源储能与受端协调的频率响应特性,则建立多源储能与受端电网协调的频率响应传递函数为
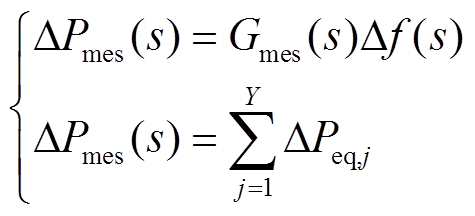 (22)
(22)
式中,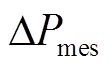 为多源储能提供的受端电网频率变化响应支撑功率;
为多源储能提供的受端电网频率变化响应支撑功率;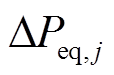 为多源储能设备j提供的惯量支撑的有功出力;
为多源储能设备j提供的惯量支撑的有功出力;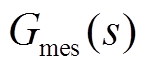 为多源储能的频率响应传递函数,
为多源储能的频率响应传递函数,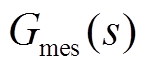 为电动汽车、电制氢、电制气等多个设备等效后的传递函数;Y为多源储能设备总量。考虑多源储能惯量支撑的受端电网频率响应模型如图5所示。
为电动汽车、电制氢、电制气等多个设备等效后的传递函数;Y为多源储能设备总量。考虑多源储能惯量支撑的受端电网频率响应模型如图5所示。
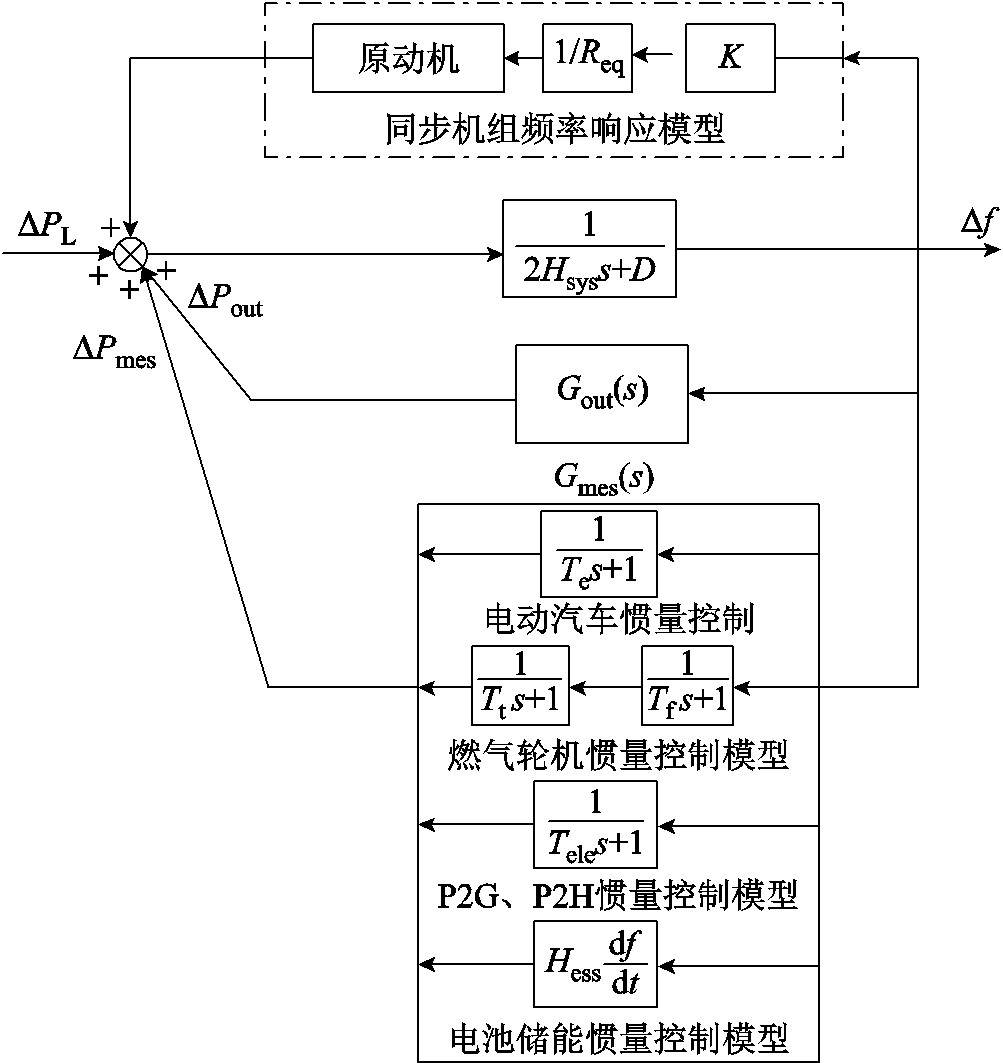
图5 考虑多源储能惯量支撑的受端电网频率响应模型
Fig.5 Frequency response model considered inertia support capacity of energy storage
从图5中可以看出,受端电网的频率响应过程主要包括内部响应、外部响应、多源储能响应三个部分。内部响应考虑有功调节时的原动机和调速器的响应。多源储能响应为虚拟同步控制下的频率响应。外部响应中包含原动机、调速器的响应和虚拟同步控制下的频率响应,利用参数辨识方法进行等值。可将被研究区域的内部、外部和多源储能系统的功率施加在等值转子上,获得计及储能系统惯量支撑的频率响应模型。
当受端电网有频率支撑需求时,可以提供惯量支撑的包括传统的调频机组和多源储能,因此基于本文建立的模型,可利用调频机组和多源储能直接参与受端电网的扰动功率分配。则得到考虑多源储能的受端电网等效惯性时间常数为
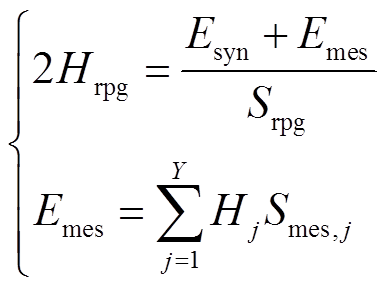 (23)
(23)
式中,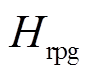 为考虑多源储能的受端电网等效惯性时间常数;
为考虑多源储能的受端电网等效惯性时间常数;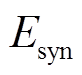 为同步机组动能;
为同步机组动能;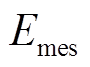 为多源储能提供的虚拟动能;
为多源储能提供的虚拟动能;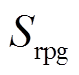 为受端电网总容量;
为受端电网总容量;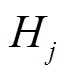 为第j个多源储能设备的惯性时间常数;
为第j个多源储能设备的惯性时间常数;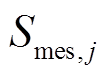 为第j个多源储能设备对应的额定容量。
为第j个多源储能设备对应的额定容量。
其中对于多源储能设备的惯性时间常数,本文基于虚拟同步技术,通过控制多能源储能每一个设备的虚拟惯性常数对受端电网频率进行优化控制。对于多源储能虚拟同步控制而言,虚拟惯量的选取不会受到物理条件的限制,可根据实际系统调节需求选择不同的值。
多能源系统中受端电网频率稳定性主要受送端电网的输出功率、受端电网负荷功率及高比例新能源接入对系统调频关键参数的影响,将影响频率稳定性的评估指标F分为两部分:频率变化速度指标和频率跌落指标。
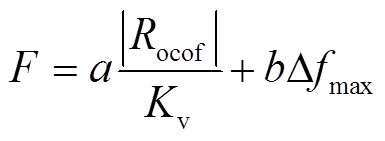 (24)
(24)
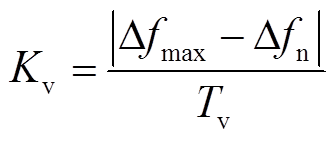 (25)
(25)
式中,a、b分别为电网频率的变化速度及频率跌落所占权重,且a+b=1;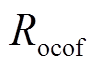 为受端电网的频率变化率;
为受端电网的频率变化率;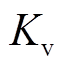 为受端电网频率受到扰动时的恢复速度;
为受端电网频率受到扰动时的恢复速度;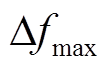 为受端系统中最大频率偏差;
为受端系统中最大频率偏差;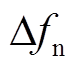 为受端系统到稳态时的频率偏差值;
为受端系统到稳态时的频率偏差值;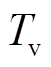 为受端系统中电网频率最低点时刻与恢复稳态时之间的时间。
为受端系统中电网频率最低点时刻与恢复稳态时之间的时间。
若多源储能参与调频,发生故障后系统的功率不平衡量会不断减弱。因此电网的惯量需求在频率变化开始时较大,然后不断减小,多源储能提供的动能也不断减小,随即多源储能虚拟惯量也会降低。
基于此,本文引入附加虚拟惯量系数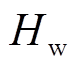 ,可表示为
,可表示为
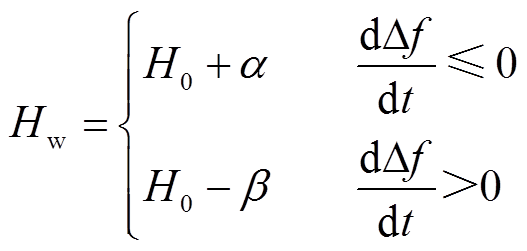 (26)
(26)
式中,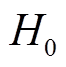 为多源储能的虚拟惯量系数初值;
为多源储能的虚拟惯量系数初值;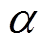 、
、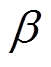 为多源储能的附加虚拟惯量系数,即
为多源储能的附加虚拟惯量系数,即
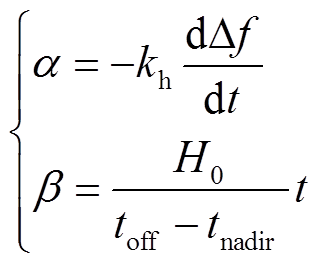 (27)
(27)
式中,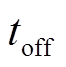 、
、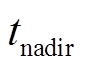 分别为多源储能退出调频时刻和频率最低点时间。
分别为多源储能退出调频时刻和频率最低点时间。
从式(27)中可看出,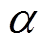 与频率变化率相关,频率变化率逐步降低为0,
与频率变化率相关,频率变化率逐步降低为0,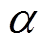 也降低,
也降低,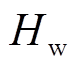 逐渐减小至
逐渐减小至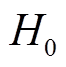 。
。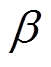 与时间变化相关,在频率恢复时
与时间变化相关,在频率恢复时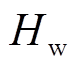 从
从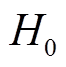 开始减小,直到多源储能退出调频
开始减小,直到多源储能退出调频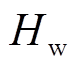 减小至0。
减小至0。
通过对频率稳定性影响因素的影响分析,以多源储能的虚拟惯量和多源储能退出调频时刻为控制量,多源储能虚拟惯量过小,会导致调频效果差[27-28]。多源储能虚拟惯量过大,不利于频率的恢复。多源储能退出调频过早无法充分发挥多源储能的惯量支撑能力,对于频率改善效果不佳。多源储能退出调频过晚,可能会影响其他能源供需平衡。本文提出系统稳定性评估指标F,为了保障受端电网的频率稳定性,以频率稳定性评估指标F最小为目标函数。目标函数定义为
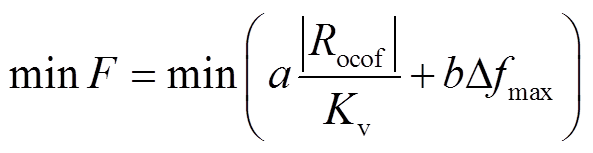 (28)
(28)
约束条件:受端电网功率约束
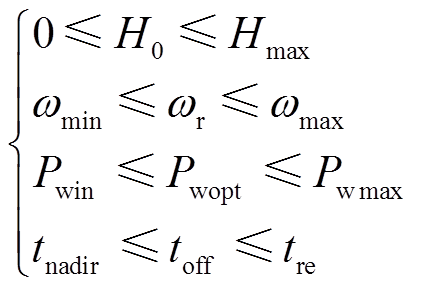 (29)
(29)
式中,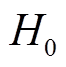 为初始虚拟惯性系数;
为初始虚拟惯性系数;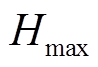 为多源储能最大虚拟惯性系数;
为多源储能最大虚拟惯性系数;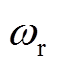 为多源储能虚拟的转子转速;
为多源储能虚拟的转子转速;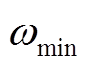 和
和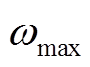 为多源储能虚拟的转子转速限制;
为多源储能虚拟的转子转速限制;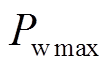 为多源储能最大输出功率;
为多源储能最大输出功率;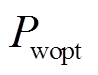 为多源储能输出功率;
为多源储能输出功率;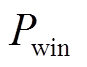 为多源储能最小输出功率;tre为频率恢复正常值的时刻。
为多源储能最小输出功率;tre为频率恢复正常值的时刻。
本文提出一种改进量子粒子群算法求解受端电网频率稳定控制的优化算法,步骤如下。
1)编码改进。
改进量子粒子群算法进行粒子位置编码,以影响受端系统频率稳定性的各因素的概率作为粒子群输入,即粒子群的当前编码为
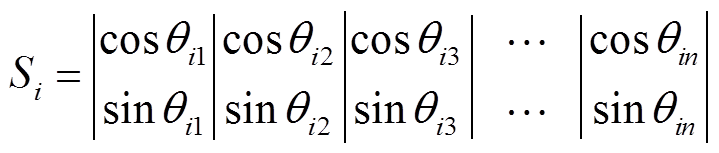 (30)
(30)
式中,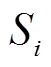 为受端电网第i个解的粒子位置;n为所求解的维数;
为受端电网第i个解的粒子位置;n为所求解的维数;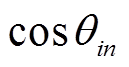 、
、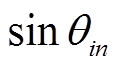 分别为所求的第i个解的第n维空间所对应的余弦和正弦位置。
分别为所求的第i个解的第n维空间所对应的余弦和正弦位置。
对所求的受端电网解集进行优化,转变为
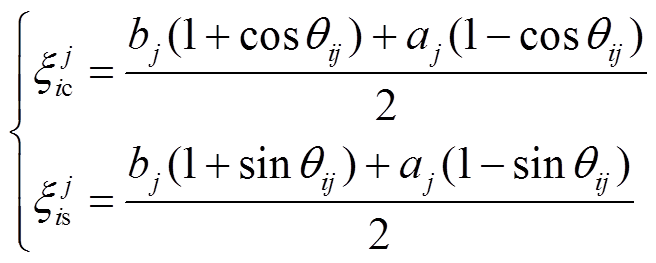 (31)
(31)
式中,aj、bj分别为受端电网中进行求解过程中第j个控制变量的最大及最小值。
2)粒子位置更新。
为得到更优计算结果,利用量子行为位置更新方程对更优位置进行更新,计算后返回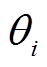 值,受端电网控制优化求解的位置更新方程为式(32)~式(35)所示。
值,受端电网控制优化求解的位置更新方程为式(32)~式(35)所示。
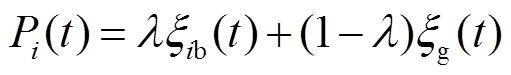 (32)
(32)
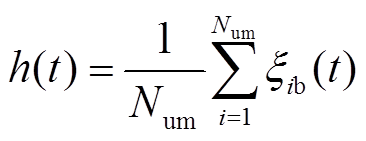 (33)
(33)
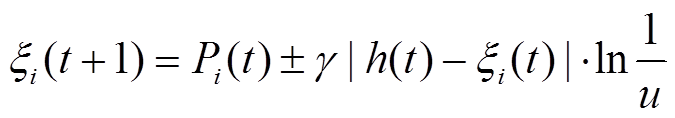 (34)
(34)
 (35)
(35)
式中,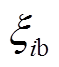 、
、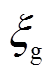 分别为受端电网在进行最优位置求解过程中单个解的最优位置及所有解集的全局最优;λ和u是取值为[0,1]的有理数;Num为解的空间内种群大小;h为受端电网求解种群中所粒子的平均值;α为解的收缩-扩张因子。
分别为受端电网在进行最优位置求解过程中单个解的最优位置及所有解集的全局最优;λ和u是取值为[0,1]的有理数;Num为解的空间内种群大小;h为受端电网求解种群中所粒子的平均值;α为解的收缩-扩张因子。
通过以上位置更新方程,求解得到系统各稳定性评估指标参数作为输出。
3)算法求解流程。
根据前文所述,受端电网频率优化控制策略流程如图6所示。
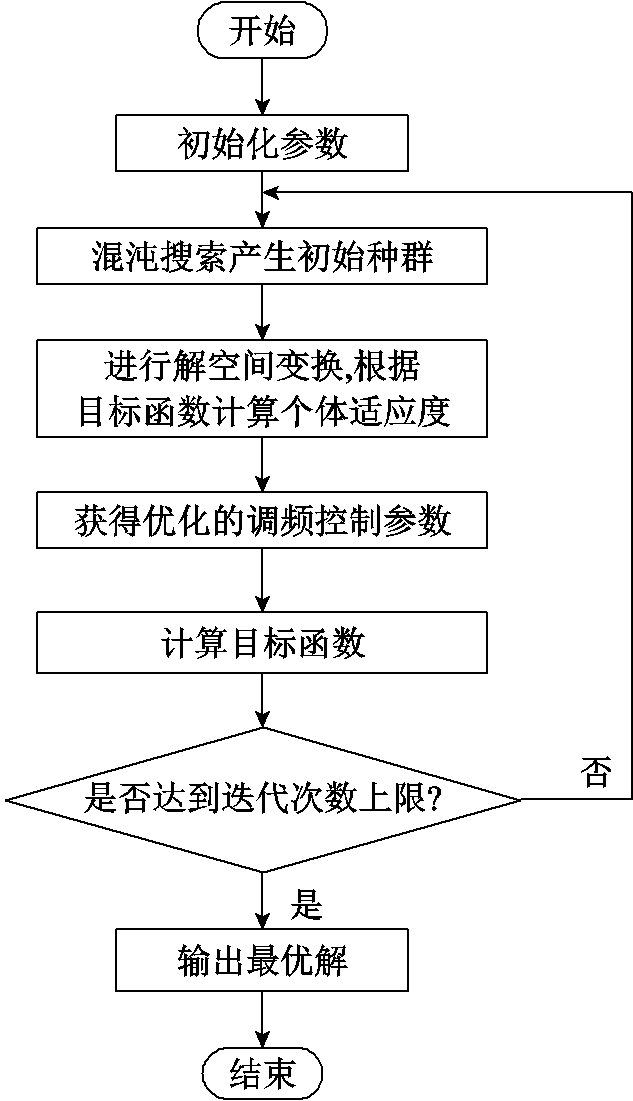
图6 模型求解流程
Fig.6 Model solution process
本文以华东某区域电网2021年夏季高峰典型潮流为背景数据,基于Matlab搭建由新能源发电机组、火电机组、直流馈入、多源储能系统及负荷组成的仿真系统,对提出的基于储能的受端电网频率稳定控制方法的有效性进行验证。采用熵权法求得目标函数权重系数a和b分别为0.46和0.54。仿真系统装机容量及设备具体调频参数见表1、表2。表3为外部电网频率响应等值参数。改进量子粒子群算法的最大迭代次数的值设置为200次。
表1 系统参数表
Tab.1 System parameter table

参数数值 非调频火电机组/MW0 调频火电机组/GW2.26
(续)

参数数值 总装机容量/GW3.18 负荷/GW3.08 直流输电馈入/GW0.48 多源储能/MW25.6
表2 设备调频参数
Tab.2 Equipment frequency modulation parameters

设备参数数值 调频火电机组机组功频静态特性系数20 惯性时间常数/s9.27 调速器动作时间常数/s20 调频频率响应死区/Hz±0.034 多源储能装置响应紧急调频响应死区/Hz±0.2 负荷负荷频率调节效应系数2
表3 外部电网频率响应等值参数
Tab.3 Equivalent parameters of external power grid frenquencg response

参数数值 a0-0.131 a11.212 a2103.181 b00.097 b11.971 b22.012 b31
在仿真系统中,设置某段系统线路发生直流馈入双极闭锁故障,损失功率为6 000 MW,系统输出的频率变化曲线如图7所示。由图7可知,扰动发生后,受端电网频率急剧减小,并在30 s后有所恢复。
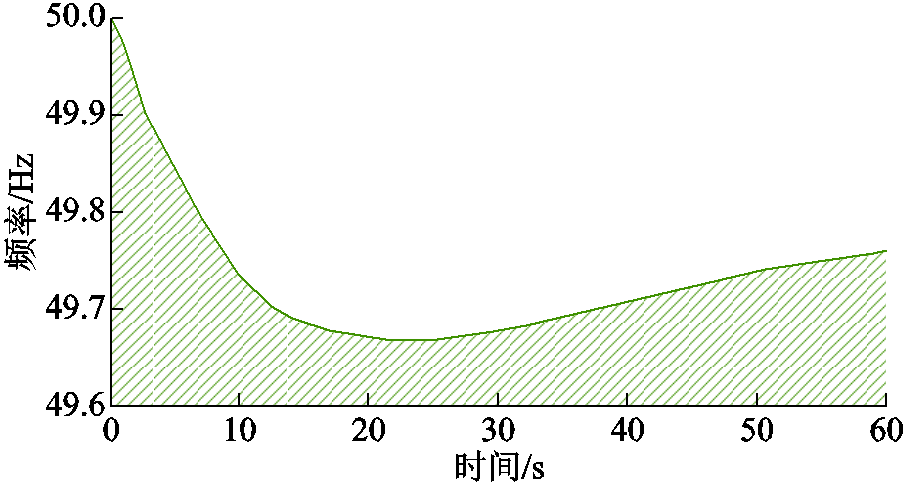
图7 直流闭锁后受端电网频率曲线
Fig.7 The frequency curve of the receiving end grid after DC blocking
将系统中的风电机组的风速上下限分别设置为1.0(pu)和1.2(pu)。采用本文提出策略在考虑多能源协调后对受端电网进行频率控制时,虚拟惯量系数随时间变化的曲线如图8所示。由图8可知本文提出的频率控制策略下,虚拟惯量系数在初始阶段达到最大值,并随响应时间延长而减小,最后在风电机组调频工作结束时达到0值,与预期目标相符。
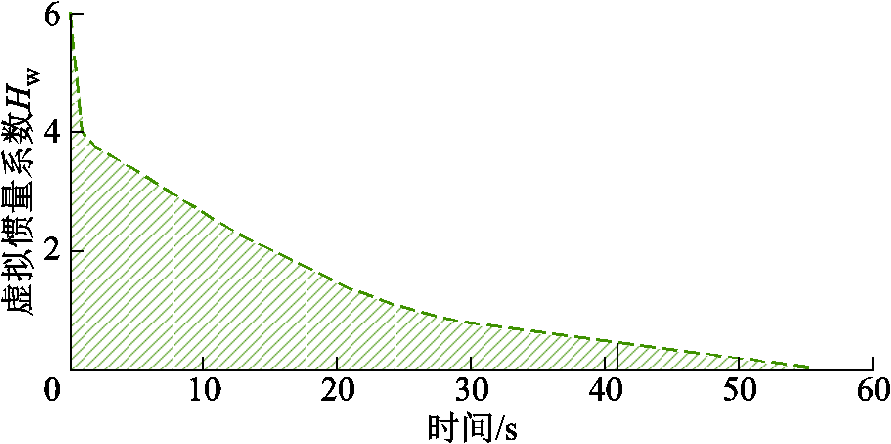
图8 虚拟惯量系数曲线
Fig.8 Virtual inertia coefficient curve
为验证本文提出频率控制策略的有效性,另外采用三种形式控制策略对受端电网频率进行调节,并作对比分析。第一种控制策略是不计及多源储能的传统频率控制方法,记为S1;第二种控制策略是计及多源储能,不考虑外部电网对本区域电网频率响应的影响,记为S2;第三种控制策略是本文计及多源储能和考虑外部区域频率响应的频率优化控制算法,记为S3。三种形式控制策略的算法均采用本文提出的改进量子粒子群算法求解受端电网频率稳定控制的优化算法。
三种控制策略下,系统扰动故障后的受端电网频率偏差曲线对比如图9所示。
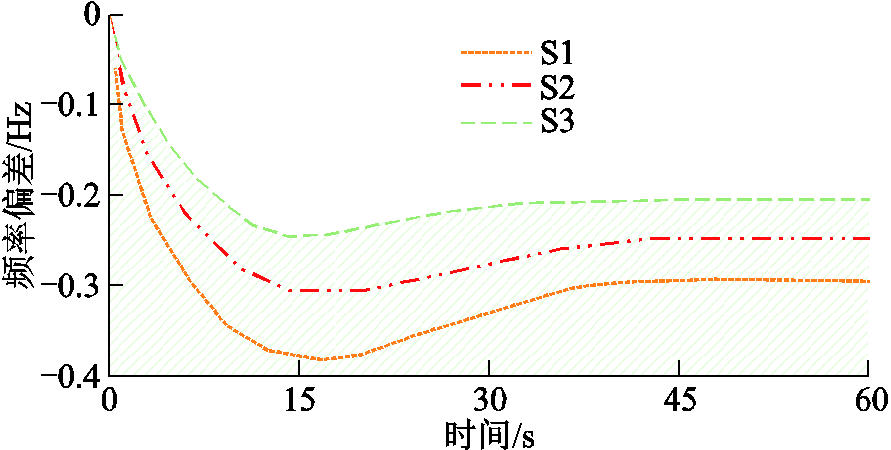
图9 频率偏差对比
Fig.9 Frequency deviation comparison chart
由图9可知,在S1中,未采用多源储能时可以看到频率跌落较大。S2考虑多源储能后减小了频率偏差。S3采用本文的基于多源储能支撑的受端电网频率稳定优化控制方法,且在考虑外部电网频率响应后,可以提升系统总惯量水平,减小频率偏差增大速率,最大频率偏差绝对值相对于其他两种策略明显减少。由于本文多源储能的设备较多,可以自适应对惯量进行调整,使频率的恢复速度较快。因此,应用本文提出的控制策略能够显著提升受端电网在直流故障后的频率稳定性和恢复能力,提升系统运行可靠性。
为验证本文提出控制策略对新能源发电设备及多源储能系统频率调节潜力的利用情况,将三种运行状态下的风电机组转子转速曲线与多源储能系统充放电曲线进行对比。在三种控制策略下,当直流发生闭锁故障时,风力发电设备转子转速如图10所示,多源储能装置充放电功率如图11所示。
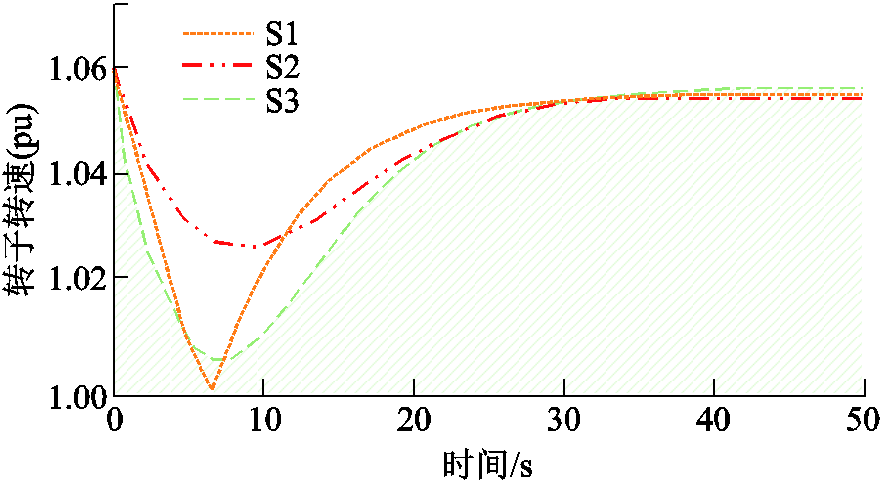
图10 风机转子转速对比
Fig.10 Fan rotor speed comparison chart
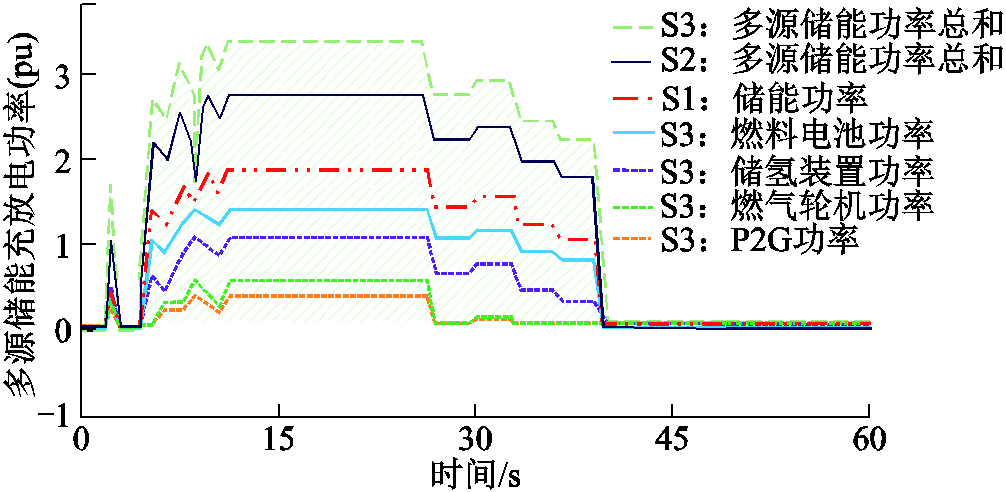
图11 多源储能装置充放电功率对比
Fig.11 Mullti-energy storage charging and discharging power comparison chart
由图10可知,在传统虚拟惯量控制策略下,转子转速控制较为困难,虚拟惯量偏低使得转子转速变化较小,转子动能未得到充分利用,设置过高导致转子转速变化过大,易触发转速保护,提前退出调频,难以把控。相对于传统虚拟惯量控制策略,本文提出的考虑储能的频率控制策略能够使风机转子转速变化过程相对平稳,在故障后,下降至1.0(pu)后恢复,且不存在提前退出调频情况,充分发挥出受端电网新能源发电设备频率调节潜力。
如图11所示,在第一种传统储能装置控制策略下,节点充放电功率远达不到上、下限,不能充分发挥调节潜力,造成了多源储能调节容量的浪费。第二种控制策略引入了多源储能,可以较好地发挥多能源耦合特性,为系统提供能量支撑。第三种控制策略,即本文提出的基于多源储能支撑的受端电网频率稳定优化控制策略下,对于惯量支撑方面,可以采用电动汽车、电制氢、电制气设备、燃气轮机、储能等设备通过虚拟同步技术为电网提供惯量。另一方面,不具有电力电子设备的多能源耦合设备如电锅炉、储热、储气等,可以为频率支撑提供一定的能量调节。在调节过程中电动汽车、电制氢、电制气等设备可以提高电能供给功率和惯量水平,协助少用功率或关停一些设备减少电能消耗以此进行多能源负荷的灵活调节。利用多能源协调可以在满足热、气负荷需求约束的前提下,发挥系统调频潜力。综上所述,多源储能装置为受端电网频率调节提供了稳定支撑,再次验证了本文提出频率控制策略的优越性。
为验证本文算法的有效性,对本文提出的改进的量子粒子群算法(Improved Quantum Particle Swarm Optimization, IQPSO)、粒子群算法(Particle Swarm Algorithm, PSO)、压缩因子粒子群算法(Compression Factor Particle Swarm Algorithm, CFPSO)和量子粒子群算法(Quantum Particle Swarm Optimization, QPSO)进行了对比。图12和表4为四种算法的仿真效果对比。从图12和表4中可以看出,PSO算法仿真时间短但是稳定性指标较差。可以看出本文提出的改进的量子粒子群算法(IQPSO)比QPSO的寻优性能更优,收敛速度更快。
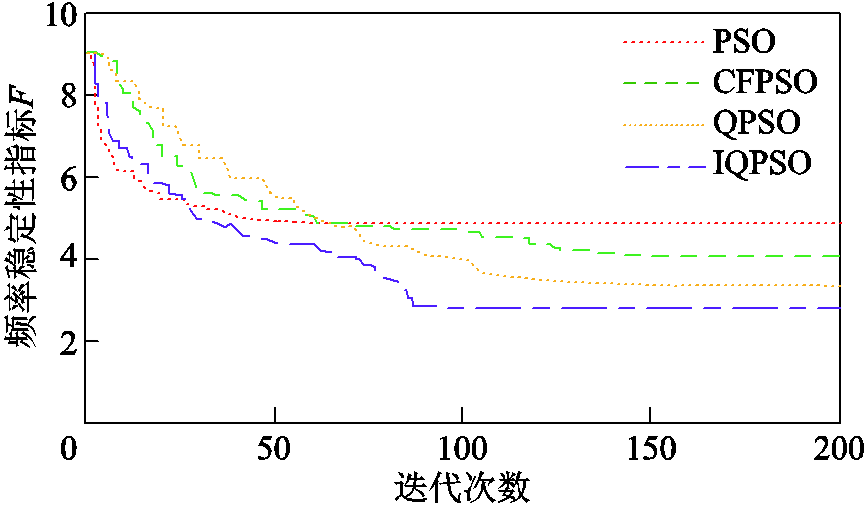
图12 算法对比
Fig.12 Algorithm comparison chart
表4 算法对比
Tab.4 Algorithm comparison

求解算法目标函数值平均求解时间/s IQPSO2.9228.76 QPSO3.5332.13 CFPSO4.0439.71 PSO4.2224.85
针对大规模可再生能源参与并网受端系统严重影响电网频率稳定的问题,为提升系统调频的能力,建立一种考虑多源储能支撑的受端电网频率响应等值模型,提出基于多源储能的频率稳定优化控制策略,并以某实际受端电网为例验证了所提频率优化控制方法的有效性。
1)分析了受端电网下多能源储能特点,以电动汽车、P2H、P2G设备和电动汽车的频率控制响应模型。
2)分析了基于多能源能量协调与多源储能对系统支撑特性,提出了考虑多源储能下的受端电网频率响应模型,建立了多源储能的频率稳定优化控制模型。
3)建立以受端电网频率变化速度指标和频率跌落指标两方面作为频率稳定指标,并利用多源储能的虚拟惯量控制进行调频。仿真证明该模型能够有效改善受端电网的频率特性,所提频率响应模型具有较高的精度。
4)基于本文的多源储能的调频优化控制方法能够充分利用转子动能,合理地调节系统惯量,提升受端系统的调频能力。
参考文献
[1] 习近平. 在第七十五届联合国大会一般性辩论上的讲话[N]. 人民日报, 2020-09-23(003).
[2] Ratnam K S, Palanisamy K, Yang Guangya. Future low-inertia power systems: requirements, issues, and solutions-a review[J]. Renewable and Sustainable Energy Reviews, 2020, 124: 109773.
[3] 李帅虎, 向丽珍, 向振宇, 等. 用于改善VSG频率响应的模型预测控制方法[J]. 高电压技术, 2021, 47(8): 2856-2864. Li Shuaihu, Xiang Lizhen, Xiang Zhenyu, et al. MPC control method for improving VSG frequency response[J]. High Voltage Engineering, 2021, 47(8): 2856-2864.
[4] 李忠文, 吴龙, 程志平, 等. 光储系统参与微电网频率调节的模糊自适应滑模控制[J]. 高电压技术, 2022, 48(6): 2065-2076. Li Zhongwen, Wu Long, Cheng Zhiping, et al. Fuzzy adaptive sliding mode control of photovoltaic and storage systems for providing frequency regulation of microgrid[J]. High Voltage Engineering, 2022, 48(6): 2065-2076.
[5] 滕云, 孙鹏, 张明理, 等. 基于农村新型产业结构的“能源-环境-经济”鲁棒优化模型[J]. 中国电机工程学报, 2022, 42(2): 614-631. Teng Yun, Sun Peng, Zhang Mingli, et al. Robust optimization model of “energy-environment-economy” based on the new rural industrial structure[J]. Proceedings of the CSEE, 2022, 42(2): 614-631.
[6] 娄源媛, 蒋若蒙, 钱峰, 等. 考虑负荷特性的解列后受端电网频率控制策略[J]. 电网技术, 2019, 43(1): 213-220. Lou Yuanyuan, Jiang Ruomeng, Qian Feng, et al. Frequency control strategy after receiving-end power grid splitting considering load characteristics[J]. Power System Technology, 2019, 43(1): 213-220.
[7] 黎静华, 骆怡辰, 杨舒惠, 等. 可再生能源电力不确定性预测方法综述[J]. 高电压技术, 2021, 47(4): 1144-1157. Li Jinghua, Luo Yichen, Yang Shuhui, et al. Review of uncertainty forecasting methods for renewable energy power[J]. High Voltage Engineering, 2021, 47(4): 1144-1157.
[8] 文云峰, 杨伟峰, 林晓煌. 低惯量电力系统频率稳定分析与控制研究综述及展望[J]. 电力自动化设备, 2020, 40(9): 211-222. Wen Yunfeng, Yang Weifeng, Lin Xiaohuang. Review and prospect of frequency stability analysis and control of low-inertia power systems[J]. Electric Power Automation Equipment, 2020, 40(9): 211-222.
[9] Syed M H, Guillo-Sansano E, Mehrizi-Sani A, et al. Load frequency control in variable inertia systems[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4904-4907.
[10] 邢鹏翔, 付立军, 王刚, 等. 改善微电网频率动态响应的虚拟同步发电机强化惯量控制方法[J]. 高电压技术, 2018, 44(7): 2346-2353. Xing Pengxiang, Fu Lijun, Wang Gang, et al. Control strategy of virtual synchronous generator with enhanced inertia for improving dynamic frequency response of microgrid[J]. High Voltage Engineering, 2018, 44(7): 2346-2353.
[11] Sun Peng, Teng Yun, Chen Zhe. Robust coordinated optimization for multi-energy systems based on multiple thermal inertia numerical simulation and uncertainty analysis[J]. Applied Energy, 2021, 296: 116982.
[12] 金红洋, 滕云, 冷欧阳, 等. 基于源荷不确定性状态感知的无废城市多能源协调储能模型[J]. 电工技术学报, 2020, 35(13): 2830-2842. Jin Hongyang, Teng Yun, Leng Ouyang, et al. Multi-energy coordinated energy storage model in zero-waste cities based on situation awareness of source and load uncertainty[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2830-2842.
[13] 李东东, 张佳乐, 徐波, 等. 考虑频率分布特性的新能源电力系统等效惯量评估[J]. 电网技术, 2020, 44(8): 2913-2921. Li Dongdong, Zhang Jiale, Xu Bo, et al. Equivalent inertia assessment in renewable power system considering frequency distribution properties[J]. Power System Technology, 2020, 44(8): 2913-2921.
[14] 滕云, 吴磊, 冷欧阳, 等. 考虑垃圾处理与多源储能协调的多能源微网优化运行模型[J]. 电工技术学报, 2020, 35(19): 4120-4130. Teng Yun, Wu Lei, Leng Ouyang, et al. Multi-energy microgrid optimization operation model considering waste disposal and multi-source coordinated energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4120-4130.
[15] 王晶晶, 廖思阳, 姚良忠, 等. 基于一致性算法的直流受端电网分布式调频资源协同频率控制[J]. 电网技术, 2022, 46(3): 888-900. Wang Jingjing, Liao Siyang, Yao Liangzhong, et al. Coordinated frequency control strategy for DC receiving-end power grid with distributed frequency regulation resources using consensus algorithm[J]. Power System Technology, 2022, 46(3): 888-900.
[16] 边晓燕, 张菁娴, 丁炀, 等. 基于DFIG虚拟惯量的微电网双维自适应动态频率优化控制[J]. 高电压技术, 2020, 46(5): 1476-1485. Bian Xiaoyan, Zhang Jingxian, Ding Yang, et al. Double layer adaptive dynamic frequency optimization control of microgrid based on DFIG virtual inertia[J]. High Voltage Engineering, 2020, 46(5): 1476-1485.
[17] 孙玉树, 杨敏, 师长立, 等. 储能的应用现状和发展趋势分析[J]. 高电压技术, 2020, 46(1): 80-89. Sun Yushu, Yang Min, Shi Changli, et al. Analysis of application status and development trend of energy storage[J]. High Voltage Engineering, 2020, 46(1): 80-89.
[18] 张祥宇, 朱正振, 付媛. 风电并网系统的虚拟同步稳定分析与惯量优化控制[J]. 高电压技术, 2020, 46(8): 2922-2932. Zhang Xiangyu, Zhu Zhengzhen, Fu Yuan. Virtual synchronous stability analysis and optimized inertia control for wind power grid-connected system[J]. High Voltage Engineering, 2020, 46(8): 2922-2932.
[19] 颜湘武, 王德胜, 杨琳琳, 等. 直驱风机惯量支撑与一次调频协调控制策略[J]. 电工技术学报, 2021, 36(15): 3282-3292. Yan Xiangwu, Wang Desheng, Yang Linlin, et al. Coordinated control strategy of inertia support and primary frequency regulation of PMSG[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3282-3292.
[20] 赵冬梅, 王闯, 谢家康, 等. 考虑惯量中心频率偏移的自编码器暂态稳定评估[J]. 电网技术, 2022, 46(2): 662-670. Zhao Dongmei, Wang Chuang, Xie Jiakang, et al. Transient stability assessment of auto encoder considering frequency shift of inertia center[J]. Power System Technology, 2022, 46(2): 662-670.
[21] 赵晋泉, 汤建军, 吴迪, 等. 直流馈入受端电网暂态电压与频率稳定紧急协调控制策略[J]. 电力系统自动化, 2020, 44(22): 45-53. Zhao Jinquan, Tang Jianjun, Wu Di, et al. Emergency coordination control strategy for transient voltage and transient frequency stability in HVDC infeed receiving-end power grid[J]. Automation of Electric Power Systems, 2020, 44(22): 45-53.
[22] 孙鹏, 滕云, 回茜, 等. 考虑异质能流输运特性的多能源系统惯量极限优化[J]. 中国电机工程学报, 2022, 42(10): 3642-3656. Sun Peng, Teng Yun, Hui Qian, et al. Inertia limit optimization of multi-energy system considering the transport characteristics of heterogeneous energy flow[J]. Proceedings of the CSEE, 2022, 42(10): 3642-3656.
[23] 李少林, 王伟胜, 张兴, 等. 基于频率响应区间划分的风电机组虚拟惯量模糊自适应控制[J]. 电网技术, 2021, 45(5): 1658-1665. Li Shaolin, Wang Weisheng, Zhang Xing, et al. Fuzzy adaptive virtual inertia control strategy of wind turbines based on system frequency response interval division[J]. Power System Technology, 2021, 45(5): 1658-1665.
[24] 王博, 杨德友, 蔡国伟. 大规模风电并网条件下考虑动态频率约束的机组组合[J]. 电网技术, 2020, 44(7): 2513-2519. Wang Bo, Yang Deyou, Cai Guowei. Dynamic frequency constraint unit commitment in large-scale WindPower grid connection[J]. Power System Technology, 2020, 44(7): 2513-2519.
[25] 周雷, 田蓓, 卓谷颖, 等. 考虑多能互补的多区域交直流系统频率稳定联合控制模型[J]. 可再生能源, 2021, 39(5): 681-686. Zhou Lei, Tian Bei, Zhuo Guying, et al. Multi-zone AC/DC system frequency stability joint control model considering multi-energy complementation[J]. Renewable Energy Resources, 2021, 39(5): 681-686.
[26] 林恒先, 侯凯元, 陈磊, 等. 高比例风电电力系统考虑频率安全约束的机组组合[J]. 电网技术, 2021, 45(1): 1-13. Lin Hengxian, Hou Kaiyuan, Chen Lei, et al. Unit commitment of power system with high proportion of wind power considering frequency safety constraints[J]. Power System Technology, 2021, 45(1): 1-13.
[27] Cheng Xueyang, Lee W J, Sahni M, et al. Dynamic equivalent model development to improve the operation efficiency of wind farm[J]. IEEE Transactions on Industry Applications, 2016, 52(4): 2759-2767.
[28] 胡石阳, 刘国荣. 基于虚拟同步机的新能源并网智能控制研究[J]. 电气技术, 2022, 23(10): 10-17. Hu Shiyang, Liu Guorong. Research on intelligent control of grid connected new energy based on virtual synchronous machine[J]. Electrical Engineering, 2022, 23(10): 10-17.
Abstract In view of the problem that the equivalent inertia and frequency modulation capability of the receiving power grid are constantly reduced due to large-scale renewable energy access, and the frequency stability of the receiving power grid is seriously affected, this paper proposes an optimal control method for frequency stability of the receiving power grid considering energy storage support. Firstly, the frequency response characteristics of multi-source energy storage in the receiving power grid are analyzed. Secondly, the relationship between multi-energy energy coordination and frequency change based on multi-source energy storage is analyzed, a frequency support characteristic model considering multi-energy energy storage sup-port is established, and the equivalent model of the frequency response of the receiving-end power grid based on multi-energy coordination is modified. Then, the frequency change speed index and frequency drop index of the receiving power grid are established as the frequency stability index, and an optimal control method for frequency stability of the receiving-end power grid based on multi-source energy storage support is proposed. Finally, a simulation model is established by taking an actual receiving-end power grid as an example. The results of the example verify the validity of the model in this paper. Based on the multi-energy energy storage support, the frequency stability performance of the receiving-end power grid can be improved.
The innovations of this paper are as follows:
(1) In this paper, the response characteristics of multi-source energy storage equipment to frequency through virtual inertia control are analyzed, and the frequency control model of multi-source energy storage inertia support is established.
(2) The internal response considers the response of the prime mover and the governor when the active power adjustment is considered, and the external response is equivalent using the parameter identification method. On this basis, a frequency response model of receiving-end power grid considering multi-source energy storage support is established.
(3) Taking the frequency change speed index and frequency drop index of the receiving-end power grid as the frequency stability index, the frequency stability optimization control method of the receiving-end power grid based on multi-source energy storage support is proposed. An improved quantum particle swarm optimization algorithm is proposed to solve the frequency stability control of the receiving-end power grid. Finally, the simulation model is established by taking the actual receiving-end power grid in East China as an example. The results of the example verify the effectiveness of the model in this paper.
The following conclusions can be drawn from the simulation analysis: (1) The characteristics of multi-energy storage in the receiving-end power grid are analyzed, and the frequency control response models of electric vehicles, P2H, P2G equipment and electric vehicles are analyzed. (2) The support characteristics of the system based on multi-energy energy coordination and multi-source energy storage are analyzed. The frequency response model of the receiving-end power grid considering multi-source energy storage is proposed, and the frequency stability optimization control model of multi-source energy storage is established. (3) A frequency stability index is established, which is composed of the frequency change speed index and the frequency drop index of the receiving power grid, and the virtual inertia control of multi-source energy storage is used for frequency regulation. The simulation results show that the model can effectively improve the frequency characteristics of the receiving end power grid, and the proposed frequency response model has high accuracy. (4) The frequency modulation optimization control method based on multi-source energy storage in this paper can make full use of the rotor kinetic energy, reasonably adjust the system inertia, and improve the frequency modulation ability of the receiving end system.
keywords:Energy storage, receiving end grid, frequency stability, optimal control
DOI: 10.19595/j.cnki.1000-6753.tces.230466
中图分类号:TM614
国家电网公司科技项目资助(SGHD0000DKJS2200172)。
收稿日期 2023-04-08
改稿日期 2023-05-24
张怡静 女,1983年生,高级工程师,研究方向电力系统稳定与控制。E-mail:supeng1024@163.com(通信作者)
李 智 女,1994年生,中级工程师,研究方向为风电功率模型预测控制研究及电力系统稳定运行等。E-mail:lizhi_0801@163.com
(编辑 赫 蕾)