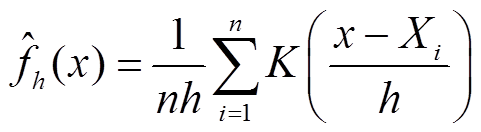 (1)
(1)
摘要 5G的快速发展使得5G基站储能容量大幅增加,如何充分发挥时常处于休眠状态的基站储能资源,使其参与配电网供电恢复,降低配电网失电量问题亟待研究。该文通过协调基站储能参与配电网供电恢复,以发挥其储能价值。首先,建立风光联合出力场景集,通过赤池信息准则和平方欧式距离确定各时段最优Copula函数,进而对其进行抽样聚类,获得风光典型出力场景集;然后,建立基站备用储能模型,通过正弦函数叠加建立不同区域的通信量模型,利用泰尔熵和修正基尼系数建立综合脆弱度模型确定各基站储能备用时间及备用储能模型,进而获得不同基站储能的可调度容量;最后,以失负荷量损失最小为目标,建立考虑基站储能参与及风光出力波动的含可调参数的两阶段鲁棒优化模型。以改进的IEEE 33节点模型为例进行仿真验证,分别对比了定基站备用时间与该文所提方法确定备用时间、鲁棒优化与确定性优化等方案下系统失负荷量的变化情况。仿真结果表明,5G基站储能可降低失负荷量损失成本,提高风光消纳率。
关键词:5G基站 备用储能 供电恢复 修正基尼系数
自2019年我国正式迈出5G商用第一步,截至2022年底,我国已累计建设5G基站231万个。同时,工信部发布《关于推动5G加快发展通知》,对于我国加快5G、工业物联网等新型信息基础设施建设与应用具有进一步的推动作用[1]。5G频率特性使其相较于4G通信,基站功耗增加了3~4倍,因此增加了5G基站对于基站储能容量的需求,据工信部预计,截至2023年,我国5G基站储能需求将会达到31.8 GW·h[2]。由于电网供电可靠性的提升,基站储能一般都处于休眠闲置状态(长期备电模式)[3-4],从而造成大量储能资源的浪费,资产利用率较低[5-6]。因此调动这些储能资源发挥其价值,将有利于减少基站储能资源浪费和提高其经济性。2022年12月在深圳市虚拟电厂聚合商签约仪式上,深圳供电局预估2023年有望深圳全市5G基站储能将接入虚拟电厂,推动了基站储能与电网之间的协调交互[7];国内部分铁塔公司通过定时关闭某一部分5G基站以降低基站能耗,在此时间段内基站的储能资源完全可用[8]。文献[2]指出,5G基站储能的自主调控、控制灵活等特性使得其调控策略有别于传统储能。相比于传统配电网储能初始投资成本昂贵,基站储能可通过与相关通信运营商合作,协调调度储能资源以最大化其经济价值。文献[9]提到5G基站储能在保证自身供电可靠性的同时,具有在相关变电站供区范围内发生故障后参与同一馈线上的其他电力负荷供电的可行性。而且5G基站的密集性与分散性,使得基站储能与电力用户之间距离密切。当用户负荷失电后,便可快速控制相关基站储能参与失电负荷供电。因此本文考虑将基站储能作为一种可调资源用于配电网供电恢复。
对配电网失电负荷应急供电可调资源的研究,相关学者做了许多工作:文献[10]考虑电网中电动汽车数量大幅增加,将电动汽车作为一种辅助电源,用于配合应急供电车对失电负荷进行快速供电;文献[11]通过调控储能和可控负荷,针对短时供电中断事件,对失电负荷进行应急供电;文献[12]协调包括独立燃料发电机、应急电源、储能等资源,在配电网发生供电中断后,对失电区域进行应急供电。以上可调资源在电网恢复供电中的研究已经颇为成熟,但对于5G基站储能参与电网供电恢复鲜有研究。
现有针对5G基站储能的研究多体现在基站储能参与电网需求响应和光伏消纳方面:文献[13]分析了5G基站的设备组成与通信特性,结合5G基站的功耗变化特性,给出了基站储能的动态划分思路,以及基站储能的可调用容量确定方式;文献[14]通过协调移动用户通信接入,动态调整各基站的功耗,进而改变基站的可调用容量,从而将这部分调用容量用来参与电网需求响应当中;文献[15]将5G基站储能纳入虚拟电厂优化调度中,用于参与电网调度、风光消纳等;文献[9]通过调控各个基站的工作状态,进而控制不同基站储能的动态划分,以利用基站冗余储能参与电网负荷的削峰填谷;文献[16]通过研究基站储能租赁定价,深入研究基站储能参与电网需求响应的租赁收益;文献[17]分析5G基站的负载特性与屋顶光伏发电特性,建立计及通信负载迁移的基站储能动态备电模型,进而确定基站储能与光伏协调运行的调度模型,实现光伏消纳,降低基站储能运行成本。
从以上对于5G基站储能参与电网调度的研究可以看出,5G基站储能的利用具有一定前景。对于配电网失电负荷供电,仅通过5G基站储能难以支撑,需协同配电网中的分布式电源进行应急供电,但分布式电源存在波动性、间歇性等特点[18-19],因此在进行协同供电恢复当中需考虑对分布式电源出力波动性的处理。已有研究针对波动性的处理方法,可分为随机优化和鲁棒优化。其中随机优化需要确定随机因素的概率分布,鲁棒优化无需确定随机参数的概率分布;随机优化存在得到的方案可能难以适应极端波动场景的问题,鲁棒优化通过寻找最恶劣场景,使其优化出的方案完全满足约束条件,因此已有研究多使用鲁棒优化对波动性进行描述求解[20]。文献[21]利用点估计仿射处理风电不确定性,进而利用鲁棒优化将不确定问题转换为确定性问题求解;文献[22]针对风电的随机波动性,通过对发电计划与风电出力差进行小波分解,确定各频段波动的置信区间,进而建立两阶段鲁棒优化模型。
根据以上分析,本文提出了一种考虑5G基站储能参与配电网供电恢复的两阶段鲁棒优化调度模型。首先对于配电网内电源——光伏和风电构建相应的出力集:根据历史数据,利用非参数核密度估计与Copula函数,结合赤池信息准则(Akaike Information Criterion, AIC)和平方欧式距离,确定各个时段的最优Copula函数,对各时段风出力进行拟合,并进行抽样聚类,以获得风光典型出力集;其次结合基站通信量模型,利用泰尔熵和修正基尼系数,建立5G基站储能的备用容量模型,进而确定基站储能的可调度容量;再次建立计及5G基站储能的配电网应急供电调度模型,并利用含可调参数的两阶段鲁棒优化模型进行优化求解;最后通过算例仿真,验证了5G基站储能参与微电网供电恢复的可行性,提升了5G基站资源的利用率。
对于风光出力的建模,已有研究包括利用概率分布模型进行相关出力拟合,如威布尔分布和beta分布来分别拟合风速和太阳辐射强度,进而获得风光出力场景;结合历史数据,可通过非参数核密度估计进行拟合,以获得风光出力的概率分布函数,并构建联合Copula函数对其进行抽样以获得相关出力场景[23]。本文利用后者进行风-光联合出力联合建模,并通过抽样聚类方式,对获得的风-光联合出力场景进行缩减以获得风-光典型出力场景,作为后续5G基站储能参与供电恢复中光伏和风电的出力预测结果。
非参数核密度估计定义为
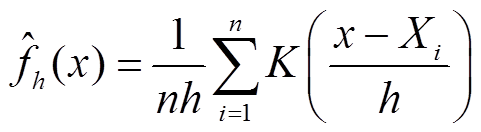 (1)
(1)
式中,K(·)为核函数;h为窗宽;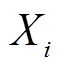 为第i个样本点的数值;n为样本总数。本文采用Gaussian函数作为核密度估计的核函数。
为第i个样本点的数值;n为样本总数。本文采用Gaussian函数作为核密度估计的核函数。
Copula函数主要用于描述变量之间的相关性,其联合分布函数和联合密度函数分别为
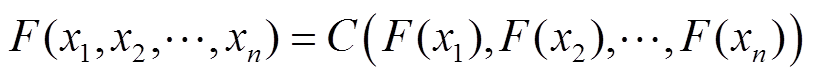 (2)
(2)
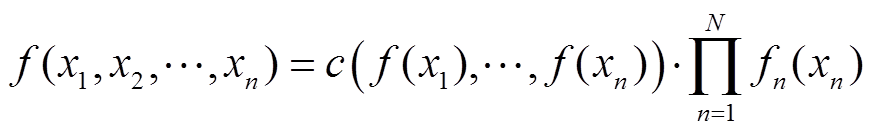 (3)
(3)
式中,F(xn)和f(xn)分别为输入变量的边缘分布函数和密度函数。
不同的Copula函数反映了变量之间不同的相关性[24]。对于不同Copula函数拟合效果的检验,多采用赤池信息准则、贝叶斯信息准则等指标进行Copula函数的拟合效果检验。本文采用AIC和平方欧式距离评判拟合效果,以选择各时段最优的Copula函数。
AIC和平方欧式距离分别为
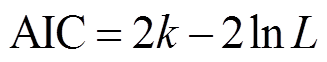 (4)
(4)
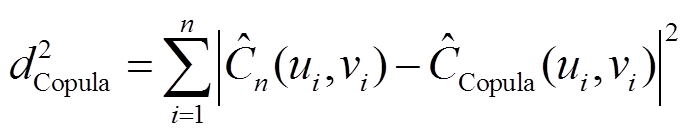 (5)
(5)
式中,k为模型参数的个数;L为极大似然估计结果;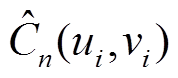 为经验Copula函数;
为经验Copula函数;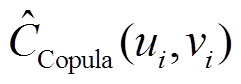 为常见Copula函数;
为常见Copula函数;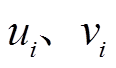 为两个随机变量的边缘累计分布函数。
为两个随机变量的边缘累计分布函数。
通过AIC和平方欧式距离得到各时段的最优Copula函数后,对其进行抽样获得原始风光联合出力集;利用K-means对原始风光联合出力集进行聚类以达到场景缩减的目的,最终得到风光联合典型出力结果。
基站功耗主要取决于基站所承载的通信业务量,而基站业务通信量取决于基站所在位置覆盖范围内用户数量和通信行为特征,其中用户的日常行为特征决定了基站通信量在空间和时间上存在差异性。文献[2]分析了24 h内,基站通信量的时空差异:基站通信量时刻处于一种波动状态,同电网负荷一样存在通信高峰和低谷;以居民区和办公区为例,工作时段办公区通信量高于居民区,非工作时段居民区高于办公区,呈现一种“潮汐效应”状态。
对于基站通信量的建模,大致可以分为利用历史数据进行拟合抽样和利用数学曲线进行叠加模拟;文献[25]通过正弦函数叠加方式,生成一天中业务流量的时域变化模型。由于具体区域通信量变化数据较难获取,本文采用后者方式建立不同区域的通信量模型,其正弦函数叠加表达式为
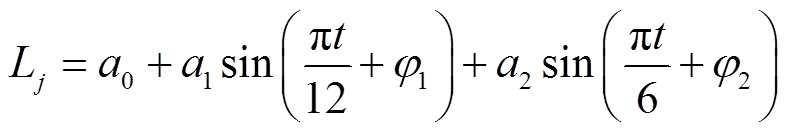 (6)
(6)
式中,Lj为基站j生成的通信量结果,通过改变式中的系数,模拟生成不同区域下的通信量时域变化结果;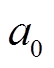 、
、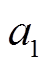 和
和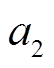 为正弦叠加函数的常系数;
为正弦叠加函数的常系数;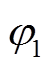 和
和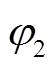 为正弦叠加函数的初相角。
为正弦叠加函数的初相角。
通信基站储能区别于传统储能,往往需要留有一定的备用储能,而5G基站备用储能容量主要取决于基站功耗。因此在对基站备用储能进行建模时,需要确定通信基站的功耗构成。
1.3.1 基站功耗组成
对于5G通信基站,其状态可以分为工作状态和休眠状态,不同状态下对应的设备功耗为
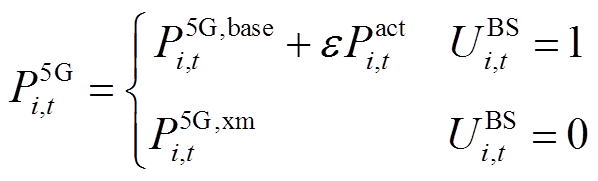 (7)
(7)
式中,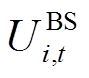 为基站状态,1为工作,0为休眠;
为基站状态,1为工作,0为休眠;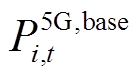 为工作状态下的固定功耗,大小取决于基站设备本身;
为工作状态下的固定功耗,大小取决于基站设备本身;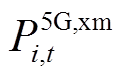 为基站处于休眠状态下的功耗;
为基站处于休眠状态下的功耗;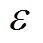 为基站动态功耗的权重;
为基站动态功耗的权重;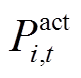 为基站动态功耗,主要取决于基站通信量,其计算式为[17]
为基站动态功耗,主要取决于基站通信量,其计算式为[17]
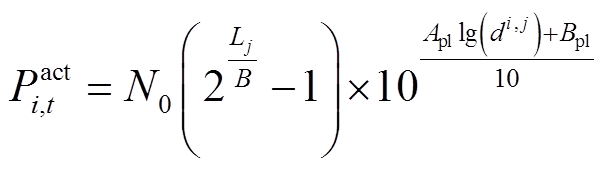 (8)
(8)
式中,N0为噪声功率,是一定值;B为信道带宽;di,j为用户j和基站i之间的距离;Apl和Bpl为信道衰落系数。因此,基站的动态功耗主要取决于用户与基站之间的距离di,j及用户的通信量Lj。
1.3.2 5G基站备用储能确定
由于基站储能要留有一定容量支撑其在市电断供后对基站进行应急供电,因此可将基站储能分为备用储能和可调用储能[26]。其中可调用储能的大小取决于备用储能的大小,因此,通过对备用储能进行研究,进而确定基站可调用储能容量,最终实现基站储能参与微电网应急供电调控。
相比于传统储能装置之间出力范围固定的特点,通信基站因其决定备用储能大小的因素具有动态特性,使得其备用储能大小在空间上存在差异,这就决定了其可调用储能也在空间上存在差异。因此确定影响基站备用储能大小的因素,就可以准确地描述不同区域内基站的可调用储能,进而提高基站储能的利用率和经济性。
针对不同区域内基站备用储能的确定,本文主要考虑基站所在的电网节点供电可靠性(电网节点可靠度)、电网节点负荷等级和通信负载量三个因素。其中负荷等级、供电可靠性可视作负指标,即数值越大,基站备用储能越小;通信负载量可视作正指标,即数值越大,基站备用储能越大。
基站备用容量 为
为
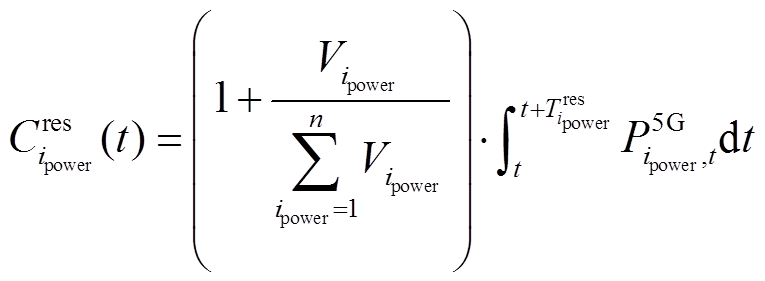 (9)
(9)
式中,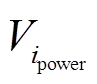 为电网节点
为电网节点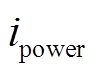 处的综合节点可靠度;
处的综合节点可靠度;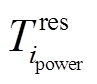 为基站储能备用时间;
为基站储能备用时间;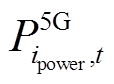 为t时刻由电网节点
为t时刻由电网节点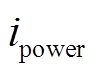 供电的基站的功耗;设基站最大备用时间为T0res。由于基站备用储能时间受配电网可靠性等因素影响,因此引入节点综合脆弱度和负荷等级来改变不同节点处的基站备用储能时间,其中电网节点可靠度越高,基站备用储能时间越长;负荷等级越高,其供电可靠性也越高,对应的基站备用储能时间就可以减少。即基站备用储能时间与电网节点可靠度之间成正比关系,与节点负荷等级成反比关系。建立不同电网节点处的基站备用时间
供电的基站的功耗;设基站最大备用时间为T0res。由于基站备用储能时间受配电网可靠性等因素影响,因此引入节点综合脆弱度和负荷等级来改变不同节点处的基站备用储能时间,其中电网节点可靠度越高,基站备用储能时间越长;负荷等级越高,其供电可靠性也越高,对应的基站备用储能时间就可以减少。即基站备用储能时间与电网节点可靠度之间成正比关系,与节点负荷等级成反比关系。建立不同电网节点处的基站备用时间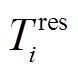 为
为
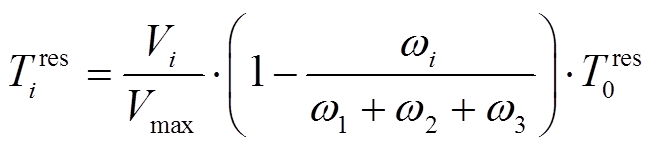 (10)
(10)
式中,ωi为节点i处的负荷等级,共分为3个等级;Vmax为最大电网节点可靠度。为保证求解出的基站备用时间大于等于最小备用时间T0,对基站备用时间Tires进行修正,得到修正后的基站备用时间为
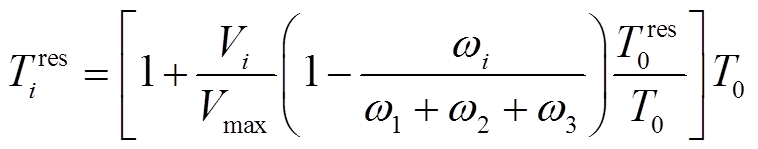 (11)
(11)
对于电网节点i处的综合可靠Vi的求解,本文从系统状态和系统拓扑两个方面进行描述计算。其中系统状态可靠度通过电压泰尔熵进行计算,系统拓扑可靠度通过基尼系数进行求解。
电压泰尔熵反映了电网节点负荷变化对于整个电网状态的影响[27],其计算方法如式(12)~式(16)。
利用电压变化量和电压裕度之间的比值yij表征电压的越限概率,其计算式为
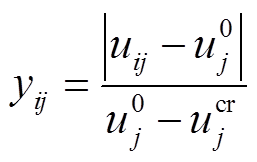 (12)
(12)
式中,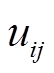 为节点i发生单位功率变化后,节点j处的电压值;
为节点i发生单位功率变化后,节点j处的电压值;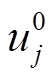 为节点j处的原始电压结果;
为节点j处的原始电压结果;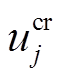 为节点j的临界电压值。则拓扑内的节点电压泰尔熵
为节点j的临界电压值。则拓扑内的节点电压泰尔熵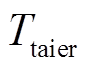 为
为
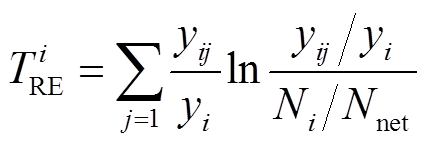 (13)
(13)
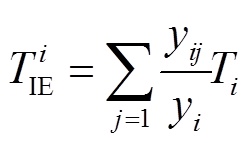 (14)
(14)
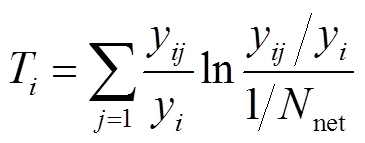 (15)
(15)
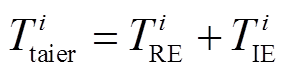 (16)
(16)
式中,Nnet为拓扑内总的节点数;Ni为电压等级i内的节点数;yi为节点i发生单位功率变化对于拓扑内其余所有节点造成的电压变化影响之和,有
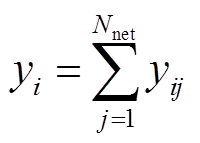 (17)
(17)
因此,通过改变每一个节点的功率变化,由式(16)便可计算出每一个电网节点的节点电压泰尔熵。
传统基尼系数在反映电网拓扑的均衡程度时,其结果往往会受电网本身负荷的影响。文献[28]针对传统基尼系数的不足,通过引入加权平均节点度对基尼系数进行修正,但是其修正后的结果反映的是电网整体结构的脆弱度,难以反映各个节点对于整体的影响程度。因此,本文在文献[28]的基础上,引入影响率指标,进一步修正基尼系数以更好地量化电网局部对于整体的影响程度。
加权平均节点度ρn为
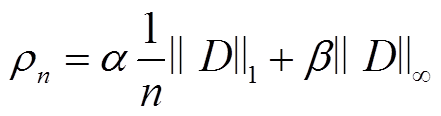 (18)
(18)
式中,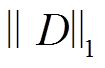 和
和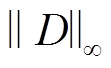 分别为电网节点度数集合D的1范数和无穷范数;α和β分别为电网节点度数集合1范数和无穷范数的权重,并满足α+β=1的关系。
分别为电网节点度数集合D的1范数和无穷范数;α和β分别为电网节点度数集合1范数和无穷范数的权重,并满足α+β=1的关系。
影响率Ri为
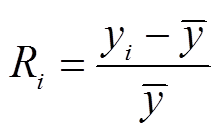 (19)
(19)
式中,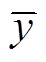 为节点度数或节点介数的均值。
为节点度数或节点介数的均值。
利用式(18)和式(19)对基尼系数进行修正,得到修正后的基尼系数为
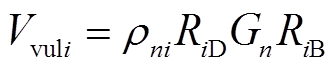 (20)
(20)
式中,Gn为原始基尼系数结果;RiD和RiB分别为电网节点度数和电网节点介数的影响率指标。
根据节点电压泰尔熵和修正后的基尼系数,建立综合可靠度指标Vi为
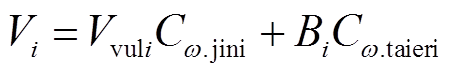 (21)
(21)
式中,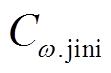 为修正基尼系数的权重;Bi为电网节点i处的节点电压泰尔熵结果;
为修正基尼系数的权重;Bi为电网节点i处的节点电压泰尔熵结果;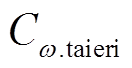 为泰尔熵的权重,其计算式如式(22)~式(24)所示。
为泰尔熵的权重,其计算式如式(22)~式(24)所示。
设修正后的基尼系数和泰尔熵的重要系数分别为μi和λi,有
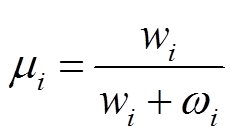 (22)
(22)
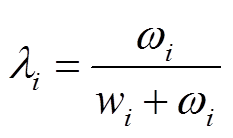 (23)
(23)
式中,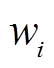 和
和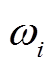 分别为节点i的修正基尼系数和泰尔熵结果,根据两者的重要系数计算修正基尼系数和泰尔熵的权重,有
分别为节点i的修正基尼系数和泰尔熵结果,根据两者的重要系数计算修正基尼系数和泰尔熵的权重,有
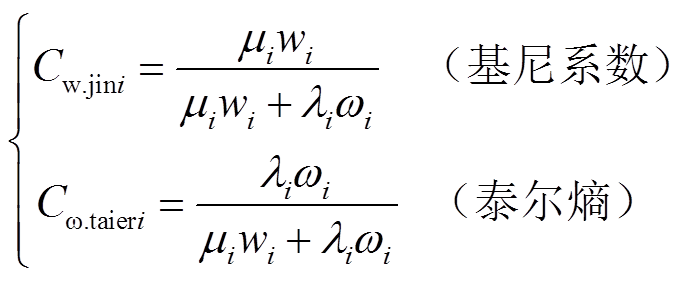 (24)
(24)
对于从市电失去供电,仅依靠分布式电源5G基站储能供电的系统,建立以运行成本最小化的目标函数为
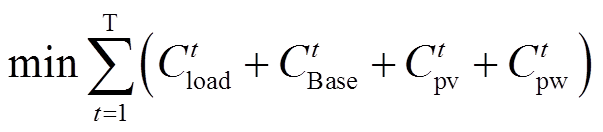 (25)
(25)
式中,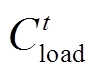 为系统失负荷量损失成本;
为系统失负荷量损失成本;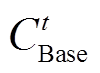 为5G基站储能充放电成本;
为5G基站储能充放电成本;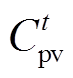 和
和 分别为光伏和风电成本。其计算方式及相关约束如下。
分别为光伏和风电成本。其计算方式及相关约束如下。
1)失负荷量损失成本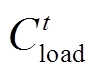
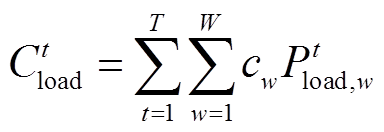 (26)
(26)
式中,T为系统运行时长;W为相应负荷等级,本文取3;cw为不同负荷等级下的失负荷量的单位成本;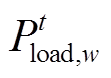 为时段t内负荷等级为w的失负荷量。
为时段t内负荷等级为w的失负荷量。
2)基站储能充放电成本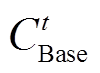
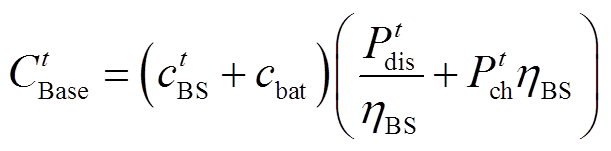 (27)
(27)
式中,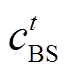 为基站储能单位充放电成本;cbat为基站储能充放电损耗成本;
为基站储能单位充放电成本;cbat为基站储能充放电损耗成本;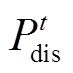 和
和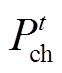 分别为t时刻基站储能的放电功率和充电功率;
分别为t时刻基站储能的放电功率和充电功率;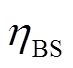 为基站储能充放电效率。
为基站储能充放电效率。
3)风光出力成本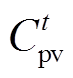 、
、
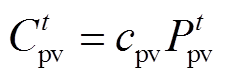 (28)
(28)
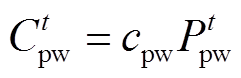 (29)
(29)
式中,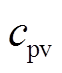 、
、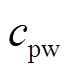 分别为光伏和风电的单位发电成本系数;
分别为光伏和风电的单位发电成本系数;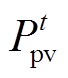 、
、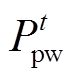 分别为t时刻光伏和风电出力。
分别为t时刻光伏和风电出力。
4)相关约束条件
基站储能充放电约束为
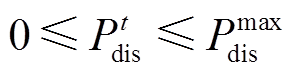 (30)
(30)
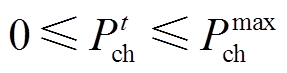 (31)
(31)
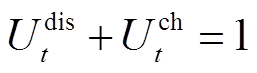 (32)
(32)
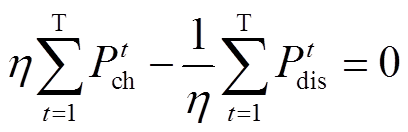 (33)
(33)
 (34)
(34)
式中,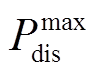 和
和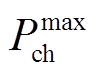 分别为基站储能最大允许放、充电功率。式(32)表示t时刻基站充放电状态唯一,其中
分别为基站储能最大允许放、充电功率。式(32)表示t时刻基站充放电状态唯一,其中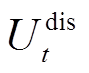 和
和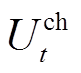 分别为t时刻基站储能运行状态(0-1变量),1表示其处于放电或充电状态;式(33)表示储能在T时间段内储能始末状态不变;式(34)表示t时刻储能的容量约束,其中
分别为t时刻基站储能运行状态(0-1变量),1表示其处于放电或充电状态;式(33)表示储能在T时间段内储能始末状态不变;式(34)表示t时刻储能的容量约束,其中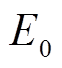 为基站储能初始容量,
为基站储能初始容量,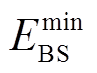 为最小基站储能容量,可通过基站备用储能进行确定;
为最小基站储能容量,可通过基站备用储能进行确定;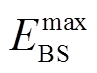 为基站储能容量上限。
为基站储能容量上限。
光伏和风力发电出力约束为
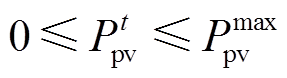 (35)
(35)
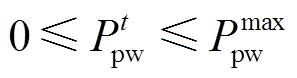 (36)
(36)
式中, 和
和 分别为光伏和风电的最大出力。
分别为光伏和风电的最大出力。
功率平衡约束为
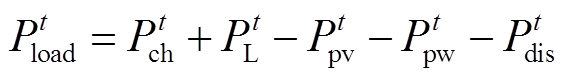 (37)
(37)
式中,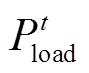 为时段t内配电网失负荷量;
为时段t内配电网失负荷量;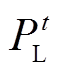 为t时刻配电网的负荷。
为t时刻配电网的负荷。
在忽略分布式电源出力的波动性情况下,式(25)为确定性模型,构建其紧凑型模型[29]为
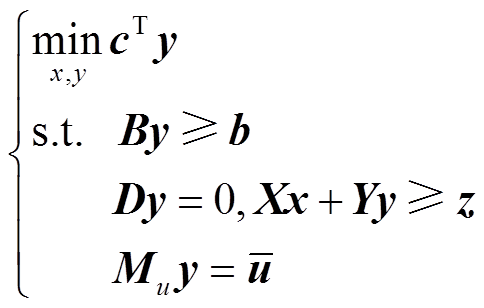 (38)
(38)
式中,c为式(25)的系数向量;B、D、X、Y、Mu分别为不等式约束、等式约束变量的系数矩阵;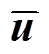 、b、z为常数列向量;x、y为优化变量,有
、b、z为常数列向量;x、y为优化变量,有
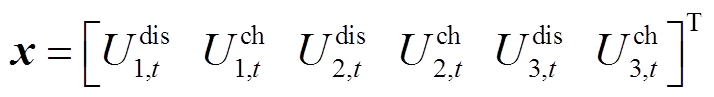 (39)
(39)
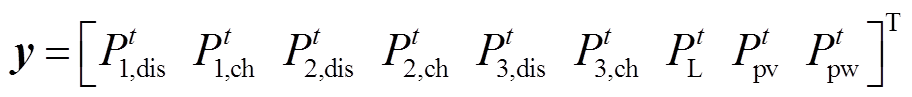 (40)
(40)
风-光-荷的不确定性采用不确定性集U进行描述,有
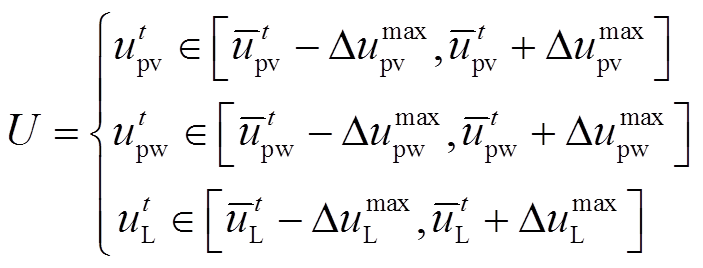 (41)
(41)
式中,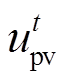 为t时段光伏的出力;
为t时段光伏的出力;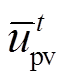 为t时段光伏的出力的预测值;
为t时段光伏的出力的预测值;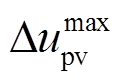 为光伏出力波动的最大值;
为光伏出力波动的最大值;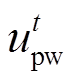 为t时段风电的出力;
为t时段风电的出力;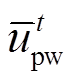 为t时段风电的出力的预测值;
为t时段风电的出力的预测值;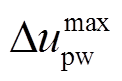 为风电出力波动的最大值;
为风电出力波动的最大值;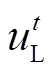 为t时段系统的负荷量;
为t时段系统的负荷量;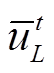 为t时段系统的负荷量的预测值,
为t时段系统的负荷量的预测值,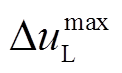 为系统的负荷量的最大值。
为系统的负荷量的最大值。
进而得到两阶段鲁棒优化模型为
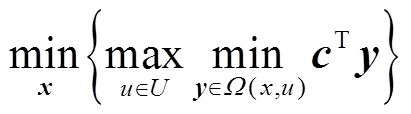 (42)
(42)
式中,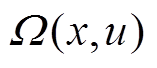 为给定一组(x,u)时优化变量y的可行域。外层最小化为第一阶段目标最小化系统运行成本,内层最大最小化为第二阶段目标用于在内层最小化成本情况下获得最恶劣运行场景。
为给定一组(x,u)时优化变量y的可行域。外层最小化为第一阶段目标最小化系统运行成本,内层最大最小化为第二阶段目标用于在内层最小化成本情况下获得最恶劣运行场景。
对于两阶段鲁棒优化模型,本文采用列与约束生成(Column-and-Constraint Generation, C&CG)算法进行求解,从而将原目标函数拆分为主目标函数和子目标函数,通过对主目标和子目标函数进行迭代交替求解,进而获得原目标函数的最优解。
采用文献[29]提出的目标函数分解方法,将式(42)分解为如式(43)和式(44)的主目标函数和子目标函数。
主目标函数为
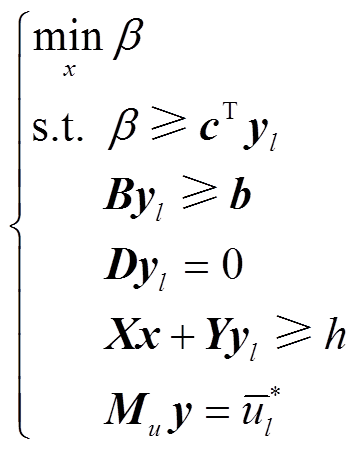 (43)
(43)
式中,yl为迭代l次后子问题的解;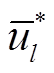 为迭代l次后的最恶劣场景下的不确定变量u的值。
为迭代l次后的最恶劣场景下的不确定变量u的值。
子目标函数为
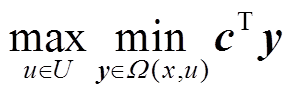 (44)
(44)
对其进行对偶处理后将最大最小问题转换为最大问题,得到转换后的子目标函数为
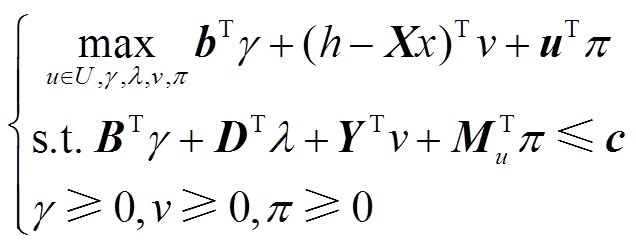 (45)
(45)
式中,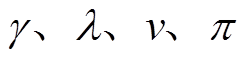 分别为原目标函数式(38)中第一行、第二行、第三行和第四行约束条件对应的对偶变量。
分别为原目标函数式(38)中第一行、第二行、第三行和第四行约束条件对应的对偶变量。
对于鲁棒优化保守性处理,文献[29]通过引入可调参数来改变传统鲁棒优化的保守性。本文对鲁棒优化的保守性出力调节采用文献[29]方法。
5G基站储能参与配电网供电求解流程如图1所示。通过Copula函数拟合抽样得到原始风光出力集合,利用K-means算法进行场景缩减;通过可调参数得到风-光-荷出力预测值和其出力区间;通过计算基站备用储能获得基站储能出力区间;将风-光-荷与基站储能出力区间代入主问题中进行求解,得到初始场景γ及下界LBk,并将其代入子目标函数中求解此时对应的风-光-荷储出力场景,将其纳入最恶劣场景集S中,并得到上界UBk,通过判断|UBk-LBk|/LBk与阈值r之间的关系判断算法是否收敛,若收敛便退出求解,若未收敛则继续迭代计算。
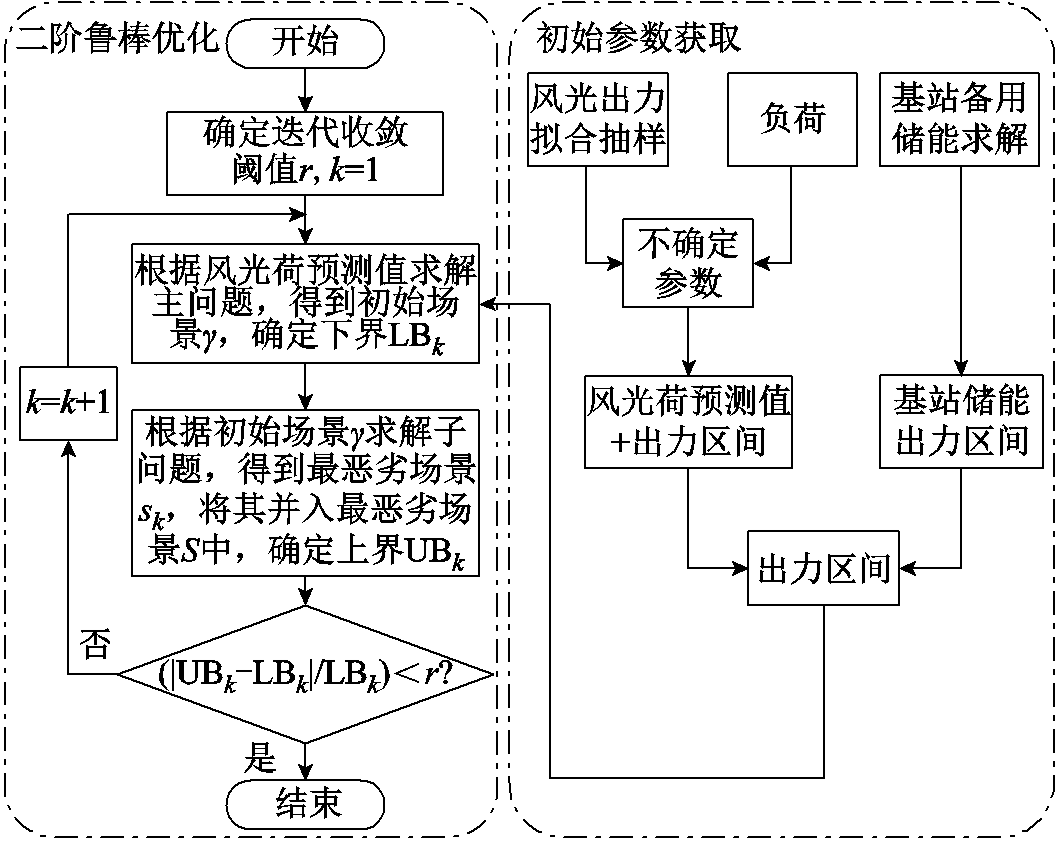
图1 基站储能参与配电网供电求解流程
Fig.1 Process of base station energy storage participation in distribution network power supply
本文采用改进后的IEEE 33节点模型为研究对象进行仿真验证,其拓扑结构如图2所示。
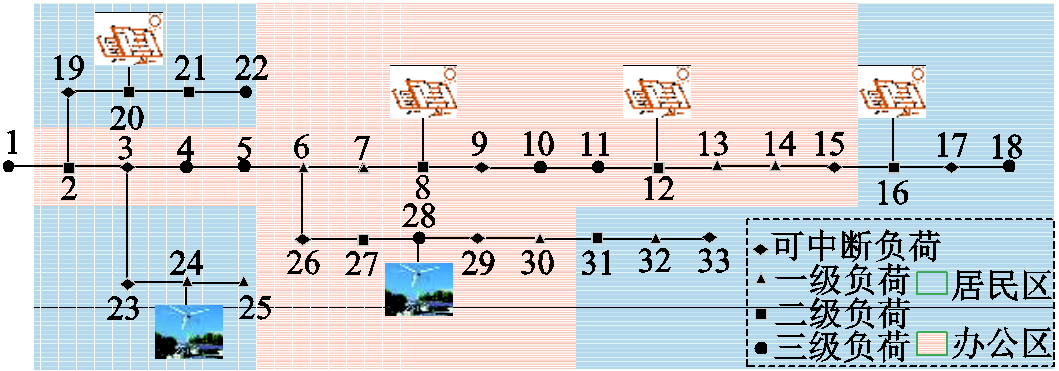
图2 改进的IEEE 33节点拓扑结构
Fig.2 Improved IEEE 33 node topology
系统基准电压为12.66 kV,在节点8、12、16、20分别接入光伏发电系统,其额定容量均为200 kW;在节点24、28分别接入风力发电系统,额定容量分别为450 kW和400 kW;将整个电网区域划分为居民区和办公区,设置一级负荷、二级负荷和三级负荷的权重分别为10、1和0.1。式(18)中,α=0.5, β=0.5。
改进的IEEE 33拓扑节点间距离见表1。
表1 各节点间距离
Tab.1 Distance between each node(单位:km)

节点距离节点距离节点距离 1~20.7812~132.3523~243.11 2~39.813~143.3424~250.92 3~411.514~150.8925~2611.23 4~59.0615~1610.9826~271.49 5~66.2816~174.4327~281.77 6~70.1517~185.6428~290.49 7~87.112~190.5329~300.41 8~93.2119~204.1830~311.11 9~106.3120~2114.6731~320.16 10~117.2121~220.5232~330.81 11~125.4122~231.77
设5G基站覆盖半径为700 m,由文献[30]方法得本文算例拓扑共有基站115个,各个节点对应的基站数量见表2。其中基站储能额定容量为20 kW·h,基站静态功耗为2.3 kW,能量效率系数为2.857 1[17],N0=10.9 W,Apl=37.6, Bpl=128.1,B=100 MHz,基站储能充放电效率为0.95,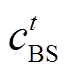 由电网分时电价决定,
由电网分时电价决定,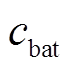 =0.14元/(kW·h),
=0.14元/(kW·h),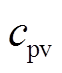 =0.715元/(kW·h),
=0.715元/(kW·h), 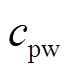 =0.56元/(kW·h)。
=0.56元/(kW·h)。
本文以ISO New England网站某月风光出力数据作为风光原始数据集,其原始出力结果如图3所示。
表2 各电网节点覆盖基站数量
Tab.2 Number of base stations at each power grid node
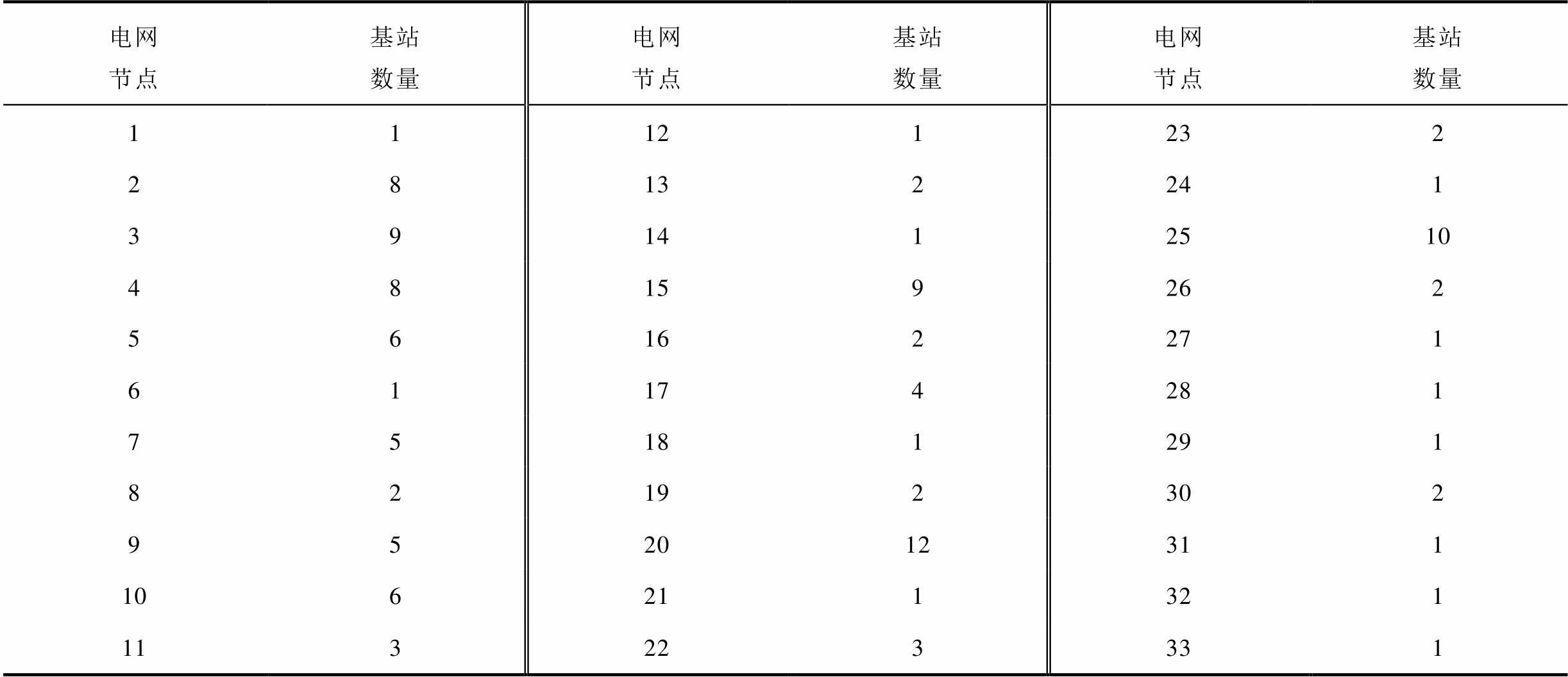
电网节点基站数量电网节点基站数量电网节点基站数量 11121232 28132241 391412510 48159262 56162271 61174281 75181291 82192302 952012311 106211321 113223331
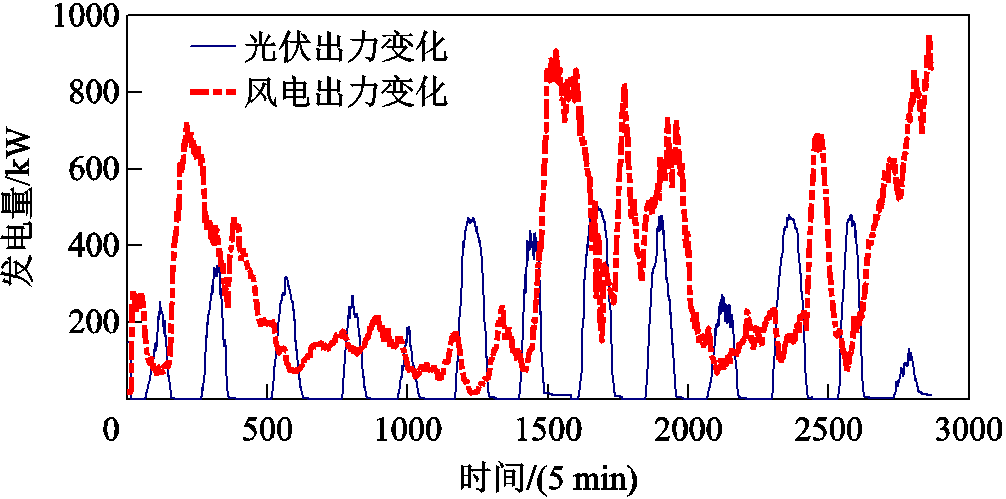
图3 风光出力原始数据
Fig.3 Raw data of wind and PV output
在原始数据基础上,构建联合Copula函数确定风光联合出力概率密度函数;同时因为夜晚光伏出力很小甚至是不出力,因此本文在建立联合Copula函数时,考虑风光联合出力的时间段为7:00—19:00,剩余时间段只考虑风机出力。
从图3原始风光出力数据中可以看出,风光大体呈现一种负相关特性,在一定程度上反映了风光联合出力具有良好的互补特性。但由于风光出力大小之间存在差异,导致风光联合出力仍具有较大的波动性,因此通过5G基站储能的参与,进一步缓解这种波动性,以提高风光利用率。
利用非参数核密度估计,拟合图3中风-光原始数据以获得风-光出力的边缘分布函数,拟合后的边缘分布结果如图4所示。同时本文对比了核密度估计与对数正态分布对于原始数据的拟合效果,从图4中可以看出核密度对于原始数据的拟合效果更好。
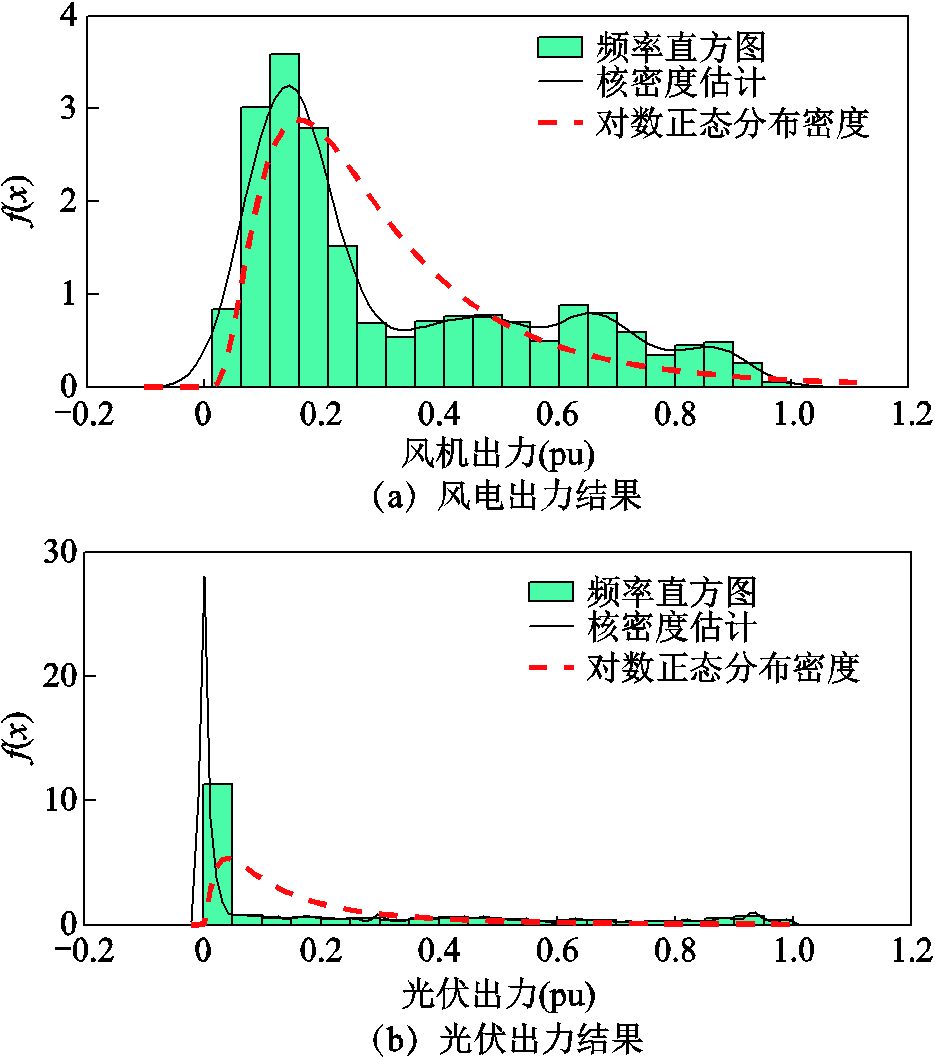
图4 不同估计方法对比
Fig.4 Comparison of different estimation methods
以AIC和平方欧式距离作为拟合优度评判准则,分别计算7:00—20:00这13个时间段内五种Copula函数的拟合效果,进而确定各个时段的最优拟合函数,其中各时段的AIC和平方欧式距离结果如图5所示。
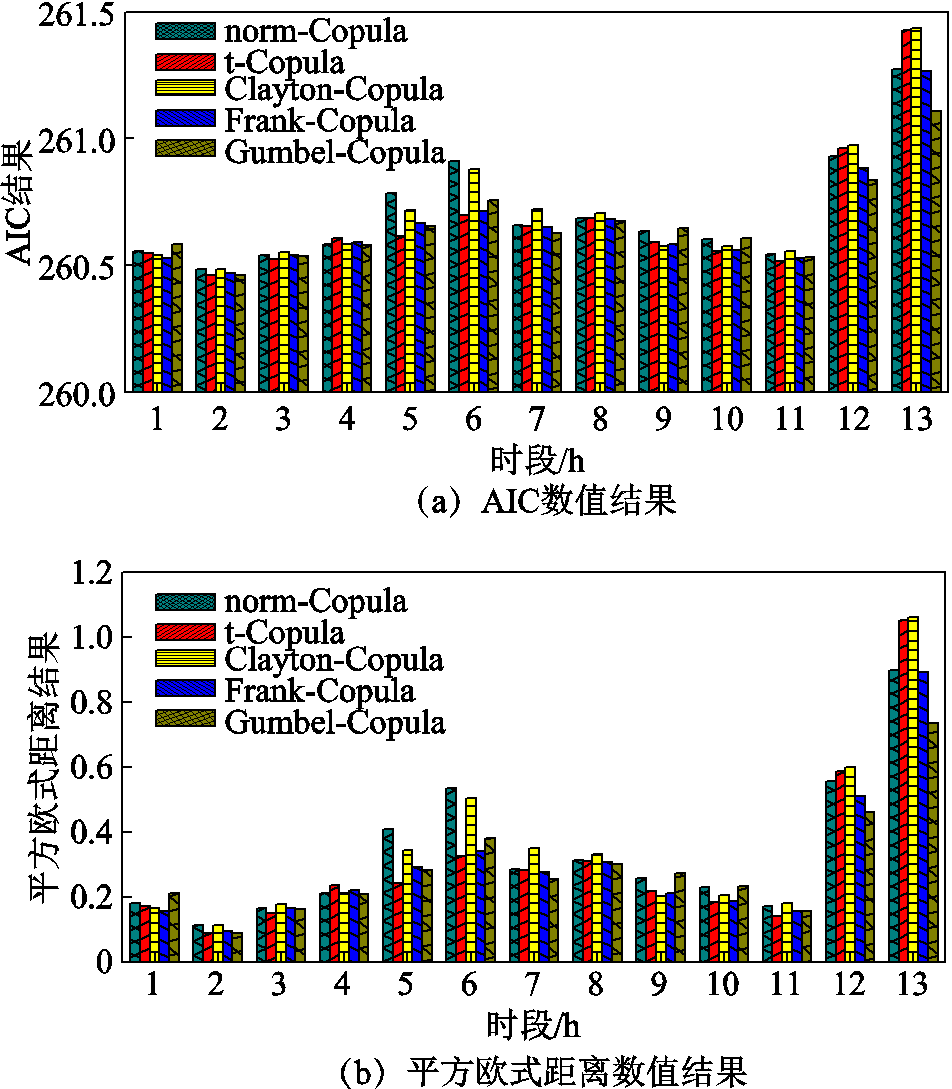
图5 不同时段拟合优度比较
Fig.5 Comparison of the fit goodness for different time periods
将AIC结果和平方欧式距离结果最小作为Copula函数的选取原则,得到各时段最优Copula函数见表3。
表3 各时段最优Copula函数
Tab.3 Optimal copula function for each time period

时段/hCopula时段/hCopula时段/hCopula 7Frank12t17t 8t13Gumbel18Gumbel 9t14Gumbel19Gumbel 10Gumbel15Clayton 11t16t
对以上各时段Copula函数进行抽样,通过K-means对抽样集进行聚类以达到场景缩减的目的;对于其余时段,针对风力原始数据同样采用K-means进行聚类,两次聚类数均设置为10。
除表3中的时间段外,其余时间光伏出力用0填充,最终将各时段风光处理分别进行拼接生成完整的24 h典型出力场景集。出力结果如图6所示。
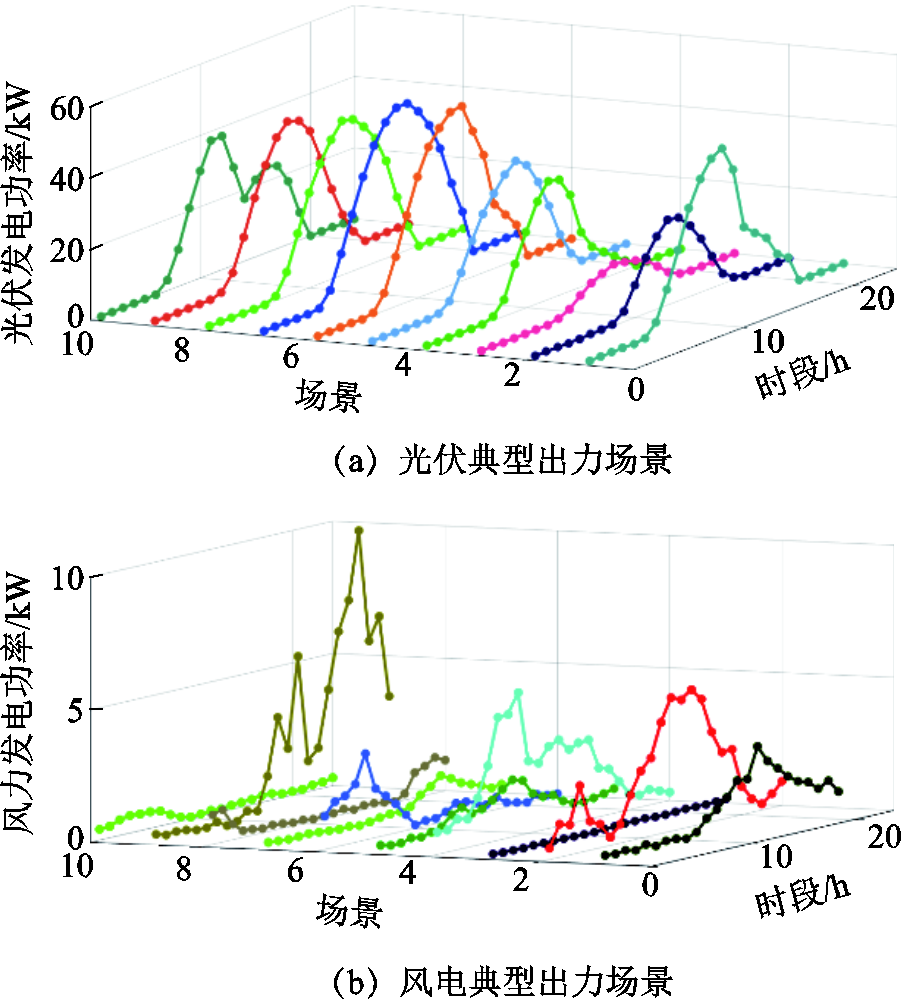
图6 风-光出力典型场景
Fig.6 Typical scenes of wind and PV out of force
3.3.1 基站功耗计算
本文通过式(6)正弦函数叠加的方式,确定不同区域内基站的通信量Lj,其参数分别为
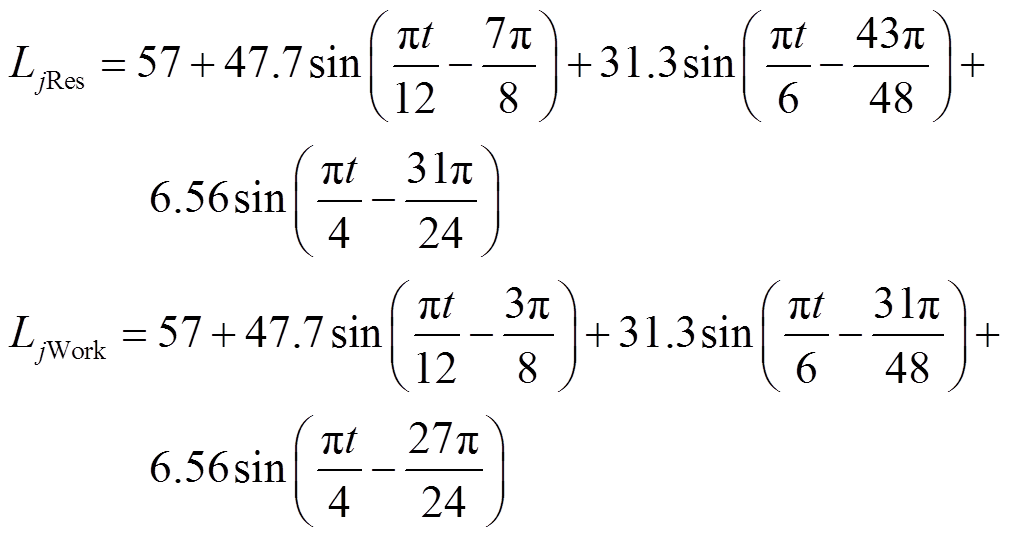
仿真结果如图7所示。
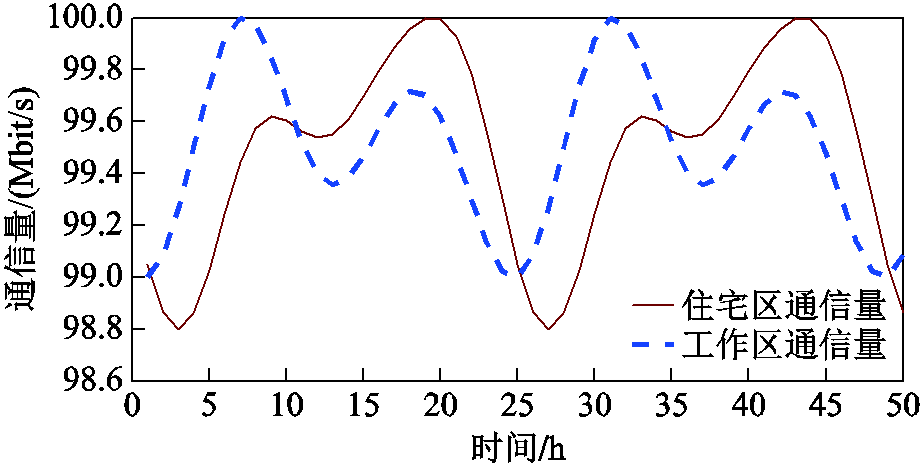
图7 不同区域基站通信量变化
Fig.7 Variation of base station traffic in different areas
将图7中不同区域基站的通信量代入式(8)中,得到不同区域内基站的功耗变化如图8所示。从图8和式(8)可以看出,基站功耗与区域内基站的通信量成正比。
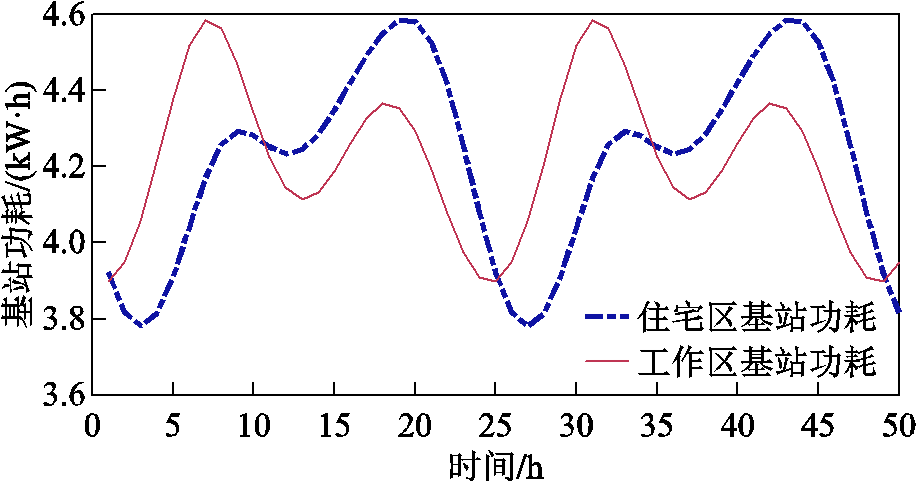
图8 基站功耗变化
Fig.8 Variation of power consumption of base stations
3.3.2 基站备用储能确定
基站备用储能往往与基站所在位置负荷等级、供电可靠性和通信负荷量有关。本文通过泰尔熵和修正基尼系数来量化不同电网节点的供电可靠性。
对于系统节点电压泰尔熵,分别计算各个节点发生0.01 kW功率波动下的电压变化情况,如图9所示。
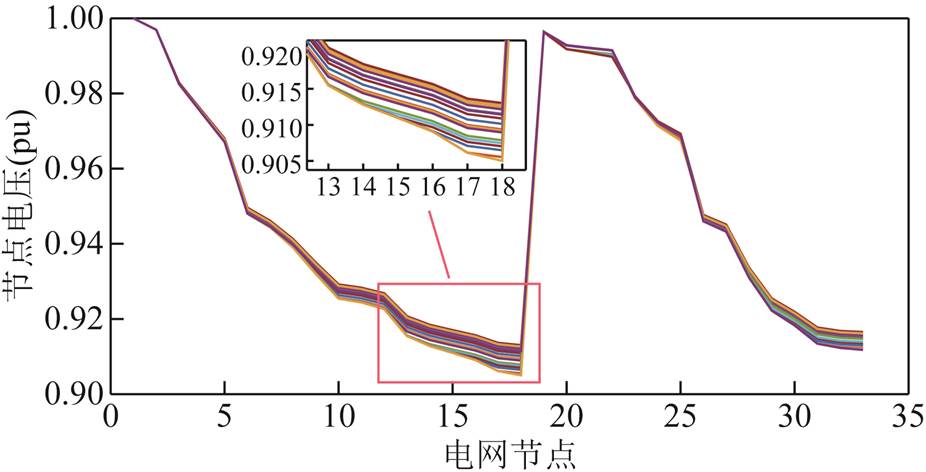
图9 节点电压变化
Fig.9 Changes in node voltage
进而根据式(16)计算得到电网各节点处的电压泰尔熵。对于传统基尼系数的修正,利用式(20)进行确定,其中拓扑节点度数和节点度数修正量的结果如图10所示。
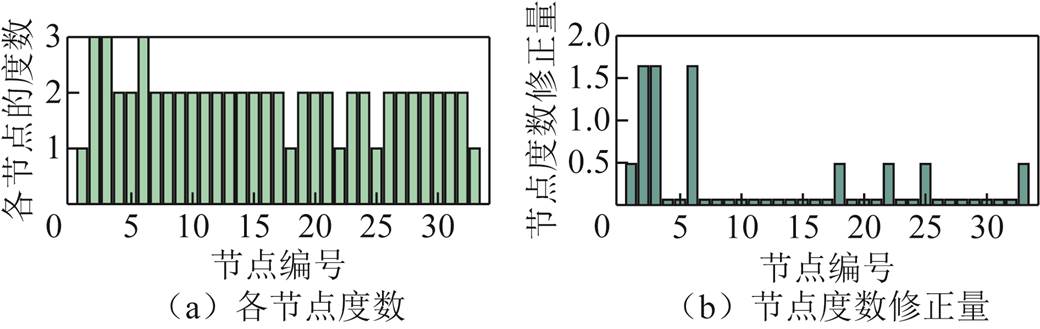
图10 拓扑度数修正结果
Fig.10 Correction results of topological degrees
通过影响率修正基尼系数,将整体结构不均衡度反映为各节点对整体的影响,同时降低拓扑对于不均衡度的影响,其计算结果如图11所示。
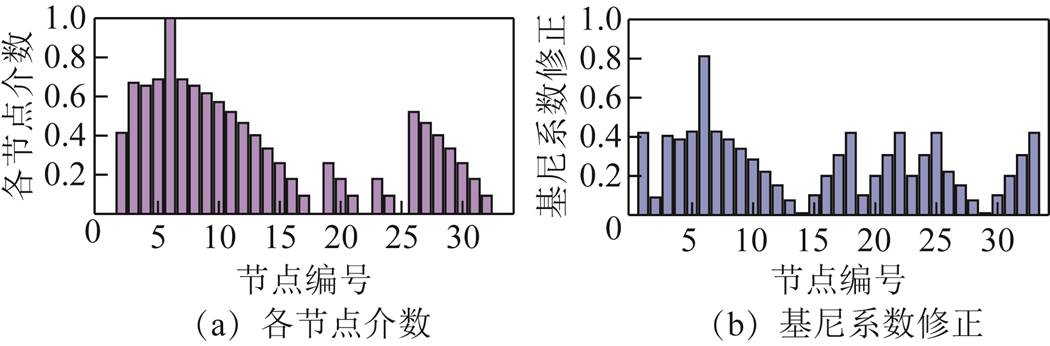
图11 修正后的基尼系数
Fig.11 Modified Gini coefficient results
通过式(20)融合节点度数修正量和基尼系数,将计算出的结果作为电网的拓扑可靠度结果。
将节点电压泰尔熵作为系统的状态可靠度结果;两种可靠度结果如图12所示。根据系统状态可靠度和系统拓扑可靠度结果,便可根据式(21)计算得到系统各节点的综合可靠度结果,如图13所示。
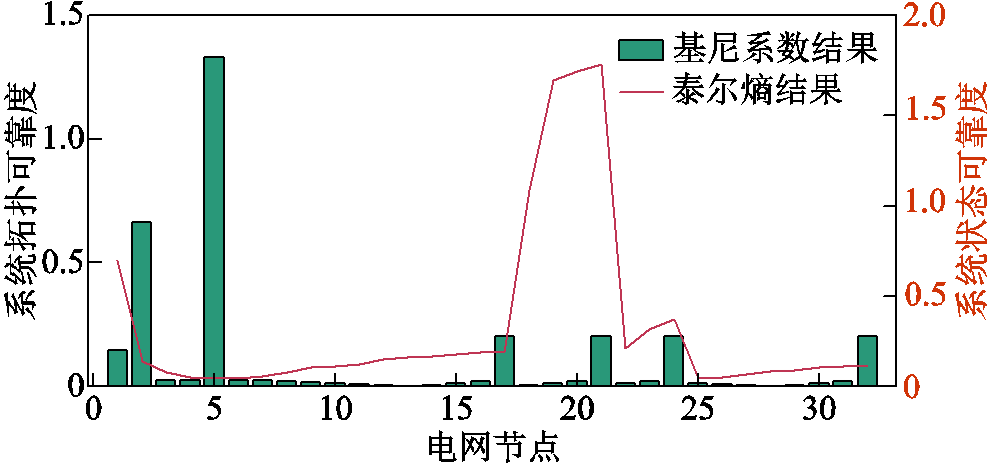
图12 系统可靠度
Fig.12 Reliability for system
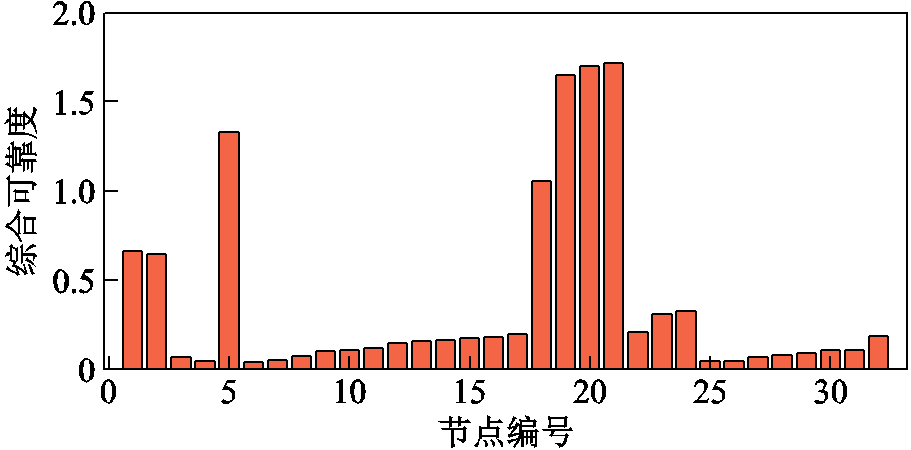
图13 系统节点综合可靠度
Fig.13 Comprehensive reliability of system nodes
本文设5G基站的最小备用时间T0=2 h,将其与系统节点综合可靠度结果代入式(11)中得到系统各节点处的基站备用时间(对结果进行取整),如图14所示。
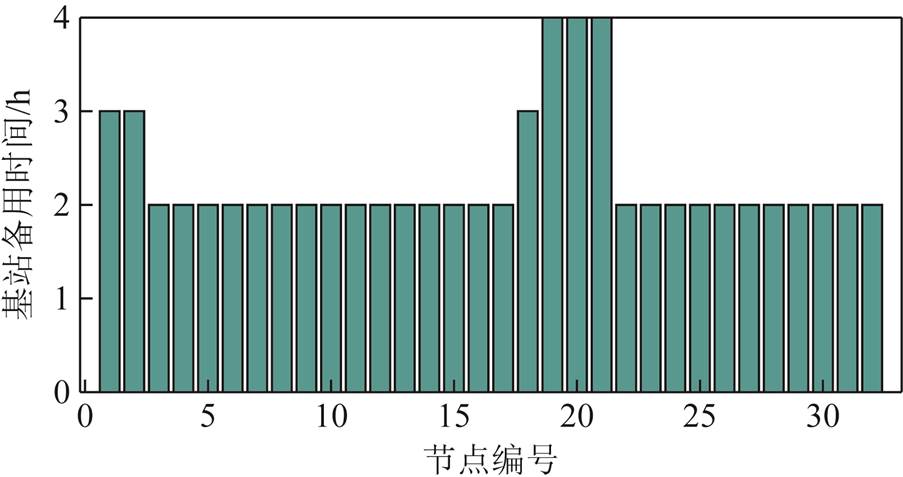
图14 基站储能备用时间
Fig.14 Backup time for base station energy storage
基站储能备用时间决定了基站备用储能容量的大小,进而可以确定基站的可调用容量,其结果如图15所示。
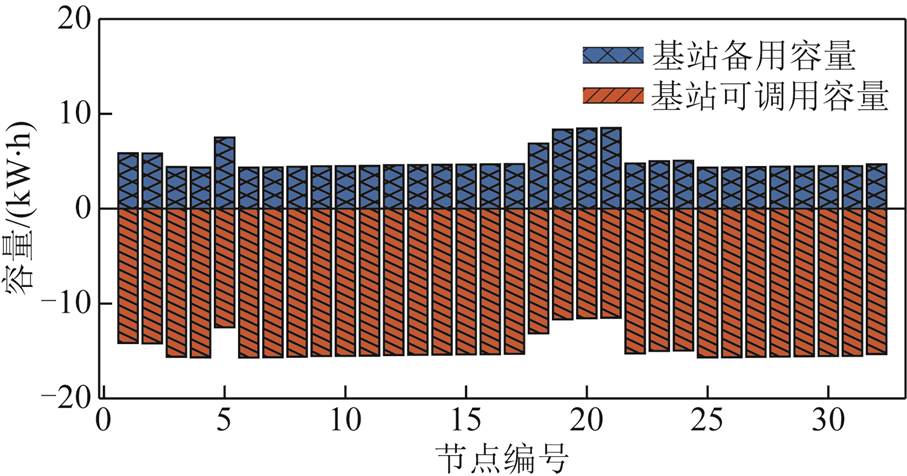
图15 各节点处基站可调用储能
Fig.15 Callable energy storage of the base station
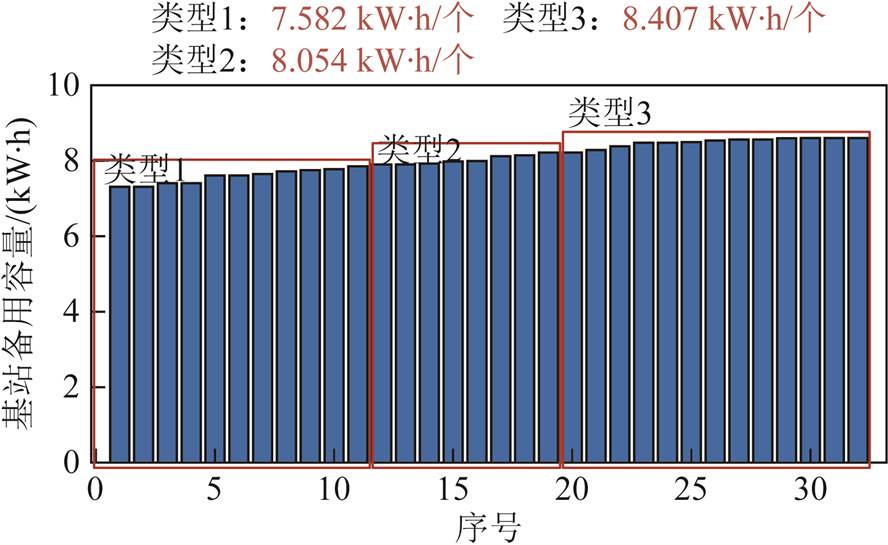
在进行基站储能调度时可将基站备用储能作为储能充放电的容量下限。由于不同节点处基站备用储能的大小存在差异,增加了调度运算时的变量个数及计算量,因此为了简化计算,对图15所示的基站备用容量进行大小排序,并将其划分为三部分,每个部分的基站备用容量取其均值,进而降低变量个数,缩短计算时间。排序分区后各节点基站备用储能容量如图16所示;其中各节点对应储能类型如图17所示。
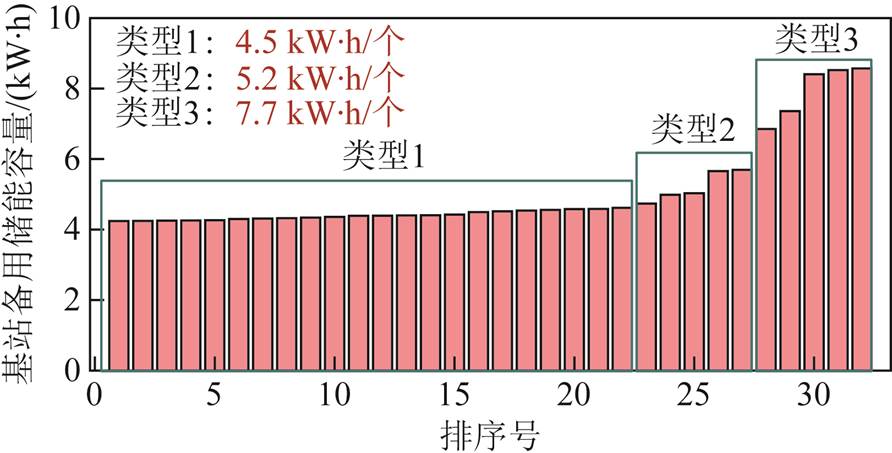
图16 不同类型备用储能容量
Fig.16 Simplification of different types of backup energy storage capacity
根据表2中各电网节点处的基站数量,结合图16和图17的结果,得到各类型储能总备用和总调用容量见表4。
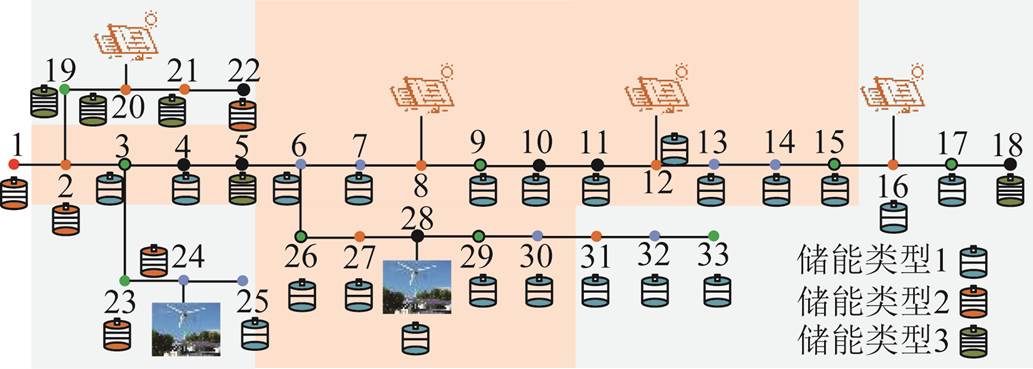
图17 各节点对应储能类型
Fig.17 Corresponding energy storage types of each node
表4 储能备用容量和可调用容量
Tab.4 Backup energy storage and callable capacity(单位:kW·h)

储能类型备用总容量可调用总容量 13511 053 278192 3169.4226.6
本节以如图2所示拓扑模型为研究对象,验证5G基站储能参与电网负荷应急供电的可行性。
3.4.1 基站储能参与应急供电
从风光联合出力场景集中选取一组,与负荷变化曲线构建风-光-荷出力预测值。设置风光出力波动为原始出力的15%,负荷出力波动为原始出力的10%,风-光-荷的预测值如图18所示。将其作为两阶段鲁棒优化模型的输入量,同时设置可调参数为:[ΓL, Γpv, Γpw]=[12,6,6];求解此场景下基站储能参与系统供电恢复下的失负荷量。
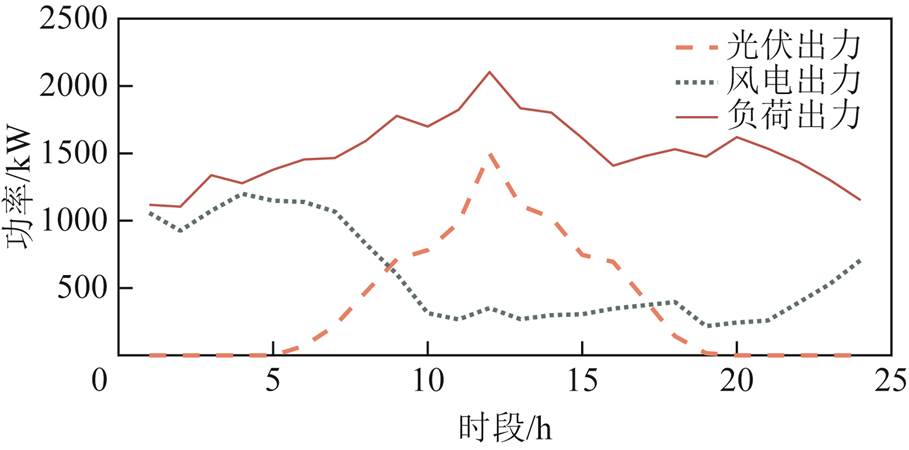
图18 风-光-荷预测出力结果
Fig.18 Predicted output results of wind-solar-loads
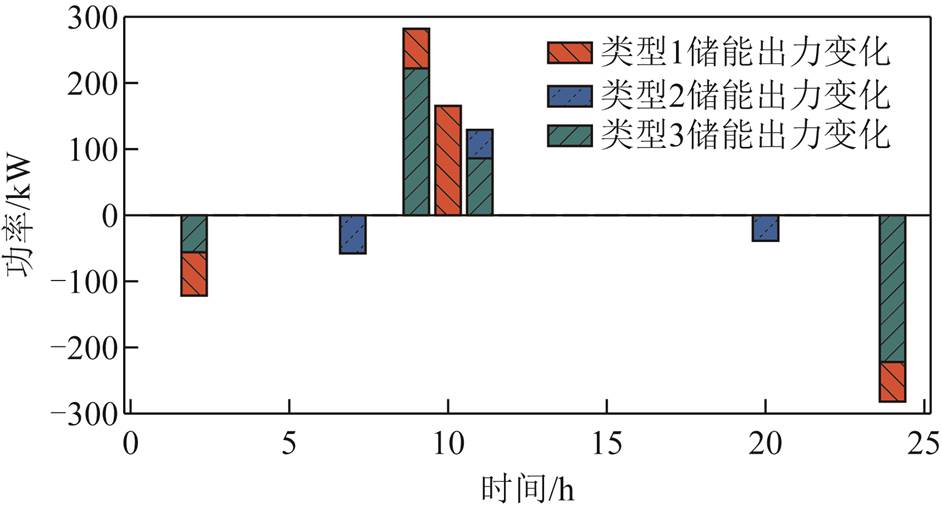
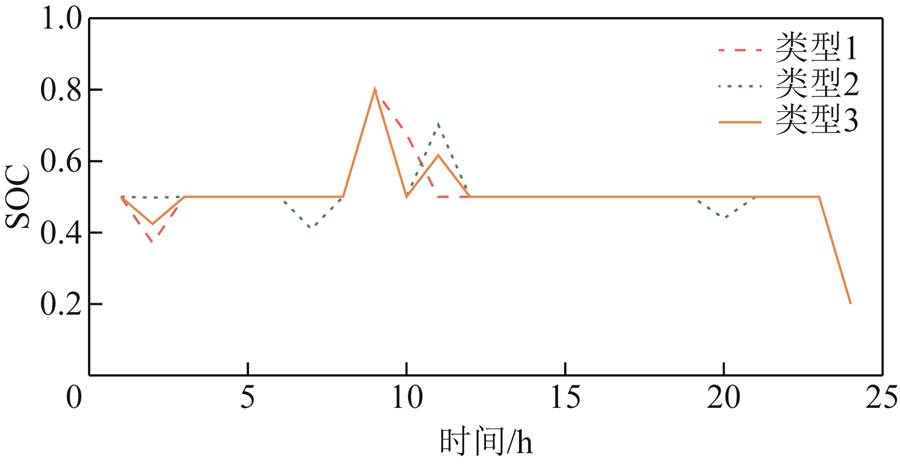
图19为两阶段鲁棒优化后风-光-荷实际出力曲线。区域内5G基站储能充放电结果如图20所示(各类型储能荷电状态变化如附图1所示)。
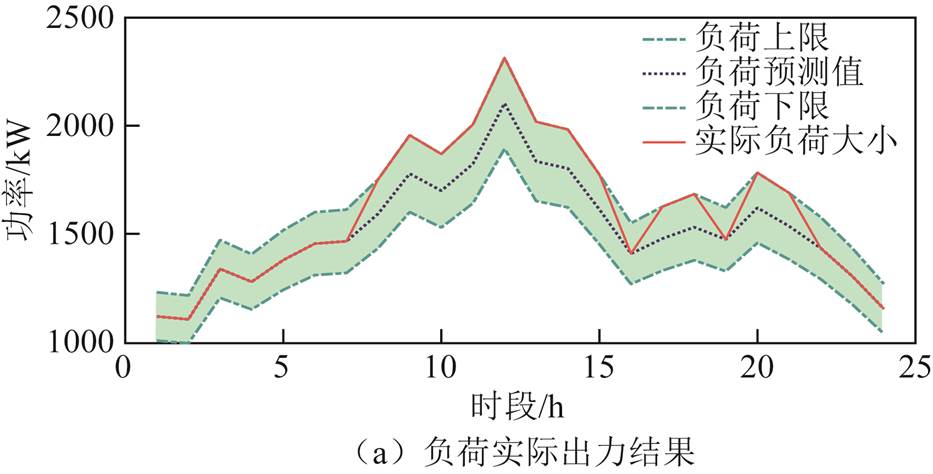
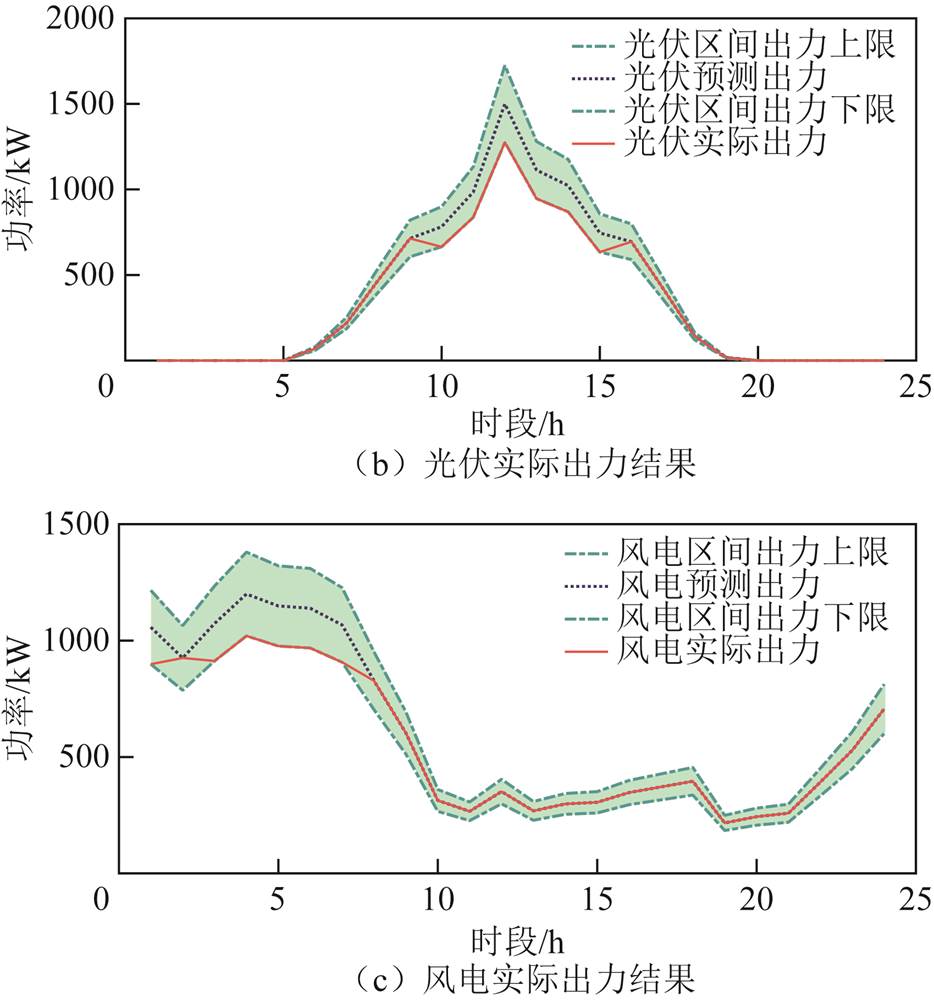
图19 原始场景风-光-荷实际出力结果
Fig.19 The actual output results of wind-solar-load in the original scenario
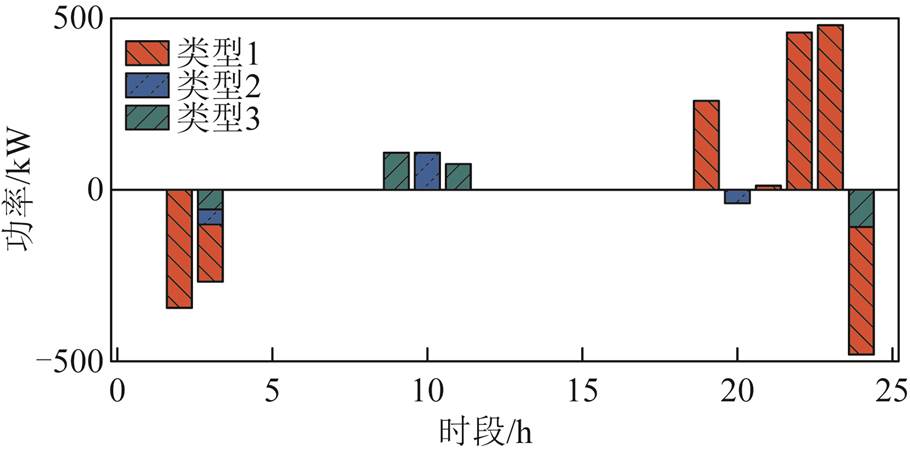
图20 不同类型储能出力
Fig.20 The energy storage output of base station in different types
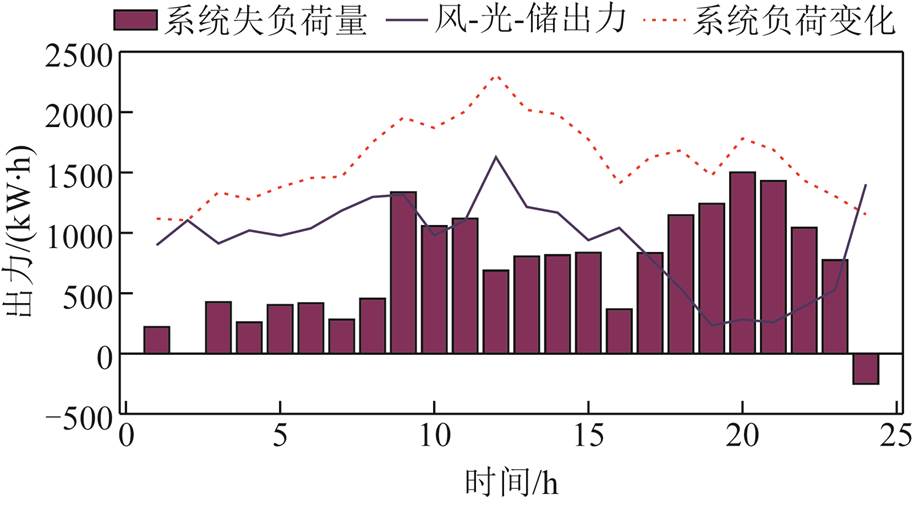
从图20中可以看出,基站储能在2~3 h、20 h和24 h进行充电,此时系统中负荷处于较低水平,且风力发电处于较高水平,不仅在分时电价的背景下降低储能充电成本,同时提升储能对于风电的消纳;在8~11 h、19 h、21~23 h,储能放电,进而降低系统失负荷量,减少负荷失电损失。
系统失负荷量变化如图21所示。其中不同负荷等级的失负荷量的单位成本见表5[31]。进而计算得到原始风-光-荷出力下系统失负荷量的成本为457 034元。
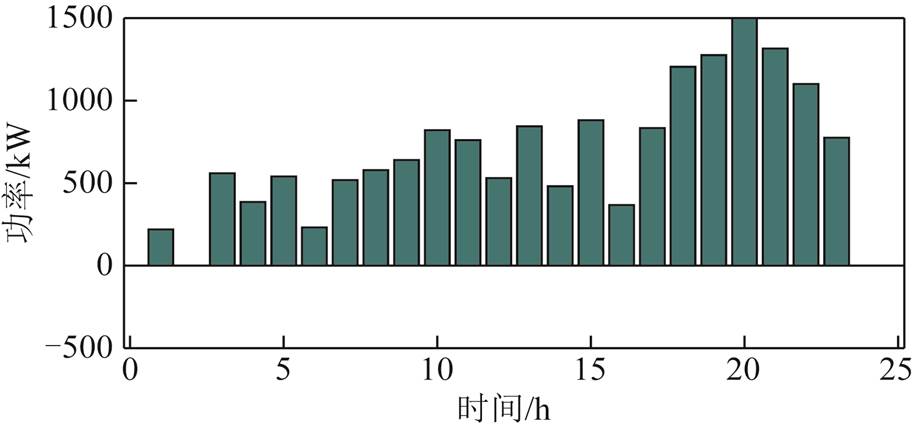
图21 原始场景下系统失负荷量
Fig.21 The system loss of load in the original scenario
表5 不同负荷等级下失负荷单位成本
Tab.5 Lost load unit cost at different load levels

负荷等级一级负荷二级负荷三级负荷 单位成本/(元/kW)84.3726.113.427
3.4.2 方案对比
针对协调5G基站储能参与配电网供电恢复,考虑基站储能参与负荷供电的可行性,本文拟从四个方面进行对比:①定备用时间和本文方法下基站备用储能容量对比;②鲁棒优化与确定性优化下系统失负荷量对比;③不同风-光出力场景下储能参与负荷供电系统失负荷量对比;④不同可调参数下系统失负荷量对比。
1)定备用时间和本文方法下基站备用储能容量对比
对于定备用时间下的基站备用容量,假设电网各节点处的基站备用时间均为3 h,其余参数不变。得到定基站备用时间下各电网节点处的基站备用容量结果如图22所示。
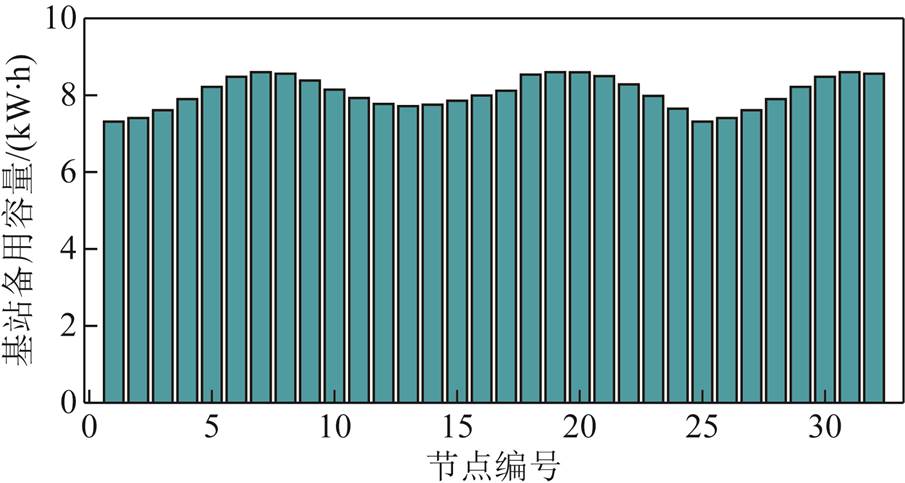
图22 定备用时间下的基站储能备用容量
Fig.22 Reserve capacity under fixed reserve time
进而对比定备用时间和变备用时间下各节点处基站的可调用容量结果如图23所示。
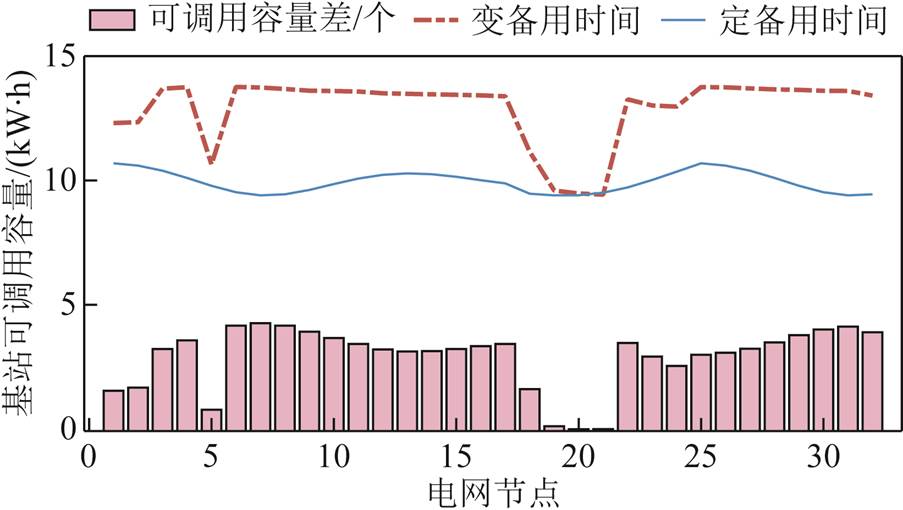
图23 可调用储能对比结果
Fig.23 Callable energy storage comparison results
图23为各节点处单个基站的可调用容量差,结合算例所用拓扑中各节点的基站数,得到不同备用时间下,基站储能可调用容量对比见表6。
从表6可以看出,考虑电网节点脆弱度等影响基站备用储能的因素下,改变基站储能备用时间,相比于定备用时间,拓扑中总基站可调用储能提高了317 kW·h,提高了基站储能的利用率。
表6 基站储能可调用容量对比
Tab.6 Comparison of callable capacity for energy storage

可调总容量(变备用时间)/(kW·h)可调总容量(定备用时间)/(kW·h)差值/ (kW·h) 1 4561 139317
在此基础上,对比定备用时间和本文方法下,5G基站储能对于系统失负荷量以及风-光消纳的影响,各方法对比结果见表7(定备用时间下,各电网节点处的单个基站备用储能容量、系统失负荷量变化、基站储能出力及相应荷电状态(State of Charge, SOC),结果分别如附图2~附图5所示)。
表7 方法对比
Tab.7 Method comparison
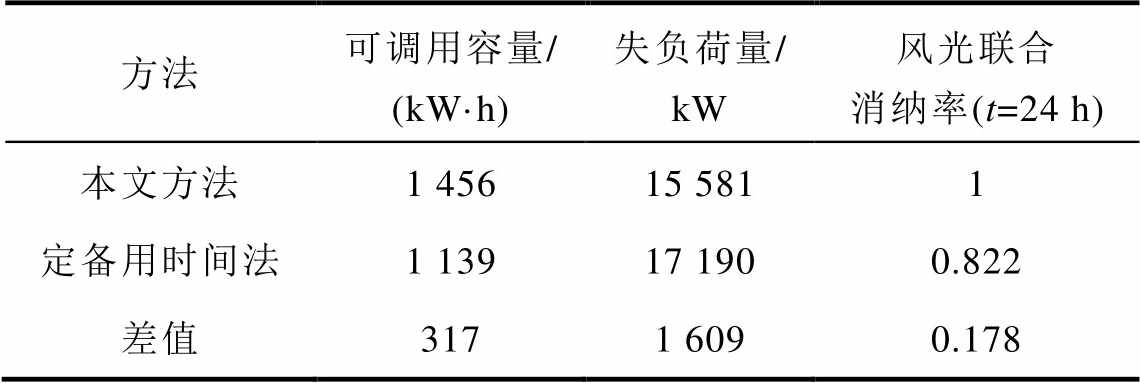
方法可调用容量/ (kW·h)失负荷量/ kW风光联合消纳率(t=24 h) 本文方法1 45615 5811 定备用时间法1 13917 1900.822 差值3171 6090.178
以文献[32]中的光伏消纳率公式为依据,建立分光联合出力消纳率计算公式为
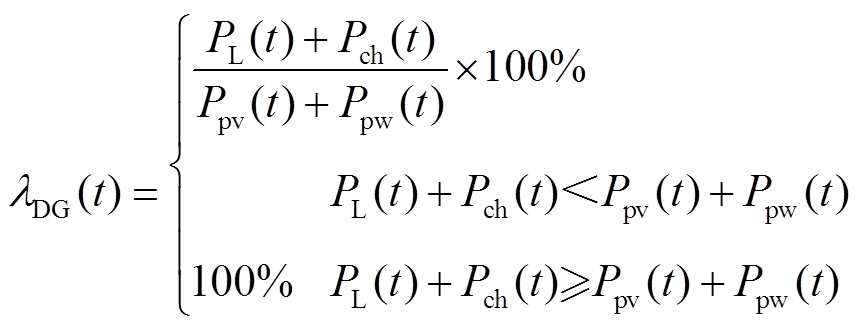 (47)
(47)
表7中系统的运行成本见附表1。
2)鲁棒优化与确定优化下系统失负荷量对比
鲁棒优化通过建立波动区间来反映相关参数的波动性,并通过优化求解至场景集中的最恶劣场景来计算相应的目标结果,而确定性优化不考虑相关参数的波动性。本文拟通过整数线性规划计算风-光-荷出力固定下的失负荷量,其目标函数同式(25),进而比较两种情况下的系统失负荷量。两种优化方式下失负荷量变化如图24所示。
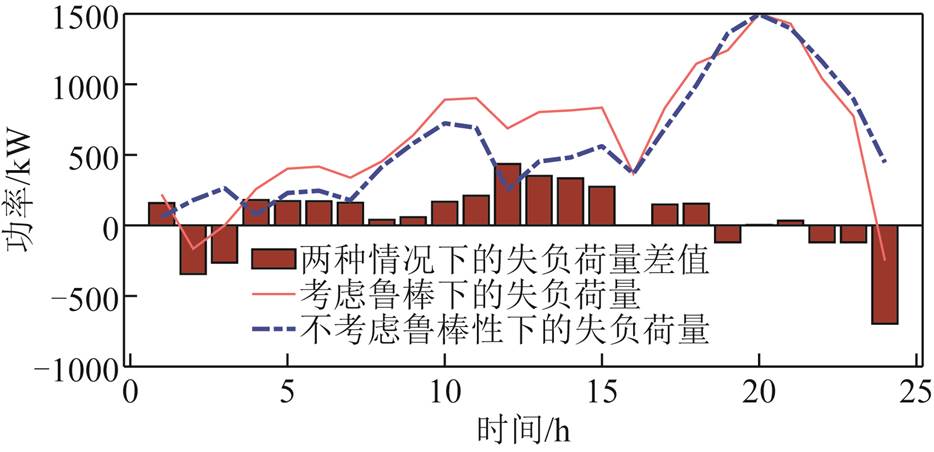
图24 鲁棒与确定性优化结果对比
Fig.24 Comparison of results between robust and deterministic optimization
从图24中可以看出,采用鲁棒优化系统失负荷量大于确定性优化,鲁棒优化最终优化出来的场景较为恶劣,其结果相比于确定性优化具有保守性,但其考虑相关参数的波动性,有利于确定系统失负荷量的最恶劣情形,进而指导相关调度工作。两种优化方式下具体失负荷量对比见表8。
表8 失负荷量对比
Tab.8 Comparison of the amount of load loss

不同算法对比失负荷量(t=24 h)/kW 确定性优化14 199 鲁棒优化15 581 差值1 382
3)不同风-光出力场景下储能参与负荷供电系统失负荷量对比
通过在风-光出力场景集中选取三组不同风-光出力特性曲线,分别利用鲁棒优化确定基站储能在三种场景下对于失负荷量的影响情况。三种场景下失负荷量结果如图25所示(各场景下基站储能的荷电状态变化如附图6所示)。
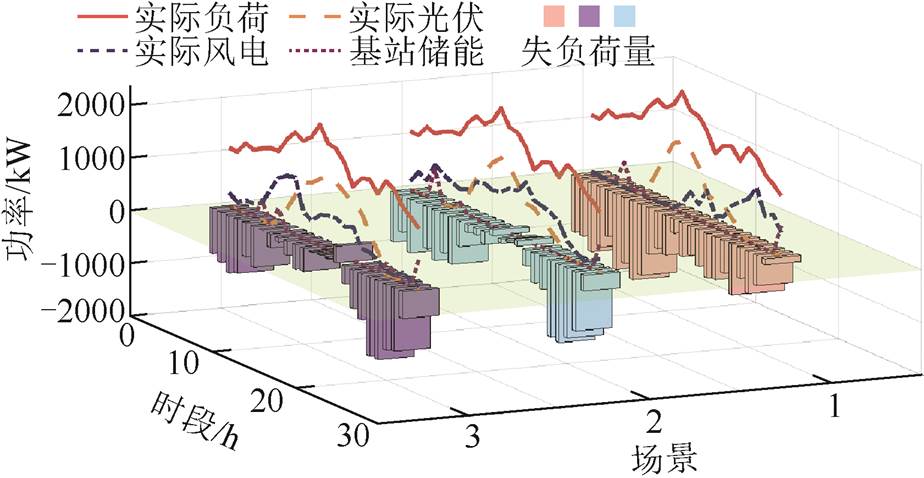
图25 不同风-光出力场景下失负荷量对比
Fig.25 Comparison of load loss under different wind and solar output scenarios
从图25可以看出,对于场景1,其风力发电主要集中于13 h之后,且其出力较大的时间段主要在下午及晚上,光伏出力主要集中于8~17 h,凌晨至8:00这个时间段内风光联合出力较低,可以看出此时基站储能进行放电,有效地降低系统失负荷量;对于场景2,光伏出力趋势与场景1类似,但风电出力时间跨度长,且出力较为稳定,此时基站储能不仅参与负荷供电,且在风-光出力大于负荷需求时进行风-光出力消纳(13 h、16 h);对于场景3,从图25中可以看出该场景下风光出力具有明显互补特性(5~20 h),此时基站储能作用同场景2,可在参与供电恢复的同时进行一定程度上的风光消纳。
三种场景下基站储能对于风光联合消纳的影响如图26所示。场景1,由于风光联合出力各时段均小于负荷量,因此对于风光的消纳率均为1;场景2,其在t=13、15、16 h存在弃风、弃光现象,在加入储能后,由于储能充电时间不在t=13、15、16 h这三个时间段内,因此对于风光消纳率无影响;场景3,在不考虑基站储能参与情况下,其在t=14、15、16 h存在弃风弃光现象,而在储能参与后,在t=14、15、16 h时段内,储能充电,使得负荷量大于风光出力,三个时间段风光消纳率为1。
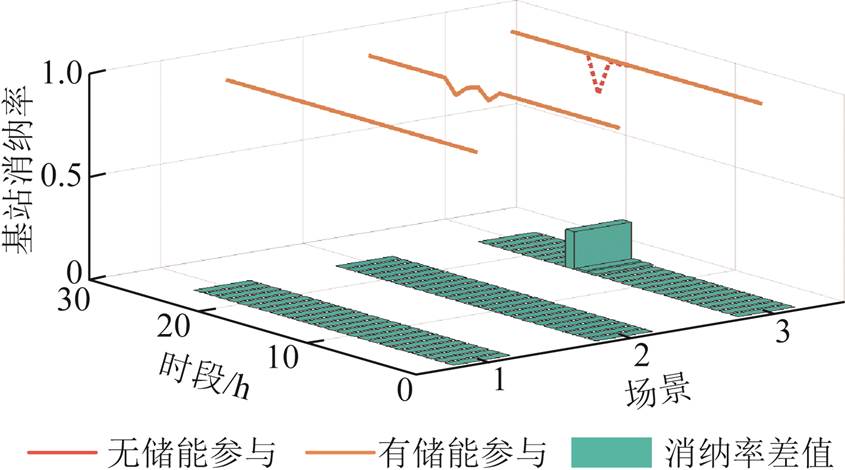
图26 基站储能对风光消纳的影响
Fig.26 The impact of base station energy storage on wind and solar energy consumption
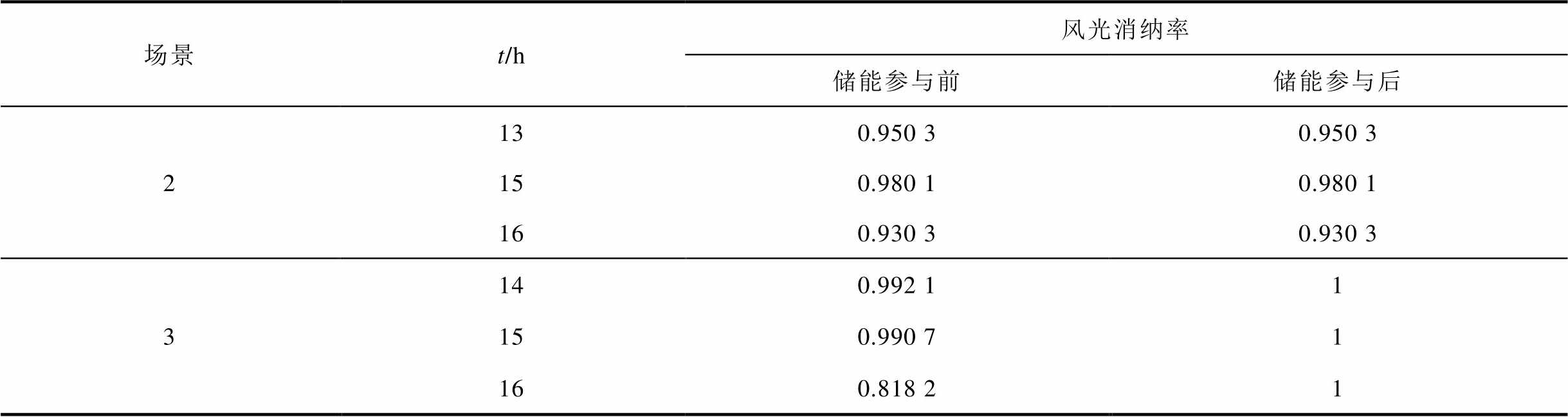
储能参与前后,各场景风光消纳率在上述时间段内的变化结果见表9。
表9 风光消纳率变化结果
Tab.9 Change in wind-light absorption rate
场景t/h风光消纳率 储能参与前储能参与后 2130.950 30.950 3 150.980 10.980 1 160.930 30.930 3 3140.992 11 150.990 71 160.818 21
从表9中可得,对于场景3,基站储能参与后,在t=14、15、16 h时段分别对风光消纳率提高了0.007 9、0.009 3和0.181 8。
4)不同可调参数下系统失负荷量对比
可调参数会影响鲁棒优化中风-光-荷实际出力结果,文献[29]通过可调参数来改变鲁棒优化的保守性,因此本文在对比4中建立五种可调参数向量,对比不同可调参数对系统失负荷量的影响。五组可调参数取值和失负荷量见表10。
各组可调参数下风-光-荷出力变化如图27所示。从图27可以看出,随着可调参数数值的增加,鲁棒优化越保守,即风光出力越接近波动区间的下界,负荷变化越接近其波动区间的上界,进而系统失负荷量增大。各场景下系统失负荷量变化如图28所示,各场景下基站储能的荷电状态变化如附图7所示。
表10 不同可调参数下相应失负荷量
Tab.10 Loss of load at different adjustable parameters
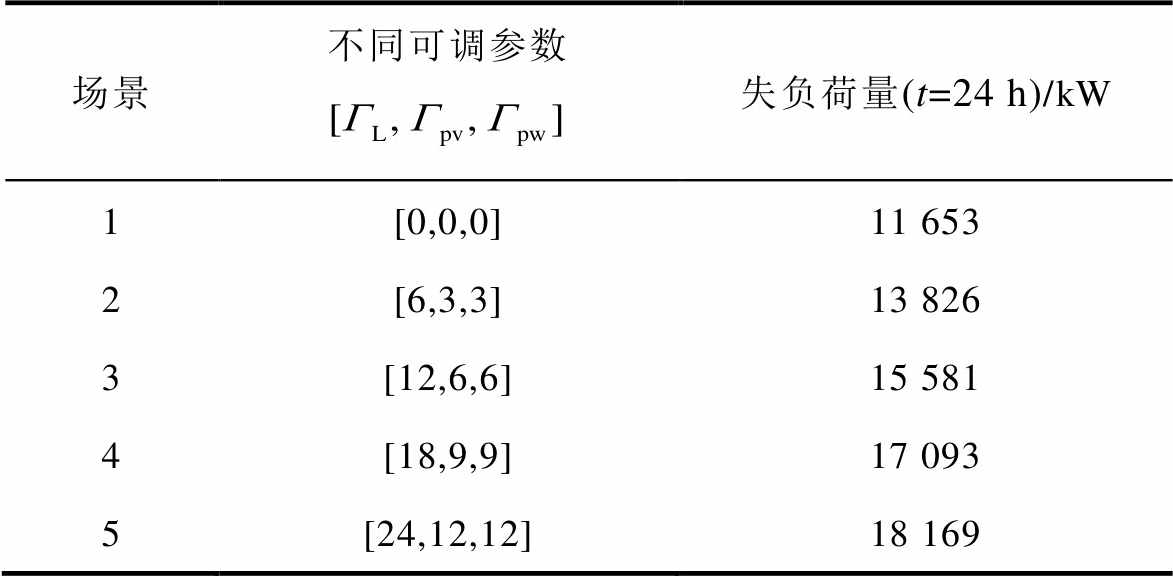
场景不同可调参数失负荷量(t=24 h)/kW 1[0,0,0]11 653 2[6,3,3]13 826 3[12,6,6]15 581 4[18,9,9]17 093 5[24,12,12]18 169
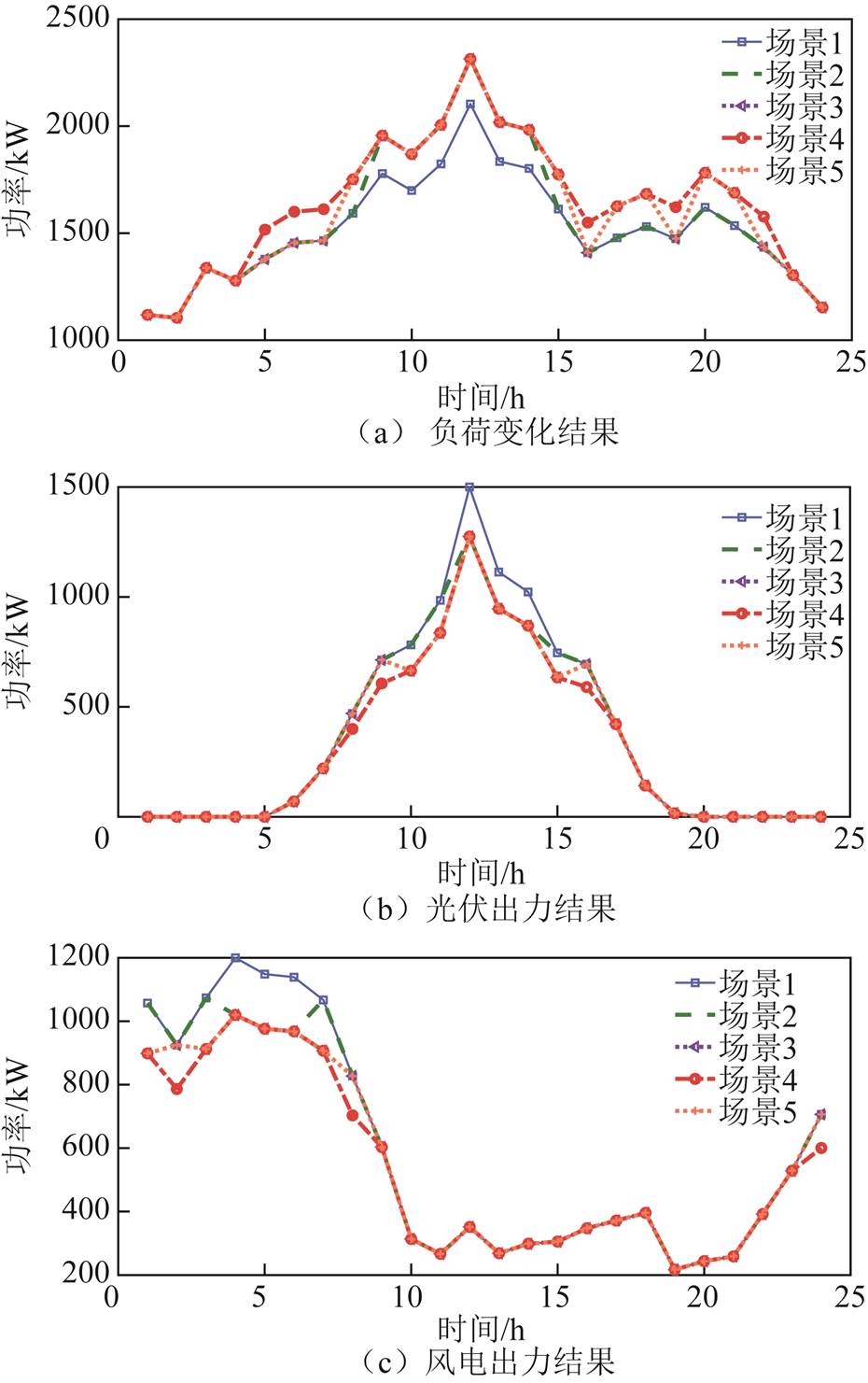
图27 不同可调参数下风-光-荷出力结果
Fig.27 Wind-solar-load actual output results with different adjustable parameters
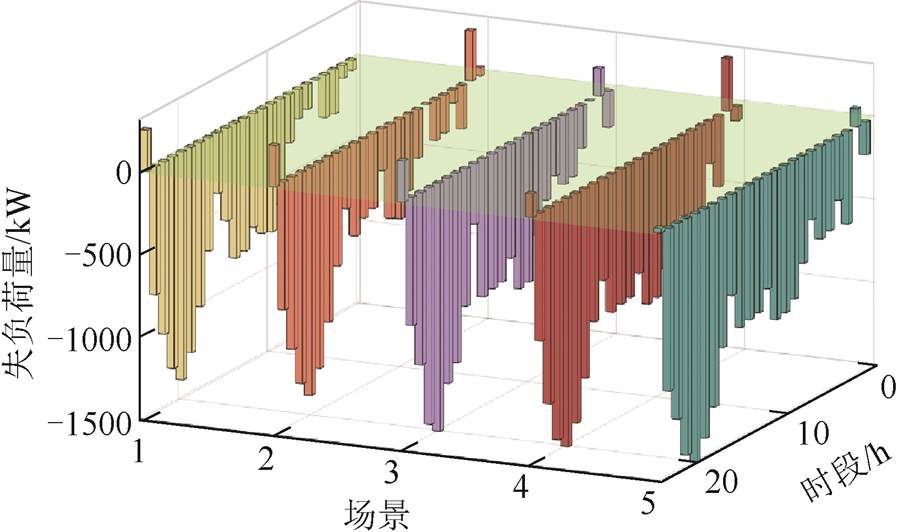
图28 不同可调参数下失负荷量对比
Fig.28 Loss of load at different adjustable parameters
上述场景中相关运行成本见附表1。
本文为最大化基站储能参与配电网失电负荷的供电恢复,提出考虑电网节点脆弱度、负荷等级和通信量等影响因素,建立不同区域基站备用储能模型。在满足不同区域基站备电需求的同时,提高基站储能的利用效率。同时建立两阶段鲁棒优化模型,量化基站储能参与失电负荷供电恢复过程中风-光-荷出力的波动性。通过在改进的IEEE 33节点模型上对比验证了所提方法的有效性,并得到以下结论:
1)相比于传统的定基站备用储能容量,结合基站所在位置的电网节点脆弱度、负荷等级和通信量等影响因素来动态确定基站的备用储能容量,提高了317 kW·h的可调用储能容量,提升了基站储能的利用效率。
2)相较于确定性优化,鲁棒优化下的配电网失负荷量较确定性优化高了1 382 kW,但利用鲁棒优化得到的方案相比于确定性优化有更好的鲁棒性,有利于提升配电网恢复供电中抵御负荷等影响因素波动的能力。
3)5G基站储能参与配电网失电负荷供电,在提高储能利用率的同时,可降低配电网的失负荷量。同时,基站储能在某些时段内对风光出力进行一定程度的消纳:其中,在t=14、15、16 h时段,风-光联合消纳率分别提高了0.007 9、0.009 3和0.181 8,进而降低了系统的弃风弃光率,提高了配电网的经济性。
未来我国5G发展仍会快速推进,5G基站的部署密度也将会进一步增加,同时配电网的可靠性也在不断提升,5G基站储能可调度资源量也将会不断提升。充分利用5G基站储能资源,可以降低配电网运行成本,提高基站储能利用效能,具有广阔的应用前景。
附 录
原始场景下不同储能的荷电状态变化如附图1所示。
在定备用时间T=3时,得到各电网节点处的基站备用储能如附图2所示。
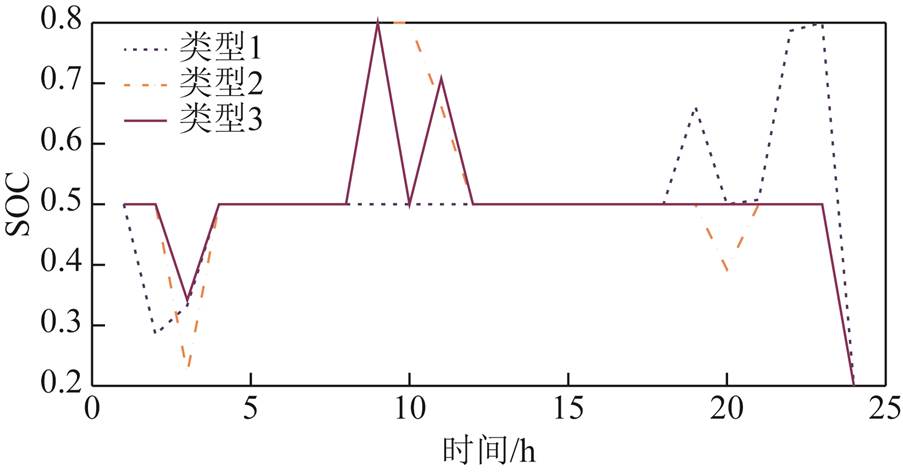
附图1 原始场景下不同储能的SOC
App.Fig.1 SOC of different energy storage in the original scenario
附图2 定备用时间下基站备用储能容量
App.Fig.2 Backup capacity under fixed backup time
系统失负荷量如附图3所示。
附图3 系统失负荷量结果
App.Fig.3 Result of system load loss
各类型储能出力结果如附图4所示。
附图4 各类型储能出力
App.Fig.4 Power output of each type of energy storage
储能荷电状态变化如附图5所示。
附图5 对比方案中各类型储能SOC
App.Fig.5 SOC of various types of energy storage in scheme comparison
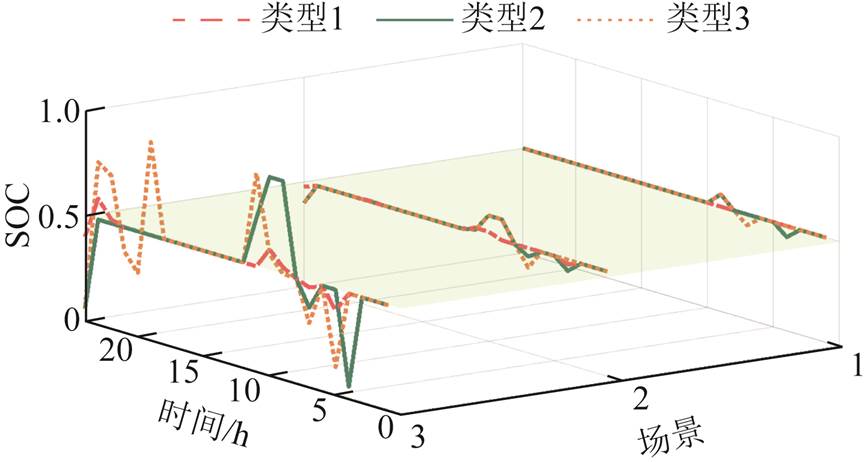
附图6 储能荷电状态变化
App.Fig.6 Change in state of charge of energy storage
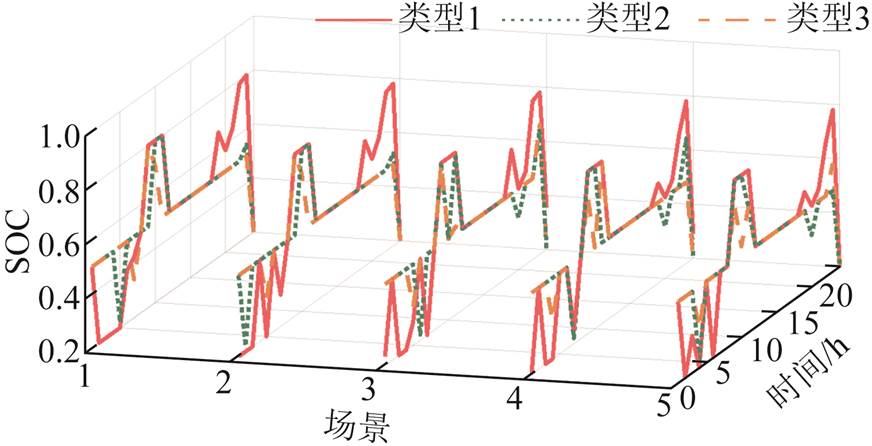
附图7 不同场景下储能荷电状态变化
App.Fig.7 Changes in the SOC of different scenarios
附表1 各场景系统运行成本
App.Tab.1 The operating cost of the system in each scenario(单位:元)
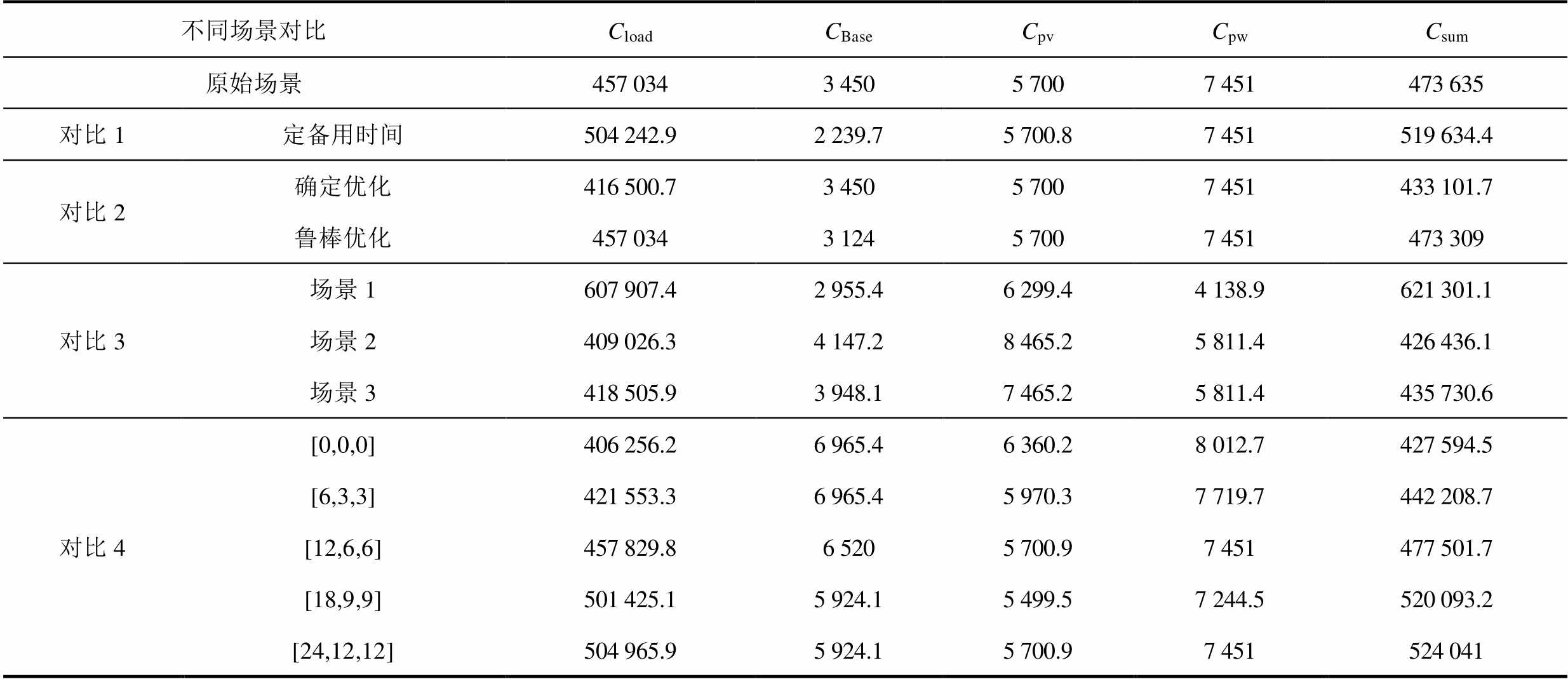
不同场景对比CloadCBaseCpvCpwCsum 原始场景457 0343 4505 7007 451473 635 对比1定备用时间504 242.92 239.75 700.87 451519 634.4 对比2确定优化416 500.73 4505 7007 451433 101.7 鲁棒优化457 0343 1245 7007 451473 309 对比3场景1607 907.42 955.46 299.44 138.9621 301.1 场景2409 026.34 147.28 465.25 811.4426 436.1 场景3418 505.93 948.17 465.25 811.4435 730.6 对比4[0,0,0]406 256.26 965.46 360.28 012.7427 594.5 [6,3,3]421 553.36 965.45 970.37 719.7442 208.7 [12,6,6]457 829.86 5205 700.97 451477 501.7 [18,9,9]501 425.15 924.15 499.57 244.5520 093.2 [24,12,12]504 965.95 924.15 700.97 451524 041
注:Csum为系统运行成本。
参考文献
[1] 刘育英. 中国工信部:加快5G、工业互联网等新型信息基础设施建设和应用[EB/OL]. [2023-03-14]. https://new.qq.com/rain/a/20230314A08RJ300.
[2] 麻秀范, 孟祥玉, 朱秋萍, 等. 计及通信负载的5G基站储能调控策略[J]. 电工技术学报, 2022, 37(11): 2878-2887. Ma Xiufan, Meng Xiangyu, Zhu Qiuping, et al. Control strategy of 5G base station energy storage considering communication load[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2878-2887.
[3] 蒋廷耀, 谢龙恩, 杜雨, 等. 基于深度强化学习的5G基站储能调度策略[J]. 电力系统自动化, 2023, 47(9): 147-157. Jiang Tingyao, Xie Longen, Du Yu, et al. Dispatching strategy of energy storage for 5G base stations based on deep reinforcement learning[J]. Automation of Electric Power Systems, 2023, 47(9): 147-157.
[4] Yong Pei, Zhang Ning, Hou Qingchun, et al. Evaluating the dispatchable capacity of base station backup batteries in distribution networks[J]. IEEE Transactions on Smart Grid, 2021, 12(5): 3966-3979.
[5] 刘友波, 王晴, 曾琦, 等. 能源互联网背景下5G网络能耗管控关键技术及展望[J]. 电力系统自动化, 2021, 45(12): 174-183. Liu Youbo, Wang Qing, Zeng Qi, et al. Key technologies and prospects of energy consumption management for 5G network in background of energy Internet[J]. Automation of Electric Power Systems, 2021, 45(12): 174-183.
[6] 岑海凤, 许苑, 王军伟, 等. 通信基站备用电池的云储能系统设计与应用[J]. 电源技术, 2020, 44(6): 902-904. Cen Haifeng, Xu Yuan, Wang Junwei, et al. Design and application of cloud energy storage system for backup battery in communication base station[J]. Chinese Journal of Power Sources, 2020, 44(6): 902-904.
[7] 郑小红. 深圳5G基站储能将全部接入深圳虚拟电厂管理中心[EB/OL]. [2022-12-14]. https:// baijiahao. baidu.com/s?id=1752198644606400924&wfr=spider&for=pc.
[8] 林固静, 高赐威, 宋梦, 等. 含通信基站备用储能的虚拟电厂构建及调度方法[J]. 电力系统自动化, 2022, 46(18): 99-107. Lin Gujing, Gao Ciwei, Song Meng, et al. Construction and scheduling method of virtual power plant with backup energy storage of communication base station[J]. Automation of Electric Power Systems, 2022, 46(18): 99-107.
[9] 麻秀范, 冯晓瑜. 考虑5G网络用电需求及可靠性的变电站双Q规划法[J]. 电工技术学报, 2023, 38(11): 2962-2976. Ma Xiufan, Feng Xiaoyu. Double Q planning method for substation considering power demand of 5G network and reliability[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2962-2976.
[10] 胡思洋, 廖凯, 杨健维, 等. 基于V2G技术的城市电网供电恢复策略[J]. 电力自动化设备, 2023, 43(6): 53-61. Hu Siyang, Liao Kai, Yang Jianwei, et al. Power supply restoration strategy of urban power grid based on V2G technology[J]. Electric Power Automation Equipment, 2023, 43(6): 53-61.
[11] 刘伟佳, 孙磊, 林振智, 等. 含间歇电源、储能和电动汽车的配电孤岛短时恢复供电策略[J]. 电力系统自动化, 2015, 39(16): 49-58. Liu Weijia, Sun Lei, Lin Zhenzhi, et al. Short-period restoration strategy in isolated electrical islands with intermittent energy sources, energy storage systems and electric vehicles[J]. Automation of Electric Power Systems, 2015, 39(16): 49-58.
[12] 许寅, 王颖, 和敬涵, 等. 多源协同的配电网多时段负荷恢复优化决策方法[J]. 电力系统自动化, 2020, 44(2): 123-131. Xu Yin, Wang Ying, He Jinghan, et al. Optimal decision-making method for multi-period load restoration in distribution network with coordination of multiple sources[J]. Automation of Electric Power Systems, 2020, 44(2): 123-131.
[13] 雍培, 张宁, 慈松, 等. 5G通信基站参与需求响应:关键技术与前景展望[J]. 中国电机工程学报, 2021, 41(16): 5540-5552. Yong Pei, Zhang Ning, Ci Song, et al. 5G communication base stations participating in demand response: key technologies and prospects[J]. Proceedings of the CSEE, 2021, 41(16): 5540-5552.
[14] 周宸宇, 冯成, 王毅. 基于移动用户接入控制的5G通信基站需求响应[J]. 中国电机工程学报, 2021, 41(16): 5452-5462. Zhou Chenyu, Feng Cheng, Wang Yi. Demand response of 5G communication base stations based on admission control of mobile users[J]. Proceedings of the CSEE, 2021, 41(16): 5452-5462.
[15] 刘雨佳, 樊艳芳. 计及5G基站储能和技术节能措施的虚拟电厂调度优化策略[J]. 电力系统及其自动化学报, 2022, 34(1): 8-15. Liu Yujia, Fan Yanfang. Optimal scheduling strategy for virtual power plant considering 5G base station technology, energy-storage, and energy-saving measures[J]. Proceedings of the CSU-EPSA, 2022, 34(1): 8-15.
[16] 刘战捷. 计及基站备用储能的电力系统经济调度[D]. 济南: 山东大学, 2019.
[17] 麻秀范, 刘子豪, 王颖, 等. 考虑通信负载迁移及储能动态备电的5G基站光伏消纳能力研究[J]. 电工技术学报, 2023, 38(21): 5832-5845. Ma Xiufan, Liu Zihao, Wang Ying, et al. Research on photovoltaic absorption capacity of 5G base station considering communication load migration and energy storage dynamic backup[J]. Transactions of China Electrotechnical Socity, 2023, 38(21): 5832-5845.
[18] 陈泽雄, 张新民, 王雪锋, 等. 分布式光伏电站接入配电网的分布鲁棒优化配置方法[J]. 电力系统保护与控制, 2021, 49(13): 30-42. Chen Zexiong, Zhang Xinmin, Wang Xuefeng, et al. A distributionally robust optimal allocation method for distributed photovoltaic generation stations integrated into a distribution network[J]. Power System Protection and Control, 2021, 49(13): 30-42.
[19] Zare A, Chung C Y, Zhan Junpeng, et al. A distributionally robust chance-constrained MILP model for multistage distribution system planning with uncertain renewables and loads[J]. IEEE Transactions on Power Systems, 2018, 33(5): 5248-5262.
[20] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477. Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two-stage robust optimization method for the whole process of power system restoration considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5462-5477.
[21] 瞿凯平, 苏伟行, 姜宇轩, 等. 基于点估计仿射可调鲁棒优化的含储能电力系统实时调度[J/OL]. 电网技术, 2023: 1-12[2023-03-16]. http://kns.cnki.net/ kcms/detail/11.2410.TM.20221208.1418.003.html. Qu Kaiping, Su Weihang, Jiang Yuxuan, et al. Real-time power dispatch with storages using a point estimate- based affinely adjustable robust optimization[J/OL]. Power System Technology, 2023: 1-12[2023-03-16]. http://kns.cnki.net/kcms/detail/11.2410.TM.20221208.1418.003.html.
[22] 包广清, 周家武, 马明, 等. 考虑风电波动不确定性的两阶段鲁棒优化分频调度方法[J]. 电网技术, 2020, 44(12): 4530-4538. Bao Guangqing, Zhou Jiawu, Ma Ming, et al. Two-stage frequency division robust optimal dispatching method considering wind power fluctuation uncertainty[J]. Power System Technology, 2020, 44(12): 4530-4538.
[23] Xu Xiaoyuan, Yan Zheng, Shahidehpour M, et al. Data-driven risk-averse two-stage optimal stochastic scheduling of energy and reserve with correlated wind power[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1): 436-447.
[24] 段偲默, 苗世洪, 霍雪松, 等. 基于动态Copula的风光联合出力建模及动态相关性分析[J]. 电力系统保护与控制, 2019, 47(5): 35-42. Duan Simo, Miao Shihong, Huo Xuesong, et al. Modeling and dynamic correlation analysis of wind/solar power joint output based on dynamic Copula[J]. Power System Protection and Control, 2019, 47(5): 35-42.
[25] 关磊. 基于蜂窝网络业务空时分布规律的高能效服务机制研究[D]. 北京: 北京邮电大学, 2014.
[26] Yong Pei, Zhang Ning, Liu Yuxiao, et al. Exploring the cellular base station dispatch potential towards power system frequency regulation[J]. IEEE Transactions on Power Systems, 2022, 37(1): 820-823.
[27] 张弘历, 李华强, 杨植雅, 等. 基于潮流增长率泰尔熵的脆弱支路辨识[J]. 电网技术, 2017, 41(7): 2340-2346. Zhang Hongli, Li Huaqiang, Yang Zhiya, et al. Identification of vulnerable line based on the theil entropy of flow growth rate[J]. Power System Technology, 2017, 41(7): 2340-2346.
[28] 李雪. 基于均匀性理论的电网脆弱性评估与应用[D]. 徐州: 中国矿业大学, 2020.
[29] 刘一欣, 郭力, 王成山. 微电网两阶段鲁棒优化经济调度方法[J]. 中国电机工程学报, 2018, 38(14): 4013-4022, 4307. Liu Yixin, Guo Li, Wang Chengshan. Economic dispatch of microgrid based on two stage robust optimization[J]. Proceedings of the CSEE, 2018, 38(14): 4013-4022, 4307.
[30] 郭亮, 王晓卫, 康乾坤, 等. 基于粒子群优化与K-means聚类的配电网5G改造经济性评价方法[J]. 电网与清洁能源, 2022, 38(6): 31-36, 43. Guo Liang, Wang Xiaowei, Kang Qiankun, et al. An economic evaluation method for 5G transformation of distribution network based on particle swarm optimization and K-means clustering[J]. Power System and Clean Energy, 2022, 38(6): 31-36, 43.
[31] 闫涵, 王建华, 范须露, 等. 基于用户停电损失评估的有源配电网灾后供电恢复模型[J]. 电力系统自动化, 2022, 46(5): 31-42. Yan Han, Wang Jianhua, Fan Xulu, et al. Post-disaster power supply restoration model for active distribution network based on customer interruption cost assessment[J]. Automation of Electric Power Systems, 2022, 46(5): 31-42.
[32] 丁浩然, 张博, 唐巍, 等. 考虑源-网-荷-储协同的配电台区分布式光伏消纳能力评估[J]. 供用电, 2023, 40(3): 2-8, 31. Ding Haoran, Zhang Bo, Tang Wei, et al. Evaluation of distributed photovoltaic consumption capacity of distribution station area considering source-network-load-storage collaboration[J]. Distribution & Utilization, 2023, 40(3): 2-8, 31.
Abstract China has vigorously promoted the development of 5G communication in recent years. The number of 5G base stations is growing rapidly, greatly demanding energy storage capacity. At present, China's power supply reliability has improved. Base stations' energy storage is often in a dormant state, thus causing a large amount of energy storage resource waste. It is urgent to study how to use the base station's energy storage resources and play its energy storage value. This paper proposed a 5G base stations' energy storage scheduling model, which jointly participates in the power supply restoration of the distribution network by combining wind-solar output, thus reducing the power loss load of the distribution network.
Firstly, the wind-solar combined output scenario set is established. The optimal Copula function in each period is determined by the Akaike information criterion and squared Euclidian distance, obtained the typical wind-solar output scenario set by sampling and clustering. Second, a backup energy storage model for 5G base stations is established. Different regions communication traffic volume models are established through sine function superposition. The synthetic vulnerability model is established by using the Theil's entropy and the modified Gini coefficient to determine the backup time and the backup storage model of each base station energy storage. Then the schedulable capacity of different base stations' energy storage is obtained. Finally, a two-stage robust optimization model considering the synergistic scheduling of base stations' energy storage and wind-solar output is established with the objective of minimizing the loss of load volume.
Simulations are performed with the improved IEEE 33 node model. The results indicate that the reserve capacity of 5G base station' energy storage is directly proportional to the node vulnerability of the power grid and inversely proportional to the load level. Compared with the traditional fixed backup time, this paper's method can increase the base stations' callable capacity by 317 kW·h. When performing emergency power restoration to the distribution network, it reduced the lost load by 1 609 kW and the cost of lost power by ¥47 208.9 compared to the fixed backup time approach. At the same time, it can use the 5G base station's energy storage for wind power and photovoltaic absorption during the restoration of the power supply in the distribution network. Among them, the wind-light absorption rate increases by 0.007 9, 0.009 3, and 0.181 8 at the moments of t=14 h, t=15 h, and t=16 h, respectively, which in turn reduces the wind and light abandonment rate of the system and improves the distribution network economics.
The following conclusions can be drawn from the simulation analysis: (1)Make full use of base station energy storage, improve the utilization rate of base station energy storage, and reduce the amount of distribution network load loss. At the same time, it can enhance the wind-solar absorption rate and reduce the degree of wind and light abandonment. (2)Combining the vulnerability of the grid node where the base station is located and the communication volume, the backup energy storage is dynamically determined, which can make full use of the energy storage resources of the base station and bring its value into play.
keywords:5G base station, backup energy storage, power supply restoration, corrected Gini coefficient
DOI: 10.19595/j.cnki.1000-6753.tces.230341
中图分类号:TM732
国家自然科学基金(52177114, 61403127)和国网江西省电力有限公司科技项目(521820210005, 521820220016)资助。
收稿日期 2023-03-23
改稿日期 2023-05-17
王晓卫 男,1983年生,博士,副教授,博士生导师,研究方向为配电网故障选线与定位、高阻故障检测、5G在配电网中的应用。E-mail:proceedings@126.com(通信作者)
康乾坤 男,1999年生,硕士研究生,研究方向为5G在配电网中的应用。E-mail:kangqk_edu@126.com
(编辑 赫 蕾)