图1 三种横磁-纵磁触头仿真模型
Fig.1 Three kinds of transverse magnetic-axial magnetic contact models
摘要 触头作为真空灭弧室的核心元件,其灭弧能力会直接影响直流开断过程。该文通过有限元仿真软件建立了三种触头模型,计算了高频电流下触头产生的磁场分布。电流峰值时的触头间隙中心可产生约为21 mT的纵向磁场,横向磁感应强度约为71 mT,纵向磁场分布不均匀。为了进一步提高触头间隙磁场强度以及分布均匀度,在触头模型中增加铁心及改变铁心结构来提升触头产生的磁场强度,基于BP神经网络与智能优化算法联合的方法对触头模型进行优化设计。优化结果显示:当触头的结构参数外触头非径向开槽夹角α为31.8°、外触头内外半径差值Δ为8.3 mm、内触头片半径r为15.2 mm、外触头杯斜槽高度h为16.1 mm、铁心结构开槽宽度d为1.1 mm时,触头间隙中心产生了74.99 mT的横向磁场;电流峰值时刻的触头间隙中心可产生44.02 mT的纵向磁场,不均匀度从优化前的7.44减小到4.67,均匀度得到了较大提升,提高了磁场对真空电弧的调控能力。
关键词:真空灭弧室触头 横向磁场 纵向磁场 算法优化 BP神经网络
“双碳”目标的提出,推动了光伏、风电等新能源的快速发展。直流输电系统作为分布式新能源大规模接入的最佳解决办法[1-2],大量应用会引起短路电流水平不断提升,直流断路器作为故障电流的切除设备将面临巨大的压力。实际中正在使用的断路器包括固态式、机械式和混合式三种,其中机械式断路器因其损耗小、带载能力强的特性被大量应用[3]。SF6断路器因其具有较强的电负性被应用于高压领域,真空断路器通常用于中低压领域。SF6因其具有极强的温室效应(约为CO2的32 400倍)以及对环境危害较大等被限制使用,因此,研制一种开断能力较强的真空断路器成为亟须解决的问题。
触头作为真空断路器的关键元件[4-11],对能否正常开断故障电流具有较大的影响。文献[12]通过实验对横向磁场(Transverse Magnetic Field, TMF)下的真空电弧形态和电弧电压进行了研究分析,结果表明在电流增大到一定值时,真空电弧开始旋转。文献[13]通过仿真对多种横磁触头进行研究,得到螺旋形横磁触头产生的磁感应强度最大,对真空电弧的控制能力最强。文献[14]研究了在纵向磁场(Axial Magnetic Field, AMF)作用下触头材料和触头半径对真空电弧的影响。文献[15]研究了频率对磁场仿真的影响。文献[16]对杯状纵磁触头模型进行磁场仿真计算,结果表明涡流的影响作用在触头中心处最大,在槽口处上方最小。在横磁和纵磁触头被广泛关注的同时,有学者提出了一种将横磁和纵磁相结合的触头。沈阳工业大学的学者设计了一种新型混合磁场的真空灭弧室触头模型,仿真结果证明该触头产生的磁场优于杯状纵磁触头[17];大连理工大学的学者提出一种新型嵌合式AMF- TMF触头结构,并进行了磁场仿真计算和分析[18]。
传统优化方式通常利用磁场仿真模型和算法相结合对触头模型的结构参数进行优化,需要借助大内存的计算机,消耗大量时间进行仿真计算。文献[19-21]采用了BP(back propagation)神经网络和多目标优化算法相结合的方法对模型结构进行联合优化,在保证求解精度的同时大大减少了仿真计算的时间。文献[22-24]通过联合优化的方式,对触头模型的结构参数进行优化,优化前后的磁场对比证明了联合优化这一方法的可行性。
综上所述,本文采用中心复合设计(Central Composite Design, CCD)试验与有限元仿真结合的方式获取数据样本,通过BP神经网络[25]与智能优化算法的联合实现对触头结构的优化设计。对比优化前后触头间隙中心的磁场分布可知,优化后触头间隙中心产生的磁场增强了对真空电弧的调控能力。
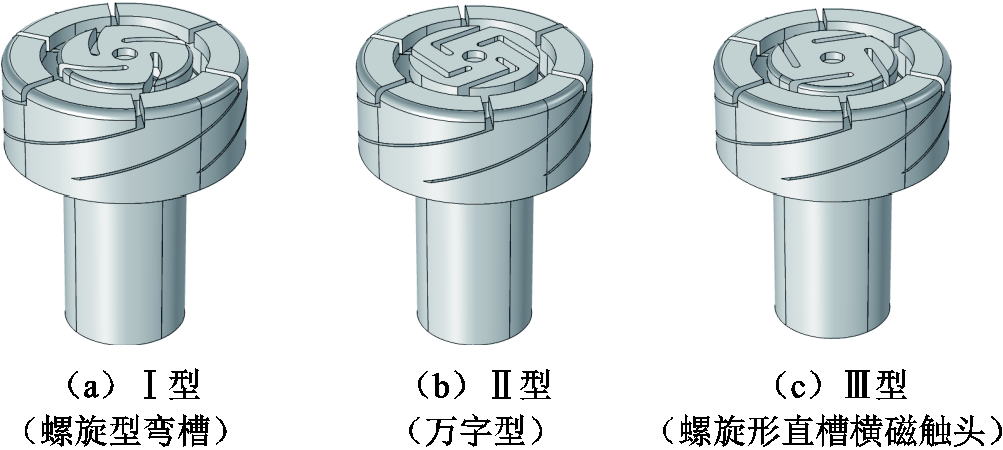
横向磁场和纵向磁场产生的电磁力对真空电弧的作用方向不同,都具有一定的调控作用。本文以杯状纵磁的触头杯和圆环形的触头片组成外触头,建立了以螺旋型弯槽、万字型、螺旋形直槽横磁触头作为内触头的三种横磁-纵磁触头。触头的仿真模型如图1所示。

图1 三种横磁-纵磁触头仿真模型
Fig.1 Three kinds of transverse magnetic-axial magnetic contact models
触头模型的主要设计思想是:横磁触头表面产生的真空电弧受到电磁力的作用,向纵向磁场中旋转和扩散,电弧在纵向磁场的作用下呈扩散态向间隙外运动,可以极大地减少对触头表面的烧蚀[26-28]。触头模型的结构参数见表1。
表1 触头模型的结构参数
Tab.1 Structural parameters of contact model

参数数值 触头杯高度/mm20 外触头片槽数6 外触头片内外径差/mm9 斜槽倾斜角度/(°)25 内触头半径/mm16 触头表面开槽宽度/mm2 触头片厚度/mm4 触头开距/mm12
直流开断过程中的电流过零点由短路电流叠加高频反向电流产生,三维仿真模型在进行磁场仿真计算时的激励源为1 000 Hz、10 kA的高频电流。
三种横磁-纵磁触头模型在触头间隙中心平面产生的横向、纵向磁场分布如图2与图3所示。由图2和图3可知,三种触头在触头间隙中心产生的横向磁感应强度最大值分别为71.51、71.43、71.52 mT,横向磁感应强度的最大值及磁场的分布均匀度较为接近,差距较小;各种触头产生的纵向磁感应强度最大值分别为21.65、21.01、21.80 mT,纵向磁场不均匀度(纵向磁感应强度最大值与最小值的比值)分别为9.45、9.30、8.90,纵向磁场的分布差异较大,其中Ⅲ型触头产生的纵向磁感应强度最大、纵向磁场分布较为均匀。三种触头产生的磁感应强度对比见表2。
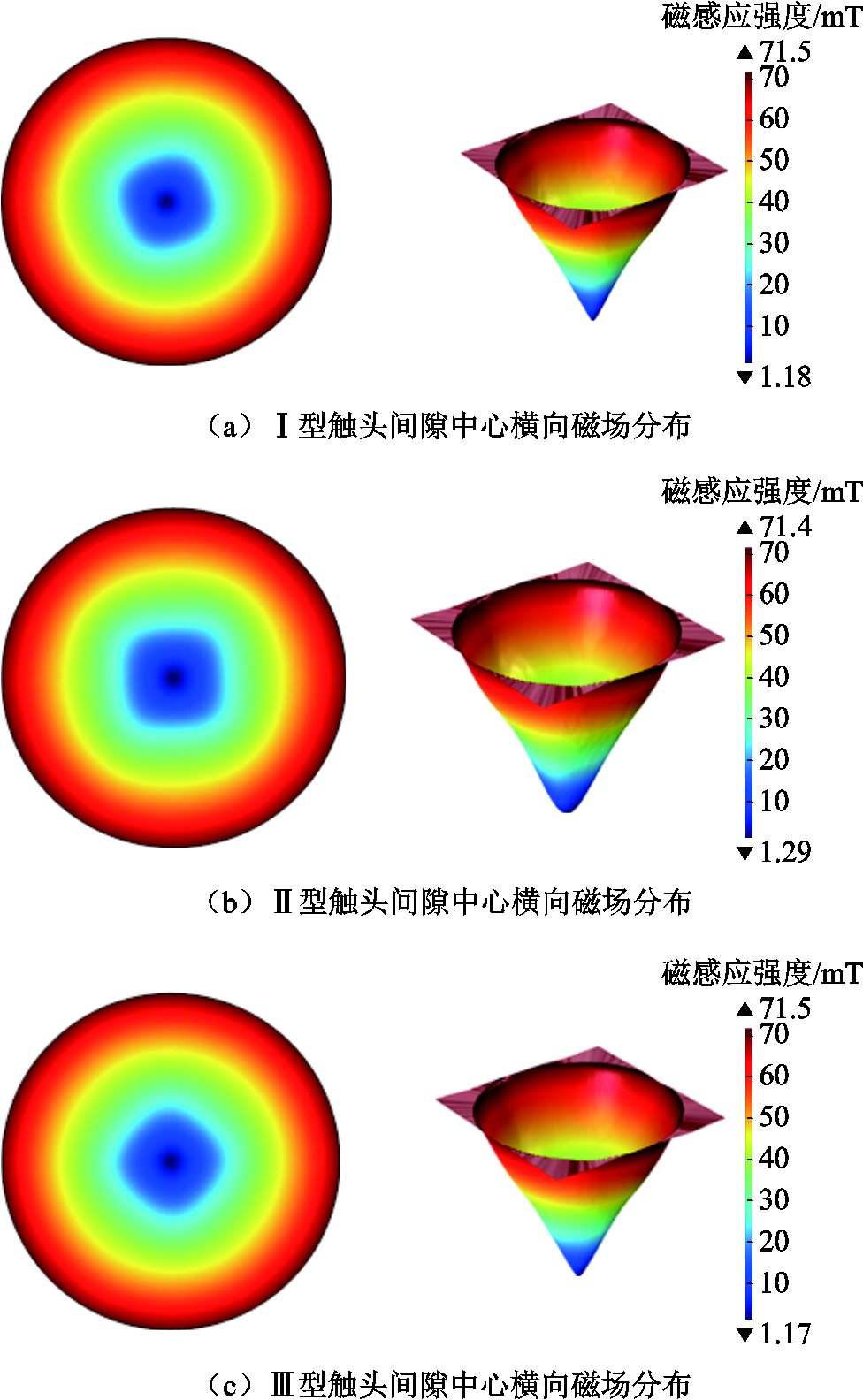
图2 三种触头间隙中心横向磁场分布
Fig.2 Transverse magnetic field distribution of three kinds of contact gap centers
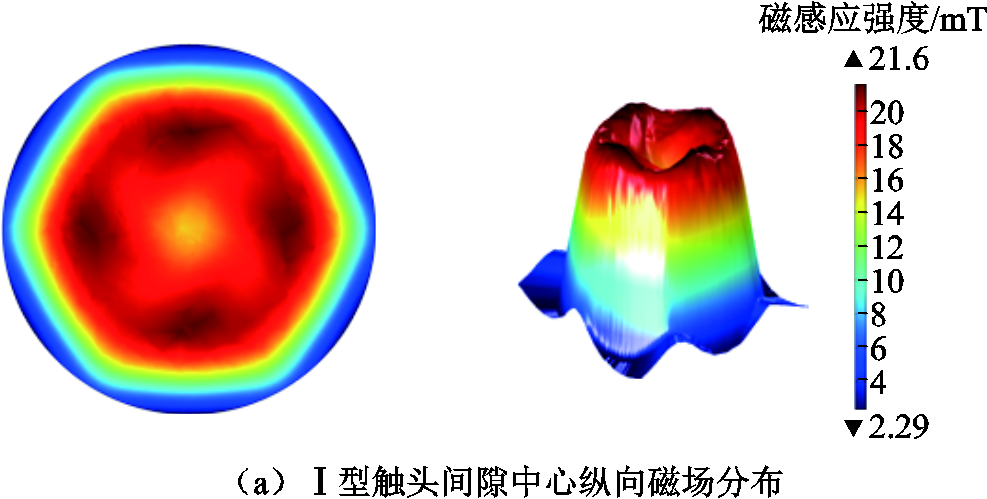
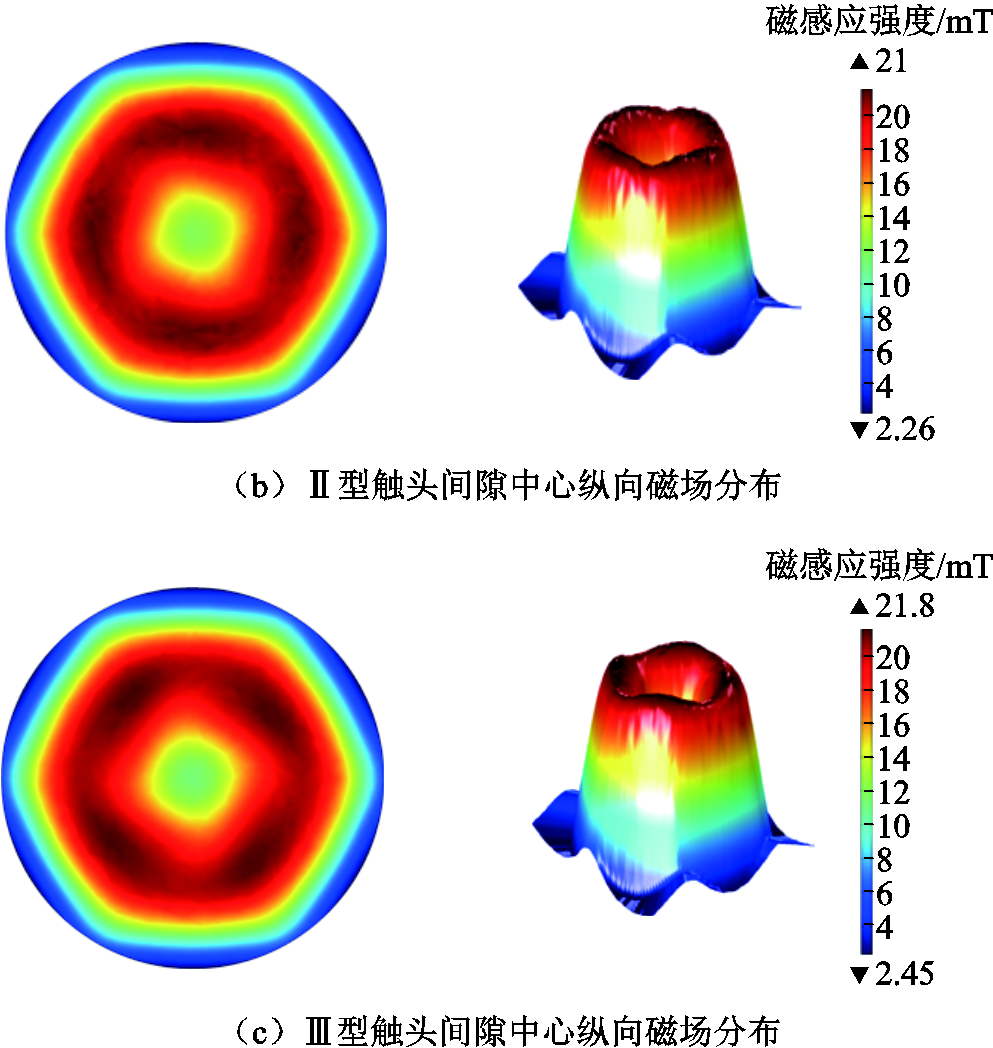
图3 三种触头间隙中心纵向磁场分布
Fig.3 Longitudinal magnetic field distribution of three kinds of contact gap centers
表2 触头间隙中心磁感应强度对比
Tab.2 Comparison of magnetic field intensity in the center of contact gap
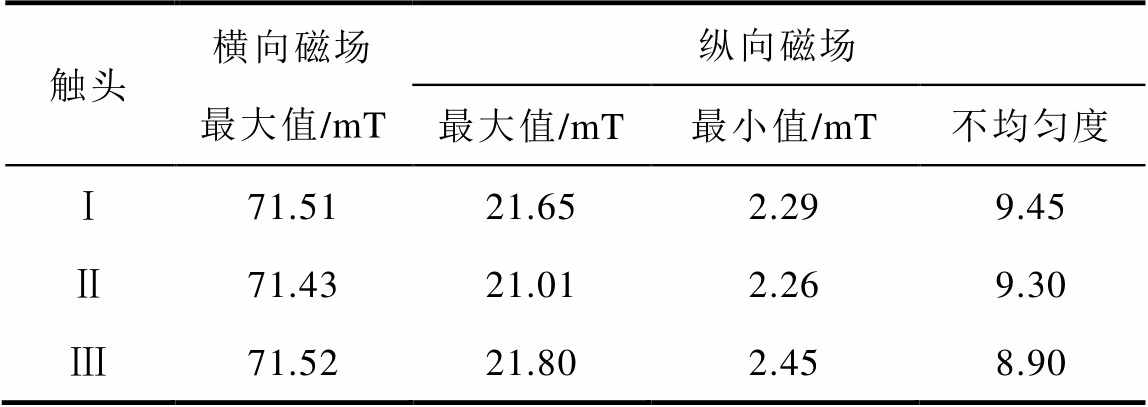
触头横向磁场最大值/mT纵向磁场 最大值/mT最小值/mT不均匀度 Ⅰ71.5121.652.299.45 Ⅱ71.4321.012.269.30 Ⅲ71.5221.802.458.90
为了增强触头间隙产生的磁感应强度、降低纵向磁场分布不均匀度,本文选择产生纵向磁感应强度最大且分布较为均匀的Ⅲ型触头进行结构改进。改进后触头间隙产生的磁场可以更好地对真空电弧进行调控,减少触头表面的烧蚀,提高真空断路器对真空电弧的控制能力。
本文在触头模型中增加了铁心结构,可将原本发散的磁场束缚到一定的空间中,增强触头间隙中的磁感应强度。含铁心触头模型剖面图如图4所示,其中铁心结构的材料为电工纯铁,电导率为1.0×107 S/m,磁导系数为B-H曲线。
触头模型中的铁心结构由上、下两层组成,内部为中空结构。铁心结构包含不开槽和开槽两种,其中开槽结构是在其上、下两层的基础结构上增加24处开槽,通过改变铁心中的涡流分布影响触头间隙中产生的磁场分布。铁心结构如图5所示。
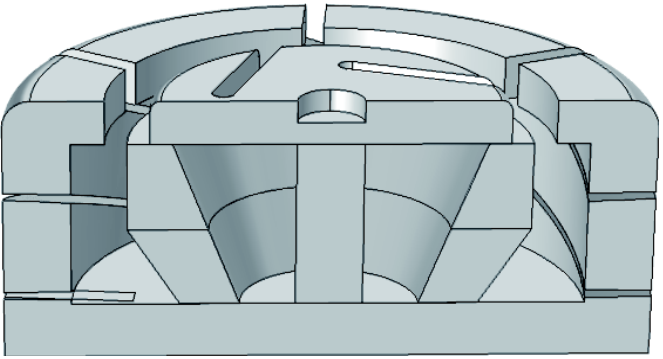
图4 含铁心触头模型剖面图
Fig.4 Section of contact with iron core
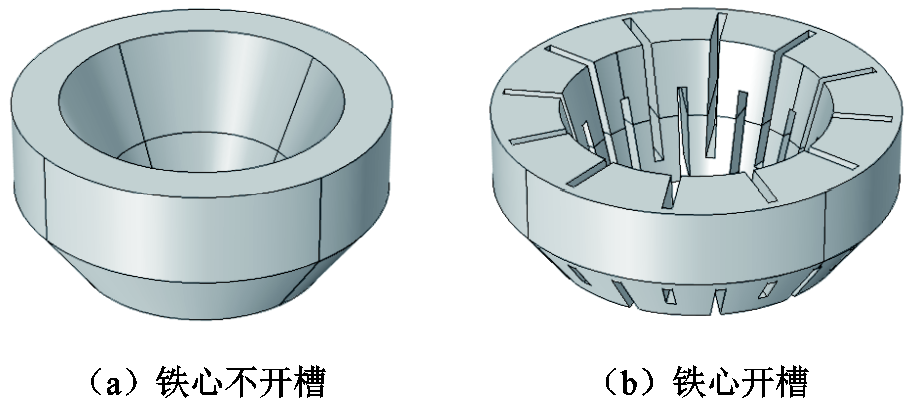
图5 触头模型中的铁心结构
Fig.5 Structure diagram of iron core in contact
触头模型中加入两种铁心后,电流峰值时刻触头间隙中心横向磁场、纵向磁场的二维、三维分布如图6和图7所示。其中铁心不开槽时的横向磁感应强度最大值为72.74 mT,纵向磁感应强度最大值为26.53 mT,纵向磁场分布不均匀度为7.39;铁心开槽后的横向磁感应强度最大值为72.99 mT,纵向磁感应强度最大值为27.02 mT,纵向磁场分布不均匀度为7.44。触头模型改进前后的磁感应强度和纵向磁场分布不均匀度对比见表3。
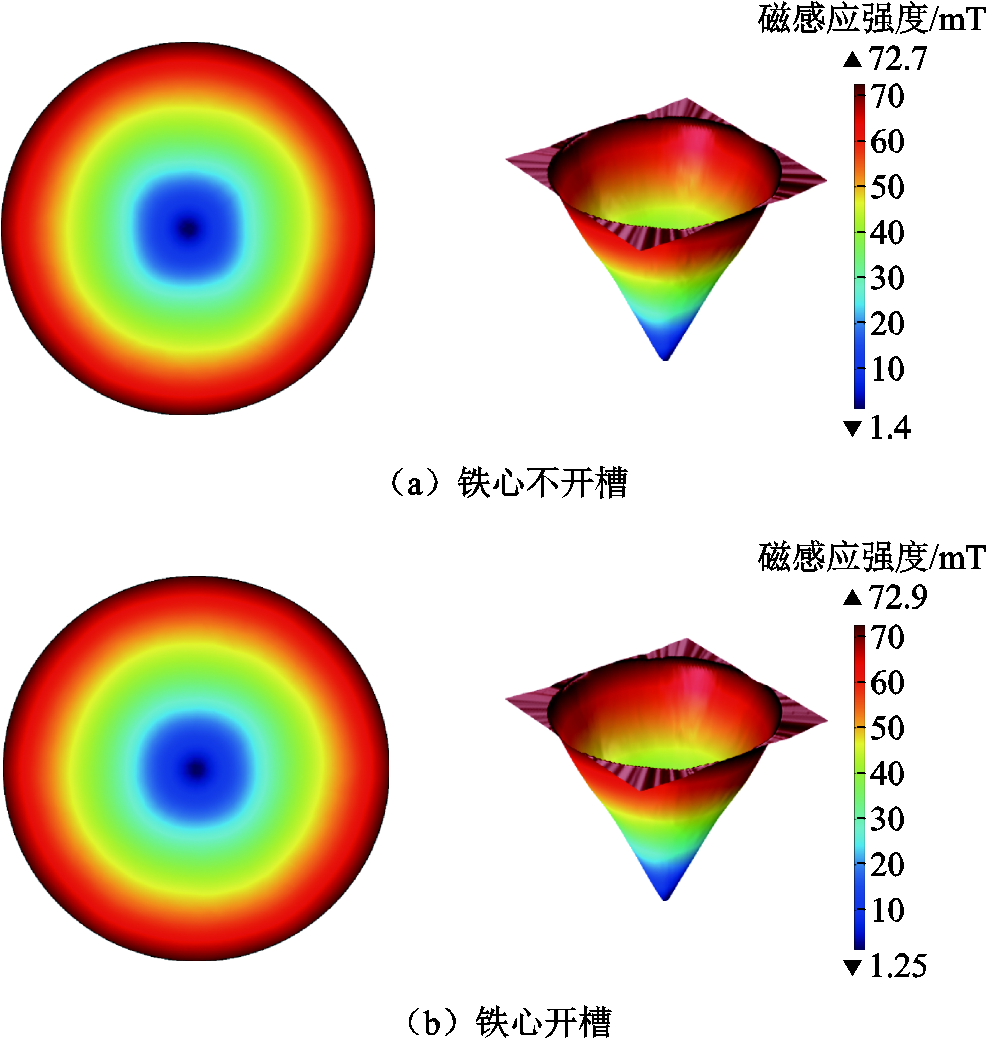
图6 触头加入铁心后间隙中心横向磁场分布
Fig.6 Transverse magnetic field distribution in gap center after contact is added with iron core
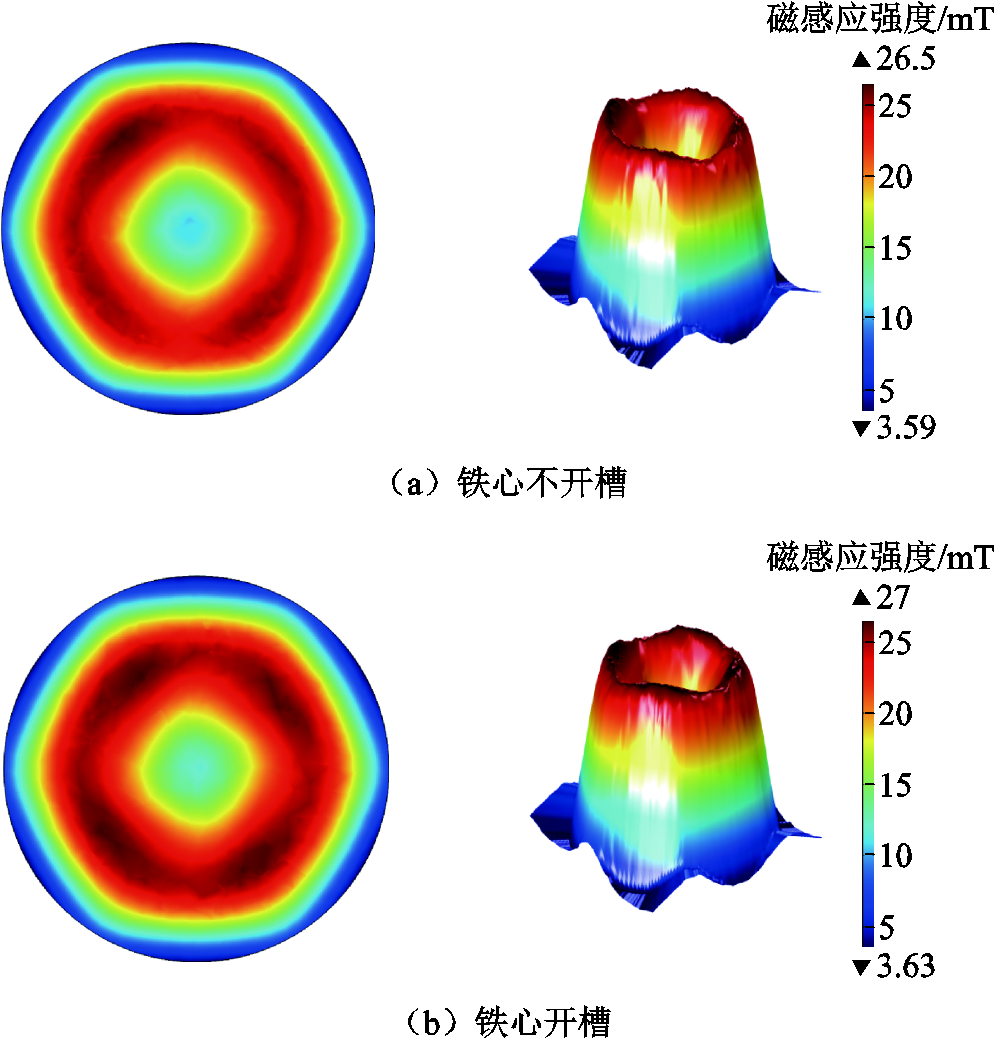
图7 触头加入铁心后间隙中心纵向磁场分布
Fig.7 Longitudinal magnetic field distribution in gap center of contact after adding iron core
表3 触头模型改进前后磁感应强度对比
Tab.3 Comparison of magnetic field intensity before and after improvement of contact model

触头类型横向磁场/mT纵向磁场/mT纵向磁场不均匀度 不加铁心71.5221.808.90 加铁心不开槽72.7426.537.39 开槽72.9927.027.44
与触头模型结构加入铁心前相比,加入铁心后模型纵向磁感应强度均得到了增强,增加了4.73 mT,纵向磁场分布的不均匀度降为7.39,磁场分布更加均匀;横向磁感应强度与加入铁心之前的变化幅度较小,反而增加了1.22 mT。除此之外,铁心开槽对间隙中心产生的横向磁场影响较小,磁感应强度仅增加了0.25 mT,;纵向磁感应强度在开槽和不开槽时相比增加了0.49 mT,但纵向磁场分布的不均匀度由7.39增加到7.44,磁场分布变得更加集中,将抑制真空电弧在触头间隙中的扩散。
触头在加入具有开槽的铁心结构后产生的纵向磁感应强度增幅较小,纵向磁场分布不均匀度仍较大,对真空电弧的调控效果有限。本文采取BP神经网络[29]和多目标智能优化算法相结合的方法对触头进行联合优化,使优化后的触头可产生较强且分布均匀的磁场,提高对触头间隙中真空电弧的调控作用。
带铁心横磁-纵磁触头的优化流程如图8所示。首先本文利用中心复合试验产生输入参数的数据样本,将样本导入有限元仿真软件中获得触头模型的完整数据样本;其次通过BP神经网络算法建立触头的预测模型,在保证精度的前提下极大地减少模型的仿真计算量以及计算需要的时间;最后使用三种多目标智能优化算法进行优化,获得触头模型的Pareto前沿最优非支配解集,再把最优解集的触头结构参数导入有限元仿真模型中进行磁场仿真计算,选择最优的结果作为触头的结构参数。
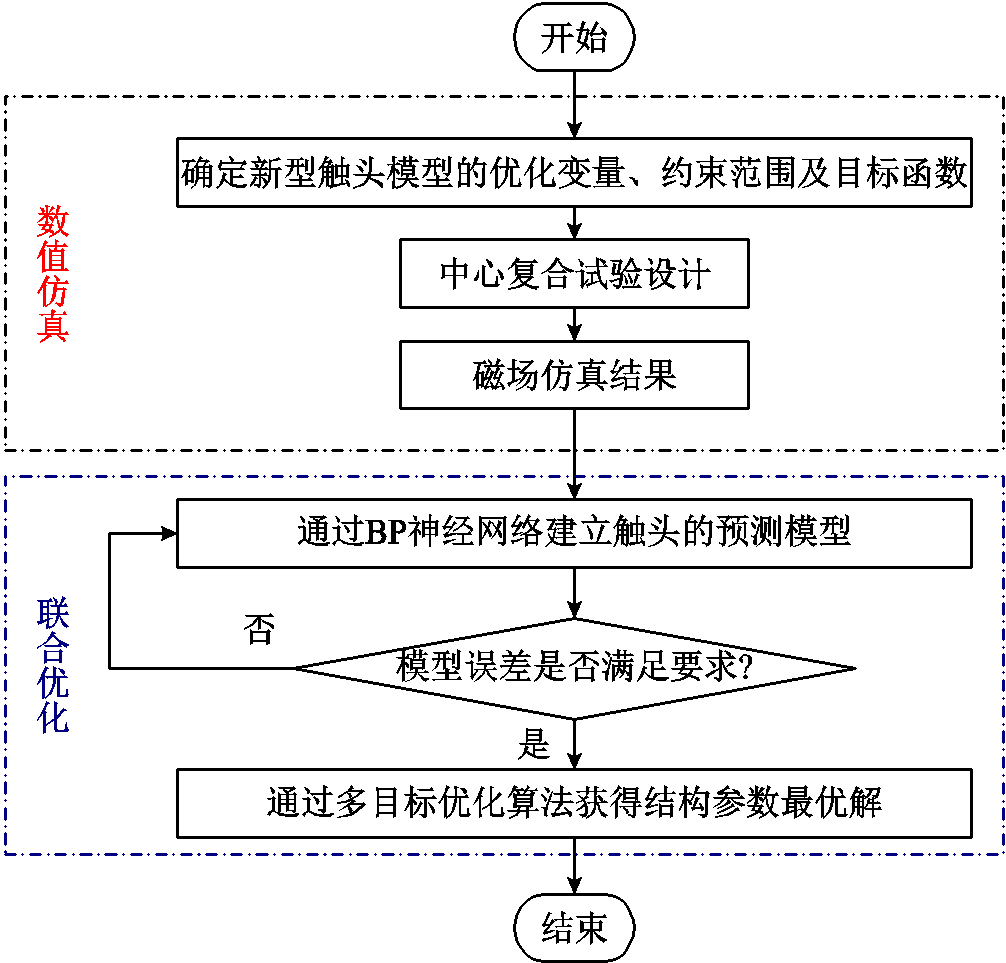
图8 触头优化流程
Fig.8 Flow chart of contact optimization
由2.2节可知,触头在开断高频电流时,触头间隙产生的磁场较弱且分布不够均匀,较难促进真空电弧形态的转变,容易影响开断结果。为了减少仿真计算时间、提高计算效率,本文采用CCD方法与仿真模型结合的方式获得试验设计的数据样本,通过BP神经网络建立预测模型,最后使用优化算法对触头模型的结构参数进行寻优,为触头模型选择最佳的结构参数。
触头模型和开槽铁心参数会影响电流及涡流的流经路径,进而改变触头间隙中的磁场强度和分布,影响真空电弧的扩散以及形态的转变。本文选取外触头非径向开槽夹角α(杯状纵磁触头片表面开槽的旋转角度与触头径向开槽的夹角)、外触头内外半径差值Δ、内触头片半径r、外触头杯斜槽高度h、铁心结构开槽宽度d作为触头模型的参数变量。触头结构优化参数如图9所示。
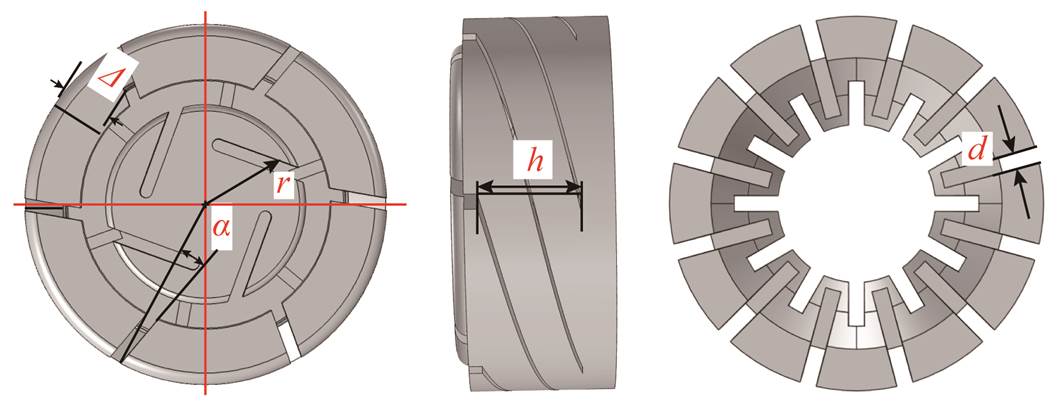
图9 触头结构优化参数
Fig.9 Optimization parameters of contact structure
触头对真空电弧的调控作用原理为:横磁触头表面产生的真空电弧受到电磁力的作用,向纵向磁场中旋转和扩散,在纵向磁场的作用下电弧呈现出扩散态,向间隙外运动。
综上所述,触头间隙中心的磁感应强度最大值和磁场分布的不均匀度将很大程度地影响触头间隙中的等离子体密度,决定弧后介质强度的恢复速度,最终对直流开断产生影响。因此,本文选取纵向磁感应强度最大值M、纵向磁场分布不均匀度h和横向磁感应强度最大值N作为触头模型的输出值。
中心复合试验作为一种经典的方法被广泛使用在工程优化设计领域,能较好地反映模型变量值与输出值之间的联系。本文采用CCD方法建立了试验样本,将数据导入三维仿真模型中进行磁场仿真计算,得到了表4所示的完整样本。
表4 中心复合试验设计样本
Tab.4 Central composite experimental design sample
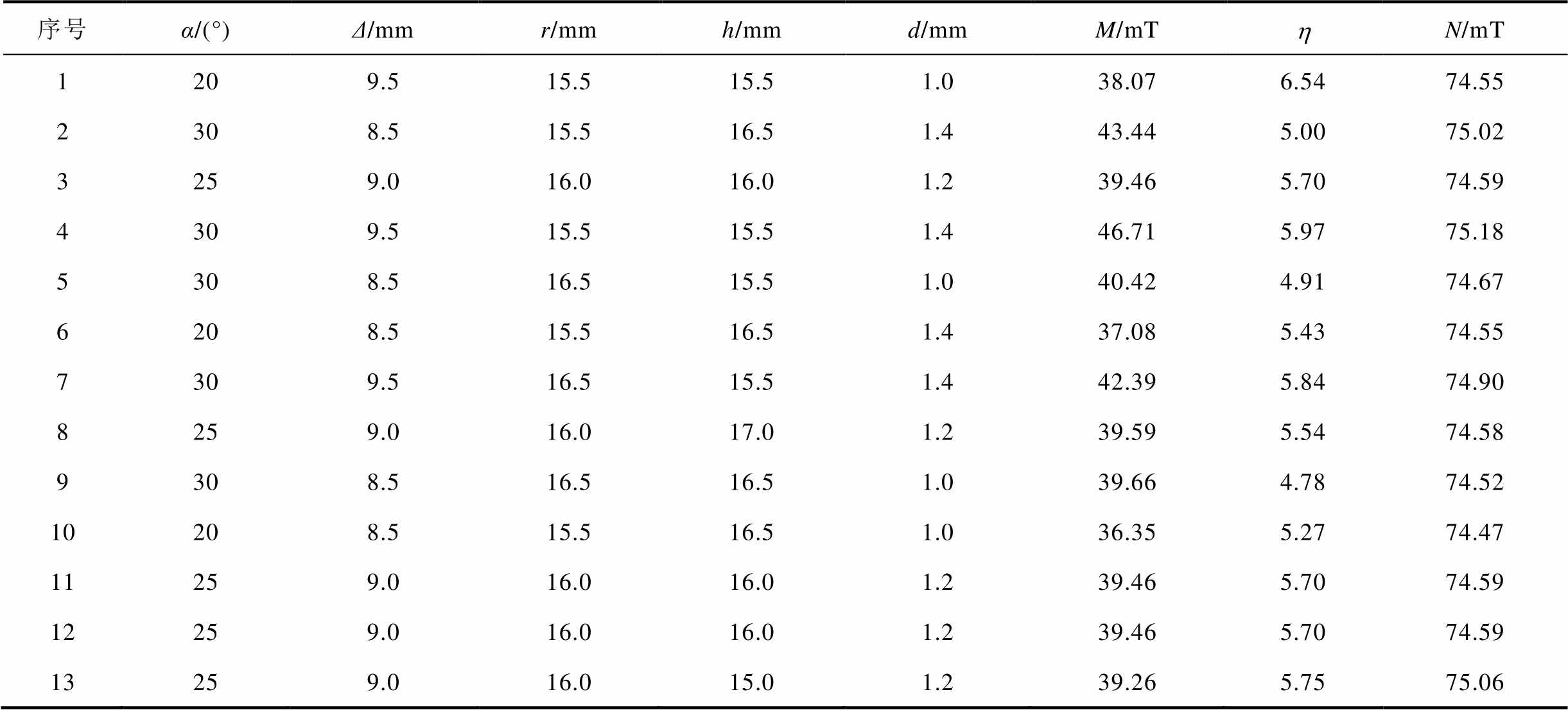
序号α/(°)Δ/mmr/mmh/mmd/mmM/mThN/mT 1209.515.515.51.038.076.5474.55 2308.515.516.51.443.445.0075.02 3259.016.016.01.239.465.7074.59 4309.515.515.51.446.715.9775.18 5308.516.515.51.040.424.9174.67 6208.515.516.51.437.085.4374.55 7309.516.515.51.442.395.8474.90 8259.016.017.01.239.595.5474.58 9308.516.516.51.039.664.7874.52 10208.515.516.51.036.355.2774.47 11259.016.016.01.239.465.7074.59 12259.016.016.01.239.465.7074.59 13259.016.015.01.239.265.7575.06
(续)
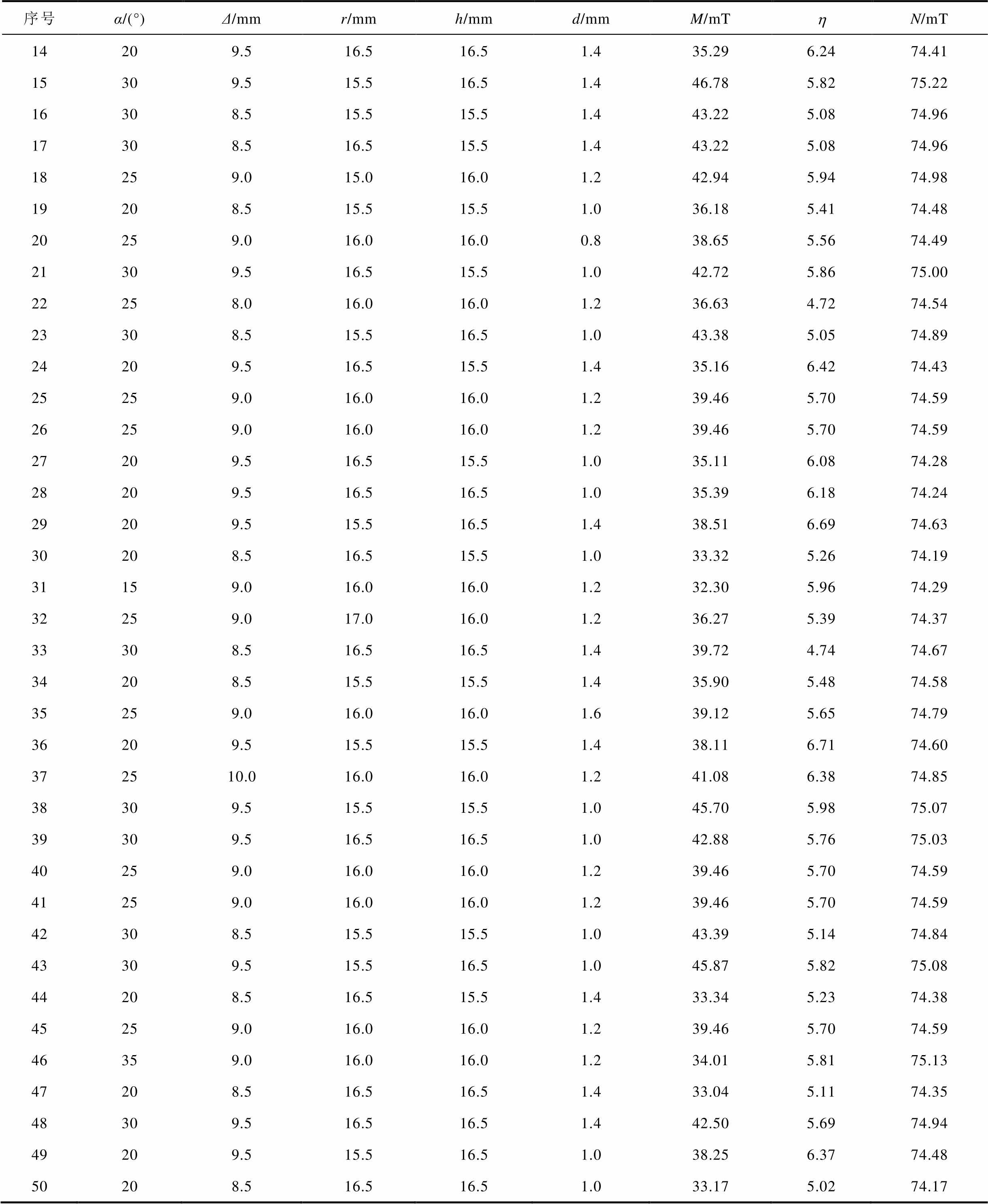
序号α/(°)Δ/mmr/mmh/mmd/mmM/mThN/mT 14209.516.516.51.435.296.2474.41 15309.515.516.51.446.785.8275.22 16308.515.515.51.443.225.0874.96 17308.516.515.51.443.225.0874.96 18259.015.016.01.242.945.9474.98 19208.515.515.51.036.185.4174.48 20259.016.016.00.838.655.5674.49 21309.516.515.51.042.725.8675.00 22258.016.016.01.236.634.7274.54 23308.515.516.51.043.385.0574.89 24209.516.515.51.435.166.4274.43 25259.016.016.01.239.465.7074.59 26259.016.016.01.239.465.7074.59 27209.516.515.51.035.116.0874.28 28209.516.516.51.035.396.1874.24 29209.515.516.51.438.516.6974.63 30208.516.515.51.033.325.2674.19 31159.016.016.01.232.305.9674.29 32259.017.016.01.236.275.3974.37 33308.516.516.51.439.724.7474.67 34208.515.515.51.435.905.4874.58 35259.016.016.01.639.125.6574.79 36209.515.515.51.438.116.7174.60 372510.016.016.01.241.086.3874.85 38309.515.515.51.045.705.9875.07 39309.516.516.51.042.885.7675.03 40259.016.016.01.239.465.7074.59 41259.016.016.01.239.465.7074.59 42308.515.515.51.043.395.1474.84 43309.515.516.51.045.875.8275.08 44208.516.515.51.433.345.2374.38 45259.016.016.01.239.465.7074.59 46359.016.016.01.234.015.8175.13 47208.516.516.51.433.045.1174.35 48309.516.516.51.442.505.6974.94 49209.515.516.51.038.256.3774.48 50208.516.516.51.033.175.0274.17
由表4可知,触头间隙中心平面的纵向磁感应强度最大值和最小值分别为46.78 mT和32.30 mT,纵向磁场分布不均匀度的最大值和最小值分别为6.71和4.72,触头间隙中心平面最大和最小的横向磁感应强度值分别为75.22 mT和74.17 mT。相比较而言,触头和铁心结构的改变对纵向磁感应强度和纵向磁场分布不均匀度的影响较大,对横向磁感应强度的影响较小。
在建立触头的预测模型中选择杯状纵磁外触头的非径向开槽夹角α、外触头片的内外半径差值Δ、内触头片半径r、杯状纵磁外触头杯的斜槽高度h、铁心结构开槽宽度d为模型的输入值,纵向磁场强度最大值M、磁场分布不均匀度h和横向磁场强度最大值N为输出,得到通过BP神经网络建立的触头预测模型的输入输出结构如图10所示。其中预测模型的输入层数为5,隐含层数为10,输出层数为3。
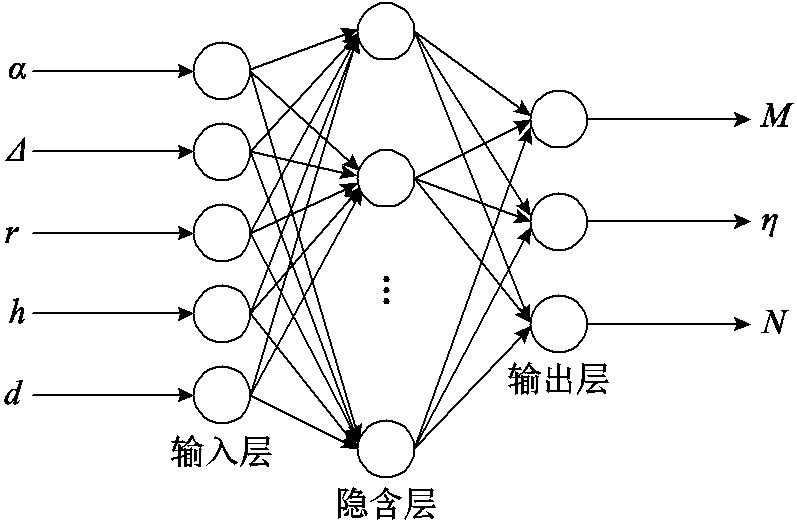
图10 神经网络模型
Fig.10 Neural network model
本文通过编程软件完成了BP神经网络模型的训练和预测。其中将数据样本中的前40组数据作为训练集,剩余数据去除重复数据后用作测试集。图11所示为预测模型输出值与期望值的对比,预测模型的误差如图12所示。
由图11和图12可知,预测模型的预测值与期望值之间的误差较小,根据式(1)可计算出纵向磁感应强度最大值、纵向磁场不均匀度和横向磁感应强度最大值的方均根误差分别为0.357 mT、0.048、0.019 mT。根据BP神经网络建立预测模型可较好地反映带铁心横磁-纵磁触头模型结构变量与纵向磁感应强度、纵向磁场分布不均匀度和横向磁感应强度之间的关系。
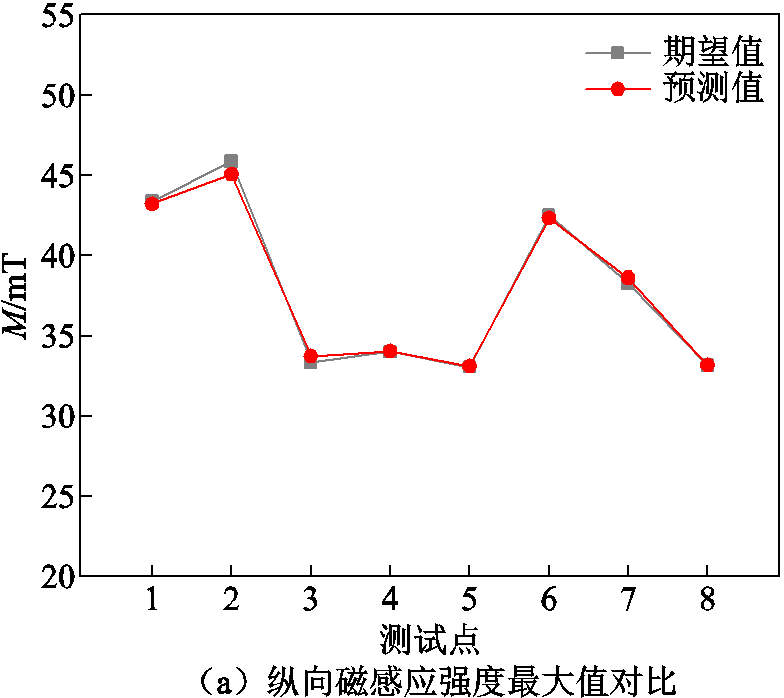
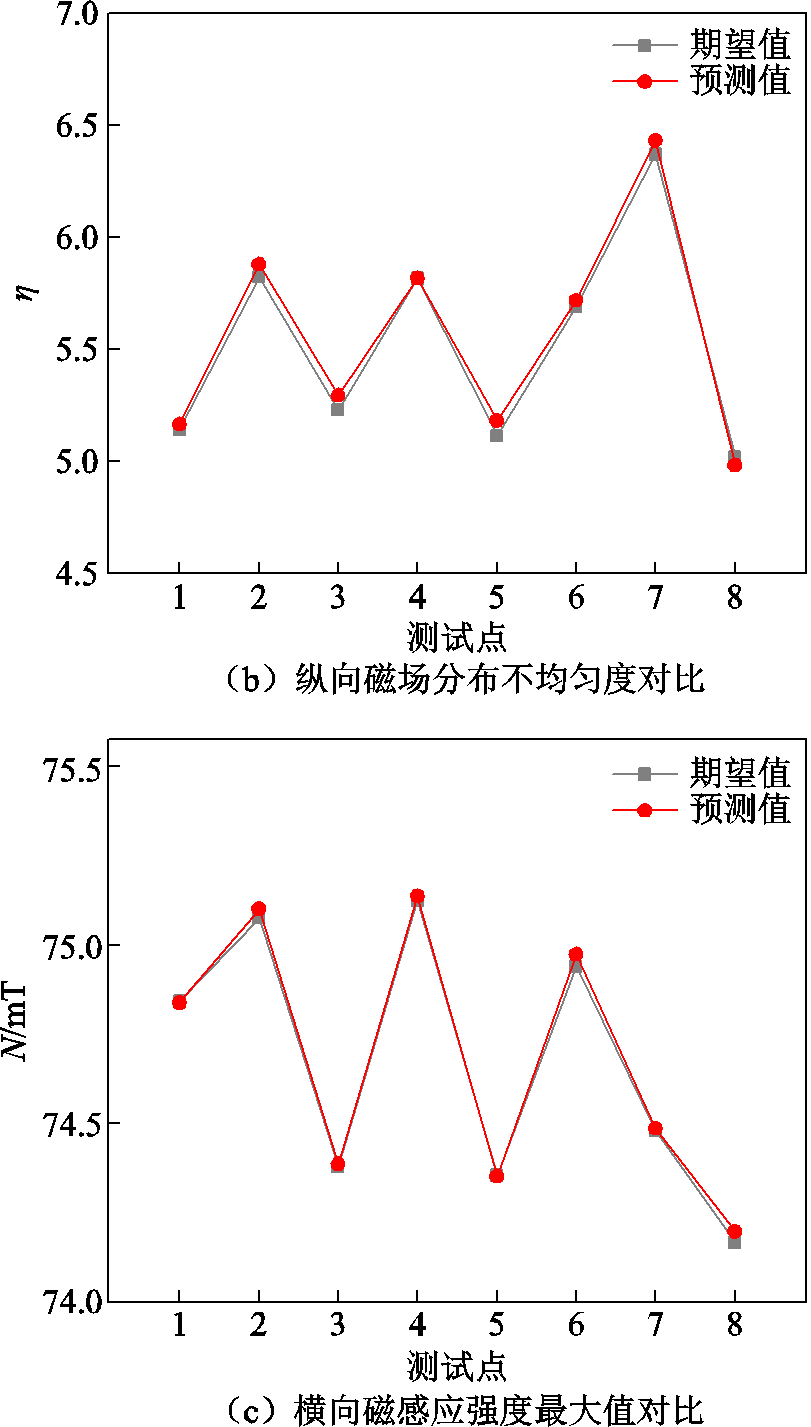
图11 BP神经网络模型预测与期望对比
Fig.11 Comparison between BP neural network model prediction and expected output
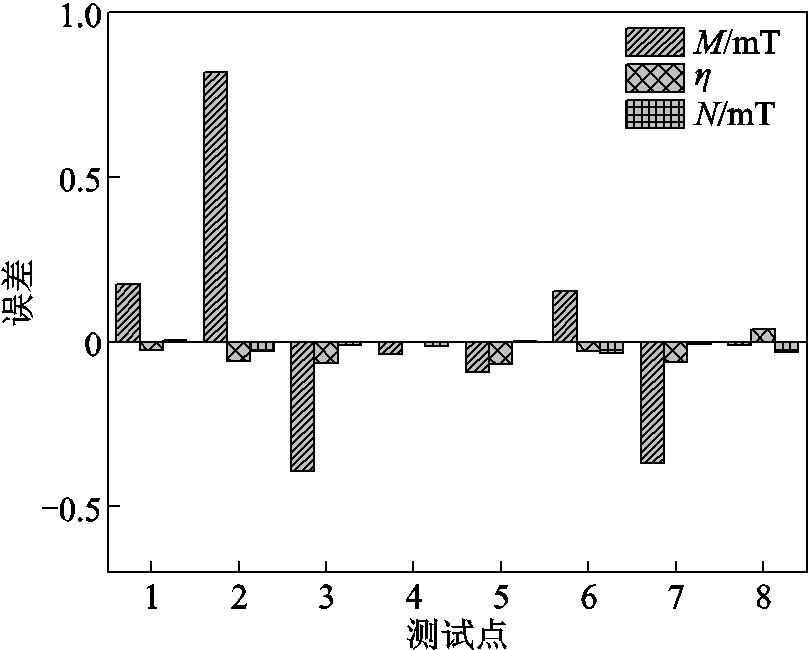
图12 模型预测误差
Fig.12 Model prediction error
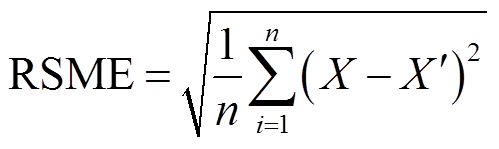 (1)
(1)
式中,RMSE为测试点的方均根误差;n为测试点个数;X为期望值;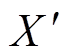 为BP神经网络模型的输出值。
为BP神经网络模型的输出值。
多目标粒子群算法(Multiple Objective Particle Swarm Optimization, MOPSO)、第二代遗传算法(Non-dominated Sorting Genetic Algorithm Ⅱ, NSGA-Ⅱ)和非支配领域免疫算法(Nondominated Neighbor Immune Algorithm, NNIA)作为多目标优化算法的典型代表[30-32],在其他领域中被广泛应用。本文将通过三种算法同时对触头模型进行优化,最终选择最佳的结构参数。
触头间隙中心的磁感应强度越大,对真空电弧等离子体的控制能力越强,同时纵向磁场的均匀分布可帮助调控真空电弧的形态。在改变触头结构参数时,触头间隙中的横向磁感应强度变化较小,但其产生的电磁力可使真空电弧高速旋转到纵向磁场中进行扩散,因此触头的优化目标设置为间隙中心纵向磁感应强度最大值M、纵向磁场分布不均匀度η和横向磁感应强度最大值N。确定触头模型结构优化为式(2)所示的三目标优化问题。
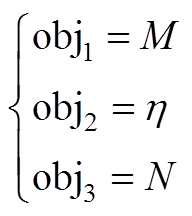 (2)
(2)
结合工程的设计经验,带铁心横磁-纵磁触头结构参数优化变量取值范围为
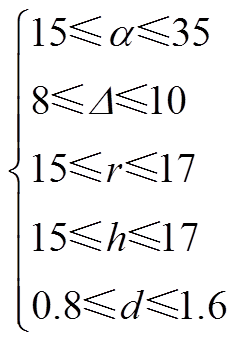 (3)
(3)
三种优化算法的种群规模设置为50,在100次迭代后得到Pareto前沿非支配解集如图13所示,三种算法的优化结果对比见表5。为了提高真空灭弧室的灭弧能力,以磁感应强度较大且分布不均匀度小为目标对结果进行比较,选择NNIA优化后得到的最优解集作为杯状纵磁触头的最优结构,即将α=31.8°、Δ=8.3 mm、r=15.2 mm、h=16.1 mm、d=1.1 mm的结构参数作为杯状纵磁触头的优化结果,导入触头仿真模型中进行计算,得到横向磁场和纵向磁场分布如图14所示。
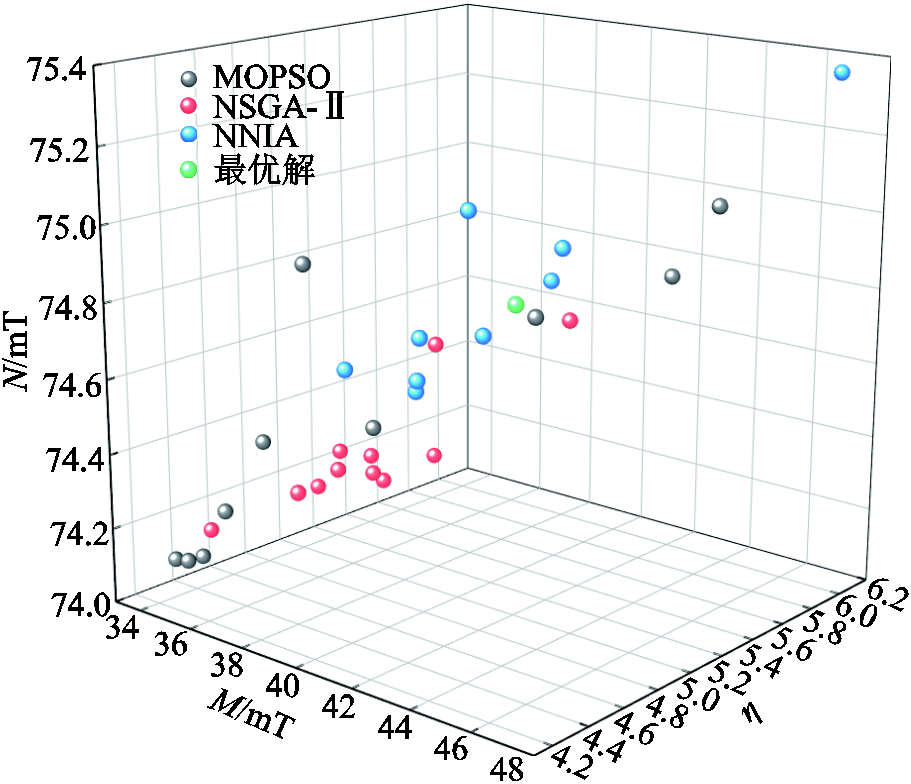
图13 Pareto前沿非支配解集
Fig.13 Pareto frontier non-dominated solution set
表5 三种算法的优化结果对比
Tab.5 Comparison of optimization results of three algorithms

算法α/(°)Δ/mmr/mmh/mmd/mmM/mThN/mT NSGA-Ⅱ29.98.915.415.50.944.605.4974.87 NNIA31.88.315.216.11.144.024.6774.99 MOPSO26.28.716.216.41.338.875.0574.66 优化前25.09.016.016.01.027.027.4472.99
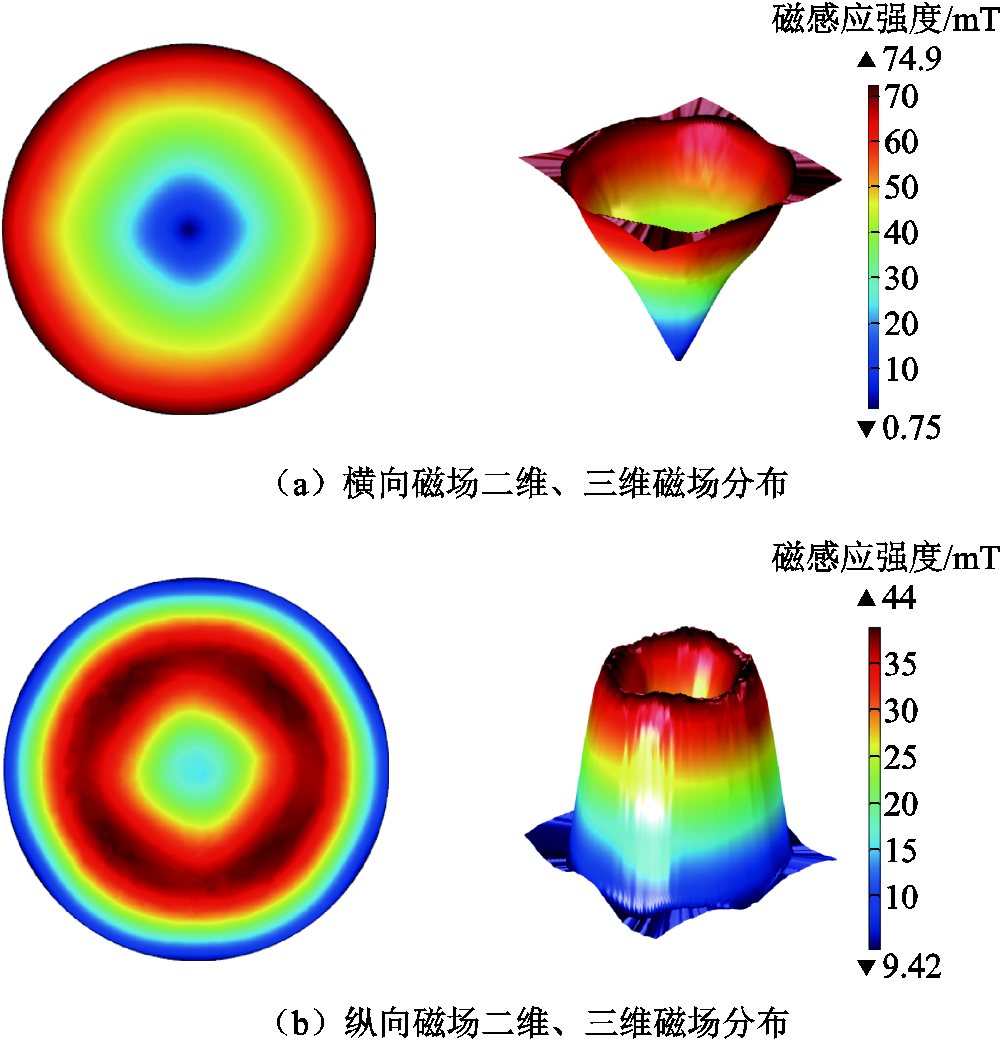
图14 优化后触头间隙中心磁场分布
Fig.14 Magnetic field distribution of contact gap center after optimization
与优化前相比,优化后触头间隙中心产生的横向磁感应强度增加了2.00 mT,纵向磁感应强度值增加了17.00 mT,纵向磁场分布不均匀度由7.44降到了4.67。横磁-纵磁触头结构优化后,真空电弧在横向磁场电磁力的驱动下做高速旋转运动,电弧能量分布均匀,减小了对触头表面的烧蚀,在强度较高且分布更加均匀的纵向磁场中进行扩散。因此,结构优化后横磁-纵磁触头产生的磁场可加强对真空电弧形态的调控作用。
带铁心横磁-纵磁触头结构参数优化后,间隙中心产生的磁感应强度较高且分布较为均匀,因此本文将通过间隙中心的磁场分布情况与优化后的杯状纵磁触头进行对比分析。优化后的杯状纵磁触头磁场分布如图15所示,两种触头结构优化后的结果对比见表6。

图15 优化后的杯状纵磁触头磁场分布
Fig.15 Optimized magnetic field distribution diagram of cup-shaped longitudinal magnetic contact
表6 两种触头结构优化后的结果对比
Tab.6 Comparative analysis of the results of two kinds of contact structure optimization

触头模型M/mTN/mT 带铁心横磁-纵磁44.024.6774.99 杯状纵磁43.413.3966.40
结合图14和图15的磁场分布可知,杯状纵磁触头产生的横向磁场在中心位置呈正六边形,在向边缘移动的过程中呈现出六角形,与带铁心横磁-纵磁触头产生的横向磁场相比,磁场分布不均匀,对真空电弧的扩散有一定程度的影响。杯状纵磁触头在结构优化后产生的纵向磁感应强度较强,纵向磁场分布不均匀度也较小,但仍存在6个磁感应强度较高的峰值区域,真空电弧在磁场作用下将会在峰值区域聚集,不利于真空电弧的均匀分布;带铁心横磁-纵磁触头优化后在间隙中心产生的纵向磁场呈现圆形分布,减少了6个纵向磁感应强度较高的峰值区域,能够有效抑制真空电弧在触头表面聚集,推动真空电弧形态的转变。因此,带铁心横磁-纵磁触头产生的磁场可以更好地对真空电弧进行调控,帮助直流断路器进行开断。
本文建立了三种横磁-纵磁触头的有限元仿真模型,通过优化算法与BP神经网络模型相结合的方式对触头结构进行了联合优化,得到以下结论:
1)建立了三种横磁-纵磁触头模型,使用有限元仿真软件计算了间隙中心的磁场分布情况。仿真结果表示:三种触头产生的横向磁感应强度差异较小,都在71.5 mT附近,纵向磁感应强度均大于21 mT,纵向磁场分布不均匀度的差异较大,分别为9.45、9.30、8.90,其中Ⅲ型触头产生的纵向磁感应强度较高且分布较为均匀。
2)在触头模型中增加铁心结构后进行磁场仿真计算,结果表明:铁心结构使横向磁感应强度增加了1.22 mT,纵向磁感应强度最大值从21.80 mT增加为26.53 mT,纵向磁场分布不均匀度由8.90减小为7.39,磁场分布变得更加均匀;铁心结构的开槽处理会使横向、纵向的磁感应强度有小幅增加,但纵向磁场的分布不均匀度由7.39增加至7.44。整体而言,铁心结构的加入可将原本发散的磁场束缚到一定的空间中,增强了触头间隙中的磁感应强度,优化了磁场分布情况,加强了对真空电弧的调控。
3)通过BP神经网络和三种优化算法结合的方式对触头模型的结构参数进行联合优化,优化后的触头模型在间隙中心产生了74.99 mT的横向磁场,纵向磁感应强度达到了44.02 mT,磁场分布不均匀度下降为4.67。同优化前相比,横向磁场和纵向磁感应强度都有所增加,纵向磁场分布更加均匀,可以加强对真空电弧的调控。
4)通过杯状纵磁触头与带铁心横磁-纵磁触头在结构优化后产生的磁场进行对比分析得到,带铁心横磁-纵磁触头产生的磁场可以更好地对真空电弧进行调控,帮助直流断路器进行开断。
参考文献
[1] 温家良, 吴锐, 彭畅, 等. 直流电网在中国的应用前景分析[J]. 中国电机工程学报, 2012, 32(13): 7-12, 185. Wen Jialiang, Wu Rui, Peng Chang, et al. Analysis of DC grid prospects in China[J]. Proceedings of the CSEE, 2012, 32(13): 7-12, 185.
[2] Zhang Shao, Tseng K J, Vilathgamuwa D M, et al. Design of a robust grid interface system for PMSG-based wind turbine generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(1): 316-328.
[3] 贾申利, 史宗谦, 王立军. 真空断路器用于直流开断研究综述[J]. 高压电器, 2017, 53(3): 12-16. Jia Shenli, Shi Zongqian, Wang Lijun. Review on the research of vacuum circuit breaker for DC breaking[J]. High Voltage Apparatus, 2017, 53(3): 12-16.
[4] 于海. 直流断路器的现状及发展[J]. 电力工程技术, 2018, 37(2): 114-120. Yu Hai. The status and development of DC circuit breaker[J]. Electric Power Engineering Technology, 2018, 37(2): 114-120.
[5] 王灿, 杜船, 徐杰雄. 中高压直流断路器拓扑综述[J]. 电力系统自动化, 2020, 44(9): 187-199. Wang Can, Du Chuan, Xu Jiexiong. Review of topologies for medium-and high-voltage DC circuit breaker[J]. Automation of Electric Power Systems, 2020, 44(9): 187-199.
[6] 徐殿国, 刘瑜超, 武健. 多端直流输电系统控制研究综述[J]. 电工技术学报, 2015, 30(17): 1-12. Xu Dianguo, Liu Yuchao, Wu Jian. Review on control strategies of multi-terminal direct current transmission system[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 1-12.
[7] 陈名, 徐敏, 黎小林, 等. 高压直流断路器开断试验方法综述[J]. 高压电器, 2018, 54(7): 37-43. Chen Ming, Xu Min, Li Xiaolin, et al. Review of HVDC circuit breaker breaking test method[J]. High Voltage Apparatus, 2018, 54(7): 37-43.
[8] 卫思明. 高压直流断路器关键技术研究[D]. 北京: 华北电力大学, 2015. Wei Siming. Research on key technologies of high voltage DC circuit breaker[D]. Beijing: North China Electric Power University, 2015.
[9] 李培源. 低压直流真空断路器换流回路拓扑与灭弧室结构优化设计[D]. 天津: 天津工业大学, 2020.
[10] 张梓莹, 梁德世, 蔡淼中, 等. 机械式高压直流真空断路器换流参数研究[J]. 电工技术学报, 2020, 35(12): 2554-2561. Zhang Ziying, Liang Deshi, Cai Miaozhong, et al. Research on commutation parameters of mechanical HVDC vacuum circuit breaker[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2554-2561.
[11] Franck C M. HVDC circuit breakers: a review identifying future research needs[J]. IEEE Transactions on Power Delivery, 2011, 26(2): 998-1007.
[12] 朱立颖, 武建文.横向磁场下中频真空电弧形态及电弧电压特性[J]. 中国电机工程学报, 2011, 31(1): 131-137.Zhu Liying, Wu Jianwen. Modes of intermediate-frequency vacuum arc and characteristics of arc VoltageUnder transverse magnetic field[J]. Proceedings of the CSEE, 2011, 31(1): 131-137.
[13] 杨兰索, 李敏, 王晓琴, 等. 真空开关触头结构形式对磁感应强度和电磁力的影响[J]. 高压电器, 2015, 51(5): 193-198. Yang Lansuo, Li Min, Wang Xiaoqin, et al. Effects of vacuum switchgear contact structure on magnetic flux density and electromagnetic force[J]. High Voltage Apparatus, 2015, 51(5): 193-198.
[14] 蒋原, 武建文. 纵向磁场中触头材料和直径对中频真空电弧特性的影响[J]. 中国电机工程学报, 2015, 35(20): 5367-5374. Jiang Yuan, Wu Jianwen. Effects of contact materials and diameters on characteristics of intermediate-frequency vacuum arc in axial magnetic field[J]. Proceedings of the CSEE, 2015, 35(20): 5367-5374.
[15] 蒋原, 李擎, 夏丽娜, 等. 中频条件下真空灭弧室的纵向磁场仿真[J]. 电工技术学报, 2021, 36(11): 2424-2432. Jiang Yuan, Li Qing, Xia Lina, et al. Simulation of axial magnetic field in vacuum arc interrupters at intermediate frequency[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2424-2432.
[16] 刘志远, 王季梅, 王政, 等. 杯状纵磁真空灭弧室三维纵向磁场及涡流的有限元分析[J]. 高压电器, 2000, 36(2): 18-21. Liu Zhiyuan, Wang Jimei, Wang Zheng, et al. Finite element analysis on 3D axial magnetic field and eddy current in cup shape axial magnetic vacumm[J]. High Voltage Apparatus, 2000, 36(2): 18-21.
[17] 钱奇锋. 基于直流真空断路器的混磁触头结构设计及磁场分析[D]. 沈阳: 沈阳工业大学, 2017. Qian Qifeng. Design and analysis on hybrid magnetic contact structure and magnetic field for DC vacuum circuit breaker[D]. Shenyang: Shenyang University of Technology, 2017.
[18] 蔡淼中. 基于直流真空断路器的复合触头磁场调控[D]. 大连: 大连理工大学, 2020. Cai Miaozhong. Magnetic arc control of composite contact based on DC vacuum circuit breaker[D]. Dalian: Dalian University of Technology, 2020.
[19] 张缙, 刘智, 刘意, 等. 基于智能算法的双面散热SiC功率模块多目标优化设计[J]. 电工技术学报, 2023, 38(20): 5515-5529. Zhang Jin, Liu Zhi, Liu Yi, et al. Research on multi-objective optimization design of double-sided cooling SiC power module based on intelligent algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5515-5529.
[20] 张春雷, 张辉, 叶佩青. 高霍尔位置检测精度的圆筒型永磁同步直线电机设计[J]. 电工技术学报, 2022, 37(10): 2481-2490. Zhang Chunlei, Zhang Hui, Ye Peiqing. Design of tubular permanent magnet synchronous linear motor by reliability-based robust design optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2481-2490.
[21] 颜华, 张馨, 王伊凡. 基于RBF神经网络和遗传算法的ERT传感器优化[J]. 沈阳工业大学学报, 2021, 43(3): 295-300. Yan Hua, Zhang Xin, Wang Yifan. ERT sensor optimization based on RBF neural network and genetic algorithm[J]. Journal of Shenyang University of Technology, 2021, 43(3): 295-300.
[22] 臧谦, 贾伯岩, 范辉, 等. 基于磁场与电弧互作的真空断路器触头结构设计[J]. 高压电器, 2022, 58(12): 42-48. Zang Qian, Jia Boyan, Fan Hui, et al. Design of contact structure of vacuum circuit breaker based on interaction between magnetic field and arc[J]. High Voltage Apparatus, 2022, 58(12): 42-48.
[23] 丁璨, 李江, 袁召, 等. 基于NSGA-II和BP神经网络的杯状纵磁触头结构优化设计[J]. 电工技术学报, 2022, 37(23): 6074-6082. Ding Can, Li Jiang, Yuan Zhao, et al. Structural optimization design of cup-shaped longitudinal magnetic contact based on NSGA-Ⅱ and BP neural network[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6074-6082.
[24] 董华军, 温超阳, 孙鹏, 等. 基于正交实验新型真空灭弧室触头磁场仿真与参数优化设计[J]. 电工技术学报, 2022, 37(21): 5598-5606. Dong Huajun, Wen Chaoyang, Sun Peng, et al. Simulation and optimization of the contact magnetic field of a new type of vacuum interrupter based on orthogonal experiment[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5598-5606.
[25] Wang Zheng, Wang Bo, Liu Chun, et al. Improved BP neural network algorithm to wind power forecast[J]. The Journal of Engineering, 2017, 2017(13): 940-943.
[26] 宋晓川. 基于人工过零的直流开断中真空电弧动态特性的研究[D]. 西安: 西安交通大学, 2013. Song Xiaochuan. Research on the dynamic characteristics of vacuum arc in DC interruption based on artificial current zero[D]. Xi′an: Xi′an Jiaotong University, 2013.
[27] 董华军, 杨海军, 郭英杰, 等. 一种具有横纵磁场的新型真空灭弧室触头三维磁场仿真[J]. 电工技术学报, 2015, 30(5): 111-118. Dong Huajun, Yang Haijun, Guo Yingjie, et al. 3-D magnetic field simulation of a new-type contact with TMF-AMF for vacuum interrupters[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 111-118.
[28] 修士新, 刘紫熹, 王婷, 等. 一种铁芯式杯状横磁真空灭弧室触头: CN106531543A[P]. 2017-03-22.
[29] Wang Jing, Fang Jiandong, Zhao Y. Visual prediction of gas diffusion concentration based on regression analysis and BP neural network[J]. The Journal of Engineering, 2019, 2019(13): 19-23.
[30] Han Honggui, Zhang Linlin, Hou Ying, et al. Adaptive candidate estimation-assisted multi-objective particle swarm optimization[J]. Science China Technological Sciences, 2022, 65(8): 1685-1699.
[31] 赵士伟, 卓力, 王素玉, 等. 一种基于NNIA多目标优化的代价敏感决策树构建方法[J]. 电子学报, 2011, 39(10): 2348-2352, 2396. Zhao Shiwei, Zhuo Li, Wang Suyu, et al. A multi-objective optimization based constructing cost-sensitive decision trees method[J]. Acta Electronica Sinica, 2011, 39(10): 2348-2352, 2396.
[32] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
Abstract As the core component of vacuum interrupter, the contact's arc extinguishing ability will directly affect the DC breaking process. The existing contact models usually rely on transverse magnetic field or axial magnetic field to regulate the vacuum arc and help the vacuum circuit breaker to break. In this paper, a type of contact which can generate both transverse magnetic field and axial magnetic field is designed. The main design idea of the contact is that the vacuum arc generated on the surface of the transverse magnetic contact rotates and diffuses into the axial magnetic field under the action of electromagnetic force, and the arc changes from the concentrated state to the diffused state under the action of the axial magnetic field. The vacuum arc in the diffused state can greatly reduce the ablation on the contact surface and improve the service life of the contact.
Firstly, three contact models are established by finite element simulation software, and the magnetic field distribution generated by the contact under high frequency current is calculated. At the peak of current, the contact gap center can generate an axial magnetic field of about 21 mT, the transverse magnetic field intensity is about 71 mT, and the axial magnetic field distribution is uneven.
Secondly, due to the increase of iron core structure, the original divergent magnetic field can be bound into a certain space, and the magnetic field intensity in the contact gap can be enhanced. In this paper, an iron core structure is added between the inner and outer contacts, and the iron core structure is slotted. The simulation structure shows that after adding the iron core, the transverse magnetic field intensity increases by 1.22 mT, the maximum axial magnetic field intensity increases from 21.80 mT to 26.53 mT, the magnetic field intensity increases by 4.73 mT, the axial magnetic field distribution unevenness decreases from 8.90 to 7.39, and the magnetic field distribution becomes more uniform. Adding grooving treatment in the iron core structure increases the transverse magnetic field intensity in the contact gap by 0.25 mT, and the maximum axial magnetic field intensity also slightly increases by 0.49 mT, but the uneven distribution of axial magnetic field increases from 7.39 to 7.44, which is not conducive to the diffusion of vacuum arc.
Finally, in order to further improve the strength and distribution uniformity of the magnetic field in the contact gap, this paper proposes a joint optimization method based on BP neural network and multi-objective intelligent optimization algorithm to optimize the contact model, establishes a BP neural network model with α, Δ, r, h and d as inputs and M, η and N as outputs, and optimizes the contact model through multi-objective intelligent optimization algorithm. The optimization results show that when the contact structure parameters α is 31.8°, Δ is 8.3 mm, r is 15.2 mm, h is 16.1 mm, and d is 1.1 mm, a transverse magnetic field of 74.99 mT is generated in the contact gap center. The axial magnetic field of 44.02 mT can be generated at the contact gap center of the peak current, and the unevenness is reduced from 7.44 before optimization to 4.67, which greatly improves the uniformity and improves the ability of magnetic field to regulate vacuum arc.
keywords:Vacuum interrupter contact, transverse magnetic field, axial magnetic field, algorithm optimization, BP neural network
DOI:10.19595/j.cnki.1000-6753.tces.230474
中图分类号:TM561
国家自然科学基金面上项目资助(52177143)。
收稿日期 2023-04-13
改稿日期 2023-05-24
丁 璨 男,1982年生,博士(后),讲师,研究方向为高压电器设计、模拟及实验。E-mail:dingcan@ctgu.edu.cn
袁 召 男,1985年生,博士(后),副研究员,研究方向为电气设备设计、仿真模拟与优化。E-mail:hustyuanzhao@qq.com(通信作者)
(编辑 李 冰)