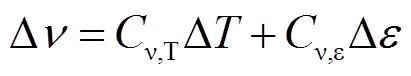（1）
摘要 变压器绕组的温度分布一直是电网运行人员重点关注的对象。与传统传感器相比，分布式光纤传感具有抗电磁干扰能力强、可实现分布式测量等优势，其中布里渊光时域分析技术（BOTDA）的性能稳定，适用于大多数场景，但BOTDA的空间分辨率为m级，难以分辨绕组运行中的局部热点。该文从布里渊散射增益谱的机理入手，利用双峰拟合算法，并结合对异常峰值曲线的边沿分析，提出了一种在不增加系统硬件复杂度的基础上提升BOTDA空间分辨率的方法，以满足局部热点检测要求。通过对光纤沿线不同位置、不同热点长度及不同热点温度下的模拟试验验证了该方法的有效性，在实验室条件下可将准确传感的热点长度提升至原空间分辨率的一半以内。基于变压器实际绕组的局部升温试验，实现了绕组异常热点的精确定位和长度感知，并准确解调了绕组局部热点的温度，进一步验证了该方法的实际可行性和检测优越性，温度相对误差控制在5%以内，为提高变压器绕组温度在线监测的经济性和可行性提供新的思考，同时也为变压器绕组局部故障的提前感知和预警提供了新的思路。
关键词：光纤传感 变压器 绕组热点温度 布里渊光时域分析技术 空间分辨率
变压器作为电网中电压转换、电能输送的关键设备，价格昂贵，一旦发生事故，将造成巨大的经济损失，甚至导致人员伤亡。因此，时刻监测变压器的运行状态对保证供电可靠性、提高电能质量具有重大意义。变压器内部绝缘问题是造成变压器故障的主要原因之一，大多数绝缘故障均以局部异常温升为前兆，监测绕组热点温度对变压器的绝缘老化程度判断及提高变压器带负载能力具有指导意义[1-4]。国内外学者对变压器绕组的温度监测方法进行了大量的研究，目前主要分为间接计算法和直接测量法两大类。间接计算法应用最为广泛的是IEEE Std C57.91标准中推荐的热点温度计算模型和国标GB/T 15164推荐的电力变压器绕组温度模拟计算模型[5]，还有将数值建模应用于变压器温度场的分布计算[6-10]；直接测量法主要包括利用红外测温仪、热电偶或热电阻的传统测量法和利用荧光光纤温度传感器[11]、光纤光栅传感器[12-13]等新型手段的光纤测温法。
分布式光纤传感技术由于具有绝缘性能强、电磁兼容能力强及能实现分布式测量等优点[14]，可以弥补传统传感器工作时的缺陷，近年来已有研究将其应用于变压器绕组的温度监测。文献[15]在一台35 kV油浸式变压器上采用单模光纤和多模光纤结合绕制的方法实现了光纤在变压器内部的成功布置，并通过了变压器的出厂试验，在温升试验中实现了变压器温度的分布式监测。文献[16]考虑光纤与绕组电磁线的稳定紧密结合，提出了嵌入式的光电复合电磁线结构与实现工艺，在一台10 kV变压器的温度监测中表现出良好性能。文献[17]改造了一台110 kV油浸式变压器，以探究不同的光纤布置方式，并通过温升试验实现了变压器在运行过程中的绕组温度分布监测，且稳定性较高。文献[18]基于分布式光纤传感技术，在温升试验中获得了精细的绕组温度分布，研究发现绕组内部温度分布呈周期性波动，且与空间位置和散热有较强的相关性。
分布式光纤传感技术中，布里渊光时域分析技术（Brillouin Optical Time Domain Analysis, BOTDA）的传感距离长、空间分辨率高、测量精度高[19-20]，在实际应用中远远超过其他光纤传感技术。传统的BOTDA受限于声子的寿命，整个系统的空间分辨率最高只能达到1 m[21-22]。对于变压器绕组来说，若运行中存在小于空间分辨率的局部热点，则会导致在线监测温度时出现较大的误差，不能及时发现潜在风险、预警局部故障。
本文从布里渊散射增益谱的机理入手，利用双峰拟合算法，结合对异常峰值曲线的边沿分析，提出一种在不增加系统硬件复杂度的基础上提升BOTDA空间分辨率的方法——基于BOTDA的异常峰值边沿分析（BOTDA Peak Edge Analysis, BOTDA-PEA），在实验室条件下从位置、长度、温度三个方面研究该方法的性能并验证其有效性。通过变压器实际绕组的局部升温试验，准确定位绕组热点并解调温度，验证该方法的实际可行性和检测优越性，为预警变压器绕组局部故障、提高绕组温度在线监测的经济性和可行性提供新的思考。
BOTDA是利用光纤的受激布里渊散射光频移变化量与温度和应变呈线性关系来实现分布式传感[23-25]，表示为
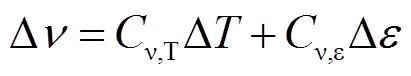（1）
式中，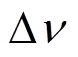
为布里渊频移变化量；
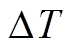和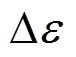
分别为光纤初始设定条件下的温度和应变变化量；Cn,T和Cn,e分别为光纤布里渊频移变化的温度和应变系数，当入射光波长为1 553.8 nm时，Cn,T=1.1 MHz/℃，Cn,e=0.048 3 MHz/με[25]。
传统的BOTDA存在空间分辨率和测量精度互相制约的问题，空间分辨率被限制在1 m。要想提高空间分辨率，脉冲光的脉宽越窄越好。但受声子寿命的影响，脉宽小于10 ns时会在光纤中出现严重的非线性效应，布里渊增益谱随之展宽，探测误差增大，不利于布里渊频移测量精度的提高。
光脉冲沿着光纤传播时与探测光相互作用，可得到整条光纤的布里渊增益谱，但光纤上某一点对应的布里渊增益谱是由有效脉冲长度对应的空间分辨率的每一段光纤产生的增益总和构成[26-28]。
假定沿线光纤的布里渊频移一致，忽略光纤衰减损耗，则光纤中产生的布里渊增益谱形状呈洛伦兹型，具体方程为
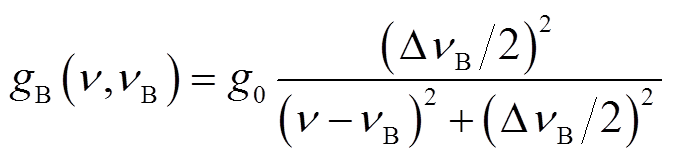（2）
式中，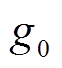
为布里渊增益谱的峰值功率；
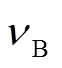为布里渊频移；
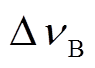为布里渊增益谱的半峰全宽（Full Width at Half Maximum, FWHM）。
当光纤存在温度或应变扰动事件时，忽略光纤衰减损耗，实际测量的布里渊增益谱[29]为
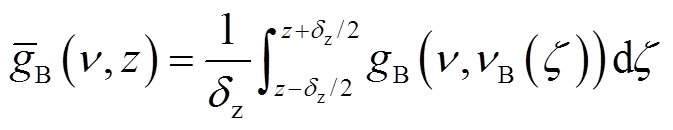（3）
式中，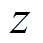
为沿传感光纤的位置；
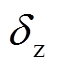为空间分辨率。在BOTDA传感系统中，空间分辨率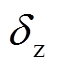通常取决于入射脉冲宽度t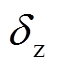，=ct/(2n)，其中，
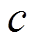为光波速度，
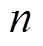为光纤折射率，一般单模光纤纤芯的折射率为1.46。
若将对应空间分辨率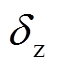按照BOTDA传感系统的采样分辨率l进行划分，则有dz=2ml，
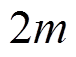为划分的总段数，可以得到离散形式为
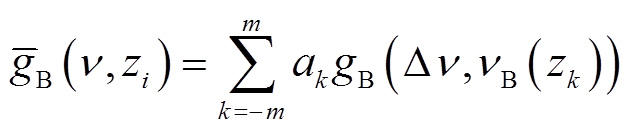（4）
式中，ak为第k段对应的权重因子；zi为沿传感光纤的位置，zi+1-zi=l。
当光纤感知存在局部热点时，背景光纤与过热点间过渡区域的布里渊散射谱不再是单一的洛伦兹型谱线，而是存在双峰的散射谱。若仍对异常的布里渊散射谱进行单峰洛伦兹拟合，则会导致拟合效果达不到精度要求，布里渊频移存在巨大偏差，不能准确地反映温度变化量的实际值。由1.2节可知，布里渊频移的误差是因为背景光纤段和过热段的共同贡献造成布里渊增益谱从标准洛伦兹型曲线上失真。失真程度既与过热段的实际长度有关，又与过热段和背景光纤段的布里渊频移差有关，即过热段的实际温度变化量。
假设背景光纤段的布里渊频移保持不变，过热段的温度在短时间内保持均匀，忽略光纤损耗，利用双洛伦兹型曲线拟合过渡区域的双峰布里渊散射谱，具体为
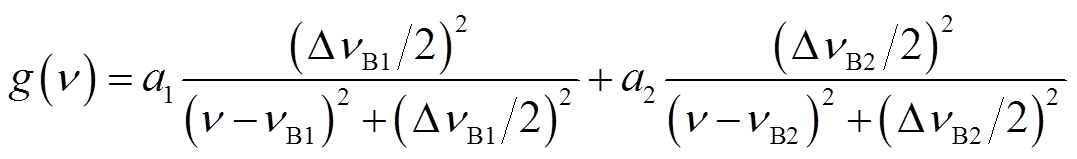（5）
式中，a1和a2分别为背景光纤段和过热段的强度因子；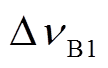
和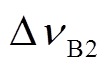
分别为各自布里渊增益谱的FWHM；
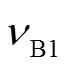和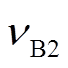
分别为对应的布里渊频移。
利用非线性最小二乘算法中的列文伯格-马夸尔特（Levenberg-Marquardt, LM）算法分别对过渡区域的散射谱现象进行单峰洛伦兹拟合和双峰洛伦兹拟合，示例结果如图1所示。可以明显看出，双峰拟合曲线与实际现象更加吻合，主、次两峰分别对应着不同段的温度信息。
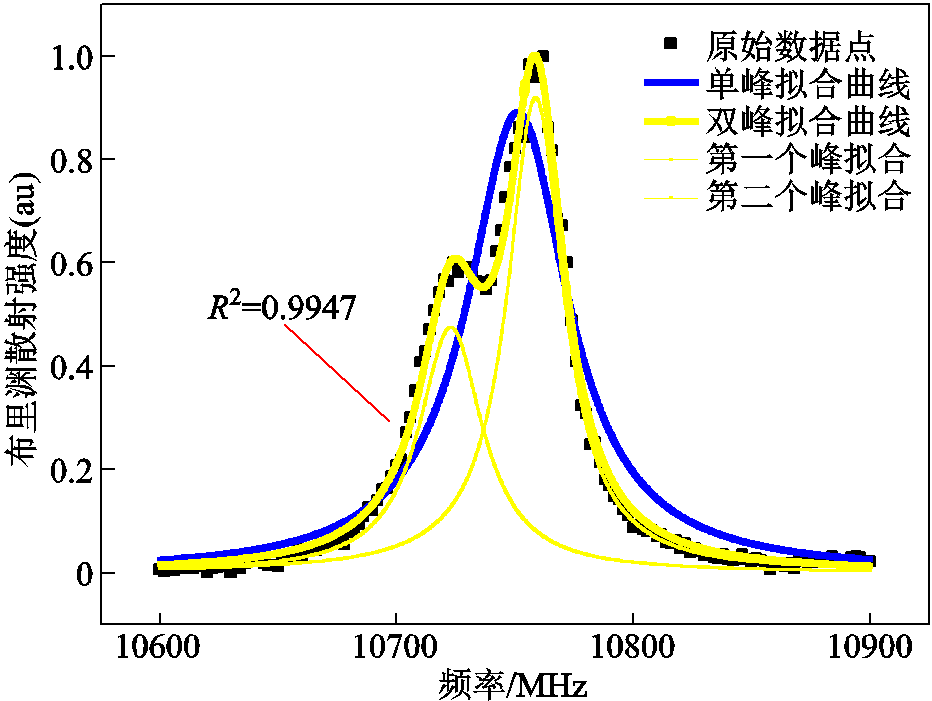
图1 单/双峰洛伦兹拟合曲线
Fig.1 Unimodal/bimodal Lorentz fitting curve
当出现的扰动事件的实际长度小于空间分辨率时，过渡区域点的布里渊散射谱就会包含异常扰动信息和正常背景光纤的散射信息，导致其不是标准的洛伦兹型谱线，也就是散射谱发生了畸变，此时采用双峰拟合算法来提取两种频移信息。BOTDA传感系统中包含热点段的光纤沿线布里渊散射谱示意图如图2所示。
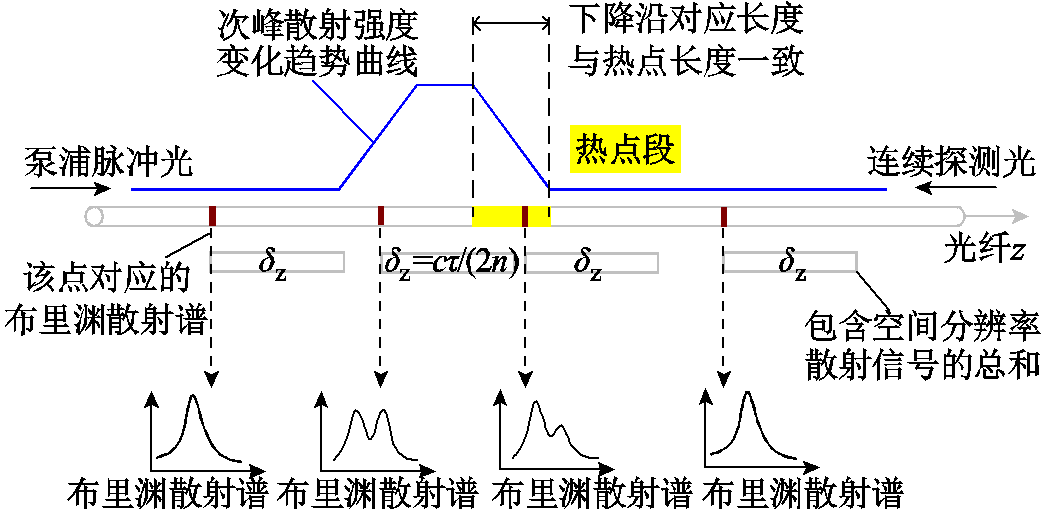
图2 BOTDA传感系统中包含热点段的光纤沿线布里渊散射谱示意图
Fig.2 Schematic diagram of Brillouin scattering spectra along optical fibers containing hot spots in BOTDA sensor system
图2显示了当热点段附近点的布里渊散射谱包含热点段或者其部分区域时，散射谱会出现双峰现象。双峰区域中次峰对应的洛伦兹型曲线代表热点段的温度信息，主峰对应的布里渊频移与单峰区域的布里渊频移基本一致，反映光纤中未受干扰的部分。因此，当热点段的长度小于空间分辨率时，借助双峰区域中布里渊频移异于单峰区域的次峰的拟合信息来判断热点段的布里渊频移和实际长度，以达到在不增加系统硬件复杂度的基础上提高BOTDA传感系统空间分辨率的目的。
图2中蓝色曲线为次峰洛伦兹拟合后的散射强度随光纤位置变化的趋势。通过分析异常峰值曲线的边沿，当采样分辨率足够高时，次峰强度曲线的下降沿投影至光纤上的长度即代表实际热点长度，次峰对应的布里渊频移代表热点段的频移信息。
由于人工测量异常光纤段与光纤首端的距离不仅耗时费力，且容易造成较大误差，因此BOTDA-PEA技术先利用单峰洛伦兹拟合进行光纤全段探测，结合三维布里渊散射谱判断异常段及其周围光纤的位置，再对其进行双峰洛伦兹拟合。使用LM算法拟合曲线时非常依赖初始值，若设置的初始值偏离实际值太多，则会导致LM算法陷入局部最优解，造成布里渊频移产生更大的误差。因此，本文针对过渡区域的布里渊散射谱，采用粒子群优化（Particle Swarm Optimization, PSO）算法和LM算法相结合的方式提取代表光纤异常段的次峰的布里渊散射信息。PSO算法与LM算法的结合可互相弥补各自的缺点，解决双峰洛伦兹拟合过分依赖初始值、容易陷入局部最优解的问题。
确定二次拟合范围后，采用PSO算法先进行大范围搜索求解，得到散射信息近似值，再以此值作为LM算法的初始值迭代求解，根据次峰散射强度曲线的下降沿对应实际热点位置与长度，次峰布里渊频移代表热点频移信息，判断得到修正后的光纤布里渊频移，从而解调出异常光纤段的温度信息。具体处理流程如图3所示。
试验采用的BOTDA传感系统是鞍山睿科光电公司生产的分布式布里渊光时域分析仪，具体型号为RP1020。使用差分脉冲对布里渊光时域分析技术实现温度/应变的分布式测量、传感和分析，现场装置实物如图4a所示。为了模拟调节光纤热点段的温度，选择恒温水浴锅及二级标准温度计作为温度指示标，设备控温精度为±0.01℃，温度可调范围为-10～90℃，槽容积为15 L，槽开口为250 mm×160 mm，槽深度为200 mm，内置的循环水系统保证锅内温度调节速度快、性能稳定、易于控制，实物如图4b所示。设置BOTDA系统的采集参数和扫频参数见表1。
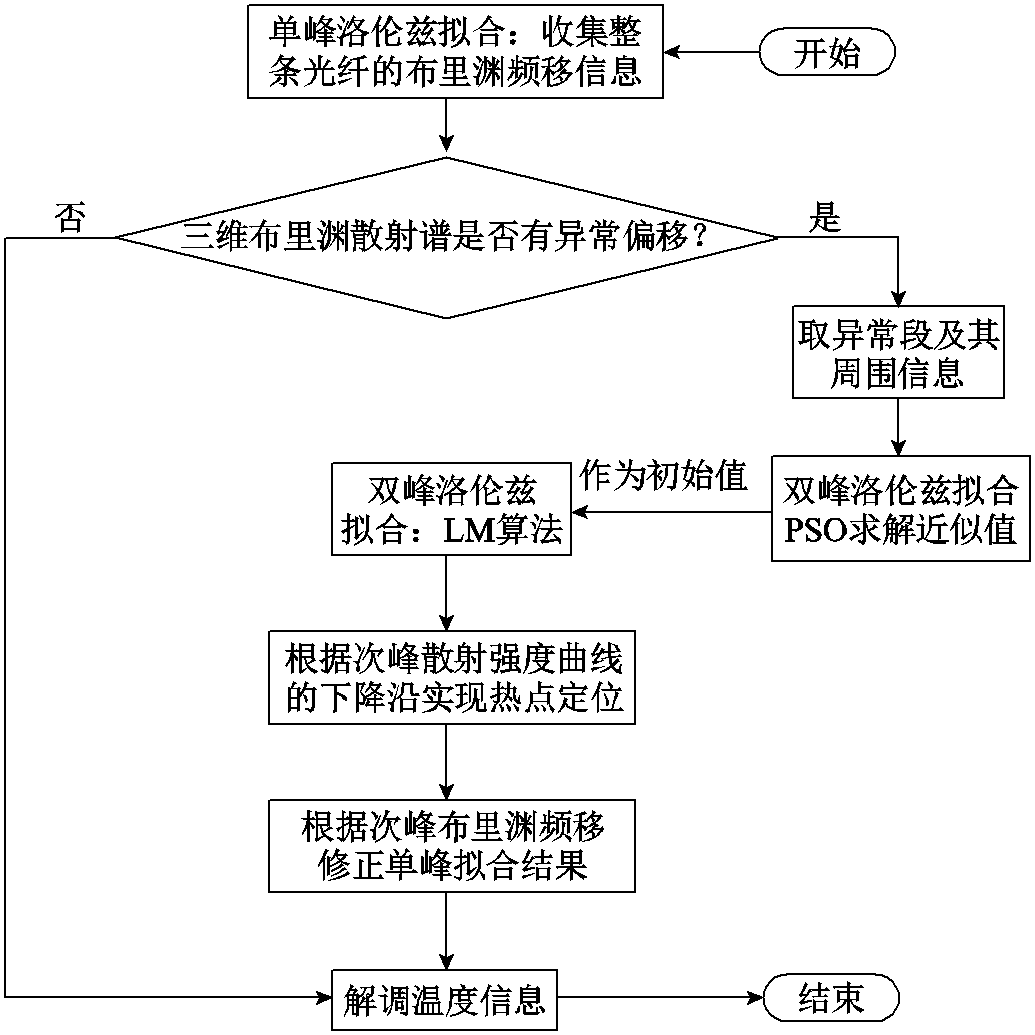
图3 BOTDA-PEA技术处理流程
Fig.3 BOTDA-PEA technology processing flow chart
图4 试验设备实物图
Fig.4 Physical diagram of test equipment
表1 系统参数设置
Tab.1 System parameter settings
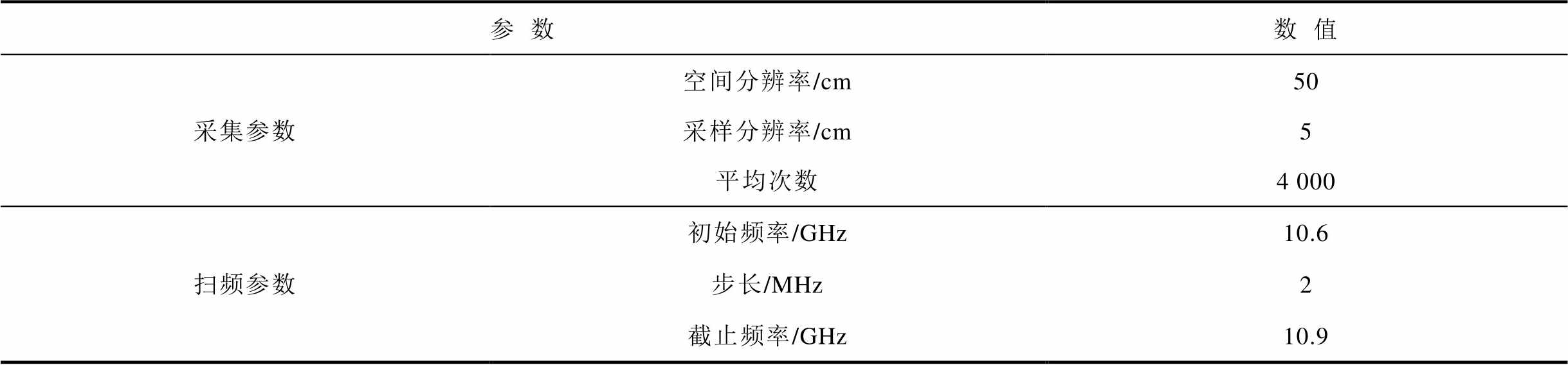
参数数值 采集参数空间分辨率/cm50 采样分辨率/cm5 平均次数4 000 扫频参数初始频率/GHz10.6 步长/MHz2 截止频率/GHz10.9
室温稳定在25℃，取一小卷护套材料为海翠、外径为900 mm的待测光纤，将其部分放入恒温水浴锅中。光纤的两端分别连接BOTDA设备的两个端口，通过调节水浴锅的温度以及没入水浴锅中光纤的位置和长度，设计了三组试验研究BOTDA-PEA的性能，采用控制变量法分别对异常光纤段的位置、长度及温度进行研究。试验示意图如图5所示。
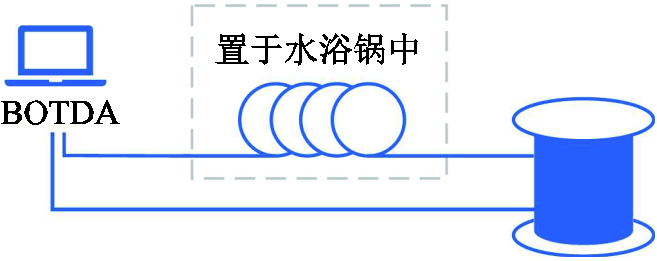
图5 试验示意图
Fig.5 Test schematic
考虑到温度越高时水蒸发越快，与外界能量交换也越快，且试验整体时间较长，若选择的水温较高可能会带来更多的人工误差。因此，为了保持水温恒定，减小不必要的误差，选择在水浴锅温度为5℃时进行异常光纤段的位置与长度对布里渊散射谱影响的研究。
2.2.1 位置试验分析
固定恒温水浴锅的温度为5℃，没入水浴锅中的光纤长度为20 cm，以光纤92.5 m处为起点，依次间隔5 cm移动水浴锅中光纤的位置，距起点50 cm时停止试验，共记录11组数据，利用BOTDA- PEA技术处理，观察异常光纤段位置的变化带来的整条光纤的散射谱的变化。
为了便于分辨，本文将布里渊散射谱上背景光纤段对应的拟合曲线命名为主峰曲线，异常光纤段代表的拟合曲线命名为次峰曲线，作出主峰及次峰曲线布里渊散射强度和布里渊频移与光纤位置的关系，如图6所示。
由于覆盖的异常光纤段的长度不同，试验保持受扰动区域的温度处于5℃不变，随着异常光纤段位置的变化，双峰曲线中的次峰强度发生变化，但对应的布里渊频移基本保持不变，说明次峰中携带了异常温度的信息，验证了温度不变，布里渊频移不会变化，受扰动光纤的位置改变不影响频移的改变。
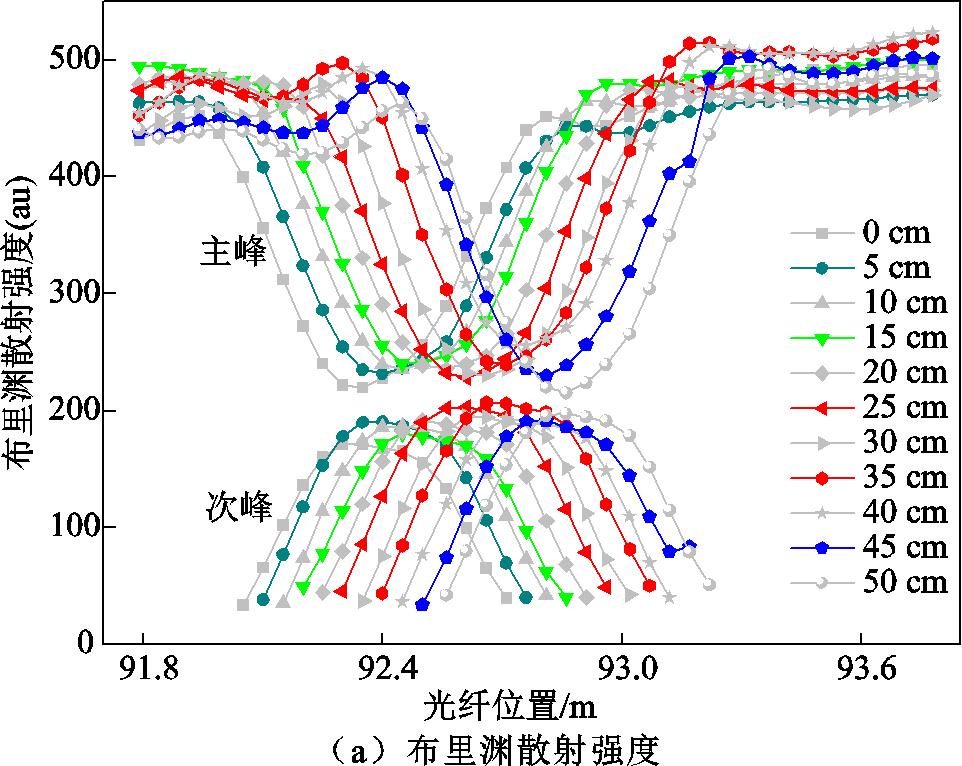
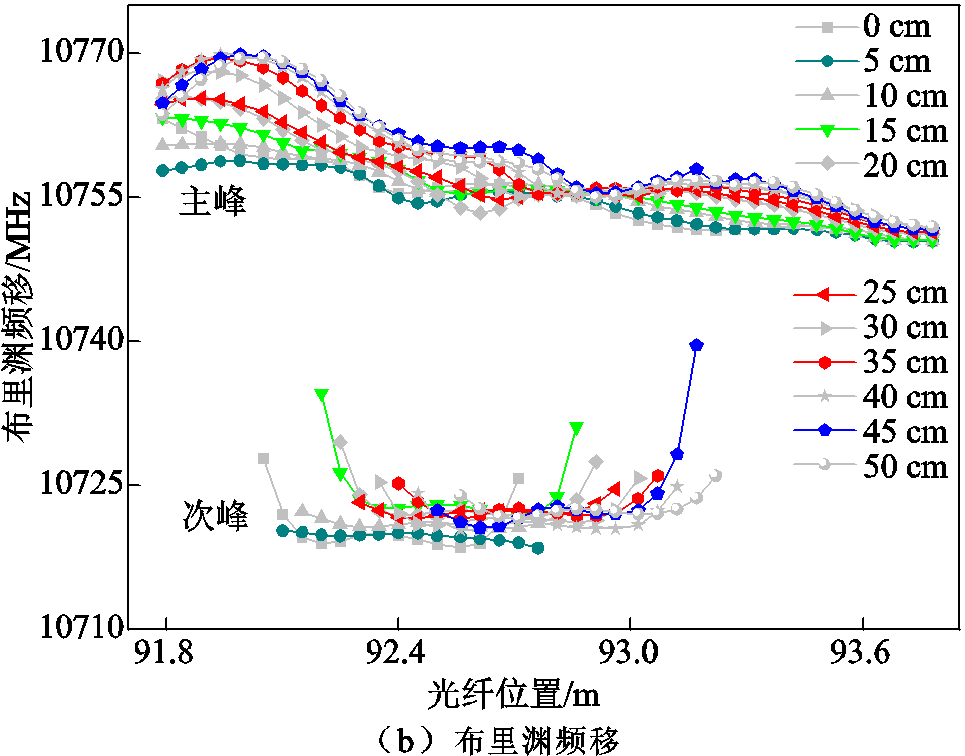
图6 位置试验结果
Fig.6 Position test results
从强度和频移曲线可以看出，随着异常光纤段以5 cm采样分辨率的间隔水平移动，布里渊散射谱的双峰整体位置也跟着以采样分辨率的间隔移动，验证了采集到的各点的布里渊散射谱是以该点为始端的光纤上、包含空间分辨率内各微小单元的散射谱的线性叠加。
在双峰区域处，主峰对应的布里渊散射强度低于具有单峰的散射谱，区域的能量转移到了次峰上。次峰的布里渊散射强度呈现等腰梯形的形状，如图7所示，对该峰值曲线进行边沿分析，可知随着空间分辨率内覆盖的异常光纤段长度的增长，次峰散射强度线性增加，且下降沿对应的投影长度等于异常光纤段的长度20 cm，与原理阐述中的图2一致。
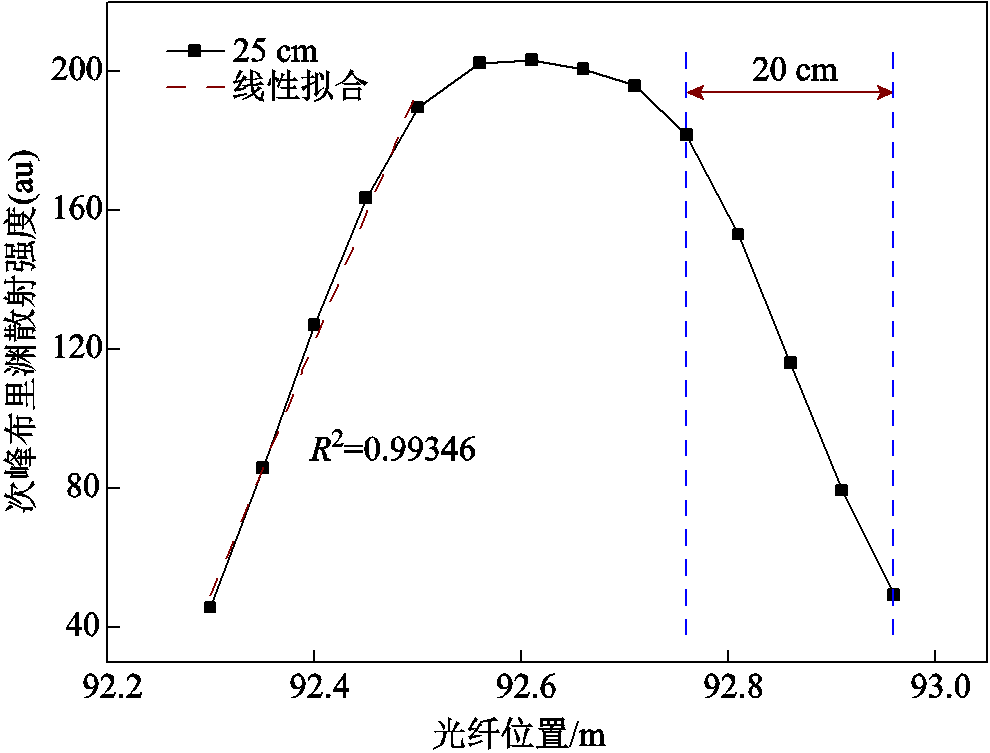
图7 次峰散射强度曲线
Fig.7 Subpeak scattering intensity curve
2.2.2 长度试验分析
固定恒温水浴锅的温度为5℃、异常光纤段的起点位置为92.5 m，以长度10 cm为起始，长度 5 cm为间隔依次增加没入水浴锅中的光纤长度，直至70 cm停止试验，共记录13组数据，结合BOTDA-PEA技术进一步探究异常光纤段的长度对传感系统空间分辨率的影响。做出主峰及次峰曲线布里渊散射强度和布里渊频移与光纤位置的关系如图8所示，研究不同的扰动事件长度的散射规律。
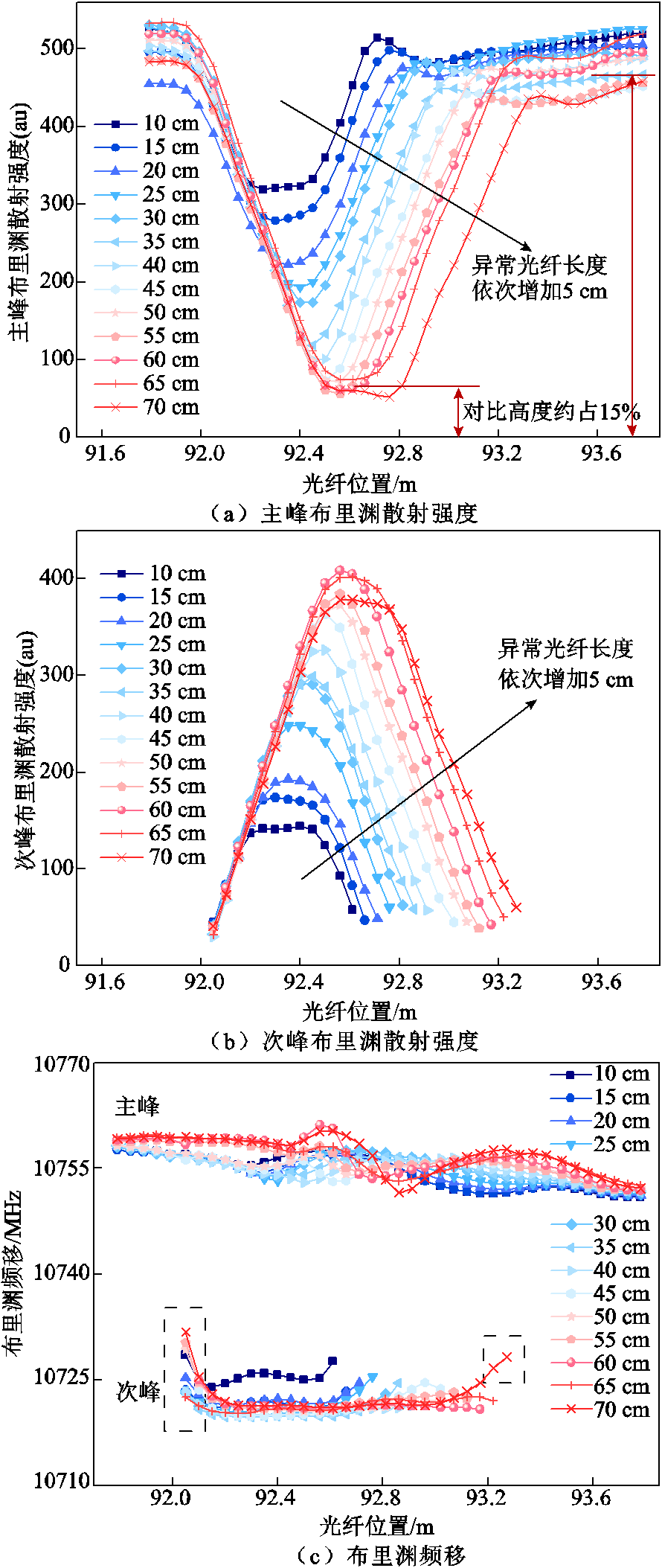
图8 长度试验结果
Fig.8 Length test results
随着异常光纤段长度的增加，双峰区域中次峰散射强度由等腰梯形逐渐向等腰三角形转换。当放入水浴锅的光纤长度较小时，部分光纤采样位置点在其空间分辨率内包含完整的受扰动区域，各个微元散射谱的叠加形成了稳定的双峰现象，由此出现了等腰梯形的“高”。试验控制了受温度扰动的光纤长度始端保持不变，从图8b强度图中可以明显看出这种现象，随着异常光纤末端位置的移动，不同光纤长度下次峰强度曲线均以相同的斜率增大。
以采样分辨率为最小单位，各种情况下次峰散射强度下降沿的距离与温度受扰动区域的光纤长度的关系如图9所示，当长度小于空间分辨率50 cm时，下降沿的宽度等于受扰动区域的光纤长度；当长度大于或等于空间分辨率50 cm时，下降沿宽度等于空间分辨率，与单峰拟合时定义的可识别的最小单位长度一致。由此验证了次峰散射强度的下降沿即反映了区域小于空间分辨率的异常光纤段的长度，且下降沿对应的光纤位置与实际异常光纤段的位置一致，其对应的布里渊频移即代表异常光纤段的频移信息。
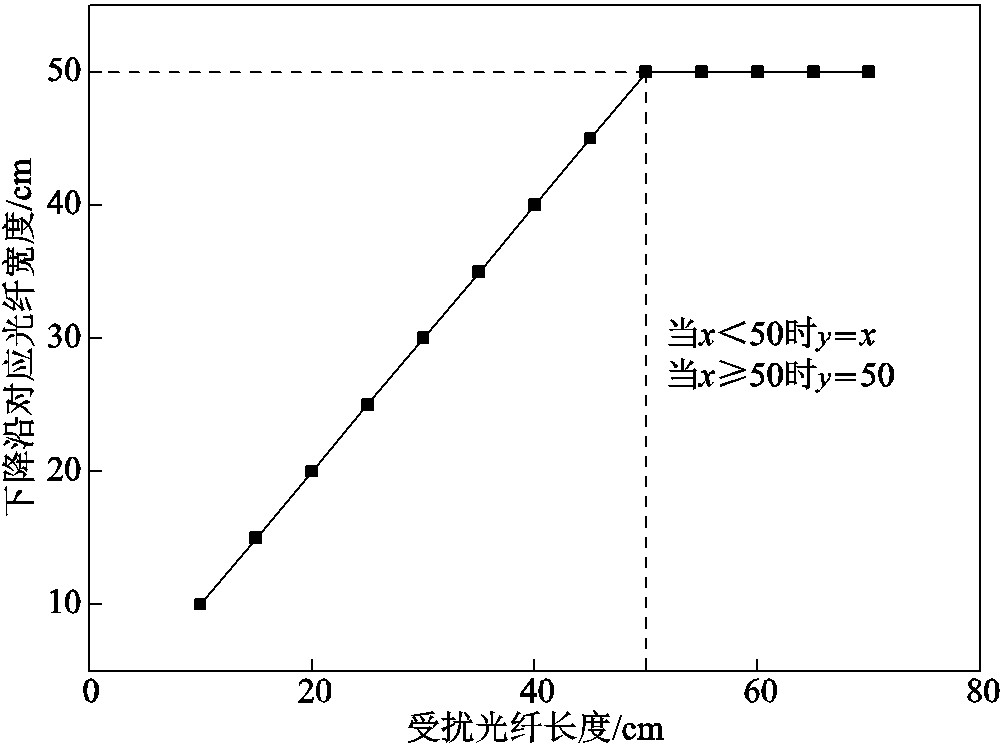
图9 下降沿对应光纤长度的关系
Fig.9 Falling edge corresponds to fiber length
随着距离的增加，双峰区域内主峰向次峰转移的能量逐渐增多，达到空间分辨率后，各峰峰值基本保持稳定。理论上对于扰动大于50 cm长度的情况，布里渊散射谱会出现主峰能量完全转移到次峰上的情况，即此位置的散射谱信息全部来自于异常光纤段，但结合图8a和图8b中55～70 cm的曲线可以看出，虽然次峰等腰梯形的“高”对应了理论上的单峰区域，但实际此区域仍存在一定的双峰状态，主峰散射强度约占不受扰动时的单峰散射强度的15%。经过分析，本文认为水浴锅中循环水浴保温时会造成光纤边缘的微小波动与散射不稳定，是导致这种问题产生的原因。
取不同长度情况下的次峰峰值平均值，这些峰值包含了全部受扰区域点的次峰布里渊散射强度，做出其强度与受扰光纤长度关系的曲线如图10所示。光纤长度小于或等于系统空间分辨率时，通过线性拟合可以得到关系y=83.29302x+6.03389，确定系数R2高达0.979 7，侧面验证了各个点的布里渊散射谱是各微小散射单元的线性集合；光纤长度大于系统空间分辨率时，散射强度基本保持不变，各点的波动范围均不大于8%，由此可预测该光纤在5℃时不同受扰光纤长度稳定区域的散射强度。
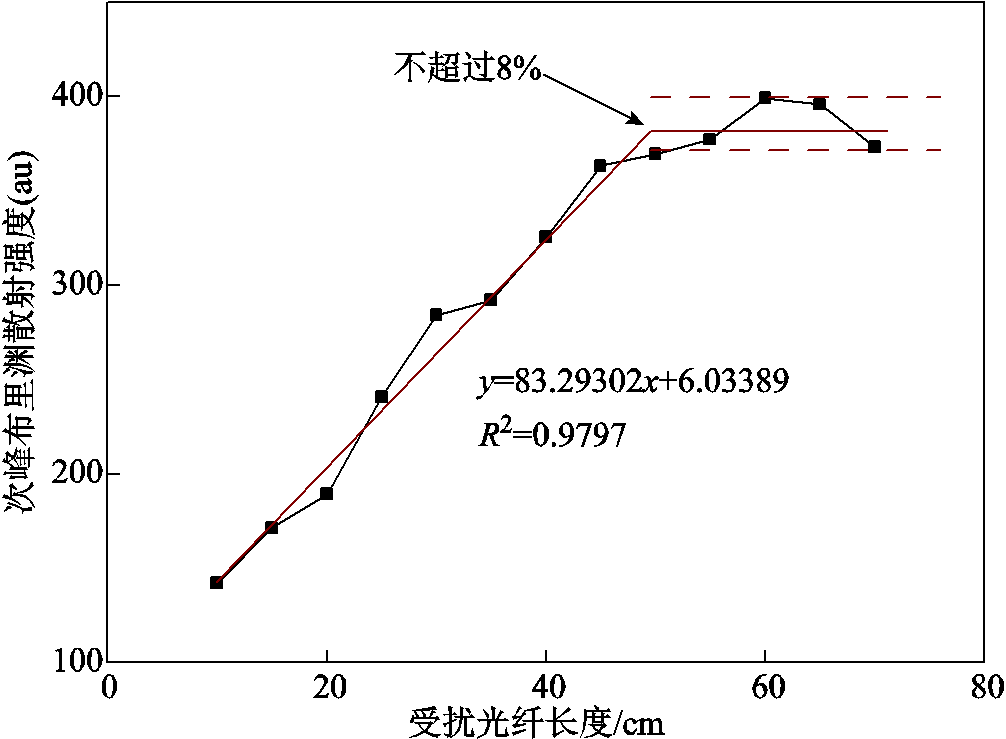
图10 次峰散射强度与受扰光纤长度关系
Fig.10 Relationship between subpeak scattering intensity and length of disturbed fiber
双峰频移曲线中主峰频移和次峰频移基本在两条平行线上下波动，随着受扰动光纤的长度增大，布里渊散射谱影响的范围也变大，但温度不变，双峰区域中代表温度扰动事件的次峰频移基本保持不变，与受扰光纤的长度无关，从侧面验证了各点的散射谱是其空间分辨率内微元单位布里渊散射的叠加。
各双峰散射谱频移曲线的边缘处均有偏离稳定值较大处的情况，如图8c中黑色虚线方框处所示。经过分析，认为是边缘光纤处于水浴锅5℃与室温25℃边界处，室温对此处的光纤温度造成了一定的影响；加之水浴锅处于循环状态，放置的光纤边界处与空气接触，在水的作用下有一定的波动，从而导致位于水浴锅边沿处的光纤温度并非标准的5℃，而是大于5℃，频移曲线的边沿处次峰均向主峰的频移靠近验证了这一点。
2.2.3 温度试验分析
固定没入水浴锅中的光纤位置为92.65～92.85 m，异常温度光纤长度为20 cm，改变水浴锅的温度，即改变光纤异常段的温度，从45～70℃，以5℃为间隔依次增加，共6组数据，验证双峰区域的温度特性，做出温度试验的结果如图11所示。
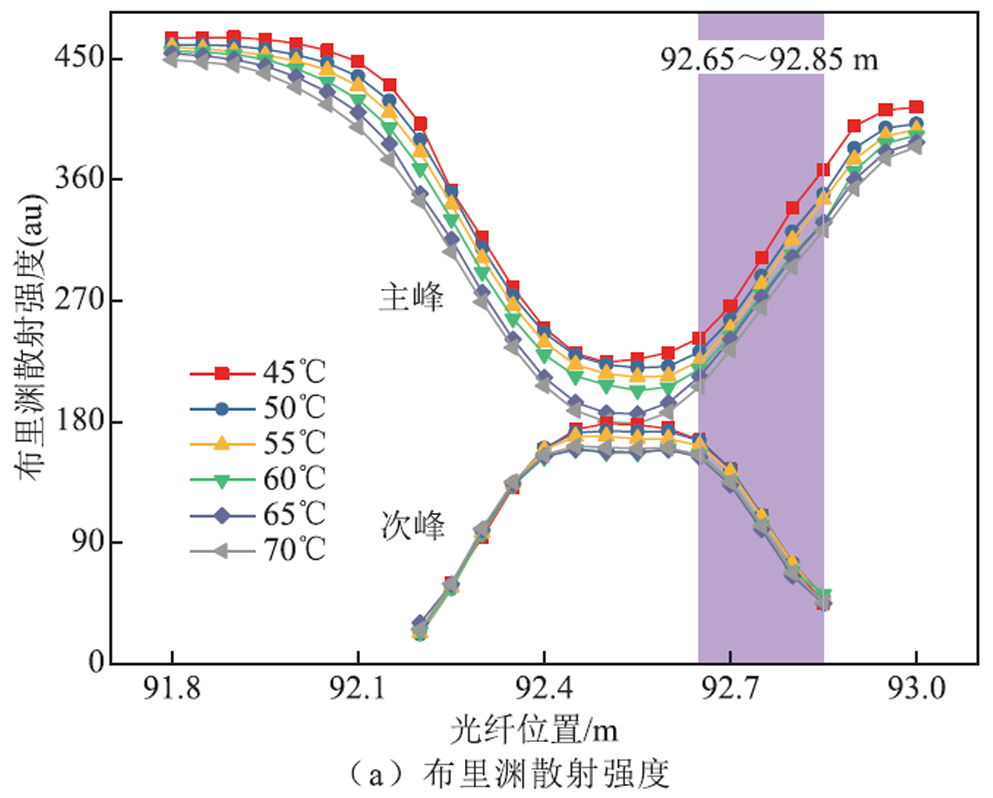
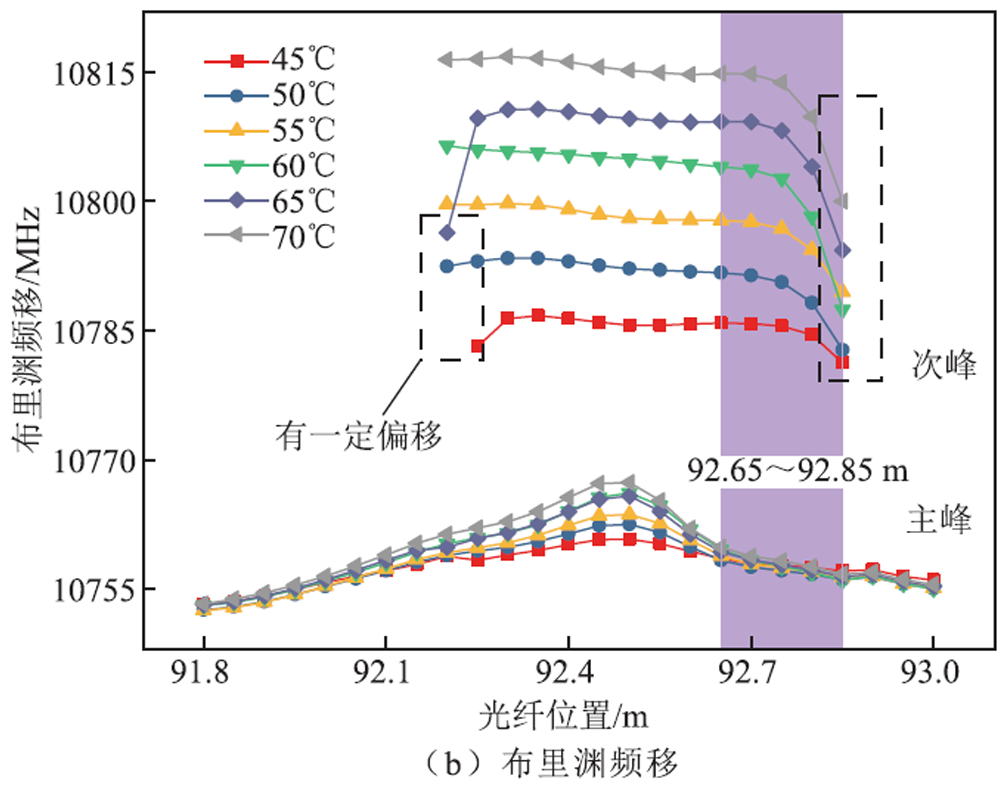
图11 温度试验结果
Fig.11 Temperature test results
受扰光纤段的次峰布里渊散射强度曲线接近于等腰梯形，随着温度的增加，强度略有波动，因为其对温度不敏感，但下降沿对应的长度不变，即代表了当受扰光纤长度不变时，温度的变化不影响通过下降沿的长度判断受温度扰动的光纤的长度。
从频移曲线可以看出，在同一温度下，光纤受扰区域频移保持稳定不变，随着温度的变化，双峰区域中代表温度扰动事件的次峰频移也发生变化。取光纤各温度稳定的布里渊散射频移作均值处理，得到其随温度差变化的曲线，如图12所示，经过线性拟合后得到光纤的温度系数为1.421 MHz/℃，R²为0.993，拟合程度较好。
双峰区域边界处的次峰布里渊频移与中心处的频移相差较大，随着水浴锅温度的上升，边缘处的频移与中心处的频移偏差逐渐明显，到达60℃时，甚至已高达20 MHz，如图11b中黑色虚线方框所示。光纤放入水浴锅，受扰区域边缘与空气接触，存在一定的热量交换，使边缘的温度向室温靠近，从而导致每个温度下边缘处的布里渊频移小于中心处的频移，在高温时热量交换更加明显，温度升高，温差越大，热交换的速率越快，高温时越容易出现明显的次峰频移下跌的现象。
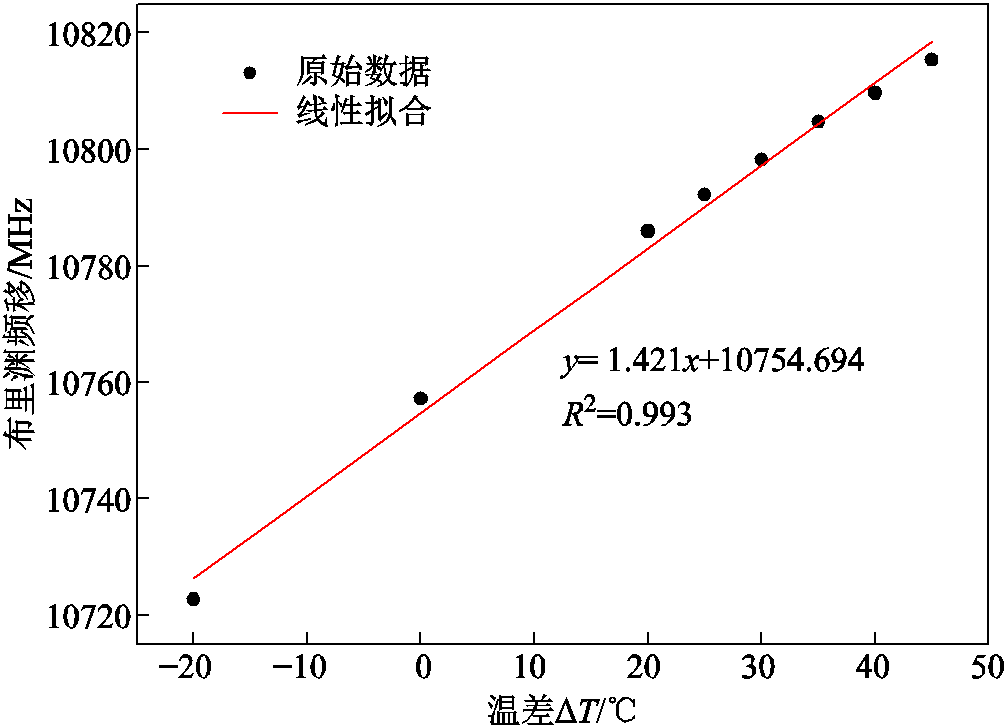
图12 光纤温度系数拟合图
Fig.12 Optical fiber temperature coefficient fitting diagram
2.2.4 对比分析
当温度异常区域的长度小于光纤传感系统的空间分辨率时，单峰拟合不能准确地反映温度异常信息，获得的温度与实际温度有较大的差距，而由于每一点的布里渊散射谱是该点向后一个空间分辨率内光纤的微元散射单元的叠加，若采用本文提出的BOTDA-PEA技术处理，则可以较为准确地反映实际的温度信息。以位于光纤94.35～94.55 m处一段长为20 cm的温度为50℃的热点加以验证，对布里渊散射谱分别进行传统拟合和BOTDA-PEA处理，当温度系数为1.421 MHz/℃时，由式（1）可计算得到光纤沿线温度分布如图13所示。
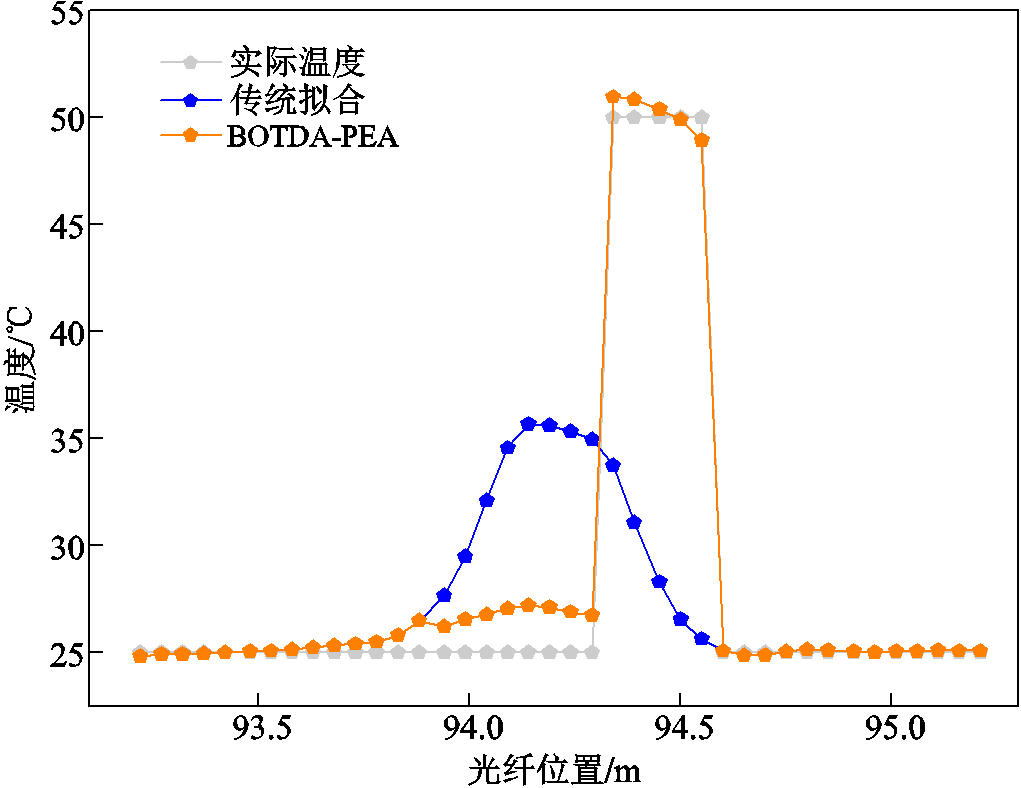
图13 50℃拟合对比
Fig.13 Fitting comparison at 50℃
对于传统拟合方法，取温度最大值所在点的周围温度，BOTDA-PEA方法则取对应光纤热点段的温度值，分别计算温度相对误差，可以得到采用BOTDA-PEA处理后的热点温度相对误差在2%左右，而传统拟合的相对误差高达30%，与实际温度相差太大，且传统单峰拟合在热点定位时有较小位置误差，如图13中实际曲线的峰值对应光纤位置所示。单峰拟合的温度峰值出现在热点实际位置前侧，通过BOTDA-PEA技术，分析次峰布里渊散射强度曲线的下降沿，结合对应次峰布里渊频移，可以修正位置误差，反映热点真实位置及温度。
理论上，利用BOTDA-PEA技术可以将空间分辨率提高至采样分辨率，但若采样分辨率过小，该微元的散射信号对空间分辨率内的布里渊散射信号贡献较小，就会导致在拟合确定布里渊频移的过程中将其认定为噪声，造成信息的丢失，从而无法分辨。在本文的试验中，异常光纤段的长度为10 cm时取得的次峰散射强度曲线已较为稳定，可以准确地定位热点位置及其长度。因此，考虑到布里渊散射谱固有的频谱展宽以及非线性效应带来的噪声，认为BOTDA-PEA技术可以稳定地将空间分辨率提升至原空间分辨率的一半以内，本文将其提高至采样分辨率的2倍。
变压器绕组内部绝缘部分损坏时，在运行过程中常以局部热点的形式表现，若能及时检测到过热点并精确定位，可以预警绕组局部故障的产生。为了验证BOTDA-PEA技术在变压器绕组热点检测中的可行性与有效性，本文设计了变压器的局部升温试验。
课题组在之前的研究中[30]已经成功地绕制了光纤复合式变压器绕组，两根单模光纤并排使用变压器用白乳胶固定于绕组导线宽面上开的小槽内，保证光纤能准确感知绕组的细微变化，且两根光纤互为补充。整个绕组内径为40 cm，外径为50 cm，共40饼导线，每饼10匝，绕组内光纤总长约为570 m。为了消除光纤首端测量盲区、实现精准定位和减少光纤末端端面菲涅尔反射造成的散射非线性效应，在绕组光纤的首尾端均焊接一段长约5 m的光纤，该光纤段的布里渊频移应与绕组内光纤的布里渊频移有较大差异。
设置BOTDA传感系统的空间分辨率为50 cm，采样分辨率为5 cm，经过测试，设置扫频范围为11～11.5 GHz，以2 MHz为步长，平均次数为3 000次时，既能满足去除高斯噪声的目的，又能限制总测量时间。
试验在室温保持为25℃的实验室中进行。首先测量绕组室温状态下的初始布里渊频移，为排除在缠绕光纤时人为导致的细微拉伸或压缩现象带来的影响，两根内置光纤分别用BOTDA传感系统测量两次。变压器绕组的局部升温试验用可控温加热条实现。将20 cm加热条贴于绕组第18饼最外匝导线，设置温度加热至70℃，稳定后用系统进行第一次测量，测量结束后等待10 min，使绕组整体完全恢复至室温状态下，再控制加热条升温至70℃，稳定后进行第二次测量。其测量示意图如图14所示。
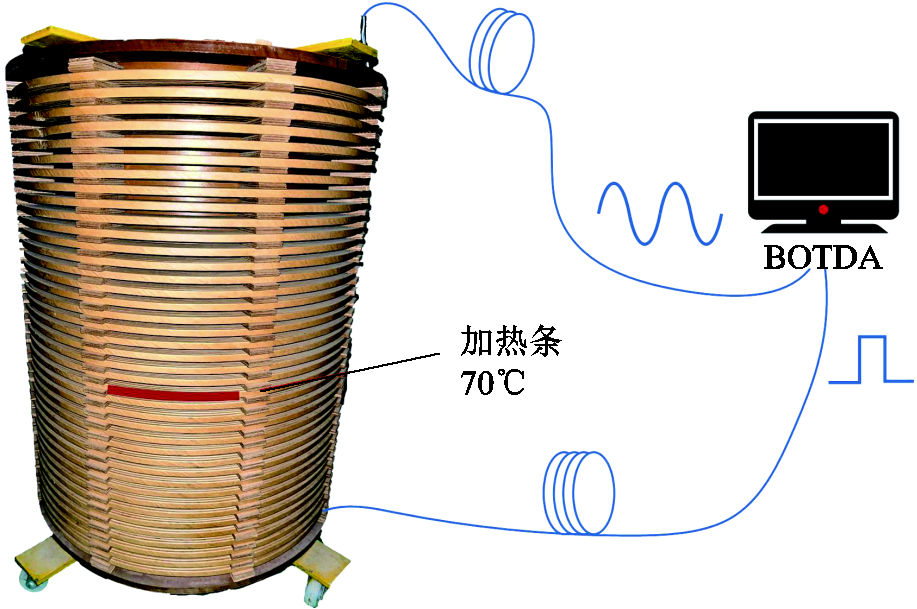
图14 变压器绕组局部升温测量示意图
Fig.14 Transformer winding local temperature measurement diagram
利用BOTDA-PEA技术对25℃和70℃的两次测量分别处理后取平均值作为最终的布里渊频移结果，如图15a所示。整条光纤各个位置散射谱拟合的相关系数R2均非常接近于1，试验数据与拟合的数据吻合程度非常高。
将25℃下测得的布里渊频移曲线作为标准，计算70℃与其的频移差，得到变压器绕组中布里渊频移有明显变化的一段绕组的频移差分布如图15b所示。由于光纤拉伸或压缩造成的应变影响已经被标准曲线消除，根据内置传感光纤的温度系数为1.725 MHz/℃，可换算得到实际温度如图15b右轴所示。
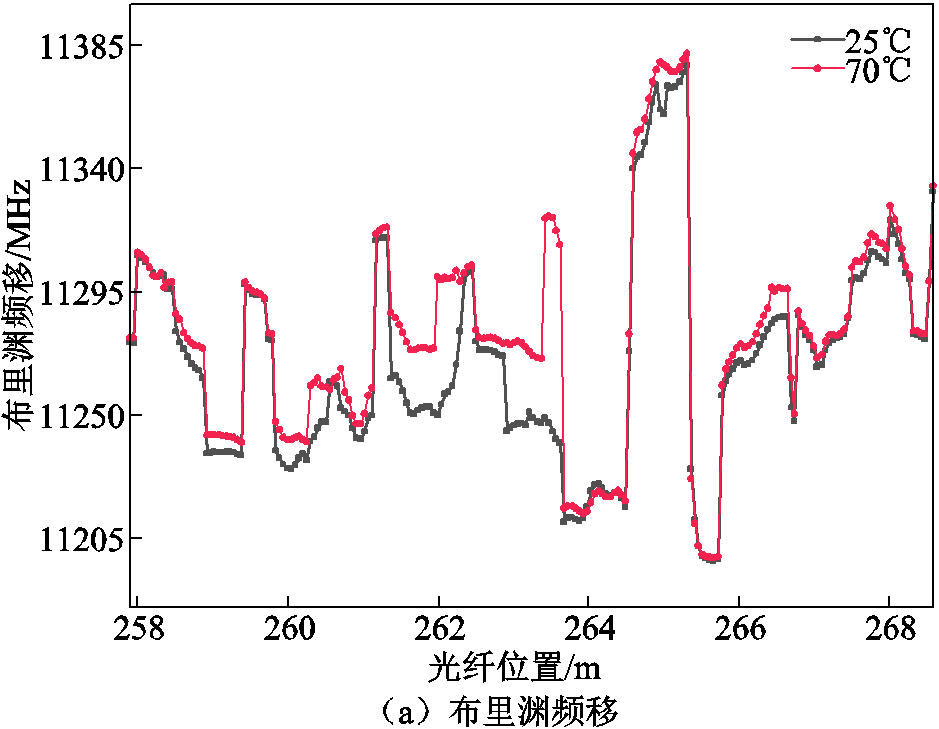
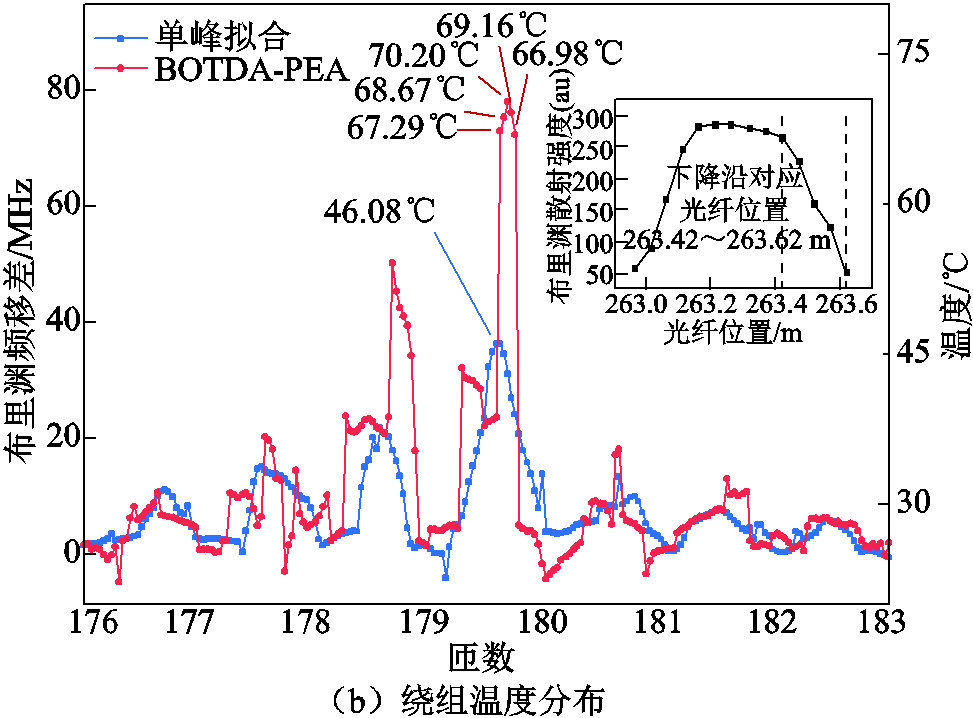
图15 变压器局部升温试验结果
Fig.15 Transformer local temperature rise test results
为了在变压器绕组热点检测的应用中验证BOTDA-PEA技术的有效性与可靠性，同时绘制了传统单峰拟合下的布里渊频移差曲线，如图15b中蓝色曲线所示。取两种方法处理后的热点温度值及具体位置，计算相对误差见表2。通过次峰散射强度曲线的下降沿分析判断热点对应光纤位置为263.42～263.62 m处，位于绕组第180匝，热点长度为20 cm，与实际情况一致，温度相对误差不超过5%；而传统单峰拟合曲线的温度相对误差大于34%，这种情况较容易被误判为散热不及时导致的升温，但实际绕组已经出现过热趋势。若变压器绕组某处长期处于这种状态，易造成局部绝缘的损坏，会带来不可估量的损失。
表2 变压器热点位置及温度对比
Tab.2 Transformer hot spot location and temperature comparison
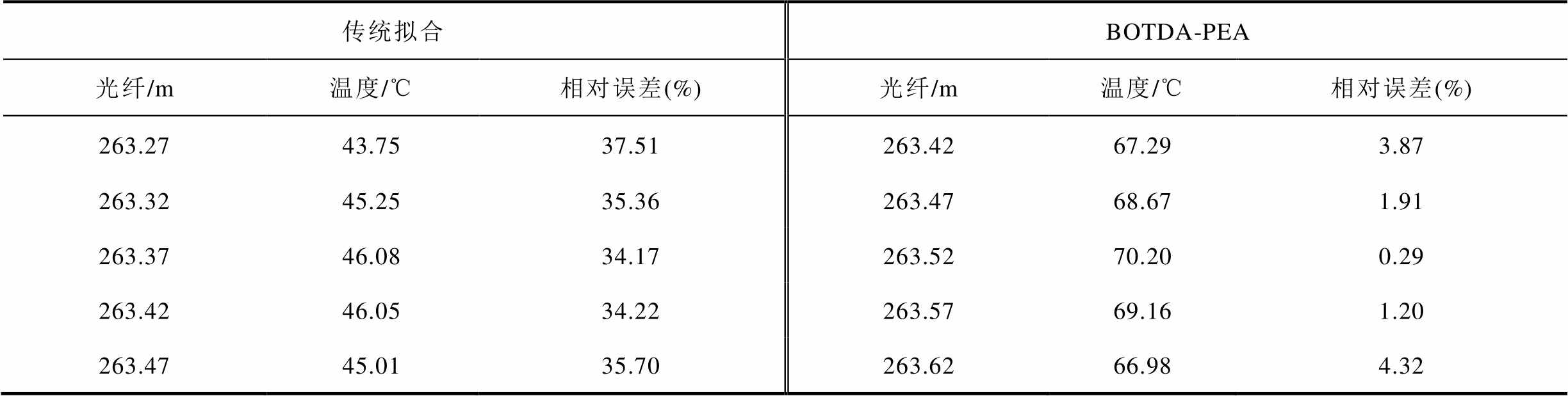
传统拟合BOTDA-PEA 光纤/m温度/℃相对误差(%)光纤/m温度/℃相对误差(%) 263.2743.7537.51263.4267.293.87 263.3245.2535.36263.4768.671.91 263.3746.0834.17263.5270.200.29 263.4246.0534.22263.5769.161.20 263.4745.0135.70263.6266.984.32
由于绕组导线的热传导和空气的对流，绕组匝间联系紧密，加热条升温后的热量会影响其所在绕组饼数周围匝的导线，造成另外的局部过热点，如图15b红色曲线所示的频移差峰值极大值点，相邻峰间隔约为一匝导线的长度，由此可以看出绕组局部过热点产生的连锁影响，匝间热量传递现象尤为明显，若不及时发现这类情况，无疑会损坏相邻导线间的绝缘，进而缩短变压器绕组的寿命。因此，绕组匝间绝缘的要求较高，在变压器运行过程中利用BOTDA-PEA技术及时发现绕组的局部过热点很有必要。
观察图15的两组曲线可以看出，单峰拟合的曲线整体比较平滑，而通过BOTDA-PEA技术得到的频移差分布曲线的各个峰都较为尖锐，突变比较明显。这是因为在过渡区域，温度异常段的散射贡献使单峰拟合偏离了主峰，既不能体现主峰信息，又不能体现异常信息，得到的频移结果受异常峰的影响逐渐偏移，而BOTDA-PEA技术主要进行双峰拟合，能即刻显示异常段的温度信息，对于热点长度小于空间分辨率的情况也能及时地反映出来，证明了BOTDA-PEA技术能提高光纤传感的空间分辨率，进一步提升系统的性能。
本文针对变压器绕组存在局部过热点可能进一步破坏匝间绝缘、影响变压器寿命的情况，利用分布式光纤传感技术实现绕组热点检测，主要得到了以下结论：
1）通过详述布里渊增益谱原理和双峰拟合原理，对受扰光纤处的异常峰值强度曲线进行边沿分析，提出了一种在不增加系统硬件复杂度的情况下提高BOTDA空间分辨率的方法——BOTDA-PEA技术。当受扰光纤长度小于空间分辨率时，根据次峰散射强度曲线的下降沿实现热点精确定位，次峰对应布里渊频移修正传统拟合结果，解调实际热点温度。
2）在实验室条件下设计了三组试验研究BOTDA-PEA的性能，当受扰动光纤段长度小于BOTDA的空间分辨率时，采用控制变量法分别研究受扰光纤所处的位置、长度及温度对布里渊增益谱的影响。试验结果验证了布里渊散射谱双峰区域的次峰强度曲线下降沿所对应的位置即为受扰光纤段的精确位置，其频移即代表受扰光纤段的温度信息。BOTDA-PEA技术可以稳定地将BOTDA传感系统的空间分辨率提高至原空间分辨率的一半以内，最高可至采样分辨率的2倍。
3）通过设置加热条进行了变压器绕组的局部升温试验，利用BOTDA-PEA技术处理数据，得到了绕组局部热点及其附近的温度分布曲线，结果表明传统BOTDA采用的单峰拟合技术不能准确地识别热点长度小于空间分辨率的情况，温度误差较大；而BOTDA-PEA技术可以成功地解调其温度，相对误差控制在5%以内。
通过BOTDA-PEA技术可以准确地解调变压器绕组的局部过热点，将传统BOTDA的空间分辨率提高至采样分辨率的2倍，从而达到提高温度监测精度的目的，为实现变压器绕组的温度在线监测提供新的思路。由于布里渊增益谱本身的展宽限制，当空间分辨率内所有散射单元的贡献差别不大，包含热点信息的光纤段贡献较小时，有用信号易被掩盖于该处光纤的总布里渊散射谱的展宽下，无法识别，造成频移拟合产生较大的误差。因此，当变压器绕组热点长度过小或与背景光纤的差异较小时，需要进一步提高信噪比，降低光纤散射非线性效应带来的噪声，针对此种情况还需要进行更深入的研究。
参考文献
[1] 陈伟根, 滕黎, 刘军, 等. 基于遗传优化支持向量机的变压器绕组热点温度预测模型[J]. 电工技术学报, 2014, 29(1): 44-51. Chen Weigen, Teng Li, Liu Jun, et al. Transformer winding hot-spot temperature prediction model of support vector machine optimized by genetic algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 44-51.
[2] 邓永清, 阮江军, 董旭柱, 等. 基于流线分析的10kV油浸式变压器绕组热点温度反演模型建立及验证研究[J]. 中国电机工程学报, 2023, 43(8): 3191-3204. Deng Yongqing, Ruan Jiangjun, Dong Xuzhu, et al. Establishment and verification of 10kV oil immersed transformer winding hot spot temperature inversion model based on streamline analysis[J]. Proceedings of the CSEE, 2023, 43(8): 3191-3204.
[3] 范贤浩, 刘捷丰, 张镱议, 等. 融合频域介电谱及支持向量机的变压器油浸纸绝缘老化状态评估[J]. 电工技术学报, 2021, 36(10): 2161-2168. Fan Xianhao, Liu Jiefeng, Zhang Yiyi, et al. Aging evaluation of transformer oil-immersed insulation combining frequency domain spectroscopy and support vector machine[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2161-2168.
[4] 曲岳晗, 赵洪山, 程晶煜, 等. 基于物联感知数据和张量融合的电力变压器绕组绝缘劣化评估方法[J]. 电工技术学报, 2024, 39(4): 1208-1220. Qu Yuehan, Zhao Hongshan, Cheng Jingyu, et al. Evaluation method for power transformer winding insulation degradation based on iot sensing data and tensor fusion[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1208-1220.
[5] 彭道刚, 陈跃伟, 钱玉良, 等. 基于粒子群优化-支持向量回归的变压器绕组温度软测量模型[J]. 电工技术学报, 2018, 33(8): 1742-1749, 1761. Peng Daogang, Chen Yuewei, Qian Yuliang, et al. Transformer winding temperature soft measurement model based on particle swarm optimization-support vector regression[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1742-1749, 1761.
[6] Rosillo M E, Herrera C A, Jaramillo G. Advanced thermal modeling and experimental performance of oil distribution transformers[J]. IEEE Transactions on Power Delivery, 2012, 27(4): 1710-1717.
[7] 谢裕清, 李琳, 宋雅吾, 等. 油浸式电力变压器绕组温升的多物理场耦合计算方法[J]. 中国电机工程学报, 2016, 36(21): 5957-5965, 6040. Xie Yuqing, Li Lin, Song Yawu, et al. Multi-physical field coupled method for temperature rise of winding in oil-immersed power transformer[J]. Proceedings of the CSEE, 2016, 36(21): 5957-5965, 6040.
[8] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491. Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal-fluid model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4483-4491.
[9] 张健, 胡玉耀, 宋士瞻, 等. 基于数值求解的油浸式变压器瞬态热点温度计算[J]. 高压电器, 2023, 59(6): 103-110, 127. Zhang Jian, Hu Yuyao, Song Shizhan, et al. Transient hot spot temperature calculation of oil immersed transformer based on numerical calculation[J]. High Voltage Apparatus, 2023, 59(6): 103-110, 127.
[10] 朱涛, 王丰华. 地磁感应电流作用下大型变压器的温升特性计算[J]. 电工技术学报, 2022, 37(8): 1915-1925. Zhu Tao, Wang Fenghua. Calculation of temperature rise of large transformer under geomagnetically induced current[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 1915-1925.
[11] Arabul A Y, Keskin Arabul F, Senol I. Experimental thermal investigation of an ONAN distribution transformer by fiber optic sensors[J]. Electric Power Systems Research, 2018, 155: 320-330.
[12] 邓建钢, 王立新, 聂德鑫, 等. 内置光纤光栅油浸式变压器的研制[J]. 中国电机工程学报, 2013, 33(24): 160-167, 23. Deng Jiangang, Wang Lixin, Nie Dexin, et al. Development of oil-immersed transformers with built-in fiber Bragg grating sensors[J]. Proceedings of the CSEE, 2013, 33(24): 23, 160-167.
[13] 王恩, 赵振刚, 曹敏, 等. 基于光纤Bragg光栅的油浸式变压器多点温度监测[J]. 高电压技术, 2017, 43(5): 1543-1549. Wang En, Zhao Zhengang, Cao Min, et al. Multi point temperature monitoring of oil immersed transformer based on fiber Bragg grating[J]. High Voltage Engineering, 2017, 43(5): 1543-1549.
[14] 苑立波, 童维军, 江山, 等. 我国光纤传感技术发展路线图[J]. 光学学报, 2022, 42(1): 9-42. Yuan Libo, Tong Weijun, Jiang Shan, et al. Road map of fiber optic sensor technology in China[J]. Acta Optica Sinica, 2022, 42(1): 9-42.
[15] 刘云鹏, 李昕烨, 李欢, 等. 内置分布式光纤传感的35 kV油浸式变压器研制[J]. 高电压技术, 2020, 46(6): 1886-1894. Liu Yunpeng, Li Xinye, Li Huan, et al. Development of 35 kV oil-immersed transformer with built-in distributed optical fiber[J]. High Voltage Engineering, 2020, 46(6): 1886-1894.
[16] 徐征宇, 张书琦, 廖和安, 等. 传感光纤与变压器电磁线一体化技术[J]. 中国电机工程学报, 2021, 41(19): 6816-6827. Xu Zhengyu, Zhang Shuqi, Liao Hean, et al. Integrated technology of distributed optical fiber and transformer electromagnetic wire[J]. Proceedings of the CSEE, 2021, 41(19): 6816-6827.
[17] 刘云鹏, 李欢, 高树国, 等. 分布式光纤传感在大型变压器温度和绕组变形监测中的应用研究[J]. 中国电机工程学报, 2022, 42(16): 6126-6135, 6186. Liu Yunpeng, Li Huan, Gao Shuguo, et al. Research on application of distributed optical fiber sensing in monitoring of temperature and winding deformation of large transformer[J]. Proceedings of the CSEE, 2022, 42(16): 6126-6135, 6186.
[18] Li Huan, Liu Yunpeng, Zhuang Xinyu, et al. Test and analysis on extended temperature rise of 110 kV transformer based on distributed temperature sensing[J]. IEEE Transactions on Power Delivery, 2023, 38(2): 1030-1041.
[19] 饶云江. 长距离分布式光纤传感技术研究进展[J]. 物理学报, 2017, 66(7): 074207. Rao Yunjiang. Recent progress in ultra-long distributed fiber-optic sensing[J]. Acta Physica Sinica, 2017, 66(7): 074207.
[20] Dong Yongkang. High-performance distributed Brillouin optical fiber sensing[J]. Photonic Sensors, 2021, 11(1): 69-90.
[21] Fellay A, Thévenaz L, Facchini M, et al. Distributed sensing using stimulated Brillouin scattering: towards ultimate resolution[C]//12th International Conference on Optical Fiber Sensors, Williamsburg, Virginia, 1997: 324-327.
[22] Denisov A, Soto M A, Thévenaz L. Going beyond 1000000 resolved points in a Brillouin distributed fiber sensor: theoretical analysis and experimental demonstration[J]. Light: Science & Applications, 2016, 5(5): e16074.
[23] Horiguchi T, Tateda M. BOTDA-nondestructive measurement of single-mode optical fiber attenuation characteristics using Brillouin interaction: theory[J]. Journal of Lightwave Technology, 1989, 7(8): 1170-1176.
[24] Lu Ping, Lalam N, Badar M, et al. Distributed optical fiber sensing: review and perspective[J]. Applied Physics Reviews, 2019, 6(4): 041302.
[25] Parker T R, Farhadiroushan M, Handerek V A, et al. Temperature and strain dependence of the power level and frequency of spontaneous Brillouin scattering in optical fibers[J]. Optics Letters, 1997, 22(11): 787-789.
[26] Sun Xizi, Hong Xiaobin, Wang Sheng, et al. Frequency shift estimation technique near the hotspot in BOTDA sensor[J]. Optics Express, 2019, 27(9): 12899.
[27] Brown A W, DeMerchant M, Bao Xiaoyi, et al. Spatial resolution enhancement of a Brillouin-distributed sensor using a novel signal processing method[J]. Journal of Lightwave Technology, 1999, 17(7): 1179-1183.
[28] Jiang Chao, Ma Jie, Li Min, et al. A long pulse bidirectional BOTDA technology developed for strain positioning and measurement[J]. Optics & Laser Technology, 2021, 143: 107361.
[29] Murayama H, Kageyama K, Shimada A, et al. Improvement of spatial resolution for strain measurements by analyzing Brillouin gain spectrum[C]//17th International Conference on Optical Fibre Sensors, Bruges, Belgium, 2005: 551-554.
[30] 刘云鹏, 李欢, 田源, 等. 基于分布式光纤传感的绕组变形程度检测[J]. 电工技术学报, 2021, 36(7): 1347-1355. Liu Yunpeng, Li Huan, Tian Yuan, et al. Winding deformation detection based on distributed optical fiber sensing[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1347-1355.
Abstract The temperature distribution of transformer windings has always been the focus of power grid operators. Compared with traditional sensors, distributed fiber sensing has great advantages such as strong anti-electromagnetic interference ability and distributed measurement. Brillouin optical time domain analysis (BOTDA) has stable performance and is suitable for most scenarios. However, the spatial resolution of BOTDA is on the order of meters, making it difficult to distinguish local hot spots in winding operation. Starting from the mechanism of Brillouin scattering gain spectrum, this paper proposes a Brillouin optical time domain peak edge analysis (BOTDA-PEA) technique to improve the spatial resolution of BOTDA without increasing the complexity of the system hardware by describing the bimodal fitting principle and analyzing the edge of the abnormal peak intensity curve in the disturbed fiber, so as to meet the requirements of local hot spot detection in transformer windings. The basic principle of this technology is that when the length of the disturbed fiber is less than the spatial resolution, the hot spot is precisely located according to the descending edge of the subpeak scattering intensity curve, the traditional fitting results are modified according to the corresponding Brillouin frequency shift of the subpeak, and the actual hot spot temperature is demodulated.
Firstly, three sets of simulation experiments were designed under laboratory conditions to study the performance of BOTDA-PEA in terms of different locations, different hot spot lengths and different hot spot temperatures along the fiber. When the length of the disturbed fiber segment was less than the spatial resolution of BOTDA, the influence of different variables on the Brillouin gain spectrum is obtained by using the control variable method. The experimental results verify that the position corresponding to the declining edge of the subpeak intensity curve in the bimodal region of Brillouin scattering spectrum is the exact position of the disturbed fiber segment, and its frequency shift represents the temperature information of the disturbed fiber segment. Compared with traditional single-peak fitting technology, BOTDA-PEA technology can stably improve the spatial resolution of BOTDA sensor system to less than half of the original spatial resolution, and up to 2 times of the sampling resolution.
The local temperature test of transformer winding was simulated by setting heating strips, and the temperature distribution curves of local hot spots and their vicinity were obtained by using BOTDA-PEA technique to process the data. The experimental results show that the single-peak fitting technique used by traditional BOTDA cannot accurately identify the hot spot length less than the spatial resolution, and the temperature error is as high as 34%. However, BOTDA-PEA technique can successfully demodulate the temperature, and the relative error is controlled within 5%. It is concluded that BOTDA-PEA technology can realize the accurate location and length perception of winding abnormal hot spots and accurately demodulate the temperature of local hot spots in winding, which further verifies the practical feasibility and detection superiority of this method, and provides new thinking for improving the economy and feasibility of online monitoring of transformer winding temperature. At the same time, it provides a new idea for the early warning of local winding fault.
keywords：Fiber sensing, transformer, winding hot spot temperature, Brillouin optical time domain analysis technology, spatial resolution
DOI: 10.19595/j.cnki.1000-6753.tces.230356
中图分类号：TM41
国家电网公司科技项目资助（5206002000D6）。
收稿日期 2023-03-24
改稿日期 2023-04-17
刘云鹏 男，1976年生，教授，博士生导师，研究方向为电力设备故障检测与诊断。E-mail：liuyunpeng@ncepu.edu.cn
黎晏霖 女，1999年生，硕士研究生，研究方向为分布式光纤传感技术及电力设备故障检测与诊断。E-mail：lylncepu2021@163.com（通信作者）
（编辑 李 冰）