图1 水中脉冲放电试验平台
Fig.1 Experimental platform for pulse discharge in water
摘要 水中脉冲放电的电弧通道发育具有强随机性,难以固定时域进行放电阶段划分,故水中脉冲放电阶段的辨识方法研究极为重要。首先,该文建立了水中脉冲放电等效电路模型并阶段化分析了电阻时变特性,得到了判定放电阶段的临界参数阈值;其次,采用扩展卡尔曼滤波算法将离散电阻数据连续化,同时降低随机放电带来的噪声,从而获得辨识时变电阻模型;再次,计算辨识电阻斜率,并依据斜率变化特性及变化系数判定预击穿放电阶段和剧烈放电阶段;最后,通过水中脉冲放电观测试验平台验证了该辨识方法的有效性。结果表明,基于扩展卡尔曼滤波算法得到的水中脉冲放电电阻较试验值的方差小于1.717 Ω2,电阻斜率方差小于1.899,故该方法可用于水中脉冲放电阶段的判定。
关键词:水中脉冲放电 时变电阻 扩展卡尔曼滤波 放电阶段辨识
水中脉冲放电广泛应用于工业、医疗和国防领域,例如岩石粉碎、体外碎石、杀菌除垢、震源模拟、油气解堵[1-4]等。水中脉冲放电基于“液电效应”发生,即液体介质因高压击穿放电引发的光、热和冲击波等综合物理效应,又因伴生冲击波被称为“电水锤效应”[5-6]。随着石油开采技术的发展,水中脉冲放电因其相较于炸药起爆具有便捷、可生成复频冲击波等优势而得到广泛应用[7-8]。
为提升水中放电冲击波压力峰值及脉冲放电装备能耗比,需深化水中脉冲放电各阶段的能量转化研究工作。现有研究表明,水中脉冲放电主要分为三个阶段:预击穿放电阶段、剧烈放电阶段和振荡放电阶段[9]。预击穿放电阶段和剧烈放电阶段是能量消耗与转化的主要阶段,因此准确区分两个阶段具有重要的研究意义。黄仕杰等建立了基于液电效应的岩石破碎技术中的电弧通道阻抗模型,通过迭代法求解了模型参数及初值,结果表明该模型能够有效地表征该应用场景中电弧阻抗的时变特性[10]。Li Xiandong等提出了以电弧通道沉积能量为参照的平均电弧阻抗的计算方法[11]。刘毅等研究了水中脉冲放电过程中电弧通道的阻抗特性,建立了改进的Braginskii-Martin液中电弧阻抗模型,为时变电阻分析提供了理论基础[12]。
目前,水中放电电压、电流等关键参数主要基于实验方法测量,但电弧通道的发育路径具有较强的随机性,且测量数据存在电磁干扰导致的噪声。为消除这一误差,获得普适性阻抗特性变化规律,本文采用非线性滤波器对原生数据进行降噪及连续化。其中,扩展卡尔曼滤波(Extended Kalman Filter, EKF)算法在参数辨识领域有着广泛的应用和较高的成熟度[13-14]。Liu Weijie等构建了电容动态模型,运用EKF算法对阻容模型参数进行辨识,较传统算法提高了电池充电状态估计精度[15]。C. M. Greve等基于EKF算法估计脉冲放电过程中等离子体反应速率系数和吸收电子输入功率等未知系统状态,有效分析估算了时变系统的等离子体性质和过程[16]。为深入研究水中脉冲放电参数变化、判定放电阶段,本文将EKF算法引入水中脉冲放电过程,对测量的电压、电流数据进行辨识,有效降低测量数据尖峰误差,分析阻抗的时变特性。
为精确划分放电阶段,搭建了水中高压脉冲放电试验平台,测量放电电压、电流数据。同时提出基于EKF算法的水中脉冲放电参数辨识方法,建立水中脉冲放电等效电路模型,利用EKF算法对测量参数进行辨识,最终得到准确的时变电阻数据。采用斜率法分析阻抗时变特性曲线,并开展了方法的离散性分析工作。结果表明,基于EKF算法获得的辨识电阻可有效应用于判定水中脉冲放电阶段,为能量沉积特性分析及冲击波压力控制提供理论基础。
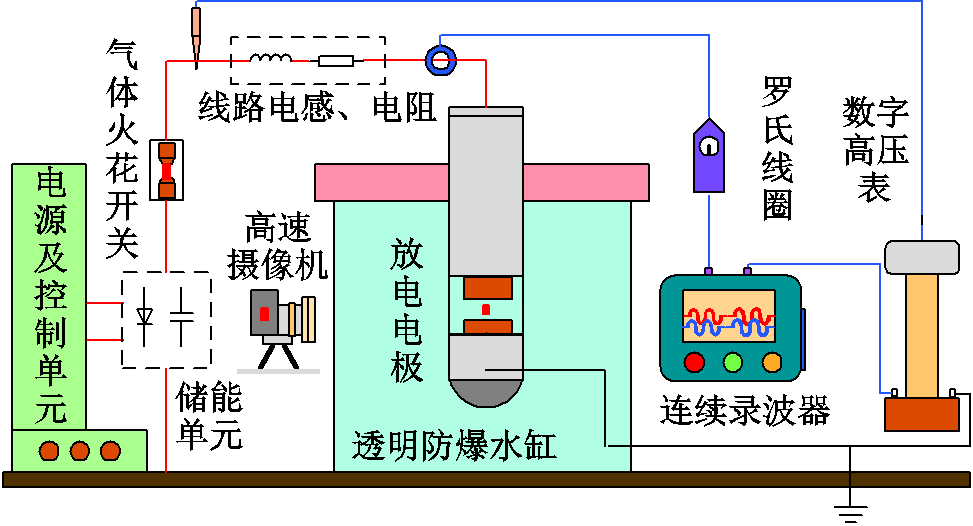
水中脉冲放电试验平台如图1所示,主要由电源及控制单元、储能单元、脉冲放电单元和测量分析单元四部分组成。

图1 水中脉冲放电试验平台
Fig.1 Experimental platform for pulse discharge in water
1)电源及控制单元:电源控制装置通过整流桥将380 V输入电压转换为0~500 V、0.5~2.5 kHz的可控交流电输出,持续为储能单元充能。
2)储能单元:储能单元由4倍压整流电路组成,将输出的低压交流电转换为高压直流电,等效电容值为8 μF;最大工作电压为30 kV,通过铠装电缆(绝缘电压30 kV,最大牵引质量3 500 kg)供给脉冲放电单元。
3)脉冲放电单元:脉冲放电单元由气体火花开关(板-板结构,电极直径为10 mm,大气压下放电)、板-板结构水中放电电极(阴极直径50 mm,阳极直径10 mm,钨铜合金)组成,最大工作电压为30 kV,脉冲放电最高频率为50 Hz。其中,电极沉浸于0.38 m´0.28 m´0.32 m的长方体透明防爆水缸中,缸内流体为以氯化钠为溶质的去离子水溶剂,电极阳极与装置外壳连接(负极性放电),外壳接地。
4)测量分析单元:主要由连续录波器(YOKOGAWA DL350,采样间隔1 μs)、罗氏线圈(CWT Mini/Mini HF)、分压式数字高压表(SGB-50C)和高速摄像机(Phantom V2512,作业频率5 MHz)组成,高速摄像机采用后触发模式。
电极两端电压、电流数据依靠分压式数字高压表及罗氏线圈测量,并通过连续录波器记录,数据线表面二次覆设金属屏蔽网。其中,罗氏线圈测量点为气体火花开关和电极之间的导线,负责测量输入端到放电电极的工作电流值,电火花开关放置于不锈钢316L材质的筒体内,并通过四氟乙烯材料封堵;分压式数字高压表测量端通过探头钳夹在导线与电极相连的端子上,数据传输端与连续录波器相连并记录时变数据,第三端接地。为保证相机拍摄到的电弧形态完整且可靠,相机安装过程中保证高速摄像机的镜头轴线与电极间隙中点保持在同一水平面上。
1.2.1 标准放电数据
水中脉冲放电观测试验通过连续录波器进行数据采集,采样率为1 MHz,水溶液电导率为 1 734 μS/cm,放电电压为-16 kV,电极间隙分别为0.62、1.01、1.38 mm。通过录波器精确测定了放电电压、电流数据。电极间隙为1.01 mm时,水中连续脉冲放电数据如图2所示。
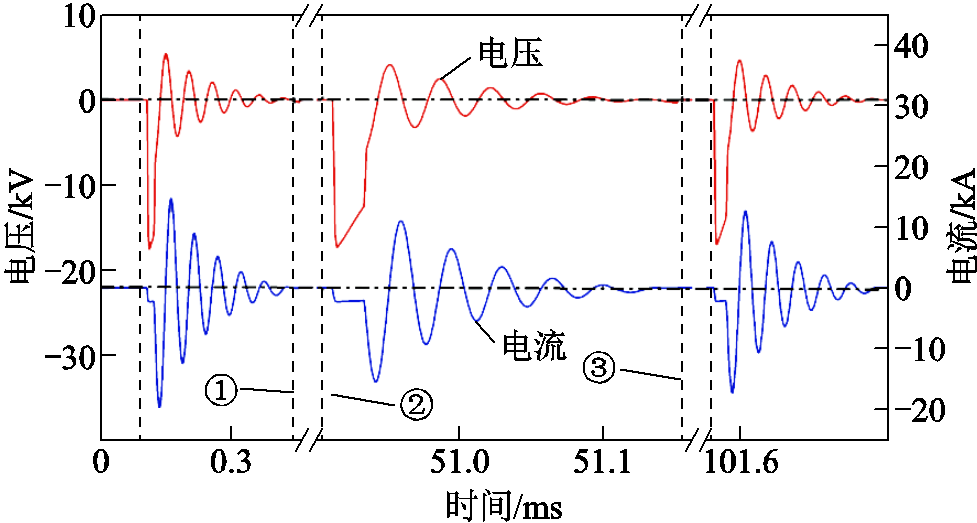
图2 水中连续脉冲放电数据
Fig.2 Data of continuous pulse discharge in water
试验中脉冲放电频率近似为20 Hz。为了体现连续放电波形,绘制过程中忽略放电间歇(电极间无电压、电流)数据,如图2中分割线①0.39 ms和②50.85 ms之间,时长约为50 ms。分割线②50.85 ms和③51.17 ms之间为一次完整的放电过程,放电周期为320 ms。图2中曲线直观地表现出电压先升高到-16 kV左右,随后缓慢下降至-13 kV,与此同时电流持续缓慢上升,该阶段即为初始电弧通道形成与发育的预击穿阶段;随后电压急剧下降,电流迅速增大,该阶段为稠密电弧形成及膨胀的剧烈放电阶段;最后电压、电流振荡直至数值为0。
1.2.2 含噪声放电数据
目前,关于水中脉冲放电阶段的判定主要根据电极两端电压、电流波形的变化特性开展。而在实际工程应用中,无法完全保证测定的电压、电流数据持续稳定且不受干扰。这是因为电火花开关与水中电极导通瞬间会形成电弧,此时存在剧烈的能量转化,伴随着强烈的电磁辐射,并且在高压放电回路中存在电压、电流的突变。特别是在复频放电过程中,外部的强电磁干扰会对电压表及罗式线圈产生较大影响,导致测量的电压和电流波形在正常变化基础上出现更明显的毛刺尖峰,如图3所示。因此,在开展水中高压脉冲放电研究过程中,需要运用滤波算法降低外部干扰影响,并求解有效放电参数用于阶段辨识分析。
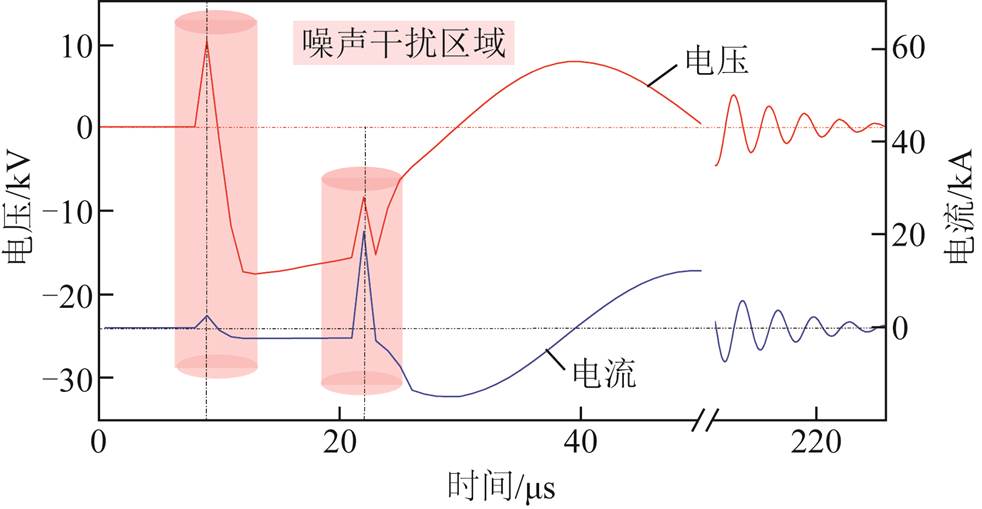
图3 电压、电流尖峰波形示意图
Fig.3 Voltage and current waveforms with spikes
预击穿放电阶段是初始电弧通道(等离子体通道)形成及发育的过程。当电极两端施加高电压后,在极板间的极不均匀流体中形成局部电场,自由电子在电场力的作用下于电极表面附近聚积形成先导,随即形成初始等离子体通道,用时约为10~25 ns[17]。此过程电极间不存在主形态的电流通道,故仅考虑电极间水介质的泄漏电流,且其电阻受液体电导率影响。
当初始等离子体通道形成后,通道内的等离子体在外部电场作用下具有一定的导流能力。但初始通道直径较小为mm级,且内部电子密度较低,导致通道内无法直接形成稠密的电弧用于电能能量沉积[18]。因此,通道形成后通道外壁面持续对周围水介质辐射加热使其达到“边界沸腾温度”来降低边界介电常数,促进通道再发育[19]。随着通道的不断发育,电极间电阻呈时变特性,且受不均匀电场的影响(随机放电),电阻呈非线性变化。受通道内电子密度与通道体积影响,此阶段等效电阻会比剧烈放电阶段电阻高10~103倍。因没有电弧产生,故该阶段没有电弧电感,可视为一个时变电阻等效电路模型,如图4所示。图中,UC为倍压整流输出的直流高电压;U为测量电压;L0为线路电感,其测定值为1.32´10-5 H;线路电阻R0为0.03 W;S为气体火花开关;R(t)为电极间隙的时变等效电阻。由此可建立等效回路方程为
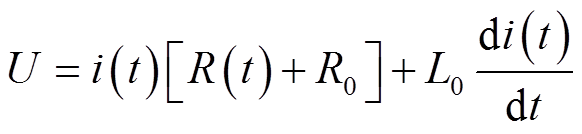 (1)
(1)
式中,i(t)为线路电流。
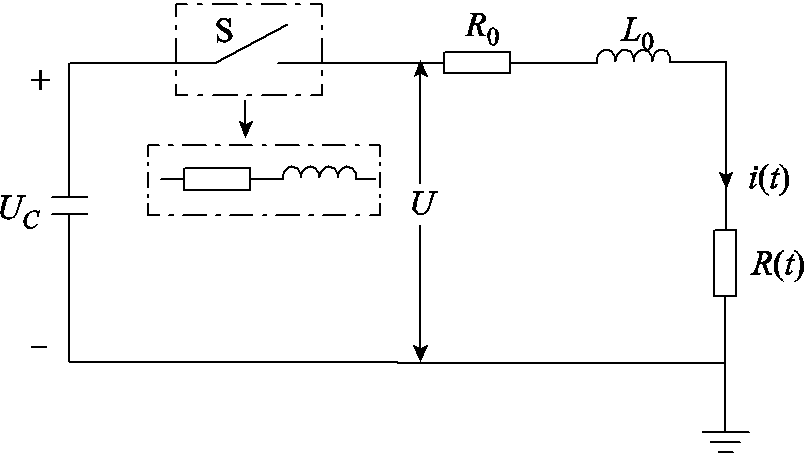
图4 预击穿放电阶段等效电路
Fig.4 Equivalent circuit of pre-breakdown discharge stage
随着雪崩电离的进行,初始等离子体通道内水蒸气、离子密度到达临界值,通道内形成稠密的电弧,电极间电阻急剧下降[20]。主放电阶段放电电弧半径有所变化,但其变化范围较小,这一结论与高速摄像机拍摄到的电弧通道形态变化特征一致,如图5所示。因此,在102 ns~102ms的情况下电弧半径可认为是常数。又因电弧电感与电弧半径呈正相关,故电弧电感可按常数参与分析[21]。

图5 水中放电电弧通道形态
Fig.5 Morphology of the arc channel of the discharge in water
电弧电感和电弧半径的关系[22-23]为
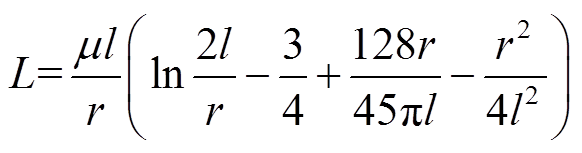 (2)
(2)
式中,L为电极之间的电弧电感;m为等离子体通道等效磁导率,此时m=m0,m0为真空磁导率,其值为4p´10-7 H/m;l为电极间隙距离,即电弧长度;r为电弧半径。基于上述阶段特征,剧烈放电阶段等效电路模型如图6所示。
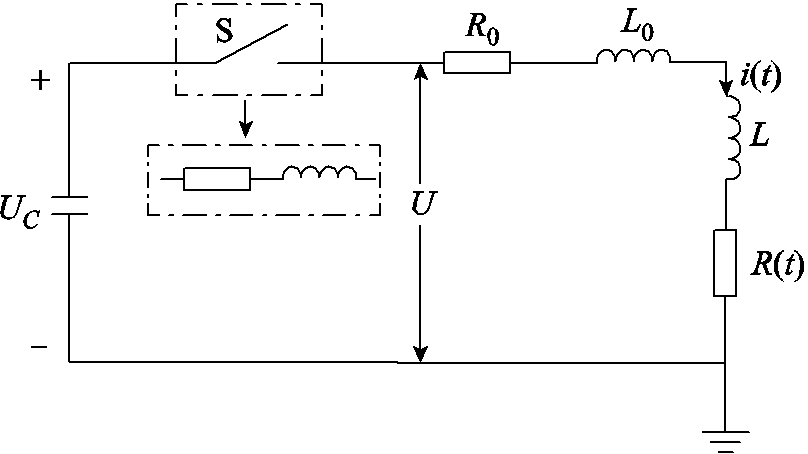
图6 剧烈放电阶段等效电路
Fig.6 Equivalent circuit of primary discharge stage
通过图5中像素点标定,测得电弧半径约为0.72 mm,依据式(2)求解电极间隙为0.62、1.01、1.38 mm时的电弧电感分别为4.13´10-7、1.30´10-6、2.43´10-6 H。与线路电感L0相比,电弧电感L较小,对辨识过程影响甚微,故求解过程中将剧烈放电阶段电路模型中的电弧电感等效为定值。
随着通道内稠密电弧的出现,储能单元内储存的电能在通道内快速沉积,等离子体通道径向方向急剧膨胀,电弧等效电阻迅速减小,因此等效电路中电阻是时变的。其中,放电过程的电阻值可通过变换式(1)进一步推导得到,表示为
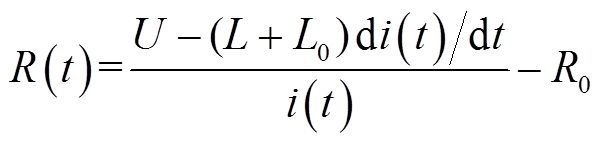 (3)
(3)
其中,不同条件下的电弧电感值可通过式(2)求得。将试验测得的放电电压、电流数据及相关参数代入式(3)进行求解,从而获得电阻值。
为进一步明晰水中放电过程中的阻抗变化特征,依据1.2节中试验环境开展水中重复脉冲放电试验,测量电压、电流数据50组。由于数据采样率较高,单个放电周期采集数据点共计约3×104个,因此本文以单放电周期内预击穿放电阶段、剧烈放电阶段及振荡放电阶段第3 s时的电阻数据为例开展研究。其中,各放电阶段起止时刻的划分标准以放电电压变化特征为主(电压突变时刻),同时以高速摄像机拍摄数据为辅[24]。将相关电压、电流数据按照放电阶段代入式(1)~式(3),可获得对应阶段及各时刻电阻,结果如图7所示。图7中数据点整体呈离散且非线性分布,这是不均匀电场下随机放电特性造成的普遍现象。该特征造成无法直接定量描述该时刻的电阻值,故以某一恒定电阻值作为放电阶段的判定依据是不严谨的。
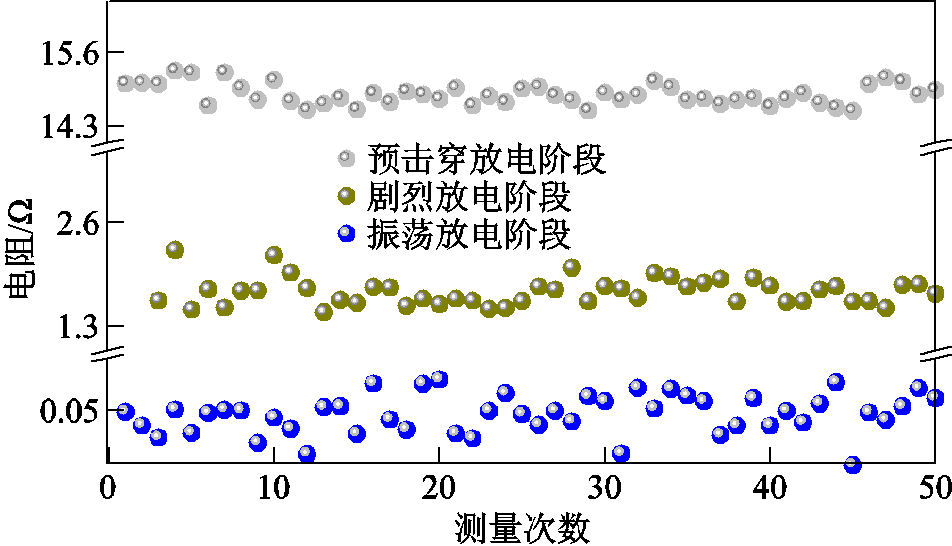
图7 不同放电阶段测量电阻对比
Fig.7 Comparison of measured resistance at each stage of discharge stage
依据相关理论开展电阻值预测,设非线性系统的状态方程和量测方程[25-27]分别为
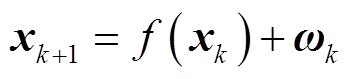 (4)
(4)
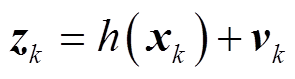 (5)
(5)
式中,xk+1为状态变量,表示t时刻第k+1次算法得出的预测电阻值;xk为第k次预测电阻值;zk为t时刻第k次试验实际测量电阻值(可由式(3)计算得到);f (xk)、h(xk)分别为t时刻第k次系统状态函数和量测函数;wk、vk分别为第k次的过程高斯白噪声和测量高斯白噪声。
对非线性系统状态方程进行一阶泰勒展开,并忽略高阶项,可得到电阻值预测计算式为
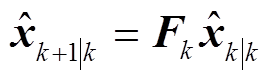 (6)
(6)
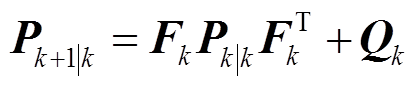 (7)
(7)
式中,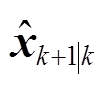 为利用状态转移矩阵Fk得到的第k+1次的系统状态量的预测值;Pk+1|k为第k+1次预测误差协方差矩阵;Qk为系统误差方差矩阵,满足均值为0的高斯白噪声。
为利用状态转移矩阵Fk得到的第k+1次的系统状态量的预测值;Pk+1|k为第k+1次预测误差协方差矩阵;Qk为系统误差方差矩阵,满足均值为0的高斯白噪声。
同理,对量测方程式(5)分析可得量测系统预测值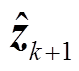 及误差协方差矩阵
及误差协方差矩阵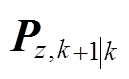 ,计算式为
,计算式为
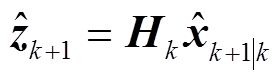 (8)
(8)
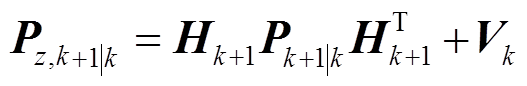 (9)
(9)
式中,Hk为第k次量测方程的雅可比矩阵;Vk为测量噪声协方差矩阵,满足均值为0的高斯白噪声。
进一步对电阻值滤波,首先对系统量测函数进行一阶泰勒展开,并忽略高阶项,可得到电阻值滤波计算式为
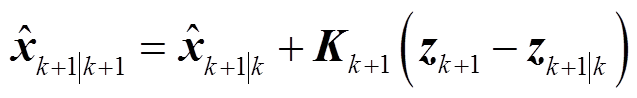 (10)
(10)
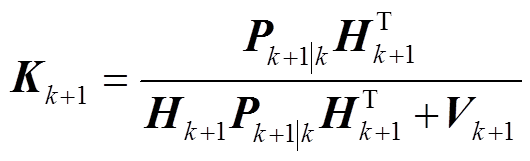 (11)
(11)
式中,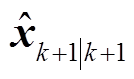 为第k+1次电阻参数先验估计值;Kk+1为第k+1次状态增益矩阵。
为第k+1次电阻参数先验估计值;Kk+1为第k+1次状态增益矩阵。
此时状态估计误差协方差矩阵Pk+1|k+1为
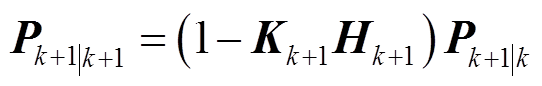 (12)
(12)
基于第2节的理论模型对采集的放电电压和电流数据开展分析求解,研究数据点的有效性。在2.2节试验条件下进一步增加放电试验次数,并将水中脉冲放电的试验数据作为样本,结合EKF对数据进行辨识处理,辨识流程如图8所示。图中,Rest为辨识电阻;Eest为估计误差;Emea为测量误差。
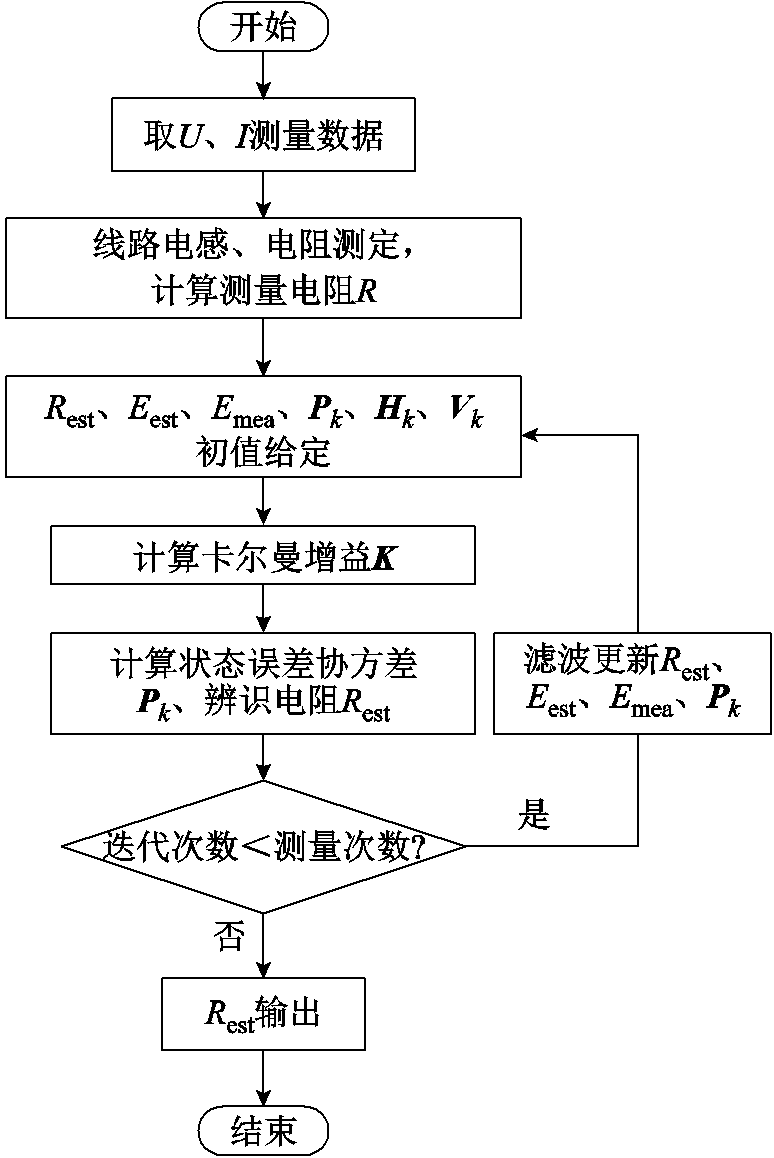
图8 基于EKF的水中脉冲放电参数辨识流程
Fig.8 Process for identifying parameters of pulse discharge in water based on EKF
通过EKF算法对放电电压、电流进行辨识处理,得到预击穿放电阶段和剧烈放电阶段的辨识电阻值见表1。结果表明,预击穿阶段辨识电阻明显大于剧烈放电阶段的辨识电阻。例如,电极间隙为0.62 mm时,其预击穿阶段15 ms的辨识电阻值为5.253 W,明显大于剧烈放电阶段20 ms的0.435 W。
表1 电极间隙等效电阻辨识数据
Tab.1 Equivalent resistance identification data of electrode gap
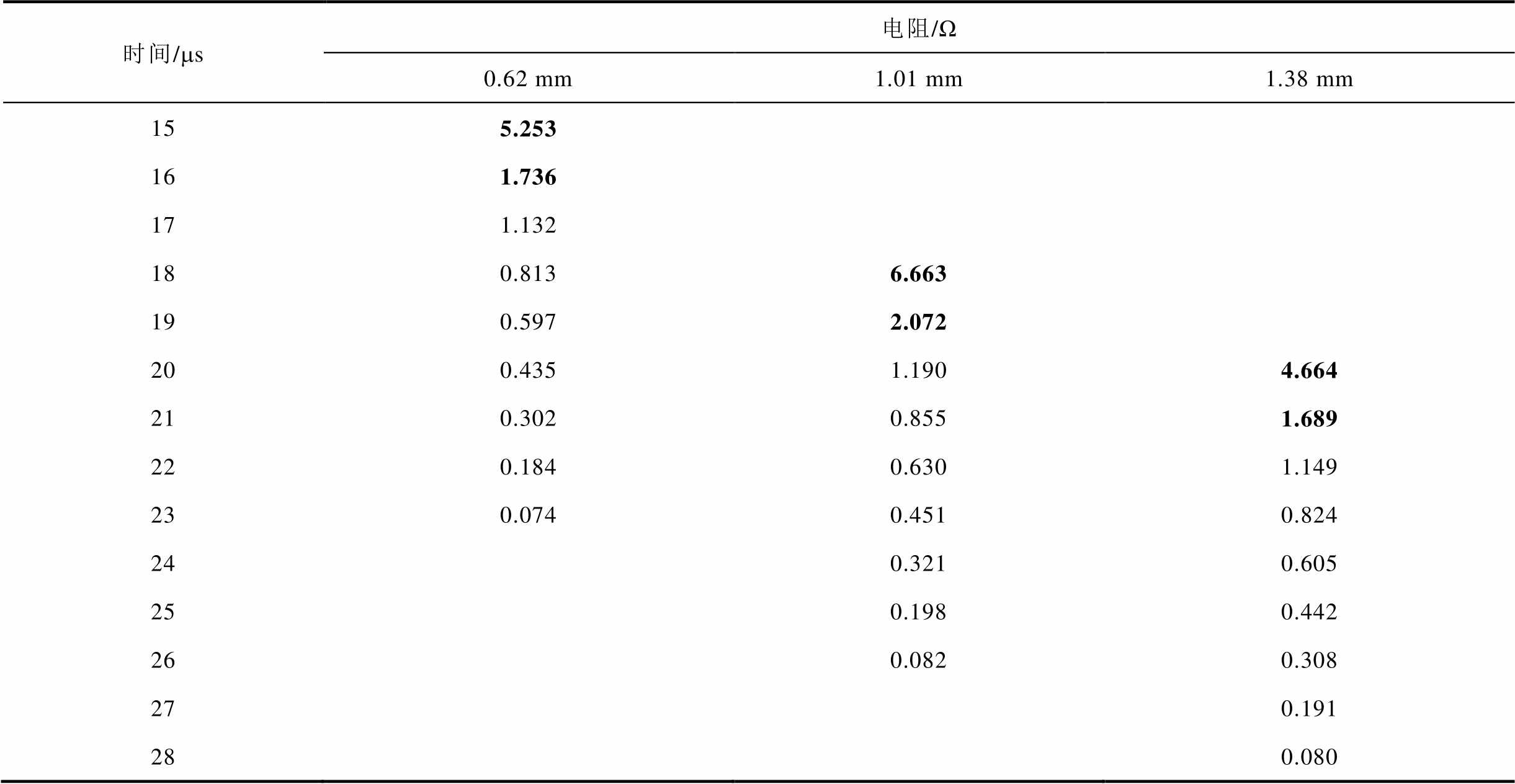
时间/ms电阻/Ω 0.62 mm1.01 mm1.38 mm 155.253 161.736 171.132 180.8136.663 190.5972.072 200.4351.1904.664 210.3020.8551.689 220.1840.6301.149 230.0740.4510.824 240.3210.605 250.1980.442 260.0820.308 270.191 280.080
其中,剧烈放电阶段辨识电阻变化明显,故对于未知条件下的放电过程仅凭单一时刻电阻值难以判定放电阶段。同时,预击穿放电阶段时间会随着电极间隙增大而变长(即剧烈放电起始时刻延后),但对剧烈放电阶段时延影响较小。这一现象进一步表明外部环境对放电阶段时间变化影响较大,故研究基于EKF算法进行放电阶段辨识具有实际意义。
基于第2节中理论分析及表1数据可知,不同放电阶段电弧通道电阻差值明显,故将这一特性作为放电阶段判定参照。首先,求解辨识电阻数据一阶导数,得到辨识电阻斜率SR为
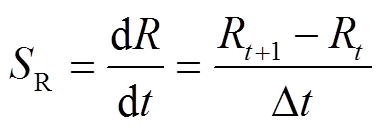 (13)
(13)
式中,Rt+1为t+1时刻的辨识电阻;Rt为t时刻的辨识电阻。
其次,SR随放电时间推移而改变,且在剧烈放电阶段会明显增大,因此基于此数据的区间分布特性进行阈值l、b的选取。SR和l、b的关系为
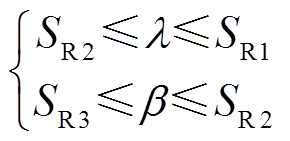 (14)
(14)
式中,SR1、SR2、SR3分别为未击穿阶段、预击穿放电阶段和剧烈放电阶段的斜率变化临界值。基于上述试验数据集,该条件下l取值范围为(0.40, 0.55),b取值范围为(-0.31, -0.13)。
最后,当SR由SR1变化至SR2时,表示放电进入预击穿放电阶段;当SR由SR2变化至SR3时,表示放电进入剧烈放电阶段;当电压上升至正值时,表示放电进入振荡放电阶段。
基于上述方法对试验测量的放电波形开展分析,根据实际电阻的斜率变化判定具体放电阶段,流程如图9所示。
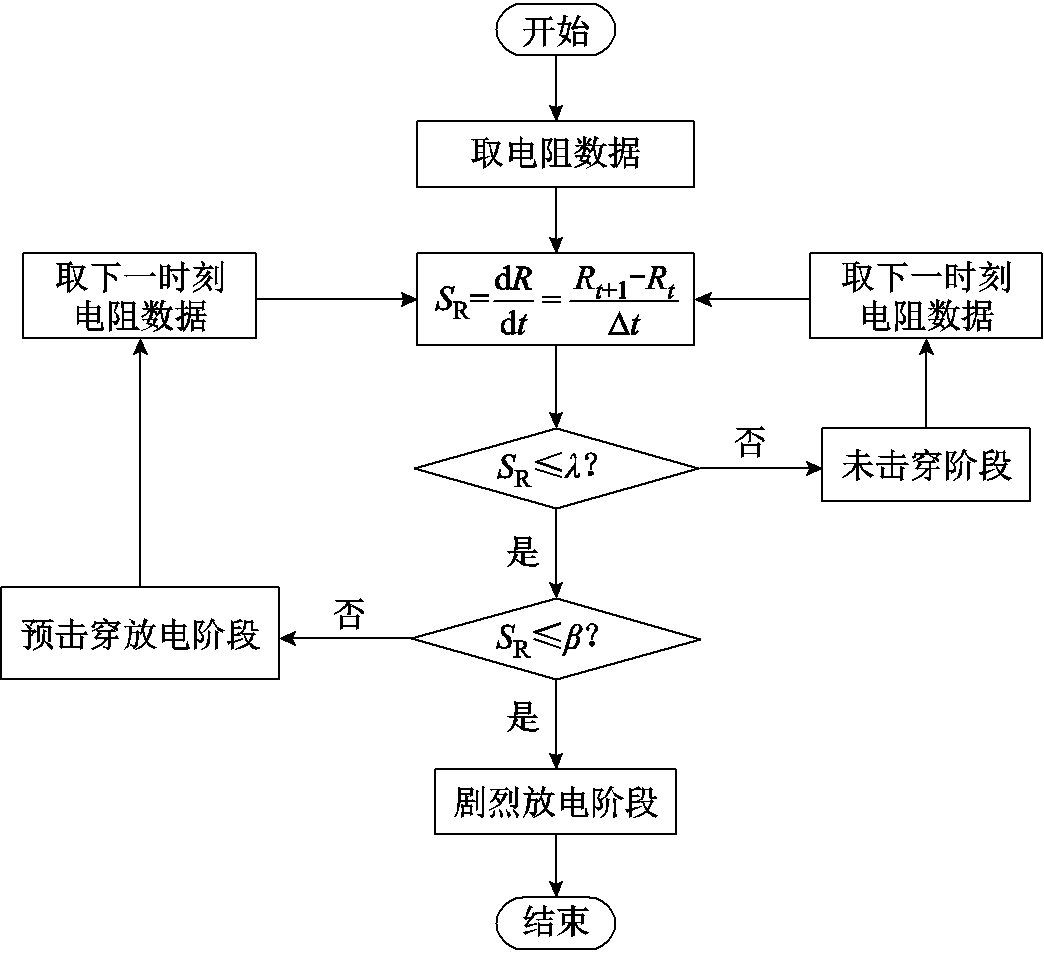
图9 放电阶段判定流程
Fig.9 Determination flow of discharge stage
通过分析处理试验数据,电极间隙为0.62 mm时,有效数据点共计82组;电极间隙为1.01 mm时,有效数据点共计72组;电极间隙为1.38 mm时,有效数据点共计78组。基于EKF算法进行电阻参数辨识,结果如图10所示。
图10a为电极间隙为0.62 mm的试验数据辨识结果,整个水中脉冲放电阶段每个时刻均迭代82次。结果表明,电阻在预击穿放电阶段约为15.00 W,呈现类线性变化,随着放电过程的推进电阻缓慢减小;16 ms时刻电阻突降至1.74 W;在23 ms时刻电阻下降至0.07 W。由此可见,预击穿放电阶段为3~14 ms,预击穿阶段时延为11 ms;剧烈放电阶段处于14~23 ms,剧烈放电时间为9 ms。
图10b为电极间隙为1.01 mm的试验数据辨识结果,每个时刻电阻数据均迭代72次。结果表明,辨识电阻在预击穿放电阶段趋近于16.00 W;19 ms时突降至2.07 W;在26 ms时下降至0.08 W。由此可见,预击穿放电阶段在3~17 ms,预击穿时间为14 ms;剧烈放电阶段在17~26 ms,剧烈放电时间为9 ms。辨识电阻数据整体变化趋势同间隙0.62 mm时相一致。
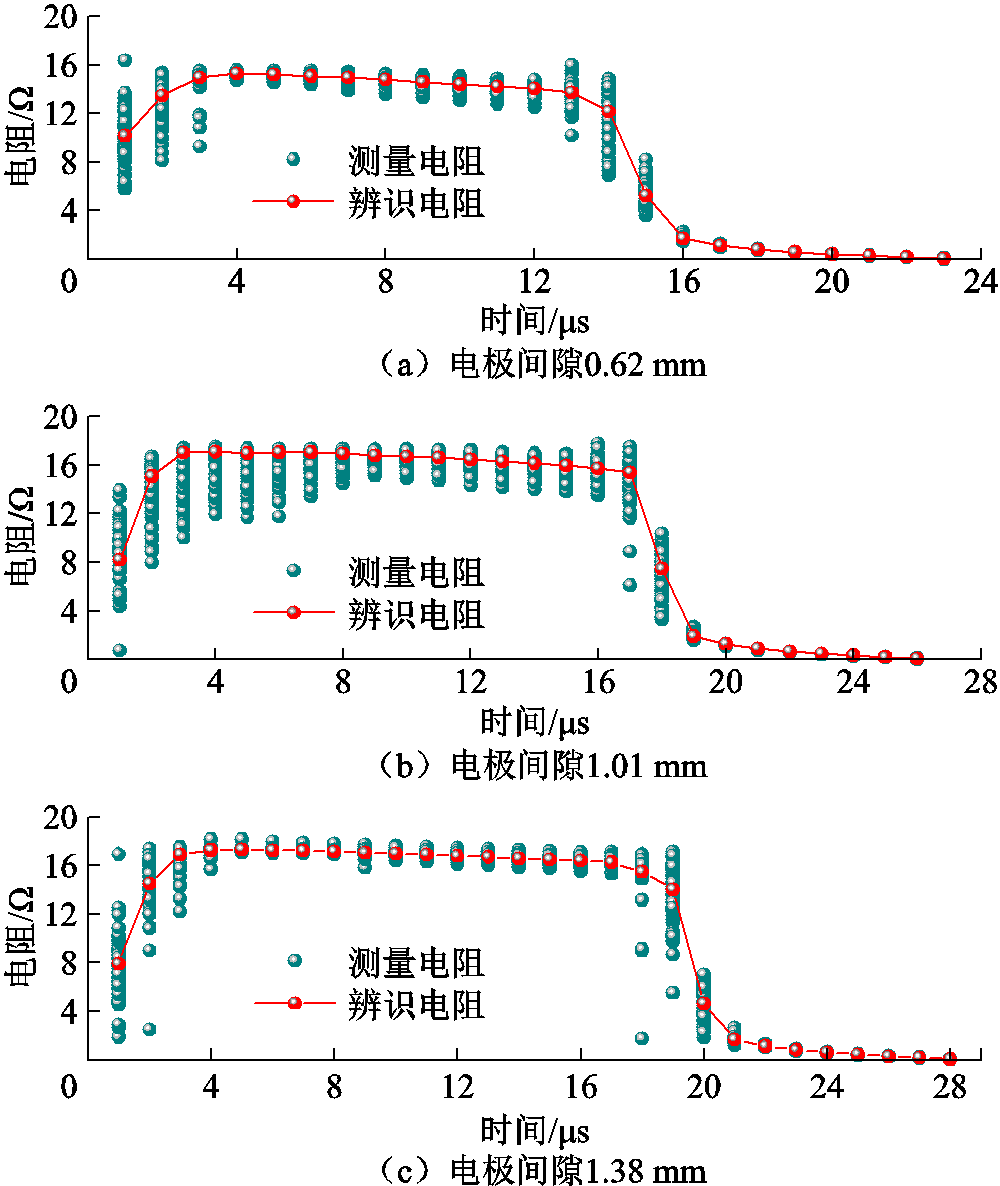
图10 辨识电阻与测量电阻对比
Fig.10 Comparison of identification resistance with the measurement resistance
图10c为电极间隙为1.38 mm的试验数据辨识结果,每个时刻电阻数据均迭代78次。结果表明,辨识电阻在预击穿放电阶段约为17.00 W,呈现类线性变化;21 ms时刻下降至1.69 W,在28 ms时刻下降至0.08 W。由此可见,预击穿放电阶段在3~19 ms,预击穿时间为16 ms;剧烈放电阶段在19~28 ms,剧烈放电时间为9 ms。数据变化趋势同上。
在上述辨识结果基础上,引用式(13)求解辨识电阻斜率,如图11所示。基于图11中电阻斜率曲线变化特性及突变时刻,可直观地分辨出预击穿放电阶段和剧烈放电阶段。预击穿放电阶段电阻斜率曲线较为平缓,斜率值稳定在-0.21~0.53内;剧烈放电阶段电阻斜率突增,三种电极间隙下的电阻斜率分别增大至-6.90、-8.05、-9.37。这一现象的主要原因为预击穿阶段等离子体通道发育平缓,边界物理场稳定,电阻值稳定变化,斜率较小;剧烈放电过程电弧通道电导率陡升,电阻值骤降,斜率较大。
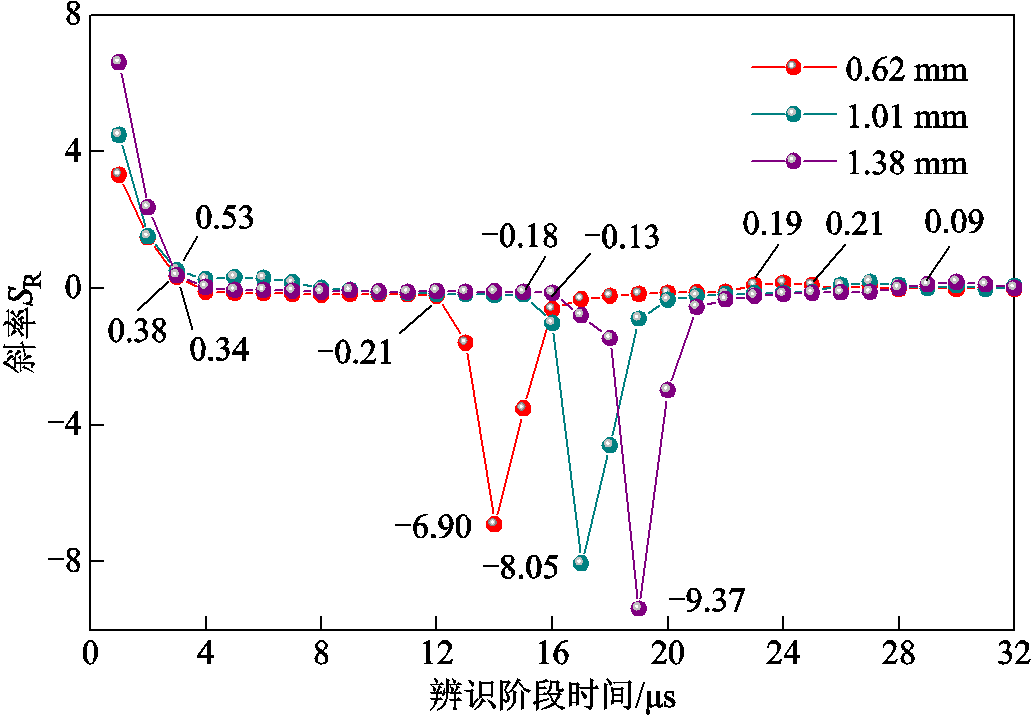
图11 辨识电阻斜率曲线
Fig.11 Slope curves of the identified resistance
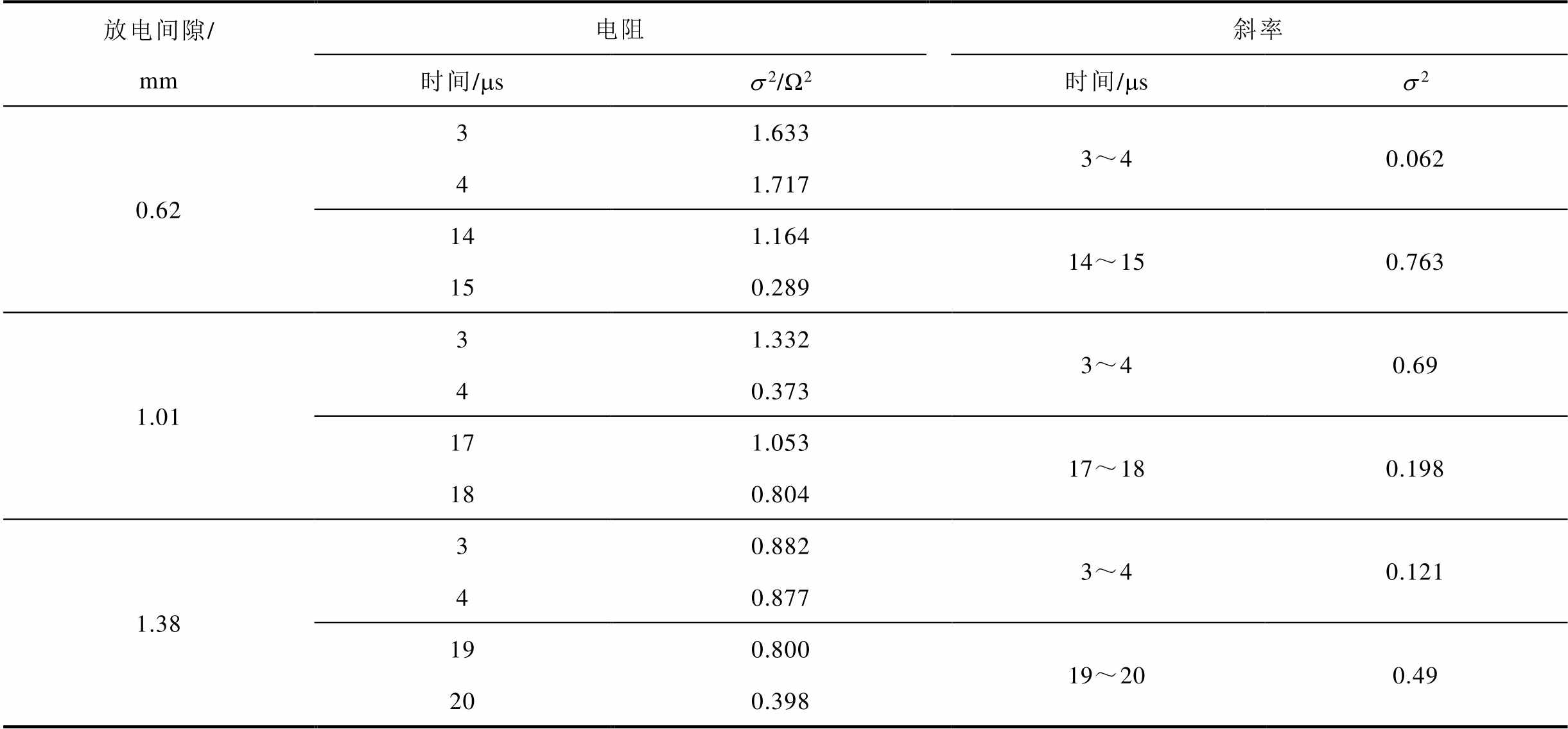
为验证上述方法的有效性及准确性,分别提取三种放电间隙下的预击穿放电阶段和剧烈放电阶段起始点的测量电阻,基于方差理论进行误差分析,从而量化辨识电阻和测量电阻关系,并定量分析斜率的拟合程度,相关结论见表2。其中,数据方差求解式为
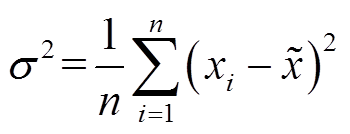 (15)
(15)
式中,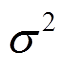 为数据方差;xi为第i次测量数据;
为数据方差;xi为第i次测量数据;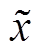 为辨识数据;n为测量次数。
为辨识数据;n为测量次数。
表2 基于方差理论的辨识电阻误差分析
Tab.2 Identification resistance error analysis based on variance theory
放电间隙/ mm电阻斜率 时间/mss2/Ω2时间/mss2 0.6231.6333~40.062 41.717 141.16414~150.763 150.289 1.0131.3323~40.69 40.373 171.05317~180.198 180.804 1.3830.8823~40.121 40.877 190.80019~200.49 200.398
受气体火花开关导通特性及录波器采样率影响,测定脉冲有效上升时延约为3 ms,故三种电极间隙预击穿放电阶段起始时刻均为3 ms时刻。其中,电极间隙0.62、1.01、1.38 mm下的验证试验中,剧烈放电阶段起始时刻分别为14、17、19 ms。通过表2可知,电阻方差最小值为0.62 mm间隙下15 ms对应值0.289 Ω2,最大值为0.62 mm间隙下 4 ms对应值1.717 Ω2,上述两个最值点对应的测量电阻值区间分别为5.20~5.40 W和15.20~15.40 W,且区间内数据的相对偏差小于3.8%。结果表明,基于扩展卡尔曼滤波得到的辨识电阻和测量电阻近似相等,故扩展卡尔曼滤波辨识水中放电电阻是有效且准确的。
在明确该方法的有效性后,进一步开展了该条件下的放电阶段辨识准确性研究,即开展电极间隙为0.62、1.01、1.38 mm的预击穿放电及剧烈放电起始时刻的电阻斜率的误差分析,相关结论见表2。电阻斜率方差数值最小为0.062,最大为0.763,上述两斜率区间分别为(-3.7, -3.5)、(-0.1, 0.05)。结果表明,辨识电阻与测量电阻在预击穿放电起始阶段和剧烈放电起始阶段的斜率近似等值,故通过此方法判定放电阶段是准确的。
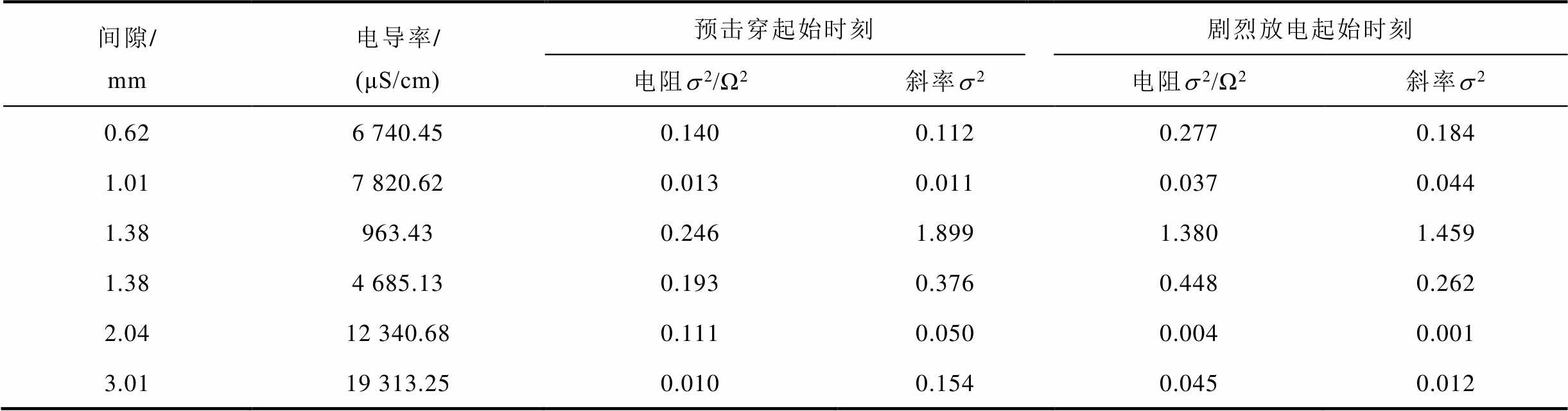
在明确方法的可靠性后,依据搭建的水中脉冲放电试验平台验证本文所提出的水中放电阶段辨识方法的普适性。试验过程中以电极间隙、溶液电导率为主变量,电极间隙取0.62、1.01、1.38、2.04、3.01 mm,对应溶液电导率分别为6 740.45、7 820.62、963.43与4 685.13、12 340.68、19 313.25 μS/cm,放电电压为12 kV。上述电极间隙及溶液电导率在覆盖现有相关研究参考范围的基础上进一步增大,将测得电压、电流数据依据第2节与第3节所述理论及方法进行处理,求解并分析预击穿与剧烈放电起始时刻的电阻及斜率误差,旨在凸显方法的适用性,结果见表3。
表3 相关辨识参数误差分析
Tab.3 Error analysis of relevant identification parameters
间隙/ mm电导率/(μS/cm)预击穿起始时刻剧烈放电起始时刻 电阻s2/Ω2斜率s2电阻s2/Ω2斜率s2 0.626 740.450.1400.1120.2770.184 1.017 820.620.0130.0110.0370.044 1.38963.430.2461.8991.3801.459 1.384 685.130.1930.3760.4480.262 2.0412 340.680.1110.0500.0040.001 3.0119 313.250.0100.1540.0450.012
通过表3中电阻方差数据可知,预击穿起始时刻电阻数据方差区间为0.010~0.246 Ω2,剧烈放电起始时刻电阻数据方差区间为0.004~1.380 Ω2,最小值为间隙2.04 mm且电导率为12 340.68 μS/cm情况下的剧烈放电起始时刻对应值0.004 Ω2,最大值为间隙1.38 mm且电导率为963.43 μS/cm情况下的剧烈放电起始时刻对应值1.380 Ω2,其对应的电阻区间分别为2.88~2.97 W、19.87~21.79 W,且区间内数据相对偏差小于8.8%。同时,将表3与表2数据对照分析可知,电极间隙一致时,电阻误差与溶液电导率呈负相关。例如,当电极间隙为0.62 mm、电导率增大至6 740.45 μS/cm时,电阻方差由1.717 Ω2降至0.140 Ω2;当电极间隙为1.38 mm、电导率降至963.43 μS/cm时,电阻方差由0.800 Ω2增至1.380 Ω2。造成这一现象的主要原因为电导率降低,电弧通道直径增大,路径形成更易受外部环境影响,放电更为容易且随机性更强[28-29]。但通过电阻取值范围及误差分析可知,基于本文提出的方法仍可有效辨识出放电阶段。
同理,通过表3电阻斜率方差数据可知,预击穿起始时刻斜率数据方差区间为0.011~1.899,剧烈放电阶段起始时刻电阻数据方差区间为0.001~1.459,最小值为间隙2.04 mm且电导率为12 340.68 μS/cm情况下的剧烈放电起始时刻对应值0.001,最大值为间隙1.38 mm且电导率为963.43 μS/cm情况下的预击穿起始时刻对应值1.899。上述两斜率区间分别为(-0.467, -0.403)、(-4.324, -3.970),相对偏差小于8.9%。与表2数据对照分析可知,当电极间隙一定时,电阻斜率误差多随着电导率的增高而降低,具体情况及原因同电阻方差分析过程一致。
最后,为进一步证明该方法的普适性,设置两组大电极间隙2.04 mm与3.01 mm,并将溶液电导率随机增大,分别提高至12 340.68 μS/cm和19 313.25 μS/cm。采用与前述研究同一方法和计算模型对测定的电压、电流开展处理,得到辨识电阻与电阻斜率值。误差分析结果表明,辨识电阻值与变化率与试验测量值更为贴合,数据离散度低,进而表明该方法同样适用于电极间隙及电导率阶跃式变化的环境。
为提升水中放电冲击波幅值压力及脉冲放电装备能耗比,需明确各放电阶段阻抗特性及能量转化总量。本文依据水中脉冲放电试验平台探明并解释了复频放电随机特性及测量噪声机理;基于等离子体理论分析了放电过程阻抗变化特性,分阶段建立了水中放电时变等效电路模型;通过EKF算法处理并分析试验测量电阻数据,得到了对应辨识电阻。离散性分析结果表明,二者相对误差小于3.8%,且时变特征相一致;采用斜率法分析辨识电阻的斜率曲线变化特性,提出用于判定预击穿放电阶段和剧烈放电阶段的辨识电阻斜率SR及其取值方法,并通过验证试验证明了方法的有效性。研究结果表明,该方法能够准确地判定ms级放电过程中的预击穿放电阶段和剧烈放电阶段,为水中放电研究提供理论支撑。有关提升高噪声及其他极端场景下的放电阶段辨识方法鲁棒性有待进一步深入研究。
参考文献
[1] 刘毅, 李志远, 李显东, 等. 水中脉冲激波对模拟岩层破碎试验[J]. 电工技术学报, 2016, 31(24): 71-78. Liu Yi, Li Zhiyuan, Li Xiandong, et al. Experiments on the fracture of simulated stratum by underwater pulsed discharge shock waves[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 71-78.
[2] 董冰岩, 甘青青, 孙宇, 等. 高压脉冲放电协同复合型催化剂去除甲醛的实验[J]. 电工技术学报, 2017, 32(8): 108-113. Dong Bingyan, Gan Qingqing, Sun Yu, et al. Degradation of formaldehyde by high voltage pulse discharge combined with compound catalyst[J]. Transactions of China Electrotechnical Society, 2017, 32(8): 108-113.
[3] Smirnov A P, Zhekul V G, Taftai E I, et al. Effect of parameters of liquids on amplitudes of pressure waves generated by electric discharge[J]. Surface Engineering and Applied Electrochemistry, 2019, 55(1): 84-88.
[4] 王瑞雪, 李忠文, 虎攀, 等. 低温等离子体化学毒剂洗消技术研究进展[J]. 电工技术学报, 2021, 36(13): 2767-2781. Wang Ruixue, Li Zhongwen, Hu Pan, et al. Review of research progress of plasma chemical warfare agents degradation[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2767-2781.
[5] 李元, 孙滢, 刘毅, 等. 液电效应及电火花震源的研究现状与展望[J]. 高电压技术, 2021, 47(3): 753-765. Li Yuan, Sun Ying, Liu Yi, et al. Electrohydraulic effect and sparker source: current situation and prospects[J]. High Voltage Engineering, 2021, 47(3): 753-765.
[6] 王志强, 曹云霄, 邢政伟, 等. 高压脉冲放电破碎菱镁矿石的实验研究[J]. 电工技术学报, 2019, 34(4): 863-870. Wang Zhiqiang, Cao Yunxiao, Xing Zhengwei, et al. Experimental study on fragmentation of magnesite ores by pulsed high-voltage discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 863-870.
[7] Kang Zhongjian, Gao Chong, Gong Dajian, et al. Effect and mechanism analysis of resonance on physical parameters of unconventional reservoirs[J]. Energy Reports, 2022, 8: 12522-12533.
[8] 戴栋, 宁文军, 邵涛. 大气压低温等离子体的研究现状与发展趋势[J]. 电工技术学报, 2017, 32(20): 1-9. Dai Dong, Ning Wenjun, Shao Tao. A review on the state of art and future trends of atmospheric pressure low temperature plasmas[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 1-9.
[9] 聂云良, 康忠健, 王聪, 等. 水中脉冲放电电极的烧蚀特性[J]. 高电压技术, 2021, 47(7): 2607-2614. Nie Yunliang, Kang Zhongjian, Wang Cong, et al. Electrodes erosion characteristics of pulse discharge in water[J]. High Voltage Engineering, 2021, 47(7): 2607-2614.
[10] 黄仕杰, 刘毅, 林福昌, 等. 高压脉冲放电破岩电弧阻抗特性分析[J]. 电工技术学报, 2022, 37(19): 4978-4988. Huang Shijie, Liu Yi, Lin Fuchang, et al. Analysis of arc impedance characteristics in high-voltage electric pulse discharge rock destruction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4978-4988.
[11] Li Xiandong, Liu Yi, Liu Siwei, et al. Influence of deposited energy on shock wave induced by underwater pulsed current discharge[J]. Physics of Plasmas, 2016, 23(10): 103104.
[12] 刘毅, 黄仕杰, 赵勇, 等. 液中大电流脉冲放电电弧阻抗特性分析[J]. 高电压技术, 2021, 47(7): 2591-2598. Liu Yi, Huang Shijie, Zhao Yong, et al. Analysis of arc impedance characteristics of high current pulsed discharge in liquid[J]. High Voltage Engineering, 2021, 47(7): 2591-2598.
[13] Tahir S, Raja M M, Razzaq N, et al. Extended Kalman filter-based power line interference canceller for electrocardiogram signal[J]. Big Data, 2022, 10(1): 34-53.
[14] 赵宏晨, 刘晓明, 李龙女. 采用遗传算法的低压开关电弧反演[J]. 高压电器, 2017, 53(4): 25-30. Zhao Hongchen, Liu Xiaoming, Li Longnü. Arc inversion with genetic algorithm for low voltage switch[J]. High Voltage Apparatus, 2017, 53(4): 25-30.
[15] Liu Weijie, Zhou Hongliang, Tang Zeqiang, et al. State of charge estimation algorithm based on fractional-order adaptive extended Kalman filter and unscented Kalman filter[J]. Journal of Electrochemical Energy Conversion and Storage, 2022, 19(2): 021005.
[16] Greve C M, Hara K. Estimation of plasma properties using an extended Kalman filter with plasma global models[J]. Journal of Physics D: Applied Physics, 2022, 55(25): 255201.
[17] Ushakov V I. Impulse Breakdown of Liquids[M]. Berlin: Springer, 2007.
[18] Kolb J F, Joshi R P, Xiao S, et al. Streamers in water and other dielectric liquids[J]. Journal of Physics D: Applied Physics, 2008, 41(23): 234007.
[19] 王一博. 水中等离子体声源的理论与实验研究[D]. 长沙: 国防科学技术大学, 2012. Wang Yibo. Theoretical and experimental study of the underwater plasma acoustic source[D]. Changsha: National University of Defense Technology, 2012.
[20] 赵勇, 刘毅, 任益佳, 等. 水中大电流脉冲放电的激波传播特性[J]. 高电压技术, 2021, 47(3): 876-884. Zhao Yong, Liu Yi, Ren Yijia, et al. Shock wave propagation characteristics of pulsed high-current discharge in water[J]. High Voltage Engineering, 2021, 47(3): 876-884.
[21] 李宁, 雷开卓, 黄建国, 等. 采用时变电阻的水下高压放电模型[J]. 高电压技术, 2009, 35(12): 3060-3064. Li Ning, Lei Kaizhuo, Huang Jianguo, et al. Model of underwater high-voltage discharge using time-varying resistance[J]. High Voltage Engineering, 2009, 35(12): 3060-3064.
[22] 李显东, 刘毅, 李志远, 等. 不均匀电场下水中脉冲放电观测及沉积能量对激波的影响[J]. 中国电机工程学报, 2017, 37(10): 3028-3036. Li Xiandong, Liu Yi, Li Zhiyuan, et al. Observation of underwater pulse discharge and influence of deposited energy on shock wave in non-uniform electric field[J]. Proceedings of the CSEE, 2017, 37(10): 3028-3036.
[23] (苏)卡兰塔罗夫, (苏)采依特林. 电感计算手册[M]. 陈汤铭, 等译. 北京: 机械工业出版社, 1992.
[24] 刘毅, 赵勇, 任益佳, 等. 水中大电流脉冲放电电弧通道发展过程分析[J]. 电工技术学报, 2021, 36(16): 3525-3534. Liu Yi, Zhao Yong, Ren Yijia, et al. Analysis on the development process of arc channel for underwater high current pulsed discharge[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3525-3534.
[25] 王竞才, 李琰, 徐天奇. 基于扩展卡尔曼滤波的智能电网虚假数据检测[J]. 智慧电力, 2022, 50(3): 50-56. Wang Jingcai, Li Yan, Xu Tianqi. Detection of false data in smart grid based on extended Kalman filter[J]. Smart Power, 2022, 50(3): 50-56.
[26] 田勇, 杨昊, 胡超, 等. 基于毫米波雷达的电动汽车无线充电运动异物检测与跟踪[J]. 电工技术学报, 2023, 38(2): 297-308. Tian Yong, Yang Hao, Hu Chao, et al. Moving foreign object detection and track for electric vehicle wireless charging based on millimeter-wave radar[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 297-308.
[27] 师蔚, 骆凯传, 张舟云. 基于热网络法的永磁电机温度在线估计[J]. 电工技术学报, 2023, 38(10): 2686-2697. Shi Wei, Luo Kaichaun, Zhang zhouyun. On-line temperature estimation of permanent magnet motor based on lumped parameter thermal network method[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2686-2697.
[28] 喻越, 朱鑫磊, 黄昆, 等. 应用于石油解堵增产的水中脉冲放电特性实验研究[J]. 高电压技术, 2020, 46(8): 2951-2959. Yu Yue, Zhu Xinlei, Huang Kun, et al. Experimental study on pulse discharge characteristics in water applied to oil plugging and increasing production[J]. High Voltage Engineering, 2020, 46(8): 2951-2959.
[29] 付思, 陈文清, 曹云东. 小电流下弧根运动对空气直流电弧的影响[J]. 高压电器, 2023, 59(11): 224-230. Fu Si, Chen Wenqing, Cao Yundong, et al. Influence of arc root motion on air DC arc under small current[J]. High Voltage Apparatus, 2023, 59(11): 224-230.
Abstract High-voltage pulsed discharge in water is a complex plasma generation and collapse process involving coupled physical processes, such as electricity, light, and heat. The discharge process consists of pre-breakdown, violent, and oscillatory discharge stages. The main existing method for determine the discharge stage is by using high-speed camera photography, but this approach is not suitable for practical applications environment of pulsed discharge technology in water. Additionally, the development of the arc channel during repeated discharges exhibits strong randomness, making it difficult to classify discharge stages within a fixed time domain. Therefore, studying the identification method of the underwater discharge stage is crucial. This paper proposes a corresponding method based on the arc impedance change characteristics of the discharge in water.
Firstly, the plasma change characteristics observed at each discharge stage are amalgamated to elucidate the variations in resistance. The initial plasma channel is formed during the pre-breakdown discharge stage. It continues to ionize to form a more robust initial arc channel under the action of an external electric field, with a more stable and linear decline in resistance. Subsequently, a dense arc is established once the plasma density within the channel surpasses a critical threshold, leading to a sudden surge in plasma density and a rapid decrease in resistance. Nevertheless, with the diminishing strength of the external electric field, sustaining a balanced arc discharge becomes impracticable, resulting in the extinction of the arc. The channel retains a substantial plasma that gradually diminishes over time at this stage and makes the resistance progressive increase.
Secondly, the discharge process in water is mainly carried out in an inhomogeneous medium. Hence, the arc channel morphology and spatial location are random, and the resistance values within each discharge cycle in a repetitive discharge environment also vary. The Extended Kalman Filtering algorithm filters the measured resistance data against the randomness, thus obtaining a representative value of the identified resistance. Solving the slope of the resistance change at each moment and combining it with the characteristics of the changes in each discharge stage, a threshold value for the resistance change rate is derived. This threshold value serves as a criterion to determine the transition of the discharge stage.
Finally, the experimental platform for pulse discharge observation in water confirmed the effectiveness of the method, and an analysis of errors was conducted. Further experimental validation analyses were carried out at the biggest distance electrode gaps of 2.04 mm and 3.01 mm based on gap distances equal to 0.62 mm, 1.01 mm, and 1.38 mm. Additionally, the conductivity of the solution is increased to 4 685.13 μS/cm, 6 740.45 μS/cm, 7 820.62 μS/cm, 12 340.68 μS/cm, and 19 319.25 μS/cm, respectively. The results indicate that the variance of the identified resistance values obtained based on the Extended Kalman Filter algorithm for underwater pulse discharge is less than 1.717 Ω2 compared to the experimentally measured resistance values. Moreover, the variances of the two type's resistance slopes are less than 1.899, with a relative error of the resistance slope being less than 8.9%. Despite variations in electrode gap distance and solution conductivity, this method maintains high accuracy. Thus, it is suitable for determining discharge stages in the underwater pulse discharge process.
keywords:Pulse discharge in water, time-varying resistance, extended Kalman filtering (EKF), discharge stage identification
DOI: 10.19595/j.cnki.1000-6753.tces.230336
中图分类号:TM89
国家重大科技专项(2016ZX05034004)和中国石油大学(华东)研究生创新基金(YCX2021109)资助项目。
收稿日期 2023-03-21
改稿日期 2023-06-15
高 崇 男,1995年生,博士研究生,研究方向为脉冲功率技术应用及优化。E-mail:kmlggc@163.com
康忠健 男,1971年生,教授,博士生导师,研究方向为脉冲功率技术应用、脉冲谐波共振破岩技术。E-mail:kangzjzh@163.com(通信作者)
(编辑 李 冰)