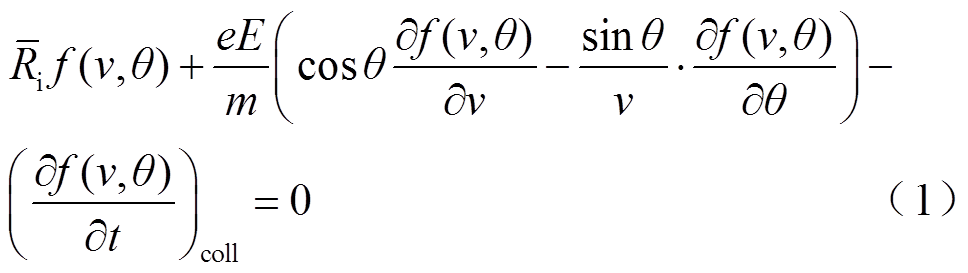
摘要 在气体放电等离子体中,电子的输运行为可由Boltzmann方程精确描述,该方程的解是许多等离子体仿真模型的基础。物理信息神经网络作为一种求解Boltzmann方程的新型方法,虽克服了传统数值方法网格剖分和方程离散的缺陷,但其参数空间规模大,在求解多任务时训练效率较低。为此,该文构建了一种基于元学习的双循环物理信息神经网络,在内循环中对多个Boltzmann方程求解任务进行优化训练,得到各任务优化后的元损失函数,用于在外循环中进行网络参数更新,从而提高网络在求解新任务时的计算效率。计算结果表明,基于元学习的双循环物理信息神经网络在求解新的Boltzmann方程时,网络损失函数值和L2误差值的下降速度均显著快于普通的物理信息神经网络。此外,该文还研究了网络容量和内循环迭代次数对Boltzmann方程多任务求解效率的影响,结果显示计算效率并不随网络容量的增大而提高,且受内循环迭代次数影响较小。
关键词:气体放电等离子体 Boltzmann方程 元学习 物理信息神经网络
Boltzmann方程是奥地利物理学家路德维希·玻耳兹曼于1872年提出的一种偏微分方程,描述了非热力学平衡系统中粒子数的变化,被广泛应用于物理学、医学、工程等领域[1-4]。在气体放电等离子体中,通过求解描述电子输运行为的Boltzmann方程可以获得气体放电过程的电子能量分布函数(Electron Energy Distribution Function, EEDF),基于EEDF可进一步计算获得迁移率、扩散率等电子输运系数,而这些参数是电晕放电、辉光放电、弧光放电等许多放电等离子体仿真模型的关键输入参数[5-8]。因此,研究气体放电等离子体电子Boltzmann方程的高效数值求解,对于气体放电等离子体的仿真建模具有重要意义。
目前,气体放电等离子体电子Boltzmann方程的数值求解方法主要分为两类:一类是蒙特卡罗模拟法,该方法的主要思路是通过随机过程模拟电子的运动,进而实现对Boltzmann方程的求解[9]。蒙特卡罗模拟法具有计算灵活、模拟精度高等优点,然而由于蒙特卡罗法的随机性[10],此类方法具有小信号分析难和计算量大的缺点[11]。另一类是利用球谐波函数获得Boltzmann方程的近似展开公式,然后对展开后的方程采用一定的数值算法进行求解,如有限差分法、有限元法、有限体积法等[12-16]。然而,此类方法需进行网格剖分,且计算精度受网格剖分质量影响。
Boltzmann方程的数学本质是偏微分方程。近年来,随着人工智能技术的发展,研究人员开始思考应用能够融合物理信息的深度学习模型,即物理信息神经网络(Physics-Informed Neural Networks, PINN)[17-22]求解偏微分方程。与传统的数值求解方法相比,PINN方法无需网格剖分,节约了网格剖分占用的计算和存储内存。同时,PINN具有极强的非线性表达能力,能够直接学习方程自变量与方程解之间的非线性映射关系,因而也不会引入因方程近似展开带来的误差。目前已有基于PINN网络求解Boltzmann方程的相关研究[23],但是PINN方法在求解多任务Boltzmann方程时依然存在显著缺陷。例如,在气体放电等离子体研究中,常常需要获得不同气体种类、不同混合比例等条件下的EEDF数据[24-25],PINN方法在处理此类问题时需根据不同任务重新训练其网络参数,计算消耗大、时间成本高、求解效率低。
元学习(meta learning)方法作为一种新兴的人工智能技术,能够根据以往及当前的任务数据进行快速学习,在多任务处理方面展示出了巨大的应用潜力[26-30]。但目前元学习在电气工程领域的应用还较少,主要集中在异常数据检测方面。例如,文献[31]提出基于元学习的基检测器动态选择集成策略,设计了使用多指标元特征进行训练的元分类器,实现了电力调度数据的异常检测;文献[32]则通过设计不同的初级学习器和元学习器,构建了用于异常窃电行为检测的集成学习模型。目前使用较为广泛的元学习算法是C. Finn等[33]提出的MAML(model-agnostic meta-learning)算法。MAML通过历史任务学习得到一个初始化的权重,以替代网络本身的初始化权重,从而有效提高网络在学习新任务时的训练效率。本文将MAML与PINN相结合,构造了具有内外两个循环结构的元PINN模型(Meta-PINN),分别进行多约化场强任务和多混合气体配比任务的气体放电等离子体电子Boltzmann方程数值求解,并在此基础上分析网络容量和内循环迭代次数对计算效率的影响。相关数值计算结果显示,该方法能够显著地提高面向气体放电等离子体的多任务电子Boltzmann方程求解效率,可为放电等离子体模型的高效计算提供支撑。
气体放电等离子体是指在气体放电作用下形成的、由电离化气体组成的等离子体。电晕放电、辉光放电、弧光放电等都是人工产生气体放电等离子体的放电形式。在此类气体放电模型中,电子的输运过程可由式(1)所示Boltzmann方程描述[34]。
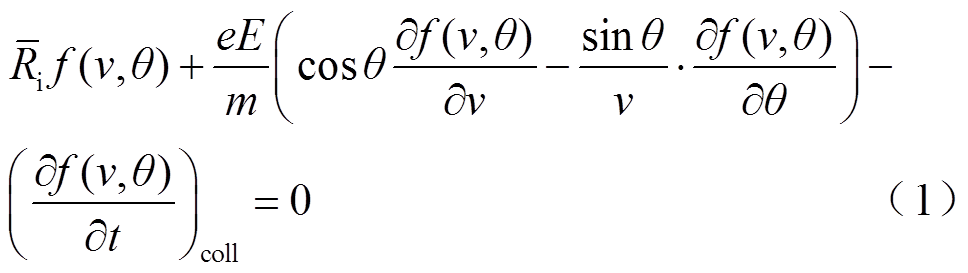
式中,f(v, θ)为电子速度分布函数;v为电子速度标量;θ为速度相对于空间坐标的偏转角;e为电子电荷量;E为电场强度;m为电子质量;t为时间;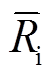 为有效电离碰撞频率,可展开为
为有效电离碰撞频率,可展开为
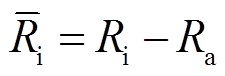 (2)
(2)
其中
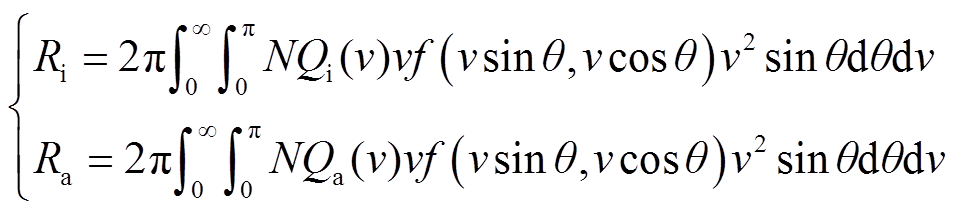
式中,Ri为电离碰撞频率;Ra为电子吸附碰撞频率;N为气体分子数密度;Qi为电离碰撞截面;Qa为电子吸附截面。
式(1)中第三项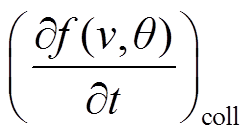 为碰撞项,可展开为
为碰撞项,可展开为
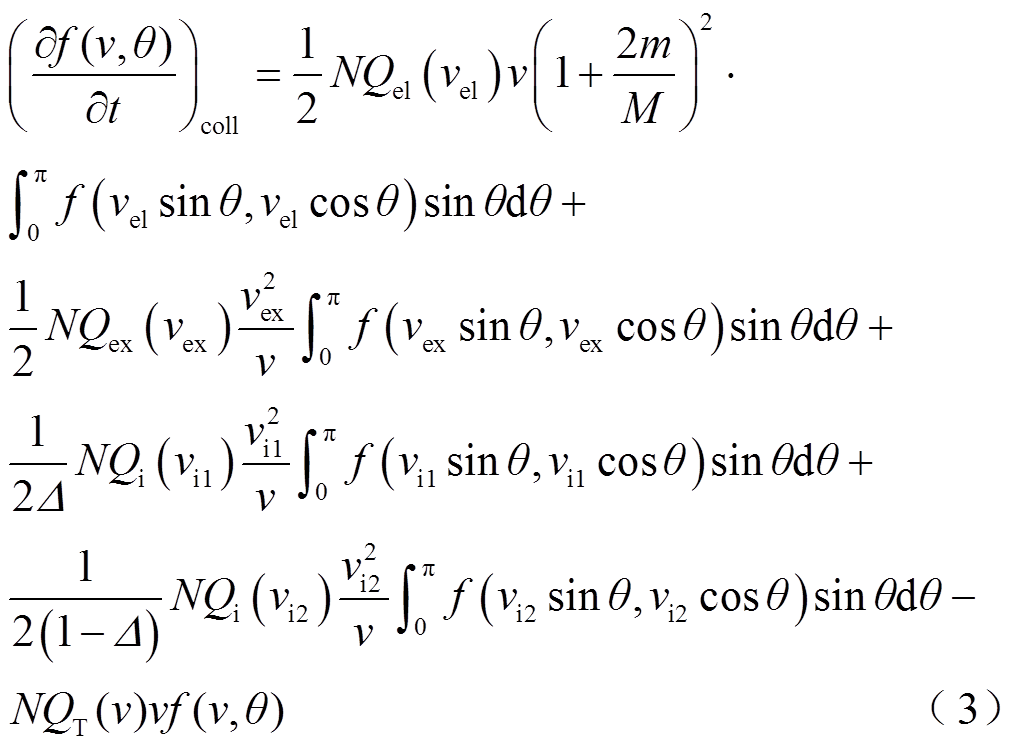
式中,M为气体分子质量;Δ为电离碰撞后的电子能量分配率;Qel为弹性碰撞截面;Qex为激发碰撞截面;QT为总碰撞截面,等于各碰撞截面之和,即
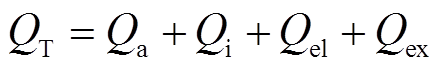 (4)
(4)
各碰撞过程电子速度vel、vex、vi1、vi2分别为
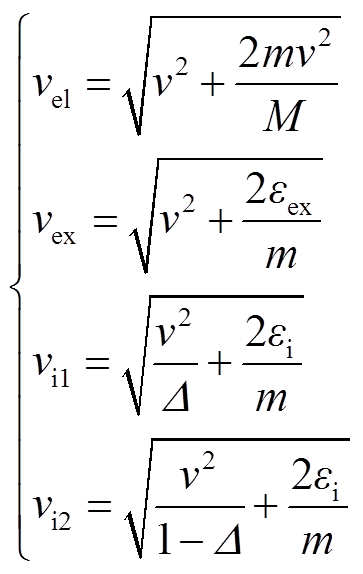 (5)
(5)
式中,εex和εi分别为Qex和Qi的能量阈值。
电子速度分布函数f的勒让德多项式展开形式为
 (6)
(6)
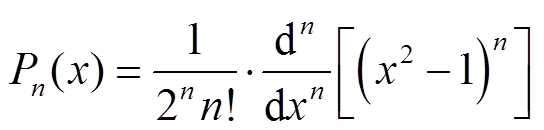 (7)
(7)
式中,n为勒让德多项式的阶数。
其中,各向同性部分f0(v)被归一化为
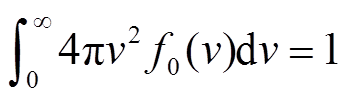 (8)
(8)
则电子能量分布函数F为
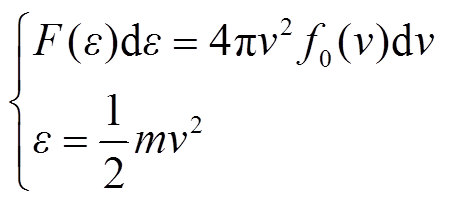 (9)
(9)
式中,ε为电子能量。
综上所述,求解气体放电等离子体的电子Boltzmann方程,需要弹性碰撞截面、激发碰撞截面、电离碰撞截面、电子吸附截面等电子-中性粒子碰撞截面数据。在本文算例中,相关截面数据选取自LXCat数据库。
在双循环Meta-PINN网络架构下,求解上述Boltzmann方程的流程如图1所示。Meta-PINN网络中有两类任务:元训练任务集(training task set)和元测试任务集(testing task set)。每个任务集均由数个任务组成,且每个任务数据又分为支持数据(support data)和测试数据(query data)以确保网络的泛化能力。同时,Meta-PINN网络中也具有两类训练网络:PINN网络和元网络。训练时,首先在内循环中使用PINN网络对多个训练任务进行优化训练,得到各任务优化后的损失函数;然后,将其用于在外循环的元网络中进行网络参数的迭代更新,网络收敛后输出权重参数;最后,利用得到的权重参数初始化PINN网络并求解新任务。Meta-PINN网络的双循环优化结构如图2所示。
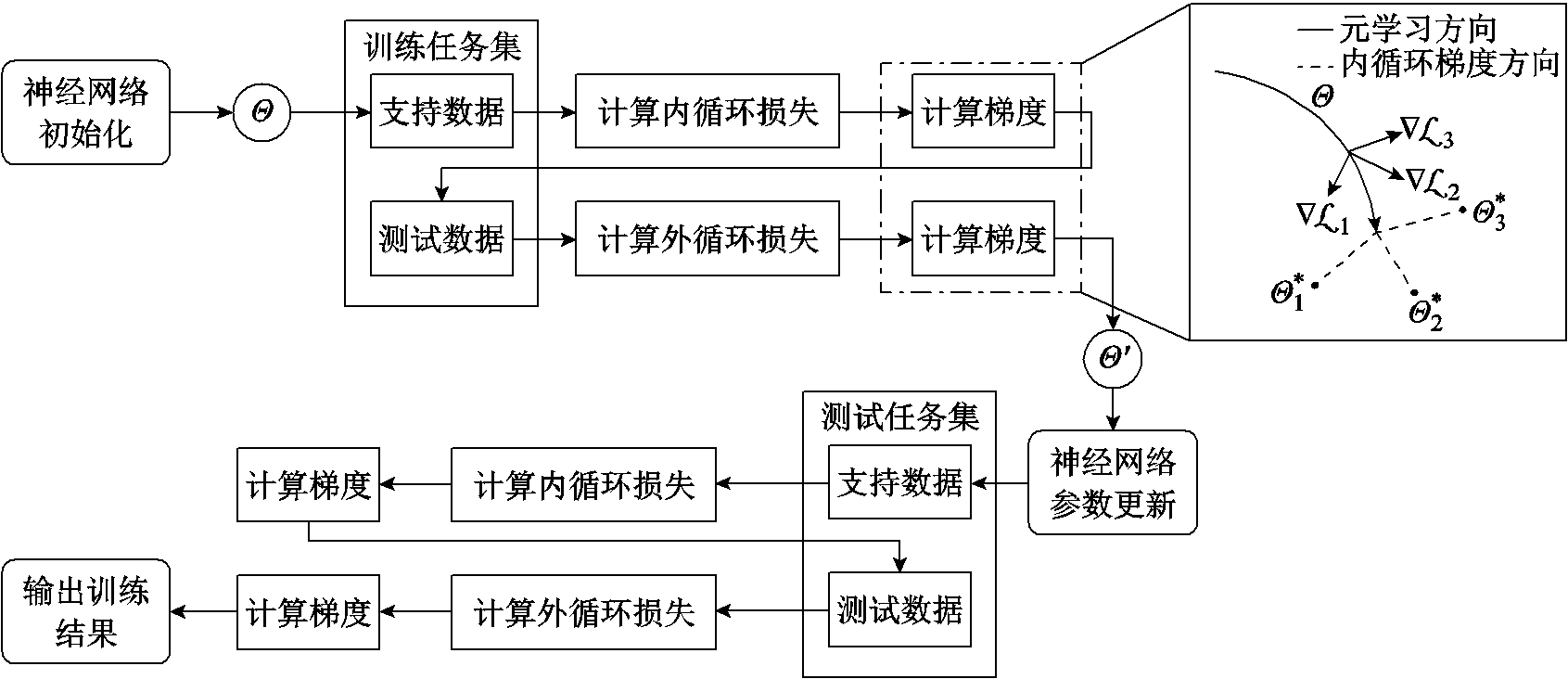
图1 Meta-PINN训练流程
Fig.1 Training process of Meta-PINN
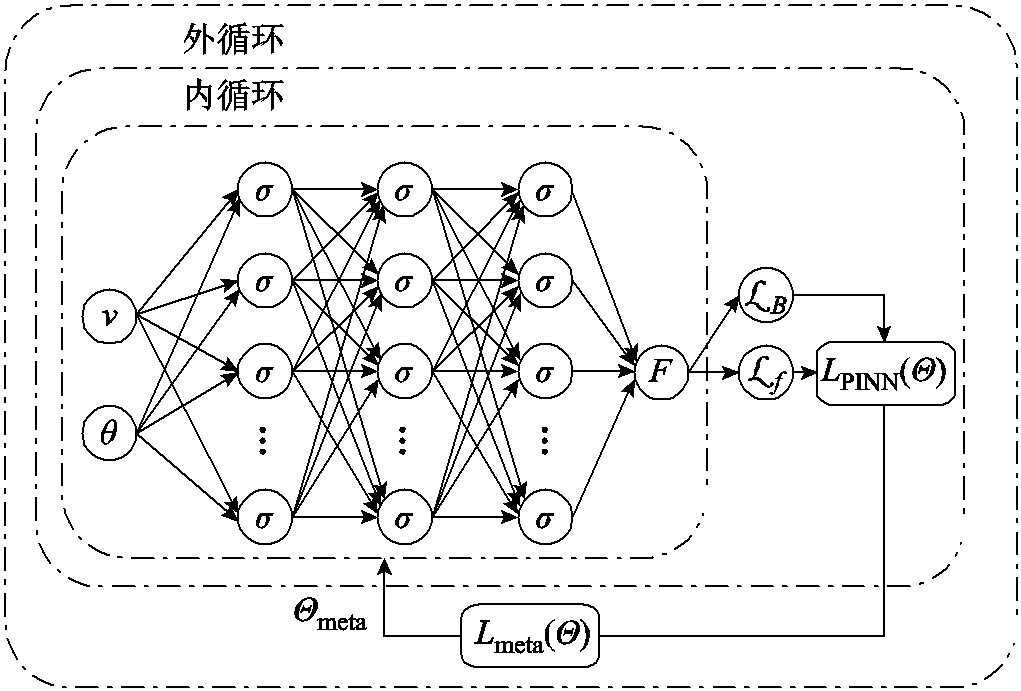
图2 Meta-PINN网络双循环优化结构
Fig.2 Two-loop optimization diagram of Meta-PINN
在PINN网络中,以v、θ为输入,电子能量分布函数F为输出,元网络的初始权重参数为Θmeta。v取值范围为[0, vm],θ取值范围为[-π, π],其中vm为电子速度上界。通过对支持数据采样计算,得到第j个训练任务对应的损失函数LPINN(Θj)为
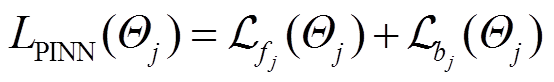 (10)
(10)
其中
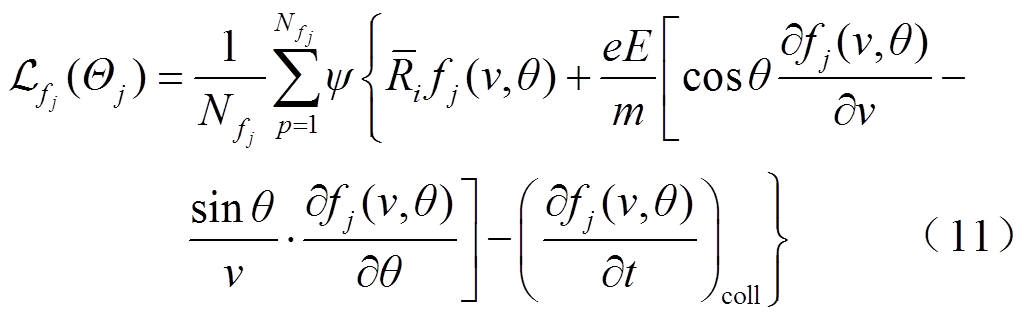
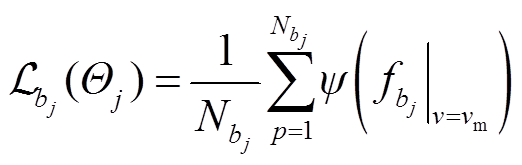 (12)
(12)
式中,ψ为Huber函数;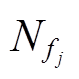 和
和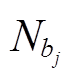 分别为第j个训练任务计算域和边界上采样点的数量。
分别为第j个训练任务计算域和边界上采样点的数量。
得到损失函数值LPINN(Θj)后,在第j个训练任务的支持数据上通过随机梯度下降算法优化Ninner步(即内循环次数),得到更新后的网络权重参数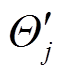 ,此时可以计算得到PINN网络在第j个训练任务的测试数据上的损失函数
,此时可以计算得到PINN网络在第j个训练任务的测试数据上的损失函数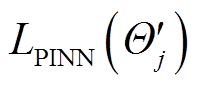 为
为
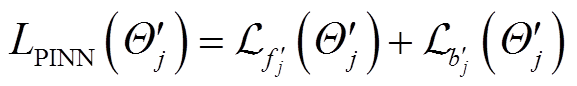 (13)
(13)
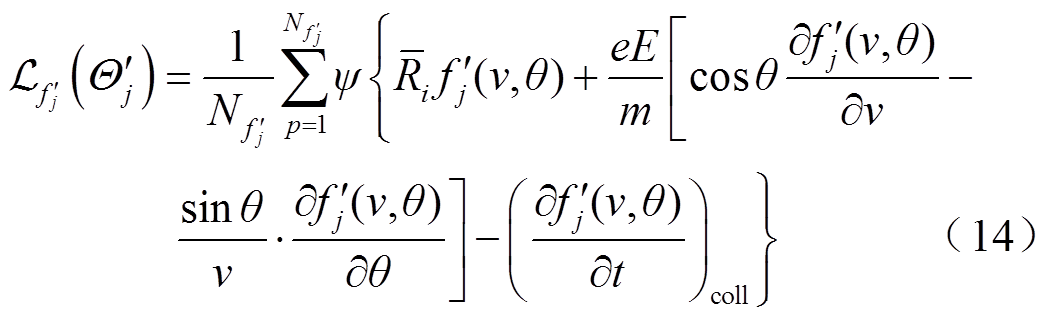
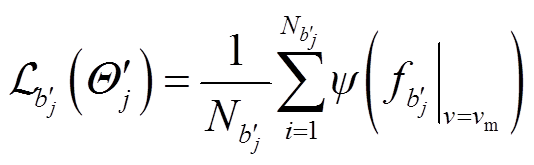 (15)
(15)
式中,上角标“′”代表测试数据上的对应变量。
PINN网络完成所有训练任务的优化之后,可以得到对应的元网络损失函数Lmeta(Θmeta)为
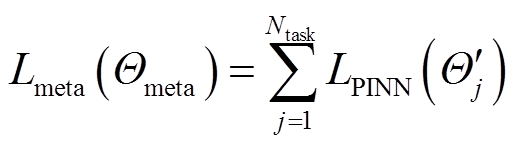 (16)
(16)
式中,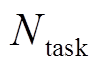 为训练任务总数。
为训练任务总数。
获得Lmeta(Θmeta)后,元网络通过随机梯度下降算法更新网络权重参数Θmeta,得到
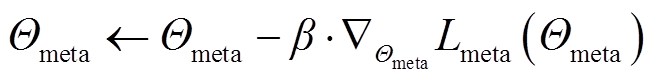 (17)
(17)
式中,β为网络的学习率。
Meta-PINN通过不断地优化元网络损失函数Lmeta(Θmeta)进行训练,迭代训练给定次数后(本文设置为10 000次),网络输出优化后的网络权重参数Θmeta。将Θmeta代入PINN网络中作为初始权重进行元测试任务(即新任务)的训练,得到对应测试任务下Boltzmann方程的计算结果。
在气体放电等离子体研究中,常常需要计算各种不同条件下的EEDF。本文以不同约化场强(E/N,单位为Td,1 Td=10-17 V·cm2)和不同混合气体配比(Ratio)下的气体放电等离子体为例,分析Meta-PINN方法求解电子Boltzmann方程的性能。同时,以广泛使用的Boltzmann方程求解器Bolsig+的计算结果为基准,验证Meta-PINN的求解精度。
本文构造的Meta-PINN网络主要参数设置如下:神经网络隐藏层层数为3层,每层500个神经元,内循环迭代次数为5次,外循环迭代次数为10 000次,内循环学习率为10-4,外循环学习率为10-4。PINN网络主要参数设置为:神经网络隐藏层层数为3层,每层500个神经元,迭代次数20 000次,学习率为10-4。
以氩气等离子体为例,设置元训练任务集为E/N={100 Td, 200 Td, 300 Td, 400 Td, 500 Td},元测试任务集为E/N={50 Td, 150 Td, 250 Td, 350 Td, 450 Td, 550 Td},在元网络训练的基础上对训练集之外的测试任务集开展测试。
图3展示了各测试任务下Meta-PINN与PINN计算得到的氩气等离子体EEDF、损失函数值LPINN和L2误差。从图中可以看出,当E/N=150、250、350、450、550 Td时,在20 000次迭代后,Meta-PINN和PINN计算得到的EEDF均与Bolsig+的结果相当。但在E/N=50 Td时,Meta-PINN和PINN的计算精度均不及Bolsig+。原因可能是此时的E/N值在元训练任务区间外,网络学习效果较差,需要更多的迭代次数。同时本文还发现,网络的训练难度随着E/N的减小而增大,因此虽然E/N=550 Td也在元训练任务区间外,但在20 000次训练之后,Meta-PINN和PINN还是能够计算得到较为准确的EEDF。
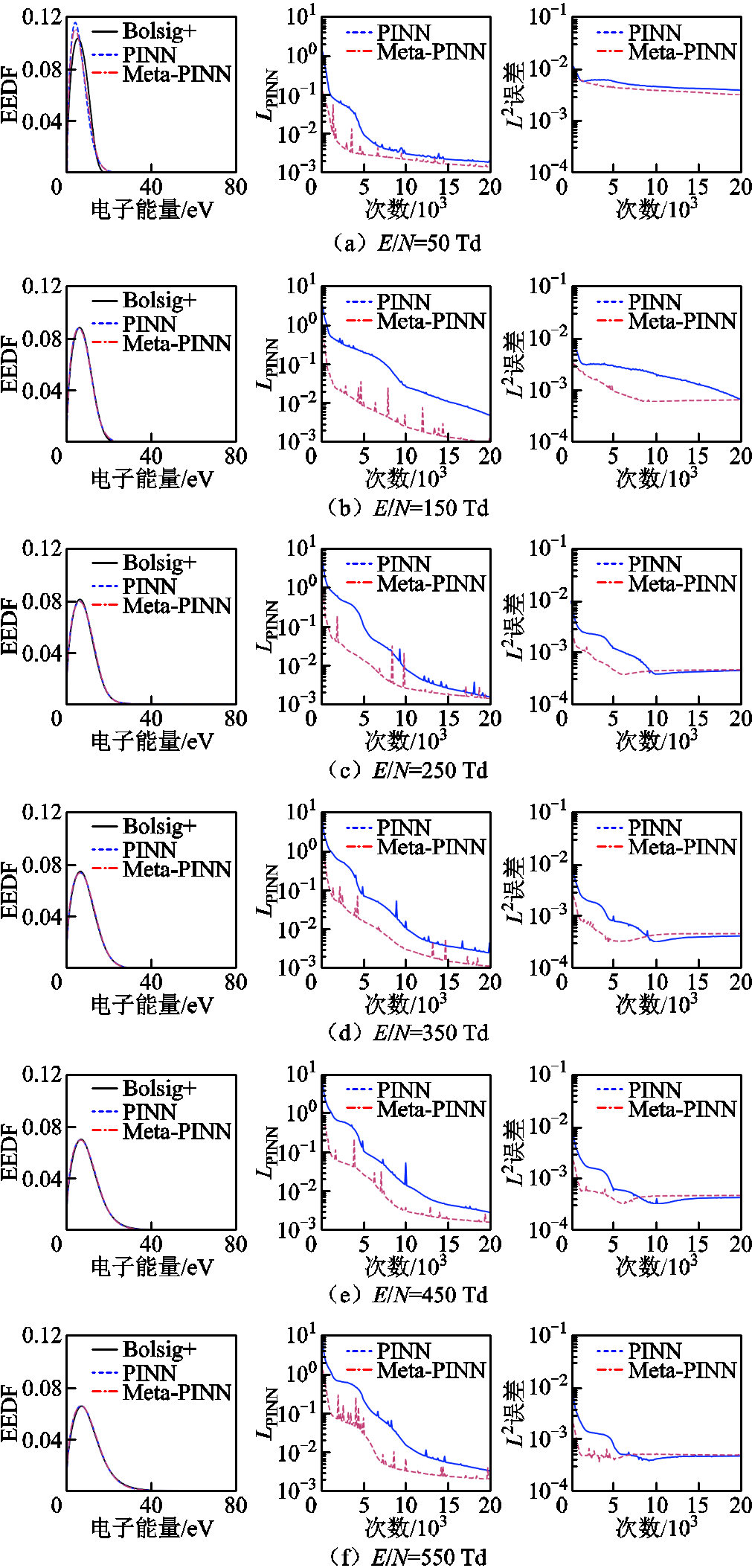
图3 不同E/N情况下氩气等离子体的Boltzmann方程求解结果
Fig.3 Solution of Boltzmann equation for Ar plasma under different values of E/N
图3中的结果还显示,Meta-PINN的损失函数值LPINN和L2误差的收敛速度均快于PINN。为了进一步对比Meta-PINN和PINN的训练效果,本文定量比较了二者在优化过程中LPINN和L2误差下降到给定阈值所需的迭代次数,见表1。结果表明,在LPINN方面(阈值分别取为10-1、10-2和5×10-3),Meta-PINN的收敛速度最高分别达到了PINN的10.9、3.4和2.8倍;在L2误差方面(阈值分别取为5×10−3、10−3和5×10−4),Meta-PINN的收敛速度最高分别达到了PINN的7、8和3.45倍。可见,Meta-PINN的收敛速度显著快于PINN。
表1 氩气等离子体在不同E/N情况下PINN和Meta-PINN达到给定LPINN值和L2误差值所需迭代次数
Tab.1 Optimizing epochs for PINN and Meta-PINN to reach the given LPINN values and L2 errors with different values of E/N in Ar plasma
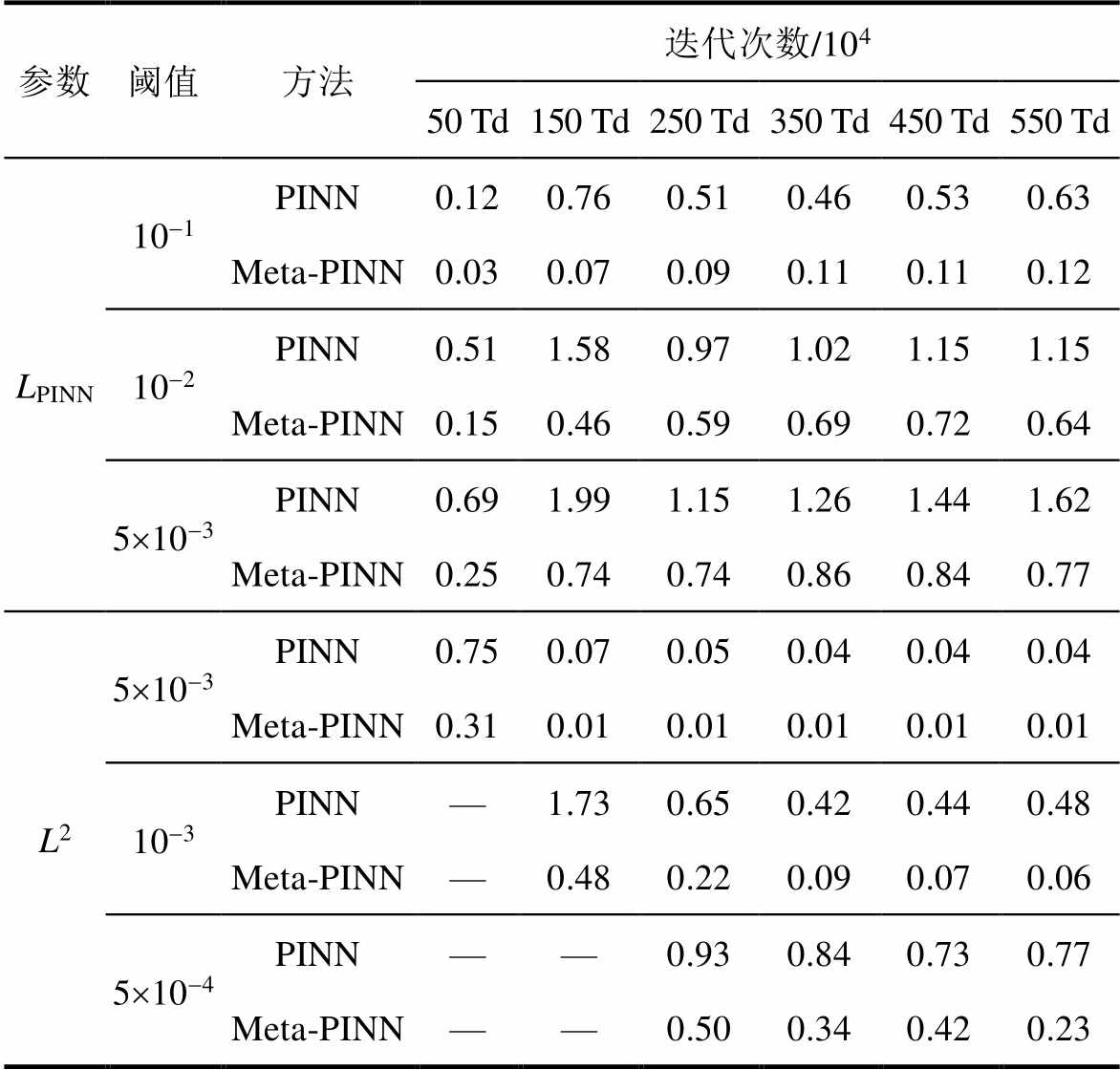
参数阈值方法迭代次数/104 50 Td150 Td250 Td350 Td450 Td550 Td LPINN10-1PINN0.120.760.510.460.530.63 Meta-PINN0.030.070.090.110.110.12 10-2PINN0.511.580.971.021.151.15 Meta-PINN0.150.460.590.690.720.64 5´10-3PINN0.691.991.151.261.441.62 Meta-PINN0.250.740.740.860.840.77 L25´10-3PINN0.750.070.050.040.040.04 Meta-PINN0.310.010.010.010.010.01 10-3PINN—1.730.650.420.440.48 Meta-PINN—0.480.220.090.070.06 5´10-4PINN——0.930.840.730.77 Meta-PINN——0.500.340.420.23
混合气体的放电性能受气体配比影响,因此选择合适的混合气体配比是气体放电研究的重要课题。本文以SF6-Ar混合气体为例,计算了不同气体配比下的EEDF。其中,元训练任务集为Ratio={10%, 20%, 30%, 40%, 50%},元测试任务集为Ratio={5%, 15%, 25%, 35%, 45%, 55%},Ratio代表该混合气体中SF6的体积分数。
各测试任务下Meta-PINN与PINN计算得到的SF6-Ar等离子体的EEDF、损失函数值LPINN和L2误差如图4所示。从图中可以看出,经过20 000次迭代更新后,Meta-PINN和PINN计算得到的EEDF均与Bolsig+的结果相当,且Meta-PINN的LPINN和L2误差的收敛速度均快于PINN。表明在该情况下,即使对于训练任务区间以外的计算任务,Meta-PINN仍能较好地进行训练。
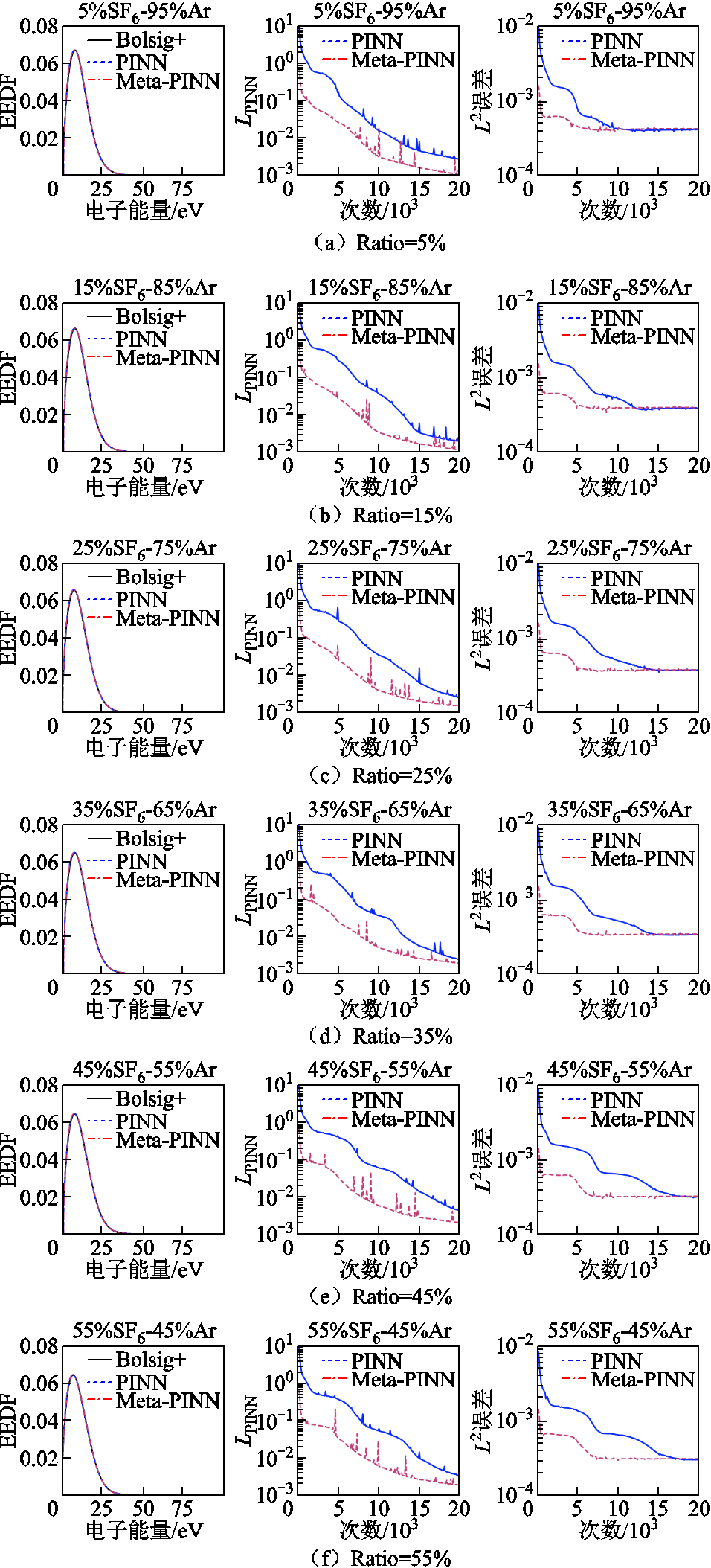
图4 不同气体配比情况下SF6-Ar等离子体的Boltzmann方程求解结果
Fig.4 Solution of Boltzmann equation for SF6-Ar plasma under different gas mixing ratios
同时,为了定量对比Meta-PINN和PINN的训练效果,本文比较了不同气体配比情况下,两种方法在优化过程中LPINN和L2误差达到给定阈值所需的迭代次数,见表2。结果表明,在LPINN方面(阈值分别取为10-1、10-2和5×10−3),Meta-PINN的收敛速度最高分别达到了PINN的11.1、2.1和1.75倍;在L2误差方面(阈值为10−3和5×10−4),Meta-PINN的收敛速度最高分别达到了PINN的23和2.69倍。
表2 SF6-Ar等离子体在不同气体配比情况下PINN和Meta-PINN达到给定LPINN值和L2误差值所需迭代次数
Tab.2 Optimizing epochs for PINN and Meta-PINN to reach the given LPINN values and L2 errors with different gas mixing ratios in SF6-Ar plasma
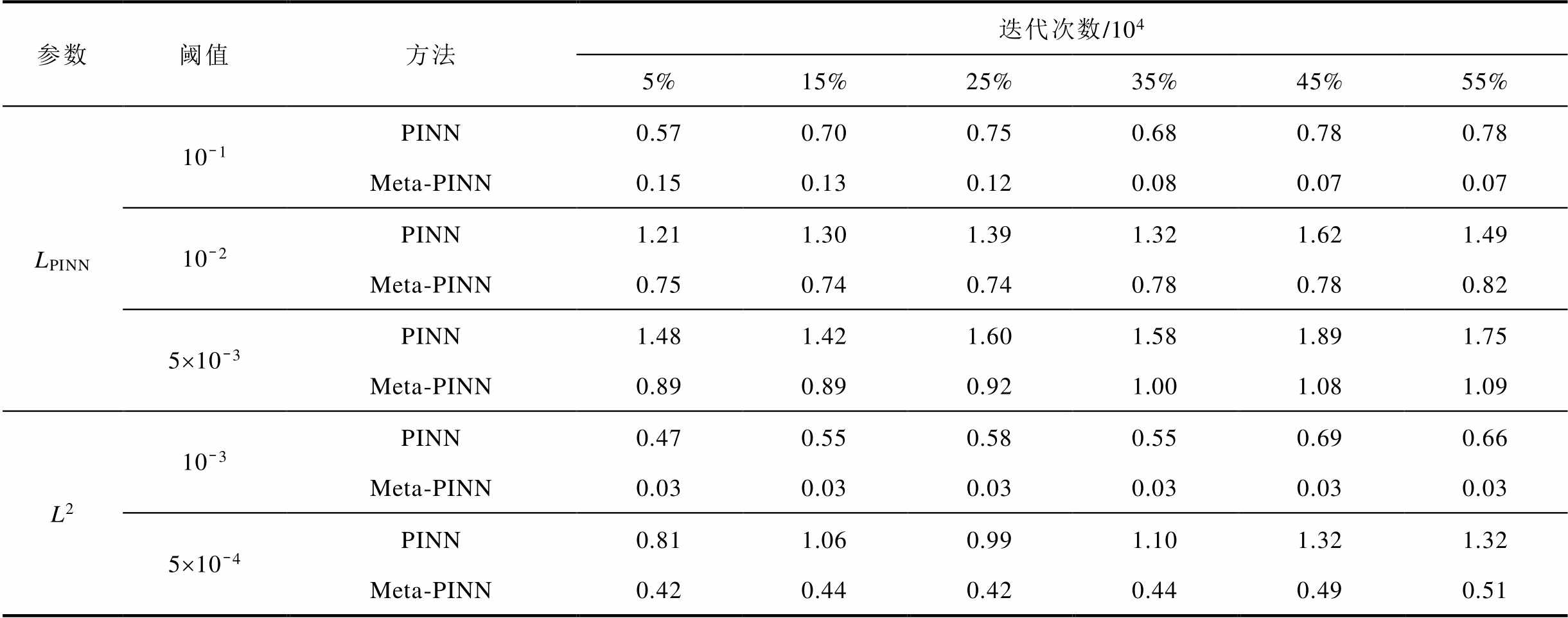
参数阈值方法迭代次数/104 5%15%25%35%45%55% LPINN10-1PINN0.570.700.750.680.780.78 Meta-PINN0.150.130.120.080.070.07 10-2PINN1.211.301.391.321.621.49 Meta-PINN0.750.740.740.780.780.82 5´10-3PINN1.481.421.601.581.891.75 Meta-PINN0.890.890.921.001.081.09 L210-3PINN0.470.550.580.550.690.66 Meta-PINN0.030.030.030.030.030.03 5´10-4PINN0.811.060.991.101.321.32 Meta-PINN0.420.440.420.440.490.51
本文采用的深度神经网络为前馈网络,其网络容量主要受两类参数控制:网络隐藏层数和每个隐藏层的神经元数,因此在构建神经网络时需选择合适的网络容量使模型具备较好的表达能力。为此,本文在Meta-PINN的计算框架下研究了不同隐藏层数和神经元数对Boltzmann方程求解效率的影响。
2.3.1 不同隐藏层数对求解效率的影响
在2.1节Meta-PINN模型其余参数不变的情况下,将网络隐藏层数分别设置为2、3、4层,求解多约化场强任务的电子Boltzmann方程。
以E/N=350 Td为例,图5展示了各Meta-PINN网络计算得到的元损失函数值Lmeta、损失函数值LPINN和L2误差。各Meta-PINN的Lmeta达到给定阈值的迭代次数见表3。从图5和表3可以看出,各Meta-PINN之间,2层、3层、4层时的L2误差收敛速度没有显著差别,但3层和4层时的Lmeta和LPINN收敛速度显著快于隐藏层为2层时的结果,且2层网络的Lmeta无法下降至0.5。同时,相较于4层网络,3层网络的稳定性更强。可见,在氩气等离子体的多约化场强Boltzmann方程计算中,3层Meta-PINN网络的性能最佳。
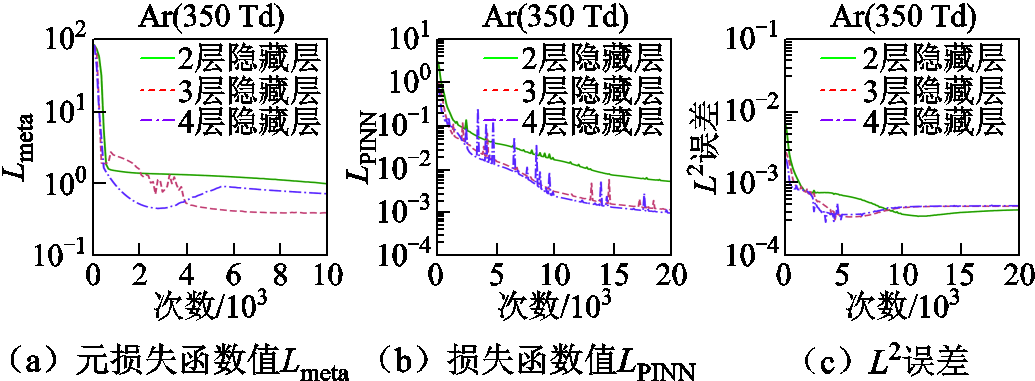
图5 Meta-PINN在不同隐藏层数下的训练过程
Fig.5 Training process of Meta-PINN with different hidden layers
表3 Meta-PINN在不同隐藏层数下达到给定Lmeta损失值所需迭代次数
Tab.3 Optimizing epochs for Meta-PINN to reach the given Lmeta value with different hidden layers

Lmeta迭代次数/104 2层隐藏层3层隐藏层4层隐藏层 5×10-1—0.440.23
2.3.2 不同神经元数对求解效率的影响
类似地,在2.1节Meta-PINN模型其余参数不变的情况下,将网络的每层神经元数分别设置为300、400、500、600,以此求解多约化场强任务下的电子Boltzmann方程。
以E/N=350 Td为例,各Meta-PINN网络计算得到的元损失函数值Lmeta、损失函数值LPINN和L2误差如图6所示。表4展示了各Meta-PINN的Lmeta达到给定阈值的迭代次数。从图6和表4可以看出,各Meta-PINN之间L2误差的收敛速度差距较小,但400与600个神经元对应的LPINN收敛速度要明显慢于其他两类设置。在Lmeta方面,300个神经元对应的Lmeta最先下降至阈值5×10-1,其次是500和600个神经元,而400个神经元对应的Lmeta下降最慢。因此,对于氩气等离子体的多约化场强Boltzmann方程计算,神经元数为300的Meta-PINN网络性能最佳。
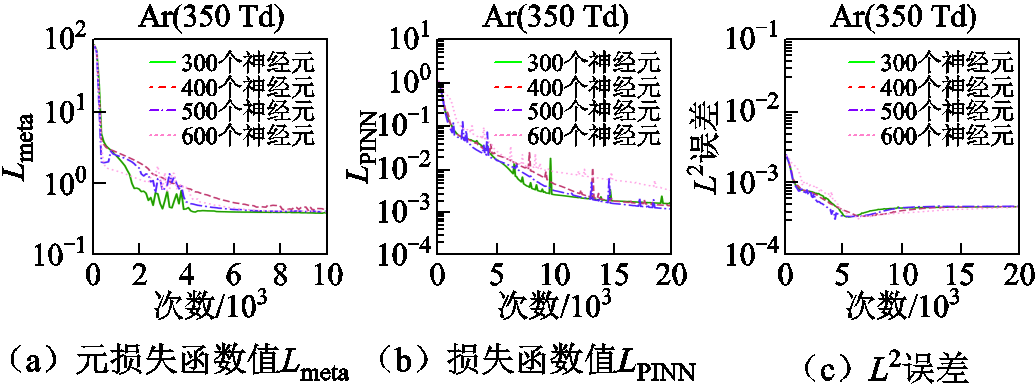
图6 Meta-PINN在不同神经元数下的训练过程
Fig.6 Training process of Meta-PINN with different neurons numbers
表4 Meta-PINN在不同神经元数下达到给定Lmeta损失值所需迭代次数
Tab.4 Optimizing epochs for Meta-PINN to reach the given Lmeta value with different neurons numbers

Lmeta迭代次数/104 300个400个500个600个 5×10-10.260.660.440.52
在此基础上,本文进一步分析了Meta-PINN的超参数——内循环迭代次数Ninner对Boltzmann方程求解效率的影响。
内循环迭代次数分别设置为1、3、5、10步时各Meta-PINN网络计算得到的元损失函数值Lmeta、损失函数值LPINN和L2误差如图7所示。表5展示了各Meta-PINN的Lmeta达到给定阈值的迭代次数。从图7和表5可以看出,各Meta-PINN之间,LPINN和L2误差的收敛速度没有显著差距,最终均会收敛到同一区间内。各Meta-PINN在双循环阶段的Lmeta的收敛速度也没有显著差异,Ninner=5时网络以略快于其他网络的收敛速度下降至阈值5×10-1。可见,Meta-PINN的内循环迭代次数对Boltzmann方程的求解效率影响较小。
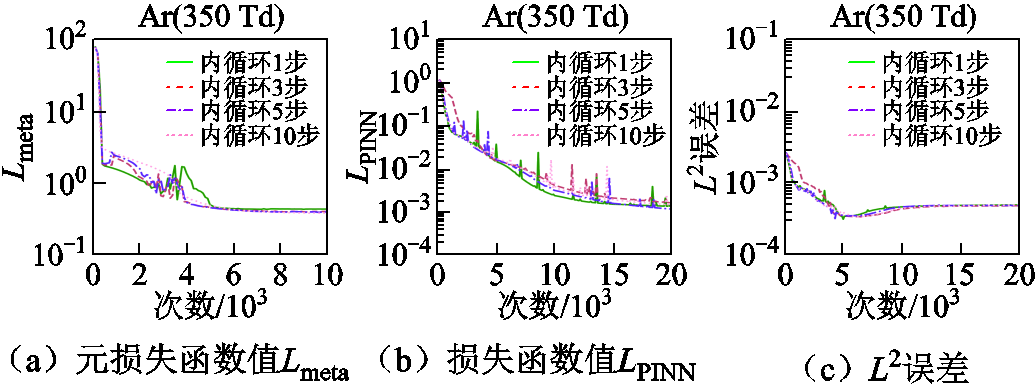
图7 Meta-PINN在不同内循环迭代次数下的训练过程
Fig.7 Training process of Meta-PINN with different inner steps
表5 Meta-PINN在不同内循环迭代次数下达到给定Lmeta损失值所需迭代次数
Tab.5 Optimizing epochs for Meta-PINN to reach the given Lmeta value with different inner steps

Lmeta迭代次数/104 1步3步5步10步 5×10-10.510.450.440.50
为解决物理信息神经网络PINN在求解多任务电子Boltzmann方程时训练效率较低的问题,本文提出了一种基于元初始化的深度学习方法,构造了具有内外两个循环结构的Meta-PINN模型,分别进行了多约化场强任务和多混合气体配比任务的气体放电等离子体电子Boltzmann方程求解,并研究了网络容量和内循环迭代次数对计算效率的影响。主要结论如下:
1)Meta-PINN在求解新任务时损失函数值和L2误差值的下降速度均显著快于PINN。在本文算例中,Meta-PINN的收敛速度最低提升75%,最高提升22倍。可见,Meta-PINN能够有效提高气体放电等离子体电子Boltzmann方程的求解效率。且在某些情况下,Meta-PINN的损失函数值和L2误差值能够比PINN下降到更低量级,表明其计算精度也优于PINN。
2)在电子Boltzmann方程求解中,Meta-PINN的计算效率并不随网络容量的增大而提高,在2~4层网络隐藏层和300~600个神经元的区间内,最适合求解氩气等离子体多约化场强电子Boltzmann方程的神经网络隐藏层为3层,每层神经元为300个。
3)Meta-PINN的计算效率也并不随着内循环迭代次数的增大而提高,在1~10步内循环步数区间内,最适合求解氩气等离子体多约化场强电子Boltzmann方程的神经网络内循环步数为5步。
总体而言,本文设计的Meta-PINN网络框架具有通用性,理论上能够将其扩展应用于其他等离子体方程的求解中,具有一定的推广应用价值。
参考文献
[1] Reid I D. An investigation of the accuracy of numerical solutions of Boltzmann's equation for electron swarms in gases with large inelastic cross sections [J]. Australian Journal of Physics, 1979, 32(3): 231-254.
[2] 赵谡, 邓云坤, 钟蕊霜, 等. 基于Boltzmann方程的CF3I混合气体协同效应分析[J]. 电工技术学报, 2019, 34(7): 1553-1558.
Zhao Su, Deng Yunkun, Zhong Ruishuang, et al. Investigation on the synergistic effect of CF3I gas mixtures using Boltzmann Equation[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1553-1558.
[3] 徐玲铃, 程林, 杜玮杰, 等. CF3I三元混合气体绝缘特性的Boltzmann分析[J]. 高电压技术, 2017, 43(3): 721-726.
Xu Lingling, Cheng Lin, Du Weijie, et al. Analysis of the insulation characteristic of CF3I ternary gas mixture using Boltzmann's equation[J]. High Voltage Engineering, 2017, 43(3): 721-726.
[4] 李冰, 邓云坤, 肖登明. 基于Boltzmann方程的C3F8及C3F8-N2混合气体绝缘性能[J]. 高电压技术, 2015, 41(12): 4150-4157.
Li Bing, Deng Yunkun, Xiao Dengming. Insulation characteristics of C3F8 and C3F8-N2 gas mixture using Boltzmann equation method[J]. High Voltage Engineering, 2015, 41(12): 4150-4157.
[5] 陈赦, 刘红梅, 吴婷, 等. 低温等离子体增强催化氨合成机理的一维流体动力学模型[J]. 电工技术学报, 2021, 36(13): 2730-2739.
Che She, Liu Hongmei, Wu Ting, et al. 1D fluid model of catalytic ammonia synthesis enhanced by low temperature plasma[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2730-2739.
[6] 何彦良, 丁未, 孙安邦, 等. 电场不均匀系数对SF6/N2混合气体负直流电晕电流脉冲特性的影响[J]. 电工技术学报, 2021, 36(15): 3124-3134.
He Yanliang, Ding Wei, Sun Anbang, et al. Effect of electric field non-uniformity coefficient on current pulse characteristics of negative DC corona in SF6/N2 gas mixtures[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3124-3134.
[7] 郝莎, 徐建源, 林莘. 隔离开关电弧流体数学模型研究与应用[J]. 电工技术学报, 2021, 36(13): 2710-2718.
Hao Sha, Xu Jianyuan, Lin Xin. Study on the application of fluid arc model in disconnector[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2710-2718.
[8] 李泳霖, 黄世龙, 刘云鹏, 等. 考虑湿度气压影响的瓷绝缘子沿面类辉光放电仿真及其紫外光谱特性分析[J]. 电工技术学报, 2023, 38(7): 1956-1969.
Li Yonglin, Huang Shilong, Liu Yunpeng, et al. Simulation and ultraviolet spectral characteristics of glow-like discharge along the surface of porcelain insulators considering the influences of the humidity and atmospheric pressure[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1956-1969.
[9] Alder B J, Wainwright T E. Studies in molecular dynamics. I. General method[J]. The Journal of Chemical Physics, 1959, 31(2): 459-466.
[10] Itoh H, Ikuta N, Toyota K. Boltzmann equation analysis of electron swarms for model cases with power-law elastic scattering[J]. Journal of Physics D: Applied Physics, 1983, 16(3): 293.
[11] 刘宇琦, 李硕, 刘世宇, 等. 基于二项近似解玻尔兹曼方程计算CF3I/N2混合气体的绝缘特性[J]. 电气技术, 2019, 20(4): 32-36.
Liu Yuqi, Li Shuo, Liu Shiyu, et al. Solving the boltzmann equation to obtain insulation properties of CF3I/N2 gas mixtures based on two-term approximation[J]. Electrical Engineering, 2019, 20(4): 32-36.
[12] Vecchi M C, Rudan M. Modeling electron and hole transport with full-band structure effects by means of the spherical-harmonics expansion of the BTE[J]. IEEE Transactions on Electron Devices, 1998, 45(1): 230-238.
[13] Hennacy K A, Wu Y J, Goldsman N, et al. Deterministic MOSFET simulation using a generalized spherical harmonic expansion of the Boltzmann equation[J]. Solid-State Electronics, 1995, 38(8): 1485-1495.
[14] 蔡新景, 王新新, 邹晓兵, 等. 基于改进的多项近似法解玻尔兹曼方程计算电子输运系数[J]. 中国电机工程学报, 2016, 36(4): 1148-1155.
Cai Xinjing, Wang Xinxin, Zou Xiaobing, et al. Computation of electron transport coefficients based on improved multi-term approximation of the Boltzmann equation[J]. Proceedings of the CSEE, 2016, 36(4): 1148-1155.
[15] Rupp K, Jüngel A, Grasser T. Matrix compression for spherical harmonics expansions of the Boltzmann transport equation for semiconductors[J]. Journal of Computational Physics, 2010, 229(23): 8750-8765.
[16] Hong S M, Matz G, Jungemann C. A deterministic Boltzmann equation solver based on a higher order spherical harmonics expansion with full-band effects[J]. IEEE Transactions on Electron Devices, 2010, 57(10): 2390-2397.
[17] Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707.
[18] Yang Yibo, Perdikaris P. Adversarial uncertainty quantification in physics-informed neural networks[J]. Journal of Computational Physics, 2019, 394: 136-152.
[19] Pang Guofei, Lu Lu, Karniadakis G E. fPINNs: fractional physics-informed neural networks[J]. SIAM Journal on Scientific Computing, 2019, 41(4): A2603-A2626.
[20] Meng Xuhui, Li Zhen, Zhang Dongkun, et al. PPINN: Parareal physics-informed neural network for time-dependent PDEs[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 370: 113250.
[21] Chen Xiaoli, Duan Jinqiao, Karniadakis G E. Learning and meta-learning of stochastic advection-diffusion-reaction systems from sparse measurements[J]. European Journal of Applied Mathematics, 2021, 32(3): 397-420.
[22] Zhong Linlin, Wu Bingyu, Wang Yifan. Low-temperature plasma simulation based on physics-informed neural networks: frameworks and preliminary applications[J]. Physics of Fluids, 2022, 34(8): 087116.
[23] Kawaguchi S, Takahashi K, Ohkama H, et al. Deep learning for solving the Boltzmann equation of electrons in weakly ionized plasma[J]. Plasma Sources Science and Technology, 2020, 29(2): 025021.
[24] 孙广雷, 林莘, 夏亚龙, 等. 热态SF6/CF4击穿特性研究[J]. 高压电器, 2021, 57(3): 65-70.
Sun Guanglei, Lin Xin, Xia Yalong, et al. Study on breakdown characteristic of hot SF6/CF4[J]. High Voltage Apparatus, 2021, 57(3): 65-70.
[25] 李祎, 张晓星, 傅明利, 等. 环保绝缘气体C4F7N研究及应用进展Ⅰ: 绝缘及电、热分解特性[J]. 电工技术学报, 2021, 36(17): 3535-3552.
Li Yi, Zhang Xiaoxing, Fu Mingli, et al. Research and application progress of eco-friendly gas insulating medium C4F7N, part Ⅰ: insulation and electrical, thermal decomposition properties[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3535-3552.
[26] Psaros A F, Kawaguchi K, Karniadakis G E. Meta-learning PINN loss functions[J]. Journal of Computational Physics, 2022, 458: 111121.
[27] Wang J X. Meta-learning in natural and artificial intelligence[J]. Current Opinion in Behavioral Sciences, 2021, 38: 90-95.
[28] Zhong Linlin, Wu Bingyu, Wang Yifan. Accelerating physics-informed neural network based 1D arc simulation by meta learning[J]. Journal of Physics D: Applied Physics, 2023, 56(7): 074006.
[29] Kayaalp M, Vlaski S, Sayed A H. Dif-MAML: Decentralized multi-agent meta-learning[J]. IEEE Open Journal of Signal Processing, 2022, 3: 71-93.
[30] Penwarden M, Zhe S, Narayan A, et al. A metalearning approach for physics-informed neural networks (PINNs): application to parameterized PDEs[J]. Journal of Computational Physics, 2023, 477: 111912.
[31] 傅世元, 高欣, 张浩, 等. 基于元学习动态选择集成的电力调度数据异常检测方法[J]. 电网技术, 2022, 46(8): 3248-3261.
Fu Shiyuan, Gao Xin, Zhang Hao, et al. Anomaly detection for power dispatching data based on meta-learning dynamic ensemble selection[J]. Power System Technology, 2022, 46(8): 3248-3261.
[32] 游文霞, 李清清, 杨楠, 等. 基于多异学习器融合Stacking集成学习的窃电检测[J]. 电力系统自动化, 2022, 46(24): 178-186.
You Wenxia, Li Qingqing, Yang Nan, et al. Electricity theft detection based on multiple different learner fusion by Stacking ensemble learning[J]. Automation of Electric Power Systems, 2022, 46(24): 178-186.
[33] Finn C, Rajeswaran A, Kakade S, et al. Online meta-learning[C]//International Conference on Machine Learning, California, USA, 2019: 1920-1930.
[34] 邓云坤, 马仪, 赵谡, 等. 基于电子输运参数的CF3I及CF3I-N2混合气体绝缘性能分析[J]. 电工技术学报, 2018, 33(7): 1641-1651.
Deng Yunkun, Ma Yi, Zhao Su, et al. Analysis of the insulation properties of CF3I and CF3I-N2 gas mixtures from electron transport parameters[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1641-1651.
Abstract The Boltzmann equation is a partial differential equation that describes the variation of particles in a non-equilibrium thermodynamic system. In the field of gas insulation and plasma discharge, the Boltzmann equation can be used to accurately describe the electron transport in gas discharge plasmas, and its solution is the basis of many plasma simulation models. However, the traditional numerical methods for solving the Boltzmann equation all require meshing on the computational domain, and the solution accuracy significantly depends on the quality of the meshing. The physics-informed neural networks (PINNs), as a new method for solving Boltzmann equation, overcomes the shortcomings of traditional numerical methods in mesh generation and equation discretization, but its training is inefficient when dealing with multi-tasks because of huge parameter space of PINNs. To address this issue, this paper proposes a Meta-PINN network with two loops of PINNs based on meta learning. Through the training in inner and outer loops, Meta-PINN solve the Boltzmann equation in multi-tasks accurately and efficiently.
In the Meta-PINN, there are two types of networks, which are the PINN network and the meta network. In the inner loop, the PINN network solve the Boltzmann equation in multi-tasks by minimizing the loss function of PINN. After all multi-tasks are optimized, the sum of the PINN loss function, namely the meta loss function, is obtained. Then, the meta network updates the weights by minimizing the meta loss function in the outer loop.Finally, the updated weights are used to improve the training efficiency when dealing with new tasks of solving Boltzmann equations.
To validate the performance of Meta-PINN, the Boltzmann equations under different reduced electric fields and gas mixing ratios are solved under the framework of Meta-PINN. The results show that, when dealing with new tasks, the loss function values and L2 errors of Meta-PINN are reduced faster than that of PINN. Specifically, the minimum and maximum acceleration speeds increase by 75% and 22 times respectively, which indicates that the Meta-PINN outperforms the PINN in solution efficiency. Additionally, the effects of network capacities and inner steps on the computational efficiency are investigated in multi-tasks of solving Boltzmann equation. The result reveals that the computational efficiency does not improve with the increase of network capacities and is less affected by the inner steps.
The following conclusions could be drawn from the numerical experiments: (1) Meta-PINN can improve the efficiency of solving Boltzmann equation describing electron transport in gas discharge plasmas. Moreover, in some cases, the loss function value and L2 error of Meta-PINN can be reduced to a lower order of magnitude than PINN, indicating that solution accuracy of Meta-PINN is also better than that of PINN. (2) In solving the Boltzmann equation, the computation efficiency is not improved with the increase of network capacity. The most suitable network for solving the Boltzmann equation under different reduced electric fields in argon plasma is the neural network with 3 hidden layers and 300 neurons per layer. (3) The computation efficiency is either not improved with the increase of inner steps. The most suitable inner steps for solving the Boltzmann equation under different reduced electric fields in argon plasma is 5 steps. Generally, the Meta-PINN can be extended easily to other numerical solution of plasma governing equations.
keywords:Gas discharge plasma, Boltzmann equation, meta learning, physics-informed neural network
DOI:10.19595/j.cnki.1000-6753.tces.230573
中图分类号:TM11
国家自然科学基金(92066106)、江苏省科协青年科技人才托举工程(2021031)和东南大学“至善青年学者”支持计划(中央高校基本科研业务费)(2242022R40022)资助项目。
收稿日期 2023-04-28
改稿日期 2023-05-30
仲林林 男,1990年生,副研究员,博士生导师,研究方向为高电压技术、放电等离子体技术、人工智能技术。E-mail:linlin@seu.edu.cn(通信作者)
吴冰钰 女,1998年生,硕士研究生,研究方向为放电等离子体技术。E-mail:wubingyu@seu.edu.cn
(编辑 李 冰)