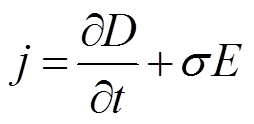 (1)
(1)
摘要 换流变压器是特高压直流输电工程中的关键设备,换流变压器油纸复合绝缘的界面处在直流电压下易积聚电荷,诱发局部放电甚至击穿。当前对于界面电荷的积聚分布,多采用传统的阻容模型进行计算,存在较大的误差。该文提出一种简易的非线性电路等效模型,首先,分别测量变压器油和油浸纸板的电容、电阻参数与极化电流,获得油纸的拓展Debye模型;其次,在拓展Debye模型的基础上,将变压器油和油浸纸板的恒定电阻模型改为随电场变化的非线性模型,并加入反映极性效应的界面势垒限制电流源,以此建立等效模型;最后,将电路等效模型仿真结果与实际测量结果进行对比。结果表明,与实际测量结果相比,该等效模型具有良好的适用性。该文模型为油纸绝缘的电场分布、界面电荷积聚量的计算提供了一种准确度较高的简便方法。
关键词:油纸绝缘 界面电荷 界面极化 拓展Debye模型 电路等效模型
换流变压器是特高压直流输电工程中的关键设备,特高压换流变压器因内部放电引起燃爆事故对电力系统构成严重威胁。油纸复合绝缘界面处在直流电压下易积聚电荷,诱发局部放电甚至击穿。界面电荷成为影响油纸绝缘性能的关键因素之一,不同条件下界面电荷的积聚特性一直是国内外研究的重点[1]。
对于油纸绝缘界面电荷的分析研究主要分为试验测量和仿真计算两类。周远翔等研究了直流电压下的双层绝缘结构,即“纸+纸”和“油+纸”两种情况[2];郝建等研究了“纸+油+纸”三层绝缘结构[3];高春嘉基于Kerr效应进一步研究了直流电压下“油隙+多层纸”结构的界面电荷特性[4],均发现油纸界面电荷特性存在极性效应:绝缘纸对负电荷的吸附作用更强,界面负电荷的积聚速度大于正电荷的积聚速度,并且随着纸层数的增加,吸附作用逐渐增强。无论正极性还是负极性,界面电荷的积聚量随着电场强度的升高而增大。
关于油纸绝缘的等效模型,常用双极性载流子输运模型[5],该模型考虑了直流电压下电介质中存在电子和空穴两类不同极性的载流子[6-7]。2006年,有学者提出了离子迁移-扩散模型,认为在外施电场的作用下,液体中载流子发生分离,并且进行迁移和扩散;纸中电荷同样存在这个过程,但是其影响较小[8]。2012年,吴锴等在双极性载流子模型的基础上结合陷阱势垒理论,建立了油纸绝缘载流子迁移模型,描述了空间电荷注入、迁移、入陷、脱陷等过程,仿真得到了单层、双层油浸纸的电荷分布特性[9]。
综上所述,油纸绝缘界面处易积聚电荷,并对电场分布产生影响[10]。油纸绝缘的双极性载流子输运模型等选取的参数大多为经验值,缺乏试验依据,并且计算量较大,较为繁琐。而用于多层介质电场分布计算的电阻-电容先并联后串联的模型,即RC模型,其计算结果与实际测量结果存在较大偏差[11]。因此迫切需要根据试验的结果,结合油纸自身特性,建立准确度较高、适用性较好的油纸等效模型。
本文基于Kerr光电效应,搭建油纸绝缘电场测量系统,测量不同条件下油纸绝缘的电场分布及界面电荷特性,并根据实测的油纸电导、松弛极化、界面势垒等特性,获取仿真模型关键参数,在RC模型的基础上,建立改进的油纸等效模型。
由电流连续性方程可知,当介质中的电流不连续时即发生电荷积聚,而在电场的作用下,介质中的电流由位移电流和传导电流两部分组成,如式(1)所示[12],因此,任何影响介质位移电流和传导电流的因素都会导致界面电荷的积聚。
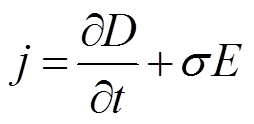 (1)
(1)
式中,j为电流密度;D为电位移;t为时间;σ为电导率;E为电场强度。
对于油纸绝缘材料而言,影响位移电流的因素包括瞬时极化和松弛极化,但是瞬时极化主要由电子位移产生,极化过程很快,而松弛极化则要复杂很多;影响传导电流的主要是电导率。
油纸绝缘材料的电导率与温度、电场强度等因素息息相关[13]。变压器油的电导率与油中带电粒子的浓度有关,当施加外电场时,油中正负离子的复合过程改变,带电粒子的浓度发生相应变化,导致变压器油的电导率改变。油浸纸板的电导主要由杂质离子电导和电子电导组成,温度和电场强度的变化使得油浸纸板内部的载流子数目发生变化,因此油浸纸板的电导率也呈现非线性变化。
由于绝缘纸内部含有纤维素分子链、水分、纤维素降解产物等极性分子,在外施电压作用下,油纸绝缘内部的极性分子会发生沿电场方向的转向,以及空间电荷在电极附近缓慢积聚的弛豫过程,从而在电极表面产生极性相反的电荷[11]。介质中空间电荷的入陷和脱陷行为会直接影响油纸绝缘的低频弛豫过程[14]。
松弛极化过程常用扩展Debye模型[15-16]表示,即一系列电容和电阻经过串、并联后形成的电路模型,如图1所示。图中,C0为几何电容,其值近似为工频电容值;R0为电阻,与前述电导率相关;Ck、Rk分别代表等效电路模型中第k条支路的电容值和电阻值,k=1, 2,…, n。
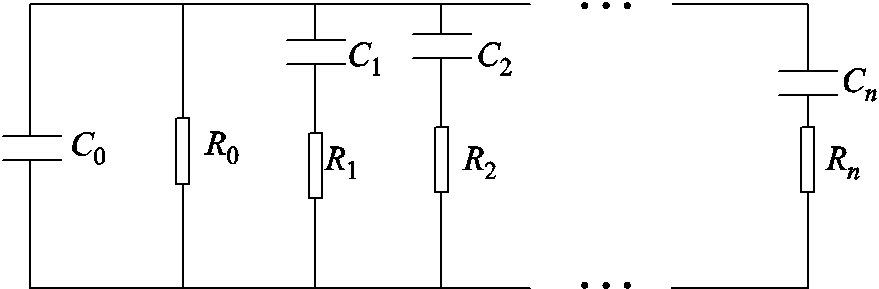
图1 扩展Debye模型等效电路
Fig.1 Equivalent circuit of extended Debye model
扩展Debye模型各RC串联支路表征不同弛豫时间的松弛极化过程,可根据式(2)~式(4)和极化电流曲线计算得到[17]。
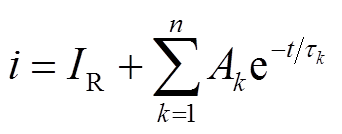 (2)
(2)
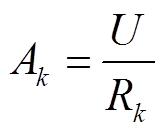 (3)
(3)
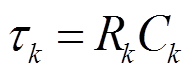 (4)
(4)
式中,U为外施电压;i为极化电流;τk为第k条支路时间常数;Ak为第k条支路的电流幅值;IR为电导电流。
对于多层介质而言,除了上述因素以外,界面势垒也是导致界面电荷积聚的一个关键因素[16]。研究表明,油纸绝缘中的变压器油和油浸纸板之间的界面存在界面势垒,载流子受到界面势垒的阻挡停留在界面处成为界面电荷。油纸界面势垒对电荷的阻挡作用可用界面势垒限制电流表示,常用Poole-Frenkel方程[18]表征,即
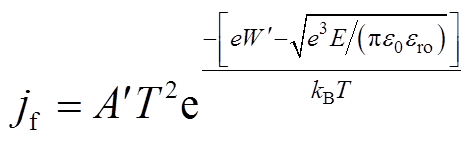 (5)
(5)
式中,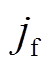 为界面势垒限制电流;
为界面势垒限制电流;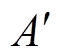 为理查德森常数;T为热力学温度;
为理查德森常数;T为热力学温度;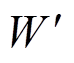 为界面势垒;e为元电荷;ε0为真空介电常数;εro为油纸相对介电常数;kB为玻耳兹曼常数。
为界面势垒;e为元电荷;ε0为真空介电常数;εro为油纸相对介电常数;kB为玻耳兹曼常数。
当不考虑上述三种因素的影响时,多层介质的介电常数和电导率的差异导致界面处积聚电荷,此时常用RC模型等效。根据RC模型,施加直流电压后,油纸复合绝缘结构中的电场由容性电场逐渐向阻性电场过渡[19-20]。
试验中所用油为KI 25X变压器油。为防止变压器油中的杂质离子和微水对试验产生干扰,先对变压器油进行过滤。过滤使用0.2 μm微孔滤纸,重复过滤2~3遍后,放入85℃真空干燥箱中脱水脱气,48 h后冷却至室温取出,经微水含量测量仪检测水分含量小于10×10-6。试验使用的纸板为ABB公司的2 mm纤维素纸板。纸板放入鼓风干燥箱中,在105℃下干燥48 h后,在真空干燥箱中浸油,并在85℃下脱水脱气48 h,冷却至室温后经测定油浸纸板中水分小于0.5%,满足试验要求。
采用Haefely 2830/2831高精度固-液绝缘材料介电性能分析系统对变压器油和油浸纸板的介电常数进行测量。油浸纸板与变压器油的电导率和极化电流的测量使用标准三电极结构,其测量平台如图2所示。
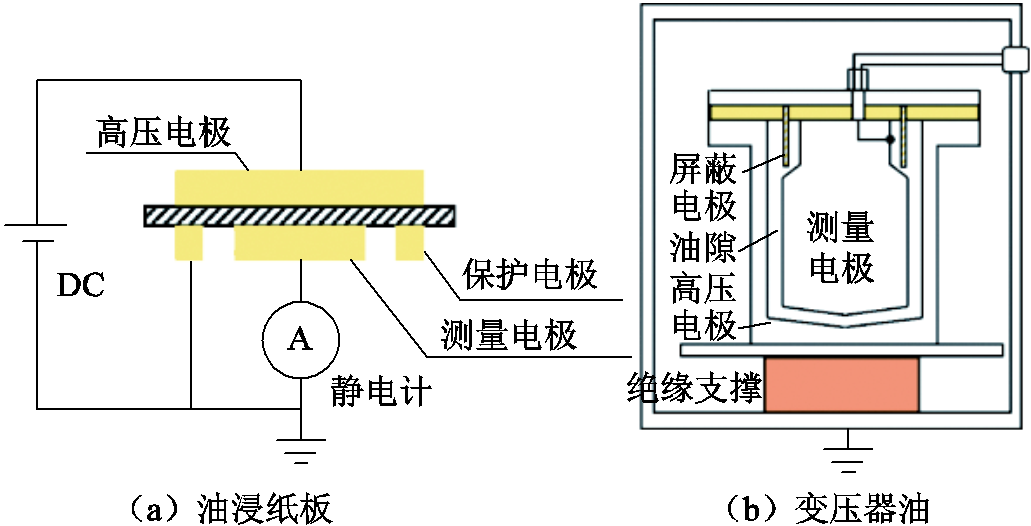
图2 电导率测量平台
Fig.2 Conductivity measurement platform
试验中采用2 mm油浸纸板+ 3 mm油隙的双层结构,其中油浸纸板尺寸略大于下电极,将下电极完全覆盖;调节高压电极高度,保持上下电极平行;控制油隙为3 mm。试验模型如图3所示。
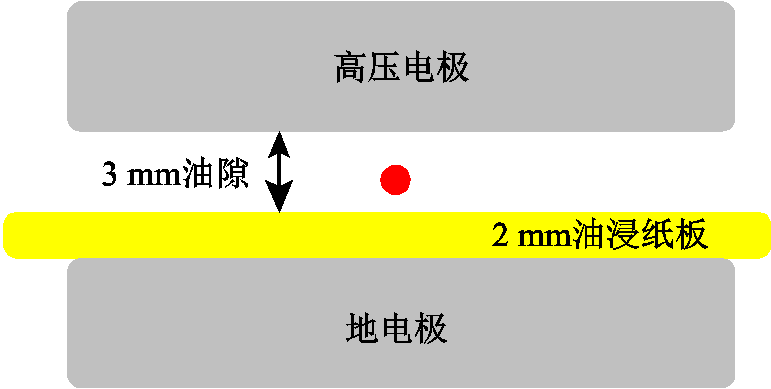
图3 试验模型
Fig.3 Test model
油中电场测量基于交流调制法的Kerr效应原理[6],激光束平行于极板从油隙的中间位置射入,在光环区域内的光强分布均匀,并且假设油中电场均匀分布,其试验平台如图4所示,其中直流+交流偏置通过信号发生器(Tektronix AFG 31000)与功率放大器(AMP-40B20)实现。经试验,直流电场测试最大误差不超过3.5%。
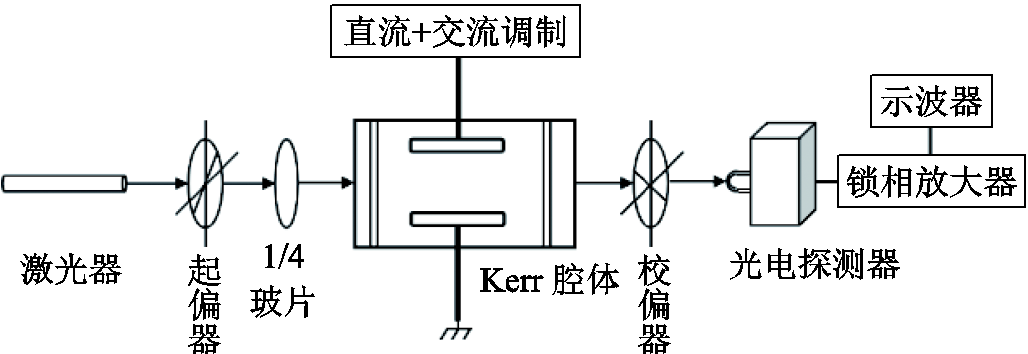
图4 Kerr效应电场测量试验平台
Fig.4 Kerr effect electric field measurement platform
3.1.1 基本介电参数
油浸纸板及变压器油介电参数的测量结果见表1,其中,油浸纸板电导率测量电场强度为1 kV/mm,变压器油电导率测量电场强度为500 V/mm。结果表明,所用2 mm油浸纸板的相对介电常数约为变压器油的1.6倍,而变压器油的电导率约为油浸纸板的117倍。
表1 相对介电常数和电导率测量结果
Tab.1 Measured relative permittivity and conductivity

检测项目相对介电常数电导率/(S/m) 油浸纸板3.801.96×10-15 变压器油2.362.29×10-13 油浸纸板:油1.6:11:117
3.1.2 电场的暂态变化规律
利用Kerr效应可测得变压器油中电场强度Eoil,油浸纸板中的平均电场强度Eop计算式[21]为
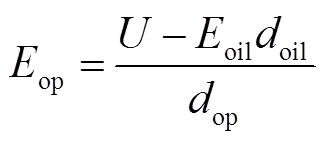 (6)
(6)
式中,dop和doil分别为油浸纸板的厚度和变压器油隙的距离。
10 kV电压下变压器油和油浸纸板中电场强度随时间的变化过程如图5所示,可以看出变压器油中电场强度达到稳态的速度较快。加压初始时,变压器油中电场强度大于油浸纸板中电场强度,变压器油中初始电场强度为2.279 kV/mm,约为油浸纸板中电场强度的1.4倍,满足与介电常数成反比的规律。但随着时间增加,介质中发生极化和电荷积聚,导致变压器油中电场强度不断减小,油浸纸板中电场强度不断增大。最终稳态时变压器油中电场强度仅为0.035 9 kV/mm,油浸纸板中平均电场强度远大于变压器油中电场强度,约为后者的138倍。
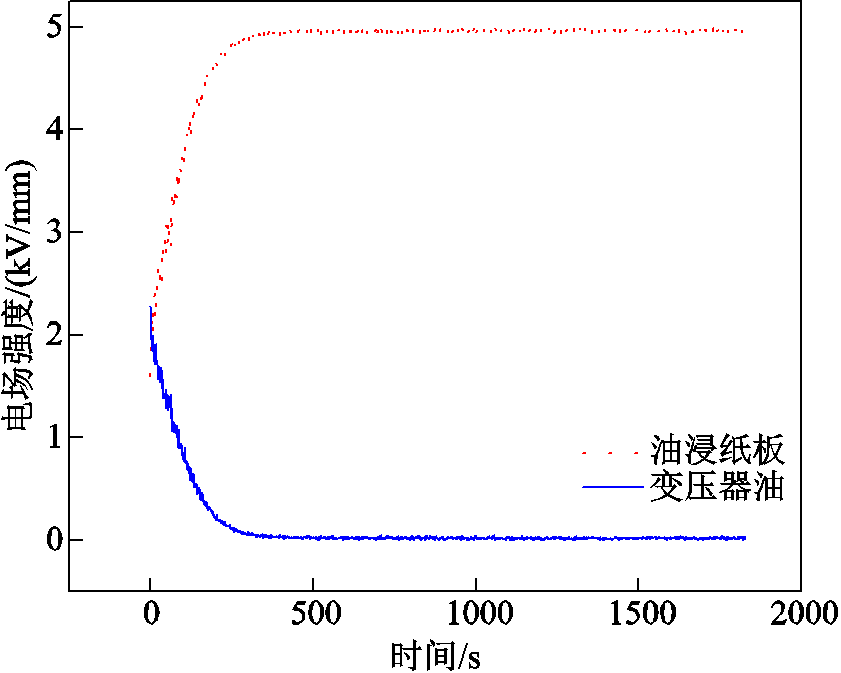
图5 10 kV电压下油纸中电场变化过程
Fig.5 Variation process of electric field in oil-paper under 10 kV voltage
3.1.3 外施电压幅值的影响
为探究不同外施电压幅值对电场分布的影响,分别进行了5、10、15、20、25 kV电压下的电场测量,油纸中初始与稳态电场强度如图6所示。可以看到,不同电压下,初始时刻变压器油中电场均大于油浸纸板中电场;随着时间的推移,油浸纸板中电场增加,变压器油中电场减小;最终达到稳态时,油浸纸板中电场远大于变压器油中电场。其中25 kV电压下初始时刻变压器油中电场强度为6.450 kV/mm,油浸纸板中电场强度为2.825 kV/mm,变压器油中电场强度为油浸纸板中电场强度的2.28倍;稳态时变压器油中电场强度为0.063 2 kV/mm,油浸纸板中电场强度为12.405 kV/mm,变压器油中电场强度仅为油浸纸板中电场强度的1/196。
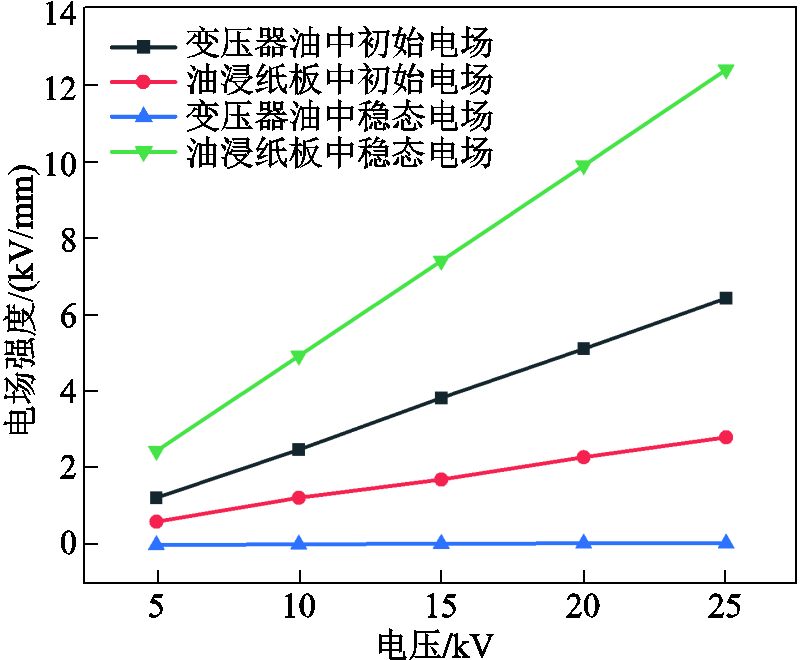
图6 不同外施电压下的电场分布
Fig.6 Electric field distribution under different applied voltages
3.1.4 外施电压极性的影响
为探究外施电压极性对电场分布的影响,测量了负极性电压下变压器油中的电场强度,并与正极性的测量结果进行对比,如图7所示。负极性下电场的变化规律与正极性下大致相同。负极性下稳态电场与外施电压整体呈非线性关系:在15 kV以下,近似呈线性增长,增长速率较快;当外施电压大于 15 kV时,增长幅度变小。对比正负极性下的结果可知,变压器油中电场存在明显的极性效应:在负极性电压下,变压器油中电场更低;在低电压下,正负极性的差异较小,随外施电压升高,正负极性下的差异增大。在25 kV电压下,正极性下变压器油中稳态电场强度为0.063 2 kV/mm,而负极性下变压器油中稳态电场强度为0.042 5 kV/mm,正极性是负极性的1.49倍。
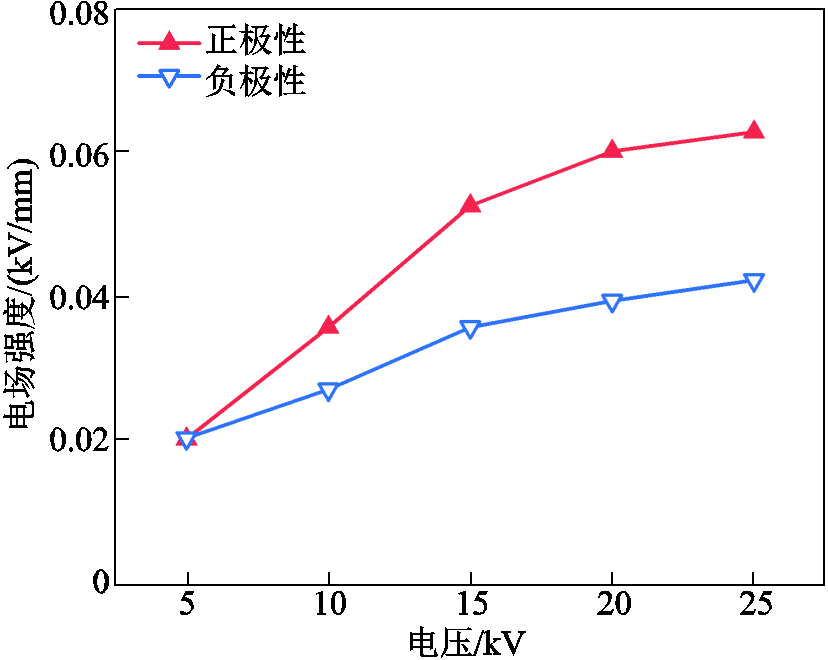
图7 正负极性电压下变压器油中电场强度
Fig.7 Electric field in oil under positive and negative voltages
正负极性电压下油浸纸板与变压器油中稳态电场强度的比值如图8所示。结果表明,相较于正极性,负极性下二者电场强度的比值更大,这说明外施电压相同时,负极性下油浸纸板中的平均电场强度高于正极性下油浸纸板中的平均电场强度,且负极性下油浸纸板中电场强度随外施电压的增长速率更大。
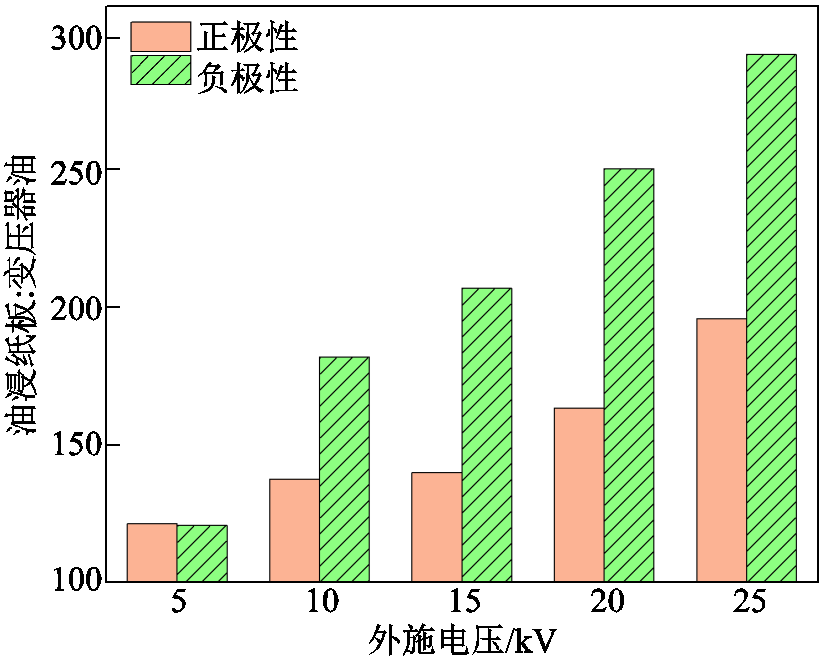
图8 正负极性下油浸纸板与变压器油中稳态电场的比值
Fig.8 Steady-state electric field ratio under positive and negative voltages
3.2.1 RC等效模型计算
根据RC模型,变压器油中稳态电场强度和暂态电场强度分别为[22]
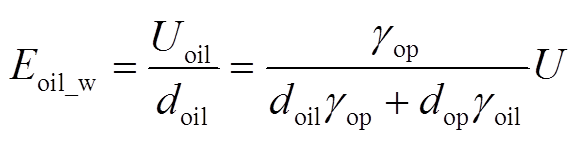 (7)
(7)
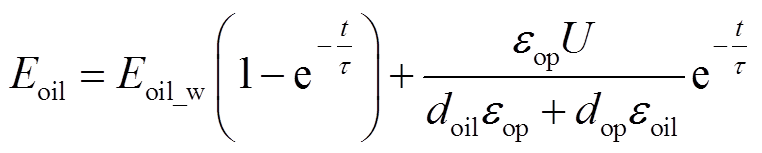 (8)
(8)
式中,γoil、γop、εoil、εop分别为变压器油及油浸纸板的电导率和介电常数;Eoil_w为变压器油中稳态电场强度;τ为时间常数,计算式为
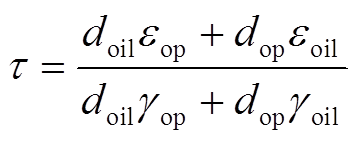 (9)
(9)
采用表1中参数,将RC模型计算的油中稳态电场强度与实测结果进行比较,如图9所示。
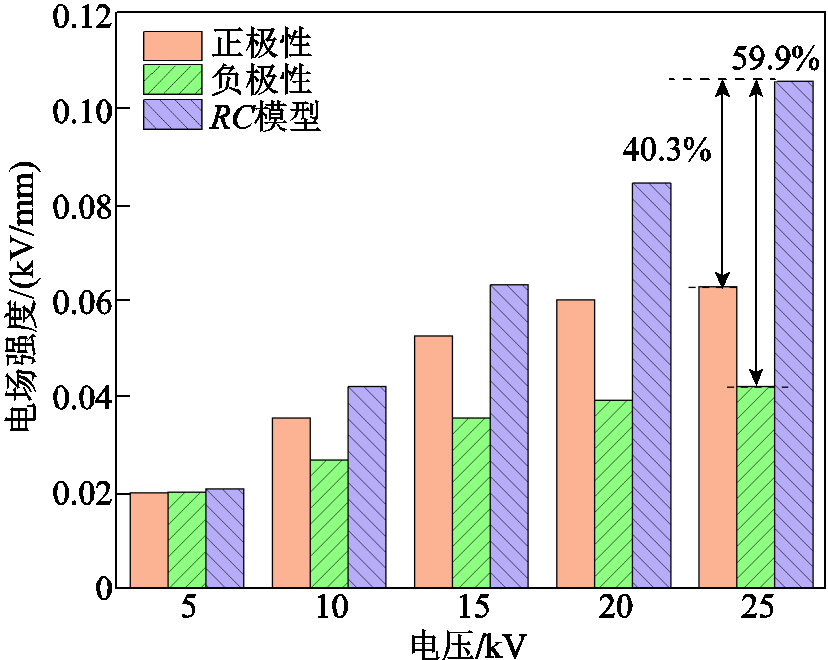
图9 不同条件下变压器油中的稳态电场强度
Fig.9 Steady-state electric field in oil under different conditions
结果表明,RC模型计算的变压器油中电场强度与外施电压成正比。低电压下的计算结果与实测结果接近,但是随着外施电压的增大,RC模型计算结果与实测结果的差距逐渐增大。在25 kV电压下,RC模型计算结果与正极性实测结果相差40.3%,与负极性实测结果相差59.9%。
分别采用高电场下(变压器油8 kV/mm,油浸纸板10 kV/mm)和低电场下(变压器油500 V/mm,油浸纸板1 kV/mm)的电导率,通过RC模型计算出油浸纸板和变压器油中电场变化过程如图10所示。从图10可以看出,两组曲线的整体变化规律与图5一致,采用高电场下电导率计算的RC模型结果更准确,在大约700 s时达到稳态。但无论采用哪种电导率,到达稳态的时间均明显晚于图5。
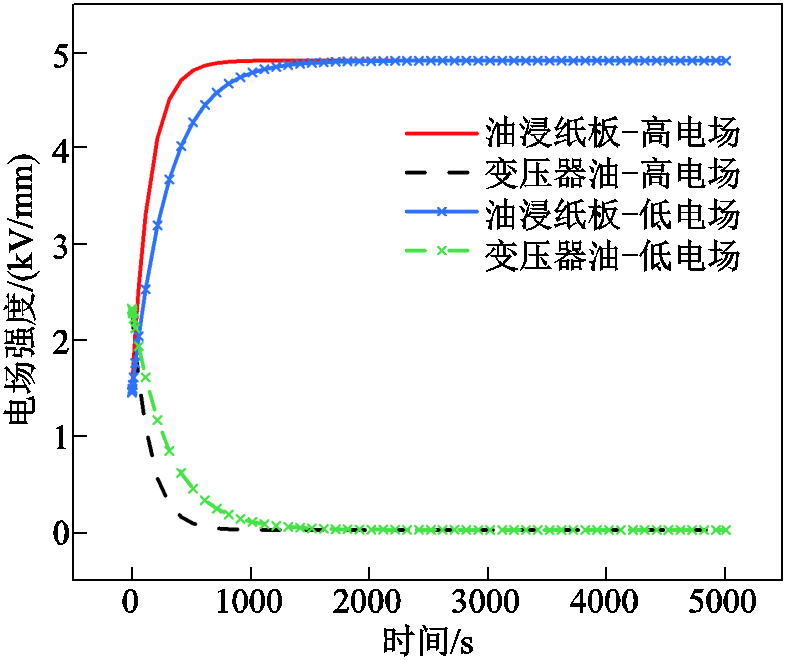
图10 RC模型计算的油纸电场变化过程
Fig.10 Dynamic change of electric field in oil-paper calculated by the RC model
图9和图10的结果表明,RC模型的计算结果在稳态值和暂态过程方面均与实测结果有较大差异,而由式(8)和式(9)可知,电导率影响稳态值,电导率和松弛极化影响暂态过程。
3.2.2 非线性电导的影响
油纸绝缘材料的电导率与电场强度有关[11]。根据Kerr试验结果可知,变压器油和油浸纸板中的电场强度变化范围分别约为0.2~7 kV/mm和2~15 kV/mm,因此选择测试变压器油在0.25~ 10 kV/mm、油浸纸板在2~20 kV/mm的电导率变化规律,结果如图11所示。
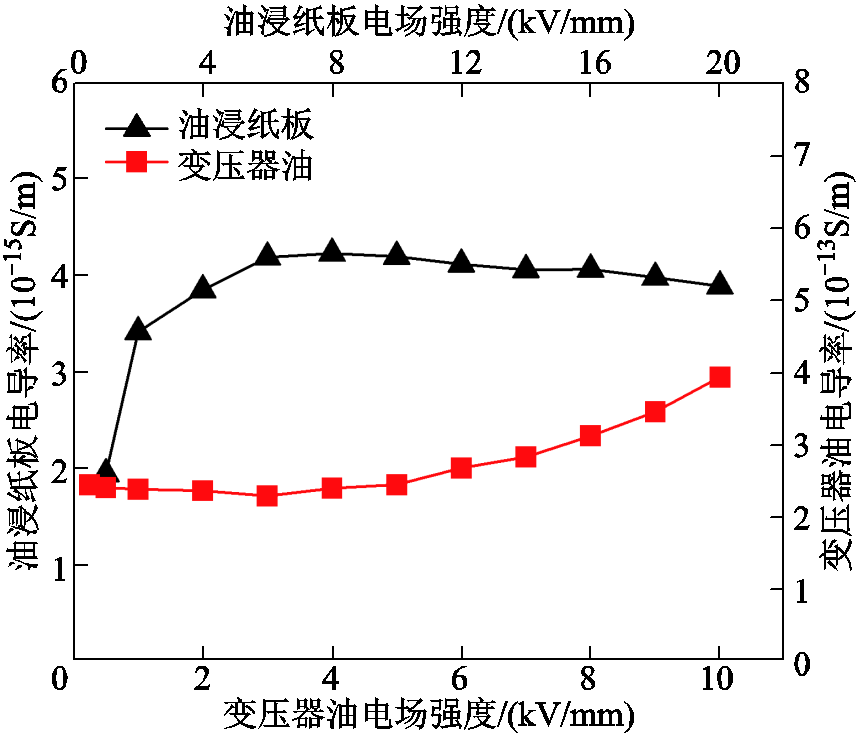
图11 变压器油和油浸纸板的电导率变化规律
Fig.11 Conductivity of transformer oil and oil-impregnated paperboard
结果表明,变压器油与油浸纸板的电导率均随着电场强度增加而增大,变压器油的电导率随电场强度的变化较为明显,而油浸纸板的电导率随电场强度增大先快速增大然后基本不变。这是因为在电场强度增大的过程中,由电极注入油中的电子动能逐渐增大,并且不易被俘获,同时在碰撞中会产生更多电子,因此电导率随着电场强度的增加呈指数型增大。对油浸纸板来说,电场强度的增大使得油浸纸板中的自由电子和带电粒子运动更剧烈,但电子注入过程不如油中明显,因此电导率变化不如变压器油显著[23]。
正极性电压下初始和稳态时刻油浸纸板与变压器油中电场强度比值如图12所示,可以看到,初始时刻的电场强度比值几乎不随外施电压变化,但是稳态下的比值随着外施电压的增大而增大。根据图6中不同外施电压下的稳态电场强度值和图11中的电导率变化曲线计算出稳态电场下变压器油与油浸纸板电导率的比值,一并绘制在图12中。可以看出,稳态下电场强度的比值与电导率的比值在数值上仍存在较大差距。
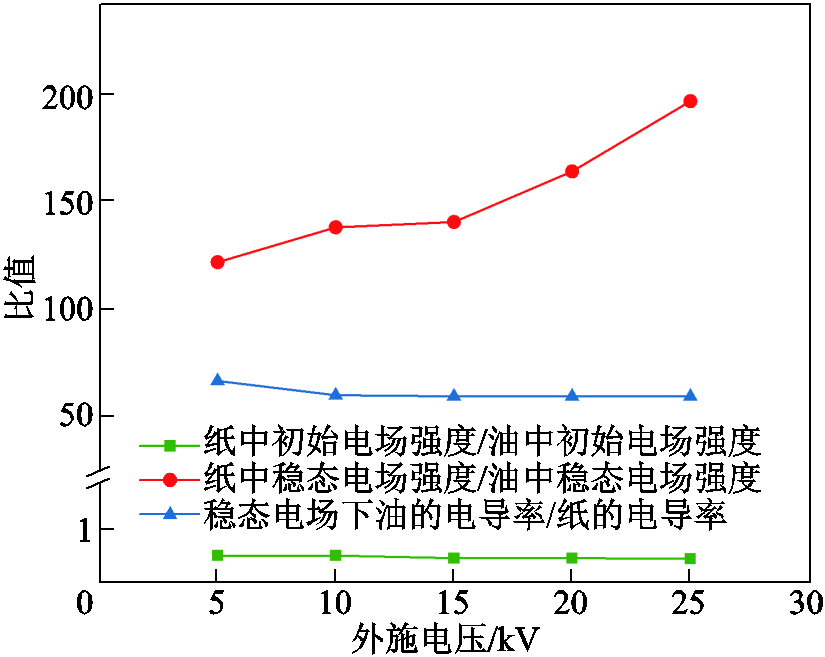
图12 不同外施电压下电场强度和电导率的比值
Fig.12 Ratio of electric field and conductivity under different voltages
3.2.3 松弛极化的影响
在低电场下(变压器油500 V/mm,油浸纸板 1 kV/mm)分别测得变压器油和油浸纸板的极化电流,如图13所示。
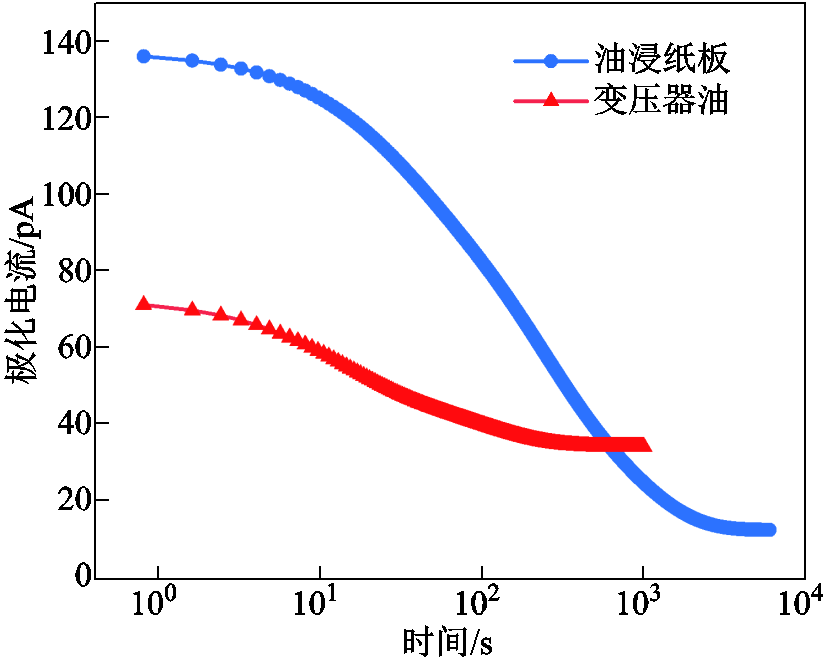
图13 变压器油和油浸纸板的极化电流
Fig.13 Transformer oil and oil-impregnated cardboard polarization current
油浸纸板的极化电流从138 pA经2 000 s衰减到10 pA,变压器油的极化电流从72 pA经300 s衰减到34 pA。可以发现,变压器油的电导电流大于油浸纸板的电导电流,但是吸收电流小于油浸纸板的。变压器油的电导率大于油浸纸板的电导率导致界面产生正电荷积聚,而油浸纸板中的松弛极化过程会产生负电荷积聚,由式(1)可知,它们将导致界面积聚的电荷极性相反。
通过拟合极化电流曲线可求得变压器油和油浸纸板扩展Debye模型各支路的电阻、电容参数,见表2。可以看出,由于变压器油为弱极性介质,其中的松弛极化主要为杂质的空间电荷极化[24],因此只需要两条支路,而油浸纸板极化时间更长,支路数也多于变压器油。
表2 RC串联模型电容电阻参数
Tab.2 RC model capacitor resistor parameters

R/TΩC/pF 支路1支路2支路3支路1支路2支路3 变压器油7.6410.921.638.82 绝缘纸板13.026.607.721.9926.3297.11
图14所示是根据串联扩展Debye模型,采用表1和表2中参数计算的10 kV电压下油浸纸板和变压器油中电场变化过程。可以看出,其变化规律与图5和图10一致。由于扩展Debye模型中考虑了松弛极化的影响,油浸纸板的弛豫时间长,导致界面处夹层极化变慢,所以油纸电场暂态变化速度稍慢,与图5的实测结果仍存在差距。
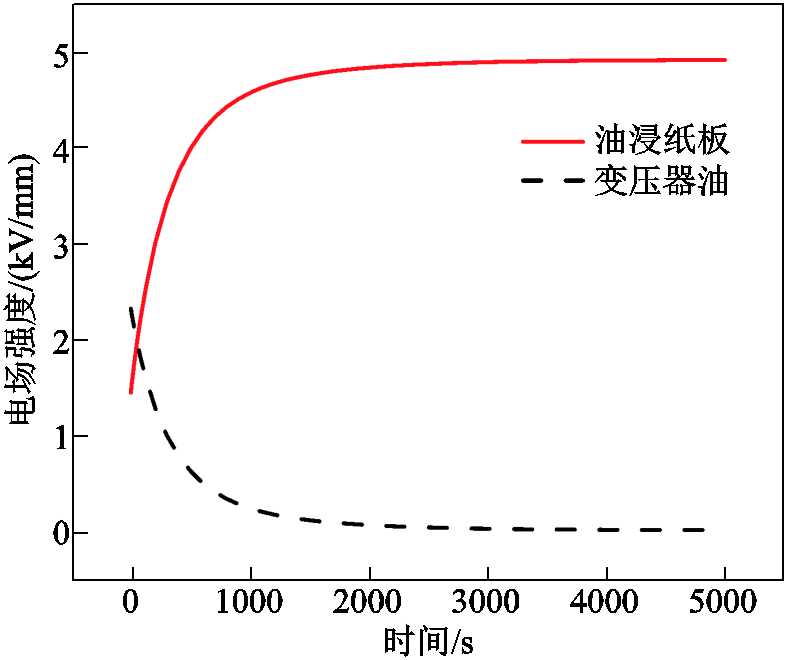
图14 扩展Debye模型计算的油纸电场变化过程
Fig.14 Dynamic change process of electric field in oil-paper calculated by the extended Debye model
3.3.1 双层油纸结构的极化电流
由上述结果可知,无论是RC模型,还是考虑非线性电导和松弛极化过程,计算结果与实测结果均存在一定差异。而且RC模型、非线性电导和扩展Debye模型中的元件特性均与极性无关,不能体现出界面电荷实测结果中的极性效应。为了分析界面势垒的影响,本文测量了双层油纸复合介质的极化电流。由于6517A高阻计电压幅值的限制,此处的测量对象采用0.13 mm油浸纸+1 mm油隙的双层结构,测量结果如图15所示。可以看出,双层油纸复合介质的极化电流存在极性效应,当外施电压为负极性时,其极化电流要大于正极性的情况。无论外施电压是正极性还是负极性,极化电流初始值均较大,然后逐渐衰减到稳态值。
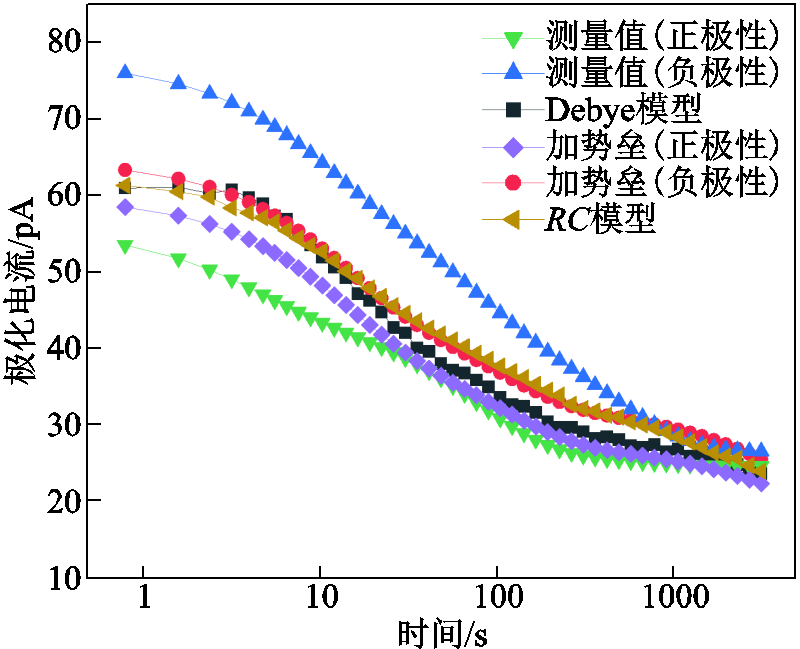
图15 双层油纸结构中极化电流的实测与仿真曲线
Fig.15 Measured and calculated polarization current curve of double-layer oil-paper
图15中同时展示了RC模型和串联扩展Debye模型的计算结果,模型参数来自文献[25]。从图15可知,RC模型的计算结果与实测结果偏差较大;通过扩展Debye模型计算的极化电流初始值介于正负极性实测值之间,并且衰减速度较快。这是因为RC模型忽略了介质松弛极化的影响,而在扩展Debye模型中,每条RC串联支路都表征不同弛豫时间的松弛极化过程,但是与实测结果依然存在差距。
3.3.2 界面势垒参数的获取
多层介质界面势垒对电荷的阻挡作用在界面电荷仿真中常用界面势垒限制电流模型表示[20],并且有研究表明,油浸纸和油浸纸板的纤维素对负电荷存在吸附作用,导致油纸绝缘界面处更容易积聚负电荷[21],因此正负极性下的界面势垒不同。在串联扩展Debye模型的基础上,将界面势垒限制电流的影响等效为在油隙侧并联一个受控电流源,受控方程如式(5)所示,极性与外施电压相反,表示这部分电流没有在油浸纸或纸板中流通,而是在界面处积聚形成界面电荷。
界面势垒限制电流的界面势垒参数通过双层油纸复合绝缘的极化电流提取[22]。采用上述串联扩展Debye模型的参数,通过反复试探发现,当正、负极性下油纸复合绝缘界面势垒分别取1.35 eV和1.20 eV时,计算的极化电流已比较接近测量值,结果如图15所示。可以看到,加入界面势垒限制电流后,虽然计算结果与实测结果仍然存在差异,但是极化电流的极性效应和弛豫过程等关键特征能较好地体现出来。
本文融合油纸非线性电导、松弛极化、界面势垒限制电流特性,建立了一种油纸绝缘非线性电路等效模型,如图16所示,以非线性电阻元件表征油纸电导随电场的变化规律,以不同弛豫时间的电容电阻串联支路表征松弛极化过程,以电压控制电流源表征界面势垒限制电流。
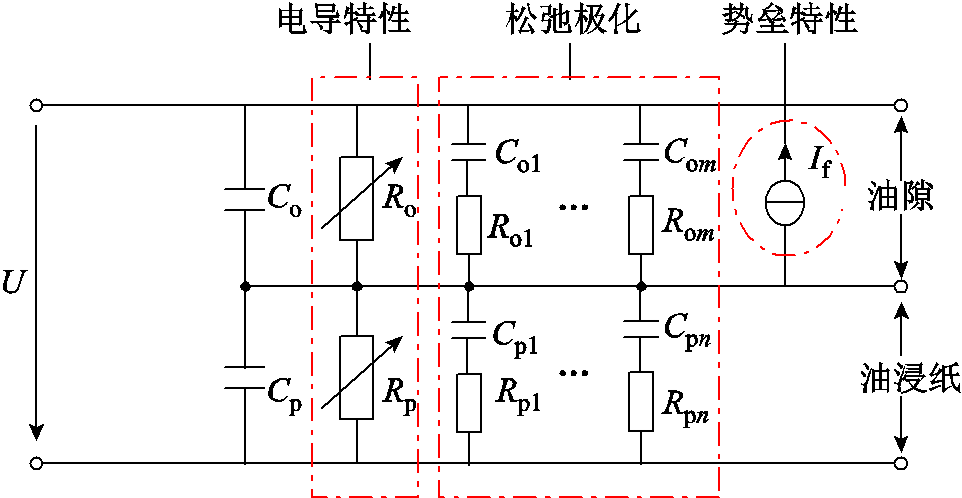
图16 电路等效模型
Fig.16 Circuit diagram of equivalent model
基于所建立的油纸绝缘等效模型,采用表1和表2中参数及前文提取的界面势垒,计算10 kV电压下油浸纸板和变压器油中电场变化过程如图17所示,同时与实测结果、RC模型与Debye模型的计算结果进行了对比。可以看出,其变化规律与图14一致,通过与RC模型和扩展Debye模型对比可知,由于在等效模型中考虑了非线性电导率的影响,到达稳态的时间减小至500 s左右,更接近图5的实测结果。
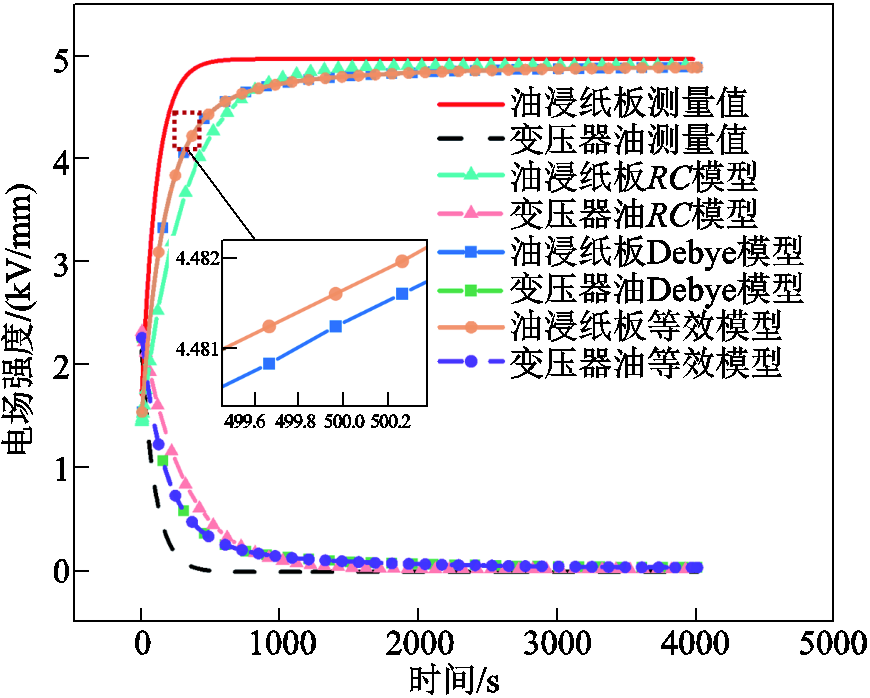
图17 电场动态变化过程的验证
Fig.17 Verification of the dynamic change process of electric field
2 mm绝缘纸板+3 mm油隙的三种模型计算结果与油中电场实测结果比较如图18a所示。RC模型和扩展Debye模型在5~25 kV电压下的计算结果与实测结果的差距随电压的升高逐渐增大,而等效模型在正负极性下的计算结果与实测结果的误差均小于5%,25 kV直流下与实测结果的误差最大,此时最大误差为4.8%,模型计算准确度相较于RC模型、串联扩展Debye模型有了极大的提高,且普适性较好,可适用于不同极性和幅值的外施电压。
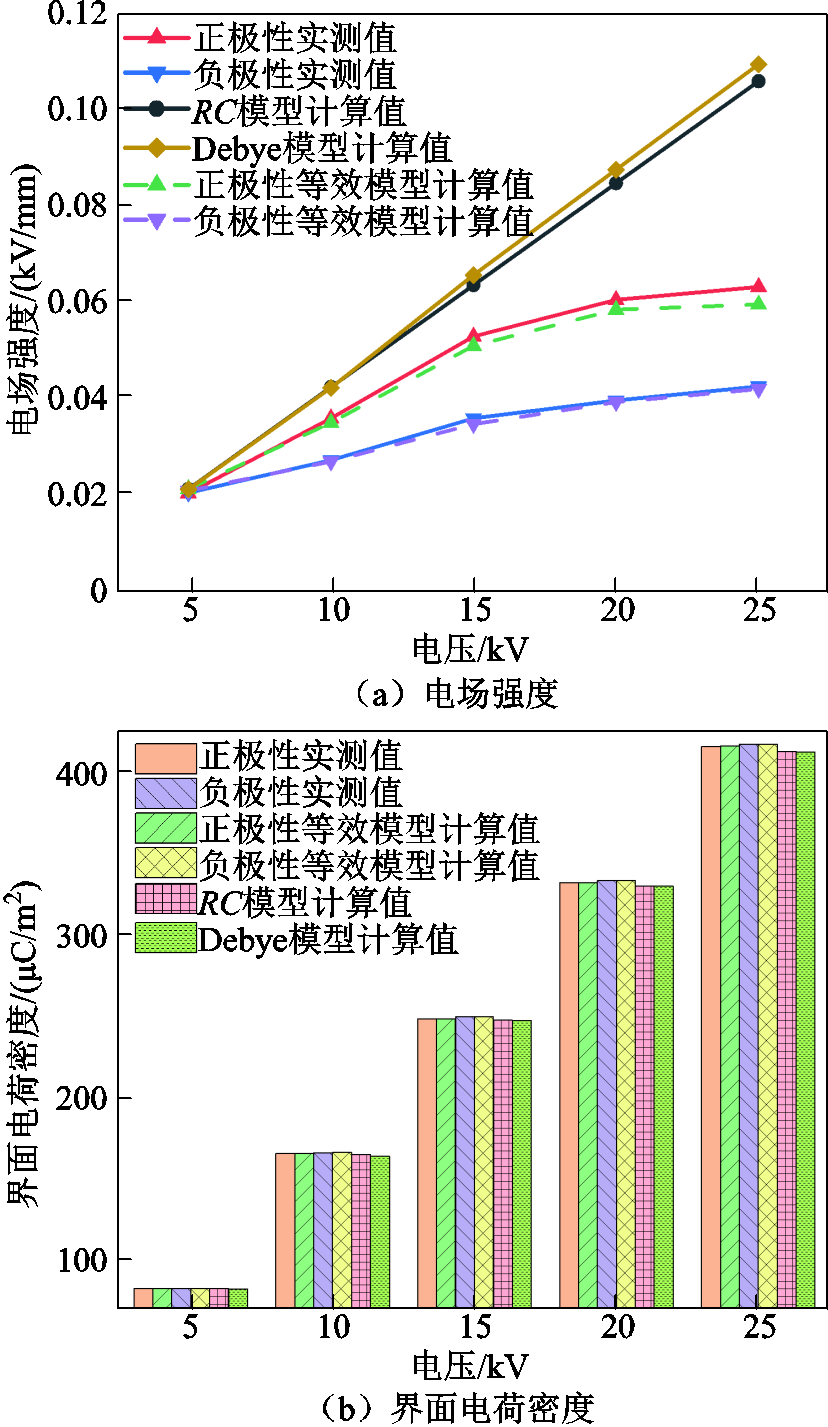
图18 稳态电场和界面电荷密度验证
Fig.18 Verification of steady-state electric fields and interfacial charge densities
将三种模型的界面电荷密度计算结果与正负极性下实际测量的绝对值进行比较,结果如图18b所示。计算结果表明,等效模型较RC模型和扩展Debye模型计算得到的界面电荷密度更接近实测值,并且等效模型能反映极性效应,与实际情况更加贴切。等效模型计算结果在低电压下误差较小,虽然其偏差随着外施电压的升高略有增大,但是依然很小。25 kV电压下负极性界面电荷实测结果的绝对值比等效模型计算结果高出1.07%,正极性界面电荷实测结果比等效模型计算结果高出0.95%。
通过测量与计算发现,变压器油的电导率随着电场强度升高呈指数增长,油浸纸板的电导率先增长后不变,因此对直流电压下油纸复合模型中的电场分布影响较大。极化电流的电导分量和弛豫分量共同作用于界面电荷积聚,但电导分量与弛豫分量积聚的界面电荷极性相反,总界面电荷极性始终与外施电压极性相同。界面势垒对正负电荷的阻挡作用存在极性差异,在实际的测量过程中,无论是界面电荷密度还是电场分布,均存在极性效应,因此需要考虑界面势垒对界面电荷与电场分布的影响。
综上所述,加入表征电导随电场变化的非线性电阻元件、表征不同弛豫时间的RC串联支路、表征界面势垒限制电流的电压控制电流源后,所建立的油纸等效模型在不同幅值、不同极性电压下的计算结果与油中电场强度实际测量结果的最大误差不超过5%,表明非线性电路模型具有较高的准确性。
1)外施电压较低时,变压器油中电场随外施电压线性增大且极性效应不明显,此时界面电荷主要由界面极化产生;高电场下存在其他形式的电荷积聚,导致变压器油中电场随外施电压非线性增大,并且极性效应明显。
2)油纸绝缘的非线性电导、松弛极化过程和界面势垒限制电流非常明显,它们会影响油纸绝缘的界面电荷积聚和电场分布特性,其中界面势垒限制电流是影响极性效应的关键因素。
3)本文提出的油纸等效模型融合了电导率变化、松弛极化、界面势垒等影响因素,对不同条件下油纸绝缘界面电荷的计算具有良好的适用性,界面电荷密度最大误差为1.07%。
参考文献
[1] 张书琦, 赵晓林, 齐波, 等. 直流和极性反转电压下石蜡基与环烷基变压器油纸界面电荷积聚特性及动态过程[J]. 电工技术学报, 2022, 37(3): 767-774, 792. Zhang Shuqi, Zhao Xiaolin, Qi Bo, et al. Interface charge accumulation characteristics and dynamic process of paraffine-base and naphthene-base transformer oils under DC and polarity reversal voltage[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 767-774, 792.
[2] Huang Meng, Zhou Yuanxiang, Chen Weijiang, et al. Influence of voltage reversal on space charge behavior in oil-paper insulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2014, 21(1): 331-339.
[3] 郝建, 黄博, George Chen, 等. 空间电荷在多层结构油纸绝缘混合体系的积聚规律及其对电场分布的影响[J]. 高电压技术, 2017, 43(6): 1973-1979. Hao Jian, Huang Bo, Chen G, et al. Space charge accumulation behavior of multilayer structure oil-paper insulation and its effect on electric field distribution[J]. High Voltage Engineering, 2017, 43(6): 1973-1979.
[4] 高春嘉. 直流电场下油纸绝缘界面电荷产生机制及影响因素的研究[D]. 北京: 华北电力大学, 2020. Gao Chunjia. Research on generation mechanism of interface charge and the impacting factors in oil-pressboard insulation structure under DC voltage[D]. Beijing: North china Electric Power University, 2020.
[5] Huang Bo, Hao Miao, Hao Jian, et al. Space charge characteristics in oil and oil-impregnated pressboard and electric field distortion after polarity reversal[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(2): 881-891.
[6] Zahn M, Takada T. High voltage electric field and space-charge distributions in highly purified water[J]. Journal of Applied Physics, 1983, 54(9): 4762-4775.
[7] Hao Miao, Zhou Yuan, Chen G, et al. Space charge behavior in oil gap and impregnated pressboard combined system under HVDC stresses[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(2): 848-858.
[8] Gafvert U, Hjortstam O, Serdyuk Y, et al. Modeling and measurements of electric fields in composite oil/cellulose insulation[C]//2006 IEEE Conference on Electrical Insulation and Dielectric Phenomena, Kansas City, MO, USA, 2006: 154-157.
[9] 吴锴, 朱庆东, 王浩森, 等. 温度梯度下双层油纸绝缘系统的空间电荷分布特性[J]. 高电压技术, 2012, 38(9): 2366-2372. Wu Kai, Zhu Qingdong, Wang Haosen, et al. Space charge distribution characteristic in double-layer oil impregnated papers under temperature gradient[J]. High Voltage Engineering, 2012, 38(9): 2366-2372.
[10] 吴洁, 郝建, 高春嘉, 等. 直流电压下界面电荷积聚对“液-固”油纸绝缘电场分布影响的仿真分析及试验验证[J]. 高电压技术, 2022, 48(5): 1737-1750. Wu Jie, Hao Jian, Gao Chunjia, et al. Simulation and verification of interface charge accumulation influence on electric field distribution of “liquid-solid” oil-paper insulation under DC voltage[J]. High Voltage Engineering, 2022, 48(5): 1737-1750.
[11] 李国倡, 王家兴, 魏艳慧, 等. 高压直流电缆附件XLPE/SIR材料特性及界面电荷积聚对电场分布的影响[J]. 电工技术学报, 2021, 36(14): 3081-3089. Li Guochang, Wang Jiaxing, Wei Yanhui, et al. Effect of material properties of XLPE/SIR and interface charge accumulation on electric field distribution of HVDC cable accessory[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 3081-3089.
[12] 黎枝鑫, 王东阳, 温荣婷, 等. 基于时变指前因子和频域介电谱平移系数的油浸纸热老化评估方法[J]. 电工技术学报, 2022, 37(17): 4487-4496, 4516. Li Zhixin, Wang Dongyang, Wen Rongting, et al. Thermal aging assessment method of oil impregnated paper based on time-varying pre-exponential factor and translation coefficient of frequency domain spectroscopy[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4487-4496, 4516.
[13] 黄峻峰, 秋向飞, 刘志华, 等. 交直流复合电压下纳米Al2O3改性绝缘纸板介电与电荷特性研究[J]. 高压电器, 2022, 58(12): 138-146. Huang Junfeng, Qiu Xiangfei, Liu Zhihua, et al. Study on dielectric and charge properties of nano-Al2O3 modified paperboard under AC-DC composite voltage[J]. High Voltage Apparatus, 2022, 58(12): 138-146.
[14] 徐晴川, 王圣康, 林福昌, 等. 基于时频域介电响应的绝缘油弛豫过程分析[J]. 电工技术学报, 2022, 37(9): 2355-2365. Xu Qingchuan, Wang Shengkang, Lin Fuchang, et al. Analysis of relaxation process of insulating oil based on dielectric response in time and frequency domain[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2355-2365.
[15] 邹阳, 林锦煌, 何津, 等. 基于频谱解构法的油纸绝缘扩展德拜模型参数辨识[J]. 电工技术学报, 2023, 38(3): 622-632. Zou Yang, Lin Jinhuang, He Jin, et al. Parameter identification of oil paper insulation extended Debye model based on spectrum deconstruction method[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 622-632.
[16] 胡一卓, 董明, 谢佳成, 等. 油纸绝缘宽频介电响应谱分析及等效模型研究[J]. 中国电机工程学报, 2019, 39(23): 7065-7073, 7119. Hu Yizhuo, Dong Ming, Xie Jiacheng, et al. Spectrum analyzing and modeling of wide-band frequency dielectric response of oil-paper insulation[J]. Proceedings of the CSEE, 2019, 39(23): 7065-7073, 7119.
[17] Wei Yanhui, Mu Haibao, Deng Junbo, et al. Effect of space charge on breakdown characteristics of aged oil-paper insulation under DC voltage[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(5): 3143-3150.
[18] 连启祥, 杜志叶, 杨知非, 等. 油纸绝缘内部合成电场数值模拟方法[J]. 电工技术学报, 2017, 32(20): 53-61. Lian Qixiang, Du Zhiye, Yang Zhifei, et al. Numerical simulation method of electric field in oil-paper insulation[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 53-61.
[19] 黄猛, 葛扬, 单秉亮, 等. TiO2纳米粒子几何形貌对冲击电压下变压器油中流注发展速度的影响[J]. 高电压技术, 2020, 46(11): 3986-3993. Huang Meng, Ge Yang, Shan Bingliang, et al. Influence of TiO2 nanoparticle’s geometry on propagation velocity of streamers in transformer oil under impulse voltage[J]. High Voltage Engineering, 2020, 46(11): 3986-3993.
[20] 朱庆东, 吴锴, 朱文兵, 等. 温度梯度下油纸绝缘空间电荷特性的数值仿真[J]. 高电压技术, 2016, 42(3): 923-930. Zhu Qingdong, Wu Kai, Zhu Wenbing, et al. Numerical simulation of space charge property in oil-paper insulation space under temperature gradient[J]. High Voltage Engineering, 2016, 42(3): 923-930.
[21] Gabler T, Backhaus K, Großmann S, et al. Dielectric modeling of oil-paper insulation systems at high DC voltage stress using a charge-carrier-based approach[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2019, 26(5): 1549-1557.
[22] Qi Bo, Gao Chunjia, Zhao Xiaolin, et al. Interface charge polarity effect based analysis model for electric field in oil-pressboard insulation under DC voltage[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(5): 2704-2711.
[23] 关毅. 动态参数下换流变压器油纸绝缘电场分布与放电特性[D]. 哈尔滨: 哈尔滨理工大学, 2022. Guan Yi. Electric field distribution and discharge characteristics of oil-pressboard insulation of converter transformer with dynamic parameters[D]. Harbin: Harbin University of Science and Technology, 2022.
[24] 应宇鹏, 黄猛, 吕玉珍, 等. TiO2纳米粒子浓度对油纸复合绝缘击穿特性和界面电荷的影响[J]. 中国电机工程学报, 2019, 39(增刊1): 249-257. Ying Yupeng, Huang Meng, Lü Yuzhen, et al. Influence of TiO2 nanoparticles concentration on breakdown characteristic and interface charge of oil-paper insulation[J]. Proceedings of the CSEE, 2019, 39(S1): 249-257.
[25] 应宇鹏. 纳米粒子对油纸复合绝缘直流击穿强度的影响[D]. 北京: 华北电力大学, 2020. Ying Yupeng. Influence of nanoparticles on DC breakdown strength of oil-paper composite insulation[D]. Beijing: North China Electric Power University, 2020.
Abstract In the operation of a converter transformer, the interface of its oil-paper composite insulation is prone to charge accumulation under DC voltage. A simple non-linear equivalent circuit model is proposed based on the extended Debye model in this paper, which can calculate the electric field distribution and interface charge amount of oil-paper insulation more easily and accurately.
Firstly, the capacitance and resistance parameters of the transformer oil and the oil-immersed paperboard are separately measured, and the electric field strength in the oil is measured based on the Kerr effect method at applied voltages from 5 to 25 kV respectively. The electric field distribution in the oil-paper composite insulation is calculated for different applied voltages as well as different voltage polarities, and the measured results are compared with the calculated results from the RC model. Secondly, the conductivity of the transformer oil and oil-immersed paperboard are measured under different electric field strength to establish a non-linear conductivity model for the oil-paper composite insulation. Then the polarisation currents of the transformer oil and oil-immersed paperboard are separately measured and fitted to extract the branch parameters of extended Debye model. Finally, the interface potential barriers are derived from the measured polarisation currents, and the polarity determined interface potential barrier is then added to the model to limit the current through the interface, thus establishing a non-linear equivalent circuit model for the transformer oil and oil-impregnated paperboard where the resistances are the electric field strength dependent.
The electric field distribution in the oil-paper composite insulation calculated by the established non-linear equivalent model is compared with those by the RC model, extended Debye model and actual measured results. The time to steady state calculated by the equivalent model is reduced to about 500 s, which is shorter than that calculated by the RC and Debye models, and is closer to the measured results. As regards the steady state electric field in oil at different applied voltages, it can be seen that the error between those by the equivalent model and measurment is less than 5% for both positive and negative polarities. The error between the electric field in oil calculated by the equivalent model and the measured results is greatest at DC voltage of 25 kV, but the maximum error is 4.8%. These indicate that the accuracy of this model is greatly improved compared to the RC and series extended Debye model. Comparing the results of the three models with the measured values for positive and negative polarities, the equivalent model is much closer to the measured values than the RC and extended Debye model, and just the equivalent model reflects a polarity effect. The absolute value of the measured negative interface charge amount at 25 kV is merely 1.07% higher than the proposed equivalent model calculation, and the measured positive interface charge amount is 0.95% higher than the proposed equivalent model calculation.
The following conclusions can be drawn from the above: (1) Compared with the RC and extended Debye model, the dynamics of electric field distribution of the oil-paper insulation calculated by the proposed model reach the steady state faster and is closer to the measured situation. (2) The proposed model takes into account the polarity determined interface barrier to limit the current through the interface, so its calculation can reflect the polarity effect and the error between the calculated and measured electric field is less than 5%. (3) The model has incorporated the influence of nonlinear conductivity, relaxation polarisation and interfacial potential barrier limiting current, so it has a good applicability to the calculation of the interfacial charge of oil-paper insulation under different conditions more easily and accurately.
keywords:Oil-paper insulation, interface charge, interface polarization, extended Debye model, equivalent circuit model
DOI: 10.19595/j.cnki.1000-6753.tces.230367
中图分类号:TM132
国家自然科学基金(51807062)和北京市自然科学基金(3212035)资助项目。
收稿日期 2023-03-27
改稿日期 2023-06-08
黄 猛 男,1988年生,副教授,硕士生导师,研究方向为油纸绝缘、电介质空间电场/电荷测量、电气设备在线监测与故障诊断等。E-mail:huang_m2011@163.com
李怡然 女,1998生,硕士研究生,研究方向为变压器油纸绝缘。E-mail:365066122@qq.com
(编辑 李 冰)