 , pagg(T)},设备n功耗序列可表示为Pn={pn(1), pn(2),
, pagg(T)},设备n功耗序列可表示为Pn={pn(1), pn(2),  , pn(T)},则t时刻聚合值Pagg(t)可表示为
, pn(T)},则t时刻聚合值Pagg(t)可表示为摘要 精细化负荷预测为制定家庭新型需求响应策略或能效管理模式提供了可靠的指导信息与理论基础,而负荷监测系统的广泛研究与发展为家庭设备层的负荷预测提供了有力的数据支撑。基于家庭负荷智能电能表集中数据,该文提出一种集分解-预测一体化的家庭负荷两阶段超短期负荷预测方法。该方法第一阶段提出了基于卷积神经网络(CNN)和双向门控单元(BiGRU)神经网络的非侵入式负荷分解(NILM)模型,解决了目前深度分解模型中特征提取不充分、分解精度低等问题。第二阶段构建了基于时间模式注意力机制(TPA)的时间卷积神经网络(TCN)负荷预测模型,深度挖掘NILM分解数据、集中负荷数据及日期特征等输入变量的深层交互信息,实现家庭设备层的负荷预测。算例部分通过UK-DALE数据集对所提方法进行验证,结果表明,该方法能够获得较高的分解精度和预测效果,为家庭负荷预测提供了良好的条件。
关键词:非侵入式负荷分解 负荷预测 卷积神经网络 双向门控单元神经网络 时间卷积网络 注意力机制
随着高级测量体系、通信技术、人工智能及电力交易市场体制改革的不断发展和深入,具备丰富柔性负荷的居民用户逐步成为“源-网-荷-储”协同互动的重要资源,将有力推动我国数字化电网建设和能源转型变革[1-2]。然而,居民用电行为的随机性、市场信息的不确定性以及决策主体的多样性,使得居民参与快速需求响应极具挑战性[3]。因此准确预测用户负荷及获悉用电设备的运行特性对于深入挖掘用户超短时间尺度可调度资源至关重要。
目前,关于家庭电器设备负荷预测的研究文献较少,预测模型较为简单。文献[4-5]提出了一种基于序列翻译模型的单个设备负荷预测方法,序列翻译模型的基本组成单元分别为长短期记忆网络(Long Short-Term Memory, LSTM)和Q学习。文献[6]利用深度神经网络构建了设备级用电需求估计模型,并将其与基于支持向量机(Support Vector Machine, SVM)的预测结果进行了对比分析。文献[7]考虑外界因素和设备自身运行特性,构建了设备分类模块、门控单元(Gated Recurrent Unit, GRU)神经网络预测模块、多任务学习模块,实现对不同类设备的预测。文献[8]利用卡尔曼滤波强大的动态状态估计能力建立了电器设备层面的负荷预测模型,并采用自下而上的建模方式实现了家庭级负荷预测。由于家庭用电需求与用户行为活动息息相关,具有很强的随机性、不确定性和非线性,且单个负荷规模较小,现有预测模型依赖负荷长期运行模式,面向波动性较大的家庭负荷时无法灵活适应。
近年,时间卷积网络(Temporal Convolutional Network, TCN)因其强大的网络感受野和并行处理序列数据能力,在长时间序列预测领域取得了显著成就[9]。文献[10]对比了TCN与LSTM、GRU、循环神经网络(Recurrent Neural Network, RNN)等网络在多种时间序列模型中的预测性能,结果表明,TCN预测精度更高。文献[11]针对TCN、SVM、高斯回归、前向神经网络等经典模型在应用于短期电力负荷预测的适用性和效果进行了分析,进一步证明了TCN在处理含非线性特征的短期电力数据方面更具优势。但上述研究主要针对负荷序列的历史数据,忽略了其他负荷特征的非线性内在联系,易出现信息丢失、数据间结构信息难以建模等问题。
此外,上述针对电器设备的负荷需求研究均是通过侵入式负荷监测(Intrusive Load Monitoring, ILM)方法对电器设备进行监测与感知,该方法虽能准确获取用电信息,但侵犯用户隐私的同时也增加了负荷监测系统的运行和维护成本,实际应用中具有较大局限性。随着机器学习和人工智能技术的快速发展,非侵入式负荷监测(Non-Intrusive Load Monitoring, NILM)[12-13]作为一种经济有效的负荷监测方式受到越来越多研究者的关注,各种先进算法相继被提出,如组合优化[14]、卷积神经网络(Convolutional Neural Network, CNN)[15]、LSTM[16-17]、注意力模块[18]及多任务学习[19]等。用户使用的电器设备具有一定规律性,基于负荷开关事件持续模式,通过NILM获得各电器设备历史数据曲线及其用电行为特征,进而可以实现对相关典型电器设备的用电曲线预测[20-21]。文献[20]利用动态时间规划算法对家庭电动汽车负荷充电模式进行非侵入式提取,并采用CNN-Attention-LSTM网络预测短期内电动汽车充电情况。该方法只对运行模式较为特殊的电动汽车进行负荷分解与预测建模,难以适用于家庭多负荷运行场景。文献[21]提出了一种基于粒子群优化求解的NILM方法,并通过人工神经网络对商业建筑用电设备的状态变化进行预测,然后利用状态变化重构了商业负荷曲线。但在构建分解与预测模型时,该方法进行了大量的线性简化,只分解与预测了电器设备的开关状态,模型的准确性有一定程度的损失。
基于上述研究,本文并未直接采用现有的ILM或NILM算法与预测模型相结合,而是通过引入泛化能力较强的NILM深度学习网络,结合TCN模型在处理含非线性特征的波动性短期电力数据方面的优势,从数据驱动模型的角度出发衡量了两个不同任务阶段的时间序列特征和网络结构特征,从而实现家庭负荷设备层的负荷预测。该方法首先利用CNN-BiGRU分解模型获取电器设备功耗数据,不仅节约了负荷监测成本,也为负荷预测提供数据支撑;其次通过融合时间模式注意力(Temporal Pattern Attention, TPA)机制的TCN模型预测不同电器的负荷值,并在预测阶段充分考虑了基于NILM的功耗数据特征、智能电表数据特征及时间因素特征,以应对电器设备负荷的随机波动;最后,通过公开数据集对所提基于NILM的两阶段负荷预测方法的准确性和适用性进行了分析和验证。
NILM技术致力于通过各种优化组合、信号处理技术或机器学习算法将目标电器的能耗信息从入户集中分离出来。从智能电能表获取包含T个时刻聚合样本可表示为Pagg={pagg(1), pagg(2),  , pagg(T)},设备n功耗序列可表示为Pn={pn(1), pn(2),
, pagg(T)},设备n功耗序列可表示为Pn={pn(1), pn(2),  , pn(T)},则t时刻聚合值Pagg(t)可表示为
, pn(T)},则t时刻聚合值Pagg(t)可表示为
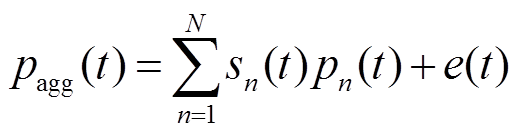 (1)
(1)
式中sn(t)为设备n在t时刻的启停状态;pn(t)为设备n在t时刻的功耗值;N为设备数量;e(t)为干扰信号。
负荷分解目标:从pagg(t)中推断出pn(t)的估值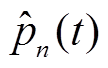 ,pn(t)、
,pn(t)、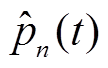 均与同一时刻的pagg(t)有关,有确定的输入与输出值,属于典型的回归问题,因此可以通过训练神经网络模型,对Pagg(t)与pn(t)的统计关系进行定量描述。2015年,J. Kelly等[22]将深度学习引入负荷分解,自此,基于CNN[23]、RNN[24]、LSTM网络模型的解决方案逐渐引起该领域研究人员的关注。CNN具有较强的特征提取能力,并能降低输入信息的维度,但卷积核的存在限制了CNN处理时间序列的能力。对于洗衣机、洗碗机等设备,其工作周期通常包含多个工作状态,运行时间较长,且有功功率随着工作状态的切换出现较大的波动,因此分解模型需要能够在较长时间跨度上挖掘数据间依赖关系。
均与同一时刻的pagg(t)有关,有确定的输入与输出值,属于典型的回归问题,因此可以通过训练神经网络模型,对Pagg(t)与pn(t)的统计关系进行定量描述。2015年,J. Kelly等[22]将深度学习引入负荷分解,自此,基于CNN[23]、RNN[24]、LSTM网络模型的解决方案逐渐引起该领域研究人员的关注。CNN具有较强的特征提取能力,并能降低输入信息的维度,但卷积核的存在限制了CNN处理时间序列的能力。对于洗衣机、洗碗机等设备,其工作周期通常包含多个工作状态,运行时间较长,且有功功率随着工作状态的切换出现较大的波动,因此分解模型需要能够在较长时间跨度上挖掘数据间依赖关系。
GRU[25-26]是一种基于LSTM的优化网络,其将输入门和遗忘门集成单一的更新门,使网络参数减少了1/3,有效地减少迭代次数和收敛时间。GRU循环计算特性有利于提取功率时序特征,因此更适用于非侵入式负荷分解领域。本文在文献[23]序列到点结构基础上对分解算法进行了自主设计,构建了融合CNN和BiGRU的神经网络分解模型,利用1D-CNN逐层抽象提取电器设备运行过程中蕴含的高级时序特征,再利用BiGRU网络全局处理能力得到Pagg(t)与pn(t)之间的非线性关系。
NILM算法有以下优点:①具有较高分解精度;②能准确地定位到设备状态的投切时刻点;③对电器设备的运行状态有较好的趋势跟踪效果;④可以使用大量数据离线训练,在线分解,为提升预测的实时性提供支撑;⑤保护用户数据隐私性。因此,可以通过NILM思想将分解样本应用于预测场景,辅助预测模型学习。基于NILM场景,一般有两类样本可以应用:其一为离线存储的大量历史场景样本;其二为基于在线分解的新场景样本。从负荷预测场景角度看,可借助历史场景样本进行模型训练,对新场景样本进行在线预测得到未来某一段时间内设备运行信息。考虑到负荷分解存在误差,仅用NILM分解样本作为预测模型的输入会将分解误差进一步引入最终预测结果,因此本文将智能电表的集中数据也作为模型的输入。
不同于以往系统级、聚合级负荷与许多环境变量密切相关,家庭用电需求更多地受用户行为活动影响,且缺乏平滑效应,具有很强的随机性、波动性和不确定性,任何一个电器的运行状态都会影响整个用户的负荷曲线。因此需采用非线性映射能力更强的算法以达到准确的预测效果。本文提出一种基于TCN-TPA的负荷预测方法,旨在利用TCN-TPA网络深度特征提取能力及时序相关性学习感知能力,以获得与前沿深度学习模型相比更好的预测精度。
CNN采用局部连接和权重共享方式对数据进行高层次抽象处理,能够以较小的计算量从高维数据中自动提取输入特征[27],为复杂映射关系的定量表征提供有力的数学模型支撑。多个卷积层和池化层交替组成了CNN主体,卷积层主要是挖掘数据特征,池化层可以降低特征维度,从而提高CNN网络的收敛速度,末端由全连接层将其转换输出。智能电表功率数据是一维时间序列,因此需采用一维卷积神经网络(1D-CNN)挖掘数据间深层特征,用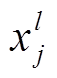 表示1D-CNN第l层的第j个特征映射,其数学模型为
表示1D-CNN第l层的第j个特征映射,其数学模型为
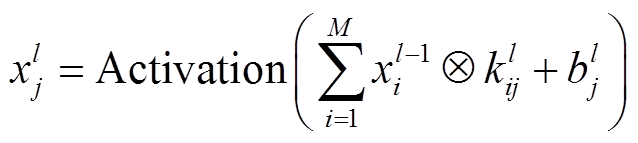 (2)
(2)
式中,Activation(·)为激活函数;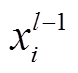 为第l-1层的第i个输出特征映射;
为第l-1层的第i个输出特征映射;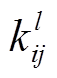 为卷积核;
为卷积核; 为卷积运算;M为输入特征映射数量;
为卷积运算;M为输入特征映射数量;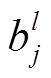 为第l层第j个输出特征映射对应的网络偏置量。
为第l层第j个输出特征映射对应的网络偏置量。
将上述CNN提取的特征向量以时序序列方式构造,并作为GRU网络输入。经典GRU状态从前往后单向传输,t时刻只与过去状态有关,仅考虑正向信息,不考虑反向信息。因此,使用GRU处理一维特征数据时,数据作为单时间片段数据输入,无法充分发挥GRU的循环特性。为提高模型分解性能,本文构建了一种双向GRU(BiGRU)模型,其输出由一个正向GRU和一个反向GRU的状态共同决定,该数据处理方式可充分利用过去和未来的信息,有助于提升序列建模能力,输出为
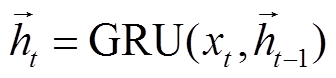 (3)
(3)
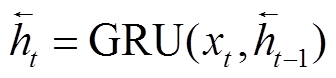 (4)
(4)
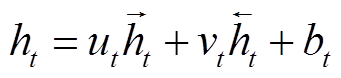 (5)
(5)
式中,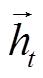 、
、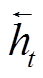 分别为t时刻正向隐藏层和反向隐藏层的输出;ut、vt分别为
分别为t时刻正向隐藏层和反向隐藏层的输出;ut、vt分别为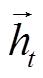 、
、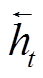 对应的可训练权重系数;bt为t时刻隐藏层状态ht对应的偏置量。本文所构建的CNN-BiGRU模型结构如图1所示,参数见表1。考虑到经预处理后的集中数据是每1 min 1个点,为获取更宽时间段的负荷特征,本文将两个卷积层的卷积核分别设为10和8,BiGRU神经元个数分别为64和128,并在全连接层前采用随机失活方法防止模型过拟合。
对应的可训练权重系数;bt为t时刻隐藏层状态ht对应的偏置量。本文所构建的CNN-BiGRU模型结构如图1所示,参数见表1。考虑到经预处理后的集中数据是每1 min 1个点,为获取更宽时间段的负荷特征,本文将两个卷积层的卷积核分别设为10和8,BiGRU神经元个数分别为64和128,并在全连接层前采用随机失活方法防止模型过拟合。
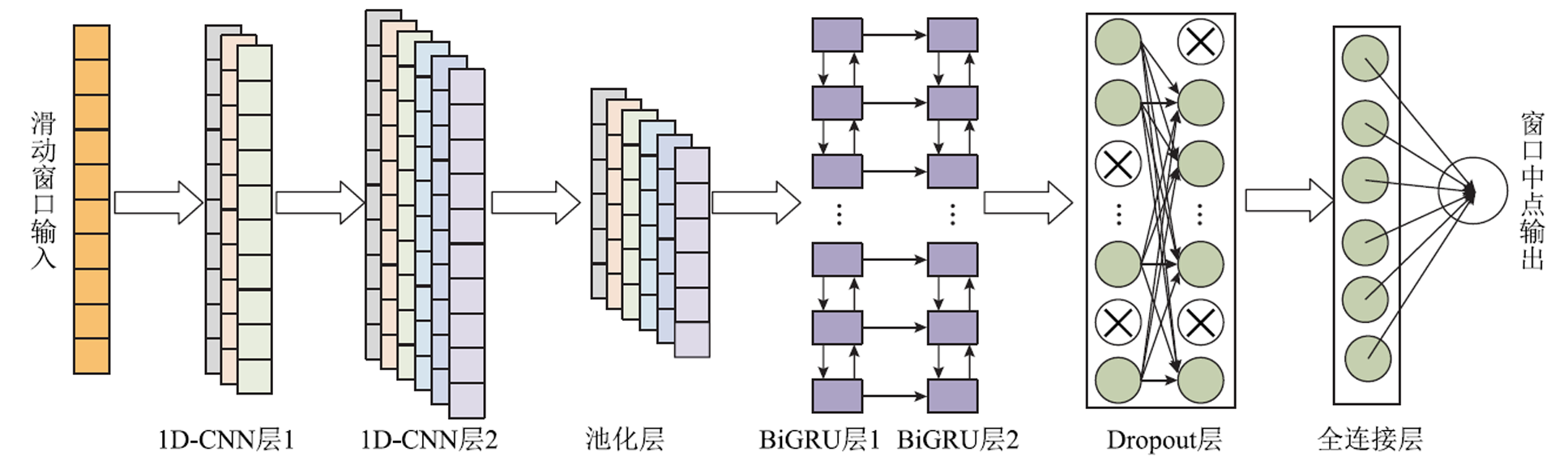
图1 CNN-BiGRU模型结构
Fig.1 Structure diagram of CNN-BiGRU model
表1 CNN-BiGRU模型具体参数
Tab.1 Parameters of CNN-BiGRU model

网络层卷积核个数卷积核大小隐藏节点数失活率 1D-CNN层13210´1 1D-CNN层2648´1 池化层3´1 BiGRU层164 BiGRU层2128 Dropout层0.1 全连接层512
在以往的短期负荷预测领域,很多研究采用LSTM[28]及其变体网络[29]捕捉长序列之间的特征关联,但这类循环神经网络易出现梯度消失、梯度爆炸问题[30]。TCN是一种基于CNN改进和优化的神经网络模型,其主要结构融合了适用时间序列建模的扩张因果卷积及解决了深度模型性能退化问题的残差模块,可以并行处理时间序列,有效地缓解梯度爆炸和梯度消失问题。扩张因果卷积(Dilated Causal Convolution, DCC)在因果卷积的基础上引入扩张系数d,使有效窗口大小随层数呈指数增长,增大了感受野范围,即可以捕捉到长序列功率数据之间的关联信息。图2为4层DCC结构示意图,该网络卷积核大小为3,扩张系数依次为1、2、4,相应的感受野依次3、5、9。由图2可知,卷积层在t时刻的输出值yt只依赖t时刻和t时刻之前的输入序列,而与t时刻之后的输入序列无关,因此不会引起未来信息的泄露。设x为输入时间序列,则DCC对x卷积运算可表达为
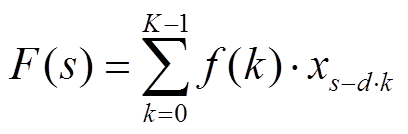 (6)
(6)
式中,f(k)为滤波器;k为卷积核大小;d为扩张系数;s为x中第s个元素。
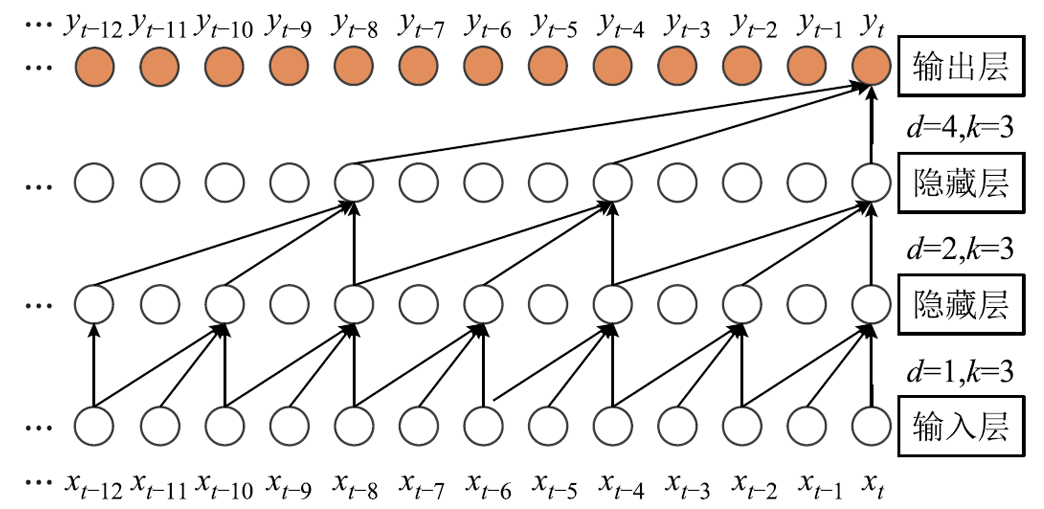
图2 扩大因果卷积结构示意图
Fig.2 Structure of dilated causal convolution
TCN网络可通过多个DCC的堆叠达到较大的感受野,并通过调整卷积层数、卷积核个数及扩张系数等参数伸缩自如地实现对任意长度功率时间序列的整体感知。网络深度的增加有利于挖掘负荷时间序列之间的关联信息,但会带来模型学习能力退化及梯度问题。为此,TCN引入残差连接进行误差修正,使得网络以跨层的方式传递信息。
本文提出的预测模型是以分解数据、智能电能表集中数据和日期特征为网络输入,当输入时间序列为多个变量时,TCN网络易忽略特征内部复杂的非线性内在联系,出现信息丢失、数据间结构信息难以建模等问题。时间模式注意力机制(Temporal Pattern Attention, TPA)可以从TCN隐藏状态行向量抽取特征,根据预测任务动态调整深度网络对不同特征的关注度,使模型更容易捕获序列中多变量之间相互依赖关系,避免序列过长信息丢失问题[31]。因此,为耦合上述负荷特征信息,本文在TCN中结合时间模式注意力机制,在最后一个残差模块后引入TPA层,实现对输入的动态加权,突出关键特征对预测任务的影响,抑制不必要的特征。本文所提基于时间模式注意力机制的时间卷积网络负荷预测模型如图3所示。
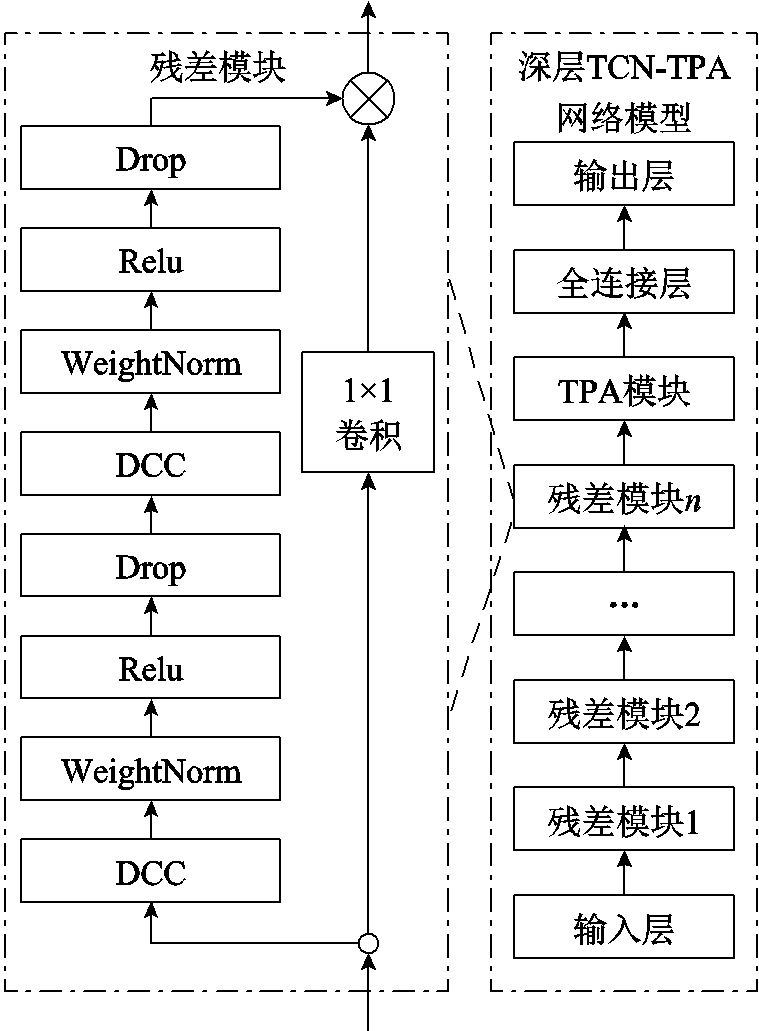
图3 基于时间模式注意力机制的时间卷积网络负荷预测模型
Fig.3 Load forecasting model of time convolutional networks based on time pattern attention mechanism
TPA层输入为TCN层提取的特征向量,输出为经注意力机制优化的结果。定义如下注意力函数计算相关性。
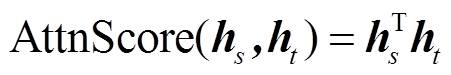 (7)
(7)
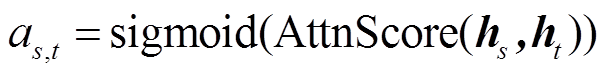 (8)
(8)
式中,hs为时间模式堆叠矩阵;ht为t时间步的隐状态向量;AttnScore(·)为注意力分数计算机制函数;Sigmoid(·)为激活函数;as,t为注意力权重。利用注意力权重as,t与hs加权求和,获得新的特征向量ct为
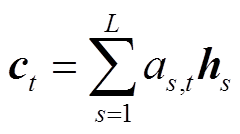 (9)
(9)
式中,L为输入变量特征数。将ct和ht线性映射后相加得到最终预测结果,有
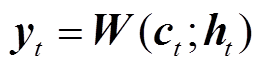 (10)
(10)
式中,W为对应变量的权重矩阵。
本文所提模型仅需智能电表总有功消耗即可实现家庭单个电器设备的负荷预测,主要框架如图4所示。对于不同的电器,本文分别构建了分解模型和预测模型,并对其进行训练。不同电器设备对应的网络架构完全相同,具体步骤如下所述。
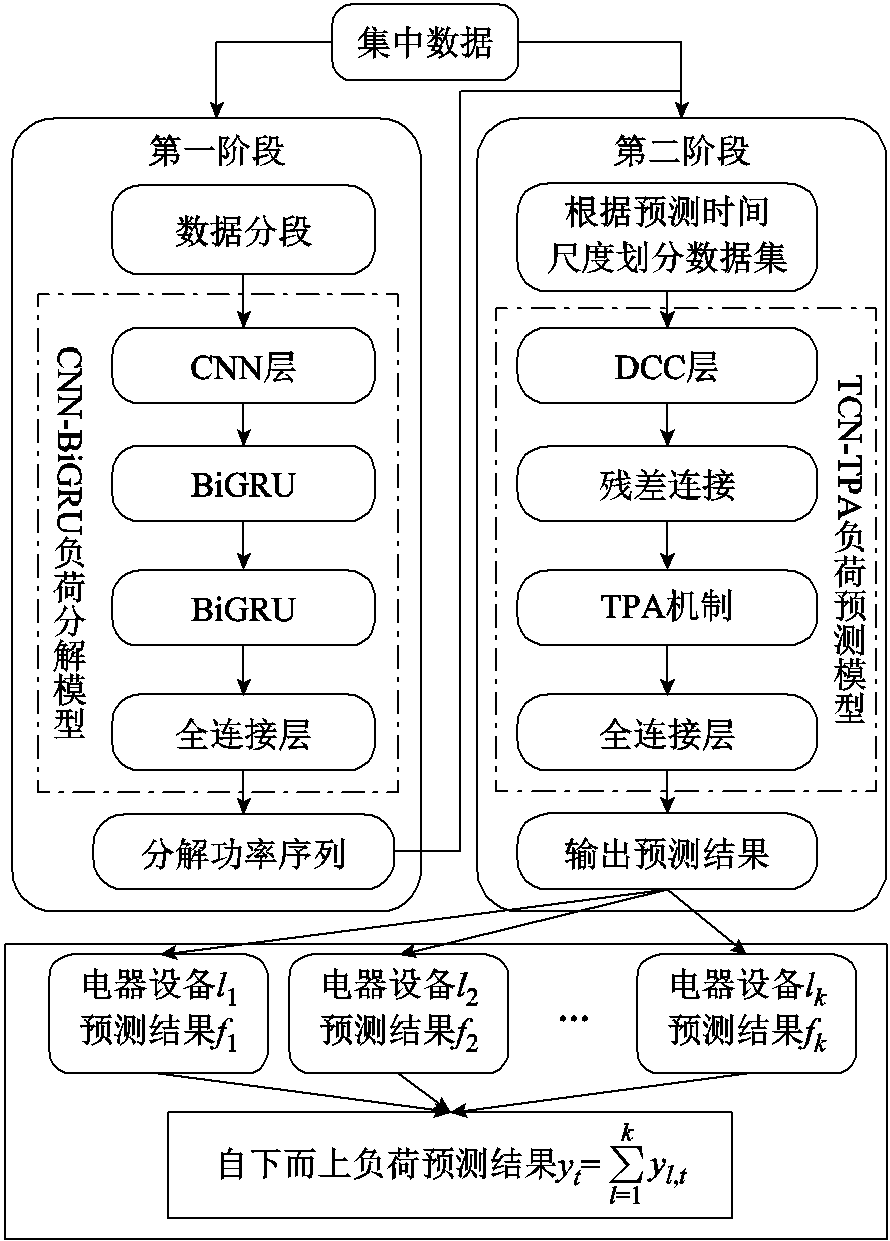
图4 基于NILM的家庭电器负荷预测结构框架
Fig.4 Structure framework of household appliance-level load forecasting based on NILM
1)将智能电表总功率数据和各个电器设备的有功功率作为分解模型的训练样本,对数据样本进行预处理及归一化,并对不同电器设定不同的序列长度进行数据分段。
2)构建负荷分解模型,将处理好的数据输入CNN-BiGRU网络进行特征提取,采用Adam优化器进行训练调参,直到网络学习到设备运行模式。
3)基于预训练完成的分解模型,输入总功率数据,即可得到电器设备的能耗数据,完成负荷能量的分解。
4)基于上述电器设备的能耗数据、总功率数据,并选择时间因素作为负荷的关联特征,即可构建预测模型的训练样本,通过滑动窗口将其分割为若干子序列。
5)构建负荷预测模型,用训练样本对TCN-TPA进行训练,并在验证集上采用Adam优化器调节模型参数,完成最终的预测模型训练。
6)基于预训练完成的预测模型,输入负荷分解数据,即可实现家庭电器的超短期负荷预测。
算例中使用公开数据集UK-DALE[32]对本文所提负荷分解及负荷预测方法进行实验与分析。数据集中包含五个家庭的单个电器设备的用电数据及集中数据,其中设备级数据采样频率为16 kHz,集中数据采用频率1/6 Hz。综合考虑设备的运行时长、房屋居住人数和数据质量等因素,本文选择房屋1中洗衣机、洗碗机、微波炉、冰箱共四种可控电器设备作为负荷分解与预测的目标。其中,NILM的训练集和验证集由房屋1(2013数据)、房屋2及房屋5的负荷数据组成;测试集中为房屋1中2014年1月1日—2014年3月31日的数据。利用训练好的模型对2014年1月1日—2014年6月30日集中数据总功率进行分解,再将分解结果与集中数据总功率输入预测模型,对2014年7月1日—2014年7月31日的数据进行预测分析。
通过所提CNN-BiGRU网络在序列到点结构基础上实现了对负荷的分解,输入为基于滑动窗口负荷数据序列,输出为窗口中心所对应的数据值。对于洗衣机、洗碗机、冰箱等运行周期较长的电器,滑动窗口序列的大小为512,对于运行周期较短的微波炉,滑动窗口序列的大小为128。训练前对负荷数据进行标准化处理,即
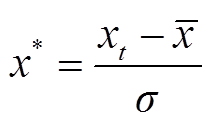 (11)
(11)
式中,x*为标准化后的数据;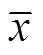 、σ分别为输入序列的平均值和标准差。
、σ分别为输入序列的平均值和标准差。
将上述分解后的电器负荷数据、集中数据及日期特征作为预测模型输入特征,并采用滚动窗口的方式构建预测模型的训练集和测试集。确定训练集和测试集之后,需要对其进行数据预处理,本文将负荷数据归一化至[-1,1]之间,如式(12)所示。对于日期数据,将一周7天转换为数字1~7,并采用独热编码形式对日期进行编码,工作日用1表示,节假日用0表示。
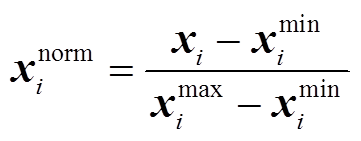 (12)
(12)
式中,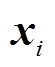 和
和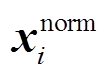 分别为第i个特征向量归一化前和归一化后数据;
分别为第i个特征向量归一化前和归一化后数据;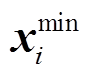 和
和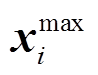 分别为第i个特征向量的最小值和最大值。
分别为第i个特征向量的最小值和最大值。
分解与预测模型的batchsize均为256,训练次数epochs为200,采用Adam进行损失函数优化。TCN扩大因子d=2, 4, 8, 16,卷积核k=5´1。模型训练均以pycharm为实验平台,借助Keras深度学习框架实现,处理器为Intel(R) Core(TM) i7-8550U CPU@1.80 GHz 2.00 GHz,内存为8G。
负荷分解与负荷预测都属于回归任务,可以采用相同的性能评估指标。考虑到家用电器运行时间有限,存在某些时刻负荷为零的情况,因此,本文采用方均根误差eRMSE、平均绝对误差eMAE作为描述模型预测效果的评价指标,有
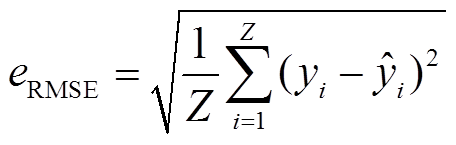 (13)
(13)
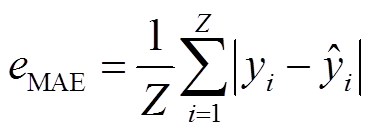 (14)
(14)
式中,yi为实际负荷数据;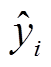 为预测值;Z为预测序列的样本点个数。
为预测值;Z为预测序列的样本点个数。
此外,为衡量所有设备预测精度的平均值,分别对上述两种预测效果评价指标取均值,即可得到eRMSE和eMAE的平均误差emRMSE和emMAE分别为
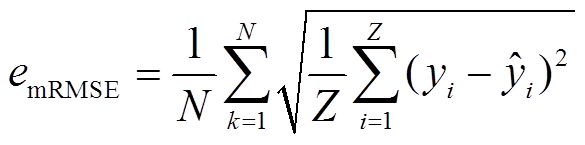 (15)
(15)
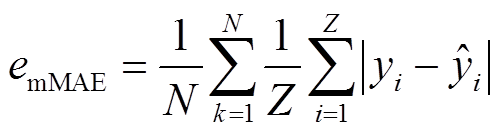 (16)
(16)
式中,N为负荷设备的数量。
为验证分解模型的性能,综合现有的研究成果,本文结合了多个深度学习模型进行对比分析,即循环神经网络(Recurrent Neural Network, RNN)模型[22]、去噪自编码(Denosing Autoencoder, DAE)模型[22]、基于CNN网络的序列到序列(sequence to sequence, seq2seq)模型[23]以及基于CNN网络的序列到点(sequence to point, seq2point)模型[23]。所有模型的输入窗口大小参数都相同,对于RNN、DAE、seq2seq+CNN模型,输出窗口大小与输入窗口参数相同。表2给出了分解模型在UK-DALE数据集上的实验结果,每个指标最佳性能以粗体显示。可以看出,CNN-BiGRU模型性能明显优于传统模型,显著降低了分解误差。相较于seq2point模型的负荷分解结果,洗衣机、微波炉、洗碗机、冰箱等基于本文所提方法的eMAE分别减少了59.39%、8.93%、36.02%与18.41%,emMAE减少了32.14%。另外,对于洗衣机、微波炉、洗碗机等功率较高且具有较为固定的运行模式的电器设备,本文所提模型具有较高的分解准确率,冰箱的运行功率较低,且频繁启动,容易淹没在大功率用电设备产生的噪声中,使得其分解准确度有所下降。
表2 不同模型负荷分解误差对比
Tab.2 Comparison of load disaggregation error of different models(单位:W)

电器种类不同算法eMAE RNNDAEseq2seqseq2pointCNN-BiGRU 洗衣机8.6819.9716.2712.515.08 微波炉12.6610.759.647.847.14 洗碗机4.258.363.303.722.38 冰箱14.3218.6715.0912.7610.41 emMAE9.9814.4411.089.216.25
考虑到家用电器运行时间有限,图5仅展示了电器设备在一段具体工作区间内的真实功率曲线与模型分解曲线的差异程度。由图5可知,对于洗衣机、微波炉、洗碗机等电器设备,模型不仅可以准确地捕捉到设备的开启与结束时段,且具有较好的趋势跟踪效果。对于冰箱,受噪声及设备频繁起停的影响,分解功率值出现偏差,但仍可以准确地辨识设备开启和关闭时间,说明模型可以实现对设备运行状态的精确感知。
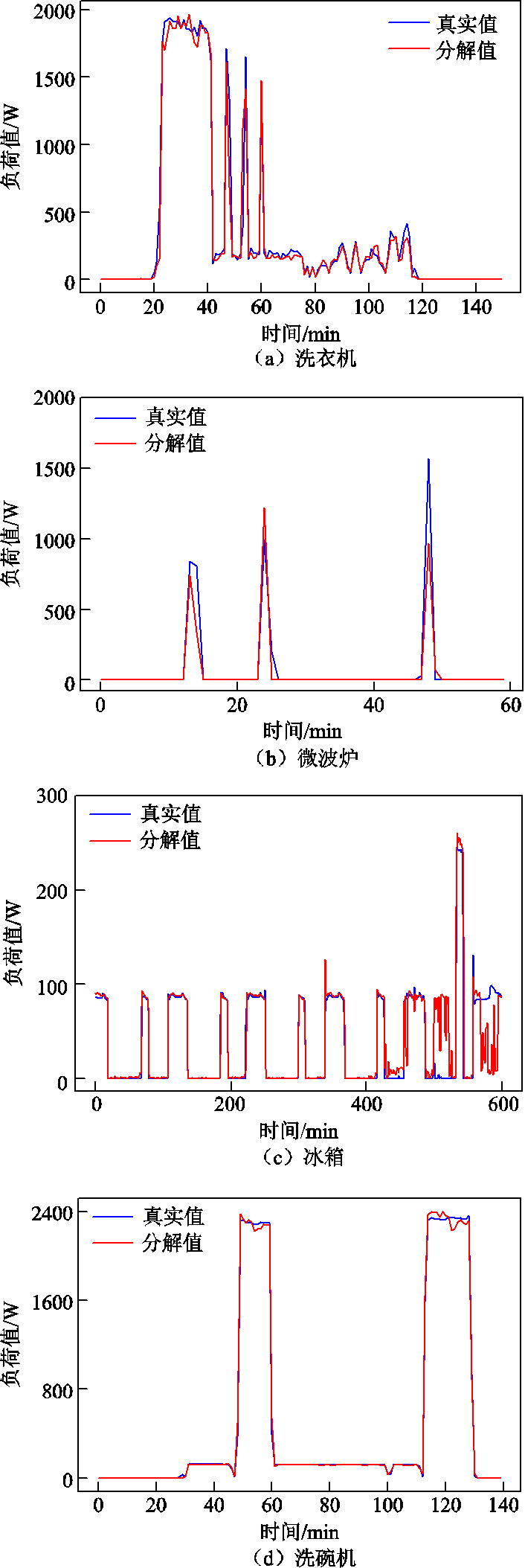
图5 不同电器设备真实功率与分解功率对比结果
Fig.5 Comparison results of ground truth power and prediction power of different appliances
面向家庭用电高峰场景,以洗衣机、冰箱、微波炉、洗碗机等可调控负荷为研究对象,对未来 15 min的家庭柔性负荷进行预测。考虑到气象信息对家庭超短期负荷预测效果影响较小,故在构造滑动时间窗口输入特征时只考虑预测时刻前2 h的电器的分解值、集中功率及日期特征。为展现所提预测模型仿真效果,本文采用迭代负荷预测方式对连续7天的负荷数据进行预测。
3.6.1 不同模型预测结果对比
为验证本文所提TCN-TPA算法的预测效果,本节设置了四种不同的负荷预测模型作对比实验,分别为LSTM、CNN-LSTM、反向传播神经网络(Back Propagation Neural Network, BPNN)与TCN。为保证对照实验的公平性和客观性,三种方法均需通过逐一建模、训练优化再预测的方法完成所有柔性电器的负荷预测。图6给出了7月份某一周上述四种模型预测曲线与真实值曲线的对比情况。
图6中,观察洗衣机、洗碗机、微波炉、冰箱的运行变化趋势,TCN-TPA与TCN的拟合效果明显优于其他对比模型,能及时跟踪负荷变化,尤其在起停阶段及局部峰值处,TCN-TPA相较于TCN的预测曲线更贴合负荷真实值。值得注意的是,微波炉虽然功率高达1 500 W,但其运行时间尺度较小,典型工作时间仅为2~5 min级。模型可以捕捉到设备的开启与结束时段,但无法准确地拟合到设备局部峰值,微波炉的负荷曲线出现了较大的偏差。
表3、表4分别给出了基于所提方法和四种对比算法的预测误差指标。由表3、表4可知,TCN-TPA在多个场景上的预测精度和平均精度都优于TCN模型,这表明TPA可以帮助TCN网络学习到时序特征复杂耦合关系,从而实现对输入的动态加权,有效提升模型的可解释性和预测精度。相较于基于LSTM的负荷预测结果,洗衣机、微波炉、洗碗机、冰箱基于本文所提方法的eMAE和eRMSE分别减少了18.65%与4.99%、13.28%与0.72%、32.04%与5.55%、4.53%与5.70%。对比基于LSTM负荷预测误差平均值,本文所提方法的emRMSE和emMAE分别减少了16.42%和4.24%。BPNN由于不能处理多维数据,相应地损失了数据的时空相关性,预测结果相对其他模型较差。较其他模型,TCN-TPA模型对不同电器设备的预测不存在局限性,两个指标的表现最为均衡,电器运行期间预测精度更高,说明模型能够充分挖掘与短期负荷波动具有强关联性的负荷特征,具有更佳的非线性映射能力。
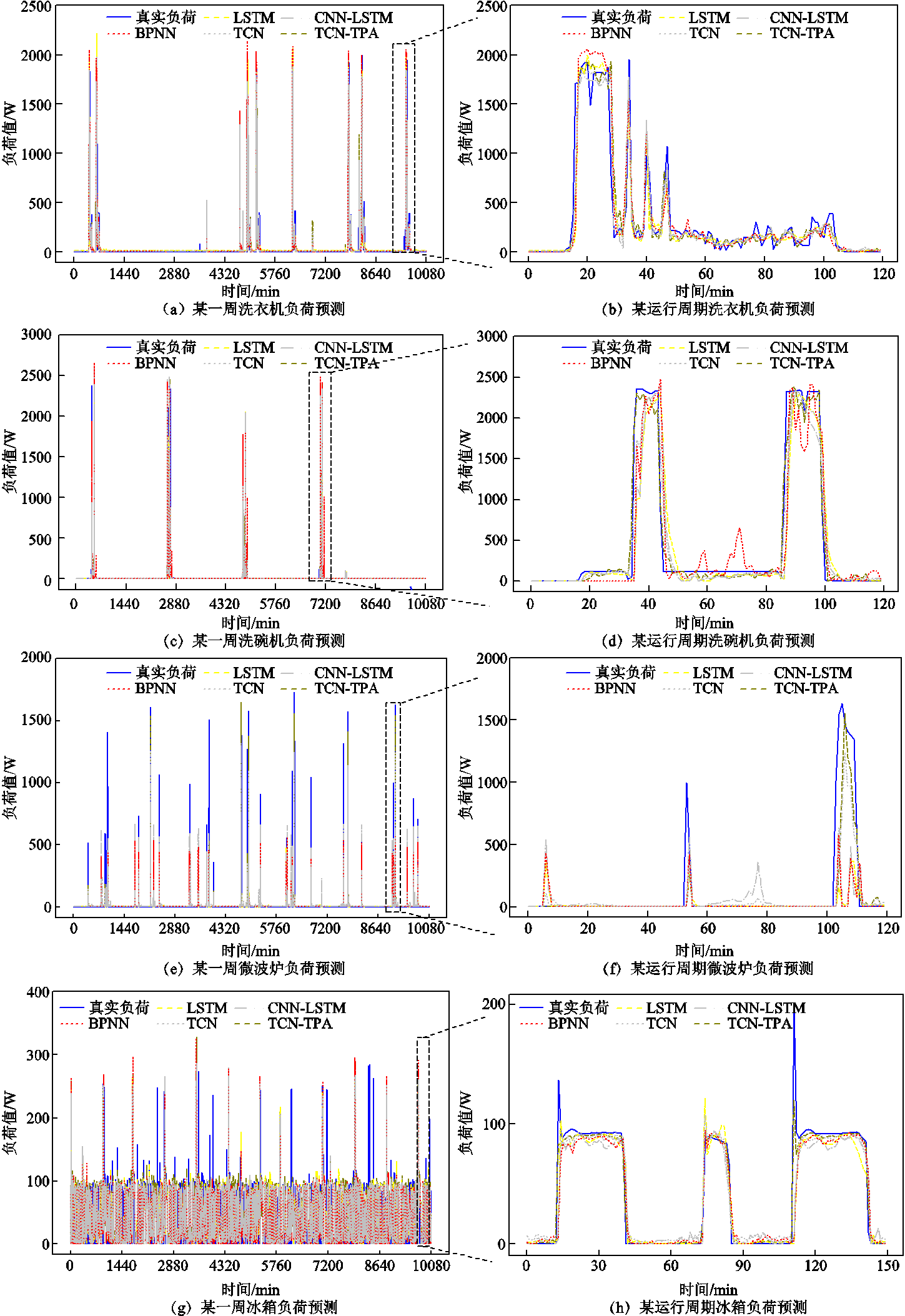
图6 不同模型预测结果对比
Fig.6 Comparison of forecasting results of different models
表3 不同模型负荷预测误差对比(eMAE/emMAE)
Tab.3 Comparison of load forecasting error of different models (eMAE/emMAE)(单位:W)
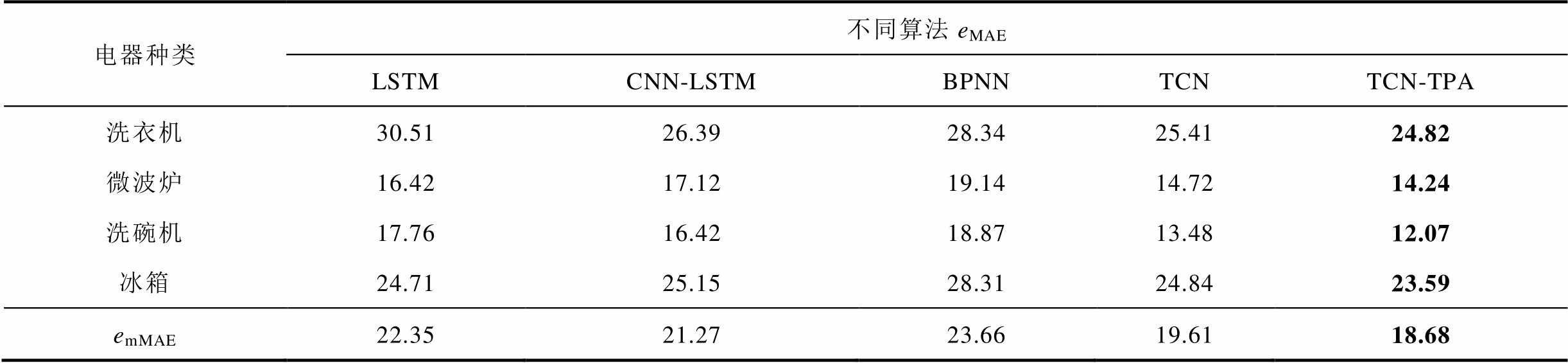
电器种类不同算法eMAE LSTMCNN-LSTMBPNNTCNTCN-TPA 洗衣机30.5126.3928.3425.4124.82 微波炉16.4217.1219.1414.7214.24 洗碗机17.7616.4218.8713.4812.07 冰箱24.7125.1528.3124.8423.59 emMAE22.3521.2723.6619.6118.68
表4 不同模型负荷预测误差对比(eRMSE/emRMSE)
Tab.4 Comparison of load forecasting error of different models(eRMSE/emRMSE)(单位:W)
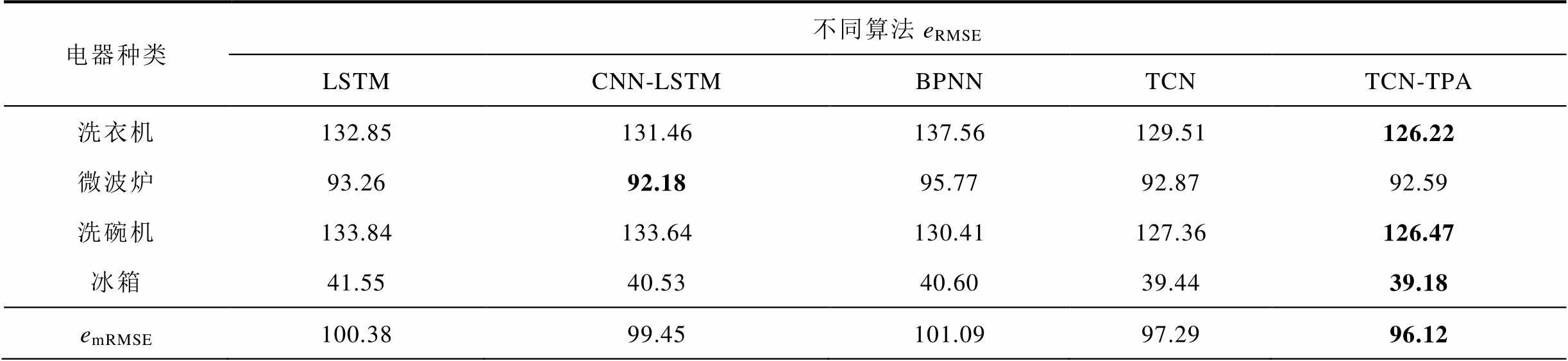
电器种类不同算法eRMSE LSTMCNN-LSTMBPNNTCNTCN-TPA 洗衣机132.85131.46137.56129.51126.22 微波炉93.2692.1895.7792.8792.59 洗碗机133.84133.64130.41127.36126.47 冰箱41.5540.5340.6039.4439.18 emRMSE100.3899.45101.0997.2996.12
3.6.2 不同输入数据预测结果对比
为了验证本文所提出的基于NILM负荷预测方法的适用性,在模型参数设置、训练轮数相同且使用相同时间段的数据进行训练与测试情况下,将基于设备真实数据的预测结果与基于NILM分解数据的预测结果做对比分析。不同输入数据的负荷预测结果对比如图7所示。由图7可知,本文模型在面对不同用电场景时,洗衣机、微波炉、洗碗机、冰箱的预测误差指标eMAE控制在15%以内,eRMSE控制在了6%以内,两种方法预测误差较小,说明基于非侵入式负荷分解的设备数据对于超短期负荷预测而言有效,能够满足不同类型电器负荷预测需求。
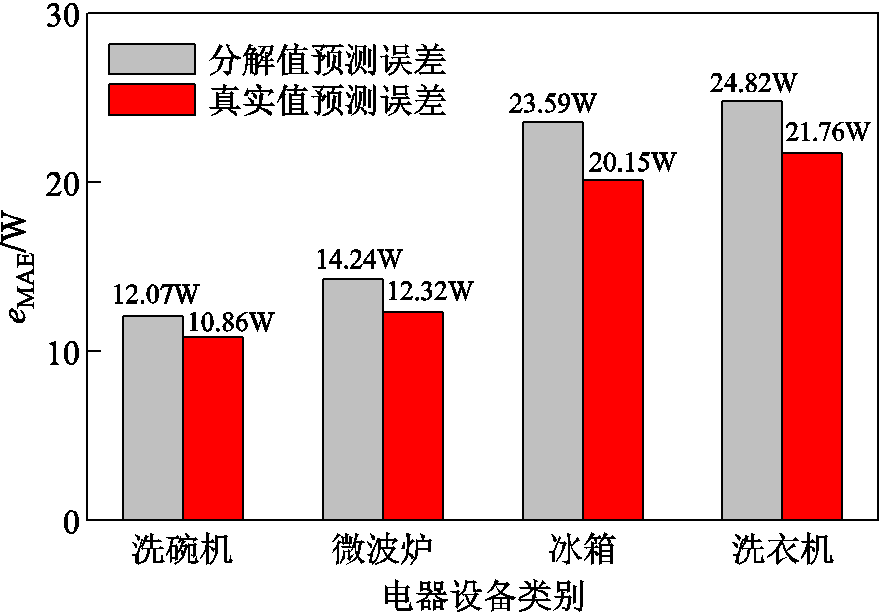
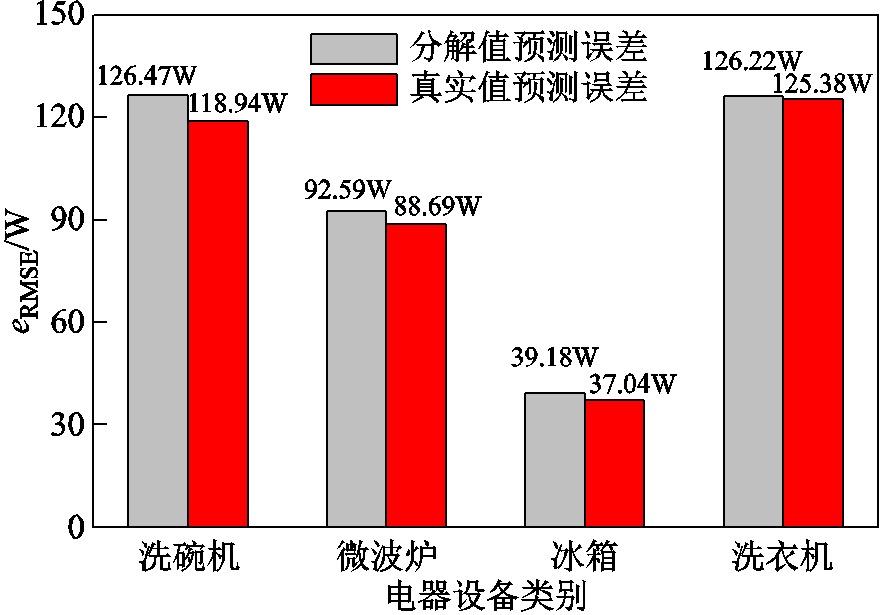
图7 不同输入数据的负荷预测结果对比
Fig.7 Comparison of load forecasting results of different input data
3.6.3 群体用户柔性负荷预测结果
电器设备之间的预测结果相互独立且符合高斯分布,因此可以通过自下而上的负荷建模方式,分别累加预测值得到家庭柔性负荷值。为进一步分析群体用户或社区未来柔性负荷预测情况,对房屋1中洗衣机、微波炉、洗碗机、冰箱等30天的连续预测结果叠加到1天,仿真出集群柔性负荷用电需求曲线。洗衣机与洗碗机属于功能模式较为复杂的电器,微波炉具有持续时间短功率值较大的特征,冰箱可作为典型的周期性起停负荷,这几种电器的组合可较为全面地反映预测模型的整体性能。如图8所示,预测功率与实际功率拟合效果偏差较小,波动大致相同,能够有效地反映区域用户柔性负荷的变化趋势。负荷曲线除剧烈波动外的其他时间均有较好的预测效果,基本与实际数值曲线相吻合。
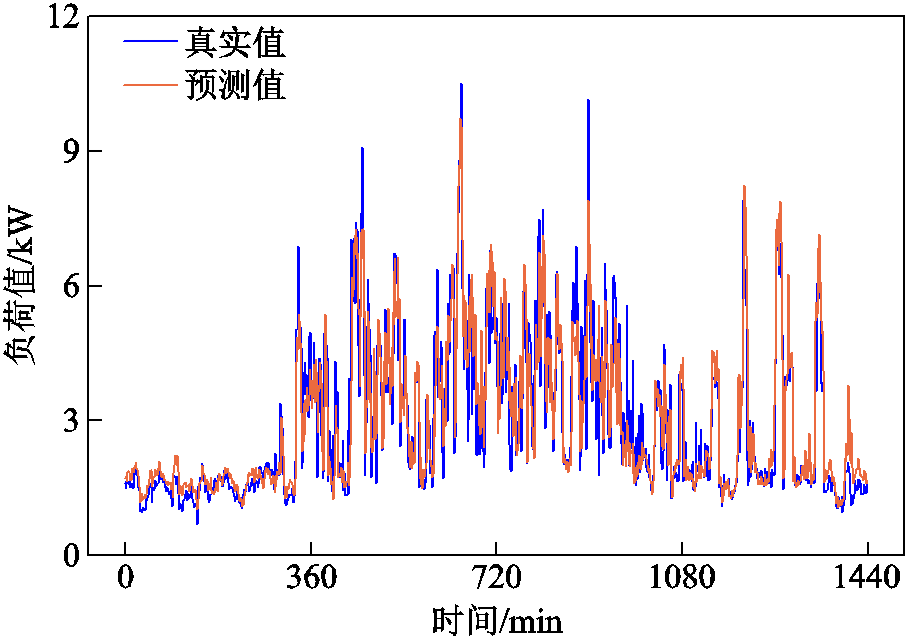
图8 集群柔性负荷预测结果
Fig.8 Cluster flexible load prediction results
本文以家庭电器设备负荷预测为研究对象,提出一种基于非侵入式负荷分解的间接预测方法,并利用公开数据集验证了该方法的准确性和适用性。主要结论如下:
1)本文利用基于NILM分解数据实现了对家庭电器设备的负荷预测,减少了对侵入式监测装置的依赖,具有较好的适应性和可扩展性,为家庭能源管理系统相关业务开展提供了新思路和新方法。
2)本文所提改进的CNN-BiGRU模型与传统seq2point相比,预测误差指标emMAE降低了32.14%,在负荷分解及设备状态检测方面具有更高的精度。
3)针对电器设备的随机性和波动性特点,利用TCN网络在处理时间序列问题的优势,并融入TPA提升对分解数据中设备运行信息提取和利用能力。与传统深度学习方法LSTM相比,该方法预测误差指标emRMSE和emMAE分别减少了16.42%和4.24%。
参考文献
[1] 徐明杰, 赵健, 王小宇, 等. 基于多任务联合模型的居民用电模式分类方法[J]. 电工技术学报, 2022, 37(21): 5490-5502. Xu Mingjie, Zhao Jian, Wang Xiaoyu, et al. Residential electricity consumption pattern classification method based on multi-task joint model[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5490-5502.
[2] 贾雁冰, 杨阳方, 刘继春, 等. 售用双方协同优化的家庭柔性负荷管理策略[J]. 电网技术, 2019, 43(4): 1430-1438. Jia Yanbing, Yang Yangfang, Liu Jichun, et al. Management strategy for domestic flexible load to achieve retailer-user coordinated optimization[J]. Power System Technology, 2019, 43(4): 1430-1438.
[3] 郑若楠, 李志浩, 唐雅洁, 等. 考虑居民用户参与度不确定性的激励型需求响应模型与评估[J]. 电力系统自动化, 2022, 46(8): 154-162. Zheng Ruonan, Li Zhihao, Tang Yajie, et al. Incentive demand response model and evaluation considering uncertainty of residential customer participation degree[J]. Automation of Electric Power Systems, 2022, 46(8): 154-162.
[4] Razghandi M, Zhou Hao, Erol-Kantarci M, et al. Short-term load forecasting for smart home appliances with sequence to sequence learning[C]//ICC 2021 - IEEE International Conference on Communications, Montreal, QC, Canada, 2021: 1-6.
[5] Razghandi M, Zhou Hao, Erol-Kantarci M, et al. Smart home energy management: sequence-to-sequence load forecasting and Q-learning[C]//2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 2022: 1-6.
[6] Mohi Ud Din G, Mauthe A U, Marnerides A K. Appliance-level short-term load forecasting using deep neural networks[C]//2018 International Conference on Computing, Networking and Communications (ICNC), Maui, HI, USA, 2018: 53-57.
[7] Wang Shouxiang, Deng Xinyu, Chen Haiwen, et al. A bottom-up short-term residential load forecasting approach based on appliance characteristic analysis and multi-task learning[J]. Electric Power Systems Research, 2021, 196: 107233.
[8] Zheng Zhuang, Chen Hainan, Luo Xiaowei. A Kalman filter-based bottom-up approach for household short-term load forecast[J]. Applied Energy, 2019, 250: 882-894.
[9] 唐贤伦, 陈洪旭, 熊德意, 等. 基于极端梯度提升和时间卷积网络的短期电力负荷预测[J]. 高电压技术, 2022, 48(8): 3059-3067. Tang Xianlun, Chen Hongxu, Xiong Deyi, et al. Short-term power load forecasting based on extreme gradient boosting and temporal convolutional network[J]. High Voltage Engineering, 2022, 48(8): 3059-3067.
[10] Bai Shaojie, Kolter J Z, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling[EB/OL]. arXiv, 2018: 1803.01271. https://arxiv.org/abs/1803.01271.
[11] 赵洋, 王瀚墨, 康丽, 等. 基于时间卷积网络的短期电力负荷预测[J]. 电工技术学报, 2022, 37(5): 1242-1251. Zhao Yang, Wang Hanmo, Kang Li, et al. Temporal convolution network-based short-term electrical load forecasting[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1242-1251.
[12] 雷怡琴, 孙兆龙, 叶志浩, 等. 电力系统负荷非侵入式监测方法研究[J]. 电工技术学报, 2021, 36(11): 2288-2297. Lei Yiqin, Sun Zhaolong, Ye Zhihao, et al. Research on non-invasive load monitoring method in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2288-2297.
[13] Li Yanzhen, Wang Haixin, Yang Zihao, et al. Stacking ensemble learning-based load identification considering feature fusion by cyber-physical approach[J]. IEEE Sensors Journal, 2023, 23(6): 5997-6007.
[14] Liu Bo, Luan Wenpeng, Yang Jinnan, et al. The balanced window-based load event optimal matching for NILM[J]. IEEE Transactions on Smart Grid, 2022, 13(6): 4690-4703.
[15] Ding Dong, Li Junhuai, Zhang Kuo, et al. Non-intrusive load monitoring method with inception structured CNN[J]. Applied Intelligence, 2022, 52(6): 6227-6244.
[16] 廖荣文, 刘刚, 肖刚. 基于时间模糊化长短时记忆的非侵入式负荷分解方法[J]. 电力系统自动化, 2021, 45(24): 73-80. Liao Rongwen, Liu Gang, Xiao Gang. Non-intrusive load decomposition method based on time-fuzzified long short-term memory[J]. Automation of Electric Power Systems, 2021, 45(24): 73-80.
[17] Kaselimi M, Doulamis N, Voulodimos A, et al. Context aware energy disaggregation using adaptive bidirectional LSTM models[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 3054-3067.
[18] 徐晓会, 赵书涛, 崔克彬. 基于卷积块注意力模型的非侵入式负荷分解算法[J]. 电网技术, 2021, 45(9): 3700-3706. Xu Xiaohui, Zhao Shutao, Cui Kebin. Non-intrusive load disaggregate algorithm based on convolutional block attention module[J]. Power System Technology, 2021, 45(9): 3700-3706.
[19] 邓旭晖, 陈中, 杨凯, 等. 基于多任务学习卷积网络的非侵入式负荷监测方法[J]. 电力系统自动化, 2023, 47(8): 189-197. Deng Xuhui, Chen Zhong, Yang Kai, et al. Non-intrusive load monitoring method based on multi-task learning convolutional network[J]. Automation of Electric Power Systems, 2023, 47(8): 189-197.
[20] 周润, 向月, 王杨, 等. 基于智能电表集总数据的家庭电动汽车充电行为非侵入式辨识与负荷预测[J]. 电网技术, 2022, 46(5): 1897-1908. Zhou Run, Xiang Yue, Wang Yang, et al. Non-intrusive identification and load forecasting of household electric vehicle charging behavior based on smart meter data[J]. Power System Technology, 2022, 46(5): 1897-1908.
[21] Brucke K, Arens S, Telle J S, et al. A non-intrusive load monitoring approach for very short-term power predictions in commercial buildings[J]. Applied Energy, 2021, 292: 116860.
[22] Kelly J, Knottenbelt W. Neural NILM: deep neural networks applied to energy disaggregation[C]// Proceedings of the 2nd ACM International Conference on Embedded Systems for Energy-Efficient Built Environments, Seoul, South Korea, 2015: 55-64.
[23] Zhang Chaoyun, Zhong Mingjun, Wang Zongzuo, et al. Sequence-to-point learning with neural networks for non-intrusive load monitoring[C]//the 32nd AAAI Conference on Artificial Intelligence, New Orleans, LA, 2018: 2604-2611.
[24] 沙建峰, 席乐, 冯亚杰, 等. 基于注意力时序网络的非侵入式负荷分解[J]. 南京信息工程大学学报(自然科版), 2023, 15(4): 448-459.
Sha Jianfeng, Xi Le, Feng Yajie, et al. Non-intrusive load decomposition based on attention recurrent network model[J]. Journal of Nanjing University of Information Science & Technology (Natural Science Edition), 2023, 15(4): 448-459.
[25] 杨童亮, 胡东, 唐超, 等. 基于SMA-VMD-GRU模型的变压器油中溶解气体含量预测[J]. 电工技术学报, 2023, 38(1): 117-130. Yang Tongliang, Hu Dong, Tang Chao, et al. Prediction of dissolved gas content in transformer oil based on SMA-VMD-GRU model[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 117-130.
[26] Çimen H, Çetinkaya N, Vasquez J C, et al. A microgrid energy management system based on non-intrusive load monitoring via multitask learning[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 977-987.
[27] 唐斯, 陈新楚, 郑松. 基于注意力与多尺度卷积神经网络的电机轴承故障诊断[J]. 电气技术, 2020, 21(11): 32-38. Tang Si, Chen Xinchu, Zheng Song. Fault diagnosis method of motor bearing based on attention and multi-scale convolution neural network[J]. Electrical Engineering, 2020, 21(11): 32-38.
[28] 王琛, 王颖, 郑涛, 等. 基于ResNet-LSTM网络和注意力机制的综合能源系统多元负荷预测[J]. 电工技术学报, 2022, 37(7): 1789-1799. Wang Chen, Wang Ying, Zheng Tao, et al. Multi-energy load forecasting in integrated energy system based on ResNet-LSTM network and attention mechanism[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1789-1799.
[29] 孙辉, 杨帆, 高正男, 等. 考虑特征重要性值波动的MI-BILSTM短期负荷预测[J]. 电力系统自动化, 2022, 46(8): 95-103. Sun Hui, Yang Fan, Gao Zhengnan, et al. Short-term load forecasting based on mutual information and Bi-directional long short-term memory network considering fluctuation in importance values of features[J]. Automation of Electric Power Systems, 2022, 46(8): 95-103.
[30] 张鹏飞, 胡博, 何金松, 等. 基于时空图卷积网络的短期空间负荷预测方法[J]. 电力系统自动化, 2023, 47(13): 78-85. Zhang Pengfei, Hu Bo, He Jinsong, et al. Short-term spatial load forecasting method based on spatio-temporal graph convolutional network[J]. Automation of Electric Power systems, 2023, 47(13): 78-85.
[31] 王渝红, 史云翔, 周旭, 等. 基于时间模式注意力机制的BiLSTM多风电机组超短期功率预测[J]. 高电压技术, 2022, 48(5): 1884-1892. Wang Yuhong, Shi Yunxiang, Zhou Xu, et al. Ultra-short-term power prediction for BiLSTM multi wind turbines based on temporal pattern attention[J]. High Voltage Engineering, 2022, 48(5): 1884-1892.
[32] Kelly J, Knottenbelt W. The UK-DALE dataset, domestic appliance-level electricity demand and whole-house demand from five UK homes[J]. Scientific Data, 2015, 2: 150007.
Abstract Due to the impact of large-scale renewable energy on the safe and stable operation of power systems, the demand for flexible sources is increasing. The home energy management system is a promising approach to enhance the flexible regulation capability of power systems and improve grid energy efficiency. However, the randomness of residents' electricity behavior, the uncertainty of market information, and the diversity of decision-making subjects make it extremely challenging for residents to participate in fast demand responses. To address these issues, this paper proposes a two-stage household load forecasting method based on the integration of load disaggregation and forecasting. By learning the correlation information from historical electricity consumption data of each appliance obtained by non-intrusive load monitoring (NILM) technology, it accurately realizes the load forecasting of household appliances and flexible cluster load prediction.
First, a NILM model based on convolutional neural network (CNN) and bi-directional gated unit (BiGRU) neural network is established to solve the problem of obtaining the operation data of appliances. Subsequently, considering the randomness and uncertainty of user behavior, a time convolutional network (TCN) load forecasting model based on the time pattern attention (TPA) mechanism is constructed to mine the deep interaction information of input variables. Finally, the proposed method is verified by the UK-DALE data set. The results show that the proposed method can obtain high disaggregation accuracy and prediction effect.
This paper implements two simulations using Keras with a TensorFlow backend. The first one is designed to monitor the appliance-level energy consumption with the proposed CNN-BiGRU-enabled NILM. The results show that the proposed NILM-Based model can accurately capture the start and end time of the appliance, and has a good trend-tracking effect. With the NILM results, the second one is conducted to verify the effectiveness of the proposed load forecasting model. Compared with other deep learning models such as long short-term memory, the eMAE and eRMSE of washing machines, microwave ovens, dishwashers and refrigerators based on the proposed forecasting method are reduced by 18.65% and 4.99%, 13.28% and 0.72%, 32.04% and 5.55%, 4.53% and 5.70%, respectively. The comparison of load forecasting results between the ground truth data and the NILM-based data shows that the eMAE is controlled within 15% and the eRMSE is controlled within 6%. Finally, to verify the robustness of the proposed model in cluster load forecasting, a bottom-up strategy is applied to obtain the flexible load prediction of group users or communities based on appliance prediction.
The following conclusions can be drawn from the simulation analysis: (1) The load forecasting framework based on NILM reduces the dependence on intrusive monitoring systems, and has strong adaptability and scalability, which can provide a new method for the development of household energy management system-related businesses. (2) Compared with shallow neural networks, CNN-BiGRU has powerful mapping ability and can achieve high accuracy in load disaggregation and event detection. (3) The proposed forecasting model extracts temporal informative features using TCN and subsequently implements dynamic weighting of inputs using TPA to highlight the impact of key features. The case study shows that the proposed method can improve forecasting accuracy compared with traditional deep learning models.
keywords:Non-intrusive load disaggregation, load forecasting, convolutional neural network, bidirectional gated unit neural network, time convolutional network, attention mechanism
DOI: 10.19595/j.cnki.1000-6753.tces.230554
中图分类号:TM714
高等学校学科创新引智计划资助项目(D23005)。
收稿日期 2023-04-27
改稿日期 2023-06-15
李延珍 女,1987年生,博士研究生,研究方向非侵入式负荷监测,家庭能源管理与优化。E-mail:yanzhenlisut@163.com
杨俊友 男,1963年生,教授,博士生导师,研究方向为新能源发电与智能微电网、特种电机先进控制等。E-mail:junyouyang@sut.edu.cn(通信作者)
(编辑 赫 蕾)