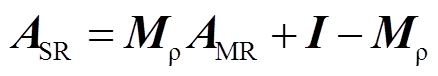（1）
摘要 现代有源配电网呈现复杂多变、多时间尺度的特征，采用单一仿真速率难以同时兼顾计算效率与精度，对此该文提出基于特征矩阵分区等值和自适应插值切换的有源配电网多速率并行仿真方法。首先，构建系统状态空间矩阵，并基于状态矩阵特征值的量级将系统拆分为多个动态特性差异的子系统，通过将系统的状态矩阵进行分块等效，实现子区域在小步长时刻的独立仿真解算与在大步长时刻的等效补偿，在保证仿真精度的基础上大幅降低了系统仿真规模；然后，针对各区域间数据交互不同步问题，通过倍率步长相量法分析线性插值误差产生原理及主要影响因素，并提出基于二阶泰勒展开式的多步自适应插值仿真算法，可以根据系统频率与仿真步长需求调节相关插值参数，显著降低插值误差；最后，采用改进型IEEE 123节点配电网算例，通过分区等值/插值计算与仿真结果的对比，验证了所提多速率并行仿真方法的可行性与有效性。
关键词：有源配电网 多速率并行仿真 状态空间方程 等效模型 自适应插值
随着分布式发电的持续发展，配电网逐渐演变为“源-网-荷-储”协同、柔性互动的有源配电网运行模式[1-3]。有源配电系统中同时具有快暂态特性的电力电子装置和慢动态特性的配电线路、用电负荷等设备，呈现出复杂多变、多时间尺度特点[4-7]，对单一速率电磁暂态仿真在计算速度和精度方面提出了挑战。若统一采用小步长仿真，虽能确保系统精度但会造成计算资源的浪费，若采用大步长仿真则无法保证仿真精度甚至造成失稳，一般通过多速率并行仿真解决计算速度和精度这一矛盾[8]，其主要内容包括多速率分区方法、并行仿真策略和区间协同交互三部分。
多速率分区方法是指对有源配电网进行快慢暂态仿真子区域的划分，为并行仿真提供结构基础。J. R. Marti等提出了多区域戴维南等值（Multi-Area Thevenin Equivalent, MATE）技术[9-10]，该方法主要根据电网物理特性对网络进行划分并设计接口位置，显著提高计算速度，但网络划分单一且缺乏理论依据，无法解决电力电子器件造成的网络拓扑高频变化问题。文献[11]将分布式电源（Distributed Generation, DG）等效为受控源，并对配电网进行暂态详细建模，提出了基于节点分裂的区域并行暂态仿真算法，但对高渗透率分布式电源接入暂态过程需进一步研究。文献[12]提出了以CPU多核计算均衡和核间交互数据量最小为目标的有源配电网优化分网策略，但优化过程不可避免地增加了计算复杂性，难以满足大规模系统快速仿真的精度需求。状态空间特征值是描述系统特性的重要参数之一，可用于描述系统相应状态的稳定性、振荡性及动态变化快慢，基于此，文献[13]提出了配电网多速率离散模型状态空间特征值计算方法，将其用于评估多速率仿真的数值准确性和计算速度，可显著减轻大规模配电网仿真计算复杂性。文献[14]在文献[13]基础上，将并行计算平衡度和分网精度等因素，进一步引入基于状态矩阵特征值的仿真分区结果，提高分区合理性。总而言之，现有分区策略大多基于暂态模型状态或区域资源优化分配，将网络划分为几个相互独立的子网络，然而忽略了子区域快慢动态下耦合交互特性对计算稳定性和准确性的作用，分区后对多速率并行仿真误差的影响尚未引起关注。
目前已有文献对分区后并行仿真算法进行研究。文献[15]首次对机电、电磁暂态构建子网络等值模型并进行系统解耦。文献[16]建立基于RT-LAB-OPNET和控制平台的信息物理混合仿真平台，通过元件并行和网络并行将多重耦合模块拆分。天津大学将微电网电气和控制系统分解为多个子网络，考虑到FPGA(field programmable gate array)硬件资源有限，利用多端口等效原理建立子网络联立方程，并设计有源配电网实时仿真I/O接口，通过接口与外部设备互联实现硬件在环仿真[17]。同时国内外研究团队也对GPU(graphics processing unit)、FPGA、RTDS(real time digital simulation)等硬件间等值交互仿真进行了系统研究，建立了机电-电磁混合仿真架构[18-20]。此外，A. Monti等将延迟插入方法引入电磁暂态仿真，提出快慢系统交替求解的多速率仿真算法[21]，然而MATE与延迟插入的迭代计算影响了数字仿真实时性。在此基础上，文献[22-23]分别从二次等值和多速率分区的角度进行改进，提高了MATE等值并行仿真的计算效率，然而MATE等值方法是基于系统拓扑结构构建的，当系统拓扑出现较大改变时等效电路需要重新计算，在大规模配电网仿真中显著增加了计算量。
对于分区交互协同方法，目前大多基于传统线性插值算法及其改进形式，以补偿由分区不同步引起的仿真误差。文献[24]针对并行计算时多速率区域间数据不同步，提出了基于模型状态空间的线性外插法，有效地补偿了多速率子区域交互时的缺失数据。文献[25]将并网逆变器电气区域和控制区域分区，分别通过FPGA、CPU对主电路、控制回路加速仿真，并采用基于拉格朗日插值的改进补偿算法，降低了由硬件交互时仿真时步、变量数据不同步产生的误差，提升两者交互协调及仿真进度。文献[26]提出了一种基于最小二乘法的交互数据拟合方法，运用拟合值对不同步数据进行补偿，较线性插值算法具有更高的精度，但同时也大幅增加了计算量。文献[27]基于分段分形插值算法对仿真中的缺失数据进行补偿，并对插值点位置的选取进行了分析优化，该方法在单相接地故障测试中有优于线性插值算法的表现，但在具有一定规模的配电系统中的应用效果有待提升。
为了提升多速率仿真数据精度和计算效率，本文提出了基于特征矩阵分区等值和自适应插值切换的多速率并行仿真方法。首先构建全系统离散状态空间矩阵，基于矩阵特征值和矩阵对角化评估分区耦合误差并进行子区域模型修正；然后基于二阶泰勒展开对多速率数据交互引起的误差进行自适应插值补偿。具体创新点如下：①基于离散状态空间矩阵对系统多速率分区后，通过矩阵对角化特征评估快慢区域耦合对多速率仿真数值准确性的影响，并进行分区子系统模型的等值解耦，实现了子区域在小步长的独立解算与大步长的等效补偿，在保证仿真精度时显著降低了计算量；②针对多速率区域数据交互不同步问题，通过倍率步长相量法分析常规线性插值法的误差原因，并推导出误差与系统频率、步长的关系；③基于二阶泰勒展开式提出多速率多步自适应插值算法，根据仿真需求调整插值算法参数使其满足最小误差条件，并进行多种插值算法的优选切换，提升了区间交互协调与仿真的准确性。
高密度分布式电源通过电力电子器件接入配电网，高频电力电子开关与配电网传输线路元件具有较大的时间尺度差异，一般采用多速率并行仿真方法，即针对不同时间常数的电网区域采用不同的仿真时间步长以兼顾仿真速度和仿真精度。主要包含多速率分区、并行仿真、交互协调等方面，本文将重点阐述多速率分区等值和交互协调。
现有分区策略大多基于暂态模型状态进行研究[11,13], 即确定各区域时间尺度下可根据不同的步长需求，对区域离散化并进行子区域分割以对应不同的仿真时间步长。目前典型的多速率分区并行状态空间模型为
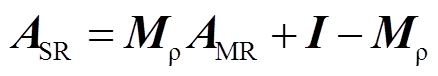（1）
式中，ASR为多速率等效的状态矩阵；Mρ为考虑线性插值的修正矩阵；AMR为初始的多速率离散化状态矩阵；I为单位矩阵。各矩阵的具体含义见文献[13]。考虑到矩阵ASR和初始矩阵AMR具有相同的阶数，在计算时所消耗的仿真资源近似，同时不同分区间动态耦合对全局准确性具有影响，本文将从矩阵降阶的角度出发，对等值模型进行解耦补偿。
全系统多速率分区后，针对快慢区域数据交互不同步导致仿真误差甚至系统失稳问题，多采用插值算法对缺失数据进行补偿，目前最常用的线性插值算法为
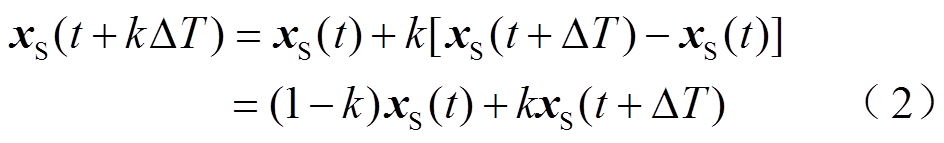
式中，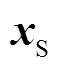
为状态向量；ΔT为步长；t为仿真时刻；k为插值位置，
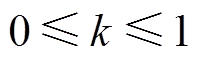。由于线性插值算法采用线性模拟非线性，对精度的提高有限，且该算法在计算较高变化频率的变量时误差较大。对此，本文建构仿真误差与系统频率、步长等仿真参数的对应关系，通过优化插值参数提出自适应插值切换算法，在提高精度的同时尽可能地减小插值数据的计算量。本文研究框架如图1所示，后续围绕两部分具体开展。
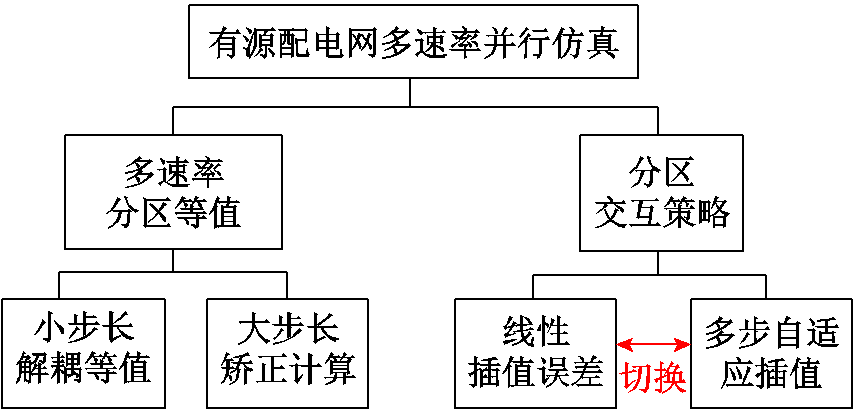
图1 本文研究框架
Fig.1 Research framework of this article
基于状态空间矩阵特征值评估多速率系统的仿真时间步长、接口位置等[13]，相比于其他评估方法可减轻大规模配电网多速率仿真计算负担，并提升多速率仿真性能。因此，将此方法作为本文所提出的多速度分区等值补偿模型的基础，这里将对其方法原理进行叙述。
对于含分布式电源的配电网络系统，首先构建系统模型，将全系统中所有状态，包括流经电感的电流以及电容两端的电压等作为状态变量，基于基尔霍夫电压电流定律，得到系统暂态模型表达式为
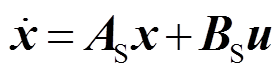（3）
式中，x为系统的状态向量；AS为该配电网络系统的连续型状态空间矩阵；BS为系统的连续型输入量关联矩阵；u为系统的输入变量组成的矩阵，主要与系统中的电压源、电流源大小和位置有关。
假定系统的状态矩阵AS具有n个特征值，分别与n个状态变量对应。每个特征值λi（i=1, 2, 3, …, n）为
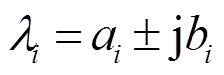（4）
式中，ai和bi分别为特征值的实部和虚部。根据自然频率与特征值的关系，可运用式（5）计算每个特征值所对应的自然频率。
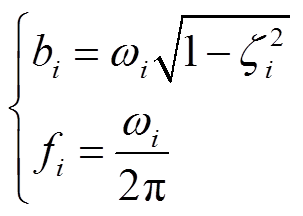（5）
式中，ωi为特征值所对应状态量的角频率；ζi为系统的阻尼比，近似计算时可取0；fi为状态量的自然频率。根据系统的特征值与动态特性对应关系，特征值的虚部对应相应状态变量的角频率，角频率越高，状态量的动态特性变化越快，保证其精度所需的仿真步长越小；角频率越低，状态量的动态特性变化越慢，保证其精度所允许的仿真步长越大。因此可根据n个状态变量各自对应的自然频率量级，将状态变量进行分区。相比于常规考虑物理结构、网络结构差异性的仿真分区方法，基于状态空间特征根的分区方法重点关注状态量/元件的动态特性，定量分析上述差异引起的自然频率变化，将动态特性与仿真步长需求对应，从而获得多速率分区方案。
假设系统存在三个不同的自然频率数量级，并被划分成三个区域，则在选择每个区域的数值仿真步长时，可依据奈奎斯特-香农采样定理进行计算。
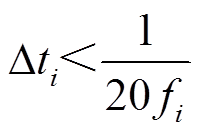（6）
式中，fi为第i个区域自然频率所对应的数量级；i=1, 2, 3。根据式（6）计算得到的仿真步长，可以保证各子区域数值仿真时的精度及数值稳定性。在确定每个子系统的仿真步长后，即可对系统进行离散化处理。首先从单一步长离散化系统出发，以此为基础推导多速率系统等值模型。假定某一有源配电系统的离散型状态空间方程为
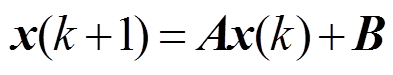（7）
假设该系统按自然频率数量级划分为三个子区域：快速率子区域F，区域中的a1个状态变量形成a1维列向量xF，该区域仿真步长为Δt1；中速率子区域M，区域中的a2个状态变量形成a2维列向量xM，仿真步长为Δt2；慢速率子区域S，区域中的a3个状态变量形成a3维列向量xS，仿真步长为Δt3。并假定Δt3=n2Δt2，Δt2=n1Δt1，其中n1、n2均为正整数。
对式（7）按三个子区域进行分块，可以得到分块后的统一速率状态空间方程为
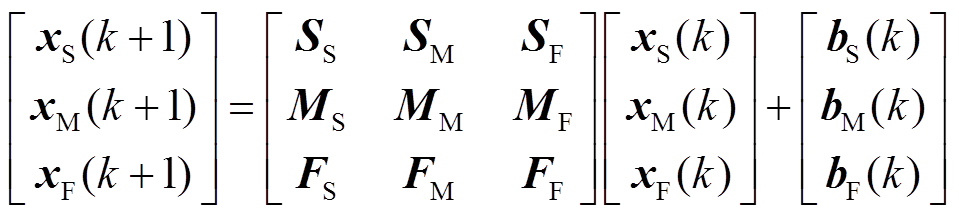（8）
式中，SS反映了慢速率状态变量对自身的状态影响；SM反映了中速率状态变量对慢速率状态变量的影响；其余各分块矩阵的含义以此类推。
根据多速率并行仿真理论，在每个小步长Δt1时刻，只有xF中的状态量需要更新，xM和xS保持不变；在每个中步长Δt2时刻，xF和xM中的状态量更新，xS继续保持不变；只有在大步长Δt3时刻，xF、xM和xS均会更新。基于此，首先考虑每个小步长Δt1时刻，状态空间方程式（8）可写为
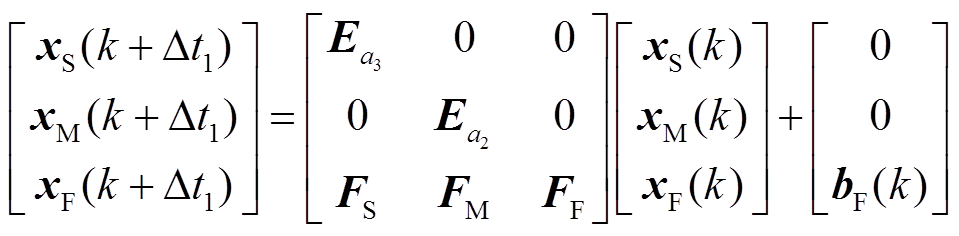（9）
式中，E为单位矩阵，其下标表示矩阵的维数，与对应的状态向量维数保持一致。将式（9）中的状态矩阵看作是两个矩阵A1、A2的和，其中A1=diag[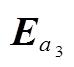
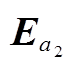FF]，A2=[0 0 0;0 0 0;FSFM 0]。
假定外部输入矩阵BF（对于电力电子换流器而言，主要为直流输入或者交流的dq分量）在小步长Δt1并未发生变化，则每个中步长Δt2的前两个小步长Δt1时刻，状态量表达式为
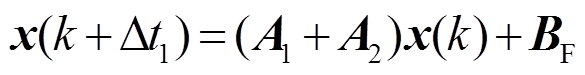（10）
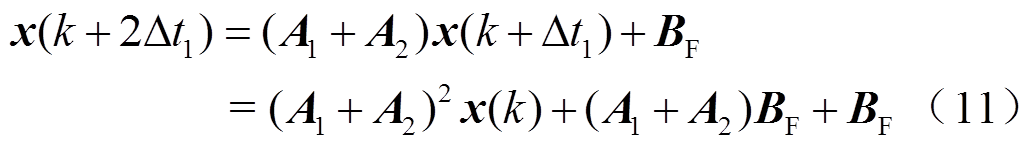
据此，其他小步长依此类推。在每个中步长Δt2中，状态量的变化可拆分成两个部分，第一部分为经过n1个小步长Δt1的迭代结果；第二部分为上一个中步长时刻t-Δt2状态的迭代结果。第一部分可在式（11）的基础上，根据式（12）推导。
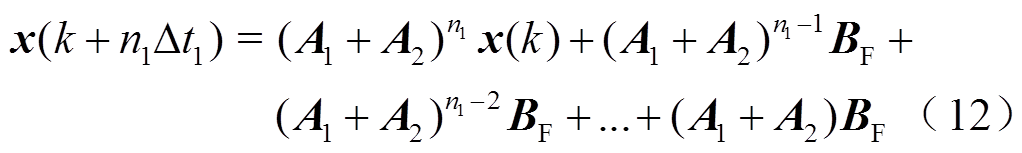
式（12）右式是由两部分构成，前半部分为状态量的迭代；后半部分相当于扰动量的迭代，可合并为一个常数向量。对于前半部分的矩阵，可以将其二项式展开，有
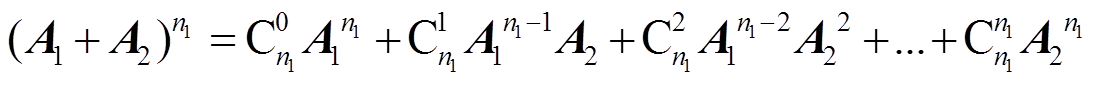（13）
观察矩阵A2，易知A22=0，因此，式（13）可进一步化简为
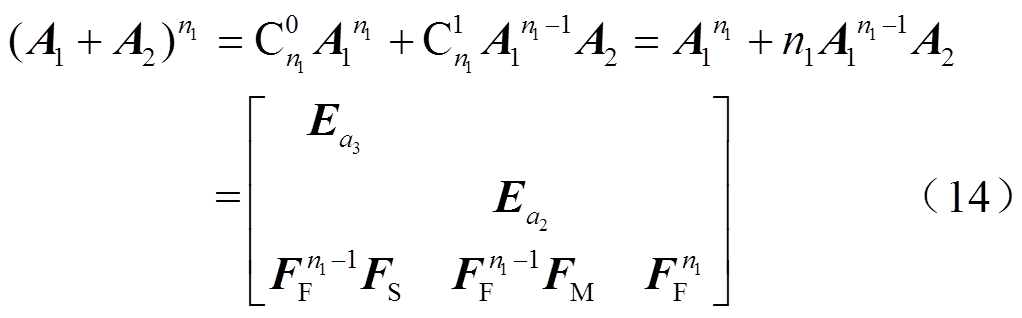
对于式（12）的后半部分，注意到矩阵A和向量BF满足
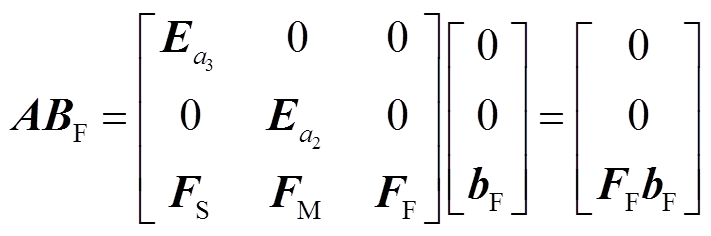（15）
根据式（15）可对式（12）的后半部分进行简化，结果为
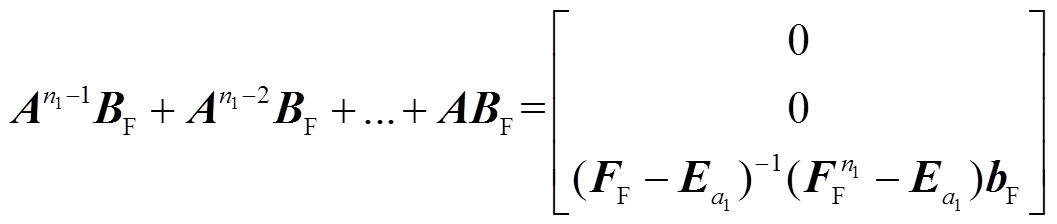（16）
综上所述，可将一个中步长Δt2内，区域F、M、S对区域F的影响用式（17）所示的状态空间方程描述，在本文中称其为xF在Δt2尺度下的修正状态空间方程式，需要注意的是，该表达式仅用作在Δt2时刻更新xF，并不用作更新xS和xM。
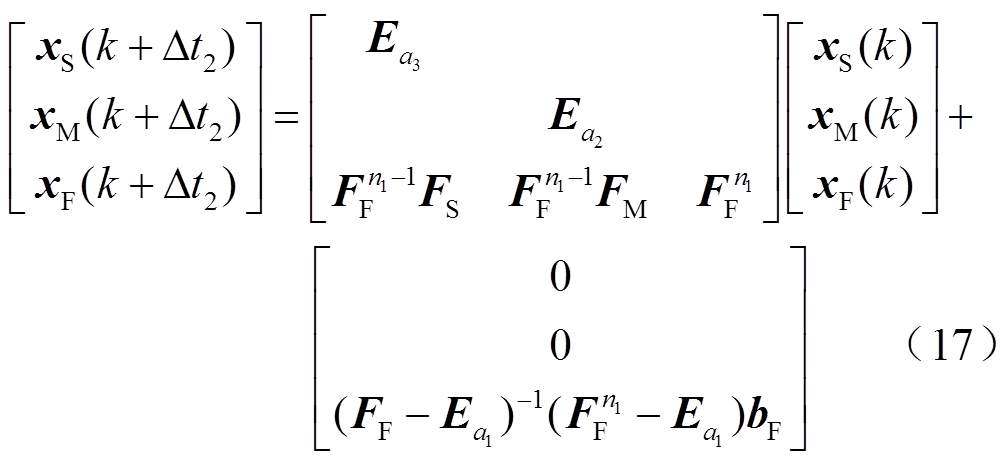
观察式（17），可以发现如果在每一个小步长Δt1时刻不计xM、xS对自身的影响，仅用区域F自身的状态空间方程求解，则需在每一个中步长Δt2的时刻，采用式（17）进行校正，即可得到该仿真时刻准确的值。因此，本节所提方法实现了各子区域在Δt1时间尺度上的解耦。解耦后，在每个仿真时步Δt1内，各子区域的迭代为
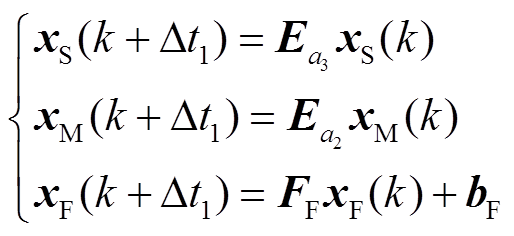（18）
在实际仿真求解时，xS和xM始终保持不变，而只有xF在进行计算，从而实现了小步长时系统各区域的解耦。
根据式（8），进行传统分区并行计算时，在一个中步长Δt2内的每个小步长Δt1时步，xF的实际计算过程为
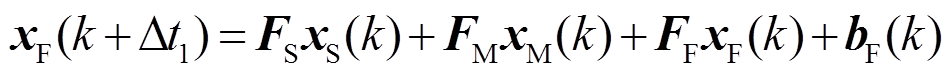（19）
Δt2内的每一个Δt1时刻，只有xF在变化，xS和xM保持不变，考虑Δt2内到xS和xM保持不变，可将FSxS(k)+FMxM(k)看作区域F的恒定扰动向量d，对比式（19）可知d即为每个小步长Δt1所产生的误差。该误差随着每次的迭代逐渐增大，即
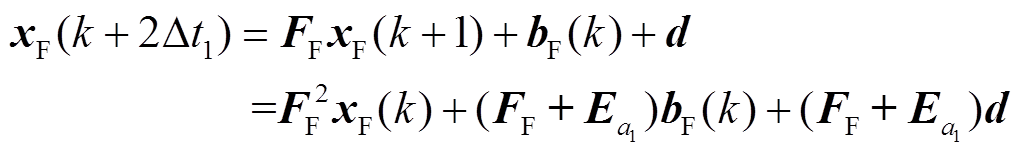（20）
易证，在第v次迭代后，误差向量e计算式为
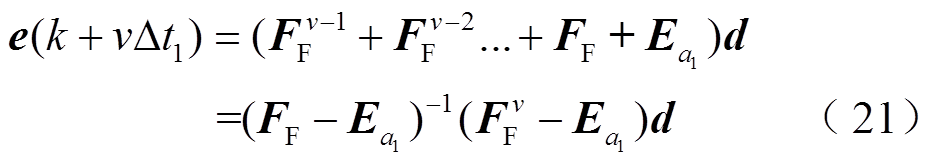
在进行到Δt2整数倍时刻时，应用式（17）进行计算。由于计算xF时直接采用Δt2时长前的状态量，并且应用式（17）对子分区F的状态向量xF进行了补偿，该计算结果与式（8），即与传统分区仿真方法的计算结果一致。由于在Δt2整数倍时刻校正了xF的值，从而确保误差仅存在于小步长Δt1时刻，中步长的值是准确的。
在每个中步长Δt2对应的时刻，状态向量xM也需要更新，这部分较为简单，只需将原始状态空间方程式（8）和修正状态空间方程式（17）进行结合，该状态空间表达式为
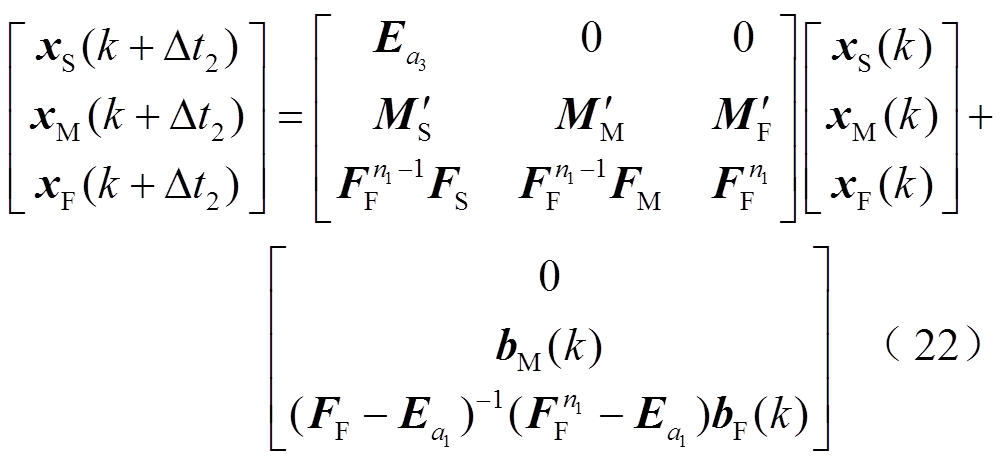
式中，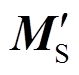
、
、
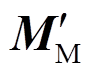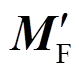均为基于中步长Δt2离散后的分块状态矩阵。
如果采用单一速率小步长进行一个中步长Δt2的计算，则至少需进行n1次a1+a2+a3阶矩阵运算，而采用2.2节所提的解耦等值及校正的方法，仅需计算n1次a1阶矩阵、1次a1+a2+a3阶矩阵运算，理论计算量大幅降低。对于一个Δt3内每个Δt2的等值解耦计算以及xM在Δt3尺度下的修正状态空间方程式，可以采用同样的基于分块矩阵的方法进行推导。
对于状态空间方程的稳定性验证，一方面，在进行多速率仿真步长确定时所采用的奈奎斯特采样定理能够使步长满足稳定性充分条件；另一方面，在等值模型建立后，可以通过对式（18）中的矩阵FF和式（22）中的迭代矩阵求取特征值，当所有特征值模的最大值小于1，系统稳定。本文不再赘述。
多速率分区后由于子区域间的步长差异及时序不同步，并行仿真会产生一定计算误差。假定两个子区域分别为小步长子区F和大步长子区S对应的仿真步长为Δt和ΔT，且两者相差整数倍n，即ΔT=nΔt，并行仿真的同步过程如图2所示。
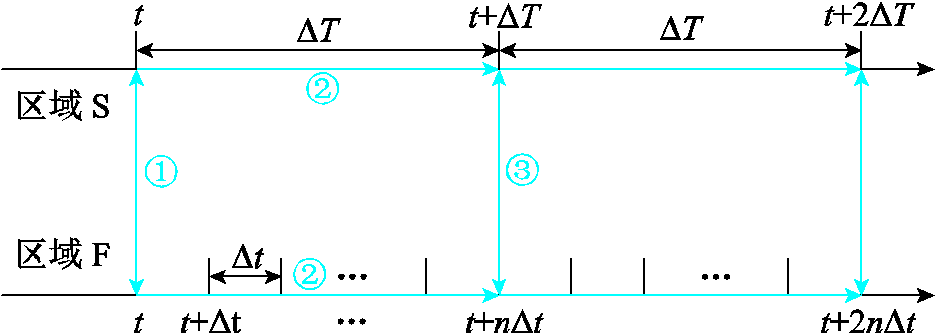
图2 并行仿真同步过程
Fig.2 Parallel simulation synchronization process
其主要步骤如下：①在t时刻，将区域S中各状态量的值传入区域F，同时将区域F中各状态量的值传入区域S；②对区域F进行以Δt为步长的离散化状态空间迭代，与此同时，对区域S进行以ΔT为步长的离散化状态空间迭代，在迭代过程中，仿真所采用的对侧区域值均为第①步中获得的；③重复步骤①，进行下一个步长ΔT的仿真计算。这种方法的数据误差来源主要为：在每个步长计算区域F中状态量时所代入的区域S中的变量值都是t时刻的值，未进行实时更新。因此需要采用插值算法对由时序交互所产生的误差进行补偿，以提高小步长区域仿真时的数值精度。目前在电气工程领域最常用的插值算法为线性插值算法，该方法通过线性模拟非线性，仿真中占用的计算资源较小，计算效率较高。小步长区域的状态向量表示为xF，大步长区域的状态向量表示为xS，对区域S采用线性插值算法后的连续型插值公式为
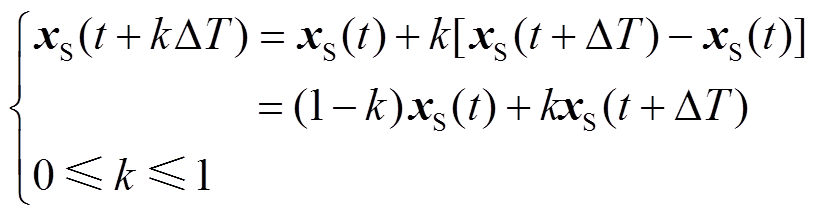（23）
考虑到本文以离散的状态空间方程作为仿真解算工具，将式（23）改为离散形式，有
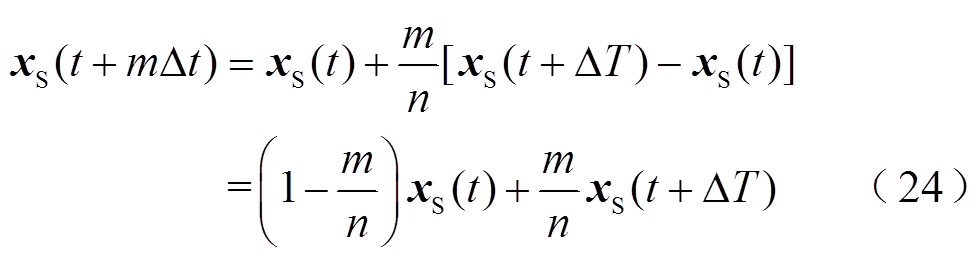
式中，m=0, 1, 2, …, n。考虑到问题描述的方便，后文中将m/n简记为p。
由于线性插值算法是一种线性过程模拟非线性动态过程的方法，必然存在误差，其原理如图3所示。对于一个大步长ΔT，设状态量变化曲线起始位置坐标为（t1, y1），终点位置坐标为（t2, y2），中间某一点对应的真实坐标为（t, yr），插值所得到的坐标为（t, y）。本节首先对该算法的误差进行详细分析。
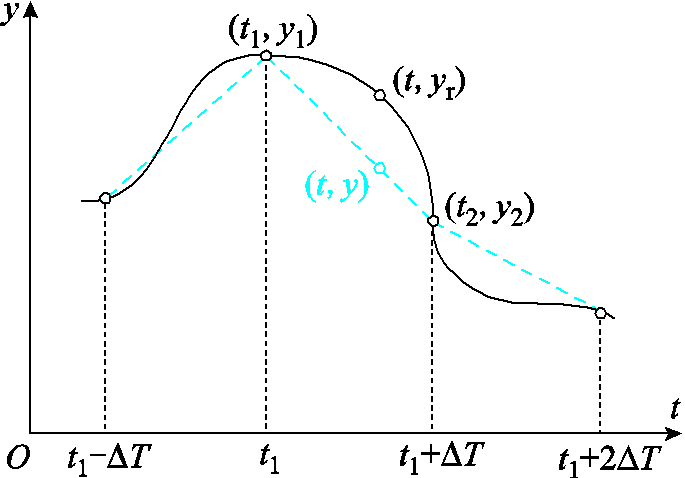
图3 线性插值误差机理示意图
Fig.3 Schematic diagram of linear interpolation error mechanism
根据相量法可以在谐波频率f的尺度下将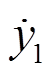
、
、
、
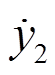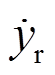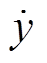分别表示为
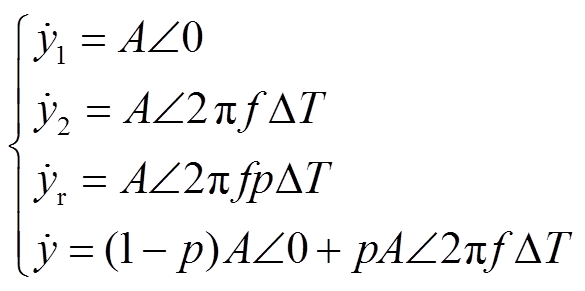（25）
式中，A为相量的幅值。根据式（25），易得插值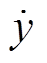的幅值误差与相角误差为
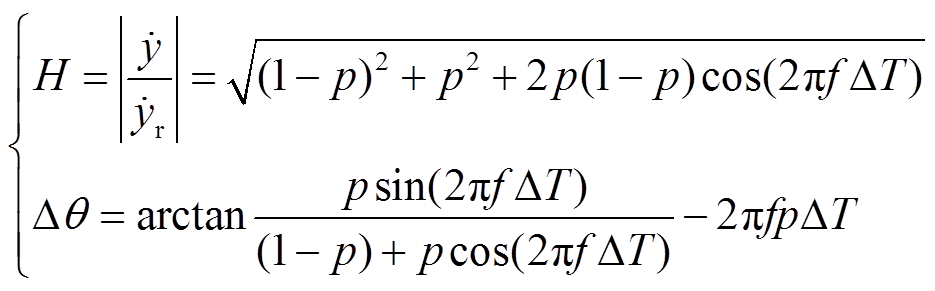（26）
为获取插值误差大小关于插值位置的关系，可用式（26）中的H对p求偏导，结果为
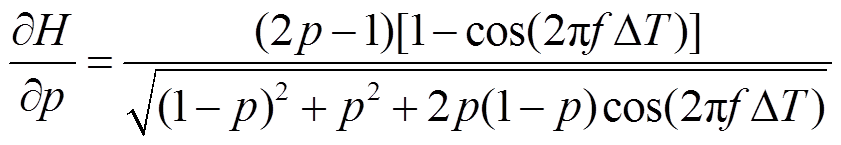（27）
根据式（27），无论频率f取何值，H总是随着p的增加，先减小后增大，在p=0.5处具有增益最小值。考虑到H(0)=H(1)=1，增益最小值即误差最大值。从而证明了在一个大步长ΔT内，线性插值算法的误差大小随着时间先逐渐增大，至中点达到最大值，而后逐渐减小。
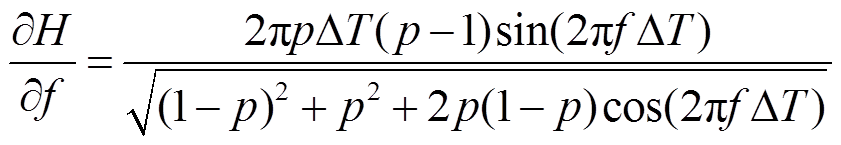（28）
观察式（28）可知，谐波频率对误差的影响与大步长ΔT有关，考虑到0≤p≤1，当sin(2πfΔT)＜0时，增益随f增大，误差随f减小；当sin(2πfΔT)＞0时，增益随f减小，误差随f增大。考虑到实际应用情况，ΔT为ms级时，误差可能会随f出现增减交替的情况；ΔT为ms级时，通常误差随f的增大而增大。因此，当区域S中高频谐波分量较大时，采用线性插值算法的误差较大，这与实际情况相吻合。对此，需要对多速率插值算法进行一定的改进，以优化其在不同谐波频率下的精度。
在实际工程应用时，插值算法按状态量已知和未知又可分为内插法和外插法。在并行仿真时，下一个大步长ΔT结束时的状态量通常是未知的，因此需要先对该状态量进行估计，并将估值和本时刻的值分别作为终点位置和起始位置进行插值，即线性外插法。为了问题描述的方便，后文均以连续函数为例进行说明，离散函数同理。线性外插法的一般数学格式为
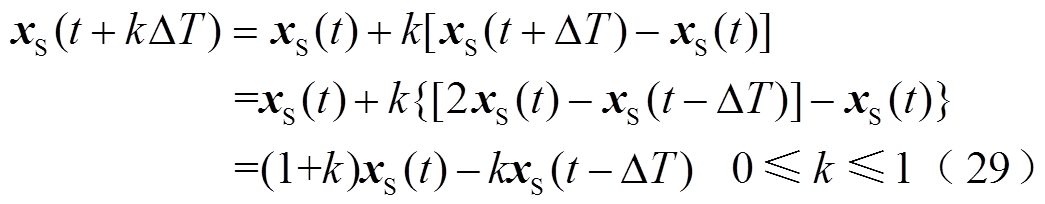
式（29）与内插法式（24）的区别在于，由于xS(t+ΔT)未知，故需要采用上一个大步长的xS(t-ΔT)和本步长的xS(t)对其进行估计。根据3.1节中的内容，类推线性外插法的幅值增益为
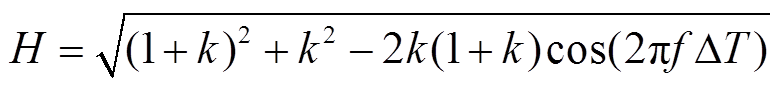（30）
同样，对k求偏导，可得
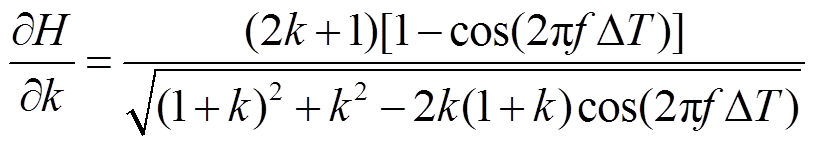（31）
根据式（31）易知H关于k单调递增，而H(0)=1，所以误差也随k单调递增，在H(1)处达到最大值。为了减小误差，可首先考虑减小H(1)的大小。采用线性外插时，H(1)为
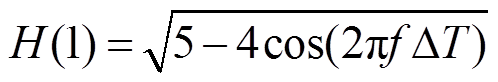（32）
基于以上，本文提出一种基于二阶泰勒展开式的校正插值算法，对插值算法所产生的误差进行削弱。首先，在t处将xS泰勒展开，保留至二次项，有
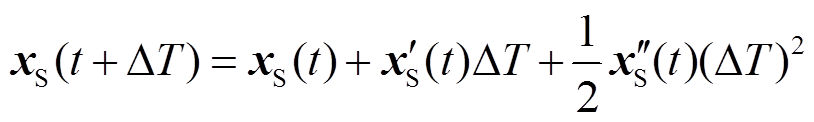（33）
而后分别用一阶差商和二阶差商代替式（33）中的一阶导数及二阶导数，可得H(1)，即xS(t+ΔT)的近似表达式为
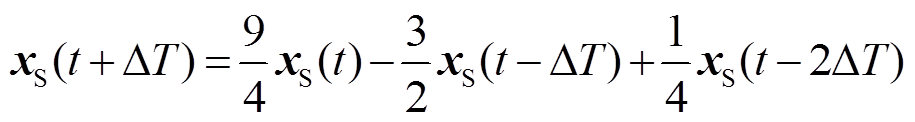（34）
显然，xS(t+ΔT)由xS(t)、xS(t-ΔT)和xS(t-2ΔT)加权组合而成，因此本文在二阶泰勒展开的基础上，引入参数a、b对传统插值方法进行改进。改进后的插值算法一般形式为
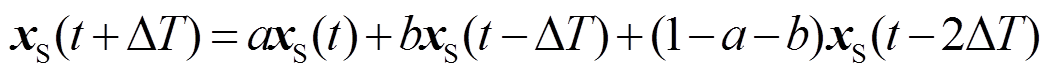（35）
采用式（35）方法外插时理论误差最大值H(1)处的值为
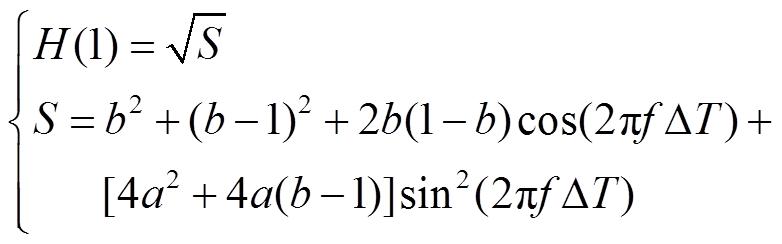（36）
通常仿真步长ΔT约为10-4～10-2 s，大步长子区域（主要为配电网线路）主要的谐波频率f取值为0～1 000 Hz，记fΔT=r，则r的取值范围为10-4～10。对于任意给定的r，可以通过a、b的选择匹配，得到H(1)的最小值，这组参数a、b所对应的插值算法理论误差是最小的。通过分别对a、b求偏导数，结果为
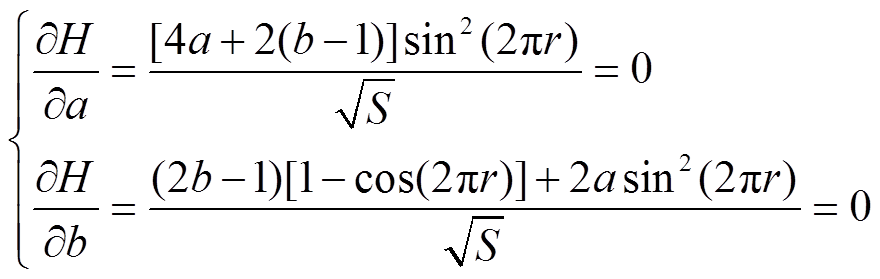（37）
可得最小值点所对应的参数a、b的值分别为
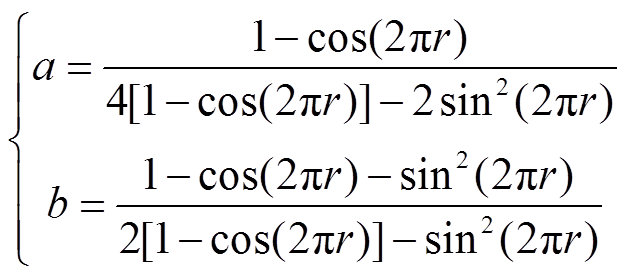（38）
将式（38）中的a、b的值代入式（35）即可得到改进后的插值算法表达式。
相比于传统线性插值算法，本节所提方法可根据系统的频率、步长差异，通过配置参数选择具体的插值计算方法，具有较高的通用性与数值精度。但多步自适应插值计算量略大于传统线性插值算法，因此在实际仿真时，可根据系统的r值，选取合适的插值算法，具体选择流程如图4所示。其核心为将式（38）中所求得的参数a、b值代入式（36），得到多步自适应插值算法的具体误差，并将其与线性外插的误差式（32）进行对比，即可确定在系统参数r已知时，何种插值算法的误差更小。具体比较过程以仿真4.2节为例进行说明。
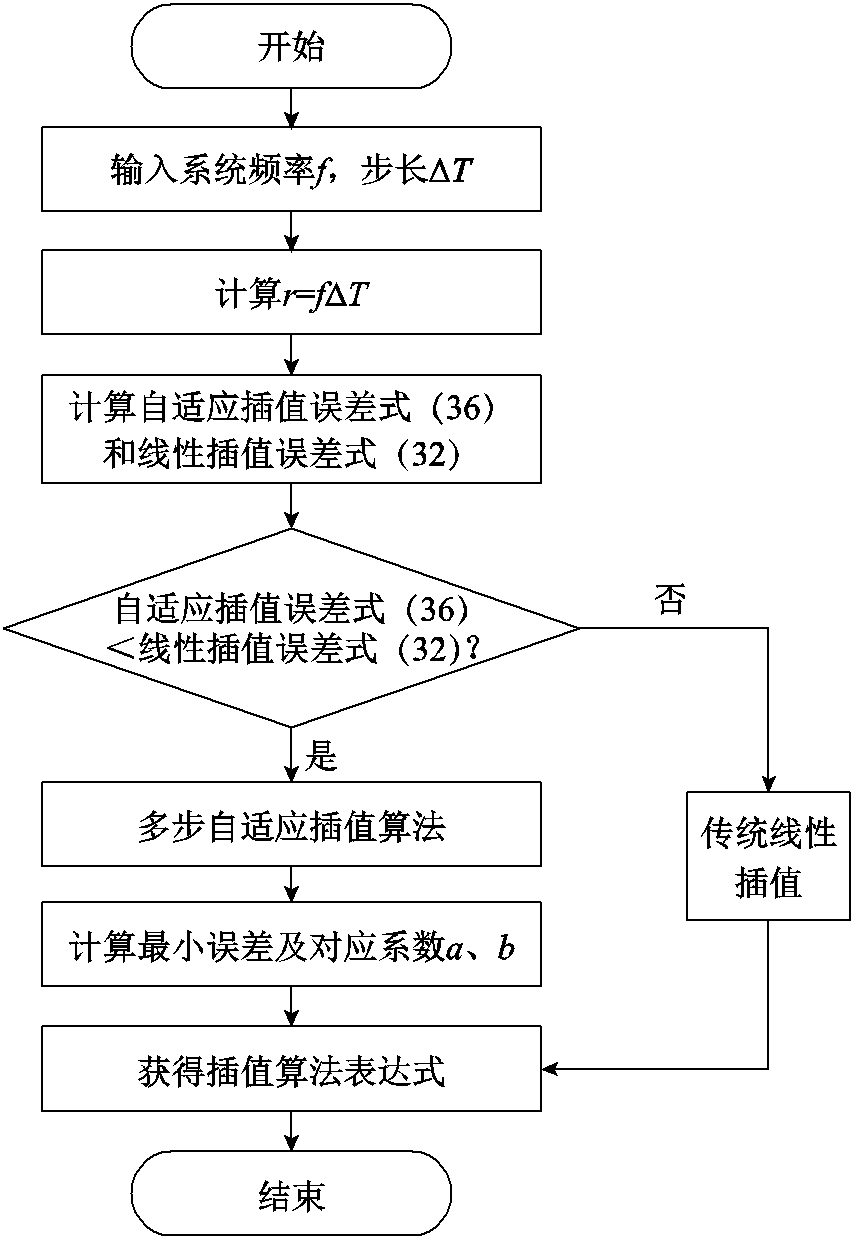
图4 插值算法选择流程
Fig.4 Interpolation algorithm selection process
为验证本文所提多速率解耦等值模型的有效性，本节通过仿真算例将本文模型与传统状态空间特征值多速率仿真[13]、单一仿真速率模型进行对比。仿真算例采用改进的IEEE 123节点有源配电网，其结构如图5所示，系统电压等级为4.16 kV，频率为50 Hz，在节点3、20、24、51、59、75、83、88、92、114位置分别接入电压源型分布式电源，该配电网馈线线路参数可参考文献[28]。
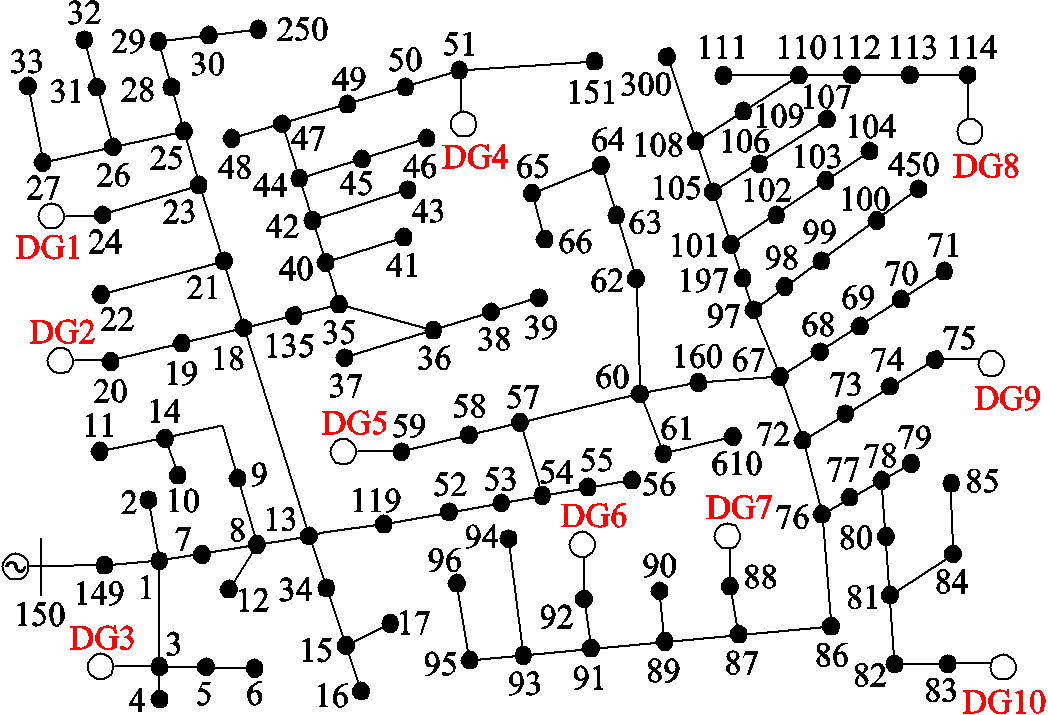
图5 有源配电网仿真算例结构
Fig.5 Structure diagram of active distribution network simulation example
假定总仿真时长为3 s。所有逆变器均采用PQ控制，控制目标Pref=20 kW，Qref=20 kvar。在系统进行至1 s时，Pref变为14 kW，Qref变为24 kvar，在1.5 s时恢复。在2 s时，节点60出现三相短路故障，并在2.2 s时恢复正常。系统求解时统一采用梯形法离散。比较以下四种方法的仿真结果与仿真耗时。
方法一：全系统采用小步长单一速率Δt=5 μs。
方法二：全系统采用大步长单一速率ΔT=100 μs。
方法三：系统采用传统状态空间特征值[13]划分为高、低速率两个子系统，文本侧重于多速率分区等值补偿模型的研究，特征值分区过程不在此赘述。根据特征值状态，分区结果为将各DG和节点的连接线路作为边界，DG侧为高速率子系统Δt=5 μs，网侧为低速率子系统ΔT=100 μs。
方法四：高低速率子系统分区及步长同方法三，并行方法采用本文所提的多速率等值解耦模型。
选取不同方法仿真所得的DG并网节点3、枢纽节点13、故障节点60的部分典型电流、电压波形如图6所示。
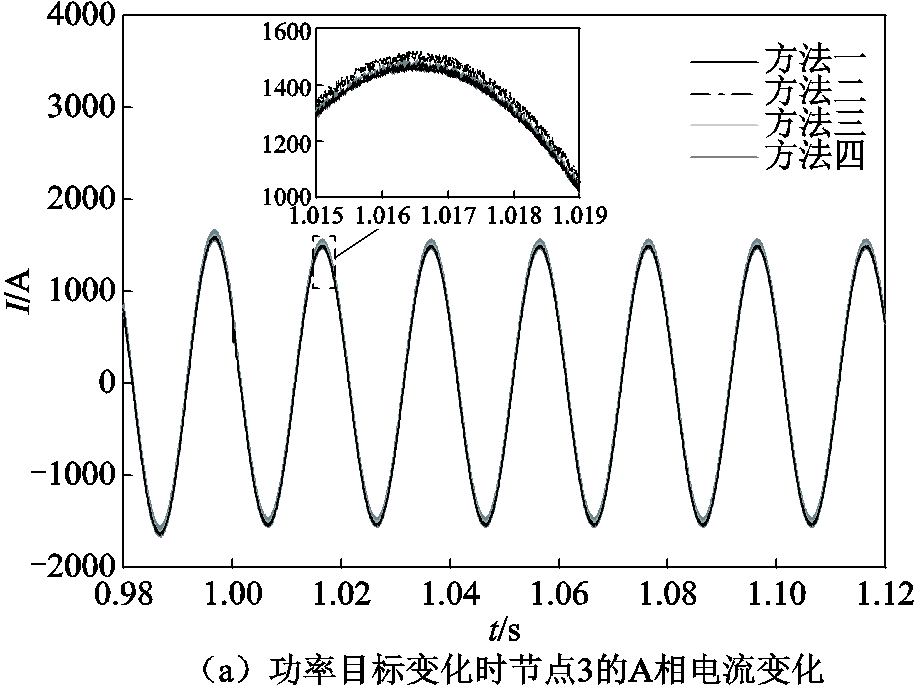
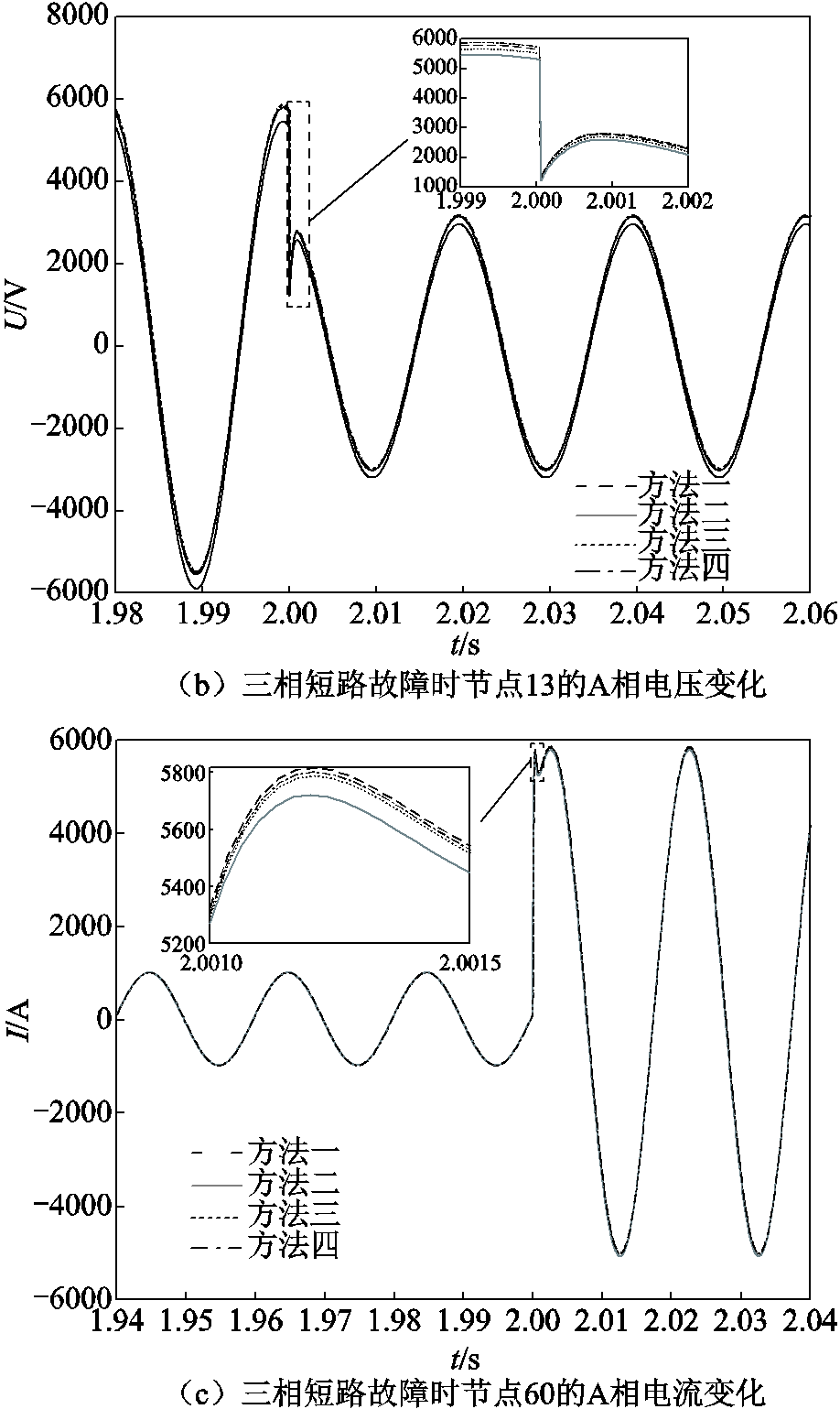
图6 部分典型仿真波形对比
Fig.6 Comparison of Some Typical Simulation Waveforms
从图6a可看出，仿真精度的由高到低排序为：方法一、方法四、方法三、方法二。而图6b、图6c中，方法一、三、四的计算结果近似，均优于方法二。为进一步对比仿真精度，本节在Simulink中基于四阶龙格-库塔法搭建仿真步长为1 μs的单一速率模型，将结果作为参考波形，并与上述四种方法进行精度对比。其中，各种方法的误差由式（39）计算所得。
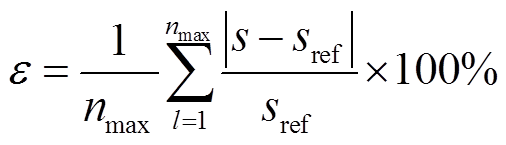（39）
式中，s代表任一状态量，可以为任意位置的电压、电流；sref为状态量的参考值；l为离散的仿真时步；nmax为总的仿真步长数。为了对各方法的精度与效率进行比对，分别对节点3的A相电流、节点13的A相电压、节点60的A相电流求取误差的平均值作为比较对象；同时对四种方法进行10次仿真运行，取总的仿真耗时，对比结果如图7所示。为了说明与单速率小步长算法的比对效果，各方法与方法一的性能指标见表1。
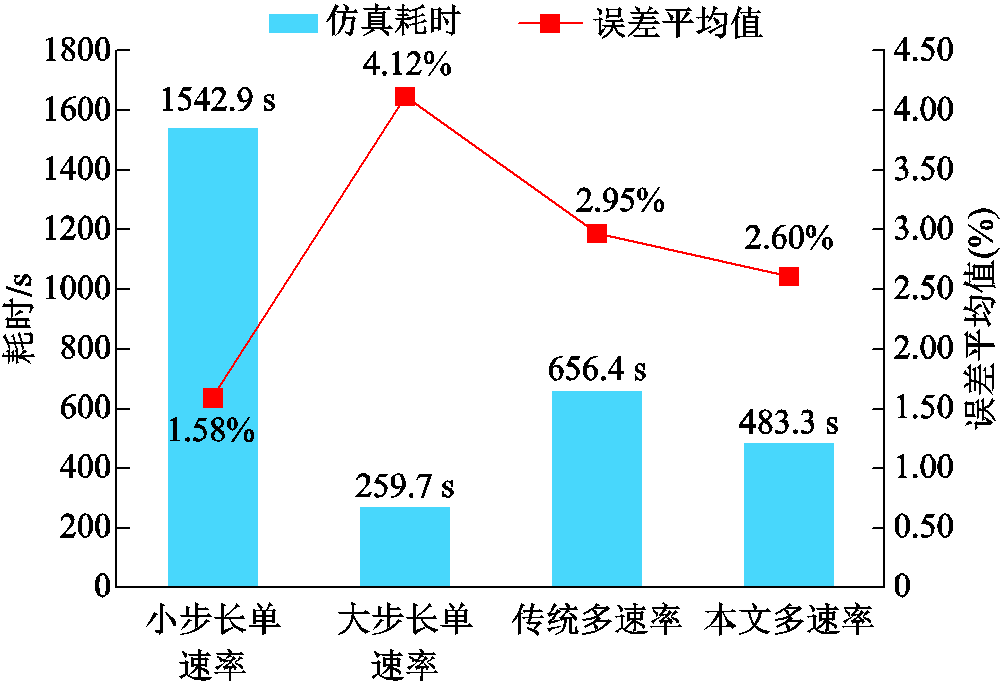
图7 各方法的误差、耗时对比
Fig.7 Comparison of errors and time consumption of various methods
表1 四种方法的误差、仿真耗时相对值
Tab.1 Comparison of errors and time consumption of four methods（%）
方法平均误差相对增加仿真耗时相对降低 小步长单速率—— 大步长单速率2.5483.17 传统多速率[13]1.3757.46 本文多速率1.0268.67
在本算例基础上，将两个子区域步长提升至原来的10倍，分别为50 ms和1 ms，进行四种方法的仿真，仿真结果如图8所示。
根据图8a的对比结果，由于该场景下大步长接近换流器频率，因此采用单一速率大步长仿真的精度已经无法模拟实际运行情况。而根据图8b采用小步长单速率、多速率分区方法时，由于小步长远小于换流器的周期，因此仍具有较高的精度。具体误差及仿真时间见表2。
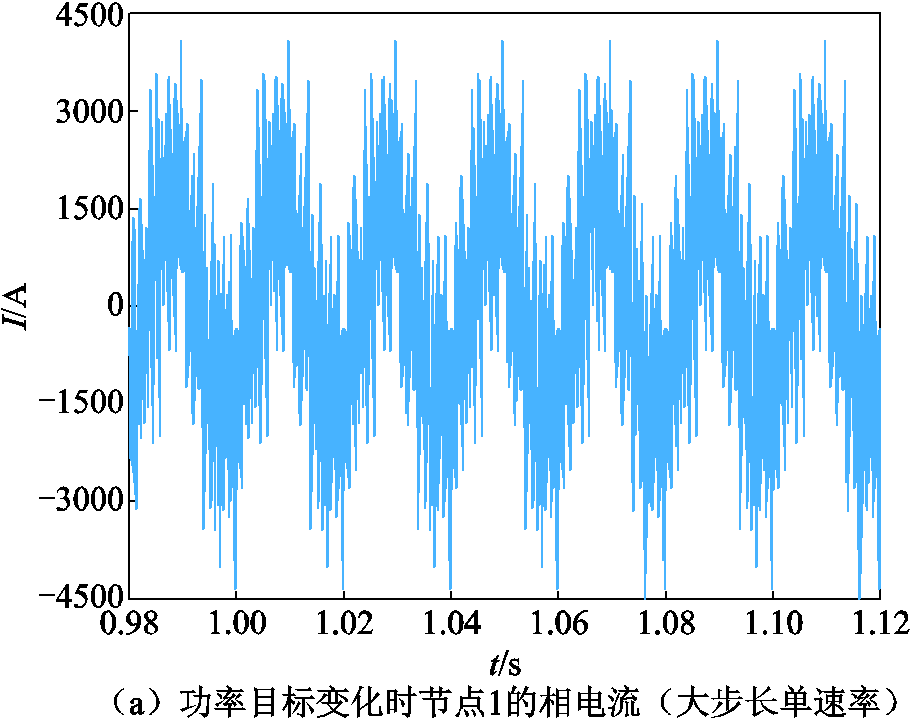
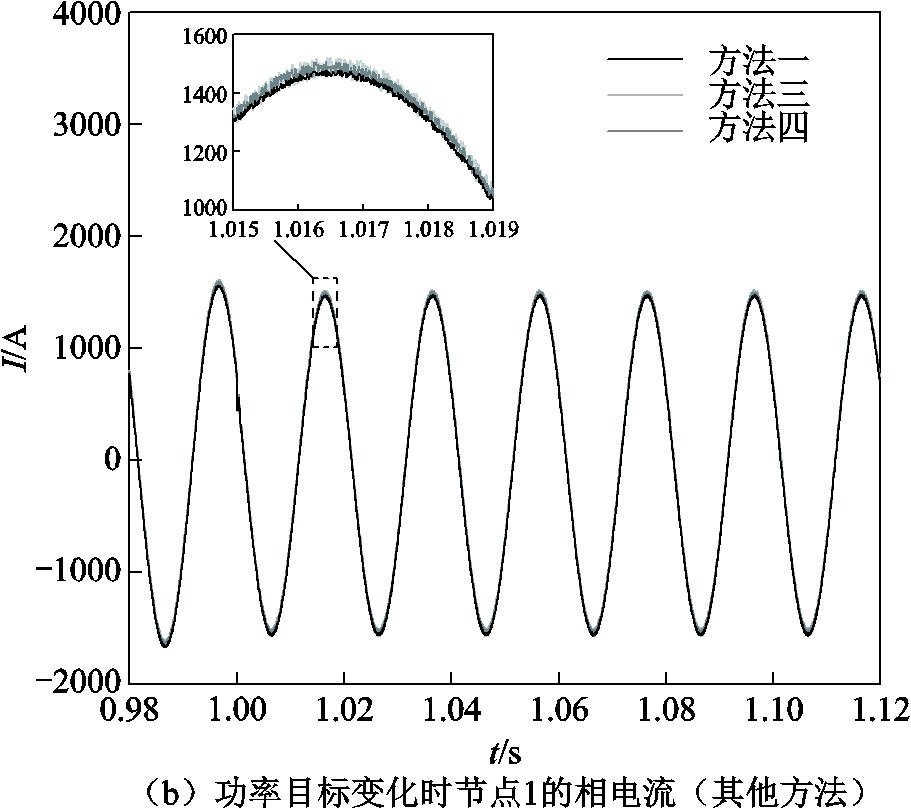
图8 增大步长后部分典型仿真波形对比
Fig.8 Comparison of typical simulation waveforms after increasing step size
表2 增大步长后四种方法误差、仿真耗时对比
Tab.2 Comparison of errors and time consumption of four methods
方法平均误差(%)仿真耗时/s 小步长单速率3.29507.2 大步长单速率31.5890.6 传统多速率[13]4.92288.4 本文多速率4.70225.8
由于本文模型在仿真过程中实现了子区域间的解耦，因此具有效率优势，相比于全系统采用小步长仿真，减少了约69%的仿真用时，相比于方法三亦有约27%的提升。同时由于校正环节的存在，精度较传统多速率方法也有一定提升。综合本节仿真结果，本文所提的基于多速率解耦等值的并行仿真模型相比于现有方法具有较大的仿真精度与仿真效率的提升。
为了对比多步自适应插值算法与线性插值算法的理论误差，将式（38）中的a、b的值代入式（36）即可得H(1)，即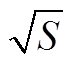
关于r的表达式，化简后为
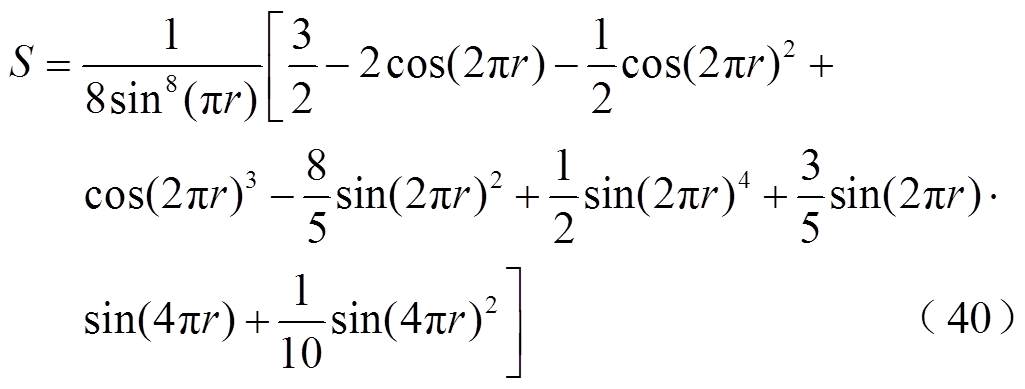
式（40）与式（32）均是关于r的函数，取定义域为r∈（10-4, 10），并比较相应的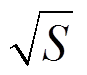
与式（36），可知当r位于如式（41）所示区间内，本文插值算法所得的理论误差最大值H(1)小于线性插值算法，即
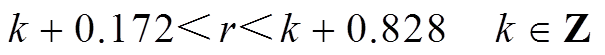（41）
可见本文方法对于r（即频率与仿真步长的乘积fΔT）的适用范围比线性插值更大，在实际应用时应首先根据系统频率及仿真步长计算r，再根据r的值及式（38）、式（41）选择合适的参数a、b进行插值。
由线性插值算法误差表达式（32）和本文算法误差表达式（36）易知，这两种算法的理论最大误差H(1)关于r的函数关系式周期均为1。为了验证本文所提的多步自适应插值算法的有效性，首先分析验证当r取值由0变化至1的过程中，本文算法的理论最大误差H(1)与线性插值算法的理论最大误差的比较，该对比结果如图9所示。
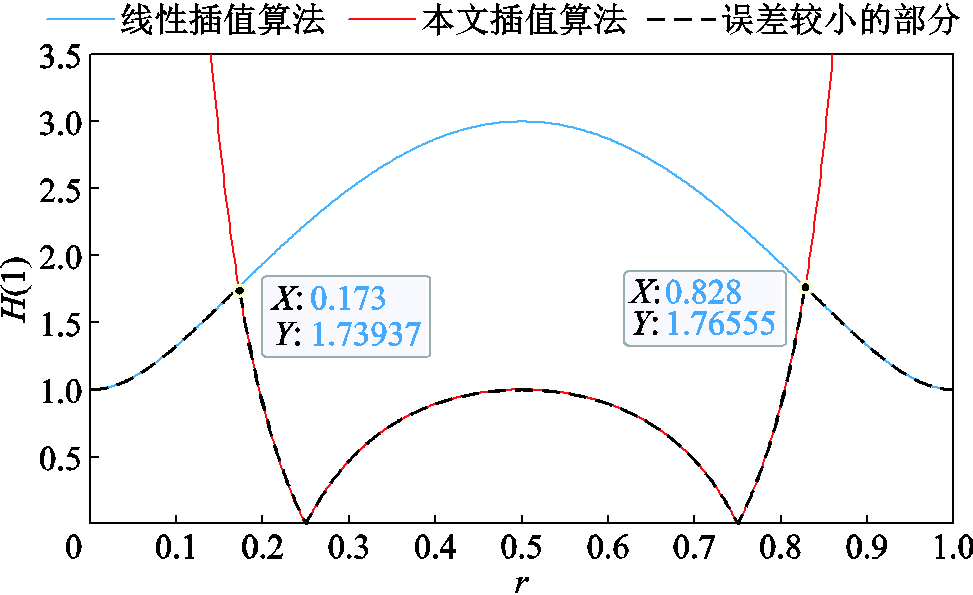
图9 本文插值算法与线性插值算法最大误差对比
Fig.9 Comparison of maximum error between interpolation algorithm in this paper and linear interpolation algorithm
由图9可见，本文插值算法在近似区间r∈（0.173, 0.828）内误差小于线性插值算法，该结果与理论值式（40）基本一致。在实际应用时，可根据r的值小数部分的差异选择最适合的插值算法。
为进一步验证本文所提插值算法在有源配电网多速率分区交互中的优势，本节仍采用4.1节算例，并对比不同插值算法的仿真结果。算例中逆变器采用PQ控制，控制目标Pref=20 kW，Qref=20 kvar。在系统进行至1 s时，Pref变为14 kW，Qref变为24 kvar，在1.1 s时恢复。经计算可调参数a=0.723 6，b=-0.447 2。
在有功功率参考值变化时，节点24处DG输出的电流、电压、有功、无功功率的波形变化对比分别如图10所示。
根据图10波形结果，相比于传统线性插值算法，本文插值算法的暂态过程波动更小，且收敛至稳态的速度较快。这就验证了3.2节所述的插值算法误差理论的正确性。同时，本算例所取的r值对应的精度结果也符合图9所示的插值算法精度对比结果。采用本文插值算法与传统线性插值算法对该算例进行仿真，取仿真过程中A相电流、A相电压、有功功率、无功功率最大误差百分数（对比场景同算例4.1节）的平均值作为综合误差，并记录总仿真耗时以及暂态调节时间，对比结果见表3。
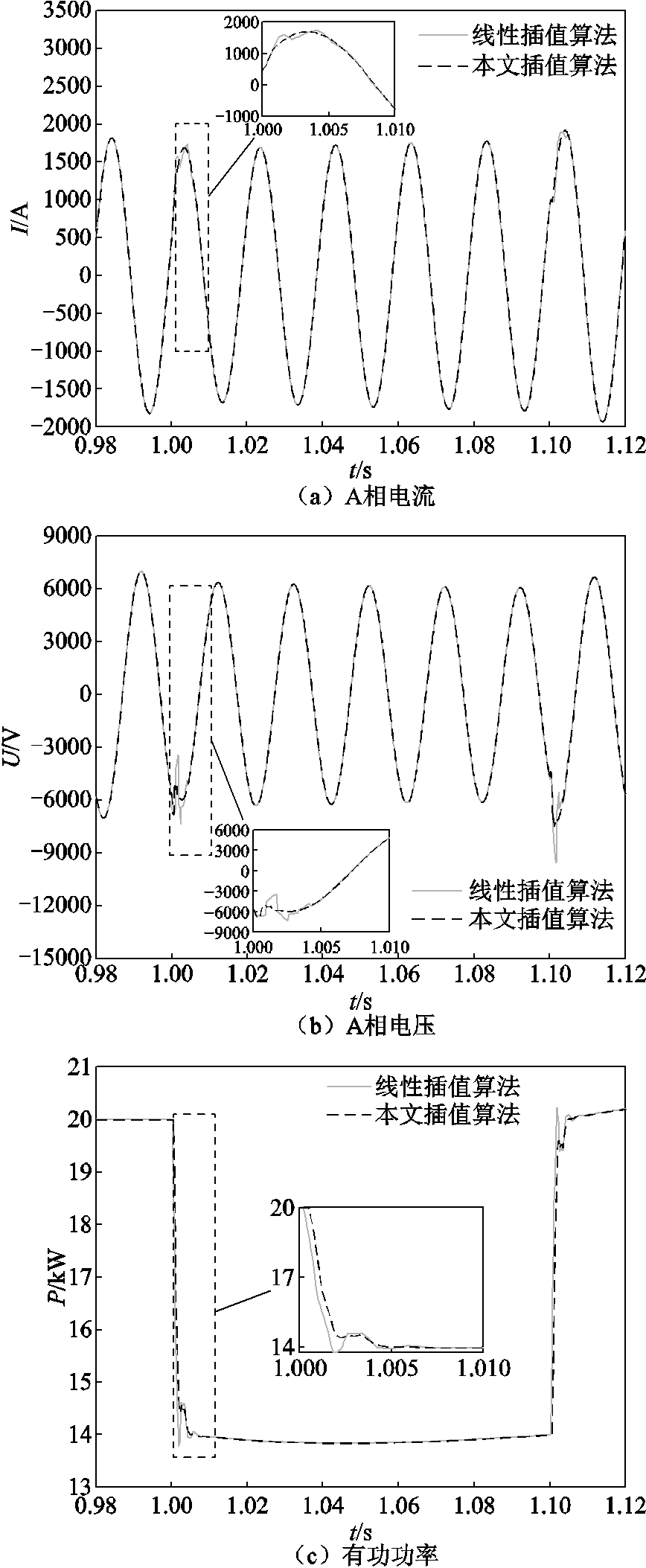
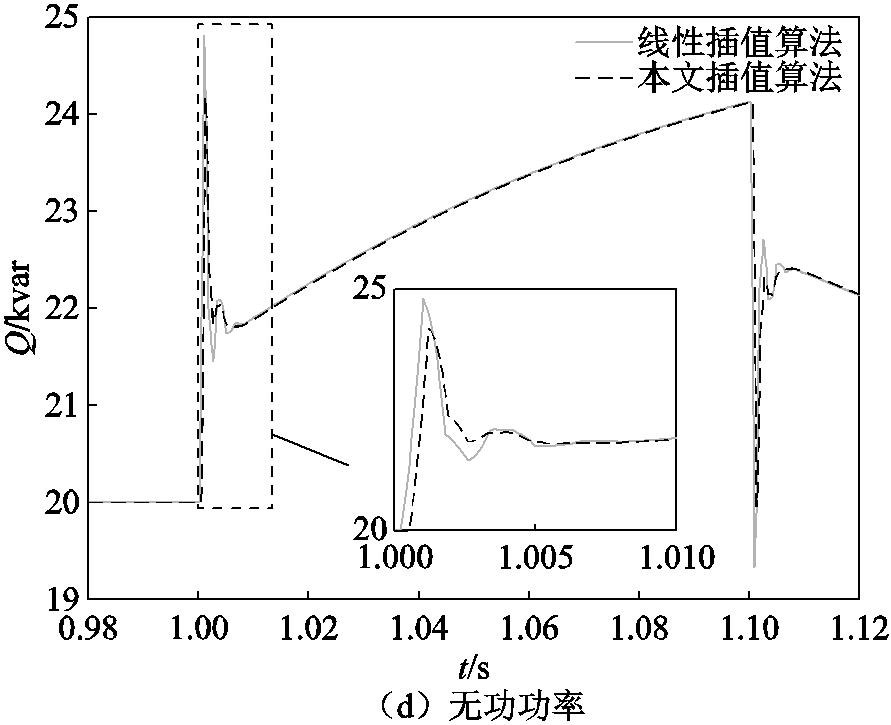
图10 有功参考值变化时DG输出波形
Fig.10 DG output waveforms when active reference value changes
表3 不同插值算法的误差、耗时对比
Tab.3 Comparison of errors and time consumption of different interpolation algorithms
方法最大设定值误差(%)仿真耗时/s调节时间/s 线性插值算法29.64178.72.645 本文插值算法17.33189.81.320
由于本文所提出的插值算法采用了三个步长的值进行外插，因此仿真耗时比传统线性插值算法略多。但考虑到本文算法在仿真精度（提升41.5%）和调节时间性能（提升50.1%）上均具有较大提升，因此在对精度及稳定性需求较高的仿真场景中具有一定的优势。
本文提出了基于特征矩阵分区等值和自适应插值的有源配电网多速率并行仿真方法，以提升多速率仿真的数值准确性与计算速度。
1）该方法评估快慢分区耦合对多速率仿真数值准确性的影响，并进行子系统模型等值解耦，实现子区域在小步长的独立解算与大步长的等效补偿，降低了仿真时状态迭代矩阵的阶数，在保证计算精度时显著提高了效率。
2）在分析线性插值误差产生原理和影响因素的基础上，提出了自适应插值切换仿真算法，根据系统频率和仿真步长需求调节相关插值参数，进行插值算法优选，提升了并行仿真的准确性和稳定性。
参考文献
[1] 蔡瑶, 卢志刚, 潘尧, 等. 计及多重差异的交直流混合多能微网多时间尺度优化调度[J/OL]. 电工技术学报: 1-19[2023-11-11]. https://doi.org/10.19595/ j.cnki.1000-6753.tces.230645. Cai Yao, Lu Zhigang, Pan Yao, et al. Multi-time-scale optimal scheduling of AC-DC hybrid multi-energy microgrid considering multiple differences[J/OL]. Transactions of China Electrotechnical Society: 1-19[2023-11-11].https://doi.org/10.19595/j.cnki.1000- 6753.tces.230645.
[2] 马钊, 安婷, 尚宇炜. 国内外配电前沿技术动态及发展[J]. 中国电机工程学报, 2016, 36(6): 1552-1567. Ma Zhao, An Ting, Shang Yuwei. State of the art and development trends of power distribution technologies[J]. Proceedings of the CSEE, 2016, 36(6): 1552-1567.
[3] 张玉莹, 曾博, 周吟雨, 等. 碳减排驱动下的数据中心与配电网交互式集成规划研究[J]. 电工技术学, 2023, 38(23): 6433-6450. Zhang Yuying, Zeng Bo, Zhou Yinyu, et al. Research on interactive integration planning of data centers and distribution network driven by carbon emission reduction[J/OL]. Transactions of China Electrotechnical Society, 2023, 38(23): 6433-6450.
[4] Hadjsa N. 有源智能配电网[M]. 陶顺, 肖湘宁, 彭骋, 译. 北京: 中国电力出版社, 2012.
[5] 王成山, 王丹, 周越. 智能配电系统架构分析及技术挑战[J]. 电力系统自动化, 2015, 39(9): 2-9. Wang Chengshan, Wang Dan, Zhou Yue. Framework analysis and technical challenges to smart distribution system[J]. Automation of Electric Power Systems, 2015, 39(9): 2-9.
[6] 江岳文, 罗泽宇, 程诺. 基于线性化方法的交直流混合配电系统网架规划[J/OL]. 电工技术学报: 1-16[2023-11-11]. https://doi.org/10.19595/j.cnki. 1000-6753.tces.222363. Jiang Yuewen, Luo Zeyu, Cheng Nuo. Network planning of AC/DC hybrid distribution system based on linearization method [J/OL]. Transactions of China Electrotechnical Society: 1-16. [2023-11-11].https:// doi.org/10.19595/j.cnki.1000-6753.tces. 222363.
[7] 何绍民, 张喆, 卢倚平, 等. 基于计算前沿面的实时仿真数值积分并行构造及其数值模型解耦加速方法[J]. 电工技术学报, 2023, 38(16): 4246-4262. He Shaomin, Zhang Zhe, Lu Yiping, et al. Numerical model decoupling acceleration method with numerical integration parallelism construction based on computation front in real-time simulation[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4246-4262.
[8] Hariri A, Faruque M O. A hybrid simulation tool for the study of PV integration impacts on distribution networks[J]. IEEE Transactions on Sustainable Energy, 2017, 8(2): 648-657.
[9] Armstrong M, Marti J R, Linares L R, et al. Multilevel MATE for efficient simultaneous solution of control systems and nonlinearities in the OVNI simulator[J]. IEEE Transactions on Power Systems, 2006, 21(3): 1250-1259.
[10] Tomim M A, Martí J R, De Rybel T, et al. MATE network tearing techniques for multiprocessor solution of large power system networks[C]//IEEE PES General Meeting, Minneapolis, MN, USA, 2010: 1-6.
[11] 邓潘, 盛万兴, 刘科研, 等. 有源配电网典型暂态模型及区域分割并行仿真方法研究[J]. 电网技术, 2020, 44(4): 1211-1219. Deng Pan, Sheng Wanxing, Liu Keyan, et al. Methods of transient model and parallel simulation of region segmentation in active distribution network[J]. Power System Technology, 2020, 44(4): 1211-1219.
[12] 王照琪, 唐巍, 张博, 等. 基于优化分网策略的有源配电网多速率并行暂态仿真分析[J]. 电网技术, 2020, 44(2): 673-682. Wang Zhaoqi, Tang Wei, Zhang Bo, et al. Multi-rate parallel transient simulation of active distribution network based on optimization decomposition strategy[J]. Power System Technology, 2020, 44(2): 673-682.
[13] 刘科研, 叶华, 裴玮, 等. 基于特征值分析的配电网多速率暂态仿真性能评估方法研究[J]. 电网技术, 2020, 44(11): 4088-4096. Liu Keyan, Ye Hua, Pei Wei, et al. Research on computational performance of multi-rate transient simulation in distribution network based on eigen-value analysis[J]. Power System Technology, 2020, 44(11): 4088-4096.
[14] 魏松韬. 复杂有源配电网电磁暂态多速率并行仿真理论与方法[D]. 南京: 东南大学, 2022.
[15] Heffernan M D, Turner K S, Arrillaga J, et al. Computation of AC-DC system disturbances - part I. interactive coordination of generator and convertor transient models[J]. IEEE Power Engineering Review, 1981, PER-1(11): 15-16.
[16] 王耀坤, 赵煜, 梁英, 等. 基于信息物理系统的配电网故障处理仿真研究[J]. 智慧电力, 2019, 47(12): 103-109. Wang Yaokun, Zhao Yu, Liang Ying, et al. Simulation on distribution network fault handling based on CyberPhysical system[J]. Smart Power, 2019, 47(12): 103-109.
[17] 李鹏, 曾凡鹏, 王智颖, 等. 基于FPGA的有源配电网实时仿真器I/O接口设计[J]. 中国电机工程学报, 2017, 37(12): 3409-3417, 3668. Li Peng, Zeng Fanpeng, Wang Zhiying, et al. I/O interface design for FPGA based real-time simulator of active distribution networks[J]. Proceedings of the CSEE, 2017, 37(12): 3409-3417, 3668.
[18] 陈颖, 宋炎侃, 黄少伟, 等. 基于GPU的大规模配电网电磁暂态并行仿真技术[J]. 电力系统自动化, 2017, 41(19): 82-88. Chen Ying, Song Yankan, Huang Shaowei, et al. GPU-based techniques of parallel electromagnetic transient simulation for large-scale distribution network[J]. Automation of Electric Power Systems, 2017, 41(19): 82-88.
[19] 周斌, 汪光森, 李卫超, 等. 基于FPGA的电力电子系统电磁暂态实时仿真通用解算器[J]. 电工技术学报, 2023, 38(14): 3862-3874. Zhou Bin, Wang Guangsen, Li Weichao, et al. An FPGA-based general solver for electromagnetic transient real-time simulation of power electronic systems[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3862-3874.
[20] 占鹏. 基于多核CPU的电力系统多速率电磁暂态仿真[D]. 北京: 华北电力大学, 2018.
[21] Benigni A, Monti A, Dougal R A. Latency-based approach to the simulation of large power electronics systems[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 3201-3213.
[22] Li Yupeng, Shu Dewu, Hu Jingwei, et al. A multi-area Thevenin equivalent based multi-rate co-simulation for control design of practical LCC HVDC system[J]. International Journal of Electrical Power & Energy Systems, 2020, 115: 105479.
[23] 韩佶, 董毅峰, 苗世洪, 等. 基于MATE的电力系统分网多速率电磁暂态并行仿真方法[J]. 高电压技术, 2019, 45(6): 1857-1865. Han Ji, Dong Yifeng, Miao Shihong, et al. Multi-rate electromagnetic transient parallel simulation of power system based on MATE[J]. High Voltage Engineering, 2019, 45(6): 1857-1865.
[24] Bartel A, Günther M. A multirate W-method for electrical networks in state-space formulation[J]. Journal of Computational and Applied Mathematics, 2002, 147(2): 411-425.
[25] 李珂, 顾伟, 柳伟, 等. 基于FPGA的变流器并行多速率电磁暂态实时仿真方法[J]. 电力系统自动化, 2022, 46(13): 151-158. Li Ke, Gu Wei, Liu Wei, et al. Real-time parallel multi-rate electromagnetic transient simulation method for converters based on field programmable gate array[J]. Automation of Electric Power Systems, 2022, 46(13): 151-158.
[26] do Couto Boaventura W, Semlyen A, Iravani M R, et al. Robust sparse network equivalent for large systems: part I-methodology[J]. IEEE Transactions on Power Systems, 2004, 19(1): 157-163.
[27] 郑雷, 王斌, 喻敏. 基于分形插值的电力系统故障录波数据压缩与还原算法研究[J]. 计算机测量与控制, 2014, 22(4): 1185-1188. Zheng Lei, Wang Bin, Yu Min. Research about compression and reproduction algorithm of digital recorded data from a faulted power system based on fractal interpolation[J]. Computer Measurement & Control, 2014, 22(4): 1185-1188.
[28] Xu Junjun, Wu Zaijun, Yu Xinghuo, et al. An interval arithmetic-based state estimation framework for power distribution networks[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8509-8520.
Abstract With the rapid development of power electronics technology and increasing penetration of distributed generations, modern active distribution networks exhibit complex dynamic characteristics due to the multiple time scales of system operation, which poses challenges to the simultaneous demand of computational efficiency and accuracy in the conventional simulation method with a single simulation-rate. This paper proposes a multi-rate parallel simulation method based on the characteristic matrix partition equivalence and adaptive interpolation switching. Firstly, a state space matrix is constructed for the whole active distributed system, and the system is divided into multiple subsystems with different dynamic characteristics based on the magnitude of the eigenvalues of the state matrix and their corresponding natural frequencies. The iterative computation of the high-speed subsystem is equivalently calculated within a certain period of time through binomial expansion and multidimensional matrix summation formulas, and then the block equivalence of the system's state matrix is achieved. This method transforms the original full-region state quantity iterative computation into the independent simulation solutions for subregions at small step sizes and equivalent compensation at large step sizes, simplifying the original high-order matrix iterative computation to the low-order matrix iterative computation, thereby significantly reducing the simulation complexity while ensuring simulation accuracy. For the problem of asynchronous data interaction between regions, the error generation principle and main influencing factors of the traditional linear interpolation method are analyzed through the magnification step length vector method. Based on the second-order Taylor expansion, the interpolation algorithm is improved by introducing undetermined coefficients. A multi-step adaptive interpolation simulation algorithm is proposed, which can adjust relevant interpolation parameters according to the system frequency and simulation step length requirements, significantly reducing interpolation errors. Finally, using the improved IEEE 123 node distribution network example, the feasibility and effectiveness of the proposed multi-rate parallel simulation method are verified through the comparison of partition equivalence/interpolation calculations and simulation results. The specific innovations of this article are as follows: Based on the discrete state space matrix, the system is considered as a multiple-rate counterpart due to different dynamic characteristics, and then the influence of coupling between fast and slow system regions on the accuracy of multi-rate simulation is evaluated through diagonalizing the matrix. The equivalent decoupling of the partitioned subsystem models is implemented to achieve independent resolution of subregions in small steps and equivalent compensation in large steps, significantly reducing the computational load while ensuring simulation accuracy. For the problem of asynchronous data interaction in multi-rate regions, the error caused by the conventional linear interpolation methods are analyzed by using the magnification step length vector method, and the relationships between the error and the system frequency and step length are also derived. Based on the second-order Taylor expansion, a multi-rate multi-step adaptive interpolation algorithm is proposed, which adjusts the interpolation algorithm parameters according to the simulation requirements for the first time to meet the minimum error condition, and performs optimal switching among multiple interpolation algorithms to improve the inter-region interaction coordination and simulation accuracy. Through simulation comparison, the following conclusions can be drawn:
(1) This method evaluates the impact of fast and slow partition coupling on the accuracy of multi rate simulation numerical values, and decouples the subsystem model equivalently to achieve independent solution of the subregion in small steps and equivalent compensation in large steps, reducing the order of the state iteration matrix during simulation and significantly improving efficiency while ensuring computational accuracy.
(2) On the basis of analyzing the principle and influencing factors of linear interpolation errors, an adaptive interpolation switching simulation algorithm is proposed. Relevant interpolation parameters are adjusted according to the system frequency and simulation step size requirements, and interpolation algorithm optimization is carried out to improve the accuracy and stability of parallel simulation.
keywords: Active distribution network, multi-rate parallel simulation, state space equation, equivalent model, adaptive interpolation algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.230808
中图分类号：TM743
国家电网有限公司科技项目资助（5400-202122147A-0-0-00）。
收稿日期 2023-05-31
改稿日期 2023-11-19
楼冠男 女，1986年生，副教授，博士生导师，研究方向为分布式新能源接入配电网运行，微电网运行与控制，电力系统实时仿真等。E-mail：glou@seu.edu.cn（通信作者）
蒋啸宇 男，1998年生，硕士研究生，研究方向电力系统实时仿真技术。E-mail：929177591@qq.com
（编辑 赫 蕾）