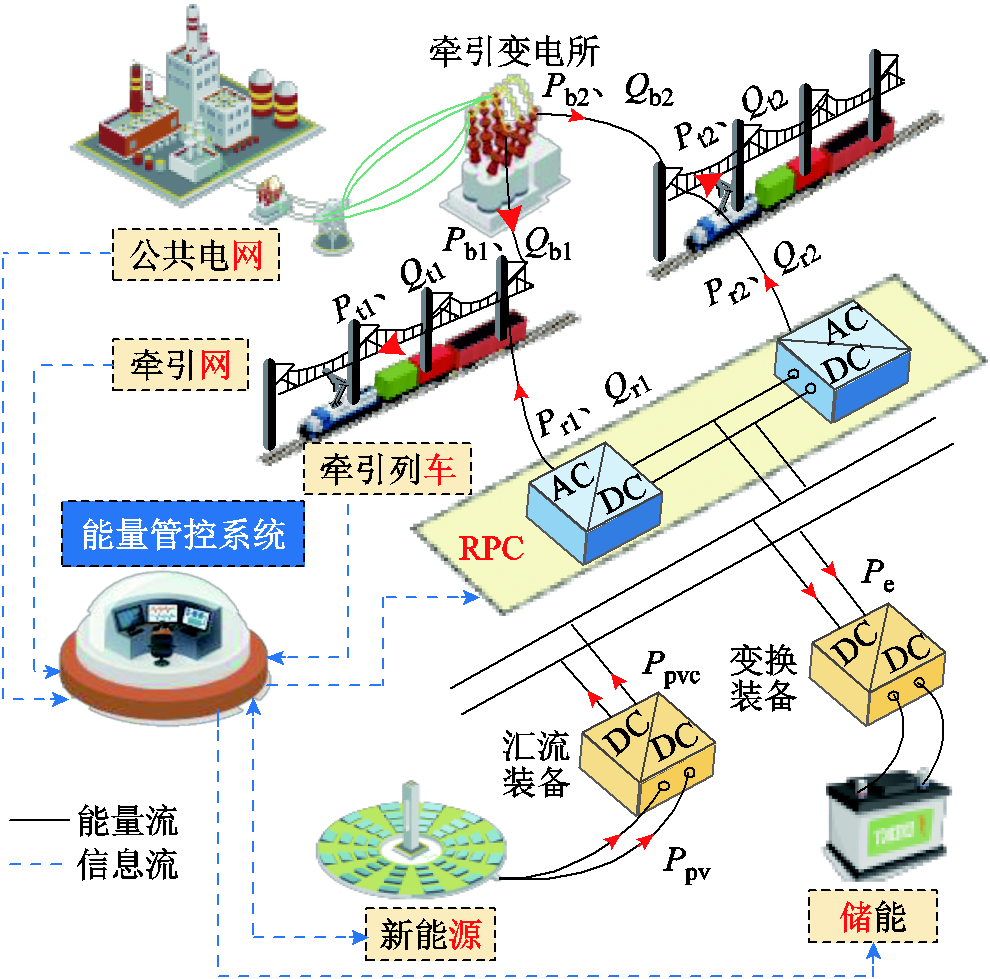
图1 电气化铁路“网-源-储-车”协同供电系统
Fig.1 Electrified railroad "network-source-storage-train" cooperative power supply system
摘要 构建“网-源-储-车”协同供电架构以实现电气化铁路的实时、可靠、高效能量管控，对推进“双碳”目标的实现具有重要意义。然而，既有规则管控策略主要针对“网-储-车”架构、管控，效果有限；优化管控策略往往关注于经济性等单一指标，可靠性较低。为此，该文首先补充了适用于“网-源-储-车”架构的规则管控策略，并构建了计及经济性与电压不平衡度的多目标管控优化模型；然后，提出一种基于“规则+优化”的电气化铁路站点实时能量管控策略，采用优化管控为主、规则管控为辅的形式，以实时管控时间阈值为导向，有序切换输出指令，在保证站点能量管控的可靠性与实时性的同时，实现整体运行效果的优化提升；最后，基于刘家沟牵引变电所实测数据对所提策略进行验证，结果表明，该文所提策略在实现新能源就地消纳与再生制动能量高效利用的同时，可改善牵引网电压水平与公共电网电能质量。
关键词：电气化铁路 网-源-储-车 实时能量管控 规则管控 优化管控
截至2022年底，我国电气化铁路运营总里程已突破15.5万 km，其中高速铁路总里程达4.2万 km。在促进国民经济增长的同时，电气化铁路的飞速发展加重了系统的能源消耗与节能减排压力。幸运的是，我国交通网与能源网存在交集，铁路沿线新能源丰富[1-2]。同时，牵引列车产生的再生制动能量具备较大消纳潜能[3]。构建“网-源-储-车”协同供电系统，实现新能源就地消纳与再生制动能量的回收利用，已成为电气化铁路运输助力“双碳”目标实现的重要举措。
然而，在电气化铁路“网-源-储-车”协同供电系统中，列车牵引负荷功率大且波动性强[4]，新能源与牵引负荷的时空差异性显著，源、荷平衡难以维持[5]，给系统的能量管控带来严峻的挑战。如何实现协同供电系统能量的稳定、实时、高效管控，在保障牵引负荷稳定供能的同时，提升系统的低碳、经济运行能力，是当前电气化铁路“网-源-储-车”协同供电系统亟待解决的难题。
目前，电气化铁路牵引供电系统的能量管控策略主要集中在规则管控与优化管控两方面。前者通过对供电系统各单元运行状态进行逻辑分析及判断以得到相应的能量管控指令；后者则通过求解优化模型，得到供电系统中可管控单元的功率指令。在规则管控方面，现有研究多为“网-储-车”架构下的能量管控策略，其主要通过探究不同储能介质下再生制动能量的消纳能力[6]，或对牵引供电系统运行工况进行分类及逻辑判断[7-8]，实现对储能功率指令的实时分配，最终达到有效回收列车再生制动能量的目的。然而，上述研究仅针对储能管控，未考虑新能源引入后系统内部双向功率不确定性、源荷突变性以及装置功率约束等问题，难以适应新能源并网与绿色能源发展的趋势。因此，关于“网-源-储-车”协同供电系统的规则管控策略有待进一步补充。此外，尽管凭借计算量小、实时管控能力强、可靠性高等优势，规则管控常用于实际工程中[9-10]，但受限于逻辑分析的单一目标判定机制，规则管控无法实现各部分能量传输损耗、运维成本与三相不平衡度等多目标的同步优化，难以保证新能源与再生制动能量的全局最优利用。
在优化管控方面，前期研究多为基于列车运行图的日前优化管控策略，如文献[11-12]分别针对“源-网-储-车”协同供电系统与同相牵引供电系统建立日前能量管控优化模型，并根据求解结果制定能量管控策略以实现系统经济运行水平的提升。然而，此类研究能量实时管控能力弱，难以适用于无日前列车负荷信息（如重载铁路牵引供电系统）的能量管控系统。为此，相关学者对优化模型或求解算法进行改进，以达到求解速度满足实时管控需求的目的。如文献[13]对所建立的两阶段鲁棒优化模型进行了线性化处理，且采用列和生成算法求解，大幅缩短了求解时间。文献[14]提出一种牵引供电系统有功、无功联合管控策略，采用模型预测控制算法对优化模型进行求解，并对模型进行了线性化处理，实现了求解精度与速度上的同步提升。然而，在实际情况中，优化模型的求解计算相对复杂，程序运行易存在“跑飞”现象[15]，进而导致优化管控指令缺失，严重影响牵引供电系统的稳定运行。因此，对于优化管控，指令发布的时效性与可靠性是其需重点突破的问题。
综上所述，规则管控与优化管控各具优劣，且二者之间存在较大的优势互补空间。基于此，本文提出一种基于“规则+优化”的电气化铁路站点实时能量管控策略。首先，以系统低碳经济运行为导向，确定“网-源-储-车”协同供电机制，并通过逻辑分析及判断，确定各工作模式下能量管控指令，从而完善“网-源-储-车”协同供电架构下的能量规则管控策略。然后，计及牵引变压器、铁路功率调节器（Railway Power Conditioner, RPC）功率传输损耗，以及新能源、列车再生制动能量弃能成本，完善系统运行成本函数以提升系统全局优化能力。进一步地，构建以站点运行成本最小及牵引变压器高压侧三相电压不平衡度最低为目标的站点多目标能量管控优化模型，采用逻辑前置方式实现模型简化，并根据求解结果制定站点能量优化管控策略。基于此，设计规则管控与优化管控的配合机制，以二者程序并行为始，以实时管控时间阈值为止，实现管控指令的有序切换及管控策略的优势互补。最后，基于刘家沟变电站实测数据验证本文所提能量管控策略的有效性与先进性。
为避免对现有线路进行过多改造，工程中常采用融通型供电架构建立电气化铁路“网-源-储-车”协同供电系统[16]，如图1所示。其中，新能源与储能系统RPC共直流端接入供电系统，在减轻公共电网供电压力的同时，又可利用储能系统的平峰填谷功效，有效地消纳新能源及列车再生制动能量[17-18]。
图1 电气化铁路“网-源-储-车”协同供电系统
Fig.1 Electrified railroad "network-source-storage-train" cooperative power supply system
能量管控系统是电气化铁路“网-源-储-车”协同供电系统的“大脑”，其接收来自系统各单元的运行状态信息，并对可管控单元发布功率运行指令，以保障供电系统的高效稳定运行。在图1中，能量管控系统接收的信息包括：①牵引变电所向牵引网两供电臂输送功率Pb1、Pb2、Qb1、Qb2；②两牵引供电臂范围内列车牵引负荷Pt1、Pt2、Qt1、Qt2；③储能荷电状态Soc；④光伏发电系统实时发电量Ppv。
基于上述接收的信息，通过逻辑分析或建模求解确定可管控单元的功率参考指令。能量管控系统向可管控单元发布的指令包括：①RPC传输功率Pr1、Pr2、Qr1、Qr2；②光伏发电系统输出功率Ppvc；③储能系统充放电功率Pe。
相比于“网-储-车”架构而言，电气化铁路“网-源-储-车”架构属多源供电系统，其牵引负荷的电力来源可为公共电网、新能源、储能及列车再生制动，内部能量流动错综复杂，可管控对象丰富多样。因此，有必要深度分析“网”“源”“储”“车”等各单元运行机制，确定系统工作状态，以充分调动各单元参与系统调控的潜力。
本文针对“网-源-储-车”协同供电系统设计的能量规则管控策略如图2所示。首先，根据协同供电系统保障牵引负荷供电、促进新能源与再生制动能量消纳的能量管控需求，确定协同供电系统运行机制。在供电环节，牵引网仅在新能源、再生制动能量以及储能供电后仍不满足列车牵引负荷需求时进行补充供电，以此提升新能源与再生制动能量消纳率；在电能消纳环节，新能源与再生制动能量优先由牵引列车消纳，当能量尚有富余时则由储能单元进行消纳，如此可避免储能频繁充放电以及能量的浪费。
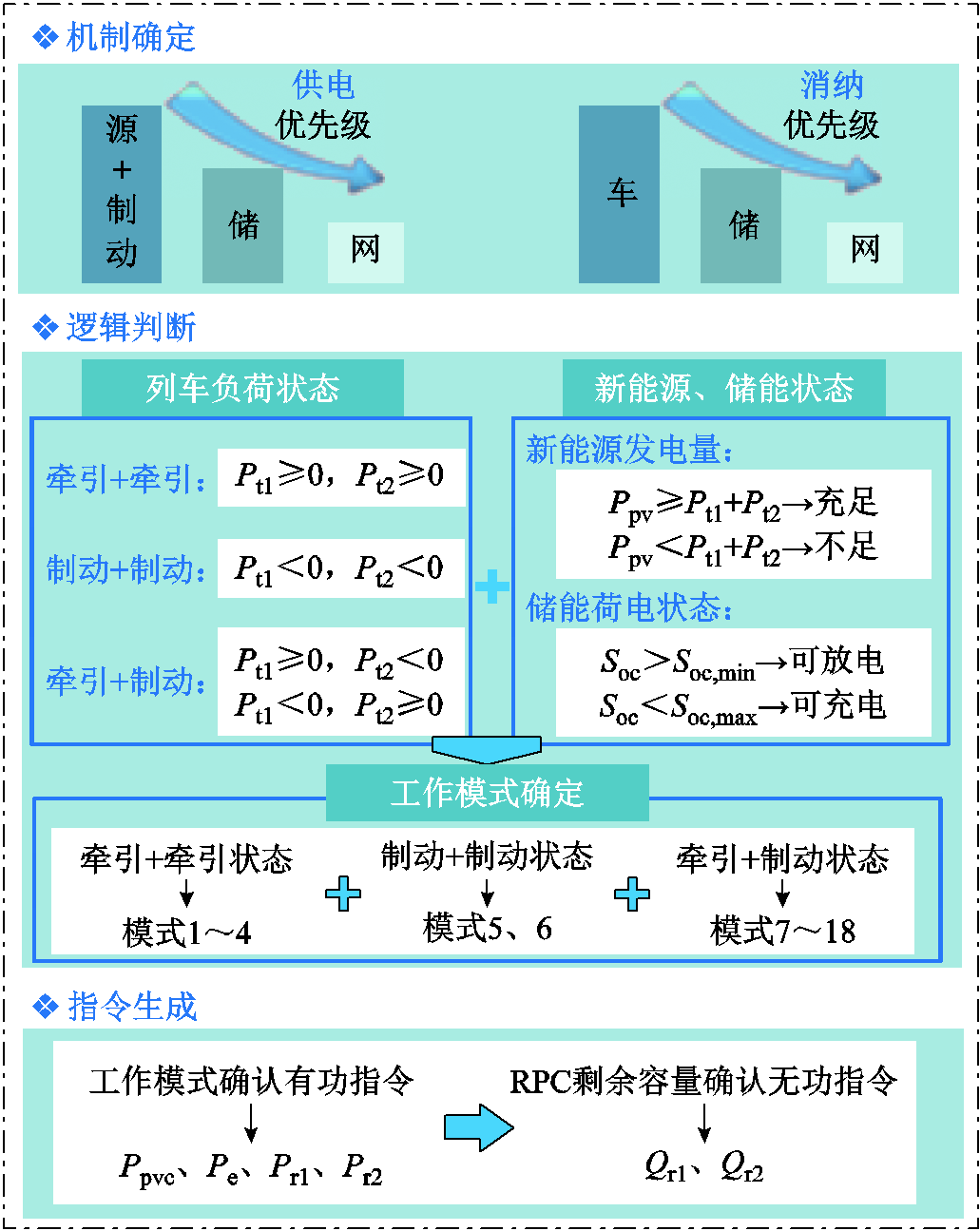
图2 “网-源-储-车”协同供电系统下的能量规则管控策略
Fig.2 Energy rule management strategy under "network-source-storage-train" cooperative power supply system
然后，剖析牵引变电所两侧供电臂上的列车负荷、新能源以及储能状态，通过逻辑判断确定协同供电系统工作模式。本文根据两相牵引负荷整体功率方向，将系统分为“牵引+牵引”、“制动+制动”以及“牵引+制动”三种工作状态。进一步地，结合新能源实时发电功率大小与储能荷电状态等信息，确定协同供电系统18种工作模式，具体模式分类流程如附图1所示。最后，确定各工作模式下新能源出力Ppvc、储能充放电Pe以及RPC有功传输功率Pr1、Pr2等有功功率指令，并根据RPC剩余容量确定其无功传输功率Qr1、Qr2等无功功率指令。具体有功、无功功率指令分别见附表1、附表2。
2.2.1 目标函数
对站点能量进行管控时，除考虑系统经济运行外，还需关注其能量流动对公共电网电能质量的影响，其中最突出的为由负序引起的三相电压不平衡度，然而，通过规则管控无法实现多目标的综合最优（具体论证见附录）。因此，为充分发挥“网-源-储-车”协同供电系统的灵活性以及降低其对公共电网不平衡度的危害，本文以最小化系统运行成本以及最小化牵引变压器高压侧三相电压不平衡度为目标，建立多目标优化模型。目标函数为
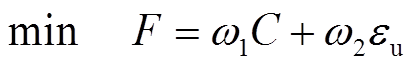（1）
式中，ω1、ω2为多目标权重，本文经熵权法确定[19]（具体流程见附录）；C为协同供电系统运行成本；εu为牵引变压器高压侧三相电压不平衡度。
对于协同供电系统运行成本，本文除购电成本、新能源发电运维以及储能运维等费用外，还考虑了牵引变压器与RPC等关键设备运行损耗费用以及新能源与再生制动能量的弃能成本，进一步完善协同供电系统运行成本函数，提升系统全局优化能力。运行成本表达式为
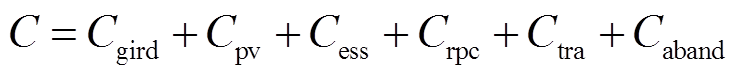（2）
式中，Cgrid为站点购电费用；Cpv为新能源发电运维费用；Cess为储能充放电运维费用；Crpc为RPC功率传输运行损耗费用；Ctra为牵引变压器功率传输运行损耗费用；Caband为新能源与再生制动能量弃能成本。各部分成本具体计算公式为
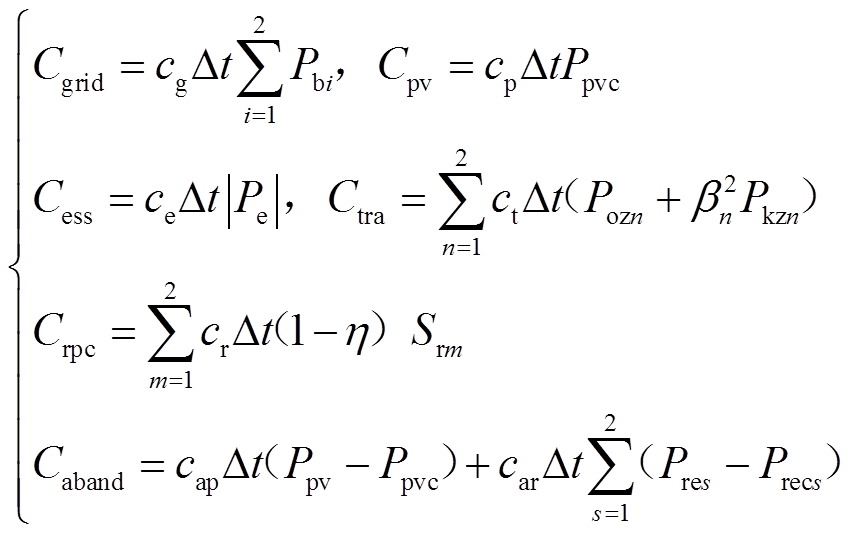（3）
式中，cg、cp、ce、ct、cr、cap、car分别对应各部分成本系数；Δt为管控周期；Pbi为牵引变压器i输出有功功率；Ppvc为新能源发电系统实际输出功率，即光伏消纳功率；Pe为储能实时充放电功率，充电为正，放电为负；Poz、Pkz分别为牵引变压器空载损耗与短路损耗；β为牵引变压器负载率；Srm为RPCm传输功率；η为RPC功率传输效率；Ppv为新能源系统预测发电功率；Pres为变电所两侧列车产生的再生制动功率大小；Precs为再生制动实际回收的功率。
根据文献[20]，牵引变压器高压侧三相电压不平衡度表达式为
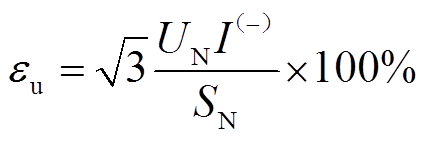（4）
式中，UN、SN分别为三相电网侧额定线电压与额定短路容量；I(-)为牵引变压器负序电流，其具体计算参考文献[21]，本文不再赘述。
2.2.2 约束条件
对于“网-源-储-车”协同供电系统中“网”而言，牵引变压器与RPC等设备需满足容量约束。此外，本文不考虑有功馈网，即牵引变压器输出非负。故共有约束条件为
（5）
式中，Qbi为牵引变压器i输出无功功率；Prm、Qrm分别为RPCm输出有功功率与无功功率；SbN、SrN分别为牵引变压器与RPC端口的额定容量。
对于“网-源-储-车”协同供电系统中“源”而言，需新能源输出非负且小于预测发电量约束，即
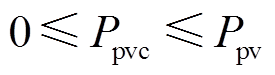（6）
对于“网-源-储-车”协同供电系统中“储”而言，需满足储能充放电功率限制以及储能荷电状态约束，即
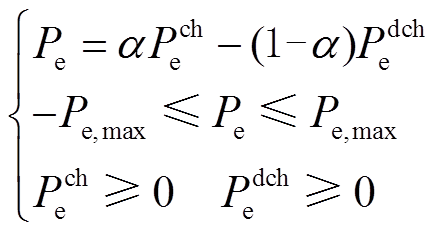（7）
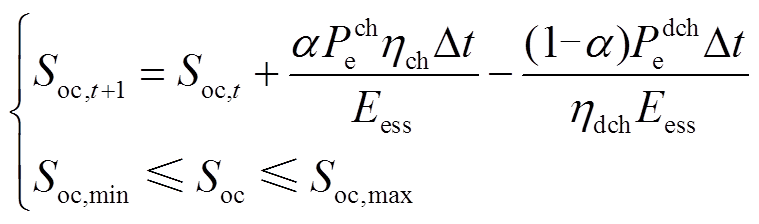（8）
式中，Pech与Pedch分别为充、放电功率；α为充放电标志，0表示储能放电，1表示储能充电；ηch与ηdch分别为储能充、放电效率；Eess为储能容量。
对于“网-源-储-车”协同供电系统中“车”而言，回收的列车再生制动能量需非负，且小于列车再生制动产生的总能量，即
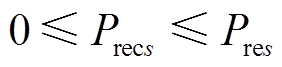（9）
此外，对于整个“网-源-储-车”协同供电系统，需满足潮流约束，有
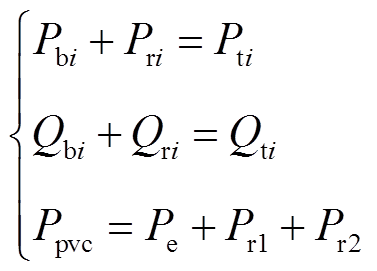（10）
式中，Pti、Qti分别为牵引列车有功与无功负荷。
2.2.3 能量优化管控策略
计及经济性与电压不平衡度的多目标优化管控策略如图3所示。首先，建立以运行成本最小和牵引变压器高压侧三相电压不平衡度最低为目标的优化模型。然后，通过逻辑前置的方式缩减优化模型中需求解的模型变量。模型的简化主要表现在两方面：一是通过逻辑判断，确定牵引变压器是否需输出能量，即确定Pb1与Pb2是否为0，可缩减求解变量个数；二是根据新能源发电情况判断储能的功率传输方向，即确定储能为充电（Pe≥0）或为放电（Pe≤0）状态，如此可去除式（3）中储能运维费的绝对值符号，线性化优化模型。模型简化具体过程如附图2所示。最后，在Matlab环境下，通过Cplex商业规划求解器对简化后的优化模型进行求解，得到协同供电系统的能量优化管控指令。
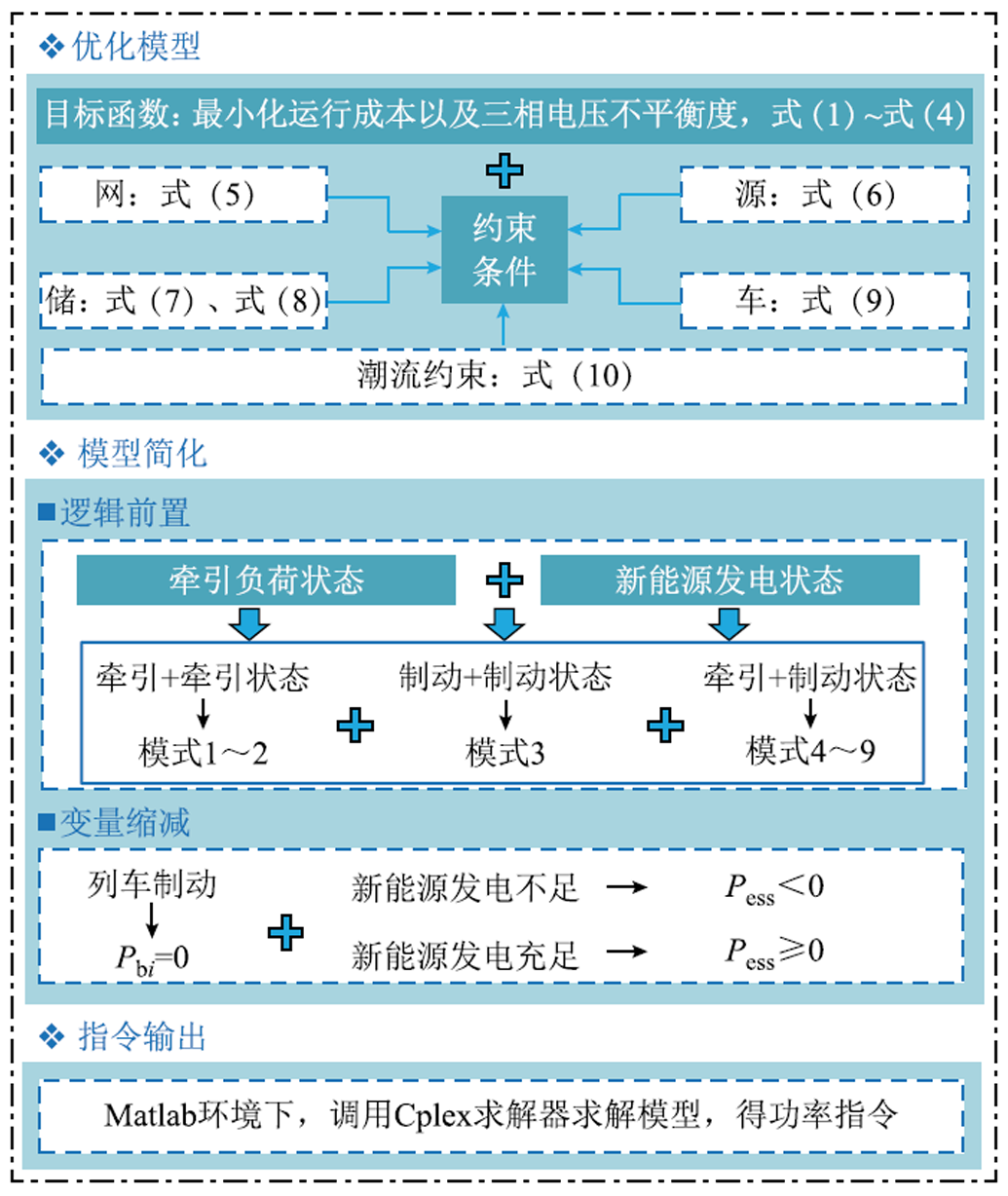
图3 计及经济性与电压不平衡度的多目标优化管控策略
Fig.3 Multi-objective optimal management strategy for economy and voltage imbalance
能量管控策略作为能量管控系统的核心组成部分，其设计的合理性直接影响整个协同供电系统的稳定与高效运行。由前文分析可知，规则管控的实时管控能力强、指令输出稳定可靠，但管控目标单一、全局增益能力较弱。优化管控可提升系统全局优化运行能力，但受制于其时效性与可靠性的限制，难以进行工程应用。因此，本文提出一种规则与优化并行的能量实时优化管控策略，其综合了上述两种策略的优势，在保证时效性与可靠性的同时，又可提升系统低碳经济运行水平，规则管控与优化管控配合示意图如图4所示。图4中，tL为逻辑管理策略得到指令所需时间，tY为优化管理策略得到指令所需时间。
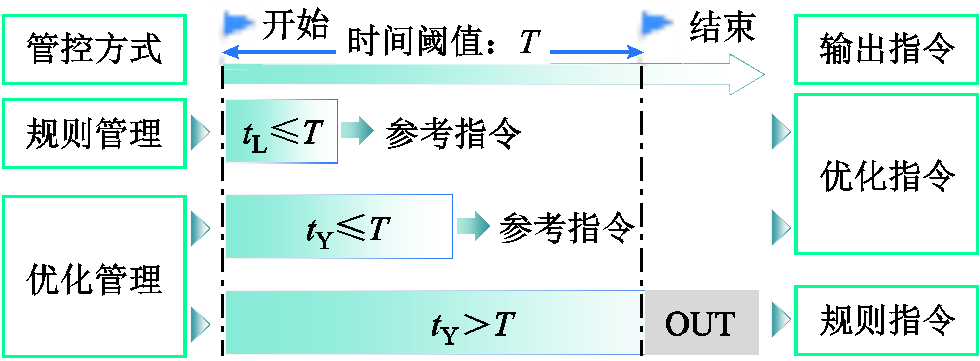
图4 规则管控与优化管控配合示意图
Fig.4 Rule management and optimization management with the schematic diagram
本文通过设置时间阈值T作为规则指令与优化指令输出的筛选依据，以保障整体策略的时效性。指令输出具体过程为：能量管理系统接收来自各单元运行状态信息后，两类能量管控策略的程序同时运行。当基于“优化”的能量管控策略程序在时间阈值T约定范围内可给出参考指令时，能量管控系统则向可管控单元发布优化指令，以实现供电系统的全局最优运行。反之，则发布经基于“规则”的能量管控策略程序得到的规则指令，以维持本文能量管控策略下功率指令输出的可靠性。两种能量管控策略相互配合，最终实现协同供电系统能量的实时、可靠、高效管控。
本文基于刘家沟牵引变电所实测牵引负荷数据对本文能量管控策略进行验证分析。在24 h内，光伏发电系统的光伏发电总量为49.34 MW·h，列车再生制动产生的总能量为7.08 MW·h，如图5所示。硬件平台为12th Gen Intel(R) Core(TM) i5-12600KF 3.7 GHz和16 GB RAM。软件平台为Matlab R2021a，集成优化工具箱YALMIP（版本20200116）和求解器IBM ILOG CPLEX（版本12.9.0）。
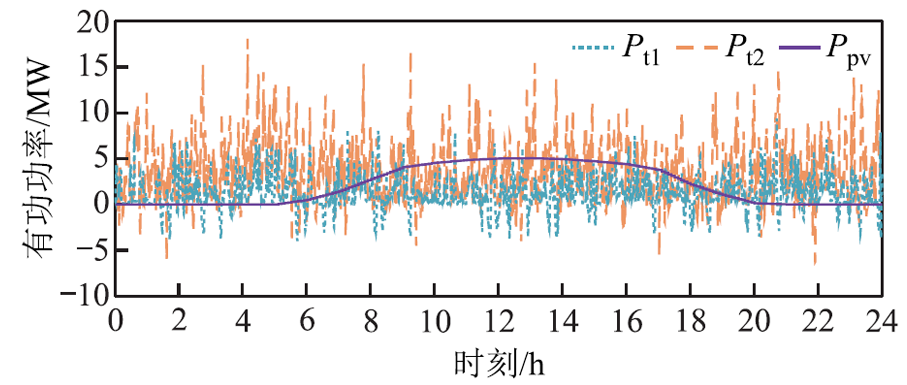
图5 牵引负荷与光伏发电数据
Fig.5 Traction load and PV power generation data
基于图5数据，确定多目标优化模型权重为ω1=0.838，ω2=0.162。实时能量管控时间阈值T设为0.5s。牵引变压器与RPC损耗成本系数以及光伏、再生制动能量弃能成本系数同电网电价，均取0.557元/(kW·h)[11]；光伏发电系统与储能系统运维成本系数均取0.05元/(kW·h)[22]。其余仿真参数见表1。
表1 仿真参数
Tab.1 Simulation parameters
参数数值 RPC端口容量SrN/MW10 储能储能容量Eess/(MW·h)2 最大充/放电功率/MW4 初始荷电状态0.5 荷电状态区间[0.1,0.9] 充（放）电效率[23]0.9 (0.9) 光伏装机容量/MW6.3 变电所变压器容量SbN/MW20 变压器空载损耗Poz/kW21 变压器短路损耗Pkz/kW77
为说明本文综合“规则”与“优化”能量管控策略的合理性，需要对规则管控与优化管控下的协同供电系统的运行效果以及功率指令输出时效性进行对比分析。
3.1.1 协同供电系统运行效果对比
首先，在光伏与再生制动能量消纳方面，图6给出了对比图，对应消纳率情况见表2。其中，优化管控下光伏消纳率可达96.82%，再生制动能量消纳率可达99.09%，均高于规则管控下的96.37%与92.96%，且整体上优化管控消纳能量比规则管控高0.77 MW·h/天。
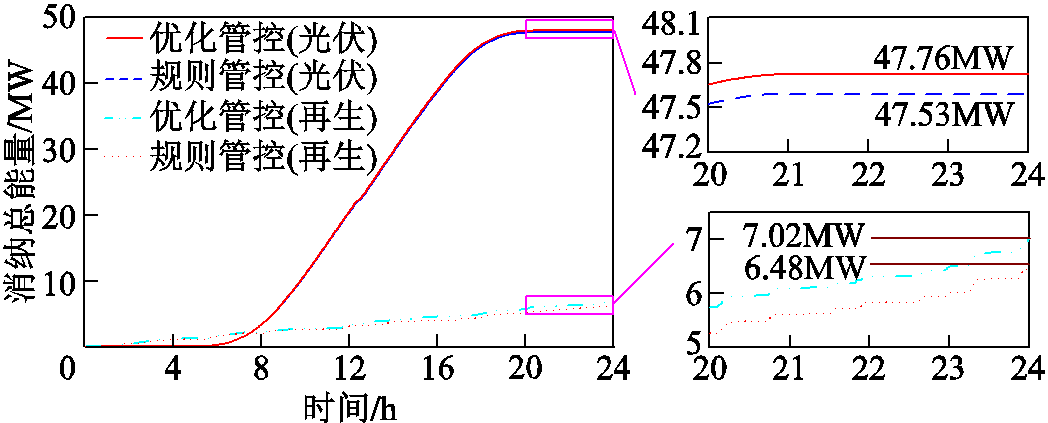
图6 不同能量管控策略下光伏与再生制动能量对比
Fig.6 Comparison of photovoltaic and regenerative braking energy under different energy management strategies
表2 光伏、再生制动消纳量与消纳率情况
Tab.2 Photovoltaic energy, regenerative braking energy consumption and consumption rate
类别总能量/ (MW·h)规则管控优化管控 消纳量/ (MW·h)消纳率(%)消纳量/ (MW·h)消纳率(%) 光伏49.3447.5396.3747.7696.82 再生制动7.086.4892.967.0299.09
其次，对比不同能量管控策略下的系统运行成本，如图7所示。由图7可知，两种能量管控策略下运行成本均要低于初始未管控时的成本。其中，规则管控相比初始成本降低42.04%，而优化管控可进一步降低运行成本，其下降比率达42.59%。
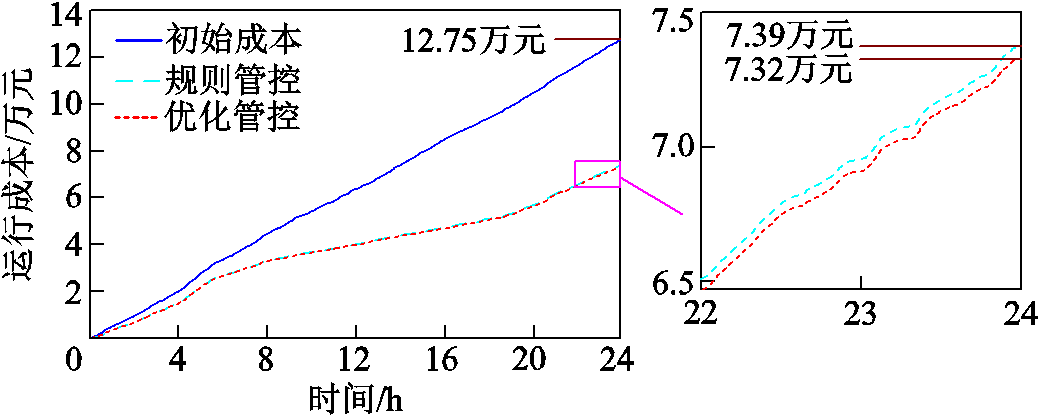
图7 不同能量管控策略下系统运行成本对比
Fig.7 Comparison of system operating costs under different energy management strategies
此外，对比不同管控策略下牵引变压器高压侧三相电压不平衡度，其对比如图8所示。由图8可知，未进行能量管控时，电压不平衡度最大值达到了3.21%且多次超出国标（εu≤2%）要求。进行能量管控后，电压不平衡度得到显著改善，但相比规则管控，优化管控的降低程度更明显，且最大值仅为1.24%（所有测试时刻均符合国标限定）。
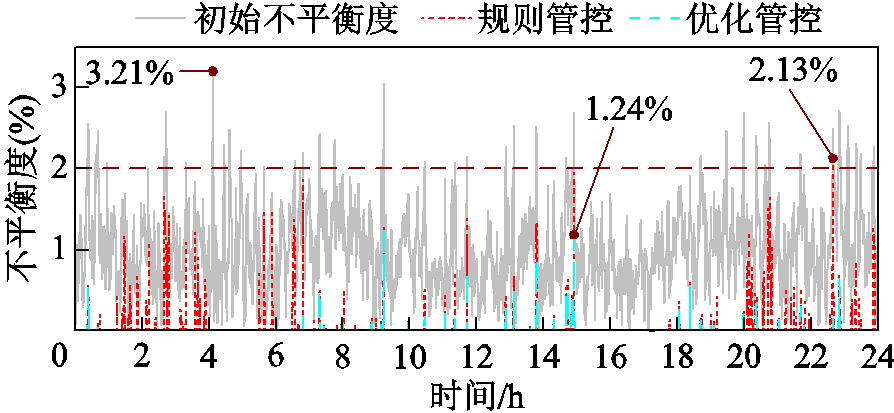
图8 牵引变压器高压侧三相电压不平衡度对比
Fig.8 Comparison of three-phase voltage unbalance on the high-voltage side of the traction transformer
3.1.2 功率指令输出时效性对比
规则管控与优化管控的指令生成时间对比如图9所示。由图9可知，规则管控的指令生成时间为ms级（最大值为4 ms），完全满足实时管控时间阈值（T=0.5 s）的限定。相比之下，优化管控虽大部分指令生成时间符合实时能量管控要求，但仍有不少的优化指令生成时间超出实时管控限定，其中最大值达到了1.7 s。
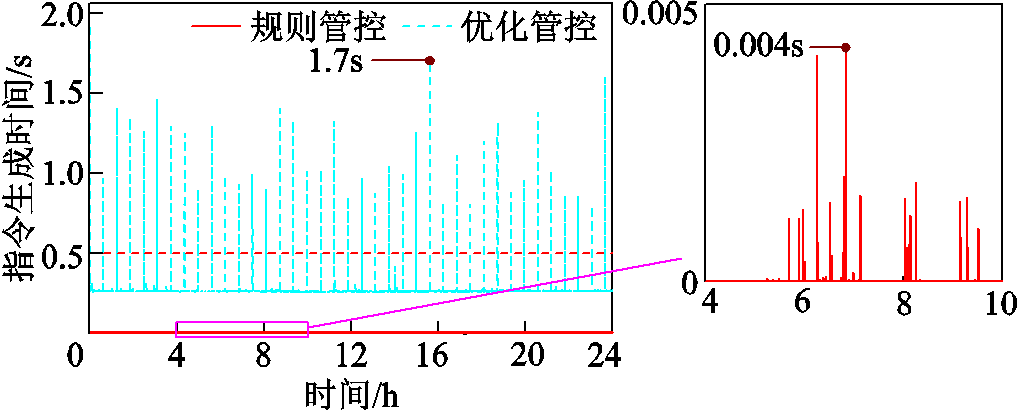
图9 不同能量管控策略的指令生成时间对比
Fig.9 Comparison of command generation time for different energy management strategies
综上分析可知，优化管控可在规则管控基础上进一步提升协同供电系统的经济运行能力与电能质量水平，但仅凭优化管控又难以满足系统能量的实时管控需求。因此，可通过两种策略相互配合以充分发挥各自优势，进而实现协同供电系统中新能源与再生制动能量的高效利用、三相电压不平衡度的显著降低，以及系统能量的可靠、实时管控。
本文基于“规则+优化”的能量管控策略的指令生成时间不会超过实时能量管控时间阈值（0.5 s），如图10所示。由其局部展开图可知，优化管控的指令生成时间低于0.5 s时（图中阴影区域），能量管控系统会输出优化指令；当指令生成时间超过0.5 s时，能量管控系统会输出早已生成的规则指令以保证能量实时管控需求。
图10 能量管控指令生成时间
Fig.10 Generation time of energy management command
对比未进行能量管控的传统牵引供电系统（无新能源、储能装置以及RPC，传统方案）与基于“规则+优化”的能量管控策略下的“网-源-储-车”协同供电系统（本文方案）仿真结果见表3。由表3可知，在本文方案下，光伏与再生制动能量的消纳率分别为96.82%与98.38%，可单日降低42.51%的运行成本，实现了协同供电系统低碳、经济运行。
表3 不同方案下仿真结果
Tab.3 Simulation results under different schemes
方案光伏消纳/MW（消纳率）再生消纳/MW（消纳率）运行成本/万元 传统方案0012.75 本文方案47.76（96.82%）6.96（98.38%）7.33
图11是传统方案与本文方案下牵引变压器低压侧电压波动情况。可知，传统方案下变压器桥臂1电压波动范围为[0.945 pu, 1.006 pu]，桥臂2电压波动范围为[0.923 pu, 1.028 pu]。本文方案变压器两侧的电压波动均在[0.996 pu，1 pu]范围内，波动范围缩减比例可达93.44%。由此说明，在本文能量管控策略下，两侧牵引网电压水平都得到了整体提升，有助于提升牵引网的能量传输效能。
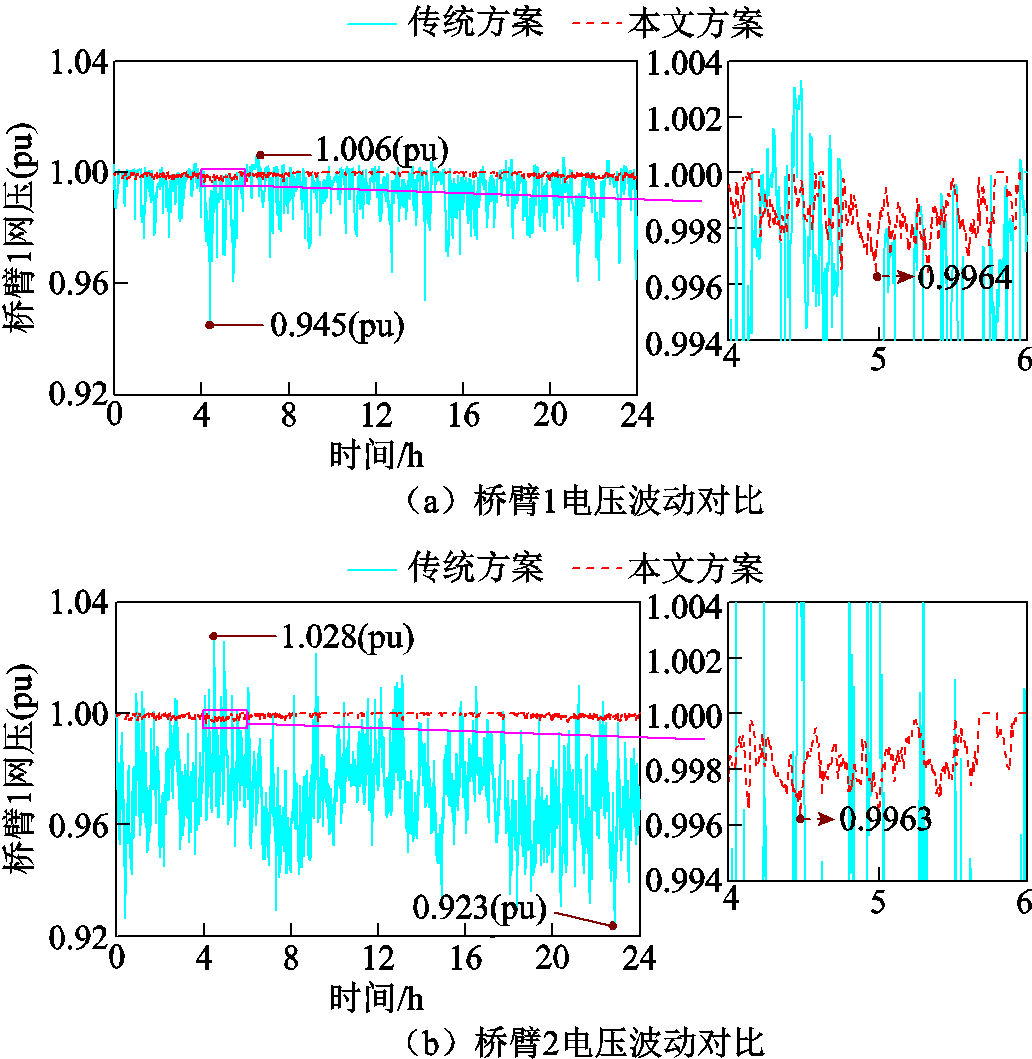
图11 牵引变压器低压侧电压波动对比
Fig.11 Comparison of voltage fluctuations on the low voltage side of the traction transformer
对比本文方案与传统方案下牵引变压器两臂输出功率与高压侧三相电压不平衡度，如图12所示。由图12a、图12b可知，未进行能量管控时，牵引变压器左右桥臂输出功率差值最大可达17.73 MW；而在本文能量管控策略下，牵引变压器左右桥臂功率输出基本平衡，最大差值仅为6.93 MW。由图12c可知，在本文能量管控策略下，电压不平衡度最大值由3.21%降为1.81%，符合三相电压不平衡度国标要求。
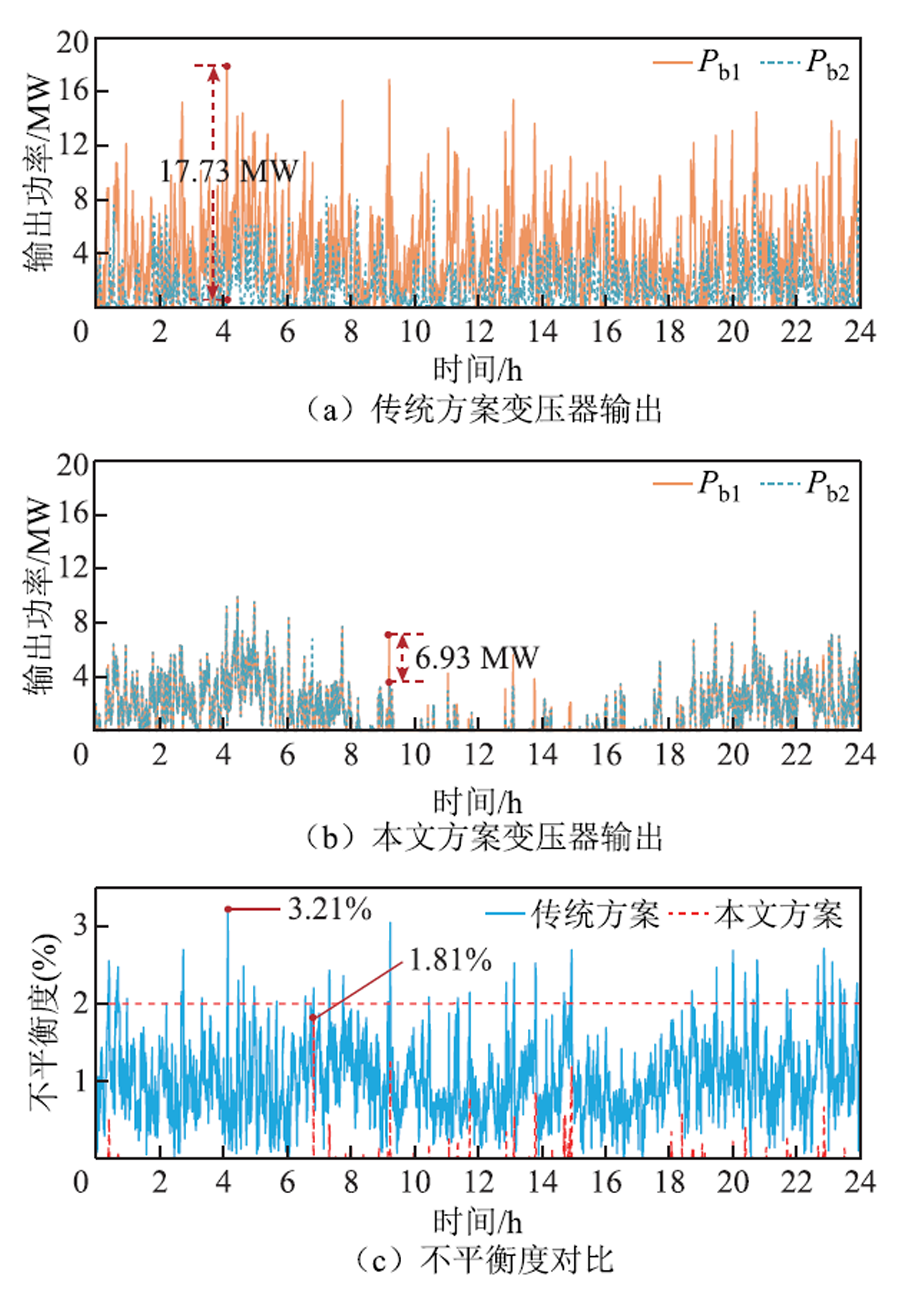
图12 牵引变压器输出与三相电压不平衡度对比
Fig.12 Comparison of traction transformer output and three-phase voltage unbalance
相对于传统牵引供电系统，“网-源-储-车”协同供电系统引入了新能源和储能，且在牵引变电所设置了RPC，这在一定程度上增加了牵引供电系统的建造成本。为验证本文基于“规则+优化”的能量管控策略的工程可行性，对该策略管控下的“网-源-储-车”协同供电系统进行经济性分析。传统牵引供电系统改造成本见表4，表4中参数源于刘家沟示范工程。
表4 传统牵引供电系统改造成本
Tab.4 Traditional traction power supply system renovation cost
类别容量单价总价/万元 RPC10 MW100万元/MW1 000 储能2 MW·h160万元/(MW·h)320 光伏6.3 MW450万元/MW2 835 总成本4 155
由表3可知，本文方案可单日节省5.42万元。若以该日测量数据进行投资分析，本文能量管控策略下，每年可节省约1 978万元。由表4可知，“网-源-储-车”协同供电系统建设改造成本为4 155万元。在此基础上，绘制两种方案下的成本年变化曲线，如图13所示。可知，本文方案预计经2.1年可实现投资回本。此外，综合考虑光伏发电系统、储能系统以及变流器的平均寿命[24-25]，本文取协同供电系统的全寿命周期为15年。在此年限内，本文方案预估节省2.55×104万元。
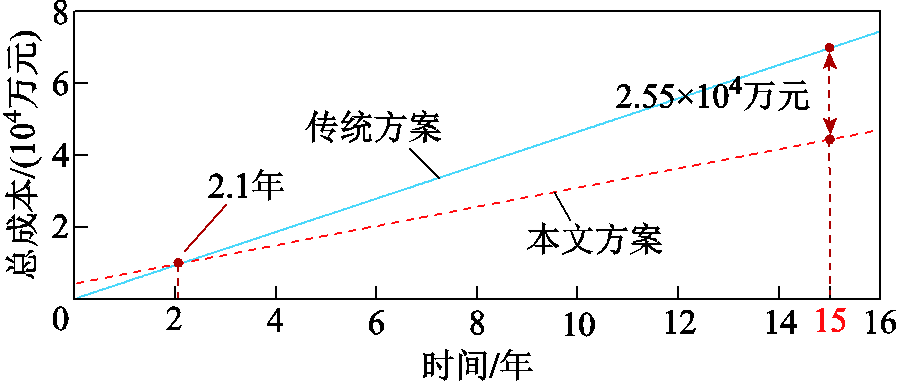
图13 协同供电系统投资分析
Fig.13 Investment analysis of cooperative power supply system
针对电气化铁路“网-源-储-车”协同供电系统能量实时管控难，新能源与再生制动能量利用率低等问题，本文设计了基于“规则+优化”的电气化铁路站点实时能量管控策略。通过实测数据算例验证，可得如下结论：
1）针对“网-源-储-车”架构，本文设计的规则管控策略可实现ms级指令输出，可弥补优化管控在实时管控要求内无法可靠输出指令的缺陷。
2）相比规则管控，本文设计的多目标优化管控策略可单日多消纳能量0.77 MW、运行成本可多降低0.55%且电压不平衡度无超国标现象，可填充规则管控在系统多目标优化运行上的不足。
3）基于规则管控与优化管控的特点，本文制定了基于“规则+优化”的能量管控策略。相比于未管控的传统牵引供电系统，本文策略下的系统单日运行成本可降低42.51%，牵引变压器低压侧电压波动范围可缩减93.44%，且高压侧三相电压不平衡度最高值仅为1.81%（所有测试时刻均满足国标要求）。
4）基于“规则+优化”的实时能量管控策略下，“网-源-储-车”协同供电系统的投资回本年限预估为2.1年，全寿命周期内可节省2.55×104万元，为实际工程的实施提供了有力支撑。
值得说明的是，本文采用熵权法确定多目标权重，暂未从主观因素层面评价各目标重要程度，后续可结合层次分析法、专家调查法等主观评价方法对目标进行权重分配。
附 录
1. 规则管控策略无法保障多目标最优的论证
1）规则管控策略解决多目标问题流程
多目标优化问题即在非单一目标的情况下，综合考虑各决策变量对每个目标的影响程度，使整体目标达到综合最优，其数学模型一般由多个目标函数以及与其相关的约束条件组成，可表示为
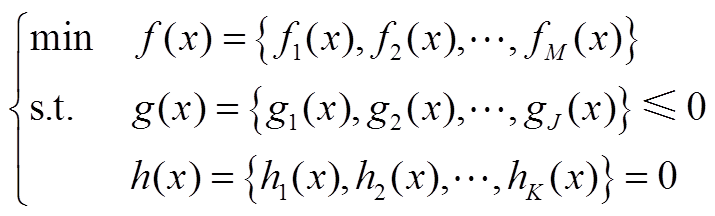（A1）
式中，M、J、K分别为子目标函数的总数、不等式约束总数以及等式约束总数；f(x)、g(x)、h(x)分别为目标函数、不等式约束与等式约束的集合。
规则管控通过对系统工作状态进行逻辑判断，并根据管控目标制定赋值规则，从而确定各工作状态下的功率指令。值得说明的是，在同一规则管控策略中，逻辑判断顺序以及确定功率指令的规则不发生改变。面对多目标问题时，规则管控策略给出功率指令的流程如附图3所示。
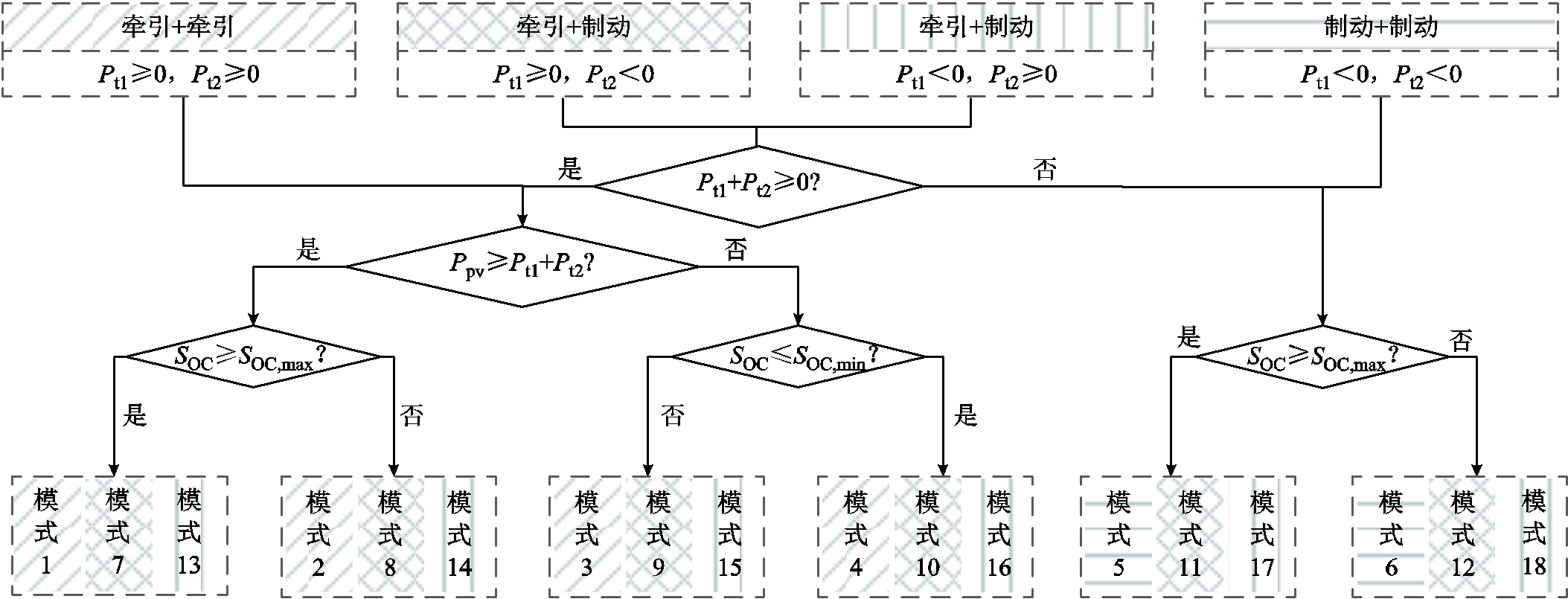
附图1 模式分类具体流程
App.Fig.1 Specific process of pattern classification
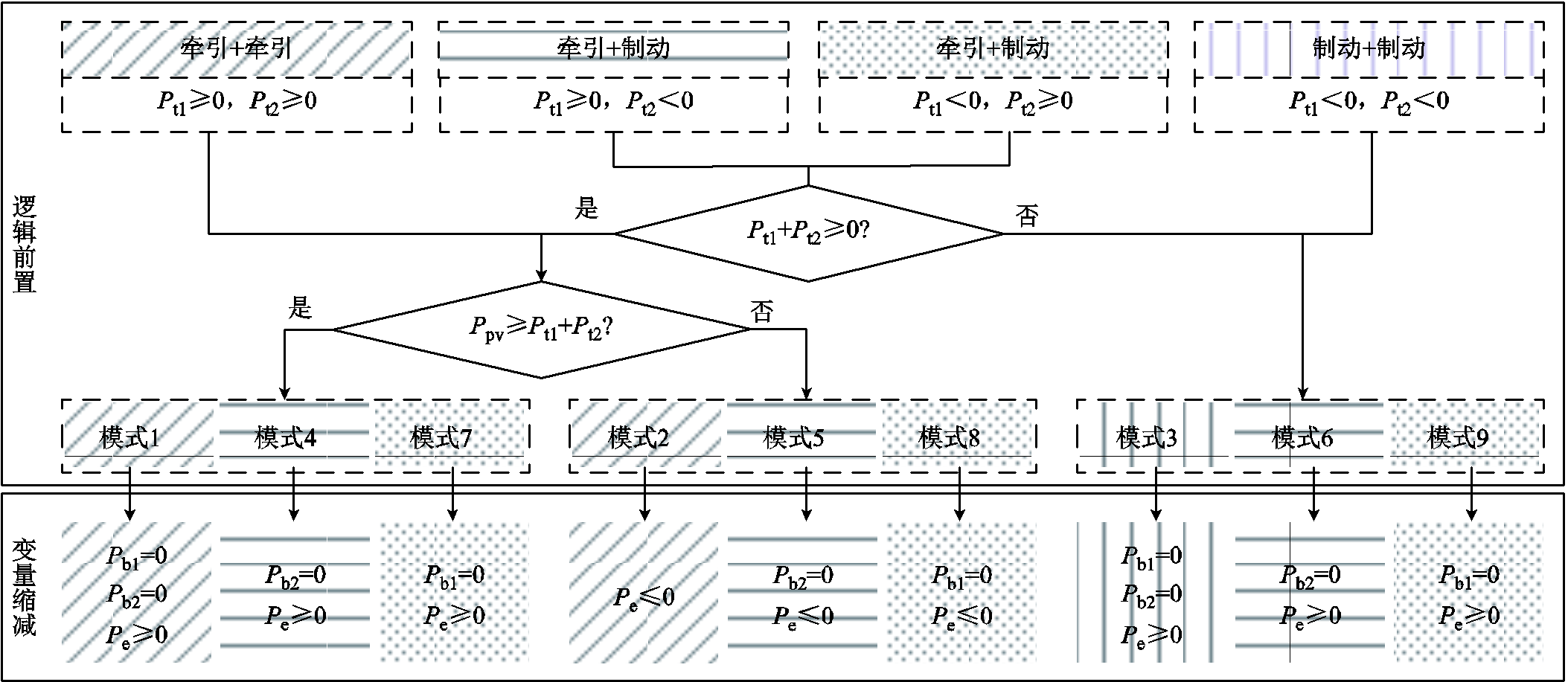
附图2 模型简化示意图
App.Fig.2 Schematic diagram of model simplification
附表1 规则管控有功功率指令分配表
App.Tab.1 Rule management active power command distribution table
状态模式牵引供电系统状态功率指令 牵引+牵引1Pt1≥0, Pt2≥0Pt1+Pt2≤Ppv, SOC≥SOC,maxPr1=Pt1, Pr2=Pt2, Pe=0, Ppvc=Pt1+Pt2 2Pt1+Pt2≤Ppv, SOC＜SOC,maxPt1+Pt2+Pe,max≤PpvPr1=Pt1, Pr2=Pt2, Pe=Ppv-Pt1-Pt2, Ppvc=Ppv Pt1+Pt2+Pe,max＞PpvPr1=Pt1, Pr2=Pt2, Pe=Pe,max, Ppvc=Pe+Pt1+Pt2 3Pt1+Pt2＞Ppv, SOC＞SOC,minPt1+Pt2≤Ppv+Pe,maxPr1=Pt1, Pr2=Pt2, Pe=Pt1+Pt2-Ppv, Ppvc=Ppv Pt1+Pt2＞Ppv+Pe,maxPr1=Pr2=(Pe,max+Ppv)/2, Pe=Pe,max, Ppvc=Ppv 4Pt1+Pt2＞Ppv, SOC≤SOC,minPr1=Pr2=Ppv/2, Pe=0, Ppvc=Ppv 制动+制动5Pt1＜0, Pt2＜0SOC≥SOC,maxPr1=Pr2=0, Pe=0, Ppvc=0 6SOC＜SOC,maxPpv-Pt1-Pt2＜Pe,maxPr1=Pt1, Pr2=Pt2, Pe=Ppv-Pt1-Pt2, Ppvc=Ppv Ppv-Pt1-Pt2≥Pe,maxPr1=Pt1, Pr2=Pt2, Pe=Pe,max, Ppvc=Ppv 牵引+制动（整体牵引）7Pt1≥0, Pt2＜0, Pt1+Pt2≥0Pt1+Pt2≤Ppv, SOC≥SOC,maxPr1=Pt1, Pe=Ppv-Pt1-Pt2, Pr2=-Pt1Pt2/(Ppv-Pt2), Ppvc=Pt1Ppv/(Ppv-Pt2) 8Pt1+Pt2≤Ppv, SOC＜SOC,maxPpv-Pt2＜Pt1+Pe,maxPr1=Pt1, Pe=Ppv-Pt1-Pt2, Pr2=-(Pt1+Pe)Pt2/(Ppv-Pt2), Ppvc=(Pt1+Pe)Ppv/(Ppv-Pt2) Ppv-Pt2≥Pt1+Pe,maxPr1=Pt1, Pe=Pe,max, Pr2=-(Pt1+Pe)Pt2/(Ppv-Pt2), Ppvc=(Pt1+Pe)Ppv/(Ppv-Pt2) 9Pt1+Pt2＞Ppv, SOC＞SOC,minPt1+Pt2≤Ppv+Pe,maxPr1=Pt1, Pr2=Pt2, Pe=Pt1+Pt2-Ppv, Ppvc=Ppv Pt1+Pt2＞Ppv+Pe,maxPr1=Ppv-Pt2+Pe,max, Pr2=Pt2, Pe=Pe,max, Ppvc=Ppv 10Pt1+Pt2＞Ppv, SOC≤SOC,minPr1=Ppv-Pt2, Pr2=Pt2, Pe=0, Ppvc=Ppv 牵引+制动（整体制动）11Pt1≥0, Pt2＜0, Pt1+Pt2＜0SOC≥SOC,maxPr1=Pt1, Pr2=-Pt1, Pe=0, Ppvc=0 12SOC＜SOC,maxPpv-Pt2＜Pt1+Pe,maxPr1=Pt1, Pe=Ppv-Pt1-Pt2, Pr2=-(Pt1+Pe)Pt2/(Ppv-Pt2), Ppvc=(Pt1+Pe)Ppv/(Ppv-Pt2) Ppv-Pt2≥Pt1+Pe,maxPr1=Pt1, Pe=Pe,max, Pr2=-(Pt1+Pe)Pt2/(Ppv-Pt2), Ppvc=(Pt1+Pe)Ppv/(Ppv-Pt2) 牵引+制动（整体牵引）13Pt1＜0, Pt2≥0, Pt1+Pt2≥0Pt1+Pt2≤Ppv, SOC≥SOC,maxPr2=Pt2, Pe=Ppv-Pt1-Pt2, Pr1=-Pt2Pt1/(Ppv-Pt1), Ppvc=Pt2Ppv/(Ppv-Pt1) 14Pt1+Pt2≤Ppv, SOC＜SOC,maxPpv-Pt1＜Pt2+Pe,maxPr2=Pt2, Pe=Ppv-Pt1-Pt2, Pr1=-(Pt2+Pe)Pt1/(Ppv-Pt1), Ppvc=(Pt2+Pe)Ppv/(Ppv-Pt1) Ppv-Pt1≥Pt2+Pe,maxPr2=Pt2, Pe=Pe,max, Pr1=-(Pt2+Pe)Pt1/(Ppv-Pt1), Ppvc=(Pt2+Pe)Ppv/(Ppv-Pt1) 15Pt1+Pt2＞Ppv, SOC＞SOC,minPt1+Pt2≤Ppv+Pe,maxPr1=Pt1, Pr2=Pt2, Pe=Pt1+Pt2-Ppv, Ppvc=Ppv Pt1+Pt2＞Ppv+Pe,maxPr1=Pt1, Pr2=Ppv-Pt1+Pe,max, Pe=Pe,max, Ppvc=Ppv 16Pt1+Pt2＞Ppv, SOC≤SOC,minPr1=Pt1, Pr2=Ppv-Pt1, Pe=0, Ppvc=Ppv
（续）
状态模式牵引供电系统状态功率指令 牵引+制动（整体制动）17Pt1＜0, Pt2≥0, Pt1+Pt2＜0SOC≥SOC,maxPr1=-Pt2, Pr2=Pt2, Pe=0, Ppvc=0 18SOC＜SOC,maxPpv-Pt1＜Pt2+Pe,maxPr2=Pt2, Pe=Ppv-Pt1-Pt2, Pr1=-(Pt2+Pe)Pt1/(Ppv-Pt1), Ppvc=(Pt2+Pe)Ppv/(Ppv-Pt1) Ppv-Pt1≥Pt2+Pe,maxPr2=Pt2, Pe=Pe,max, Pr1=-(Pt2+Pe)Pt1/(Ppv-Pt1), Ppvc=(Pt2+Pe)Ppv/(Ppv-Pt1)
附表2 规则管控无功功率指令分配表
App.Tab.2 Rule management reactive power command allocation table
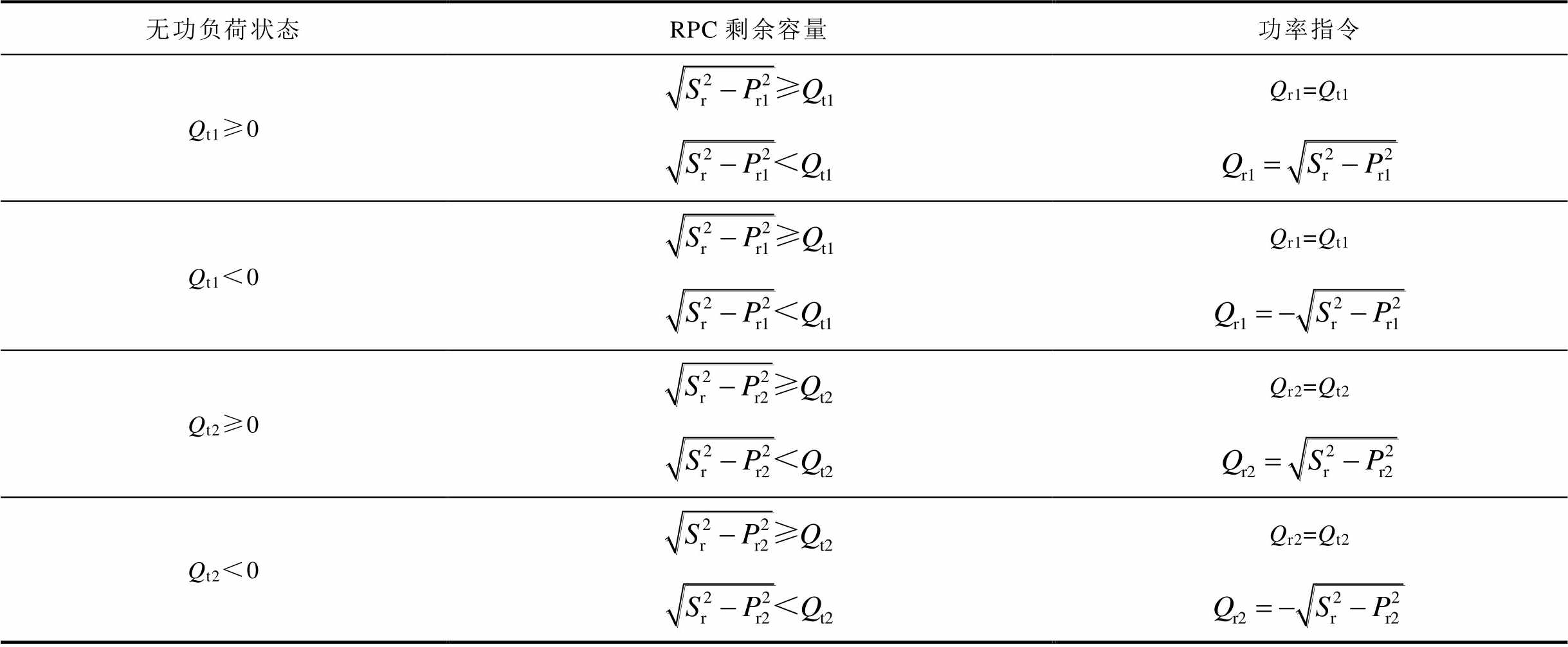
无功负荷状态RPC剩余容量功率指令 Qt1≥0Qr1=Qt1 Qt1＜0Qr1=Qt1 Qt2≥0Qr2=Qt2 Qt2＜0Qr2=Qt2
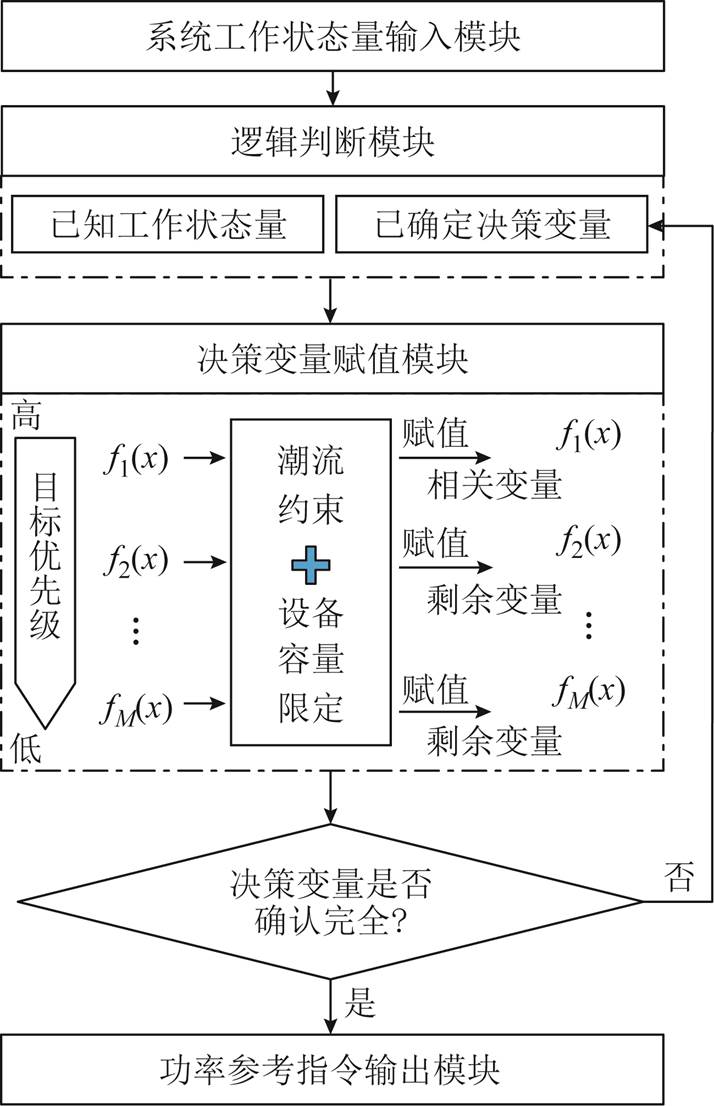
附图3 规则管控策略处理多目标流程
App.Fig.3 The flow chart of handling multi-objective problems through rule control strategies
为方便描述，设多目标优化中目标优先级排序为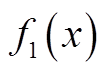
, 
, 
, 
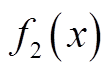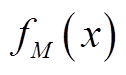，与各目标相关的决策变量集合分别为
, 
, , 
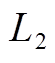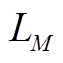。由附图3可知，在潮流以及设备容量等条件的限定下，规则管控策略依次对与各级目标相关的决策变量进行赋值。由于决策变量被赋值后，后续不会再改变，因此，各级目标可确定的决策变量见附表3。
附表3 各级目标可确定的决策变量范围
App.Tab.3 The range of decision variables that can be determined for each level of goal
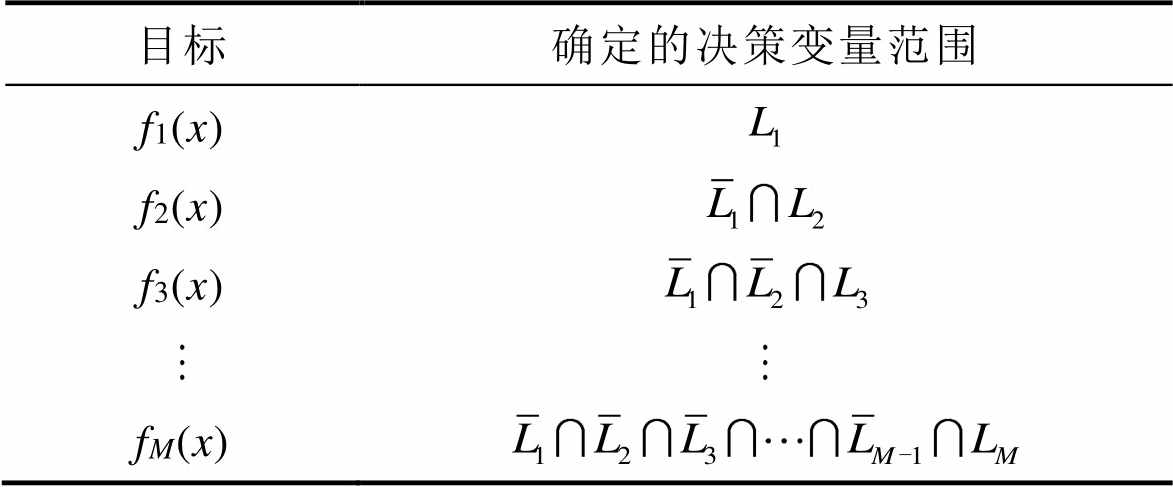
目标确定的决策变量范围 f1(x) f2(x) f3(x) fM(x)
2）规则管控策略主要缺陷
当通过优化算法求解多目标问题时，最终实现的是整体目标的综合最优。为达到这一目的，各目标之间的决策变量确定顺序不存在先后，且可根据综合效益相互调整，最终确定一组Pareto最优解[26-27]。然而，由附表3可知，规则管控策略中不存在fn(x)确定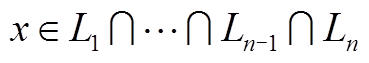
，n=2,3,,M（优先级靠后的目标改变前级目标已确定决策变量）来提升综合优化效果的行为。因此，规则管控策略不进行Pareto最优解的判定，由其给出的功率参考指令常为一组次优解[28]。
值得说明的是，在某一系统工作状态下，通过规则管控策略的逐级赋值方式可能给出同优化管控策略一样的功率指令，即此时的规则管控策略中人为选定的赋值规则刚好匹配优化管控策略中的最优分配比例。然而，此类情况存在偶然性，对于工作状态复杂、决策变量众多、数据量庞大的牵引供电系统来说，规则管控策略中固定单一的赋值规则往往无法实现多目标的最优化。
3）图例补充论证
为更方便读者理解上述证明过程，以图示方式对规则管控策略无法实现多目标最优进行说明。设求解多目标问题max: x+y，其约束条件组成的可行域为半径为1的圆，如附图4所示。当通过规则管控策略求解该多目标问题时，首先会根据逻辑判断条件，制定对应的赋值规则。设图2中平行于x轴的直线即为y的赋值规则，则其共有七种赋值选择（y1, y2, , y7），同理，x也有x1, x2, , x7共七种赋值选择，故附图4中可行域内两直线的交点即为规则管控策略下x+y可能得到的目标值。然而，由附图4可知，仅在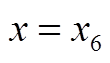
且
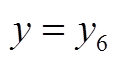时（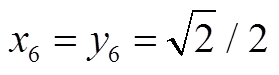
），才能取得最优解，其余蓝色圆交点均为次优解。
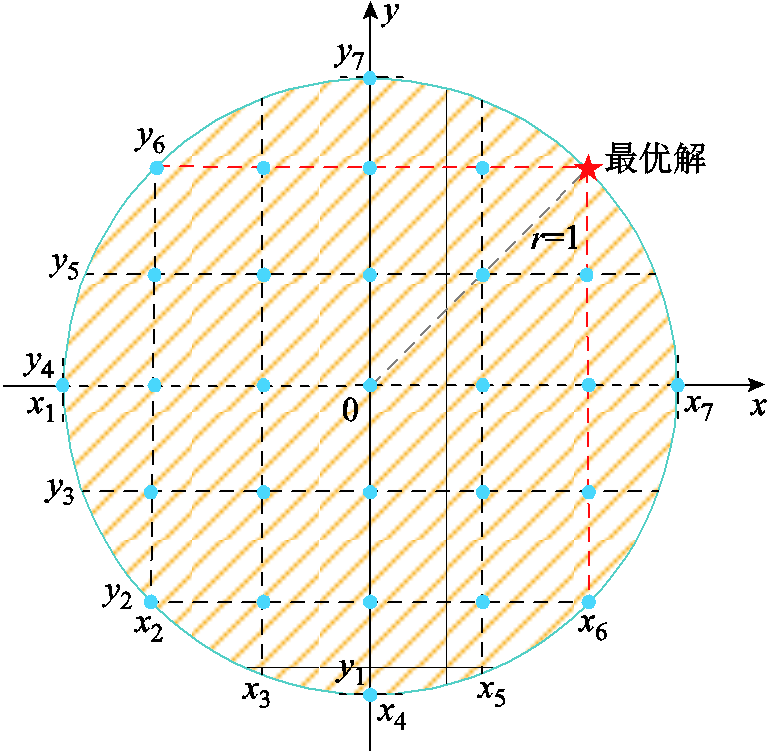
附图4 规则管控策略中决策变量赋值示意图
App.Fig.4 Schematic diagram of assigning values to decision variables in rule control strategies
综上可知，规则管控有可能取得与优化管控相同的解，但其不仅要求存在同优化管控相匹配的赋值规则，且需经逻辑判断后能执行该赋值规则。因此，鉴于规则管控策略小概率取得最优解，大概率取得次优解的特性，其无法保障工作状态复杂、决策变量众多、数据量庞大的牵引供电系统的最优管控。
2. 多目标权重确定流程
1）原始数据计算
计算未进行能量时系统的运行成本以及三相电压不平衡度，记运行成本为M、三相电压不平衡度为U，其中M、U均为N维向量（N取决于数据采集量）。
2）熵权法计算权重[8]
首先，对数据进行归一化处理，归一化处理公式为
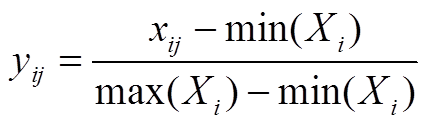（A2）
式中，Xi={xi1,xi2,,xiN}，在本文算例中，有X=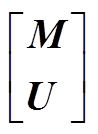
。将M与U代入式（A2）中，求得数据的归一化结果如附图5所示。
然后，根据信息熵计算公式计算各特征值的信息熵。在有S个特征指标和N个评估对象的问题中，第i个指标的熵值计算公式为
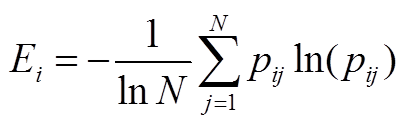（A3）
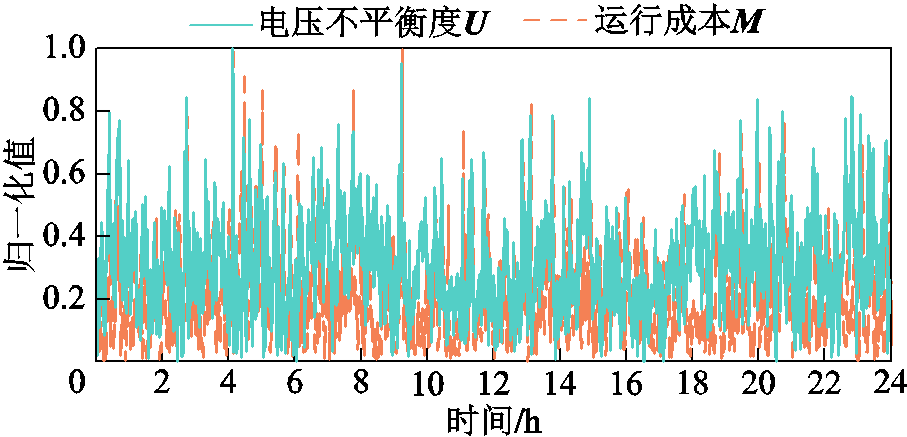
附图5 数据归一化结果
App.Fig.5 Data normalization results
式中，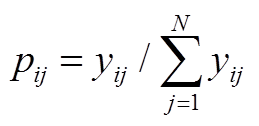
。此处有一特殊定义：若
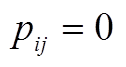，则有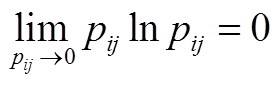
。
最后，计算各特征值的权重值，其计算公式为
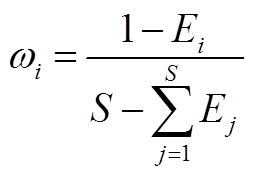（A4）
在本文算例中，S=2，即两个特征指标；N=86 400，即24 h内共采集86 400个数据作为评估对象。将运行成本M与三相电压不平衡度U归一化结果相继代入式（A3）、式（A4）中，最终可求得多目标权重为：运行成本权重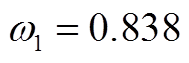
、三相电压不平衡度权重
。
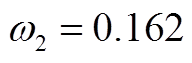参考文献
[1] Cheng Peng, Liu Wenquan, Ma Jing, et al. Solar-powered rail transportation in China: potential, scenario, and case[J]. Energy, 2022, 245: 123221.
[2] 何正友, 向悦萍, 廖凯, 等. 能源-交通-信息三网融合发展的需求、形态及关键技术[J]. 电力系统自动化, 2021, 45(16): 73-86. He Zhengyou, Xiang Yueping, Liao Kai, et al. Demand, form and key technologies of integrated development of energy-transport-information networks[J]. Automation of Electric Power Systems, 2021, 45(16): 73-86.
[3] 胡海涛, 陈俊宇, 葛银波, 等. 高速铁路再生制动能量储存与利用技术研究[J]. 中国电机工程学报, 2020, 40(1): 246-256, 391. Hu Haitao, Chen Junyu, Ge Yinbo, et al. Study on storage and utilization technology of regenerative braking energy for high-speed railway[J]. Proceedings of the CSEE, 2020, 40(1): 246-256, 391.
[4] 张恒, 王辉, 李群湛, 等. 采用自耦变压器供电的重载铁路牵引电缆贯通供电系统供电方案[J]. 电力自动化设备, 2021, 41(1): 204-213. Zhang Heng, Wang Hui, Li Qunzhan, et al. Power supply scheme of heavy-haul railway traction cable through power supply system with autotransformer power supply[J]. Electric Power Automation Equipment, 2021, 41(1): 204-213.
[5] 胡海涛, 葛银波, 黄毅, 等. 电气化铁路“源-网-车-储”一体化供电技术[J]. 中国电机工程学报, 2022, 42(12): 4374-4391. Hu Haitao, Ge Yinbo, Huang Yi, et al. “source-network-train-storage” integrated power supply system for electric railways[J]. Proceedings of the CSEE, 2022, 42(12): 4374-4391.
[6] 耿安琪, 胡海涛, 张育维, 等. 基于阶梯能量管理的电气化铁路混合储能系统控制策略[J]. 电工技术学报, 2021, 36(23): 4916-4925. Geng Anqi, Hu Haitao, Zhang Yuwei, et al. Control strategy of hybrid energy storage system for electrified railway based on increment energy management[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4916-4925.
[7] 黄文龙, 胡海涛, 陈俊宇, 等. 枢纽型牵引变电所再生制动能量利用系统能量管理及控制策略[J]. 电工技术学报, 2021, 36(3): 588-598. Huang Wenlong, Hu Haitao, Chen Junyu, et al. Energy management and control strategy of regenerative braking energy utilization system in hub traction substation[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 588-598.
[8] Chen Junyu, Hu Haitao, Ge Yinbo, et al. An energy storage system for recycling regenerative braking energy in high-speed railway[J]. IEEE Transactions on Power Delivery, 2021, 36(1): 320-330.
[9] 高锋阳, 张浩然, 王文祥, 等. 氢燃料电池有轨电车混合储能系统的节能运行优化[J]. 电工技术学报, 2022, 37(3): 686-696. Gao Fengyang, Zhang Haoran, Wang Wenxiang, et al. Energy saving operation optimization of hybrid energy storage system for hydrogen fuel cell tram[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 686-696.
[10] 黄文强, 李奇, 陈维荣, 等. 基于制动速度优化策略的新型供电方式有轨电车再生制动能量回收方法[J]. 中国电机工程学报, 2019, 39(18): 5406-5414, 5588. Huang Wenqiang, Li Qi, Chen Weirong, et al. A regenerative braking energy recovery method based on braking speed optimization strategy for novel power supply model tram[J]. Proceedings of the CSEE, 2019, 39(18): 5406-5414, 5588.
[11] 廖海朱, 胡海涛, 黄毅, 等. 电气化铁路“源-网-车-储”协同供能系统日前能量优化与调度策略[J]. 机车电传动, 2022(3): 1-9. Liao Haizhu, Hu Haitao, Huang Yi, et al. Day-ahead energy optimization and scheduling strategy of “source-networktrain-storage” coordinated power supply system for electrified railways[J]. Electric Drive for Locomotives, 2022(3): 1-9.
[12] 刘元立, 李群湛. 含光伏和混合储能的同相牵引供电系统日前优化调度[J]. 西南交通大学学报, 2023, 58(1): 30-39. Liu Yuanli, Li Qunzhan. Day-ahead optimal scheduling of co-phase traction power supply system with photovoltaic and hybrid energy storage[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 30-39.
[13] Liu Yuanli, Chen Minwu, Cheng Zhe, et al. Robust energy management of high-speed railway co-phase traction substation with uncertain PV generation and traction load[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(6): 5079-5091.
[14] Ge Yinbo, Hu Haitao, Chen Junyu, et al. Combined active and reactive power flow control strategy for flexible railway traction substation integrated with ESS and PV[J]. IEEE Transactions on Sustainable Energy, 2022, 13(4): 1969-1981.
[15] 谭敏哲. 多核心表决式控制系统的研究[J]. 机电工程技术, 2013, 42(12): 9-12, 61. Tan Minzhe. Research of a multi-core control system based on voting logic[J]. Mechanical & Electrical Engineering Technology, 2013, 42(12): 9-12, 61.
[16] 高仕斌, 罗嘉明, 陈维荣, 等. 轨道交通“网-源-储-车”协同供能技术体系[J/OL]. 西南交通大学学报, 2022: 1-18. https://kns.cnki.net/kcms/detail//51.1277. U.20221130.1759.003.html Gao Shibin, Luo Jiaming, Chen Weirong, et al. Rail transit "network source storage train" collaborative energy supply technology system [J/OL]. Journal of Southwest Jiaotong University, 2022: 1-18. https://kns. cnki.net/kcms/detail//51.1277.U.20221130.1759.003.html.
[17] 李勇, 姚天宇, 乔学博, 等. 基于联合时序场景和源网荷协同的分布式光伏与储能优化配置[J]. 电工技术学报, 2022, 37(13): 3289-3303. Li Yong, Yao Tianyu, Qiao Xuebo, et al. Optimal configuration of distributed photovoltaic and energy storage system based on joint sequential scenario and source-network-load coordination[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3289-3303.
[18] 高锋阳, 宋志翔, 高建宁, 等. 计及光伏和储能接入的牵引供电系统能量管控策略[J]. 电工技术学报, 2024, 39(3): 745-757. Gao Fengyang, Song Zhixiang, Gao Jianning, et al. Traction power supply system energy management strategy considering photovoltaic and energy storage access[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 745-757.
[19] Wang Jianyuan, Gu Chengcheng, Liu Kechen. Anomaly electricity detection method based on entropy weight method and isolated forest algorithm[J]. Frontiers in Energy Research, 2022, 10: 984473.
[20] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 电能质量三相电压不平衡: GB/T 15543—2008 [S]. 北京: 中国标准出版社, 2009.
[21] 王鑫, 郭祺, 涂春鸣, 等. 新型混合式贯通牵引供电系统及其复合控制策略[J/OL]. 中国电机工程学报, 2023: 1-11. https://doi.org/10.13334/ j.0258-8013.pcsee.222449. Wang Xin, Guo Qi, Tu Chunming, et al. New type hybrid through traction power supply system and its composite management strategy[J/OL]. Chinese Journal of Electrical Engineering, 2023: 1-11. https:// doi.org/10.13334/j.0258-8013.pcsee.222449.
[22] Liu Yuanli, Chen Minwu, Chen Yinyu, et al. Energy management of connected co-phase traction power system considering HESS and PV[C]//2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi'an, China, 2019: 1408-1412.
[23] Liu Fang, Liu Qianyi, Tao Qing, et al. Deep reinforcement learning based energy storage management strategy considering prediction intervals of wind power[J]. International Journal of Electrical Power & Energy Systems, 2023, 145: 108608.
[24] 王磊, 石家瑞, 吴源鑫, 等. 基于光伏系统可靠性的组件与逆变器最优容配比研究[J]. 太阳能学报, 2021, 42(12): 498-504. Wang Lei, Shi Jiarui, Wu Yuanxin, et al. Research on optimal capacity ratio of module and inverter based on reliability of photovoltaic system[J]. Acta Energiae Solaris Sinica, 2021, 42(12): 498-504.
[25] 张育维, 胡海涛, 耿安琪, 等. 考虑削峰填谷的电气化铁路混合储能系统容量优化配置[J]. 电力自动化设备, 2023, 43(2): 44-50. Zhang Yuwei, Hu Haitao, Geng Anqi, et al. Optimal capacity allocation of hybrid energy storage system for electrified railway considering peak load shedding and valley filling[J]. Electric Power Automation Equipment, 2023, 43(2): 44-50.
[26] 张维海, 彭称称, 蒋秀珊. 多目标动态优化中Pareto随即合作博弈研究综述[J]. 控制与决策, 2023, 38(7): 1669-1801. Zhang Weihai, Peng Weigao, Jiang Xiushan. A review of research on Pareto's stochastic cooperative game in multi-objective dynamic optimization [J]. Control and Decision, 2023, 38(7): 1669-1801.
[27] 李鹏, 韩建沛, 殷云星, 等. 电转氢作为灵活性资源的微网容量多目标优化配置[J]. 电力系统自动化, 2019, 43(17): 28-35, 139. Li Peng, Han Jianpei, Yin Yunxing, et al. Multi-objective optimal capacity configuration of microgrid with power to hydrogen as flexible resource[J]. Automation of Electric Power Systems, 2019, 43(17): 28-35, 139.
[28] Shehata M, Abdelnaeem M, Mokhiamar O. Integrated multiple criteria decision-making framework for ranking Pareto optimal solutions of the multiobjective optimization problem of tuned mass dampers[J]. Ocean Engineering, 2023, 278: 114440.
Abstract While promoting national economic growth, the rapid development of electrified railroads has increased the pressure of energy consumption, energy saving and emission reduction of the system. The construction of "network-source-storage-train" cooperative power supply system is conducive to the local consumption of new energy and the recycling of regenerative braking energy, which is of great significance to achieve the goal of "double carbon". However, the existing rules management strategy mainly focuses on the "network-storage-train" architecture and has limited management effect; the optimized management strategy often focuses on a single indicator such as economy and has low reliability. Therefore, this paper proposes a real-time energy management strategy based on "rules + optimization" for electrified railroad stations, which can improve the traction network voltage level and public grid power quality while achieving efficient utilization of new energy and regenerative braking energy.
First of all, the "network-source-storage-train" cooperative power supply mechanism is determined with the low-carbon economic operation of the system as the guide, and the energy management instructions in each working mode are determined through logical analysis and judgment to improve the energy rule management strategy under the "network-source-storage-train" cooperative power supply architecture. Then, taking into account the traction transformer, railway power conditioner power transmission losses and new energy, train regenerative braking energy disposal costs, the system operation cost function is improved to enhance the system global optimization capability. Further, a multi-objective site energy management optimization model is constructed with the objectives of minimizing the site operation cost and minimizing the three-phase voltage imbalance on the high-voltage side of the traction transformer, and the model is simplified by using a logical front, and the site energy optimization management strategy is formulated based on the solution results. Finally, the cooperation mechanism of rule management and optimization management is designed, starting with the parallelism of the two procedures and ending with the real-time management time threshold, so as to realize the orderly switching of management instructions and the complementary advantages of management strategies.
Through the simulation verification of the measured data, the following conclusions can be drawn: (1) The rule management can achieve ms-level output, which makes up for the defect that the optimization management cannot reliably output instructions within the real-time management requirements. (2) The multi-objective optimal management strategy designed in this paper can consume 0.77 MW more clean energy in a single day, reduce the operating cost by 0.55% more and the voltage imbalance does not exceed the national standard, which fills the shortage of rule management in the multi-objective optimal operation of the system. (3) Compared with the traditional traction power supply system without energy management, the single-day operating cost of the system under the energy management strategy based on "rules + optimization" in this paper can be reduced by 42.51%, the voltage fluctuation range of the low-voltage side of the traction transformer can be reduced by 93.44%, and the highest value of the three-phase voltage unbalance on the high-voltage side is only 1.81%. All test moments can meet the national standard requirements. (4) Under the real-time energy management strategy based on "rules + optimization", the estimated payback time of the "network-source-storage-train" cooperative power supply system is 2.1 years, and the final benefit is 2.55×104 million RMB, which provides strong support for the implementation of the actual project.
keywords：Electrified railroad, network-source-storage-train, real-time energy management, rules management, optimized management
DOI: 10.19595/j.cnki.1000-6753.tces.230320
中文图分类号：TM922.3
国家重点研发计划资助项目（2021YFB2601504）。
收稿日期 2023-03-23
改稿日期 2023-05-22
李俊豪 男，1998年生，硕士研究生，研究方向为微能源网优化管控。E-mail：lih17wo@hnu.edu.cn
王 鑫 男，1997年生，博士研究生，研究方向为分布式能源与微电网、电气化铁路贯通牵引供电系统。E-mail：wx815307656@foxmail.com（通信作者）
（编辑 赫 蕾）