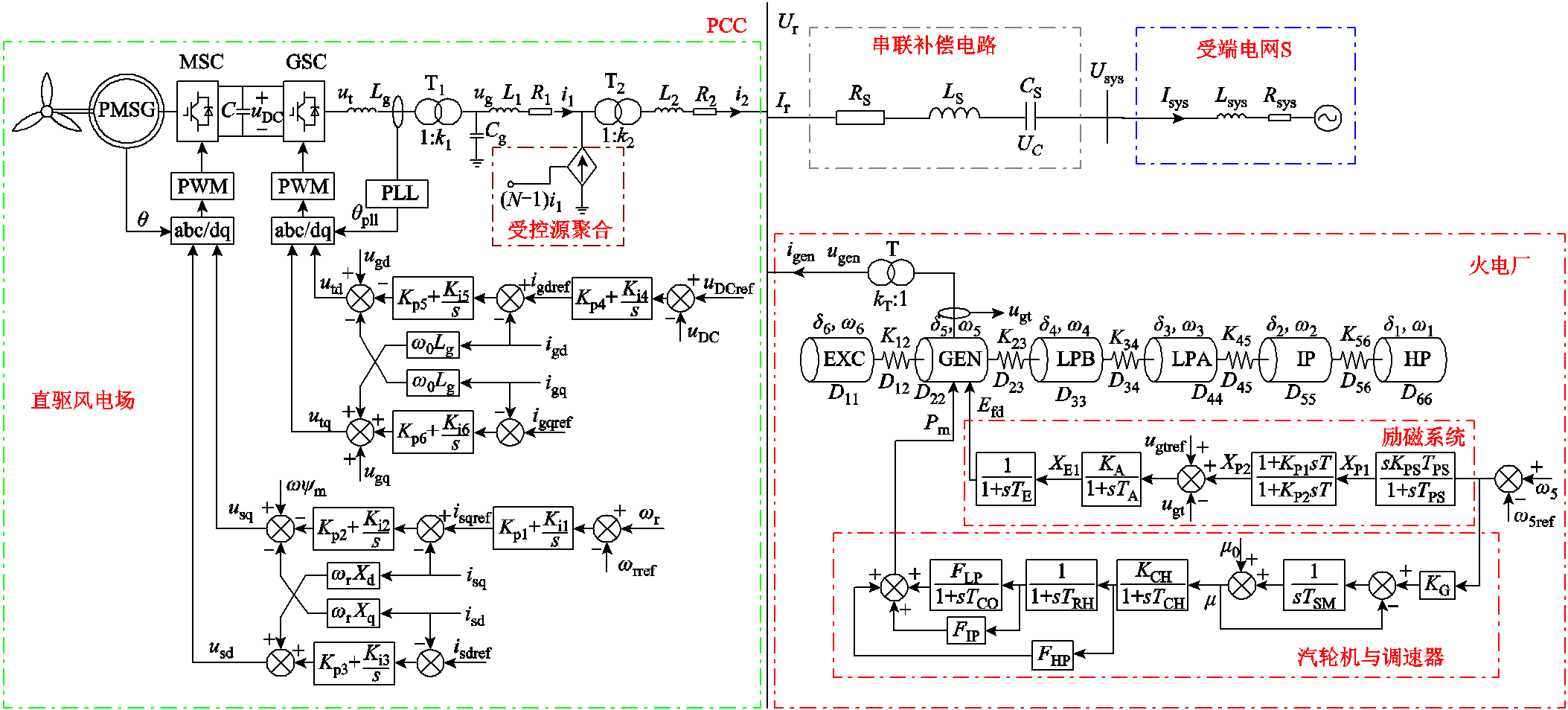
图1 风火打捆经串补送出的点对网型系统拓扑结构
Fig.1 The point-to-net structure of D-DWF-thermal bundled system integrated with series supplementation
摘要 直驱风电场（D-DWF）接入火电经串补外送系统后，其对火电机组的次同步谐振（SSR）影响机理尚不明确。针对风火打捆经串补点对网型系统，采用适用于模块化建模的状态变量消去方法，建立模块化的耦合小信号模型；利用特征值分析法研究D-DWF接入后系统的SSR情况；结合特征值分析结果阐释SSR机理，并针对D-DWF及串补线路参数进行阻尼分析。研究结果表明：D-DWF会引入与SSR频率相近并引起“共振”的一个新模态，使得“机电谐振”与“模态频率接近”的振荡机理耦合共存。在跟网型风机的控制策略及参数下，D-DWF并入会导致SSR模态阻尼大幅降低，恶化系统的SSR。随着D-DWF的容量、风速和系统串补度降低，系统阻尼将提高，SSR的风险将降低。基于PSCAD/EMTDC平台的电磁暂态仿真，验证了机理分析的正确性。
关键词：直驱风电场 串联补偿 风火打捆 特征值分析 次同步谐振
近年来，我国新能源发电比例不断提高[1-3]，截至2022年10月，年风电装机容量达到3.5亿kW，同比增长16.6%[4]。《“十四五”可再生能源发展规划》指出：需提高火电“点对网”输电通道的利用率，推动其外送新能源[5]。一方面，我国能源呈现逆向分布，新能源场站远离负荷中心、就地消纳能力不足；另一方面，新能源发电并网系统存在电能波动、间歇发电的特征，系统灵活性差[6]。因此，直驱风电场（Direct-Drive Wind Farm, D-DWF）与火电打捆经串补线路送出的点对网型系统因其传输容量大、技术成熟可靠等优点，已成为近年来能源消纳的主要方式，工程上对其稳定性的研究有迫切需求。
当D-DWF并入弱电网时，直驱永磁同步发电机（Direct-drive Permanent Magnet Synchronous Generator, D-PMSG）与电网间的次同步交互可能不稳定，存在诱发次同步振荡（Subsynchronous Oscillation, SSO）的风险[7-10]。D-DWF振荡频率与火电机组轴系扭振模态（简称扭振模态）频率匹配时会激发严重的轴系扭振，D-DWF与火电轴系的开环模态频率接近时也会诱发系统失稳。文献[11-13]研究了D-DWF经串补送出系统的SSO特性，结果表明部分D-DWF并网系统中存在D-DWF参与的SSO模态，且SSO由控制或与电网间的相互作用引起。次同步谐振（Subsynchronous Resonance, SSR）指轴系扭振频率和串补频率在工频接近互补时引发[14-15]，但是上述振荡问题与SSR问题有显著区别。因此，对含D-DWF系统SSR问题的深入研究具有一定意义。
目前针对含D-DWF复杂系统的相关振荡问题，主要围绕D-DWF经高压直流外送系统，是主要与控制相关的SSO问题[16-18]，针对风火打捆SSR问题的相关研究不足[19-20]。文献[19]的研究结果表明D-DWF中存在锁相环（Phase Locked Loop, PLL）主导的SSO，PLL与火电轴系的开环模式谐振会造成扭振失稳；文献[20]指出弱连接下的D-DWF向火电注入的电阻尼增加，降低发电机轴系的稳定性。但是所提及的风火打捆系统不涉及串联补偿线路，即不针对SSR问题。因此，有必要研究风火打捆系统中D-DWF并网对火电机组的SSR的影响。
现有文献对风火打捆经串补送出系统的研究主要集中在双馈风电场。在系统的补偿度和潮流不变的前提下，双馈风电场并入后，系统阻尼下降，火电机组扭振模态频率不会改变[21-22]，但系统的SSO模态（不特指轴系）会发生变化[23-24]。文献[25-28]基于双馈风电场与串补的场景，研究发现，串联补偿和双馈风机之间的不规则能量交换会引发次同步控制交互，双馈风电场的容量、风速、风机数量、转速和转子换流器的控制参数均会增加发生SSO的风险，与双馈风机与火电打捆系统中SSR的影响因素保持一致。但是由于D-DWF和双馈风电场在结构、动态特性上存在较大的差异，因此有必要研究D-DWF与火电打捆经串补线路送出系统的SSR情况。
特征值分析法广泛用于电力系统稳定性分析，往往与时域仿真法联合使用，该方法成熟、可靠，针对实际工程具有一定的可信性[29-30]。本文采用特征值分析法，通过特征值结果和参与因子研究系统的扭振模态，分析D-DWF并网以及并网后系统参数对SSR的阻尼影响，基于此揭示阻尼变化的机理。
本文首先基于D-DWF与火电打捆经串补外送的点对网型系统线性化数学模型，采用适用于模块化建模的状态变量消去方法，在Matlab/Simulink中建立基于模块化建模思想的系统小信号模型，并通过阶跃响应验证其可靠性；其次，求解D-DWF并网前后系统的小信号模型，并进行SSR特性分析；然后，阐释D-DWF接入后系统的SSR机理，结合时域仿真验证SSR机理；最后，以D-DWF的容量、风速以及系统串补度为研究对象，从阻尼特性及时域响应情况的角度，分析系统发生SSR的风险。
图1为D-DWF与火电打捆经串补外送的点对网型系统（以下简称为“点对网”系统）的拓扑结构，系统主要由火电厂、D-DWF、串补线路以及受端电网S组成。系统中的火电厂子系统参数参考文献[15]，关键参数见附表1。其他子系统的主拓扑参数详见附表2，D-DWF系统控制参数见附表3。
图1 风火打捆经串补送出的点对网型系统拓扑结构
Fig.1 The point-to-net structure of D-DWF-thermal bundled system integrated with series supplementation
火电厂、串补线路以及受端电网S采用IEEE第一标准模型的结构[15]。火电厂的额定容量为892.4 MV·A，额定频率为60 Hz。机组采用包括高压缸（HP）、中压缸（IP）、低压缸（LPA和LPB）、发电机（GEN）和励磁机（EXC）的六质量块轴系模型，经过变压器T（正序阻抗0.14(pu)）升压至500 kV汇流母线。串补线路采用23.5%的串补度。由于本文研究直驱风电场并入对火电SSR的影响，受端电网S非研究重点，所以电网S基于戴维南定理等效为电压源串联阻抗的形式，且电网S强度足够大。
D-DWF采用适用于振荡分析的单机倍乘受控源聚合等值模型[31]，由80台额定功率为5 MW的风机构成，额定风速为11 m/s。D-DWF主要由考虑单质量块的D-PMSG、机侧换流器（Machine-Side Converter, MSC）、解耦电容、网侧换流器（Grid-Side Convertor, GSC）和控制系统等组成。D-PMSG发出的电能经变压器T1升压至35 kV汇流母线，经受控源聚合模型后模拟D-DWF，最后经变压器T2升压至500 kV汇流母线。
本文通过改变D-DWF的运行状态及串补线路的参数，研究D-DWF与火电打捆经串补外送系统中SSR的情况，分析系统的SSR特性。稳态运行时，风火打捆的“点对网”型系统的新能源占比约为30%，串补谐振频率[32]在29 Hz左右，500 kV汇流母线为公共耦合点（Point of Common Coupling, PCC）。
图1的主要变量定义如下：D-DWF子系统中，ωr和uDC分别为直驱风机转子角频率和解耦电容电压，分别是MSC和GSC的外环控制量；us和ut分别为MSC入口电压和GSC出口电压；is、ig和ug分别为D-PMSG机侧电流、网侧电流和电压；Lg和Cg分别为滤波电感和线路等效并联电容；θ和θpll分别为转子位置角和电网锁相角；R1和L1与R2和L2依次为35 kV、500 kV线路阻抗，i1、i2为线路电流。火电厂子系统中，ω1～6、δ1～6对应六个质量块的转子角速度和角度；μ为汽轮机气门开度；ugt为发电机端电压；XP1、XP2与XE1为励磁系统中间变量；ugen和igen为发电厂输出电压和电流。在串补电路子系统中，RS、LS和CS分别为串补线路等效电阻、等效电感和补偿电容；Ir为流入子系统的电流；UC为CS端电压；Ur为PCC处电压。受端电网S子系统中，Usys为受端电网S母线电压。
火电厂系统的数学模型主要包括：汽轮机与调速器模型、六质量块轴系模型、同步发电机模型、励磁系统模型、变压器简化模型等，限于篇幅，详细数学模型参考文献[15]。
D-DWF系统的数学模型主要包括：单质量块轴系模型、D-PMSG模型、变流器及其控制模型、解耦电容模型、滤波器与锁相环模型、受控源聚合等值模型、含两级变压器的输电线路模型等，详细模型参考文献[20]。
串补线路子系统的数学模型由电路等值模型构成二阶系统，即
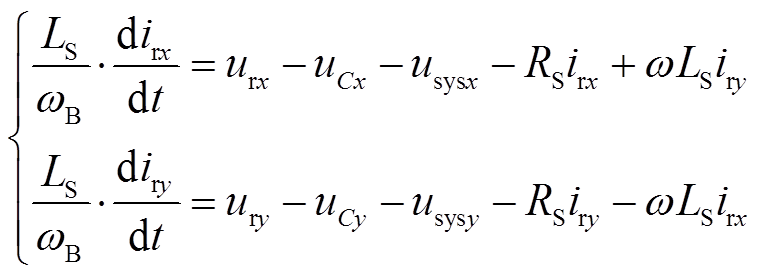（1）
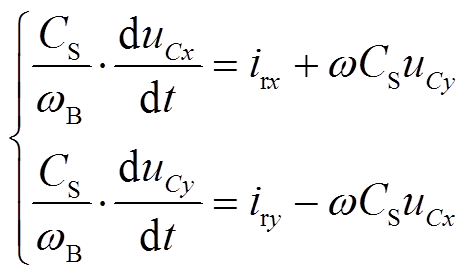（2）
式中，ωB、ω分别为系统的角速度基准值和Ur的旋转角频率；irx、iry、urx、ury、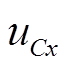
、
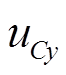、usysx、usysy分别为Ir、Ur、UC、Usys在xy旋转坐标系下的分量。
2.2.1 模型搭建
考虑到待研系统较为复杂，本文以火电厂子系统参数为基准值，采用模块化建模的方法，在Matlab/Simulink中搭建“点对网”系统的小信号模型。模块化建模法具有灵活性好、可扩展性强的优点，便于D-DWF与火电厂之间的耦合建模。
首先分离系统各子模块并建立状态空间模型，然后将子模块间的输入、输出信号互相连接，最后得到系统的闭环小信号模型。
具体过程为：线性化处理2.1节的系统数学模型，以串补线路子系统中CS为例，式（2）的线性化方程为
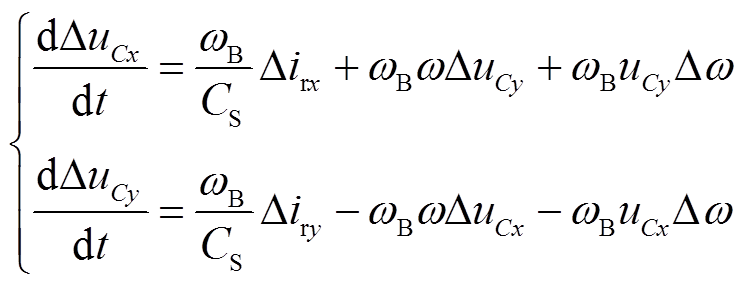（3）
式中，∆表示信号的小扰动量。
系统各子模块作类似于式（3）的线性化处理，分别在Matlab/Simulink中形成各子模块的状态空间模型，表达形式为
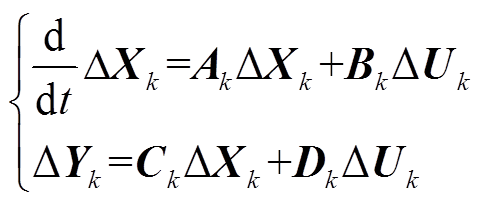（4）
式中，下标k表示各子模块；Xk、Uk、Yk分别为子模块k的状态变量矩阵、输入变量矩阵、输出变量矩阵；Ak、Bk、Ck、Dk分别为第k个子模块的系数矩阵、输入矩阵、输出矩阵、传递矩阵，各矩阵中的元素由系统稳态获得[33]。
本文所研究系统的各子模块在独立坐标系下建模：火电厂和串联补偿电路子模块处于xy坐标系下[32]，D-DWF处于dq坐标系下。子模块间通过输入矩阵Ui和输出矩阵Yj中的元素连接，即当i=k时，j≠k。为使各子模块相互连接成闭环系统，将系统统一在同一坐标系下，即利用坐标变换将D-DWF模型转换到xy坐标下。
坐标耦合处xy坐标系和dq坐标系需相互转换，变换式为
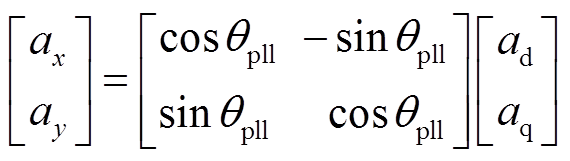（5）
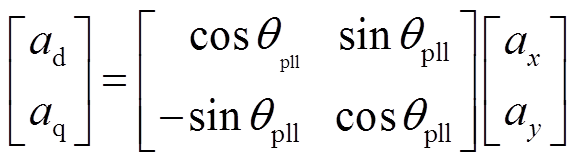（6）
式中，ax、ay、ad、aq分别为变量a在x轴、y轴、d轴、q轴下的分量。
将式（5）和式（6）搭建成形如式（4）的子模块，D-DWF子系统基于此模块转换至xy坐标系下，与火电厂和串补线路子系统经PCC耦合，下面基于串补子系统介绍耦合过程。
火电厂和D-DWF子系统耦合处子模块下标分别记为gen和pmsg，则Uk、Yk分别为Ugen、Ygen和Upmsg、Ypmsg。由图1可知，PCC处三个子系统的电压和电流相互耦合，小信号模型中子系统的耦合变量表示为
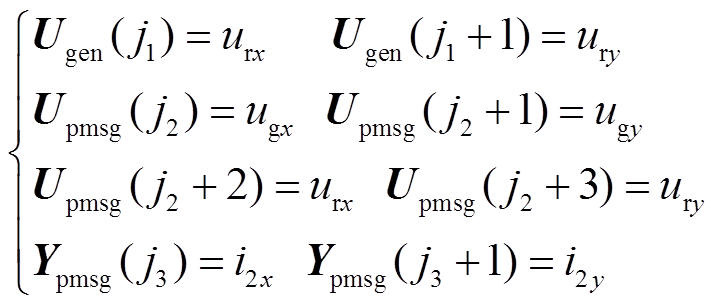（7）
式中，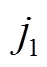
、
、
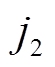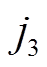分别为Ugen、Upmsg、Ypmsg中元素位置；ugx、ugy、i2x、i2y分别为ug、i2在xy坐标下分量，并与串补线路子系统耦合。
由式（1）和式（2）可知，串补系统有四个独立的状态量，但由于PCC处i2和igen汇流成ir，所以irx和iry是非线性独立的状态量，需将两者排除[15]。式（1）的线性化模型如式（8）所示，为耦合处建模的关键。下面介绍适用于模块化建模方法的小信号模型状态变量的关键消去方法。
（8）
串补子系统耦合处子模块下标记为rlc，Urlc与Ugen、Ygen、Upmsg、Ypmsg部分元素连接；Yrlc与Ugen、Upmsg部分元素连接。由于式（3）中irx、iry不以微分形式出现，Arlc和Brlc不涉及状态量的排除问题；将Agen、Bgen中i2和Apmsg、Bpmsg中igen四个xy坐标下的状态量的元素线性组合，代入式（8）中，便可排除irx和iry状态量，得到Crlc和Drlc，即
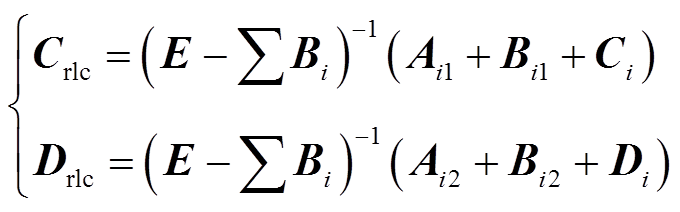（9）
式中，Bi为Bgen和Bpmsg对应式（7）中urx、ury位置的元素；Ai1、Ai2、Bi1、Bi2为消除状态量时，在Agen、Apmsg、Bgen、Bpmsg引入的元素所构成的矩阵，对应Xrlc与Urlc的系数；Ci和Di为式（8）中Xrlc与Urlc的系数所构成的矩阵。
状态变量消去法从矩阵元素的角度出发，更适用于模块化建模。如式（9）所示，基于串联补偿子系统独立模块进行状态变量消去，完成耦合处建模。状态变量消去法的应用场景得到进一步丰富。由于篇幅的限制，式（9）详细的数学描述与解释见附录。
结合式（4）～式（9），在Matlab/Simulink中建立第1节系统的闭环小信号模型。如图2所示，D-DWF子系统分成风机轴系模块、GSC模块等10个模块，火电厂子系统分为同步发电机模块、火电轴系模块等5个模块，串补线路子系统为1个串补线路模块。连接16个子模块，得到如式（10）所示的风火打捆经串补送出的点对网型系统的小信号模型。
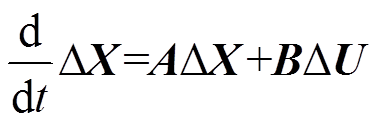（10）
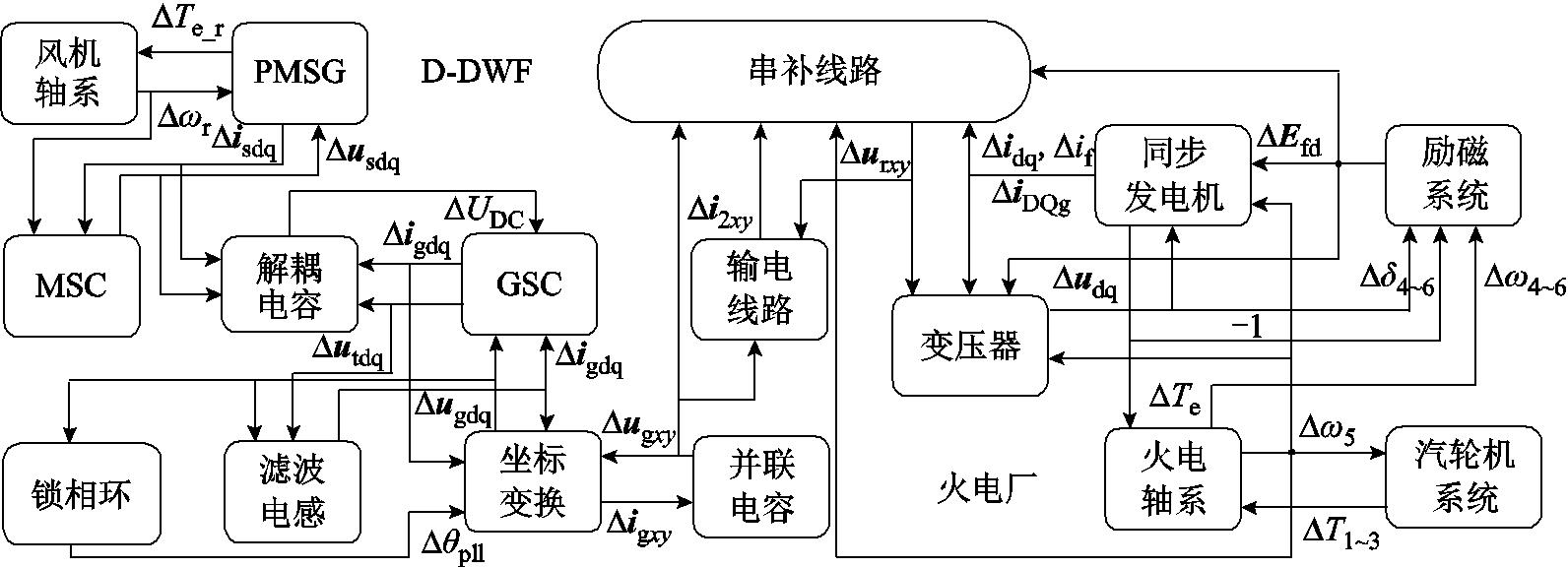
图2 闭环小信号模型示意图
Fig.2 Closed-loop schematic of the small signal mode
式中，∆X为16个子模块中的状态变量，其含义见表1；∆U为系统控制给定量组成的输入矩阵，系统闭环后为零矩阵。
表1 系统状态变量
Tab.1 State variables of the systems
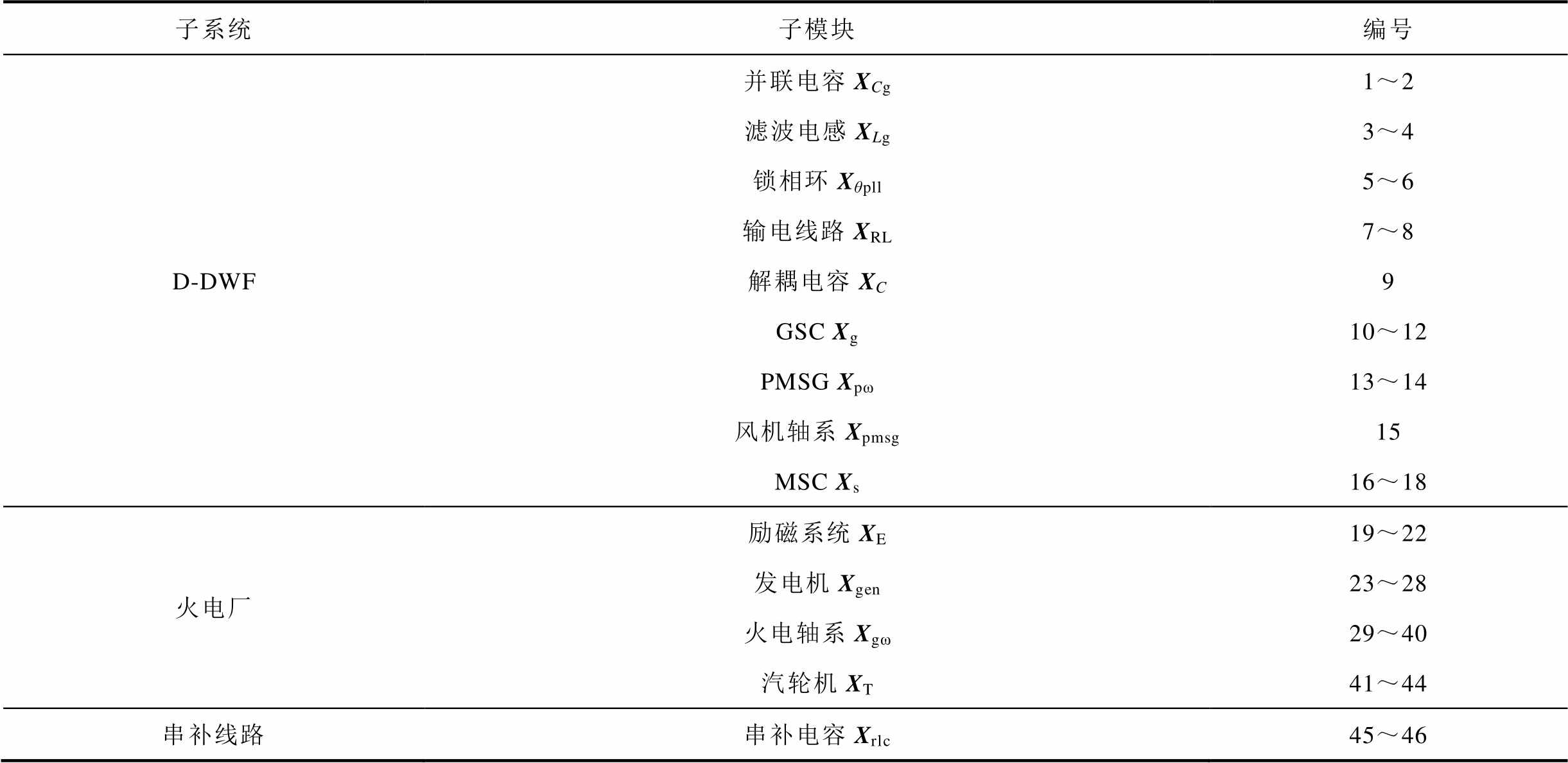
子系统子模块编号 D-DWF并联电容XCg1～2 滤波电感XLg3～4 锁相环Xθpll5～6 输电线路XRL7～8 解耦电容XC9 GSC Xg10～12 PMSG Xpω13～14 风机轴系Xpmsg15 MSC Xs16～18 火电厂励磁系统XE19～22 发电机Xgen23～28 火电轴系Xgω29～40 汽轮机XT41～44 串补线路串补电容Xrlc45～46
2.2.2 模型验证
小信号模型的准确性通过阶跃响应曲线对比验证[17]。在SSO分析方法中，时域仿真由于采用数值积分方法，精度较高，当小信号模型的阶跃响应曲线与时域仿真结果基本一致时，可验证小信号模型的准确性。
按照图1设置系统采用低串补度（7%），其他子系统参数不变，在PSCAD/EMTDC仿真平台中搭建电磁暂态模型，并与小信号模型均仿真20 s。仿真运行开始至15 s时，在D-DWF子系统中GSC电压外环给定uDCref上设置10%的阶跃，其他参数保持不变，分别得到两类模型的阶跃响应曲线。截取13～18 s的波形进行对比，结果如图3所示，其中图3a～图3d依次为：解耦电容的电压uDC、 D-DWF并网电流d轴分量igd、D-DWF并网电压q轴分量ugq、发电机的转速ω5。
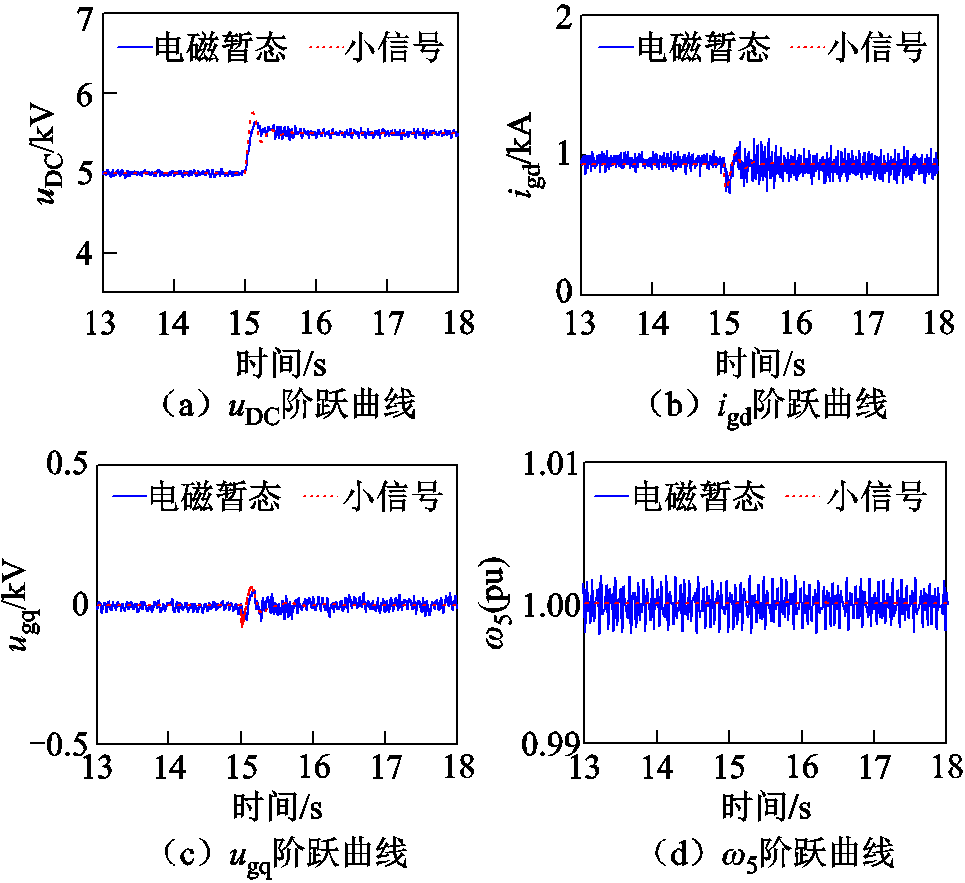
图3 响应对比曲线
Fig.3 Response contrast curves
如图3所示，小信号模型和电磁暂态模型的阶跃响应曲线在数值和趋势上的变化基本一致，阶跃前后达到相同的稳态，验证了用小信号模型分析的可靠性。图3d基本不体现阶跃变换，在一定程度上说明D-DWF在不失稳的前提下，控制上的小扰动不会引起ω5的变化。
本节通过研究火电机组的扭振模式，分析D-DWF接入对SSR的影响。首先求解有无D-DWF的小信号模型并筛选轴系参与的模态；其次观测模态频率与模态阻尼比（简称阻尼比）；然后分析模态的参与因子；最后研究D-DWF和串补线路对SSR模式的参与情况。
为方便叙述，分别称D-DWF接入前后的系统为系统Ⅰ、系统Ⅱ。为了研究系统Ⅱ中D-DWF对SSR的影响，在保证点对网系统潮流不变的前提下，基于系统Ⅱ，仅将D-DWF等效为400 MW的电源，对系统Ⅰ进行建模，小信号模型与系统Ⅱ类似，此处不再赘述。筛选两个系统的扭振模态，观察D-DWF接入对扭振模态的影响，结果见表2。
表2 有无D-DWF接入的系统扭振模态结果
Tab.2 Torsional vibration modal results ofthesystem with or without D-DWF
工况扭振模态特征值频率/Hz阻尼比 系统Ⅰ（不含D-DWF）模态1(λ1,2)0.126±j99.54815.84-1.28×10-3 模态2(λ3,4)0.013 2±j127.05720.22-1.04×10-4 模态3(λ5,6)0.078 2±j160.73925.58-4.87×10-4 模态4(λ7,8)0.346±j203.15732.34-1.71×10-3 模态5(λ9,10)-6.89×10-6±j298.17747.462.31×10-6
（续）
工况扭振模态特征值频率/Hz阻尼比 系统Ⅱ（含D-DWF）模态0.063 8±j99.77615.88-6.39×10-4 模态6.48×10-3±j127.07920.23-5.10×10-5 模态0.046 0±j160.84525.60-2.86×10-4 模态1.60±j204.71632.58-7.82×10-3 模态-6.82×10-4±j298.17747.462.29×10-6
由表2可知，系统Ⅰ和系统Ⅱ中均存在五种扭振模态[21]，且模态1～5频率的整数部分对应相等，因此D-DWF的并入基本不改变扭振模态频率。模态4的频率与串补谐振的互补频率（31 Hz）相差约1 Hz，即模态4与串补谐振频率接近互补[15]，因此称模态4为SSR模态。由于SSR模态的存在，系统具有发生SSR的风险。
D-DWF接入前后，系统Ⅰ、系统Ⅱ的模态1～4阻尼比均为负，是不稳定的模态；模态5阻尼比均为正，是稳定模态。系统Ⅱ相比于系统Ⅰ，SSR模态的特征值实部增大，阻尼比明显降低，模态阻尼被削弱；模态1～3的特征值实部减小，阻尼比均升高，模态阻尼得到增强。
因D-DWF的接入，系统Ⅱ中SSR模态阻尼减弱，“点对网”系统将发生更严重的SSR；模态1～3因阻尼增强，对应的轴系扭振将被削弱。
模态与状态变量的关联程度可以用参与因子表示[17]。一般来讲，参与因子越大，关联程度越强，影响状态变量的参数对模态的作用就越大。为分析与扭振模态参与度较高的影响因素，本节对系统Ⅰ和系统Ⅱ的小信号模型进行参与因子分析，结果如图4所示。
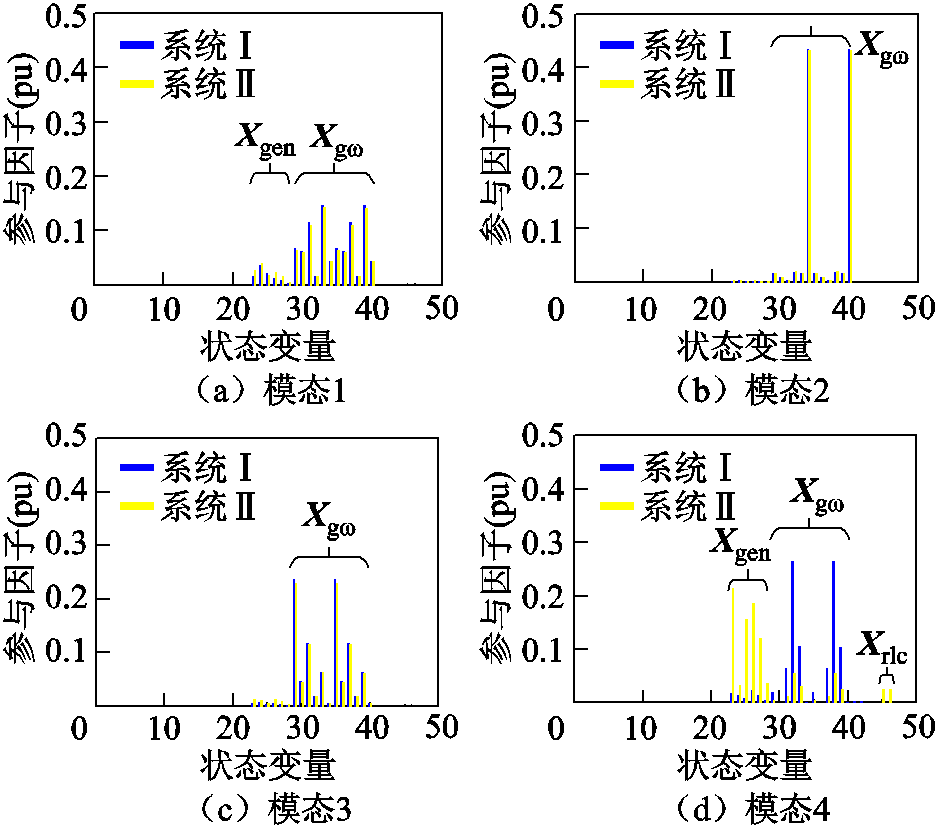
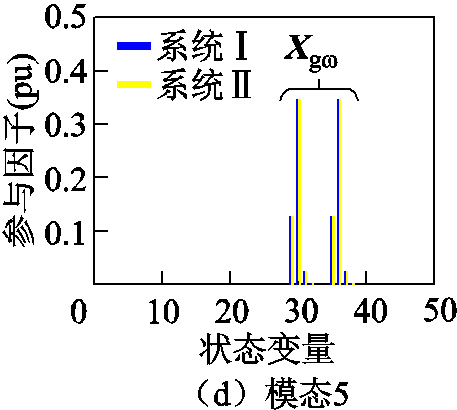
图4 扭振模态参与因子
Fig.4 Participation factor of torsional vibration
图4中，Xgω=[δ1～6 ω1～6]T，参数与图1保持一致，表示六个质量块的转子角速度和角度；Xgen=[ID1～3 IQ1～3]T。ID1～3分别为发电机d、f、D绕组电流；IQ1～3分别为发电机q、g、Q绕组电流。
图4表明，在系统Ⅰ中，模态1～5均是由状态量Xgω强参与的扭振模态，同时模态1、SSR模态由Xgen弱参与，绕组电流的变化会对SSR模态产生影响。相较于系统Ⅰ，系统Ⅱ中模态1～3、模态5的参与因子分布几乎不变，且由Xgω、Xgen的主导程度相同；SSR模态的Xgen参与度增强、Xgω参与度减弱，状态量Xrlc也弱参与SSR模态。
当系统不含D-DWF时，扭振模态（包括SSR模态）主要受发电机和火电轴系本身参数的影响。当系统存在D-DWF时，“点对网”系统中SSR模态的参与因子侧重于绕组电流状态量、串补线路参数，其中定子绕组d、q电流的参与度最高。
“点对网”系统中的SSR模态由Xgen、Xgω、Xrlc共同参与。由于火电厂子系统和D-DWF子系统经PCC处电流耦合流入串补线路子系统，因此D-DWF中电流变化将间接通过Xgen影响SSR模态的阻尼，影响i2的因素均可能影响SSR。Xgω反映火电机组的固有属性，难以通过改变参数影响SSR。D-DWF的存在将提高Xrlc在SSR模态中的参与度，从而影响系统Ⅱ的SSR风险。
本节基于特征值分析结果研究“点对网”系统的SSR机理，基于电磁暂态仿真结果验证SSR机理。
本文重点关注SSR的情况，因此主要研究SSR模态及其次同步交互过程。分析表2可知，D-DWF并入后，SSR模态的特征值实部增大明显，其次同步交互作用增强；模态1～3的特征值实部降低，其次同步交互作用减弱。
下面阐释“点对网”系统的次同步交互机理。传统火电串补送出系统，将发生SSR归因于机电谐振[32]。在风火打捆系统中，D-DWF并网引发的SSO模态与火电扭振模态频率接近时，会诱发轴系振荡[8-9]。为验证系统Ⅱ是否新增频率相近模态，再次求解系统Ⅰ、Ⅱ的小信号模型，筛选出与模态1～5相近、且仅存在于系统Ⅱ的模态，此模态即为D-DWF新引入的模态，结果见表3。
表3 D-DWF并网后的激励模态
Tab.3 Excitation mode of D-DWF after grid connection
模态特征值频率/Hz SSR模态()1.60±j204.71632.58 SSO模态()-1.78±j206.91832.92
由表3可知，系统Ⅱ中新增SSO模态与SSR模态频率相近。D-DWF并入后，尽管由于SSO模态的特征值实部为负，系统受到扰动时不发生SSO，但是新增32.92 Hz的次同步分量，其与SSR分量频率几乎相等。当系统受到扰动后，将产生次同步分量耦合过程，SSO模态对SSR模态的次同步分量形成激励效果。一般来说，D-DWF中由于D-PMSG型号相同，因此引入的SSO模态频率基本相同。但是电网中不同火电机组的扭振模态频率不同，而且两个或几个模态频率位于某一区间内具有激励效果，因此风火打捆经串补外送系统中“激励”发生的风险较大。
为探究SSO模态的成因，求解其参与因子，并与SSR模态做对比，结果如图5所示。
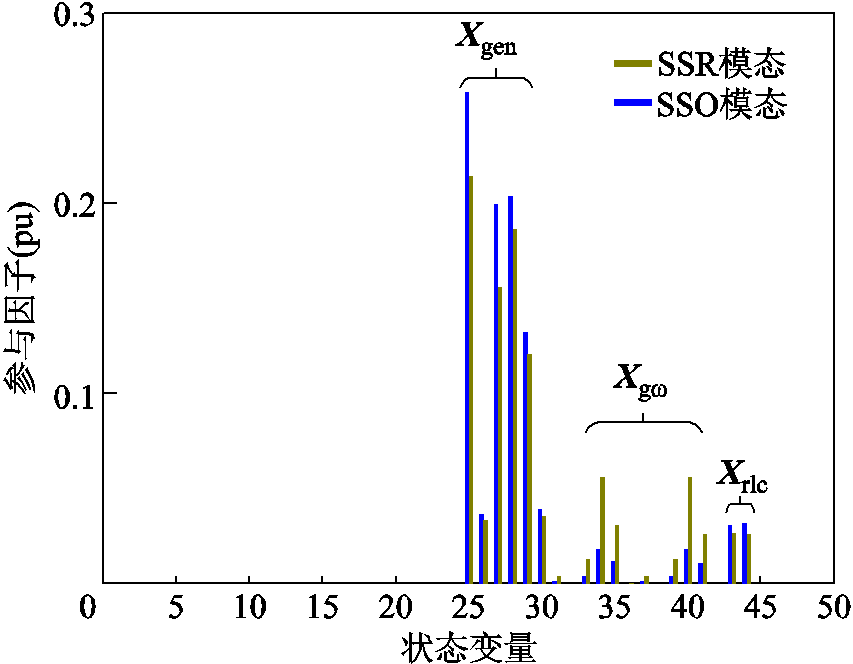
图5 参与因子分析
Fig.5 Participation factors analysis
由图5可知，SSR模态和SSO模态的参与因子分布情况不变，均主要由Xgen、Xgω、Xrlc参与，参与程度略有变化但总体上相差不大。尽管SSO模态是D-DWF并入后引入的，但是D-DWF系统参与度极低，对其几乎没有影响。SSO模态受火电厂子系统、串补线路子系统参数主导。可以认为，SSO模态虽然是由D-DWF引入的，但和D-DWF本身参数关系不大。
本文研究的“点对网”系统，在D-DWF接入传统火电串补送出系统后，其SSR振荡机理兼具“机电谐振”与“模态频率接近”的耦合作用，作用过程如图6所示。
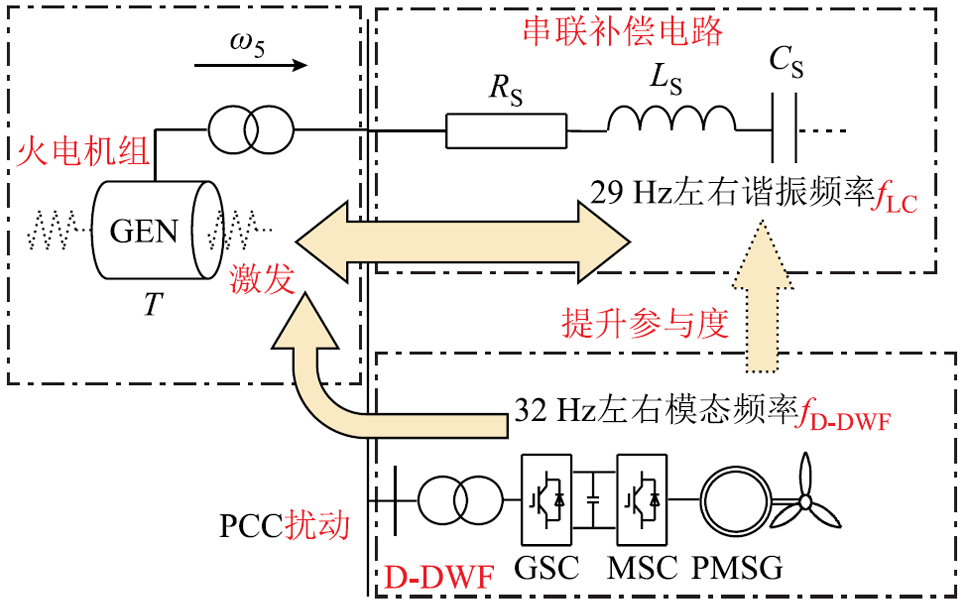
图6 频率耦合作用过程
Fig.6 The process of frequency coupling
当串补度为23.5%时，对应谐振频率在29 Hz左右，与SSR模态的频率互补。此时系统受到扰动时，次同步分量通过PCC作用于火电机组，诱发振荡。当D-DWF中存在32 Hz左右的模态时，扰动出现后，次同步分量也会经PCC作用于火电机组，加剧振荡。由3.2节SSR模态参与因子分析结果可知，D-DWF的并入会加强Xrlc的参与度，说明此时D-DWF与串补线路的次同步分量产生耦合，前者对后者有加强作用。当火电机组产生SSR时，火电机组通过转速信号将次同步分量反馈至PCC，次同步分量流过闭环。
综上所述，D-DWF与串补线路共同影响“点对网”系统中的SSR。由于发电机和D-DWF在PCC处i2和igen耦合流过串补线路，而且从参与因子的角度看，D-DWF参数并不直接参与SSR模态的阻尼变化。因此，D-DWF中电流变化将间接影响SSR模态阻尼；串补线路则直接影响SSR模态阻尼。
为验证模态1～5的阻尼变化情况，在PSCAD/ EMTDC中对系统Ⅰ、系统Ⅱ进行电磁暂态时域仿真。设系统Ⅰ、Ⅱ均仿真50 s，PCC处在8 s时发生B相接地故障，持续时间为33 ms（系统基频下两个周波），以激发出SSR。火电机组SSR情况用火电机组转速表示[34]，通过带宽为3 Hz的带通滤波器提取其次同步分量，并用ω5_4表示。图7为火电机组转速快速傅里叶分解（Fast Fourier Transform, FFT）的结果。
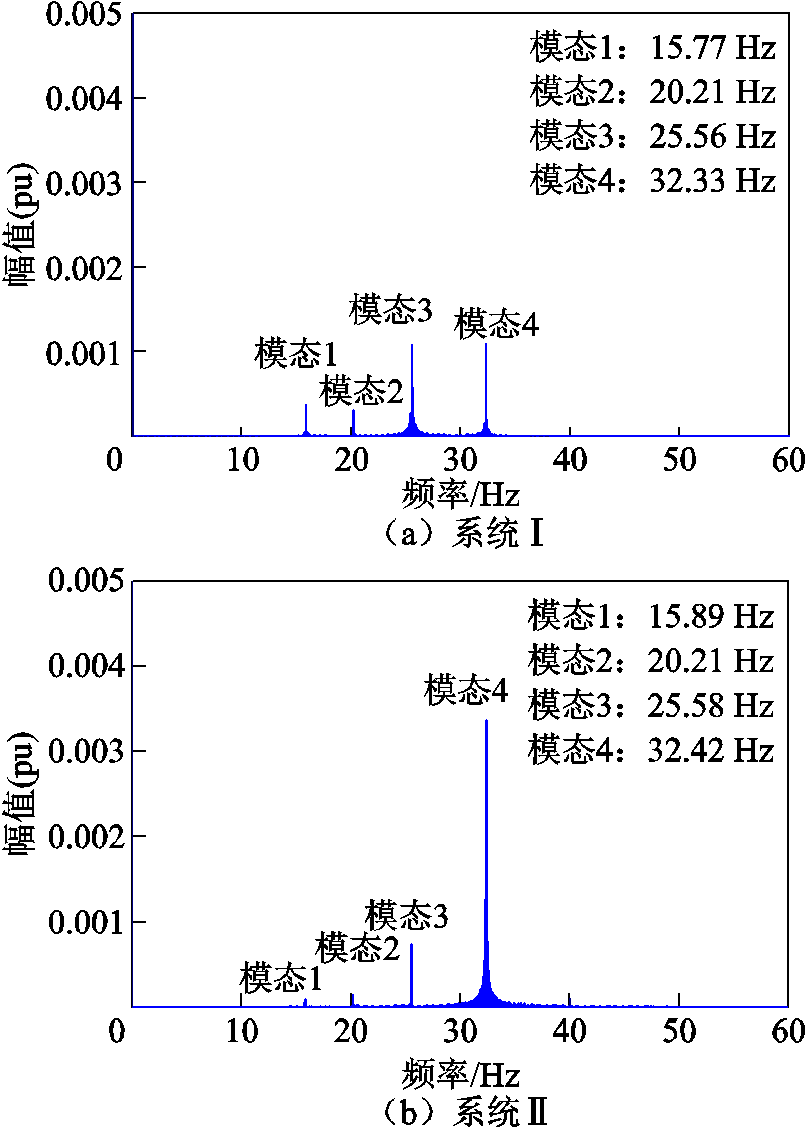
图7 火电机组转速的FFT结果
Fig.7 FFT results ofthethermal power unit speed
由图7可知，当故障发生后，系统Ⅰ中出现15.77 Hz、20.21 Hz、25.56 Hz、32.33 Hz的振荡，系统Ⅱ中出现15.89 Hz、20.21 Hz、25.58 Hz、32.42 Hz的振荡，均与表2中模态1～4一致。模态1～3对应振荡的幅值在系统Ⅱ中有所减小。SSR的幅值在系统Ⅱ中明显增加，系统发生严重的SSR。模态5在FFT中几乎观察不到。图7中4个模态的频率分布和幅值大小验证了特征值分析结果。为观察D-DWF并入的作用效果，对比系统Ⅰ和系统Ⅱ模态4在8～20 s的SSR波形，如图8所示。由图7和图8可知，系统Ⅱ比系统Ⅰ发生的SSR幅度明显大。由于D-DWF的并入，“点对网”系统中的SSR将严重。此外，由于PSCAD/EMTDC中采用3 Hz带宽的滤波器滤出SSR，所以图8的振荡幅度比图7中FFT分析的幅值大。
为研究系统Ⅱ中次同步分量的流通，保持和4.2节相同的仿真条件，并观测火电厂、D-DWF并入PCC处以及电网侧的电流有效值波形，截取7.5～50 s，如图9所示。
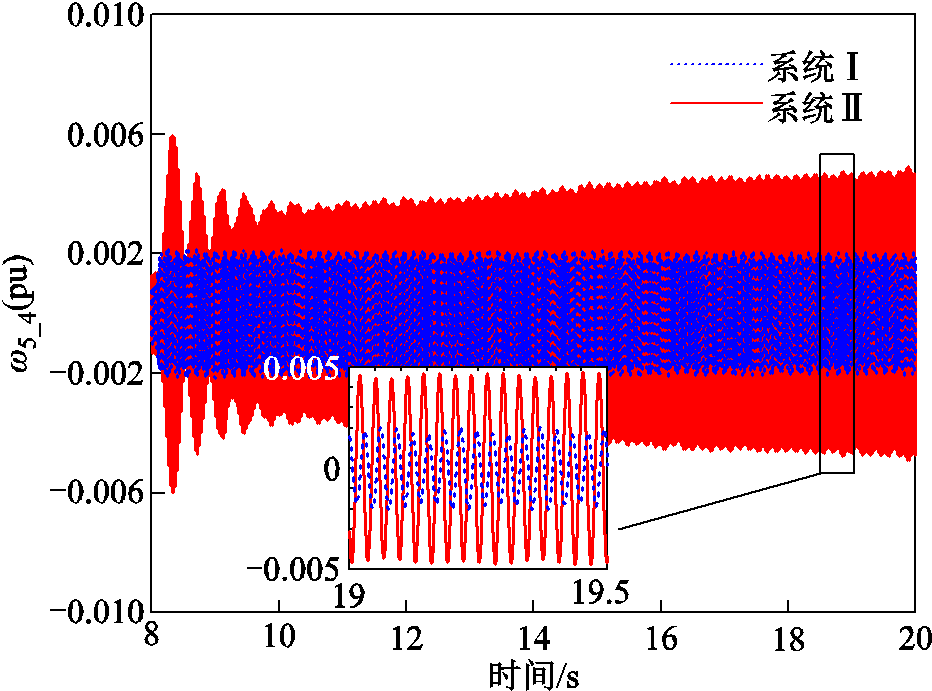
图8 系统Ⅰ和系统Ⅱ的SSR
Fig.8 The shafting SSR of System I and System II
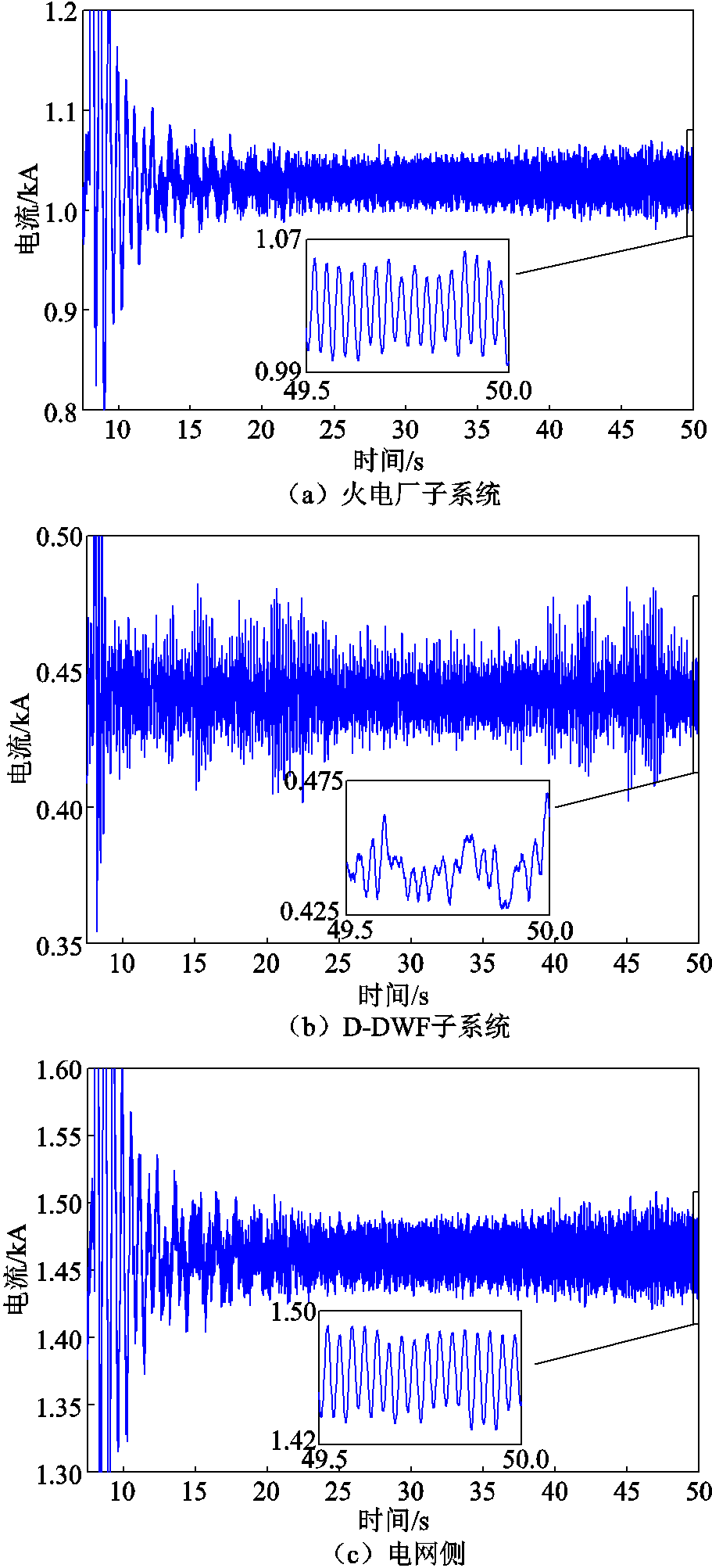
图9 系统Ⅱ电流有效值
Fig.9 RMS current of SystemⅡ
图9表明，火电厂子系统、电网侧中电流仅产生32 Hz的次同步分量，对应SSR模态；D-DWF子系统中有包含32 Hz在内的多种次同步分量，但是除32 Hz的次同步分量外，其他分量并没有形成如图6所示的闭环通路。
因此，系统中各处存在32 Hz的SSR分量，且SSR分量主要在火电厂与串补线路之间传递。SSR分量最终将汇入电网，威胁电力系统运行安全。
本节研究D-DWF子系统和串补线路子系统对火电厂子系统SSR的影响情况。从阻尼变化及时域仿真的角度，重点分析D-DWF的容量、风速、线路串补度对系统稳定性的影响。
D-DWF子系统中的风机数以5为步长从80个减到40个，对应D-DWF的容量以25 MW步长由400 MW减至200 MW，“点对网”系统的其他参数不变，根据小信号模型求解模态4的灵敏度，结果如图10所示。
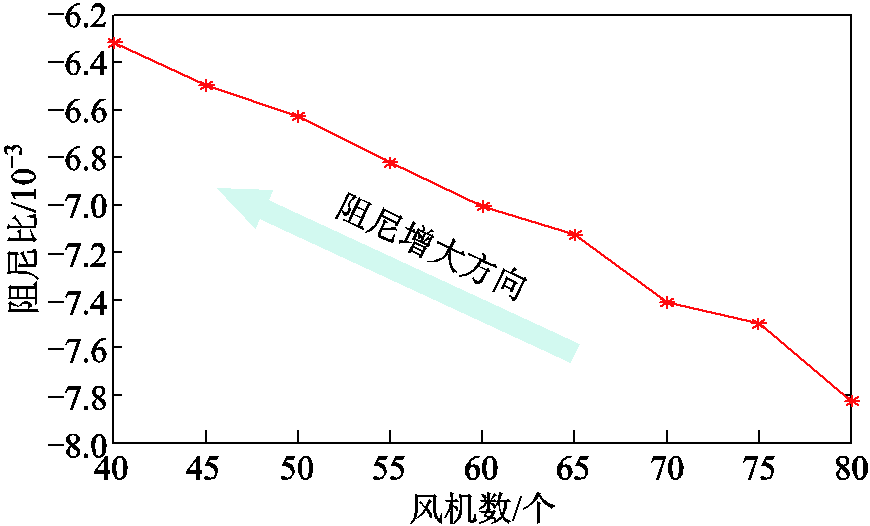
图10 风机数量改变对阻尼的影响
Fig.10 Influence of PMSG nummber variation on damping
由图10分析知，当D-DWF的容量减少时，SSR模态的阻尼变大，对应的SSR将会减弱。但是阻尼比的变化范围仅在-8×10-3到-6.2×10-3，容量对SSR的影响程度有限。其机理为：虽然D-DWF并入后新增SSO模态与SSR模态激励，形成更严重的SSR，但是D-DWF是通过改变汇入PCC的电流，间接参与SSR模态的阻尼变化，参与影响效果只在一定范围内明显。
在PSCAD/EMTDC中对上述分析进行时域验证：选取三组仿真，设置风机数分别为80、60、40，对应容量分别为400 MW、300 MW、200 MW，设置同4.2节的故障扰动以激发SSR，得到SSR模态对应SSR激发后的时域仿真波形，结果如图11所示。
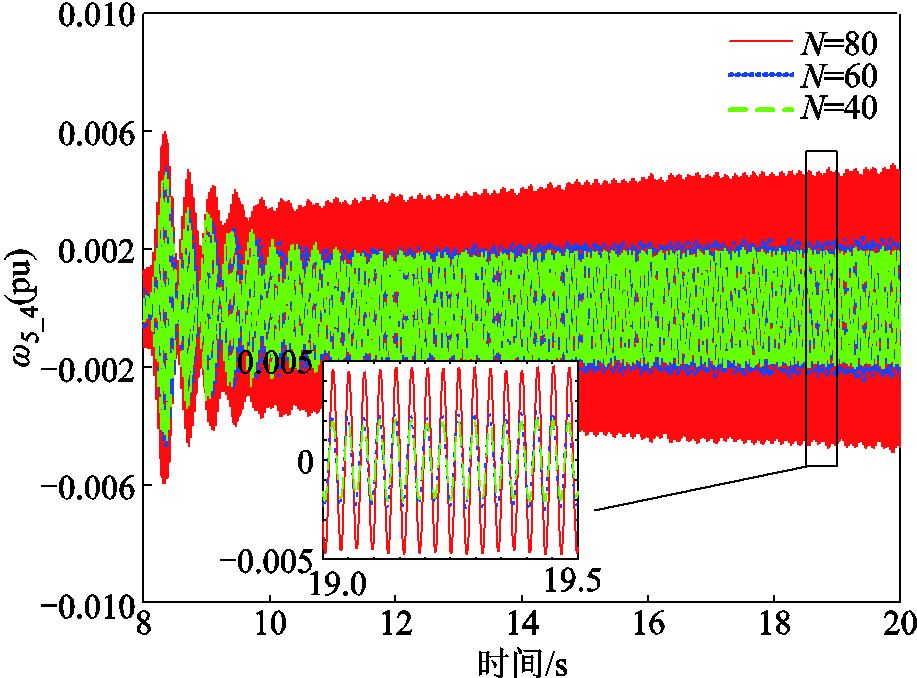
图11 风机数量变化时的仿真结果
Fig.11 Simulation resultes of PMSG nummber variation
由图11可知，随着D-DWF风机数量减少，即容量下降，系统阻尼增强，SSR幅度降低，时域仿真结果与灵敏度分析保持一致。同时，可以看到当D-DWF容量减少到一定程度（本算例下为300 MW），D-DWF子系统对SSR的影响将不明显，与图10中阻尼变化范围小的结果保持一致。
D-DWF子系统中的风速以0.5 m/s步长从 11 m/s减至8 m/s，“点对网”系统的其他参数不变，求解小信号模型得到SSR模态的灵敏度曲线，结果如图12所示。
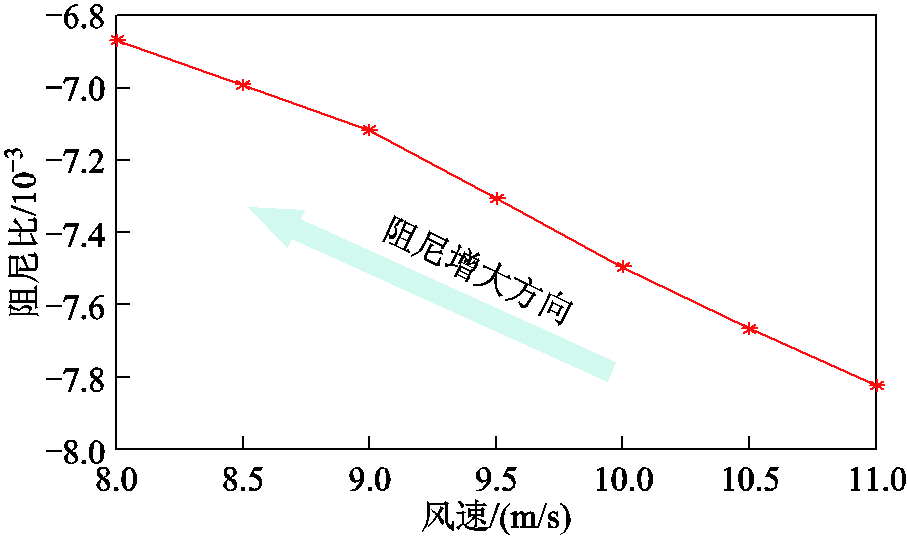
图12 风速改变对阻尼的影响
Fig.12 Influence of wind speed variation on damping
由图12可知，随着D-DWF中风速的降低，灵敏度曲线走势向上，系统的阻尼变大、更加稳定，其机理与D-DWF容量类似，通过影响串补系统间接参与SSR模态的阻尼变化。
在PSCAD/EMTDC中验证上述分析：保持系统其他参数不变，更改D-DWF的风速，选取风速分别为11 m/s、10.5 m/s、10 m/s的三组仿真，设置相同的故障激发SSR，电磁时域波形如图13所示。
由图13可知，当D-DWF中风速下降时，系统的阻尼增强，SSR幅值降低，与图12灵敏度曲线相一致。同5.1节分析，D-DWF中风速对火电厂的影响也有限，风速在额定值下降后，系统SSR的幅值被削弱，但风速的下降并不会使SSR明显地减弱，也验证了图12中的阻尼变化范围小的结果。
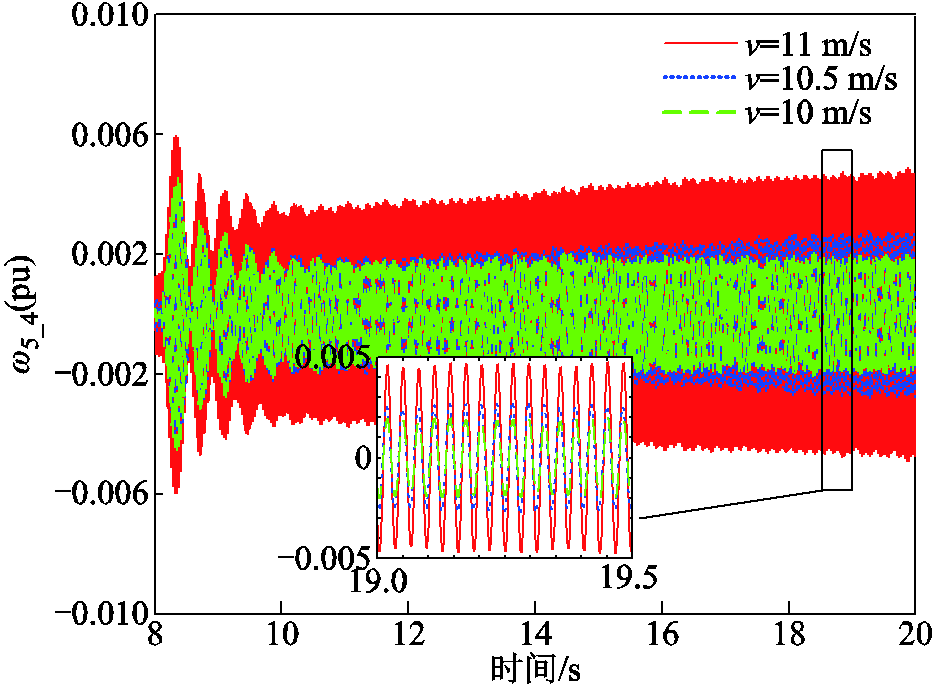
图13 风速改变时的仿真结果
Fig.13 Simulation resultes of wind speed variation
串补线路子系统中电容以5 μF的步长从100 μF增至150 μF，对应串补度从23.5%降至15.6%，保持“点对网”系统的其他参数不变，求解小信号模型得到SSR模态的灵敏度曲线，结果如图14所示。
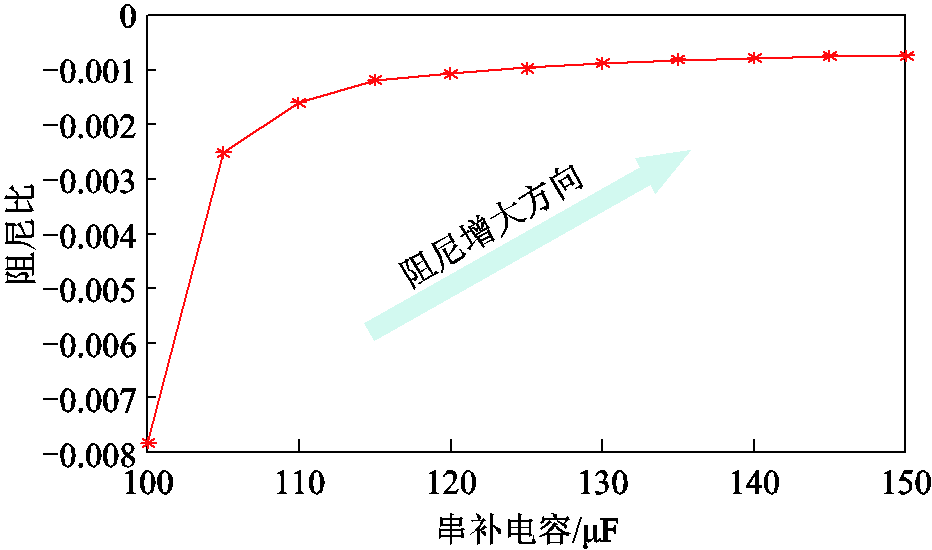
图14 串补度的变化对阻尼的影响
Fig.14 Influence of series compensation degree variation on damping
由图14可知，随着线路串补度的降低，系统的阻尼逐渐变大。其机理可以解释为：串补度降低，破坏了SSR的发生条件，导致SSR模态的阻尼增大。串补度降低后，谐振频率减小，对应互补频率增大，即发生SSR需要更高扭振频率的模态。因此，针对本系统不会产生新的SSR问题。
改变线路电容，设置线路串补度分别为23.5%、21.3%、19.5%，系统的其他参数以及SSR的激发条件不变，在PSCAD/EMTDC模型中运行得到电磁时域波形，如图15所示。
由图15可知，当系统串补度降低时，系统中的SSR明显被削弱。时域暂态波形与灵敏度曲线变化趋势吻合，验证了灵敏度分析的有效性。对比图8可知，当系统串补度降低到19.5%时，SSR谐振的幅度远远小于无D-DWF并入的系统。因此，D-DWF并入系统后，串补度仍是系统发生SSR的主要影响因素。结合图11、图13分析可知，D-DWF的容量或风速减小到一定程度，将对SSR的影响不大，因此控制D-DWF的容量和风速将有效避免发生严重的SSR，改变线路串补度基本可以避免SSR的发生。
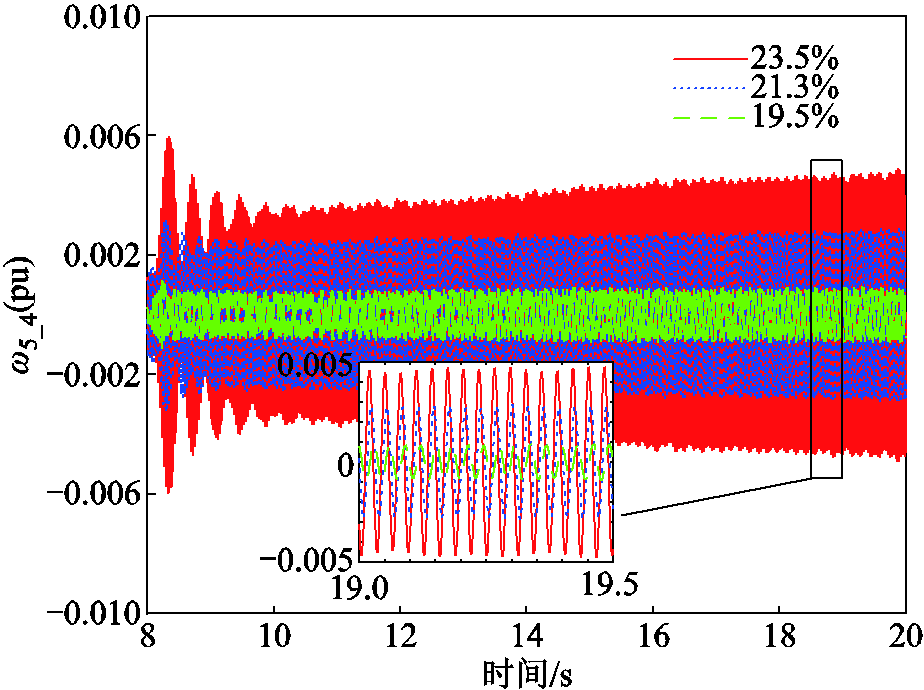
图15 串补度变化时的仿真结果
Fig.15 Simulation resultes of series compensation degree variation
由上述分析可知，D-DWF子系统和串补线路子系统均会影响SSR，而且前者并不直接参与SSR模态，仅通过PCC间接使SSR的阻尼产生较小幅度的变化，其影响程度有限；后者会直接参与SSR模态，对SSR的阻尼变化影响较大，为主要的影响因素。当D-DWF容量降低、D-DWF风速降低、串补度降低时，均有利于提高“点对网”系统的阻尼。
本文结合特征值与时域仿真的方法，分析了“点对网”系统中的SSR问题，研究了相关参数对其阻尼特性的影响。主要结论如下：
1）针对“点对网”系统，采用适用于模块化建模方法的小信号模型状态变量消去方法，建立小信号模型，并通过阶跃响应验证了可靠性、准确性。
2）D-DWF接入前后，系统均存在四种负阻尼的扭振模态，包含一个SSR模态。D-DWF接入后，其会与串补线路、火电机组形成次同步激励回路。振荡机理呈现“机电谐振”与“模态频率接近”耦合现象。SSR模态阻尼降低，“点对网”系统SSR发生的风险升高，其他负阻尼的扭振模态阻尼得到改善。
3）D-DWF的容量降低、风速下降、串补度减小，会提高SSR模态的阻尼，降低SSR的风险。D-DWF并入后串补度仍是系统SSR的主要影响因素，D-DWF的影响效果有限。此结论对实际工程存在一定的指导意义。
附 录
1.“点对网”型系统参数
附表1 火电厂参数
App.Tab. 1 Parameters of thermal power plant
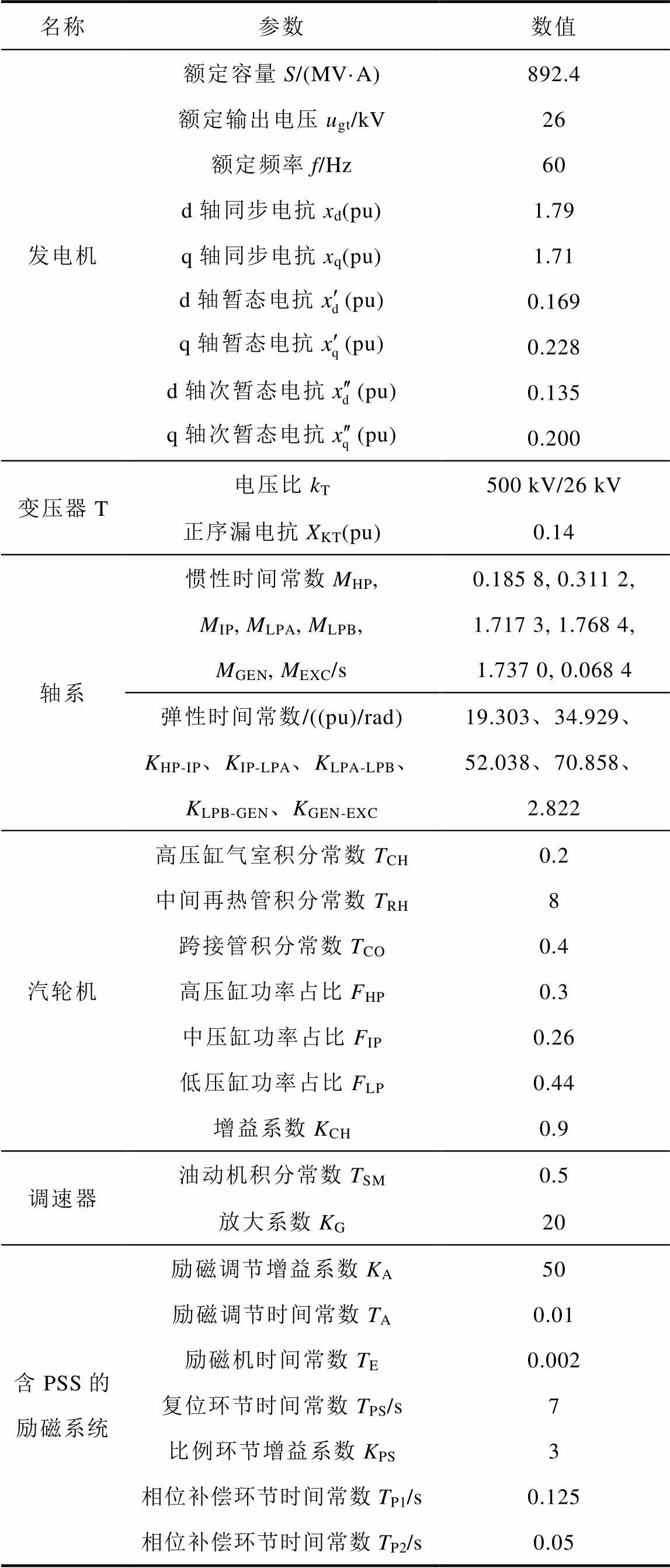
名称参数数值 发电机额定容量S/(MV·A)892.4 额定输出电压ugt/kV26 额定频率f/Hz60 d轴同步电抗xd(pu)1.79 q轴同步电抗xq(pu)1.71 d轴暂态电抗(pu)0.169 q轴暂态电抗(pu)0.228 d轴次暂态电抗(pu)0.135 q轴次暂态电抗(pu)0.200 变压器T电压比kT500 kV/26 kV 正序漏电抗XKT(pu)0.14 轴系惯性时间常数MHP, MIP, MLPA, MLPB, MGEN, MEXC/s0.185 8, 0.311 2, 1.717 3, 1.768 4, 1.737 0, 0.068 4 弹性时间常数/((pu)/rad)KHP-IP、KIP-LPA、KLPA-LPB、KLPB-GEN、KGEN-EXC19.303、34.929、52.038、70.858、2.822 汽轮机高压缸气室积分常数TCH0.2 中间再热管积分常数TRH8 跨接管积分常数TCO0.4 高压缸功率占比FHP0.3 中压缸功率占比FIP0.26 低压缸功率占比FLP0.44 增益系数KCH0.9 调速器油动机积分常数TSM0.5 放大系数KG20 含PSS的励磁系统励磁调节增益系数KA50 励磁调节时间常数TA0.01 励磁机时间常数TE0.002 复位环节时间常数TPS/s7 比例环节增益系数KPS3 相位补偿环节时间常数TP1/s0.125 相位补偿环节时间常数TP2/s0.05
附表2 主拓扑参数
App.Tab.2 Primary topology parameters
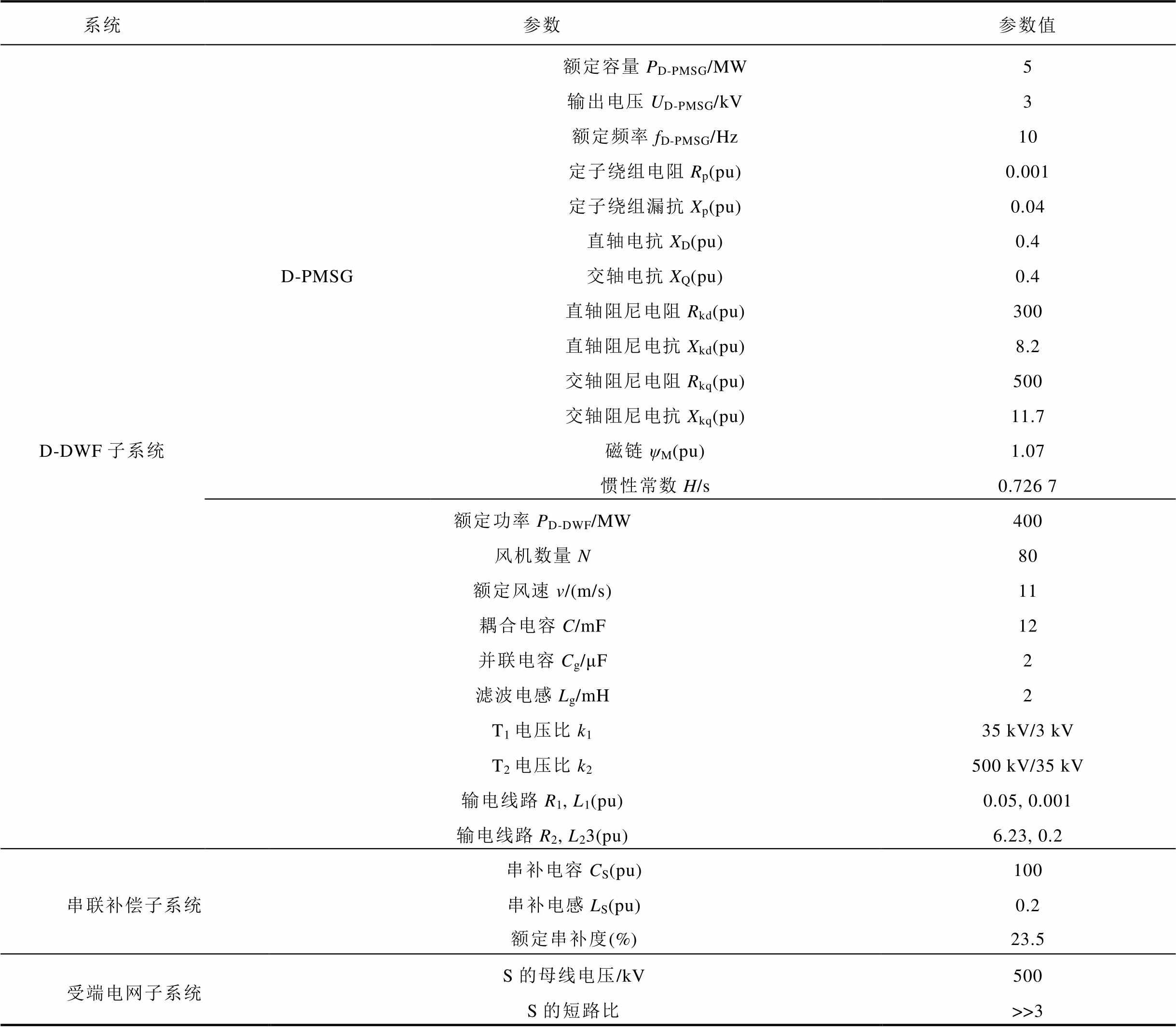
系统参数参数值 D-DWF子系统D-PMSG额定容量PD-PMSG/MW5 输出电压UD-PMSG/kV3 额定频率fD-PMSG/Hz10 定子绕组电阻Rp(pu)0.001 定子绕组漏抗Xp(pu)0.04 直轴电抗XD(pu)0.4 交轴电抗XQ(pu)0.4 直轴阻尼电阻Rkd(pu)300 直轴阻尼电抗Xkd(pu)8.2 交轴阻尼电阻Rkq(pu)500 交轴阻尼电抗Xkq(pu)11.7 磁链ψM(pu)1.07 惯性常数H/s0.726 7 额定功率PD-DWF/MW400 风机数量N80 额定风速v/(m/s)11 耦合电容C/mF12 并联电容Cg/μF2 滤波电感Lg/mH2 T1电压比k135 kV/3 kV T2电压比k2500 kV/35 kV 输电线路R1, L1(pu)0.05, 0.001 输电线路R2, L23(pu)6.23, 0.2 串联补偿子系统串补电容CS(pu)100 串补电感LS(pu)0.2 额定串补度(%)23.5 受端电网子系统S的母线电压/kV500 S的短路比>>3
附表3 D-DWF控制参数
App.Tab.3 Control parameters of D-DWF
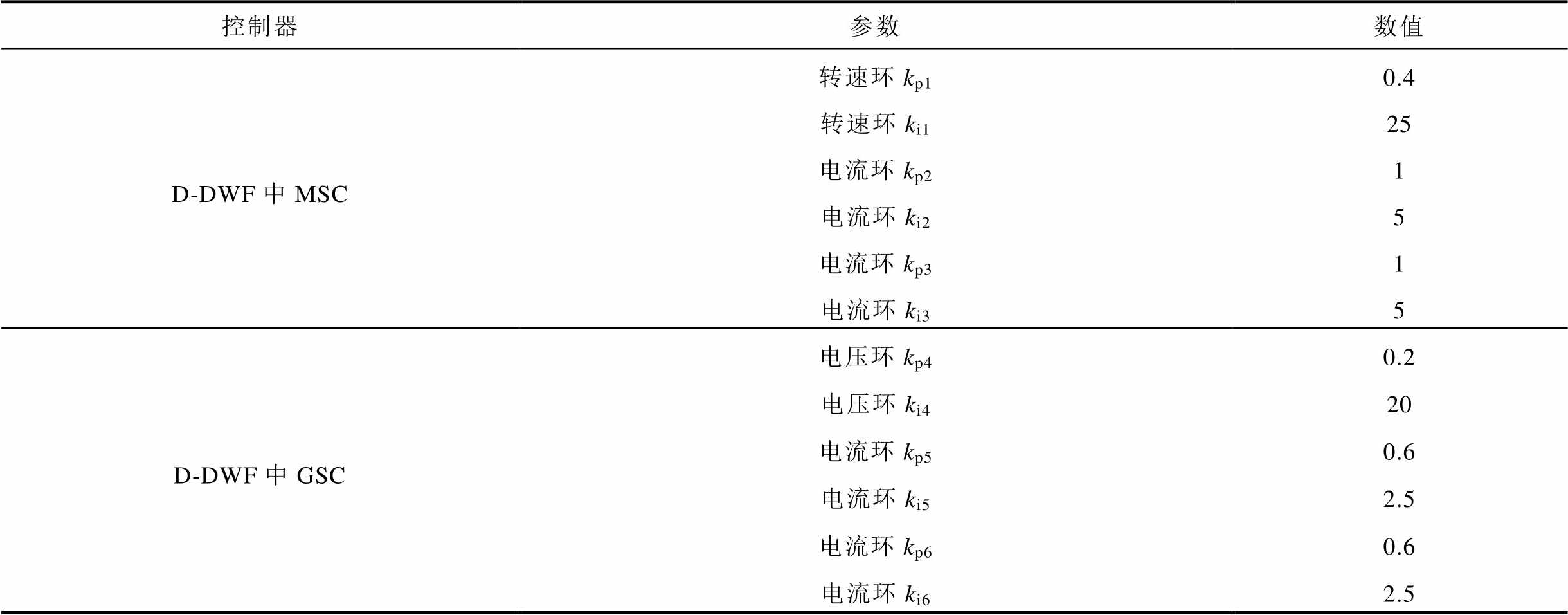
控制器参数数值 D-DWF中MSC转速环kp10.4 转速环ki125 电流环kp21 电流环ki25 电流环kp31 电流环ki35 D-DWF中GSC电压环kp40.2 电压环ki420 电流环kp50.6 电流环ki52.5 电流环kp60.6 电流环ki62.5
2. 状态变量消去方法的数学解释
1）火电厂子模块
设火电厂汇入PCC处电流的xy分量分别为ix1、iy1，根据本模块的状态空间模型可以得到
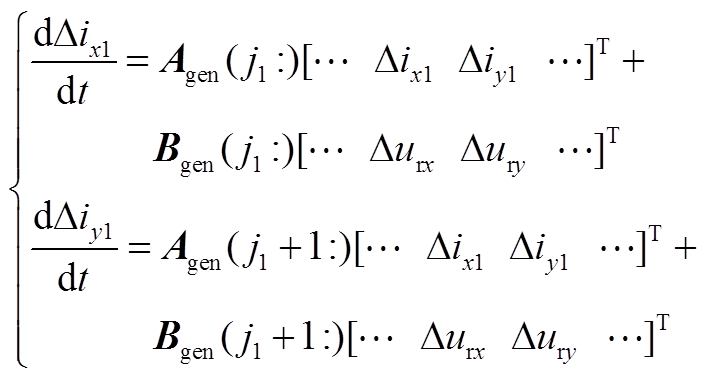（A1）
式中，Agen、Bgen分别为火电厂子模块状态空间模型的系数矩阵、输出矩阵，并省略了非关键元素。
2）D-DWF子模块
设D-DWF汇入PCC处电流的xy分量分别为ix2、iy2，根据本模块的状态空间模型可以得到
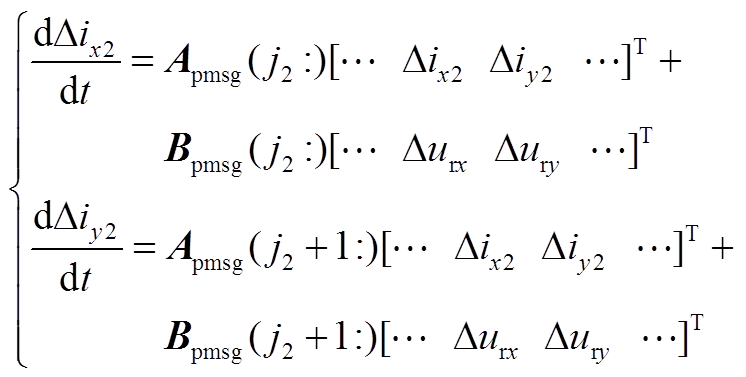（A2）
式中，Apmsg、Bpmsg分别为D-DWF子模块状态空间模型的系数矩阵、输出矩阵，并省略了非关键元素。
irx为ix1与ix2的和、iry为iy1与iy2的和，将式（A1）与式（A2）代入式（8），结合矩阵运算即可得到式（9）。
参考文献
[1] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97. Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[2] 王一珺, 杜文娟, 陈晨, 等. 基于改进复转矩系数法的风电场并网引发电力系统次同步振荡研究[J]. 电工技术学报, 2020, 35(15): 3258-3269. Wang Yijun, Du Wenjuan, Chen Chen, et al. Study on sub-synchronous oscillations of power systems caused by grid-connected wind farms based on the improved complex torque coefficients method[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3258-3269.
[3] 陈露洁, 徐式蕴, 孙华东, 等. 高比例电力电子电力系统宽频带振荡研究综述[J]. 中国电机工程学报, 2021, 41(7): 2297-2310. Chen Lujie, Xu Shiyun, Sun Huadong, et al. A survey on wide-frequency oscillation for power systems with high penetration of power electronics[J]. Proceedings of the CSEE, 2021, 41(7): 2297-2310.
[4] 国家能源局. 国家能源局发布1-10月份全国电力工业统计数据[EB/OL]. 北京: 国家能源局, 2022.(2022-11-22)[2022-12-06]. http://www.nea.gov. cn/2022-11/22/c_1310678885.htm.
[5] 中华人民共和国国家发展和改革委员会. 关于印发“十四五”可再生能源发展规划的通知[EB/OL]. 北京: 中华人民共和国国家发展和改革委员会, 2022.(2022-06-01)[2022-12-06]. https://www.ndrc.gov. cn/xwdt/tzgg/202206/t20220601_1326720.html?code=&state=123.
[6] 张蓉. “十四五”新能源消纳的思考[J]. 中国电力企业管理, 2021(4): 23-25.
[7] Liu Huakun, Xie Xiaorong, He Jingbo, et al. Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4708-4720.
[8] 张天翼, 杜文娟, 陈晨, 等. 弱连接条件下并网直驱风电场引发无串补电力系统次同步扭振机理研究[J]. 中国电机工程学报, 2020, 40(18): 5875-5885. Zhang Tianyi, Du Wenjuan, Chen Chen, et al. A mechanism investigation on SSTOs in power systems without series compensated lines induced by PMSG wind farms under the condition of weak grid connection[J]. Proceedings of the CSEE, 2020, 40(18): 5875-5885.
[9] 谢小荣, 刘华坤, 贺静波, 等. 直驱风机风电场与交流电网相互作用引发次同步振荡的机理与特性分析[J]. 中国电机工程学报, 2016, 36(9): 2366-2372. Xie Xiaorong, Liu Huakun, He Jingbo, et al. Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full-converter wind turbines and AC systems[J]. Proceedings of the CSEE, 2016, 36(9): 2366-2372.
[10] 王利超, 于永军, 张明远, 等. 直驱风电机组阻抗建模及次同步振荡影响因素分析[J]. 电力工程技术, 2020, 39(1): 170-177. Wang Lichao, Yu Yongjun, Zhang Mingyuan, et al. Impedance model and analysis of subsynchronous oscillation influence factors for grid-connected full-converter wind turbines[J]. Electric Power Engineering Technology, 2020, 39(1): 170-177.
[11] 刘文元, 任必兴, 李海峰, 等. 直驱风电场和串补之间的次同步振荡风险[J]. 电力工程技术, 2022, 41(4): 25-32. Liu Wenyuan, Ren Bixing, Li Haifeng, et al. Sub-synchronous oscillation risk between PMSG farm and series complement[J]. Electric Power Engineering Technology, 2022, 41(4): 25-32.
[12] Xu Yangkun, Zhang Miao, Fan Lingling, et al. Small-signal stability analysis of type-4 wind in series-compensated networks[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 529-538.
[13] Zhao Shuqiang, Li Ren, Gao Benfeng, et al. Sub and super synchronous oscillations between type 4 wind turbines and series compensated AC transmission systems[C]//2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 2018: 1-5.
[14] 谢小荣, 王路平, 贺静波, 等. 电力系统次同步谐振/振荡的形态分析[J]. 电网技术, 2017, 41(4): 1043-1049. Xie Xiaorong, Wang Luping, He Jingbo, et al. Analysis of subsynchronous resonance/oscillation types in power systems[J]. Power System Technology, 2017, 41(4): 1043-1049.
[15] 程时杰, 曹一家, 江全元. 电力系统次同步振荡的理论与方法[M]. 北京: 科学出版社, 2009.
[16] 刘斌, 呼斯乐, 王甲军, 等. 直驱风电场经LCC-HVDC外送系统阻抗建模及振荡机理分析[J]. 中国电机工程学报, 2021, 41(10): 3492-3504, 3674. Liu Bin, Hu Sile, Wang Jiajun, et al. Impedance modeling and oscillation mechanism analysis of D-PMSG-based wind farms integration through LCC-HVDC system[J]. Proceedings of the CSEE, 2021, 41(10): 3492-3504, 3674.
[17] 高本锋, 崔意婵, 李蕴红, 等. D-PMSG经LCC-HVDC送出系统的次同步振荡特性分析[J]. 中国电机工程学报, 2022, 42(6): 2084-2096. Gao Benfeng, Cui Yichan, Li Yunhong, et al. Analysis of subsynchronous oscillation characteristics of D-PMSG integrated with LCC-HVDC system[J]. Proceedings of the CSEE, 2022, 42(6): 2084-2096.
[18] 邵冰冰, 赵书强, 裴继坤, 等. 直驱风电场经VSC-HVDC并网的次同步振荡特性分析[J]. 电网技术, 2019, 43(9): 3344-3355. Shao Bingbing, Zhao Shuqiang, Pei Jikun, et al. Subsynchronous oscillation characteristic analysis of grid-connected DDWFs via VSC-HVDC system[J]. Power System Technology, 2019, 43(9): 3344-3355.
[19] 王旭斌, 杜文娟, 王海风. 直驱风电并网系统中锁相环引起次同步振荡的开环模式谐振机理分析[J]. 中国电机工程学报, 2018, 38(7): 1935-1950, 2209. Wang Xubin, Du Wenjuan, Wang Haifeng. Mechanism analysis of open-loop modal resonance on subsynchronous oscillations caused by PLL in power systems with integrated PMSGs[J]. Proceedings of the CSEE, 2018, 38(7): 1935-1950, 2209.
[20] Zhang Tianyi, Wang Haifeng. Method to evaluate the impact of integration of PMSG on stability of synchronous generator shaft under weak grid connection[J]. Frontiers in Energy Research, 2021, 9: 742304.
[21] 李辉, 陈耀君, 李洋, 等. 双馈风电场并网对汽轮发电机次同步振荡的影响[J]. 电机与控制学报, 2015, 19(6): 47-54. Li Hui, Chen Yaojun, Li Yang, et al. Impact of DFIG-based wind farms interconnected to power grid on subsynchronous oscillation of turbogenerator[J]. Electric Machines and Control, 2015, 19(6): 47-54.
[22] 张育硕, 郝丽丽, 周彦彤, 等. 风火打捆经串补外送系统次同步振荡分析及抑制策略研究[J]. 电力电容器与无功补偿, 2019, 40(6): 189-195. Zhang Yushuo, Hao Lili, Zhou Yantong, et al. Analysis and suppression strategy of sub-synchronous oscillation for wind-thermal-bundled power transmitted by series-compensated system[J]. Power Capacitor & Reactive Power Compensation, 2019, 40(6): 189-195.
[23] Li Jing, Zhang Xiaoping. Impact of increased wind power generation on subsynchronous resonance of turbine-generator units[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(2): 219-228.
[24] Leon A E. Integration of DFIG-based wind farms into series-compensated transmission systems[J]. IEEE Transactions on Sustainable Energy, 2016, 7(2): 451-460.
[25] Li Penghan, Wang Jie, Xiong Linyun, et al. Energy-shaping controller for DFIG-based wind farm to mitigate subsynchronous control interaction[J]. IEEE Transactions on Power Systems, 2021, 36(4): 2975-2991.
[26] Sun Bin, Ju Ping, Shahidehpour M, et al. Calculation of stable domain of DFIG-based wind farm in series compensated power systems[J]. IEEE Access, 2020, 8: 34900-34908.
[27] Fan Lingling, Kavasseri R, Miao Z L, et al. Modeling of DFIG-based wind farms for SSR analysis[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2073-2082.
[28] Peng Xiaotao, Chen Renjie, Zhou Jicheng, et al. Research on mechanism and damping control strategy of DFIG-based wind farm grid-connected system SSR based on the complex torque method[J]. Electronics, 2021, 10(14): 1640.
[29] 赵书强, 李忍, 高本锋, 等. 适用于多源系统次同步振荡分析的图形化建模方法[J]. 电工技术学报, 2017, 32(14): 184-193, 228. Zhao Shuqiang, Li Ren, Gao Benfeng, et al. A graphical modeling method applied for multi-sources system subsynchronous oscillation analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 184-193, 228.
[30] 陈宝平, 林涛, 陈汝斯, 等. 直驱风电场经VSC-HVDC并网系统的多频段振荡特性分析[J]. 电工技术学报, 2018, 33(增刊1): 176-184. Chen Baoping, Lin Tao, Chen Rusi, et al. Characteristics of multi-band oscillation for direct drive wind farm interfaced with VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 176-184.
[31] 董文凯, 任必兴, 王海风, 等. 适用于系统次同步振荡分析的风电场等值建模方法综述[J]. 电力工程技术, 2022, 41(4): 33-43. Dong Wenkai, Ren Bixing, Wang Haifeng, et al. Small-signal equivalent modeling methods of the wind farm and its application in sub-synchronous oscillations analysis of gird-connected wind power systems[J]. Electric Power Engineering Technology, 2022, 41(4): 33-43.
[32] 顾志明. 大规模风电场接入对火电机组次同步振荡阻尼特性影响研究[D]. 北京: 华北电力大学, 2021. Gu Zhiming. Study on the influence of large-scale wind farms connected to the grid on the damping characteristics of the subsynchronous oscillation of thermal power unit[D]. Beijng: North China Electric Power University, 2021.
[33] Abdeen M, Li Hui, Kamel S, et al. A recent analytical approach for analysis of sub-synchronous resonance in doubly-fed induction generator-based wind farm[J]. IEEE Access, 2021, 9: 68888-68897.
[34] 张学伟. 风火打捆送出系统的次同步振荡问题研究[D]. 北京: 华北电力大学, 2017. Zhang Xuewei. Research of sub synchronous oscillation in wind-thermal bundled system[D]. Beijing: North China Electric Power University, 2017.
Abstract The direct-drive wind farm (D-DWF) and thermal power bundled point-to-network system sent through series supply lines have become the main form of energy consumption in recent years because of its advantages of large transmission capacity and mature and reliable technology. However, there is a subsynchronous resonance problem in the thermal power series compensation system, and the direct drive wind farm system itself also has the risk of subsynchronous oscillation. Therefore, the oscillation problem of the baling system cannot be ignored. After D-DWF is connected to the thermal power series replenishment system, its influence mechanism on the subsynchronous resonance (SSR) of thermal power units is not clear.
Firstly, based on the linearization mathematical model of point-to-mesh system with D-DWF and thermal power bundled and sent by series supplementation, the state variable elimination method suitable for modular modeling is used to establish a system small signal model based on modular modeling idea in MATLAB/Simulink, and its reliability is verified by step response. Secondly, the small signal model of the D-DWF system before and after grid connection is solved, and the SSR characteristics are analyzed. Then, the SSR mechanism of the D-DWF system after access is explained, and the SSR mechanism is verified by time domain simulation. Finally, taking the capacity, wind speed and string complement of D-DWF as the research objects, the risk of SSR in the system is analyzed from the perspective of damping characteristics and time-domain response.
When the series complement is 23.5%, the corresponding resonant frequency is about 29 Hz, which is complementary to the frequency of SSR mode (corresponding to thermal shafting mode 4) in the system. At this time, when the system is disturbed, the subsynchronous component acts on the thermal power unit through the point of common coupling (PCC), inducing SSR. When there is a mode of about 32 Hz in D-DWF, after the disturbance occurs, the subsynchronous component will also act on the thermal power unit through PCC, which will excite the SSR in the system and intensify the oscillation. After the thermal power unit generates SSR, the thermal power unit feeds the subsynchronous component back to the PCC through the speed signal, and the subsynchronous component flows through the closed loop.
The main conclusions of this paper are as follows: (1) Through step response, the reliability and accuracy of the small signal model of wind-fire bundle warp supply system are verified. (2) Before and after D-DWF access, the system has four negative damping torsional vibration modes, including an SSR mode. After D-DWF is connected, it will form a subsynchronous excitation loop with series lines and thermal power units. The oscillation mechanism shows the coupling phenomenon of "electromechanical resonance" and "modal frequency approach"; SSR mode damping is reduced, the risk of system SSR occurrence is increased, and the torsional vibration mode damping of other negative damping is improved. (3) The reduction of D-DWF capacity, wind speed decrease, and series complement decrease will increase the damping of SSR mode and reduce the risk of SSR. The string complement degree after D-DWF is incorporated is still the main influencing factor of SSR in the system, and the influence effect of D-DWF is limited.
keywords：Direct-drive wind farm, series compensation, wind-thermal bundled, eigenvalue analysis, subsynchronous resonance (SSR)
DOI: 10.19595/j.cnki.1000-6753.tces.230340
中图分类号：TM712
收稿日期 2023-03-22
改稿日期 2023-04-17
高本锋 男，1981年生，副教授，研究方向为高压直流输电和电力系统次同步振荡。E-mail：gaobenfeng@126.com
刘培鑫 男，2000年生，硕士研究生，研究方向为电力系统次同步振荡。E-mail：liupeixin2022@126.com（通信作者）
（编辑 郭丽军）