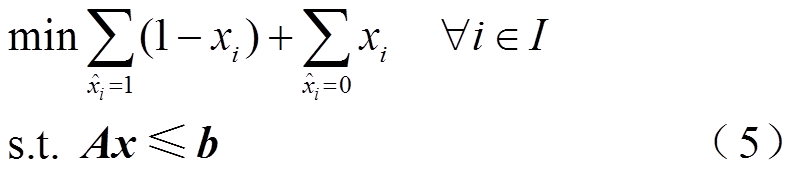电力系统混合整数线性规划问题的运筹决策关键技术综述与展望
高 倩 杨知方 李文沅
(输变电装备技术全国重点实验室(重庆大学) 重庆 400044)
摘要 机组组合、检修计划、拓扑运行优化、电力系统规划等电力系统混合整数线性规划(MILP)问题旨在实现电力资源的最佳配置,应用广泛,其精准性与高效性直接影响了电力系统的安全性与经济性。随着“双碳”目标的提出,新型电力系统MILP问题模型复杂度更高、计算效率要求更严格,对当前运筹决策技术提出了更严峻的挑战。然而,现有依赖于国外进口求解器的电力系统运筹决策技术面临“组合爆炸”,且求解器依赖进口面临“卡脖子”困境,亟须实现技术突破。为此,该文系统地梳理了电力系统MILP问题的运筹决策技术,以及近年来通用MILP问题的最新进展,并展望了电力系统MILP问题运筹决策关键技术未来的研究方向,旨在为我国相关研究工作提供参考和思路。
关键词:电力系统优化 混合整数线性规划 运筹决策 混合整数线性规划(MILP)求解器
0 引言
组合优化问题(Combinatorial Problem, CO)是一类在离散空间中运用运筹决策(Operations Research, OR)技术寻找最优决策的问题,被广泛应用在国防、交通、能源等重要领域。其中,电力系统组合优化问题旨在实现电力资源的最佳配置,从而提高能源利用效率,其求解的精准性与高效性直接影响电力系统的安全性与经济性。电力系统组合优化问题求解的关键难点在于非凸特性和离散特性。非凸特性包括约束和目标函数中的交流潮流方程、机组阀点效应等,当前通常采用以下几种方式进行处理:①线性化,电力系统的一些组成部分具有近似线性的特点,因此可采用例如直流潮流方程、分段线性化等方式进行低误差的线性化建模,使得原模型转换为混合整数线性规划(Mixed-Integer Linear Programming, MILP)问题;②凸化,根据原模型的结构特性,可转换成半正定规划(Semidefinite Programming, SDP)、二阶锥规划(Second-Order Cone Programming, SOCP)等更容易求解的问题;③直接求解,利用内点法、梯度下降算法等非线性优化算法直接求解,但容易面临收敛性、鲁棒性的问题。本文中针对电力系统组合优化问题的讨论,通过线性化简化了非凸特性,专注于离散特性带来的求解困难,即电力系统MILP问题。MILP问题中,决策变量由连续变量和离散变量构成,同时需考虑电力系统线性或经线性化处理的物理约束。其优势在于建模的泛用性和求解的收敛性、鲁棒性,因此在电力系统组合优化领域应用广泛。典型的电力系统MILP问题包括机组组合、检修计划、拓扑运行优化、电力系统规划等。
作为一种典型的NP难(Non-deterministic Polynomial-time hardness)问题,MILP问题的可行解数目随着离散变量的规模呈指数型增长,无法在多项式时间内通过穷举得到问题的最优解。电力工业领域求解电力系统MILP问题的运筹决策技术见表1[1-2],通常有两种应用方式:①直接调用内嵌不同算法的求解器,简便可行,具有一定的泛用性,然而对于大规模问题仍然面对收敛缓慢或者难以收敛的实际瓶颈;②使用自研算法,能够应对难以直接调用求解的问题,但在特定问题结构下的适用性难以保证。近年来以分支定界为核心算法的开源和商业求解器快速发展,MILP问题的求解效率、稳定性和通用性都得到了极大提升,MILP求解器已成为电力系统MILP问题的主流运筹决策技术,如中国、美国等国家均采用CPLEX、GUROBI等商用求解器求解日前机组组合等大规模电力系统MILP问题[3]。
表1 几种常见的混合整数线性规划运筹决策技术
Tab.1 Several solution methods for mixed-integer linear programming problem
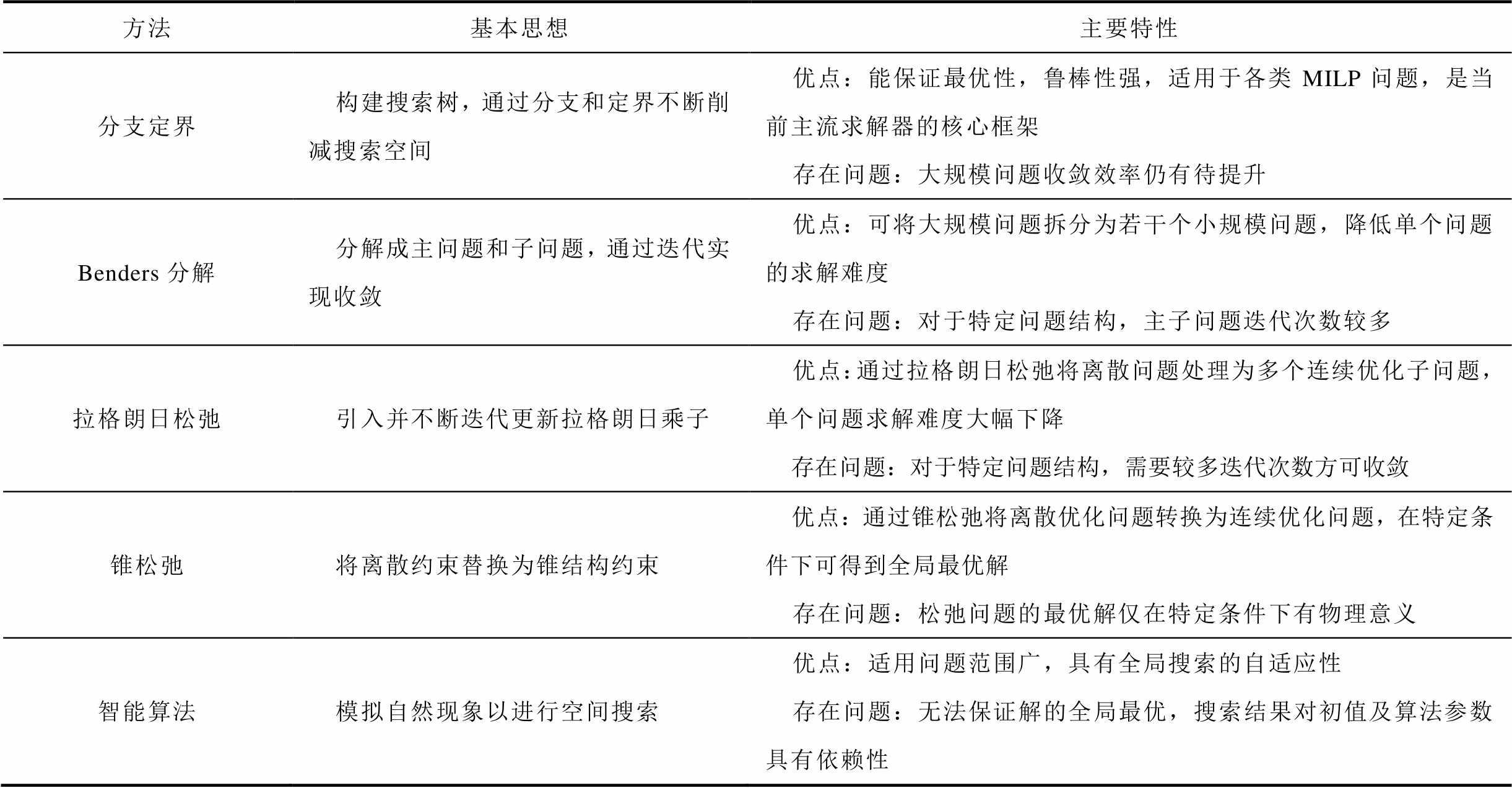
方法基本思想主要特性 分支定界构建搜索树,通过分支和定界不断削减搜索空间优点:能保证最优性,鲁棒性强,适用于各类MILP问题,是当前主流求解器的核心框架存在问题:大规模问题收敛效率仍有待提升 Benders分解分解成主问题和子问题,通过迭代实现收敛优点:可将大规模问题拆分为若干个小规模问题,降低单个问题的求解难度存在问题:对于特定问题结构,主子问题迭代次数较多 拉格朗日松弛引入并不断迭代更新拉格朗日乘子优点:通过拉格朗日松弛将离散问题处理为多个连续优化子问题,单个问题求解难度大幅下降存在问题:对于特定问题结构,需要较多迭代次数方可收敛 锥松弛将离散约束替换为锥结构约束优点:通过锥松弛将离散优化问题转换为连续优化问题,在特定条件下可得到全局最优解存在问题:松弛问题的最优解仅在特定条件下有物理意义 智能算法模拟自然现象以进行空间搜索优点:适用问题范围广,具有全局搜索的自适应性存在问题:无法保证解的全局最优,搜索结果对初值及算法参数具有依赖性
随着“双碳”目标的提出,构建以新能源为主体的新型电力系统已成为我国能源发展转型的关键战略。新型电力系统下源、网、荷、储等可调节资源配置范围更广、不确定性增强,可调度主体/时段颗粒度的增加及随机性约束/碳减排机理的构建使得电力系统MILP问题模型复杂度更高、计算效率要求更严格,对当前运筹决策技术提出了更严峻的挑战。电力工业的体量大,通过优化决策的资源总量多,即使是小幅度的运筹决策精度和效率提升也能够产生巨大的经济效益。反而言之,若运筹决策技术未能在工程需求时间内达到全局最优,将会引起决策精准性不足问题,从而制约电网方式调整空间,增加电网成本,影响新能源消纳。据美国联邦能源管理委员会(Federal Energy Regulation Commission, FERC)估计,全球电力系统调度决策精准性问题每年造成数百亿美元的经济损失[4]。
一方面,CPLEX、GUROBI等商用求解器在大规模电力系统MILP问题求解中已面临求解瓶颈,难以破解“组合爆炸”难题。以我国某区域电网日前机组组合为例,该问题模型约有70万约束数目和16万离散变量,部分算例无法在1 h内获得可行解,成为制约区域乃至全国统一电力市场建设的瓶颈。另一方面,商用求解器依赖国外进口,内部算法“黑箱”调用难以深度调试,而SCIP、CBC等开源求解器在求解效率上仍存在较大差距[5]。国内企业也相继发布了国产自研求解器,如杉数科技的COPT、阿里巴巴达摩院决策智能实验室的MindOpt等,但面向省网及区域电网的超大规模机组组合等MILP问题,其求解效率与国外求解器尚存在差距。可见,电力系统MILP问题运筹决策技术的自主知识产权已成为国家能源领域的“卡脖子”问题,亟须研发突破性技术。
为此,本文系统地梳理了电力系统MILP问题的运筹决策技术,以及近年来通用MILP问题的最新进展,并展望了电力系统MILP问题运筹决策关键技术未来的研究方向,旨在为我国相关研究工作提供参考和思路。
1 电力系统MILP问题概述
本节分别概述几个典型电力系统MILP问题,并构建通用数学模型。
1)机组组合(Unit Commitment, UC)。机组组合在电力系统短期运行中应用广泛,尤其是近年来随着电力现货市场建设,日前机组组合的求解效率需满足市场出清的时效性要求,成为学术界和工业界关注的重点[3]。机组组合旨在满足供需平衡约束、线路传输约束以及机组物理约束等要求的基础上,制定电网运行成本最小的开停机方案及机组发电计划。其开停机决策作为0-1离散变量,规模与机组数目、调度时段精细度等成正比。考虑电网交流潮流方程[6]、机组阀点效应等非线性约束,机组组合本质上是混合整数非线性规划问题,但受限于求解鲁棒性要求,通常采用直流潮流方程等线性处理方法转换为MILP问题[1,7]。省级电网机组组合,不仅具有大规模参与决策的机组,更需要考虑含N-1安全校核的大量线路约束;为应对新能源强不确定性,进一步考虑随机性约束、细化机组组合调度时段颗粒度的需求凸显[8-10];构建全国统一电力市场已成为国家重大战略需求,机组组合的优化范围将从单一省份扩展至多区域联合决策。可见,随着新型电力系统的构建,机组组合问题复杂度陡增,面临极大的计算负担。
2)检修计划(Maintenance Scheduling, MS)。电力系统检修计划旨在以发电机、输电线路、变压器、断路器等设备实际状态为基础,考虑当前系统电源容量、拓扑冗余度、用电负荷、人力成本等条件,确定各个设备的最优检修时机[11]。与机组组合类似,检修计划模型中含有大量表示设备检修状态的离散变量、大量电力系统复杂物理约束以及时序周期性约束等,具有较大计算负担。随着电网运营的精细化要求逐渐提高,迫切需要通过优化制定满足电网多维安全要求、节省电网运行成本的检修计划,当前检修制定方法仍需进一步提升计算效率以适应电网运行要求。
3)拓扑运行优化(Optimal Transmission Switching, OTS)。传统电网运行通常认为网架结构是给定参量,然而,已有研究表明,在运行阶段对电网拓扑进行合理优化可有效消除电磁环网等不利电网运行状态,有效缓解阻塞,提升电网运行的经济性和安全性[12]。由于电力系统线路数目众多,该问题进一步引入了大量离散变量,优化难度加剧;同时,由于网络拓扑结构变化对系统潮流等运行状态影响大,为寻优带来了额外难度,尤其在要求快速调度的电力系统实时运行中仍面临很大的计算瓶颈。当前的拓扑运行优化研究通常需要通过限制线路切断数目等方式缩减优化空间。
4)电力系统规划(Power System Planning, PSP)。电力系统规划是发电资源、网架结构、市场运营等因素在短期和中长期的规划和管理问题,旨在保障电力系统的可靠性、经济性等需求。与电力系统运行问题相比,电力系统规划问题涉及的时间尺度通常更宽。特别是在实现“双碳”目标的背景下,高比例新能源接入电力系统带来的不确定性问题,设备规模和类型的显著增加,以及对碳减排等新型指标的优化需求,进一步增加了电力系统规划的求解难度[13]。
除上述问题之外,对电力系统中非线性特性的分段线性处理也会引入大量离散变量,包括:模型分段线性处理(Piecewise Linear Formulation, PLF)、逻辑描述(Logical Constraints, LC)等。如通过分段报价将发电机的二次成本曲线线性化处理等。分段线性化一方面能增强模型的收敛性和鲁棒性;另一方面也使得MILP问题规模进一步增长。此外,针对部分电力系统状态的逻辑描述(如柔性输电设备动作对潮流方向的影响、绝对值函数等)通常也会引入离散变量,形成MILP问题。可见,电力系统MILP问题具有广泛的工程意义,本文旨在针对这一广义问题探讨其关键技术。需要注意的是,相比于电力系统规划问题,电力系统运行问题对MILP的求解效率要求更加严格;其中,机组组合在日前电力市场的应用及其时效性要求引起了重点关注。因此,本文主要关注电力系统运行层面的运筹决策相关研究。
除离散特性外,本文仅考虑电力系统线性或经线性化处理的物理特性,因此,上述问题的数学本质均可以构建为具有m条约束和n个决策变量的通用MILP模型,即
式中,A、b为约束系数矩阵及其右端项;c为成本系数;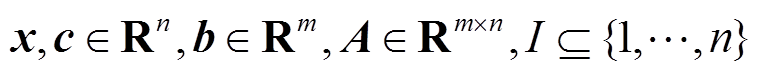 。对于不同的电力系统MILP问题,A、b、c具有不同的物理意义。若将模型式(1)中的离散决策变量由连续决策变量替代,则原问题转变为线性规划(Linear Programming, LP)问题,这一过程被称为LP松弛(Relaxation)。
。对于不同的电力系统MILP问题,A、b、c具有不同的物理意义。若将模型式(1)中的离散决策变量由连续决策变量替代,则原问题转变为线性规划(Linear Programming, LP)问题,这一过程被称为LP松弛(Relaxation)。
2 MILP运筹决策关键技术基本框架
本节概述了在通用MILP问题及电力系统MILP问题的运筹决策基本框架和方法。
2.1 MILP模型基本求解框架
根据问题特性构建由优化目标和物理约束组成的通用MILP模型式(1)后,该模型的基本求解流程如图1所示,可以分为以下几个步骤:①外围模型处理,调用求解器之前,通常会利用电力系统专家经验或领域知识对模型式(1)中的变量、约束、建模方式进行削减和重构,旨在尽可能降低求解器处理模型的复杂度;②预求解和割平面,求解器调用后,首先基于通用MILP理论对加载模型进行一系列预求解,接着计算预求解后模型的松弛解(即根松弛),然后不断添加割平面以提高松弛起点;③分支定界,从松弛起点出发建立由分支选择、节点选择、启发式三个主要模块组成的搜索树,在搜寻最优解的同时估计最优解的上下界,最终获得并证明最优解;④参数调整,该环节调整上述几个步骤内的算法参数,旨在适应问题结构,实现整体效率提升。
2.2 外围模型处理
外围模型处理指的是在调用求解器之前的处理,包括变量处理、约束处理、建模方式处理等。部分处理方式不影响MILP模型的最优性(如采用不同的建模方式等),而为了大幅提高计算效率,部分电力系统MILP问题外围模型处理会采用启发式的方法削减寻优空间。当前电力系统MILP问题的运筹决策关键技术大部分集中在外围模型处理环节。
2.2.1 变量处理
由于MILP模型的求解难度与离散变量数目呈正向关联,对离散变量数目的削减可有效降低求解负担。变量处理旨在求解之前通过运筹决策技术对部分离散变量进行聚合或固定,从而大幅削减离散变量数目。
离散变量聚合的基本思想在于将作用相似、优化结果相似的变量聚合在等效的变量簇中,用变量簇替代原始离散变量直接参与优化,从而使得MILP模型中的离散变量实际数目大幅减少。以机组组合为例,离散变量聚合方法可分别应用于机组聚合与调度时段聚合。其中,机组聚合根据机组参数、地理位置等条件将相似的机组群聚合,但每个机组群的优化结果相同,将影响实际调度指令下达、电力市场竞价等环节[14]。由于机组聚合后产生虚拟节点影响网络拓扑结构,文献[15-16]提出一种计及线路潮流的方法,提高了机组聚合对网络约束构建的精准性。调度时段聚合则以负荷曲线为基础,通过提取关键时段、聚合相似时段减少MILP模型在时序维度上的复杂度,与机组聚合相比对运行的影响更小。文献[17]提出基于均匀取样的聚合方法,而文献[18]通过分析负荷曲线的极值点、爬坡点等关键特征,实现时段的不均匀聚合。
离散变量固定一方面基于启发式思想,如文献[19]构建辅助LP模型,通过辅助松弛解中离散变量的取值确定是否在原MILP模型中固定该变量;另一方面则以数据驱动为支撑,利用近年来兴起的大数据和机器学习等技术,挖掘历史决策结果并以端对端的模式应用于当前MILP模型中,如文献[20]提出一种仿射子空间预测方法,预测各离散变量及其相邻时段是否能以较高的置信度取特定值。该方法的特点与常规数据驱动方法一致,需要耗费大量时间收集标签数据,并且容易发生泛化性问题,即难以保证分布外(Out-of-Distribution, OOD)预测的正确性。对于电力系统MILP问题,一方面需要收集大量最优解的计算负担更加严峻;另一方面电力系统工况多变,泛化性难以得到保证。
离散变量聚合与固定都会带来离散变量规模上的大量削减,因此对求解效率的提升是显著的。文献[18]验证了所提聚合方法在省级电网规模系统上能够实现4倍以上的加速,文献[20]则能实现约10倍的加速。此外,变量处理容易发生不可行问题,即使经过不可行修复等启发式方法仍然难以确保原MILP模型的可行域不被更改,从而导致局部最优。
2.2.2 约束处理
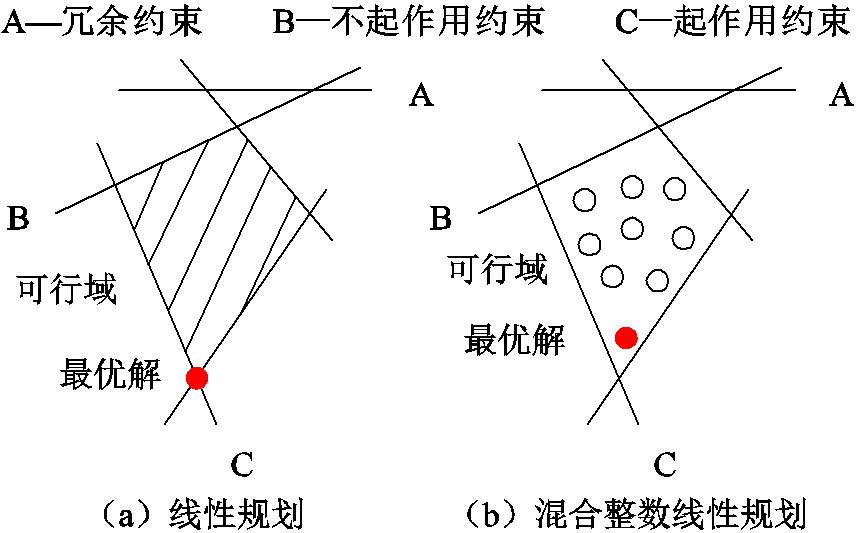
由于MILP模型的求解需要反复求解松弛LP问题,约束规模会影响其求解效率,进而影响原MILP模型的求解进程。约束处理的目的是区分冗余约束(redundant constraints)、不起作用约束(non-binding constraints)和起作用约束(binding constraints),其关系如图2所示。冗余约束指的是不参与构成可行域的约束,如图2中约束A;不起作用约束指的是参与构成可行域、但不参与限制最优解的约束,如果目标函数形式发生改变,则不起作用约束有可能转变为起作用约束,如图2中约束B;起作用约束指的是参与限制最优解的约束,如图2中约束C。倘若仅保留起作用约束,就能在大幅度削减约束规模的基础上保证不影响原MILP模型的最优性。对于LP模型,起作用约束在最优解处是达界的,即约束不等式的左右两端相等,如图2a所示;对于MILP模型,由于可行域非凸(可行解集合不连续),起作用约束在最优解处不一定是达界的,如图2b所示,倘若去除这部分约束,MILP模型的最优解将会发生改变。
电力系统MILP问题在起作用约束辨识领域已有大量研究,其研究对象以线路潮流约束为主。这是由于电力系统MILP问题约束中网络拓扑结构关联约束(即线路潮流约束)占比最高。例如,若系统考虑所有线路N-1场景下的潮流安全,网络约束比例的规模与线路数目二次方呈正相关。然而,大量线路潮流约束呈冗余或不起作用状态,辨识其起作用状态可大幅削减约束规模。
当前主要的线路潮流起作用约束辨识方法整理如下:①迭代法,文献[21-22]构建了一系列辅助LP模型,每次迭代寻找当前可行域中使得约束条件达界最多的顶点,直到可行域所有的顶点都被搜索完成为止;文献[23]以无约束MILP模型为迭代起点,不断将求解后越界的约束条件添加到初始模型中,直到不再出现越界为止;文献[24]基于相似约束辨识和聚合,大幅减少了N-k场景遍历带来的海量约束;文献[25]基于约束耦合关系分析辨识潜在起作用约束。②变量上下界约束法,通过变量的上下界以及变量在约束中的系数估计某条约束可能取得的极限值,如通过发电机的出力上下限以及发电机的功率转移分布因子(Power Transfer Distribution Factor, PTDF),计算一条线路的理论负载并与线路容量对比[26]。③重要性筛选法,从全部的场景集合中删除一些不重要,或者不影响最优解的场景以及对应的场景约束。文献[27]提出根据不同场景下线路潮流约束的违反程度,确定关键场景;文献[28]提出严重指标排序法,表征一个场景对系统影响的严重程度并优先保留影响较大的场景;文献[29]结合迭代方法和重要性筛选方法,每次迭代添加5~15条违反程度最大的约束。④数据驱动方法,依赖于对历史运行信息的分析辨识起作用约束[20,30-32]。
与变量处理不同的是,在起作用约束辨识后往往会将剩余约束作为一种惰性约束参与模型求解,倘若违反则会添加回模型中继续迭代,从而保证重要性筛选方法或数据驱动方法下原MILP模型的最优性[3]。因此约束处理也是电力系统实际工业中广泛使用的方法,例如将重点线路添加到监视列表(Watchlist)中,通过同步安全校核(Simultaneous Feasibility Test, SFT)[33]修正结果等。
2.2.3 建模方式处理
MILP模型的建模方式包括变量和约束的构建及其顺序,约束的凸包处理等。不同的建模方式会影响求解进程和效率[34-35]。一般认为建模方式有两个维度的评价指标,即紧凑性(Compactness)和紧密性(Tightness)[35]。紧凑性着重于变量和约束的数目最小,即与变量处理和约束处理相关;而紧密性则要求MILP模型(以模型式(1)极小化目标函数为例)的松弛LP模型目标函数最大,从而使得原模型与松弛模型之间的间隙最小。当该间隙为0时,求解松弛LP模型即可得到原MILP模型的最优解,此时的松弛LP模型被称为原问题的凸包。紧凑性和紧密性在一定程度上是互斥的,但均不会损失原MILP模型的最优性。
以机组组合建模方式为例,典型的紧凑性处理包括三变量建模方式和单(双)变量建模方式等,典型的紧密性处理则集中于如何构造单个机组的凸包。单机物理约束包括最小启停时间约束、爬坡约束、时序相关的启动成本和分段线性运行成本等,现有研究往往针对其中一种或两种约束构建局部凸包建模方式。文献[35]详细综述了不同的机组组合建模方式以及各种建模方式下求解效率的数值结果,表明了建模方式对求解进程和效率的影响。需要注意的是,建模方式带来的效率提升受外部因素影响较大,包括MILP问题的类型、实际运行边界条件、求解器的种类及优化参数等,需根据实际需求动态测试,通常难以获得在所有场景下均表现最佳的建模方式,建模方式对计算效率的提升难以获得理论保障。
此外,也有部分目标函数诱导方法和凸包刻画方法研究。目标函数诱导方法通过修改原MILP模型中的目标函数系数诱导离散决策变量在求解过程中的取值。由于没有改变约束,该算法得到的解能够保证可行性,但不能保证最优性[36]。凸包刻画方法研究通过枚举离散变量的可能性组合构造相应的凸包刻画约束[37],如析取规划枚举法[38]、网络流枚举法[39]、动态规划枚举法[40]。然而凸包刻画会引入大量约束,损失紧凑性,不一定能提高求解效率,当前多应用于市场定价等电力系统领域[37]。
2.3 预求解和割平面
本节开始将概述求解器内部求解流程,相关运筹决策技术以通用MILP研究为主。当前电力系统MILP还罕有涉及求解器内部流程的算法研究,本文将简要叙述当前电力系统MILP问题的前沿思想。
2.3.1 预求解
预求解是求解器求解MILP模型的第一个环节,通常在求解第一个松弛LP模型(又称为根松弛)之前调用,用于检查错误、简化模型和辨识结构特征,直接影响后续求解效率[41]。预求解工作与外围模型处理相似,即通过一系列集成算法对变量、约束和建模方式提出改进,从而更紧凑、紧密地描述MILP模型的可行域。但不同的是,预求解的改进以通用数学模型为基础,并未充分考虑电力系统物理特性。同时,预求解以最优性保证为前提。
以GUROBI为例,根据算法耗时可将预求解算法分成三个层次,并形成嵌套式的循环预求解流程:①底层循环包括大部分单条约束或单个变量的削减计算,速度最快;②中层循环考虑多条约束或多个变量的联合评估;③上层循环中则包含最耗时的预求解算法,对模型整体结构进行辨识。在此结构下各层算法相互影响,最终实现对MILP模型的削减。文献[41]详细介绍了GUROBI中应用的预求解算法,并基于算例分析了各算法对整体求解效率的影响,本文不再赘述。
2.3.2 割平面
预求解后,求解器计算根松弛从而生成根节点,大部分割平面都在此时添加。割平面的本质是线性不等式,属于一种紧密性建模方式,后成为求解器的重要组成部分。尽管增加了MILP模型的约束规模,但割平面通常会更好地凸化MILP模型可行域,直观而言会提高根松弛的目标函数,有利于后续求解过程。
以CPLEX为例,常用的割平面类型包括覆盖割平面、广义上限(Generalized Upper Bound, GUB)覆盖割平面、团分割、流覆盖割平面、流路径割平面、隐式边界割平面、Gomory小数割平面、混合整数舍入(Mixed Integer Rounding, MIR)割平面、零-半分割等[42]。
2.4 分支定界
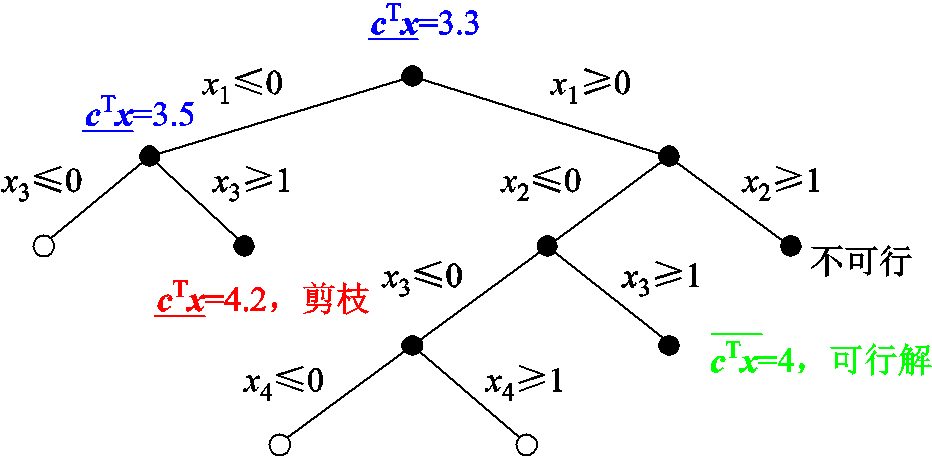
从根节点开始直到证明最优的求解过程即为分支定界算法的核心部分。分支定界算法的原理在于通过构建搜索树,依次求解一系列LP模型的同时动态评估最优解的上下界,从而实现对具有最优解可能性的可行解的策略性穷举,如图3所示(以0-1规划为例)。图中上划线和下划线分别表示最优解目标函数的当前上界和下界。因此,分支定界算法有三个主要组成部分,分别是:分支选择(Variable Selection)策略、节点选择(Node Selection)策略和启发式(Heuristic)策略。
2.4.1 分支选择策略
从根节点出发,搜索树中的每个节点都表示一个可行域被切割的松弛LP模型,通过求解该模型得到的解被称为松弛解,其中有一部分离散变量的取值是连续的,即待选变量。分支选择指的是通过算法评估待选变量的分支价值,生成进一步切割可行域的分支,使得子节点LP模型的目标函数尽可能提高,从而减少节点生成的数目。如图3所示,分别对被选择的变量向上取整和向下取整构建约束,从而生成可行域互补的子节点,并且子节点的松弛目标函数不断提高。
强分支(Strong Branching, SB)是一种典型的前瞻性(Look-ahead)分支选择策略,计算每一个待选变量生成子节点的松弛目标函数,并转换成SB分数用于最终的分支选择,即
式中,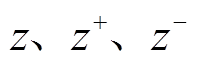 分别为当前节点、所选变量向上和向下分支后生成节点的松弛目标函数;
分别为当前节点、所选变量向上和向下分支后生成节点的松弛目标函数;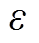 为一个小量。式(2)的内涵在于任一子节点目标函数的微小变化均会影响SB分数[43]。数值分析表明SB生成的搜索树节点规模较少,但由于需要求解大量LP模型,造成的计算负担使得分支定界整体搜索效率较低。
为一个小量。式(2)的内涵在于任一子节点目标函数的微小变化均会影响SB分数[43]。数值分析表明SB生成的搜索树节点规模较少,但由于需要求解大量LP模型,造成的计算负担使得分支定界整体搜索效率较低。
伪分支(Pseudocost Branching, PC)是另一种典型的历史信息分支选择策略,统计每一个待选变量在历史分支后造成的目标函数变化量,并转换成PC分数用于最终的分支选择,即
式中,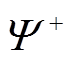 、
、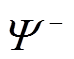 分别为该变量在历史向上和向下分支后目标函数变化量的平均值;
分别为该变量在历史向上和向下分支后目标函数变化量的平均值; 、
、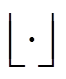 分别表示向上取整和向下取整。式(3)随着搜索深入,历史信息越多,评估越准确。由于不需要额外计算LP问题,PC的整体效率更高。
分别表示向上取整和向下取整。式(3)随着搜索深入,历史信息越多,评估越准确。由于不需要额外计算LP问题,PC的整体效率更高。
其他分支选择策略大多衍生于SB和PC的基本思想,旨在平衡分支选择的精准性和高效性[44]。可靠性分支(Reliability Branching)使用SB计算部分初始节点,收集分支信息后采用含置信度校验的PC完成剩余分支;混合分支(Hybrid Branching)则收集包括起作用约束在内的更多节点信息,用以构建多指标加权的分数函数;后门分支(Backdoor Branching)通过多次小规模迭代重启选择更重要的待选变量。
近年来由于数据驱动方法的发展,兴起了采用机器学习、图神经网络等技术模仿SB的研究。其基本思想在于通过人工或图卷积的方式提取MILP模型的静态特征和分支定界搜索过程中的动态特征,构建由历史SB决策结果为标签的训练集,利用数据驱动的快速映射特性实现更高效的分支选择策略。文献[45]基于排序学习提出了一种即插即用的数据驱动分支选择策略框架,通过SB收集部分初始节点的分支决策后转用数据驱动方法完成剩余搜索;文献[46]提出以图卷积神经网络代替人工特征工程,将MILP模型转换为两顶点或三顶点图,图的边即代表模型系数,从而实现特征自动提取;文献[47]基于交替乘子法(Alternating Directions Method of Multipliers, ADMM)重构了并行LP求解器以更高效地获得SB标签数据;文献[43]提出一种对广义SB的学习策略,即同时对多个待选变量分支。
这种方法在电力系统MILP领域也有研究。文献[47]在PJM公开数据构建的机组组合问题中验证了所提分支选择策略,10 000 s后的解质量优于开源求解器SCIP两倍;文献[48]根据机组组合的性质,提出基于离散变量分组的联合分支选择策略,将离散变量分别按机组、时段和类型分组,并对每组构建单独预测器。然而上述研究大多基于开源求解器,实际效率与商业求解器相比仍存在一定的差距。
2.4.2 节点选择策略
经过多次分支选择后,搜索树中存在大量尚未计算松弛LP的未探索节点,如图3中的白色节点。而节点选择策略指的是如何决定未探索节点的探索顺序,从而引导分支定界尽早探索最优解所在节点,避免陷入局部最优。因此,分支选择和节点选择是一种循环耦合关系。
典型的节点选择策略包括价值优先(Best-first)和深度优先(Depth-first),分别以节点松弛目标函数和所在深度作为评估准则[44]。前者旨在证明最优,探索节点更少,但对内存的占用也更高;后者旨在获得更好的解,但往往需要探索更多节点,尤其是在初始决策欠佳的极端情况。其他节点选择策略往往是上述两种策略的结合,并根据具体问题适应性调整。
另一类节点选择策略从强化学习的角度出发,采取探索(Exploration)与利用(Exploitation)的平衡。“探索”对应广度搜索,旨在探索未知空间;“利用”对应深度搜索,旨在利用当前信息,从而共同实现全局最优。文献[49]将上限置信区间(Upper Confidence Bound Apply to Tree, UCT)算法应用于节点选择中,即
式中,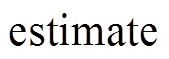 表示对当前节点的评估(如松弛目标函数);
表示对当前节点的评估(如松弛目标函数);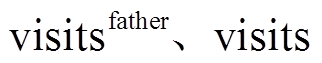 分别为对父节点和当前节点的历史选择信息;
分别为对父节点和当前节点的历史选择信息;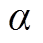 为权重。式(4)的内涵在于优先利用评估理想的节点(第一项),同时考虑在邻近节点中较少探索的部分(第二项)。
为权重。式(4)的内涵在于优先利用评估理想的节点(第一项),同时考虑在邻近节点中较少探索的部分(第二项)。
2.4.3 启发式策略
在获得的松弛解中,如果所有离散变量的取值都是离散的,则松弛解也是可行解。目标函数最小的可行解即为最优解的当前上界(见图3中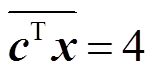 ),未探索节点中最小的松弛解即为最优解的当前下界(见图3中
),未探索节点中最小的松弛解即为最优解的当前下界(见图3中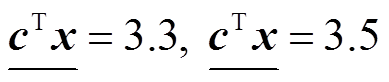 )。因此,倘若节点的松弛目标函数高于当前上界,最优解必定不存在于这部分子树下,该节点被剪除(Prune),如图中3
)。因此,倘若节点的松弛目标函数高于当前上界,最优解必定不存在于这部分子树下,该节点被剪除(Prune),如图中3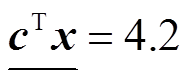 。由于下界变化依赖于节点的穷举式探索,提升相对困难,因此启发式策略的基本思想是快速降低上界,从而引导分支定界算法剪除更多冗余搜索空间。
。由于下界变化依赖于节点的穷举式探索,提升相对困难,因此启发式策略的基本思想是快速降低上界,从而引导分支定界算法剪除更多冗余搜索空间。
启发式策略需要构建辅助模型优化当前上界,根据辅助模型性质又可分为基于LP辅助模型的启发式和基于MILP辅助模型的启发式。可行性泵(Feasibility Pump, FP)[50]是一种典型的基于LP辅助模型的启发式,将现有松弛解通过四舍五入构造辅助可行解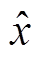 ,并建立辅助LP模型(以0-1规划为例),有
,并建立辅助LP模型(以0-1规划为例),有
与原MILP模型式(1)相比,辅助LP模型式(5)保留了除离散约束之外的约束条件,并修改了目标函数。求解模型式(5)后得到新的松弛解,即可通过四舍五入构造以该松弛解为基础的新的辅助可行解,从而更新模型式(5)的目标函数继续求解。重复上述过程实现迭代,直到模型式(5)目标函数为0(即四舍五入得到的辅助可行解也是原MILP模型的可行解)为止。其内涵是沿着松弛解和辅助可行解之间的距离在邻域内搜索可行解。辅助LP模型式(5)可以推广到一般化的MILP模型中。若将目标函数作为约束左端项、原目标函数的取值作为约束右端项,添加小于约束到模型式(5)中,能保证迭代得到可行解的质量逐渐提高。
与基于辅助LP模型的启发式相比,基于MILP辅助模型的启发式往往拥有更高的可行解质量和更慢的计算效率。松弛诱导邻域算法(Relaxation Induced Neighbourhood Search, RINS)[51]是一种经典且有效的基于MILP辅助模型的启发式,其核心思想在于利用当前获得的松弛解和可行解信息,以两者之中取值相同的离散变量为中心构建邻域,通过固定这部分离散变量构建小规模MILP辅助模型。由于RINS以现有可行解为基础,不改变原MILP模型的约束,因此求解小规模MILP辅助模型得到新的解也是原MILP模型的可行解。文献[52]在此基础上提出了松弛强化邻域算法(Relaxation Enforced Neighbourhood Search, RENS),仅固定在松弛解中取值离散的离散变量,适用于难以获得可行解的困难问题。
除面向通用MILP领域的启发式外,也有部分特殊结构启发式,基于旅行商(Travelling Salesman Problem, TSP)、装箱(Bin Packing Problem)等具体问题的约束边界条件构建特殊策略,从而根据问题属性有针对性地降低上界。如TSP问题中的Subtour启发式[53]、Swap启发式[54]等,辨识当前路径中的局部环、交叉环等特殊结构。在电力系统优化领域,文献[55]提出了一种针对含线路越限罚项机组组合的启发式策略,通过PTDF灵敏度辨识当前对阻塞缓解影响最大的机组。针对省级电网规模系统的测试表明,该方法在不损失最优性的前提下能实现平均2.05倍的加速。
此外,由于启发式策略与分支选择、节点选择的耦合性不强,往往作为一种外挂模块应用在求解器中,如GUROBI具有几十种不同的启发式算法。这种外挂模块的性质一方面使得启发式策略不影响分支定界算法的最优性;另一方面使得启发式策略可以通过并行结构实施。文献[56]提出一种并行结构的可行性泵算法,将多个参数不同的可行性泵分布在多个子进程中,最后取其中最好的结果。与之相反,分支选择、节点选择往往具有时序性,并行处理带来的提升有限[57]。
2.5 参数调整
综上所述,MILP模型的求解过程本质是大量算法模块的集成,而各个算法都具有大量参数需要调整,例如:外围模型的处理方式,预求解的时间限制,割平面的种类,分支选择和节点选择的策略倾向,启发式的调用频率、调用条件、求解时间等。合理的参数能根据不同的问题调整算法倾向,并更好地集成算法模块,实现整体效率的提升。文献[58]数值结果表明,参数调整在MILP模型求解中能带来最高52倍的效率提升。然而,一方面算法模块的求解参数具有规模较大的、离散的自由度空间;另一方面由于非凸性,MILP模型的求解过程往往具有较强的随机性,给参数调整带来极大的困难。
穷举法是最基础的参数调整策略。通过人工经验确定数组参数组合后,分别求解得到各自的计算效率,从而筛选最优的参数组合。穷举法一方面依赖于人工经验设置穷举范围;另一方面高额的计算负担使得对参数组合的评估效率较低,不适合实际应用中的大规模求解。
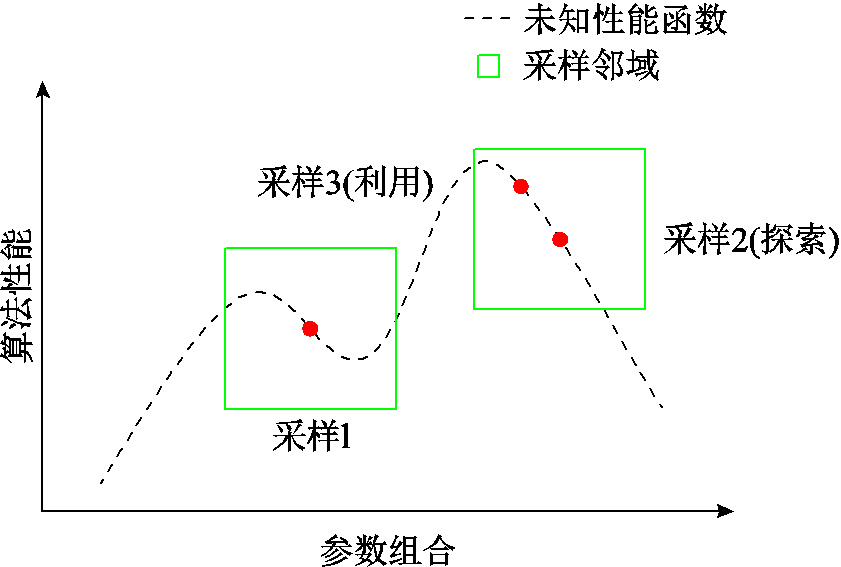
以贝叶斯优化(Bayesian Optimization)为典型算法的采样法,旨在通过有限次模拟采样逼近真实的性能曲线,其基本思想同样在于探索与利用,如图4所示。经采样1后,采样2探索采样1邻域之外的未知空间,采样3则进一步利用采样2邻域空间,经多次采样后在提升参数性能的同时避免局部最优。贝叶斯优化通过高斯过程回归(Gaussian Process Regression)计算现有采样点的均值和方差(即邻域),再构建采集函数评估下一个采样点位置。
在MILP领域,近年来的参数调整研究与数据驱动方法紧密结合,以单一种类算法的参数调整为主要研究对象。文献[59]基于强化学习提出一种对不同割平面生成顺序的参数调整策略;文献[60]针对0-1规划问题提出了一种通用的启发式及其参数自动选择策略;文献[61]构建了混合整数二次规划(Mixed Integer Quadratic Programming, MIQP)学习模型,调整不同启发式在搜索树节点中的调用顺序和调用时间。CPLEX、GUROBI等求解器均具有参数自动调整工具,调整范围不仅针对单一种类算法,且与内部求解信息联系更紧密。
还有一类研究与参数调整密切联系,即MILP问题的求解时间估计[62],其本质可以理解为一种元(meta)分析。MILP问题的模型约束、求解算法等的复杂耦合使得难以从理论或实验中给出MILP问题求解时间的下界[63](求解时间上界与离散变量的规模呈正指数关系),也导致电力系统实际MILP问题的求解效率千差万别,难以提前判断是否满足工程效率需求,只能在优化之后才能评估当前优化的效果以及是否需要改进。例如,当前优化的收敛性无法满足效率需求时,需要综合考虑收敛性和精准性之间的平衡决定是否修改模型(是否使用线性化等方法降低模型的非凸特性、是否使用缩减降维等模型处理方法缓解离散特性的维数灾等)。因此,求解时间估计旨在基于模型特性、历史或实时求解信息评估当前MILP问题的求解进程,辅助调整阶段性参数倾向[64],或提前判断能否在一定时间内满足该问题具有的求解需求[62]。同时,这也是一种对于何种元素造成MILP问题求解困难的探讨,尚待进一步研究。
3 电力系统运筹决策关键技术展望
当前以通用运筹决策技术为核心的求解器无法满足新型电力系统MILP问题求解瓶颈,其关键问题在于电力系统MILP问题具有鲜明特异的物理特征,而面向通用数学研发的运筹决策技术缺乏电力系统领域知识驱动的定制化高效求解策略。例如,机组组合、检修计划、拓扑运行优化都具有海量但稀疏性强的安全运行约束,受到线路阻塞状况、系统潮流分布等电力系统网络拓扑特征影响大;同时机组组合和检修计划还具有多类型时间相依的离散变量,需要考虑设备成本特性、运行特性等。通用的数学求解工具并未充分利用上述特征,导致运筹决策技术的加速效能未得到充分挖掘。
因此,本节展望了电力系统MILP问题运筹决策关键技术未来研究方向,提出了“电力系统物理特征构建-求解过程信息挖掘-加速算法深度内嵌”的基础研究脉络。
3.1 电力系统物理特征构建
在电力系统MILP问题研究中,电力系统领域知识或专家经验具有支撑和指导作用,是将电力系统MILP问题区别于其他领域MILP问题的关键。因此,如何分析电力系统物理特性,从而转换为可应用在运筹决策技术研究中的数学特征,是一个有待解决的重要问题,可以从以下几个方面出发。
1)资源特征。可调用资源有两方面特征:①资源与资源之间的差异化特征,如不同机组的类型、地理位置、成本、容量等因素,这种差异化使得运筹决策总是向成本更低、更容易满足需求的关键资源偏移。因此,辨识关键资源能更好地分配求解性能,并引导求解方向。文献[3]根据市场定价结果将机组分为成本已覆盖和未覆盖两种,通过邻域搜索改进当前决策;文献[48]将每个机组的离散变量作为一组,分别研究其分支选择策略;文献[55]根据地理位置衡量哪些机组能更显著地改善当前决策中的线路阻塞。②资源本身的特性,如机组爬坡过程、设备检修过程中的多时段状态耦合等,隐含着离散变量的关联关系,有利于削减组合空间。文献[19]认为大部分机组在所有时段都处于必开或必关;文献[20]将相邻两个时段的状态是否一致作为学习目标。
2)网络约束特征。电力系统网络约束是一种电力特有的稀缺性资源,也是电力系统MILP问题中占比最高的约束类型。相比于其他能源系统的网络传输约束,以潮流方程描述的电力系统网络约束将电力系统所有决策变量通过稠密的PTDF矩阵紧密耦合,极大地提升了决策难度。若能够辨识电力系统网络约束瓶颈,即可准确定位电力系统MILP问题中的起作用约束,从而引导求解方向,提高求解效率。文献[29]在迭代过程中优先添加越限最严重的线路潮流约束;文献[55]同样将越限最严重的线路作为优先改善目标。
3)负荷特征。由于电力系统需满足供需实时平衡,负荷特征主要体现在时段层面,一方面引入不同时段的大量相似约束;另一方面在峰、谷、陡增、陡降等特殊时段制约组合决策。文献[18]分析了负荷曲线的极值点、爬坡点等关键特征,从而将状态相似的时段聚合,削减了MILP问题的复杂度;文献[48]将每个时段的离散变量作为一组,分别研究其分支选择策略。
4)可分解特征。电力系统MILP问题的可分解特征体现在时间可分解[65]和空间可分解两方面[66]。时间可分解特征在于电力系统中存在大量时段弱耦合的约束,而空间可分解特征在于电力系统中存在多个互相弱联通的区域。因此,若能通过分解算法将电力系统MILP问题转换为相对独立的子问题,并且基于分布式并行计算的架构实现与求解器的结合,有助于进一步提高整体计算的效率[67]。
5)实用化决策要求。实际应用中的电力系统MILP问题往往在决策精度和决策效率之间取得平衡,如MISO日前机组组合以1 200 s内获得误差在0.1%以内的决策为总体目标,并不一定需要获得最优解[3]。因此,以可接受的最优性损失为代价,大幅提升求解效率,从而尽快获得高质量可行解,更有利于工程实际。但同时,工程实际也需要保证最终决策的质量,即确定运筹决策技术的误差边界。而现有集中在外围模型处理的电力系统运筹决策技术难以兼顾高决策效率和低决策误差边界的需求。
3.2 求解过程信息挖掘
上述电力系统物理特性是不会随着求解进程发生改变的静态信息,此外,与求解器的深度交互也能挖掘大量与求解进程有关的内部动态信息。电力系统物理特性和求解过程信息互相支撑、补足,才能更好地分析问题特性,设计加速算法的核心内容。然而,现有电力系统MILP问题研究往往只基于最优决策结果等有限信息,对求解器内部信息的收集和利用程度较低。
例如,经求解器预求解后的MILP模型规模得到了大幅削减,不仅去除了冗余约束,也修改了变量的边界。而电力系统MILP研究往往基于预求解之前的模型,如原始松弛解、原始约束等,未能最大限度地利用当前信息。
分支定界过程中产生的大量可行解和松弛解也是重要的求解信息。文献[47,68]构建以可行解为基础的数据集,实现离散变量取值预测,避免了实际应用中难以获得最优解的问题;文献[55]提出通过动态对比可行解和松弛解之间在线路越限上的差距,提前引导分支定界算法向减少差距的方向搜索。
分支定界的分支决策和历史搜索路径等信息也是一大信息来源。文献[69-70]提出根据预求解模型和历史搜索路径不断重启搜索树,从而找到更好的搜索起点,加快后续搜索进程;文献[45]提出一种在线收集和在线学习的框架,收集分支决策及其辅助信息用于对分支选择策略的模仿学习;文献[71]提出根据历史搜索路径构建集合覆盖模型,辨识可用于优先分支的离散变量。
3.3 加速算法深度内嵌
结合电力系统物理信息和求解过程信息的算法,需要深度内嵌于求解流程,从而实现求解效率的提升。加速算法深度内嵌的优势在于:①考虑了电力系统MILP问题的特殊结构和特殊性质,同时也能收集大量求解内部信息;②与部分外围模型处理方式不同,内嵌求解流程不会影响最优性,有利于确保误差边界;③支撑国产自研求解器发展,使其效率进一步提升。内嵌求解与求解器交互接口的开放程度有关,目前商业或开源求解器均有一定程度的接口开放,从而支持定制化策略设计。
在预求解环节,热启动是最基础的内嵌方法。电力系统MILP问题往往需要求解一系列运行工况相似的模型,因此历史决策结果在一定程度上能运用在当前决策中。热启动将解或解的一部分输入求解器中,经修复后成为初始上界,帮助求解器更好地启动。然而,一方面求解器的解修复功能并不能保证得到可行解;另一方面由于MILP问题的NP难特性,即使最优解作为热启动对求解效率的提升仍然是有限的。文献[32]以随机机组组合为例分析了热启动的效率。惰性约束是另一种常用于约束处理中的内嵌方法,将大量辨识得到的不起作用设置成惰性约束,即可在减少LP计算负担的同时避免损失原MILP模型最优性[3]。
割平面的构建理论和调用策略是两种研究方向。当前,包括电力系统在内的多种MILP问题中,仍以几种传统割平面为主,专家经验或领域知识一方面难以形成数学描述的割平面形式;另一方面难以评估对于非凸可行域的影响。电力系统MILP问题约束复杂,存在大量不可行解,但当前研究多关注于可行性,对不可行这一性质的挖掘尚不明晰;以构建割平面的形式有望利用不可行性,从而更好地描述可行域。割平面的调用策略与参数调整类似,过多或过少地添加割平面都会降低求解效率,因此,添加割平面的种类和数目需要根据具体的问题调整[72]。此外,求解器中割平面往往在根节点处添加,对整个求解流程都产生影响,因此趋向保守;而分支定界过程中的割平面旨在辅助当前子树快速收敛,和当前子树状态相关,对其他子树状态影响小,因此可能成为一种行之有效的专家经验应用方式。
在分支定界环节,显著的挑战在于嵌入算法可能会影响求解器内部复杂流程之间的相互作用,反而降低了整体求解效率。相较于直接修改求解器的分支选择策略,优先分支是一种更易结合电力系统物理特性的内嵌方法。通过提升部分关键离散变量的分支优先级,可以在不过多干涉求解器内部运行的前提下更改分支的倾向,从而减少搜索树的规模。另一方面,由于启发式模块相对独立且具有可并行的结构,基于邻域搜索的启发式可以有效地结合多种现有电力系统运筹决策技术。文献[47,68]预测可固定的离散变量后,通过邻域搜索切分可行域,从而保证原MILP模型的最优性;文献[55]通过启发式回调动态更新分支定界上界,并应用在电力系统MILP问题中;热启动也可以通过邻域搜索转换成约束形式,从而更直接地削减搜索空间。
参数调整的难点在于搜索空间大,但对于一个具体的电力系统MILP问题,其模式在不同的工况下依然是相似的,利用专家经验有助于划分参数搜索空间,从而在少数迭代中快速找到适合当前工况的参数。因此,如何将这种相似模式加以固化描述、实现模型结构与参数空间的匹配,是参数调整的关键。另外,求解时间估计对电力系统MILP问题的实用化决策需求意义重大,有助于探讨某个实例是否适用于直接调用求解器,是否需要修改建模方式,是否无法在工程时间内达到求解需求。要实现这一点,需要基于电力系统MILP问题的具体模型分析其构成元素对于求解过程的影响,以及这种影响如何通过求解信息反映,从而指导加强对电力系统MILP问题的认知。
此外,上述环节均可与并行计算相结合,从而进一步提高算法效率。一方面,并行计算可以将分支定界的子树合理分配于多个计算资源上,但需考虑通信设计,避免降低整体效率;另一方面,在领域知识指导下,可以同时计算多种具有并行结构的策略以获得最佳结果。例如,文献[73]通过机组成本系数波动产生多个MILP模型,基于并行计算在不增加耗时的前提下收集更多求解信息。
综上所述,已有部分前沿研究以电力系统领域知识驱动的定制化高效求解策略为核心,以提升电力系统MILP问题求解效率,例如文献[48, 55]将离散变量物理意义、电力系统阻塞情况等物理特性与分支、上界和下界等求解信息相融合,并内嵌于MILP问题求解过程。要实现电力系统领域知识的深度嵌入,需要先掌握针对MILP问题的数学运筹决策基本流程,从而了解哪些运筹决策环节适合领域知识嵌入、如何用领域知识引导运筹决策效率提升。然而,当前研究成果较少、学术关注度不足,因此本文对MILP问题的通用求解流程做了详细介绍,并结合内容讨论了电力系统领域知识驱动的运筹决策研究现状及可行思路,提出了电力系统运筹决策技术的未来研究方向应以“电力系统物理特征构建-求解过程信息挖掘-加速算法深度内嵌”为基础脉络。本文旨在扩展现有的电力系统运筹决策框架,启发全新的电力系统运筹决策技术,从而为我国相关研究工作提供参考和思路,最终实现具有自主知识产权的电力系统MILP领域突破。
最后,为扩展读者对此的阅读与了解,以下介绍部分国外前沿攻关科研小组在MILP领域及更一般化组合优化领域的工作成果。
1)在学术研究方面,2021年,图灵奖得主、人工智能领域专家Y. Bengio以及传统非凸优化理论领域专家A. Lodi等共同撰写了一篇综述,探讨机器学习在组合优化问题中的方法论,获得了学术界广泛关注[74]。该综述认为,传统非凸优化求解尚且依赖于大量人工设计、性能较低的启发式算法,而机器学习的特性有望在这一方面提出改进。为此,该综述首先回顾了近年来相关领域的研究成果,总结出机器学习主要通过模仿或发掘专家经验进行学习;然后讨论了机器学习和组合优化结合过程中的交互影响;最后,构建了机器学习在组合优化中的通用学习框架及其关键算法概念,并展望了这一方法论的未来挑战,对深入研究和创新具有借鉴意义。
2)在工程应用方面,近年来Zuse Institute Berlin、Gurobi 、DeepMind Google等求解器研发团队和人工智能科研团队纷纷投入到这一交叉领域中。其中,Gurobi Optimization在新发布的求解器版本10.0中已经包含少量人工智能算法,部分模型通过内嵌含ReLU激活函数的神经网络实现了组合优化10倍以上加速[75];DeepMind基于其在人工智能方面世界前沿的研究经验和计算资源设计了Neural Diving和Neural Branching两种算法,分别预测离散变量取值和模仿离散变量分支,并应用于包括电力系统机组组合问题在内的六种工程实际数据集中,提升了开源求解器SCIP的计算效率[47]。可见,目前针对非凸系统解的工程应用已有一部分成功案例,但由于面临诸多实用性挑战而整体应用较为有限,需要进一步探索。
3)在电力系统方面,以美国为主,国外前沿研究团队包括佐治亚理工学院、Argonne国家实验室、西北太平洋国家实验室(Pacific Northwest National Laboratory, PNNL)、MISO等高等院校、科研院所和电力系统运营机构。其中,MISO、PNNL、Gurobi Optimization等曾组建团队实施美国能源局项目HIPPO(High-Performance Power-Grid Optimization),包括致力于提供规模不断扩大、复杂性不断增强的未来场景所需的求解效率[3];2023年,IEEE Task Force on Solving Large Scale Optimization Problems in Electricity Market and Power System Applications发表了一篇综述讨论电力市场中机组组合问题的建模、求解及未来挑战[67]。可见,这一问题在电力系统领域也正受到广泛关注,亟须科研攻关。
4 结论
为了应对电力系统大规模MILP问题的“组合爆炸”计算效率难题,突破依赖于国外进口“黑箱”求解器的核心技术“卡脖子”封锁现状,迫切需要开展MILP的底层算法研究及其与电力系统特征的结合研究。为此,本文旨在为从事电力系统领域MILP问题的研究者提供如下信息:①电力系统MILP问题求解效率的主要影响因素;②求解MILP问题的分支定界算法基本流程及其加速方法;③电力系统MILP问题加速求解的可行思路,即“电力系统物理特征构建-求解过程信息挖掘-加速算法深度内嵌”的基础研究脉络。本文综述与展望的运筹决策技术并未面向电力系统组合优化问题的非凸特性,但仍希望能够通过MILP问题的技术基础,启发研究者在更一般化组合优化问题中进一步的思考与拓展。
另外,“双碳”目标下这一问题仍然存在,甚至更加严峻,需要考虑两个方面的研究思路:①建模方式需平衡精准性和计算复杂度。例如对于新能源接入的随机性约束、系统碳减排目标的机理约束等,需要考虑如何精细化处理模型中的非凸非线性因素。②求解效率需进一步提升。在随机性影响下,系统的响应频率相应提升(即调度颗粒度增加)以跟随新能源和需求响应的变化,而逐渐增加的变量和约束规模使得求解效率更加难以满足需求。在“双碳”目标下,运筹决策技术的未来发展尚待进一步研究,希望本文相关内容能够为我国在本领域的研究提供参考和思路。
参考文献
[1] 李文沅. 电力系统安全经济运行: 模型与方法[M]. 重庆: 重庆大学出版社, 1989.
[2] Quarm E, Madani R. Scalable security-constrained unit commitment under uncertainty via cone programming relaxation[J]. IEEE Transactions on Power Systems, 2021, 36(5): 4733-4744.
[3] Chen Yonghong, Pan Feng, Holzer J, et al. A high performance computing based market economics driven neighborhood search and polishing algorithm for security constrained unit commitment[J]. IEEE Transactions on Power Systems, 2021, 36(1): 292-302.
[4] Cain M, O’Neill R, Castillo A. History of optimal power flow and formulations[J]. Federal Energy Regulatory Commission, 2012, 1: 1-36.
[5] Mittelmann H. Decison tree for optimization software[EB/OL]. [2023-04-13]. http://plato.asu.edu/ bench.html.
[6] 吴熙, 陆瑶, 蔡晖, 等. 计及风电不确定性的含线间潮流控制器的电力系统经济调度[J]. 电工技术学报, 2023, 38(3): 781-792. Wu Xi, Lu Yao, Cai Hui, et al. Economic dispatching of power system with interline power flow controller considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 781-792.
[7] 徐玉琴, 方楠. 基于分段线性化与改进二阶锥松弛的电-气互联系统多目标优化调度[J]. 电工技术学报, 2022, 37(11): 2800-2812.Xu Yuqin, Fang Nan. Multi objective optimal schedulingof integrated electricity-gas system based on piecewise linearization and improved second order cone relaxation[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2800-2812.
[8] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485. Wu Mengxue, Fang Fang. Distributionally robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[9] 周博, 艾小猛, 方家琨, 等. 计及超分辨率风电出力不确定性的连续时间鲁棒机组组合[J]. 电工技术学报, 2021, 36(7): 1456-1467. Zhou Bo, Ai Xiaomeng, Fang Jiakun, et al. Continuous-time modeling based robust unit commitment considering beyond-the-resolution wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1456-1467.
[10] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477. Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two stage robust optimization method for the whole-process power system restoration considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5462-5477.
[11] 王怡, 杨知方, 余娟, 等. 考虑可靠性需求的配网多种设备统一优化配置方法[J]. 电工技术学报, 2023, 38(24): 6727-6743. Wang Yi, Yang Zhifang, Yu Juan, et al. A unified optimal placement method for multiple types of devices in distribution networks considering reliability demand[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6727-6743.
[12] 杨知方, 钟海旺, 夏清, 等. 输电网结构优化问题研究综述和展望[J]. 中国电机工程学报, 2016, 36(2): 426-434. Yang Zhifang, Zhong Haiwang, Xia Qing, et al. Review and prospect of transmission topology optimization[J]. Proceedings of the CSEE, 2016, 36(2): 426-434.
[13] 赵伟, 熊正勇, 潘艳, 等. 计及碳排放流的电力系统低碳规划[J]. 电力系统自动化, 2023, 47(9): 23-33. Zhao Wei, Xiong Zhengyong, Pan Yan, et al. Low-carbon planning of power system considering carbon emission flow[J]. Automation of Electric Power Systems, 2023, 47(9): 23-33.
[14] Meus J, Poncelet K, Delarue E. Applicability of a clustered unit commitment model in power system modeling[J]. IEEE Transactions on Power Systems, 2018, 33(2): 2195-2204.
[15] Du Ershun, Zhang Ning, Kang Chongqing, et al. A high-efficiency network-constrained clustered unit commitment model for power system planning studies[J]. IEEE Transactions on Power Systems, 2019, 34(4): 2498-2508.
[16] Yin Yue, He Chuan, Liu Tianqi, et al. Risk-averse stochastic midterm scheduling of thermal-hydro-wind system: a network-constrained clustered unit commitment approach[J]. IEEE Transactions on Sustainable Energy, 2022, 13(3): 1293-1304.
[17] Pineda S, Fernández-Blanco R, Morales J M. Time-adaptive unit commitment[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3869-3878.
[18] Zhang Menghan, Yang Zhifang, Lin Wei, et al. Enhancing economics of power systems through fast unit commitment with high time resolution[J]. Applied Energy, 2021, 281: 116051.
[19] 汪洋, 夏清, 康重庆. 机组组合算法中起作用整数变量的辨识方法[J]. 中国电机工程学报, 2010, 30(13): 46-52. Wang Yang, Xia Qing, Kang Chongqing. Identification of the active integer variables in security constrained unit commitment[J]. Proceedings of the CESS, 2010, 30(13): 46-52.
[20] Xavier Álinson S, Feng Qiu, Shabbir A. Learning to solve large-scale security-constrained unit commitment problems[J]. Informs Journal on Computing, 2020, 33(2): 739-756.
[21] Ardakani A J, Bouffard F. Identification of umbrella constraints in DC-based security-constrained optimal power flow[J]. IEEE Transactions on Power Systems, 2013, 28(4): 3924-3934.
[22] Ardakani A J, Bouffard F. Acceleration of umbrella constraint discovery in generation scheduling problems[J]. IEEE Transactions on Power Systems, 2015, 30(4): 2100-2109.
[23] Thompson G L, Tonge F M, Zionts S. Techniques for removing nonbinding constraints and extraneous variables from linear programming problems[J]. Management Science, 1966, 12(7): 588-608.
[24] Yang Yafei, Guan Xiaohong, Zhai Qiaozhu. Fast grid security assessment with N-k contingencies[J]. IEEE Transactions on Power Systems, 2017, 32(3): 2193-2203.
[25] 袁泉, 孙宇军, 张蔷, 等. 考虑安全约束耦合辨识的日前发电计划求解[J]. 电力系统自动化, 2022, 46(21): 143-151. Yuan Quan, Sun Yujun, Zhang Qiang, et al. Day-ahead generation schedule solving considering identification of security constraint coupling[J]. Automation of Electric Power Systems, 2022, 46(21): 143-151.
[26] Brearley A L, Mitra G, Williams H P. Analysis of mathematical programming problems prior to applying the simplex algorithm[J]. Mathematical Programming, 1975, 8(1): 54-83.
[27] Capitanescu F, Glavic M, Ernst D, et al. Contingency filtering techniques for preventive security-constrained optimal power flow[J]. IEEE Transactions on Power Systems, 2007, 22(4): 1690-1697.
[28] Capitanescu F, Wehenkel L. A new iterative approach to the corrective security-constrained optimal power flow problem[J]. IEEE Transactions on Power Systems, 2008, 23(4): 1533-1541.
[29] Santos Xavier Á, Qiu Feng, Wang Fengyu, et al. Transmission constraint filtering in large-scale security-constrained unit commitment[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2457-2460.
[30] Pineda S, Morales J M, Jiménez-Cordero A. Data-driven screening of network constraints for unit commitment[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3695-3705.
[31] Zhang Shubo, Ye Hongxing, Wang Fengyu, et al. Data-aided offline and online screening for security constraint[J]. IEEE Transactions on Power Systems, 2021, 36(3): 2614-2622.
[32] Mohammadi F, Sahraei-Ardakani M, Trakas D N, et al. Machine learning assisted stochastic unit commitment during hurricanes with predictable line outages[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5131-5142.
[33] Holzer J T, Chen Yonghong, Wu Zhongyu, et al. Fast simultaneous feasibility test for security constrained unit commitment[J]. IEEE Transactions on Power Systems, 2023, PP(99): 1-10.
[34] Tejada-Arango D A, Lumbreras S, Sánchez-Martín P, et al. Which unit-commitment formulation is best? A comparison framework[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2926-2936.
[35] Knueven B, Ostrowski J, Watson J. On mixed-integer programming formulations for the unit commitment problem[J]. Informs Journal on Computing, 2020, 32(4): 857-876.
[36] Ma Ziming, Zhong Haiwang, Xia Qing, et al. A unit commitment algorithm with relaxation-based neighborhood search and improved relaxation inducement[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3800-3809.
[37] Yu Yanan, Guan Yongpei, Chen Yonghong. An extended integral unit commitment formulation and an iterative algorithm for convex hull pricing[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4335-4346.
[38] Schiro D A, Zheng Tongxin, Zhao Feng, et al. Convex hull pricing in electricity markets: formulation, analysis, and implementation challenges[J]. IEEE Transactions on Power Systems, 2016, 31(5): 4068-4075.
[39] Álvarez C, Mancilla-David F, Escalona P, et al. A bienstock–zuckerberg-based algorithm for solving a network-flow formulation of the convex hull pricing problem[J]. IEEE Transactions on Power Systems, 2020, 35(3): 2108-2119.
[40] Yan Bing, Luh P B, Zheng Tongxin, et al. A systematic formulation tightening approach for unit commitment problems[J]. IEEE Transactions on Power Systems, 2020, 35(1): 782-794.
[41] Achterberg T, Bixby R E, Gu Zonghao, et al. Presolve reductions in mixed integer programming[J]. Informs Journal on Computing, 2020, 32(2): 473-506.
[42] CPLEX. What are cuts?-IBM Documentation[EB/OL]. [2023-04-13]. https://www. ibm.com/docs/en/icos/22. 1.0?topic=cuts-what-are.
[43] Yang Yu, Boland N, Dilkina B, et al. Learning generalized strong branching for set covering, set packing, and 0-1 knapsack problems[J]. European Journal of Operational Research, 2022, 301(3): 828-840.
[44] Lodi A, Zarpellon G. On learning and branching: a survey[J]. TOP, 2017, 25(2): 207-236.
[45] Khalil E B, Le Bodic P, Song Le, et al. Learning to branch in mixed integer programming[C]// Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, Arizona, 2016: 724-731.
[46] Gasse M, Chetelat D, Ferroni N, et al. Exact combinatorial optimization with graph convolutional neural networks[C]//Advances in Neural Information Processing Systems: Curran Associates, Inc., Vancouver, Canada, 2019: 15580-15592.
[47] Nair V, Bartunov S, Gimeno F, et al. Solving mixed integer programs using neural networks[EB/OL]. arXiv, 2020: 2012.13349. https://arxiv.org/abs/2012. 13349.pdf.
[48] Gu Xiaoyi, Dey S, Xavier A, et al. Exploiting instance and variable similarity to improve learning-enhanced branching[EB/OL]. arXiv, 2022: 2208.10028. https:// arxiv.org/abs/2208.10028.pdf.
[49] Sabharwal A, Samulowitz H, Reddy C. Guiding combinatorial optimization with UCT[C]//International Conference on Integration of Artificial Intelligence (AI) and Operations Research (OR) Techniques in Constraint Programming, Berlin, Germany, 2012: 356-361.
[50] Berthold T, Lodi A, Salvagnin D. Ten years of feasibility pump, and counting[J]. EURO Journal on Computational Optimization, 2019, 7(1): 1-14.
[51] Danna E, Rothberg E, Le Pape C. Exploring relaxation induced neighborhoods to improve MIP solutions[J]. Mathematical Programming, 2005, 102(1): 71-90.
[52] Rothberg E. An evolutionary algorithm for polishing mixed integer programming solutions[J]. Informs Journal on Computing, 2007, 19(4): 534-541.
[53] Pferschy U, Staněk R. Generating subtour elimination constraints for the TSP from pure integer solutions[J]. Central European Journal of Operations Research, 2017, 25(1): 231-260.
[54] Wang Kangping, Huang Lan, Zhou Chunguang, et al. Particle swarm optimization for traveling salesman problem[C]//Proceedings of the 2003 International Conference on Machine Learning and Cybernetics (IEEE Cat. No.03EX693), Xi'an, China, 2004: 1583-1585.
[55] Gao Qian, Yang Zhifang, Yin Wotao, et al. Internally induced branch-and-cut acceleration for unit commitment based on improvement of upper bound[J]. IEEE Transactions on Power Systems, 2022, 37(3): 2455-2458.
[56] Koc U, Mehrotra S. Generation of feasible integer solutions on a massively parallel computer using the feasibility pump[J]. Operations Research Letters, 2017, 45(6): 652-658.
[57] Koch T, Ralphs T, Shinano Y. Could we use a million cores to solve an integer program?[J]. Mathematical Methods of Operations Research, 2012, 76(1): 67-93.
[58] Hutter F, Hoos H H, Leyton-Brown K. Automated configuration of mixed integer programming solvers[C]//International Conference on Integration of Artificial Intelligence (AI) and Operations Research (OR) Techniques in Constraint Programming, Berlin, Germany, 2010: 186-202.
[59] Tang Yunhao, Agrawal S, Faenza Y. Reinforcement learning for integer programming: learning to cut[EB/OL]. arXiv, 2019: 1906.04859. https://arxiv. org/abs/1906.04859.pdf.
[60] Chmiela A, Khalil E B, Gleixner A, et al. Learning to schedule heuristics in branch-and-bound[EB/OL]. arXiv, 2021: 2103.10294. https://arxiv.org/abs/2103. 10294.pdf.
[61] de Souza M. Automatic design of heuristic algorithms for binary optimization problems[C]//Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, Montreal, Canada, 2021: 4881-4882.
[62] Fischetti M, Lodi A, Zarpellon G. Learning MILP resolution outcomes before reaching time-limit[C]// International Conference on Integration of Constraint Programming, Artificial Intelligence, and Operations Research, Thessaloniki, Greece, 2019: 275-291.
[63] Gregor H, Daniel A, Pierre L B, et al. Estimating the size of branch-and-bound trees[J]. Informs Journal on Computing, 2021, 34(2): 934-952.
[64] Berthold T, Hendel G, Koch T. From feasibility to improvement to proof: three phases of solving mixed-integer programs[J]. Optimization Methods and Software, 2018, 33(3): 499-517.
[65] Safdarian F, Mohammadi A, Kargarian A. Temporal decomposition for security-constrained unit commitment[J]. IEEE Transactions on Power Systems, 2020, 35(3): 1834-1845.
[66] Feizollahi M J, Costley M, Ahmed S, et al. Large-scale decentralized unit commitment[J]. International Journal of Electrical Power & Energy Systems, 2015, 73: 97-106.
[67] Chen Yonghong, Pan Feng, Qiu Feng, et al. Security-constrained unit commitment for electricity market: modeling, solution methods, and future challenges[J]. IEEE Transactions on Power Systems, 2023, 38(5): 4668-4681.
[68] Ding Jianya, Zhang Chao, Shen Lei, et al. Accelerating primal solution findings for mixed integer programs based on solution prediction[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(2): 1452-1459.
[69] Berthold T, Hendel G, Salvagnin D. Transferring information across restarts in MIP[C]//International Conference on Integration of Constraint Programming, Artificial Intelligence, and Operations Research, Los Angeles, CA, USA, 2022: 24-33.
[70] Anderson D, Hendel G, Le Bodic P, et al. Clairvoyant restarts in branch-and-bound search using online tree-size estimation[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1): 1427-1434.
[71] Fischetti M, Monaci M. Backdoor branching[C]// International Conference on Integer Programming and Combinatorial Optimization, Berlin, Heidelberg, 2011: 183-191.
[72] Claudio C, Andrea L, Andrea T. Cutting planes from the branch-and-bound tree: challenges and opportunities[J]. Informs Journal on Computing, 2022, 35(1): 2-4.
[73] Gao Qian, Yang Zhifang, Li Wenyuan, et al. Online learning of stable integer variables in unit commitment using internal information[J]. IEEE Transactions on Power Systems, 2023, 38(3): 2947-2950.
[74] Bengio Y, Lodi A, Prouvost A. Machine learning for combinatorial optimization: a methodological tour d’horizon[J]. European Journal of Operational Research, 2021, 290(2): 405-421.
[75] World Wind Energy Association. Wind power capacity worldwide reaches 597 GW, 50.1 GW added in 2018[EB/OL]. [2019-07-04]. http://wwindea. org/blog/2019/02/25/wind-power-capacity-worldwide-reaches-600-gw-539-gw-added-in-2018.
Prospect on Operations Research for Mixed-Integer Linear Programming Problems in Power Systems
Gao Qian Yang Zhifang Li Wenyuan
(State Key Laboratory of Power Transmission Equipment Technology Chongqing University Chongqing 400044 China)
Abstract The mixed-integer linear programming (MILP) problem is formulated to find the optimal decision in a discrete search decision space, which is wildly used in power systems, such as the unit commitment, maintenance scheduling, optimal transmission switching, power system planning, etc. MILP aims to achieve the best allocation of resources, whose accuracy and efficiency directly affect the security and economy of power systems. In a MILP model, both discrete and continuous decision variables are considered, and the physical constraints in power systems are linearly formulated because of the robustness and the convergence.
Under the non-deterministic polynomial-time hardness, the number of feasible solutions to MILP is exponential to the scale of discrete decision variables, and cannot obtain the optimal solution by enumeration within the polynomial-time. Many methods and algorithms are proposed for MILP in power systems. Recently, the MILP solvers with the branch-and-bound (B&B) algorithm as the core is developing rapidly, and bring a considerable improvement to the solution efficiency, stability, and generality. Commercial MILP solvers, such as CPLEX, GUROBI, etc., have been the dominated technology for MILP in power industries.
However, MILP solvers still suffers from “combinatorial explosion” for large-scale MILP in power systems, and the independent intellectual property rights are restricted. Compared with commercial solvers, the open-source or the domestic MILP solvers has a gap in the solution efficiency. It is essential to develop a technological breakthrough for MILP in power systems. Therefore, this paper reviews the operation research in power systems and the latest developments in general MILP, and provides a future prospect on this topic, in order to offer a reference.
First, this paper suggests several typical problems in power systems, including the unit commitment, maintenance scheduling, optimal transmission switching, power system planning, etc., that can be formulated with a general MILP form. Second, this paper introduces a unified framework to solve the MILP model, while existing research is divided into different modules in the framework, i.e., the solution process: (1) External model processing, including the processing of variables, constraints, and formulations; (2) presolve and cutting planes; (3) the branch-and-bound algorithm, including the variable selection strategy, the node selection strategy, and the heuristic; (4) parameter tuning, including the solution time prediction. Third, this paper summaries that the bottleneck of operation research in power systems is: (1) The wildly-studied external model processing methods cannot balance the optimality guarantee and the solution efficiency; (2) the internal algorithms are designed for general MILP instead of specific for MILP in power systems. Therefore, this paper presents the prospect for the future research of operations research in power systems that customized strategies should be developed based on both the physical feature of power systems and the mathematical information of MILP solvers. This idea is composed of three steps: (1) To build the physical feature of power systems; (2) to dig out the internal information during the solution process; (3) to embed the customized strategies into the solution process.
In conclusion, this paper aims to draw the academic attention to the innovative research idea for MILP in power systems, and to provide a reference for related work in China. Although this paper does not consider the nonlinear nature of operation research in power systems, the main content should provide an inspiration for the general combinational problem.
Keywords:Power system optimization, mixed-integer linear programming, operations research, mixed-integer linear programming (MILP) solver
DOI: 10.19595/j.cnki.1000-6753.tces.230478
中图分类号:TM73
国家重点研发计划(2021YFE0191000)和国家自然科学基金(52177072)资助项目。
收稿日期 2023-04-17
改稿日期 2023-10-16
作者简介
高 倩 女,1997年生,博士研究生,研究方向为电力系统优化、混合整数线性规划、机器学习。E-mail:gaoqianmail@cqu.edu.cn
杨知方 男,1992年生,博士,教授,博士生导师,研究方向为电力系统优化、电力市场。E-mail:zfyang@cqu.edu.cn(通信作者)
(编辑 赫 蕾)

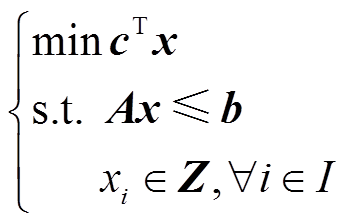 (1)
(1)
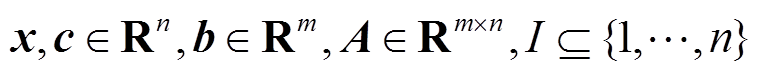 。对于不同的电力系统MILP问题,A、b、c具有不同的物理意义。若将模型式(1)中的离散决策变量由连续决策变量替代,则原问题转变为线性规划(Linear Programming, LP)问题,这一过程被称为LP松弛(Relaxation)。
。对于不同的电力系统MILP问题,A、b、c具有不同的物理意义。若将模型式(1)中的离散决策变量由连续决策变量替代,则原问题转变为线性规划(Linear Programming, LP)问题,这一过程被称为LP松弛(Relaxation)。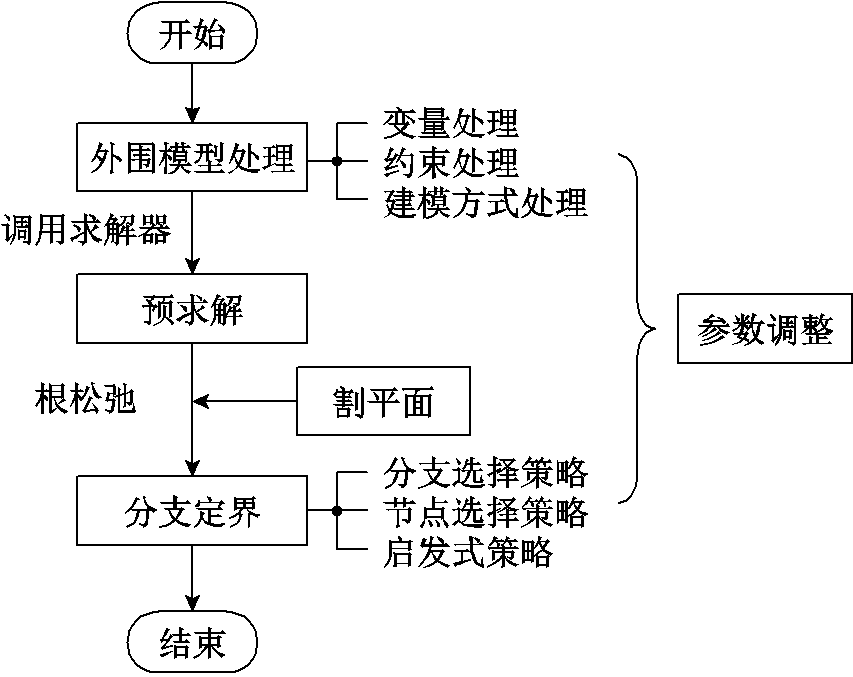
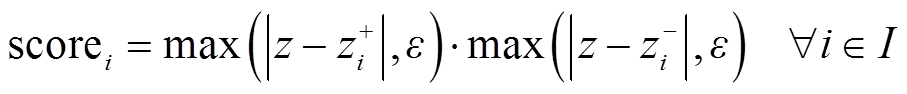 (2)
(2)
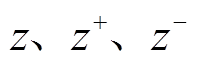 分别为当前节点、所选变量向上和向下分支后生成节点的松弛目标函数;
分别为当前节点、所选变量向上和向下分支后生成节点的松弛目标函数;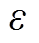 为一个小量。式(2)的内涵在于任一子节点目标函数的微小变化均会影响SB分数
为一个小量。式(2)的内涵在于任一子节点目标函数的微小变化均会影响SB分数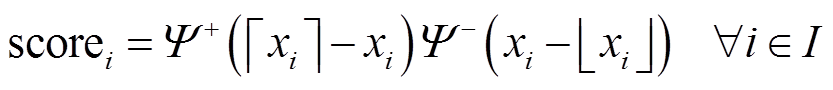 (3)
(3)
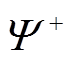 、
、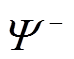 分别为该变量在历史向上和向下分支后目标函数变化量的平均值;
分别为该变量在历史向上和向下分支后目标函数变化量的平均值; 、
、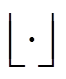 分别表示向上取整和向下取整。式(3)随着搜索深入,历史信息越多,评估越准确。由于不需要额外计算LP问题,PC的整体效率更高。
分别表示向上取整和向下取整。式(3)随着搜索深入,历史信息越多,评估越准确。由于不需要额外计算LP问题,PC的整体效率更高。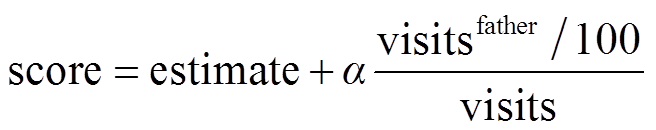 (4)
(4)
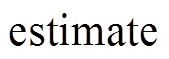 表示对当前节点的评估(如松弛目标函数);
表示对当前节点的评估(如松弛目标函数);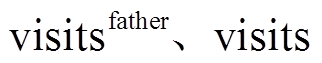 分别为对父节点和当前节点的历史选择信息;
分别为对父节点和当前节点的历史选择信息;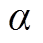 为权重。式(4)的内涵在于优先利用评估理想的节点(第一项),同时考虑在邻近节点中较少探索的部分(第二项)。
为权重。式(4)的内涵在于优先利用评估理想的节点(第一项),同时考虑在邻近节点中较少探索的部分(第二项)。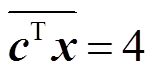 ),未探索节点中最小的松弛解即为最优解的当前下界(见图3中
),未探索节点中最小的松弛解即为最优解的当前下界(见图3中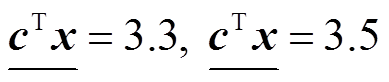 )。因此,倘若节点的松弛目标函数高于当前上界,最优解必定不存在于这部分子树下,该节点被剪除(Prune),如图中3
)。因此,倘若节点的松弛目标函数高于当前上界,最优解必定不存在于这部分子树下,该节点被剪除(Prune),如图中3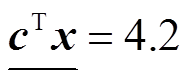 。由于下界变化依赖于节点的穷举式探索,提升相对困难,因此启发式策略的基本思想是快速降低上界,从而引导分支定界算法剪除更多冗余搜索空间。
。由于下界变化依赖于节点的穷举式探索,提升相对困难,因此启发式策略的基本思想是快速降低上界,从而引导分支定界算法剪除更多冗余搜索空间。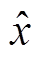 ,并建立辅助LP模型(以0-1规划为例),有
,并建立辅助LP模型(以0-1规划为例),有