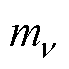 (
(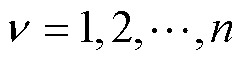 )进行非线性映射
)进行非线性映射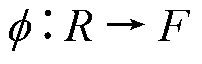 ,可得到
,可得到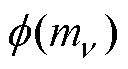 (
(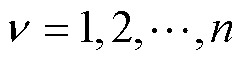 ),从而建立协方差矩阵
),从而建立协方差矩阵 ,同时为求解该矩阵,引入核矩阵
,同时为求解该矩阵,引入核矩阵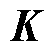 。H和K分别为
。H和K分别为摘要 锂离子电池的剩余使用寿命(RUL)是健康管理中重要参数,其准确评估对于保证电池设备的安全稳定运行非常重要。该文提出一种数据预处理联合变分模态分解(VMD)、长短期记忆网络(LSTM)和高斯回归过程(GPR)的预测框架。首先选取充放电循环过程中的信息作为间接健康因子(HI),并通过核主元分析方法(KPCA)实现间接HI的特征提取,完成数据预处理;其次通过VMD-LSTM方法实现健康因子的分解、预测和重构,并将重构得到的数据应用于RUL预测的GPR模型,完成预测模型搭建;最后以NASA锂电池数据集作为算法测试数据,结果表明,所提取的健康因子能够准确跟踪锂电池的退化过程;所提预测方法能够准确地估计电池的剩余寿命,同时具有较高的可靠性和稳定性。
关键词:锂离子电池 剩余寿命 健康因子 变分模态分解 高斯回归过程 长短期记忆
随着能源和环境危机加剧,锂离子电池作为一种清洁能源、同时兼有能量密度高、自放电低、寿命长等优点,在船舶、航空、卫星以及军工等领域得到了广泛的应用和发展[1-4]。然而在锂离子电池的连续充放电过程中,锂离子电池性能会随着容量的降低和阻抗的增加而恶化,这将导致设备和系统故障甚至造成灾难性损失,因此实现准确可靠的锂离子电池剩余使用寿命(Remaining Useful Life, RUL)预测在电池管理系统设计的科学研究中和实际应用过程中至关重要[5]。
电池健康状态(State of Health, SOH)是表征电池老化程度的重要指标,一般定义为当前可用最大容量与出厂额定容量之间的比值。随着电池老化程度增加,SOH逐步降低,当SOH下降至70%~80%时,电池寿命达至终点[6]。通过预测锂电池健康状态和参数未来变化趋势,可以实现准确的RUL预测,目前基于模型、经验公式以及数据驱动的方法都已用于锂电池的健康管理中,其中基于模型的方法根据建模机理差异又可以分为电化学模型和等效电路模型[7]。电化学模型是通过一系列的偏微分方程来描述电池的动态性能,能够直接反应电池内部的状态信息,同时表征了内部锂离子、电化学和材料特征之间的传输过程,文献[8]中对电化学模型的建模以及参数识别方法进行了全面综述,但是该类模型常常受限于复杂的微分方程和繁多的模型参数,难以在实际中应用。等效电路模型使用基本电路元件来模拟电池的输出特性,具有结构简单、模型参数少以及计算高效等特点,文献[9]中构建了Thevenin等效电路模型,提出使用改进卡尔曼滤波算法对电池内阻进行辨识,进而根据欧姆内阻与电池SOH的函数关系,估算SOH,文献[10]中建立了Thevenin等效电路模型和容量交换模型,应用多尺度卡尔曼滤波方法,提出了锂离子充电状态和健康状态的联合估计模型,但是该类模型存在适应性差、模型参数辨识困难等问题。由于实际电路模型的复杂性,基于经验公式的方法常被应用到工程中,经验公式是基于电池的历史运行数据而构建的经验老化公式,并在此基础上结合粒子滤波等数理算法进行参数估算,Duan Bin等基于一般经验模型,提出使用扩展卡尔曼滤波优化粒子滤波方法,成功搭建剩余使用寿命(RUL)预测框架[11],考虑到电池外部因素会影响电池内部的退化行为,贺宁等将双指数模型与神经网络模型结合来描述容量退化趋势,进一步使用改进粒子滤波算法实现模型参数更新,完成了RUL的准确预测[12],但是该类模型对SOH的估计精度很大程度依赖经验公式和数据的准确性,但由于神经网络的引入反而增加了模型的复杂性。
随着人工智能的发展,基于数据驱动的方法越来越受到众多学者的重视,因该方法不需要考虑电池内部复杂的化学反应,而是直接从原始数据中挖掘锂电池的劣化信息和演化信息,通过人工智能算法实现锂电池的RUL预测。目前相关学者已经分别将支持向量机[13]、相关向量机[14]、极限学习机[15]以及深度神经网络[16]与优化算法相结合,以表征电池性能退化的健康因子为数据研究对象,实现了锂电池的健康状态估计和剩余寿命预测。但是上述的预测方法存在两个问题:①此类机器学习方法仅支持点预测而无法支持概率预测,对预测结果的置信度没有明确的数学表示;②忽视了原始数据中存在的噪声和容量回升现象。数理统计中基于贝叶斯理论和统计学习理论的高斯回归过程可以用概率分布描述回归过程,文献[17]从充放电曲线中提取电池健康特征,利用高斯过程回归(Gaussian Regression Process, GPR)建立老化模型,实现了SOH估计,并给出了预测结果的概率表达式,考虑到容量回升和噪声影响,文献[18]将经验模态分解(Empirical Mode Decomposition, EMD)方法和SOH结合,建立了SOH估计和RUL预测模型,模型中EMD方法能够有效地消除噪声信号,提高预测精度,但是EMD方法在分解过程中可能会出现模态重叠的现象,为此,文献[19-20]提出了集合经验模态分解方法(Complete Ensemble Empirical Mode Decom- position with adaptive Noise, CEEMDN)对原始数据进行去噪,并分别联合长短期记忆网络(Long Short Term Memory, LSTM)和支持向量回归(Support Vector Regression, SVR)方法,建立了锂离子电池的RUL预测模型,除此之外,Sun Chuan等提出使用鲸鱼优化算法优化的变分模态分解(Variational Modal Decomposition, VMD)算法将锂电池容量数据集分解为残余成分和再生分量,而后分别通过LSTM方法和GPR方法建立预测模型,最后整合预测结果得到最终预测的锂离子电池容 量[21],但是反向长短期记忆神经网络(Bi-Long Short Term Memory, Bi-LSTM)数据集中容量的测量易受随时间变化的放电速率和温度的影响,通过容量直接预测电池RUL会产生累计误差且在线测量困难。
基于上述分析,本文提出来一种新的预测框架,首先从充放电曲线中提取反映电池寿命退化趋势的间接健康因子(Health Indicator, HI),同时采用核主元分析(Kernel Principal Component Analysis, KPCA)特征提取方法去除冗余分量变换为融合HI,其次应用VMD分解方法并结合LSTM神经网络,实现融合HI的分解、预测以及重构,最后以重构HI和容量分别作为GPR模型的输入和输出,实现锂离子电池的RUL预测。
KPCA算法的思想是利用少数变量反映全部变量的大部分信息,并且这些少数变量所含的信息线性不相关。
假设对原始数据序列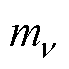 (
(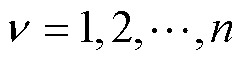 )进行非线性映射
)进行非线性映射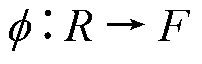 ,可得到
,可得到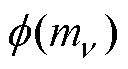 (
(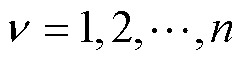 ),从而建立协方差矩阵
),从而建立协方差矩阵 ,同时为求解该矩阵,引入核矩阵
,同时为求解该矩阵,引入核矩阵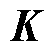 。H和K分别为
。H和K分别为
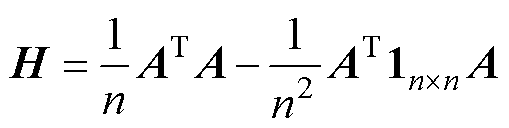 (1)
(1)
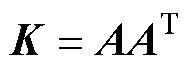 (2)
(2)
式中,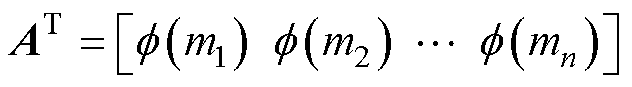 ,设协方差矩阵的特征值分别为
,设协方差矩阵的特征值分别为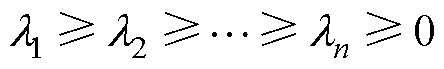 ,特征值又称为主元,对应的特征向量称为主成分,累计贡献度定义为所选顺序特征值与总特征值的比值,即
,特征值又称为主元,对应的特征向量称为主成分,累计贡献度定义为所选顺序特征值与总特征值的比值,即
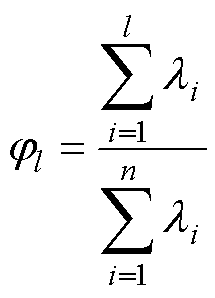 (3)
(3)
式中,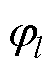 为前
为前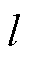 个主元的贡献度之和,代表前
个主元的贡献度之和,代表前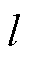 个主成分在所有主成分中所占的比重,为尽可能保留原始数据中有用信息,
个主成分在所有主成分中所占的比重,为尽可能保留原始数据中有用信息,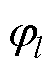 通常设定为不小于0.9。
通常设定为不小于0.9。
VMD是一种非递归信号变分分解方法,可以自适应地将信号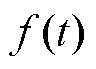 分解成一系列较为规律的本征模态分量,相较于EMD分解方法,它克服了模态混叠和虚假分量等缺点。
分解成一系列较为规律的本征模态分量,相较于EMD分解方法,它克服了模态混叠和虚假分量等缺点。
VMD分解过程实质上是变分问题的求解过程,目的是使所有模态分量带宽之和最小,首先通过Hibert变换获取每个模态分量的单边频谱,然后加入调整项使各个频谱调制基带宽,最后对解调信号进行处理,计算各模态分量带宽,由此引出的约束变分模型为
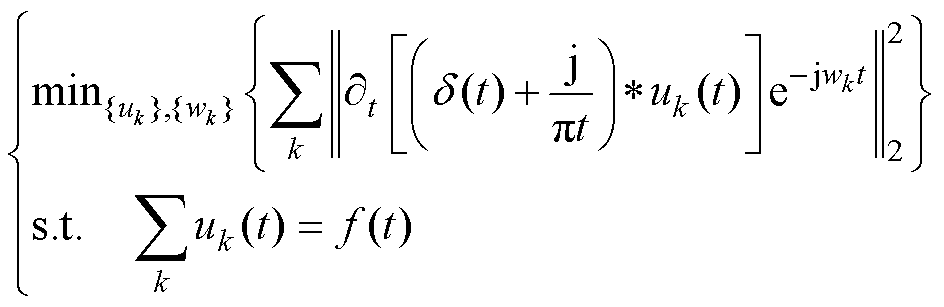 (4)
(4)
式中,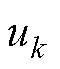 和
和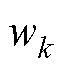 分别表示VMD分解的第
分别表示VMD分解的第 个模态分量和对应的中心频率;*表示卷积运算;
个模态分量和对应的中心频率;*表示卷积运算;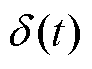 为狄克拉函数;
为狄克拉函数;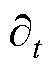 为梯度运算。
为梯度运算。
为求解变分模型,第一步引入惩罚因子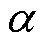 和拉格朗日算子
和拉格朗日算子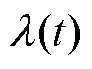 ,将约束问题转化为非约束问题,即
,将约束问题转化为非约束问题,即
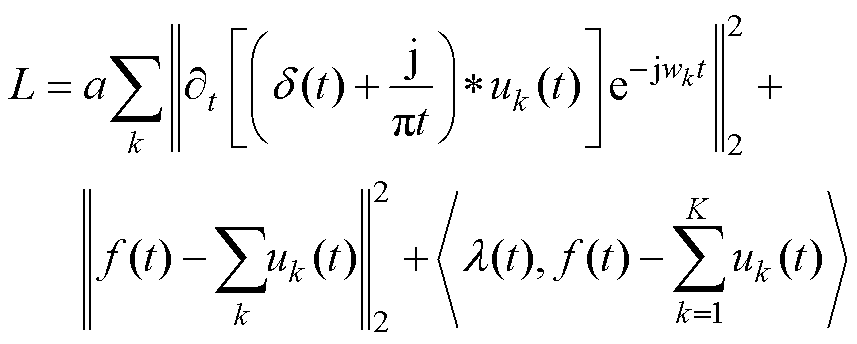 (5)
(5)
第二步引入乘法算子采用交替方向法迭代更新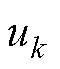 、
、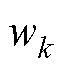 和
和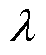 ,寻找式(5)的鞍点,即为约束变分方程的最优解,
,寻找式(5)的鞍点,即为约束变分方程的最优解,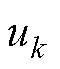 、
、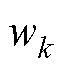 和
和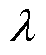 的更新公式分别为
的更新公式分别为
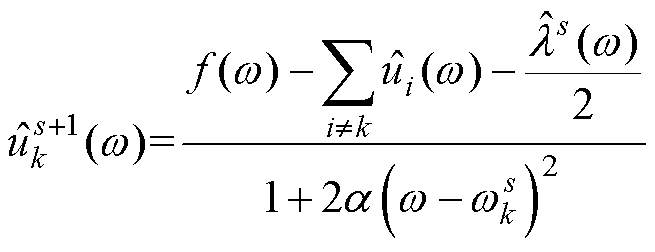 (6)
(6)
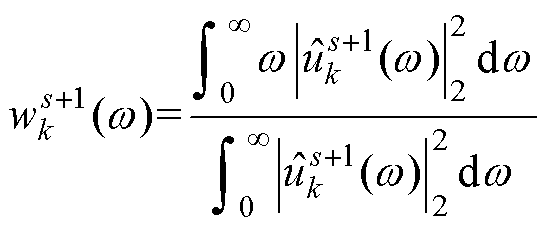 (7)
(7)
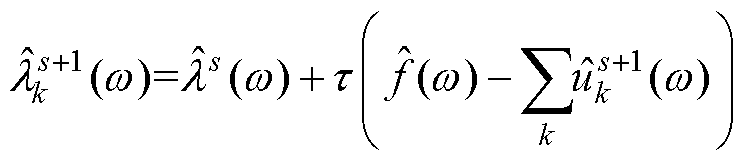 (8)
(8)
式中,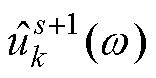 、
、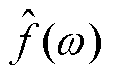 、
、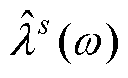 分别为
分别为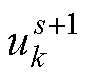 、
、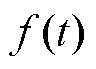 、
、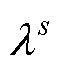 所对应的傅里叶变换。
所对应的傅里叶变换。
迭代终止条件为
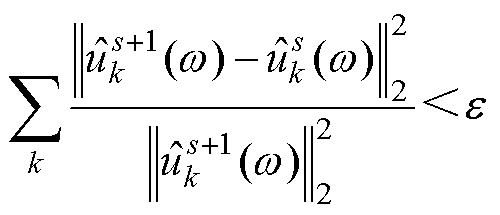 (9)
(9)
式中,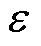 为收敛精度。
为收敛精度。
LSTM是一种递归神经网络,其基本神经元由输入门、遗忘门和输出门三部分组成,这些门被用于更新或者丢弃历史信息,这使LSTM获得了长期记忆能力,相较于循环神经网络,它克服了梯度爆炸和梯度消失的缺点。目前在语音识别、寿命预测、机器翻译等领域有了广泛的应用,其原理公式为
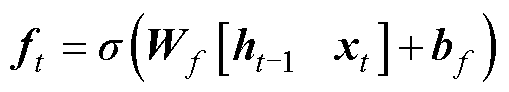 (10)
(10)
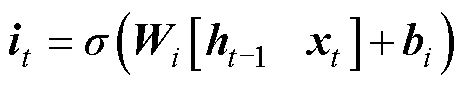 (11)
(11)
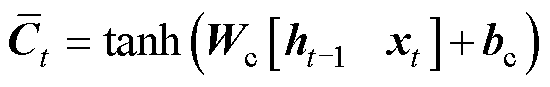 (12)
(12)
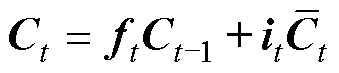 (13)
(13)
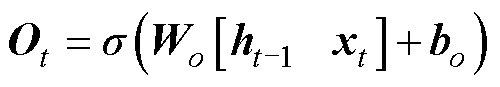 (14)
(14)
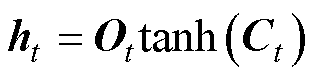 (15)
(15)
式中,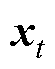 、
、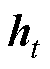 分别为时间
分别为时间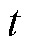 对应的输入和输出;
对应的输入和输出;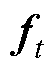 、
、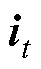 和
和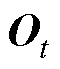 分别为t时刻遗忘门、输入门和输出门的状态;
分别为t时刻遗忘门、输入门和输出门的状态;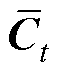 和
和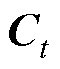 分别为t时刻待更新神经元和单元状态;
分别为t时刻待更新神经元和单元状态;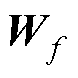 、
、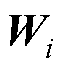 、
、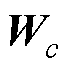 、
、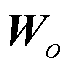 和
和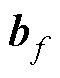 、
、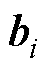 、
、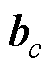 、
、 分别为对应门的权值矩阵和偏置项;
分别为对应门的权值矩阵和偏置项; 为隐藏层中的Sigmoid激活函数。
为隐藏层中的Sigmoid激活函数。
GPR是一种用概率分布描述回归函数的模型,由输入的均值函数和协方差函数定义。假定训练集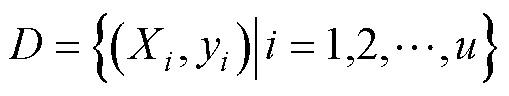 ,其中
,其中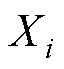 和
和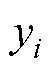 分别为第
分别为第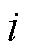 个输入向量和函数输出,构建回归模型为
个输入向量和函数输出,构建回归模型为
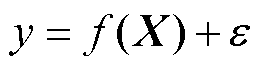 (16)
(16)
式中,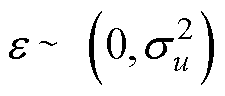 ,
,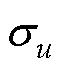 为噪声的标准差。
为噪声的标准差。
对于输入向量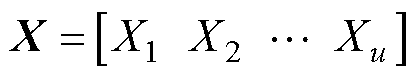 ,假定
,假定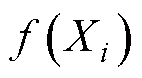 服从高斯分布,则
服从高斯分布,则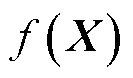 服从多元高斯分布
服从多元高斯分布
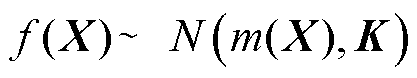 (17)
(17)
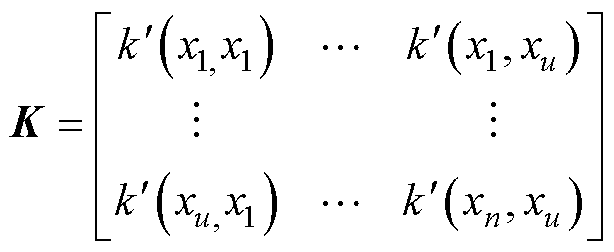 (18)
(18)
式中,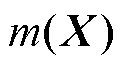 和
和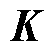 分别为该多元高斯分布的均值向量和协方差矩阵;
分别为该多元高斯分布的均值向量和协方差矩阵;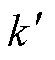 为协方差矩阵中采用的核函数。一般情况下,会经过数据变换使均值函数
为协方差矩阵中采用的核函数。一般情况下,会经过数据变换使均值函数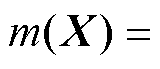
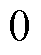 ,则
,则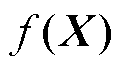 服从如下形式的多元高斯分布
服从如下形式的多元高斯分布
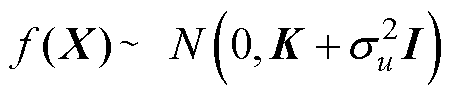 (19)
(19)
在上述多元高斯分布的基础上,假设预测集 对应的高斯过程为
对应的高斯过程为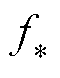 ,则有
,则有
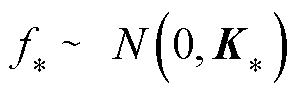 (20)
(20)
从而训练集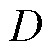 的输出值
的输出值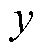 与预测集
与预测集 的输出
的输出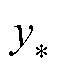 的联合先验分布为
的联合先验分布为
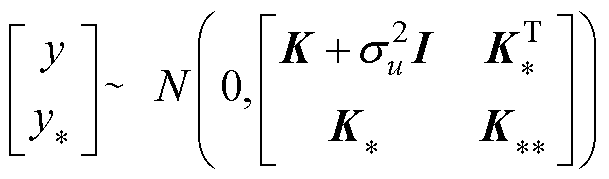 (21)
(21)
式中,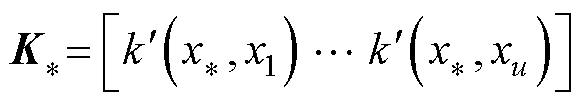 ;
;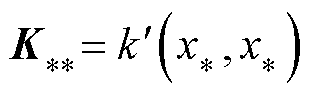 ,根据高斯分布的数学推导,推得
,根据高斯分布的数学推导,推得 的后验证分布为
的后验证分布为
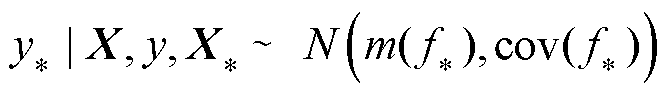 (22)
(22)
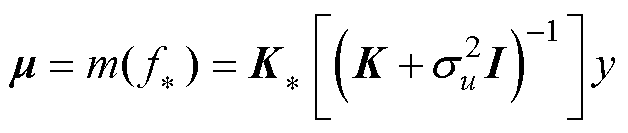 (23)
(23)
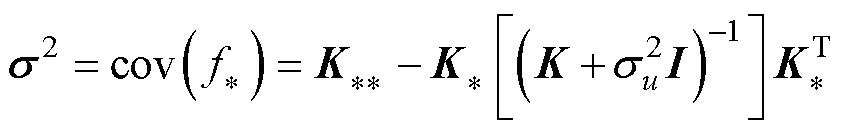 (24)
(24)
式中,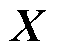 和
和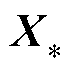 分别为训练集和测试集输入向量的列向量矩阵;
分别为训练集和测试集输入向量的列向量矩阵;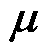 和
和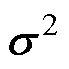 分别为均值矩阵和协方差矩阵,其中GPR预测模型的95%置信区间为
分别为均值矩阵和协方差矩阵,其中GPR预测模型的95%置信区间为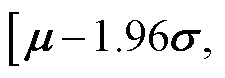
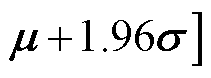 。
。
基于上述提出的算法,本文的锂离子电池RUL预测框架如图1所示,该框架主要由三部分组成:
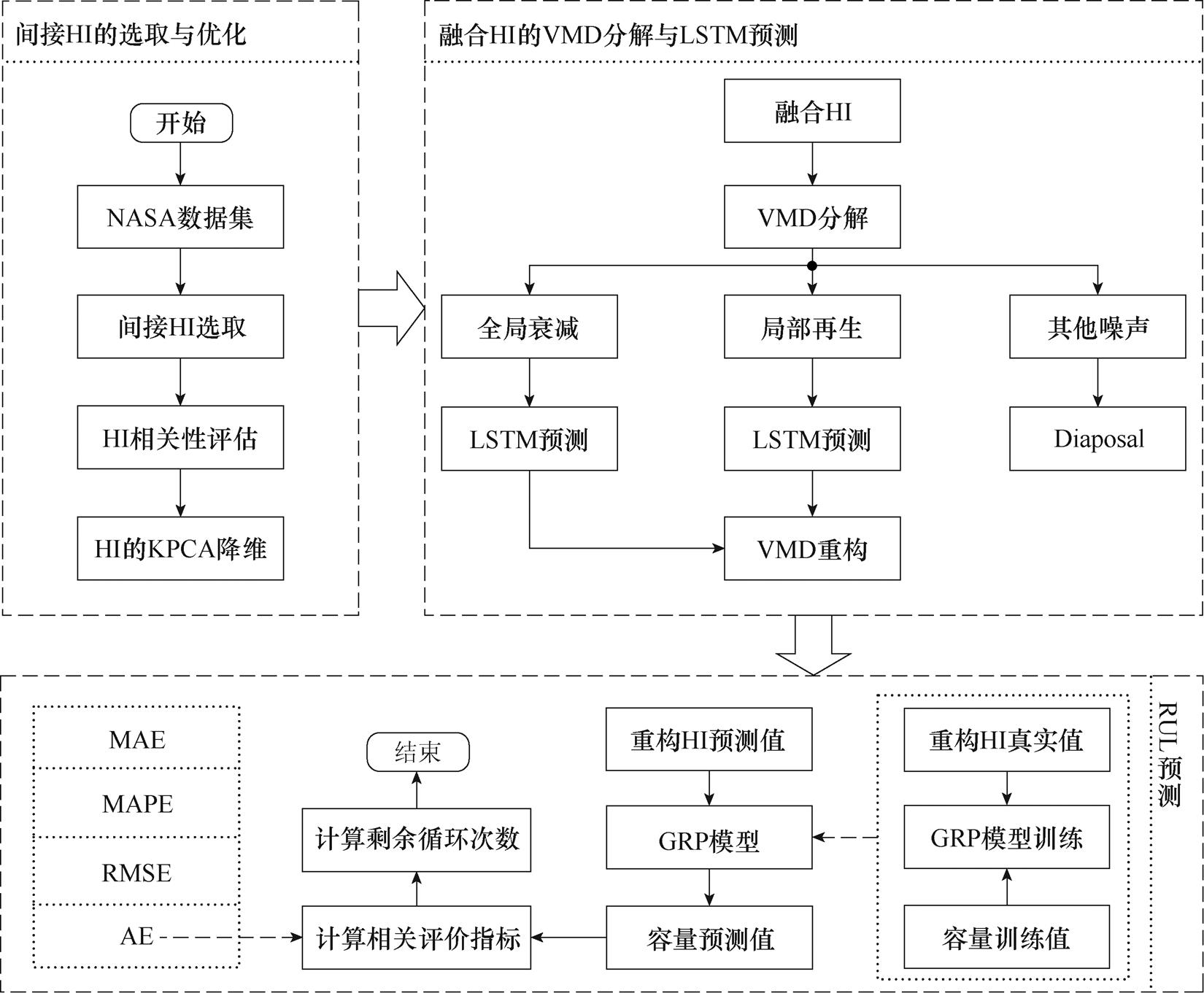
图1 本文所提方法预测流程框架
Fig.1 Prediction framework of the paper
(1)第一部分,选取反映RUL退化趋势的间接HI,对间接HI做相关性评估和KPCA特征提取,得到融合HI。
(2)第二部分,首先采用VMD分解方法将得到的融合HI分解为多个模态分量,依据各个模态分量中心频率和与容量相关系数分为全局衰减、局部再生和其他噪声三部分,而后用LSTM神经网络分别对全局衰减和局部再生分量进行时间序列预测,得到预测起点后的预测值,最后将各个部分的值相加得到重构HI。
(3)第三部分,设定第二部分LSTM预测起点为分隔点,选取分隔点前的重构HI的真实值作为输入,对应容量作为输出,建立GPR模型,而后将分隔点后的重构HI的预测值作为测试集,输入高斯回归模型中,得到分隔点后各个循环容量的预测值,最终根据终止阈值计算锂电池的RUL。
NASA研究中心对多组锂离子电池进行不同工况下的电池寿命退化实验,本文采用额定容量为2 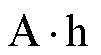 ,标号分别为B05、B06、B07和B18锂离子电池为实验对象,具体实验过程如下[22]。
,标号分别为B05、B06、B07和B18锂离子电池为实验对象,具体实验过程如下[22]。
(1)充电过程:环境温度保持24℃,电池以1.5 A恒流充电至电压为4.2 V,然后以4.2 V恒压充电至电流降为20 mA,充电过程结束。采集数据包括:电池输出电流、电池端电压、电池温度以及数据采集时间。
(2)放电过程:环境温度保持24℃,电池以2 A恒定电流进行放电,当B05、B06、B07、B18锂离子电池电压分别降至2.7 V、2.5 V、2.2 V和2.5 V,放电过程结束。采集数据包括:电池输出电流、电池端电压、电池温度、数据采集时间以及对应电池容量。
锂离子电池的健康因子是表征电池健康状态与剩余寿命的变量,由于电池容量与电池内部化学反应密切相关,一般情况下,常使用电池容量作为直接健康因子,当电池实际容量降至额定容量的70%~80%时认为电池寿命终止。本文采用的NASA数据集将寿命的终止阈值设定为额定容量的70%,即为1.4 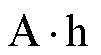 ,鉴于实验中B7号电池容量没有下降到1.4
,鉴于实验中B7号电池容量没有下降到1.4 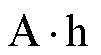 ,故选取1.45
,故选取1.45 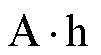 作为终止阈值,四种电池的容量退化曲线如图2所示。
作为终止阈值,四种电池的容量退化曲线如图2所示。
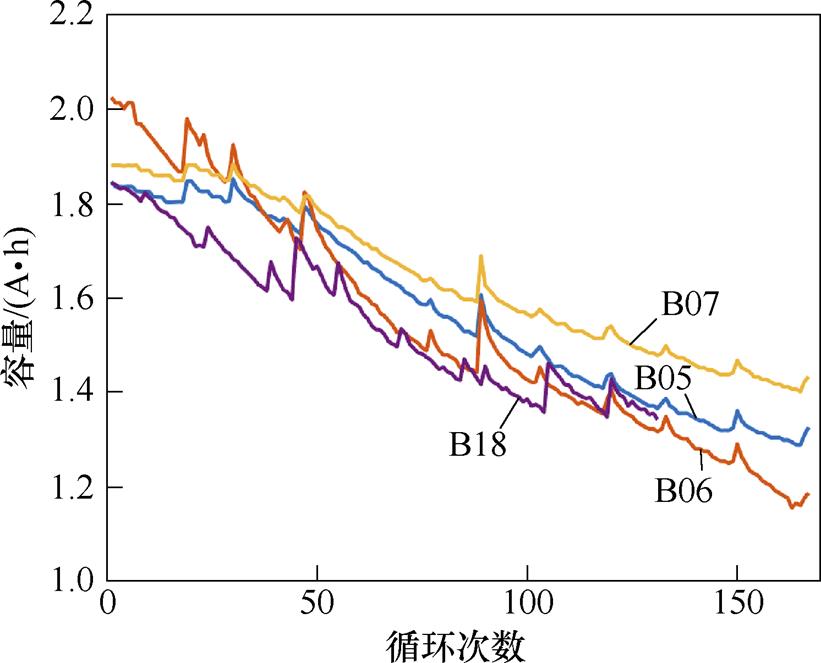
图2 NASA数据集容量退化曲线
Fig.2 NASA dataset capacity degradation curves
但是在电池老化的过程中,测量容量不仅需要标准严格的实验条件,而且需要昂贵精确的测量设备,同时侵入性的测量方式对电池具有一定损害,而从电压、电流和温度变化曲线中提取的间接健康因子同样可以反映电池的老化情况,考虑到篇幅限制,仅给出B05号电池在不同循环周期下充电电流和充电电压变化曲线,如图3和图4所示,颜色从黑到红依次表示循环次数从低到高。本文依据电池老化特征并结合参考文献[23-26],从电流、电压和温度充放电循环曲线中选取8个健康因子,在充电过程中:选取等压升充电时间、恒流阶段充电时间、充电温度达到峰值的时间,分别记为HI1、HI2、HI3,在放电过程中:选取等压降放电时间、放电电压达到最低点的时间、等时间间隔放电电压差、放电温度达到峰值的时间、等时间间隔放电温度差,分别记为HI4、HI5、HI6、HI7、HI8,经标准化处理后,提取的间接HI如图5所示。
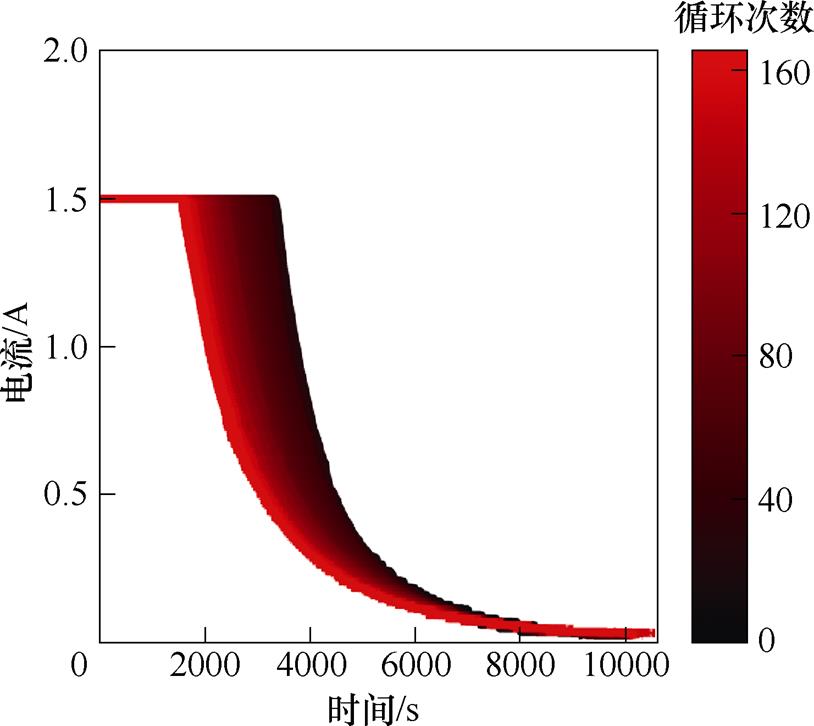
图3 不同循环周期下充电电流变化曲线
Fig.3 Charging current change curve under different cycle
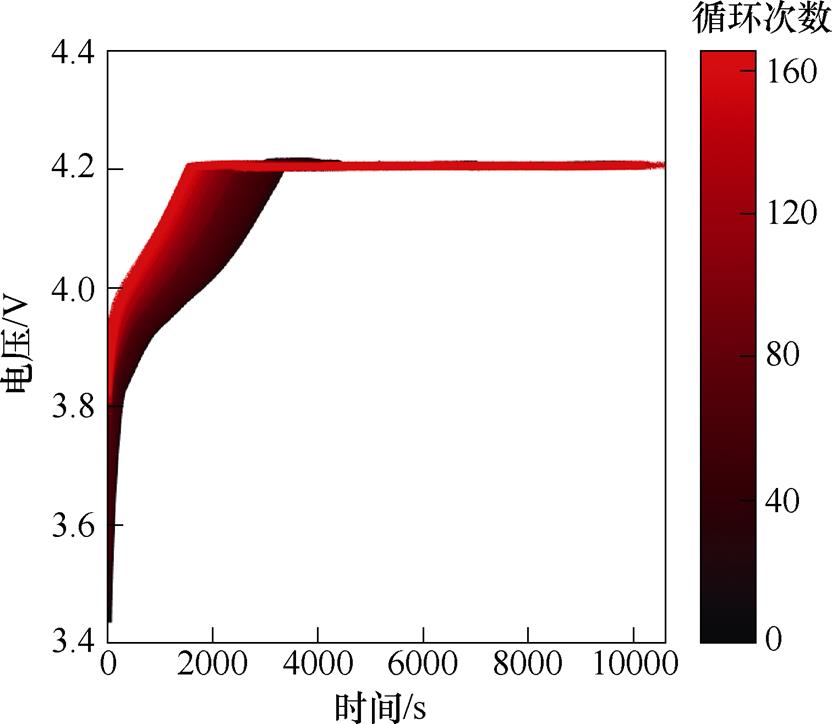
图4 不同循环周期下充电电压变化曲线
Fig.4 Charging voltage change curve under different cycle
统计学中常用来描述两组数据序列相关性的分析方法有Pearson积矩相关系数和Spearman秩相关系数。其中Pearson只能衡量样本总体服从正态分布变量的线性相关关系,Spearman秩相关系数无上述约束,是一种基于秩相关系数度量变量间相关性的非参数分析方法,二者计算公式分别为

图5 不同循环周期下健康因子变化曲线
Fig.5 Change curves of health indicator under different cycles
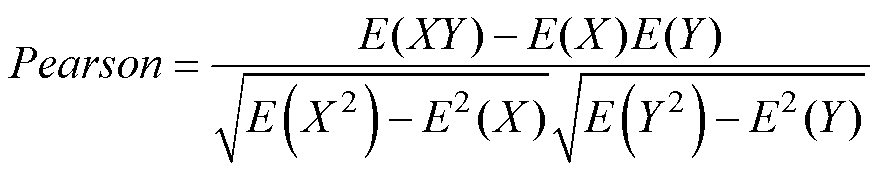 (25)
(25)
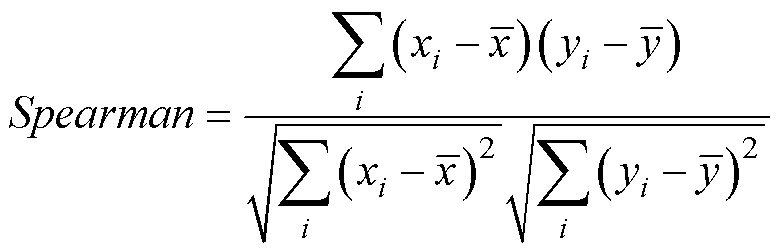 (26)
(26)
式中,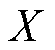 和
和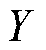 分别为两类样本总体;
分别为两类样本总体;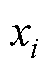 和
和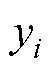 分别代表两类样本个体。
分别代表两类样本个体。
相关系数的取值范围均为[-1, 1],其绝对值越大表明两类样本相关程度越高,为了衡量选取的间接HI与容量的相关程度,本文采用Pearson和Spearman相关系数方法量化处理。各个电池间接健康因子与容量的相关系数见表1和表2,分析可知,每个电池的间接HI与容量的相关系数均大于0.95,说明本文选取的间接HI是合理的,能够准确地跟踪锂离子电池的退化过程。
表1 间接HI的Spearman的相关系数
Tab.1 Spearman correlation coefficient of indirect HI

SpearmanHI1HI2HI3HI4HI5HI6HI7HI8 B050.990 50.990 80.990 60.996 70.999 70.993 80.999 5-0.985 3 B060.993 50.993 20.992 70.998 90.999 90.997 80.999 8-0.984 6 B070.989 60.989 70.991 70.995 60.999 00.991 50.998 6-0.967 5 B180.974 80.961 60.975 70.997 90.999 50.996 60.998 8-0.988 1
表2 间接HI的Pearson相关系数
Tab.2 Pearson correlation coefficients of indirect HI

PearsonHI1HI2HI3HI4HI5HI6HI7HI8 B050.995 20.996 50.996 20.996 20.999 90.978 00.999 8-0.984 4 B060.990 60.991 70.992 30.994 80.999 90.970 10.999 9-0.969 5 B070.988 70.994 50.995 90.998 10.999 70.985 30.999 2-0.980 4 B180.985 80.978 40.986 50.998 00.999 80.980 40.999 4-0.975 1
上述所提取的健康因子与容量之间均具有较高的相关性,则相互之间必然存在冗余信息,为减少后续RUL预测计算复杂度,本文采用KPCA算法对所选取的间接HI进行优化,将重叠信息分离。KPCA能将大量的冗余变量转化为少量不相关的综合变量,同时尽可能多地保留信息。表3列出了各电池间接HI经KPCA方法特征提取后主成分1的贡献率以及主成分1与容量的Spearman和Pearson相关系数,可以看出,主成分1贡献率均超过95%,且Spearman和Pearson相关系数的绝对值也均大于0.99,因此,本文选取主成分1作为融合HI来进行后续的剩余寿命预测,该方法不仅消除了多变量之间的冗余信息,也减少了计算量,完成了前期数据预处理的工作。
表3 融合HI的贡献率和相关系数
Tab.3 Contribution and correlation coefficient of fusion HI
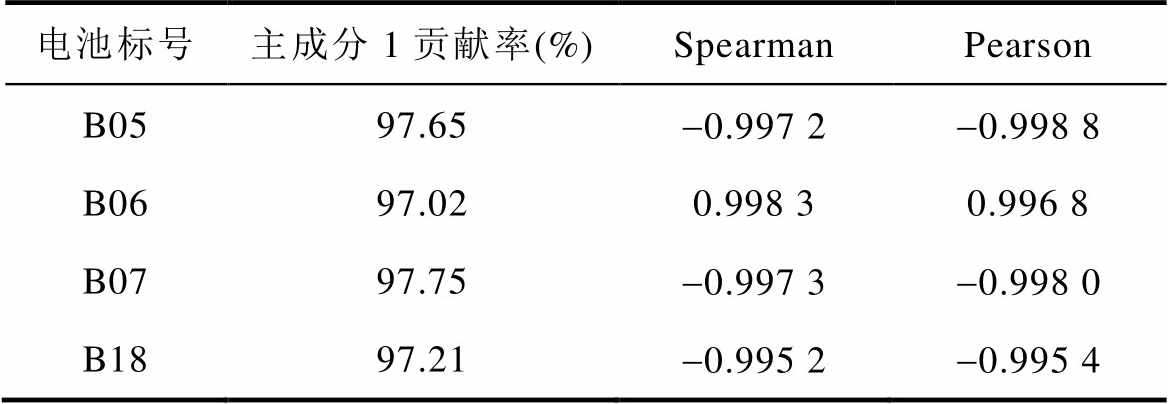
电池标号主成分1贡献率(%)SpearmanPearson B0597.65-0.997 2-0.998 8 B0697.020.998 30.996 8 B0797.75-0.997 3-0.998 0 B1897.21-0.995 2-0.995 4
为避免容量回升的局部波动和测试噪声对RUL预测结果造成干扰,本文应用VMD方法将融合HI分解为全局衰减、局部再生和其他噪声三部分。VMD的主要参数中,惩罚因子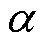 、凸函数优化参数
、凸函数优化参数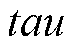 、中心频率初始化值
、中心频率初始化值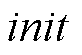 、直流分量
、直流分量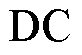 以及终止条件
以及终止条件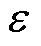 对分解结果影响较小,根据经验分别设置为100、0、1、0以及
对分解结果影响较小,根据经验分别设置为100、0、1、0以及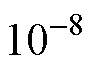 ;但是模态分量个数
;但是模态分量个数 对分解结果影响较大,
对分解结果影响较大, 值过小,分解不充分;
值过小,分解不充分; 值过大,则会过分分解导致产生虚假分量,一般情况下
值过大,则会过分分解导致产生虚假分量,一般情况下 的取值范围为[3, 7]。为选择合理的
的取值范围为[3, 7]。为选择合理的 值,本文采用一种依据能量差来选择模态数的方法,以克服其随机选择带来的缺陷[27]。从VMD分解的最优理论结果来看,每个分量的能量之和应等于原始信号,当
值,本文采用一种依据能量差来选择模态数的方法,以克服其随机选择带来的缺陷[27]。从VMD分解的最优理论结果来看,每个分量的能量之和应等于原始信号,当 值太大时,虚拟分量的产生将导致分量的能量总和太高。基于此,根据式(27),当
值太大时,虚拟分量的产生将导致分量的能量总和太高。基于此,根据式(27),当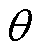 值较小时,信号会分解不完全,当
值较小时,信号会分解不完全,当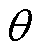 值较大时,则会分解过度。因此,随着
值较大时,则会分解过度。因此,随着 值增大,相应的
值增大,相应的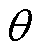 值会显著增加。在这种情况下,可以将
值会显著增加。在这种情况下,可以将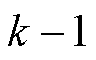 视为VMD分解的最佳模态个数。
视为VMD分解的最佳模态个数。
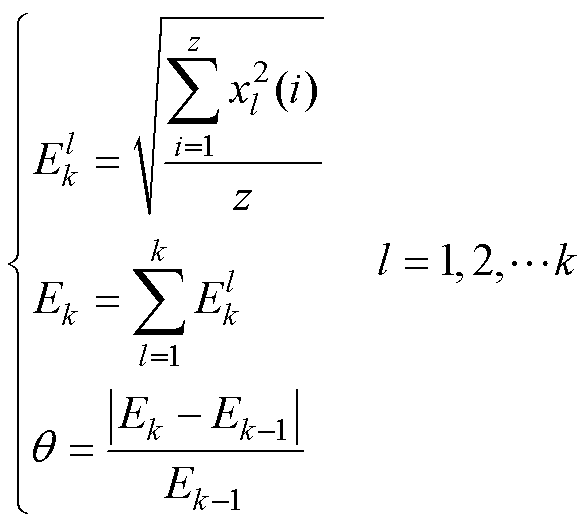 (27)
(27)
式中,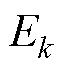 为模态分量个数为
为模态分量个数为 时所有分量能量之和;
时所有分量能量之和;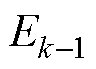 为模态分量个数为
为模态分量个数为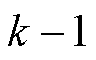 时所有分量能量之和;
时所有分量能量之和;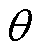 为能量差值;
为能量差值;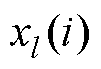 为当模态分解下第
为当模态分解下第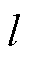 个分量序列的第
个分量序列的第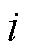 个采样点;z为采样点个数。
个采样点;z为采样点个数。
以B05号电池为例,图6给出了模态分量的能量差值曲线,可以看出当分解为5层时,它的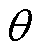 值相对于分解层为4时显著增加,表明以此模态数分解产生了虚假分量,故模态分量个数设置为4。依据上述参数设置,图7为该电池融合HI的原始曲线以及VMD分解后的模态分量曲线,表4为各个模态分量对应的中心频率和与容量的相关系数,其中,残余分量的中心频率低、相关性高,较好地反映了电池容量的退化趋势;IMF1和IMF2分量中心频率和相关性均相对较低,表示了电池容量的随机再生分量;IMF3分量中心频率大、相关性低,代表了其余噪声分量。VMD分解方法的应用解决了原始数据中存在的容量回升和噪声现象,为后续RUL预测提供了基础。
值相对于分解层为4时显著增加,表明以此模态数分解产生了虚假分量,故模态分量个数设置为4。依据上述参数设置,图7为该电池融合HI的原始曲线以及VMD分解后的模态分量曲线,表4为各个模态分量对应的中心频率和与容量的相关系数,其中,残余分量的中心频率低、相关性高,较好地反映了电池容量的退化趋势;IMF1和IMF2分量中心频率和相关性均相对较低,表示了电池容量的随机再生分量;IMF3分量中心频率大、相关性低,代表了其余噪声分量。VMD分解方法的应用解决了原始数据中存在的容量回升和噪声现象,为后续RUL预测提供了基础。
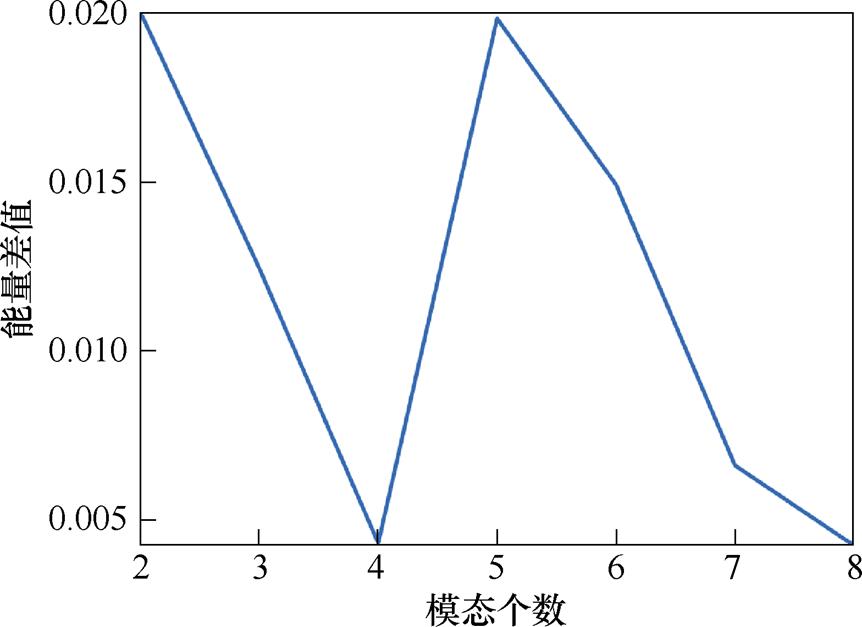
图6 模态分量能量差值曲线
Fig.6 Modal component energy difference curve
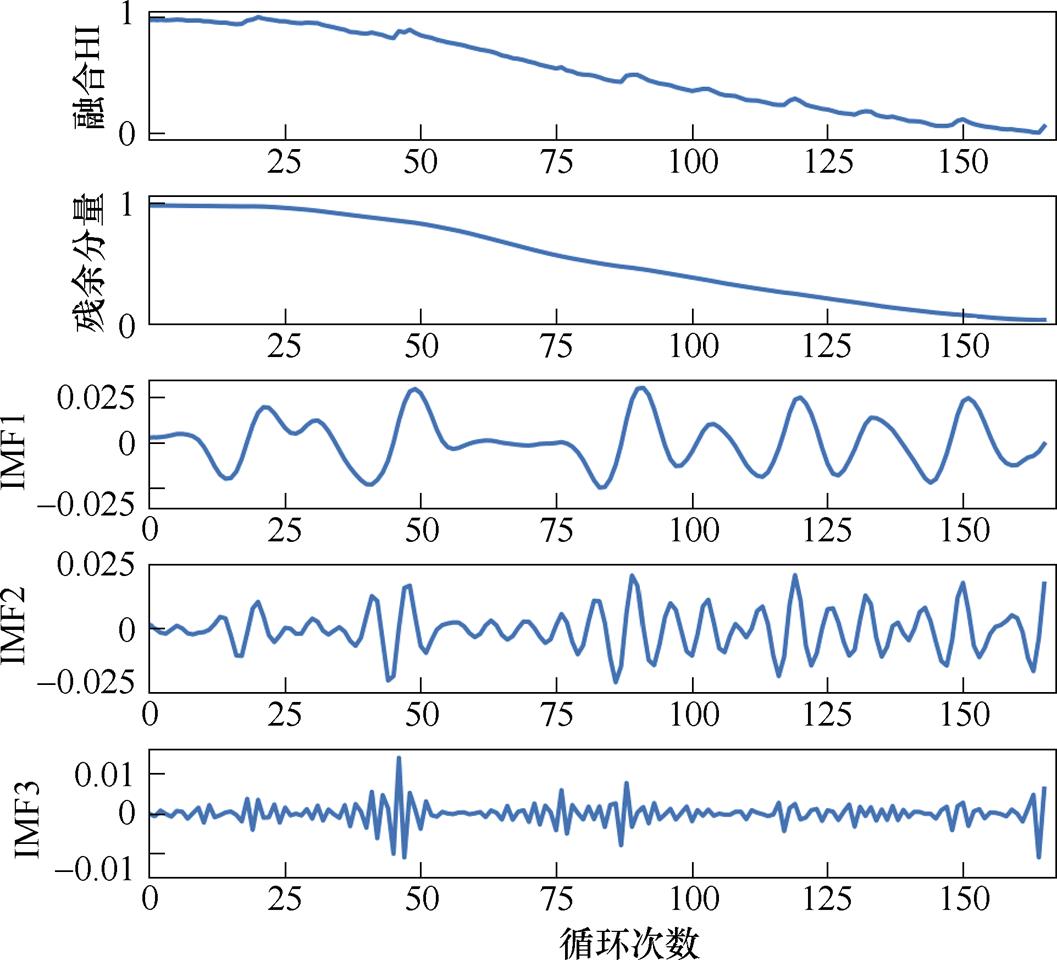
图7 融合HI的VMD分解曲线
Fig.7 VMD decomposition curves of fusion HI
表4 模态分量的中心频率和相关系数
Tab.4 Center frequency and correlation coefficient of modal components
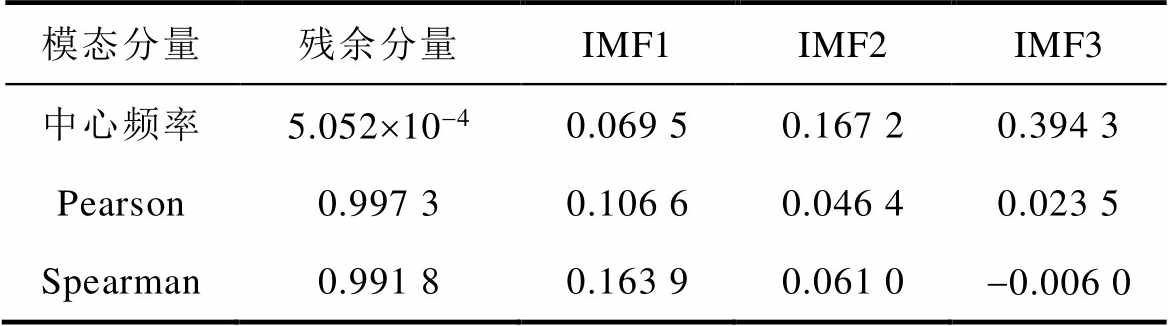
模态分量残余分量IMF1IMF2IMF3 中心频率5.052´10-40.069 50.167 20.394 3 Pearson0.997 30.106 60.046 40.023 5 Spearman0.991 80.163 90.061 0-0.006 0
在上述VMD分解的基础上,分别构建全局衰减、局部再生部分的LSTM预测模型,LSTM模型的主要参数设置见表5,为研究超参数选取对模型的影响,以残余分量的前50%数据作为训练集,以RMSE作为评价指标,采用网络搜索法和交叉验证法搜寻最优参数。首先保持其他参数不变,将设LSTM-1层和LSTM-2层神经元数目均设置为[25, 50, 75, 100, 125, 150],获得三折交叉验证(3-folds Cross-Validation, 3-fold CV)下的RMSE,如图8a所示,而后对优化器初始学习率、批量大小、迭代次数进行相同的操作,如图8b~图8d所示。由图分析可得,首先LSTM神经元数目设置为50和100时测试效果最好,合适的神经元个数可以提高预测精度和计算效率;其次优化器学习率与目标函数的局部极小值的收敛性有关,适当的学习率有利于其收敛,模型中的学习率应设置为0.01;同时批量大小也是影响模型准确性的重要因素,大批量不利于损失函数的优化和梯度下降,小批量则会导致训练时间过长,当批量大小设置为32时训练时间较短以及测试误差最小;最后模型迭代次数过大可能会导致过度拟合问题,交叉验证结果表明迭代次数应设置为100。
表5 LSTM网络参数设置
Tab.5 LSTM network parameter settings
网络模型实验参数数 值 LSTMLSTM-1神经元数目50 LSTM-2神经元数目100 全连接层-1输出数目100 全连接层-2输出数目1 优化器初始学习率0.01 批量大小32 迭代次数100
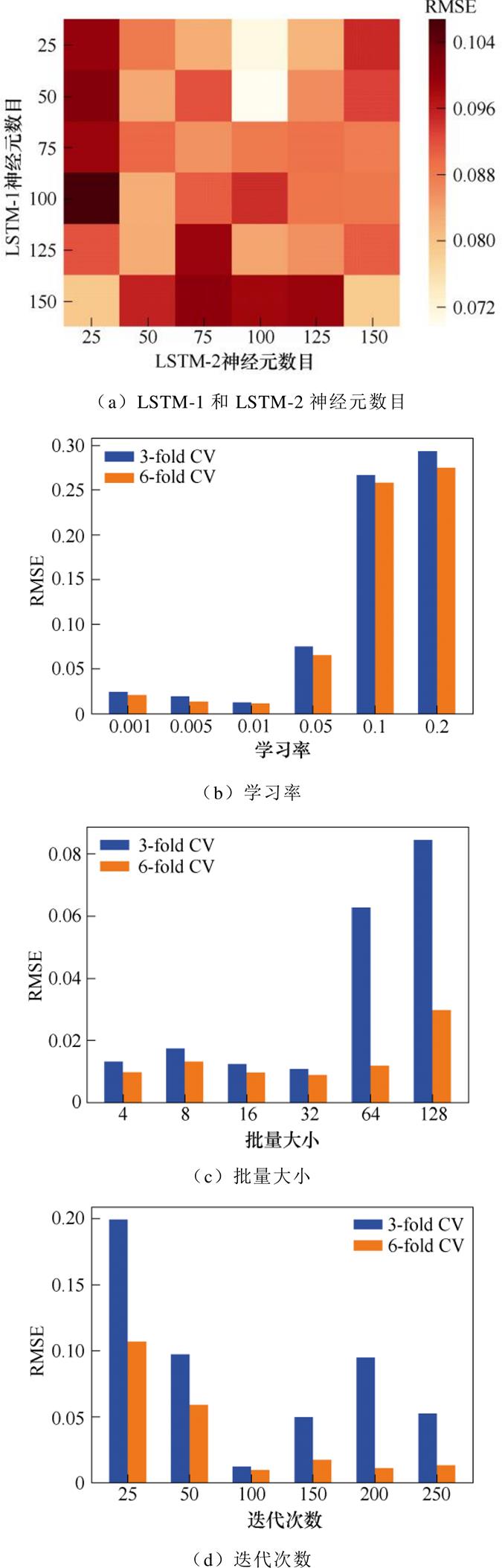
图8 神经网络超参数k-fold交叉验证的RMSE值
Fig.8 RMSE value of neural network hyperparameter k-fold cross validation
以B05电池为例,该电池融合HI经VMD分解共计166组循环数据,首先根据LSTM时间步长分别进行数据变换,并设定预测起点将数据分为训练集和测试集,而后依据训练集建立LSTM预测模型,模型测试集的测试结果如图9所示,由图9可得,LSTM预测模型不仅可以准确地预测出电池容量的退化趋势,并且对电池容量再生也有良好的估计能力,最后将残余分量与两个IMF分量重构,重构后HI的真实值及预测值如图10所示。
电池RUL定义为预测起点至电池实际容量退化至终止阈值时的循环次数。设定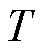 为起始循环周期,TEOL为实际状态下电池容量达到阈值时所在周期数,
为起始循环周期,TEOL为实际状态下电池容量达到阈值时所在周期数,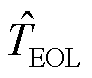 为预测状态下电池容量达到阈值时所在周期数。电池RUL的真实值TRUL和预测值
为预测状态下电池容量达到阈值时所在周期数。电池RUL的真实值TRUL和预测值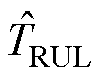 分别定义为
分别定义为
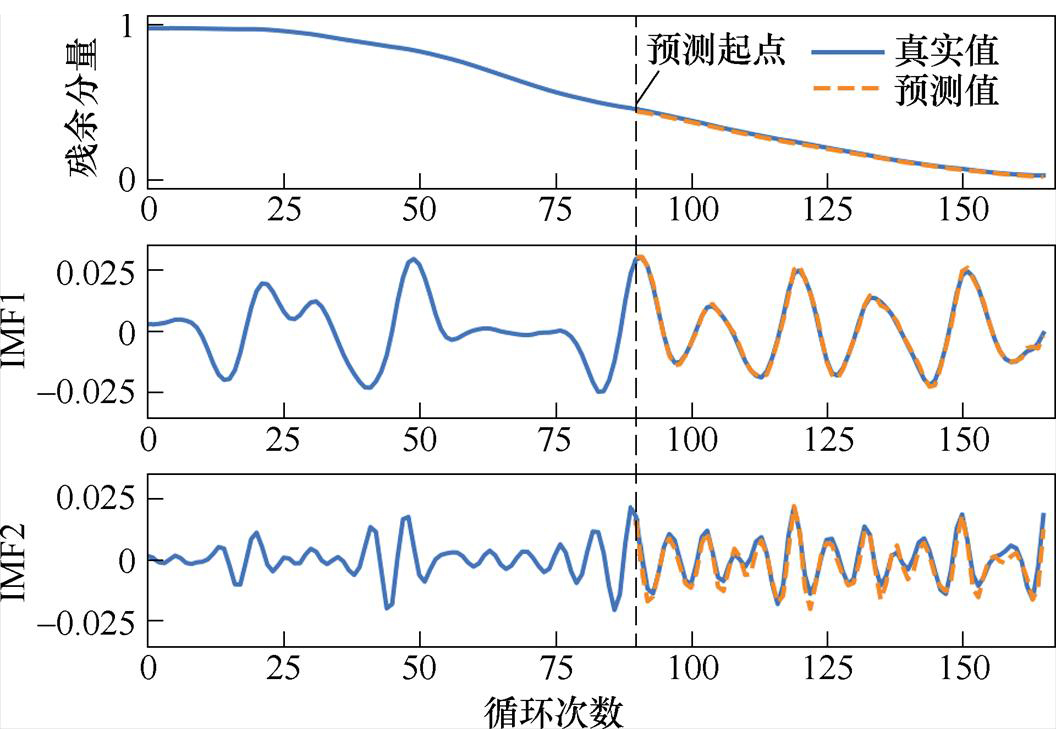
图9 模态分量的预测曲线
Fig.9 Prediction curves of modal components
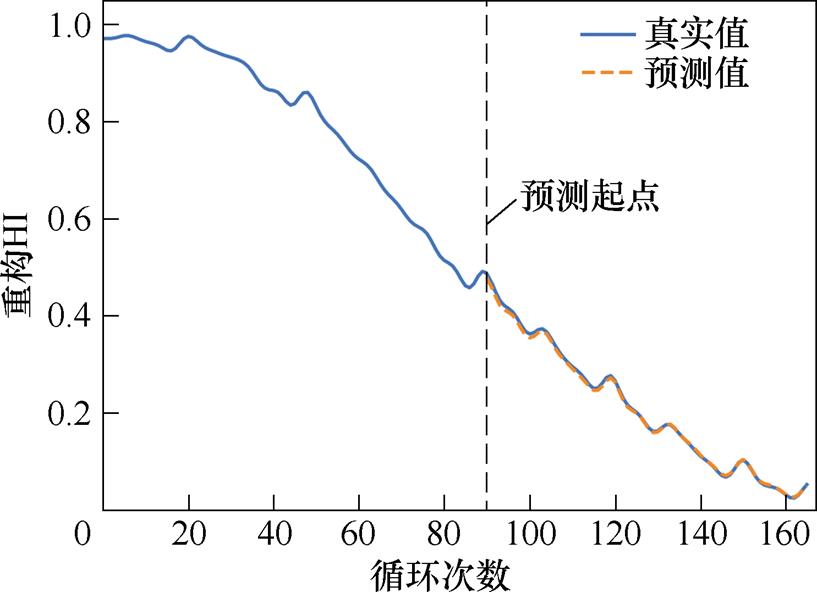
图10 重构HI的预测曲线
Fig.10 Prediction curve of reconstructed HI
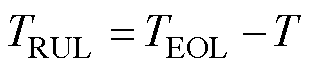 (28)
(28)
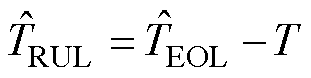 (29)
(29)
本文选用GPR模型用作锂电池寿命预测,模型中选用二次方指数协方差函数作为核函数,首先设置与LSTM预测模型等同的预测起点,而后将预测起点前重构HI的真实值和电池容量作为训练集输入GPR模型,完成对模型的训练,模型训练完成后,将预测起点后重构HI的预测值作为测试集输入到GPR模型,完成对锂离子电池剩余寿命的预测,最后采用下述评价指标完成对预测模型的评价。
模型评价指标包括绝对误差(Absolute Error, AE)、平均绝对误差(Mean Absolute Error, MAE)、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)以及方均根误差(Root Mean Square Error, RMSE),公式分别为
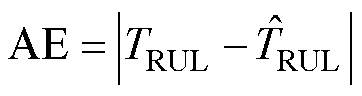 (30)
(30)
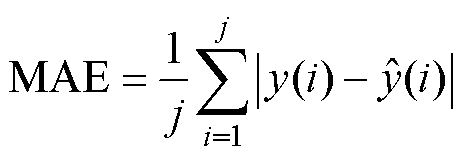 (31)
(31)
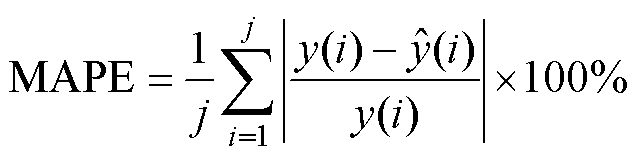 (32)
(32)
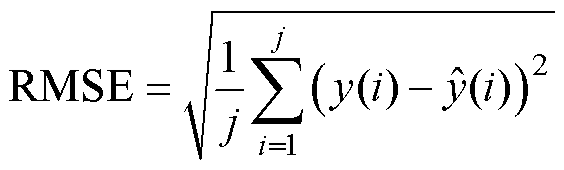 (33)
(33)
式中,j为预测起点至循环终止周期数;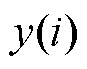 为容量真实值;
为容量真实值;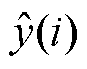 为容量预测值,其中AE、MAE、MAPE和RMSE的值越小,表明预测效果越好。
为容量预测值,其中AE、MAE、MAPE和RMSE的值越小,表明预测效果越好。
为验证本文提出基于KPCA数据预处理和VMD- LSTM-GPR预测模型的可靠性、稳定性以及准确性,本文采用NASA数据集标号为B05、B06、B07和B18的锂电池进行实验验证,对每种电池设置多种不同的预测起点T,见表6,起点均设置为总循环周期约40%处,由于B06在110周期和B18在90周期,其电池容量已经分别下降到终止阈值和接近终止阈值,故不作讨论,容量预测结果和相关评价指标以及锂离子电池RUL预测结果分别如图11、图12和表7所示。
表6 预测起点设置
Tab.6 Prediction starting point settings
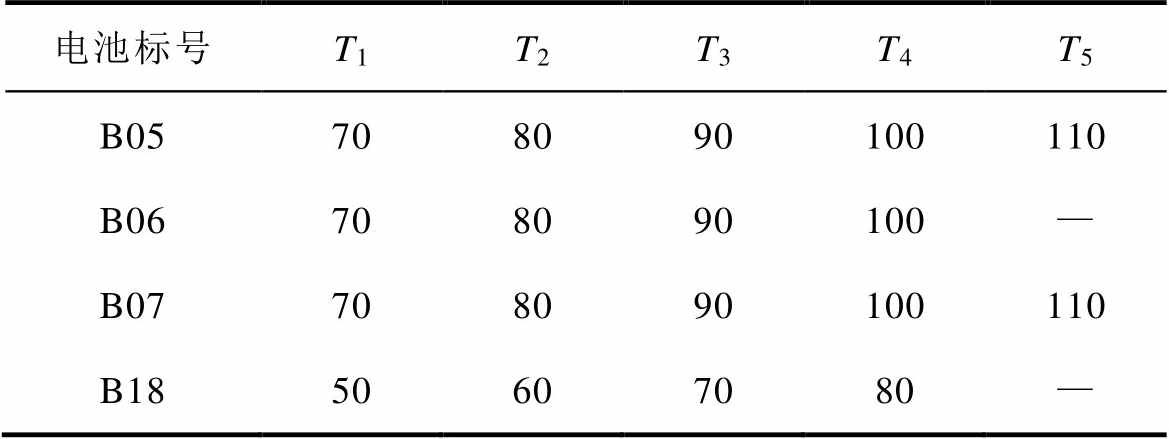
电池标号T1T2T3T4T5 B05708090100110 B06708090100— B07708090100110 B1850607080—
通过容量预测结果、RUL预测结果以及相关评价指标可以得到如下结论:
(1)在图11中,蓝色曲线代表容量的真实值,黄色虚线代表容量的预测值,淡蓝色覆盖区域代表预测值的95%置信区间,表示真实值有95%的概率落在该区间内,同时置信区间的宽度大小与模型可靠性的高低呈正相关。由图11分析可得,容量的预测值可以很好地跟踪电池老化趋势,并且对老化过程中容量再生的局部波动现象也有良好的估计和预测能力。
对于B05、B07和B18号电池,所有预测起点下,除小部分容量回升阶段外,包含终止阈值在内的大部分循环周期,容量的真实值基本落在预测值的95%置信区间;对于B06号电池,70和80预测起点下,在容量回升幅度较大阶段以及循环终止阶段,容量真实值与预测值偏差较大,偏离置信区间,但是在终止阈值附近的循环周期内,容量的真实值也基本落在预测值的95%置信区间,90以及100预测起点下,预测效果得到明显改善,真实值与预测值基本一致,这说明所提方法的预测模型具有理想的可靠性。
(2)由图12分析可得,在合理的预测区间内,不同的预测起点容量预测效果会有一定差异,但是对于所有标号电池,预测起点靠后的预测结果均优于预测起点靠前的预测结果,这是由于预测起点越高,训练数据越多,模型的学习效果越好,预测越准确,评价指标越优异。
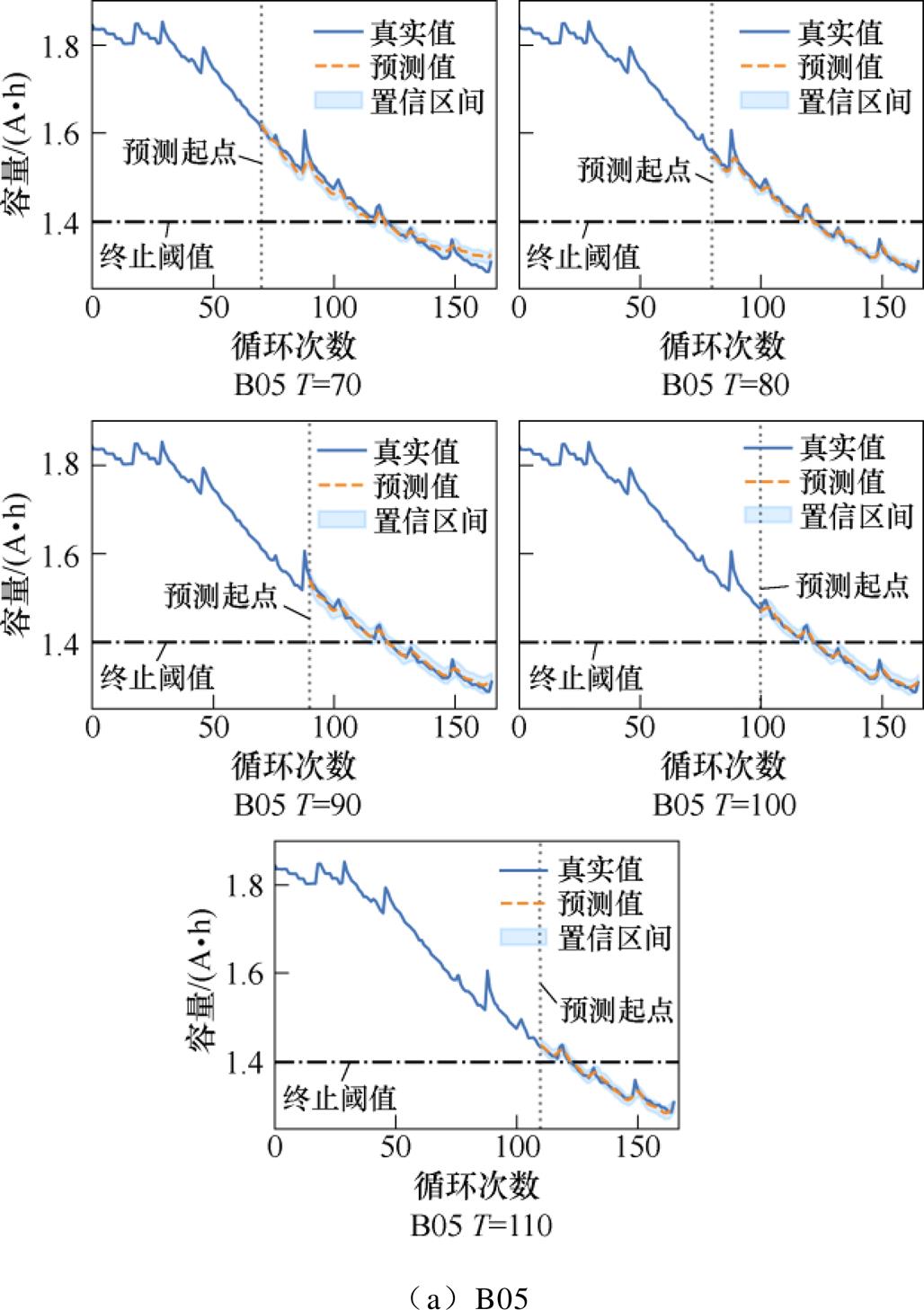
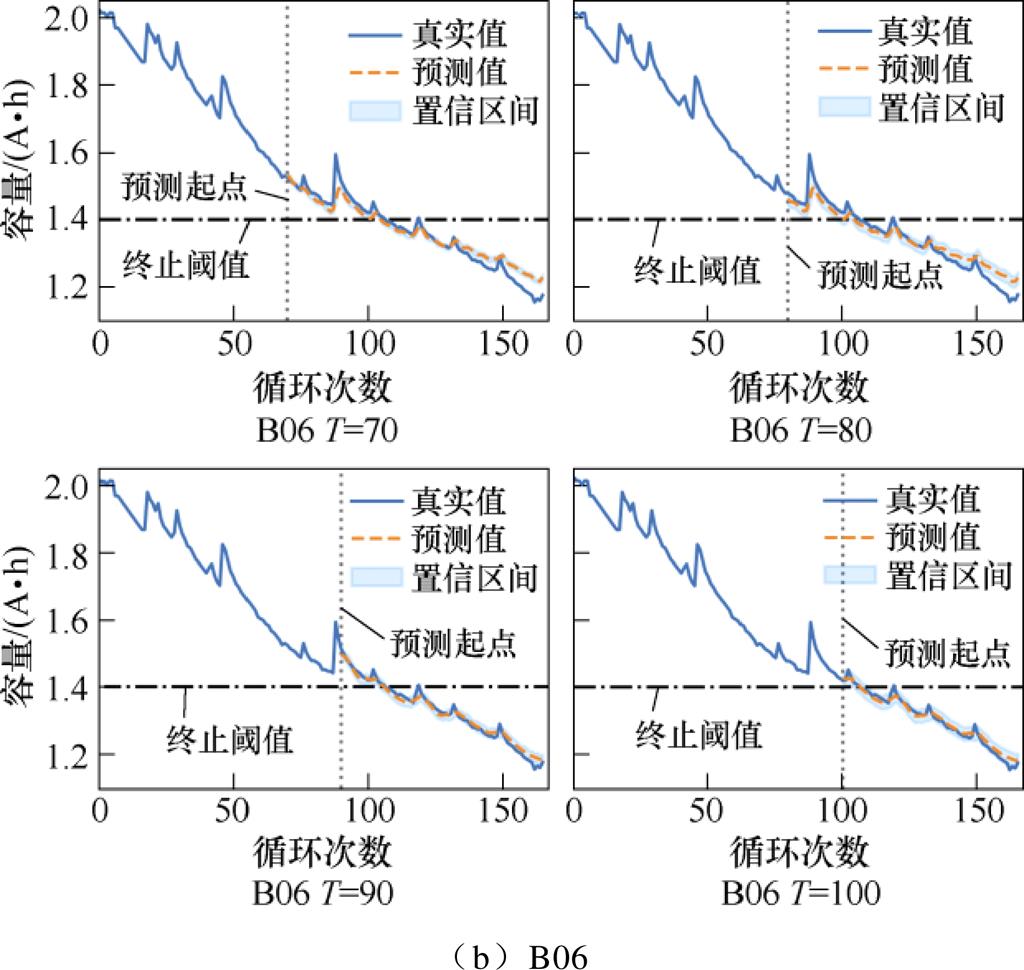
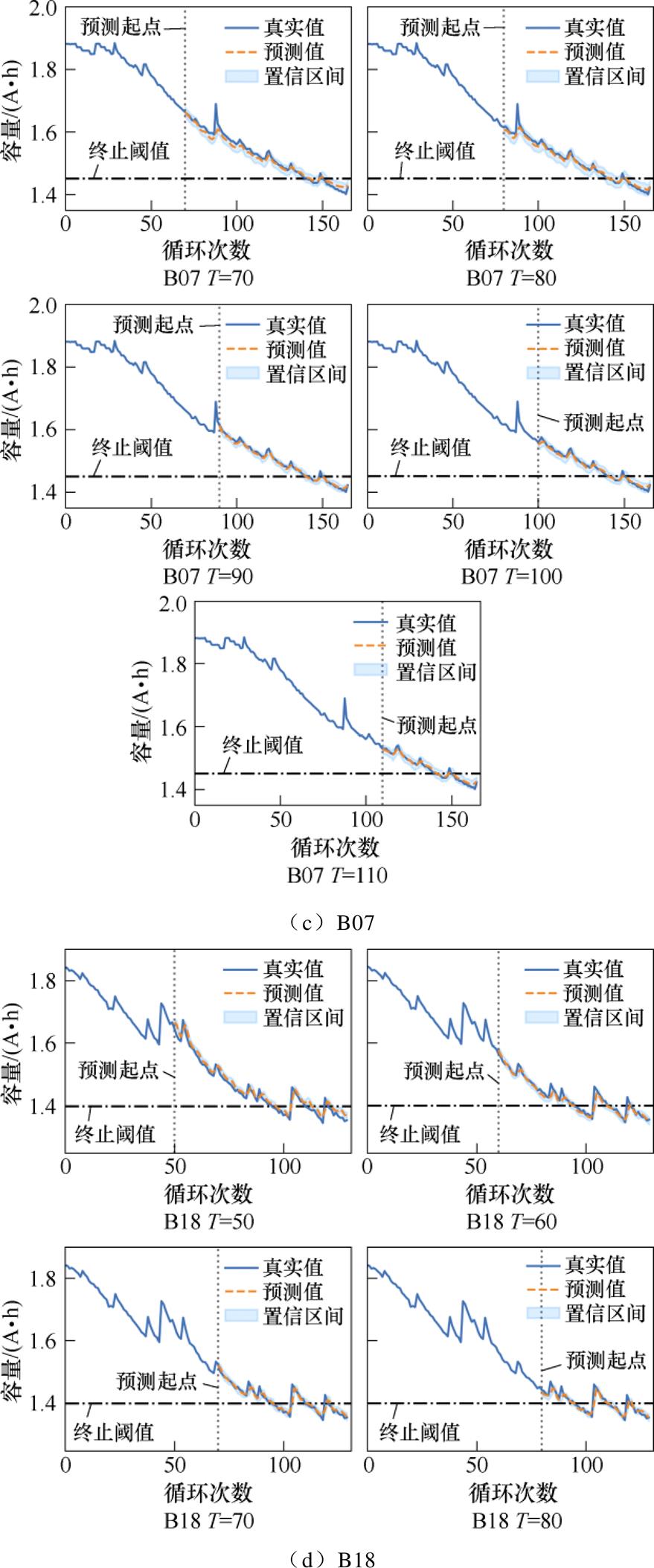
图11 NASA锂电池容量预测结果
Fig.11 NASA lithium-ion battery capacity prediction results
对于B05和B07号电池,各个预测起点下,三种评价指标均在1.5%以内;对于B18型号电池,各个预测起点下,三种评价指标基本在2.0%内;对于B06型号电池,在90和100预测起点下,三种评价指标均在2.0%内,在70和80预测起点下,方均根误差值分别达到了2.98%和2.78%,平均绝对误差分别达到了2.34%和2.03%,均超过了2%,这是由于相对于训练数据,测试集的电池容量发生了较大回升,模型的适应度降低导致预测效果变差。但是总体而言,预测起点的降低并未引起评价指标的大幅变动,仅仅略有升高,这说明所提方法的预测模型具有理想的稳定性。
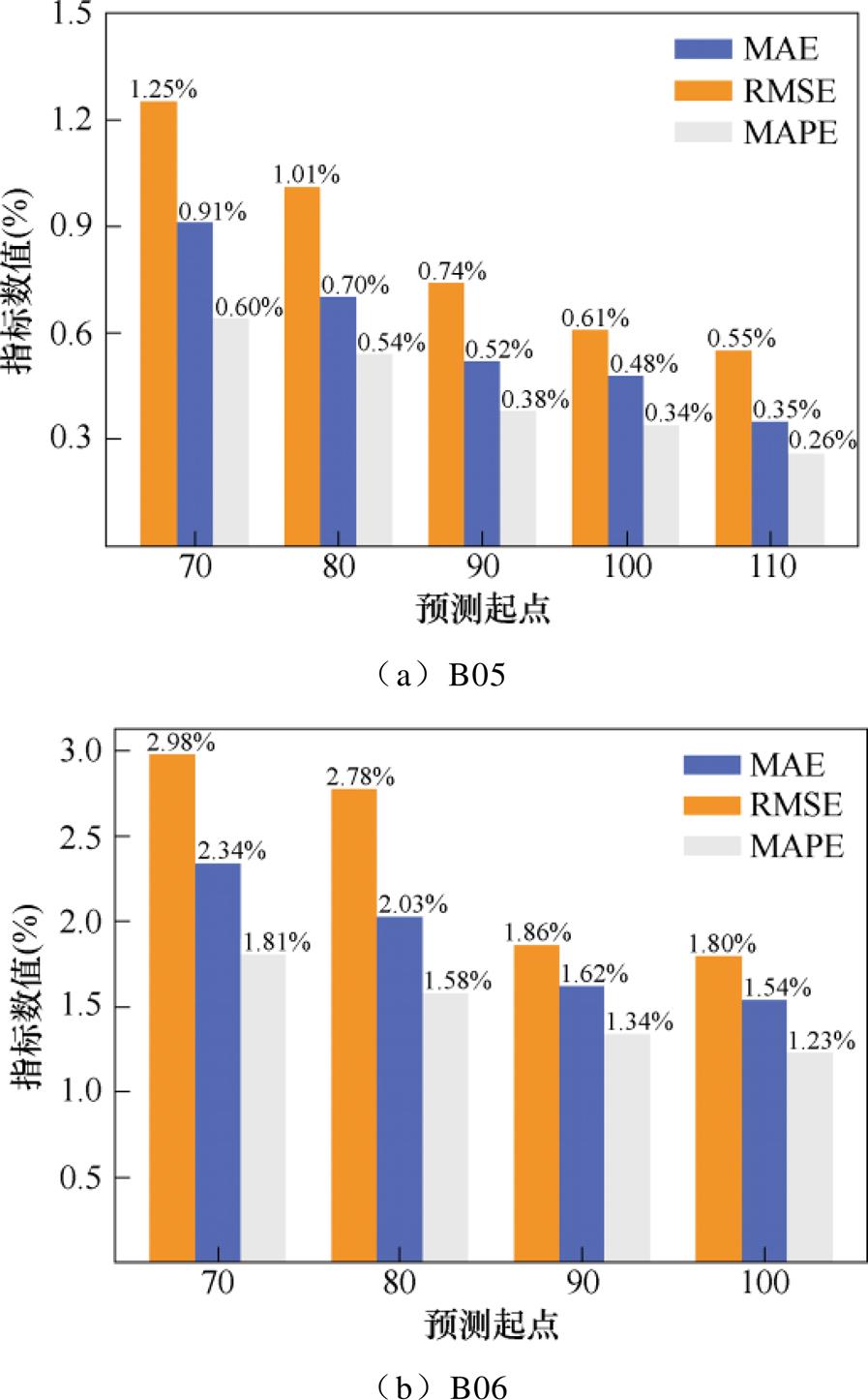
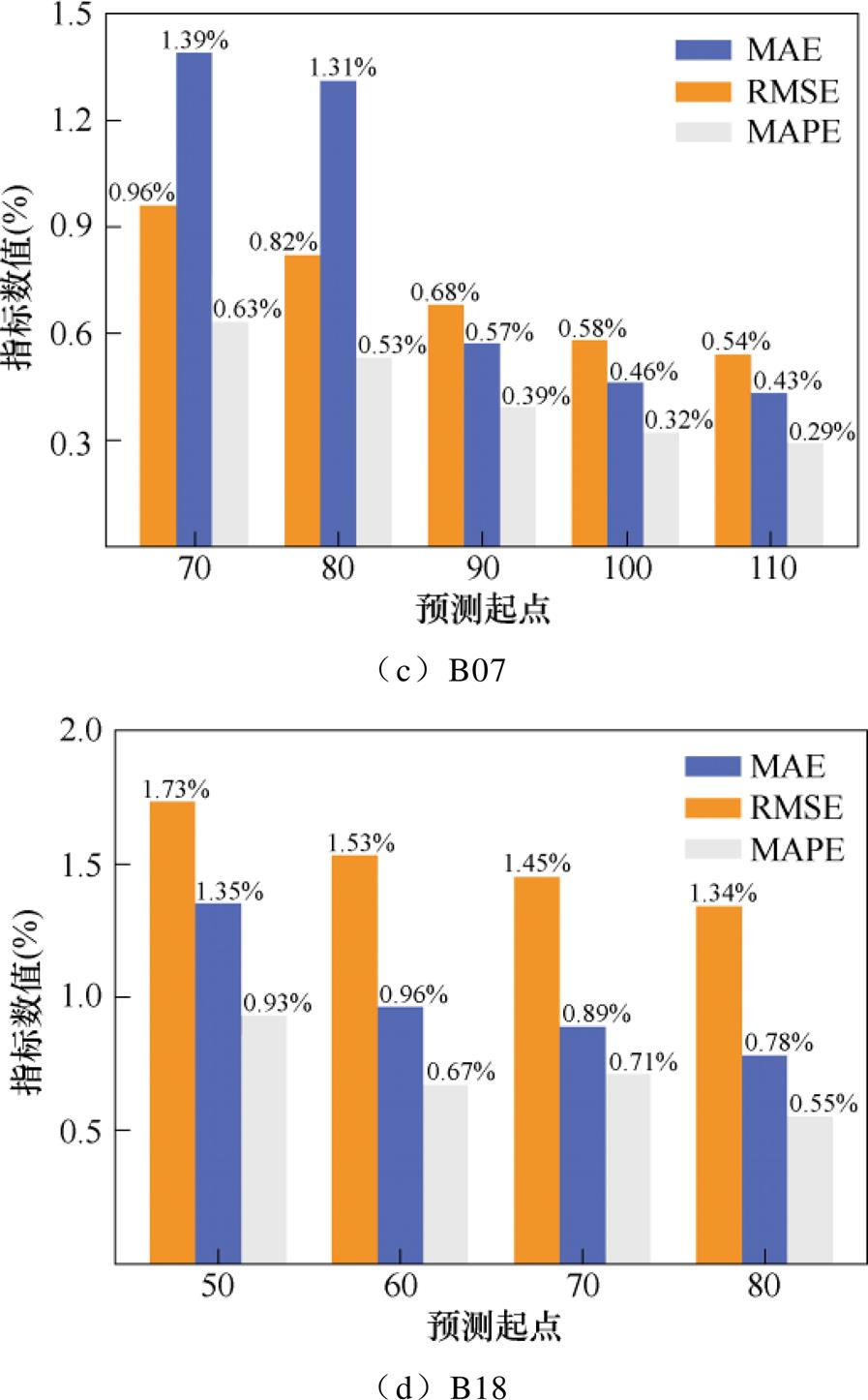
图12 不同预测起点下容量预测结果评价指标
Fig.12 Evaluation indicators of capacity prediction results at different prediction starting point
表7 NASA锂电池RUL预测结果
Tab.7 RUL prediction results of NASA lithium-ion battery
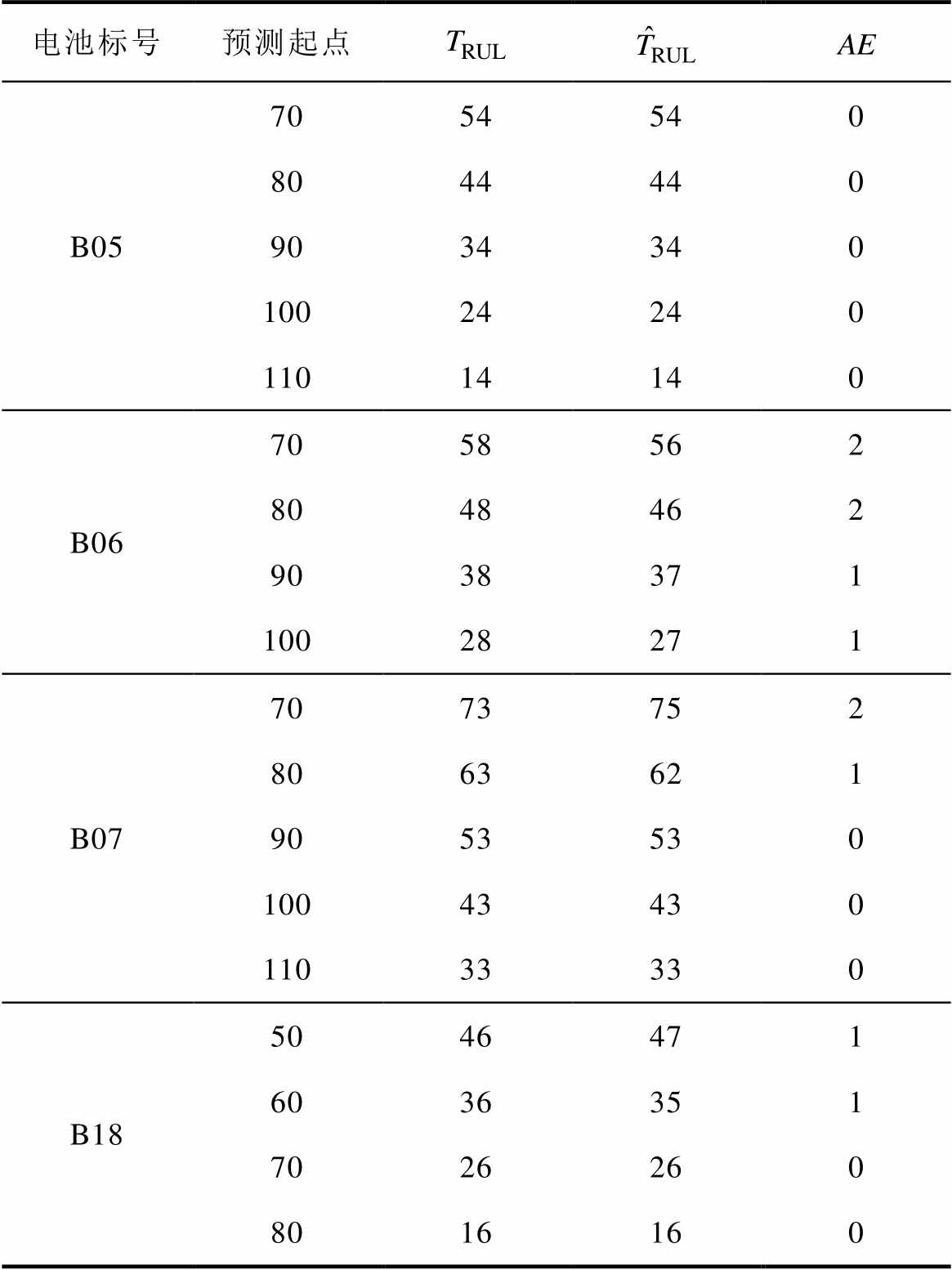
电池标号预测起点 B057054540 8044440 9034340 10024240 11014140 B067058562 8048462 9038371 10028271 B077073752 8063621 9053530 10043430 11033330 B185046471 6036351 7026260 8016160
(3)在表7中,记录了在不同预测起点下RUL的真实值、预测值以及差值。对于B05电池,所有预测起点下剩余寿命的预测值与真实值的差值均为零;对于B06号电池,在70和80预测起点下,提前2个循环周期达到终止阈值,在90和100预测起点下,提前1个循环周期达到终止阈值;对于B07电池,在70和80预测起点下,分别延迟2个和提前1个循环周期达到终止阈值,其余预测起点下差值为0;对于B18号电池,在50预测起点下,延迟1个循环周期达到终止阈值,在60预测起点下,提前1个循环周期达到终止阈值,其余预测起点下差值为0。总体而言,所有锂电池的最大RUL预测误差在2个循环周期内,这说明所提方法的预测模型具有理想的准确性。
此外,为进一步验证所提方法的优越性,与现有文献中在锂电池寿命预测领域应用广泛的SVM、RVM等机器学习方法进行比较,规定A1为本文所提方法;A2为蚁狮优化(Ant Lion Optimization, ALO)算法支持向量回归机(Support Vector Regression, SVR)的组合方法[28];A3为灰狼优化(Gray Wolf Optimization, GWO)算法最小二乘支持向量机(Least Square Support Vector Machine, LSSVM)的组合方法;A4为粒子群优化(Particle Swarm Optimization, PSO)算法极限学习机(Extreme Learning Machine, ELM)的组合方法;同时设定预测起点均为总循环周期的50%,采用MAE和RMSE这两种评价指标,方法的对比结果见表8,分析可得,本文所提预测方法的评价指标在等同条件下都是最小值,具备较高的预测性能。
表8 不同预测方法对比结果
Tab.8 Comparison results of different prediction methods

电池标号方法预测起点MAE(%)RMSE(%) B05A1830.550.93 A2830.711.38 A3831.511.83 A4832.492.91 B06A1832.002.52 A2833.563.94 A3832.243.06 A4832.633.44 B07A1831.230.71 A2831.361.80 A3831.231.69 A4831.481.84 B18A1650.891.46 A2652.382.63 A3651.862.52 A4651.792.43
本文提出一种基于数据预处理和VMD-LSTM- GPR的锂电池剩余寿命预测方法。首先从充放电循环曲线中提取间接HI,使用KPCA算法进行间接HI的特征提取,从而得到融合HI。在此基础上,采用VMD算法对融合HI进行分解、重构,过程中使用LSTM算法对分解后的模态分量进行预测,进一步得到重构HI,最后将重构HI、电池容量分别作为GPR模型的输入和输出,建立预测模型并进行实验验证,得出结论如下:
1)Pearson和Spearman两种相关系数证明了所提取的健康间接HI与容量之间的高相关性,KPCA算法去除了各变量之间的冗余信息,减少了数据复杂度,达到了数据预处理效果。
2)VMD分解方法可以挖掘数据中的内在信息,捕捉融合HI中隐含的长期下降趋势、局部回升以及噪声信息;LSTM神经网络通过学习前期的容量退化趋势和局部回升可以建立精准的预测模型,适用于时间序列预测;GPR模型能够支持概率预测,给出容量预测结果的置信区间。
3)采用NASA锂电池公开数据集进行实验验证,设置多种不同的预测起点,同时与现有其他文献中所提方法进行对比。结果证明,在相同的预测条件下,本文所提方法的评价指标更加优异,以总循环周期数的50%作为预测起点时,MAE、RMSE和MAPE分别保持在2.00%、2.52%以及1.45%以内,RUL预测误差在2个循环周期以内,真实值也基本落在预测值的95%置信区间内。
综上所述,本文所提的预测方法具有理想的可靠性、稳定性和准确性,对现有的锂离子电池寿命预测研究有一定的借鉴意义。
参考文献
[1] 申江卫, 高承志, 舒星, 等. 基于迁移模型的锂离子电池宽温度全寿命SOC与可用容量联合估计[J]. 电工技术学报, 2023, 38(11): 3052-3063.
Sheng Jiangwei, Gao Chengzhi, ShuXing, et al. Joint estimation of SOC and usable capacity of lithium-ion battery with wide temperature and full life based on migration model[J]. Transactions of China Electro- technical Society, 2023, 38(11): 3052-3063.
[2] 黄凯, 丁恒, 郭永芳, 等. 基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测[J]. 电工技术学报, 2022, 37(15): 3753-3766.
Huang Kai, Ding Heng, Guo Yongfang, et al. Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3753-3766.
[3] 杨梦洁, 杨爱军, 叶奕君, 等. 基于气体分析的锂离子电池热失控早期预警研究进展[J]. 电工技术学报, 2023, 38(17): 4507-4538.
Yang Mengjie, Yang Aijun, Ye Yijun, et al. Research progress on early warning of thermal runaway of Li-ion batteries based on gas analysis[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4507-4538
[4] 顾菊平, 蒋凌, 张新松, 等. 基于特征提取的锂离子电池健康状态评估及影响因素分析[J]. 电工技术学报, 2023, 38(19): 5330-5342.
Gu Juping, Jiang Ling, Zhang Xinsong, et al. Estimation and influencing factor analysis of lithium- ion batteries state of health based on features extraction[J]. Transactions of China Electro- technical Society, 2021, 36(24): 5201-5212.
[5] Liu Jian, Chen Ziqiang. Remaining useful life prediction of lithium-ion batteries based on health indicator and Gaussian process regression model[J]. IEEE Access, 2019, 7:39474-39484.
[6] Ding Guorong, Wang Wenbo, Zhu Ting. Remaining useful life prediction for lithium-ion batteries based on CS-VMD and GRU[J]. IEEE Access, 2022, 10: 89402-89413.
[7] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J].Automation of Electric Power Systems, 2022, 46(14): 193-207.
[8] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703- 1725.
[9] 颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3948.
Yan Xiangwu, Deng Haoran, Guo Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Electro- technical Society, 2019, 34(18): 3937-3948.
[10] Bian Zengyuan, Ma Yan. An improved particle filter method to estimate state of health of lithium-ion battery[J]. IFAC-Papers On Line, 2021, 54(10): 344- 349.
[11] Duan Bin, Zhang Qi, Geng Fei, et al. Remaining useful life prediction of lithium-ion battery based on extended Kalman particle filter[J]. International Journal of Energy Research, 2019, 44(3): 1724-1734.
[12] 贺宁, 钱成, 李若夏. 自适应模型与改进粒子滤波的电池RUL预测[J]. 哈尔滨工业大学学报, 2022, 54(9): 111-121.
He Ning, Qian Cheng, Li Ruoxia. RUL prediction for lithium-ion batteries via adaptive modeling and improved particle filter[J]. Journal of Harbin Institute of Technology, 2022, 54(9): 111-121.
[13] 徐佳宁, 倪裕隆, 朱春波. 基于改进支持向量回归的锂电池剩余寿命预测[J]. 电工技术学报, 2021, 36(17): 3693-3704.
Xu Jianing, Ni Yulong, Zhu Chunbo. Remaining useful life prediction for lithium-ion batteries based on improved support vector regression[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(17): 3693-3704.
[14] Liu Datong, Zhou Jianbao, Pan Dawei, et al. Lithium-ion battery remaining useful life estimation with an optimized relevance vector machine algorithm with incremental learning[J]. Measurement, 2015, 63: 143-151.
[15] Zhu Jun, Tan Tianxiong, Wu Lifeng, et al. RUL prediction of lithium-ion battery based on improved DGWO-ELM method in a random discharge rates environment[J]. IEEE Access, 2019, 7: 125176-125187.
[16] Phattara K, Yodo N. A data-driven predictive prognostic model for lithium-ion batteries based on a deep learning algorithm[J]. Energies, 2019, 12(4): 660.
[17] 王萍, 范凌峰, 程泽. 基于健康特征参数的锂离子电池SOH和RUL联合估计方法[J]. 中国电机工程学报, 2022, 42(4): 1523-1534.
Wang Ping, Fan Lingfeng, Cheng Zhe. A joint state of health and remaining useful life estimation approach for lithium-ion batteries based on health factor parameter[J]. Proceedings of the CSEE, 2022, 42(4): 1523-1534.
[18] Cheng Gong, Wang Xinzhi, He Yurong. Remaining useful life and state of health prediction for lithium batteries based on empirical mode decomposition and a long and short memory neural network[J]. Energy, 2021, 232: 121022.
[19] Qu Jingtao, Liu Feng, Ma Yuxing, et al. A neural- network-based method for RUL prediction and SOH monitoring of lithium-ion battery[J]. IEEE Access, 2019, 7: 87178-87191.
[20] 杨彦茹, 温杰, 史元浩, 等. 基于CEEMDAN和SVR的锂离子电池剩余使用寿命预测[J]. 电子测量与仪器学报, 2020, 34(12): 197-205.
Yang Yanru, Wen Jie, Shi Yuanhao, et al. Remaining useful life prediction for lithium-ion battery based on CEEMDAN and SVR[J]. Journal of Electronic Measurement and Instrument, 2020, 34(12): 197-205.
[21] Sun Chuang, Qu An, Zhang Jun, et al. Remaining useful life prediction for lithium-ion batteries based on improved variational mode decomposition and machine learning algorithm[J]. Energies, 2023, 16(1): 313.
[22] Saha B, KG. Battery data set. NASA ames prognostics data repository[DB/OL]. NASA Ames Research Center, Moffett Field, CA 2017, https://ti. arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data- repository.
[23] Hell S M, Kim C D. Development of a data-driven method for online battery remaining-useful-life prediction[J]. Batteries, 2022, 8(10): 192.
[24] Jia Shun, Ma Bo, Guo Wei, et al. A sample entropy based prognostics method for lithium-ion batteries using relevance vector machine[J]. Journal of Manufacturing Systems, 2021, 61: 773-781.
[25] 王竹晴, 郭阳明, 徐聪. 基于SAE-VMD的锂离子电池健康因子提取方法[J]. 西北工业大学学报, 2020, 38(4): 814-821.
Wang Zhuqing, Guo Yangming, Xu Cong. An HI extraction framework for lithium-ion battery prognostics based on SAE-VMD[J]. Journal of Northwestern Polytechnical University, 2020, 38(4): 814-821.
[26] Jia Jianfang, Liang Jianyu, Shi Yuanhao, et al. SOH and RUL Prediction of lithium-ion batteries based on Gaussian process regression with indirect health indicators[J]. Energies, 2020, 13(2): 375.
[27] Zhang Yagang, Li Ruixuan, Zhang Jinghui. Optimi- zation scheme of wind energy prediction based on artificial intelligence[J]. Environmental Science and Pollution Research, 2021, 28(29): 39966-39981.
[28] 王瀛洲, 倪裕隆, 郑宇清, 等. 基于ALO-SVR的锂离子电池剩余使用寿命预测[J]. 中国电机工程学报, 2021, 41(4): 1445-1457, 1550.
Wang Yingzhou, Ni Yulong, Zheng Yuqing, et al. Remaining useful life prediction of lithium-ion batteries based on support vector regression optimized and ant lion optimizations[J]. Proceedings of the CSEE, 2021, 41(4): 1445-1457, 1550.
Abstract The performance of lithium-ion batteriescandeteriorate with the decrease of capacity and the increase of impedance during continuous charging and discharging process, which poses a risk of equipment and system failures, includingcatastrophic losses. Accurate and reliable prediction of the remaining useful life (RUL) of lithium-ion batteries is crucial. However, previous prediction methods mainly supportedpoint predictions without offering a clear mathematical representation of the confidence level of the prediction results. The noise and capacity rebound phenomena in the original data are ignored. Therefore, this paper proposes a prediction framework based on data pre-processing combined with variational mode decomposition (VMD), long and short-term memory network (LSTM), and Gaussian regression process (GPR).
Firstly, anindirect health indicator (HI) reflecting the life degradation trend of lithium-ion batteriesisextracted from the charge/discharge curve. Pearson and Spearman correlation coefficients are used to verify the correlation between the extracted indirect HI and capacity. The kernel principal element analysis (KPCA) method reduces computational complexity by removingredundant components of indirect HI, transform them into fusion HI. Then, the VMD decomposition method decomposes the fusion HI into multiple modal components. Based on the central frequency of modal components and capacity-related coefficients, multiple modal components are divided into three parts: global attenuation, local regeneration, and other noise. Time series prediction of the global attenuation and local regeneration components are performed separately using LSTM neural networks to obtain the predicted values after the prediction starting point. The values of each component aresummed up to obtain the reconstructed HI. Finally, the reconstructed HI and capacity serve as the input and output of the GPR model RUL prediction, respectively.
NASA lithium-ion battery public data set is used for experimental validation, and different prediction starting points are set for each battery. The starting point set is at about 40% of the total cycle. The experimental results show that the predicted capacity values closely track the battery aging trend and effectively estimate the local regeneration phenomenon during the aging process. The true capacity values generally fall within the 95% confidence interval of the predicted value, and the prediction effect improves as the training data increase. Regarding evaluation indexes for capacity prediction results, the maximum root mean square error, mean absolute error, and mean absolute percentage error are 2.98%, 2.34%, and 1.81%, respectively. Errors in the remaining useful life prediction are all within 2 cycles.
The following conclusions can be drawn from the experimental analysis: (1) The KPCA algorithm removesredundant information between indirect health indicators to reduce data complexity and achieve data pre-processing. (2) The VMD decomposition method minesintrinsic information, capturing the long-term downward trend, local regeneration, and noise component to remove implied noise in the data. (3) The GPR model supports probabilistic prediction and provides confidence intervals for capacity prediction results.
keywords:Lithium-ion battery, remaining useful life, health indicator, variational mode decomposition, Gaussian regression process, long and short-term memory
DOI: 10.19595/j.cnki.1000-6753.tces.230210
中图分类号:TM912
辽宁省“兴辽英才计划”资助项目(XLYC1903015)。
收稿日期 2023-02-22
改稿日期 2023-05-24
李英顺 女,1971年生,博士,教授,研究方向为火控系统的故障预测与健康管理。E-mail: 1982215089@qq.com
阚宏达 男,1997年生,硕士,研究方向为火控计算机的故障诊断与锂电池的寿命预测。E-mail: 1780623034@mail.dlut.edu.cn(通信作者)
(编辑 郭丽军)