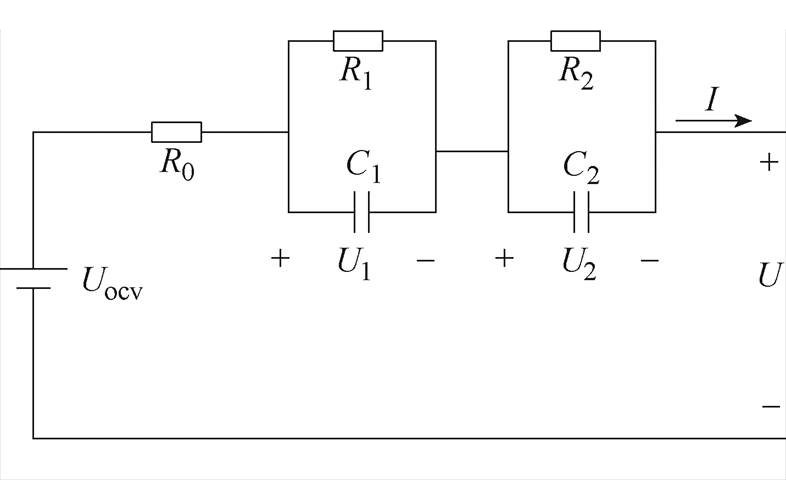
图1 二阶RC等效电路模型
Fig.1 Second-order RC equivalent circuit model
摘要 针对电池SOC与SOH估计结果相互影响,单独估计准确度不高的问题,该文提出了一种基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法。通过构建考虑老化和SOC的电池二阶RC等效电路模型,采用带遗忘因子的递推最小二乘法,在不同SOC和SOH的情况下,对电池的参数进行在线辨识,实现电池参数在线辨识与电池SOC和SOH估计的耦合。以锂离子电池自SOC=20%到恒流充电阶段结束所需时间为输入,电池SOH值为输出,训练GPR模型,实现电池SOH估计。将输出的SOH估计值与电池的额定容量相乘,得到电池的实际容量,更新二阶RC状态空间方程,采用扩展卡尔曼滤波算法对电池进行SOC估计,实现电池SOH估计和SOC估计之间的联合。采用牛津大学电池退化数据集和NASA随机使用电池数据集进行算法验证,结果表明,所提联合估计方法能够在电池的生命周期内较准确地跟随锂离子电池SOC和SOH的真实值。
关键词:锂离子电池 荷电状态 健康状态 高斯过程回归 带遗忘因子的递推最小二乘法
锂离子电池被广泛应用于电网储能系统中[1-2],其电池管理系统(Battery Management System, BMS)能保障电池的健康稳定运行。BMS的重要功能为电池状态估计,包括荷电状态(State of Charge, SOC)估计和健康状态(State of Health, SOH)估计等[3]。
SOC是储能电池管理系统的重要参数,SOC估计的方法大致有放电实验法、开路电压法、安时积分法、卡尔曼滤波法及神经网络法等[4-6]。前三种估算方法对SOC估算简单易实现。其中放电实验法只能用于离线估计。开路电压法[7-8]需要定期校正开路电压。安时积分法[9]对SOC初始值依赖程度较高,且仪器的测量误差而产生的电流测量误差会随着积分环节的进行而不断累积,随着电池的运行,电池容量不是一个恒定值,会随着老化程度而降低。因此安时积分法容易受SOC初值和SOH的影响,电池运行时间越长,SOC误差越大,这意味着一旦电池处于连续充放电状态,安时积分法的精度将受到很大影响。由此,卡尔曼滤波算法及其改进算法[10-13]在电池SOC识别中的应用越来越受到重视。锂离子电池是一个复杂的非线性动态系统,而神经网络算法[14-16]具有高度的非线性及自学能力,可以估算各种电池,实现在线估计,但对训练样本的依赖性强。
SOH表示电池满充容量与额定容量的比值,能体现电池容量或者功率的退化现象,是度量电池老化程度的指标[17-18]。SOH估计方法大致分为基于耐久性模型的开环方法和基于电池模型的闭环方法[18-19]。开环方法利用电池耐久性实验数据构建模型,能直接对电池容量和内阻进行估计,得出电池SOH,但是该方法计算量大,需要进行大量实 验[20-22]。闭环方法则采用卡尔曼滤波算法及其改进算法[23-24]和自适应算法[25]对现有的电池模型内阻等参数进行辨识,从而实现对电池SOH的估计。
电池老化会严重影响SOC的估计结果[26],且SOH的校准会受到不准确SOC估计结果的误导[27]。现有研究大多对SOC或SOH进行单独估计,忽略了两者之间的紧密联系。充分了解电池SOC与SOH之间的影响机理,研究SOC和SOH进行联合估计的方法,能在一定程度上解决两者之间的相互影响,达到提高估计准确度的目的。
因此,本文提出了一种基于等效电路模型和数据驱动模型融合的SOC和SOH的联合估计方法。通过构建考虑老化和SOC的电池二阶RC等效电路模型,在不同SOC和SOH的情况下,采用带遗忘因子的递推最小二乘法(Forgetting Factor Recursive Least Squares, FFRLS)对电池的参数进行实时在线辨识,实现电池参数在线辨识与电池SOC和SOH估计的联合。以锂离子电池恒流充电时间为输入,电池SOH值为输出,训练高斯过程回归模型,实现电池SOH估计。将输出的SOH估计值与电池的额定容量相乘,得到电池的实际容量,更新二阶RC状态空间方程,采用扩展卡尔曼滤波算法对电池进行SOC估计,实现电池SOH估计和SOC估计之间的联合。采用牛津大学电池退化数据集和NASA随机使用数据集进行算法验证,结果表明,所提联合估计方法能够在电池的生命周期内较准确地跟随锂离子电池SOC和SOH的真实值。
本文的电池数据来源于牛津大学电池退化数据集和NASA随机使用数据集,采用电池寿命终止(End of Life, EOL)状态表征电池寿命结束。牛津大学电池退化数据集包含8个Kokam制造的740 mA×h锂离子软包电池数据,记为Cell 1~Cell 8,设EOL=0.8,详细介绍见参考文献[28]。NASA随机使用数据集包含28个2 A·h的LCO18650电池数据,选取编号为RW 3~RW 6的电池进行验证,设EOL=0.7,详细介绍见参考文献[29]。
二阶RC等效电路模型计算量适中,精度较高,比较接近锂离子电池的真实特性,故本文采用二阶RC等效电路作为锂离子电池模型,如图1所示。
图1中,Uocv为开路电压;U为端电压;I为放电电流;R0为欧姆电阻;R1、R2为极化电阻;C1、C2为极化电容[30]。
根据电路基尔霍夫定律及电容电压电流关系,图1所示的二阶RC电路的状态方程为

图1 二阶RC等效电路模型
Fig.1 Second-order RC equivalent circuit model
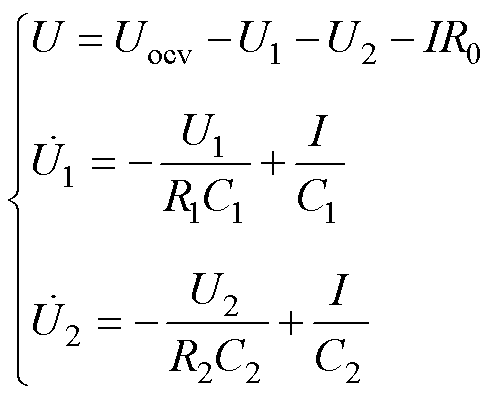 (1)
(1)
由于锂离子电池的OCV-SOC曲线受SOH的影响较小[31-32],故本文选用新电池的OCV-SOC曲线[32]。
考虑电池老化对二阶RC等效电路模型参数的影响,电池模型参数应随电池充放电循环次数在线更新,以提高SOC估计精度。结合二阶RC电路的状态方程,可以得出不同循环次数下电池端电压的变化特性为
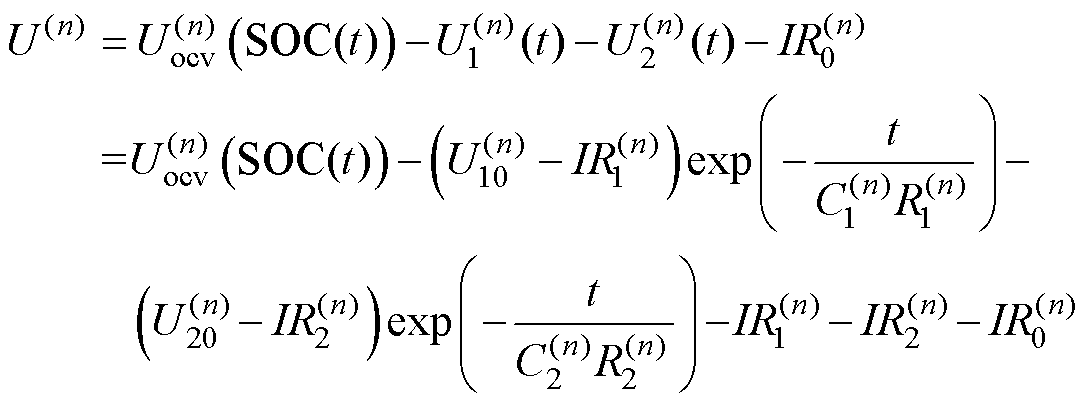 (2)
(2)
式中,n为充放电循环次数。
本文采用带遗忘因子的递推最小二乘法对二阶RC电路模型进行参数辨识。根据图1所示,二阶RC等效电路需要辨识的参数有R0、R1、R2、C1、C2。对式(1)表示的状态方程进行离散化处理,可得二阶RC等效电路模型的最小二乘法公式[33]为
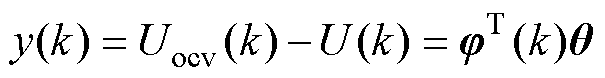 (3)
(3)
式中,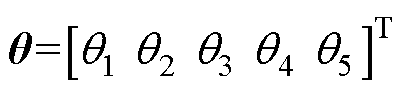 ;
;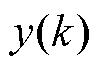 为k时刻输出响应;
为k时刻输出响应;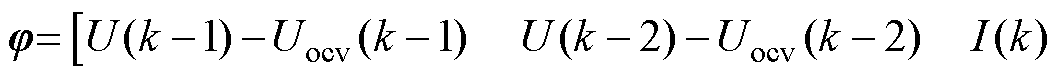
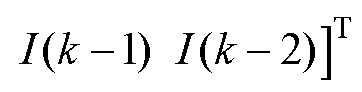 ;
;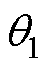 ~
~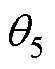 的公式为
的公式为
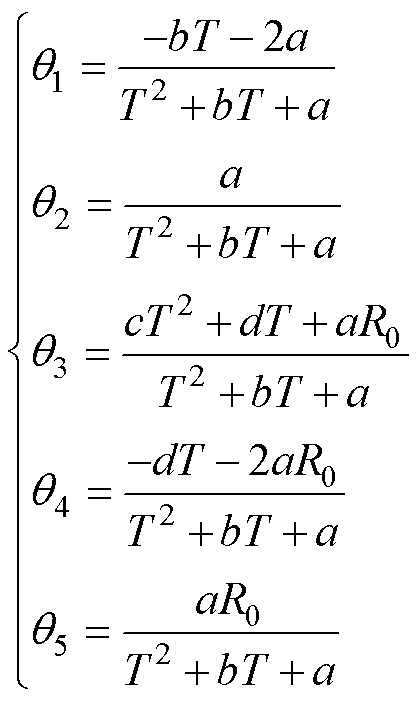 (4)
(4)
根据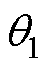 ~
~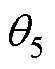 可以得出a、b、c、d的值,令
可以得出a、b、c、d的值,令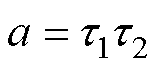 ,
,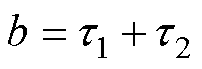 ,最后可以通过式(5)求出二阶RC电路模型的阻容参数。
,最后可以通过式(5)求出二阶RC电路模型的阻容参数。
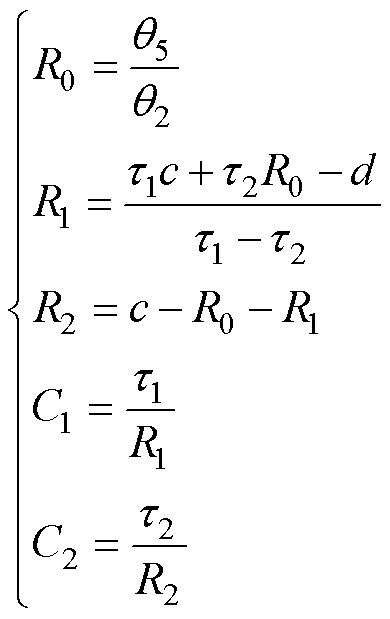 (5)
(5)
本文采用FFRLS算法在线辨识二阶RC电路模型的阻容参数,以Cell 1为例,R0、R1、R2、C1、C2随电池SOC的变化情况如图2所示。从图2中可以看出,电池各参数随SOC出现不同程度地变化,由此说明,根据SOC实时更新二阶RC电路模型参数很有必要。
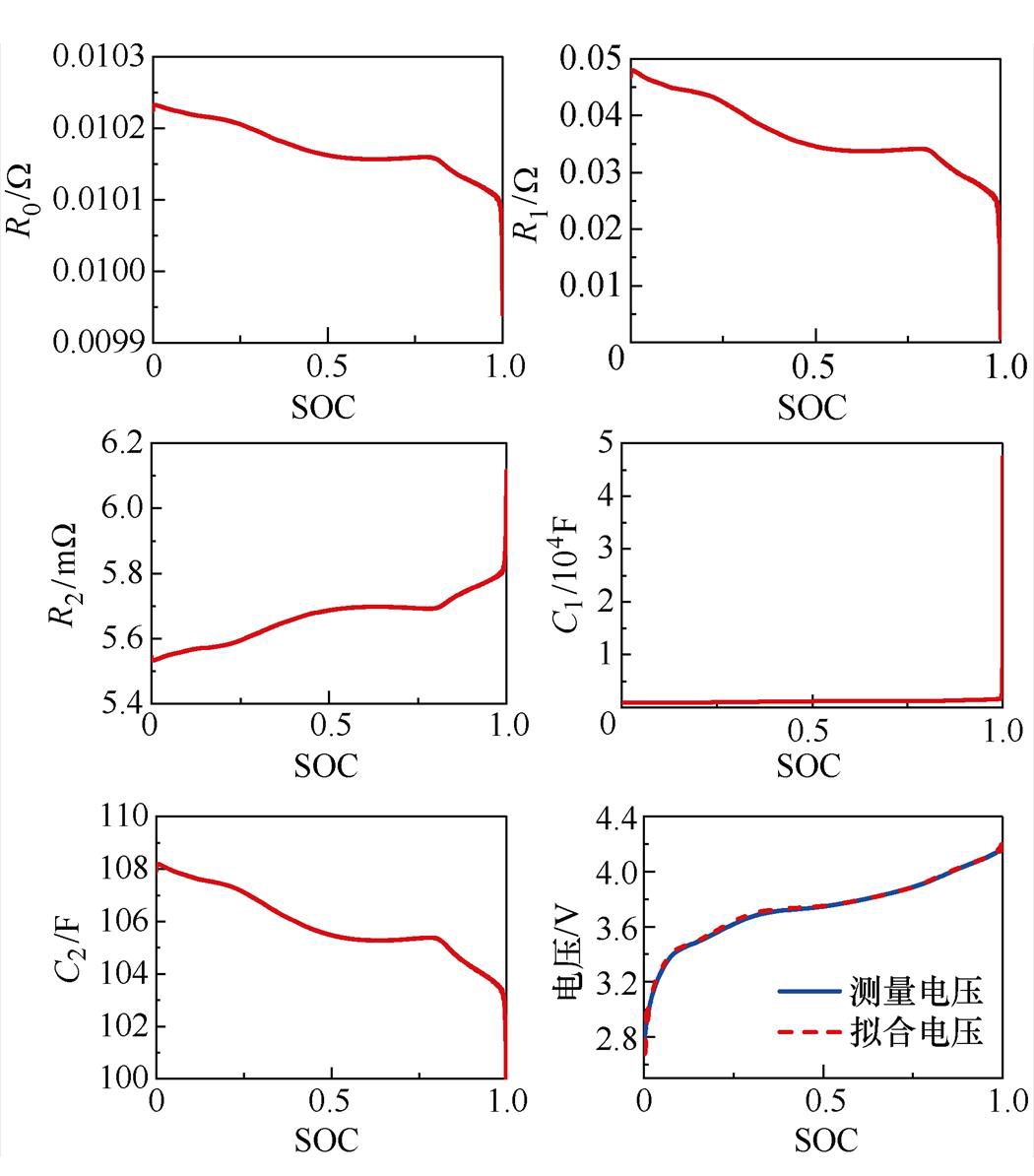
图2 Cell 1阻容参数随SOC变化结果
Fig.2 The results of Cell 1 parameters with SOC change
为验证二阶RC等效电路模型及其参数精度,本文比较了不同SOH下模型的拟合电压和测量电压。以Cell 1为例,结果如图3所示。从图3中可以看出,电池老化程度加深时,二阶RC电路模型的拟合误差较SOH=1时大,这是因为本文选用的OCV-SOC曲线恒定而造成的,但仿真得到的电压整体能够较好地跟踪实际电压。由此可见,基于FFRLS辨识的参数是准确的,在老化的情况下,依旧能较好刻画电池的外特性。基于FFRLS算法辨识的R0、R1、R2、C1、C2,会用于该循环的SOC估计,详细介绍见2.3节。
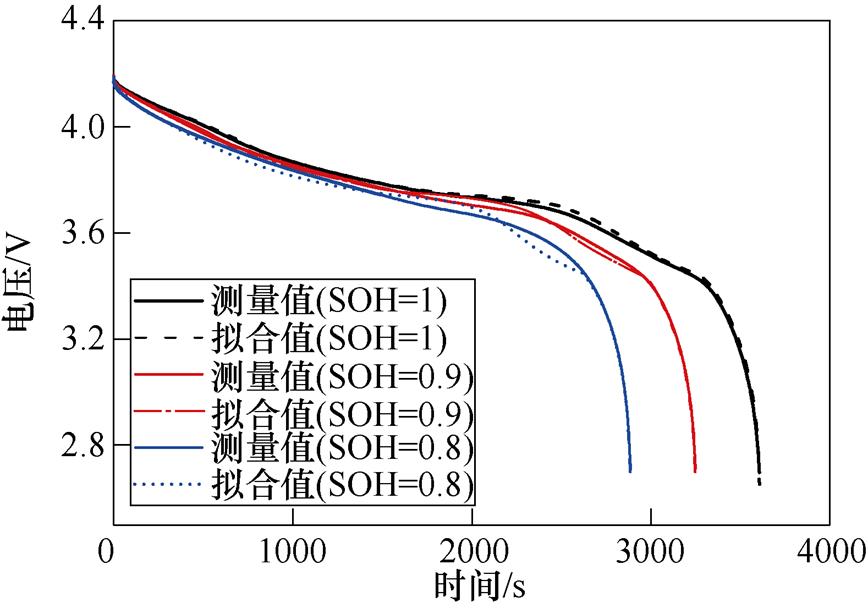
图3 Cell 1参数辨识结果
Fig.3 Parameter identification results of Cell 1
随着电池充放电循环次数的增加,电池额定容量逐渐减小,出现容量退化现象,SOH会呈现下降的趋势。与此同时,随着电池的充放电次数增多,电池的恒流充电时间会逐渐下降。由于电池在实际使用中不能保证从SOC=0开始充电,本文提取电池自SOC=20%到恒流充电阶段结束所需时间,标定此时间为恒流充电时间。
以Cell 1电池为例,电池SOH和恒流充电时间随电池充放电循环次数变化情况如图4所示。图4中,随着电池充放电次数的增加,曲线颜色由浅到深,电池恒流充电时间减少,老化程度加深,电池恒流充电时间与电池容量退化具有一定的对应关系。
本文依据Pearson和Spearman相关系数,评估电池充电时间与容量的相关性。其计算公式分别为
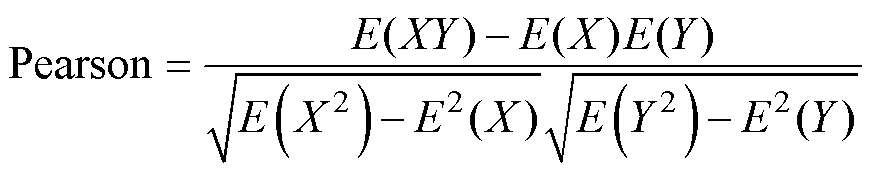 (6)
(6)
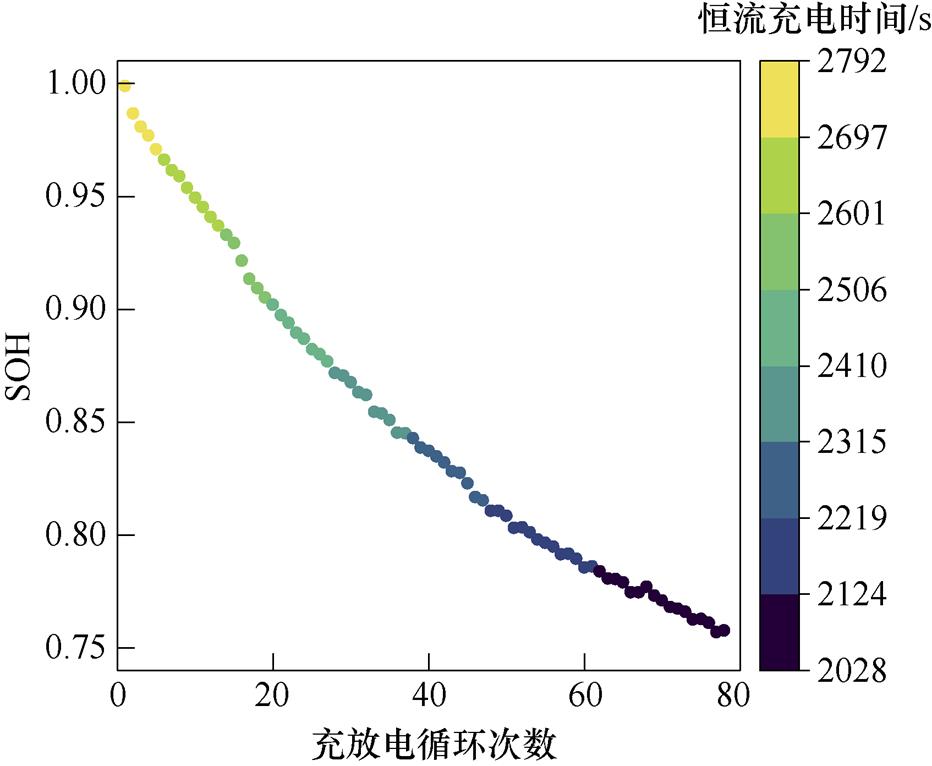
图4 Cell 1恒流充电时间和SOH变化情况
Fig.4 Constant current charging time and SOH change of Cell 1
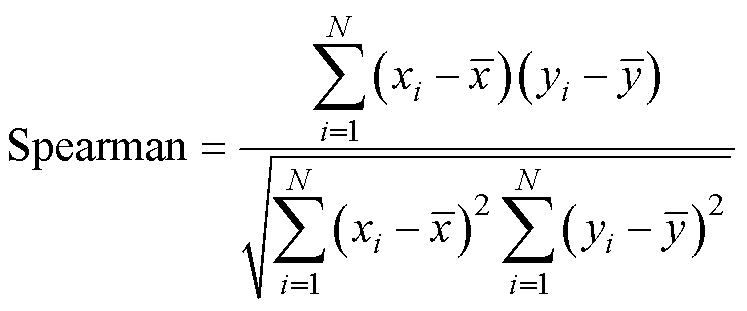 (7)
(7)
式中,X和Y分别为锂离子20%SOC恒流充电时间和SOH值;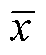 和
和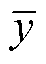 分别为锂离子20%SOC恒流充电时间和SOH的均值;N为样本总数。
分别为锂离子20%SOC恒流充电时间和SOH的均值;N为样本总数。
Pearson和Spearman相关系数可用于评价两个变量之间的相关性,其值介于[-1, 1]之间。若值大于0,则为正相关;反之,为负相关,绝对值越大,则表明相关程度越高。分别计算Cell 1~Cell 8、RW 3~RW 6锂离子恒流充电时间与SOH之间的Pearson相关系数和Spearman相关系数,计算结果见表1。
表1 电池SOH与恒流充电时间的相关系数
Tab.1 Correlation between SOH and constant current charging time
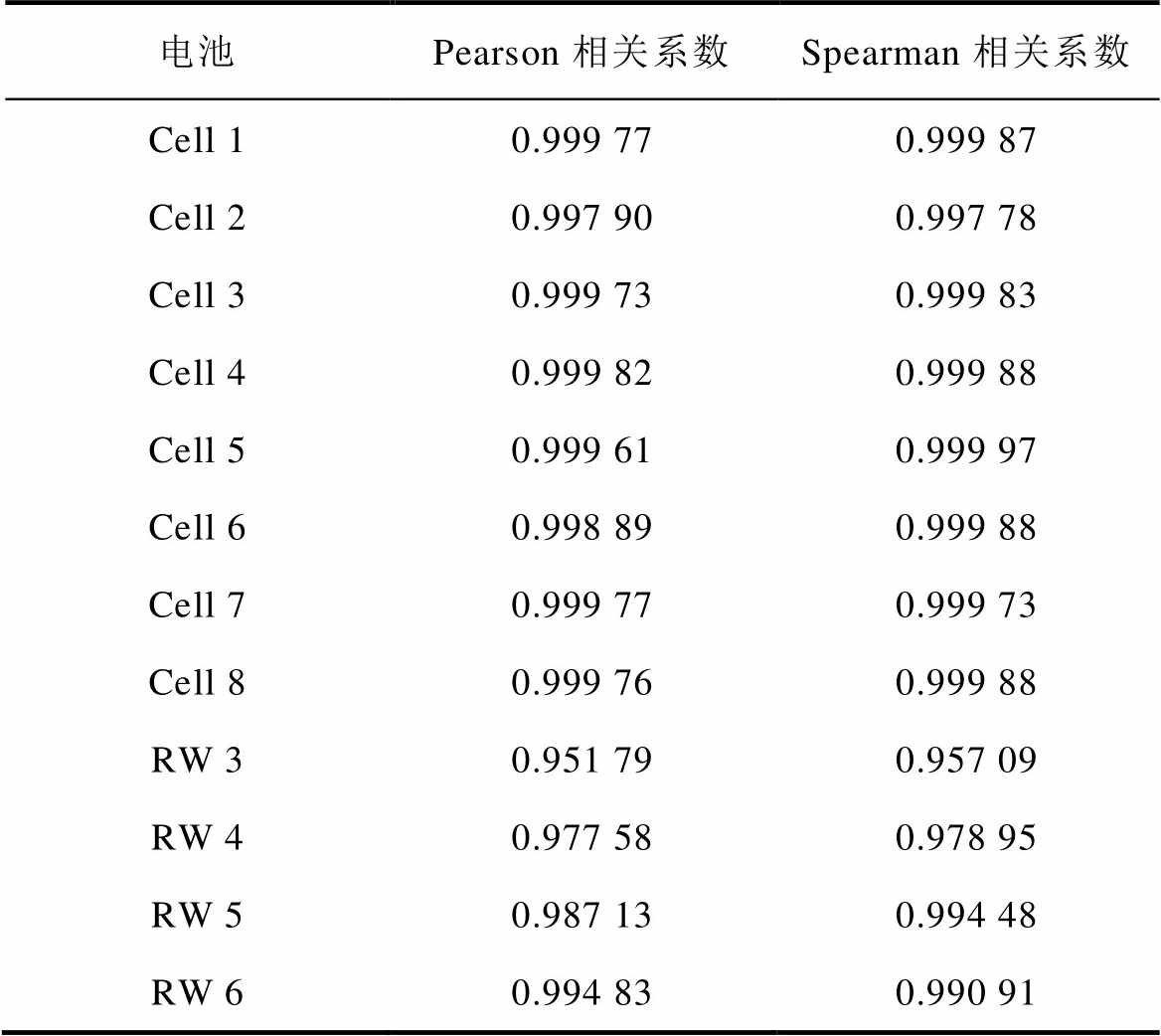
电池Pearson相关系数Spearman相关系数 Cell 10.999 770.999 87 Cell 20.997 900.997 78 Cell 30.999 730.999 83 Cell 40.999 820.999 88 Cell 50.999 610.999 97 Cell 60.998 890.999 88 Cell 70.999 770.999 73 Cell 80.999 760.999 88 RW 30.951 790.957 09 RW 40.977 580.978 95 RW 50.987 130.994 48 RW 60.994 830.990 91
由表1可知,Cell 1~Cell 8的Pearson相关系数均在0.99以上,Spearman相关系数基本在0.999以上。RW 3~RW 6的Pearson和Spearman相关系数均在0.9以上。结果表明,各电池的容量衰退与电池恒流充电时间具有较强的正相关性,采用电池的恒流充电时间对电池SOH进行估计是可行的。
锂离子电池本身是一个非线性系统,针对线性系统的卡尔曼滤波无法直接使用。扩展卡尔曼滤波(Extended Kalman Filter, EKF)算法是标准卡尔曼滤波在非线性情形下的一种扩展形式。EKF算法将非线性系统线性化,得到系统的状态估计值。
非线性系统的状态方程和观测方程为
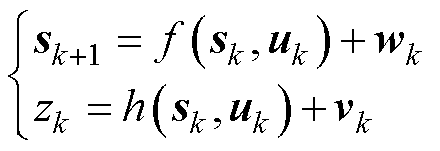 (8)
(8)
式中,sk为k时刻的系统状态量;uk为k时刻系统的输入量;zk为k时刻系统的观测量;wk为系统过程噪声;vk为系统观测噪声。
非线性系统近似线性化的状态方程和观测方程为
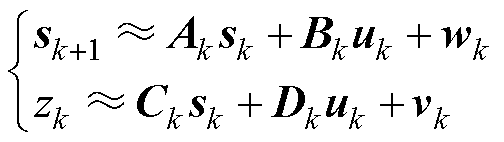 (9)
(9)
式中,Ak为状态转移矩阵;Bk为系统控制输入矩阵;Ck、Dk为系统观测矩阵。
EKF算法的具体实现步骤如下。
(1)初始化
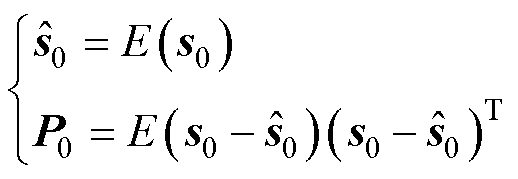 (10)
(10)
式中,s0和P0分别为系统状态变量初始值和状态变量误差协方差矩阵初始值。
(2)状态变量预测估计
状态向量预测
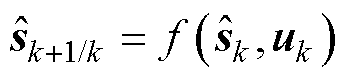 (11)
(11)
误差协方差矩阵预测
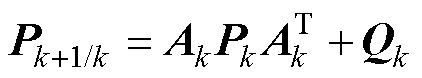 (12)
(12)
式中,Pk为k时刻的状态误差协方差矩阵;Qk为系统过程噪声方差矩阵;下标k+1/k为基于k时刻对k+1时刻系统变量的递推结果。
(3)状态变量测量更新
卡尔曼增益计算
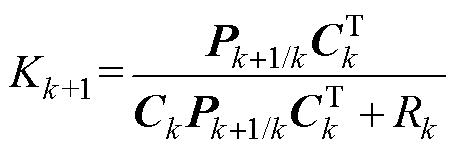 (13)
(13)
式中,Kk+1为k+1时刻的卡尔曼增益;Rk为系统观测噪声方差。
状态向量更新
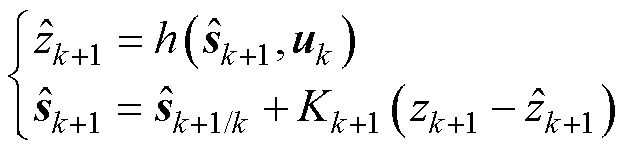 (14)
(14)
误差协方差矩阵更新
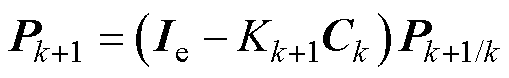 (15)
(15)
式中,Ie为单位矩阵。
高斯过程回归(Gaussian Process Regression, GPR)是使用高斯过程(Gaussian Process, GP)先验对数据进行回归分析的非参数模型。
GP是一个随机变量的集合,处理高维度、小样本和非线性复杂问题时,具有很好的适应能力。
给定的样本D={(xi, yi)},其均值函数、协方差函数分别为m(x)、k(x, x')。高斯过程表示为
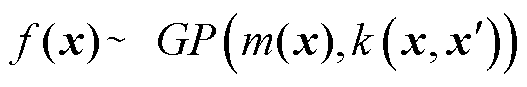 (16)
(16)
对任意输入量xi,其对应的输出量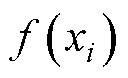 均服从联合高斯分布。
均服从联合高斯分布。
考虑含有噪声的回归问题,有
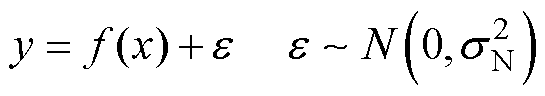 (17)
(17)
式中,x为输入向量;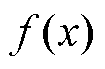 为函数值;y为受白噪声干扰的输出观测值;
为函数值;y为受白噪声干扰的输出观测值;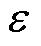 为均值为0,方差为
为均值为0,方差为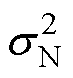 的噪声。
的噪声。
观测值的先验分布
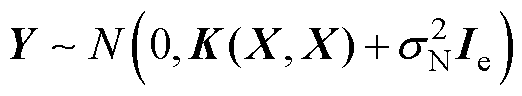 (18)
(18)
式中,Y=[y1 y2 …yn]为观测值集合;X=[x1 x2 …xn]为训练样本集合;K(X, X)=(Kij)n×n为对称正定协方差矩阵,Kij=k(xi, xj)为核函数,本文选取零均值函数和平方指数核函数(Squared Exponential, SE)作为GPR模型的核函数。
观测值和预测值的联合先验分布符合联合高斯分布为
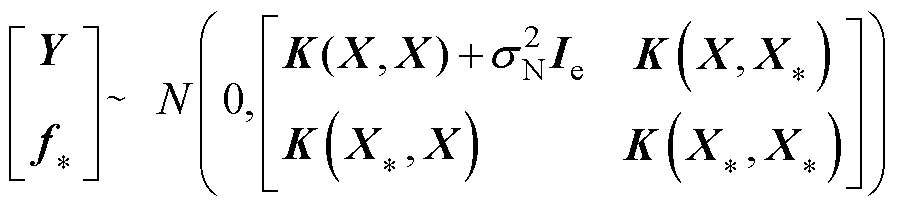 (19)
(19)
式中,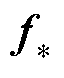 为预测值;X*=[x1* x2* … xn*]为测试样本集合;
为预测值;X*=[x1* x2* … xn*]为测试样本集合;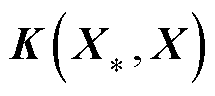 和
和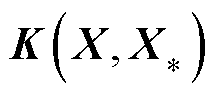 为X和X*构成的协方差矩阵;
为X和X*构成的协方差矩阵;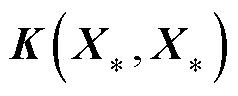 为
为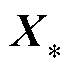 构成的协方差矩阵。
构成的协方差矩阵。
预测值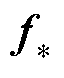 的后验分布为
的后验分布为
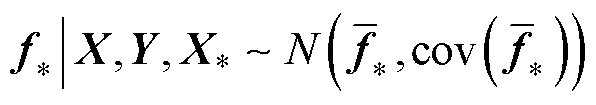 (20)
(20)
式中,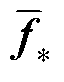 为预测值均值。
为预测值均值。
训练集训练得到的GPR模型,结合预测值的后验分布,若测试集输入向量已知,可得测试集的均值矩阵以及协方差矩阵。
均值矩阵为
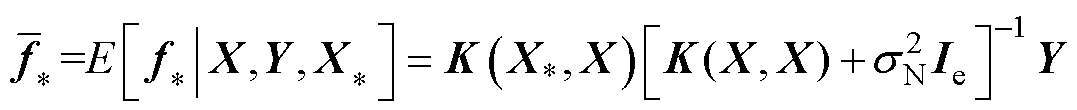 (21)
(21)
协方差矩阵为
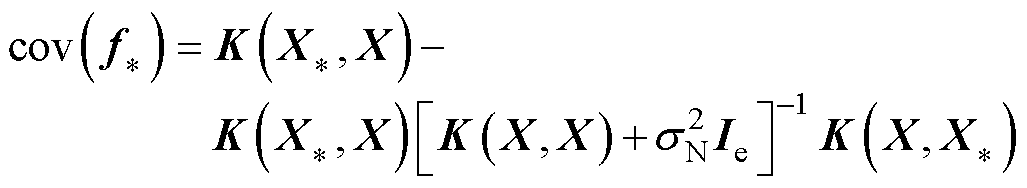 (22)
(22)
GPR模型预测输出的95%的置信区间为
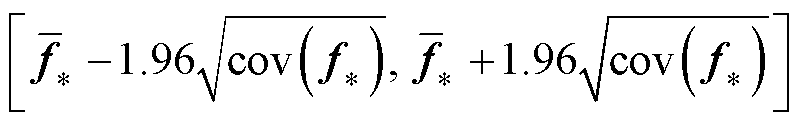 (23)
(23)
针对电池SOC与SOH估计结果相互影响,单独估计准确度不高的问题,本文提出了一种基于等效电路模型和数据驱动模型融合的锂离子电池SOC和SOH联合估计方法,联合估计流程如图5所示,分为电池参数在线辨识和电池状态联合估计两个部分。其中,电池状态联合估计又分为电池SOC估计和电池SOH估计。
电池在线参数辨识部分:本文构建考虑SOH和SOC的动态电池二阶RC等效电路模型,在不同SOH和SOC状态下,采用FFRLS对电池的R0、R1、R2、C1、C2进行实时在线辨识。首先,根据样本电池数据拟合电池的SOC-OCV函数关系式;其次,找到电池SOC估计过程中SOC估计值对应的电池开路电压值;最后,根据当前循环的电池数据,基于FFRLS在线辨识二阶RC电池模型阻容参数,将输出的R0、R1、R2、C1、C2用于电池SOC估计,确定其二阶RC状态方程。直至电池SOH<EOL时,结束循环,实现电池参数在线辨识与电池SOC估计及SOH的联合。由于锂离子电池的OCV-SOC曲线受SOH的影响较小[31-32],故图5所示的流程框图中,SOC-OCV关系式根据新电池的数据拟合所得。
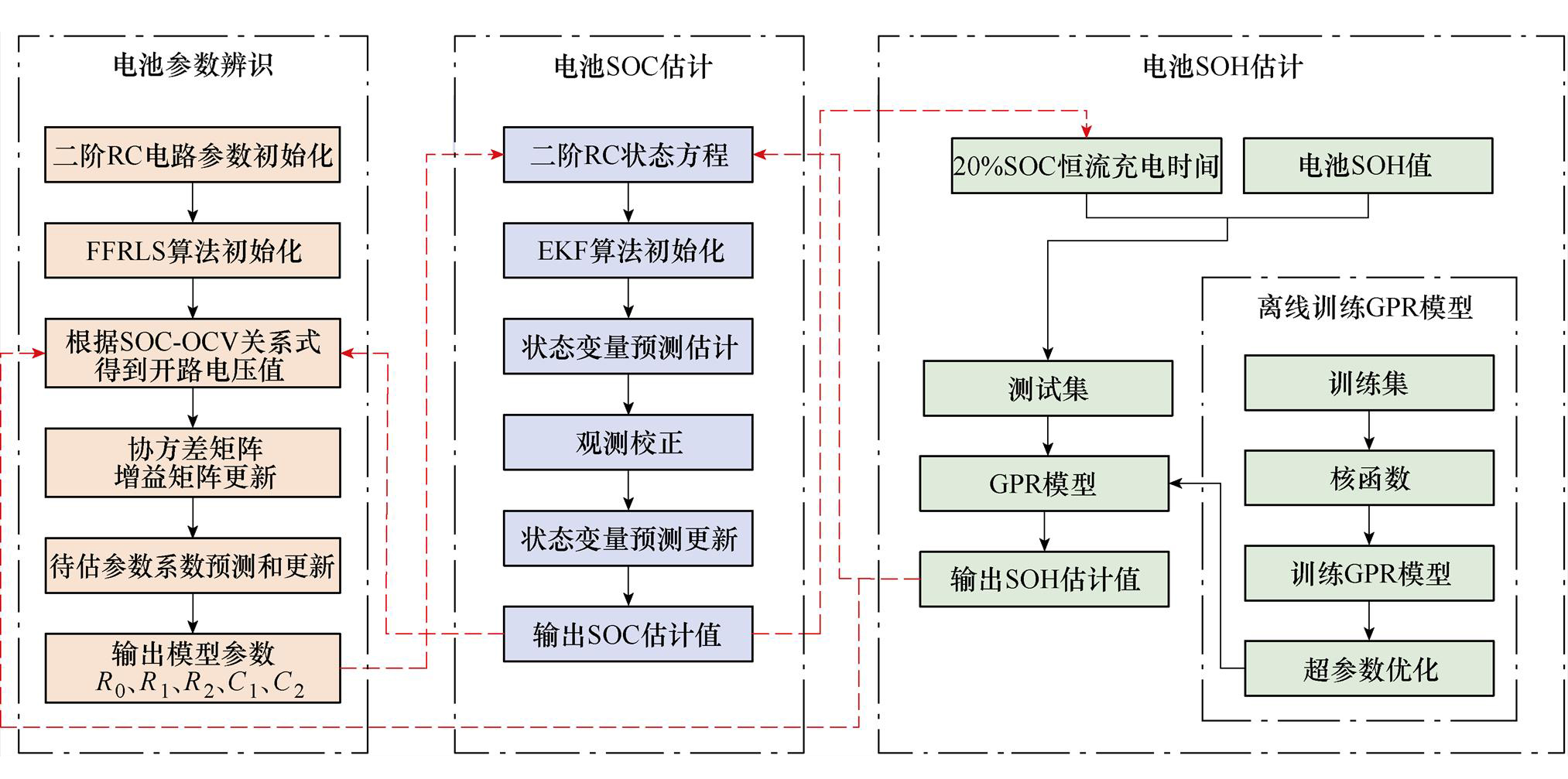
图5 锂离子电池SOH和SOC联合估计流程框图
Fig.5 Flow chart of joint estimation of SOH and SOC of lithium-ion battery
状态联合估计部分:
1)电池SOH估计
本文采用留一法对GPR模型进行验证。以实际锂离子电池自SOC=20%到恒流充电阶段结束所需时间为输入,电池SOH值为输出,离线训练GPR模型。将训练得到的GPR模型进行超参数优化,用于测试集的预测估计。最后,将测试集中的锂离子SOC=20%恒流充电时间输入GPR模型中,进行电池SOH估计。将输出的SOH估计值与电池的额定容量相乘,得到电池的实际容量,用于更新二阶RC状态空间方程,实现电池SOH估计和SOC估计之间的联合。
2)电池SOC估计
本文构建二阶RC等效电路模型,结合EKF算法对电池SOC进行估计,选取电池SOC值、极化电压U1和U2作为状态变量。二阶RC电路模型的状态空间方程和观测方程为
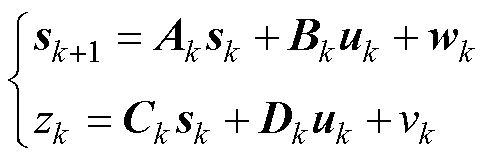 (24)
(24)
式中,sk=[SOC(k) U1(k) U2(k)]T;zk=U(k);uk=I(k)。
各矩阵表达式为
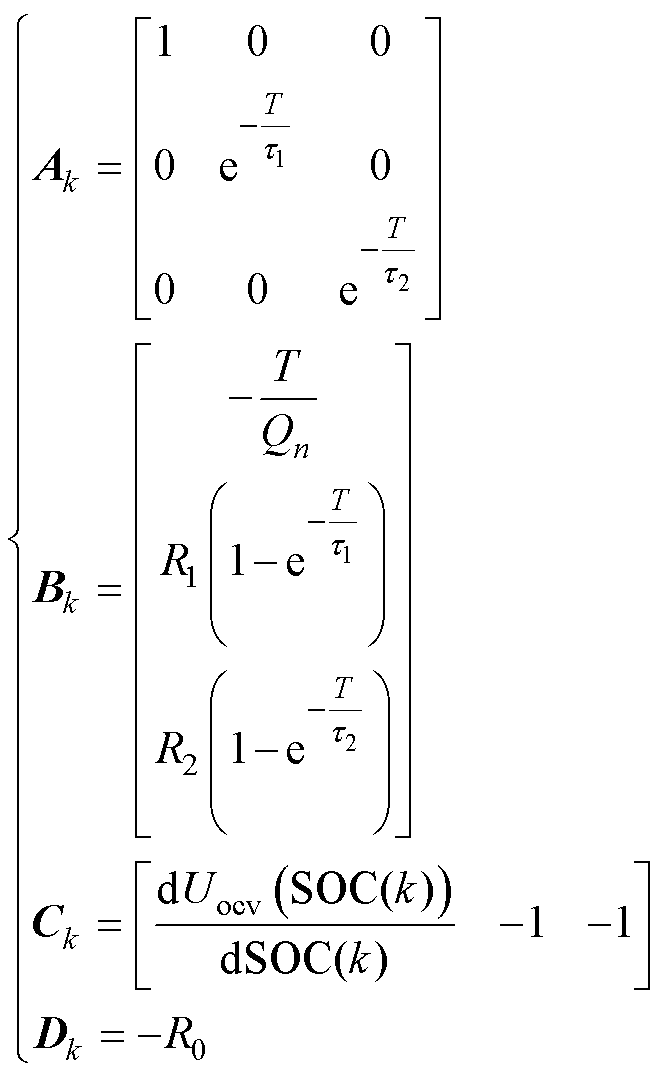 (25)
(25)
式中,Qn为第n次电池SOH估计值与电池额定容量的乘积。
将电池SOH估计值应用于电池SOC估计中,可以保证电池的SOC状态值随着电池的老化进行调整,从而达到准确估计电池SOC的目的。并且,将考虑老化的电池SOC估计值应用于电池参数辨识中,使电池此刻的模型参数最接近当前时刻电池的实际状态,达到电池模型实时更新的目的,实现电池SOC估计和参数在线辨识之间的联合。
用于电池SOC和SOH估计的电池数据来源于牛津大学提供的电池退化数据集和NASA随机使用数据集。本文只考虑SOH>EOL时,SOC和SOH估计结果。采用平均绝对误差(Mean Absolute Error, MAE)和方均根误差(Root Mean Squared Error, RMSE)作为预测效果的评判标准。
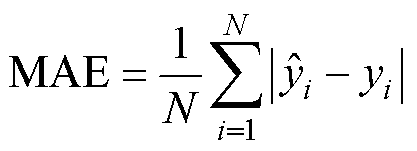 (26)
(26)
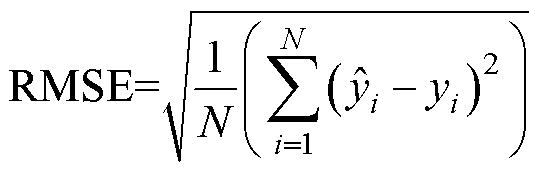 (27)
(27)
式中,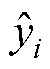 和
和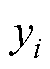 分别为样本估计值与实际值。
分别为样本估计值与实际值。
实际的SOC初始值是1,本文将初始值设为0.7,以便检验算法的鲁棒性。
图6所示为联合估计SOC与单独估计SOC误差对比。图6a为平均MAE对比,图6b为平均RMSE对。图6中,实线和虚线分别代表单独估计SOC和联合估计SOC的误差。联合估计SOC和EKF单独估计SOC的误差结果见表2和表3。本文Cell 1~Cell 8和RW 3~RW 6的SOC误差采用平均MAE和平均RMSE表示。
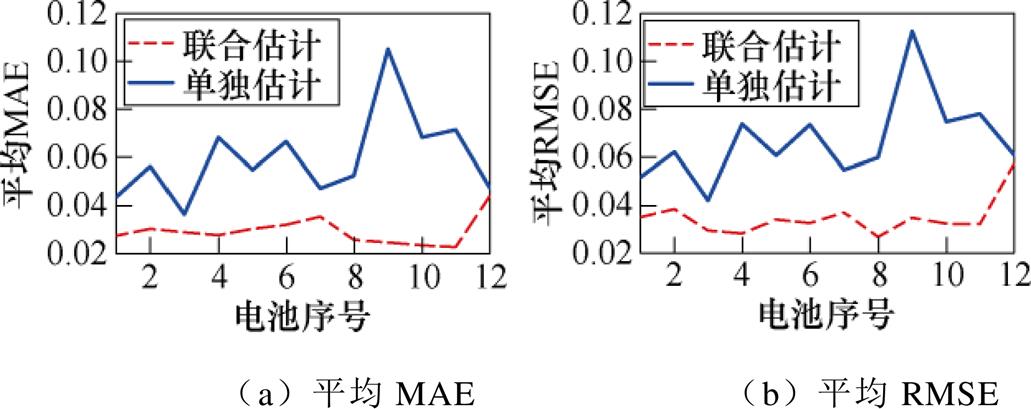
图6 联合估计SOC与单独估计SOC误差对比
Fig.6 Comparison of SOC error between joint estimation and individual estimation
从图6可以看出,采用本文提出的联合估计方法对SOC估算的平均MAE和平均RMSE基本上小于0.04,即使Cell 1~Cell 8和RW 3~RW 6是在不同工况下进行的老化实验,其平均MAE和平均RMSE均较为平稳,而采用EKF单独估计SOC,平均MAE和平均RMSE均比联合估计下的要高,且随电池工况有较大的波动。由此说明,联合估计方法适用性较好。
本文以SOH=0.1为间隔,分别选取了Cell 1~Cell 8和RW 3~RW 6从SOH=1到SOH=0.8三个放电循环过程的SOC估计情况。以Cell 1和RW 3为例,图7中,(黑色)实线代表SOC实际值,(红色)点线代表SOC联合估计值,(蓝色)虚线代表SOC单独估计值,右图代表联合估计实时误差。从图7中可以看出,即使电池SOC初始值设为0.7,随着电池容量的衰退,电池的SOC联合估计值依旧能较准确地跟随锂离子电池SOC实际值,而采用EKF单独估计SOC时,随着电池老化程度的加深,SOC估计值与实际值误差越来越大。由此说明,联合估计算法的鲁棒性和准确性均较好。
表2 联合方法估计SOC误差结果
Tab.2 The SOC error results of the joint method
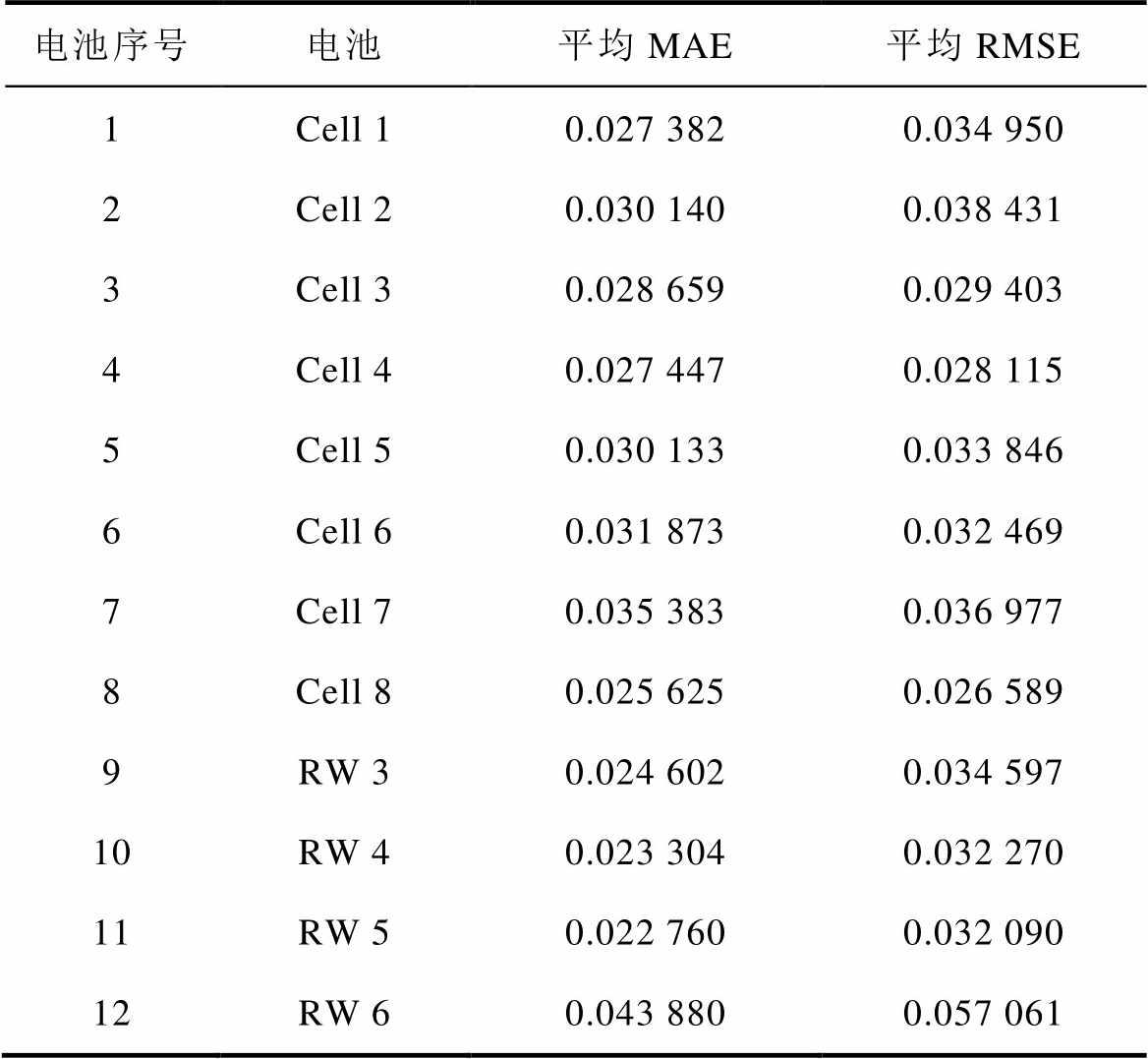
电池序号电池平均MAE平均RMSE 1Cell 10.027 3820.034 950 2Cell 20.030 1400.038 431 3Cell 30.028 6590.029 403 4Cell 40.027 4470.028 115 5Cell 50.030 1330.033 846 6Cell 60.031 8730.032 469 7Cell 70.035 3830.036 977 8Cell 80.025 6250.026 589 9RW 30.024 6020.034 597 10RW 40.023 3040.032 270 11RW 50.022 7600.032 090 12RW 60.043 8800.057 061
表3 EKF单独估计SOC误差结果
Tab.3 The SOC error results of the EKF alone

电池序号电池平均MAE平均RMSE 1Cell 10.043 4330.051 583 2Cell 20.056 2390.062 106 3Cell 30.036 2740.041 916 4Cell 40.068 2910.073 762 5Cell 50.054 8450.060 599 6Cell 60.066 5690.073 555 7Cell 70.047 1350.054 608 8Cell 80.052 5230.059 876 9RW 30.105 0820.112 619 10RW 40.068 3250.074 820 11RW 50.071 4950.077 877 12RW 60.047 2170.060 911
SOC的估计结果说明,与采用EKF单独估计SOC相比,本文采用联合估计的方法对电池SOC进行估计,可以实时根据电池SOC和充放电循环的变化在线辨识二阶RC等效电路的参数,并且根据SOH的变化实时调整最大可用容量,因此在电池老化的情况下,能较准确地跟随锂离子电池SOC的实际值。
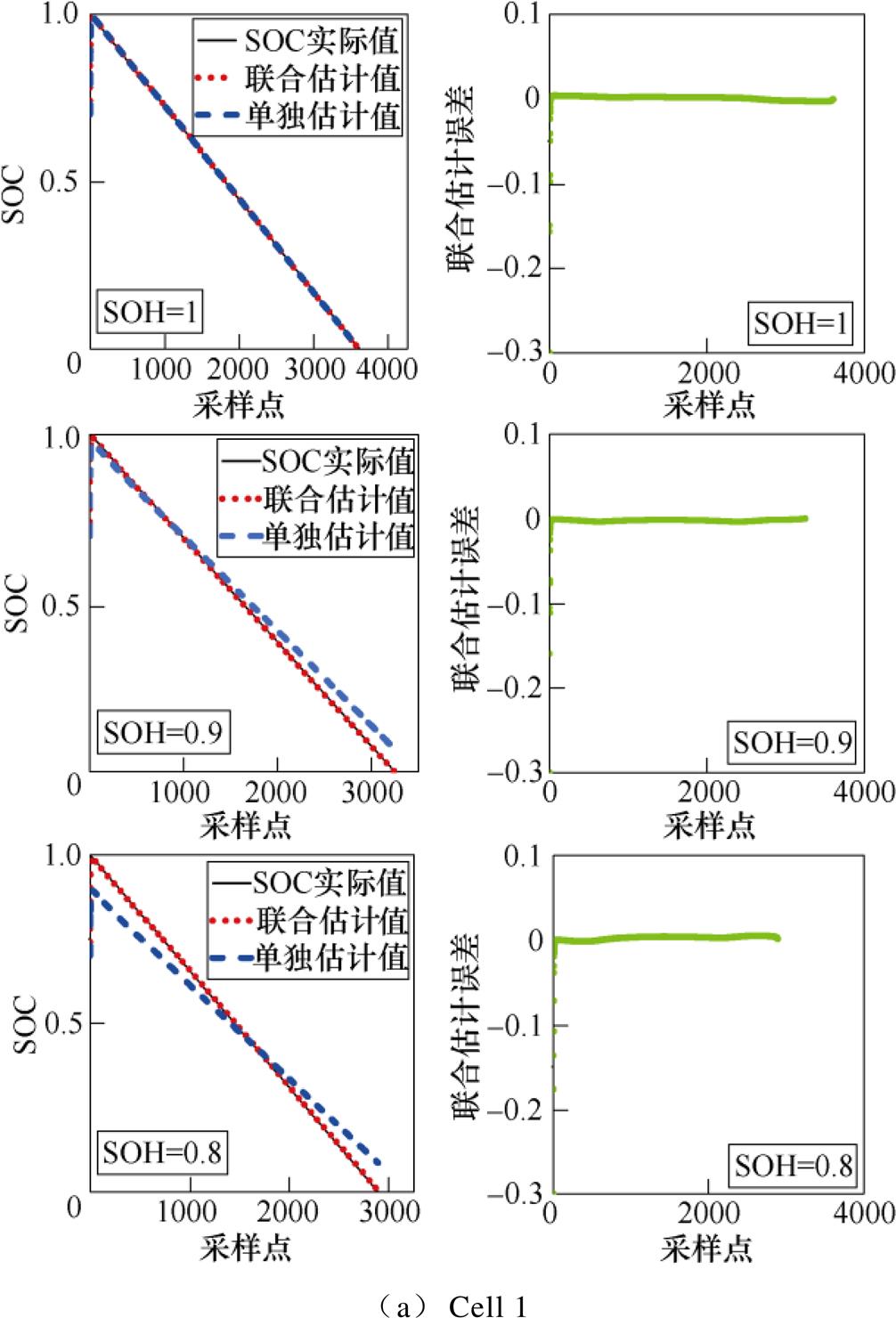
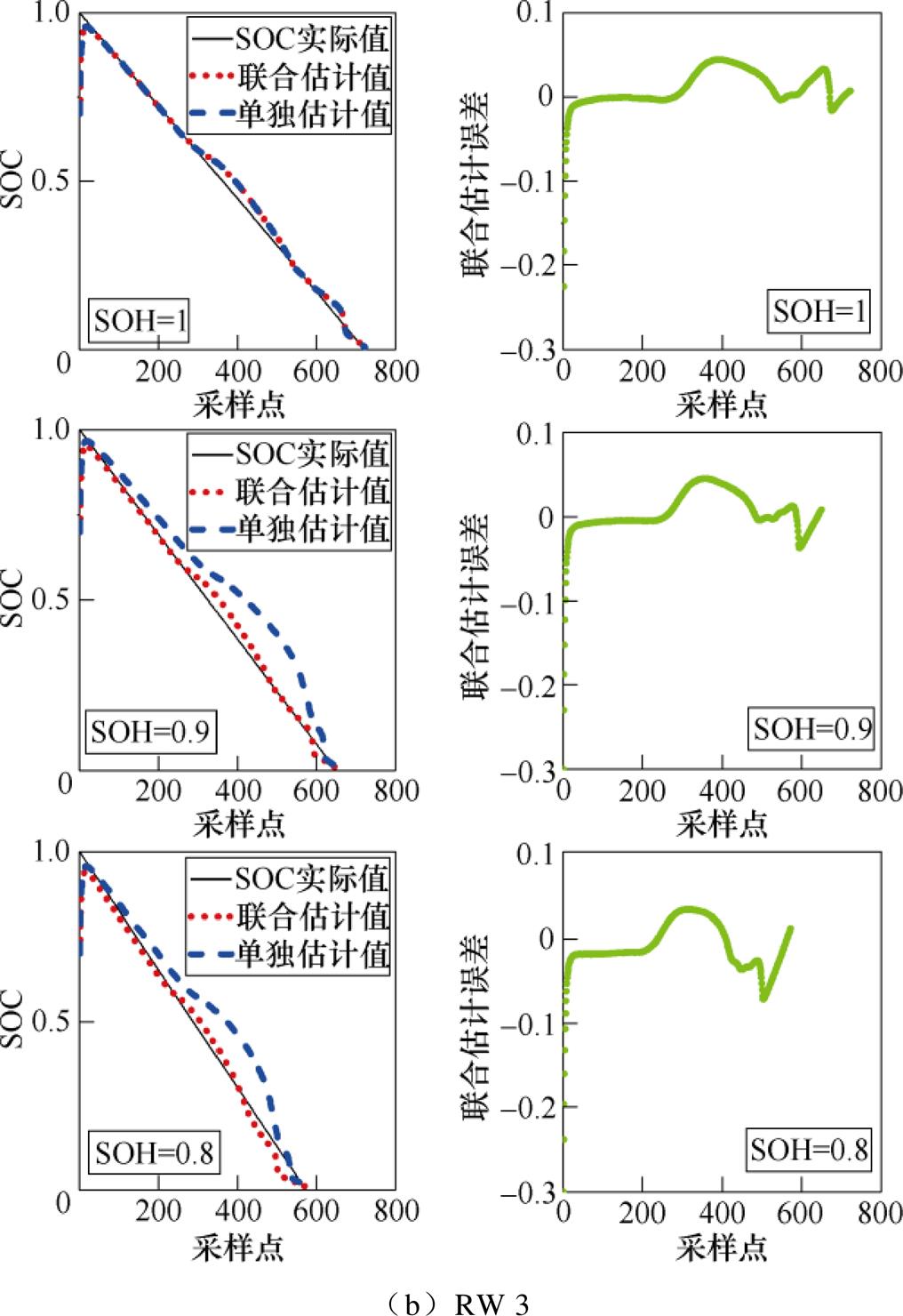
图7 Cell 1和RW 3的SOC估计结果
Fig.7 SOC estimation results of Cell 1 and RW 3
训练集和测试集具有相同的容量衰退特性,能够有效提取更多反馈待测电池容量变化的信息。本文采用留一法进行验证,即当Cell 1为待测电池时,选取同一工况下剩下七组电池Cell 2~Cell 8的SOC为20%恒流充电时间和SOH序列作为GPR模型的训练集。
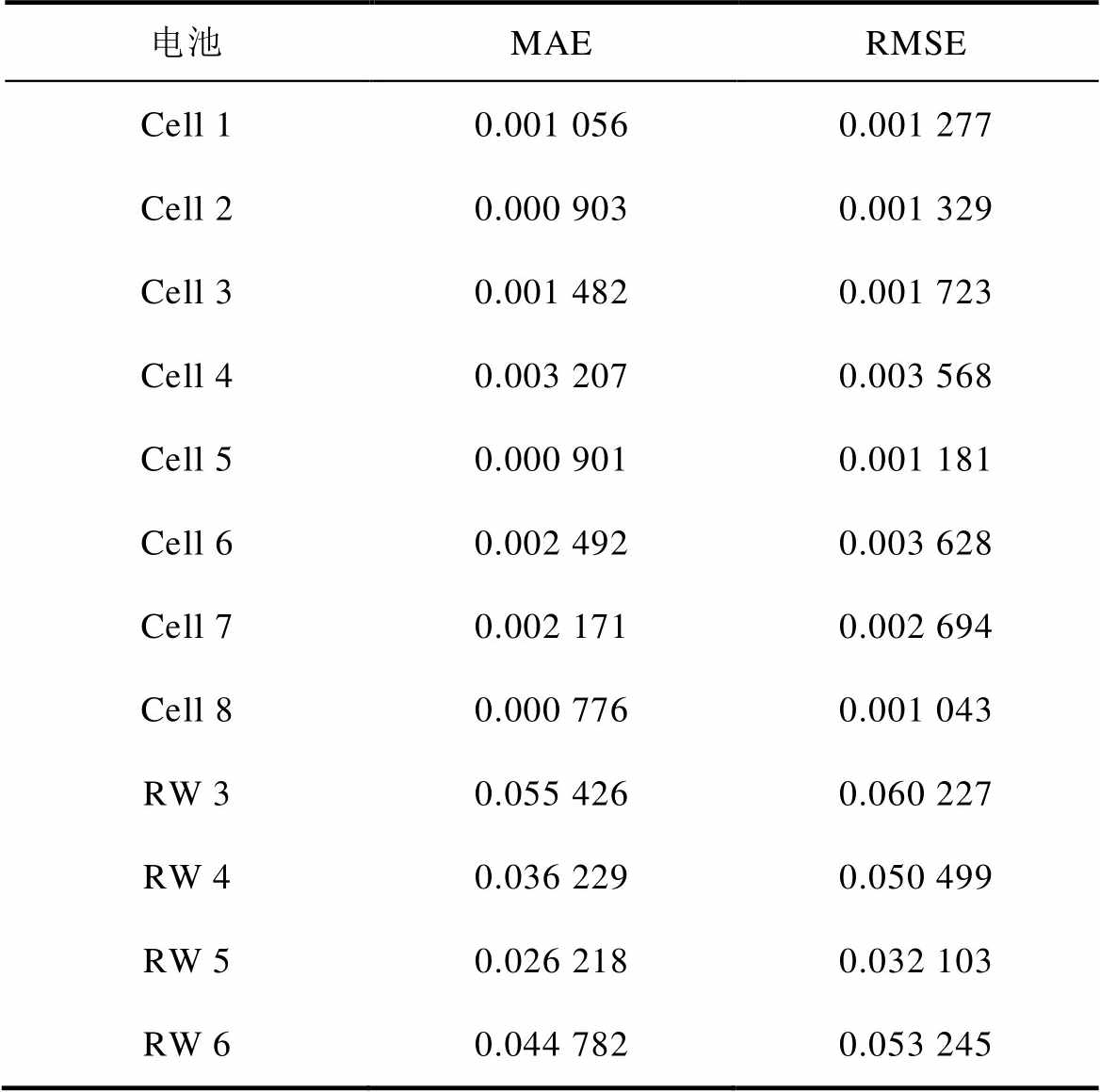
表4展示了12块电池的SOH预测误差,包括MAE和RMSE。从表4中,可以看出,Cell 1~Cell 8的SOH预测MAE和RMSE均小于0.5%,RW 3~RW 6的SOH预测MAE和RMSE在0.05左右。这是因为对RW 3~RW 6进行SOH预测时,采用的样本数较少,不及Cell 1~Cell 8的1/10,即使样本数较少,对SOH的预测MAE和RMSE基本在0.05附近,这说明本文采用的联合估计方法具有较好的准确性。
表4 各电池的SOH预测误差
Tab.4 SOH prediction error of each battery
电池MAERMSE Cell 10.001 0560.001 277 Cell 20.000 9030.001 329 Cell 30.001 4820.001 723 Cell 40.003 2070.003 568 Cell 50.000 9010.001 181 Cell 60.002 4920.003 628 Cell 70.002 1710.002 694 Cell 80.000 7760.001 043 RW 30.055 4260.060 227 RW 40.036 2290.050 499 RW 50.026 2180.032 103 RW 60.044 7820.053 245
图8和图9分别展示了电池Cell 1~Cell 8和RW 3~RW 6随充放电循环次数变化的SOH预测误差。以Cell 1为例,图10展示了Cell 1的SOH随着充放电循环次数变化的整体情况。图10中,预测区间上下界包络的区间为95%的置信区间。从图10可以看出,电池的SOH预测值能够较好地跟随真实值,预测值均位于置信区间中,且置信区间较窄,说明本文建立的GPR模型对SOH预测具有较高的准确性和可靠性。
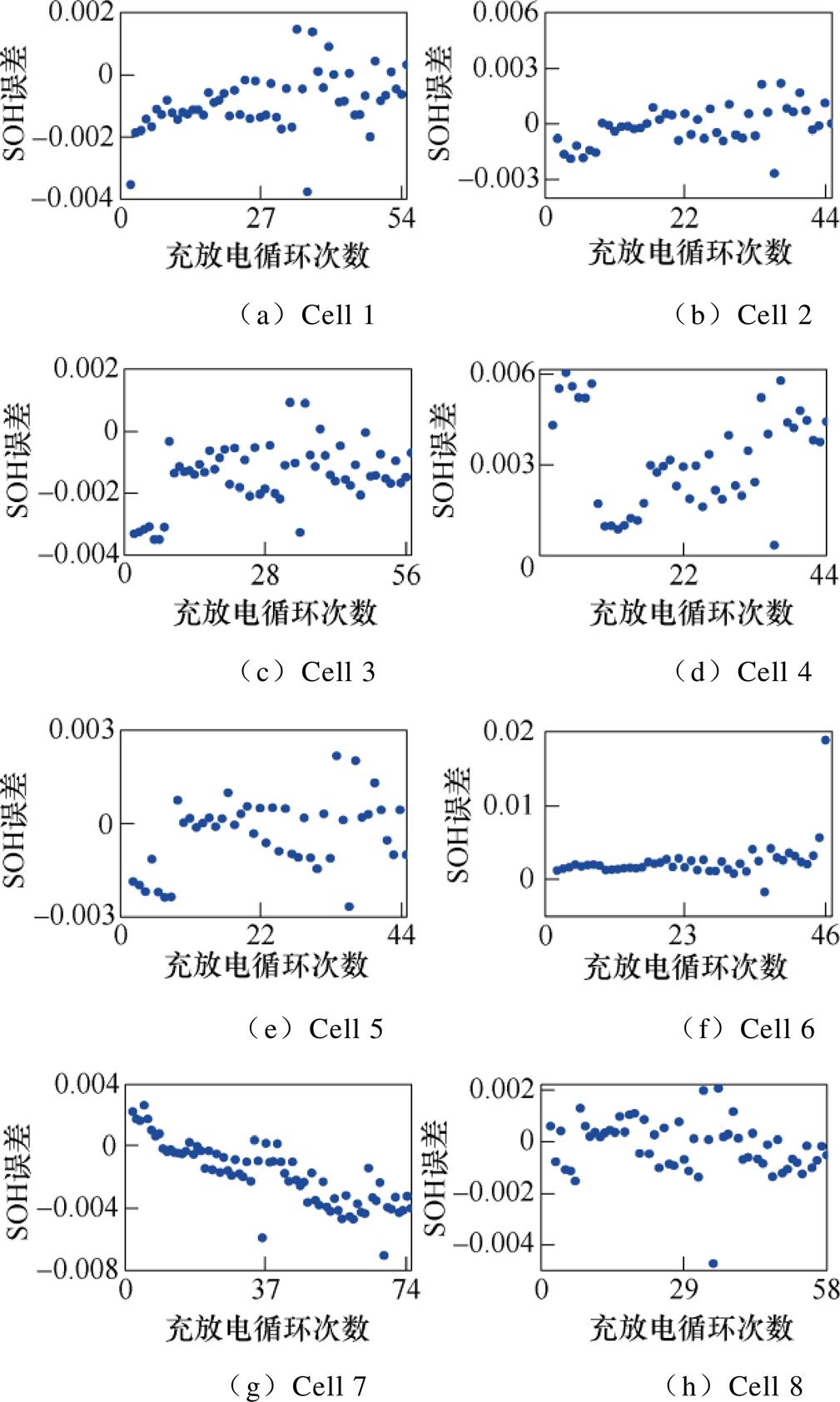
图8 Cell 1~Cell 8的SOH预测误差
Fig.8 SOH prediction error of Cell 1~Cell 8
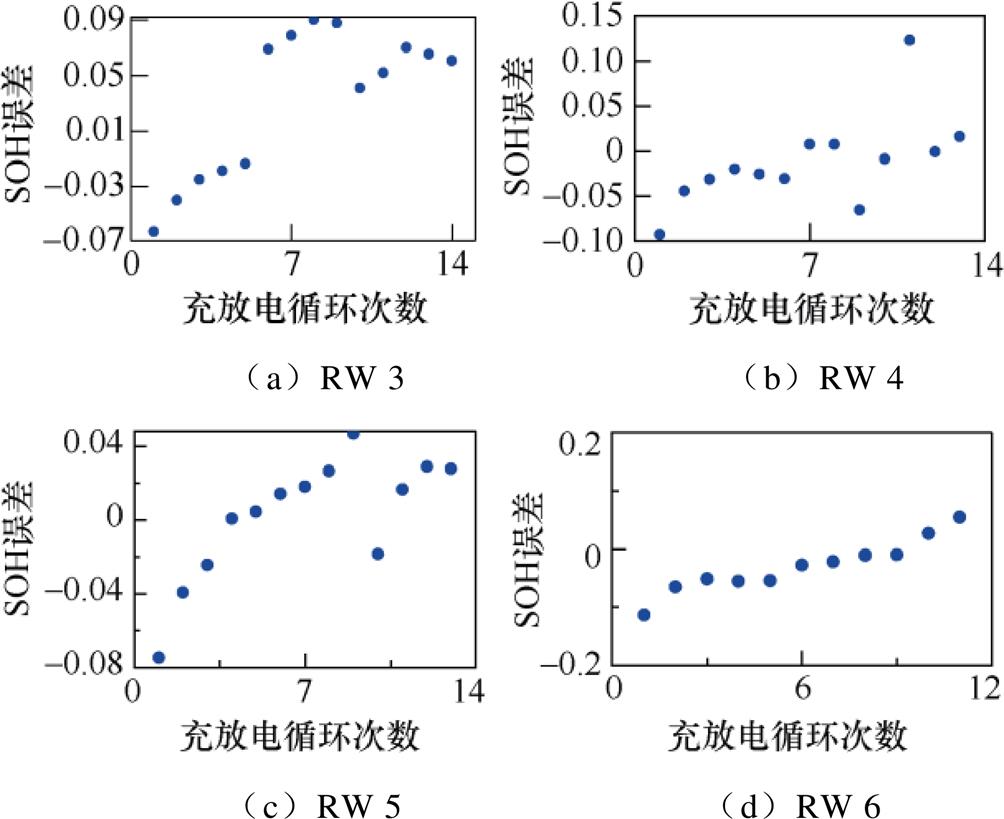
图9 RW 3~RW 6的SOH预测误差
Fig.9 SOH prediction error of RW 3~RW 6
本文提出了一种基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法。通过构建考虑老化和SOC的电池二阶RC等效电路模型,采用FFRLS算法,在不同SOC和SOH的情况下,对电池的参数进行在线辨识,实现电池参数在线辨识与电池SOC和SOH估计的联合。以锂离子电池自SOC= 20%到恒流充电阶段结束所需时间为输入,电池SOH值为输出,训练GPR模型,实现电池SOH估计。将输出的SOH估计值与电池的额定容量相乘,得到电池的实际容量,用于更新二阶RC电路空间状态方程,实现电池SOC的估计。采用牛津大学电池退化数据集和NASA随机使用数据集进行算法验证,结果表明,所提联合估计方法能够在电池的生命周期内较准确地跟随锂离子电池SOC和SOH的真实值。
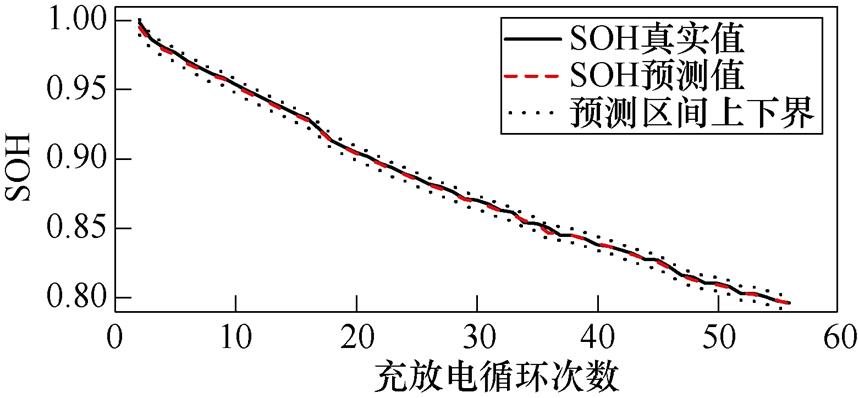
图10 Cell 1的SOH预测结果
Fig.10 SOH prediction results of Cell 1
参考文献
[1] 甘露雨, 陈汝颂, 潘弘毅, 等. 锂电池安全性多尺度研究策略: 实验与模拟方法[J]. 储能科学与技术, 2022, 11(3): 852-865.
Gan Luyu, Chen Rusong, Pan Hongyi, et al. Multiscale research strategy of lithium ion battery safety issue: experimental and simulation methods[J]. Energy Storage Science and Technology, 2022, 11(3): 852-865.
[2] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.
[3] Rahimi-Eichi H, Ojha U, Baronti F, et al. Battery management system: an overview of its application in the smart grid and electric vehicles[J]. IEEE Industrial Electronics Magazine, 2013, 7(2): 4-16.
[4] 谭必蓉, 杜建华, 叶祥虎, 等. 基于模型的锂离子电池SOC估计方法综述[J]. 储能科学与技术, 2023, 12(6): 1995-2010.
Tan Birong, Du Jianhua, Ye Xianghu, et al. Overview of SOC estimation methods for lithium-ion batteries based on model[J]. Energy Storage Science and Technology, 2023, 12(6): 1995-2010.
[5] How D N T, Hannan M A, Hossain Lipu M S, et al. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: a review[J]. IEEE Access, 2019, 7: 136116-136136.
[6] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703- 1725.
[7] Yu Quanqing, Wan Changjiang, Li Junfu, et al. An open circuit voltage model fusion method for state of charge estimation of lithium-ion batteries[J]. Energies, 2021, 14(7): 1797.
[8] Somakettarin N, Funaki T. Study on factors for accurate open circuit voltage characterizations in Mn-type Li-ion batteries[J]. Batteries, 2017, 3(4): 8.
[9] 于海芳, 逯仁贵, 朱春波, 等. 基于安时法的镍氢电池SOC估计误差校正[J]. 电工技术学报, 2012, 27(6): 12-18.
Yu Haifang, Lu Rengui, Zhu Chunbo, et al. State of charge estimation calibration for Ni-MH battery based on ampere-hour method[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 12-18.
[10] 程泽, 杨磊, 孙幸勉. 基于自适应平方根无迹卡尔曼滤波算法的锂离子电池SOC和SOH估计[J]. 中国电机工程学报, 2018, 38(8): 2384-2393, 2548.
Cheng Ze, Yang Lei, Sun Xingmian. State of charge and state of health estimation of Li-ion batteries based on adaptive square-root unscented Kalman filters[J]. Proceedings of the CSEE, 2018, 38(8): 2384-2393, 2548.
[11] 郝文美, 张立伟, 彭博, 等. 动车组钛酸锂电池荷电状态估计[J]. 电工技术学报, 2021, 36(增刊1): 362-371.
Hao Wenmei, Zhang Liwei, Peng Bo, et al. State of charge estimation of lithium titanate battery for EMU[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 362-371.
[12] Luo Jiayi, Peng Jiankun, He Hongwen. Lithium-ion battery SOC estimation study based on Cubature Kalman filter[J]. Energy Procedia, 2019, 158: 3421- 3426.
[13] 魏克新, 陈峭岩. 基于自适应无迹卡尔曼滤波算法的锂离子动力电池状态估计[J]. 中国电机工程学报, 2014, 34(3): 445-452.
Wei Kexin, Chen Qiaoyan. States estimation of Li-ion power batteries based on adaptive unscented Kalman filters[J]. Proceedings of the CSEE, 2014, 34(3): 445- 452.
[14] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051- 2062.
[15] 李宁, 何复兴, 马文涛, 等. 基于经验模态分解的门控循环单元神经网络的锂离子电池荷电状态估计[J]. 电工技术学报, 2022, 37(17): 4528-4536.
Li Ning, He Fuxing, Ma Wentao, et al. State-of- charge estimation of lithium-ion battery based on gated recurrent unit using empirical mode decom- position[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4528-4536.
[16] Jiao Meng, Wang Dongqing, Qiu Jianlong. A GRU- RNN based momentum optimized algorithm for SOC estimation[J]. Journal of Power Sources, 2020, 459: 228051.
[17] 周才杰, 汪玉洁, 李凯铨, 等. 基于灰色关联度分析-长短期记忆神经网络的锂离子电池健康状态估计[J]. 电工技术学报, 2022, 37(23): 6065-6073.
Zhou Caijie, Wang Yujie, Li Kaiquan, et al. State of health estimation for lithium-ion battery based on gray correlation analysis and long short-term memory neural network[J]. Transactions of China Electro- technical Society, 2022, 37(23): 6065-6073.
[18] 姚芳, 张楠, 黄凯. 锂离子电池状态估算与寿命预测综述[J]. 电源学报, 2020, 18(3): 175-183.
Yao Fang, Zhang Nan, Huang Kai. Review of state estimation and life prediction for lithiumion batteries[J]. Journal of Power Supply, 2020, 18(3): 175-183.
[19] 陈霖华, 陈剑, 徐志强, 等. 基于实时电路模型的储能系统锂离子电池状态估算[J]. 中南大学学报(自然科学版), 2021, 52(2): 458-464.
Chen Linhua, Chen Jian, Xu Zhiqiang, et al. State estimation of lithium ion battery in energy storage system based on real time circuit model[J]. Journal of Central South University (Science and Technology), 2021, 52(2): 458-464.
[20] Spotnitz R. Simulation of capacity fade in lithium-ion batteries[J]. Journal of Power Sources, 2003, 113(1): 72-80.
[21] Bloom I, Cole B W, Sohn J J, et al. An accelerated calendar and cycle life study of Li-ion cells[J]. Journal of Power Sources, 2001, 101(2): 238-247.
[22] Matsushima T. Deterioration estimation of lithium- ion cells in direct current power supply systems and characteristics of 400-Ah lithium-ion cells[J]. Journal of Power Sources, 2009, 189(1): 847-854.
[23] Remmlinger J, Buchholz M, Meiler M, et al. State- of-health monitoring of lithium-ion batteries in electric vehicles by on-board internal resistance estimation[J]. Journal of Power Sources, 2011, 196(12): 5357-5363.
[24] Liu Enhui, Niu Guangxing, Wang Xuan, et al. SOH diagnostic and prognostic based on external health indicator of lithium-ion batteries[C]//IECON 2021- 47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 2021: 1-6.
[25] 樊欣欣, 丁晖, 陈秀国, 等. 基于模糊逻辑的变电站蓄电池在线健康状态评估[J]. 电子器件, 2021, 44(1): 136-140.
Fan Xinxin, Ding Hui, Chen Xiuguo, et al. On-line health assessment of substation battery based on fuzzy logic[J]. Chinese Journal of Electron Devices, 2021, 44(1): 136-140.
[26] 申江卫, 高承志, 舒星, 等. 基于迁移模型的锂离子电池宽温度全寿命SOC与可用容量联合估计[J]. 电工技术学报, 2023, 38(11): 3052-3063.
Shen Jiangwei, Gao Chengzhi, Shu Xing, et al. Joint estimation of SOC and usable capacity of lithium-ion battery with wide temperature and full life based on migration model[J]. Transactions of China Electro- technical Society, 2023, 38(11): 3052-3063.
[27] 赵靖英, 胡劲, 张雪辉, 等. 基于锂电池模型和分数阶理论的SOC-SOH联合估计[J]. 电工技术学报, 2023, 38(17): 4551-4563.
Zhao Jingying, Hu Jin, Zhang Xuehui, et al. Joint estimation of the SOC-SOH based on lithium battery model and fractional order theory[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4551- 4563.
[28] Birkl C. Oxford battery degradation dataset 1[DB/OL]. University Oxford, Oxford, UK, 2017.
[29] Bole B, Kulkarni C, Daigle M. Randomized battery usage data set, NASA prognostics data repo- sitory[DB/OL]. NASA Ames Research Center, Moffett Field, CA, USA.
[30] Yun Xiang, Zhang Xin, Wang Chao, et al. Online parameters identification and state of charge esti- mation for lithium-ion batteries based on improved central difference particle filter[J]. Journal of Energy Storage, 2023, 70: 107987.
[31] Abu-Sharkh S, Doerffel D. Rapid test and non-linear model characterisation of solid-state lithium-ion batteries[J]. Journal of Power Sources, 2004, 130(1/2): 266-274.
[32] 王萍, 彭香园, 程泽, 等. 基于数据驱动模型融合的锂离子电池多时间尺度状态联合估计方法[J]. 汽车工程, 2022, 44(3): 362-371, 378.
Wang Ping, Peng Xiangyuan, Cheng Ze, et al. A multi-time scale joint state estimation method for lithium-ion batteries based on data-driven model fusion[J]. Automotive Engineering, 2022, 44(3): 362- 371, 378.
[33] 廖根兴, 赵盈盈, 高雁凤, 等. 锂离子电池模型参数辨识与荷电状态估算[J]. 电源技术, 2021, 45(9): 1136-1139.
Liao Genxing, Zhao Yingying, Gao Yanfeng, et al. Parameter identification and SOC estimation of lithium-ion battery model[J]. Chinese Journal of Power Sources, 2021, 45(9): 1136-1139.
Abstract The accuracy of state of charge (SOC)can be significantly affected by battery aging, leading to misguidance in the calibration of state of health(SOH). Existing studies often estimate SOC and SOH separately, neglecting their close relationship and resulting in reduced estimation accuracy. This paper proposes a joint estimation method for SOC and SOH based on the fusion of an equivalent circuit model and a data-driven model. The influence mechanism between battery SOC and SOH is revealed, mitigating their mutual influence and enhancing the accuracy of SOC and SOH estimation.
Firstly, by constructing a second-order RC equivalent circuit model of the battery considering aging and SOC, the recursive least square method with a forgetting factor isused to identify battery parameters online under different SOC and SOH conditions. Secondly, the required time from 20%SOC to the end of the constant-current charging stage is extracted. Pearson and Spearman relationships between constant current charge time and SOH of lithium-ion batteries arecalculated. Thirdly, the actual time required from 20%SOC to the end of the constant-current charging phase of lithium-ion batteries is taken as input and battery SOH as output to train the GPR model offline. The trained GPR model is optimized by hyper parameters and used for SOH prediction. Finally, the estimated SOH output ismultiplied by the rated capacity of the cell to obtain the actual cell capacity, which is used to update the second-order RC state space equation. Based on the second-order RC equivalent circuit model, the battery SOC was estimated by the EKF.
The Oxford University battery degradation data set and NASA random battery data set are used to verify the joint estimation method. The results show that the proposed method achieves low average MAE and RMSE for SOC estimation (typicallyless than 0.04). In aging experiments of Cell 1~Cell 8 and RW 3~RW 6 under different working conditions, the average MAE and average RMSE are stable. The actual initial SOC value is 1, and the initial value is set to 0.7 in this paper. With the decline in battery capacity, the joint estimate of battery SOC can follow the actual SOC more accurately. The joint estimation algorithm is robust and accurate. Meanwhile, the reservation-one method is used to verify the Gaussian process regression model. The MAE and RMSE predicted by SOH for Cell 1~Cell 8 are less than 0.5%, and the MAE and RMSE predicted by SOH for RW 3~RW 6 are about 0.05. All the predicted SOH values are in a narrow confidence interval.
The following conclusions can be drawn from the simulation analysis: (1) Compared with the existing battery model, the dynamic second-order RC equivalent circuit model considering battery aging and SOC is constructed. In the case of battery aging, the voltage obtained by fitting the identified circuit parameters can track the actual voltage well. (2) The joint estimation method applies the real-time online modified battery parameters and battery SOH to ensure that the battery SOC is adjusted with battery aging. The SOC estimation is accurate. (3) The combined method applies the estimated SOC to ensure effective health feature extraction and improve the accuracy of SOH prediction.
keywords:Lithium-ion battery, state of charge, state of health, Gaussian process regression, forgetting factor recursive least squares
DOI: 10.19595/j.cnki.1000-6753.tces.230261
中图分类号:TM912
湖南省科技创新人才计划科技创新团队资助项目(2021RC4061)。
收稿日期 2023-03-07
改稿日期 2023-04-18
刘 萍 女,1999年生,硕士研究生,研究方向为电池参数辨识与状态估计。E-mail: 1985259625@qq.com
李泽文 男,1975年生,博士,博士生导师,研究方向为电力系统保护与控制。E-mail: lzw0917@163.com(通信作者)
(编辑 郭丽军)