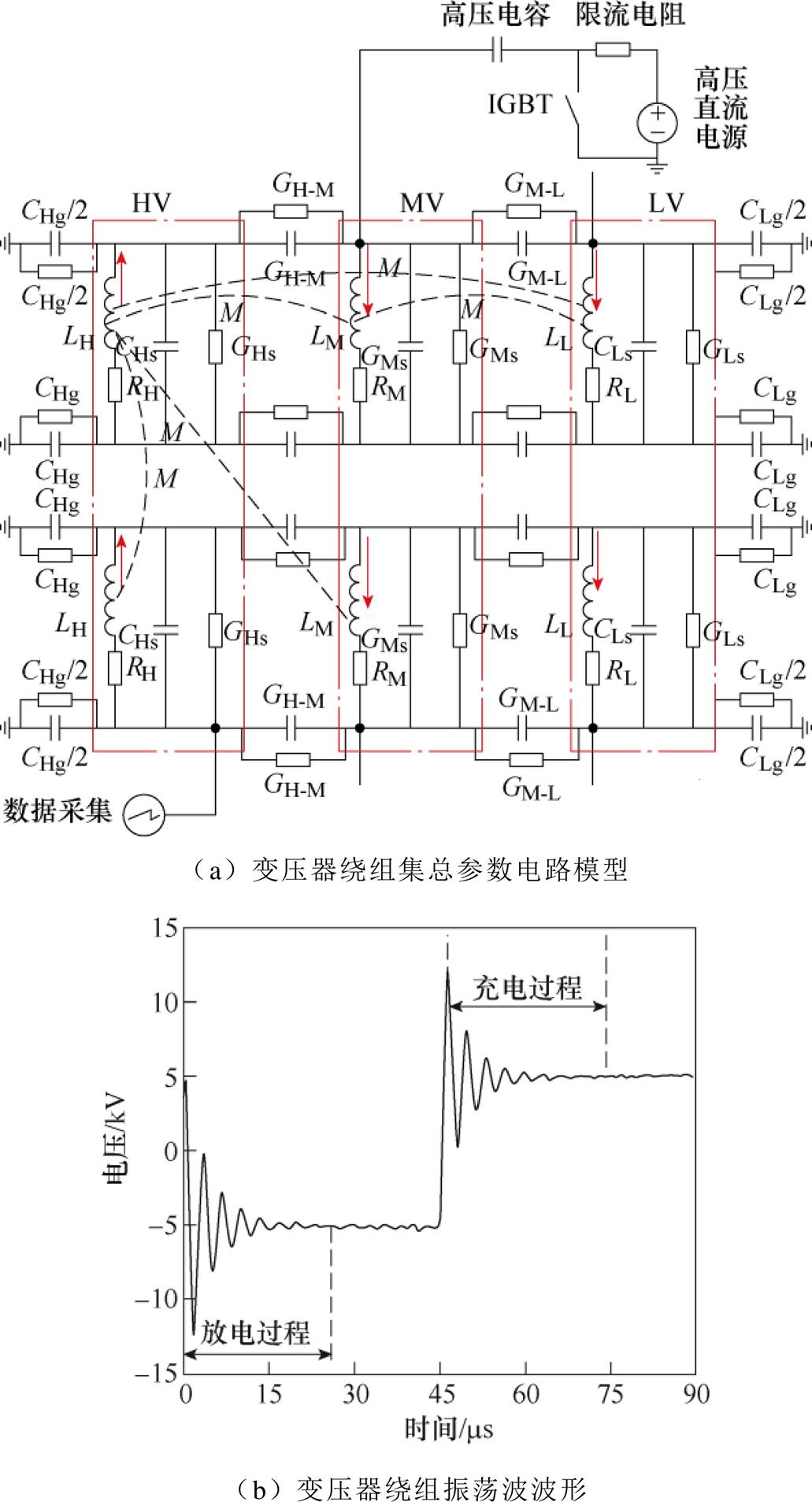
图1 变压器绕组振荡波原理分析
Fig.1 Schematic of transformer winding oscillation wave
摘要 变压器绕组振荡波能够有效地反映绕组状态变化,实际应用中发现振荡波末期存在不规律振荡行为,影响了基于振荡波的变压器绕组故障诊断准确性。该文针对此问题,首先,搭建变压器绕组故障模拟平台,获取轴向移位、局部翘曲、饼间短路和匝间短路四种故障下绕组振荡波数据;其次,通过定义的能量衰减因子,提出了一种基于电压阻尼振荡的变压器绕组振荡波有效波段动态选取方法;再次,基于确定的有效波段,提出了基于二值化的Tamura纹理特征的特征参数提取方法,并结合波形特征关联度(FCD),提出了用于故障类型(轴向移位、局部翘曲、饼间短路和匝间短路)、区域、程度诊断的特征参数组合并分析了其分布规律;最后,基于特征参数组合的分布规律通过实际变压器进行了应用分析。结果表明,动态选取出的波段干扰信息少、衰减振荡规律性明显且包含丰富的特征信息,可实现对故障类型、故障程度和故障区域的识别分类。
关键词:变压器 振荡波 绕组故障 动态波段 波形特征 纹理特征
大型电力变压器作为电力系统的核心设备,在短路冲击等作用下易发生绕组故障[1],如轴向移位或径向移位、局部翘曲、饼间短路、匝间短路等。据统计,50%左右的电力变压器故障是由于绕组故障引发的[2]。因此,有效诊断绕组故障对于变压器安全可靠运行具有重要意义。
针对变压器绕组故障检测,目前国内外学者陆续提出了多种检测方法。例如,振动法[3]、短路阻抗法[4]、频率响应法(Frequency Response Analysis, FRA)[5-7]。振动法能够实现绕组故障的在线监测,但由于受到现场噪声干扰及传感器本身局限性等问题,容易对信号的采集和分析产生影响。短路阻抗法操作简单、可重复性高,但灵敏度低、检测时间较长。FRA具有稳定性好、可重复测试性强等优点,是目前较为广泛应用的绕组故障检测方法,国内外学者针对基于FRA的绕组故障诊断方法,在原有标准的基础上提出了二值形态学[8]、欧氏距离和偏移面积比[9]、极坐标图[10]、权重函数[11]等多维指标。上述研究为变压器绕组故障检测提供了有效帮助,但在现场实际开展FRA测试时,测试结果受测试引线长度、测试地线长度和信号源位置等多种因素影响,且对于局部扭曲等轻微故障不敏感[12-14],为此文献[15]提出了一种基于振荡波的变压器绕组状态检测方法,该方法经试验验证可以有效地反映绕组状态变化,且抗干扰能力强,能够作为现有检测方法的一种有效补充。
然而,变压器绕组振荡波在充放电将要结束的一段时间内仍持续微小的波动[15-17],这个过程中会出现大量不规律的振荡波段及极大值点、极小值点,这些不规律的振荡波段及无效的极值点会对振荡波的后续特征处理分析产生干扰[18-19]。因此,选取出振荡波的有效波段对于提高绕组故障诊断的准确率十分重要。
为此,本文利用机械阻尼系统和电磁振荡系统类比的有效性,从能量转化的角度分析了振荡波衰减的特性,通过定义能量衰减因子Q动态选取出振荡波的有效波段。此外,为了消除现场测试的微小偏差并获取更加稳定的特征信息,本文构建基于数学形态学的振荡波二值图像,结合波形特征关联度(Feature Correlation Degree, FCD)[20]和Tamura纹理特征提出了用于故障区域、故障程度识别的特征参数组合。最后,基于现场变压器对所提方法进行了应用案例分析。
当变压器的注入激励处于高频段时,其绕组整体结构可视为由电阻、电感和电容构成的无源非线性电路网络[21-22],图1a所示为其集总参数电路模 型[23-24]。图1a中,CHS、CMS、CLS为纵向等值电容,CHg、CLg为对地电容,CH-M、CM-L为高中低压绕组间耦合电容,GHS、GMS、GLS、GHg、GLg为电容并联电导,RH、RM、RL为等值电阻,LH、LM、LL与M分别为绕组自感与绕组间互感。振荡波测试原理如下:初始高压电力电子开关-绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)处于断开状态,高压直流电源通过限流电阻和高压电容向变压器绕组充电,绕组中电感和电容开始蓄能。在某一时刻,IGBT动作接地,高压直流电源与限流电阻和大地之间形成回路并不再向绕组供电,由于电感和电容维持电荷的固有特性,绕组进行反复充放电以至在输出端形成阻尼振荡信号,波动过程中出现的波峰和波谷称为极大值点和极小值点。根据标准IEC 60071-2可知,相同激励下的暂态响应(即振荡波)与变压器绕组自身属性相关,因此,振荡波可用于分析变压器绕组的结构变化[15]。
变压器绕组振荡波波形如图1b所示。当IGBT断开时,高压直流电源经限流电阻和高压电容向绕组充能,由于绕组电容和电感作用产生反生振荡,最终趋于能量稳定,此过渡过程为充电过程,当IGBT动作接地时,绕组中储存的能量以阻尼振荡的形式释放,此过程为放电过程。

图1 变压器绕组振荡波原理分析
Fig.1 Schematic of transformer winding oscillation wave
本文搭建了等比例变压器绕组故障模拟试验平台,如图2a所示。该变压器为双柱三绕组结构,距铁心由内而外依次为低压绕组(LV)、中压绕组(MV)、高压绕组(HV),如图2b所示,本文振荡波测试通过高压绕组完成。试验变压器绕组为连续式双饼结构,高、中、低压绕组均由18饼构成,变压器的主要结构参数见表1。
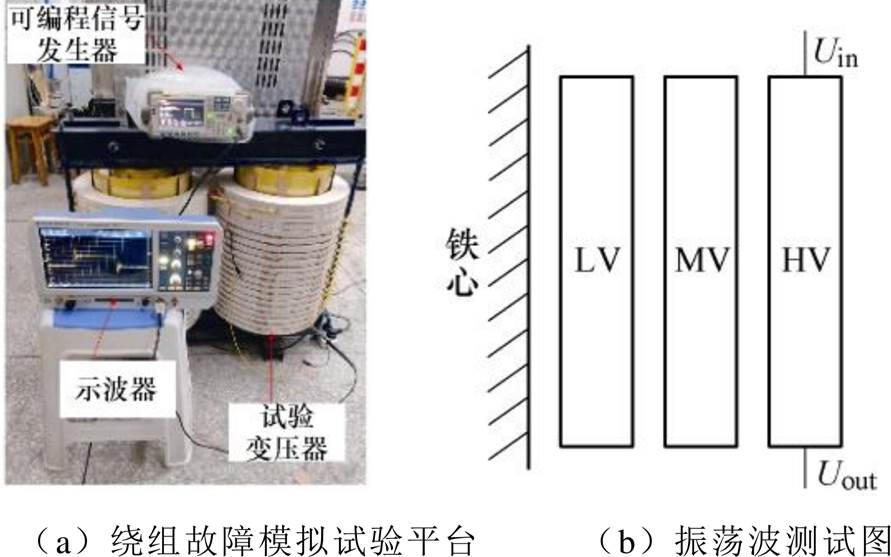
图2 振荡波测试平台
Fig.2 The test platform of oscillation wave
表1 变压器主要部件参数
Tab.1 Parameters of main components of transformer

参 数数 值 铁心高度/mm530 铁心半径/mm53 绕组高度/mm450 高压绕组单饼匝数24 中压绕组单饼匝数16 低压绕组单饼匝数8
为了探究不同故障下变压器绕组的振荡波表现出的差异性,通过绕组故障模拟平台针对高压绕组HV进行轴向移位、局部翘曲、饼间短路和匝间短路多种故障模拟,试验变压器故障设置如图3所示。

图3 试验故障模拟
Fig.3 Test fault simulation
(1)轴向移位故障通过在两线饼间增加某一数量的垫块模拟,其移位程度D[25]为
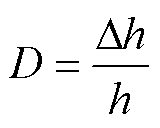 (1)
(1)
式中,Dh为轴向移位高度;h为绕组总高度。
分别将绕组的18个线饼从顶部到底部标记为1~18号,将第4饼、第10饼、第16饼分别设置为上部、中部、下部故障饼。在这3个位置均模拟了1%、3%、5%和7%故障程度的轴向移位故障,每种故障重复试验20次,共进行240组试验。
(2)局部翘曲故障是变压器绕组线饼间的距离发生变化或物理结构受外力影响产生形变,其反映至绕组等效参数上为饼间纵向等值电容发生改变[26]。因此,可采取饼间并联电容模拟此故障。文献[27]中的串联电容解析式,选取150 pF电容模拟局部翘曲故障,分别在试验变压器的上部(第2饼与第3饼,第5饼与第6饼)、中部(第8饼与第9饼,第11饼与第12饼)、下部(第14饼与第15饼,第17饼与第18饼)进行故障模拟,每种故障重复试验20次,共进行120组试验。
(3)饼间短路故障通过短接试验变压器绕组的上部(第2饼与第3饼,第5饼与第6饼)、中部(第8饼与第9饼,第11饼与第12饼)、下部(第14饼与第15饼,第17饼与第18饼)对应的铜鼻子进行故障模拟,每种故障重复试验20次,共进行120组试验。
(4)匝间短路故障由上而下设定将第4饼、第10饼、第16饼分别设置为上部、中部、下部故障饼。
本文以短路匝数占比表征匝间短路故障程度[28]。试验由外向内将每一故障饼的第3匝、第8匝、第13匝、第18匝、第23匝处引出导线模拟不同短路匝数。每一故障饼的第3匝分别与第8匝、第13匝、第18匝、第23匝短接形成短路匝数占比为1%、2%、3%、4%的匝间短路故障,每种故障重复试验20次,共进行240组试验。
基于搭建的振荡波试验平台开展了上述四种故障情况下的数据测试,由于振荡波的充电过程和放电过程呈镜像分布,所以本文针对充电过程对数据进行分析,测试结果如图4所示。图中,轴向移位和匝间短路的图例m-n%表示在m饼(或匝)上设置n%程度的故障;局部翘曲和饼间短路的图例p-q表示在第p饼和第q饼间设置故障;ZC表示绕组正常情况。
由图4可知,在正常情况和四种故障情况下振荡波充电末期均存在大量的不规律极值点和异常波动,且当同种故障发生的位置和程度相近时振荡波提取的特征受干扰严重,因此以现有的振荡波分析方法难以精确地辨别不同故障类型下位置、程度的故障情况。为有效辨识变压器绕组四种故障类型、故障程度、故障区域,需对振荡波数据进一步分析处理。
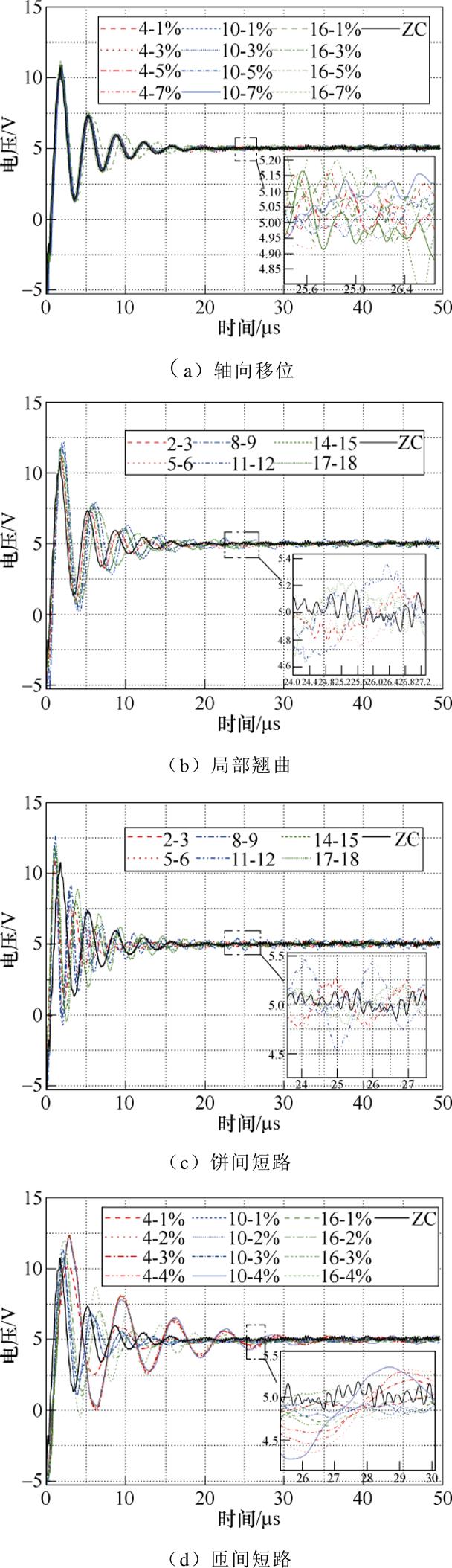
图4 振荡波测试结果
Fig.4 The test results of oscillation waves
针对以上存在的问题,振荡波有效波段具体选取的理论依据如下:
文献[29-30]阐述了电气系统与机械系统类比的有效性,RLC电磁振荡与机械振动有如下类比 关系:
(1)机械阻尼振动中对象的位移(受力)、速度分别与RLC电磁振荡中输出端电压、电流呈对应 关系。
(2)机械阻尼振动中对象的位移-时间二维曲线的振荡是动能和势能不断互相转化的过程,其极大值点和极小值点则表征了动能转化为势能的转折点;RLC电磁振荡中输出端电压-时间二维曲线的振荡是电容存储的电能和电感存储的磁能不断互相转化的过程,其极大值点和极小值点则表征了磁能完全转化为电能的转折点。
(3)机械阻尼与电阻R呈对应关系。在机械阻尼振动中,由于阻尼不断耗能,当动能与势能之和转化为阻尼生成的热能后,振动过程结束;在RLC电磁振荡中当电能与磁场之和转化为电阻生成的热能后,振荡过程结束。
由以上分析可知,随着振荡波充电过程的进行,其振幅的减小是由于电感和电容存储的电磁能耗散为电阻的热能。在工程上,当振荡波的电磁能小于一定阈值时,则可认为其不再波动[31]。但在实际绕组振荡波的分析中,求取每时刻绕组电磁能几乎是不可能的。因此,选取合适的特征参量来表征绕组RLC能量转化情况是确定振荡波有效波段的关键。在机械阻尼振动中,将质点处于静止的位置称为平衡点,质点连续两次通过平衡位置并沿相同方向运动所需的时间间隔T是相同的[32],将此定义映射到电磁振荡中,如图5所示。u=u0为电压振荡的平衡位置,电压沿相同方向振荡趋势连续两次与平衡位置的交点称为平衡点,其坐标分别为(t1, u0)、(t2, u0)、(t3, u0),两平衡点间的时间间隔记为周期T,T=t3-t2=t2-t1。u1、u2和u3、u4分别为相邻周期内的波峰值、波谷值。
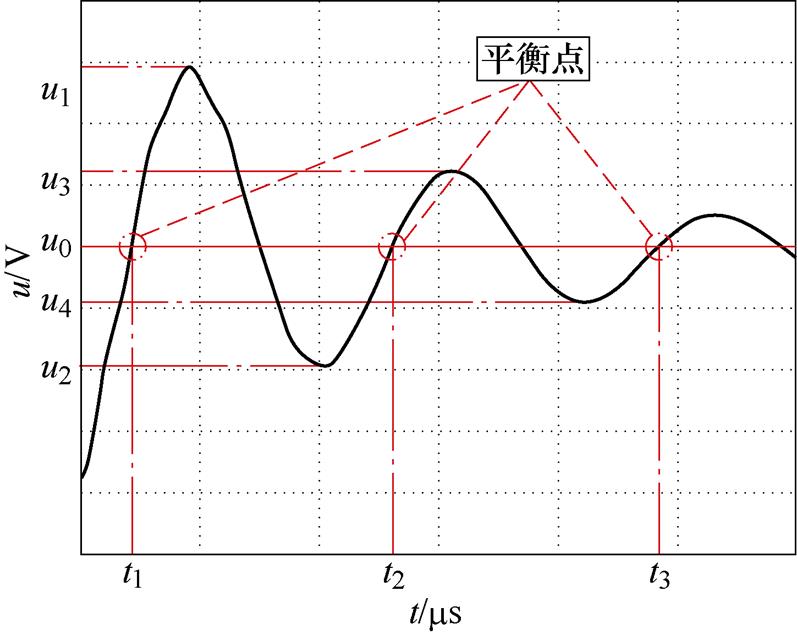
图5 电磁振荡的平衡点
Fig.5 Equilibrium point of electromagnetic oscillation
由于机械阻尼振动的机械能与位移振幅的二次方成正比[32],如式(2)所示,则通过上述类比关系可得电磁振荡的电磁能与电压幅值的二次方成正比,电压振荡波在每个周期内(即每两相邻平衡点间)的能量是逐渐衰减的。因此,可利用两相邻平衡点之间电压振幅二次方值的衰减变化情况反映阻尼特性下能量转化情况,当衰减至某一状态时,可认为振荡行为完毕,从而不再分析后续存在大量异常振荡行为的波段,进而判断出利于振荡波后续特征提取与分析的有效波段。
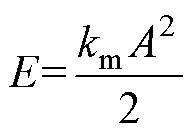 (2)
(2)
式中,E为机械能;km为劲度系数;A为位移振幅。
结合文献[33]中衰减系数的定义方法和振荡波衰减的本质特征,定义能量衰减因子为
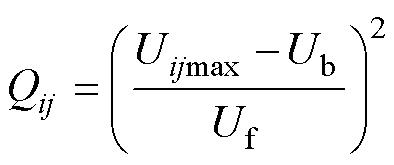 (3)
(3)
式中,Qij为两相邻平衡点i和j间的能量衰减因子,i=0, 1, 2,…,j=1, 2, 3,…,j=i+1;Uijmax为两相邻平衡点i和j间电压波峰值;Ub为振荡波衰减完毕时的稳定值;Uf为第一、二个平衡点间的电压波峰值。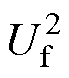 表征了在整个衰减过程中电压振荡波能量的基值,随着电能与磁能间不断转化和阻尼的不断耗能,电压开始衰减振荡(即电压波峰值逐渐下降),当电压下降至Ub时,电磁能之间不再发生交换,振荡完毕。(Uijmax-Ub)2表征了电压振荡波在两相邻平衡点i和j间具有的进行电磁转化的能量值,(Uijmax-Ub)2/
表征了在整个衰减过程中电压振荡波能量的基值,随着电能与磁能间不断转化和阻尼的不断耗能,电压开始衰减振荡(即电压波峰值逐渐下降),当电压下降至Ub时,电磁能之间不再发生交换,振荡完毕。(Uijmax-Ub)2表征了电压振荡波在两相邻平衡点i和j间具有的进行电磁转化的能量值,(Uijmax-Ub)2/ 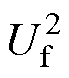 则表征了在每个周期内振荡波进行电磁转化的能量的耗散情况。当Qij小于某一阈值m时,认为包含前j个极小值点的振荡波为有效的波段,后续波段不再进行分析。
则表征了在每个周期内振荡波进行电磁转化的能量的耗散情况。当Qij小于某一阈值m时,认为包含前j个极小值点的振荡波为有效的波段,后续波段不再进行分析。
根据文献[31],当响应动态值下降至响应初始值的4.98%时,在工程上可认为动态电路的过渡过程结束。因为上述已知电磁振荡的电磁能与电压幅值的二次方成正比,所以可推得:当能量下降至初始值0.248%时,动态电路的过渡过程结束。因此,本文选取阈值m=0.248%。基于本文搭建的试验平台进行了大量试验验证,当Qij≤0.248%时,振荡波几乎不发生明显波动,且在此时域区间内波形具有平滑性、规律性的特点,适于进行后续特征提取及故障诊断分析。
动态波段选取的流程如图6所示,具体步骤 如下:
(1)通过Matlab获得正常和故障情况下的振荡波数据。
(2)采用滑动平均法去除曲线上的较大毛刺 干扰。
(3)计算相邻平衡点ti和tj间的能量衰减因子Qij,当Qij小于阈值m时,取包含前j个极小值点的振荡波为有效的波段。
(4)根据以上流程可确定出振荡波有效、受干扰较小的时域区间,后续特征提取与诊断分析在此区间展开。
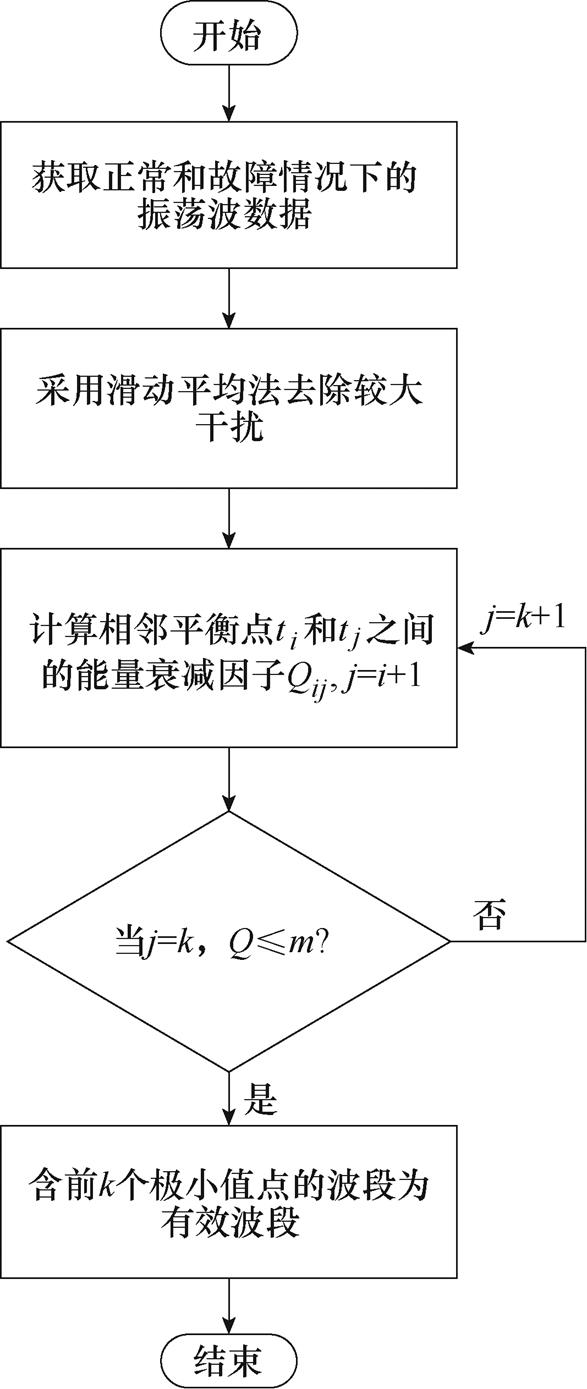
图6 动态波段选取流程
Fig.6 Dynamic wave band selection process
振荡波有效波段的选取结果如图7所示。从图中可以看出,经过动态选取后的四种故障下的振荡波波形呈现出规律的衰减振荡,且较正常情况具有丰富的特征变化:
(1)轴向移位故障下振荡波有效波段均具有5个波峰,上部和中部故障整体波形向右移动,下部故障除7%故障程度外均向右偏移,随故障程度加深波形整体具有向左移动趋势,下部故障1%故障程度下振荡波振荡时间明显增大。
(2)局部翘曲故障下振荡波有效波段均具有5个波峰,上、中、下部故障波形均向右偏移,中、下部故障的振荡波振幅明显增大,且其振荡时间明显增大。
(3)饼间短路上部故障的振荡波有效波段具有5个波峰,中部故障的振荡波具有6个波峰,下部故障的振荡波最高达7个波峰,上、中、下部故障波形均向左偏移,上、中部故障的振荡波振荡时间明显减小,中、下部故障的振荡波振幅增大。
(4)匝间短路上部故障除1%故障程度外振荡波有效波段均具有5个波峰,1%故障程度则较正常情况下缩减为3个波峰,中部故障除4%故障程度外缩减为4个波峰,4%故障程度具有5个波峰,下部故障1%故障程度具有5个波峰,2%和3%故障程度具有4个波峰,4%故障程度具有6个波峰,上、中、下部故障波形均向右偏移且偏移程度较大,上部故障除1%故障程度外振荡时间明显增大,中部故障和除4%故障外振荡时间略微减小,下部故障除2%故障程度振荡时间均明显增大。
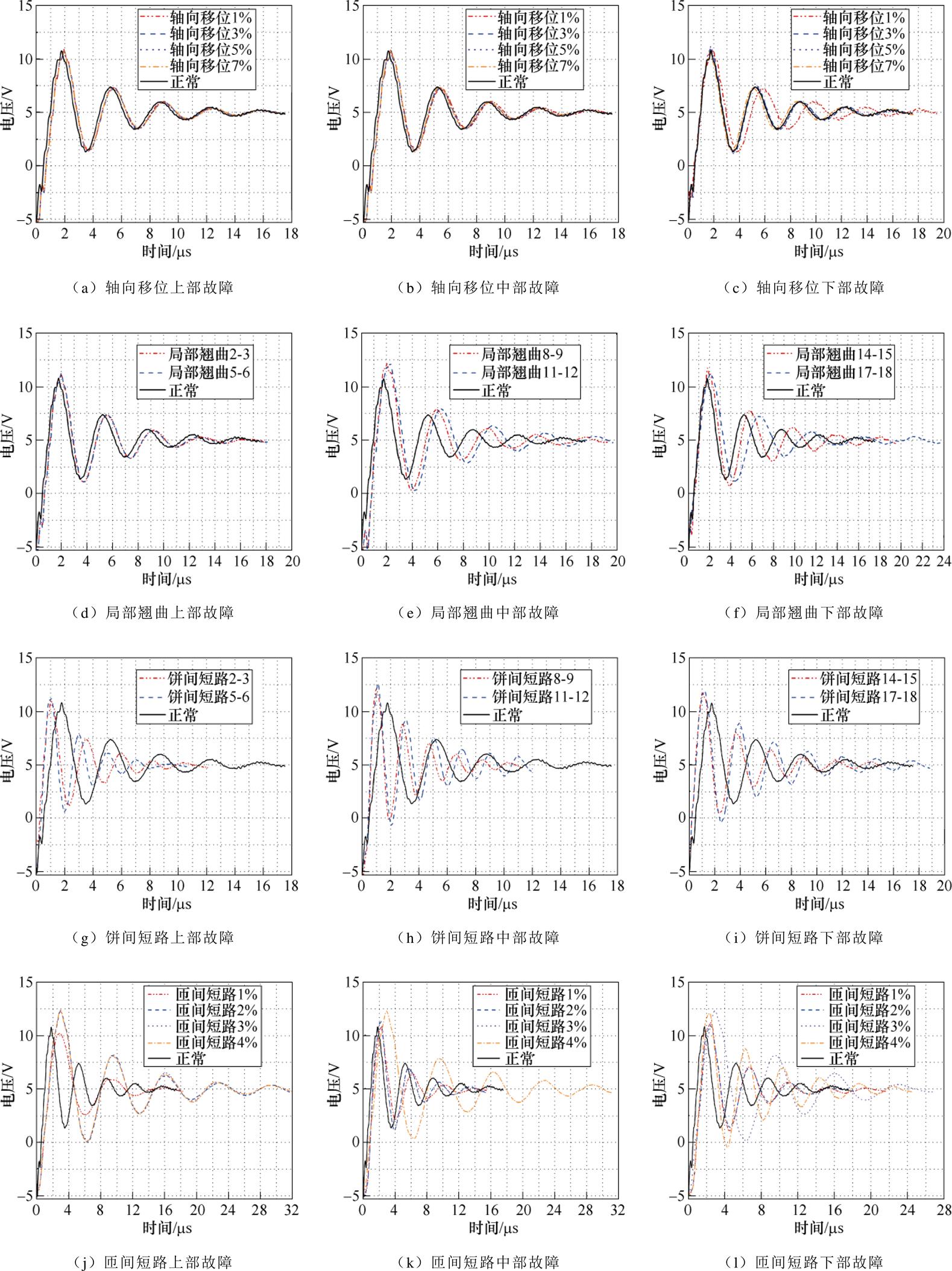
图7 振荡波波段选取结果
Fig.7 Selection results of oscillation waves band
由动态选取出的振荡波有效波段在不同故障下展现出的差异表明其对绕组状态具有高灵敏性,可在此基础上通过提取特征进行细致分析。
4.1.1 波形特征
波形特征提取作为常用的数据分析工具,可以有效地表征振荡波的信息。常用以下统计指标描绘波形特征[9, 16]:方差(variance)、峭度(kurtosis)、方均根(root mean square)、波形因子(waveform factor)、峰值因子(peaking factor)、裕度因子(clearance factor)、脉冲因子(impulse factor)、方根幅值(mean square amplitude)。由于波形特征中存在多个指标含义相近,因此,为了使提取的波形特征更加直观,本文采用特征关联度FCD对波形特征进行描绘说明,特征关联度公式为
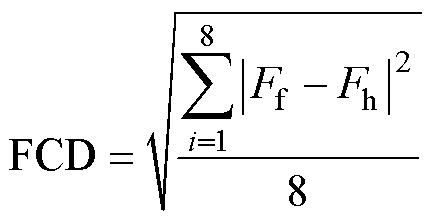 (4)
(4)
式中,Ff和Fh分别为故障和正常情况下的特征值。
4.1.2 基于二值化的Tamura纹理特征
由于特征变化通常出现在极值点中[34],且现有变压器的振荡波时域特征提取仅针对单一的曲线特征进行分析,辨识精度较差,所以本文通过构建极值点间的二值化图像来获取更多的辨识信息[35-37],如图8所示。
考虑到振荡波现场测试时的复杂干扰[18],本文利用数学形态学分析方法中的扩张和腐蚀对二值图像进行处理[38],二值化具体处理方法可见文献[39-40]。基于上述二值化图像,本文利用Tamura纹理特征进行特征信息的提取。Tamura纹理特征具有图像的重要视觉特征,有较好的适应性与鲁棒性,其共有六个指标,分别为粗糙度(coarseness, Fcrs)、对比度(contrast, Fcon)、方向度(directionality, Fdir)、线性度(line-likeness, Flin)、规则度(regularity, Freg)、粗略度(roughness, Frgh)[41]。对于构建的极值点间的二值化图像来说,振荡周期、衰减速度和极值点的相对位置等包含丰富的辨识信息。
图8 构建的振荡波二值化图像
Fig.8 Binary image of oscillation wave
因此,本文针对振荡波二值化图像的粗糙度、对比度、方向度、粗略度进行分析,具体计算公式如下:
1)粗糙度Fcrs
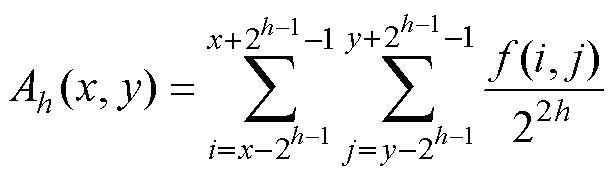 (5)
(5)
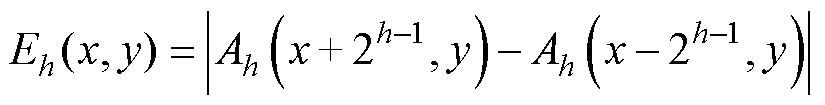 (6)
(6)
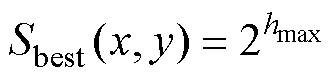 (7)
(7)
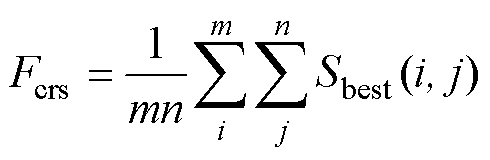 (8)
(8)
式中,在2h×2h个像素的活动窗口,A(x, y)为像素的平均强度值;f(i, j)为位于(i, j)处像素的灰度值;Eh(x, y)为水平方向上互不重叠的窗口之间的平均强度差(垂直方向同理可写出);hmax为使水平和垂直方向的Eh(x, y)达到最大值时的h值;Sbest为最佳尺寸;m和n为图片有效的宽度和高度。
2)对比度Fcon[41]
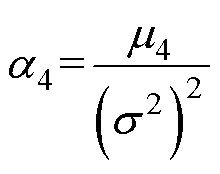 (9)
(9)
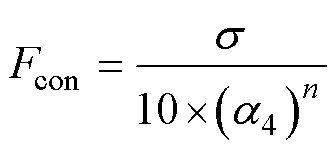 (10)
(10)
式中,a4为峭度;m4为四次矩;s 为标准差;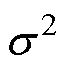 为方差;n为一个优化对比度的正数,本文取n=1/4。
为方差;n为一个优化对比度的正数,本文取n=1/4。
3)方向度Fdir
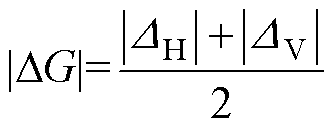 (11)
(11)
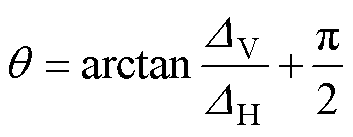 (12)
(12)
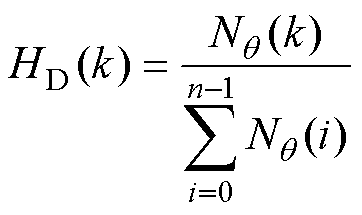 (13)
(13)
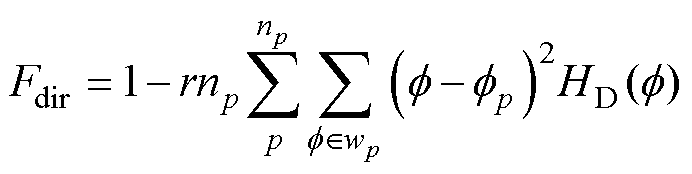 (14)
(14)
式中,|DG|为直方图像素梯度的幅值;DH和DV分别为图像卷积预设三维卷积核所得水平和垂直方向上的变化量;q 为直方图像素梯度的局部边缘方向;Nq (k)为(2k-1)p/(2n)≤q<(2k+1)/(2n)和|DG|大于等于一定阈值t(本文取t =12)的条件下定义的像素点的数量,k=0, 1,…, n-1(本文取n=16);np为峰值的数量;fp为HD中第p个峰值的位置;wp为波谷间第p个峰值的范围;f 为量化方向码;r为与f 量化程度相关的标准化因子。
4)粗略度Frgh
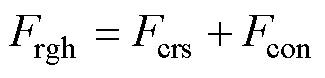 (15)
(15)
基于二值化的Tamura纹理特征提取具体步骤如下:
(1)获得振荡波有效波段的三原色光(Red- Green-Blue, RGB)模式图。
(2)连接振荡波原点与第一个极小值点构成线段l1,第一个极小值点与第二个极小值点构成l2,第二个极小值点与第三个极小值点构成l3,…,依次连接两两相邻的极小值点,与数据曲线形成闭合 区域。
(3)将振荡波图像进行二值化处理,二值图像矩阵元素中的1表示图像背景颜色,0表示振荡波与极小值点连线间的区域。
(4)利用数学形态学分析方法中的扩张和腐蚀对二值图像进行处理,运算的基本表达式为
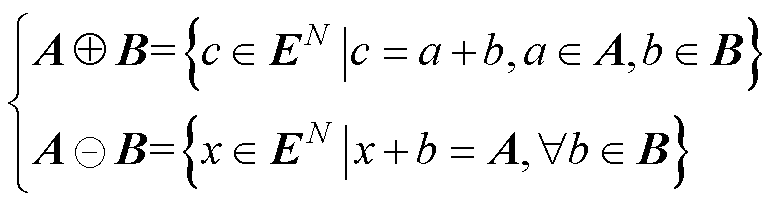 (16)
(16)
式中,A为二值图像矩阵;B为结构元素;A和B分别为N维空间(EN)中的具有元素a和b的集合。
(5)基于上述二值化图像,提取粗糙度Fcrs、对比度Fcon、方向度Fdir、粗略度Frgh进行故障诊断分析。
本文基于上述选取出的原始波段,利用波形FCD对轴向移位、饼间短路、局部翘曲和匝间短路四种故障类型进行划分,分类结果如图9所示。可以看出,据波形FCD对四种故障分类效果明显,轴向移位FCD分布在1.15左右,局部翘曲FCD分布在1.21~1.33之间,主要集中在1.28附近,饼间短路FCD分布在1.80~1.83之间,匝间短路FCD分布在1.59~1.64之间,整体分类效果显著,故障类型辨识度高。
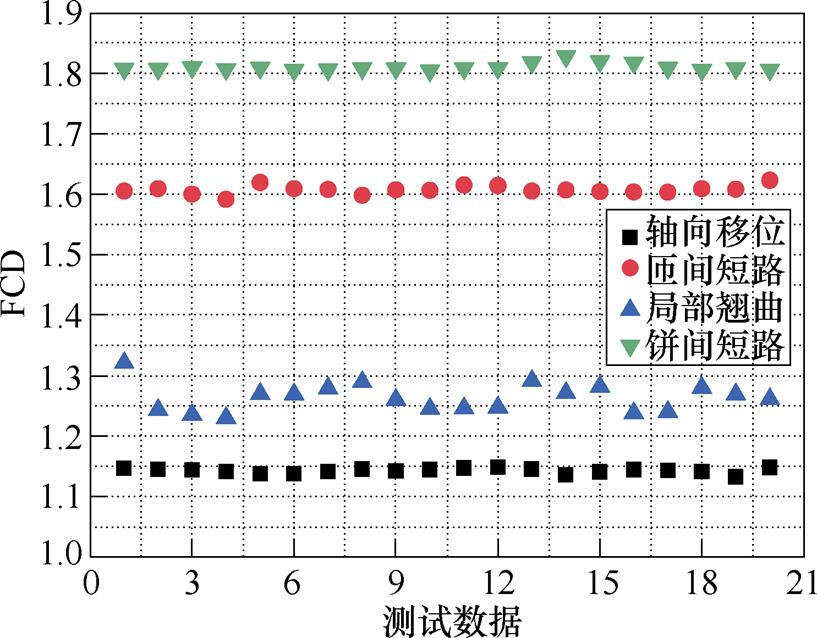
图9 绕组故障类型特征分析
Fig.9 The characteristics analysis of winding fault types
本文基于上述选取出的波段的二值化图像,利用Tamura纹理特征中的粗糙度Fcrs、方向度Fdir和粗略度Frgh分析轴向移位的故障程度;利用粗糙度Fcrs、对比度Fcon和方向度Fdir分析匝间短路的故障程度,结果如图10所示,将正常情况作为基值进行标准化处理,具体分析如下:
(1)轴向移位故障:1%故障下Fdir集中在0.81~1.02区间内,其他故障程度均不在此区间内;3%故障下Fdir集中在1.02~1.15区间内,均大于其他故障程度的Fdir值;5%故障下Fcrs处于1.08~1.10区间内,其他故障程度均不在此区间;7%故障Fcrs处于1.05~1.13区间内,与其他故障程度区分明显。
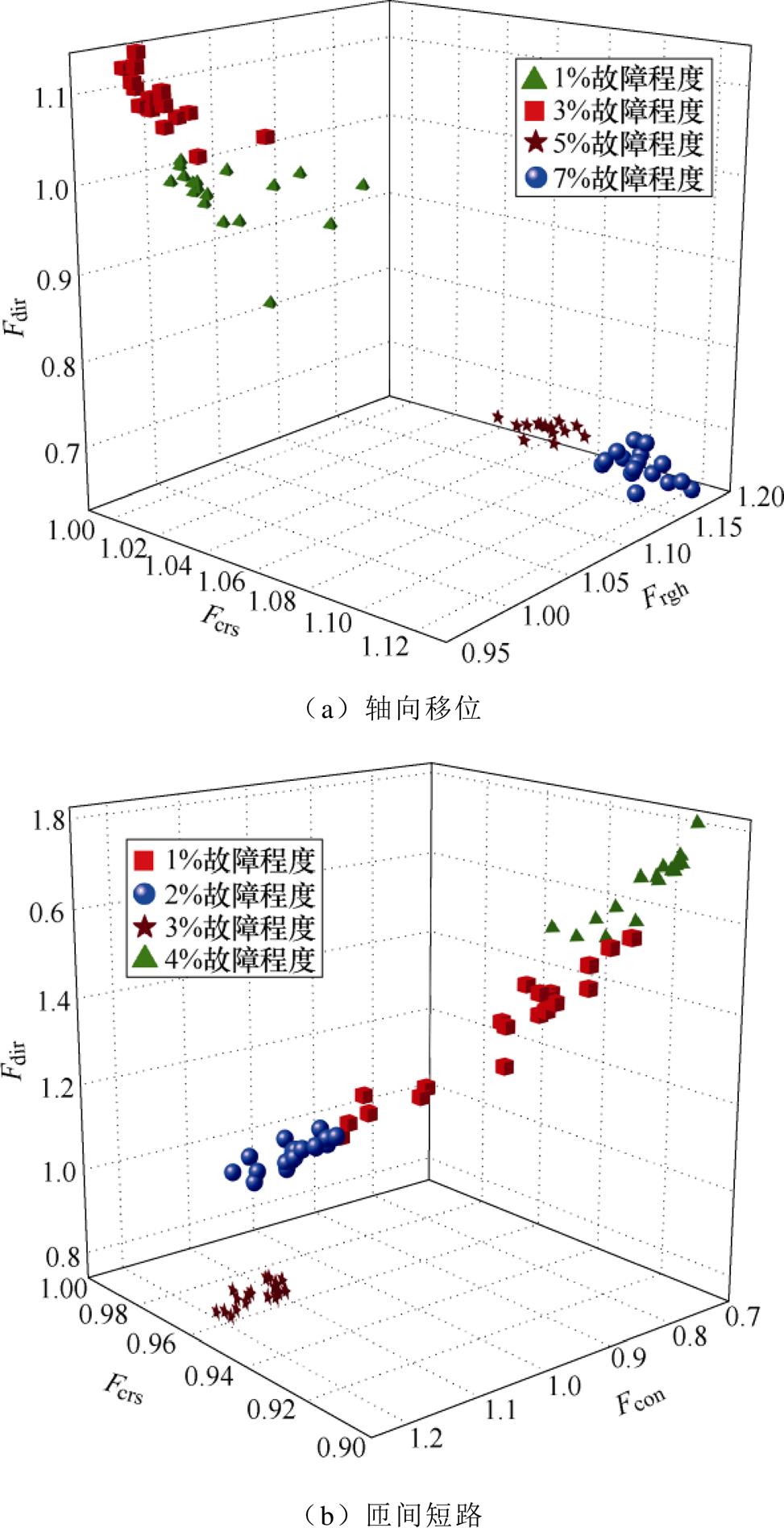
图10 绕组故障程度特征分析
Fig.10 Characteristic analysis of winding fault degree
(2)匝间短路故障:1%故障下Fcon在0.80~1.00区间内,Fdir处于1.06~1.57之间,通过Fcon和Fdir与其他故障程度区分明显;2%故障下Fcrs处于0.97~1.00区间内,其他故障程度均不在此区间内;3%故障下Fdir处于0.74~0.87之间,其他故障程度均不在此区间;4%故障下Fcon处于0.71~0.80之间,与其他故障程度区分明显。
本文基于上述选取出的波段的二值化图像,利用Tamura纹理特征中方向度Fdir、粗略度Frgh分析轴向移位和饼间短路的故障区域;利用粗糙度Fcrs、对比度Fcon分析局部翘曲和匝间短路的故障区域,结果如图11所示,将正常情况作为基值进行标准化处理,具体分析如下:
(1)轴向移位故障:上部故障与中部故障大致以Fdir=1.08为分界线,其中上部故障的Fdir最小值为0.95,中部故障的Fdir最大值为1.14,上部故障的Frgh值相较于中部故障整体偏大;下部故障的Fdir值处于0.62~0.72之间,整体聚类效果明显。
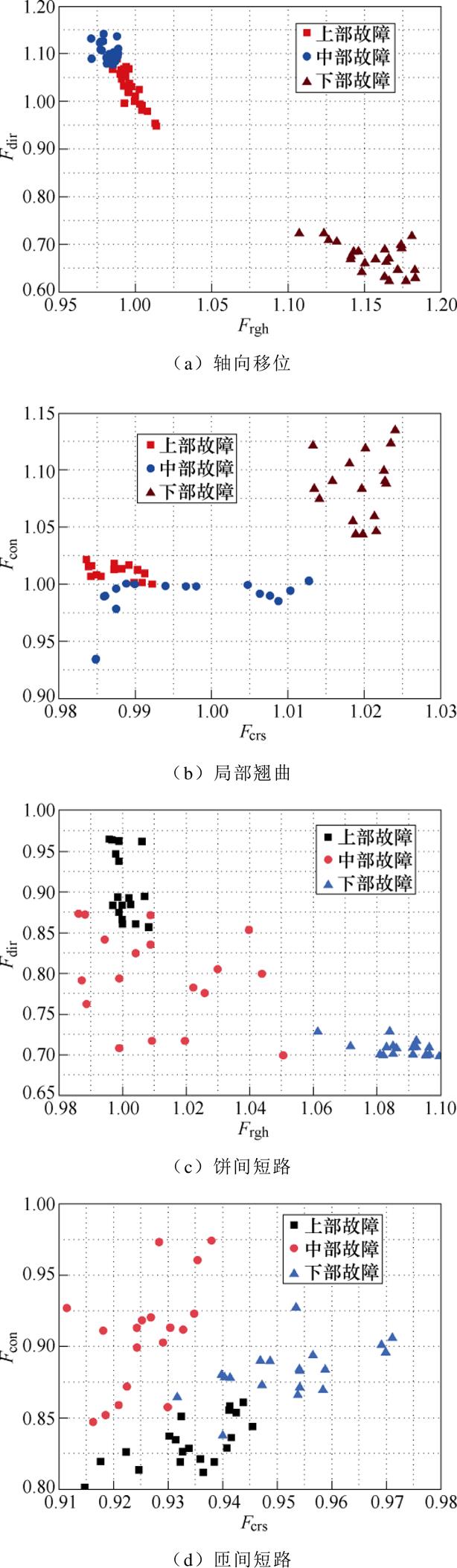
图11 绕组故障区域特征分析
Fig.11 Characteristic analysis of winding fault area
(2)局部翘曲故障:上部故障和中部故障大致以Fcon=1.00为分界线,上部故障的Fcon最大值为1.02,中部故障的Fcon最小值为0.93;下部故障的Fcon值处于1.04~1.13之间,整体聚类效果明显。
(3)饼间短路故障:上部故障的Fdir分布在0.86~0.97之间;中部故障的Fdir大多数处于0.70~0.85之间,Frgh分布在0.99~1.05之间;下部故障与其他故障的分界线为Frgh=1.06,其最大值为1.10。
(4)匝间短路故障:匝间短路上部故障的Fcon最大值为0.86,最小值为0.80,中部故障和下部故障的Fcon值大多数大于0.86;中部故障的Fcon大体分布在0.85~0.97之间,Fcrs大体分布在0.91~0.94之间;下部故障的Fcon大体分布在0.86~0.92之间,Fcrs大体分布在0.94~0.97之间。
本文以沈阳变压器研究院110 kV电力变压器为研究对象开展相关测试研究,如图12所示。变压器部分参数见表2。高压绕组和中压绕组为星形联结,低压绕组为三角形联结。分别对高、中、低压绕组的A、B、C三相绕组进行测试,测试方案为:高压、中压绕组以中心点O为信号注入点,分别以A、B、C三相的套管末屏作为信号采集点;低压绕组选取A、B、C三相中的任意两相,互相作为信号注入点和信号采集点。

图12 110 kV电力变压器试验测试
Fig.12 110 kV power transformer test
表2 110 kV电力变压器参数
Tab.2 110 kV power transformer parameters
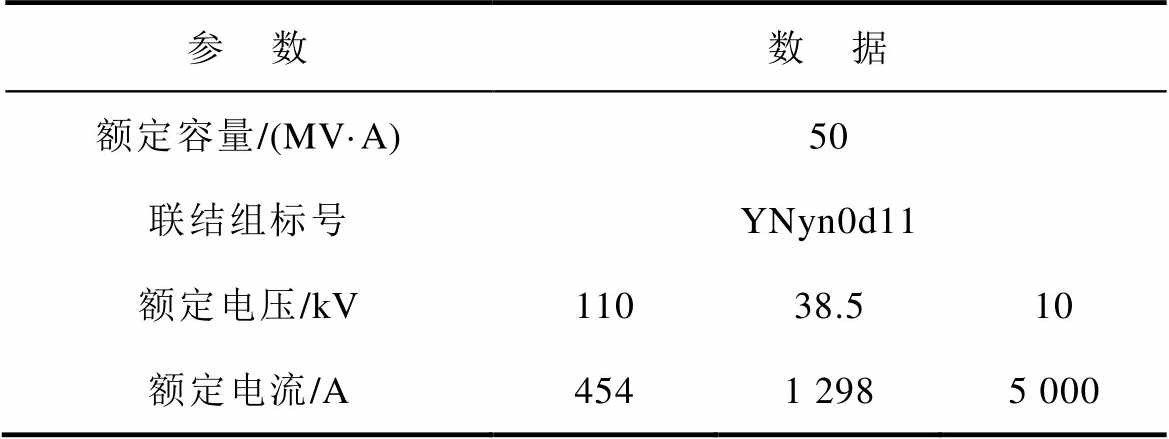
参 数数 据 额定容量/(MV·A)50 联结组标号YNyn0d11 额定电压/kV11038.510 额定电流/A4541 2985 000
测试结果表明:高压绕组与低压绕组的测试曲线基本无明显变化,波形FCD稳定在0附近,波动较小可以忽略,在此不详细描述。A相中压绕组测试曲线与参考曲线相比存在一定差异,结果如图13所示。
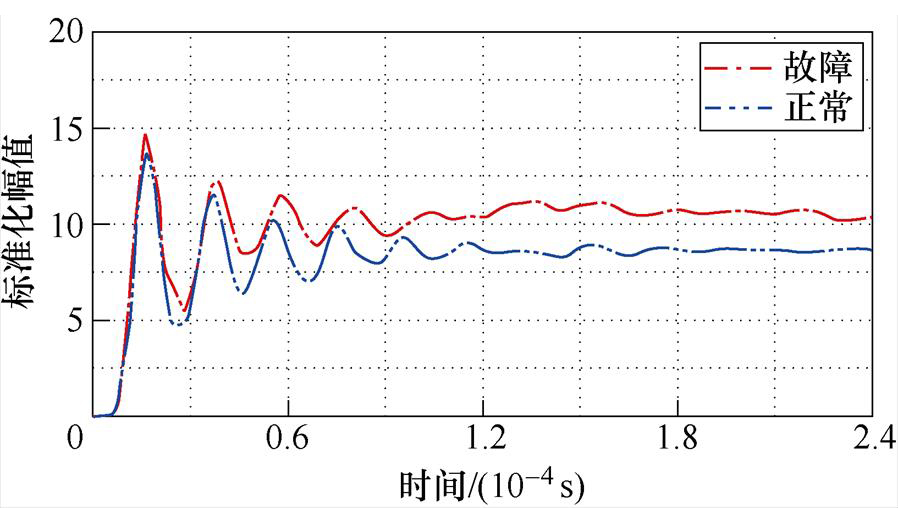
图13 110 kV电力变压器测试曲线
Fig.13 Test curves of 110 kV power transformer
按照本文上述方法选取110 kV电力变压器原始测试曲线的有效波段,结果如图14所示。在有效波段内提取波形FCD及基于二值化的Tamura纹理特征,结果见表3。
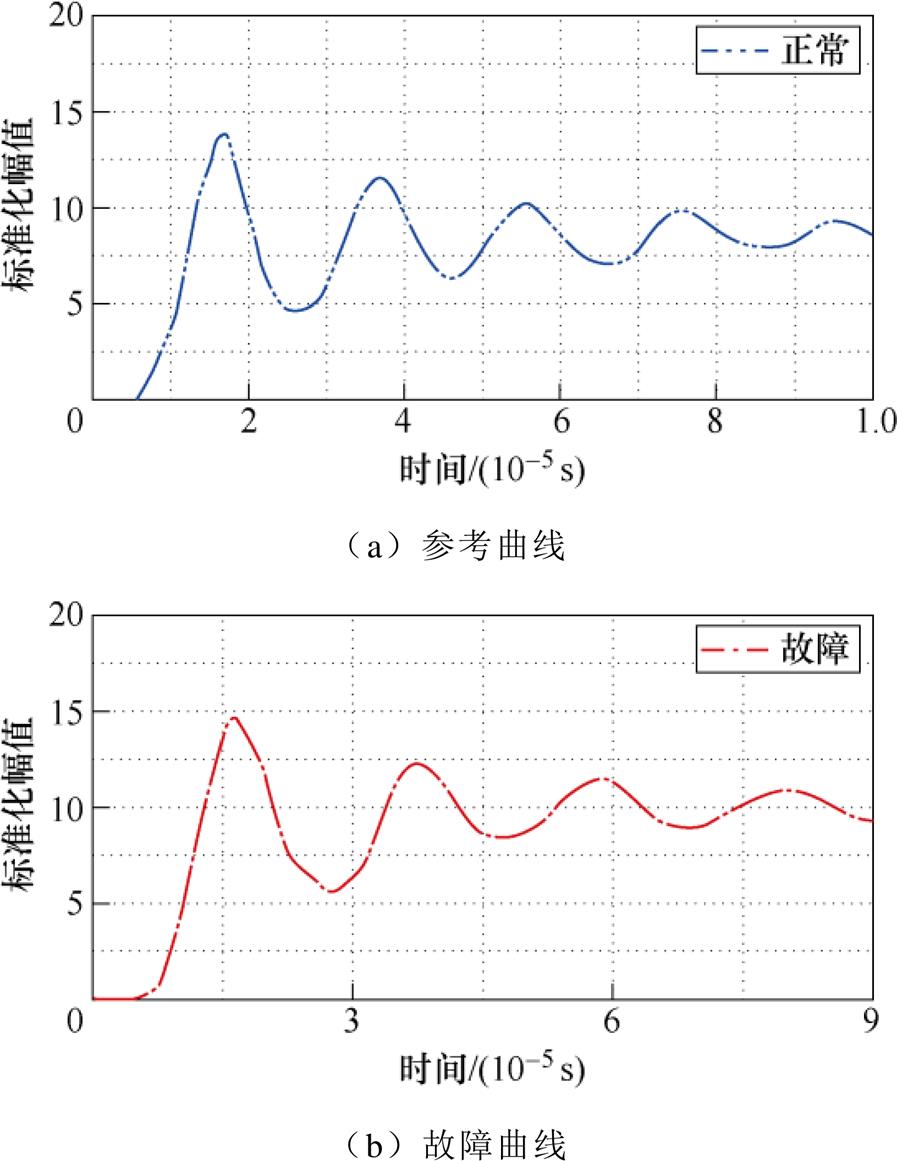
图14 测试曲线的有效波段
Fig.14 Effective band of test curves
表3 电力变压器特征参数
Tab.3 Characteristic parameters of power transformer
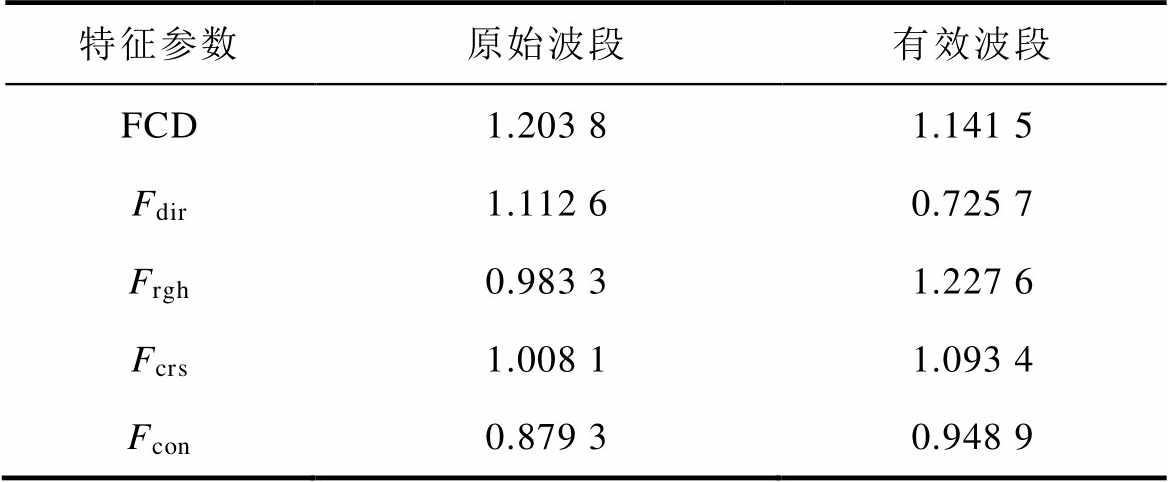
特征参数原始波段有效波段 FCD1.203 81.141 5 Fdir1.112 60.725 7 Frgh0.983 31.227 6 Fcrs1.008 11.093 4 Fcon0.879 30.948 9
相似结构的变压器在某一故障下的阻尼振荡曲线的变化规律是大致相似的[42],且FCD和Tamura均为相对值,因此等比例试验平台的特征值变化规律可为现场变压器提供参考。参考图9~图11分析实际变压器的故障情况。根据表3的计算可知:测试曲线原始波段FCD值为1.203 8,区分轴向移位和局部翘曲困难;根据测试曲线有效波段的FCD值和基于二值化的Tamura纹理特征,可推断出电力变压器上部区域存在重度轴向移位故障。
为了验证上述分析方法的有效性,现场开展变压器检修。利用起吊有载调压开关,通过视频探头对内部绕组结构进行分析。检修结果表明,电力变压器中压绕组的上部区域存在线圈明显移位的情况。检修结果与上述理论分析一致,验证了本文分析方法的有效性。
1)经过动态选取出的有效波段衰减振荡规律性明显且干扰信息少,可提取特征丰富,有利于后续通过特征提取进行绕组故障诊断。轴向移位、局部翘曲、饼间短路和匝间短路四种故障下的振荡波波形彼此间有一定的差异性,而且相比于正常绕组表现出较明显的变化规律,利用波形FCD在识别绕组故障类型时效果突出;同一故障类型下的振荡波在不同故障区域和故障程度下表现出的差异性较小,利用四种Tamura纹理特征的不同组合在识别故障程度和故障种类时均表现出良好的分类效果。
2)本文提出的基于振荡波动态波段选取方法应用在变压器绕组故障分析时,通过判断能量衰减因子Qij≤0.248%时包含前j个极小值点的振荡波波段为有效波段,从而确定出后续特征提取所在的波段,结合波形FCD和基于二值化的Tamura纹理特征诊断轴向移位、局部翘曲、饼间短路和匝间短路四种故障类型及其故障区域和故障程度,少部分特征存在重叠混淆现象,但整体具有良好的分离与聚类性。
参考文献
[1] 张冰倩, 咸日常, 于洋, 等. 匝间短路故障下电力变压器绕组的物理特征分析[J]. 高电压技术, 2021, 47(6): 2177-2185.
Zhang Bingqian, Xian Richang, Yu Yang, et al. Analysis of physical characteristics of power trans- former windings under inter-turn short circuit fault[J]. High Voltage Engineering, 2021, 47(6): 2177-2185.
[2] 韩金华, 张健壮. 大型电力变压器典型故障案例分析与处理[M]. 北京: 中国电力出版社, 2012.
[3] 汲胜昌, 王世山, 李清泉, 等. 用振动信号分析法监测变压器绕组状况[J]. 高电压技术, 2002, 28(4): 12-13, 15.
Ji Shengchang, Wang Shishan, Li Qingquan, et al. The application of vibration method in monitoring the condition of transformer winding[J]. High Voltage Engineering, 2002, 28(4): 12-13, 15.
[4] 黄华, 周建国, 姜益民, 等. 阻抗法和频响法诊断电力变压器绕组变形[J]. 高电压技术, 1999, 25(2): 70-73.
Huang Hua, Zhou Jianguo, Jiang Yimin, et al. Diagnosis of winding deformation of transformer by impedance method and FRA[J]. High Voltage Engin- eering, 1999, 25(2): 70-73.
[5] Akhmetov Y, Nurmanova V, Bagheri M, et al. A new diagnostic technique for reliable decision-making on transformer FRA data in interturn short-circuit con- dition[J]. IEEE Transactions on Industrial Informatics, 2021, 17(5): 3020-3031.
[6] Nurmanova V, Bagheri M, Zollanvari A, et al. A new transformer FRA measurement technique to reach smart interpretation for inter-disk faults[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1508- 1519.
[7] Tahir M, Tenbholen S, Miyazaki S. Analysis of statistical methods for assessment of power trans- former frequency response measurements[J]. IEEE Transactions on Power Delivery, 2021, 36(2): 618-626.
[8] 赵仲勇, 唐超, 李成祥, 等. 基于频率响应二值化图像的变压器绕组变形故障诊断方法[J]. 高电压技术, 2019, 45(5): 1526-1534.
Zhao Zhongyong, Tang Chao, Li Chengxiang, et al. Diagnosis method of transformer winding defor- mation faults based on frequency response binary image[J]. High Voltage Engineering, 2019, 45(5): 1526-1534.
[9] 付强, 宁文瑶, 刘代飞. 基于多指标融合的绕组混合故障分析方法[J]. 高电压技术, 2021, 47(2): 537-545.
Fu Qiang, Ning Wenyao, Liu Daifei. Analysis method for mixed faults in winding based on multi-index fusion[J]. High Voltage Engineering, 2021, 47(2): 537-545.
[10] Aljohani O, Abu-Siada A. Application of DIP to detect power transformers axial displacement and disk space variation using FRA polar plot signature[J]. IEEE Transactions on Industrial Informatics, 2017, 13(4): 1794-1805.
[11] Rahimpour E, Jabbari M, Tenbohlen S. Mathematical comparison methods to assess transfer functions of transformers to detect different types of mechanical faults[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2544-2555.
[12] 孙翔, 何文林, 詹江杨, 等. 电力变压器绕组变形检测与诊断技术的现状与发展[J]. 高电压技术, 2016, 42(4): 1207-1220.
Sun Xiang, He Wenlin, Zhan Jiangyang, et al. Current status and development of test and diagnostic technique of transformer winding deformation[J]. High Voltage Engineering, 2016, 42(4): 1207-1220.
[13] 刘勇, 汲胜昌, 杨帆, 等. 检测变压器故障的扫频阻抗法特性研究及应用[J]. 高电压技术, 2016, 42(10): 3237-3245.
Liu Yong, Ji Shengchang, Yang Fan, et al. Characteri- stics and application of sweep frequency impedance method for detecting transformer fault[J]. High Voltage Engineering, 2016, 42(10): 3237-3245.
[14] 赵新. 变压器绕组变形检测技术分析研究[J]. 技术与市场, 2020, 27(10): 77-78.
Zhao Xin. Analysis and research of transformer winding deformation detection technology[J]. Tech- nology and Market, 2020, 27(10): 77-78.
[15] 吴振宇, 周利军, 周祥宇, 等. 基于振荡波的变压器绕组故障诊断方法研究[J]. 中国电机工程学报, 2020, 40(1): 348-357, 401.
Wu Zhenyu, Zhou Lijun, Zhou Xiangyu, et al. Research on fault diagnosis method of transformer winding based on oscillatory wave[J]. Proceedings of the CSEE, 2020, 40(1): 348-357, 401.
[16] 周利军, 周猛, 李沃阳, 等. 基于振荡波多特征融合的变压器绕组故障诊断方法[J]. 电力自动化设备, 2022, 42(12): 191-196, 203.
Zhou Lijun, Zhou Meng, Li Woyang, et al. Trans- former winding fault diagnosis method based on oscillating wave multi-feature fusion[J]. Electric Power Automation Equipment, 2022, 42(12): 191-196, 203.
[17] Wu Zhenyu, Zhou Lijun, Lin Tong, et al. A new testing method for the diagnosis of winding faults in transformer[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(11): 9203-9214.
[18] Gonzales Arispe J C, Mombello E E. Detection of failures within transformers by FRA using multire- solution decomposition[J]. IEEE Transactions on Power Delivery, 2014, 29(3): 1127-1137.
[19] Wu Zhenyu, Zhou Lijun, Wang Dongyang, et al. Feature analysis of oscillating wave signal for axial displacement in autotransformer[J]. IEEE Transa- ctions on Instrumentation and Measurement, 2021, 70: 1-13.
[20] 周利军, 林桐, 江飞明, 等. 频响多级分解与图像特征在自耦变压器绕组故障的应用研究[J]. 高电压技术, 2021, 47(10): 3617-3627.
Zhou Lijun, Lin Tong, Jiang Feiming, et al. Application research of autotransformer winding fault by using FRA multi-decomposition and image features[J]. High Voltage Engineering, 2021, 47(10): 3617-3627.
[21] 范学鑫, 杨北超, 揭贵生, 等. 考虑漏感频变特性的三相立体卷铁心变压器建模及分析[J]. 电工技术学报, 2023, 38(1): 140-152.
Fan Xuexin, Yang Beichao, Jie Guisheng, et al. Modeling and analysis of 3D wound core transformer considering frequency-dependent characteristics of leakage inductance[J]. Transactions of China Elec- trotechnical Society, 2023, 38(1): 140-152.
[22] 杨北超, 范学鑫, 王瑞田, 等. 考虑铁心非线性的三相立体卷铁心变压器建模及空载特性分析[J]. 电工技术学报, 2022, 37(9): 2263-2274.
Yang Beichao, Fan Xuexin, Wang Ruitian, et al. Modeling and no-load characteristics analysis of 3D wound core transformer considering core non- linearity[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2263-2274.
[23] Insulation coordination in part 2: application guide- lines: the international electrotechnical commission IEC 60071-2[S]. Geneva: International Electrotech- nical Commission, 2018.
[24] 严静荷. 基于属性选择和支持向量机的高铁自耦变压器绕组故障诊断研究[D]. 成都: 西南交通大学, 2019.
[25] Hashemnia N, Abu-Siada A, Islam S. Improved power transformer winding fault detection using FRA diagnostics-part 1: axial displacement simulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(1): 556-563.
[26] Usha K, Usa S. Inter disc fault location in transformer windings using SFRA[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(6): 3567-3573.
[27] Abeywickrama N, Serdyuk Y V, Gubanski S M. High- frequency modeling of power transformers for use in frequency response analysis (FRA)[J]. IEEE Transa- ctions on Power Delivery, 2008, 23(4): 2042- 2049.
[28] 张宗成. 基于小波分析的变压器绕组匝间短路检测方法研究[D]. 北京: 华北电力大学, 2015.
[29] Bertuccio G. On the physical origin of the electro- mechano-acoustical analogy[J]. The Journal of the Acoustical Society of America, 2022, 151(3): 2066- 2076.
[30] Bloch A. Electromechanical analogies and their use for the analysis of mechanical and electromechanical systems[J]. Journal of the Institution of Electrical Engineers-Part I: General, 1945, 92(52): 157-169.
[31] 邱关源原著, 罗先觉修订. 电路[M]. 5版. 北京: 高等教育出版社, 2006.
[32] Ginsberg J H. Mechanical and structural vibrations: theory and applications[M]. New York: Wiley, 2001.
[33] 李谦, 张波, 蒋愉宽, 等. 变电站内短路电流暂态过程及其影响因素[J]. 高电压技术, 2014, 40(7): 1986-1993.
Li Qian, Zhang Bo, Jiang Yukuan, et al. Transient process of short-circuit current in substations and its influential factors[J]. High Voltage Engineering, 2014, 40(7): 1986-1993.
[34] 赵耀, 陆佳煜, 李东东, 等. 基于机电信号融合的电励磁双凸极电机绕组匝间短路故障诊断[J]. 电工技术学报, 2023, 38(1): 204-219.
Zhao Yao, Lu Jiayu, Li Dongdong, et al. A fault diagnosis strategy for winding inter-turn short-circuit fault in doubly salient electro-magnetic machine based on mechanical and electrical signal fusion[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 204-219.
[35] 李斌, 屈璐瑶, 朱新山, 等. 基于多尺度特征融合的绝缘子缺陷检测[J]. 电工技术学报, 2023, 38(1): 60-70.
Li Bin, Qu Luyao, Zhu Xinshan, et al. Insulator defect detection based on multi-scale feature fusion[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 60-70.
[36] 刘会兰, 许文杰, 赵书涛, 等. 面向高压断路器故障分类的电流-振动信号类聚几何敏感特征优选方法[J]. 电工技术学报, 2023, 38(1): 26-36.
Liu Huilan, Xu Wenjie, Zhao Shutao, et al. Opti- mization method of clustering geometric sensitive features of current vibration signals for fault classification of high voltage circuit breakers[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 26-36.
[37] Ghanizadeh A J, Gharehpetian G B. ANN and cross-correlation based features for discrimination between electrical and mechanical defects and their localization in transformer winding[J]. IEEE Transa- ctions on Dielectrics and Electrical Insulation, 2014, 21(5): 2374-2382.
[38] Zhao Zhongyong, Yao Chenguo, Li Chengxiang, et al. Detection of power transformer winding deformation using improved FRA based on binary morphology and extreme point variation[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3509-3519.
[39] Hedberg H, Dokladal P, Owall V. Binary morphology with spatially variant structuring elements: algorithm and architecture[J]. IEEE Transactions on Image Processing, 2009, 18(3): 562-572.
[40] Dai Xiaolong, Khorram S. A feature-based image registration algorithm using improved chain-code representation combined with invariant moments[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2351-2362.
[41] Tamura H, Mori Shunji, Yamawaki T. Textural features corresponding to visual perception[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1978, 8(6): 460-473.
[42] Hashemnia N, Abu-Siada A, Islam S. Improved power transformer winding fault detection using FRA diagnostics-part 2: radial deformation simulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(1): 564-570.
Abstract The voltage damping oscillation method is effective for diagnosing winding faults, but it still has the following problems. The voltage-damping oscillation of transformer winding continues to fluctuate slightly for a period before the end of charging and discharging. In this process, there are a lot of irregular maximum points, minimum points, and burrs, which interfere with the subsequent characteristic processing and oscillation wave analysis. According to the existing literature, the oscillation ends when it attenuates to 5% of the maximum value, and all poles in this band are effective extreme points. Through a large number of experiments, it is observed that when the voltage-damping oscillation is no longer attenuated, its stable value often exceeds this threshold. As a result, the definition of the effective wave band of the above voltage-damping oscillation is inapplicable. Due to the complexity of on-site testing and external interference, two voltage-damping oscillation signals measured at different time intervals on the same transformer may have small deviations. However, the time-domain feature extraction of the oscillation wave is distinguished only by a single curve feature, and the identifiable accuracy is low when diagnosing the fault location and degree.
Therefore, this paper presents a transformer winding fault analysis method for selecting a dynamic wave band of voltage-damping oscillations. First, a transformer winding fault simulation platform is built, considering four kinds of faults: axial displacement, inter-disk capacitance, inter-pie, and inter-turn short circuits. Secondly, the characteristics of oscillation wave attenuation are analyzed from the perspective of energy conversion, selecting the effective wave band through a defined energy attenuation factor. Then, the waveform feature correlation degree (FCD) is obtained for fault type identification. At the same time, considering the rich feature information between the extreme point and the waveform, the oscillating wave binary image is constructed based on mathematical morphology to eliminate interference and extract more stable Tamura texture features. Finally, according to the distribution rule of characteristic parameter combination, the application analysis is carried out through the actual transformer.
The dynamically selected band shows minimal interference, clear attenuation oscillation regularity, and rich feature information. Oscillation waves under four fault types are different from each other, exhibiting significant variation patterns compared to normal windings. The waveform FCD is effective in identifying winding fault types. Oscillation waves exhibit minor differences in fault areas and degrees under the same fault type. Different combinations of four Tamura texture features demonstrate good performance in classifying fault degrees and types. In general, the waveform FCD and Tamura texture feature based on binarization values extracted under different faults have apparent separation and clustering, which can recognize fault type, degree, and region.
keywords:Transformer, voltage damping oscillation, winding fault, dynamic band, waveform feature, texture feature
DOI: 10.19595/j.cnki.1000-6753.tces.230314
中图分类号:TM614
收稿日期 2023-03-16
改稿日期 2023-04-03
周利军 男,1978年生,教授,博士生导师,研究方向为电气设备状态检测与故障诊断等。E-mail: ljzhou10@163.com(通信作者)
员秀程 男,1998年生,硕士研究生,研究方向电气设备状态检测及故障诊断。E-mail: 13685480501@163.com
(编辑 崔文静)