图1 接触器结构
摘要 该文对接触器的优化设计进行研究,将磁链闭环控制引入接触器本体优化设计中,实现控制策略与本体优化设计的协同。首先,综合考虑接触器的外部漏磁和磁场分布特性,在三维有限元动态仿真的基础上构建改进的磁路模型,以实现磁路模型的参数化计算。然后,提出了一种改进的非支配排序遗传算法(NSGA-Ⅱ)与磁路模型相结合进行优化设计,以Pareto前沿个数判断种群进化进程,实现自适应遗传-差分混合进化策略,提高了多目标优化设计算法的全局收敛性和收敛速度。最后,将恒磁链闭环控制策略与多目标优化设计相结合,通过减小接触器的电磁惯性、机械惯性及提高控制磁通密度,来提高机构响应速度和磁性材料利用率,同时减小触头弹跳。仿真及实验验证了改进磁路模型及多目标优化设计方法的有效性。
关键词:接触器 优化设计 磁路法 改进的非支配排序遗传算法(NSGA-Ⅱ)
接触器是一种常用的控制电器,在电力系统中承担着频繁断开和接通主电路的任务。传统接触器存在工作电压范围窄、触头弹跳严重、运行功耗大等问题,影响其使用寿命及可靠性[1-5]。目前,多通过本体优化设计并配合智能控制策略,来改善接触器性能[6-8]。接触器本体设计一般先采用经验公式和理论计算,进行机构的粗略设计,然后利用计算机仿真技术建立样机模型,进行数值仿真,将新产品的设计问题转化为优化问题,显著减少研发成本,提高了设计质量[9-11]。当前,国内外学者已对永磁接触器动作和保持特性、电磁接触器的弹跳特性等进行了有限元仿真研究[12-15],但有限元仿真计算量大、计算时间长,适用于迭代次数少的局部优化设计[16-18],且多为单目标优化,对于多目标问题往往通过加权转化为单目标后进行处理。而智能优化算法需要进行大规模迭代计算,如果在每个迭代过程中均结合有限元仿真,则需要耗费大量的计算时间,为此,需要建立接触器的快速计算模型,便于智能优化算法的实施。
传统交流接触器的激励是工频交流电压,磁场存在交变,运行时有诸多问题[19],不同合闸相位下,吸合时间、吸合速度存在较大差异[20],通常通过电流闭环控制进行直流化运行以解决该问题[21]。为了进一步抑制触头弹跳,在电流闭环基础上需要再结合优化控制,如无模型自适应控制[22]、模糊控制[23]等手段调整强励磁时间和励磁电压,从而调整动静铁心碰撞速度,虽然可以达到一定的弹跳抑制效果,但控制过程较为复杂。文献[24]在接触器起动及保持过程中采用磁链外环控制电流内环的双闭环结构,实现了接触器的磁链闭环控制,仅采用恒磁链运行即可达到较好的弹跳抑制及节能保持效果,降低了接触器优化控制的难度。在电流闭环及磁链闭环控制下,接触器的线圈励磁电压为受反馈控制的高频方波信号,励磁状态受控制器软硬件及开关本体参数的综合制约。在控制策略确定的情况下,如何合理设计接触器本体,减小电磁惯性和机械惯性,提高电磁力响应速度,以进一步提高整体性能,是值得探讨的问题。
本文首先提出了一种考虑线圈外部漏磁分布和铁心磁场不均匀分布的改进磁路模型,将漏磁和铁心磁场不均匀等效方法与电磁机构的几何参数紧密联系,保证模型准确的同时,可用于快速参数化计算,便于电磁机构的智能迭代优化;然后,提出了一种基于Pareto前沿个体数的差分-遗传混合进化算法,对种群进化不同阶段的个体分布特性和收敛性进行分析,以Pareto前沿个数作为指标,在不同进化阶段合理分配遗传算法和差分算法,提高了快速非支配排序多目标优化遗传算法(Non dominated Sorting Genetic Algorithm-Ⅱ, NSGA-Ⅱ)的全局收敛性和计算效率,为接触器的多目标优化设计提供了高效准确的全局智能优化算法;最后,将磁路快速计算模型与改进的NSGA-Ⅱ多目标优化设计方法相结合,对恒磁链闭环控制下的接触器本体进行优化设计,以吸合时间-吸合末速度构建双目标适应度函数,通过减小电磁惯性及机械惯性,提高控制磁通密度,在提高机构响应速度和磁性材料利用率的同时,减少触头弹跳。本文所做研究对于闭环控制下接触器的本体优化设计具有一定的参考价值。
磁路模型由于漏磁和分布参数的影响,准确性较差,部分学者采用补偿矩阵和漏磁曲线拟合的方式对磁路模型进行补偿[25-27]。但在电磁机构几何参数变化较大的情况下磁场分布发生变化,补偿失效,模型精度降低。本文通过对有限元仿真结果进行分析,将线圈外部漏磁和铁心磁场不均匀分布纳入考虑,在COMSOL中实现磁路模型的参数化仿真,为后续接触器多目标优化设计提供可快速准确计算的参数化模型。
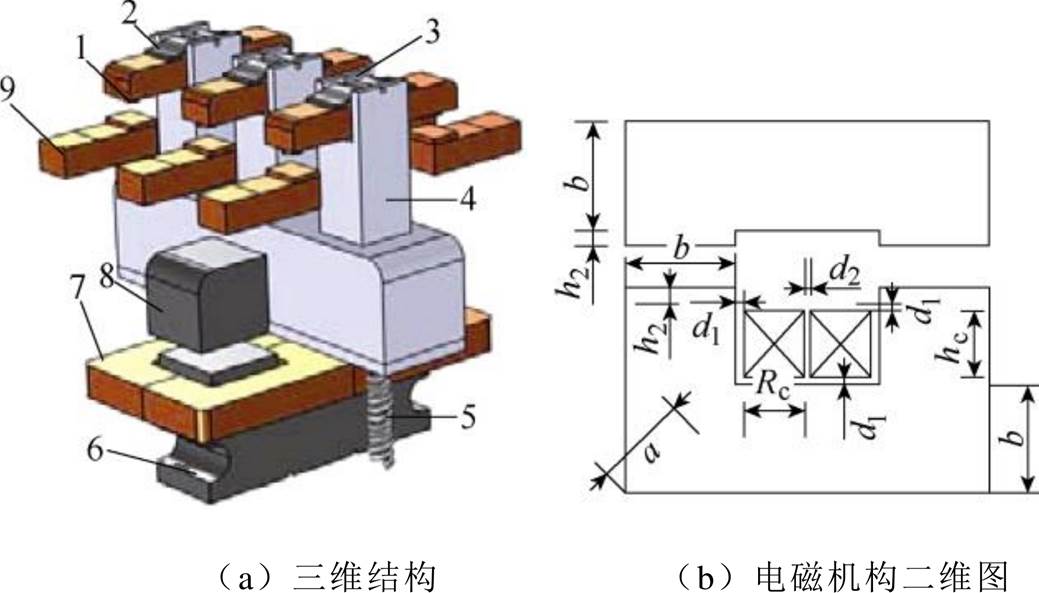
仿真对象为CJ20-630交流接触器,其结构如图1所示。根据接触器二维平面图将其电磁机构分割为诸多部分并测量相应尺寸,其中,a为铁心厚度,b为动静铁心接触面宽度,h2为静铁心端面与线圈骨架顶部之间的线圈凹槽高度,d1为线圈骨架厚度,Rc为线圈厚度,hc为线圈高度,d2为两个线圈之间的间隔。

图1 接触器结构
1—静触头 2—触头弹簧 3—顶杆 4—连杆 5—铁心弹簧 6—静铁心 7—线圈 8—动铁心 9—动触头
Fig.1 The structure of the contactor
磁路的动态计算步骤如图2所示。首先,将磁路的电压平衡方程改写成积分形式,计算磁链y,进而确定静铁心磁通密度B。图2中,N为线圈匝数,S为铁心端面积。求解接触器的动态过程,需要利用工作气隙磁通密度Bd 来确定电磁力的大小,并与反力一起计算合力,通过达朗贝尔运动方程计算动铁心位移x。K为漏磁系数,为求解K需建立等效磁路,以确定各部分区域的磁阻。静铁心磁通密度和工作气隙磁通密度确定后,可以从各自的B-H曲线中反推动铁心和静铁心的相对磁导率m1和m2,同时可确定不均匀分布系数k1和k2,以求解静铁心磁阻Rj和动铁心磁阻Rd。通过位移x可计算工作气隙磁阻Rd 及漏磁阻Rl。klc为外部线圈漏磁等效系数,Rln为内部线圈漏磁阻。最后,通过磁路磁阻进一步计算线圈电感L及漏磁系数K,K返回到Bd的求解模块中;通过电感定义求得电流并返回到磁链求解模块中。通过对上述步骤反复迭代,即可实现考虑线圈外部漏磁及铁心磁场不均匀分布时磁路的动态计算。
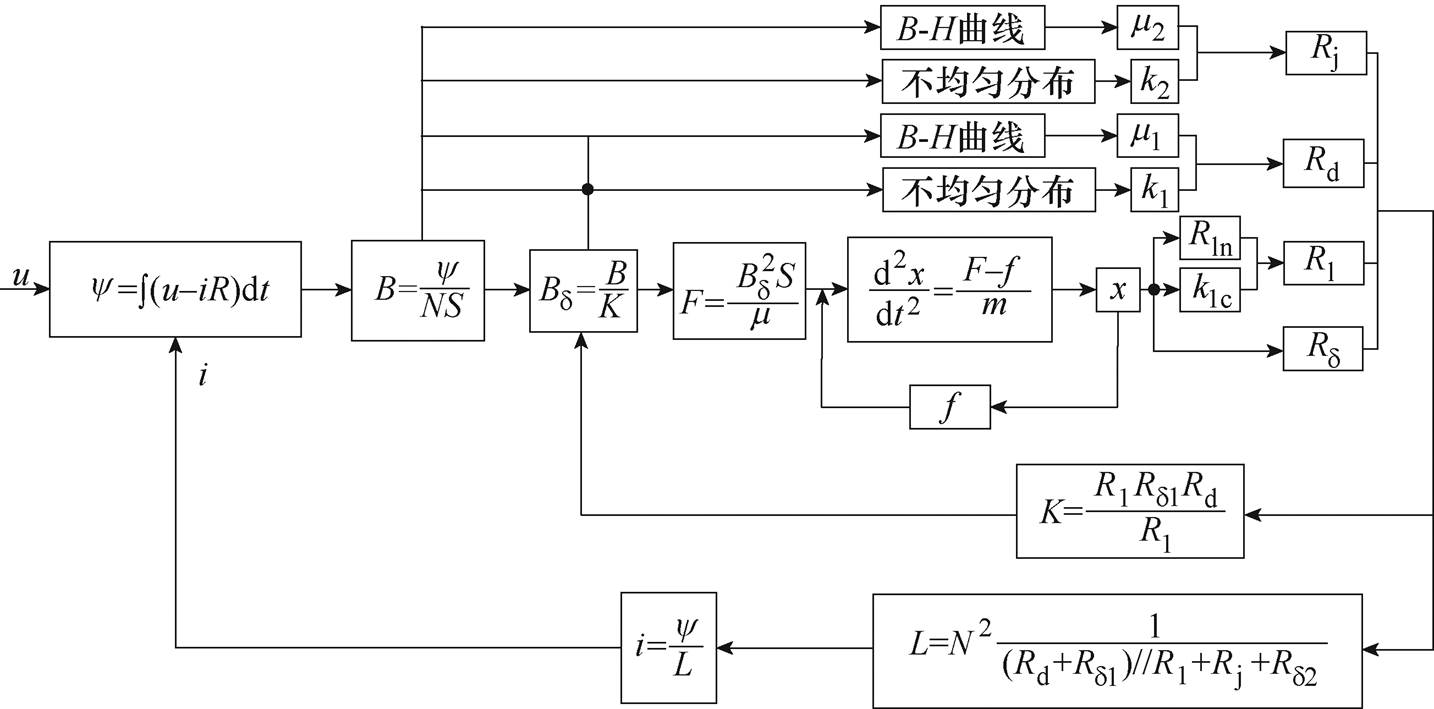
图2 磁路动态计算步骤
Fig.2 Calculation steps of magnetic circuit
计算磁阻时,首先需要绘制图3所示等效磁路,图中,Rd为动铁心磁阻,Rd11、Rd12为工作气隙磁阻,Rl漏磁磁阻,Rj1~Rj4为静铁心磁阻,Rd2为非工作气隙磁阻;Rd1为简化后的工作气隙磁阻,Rj为简化后的静铁心磁阻。
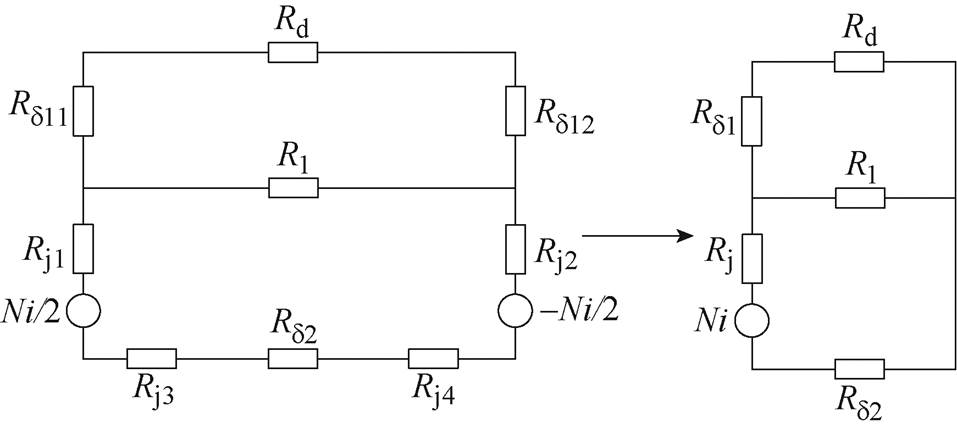
图3 等效磁路
Fig.3 Equivalent diagram of magnetic circuit
磁路可以类比为电路,磁阻为
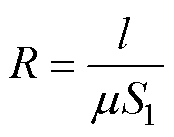 (1)
(1)
式中,R为磁阻;l为磁路等效长度;m 为磁导率;S1为磁路等效截面积。
计算工作气隙磁阻时,由于存在端部磁通,引入工程经验系数kd[1-3],来考虑端部磁通的影响。
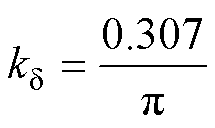 (2)
(2)
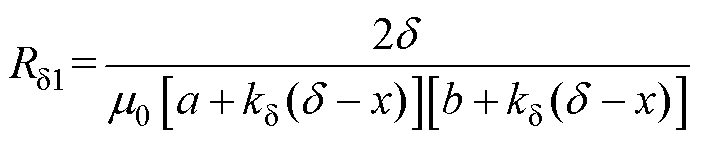 (3)
(3)
式中,m0为空气磁导率;d 为工作气隙长度。
对于非工作气隙,由于气隙较小,忽略端部磁通影响,其磁阻为
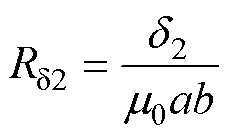 (4)
(4)
式中,d2为非工作气隙长度。
传统磁路模型中,认为磁通密度在铁心中是均匀分布的,且仅考虑了内部漏磁,而忽略了外部漏磁的影响。本文根据三维有限元仿真结果,结合安培环路定理对铁心磁场的不均匀分布进行等效,并建立环绕线圈分布的漏磁模型,将外部漏磁纳入考虑,改进模型与电磁系统几何参数密切联系,提高模型准确性的同时,还可适用于参数化仿真,便于优化设计。
1.2.1 铁心磁场的不均匀分布
引入磁场不均匀分布系数k,并用k1、k2分别表征动、静铁心的不均匀分布系数。动、静铁心磁阻分别为
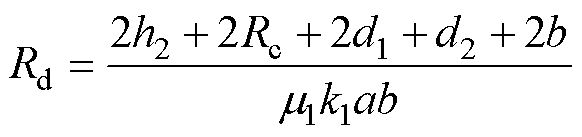 (5)
(5)
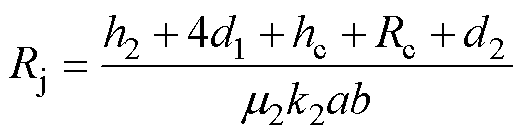 (6)
(6)
在吸合过程中,铁心磁通密度的分布是不均匀的,越靠近铁心内侧线圈,磁通密度越大,靠近铁心外侧磁通密度较小。引入k作为衡量铁心磁通密度不均匀程度,称为不均匀分布系数,铁心磁场等效分布如图4所示,图中,静铁心内侧磁场强度为H1,铁心部分长度为2h2+6d1+2hc+2Rc+d2,用l1表示;外侧磁场强度为H2,铁心部分长度为l1+4b,用l2表示;在铁心中任一位置,假设磁场强度为H,铁心部分长度为l1+4x,记为l,x为该位置到Y轴的垂直距离。
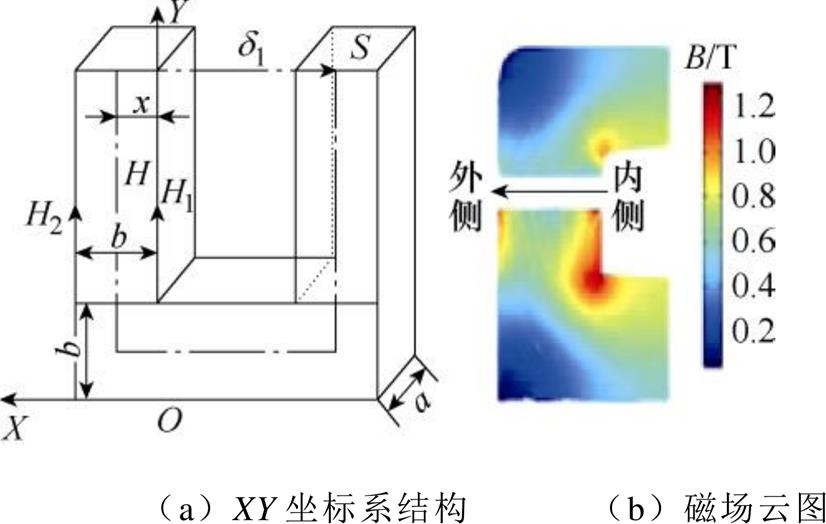
图4 铁心磁场等效分布
Fig.4 Distribution of iron core magnetic field
根据安培环路定律可得
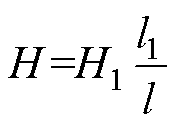 (7)
(7)
进一步将H沿铁心截面进行积分,可得平均磁通。
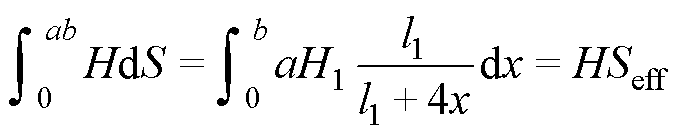 (8)
(8)
式中,Seff为平均磁通所经过的铁心等效截面积。
将式(7)代入(8)可得
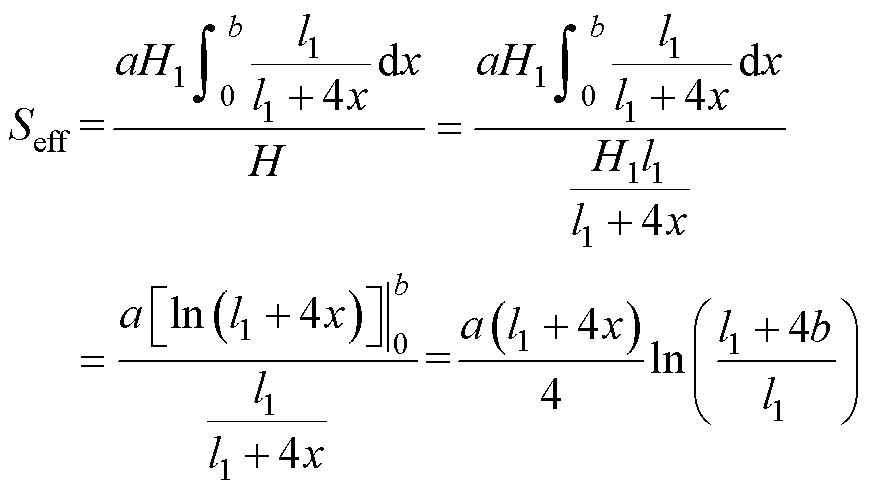 (9)
(9)
铁心磁通密度不均匀分布系数k为
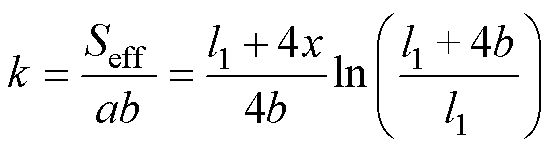 (10)
(10)
当磁通密度较小时,沿铁心边缘分布;当磁通密度较大时,铁心中磁通密度分布变得均匀,平均磁通密度B的位置接近X轴铁心中线位置,对有限元仿真结果中的截面平均磁通密度进行线性化处理,将平均磁通密度的X轴坐标x视为磁通密度B的线性函数,有
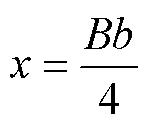 (11)
(11)
将式(11)及l1代入式(10),得到考虑磁场不均匀分布的静、动铁心面积等效系数k1、k2分别为
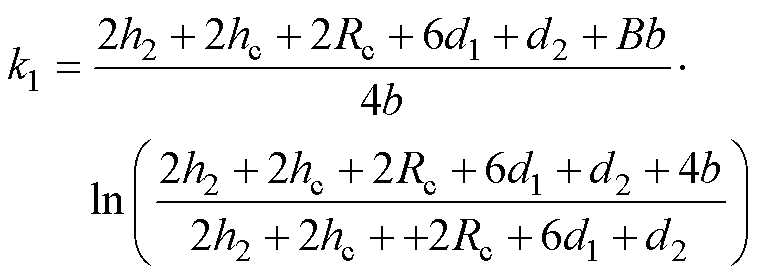 (12)
(12)
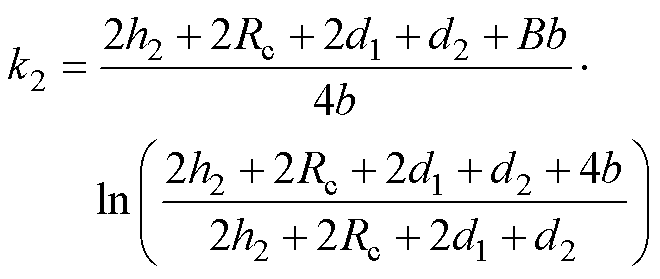 (13)
(13)
由此可求得静、动铁心磁阻Rj、Rd。
1.2.2 环绕线圈的漏磁分布模型
本文将电磁机构的线圈通电励磁,用三维有限元仿真磁力线分布来分析接触器中的漏磁。漏磁通分布如图5所示,图中两个线圈产生的磁场相互叠加,铁心外部漏磁分成红色箭头部分和蓝色箭头部分。其中,红色箭头部分为端部漏磁,交链动、静铁心,可归算为工作气隙端部磁通;蓝色箭头部分为线圈外部漏磁,在铁心内部交链静铁心两端,对电磁机构运动无贡献。
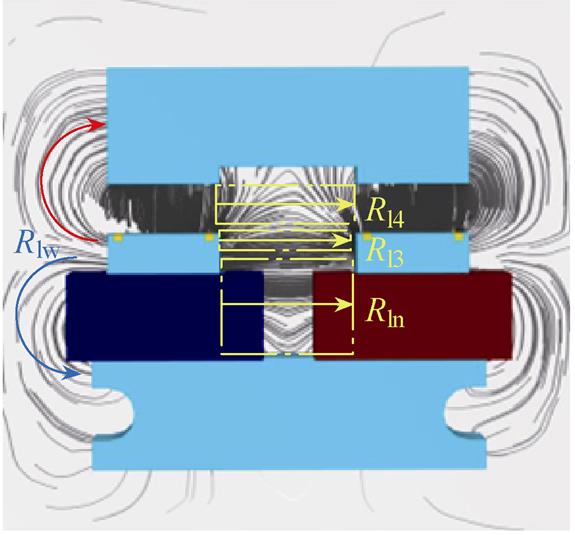
图5 漏磁通分布
Fig.5 Distribution of leakage flux
如图5中黄线部分所示,将铁心内部漏磁分割为Rln、Rl3和Rl4。其中,Rln为线圈内部漏磁,Rl3为线圈骨架与铁心端面之间的侧面漏磁,Rl4为工作气隙侧面漏磁,与工作气隙大小有关。
将几何尺寸代入磁阻计算式(1)中,则Rln、Rl3和Rl4分别为
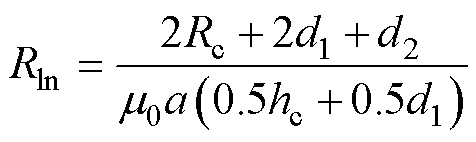 (14)
(14)
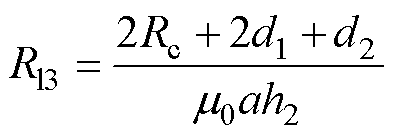 (15)
(15)
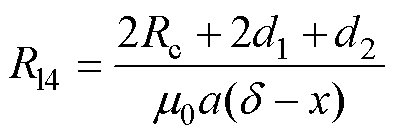 (16)
(16)
漏磁通分布等效磁路如图6所示,将线圈漏磁单独排列,其中,Rl1为左侧线圈单独作用时产生的漏磁阻,为左侧线圈的外部和内部漏磁阻并联而成。Rl11为左侧线圈产生的内部漏磁阻;Rl12、Rl13和Rl14为左侧线圈在其余三个边的法线方向上产生的外部漏磁阻,后文用Rlw表示Rl12、Rl13和Rl14的总等效磁阻。同理可得右侧线圈漏磁阻。
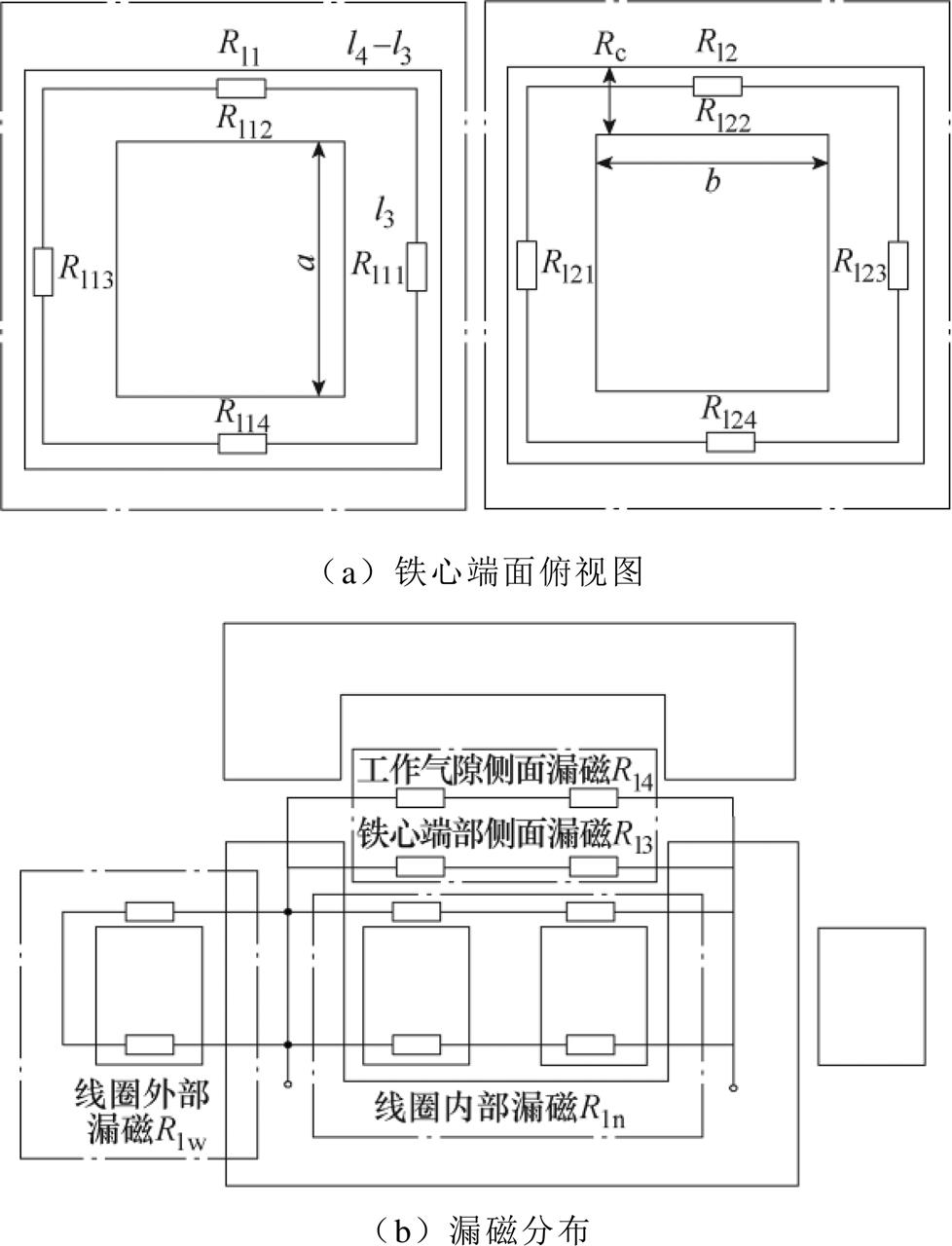
图6 漏磁通分布等效磁路
Fig.6 Equivalent magnetic circuit diagram of leakage flux distribution
两个铁心内部漏磁阻为两个线圈的内部漏磁阻串联而成,且二者对称,有
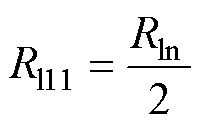 (17)
(17)
将内部漏磁流经宽度记为l3,线圈一匝总长度为l4,则有外部漏磁流经长度为l4-l3,线圈漏磁阻为并联形式,因此有
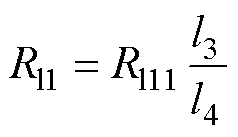 (18)
(18)
同理可得,线圈外部漏磁为
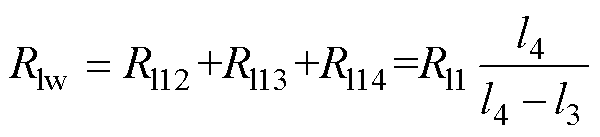 (19)
(19)
将线圈等效漏磁记为Rlc,为外部漏磁阻与内部漏磁阻的并联,则有
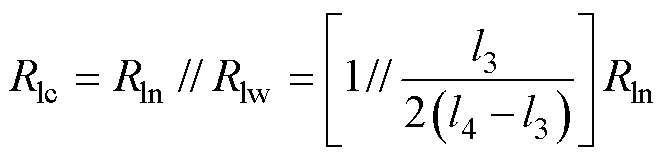 (20)
(20)
进一步求解磁路总漏磁阻Rl为
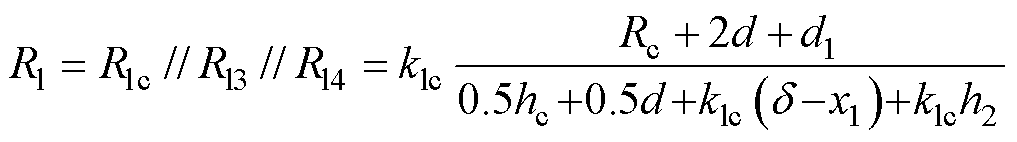 (21)
(21)
本节改进传统磁路模型:利用安培环路定律,将磁路的等效几何特征用磁场强度进行线性化处理,并将外部漏磁归算到内部漏磁,实现了总漏磁阻的计算,最终完成静铁心磁阻Rj、动铁心磁阻Rd、气隙磁阻Rd1及漏磁阻Rl的计算,且计算公式均与几何结构紧密相关,便于实现电磁机构迭代优化时的快速参数化计算。
按照表1参数加工两种接触器铁心,并绕制三种匝数的线圈与铁心配合,构成电磁机构。利用NI- CompactRIO构建快速控制原型验证系统,得到不同控制方案下设计电磁机构的实验波形;同时在仿真系统中设定所加工电磁机构的几何参数,并结合相应控制策略进行仿真,将实验波形与仿真波形对比,以验证改进磁路模型的有效性。
表1 接触器铁心尺寸
Tab.1 Core size of contactor (单位: mm)

铁心铁心厚度a接触面宽度b静铁心柱高度hU型槽宽度w 162.830.235.437.0 280.040.034.052.0
图7为分别对铁心1和铁心2配合2×730匝、2×490匝、2×430匝线圈,采用全波整流电压激励、1.5 Wb高频恒磁链激励、3.5 A恒电流激励三种不同激励方式下进行实验及仿真的对比波形。在不同控制策略及不同铁心及线圈参数下,仿真结果与实验结果均较为一致,证实了该改进磁路模型的有效性。同时,该改进磁路模型进行一次动态过程计算耗时约1 min,相较于计算高达数小时的有限元动态仿真,大大提升了计算速度,便于后续电磁系统优化设计。
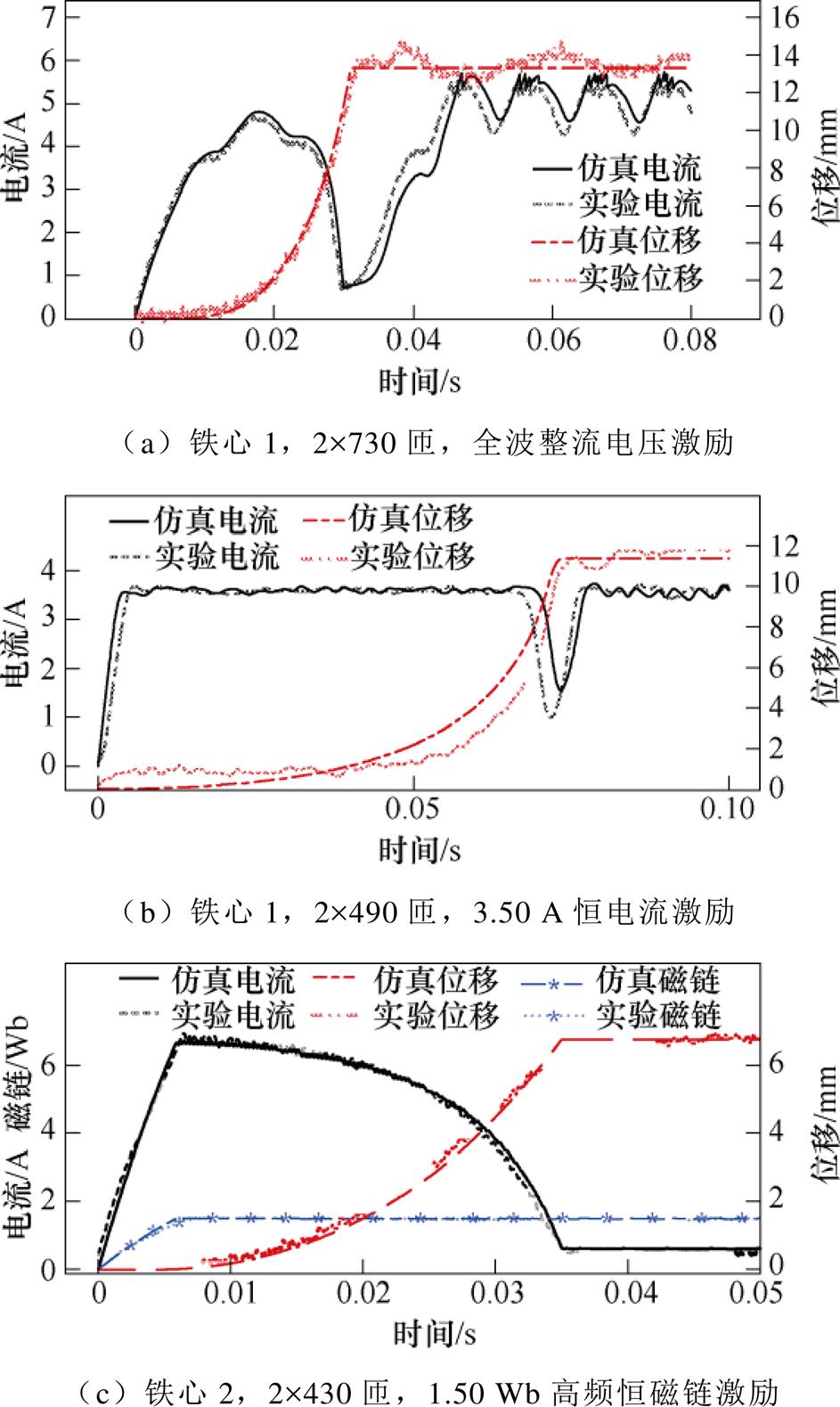
图7 磁路模型实验与仿真对比
Fig.7 The results of test and simulation
本文采用卡方检验进行电流拟合优度检验,同时计算仿真吸合时间相对误差。电流拟合优度检验与吸合时间误差分析见表2。表中,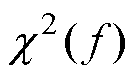 表示在自由度为f的情况下,电流拟合优度检验的卡方值,当
表示在自由度为f的情况下,电流拟合优度检验的卡方值,当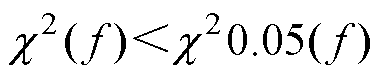 时,说明在自由度为f、显著性水平为0.05的情况下,可以认定仿真电流与实验电流拟合较好。如表2所示,对图7中的电流采用卡方检验进行拟合优度检验,四组数据中
时,说明在自由度为f、显著性水平为0.05的情况下,可以认定仿真电流与实验电流拟合较好。如表2所示,对图7中的电流采用卡方检验进行拟合优度检验,四组数据中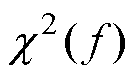 都小于
都小于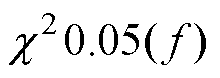 ,因此,在0.05的显著性水平上,认定电流仿真值与实验值拟合度较优;此外,对吸合时间进行相对误差分析,相对误差皆小于3%,仿真与实验结果较为接近。
,因此,在0.05的显著性水平上,认定电流仿真值与实验值拟合度较优;此外,对吸合时间进行相对误差分析,相对误差皆小于3%,仿真与实验结果较为接近。
仿真与实验数据存在误差的原因可能有:①数值仿真潜在误差,步长、容差、迭代次数等对结果都会造成影响,步长和容差设置得越小,或迭代次数设置得越大,则误差越小,但计算时间和计算量越大;②磁链、电阻测量可能存在系统误差,导致控制过程不准确,实验数据与理想数据存在误差;③电磁机构几何参数可能存在测量误差,铁心材料所用的DW360-50的B-H曲线的测量可能存在误差,这两种误差导致仿真时磁阻计算存在误差;④邻近吸合瞬间,由于气隙很小,磁场主要沿主磁路分布,漏磁分布发生剧烈改变,铁心内部磁场在边角处由沿边界分布迅速变化为呈带状减小,导致电流急剧变化产生误差;⑤摩擦力、阻力等因素导致的误差,这致使仿真接触器运动过程中,运动较实际过程偏快。这些导致误差的因素不易精确测量,因此难以进行误差的实验分析。
表2 电流拟合优度检验与吸合时间误差分析
Tab.2 Test of goodness of fit of current and analysis of pull-in time error
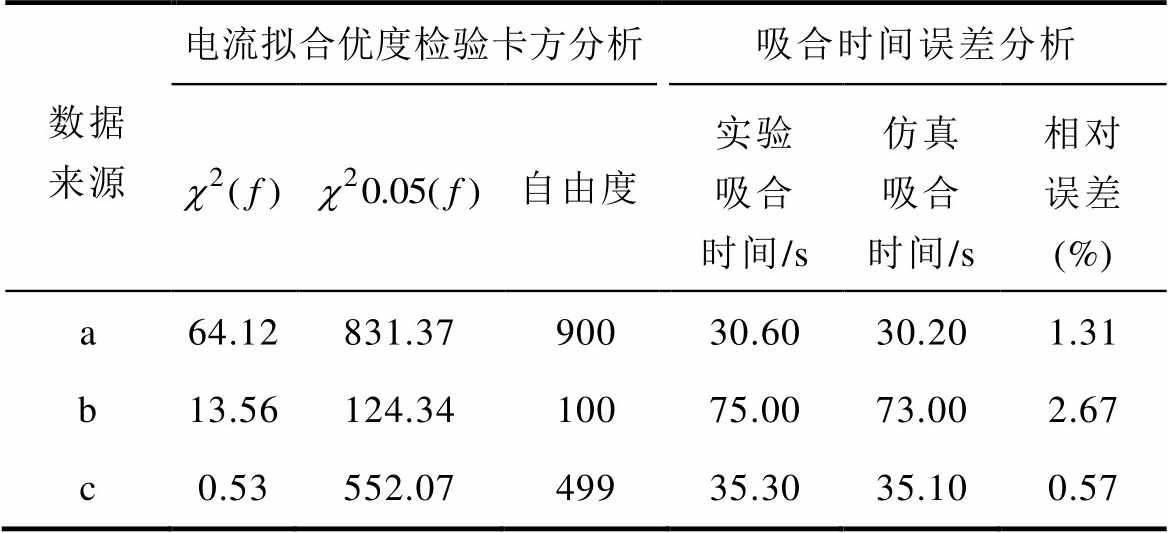
数据来源电流拟合优度检验卡方分析吸合时间误差分析 自由度实验吸合时间/s仿真吸合时间/s相对误差 (%) a64.12831.3790030.6030.201.31 b13.56124.3410075.0073.002.67 c0.53552.0749935.3035.100.57
实验结果表明,在误差允许的范围内,该磁路模型可以体现不同控制策略下,电磁系统和线圈参数变化时接触器的动态特性变化规律。
NSGA-Ⅱ算法作为一种多目标全局自适应概率搜索算法,求解规模大,且由于采用随机性强的遗传算法作为基础,收敛性较差,若交叉概率和变异概率设置不当,存在局部收敛、过早收敛或者收敛慢的情况,针对这些缺陷,本文提出了一种基于Pareto前沿个数的自适应差分-遗传混合进化算法。在Matlab中对遗传算法、差分进化算法、自适应NSGA-Ⅱ算法和DENSGA-Ⅱ算法在测试函数上进行构建和计算,总结收敛性、适应度函数等参数的变化规律,根据Pareto前沿个体数,将种群进化过程进行分段处理,并根据不同阶段的特性进行针对性算法优化。
改进NSGA-Ⅱ算法基本流程如图8所示。根据当前Pareto前沿个体数,判断种群进化进程,进行算法针对性优化。非支配排序时个体会按照支配关系进行分层,最低层为非支配前沿,只有进化后期,种群较成熟时才有可能形成较优越的前沿个体,在进化前中期,种群多样性丰富,前沿个体较少;同层个体根据种群拥挤度进行升序排序并整合,序号越小的个体越优越,其中,序号小于前沿个体数的子代为前沿个体,序号大于前沿个体数的子代为非前沿个体。
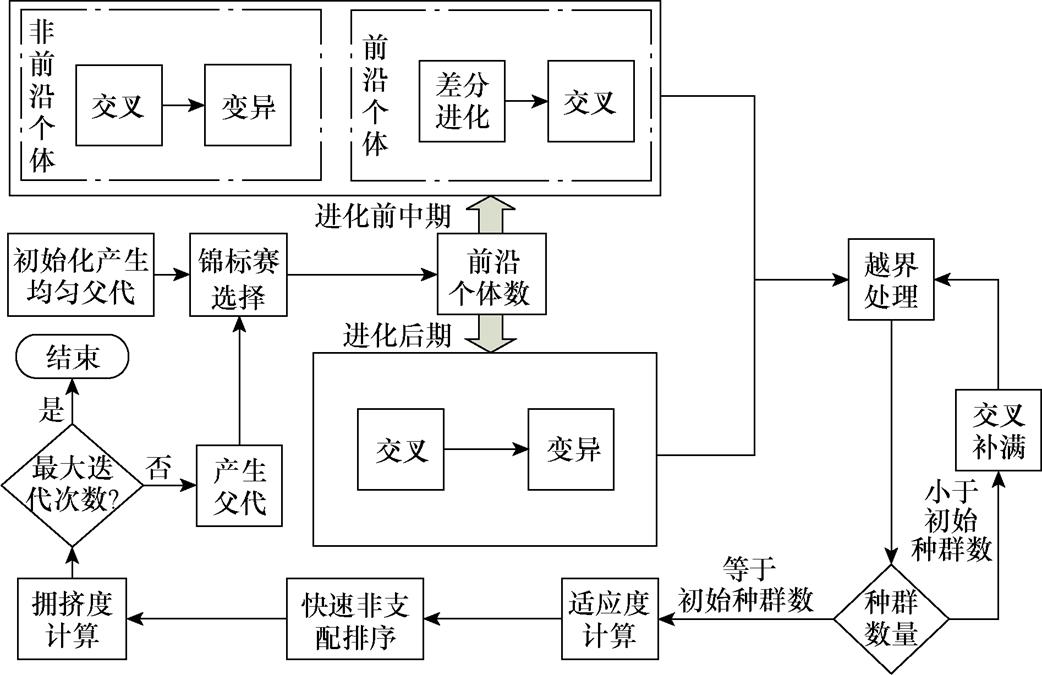
图8 改进NSGA-Ⅱ算法基本流程
Fig.8 The basic flow of the improved NSGA-Ⅱ algorithm
产生初始种群时进行均匀化处理,保证解空间的多样性和分布性,采用锦标赛选择,提高收敛速度。根据当前Pareto前沿个数,判断种群进化进程,对变异概率和交叉概率进行分段处理。在种群进化前期,交叉概率和变异概率分别为pc1和pm1;在种群进化中期,分别为pc2和pm2;在种群进化后期,分别为pc3和pm3。
在种群进化前中期,种群多样性丰富,但个体素质较差,采用差分进化算子和交叉、变异算子的混合进化策略:前沿个体素质相对非前沿个体更优,由父代个体通过锦标赛法选择三个不同的个体,进行差分后直接作为子代进行适应度计算,以加快收敛速度;对非前沿个体进行交叉、变异从而产生子代,以保证种群多样性。
在种群进化后期,个体较优越,但种群多样性较差,容易陷入局部收敛,全部子代由搜索能力更强的交叉、变异操作产生,从而提高收敛性和减少种群进化代数。采用差分进化算法与遗传算法混合进化的形式,可以减少迭代次数,同时避免因差分进化操作陷入局部收敛或者过早收敛。差分进化方式为
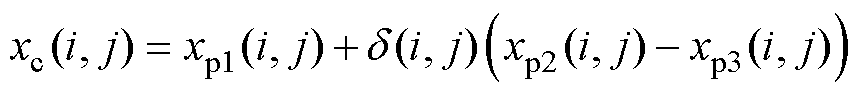 (22)
(22)
式中,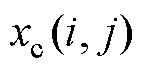 为子代个体;
为子代个体;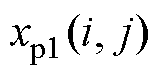 、
、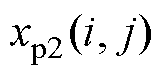 、
、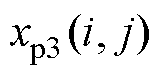 为互不相同的父代个体;
为互不相同的父代个体;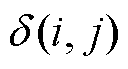 为介于0~1之间的随机数。
为介于0~1之间的随机数。
种群进化完成后需要进行越界处理。最后,计算种群的适应度函数,并进行快速非支配排序和拥挤度计算。判断算法是否到达最大迭代次数,若到达最大迭代次数,则输出Pareto前沿个体作为多目标优化解集;若未到达最大迭代次数,则选择最优的M个个体作为新的父代,进行下一次种群进化。
本节用前沿个体数判断种群进化进程,对种群中不同阶段的不同个体采用特定进化策略,实现遗传进化和交叉进化的混合进化过程,并实现交叉、变异概率的自适应设置,以提高算法的全局收敛性和收敛速度。
为了验证改进后的NSGA-Ⅱ算法,用常规的自适应NSGA-Ⅱ算法、DENSGA-Ⅱ算法以及改进的NSGA-Ⅱ算法分别进行测试,选择测试函数ZDT4,最大迭代次数为1 000次,变量个数为10个。为了判断算法的收敛性,采用世代距离(Generational Distance, GD)作为指标,计算结果如图9所示。图中,柱状图为实际数据的分布直方图,曲线为根据数据的平均值、方差等参数生成的正态分布曲线,图9a横坐标表示1 000次计算中算法收敛时的迭代次数,纵坐标表示1 000次计算过程中收敛迭代落于该区间范围内的次数;图9b横坐标表示1 000次计算中算法收敛时的GD,纵坐标表示1 000次计算过程中GD落于该区间范围内的次数。
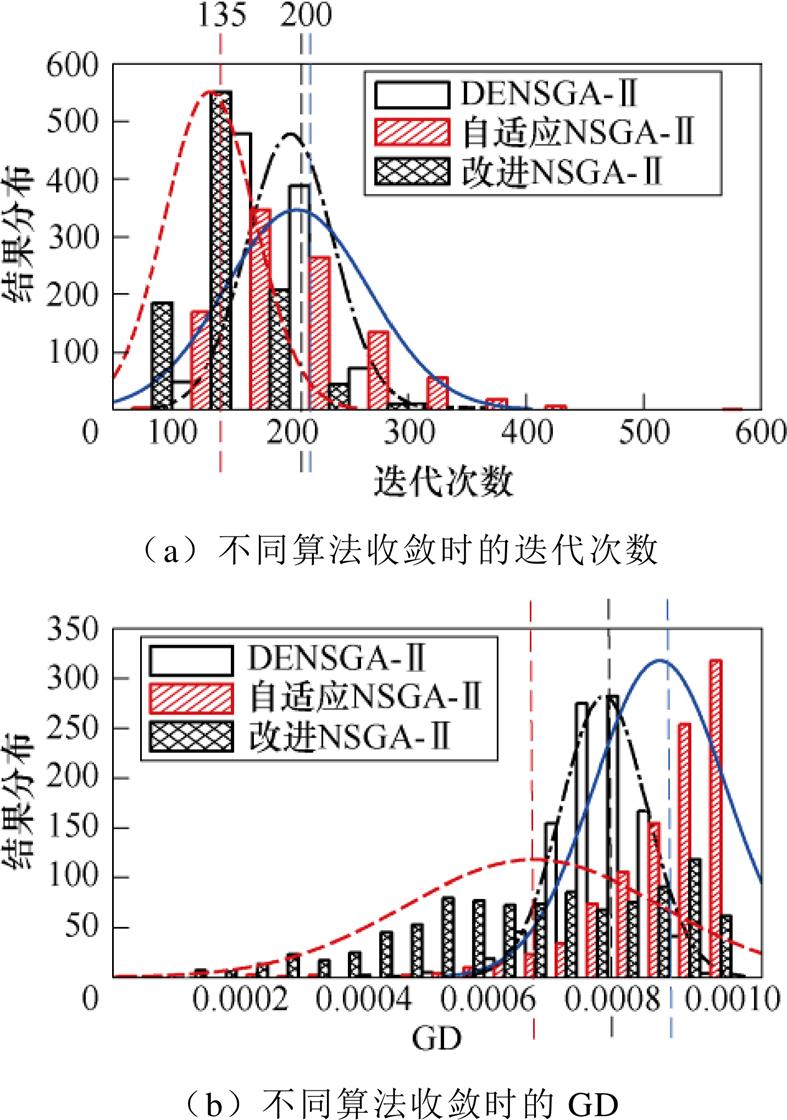
图9 DENSGA-Ⅱ、自适应NSGA-Ⅱ与改进NSGA-Ⅱ在ZDT4测试函数上的性能
Fig.9 The performance of DENSGA-Ⅱ, adaptive NSGA-Ⅱ and improved NSGA-Ⅱ on the ZDT4 test function
如图9a所示,采用自适应NSGA-Ⅱ、DENSGA- Ⅱ算法和改进NSGA-Ⅱ算法时,在1 000次计算中,ZDT4测试函数都能实现全局收敛;蓝色实线为自适应NSGA-Ⅱ算法收敛时的平均迭代次数,黑色点画线为DENSGA-Ⅱ算法收敛时的平均迭代次数,二者几乎相同,平均迭代次数在200次附近,即需要进行200 000次左右的磁路模型计算;红色虚线为采用改进NSGA-Ⅱ算法计算时的平均迭代次数,减少到了135次附近,即需要进行135 000次磁路模型计算,减少了32.5%的迭代次数;图9b中,黑、蓝、红色的曲线分别为采用DENSGA-Ⅱ,自适应NSGA-Ⅱ和改进NSGA-Ⅱ计算,算法收敛时的平均世代距离GD,可知,改进NSGA-Ⅱ算法收敛时的平均世代距离最小、收敛性最好。
传统接触器优化设计时,追求增大电磁系统的出力性能以减小吸合时间,但这往往导致吸合速度增大,弹跳严重。恒磁链闭环控制下,磁链保持不变,电磁力的变化由气隙大小及漏磁系数决定,因此,本文将恒磁链闭环控制与接触器本体多目标优化设计相结合,通过减小电磁机构的电磁惯性和机械惯性来提高机构的响应速度及磁性材料利用率,并针对吸合末速度和运动部件质量进行优化以减小触头弹跳。一般以电磁时间常数衡量电磁惯性,以运动部件质量衡量机械惯性,但在接触器本体优化设计时,关注电磁惯性的实质是关注电磁力的响应速度,而电磁力不仅与磁通密度相关,还受铁心截面和漏磁系数影响,优化设计时电磁系统结构的变化导致了漏磁系数和铁心截面发生较大变化,因此,磁通密度响应快仅是电磁响应快的必要条件之一。
吸合时间由触动时间和吸动时间构成,对于吸合时间-吸合末速度构成的非支配解,要求吸合时间和吸合末速度都尽可能小,因此这两个目标是相互对抗的。本文将吸合时间t、运动部件质量m、控制磁通密度B这三个参数通过加权函数整合为复合目标函数1,将吸合末速度v单独作为目标函数2,两个目标函数互相对抗,从而进行双目标优化设计。
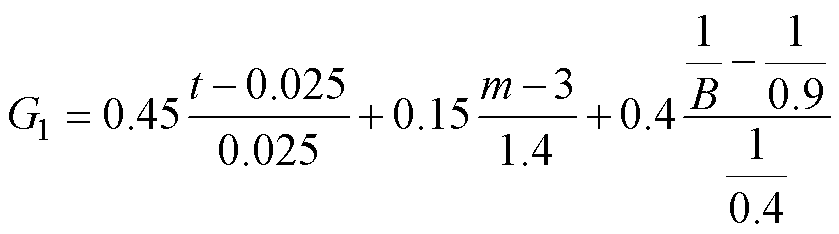 (23)
(23)
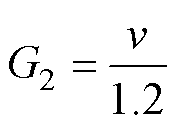 (24)
(24)
对目标参数根据约束值进行了归一化处理。
受限于现有接触器框架,电磁机构的约束条件如下:线圈匝数N为(0.5~2)×572;线圈高度hc为(0.5~2)×11 mm;铁心厚度a为40~80 mm;线圈凹槽高度h2为1.0~3.0 mm;控制磁通密度B为0.4~1 T。在Matlab上编写基于改进NSGA-Ⅱ算法的接触器多目标优化程序并调用COMSOL上构建的改进磁路模型,实现联合仿真。
多目标优化结果如图10所示。由图10a可知,在Pareto前沿中,两个目标为负相关,表明两个目标间存在对抗性,因此仅存在相对最优解。由于多目标优化所得结果是一个含复数的解集,如何折中选取满足需求的最优解至关重要。本文采用模糊隶属度法选取最优解,为了更加直观,处理时乘上个体数,以保证数值分布于1附近。如图10b所示,前14个个体的模糊隶属度较为接近,且大于后面的个体,因此最优解从前14个个体中产生。由图10a可知,所有个体的速度是降序分布的,由于速度较小时弹跳较小,因此最终选择14为最优个体,其参数见表3。
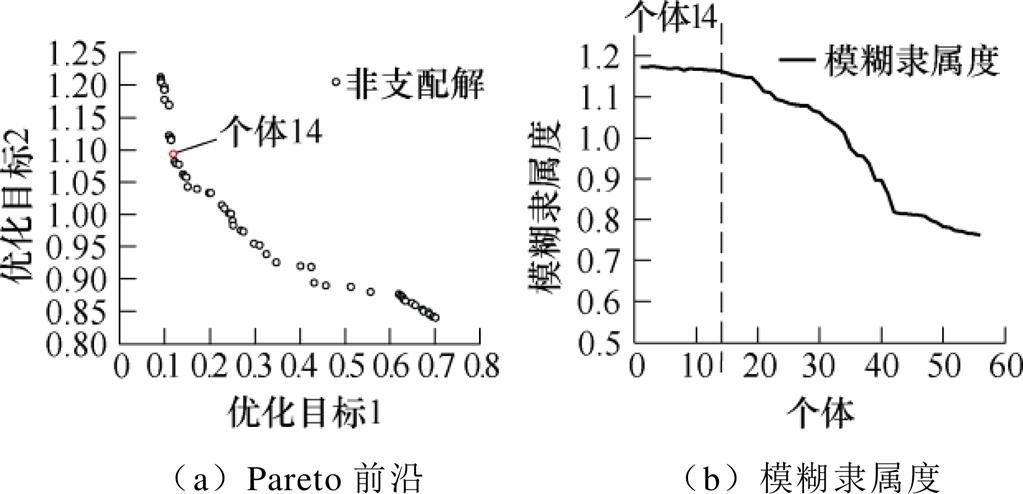
图10 多目标优化结果
Fig.10 Results of multi-objective optimization
表3 优化铁心参数
Tab.3 The optimized iron core parameters

参 数数 值 线圈高度hc/mm14 线圈匝数N1 304 铁心厚度a/mm40 控制磁通密度B/T0.73 线圈凹槽高度h2/mm2
根据优化后的参数对接触器的线圈和铁心进行加工,与原样机框架进行组装,并在高频恒磁链控制下对优化样机和原样机进行对比实验。
恒磁链吸合实验结果如图11所示,优化样机在1.5 Wb磁链下即可进行恒磁链起动,原样机需要在2.0 Wb磁链下进行恒磁链起动,此时二者吸合时间分别为29.2 ms和30.8 ms。在保持过程,优化样机保持电流为0.2 A,线圈损耗为0.72 W;而原样机保持电流为0.23 A,线圈损耗为2.20 W。优化样机发生了2次弹跳,弹跳时间为0.6 ms;原样机发生了3次弹跳,弹跳时间为1.8 ms。优化样机达到磁链闭环状态的时间仅为8 ms,而原样机为18 ms,可见优化样机的磁通密度增长更快,这是因为优化设计时吸合时间-吸合末速度非支配关系要求相同吸合时间下触动时间更短,电磁响应速度更快。
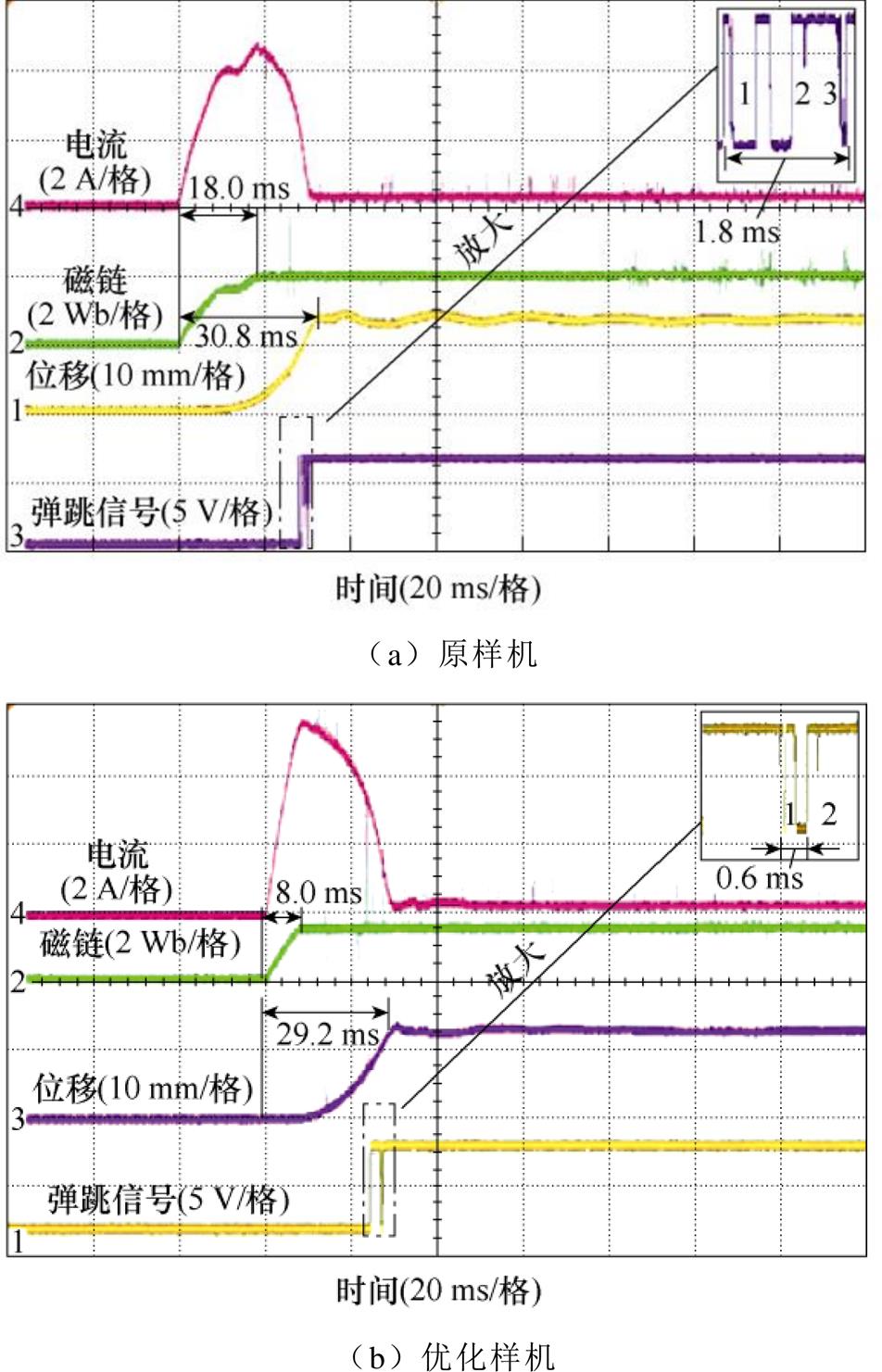
图11 恒磁链吸合实验结果
Fig.11 The results of the pull-in experiment under the constant flux linkage
对优化前后样机进行20次实验,记录其弹跳时间和弹跳次数,分布如图12所示。柱状图为实验数据的分布直方图,曲线为根据数据的平均值、方差等参数生成的正态分布曲线,原样机平均弹跳次数为2.9次,平均弹跳时间为2.0 ms;优化样机的平均弹跳次数为2.0次,平均弹跳时间为0.7 ms。由上述实验数据可知,在恒磁链控制下,优化样机在保持较小吸合时间的同时,减小了弹跳次数,并充分降低了弹跳时间。
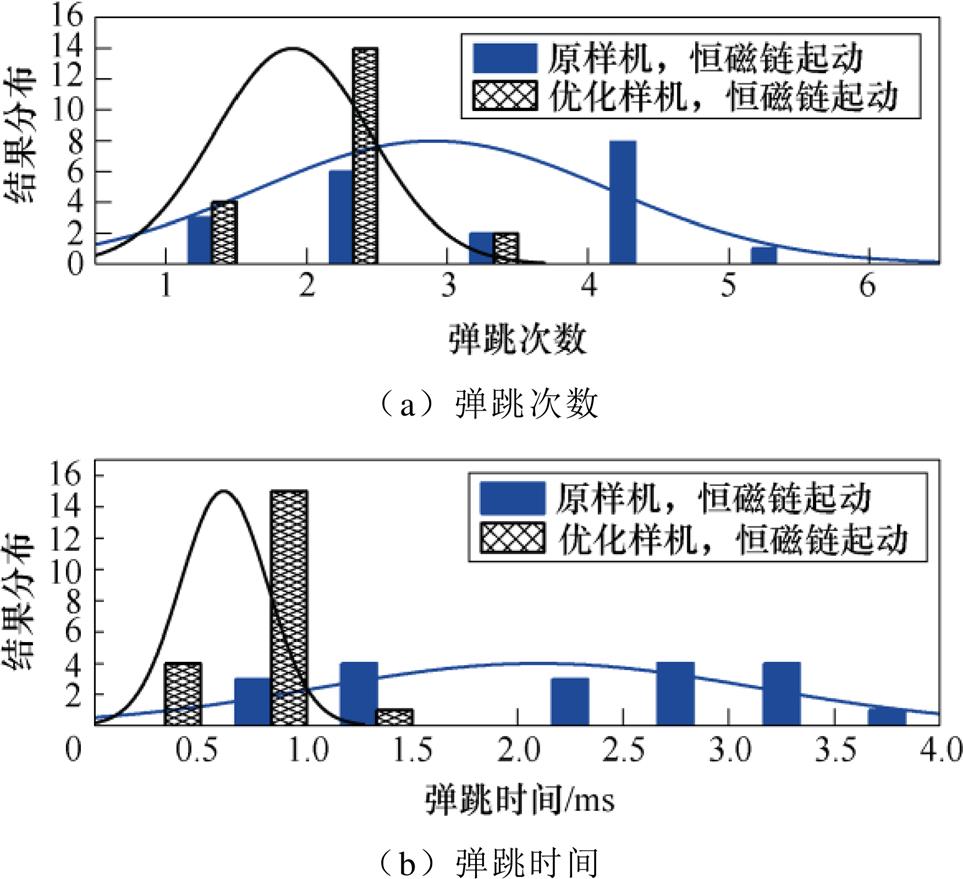
图12 弹跳特性
Fig.12 Bounce characteristics
综上所述,原样机和优化样机的吸持功率Px、电阻R、平均弹跳时间tb、平均弹跳次数nb、线圈匝数N、控制磁通密度B的数据对比列于表4,可知,优化样机的吸持功率减小到了0.72 W,电阻为18 W,平均弹跳时间减小到了0.7 ms,平均弹跳次数减小到了2.0次,匝数减小到了1 304匝,且控制磁通密度值由0.54 T增加到了0.73 T,提高了磁性材料利用率,降低了保持功耗。
表4 优化样机与原样机对比
Tab.4 Comparison of optimized contactor and original contactor
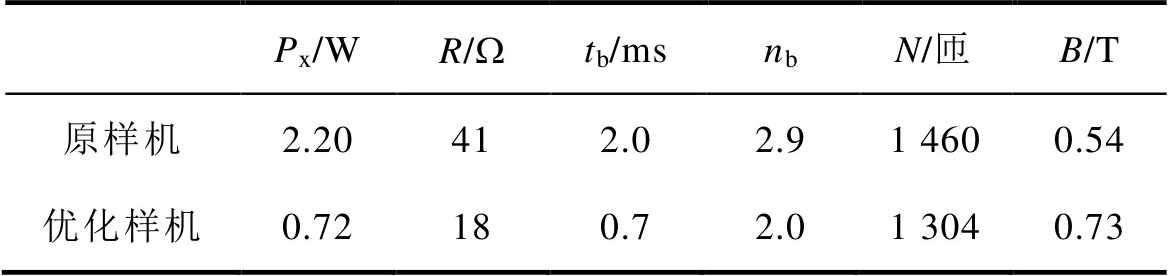
Px/WR/Wtb/msnbN/匝B/T 原样机2.20412.02.91 4600.54 优化样机0.72180.72.01 3040.73
本文将恒磁链PWM闭环控制与接触器本体优化设计结合,通过理论分析、仿真与实验验证得到如下结论:
1)考虑外部漏磁分布和动态过程磁场不均匀分布的改进磁路模型,计算效率高,能够在几何参数变化和控制策略变化的情况下保持准确性,适用于不同控制策略下电磁机构以参数化形式进行优化 设计。
2)改进的NSGA-Ⅱ算法用Pareto前沿个体数判断种群进化进程,根据种群进化不同阶段的特性选择不同的进化策略和概率设置,能够有效减少适应度函数计算次数,增强全局收敛能力。
3)恒磁链闭环控制下,将接触器的电磁惯性、机械惯性、触头弹跳特性和铁心材料利用率作为主要优化指标,设计出的样机具有触动快、触头弹跳时间短、铁心材料利用率高、吸持功率小等优点。
该优化设计方法对于智能控制下的接触器本体优化有一定的参考和借鉴意义。
参考文献
[1] 许志红. 电器理论基础[M]. 北京: 机械工业出版社, 2014.
[2] 贾博文, 武建文, 夏尚文, 等. 直流自然换流式接触器设计与均压开断研究[J]. 电工技术学报, 2021, 36(20): 4371-4378.
Jia Bowen, Wu Jianwen, Xia Shangwen, et al. Design and uniform voltage breaking research of a DC natural current commutation contactor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(20): 4371-4378.
[3] 刘树鑫, 宋健, 刘洋, 等. 交流接触器触头系统运动分析及故障诊断研究[J]. 电工技术学报, 2021, 36(增刊2): 477-486.
Liu Shuxin, Song Jian, Liu Yang, et al. Research on motion analysis and fault diagnosis of contact system of AC contactor[J]. Transactions of China Electro- technical Society, 2021, 36(S2): 477-486.
[4] 李奎, 张国盼, 郑淑梅, 等. 基于实时服役参数的交流接触器电寿命最大化控制策略[J]. 电工技术学报, 2021, 36(9): 1976-1985.
Li Kui, Zhang Guopan, Zheng Shumei, et al. A control strategy for maximizing the electrical life of AC contactors based on real-time operating par- ameters[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1976-1985.
[5] 于洪乾, 申笑菱, 曾伟, 等. 基于柔性切换的交流接触器晃电保持方案[J]. 电气技术, 2023, 24(3): 16-22.
Yu Hongqian, Shen Xiaoling, Zeng Wei, et al. Voltage sag retainment scheme for AC contactors based on flexible switching[J]. Electrical Engineering, 2023, 24(3): 16-22.
[6] 唐昭晖, 许志红. 基于响应面法的交流接触器弹簧系统优化设计方法[J]. 电工技术学报, 2022, 37(2): 515-527.
Tang Zhaohui, Xu Zhihong. Optimal design method for AC contactor spring system based on response surface method[J]. Transactions of China Electro- technical Society, 2022, 37(2): 515-527.
[7] 刘向军, 杨程, 周煜源. 基于多反馈参量的交流接触器自适应吸持控制策略[J]. 电工技术学报, 2023, 38(2): 554-562.
Liu Xiangjun, Yang Cheng, Zhou Yuyuan. Adaptive holding control strategy of AC contactor based on multiple feedback parameters[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 554-562.
[8] 刘颖异, 陈德桂, 袁海文, 等. 带电流反馈的永磁接触器动态特性仿真与分析[J]. 中国电机工程学报, 2010, 30(15): 118-124.
Liu Yingyi, Chen Degui, Yuan Haiwen, et al. Simulation and analysis on dynamic characteristics of permanent magnetic contactor with current feed- back[J]. Proceedings of the CSEE, 2010, 30(15): 118-124.
[9] 周茂祥主编. 低压电器设计手册[M]. 北京: 机械工业出版社, 1992.
[10] 王雨诗. 带有动态开距的控制与保护开关电器电磁机构设计[D]. 沈阳: 沈阳工业大学, 2019.
[11] 何晓燕, 许志红. 交流接触器虚拟样机设计技术[J]. 电工技术学报, 2016, 31(14): 148-155.
He Xiaoyan, Xu Zhihong. Virtual prototyping tech- nology of AC contactor[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 148-155.
[12] Shu Liang, Wu Lang, Wu Guichu, et al. A fully coupled framework of predicting the dynamic characteristics of permanent magnet contactor[J]. IEEE Transactions on Magnetics, 2016, 52(8): 1-7.
[13] Kang J W, Jung H K, Ro J S, et al. Design of an AC magnetic contactor with a permanent magnet[C]// 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea (South), 2018: 2826-2828.
[14] 林抒毅, 许志红. 交流接触器三维动态过程数值计算与分析[J]. 中国电机工程学报, 2014, 34(18): 2967-2975.
Lin Shuyi, Xu Zhihong. Simulations and numerical analysis on 3D dynamic process of alternating current contactors[J]. Proceedings of the CSEE, 2014, 34(18): 2967-2975.
[15] 杨文英, 刘兰香, 翟国富. 热场影响下新能源用接触器弹跳特性研究[J]. 电工技术学报, 2019, 34(22): 4687-4698.
Yang Wenying, Liu Lanxiang, Zhai Guofu. The bounce characteristics of contactors for new energy under the influence of thermal field[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4687-4698.
[16] Chen Zhiwei, Bai Baodong, Chen Dezhi, et al. Design of distribution devices for smart grid based on magnetically tunable nanocomposite[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(3): 2083- 2099.
[17] Liu Shaowei, Sun Liqiong, Ma Hui, et al. Design method of electromagnetic mechanism for vacuum contactors by using twice orthogonal analyses with multi-physical simulation[C]//2019 5th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Kitakyushu, Japan, 2019: 641-644.
[18] Fang Shuhua, Chen Yong, Yang Yanju. Optimization design and energy-saving control strategy of high power dc contactor[J]. International Journal of Elec- trical Power & Energy Systems, 2020, 117: 105633.
[19] 张长坤, 许志红. 基于磁链反馈的智能交流接触器串级控制策略[J]. 中国电机工程学报, 2020, 40(4): 1329-1338, 1424.
Zhang Changkun, Xu Zhihong. A cascade control strategy for intelligent AC contactors based on flux linkage feedback[J]. Proceedings of the CSEE, 2020, 40(4): 1329-1338, 1424.
[20] dos Santos Dias de Moraes P M, Perin A J. An electronic control unit for reducing contact bounce in electromagnetic contactors[J]. IEEE Transactions on Industrial Electronics, 2008, 55(2): 861-870.
[21] Han Zhiping, Tang Longfei. HIL simulation for the closure process of contactors based on neural network[C]//2019 4th International Conference on Intelligent Green Building and Smart Grid (IGBSG), Yichang, China, 2019: 300-303.
[22] 吴敬轩, 许志红. 电磁接触器吸合过程无模型自适应控制策略[J]. 中国电机工程学报, 2020, 40(5): 1663-1673.
Wu Jingxuan, Xu Zhihong. A model-free adaptive control strategy for actuation of electromagnetic contactors[J]. Proceedings of the CSEE, 2020, 40(5): 1663-1673.
[23] Tang Longfei, Han Zhiping, Xu Zhihong. A sequ- ential adaptive control strategy for the contact colliding speed of contactors based on fuzzy control[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(7): 6064-6074.
[24] Tang Longfei, Qu He, Xu Zhihong. Research on double closed-loop control strategy of contactors based on flux linkage observers[J]. IEEE Transactions on Industrial Electronics, 2022, 69(3): 2769-2779.
[25] Ramirez-Laboreo E, Sagues C, Llorente S. A new model of electromechanical relays for predicting the motion and electromagnetic dynamics[J]. IEEE Transactions on Industry Applications, 2016, 52(3): 2545-2553.
[26] Shu Liang, Zhao Sheng, Wu Ziran, et al. Optimal design and control of a new permanent magnet AC contactor with forced breaking mechanism[J]. IET Electric Power Applications, 2020, 14(2): 157-164.
[27] Yang Wenying, Liu Peng, Wang Yingqi, et al. Research on dynamic characteristics optimization via analytical modeling for typical rotational electro- magnetic system[J]. IEEE Transactions on Magnetics, 2014, 50(11): 1-4.
Abstract The traditional contactor’s optimization design process requires static calculation, prototype production, and repeated testing, which consumes much time and is high cost, demanding substantial human and material resources. The finite element dynamic simulation method has become the main way to optimize the contactor design but it is hindered by prolonged calculation time. The optimization design method is mainly based on the orthogonal experimental method, which can only generate the local optimal solutions at the experimental level. Intelligent optimization design algorithms can achieve global optimal solutions but require a lot of iterative calculations. Therefore, this paper proposes an improved optimization algorithm for the dynamic process of contactors to reduce the electromagnetic and mechanical inertia of contactors and increase the magnetic density. The response speed of the mechanism and the utilization rate of magnetic materials are improved, reducing contact bounces.
Firstly, considering the external leakage flux and magnetic field’s distribution characteristics in contactors, an improved magnetic circuit model is constructed based on the three-dimensional finite element dynamic simulation to calculate parameters. Then, an improved NSGA-Ⅱ algorithm is introduced for optimization design. The number of Pareto fronts is used to judge the evolution process of the population, and the adaptive genetic differential hybrid evolution strategy is realized, improving global convergence and convergence speed. Finally, combined with a constant flux closed-loop control strategy and multi-objective optimization design, the speed response and magnetic material utilization are improved by reducing electromagnetic and mechanical inertia while increasing magnetic density to mitigate contact bounces.
Simulations and experiments are conducted on the improved magnetic circuit model. The results show that the simulation and experimental waveforms are almost consistent, with errors of less than 3% within the allowable range. Combined with the improved magnetic circuit model and the improved NSGA-Ⅱ algorithm, the contactor design is optimized by the flux linkage closed-loop. The optimization results show that the prototype's holding power is reduced to 0.72 W, the average bounce time is reduced to 0.7 ms, the average number of bounce times is reduced to 2, the number of coil turns is reduced to 1 304, and the magnetic density is increased from 0.54 T to 0.73 T, improving the utilization rate of magnetic materials and reducing the power consumption.
The following conclusions can be obtained: (1) An improved magnetic circuit model, considering the external magnetic leakage and magnetic field distributions in the dynamic process of the contactors, maintains computational efficiency and accuracy across structural parameters and control strategy variations, suitable for optimizing electromagnetic mechanisms with diverse parametric forms. (2) The improved NSGA-Ⅱ algorithm judges the population evolution using the number of individuals in the Pareto frontier and selects evolution strategies and probability settings according to different stages of population evolution, thereby effectively reducing the calculation number of fitness functions and enhancing the global convergence. (3) Under constant flux closed-loop control, the electromagnetic and mechanical inertia, contact bounces, and material utilization rate are taken as the main optimization indicators. The designed prototype has advantages such as fast response, short contact bounce time, high material utilization rate, and low holding power.
keywords:Contactor, optimized design, magnetic circuit method, non dominated sorting genetic algorithm-Ⅱ (NSGA-Ⅱ)
DOI: 10.19595/j.cnki.1000-6753.tces.230377
中图分类号:TM572
福建省自然科学基金资助项目(2021J01634)。
收稿日期 2023-03-31
改稿日期 2023-07-14
汤龙飞 男,1987年生,博士,教授,研究方向为电器及其智能化技术。E-mail: tlftel@fzu.edu.cn(通信作者)
姚林睿 男,1998年生,硕士研究生,研究方向为电器及其智能化技术。E-mail: 1456691792@qq.com
(编辑 崔文静)