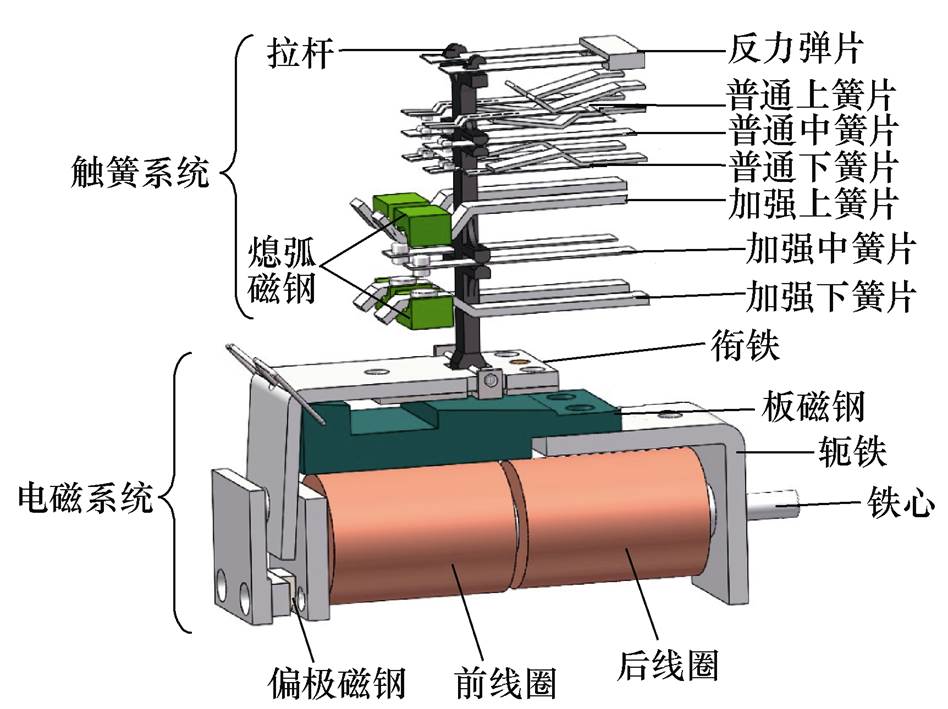
图1 磁保持继电器结构示意图
Fig.1 The structure of magnetic latching relay
摘要 多簧片结构的磁保持继电器衔铁转动引起的触点碰撞、弹跳现象使运动过程复杂，静、动态特性理论分析和仿真模型建立困难。以某型号多簧片结构的磁保持继电器为研究对象，理论分析结构拓扑及工作机理，考虑触点间切入深度，引入狄拉克函数和赫维赛德函数，解决簧片受力分散及触点由于碰撞、弹跳引起的作用力不连续问题；将簧片等效为悬臂梁，基于欧拉-伯努利梁理论建立触簧系统三簧片分段耦合动力学模型。利用Ansys Maxwell引入基于误差的自适应网格划分方法求解电磁机构静态特性；考虑触簧系统簧片运动变形效应，通过ADAMS基于模态理论，构建刚柔耦合动力学仿真模型。基于分段动力学思想，搭建电-磁-机械运动多物理场刚柔耦合仿真模型。利用高速摄像机、电流探头等设计磁保持继电器实验方案，搭建实验平台，测试并分析磁保持继电器触点吸合运动时间、触点压力、弹跳时间、线圈电流，并分析人工装配簧片引起触点压力不同使继电器动作过程存在的不一致性问题，验证该文所提多簧片结构的磁保持继电器特性分段耦合分析方法和多物理场刚柔耦合仿真模型的有效性。
关键词：磁保持继电器 多簧片结构 碰撞弹跳 分段耦合动力学模型 多物理场刚柔耦合
“十四五”规划提出，在综合交通运输发展的铁路主要指标方面，铁路营业里程将从2020年的14.6万km发展为2025年的16.5万km；其中高速铁路营业里程将从2020年的3.8万km发展为2025年的5万km，铁路用电磁继电器的需求和发展日益增加。立足于“双碳”战略，倡导绿色、环保、低碳的行为方式，传统的无磁钢电磁继电器结构简单，线圈通断电后不具有磁保持效果，线圈长时间通电引起的电能损耗给继电器工作性能带来明显影响的同时，也不利于绿色发展。相比于无磁钢电磁继电器，有磁钢电磁继电器线圈通电后实现磁保持，性能可靠、绿色节能。
磁保持继电器结构复杂，部件间一致性较差，各参数间配合不佳，会引起衔铁与铁心以及动、静触头间弹跳次数增多，导致电弧侵蚀与触头磨损加重，严重时会产生触点熔焊粘连，引起吸合时间、吸合电压及触头压力等静、动态特性参数发生显著变化[1]。为满足铁路、航空航天等场景下磁保持继电器高可靠性需求，确定理论分析静、动态特性的方法，建立静、动态特性理论与仿真模型，分析静、动态变化规律。
近年来，国内外学者对电磁继电器等电器产品的静、动态特性仿真建模与实验测试进行了大量研究。在仿真建模方面，E. Ramirez-Laboreo等基于等效磁路法计算电磁转矩，将电磁继电器建模为由4个刚性体组成的平面四连杆机构，模拟实际运动，基于牛顿第二定律分析计算动态特性[2]。J. R. Riba等考虑边缘磁通量及短路环的影响，建立能够同时预测交、直流接触器动态行为的统一参数模型[3]。N. Lambrecht等利用触点闭合与断开时触点两端电压分别为低电平与高电平两种不同现象，将低电平时间和高电平时间作为随机变量表征触点随机弹跳现象，基于电路编辑器将电磁继电器替换为可控电压开关，建模触点弹跳过程[4]。鲍光海等引入Ansys LS-DYNA，基于继电器运动方程、材料本构方程和边界条件，处理动、静簧片的弹性变形[5]。杨文英等将微小型继电器簧片等效为欧拉-伯努利梁分析单柔性体簧片与刚性体耦合系统动力学方程[6]。曹云东等将继电器簧片等效为欧拉-伯努利梁，建立单簧片计算模型，采用Bathe复合时间积分算法求解簧片固有振动特性[7]。翟国富等采用分段线性结构动力学思想以及Kelvin-Voigt模型，考虑能量损失、碰撞变形等因素分段分析弹簧系统动力学特征，提出基于瞬态特性的快速耦合直流接触器机-电-磁-运动多物理场计算方法[8]。许志红等基于连续介质力学有限元法，研究接触器缓冲垫大变形引起的几何非线性、非线性接触等非线性问题[9]。汤龙飞等将永磁接触器永磁磁链和电磁磁链分开考虑，改进传统电磁接触器等效电路，基于COMSOL有限元仿真与电磁操动机构等效磁路提出永磁接触器全过程等效电路模型，基于LabVIEW和Multisim搭建单稳态永磁接触器联合仿真模型[10]。梁慧敏等基于Ansys制作静态特性数据表，耦合电压平衡方程、达朗贝尔方程以及麦克斯韦方程，借助Matlab/ Simulink模块调用ADAMS模型、线圈回路子模型完成双磁钢差动式继电器动态特性联合仿真分析[11]。叶雪荣等基于斯通纳-沃尔法斯模型建立单轴单畴磁性微粒磁特性模型，采用改进Preisach模型建立磁钢宏观磁感应强度模型，建立航天电磁继电器磁钢局部磁滞回线数学模型[12]。李东晖等基于改进Lankarani- Nikravesh接触模型建模转臂与转臂套筒间的接触力和摩擦力，采用Gerber模型建模转臂裂纹萌生周期，建立虚拟样机模型仿真真空交流接触器转臂的断裂周期[13]。周学等考虑裂纹为椭圆形，基于S-N曲线和Gerber模型计算打击杆裂纹萌生周期，采用Pairs公式建立万能式断路器打击杆裂纹扩展模型[14]。实验测试方面，C. R. Tung等利用多普勒激光测振仪从多时间尺度角度测试直流悬臂式接触开关弹跳现象，发现触点高频弹跳来源于悬臂结构第二本征模态的瞬态激励[15]。姚帅亮利用滚珠丝杠配合步进电机，基于拉压力传感器制作螺管式电磁机构静态吸力测试装置，实现静态吸力特性的自动测量[16]。汤龙飞等在动、静铁心间嵌入多层云母片测量恒定气隙下线圈电压和电流，结合理论公式间接测量接触器静态磁链和静态电磁吸力[17]。陈德为等通过高速摄像机拍摄接触器动态过程，基于刚体运动方程和投影关系约束方程分析二维序列图像特征点，获取接触器三维动态特性[18]。刘向军等基于高速摄像机、平面镜成像系统，将电磁系统被测面与成像平面呈45°摆放，基于Image-Pro Plus软件处理，获取电磁机构三维动态特性[19]。刘亚魁等基于霍夫变换自动定位关键角点，采用Lucas- Kanade光流法获取角点运动轨迹，完成高压断路器机械特性的机器视觉测试[20]。许志红等基于选相分合闸装置控制交流接触器线圈合闸相位，基于激光位移传感器测量动铁心位移，基于直流电源测量触头弹跳信号[21]。孙曙光等基于霍尔传感器测量线圈和触头回路电压、电流信号，基于聚偏氟乙烯压电薄膜传感器配合电荷放大器测量触头压力[22]。目前，国内外研究大多聚焦于传统无磁钢、无簧片式结构的继电器等产品，针对不对称双磁钢和不对称双线圈之间永磁磁通与电磁磁通相互耦合和多组簧片配合工作的永磁继电器静、动态特性理论分析，仿真建模与实验测试鲜见报道。
本文在电器仿真建模与实验测试方法的基础上，考虑不对称永磁磁通与电磁磁通相互耦合作用、多组可变形簧片间簧片运动变形效应和触点间非线性高速碰撞与弹跳现象，提出多簧片结构的磁保持继电器电-磁-机械运动多物理场刚柔耦合仿真模型。基于Solidworks建模磁保持继电器拍合式电磁机构和触簧系统三维实体；基于牛顿力学理论分析触簧系统分段运动过程，并将簧片等效为欧拉-伯努利梁构建三簧片分段耦合动力学等效模型。基于Ansys Maxwell搭建电磁机构永磁磁通与电磁磁通电磁耦合仿真模型，求解静态电磁特性；基于ADAMS，采用嵌入式MSC Nastran程序，基于模态理论创建触簧系统可变形簧片，并基于数显式推拉力计测试柔性体力-形变量曲线，提高金属簧片柔性体建模精度，建立磁保持继电器刚柔耦合动力学仿真模型。结合电磁特性，基于三簧片分段耦合动力学模型，引入分段动力学思想，构建磁保持继电器电-磁-机械运动多物理场刚柔耦合仿真模型。基于电流探头测试磁保持继电器电磁机构线圈电流，基于高速摄像机拍摄触簧系统动态特性，并分析因人工装配簧片而引起触点压力不同使继电器动作过程存在不一致性的问题。验证多簧片结构的磁保持继电器理论分析和多物理场刚柔耦合仿真模型的有效性。
本文选用某型号磁保持继电器为研究对象，三维实体模型如图1所示。电磁机构为含不对称双磁钢和不对称双线圈的直流极化拍合式电磁系统。触簧系统包括24组触点和13组可变形金属簧片。相关参数见表1。
图1 磁保持继电器结构示意图
Fig.1 The structure of magnetic latching relay
表1 磁保持继电器相关参数
Tab.1 Related parameters of magnetic latching relay
参 数数 值 线圈额定电压/V24 线圈额定电流/A0.15 线圈电阻/W160 线圈匝数5 100 衔铁最大转角/(°)8.5
电磁机构包括两块材质、形状、大小不同的磁钢、两个不同线圈；触簧系统包括加强上触点、加强中触点、加强下触点、普通上触点、普通中触点、普通下触点、加强静簧片、加强动簧片、普通静簧片、普通动簧片、上托片、下托片、顶部托片、反力弹片、拉杆、熄弧磁钢等部件。拍合式电磁机构主磁通分布如图2所示。如图2a所示，衔铁处于反位落下稳定状态，给前线圈两端施加恒定直流额定电压，铁心内部产生从左向右的电磁通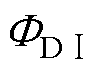
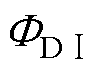，通过削弱衔铁与板磁钢间合成磁通、加强工作气隙合成磁通，进而增大衔铁和铁心间电磁吸力，使衔铁与铁心吸合。如图2b所示，衔铁处于定位吸合稳定状态，工作原理类似，区别是给后线圈两端施加恒定直流额定电压，铁心内部产生与电磁通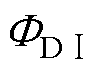方向相反的电磁通
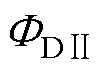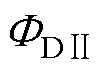，通过削弱衔铁和铁心间的合成磁通，增加工作气隙内合成磁通，进而增大衔铁与板磁钢间电磁吸力，衔铁动作与铁心断开，触簧系统通过衔铁来回运动带动拉杆完成触点通断。
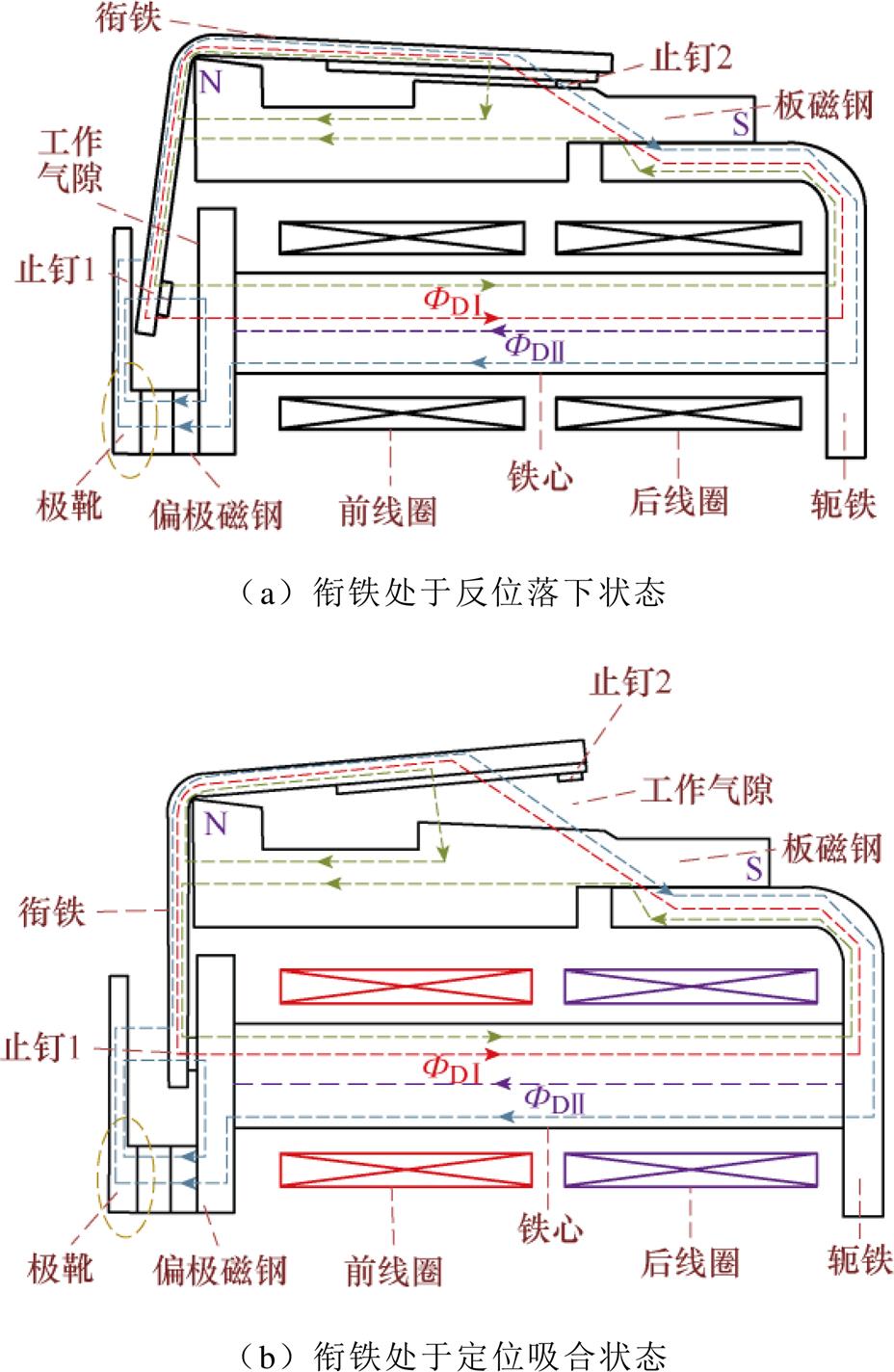
图2 拍合式电磁系统主磁通分布
Fig.2 The distribution of main magnetic flux of clapper type electromagnetic system
高速碰撞、弹跳引起的间歇性接触现象存在于电磁继电器衔铁和触点运动过程中，其中触点接触时，在触点间由于电流线收缩产生电动斥力，因此有必要对运动过程进行分段受力分析，研究动力学特征突变成因。
根据柔性体簧片运动特性，将簧片等效为悬臂梁结构，采用欧拉-伯努利梁理论进行动力学分析。假定簧片变形前垂直于簧片轴线的平截面，在受力发生弯曲变形后，仍保持为平面且垂直于变形后的簧片轴线。根据继电器触点间面-面接触特性，基于导电斑点模型分析触点间电动斥力，将触点间所有导电斑点假定为一个较大圆形导电斑点，且导电斑点与触点材料相同[6]。磁保持继电器触簧系统运动中为三簧片耦合运动碰撞过程，区别于单簧片与刚性体之间的碰撞接触，需要同时考虑三个柔性体簧片在受力弯曲变形之后的耦合运动。
基于上述分析，建立如图3所示考虑碰撞接触的磁保持继电器簧片等效动力学耦合模型。图3中，以中触点簧片固定端为原点O，中触点簧片轴线为x轴，并过原点O和上、下触点簧片固定端作y轴，建立二维平面坐标系表征簧片位置。L为簧片等效长度；d0为簧片等效厚度；x1为簧片拉杆等效作用点距原点距离；x2为触点等效接触作用点距原点距离；y1为上触点簧片和下触点簧片固定端等效位置距原点距离；y2为上触点簧片和下触点簧片自由端等效最大位移；y3为下触点簧片自由端等效最大上移距离；f1为拉杆等效作用力；fjU、fjM、fjD分别为上、中、下触点运动碰撞等效接触力；fiU、fiM、fiD分别为上、中、下触点间等效电动斥力；P1为触点等效接触点；yU、yM、yD分别为上、中、下触点等效位移。
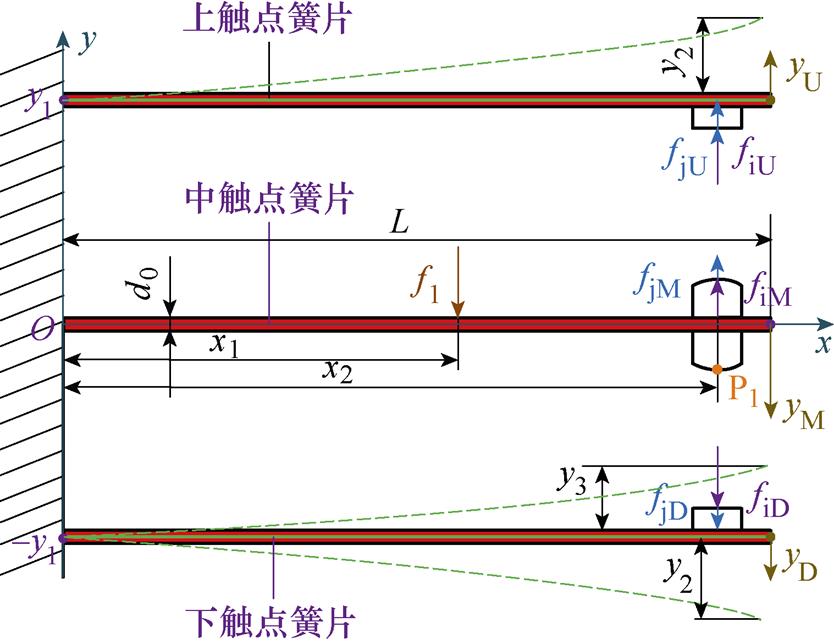
图3 磁保持继电器簧片等效动力学耦合模型
Fig.3 The equivalent dynamic coupling model of magnetic latching relay reed
衔铁在与铁心断开到吸合过程中，中触点从与下触点稳定接触开始运动，直到与上触点稳定接触，运动过程中触点簧片受力状态不同，动力学特征产生突变。整个运动过程可等效为以下三个不同的运动阶段（其中规定向上为正方向，忽略触点高度）：
（1）当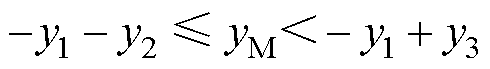
时，中触点与下触点接触，中触点簧片受到拉杆向上拉力f1、触点间接触力fjM和电动斥力fiM，下触点簧片受到触点间接触力fjD和电动斥力fiD。此时，中触点、下触点簧片间产生耦合运动，中触点、下触点簧片动力学方程分别表示为
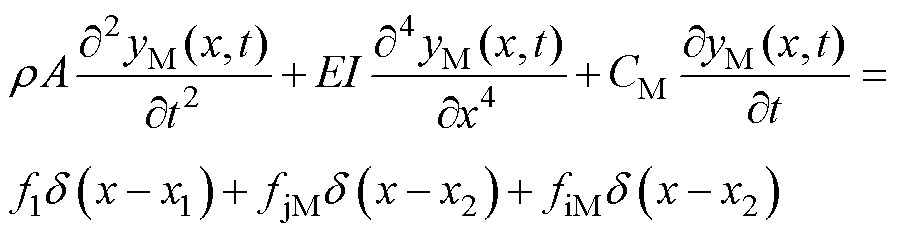（1）
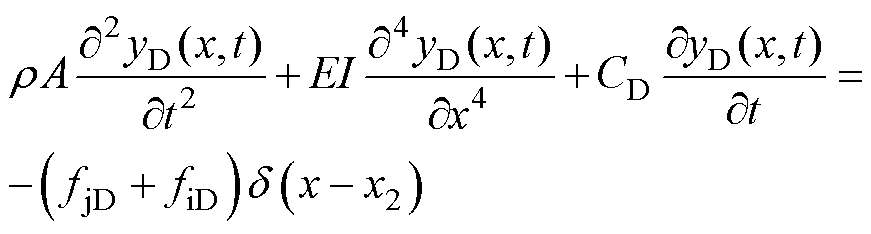（2）
式中，r 为簧片密度；A为簧片横截面积；E为簧片弹性模量；I为继电器簧片惯性矩；CD、CM分别为下、中触点簧片等效阻尼。
基于牛顿第三定律可知，触点间接触力、电动斥力分别为一对反作用力，表示为
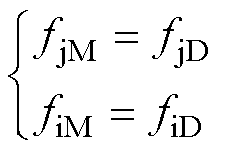（3）
此阶段边界条件为：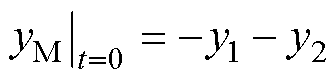
；
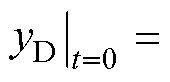
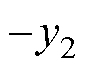。本文考虑簧片实际受力为分散状态，引入狄拉克函数d(x)解决簧片实际中仅在有限个位置处受力的问题。
（2）当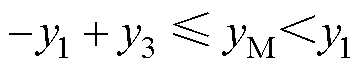
时，中触点与下触点分离，触点间接触力和电动斥力消失，中触点簧片仅受拉杆向上拉力f1，下触点簧片不受任何外力。此时，中触点簧片继续向上触点运动；下触点簧片单独运动，直至稳定。中触点、下触点簧片动力学方程分别表示为
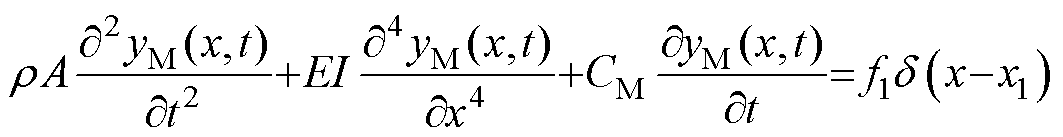（4）
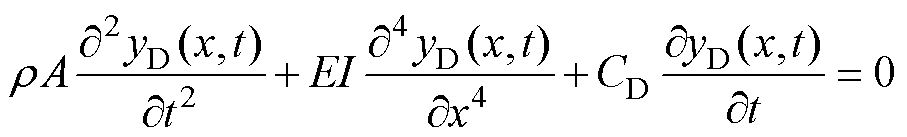（5）
此阶段边界条件为：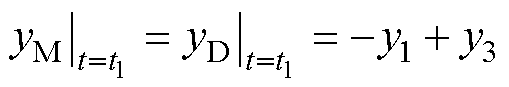
；
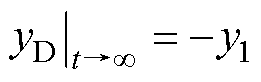。其中，t1为第一阶段运动结束时刻。
（3）当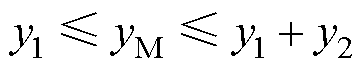
时，中触点与上触点接触，触点间首先产生不规则弹跳发生间歇性接触，然后触点间持续接触，直至簧片运动结束，此时中触点簧片受到拉杆向上拉力f1、触点间向下接触力fjM和向下电动斥力fiM，上触点簧片受到触点间向上接触力fjU和向上电动斥力fiU，中触点、上触点簧片动力学方程分别表示为
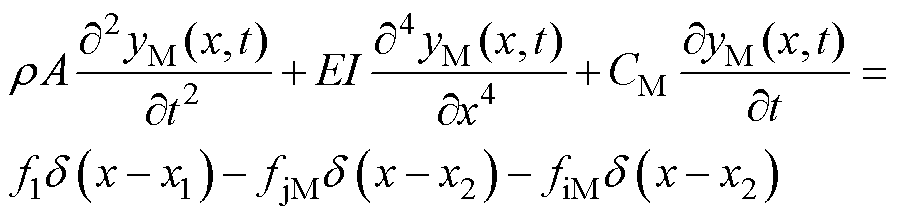（6）
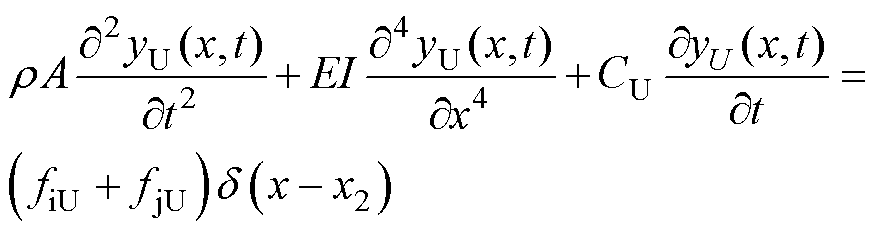（7）
式中，CU为上触点簧片等效运动阻尼。
同样，基于牛顿第三定律得
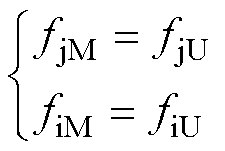（8）
此阶段边界条件为：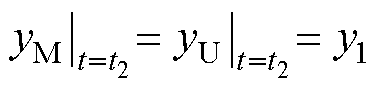
；
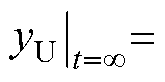
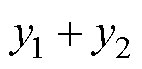。同理，t2为第二阶段运动结束时刻。
上述三个阶段簧片被等效为欧拉-伯努利梁，簧片运动过程中固定端的挠度、转角为零，自由端的弯矩、剪力为0。三个阶段边界条件都服从于
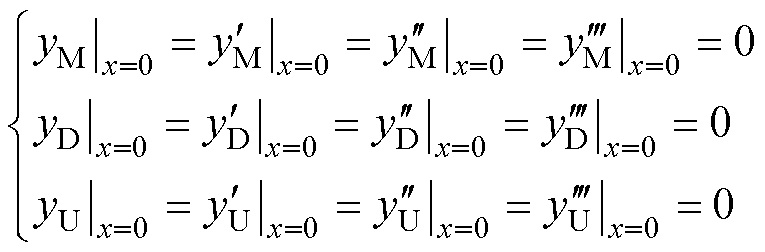（9）
簧片运动过程中触点间会发生间歇性接触，引起触点间接触力和电动斥力作用不连续。本文考虑触点间切入深度引入赫维赛德函数e( y)处理触点间作用力不连续问题。根据触点间面-面接触特性，基于电动力理论引入接触桥模型[6]，触点间电动斥力fi表示为
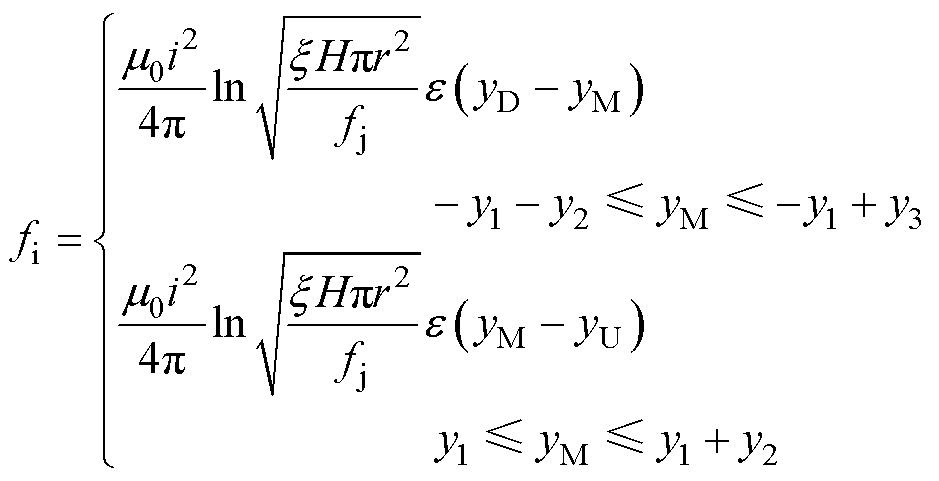（10）
式中，i为触点间等效电流；m0为真空磁导率；x 为触点等效表面接触系数；H为触点等效材料布氏硬度；r为触点等效接触半径；fj为触点间接触力。
基于赫兹接触理论，引入冲击函数（impact）模型，触点间碰撞接触力表示为
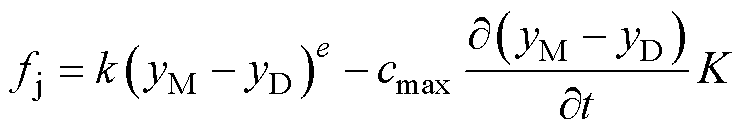（11）
式中，k为触点间等效接触刚度系数；cmax为触点间等效最大阻尼系数；e为触点间等效碰撞指数；K为系数。
为解决触点间开始接触瞬间前由于尚未真正接触阻尼力为零到开始接触瞬间后由于触点切入速度不为零引起阻尼力不为零的不连续问题，引入系数K，表示为
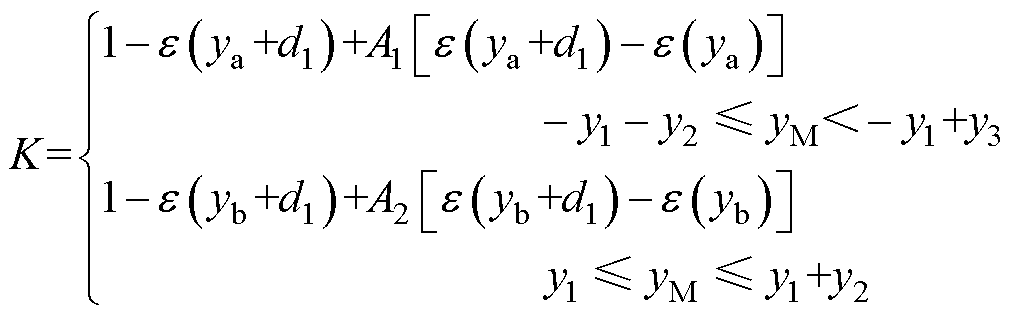（12）
其中
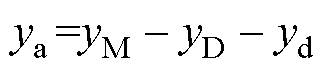
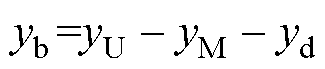
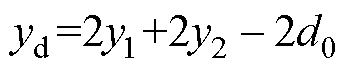
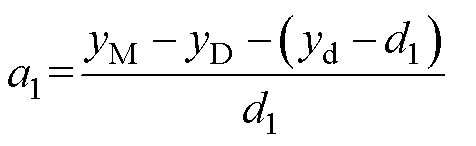
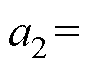
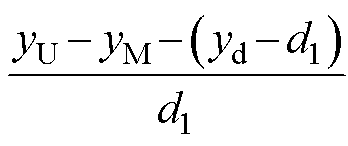
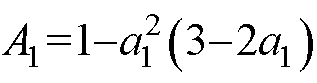
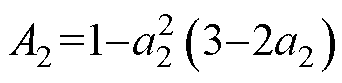
式中，d1为触点间切入过程中阻尼力达到最大时的等效切入深度。
磁保持继电器静、动态特性仿真建模牵涉到电-磁-机械运动多物理场耦合分析。分别建立磁保持继电器三维电磁场仿真模型和刚柔耦合动力学仿真模型，基于线圈电压平衡方程搭建磁保持继电器电-磁-机械运动多物理场刚柔耦合仿真模型。磁保持继电器多物理场刚柔耦合仿真流程如图4所示。
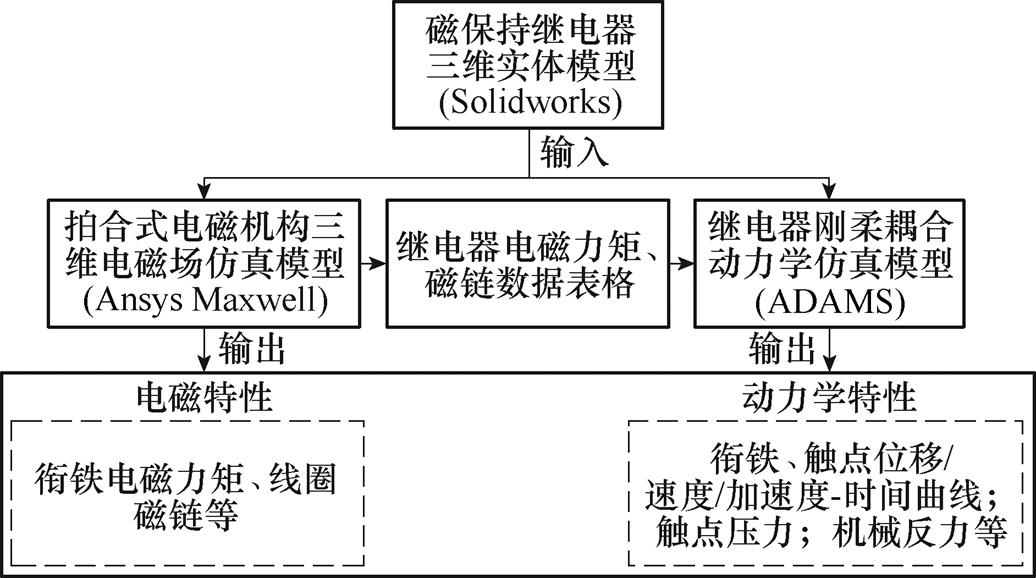
图4 磁保持继电器多物理场刚柔耦合仿真流程
Fig.4 The flow chart of the multiphysics rigid flexible coupling simulation of magnetic latching relay
电磁机构静态特性分析中磁场不随时间发生变化，在Ansys Maxwell中，选择三维静磁场求解器建立如图5所示的拍合式电磁机构三维电磁仿真模型，并分析求解。
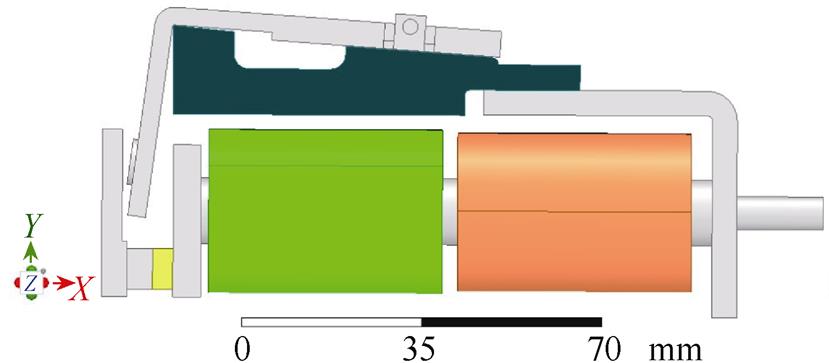
图5 磁保持继电器拍合式电磁机构电磁仿真模型
Fig.5 The electromagnetic simulation model of clapper type electromagnetic system of magnetic latching relay
首先，分别赋予拍合式电磁机构部件对应材料属性，定义不对称双磁钢实际充磁方向。其次，为模拟拍合式电磁机构磁力线在周围空气中的分布，考虑拍合式电磁机构整体为方形结构，建立电磁机构三维长方体求解域，并设置求解域所有外表面上的矢量磁位为零，即求解域边界磁力线平行于求解域外表面。然后，划分拍合式电磁机构网格，在三维静磁场分析中，传统分析方法依赖人为判断所需网格类型与数目，基于网格划分参数一次性产生整个求解过程中全部网格，精度无法保证。考虑拍合式电磁机构结构复杂性引起永磁磁通和电磁磁通耦合复杂性，本文引入内嵌于Ansys Maxwell的基于误差的自适应网格划分求解方法，自适应迭代细化拍合式电磁机构初始网格，减小高误差区域内网格尺寸，提升电磁模型求解精度。
考虑拍合式电磁机构衔铁所受转矩与导体中流过电流时导体所受洛伦兹转矩不同的特点，本文引入虚功原理法，基于能量守恒原理，在电磁机构有限元求解过程中，沿电磁机构外表面分布的网格会发生变形，电磁机构磁共能变化由已变形网格磁共能变化求出。考虑铁磁材料的非线性，磁共能Wc表示为
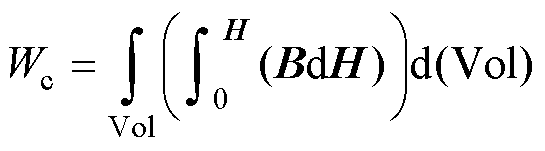（13）
式中，B为电磁机构磁通密度；H为电磁机构磁场强度；Vol为电磁机构体积。
衔铁所受虚功转矩表示为
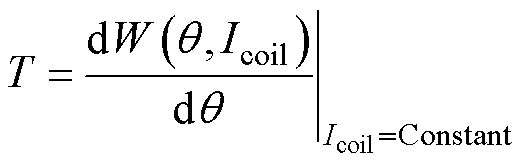（14）
式中，T为虚功转矩；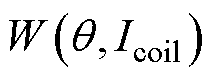
为电磁机构磁共能；
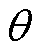为电磁机构衔铁转角；
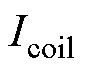为电磁机构线圈电流且保持为恒值。
考虑拍合式电磁机构不对称双磁钢与不对称双线圈间永磁磁通与电磁磁通相互耦合作用，线圈总磁链表示为
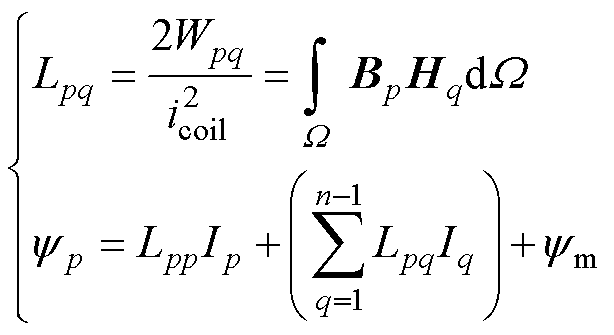（15）
式中，p、q分别为电磁机构前线圈和后线圈；Wpq为前线圈和后线圈耦合系统中，磁场存储的能量；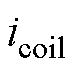
为前线圈中的电流；Bp为前线圈流过1 A电流时的磁通密度；Hq为后线圈中流过1 A电流时的磁场强度；
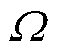为线圈空间位置分布；
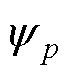为前线圈总磁链；LppIp为线圈自感磁链；
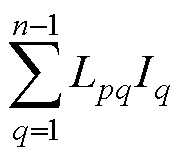为线圈互感磁链；
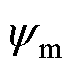为永磁磁链；n为线圈数目。
最后，设计拍合式电磁机构衔铁旋转角度和线圈电流参数化方案，批量求解不同电流、不同角度下衔铁静态力矩和线圈静态磁链，分析继电器静态特性并制作静态特性数据表格。衔铁吸合过程中拍合式电磁机构静态磁链和静态转矩仿真结果如图6和图7所示。
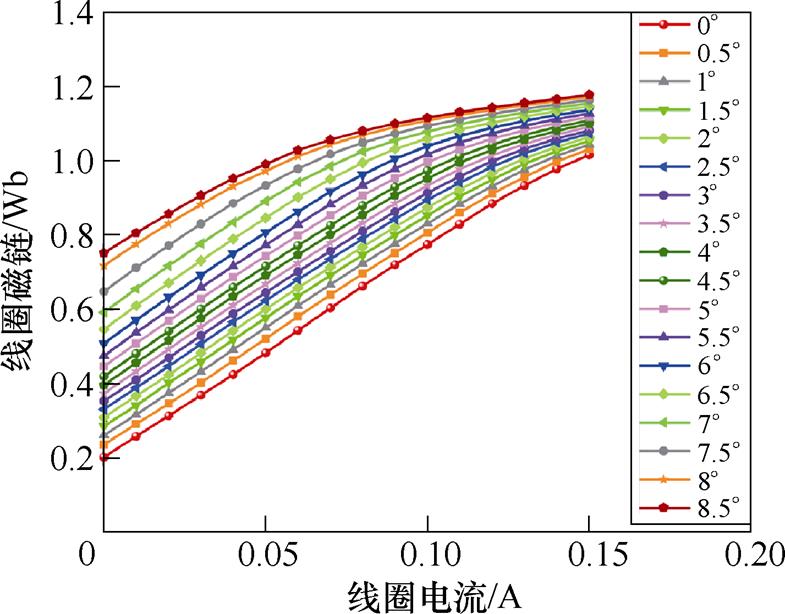
图6 拍合式电磁机构静态磁链仿真曲线
Fig.6 The simulation curves of the static magnetic linkage of clapper type electromagnetic system
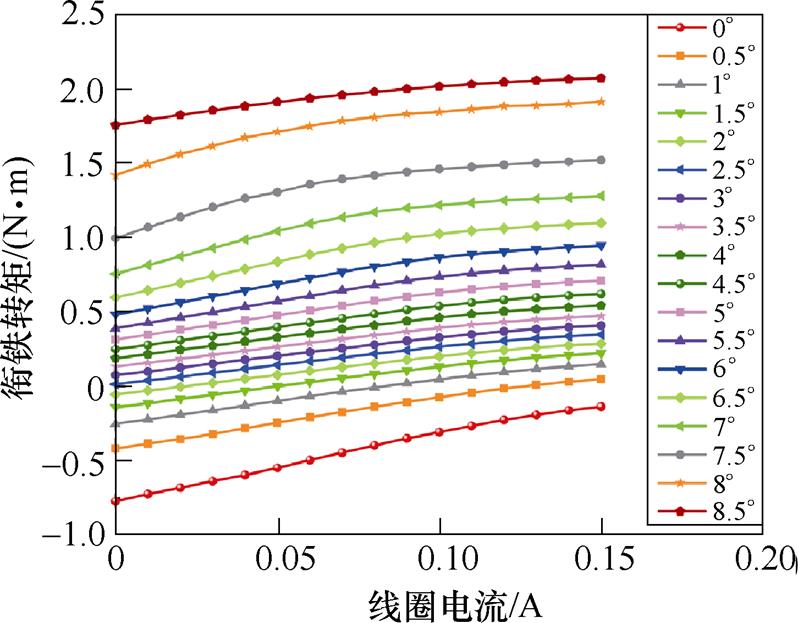
图7 拍合式电磁机构静态转矩仿真曲线
Fig.7 The simulation curves of the static torque of clapper type electromagnetic system
图6、图7显示，磁保持继电器吸合过程中，当拍合式电磁机构衔铁转动较小角度时，衔铁与铁心间气隙较大，总磁路磁阻中气隙磁阻占主要成分，磁路尚未饱和，线圈磁链和衔铁所受转矩随线圈电流呈线性增加。当衔铁转动较大角度时，气隙磁阻减小，铁心磁阻占主要成分，随着线圈电流增加，线圈磁链和衔铁所受转矩增加趋于平缓，呈现出非线性铁磁材料典型的饱和特性。
基于继电器静态特性，动态特性分析包含电-磁-机械运动多物理场互相耦合产生的效应，遵循动态微分方程组为
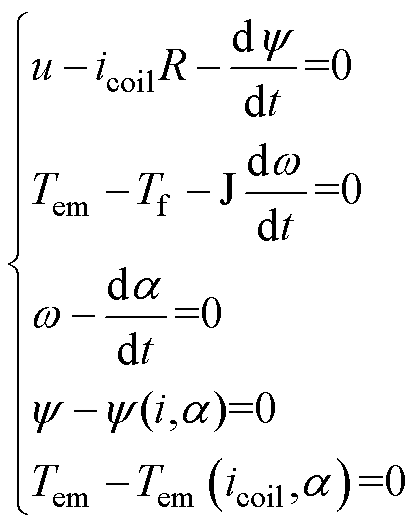（16）
式中，u为线圈电压；R为线圈电阻；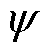
为线圈磁链；Tem为衔铁所受电磁转矩；Tf为衔铁所受反作用力矩；w 为衔铁角速度；a 为衔铁角位移。
磁保持继电器多物理场刚柔耦合仿真模型逻辑如图8所示。
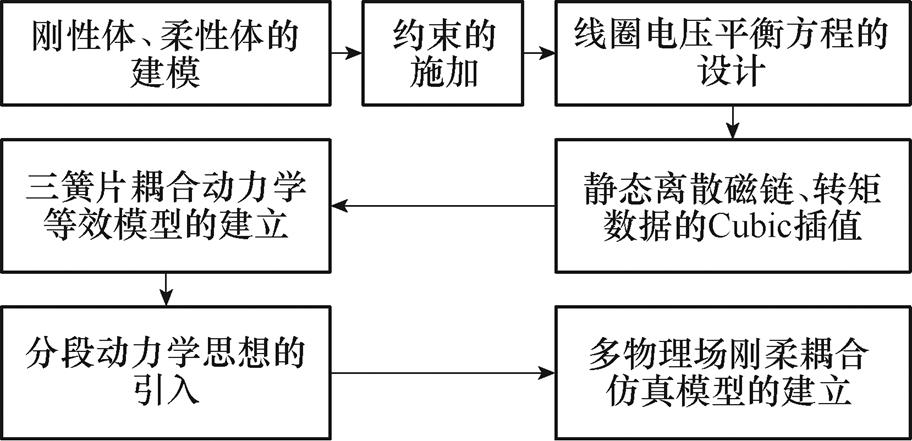
图8 磁保持继电器多物理场刚柔耦合仿真模型逻辑
Fig.8 The logic diagram of the multiphysics rigid flexible coupling simulation model of magnetic latching relay
在多体动力学软件ADAMS中，建立如图9所示磁保持继电器刚柔耦合动力学仿真模型。
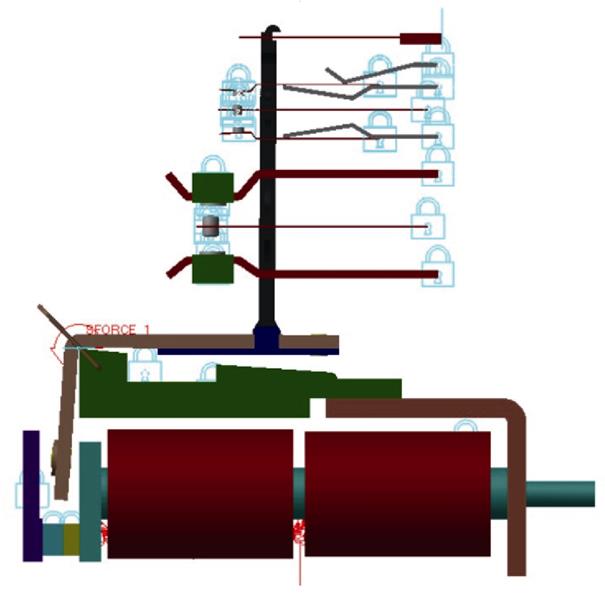
图9 磁保持继电器刚柔耦合动力学仿真模型
Fig.9 The rigid flexible coupling dynamic simulation model of magnetic latching relay
首先，建模电磁机构为刚性体，为精确模拟13个簧片的实际变形效果，考虑簧片运动变形效应，基于模态理论，利用嵌入式MSC Nastran程序将簧片建模为柔性体，区别于Ansys APDL联合ADAMS使簧片柔性化，虽然两者均是基于有限元技术通过制作模态中性文件创建柔性体，但是基于Ansys APDL的模态中性文件导入ADAMS替换刚性体过程中，不同零部件需分别多次导入，零部件参数发生变化时需要重新制作文件，过程繁琐。考虑磁保持继电器具有13个可变形簧片，数目较多，本文基于ADAMS ViewFlex模块嵌入式MSC Nastran程序，直接在磁保持继电器三维实体模型创建簧片柔性体，提高建模效率，磁保持继电器部件建模类型见表2。并对刚柔耦合结构模型添加正确的固定副、运动副、衔铁所受力矩、部件间接触等约束，磁保持继电器部件接触类型见表3。
表2 磁保持继电器部件建模类型
Tab.2 Component modeling types of magnetic latching relay
部件类型建模类型 衔铁刚性体 铁心刚性体 轭铁刚性体 极靴刚性体 线圈刚性体 板磁钢刚性体 永久磁钢刚性体 蝶形卡扣刚性体 拉杆刚性体 拉杆轴刚性体 触点刚性体 熄弧磁钢刚性体 止钉刚性体 上、下托片刚性体 顶部托片刚性体 反力弹片柔性体 加强下触点簧片柔性体 加强中触点簧片柔性体 加强上触点簧片柔性体 普通下触点簧片柔性体 普通中触点簧片柔性体 普通上触点簧片柔性体
触簧系统柔性体簧片位移公式表示为
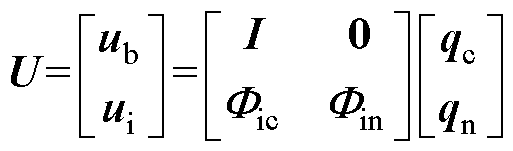（17）
表3 磁保持继电器部件接触类型
Tab.3 Component contact types of magnetic latching relay
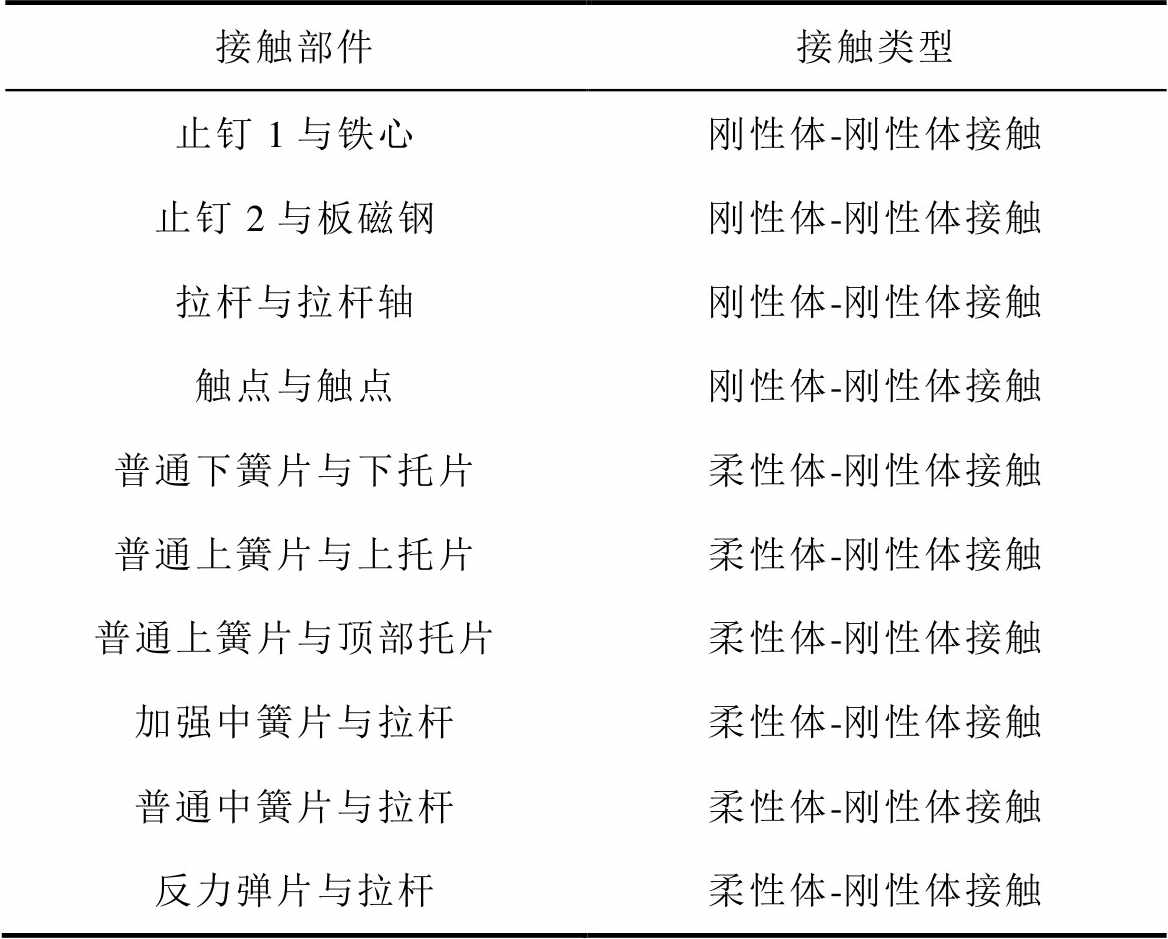
接触部件接触类型 止钉1与铁心刚性体-刚性体接触 止钉2与板磁钢刚性体-刚性体接触 拉杆与拉杆轴刚性体-刚性体接触 触点与触点刚性体-刚性体接触 普通下簧片与下托片柔性体-刚性体接触 普通上簧片与上托片柔性体-刚性体接触 普通上簧片与顶部托片柔性体-刚性体接触 加强中簧片与拉杆柔性体-刚性体接触 普通中簧片与拉杆柔性体-刚性体接触 反力弹片与拉杆柔性体-刚性体接触
式中，U为簧片位移；ub为簧片外连点位移；ui为簧片内部点位移；I为单位矩阵；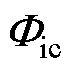
为簧片内部节点约束模态的模态位移；
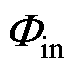为簧片内部节点正交模态的模态位移；qc为簧片约束模态的模态坐标值；qn为簧片正交模态的模态坐标值。
基于面-面碰撞接触理论，引入Kelvin-Voigt模型[8]计算触点间切入深度。设触点间接触面为圆形，则触点间平均变形D 为
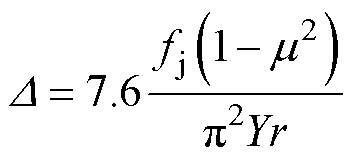（18）
式中，m 为触点材料泊松比；Y为触点材料杨氏模量。
触点间切入深度d 为两触点变形之和，可表示为
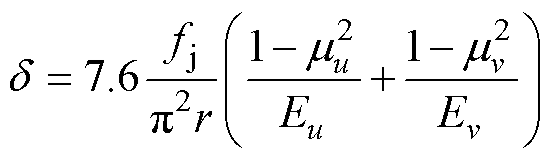（19）
式中，下角u、v为两个接触触点。
基于胡克定律，触点间等效接触刚度可表示为
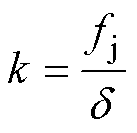（20）
根据厂家技术手册银-银材质摩擦系数数量级约为10-1，仿真中触点间摩擦系数设置为厂家实验参考值0.8[9]。触点间等效接触阻尼C设置为
[8]，用来模拟触点间碰撞弹跳过程中的能量损失。
然后，为耦合磁保持继电器机械运动方程和电磁场方程，设计线圈电压平衡微分方程，并以三维样条线性数据分别导入静态磁链和静态转矩数据表格。考虑求解电压平衡方程时涉及磁链的一阶导数，本文引入Cubic插值法，插值静态离散磁链数据。区别于Akima插值方法，Cubic插值法属于全局插值，即同时利用所有已知线圈磁链数据插值某一未知磁链数据，不必考虑离散磁链数据点分布的均匀性，获得良好的线圈磁链一阶和二阶导数插值结果，减少静态特性数据的离散性对连续动态特性求解精度的影响，完成离散数据到连续数据的合理扩充。
最后，考虑磁保持继电器吸合过程为衔铁从与铁心间距最大开始，通电运动直到衔铁与铁心完全闭合，结合所建刚柔耦合动力学模型，本文基于三簧片耦合动力学等效模型，引入分段动力学思想，首先使磁保持继电器运动，直到衔铁与铁心之间稳定保持最大距离，此时中触点与下触点稳定接触。然后线圈通电，衔铁开始吸合，直到衔铁与铁心稳定接触，中触点与上触点停止弹跳，建立完整的磁保持继电器电-磁-机械运动多物理场刚柔耦合仿真模型。
采用高精度韦度数显式推拉力计、德力西不锈钢数显式游标卡尺以及固定夹具，测试磁保持继电器簧片受力与形变量之间的关系，其中，数显式推拉力计采集簧片受力大小，上限负荷值为2 N，负荷分度值为0.001 N，测量精度为±0.5%；数显式游标卡尺用来测量簧片受力弯曲形变量，量程为0～150 mm，分度值为0.01 mm，误差值为±0.03 mm。普通中触点簧片和加强中触点簧片力-形变量曲线如图10和图11所示。
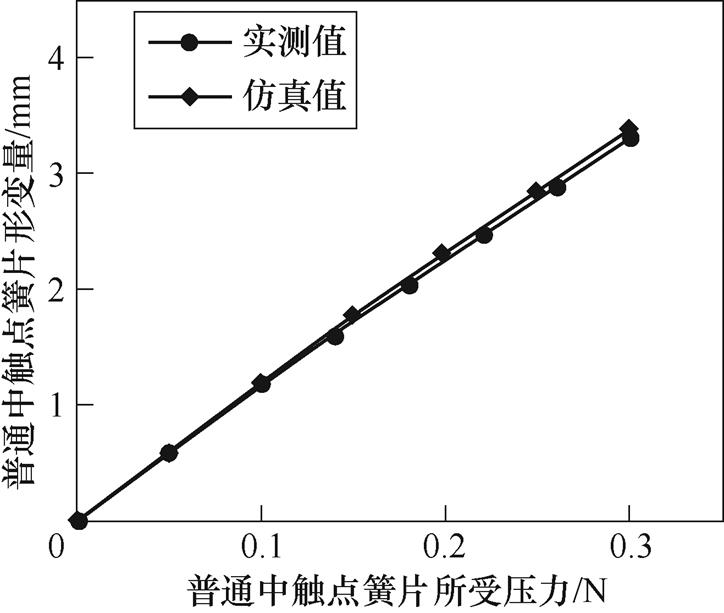
图10 普通中触点簧片力-形变量仿真与实验对比
Fig.10 The comparison of force-displacement simulation and measurement of common middle contact reed
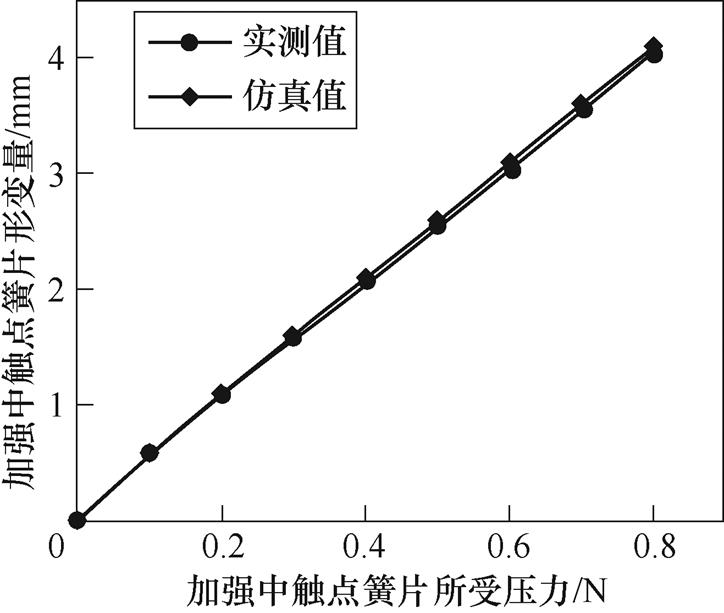
图11 加强中触点簧片力-形变量仿真与实验对比
Fig.11 The comparison of force-displacement simulation and measurement of reinforce middle contact reed
图10和图11显示，磁保持继电器普通中触点簧片和加强中触点簧片在形变量较大处百分比误差较小；在形变量较小处百分比误差较大，最大百分比误差在3%左右。原因为，在仿真建模过程中簧片柔性体模态阶数与网格数量难以准确设定；在实际测试过程中对于越小的力和越小的形变量，推拉力计和游标卡尺越难以精确测试。
本节建立磁保持继电器电-磁-机械运动多物理场刚柔耦合仿真模型，完成磁保持继电器动态特性仿真计算。
设计基于高速摄像机的运动轨迹测试平台，包括pco.dimax S高速摄像机、直流恒压恒流线性电源、照明灯、计算机等，如图12所示。直流恒压恒流电源提供磁保持继电器动作线圈所需直流电压；考虑触簧系统触点为对称结构，照明灯采用对称双灯方案，使触簧系统对称两侧触点均匀受光，减少反光，保证清晰捕捉触点运动轨迹；基于采集和存储的系列照片，分析计算触点运动关系，提取触点运动过程中位移-时间关系、速度-时间关系以及加速度-时间关系，进行动态特性仿真与实验对比分析。
图12 磁保持继电器触点运动轨迹测试平台
Fig.12 The experimental platform for contact movement track of magnetic latching relay
图13为磁保持继电器运动过程中高速摄像机拍摄的开始时刻对应照片。拍摄前在拉杆轴正面粘贴标尺，通过跟踪像素点的移动轨迹获取触点动态特性数据。
图13 磁保持继电器开始运动时刻照片
Fig.13 The photo of magnetic latching relay at the beginning of movement
磁保持继电器触点吸合运动时间仿真与实验对比见表4。
表4 触点吸合运动时间仿真与实验对比
Tab.4 The simulation and measurement comparison of contact pick-up movement time
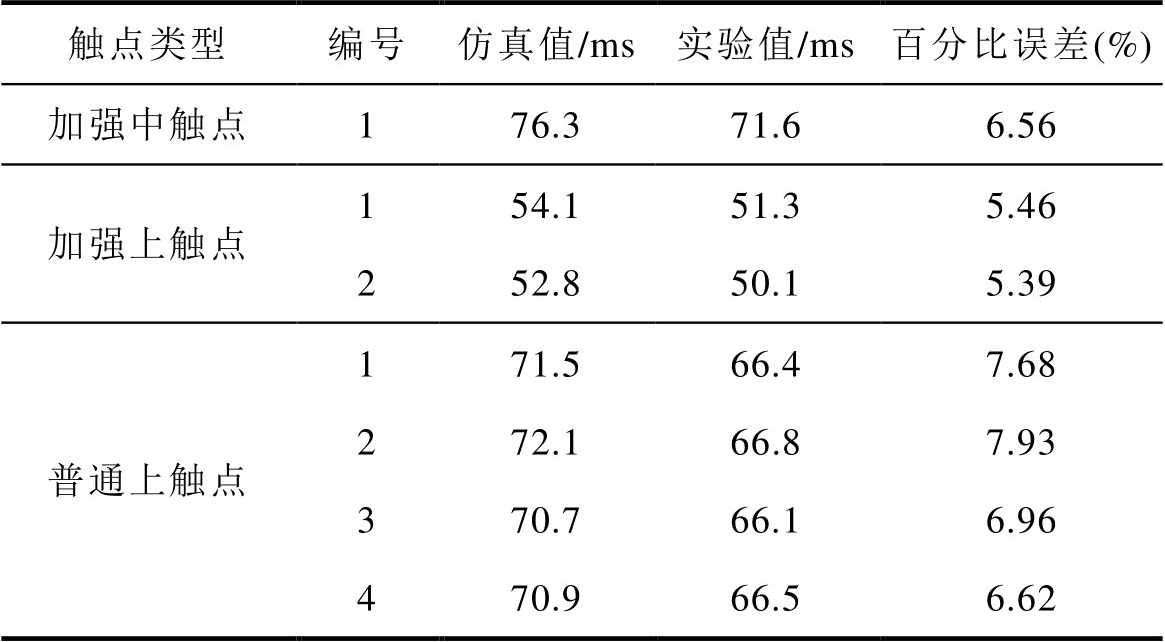
触点类型编号仿真值/ms实验值/ms百分比误差(%) 加强中触点176.371.66.56 加强上触点154.151.35.46 252.850.15.39 普通上触点171.566.47.68 272.166.87.93 370.766.16.96 470.966.56.62
表4显示，加强中触点的吸合时间比加强上触点吸合时间大20 ms左右。原因为线圈通电后，衔铁先带动加强中触点运动20 ms，直到与加强上触点接触，再带动加强上触点开始运动。此外，普通上触点吸合时间均大于加强上触点吸合时间，原因为普通上触点簧片相比于加强上触点簧片薄，受力之后更易运动，持续时间更长。表4中触点吸合时间仿真与实验结果对比误差最大为7.93%。
磁保持继电器触点压力、弹跳时间仿真与实验对比见表5、表6。
表5、表6显示，对触点压力分别连续测量3次，加强上触点、普通上触点压力实测平均值与仿真值误差分别为6.17%、7.91%。触点弹跳时间仿真值略大于实验值。加强上触点、普通中触点弹跳时间仿真与实验值误差分别为8.47%、7.49%。
表5 触点压力仿真与实验对比
Tab.5 The simulation and measurement comparison of contact pressure
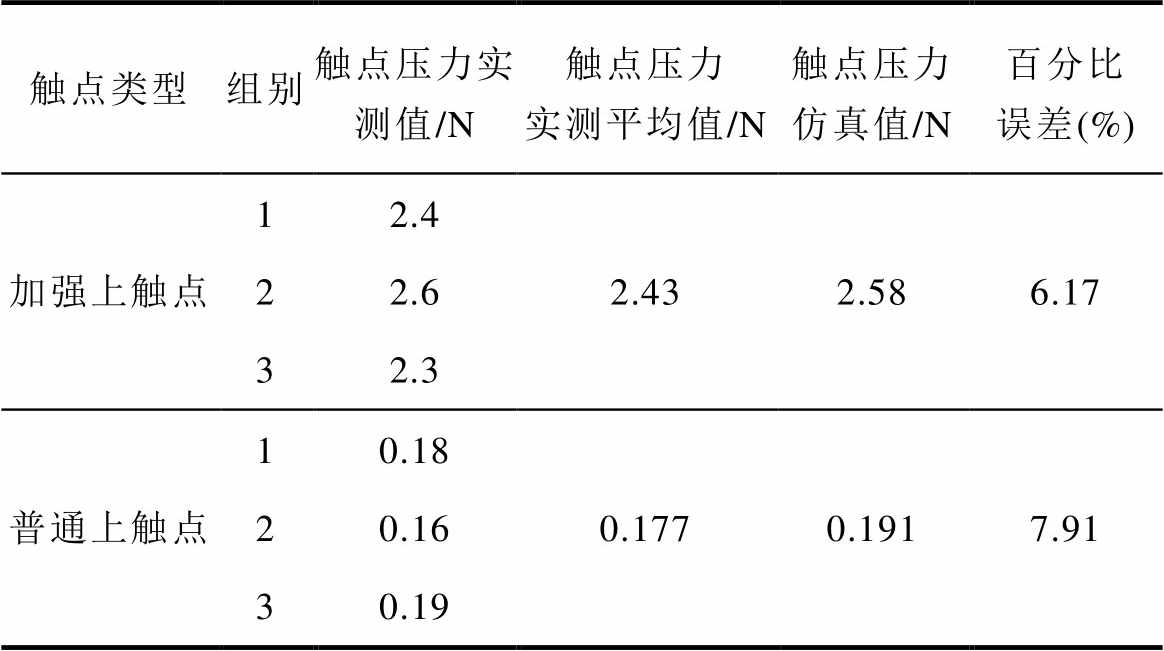
触点类型组别触点压力实测值/N触点压力实测平均值/N触点压力仿真值/N百分比误差(%) 加强上触点12.42.432.586.17 22.6 32.3 普通上触点10.180.1770.1917.91 20.16 30.19
表6 触点弹跳时间仿真与实验对比
Tab.6 The simulation and measurement comparison of bounce time
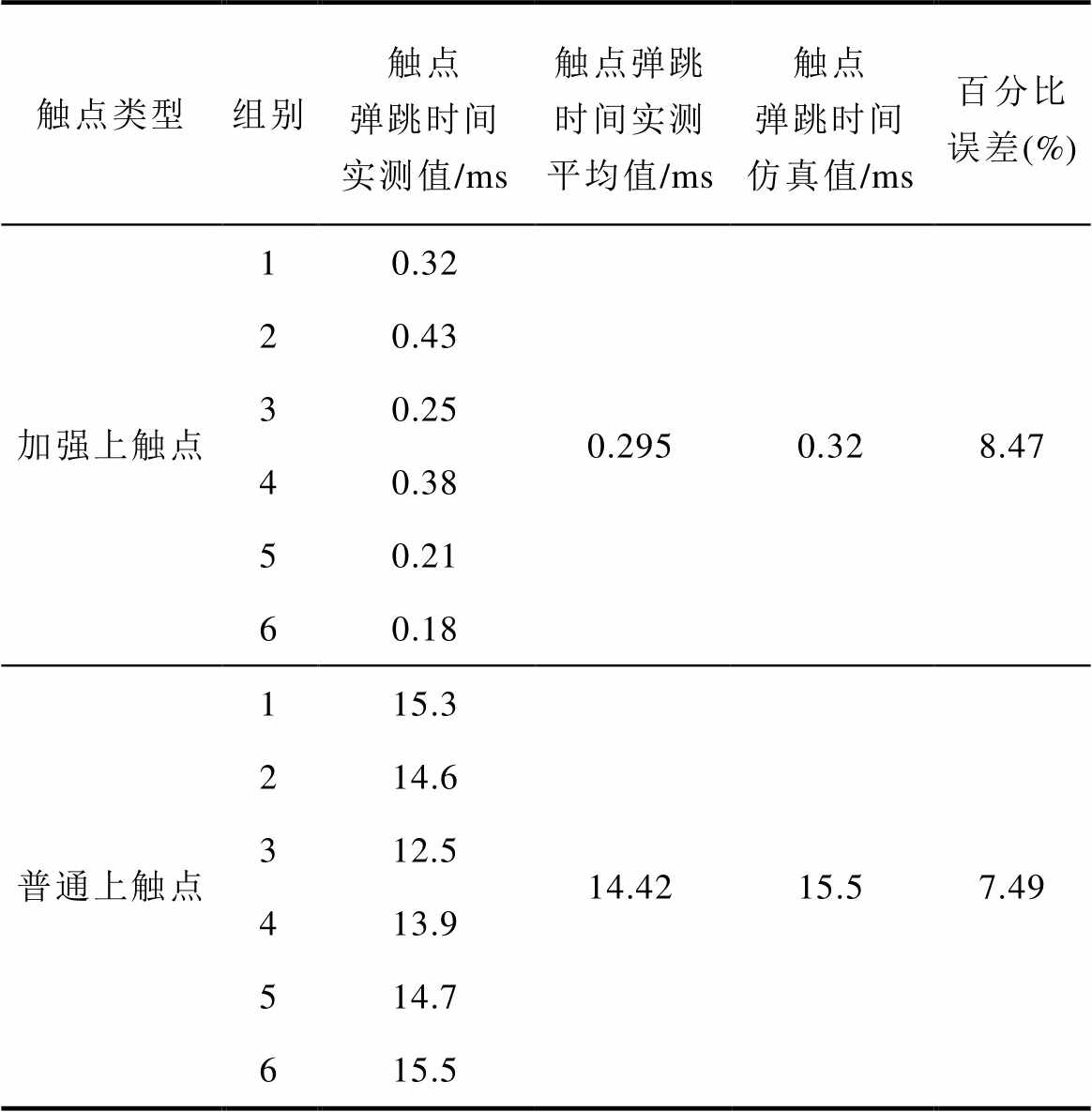
触点类型组别触点弹跳时间实测值/ms触点弹跳时间实测平均值/ms触点弹跳时间仿真值/ms百分比误差(%) 加强上触点10.320.2950.328.47 20.43 30.25 40.38 50.21 60.18 普通上触点115.314.4215.57.49 214.6 312.5 413.9 514.7 615.5
触点压力、弹跳时间仿真与实验误差原因为：仿真建模过程中，设置簧片材料属性与实际材料属性存在差别，加强上触点簧片柔性体和普通上触点簧片柔性体较实际簧片偏硬；在实验测试过程中标尺粘贴在拉杆上，当衔铁带动拉杆运动时标尺会发生偏斜，引起实验误差。
采用电流探头、电压探头、MSO2024示波器和直流电源测试电磁机构额定状态下线圈动态电流，平台如图14所示。电流探头测试线圈动态电流，电压探头测试线圈端电压，直流电源提供继线圈24 V直流额定电压。示波器界面中，黄色线是线圈电流实测变化曲线，蓝色线是线圈两端电压实测变化曲线。实测线圈动态电流仿真与实验曲线数据对比如图15所示。
图14 磁保持继电器线圈电流测试平台
Fig.14 The experimental platform of magnetic latching relay coil current
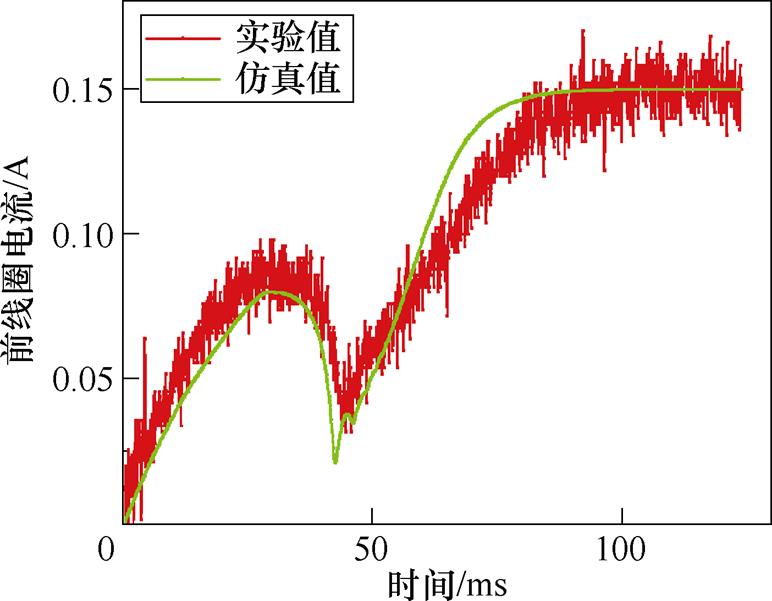
图15 磁保持继电器线圈电流-时间仿真与实验对比
Fig.15 The comparison diagram current-time simulation and experiment of magnetic latching relay coil
图15实测和仿真电流曲线表明，实验测得电磁机构线圈电流从零时刻开始增加，在30 ms左右电流开始减小，之后在45 ms时刻左右开始重新上升，直到100 ms时刻左右线圈电流达到稳态。其中，线圈电压、电流满足
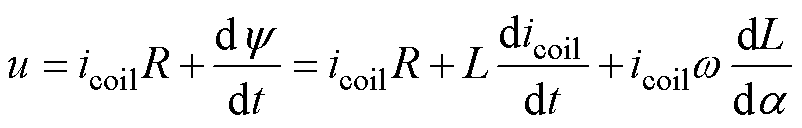（21）
式中，L为线圈电感。
式（21）表明，当电磁机构处于触动阶段时，衔铁尚未运动，运动反电动势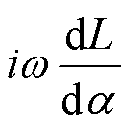
为零，电流逐渐增大；当衔铁所受电磁吸力矩大于反作用力矩时，衔铁开始运动，电磁机构进入吸合运动阶段，由于最初衔铁速度较小，运动反电动势在总反电动势
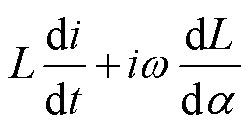中尚未占主要地位，线圈电流继续增大，但因存在运动反电动势，线圈电流上升过程中斜率减小，运动反电动势随衔铁速度增大而逐渐增加，直到30 ms左右衔铁速度增大到某一数值，运动反电动势占主要地位，为维持线圈电压平衡，线圈电流逐渐减小。当衔铁与铁心稳定吸合即45 ms之后，衔铁速度为零，运动反电动势变为零，线圈电流重新增大，此时电磁机构机械运动过程虽然已经结束，但是电磁过渡过程仍在继续，直到100 ms左右，线圈电流达到150 mA，至此电磁机构电磁过渡过程结束，电磁机构进入稳态阶段。
图15显示，仿真与实测电流全过程变化趋势基本一致。其中，仿真电流在42 ms时刻达到最小值，实验电流在45 ms时刻达到最小值，百分比误差为6.67%，原因为仿真过程中忽略衔铁与转轴间摩擦阻力引起衔铁仿真转动速度较实验值偏大所致。仿真电流在重新上升之后短时间内又出现下降现象，是衔铁与铁心碰撞之后发生二次弹跳所致。仿真电流在接近稳态时电流增长斜率明显大于实验电流增长斜率，百分比误差达到7.25%，原因为伴随线圈电流逐渐增大，直流电磁机构内涡流效应逐渐增强，而仿真模型忽略涡流效应所致。
触点吸合运动时间、触点压力、触点弹跳时间和线圈动态电流仿真与实验误差主要原因为：仿真建模难以精确模拟衔铁运动过程中电磁机构内部不对称双磁钢间永磁磁通相互耦合使磁钢工作点偏移的现象，并且衔铁吸合过程中忽略含有不同频率交流分量的线圈电流中不同频率对铁心、衔铁及轭铁等非线性铁磁材料磁滞回线的影响；实验测试方面，像素点跟踪过程中不同照片像素点对应位置像素变化不明显引起像素点漂移现象，也会产生实验误差。
人工装配继电器过程中，触点簧片经过人工调试满足触点压力等指标要求，会造成触点簧片间运动不一致。通过高速摄像机拍摄磁保持继电器系列照片，经高速运动分析软件TEMA跟踪像素点的移动，利用标尺标定实际距离，分析继电器触点运动-时间关系，如图16～图18所示。
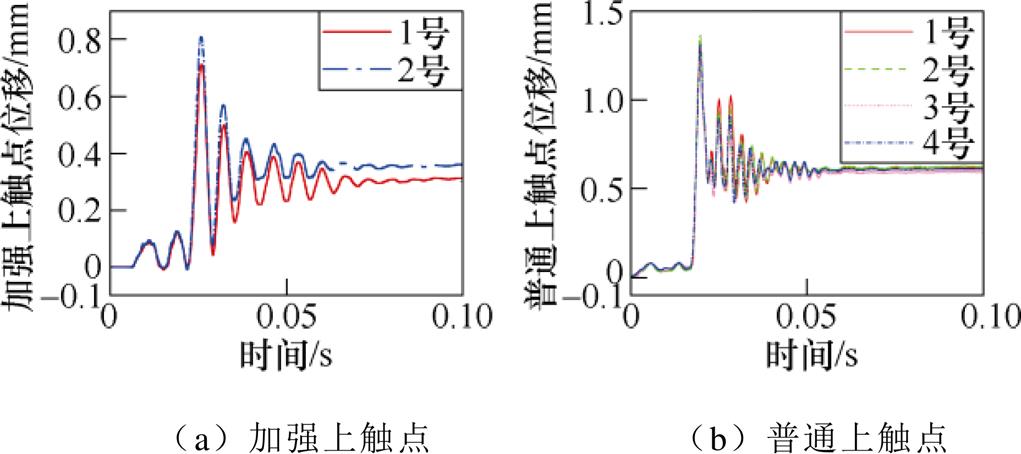
图16 磁保持继电器触点实测位移-时间曲线
Fig.16 The measured displacement-time curves of magnetic latching relay contact
图16～图18显示，触头位移-时间实测曲线上下多次波动，持续较长时间，原因为：中触点与上触点发生接触时，触点间首先产生短时不规则弹跳，然后中触点与上触点接触开始上下同步运动。1号加强上触点位移基本位于2号加强上触点位移之上，触点运动稳定后，1号加强上触点稳定后位移量高于2号加强上触点14.63%，并且1号加强上触点最大峰值速度、最大峰值加速度分别高于2号加强上触点14.29%、15.39%。普通上触点稳定后位移量最大相差5%，并且普通上触点最大峰值速度、最大峰值加速度分别相差10.62%、10.11%。
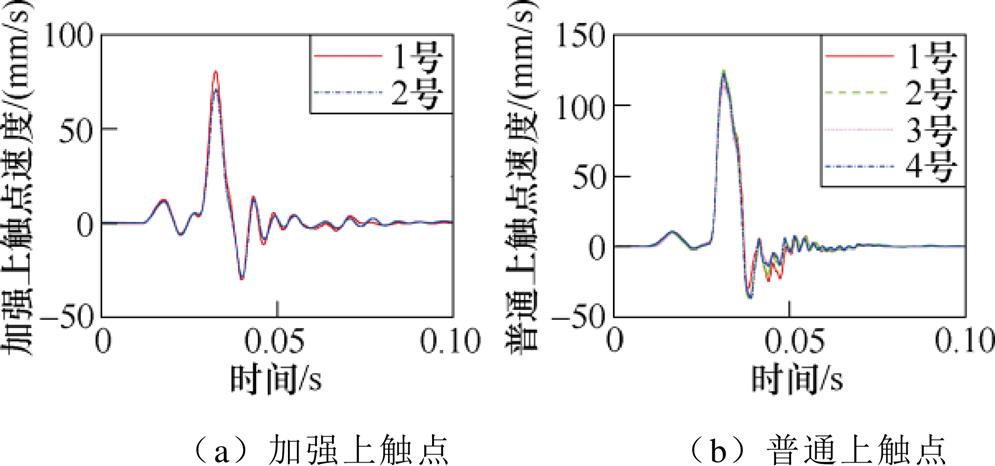
图17 磁保持继电器触点实测速度-时间曲线
Fig.17 The measured speed-time curves of magnetic latching relay contact
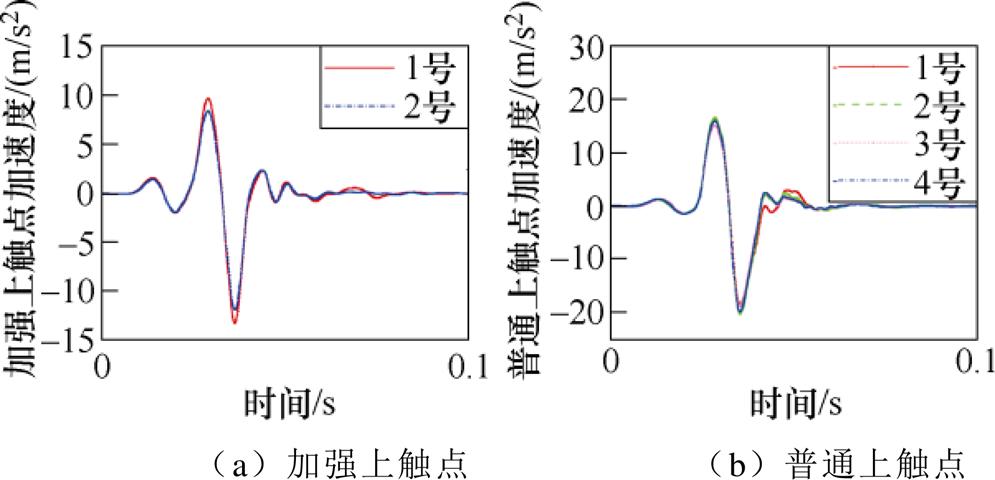
图18 磁保持继电器触点实测加速度-时间曲线
Fig.18 The measured acceleration-time curves of magnetic latching relay contact
上述分析表明，经人工调试簧片触点压力的磁保持继电器，参数的不一致造成触点动作过程存在不一致现象；在实际工作过程中，轻则延迟主电路通断，重则使率先闭合触点短时承受多倍大电流，加重触点电磨损，缩短磁保持继电器电寿命。
本文理论分析了多簧片结构的磁保持继电器电磁系统和触簧系统的结构拓扑及工作原理。基于分段动力学思想建立磁保持继电器触簧系统三簧片耦合动力学模型，提出磁保持继电器电-磁-机械运动多物理场刚柔耦合仿真模型，设计磁保持继电器动态特性实验平台和方案，验证了磁保持继电器多物理场刚柔耦合仿真模型的有效性。
1）将磁保持继电器触簧系统簧片等效为悬臂梁，基于欧拉-伯努利梁理论，分析簧片动力学特征突变成因。引入狄拉克函数d(x)和赫维赛德函数e( y)，建立考虑触点间切入深度时三簧片耦合动力学模型，并处理触点间碰撞接触力、电动斥力由于触点间碰撞弹跳引起的作用力不连续问题。
2）引入内嵌于Ansys Maxwell的基于误差的自适应网格划分方法，求解电磁机构静态特性。基于模态理论，利用嵌入式MSC Nastran程序，建立磁保持继电器触簧系统刚柔耦合仿真模型，来进行动态特性仿真计算。基于三簧片分段耦合动力学模型，引入分段动力学思想，解决磁保持继电器动力学仿真模型初始时刻衔铁无法处于稳定状态的问题。
3）设计基于高速摄像机的运动轨迹测试平台，给出磁保持继电器电磁机构线圈动态电流和触点运动轨迹实验方案，结果表明：普通中触点簧片和加强中触点簧片力-形变量实验与仿真误差分别在3%左右；触点吸合运动时间、触点压力、弹跳时间、线圈动态电流实验与仿真误差最大分别为7.93%、7.91%、8.47%、7.25%，验证了本文所提磁保持继电器电-磁-机械运动多物理场耦合仿真模型的有效性。同时，分析了加强上触点和普通上触点动作过程存在的不一致现象，为提升产品可靠性提供了 支撑。
参考文献
[1] 袁百慧. 微型航天磁保持继电器抗浪涌性能优化方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2021.
[2] Ramirez-Laboreo E, Sagues C, Llorente S. A new model of electromechanical relays for predicting the motion and electromagnetic dynamics[J]. IEEE Transactions on Industry Applications, 2016, 52(3): 2545-2553.
[3] Riba J R, Garcia A, Cusidó J, et al. Dynamic model for AC and DC contactors-simulation and experi- mental validation[J]. Simulation Modelling Practice and Theory, 2011, 19(9): 1918-1932.
[4] Lambrecht N, Pues H, De Zutter D, et al. Modeling of contact bounce in a transient electromagnetic com- patibility test for the analysis and optimization of nonlinear devices[J]. IEEE Transactions on Electro- magnetic Compatibility, 2017, 59(2): 541-544.
[5] 鲍光海, 王金鹏, 王毅龙. 磁保持继电器多物理场耦合模型设计与触头弹跳影响因素分析[J]. 电工技术学报, 2023, 38(3): 828-840.
Bao Guanghai, Wang Jinpeng, Wang Yilong. Design of multi-physical field coupling model of magnetic latching relay and analysis of influencing factors of contact bounce[J]. Transactions of China Electro- technical Society, 2023, 38(3): 828-840.
[6] 刘兰香, 杨文英, 柴玉阳, 等. 微小型继电器的刚柔耦合碰撞动力学建模方法与弹跳行为分析[J]. 中国电机工程学报, 2022, 42(2): 808-818.
Liu Lanxiang, Yang Wenying, Chai Yuyang, et al. Modeling method of rigid-flexible coupling impact dynamics and analysis of bounce behavior of the micro-relay[J]. Proceedings of the CSEE, 2022, 42(2): 808-818.
[7] 张高廷, 曹云东, 刘炜. 簧片式继电器固有振动特性研究[J]. 电工技术学报, 2020, 35(2): 292-299.
Zhang Gaoting, Cao Yundong, Liu Wei. The natural vibration characteristics of reed relay[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 292- 299.
[8] 杨文英, 刘兰香, 刘洋, 等. 考虑碰撞弹跳的接触器动力学模型建立及其弹跳特性影响因素分析[J]. 电工技术学报, 2019, 34(9): 1900-1911.
Yang Wenying, Liu Lanxiang, Liu Yang, et al. Establishing of contactor dynamic model considering collision bounce and analysis of influencing factors of bounce characteristics[J]. Transactions of China Elec- trotechnical Society, 2019, 34(9): 1900-1911.
[9] 何晓燕, 许志红. 交流接触器虚拟样机设计技术[J]. 电工技术学报, 2016, 31(14): 148-155.
He Xiaoyan, Xu Zhihong. Virtual prototyping tech- nology of AC contactor[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 148-155.
[10] 汤龙飞, 柯昌辉, 许志红. 智能单稳态永磁接触器动作特性的联合仿真[J]. 中国电机工程学报, 2023, 43(4): 1641-1651.
Tang Longfei, Ke Changhui, Xu Zhihong. Co- simulation of action characteristics of intelligent monostable permanent magnet contactor[J]. Pro- ceedings of the CSEE, 2023, 43(4): 1641-1651.
[11] 梁慧敏, 于海丹, 唐钰杰, 等. 双磁钢差动式电磁继电器虚拟样机与参数优化研究[J]. 中国电机工程学报, 2016, 36(1): 258-267.
Liang Huimin, Yu Haidan, Tang Yujie, et al. Virtual prototyping and parameter optimization of differential electromagnetic relays with double permanent mag- nets[J]. Proceedings of the CSEE, 2016, 36(1): 258- 267.
[12] 陈昊, 叶雪荣, 梁慧敏, 等. 磁保持型航天电磁继电器性能提升与质量一致性设计[J]. 电工技术学报, 2023, 38(4): 1076-1087.
Chen Hao, Ye Xuerong, Liang Huimin, et al. Per- formance enhanced and quality consistency design optimization of magnetically latching aerospace electromagnetic relay[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1076-1087.
[13] 李东晖, 周学, 王傲, 等. 考虑制造参数的批量化真空交流接触器机械寿命预测[J]. 电工技术学报, 2023, 38(7): 1982-1990.
Li Donghui, Zhou Xue, Wang Ao, et al. Mechanical life prediction of batch electromagnetic switches considering manufacturing parameters[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(7): 1982-1990.
[14] 周学, 李东晖, 金玥, 等. 考虑空间形位偏差的万能式断路器关键零件断裂失效研究[J]. 电工技术学报, 2022, 37(6): 1595-1605.
Zhou Xue, Li Donghui, Jin Yue, et al. Fracture failure process of key part of air circuit breaker considering spatial shape and position deviation[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1595- 1605.
[15] Tung R C, Fruehling A, Peroulis D, et al. Multiple timescales and modeling of dynamic bounce pheno- mena in RF MEMS switches[J]. Journal of Microele- ctromechanical Systems, 2014, 23(1): 137-146.
[16] 姚帅亮. 新型双电源转换开关用螺管式电磁铁的设计与性能测试技术研究[D]. 天津: 河北工业大学, 2016.
[17] 汤龙飞, 谌浩, 柯昌辉. 接触器静态特性测量方法的研究[J]. 中国电机工程学报, 2023, 43(3): 1241- 1251.
Tang Longfei, Chen Hao, Ke Changhui. A method for measuring the static characteristics of contactors[J]. Proceedings of the CSEE, 2023, 43(3): 1241-1251.
[18] 陈德为, 庄煜祺, 黄航宇. 智能交流接触器三维动态测试与分析[J]. 电工技术学报, 2014, 29(11): 162-168.
Chen Dewei, Zhuang Yuqi, Huang Hangyu. 3D dynamic testing and analysis of intelligent AC contactor[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 162-168.
[19] 刘向军, 许雄, 兰太寿. 电磁机构三维动态特性测试及数据处理与分析[J]. 仪器仪表学报, 2014, 35(10): 2208-2215.
Liu Xiangjun, Xu Xiong, Lan Taishou. Three- dimensional dynamic characteristic testing, and data processing analysis for electromagnetic mechanism[J]. Chinese Journal of Scientific Instrument, 2014, 35(10): 2208-2215.
[20] 刘亚魁, 李红运, 林天然, 等. 基于机器视觉的高压断路器机械特性测量方法[J]. 电工技术学报, 2023, 38(增刊1): 222-230.
Liu Yakui, Li Hongyun, Lin Tianran, et al. Research on mechanical characteristic measurement method of high voltage circuit breaker based on machine vision[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 222-230.
[21] 唐昭晖, 许志红. 基于响应面法的交流接触器弹簧系统优化设计方法[J]. 电工技术学报, 2022, 37(2): 515-527.
Tang Zhaohui, Xu Zhihong. Optimal design method for AC contactor spring system based on response surface method[J]. Transactions of China Electro- technical Society, 2022, 37(2): 515-527.
[22] 孙曙光, 宗俊吉, 王景芹, 等. 振动因素对交流接触器动态特性影响的测试分析[J]. 仪器仪表学报, 2020, 41(11): 155-167.
Sun Shuguang, Zong Junji, Wang Jingqin, et al. Test and analysis of influence of vibration factors on the dynamic characteristics for AC contactor[J]. Chinese Journal of Scientific Instrument, 2020, 41(11): 155- 167.
Abstract The magnetic latching relay exhibits a complex structure with weak consistency between components, leading to issues such as arc erosion and severe contact wear caused by increased bounce frequencies of the armature and iron core, affecting dynamic and static contacts. In extreme cases, contact welding adhesion causes significant changes in static and dynamic characteristic parameters, including pick-up time, pick-up voltage, and contact pressure. Therefore, theoretical analysis methods and simulation models for the magnetic latching relay are established, and changes in static and dynamic characteristics are analyzed.
To improve the accuracy of simulation models, a multiphysics rigid flexible coupling simulation model is established. The magnetic latching relay serves as the research object. The structure topology and operation mechanisms of the relay are analyzed theoretically. The penetration depth between contacts is considered, and the Dirac delta function and the Heaviside function are introduced to solve problems of reed force dispersion and discontinuity between contacts due to collision and bounce. The reeds are equivalent to the cantilever beam, and a triple reed piecewise coupling dynamic model of the relay contact reed system is established based on the Euler-Bernoulli beam theory. Moreover, an error-based adaptive mesh generation method is introduced to solve the static characteristics of the electromagnetic mechanism in Ansys Maxwell. Considering the deformation effect of reed movement, a rigid-flexible coupling dynamic simulation model is developed based on modal theory in ADAMS. Finally, a rigid, flexible couplingsimulation model for the multiphysics of electro-magnetic- mechanical motion is structured based on piecewise dynamics.
An experimental scheme for the magnetic latching relay is devised using a high-speed camera and a current probe. An experimental platform is established to analyze the contact pick-up motion time, contact pressure, bounce time, and coil current to verify the effectiveness of the proposed analysis method and the multiphysics rigid-flexible coupling simulation model for the magnetic latching relay with a multi-reed structure. The inconsistency caused by different contact pressures during the manual assembly of reeds is analyzed in the relay operation process.
The simulation results of magnetic latching contact pick-up motion time, contact displacement-time relationship, contact pressure, bounce time, and coil current are consistent with the experimental results. The following conclusions can be drawn.
(1) Based on the Euler-Bernoulli beam theory, the reeds of the magnetic latching relay are equivalent to cantilever beams, addressing sudden changes in dynamic characteristics by introducing the Dirac delta function and the Heaviside function.
(2) The static characteristics are solved using the error-based adaptive mesh generation method in Ansys Maxwell. Based on modal theory, a rigid-flexible coupling dynamic simulation model of magnetic latching relay reeds is established, overcoming challenges in the initial moment of dynamic simulation.
(3) An experimental platform is designed for the dynamic current of the coil and contact movement of the magnetic latching relay. The experiment and simulation errors for force-deformation relationships are around 3% for the common middle contact and reinforced middle contact reeds. The maximum errors of the contact pick-up motion time, contact pressure, bounce time, and coil dynamic current are 7.93%, 7.91%, 8.47%, and 7.25%.
keywords：Magnetic latching relay, multi-reed structure, collision bounce, piecewise coupling dynamic model, rigid flexible coupling multiphysics
DOI: 10.19595/j.cnki.1000-6753.tces.230381
中图分类号：TM572
国家自然科学基金（51777057）和河北省自然科学基金（E2021202136）资助项目。
收稿日期 2023-03-31
改稿日期 2023-04-20
赵靖英 女，1974年生，教授，硕士生导师，研究方向为电工装备可靠性理论及应用、智能电网、无线传能。E-mail: zhaojy931@hebut.edu.cn（通信作者）
李 宁 男，1999年生，硕士研究生，研究方向为电工装备可靠性理论及应用。E-mail: 422091990@qq.com
（编辑 崔文静）