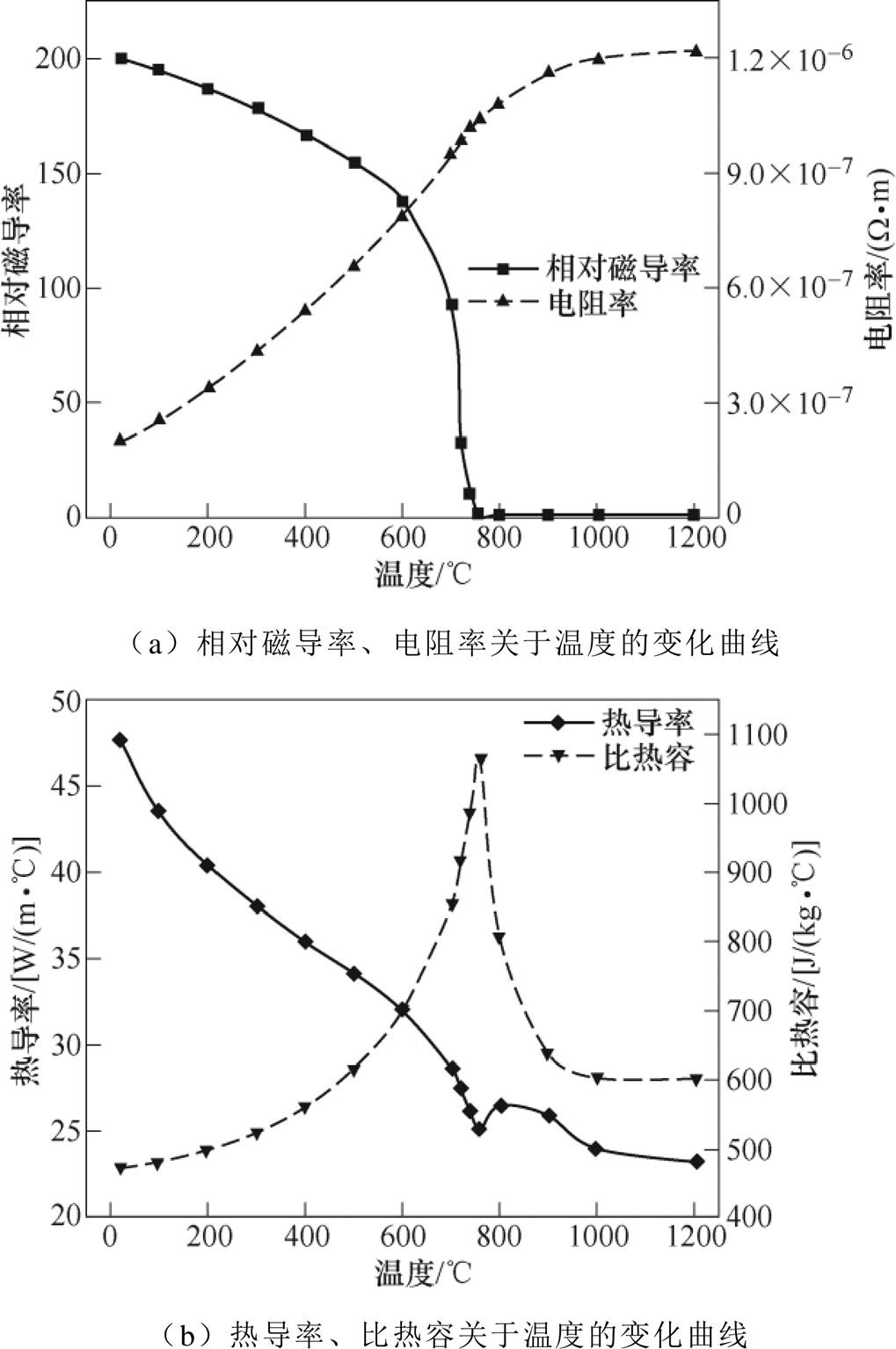
图1 45号钢关于温度的材料特性曲线
Fig.1 Material property curves of 45号 steel with temperature
摘要 对金属带材进行横向磁通感应加热（TFIH）时，通常会存在加热温度分布不均匀以及加热温度偏离目标值两个问题。该文研究了加热器结构参数与电源参数对45号钢带材回火热处理温度的影响，并对两种参数分别进行优化，使带材在加热器出口处的平均温度达到目标值600℃，同时获得均匀的温度分布。采用Morris法对加热器结构参数进行全局灵敏度分析，选取显著影响相对不均匀度的参数并建立径向基函数（RBF）神经网络预测模型。使用多岛遗传算法（MIGA）对筛选的结构参数进行优化，初步获得均匀的温度分布。最后以降低温度分布的相对不均匀度和达到理想平均温度为目标，在优化后的加热器结构基础上使用响应面法（RSM）优化电源参数，实现多目标优化设计。仿真验证结果表明，45号钢带材在加热器出口处的平均温度为600.06℃、相对不均匀度为2.36%，满足45号钢回火热处理的要求。
关键词：横向磁通感应加热 全局灵敏度分析 径向基函数神经网络模型 多岛遗传算法 响应面法
随着工业的发展，市场对钢铁产品的要求越来越高，改进热处理工艺以改善加热效果，有利于提高产品的性能。根据Faraday电磁感应定律，交变磁场穿过金属工件时，会在工件内部产生感应电流，即为涡流。感应加热就是利用涡流的热效应对工件进行加热[1-3]。与传统的明火加热方式相比，感应加热具有节能、高效、环保、灵活等优点，因此感应加热广泛应用于生产生活的各个方面[4-7]。目前常见的感应加热方式有横向磁通感应加热（Transverse Flux Induction Heating, TFIH）和纵向磁通感应加热（Longitudinal Flux Induction Heating, LFIH）两种。TFIH中，线圈产生的磁感线垂直穿过工件，因此主要用于加热带材等平板类工件；LFIH中，线圈产生的磁感线平行穿过工件，因此主要用于加热棒材等柱类工件。
为了评估TFIH的效果，通常引入加热器出口处带材表面温度分布的相对不均匀度drel和加热器出口处带材表面的平均温度Tav作为加热结果的评价指标。一般来说，希望Tav满足热处理工艺要求的同时drel保持在一个较低的水平。
近年来，为了实现这一目标，国内外学者进行了广泛而有效的探索，并取得了许多成果。文献[8] 提出了一种利用磁屏蔽结构降低带材边缘温度的加热器模型。该模型可以提高加热器出口处带材表面温度的均匀性，但是该方案仅对线圈结构简单的加热器有较好的效果，而且会导致加热效率降低。文献[9]使用改进后的粒子群算法对部分加热器参数进行优化，得到了均匀的带材表面温度分布。文献[10]提出了一种带铁轭的新型加热器磁极，有效地提高了加热的均匀性并减少了装置的漏磁。文献 [11]通过改变磁极的形状来改变气隙的高度，从而影响用于加热带材的交变磁场有效值大小。
除优化加热器的结构之外，利用反馈控制实现对电源参数的动态调整同样可以起到改善加热效果的作用。感应加热系统具有强耦合性、强非线性以及时滞性的特点，经典的PID控制难以给出具体的控制参数，不能实现精确控制。为了克服经典PID控制的局限性与依赖性，文献[12]提出一种基于改进粒子群优化的模糊PID控制算法，并应用于感应加热系统，提高了控制器的自适应能力并减少了调整时间。文献[13]在感应加热过程中使用自整定模糊控制器，实现了对加热工件的稳定温度以及温度变化速度的动态控制。对于TFIH而言，反馈控制引起电源参数的变化可以显著影响Tav的数值，但是由于线圈在电源端串联，无法通过改变流过任一部分线圈的电流大小与频率来实现各部分独立加热并达到降低drel的目的。文献[14]提出了一种新型行波感应加热装置，使工件内涡流密度和温度分布更加均匀，但是需要复杂的供电系统。文献[15]提出可以先使用直流超导线圈在工件中产生强直流磁场使之饱和以增加电流透入深度，然后再使用交流线圈可以实现对工件更为均匀、快速地加热。但是受限于超导技术的成熟程度以及经济成本问题，目前该方案难以得到广泛应用。
上述研究都仅是改变加热器结构参数或电源参数来满足加热结果对均匀度或加热温度的要求，而没有考虑参数变化对二者的综合影响，这可能会导致由于加热温度偏离目标值或温度分布不均匀而失去最佳热处理效果。为了解决这一问题，本文将优化参数分为加热器结构参数与电源参数，并分别使用不同的方法进行优化。对结构参数而言，本文在基于Morris全局灵敏度分析筛选加热器结构参数的前提下，采用径向基函数（Radial Basis Function, RBF）神经网络预测模型和多岛遗传算法（Multi- Island Genetic Algorithm, MIGA），得到了加热器结构参数的最优组合，使drel在一定温度范围内降到最小。然后，基于优化后的加热器结构，采用响应面法（Response Surface Method, RSM）对电源参数进行优化，最终使Tav达到理想的热处理温度，同时drel保持在较低水平。
TFIH是一个复杂的磁热耦合过程。考虑到带材运动等实际工况，本文使用COMSOL软件对TFIH过程进行了有限元分析。
本文所用的加热工件是45号钢带材，它是一种强度高、抗形变能力强的优质碳素钢。对带材进行回火热处理可以消除其内应力并提高韧性与延展性，45号钢的理想回火温度为600℃。在对45号钢带材进行加热的过程中，其材料特性会随温度的变化而发生非线性变化。图1为带材的相对磁导率、电阻率、热导率和比热容关于温度的变化曲线[16]。
图1 45号钢关于温度的材料特性曲线
Fig.1 Material property curves of 45号 steel with temperature
TFIH装置的分解结构模型如图2a所示，在带材的每一侧都有一个由双六边形线圈和开槽磁极组成的感应加热器，其中双六边形线圈经过串联接在电源端，这样可以保证内外线圈流过的电流相同，降低了供电的复杂性。其中带材的宽度为600 mm，厚度为0.5 mm；磁极由厚度为0.3 mm的30Q130硅钢片制成，整体尺寸为400 mm×600 mm×60 mm。图2b是TFIH装置的全结构模型，带材以v=0.1 m/s的速度穿过加热器之间的气隙。从垂直带材运动方向的结构可以看出，带材两侧与磁极之间均存在气隙，在正常工作情况下两侧气隙的高度始终保持相等。图2c为单侧加热器的结构模型。线圈按照各部分的相对位置可分为“边缘线圈”和“中间线圈”，从图中可以看出线圈的结构由六个参数决定：外线圈顶端突出磁极边缘的距离A，内线圈顶端与磁极边缘的距离B，内线圈的顶角角度C，外线圈的顶角角度D，内线圈沿带材运动方向的宽度E，外线圈沿带材运动方向的宽度F。
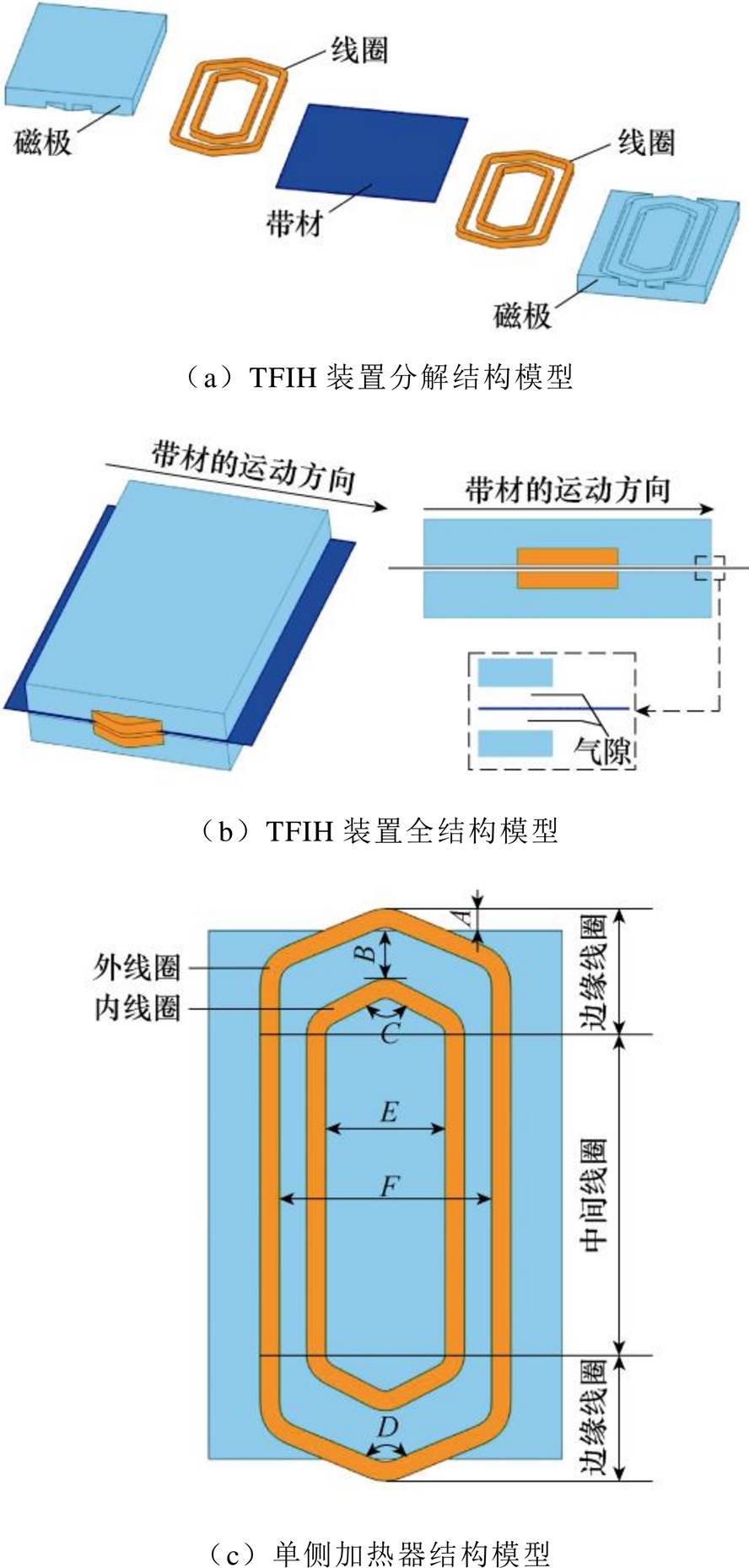
图2 TFIH装置结构模型
Fig.2 Structure model of the TFIH device
根据图2可以发现，TFIH装置的有限元模型在水平和垂直方向上都是对称的，所以通常使用TFIH装置的1/4模型进行有限元仿真计算，如图3a所示。
生成网格时，由于带材的厚度较薄，所以先在带材表面进行自由三角形网格剖分，然后扫掠形成棱柱单元。对于其他域，则使用自由四面体网格。图3b是隐藏空气域后的1/4 TFIH装置有限元模型网格剖分结果。使用这种网格剖分方法得到的网格质量较高，计算结果更加准确，所需要的计算时间更少。
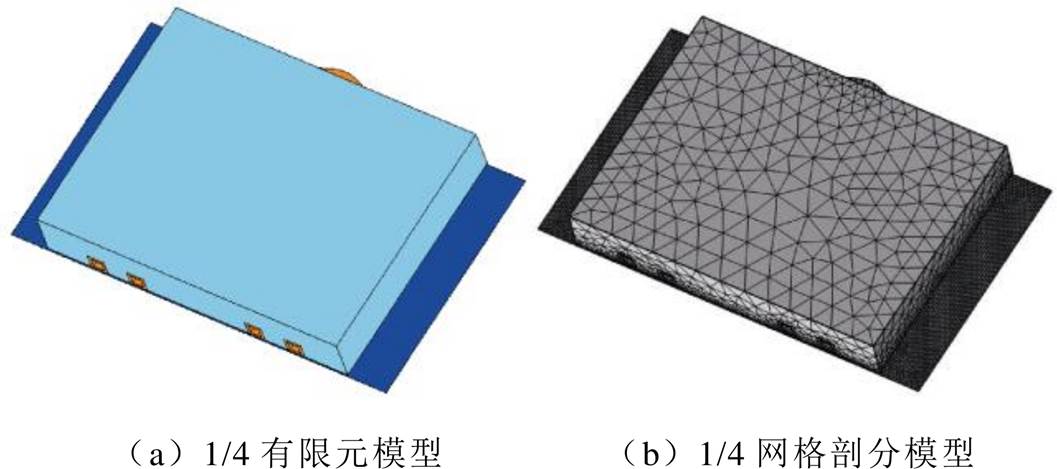
图3 TFIH装置1/4有限元模型
Fig.3 A quarter finite element model of the TFIH device
假设加热器出口处带材表面有n个温度采样点，Ti为第i个采样点所采集到的温度。温度采样点分布如图4所示，图中，温度采样区域即为图中红色直线部分，直线的起点坐标与终点坐标分别为（200 mm, 0 mm, 0.25 mm）和（200 mm, 600 mm, 0.25 mm）。一般而言，总是希望沿该直线的温度分布尽可能均匀，同时平均温度更加接近目标值。
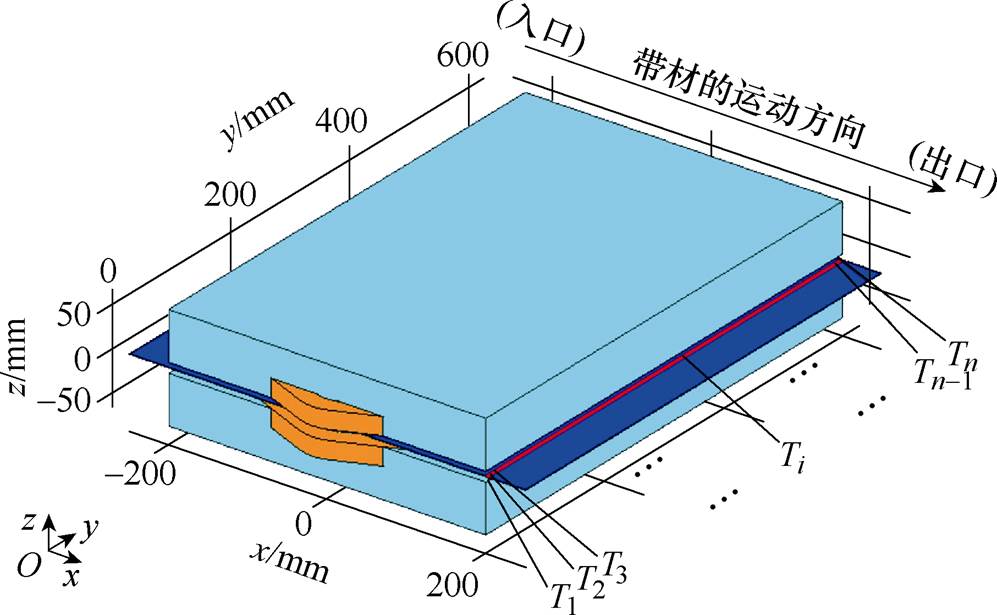
图4 温度采样点分布
Fig.4 Distribution of temperature sampling points
当带材的加热状态达到稳定时，在加热器出口处带材表面的平均温度Tav可以表示为
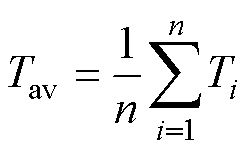（1）
进一步得到相对不均匀度drel可以表示为
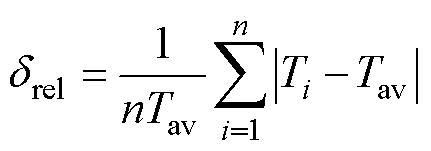（2）
drel越小，加热器出口处的带材表面温度波动幅度越小，温度的均匀性越好。
对TFIH装置而言，一经制造就很难再改变加热器的结构。根据“线圈投影定律”，带材中的涡流路径近似对应于线圈在带材表面的投影，而涡流产生的焦耳热就是使带材温度升高的热源，所以线圈的形状就决定了带材表面的热源分布，并进一步影响了drel的大小。
尤其是当外线圈的顶端突出磁极时，在电磁场的边缘效应影响下，带材边缘的热源值将高于中间部分，并使带材边缘区域的温度进一步提高；否则，由于边缘线圈产生的磁感线通过的磁路空气所占比例较大，带材边缘处的热源值将会低于中间区域，从而产生低温区，这两种情况都会导致drel增加。而对带材的中间区域来说，中间线圈的投影是相对均匀的，所以带材中部产生的温度波动很小。基于以上原因，本文选择双六边形线圈结构，并使外侧线圈顶端突出磁极边缘以改善较大空气磁阻所引起的低热源，起到使带材边缘温度接近中间区域的效果。本节进行有限元仿真计算时取电源电流I=800 A，频率f=800 Hz。
如图2所示，在加热器整体尺寸确定的前提下，通常还需要七个参数来确定加热器的结构，包括图2b中的气隙高度以及图2c中的六个线圈结构参数。为了降低优化的复杂性，有必要对设计参数进行筛选，去除不必要的参数。根据工程要求和磁热耦合原理，本文开展了以下工作。
对于带材与磁极表面之间的气隙高度。硅钢片的磁导率远远大于空气的磁导率，且磁路的磁阻Rm可以表示为
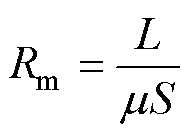（3）
式中，L为磁路的长度（m）；S为磁路的横截面积（m2）；m 为磁路通过介质的磁导率（H/m）。由式（3）可知，气隙高度越大，磁路磁阻越大，加热器的加热效率越低。因此，在保证加工工艺的前提下，气隙应尽可能地小。本文设定气隙高度为4 mm。
对于其他结构参数，整体优化流程如图5所示。
灵敏度分析可用于研究模型输入参数的变化如何影响其输出响应的变化。灵敏度分析可分为局部灵敏度分析（Local Sensitivity Analysis, LSA）和全局灵敏度分析（Global Sensitivity Analysis, GSA）[17-18]。前者多适用于一些因素之间没有很强关联性的分析模型，而TFIH是一个非线性、强耦合的过程，各因素之间通常存在较强的交互作用，因此本文采用GSA进行灵敏度分析。
GSA包括定性灵敏度分析和定量灵敏度分析。定性灵敏度分析包括Morris法等，它能以较少的计算成本获得更可靠的灵敏度排序结果。定量灵敏度分析包括Sobol’法等，它可以定量计算输入参数对系统响应的影响系数，但需要进行大量的计算。本文进行灵敏度分析的目的是为了筛选出对系统响应有显著影响的结构参数，所以选择Morris法进行后续分析。
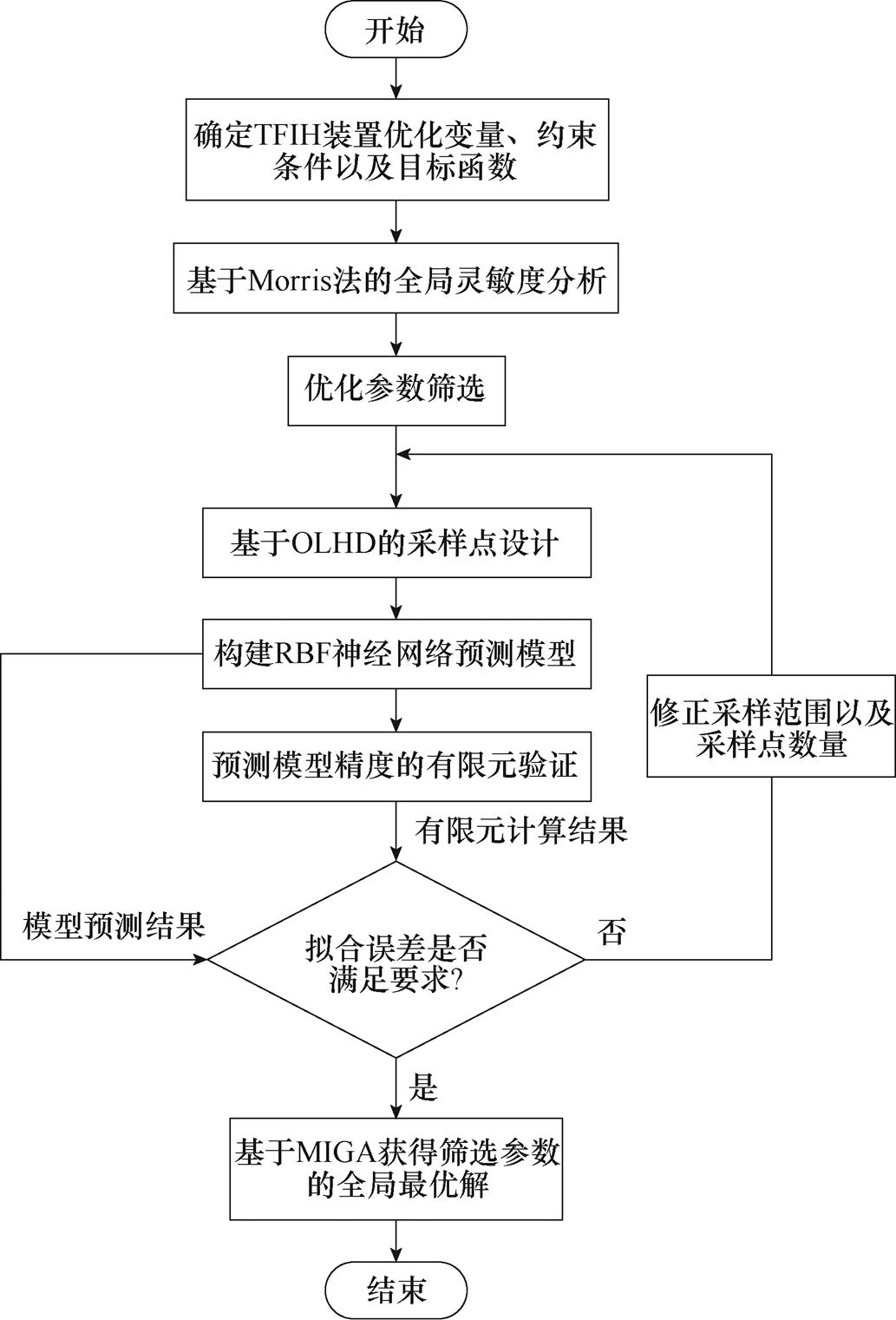
图5 结构参数优化流程
Fig.5 Flow chart of structural parameters optimization
Morris法是一种基于基本因子法和参数空间离散搜索法的灵敏度分析方法[19]，可用于确定输入参数是否对系统响应有可忽略性、可加性、非线性或交互性等影响。
对于有k个输入参数的模型，假设每个输入参数有p个采样等级，将每个输入参数的变化范围映射到[0, 1]区间内，并根据采样等级进行离散化处理。
对任一个系统输入向量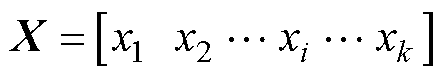
，假设对应的输出响应y(X)为
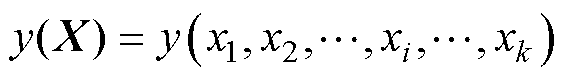（4）
那么X中第i个参数的基本影响（Elementary Effect, EE）可以表示为
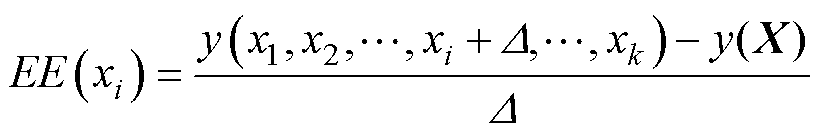（5）
式中，xi在[0, 1/( p-1), 2/( p-1),…, 1-D]中随机取值，D 为1/( p-1)的整数倍。
通常来说，p一般选择为偶数且D =p/[2(p-1)]，这样做可以保证对输入变量的对称性处理。
将(k+1)×k维输入矩阵B表示为
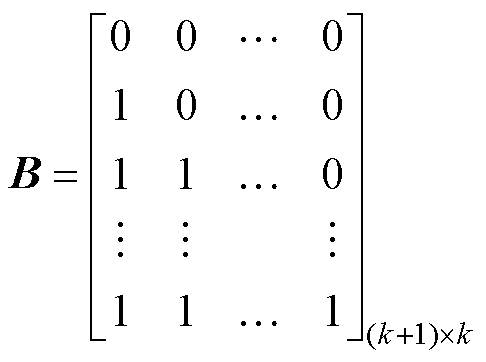（6）
在矩阵B中，第一行所有的“0”元素即代表初始采样点；其余各行的“1”代表输入参数发生了变化，“0”代表输入参数保持不变。可以发现，相邻两行之间只有一个参数发生了变化，而且变化量为D。
为了使抽样矩阵具有随机性，可以将输入矩阵B按照式（7）的方法进行处理，并得到最终的抽样矩阵B*为
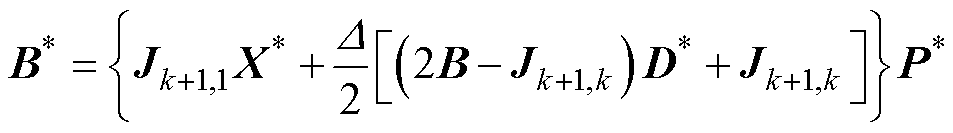（7）
式中，Jk+1,k为所有元素均为1的(k+1)×k维矩阵；X*为在X中随机选取的一组初始输入向量；D*为k×k维对角矩阵，其中对角线的元素在1或-1中随机取值；P*为k×k维随机置换矩阵，该矩阵的每行和每列中只有一个元素为1，其余元素均为0。X*、D*和P*中的元素均为随机取值且相互独立，从而可以确保采样矩阵B*具有随机性。
B*中的每一行元素都是一组系统的输入参数，将矩阵中的元素映射回原范围进行计算，可以得到对应输入参数下的系统响应。为了提高结果的可靠性，通常会选择新的样本点并重复上述步骤r次，共进行(k+1)×r次计算。一般认为p=4和r=10可以满足分析要求。
灵敏度评价指标为
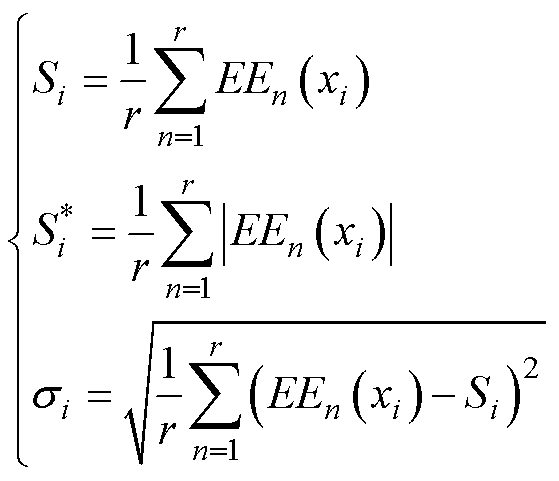（8）
式中，i=1, 2, 3,…, k。
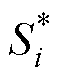越大，说明对应参数对输出响应的影响越大；si越大，说明相应参数的非线性越强，或与其他参数的交互作用越强[20]。
待优化的加热器结构参数及其概率分布见表1。
表1 结构参数及其概率分布
Tab.1 Structural parameters and their probability distributions
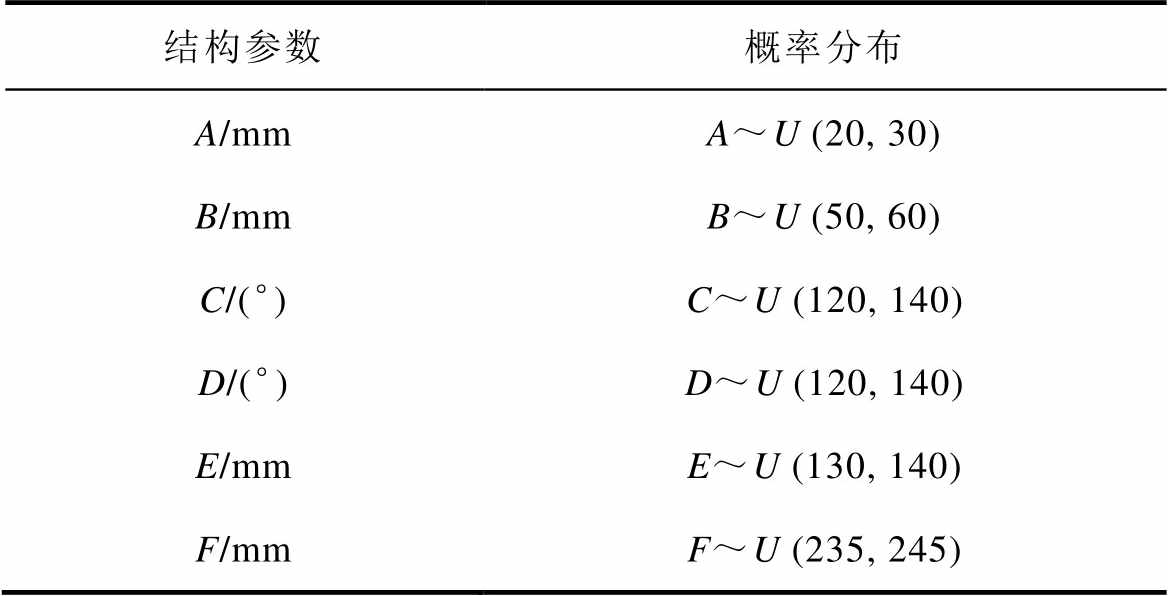
结构参数概率分布 A/mmA～U (20, 30) B/mmB～U (50, 60) C/(°)C～U (120, 140) D/(°)D～U (120, 140) E/mmE～U (130, 140) F/mmF～U (235, 245)
在完成对所有结构参数的计算后，根据Morris法分析步骤计算得到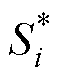和si，见表2。
表2 灵敏度指数计算结果
Tab.2 Calculation results of sensitivity indexes
结构参数si A/mm5.01´10-46´10-4 B/mm1.26´10-31.26´10-3 C/(°)2.67´10-43.48´10-4 D/(°)3.61´10-44.06´10-4 E/mm1.58´10-42.03´10-4 F/mm2.78´10-43.09´10-4
图6显示了drel对各结构参数灵敏度的对比。
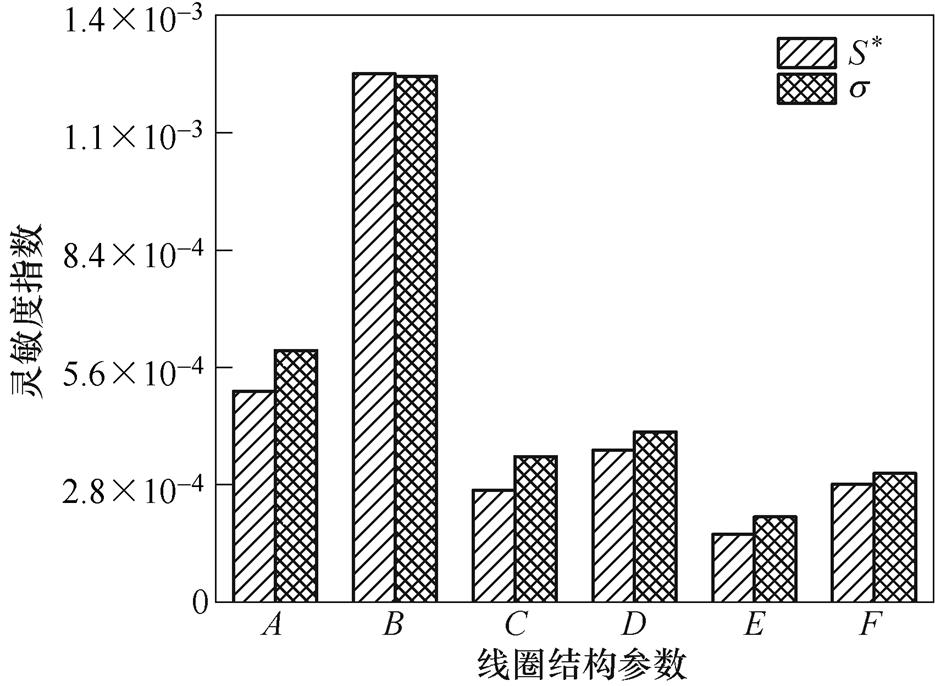
图6 drel关于结构参数的灵敏度对比
Fig.6 Comparison of the sensitivity of drel on the structure parameters
最后，选择对结果有较大影响的四个结构参数A、B、D、F进行下一步分析，同时保持C=125°和E=135 mm不变。
TFIH是一个非常复杂的物理过程，而且随着计算精度的提高，计算机有限元仿真计算消耗的时间会不断增加。预测模型可以用来近似代替有限元模型，其本质是对离散数据进行拟合或插值来预测未知数据。该方法可以极大地缩短计算时间，并且在自变量的变化范围内获得较高的计算精度[21]。
2.2.1 最优拉丁超立方设计采样
在构建预测模型之前，需要在设计空间中选择一些样本点，并使之尽可能均匀地分布在整个空间中，这有助于提供全空间的信息。
本文使用最优拉丁超立方设计（Optimal Latin Hypercube Design, OLHD）进行采样，与传统拉丁超立方设计相比，该采样方式具有更好的空间填充均匀性和平衡性[22-23]。选取100个训练样本点，得到采样点的空间分布如图7所示。
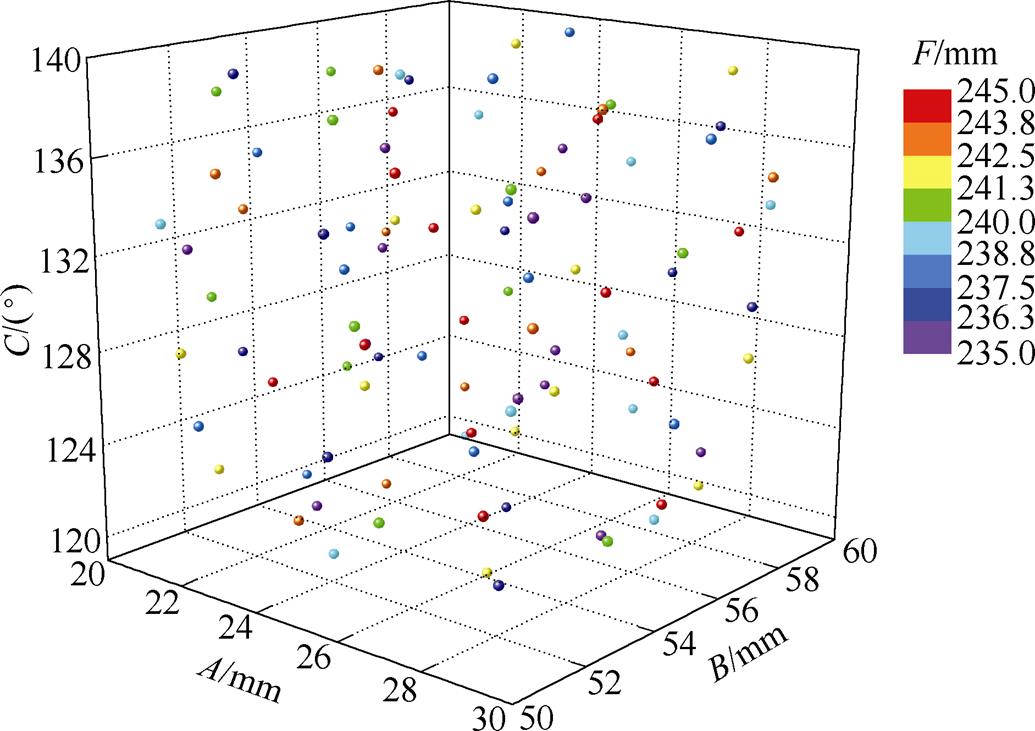
图7 基于OLHD的采样点空间分布
Fig.7 Distribution of sampling points based on OLHD
2.2.2 RBF神经网络预测模型
RBF神经网络模型是一种涵盖输入层、中间层和输出层的神经网络结构，可广泛应用于函数逼近、智能优化等方面[24-25]。因为该模型具有逼近复杂非线性函数能力强且容错率高等特点，所以适用于建立drel关于结构参数的预测模型。
将OLHD得到的100组训练样本点用于训练RBF神经网络模型，部分样本点计算结果见表3，其中drel为有限元仿真计算结果。
重新选取15个验证样本点进行误差分析，部分计算结果与相应的模型预测结果见表4。其中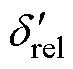
为模型的预测结果。
模型的预测相对误差erel可以表示为
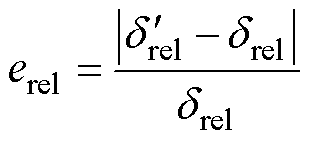（9）
表3 训练样本点的计算结果
Tab.3 Calculation results of the training sample points
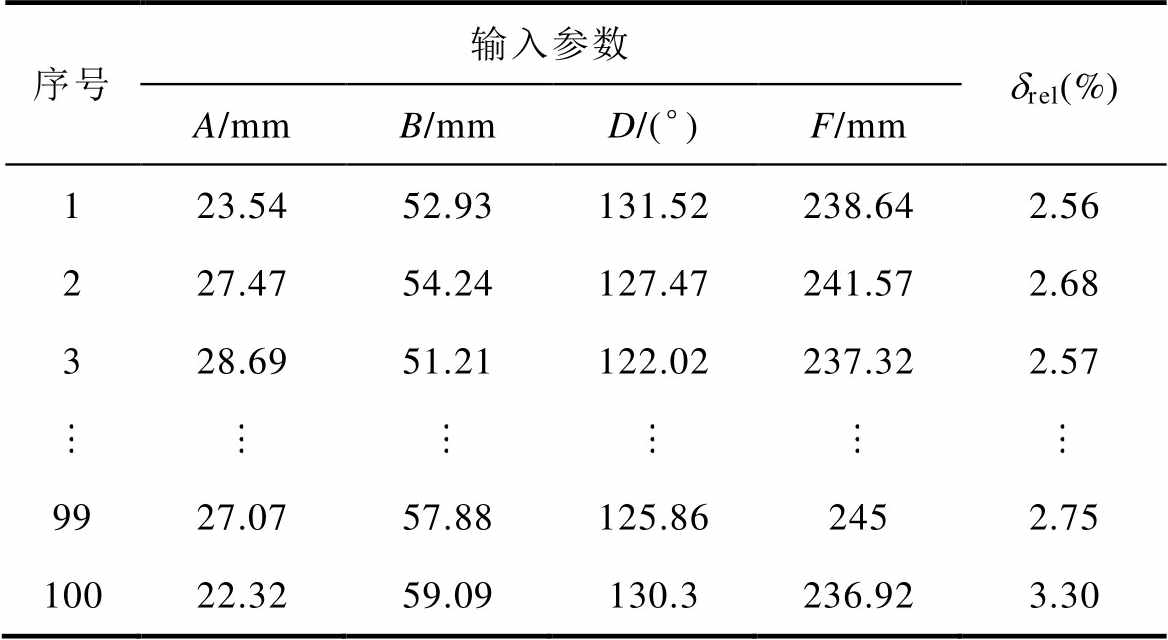
序号输入参数drel(%) A/mmB/mmD/(°)F/mm 123.5452.93131.52238.642.56 227.4754.24127.47241.572.68 328.6951.21122.02237.322.57 9927.0757.88125.862452.75 10022.3259.09130.3236.923.30
表4 验证样本点的计算结果
Tab.4 Calculation results of the verification sample points
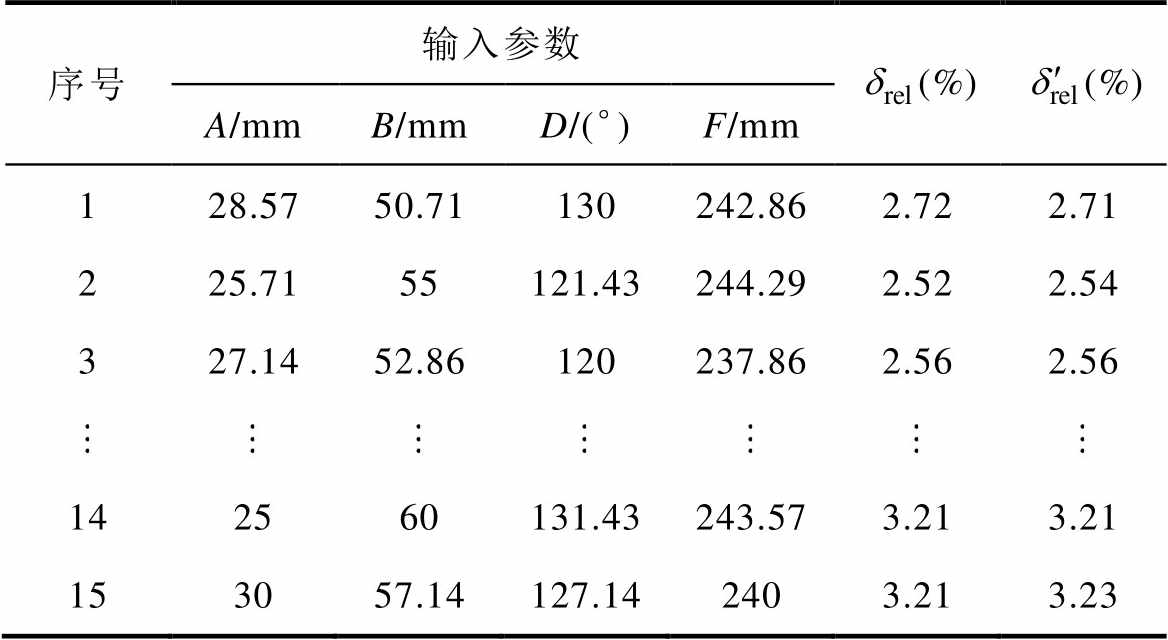
序号输入参数(%)(%) A/mmB/mmD/(°)F/mm 128.5750.71130242.862.722.71 225.7155121.43244.292.522.54 327.1452.86120237.862.562.56 142560131.43243.573.213.21 153057.14127.142403.213.23
经检验，RBF神经网络模型的最大预测相对误差为2.21%。这说明该模型具有足够的预测精度，可以用于代替有限元模型分析TFIH问题。
传统的遗传算法（Genetic Algorithm, GA）是根据自然界的生物进化规律而提出的一种寻找最优解的方法，该算法的计算效率高、鲁棒性好，因此广泛应用于对工程问题的优化处理[26]。为了避免在优化过程中陷入局部最优，针对GA中经常出现的早熟问题，有学者提出了MIGA，即把整个种群分成多个子种群，并引入迁移等方式增加种群的多样性，提高算法的全局搜索能力和计算效率[27]。本文设置MIGA控制参数见表5。
表5 MIGA的控制参数
Tab.5 Control parameters of MIGA
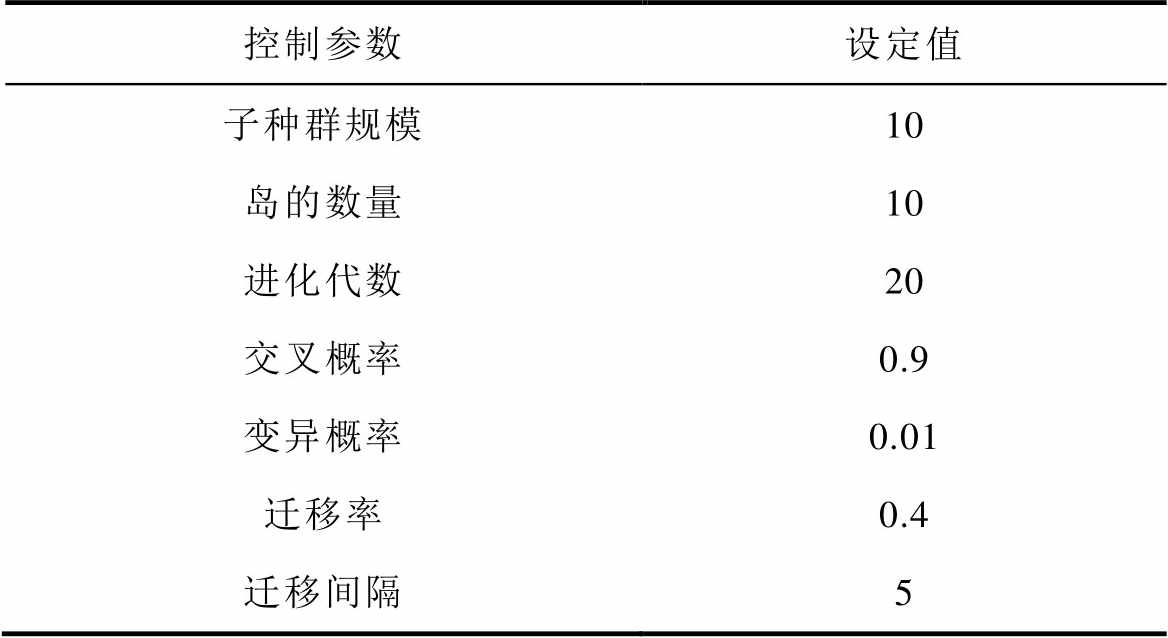
控制参数设定值 子种群规模10 岛的数量10 进化代数20 交叉概率0.9 变异概率0.01 迁移率0.4 迁移间隔5
基于RBF神经网络预测模型使用MIGA进行优化，经过1 972次计算得到最优解。drel优化过程如图8所示。
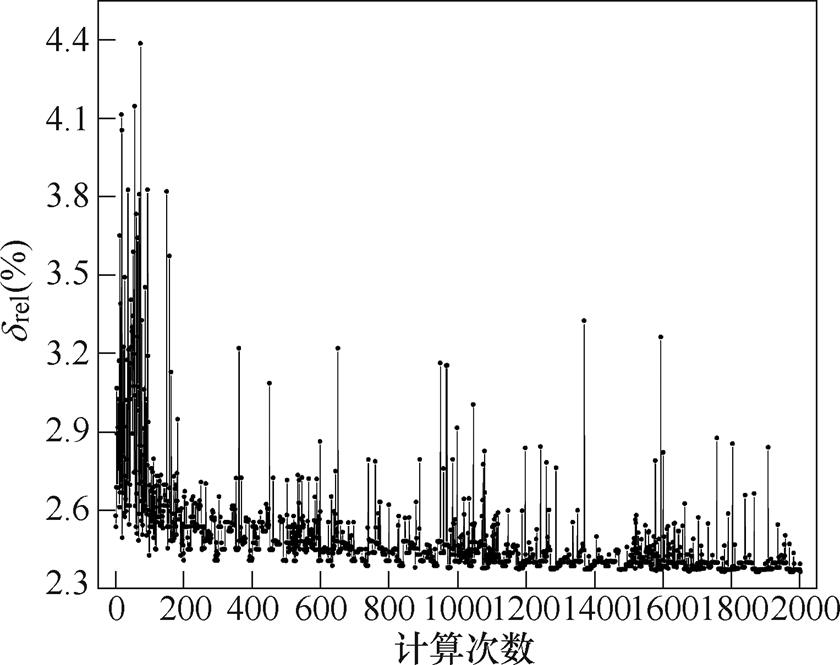
图8 drel优化过程
Fig.8 Optimization process of drel
优化前后TFIH装置的结构参数和对应的有限元仿真计算结果见表6。
表6 结构参数优化前后对比
Tab.6 Comparison of structural parameters before and after optimization
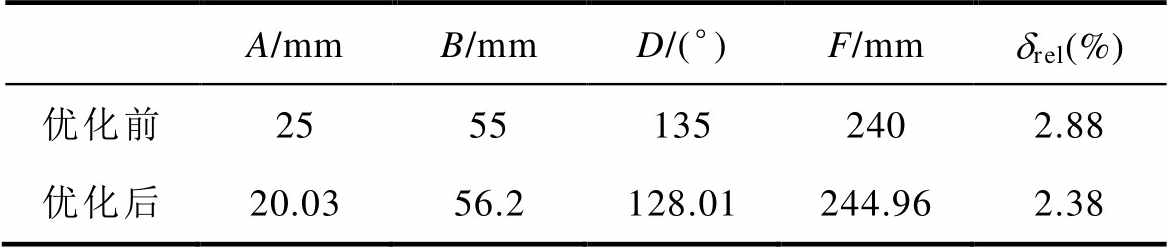
A/mmB/mmD/(°)F/mmdrel(%) 优化前25551352402.88 优化后20.0356.2128.01244.962.38
为了使优化前后的对比更具有参考性，优化前的结构参数是根据多次有限元分析的结果依据经验所得。结果显示，优化后，drel从2.88%下降到2.38%，接近MIGA的预测结果2.37%，这表明MIGA有效地优化了TFIH装置的结构参数。优化前后加热器出口处带材表面的温度分布曲线如图9所示。
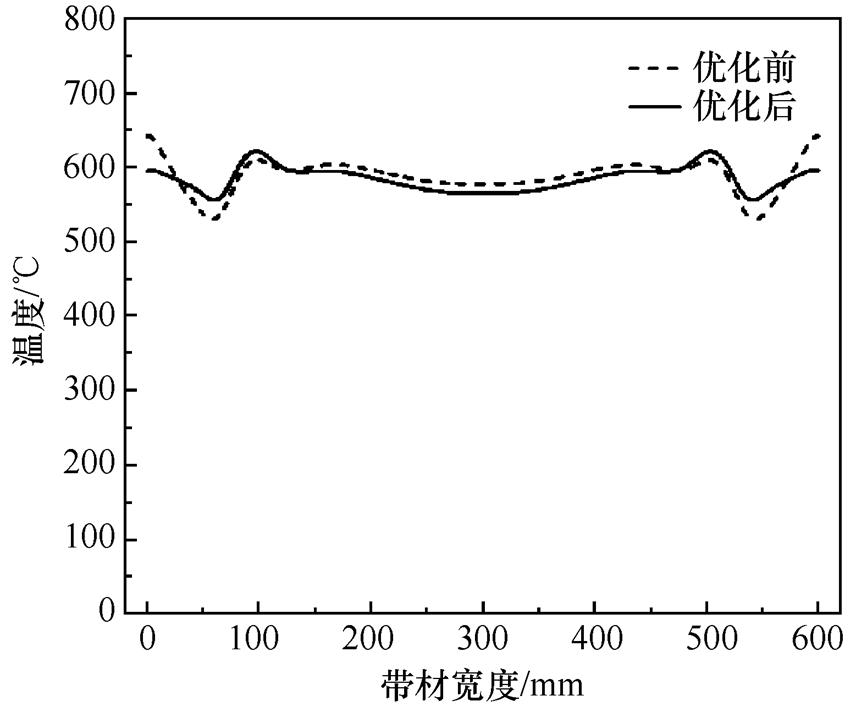
图9 优化前后带材在加热器出口处温度分布曲线
Fig.9 Temperature distribution curves of the strip at the heater outlet before and after optimization
通过优化加热器结构参数可以初步获得理想的drel，但此时Tav与理想回火温度600℃之间仍有大约20℃的差距，本节将通过调整电源参数I和f使Tav达到目标值同时尽可能减小drel。
在进行热处理时，电源参数I和f是可以灵活调整的，且调整精度较高。无论哪一个电源参数发生变化，都会同时对Tav和drel产生影响。
本节使用最小二乘法（Least Square Method, LSM）拟合Tav与drel的二阶响应面模型，表达式为
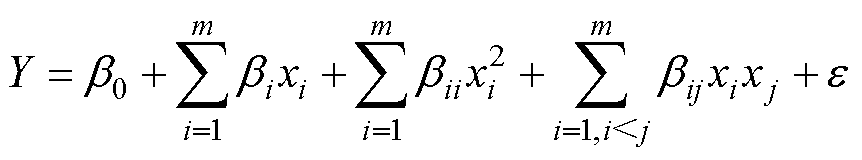（10）
式中，b0、bi、bii和bij为设计参数x的回归系数；m为设计参数的数量；e 代表随机误差[28-29]。
为防止计算结果与目标值相差太大而失去参考意义[30]，I和f的范围被设定为
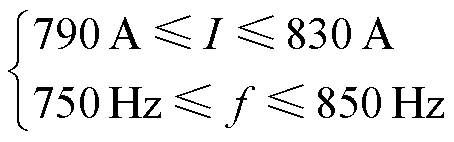（11）
RSM采样点设计同样选择OLHD来获得分布更加均匀的样本点。采样点数设定为20，RSM设计表和有限元仿真计算结果见表7。
表7 RSM设计表及计算结果
Tab.7 RSM design table and calculation results
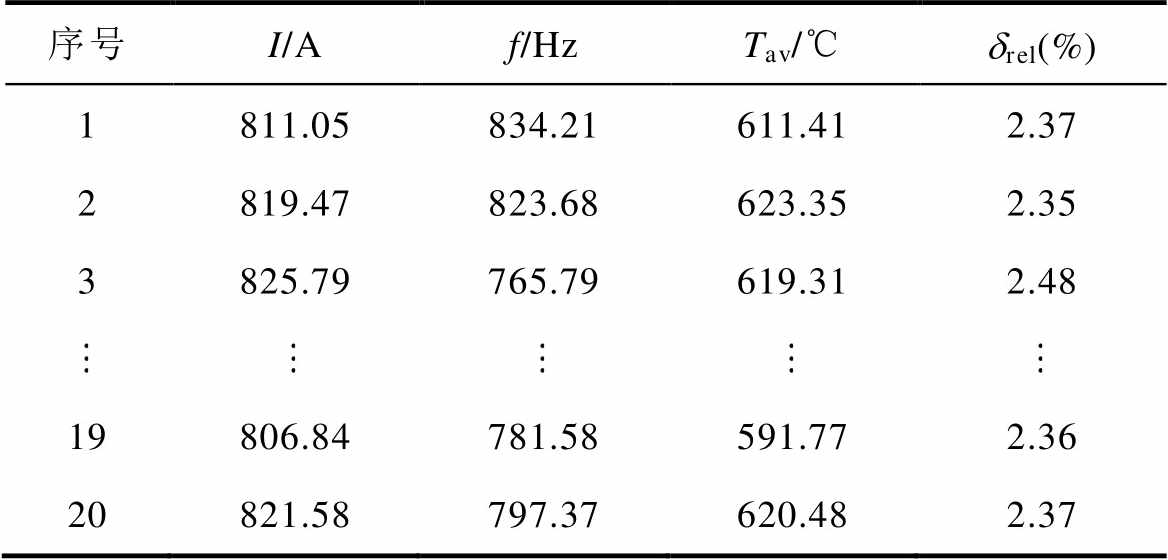
序号I/Af/HzTav/℃drel(%) 1811.05834.21611.412.37 2819.47823.68623.352.35 3825.79765.79619.312.48 19806.84781.58591.772.36 20821.58797.37620.482.37
拟合建立Tav和drel的二阶响应面模型后，使用方差分析（Analysis of Variance, ANOVA）来检验模型质量，方差分析结果见表8和表9。
表8 Tav的方差分析结果
Tab.8 ANOVA results for Tav
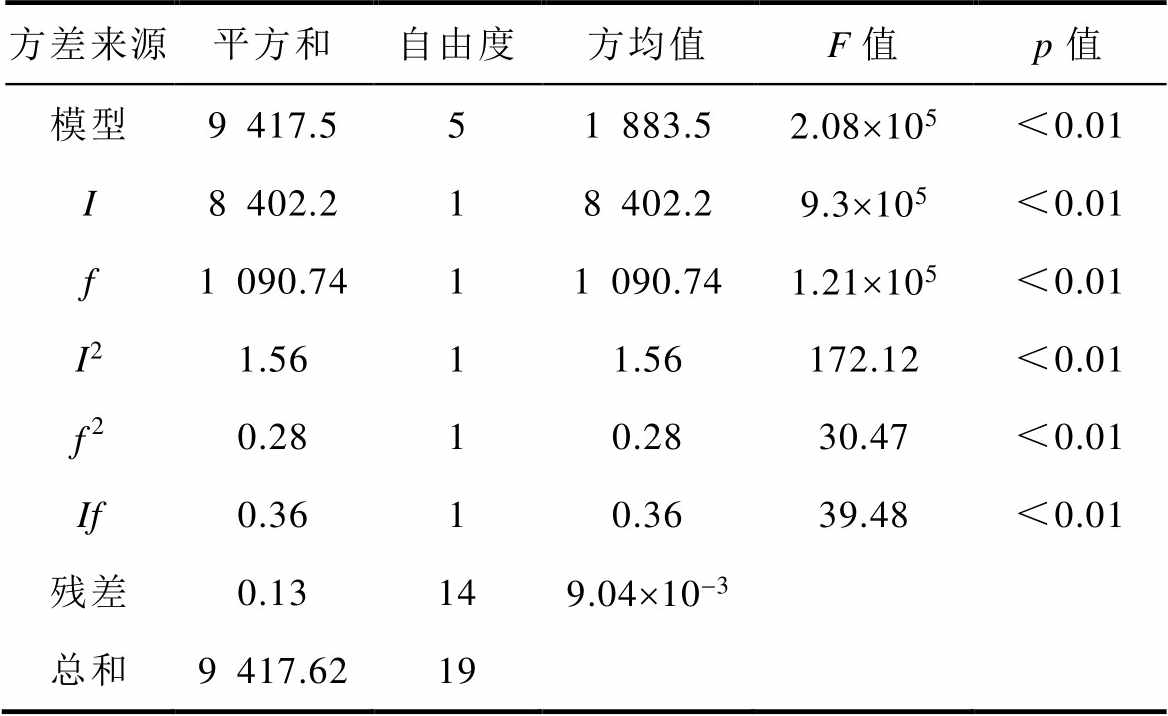
方差来源平方和自由度方均值F值p值 模型9 417.551 883.52.08´105＜0.01 I8 402.218 402.29.3´105＜0.01 f1 090.7411 090.741.21´105＜0.01 I21.5611.56172.12＜0.01 f20.2810.2830.47＜0.01 If0.3610.3639.48＜0.01 残差0.13149.04´10-3 总和9 417.6219
表9 drel的方差分析结果
Tab.9 ANOVA results for drel
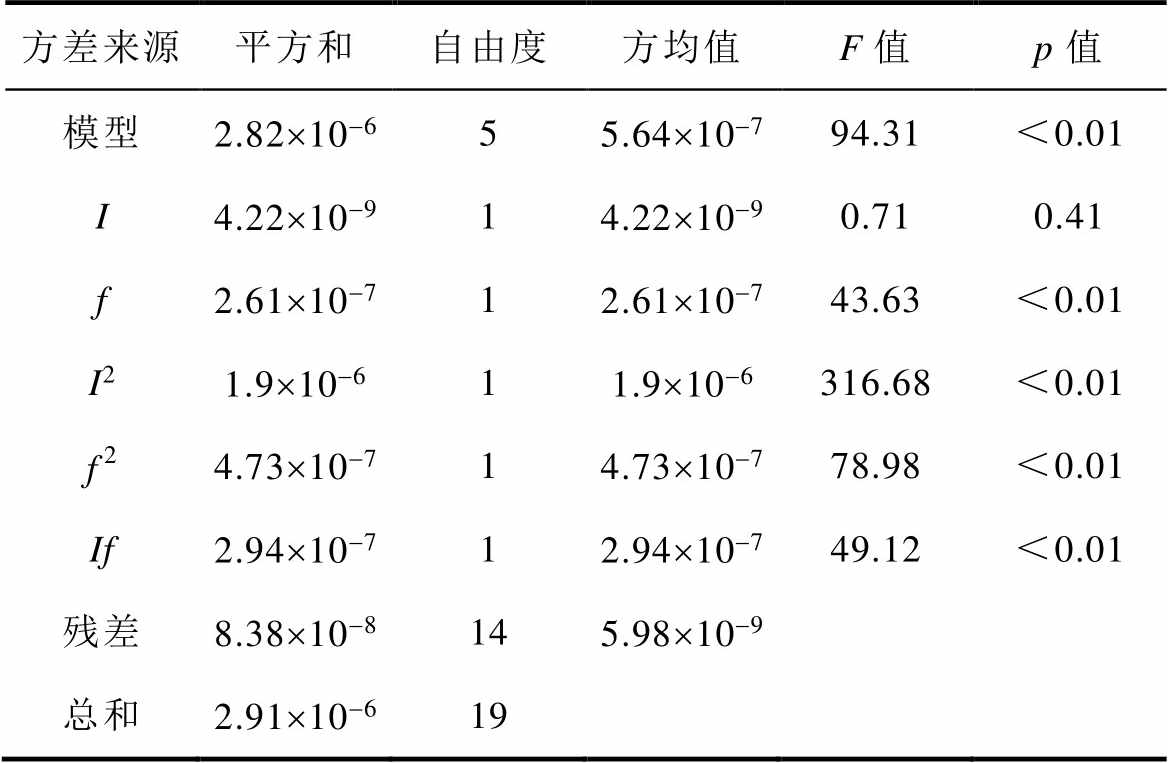
方差来源平方和自由度方均值F值p值 模型2.82´10-655.64´10-794.31＜0.01 I4.22´10-914.22´10-90.710.41 f2.61´10-712.61´10-743.63＜0.01 I21.9´10-611.9´10-6316.68＜0.01 f24.73´10-714.73´10-778.98＜0.01 If2.94´10-712.94´10-749.12＜0.01 残差8.38´10-8145.98´10-9 总和2.91´10-619
通常用Adj.R2来评价模型的拟合与预测效果，Adj.R2越接近1说明所获得的模型拟合精度越高。当p＜0.05时，则认为对应项对模型输出响应有显著影响[31-32]。
表8中，模型中的所有项均对Tav有显著影响。Tav的二阶响应面模型为
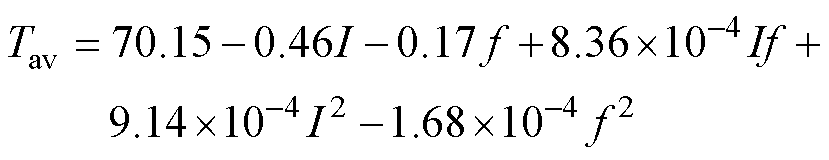（12）
对模型进行检验，Adj.R2≈1，说明该模型具有很好的拟合精度和预测能力。
表9中，对drel而言，除I外，其他项对结果均有显著影响，但I为基本项，不能忽略，因此可以得到drel的二阶响应面模型为
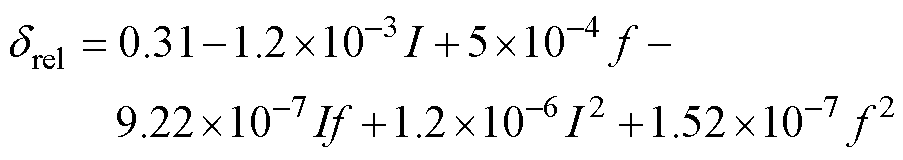（13）
经过检验，Adj.R2=96.09%，说明该模型同样有较好的拟合精度和预测能力。
响应面的拟合质量取决于每次实验的精度和设计参数的变化范围。本文中，RSM的样本点是通过有限元仿真计算得到的，计算结果不受环境等不可控因素的影响，可以保证每次实验的精度。此外，设计参数的变化范围越小，拟合精度越高[33]，因此得到的Tav与drel响应面模型均具有较高的质量。
根据式（12）和式（13）可以绘制得到Tav与drel的响应面如图10所示。图10直观地显示了当输入参数发生变化时输出响应的变化情况。
图10a显示了I、f和Tav之间的关系。Tav主要与I和f呈线性关系，受二次方项和交互项的影响较小。I或f增大，带材表面的热源值增加，Tav随之增大。
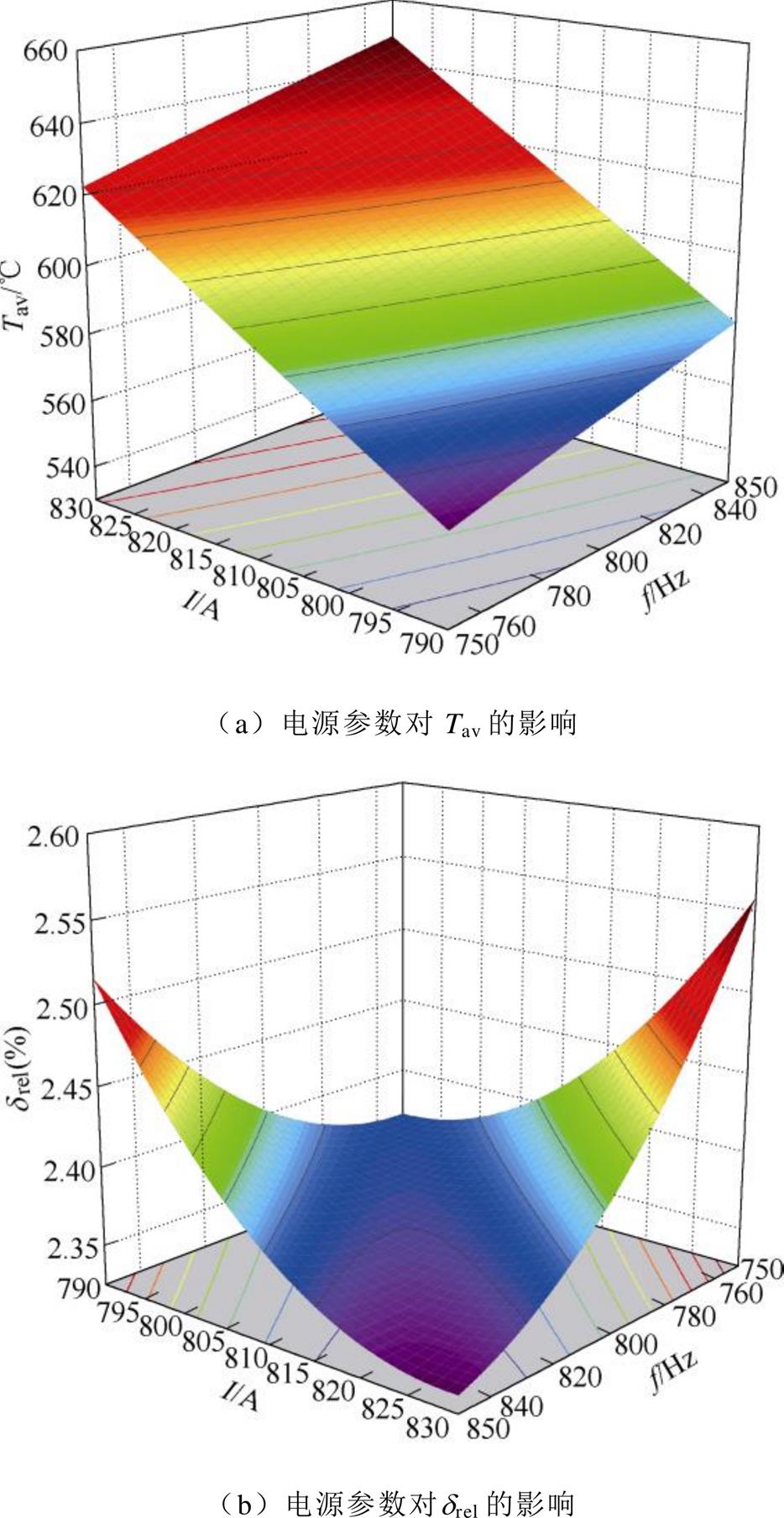
图10 Tav、drel关于电源参数的响应面
Fig.10 Response surface diagrams of Tav and drel to power supply parameters
图10b显示了I、f和drel之间的关系，可以发现响应面出现了明显的弯曲。然而，受输入参数范围的限制，响应面没有出现极值点。根据等高线图可以推测使drel取到极小值的点应该出现在I≥830 A且f≥850 Hz的范围内。
根据Tav和drel的表达式，使用Design-Expert中的响应优化器对电源参数进行多目标优化设计。对于Tav，选择“目标-600”，使其尽可能地接近600℃。对于drel，选择“最小化”以使该值尽可能小。优化结果见表10。可以看出，RSM的预测结果与有限元仿真计算结果接近，这表明得到的响应面模型可以用来预测电源参数的最佳组合。
使用优化后的结构参数与电源参数进行有限元仿真计算，最终得到在加热器出口处带材表面的温度分布曲线和带材表面的温度分布云图分别如图11a和图11b所示。结果表明，当带材的加热状态达到稳定时，带材在加热器出口处可以获得均匀的温度分布，而且平均温度稳定在600℃左右，满足45号钢带材的回火工艺要求。
表10 RSM优化结果
Tab.10 Optimization results by RSM
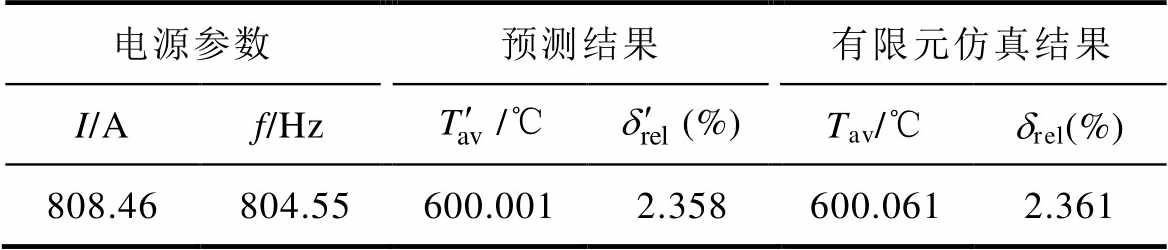
电源参数预测结果有限元仿真结果 I/Af/Hz/℃(%)Tav/℃drel(%) 808.46804.55600.0012.358600.0612.361
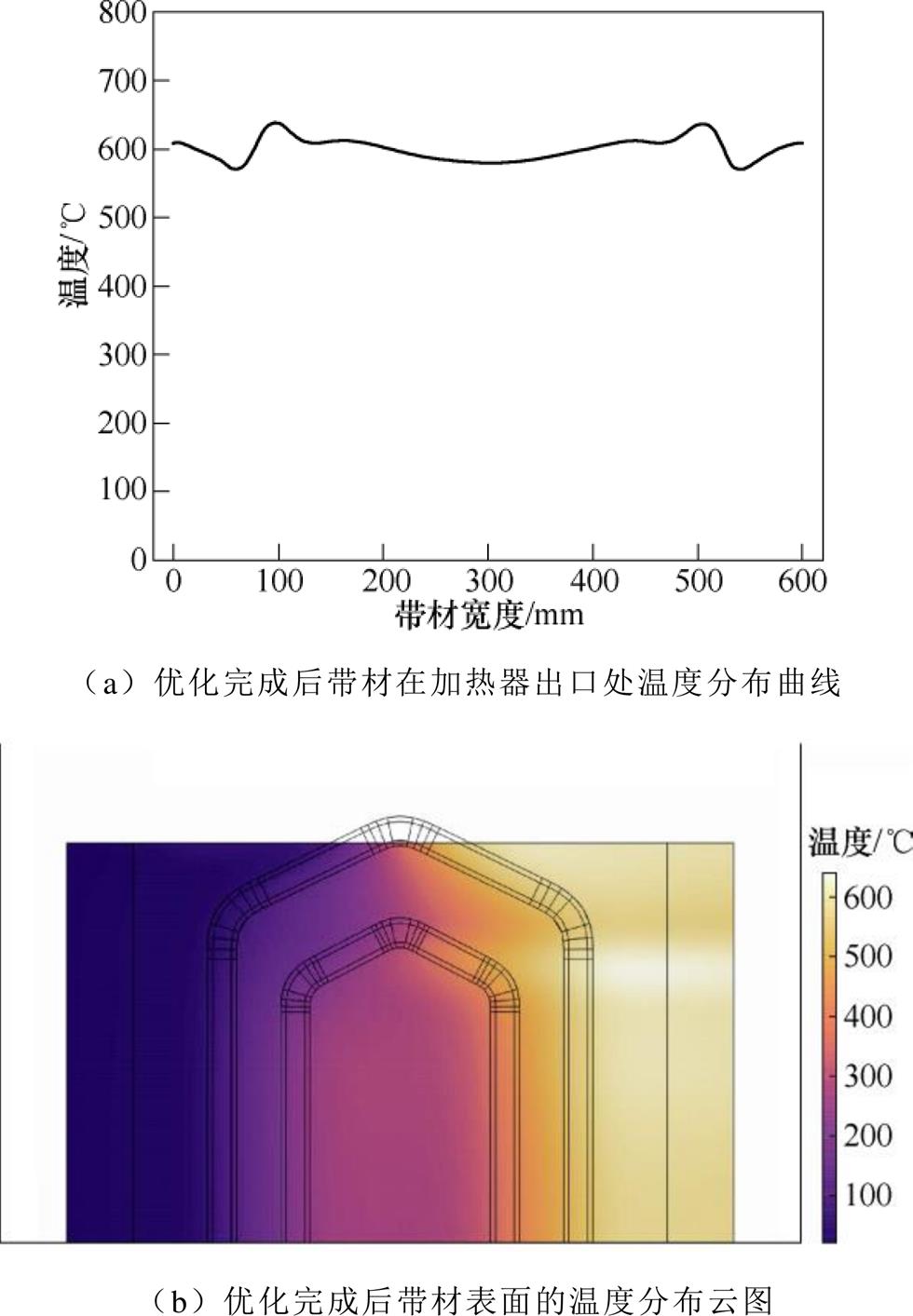
图11 TFIH装置优化结果
Fig.11 Optimization results of the TFIH device
本文针对45号钢带材进行TFIH回火热处理时出现的一系列问题提出了相应的解决方案，并通过COMSOL软件进行了验证。经过参数优化，当带材的加热状态达到稳定时，加热器出口处带材表面温度分布的均匀性得到了改善，且平均温度达到目标值。
1）为了降低优化难度同时提高优化精度，本文提出将优化参数分为加热器结构参数和电源参数，并使用不同方法进行优化。
2）针对加热器结构参数过多、计算量过大的问题，本文提出采用Morris法进行全局灵敏度分析，在六个结构参数中选择出四个对结果影响较大的参数进行下一步分析。
3）利用基于OLHD的RBF神经网络预测模型建立了被筛选结构参数与相对不均匀度之间的关系，并利用MIGA进行全局优化，将相对不均匀度从2.88%降至2.38%。
4）在优化后的加热器结构基础上，采用RSM求解电源参数的最优组合，实现多目标优化设计。验证结果表明，当带材的加热状态达到稳定时，加热器出口处带材表面温度分布的相对不均匀度为2.361%，平均温度为600.061℃，满足45号钢带材回火热处理的要求。
参考文献
[1] 黄亚飞, 蒋兴良, 任晓东, 等. 采用涡流自热环防止输电线路冰雪灾害的方法研究[J]. 电工技术学报, 2021, 36(10): 2169-2177.
Huang Yafei, Jiang Xingliang, Ren Xiaodong, et al. Study on preventing icing disasters of transmission lines by use of eddy self-heating ring[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2169-2177.
[2] 段志荣, 解社娟, 李丽娟, 等. 基于磁力传动式阵列涡流探头的管道缺陷检测[J]. 电工技术学报, 2020, 35(22): 4627-4635.
Duan Zhirong, Xie Shejuan, Li Lijuan, et al. Detection of defects in pipeline structures based on magnetic transmission eddy current array probe[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4627-4635.
[3] 涂彦昕, 梅红伟, 刘立帅, 等. 基于动态扫描涡流热成像技术的碳钢结构损伤检测[J]. 电工技术学报, 2023, 38(11): 2999-3008.
Tu Yanxin, Mei Hongwei, Liu Lishuai, et al. Structural damage evaluation of carbon steel based on dynamic scanning eddy current infrared thermo- graphy[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2999-3008.
[4] Xu H, Kamada H, Isobe T, et al. Feasibility study on a real-scale high-frequency electromagnets for mag- netic hyperthermia base on a magnetic scaling law[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(6): 1-5.
[5] Bao Li, Wang Bo, You Xiaoping, et al. Numerical and experimental research on localized induction heating process for hot stamping steel sheets[J]. International Journal of Heat and Mass Transfer, 2020, 151: 119422.
[6] 冷朝霞, 刘庆丰. 基于多电平逆变器的感应加热双频率输出设计[J]. 电工技术学报, 2016, 31(24): 195-204.
Leng Zhaoxia, Liu Qingfeng. Design of dual frequency output of induction heating based on multilevel inverter[J]. Transactions of China Elec- trotechnical Society, 2016, 31(24): 195-204.
[7] Plumed E, Lope I, Acero J. Modeling and design of cookware for induction heating technology with balanced electromagnetic and thermal characteri- stics[J]. IEEE Access, 2022, 10: 83793-83801.
[8] Peng Wen, Chen Xiaorui, Zhang Li, et al. Finite element analysis of temperature uniformity in transverse induction heating process in ESP rolling[J]. The International Journal of Advanced Manufacturing Technology, 2021, 115(11-12): 3423-3439.
[9] Wang Youhua, Li Bin, Yin Liuxia, et al. Velocity- controlled particle swarm optimization (PSO) and its application to the optimization of transverse flux induction heating apparatus[J]. Energies, 2019, 12(3): 487.
[10] 汪友华, 吴建成, 李宾, 等. 新型带材横向磁通感应加热器设计与相关激励参数优选[J]. 电工技术学报, 2020, 35(4): 745-757.
Wang Youhua, Wu Jiancheng, Li Bin, et al. Design and optimization of relative excitation parameters for a new strip transverse flux induction heating apparatus[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 745-757.
[11] Song Huabin, Wang Youhua, Peng Jiangpai, et al. Study on the uniformity of temperature distribution of transverse flux induction heating based on a new magnetic pole[J]. Energies, 2022, 15(19): 7450.
[12] 许家忠, 赵辉, 付天宇, 等. 感应加热CFRP温度控制算法[J]. 东北大学学报(自然科学版), 2022, 43(1): 17-23, 39.
Xu Jiazhong, Zhao Hui, Fu Tianyu, et al. Temperature control algorithm of induction heating CFRP[J]. Journal of Northeastern University (Natural Science), 2022, 43(1): 17-23, 39.
[13] Chang C J, Chiang T H, Tai C C. A modified self-tuning fuzzy logic temperature controller for metal induction heating[J]. The Review of Scientific Instruments, 2020, 91(6): 064905.
[14] Wang Junhua, Wang Youhua, Ho S L, et al. Design and FEM analysis of a new distributed vernier traveling wave induction heater for heating moving thin strips[J]. IEEE Transactions on Magnetics, 2011, 47(10): 2612-2615.
[15] Morandi A, Fabbri M. In-depth induction heating of large steel slabs by means of a DC saturating field produced by superconducting coils[J]. IEEE Transa- ctions on Applied Superconductivity, 2016, 26(4): 1-7.
[16] 汪友华, 吴建成, 刘成成, 等. 横向磁通连续感应加热过程中带材涡流场和温度场的仿真分析[J]. 金属热处理, 2019, 44(1): 229-234.
Wang Youhua, Wu Jiancheng, Liu Chengcheng, et al. Simulation and analysis of eddy current field and temperature field of strips during transverse flux continuous induction heating[J]. Heat Treatment of Metals, 2019, 44(1): 229-234.
[17] 王晗, 侯恺, 刘晓楠, 等. 基于全局灵敏度分析的电气互联系统韧性提升方法[J]. 电力系统自动化, 2023, 47(3): 59-67.
Wang Han, Hou Kai, Liu Xiaonan, et al. Resilience enhancement method for electricity-gas intercon- nection system based on global sensitivity analysis[J]. Automation of Electric Power Systems, 2023, 47(3): 59-67.
[18] 何琨, 严正, 徐潇源, 等. 基于Sobol’法的孤岛微电网潮流全局灵敏度分析[J]. 电力系统自动化, 2018, 42(14): 99-106.
He Kun, Yan Zheng, Xu Xiaoyuan, et al. Sobol’ method based global sensitivity analysis of power flow in islanded microgrid[J].Automation of Electric Power Systems, 2018, 42(14): 99-106.
[19] Morris M D. Factorial sampling plans for preliminary computational experiments[J]. Technometrics, 1991, 33(2): 161-174.
[20] Campolongo F, Cariboni J, Saltelli A. An effective screening design for sensitivity analysis of large models[J]. Environmental Modelling & Software, 2007, 22(10): 1509-1518.
[21] 戴睿, 张岳, 王惠军, 等. 基于多物理场近似模型的高速永磁电机多目标优化设计[J]. 电工技术学报, 2022, 37(21): 5414-5423.
Dai Rui, Zhang Yue, Wang Huijun, et al. Multi- objective optimization design of high-speed per- manent magnet machine based on multi-physics approximate model[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5414- 5423.
[22] McKay M D, Beckman R J, Conover W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technimetrics, 1979, 21(2): 239- 245.
[23] Park J S. Optimal Latin-hypercube designs for computer experiments[J]. Journal of Statistical Planning and Inference, 1994, 39(1): 95-111.
[24] 吴月宝, 赵晋斌, 张少腾, 等. 基于径向基神经网络的多负载无线电能传输系统自适应阻抗匹配方法[J]. 电工技术学报, 2021, 36(19): 3969-3977.
Wu Yuebao, Zhao Jinbin, Zhang Shaoteng, et al. An adaptive impedance matching method based on radial basis function neural network in multi-load wireless power transfer systems[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 3969-3977.
[25] 陈宗遥, 卜旭辉, 郭金丽. 基于神经网络的数据驱动互联电力系统负荷频率控[J]. 电工技术学报, 2022, 37(21): 5451-5461.
Chen Zongyao, Bu Xuhui, Guo Jinli. Neural network based data-driven load frequency control for inter- connected power systems[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5451-5461.
[26] 王超, 李文栋, 陈泰然, 等. 550kV GIS盆式绝缘子小型化设计（一）——几何形状优化[J]. 电工技术学报, 2022, 37(7): 1847-1855.
Wang Chao, Li Wendong, Chen Tairan, et al. Compact design of 550kV basin-type spacer in gas insulated switchgear (part I)—structure optimi- zation[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1847-1855.
[27] Zhang Wenwen, Qi Hong, Yu Zhiqiang, et al. Optimization configuration of selective solar absorber using multi-island genetic algorithm[J]. Solar Energy, 2021, 224: 947-955.
[28] 罗玉涛, 卢若皓. 基于结构参数分级优化的电机电磁噪声抑制[J]. 电工技术学报, 2021, 36(14): 2957- 2970.
Luo Yutao, Lu Ruohao. Hierarchical optimization of structural parameters for motor electromagnetic noise suppression[J]. Transactions of China Electrotech- nical Society, 2021, 36(14): 2957-2970.
[29] 张嘉伟, 曾正, 孙鹏, 等. 基于响应面的车用功率模块Pin-Fin优化设计[J]. 电工技术学报, 2022, 37(22): 5836-5850.
Zhang Jiawei, Zeng Zheng, Sun Peng, et al. Optimized Pin-Fin design of power module for electric vehicle application by response surface[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5836-5850.
[30] 吉敬华, 沈人洁, 徐亮, 等. 考虑运行工况的模块化双永磁游标电机多工作点优化设计[J]. 电工技术学报, 2022, 37(22): 5649-5659.
Ji Jinghua, Shen Renjie, Xu Liang, et al. Multi- working point optimization of modular double permanent-magnet vernier motor considering oper- ation condition[J]. Transactions of China Electro- technical Society, 2022, 37(22): 5649-5659.
[31] Paese E, Geier M, Homrich R P, et al. Assessment of process parameters in the optimization of the metal sheet electromagnetic forming process[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(6): 1-6.
[32] 唐昭晖, 许志红. 基于响应面法的交流接触器弹簧系统优化设计方法[J]. 电工技术学报, 2022, 37(2): 515-527.
Tang Zhaohui, Xu Zhihong. Optimal design method for AC contactor spring system based on response surface method[J]. Transactions of China Electro- technical Society, 2022, 37(2): 515-527.
[33] Zhang Bangfu, Cheng Ming, Cao Ruiwu, et al. Analysis of linear flux-switching permanent magnet motor using response surface methodology[J]. IEEE Transactions on Magnetics, 2014, 50(11): 1-4.
Abstract Transverse flux induction heating (TFIH) devices are widely used in the heat treatment process of flat workpieces, such as metal strips. The heating results affect the application performance of metal strips. Ideal average temperature and uniform temperature distribution of the strip at the heater outlet are desired when the heating state of the strip is stable. The standard tempering temperature of 45# steel is 600℃. This paper divides the optimization parameters into structural and power supply parameters to meet heat treatment requirements. Different methods are used to reduce optimization difficulties while maintaining optimization accuracy.
The structure of the TFIH device is determined by seven parameters. The air gap between the magnetic pole and the strip should be as small as possible to meet the processing technology. A global sensitivity analysis (GSA) based on the Morris method ranks the sensitivity of the relative non-uniformity to the six coil structural parameters. The top four structural parameters with significant effects are screened out, ensuring optimization accuracy while reducing calculation time.
Due to the strong robustness, the radial basis function (RBF) neural network prediction model replaces the finite element calculation model to estimate nonlinear functions. The optimal Latin hypercube design (OLHD) samples 100 times, and the sampling results are used as the training sample points of the prediction model. After testing, the RBF neural network model has high prediction accuracy within the variation range of the input parameters. The multi-island genetic algorithm (MIGA) optimizes the screened structural parameters globally. The results show that the relative non-uniformity is reduced from 2.88% to 2.38% after optimization, effectively improving the temperature distribution uniformity.
Based on the optimized structural parameters, the response surface method (RSM) is used to optimize the current and frequency. Consequently, the average temperature is close to the target value, and the relative non-uniformity is maintained at a low level. The relative non-uniformity and the average temperature expressions for power supply parameters are fitted separately using a second-order polynomial. Both models are tested by the variance (ANOVA) analysis. The multi-objective optimization is then performed using the response optimizer in Design-Expert. The results show that after the optimization of structural parameters and power supply parameters, when the strip heating state reaches stability, the relative non-uniformity of the strip surface temperature distribution at the heater outlet is 2.36%, and the average temperature is 600.06°C, which can meet the tempering requirements of 45# steel strip.
keywords：Transverse flux induction heating, global sensitivity analysis, radial basis function neural network model, multi-island genetic algorithm, response surface method
DOI: 10.19595/j.cnki.1000-6753.tces.230429
中图分类号：TG155.2
河北省省级科技计划资助项目（215676146H, 225676163GH）。
收稿日期 2023-04-06
改稿日期 2023-06-19
刘志赢 男，1999年生，硕士研究生，研究方向为横向磁通感应加热技术。E-mail: 202121401079@stu.hebut.edu.cn
汪友华 男，1964年生，教授，博士生导师，研究方向为工程电磁场综合效应。E-mail: wangyi@hebut.edu.cn（通信作者）
（编辑 郭丽军）