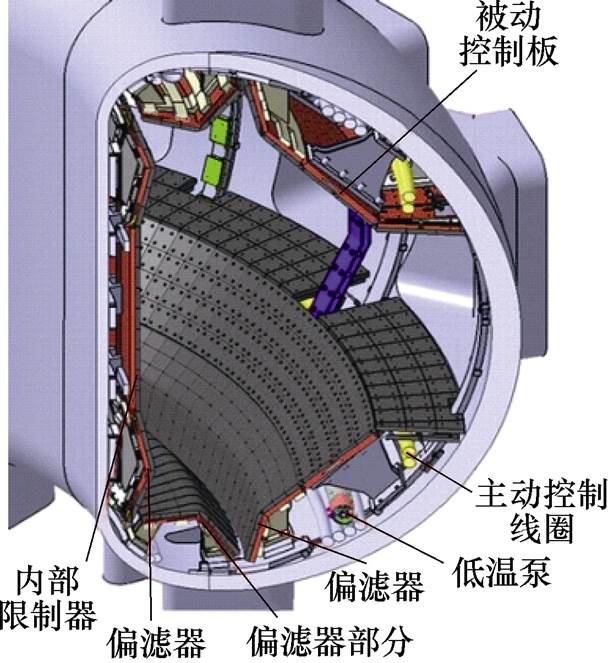
图1 EAST装置剖面
Fig.1 EAST device profile
摘要 全超导托卡马克核聚变发电装置(EAST)快控电源的首要性能指标是快速跟踪参考信号,以输出电流实现负载线圈的励磁,对等离子体的垂直位移进行反馈控制。EAST快控电源负载线圈受装置内部部件和真空内等离子体的影响,线圈感值会出现小范围内慢时变波动以及线圈上存在互感电动势干扰,传统比例-积分(PI)控制方法在电流跟踪控制过程中存在不足。为了实现干扰的抑制和应对负载波动,提出一种带干扰抑制的离散积分滑模控制方法,根据系统状态方程设计离散积分滑模控制器,结合滑模干扰观测器实现集总干扰的观测,对集总干扰进行前馈补偿控制。为了抑制抖振和加快收敛速度,设计一种新型平滑饱和函数和增益自适应观测器,根据观测电流误差和跟踪电流误差自适应调整观测器增益。对比传统PI控制,仿真和实验验证了所提控制方法具有更加优良的电流跟踪特性,在输出电流超调更小的情况下动态响应更快,能够有效地抑制负载侧扰动,具有良好的鲁棒性。
关键词:EAST快控电源 离散积分 滑模控制 滑模干扰 观测器前馈补偿
全超导托卡马克核聚变发电装置(Experimental Advanced Superconducting Tokamak, EAST)是我国自主研发的实现可控核聚变的重要装置,其中控制等离子体垂直方向位移的快速控制电源是其重要组成部分。EAST快控电源跟踪控制室给定的参考电流信号输出电流,输出电流将对全超导托卡马克装置真空室内的超导快控主动控制电感线圈励磁,以产生磁场主动约束等离子体垂直方向的位移。
快速精确跟踪给定参考电流信号是EAST快控电源的重要性能指标,现阶段采用比例-积分(Proportional-Integral, PI)控制实现输出电流的跟踪目的。EAST装置剖面如图1所示,实际工程中快控电源主动控制超导线圈的电流受多因素影响[1],真空室内运动的等离子体、被动控制板上的涡流、偏滤器的鞘层和上下主动控制线圈互感等因素,均会在一定范围内影响主动控制线圈的电感值以及在线圈上产生相应的互感电动势。在考虑到EAST快控电源负载存在小范围慢时变以及存在交流互感电动势扰动的情况下,传统PI控制方式简单可靠,但是存在着抗扰动性能不足和控制精度不高的问题。

图1 EAST装置剖面
Fig.1 EAST device profile
滑模控制具有强鲁棒性和控制简单可靠的优点,在三电平并网逆变器[2]、永磁同步电机控制[3-4]、高速磁悬浮列车电机驱动[5]、铁路牵引供电系统[6]和DC-DC变换器[7]等场合已广泛应用。在EAST快控电源输出电流跟踪控制过程中,数字控制方式高效便捷[8],而离散滑模积分也得到诸多应用[9],为EAST快控电源中的离散滑模应用提供了良好的基础。传统滑模控制过程中存在着抖振和收敛速度不够快等问题,为了抑制抖振同时加快收敛速度,文献[10]提出了一种基于模糊神经网络的全局滑模控制方法应用在有源电力滤波器中,实现了全局鲁棒无抖振控制。文献[11]引入了正切函数以及对传统幂次趋近律进行改进,达到趋近律快速收敛和无抖振目的。文献[12]提出了一种组合趋近律实现了柔性直流输电系统的稳定控制。文献[13]利用直接转矩超螺旋二阶滑模控制,实现了笼型异步电动机系统的快速鲁棒控制。文献[14]为了实现燃料电池系统应对不同工况能快速调节,提出了基于状态误差的分段函数和双曲正切函数幂次趋近律滑模控制方法。文献[15]设计了基于双曲正切函数与边界层厚度相结合的饱和函数抑制抖振,实现永磁直线同步电机反推终端滑模控制。以上组合趋近律以及新型饱和函数均能实现抖振抑制和快速收敛的目的,但是在EAST快控电源的ms级输出电流跟踪控制过程中较为复杂,不利于工程的实现。考虑到EAST快控电源负载线圈上存在互感电动势干扰以及负载电感值的变化,因此需要对干扰进行抑制,文献[16]提出了一种结合干扰观测器的改进非奇异快速终端滑模控制方法,实现永磁同步电机中参数摄动带来的干扰抑制。文献[17]设计了一种新型超螺旋滑模自适应观测器,实现永磁同步电机转速的准确观测。文献[18]为了抑制Buck-Boost变换器中参数不匹配带来的扰动,提出一种基于线性扩张状态观测器的滑模控制方法。文献[19]设计一种滑模负载转矩观测器对负载转矩进行实时辨识,同时设计一种可快速收敛的自适应系数指数趋近律来提高负载转矩观测器性能。文献[20]提出了一种基于滑模观测器误差补偿的永磁同步电机无位置传感器控制策略,并且利用临界饱和切换函数改进滑模观测器收敛性能。文献[21]利用高增益观测器结合滑模控制,实现并网中性点钳位变换器控制。文献[22]将二阶滑模控制和递归径向基神经网络相结合,实现永磁同步直线电机强鲁棒控制。以上滑模控制结合观测器的控制方法能够良好地抑制负载端扰动,但是观测器设计较为复杂且观测器增益难以确定。文献[23-24]利用模糊控制和神经网络自适应调整滑模观测器增益,实现了增益的自适应在线调整,但是自适应结构复杂,需要大量的计算过程,不利于EAST快控电源工程上的实现。
在EAST快控电源输出负载端存在干扰电动势和负载慢时变情况下,为解决传统PI控制抗扰动性能不足和控制精度变差的问题,提出一种带干扰抑制的离散积分滑模控制策略,根据离散状态方程建立离散滑模控制器,设计滑模观测器实现扰动的观测,结合观测器的前馈补偿实现输出电流的离散滑模跟踪控制。为了抑制滑模控制过程的抖振和加快收敛速度,设计了一种新型饱和函数,同时根据输出电流跟踪误差和观测误差,设计了观测器的自适应变增益系数,达到了抑制抖振和加快收敛速度的目的。仿真和实验结果验证了设计的干扰抑制前馈离散积分滑模控制器具有良好的控制性能,能够实现EAST快控电源输出电流的快速准确跟踪。
EAST快控电源主电路采用单相H桥逆变电路级联成单支路的模式,电路结构如图2所示。图2中,uH为级联单相H桥逆变输出端电压,io为输出电流,L为内部真空室负载电感,R为负载电感与线路等效电阻总和,E为单H逆变桥直流侧电压。
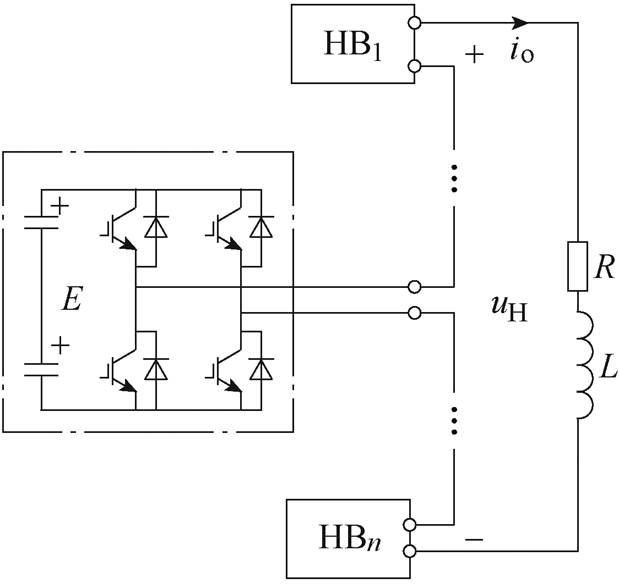
图2 EAST快控电源支路结构
Fig.2 EAST fast control power supply branch structure
考虑到真空室中其他偏置部件以及被动控制板对EAST快控电源支路线圈负载上产生的感应电动势影响,将所有环节在负载线圈上产生的互感电动势等效为一交流扰动电源,同时负载线圈电感值会受到周围等离子体运动的影响,产生负载的变化,将交流扰动和负载变化扰动总和等效为集总外部干扰d。忽略超导线圈内阻情况下EAST快控电源的单支路等效支路如图3所示。
传统的EAST快控电源采用PI控制,当输入相应的参考信号时,控制器按照相应的比例输出电流。当考虑到慢时变的交流外部集总扰动时,以输出电流快速精确跟踪参考信号为控制目的的情况下,PI控制在快速性和精确性之间难以实现均衡,存在不足之处。滑模控制具有鲁棒性强和控制精度高的优点,利用观测器实现干扰的前馈补偿,则能够实现良好的输出电流跟踪控制。
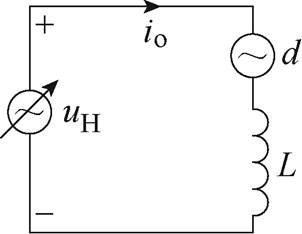
图3 等效支路
Fig.3 Equivalent branch circuit
根据图3,考虑集总干扰信号d,可建立EAST快控电源支路模型为
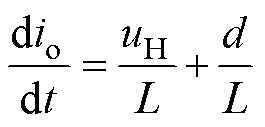 (1)
(1)
将式(1)表示为离散状态形式,即
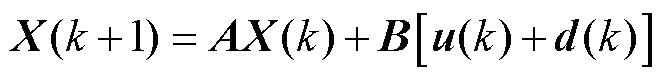 (2)
(2)
式中,X(k+1)为下一时刻的状态量;X(k)为当前时刻状态输出量;A和B为系数矩阵;d(k)为干扰量;u(k)为控制量。且有X(k)=[io(k)],A=[1],B=[Ts/L],Ts为开关周期。
输出负载端存在交流集总扰动情况下,在EAST快控电源输出电流的传统PI控制过程中,存在较大的跟踪误差,为了减小跟踪误差,建立离散积分滑模控制器,滑模函数表示为
 (3)
(3)
式中,c1和c2分别为误差系数和积分系数;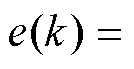
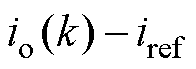 为跟踪误差,iref为输出电流目标参考值;
为跟踪误差,iref为输出电流目标参考值;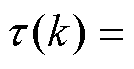
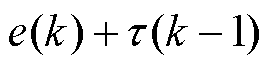 为误差的离散积分。
为误差的离散积分。
为了实现良好的控制性能,采用离散指数趋近控制率设计控制器,离散指数趋近控制率表示为
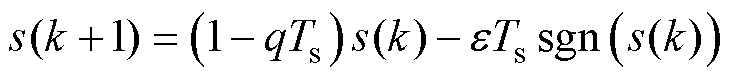 (4)
(4)
式中,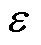 和q为滑模系数,且
和q为滑模系数,且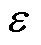 >0,0<1-qTs<1;sgn( )为符号函数。
>0,0<1-qTs<1;sgn( )为符号函数。
联立式(2)~式(4)可得控制量为
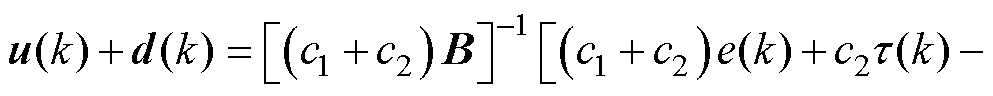
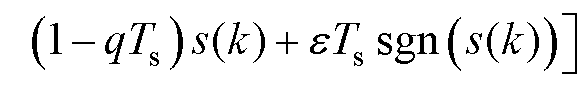 (5)
(5)
假设干扰观测量为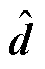 ,将式(5)改为
,将式(5)改为
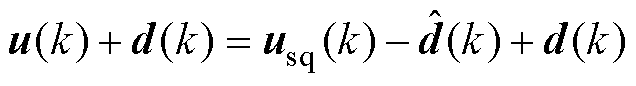 (6)
(6)
在理想情况下,可得标准控制量
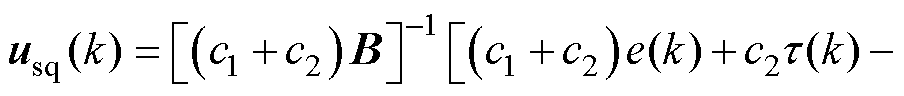
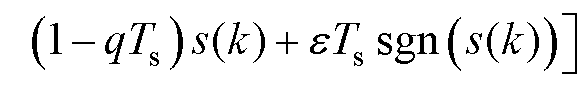 (7)
(7)
为了实现输出端的扰动抑制,利用滑模干扰观测器观测输出端集总扰动量,在标准控制量的基础上再实现前馈补偿,基于滑模干扰观测器的离散积分滑模控制结构框图如图4所示。
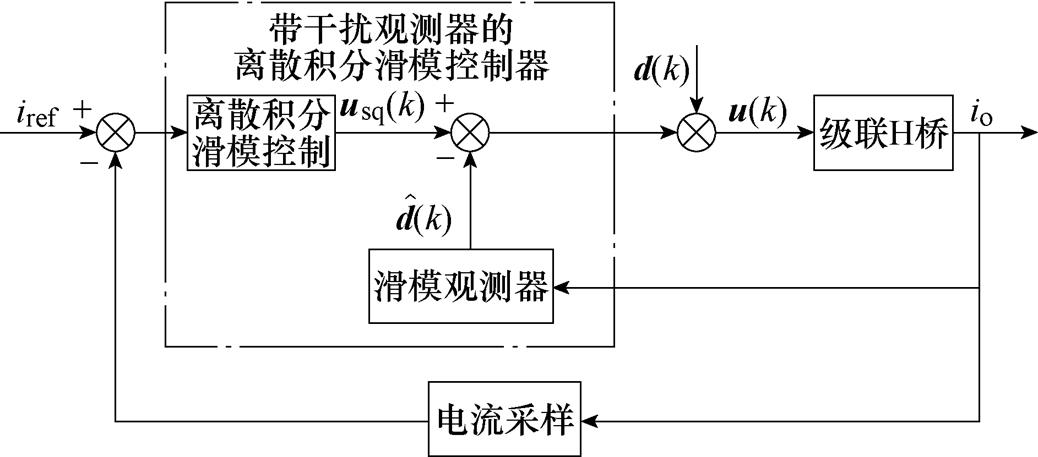
图4 基于干扰抑制的离散积分滑模控制结构框图
Fig.4 Diagram of discrete integral sliding mode control based on disturbance suppression
基于式(1),以输出电流和集总干扰量构造滑模观测器,离散状态下有
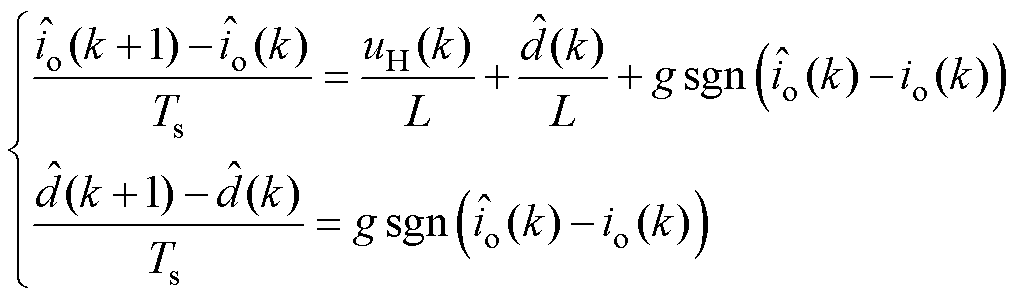 (8)
(8)
式中,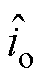 和
和 为电流和干扰观测量;g为观测增益。
为电流和干扰观测量;g为观测增益。
因此,滑模观测器观测的干扰值可表示为
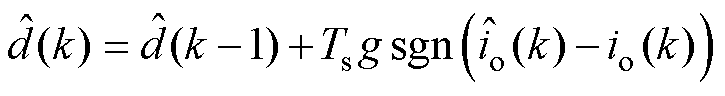 (9)
(9)
取观测器滑模函数为电流观测误差为
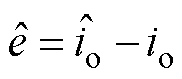 (10)
(10)
可得电流观测状态方程为
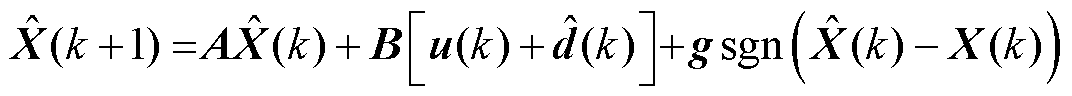 (11)
(11)
当k时刻干扰观测误差足够小时,将式(11)与式(2)相减可得
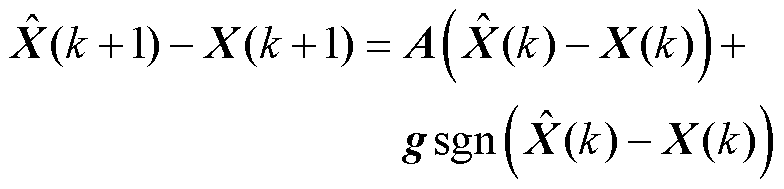 (12)
(12)
在滑模控制过程中,常用饱和函数代替sgn函数以抑制抖振,利用新型饱和函数抑制抖振时,在滑模边界层内存在
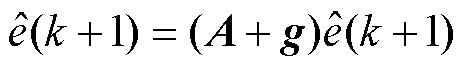 (13)
(13)
若矩阵A+g的所有特征值均在z平面单位圆内,则观测器误差系统渐近稳定,从而在任意初始误差下观测误差最终都将趋向于零。为了保证观测误差在k+1时刻也能收敛到零值,因此可将增益配置为g=-A。当g=-A存在时,若干扰观测器在k时刻有界,则k+1时刻必严格收敛。滑模观测器增益取值将会直接影响收敛速度和抖振大小,当观测器增益过小时,收敛速度将会受到影响;当观测器增益过大时,将引起较大的抖振。在EAST快控电源跟踪电流上升阶段存在一定的电流误差,此时需要较快的收敛速度,而在稳态阶段则需要较小的抖振实现平稳的电流跟踪,为了平衡抖振大小和收敛速度问题,设计变增益观测器结构,使得增益g随着观测电流误差而变化。
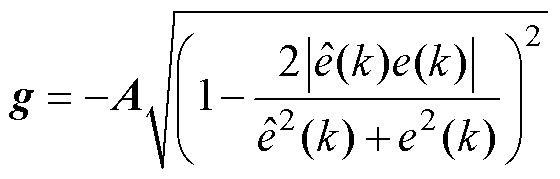 (14)
(14)
设计带有滑模干扰观测器的离散积分滑模控制结构如图4所示,设计的滑模函数表达式如式(3)和式(4)所示,基于以上条件,对滑模控制器的稳定性进行分析。
结合式(6),将实际干扰和观测干扰的误差值表示为
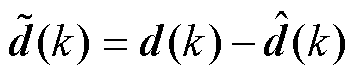 (15)
(15)
联立式(2)、式(4)~式(6)得
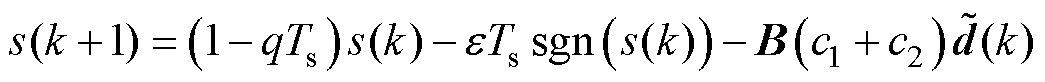 (16)
(16)
基于以上分析可知,干扰观测误差理论上可收敛到零值,假设干扰观测误差有界,令
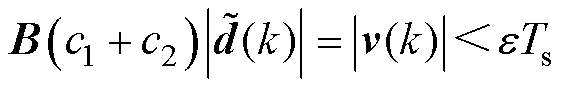 (17)
(17)
式中,v(k)为干扰边界。
将滑模控制分为趋近运动阶段和滑模运动阶段,可知0<1-qTs<1,因此可从以下四方面证明滑模控制器的稳定性。
1)当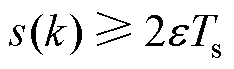 时
时
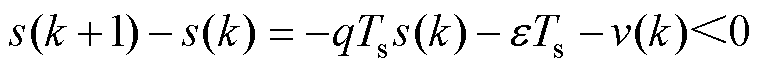 (18)
(18)
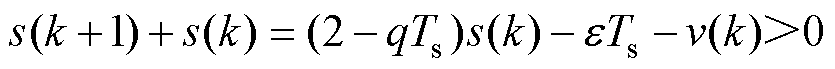 (19)
(19)
式(18)和式(19)相乘可得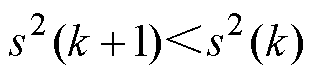 。
。
2)当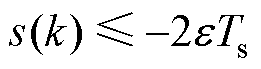 时
时
同理可推导出类似式(18)和式(19)结果,因此同理可得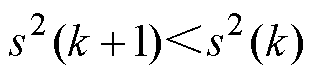 。
。
3)当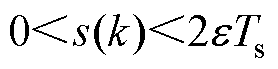 时
时
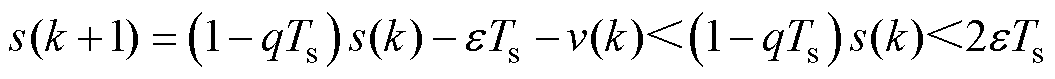 (20)
(20)
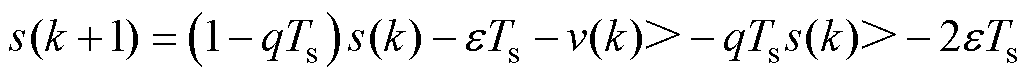 (21)
(21)
联立式(20)和式(21)可得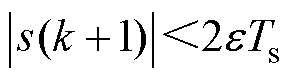 。
。
4)当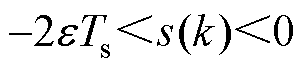 时
时
同理可推导出类似式(20)和式(21)结果,因此同理可得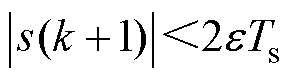 。
。
综合以上证明分析可得以下结论:
(1)当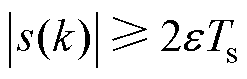 时,有
时,有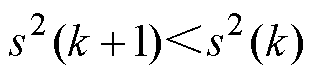 。
。
(2)当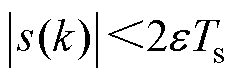 时,有
时,有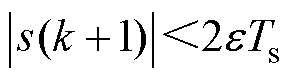 。
。
因此只需要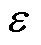 取较小正实数,则可保证
取较小正实数,则可保证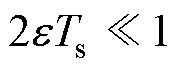 成立,即保证s(k+1)充分收敛。
成立,即保证s(k+1)充分收敛。
在滑模控制过程中,滑模的抖振抑制问题是现在许多学者关注的热点问题。在设计滑模控制器时,经常利用符号函数sgn(s)来实现控制,但是符号函数的不平滑特性使得滑模控制中出现抖振问题。为了实现抖振的抑制,经常采用线性饱和函数来抑制抖振,线性饱和函数表达式为
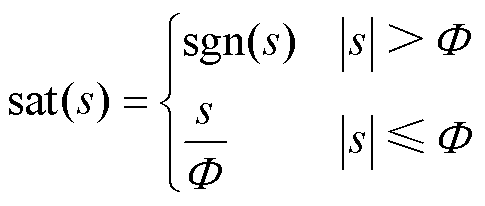 (22)
(22)
式中,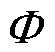 为滑模区域的边界层厚度。
为滑模区域的边界层厚度。
线性饱和函数虽然能够起到一定抑制抖振的效果,但是在s=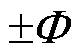 时函数不可微,而且在平滑区间内切换控制律的斜率固定不可调,且在
时函数不可微,而且在平滑区间内切换控制律的斜率固定不可调,且在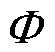 趋近于0的区间内其切换特性与符号函数类似。为了解决可微的问题,文献[8]提出了一种三角平滑饱和函数,其表达式为
趋近于0的区间内其切换特性与符号函数类似。为了解决可微的问题,文献[8]提出了一种三角平滑饱和函数,其表达式为
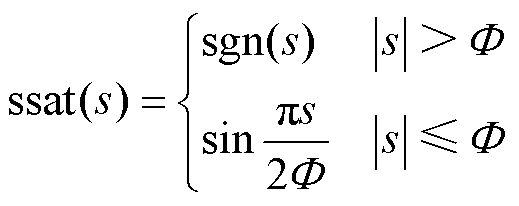 (23)
(23)
三角平滑饱和函数连续可微,但是切换增益有限,且三角函数在数字处理器中计算精度和速度有限。因此,设计一种新型平滑饱和函数为
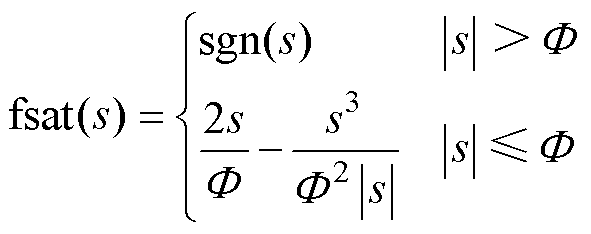 (24)
(24)
对于设计的新型平滑饱和函数fsat(s)有以下特点:①当s=0时,fsat(0)=0,即当系统状态到达滑模面时,切换控制律为0;②当s=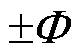 时,
时,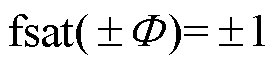 ,函数值能够完全到达[-1, 1],切换控制率能够在最大范围内输出;③fsat(s)在全定义域范围内是连续可微的。在相同平滑区间内,任取边界层厚度
,函数值能够完全到达[-1, 1],切换控制率能够在最大范围内输出;③fsat(s)在全定义域范围内是连续可微的。在相同平滑区间内,任取边界层厚度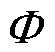 =0.1时,三种饱和函数曲线对比如图5所示。通过对比可知,设计的新型饱和函数在相同平滑区间内切换增益更大,能够更好地抑制抖振。同时,当
=0.1时,三种饱和函数曲线对比如图5所示。通过对比可知,设计的新型饱和函数在相同平滑区间内切换增益更大,能够更好地抑制抖振。同时,当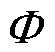 为其他值时,新型饱和函数在相同平滑区间内切换增益更大的特性也成立。
为其他值时,新型饱和函数在相同平滑区间内切换增益更大的特性也成立。
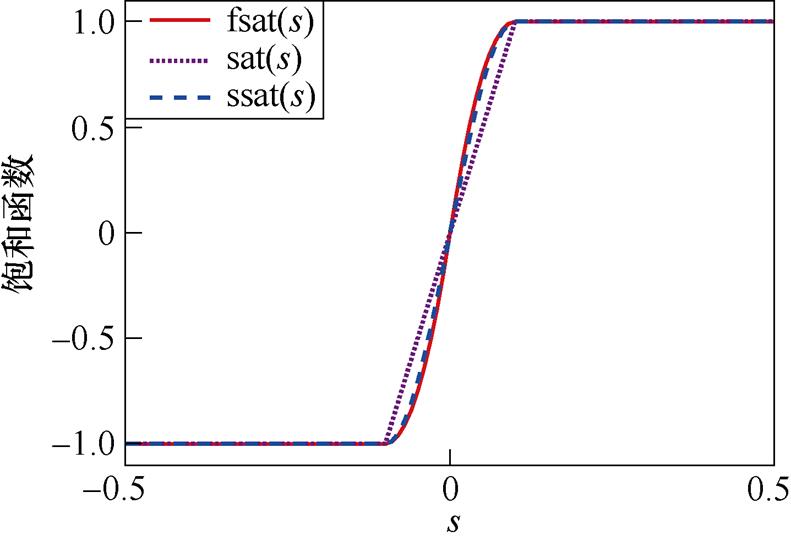
图5 三种饱和函数曲线对比
Fig.5 Comparison of three saturation function curves
收敛速度也是滑模控制器设计的重要指标,收敛速度越快,控制器性能越优良。在滑模控制过程中,系统运动状态分为从任意初始状态经有限时间t到达边界层的趋近运动阶段,以及在边界层内的滑模运动阶段。假设所提的三种饱和函数的切换增益均为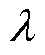 ,三种饱和函数趋近运动阶段经历时间均为
,三种饱和函数趋近运动阶段经历时间均为
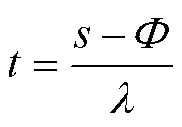 (25)
(25)
在边界层内的滑模运动阶段,线性饱和函数、三角平滑饱和函数以及新型平滑饱和函数趋近律分别为
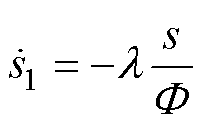 (26)
(26)
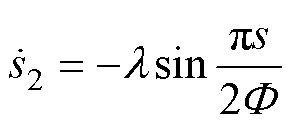 (27)
(27)
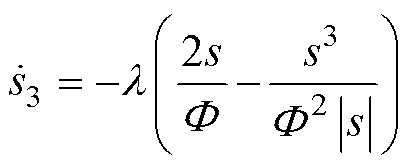 (28)
(28)
在三种函数中,从边界层到边界层内任意一点所需要的滑模运动时间分别为
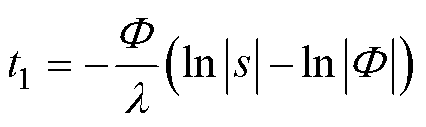 (29)
(29)
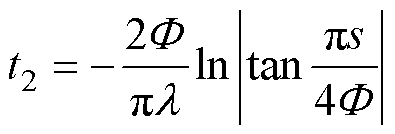 (30)
(30)
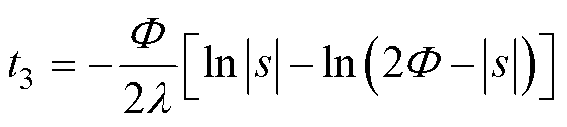 (31)
(31)
通过以上收敛时间分析可知,三种饱和函数在切换增益、边界层厚度及初始点状态相同时,所经历的趋近运动时间t相等,且与切换增益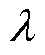 成反比。在滑模运动阶段,三种函数经历的收敛时间不同但是仍与切换增益成反比,因此可以通过增大平滑函数的切换增益来减小系统总收敛时间,进而提高滑模控制器收敛速度。
成反比。在滑模运动阶段,三种函数经历的收敛时间不同但是仍与切换增益成反比,因此可以通过增大平滑函数的切换增益来减小系统总收敛时间,进而提高滑模控制器收敛速度。
结合图5和式(29)~式(31)分析可知,在相同的边界层厚度情况下,提出的新型平滑饱和函数具有更大的函数切换增益。在切换增益相同时,所提出的新型平滑饱和函数具有最小的滑模运动阶段时间。因此当边界层厚度相同时,所提出的新型平滑饱和函数具有最小的收敛时间,对应的滑模控制器具有最快的总收敛速度。将提出的新型平滑饱和函数代替式(7)和式(9)中的符号函数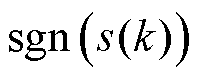 ,即可实现滑模控制器的快速收敛和抖振抑制。
,即可实现滑模控制器的快速收敛和抖振抑制。
为了验证所提带干扰抑制的离散积分滑模控制方法的有效性,在Matlab中搭建两路H桥逆变级联模型,级联H桥输出电压uH=200 V,负载电感为4 mH,开关频率取5 kHz进行移相控制,额定输出电流为10 A/100 Hz的交流方波电流。滑模控制器中有: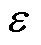 =90,q=800,
=90,q=800,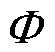 =0.5,c1=1,c2=0.7。
=0.5,c1=1,c2=0.7。
传统滑模控制存在抖振问题,稳态时控制器在滑模面上来回滑动可能会造成电流抖动,使得电流跟踪存在误差。对比传统线性饱和函数sat(s)、三角平滑饱和函数ssat(s)以及本文提出的新型平滑饱和函数fsat(s)下的滑模控制输出电流跟踪误差esat、essat和efsat,稳态下的电流跟踪误差对比如图6所示。提出的新型平滑饱和函数fsat(s)使得稳态电流跟踪误差抖动更小,具有良好的抖振抑制性能。
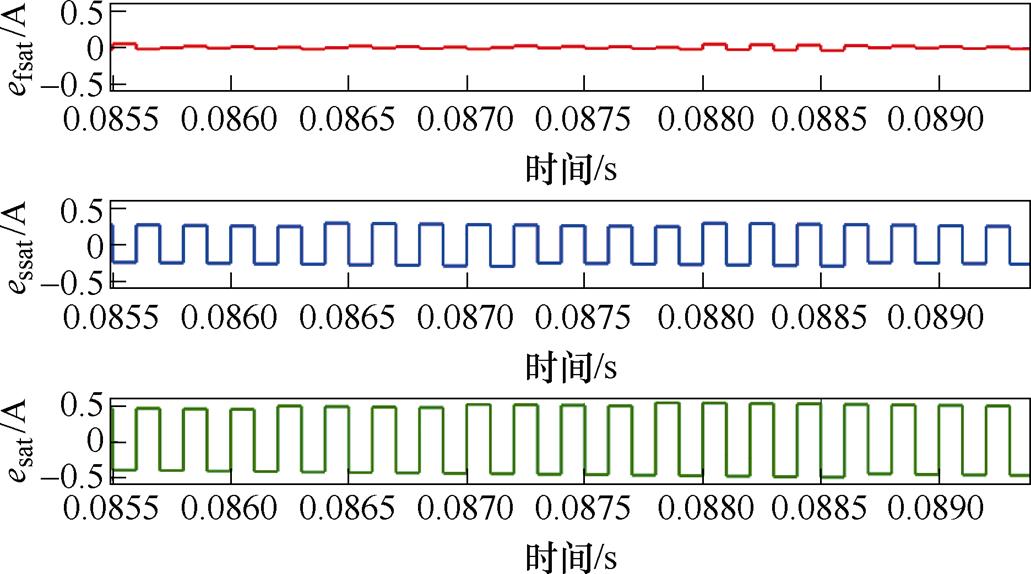
图6 稳态电流跟踪误差对比
Fig.6 Comparison of steady-state current tracking error
为了快速跟踪参考电流,工程上一般给定较大的PI控制参数以保证跟踪速度,甚至产生少量的超调。对比传统PI控制下的输出电流ioPI和所提带干扰抑制的离散积分滑模控制方法下的输出电流iofsat,结果如图7所示,所提控制方法下的输出电流iofsat具有更小的超调和更快的输出响应速度,对参考电流iref的跟踪控制性能更加优良。
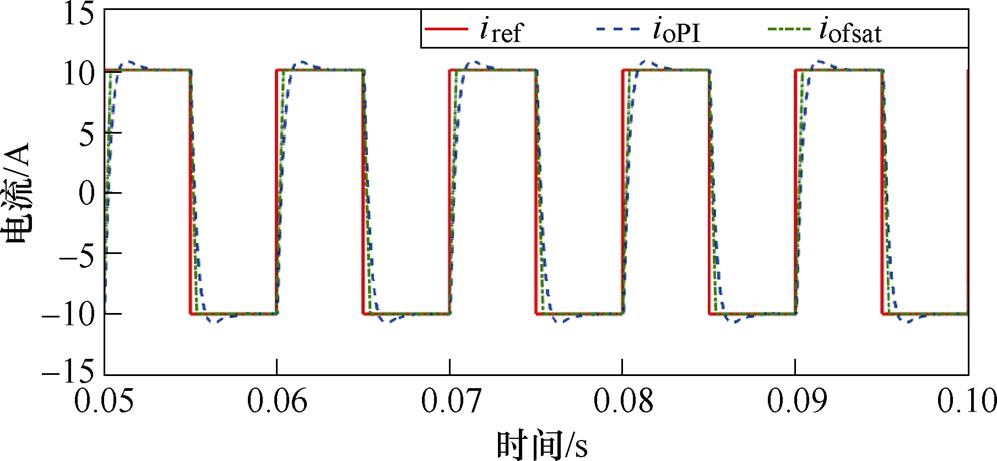
图7 输出电流跟踪性能对比
Fig.7 Comparison of output current tracking performance
为了验证所提控制方法的良好扰动抑制性能,在输出负载端串联幅值为15 V的工频交流电压信号模拟交流互感电动势扰动,存在输出端干扰时两种控制方式下电流对比如图8所示。传统PI控制下的输出电流ioPI存在一定的跟踪电流波动,干扰信号对输出电流呈现周期扰动,对参考电流iref的跟踪控制性能较差。所提控制方法下的输出电流iofsat具有良好的跟踪性能,动态响应和跟踪误差与无扰动状态下基本一致,所提控制方法对扰动实现了抑制。
EAST快控电源电感负载受周围环境影响,存在一定的慢时变波动,为了验证所提控制方法具有良好的适应参数变化性能,进行了负载突变实验验证。在0.103 5 s时将电感负载值由4 mH切换到5 mH,两种控制方法下输出电流对比如图9所示,所提控制方法下的输出电流iofsat仍具有良好的跟踪性能,能够快速且无超调跟踪参考电流iref,负载电感切换前后跟踪性能不受影响,使得负载在一定范围内变化仍具有良好的鲁棒性。传统PI控制下的输出电流ioPI在负载感值为4 mH时存在一定的超调,当负载感值变大时,超调减小但是跟踪响应时间变慢,不能满足EAST快控电源快速跟踪参考电流的需求,控制性能劣于所提的控制方法。
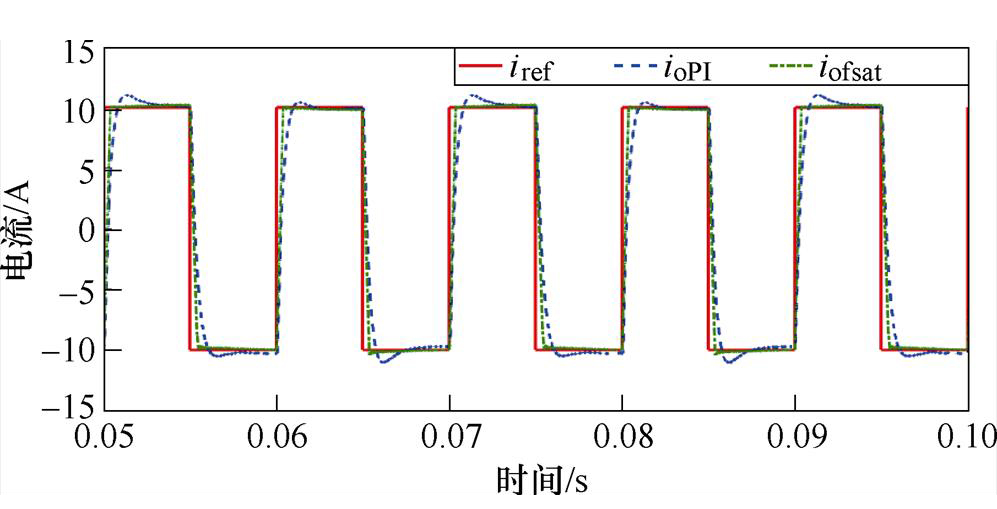
图8 扰动下输出电流跟踪性能对比
Fig.8 Comparison of output current tracking performance under disturbance
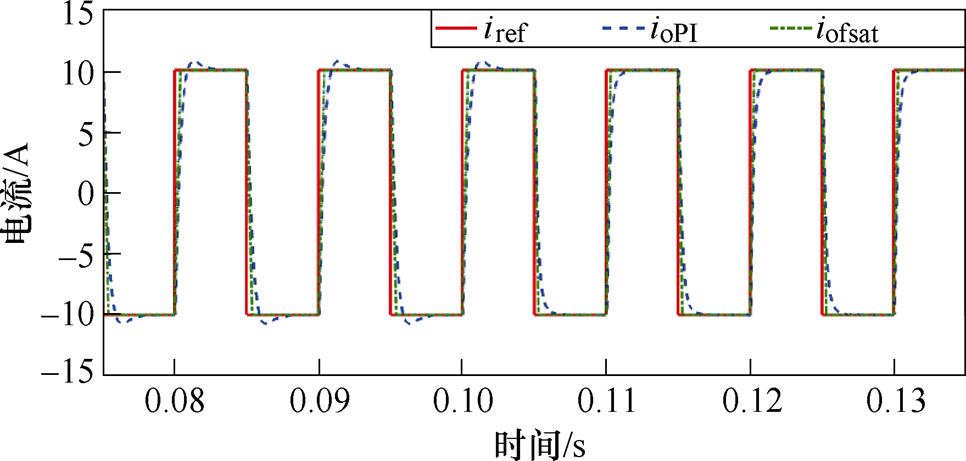
图9 负载突变下输出电流跟踪性能对比
Fig.9 Comparison of output current tracking performance under sudden load changes
为了进一步验证所提控制方法的优越性能,搭建2H桥级联样机,控制器选择TMS32028335数字处理器,直流侧电压为100 V,IGBT开关管型号为2MBI75N-060,电流传感器为1 000 1的LA55-P/ SP50电流传感器,负载电感为4 mH,指令电压Ui= ±4 V,输出额定电流io=±8 A(100 Hz),实验样机如图10所示。
1的LA55-P/ SP50电流传感器,负载电感为4 mH,指令电压Ui= ±4 V,输出额定电流io=±8 A(100 Hz),实验样机如图10所示。
传统线性饱和函数sat(s)、三角平滑饱和函数ssat(s)以及本文提出的新型平滑饱和函数fsat(s)下的滑模控制输出电流稳态归一化跟踪误差esat、essat和efsat对比如图11所示。对比图11所示的三种输出电流稳态归一化跟踪误差,efsat具有最小的抖动,说明对比ssat(s)和sat(s)控制,所提出的fsat(s)使得滑模面的抖振得到了进一步抑制。

图10 实验样机
① —三相隔离变压器 ②—整流桥 ③—滤波电容 ④—IGBT及驱动板 ⑤—参考源 ⑥—DSP控制板 ⑦—光纤通信板 ⑧—辅助电源板 ⑨—交流扰动源 ⑩—负载电感
Fig.10 Experimental prototype
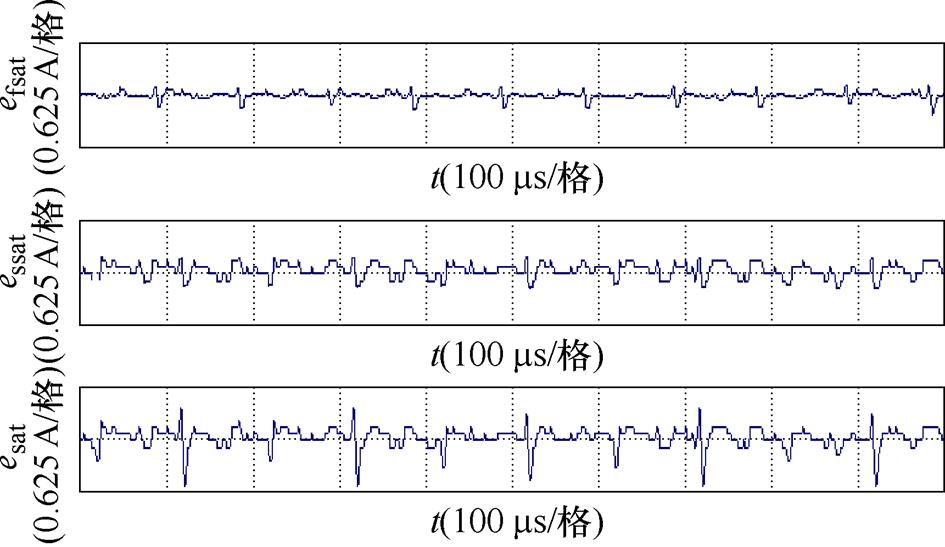
图11 三种饱和函数控制下电流稳态跟踪误差对比
Fig.11 Comparison of current steady-state tracking error under three kinds of saturation function control
在额定负载电感下,PI控制下输出电流波形如图12所示,输出电流io能够稳定跟踪参考信号值。电流跟踪的上升和下降动态响应波形如图13所示,上升过程中产生27.3%超调,整个上升调节时间为2.15 ms,下降过程中产生25.6%超调,整个下降调节时间为2.03 ms。
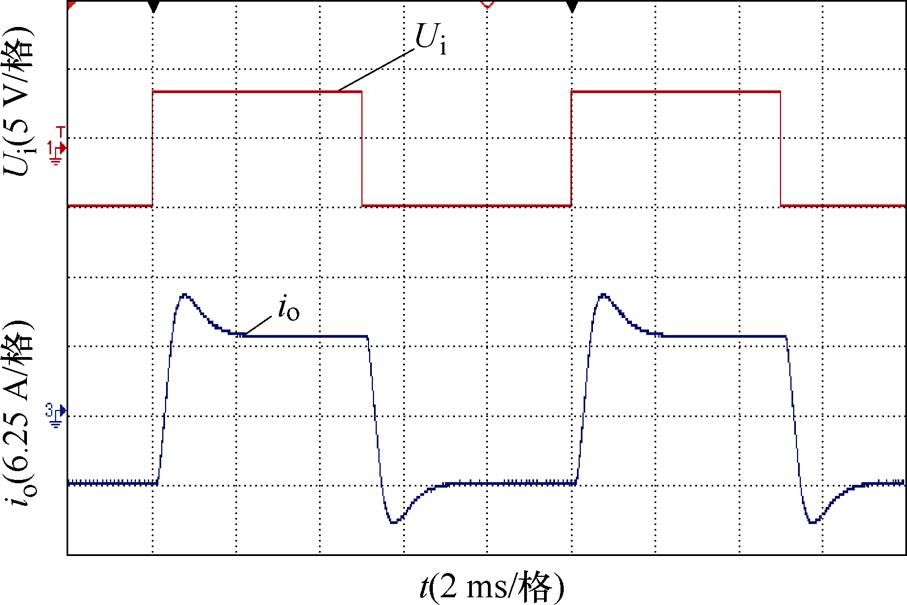
图12 PI控制下输出电流波形
Fig.12 Output current waveforms of PI control
相同工况下,所提控制方法控制输出的电流如图14所示,输出电流io同样能稳定跟踪参考信号值。所提控制方法下电流跟踪的上升和下降动态响应如图15所示,上升过程中产生8.5%的超调,整个上升调节时间为980 ms,下降过程中产生8.5%的超调,整个下降调节时间为910 ms。对比传统PI控制,所提控制方法下输出电流具有更小的超调和更快的动态响应速度。

图13 PI控制下输出电流动态波形
Fig.13 Output current dynamic waveforms of PI control
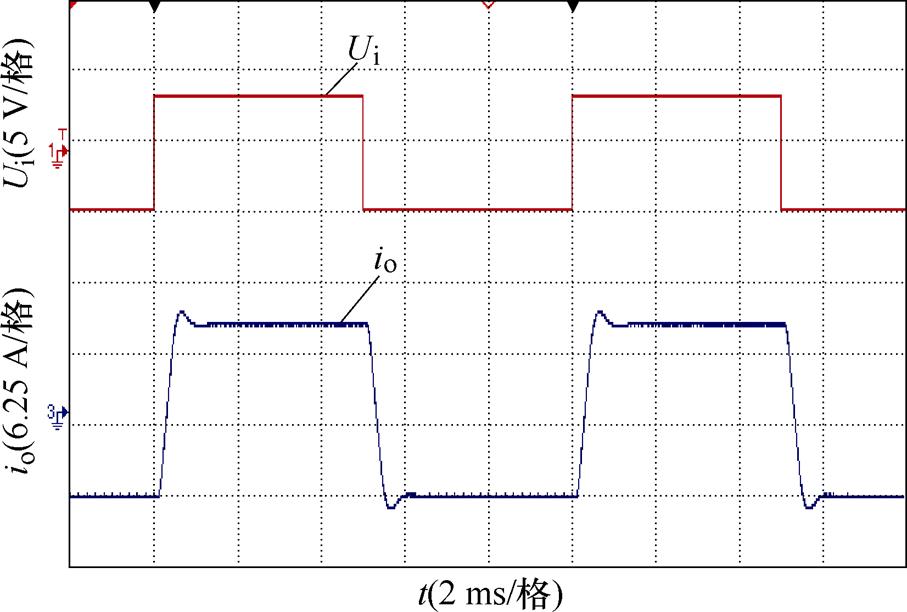
图14 所提方法控制下输出电流波形
Fig.14 Output current waveforms of proposed method
为了对比所提控制方法和传统PI控制方法的干扰抑制能力,在4 mH电感负载侧串联交流可编程电源,输出有效值为10 V的工频电压模拟线圈上的互感干扰电动势。在存在外部互感电动势干扰情况下,传统PI控制下输出电流波形如图16所示,与仿真类似,输出电流呈不规则波动,电流跟踪性能较差,受负载侧干扰影响较大。所提方法控制下输出电流波形如图17所示,输出电流跟踪性能良好,产生的超调和动态响应时间与只由额定负载时类似,所提控制方法具有很好的干扰抑制性能。
为了验证所提控制方法的鲁棒性,进行负载突变实验,在稳态跟踪时将负载由3 mH突变为4 mH,负载突变时PI控制下和所提方法控制下输出电流波形如图18和图19所示。由于输出侧电感值有限,且存在一定的等效电阻,因此在电感值突变点处电流值发生了较小的突变,且负载增大后超调均减小。负载突变时,PI控制下电流下降约2 A,经过1.3 ms后恢复到稳态,所提方法控制下电流下降约1.5 A,经过1 ms后恢复到稳态。在负载突变时,对比PI控制所提控制方法,具有更小的电流突变和更小的恢复时间,以及良好的鲁棒性。
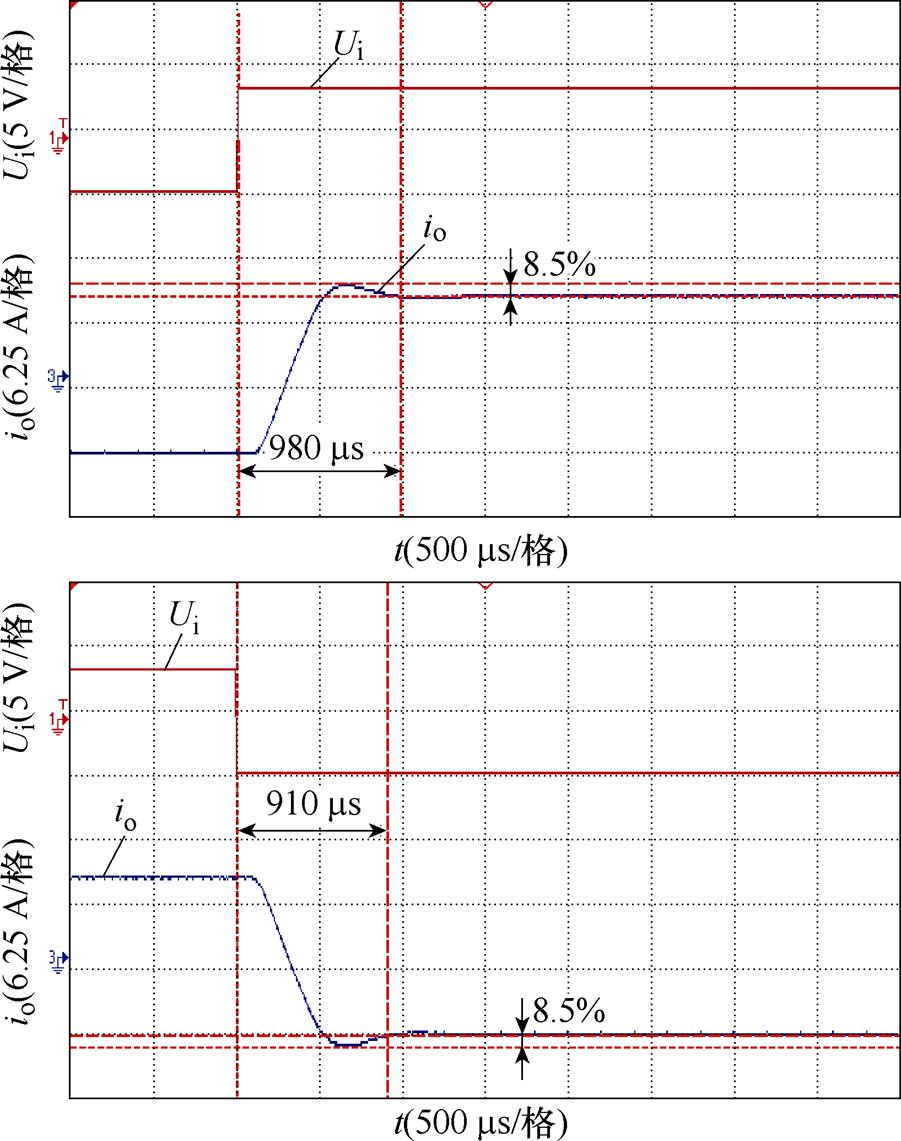
图15 所提方法控制下输出电流动态波形
Fig.15 Output current dynamic waveforms of proposed method
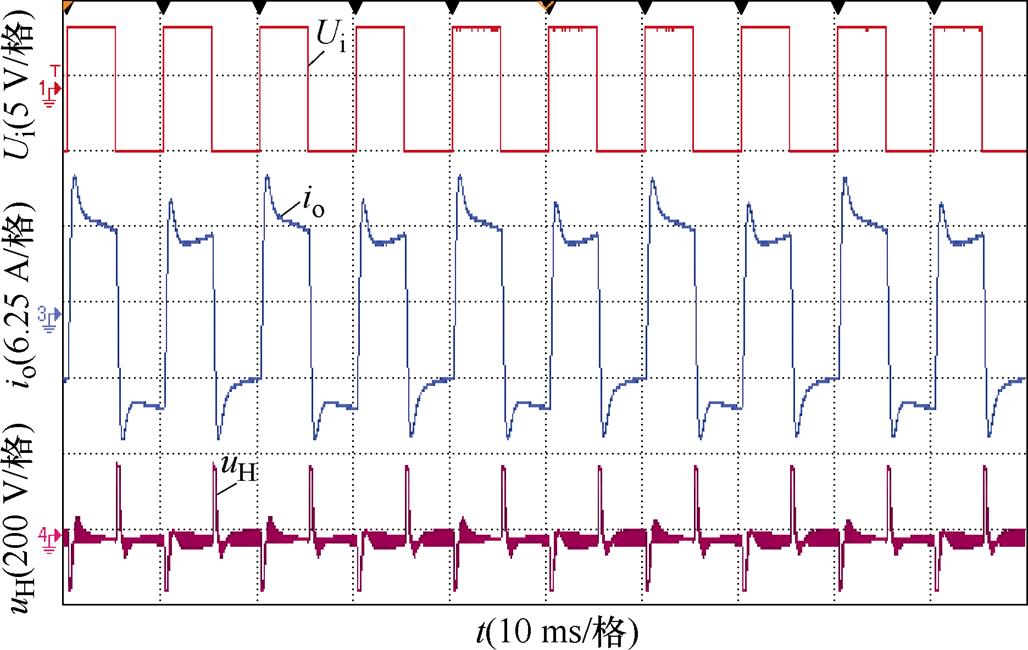
图16 输出扰动时PI控制下输出电流波形
Fig.16 Output current waveforms of PI control during output disturbance
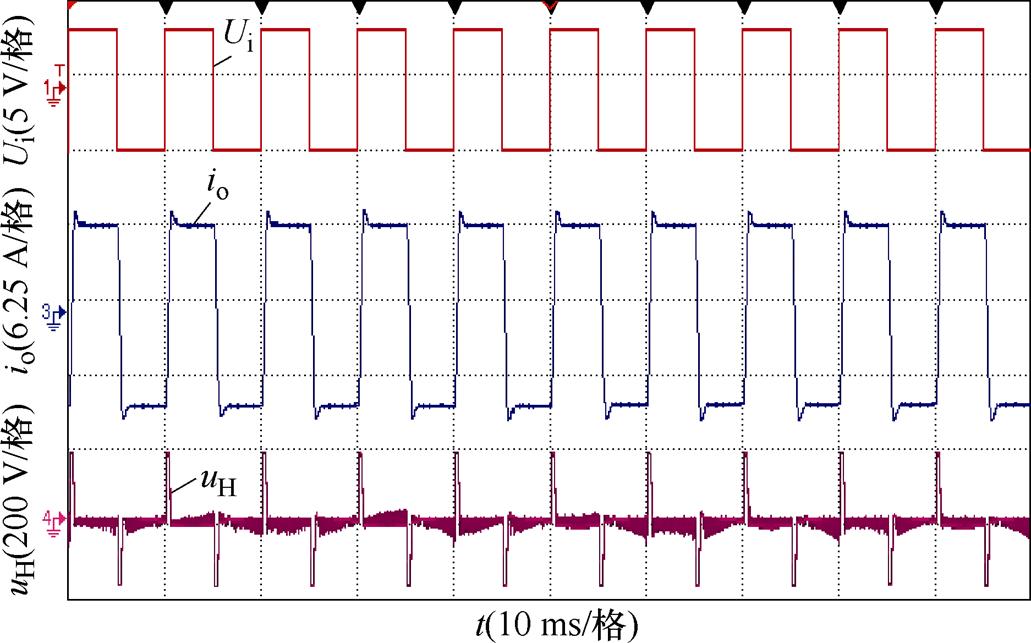
图17 输出扰动时所提方法控制下输出电流波形
Fig.17 Output current waveforms of proposed method control during output disturbance
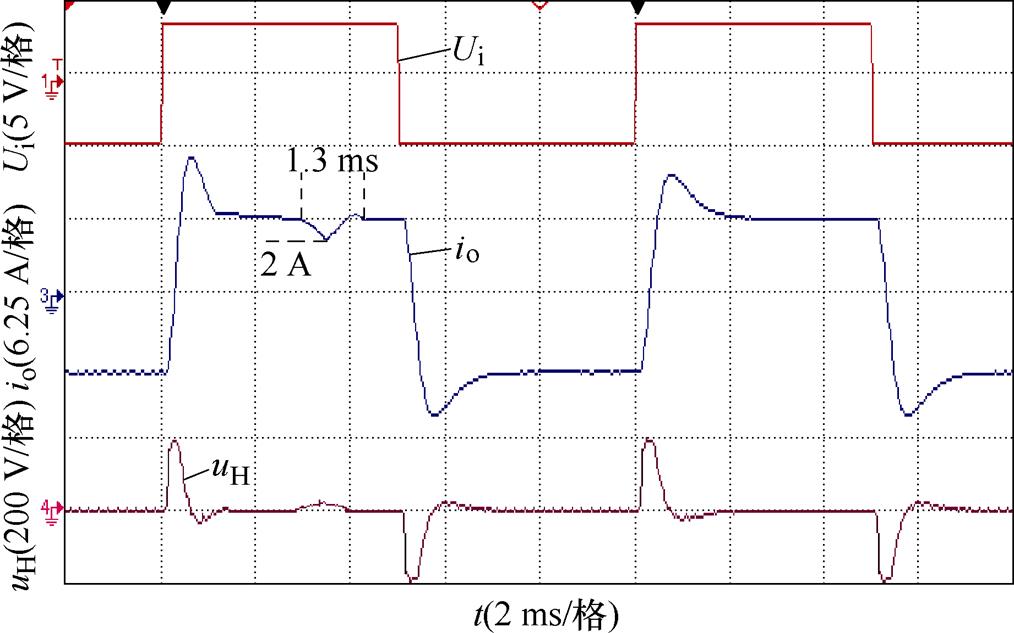
图18 负载变化时PI控制输出电流跟踪性能
Fig.18 Output current tracking performance of PI control when load changes
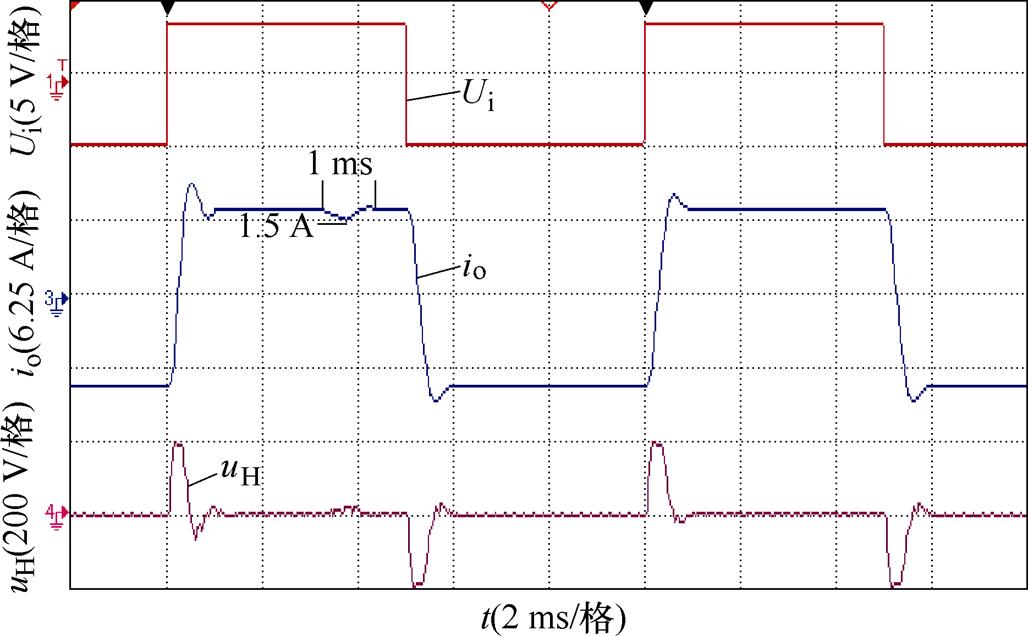
图19 负载变化时所提方法输出电流跟踪性能
Fig.19 Output current tracking performance of proposed method with load changes
为了解决EAST快控电源中传统PI控制存在的抗干扰能力不足、鲁棒性较差的问题,提出了一种带干扰抑制的离散积分滑模控制策略。考虑负载侧的集总干扰,设计了离散积分滑模控制器和滑模干扰观测器实现干扰项的前馈补偿,为了进一步抑制抖振和加速收敛,设计了新型平滑饱和函数和增益自适应滑模干扰观测器。仿真和实验验证了所提控制方法具有更加优良的输出电流跟踪性能,对比传统PI控制输出电流超调更小情况下动态响应更快,在EAST快控电源负载侧存在互感扰动电动势时具有良好的扰动抑制特性,负载出现波动时电流跟踪性能更加优良,具有较强的鲁棒性。
参考文献
[1] Ji Xin, Song Yangtian, Shen Ge, et al. Engineering design of EAST passive stabilization loop[J]. Journal of Fusion Energy, 2015, 34: 504-508.
[2] 许水清, 黄文展, 何怡刚, 等. 基于自适应滑模观测器的中点钳位型三电平并网逆变器开路故障诊断[J]. 电工技术学报, 2023, 38(4): 1010-1022.
Xu Shuiqing, Huang Wenzhan, He Yigang, et al. Open-circuit fault diagnosis method of neutral point clamped three-level grid-connected inverter based on adaptive sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1010-1022.
[3] 方馨, 王丽梅, 张康. 基于扰动观测器的永磁直线电机高阶非奇异快速终端滑模控制[J]. 电工技术学报, 2023, 38(2): 409-421.
Fang Xin, Wang Limei, Zhang Kang. High order non- singular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 409-421.
[4] 郭昕, 黄守道, 彭昱, 等. 基于改进型双幂次趋近律与全局快速终端滑模观测器的IPMSM调速系统滑模控制[J]. 电工技术学报, 2023, 38(1): 190-203.
Guo Xin, Huang Shoudao, Peng Yu, et al. Sliding mode control of IPMSM speed regulation system based on an improved double power reaching law and global fast terminal sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 190-203.
[5] 曹学谦, 葛琼璇, 朱进权, 等. 基于积分滑模的高速磁悬浮列车谐波电流抑制策略[J]. 电工技术学报, 2022, 37(22): 5817-5825.
Cao Xueqian, Ge Qiongxuan, Zhu Jinquan, et al. Harmonic current suppression strategy for high-speed maglev train based on integral sliding mode[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5817-5825.
[6] 杨朋威, 康祎龙, 苗世洪, 等. V/v牵引供电系统中铁路功率调节器的改进滑模控制策略[J]. 高电压技术, 2020, 46(6): 2218-2229.
Yang Pengwei, Kang Yilong, Miao Shihong, et al. Improved sliding mode control strategy for railway static power conditioner in V/v traction power supply system[J]. High Voltage Engineering, 2020, 46(6): 2218-2229.
[7] Zheng Changming, Tomislav D, Zhang Jiasheng, et al. Composite robust quasi-sliding mode control of DC-DC Buck converter with constant power loads[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 1455-1464.
[8] 方馨, 王丽梅, 张康. H型平台直驱伺服系统离散积分滑模平滑控制[J]. 电机与控制学报, 2022, 26(6): 101-111.
Fang Xin, Wang Limei, Zhang Kang. Discrete integral sliding mode smoothing control of H-type platform direct drive servo system[J]. Electric Machines and Control, 2022, 26(6): 101-111.
[9] Wang Zuo, Li Shihua, Li Qi. Discrete-time fast terminal sliding mode control design for DC-DC Buck converters with mismatched disturbances[J]. IEEE Transactions on Industrial Informatics, 2020, 16(2): 1204-1213.
[10] 侯世玺, 储云迪, 陈晨. 基于模糊神经网络的有源电力滤波器全局滑模控制[J]. 控制与决策, 2020, 35(10): 2330-2335.
Hou Shixi, Chu Yundi, Chen Chen. Fuzzy neural network based global sliding mode control for active power filter[J]. Control and Decision, 2020, 35(10): 2330-2335.
[11] 雷城, 蓝益鹏, 徐泽来, 等. 一种新型复合滑模趋近律设计与分析[J]. 控制与决策, 2023, 38(2): 435- 440.
Lei Cheng, Lan Yipeng, Xu Zelai, et al. Design and analysis of a new compound sliding mode reaching law[J]. Control and Decision, 2023, 38(2): 435-440.
[12] 赵书强, 邵冰冰, 高本锋, 等. 基于组合趋近律的VSC-HVDC滑模电流控制设计和稳定性分析[J]. 高电压技术, 2019, 45(11): 3603-3611.
Zhao Shuqiang, Shao Bingbing, Gao Benfeng, et al. Sliding mode current control design and stability analysis of VSC-HVDC based on combinatorial reaching law[J]. High Voltage Engineering, 2019, 45(11): 3603-3611.
[13] 谷志锋, 孙晓云, 葛孟超, 等. 直接转矩Super- Twisting滑模异步发电控制[J]. 高电压技术, 2020, 46(8): 2760-2768.
Gu Zhifeng, Sun Xiaoyun, Ge Mengchao, et al. Super-twisting sliding-mode direct-torque control for asynchronous generation[J]. High Voltage Engineering, 2020, 46(8): 2760-2768.
[14] 谭超, 韩国鹏, 戴朝华, 等. 基于改进滑模控制的PEMFC热管理控制方法[J]. 中国电机工程学报, 2022, 42(16): 5899-5909.
Tan Chao, Han Guopeng, Dai Chaohua, et al. Thermal management control method of PEMFC based on improved sliding mode control[J]. Proceedings of the CSEE, 2022, 42(16): 5899-5909.
[15] 付东学, 赵希梅. 基于径向基函数神经网络的永磁直线同步电机反推终端滑模控制[J]. 电工技术学报, 2020, 35(12): 2545-2553.
Fu Dongxue, Zhao Ximei. Backstepping terminal sliding mode control based on radial basis function neural network for permanent magnet linear syn- chronous motor[J]. Transactions of China Electro- technical Society, 2020, 35(12): 2545-2553.
[16] Xu Bo, Zhang Lei, Ji Wei. Improved non-singular fast terminal sliding mode control with disturbance observer for PMSM drives[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2753-2762.
[17] 孙恺英, 李冬辉, 姚乐乐, 等. 基于新型超螺旋滑模自适应观测器的永磁同步电机转速估计策略[J].高电压技术, 2020, 46(11): 3771-3781.
Sun Kaiying, Li Donghui, Yao Lele, et al. Speed estimation algorithm for permanent magnet syn- chronous motor based on novel super-twisting adaptive observer[J]. High Voltage Engineering, 2020, 46(11): 3771-3781.
[18] Jesus L F, Jose A J, Arturo H M, et al. Sliding mode control based on linear extended state observer for DC-to-DC Buck-Boost power converter system with mismatched disturbances[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 2753-2762.
[19] 靳东松, 刘凌. 永磁同步电机的改进无差拍预测抗扰前馈控制[J]. 西安交通大学学报, 2022, 56(7): 38-46.
Jin Dongsong, Liu Ling. Improved control strategy combining deadbeat predictive current control with disturbance rejection feedforward compensation for permanent magnet synchronous motor[J]. Journal of Xi’an Jiaotong University, 2022, 56(7): 38-46.
[20] 梅三冠, 卢闻州, 樊启高, 等. 基于滑模观测器误差补偿的永磁同步电机无位置传感器控制策略[J].电工技术学报, 2023, 38(2): 398-408.
Mei Sanguan, Lu Wenzhou, Fan Qigao, et al. Sensorless control strategy of permanent magnet synchronous motor based on error compensation estimated by sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 398- 408.
[21] Liu Jianxing, Shen Xiaoning, Abraham M A, et al. Sliding mode control of grid connected neutral- point-clamped converters via high-gain observer[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 4010-4021.
[22] 王天鹤, 赵希梅, 金鸿雁. 基于递归径向基神经网络的永磁直线同步电机智能二阶滑模控制[J]. 电工技术学报, 2021, 36(6): 1229-1237.
Wang Tianhe, Zhao Ximei, Jin Hongyan. Intelligent second-order sliding mode control based on recurrent radial basis function neural network for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1229- 1237.
[23] 禹聪, 康尔良. 永磁同步电机模糊滑模速度控制器设计[J]. 电机与控制学报, 2022, 26(7): 98-104.
Yu Cong, Kang Erliang. Design of fuzzy sliding mode speed controller for permanent magnet synchronous motor[J]. Electric Machines and Control, 2022, 26(7): 98-104.
[24] 魏惠芳, 王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J]. 电工技术学报, 2022, 37(4): 861-869.
Wei Huifang, Wang Limei. Adaptive fuzzy neural network time-varying sliding mode control for per- manent magnet linear synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 26(7): 861-869.
Abstract The primary performance of the fast control power supply for the experimental advanced superconducting Tokamak (EAST) is to quickly track the reference signal, realize the excitation of the load coil, and feedback control the vertical displacement of the plasma. The load coil of the EAST fast control power supply is affected by the internal components and the plasma in the vacuum. The coil inductance will fluctuate slowly in a small range, and there will be mutual inductance electromotive force interference on the coil. The traditional proportional-integral (PI) control has shortcomings in the current tracking control process. Sliding mode control has been widely used due to its advantages of simple control and strong robustness.
To realize disturbance suppression and cope with load fluctuation, a discrete integral sliding mode control method with disturbance suppression is proposed based on the system state equation of the EAST fast control power supply. The control disturbance caused by inductance fluctuation and mutual inductance electromotive force on the load side is equivalent to lumped disturbance. The observation of lumped disturbance is realized using a sliding mode disturbance observer. In order to compensate for the lumped disturbance on the load side, a discrete integral sliding mode controller and a sliding mode disturbance observer are combined to perform feedforward compensation control. A variable gain observer structure is designed based on the observed current error and the tracking current error to balance the chattering magnitude and convergence speed in the sliding mode control process. Thus, the gain is adaptively adjusted with the observed current error. According to the observer error stability conditions, the adaptive adjustment range of the observer gain is determined. The stability of the designed sliding mode controller is analyzed to ensure sufficient convergence of the sliding mode controller. A novel smooth saturation function is designed to address insufficient chattering suppression of traditional symbolic and linear saturation functions in sliding mode control. By analyzing the gain characteristics and convergence time characteristics of different saturation functions, the designed new smooth saturation function with continuous differentiability in the full definition domain and great switching gain is demonstrated to provide a faster overall convergence rate. Combined with a gain adaptive disturbance observer, the proposed new smooth saturation function can achieve rapid convergence and further chattering suppression of the control system.
Simulation and experimental results show that the proposed control method has better current tracking characteristics and faster dynamic response than traditional PI control under small output current overshoot. It has outstanding disturbance rejection performance, current tracking performance, and strong robustness. As a result, accurate excitation of the coil inductance can be achieved to ensure vertical displacement closed-loop feedback control of the plasma, even considering load side disturbance.
keywords:Experimental advanced superconducting Tokamak (EAST) fast control power supply, discrete integral, sliding mode control, sliding mode disturbance, observer feedforward compensation
DOI: 10.19595/j.cnki.1000-6753.tces.230275
中图分类号:TM91
国家自然科学基金区域创新发展联合基金资助项目(U22A20225)。
收稿日期 2023-03-12
改稿日期 2023-03-31
黄海宏 男,1973年生,教授,博士生导师,研究方向为新型大功率变流技术与电力电子技术等。E-mail: hhaihong741@ 126.com
陈 昭 男,1996年生,博士研究生,研究方向为电能变换技术等。E-mail: chenzhao_0202@163.com(通信作者)
(编辑 陈 诚)