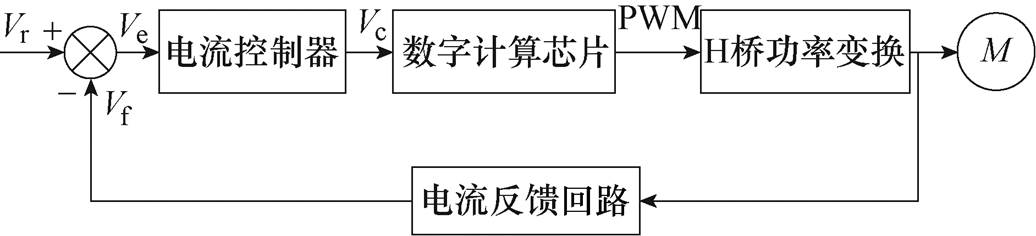
图1 本文中提及的开关功率放大器
Fig.1 Switch mode power amplifier mentioned in this paper
摘要 高频开关功率放大器具有高功率、低纹波、高响应的优点，是高加速、高精度定位系统的核心部件。为了解决高频PWM中开关频率与占空比分辨率的矛盾，该文分析调制中噪声整形的基本原理，采用误差反馈结构提取PWM量化噪声进行数字整形，阐述噪声整形滤波器设计约束条件。提出通过逆全极点无限脉冲响应（IIR）滤波器获得有限脉冲响应（FIR）噪声整形滤波器的简明设计方法，仿真及实验表明，该文提出的方法可利用低阶FIR整形滤波器获得平坦的通带和高整形衰减。在不足9位的PWM中，4阶的FIR噪声整形滤波器能够恢复调制信号在10 kHz频段内约40 dB的信噪比损失。
关键词：开关功率放大器 高频PWM 噪声整形 全极点滤波器 信噪比
以半导体制造设备为代表的超精密装备需要纳米/亚纳米级精度定位，其作动器要求超高信噪比功率变换系统以避免产生扰动力影响定位精度[1]，该信噪比指标要求每五年提升约20 dB[2]。AB类线性功率变换的电流噪声低且带宽高，但难以满足高加速运动的大功率要求。高频开关功率变换[3-4]能够在大功率下实现较低的输出电压和电流失真，C. Brecher[5]等验证了其和线性功放具有相近的电机定位抖动控制效果，并且高频开关有利于提高运动控制带宽[6-9]、简化输出滤波器设计[10-11]。
由于数字芯片基频有限，高开关频率在调制过程中无法同时实现高分辨率。如基频168 MHz的STM32F4，进行200 kHz的脉冲宽度调制（Pulse Width Modulation, PWM）时，占空比有效位数不足9位，估算其信噪比（Signal-to-Noise Ratio, SNR）不足57 dB[12]。为解决PWM高开关频率和高分辨率的矛盾，采用可配置延迟线的PWM发生器能够同时完成高频和高分辨率调制[13-14]，或者是采用高速数字序列化器，能够实现GHz的PWM计数频率[15]，但这类具有高基频的系统需要更高的运维费用。
基于过采样的噪声整形Delta-Sigma（S-D）调制方法，通过改造采样量化器的结构，提升采样速度至奈奎斯特频率的8～512倍，能够实现20位以上的分辨率，目前已在数模转换器（Digital-to- Analog Converter, DAC）和模数转换器（Analog-to- Digita Converter, ADC）中获得广泛的应用[16-18]，为实现高频高信噪比的PWM提供了新思路[13]。M. Norris[19]等对784 kHz、4位PWM器进行噪声整形，实现了超过44 dB的噪声衰减。Z. Lukic[20]等利用S-D 调制实现了10位分辨率和大于10 MHz的开关频率。M. Mauerer[12]采用高达11阶的噪声整形滤波器将100 kHz、9位的PWM信噪比提高了30 dB。噪声整形滤波器是增强高频PWM信噪比的关键，在设计研究中最早通过逼近心理声学曲线[21]，后来有限脉冲响应（Finite Impulse Response, FIR）和无限脉冲响应（Infinite Impulse Response, IIR）噪声整形滤波器成为主流。R. Schreier[18]等提供了一种IIR形式的噪声滤波器设计工具，根据滤波器阶数、过采样率和稳定性定制噪声整形传函。M. Yagyu和M. Nagahara等[22-24]根据范数条件，以最小二乘法（Least Square Method, LSM）和线性矩阵不等式（Linear Matrix Inequality, LMI）的混合方法设计FIR滤波器，实现通带内最大波纹最小化。M. R. Tariq[25-27]等同样基于整形带内量化噪声的H2、H∞范数，获得IIR和FIR形式的噪声整形滤波器设计和优化方法。基于数字滤波器的噪声整形，易于部署在各种数字计算系统中。IIR噪声整形滤波器在低阶时具有较大的截止斜率，但通带波纹大，且易引起量化和反馈的不稳定。FIR具有自身稳定的特征，计算占用少，具有广泛应用的潜力[24]。现有基于H2、H∞范数的LMI等设计方法，设计原理复杂。虽然有利于实现FIR整形滤波器的高阶设计，但不利于高频应用。而低阶设计中难以实现通带波纹控制保障整形衰减。
为了在开关功率放大器中实现高频率和高信噪比的PWM，本文指出了高频调制和高信噪比的共融困难在于调制中的量化噪声。在量化噪声建模的基础上，采用误差反馈结构，区分数字PWM过程中的有效信号和量化噪声，实现有效信号传递和量化噪声数字滤波处理的分化。在噪声整形滤波器的设计上，将整形原理和滤波器稳定性转化为整形滤波器系数固定、最小相位特征和高频增益的约束，提出了逆全极点IIR滤波器的整形滤波器设计方法，在设计约束下简化了设计流程。经过仿真和实验对比，该方法较于其他方法减小了整形带波纹，改善了整形衰减；而且低阶的设计有利于高频调制，减少计算负担。
图1所示的开关功率变换系统能够大幅提高电机出力实现高加速运动，主要结构包括电流控制器、数字计算芯片、H桥功率变换、电流反馈回路。开关变换相比于线性变换往往保真度不高，但提高开关频率能够降低失真。
图1 本文中提及的开关功率放大器
Fig.1 Switch mode power amplifier mentioned in this paper
为提高高频开关下的电流控制能力，本文采用模拟电路搭建电流控制器，电流参考信号Vr和电流反馈信号Vf通过差分运算后得到电流偏差Ve，Ve通过模拟电流控制器输出调节信号Vc。模拟信号Vc由ADC转化为高位数字信号，再换算为低位的PWM参考信号，如图2所示。H桥功率变换电路根据PWM信号调节输入到电机两端的电压，电机产生的电流经霍尔电流传感器检测，形成反馈信号Vf，整个驱动器构成了一个电流闭环控制系统。
图2 常规的数字PWM过程
Fig.2 Typical process for digital PWM
由于模数转换并不直接采样电流信号，数字系统无复杂的控制运算，只需完成控制信号采样，更新PWM并监控驱动器工作温度、输入输出状态，其主要信号处理流程如图2所示。ADC在第n次数模转换后产生M位的高位数字信号x[n]，并再量化为低位N位的PWM参考信号y[n]，由参考信号与数字载波产生比较，实现PWM的占空比更新。采用式（1）可以初步估算数字信号的信噪比，其中nbits为数字信号位数。
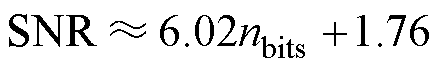（1）
从式（1）中可以看出，提高ADC位数可以直接提高数字信号x[n]的信噪比。在PWM过程中，PWM参考信号y[n]主要取决于数字计数主频率TCLK和PWM周期TPWM，数字PWM如图3所示。数字芯片以TCLK的主频计数，其中最大计数值TOP由主频TCLK和PWM周期TPWM决定，即
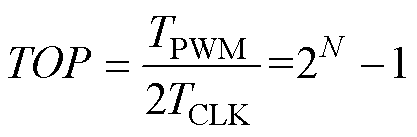（2）
式中，N为最大计数值的有效位数。
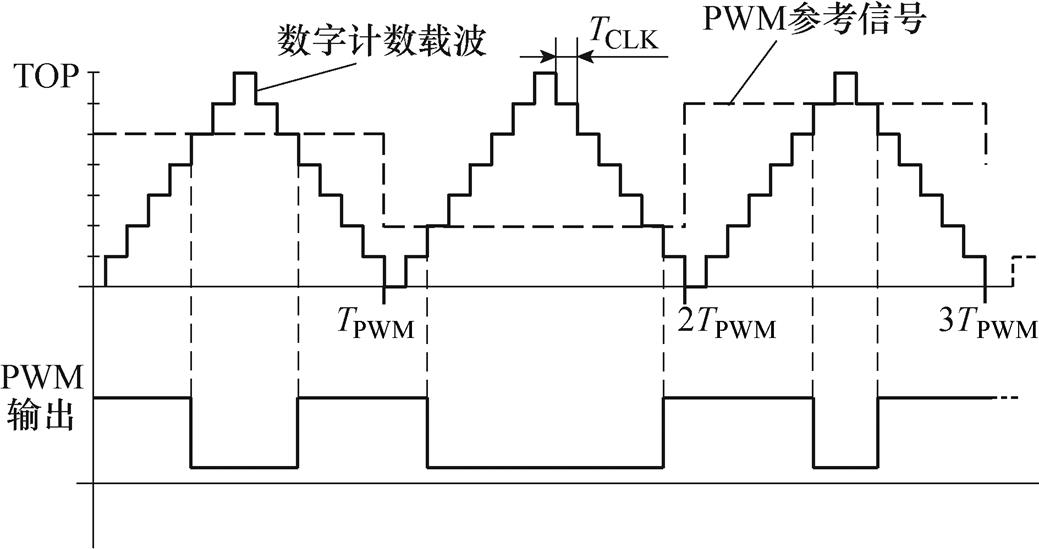
图3 数字PWM
Fig.3 Digital PWM
根据式（2），采用基频168 MHz的STM32F4，在200 kHz的数字PWM中，其参考信号最大计数值为420，有效位数不足9位，估算其信噪比不足57 dB。如果通过提高有效位数至12位来提高输出信噪比，则数字芯片主频需要高达1.6 GHz，而目前数字芯片基频普遍低于500 MHz，难以同时实现高分辨率和高频率的PWM。
在图2的数字信号处理过程中，第二次信号量化过程是导致信噪比降低的主要原因。模数量化有效抑制模拟噪声但引入了量化误差eq，增大模数转换器位数或者过采样方法能够降低该误差。而经由模数转换后的高位数字信号被重新量化为N位的PWM参考信号，引入了再量化误差ereq，该误差同样没有实质噪声源，本质上是数字整型计算时被舍弃的小数数值，这使得数字信号产生了极大的信噪比损失，是本文噪声整形的主要对象。
对于量化噪声ereq，假设其是一个独立于输入序列x[n]的白色噪声序列，在[-0.5, 0.5]中均匀分布。可知量化噪声均值为0，其方差（功率）为
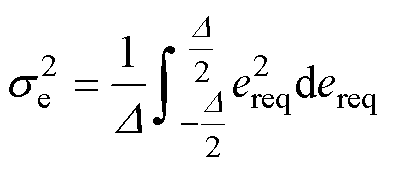（3）
式中，
为量化步长或最小量化电平，=2E/TOP，E为信号幅度，TOP为量化级数。
其自相关函数为
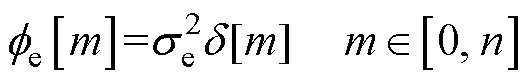（4）
根据维纳辛钦定理，平稳随机过程的功率谱密度为其自相关函数的傅里叶变换。可知量化噪声的功率谱密度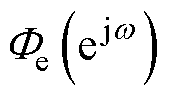
可经由其信号自相关函数
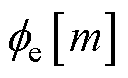求取，m为序列间隔。因此利用离散时间傅里叶变换计算出噪声的傅里叶域功率谱密度为
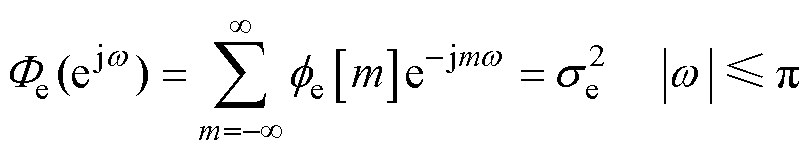（5）
式中，w 为角频率。
针对在频域范围内功率谱均匀分布的量化噪声，过采样引起的噪声整形可以降低其在目标频段内的分布。在PWM参考信号的功率频谱中，其理想成分如图4所示，主要有频率为f的期望信号Sf，以及量化噪声信号Sn，其中噪声信号不计入期望信号的基频及其整数次谐波Skf，以满足噪声与输入不相关的假设。在PWM参考信号的功率确定时，通过对量化噪声进行整形，将低频的量化噪声搬移至高频段，减小整形频带内较高的噪声以增加信噪比，而高频量化噪声可采用低通滤波等方法消除。
由于量化噪声是一种基于量化结果的假设噪声，并没有实质的噪声源。为此增加反馈回路如图5所示，对比量化前后的信号以复现量化误差，进而分化有效信号和量化噪声的信号通径。
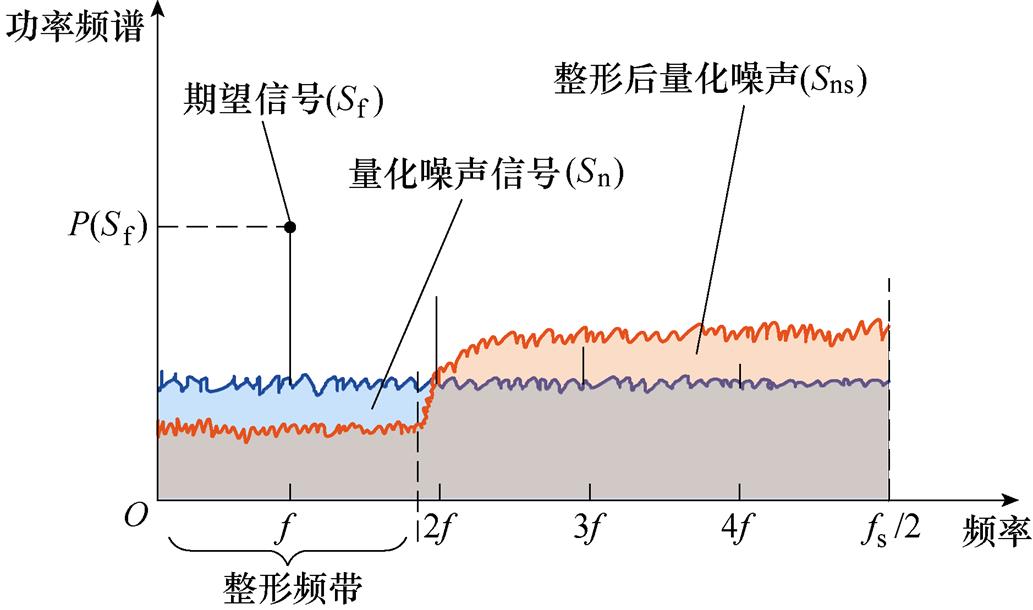
图4 PWM参考信号的功率频谱
Fig.4 The power spectrum of the PWM reference
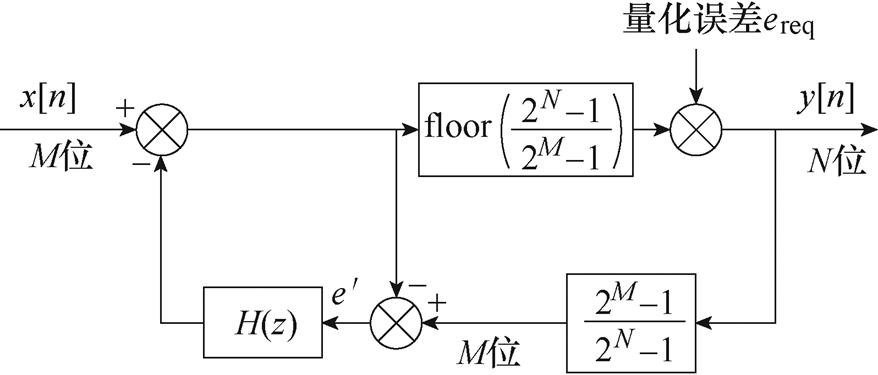
图5 量化误差反馈结构
Fig.5 The quantization error feedback struture
图5中，输入序列x[n]经由直接量化计算产生整型类型的结果y[n]，因此，在圆整过程中产生了数据损失，即量化误差ereq。将输出序列y[n]反量化为M位的数字信号后与x[n]作差，产生的误差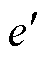
即为量化误差ereq的复现。据此经由反馈通道上的滤波函数H(z)处理后与原信号作差，便能够实现对量化误差ereq的噪声整形。该结构通常称为误差反馈结构或噪声整形编码器[18]，广泛用于S-D 类型的DAC。推导图5结构中输出信号的组成，即
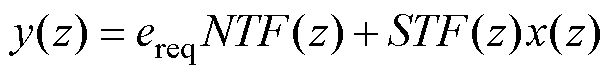（6）
其中
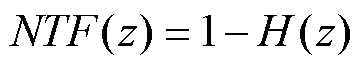
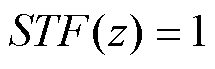
在量化误差反馈作用下，由式（6）可得噪声整形输出的等效结构如图6所示，输出序列y[n]是整形后量化噪声ereq和输入序列x[n]的总和。明显可见，使用滤波器H(z)对量化误差ereq进行处理时，并不会对输入序列x[n]产生作用，因此，该输入序列对输出序列的信号传递函数（Signal Transfer Function, STF）STF(z)=1。反而是在量化误差ereq项出现了噪声整形传递函数（Noise Transfer Function, NTF），即NTF(z)=1-H(z)。可见，该量化误差反馈结构消除了量化噪声整形过程中与输入信号的耦合。
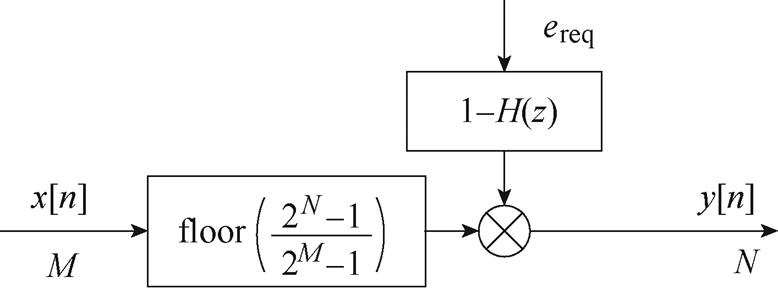
图6 噪声整形输出等效结构
Fig.6 Equivalent structure of noise-shaped output
由于噪声整形传递函数对量化噪声独立作用，噪声整形滤波器NTF(z)决定了噪声整形效果。在数字系统中实现噪声整形滤波器，其中的无延迟规则要求滤波器至少要包括一阶的延迟，因此，H(z)理应分做一级延迟和一个因果的数字滤波器。本文中的H(z)采用FIR数字滤波器为具体实施，相比IIR滤波器，FIR滤波器具有先天稳定的特点，计算量小，用于高频PWM更可靠。因此可得NTF(z)与H(z)的关系为
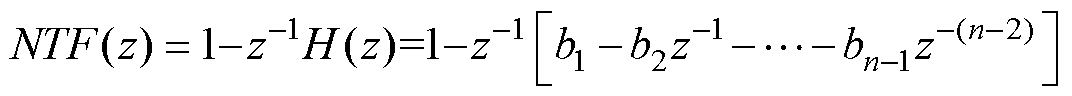（7）
从式（7）中可知，n阶NTF(z)的冲击响应h(0)=1, h(1)=b1,…, h(n)=bn。因此，其噪声增益系数为
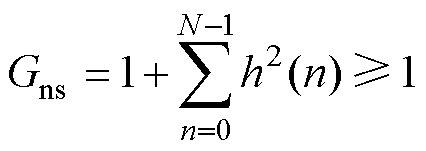（8）
而量化噪声近似于广义平稳随机过程，具有频域内均匀的功率密度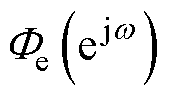，因此，整形后噪声频谱
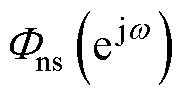与整形滤波器幅频特性有
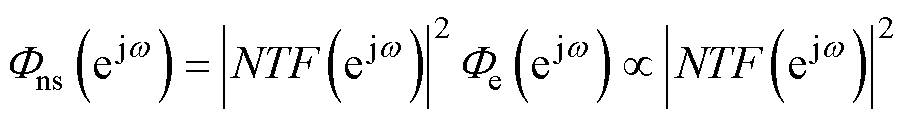（9）
结合式（8）、式（9），整形后的噪声功率谱与噪声整形传递函数具有比例关系，且该比例总是不小于1。根据帕萨瓦尔定理，可以给出式（8）在频域的表达式为
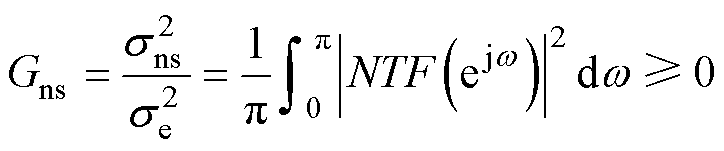（10）
由最优噪声整形定理可得：当NTF(z)满足最小相位时等式成立。其直观的几何意义是：在以线性频率的横轴和对数域幅值为纵轴的坐标系上，具有最小相位性质的NTF(z)在0 dB以上和以下的面积相等。
除此之外，噪声整形还需要具备两个稳定性条件：滤波函数稳定性和量化器非饱和。采用FIR作为噪声整形滤波器具有先天稳定的优势，在各项滤波器系数输入有界的条件下FIR总是稳定的；而量化器过载引起滤波器饱和时，量化噪声由输入信号决定不再有界，导致原先的量化噪声建模失效。为了分析量化器非饱和的特性，将饱和量化器看作是一个无限范围的量化器与一个饱和非线性级联，考虑量化器饱和的误差反馈结构如图7所示。
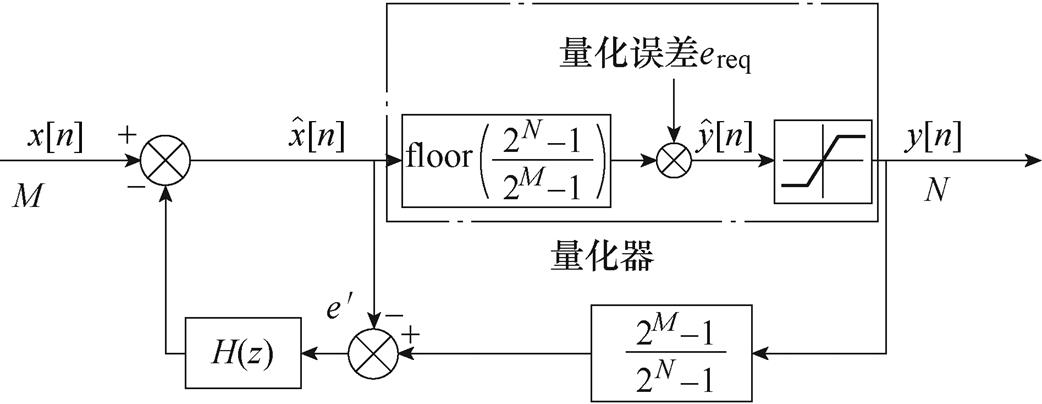
图7 考虑量化器饱和的误差反馈结构
Fig.7 Error feedback structure with quantizer saturation
当量化器不饱和，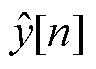
输出范围为[0, 2N-1]时，则
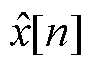作为输入，范围应为[-D/2, 2M-1+D/2]，在该范围内，量化噪声没有因为过载而产生额外的误差。根据式（6）有
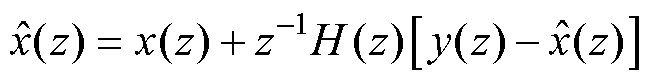（11）
可见，量化器的输入由两部分组成，输入x[n]和被NTF(z)-1整形的量化误差e'。对于没有过载的量化器，量化误差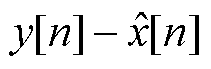
在整个奈奎斯特频段内的幅值都小于D/2。所以有
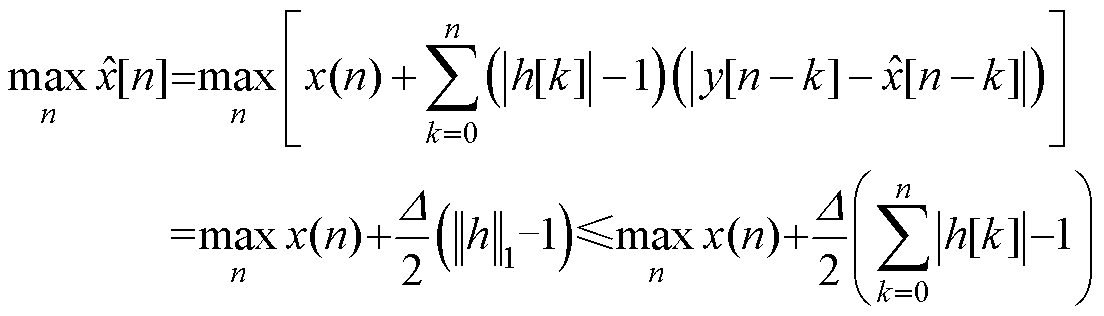（12）
式中，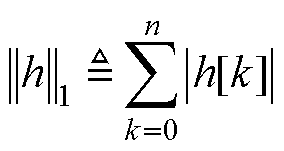
，即h[n]的1-范数。结合无饱和量化器的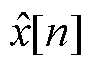输入范围，可以确定量化器不过载时x[n]的最小输入范围为
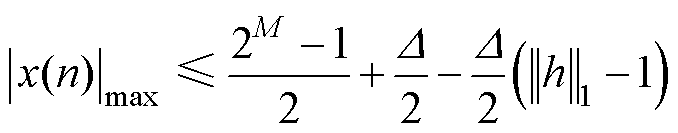（13）
为了保证整形反馈环路的稳定性，将稳定工作的最大输入，归一化为量化器的满量程输出，称为噪声整形的最大稳定幅度（Maximum Stable Amplitude, MSA），即
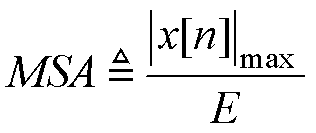（14）
明显可见，噪声整形滤波器的1-范数是影响输入最大稳定幅度的重要指标，而滤波器的1-范数是其高频增益的等效表征，因此控制滤波器的高频增益能够扩大输入的稳定幅度。
在第1节分析中，整形滤波器既不能提高信道内的信息容量，也不能降低量化噪声的功率，这和传统的高通滤波器具有实质性区别，可得其设计主要有既定约束：
（1）系数b0=1，确保滤波器可实现。
（2）具有最小相位，确保滤波器量化噪声功率不变。
（3）高频增益小，保证环路稳定。
在实际设计变量中，噪声整形滤波器主要参数有整形截止频率（归一化）wb，整形衰减Ans（dB），次要参数有高频增益开始频率（归一化）wh，以及高频增益Ahg（dB）。根据这些参数可以确定理想滤波器曲线，但是直接使用逼近的设计方法无法控制滤波器系数，且无法满足最小相位需求。为此提出一种逆全极点IIR低通滤波器简便快速方法来设计FIR噪声整形滤波器。
一个稳定的全极点IIR低通滤波器具有以下形式，其分母的最小次项系数总是为1，其余系数为a1, a2,…, ap。由于稳定性问题，该滤波器的所有极点都位于单位圆内。因此以该组系数作为FIR滤波器时，能够获得满足首个系数为1且具有最小相位的FIR高通噪声整形。
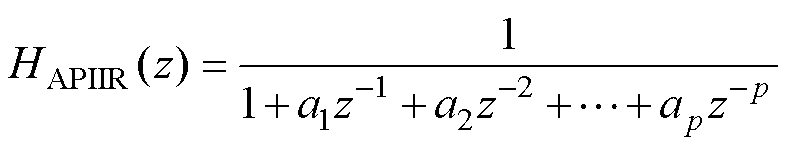（15）
在全极点的IIR滤波器设计中无法像多数IIR滤波器设计过程一样先描述其连续模拟域的滤波器理想特征，再通过如切比雪夫、椭圆这类滤波器逼近，最终由双线性变换获得离散Z域滤波器，因为这些方式会带来远离Z平面原点的零点，无法保证全极点的实现。通过Feldtkeller’s方程式，以多项式来获得模拟特征，就能够描述全极点滤波器的幅值特征。将滤波器的幅值二次方特性表示为频率变量x的实函数，即
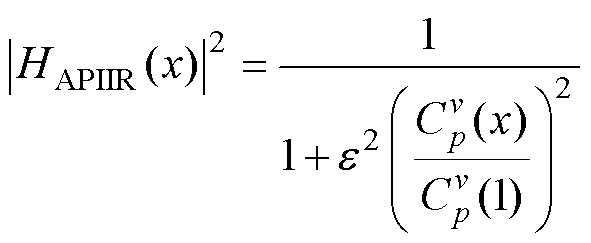（16）
式中，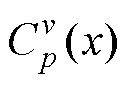
为超球多项式，也称作盖根堡多项式，实数v为类型参数，p为滤波器阶数；
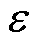与滤波器
设计中通带最大纹波幅值amax相关，有
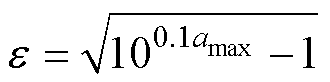（17）
而超球多项式可以表示为递归的方式，即
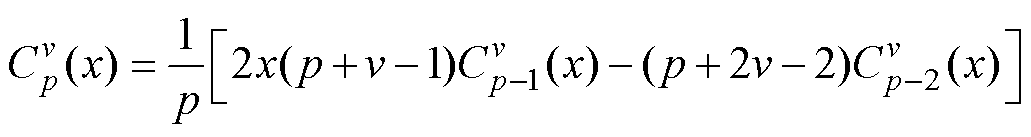（18）
式中，
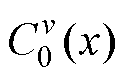=1；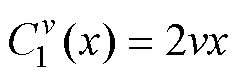
。当p为偶数时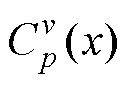，为x的偶次方多项式；反之，p为奇数时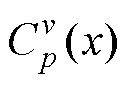，为x的奇次方多项式。v作为当中的自由参数，随着v从0到∞，超球多项式将从切比雪夫多项式一型（v→0），勒让德多项式（v=0.5），切比雪夫多项式二型（v=1），巴特沃斯多项式（v→∞）逐渐演化，主要关系为
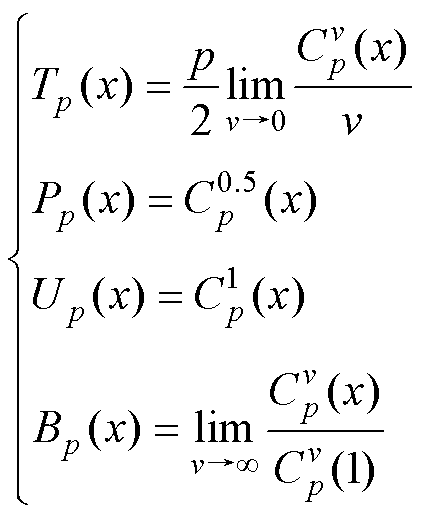（19）
可见，采用超球多项式能够囊括几种主要类型IIR滤波器形式。将多项式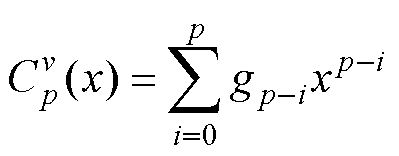
代入式（16）中展开为x的多项式有
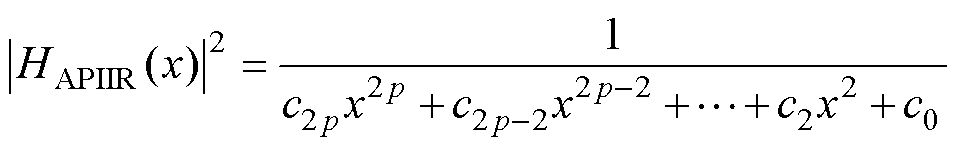（20）
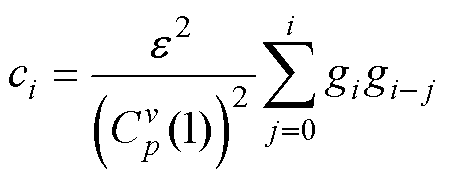（21）
式中，i=1,…, 2p。对于i=0且p为偶数时，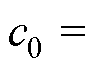
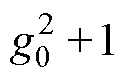；p为奇数时，c0=1。显然全极点的IIR幅值响应是关于x的偶数多项式。如果滤波器仅限于模拟域中则有x2=-s2，但若最终要取得离散滤波器的传递函数，则需要变换为
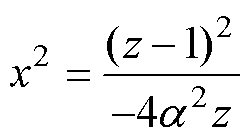（22）
式中，a =sin(wc/2)，wc为归一化的低通截止频率，在倒置为FIR滤波器后，与整形截止频率关系为wb=wcfs/(2p)，fs为离散频率。
因为HAPIIR(z)的全极点特性，因此可以令G(z)= HAPIIR(z)HAPIIR(1/z)，等效于|HAPIIR(z)|2，将式（22）代入式（20），并进一步整理，可得G(z)为
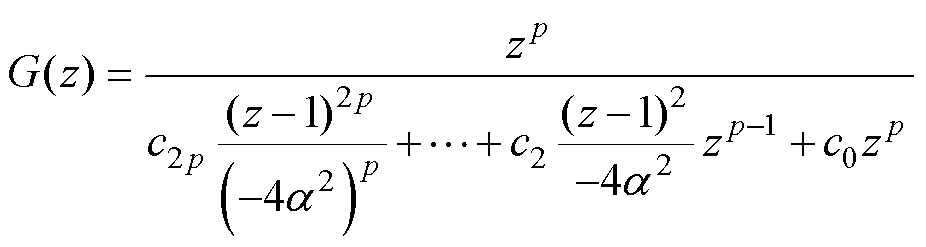（23）
G(z)的分母可以继续展开为含有变量z的多项式函数，则G(z)为z的有理函数，又(z-1)k为镜像多项式，其k次和k-2l次的多项式并乘上zl（k、l= [0, 2p]），也是镜像多项式，因此G(z)可以进一步整理为2p阶的镜像多项式，有
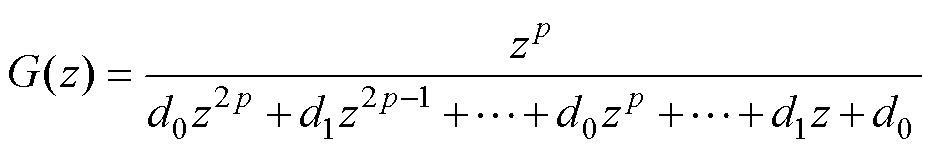（24）
其分母系数为
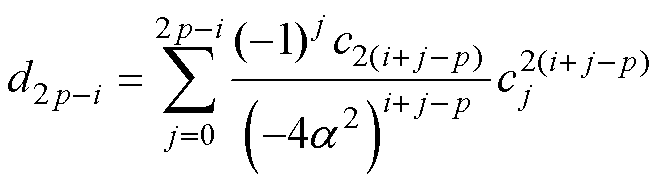（25）
求G(z)的极点，由于G(z)=HAPIIR(z)HAPIIR(1/z)，会发现其根以倒数对的形式出现。此时将处于单位圆内的根分配给HAPIIR(z)，即可求得所需的全极点IIR低通滤波器为
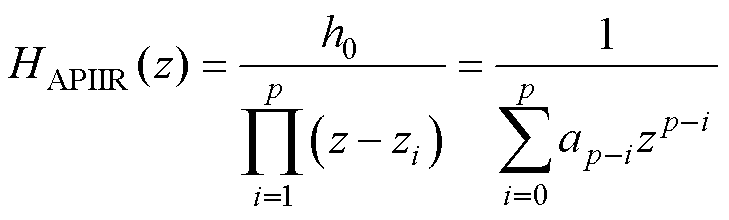（26）
其中
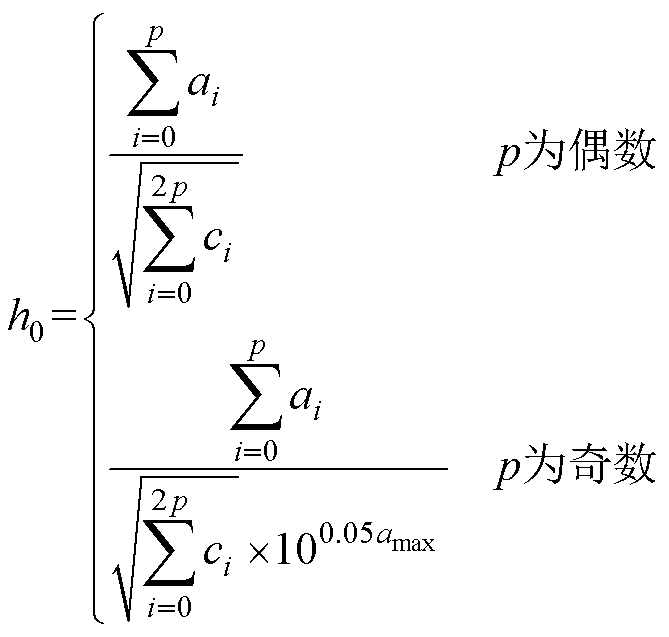（27）
h0作为常数调整全极点滤波器的增益，使低通通带幅值增益为1。当对全极点滤波器进行倒置时，h0为FIR噪声整形滤波器中整形带的衰减幅值，有Ans=20lgh0。至此，逆全极点IIR为FIR的设计过程结束，全极点IIR的系数特征为FIR满足了首系数为1的约束，而设计计算过程中的根分配也符合FIR最小相位的要求。最后合理选取滤波器阶数，降低高频增益对稳定性的影响。逆全极点的设计方法浅显明了，能够快速实现整形滤波器设计。
图8展示了根据上述方法获得的四种不同类型滤波器的幅值频率特性，其中，归一化频率是对采样系统奈奎斯特频率的标幺值。当滤波器采用相同截止频率、阶数和通带波纹值时，巴特沃斯表现出了最平坦的通带，而勒让德、切比雪夫一类、切比雪夫二类的整形衰减更高，但是伴随着较大的高频增益和通带波动，切比雪夫一类过渡阶段斜率高，截止效果好，但通带波动最大。
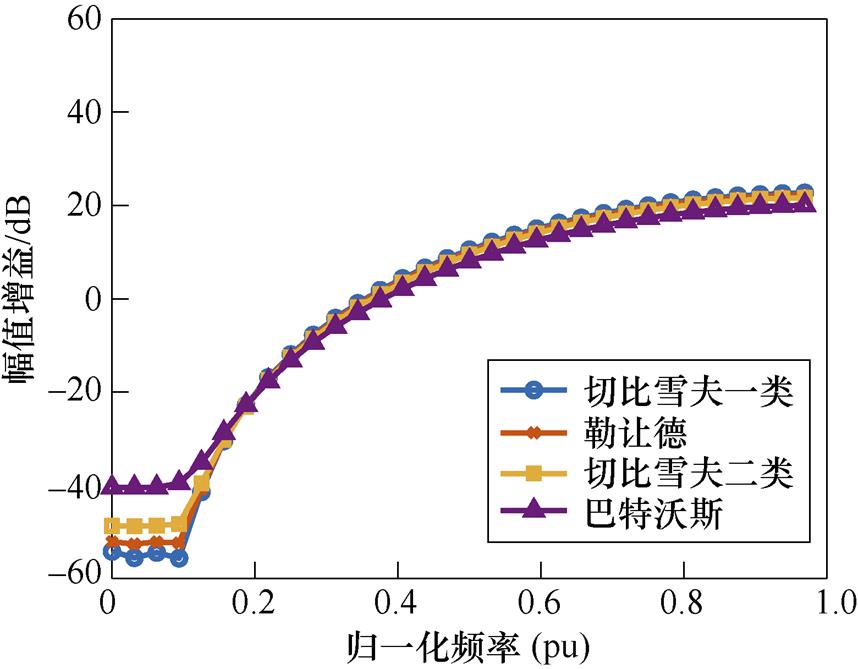
图8 四种类型的整形滤波器幅值频率特性
Fig.8 Amplitude-frequency characteristics of four types of noise shaping filters
图9、图10进一步明确滤波器阶数对整形衰减、高频增益的影响。随着滤波器的阶数增大，整形衰减和高频增益都表现出增大的趋势。在本设计方法中，6阶的切比雪夫一类能够实现80 dB的噪声整形，而巴特沃斯以无通带波纹的特性实现了60 dB的噪声整形。相比传统方法对高频增益控制采用H∞范数的约束，本文在滤波器的选取时则计算高频增益对稳定输入幅度的影响，通过调整设计参数避免在实际控制中引起稳定性问题。
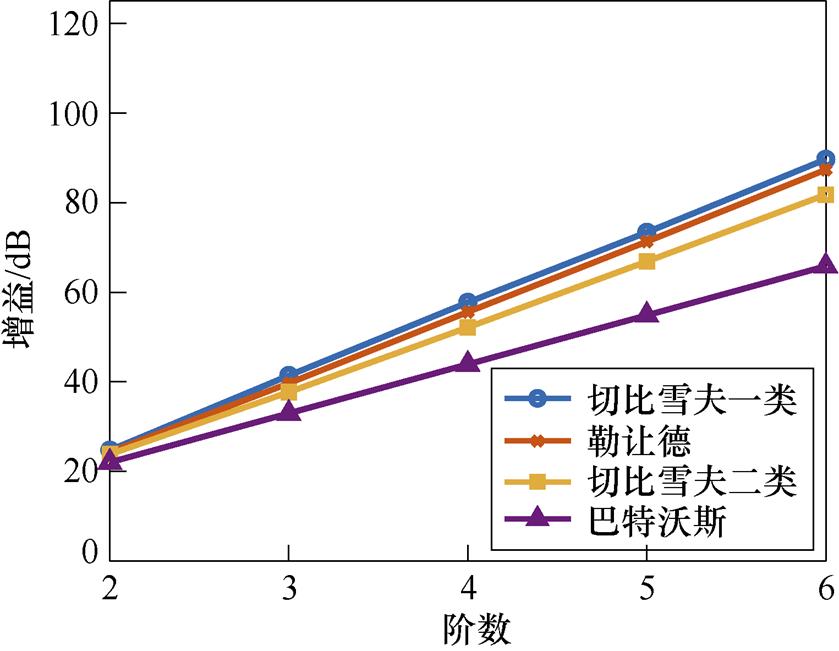
图9 整形衰减与阶数的关系
Fig.9 The correlation between noise shaping attenuation and filter order
将本文提出的设计方法与Nagahara提出的Min-Max设计方法做比较，如图11所示及见表1。Nagahara采用基于H2、H∞范数的LMI设计方法，而且设计过程中将频域进行分段LMI表征，设计流程较为复杂。本文简化了设计流程，而且提供丰富的低阶滤波器类型。图11中，本文提出的切比雪夫一类实现了Nagahara提出的FIR整形滤波器相近的幅值特性，而且减小了截止频率处的波纹。
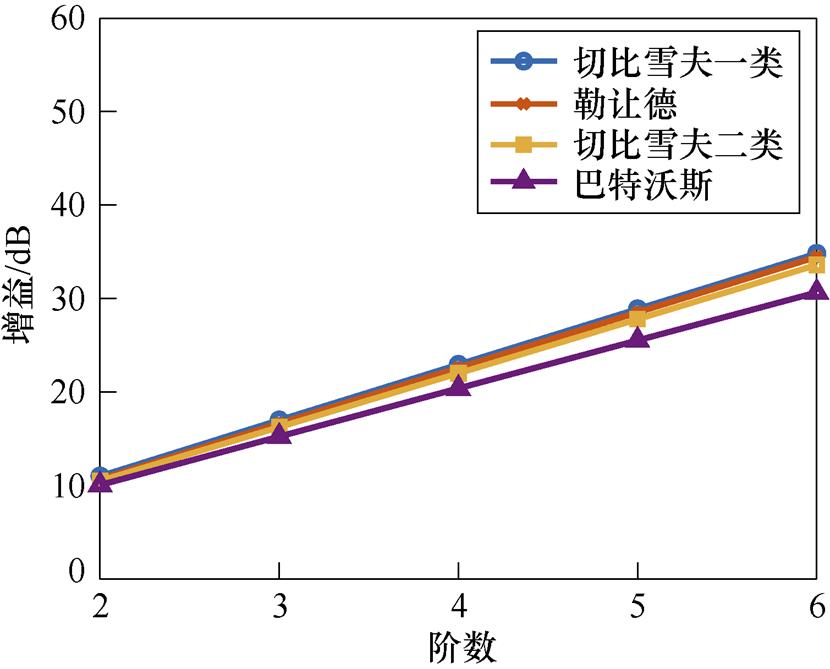
图10 高频增益与阶数的关系
Fig.10 The correlation between high-frequency gain and filter order
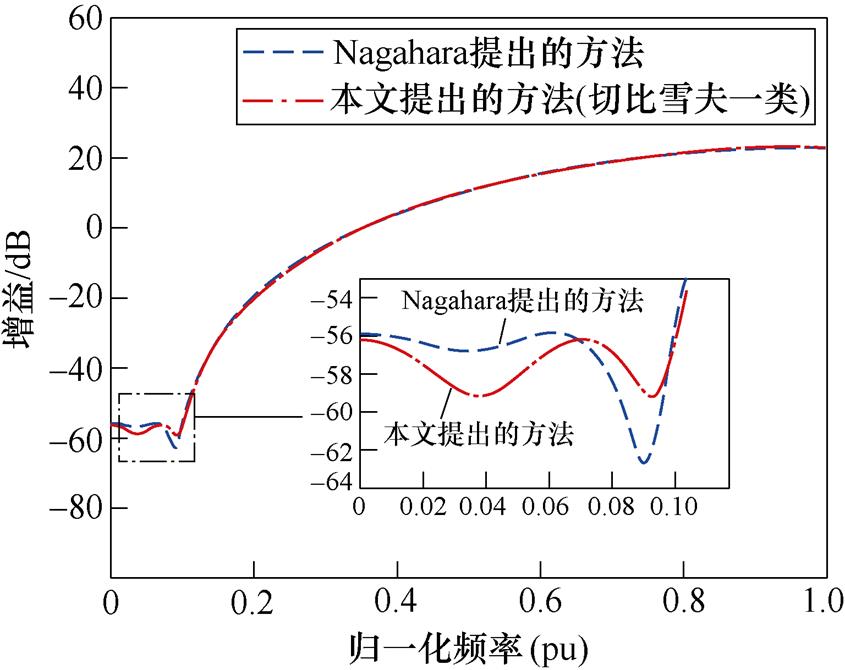
图11 FIR噪声整形滤波器设计方法对比
Fig.11 Comparison of design methods for FIR noise shaping filters
表1列出了对两种FIR整形滤波器在两种截止频率下，整形衰减随阶数的变化。从表中可以看出，在本文设计的滤波器整形衰减相较于Min-Max都较大，可见通带波纹的控制，改善了整形衰减。随着阶数的上升，本文提供的整形滤波器性能优势更突出。
本文采用的实验对象如图12所示，其中开关功率放大器的主控芯片采用168 MHz主频的STM32F4，产生200 kHz的PWM计数载波时，其最大计数值为419，不足9位，高开关频率和分辨率的矛盾显著。而ADC采用的是AD8556的多通道16位芯片，其采样幅值为-10～10 V，但是实际模拟电路的控制基准问题，真正工作中只使用了0～10 V的采样范围，因此仅有15位的分辨率。
表1 两种FIR整形滤波器的整形衰减对比
Tab.1 Comparison of noise shaping attenuation between two FIR noise shaping filters
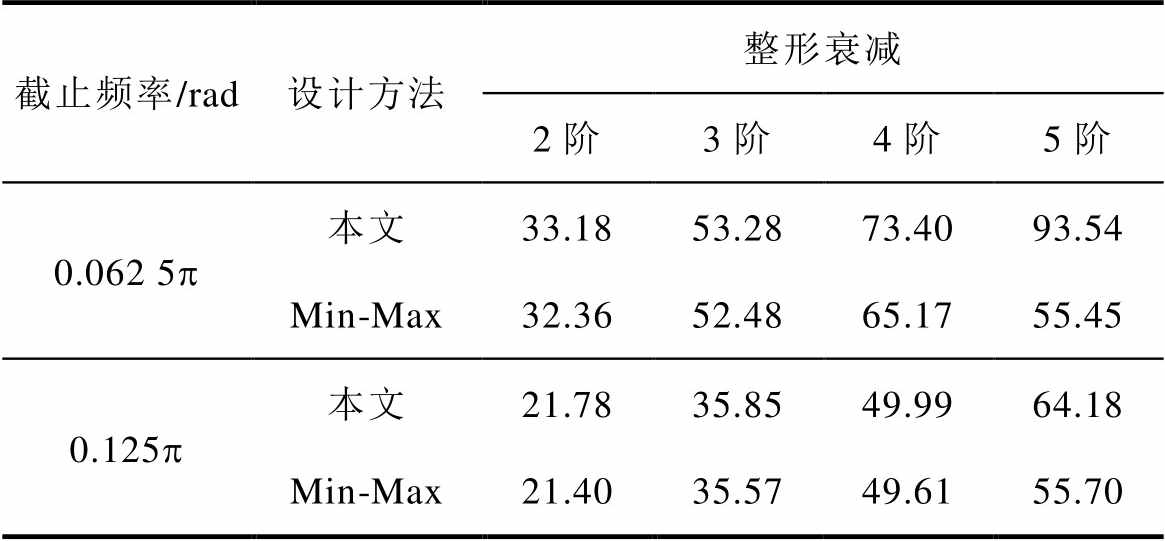
截止频率/rad设计方法整形衰减 2阶3阶4阶5阶 0.062 5p本文33.1853.2873.4093.54 Min-Max32.3652.4865.1755.45 0.125p本文21.7835.8549.9964.18 Min-Max21.4035.5749.6155.70
图12 本文中的开关功率放大器
Fig.12 Switch mode power amplifier in this paper
此外，实验过程中对于模拟信号生成仪器的输出信号幅值和信噪比要求较高，需要信号峰-峰值达到10 V，在规定频带内信噪比超过100 dB，信号频率采用170 Hz，高于一般电机位置环路带宽。本文中的实验输入采用仿真获得的高位信号来替代实际模数转换结果，保证输入的高位信号具有较高的信噪比和幅度。而在实验输出结果的选取上，如果直接测量驱动器的输出电流信噪比，将会引入PWM传输、功率变换、电流测量这几个部分的噪声影响，无法直接体现PWM的信噪比增强效果，因此直接记录PWM参考信号值进行功率谱分析。
根据实验对象的器件特征和运行情况，表2列出了驱动器中信号主要参数。
结合图7的量化反馈结构和表2中的主要参数，在Simulink进行仿真。仿真中，ADC在理想工作下对模拟信号采样的量化和PWM参考信号再量化时，两者量化噪声水平如图13所示，模数转换产生的量化噪声功率是-81.27 dB，而再量化将量化噪声提高至-43.12 dB，噪声分布满足白噪声在频谱上均匀分布的特征，符合量化噪声建模。
表2 仿真过程中的主要参数
Tab.2 Main parameters during simulation process
参 数数 值 模拟信号幅值E/V5 模拟信号频率f/Hz170 AD采样位数M/bit15 AD采样频率fs/kHz200 PWM参考信号最大计数值419
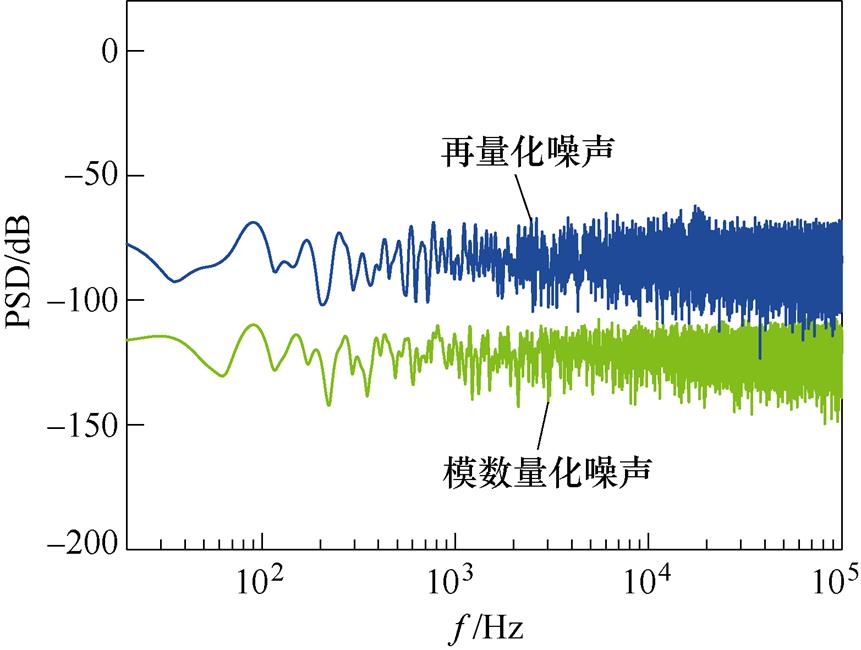
图13 量化噪声功率谱
Fig.13 Quantizaion noise power spectrum
由于噪声整形仅对再量化噪声有效，整形后信号仍然保留有模数转换产生的量化噪声，即进入数字系统的初始数字信号具有该过程中最佳保真度；但再量化的附加噪声污染了原有的信号，因此采用噪声整形的最佳效果是恢复至模数转换后的数字信号，可供整形恢复的噪声幅值最高为38.14 dB，即噪声整形滤波器需提供整形衰减约40 dB。
以10 kHz整形截止频率符合大多数超精密定位平台的功率放大器带宽；考虑系统中的功率滤波器截止频率，选定高频增益开始频率为30 kHz，更高频率的量化噪声首先会被输出端的功率滤波器滤除，其次会在感性负载中衰减。而高频增益应尽可能低以实现噪声整形稳定幅度的最大化，结合式（13），式（14）选定高频增益为20 dB，此时模拟信号输入幅度为4.9 V，噪声整形的最大稳定幅度为98%，基本实现控制量程的覆盖。结合上述分析，表3列出整形滤波器的主要设计指标。
根据表3的设计指标，按照第2节的设计方法可得4阶的巴特沃斯，提高了足够的整形衰减，且高频增益也满足要求，整形滤波器为
表3 整形滤波器的主要设计指标
Tab.3 Main design specifications of noise shaping filters
滤波器的主要设计指标数 值 整形截止频率wb/(rad/s)0.1 整形衰减Ans/dB40 高频增益开始频率wh/(rad/s)0.3 高频增益Ahg/dB20 通带波动幅值amax/dB1.5
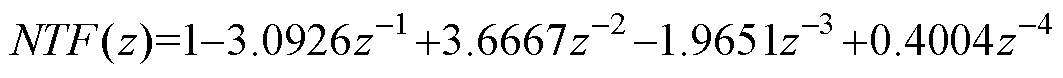（28）
将上述滤波器代入仿真模型中，并以输入幅度4.9 V、170 Hz的模拟正弦波作为有效信号成分，图14分析了仿真中主要信号的噪声整形效果。经过15位AD数模转换后，其整形带内的信噪比高达101.17 dB。经过再量化后，其整形带内的信噪比仅有62.23 dB，可见再量化明显降低了信号保真度。经过4阶巴特沃斯的滤波整形后，其信噪比回复到97.17 dB，效果明显。
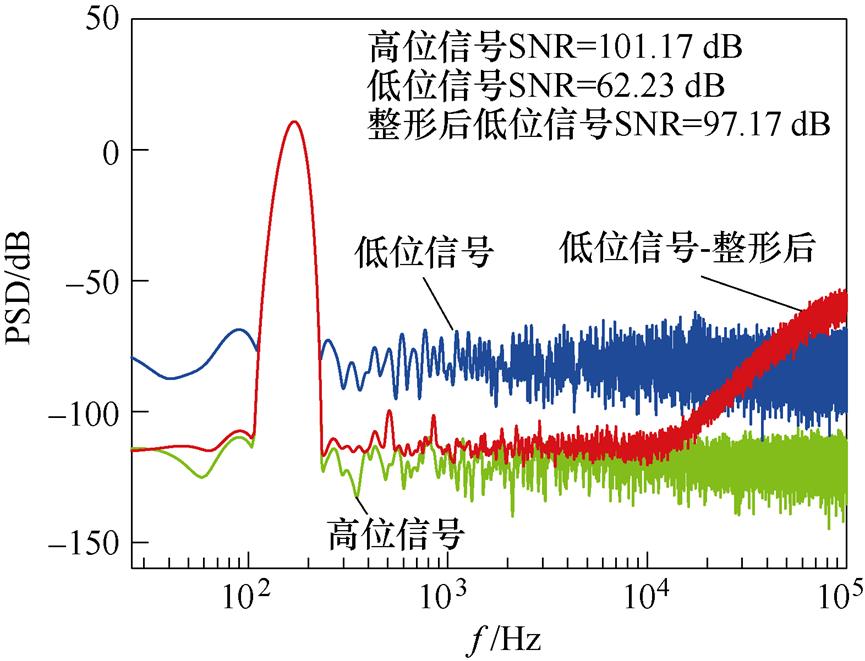
图14 仿真中噪声整形功率谱-主要信号
Fig.14 The noise shaping power spectrum of main signals in simulation
由于本文的滤波器的阶数较低，在实际部署驱动器的数字计算程序中，有利于在单个PWM短周期过程中进行滤波计算并完成结果输出。实验中噪声整形功率谱-PWM参考信号功率谱如图15所示，低位信号在实际的数字计算中完成整形滤波，在整形频带内，实现信噪比从62.30 dB到99.04 dB的提升，与仿真结果相符。
实验中噪声整形功率谱-量化噪声功率谱如图16所示。从图16中可见，量化噪声被整形后，其整形带内的噪声下降到数模转换的噪声水平，结合图15，信号的功率并没有发生改变，说明量化噪声功率的降低是输出信号信噪比提高的主要原因。
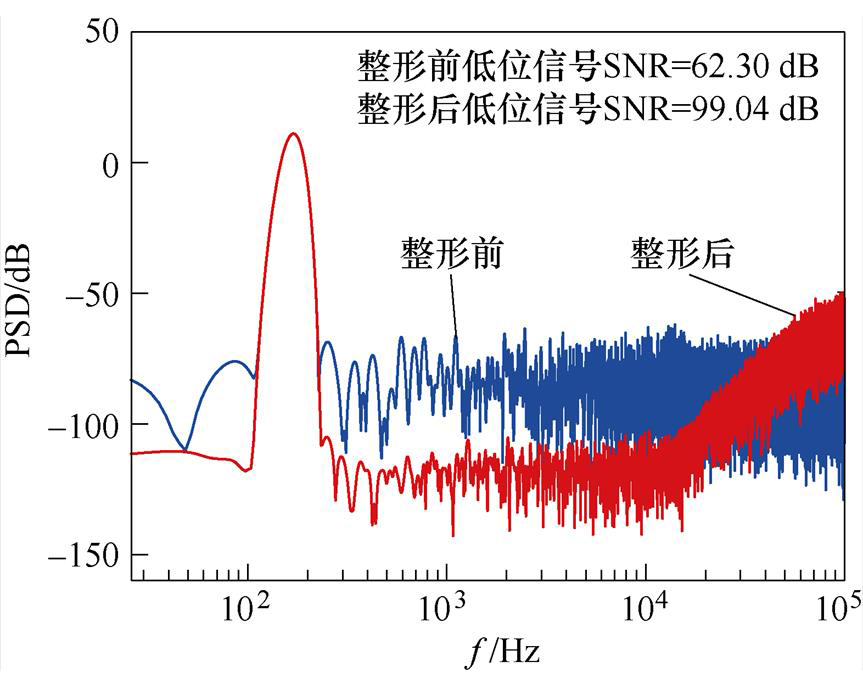
图15 实验中噪声整形功率谱-PWM参考信号功率谱
Fig.15 The noise shaping power spectrum of PWM reference in experiment
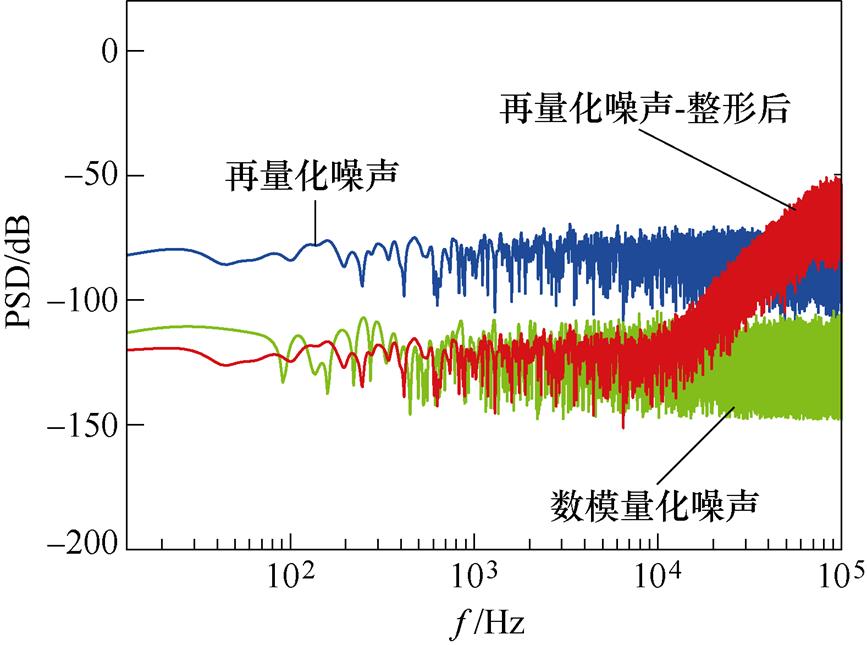
图16 实验中噪声整形功率谱-量化噪声功率谱
Fig.16 The noise shaping power spectrum of quantization noise in experiment
实验中噪声整形效果-量化噪声波形如图17所示。从量化误差波形上来看，在整形基带10 kHz频率范围内，量化误差相比整形前有大幅衰减，电压误差衰减了接近两个数量级，符合40 dB的整形衰减效果。再观察整形前后的PWM参考信号波形如图18所示，局部上来看，由于量化噪声的搬移导致高频的“毛刺”增加，连续采样样本的变化较大，即表现在高频上的噪声有所增加，但是在低频中参考信号更接近于实际模拟值。进一步可见，滤波器产生的非线性相位并没有出现在PWM的参考信号上，说明量化噪声的反馈结构能够完美地实现量化噪声和有效信号的分化，完成噪声与信号的隔离处理。
图19分析了开关频率对噪声整形的影响。通过降低开关频率可以提高PWM输出信噪比，但低开关频率增大了电流纹波，也不利于输出滤波。在不同开关频率下，噪声整形都能提高PWM参考信号的信噪比，因为噪声整形滤波器衰减了各种调制频率中产生的量化噪声。在高频开关和高信噪比的同步要求下，采用噪声整形的开关信号调制方法，降低了对硬件性能的依赖。图19中，按照本文的逆滤波器设计方法，通过控制整形带波纹，相比较Nagahara的噪声滤波器设计方法，实现了更优的信噪比，而且开关频率越高，通道波纹控制带来的信噪比提升越明显。
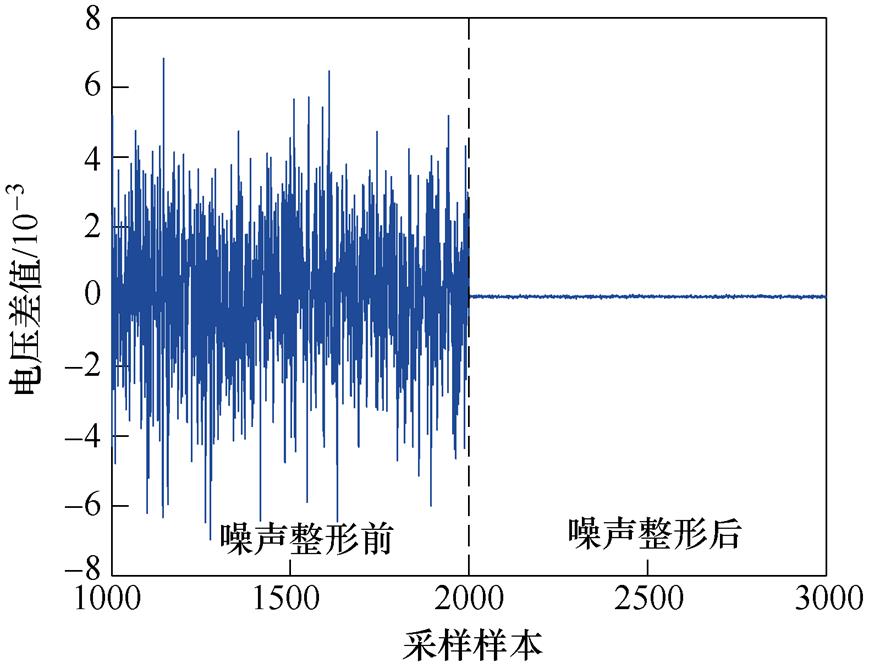
图17 实验中噪声整形效果-量化噪声波形（10 kHz内）
Fig.17 The noise shaping performance-quantization noise (with 10 kHz) in experiment
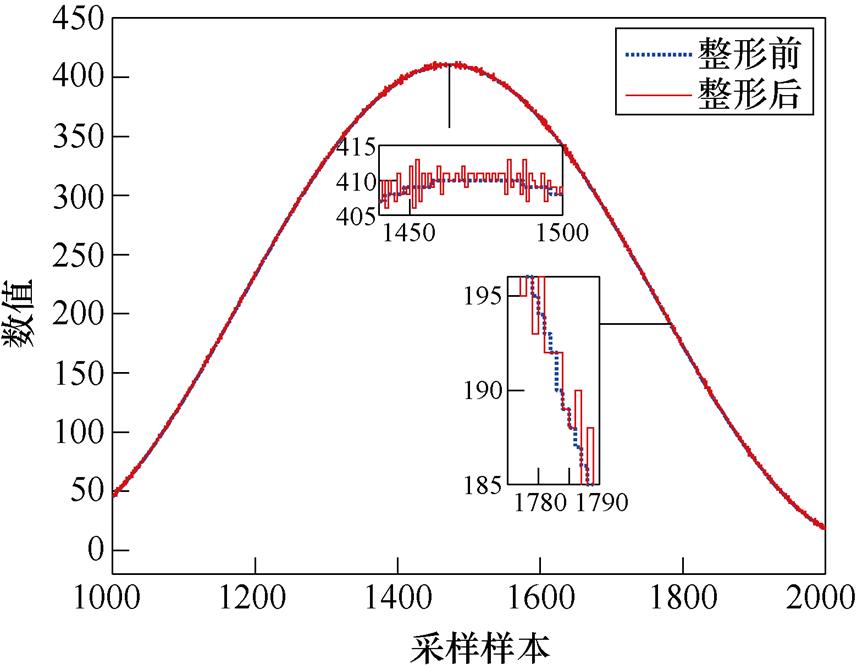
图18 实验中噪声整形效果-PWM参考信号波形
Fig.18 The noise shaping performance-PWM reference in experiment
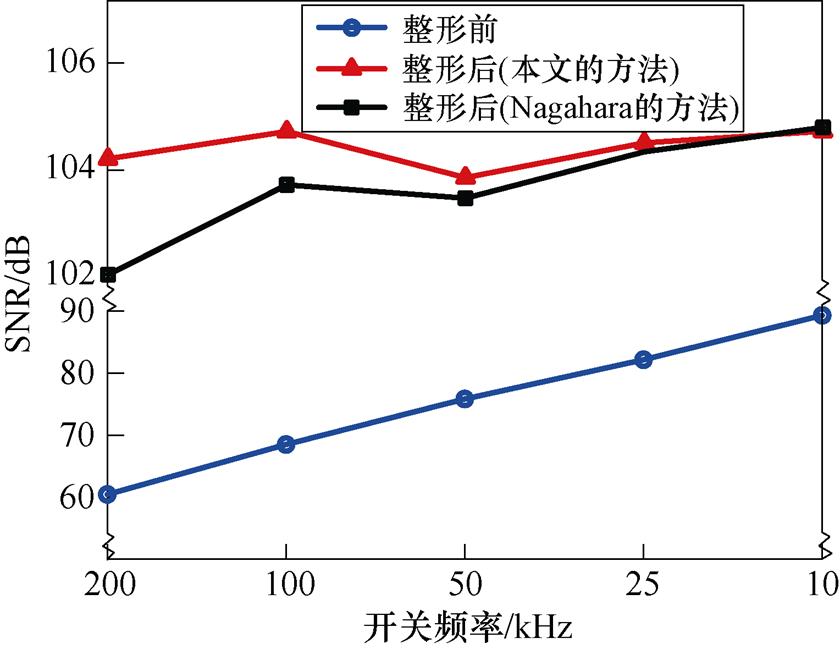
图19 实验中噪声整形效果对比
Fig.19 Comparasion of noise shaping performance in experiment
本文分析了PWM过程中由量化产生的噪声特征，并根据误差反馈结构区分再量化产生的低位参考信号和量化噪声，实现了两种信号的分化处理。分析了无实际过采样发生的数字整形滤波器的噪声整形原理和稳定性问题，提出了一种通过反转全极点IIR滤波器为FIR噪声整形滤波器的设计方法，在噪声整形滤波器系数和最小相位特征的约束下同时兼顾噪声整形需求，分析了四种类型的全极点IIR滤波器反转为噪声整形滤波器的效果。通过仿真和实验的相互验证，在15位高位信号再量化为不足9位的低位信号时，采用此快速设计方法反转4阶巴特沃斯为FIR噪声滤波器，平坦的整形通带带来了更大的噪声衰减能力，实现了信号在0～10 kHz频段内约40 dB的信噪比回复。
参考文献
[1] Lemke R, Krcher H J, Noethe L. Telescope posi- tioning and drive system based on magnetic bearings, technical challenges and possible applications in optical stellar interferometry[C]//SPIE Astronomical Telescopes+Instrumentation, Amsterdam, Netherlands, 2012: 844440.
[2] Schellekens J M. A class of robust switched-mode power amplifiers with highly linear transfer characteristics: on the elimination of zero-crossing distortion in switching converters[D]. Eindhoven: Technische Universiteit Eindhoven, 2014.
[3] Berkhout M. An integrated 200-W class-D audio amplifier[J]. IEEE Journal of Solid-State Circuits, 2003, 38(7): 1198-1206.
[4] Nyboe F, Kaya C, Risbo L, et al. A 240 W monolithic class-D audio amplifier output stage[C]//2006 IEEE International Solid State Circuits Conference, San Francisco, CA, USA, 2006: 1346-1355.
[5] Brecher C, Lindemann D, Wenzel C. Influences of closed loop control components on the performance of ultra-precision machines[J]. Key Engineering Materials, 2014, 625: 207-212.
[6] Stubenrauch F, Seliger N, Schmitt-Landsiedel D. Design and performance of a 200 kHz GaN motor inverter with sine wave filter[C]//PCIM Europe 2017; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 2017: 1-9.
[7] Tiapkin M, Balkovoi A, Samygina E. Current controller design of precision servo drive[C]//2020 27th International Workshop on Electric Drives: MPEI Department of Electric Drives 90th Anniver- sary (IWED), Moscow, Kussia, 2020: 1-6.
[8] Höllthaler J, Hagl R, Kennel R. Influence of the PWM frequency on dynamic and position stability of servo drives[C]//2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 2020: 23-29.
[9] Höllthaler J, Hagl R, Kennel R. Bandwidth improve- ments of linear direct drives with a 100 kHz PWM- frequency[C]//2019 12th International Symposium on Linear Drives for Industry Applications (LDIA), Neuchatel, Switzerland, 2019: 1-6.
[10] 孙兆君, 董腾辉, 周飞, 等. PWM开关频率对转子损耗和温升影响探究[J]. 微电机, 2020, 53(2): 37-42.
Sun Zhaojun, Dong Tenghui, Zhou Fei, et al. Influence of PWM switching frequency on rotor loss and temperature rise[J]. Micromotors, 2020, 53(2): 37-42.
[11] 胡怡婷, 赵朝会, 吉洪智, 等. PWM频率对高速无刷直流电动机转矩脉动影响分析[J]. 上海电机学院学报, 2019, 22(6): 337-344.
Hu Yiting, Zhao Chaohui, Ji Hongzhi, et al. Analysis of influence of pulse width modulation frequency on torque ripple of high speed brushless DC motor[J]. Journal of Shanghai Dianji University, 2019, 22(6): 337-334.
[12] Mauerer M. Low-noise and low-distortion switch- mode power amplifiers for nano-positioning appli- cations[D]. Zurich: ETH Zurich, 2020.
[13] Texas Instruments Co, TMS320x280x, 2801x, 2804x high resolution pulse width modulator (HRPWM)[EB/OL]. [2011-10]. https://www.ti.com/lit/pdf/spru924.
[14] de Castro A, Sutter G, Huerta S C, et al. High reso- lution pulse width modulators in fpga[C]//2007 3rd Southern Conference on Programmable Logic, Mar del Plata, Argentina, 2007: 137-142.
[15] Froidevaux C. Method and device for generating PWM signals. US08508310B2[P]. 2013.
[16] Enuchenko M S, Korotkov A S. Digital-to-analog converters based on Delta-Sigma modulators[J]. Journal of Communications Technology and Elec- tronics, 2022, 67(1): 1-16.
[17] Tan Zhichao, Chen C-H, Chae Y, et al. Incremental Delta-Sigma ADCs: a tutorial review[J]. IEEE Transactions on Circuits and Systems, 2020, 67(12): 4161-4173.
[18] Pavan S, Schreier R, Temes G C. Understanding Delta-Sigma data converters[M]. New York: Wiley, 2005.
[19] Norris M, Platon L M, Alarcon E, et al. Quantization noise shaping in digital PWM converters[C]//2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 2008: 127-133.
[20] Lukic Z, Rahman N, Prodie A. Multibit S-D PWM digital controller IC for DC-DC converters operating at switching frequencies beyond 10 MHz[J]. IEEE Transactions on Power Electronics, 2007, 22(5): 1693-1707.
[21] Verhelst W. Noise shaping filter design for minimally audible signal requantization[C]//Proceedings of the 2001 IEEE Workshop on the Applications of Signal Processing to Audio and Acoustics, New York, 2001: 147-150.
[22] Yagyu M. Design of noise shaping FIR filters by minimizing in-band peak amplitude for stable single- and multi-bit data converters[C]//Proceedings of the 2003 International Symposium on Circuits and Systems, Bangkok, Thailand, 2003: I.
[23] Yagyu M, Nishihara A. Fast and efficient algorithm to design noise-shaping FIR filters for high-order overload-free stable sigma-delta modulators[C]// 2004 IEEE International Symposium on Circuits and Systems (IEEE Cat. No.04CH37512), Vancouver, BC, Candan, 2004: I-469.
[24] Nagahara M, Yamamoto Y. Frequency domain min- max optimization of noise-shaping Delta-Sigma modulators[J]. IEEE Transactions on Signal Pro- cessing, 2012, 60(6): 2828-2839.
[25] Tariq M R, Ohno S. An indirect approach to synthesis of noise shaping IIR filters in DS modulators[C]// 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 2017: 1-4.
[26] Tariq M R, Ohno S. Unified LMI-based design of DS modulators[J]. Eurasip Journal on Advances in Signal Processing, 2016, 2016(1): 1-14.
[27] Ohno S, Tariq M R. Optimization of noise shaping filter for quantizer with error feedback[J]. IEEE Transactions on Circuits and Systems, 2016, 64(4): 918-930.
Abstract To keep track of the requirements of driving the high-precision electromechanical system in semiconductor manufacturing, the SNR of the amplifier output current needs to increase by 20 dB every five years. Compared to linear power amplifiers, switching power amplifiers have superior potential in power and efficiency. High-frequency switching power amplifiers can reduce voltage and current distortion. However, the limited digital computation causes a conflict between high switch frequency and high-duty cycle resolution. Therefore, this paper analyzes the noise shaping principles in the pulse-width modulation process and proposes a simple design method for low-order FIR noise shaping filters, which provides sufficient noise attenuation and passband flatness with the least computational cost.
Firstly, the signal processing in switch power amplifiers is demonstrated. Quantization noise in digital PWM modulation causes a trade-off between high SNR and high frequency, assumed to be uniformly distributed white noise and independent of the input. The improvement of the SNR via noise shaping is analyzed accordingly. Secondly, an error feedback structure is used to obtain the quantization noise as high-bit digital signals, separating the transmission of target signals and quantization noise shaping processing. Furthermore, the minimum phase and stability constraints of noise-shaping filters are derived. Thirdly, four different types of all-pole IIR filters are derived by the Gegenbauer polynomial. Their inverse forms are FIR filters with the origin cutoff frequency and shaping attenuation as well as the minimum phase and coefficient characteristics. Finally, the noise attenuation requirements are met by selecting the filter order reasonably. The inverse all-pole filter method reduces the complexity of the noise-shaping filter design and enhances the ability to control the ripple in the noise-shaping band. Simulation and experiment have shown that the proposed method achieves a large noise attenuation in the same order as the LMI method and has better ripple control. When PWM modulating at 200 kHz with a resolution lower than 9-bit, a 4th-order FIR noise shaping filter increases the SNR of the reference signal from 62.30 dB to 99.04 dB within a bandwidth of 10 kHz. After the noise shaping, the power level of quantization noise in the target frequency band reduces from -43.12 dB to -81.27 dB, and the quantization noise generated by PWM has been eliminated. In addition to the SNR improvement, the error feedback structure preserves the phase and amplitude characteristics of the target signal.
The following conclusions can be drawn: (1) Quantization noise can be modeled as uniform white noise and extracted through an error feedback structure, effectively separating the quantization noise and the control signal in digital signal processing. (2) The inverse all-pole filter makes the FIR noise shaping filter conform to the constraints of the first fixed coefficient and minimum phase, which is an expeditious method for low-cost noise shaping design in high-frequency PWM. (3) Performing noise shaping in PWM modulation can recover SNR loss caused by coarse quantization in modulation, but the best SNR still depends on the analog-to-digital conversion.
keywords：Switch mode power amplifier, high frequency PWM, noise shaping, all-pole filter, signal- to-noise ratio (SNR)
DOI: 10.19595/j.cnki.1000-6753.tces.230307
中图分类号：TM46
国家自然科学基金资助项目（52275112, 52075193）。
收稿日期 2023-03-16
改稿日期 2023-04-27
陈福祥 男，1997年生，博士研究生，研究方向为高频开关功率放大器、精密控制系统。E-mail: D202080294@hust.edu.cn
曾理湛 男，1973年生，副教授，研究方向为机电系统动力学及控制、超精密磁浮工作台等。E-mail: zenglizhan@hust.edu.cn（通信作者）
（编辑 陈 诚）