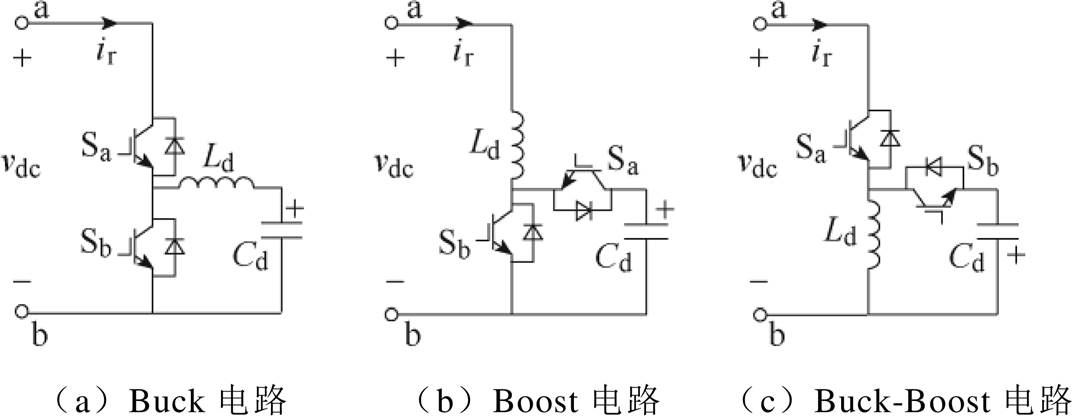
图1 解耦模块常用实现电路
Fig.1 Common circuits for active decoupling modules
摘要 有源功率解耦技术是解决单相变换器中低频二次脉动功率的有效方法。模块化电路具有标准化、独立性和通用性等优点,发展模块化的解耦电路是有源功率解耦技术的重要方向。现有控制策略仅针对单个解耦电路提出,没有考虑多个解耦模块共同工作时的协同控制问题。对此,该文提出一种基于虚拟阻抗的多解耦模块协同控制策略,通过控制解耦模块模拟无源RLC电路的阻抗特性,实现单个解耦模块的即插即用和多个解耦模块的协同功率分配。所提出的控制无需解耦模块与主电路交互电网电压和电流信息,也无需解耦模块间的相互通信,避免了集中的中央控制器和昂贵实时通信的使用。实验以两个解耦模块的功率协同控制为例验证了所提控制策略有效可行性。
关键词:单相变换器 有源功率解耦 协同控制 模块化
单相变换器在工业、商业、家用住宅等领域都有着广泛的应用[1],如LED驱动照明、电动汽车充电、电机驱动及UPS电源等[2-5],功率等级从几十W到十几kW不等。单相变换器交流侧的功率包含二倍于电网频率的脉动功率(二次脉动功率)。通常利用大电解电容吸收二次脉动功率以保证恒定的电压输出,即无源功率解耦方法,但电解电容的使用不可避免地增大了系统的体积、降低了系统的可靠性[6-7]。
为了避免电解电容的使用,有源功率解耦技术受到广泛关注,它将系统中的二次脉动功率转移到主电路外的解耦电容进行缓存。由于解耦电容电压允许在较大范围内波动,所以其容值可以较小,通常只有几十mF。目前,有源功率解耦技术在解耦电路拓扑和解耦控制策略两个方面得到了广泛的研究。已有文献[8-9]对现有解耦电路拓扑进行了总结,对拓扑的构造规律进行了提炼。根据解耦电路与主电路是否复用开关器件/无源器件,解耦电路可分为独立型和复用型[8]。常见的独立型电路如图1所示,包括Buck电路[10]、Boost电路[11]、Buck-Boost电 路[12]等,而复用型电路通常由独立型电路与原电路共用开关或者电容得到[13]。在控制策略方面,文献[14]对现有的解耦控制策略从功率平衡、谐波抑制、伏秒/电荷平衡和虚拟阻抗进行了分类总结,并对各自的优缺点进行了对比分析。

图1 解耦模块常用实现电路
Fig.1 Common circuits for active decoupling modules
随着时代的发展,有源功率解耦技术也面临着新的挑战和发展契机。由于有源功率解耦技术的最终目标是代替大电解电容,所以发展解耦电路的模块化是未来的重要方向。所谓模块化电路[15],就是指可组合成系统、具有某种确定功能和接口结构的典型通用独立电路单元,其具有标准化、独立性和通用性等优点[16-17],同时还有利于缩短系统的研发周期、便于系统容量的扩展。发展模块化解耦电路可使单相变换系统根据自身负载功率(LED驱动(10~100 W)、车载充电机(6.6 kW)、UPS电源(10~100 kW)等)灵活选择相应解耦模块进行功率解耦,对于较大功率场合也可利用多个解耦模块进行解耦。
为了实现解耦电路的模块化设计,解耦电路必须具备控制独立性[18-19],即解耦模块的控制不需要与主电路进行交互功角等信息。目前一些基于直流母线电压提取解耦控制参考和基于虚拟电容的解耦控制满足此要求。在文献[20]中,高通滤波器用于提取直流母线电压的二倍频分量,然后利用比例-谐振(PR)控制器得到解耦电路的控制参考,进而实现母线电压校准。文献[21-23]中提出的方法基于虚拟电容,均是通过构造解耦电路的端口特性来使其模拟大电容。在文献[22-23]中,解耦电路的端电流被控制为直流母线电容电流的N倍,从而模拟出N倍于母线容值的电容,实现了良好的功率解耦。
然而,当系统中二次脉动功率较大,需要两个或多个解耦模块协同工作完成解耦时,上述针对单个模块提出的控制方法均无法满足解耦模块协同工作的需求。针对此问题,本文提出了基于虚拟阻抗的解耦模块协同控制策略。通过模拟无源LC谐振电路的外电压-电流特性,在无需已知相位和功率信息情况下,实现单个模块的即插即用控制。并在此基础上,通过虚拟谐振电路中的串联电阻来实现多解耦模块在无通信情况下的功率分配,避免了集中的中央控制器和昂贵的实时通信。
本文首先介绍了虚拟阻抗控制在单个解耦模块和多个模块中的实现方式;然后以典型Buck解耦模块为例,阐述了控制器的参数设计和功率分配原则;最后通过实验结果验证了所提控制方法的有 效性。
本节提出基于虚拟阻抗的多模块解耦电路协同控制策略,首先简单介绍了有源功率解耦的基本原理,然后提出虚拟阻抗控制在单个模块中的实现方式,并在此基础上讨论增加虚拟串联电阻实现功率分配的解耦模块协同控制策略。
图2为配置并联解耦模块的单相全桥电压源型整流器拓扑。假定电网电压和电网电流分别为
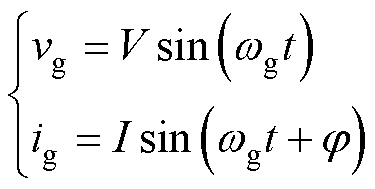 (1)
(1)
式中,V和I分别为电网电压和电网电流幅值;wg为电网角频率;j 为功率因数角。
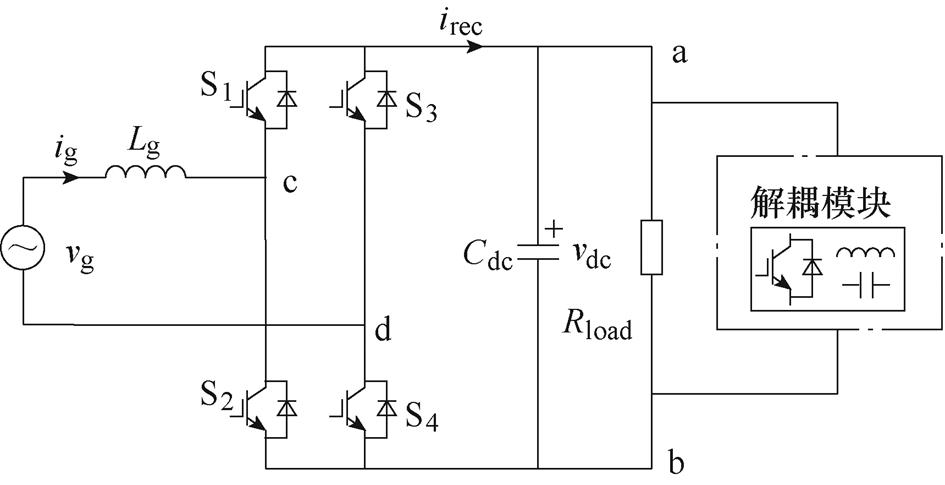
图2 单相全桥电压源整流器
Fig.2 Single-phase voltage-source rectifier
则网侧瞬时功率可表示为
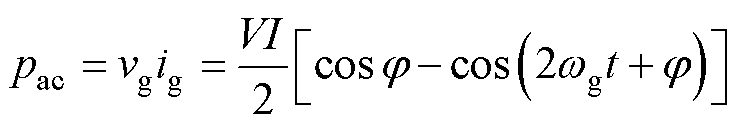 (2)
(2)
根据irec=pac/vdc,整流器的输出电流irec可表示为
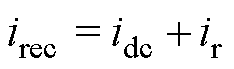 (3)
(3)
其中
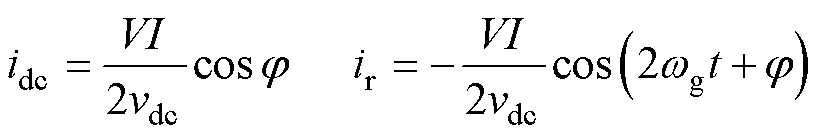
显然,式(3)中包含一个由二次脉动功率引起的纹波脉动电流。在解耦模块不工作时,直流侧电容的微分方程满足
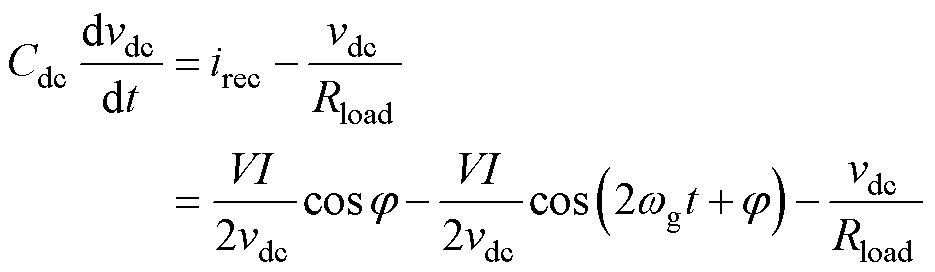 (4)
(4)
考虑初始条件vdc(t=0)=0,式(4)的稳态解为
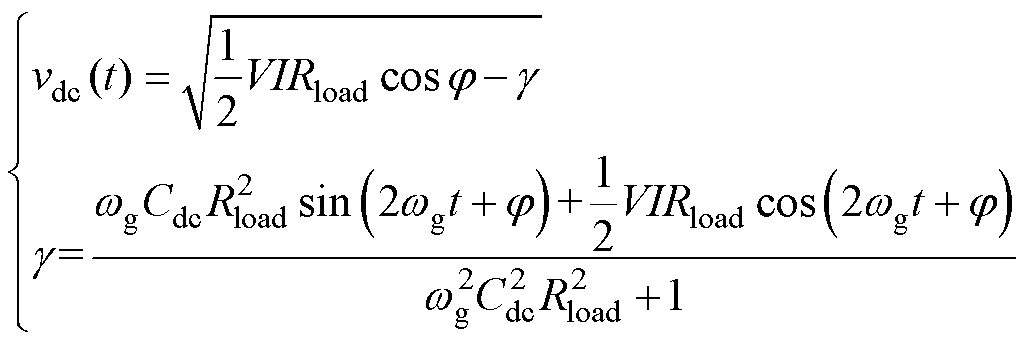 (5)
(5)
为满足母线电压纹波标准,需将g 减小到允许范围内,通常的做法是增大电容Cdc的容值。而有源功率解耦技术则是利用有源功率解耦模块产生一个电流以抵消irec的脉动部分ir,进而消除式(5)中的g 项,避免大电容的使用。
为控制有源解耦模块旁路二次纹波电流,实现解耦功能,本文首先借鉴无源LC谐振电路的解耦思想:无源LC谐振电路是通过并联一个谐振频率wr(wr=2wg)的串联LC谐振电路来旁路二次纹波电流ir,以此避免其流入负载侧。无源串联谐振解耦电路如图3所示,LC谐振电路的等效导纳为
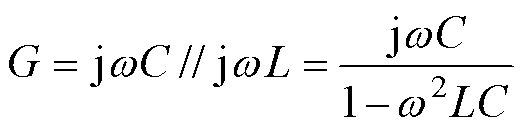 (6)
(6)
式中,L、C分别为无源谐振电路的电感、电容。
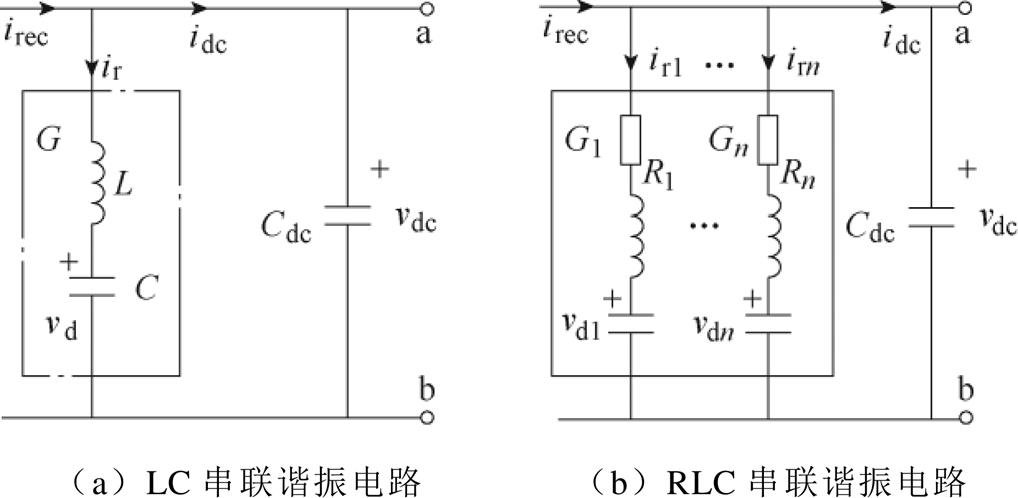
图3 无源串联谐振解耦电路
Fig.3 Passive series resonant decoupling circuit
当w=0,G=0时,说明对于irec中的直流分量idc,谐振电路等同于开路。当w=2wg,G趋于无穷大,说明对于irec中的二次分量ir,谐振电路等同于短路,二次纹波电流被谐振电路旁路。
受此启发,单个解耦模块的控制目的是保证端口输出特性与谐振电路一致,从而起到与谐振电路等价的效果。根据图3a,流入谐振电路的端口电流的传递函数可表示为
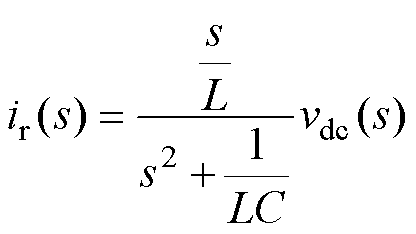 (7)
(7)
据此,解耦模块端口电流参考可选择为
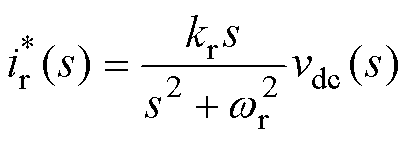 (8)
(8)
式中,kr为谐振增益,kr=1/L;wr为谐振角频率,wr= 2wg。
从式(8)可以看出,提出的虚拟阻抗控制策略只需直流母线电压vdc这一个外部信息,从而保证解耦模块与整流器的控制相互独立,不需要统一的中央控制器,可实现解耦模块即插即用。
类似地,在考虑多个解耦模块之间的功率分配问题时,可借鉴多个无源RLC串联谐振电路的功率分配原则。如图3b所示,在LC电路中串联一个小电阻R,形成RLC电路,则第i支路的等效导纳可表示为
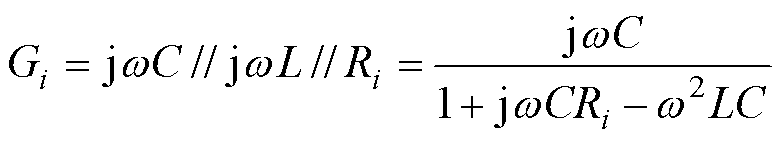 (9)
(9)
式中,Ri(i=1, 2,…, n)为第i谐振支路的功率分配电阻。
对于irec中的直流分量idc,Gi仍等于零,谐振电路开路。对于二次纹波电流ir,谐振电路导纳为
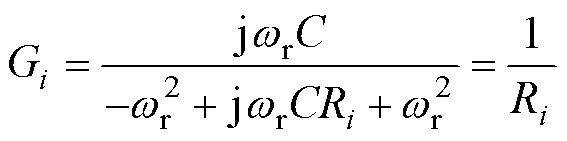 (10)
(10)
此时,串联谐振电路等效为纯电阻电路。则当多个RLC电路并联时,由于端电压相同,各支路电流满足
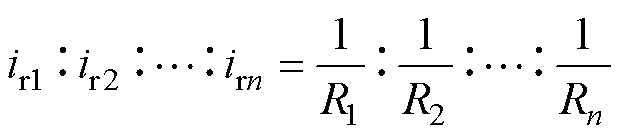 (11)
(11)
式中,iri(i=1, 2,…, n)为第i谐振支路的电流。例如,两个谐振电路并接于直流母线,若功率分配电阻的大小关系满足R1 R2=1
R2=1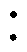 1,则两个电路之间功率均等分配;若R1
1,则两个电路之间功率均等分配;若R1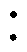 R2=1
R2=1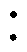 2,则功率分配关系为pd1
2,则功率分配关系为pd1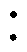 pd2=2
pd2=2 1。
1。
根据上述分析,第i个解耦模块端口电流iri参考可修正为
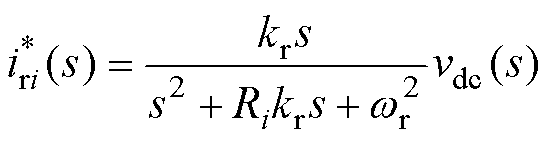 (12)
(12)
由此,在单个解耦电路的虚拟阻抗控制策略基础上,通过增加虚拟功率分配电阻,实现了无通信情况下多个解耦模块的协同控制。
根据上述分析,模块化解耦电路的控制框图如图4所示,采用本文提出的协同控制策略。由于开关器件和线路阻抗等会产生损耗,故在解耦电感电流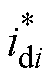 的参考塑造中增加额外项iRi以稳定解耦电容电压。
的参考塑造中增加额外项iRi以稳定解耦电容电压。
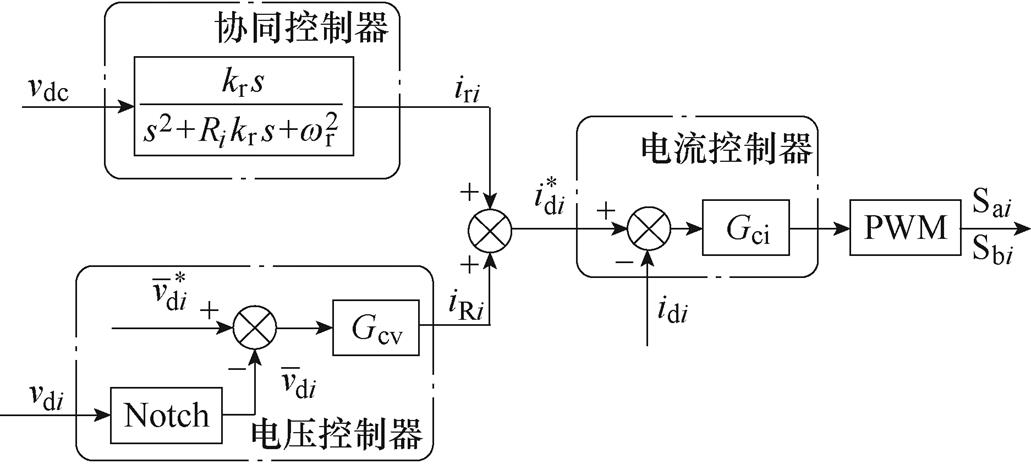
图4 第i解耦模块控制框图
Fig.4 Control block diagram of ith module
本节介绍基于虚拟阻抗的协同控制策略在典型Buck解耦模块中的具体实现,首先讨论了协同控制器设计,阐述了根据解耦电容值分配各模块缓冲功率的功率分配原则;然后介绍了解耦电压/电流控制器的具体参数设计;最后推导了解耦模块在所设计控制器下的输入导纳特性。
协同控制器中,谐振角频率根据wr=2wg(wg= 100π rad/s)确定,同时根据式(12),谐振增益kr=1/L,L一般可取较大电感值(如10~20 mH),故kr可取50~100。
为了自主地实现脉动功率分配,每个解耦模块控制中的虚拟电阻是根据解耦模块电容的大小来选择,即
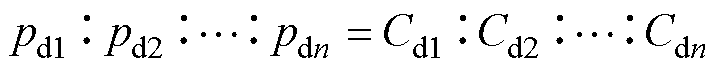 (13)
(13)
式中,pdi(i=1, 2,…, n)为第i个解耦模块缓冲脉动功率;Cdi为第i个解耦模块解耦电容。
根据式(11)和式(13),Ri可以设置为
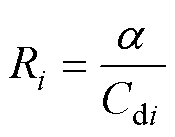 (14)
(14)
式中,a 为一个较小常数,以保证Ri足够小。
为了塑造出第1节分析的解耦模块外特性,需要对解耦电容电压、电感电流进行相应控制。根据图1a所示,Buck型解耦电路的数学模型如下
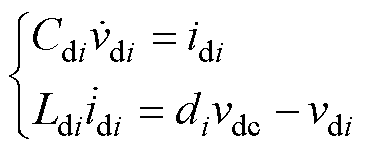 (15)
(15)
式中,di为解耦模块开关管Sai的占空比(Sai、Sbi开关状态互补);Ldi和Cdi分别为第i模块解耦电感和电容;idi和vdi分别为第i模块的电感电流和电容电压。
控制框图如图5所示。根据式(15),可将控制系统的解耦电流内环简化为图5a。则电流内环的闭环传递函数为
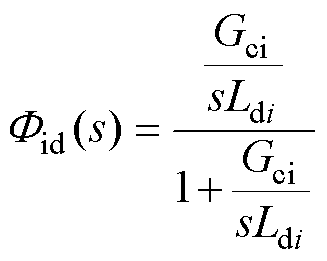 (16)
(16)
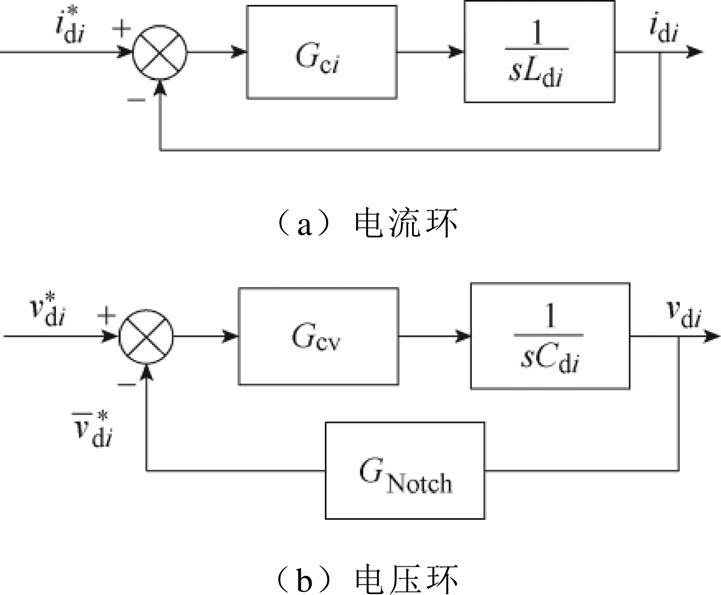
图5 控制框图
Fig.5 Control block diagram
电流控制器Gci采用经典PI控制,则
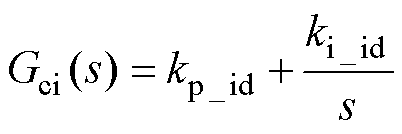 (17)
(17)
将式(17)代入式(16),得到电流内环传递函数为
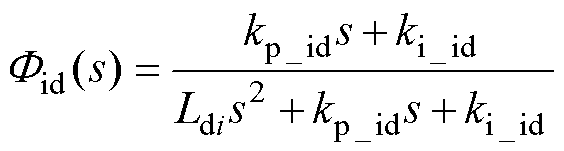 (18)
(18)
采用经典二阶系统的设计方法,可将电流环的PI参数kp_id和ki_id分别设计为
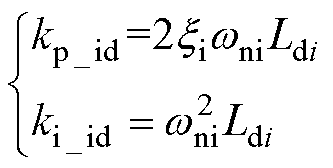 (19)
(19)
式中,wni为电流环的控制带宽,通常为获得较快的电流响应将其设计成高带宽(本文取wni=800 πrad/s);xi为阻尼比,一般选取xi=0.7~0.8。
当电流内环控制的带宽远高于电压外环控制的带宽时,在电压外环控制中可以认为实际解耦电流完全跟踪参考,因此在电压外环控制中电流内环传递函数可简化为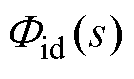 =1。此时,可将控制系统的解耦电压外环简化为图5b。类似地,采用经典PI控制器,电压外环的闭环传递函数为
=1。此时,可将控制系统的解耦电压外环简化为图5b。类似地,采用经典PI控制器,电压外环的闭环传递函数为
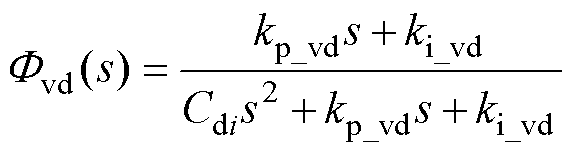 (20)
(20)
采用经典二阶系统的设计方法,可将电压环的PI参数kp_vd和ki_vd分别设计为
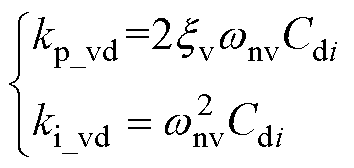 (21)
(21)
式中,wnv为电压环的控制带宽,一般而言,电压环为低控制带宽,故选取wnv=40π rad/s;xv为阻尼比,一般选取xv=0.7~0.8。
为验证控制器性能,以下将推导并分析在所设计的控制器下解耦模块的输入导纳。首先,根据图1a,补充Buck型解耦电路的端口电流方程为
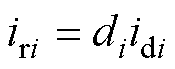 (22)
(22)
根据小信号建模方法,可以得到解耦电流idi到端口电流iri的传递函数为
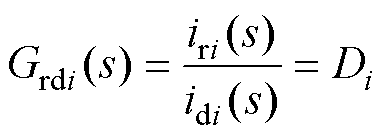 (23)
(23)
式中,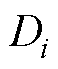 为
为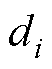 的稳态值。
的稳态值。
结合式(12)、式(18)和式(23),可求得在关联参考方向下,第i解耦模块的输入导纳Gi(s)为
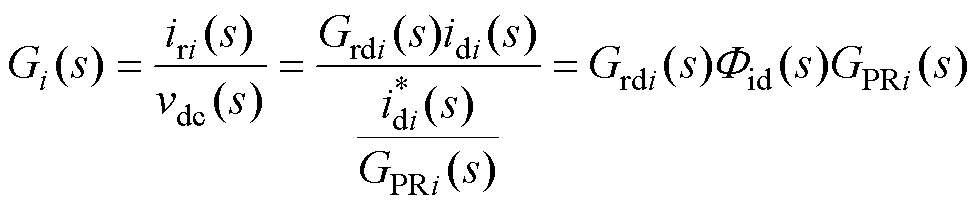 (24)
(24)
其中
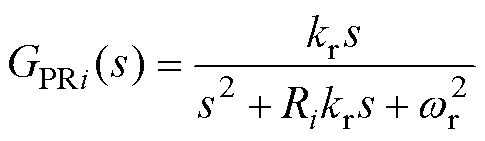
根据参数设计规则,选取kr=50,R1= 5×10-7,wni=800π rad/s,xi=0.7,并定义N=20lgN,将示例解耦模块输入导纳G1(s)的伯德图绘制于图6。可以看出,在频率接近0 Hz时,模块输入导纳G1(s)幅值接近10-5,极小的幅值增益代表着对于直流分量而言,解耦模块相当于开路;而在频率为100 Hz时,模块输入导纳G1(s)=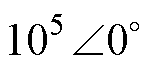 ,代表着此时解耦模块相当于阻值极小的电阻,这与式(10)推导的无源RLC外特性一致,二次脉动电流将全部流进解耦电路,纹波功率将由解耦模块吸收。同时当不同模块虚拟功率电阻Ri满足功率分配比例时,其阻抗增益与虚拟功率电阻Ri成反比,保证流入模块的端口电流按所需比例分配,进而保证分配各解耦模块的缓冲功率。例如,取R1
,代表着此时解耦模块相当于阻值极小的电阻,这与式(10)推导的无源RLC外特性一致,二次脉动电流将全部流进解耦电路,纹波功率将由解耦模块吸收。同时当不同模块虚拟功率电阻Ri满足功率分配比例时,其阻抗增益与虚拟功率电阻Ri成反比,保证流入模块的端口电流按所需比例分配,进而保证分配各解耦模块的缓冲功率。例如,取R1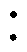 R2
R2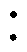 R3=1
R3=1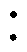 2
2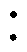 3,计算得到100 Hz时导纳G1=
3,计算得到100 Hz时导纳G1=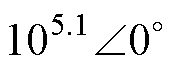 ,G2=
,G2=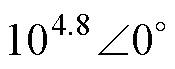 ,G3=
,G3=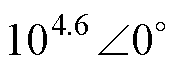 ,即|G1|约为|G2|的2倍、|G3|的3倍,符合第1节的理论分析。
,即|G1|约为|G2|的2倍、|G3|的3倍,符合第1节的理论分析。
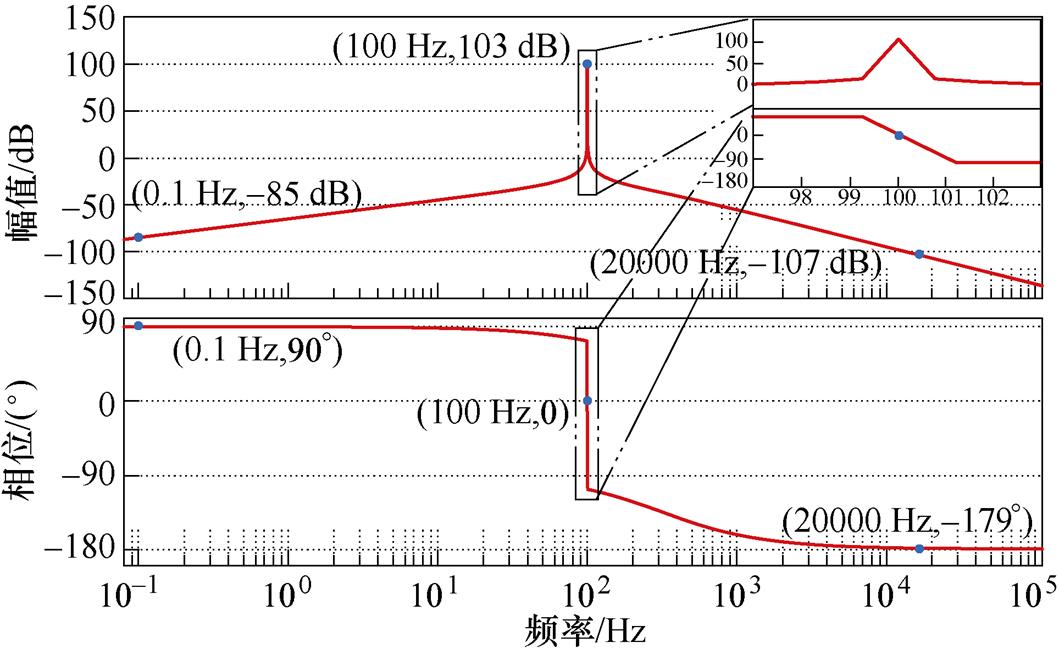
图6 输入导纳伯德图
Fig.6 Bode diagram of input conductance
为了验证所提控制策略的有效性,搭建了如图7所示电路的实验装置,包括一个单相电压源型整流电路、两个Buck解耦模块。电路主要参数如下:网侧电压vg=110Vrms,直流母线电压为400 V,解耦电容电压平均值为300 V,直流侧输出功率为800 W,网侧滤波电感Lg=3 mH,输出滤波电容Cdc=20 mF,开关频率fs=20 kHz。
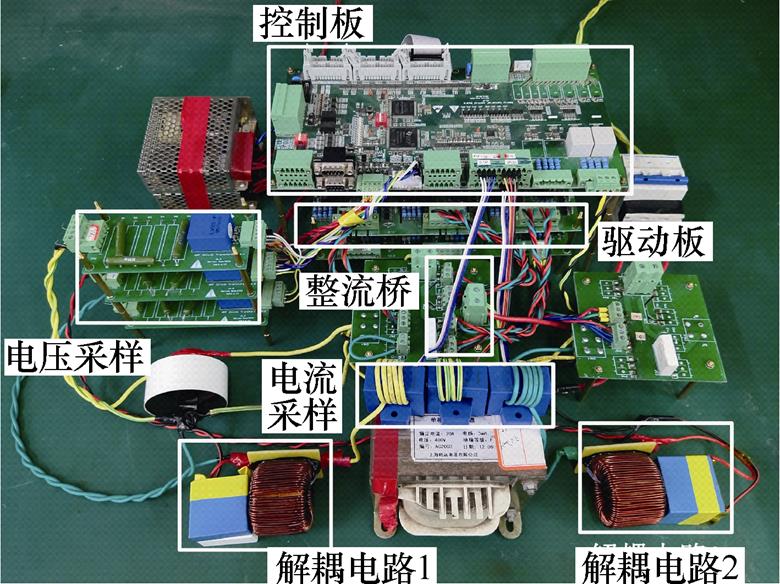
图7 实验装置
Fig.7 Diagram of experimental setup
整体的控制框图如图8所示,整流器采用经典的电压外环、电流内环控制,其中电压外环控制的是母线电压平均值以实现平均功率控制。解耦电路采用提出的协同控制策略,控制器主要参数如下:wr=200p rad/s,kr=50,α=5×10-7。
实验测试分为四组:第一组为单解耦模块实验;第二组为相同解耦电容双解耦模块实验;第三组为不同解耦电容双解耦模块实验;第四组为功率动态变化实验。
图9为解耦模块不工作时整流器的相关实验波形,包括网侧电压vg、网侧电流ig和直流母线电压vdc的波形。网侧电流与网侧电压同相,直流母线电压平均值稳定在400 V,但直流母线电压波动Dv高达280 V,不满足整流器输出电压的纹波要求。
图10为仅采用单个解耦模块(解耦电容为50 mF,最大解耦功率约为620 var)的实验波形,包括网侧电压vg、网侧电流ig、直流母线电压vdc和解耦电容电压vd的波形。对比图9可以看出,解耦电路工作后,直流母线电压纹波大大减小,但由于系统中二次纹波功率为800 var,无法实现完全解耦,母线电压仍然存在较大的纹波(约为80 V)。
图11为采用两个等额定功率解耦模块(解耦电容均为50 mF)的实验波形。图11a为整流波形,包括网侧电压vg、网侧电流ig和直流母线电压vdc的波形。t时刻前,解耦模块未接入,直流母线电压波动较大;t时刻时,同时接入两个解耦模块,可以看出,直流母线电压波动明显减小且最终稳定在400 V,直流母线电压波动Dv<20 V(电压纹波<5%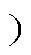 ,实现了良好的解耦效果。解耦模块相关波形如图11b所示,包括解耦电容电压vd1、vd2和电感电流id1、id2波形,两个解耦模块的工作状态基本一致,实现两个模块功率按1
,实现了良好的解耦效果。解耦模块相关波形如图11b所示,包括解耦电容电压vd1、vd2和电感电流id1、id2波形,两个解耦模块的工作状态基本一致,实现两个模块功率按1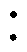 1均分。
1均分。
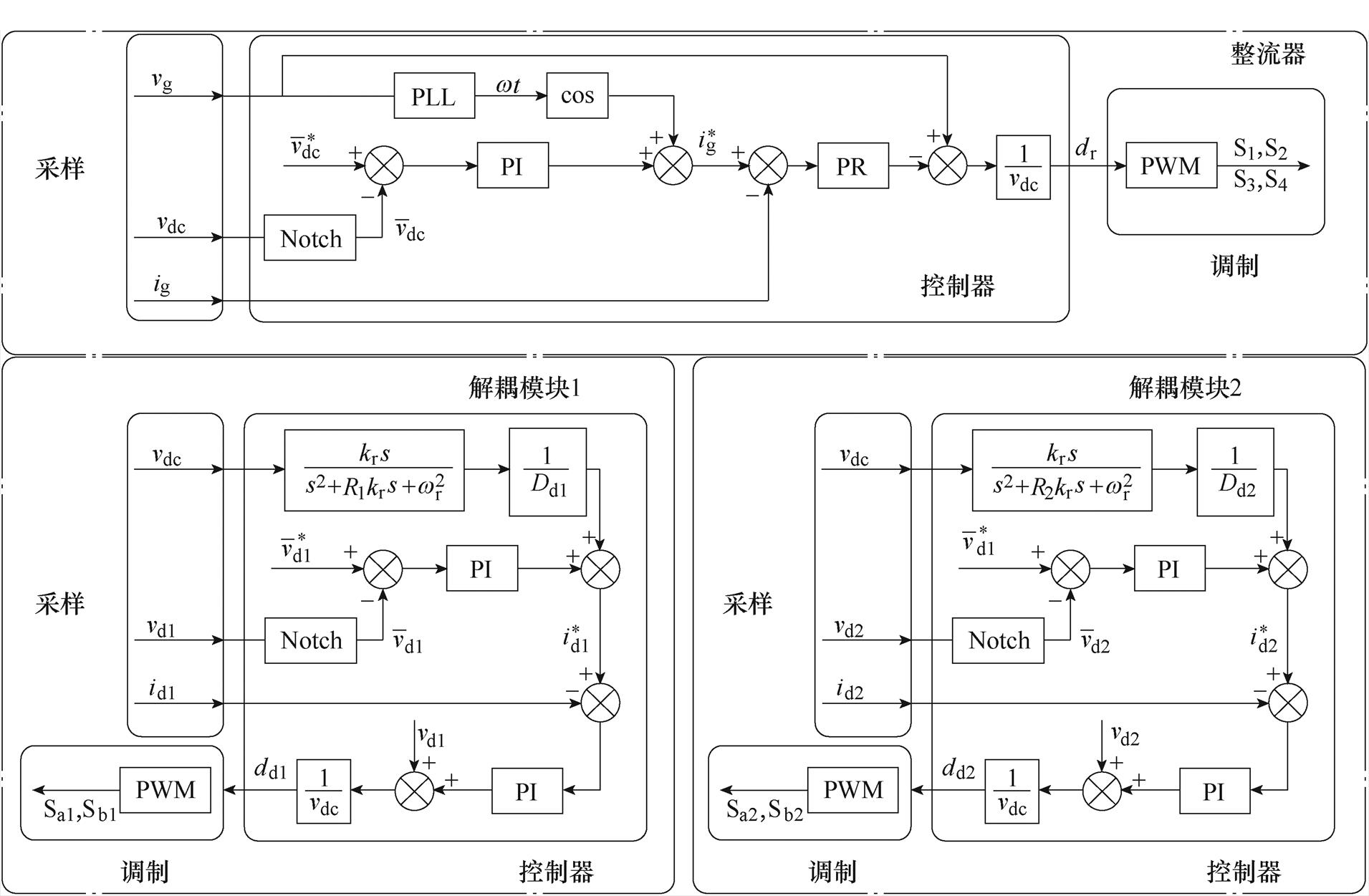
图8 系统控制框图
Fig.8 System control block diagram
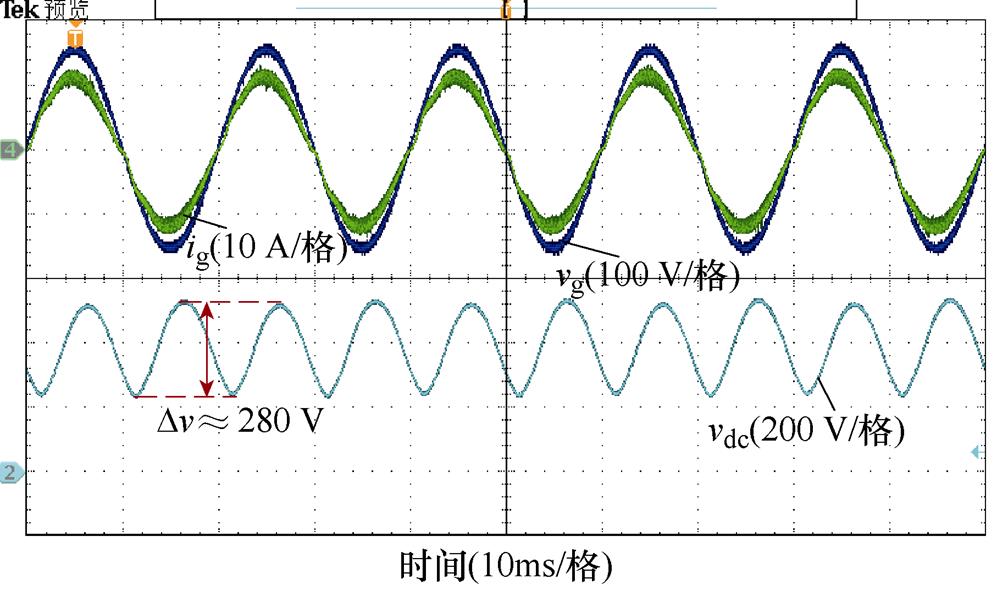
图9 仅整流器工作实验波形
Fig.9 Experimental waveforms of rectifier operation
图10 仅采用单个解耦电路实验波形
Fig.10 Experimental waveforms of adopting a single decoupling module
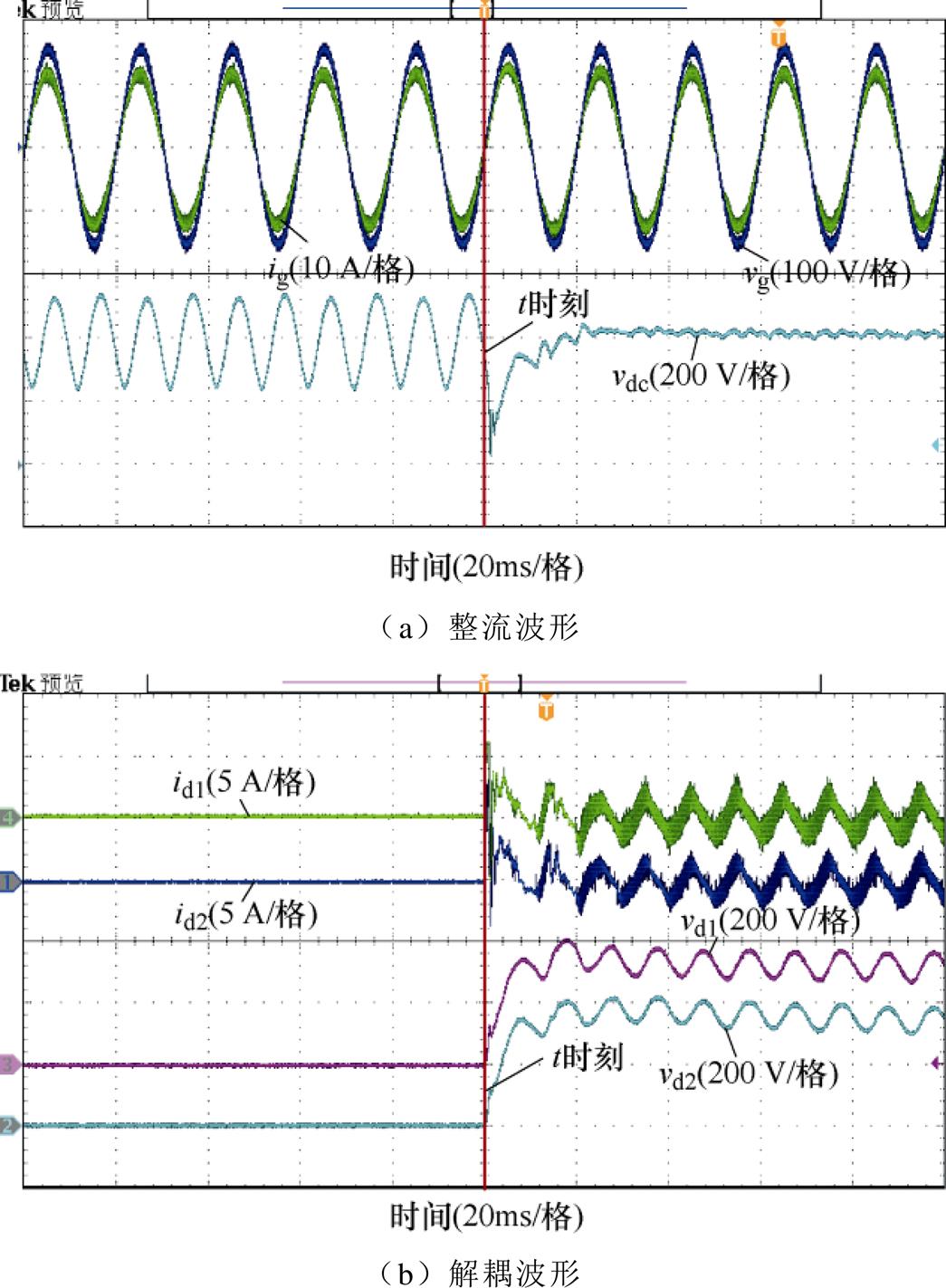
图11 相同解耦电容双解耦模块动态实验波形
Fig.11 Dynamic experimental waveforms of adopting two equally rated power decoupling modules
图12为采用两个不等额定功率解耦模块(模块1的解耦电容为60 mF,最大解耦功率约为750 var;模块2的解耦电容为30 mF,最大解耦功率约为370 var)的实验波形。同样在t时刻接入两个解耦模块,由图12a可知,直流母线电压波动明显减小并最终稳定在400 V,直流母线电压波动Dv也小于20 V,实现了良好的解耦效果。解耦模块相关波形如图12b所示,包括解耦电容电压vd1、vd2和电感电流id1、id2波形,稳态下解耦电压vd1=vd2,而解耦电流id1≈2id2,实现了两个模块功率按2 1分配。
1分配。
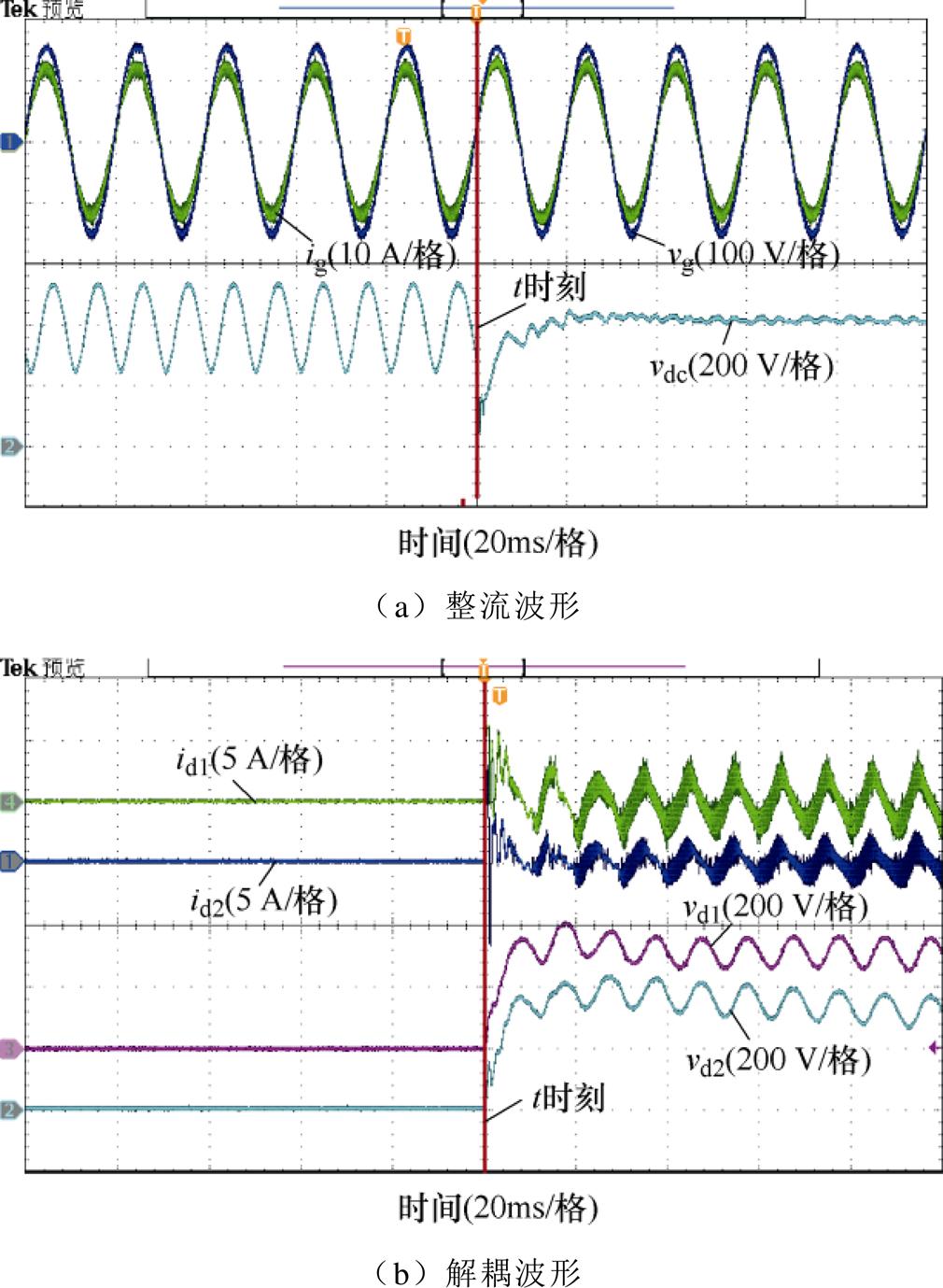
图12 不同解耦电容双解耦电路实验波形
Fig.12 Dynamic experimental waveforms of adopting unequally rated decoupling modules
图13展示了功率突然增大的动态变化实验波形,实验中采用两个等额定功率解耦模块(解耦电容均为50 mF)。如图13a所示,t1时刻前,负载功率为500 W,仅采用一个解耦模块即可实现完全解耦,直流母线电压波动Dv<20 V;t1时刻时(见图13b存在较大波动80 V,无法实现完全解耦;t2时刻时所示),输出功率增大到1 000 W,由于二次脉动功率超出单个解耦模块的极限628 var,直流母线电压(见图13c)接入第二个解耦模块,经过短暂调节,直流母线电压略微波动后进入稳态,波动值Dv<20 V,实现完全解耦。
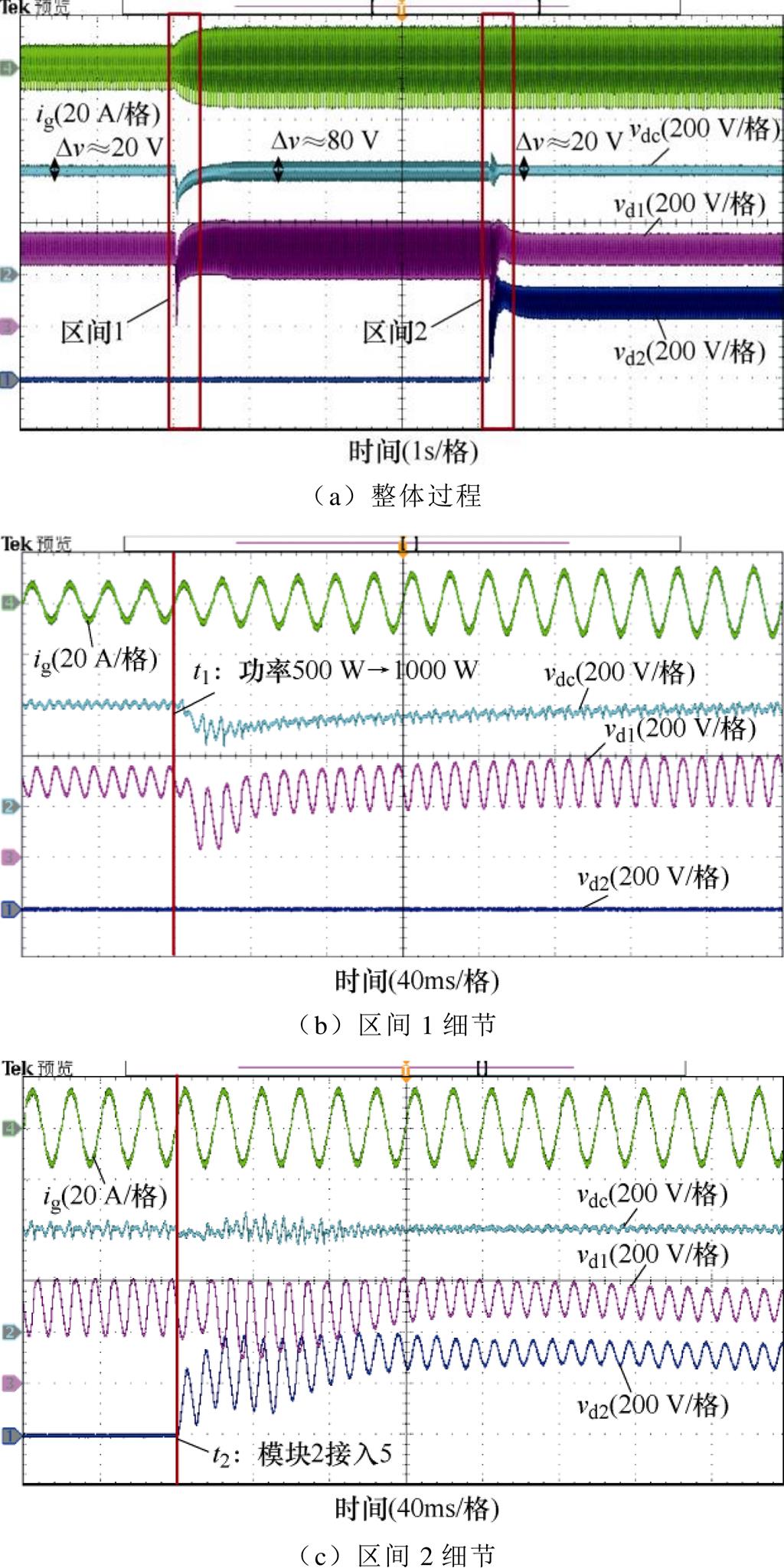
图13 功率增大动态变化实验波形
Fig.13 Experimental waveforms of forward dynamic power change
图14为功率突然减小的实验波形,如图14a所示,t1时刻前,直流侧输出功率为1 000 W,采用两个电路进行解耦,直流母线电压波动Dv<20 V;t1时刻时(见图14b),直流侧输出功率减小到500 W,直流母线电压和解耦电压波动明显减小,此时脉动功率也减小,这时不需要两个模块进行解耦;t2时刻时(见图14c),切除一个解耦模块,经过短暂波动,直流母线电压进入稳态,波动值仍为Dv<20 V;而解耦电压vd1经调节后波动增大,后进入稳态实现稳定解耦。

图14 反向功率动态变化实验波形
Fig.14 Experimental waveforms of inverse dynamic power change
本文提出一种基于虚拟阻抗的解耦模块控制策略,该方法只依赖直流母线电压的纹波信息进行解耦控制,实现了单个解耦模块的即插即用控制;在此基础上,通过增加虚拟功率分配电阻的方法实现了各模块解耦功率按照解耦电容比例进行分配,解决了多个解耦模块协同工作时的控制问题。所提出的控制无需解耦模块与主电路交互电网信息,也无需解耦模块间的相互通信,从而避免使用集中的中央控制器和昂贵的实时通信设备。
实验结果表明:
1)两个解耦能力相同的解耦模块工作时,各模块缓冲功率按照解耦电容进行分配(满足1 1分配关系),母线电压纹波被有效抑制(Dvdc/Vdc<5%)。
1分配关系),母线电压纹波被有效抑制(Dvdc/Vdc<5%)。
2)两个解耦能力不同的解耦模块工作时,各模块缓冲功率按照解耦电容进行分配(满足2 1分配关系),母线电压纹波被抑制到允许范围。
1分配关系),母线电压纹波被抑制到允许范围。
3)动态功率变化实验表明:提出的方法能够实现解耦模块灵活的插入和切除,验证了解耦模块在无通信下的即插即用性能。
4)除暂态调节过程外,整流器输入电流满足性能指标(PF=0.99, THD=3.6%)。
参考文献
[1] 周孝信, 鲁宗相, 刘应梅, 等. 中国未来电网的发展模式和关键技术[J]. 中国电机工程学报, 2014, 34(29): 4999-5008.
Zhou Xiaoxin, Lu Zongxiang, Liu Yingmei, et al. Development models and key technologies of future grid in China[J]. Proceedings of the CSEE, 2014, 34(29): 4999-5008.
[2] 钱照明, 张军明, 吕征宇, 等. 我国电力电子与电力传动面临的挑战与机遇[J]. 电工技术学报, 2004, 19(8): 10-22.
Qian Zhaoming, Zhang Junming, Lü Zhengyu, et al. Challenge and opportunity for power electronics and electrical drive in China[J]. Transactions of China Electrotechnical Society, 2004, 19(8): 10-22.
[3] 廖志凌, 阮新波. 半导体照明工程的现状与发展趋势[J]. 电工技术学报, 2006, 21(9): 106-111.
Liao Zhiling, Ruan Xinbo. Present situation and development trend of semiconductor lighting Engin- eering[J]. Transactions of China Electrotechnical Society, 2006, 21(9): 106-111.
[4] 刘晓飞, 张千帆, 崔淑梅. 电动汽车V2G技术综述[J]. 电工技术学报, 2012, 27(2): 121-127.
Liu Xiaofei, Zhang Qianfan, Cui Shumei. Review of electric vehicle V2G technology[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 121-127.
[5] 毛玲, 张钟浩, 赵晋斌, 等. 车-桩-网交融技术研究现状及展望[J]. 电工技术学报, 2022, 37(24): 6357- 6371.
Mao Ling, Zhang Zhonghao, Zhao Jinbin, et al. Research status and prospects of fusion technology of vehicle-charging pile-power grid[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6357- 6371.
[6] Wang Huai, Liserre M, Blaabjerg F. Toward reliable power electronics: challenges, design tools, and opportunities[J]. IEEE Industrial Electronics Magazine, 2013, 7(2): 17-26.
[7] 潘启军, 黄垂兵, 邓晨, 等. 电解电容与薄膜电容的对比分析[J]. 海军工程大学学报, 2014, 26(2): 5-9.
Pan Qijun, Huang Chuibing, Deng Chen, et al. Comparative analysis of electrolytic capacitor and thin film capacitor[J]. Journal of Naval University of Engineering, 2014, 26(2): 5-9.
[8] Sun Yao, Liu Yonglu, Su Mei, et al. Review of active power decoupling topologies in single-phase systems[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4778-4794.
[9] Zhang Jianhua, Ding Hao, Wang Baocheng, et al. Active power decoupling for current source con- verters: an overview scenario[J]. Electronics, 2019, 8(2): 197.
[10] 李红波, 张凯, 赵晖, 等. 基于功率解耦的高功率密度单相整流器[J]. 电工技术学报, 2011, 26(增刊1): 77-82.
Li Hongbo, Zhang Kai, Zhao Hui, et al. A high power density single rectifier with power decoupling function[J]. Transactions of China Electrotechnical Society, 2011, 26(S1): 77-82.
[11] 王立乔, 崔舒敏, 陈梅. 功率解耦型无电解电容 PFC电路并联补偿控制[J]. 电工技术学报, 2019, 34(3): 516-528.
Wang Liqiao, Cui Shumin, Chen Mei. Parallel compensation control of power factor corrector without electrolytic capacitor by power decoup- ling[J].Transactions of China Electrotechnical Society, 2019, 34(3): 516-528.
[12] 王舒, 阮新波, 姚凯, 等. 无电解电容无频闪的 LED驱动电源[J]. 电工技术学报, 2012, 27(4): 173- 178.
Wang Shu, Ruan Xinbo, Yao Kai, et al. A novel LED driver without electrolytic capacitor and flicker[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 173-178.
[13] 彭寥廓, 陈艳慧. 单相全桥离网逆变器输出侧功率解耦电路研究[J]. 电气技术, 2022, 23(1): 42-48, 55.
Peng Liaokuo, Chen Yanhui. Research on a single- phase full-bridge off-grid inverter with active power decoupling circuit at output side[J]. Electrical Engin- eering, 2022, 23(1): 42-48, 55.
[14] Liu Yonglu, Zhang Wanlu, Sun Yao, et al. Review and comparison of control strategies in active power decoupling[J]. IEEE Transactions on Power Elec- tronics, 2021, 36(12): 14436-14455.
[15] 童时中. 模块化的概念与定义[J]. 电力技术, 1995, 4(4): 22-25.
Tong Shizhong. Concept and definition of modulari- zation[J]. Electric Power Technology, 1995, 4(4): 22-25.
[16] 丁国臣, 张芳, 杨晓霞, 等. 一种AC/DC开关电源的模块化设计[J]. 电工技术, 2021(8): 69-71, 74.
Ding Guochen, Zhang Fang, Yang Xiaoxia, et al. A modular design of AC/DC switching power supply[J]. Electric Engineering, 2021(8): 69-71, 74.
[17] 王要强, 李娜, 赵朝阳, 等. 一种新型多电平逆变器及其模块化分析[J]. 电工技术学报, 2022, 37(18): 4676-4687.
Wang Yaoqiang, Li Na, Zhao Chaoyang, et al. A new type of multilevel inverter and its modular analysis[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4676-4687.
[18] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049.
Yang Jun, Hou Junhao, Liu Yawei, et al. Distributed cooperative control method and application in power system[J]. Transactions of China Electrotechnical Society, 2021,36(19): 4035-4049.
[19] 张昊, 李昱, 尹亚飞, 等. 直流微电网集成式高品质协同控制策略[J]. 电工技术学报, 2022, 37(3): 697-706.
Zhang Hao, Li Yu, Yin Yafei, et al. An integrated high-quality cooperative control strategy of DC microgrids[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 697-706.
[20] Li Sinan, Lee A T L, Tan S C, et al. Plug-and-play voltage ripple mitigator for DC links in hybrid AC-DC power grids with local bus-voltage control[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 687-698.
[21] Mutovkin A, Yuhimenko V, Mellincovsky M, et al. Control of direct voltage regulated active DC-link capacitance reduction circuits to allow plug-and-play operation[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(8): 6527-6537.
[22] Li Sinan, Qi Wenlong, Tan S C, et al. A general approach to programmable and reconfigurable emulation of power impedances[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(1): 259-271.
[23] Lin Jun, Weiss G. An indirect approach to control an active capacitor[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2898-2906.
Abstract As an important development direction of active power decoupling (APD) technology, the modularization of active decoupling circuits has the advantages of standardization, independence, and versatility. However, the existing control strategies can only be applied to individual decoupling modules without considering the power distribution problem among multiple decoupling modules. Hence, a virtual impedance- based cooperative control strategy for multiple decoupling modules is proposed.
Firstly, the impedance characteristic of a passive LC resonance circuit is analyzed: for the DC component, the resonance circuit is equivalent to an open circuit; for the double-line frequency component, it is equivalent to a short circuit, and the resonance circuit bypasses the ripple current. When the external characteristic of individual decoupling modules is controlled to be consistent with the passive LC resonance circuit, the ripple power is well buffered by decoupling modules. Meanwhile, the control of decoupling modules is independent because only one external information is needed. No unified central controller is needed, and the plug-and-play function is realized.
Secondly, when considering the power distribution problem between multiple decoupling modules, the impedance characteristic of multiple passive RLC resonance circuits can be utilized. For the DC component, the RLC resonance circuit is still equivalent to an open circuit; the double-line frequency component is equivalent to a purely resistive circuit, and the ripple current flowing through each RLC resonance circuit is inversely proportional to its branch resistor. Thus, adding virtual power distribution resistors can realize the cooperative control of multiple decoupling modules without real-time communication between decoupling modules.
Then, this paper introduces the concrete implementation of the proposed cooperative control strategy with typical Buck-type decoupling modules. The controller design is discussed, including the virtual power distribution resistor selection and the parameters of the decoupling voltage\current controller.
Finally, a series of experiments are conducted. When two same decoupling modules work, the buffer power of each module is distributed according to the decoupling capacitance (satisfying the 1 1 distribution relationship), and the bus voltage ripple is effectively suppressed (Dvdc/Vdc<5%
1 distribution relationship), and the bus voltage ripple is effectively suppressed (Dvdc/Vdc<5% . When two different decoupling modules work, the buffer power of each module is distributed according to the decoupling capacitance (satisfying the 2
. When two different decoupling modules work, the buffer power of each module is distributed according to the decoupling capacitance (satisfying the 2 1 distribution relationship), and the bus voltage ripple is also suppressed. The dynamic power variation experiments show that the proposed method can achieve flexible insertion and removal of decoupling modules, which verifies the plug-and-play performance of decoupling modules without communication. Except for the transient regulation process, the rectifier input current meets the performance index (PF=0.99, THD=3.6%).
1 distribution relationship), and the bus voltage ripple is also suppressed. The dynamic power variation experiments show that the proposed method can achieve flexible insertion and removal of decoupling modules, which verifies the plug-and-play performance of decoupling modules without communication. Except for the transient regulation process, the rectifier input current meets the performance index (PF=0.99, THD=3.6%).
According to the theoretical and experimental results, the proposed virtual impedance-based control strategy for decoupling modules relies only on the ripple information of the DC bus voltage. The decoupling power of each module is distributed in proportion to its decoupling capacitance. The problem of cooperative control is solved. The proposed control does not require the decoupling modules to interact with the main circuit for grid information, nor does it require the decoupling modules to communicate with each other. Thus, using a centralized central controller and expensive real-time communication equipment is avoided.
keywords:Single-phase converter, active power decoupling, cooperative control, modularization
DOI: 10.19595/j.cnki.1000-6753.tces.230363
中图分类号:TM46
中南大学创新驱动人才计划(2023CXQD020)、长沙市杰出创新青年培养计划(kq2206013)和省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学)开放课题基金(EERIKF2022006)资助项目。
收稿日期 2023-03-27
改稿日期 2023-05-08
刘永露 男,1989年生,博士,副教授,硕士生导师,主要研究方向为电力电子技术、可再生能源变换器。E-mail: liuyonglu@csu.edu.cn
王 辉 男,1984年,博士,副教授,博士生导师,主要研究方向为矩阵变换器、DC-DC变换器。E-mail: wanghuicp9@csu.edu.cn(通信作者)
(编辑 陈 诚)