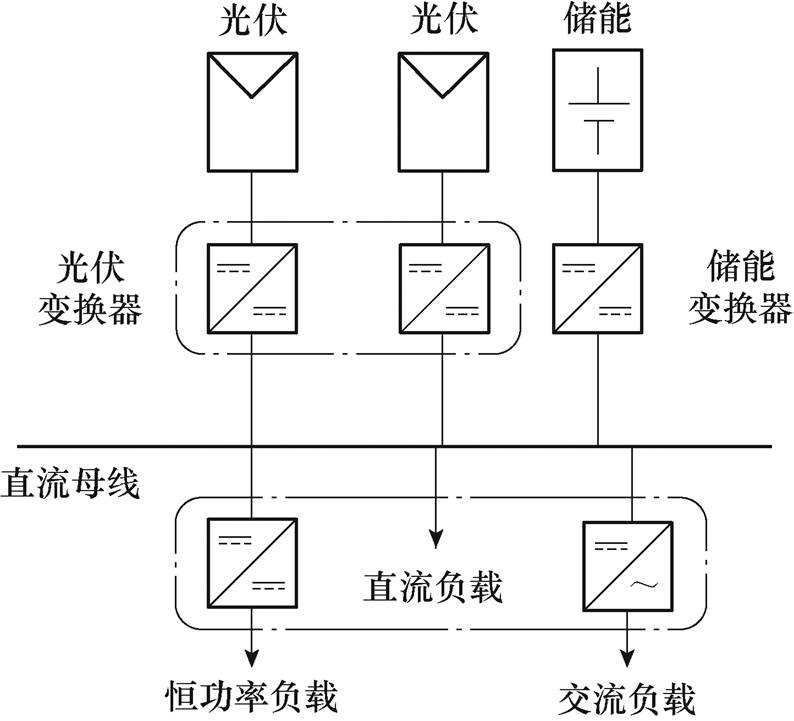
图1 独立直流微电网结构
Fig.1 Structure of stand-alone DC microgrid
摘要 在独立直流微电网中，储能系统（ESSs）和光伏（PV）是主要能源。在极端条件下，储能和光伏变换器需要进行工作模式切换以协调功率，为了优化切换性能，该文提出一种基于直流总线信号（DBS）的自主平滑模式切换控制策略，用于多个光伏电源和ESS的无通信协同工作，提高了系统的可靠性。针对多模式切换过程中的抖振和死锁问题，所提出的控制策略利用具有反馈抑制机制的PI控制器实现了在饱和与激活之间无缝切换。同时，为了进一步提升光伏能量的利用率，所提出的控制策略充分考虑了ESS的荷电状态（SOC），并使光伏电源能够直接参与直流母线电压的调节。此外，还对模式切换时间与控制器参数的设计进行了详细的分析建模，以优化模式切换性能。最后，建立了一个小型独立直流微电网实验系统，以验证所提出的直流微电网控制方法的可行性。
关键词：自主控制方案 直流微电网 储能系统（ESS） 光伏（PV）电力系统 电力管理
微电网作为一种能够有效结合可再生能源（Renewable Energy Sources, RES）、储能系统（Energy Storage System, ESS）和本地负载的方案，由于其具有灵活性和可扩展性的优势而备受关注[1-2]。与交流微电网相比，直流微电网具有更高的效率、更低的实施成本和更高的可靠性等优点[3-4]。独立直流微电网的性能在很大程度上取决于电源管理策略[5]。通常，小型独立直流微电网由ESS、RES和各种现代负载（如照明、电动汽车和消费电子产品）组成，独立直流微电网结构如图1所示。在独立的直流微电网系统中，ESS和光伏（Photovoltaic, PV）电源是主要的能源。然而，蓄电池提供的直流母线电压调节能力是有限的，并且会随着光伏渗透率的增加而降低[6]。此外，切换过程中的瞬态问题在独立直流微电网中尤其具有挑战性，这可能会导致控制装置之间的错误切换[7]。因此，直流微电网面临的关键挑战如下：①直流母线电压调节；②光伏发电-储能协调；③模式切换瞬态性能。
图1 独立直流微电网结构
Fig.1 Structure of stand-alone DC microgrid
许多研究集中于直流微电网的模式切换[8-9]。在通信关键型微电网中，分布式能源由不同位置的变换器连接，而参考功率和模式管理通过通信进行调度[10-11]，因此稳定和即时的通信至关重要。图2是微电网的控制策略，其中每个模式的控制回路由模式切换信号选择。然而，这增加了额外通信电路的成本，不适合偏远地区的小型直流微电网。
下垂控制是实现一级控制的常见分散解决方案，其中母线电压用于传达微电网的负载条件[12-13]。除了下垂控制之外，基于直流总线信号（DC Bus Signaling, DBS）的控制策略是另一种有效的直流微电网管理方法，该控制策略通过检测直流母线电压信号来保持系统的可靠性。此外，直流母线电压根据系统中电源和负载的功率消纳而变化[14]。
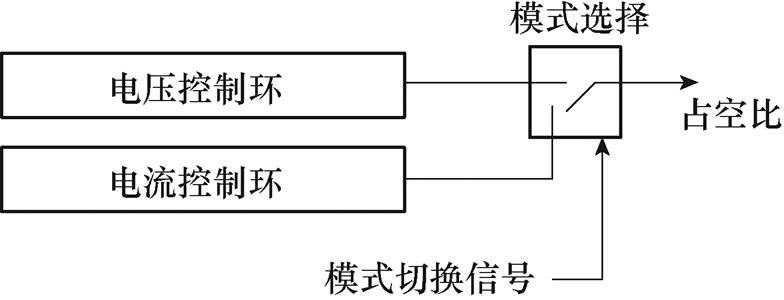
图2 传统模式切换方案
Fig.2 Concept of the conventional mode switching scheme
然而，这种方法在判断操作模式时可能会出现抖振现象[9]。在文献[15]中，基于DBS的控制方法与传统抗饱和积分策略相结合，用于自主模式切换。然而，M. A. A. Murad和F. Milano已经证明了在这些模型中可能会发生死锁现象[16]。在文献[17]中，考虑了电池储能（Battery Energy Storage, BES）系统的自主模式切换。然而，没有考虑光伏变换器的控制策略。
为了解决与模式切换相关的问题，本文提出了一种基于DBS方法的小型独立直流微电网系统的控制方案。该控制器的优点包括：①实现操作模式之间的无缝转换；②各单元无通信自主控制，减少了对通信的依赖，提高了系统的可靠性；③所提出的控制方案考虑了荷电状态（State of Charge, SOC）和储能的存储容量，并使光伏电源能够参与调节直流母线电压，增加了光伏能源的利用率。
本文首先介绍了独立直流微电网系统和不同电压区域的运行模式。然后，提出了具有抗饱和积分措施的控制方案。此外，还讨论了稳态和瞬态性能。最后，通过仿真和实验结果，验证了其可行性和有效性。
本文研究的小型独立直流微电网系统包括两个用于光伏阵列的PV变换器、一个BES变换器和本地负载；提出了一种采用DBS的电源管理方案，以保持系统的功率平衡和稳定运行。本质上，DBS方法属于主从控制策略。主模块工作在电压控制模式，主要负责直流母线电压调节；辅助模块在电流控制模式下工作，确保准确的电流输入或输出。
每个PV变换器有两种控制模式：最大功率点跟踪（Maximum Power Point Tracking, MPPT）控制和高直流母线电压调节（High DC bus Voltage Regulation, HDVR）。BES变换器有两种控制模式：恒压（Constant Voltage, CV）控制和低直流母线电压调节（Low DC bus Voltage Regulation, LDVR）。其中，HDVR和LDVR工作在电压控制模式，而MPPT和CV工作在电流控制模式。
在该方案中，系统的操作可分为模式Ⅰ（MPPT和LDVR模式，BES放电）、模式Ⅱ（MPPT与LDVR模式，BES充电）和模式Ⅲ（HVDR与CV模式，BES充电）三类，如图3所示。直流母线电压被用作信息载体，这三种操作模式由不同的直流母线电压电平标识。
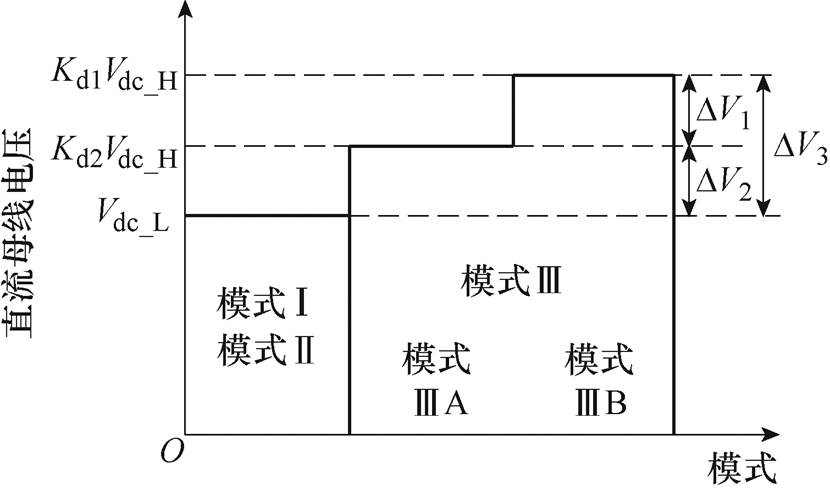
图3 直流母线电压运行区域
Fig.3 DC bus voltage regions
不同的直流母线电压参考值（Vdc_L、Kd1Vdc_H和Kd2Vdc_H）指示不同的操作模式。DV1、DV2和DV3是不同模式之间的电压差。第i个PV变换器的直流母线电压的参考值用KdiVdc_H标记。Kdi为直流母线电压检测的分散系数，它取决于电压差和采样电路参数的选择。Vdc为实际直流母线电压。第3节将描述Vdc_L、Kd1Vdc_H和Kd2Vdc_H的选择。系统的工作模式详述如下：
模式Ⅰ：当光伏发出的功率小于本地负载需求时，系统工作于模式Ⅰ。此时，直流母线电压由储能放电调节。光伏阵列的DC-DC变换器工作在MPPT模式，BES变换器工作在LDVR模式。
模式Ⅱ：当光伏发出的功率大于本地负载需求，且BES没有充满电时，系统工作于模式Ⅱ。此时，直流母线电压Vdc由BES变换器充电调节。用于光伏阵列的DC-DC变换器都在MPPT模式下工作，BES变换器在LDVR模式下工作。
模式Ⅲ：当光伏发出的功率大于本地负载需求，且BES的电荷状态足够高时，系统工作于模式Ⅲ。此时，直流母线电压由PV变换器调节。由于在该模式下PV阵列的最大功率大于本地负载需求，因此其中一个PV变换器必须将母线电压保持在Kd1Vdc_H或Kd2Vdc_H，这分别对应于模式ⅢB和模式ⅢA。此时，另一个PV变换器充当辅助变换器，根据负载需求以MPPT或待机模式运行。
如上所述，拟建微电网中的每个变换器都有两种运行模式，功率变换器功能见表1。通常，系统在模式Ⅰ和模式Ⅱ下工作，以充分利用光伏功率、BES变换器调节直流母线电压。然而，当BES充满电时，BES变换器不能再充电调节直流母线电压，为了最大限度利用光伏能量，此时，两个PV变换器中的一个用于维持直流母线电压，以防止BES过度充电，同时减小光伏弃光率。当光伏发出的功率小于本地负载需求且储能SOC低于安全阈值时，系统将进入停机模式，确保系统的安全可靠运行。
表1 功率变换器功能
Tab.1 Functions of power converters
变换器模式Ⅰ模式Ⅱ模式ⅢA模式ⅢB BESLDVR (放电)LDVR (充电)CVCV PV1MPPTMPPTMPPTHDVR PV2MPPTMPPTHDVR待机
本文的重点是提出一种基于DBS的小型独立直流微电网控制方案。本研究使用双向Buck-Boost变换器来实现所提出的控制方法。电压外环的PI补偿器根据运行模式在饱和与激活之间切换。因此，PI补偿器需要一个抗饱和积分机制。
在DBS控制策略中，部分PI补偿器的外部控制环路达到极限，反馈回路被破坏。传统的抗饱和积分控制是通过固定幅值的限幅器实现的，这可能会导致死锁和抖振现象[16]。为了解决这些问题，本文结合反馈抑制机制提出了新的控制方案。
图4显示了基于反馈抑制的PI控制器的控制框图。该系统具有由控制器的输出y(t)和限幅器的输出v(t)的差产生的额外反馈路径。信号es(t)通过反馈系数Ka被馈送到积分器的输入端。
若误差er(t)是常值E，则
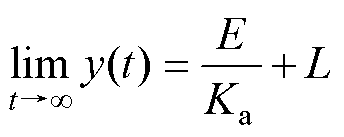（1）
式中，L为限幅器的限幅值。
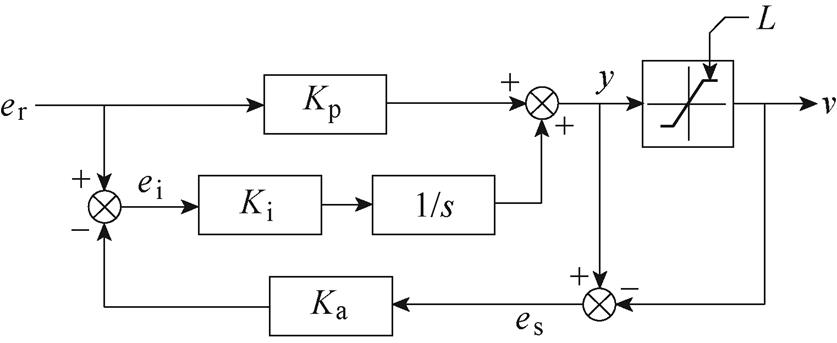
图4 基于反馈抑制的抗饱和积分控制器
Fig.4 PI controller with back-calculation
若误差er(t)=At+B，则
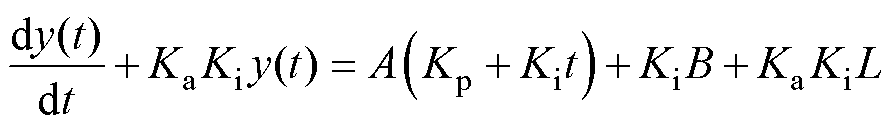（2）
式中，Kp和Ki分别为控制器的比例系数和积分系数。
求解式（2）的一阶微分方程可以得到
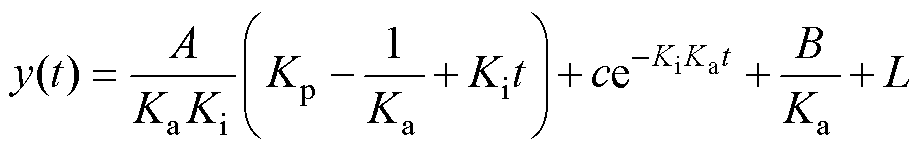（3）
式中，c为任意常数，由初始条件确定。
通过以上分析可以看出，基于反馈抑制机制，增加了额外的反馈路径，从而加快了控制器的退饱和速度，并能够改善传统模式切换下的死锁和抖振现象，实现不同模式之间的自主平滑切换。通过反馈抑制机制的动态过程可以获得模式切换时间。
2.2.1 光伏变换器的控制方法
拟议的光伏变换器的控制方案示意图如图5所示。为了便于分析，PV1变换器和PV2变换器的原理统一显示在图5中，其中PI1i和PI2i分别为第i个PV变换器的高直流母线电压控制器和内部电流控制器，Kp1i和Kp2i分别为PI1i和PI2i控制器的比例系数，Ki1i和Ki2i分别为PI1i和PI2i控制器的积分系数，Ka1i为PI1i控制器的反馈系数。y1i和e1i分别为PI1i控制器的输出和输入误差值。第i个光伏阵列的端电压用VPVi标记，电流IPVi为第i个光伏阵列的输出电流，IMPPTi为第i个光伏阵列的最大功率点电流。Di为第i个光伏变换器的占空比。此后，下标i表示第i个光伏阵列的变量。
所提出的控制方案由三个控制器组成，运行模式取决于图5中限幅器的状态。高直流母线电压控制器的输出通过调节KdiVdc_H和Vdc之间的差或限幅器IMPPTi的幅值（MPPTi控制器的输出）来产生参考电流。电流调节器通过调节电流参考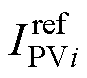
和光伏阵列电流IPVi之间的差来产生占空比Di。值得注意的是，由于高直流母线电压控制器的带宽比MPPT调节器的带宽快，因此当功率发生波动时，高直流母线电压控制首先生效。所有模式的等效控制回路都基于平均电流控制。
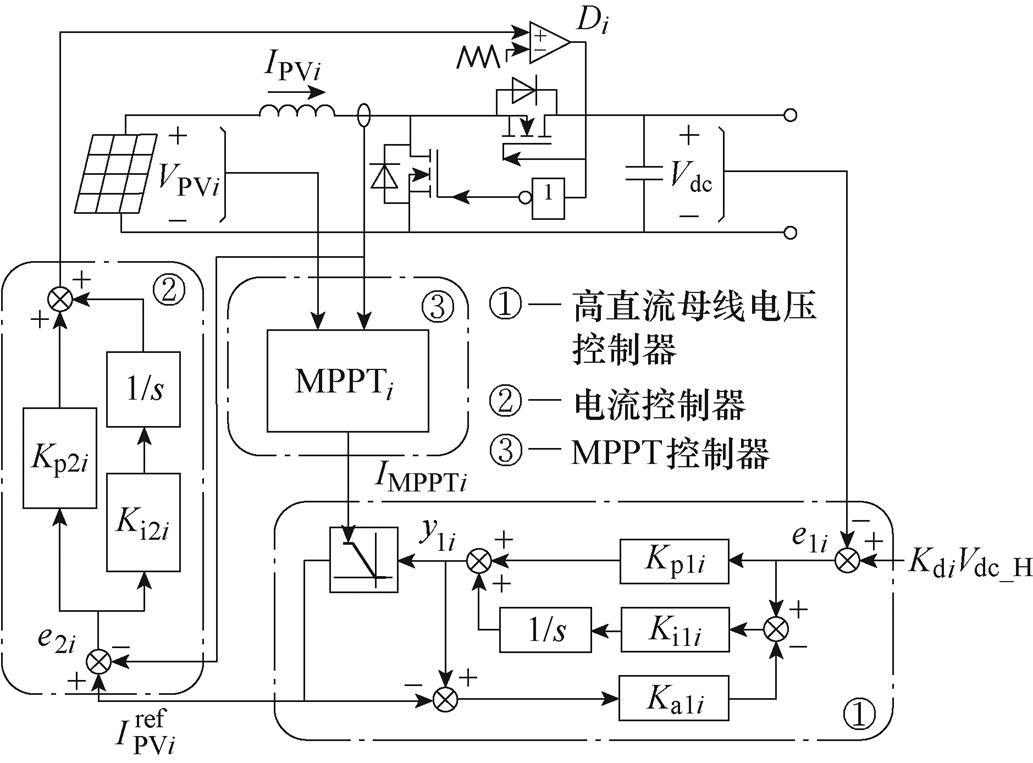
图5 拟议光伏变换器控制方案示意图
Fig.5 Schematic of the proposed PV converter control scheme
当Vdc=Vdc_L时，PV1变换器和PV2变换器都以MPPT模式运行。此时，PI11和PI12处于饱和状态，对内部电流回路PI21和PI22没有影响，PI21和PI22的输入分别由IMPPT1和IMPPT2确定。根据式（1），PI11和PI12的稳态输出如下
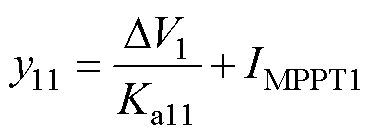（4）
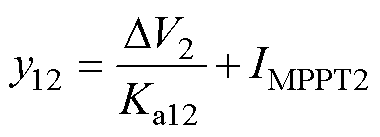（5）
当Vdc=Kd2Vdc_H时。PI12处于激活状态，MPPT2控制器被禁用。PV2变换器在HDVR模式下运行。此时，PI11仍处于饱和状态，PV1变换器以MPPT模式运行，y11如式（4）所示。
如果直流母线电压达到Kd1Vdc_H，此时，PI11处于激活状态，PV1变换器在HDVR模式下运行，PI12的输出为零，PV2变换器处于待机模式。
注意，当光伏变换器在HDVR模式下运行时，建议IPVi取值在光伏阵列的P-I曲线的上坡段，光伏阵列功率-电流曲线如图6所示。原因是上坡段的运行呈现出一个理想的特性，即当负载增加时，光伏电流增加，光伏输出功率增加。在下坡段，负荷增加，光伏电流增加，使得光伏发电量减少，从而导致电压崩溃[18]。另一个重要特性是图6所示的上坡段在文献[19]中显示出更好的阻尼特性。
2.2.2 储能变换器的控制方法
根据储能的SOC划分，储能变换器有两种控制模式。所提出的控制策略由三个控制器组成，拟议BES变换器控制方案示意图如图7所示，其中PI3和PI4分别为BES变换器的低直流母线电压控制器和内部电流控制器，Kp3和Kp4分别为PI3和PI4控制器的比例系数，Ki3和Ki4分别为PI3和PI4控制器的积分系数，Ka3和Ka4分别为PI3和PI4控制器的反馈系数。y3和y4分别为PI3和PI4控制器的输出，e3和e4分别为PI3和PI4控制器的输入误差值。VB和IB分别为储能的实际电压和电流。规定当储能放电时，储能电流IB为正。Vdc_L为低直流母线电压，如图3所示。VBH为储能的满电电压，其对应于95%的SOC状态。IBH为储能充电电流的极限。D3为储能变换器的占空比。
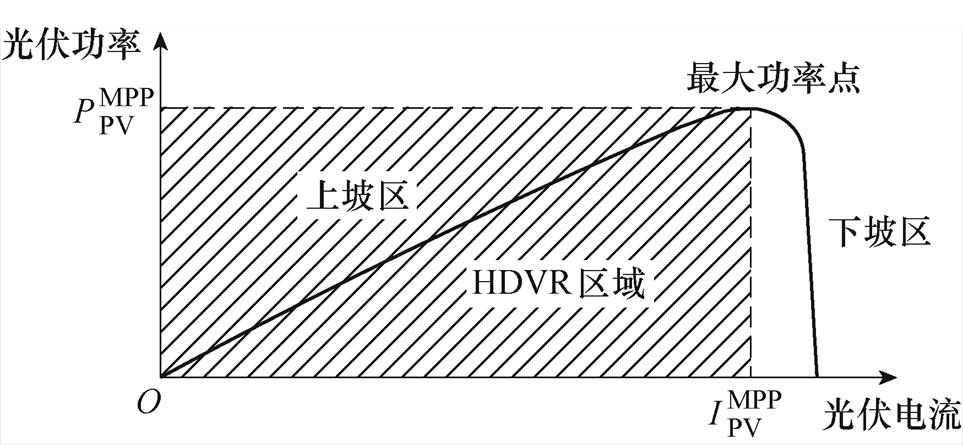
图6 光伏阵列功率-电流曲线
Fig.6 P-I curve of a PV array
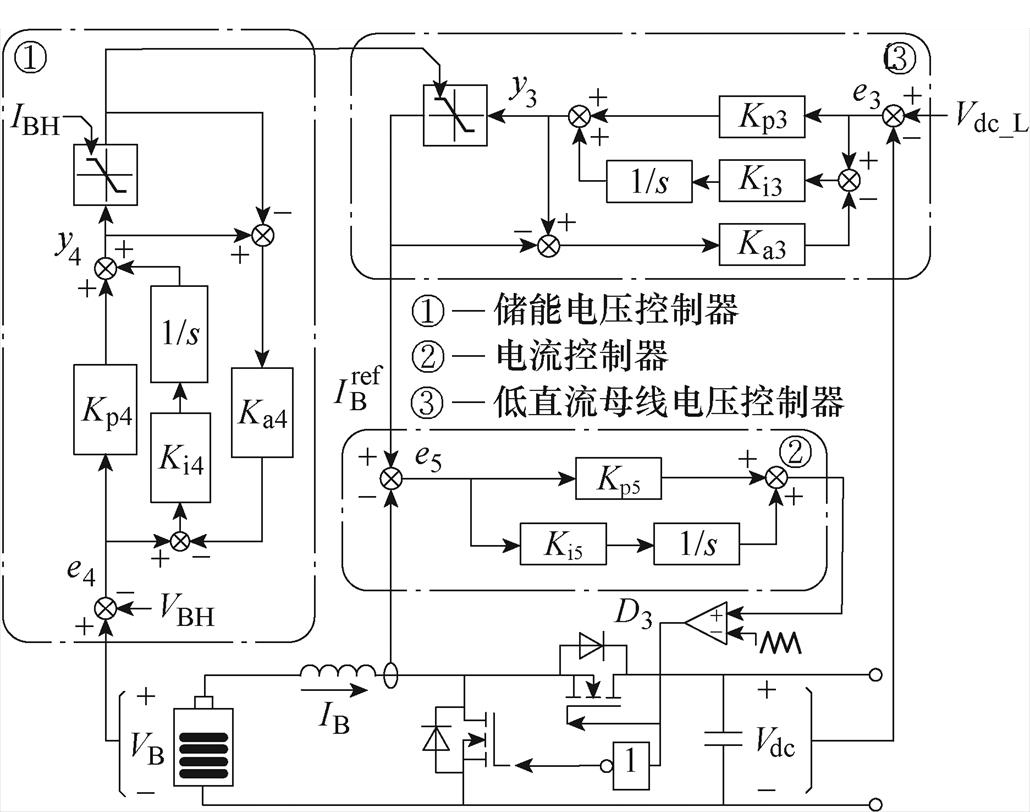
图7 拟议BES变换器控制方案示意图
Fig.7 Schematic of the proposed BES converter control scheme
图7中，限幅器的状态决定了电流控制器的参考电流，该电路通过调节参考电流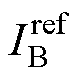
和储能实际电流IB之间的差值来产生占空比D3。储能电压控制器通过调节储能的实际电压VB和储能参考电压VBH之间的差值产生输出y4，低直流母线电压控制器通过调节低直流母线电压Vdc_L和Vdc之间的差来产生输出y3。
如果储能SOC低于95%，PI4处于饱和状态，则直流母线电压将被调节为Vdc_L。
如果储能已完全充电，PI4处于激活状态，则直流母线电压将增加，并由其中一个PV变换器调节。PI3的稳态输出可以表示为
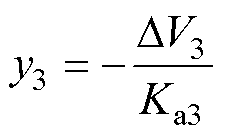（6）
基于上述分析可以看出，无论是对于光伏还是储能变换器，内部控制回路都保持不变。通过合理的参数设计和不同的外部控制回路的饱和或激活状态，这种方法可以实现平滑的模式切换，无需额外的通信电路。因此，它避免了模式切换时的不稳定性，并节省了通信设备的成本。接下来，本文将进一步分析该方法在不同模式转换下的瞬态过程。
2.2.3 协调运行和控制
图8显示了直流微电网系统中的五种典型工况。所有模式转换都基于无缝控制。模式切换波形如图9所示。
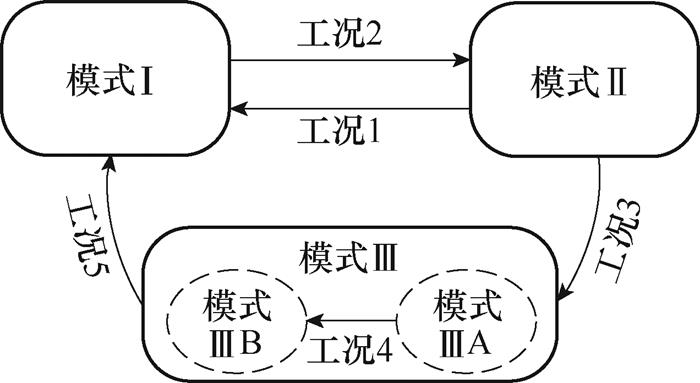
图8 所有可能的模式切换工况
Fig.8 All possible mode switching cases
1）转换条件
工况1：如图9a所示，在模式Ⅱ下，当本地负载功率增加或光伏功率降低时，储能变换器从充电模式切换为放电模式以保持Vdc。因此，在这种情况下，IB从负值变为正值。
工况2：如图9a所示，在模式Ⅰ下，本地负载功率减少或光伏功率增加，这导致光伏提供的功率大于本地负载所需的功率。储能变换器从放电模式变为充电模式，IB从正值变为负值。
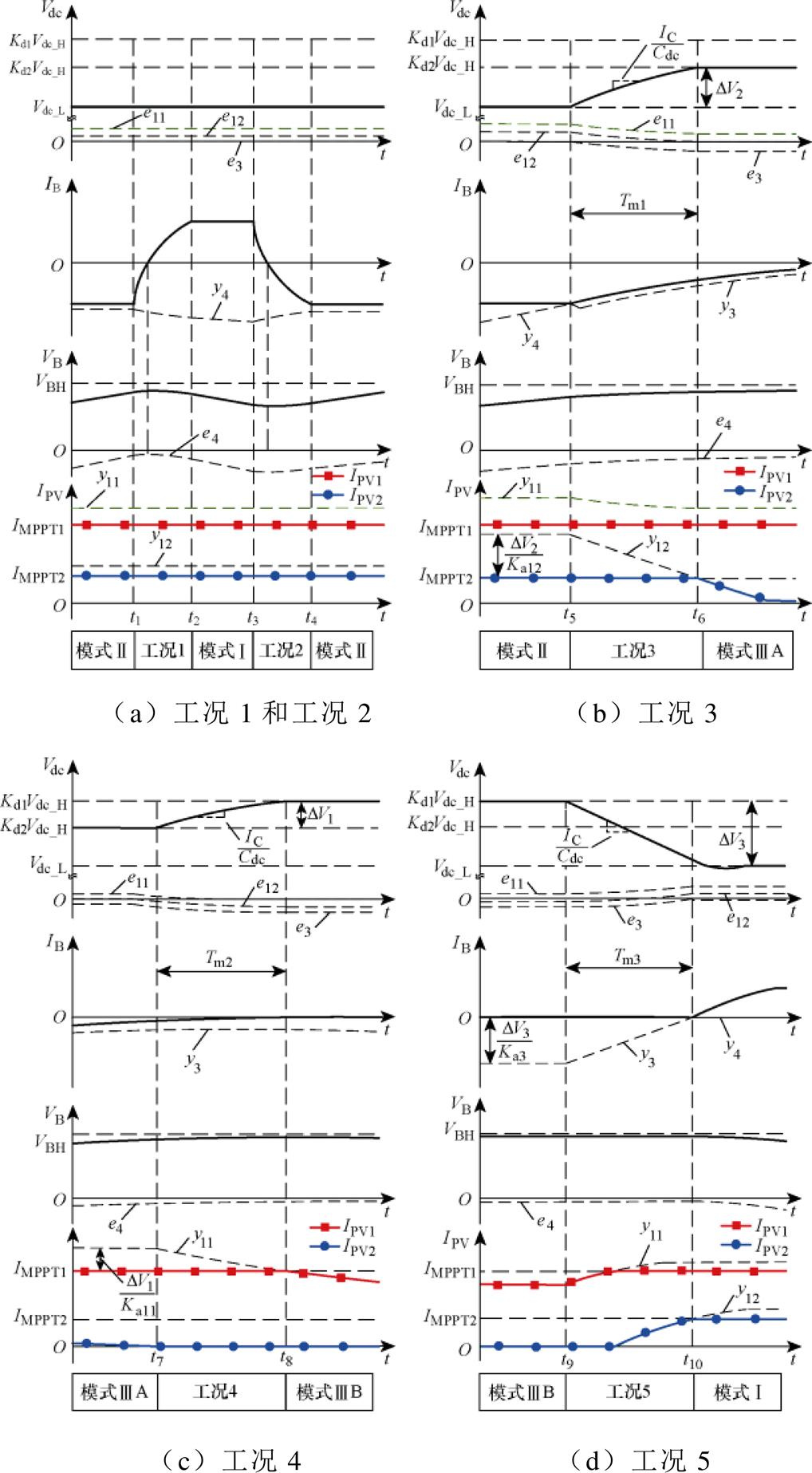
图9 模式切换波形
Fig.9 The waveforms showing the mode transition
工况3：如图9b所示，在模式Ⅱ下，储能几乎充满电，直流母线电压增加，最终接近Kd2Vdc_H。此时，IB逐渐减小，IPV2随着PV2的实际功率减小而减小。
工况4：如图9c所示，在模式ⅢA下，VB持续增加，储能充满电，直流母线电压增加，最终接近Kd1Vdc_H。IB继续下降，最后，储能变换器和PV2变换器都处于待机模式，PV1变换器工作在HDVR模式，以将Vdc保持在Kd1Vdc_H。
工况5：如图9d所示，在模式ⅢB下，负载功率增加或光伏功率减少，这使得光伏提供的功率小于本地负载所需的功率。两个光伏变换器以PV1→PV2的顺序从HVDR模式或待机模式依次切换为MPPT模式。储能需要放电以保持Vdc。
2）模式切换
为了简单起见，可以假设IMPPT1和IMPPT2在瞬时过渡期间是恒定值。图8所示的五种典型情况如图9所示，工况3、工况4和工况5的模式切换时间分别定义为Tm1、Tm2和Tm3。
当直流母线电压变化时，Vdc进入浮动状态并且可以表示为
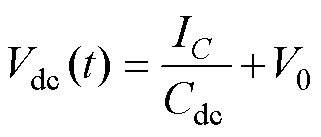（7）
式中，V0为初始电压；Cdc为母线电容；IC为通过母线电容的瞬时平均电流，即
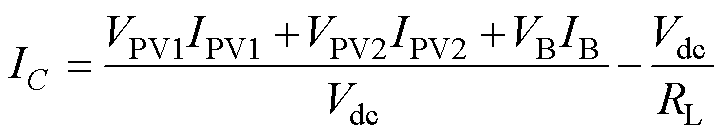（8）
式中，RL为负载电阻；VB为储能电压；IB为储能 电流。
图9a显示了工况1和工况2的模式转换。在这些工况下，完成电流的换向操作。BES变换器在LDVR模式下工作，PV变换器都在MPPT模式下工作。此时，储能尚未完全充电，y4未达到y3，这意味着PI4补偿器处于饱和状态，Vdc仍由BES变换器调节。
图9b显示了模式切换工况3，在t5之前，储能被充电，储能电压VB增加，这导致e4和y4增加。在t5，储能几乎充满电，并导致增加的y4达到y3。同时，PI4补偿器处于激活状态，Vdc增加，导致e12和y12减少。PI12补偿器从饱和变为激活。e12(t)可表示为
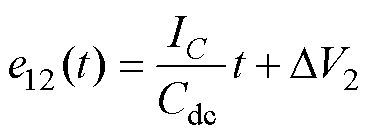（9）
在Tm1期间PI12的输出可由式（3）、式（5）和式（9）表示为
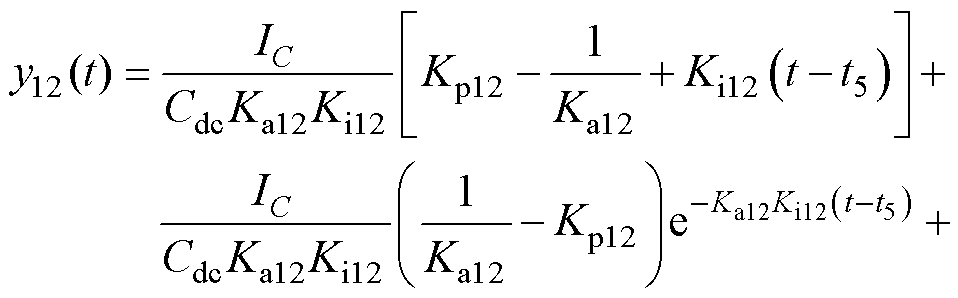
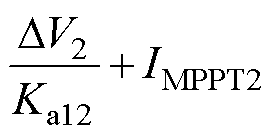（10）
根据式（10），模式切换时间Tm1可以用Lambert- W函数[20]表示为
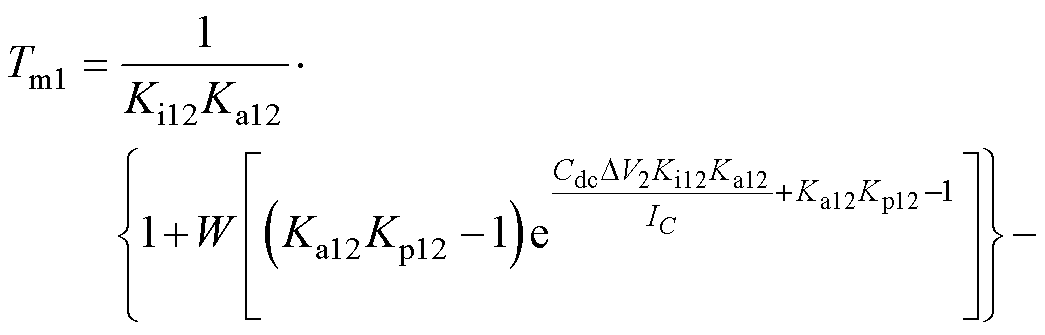
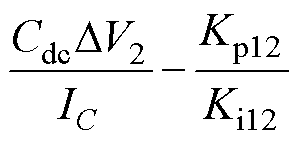（11）
图9c显示了模式变换工况4，t7之前，VB持续增加。t7时刻，IPV2减小到0 A，Vdc增大，这导致e11和y11减小，PI11补偿器从饱和变为激活。Tm2期间的e11(t)可表示为
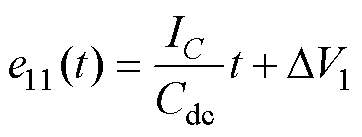（12）
Tm2期间的y11(t)可由式（3）、式（4）和式（12）得到
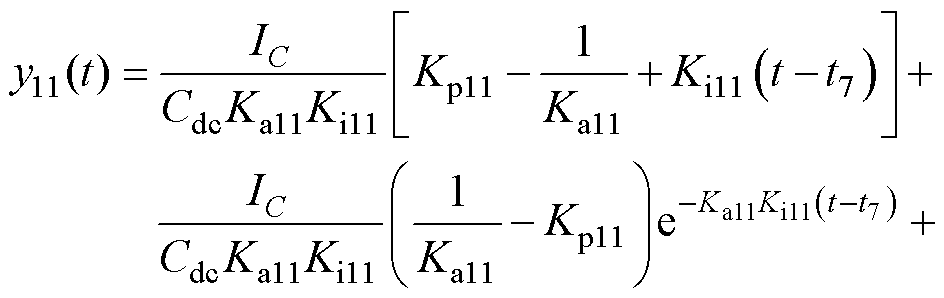
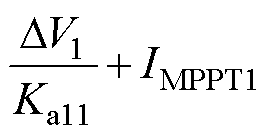（13）
从式（13）可以得出模式切换时间Tm2为
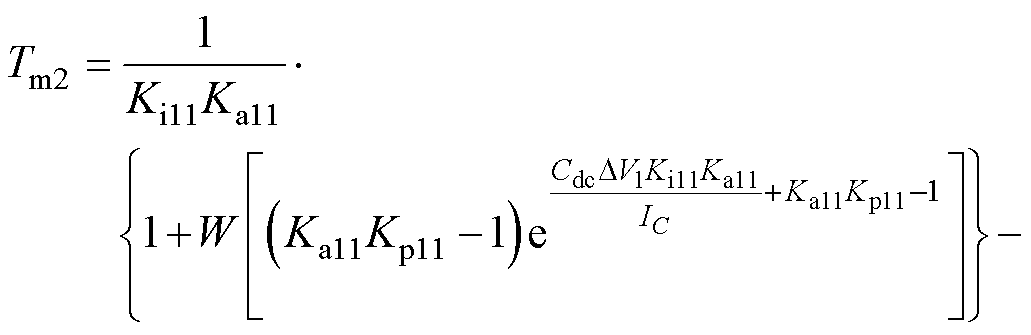
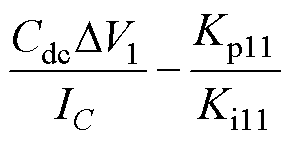（14）
图9d显示了模式转换工况5。当负载功率增加时，光伏组件提供的功率小于本地负载所需的功率。Vdc降低，导致PI11补偿器和PI12补偿器饱和。因此，PV1变换器和PV2变换器依次转变为MPPT模式。最后，PI3补偿器处于激活状态，以将Vdc维持在Vdc_L。
在Tm3期间，e3(t)为
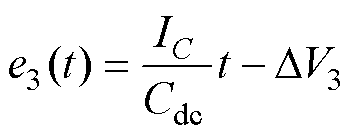（15）
根据式（3）、式（6）和式（15），可以得到PI3的输出为
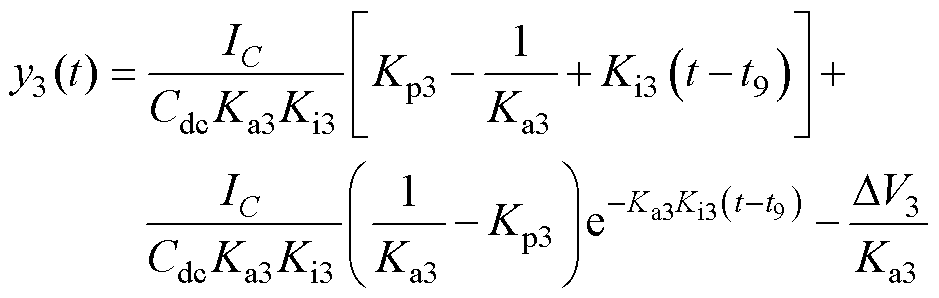（16）
Tm3可由式（16）表示为
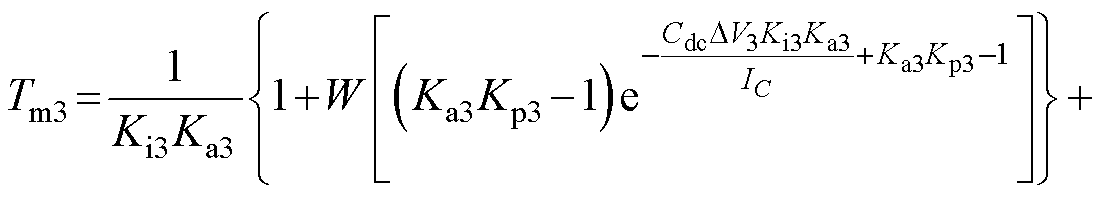
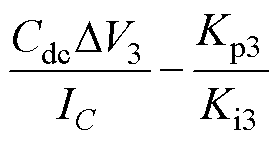（17）
3）模式切换时间Tm
Kp和Ki的设计与传统的DC-DC变换器相同，可参考文献[21]，由于篇幅问题，本文不再进行讨论。从式（11）、式（14）和式（17）可以看出，模式切换时间与IC、电压差（DV1、DV2和DV3）和抗饱和增益（Ka11、Ka12和Ka3）有关。IC由PV、储能和负载的功率决定。该系统中的标称直流母线电压为375 V。选择电压差（DV1、DV2和DV3）时应考虑以下因素：①在低电压和高电流条件下，DV越大，效率越低，过电流故障越严重[15]；②DV越小，所需的采样精度越高，干扰也可能发生。在本设计中，考虑到采样精度和开关性能的要求，Kd1Vdc_H选择为380 V，Kd2Vdc_H选择为377 V。
仿真和实验参数见表2。图10描述了表2所列条件下Ka与Tm的关系波形。从图10可以看出，Ka越大，Tm越小。但大的Ka将导致三个外环之间的干扰。为了调节Tm并避免由采样不准确和小扰动引起的干扰，应在折中的情况下选择Ka。此外，Tm还与负载、硬件规格和动态响应等有关。
表2 仿真和实验参数
Tab.2 Simulation and experiment parameters
参 数数 值 PV1短路电流Isc1/A6 PV1开路电压Voc1/V180 PV1最大功率Pmpp1/W750 PV1变换器电感L1/mH150 PV1变换器开关频率fs1/kHz100 PV2短路电流Isc2/A2.4 PV2开路电压Voc2/V300 PV2最大功率Pmpp2/W500 PV2变换器电感L2/mH150 PV2变换器开关频率fs2/kHz100 模式Ⅰ电压Vdc_L/V375 模式Ⅱ电压Vdc_L/V375 模式ⅢA电压Kd2Vdc_L/V377 模式ⅢB电压Kd1Vdc_L/V380 储能电压VB/V105 储能满电电压VBH/V110 母线电容Cdc/mF800 BES变换器电感L3/mH150 BES变换器开关频率fs3/kHz100
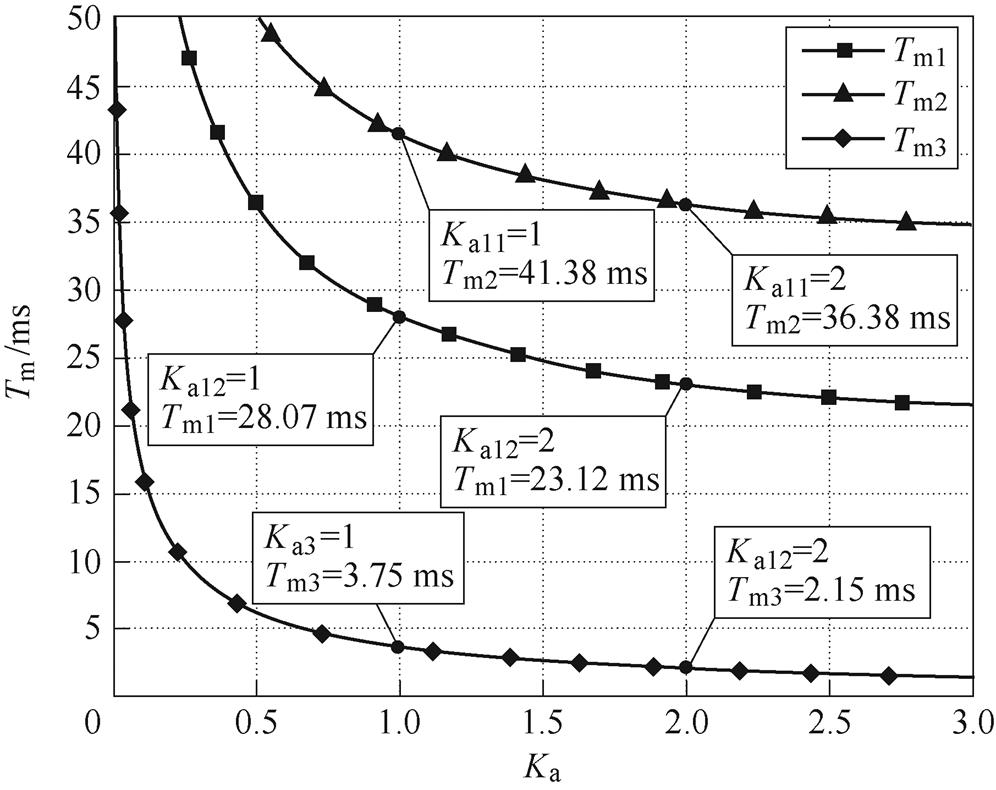
图10 不同工况下Ka与Tm的关系
Fig.10 Mode switching time according to Ka for different cases
为了验证该方法的有效性，特别是Ka对Tm的影响，本节将提供该方法工况3、工况4和工况5的仿真结果。表2显示了仿真中使用的参数。注意，为了便于测量和分析，在仿真中分别使用IB、IPV1和IPV2的平均值IB_AVG、IPV1_AVG和IPV2_AVG。
仿真波形如图11所示，Kax=2的模式切换时间短于Kax=1的模式切换时间，因此较大的Ka可以缩短切换时间。此外，较小的Ka可能会导致直流母线电压超调，因为PI补偿器的退饱和速度较慢。Tm的误差见表3。
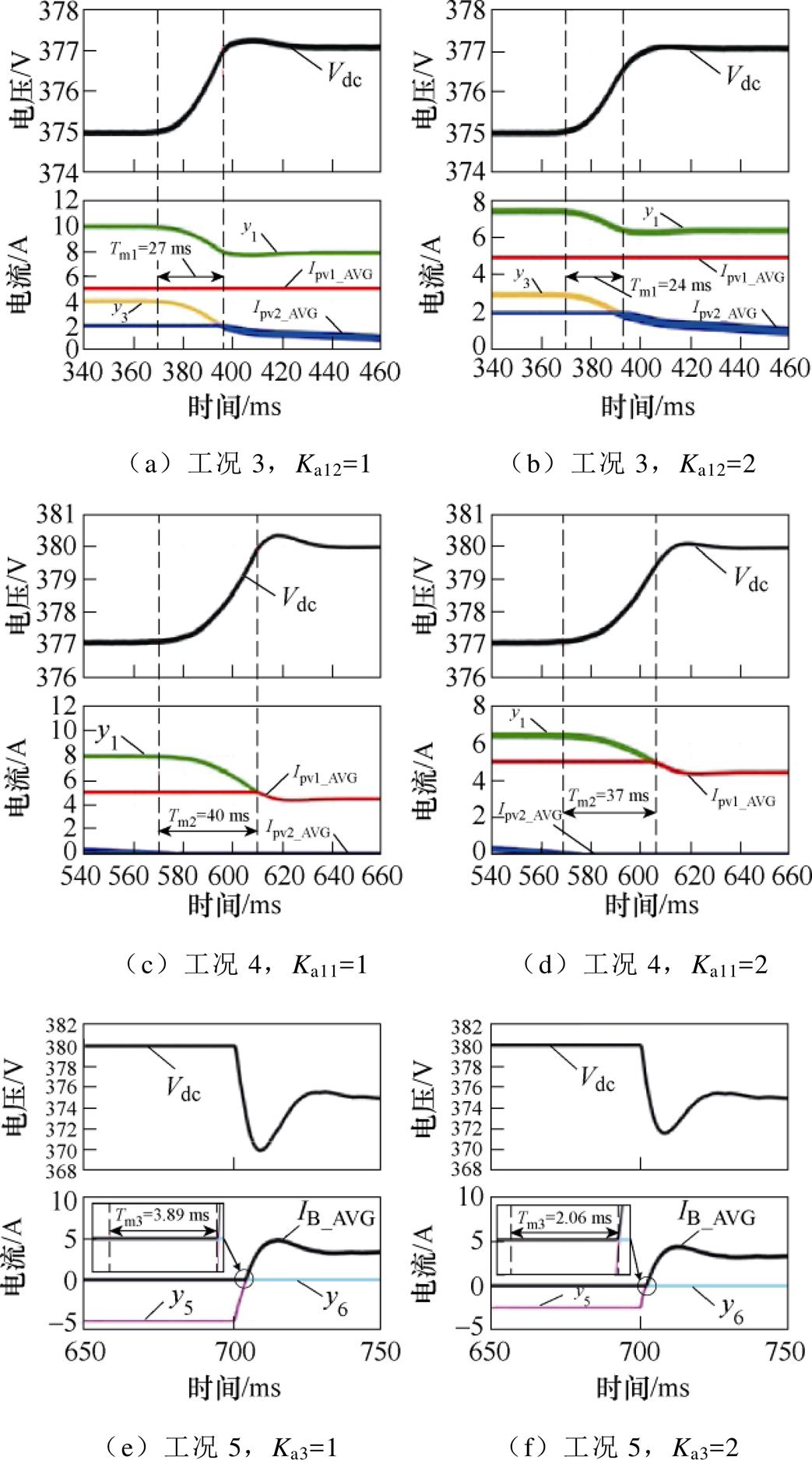
图11 仿真波形
Fig.11 Simulation waveforms
表3 Tm的误差
Tab.3 Errors of Tm
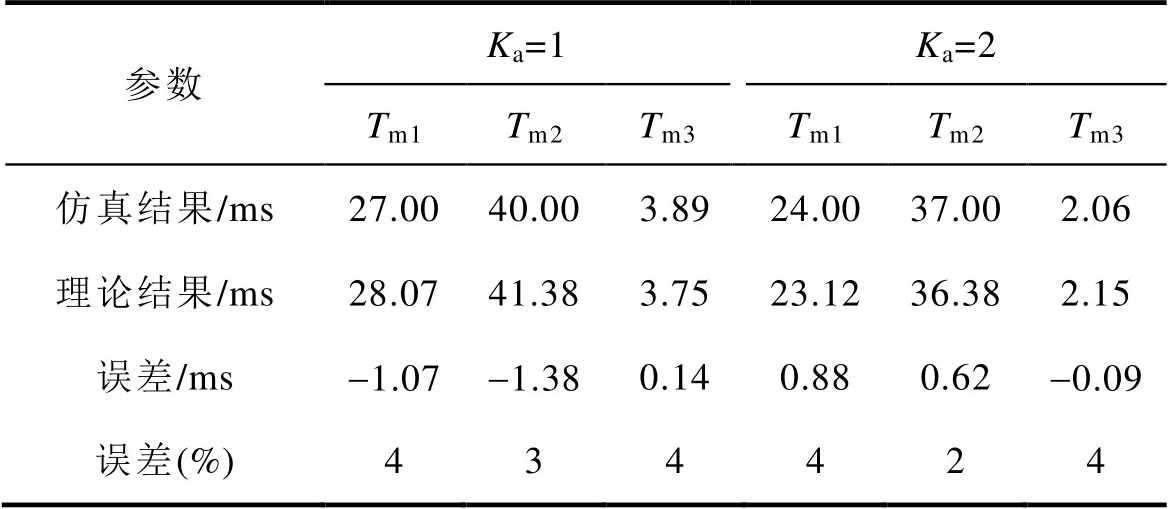
参数Ka=1Ka=2 Tm1Tm2Tm3Tm1Tm2Tm3 仿真结果/ms27.0040.003.8924.0037.002.06 理论结果/ms28.0741.383.7523.1236.382.15 误差/ms-1.07-1.380.140.880.62-0.09 误差(%)434424
应用小型独立直流微电网实验系统验证所提出的方法，实验样机如图12所示，其框图如图13所示。实验系统包含两个光伏组件，储能和通过直流母线连接的电阻负载。用于实现所提出的控制方案的控制器由数字信号处理器（TI公司的TMS320F28379D）实现。实验参数见表2。
图12 实验样机
Fig.12 Experimental prototype
模式Ⅰ中负载变化的实验结果如图14所示。在模式Ⅰ中，光伏模块提供的功率小于负载的功率。BES变换器在LDVR模式下工作，并且放电以维持直流母线电压。可以看出，当负载功率增加或减少时（负载阻值为80 W 和60 W，对应的负载功率分别为1 758 W和2 344 W），直流母线电压保持在375 V，波动较小，电压跌落分别为2.5%和2.7%。
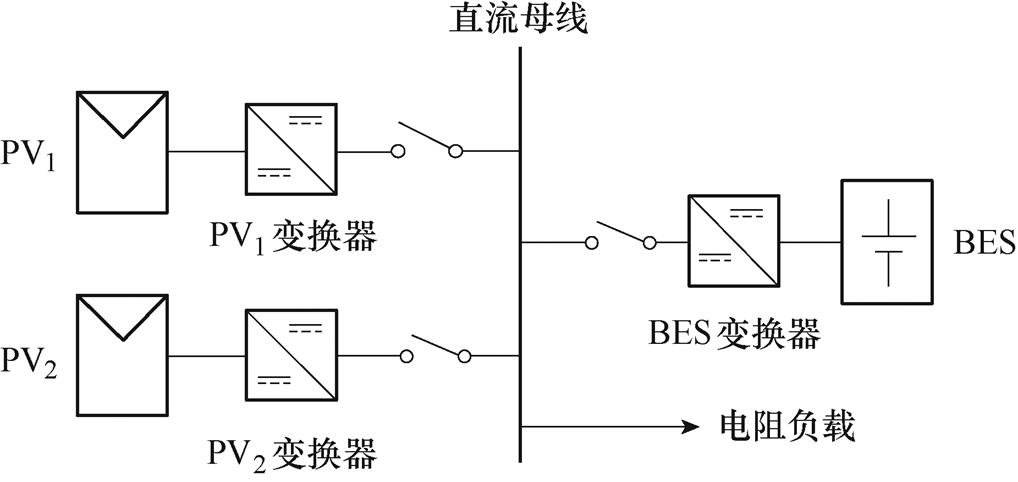
图13 实验装置框图
Fig.13 Block diagram of experimental set-up
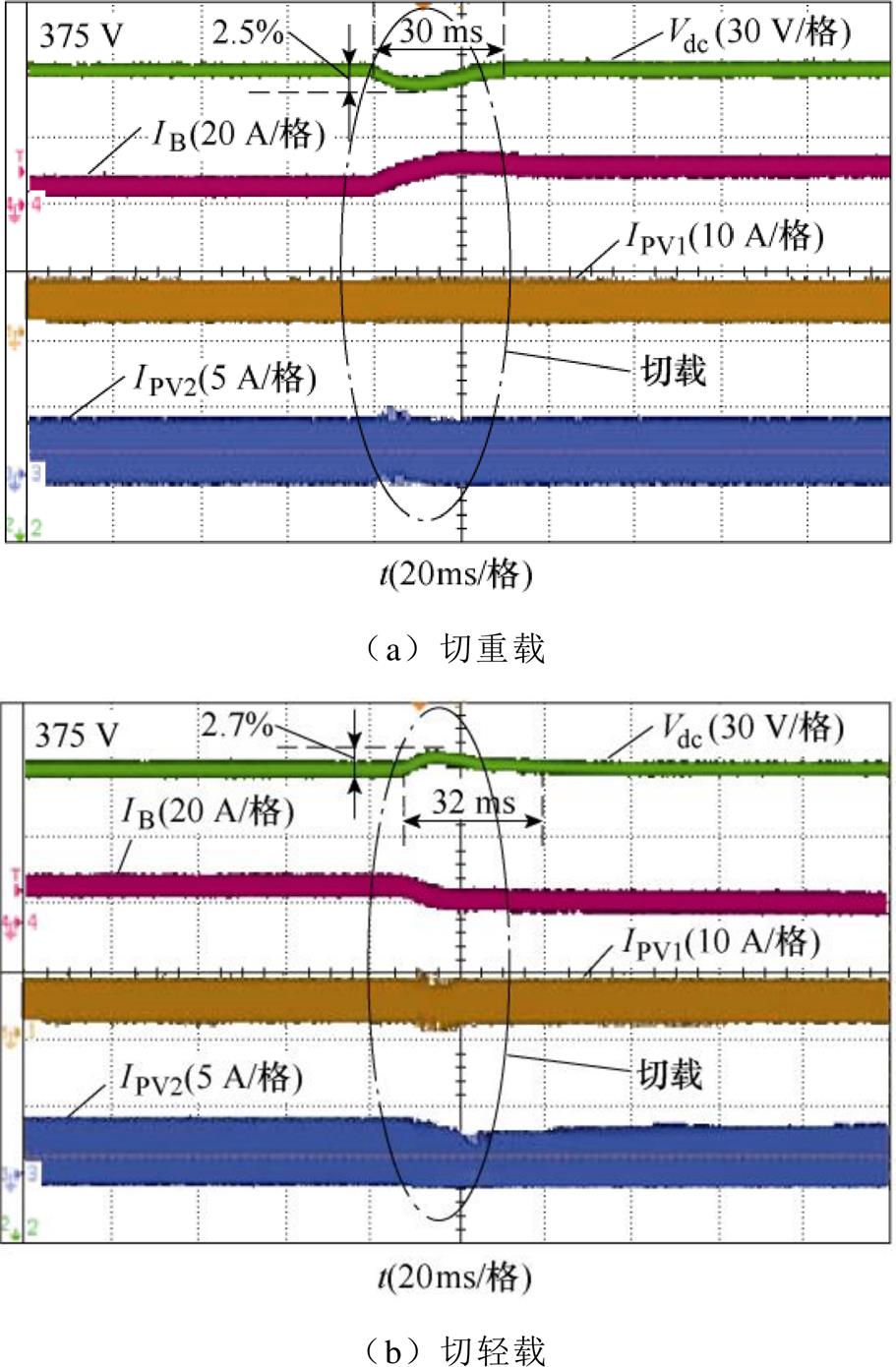
图14 模式Ⅰ实验结果
Fig.14 Experimental results in Mode Ⅰ
模式Ⅱ中负载变化的实验结果如图15所示。在此模式下，光伏功率大于负载功率，储能的SOC小于95%。因此，通过BES变换器充电调节直流母线电压。图15中，无论负载功率增加或减少（负载阻值为200 W 和260 W，对应的负载功率分别为703 W和541 W），直流母线电压在375 V左右波动，电压超调分别为1.1%和1%。
图16显示了模式Ⅲ中PV1功率变化的实验波形。在此模式下，光伏功率大于负载功率，储能的SOC大于95%。因此，直流母线电压由一个PV变换器调节。如图16a所示，当PV1功率增加时，直流母线电压增加至380 V，并由PV1变换器调节，PV1变换器从MPPT模式变为HDVR模式，PV2变换器从HDVR模式变为待机模式。类似地，当PV1功率降低时，如图16b所示，直流母线电压降至377 V，并由PV2变换器调节，PV1变换器从HDVR模式变为MPPT模式，PV2变换器从待机模式变为HDVR模式。
图15 模式Ⅱ实验结果
Fig.15 Experimental results in Mode Ⅱ
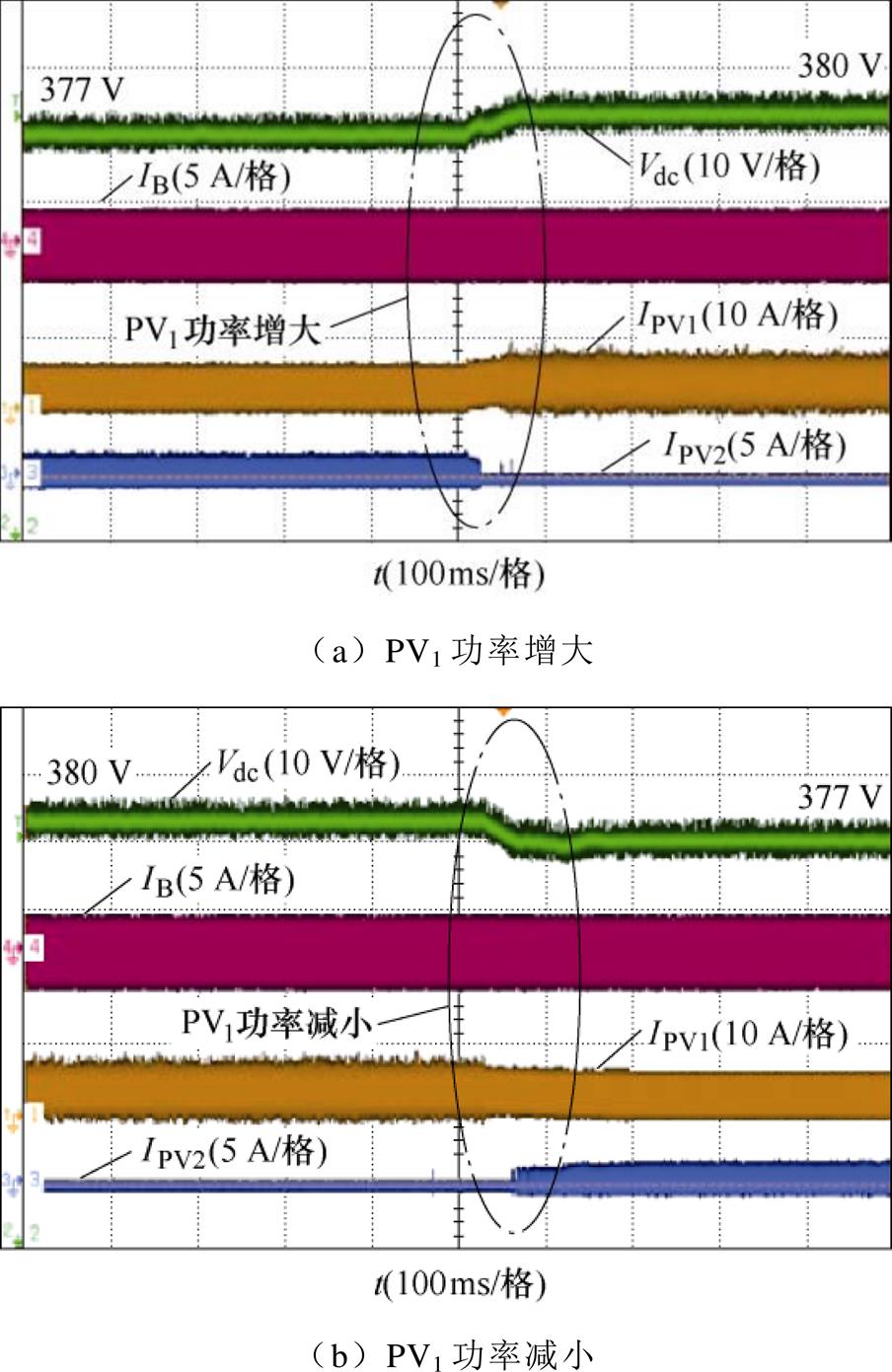
图16 模式Ⅲ实验结果
Fig.16 Experimental results in Mode Ⅲ
图17显示了工况1的实验结果。在初始状态下，BES变换器在LDVR模式下工作，储能充电，并将直流母线电压调节为375 V。所有PV变换器均在MPPT模式下工作。当负载功率增加时（负载阻值由260 W 切换到80 W，对应的负载功率分别为541 W和1 758 W），BES变换器开始放电，直流母线电压有一个小的下冲，然后在30 ms内恢复到375 V。
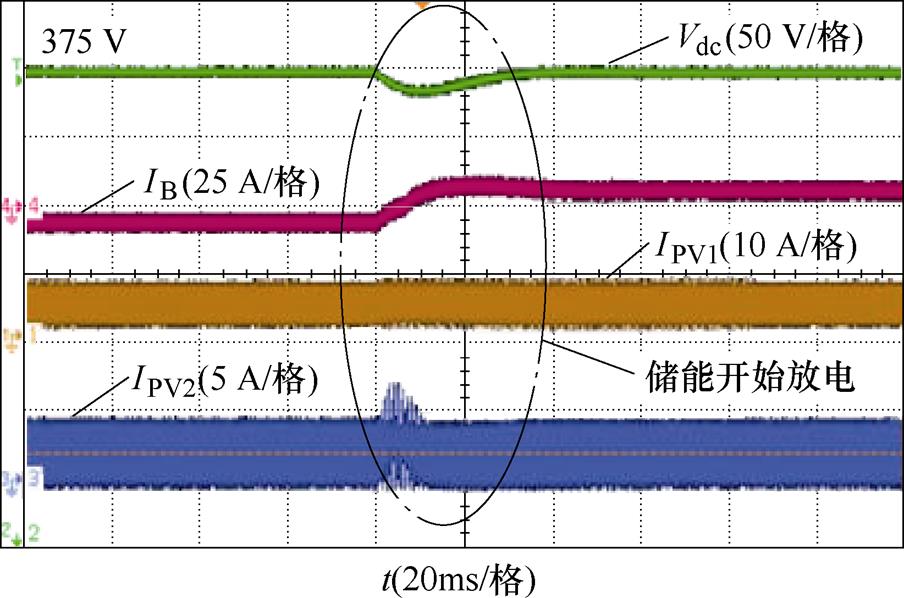
图17 工况1实验结果
Fig.17 Experimental waveforms of Case 1
图18显示了工况2的实验结果。类似地，当负载功率降低时（负载阻值由80 W 切换到260 W，对应的负载功率分别为1 758 W和541 W），BES变换器开始充电，直流母线电压有一个小的过冲，然后在30 ms内恢复到375 V。
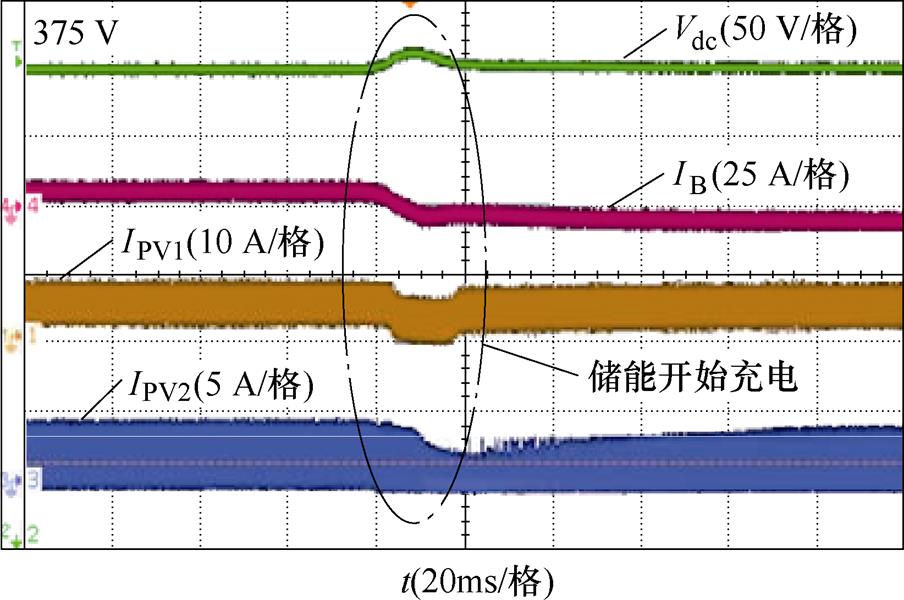
图18 工况2实验结果
Fig.18 Experimental results of Case 2
图19显示了具有不同Ka的工况3和工况4的实验结果。工况3发生在储能过充时。当检测到储能电压VB=VBH时，意味着储能的SOC达到95%，充电电流减小以避免过度充电。因此，直流母线电压增加，这导致PV2变换器从MPPT模式改变为HDVR模式，并将直流母线电压维持在377 V。IB开始减小到IPV2开始减小之间的短时间可以被视为切换时间Tm1。从图19a和图19b可以看出，当Ka=1时，Tm1=28 ms，当Ka=2时，Tm2=22 ms。在Ka较大的情况下，Tm1较短，但外部回路之间存在干扰（见图19b中，当直流母线电压等于377 V时，与图19a相比略有波动）。
图19 工况3和工况4实验结果
Fig.19 Experimental results of Case 3 and Case 4
工况4发生在储能充电电流持续降低，IPV2降至0 A时。PV1变换器开始从MPPT模式转换为HDVR模式，并将直流母线电压调整为380 V。IPV2减小到0 A到IPV1开始减小之间的短时间可以被视为切换时间Tm2。可以看出，Ka越大，Tm2越短。并且由于DV2＜DV1，则Tm2＞Tm1。
图20显示了工况5的实验结果。当负载功率增加（负载由260 W 切换到80 W，对应的负载功率分别为541 W和1 758 W），并且大于光伏功率时，直流母线电压开始降低。IB保持在0 A的短时间，可以被视为切换时间Tm3。从图20a和图20b可以看出，当Ka=1时，Tm3=3.8 ms，电压跌落为6.2%；当Ka=2时，Tm3=2.4 ms，电压跌落为5.5%。所以，Ka越大，Tm3越短，直流母线电压跌落越小。
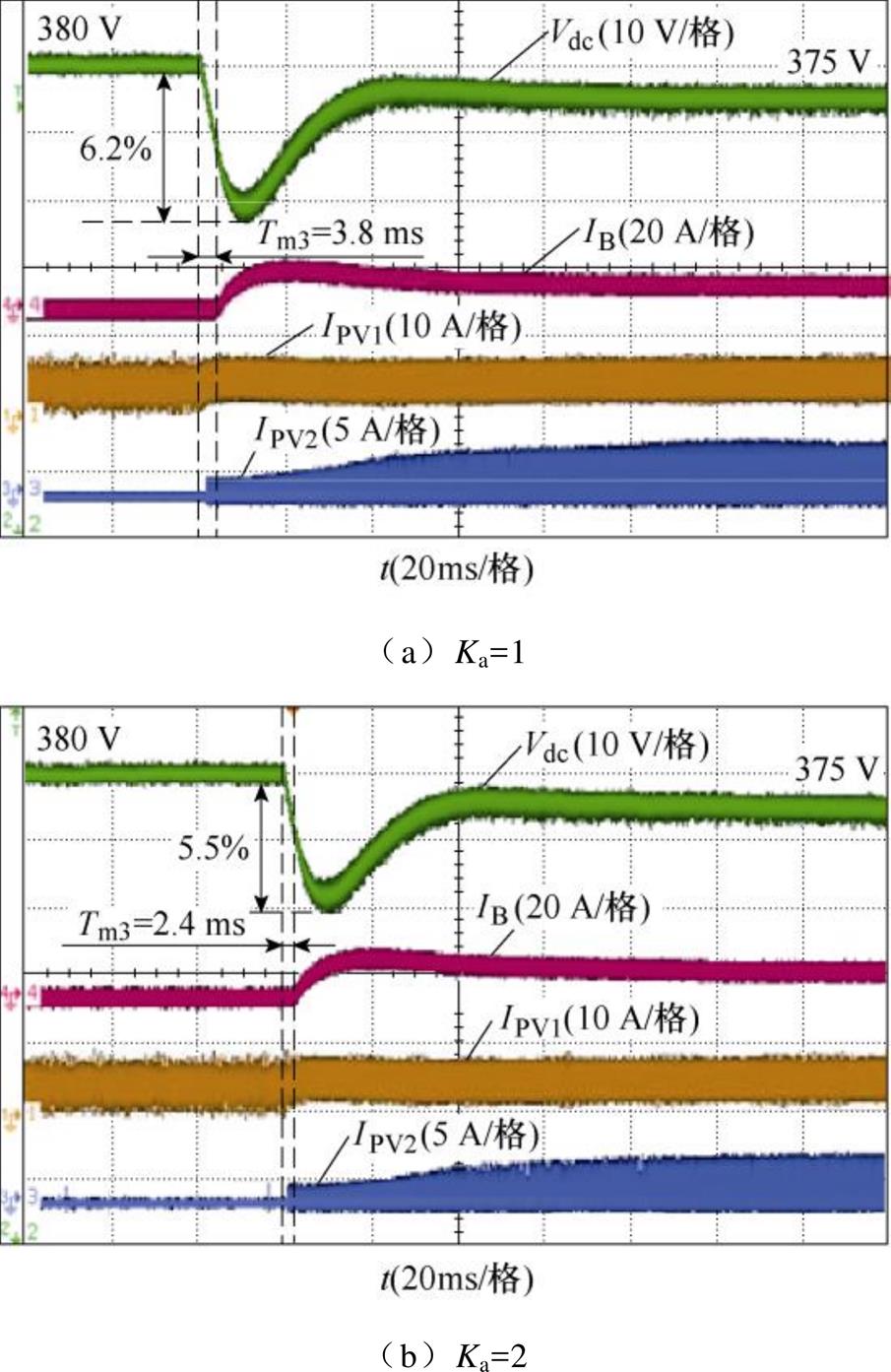
图20 工况5实验结果
Fig.20 Experimental results of Case 5
所有的实验结果都证明了自主和平滑的模式转换。由于仿真和理论结果中未考虑寄生参数，图19和图20所示的Tm1、Tm2和Tm3值与表3所示值略有不同。
本文应用反馈抑制策略对切换过程进行优化，可以缩短模式切换时间，改善由模式切换带来的母线电压跌落和超调。为了便于对比验证，以工况5为例，对本文提出的方法与文献[15]中提出的方法进行对比实验验证。为了对照，两种方法所使用的Kp和Ki参数均相同，对比实验参数见表4。实验中设置一个光伏组件、一个储能和电阻负载。
工况5中，光伏变换器由HDVR模式切换为MPPT模式，储能变换器由CV模式切换为LDVR放电模式（负载阻值设定为160 W 和80 W，对应的负载功率分别为903 W和1 758 W）。从图21和图22中可以看出，传统方法的模式切换时间为39 ms，直流母线电压跌落为15.8%，在本文提出的方法中，模式切换时间为6 ms，直流母线电压跌落为4.8%。由此可见，本文提出的方法可以缩短模式切换时间，减小母线电压的跌落和超调，实现模式的平滑过渡。
表4 对比实验参数
Tab.4 Comparative experimental parameters
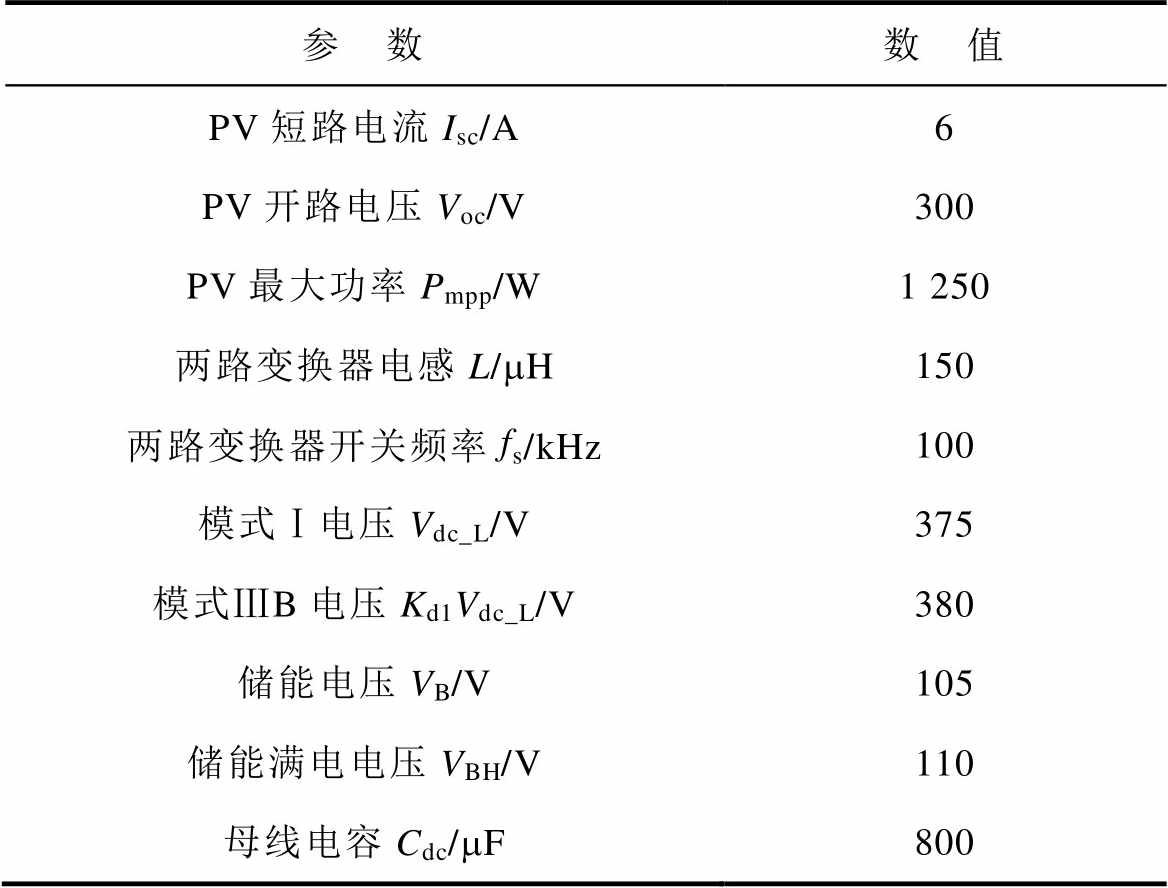
参 数数 值 PV短路电流Isc/A6 PV开路电压Voc/V300 PV最大功率Pmpp/W1 250 两路变换器电感L/mH150 两路变换器开关频率fs/kHz100 模式Ⅰ电压Vdc_L/V375 模式ⅢB电压Kd1Vdc_L/V380 储能电压VB/V105 储能满电电压VBH/V110 母线电容Cdc/mF800
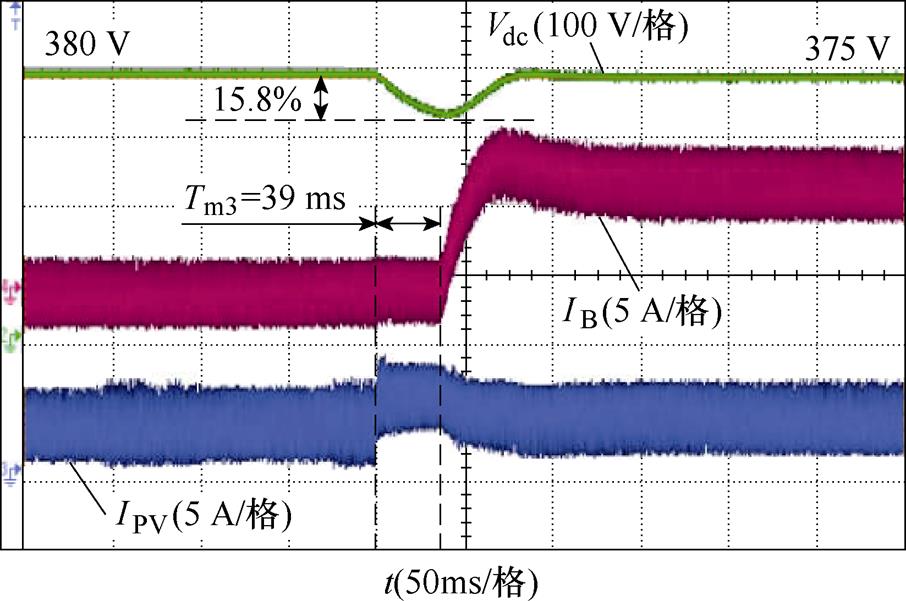
图21 工况5传统方法的实验结果
Fig.21 Experimental results of Case 5 of the traditional method
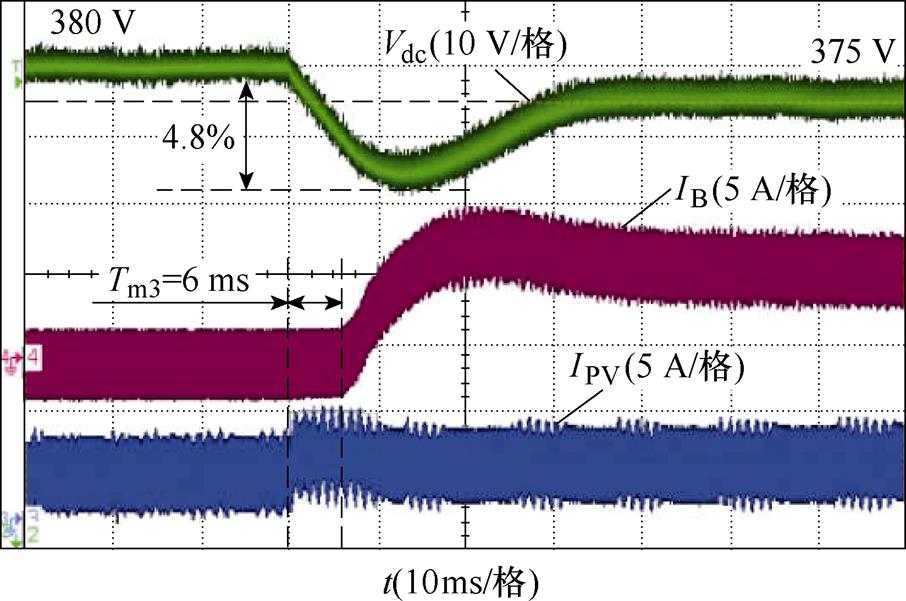
图22 工况5所提出方法的实验结果
Fig.22 Experimental results of Case 5 of the proposed method
本文在小型独立直流微电网中提出了一种基于DBS的控制器，以确保全局平滑过渡并解决与模式切换相关的问题。首先，基于反馈抑制的抗饱和积分控制方法，改变PI控制器的极限值，实现不同模式之间的自主平滑切换。通过使用DBS来划分系统的不同操作模式。然后，分别讨论了PV变换器和BES变换器的控制方法。该控制方案使光伏电源能够调节直流母线电压，并充分利用光伏能量。为了优化模式切换过程，通过分析反馈抑制PI补偿器获得模式切换时间。结果表明，模式切换时间与IC、电压差和抗饱和增益有关。仿真结果与理论结果的误差小于5%。在375 V/2 kW样机上的实验结果验证了所提出的控制策略。在实验部分，讨论了稳态和动态性能，以验证所提出的控制方案的可行性。结果表明，所提出的控制方法可以实现自主、平滑的模式切换，而不会出现抖振和死锁问题。所提出的控制方案能够自动改变控制目标，并提高了直流微电网的可靠性。
参考文献
[1] 支娜, 丁可, 黄庆辉, 等. 基于P-U下垂特性的虚拟直流电机控制策略[J]. 电工技术学报, 2021, 36(6): 1238-1248.
Zhi Na, Ding Ke, Huang Qinghui, et al. A virtual DC motor control strategy based on P-U drooping characteristics[J]. Transactions of China Electro- technical Society, 2021, 36(6): 1238-1248
[2] 郭方洪, 李赫, 王函韵, 等. 直流微电网分布式弹性二次电压恢复与电流分配控制[J]. 电力系统自动化, 2022, 46(4): 84-92.
Guo Fanghong, Li He, Wang Hanyun, et al. Distri- buted resilient secondary voltage restoration and current distribution control of DC microgrid[J]. Auto- mation of Electric Power Systems, 2022, 46(4): 84-92.
[3] 李霞林, 郭力, 王成山, 等. 直流微电网关键技术研究综述[J]. 中国电机工程学报, 2016, 36(1): 2-17.
Li Xialin, Guo Li, Wang Chengshan, et al. Key technologies of DC microgrids: an overview[J]. Pro- ceedings of the CSEE, 2016, 36(1): 2-17.
[4] 朱晓荣, 李铮, 孟凡奇. 基于不同网架结构的直流微电网稳定性分析[J]. 电工技术学报, 2021, 36(1): 166-178.
Zhu Xiaorong, Li Zheng, Meng Fanqi. Stability analysis of DC microgrid based on different grid structures[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 166-178.
[5] 李忠文, 程志平, 张书源, 等. 考虑经济调度及电压恢复的直流微电网分布式二次控制[J]. 电工技术学报, 2021, 36(21): 4482-4492.
Li Zhongwen, Cheng Zhiping, Zhang Shuyuan, et al. Distributed secondary control for economic dispatch and voltage restoration of DC microgrid[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(21): 4482-4492.
[6] Zhang Yuru, Li Yunwei. Energy management strategy for supercapacitor in droop-controlled DC microgrid using virtual impedance[J]. IEEE Transactions on Power Electronics, 2017, 32(4): 2704-2716.
[7] Sanchez S, Molinas M. Degree of influence of system states transition on the stability of a DC microgrid[J]. IEEE Transactions on Smart Grid, 2014, 5(5): 2535- 2542.
[8] Wang Huaizhi, Li Gangqiang, Wang Guibin, et al. Deep learning based ensemble approach for pro- babilistic wind power forecasting[J]. Applied Energy, 2017, 188: 56-70.
[9] Nie Jintong, Yuan Liqiang, Wen Wusong, et al. Communication-independent power balance control for solid state transformer interfaced multiple power conversion systems[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4256-4271.
[10] Chen C L, Wang Yubin, Lai J S, et al. Design of parallel inverters for smooth mode transfer microgrid applications[J]. IEEE Transactions on Power Elec- tronics, 2010, 25(1): 6-15.
[11] Li Xiangke, Jiang Wentao, Wang Junjun, et al. An autonomous control scheme of global smooth transi- tions for bidirectional DC-DC converter in DC microgrid[J]. IEEE Transactions on Energy Con- version, 2021, 36(2): 950-960.
[12] 吴琦, 邓卫, 谭建鑫, 等. 基于下垂控制的多端直流系统稳定性分析[J]. 电工技术学报, 2021, 36(增刊2): 507-516.
Wu Qi, Deng Wei, Tan Jianxin, et al. Stability analysis of multi-terminal DC system based on droop control[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 507-516.
[13] 刘彦呈, 庄绪州, 张勤进, 等. 基于虚拟频率的直流微电网下垂控制策略[J]. 电工技术学报, 2021, 36(8): 1693-1702.
Liu Yancheng, Zhuang Xuzhou, Zhang Qinjin, et al. A virtual current-frequency droop control in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1693-1702.
[14] Schonbergerschonberger J, Duke R, Round S D. DC-bus signaling: a distributed control strategy for a hybrid renewable nanogrid[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1453-1460.
[15] Sun Kai, Zhang Li, Xing Yan, et al. A distributed control strategy based on DC bus signaling for modular photovoltaic generation systems with battery energy storage[J]. IEEE Transactions on Power Elec- tronics, 2011, 26(10): 3032-3045.
[16] Murad M A A, Milano F. Modeling and simulation of PI-controllers limiters for the dynamic analysis of VSC-based devices[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3921-3930.
[17] Kwon M, Choi S. Control scheme for autonomous and smooth mode switching of bidirectional DC-DC converters in a DC microgrid[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 7094-7104.
[18] Elrayyah A, Sozer Y, Elbuluk M E. Modeling and control design of microgrid-connected PV-based sources[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(4): 907-919.
[19] Xiao Weidong, Dunford W G, Palmer P R, et al. Regulation of photovoltaic voltage[J]. IEEE Transa- ctions on Industrial Electronics, 2007, 54(3): 1365- 1374.
[20] Yi Sun, Nelson P W, Ulsoy A G. Time-delay systems: analysis and control using the Lambert W function[M]. New Jersey: World Scientific, 2010.
[21] 李洋. 直流微电网混合储能系统功率分配及稳定性研究[D]. 哈尔滨: 哈尔滨工业大学, 2020.
Abstract In a stand-alone DC microgrid system, energy storage systems (ESSs) and photovoltaic (PV) power sources are the main energy sources. However, the battery’s DC bus voltage regulation capability is limited and decreases with increasing photovoltaic penetration. In this scenario, there is an increasing demand for PV sources to participate in DC bus voltage regulating, especially in small-sized stand-alone DC microgrids. In the current control method, the control for PV generators needs to be switched to different modes according to the corresponding voltage level. During the switching, the output power of PV modules fluctuates greatly, which influences the performance of the system. Therefore, transients are particularly challenging in stand-alone DC microgrids and may cause erroneous switching between control sets. The switching control strategies must be carefully designed, especially when a time delay exists in detecting the switching situation.
This paper introduces an autonomous and smooth mode-switching control strategy based on DC Bus Signaling (DBS) to cooperate with multiple PV sources and ESS. The proposed control strategy utilizes the alternation between saturation and activation of the PI controller with a back-calculation mechanism. Some outer closed loops of the PI compensator reach the actuator limits, and the feedback loop is broken during mode switching. This method can solve the chattering and deadlock problems during mode switching, shorten the mode switching time, and reduce the overshoot of DC bus voltage. The communication between the converters is realized through the DC bus voltage, which reduces the overall cost of the system. Based on the DBS method, different operation modes of the system are divided, and the five representative cases in the DC microgrid system are indicated. In addition, the control methods for PV converters and battery energy storage (BES) converters are discussed. Particularly, to fully use PV energy, the proposed control strategy considers the state of charge (SOC) of ESS and enables PV sources to regulate the DC bus voltage.
Besides, the mode-switching time is obtained by analyzing the back-calculation PI compensators to optimize the mode-switching process. The results show that the mode switching time is related to IC, voltage difference, and the anti-windup gain. The errors between simulation results and theoretical results are less than 5%. The design method for controller parameters is also provided.
Finally, a small-scale stand-alone DC microgrid experimental system on a 375 V/2 kW prototype is set up to demonstrate the feasibility of the proposed method for DC microgrid controls. The steady-state and dynamic performances have been discussed to verify the feasibility of the proposed control scheme. The mode switching performance under different control parameters Ka is given. Compared with the traditional method, the proposed control method can achieve autonomous and smooth mode switching without chattering and deadlock problems, shorten the mode switching time, and reduce the overshoot of the DC bus voltage during the mode-switching process. The proposed control scheme can autonomously alter the control objectives without the central controller and enhance the reliability of the DC microgrid.
keywords：Autonomous control scheme, DC microgrid, energy storage system (ESS), photovoltaic (PV) power systems, power management
DOI: 10.19595/j.cnki.1000-6753.tces.230305
中图分类号：TM46
国家重大自然科学基金项目（51977146）和2021年天津市研究生科研创新项目（2021YJSO2S01, 2021YJSB152）资助。
收稿日期 2023-03-17
改稿日期 2023-05-29
翟 凡 女，1996年生，硕士研究生，研究方向为分布式光储交直流微电网系统控制。E-mail: zhaifan516@163.com
王议锋 男，1981年生，副教授，博士生导师，研究方向为高频电能变换技术、磁集成技术、软开关技术及交直流微电网中的电力电子技术等。E-mail: wayif@tju.edu.cn（通信作者）
（编辑 陈 诚）