 1,iL为电感电流,交流端口处的电感值归算至一次侧为Li。V1和i1分别为系统总的输入电压和电流,V1i为模块i的输入电压,i2i为模块i的输出电流,V2和i2分别为系统总的输出电压和电流。
1,iL为电感电流,交流端口处的电感值归算至一次侧为Li。V1和i1分别为系统总的输入电压和电流,V1i为模块i的输入电压,i2i为模块i的输出电流,V2和i2分别为系统总的输出电压和电流。摘要 针对三电平半桥型输入串联输出并联(ISOP)型双有源桥(DAB)变换器的各模块参数差异而导致的模块功率不均衡传输问题,该文首先分析多模块功率不平衡原因,然后提出基于三重移相(TPS)调制的串联侧功率平衡策略。针对ISOP系统多模块间参数差异问题,提出多模块参数差异估计方法,该方法无需增加额外的电流或电压传感器,通过注入强制分量作为扰动而采集反映模块差异的特征量变化,对控制量进行补偿实现多模块功率平衡。仿真和实验结果表明,在多种扰动条件下,所提功率平衡方法可实现样机串联侧均压,在输出电压24 V工况和10~435 W功率范围下,系统在所提控制策略下能明显提高串联侧的电压平衡,工作效率达到90%以上。
关键词:输入串联输出并联型双有源桥(ISOP-DAB)变换器 多模块功率不平衡 参数差异估计方法 串联侧均压
随着现代电力系统的发展,对系统中的电力电子变换器有了更多要求,例如,高电压化、大电流化、大功率化[1-4]等,单个变换器模块已无法满足上述要求,于是将多个模块串联或者并联,构成组合变换器系统[5]以解决上述问题,但各个模块的主电路参数不完全一致,导致模块的等效阻抗不同而出现模块间的不平衡问题,影响变换器使用寿命[6]。因此,需要调节控制参数,解决模块间不平衡问题。
现有的DC-DC类输入串联输出并联(Input- Series Output-Paralle, ISOP)型变换器的模块平衡可以分为两类:自然平衡法和多环控制法[7-10]。前者对现有的常用拓扑进行改进,使其自然均压,如在变压器设计时加入平衡绕组,平衡绕组的两端交错连接在不同模块,电流流过该绕组时补偿模块间的电流差[11-13],该方式硬件设计复杂,不便于拓展模块数量。文献[14]对多模块直接施加相同控制参数,实现ISOP系统串联侧的自然平衡,这种方式也称为共占空比控制,其控制简单,但平衡效果依赖于模块参数差异,易受变换器具体工况的影响,常常应用在均压不平衡度要求不高的场合。
在上述共占空比控制基础上,于控制环路加入一个或多个平衡环路即为多环控制[15-16]:除了输出电压环外,加入模块电压或模块电流平衡环构成双环控制[17-18],可以克服因干扰或模块参数不一致而带来的不平衡问题[19-21]。但上述控制策略需要大量的传感器来构造多模块平衡的闭环,其硬件成本和控制复杂度高,并且传感器故障时会使平衡控制策略失效。文献[22]针对输入并联输出并联(Input- Paralle Output-Paralle, IPOP)型DC-DC变换器,提出基于扰动算法估计的控制策略,其控制策略在模块占空比和等效阻抗不严格一致时不依赖于电流采集,但能否推广到其他拓扑中还有待研究。
为了解决输入串联输出并联型双有源桥(Input- Series Output-Paralle-Dual Active Bridge, ISOP-DAB)变换器各模块参数差异而导致的模块功率不均衡传输问题,本文提出了一种简化的功率平衡控制方法,该方法通过参数差异估计实现多模块功率平衡,无需增加额外的电流或电压传感器,降低了采样电路的成本和控制复杂度。最后通过仿真和实验验证了模块差异估计和功率平衡策略的有效性。
基于三电平中性点钳位(Three-Level Neutral Point Clamed, 3L-NPC)半桥-H桥结构的ISOP-DAB系统如图1所示,每个模块都由一次侧3L-NPC半桥、二次侧H桥所组成。模块i(i=1, 2,…, N)的中高频变压器的电压比为ni 1,iL为电感电流,交流端口处的电感值归算至一次侧为Li。V1和i1分别为系统总的输入电压和电流,V1i为模块i的输入电压,i2i为模块i的输出电流,V2和i2分别为系统总的输出电压和电流。
1,iL为电感电流,交流端口处的电感值归算至一次侧为Li。V1和i1分别为系统总的输入电压和电流,V1i为模块i的输入电压,i2i为模块i的输出电流,V2和i2分别为系统总的输出电压和电流。
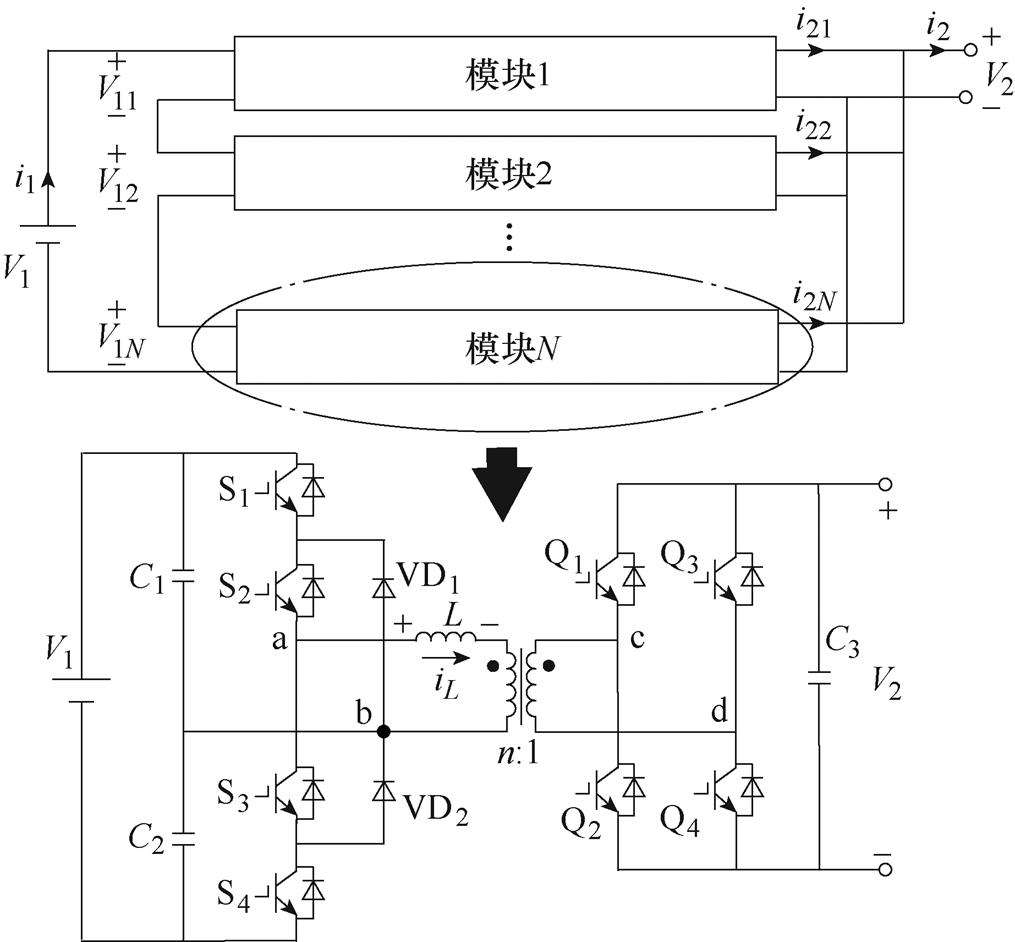
图1 基于3L-NPC半桥-H桥结构的ISOP-DAB系统
Fig.1 ISOP-DAB system based on 3L-NPC half-bridge-H bridge structure
由电路串并联关系可知,每个模块输入电流均为i1、输出电压均为V2。假设各模块效率一致且忽略损耗,则模块i的功率Pi与输入电压、输出电流关系如式(1)所示,即理论上模块功率比值与输入电压、输出电流比值相等。换言之,理论上模块功率平衡、串联侧均压、并联侧均流三者等价,实现其中一个,其余两个自动实现。
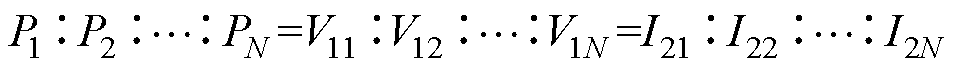 (1)
(1)
文献[23]给出了三重移相(Triple Phase Shift,TPS)调制模式下,单模块DAB变换器基于电感电流有效值优化控制策略的功率表达式P(D1, D2, Dj),根据Dj 大小,表达式分为A、B、C三段。
本文以功率范围较大的C模式为例进行分析,其他两种模式分析方法类似。功率表达式PC表示为
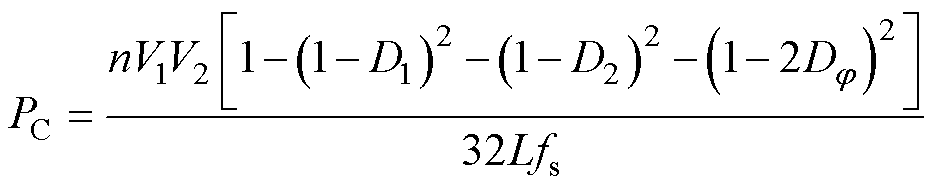 (2)
(2)
式中,fs为模块的开关频率。
对于ISOP-DAB系统,最常见的是共占空比/移相比控制方式,即每个模块的三个自由度控制参数D1、D2、Dj 一致,它们分别是3L-NPC半桥在一次侧交流端口产生的Vab的占空比、H桥在二次侧交流端口产生的Vcd的占空比、它们基波相位差j 所对应的移相占空比Dj =j/p。当每个模块参数完全一致,并且控制参数也完全一致且均为 (D1, D2, Dj) 时,则每个模块传输功率确定且均为P/N,同时可实现串联侧均压、并联侧均流。
ISOP-DAB系统在理想情况下,受到扰动能自动恢复到平衡。但实际应用中,多模块系统存在硬件参数差异会导致模块的等效阻抗不同,此时ISOP-DAB系统采用共占空比/移相比控制方式,系统受到扰动后难以恢复功率平衡状态。
在Matlab/Simulink中,对等效电感L1、L2分别为35 mH、50 mH的两模块ISOP-DAB进行仿真验证,采用共占空比/移相比控制,V1i随着负载功率Pload的变化情况如图2所示,可见V11和V12随着Pload增加而发散,串联侧会出现严重不均压的情况。
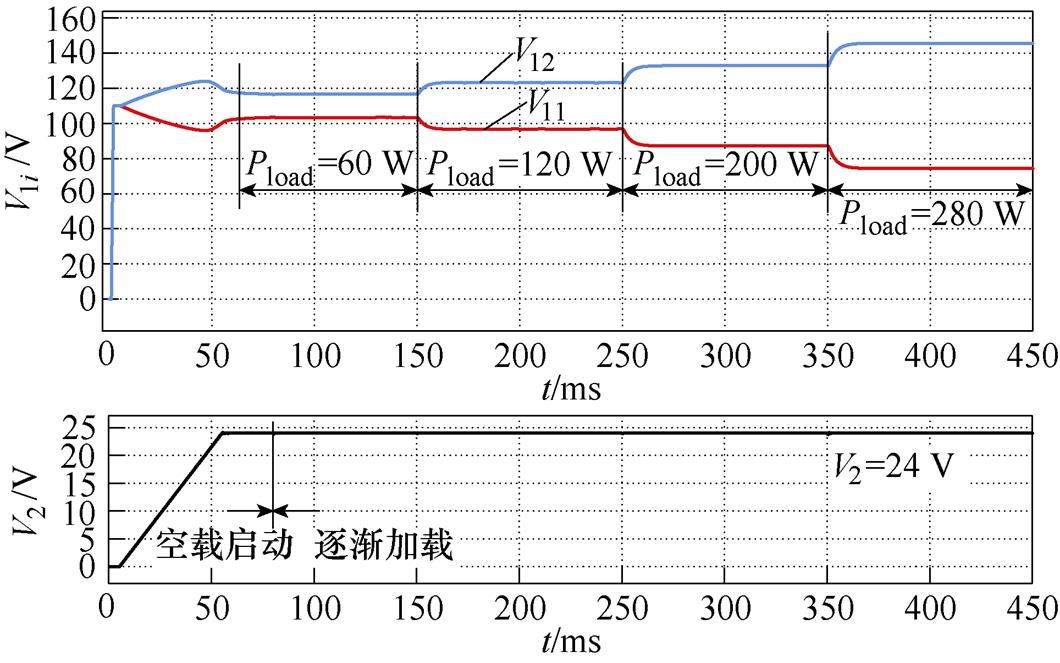
图2 存在模块差异时,模块输入电压随负载变化情况
Fig.2 Module input voltage varies with load when there is a module difference
理论上模块功率平衡、串联侧均压、并联侧均流三者等价,但实际上稳定性却不同。如果采用并联侧控制且功率正向传递时,系统虽然能保持功率恒定,但在受到扰动后串联侧不能恢复均压,V1i会逐渐偏移为V1av,极端情况下会逐渐跌落至零或者升高至V1,系统稳定性差。
相比之下,采用串联侧控制系统功率正向和反向传递时具备更好的稳定性,受到扰动后系统能恢复并实现串联均压和并联均流。为了保证双向传输时的稳定性,本文以串联侧控制作为研究方向[10, 24]。
本节以TPS调制的N模块ISOP-DAB为例,提出一种简化的功率平衡控制策略,该策略不需要采集模块的特征物理量。
以变换器工作在式(2)工作段为例,第i个模块的功率表达式为
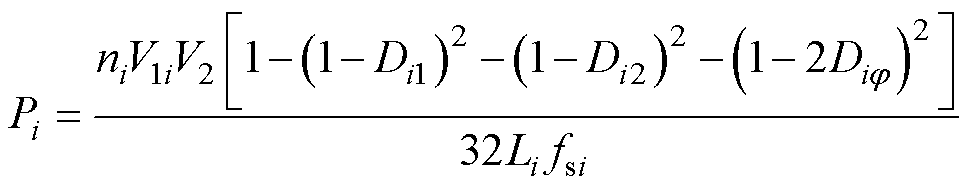 (3)
(3)
式中,Di1为i模块的D1;Di2为i模块的D2;Dij 为i模块的Dj;fsi为i模块的开关频率。
为简化分析,做出如下合理假设
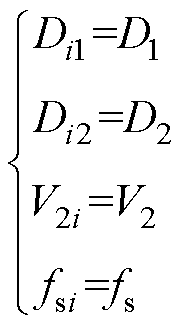 (4)
(4)
此时,不同模块的控制参数仅移相占空比Dij 有差异。因为多模块的参数不一致,所以要实现功率平衡需要调节相应的控制参数。当功率平衡时令控制参数D1j 与Dij 的关系为
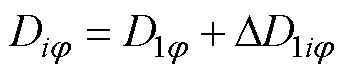 (5)
(5)
式中,DD1ij 为功率平衡时模块1控制参数D1j 与模块i控制参数Dij 的移相补偿量。将式(5)代入简化后的模块i功率表达式(2),得
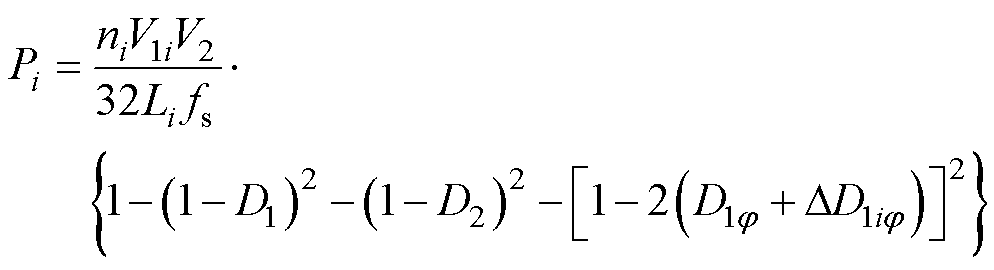 (6)
(6)
考虑到D1jÎ[0,0.5]且DD1ij<D1j,故DD1ij 的高次项数值很小并可忽略,得到
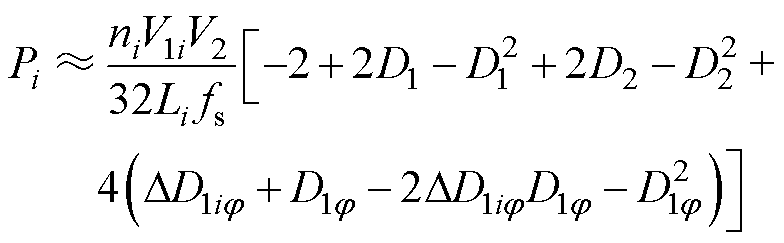 (7)
(7)
假设DD1ij 加入后,N个模块功率平衡P1= P2=…=PN,则串联侧均压V11=V12=…=V1N,故可导出工作在式(2)所需的移相补偿量DD1ij为
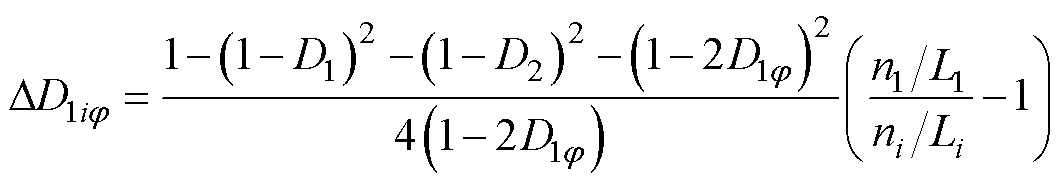 (8)
(8)
式中,ni/Li为第i个模块的变压器电压比与等效电感的比值,为便于分析,定义模块参数Hi=ni/Li。
当式(2)使用等效电感电流IL_RMS最小化控制策略,k=0.8时,所需的移相补偿量DD1ij 关于D1j 和H1/Hi的变化曲线如图3所示。
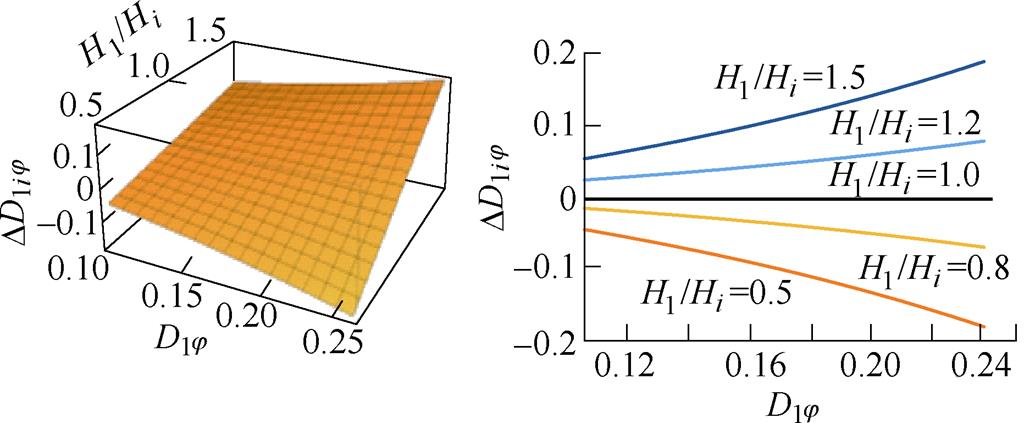
图3 移相补偿量DD1ij 关于Dj 的变化曲线
Fig.3 Variation curves of phase shift compensation DD1ij with respect to Dj
H1/Hi<1时,DD1ij =Dij -D1j<0;而H1/Hi>1时,DD1ij =Dij -D1j >0。通过类似的方法,可以求解出变换器工作在模式A和模式B时所需的移相补偿量DD1ij,则三种模式下DD1ij 的表达式见表1。
表1 三种模式下DD1ij的表达式
Tab.1 Expression of DD1ij in three modes

模式DD1ij A B C
所提出的功率控制方案为了使功率平衡,求解出N-1个从模块(2~N)相对于主模块(模块1)的移相补偿量DD1ij,因此还需要H1/Hi的估计值才能使用本文所提出的多模块功率均衡方案。
第1节提出一种简化的控制策略:若已知模块参数Hi,代入DD1ij 表达式(8)可求解出所需的移相补偿量。实际上,普遍的是模块参数Hi未知的情况,特别是模块数量较多时,想要准确测量所有的Hi将变得非常繁杂。为简化测量模块参数Hi并兼顾功率平衡控制策略,提出一种模块参数Hi差异的估计方法,本文以模式C进行推导。
本节以Vab超前Vcd的TPS调制为例,将功率表达式(2)改写为变换器输入电压的表达式,有
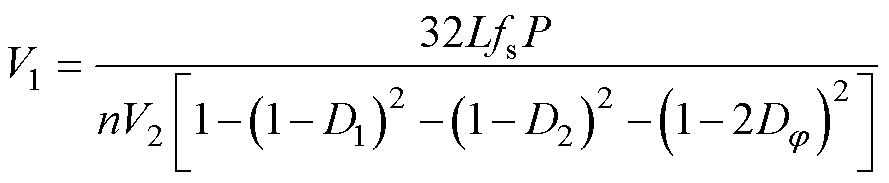 (9)
(9)
将移相补偿量DD1ij 表达式(8)重写为
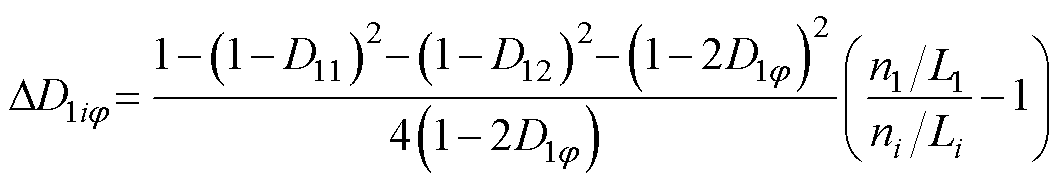 (10)
(10)
考察式(10)可以发现,对于含有未知模块参数Hi=ni/Li的DD1ij 表达式,直接解出模块参数的比值H1/Hi。根据两个模块的耦合关系,提出一种适用于ISOP-DAB的模块参数比值H1/Hi估计方法。
为了便于分析,以n1/L1>ni/Li为例,按照图4所示的流程,将估计方法及其过程分为如下三个阶段展开详细分析。
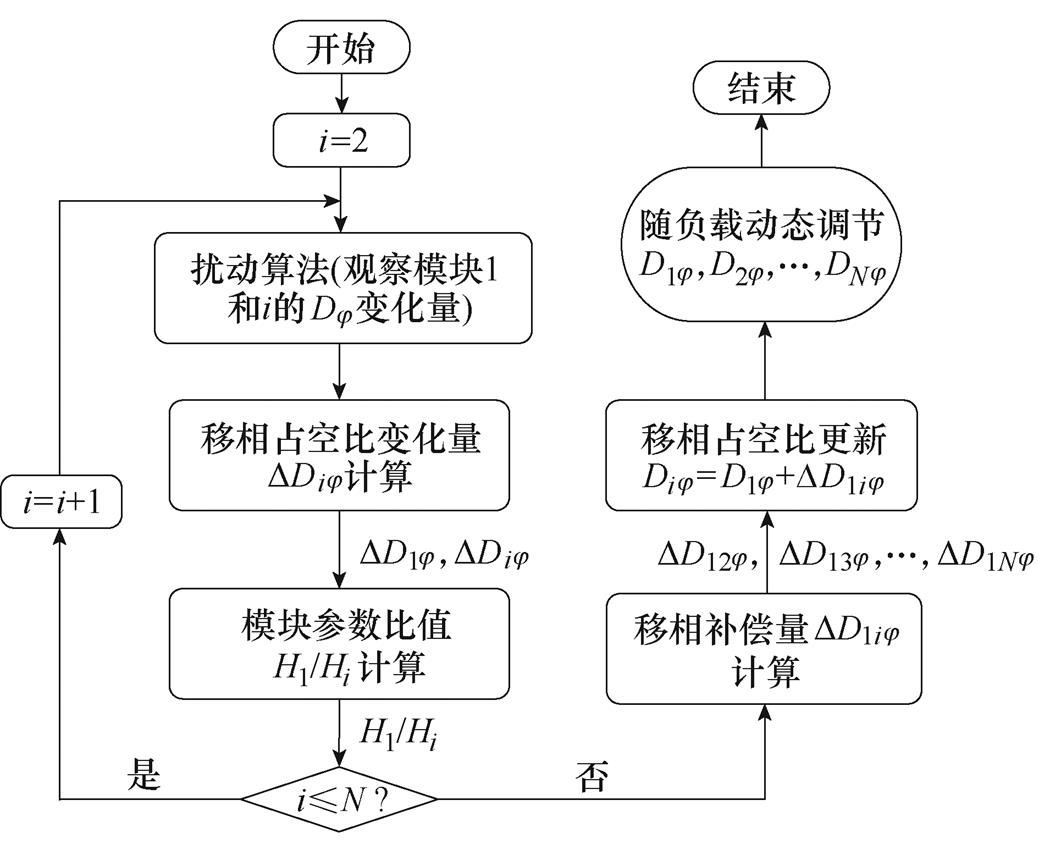
图4 差异估计法流程
Fig.4 Flowchart for difference estimation
2.1.1 阶段一:共同控制参数阶段
阶段一为系统启动阶段,N个模块以相同的控制参数D1、D2和Dj 工作并传递一定的功率。因为系统自身具备稳定性,在低功率段即使模块参数存在差异且不采取功率平衡,系统仍能工作。在该阶段,N个模块移相占空比D1j =Dij =DjPI_1,移相占空比由输出电压闭环PI确定。此时,N个模块有着相同的端口电平占空比D1和D2。在这个阶段,由式(2)知第i个模块的输入电压V1i为
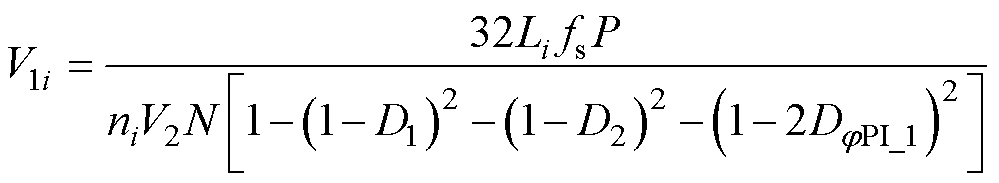 (11)
(11)
2.1.2 阶段二:参数估计阶段
阶段二开始前,模块1的控制参数D1j 完全由输出电压闭环PI确定,在阶段二开始时给D1j 叠加一个强制分量-DDjD。
在阶段二时D1j =DjPI_2-DDjD<DjPI_2,所以模块1的功率传递能力在阶段初期将降低,这使得模块1的输入侧支撑电容上积累更多的能量、V11升高。由于系统输入电压V1和负载功率P始终不变,而模块功率与串联侧分压成正比。系统重新稳定后,模块1的传递功率P1将增加,模块i的输入电压V1i和传递功率Pi相比注入强制分量前将减少。三个阶段的模块控制参数与功率的变化示意图如图5 所示。
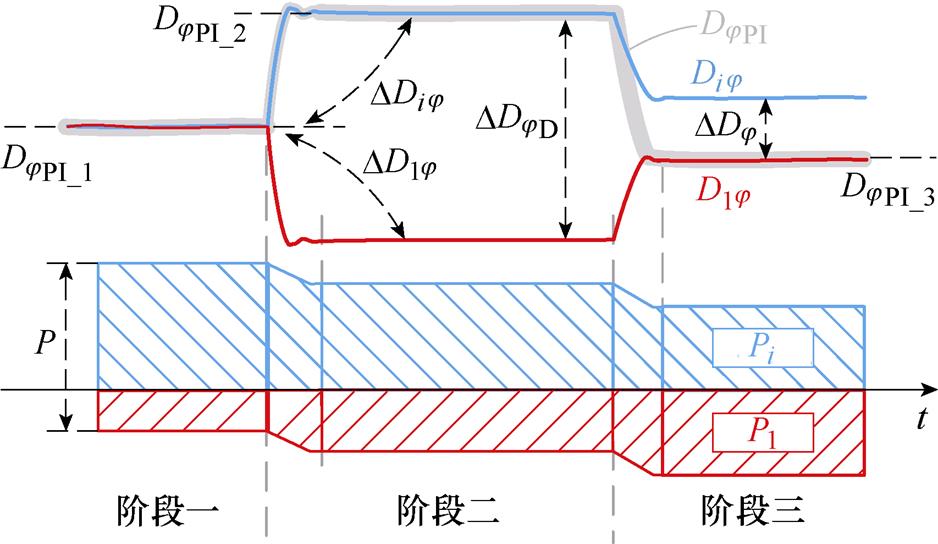
图5 差异估计法三个阶段的控制参数和功率变化示意图
Fig.5 Diagram of control parameters and power changes in three stages of difference estimation method
在注入强制分量前D1j =Dij =DjPI_1,注入后D1j =DjPI_2-DDjD,但Dij 仍然由输出电压PI确定,控制参数变化时输出电压V2必然产生变化,输出电压闭环PI调节,PI输出值从DjPI_1调节到DjPI_2且DjPI_2>DjPI_1,故系统稳定后模块i的移相占空比Dij 从DjPI_1变化到DjPI_2。
叠加强制分量前后移相占空比D1j 和Dij 变化量分别为DD1j 和DDij,并假设均为正值,则DD1j 和DDij 与DDjD、DjPI_1和DjPI_2的关系为
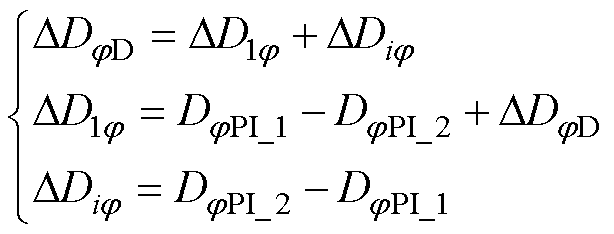 (12)
(12)
阶段二稳定后,第i个模块的输入电压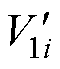 为
为
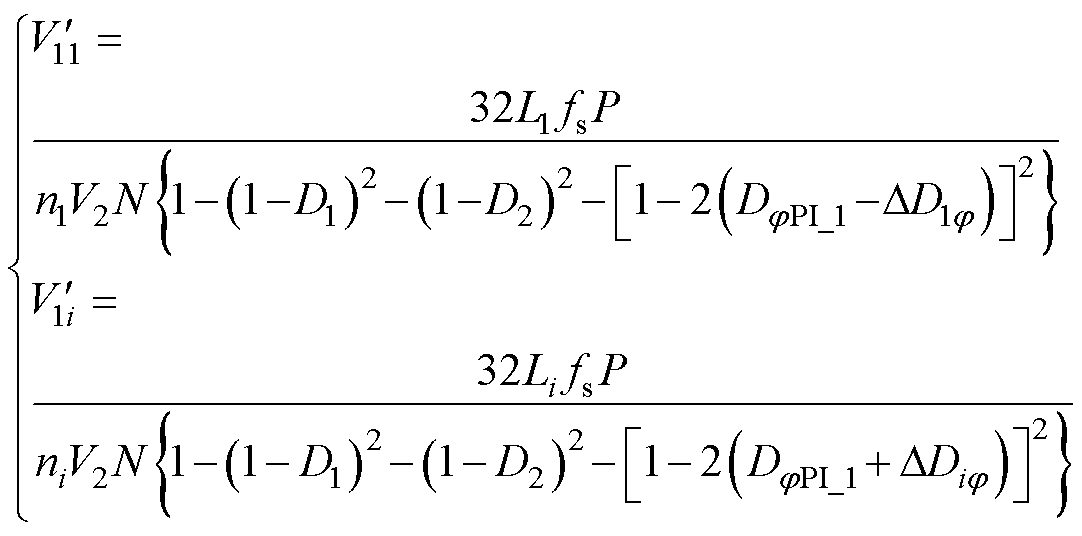 (13)
(13)
由式(11)、式(13)可知,叠加强制分量前后的模块输入电压变化量为DV1i。在叠加强制分量前后,系统功率P和系统输入电压V1不变,故模块输入电压变化量应满足DV11+DV1i=0。可得
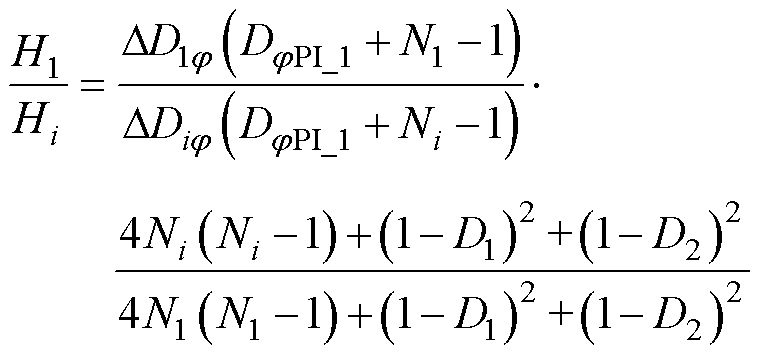 (14)
(14)
其中
N1=DPI_1-DD1j Ni=DPI_1+DDij
式中,D1、D2、DjPI_1、DDij 均可从控制器中读取或经过式(12)计算后得到。根据式(14)求解出两个模块的参数比值H1/Hi,将H1/Hi的求解结果代入式(8),可以得到移相补偿量DD1ij。
同理,可以获得模式A和B的H1/Hi表达式为
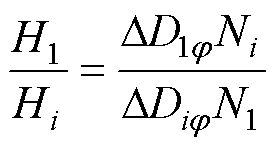 (15)
(15)
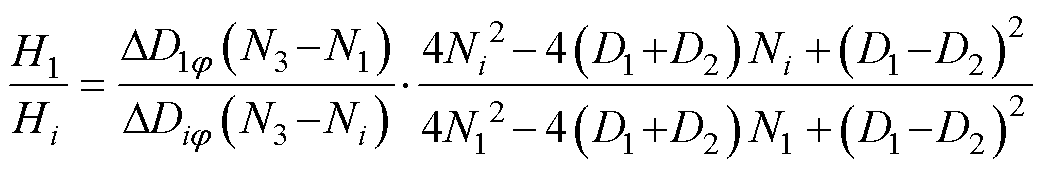 (16)
(16)
其中
N3=D1+D2-DPI_1
2.1.3 阶段三:功率平衡阶段
在估计出模块的参数比值H1/Hi后,利用估计出的模块参数比值,进一步得到了为实现模块功率平衡的移相补偿量DD1ij,系统过渡到功率平衡阶段,即阶段三。
在功率平衡控制阶段,去掉模块1控制参数D1j 中的强制分量DDjD,并重新由输出电压闭环PI所确定,此时D1j =DjPI_3。模块i的控制参数Dij 大小从DjPI_2切换到由D1j 和DD1ij 所确定的值,Dij = D1j +DD1ij,其中DD1ij 可由式(8)得出。在系统完全进入功率平衡阶段后,D1j 和DD1ij 随着负载动态调节,满足功率的传递并兼顾模块的平衡。结合1.2节提出的N模块平衡控制策略,可以整理出N模块参数差异估计与功率平衡控制的步骤,系统控制结构如图6所示。
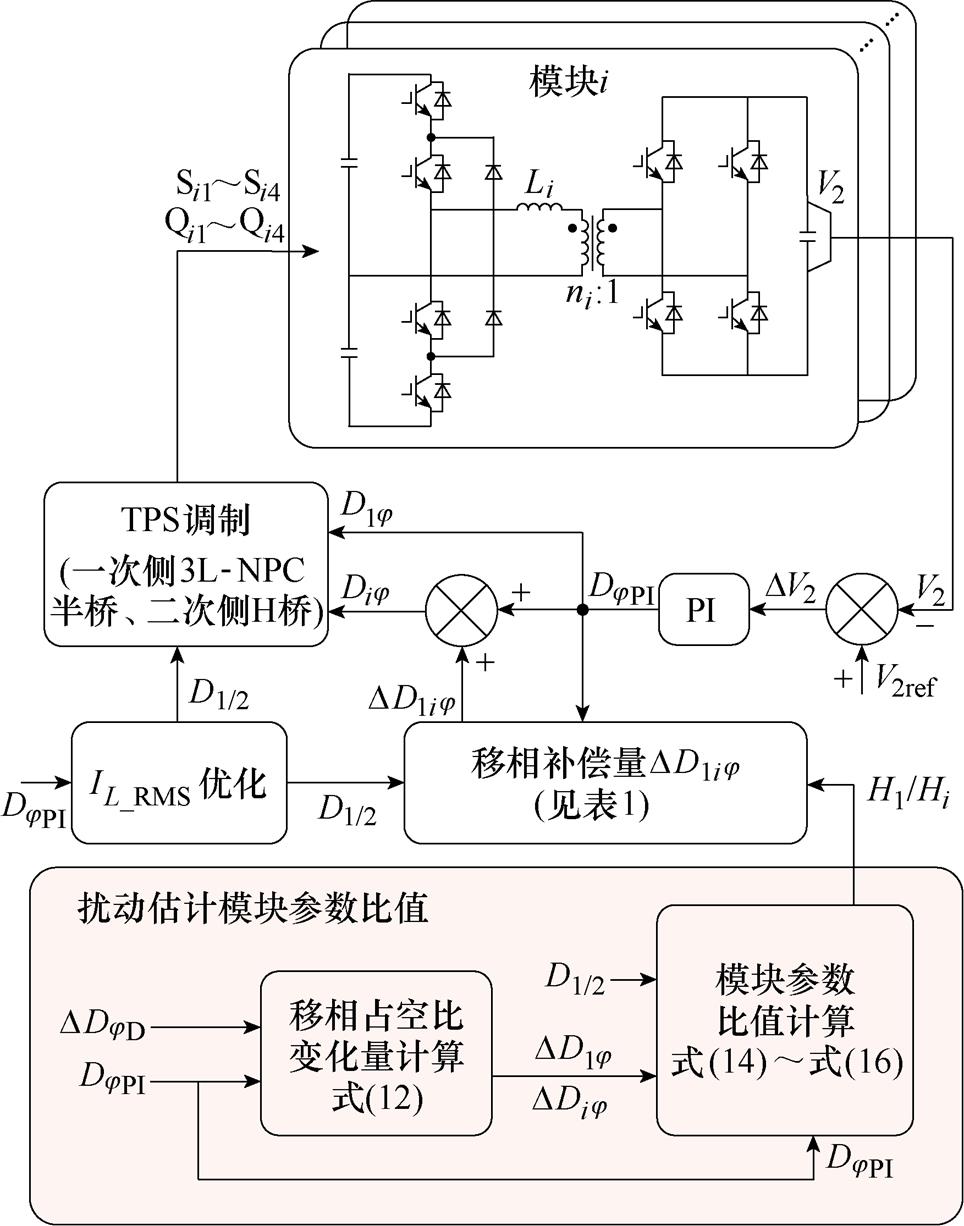
图6 系统控制结构
Fig.6 System control structure diagram
在模块出现传递功率超过其最大传递能力时,即过功率,会存在破坏电路的潜在威胁并降低系统安全性,在ISOP-DAB的模块平衡后,对系统所传递功率的边界展开进一步分析。
假设系统所能传递的最大负载功率为Pload_m,Pload_m受所有模块中传递功率能力最小的模块k约束,故需满足式(17)才能避免模块k出现过功率。
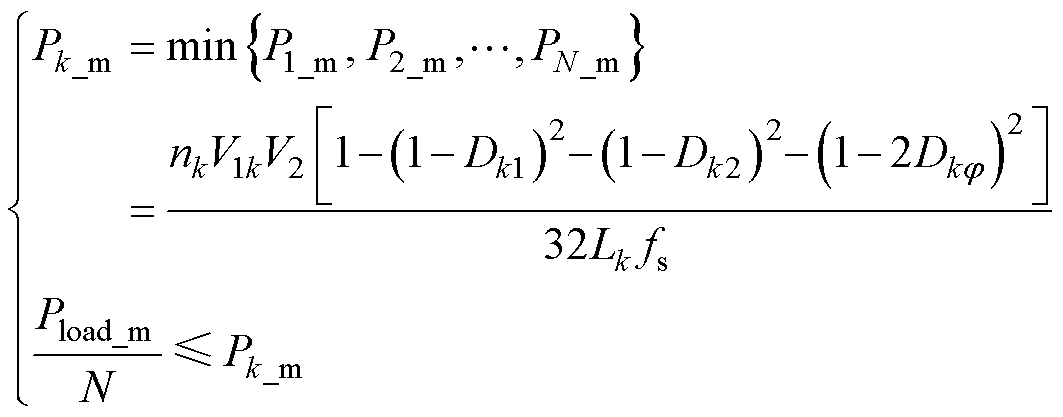 (17)
(17)
式中,Pi_m为模块i所能传递的最大功率。
为了验证本文提出的ISOP-DAB的参数差异估计和功率平衡控制策略,在Matlab/Simulink仿真软件中搭建由三个DAB模块组成的ISOP系统,仿真参数见表2。
表2 三模块ISOP-DAB仿真参数
Tab.2 Three-module ISOP-DAB simulation parameters
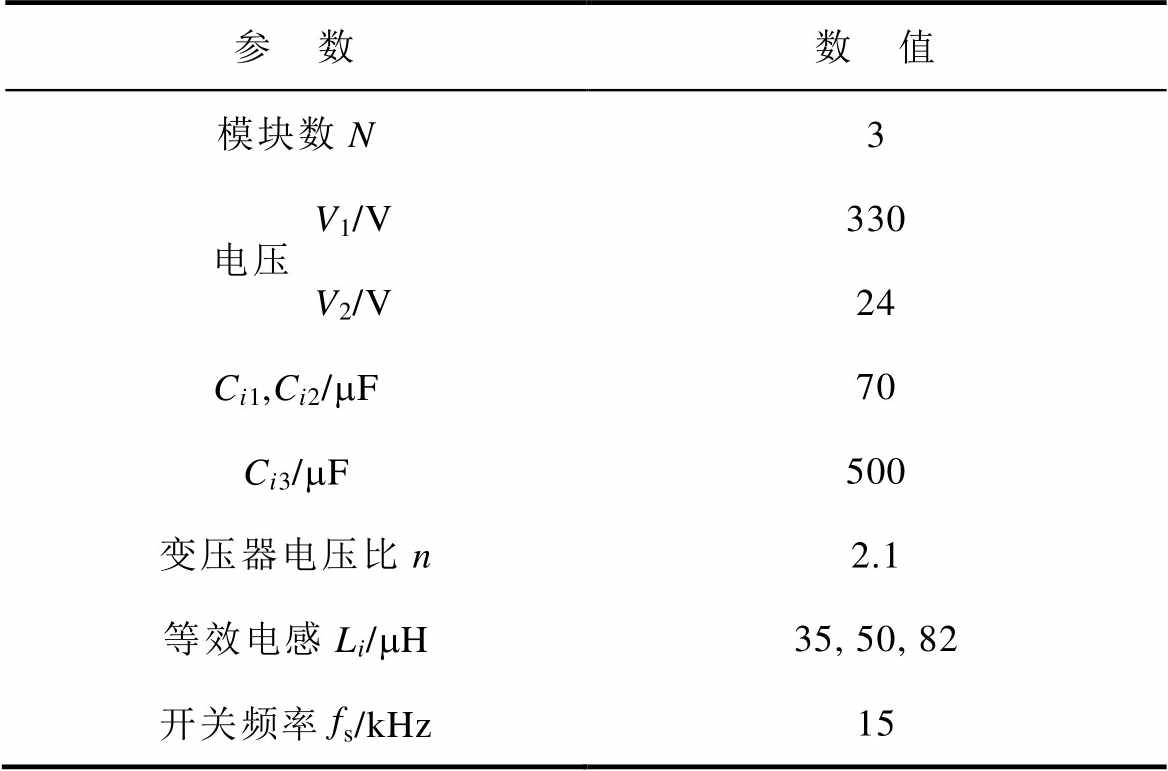
参 数数 值 模块数N3 电压V1/V330 V2/V24 Ci1,Ci2/mF70 Ci3/mF500 变压器电压比n2.1 等效电感Li/mH35, 50, 82 开关频率fs/kHz15
首先验证本文提出的参数差异估计方法,令模块1为主模块,模块2和3为从模块,注入的强制分量DDjD=-0.02。现以H1>H2>H3为例,其他两种情况(H2>H1>H3、H1<H2<H3)采用类似的分析方法。
当H1>H2>H3时,模块1~3的等效电感L1、L2、L3分别为35 mH、50 mH、82 mH,主模块参数H1=max{H1, H2, H3}。以共占空比/移相比空载启动系统后,在t≥0.8 s带载Pload=200 W;0.15 s≤t<0.25 s,模块1和2扰动期间模块3的D3j 保持不变;0.35 s≤t<0.45 s,在模块1和3扰动期间模块2的D2j 保持不变,两次扰动后分别估计出模块参数差异的比值;t≥0.45 s时,进入多模块的功率平衡控制,三个模块的输入电压V1i分别为109.8 V、110.7 V、109.5 V,整个过程中三个模块的输入电压V1i和输出电压V2如图7所示。可以明显地观察到,使用参数差异估计方法后串联侧均压效果良好。
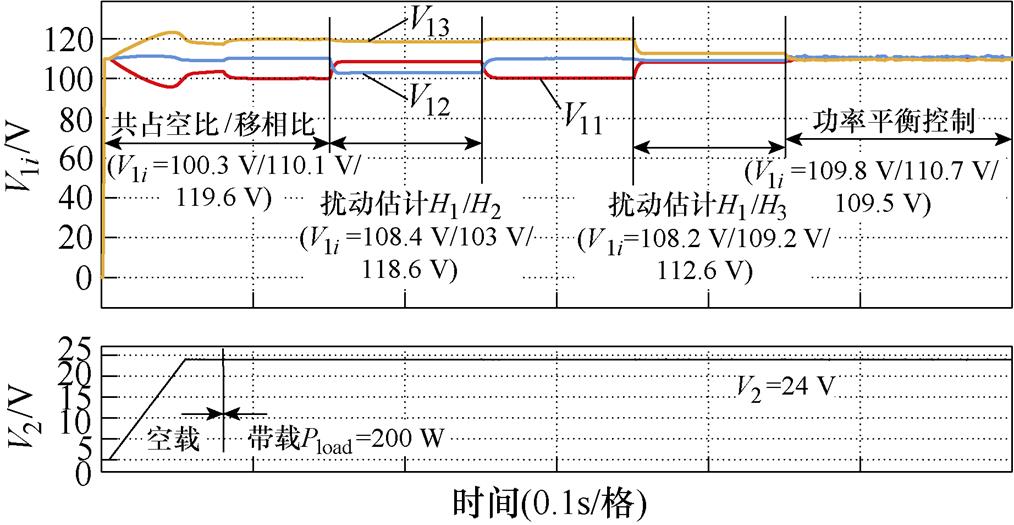
图7 模块参数差异估计过程
Fig.7 Module parameter difference estimation process
实验平台如图8所示。两个模块一次侧3L-NPC半桥中钳位二极管型号为LSIC2SD120A10;开关管均采用SiC MOSFET,但型号并不相同(以增加模块参数的差异性):模块1的开关管型号为P3M12080K3、模块2的为SCT2080KE。两个模块的二次侧H桥开关管型号均为IXFN520N075T2。

图8 实验平台
Fig.8 Experimental platform diagram
表3 实验系统硬件参数
Tab.3 Hardware parameters of experimental system
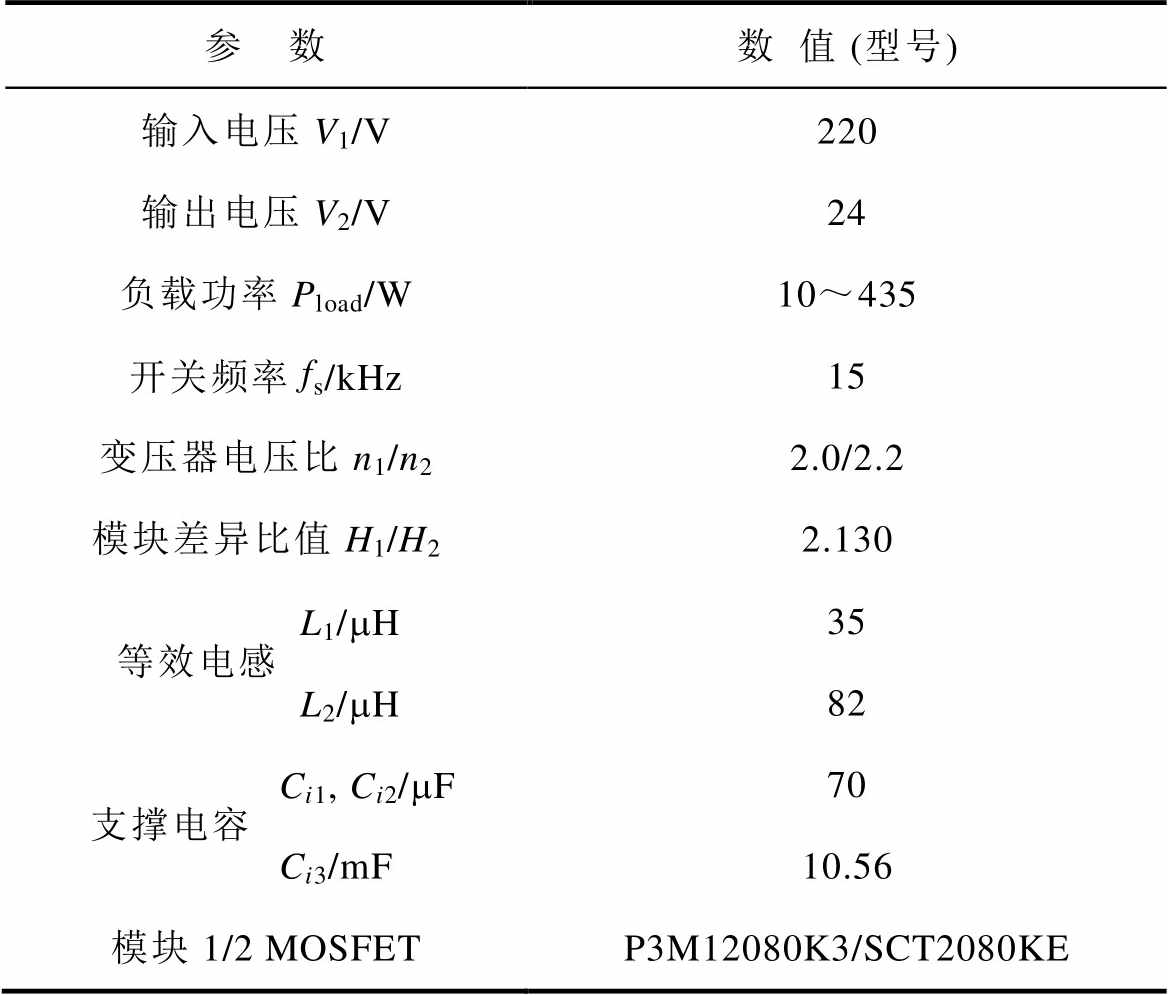
参 数数值 (型号) 输入电压V1/V220 输出电压V2/V24 负载功率Pload/W10~435 开关频率fs/kHz15 变压器电压比n1/n22.0/2.2 模块差异比值H1/H22.130 等效电感L1/mH35 L2/mH82 支撑电容Ci1, Ci2/mF70 Ci3/mF10.56 模块1/2 MOSFETP3M12080K3/SCT2080KE
本节实验条件:输入电压V1=220 V、输出电压V2= 24 V、负载功率Pload=200 W。本节以扰动量-DDjD<0为例来验证模块参数差异估计方法,估计过程可分为三个阶段。
ISOP-DAB系统的模块参数差异估计过程如图9所示,其中,图9a、图9b分别是扰动量-DDjD为-0.040和-0.086,即|-DDjD|为较小量和较大量。
在阶段一、共占空比/移相比阶段,系统功率为200 W,D1j =D2j =DjPI=0.168。此时,模块输入电压V11/V12=94.5 V/124.8 V。
在阶段二、扰动估计模块差异阶段,在模块1的控制参数D1j 叠加了一个负值的强制分量-DDjD作为扰动。该阶段为调整阶段,扰动量较小时,调整时间为0.4 s,扰动量较大时,调整时间为0.8 s。这意味着模块1的传递功率P1将减少,所以V11/V12朝着均压方向变化,并且对比图9a和图9b可知,|-DDjD|较大时模块输入电压V11和V12变化更明显。
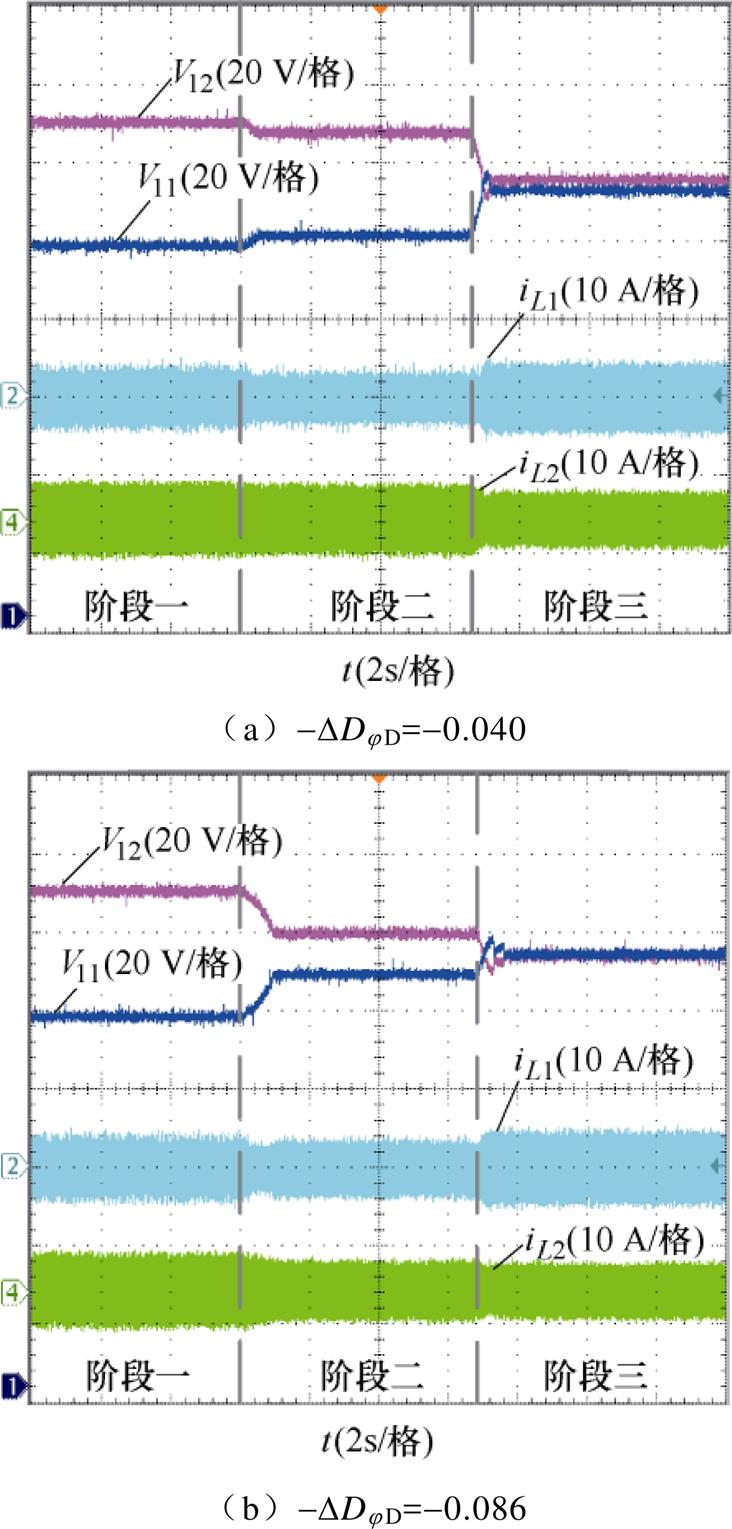
图9 模块参数差异估计过程
Fig.9 Module parameter difference estimation process
在阶段二稳定后,估计出两个模块参数比值H1/H2,系统进入阶段三,即功率平衡控制阶段,此时系统处于TPS状态,D1和D2跟随D1j 实时调节。该阶段为实际响应阶段,动态响应较慢,扰动量较小时,均压时间为0.3 s,扰动量较大时,均压时间为0.4 s。在阶段三稳定后:-DDjD=-0.04时,V11/V12= 109.0 V/110.7 V;-DDjD=-0.086时,V11/V12=110.4 V/ 109.1 V,实现了两个模块输入电压平衡,可知|-DDjD|较大和较小时都能较好地实现参数比值估计,验证了本文所提参数估计方法的可行性。
本节实验条件:V1=220 V、V2=24 V、Pload从10 W逐渐增加到系统最大功率435 W。由于实验是输入侧两模块串联分压和输出侧并联分流,故以模块1的输入电压V11和输出电流i21为例进行分析。
模块输入电压随负载功率的变化情况如图10所示。在不进行功率平衡控制时,如图10a所示,样机低功率段时V11/V12能维持一定的平衡,但在高功率Pload≥200 W(t≥t2)时系统串联侧电压出现严重不均压现象。Pload=250 W(t3~t4)时,尽管串联侧电压能稳定,但模块间不均压,系统稳定性差。当Pload=280 W(t4~t5)时,平衡已经完全破坏,触发了系统保护并停机。
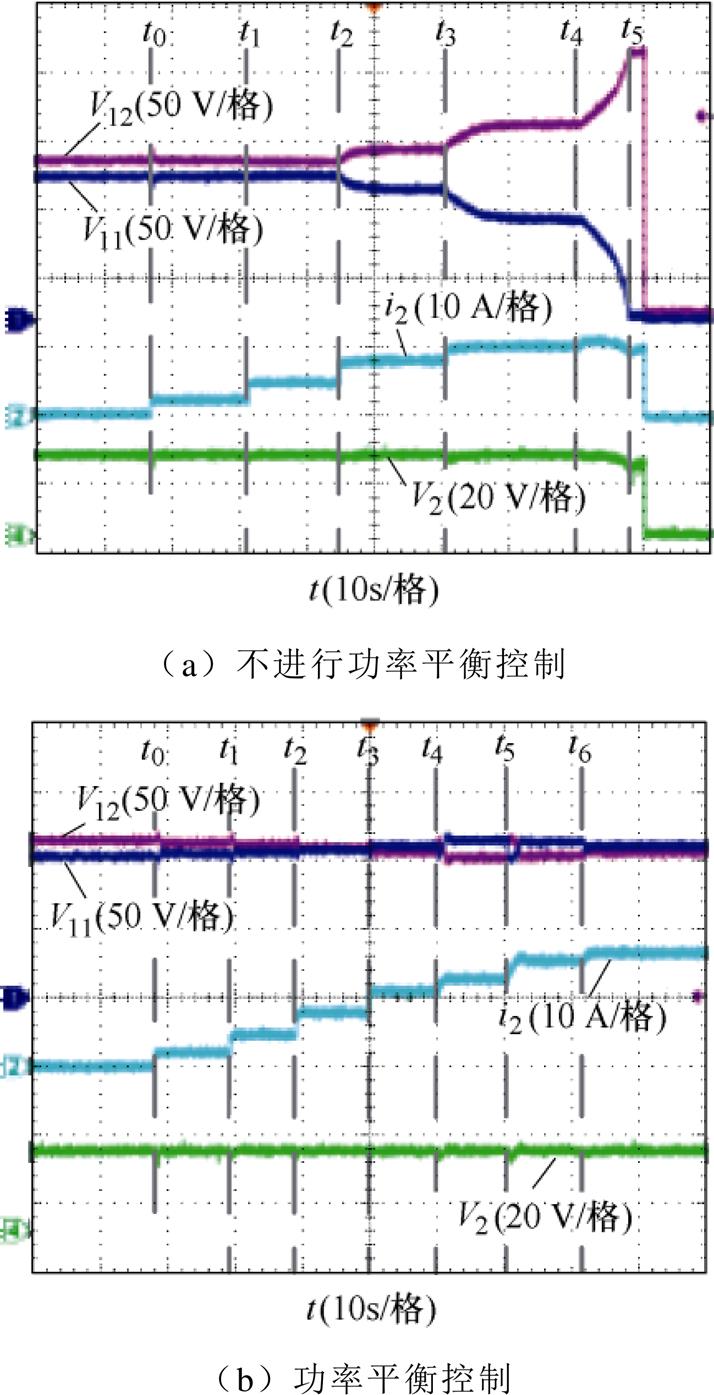
图10 模块输入电压随负载功率的变化情况
Fig.10 The change of module input voltage with load power
系统采用功率平衡控制时,如图10b所示,系统在全功率范围(Pload=10~435 W)内都能保持稳定工作。综上所述,采取平衡控制时,在Pload变化的调节过程中,模块输入电压没有过大的电压冲击或者跌落,在全功率范围内串联侧都有较好的均压效果,验证了该控制的有效性。
模块输出电流随负载功率的变化情况如图11所示。根据图11a,不采用功率平衡控制时,低功率段并联侧i21/i22能维持一定的平衡,但并联侧的均流特性随着Pload增加而变差,甚至出现Pload增加i21反而减小的现象。当Pload=280 W(t>t4)时并联侧完全失衡,此时,系统因为输入电流i1过大而触发保护。
在采取功率平衡控制后,如图11b所示,Pload≤280 W(t≤t4)时模块1输出电流i21不平衡度Di21%≤4.35%,Pload=320~380 W(t4~t6)时Di21%≈4.6%,系统没有因为模块失衡而触发保护。Pload=400 W (t>t6)时i21不平衡度维持在约3%。综上所述,模块并联侧在全功率范围内都有较好的均流效果,符合理论分析。
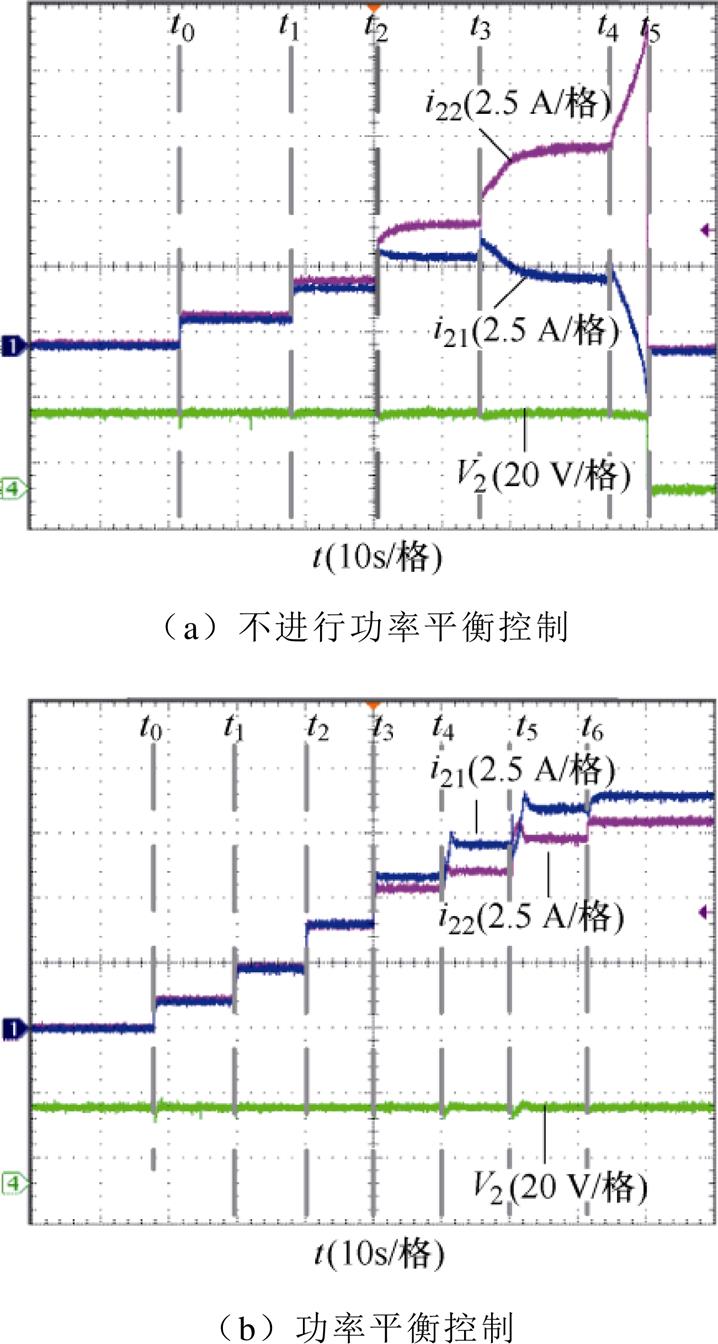
图11 模块输出电流随负载功率的变化情况
Fig.11 The change of module output current with load power
功率平衡控制前后均压不平衡度DV11%随Pload变化的实验数据拟合曲线如图12所示。不进行模块平衡时,|DV11%|均大于6%,甚至在重载时|DV11%|≥ 14%;在进行平衡控制后,全功率范围内|DV11%|明显降低。
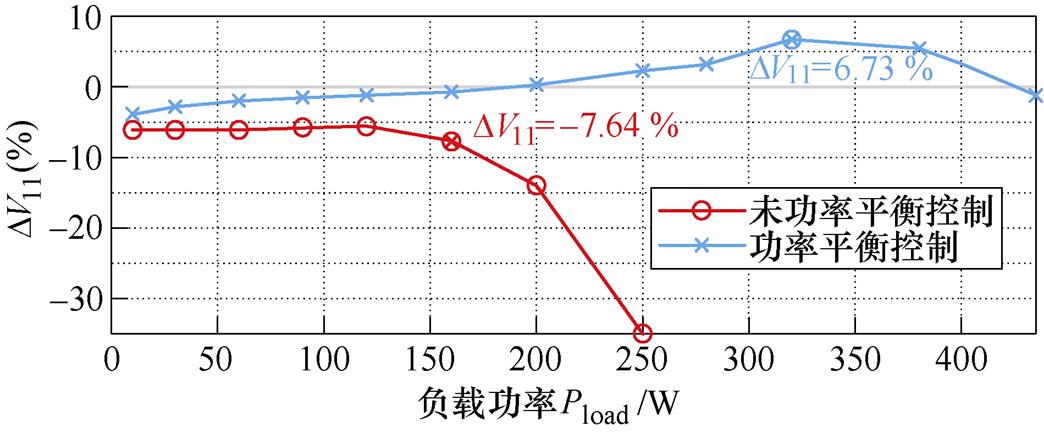
图12 两种控制下,均压不平衡度随负载功率变化的拟合曲线
Fig.12 Fitted curves of unbalance of voltage equalizationvarying with load power under two control conditions
采取功率平衡控制前后效率随Pload变化的实验数据拟合曲线如图13所示。在低功率段30 W≤Pload≤200 W时,两种控制方式都能保持一定的模块平衡。但不采取功率平衡时,当Pload>200 W后,随着串联侧严重不均压h 快速降低,与之对比的是,在200 W<Pload≤280 W范围内,采取功率平衡控制时h≥92%。考虑到系统是大电流输出的情况,故Pload≥320 W时大电流产生的欧姆损耗增加,h 稍微降低,但仍可以保持h>85%。
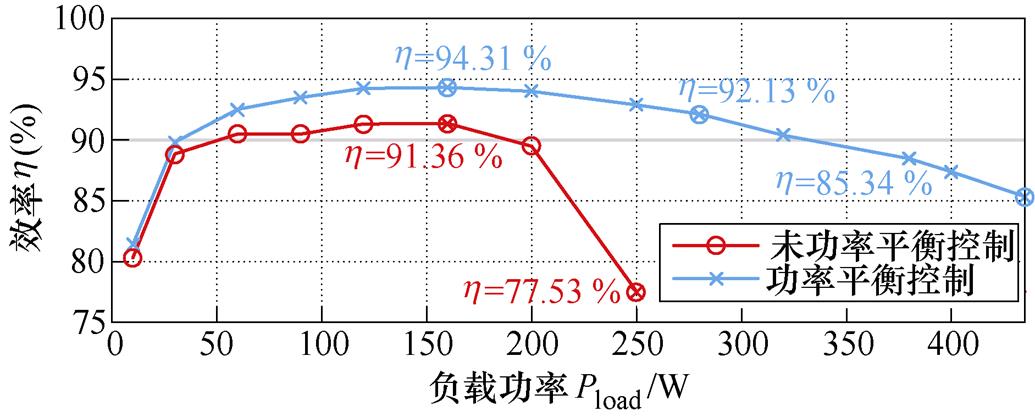
图13 两种控制下,效率随负载功率变化的拟合曲线
Fig.13 Fitted curves of efficiency versus load power under two controls
将近年发表的关于ISOP平衡控制的两篇文献与本文提出的控制方法进行对比,见表4。
表4 三种控制方法及实验结果对比
Tab.4 Comparison of three control methods and experimental results

文献电路结构传感器数量需求参数效率 (%)平衡效果模块差异 [25]两电平N+1无86~90好1.154 [15]两电平N+1漏感、电压比85~92好1.616 本文三电平+两电平1无82~94好2.130
表4中,实验模块差异为模块间不一致性的量化比值。本文所提出的平衡控制方法在模块差异较大的条件下,在DAB一次侧为三电平结构的实验平台上验证了有效性,仅需一个输出电压传感器来构成控制环路,并且无需准确测量或设计硬件参数,最高效率略优于其余文献。
本文分析了三电平半桥型ISOP-DAB变换器的各模块差异而导致的模块功率不均衡传输原因。基于TPS调制提出增加一个移相补偿量的变换器串联侧功率平衡控制策略。同时针对模块参数不一致问题,提出了多模块参数差异估计法,通过注入强制分量作为扰动进而采集反映模块差异的特征量变化,推导了差异估计表达式。仿真与实验结论表明:
1)相比现有的多模块功率平衡控制,本文提出的多模块功率平衡控制策略,使用串联侧控制策略解决了ISOP-DAB系统模块间功率不平衡问题。
2)提出了一种多模块参数差异估计方法,不需要系统的参数以及模块间的传感器采集。只要在输出侧设置一个电压传感器就能实现ISOP-DAB系统的模块间电压和传输功率均衡。
参考文献
[1] 郭小强, 魏玉鹏, 万燕鸣, 等. 新能源制氢电力电子变换器综述[J]. 电力系统自动化, 2021, 45(20): 185-199.
Guo Xiaoqiang, Wei Yupeng, Wan Yanming, et al. Review on power electronic converters for producing hydrogen from renewable energy sources[J]. Auto- mation of Electric Power Systems, 2021, 45(20): 185-199.
[2] 高范强, 李子欣, 李耀华, 等. 面向交直流混合配电应用的10kV-3MV·A四端口电力电子变压器[J].电工技术学报, 2021, 36(16): 3331-3341.
Gao Fanqiang, Li Zixin, Li Yaohua, et al. 10kV- 3MV·A four-port power electronic transformer for AC-DC hybrid power distribution applications[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3331-3341.
[3] 孙孝峰, 张绘欣, 张涵, 等. 一种用于电-氢多能互补型微电网的双有源桥集成Boost拓扑及其控制[J]. 电工技术学报, 2021, 36(10): 2092-2104.
Sun Xiaofeng, Zhang Huixin, Zhang Han, et al. Topology and control strategy of dual active bridge integrated boost circuit for electro-hydrogen multi- energy complementary microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2092- 2104.
[4] 何东欣, 张涛, 陈晓光, 等. 脉冲电压下电力电子装备绝缘电荷特性研究综述[J]. 电工技术学报, 2021, 36(22): 4795-4808.
He Dongxin, Zhang Tao, Chen Xiaoguang, et al. Research overview on charge characteristics of power electronic equipment insulation under the pulse voltage[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4795-4808.
[5] Shi Jianjiang, Gou Wei, Yuan Hao, et al. Research on voltage and power balance control for cascaded modular solid-state transformer[J]. IEEE Transactions on Power Electronics, 2011, 26(4): 1154-1166.
[6] Elserougi A A, Massoud A M, Ahmed S. A grid- connected capacitor-tapped multimodule converter for HVDC applications: operational concept and con- trol[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5523-5535.
[7] 张颖, 荆龙, 吴学智, 等. 输入串联输出串联型双向DC/DC变换器自适应均压控制策略研究[J]. 电网技术, 2018, 42(9): 2900-2907.
Zhang Ying, Jing Long, Wu Xuezhi, et al. Adaptive voltage sharing control strategy for input-series output-series connected DC/DC converter[J]. Power System Technology, 2018, 42(9): 2900-2907.
[8] Tang Yu, Zhao Zixiang, Shi Zhe, et al. Input-series output-parallel DC-DC converter based on adaptive coefficient voltage equalization control[J]. Inter- national Journal of Circuit Theory and Applications, 2022, 50(10): 3539-3550.
[9] 徐硕, 马智远, 许中, 等. ISOP-DAB的均压均流控制方法综述[J]. 北京交通大学学报, 2021, 45(6): 1-9.
Xu Shuo, Ma Zhiyuan, Xu Zhong, et al. Review of voltage and current sharing control methods for ISOP-DAB[J]. Journal of Beijing Jiaotong University, 2021, 45(6): 1-9.
[10] 杨博, 葛琼璇, 赵鲁, 等. 基于输入串联输出并联的双向全桥串联谐振DC-DC变换器系统控制策略研究[J]. 电工技术学报, 2020, 35(12): 2574-2584.
Yang Bo, Ge Qiongxuan, Zhao Lu, et al. Control strategy of dual bridge series resonant DC-DC converter system based on input series output parallel connection[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2574-2584.
[11] Liu Fei, Zhou Guangjun, Ruan Xinbo, et al. An input- series-output-parallel converter system exhibiting natural input-voltage sharing and output-current sharing[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(2): 1166-1177.
[12] 郑昊, 杜贵平, 雷雁雄, 等. 混合储能双向DC/DC变换器线性自抗扰控制研究[J]. 电力电子技术, 2022, 56(9): 80-83.
Zheng Hao, Du Guiping, Lei Yanxiong, et al. Research on linear active disturbance rejection control of hybrid energy storage bidirectional DC/DC converter[J]. Power Electronics, 2022, 56(9): 80-83.
[13] Kim S H, Kim B J, Park J M, et al. Decentralized control method of ISOP converter for input voltage sharing and output current sharing in current control loop[J]. Energies, 2020, 13(5): 1114.
[14] 张捷频, 刘建强, 杨景熙, 等. 输入串联输出并联变换器的控制器设计及稳定性分析方法[J]. 电工技术学报, 2017, 32(17): 180-188.
Zhang Jiepin, Liu Jianqiang, Yang Jingxi, et al. Controller design and stability analysis method for input-series-output-parallel converters[J]. Transactionsof China Electrotechnical Society, 2017, 32(17): 180-188.
[15] 安峰, 王嵩, 杨柯欣. 输入串联输出并联双有源全桥DC-DC变换器多模块优化功率平衡控制方法[J]. 电工技术学报, 2018, 33(16): 3732-3742.
An Feng, Wang Song, Yang Kexin. Multi-module optimized power balance control scheme of the input-series-output-parallel operated dual-active- bridge DC-DC converters[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3732-3742.
[16] Moon J, Lee T, Han Sanghun, et al. Multi-loop voltage control strategy of half-bridge voltage balancers with current sensorless scheme[J]. Journal of Power Electronics, 2020, 20(4): 1015-1024.
[17] 贾卓, 贾文超, 林宏博, 等. 双向DC/DC变换器ISOP系统功率均分策略研究[J]. 现代电子技术, 2021, 44(10): 105-109.
Jia Zhuo, Jia Wenchao, Lin Hongbo, et al. Research on power sharing strategy of ISOP system for dual active bridge DC/DC converter[J]. Modern Elec- tronics Technique, 2021, 44(10): 105-109.
[18] 谷恭山, 郑祥杰, 高明, 等. 两级结构模块化ISOP组合的DC-DC变换器均压控制策略[J]. 电工技术学报, 2019, 34(15): 3175-3185.
Gu Gongshan, Zheng Xiangjie, Gao Ming, et al. Research on voltage sharing control strategy of a combined two stage modular input-series output- parallel DC-DC converter[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3175-3185.
[19] 蔡逢煌, 石安邦, 江加辉, 等. 结合电流应力优化与虚拟电压补偿的双有源桥DC-DC变换器三重移相优化控制[J]. 电工技术学报, 2022, 37(10): 2559-2571.
Cai Fenghuang, Shi Anbang, Jiang Jiahui, et al. Triple-phase-shift optimal control of dual-active- bridge DC-DC converter with current stress optimi- zation and virtual voltage compensation[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(10): 2559-2571.
[20] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720-4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A hybrid optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720- 4731.
[21] 杨向真, 王锦秀, 孔令浩, 等. 电压不匹配运行条件下双有源桥变换器的效率优化方法[J]. 电工技术学报, 2022, 37(24): 6239-6251.
Yang Xiangzhen, Wang Jinxiu, Kong Linghao, et al. Efficiency optimization method of DAB converters under wide-voltage operating conditions[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(24): 6239-6251.
[22] Sun Zhifeng, Wang Qin, Xiao Lan, et al. A simple sensorless current sharing control for input-parallel output-parallel dual active bridge converters[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 10819-10833.
[23] 高宇, 李若愚, 李林柘, 等. 三重移相调制模式下双有源变换器的直接功率控制[J]. 电工技术学报, 2022, 37(18): 4707-4719.
Gao Yu, Li Ruoyu, Li Linzhe, et al. Triple phase shift modulation-based direct power control strategy for a dual active bridge converter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4707-4719.
[24] 曲璐. 输入串联型组合变换器控制策略关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
Qu Lu. Study on key technologies of input series combination converters control strategy[D]. Harbin: Harbin Institute of Technology, 2018.
[25] Qu Lu, Zhang Donglai, Bao Zhiyun. Output current- differential control scheme for input-series-output- parallel-connected modular DC-DC converters[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5699-5711.
Abstract The dual active bridge (DAB) has the advantages of high voltage utilization, high power density, and bidirectional power transfer capability. In medium and high voltage-low voltage DC power grids, the input-series output-parallel (ISOP) DAB improves the voltage of the series side and realizes a large voltage conversion ratio. However, problems such as power imbalance between modules exist. This paper analyzes the module difference and power balance control for ISOP-DAB with a three-level neutral point clamped (3L-NPC) half-bridge.
Firstly, this paper compares existing multi-module power balance methods, introduces their advantages and disadvantages, and analyzes the structure and principle of the ISOP-DAB system with a 3L-NPC half-bridge-H bridge. The reasons for the power imbalance of multiple modules are analyzed, focusing on the power transmission imbalance caused by different module parameters of the three-level half-bridge ISOP-DAB converter.
Secondly, this paper analyzes the relationship between voltage, current, and power among ISOP-DAB modules. The factors affecting module consistency are discussed. The self-balancing ability of the system under disturbance is analyzed, as well as the difference in control stability between series and parallel sides under bidirectional power. A power balance control strategy without sampling voltage or current module is proposed based on TPS modulation, simplifying the sampling circuit and control design. The strategy provides a backup solution in case of sensor failure.
Then, an estimation method for multi-module parameter differences is proposed. Its core idea is to inject forced components as disturbance and observe feature changes reflecting module differences. Combined with the power balance control strategy, the estimation method can be extended to N modules. Three modules are simulated in Matlab/Simulink. The constraints of the control parameter are studied to avoid overpowering. The variation trend of the power boundary margin is analyzed concerning the module number and power.
Finally, an ISOP-DAB converter experimental platform with field programmable gate arrays (FPGA) controllers is designed to realize the voltage conversion from 220 V to 24 V. Under four disturbances of different sizes and plus and minus, the module difference estimation method is verified. In the output voltage range of 24 V and 10~435 W, the system can significantly improve the voltage balance on the series side under power balance control, and the efficiency is higher than 90% under most powers.
keywords:Input series output-paralle-dual active bridge (ISOP-DAB) converter, multi-module power imbalance, parameter difference estimation method, series side pressure equalization
DOI: 10.19595/j.cnki.1000-6753.tces.230316
中图分类号:TM46
国家重点研发计划(2021YFB2601500)和国家自然科学基金(52077183)资助项目。
收稿日期 2023-03-16
改稿日期 2023-09-01
李嘉进 男,2000年生,硕士研究生,研究方向为隔离DC-DC变换器拓扑及控制策略。E-mail: iij2022@163.com
舒泽亮 男,1979年生,教授,博士生导师,研究方向为牵引供电与传动领域的电力电子变压器。E-mail: shuzeliang@swjtu.edu.cn(通信作者)
(编辑 陈 诚)