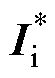 、参考输出电压矢量
、参考输出电压矢量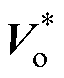 分别采用空间矢量调制策略确定整流级、逆变器开关状态。TSMC整流级、逆变级空间矢量分布如图2所示。
分别采用空间矢量调制策略确定整流级、逆变器开关状态。TSMC整流级、逆变级空间矢量分布如图2所示。摘要 Delta-Sigma调制(DSM)可在无需随机过程统计特性和复杂谐波理论分析的基础上,依托其过采样特性实现电力电子变换器变频调制。双级矩阵变换器(TSMC)作为一种理想的“全硅”交-交变换器,若能够将DSM引入TSMC,可进一步优化其电磁干扰(EMI)水平和运行效率,但TSMC的直流链电压波动问题导致TSMC-DSM策略难以直接实现。针对TSMC-DSM实现问题,该文提出一种基于参考电压修正的DSM策略。在所提方法中,通过解析TSMC整流级调制过程,将逆变级参考电压按照整流级矢量作用顺序进行修正,并依次获得各扇区参考电压修正系数。最后,在两相坐标系下分别构建两个DSM调制器,并将修正后的逆变级电压参考值引入DSM调制器以实现高性能TSMC-DSM策略。实验结果表明,所提策略能够对输出电压、电流频谱进行合理整形以减少系统对外部的电磁干扰,同时具备优良的电压传输比和动态调制性能。
关键词:双级矩阵变换器 Delta-Sigma调制器 电压传输比 双空间矢量调制
双级矩阵变换器(Two-Stage Matrix Converter, TSMC)不仅具备直接矩阵变换器无需直流滤波元件、能量输出灵活、结构紧凑等优点,而且避免了直接矩阵变换器复杂的四步换流机制,简化了调制环节,是一种具有发展潜力的电力电子变换器[1-2]。目前,采用经典双空间矢量调制的TSMC电压传输比数值仍无法突破0.866,且开关频率处因电压谐波引起的电磁噪声较为集中[3]。扩频调制技术依据特定数学规律将规则PWM序列变为不规则脉冲序列,在提升电压传输比的同时,令输出电压频谱扩展到更宽的范围,以达到降低输出谐波和电磁噪声的目的[4-6]。但是,由于TSMC功率器件数目较多,整流级-逆变级功率器件开关协同复杂,TSMC的扩频调制技术仍存在许多关键问题有待研究[7-10]。
现阶段,根据调制信号、调制参数和调制方式的不同,电力变换器扩频调制技术可分为随机PWM技术、周期PWM技术和程控PWM技术[8, 11]。随机PWM技术通常依据具有稳定统计特征的随机数来改变载波特性,以达到扩频的效果。文献[12]将随机载波序列的概率参数与频域谐波分布联系起来,提出了一种随机斜率PWM技术,降低了变流器电磁干扰和机械振动。周期PWM技术按照周期性规律变更载波密度来实现扩频调制,文献[13]在对变流器差模电压进行理论分析的基础上,讨论了正弦波、锯齿波和指数型载波密度对输出谐波峰值的抑制效果,给出了调节载波周期、形状等参数的数学依据。程控PWM是一种通过调节开关位置来实现特定谐波优化目标的扩频PWM技术,如经典的特定谐波消除PWM(Selective Harmonic Elimination- PWM, SHE-PWM)技术。文献[14]通过将采样中的Delta-Sigma调制器引入逆变器调制策略,提出一种特殊的程控PWM技术,即Delta-Sigma调制(Delta- Sigma Modulation, DSM)技术,可在无需确定随机过程统计特性和复杂谐波理论分析的基础上,借助DSM过采样特性来提高基带内信噪比,减少系统噪声。
区别于PWM技术,DSM本质上是一种模拟电路和数字电路相混合的调制器,可在量化器的辅助下完成调制波到开关信号间的转换,输出电压脉冲的密度对应于调制波的幅值,可通过低通滤波环节得到调制基波。文献[15-16]分别将一阶、二阶DSM应用于DC-DC变换器,并配合动态电流补偿器提升了电压调节动态性能,降低了系统杂散噪声。文献[17]提出了一种采用双环路六边形量化器的DSM技术,与经典DSM相比,不仅可降低两电平电压型逆变器的电压输出谐波,还极大地降低了开关损耗。文献[18-19]进一步扩展了DSM量化器的构建方式,提出了可消除共模电压的DSM技术。在总结DC-DC和DC-AC变换器DSM技术的基础上,文献[20]提出了直接矩阵变换器标量DSM策略,利用3个一阶DSM实现了参考输出电流的跟踪,但是输入功率因素仍处于失控状态。文献[21]通过引入模型预测控制环节分别实现了直接矩阵变换器的输入、输出功率调节,提出了预测DSM策略。
因DSM技术结构简单、无需复杂的随机统计特性和谐波分析过程,将其应用于电力电子变换器能够显著优化变换器输出频谱,降低变换器电磁干扰(Electromagnetic Interference, EMI)水平,并优化变流装置运行效率。然而,对于TSMC而言,可将其调制策略分为整流级算法和逆变级算法。更为重要的是,TSMC的无直流母线电容结构会导致其直流链电压处于两级波动状态[22-23]。文献[24]提出了完整的TSMC整流级DSM实现方案,有效地降低了TSMC的输入侧谐波与EMI水平。但是,DSM作为一类基于反馈控制结构的调制器,若逆变级DSM无法精确量化、跟踪整流级波动规律,将导致TSMC难以在逆变级直接实现DSM,且目前尚无文献报道相关改进成果。
为解决直流链电压波动导致的TSMC-DSM实现问题,本文提出了一种基于参考电压修正的DSM(Reference Voltage Correction based DSM, RVC- DSM)方案。在所提方案中,通过分析TSMC整流级位于不同扇区时的直流链电压波动规律,联立当前时刻的调制目标,求解得出不同直流链电压等级下的DSM参考值补偿系数。进而,将补偿系数按需、实时分配给不同扇区下的逆变级参考电压,以消除直流链电压两级波动现象对DSM零误差调制的影响,实现TSMC高效扩频效果。
TSMC由输入滤波电路、整流级电路、钳位电路和逆变级电路四部分组成,其基本电路结构如图1所示。TSMC应用最为广泛的调制技术是双空间矢量调制策略,即依据参考输入电流矢量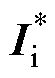 、参考输出电压矢量
、参考输出电压矢量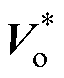 分别采用空间矢量调制策略确定整流级、逆变器开关状态。TSMC整流级、逆变级空间矢量分布如图2所示。
分别采用空间矢量调制策略确定整流级、逆变器开关状态。TSMC整流级、逆变级空间矢量分布如图2所示。
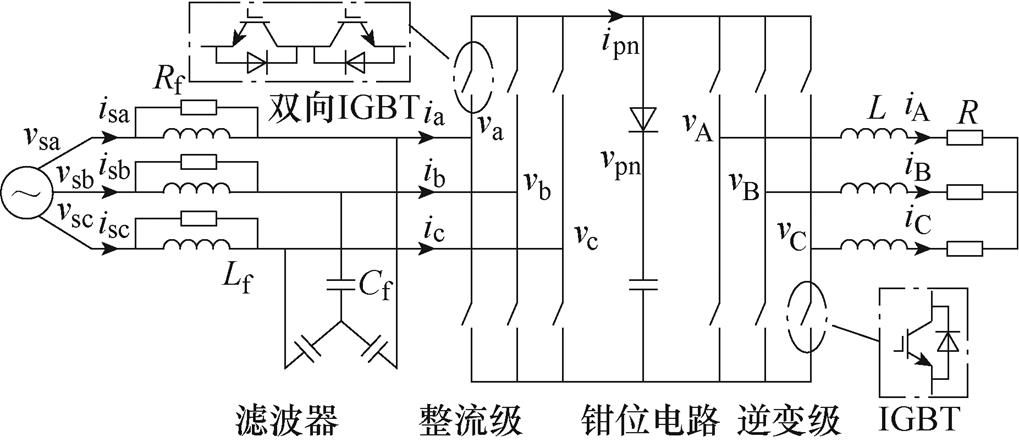
图1 TSMC拓扑结构
Fig.1 Topology diagram of TSMC
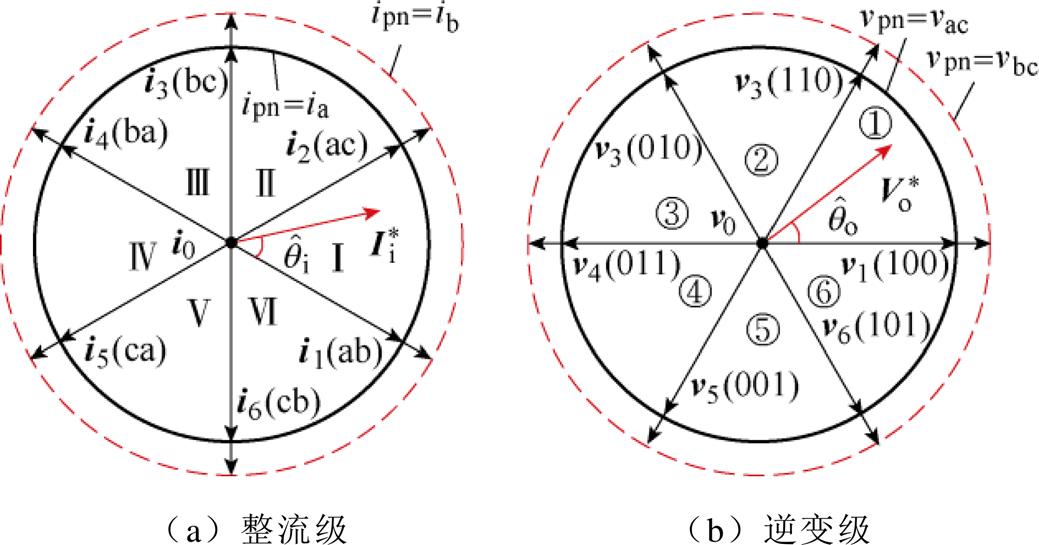
图2 TSMC空间矢量分布
Fig.2 Voltage vector diagram of TSMC
图2中,按照整流级导通相来划分,整流级共包含6个基本电流矢量ix(x=1, 2,…, 6)和3个零矢量i0(aa, bb, cc),如i1对应的导通相为整流级a相和b相,表示为i1(ab)。进而,通过这6个基本电流矢量可将输入电流矢量平面分为6个扇区,分别表示为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ。按照逆变级各开关通断状态来划分,逆变级共包含6个基本电压矢量vy(y=1, 2,…, 6)和2个零矢量v0(000, 111),如v1对应的导通开关为输出侧A相上桥臂开关和B、C相下桥臂开关,表示为v1(100),其中“1”表示对应相处于上桥臂IGBT开通、下桥臂IGBT关断状态,“0”表示对应相处于下桥臂IGBT开通、上桥臂IGBT关断状态。进而,通过这6个基本电压矢量可将逆变级电压矢量平面分为6个扇区,分别表示为①、②、③、④、⑤、⑥。
TSMC整流级的调制目标是在避免整流级电路直通的情况下获得尽可能大的直流链电压平均值,以保证TSMC的电压利用率。为此,通常选取输入扇区边界电流矢量来合成直流链电压vpn,并调节输入电流矢量以跟踪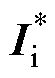 。具体来讲,通过将整流级PWM周期分为两段,并令每段占空比等于构成边界电流矢量的两个相电压瞬时值之比,定义滞后
。具体来讲,通过将整流级PWM周期分为两段,并令每段占空比等于构成边界电流矢量的两个相电压瞬时值之比,定义滞后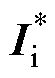 的边界矢量为
的边界矢量为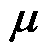 矢量,超前
矢量,超前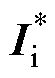 的边界矢量为
的边界矢量为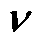 矢量,边界矢量
矢量,边界矢量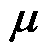 和
和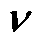 对应的占空比分别为
对应的占空比分别为
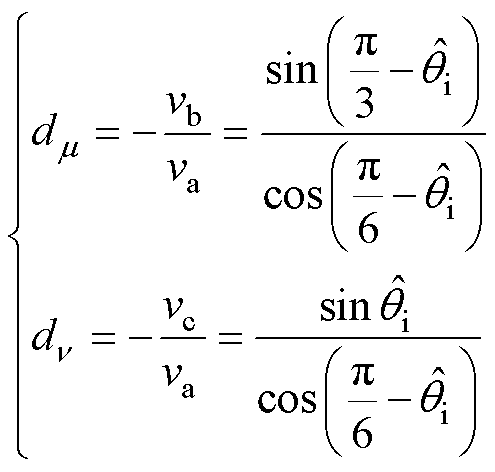 (1)
(1)
式中,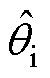 为
为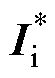 与所在扇区起始矢量间的夹角。
与所在扇区起始矢量间的夹角。
由式(1),TSMC的直流链电压vpn和电流ipn可分别表示为
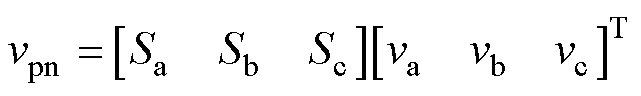 (2)
(2)
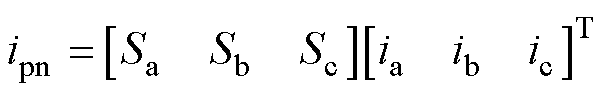 (3)
(3)
式中,Sj(j=a, b, c)为整流级三相桥臂开关状态,Sj=1表示上桥臂IGBT处于开通状态,Sj=0表示下桥臂IGBT处于开通状态。
由式(2)、式(3)可知,由于输入电压、电流均为正弦变量,三相正弦电压峰值包络线将与直流链电压波动峰值包络线重合。考虑到功率器件的开关频率要远大于输入电压频率,可将一个斩波周期内的两段输入线电压视作常量,从而可在两段输入线电压上分别进行逆变级空间矢量调制(Space Vector Modulation, SVM)。
定义TSMC电压传输比K为
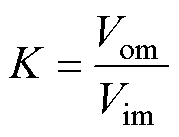 (4)
(4)
式中,Vim和Vom分别为TSMC输入、输出相电压幅值。根据SVM原理,定义滞后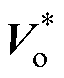 的边界矢量为m矢量,超前
的边界矢量为m矢量,超前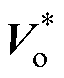 的边界矢量为n矢量,边界矢量m、n和零矢量对应的占空比dm、dn、do分别为
的边界矢量为n矢量,边界矢量m、n和零矢量对应的占空比dm、dn、do分别为
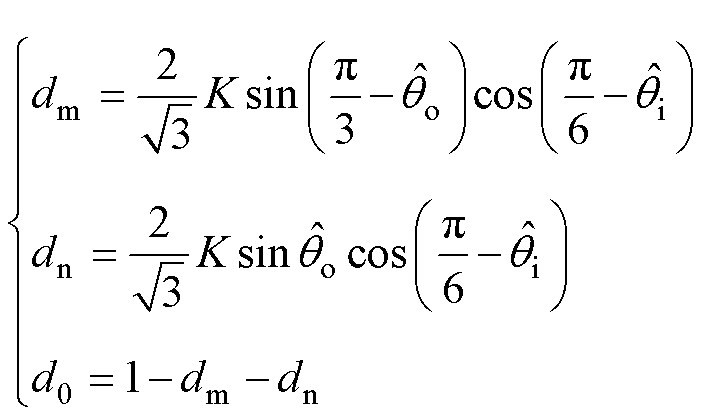 (5)
(5)
式中,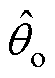 为
为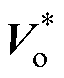 与所在扇区起始矢量间的夹角。由式(5)可知,当
与所在扇区起始矢量间的夹角。由式(5)可知,当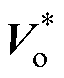 达到逆变器线性调制区边界时,dm的数值被限制为0.866。
达到逆变器线性调制区边界时,dm的数值被限制为0.866。
一阶DSM是由减法器(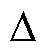 )和积分器(
)和积分器(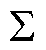 )构成的环路滤波器与量化器组成的负反馈系统,其原理框图如图3所示。
)构成的环路滤波器与量化器组成的负反馈系统,其原理框图如图3所示。
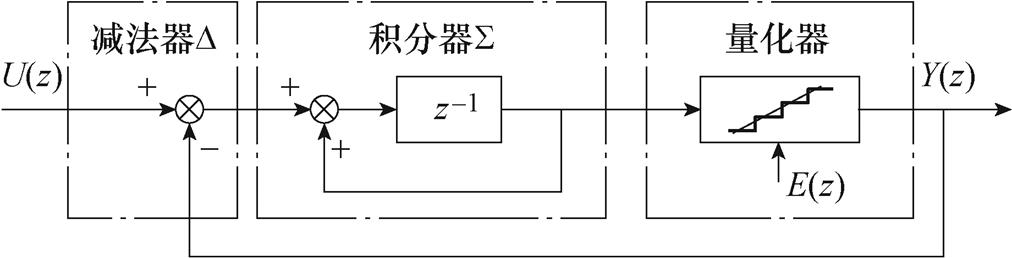
图3 一阶DSM原理框图
Fig.3 Diagram of first-order DSM
由图3,结合线性叠加原理,一阶DSM输出信号的z变换结果Y(z)可表示为
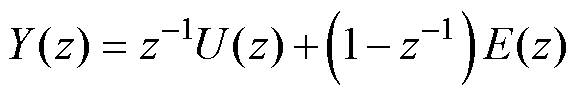 (6)
(6)
式中,U(z)、E(z)分别为输入信号、量化误差信号的z变换结果。
定义NTF=1-z-1表示噪声传递函数。根据离散控制理论可知,NTF是在z=1,即直流分量(信号频率w=0)处有一个零点的一阶高通响应,其幅频响应如图4所示。
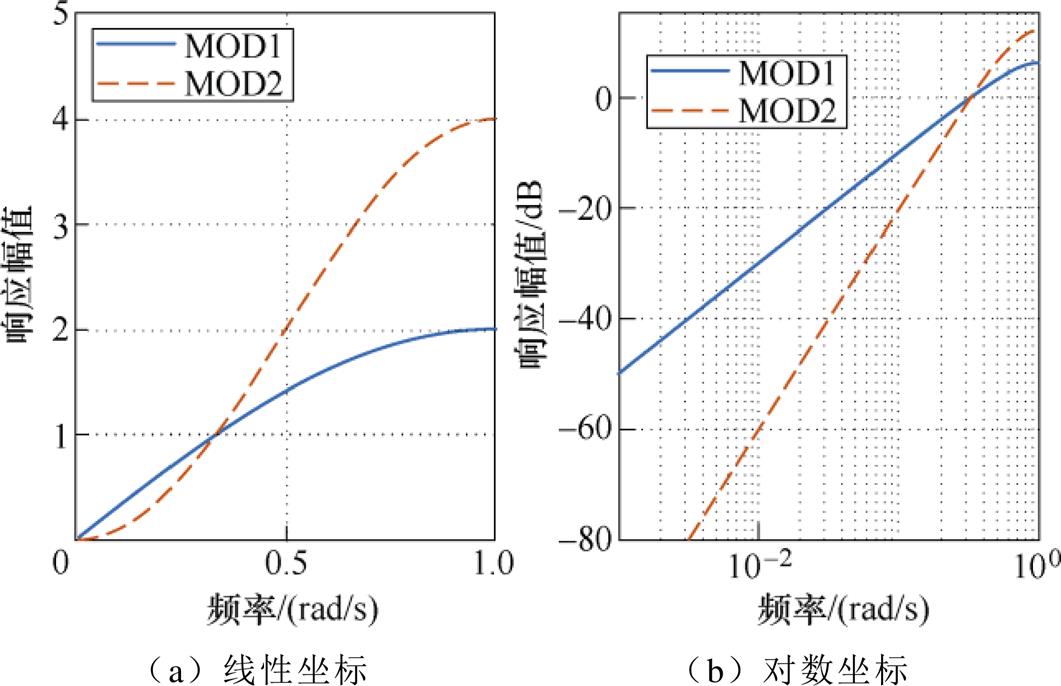
图4 NTF幅频响应
Fig.4 Logarithmic frequency response of NTF
图4说明了NTF高通响应的一阶性质(MOD1),即幅值以每10倍频程20 dB(20 dB/decade)的速率增长。由图4可知,量化噪声E(z)被高通滤波,相当于将E(z)外推至高频段,也可理解为被“整形”出信号带,即实现对量化噪声的频谱“整形”。同时,在DSM工作频率足够高时,输入传递函数z-1表现为全通特性,可以极低失真度还原输入信号U(z)。总体来看,DSM可在对TSMC输出频谱“整形”的前提下,实现对调制信号的高性能跟踪。
若在积分器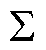 前方再串联一级积分器,即可构成二阶DSM,其原理框图如图5所示。
前方再串联一级积分器,即可构成二阶DSM,其原理框图如图5所示。
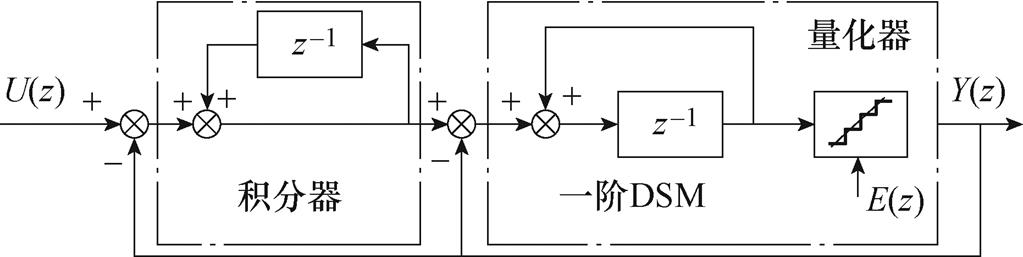
图5 二阶DSM调制器原理框图
Fig.5 Diagram of second-order DSM
由图5可知,二阶DSM的输出信号Y(z)可表 示为
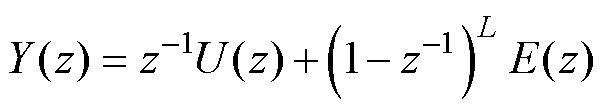 (7)
(7)
式中,L为DSM的阶数。
由式(7)可知,随着阶数L的提高,DSM在低频段对E(z)的抑制效果更优,调制器分辨率显著改善。图4同时给出了二阶DSM的NTF幅频特性,由图4可知,二阶DSM的NFT高通响应具有二阶性质,幅值以40 dB/decade的速率增长,具备更强的噪声整形效果。具体来讲,DSM工作频率每增加1倍,DSM分辨率将提高L+0.5位。然而,三阶以上DSM因稳定性设计困难,在实际工程中应用较少。
为保证TSMC电压利用率,TSMC整流级仍采用无零矢量SVM,将DSM引入TSMC逆变级中,实现TSMC扩频调制,此处以二阶DSM为例,其具体实现方案如图6所示。图6中,输出电压参考矢量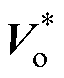 的两相静止坐标系分量
的两相静止坐标系分量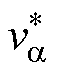 和
和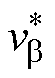 各自使用一路DSM,在与反馈矢量作差后作为积分器的输入,经积分器运算后得到偏差矢量
各自使用一路DSM,在与反馈矢量作差后作为积分器的输入,经积分器运算后得到偏差矢量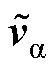 和
和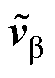 ,最后依据DSM量化器得到逆变级的开关信号SAp, SAn, SBp, SBn, SCp, SCn。
,最后依据DSM量化器得到逆变级的开关信号SAp, SAn, SBp, SBn, SCp, SCn。
DSM量化器的作用是依据偏差矢量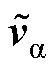 和
和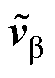 所组成的偏差矢量位置,确定合理的输出电压矢量,即TSMC开关信号,以消除TSMC输出电压矢量与
所组成的偏差矢量位置,确定合理的输出电压矢量,即TSMC开关信号,以消除TSMC输出电压矢量与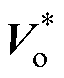 间的矢量偏差。
间的矢量偏差。
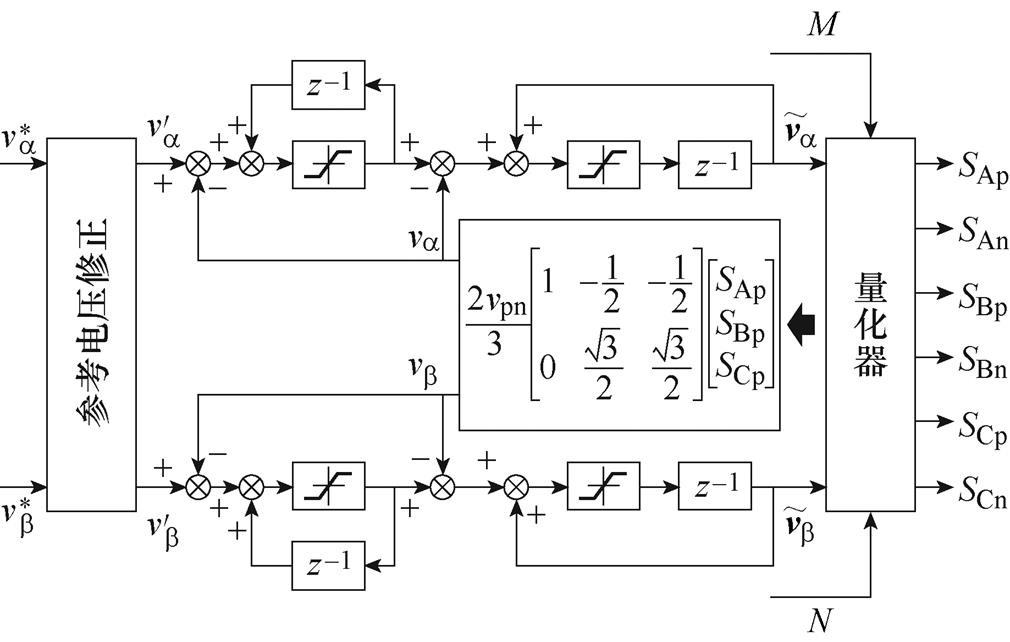
图6 TSMC DSM原理
Fig.6 Principle of TSMC DSM
对于电力电子变换器而言,在解决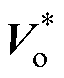 跟踪问题的同时,还需要考虑限制开关频率以降低开关损耗,一般选用形如Voronoi的空间矢量分区规则,又称“Voronoi量化器”,Voronoi量化器电压矢量分区示意图如图7所示。
跟踪问题的同时,还需要考虑限制开关频率以降低开关损耗,一般选用形如Voronoi的空间矢量分区规则,又称“Voronoi量化器”,Voronoi量化器电压矢量分区示意图如图7所示。
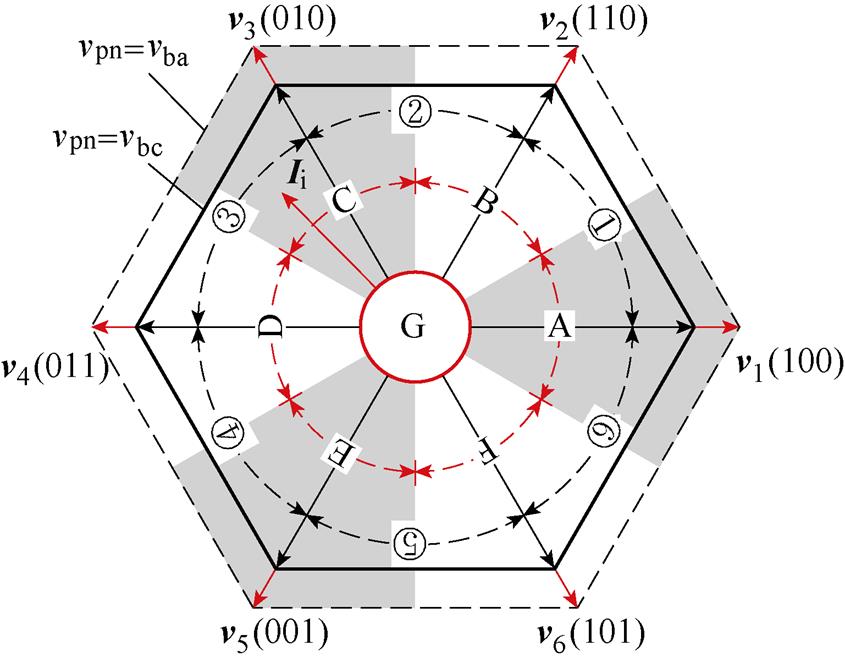
图7 Voronoi量化器电压矢量分区示意图
Fig.7 Schematic diagram of the voltage vector division of Voronoi quantizer
Voronoi量化器将电压空间矢量划分为A~G 7个区域,若由DSM输出的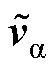 和
和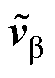 所构成偏差矢量
所构成偏差矢量 的幅值小于预定数值,即
的幅值小于预定数值,即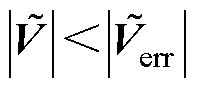 ,则量化器输出零矢量v0和v7。否则,需要按照以下规则来消除电压矢量偏差。
,则量化器输出零矢量v0和v7。否则,需要按照以下规则来消除电压矢量偏差。
(1)当前时刻参考电压矢量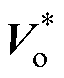 所处扇区M(M=①、②、…、⑥)与
所处扇区M(M=①、②、…、⑥)与 所处扇区N(N=A、B、…、F)有重合区域,则输出重合区域中的基本电压矢量vy(y=1, 2,…, 6)。如,N=A,M=①,重合区域的基本电压矢量为v1。
所处扇区N(N=A、B、…、F)有重合区域,则输出重合区域中的基本电压矢量vy(y=1, 2,…, 6)。如,N=A,M=①,重合区域的基本电压矢量为v1。
(2) 所处扇区N与
所处扇区N与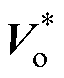 所处扇区M无重合区域,但与扇区M的相邻扇区有重合,则输出扇区M与该相邻扇区的公共边界矢量。例如,N=A,M=②,虽然扇区M和扇区N不重合,但扇区N与扇区①相重合,则输出扇区②与扇区①的公共边界矢量v2。
所处扇区M无重合区域,但与扇区M的相邻扇区有重合,则输出扇区M与该相邻扇区的公共边界矢量。例如,N=A,M=②,虽然扇区M和扇区N不重合,但扇区N与扇区①相重合,则输出扇区②与扇区①的公共边界矢量v2。
(3) 所处扇区N与
所处扇区N与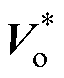 所处扇区M无重合区域,与扇区M的相邻扇区亦无重合,则输出v0和v7。
所处扇区M无重合区域,与扇区M的相邻扇区亦无重合,则输出v0和v7。
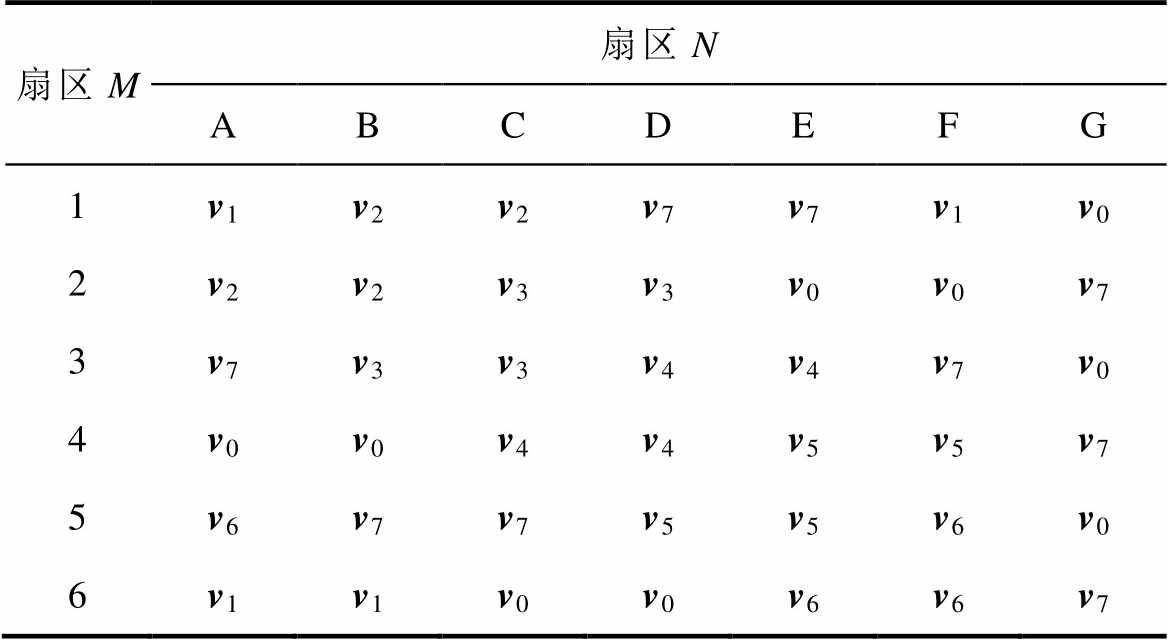
按照以上三条规则,Voronoi量化器的开关见表1。
表1 Voronoi量化器开关
Tab.1 Switching table of Voronoi quantizer
扇区M扇区N ABCDEFG 1v1v2v2v7v7v1v0 2v2v2v3v3v0v0v7 3v7v3v3v4v4v7v0 4v0v0v4v4v5v5v7 5v6v7v7v5v5v6v0 6v1v1v0v0v6v6v7
由表1可知,当判断条件落入G区时,表明输出电压与参考电压间的偏差较小,所以量化器将会选择输出零矢量,以减少不必要的开关动作,降低逆变器开关损耗。G区的设置并不会影响开关频率的上限,但若需提高逆变级开关频率,必须采用更短的控制/采样周期予以配合。
由第1节的分析可知,TSMC的直流链电压由整流级SVM得到,呈两级波动状态。进而,TSMC逆变级基本电压矢量幅值同样具有两种幅值状态。例如,假定当前时刻输入电流矢量Ii位于第Ⅲ扇区,整流级调制由基本电流矢量iba和ibc来完成,此时直流链电压vpn交替等于网侧线电压vba和vbc,如图7所示。
vpn的数值波动将导致DSM存在以下两方面问题:
(1)若单位调制周期内电压反馈估计值va和vb为波动量,则参考电压数值为固定数值。DSM设计过程中仅考虑了量化误差消除问题,电压估计误差将难以消除。
(2)由于通常难以满足逆变级开关频率远大于整流级开关频率,那么在单位调制周期内,DSM将无法在整流级开关状态切换前实现对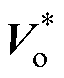 的零误差跟踪,从而导致DSM在理论上存在不可消除的调制偏差。综合以上两点,需要依照vpn的数值波动规律,对
的零误差跟踪,从而导致DSM在理论上存在不可消除的调制偏差。综合以上两点,需要依照vpn的数值波动规律,对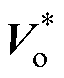 进行修正,以消除TSMC-DSM的调制 偏差。
进行修正,以消除TSMC-DSM的调制 偏差。
考虑到TSMC系统vpn数值波动仅会影响到参考电压幅值,故认为参考电压相位无需修正。分别定义整流级两端矢量作用时的幅值修正系数p和q,用以修正各自整流矢量作用时的逆变级参考电压,可分别写为
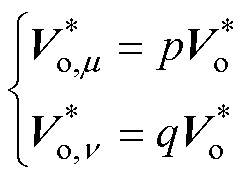 (8)
(8)
式中,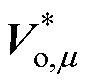 和
和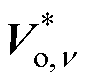 分别为整流级
分别为整流级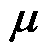 矢量和
矢量和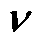 矢量作用下的修正后参考电压。同时,为保证单位控制周期对
矢量作用下的修正后参考电压。同时,为保证单位控制周期对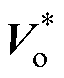 进行无差跟踪,需要满足
进行无差跟踪,需要满足
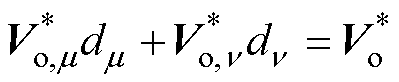 (9)
(9)
将式(1)和式(8)代入式(9),可得
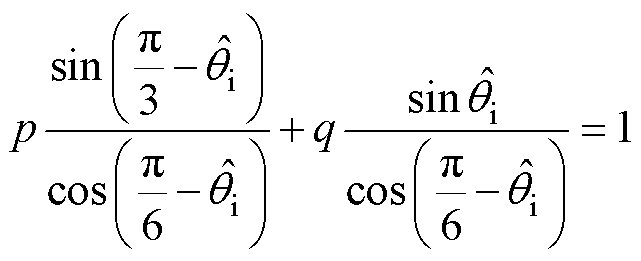 (10)
(10)
同时,p和q对参考电压的修正原理本质上是要求参考电压跟随当前网侧电压进行波动。基于这一原理,以第Ⅰ扇区为例,可得
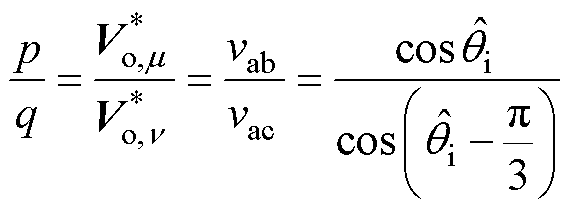 (11)
(11)
联立式(10)和式(11),可得
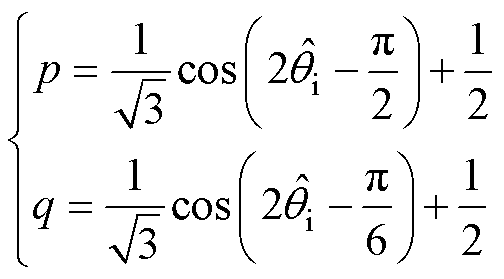 (12)
(12)
同理,可推导得到Ii位于第Ⅱ~Ⅵ扇区时的修正系数。然而,由于扇区对称性,第Ⅱ~Ⅵ扇区的修正系数表达式均与式(12)相同。
将式(12)的p、q数值代入式(8)和式(9),对参考电压进行预修正,即可得到满足DSM零误差跟踪的调制参考值,实现TSMC系统的高性能DSM策略。
大量研究表明,直接矩阵变换器的最大线性电压传输比为0.866。然而,TSMC电压传输比会受到输出/输入频率比、输入功率因数等多种因素的影 响[24]。为简化分析,假定TMSC运行于单位输入功率因数下,且输出电压初始相位为零,令TSMC逆变级零矢量占空比d0=0,即逆变级采用双有效矢量用以合成输出电压矢量,此时TMSC具有最大输出电压幅值。由式(5)可得,两个有效矢量的占空比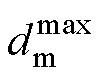 和
和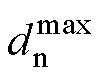 满足
满足
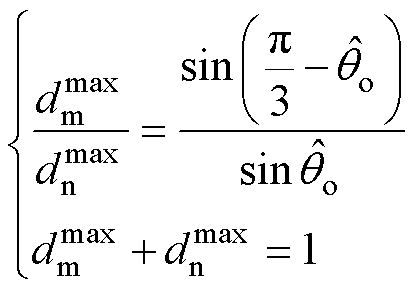 (13)
(13)
由式(13),在输入功率为1.0时,可得双有效矢量合成状态下的最大输出电压幅值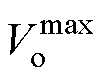 为
为
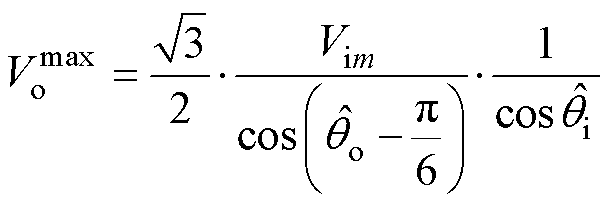 (14)
(14)
由式(14),此时TSMC的电压传输比满足
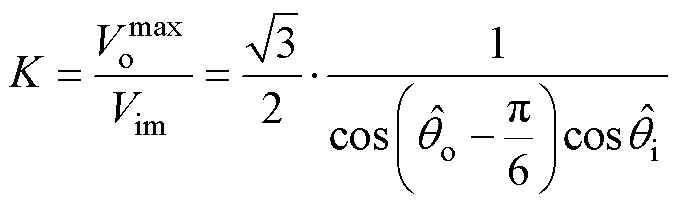 (15)
(15)
由式(15)可知,若令整流级与逆变级均工作于六拍运行模式,即令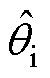 =p/3,
=p/3,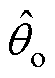 =0,可得TSMC极限电压传输比
=0,可得TSMC极限电压传输比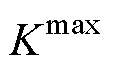 =1.155。然而,对于RVC-DSM,整流级始终工作于线性调制区,无法工作于六拍运行模式;逆变级依照表1中的开关表动作,极限情况下可进入六拍运行模式。因此,令
=1.155。然而,对于RVC-DSM,整流级始终工作于线性调制区,无法工作于六拍运行模式;逆变级依照表1中的开关表动作,极限情况下可进入六拍运行模式。因此,令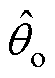 =0,即RVC- DSM逆变级工作于六拍运行模式,其电压传输比等于1/cos
=0,即RVC- DSM逆变级工作于六拍运行模式,其电压传输比等于1/cos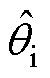 。进而可知,RVC-DSM策略的极限电压传输比随输入相位的变化在1.0~1.155之间波动。
。进而可知,RVC-DSM策略的极限电压传输比随输入相位的变化在1.0~1.155之间波动。
为验证本文所提出RVC-DSM策略的有效性,采用Intel公司产Cyclone V FPGA芯片以及TI公司产TMS320F28377D MCU芯片作为主控单元,以Ametek MX22.5可编程程控电源作为网侧电压源,采用Yokogawa公司产WT5000系列功率分析仪实测调制策略效率,对TSMC双空间矢量调制、一阶RVC-DSM和二阶RVC-DSM策略进行实验研究,实验参数见表2,TSMC系统实验平台如图8所示。
为验证不同负载范围内双空间矢量调制、一阶RVC-DSM和二阶RVC-DSM的运行性能,调节负载电阻,图9给出了不同电压传输比下的TSMC输出电流总谐波畸变率(Total Harmonic Distortion, THD)数据,图10给出了不同电压传输比下的TSMC运行效率数据。
表2 实验平台参数
Tab.2 Experimental platform parameters

参 数数 值 网侧电压频率/Hz50 输入滤波电容/mF35 输入滤波电感/mH1.37 输入滤波电阻/W10 负载电阻调节范围/W0~40 负载电感调节范围/mH10~40

图8 TSMC系统实验平台
Fig.8 Experimental platform of TSMC
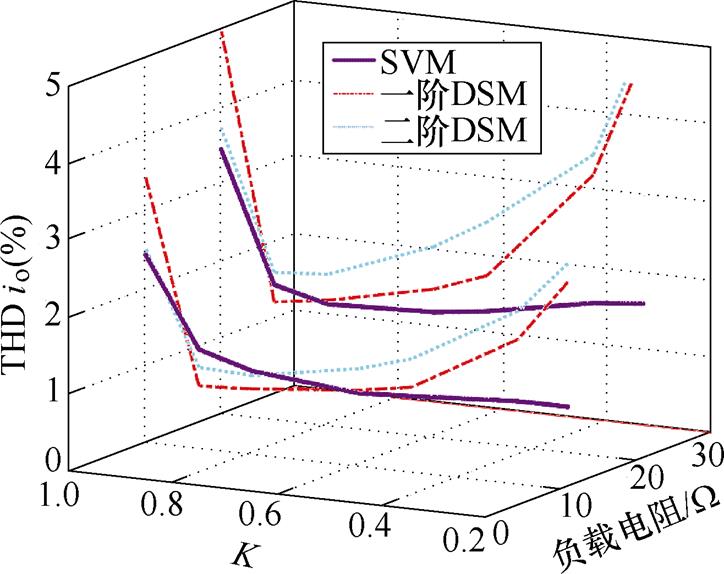
图9 不同电压传输比下输出电流THD数据
Fig.9 Output current THD data under different voltage transmission ratios
由图9可以看出,随着负载侧功率因数角的增大,相比于SVM策略,所提RVC-DSM策略的电流畸变率有所提升,但THD仍小于5%。同时,当0.5<K<0.8时,RVC-DSM策略的电流THD指标明显改善。然而,由图10可以看出,受益于RVC- DSM频谱整形效应,RVC-DSM策略的运行效率远高于SVM策略。EMI数值分析结果如图11所示。由图11可以看出,双空间矢量调制策略下的干扰电压尖峰主要集中于1 MHz以下,而RVC-DSM在10 MHz以内的干扰电压幅值较小,其干扰电压尖峰主要集中于30 MHz附近,表明RVC-DSM策略能够有效减弱TSMC在0~30 MHz内的传导干扰。
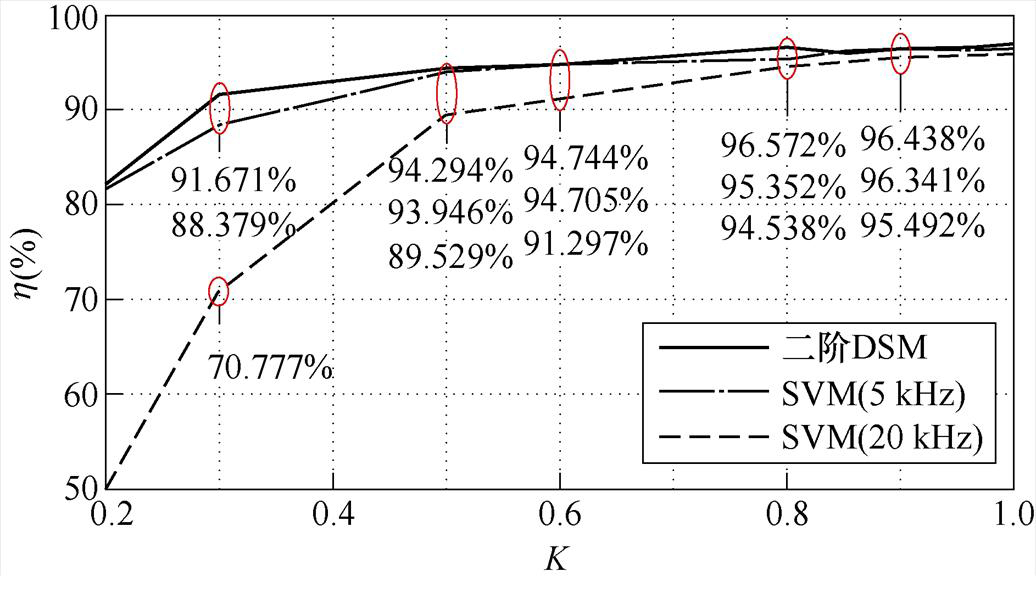
图10 不同电压传输比下运行效率数据
Fig.10 Operation efficiency data under different voltage transmission ratios
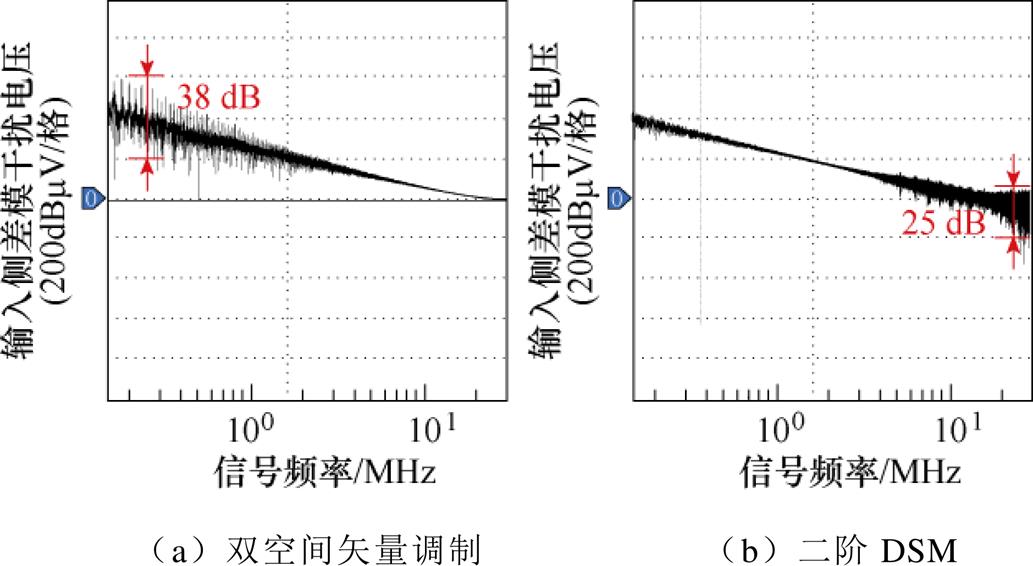
图11 EMI数值分析结果
Fig.11 EMI numerical analysis results
图12给出了K=0.6,负载电阻20 W,负载电感40 mH时TSMC分别采用SVM策略、一阶RVC- DSM策略和二阶RVC-DSM策略的输入电流、输出电流、输出线电压、THD和直流链电压波形。实验过程中,SVM策略PWM周期设定为200 ms,开关频率恒定为5 kHz;RVC-DSM策略的整流级PWM周期设定为200 ms,采样频率为5 kHz;逆变级控制周期设定为50 ms,采样频率为20 kHz,一阶DSM平均开关频率约为6.22 kHz,二阶DSM平均开关频率约为6.24 kHz。由图12可以看出,矩阵变换器网侧相电压和网侧电流相位基本一致,矩阵变换器工作于单位功率因数下。由图12a可以看出,基于固定开关频率的SVM会使得输出电压和电流在开关频率及其倍频处出现高频谐波簇。由图12b和图12c可以看出,在采用RVC-DSM策略后,原本在SVM下与开关频率(5 kHz、10 kHz、…)相关的谐波受到了较强抑制,这部分谐波能量被外推至高频段,并借助负载的低通特性滤除,有效地降低了TSMC系统对外部电子系统的电磁干扰。同时,由图12还可以看出,RVC-DSM策略输出电压的低频段性能稍有改变,但输出电流正弦度并未受到显著影响。
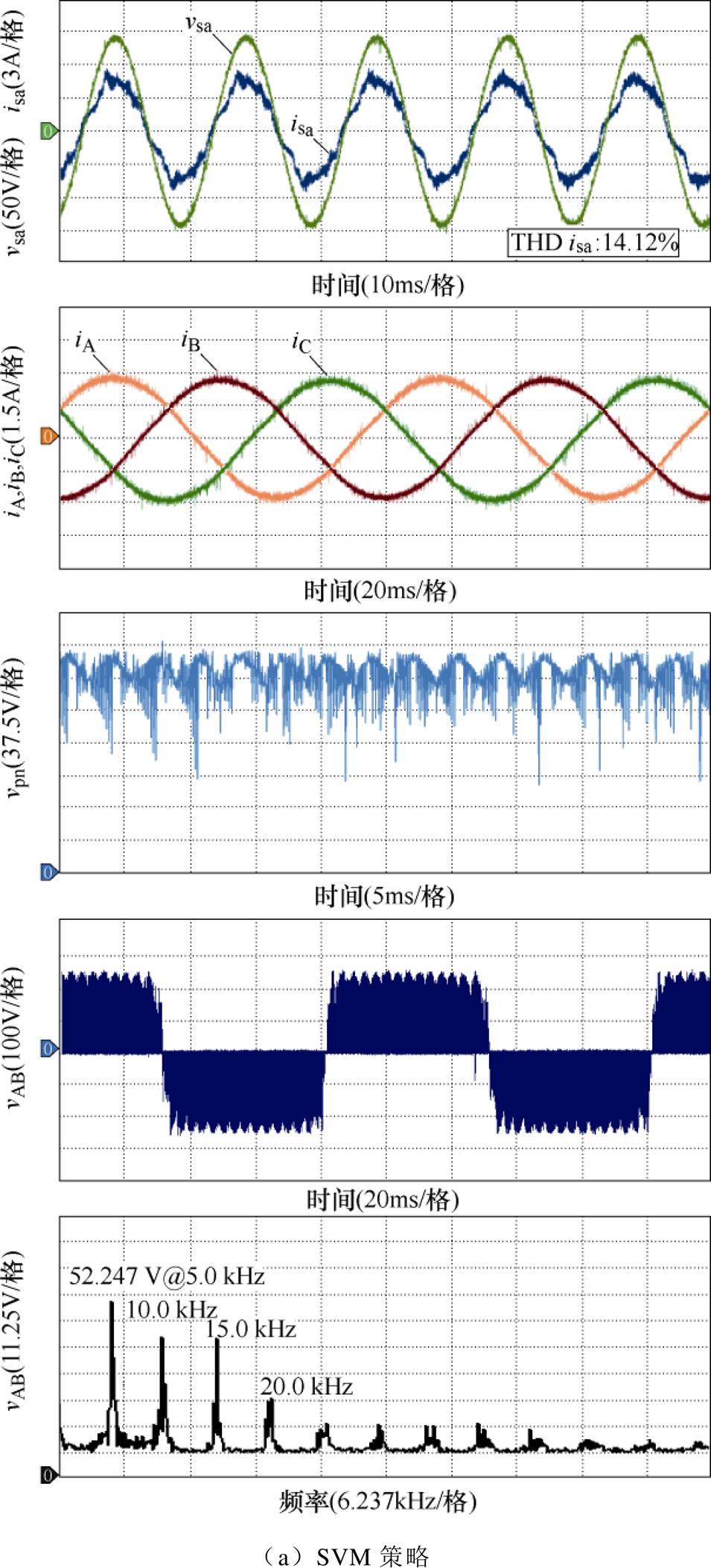
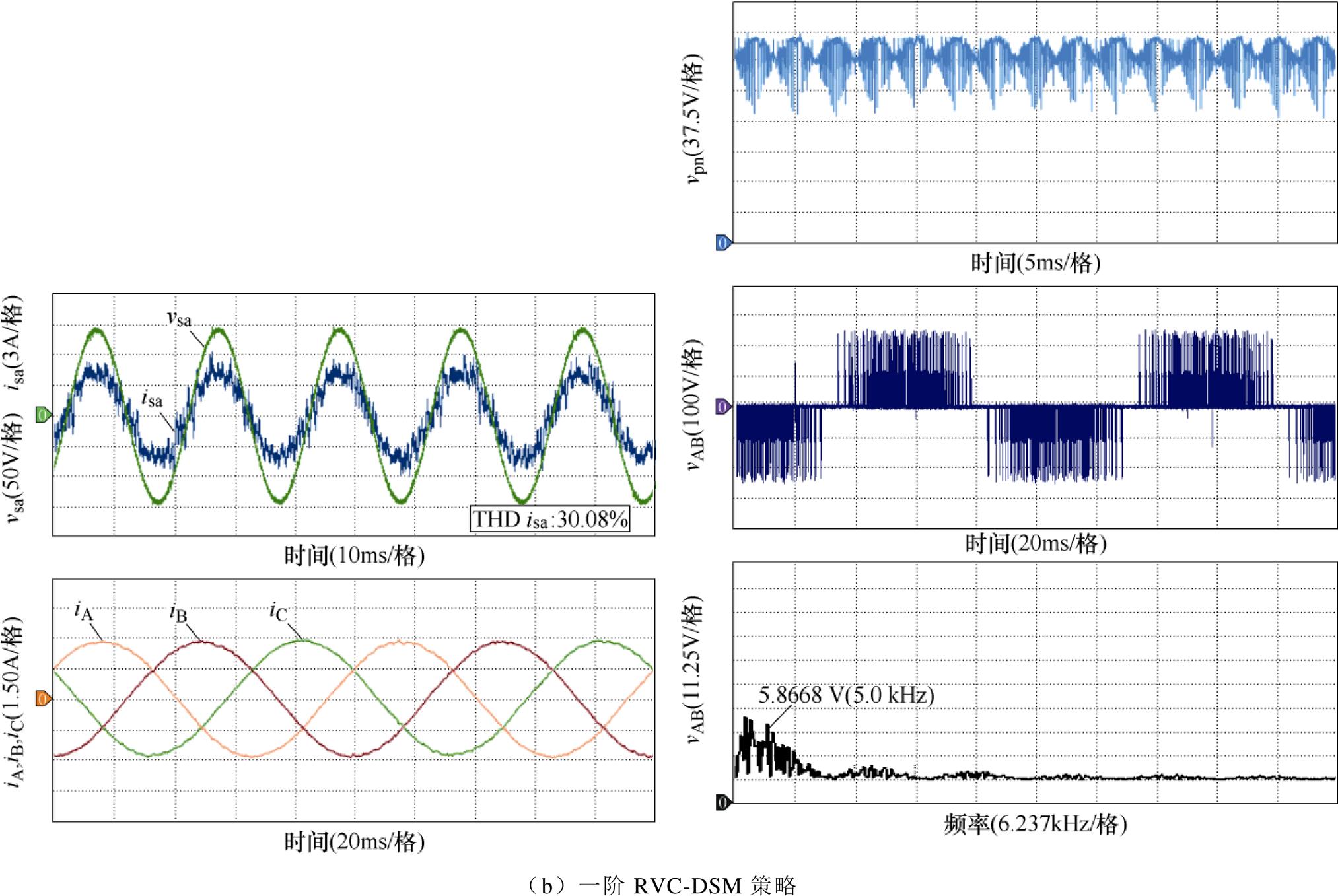
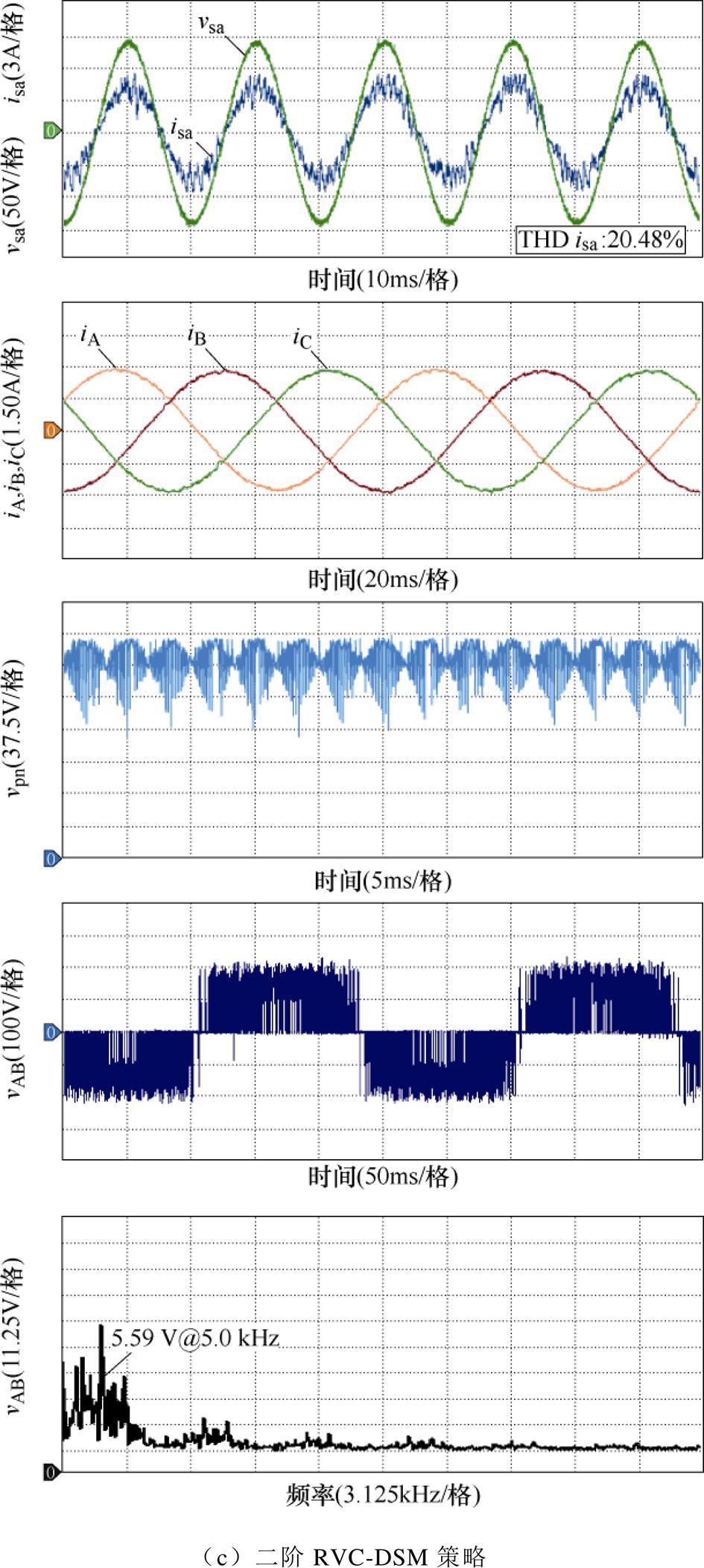
图12 TSMC稳态运行实验波形
Fig.12 Steady-state operation waveforms of TSMC
图13分别给出了采用SVM策略、一阶RVC- DSM策略和二阶RVC-DSM策略的TSMC输入侧电流和输出侧电流。实验过程中,负载电阻20 W,负载电感40 mH,K分别为0.9和1.0。实验过程中,SVM开关频率固定为2.0 kHz,RVC-DSM策略的整流级PWM周期设定为200 ms,逆变级控制周期设定为100 ms,采样频率为10 kHz,平均开关频率约为1.7 kHz,两者开关频率基本一致。由图13可以看出,SVM策略在过调制区域出现了明显的电流畸变。在通过参考电压修正后,一阶RVC-DSM和二阶RVC-DSM可直接利用逆变级基本电压矢量作为调制输出,理论调制度可达到1.0。同时,借助DSM频谱整形优势,仍可保证TSMC在过调制区具有良好运行性能。
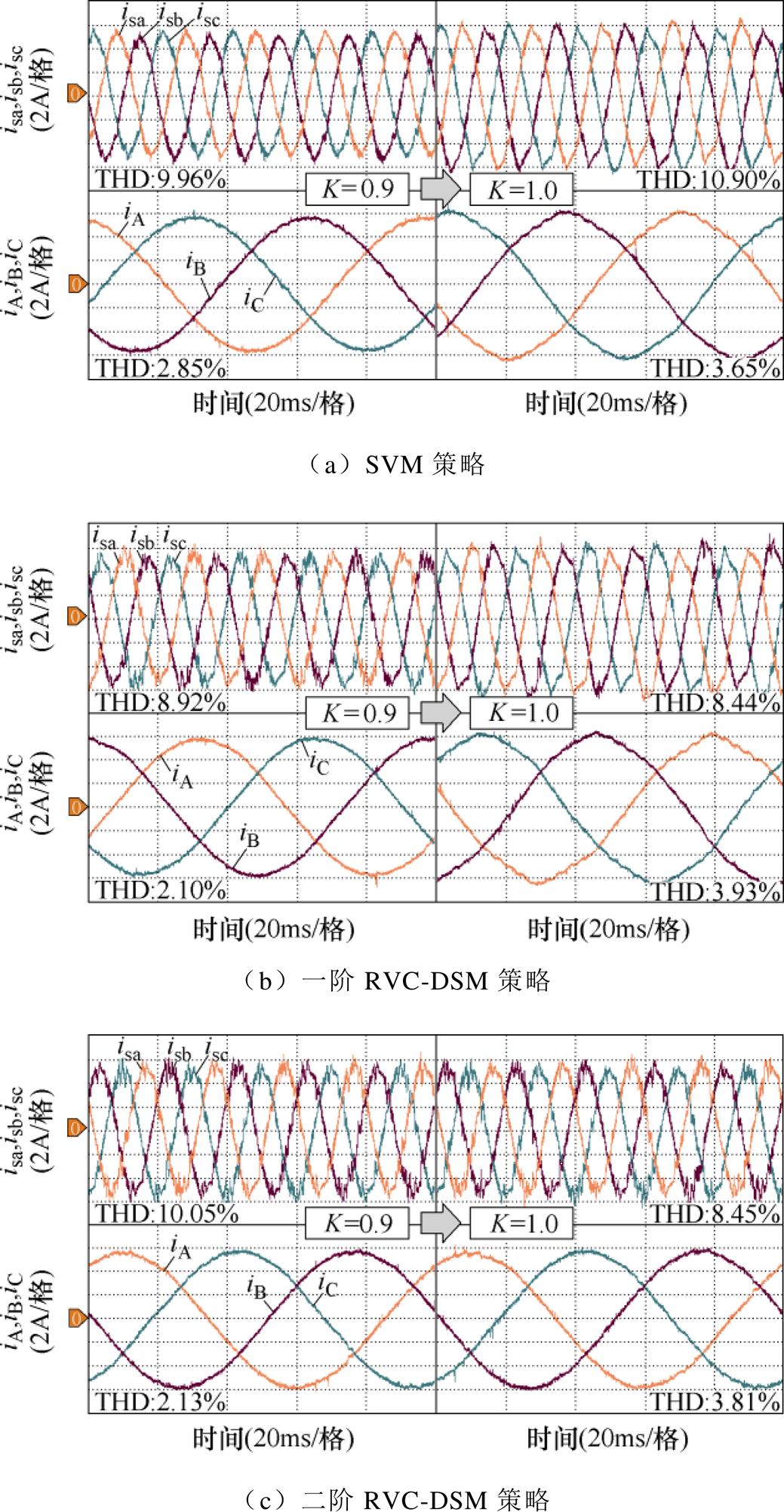
图13 过调制区域输出电流波形
Fig.13 Output current waveforms under overmodulation region
为验证RVC-DSM策略的动态调制性能,图14给出了采用二阶RVC-DSM策略的TSMC输入侧电流、输出侧电流、直流链电压和调制度实验波形。实验过程中,图14a中,负载电阻20 W,负载电感40 mH,qm由0.2阶跃至0.8;图14b中,负载电阻20 W,负载电感40 mH,参考输出电压频率由10 Hz阶跃至40 Hz。由图14可以看出,无论是参考电压幅值突变,还是参考电压频率突变,RVC-DSM策略均具有良好的动态跟踪能力。
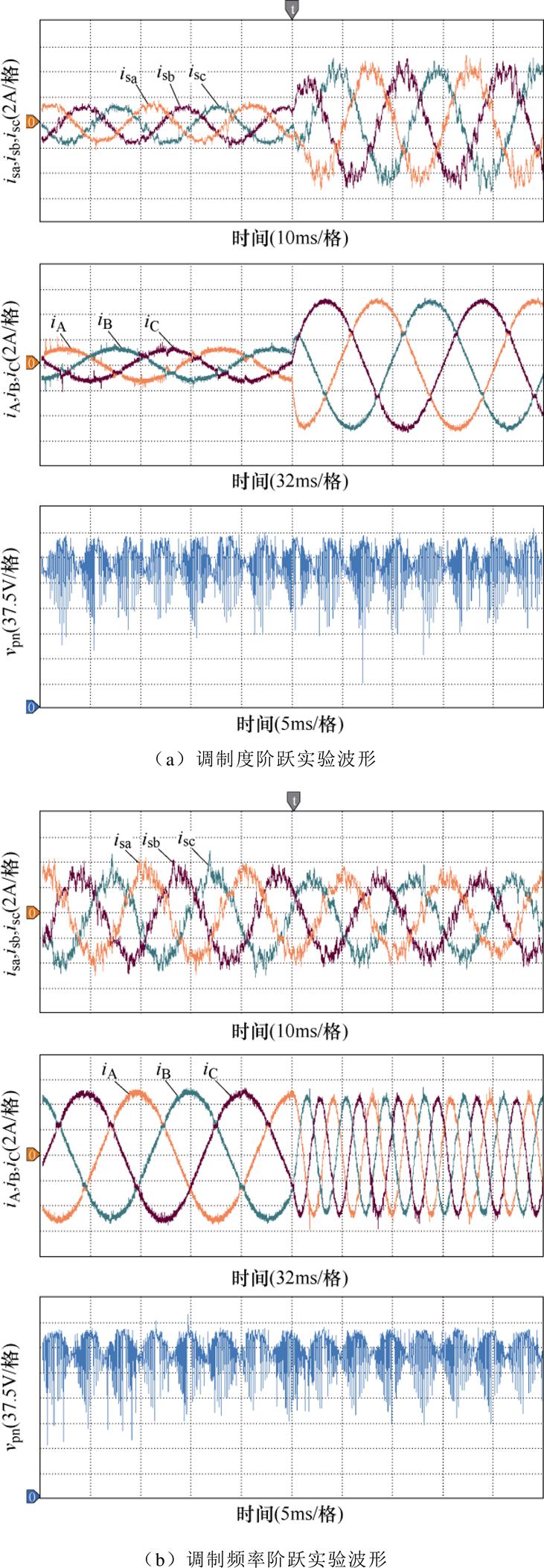
图14 TSMC动态运行实验波形
Fig.14 Dynamic operation waveforms of TSMC
本文在介绍TSMC整流级、逆变器调制原理的基础上,通过分析整流级两段基本矢量对直流链电压的影响规律,得出虑及整流级两级电压波动的逆变级参考矢量修正方法,并给出了详细的修正系数计算方案。实验结果表明,在引入参考电压修正机制后,相比于双空间矢量调制策略,RVC-DSM具有更低水平的EMI,在过调制能力和动态跟踪能力方面亦呈现出特有优势。
1)借助RVC-DSM的频谱整形能力,TSMC输出电压、电流中开关频率及其倍频分量处的高频谐波显著降低。
2)由于RVC-DSM可直接利用逆变级基本矢量跟踪调制参考值,理论极限电压传输比随输入相位的变化在1.0~1.155之间波动,提升了TSMC电压传输比。
3)RVC-DSM逆变级开关频率与其控制周期直接相关。采用更短的控制周期,可更充分地利用功率器件开关性能,发挥RVC-DSM在改善EMI方面的能力。
参考文献
[1] 梅杨, 许策, 鲁乔初. 基于零矢量嵌入的双向隔离型AC-DC矩阵变换器分段同步控制策略[J]. 电工技术学报, 2021, 36(22): 4784-4794.
Mei Yang, Xu Ce, Lu Qiaochu. Piecewise syn- chronous control strategy of bidirectional isolated matrix AC-DC converter based on zero vector embedded[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4784-4794.
[2] 齐琛, 陈希有. 一种可靠换流的双级矩阵变换器载波调制策略[J]. 电工技术学报, 2013, 28(6): 184-191.
Qi Chen, Chen Xiyou. A carrier-based modulation strategy of two stage matrix converter with reliable commutation[J]. Transactions of China Electrotech- nical Society, 2013, 28(6): 184-191.
[3] 王文圣, 李珊瑚, 刘旭, 等. 一种基于输入电流矢量相位的新型间接矩阵变换器空间矢量过调制策略[J]. 电气技术, 2020, 21(3): 1-10.
Wang Wensheng, Li Shanhu, Liu Xu, et al. A novel space vector overmodulation strategy based on input current vector phase for indirect matrix converter[J]. Electrical Engineering, 2020, 21(3): 1-10.
[4] 肖蕙蕙, 魏苏东, 郭强, 等. 优化开关序列的PWM整流器模型预测控制策略[J]. 电工技术学报, 2022, 37(14): 3665-3675, 3700.
Xiao Huihui, Wei Sudong, Guo Qiang, et al. Model predictive control strategy for PWM rectifier with optimized switching sequence[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3665- 3675, 3700.
[5] 何杰, 刘钰山, 毕大强, 等. 开关变换器传导干扰抑制策略综述[J]. 电工技术学报, 2022, 37(6): 1455-1472.
He Jie, Liu Yushan, Bi Daqiang, et al. Review of conducted electromagnetic interference suppression strategies for switching converters[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1455-1472.
[6] Chang Qingyun, Zhou Bo, Lu Chengjia, et al. Mains current distortion analysis and suppression method for third-harmonic injection two-stage matrix conver- ter[J]. IEEE Transactions on Industrial Electronics, 2023, 70(3): 2168-2177.
[7] 夏长亮, 阎彦. 矩阵变换器-永磁同步电机系统[J]. 电工技术学报, 2015, 30(23): 1-9.
Xia Changliang, Yan Yan. Matrix converter-permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 1-9.
[8] Chen Jianan, Jiang Dong, Sun Wei, et al. A family of spread-spectrum modulation schemes based on dis- tribution characteristics to reduce conducted EMI for power electronics converters[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 5142-5157.
[9] 蒋栋, 沈泽微, 刘自程, 等. 电力推进系统电力电子噪声的主动抑制技术进展[J]. 中国电机工程学报, 2020, 40(16): 5291-5302.
Jiang Dong, Shen Zewei, Liu Zicheng, et al. Progress in active mitigation technologies of power electronics noise for electrical propulsion system[J]. Proceedings of the CSEE, 2020, 40(16): 5291-5302.
[10] 邱子桢, 陈勇, 成海全, 等. 基于周期谐波扩频调制的永磁同步电机高频边带声振抑制[J]. 电工技术学报, 2022, 37(10): 2459-2468.
Qiu Zizhen, Chen Yong, Cheng Haiquan, et al. Periodic harmonic spread spectrum modulation for high-frequency sideband vibro-acoustic suppression in permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(10): 2459-2468.
[11] Jacob B, Baiju M R. Spread spectrum modulation scheme for two-level inverter using vector quantised space vector-based pulse density modulation[J]. IET Electric Power Applications, 2011, 5(7): 589.
[12] Xu Jie, Nie Ziling, Zhu Junjie. Characterization and selection of probability statistical parameters in random slope PWM based on uniform distribution[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 1184-1192.
[13] Mathe L, Lungeanu F, Sera D, et al. Spread spectrum modulation by using asymmetric-carrier random PWM[J]. IEEE Transactions on Industrial Electronics, 2012, 59(10): 3710-3718.
[14] Colodro F, Torralba A, Laguna M. Continuous-time Sigma-Delta modulator with an embedded pulsewidth modulation[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2008, 55(3): 775-785.
[15] Dunlap S K, Fiez T S. A noise-shaped switching power supply using a Delta-Sigma modulator[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2004, 51(6): 1051-1061.
[16] Hwang Y S, Chen J J, Yang J, et al. A low-EMI continuous-time Delta-Sigma-modulator Buck converter with transient response eruption techniques[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6854-6863.
[17] Lumbreras D, Zaragoza J, Berbel N, et al. Com- prehensive analysis of hexagonal Sigma-Delta modulations for three-phase high-frequency VSC based on wide-bandgap semiconductors[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 7212-7222.
[18] Mir T N, Singh B, Bhat A H. Delta-Sigma modulation based common-mode voltage elimination in direct matrix converter[J]. IEEE Transactions on Industrial Informatics, 2021, 17(2): 1048-1057.
[19] 耿乙文, 王亮, 许家斌, 等. 基于Sigma-Delta调制的双两电平逆变器调制策略[J]. 电工技术学报, 2017, 32(18): 239-247.
Geng Yiwen, Wang Liang, Xu Jiabin, et al. A modulation strategy of dual inverter using Sigma-Delta converter[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 239-247.
[20] Hirota A, Nakaoka M. A low noise three-phase matrix converter introducing Delta-Sigma modulation scheme[C]//2006 37th IEEE Power Electronics Specialists Conference, Jeju, Korea (South), 2017: 1-6.
[21] Mir T N, Singh B, Bhat A H. Predictive Delta-Sigma modulation for three-phase to three-phase matrix converters[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(1): 968-976.
[22] Xia Changliang, Li Shanhu, Yan Yan, et al. Research on linear output voltage transfer ratio for ultrasparse matrix converter[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 1811-1815.
[23] 高文科, 阎彦, 史婷娜. 传统矩阵变换器最小相位误差空间矢量过调制策略[J]. 电工技术学报, 2019, 34(2): 316-325.
Gao Wenke, Yan Yan, Shi Tingna. Minimum phase error space-vector over-modulation strategy of con- ventional matrix converter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 316-325.
[24] Ma Chaolei, Shi Tingna, Lin Zhichen, et al. A novel wider range modulation for indirect matrix converter utilizing Delta-Sigma and space vector[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 1429-1434.
Abstract A two-stage matrix converter (TSMC) has the advantages of a conventional matrix converter, such as no DC-bus capacitance, flexible energy control, and a compact structure. Moreover, it simplifies the modulation process while avoiding the complex four-step commutation mechanism of direct matrix converters, becoming a potential power electronics topology. Currently, the voltage transfer ratio of TSMC using the classical method cannot exceed 0.866, and the electromagnetic noise caused by voltage harmonic near the switching frequency is relatively concentrated. According to the specific mathematical laws, the spread spectrum modulation technology transforms PWM waveforms into irregular pulse sequences. It improves the voltage transfer ratio and expands the output voltage spectrum to a wider range, thereby reducing output harmonics and electromagnetic noise. However, TSMC has a large number of power switches, and its switching coordination between the rectifier and inverter stage is complex. There are still many key issues to be addressed in the spread spectrum modulation technology of TSMC.
Considering the simple structure and without complex random statistical characteristics, Delta-Sigma modulation (DSM) can significantly optimize the output spectrum, reduce the EMI level, and optimize the operational efficiency of the power converter. However, the modulation strategy of TSMC can be divided into rectifier-stage algorithms and inverter-stage algorithms. The absence of a DC-link capacitor of TSMC leads to fluctuations in DC-link voltage. The DSM of the inverter stage cannot accurately quantify and track the fluctuation patterns of DC-link voltage, making it difficult for TSMC to directly implement DSM in the inverter stage.
This paper proposes a DSM scheme with reference voltage correction (RVC-DSM). Firstly, the operation principle of DSM indicates that as the order L of DSM increases, the suppression effect on low-frequency harmonics of voltage is better, and the modulator resolution is significantly improved. Specifically, the DSM resolution is increased by L+0.5 bits when its operating frequency is doubled. Then, to ensure the voltage utilization of TSMC, the rectifier stage still adopts SVM without zero-vector, and DSM is only employed on the inverter stage to achieve spread spectrum modulation. Meanwhile, limiting the switching frequency for switching loss reduction and solving the problem of voltage tracking are necessary. This paper utilizes the “Voronoi quantizer”, shaped like a Voronoi diagram as the vector partitioning rule, to implement the DSM strategy of TSMC. Finally, combined with the modulation target, the compensation coefficients of the DSM under different DC-link voltages are obtained by analyzing the DC-link voltage fluctuation in different sectors. Furthermore, the compensation coefficients are allocated to the reference voltage in real-time to eliminate the impact of DC-link voltage fluctuations on DSM, achieving efficient spread spectrum modulation of TSMC.
Experiments were carried out on the platform with a dual-core controller of “FPGA+DSP” to verify the proposed RVC-DSM. The experimental results show that the harmonics originally related to the switching frequency (5 kHz, 10 kHz, …) under SVM modulation have been suppressed, and this part of harmonic energy has been extrapolated to the high-frequency band. The low-pass characteristics of the inductance load effectively reduce the conducted interference of TSMC in the 0~30 MHz band. At the same time, RVC-DSM directly employs the basic voltage vector of the inverter stage, ensuring good operating performance in the over- modulation region. Finally, benefiting from its spectrum-shaping effect, the operational efficiency of the RVC-DSM strategy is much higher than that of the SVM strategy.
The following conclusions can be drawn through theoretical analysis and experimental verification. (1) By utilizing the spectrum shaping ability of the RVC-DSM modulator, the high-frequency harmonics near switching frequencies and its octave components are significantly reduced. (2) RVC-DSM can directly use the basic vector of the inverter stage. Its theoretical limit voltage transmission ratio fluctuates between 1.0 and 1.155, improving the TSMC voltage transmission ratio. (3) The switching frequency of RVC-DSM is directly related to its control period. By adopting a shorter control period, the tracking performance of the algorithm is better, and EMI can be improved significantly.
keywords:Two stage matrix converter, Delta-Sigma modulation, voltage transmission ratio, dual space vector modulation
DOI: 10.19595/j.cnki.1000-6753.tces.230306
中图分类号:TM921
国家自然科学基金资助项目(52377066, 51777135, 51907142)。
收稿日期 2023-03-16
改稿日期 2023-06-21
周湛清 男,1989年生,博士,副教授,硕士生导师,研究方向电机系统设计与智能控制。E-mail: zhzhq@tju.edu.cn
史婷娜 女,1969年生,博士,教授,博士生导师,主要研究方向为电机及其控制。E-mail: tnshi@zju.edu.cn(通信作者)
(编辑 陈 诚)