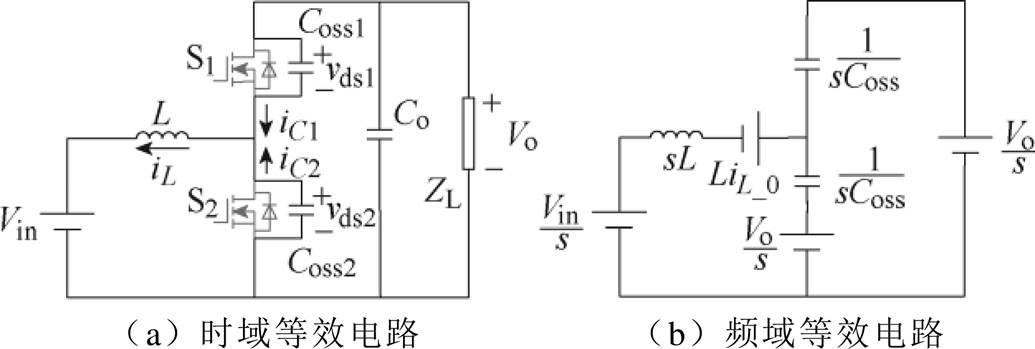
图1 死区过程示意图
Fig.1 The equivalent circuit during dead band
摘要 在变换器高频化发展的趋势中,功率器件的软开关实现对变换效率的影响更加突出。无辅助电路的临界导通工作模式下,Boost变换器主开关管在特定增益下无法实现软开关。为此,该文提出一种能量模型及相应的软开关实现方法。首先,建立死区前后储能元件能量变化的数学模型。然后,结合死区起止时刻的能量平衡方程,研究软开关无法实现的电路机理。在此基础上,考虑开关管输出电容非线性特征,提出软开关实现方法,避免了复杂谐振过程的时域精确建模,提高软开关实现的准确性。最后,搭建500 W实验样机进行实验,结果表明,相较于对谐振过程建模的传统时域模型,所提方法将实际开通电压降低47%,使峰值变换效率提升0.4%,进而验证了其有效性。
关键词:Boost变换器 临界导通模式 能量模型 软开关 开关管输出电容
Boost变换器因其结构简单、易于控制、可靠性高,在通信领域、可再生能源系统、汽车电子等多个场合得到了广泛应用[1-5]。近年来,得益于碳化硅(SiC)和氮化镓(GaN)等宽禁带半导体器件的发展和应用,Boost变换器的高频化发展加速[6-8]。然而,开关频率的提升将使开关损耗成比例增加,加剧开关管发热,导致变换器效率及可靠性降低。因此,开关损耗是影响Boost变换器高频、高效运行的重要因素,开展功率器件的软开关实现方法研究具有重要的理论与应用意义[9-10]。
Boost电路可工作在三种不同的模式下,分别为连续导通模式(Continuous Conduction Mode, CCM)、临界导通模式(Boundary Conduction Mode, BCM)及断续导通模式(Discontinuous Conduction Mode, DCM)。对于CCM下的Boost变换器,由于其电感电流连续而无法反向流动,须增加辅助电路以将电感电流转移到其他支路,从而为主开关管的零电压软开关(Zero Voltage Switching, ZVS)提供条件[11]。在大功率场合中,该方法应用广泛。然而,针对中小功率应用,辅助电路的引入增加了变换器成本,且令电路结构更加复杂,在造成额外损耗的同时,降低了变换器的可靠性[12-13]。
工作于BCM与DCM下的Boost变换器在电感电流为0时开通主开关管,可在无辅助电路的情况下降低开关损耗[14-15]。而相较于DCM,BCM具有更小的电感纹波,因此在中小功率场合备受青睐。然而,BCM仍不能保证主开关管的ZVS开通,在一定增益范围内,主开关管开通时漏-源电压仍为正,因此其效率存在进一步提升的空间。
针对BCM Boost变换器的软开关缺失和精确实现问题,研究者们开展了大量工作。文献[16-17]通过分析主开关管导通前死区内的谐振过程,建立时域模型,得到了ZVS缺失的原因:在一定增益范围内,主开关管漏-源电压vds谐振谷值仍为正,因而不具备ZVS开通条件。
同步整流技术的应用为解决这一问题提供了重要帮助。将续流二极管替换为同步整流管后,电感电流反向流通成为可能。若延迟同步整流管的关断时刻,令死区起始时电感具备一定的反向初始电流,从而调整vds的谐振轨迹,使其与原点相交,则可实现主开关管的ZVS开通。该方法能够解决BCM Boost变换器主开关管ZVS缺失的问题,但如何确定同步整流管的关断时刻又成为了新的难点。
文献[18]检测主开关管两端电压,通过定步长调节方式持续调整同步整流管的导通时间,直至vds2谷值降至0附近。该方法虽能较为准确地控制同步整流管的关断时刻,但额外的采样需求引入了控制延迟、提升了成本,且定步长调节过程需持续数个开关周期,开关损耗仍然难以避免。文献[19-20]采用传统时域模型的ZVS实现。即基于时域模型,计算电感初始电流取值,并相应调整同步整流管与主开关管的驱动信号。然而,由于时域模型所得表达式计算量较大,在实际应用中多采用近似表达式简化计算。且大多数研究工作均忽略开关管输出电容Coss的非线性特征,将其简化为定值。这降低了传统时域模型计算结果的准确性,使其在实际运用中仍然面临较严重的硬开关问题。
针对BCM Boost变换器主开关管的ZVS精确实现问题,本文提出一种基于能量模型的ZVS分析与实现方法。首先,对传统时域模型的ZVS实现存在的问题与局限性进行分析,并提出能量模型,建立死区前后各储能元件能量变化的数学模型,通过分析能量的流动与平衡,研究ZVS的缺失原因及实现条件。基于该能量模型,提出考虑Coss非线性特征的死区电感初始电流表达式。最后,通过搭建一台500 W的实验样机,对本文提出的能量模型与ZVS方法进行验证。
图1为主开关管导通前的死区过程,其中图1a为时域等效电路,图1b为拉氏变换所得频域等效电路。图中,Vin为输入电源电压,L为功率电感,S1与S2分别为同步整流管与主开关管,Coss1与Coss2分别为S1与S2的输出寄生电容,Co为输出电容,ZL为负载,iL为电感电流,iC1与iC2分别为流过Coss1与Coss2的电流,vds1与vds2分别为S1与S2的漏-源电压,Vo为输出电压。

图1 死区过程示意图
Fig.1 The equivalent circuit during dead band
从S1关断后、S2开通前的死区开始,L、Coss1及Coss2发生谐振。根据文献[16],传统时域模型的ZVS实现借助拉氏变换及其反变换,基于图1b,对上述谐振过程建模,并得到死区过程中S2漏-源电压vds2与电感电流iL的时域表达式。
由文献[16],传统时域模型的ZVS实现对死区的完整暂态过程进行建模,模型覆盖死区的每个时刻。然而,主开关管的ZVS开通往往只关注死区结束时其漏-源电压vds2的大小。此外,时域谐振模型的推导需借助拉氏变换,过程复杂、运算量大,在实际运用中需简化处理,这将导致运算结果的精度下降以及ZVS实现效果不理想。
除此之外,时域模型在建立过程中,开关管输出电容Coss被视为定值,其非线性特征被忽略。而实际开关过程中,Coss的容值随漏-源电压vds的变化呈现出显著的非线性[14],其幅度变化量可高达80%[21]。根据文献[16],传统时域模型ZVS实现中,不论是vds2与iL的时域表达式,还是电感初始电流iL_0的表达式,均包含Coss。因此,对其简化处理将直接导致时域模型及电感初始电流的计算结果偏离实际值,使得在工程应用中,ZVS仍然无法实现。然而,若计及Coss动态特征,则计算过程将更为复杂,以至难以求解。如何在保持运算量较低的同时尽可能提升结果准确性,是传统时域模型实现ZVS面临的主要问题,也是Coss容值求取的难点。
针对传统方法的局限性,本文分析了死区前后储能元件的能量变化,并基于能量模型阐述了不同工况下的死区过程,从而得到相应的ZVS实现条件。
如图1a所示,S2导通前的死区内,电路中的储能元件包括:开关管输出电容Coss1与Coss2,输入电源Vin,母线电容Co与功率电感L。电压与电流正方向见图1。
由于死区持续时间较短,通常为几十至上百ns,输入电压Vin与输出电压Vo的变化可忽略,因此分析过程中将二者均视为定值。设死区起始和终止时刻分别为ts和te,则死区前后输入电源Vin和母线电容Co的能量变化为
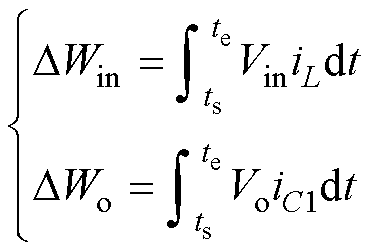 (1)
(1)
式中,DWin、DWo分别为输入电源、母线电容能量变化量。
基于图1a所示的电压和电流正方向,S2开通前的死区内,DWin、DWo均为正,即输入电源持续吸收能量,母线电容持续供出能量。
根据电感能量表达式,死区前后电感能量变化DWL为
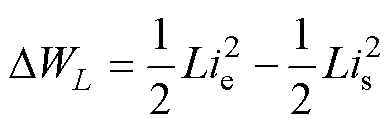 (2)
(2)
式中,is为死区起始时刻电感电流;ie为死区结束时刻电感电流。
在考虑Coss非线性特征的情况下,对Coss1与Coss2的总能量进行建模。输出电容Coss随漏-源电压vds的变化由函数Coss(vds)表示。由此可得,同步整流管S1与主开关管S2的输出电容总能量为
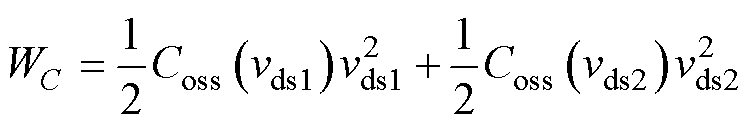 (3)
(3)
基于图1a所示的死区过程等效电路,根据基尔霍夫定律,有
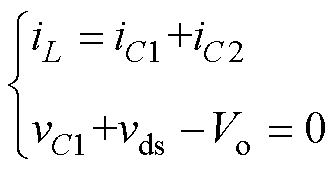 (4)
(4)
将式(4)代入式(3)消去vC1,可得
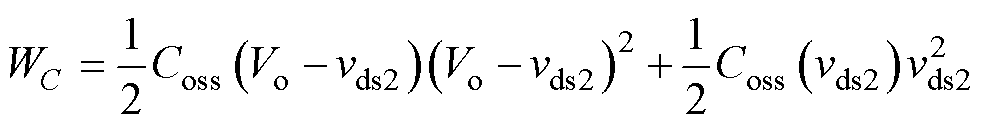 (5)
(5)
由此可见,输出电容总能量WC为S2漏-源电压vds2的一元函数。
图2为开关过程中输出电容总能量WC随vds2变化的曲线示意图。以GaN GS66516T开关器件为例,分别绘制考虑与忽略Coss非线性特征时,WC关于vds2的图像。由图2可知,不论是否考虑Coss的非线性特征,S2漏-源电压vds2从Vo放电至0 V过程中,输出电容总能量WC均关于vds2=0.5Vo对称,呈先下降后上升的趋势。当vds2≥0.5Vo时,随着vds2的下降,Coss1与Coss2整体等效供能;当vds2<0.5Vo时,随vds2的下降,Coss1与Coss2整体等效吸收能量。当死区前后S1和S2的输出电容间顺利完成能量交换时,S2实现ZVS开通。
根据能量守恒定律,死区前后各储能元件的能量变化满足
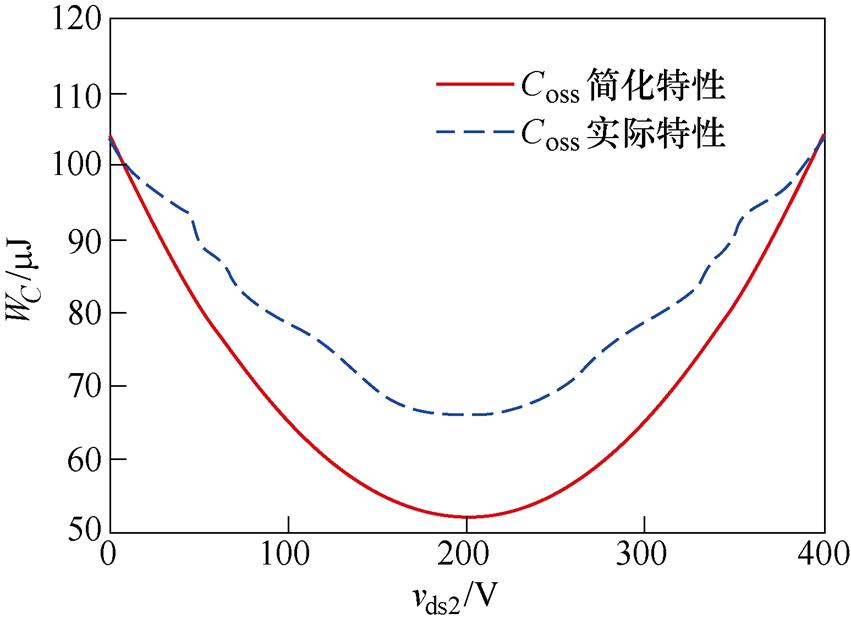
图2 开关过程中WC变化曲线
Fig.2 Variation curves of WC during one switching process
 (6)
(6)
式中,DWC为死区前后开关管输出电容总能量的变化量。
当S2实现ZVS开通时,DWC=0,则基于能量模型的ZVS实现条件为
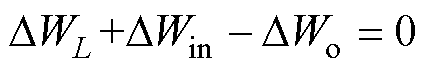 (7)
(7)
基于式(7),根据输入电源与母线电容的能量变化关系,分三种工况进行讨论,具体见表1。
表1 DWin-DWo正负性及对应工况
Tab.1 Polarity of DWin-DWo and corresponding conditions

序号DWin-DWoDWL电流关系效率优化方式 ①<0>0|ie|>|is|is=0 ②=0 = 0|ie| = |is| ③>0<0|ie|<|is|ie=0
2.2.1 DWin-DWo≤0的工况分析
ZVS实现模态示意与理论波形如图3所示。当DWin-DWo≤0时,DWL≥0,死区终止时刻电感电流绝对值大于其起始时刻,即|ie|≥|is|,此时的电路模态如图3a所示。图中,当死区结束时,电感电流iL流过S2的体二极管,此时施加驱动信号,S2实现ZVS开通。
图3b中分别给出了DWin-DWo<0与DWin-DWo=0时,vds2和iL的理论波形。此时死区前后输入电源吸收的能量不大于母线电容供出的能量,即母线电容可支撑输入电源的能量消耗,因此S1与S2间输出电容Coss的能量交换能够正常完成。即使电感死区初始电流为0(电感不具备初始储能),S2仍可实现ZVS开通。
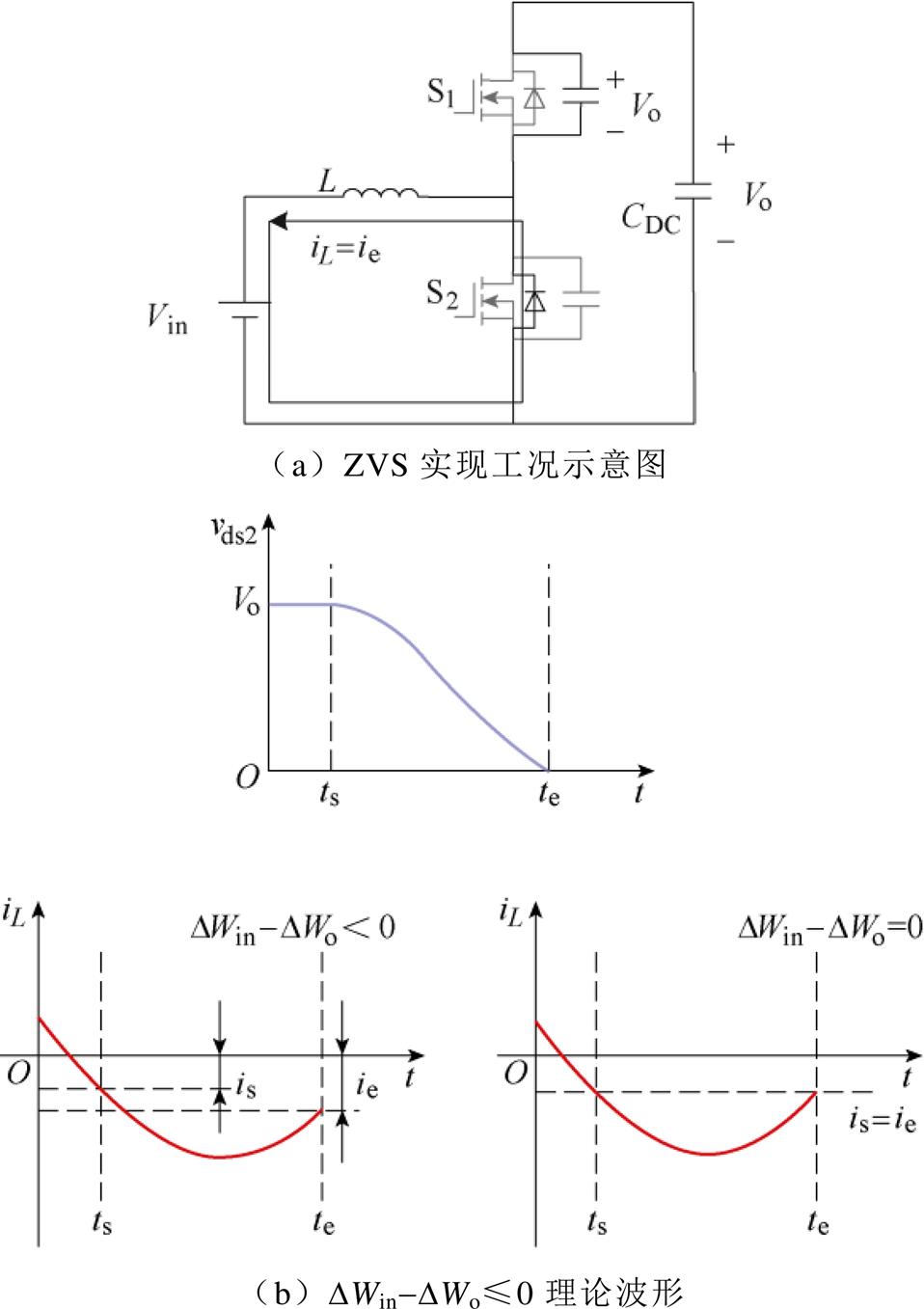
图3 ZVS实现模态示意与理论波形
Fig.3 Circuit condition and theoretical waveforms under ZVS condition
2.2.2 DWin-DWo>0的工况分析
DWin-DWo>0理论波形如图4所示。DWin-DWo>0代表输入电源吸收的能量高于母线电容释放的能量,即母线电容无法支撑输入电源的能量消耗,需从电路其他部分吸收能量。
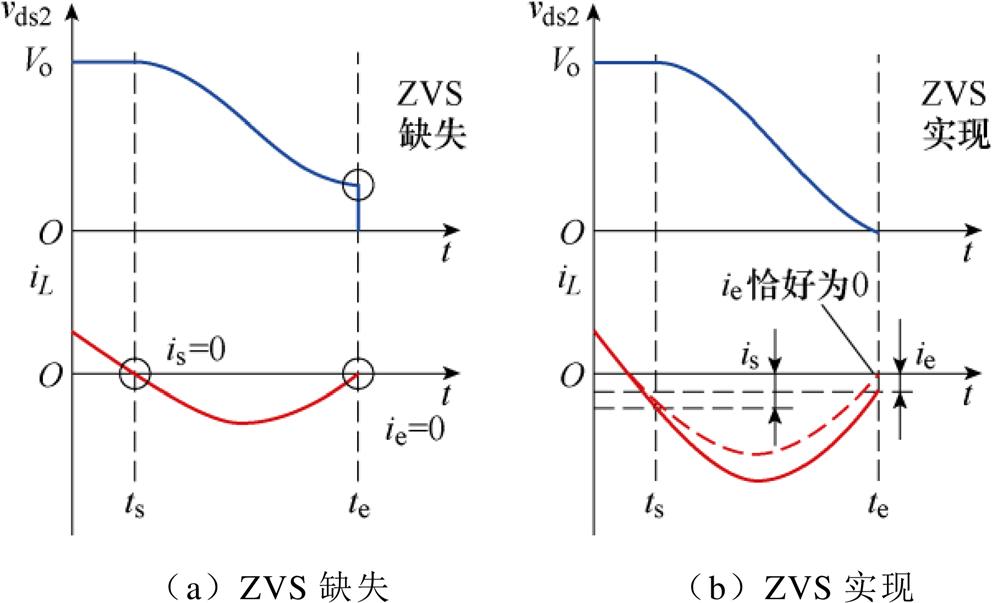
图4 DWin-DWo>0理论波形
Fig.4 Theoretical waveforms when DWin-DWo>0
图4a所示为上述工况下,电感不具备初始储能时vds2与iL的理论波形,此时S2工作于硬开关条件下。这是由于死区前后输入电源从开关管的输出电容处吸收能量,使式(6)中DWC为负值。根据图2所示能量曲线,若DWC为负,则电感电流再次降低至0时,S2漏-源电压vds2介于0~Vo之间,即ZVS开通无法实现。
基于上述分析,当DWin-DWo>0时,若令电感具备相应初始储能,能够补偿输入电源的能量消耗,则可保证S1与S2间输出电容Coss的能量交换正常完成,此时,vds2与iL的理论波形如图4b中实线所示。根据式(7),为实现S2的ZVS开通,死区电感初始储能应满足DWL≥-(DWin-DWo),即电感初始能量不小于输入电源与母线电容的净消耗量。
根据表1,DWin-DWo≤0时,BCM Boost变换器主开关管S2的ZVS实现不需死区电感初始储能。同时,额外的电感初始电流将造成电流平均值上升,引入不必要的导通损耗,此时死区电感初始电流应为0。则无电感初始储能的ZVS实现范围可表示为
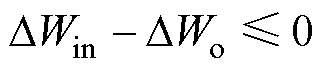 (8)
(8)
求解式(8),基于图1a所示正方向,根据电容特性表达式有
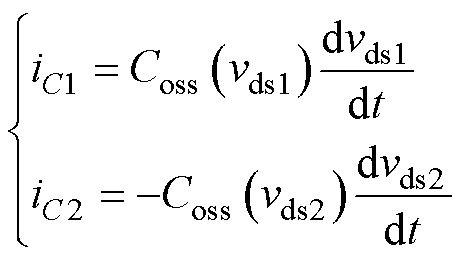 (9)
(9)
代入式(4)并消去vds1得
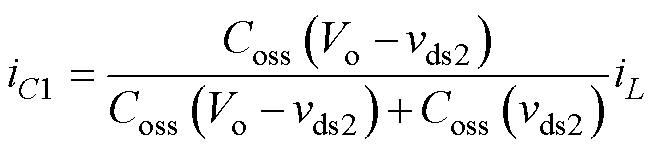 (10)
(10)
将式(10)代入式(1),消去iC1,得DWin-DWo表达式为
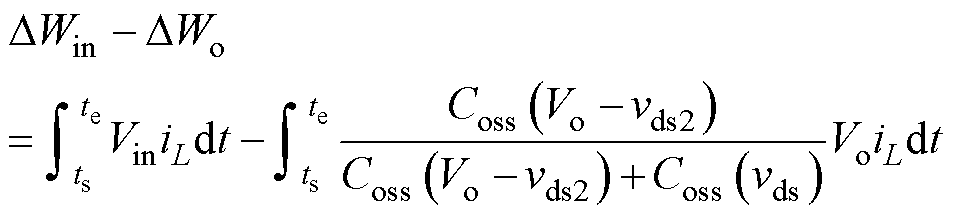
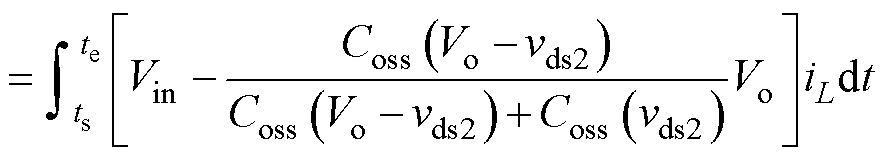 (11)
(11)
由于考虑了Coss的非线性特征,式(11)形式复杂,且仍为时域积分,计算量大、求解困难。因此,对式(11)作进一步处理。将电容特性表达式式(9)代入式(4)得
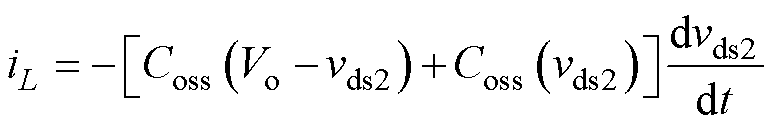 (12)
(12)
将式(12)代入式(11),替换积分算子得到
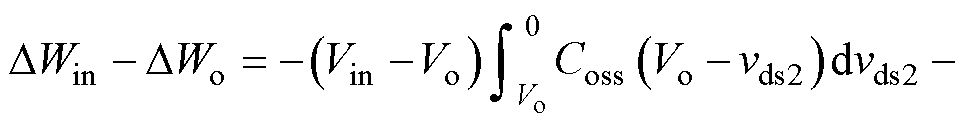
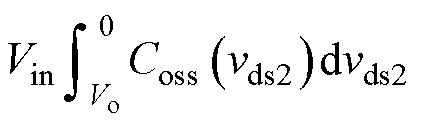 (13)
(13)
式(13)中两积分项将开关管输出电容Coss容值关于漏-源电压vds2积分,其物理意义为:漏-源电压为Vo时,Coss所携带电荷量,定义其符号为Qoss,则式(13)可进一步简化为
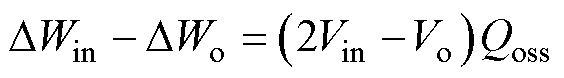 (14)
(14)
将式(14)代入式(8),得到无电感初始储能时,BCM Boost变换器主开关管ZVS实现条件, Vin≤0.5Vo。该分析结果与文献[16]中时域谐振模型结果一致,因此可验证能量模型的正确性。
与时域模型不同,能量模型的建模过程及ZVS分析仅着眼于死区的起点与终点,规避了对复杂谐振过程的研究。除此之外,得益于积分算子的替换与电荷量概念的应用,能量模型分析过程较为简单,在降低了计算量的同时计及了Coss的非线性特性。
如2.2.2节中所述,当DWin-DWo>0时,死区前后电感能量变化量DWL应满足DWL≥-(DWin-DWo)。而与DWin-DWo≤0情形相似,过大的死区电感初始电流仍将造成额外导通损耗。为得到更高的变换效率,应使电感的初始储能恰好补偿输入电源与母线电容的净消耗量,即DWL=-(DWin-DWo)。此时,vds2与iL同时过0,相应理论波形如图4b中虚线所示。
因此,当DWin-DWo>0时,为保证S2的ZVS开通和变换效率,死区电感初始电流is取值应满足
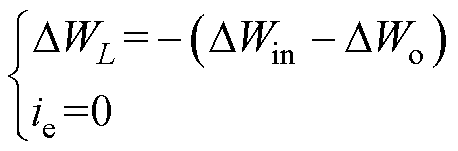 (15)
(15)
由式(15)推导is表达式。将式(2)代入式(15)并整理得到
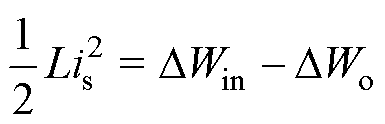 (16)
(16)
将式(14)代入式(16)有
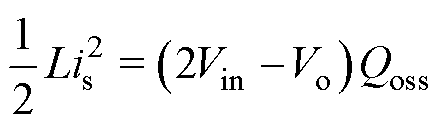 (17)
(17)
由式(17)求得满足式(15)的电感初始电流is表达式为
 (18)
(18)
式(18)即为能量模型ZVS实现方法所得死区电感初始电流表达式。其中,除Qoss外,其他物理量均可视为定值,在计算过程中直接赋值即可。
能量模型ZVS实现方法中,虽然分析过程保留了Coss,但其计算结果,即式(18),并不需确定Coss的值,只需计算其在vds2=Vo时的电荷量Qoss。一旦输出电压Vo与开关器件型号确定,则Qoss为定值。
以GaN GS66516T开关器件为例,说明Qoss计算过程。根据式(13)与式(14),可得Qoss定义为
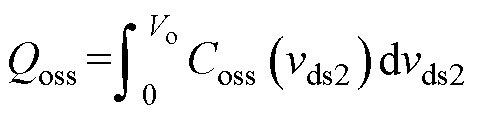 (19)
(19)
由式(19),Qoss的计算只需将Coss(vds2)关于vds2作积分即可。因此,Coss容值函数的获取是Qoss计算的关键。
本文选用Matlab曲线拟合工具,采用多项式分段拟合方式,得到较为准确的Coss容值函数。由于Coss曲线非线性较强,为提高拟合精度,对曲线进行分段,并保证在每一段曲线内均有较好的拟合效果。同时,为降低计算难度,本文采用5阶及以下多项式拟合,即每一段Coss容值函数均可由以下标准形式表示为
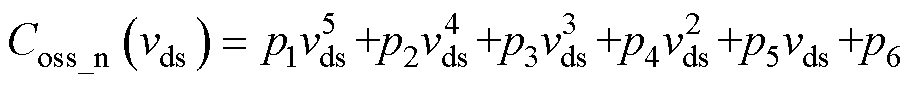 (20)
(20)
根据上述方法,对开关器件数据手册中提供的Coss曲线进行拟合,共分为5段,各段范围与参数结果见表2,原曲线及拟合结果如图5所示。
表2 曲线分段情况及参数拟合结果
Tab.2 Curve segmentation and fitting results

分段序号12345 vds范围/V[0, 48.5](48.5, 70(70, 150(150, 400(400, 500 p1-3.885 2×10-50000 p20.004 30000 p3-0.007 3-0.040 0-1.011 7×10-4-1.368 1×10-50 p43.250 47.062 90.022 60.013 00 p5-28.201 0-421.835 4-2.882 1-4.156 10 p61.036 2×1038.977 1×103471.112 8586.812 2130.081 3
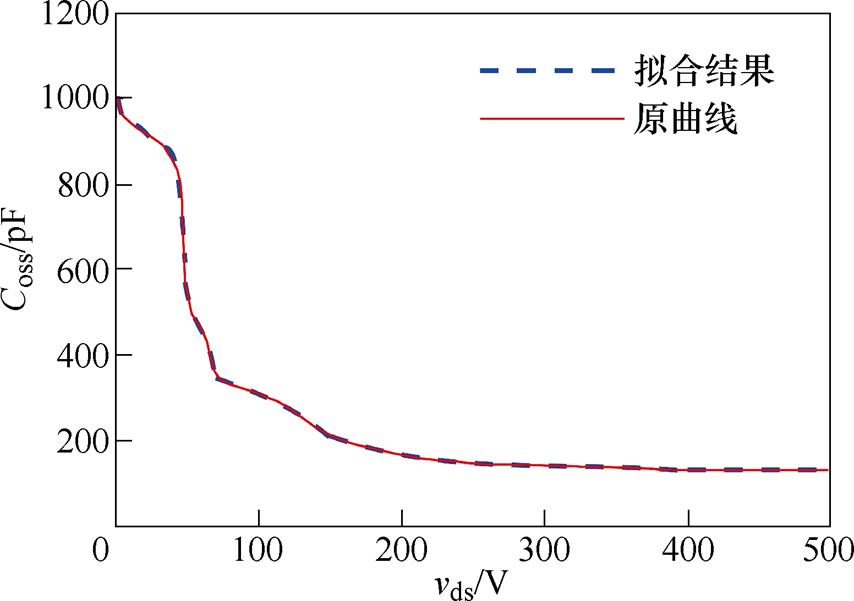
图5 曲线拟合效果示意图
Fig.5 Diagram of curves fitting result
由图5可见,曲线拟合结果体现出较高的准确性,而由于运用了多项式拟合,所得Coss函数表达式易于进行积分运算。因此,多项式分段拟合法可在保持计算量较低的同时得到较为准确的Qoss。
为测试能量模型在实际运用中的优化效果,本文搭建如图6所示Boost变换器样机,相关参数及器件型号见表3。其额定功率为500 W,功率电感为25 mH。通过实验验证从电感死区初始电流准确性与效率两方面展开对比,相关实验结果展示如下。

图6 实验样机示意图
Fig.6 The prototype for experiment
表3 实验样机参数及器件型号
Tab.3 Parameters and device type of the prototype

参 数数值 (型号) 额定功率/W500 功率电感/mH25 开关频率/kHz500 开关器件型号GS66516T
由于死区电感初始电流由同步整流管延迟关断时间tdelay控制,因此通过对比两种ZVS实现所得tdelay与实际所需取值的偏差,即可对比其理论准确度。基于上述样机,测量不同输出电压及不同增益下,满足式(15)所需的实际tdelay取值,绘制曲线如图7所示。其中,图7a~图7c分别给出了变换器输出电压分别为150、200、300 V,在增益小于2(Vin>0.5Vo)范围内,不同增益k(k=Vin/Vo)下tdelay的时域模型计算结果、能量模型计算结果及实际所需取值的对比。
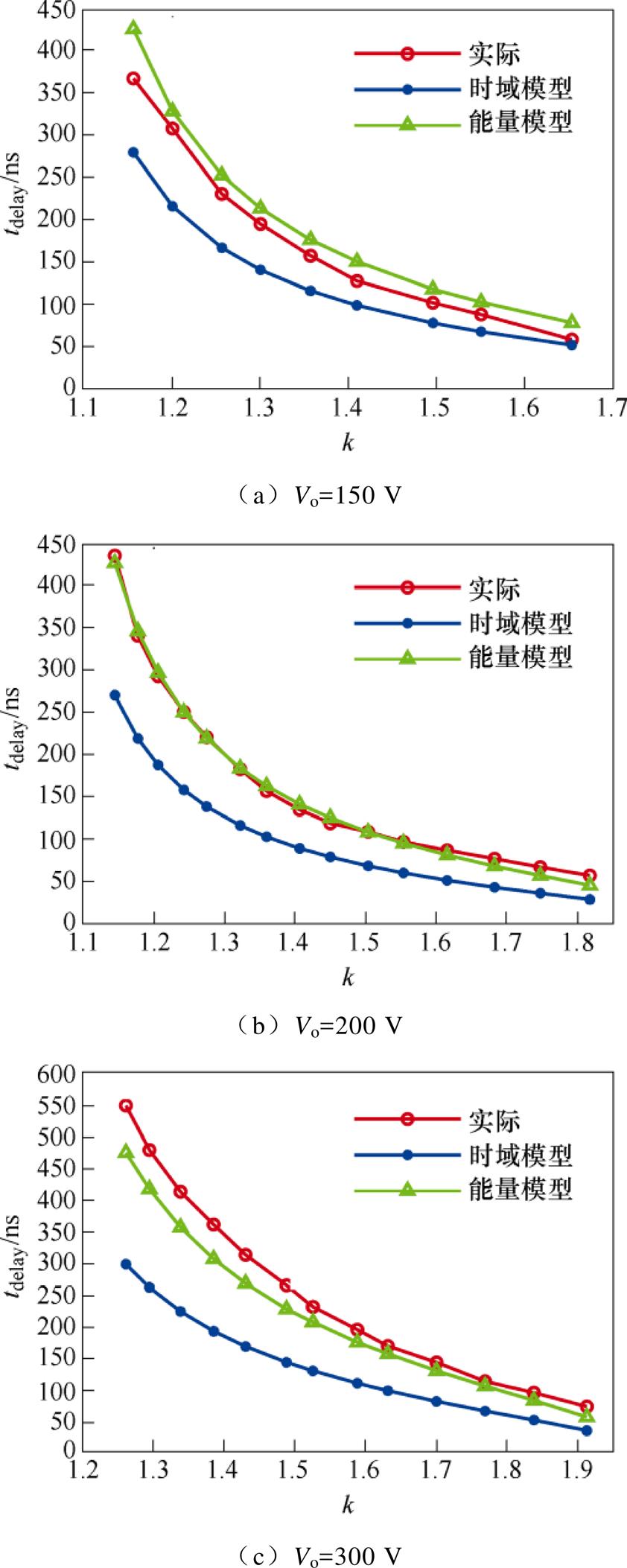
图7 理论计算结果对比示意图
Fig.7 Comparison of theoretical calculation results
由图7可见,在不同电压等级下,相较于传统时域谐振模型,能量模型所得延迟关断时间均更接近实际所需。对比不同输出电压下的曲线发现,随着输出电压的升高,时域谐振模型的偏差逐渐增大,这是忽略了Coss动态特征的结果。根据图5所示数据曲线,输出电压由150 V上升至300 V过程中,死区前后Coss的变化量明显上升,导致时域模型的偏差随之升高。而能量模型在三种输出电压下均保持着相对较低的偏差,因此能够验证其准确性的提升。
然而,能量模型所得理论结果与实际取值间的误差虽然较时域模型有所减小,但仍存在一定的误差。这是由Coss容值曲线测取过程中的误差所致。通常情况下,Coss容值曲线在特定电压及工况下测取得到,而该工况与开关管的实际工作环境存在差异,即在实际的高频开关过程中,Coss容值的变化过程与数据曲线间存在偏差,从而导致误差无法完全消除。与传统时域模型方法相比,本文所提能量模型明显降低了计算误差,实现了开关过程的优化。
分别在Vin=200 V及Vin=250 V,Vo=300 V条件下,对Boost变换器主开关管S2的实际开关过程进行测试,结果如图8、图9所示。测量Vin=200 V时,不同功率点处,BCM(无电感初始储能)、传统时域模型ZVS实现、能量模型ZVS实现三种工况下变换器的工作效率,结果如图10所示。
当输入电压为200 V时,基于传统时域模型ZVS实现求得延迟关断时间为140 ns,基于能量模型ZVS实现求得延迟关断时间为224 ns。如图8所示为500 W满载条件下,主开关管实际开通过程的实验波形,图8a~图8c分别对应BCM(tdelay=0 ns)、传统时域模型ZVS实现(tdelay= 140 ns)、能量模型ZVS实现(tdelay=224 ns)。图中,vgs1为同步整流管驱动信号,vsw为主开关管硬开关电压。
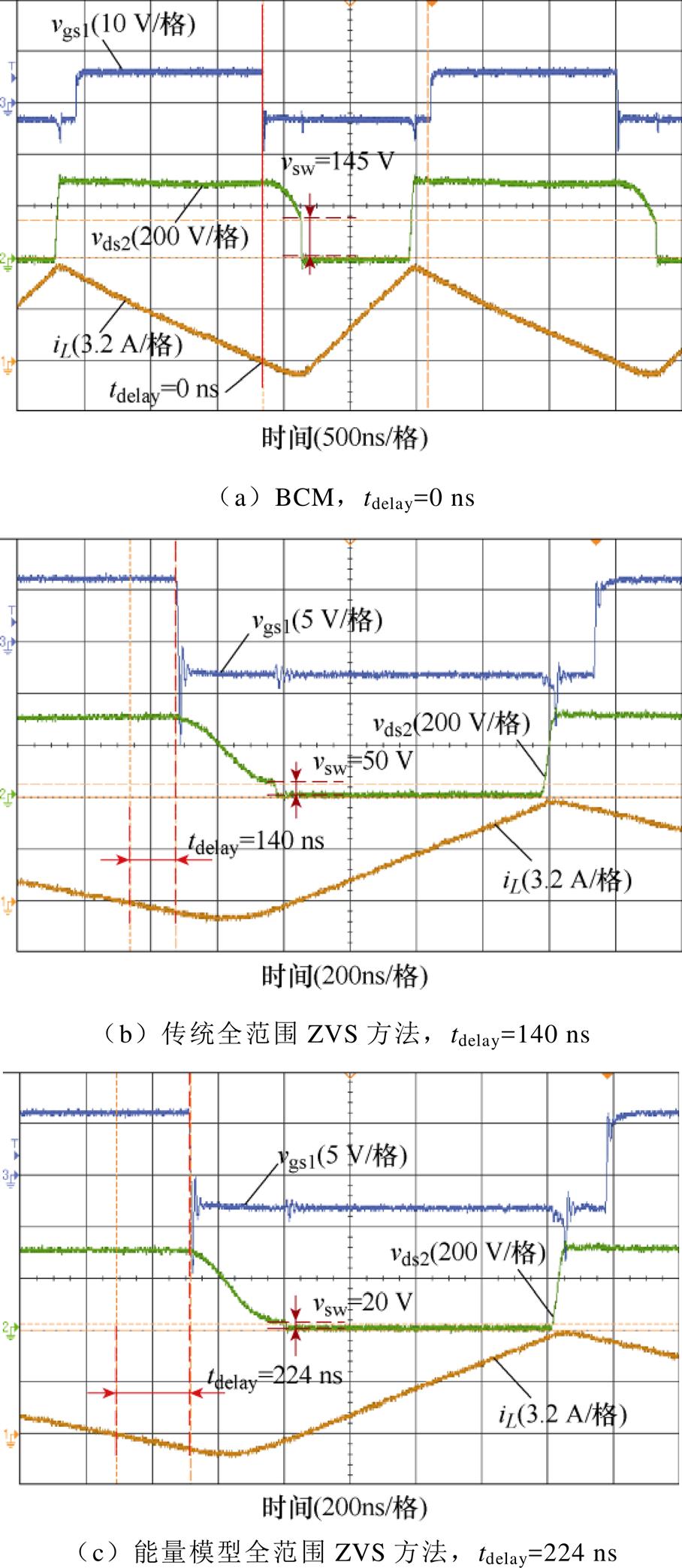
图8 Vin=200 V时主开关管开通过程波形示意图
Fig.8 Waveforms of real switching process of main switch with Vin=200 V
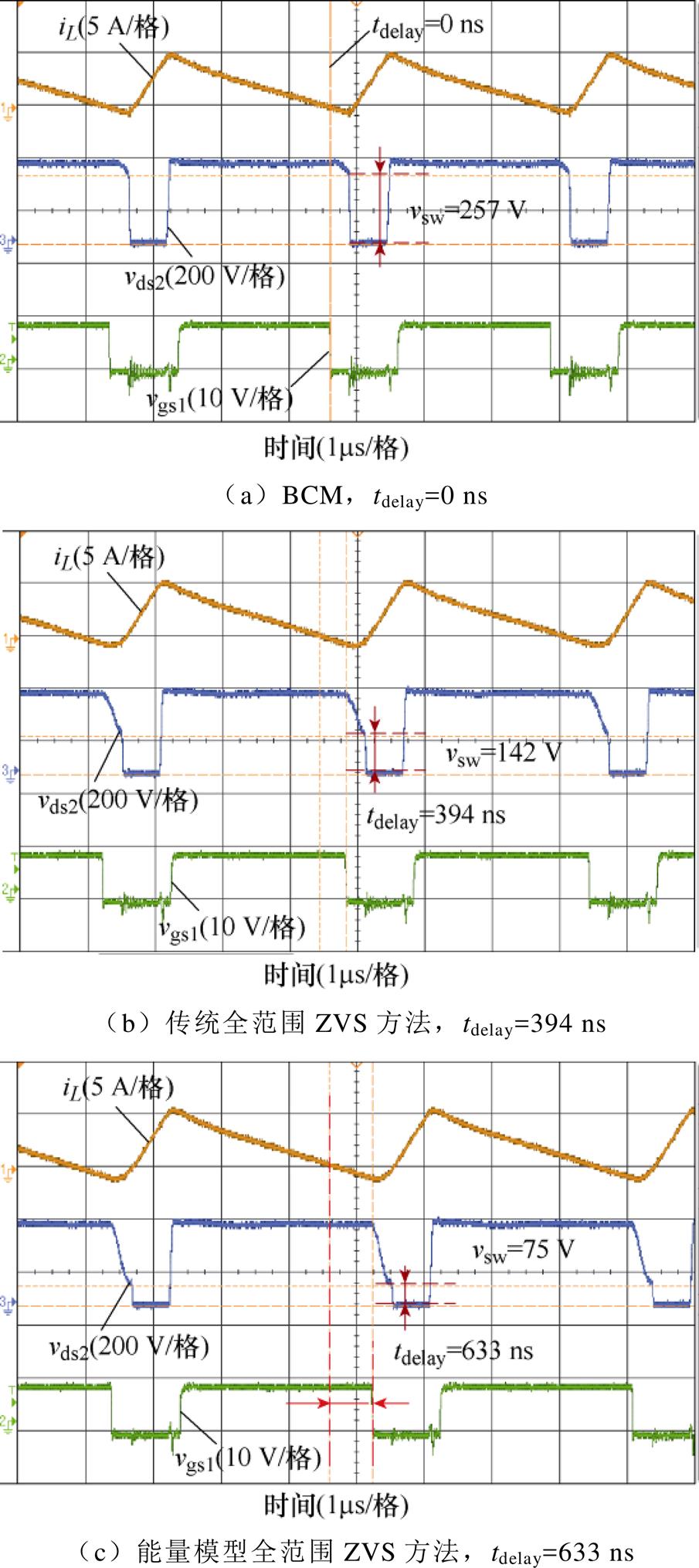
图9 Vin=250 V时主开关管开通过程波形示意图
Fig.9 Waveforms of real switching process of main switch with Vin=250 V
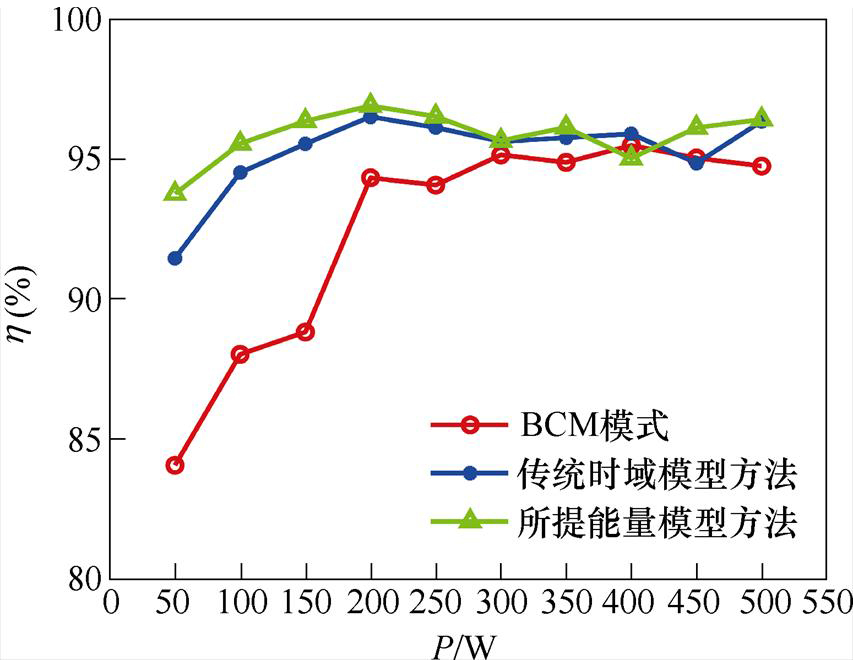
图10 BCM模式、传统ZVS及所提方法的效率曲线
Fig.10 Efficiency curves under: BCM condition, conventional ZVS method, proposed method
当输入电压为250 V时,基于传统时域模型ZVS实现求得延迟关断时间为394 ns,基于能量模型ZVS实现求得延迟关断时间为633 ns。如图9所示为500 W满载条件下,主开关管实际开通过程的实验波形,图9a~图9c分别对应BCM(tdelay=0 ns)、传统时域模型ZVS实现(tdelay=394 ns)、能量模型ZVS实现(tdelay=633 ns)。
由图8及图9可知,在不同ZVS方法下,S2开通时刻电感电流较为相近,因此可通过实际开关电压对比开关损耗。Vin>0.5Vo时,若电感无死区初始储能,主开关管ZVS缺失明显,硬开关电压高达上百伏。两种ZVS实现均降低了实际硬开关电压,传统时域模型ZVS实现下硬开关电压降幅可达44%~65%,而能量模型ZVS实现下硬开关电压降幅可达70%~86%。相较于传统方法,能量模型方法可将硬开关电压进一步降低47%~60%。因此可以验证,能量模型ZVS方法在实际运用中具有更高的准确性。
在图8及图9所示结果的基础上,本文进一步对比了三种控制方式的效率曲线,其结果如图10所示。根据图10,相较于电感无储能工况,两种ZVS实现均提升了变换器的效率。能量模型ZVS实现的效率提升更明显,在峰值处可达96.9%,较传统时域模型(96.5%)实现了0.4%的提升。则能够验证能量模型ZVS实现对变换器工作效率的优化效果。
针对BCM电路Boost变换器的ZVS实现问题,传统时域模型基于死区中的谐振过程展开分析,其数学模型复杂且计算量大。此外,由于忽略了开关管输出电容Coss的非线性特征,其计算结果与实际的偏差较大。为此,本文在计及Coss非线性特征的基础上,提出一种基于能量模型的Boost变换器ZVS实现方法,并搭建500 W的Boost变换器样机开展实验验证。所得结论如下:
1)本文建立了死区前后各储能元件能量变化的数学模型,并从能量平衡的角度,揭示了ZVS缺失原因及实现条件。所得结果与传统时域模型一致,因而验证了其正确性。由于避免了对复杂谐振过程的精确分析,该模型大大简化了软开关实现的分析与计算过程。
2)结合所提能量模型及积分算子替换,将电感初始电流is与Coss的积分关系转换为关于电荷量Qoss的数学模型,避免了难以求解的复杂时间积分运算。并通过分段曲线拟合建立了Coss与vds的非线性数学关系,大大简化了电荷量Qoss的计算,从而在降低is计算难度的同时,提升其计算精度。
3)实验结果表明,相较于传统时域模型,基于能量模型的ZVS实现方法使主开关管实际硬开关电压降低47%,并使峰值效率提升了0.4%,由此验证了能量模型ZVS实现方法的正确性和有效性。
参考文献
[1] Jabbari M, Mokhtari M. High-frequency resonant ZVS Boost converter with grounded switches and continuous input current[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 1059-1067.
[2] Jafari A, Samizadeh Nikoo M, van Erp R, et al. Optimized kilowatt-range Boost converter based on impulse rectification with 52 kW/L and 98.6% effici- ency[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7389-7394.
[3] 唐钧涛, 戚志东, 裴进, 等. 基于电荷泵的燃料电池有源网络升压变换器[J]. 电工技术学报, 2022, 37(4): 905-917.
Tang Juntao, Qi Zhidong, Pei Jin, et al. An active network DC-DC Boost converter with a charge pump employed in fuel cells[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 905-917.
[4] 林雪凤, 许建平, 周翔. 谐振软开关耦合电感高增益DC-DC变换器[J]. 电工技术学报, 2019, 34(4): 747-755.
Lin Xuefeng, Xu Jianping, Zhou Xiang. Soft-switched high step-up DC-DC converter with coupled inductor of resonance[J]. Transactions of China Electro- technical Society, 2019, 34(4): 747-755.
[5] 马小勇, 王萍, 王议锋, 等. 基于交错并联Boost变换器的耦合电感综合建模与多目标优化方法[J]. 电工技术学报, 2022, 37(24): 6399-6410.
Ma Xiaoyong, Wang Ping, Wang Yifeng, et al. Com- prehensive modeling and multi-objective optimization method for coupled inductors of interleaved Boost converters[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6399-6410.
[6] Liu Ziheng, Lin Zhen, Wang Jinyan, et al. A fully integrated heterogenous Si-CMOS/GaN 500 MHz 6 V-to-18 V Boost converter chip[J]. IEEE Transa- ctions on Power Electronics, 2023, 38(5): 5615-5618.
[7] 王忠杰, 王议锋, 陈庆, 等. 基于GaN的高频Boost变换器优化设计[J]. 电工技术学报, 2021, 36(12): 2495-2504.
Wang Zhongjie, Wang Yifeng, Chen Qing, et al. Optimal design of high frequency Boost converter based on GaN[J]. Transactions of China Electro- technical Society, 2021, 36(12): 2495-2504.
[8] 王议锋, 王忠杰, 陈博, 等. 基于耦合电感的交错Boost变换器性能优化[J]. 电工技术学报, 2022, 37(8): 2097-2106.
Wang Yifeng, Wang Zhongjie, Chen Bo, et al. Performance optimization of interleaved Boost based on coupled inductors[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2097-2106.
[9] Liu Zhengyang, Huang Xiucheng, Mu Mingkai, et al. Design and evaluation of GaN-based dual-phase interleaved MHz critical mode PFC converter[C]// Energy Conversion Congress & Exposition, Pittsburgh, 2014: 611-616.
[10] 张建丰, 许建平, 周翔, 等. 一种基于辅助网络的软开关二次型Boost高增益变换器[J]. 电工技术学报, 2017, 32(24): 71-79.
Zhang Jianxin, Xu Jianping, Zhou Xiang, et al. A soft-switched high step-up quadratic Boost converter with auxiliary circuit[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 71-79.
[11] 姚志刚. Near-CRM模式下基于零电压软开关的无传感器均流与均压技术的研究[D]. 重庆: 重庆大学, 2020.
[12] Wu Xinke, Zhang Junming, Ye Xin, et al. Analysis and derivations for a family ZVS converter based on a new active clamp ZVS cell[J]. IEEE Transactions on Industrial Electronics, 2008, 55(2): 773-781.
[13] Tang Shihuang, Chen Dan, Huang C S, et al. A new on-time adjustment scheme for the reduction of input current distortion of critical-mode power factor correction Boost converters[C]//The 2010 Inter- national Power Electronics Conference-ECCE ASIA-, Sapporo, Japan, 2010: 1717-1724.
[14] Lü Dian, Shi Guoxiong, Min Run, et al. Extended off-time control for CRM Boost converter based on piecewise equivalent capacitance model[J]. IEEE Access, 2020, 8: 155891-155901.
[15] 周玉婷, 吴羽, 任小永, 等. 基于改进恒导通时间控制的临界连续导通模式Boost功率因数校正变换器[J]. 电工技术学报, 2021, 36(20): 4329-4338.
Zhou Yuting, Wu Yu, Ren Xiaoyong, et al. Improved constant on-time control of boundary conduction mode Boost power factor correction converter[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4329-4338.
[16] 王议锋, 王忠杰, 陈博, 等. 高频Boost ZVS建模分析及其轻载效率优化[J]. 太阳能学报, 2023, 44(2): 309-316.
Wang Yifeng, Wang Zhongjie, Chen Bo, et al. High- frequency Boost ZVS modeling analysis and its light-load efficiency optimization[J]. Acta Energiae Solaris Sinica, 2023, 44(2): 309-316.
[17] Chen Yanglin, Chen Yaowming, Chen Hongjyun. On-time compensation method for CRM/DCM Boost PFC converter[C]//2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Expo- sition (APEC), Long Beach, CA, USA, 2013: 3096- 3100.
[18] Wang Kangping, Zhu Hongkeng, Wu Jiarui, et al. Adaptive driving scheme for ZVS and minimizing circulating current in MHz CRM converters[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 3633-3637.
[19] Sun Jingjing, Huang Xingxuan, Strain Nathan N, et al. Inductor design and ZVS control for a GaN-based high efficiency CRM totem-pole PFC converter[C]// 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 727-733.
[20] Marvi Mohammad, Fotowat-Ahmady Ali. A fully ZVS critical conduction mode Boost PFC[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1958-1965.
[21] (Mar. 2023) Datasheet of GS66516T. [S/OL]. Available: https://gansystems.com/wp-content/uploads/2021/10/GS66516T-DS-Rev-210727.pdf.
Abstract Soft switching is crucial for Boost converters, especially in the trend of high-frequency development. During boundary conduction mode (BCM), zero voltage switching (ZVS) of the main switch of the Boost converter is achieved without auxiliary circuits, which is favored in small and medium power applications. However, when the gain of the converter is greater than 2, ZVS based on BCM cannot be realized because of the positive resonance valley of its drain-source voltage vds in the dead zone. Therefore, a method extending the synchronized switch time is proposed based on time-domain dead zone analysis. A negative current is obtained on the inductor at the start of the dead zone, forcing the resonance valley of vds to get closer to 0. Due to the calculation of the resonance process, the complexity of the calculation process and result expression is greatly increased. However, in practice, the realization of soft switching only focuses on the start and end moment of the dead zone. Complex analysis of the resonance process is optional. Besides, nonlinear characteristics of the output capacitor Coss on power switchesare ignored in the time-domain model, causing inaccurate inductor current at the start of the dead zone and is harmful to reducing switch losses. Thus, this paper proposes a ZVS method based on the energy model.
Firstly, the energy model of passive power components is established during the dead zone. Instead of considering the entire dead zone, only energy change at the start and end of the dead zone is focused. Secondly, conditions with power variations are analyzed, and the requirement for ZVS realization is given from the energy balance perspective. Then, considering the nonlinear characteristics of Coss, an accurate expression of the negative inductance current needed is obtained. The ZVS realization method based on the power model avoids complex resonant processes oftime-domain modeling. Accordingly, less calculation is needed, and the accuracy of soft switching implementation is improved. Finally, a 500 W experimental prototype is built to verify the proposed method.
Experiments are conducted when the input voltage is 200 V and 250 V, respectively, and the output voltage is 300 V. With an input voltage of 200 V, the proposed method reduces the actual switching voltage by 86% compared with the critical conduction mode and 60% with the time-domain model. Under 250 V, the proposed method reduces the actual turn-on voltage by 70% and 47% compared with the critical conduction mode and the time-domain model, respectively. Since the switching current between different methods is almost the same, switching loss is proportional to the switching voltage. Therefore, the proposed method can effectively decrease switching loss.
Conclusions below can be drawn from experimental results.
(1) The proposed method is based on energy balancing the start and end of the dead zone, simplifying the analysis and calculation process of soft switching implementation.
(2) The proposed model considers the dynamic characteristics of the output capacitor Coss accurately, which improves the accuracy of the negative inductance current.
(3) Compared with the traditional time-domain model, the proposed model and ZVS implementation method can effectively reduce the actual switching loss and improve peak efficiency by 0.4%, which verifies the ZVS implementation method based on the energy model.
keywords:Boost converter, boundary conduction mode, energy model, soft switching, switch output capa- citance
DOI: 10.19595/j.cnki.1000-6753.tces.230385
中图分类号:TM46
收稿日期 2023-03-31
改稿日期 2023-05-08
王议锋 男,1981年生,副教授,博士生导师,研究方向为高频电能变换技术、磁集成技术、软开关技术及交直流微电网中的电力电子技术等。E-mail: wayif@tju.edu.cn
马小勇 男,1991年生,博士研究生,研究方向为高频大功率电能变换技术。E-mail: maxiaoyong@tju.edu.cn(通信作者)
(编辑 陈 诚)