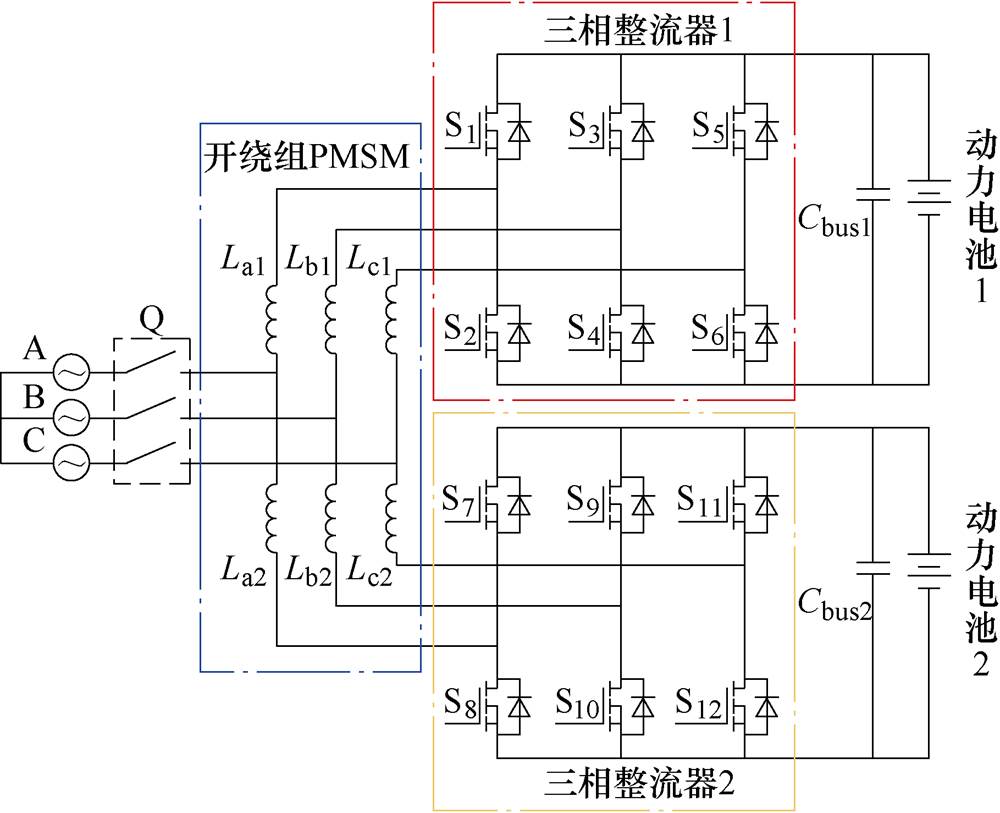
图1 基于开绕组PMSM的双电池集成充电系统拓扑
Fig.1 Topology of the dual-battery integrated charging system based on OW-PMSM
摘要 针对基于开绕组永磁同步电机和双电池组驱动的电动汽车提出一种集成化充电拓扑，充电运行时将双逆变器和电机绕组复用为双PWM整流器及其输入侧滤波电感。在三相电压源型整流器（VSR）和开绕组永磁电机数学模型的基础上，将电网坐标系和电机坐标系相统一，分析了充电状态下的电磁转矩。实际运行时存在双电池剩余电量不相等的情况，导致充电时双通道功率不平衡，因此设计了一种准直接功率控制策略，以解决功率不平衡带来的转矩脉动问题。最后通过仿真和实验验证了该集成化充电拓扑的可行性。
关键词：集成化充电拓扑 开绕组永磁同步电机 双电池组 准直接功率控制
随着我国“双碳”目标的推进，电动汽车成为了交通行业绿色低碳、节能减排的重要途经，然而电动汽车的快速发展也迎来诸多挑战，其最核心的续航能力始终受制于车载电池容量[1-2]，在电池技术未能获得革命性突破的前提下，充电问题仍是影响电动汽车进一步快速发展的关键[3]。目前，市面上绝大多数电动汽车采用非车载独立充电桩充电，该方式具有充电速度快、可靠性高等优点，但其充电便利性差、城市占地面积大、建设周期长等问题也饱受争议[4-5]。在此背景下，车载充电机（On Board Charger, OBC）直接通过家用交流电在汽车闲置时对车载电池进行充电，因其充电便利、成本低廉等优势成为众多车企的备选充电方案。然而，目前传统的OBC存在体积质量大、汽车行驶过程中冗余等问题，与提高汽车续航、整车轻量化的理念相悖，限制了其发展与应用[6]。
利用电动汽车驱动系统四象限运行特性，将其复用为车载集成充电机（Integrated Battery Charger, IBC）的理念最早于1985年由美国学者提出，增加一套隔离变压器，复用部分驱动器件，实现了单相交流供电方式下的充电功能[7]。IBC一般是在电动汽车泊车闲置时，通过继电器或切换开关改变车载驱动系统的电路连接，驱动电机系统被重构为一套充电机，无需添加额外的功率器件，将原本的车载驱动系统通过分时复用的方式实现充电功能，在提高充电便利性的同时，实现充电系统的高度集成化，能够有效解决传统OBC在体积、质量和容量上的问题。
电动汽车电气系统中通常包括高压动力电池组、备用电池组、低压电池组以及辅助电源等多种能量源[8]，不同能量源之间的电能转换始终依赖额外的车载变换器完成，不仅占用车内有限空间，更是增加了系统的复杂度，因此针对多能量源的集成充电系统引起了部分学者的研究关注。文献[9]中针对双电源供电隔离母线型的开绕组永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）驱动系统进行车载IBC的研究，充电时通过外部充电机给一次侧电池组充电，同时将三相逆变器与电机绕组重构为一个Buck-Boost变换器给二次侧电池组充电，该方案还研究了在电机运行过程中通过额外的逆变器裕度对二次侧电池进行充电补偿的方法，实现了单个充电机对双电池同时充电的方案，但是未能实现充电系统的整体集成。文献[10]研究了采用电流源型整流器作为前级直流输入的结构，通过三相电网进行充电，实现了较高的功率因数及充电电流品质，但是整个系统结构不够紧凑，额外增加的网侧LC滤波器和电流源型整流器在驱动过程中不工作，增加了系统的成本和复杂度，因此难以在实际场合有所应用。文献[11]也针对隔离母线型开绕组PMSM的双电池IBC进行了研究，将直流输出侧改为双通道独立输出，引出各相绕组的中性点，从而抵消充电过程中各相绕组的充电电流，抑制电磁转矩。此外，该拓扑通过在输出侧增加4个接地电容来解决双电池独立充电后充电电流不平衡与漏电流的问题，但增设的接地电容设计难度较大，且在充电过程中其等效串联电阻增加了系统的损耗，在双通道负载不平衡的状态下存在发热严重、系统充电效率降低的问题。
可见，由于双电源供电的特点，隔离母线型的开绕组PMSM驱动系统更加适合于双电池IBC拓扑结构[11-14]，虽然也有许多文献利用多通道隔离变压器或谐振变换器进行了多电池充电的研究，在实现电气隔离的基础上完成双电池充电的功能[15-17]，但系统中增加额外的铁心与线圈，提高了系统的复杂度和成本。
因此，本文基于开绕组永磁同步电机提出一种车载双电池集成充电系统，利用开绕组永磁电机绕组易重构、驱动系统功率器件多等优势，进行三相集成充电系统拓扑的设计，并针对双电池充电的控制策略进行研究，在基本控制策略的基础上，开展准直接功率控制（Quasi Direct Power Control, QDPC）策略的研究，实现单位功率因数控制的同时有效抑制充电过程中的转矩脉动。最后通过对稳态和动态充电过程进行仿真和实验分析，验证了所提双电池集成充电系统及其准直接功率控制策略的可行性。
图1所示为本文所提双电池集成充电拓扑，当系统处于驱动模式时，三相电网接入开关Q断开，系统等效为开绕组永磁电机双电源驱动系统；当系统处于充电模式时，开关Q闭合，三相电网接至开绕组永磁电机三相绕组中心抽头上，此时两个三相电压源型逆变器被复用为两个三相电压源型整流器（Voltage Source Rectifier, VSR），电机的两套三相绕组分别作为两个整流器的输入侧交流滤波电感，实现三相电网通过两套电机绕组与整流器同时给两个动力电池组充电。
图1 基于开绕组PMSM的双电池集成充电系统拓扑
Fig.1 Topology of the dual-battery integrated charging system based on OW-PMSM
在充电过程中，对同相两段绕组对应的各自桥臂采用同步控制，使两段绕组上流过幅值相等、相位相反的交变电流，两段绕组所产生的磁通互相抵消，从而实现电机平均输出转矩为零，保持充电过程电机静止。
但对于实际工况下的电动汽车电池，由于参数的区别，不同充电阶段双电池对应的等效负载是不同的，如双电池独立供电的开绕组PMSM驱动系统在运行过程中往往会存在两个电池组剩余电量不相等的情况，此时对双电池进行充电就存在双通道负载不平衡的问题。另外，实际电机绕组中心抽头两端的阻感参数无法达到完全一致，即充电系统的两个通道总会存在参数不对称的问题。
鉴于上述两点，若对集成充电系统的两个通道采用对称的控制方法，则会造成双通道充电功率不平衡，进而导致中心抽头两端的绕组上流过幅值不相等的交变电流，产生脉振电磁转矩，这可能导致电机在充电过程中产生振动和噪声，同时也降低了充电的效率。因此，首先需要对负载不平衡情况下复用电机绕组所产生的脉振转矩进行理论分析，然后考虑设计相应的控制策略抑制充电状态下的脉振转矩。
为分析系统负载不平衡对充电电磁转矩的影响，首先需要从复用电机绕组的三相VSR的数学模型入手。图2为复用电机三相绕组La1、Lb1、Lc1的三相VSR电路拓扑[18-19]。
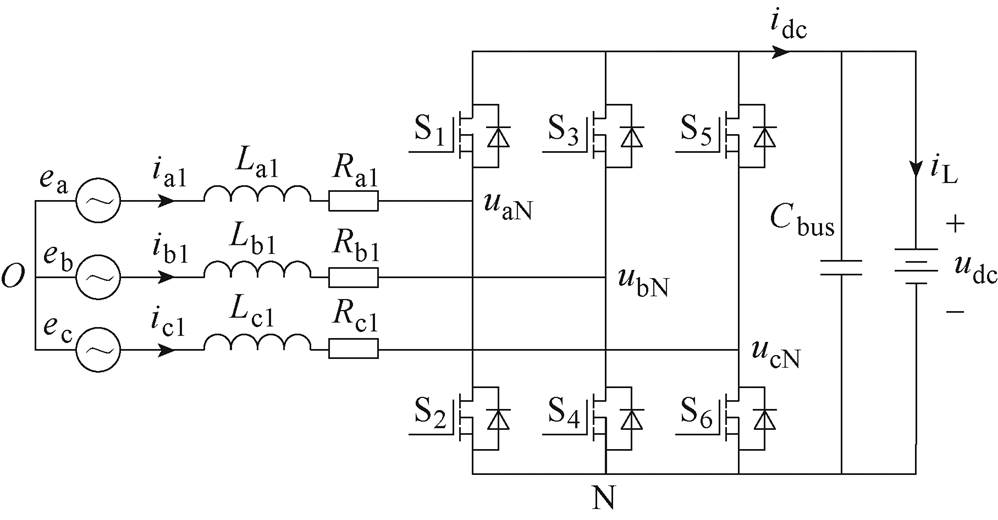
图2 三相VSR拓扑
Fig.2 Topology of three-phase VSR
由于VSR同一桥臂上下两个开关管不允许同时导通，只存在两种开关状态，因此可以定义开关函数Si为
（1）
dq旋转坐标系下的三相VSR状态方程为
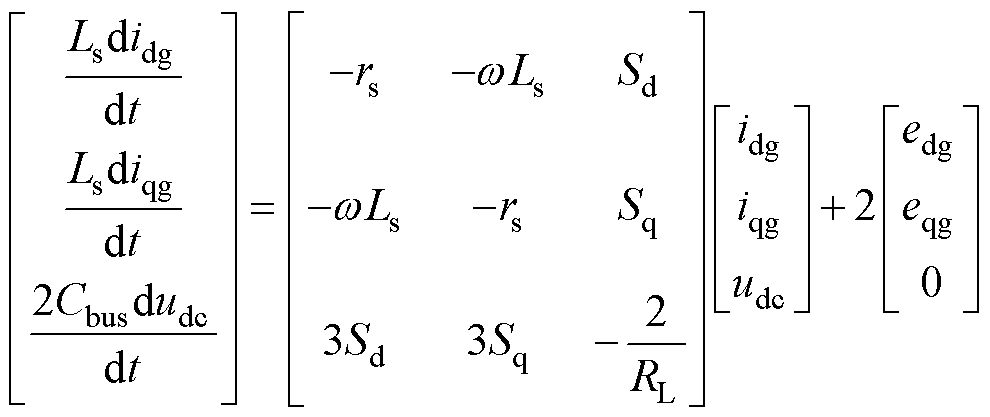（2）
式中，idg、iqg、edg、eqg、Sd、Sq分别为电网电流、电网电压以及开关函数在d、q轴上的分量，其中d轴表示网侧有功分量，q轴表示网侧无功分量；Ls为电机相电感的一半；rs为电机相电阻的一半；Cbus为直流母线电容；udc为直流侧电压；RL为直流侧负载。
将电网坐标系与电机坐标系相统一，其三相ABC坐标轴重合，如图3所示。图中，qg为电网侧d轴与A轴的夹角，dg、qg分别为电网侧的d、q轴，在充电过程中，其按照电网侧工频角速度wg同步旋转；qr为电机d轴与A轴的夹角，dr、qr分别为电机的d、q轴。
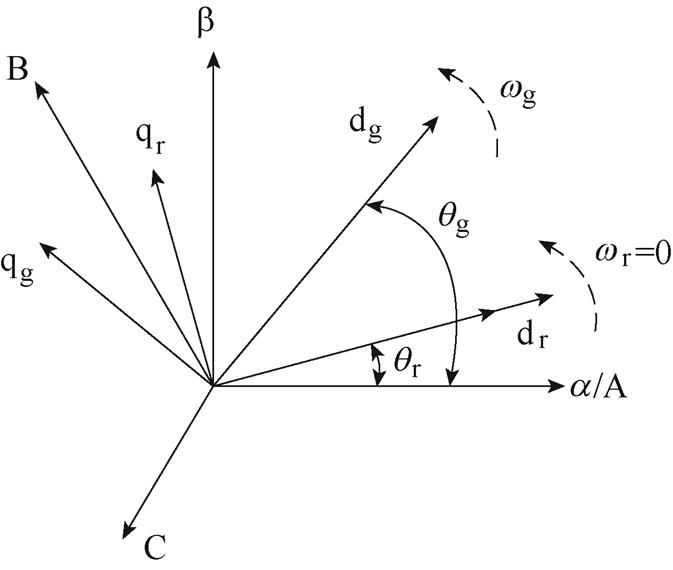
图3 电网与电机合并坐标系示意图
Fig.3 Schematic diagram of the combined grid and motor coordinate system
假设电机保持静止，则电机dq轴的角速度wr为零，可以获得两坐标系dq轴电流关系为
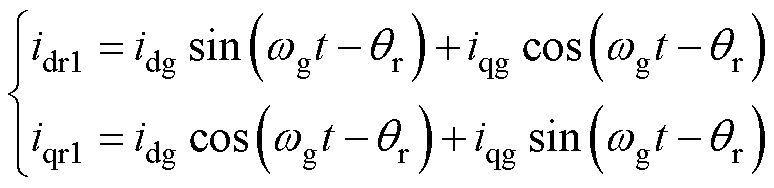（3）
式中，idr1、iqr1分别为电机第一套三相绕组等效d、q轴电流。而开绕组PMSM在同步旋转坐标系下的转矩方程为
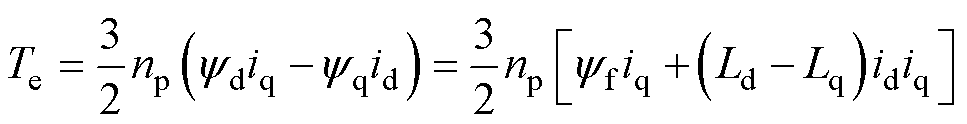（4）
式中，np为转子极对数；Ld、Lq分别为d、q轴电感；yd、yq分别为d、q轴磁链；yf为永磁体磁链。将式（3）代入式（4）可以得到第一套绕组在充电时的电磁转矩为
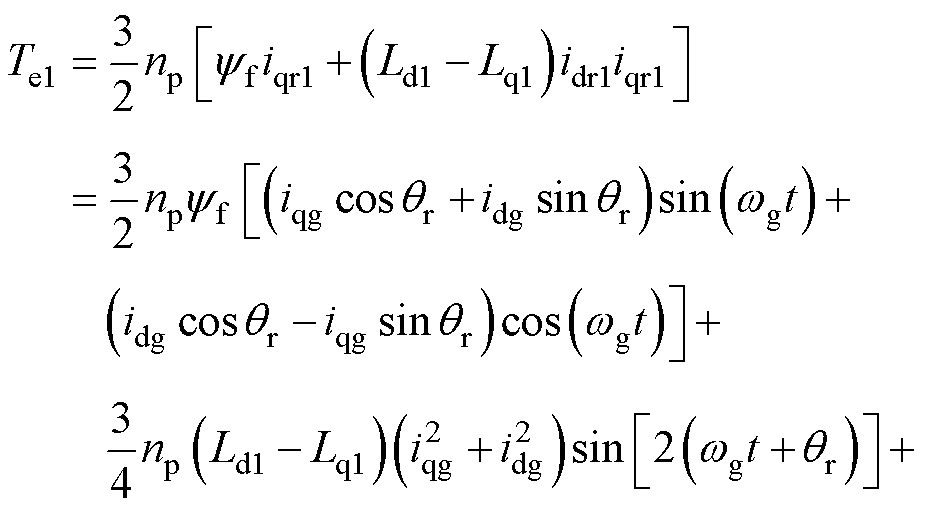
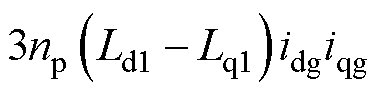（5）
式中，Ld1、Lq1分别为第一套绕组的d、q轴电感。
可见，电机所产生的脉振电磁转矩包括一个直流分量、一个以电网频率脉动的分量和一个以电网二倍频率脉动的分量。转矩中耦合了大量网侧变量，两套三相绕组的充电转矩合并后难以进一步化简分析。为了降低针对不平衡负载情况的充电控制策略的设计难度，将转子dq坐标系下的转矩方程变换到电网与电机统一的ab 坐标系进行，有
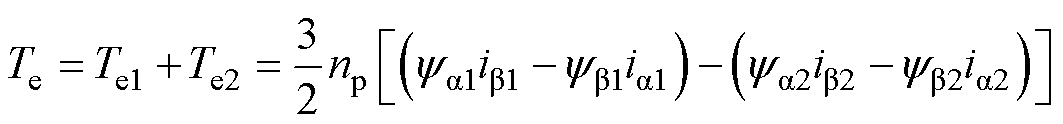（6）
式中，ya1、ya2、yb1、yb2分别为两套电机绕组在其对应两相静止a、b 坐标系下的磁链分量。假设电机两套绕组参数对称，即ya1=ya2=ya/2，yb1=yb2= yb/2，则式（6）可化简为
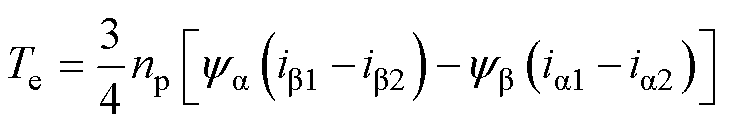（7）
式（7）中两相磁链为
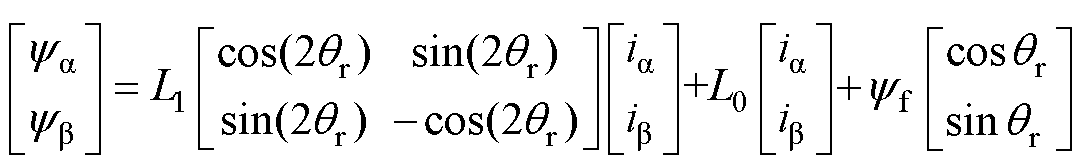（8）
其中
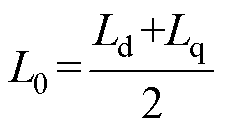
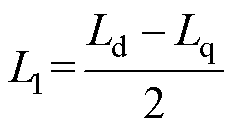
式中，ia、ib 分别为电机总三相电流在a、b 轴的分量；q 为位置角。将式（8）代入式（7）中即可得到电磁转矩Te。充电过程中电机转子保持静止，位置角q 为定值，通过合适的控制策略使两套绕组在静止坐标系的电流相等，即可抵消系统的充电转矩。
在本文提出的双电池集成充电拓扑中，系统被复用为两个三相VSR对两个独立高压电池组充电，与传统的三相并联型VSR系统结构相似，但由于输出母线相互隔离，不存在零序回路和模块间环流，因此本系统不需要额外设计零序环流抑制策略，但两通道的充电功率不平衡会导致电机在充电过程中产生脉振转矩。为抑制该转矩，本文针对复用为滤波电感的电机绕组电流平衡控制方法，开展对双通道功率平衡控制策略的研究。
一般的三相VSR控制目标分为两个部分：一个目标是输出侧的电压或电流恒定可控，面对突变负载具有快速响应的能力；另一个目标则是要求网侧三相电流正弦化，达到单位功率因数控制要求，抑制网侧无功分量。因此，VSR的基本控制策略中，通常将网侧参数进行坐标变换，从而实现有功分量与无功分量的解耦，最终通过电压电流双闭环调节完成控制目标。而对于本文所提出的双三相VSR集成充电系统，还需要实现的第三个目标则是对两套系统输入侧绕组的电流平衡控制。
为满足集成充电系统中双三相VSR的输入侧电流平衡，首先需要确保双通道充电功率一致，根据系统功率方程，有
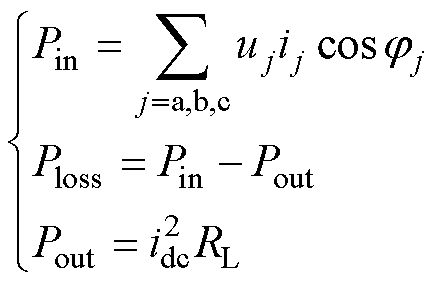（9）
式中，Pin、Pout、Ploss分别为三相VSR的输入功率、输出功率和损耗功率；uj、ij分别为j相输入电压和电流的有效值；jj为j相的输入功率因数；idc为输出侧直流电流。
本文主要目标是验证集成充电拓扑及其控制策略的可行性，故简化使用可变电阻作为双通道的负载。假设Ploss在相近工况下基本相等，双通道的负载分别用RL1、RL2表示，则根据双三相VSR的电流状态方程可得
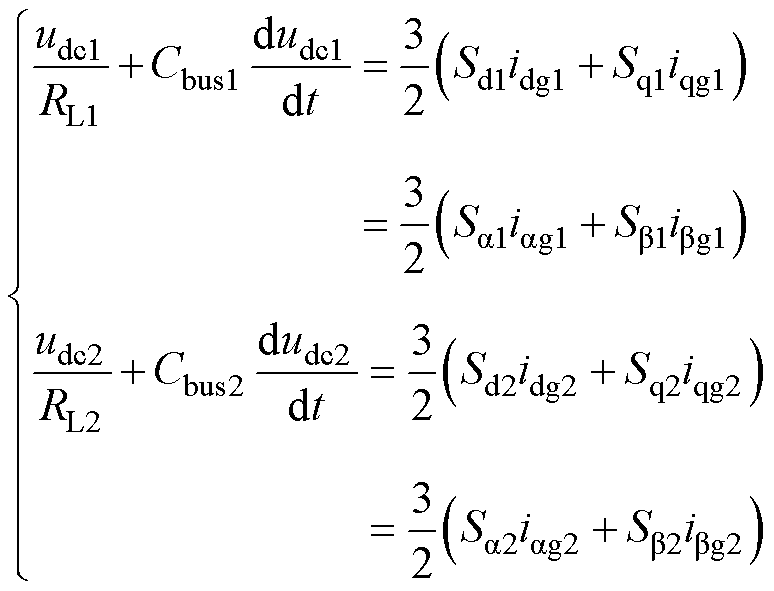（10）
式中，udc1、udc2、Cbus1、Cbus2分别为双通道的直流输出电压和支撑电容；Sd1、Sq1、Sd2、Sq2分别为两组三相VSR开关函数在d、q轴的分量；Sa1、Sb1、Sa2、Sb2分别为开关函数在a、b 轴的分量。当负载不平衡时，RL1≠RL2，若要满足直流侧输出功率一致，则需要根据双通道负载差异独立对应控制输出电压。对于VSR而言，母线电容电压纹波频率远高于电网和电机基频，因此式（10）中电压的微分项在工频运行过程可以被忽略。对于电阻负载，若要满足输入侧电流平衡，只需根据输出功率调整给定输出电压，主动控制双通道输出功率趋近于相等，给定电压应满足
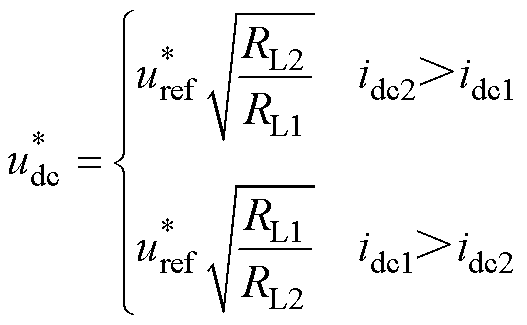（11）
式中，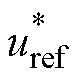
为电池组的期望充电电压；idc1和idc2分别为双通道负载电流。
式（10）给出了两通道负载不平衡工况下的电压给定计算方法，通过变输出电压的方法，利用协同控制的思想，不仅可以实现双通道给定输出功率一致，提高系统稳态过程的输出特性，此外还整合了电压外环的PI调节器，减少了数字芯片计算资源的需求。
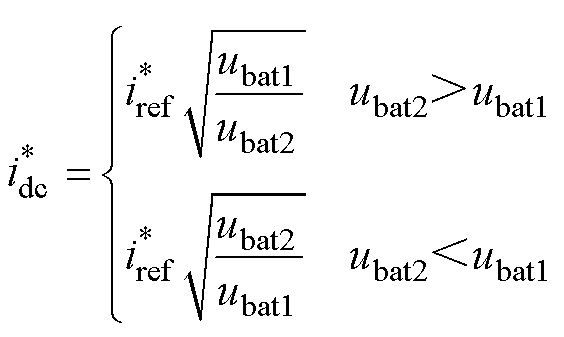（12）
式中，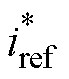
为电池组的期望充电电流；ubat1和ubat2分别为双通道电池组端电压。
针对实际系统中双通道负载的蓄电池，需要结合其不同充电模式，在式（12）的控制方式基础上，相应地对控制策略加以调整。在恒流充电模式下，将直流侧充电电流作为外环，控制参考给定如式（12）所示，将式（11）中的参考量由输出电压修改为输出电流，此时负载比RL1/RL2等效为电池组端电压之比ubat2/ubat1；对于恒压充电模式，则将直流侧电压作为外环，此时负载比RL1/RL2等效为输出电流之比idc2/idc1，需要注意的是，双通道充电电压均不应超过电池组的最大充电电压Umax。
不难看出，虽然在双通道功率平衡的方案下，外环PI控制器经过整合，可以节省部分计算资源，但基本控制策略下的整个充电系统的软件复杂度较高，在电网侧旋转坐标系下的控制方式不仅需要软件锁相环来跟踪电网相位，反复进行坐标变换，还需要在控制过程中对dq轴电压进行解耦。一方面占用了较多的数字芯片资源，增加了对车载硬件设备的要求；另一方面不利于控制参数的整定，尤其在负载变化的过程中，内环耦合项严重影响了系统的动态性能，无法满足双通道同步精准控制的要求。因此需要对该系统控制策略进行多方面的改进。
对于本系统的双三相VSR而言，控制过程中最关键的点在于滤波电感的电流是否平衡。虽然采用功率控制可以间接对输入电流进行控制，但在旋转坐标系下，电网坐标系与电机坐标系之间始终存在角度差，导致电机复用绕组由于交叉耦合的分量产生电磁转矩。此外，在旋转坐标系下的控制策略均需要对电网侧相位进行闭环计算，本系统在充电模式与驱动模式下复用同一套数字控制器，但三相充电模式需要对双通道输出功率均进行闭环控制，相比于驱动模式只对单电机进行控制所需的数字芯片计算资源更多，因此，在参考坐标关系与合理分配数控芯片资源的前提下，最优选是直接在静止坐标系下对两套绕组的ab 电流进行精确控制。为此，本文提出在静止坐标系下的准直接功率控制（QDPC）策略，直接对静止坐标系下的两相电流进行控制。
与旋转坐标系类似，在静止坐标系下通过瞬时功率定义同样可以获得网侧有功功率P与无功功率Q，有
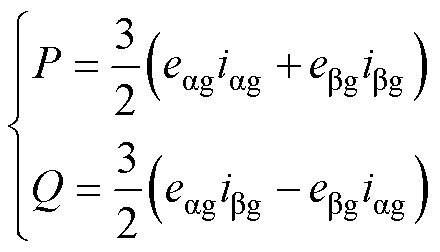（13）
式中，iag、ibg、eag、ebg分别为电网电流和电网电压在a、b 轴上的分量。
系统中功率平衡外环计算获得给定功率，假设瞬时有功功率与无功功率的给定值分别为P*和Q*，则静止坐标系下两相输入电流的给定值为
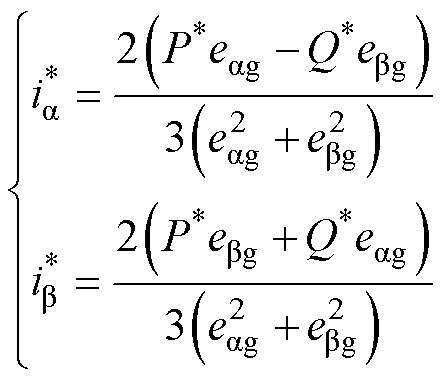（14）
在三相电网电压平衡时，式（14）中的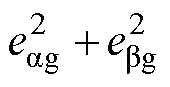
保持恒定，给定无功分量Q*=0时，给定的两相电流即与对应的两相电压同相位，从而满足单位功率因数控制的要求，使系统不再依赖软件锁相环获取电网电压相位。此外，三相VSR在两相静止坐标系下αβ轴电流没有耦合项，因此不需要解耦控制，但内环为静止坐标系下的交流量，PI调节器无法实现对交流信号的无静差跟随，而理想的PR调节器对特定频率的交流分量增益无穷大，可以准确控制内环αβ轴电流，这也满足了系统最关键的控制要求，有效地避免了双三相VSR负载不平衡时由于控制因素导致的充电转矩脉动。
图4给出了本系统在静止坐标系下采用QDPC策略的具体控制框图，将功率平衡外环输出直接代入式（14）得到静止坐标系下的两相电流的给定值，并通过PR调节器对其进行无静差跟随，在实现对两相静止坐标系电流准确控制的基础上间接实现了对网侧有功与无功功率的控制，并且还省略了电网侧软件锁相环。
本系统消除了电流坐标变换的环节，控制对象为工频交流量，传统PI调节器无法实现无静差跟随，因此，本系统中电流环采用PR调节器，并对其控制参数进行详细设计。
图5为a 轴电流环的控制框图，由于数字控制系统中存在1个控制周期的计算延时以及0.5个周期的调制延时，考虑到1.5Ts很小，故用一阶惯性环节来近似表示。
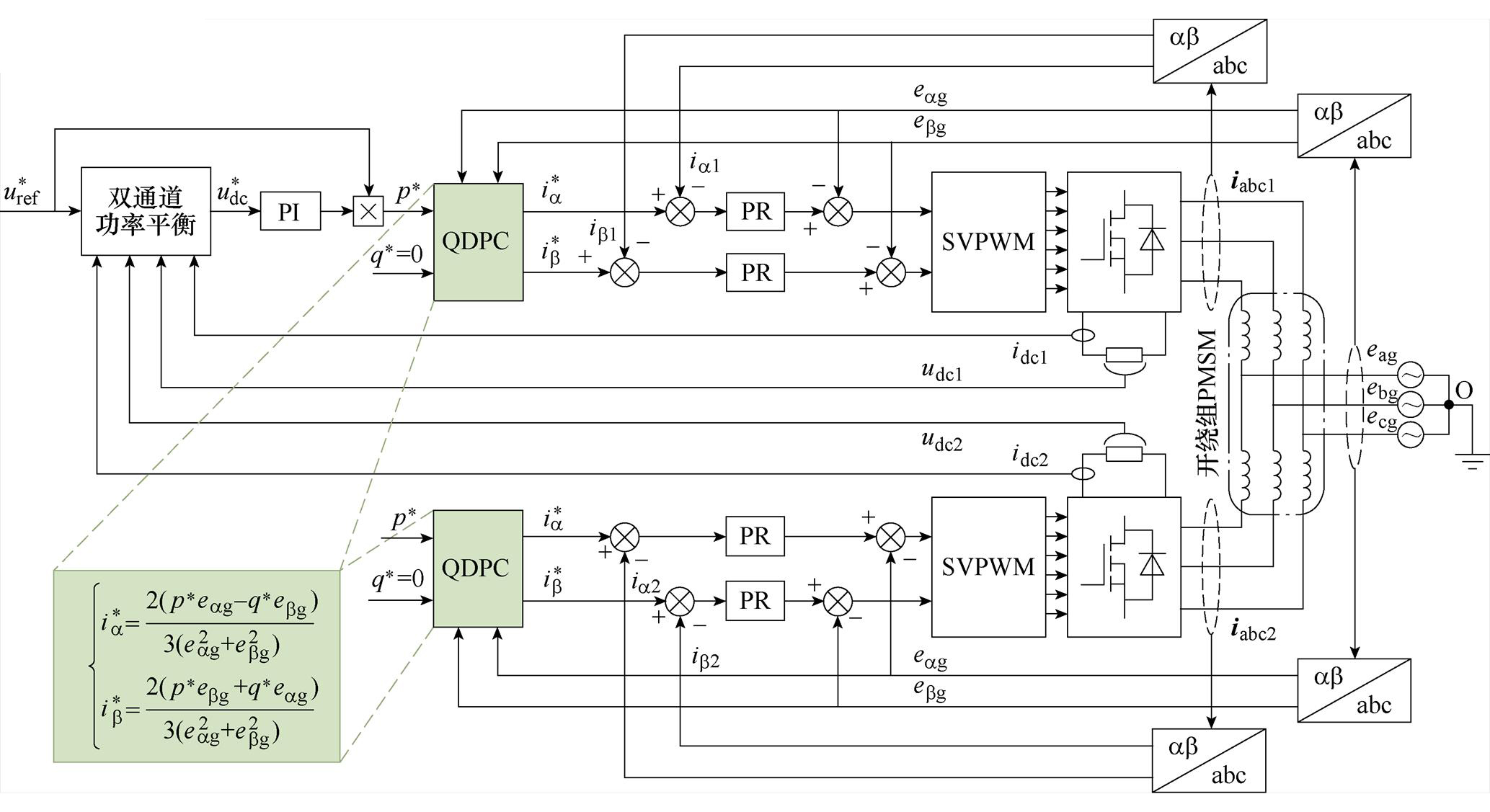
图4 双电池集成充电系统QDPC策略框图
Fig.4 Diagram of QDPC strategy for dual-battery integrated charging system
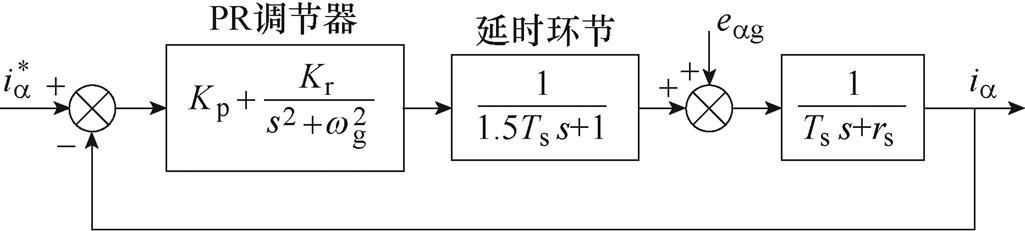
图5 a 轴电流环控制框图
Fig.5 Control block diagram of a-axis current loop
a 轴电流值计算方法为
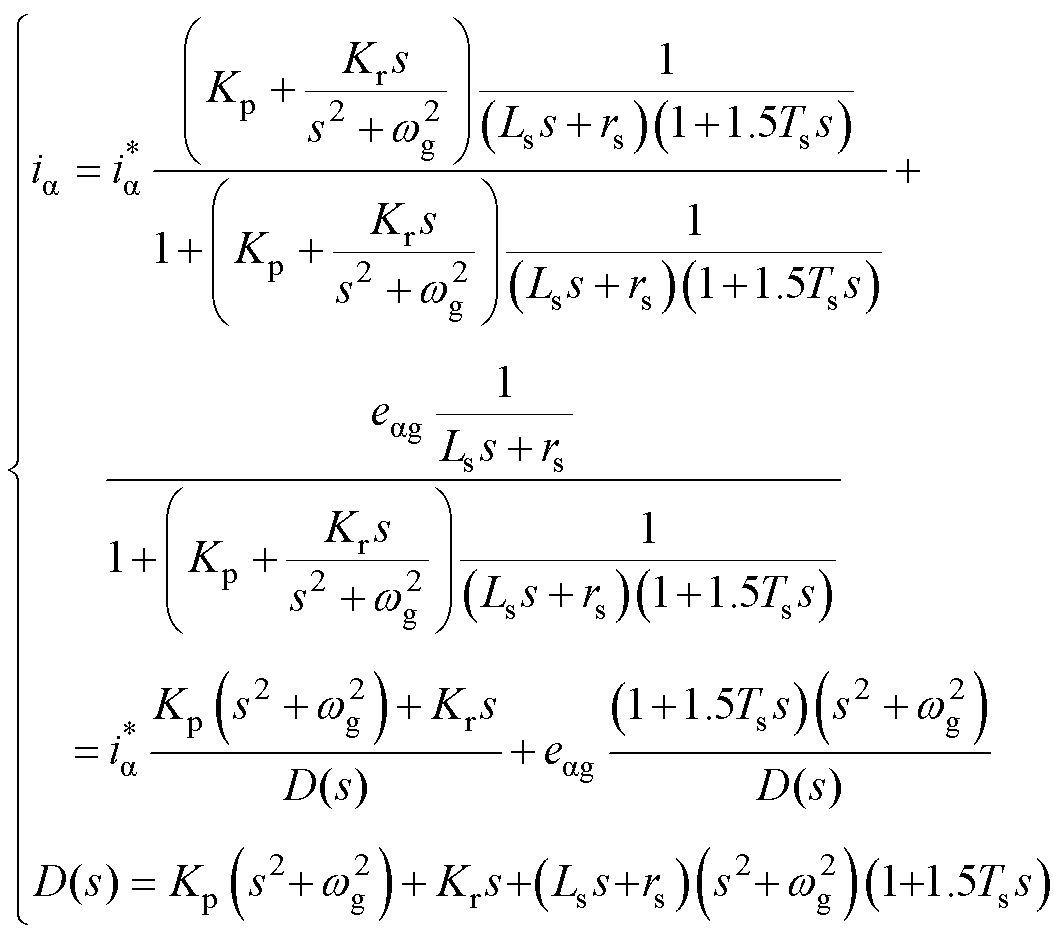（15）
式中，
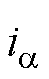和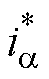
分别为a 轴电流的实际值和给定值；Kp和Kr分别为PR调节器的比例系数和谐振系数；Ts为控制周期。
采用PR调节器的电流环为四阶系统，为使电流环具有较好的动稳态性能，需要将主导极点配置为二阶，并使其阻尼比z =0.707。
根据开环传递函数的零极点分布，将Kp设为定值，作Kr由零变化到无穷时的参数根轨迹。图6给出了Kp分别为1、8、15时的电流环根轨迹，可见，当0＜Kp＜3.79时，系统的4个极点均离虚轴较近，且共轭复极点的阻尼比始终小于0.707；当3.79＜Kp＜9.57时，共轭复极点存在阻尼比大于0.707的区间，且其余两个极点距离虚轴较远；当Kp＞9.57时，系统存在两对共轭复极点，且距离虚轴较近的共轭复极点阻尼比z =0.707时，另一对共轭复极点距虚轴较远。
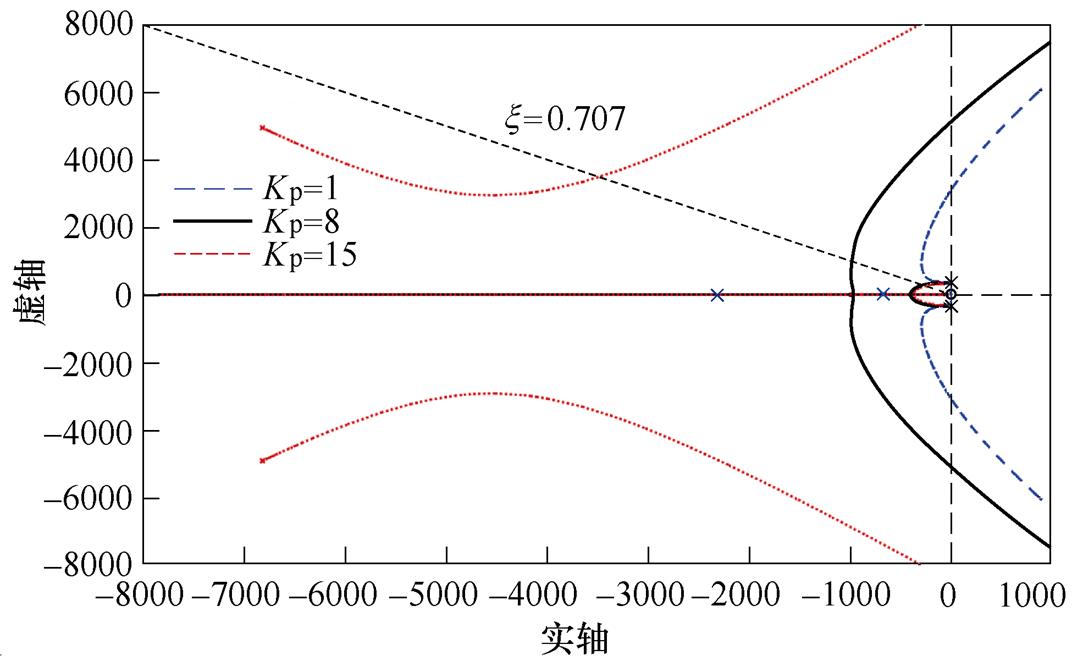
图6 不同Kp下电流环的闭环根轨迹
Fig.6 Root locus of the current loop under different Kp
综上所述，当Kp＞3.79时，可以选择合适的Kp，使电流环具有较好的动稳态性能，此外，Kp的取值还应该考虑系统的稳定裕度和带宽。因此，本系统中电流环PR调节器的参数选择为：Kp=8，Kr= 3 650。此时，电流环主导极点为-241±j241，阻尼比z =0.707，另外两个极点分别为-9 749和-3 394，离虚轴的距离远大于主导极点。
根据此控制参数绘制电流环的闭环Bode图，如图7所示，-3 dB处对应的频率为552 Hz，即电流环的带宽为552 Hz，而电网电流的频率为工频50 Hz，带宽为电流频率的10倍以上，可以满足系统快速性的要求。
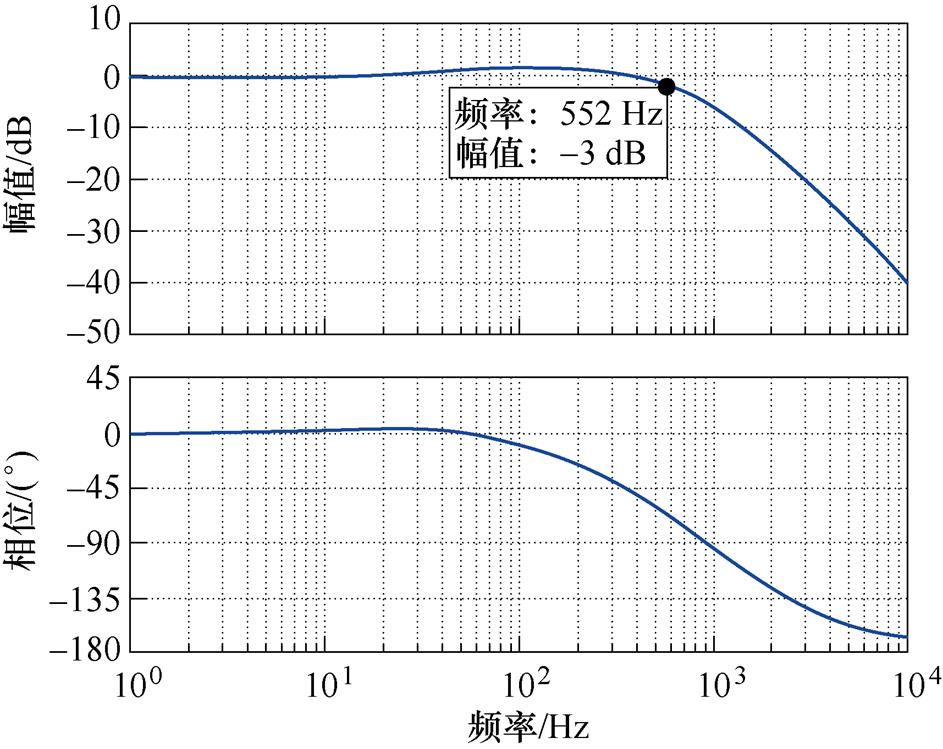
图7 电流环的闭环Bode图
Fig.7 Closed-loop Bode diagram of the current loop
图8为电压环的控制框图。由于电流内环的响应速度远高于电压外环，故可以将框图中的电流内环等效为一阶惯性环节，而直流侧负载RL和滤波电容Cbus的数值一般较大，电流环以及采样带来的延时相较于RLCbus的时间常数可以忽略，所以电压外环的闭环传递函数可以简化为
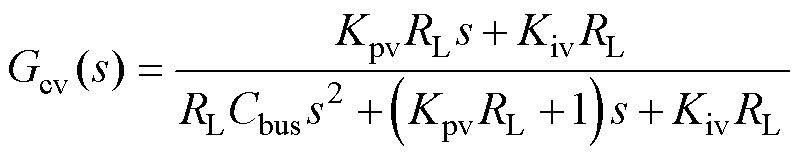（16）
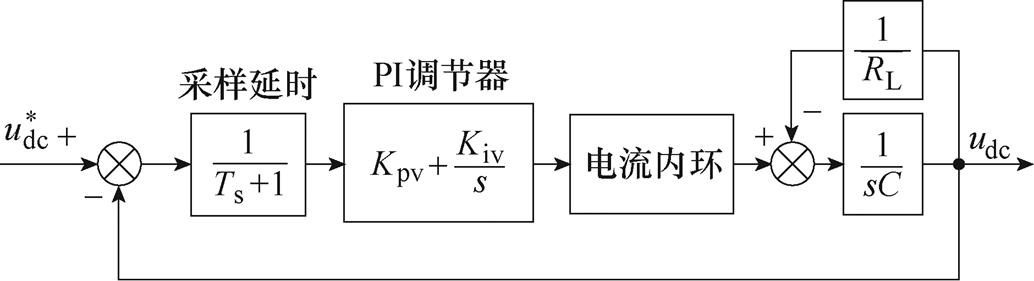
图8 电压环控制框图
Fig.8 Control block diagram of the voltage loop
由式（16）可以看出，本系统中电压环为典型二阶系统，与电流环类似，将电压环的阻尼比设置为0.707，带宽设置为电流环的1/50，即11 Hz，最终电压环的PI调节器参数设置为Kp=0.5，Ki=24。
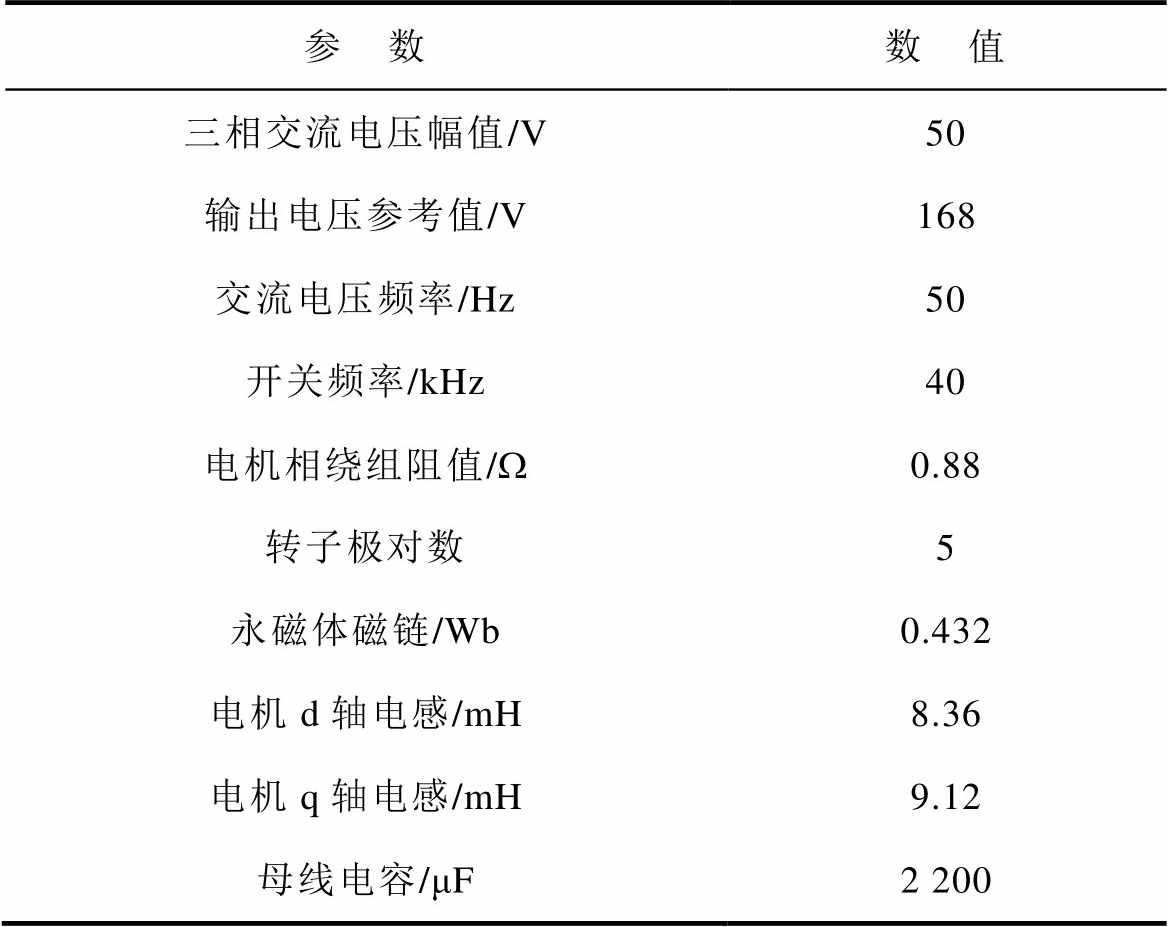
为验证本文所提集成充电系统及其控制方案的可行性，在仿真软件中基于数学模型搭建了双三相开绕组永磁同步电机本体以及QDPC方法的仿真模型。仿真系统参数与实验验证平台相一致，见表1。
表1 充电系统仿真参数
Tab.1 Simulation parameters of the charging system
参 数数 值 三相交流电压幅值/V50 输出电压参考值/V168 交流电压频率/Hz50 开关频率/kHz40 电机相绕组阻值/W0.88 转子极对数5 永磁体磁链/Wb0.432 电机d轴电感/mH8.36 电机q轴电感/mH9.12 母线电容/μF2 200
对于电池负载，双通道的充电电压的上限为电池组的最大充电电压Umax，下限为电池组的极限放电电压Umin。当等效负载RL1＞RL2时，通道1的充电电压udc1大于通道2的充电电压udc2，基于功率平衡的原则，应满足：RL1/RL2=udc1/udc2，udc1/udc2的最大值为Umax/Umin；RL1＜RL2时也是同理分析。故对于本文的充电系统，负载比应满足
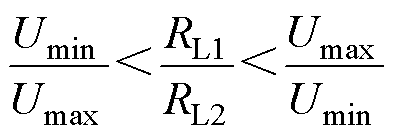（17）
本文仿真和实验中使用电阻作为负载，设通道1和通道2负载比为其负载电阻阻值之比，稳态工况下保持通道1的负载不变，改变通道2的负载，选取在通道1和通道2负载比k=1.5、k=1、k=0.75的条件下进行充电仿真，下标1、2分别表示通道1和通道2的仿真结果。三种工况下均保持通道1输出电压参考值为168 V。
图9为采用QDPC策略时在系统三种负载工况下的输入电压电流稳态仿真结果。电网输入的电流与电压相位相同，电流正弦度较高，A相电流总谐波畸变率（Total Harmonic Distortion, THD）值分别为3.62%、2.96%、3.36%，有效满足单位功率因数控制的要求，电流谐波中高次谐波的含量较低，基本为靠近基波频率的低次谐波，这也是在ab 坐标系下采用PR控制器带来的优点，针对固定频率交流信号的谐振控制相当于带通滤波器，可以有效地滤除控制上的高次谐波，但对于谐振带宽范围内频率相近的谐波会有一定的放大。
图10为采用QDPC策略在三种负载比工况下双通道的稳态功率、电压以及电机转矩仿真结果。在k=1时，双通道的输入有功功率、无功功率以及输出电压基本保持一致，电机转矩仅包含开关次的高频分量；而在k=1.5或0.75时，由于两通道负载的差异，k=1.5时，通道2直流电压的给定值为137.2 V，而k=0.75时，给定值为193.9 V，在相同的电压环控制参数下通道2的输出电压存在差异，导致输入有功功率与无功功率仍与通道1存在一定的差异。设通道1和通道2的有功功率分别为P1和P2，在k＞1时，P2＞P1，在k＜1时，P2＜P1，这也使得电机产生一定的转矩脉动，在三种工况下的转矩脉动峰峰值分别为1.26、0.42、1.03 N×m。
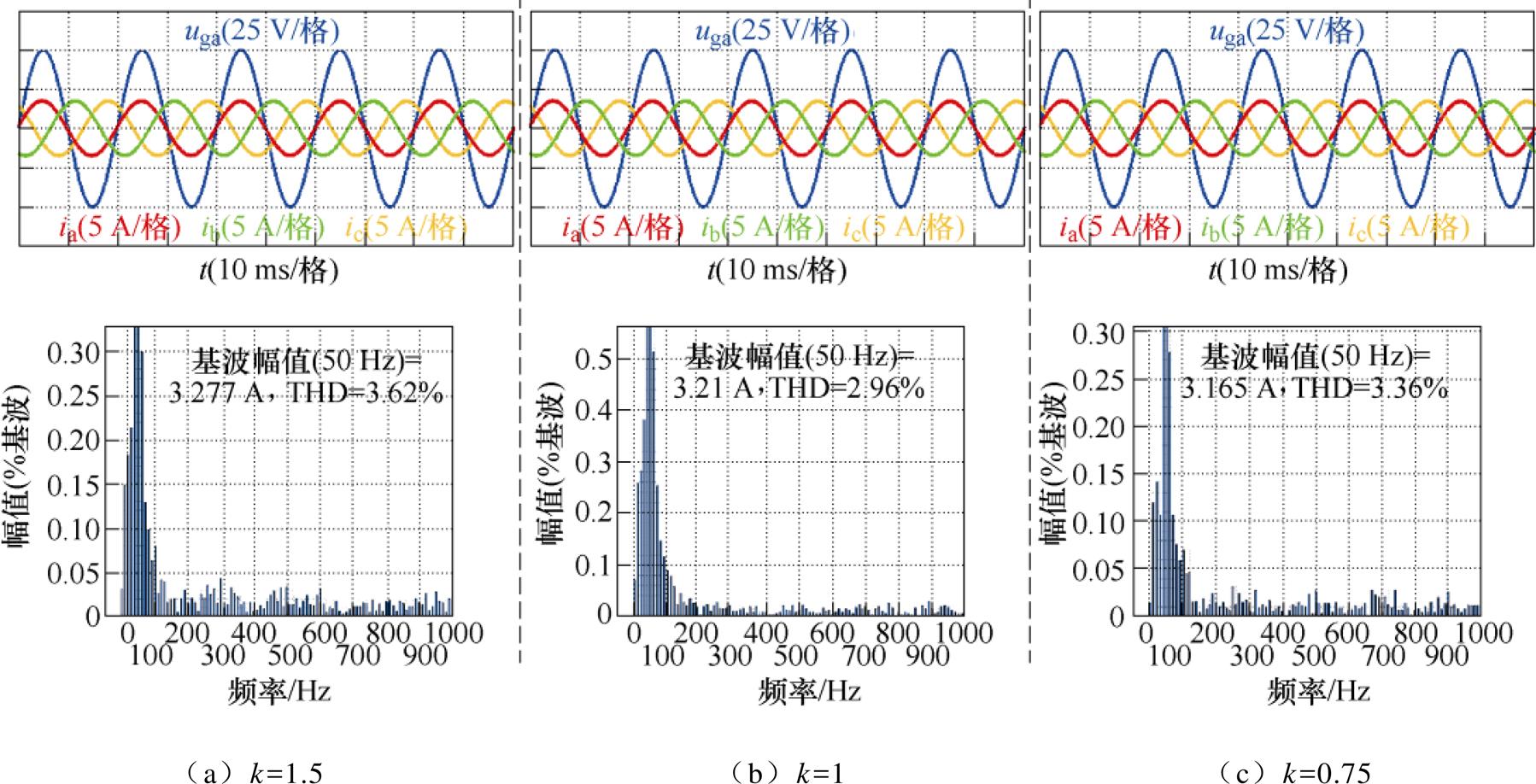
图9 稳态充电时输入电压电流的仿真波形
Fig.9 Simulation waveforms of input voltage and current during steady-state charging
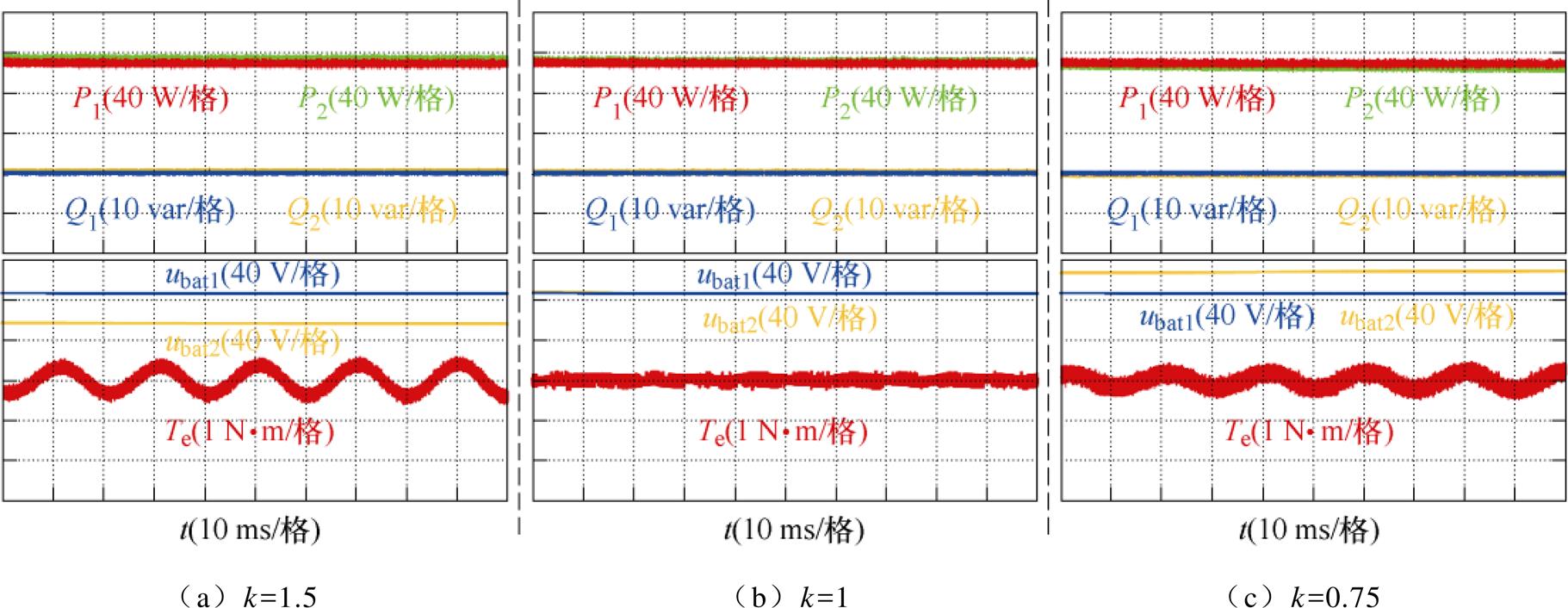
图10 稳态充电时功率、电压、电机转矩的仿真波形
Fig.10 Simulation waveforms of power, voltage, and motor torque during steady-state charging
为模拟电池充电过程中随着电量上升，端电压逐渐提高、等效负载逐渐减小的过程，动态充电仿真分为变负载与变电压两种动态工况。在变负载仿真中保持输出参考电压为168 V，通道1负载保持不变，改变通道2负载，使负载比k在1.5至0.75宽范围内变化，通过功率平衡自适应调节输出电压。
图11为QDPC策略下系统负载比k由1.5减小至0.75再变化至1.5的仿真结果。在变负载过程中，其通道1输出电压同样保持不变，通道2输出电压随负载比变化自适应调整，通道2有功功率与电压变化趋势相反，电机的转矩脉动也呈现出先减小后增大的波形，在双通道功率相等时达到最小值，整个变负载过程中，QDPC策略对功率与转矩的控制特性较好，平均有功功率的最大变化量DP为11.32 W，最大转矩脉动峰峰值为1.26 N·m。
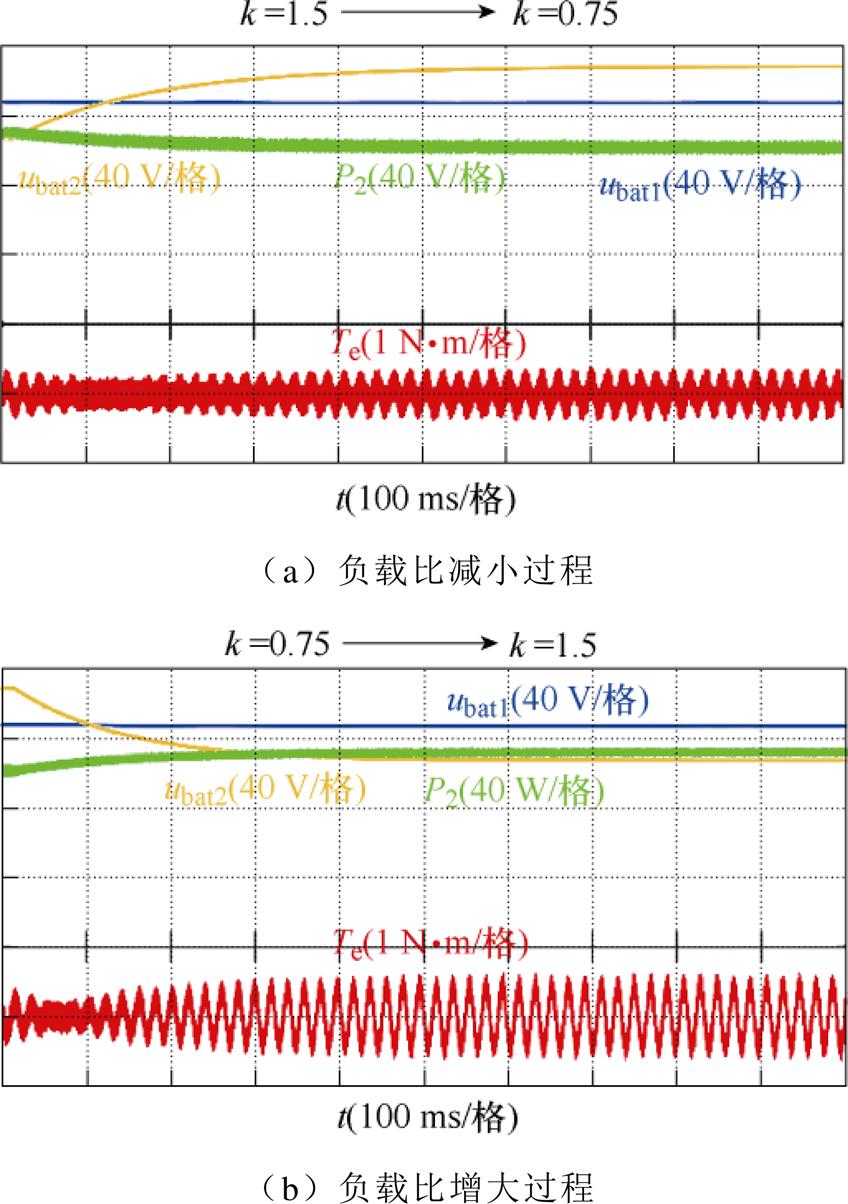
图11 充电系统变负载仿真结果
Fig.11 Simulation results of the charging system with variable load
在变电压仿真中，保持双通道负载相同，即负载比k保持为1，输入侧电压保持不变，输出给定参考电压在168～200 V变化，此时双通道输出功率均发生改变，模拟电池充电过程变电压工况。
图12为采用QDPC策略的变电压仿真结果，升压时双通道的输出电压在195 ms左右由168 V上升至200 V，动态过程中输入相电流幅值由3.2 A增至7.6 A，到达稳态后幅值降至5.1 A，升压过程平缓，未出现转矩尖峰，对转矩脉动的控制较好。降压时其双通道输出电压在约213 ms后下降至168 V并保持稳定，降压过程相电流也出现了一定的尖峰，在整个变电压仿真过程中QDPC策略对转矩脉动实现了很好的控制。
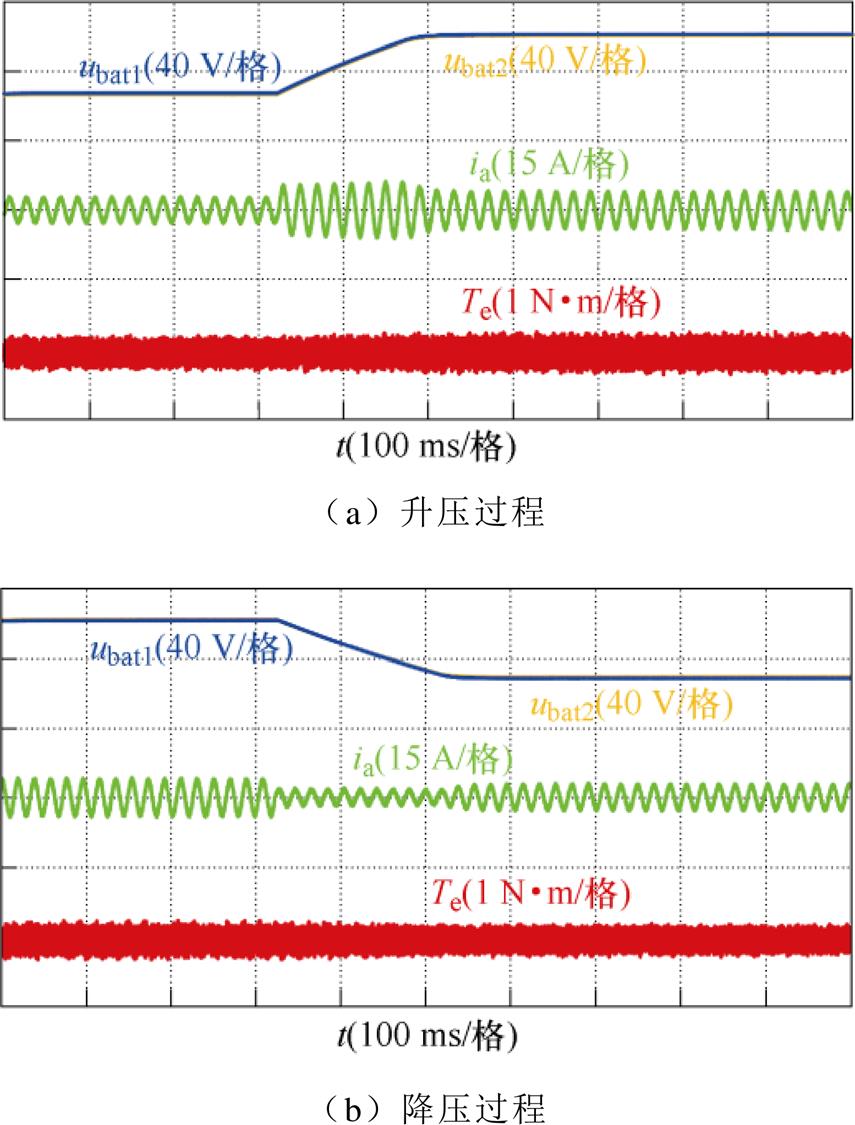
图12 充电系统变电压仿真结果
Fig.12 Simulation results of the charging system with variable voltage
在上述理论和仿真分析的基础上搭建了如图13所示的集成充电系统实验平台。开绕组PMSM与一台传统PMSM通过联轴器连接构成实验机组，在实验中通过短接PMSM的三相绕组实现对转子位置的机械固定，使用可变电子负载作为双通道的负载，电子负载运行在恒电阻模式下。
图13 集成充电系统实验平台
Fig.13 Experimental platform for the integrated charging system
稳态实验中保持通道1的负载不变，通过修改通道2的负载来实现双通道负载比k=1.5、k=1、k=0.75的三种工况。三种工况下均保持逆变器1输出电压参考值为168 V。
图14和图15为集成充电系统在三种负载工况下的稳态实验结果，其中图14为电机充电转矩、电网A相电压以及电网输入三相电流的实验波形。在三种工况下的A相电流THD值分别为4.23%、3.41%和3.76%，在不同负载比例的工况下输入电流与输入电压相位跟踪较好，在稳态时三相功率因数均大于0.98，满足单位功率因数控制的要求，但在三种负载比例下电机的充电转矩会有所变化，电机转矩脉动峰峰值分别为1.15 、0.46和0.95 N×m。
在图15中给出了双通道的有功功率、无功功率和输出电压的实验波形，通道1的有功功率和无功功率在功率平衡控制下基本保持不变，输出电压也保持在168 V的参考电压，但通道2随着负载比的减小，输出电压逐渐增大，有功功率也逐渐减小，无功功率基本维持不变，两个通道的输入功率存在不平衡，导致电机转矩脉动的变化。
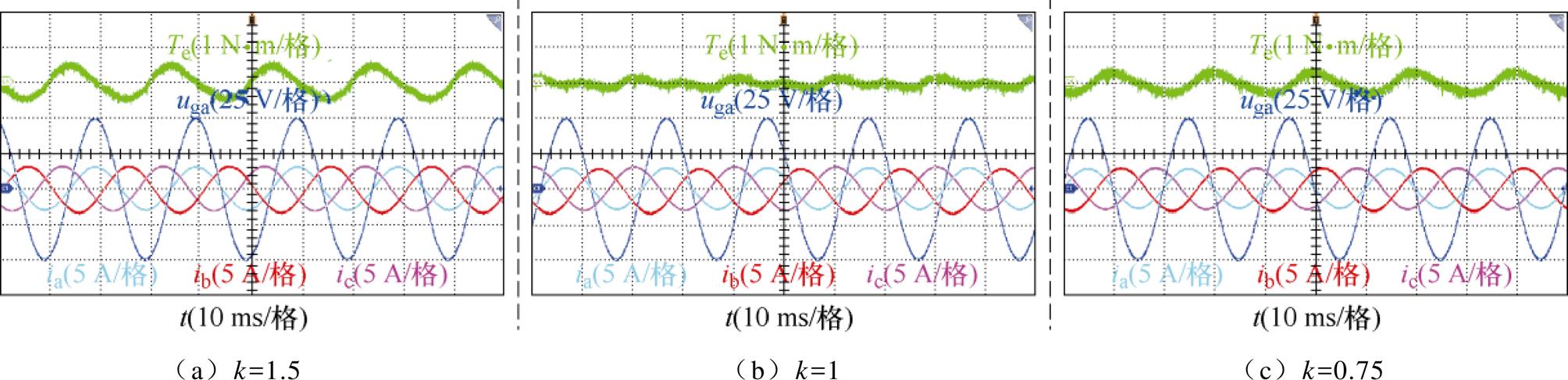
图14 稳态充电时电机转矩、输入电压、输入电流的实验波形
Fig.14 Experimental waveforms of motor torque, input voltage and input current during steady-state charging
图15 稳态充电时有功功率、无功功率、输出电压的实验波形
Fig.15 Experimental waveforms of active power, reactive power and output voltage during steady-state charging
与仿真类似，动态实验分为变负载与变电压两种动态工况。在变负载实验中保持通道1负载不变，修改通道2负载，使负载比k在0.75～1.5宽范围内变化，模拟电池在充电过程中电池电量上升、等效负载减小的情况。动态充电过程分别针对系统采用本文提出的QDPC策略和功率平衡基本控制策略，对实验结果进行对比。
图16为采用QDPC策略下负载比k由1.5下降至0.75再上升为1.5的实验结果。通过实验波形可以看到，在功率平衡的条件下，通道1的输出电压在负载变化的过程中基本保持不变，通道2的输出电压随负载比改变而实时调整。有功功率呈现与负载比相反变化的趋势，电机充电转矩脉动也表现为先减小后增大的现象。在整个变负载过程中，QDPC策略对有功功率的控制性能较好，平均有功功率的最大变化量DP=18.43 W，对应电机的最大转矩脉动峰峰值为1.21 N·m。
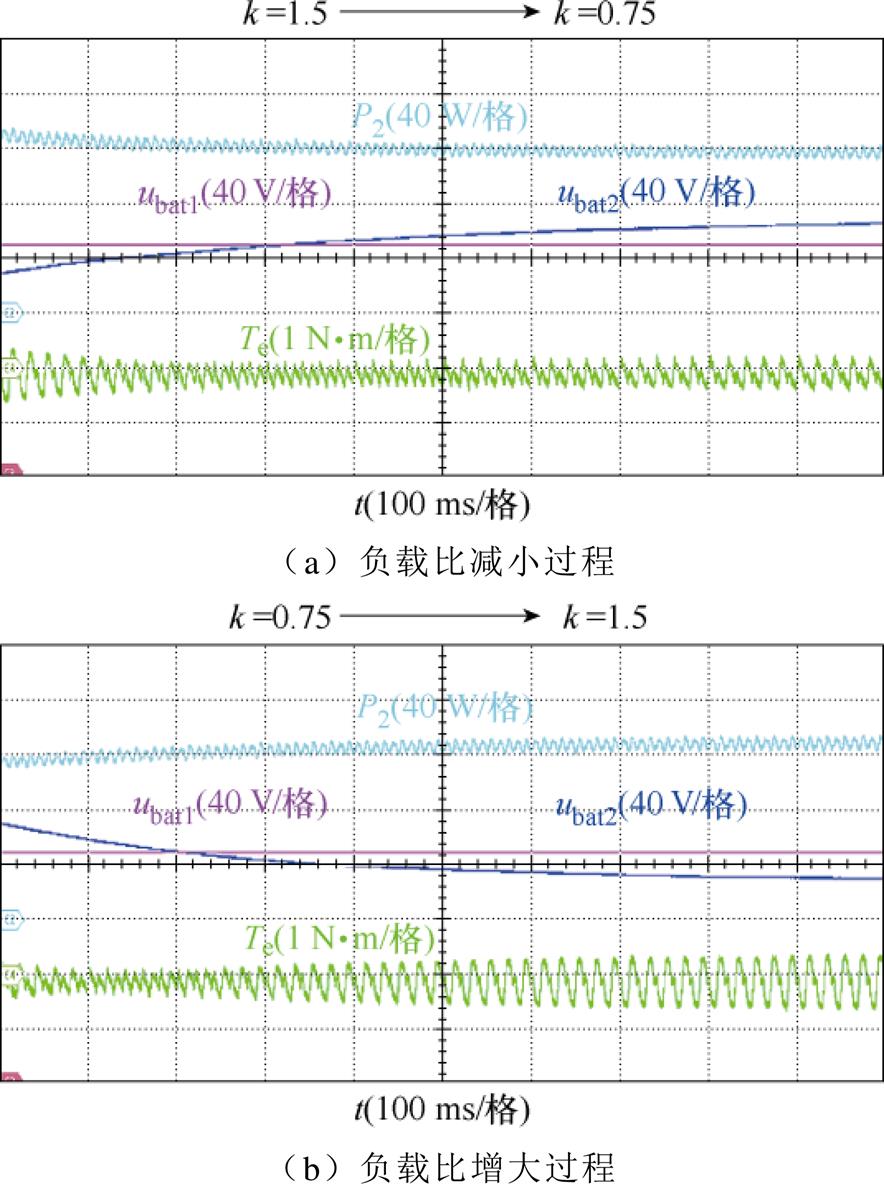
图16 采用QDPC策略的变负载实验结果
Fig.16 Experimental results of with the QDPC strategy under variable load condition
图17给出功率平衡基本控制策略下负载比k由1.5下降至0.75再上升至1.5的实验结果。从图中可以看出，整个实验过程中平均有功功率最大变化量达到32.75 W，最大转矩脉动峰峰值为1.76 N·m，相较于QDPC策略均高出许多。
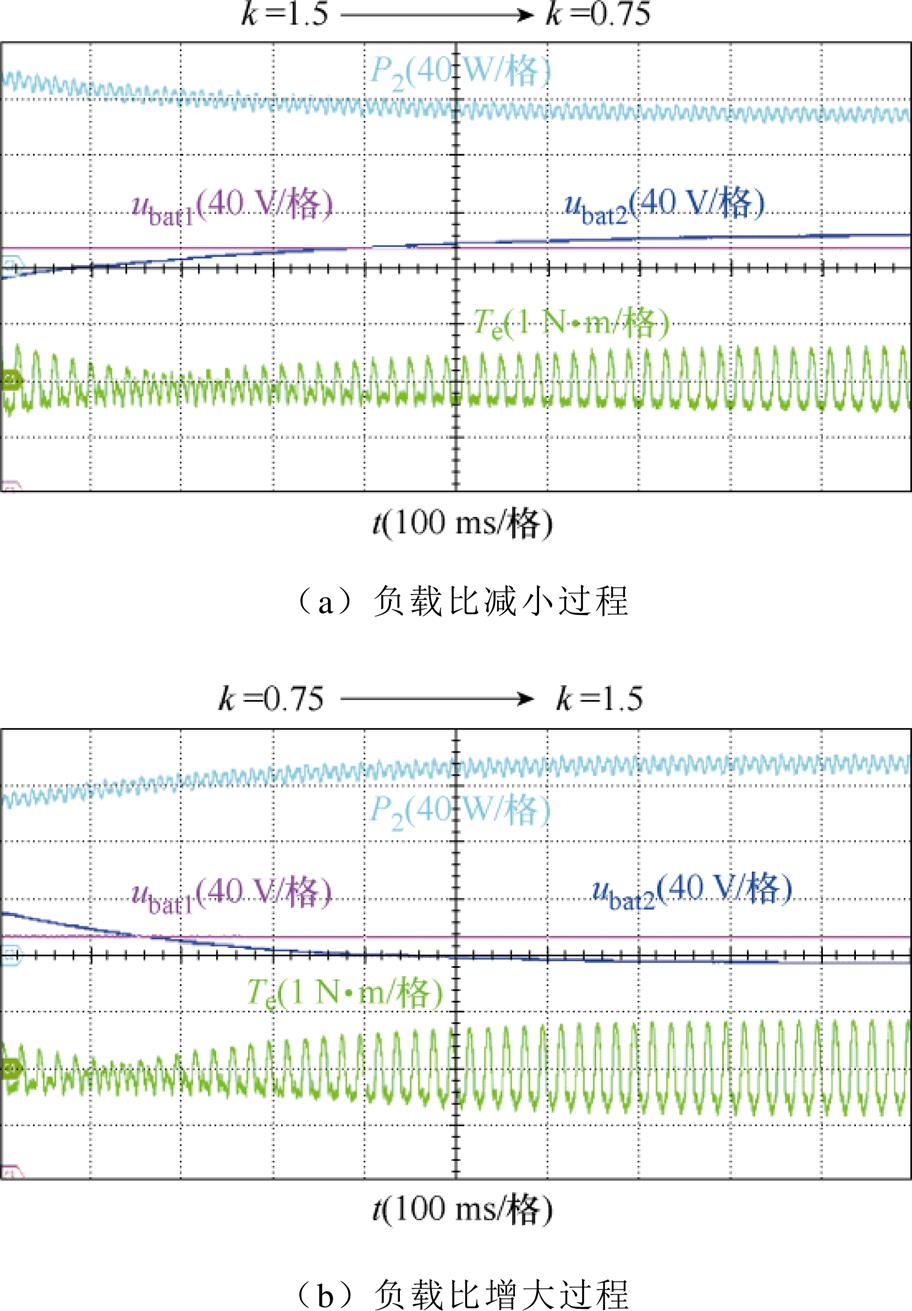
图17 采用功率平衡基本控制策略的变负载实验结果
Fig.17 Experimental results with the basic power balance control strategy under variable load condition
变电压实验中保持通道1与通道2负载不变，负载比k始终为1，输入侧电压保持不变，双通道参考输出电压在168～200 V变化，模拟电池充电过程中端电压的变化，此时双通道输出功率均改变，不再观测通道2有功功率，通道2修改为输入侧A相电流。
图18为采用QDPC策略下系统变电压动态实验结果，升压时双通道的输出电压约186 ms左右由168 V上升至200 V，输入相电流幅值由3.77 A增大至9.96 A，在电压稳定后减小为5.18 A，升压过程中充电转矩随电流幅值变化而改变，最终略微增大。与升压相对应，在系统给出降压指令后，双通道输出电压经193 ms左右下降至168 V，降压过程中转矩脉动与相电流均减小，待输出电压稳定后恢复。
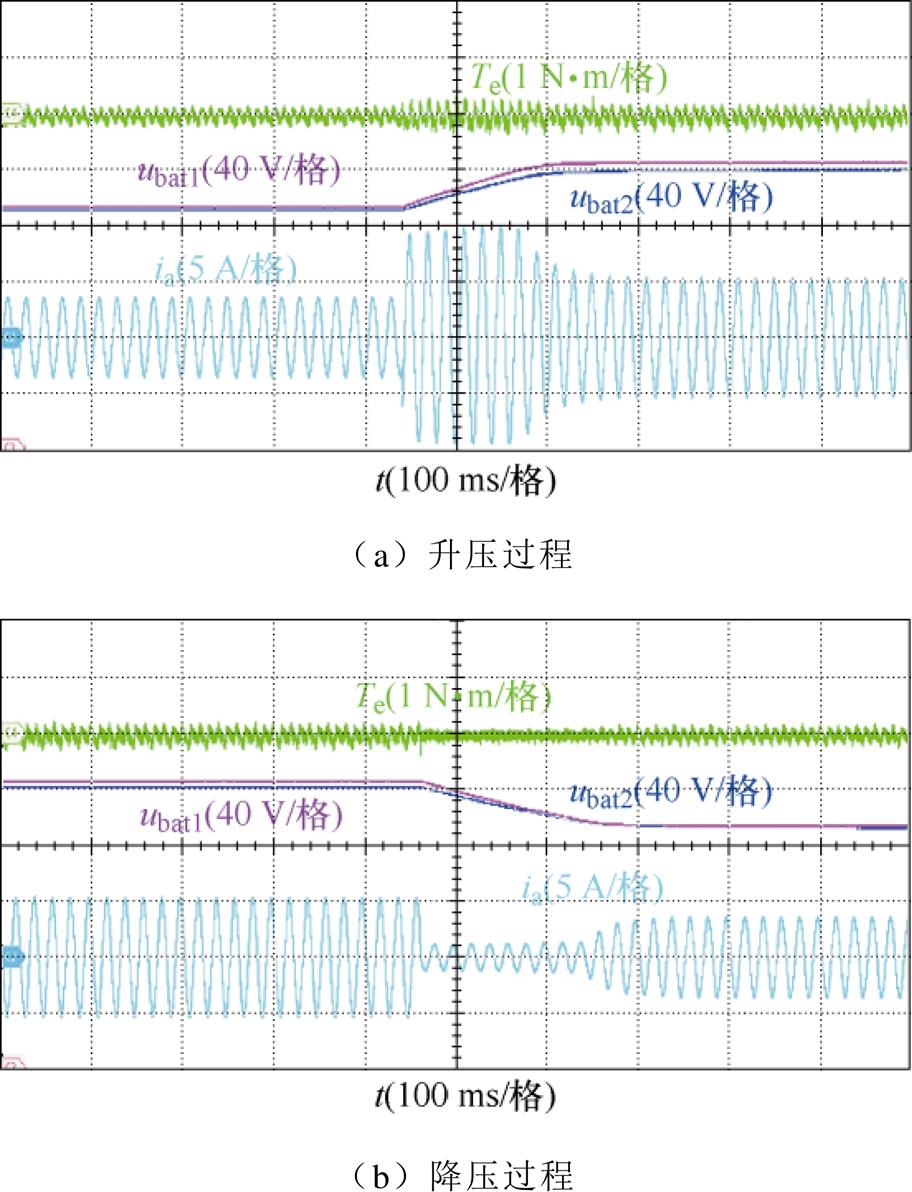
图18 采用QDPC策略的变电压实验结果
Fig.18 Experimental results of with the QDPC control strategy under variable voltage condition
图19为功率平衡基本控制策略下的变电压实验结果，双通道输出电压均在175 ms左右上升至200 V，但通道1输出电压略大于通道2，存在一定的不平衡，升压时输入侧相电流幅值从3.73 A增大至10.21 A，电压稳定在200 V附近后相电流幅值减小至5.30 A。升压过程中充电转矩随电流幅值变化而改变，最终略微增大。与升压相对应，降压时双通道输出电压经151 ms左右下降至168 V，降压过程中转矩脉动与相电流均减小，待输出电压稳定后恢复整个变压过程的充电转矩脉动变化趋势与QDPC策略相同，但其平均脉动峰峰值增加了约66%。
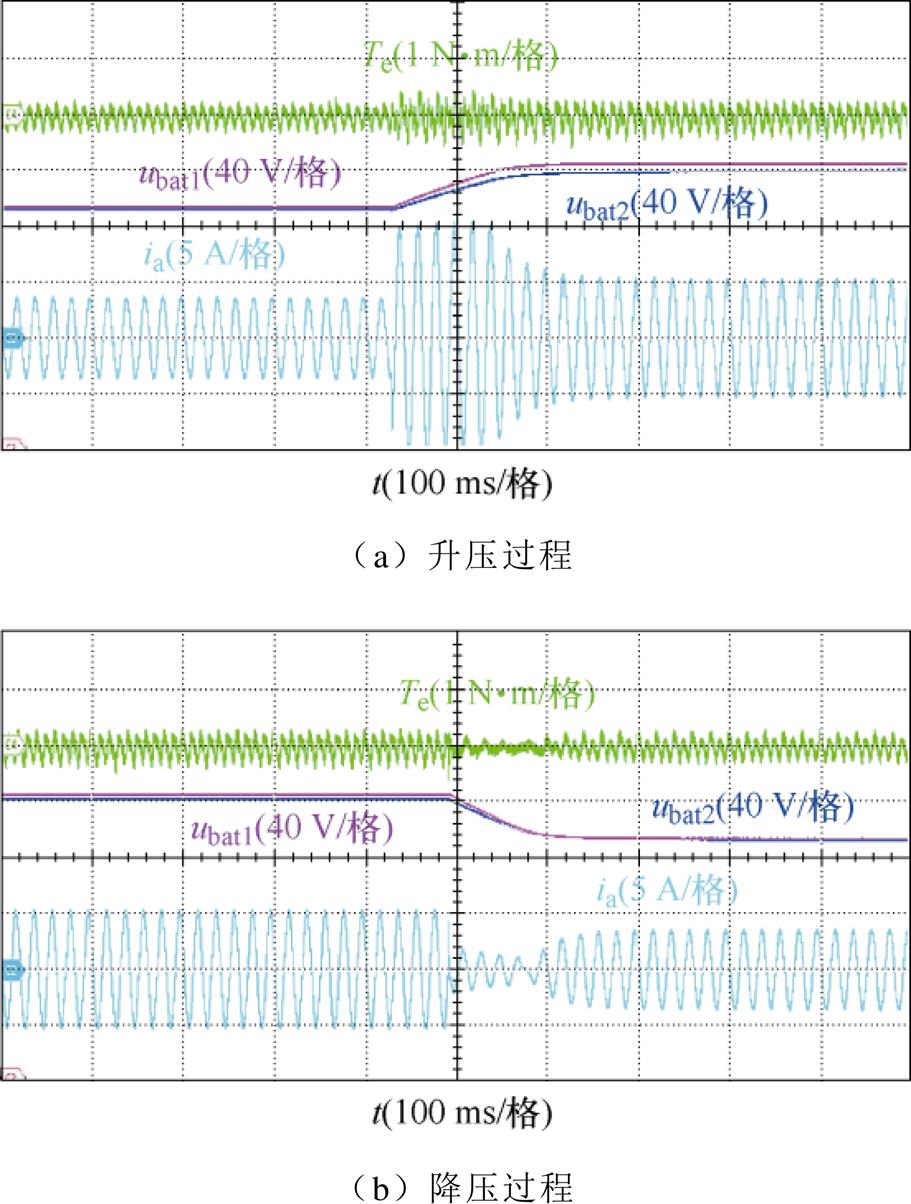
图19 采用功率平衡基本控制策略的变电压实验结果
Fig.19 Experimental results of with the basic power balance control strategy under variable voltage condition
如2.1节所述，由于采用功率平衡基本控制策略的系统电流环需要反复进行坐标变换，并对电压进行解耦，内环中的耦合项影响系统的动态性能，使系统在负载变化的过程中难以准确控制双通道的功率平衡，进一步验证了本文提出的QDPC策略可以使系统具有更好的动态性能。
本文提出一种基于开绕组永磁电机的电动汽车双电池集成充电系统，在双通道功率平衡的基本控制方案的基础上进一步设计了准直接功率控制策略，以实现三相充电时的网侧功率因数校正和充电过程中电机电磁转矩的抑制，完成了仿真模型的建立和实验平台的搭建。实验结果表明，该集成充电系统能够在双通道不同负载比稳态充电时较好地实现功率因数校正功能，不同负载比时无功功率基本保持不变，有功功率随负载比减小而减小，故稳态转矩大小有所变化，但总体不超过1.15 N×m。在变负载和变电压的动态过程中，QDPC策略能够较好地控制有功功率，有效抑制了动态过程中转矩脉动的变化，且由于QDPC策略在静止坐标系下实现，算法结构简单，具有较高的实用价值。
参考文献
[1] 王晓姬, 王道涵, 王柄东, 等. 电动汽车驱动/充电一体化系统及其控制策略综述[J]. 电工技术学报, 2023, 38(22): 5940-5958.
Wang Xiaoji, Wang Daohan, Wang Bingdong, et al. A review of drive-charging integrated systems and control strategies for electric vehicles[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(22): 5940-5958.
[2] Su Yiyan, Liang Deliang, Kou Peng. MPC-based torque distribution for planar motion of four-wheel independently driven electric vehicles: considering motor models and iron losses[J]. CES Transactions on Electrical Machines and Systems, 2023, 7(1): 45-53.
[3] Wang Yiwei, Wei Jiadan, Guo Lei, et al. The torque elimination control strategy for integrated charging system of electric vehicle with dual-battery[C]//2022 IEEE 5th International Electrical and Energy Con- ference (CIEEC), Nangjing, China, 2022: 1125-1130.
[4] 佟明昊, 程明, 许芷源, 等. 电动汽车用车载集成式充电系统若干关键技术问题及解决方案[J]. 电工技术学报, 2021, 36(24): 5125-5142.
Tong Minghao, Cheng Ming, Xu Zhiyuan, et al. Key issues and solutions of integrated on-board chargers for electric vehicles[J]. Transactions of China Elec- trotechnical Society, 2021, 36(24): 5125-5142.
[5] 王海鑫, 袁佳慧, 陈哲, 等. 智慧城市车-站-网一体化运行关键技术研究综述及展望[J]. 电工技术学报, 2022, 37(1): 112-132.
Wang Haixin, Yuan Jiahui, Chen Zhe, et al. Review and prospect of key techniques for vehicle-station- network integrated operation in smart city[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 112-132.
[6] 蒋栋, 高加楼, 李柏杨, 等. 电动汽车电机驱动系统零转矩充电复用技术简介[J]. 电工技术学报, 2022, 37(19): 4862-4871.
Jiang Dong, Gao Jialou, Li Boyang, et al. Introduction of integrated motor drive-charger technologies for electric vehicle with zero torque[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4862- 4871.
[7] Thimmesch D. An SCR inverter with an integral battery charger for electric vehicles[J]. IEEE Transa- ctions on Industry Applications, 1985, IA-21(4): 1023-1029.
[8] Shah V, Kumawat G, Payami S. Integrated power converter with G2V, V2G and direct V2V capabilities for SRM drive based electric vehicle appli- cation[C]//2022 Second International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 2022: 1-6.
[9] Hong J, Lee H, Nam K. Charging method for the secondary battery in dual-inverter drive systems for electric vehicles[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 909-921.
[10] Wang Sitan, Lehn P W. A three-phase electric vehicle charger integrated with dual-inverter drive[J]. IEEE Transactions on Transportation Electrification, 2022, 8(1): 82-97.
[11] Viana C, Pathmanathan M, Lehn P W. Dual-inverter- integrated three-phase EV charger based on split- phase machine[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 15175-15185.
[12] Viana C, Lehn P W. A drivetrain integrated DC fast charger with Buck and Boost functionality and simultaneous drive/charge capability[J]. IEEE Transa- ctions on Transportation Electrification, 2019, 5(4): 903-911.
[13] Viana C, Semsar S, Pathmanathan M, et al. Integrated transformerless EV charger with symmetrical modu- lation[J]. IEEE Transactions on Industrial Electronics, 2022, 69(12): 12506-12516.
[14] Viana C C D, Pathmanathan M, Lehn P W. Auxiliary power module elimination in EVs using dual inverter drivetrain[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12513-12524.
[15] Kougioulis I, Wheeler P, Ahmed M R. An integrated on-board charger and auxiliary power module for electric vehicles[C]//2022 IEEE Applied Power Elec- tronics Conference and Exposition (APEC), Houston, TX, USA, 2022: 1162-1169.
[16] Meher S R, Banerjee S, Vankayalapati B T, et al. A reconfigurable on-board power converter for electric vehicle with reduced switch count[J]. IEEE Transa- ctions on Vehicular Technology, 2020, 69(4): 3760- 3772.
[17] 何亦飞. 集成OBC-LDC功能的车载三端口变换器研究[D]. 哈尔滨: 哈尔滨工业大学, 2020.
HE Yifei. Research on integrated OBC-LDC multifunctional three-port converter for electric vehicles[D]. Harbin: Harbin Institute of Technology, 2020.
[18] 李山, 马雯, 郭强, 等. 非理想电网条件下PWM整流器优化预测功率控制[J]. 电工技术学报, 2022, 37(18): 4745-4756.
Li Shan, Ma Wen, Guo Qiang, et al. Optimal predictive power control of PWM rectifier under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4745-4756.
[19] 肖蕙蕙, 魏苏东, 郭强, 等. 优化开关序列的PWM整流器模型预测控制策略[J]. 电工技术学报, 2022, 37(14): 3665-3675, 3700.
Xiao Huihui, Wei Sudong, Guo Qiang, et al. Model predictive control strategy for PWM rectifier with optimized switching sequence[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3665- 3675, 3700.
Abstract Recently, electric vehicle (EVs) charging has mainly relied on DC charging piles, facing challenges such as large space occupation and high construction costs. Scholars have proposed several integrated battery chargers (IBC) based on reconfiguration relays or switches. The driving system with power converters and phase windings of the electric machine can be reused as the charger when the EV is in the standstill status. However, traditional structures of the phase windings require additional switches for reconfiguration topology. The specific open-winding PMSMs (OW-PMSMs) emerge as promising candidates for IBCs due to their high output power, fault tolerance, and other characteristics. This paper proposes an IBC topology and control strategy based on OW-PMSM with dual battery packs for EVs with new energy power. The three-phase grid power is connected to the neutral points of the three-phase windings of OW-PMSMs, enabling simultaneous charging of dual battery packs. When the residual power of dual battery packs is unequal, their equivalent loads are different, and the charging power are imbalanced. Accordingly, in the charging mode, imbalanced currents flowing in the phase windings of OW-PMSM can lead to the output torque, which has a side effect on the proposed IBC system. Therefore, a quasi-direct power control (QDPC) strategy is designed to suppress the torque pulsation.
Firstly, a mathematical model for the dual-battery integrated charging system based on OW-PMSM is carried out. The grid and motor coordinate systems are unified to simplify the electromagnetic torque expression during the charging mode. Then, to eliminate the output torque of the proposed system in the charging mode when the dual channel charging power is equal, a basic control strategy for the balanced charging power is designed. However, the phase-locked loop (PLL) and decoupling of the dq-axis voltage may consume a lot of computing resources and affect the dynamic performance of the proposed system. Thus, the QDPC strategy is derived and designed to obtain the ab-axis current control directly in the rotating coordinate system. The corresponding parameters in the dual-loop of current and voltage are also designed in detail.
Simulation and experimental results demonstrate that the output torque for the proposed IBC system with imbalanced equivalent loads can be eliminated. Steady-state experiments are conducted at load ratios of 0.75, 1, and 1.5, and dynamic experiments are conducted under variable loads and voltages. With the proposed QDPC strategy, the steady-state charging torque is less than 1.15 N·m under different load ratios, and the dynamic charging torque is less than 1.21 N·m under variable loads and voltages. Moreover, the dynamic charging torque of the proposed system is reduced by 60% compared to the basic control strategy. The proposed QDPC strategy for the proposed OW-PMSM improves dynamic performance.
keywords：Integrated dual-battery charging topology, open-winding permanent magnet synchronous motor, dual batteries, quasi-direct power control
DOI: 10.19595/j.cnki.1000-6753.tces.230426
中图分类号：TM351
江苏省自然科学基金（BK20191277）和科技创新2025重大专项（2022Z038）资助项目。
收稿日期 2023-04-06
改稿日期 2023-08-08
郭 磊 男，1999年生，硕士研究生，研究方向为电动汽车的车载集成充电。E-mail: threestones@nuaa.edu.cn
魏佳丹 男，1981年生，博士，教授，博士生导师，研究方向为航空电源系统、新能源发电、特种电机调速及数字控制。E-mail: weijiadan@nuaa.edu.cn（通信作者）
（编辑 崔文静）