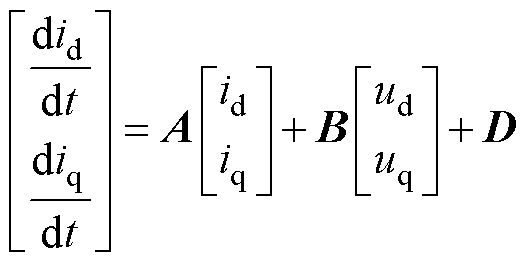 (1)
(1)
摘要 针对永磁同步电机(PMSM)采用无差拍预测电流控制(DPCC)时,性能易受电机参数失配及死区效应的影响,该文提出一种基于广义比例积分(GPI)观测器的鲁棒谐振预测电流控制(RRPCC)方法。首先,分析PMSM参数失配将产生非周期扰动及逆变器死区效应会导致周期扰动,进而建立带有非周期和周期性扰动的PMSM精确数学模型;其次,基于内模原理,将包含扰动频率的谐振多项式嵌入电流预测模型,可有效地抑制周期性扰动;最后,采用GPI观测器估计由参数失配引起的集总扰动,并通过前馈补偿消除非周期扰动。实验结果表明,该方法能提高系统面对非周期及周期性扰动时的鲁棒性。
关键词:参数失配 GPI观测器 周期扰动 鲁棒谐振预测电流控制
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)凭借其高效率、高功率密度以及优异的控制性能广泛应用于工业、航天等领域。但由于PMSM非线性、强耦合的特性,在要求动态响应快速精确及低输出转矩脉动的场合,采用线性控制方法很难在整个工作范围获得理想的动态性能。
模型预测控制具有处理非线性和多约束的能力,实现系统在目标函数下的最优控制[1]。模型预测控制包括有限集模型预测控制(Finite Control Set Model Predictive Control, FCS-MPC)和连续集模型预测控制(Continuous Control Set Model Predictive Control, CCS-MPC)[2]。FCS-MPC不需要调制器,是基于逆变器的离散开关特性,将使目标函数最小化的离散电压矢量作为输出。然而,有限的电压矢量使FCS-MPC具有电流纹波大、开关频率不固定等缺陷[3]。作为CCS-MPC的一种,无差拍预测电流控制(Deadbeat Predictive Current Control, DPCC)利用系统模型输出最优的连续电压矢量。因此,DPCC具有开关频率恒定、低电流纹波等优点[4]。但DPCC的性能依赖电机模型的准确性,参数失配会导致电流稳态误差,甚至使系统不稳定[5]。由于温度漂移、磁饱和等原因,参数不匹配是不可避免的。
解决DPCC参数不匹配问题的方法有:参数在线辨识法[6-7]、电流误差前馈补偿[8-9]及扰动观测器法[10-12]。其中,将预测控制与扰动观测器相结合,通过观测器估计参数变化导致的扰动并进行补偿的方法得到广泛关注。文献[10]基于模型参考自适应观测器校正稳态电流误差;文献[11]设计的组合观测器由两个滑模观测器并联而成,一个对DPCC的参数失配提供精确的扰动补偿,另一个用于估计负载突变扰动,进一步增强系统的鲁棒性;在文献[12]中,使用扩张状态观测器估计参数失配引起的集总扰动,得到零稳态误差的输出特性。
以上方法均要假定扰动恒定,然而PMSM参数是时变的[13]。广义比例积分(Generalized Pro- portional Integral, GPI)观测器是对扩张状态观测器的高阶化扩展,能准确地估计时变扰动,扩大了扰动观测的范围,从而得到更高的估计精度[14]。同时,由于逆变器死区效应使输出产生周期性电压扰动,导致相电流失真及转矩脉动,降低了PMSM系统的性能。因此,抑制由于死区效应引起的周期性扰动是必要的。主要方法可分为三类,即定子电流补偿法[15]、基于模型观测的方法[16]和电流谐波监测法[17]。
本文提出一种基于GPI观测器的鲁棒谐振预测电流控制(Robust Resonant Predictive Current Control, RRPCC)方法,能同时抑制参数失配产生的非周期性扰动及逆变器死区效应导致的周期性扰动。首先,分别分析由参数失配和死区效应引起的扰动,并建立带有非周期性和周期性扰动的PMSM精确数学模型;其次,设计包含扰动频率多项式的谐振预测电流控制器,消除由于死区效应导致的周期性扰动;然后,将电机电感、电阻及磁链参数失配导致的扰动视为集总扰动,并使用GPI观测器进行估计和补偿;最后,通过实验验证了所提方法的有效性。
本文以表贴式PMSM为研究对象,则在dq旋转坐标系下的PMSM电流方程可表示为
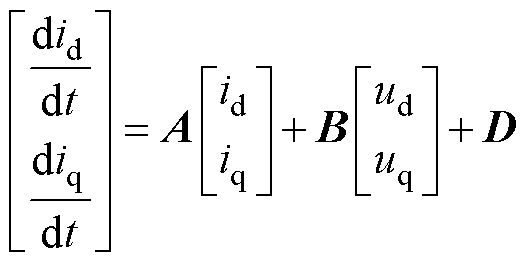 (1)
(1)
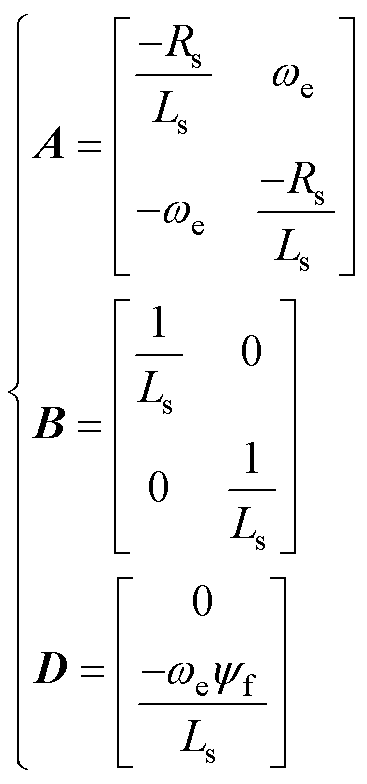
其中
 (2)
(2)
式中,ud、uq分别为d、q轴输出电压;id、iq分别为d、q轴电流;Ls为同步电感;we为电机电角频率;Rs为定子电阻;yf为永磁体磁链。
定义id(k)、iq(k)及ud(k)、uq(k)分别为k时刻的d、q轴电流和输出电压;idp(k+1)、iqp(k+1)分别为k+1时刻的d、q轴预测电流。设控制周期为Ts,采用欧拉法将式(1)进行离散化,可得到PMSM的离散数学模型,有
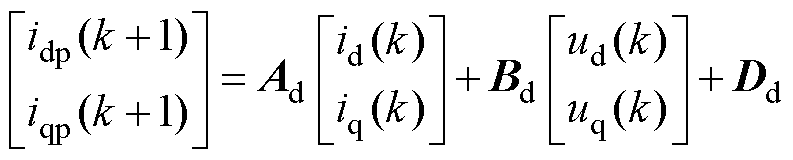 (3)
(3)
其中
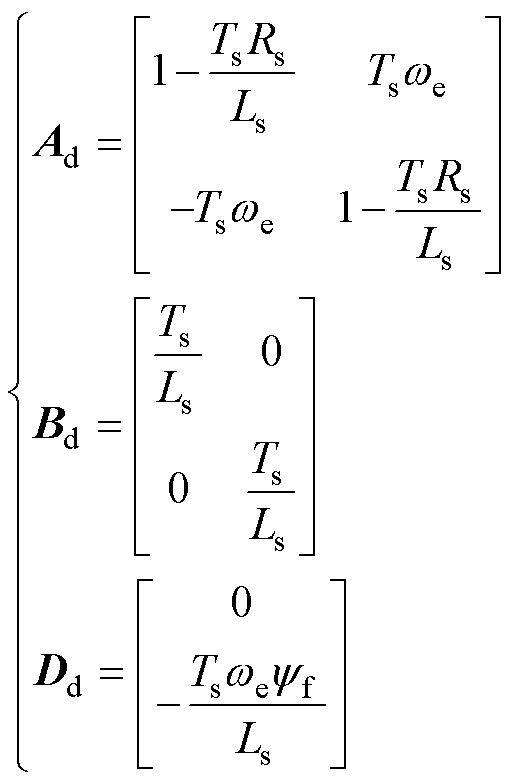 (4)
(4)
设idref(k+1)和iqref(k+1)为k+1时刻d、q轴电流参考值。由于DPCC输出是单步预测电流控制的无约束最优解,因此,根据式(3)可以得到k时刻DPCC输出的d、q轴电压ud(k)和uq(k)为
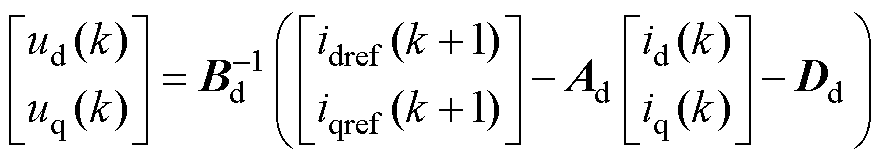 (5)
(5)
由于Ts足够小,因此Ad可近似为单位矩阵,则DPCC的输出电压可近似表示为
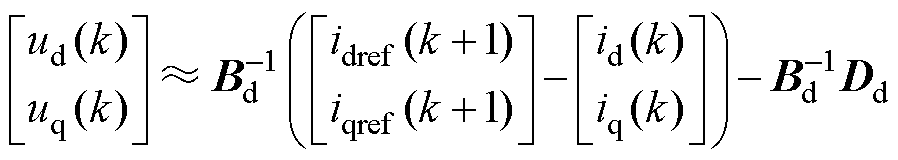 (6)
(6)
式(6)表明,DPCC等效为高增益控制加反电动势前馈补偿的控制方式,但由于缺少积分等扰动抑制措施,当受到参数失配等扰动时会产生电流稳态误差。
由于DPCC是基于PMSM数学模型的预测控制方法,这意味着DPCC的性能受PMSM电阻Rs、电感Ls及磁链yf的参数敏感性影响。
设DRs、DLs和Dyf为标称值与实际值的偏离误差,则参数失配时稳态电流预测误差iderr和iqerr分别为
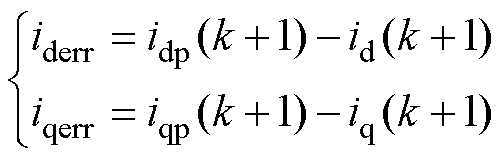 (7)
(7)
代入式(3),可得
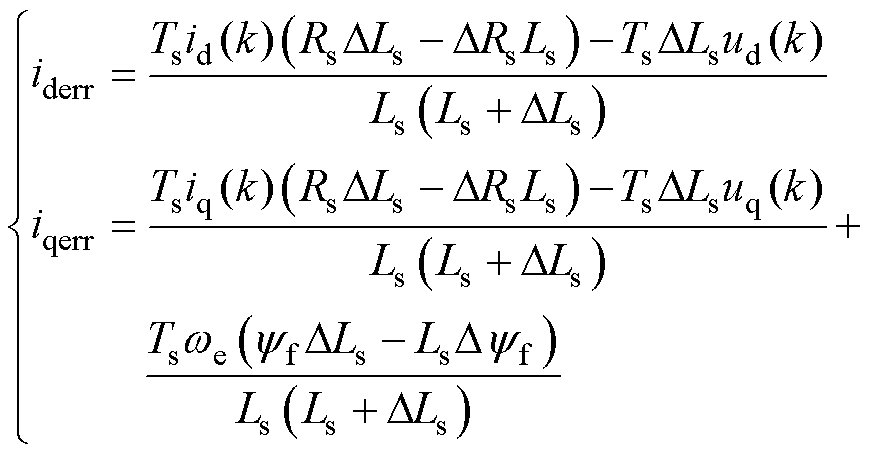 (8)
(8)
式(8)表明,PMSM参数不匹配将导致电流稳态误差,且3个参数对误差的影响程度不同,因此需要对每个参数的敏感性分别进行分析。
仅当电阻参数失配时,式(8)可简化为
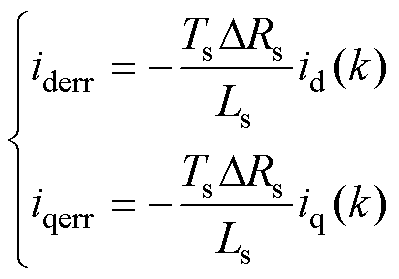 (9)
(9)
由于TsDRs远小于电感Ls,iderr和iqerr近似为零,因此电阻失配对电流误差影响很小,可忽略不计。
仅当磁链参数失配时,式(8)可表示为
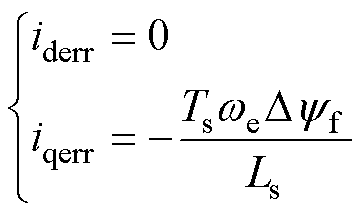 (10)
(10)
如式(10)所示,磁链参数失配对q轴电流误差的影响显著,且速度越高电流误差越大;而磁链参数失配对d轴电流没有影响。
当电感参数失配时,式(8)可对应为
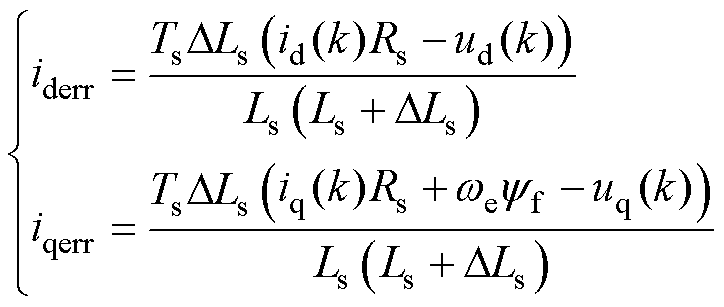 (11)
(11)
式(11)表明,电感参数失配使dq轴电流产生稳态误差,且误差与dq轴电压、电流及电机速度相耦合。电感参数失配对PMSM稳定运行有直接的影响,电感标称值偏离实际值时电流会发生振荡,当电感参数失配过大时,系统将失稳[18]。
设Dudf和Duqf分别为参数失配导致的d、q轴集总电压扰动,由式(1)可得Dudf和Duqf的表达式分别为
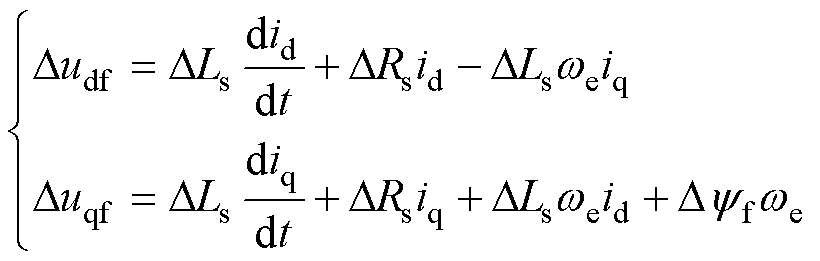 (12)
(12)
在逆变器中加入死区时间Tdt,避免了上下桥臂在开关瞬间出现直通而短路。在一个控制周期内,根据定子三相电流的方向不同,由死区时间引起的三相平均电压误差可表示[19]为
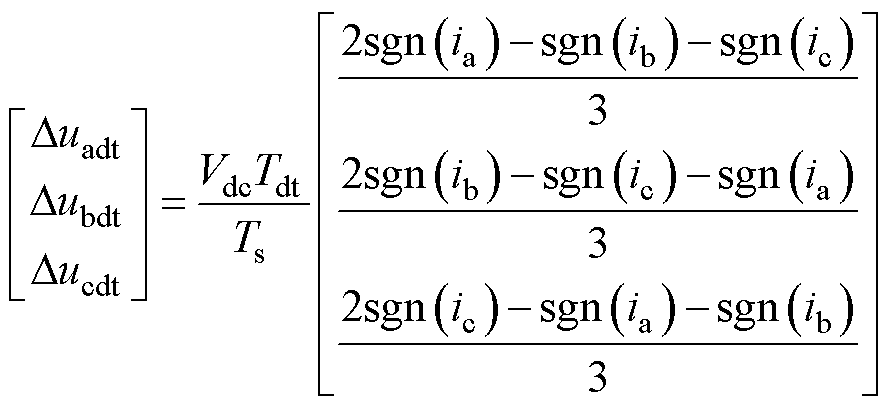 (13)
(13)
式中,Duadt、Dubdt、Ducdt为三相平均电压误差;ia、ib、ic为定子三相电流;Vdc为母线电压;sgn( · )为符号函数,定义为
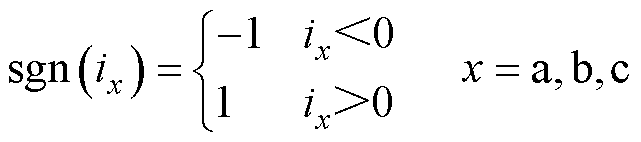 (14)
(14)
设P为dq旋转坐标系与三相静止坐标系间的变换矩阵,即
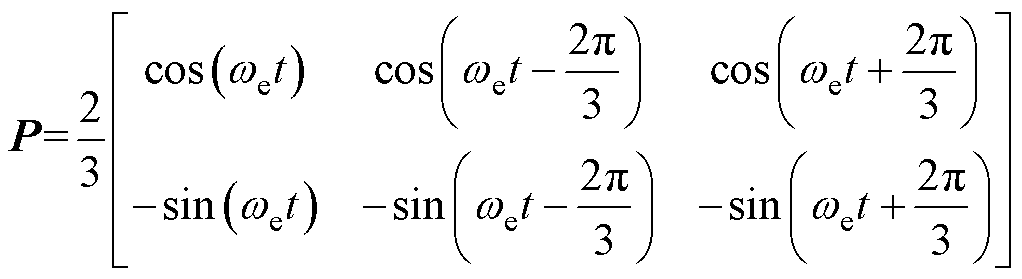 (15)
(15)
将三相平均电压误差从三相静止坐标系变换到dq旋转坐标系后,可得到dq旋转坐标系下的平均电压误差Duddt和Duqdt,有
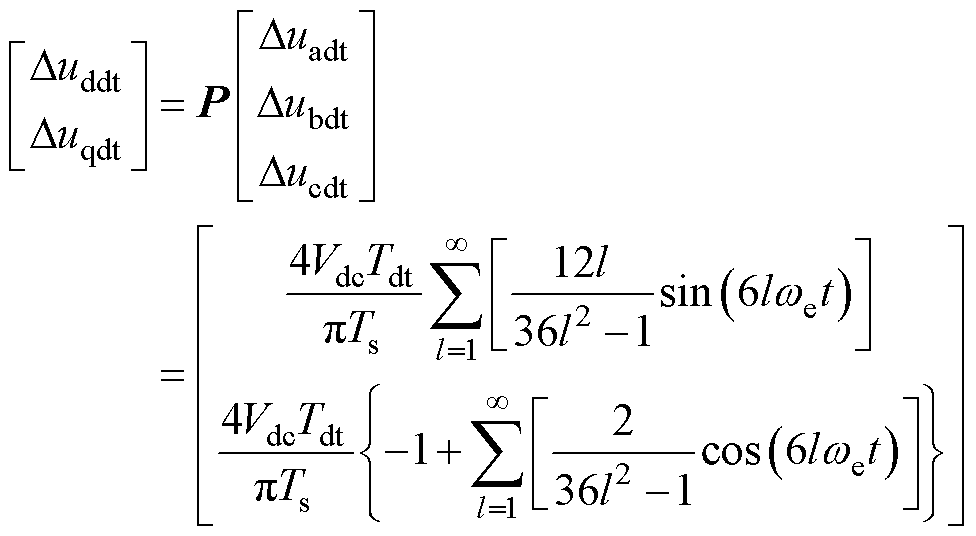 (16)
(16)
式(16)表明,逆变器死区效应使dq轴输出电压中含有与we相关、频率为6lwe(l=1, 2, 3,…)的周期性扰动电压Duddt和Duqdt,使PMSM的速度和dq轴电流出现周期性脉动。考虑到12次及以上的谐波对逆变器及电机的影响较小,因此,本文仅考虑幅值最高的6次谐波扰动。
考虑由参数失配导致的非周期扰动及死区效应引起的周期性扰动,根据式(1)、式(12)及式(16),得到带有这两种扰动的PMSM精确数学模型为
 (17)
(17)
定义电流i=[id iq]T;电压u1=[ud uq-weyf]T;非周期扰动Duf=[Dudf Duqf]T;周期扰动Dudt= [Duddt Duqdt]T。设y为状态方程的输出变量,则PMSM精确数学模型的状态方程可表示为
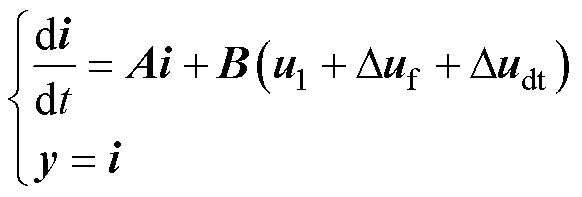 (18)
(18)
采用欧拉法将式(18)离散化,得到PMSM精确模型的离散状态方程,有
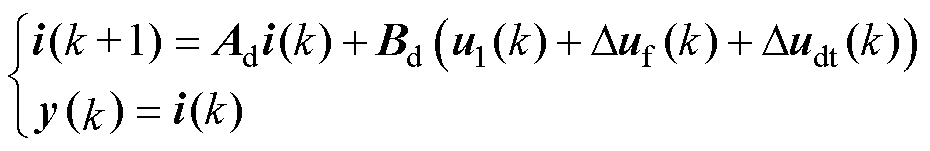 (19)
(19)
根据式(16),周期性扰动信号的频率为6we,则数字频率wd=6weTs。设正余弦信号x1(k)=sin(wdk)及x2(k)=cos(wdk),经过z变换后,正余弦信号的分母多项式为D(z),即
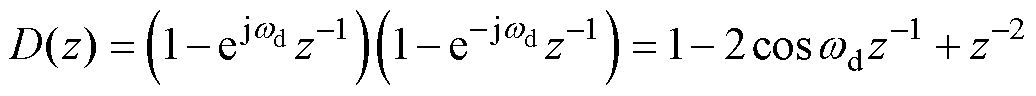 (20)
(20)
D(z)为包含wd的谐振多项式,式(21)证明,D(z)与同频率正余弦信号相乘后的输出dsin和dcos均为0。
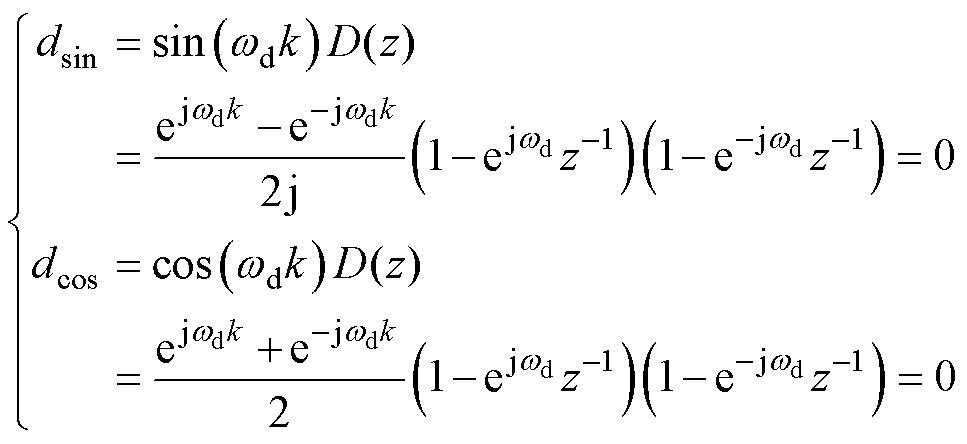 (21)
(21)
因此,在PMSM数学模型式(19)嵌入数字频率为wd的谐振内模多项式D(z)后,死区效应引起的dq轴正弦周期扰动Dudt将被抑制,即
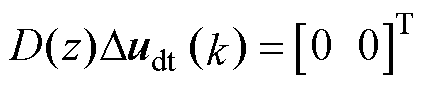 (22)
(22)
设电压向量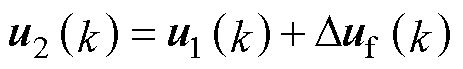 ,当在式(19)中嵌入谐振多项式D(z)后,PMSM数学模型变换为
,当在式(19)中嵌入谐振多项式D(z)后,PMSM数学模型变换为
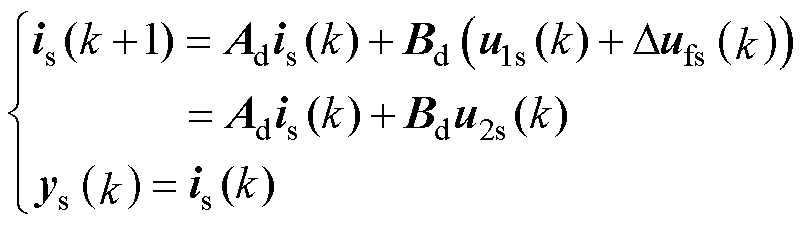 (23)
(23)
其中
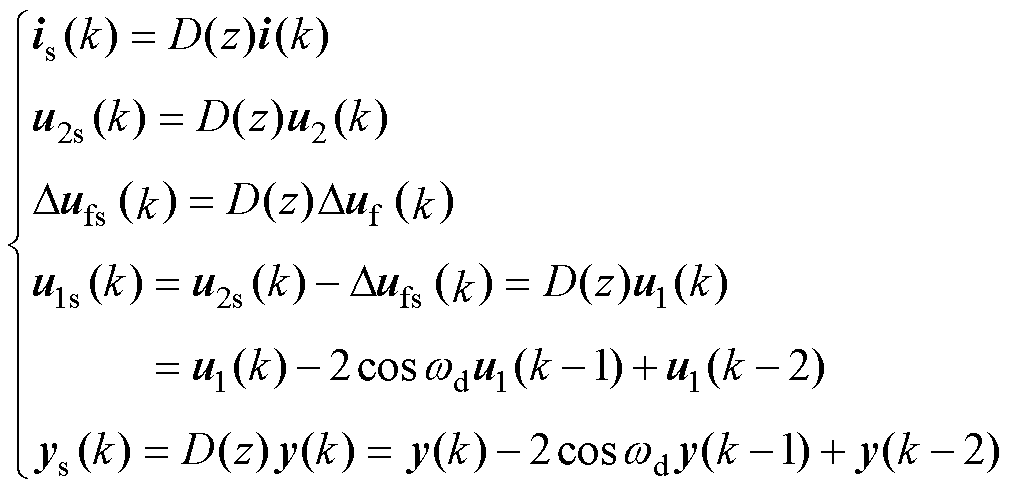 (24)
(24)
设r(k)为k时刻dq轴电流参考向量,e(k)为k时刻电流跟踪误差向量,定义增广状态变量x(k)为
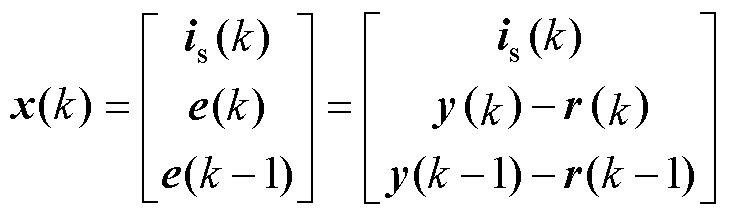 (25)
(25)
设ye(k)为输出变量,将x(k)代入式(19)及式(23),得到谐振预测电流控制器预测模型,有
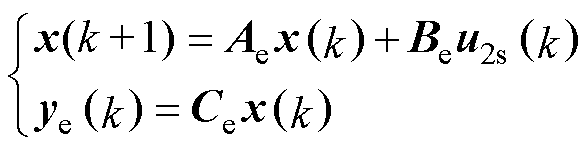 (26)
(26)
其中
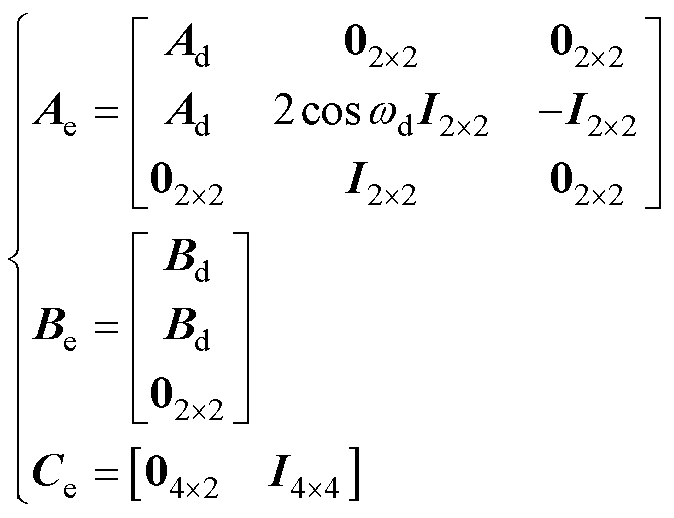 (27)
(27)
式中,矩阵0和I分别为零矩阵和单位矩阵。
为使实际电流跟随电流参考,选取目标函数J为
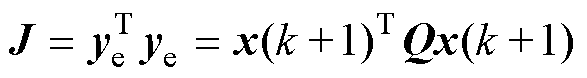 (28)
(28)
式中,Q为系数矩阵,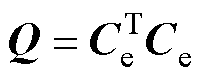 。将预测模型式(26)代入目标函数J,并令
。将预测模型式(26)代入目标函数J,并令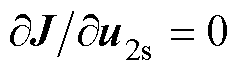 ,可求得单步谐振预测电流控制在无约束条件下的最优解
,可求得单步谐振预测电流控制在无约束条件下的最优解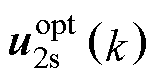 为
为
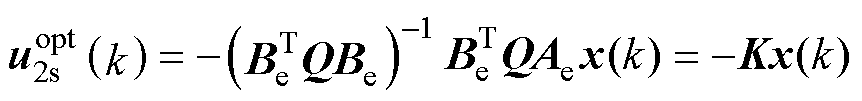 (29)
(29)
式中,K为增益矩阵。矩阵Ae和Be可由已知参数构成,因此K可通过离线计算得出,这样能降低谐振预测电流控制器的实时计算负担。
定义增益矩阵K=[K1K2K3],式(29)可变换为
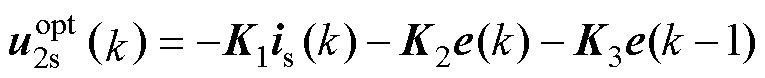 (30)
(30)
设Is(z)、U2s(z)、U2(z)和E(z)分别为is(k)、u2s(k)、u2(k)和e(k)的z变换变量,则U2s(z)可表示为
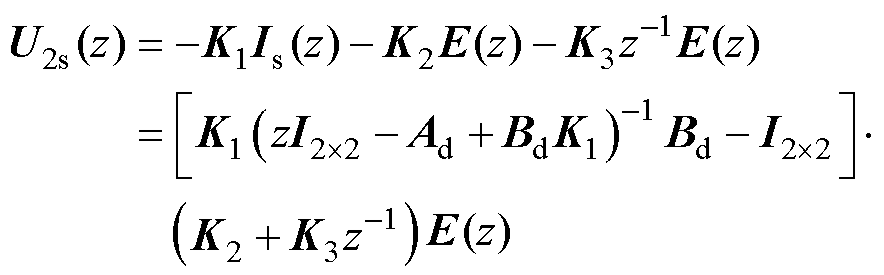 (31)
(31)
因此,谐振预测电流控制器的传递函数C(z)为
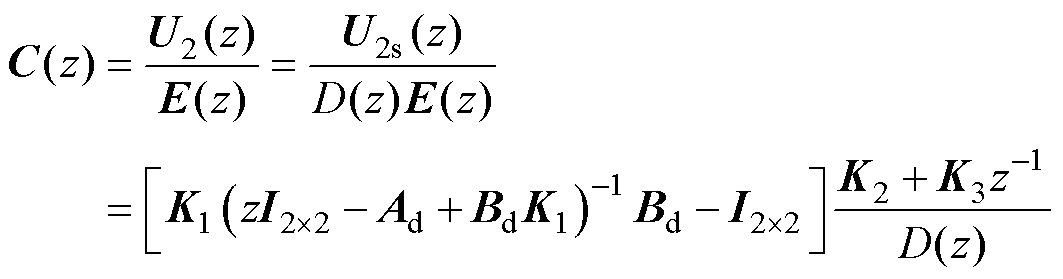 (32)
(32)
根据内模原理,控制器传递函数的分母包含扰动信号的多项式,可抑制相应扰动。式(32)中,C(z)的分母包含正余弦信号的分母多项式D(z),进一步证明谐振预测电流控制器能抑制死区效应导致的正余弦扰动。
根据式(19),可得PMSM的传递函数G(z)为
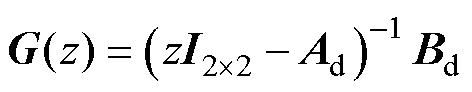 (33)
(33)
根据表1,当电机转速为800 r/min(we= 335 rad/s)时,可得出在频率6we(即2 010 rad/s)扰动信号作用下的闭环传递函数矩阵S(z)为
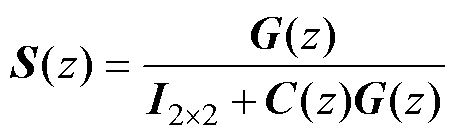 (34)
(34)
S(ejw)的幅频响应,如图1所示。图1尖峰处为谐振频率点,频率等于扰动频率2 010 rad/s,对应幅值为-210 dB和-226 dB,表明谐振预测电流控制器对该频率扰动有很强的衰减能力。
将参数失配集总扰动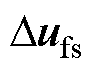 及其1阶导数
及其1阶导数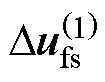 扩展为新的状态变量,则设计的GPI观测器为
扩展为新的状态变量,则设计的GPI观测器为
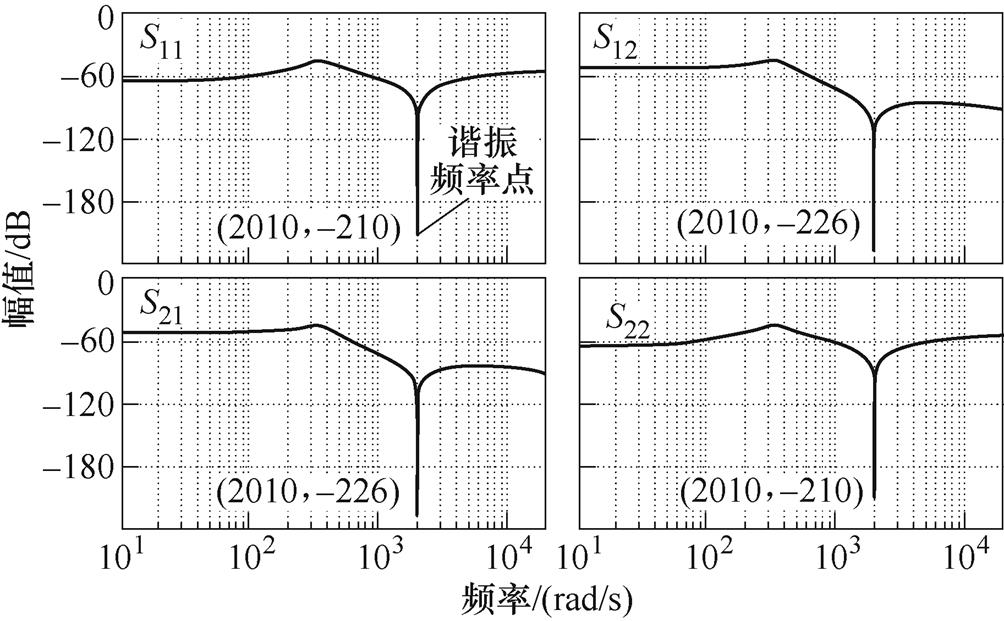
图1 S(ejw)的幅频响应
Fig.1 Amplitude response of S(ejw)
表1 PMSM参数标称值
Tab.1 Nominal parameters of PMSM

参 数数 值 额定功率/W950 额定转矩/(N×m)5.6 额定转速/(r/min)1 600 额定电流/A6.8 极对数4 定子电阻/W0.97 定子电感/mH13 永磁体磁链/Wb0.185
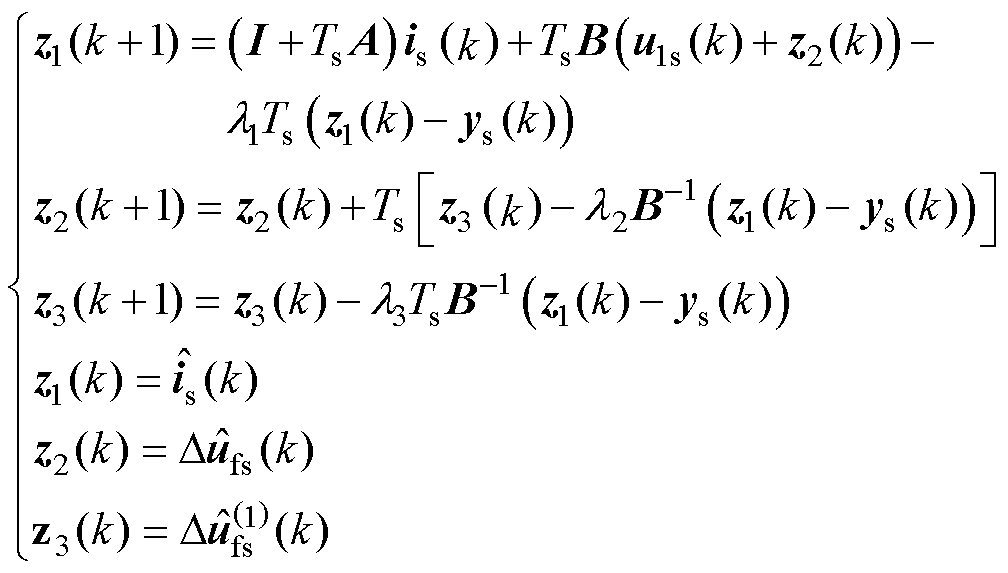 (35)
(35)
式中,l1、l2和l3为观测器增益。
通过GPI观测器可得到参数失配集总扰动及其1阶导数的估计值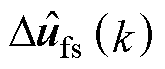 和
和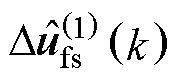 ,以及下一时刻电流is的估计值
,以及下一时刻电流is的估计值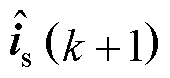 。
。
定义e1(k)、e2(k)和e3(k)分别为k时刻电流is的估计误差、集总扰动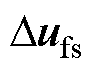 (k)的估计误差和集总扰动一阶导数
(k)的估计误差和集总扰动一阶导数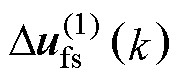 的估计误差,即
的估计误差,即
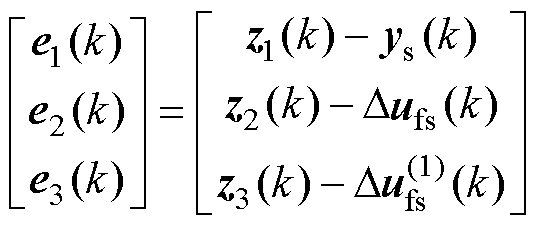 (36)
(36)
设误差矩阵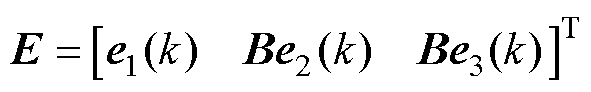 ,则
,则
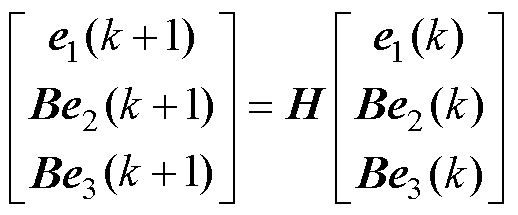 (37)
(37)
其中
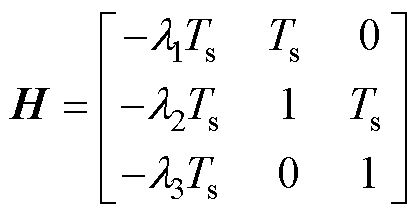 (38)
(38)
观测器的稳定性取决于H的特征根,当其都在z平面的单位圆内时,GPI观测器将渐近稳定,误差矩阵E将收敛至零。
矩阵H的特征多项式D(z)可表示为
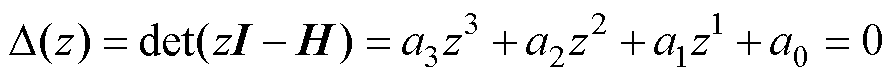 (39)
(39)
其中
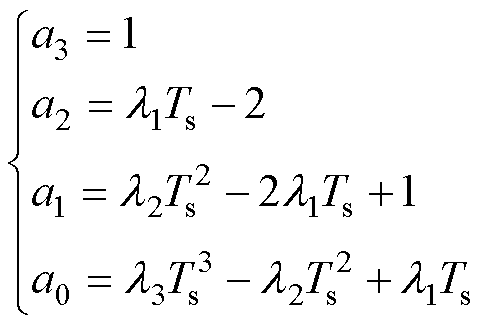 (40)
(40)
根据Jury稳定性判据,当满足不等式(41)时,特征根均在单位圆内,可保证GPI观测器的稳定性。
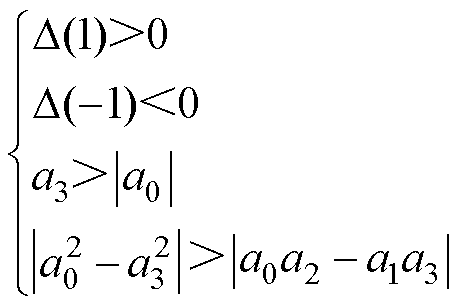 (41)
(41)
在本文中,取Ts=50 ms,l1=300,l2=30 000,l3=104,使式(41)中的不等式全部满足。因此,所设计的GPI观测器是稳定的。
设输出电压u=[ud uq]T,反电动势ue=[0 weyf]T,则输出电压u(k)=u1(k)+ue(k)。根据式(24)和式(30),可求得RRPCC在k时刻的dq轴输出电压u为
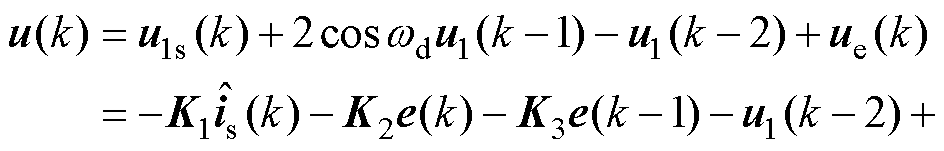
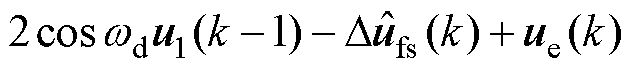 (42)
(42)
对比式(6)的常规DPCC,式(42)所示的RRPCC输出包括:k时刻的电流估计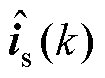 和电流误差e(k)的反馈,以及扰动估计
和电流误差e(k)的反馈,以及扰动估计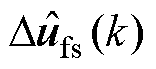 和反电动势ue(k)的前馈补偿;k-1时刻的电流误差e(k-1)和输出电压u1(k-1)的反馈;k-2时刻输出电压u1(k-2)的反馈。
和反电动势ue(k)的前馈补偿;k-1时刻的电流误差e(k-1)和输出电压u1(k-1)的反馈;k-2时刻输出电压u1(k-2)的反馈。
因此,RRPCC具有很好的电流跟踪能力,并且在面对不同扰动时均具有非常高的鲁棒性。
根据上述分析,基于GPI观测器的RRPCC电机控制系统框图如图2所示。
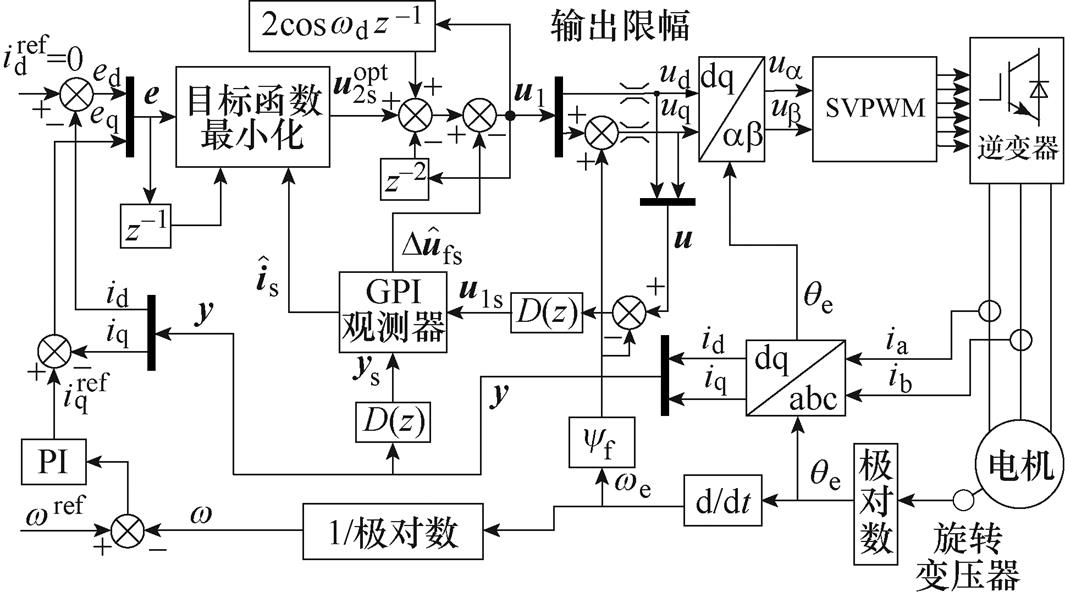
图2 基于GPI观测器的RRPCC系统框图
Fig.2 Block diagram of RRPCC system based on GPI observer
实现基于GPI观测器的RRPCC步骤如下:
(1)首先,根据k时刻电流值y(k)、电流参考值r(k)、电流估计值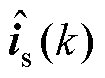 及k-1时刻电流误差e(k-1),计算状态变量x(k)。
及k-1时刻电流误差e(k-1),计算状态变量x(k)。
(2)最优化目标函数J,求出 及增益K。
及增益K。
(3)根据式(42)计算dq轴输出电压u,并对输出电压进行限幅,再经过Park逆变换及SVPWM转换为6路开关信号,最后送入三相桥逆变器。
(4)根据式(24)更新ys(k)和u1s(k),使用GPI观测器式(35),更新下一时刻参数失配集总扰动的估计值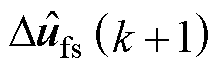 及电流估计值
及电流估计值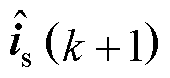 。
。
为验证本文所提方法的有效性,搭建了PMSM实验测试平台,如图3所示。测试平台主要包括PMSM、开发主机及Links-BOX实时仿真机、伺服驱动器、负载电机、转矩测量仪等。

图3 PMSM实验平台
Fig.3 PMSM experiment platform
死区效应会导致频率为6we的周期性扰动,分别采用常规DPCC和提出的RRPCC,比较dq轴电流及速度反馈的输出波形。在测试中,PMSM在额定负载条件下以800 r/min(即we=335 rad/s)的转速稳态运行。对比测试结果如图4~图6所示。
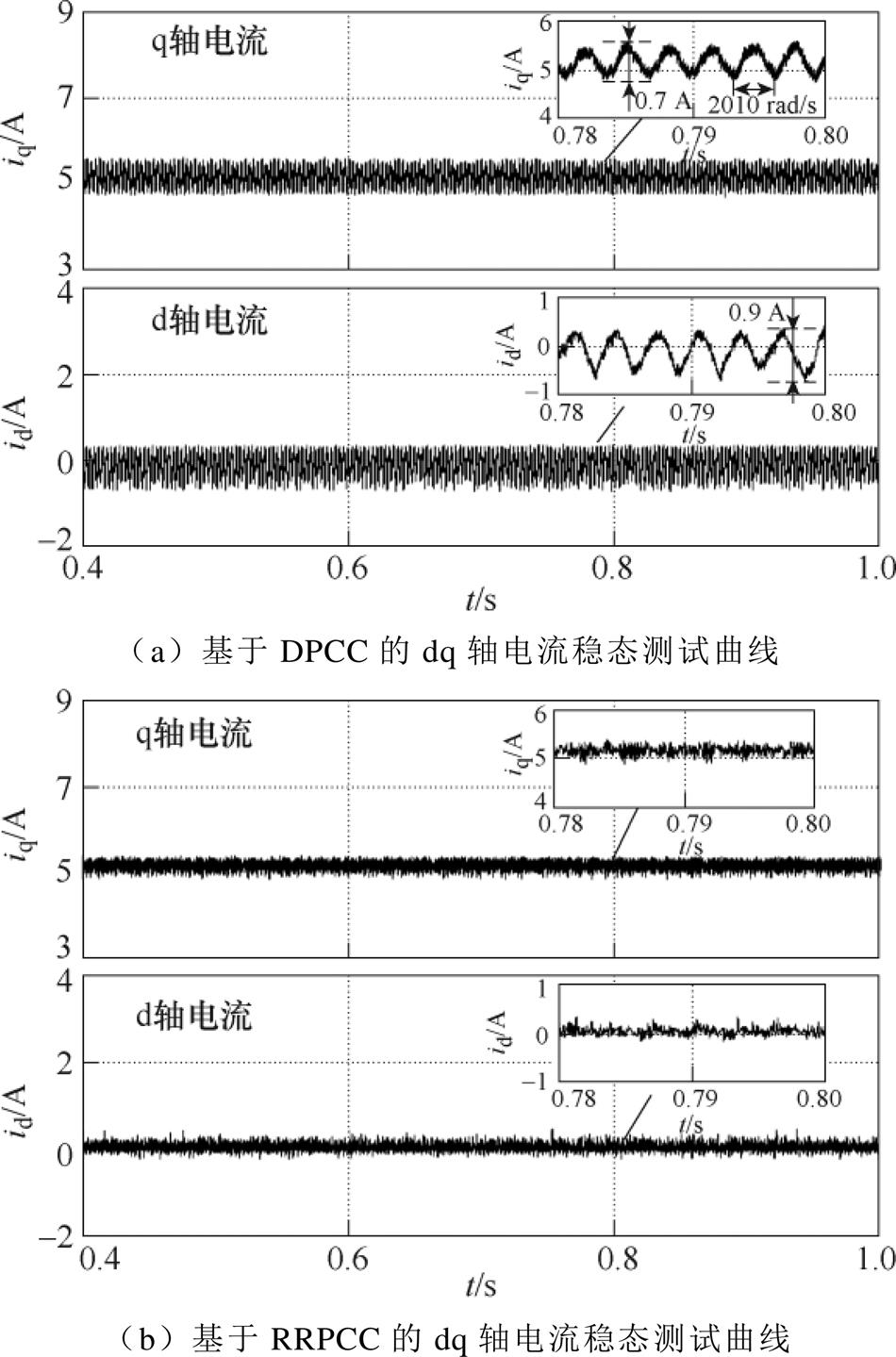
图4 dq轴电流稳态测试对比
Fig.4 Comparison of dq axis current steady-state test
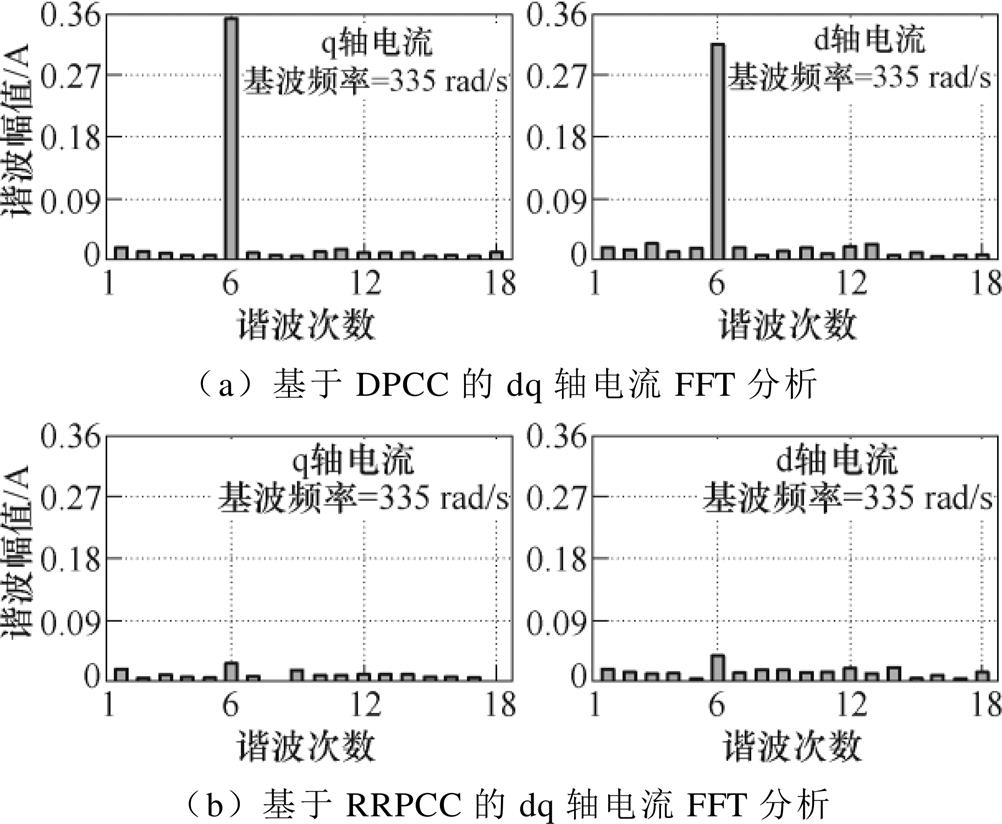
图5 dq轴电流的FFT分析对比
Fig.5 Comparison of dq axis current FFT analysis
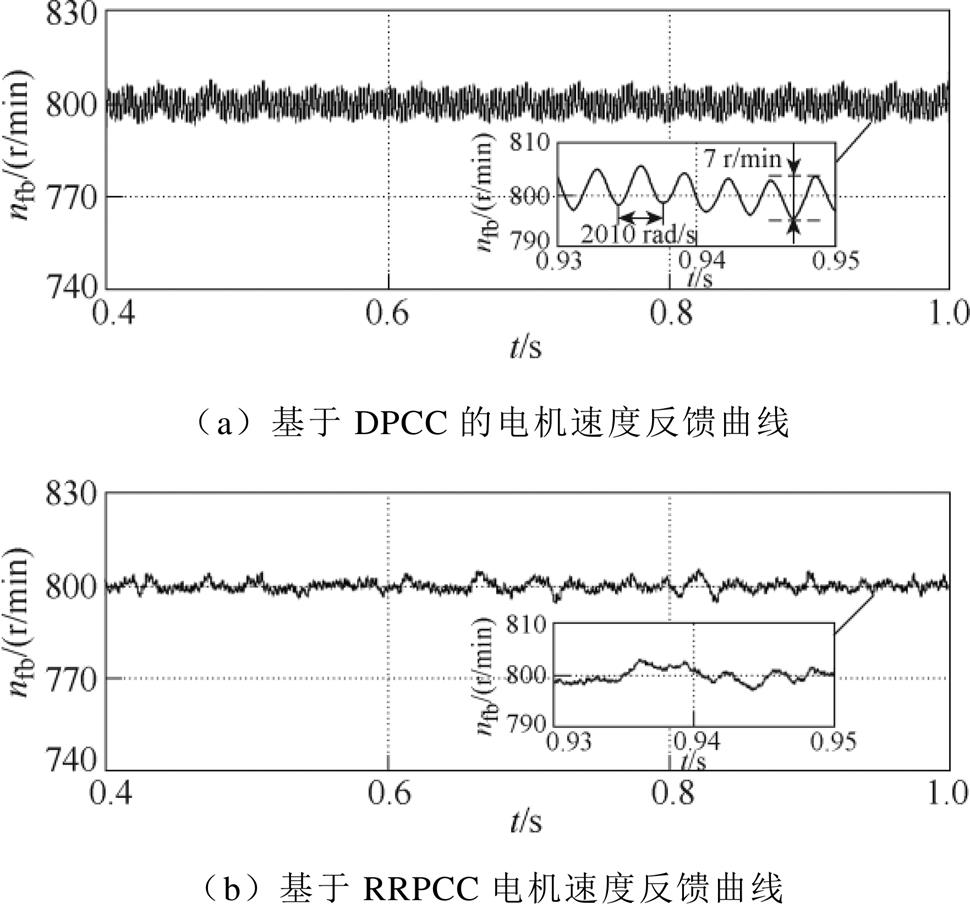
图6 电机速度稳态测试曲线对比
Fig.6 Comparison of PMSM speed steady-state test
采用常规DPCC策略时,由于没有采取扰动抑制措施,dq轴电流出现明显的电流脉动。如图4a所示,电流脉动频率为2 010 rad/s,电流iq的波动幅值为0.7 A,电流id的波动幅值为0.9 A。而采用RRPCC策略时,如图4b所示,由于谐振控制器有效抑制了正弦扰动,电流波动随之降低,电流iq的波动幅值为0.3 A,电流id的波动幅值为0.2 A。因此,RRPCC实现了更稳定的电流跟踪。
分别对dq轴稳态电流进行快速傅里叶变换(Fast Fourier Transform, FFT)分析,如图5所示。可以看出,采用常规DPCC的dq轴电流存在明显的6次谐波,而采用本文提出的RRPCC后,dq轴电流6次谐波含量明显降低。
速度对比曲线如图6所示,常规DPCC的稳态速度存在频率为2 010 rad/s的周期性脉动,脉动幅度约为7 r/min。采用RRPCC时,由于消除了dq轴电流的周期性扰动,速度的6次谐波脉动也被抑制,速度脉动显著降低,速度波动幅值降为3 r/min。
PMSM运行中因参数失配而产生非周期性扰动。由于实验过程中电机参数不能任意改变,因此可以通过修改控制器中的电机参数设定值来实现电机参数不匹配测试。
根据2.1节分析,定子电阻Rs失配对电流误差的影响轻微,因此实验中仅选择磁链yf和电感Ls作为测试参数,分别测试当PMSM的磁链和电感参数发生失配后,常规DPCC和所提RRPCC在电流跟踪性能方面的对比实验结果。
首先,当PMSM以800 r/min的速度在额定负载条件下稳态运行时,测试磁链参数按照0.5yf、yf、2yf阶跃变化时的电流跟踪性能。
当使用常规DPCC时,在yf阶跃变化下的测试如图7所示,d轴电流能跟随参考值,没有受磁链失配的影响;而q轴电流受磁链失配影响较大,出现明显的电流跟踪误差,特别当磁链参数失配值为2yf时,iq的稳态电流跟踪误差为0.9 A。从图7还可以看出,在磁链阶跃变化瞬间,iq出现了明显的暂态电流尖峰,尖峰幅值最高达到5.85 A。
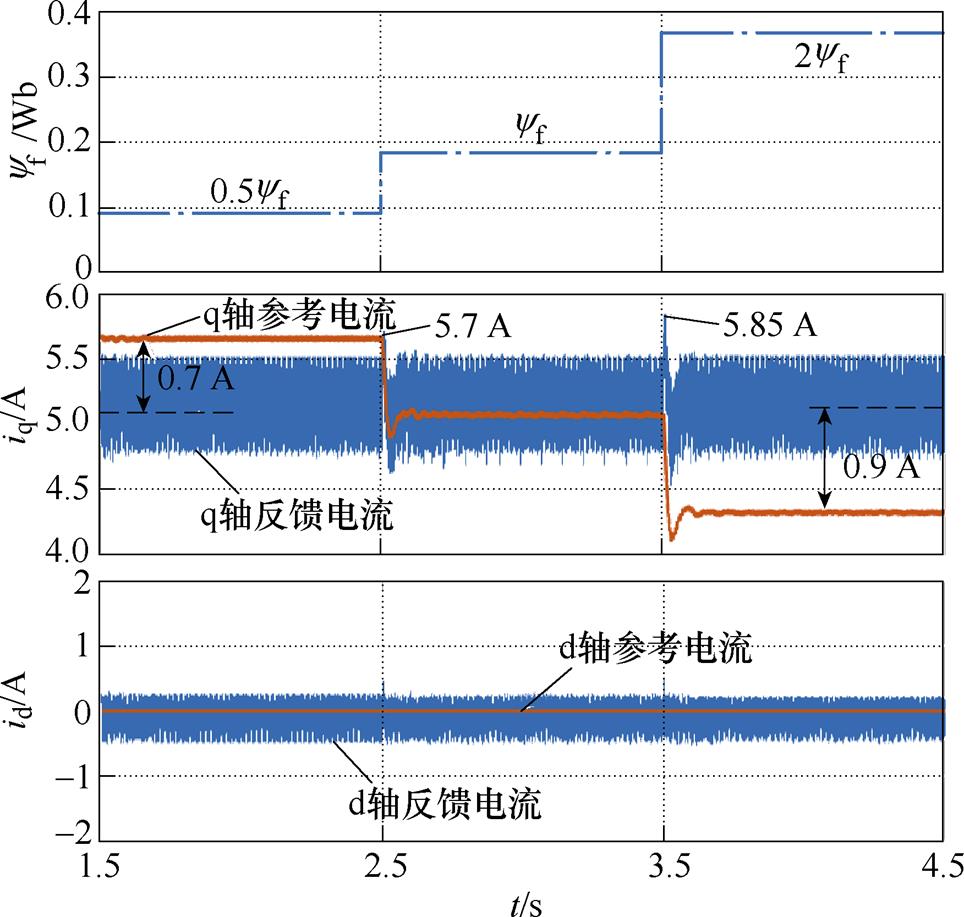
图7 常规DPCC在yf阶跃变化下的测试
Fig.7 Test of conventional DPCC with yf step change
然后,磁链参数保持失配状态为2yf,使电机速度从400 r/min上升到1 600 r/min。使用常规DPCC时,在yf失配下的测试如图8所示,速度变化使iq的参考电流发生阶跃变化。在电流动态过程中,电流iq出现振荡,iq瞬时跟踪误差达到2 A。电流稳态时,跟踪误差随速度升高明显增加,iq电流跟踪误差约为1.5 A。
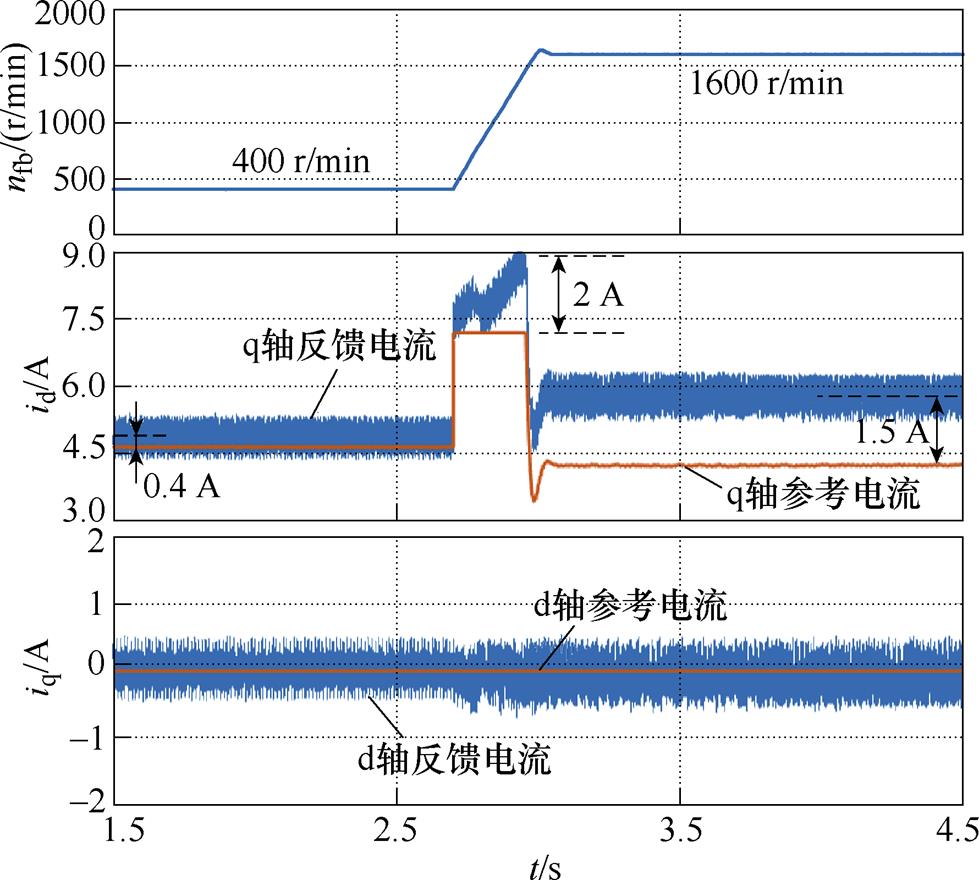
图8 速度变化时常规DPCC在yf失配下的测试
Fig.8 Test of conventional DPCC with yf mismatch when motor speed changes
在两种同样的测试工况下,采用本文提出的RRPCC方法时,结果分别如图9和图10所示,由于GPI观测器能准确估计参数失配导致的电压扰动,dq轴电流能以相对较小的波动快速收敛到它们的参考值,消除电流稳态误差,实现对id和iq的精确跟踪。因此,在磁链失配条件下,RRPCC方法表现出良好的电流跟踪性能。
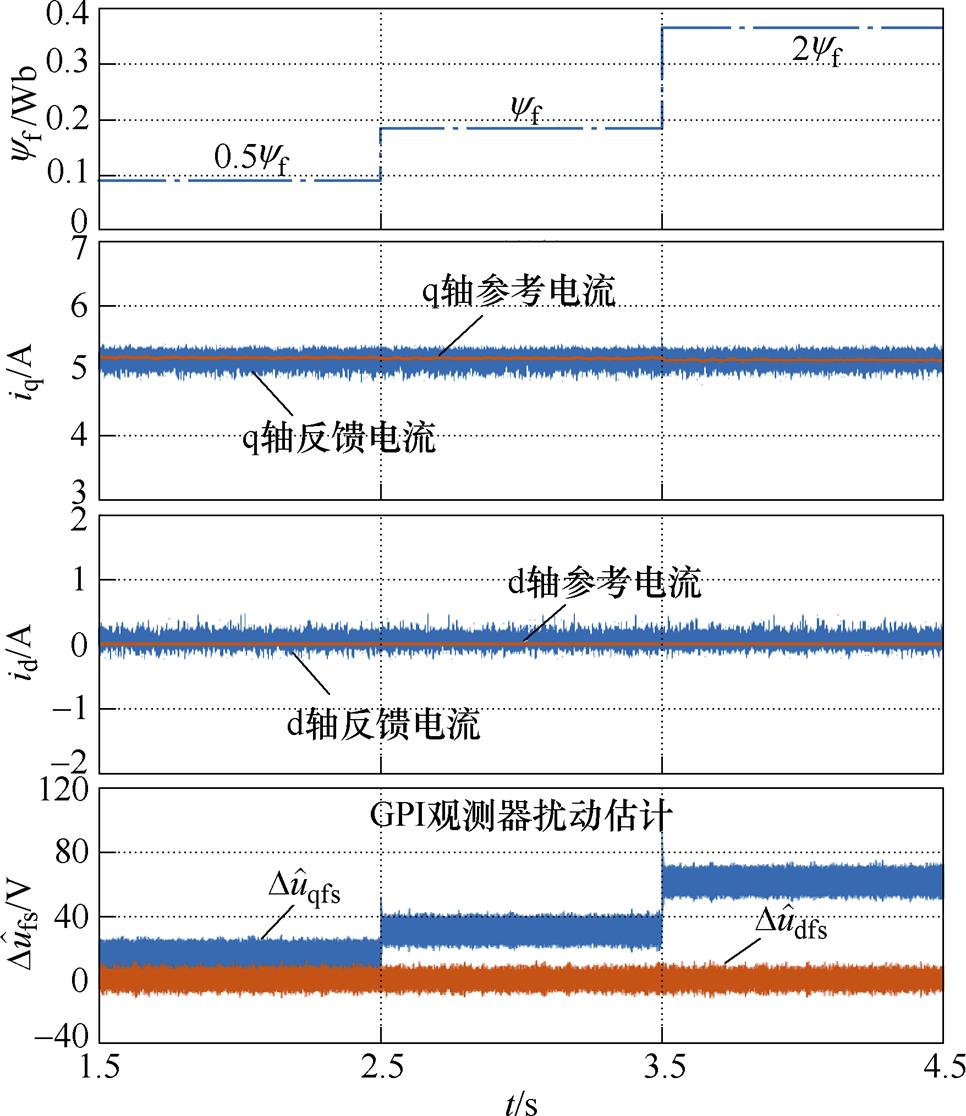
图9 所提RRPCC在yf阶跃变化下的测试
Fig.9 Test of proposed RRPCC with yf step change
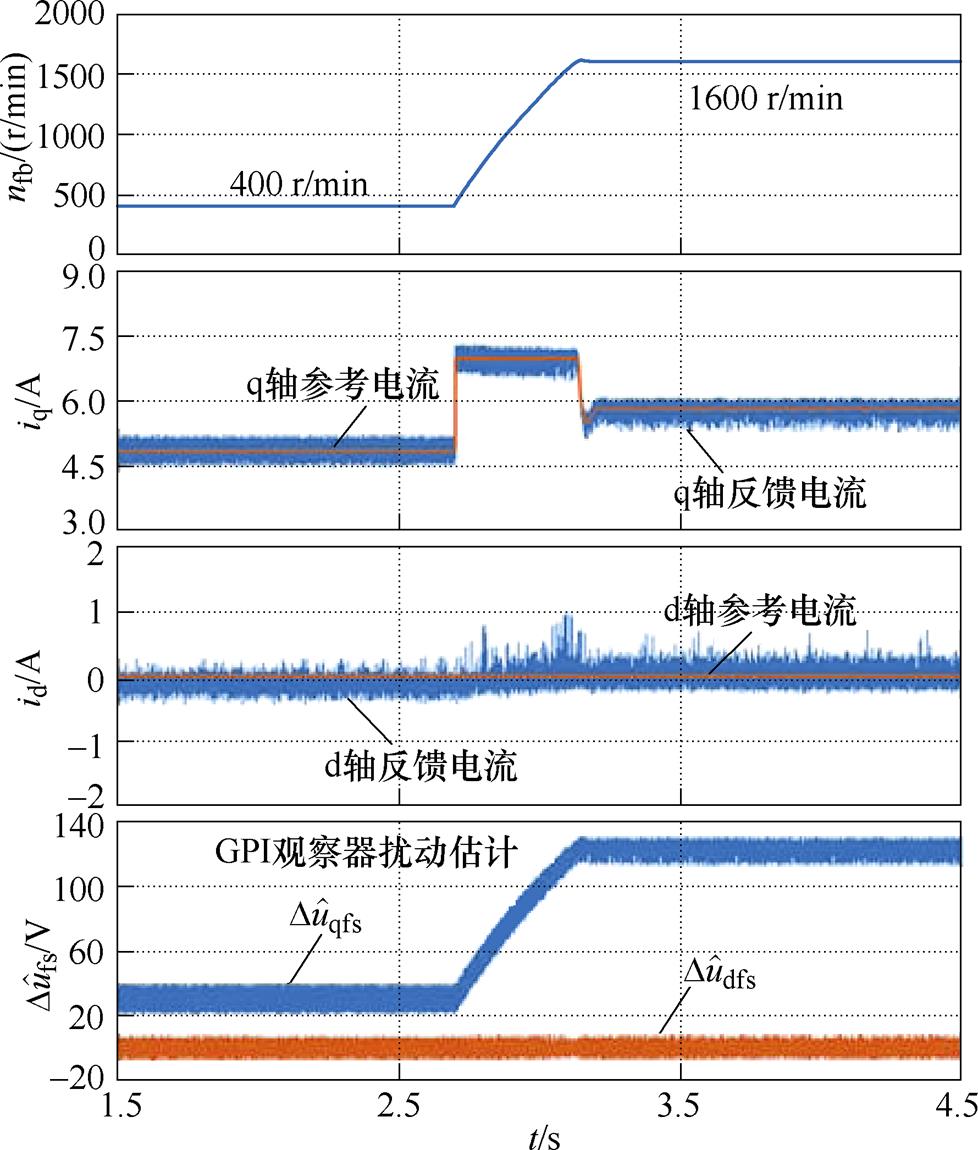
图10 速度变化时所提RRPCC在yf失配下的测试
Fig.10 Test of proposed RRPCC with yf mismatch when motor speed changes
当定子电感按照0.5Ls、Ls、2Ls阶跃变化时,图11和图12比较了两种方法的测试结果。当电感失配时,如图11所示,常规DPCC的dq轴电流不能很好地跟踪其参考值,特别当预设的定子电感值小于电机实际定子电感时,dq轴电流波动较大,iq的波动幅值达到1.1 A,稳态误差为0.3 A;id的波动幅值达到1.6 A,稳态误差为0.4 A。而采用所提RRPCC,GPI观测器补偿了电感参数失配导致的电压扰动,消除了由电感失配引起的dq轴稳态电流误差,电流波动没有因扰动发生变化,如图12所示,波动幅值保持为0.5 A及0.4 A。因此,RRPCC对电感参数失配表现出良好的鲁棒性。
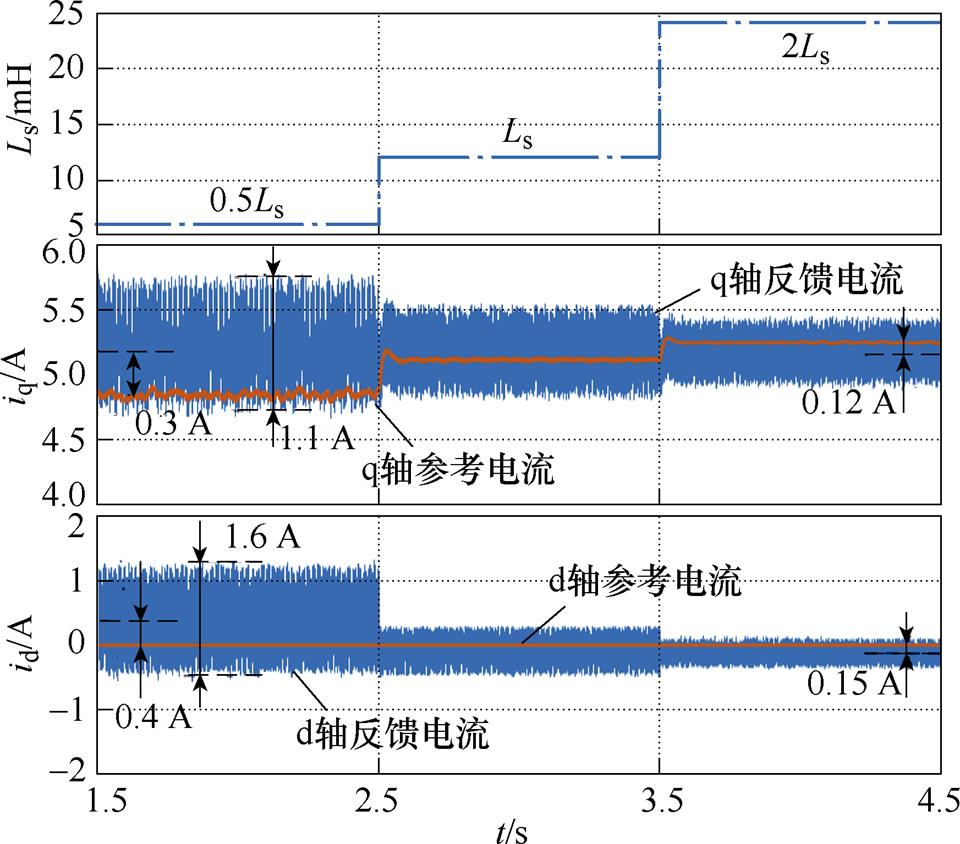
图11 常规DPCC在Ls失配下的测试
Fig.11 Test of conventional DPCC with Ls mismatch
PMSM参数失配及逆变器死区效应分别产生非周期及周期性扰动,会影响预测电流控制的性能。本文提出基于GPI观测器的RRPCC方法。经过理论分析和实验验证,得出以下结论:
1)死区效应会引起周期性扰动,常规DPCC无法抑制这些周期性扰动,使输出电流和速度出现脉动。本文将与扰动同频率的谐振内模多项式嵌入到电流预测模型中,建立谐振预测电流控制器,能抑制周期性扰动,实现更稳定的电流和转速输出。
2)PMSM参数敏感性分析表明,参数失配会降低预测控制器的性能,导致稳态电流误差。本文采用GPI观测器估计和补偿由参数失配引起的集总扰动,消除参数失配的影响,提高了鲁棒性。

图12 所提RRPCC在Ls失配下的测试
Fig.12 Test of proposed RRPCC with Ls mismatch
3)所提出的基于GPI观测器的RRPCC方法,在存在非周期性和周期性扰动的情况下表现出良好的扰动抑制能力和电流跟踪性能。
参考文献
[1] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345.
Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
[2] 赵凯辉, 周瑞睿, 冷傲杰, 等. 一种永磁同步电机的有限集无模型容错预测控制算法[J]. 电工技术学报, 2021, 36(1): 27-38.
Zhao Kaihui, Zhou Ruirui, Leng Aojie, et al. Finite control set model-free fault-tolerant predictive control for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(1): 27-38.
[3] 陈卓易, 屈稳太, 邱建琪. 一种开关频率可控的有限集模型预测控制[J]. 电工技术学报, 2022, 37(16): 4134-4142.
Chen Zhuoyi, Qu Wentai, Qiu Jianqi. A switching- frequency-controlled finite-control-set model predi- ctive control method[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4134-4142.
[4] Pei Genji, Liu Jiaxi, Gao Xiaonan, et al. Deadbeat predictive current control for SPMSM at low switching frequency with moving horizon estimator[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 345-353.
[5] 郭磊磊, 王朋帅, 李琰琰, 等. 不同代价函数下永磁同步电机模型预测控制参数失配可视化分析[J]. 电工技术学报, 2023, 38(4): 903-914.
Guo Leilei, Wang Pengshuai, Li Yanyan, et al. Visual analysis of parameters mismatch in model predictive control for permanent magnet synchronous motor under different cost functions[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 903- 914.
[6] Wang Zitan, Chai Jianyun, Xiang Xuewei, et al. A novel online parameter identification algorithm designed for deadbeat current control of the permanent-magnet synchronous motor[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 2029-2041.
[7] Zhou Ying, Zhang Shuo, Zhang Chengning, et al. Current prediction error based parameter identi- fication method for SPMSM with deadbeat predictive current control[J]. IEEE Transactions on Energy Conversion, 2021, 36(3): 1700-1710.
[8] Xu Cheng, Han Zaikun, Lu Shuai. Deadbeat predictive current control for permanent magnet synchronous machines with closed-form error com- pensation[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5018-5030.
[9] 卜飞飞, 罗捷, 刘皓喆, 等. 双绕组感应发电机系统无差拍电流预测控制策略[J]. 电工技术学报, 2021, 36(24): 5213-5224.
Bu Feifei, Luo Jie, Liu Haozhe, et al. Deadbeat predictive current control strategy of dual winding induction generator system[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5213-5224.
[10] 李争, 安金峰, 肖宇, 等. 基于自适应观测器的永磁同步直线电机模型预测控制系统设计[J]. 电工技术学报, 2021, 36(6): 1190-1200.
Li Zheng, An Jinfeng, Xiao Yu, et al. Design of model predictive control system for permanent magnet synchronous linear motor based on adaptive observer[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1190-1200.
[11] Wang Lijun, Zhao Jiwen, Yang Xing, et al. Robust deadbeat predictive current regulation for permanent magnet synchronous linear motor drivers with parallel parameter disturbance and load observer[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 7834-7845.
[12] Zhang Yongchang, Jin Jialin, Huang Lanlan. Model- free predictive current control of PMSM drives based on extended state observer using ultralocal model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 993-1003.
[13] Wang Junxiao, Wang Fengxiang, Wang Gaolin, et al. Generalized proportional integral observer based robust finite control set predictive current control for induction motor systems with time-varying dis- turbances[J]. IEEE Transactions on Industrial Infor- matics, 2018, 14(9): 4159-4168.
[14] Yang Jun, Wu Han, Hu Liang, et al. Robust predictive speed regulation of converter-driven DC motors via a discrete-time reduced-order GPIO[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(10): 7893- 7903.
[15] Geng Yiwen, Deng Renxiong, Dong Wenming, et al. An overlap-time compensation method for current- source space-vector PWM inverters[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(4): 3192- 3203.
[16] Liang Donglai, Li Jian, Qu Ronghai, et al. Adaptive second-order sliding-mode observer for PMSM sensorless control considering VSI nonlinearity[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8994-9004.
[17] Shen Zewei, Jiang Dong. Dead-time effect com- pensation method based on current ripple prediction for voltage-source inverters[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 971-983.
[18] Li Yongfei, Li Yong, Wang Qian. Robust predictive current control with parallel compensation terms against multi-parameter mismatches for PMSMs[J]. IEEE Transactions on Energy Conversion, 2020, 35(4): 2222-2230.
[19] Zhou Zhanqing, Xia Changliang, Yan Yan, et al. Disturbances attenuation of permanent magnet syn- chronous motor drives using cascaded predictive- integral-resonant controllers[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1514-1527.
Abstract To improve the control performance of a permanent magnet synchronous motor (PMSM), deadbeat predictive current control (DPCC) is adopted for the inner current loop due to its small current ripple and fast dynamic response. However, DPCC is highly dependent on accurate PMSM parameters, and any mismatch may lead to steady-state current errors and system instability. In practical PMSM operation, parameter mismatch is inevitable due to factors such as temperature drift and magnetic saturation. In addition, inverter dead time introduces periodic voltage disturbance, resulting in current distortion and torque ripple, which deteriorates the performance of the PMSM system. Therefore, this paper proposes a robust resonant predictive current control (RRPCC) strategy based on the generalized proportional integral (GPI) observer to mitigate the adverse impacts of parameter mismatch and inverter dead-time effect.
Firstly, the non-periodic disturbance generated by parameter mismatch and the periodic disturbance induced by the dead-time effect are analyzed. A precise mathematical model of the PMSM is established considering both disturbances. Secondly, based on the internal mode principle, a resonant polynomial is incorporated into the current prediction model at the same frequency as the periodic disturbance. The resonant predictive current controller is designed to reject periodic sinusoidal disturbance and achieve smooth current output. Finally, to eliminate non-periodic disturbance, a GPI observer is added to the current controller to estimate and compensate for lumped disturbances induced by parameter mismatch. The stability analysis of the GPI observer in the discrete-time domain is given.
The effectiveness of the proposed method is verified by experiments. The speed reference is set to 800 r/min (we=335 rad/s) in the periodic disturbance test. Apparent d-q axis current pulsations occur with 2 010 rad/s in the conventional DPCC. The pulsation amplitude of iq and id is 0.9 A and 0.7 A, respectively. The FFT analysis shows that 6th current harmonics are significant in the d-q axis. The RRPCC method effectively suppresses 6th harmonics. The pulsation amplitude of iq and id is reduced to 0.3 A and 0.2 A, respectively. In the flux-linkage mismatch test, the flux-linkage is changed in step from 50% to 200% of the nominal value. The flux-linkage variation in the conventional DPCC causes an obvious steady-state current error with 0.9 A in the q-axis. The flux-linkage is maintained at 2yf, and the speed increases from 400 r/min to 1 600 r/min. When the conventional DPCC is adopted, the q-axis current oscillates during the current dynamic process. The current tracking error increases to 1.5 A at 1 600 r/min in the steady state. The proposed RRPCC maintains the d-q axis current stable and smooth, exhibiting good current tracking performance. In the inductance mismatch test, the inductance step changes from 50% to 200% of the nominal value. In the conventional DPCC, current ripples are severely increased with the amplitudes of 1.1 A and 1.6 A in the d-q axis. The current quality of the proposed RRPCC is not affected by maintaining current ripples at 0.5 A and 0.4 A.
The following conclusions can be drawn from the experimental analysis: (1) The dead-time effect generates periodic sinusoidal disturbances. Compared with the conventional DPCC, the resonant predictive current controller is established in RRPCC, which can reject the periodic disturbance. (2) Steady-state current errors induced by PMSM parameter mismatch are compensated by the GPI observer in RRPCC, enhancing system robustness. (3) The proposed RRPCC exhibits good disturbance rejection ability and current tracking performance in the presence of non-periodic and periodic disturbances.
keywords:Parameter mismatch, GPI observer, periodic disturbance, robust resonant predictive current control (RRPCC)
DOI: 10.19595/j.cnki.1000-6753.tces.230331
中图分类号:TM351
辽宁省博士科研启动基金计划资助项目(2022-BS-177)。
杨 帆 男,1985年生,博士研究生,副研究员,研究方向为电机控制、电力电子、预测控制等。E-mail: sailing_0402@163.com
赵希梅 女,1979年生,教授,博士生导师,研究方向为直线伺服、智能控制、鲁棒控制等。E-mail: zhaoxm_sut@163.com(通信作者)
收稿日期 2023-03-21
改稿日期 2023-04-07
(编辑 崔文静)