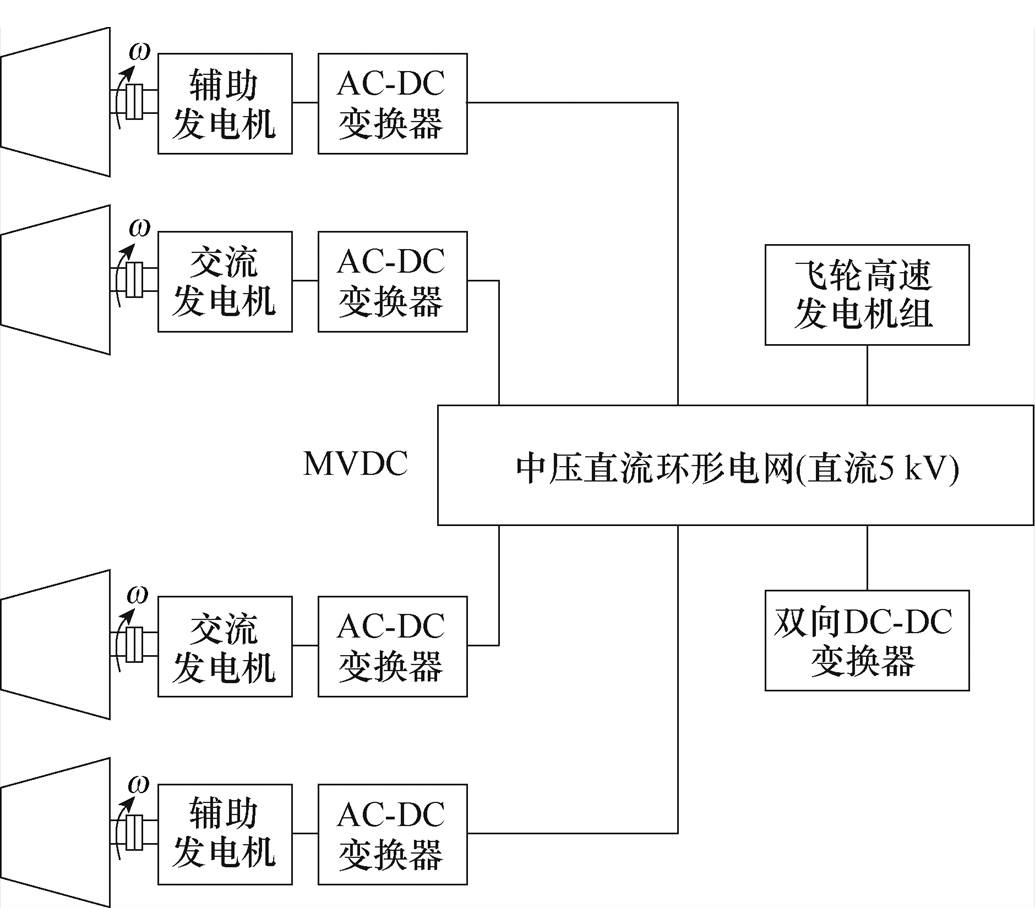
图1 美国某船MVDC综合电力系统
Fig.1 USA ship MVDC IPS
摘要 鉴于原动机调速特性对舰船中压直流(MVDC)发电机组运行影响的重要性,该文基于十二相同步发电机及其三相交流励磁机数学模型提出MVDC发电机组动态建模方法,以解决多相整流发电机及其励磁系统难以考虑原动机动态调速特性的难题。以某型燃气轮机整流发电机组动态仿真模型为基础,建立了频率不同的十二相同步发电机与三相交流励磁机组合模型,阐述原动机调速与发电机励磁调压相互耦合的计算流程。实测与仿真结果表明,该型燃气轮机发电机组在突加20%负载工况时转速跌落较大,且转速恢复过程需约20 s,但MVDC发电机组通过调节励磁系统可在1 s内使直流母线电压恢复稳定,从而为负载提供稳定直流功率输出。在校准仿真模型的基础上,通过系统分析突加不同比例负载时的转速、燃油流量、励磁电流、输出电压等性能参数变化规律,获取了燃发机组允许突加负载上限约为30%的运行边界认知,为MVDC发电机组励磁系统设计以及如何预留充足的短时强励能力提供了理论支撑。
关键词:原动机调速特性 MVDC发电机组 十二相整流发电机 动态仿真模型
舰船中压直流(Medium-Voltage Direct Current, MVDC)综合电力系统(Integrated Power System, IPS)如图1所示,与图2所示的中压交流(Medium- Voltage Alternating Current, MVAC)综合电力系统相比,前者消除了原动机转速和电网频率之间的影响,为调速特性各异且容量存在量级差异的燃气轮机发电机组、柴油机发电机组和汽轮机发电机组多机并联供电提供了有效的解决方案,这有利于舰船动力系统的灵活配置,代表了国内外舰船综合电力系统未来的发展方向[1-7]。
在MVDC综合电力系统中,为提高燃油运行经济性和供电可靠性,一般采用多机并联供电方式。若单台机组发生故障跳闸,则会引发在网机组突加负载的动态过程,此时在网机组能否承受该动态过程,并维持电网电压的稳定,是MVDC综合电力系统在设计之初就需要重点关注的问题之一,这与原动机调速性能和发电机调压性能密切相关。因此,有必要建立考虑原动机调速特性的MVDC发电机组动态仿真模型,对机组突加负载动态性能进行仿真并与实验对比验证。

图1 美国某船MVDC综合电力系统
Fig.1 USA ship MVDC IPS
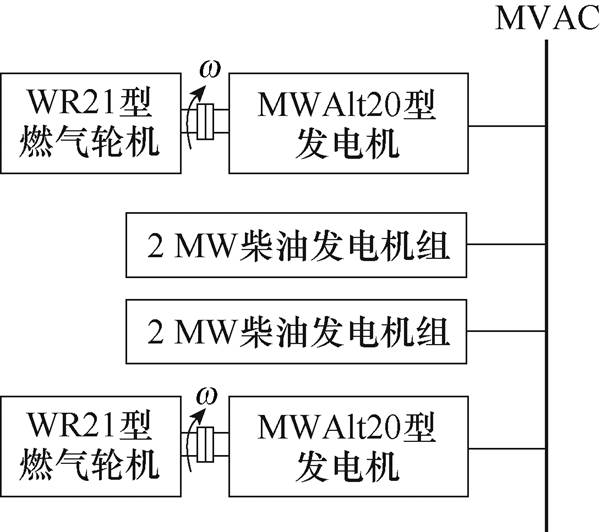
图2 英国某船MVAC综合电力系统
Fig.2 British ship MVAC IPS
MVDC发电机组系统架构既包含原动机及其调速系统,又包含主发电机、励磁机、整流器、励磁控制装置和数字式自动电压调节器(Automatic Voltage Regulator, AVR)等模块,其复杂性在于:作为机械部件的原动机存在燃油与空气混合燃烧、气体膨胀做功等多个物理化学过程,调速系统受燃油流量限制,而主发电机与励磁机的相数、频率及结构均不相同,且整流器和励磁控制装置引入具有明显非线性特征开关暂态过程[7]。上述各模块间存在机械、电气、控制等多种物理信号接口,导致考虑原动机调速特性的MVDC发电机组详细动态仿真建模非常困难,而传统多相整流发电机数值仿真模型大多未考虑励磁系统与调速系统的耦合,难以准确分析突加负载工况时动态调速特性对MVDC发电机组调压性能的影响。文献[8]利用十二相发电机数学模型及其定子4套三相绕组对称性,建立了十二相发电机整流系统的等效三相模型,推导得到了极间短路时短路电流的解析表达式;文献[9]建立了整流发电机等效电路模型,研究了多台整流发电机并联时直流中点环流产生的机理与频率特征;文献[10]建立了十二相四Y移15°绕组同步电动机的动态仿真数学模型,其中定子采用静止abc模型,转子采用多回路dq模型,对方波供电下多相电动机的起动过程进行了计算和分析;文献[11]对带线性负载的十二相飞轮储能同步发电机系统进行了设计与仿真研究,通过励磁控制实现了转子动能的释放;文献[12-13]建立了双九相储能电机带整流负载系统降阶等效平均模型并以此展开研究工作;文献[14]建立了大容量双六相储能电机系统仿真模型。上述文献均未建立考虑原动机调速特性的整流发电机组模型,难以确定此类发电机组的动态正常运行边界,为此需要在上述研究工作的基础上,建立考虑原动机动态调速特性的MVDC发电机组仿真模型。
为解决考虑原动机动态调速特性的建模难题,本文在传统同步发电机建模方法的基础上,取时间基值为1,统一十二相同步发电机及其三相励磁机数学模型的电角速度输入接口,建立计及转速变化的变系数矩阵高阶状态空间仿真模型,进而提出考虑原动机调速特性的MVDC发电机组动态建模方法。以某型燃气轮机发电机组为例,在Matlab/ Simulink软件中建立其动态仿真模型,通过仿真和实验对比,验证MVDC发电机组动态仿真模型的准确性。进一步研究可知,MVDC发电机组在转速动态调节过程中,可通过调励磁释放转子动能,维持电网电压稳定,这与传统三相交流同步发电机组“调转速调有功、调励磁调无功”的原理不同。
本文所述MVDC发电机组由原动机及其调速系、三相交流励磁机、旋转整流器、十二相同步发电机、十二相不控整流器和数字式AVR等组成,如图3所示。
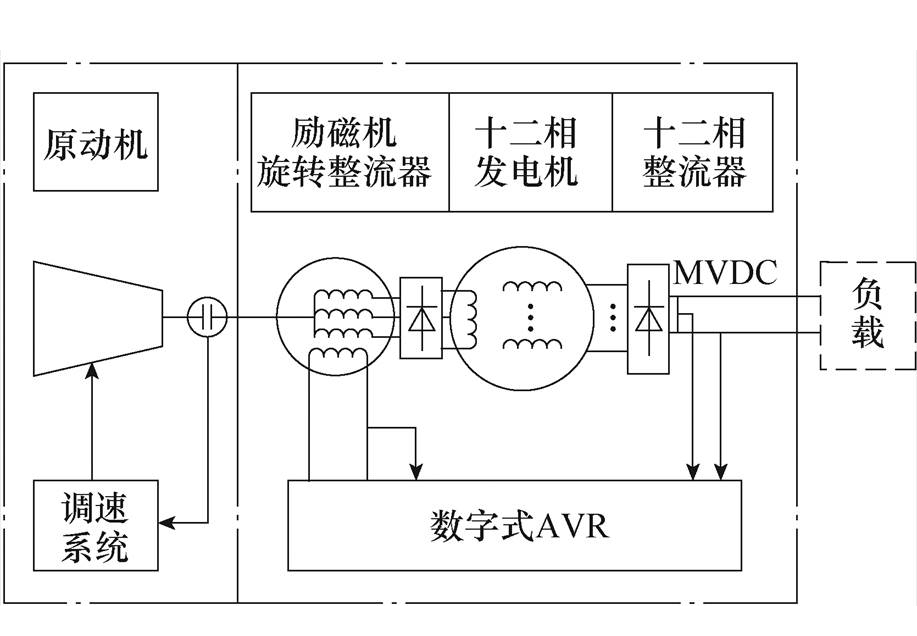
图3 MVDC发电机组系统架构
Fig.3 MVDC Generator set system architecture
在上述架构下,以某型燃气轮机发电机组为例,其工作原理是:燃气轮机为MVDC发电机组提供机械输入转矩,其调速系统通过控制燃油流量实现对机组转速的闭环控制;励磁机与十二相同步发电机转子同轴,该转子由燃气轮机驱动旋转时,励磁机旋转整流器开始工作,并通过旋转整流器为十二相同步发电机提供所需直流励磁电流,十二相发电机转子获得直流励磁及转动动能后,十二相定子绕组输出交流电能至十二相整流器,十二相整流器将交流电整流为直流电,为后续负载提供所需直流电能,发电机数字式AVR通过控制励磁机的励磁电流实现对MVDC发电机组直流电压的闭环控制。
按照电气工程领域惯例,在建立同步发电机数学模型的标幺值系统中,取额定电角速度作为电角速度的基值,而一个多电机系统存在不同额定电角速度的发电机,在对其进行数值仿真计算时,由于时间基值只能选一个,因此电角速度的基值wb只能唯一确定。为解决仿真计算时出现时间基值不统一的问题,本文提出多机系统的时间基值取为1,对应电角速度的基值wb也为1,此时数值仿真计算的各物理量时间轴保持一致,这为发电机励磁调压与原动机调速之间的耦合迭代计算提供了基础。电枢绕组和励磁绕组电压、电流的基值选取原则与传统标幺值系统保持一致。另外,考虑到自定义发电机模型为信号接口,而Matlab/Simulink软件中电力电子装置模型接口为电气接口,如不加以转换则无法联合仿真,本文参考文献[15]的方法,以电流源并联大电阻并结合电压测量元件的方式进行模型接口的转换,可对发电机与整流器、励磁器等电力电子装置组成的非线性强耦合系统实现静态、动态联合 仿真。
MVDC发电机组中的十二相发电机和三相励磁机都是同步发电机,它们的电枢绕组均为星形联结,且中性点不引出,因此不用考虑其零序分量。为便于处理转速变化问题,取时间基值为1。
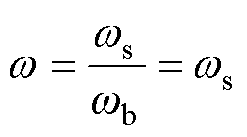 (1)
(1)
则由式(1)可知,电机角速度的标幺值w 与实际值ws相同。
此时,十二相同步发电机的磁链方程和电压方程,在dq坐标系下可分别表示为
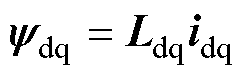 (2)
(2)
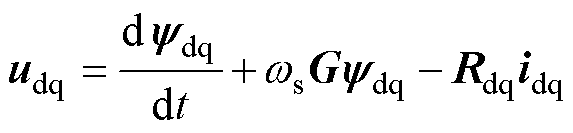 (3)
(3)
式中,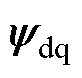 为定转子磁链;udq为定转子电压;idq为定转子电流;G为符号矩阵。电感矩阵Ldq和电阻矩阵Rdq的表达式参见文献[15],其中的元素均为发电机已知参数,详见附录。与传统发电机建模方法不同,电角速度ws已经计及了原动机调速特性对发电机组的影响。
为定转子磁链;udq为定转子电压;idq为定转子电流;G为符号矩阵。电感矩阵Ldq和电阻矩阵Rdq的表达式参见文献[15],其中的元素均为发电机已知参数,详见附录。与传统发电机建模方法不同,电角速度ws已经计及了原动机调速特性对发电机组的影响。
联立(2)和式(3),写成微分方程的形式,可表示为
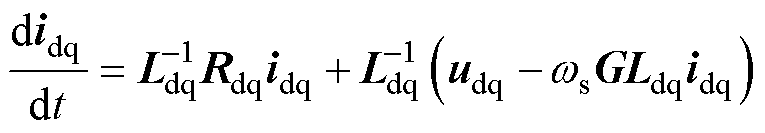 (4)
(4)
令
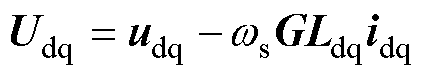 (5)
(5)
则
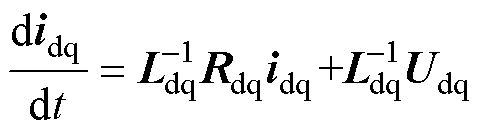 (6)
(6)
进一步,令
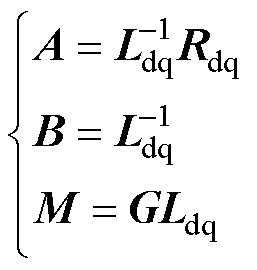 (7)
(7)
则
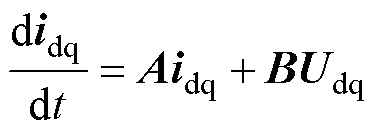 (8)
(8)
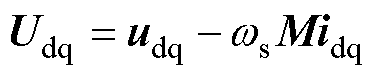 (9)
(9)
根据式(8)和式(9),即可建立考虑转速变化的发电机通用状态空间仿真模型,如图4所示,图中,C为单位矩阵,D为零矩阵。
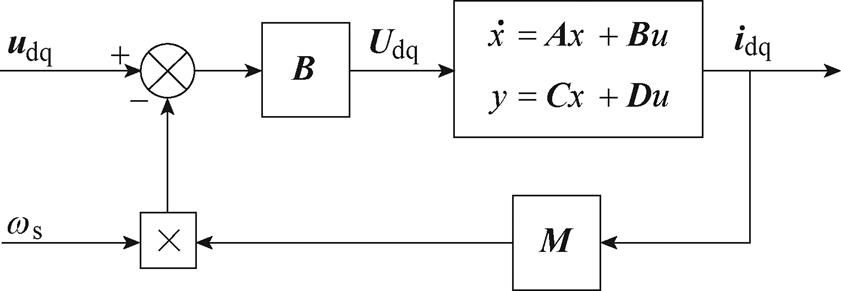
图4 考虑转速变化的发电机模型
Fig.4 Generator model considering speed variation
对于本文所述MVDC发电机组中的十二相同步发电机,定子上布置有四Y移15°十二相电枢绕组,转子上有阻尼绕组和q轴稳定绕组。因此,udq和idq均为12阶列向量,可分别表示为
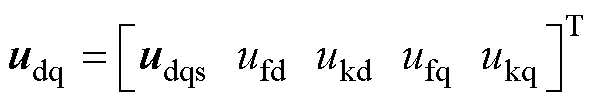 (10)
(10)
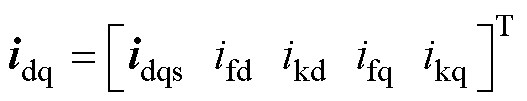 (11)
(11)
式中,ukd、ikd分别为d轴阻尼绕组电压、电流;ukq、ikq分别为q轴阻尼绕组电压、电流;ufq、ifq分别为q轴稳定绕组电压、电流,因上述绕组短接,故ukd=ukq=ufq=0;ufd、ifd分别为发电机励磁电压、电流;udqs和idqs分别为电枢绕组电压和电流向量,不考虑零序分量,均为8阶列向量。
根据Park变换及其反变换原理,按照式(12)可将dq坐标系下电枢绕组电流idqs变换至abc坐标系下的电枢绕组电流iabc,按照式(13)可将abc坐标系下电枢绕组电压uabc变换至dq坐标系下的电枢绕组电压udqs。其中,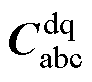 为Park变换矩阵,用式(14)和式(16)表示,
为Park变换矩阵,用式(14)和式(16)表示,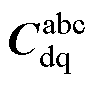 为Park反变换矩阵,用式(15)和式(17)表示。需要注意的是,uabc和iabc均为标幺值,仿真时乘以各自的基值Ub和Ib,详见附录,可得到实际值。
为Park反变换矩阵,用式(15)和式(17)表示。需要注意的是,uabc和iabc均为标幺值,仿真时乘以各自的基值Ub和Ib,详见附录,可得到实际值。
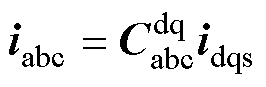 (12)
(12)
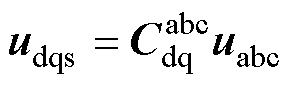 (13)
(13)
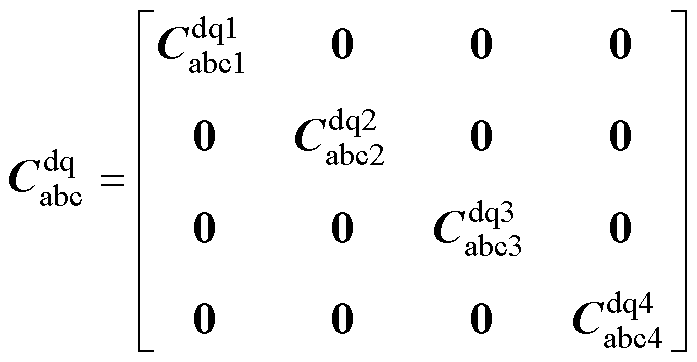 (14)
(14)
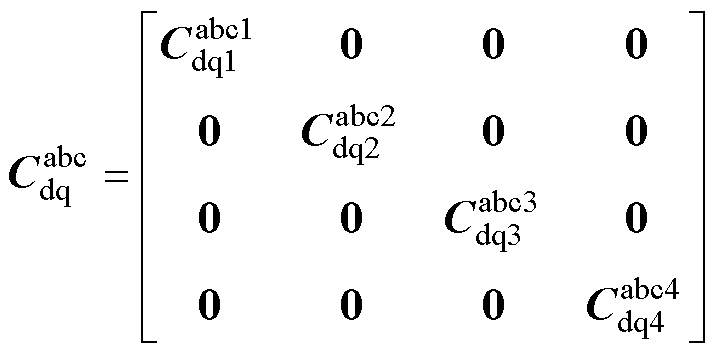 (15)
(15)
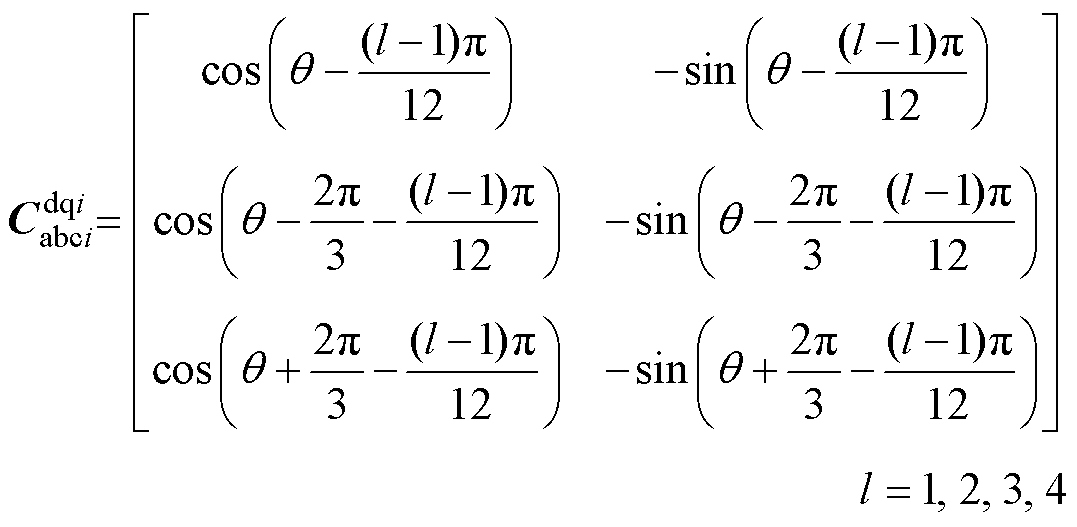 (16)
(16)
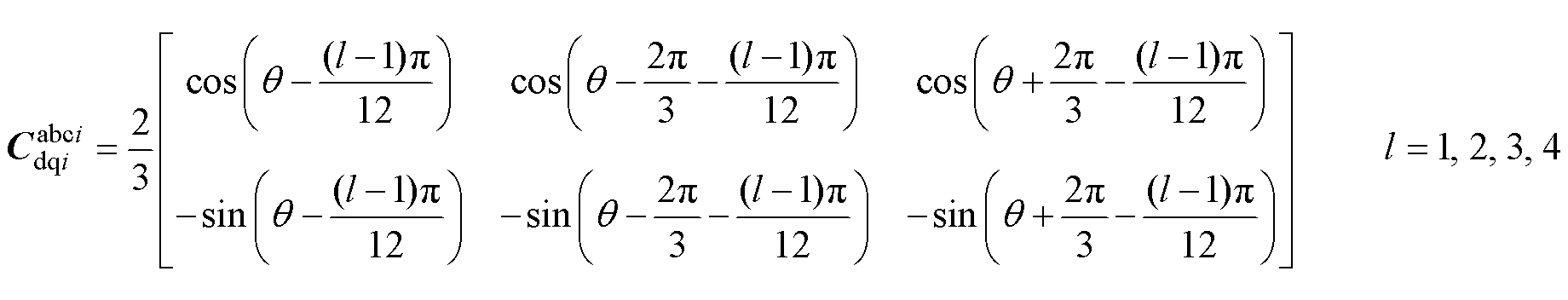 (17)
(17)
式中,q 为转子位置角;l为第l套绕组。
本文所述MVDC发电机组中的交流励磁机,定子为凸极结构布置有励磁绕组,无阻尼绕组转子上布置有三相电枢绕组。因此,励磁机在dq坐标系下的电压udqe和电流idqe均为3阶列向量,可分别表示为
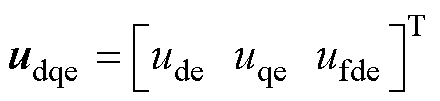 (18)
(18)
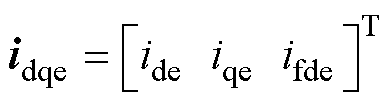 (19)
(19)
式中,ude、uqe、ide、iqe分别为励磁机电枢绕组d、q轴电压、电流;ufde、ifde分别为励磁机励磁绕组电压、电流。同理,可将dq坐标系下的电气量转换为abc坐标系下的电气量,此处不再赘述。列写十二相同步发电机和三相交流励磁机的电磁转矩方程,可分别表示为
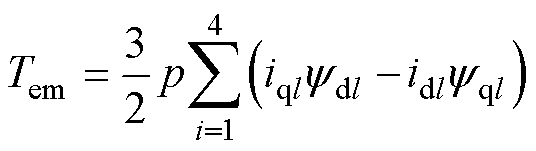 (20)
(20)
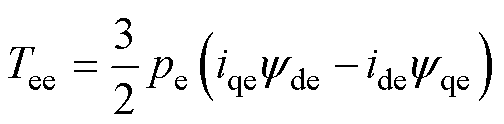 (21)
(21)
式中,Tem和Tee分别为十二相发电机和三相励磁机的电磁转矩;p和pe分别为十二相发电机和三相励磁机的极对数;ydl和yql分别为十二相发电机第l套绕组d轴和q轴磁链;yde和yqe分别为三相励磁机电枢绕组d轴和q轴磁链。
注意到式(20)和式(21)得到的是电磁转矩标幺值,而十二相同步发电机和三相励磁机的电磁转矩基值不相同,与自身额定功率成正比,联合仿真时需要统一至十二相发电机的电磁转矩基值之下,因此总的电磁转矩标幺值为
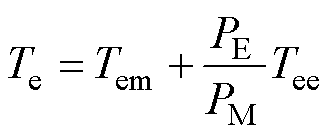 (22)
(22)
式中,PM和PE分别为十二相发电机和三相励磁机的额定功率。
设原动机输出转矩标幺值为Tm,发电机组的惯性时间常数为TJ,机组转子旋转摩擦系数lt,机械角速度标幺值为W,列写发电机组转子运动方程为
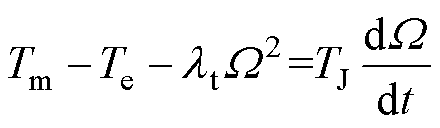 (23)
(23)
以某型燃气轮机发电机组为例,参考文献[15-16]的方法,结合式(23),建立原动机及其调速系统仿真模型,如图5所示。图中,Wref为转速参考值。
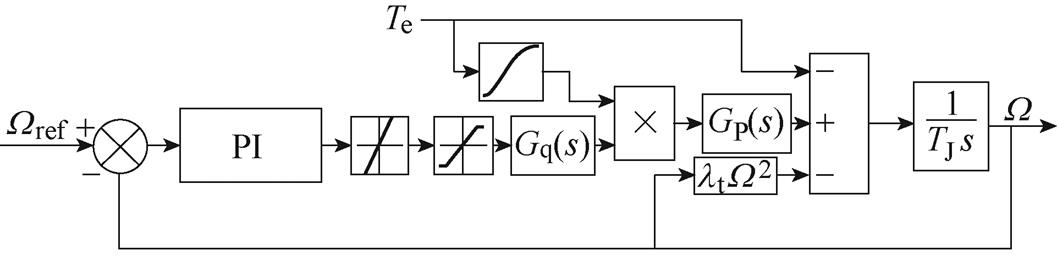
图5 某燃气轮机及其调速系统模型
Fig.5 Gas turbine and its speed control system model
图5中,燃油燃烧产生高温高压气体做功输出机械转矩的延时传递函数可近似表示为
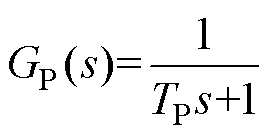 (24)
(24)
式中,TP为燃气轮机气动延时时间常数。
燃油控制系统的传递函数可近似表示为
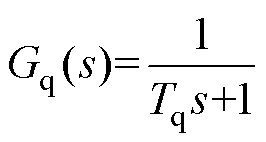 (25)
(25)
式中,Tq为燃油系统延时时间常数。
调速系统参数还包括PI控制器等参数,某燃气轮机及其调速系统的主要参数见表1。
表1 某燃气轮机及其调速系统的主要参数
Tab.1 Main parameters of the gas turbine and its speed control system
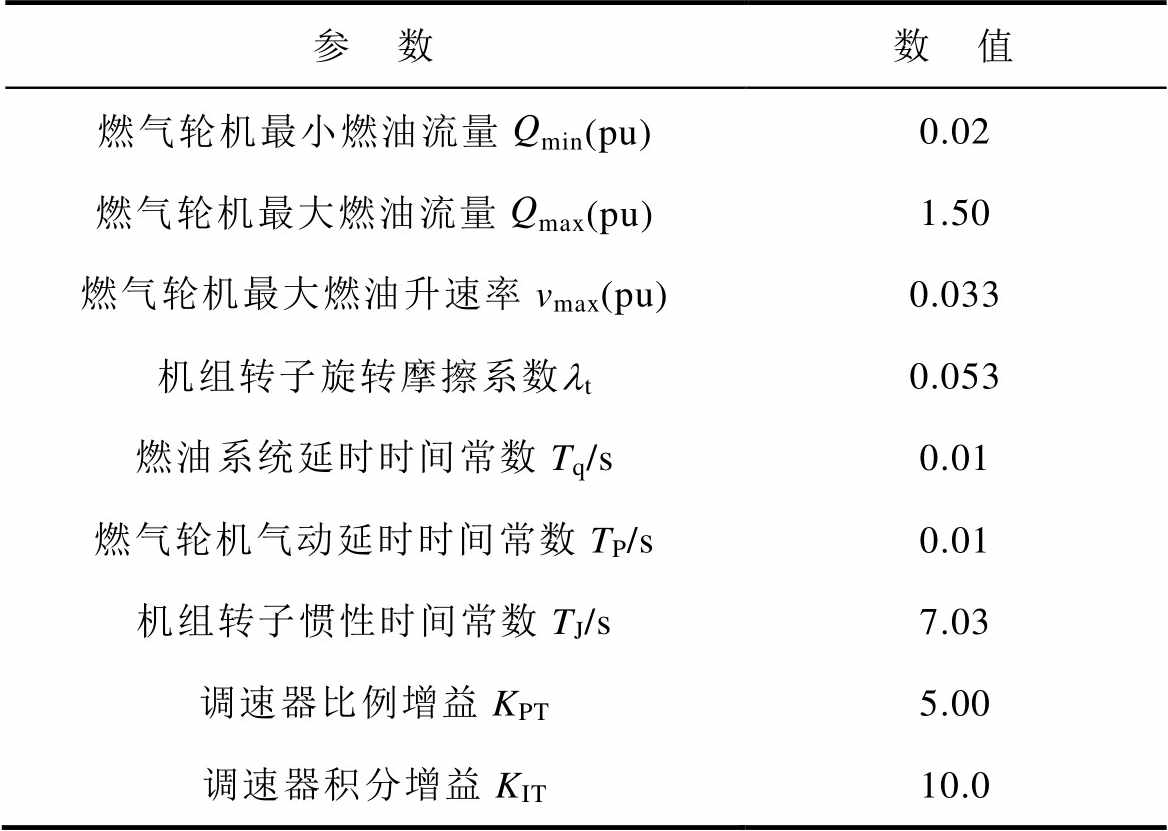
参 数数 值 燃气轮机最小燃油流量Qmin(pu)0.02 燃气轮机最大燃油流量Qmax(pu)1.50 燃气轮机最大燃油升速率vmax(pu)0.033 机组转子旋转摩擦系数lt0.053 燃油系统延时时间常数Tq/s0.01 燃气轮机气动延时时间常数TP/s0.01 机组转子惯性时间常数TJ/s7.03 调速器比例增益KPT5.00 调速器积分增益KIT10.0
将MVDC发电机及其励磁系统的输出电磁转矩引入燃气轮机及其调速系统,再把燃气轮机及其调速系统的输出转速接入MVDC发电机及其励磁系统,从而可实现原动机调速与发电机励磁调压的强耦合数值仿真计算。
为模拟实际系统的动态负载,采取添加开关和接入电阻的措施,在Matlab/Simulink软件中建立其动态仿真模型,如图6所示,实际系统中原动机、十二相同步发电机和三相励磁机三者同轴,在发电机模型中的十二相同步发电机和三相励磁机分别乘以自身极对数再乘以机械加速度基值,即可得到各自的电角频率实际值,从而实现原动机调速特性与发电机之间迭代计算机仿真计算。MVDC发电机励磁控制系统的建模过程详见文献[17],十二相不控整流器和三相旋转整流器的仿真模型可直接在软件中搭建,比较简单不再赘述。
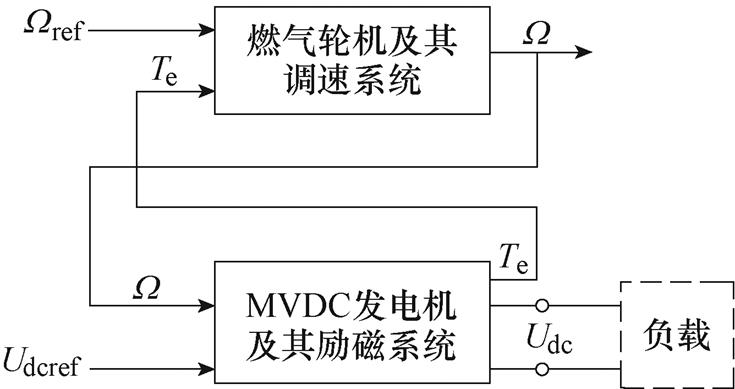
图6 MVDC发电机组调速与调压耦合计算模型
Fig.6 MVDC generator set coupling calculation model
为验证MVDC发电机组动态仿真模型的分析精度,以真实系统可能出现在网机组空载突加20%负载工况下的动态性能进行仿真,并和实际MVDC燃气轮机发电机组在突加20%负载工况下的实验结果进行对比。转速、直流电压和直流电流波形仿真与实验结果对比,分别如图7~图9所示,仿真与实验结果基本一致,验证了模型的有效性与准确度。
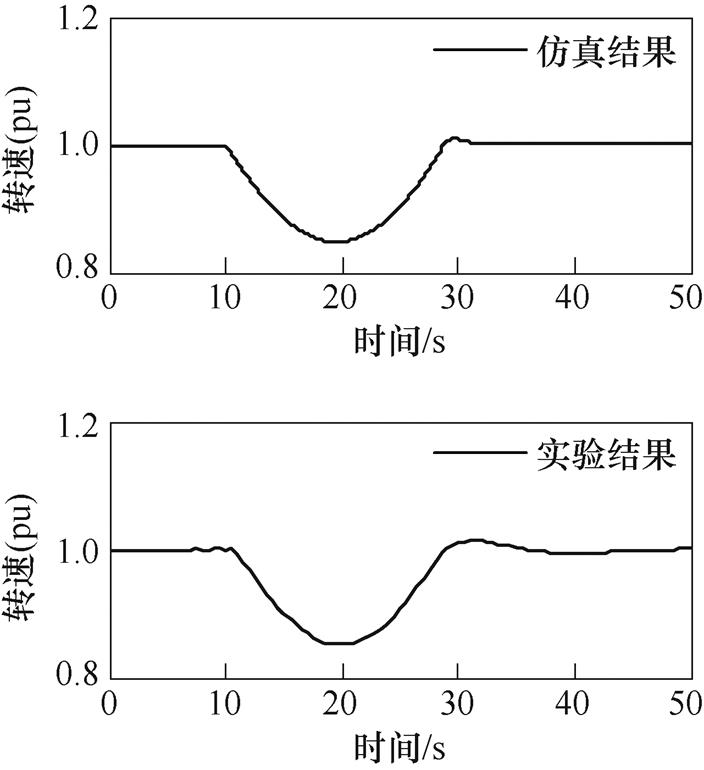
图7 转速波形对比
Fig.7 Comparison of speed waveforms

图8 直流电压波形对比
Fig.8 Comparison of DC voltage waveforms
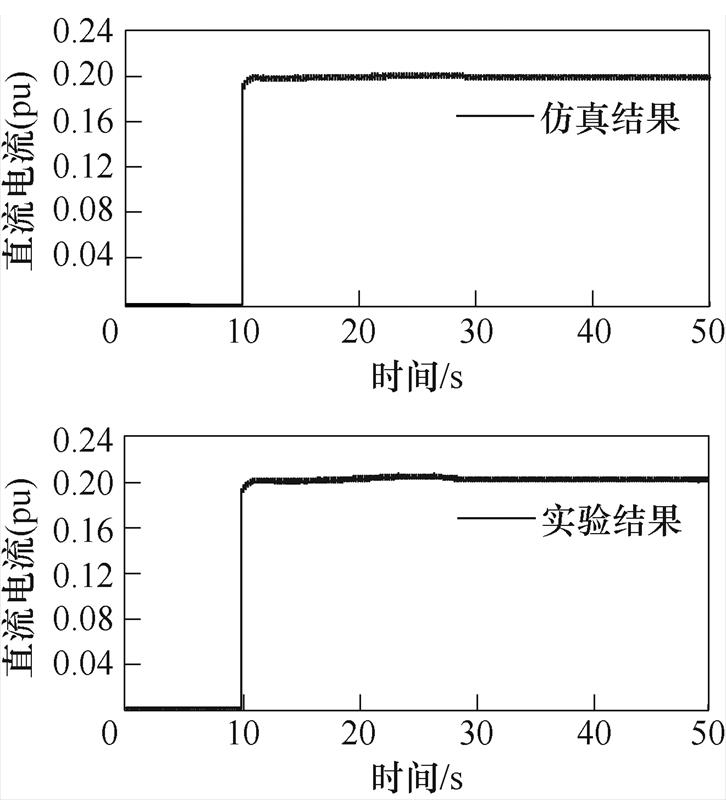
图9 直流电流波形对比
Fig.9 Comparison of DC current waveforms
进一步从仿真和实验波形中提取出该发电机组在突加20%负载动态工况下的转速和电压谷值,并计算转速和电压恢复至±3%误差带内所需的时间,见表2。对于MVDC综合电力系统重点关注的瞬态调速率、瞬态调压率以及转速、电压恢复时间等动态性能指标,表2显示仿真结果与实验结果相对误差最大为2.91%,更为有效地验证了MVDC发电机组模型的动态性能仿真分析精度。
表2 MVDC发电机组动态性能仿真与实验对比
Tab.2 Simulation and experimental comparison of dynamic performance of MVDC generator set

参 数仿真结果实验结果相对误差(%) 动态转速谷值(pu)0.8680.8571.28 动态电压谷值(pu)0.9330.9481.58 转速恢复时间/s20.020.62.91 电压恢复时间/s0.400.412.44
实测与仿真结果表明,该型燃气轮机发电机组在突加20%负载工况转速跌落较大,且转速恢复过程需约20 s,不满足船舶交流电力系统对发电用燃机瞬态调速性能的要求(<7%,5 s),但MVDC发电机组通过励磁系统的调节可在1 s内使直流母线电压恢复稳定,从而为负载提供稳定的功率。
基于此模型进行仿真分析,可以获得该型燃气轮机发电机组在突加30%、40%负载等工况下转速、燃油流量、励磁电流、输出电压等性能参数的变化规律,如图10和图11所示。
结合该模型及其仿真分析结果可知,燃气轮机调速与发电机励磁系统调压存在明显的相互耦合影响,即在动态过程中,首先燃气轮机受到了最大燃油升速率的限制,导致机组瞬态转速跌落较大,然后发电机励磁调节系统在转速跌落过程中,必须提供较大的励磁电流,才能维持机组输出电压恒定,但励磁系统存在最大励磁电流的限制。
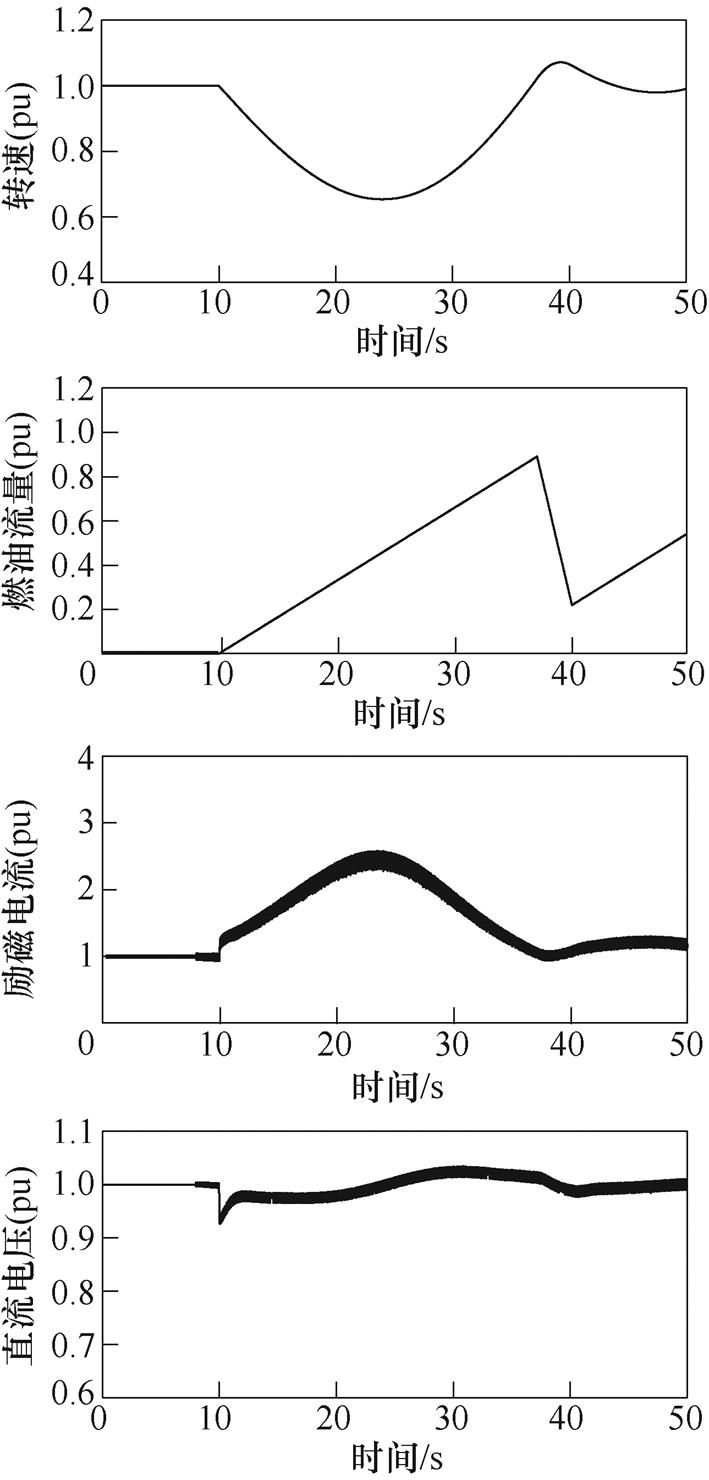
图10 突加30%负载工况下参数变化曲线
Fig.10 Charactical parameter curves under sudden increase of 30% load condition
对比图10和图11可知,受最大燃油升速率和最大励磁电流限制,该燃发机组允许突加负载上限约为30%,从而获得了该机组的动态正常运行边界。为提高此类发电机组的动态运行边界,设计其励磁系统时,建议预留充足的短时强励磁能力。
在原动机调速特性对MVDC发电机组运行有着直接且重要影响的背景,且现有研究成果并未有效解决考虑原动机动态调速特性下多相整流发电机及其励磁系统数学建模难题的问题导向下,本文基于十二相同步发电机及其三相交流励磁机数学模型提出了MVDC发电机组动态建模方法,以解决多相整流发电机及其励磁系统难以考虑原动机动态调速特性的难题。具体说来,本文以某型燃气轮机整流发电机组动态仿真模型为基础,系统建立了频率不同的十二相同步发电机与三相交流励磁机组合模型,全面阐述了原动机调速与发电机励磁调压相互耦合的计算流程。

图11 突加40%负载工况下参数变化曲线
Fig.11 Charactical parameter curves under sudden increase of 40% load condition
为验证MVDC发电机组动态仿真模型的分析精度,以真实系统可能出现在网机组空载突加20%负载工况下的动态性能进行仿真,并和实际MVDC燃气轮机发电机组在突加20%负载工况下的实验结果进行了对比。对比结果较为一致(动态转速谷值、动态电压谷值、转速恢复时间、电压恢复时间等各对比变量的最大误差为2.91%),且实测与仿真结果表明,该型燃气轮机发电机组在突加20%负载工况转速跌落较大,且转速恢复过程需要约20 s,但MVDC发电机组通过励磁系统的调节可在1 s内使直流母线电压恢复稳定,从而为负载提供稳定直流功率。在校准仿真模型基础上,通过系统分析突加不同比例负载的转速、燃油流量、励磁电流、输出电压等性能参数变化规律,获取了该燃发机组允许突加负载上限约为30%的运行边界认知,从而可为MVDC发电机组励磁系统设计以及如何预留充足的短时强励能力提供理论支持,进而可为推进MVDC综合电力系统的工程化进程提供有力支撑。
附 录
附表1 十二相同步发电机参数
App.Tab.1 Twelve-phase synchronous generator parameters
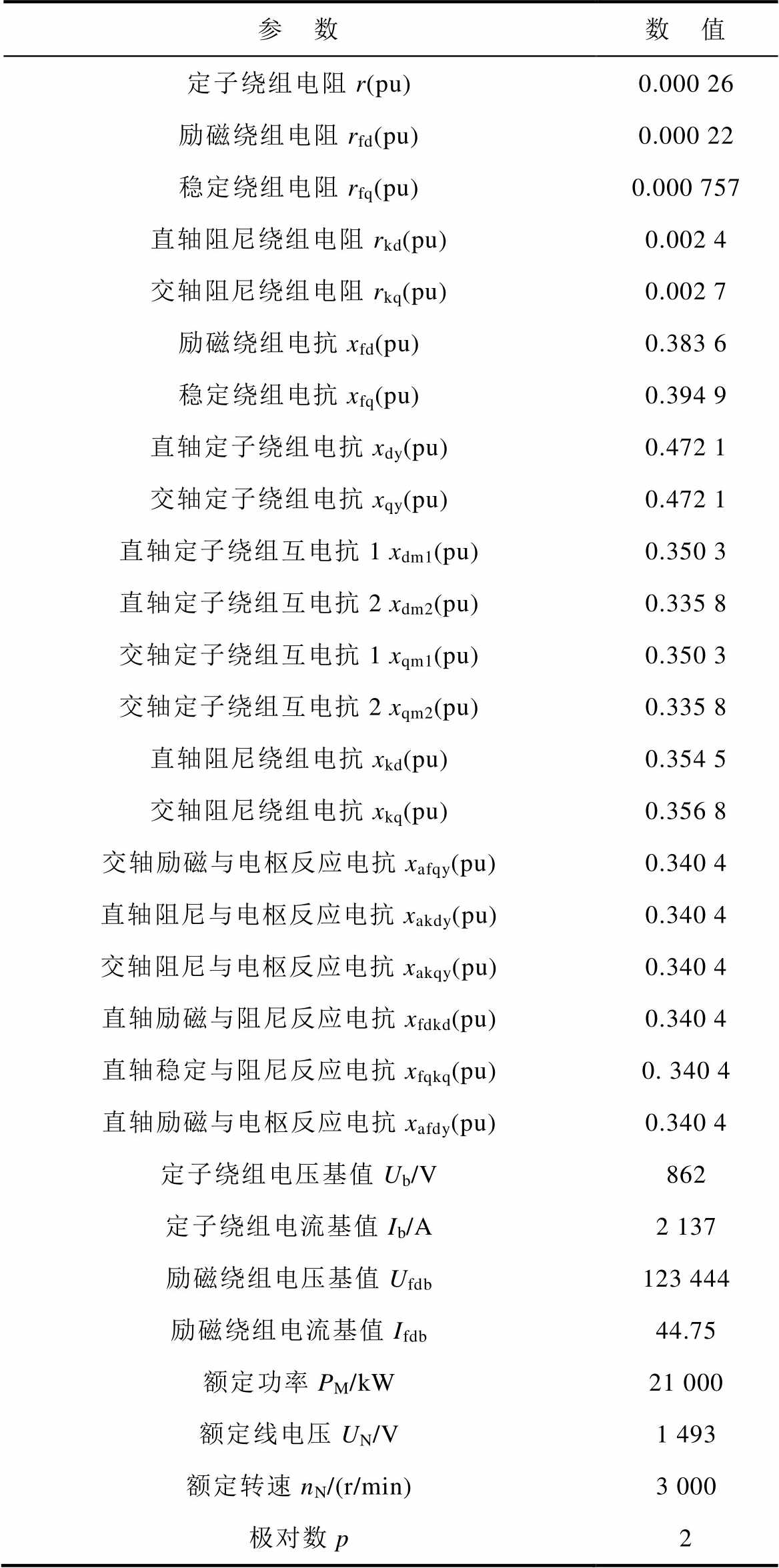
参 数数 值 定子绕组电阻r(pu)0.000 26 励磁绕组电阻rfd(pu)0.000 22 稳定绕组电阻rfq(pu)0.000 757 直轴阻尼绕组电阻rkd(pu)0.002 4 交轴阻尼绕组电阻rkq(pu)0.002 7 励磁绕组电抗xfd(pu)0.383 6 稳定绕组电抗xfq(pu)0.394 9 直轴定子绕组电抗xdy(pu)0.472 1 交轴定子绕组电抗xqy(pu)0.472 1 直轴定子绕组互电抗1 xdm1(pu)0.350 3 直轴定子绕组互电抗2 xdm2(pu)0.335 8 交轴定子绕组互电抗1 xqm1(pu)0.350 3 交轴定子绕组互电抗2 xqm2(pu)0.335 8 直轴阻尼绕组电抗xkd(pu)0.354 5 交轴阻尼绕组电抗xkq(pu)0.356 8 交轴励磁与电枢反应电抗xafqy(pu)0.340 4 直轴阻尼与电枢反应电抗xakdy(pu)0.340 4 交轴阻尼与电枢反应电抗xakqy(pu)0.340 4 直轴励磁与阻尼反应电抗xfdkd(pu)0.340 4 直轴稳定与阻尼反应电抗xfqkq(pu)0. 340 4 直轴励磁与电枢反应电抗xafdy(pu)0.340 4 定子绕组电压基值Ub/V862 定子绕组电流基值Ib/A2 137 励磁绕组电压基值Ufdb123 444 励磁绕组电流基值Ifdb44.75 额定功率PM/kW21 000 额定线电压UN/V1 493 额定转速nN/(r/min)3 000 极对数p2
附表2 三相励磁机参数
App.Tab.2 Three-phase exciter parameters

参 数数 值 电枢绕组电阻rs(pu)0.009 646 电枢绕组漏抗xl(pu)0.168 8 直轴电枢反应电抗xmd(pu)0.626 0 交轴电枢反应电抗xmq(pu)0.318 2 励磁绕组电阻rf(pu)0.001 632 励磁绕组漏抗xfdl(pu)0.072 4 电枢绕组电压基值Ube/V75.65
(续)

参 数数 值 电枢绕组电流基值Ibe/A236.6 励磁绕组电压基值Ufdeb/V14 007 励磁绕组电流基值Ifdeb/A3.833 额定功率PE/kW56 额定线电压UNe/V131 额定转速nNe/(r/min)3 000 极对数pe6 励磁机励磁电流最大值Iffdmax(pu)3
参考文献
[1] 马伟明. 舰船综合电力系统中的机电能量转换技术[J]. 电气工程学报, 2015, 10(4): 3-10.
Ma Weiming. Electromechanical power conversion technologies in vessel integrated power system[J]. Journal of Electrical Engineering, 2015, 10(4): 3-10.
[2] 付立军, 刘鲁锋, 王刚, 等. 我国舰船中压直流综合电力系统研究进展[J]. 中国舰船研究, 2016, 11(1): 72-79.
Fu Lijun, Liu Lufeng, Wang Gang, et al. The research progress of the medium voltage DC integrated power system in China[J]. Chinese Journal of Ship Research, 2016, 11(1): 72-79.
[3] 李浩然, 崔超辉, 王生东, 等. 基于二阶拟合模型的SiC双向LLC数字同步整流控制[J]. 电工技术学报, 2022, 37(24): 6191-6203.
Li Haoran, Cui Chaohui, Wang Shengdong, et al. Two-order fitting model-based digital synchronous rectifier control for SiC bidirectional LLC con- verter[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6191-6203.
[4] 宋钊, 刘明. 模块化多端口无线电能DC-DC变换器建模及其多向功率流解耦控制策略[J]. 电工技术学报, 2022, 37(24): 6262-6271.
Song Zhao, Liu Ming. Modular multiport wireless DC-DC converter with multidirectional power flow and its decoupling control strategy[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6262- 6271.
[5] 原露恬, 王琛琛, 薛尧, 等. 适用于中压领域的V形钳位多电平变换器[J]. 电工技术学报, 2021, 36(20): 4318-4328, 4338.
Yuan Lutian, Wang Chenchen, Xue Yao, et al. V- clamp multilevel converters suitable for medium- voltage fields[J]. Transactions of China Electro- technical Society, 2021, 36(20): 4318-4328, 4338.
[6] 林霖, 裴忠晨, 蔡国伟, 等. 混合式隔离型模块化多电平变换器[J]. 电工技术学报, 2021, 36(16): 3319-3330.
Lin Lin, Pei Zhongchen, Cai Guowei, et al. Hybrid isolated modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3319-3330.
[7] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636.
Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[8] 马凡, 付立军, 郭云珺, 等. 十二相同步发电机整流系统直流极间短路电流的解析计算方法[J]. 中国电机工程学报, 2021, 41(20): 7117-7126.
Ma Fan, Fu Lijun, Guo Yunjun, et al. Analytic calculation of pole-to-pole faults in twelve-phase synchronous generator-rectifier systems[J]. Proceedings of the CSEE, 2021, 41(20): 7117-7126.
[9] 黄河, 马凡, 付立军, 等. 十二相整流发电机并联供电系统直流中点环流特性及其抑制方法[J]. 电工技术学报, 2022, 37(7): 1760-1767.
Huang He, Ma Fan, Fu Lijun, et al. DC neutral point circulating current characteristics and suppression method of twelve-phase rectifier generator parallel power supply system[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1760-1767.
[10] 谢卫, 朱军. 十二相四Y移15°绕组同步电动机的数学模型及动态仿真[J]. 电工技术学报, 2004, 19(1): 2-6.
Xie Wei, Zhu Jun. Modeling and simulation of 12-phase synchronous motor with four Y-connected 3-phase symmetrical windings displaced in turn by 15°[J]. Transactions of China Electrotechnical Society, 2004, 19(1): 2-6.
[11] 魏克银, 刘德志, 欧阳斌, 等. 一种带线性动态负载的十二相飞轮储能发电机系统[J]. 电工技术学报, 2010, 25(1): 37-42.
Wei Keyin, Liu Dezhi, Ouyang Bin, et al. A 12-phase flywheel energy storage generator system with linearly dynamic load[J]. Transactions of China Elec- trotechnical Society, 2010, 25(1): 37-42.
[12] 刘金利, 马伟明, 翟小飞, 等. 双九相储能电机带整流负载系统降阶等效平均模型研究[J]. 电工技术学报, 2018, 33(17): 4052-4059.
Liu Jinli, Ma Weiming, Zhai Xiaofei, et al. Study on equivalent reduced average model of dual nine-phase energy storage electrical machine with rectifier load[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4052-4059.
[13] 晏明, 马伟明, 欧阳斌, 等. 双九相储能电机系统性能研究[J]. 中国电机工程学报, 2015, 35(15): 3770-3775.
Yan Ming, Ma Weiming, Ouyang Bin, et al. Study on the characteristics of dual nine-phase energy storage electrical machine[J]. Proceedings of the CSEE, 2015, 35(15): 3770-3775.
[14] 欧阳斌, 马伟明, 王东, 等. 大容量双六相储能电机系统建模与仿真[J]. 电机与控制学报, 2014, 18(1): 92-97.
Ouyang Bin, Ma Weiming, Wang Dong, et al. Modeling and simulation of energy storage system with dual six-phase electrical machine of great capacity[J]. Electric Machines and Control, 2014, 18(1): 92-97.
[15] 马伟明, 王东. 多相整流发电机及其系统的分析[M]. 杭州: 浙江大学出版社, 2020.
[16] 孙鹏, 张善科, 马正军, 等. 某型燃气轮机发电机组大负荷突卸时动态特性仿真与试验研究[J]. 热能动力工程, 2019, 34(7): 66-70.
Sun Peng, Zhang Shanke, Ma Zhengjun, et al. Simulation and experimental study on dynamic characteristics of a gas turbine generator unit during suddenly unloading at heavy load[J]. Journal of Engineering for Thermal Energy and Power, 2019, 34(7): 66-70.
[17] Yi Xinqiang, Wang Dong, Guo Yunjun, et al. Research on self-excited initiation of a Medium- voltage DC (MVDC) multiphase synchronous generator-rectifier system[C]//2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 2015: 368-372.
Abstract Compared with the medium voltage AC(MVAC) integrated power system, the medium voltage DC(MVDC) integrated power system eliminates the influence between the rotational speed of the prime mover and the frequency of the power grid, providing an effective solution for the parallel power supply of multiple gas turbine generator sets, diesel engine generator sets, and steam turbine generator sets with different speed regulation characteristics and magnitude differences in capacity. In MVDC integrated power systems, a multi-machine parallel power supply is commonly used to improve fuel operation economy and power supply reliability. If a single unit trips, it will trigger a dynamic process of sudden load application to units on the grid. The stability of the grid voltage is crucial at the beginning of the design of the MVDC integrated power system, which is closely related to the speed regulation of the prime mover and the voltage regulation of the generator. Therefore, it is necessary to establish a dynamic simulation model for MVDC generator units considering the speed regulation characteristics of the prime mover.
Based on traditional modeling methods for synchronous generators, this paper takes a time base value of 1, unifying the electrical angular velocity input interface of the mathematical models for twelve-phase synchronous generators and their three-phase exciters. A variable coefficient matrix simulation model with high order and state space is established considering the speed variation, as shown in Fig.A1. A dynamic modeling method for MVDC generator sets is constructed with speed regulation characteristics of prime movers. Taking a gas turbine generator unit as an example, the dynamic simulation model is established in Matlab/Simulink software, as shown in Fig.A2. The output electromagnetic torque of the MVDC generator and its excitation system is introduced into the gas turbine and its speed governing system, and the output rotational speed is connected to the MVDC generator and its excitation system, which achieves strong coupling numerical simulation calculations for the prime mover’s speed regulation and the generator excitation’s voltage regulation.
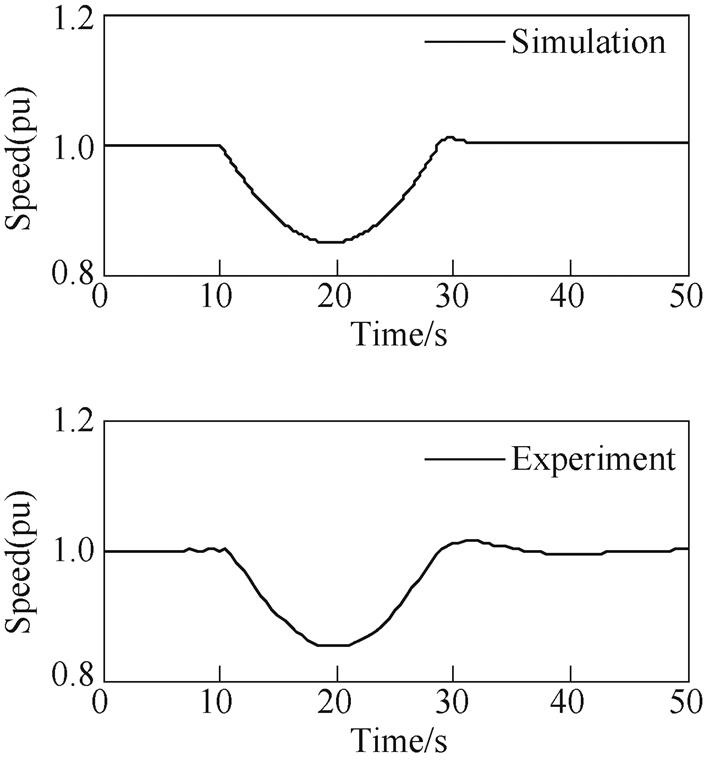
Fig.A1 Comparison of speed waveform
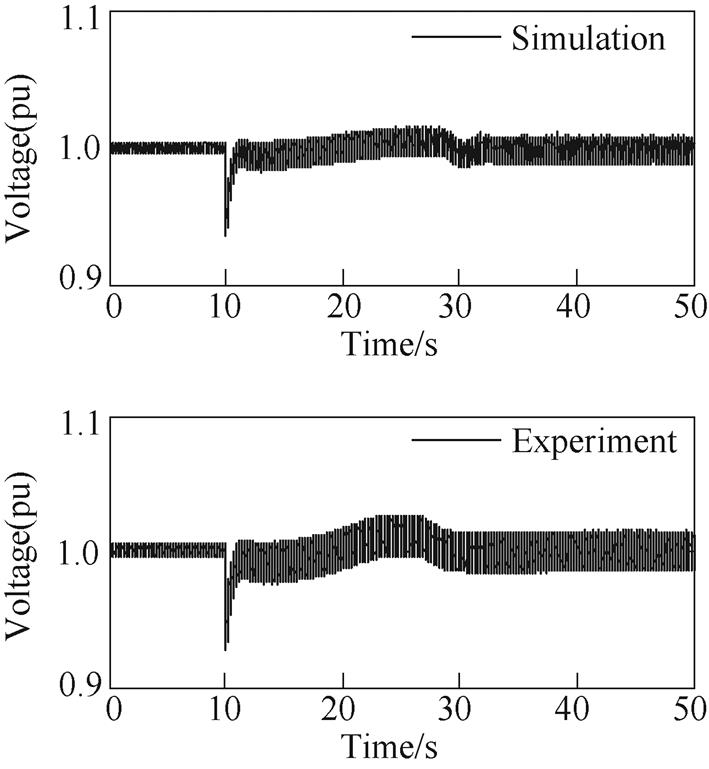
Fig.A2 Comparison of DC voltage waveform
The dynamic performance of a real system under the no-load sudden load condition is simulated, comparing the experimental data from actual MVDC gas-turbine power generation units under a sudden load condition of 20%. The comparison reveals consistent rotational speed output waveforms (Fig.A1) and DC voltage output waveforms (Fig.A2). Key dynamic performance indicators are analyzed, including transient speed regulation rate, transient voltage regulation rate, rotational speed, and voltage recovery time. The maximum relative error between the simulation and the experiment is 2.91%, verifying the accuracy of the dynamic performance simulation analysis of the MVDC generator set model.
keywords:Speed characteristics of prime mover, MVDC generator set, twelve-phase rectifier generator, dynamic simulation model
DOI: 10.19595/j.cnki.1000-6753.tces.230383
中图分类号:TM314
国家自然科学基金资助项目(52107136, 52207047)。
收稿日期 2023-03-31
改稿日期 2023-06-07
易新强 男,1986年生,副研究员,研究方向为多相整流发电机励磁控制、电力推进技术。E-mail: yixinqiang86@163.com
王 东 男,1978年生,教授,博士生导师,研究方向为电力推进、独立电源系统。E-mail: wangdongl@vip.sina.com(通信作者)
(编辑 崔文静)