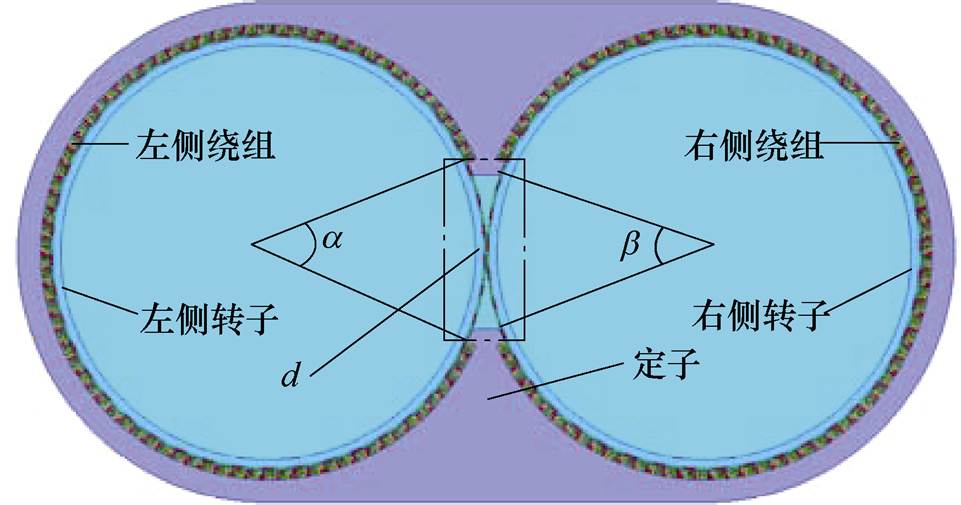
图1 DR-PMDM典型结构
Fig.1 Structure of DR-PMDM
摘要 双并列转子永磁直驱电机受轴间距限制，设计时会切掉部分定子铁心和绕组，造成转子电磁力不平衡。为最大限度地抑制转子所受的不平衡电磁力，该文从双并列转子结构出发，分析了电机绕组电感参数不对称的原因，提出通过合理设计线圈跨距和分布平衡三相电感。在此基础上，构建转子所受总电磁力的数学模型，理论分析各个分力的来源及影响因素，研究各个分力对转子所受总电磁力的影响，提出了优化占空角、优化耦合间距、采用定子端部不对称结构、采用转子偏心结构和切除部分单元电机五种优化方法，实现对转子所受电磁力的优化，探讨了不同方法的优化效果，以及其对转矩脉动的影响，总结了不同优化方法的优缺点。
关键词：双并列转子 永磁直驱电机 电磁力 优化方法
并行对驱机械设备广泛应用于二辊轧机、双螺杆泵、破碎机等领域。以二辊轧机为例，目前的驱动方式为主从驱动，即由一台三相感应电机驱动主动轴，通过主从动轴上同步机械齿轮的转矩传递作用，实现两个辊轴的反向同步旋转[1-2]。这种采用同步机械齿轮的传统驱动方式存在系统结构复杂、传动链长、系统效率低、减速箱漏油、维护复杂等问题[3-4]，而通过两个完整的低速电机分别直驱难以满足双并列轴间距尺寸要求，因此双并列转子永磁直驱电机（Dual-parallel Rotor Permanent Magnet Direct-driven Motor, DR-PMDM）逐渐进入人们的视野，其两个轴伸直接套装在二辊轧机的两个辊轴上，解决了上述由同步机械齿轮的存在而带来的一系列问题。
一台二辊轧机用DR-PMDM的典型结构如图1所示。定子可以看成由两个完全相同的传统结构电机定子各自切割掉部分单元电机后拼接而成；两个并列转子采用表贴式永磁转子结构。两个转子铁心上均匀分布永磁体，沿中心线对称位置的永磁体极性相反。两个转子之间沿单侧圆周无绕组分布的区域定义为耦合区，见图1点画线框部分，图2为其放大图。耦合区所占的圆心角定义为耦合角a。耦合区中沿单侧圆周被切割掉的定子铁心区域定义为占空区，所对应的圆心角称为占空角b。两个永磁转子之间的最小距离称为耦合间距d，单位为mm。
图1 DR-PMDM典型结构
Fig.1 Structure of DR-PMDM
DR-PMDM左右侧绕组都是非完整圆周分布，当绕组采用双层绕组时，由于单侧部分定子铁心的缺失，导致靠近耦合区附近的部分线圈无处安放。解决办法是将拼接的连体定子看成由多个分块定子组成，每个定子模块采用不等跨距绕组[5]。然而，这种方法使得三相电感参数不再对称。当电机接入三相对称电压时，产生不对称的三相电流，由负序电流产生的负序磁场会严重影响电机的性能。目前，研究电感参数的不平衡问题主要针对的是直线电机或弧线电机，通过添加定子辅助槽或绕组换位可以在一定程度上平衡电感[6-8]；也有学者提出不等匝数绕组结构[9]或设计反馈解耦器[10]来抑制电感的不对称。基于以上原因，对DR-PMDM绕组的合理设计是必要的，这是对此类电机进行优化设计的前提。
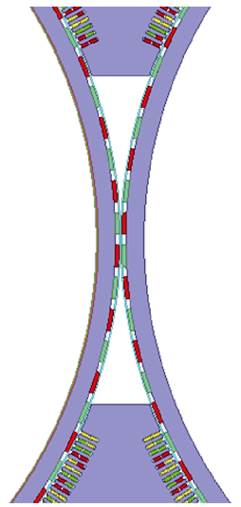
图2 DR-PMDM耦合区示意图
Fig.2 Coupling area of DR-PMDM
耦合区的存在使得电机运行时转子受到不平衡电磁力，不平衡电磁力的存在会引起转子振动，从而影响电机的稳定运行。同时，不平衡电磁力会增大转轴的挠度，影响轴承的寿命。对于不平衡电磁力，大多数文献都专注于研究因转子偏心而造成的不平衡电磁力问题[11-13]，主要关注力的谐波频率与定子振动模态频率的关系，也有学者对集中绕组永磁电机局部切向力的削弱[14]、盘式对转双转子永磁电机的轴向磁拉力的抑制[15]及用于特殊应用场合下永磁电机电磁力的解析计算做了大量研究[16-17]。然而，DR-PMDM转子所受的不平衡电磁力是由于其结构特殊性带来的特有问题，探明该类结构电机转子不平衡电磁力机理，对促进其工程应用与开发具有重要理论意义和工程实用价值。
DR-PMDM工况下转子所受的电磁力主要包含五个部分，分别为含绕组的定子与对应转子之间的电磁力、定子拼接处铁心端部与耦合区内占空区外的转子的作用力、占空区内两个永磁转子之间的作用力、占空区内转子对铁心端部的磁阻力和附加电磁力。左右两侧转子所受的总电磁力和力的各个分量大小完全相同，方向沿中心线镜像对称。本文旨在对DR-PMDM转子所受的电磁力进行分析和优化设计。在绕组的电感参数基本平衡后，分析了转子所受电磁力的来源，建立了转子不平衡电磁力的数学模型。此外，研究了削弱转子所受不平衡电磁力的方法，包括优化占空角大小、优化耦合间距、采用定子铁心端部不对称结构、采用转子偏心结构、采用切除部分单元电机的方式等，同时考虑了其对转矩脉动的影响，以此来提高此类电机运行时的可靠性，并总结了五种优化方法的优缺点，为双并列转子永磁直驱电机的研发提供了参考。
本文以某双轴并列驱动系统实际工程需求为背景，额定功率为1 200 kW、额定转速为20 r/min的DR-PMDM的主要参数及尺寸见表1，尺寸参数为单侧电机的尺寸参数。电机采用定子模块化结构，其可以视为由多个模块化单元电机组成。根据需要可以将不同模块进行串联或并联，用多个小容量变频器进行驱动，提高了电机系统的容错性和控制的灵活性。电机左右两侧绕组沿中心线对称分布，处于对称位置的两侧绕组电流完全相同，即电流幅值大小、相位相序完全相同。由此，两侧绕组在各自的气隙中产生完全相同的旋转磁场，保证两个转子严格同步旋转。
表1 DR-PMDM的主要参数和尺寸
Tab.1 Main parameters and dimension of DR-PMDM
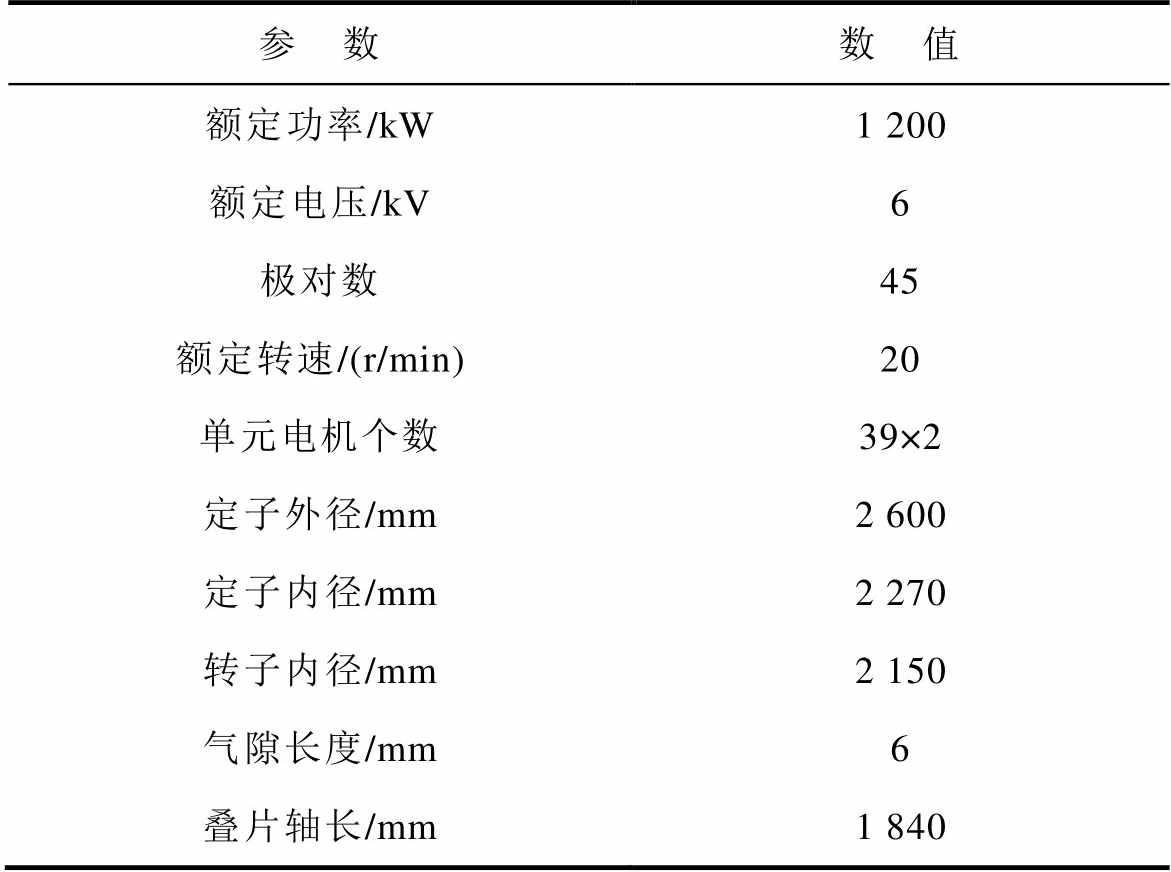
参 数数 值 额定功率/kW1 200 额定电压/kV6 极对数45 额定转速/(r/min)20 单元电机个数39×2 定子外径/mm2 600 定子内径/mm2 270 转子内径/mm2 150 气隙长度/mm6 叠片轴长/mm1 840
DR-PMDM中一个模块单元电机的电压方程为
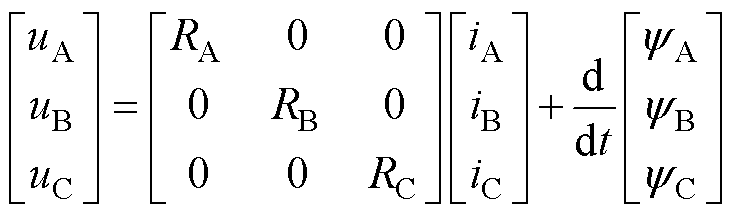（1）
式中，u为绕组相电压（V）；i为绕组相电流（A）；R为绕组相电阻（W）；y 为一相绕组的全磁链（Wb）。有
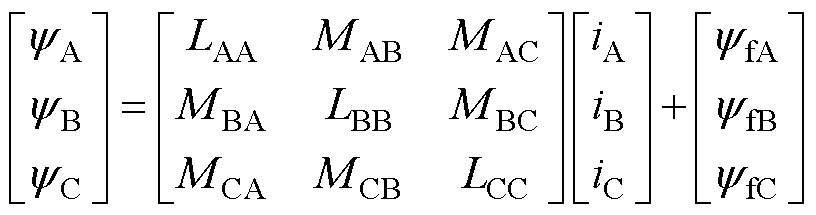（2）
式中，L和M分别为三相绕组的自感和互感（H）；yf为永磁体磁链（Wb）。单侧电机的瞬时电磁功率pe为
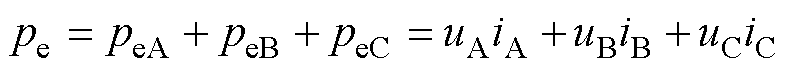（3）
根据式（3）及三相交流电路基本原理可知，当接入三相对称电源，只有三相负荷对称，其电磁功率才可以表示为pe=3UAIAcosj =3PeA，即产生恒定电磁转矩。其中，UA、IA、PeA、cosj 分别为A相电压有效值、电流有效值、产生的恒定电磁功率及功率因数。换言之，式（2）中三相绕组的自感L和互感M的对称性是保证负荷对称的必要条件。然而，由于定子的模块化结构会引入不等跨距的线圈，影响了电机绕组互感的对称性；同时，靠近耦合区边缘的定子存在端部效应，影响了靠近端部绕组的自感。
需要说明的是，不等跨距线圈的引入也会导致三相电阻参数的不对称，但由于一个模块化单元电机叠片的轴向长度（1 840 mm）远远大于周向长度（约150 mm），三相电阻参数可认为近似相等。因此，本文研究绕组参数的对称性，将主要以三相电感参数的对称性为主，忽略电阻的影响。
本文研究的DR-PMDM采用模块化设计思想，左右各有39个模块单元电机，每个模块单元电机为2极9槽，每极每相槽数q=3/2，其结构如图3所示。为了削弱5次和7次谐波电动势，绕组跨距y1一般选为
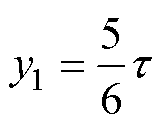（4）
式中，t 为定子极距（槽）。本文采用分数槽分布绕组，经过计算y1=3.75。因此，绕组跨距选为3或4。
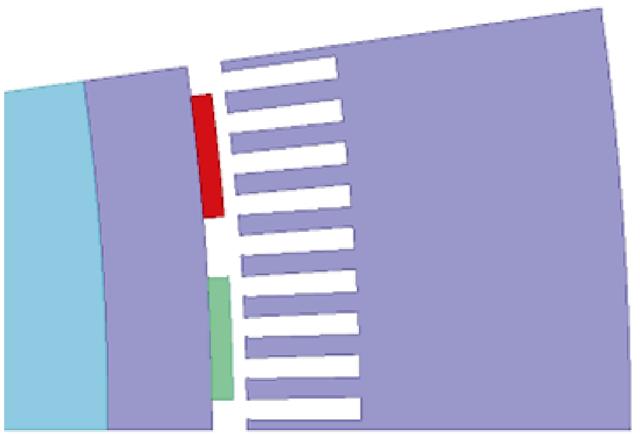
图3 模块单元电机结构
Fig.3 Structure of one module unit motor
当绕组跨距选为4时，单元电机的绕组连接如图4所示。由图4可知，A相绕组存在两个跨距为4的线圈和一个跨距为5的线圈，B相存在三个跨距为4的线圈，C相存在两个跨距为5的线圈和一个跨距为4的线圈，且无论将A相首端选在哪个槽都不能使各相大小跨距的绕组数量相同，这使得各相绕组自感不等。根据1.1节所述，模块单元电机的轴向长度远大于周向长度，即使各相绕组大小跨距线圈数量不同，但对各相自感的影响很小，三相自感可认为近似对称，即LAA≈LBB≈LCC。由图4可知，A相绕组和B相绕组在模块单元电机的两侧，C相绕组位于中部，故A相绕组和C相绕组交链的磁通，以及B相绕组和C相绕组交链的磁通均多于A相绕组和B相绕组交链的磁通，由此可以推断MAC≈MBC＞MAB。
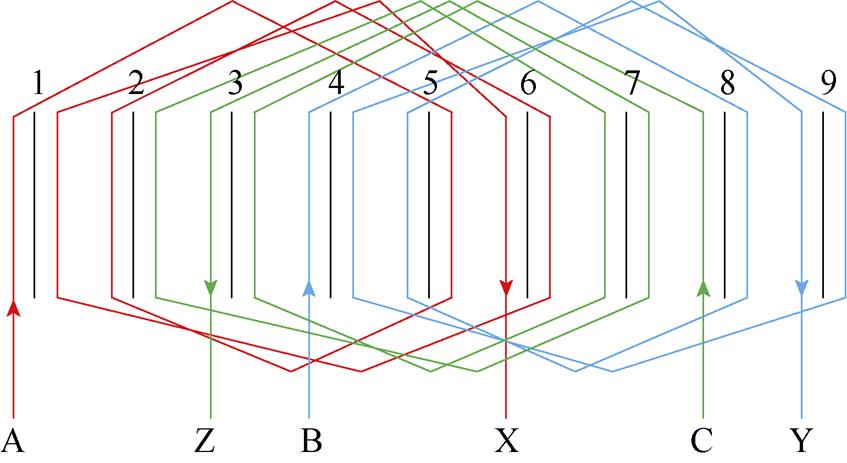
图4 跨距为4时模块单元电机绕组展开
Fig.4 Winding connection diagram of one module unit motor with the coil pitch is 4
当绕组跨距选为3，且将A相绕组的首端选在3号槽时，单元电机的绕组连接如图5所示。由图5可知，A、B、C三相绕组均由两个跨距为3的线圈和一个跨距为6的线圈组成。A、B、C三相绕组中仍可认为LAA≈LBB≈LCC。与绕组跨距为4时相比较，各相绕组之间交链磁通的均匀程度大大提高，改善了各相绕组之间的互感，此时可认为MAB≈ MBC≈MAC。
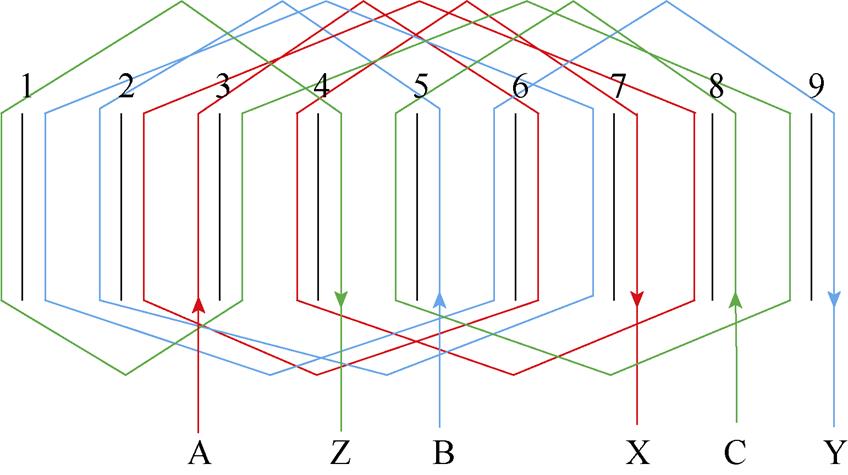
图5 跨距为3时模块单元电机绕组展开
Fig.5 Winding connection diagram of one module unit motor with the coil pitch is 3
根据以上分析，大跨距线圈的使用势必会影响三相绕组的参数，尤其是各相之间的互感。因此，对DR-PMDM进行电磁设计时，必须对绕组跨距和各相分布进行合理选择。
DR-PMDM的各个模块单元电机完全相同，考虑一个单元电机三相绕组的电感进行计算。由于采用了不等跨距的线圈，端部交叠比较复杂，采用解析法计算电感时精度难以得到保证，故本节采用有限元法来计算，能够考虑到漏电感的影响。
绕组跨距为4和3时一个模块单元电机三相绕组的自感和互感分别如图6、图7所示。根据图6、图7计算各相电感参数的平均值，并将两种跨距下的自感和互感整理见表2和表3。可知，当绕组跨距选为4时，自感的不对称度为0.36%，互感的不对称度为19.27%。当绕组跨距选为3时，自感的不对称度为2.06%，互感的不对称度为5.01%。与绕组跨距为4时的自感相比，跨距为3时绕组自感的不对称度增加的原因是，跨距为3的各相绕组线圈分布规律性不强，相对较杂乱，而跨距为4的各相绕组线圈主要集中在某几个槽内，使得各相绕组自感的不对称度增加。然而，跨距为3时绕组间互感的不对称度降低了74%，说明跨距设计为3时，能够极大地增加各相绕组互感的对称性，这与1.2节中的分析结果一致。
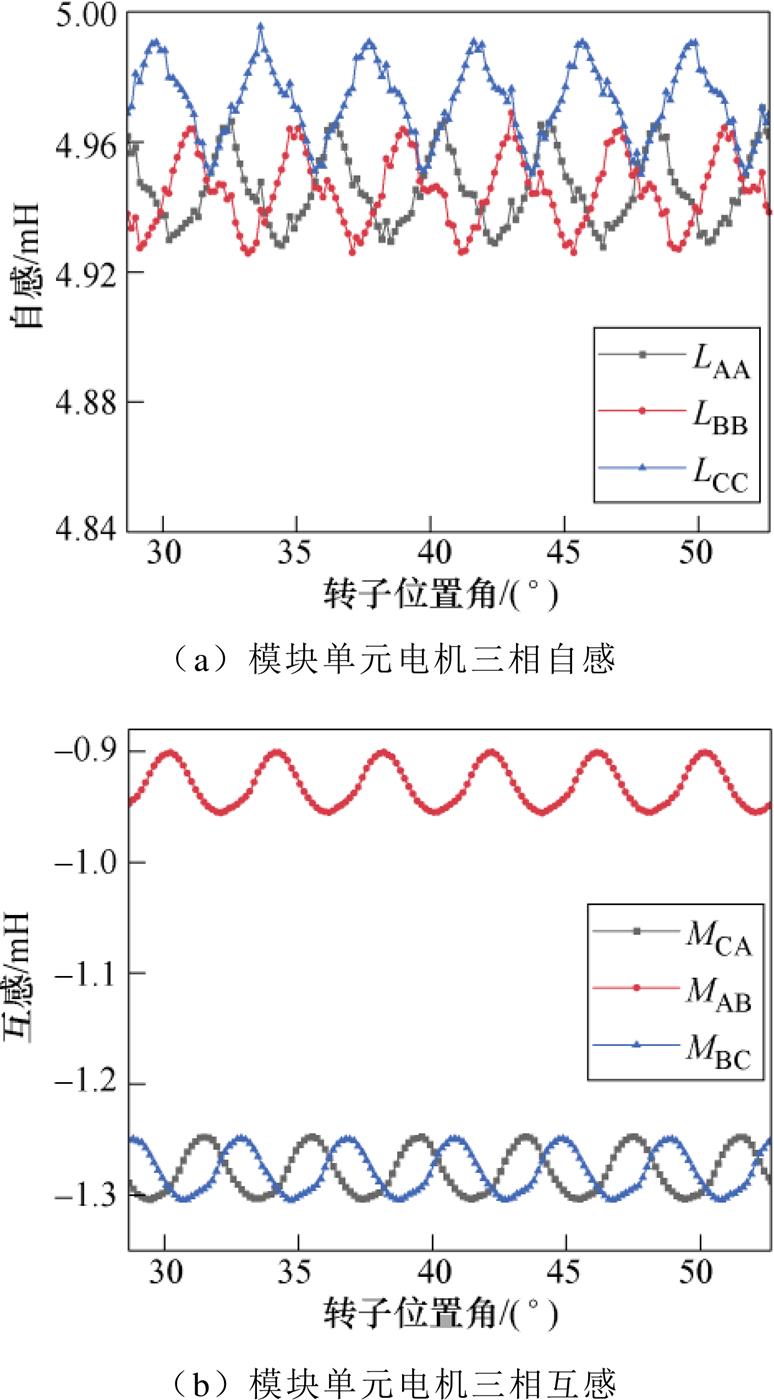
图6 跨距为4时模块单元电机电感
Fig.6 Inductance of one module unit motor with the coil pitch is 4
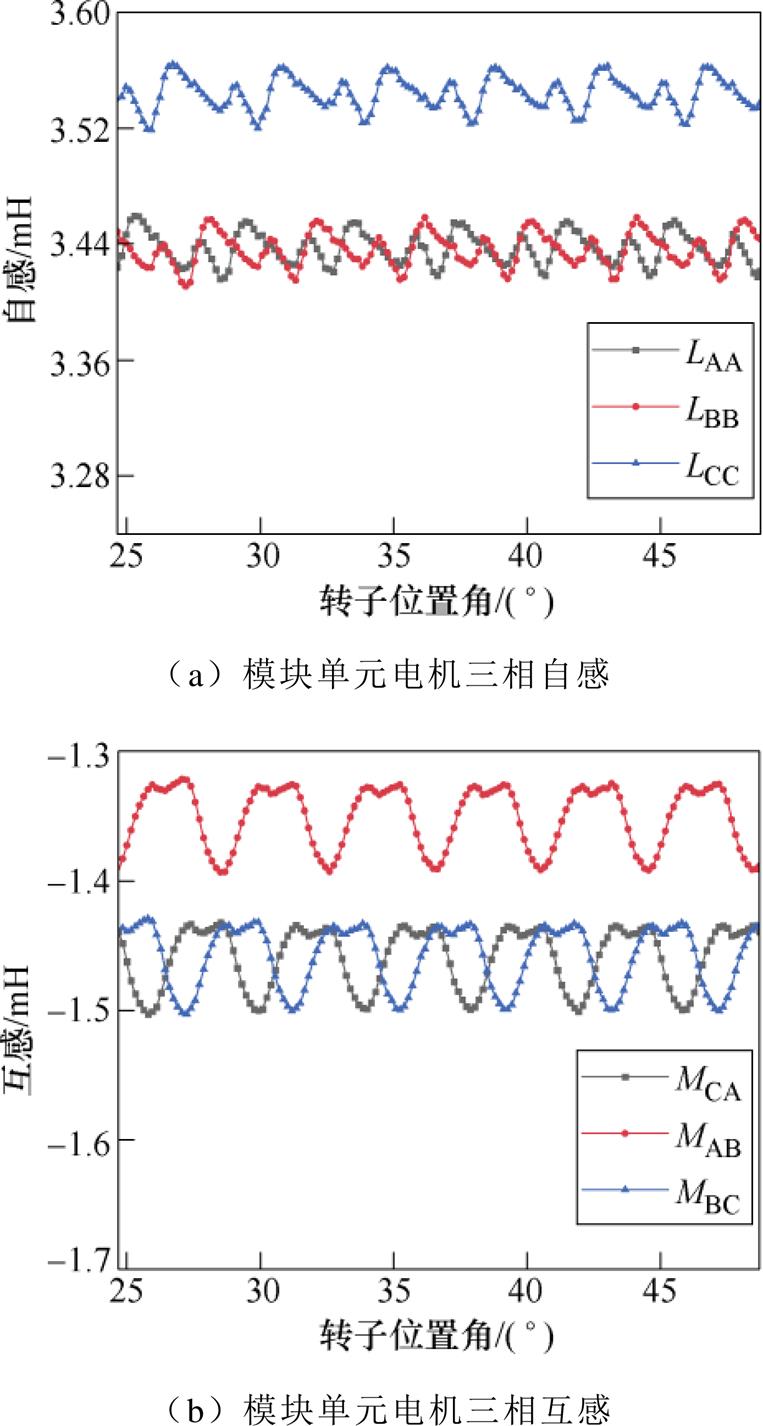
图7 跨距为3时模块单元电机电感
Fig.7 Inductance of one module unit motor with the coil pitch is 3
表2 两种跨距下的自感
Tab.2 Self-inductance under two coil pitch
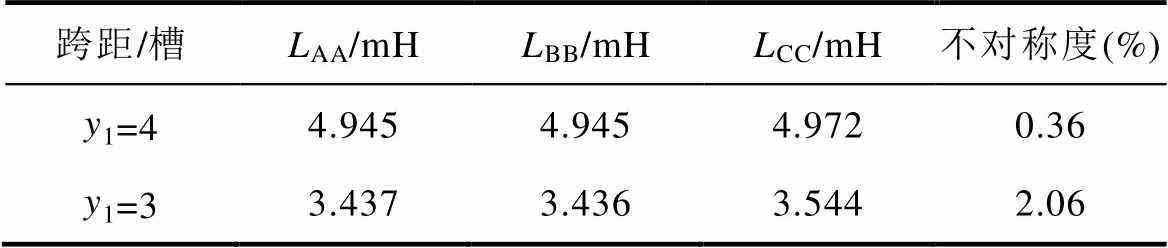
跨距/槽LAA/mHLBB/mHLCC/mH不对称度(%) y1=44.9454.9454.9720.36 y1=33.4373.4363.5442.06
表3 两种跨距下的互感
Tab.3 Mutual inductance under two coil pitch
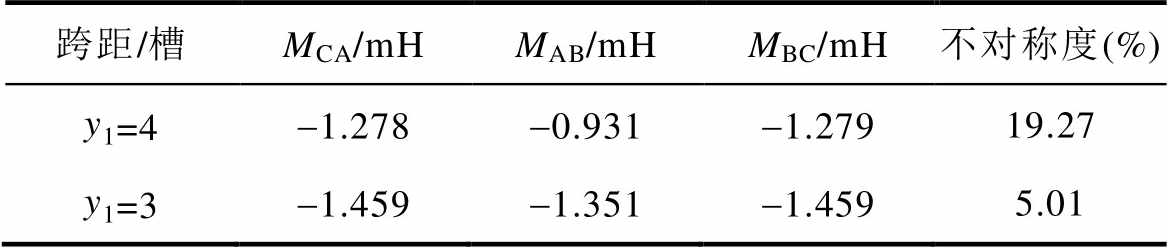
跨距/槽MCA/mHMAB/mHMBC/mH不对称度(%) y1=4-1.278-0.931-1.27919.27 y1=3-1.459-1.351-1.4595.01
根据表2和表3，计算跨距为3时单元电机的A、B、C各相的总电感L，求得
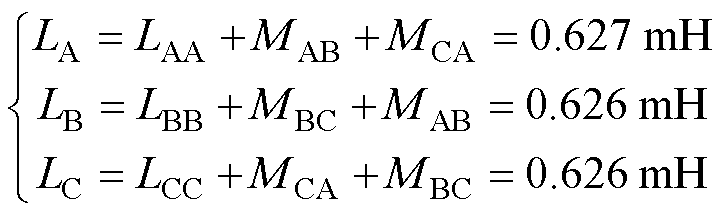（5）
由式（5）可见，A、B、C各相的总电感几近相同，由大跨距线圈的使用而带来的三相电感参数不对称问题得到了解决。特别说明，靠近耦合区的4个单元电机中靠近铁心端部线圈的磁通不得不流过端部铁心，而单元电机其他线圈的磁通通过定子齿完成闭合，从而影响了端部线圈的电感。本文研究的DR-PMDM共有78个模块单元电机，与74个模块单元电机相比，这4个单元电机相电感的微小变化对整体电机的性能影响不大，因此这种影响可以忽略。
综上所述，当设计DR-PMDM的绕组时，需要考虑三相电感参数的不对称问题。通过选择合适的绕组跨距和A相绕组的首端，可以近乎完美地平衡电感，这也是后文对DR-PMSM转子所受不平衡电磁力进行分析和优化设计的前提。
DR-PMDM左右两个转子受力情况基本相同，两个转子所受合力和各个力的分量大小相等，仅是方向不同。为了表达方便，除非特殊说明，本文所述转子所受的电磁力均以左侧转子为研究对象，分析其受力组成，右侧转子的受力情况可根据结构的对称性来分析。文中，F为矢量，既有大小又有方向，F仅表示其大小。
DR-PMDM转子所受的总电磁力表达式为
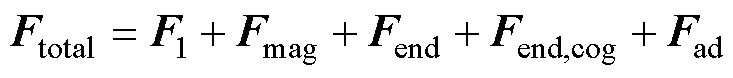（6）
式中，Ftotal为转子所受的总电磁力；F1为含绕组的定子与对应转子之间的电磁力；Fmag为占空区内两个永磁转子之间的磁力；Fend为铁心端部与耦合区内占空区外转子的作用力；Fend,cog为占空区内转子对铁心端部的磁阻力；Fad为附加电磁力。本文所涉及的力的单位均为kN。
在直角坐标系中，将式（6）分解为X方向和Y方向的分力，其表达式为
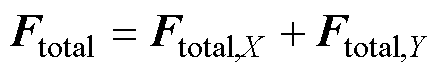（7）
式中，Ftotal,X和Ftotal,Y分别为Ftotal的X方向和Y方向的分量。
转子所受的电磁力示意图如图8所示，图中各部分电磁力的分量仅是为了说明该种电磁力的方向，箭头的数量和线段的长短并不代表力的密集程度和大小。由于转子同步旋转，各部分电磁力的大小是随时间变化的周期函数，本文对额定工况下各部分电磁力的平均值进行研究，下文将对各部分电磁力进行逐一分析。
含绕组的定子与对应转子之间的电磁力F1可参照常规永磁同步电机电磁力的求解方法。首先采用针对磁场的解析方法计算电磁力密度，然后根据Maxwell张量法求得电磁力的表达式。径向电磁力密度和切向电磁力密度分别为
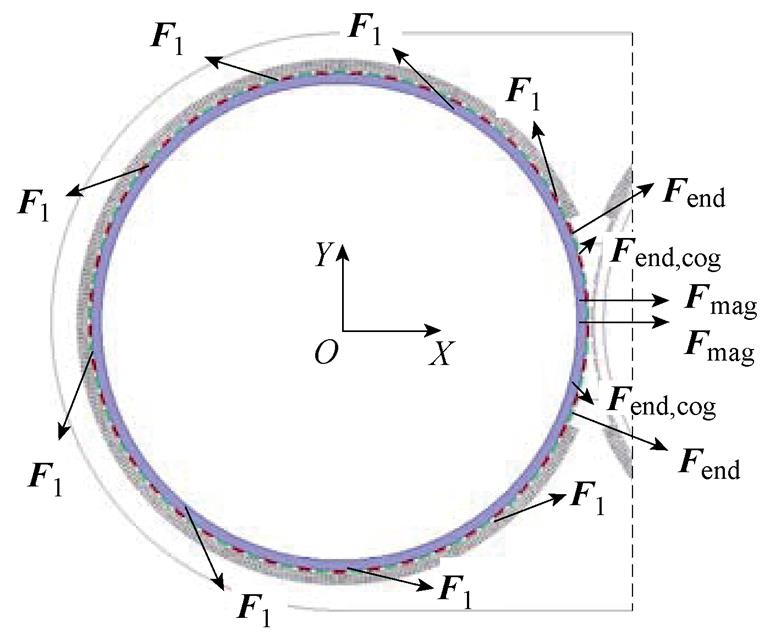
图8 转子所受电磁力示意图
Fig.8 The electromagnetic force on the rotor
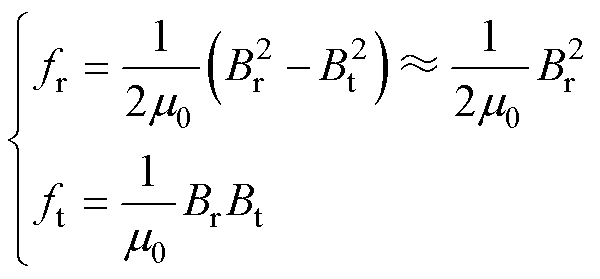（8）
式中，fr和ft分别为径向、切向电磁力密度（N/m2）；Br和Bt分别为径向、切向气隙磁通密度（T）；m0为真空磁导率（H/m）。
一般情况下，气隙磁场中Br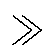
Bt，因此计算fr时常忽略Bt的影响。F1在直角坐标系中表示为
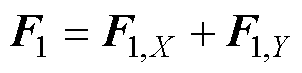（9）
式中，F1,X和F1,Y分别为F1的X方向和Y方向的分量。
由于电机结构的对称性，在转子位置角[a/2, p-a/2]中转子所受的F1和在[a/2+p, -a/2]中转子所受的F1相互抵消，实际对转子所受不平衡力起作用的是在[p-a/2, a/2+p]范围内的F1，如图9所示。在图9中，在转子位置[p-a/2, a/2+p]中任取一点A，位置角为q，点A所受的径向电磁力和切向电磁力分别为Fr,A和Ft,A，则点A所受X方向和Y方向的电磁力FX,A和FY,A分别为
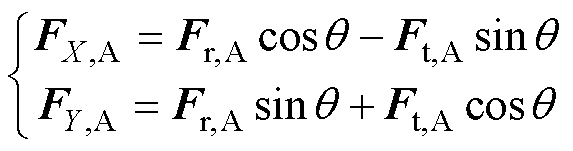（10）
由此可推导出F1,X和F1,Y的表达式分别为
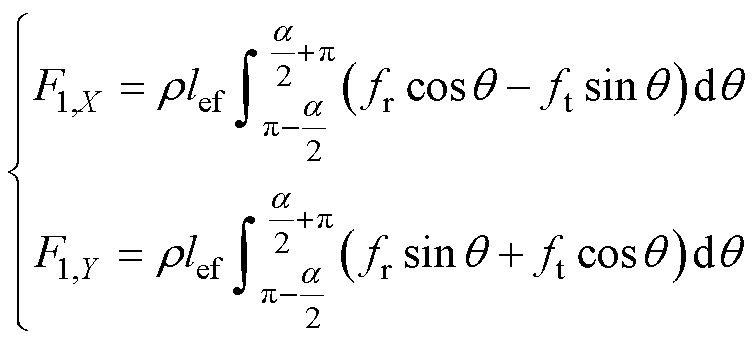（11）
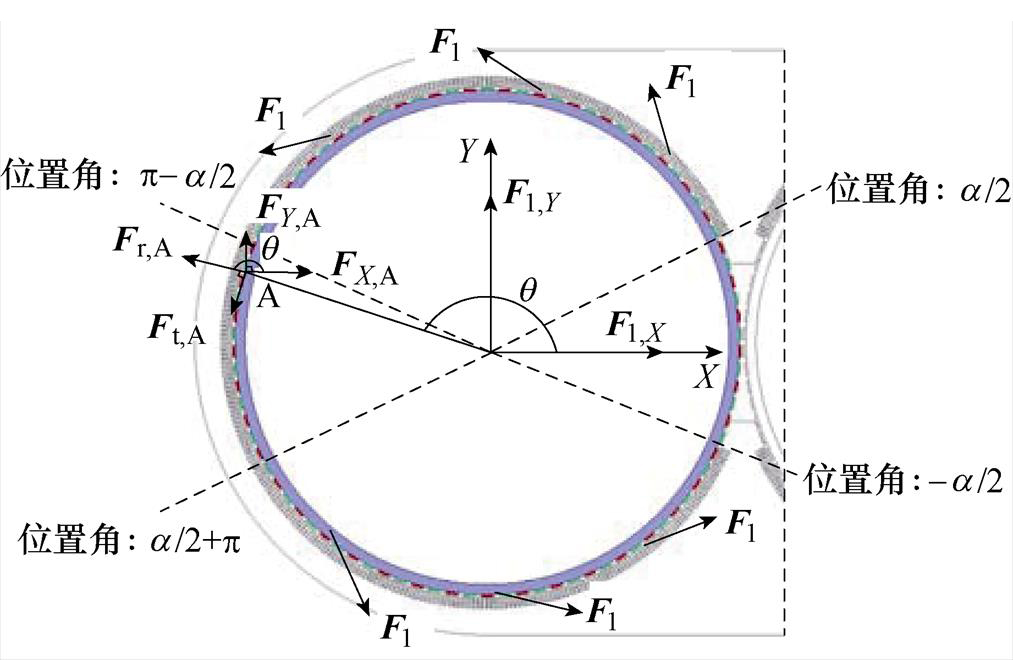
图9 F1示意图
Fig.9 Schematic diagram of F1
式中，r 为电磁力在气隙中的位置参数，可取转子外径（mm）；lef为转子的有效长度（mm）。
根据式（8）、式（9）和式（11）可知，当r、lef不变时，含绕组的定子与对应转子之间的电磁力F1仅仅与气隙磁通密度Br和Bt以及耦合角a 有关。
占空区内两个永磁转子之间的磁力Fmag由占空区内两侧转子所有永磁体之间的相互作用力所组成。根据等效磁荷理论[18]，磁荷的库仑定律为
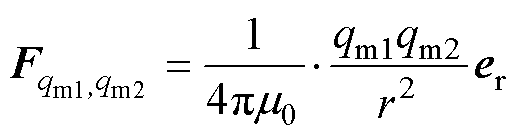（12）
式中，r为两个点磁荷之间的距离（mm）；er为两个点磁荷连线方向的单位矢量；qm1、qm2分别为磁体1、2表面的点磁荷（Wb），表示[19]为
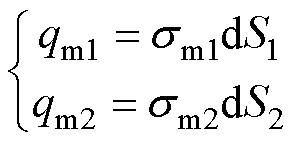（13）
式中，sm1和sm2为两个永磁体的磁荷面密度（Wb/m2），可通过式（14）求得；dS1和dS2为各自磁极面的面积微元。
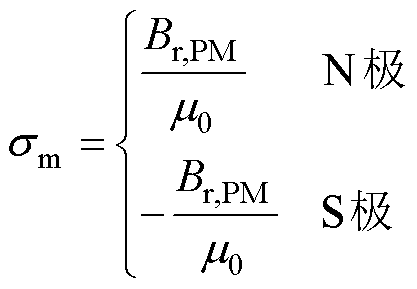（14）
式中，Br,PM为永磁体剩磁（T）。
结合式（12）～式（14），两个永磁体之间的磁力为
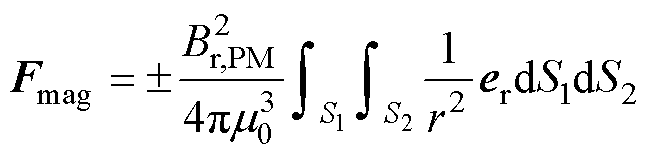（15）
式中，同名磁极之间的作用力取“+”，异名磁极之间的作用力取“-”。
占空区内两个永磁转子之间的磁力Fmag示意图如图10所示。在图10中，取占空区内沿X轴对称的两个永磁体B和C，根据式（15）可知，永磁体B和C与其他永磁体之间的磁力大小完全相同，方向沿X轴镜像对称，由此可以推断，沿X轴镜像对称位置的两个永磁体与另一侧转子永磁体之间的Y向磁力分量相互抵消，换言之，占空区内两个永磁转子之间的磁力Fmag只有X方向的分量Fmag,X，不存在Y向磁力分量Fmag,Y，即
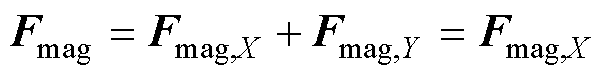（16）
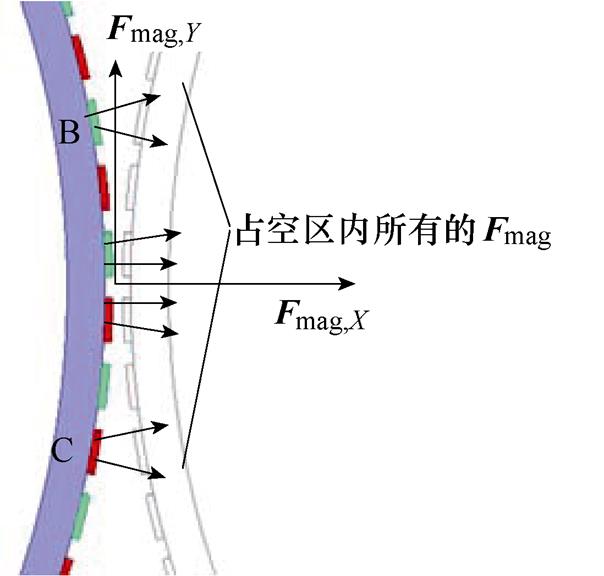
图10 Fmag示意图
Fig.10 Schematic diagram of Fmag
通过以上分析可知，占空区内两个永磁转子之间的磁力Fmag与永磁体剩磁Br,PM、永磁体的形状尺寸和永磁体之间的距离r有关，且仅存在X方向的分量。
铁心端部与耦合区内占空区外转子的作用力Fend是由于耦合区内占空区外转子永磁体与铁心端部之间的吸引力产生的，其只存在径向分量，不存在切向分量，上端部Fend示意图如图11所示。
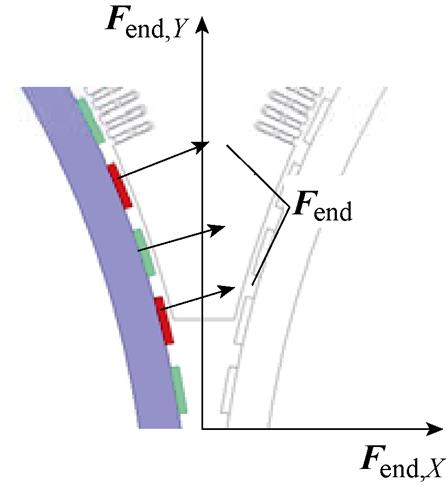
图11 上端部Fend示意图
Fig.11 Schematic diagram of Fend
上端部Fend,X和Fend,Y的表达式可根据F1,X和F1,Y的求法直接写为
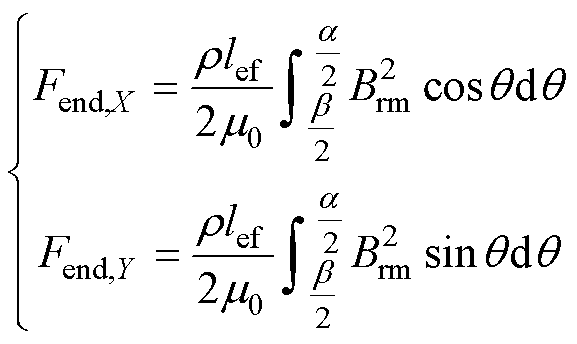（17）
式中，Brm为永磁体产生的径向气隙磁通密度（T）。
上端部的Fend方向与下端部的Fend方向沿X轴对称，因此对下端部的Fend在直角坐标系分解时，其结果与式（17）有着相同的形式，仅是积分的上下限不同，都变为上端部的负值。容易得到，上端部的Fend,Y和下端部的Fend,Y相互抵消，上端部的Fend,X和下端部的Fend,X大小相等。因此，总的Fend也只存在X方向的分量，即
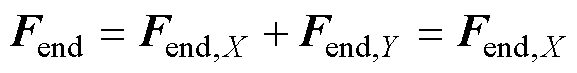（18）
根据以上分析，当r、lef不变时，铁心端部与耦合区内占空区外转子的作用力Fend与耦合角a、占空角b 和永磁体产生的径向气隙磁通密度Brm有关。
定子铁心端部磁导的突变导致了占空区内转子对铁心端部的磁阻力Fend,cog的产生，这与直线电机中因端部效应引起的边端力非常相似。上端部的Fend,cog示意图如图12所示。
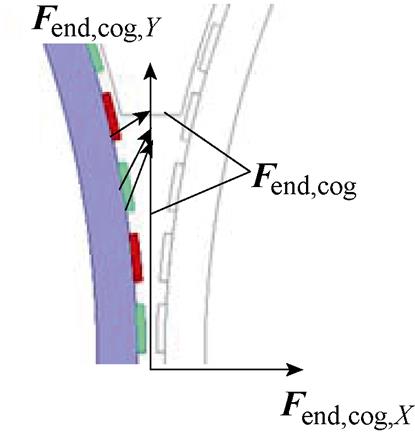
图12 上端部Fend,cog示意图
Fig.12 Schematic diagram of Fend,cog
与Fend分析相同，上端部的Fend,cog,Y和下端部的Fend,cog,Y相互抵消，因此总的Fend,cog也只存在X方向的分量，即
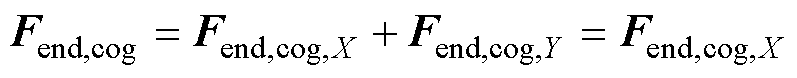（19）
目前，计算边端力大都采用许克变换计算端部附近磁场分布，从而计算出边端力。
附加电磁力Fad包括占空区内永磁体对另一侧转子铁心的作用力Fad1、耦合区内占空区外两侧永磁体之间的作用力Fad2等，如图13所示。其合力方向仍然只存在X方向的分量。
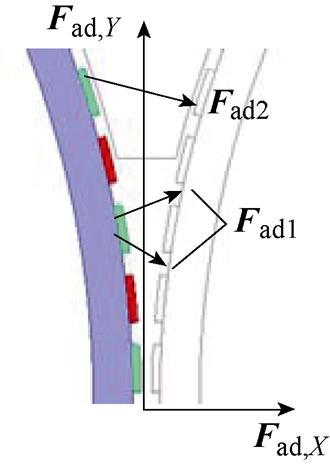
图13 Fad示意图
Fig.13 Schematic diagram of Fad
为了验证对转子所受不平衡电磁力分析的正确性，本文采用有限元法对DR-PMDM转子所受的电磁力进行仿真，电磁力线密度仿真结果如图14所示。由图14可知，Fend,cog的线密度仅为0.36× 105 N/m，Fad1的线密度约为0.85×105 N/m，虽然Fad2的线密度较大，但其上下两个端部力矢量的总数目仅为2。因此，相比于F1、Fmag和Fend，Fend,cog和Fad占转子所受总的电磁力Ftotal的比重较小。
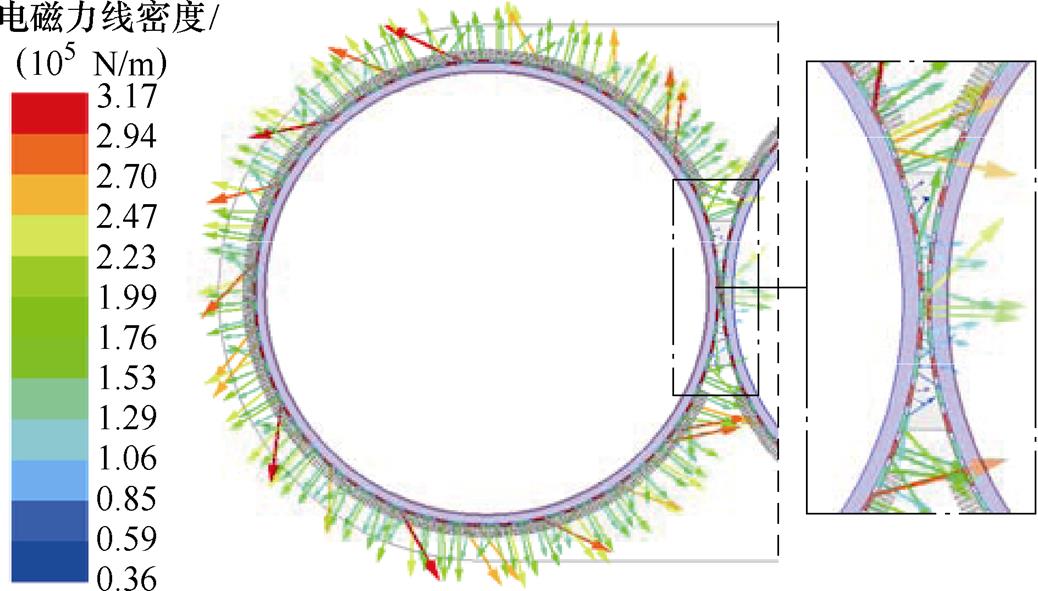
图14 电磁力线密度
Fig.14 Electromagnetic force line density
综上所述，转子所受的总电磁力Ftotal主要来源于三部分，包括含绕组的定子与对应转子之间的电磁力F1、占空区内两个永磁转子之间的磁力Fmag、铁心端部与耦合区内占空区外转子的作用力Fend。占空区内转子对铁心端部的磁阻力Fend,cog、附加电磁力Fad是Ftotal的次要来源。当定子铁心拼接处上下端部对称时，Ftotal,X与上述电磁力的分量均有关，而Ftotal,Y仅与F1有关，即
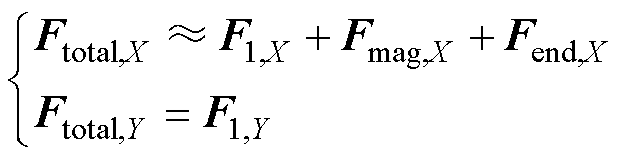（20）
根据以上对转子所受不平衡电磁力Ftotal的分析，以削弱Ftotal的大小作为优化目标。对DR-PMDM进行设计时，耦合角a 根据功率分配已经确定，不能改变。因此，优化的结构参数仅包括占空角b、耦合间距d，如图1所示。此外，采用定子端部不对称结构、转子偏心结构和切除部分单元电机的方式对Ftotal的大小进行削弱。表4给出了所研究的DR-PMDM耦合区初始参数，并给出了初始的Ftotal的大小及其分量的大小。
表4 DR-PMDM的初始参数
Tab.4 Initial parameters of DR-PMDM
参 数数 值 耦合区初始耦合角/(°)48 占空角/(°)36 耦合间距/mm12 初始电磁力/kNFtotal85.6 Ftotal,X-77.3 Ftotal,Y-36.7
占空角b 的大小决定了定子拼接处铁心端部的长度和占空区内永磁体数量，从而影响着Fend、Fmag、Fend,cog、Fad，b 的合理设计对Ftotal的削弱起着十分重要的作用。
图15给出了负载情况下转子所受的电磁力。由图15可知，随着占空角b 的增大，转子所受的总电磁力Ftotal先减小后增大，方向由右下方变为左下方。Ftotal,X先减小后增大，当占空角b =16°时，Ftotal,X≈0，其方向由正变为负，此时，-F1,X≈Fmag,X+ Fend,X+Fend,cog,X+Fad,X。Ftotal,Y基本不变，可视为一恒值，这与2.1节分析一致，因为b 的变化对F1无影响。因此，占空角b 仅影响着Ftotal,X，设计时应找到F1,X与其他力分量的和相平衡的最佳设计，尽量使Ftotal,X=0，此时转子所受的总电磁力Ftotal仅来源于F1,Y。在本例中，当占空角b=16°时，Ftotal最小，为36.3 kN，方向竖直向下。
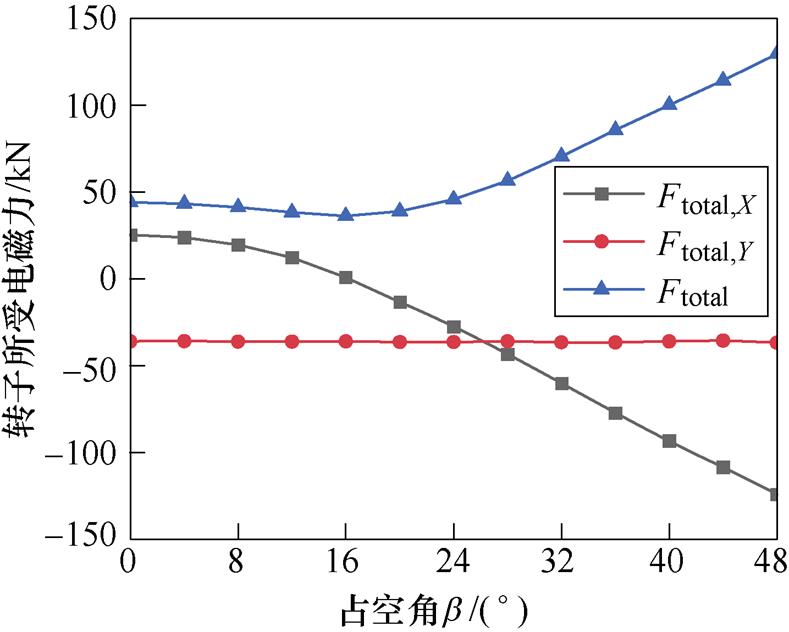
图15 不同占空角下转子所受的总电磁力
Fig.15 Electromagnetic force at different b
图16给出了不同占空角b 下Fmag、Fend的变化情况。由图16可知，随着占空角b 的增大，Fmag先明显增加后基本不变，保持在53 kN左右。可以推断，虽然占空角增大使暴露在占空区内的永磁体数量增加，但对Fmag起实际作用的是靠近X轴处两侧转子永磁体之间的磁力，当两侧转子永磁体离X轴较远时，换言之，磁极表面的磁荷距离r较大时，它们之间的磁力基本为零，这也能从式（15）看出。Fend随占空角b 的增大而减小，见式（17），当b 增大到一定程度时，二者呈线性关系。这是因为当b 较小时，定子铁心端部宽度变化不大，与永磁体之间的作用力基本保持不变。
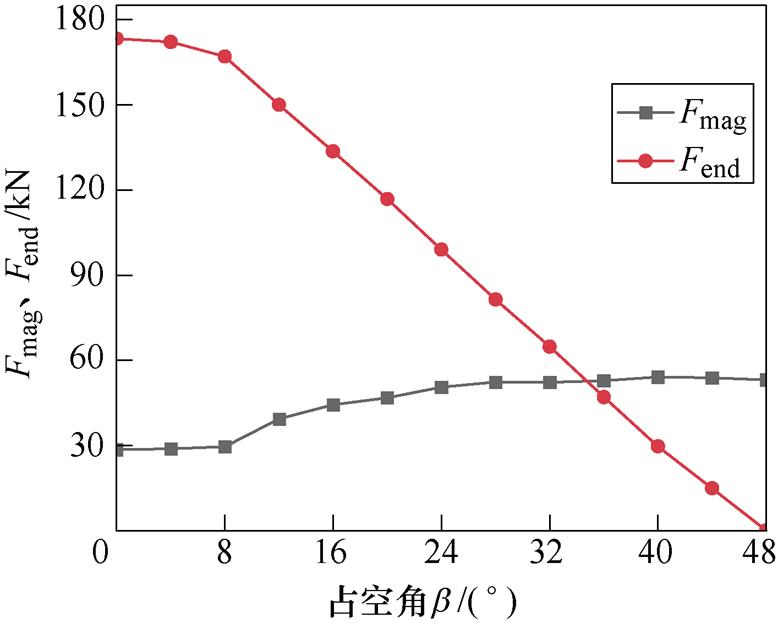
图16 不同占空角下转子所受的Fend and Fmag
Fig.16 Fend and Fmag at different b
耦合间距d决定了占空区内两侧永磁转子之间的距离和定子铁心端部宽度，其大小影响了Fmag和Fend,cog，进而对Ftotal,X产生影响。初始Ftotal,X的值为负，因此可以减小d来增加Fmag,X，从而削弱Ftotal,X。图17给出了不同耦合间距d下转子所受的电磁力。
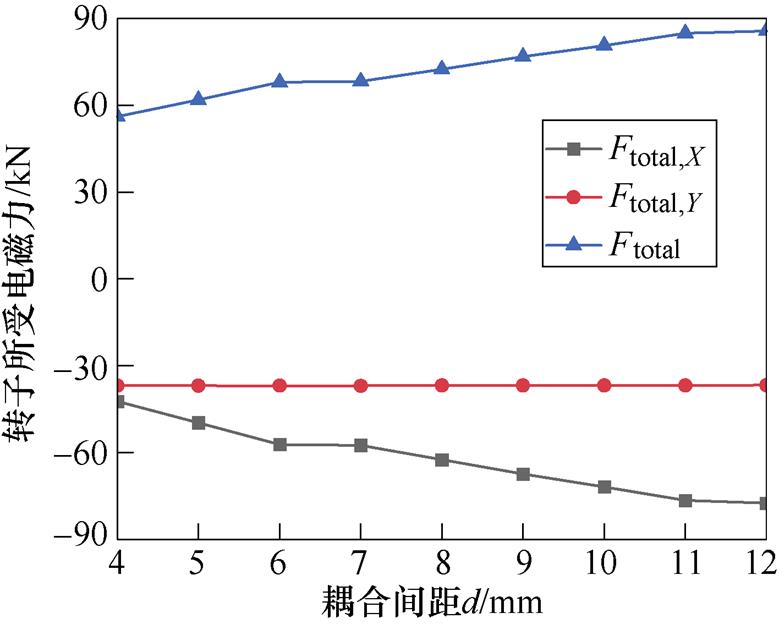
图17 不同耦合间距下转子所受的总电磁力
Fig.17 Electromagnetic force at different d
由图17可知，随着d的减小，Ftotal,X逐渐减小。d在11～12 cm时，Ftotal,X基本不变，这是因为初始两侧永磁转子距离较远，Fmag之间的作用力有限。d在6～7 cm时，Ftotal,X改变非常小，原因是受Fend,cog和Fad的影响。其他区间内二者基本呈线性关系。Ftotal,Y不随d的改变而改变，Ftotal随d的减小而减小。需要说明的是，若耦合间距过小，两侧永磁转子之间的距离太近，耦合区中心永磁体距离太小使二者磁吸力过大，不易加工制造，因此本文考虑工艺因素，将耦合间距选为4 mm，此时Ftotal为56.13 kN，方向指向左下。
根据2.3小节的分析，当定子端部对称时，上端部的Fend,Y和下端部的Fend,Y相互抵消，Fend的Y方向分量Fend,Y=0。由于定子端部对称时的Ftotal,Y仅与F1有关，因此采用定子端部不对称结构时，上端部的Fend,Y和下端部的Fend,Y不能够抵消，上、下端部的Y方向合力可以来抵消一部分由F1产生的Ftotal,Y，由此可见，采用不对称结构的定子端部，可以作为削弱转子所受不平衡电磁力的方式之一。定子端部不对称结构是指定子拼接处铁心上、下两个端部的长度不相等，其不对称程度取决于上端部占空角b1和下端部占空角b2，示意图如图18所示。
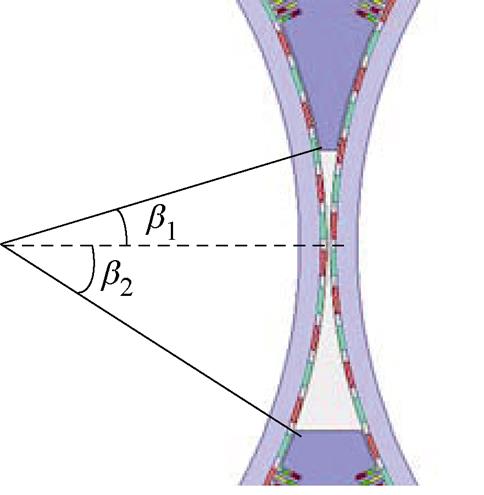
图18 定子端部不对称结构
Fig.18 Asymmetric stator end structure
由于Ftotal,Y仅与F1有关，且F1,Y为负，因此采用b1＜b2的定子端部不对称结构时，Fend,Y为正，可以抵消掉一部分负的F1,Y，但同时要注意Fend,X和Fmag,X的变化。保持b=b1+b2=16°不变，图19为不同b1下转子所受的电磁力。由图19可知，Ftotal,Y随b1的增大而减小，与2.3小节分析一致。Ftotal,X先增大后减小，当7°≤b1≤9°时，Ftotal,X≈0。同时可以发现，以b1=b2=(1/2)b=8°为界限，Ftotal,X基本呈对称分布。例如b1=3°、b2=13°和b1=13°、b2=3°两种不对称结构，Ftotal,X分别为-8.47 kN、-8.31 kN，二者基本相等，二者不完全相同是因为受Fmag,X变化的影响。可以推断，采用定子端部不对称结构时，由于F1,X不变，影响Ftotal,X最主要的分量为Fend,X。Ftotal随b1的增加而增加，最小值为32.8 kN，因此在考虑工艺要求的前提下，b1应该尽可能小。
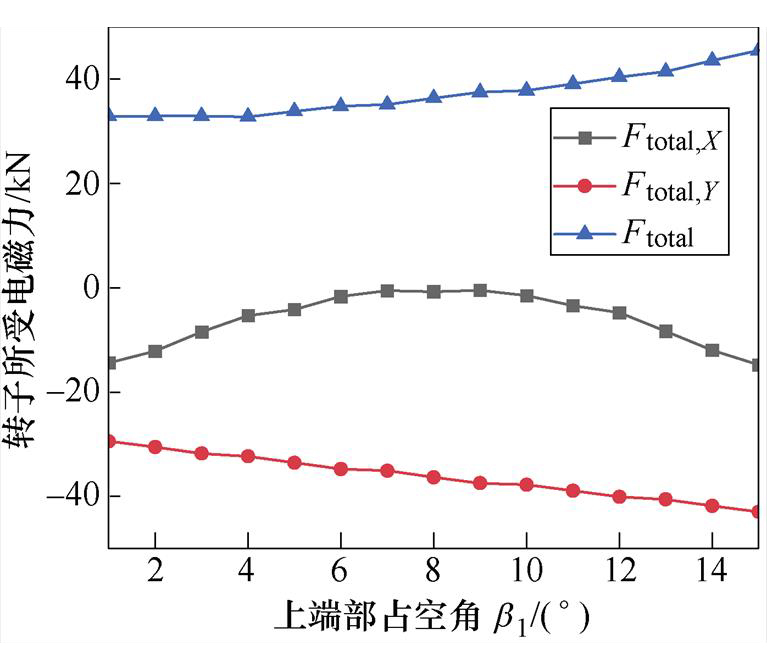
图19 定子端部不对称结构
Fig.19 Asymmetric stator end structure
对于常规电机，转子偏心会对电机的稳态性能产生影响，甚至会带来严重的振动噪声。但对于本文所研究的DR-PMDM，可利用转子静偏心结构来削弱转子所受的不平衡电磁力。这是因为，转子偏心改变了沿转子圆周的磁通密度分布，也改变了耦合区内永磁体之间的相对位置以及永磁体与定子铁心之间的相对位置，根据式（11）、式（15）、式（17）以及2.4节和2.5节中的分析，转子偏心对Ftotal五个力的分量均有影响，因此需要综合考虑偏心距的选取。初始方案中Ftotal,X和Ftotal,Y均为负，因此可将转子中心沿X轴正方向和Y轴正方向所包围的第一象限平移，偏心距离分别为dX和dY，以此来削弱转子所受总的电磁力。
图20和图21分别给出了不同dX和dY下转子所受的电磁力。由图20可知，随着dX的增加，Ftotal,X的方向发生了变化，即由原来指向X轴负方向逐步改变为指向X轴正方向，Ftotal,X的代数数值呈现出先减小后增大的规律，当dX =0.85 mm时，Ftotal,X几乎为0；Ftotal,Y基本不随dX的变化而变化；Ftotal随着dX的增大先减小后增大。由图21可知，随着dY的增加，Ftotal,Y的方向也发生了变化，即由原来指向Y轴负方向逐步改变为指向Y轴正方向，Ftotal,Y的代数数值也呈现出先减小后增大的规律，当dY = 0.35 mm时，Ftotal,Y几乎为0；Ftotal,X基本不随dY的变化而变化；Ftotal随着dY的增大先减小后增大。
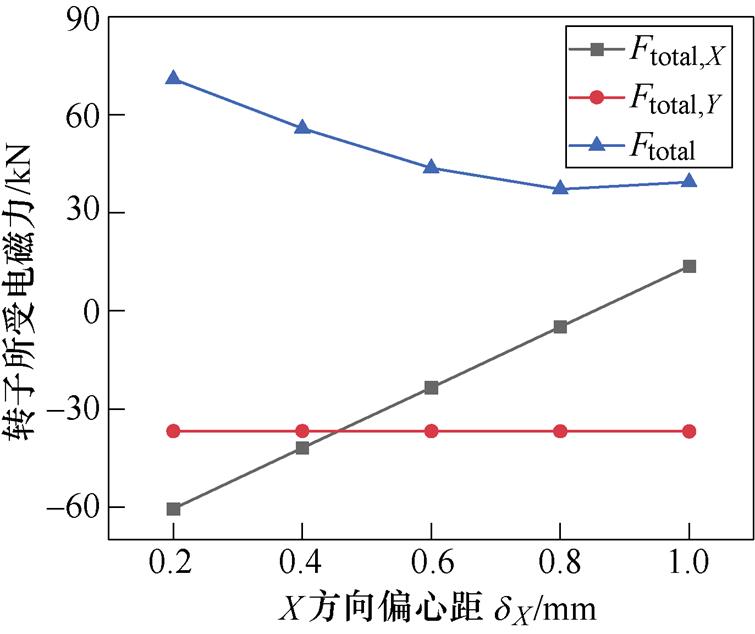
图20 不同X方向偏心距下转子所受的总电磁力
Fig.20 Electromagnetic force at different dX
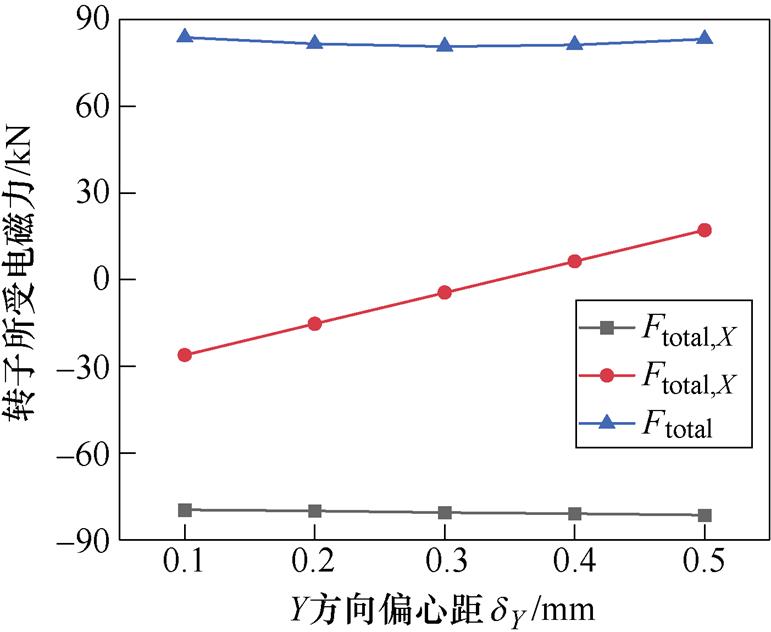
图21 不同Y方向偏心距下转子所受的总电磁力
Fig.21 Electromagnetic force at different dY
根据以上分析可认为，dX仅影响Ftotal,X，dY仅影响Ftotal,Y。因此存在一组 (dX, dY) 使Ftotal,X、Ftotal,Y都近似为0，换言之，Ftotal近似为0。综合考虑，当dX=0.85 mm，dY=0.35 mm时，Ftotal=3.3 kN，可认为近似为0。
根据式（11）可分析出，转子位置角[p-a/2, a/2+p]内的单元电机是F1产生不平衡的根源，切除转子位置角[p-a/2, a/2+p]内的单元电机可以有效削弱F1。在转子位置[p-a/2, a/2+p]中，共有5个完整单元电机，当切除单元电机1时，其结构如图22所示。为了不产生新的不平衡电磁力，使剩余单元电机的F1,X =0，切除的单元电机应沿X轴对称。因此，共有四种切除部分单元电机的方案，以切除单元电机1、2、3为例，根据图9的分析，剩余的单元电机4和电机5的F1,X大小相等，方向相反，此时单元电机4和电机5的F1,X =0。不同方案下DR- PMDM的Ftotal,X、Ftotal,Y、Ftotal整理见表5。
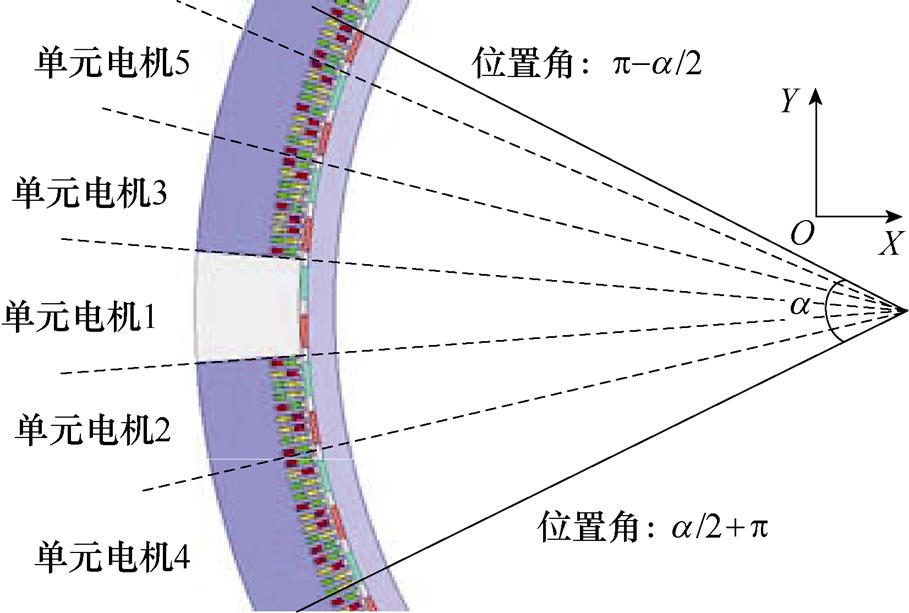
图22 在转子位置[p-a/2, a/2+p]中的单元电机
Fig.22 Unit motors at rotor position [p-a/2, a/2+p]
表5 四种切除部分单元电机的方案
Tab.5 Four ways to remove the unit motors
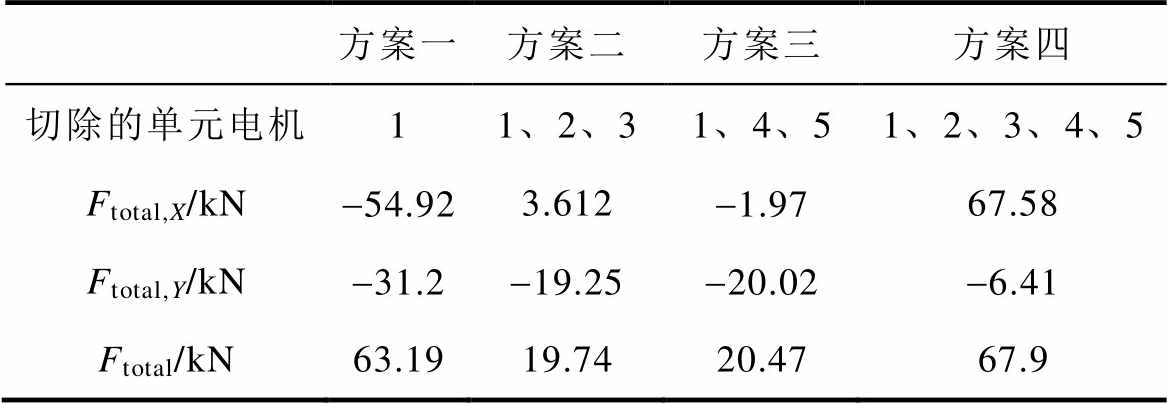
方案一方案二方案三方案四 切除的单元电机11、2、31、4、51、2、3、4、5 Ftotal,X/kN-54.923.612-1.9767.58 Ftotal,Y/kN-31.2-19.25-20.02-6.41 Ftotal/kN63.1919.7420.4767.9
由表5可知，方案二和方案三对于Ftotal,X的削弱效果最明显；方案一由于只切除一个单元电机，Ftotal,X的变化不明显且仍为负；方案四切除单元电机数量最多导致Ftotal,X反向增加显著，方向由负变为正。Ftotal,Y随着切除单元电机数量的增加而减小，这可以从2.1节的分析中得出。综合考虑，方案二对于Ftotal的削弱效果最好，此时Ftotal=19.74 kN，方向指向右下。
为了说明上述优化方法的可行性，将不同的优化方法、采用不同的优化方法后和优化前的转子所受电磁力Ftotal、转矩脉动Trip的对比整理见表6。图23为电机转子所受的初始不平衡电磁力Ftotal,0及采用五种优化方法后的不平衡电磁力Ftotal,1、Ftotal,2、Ftotal,3、Ftotal,4、Ftotal,5的示意图。由表6和图23可知，五种优化方法都能够削弱转子所受的总电磁力；采用转子偏心结构的优化方法对Ftotal的削弱效果最好，选择合适的偏心距几乎可以完全消除转子所受的不平衡力，但会增加电机的转矩脉动；采用优化耦合间距的方法对削弱转子所受电磁力的效果有限；优化占空角和采用端部不对称结构的方法可以在一定程度上削弱转子所受的电磁力，同时能够降低电机的转矩脉动；采用切除部分单元电机的方式能够大幅度削弱转子所受的电磁力，同时使转矩脉动略有降低。
表6 不同优化方法的比较
Tab.6 Comparison of different optimization methods
优化方法Ftotal/kNTrip(%) 初始优化前85.5010.33 方法1占空角优化36.348.81 方法2耦合间距优化56.1310.23 方法3端部不对称结构32.828.65 方法4转子偏心结构3.3010.52 方法5切除部分单元电机19.749.24
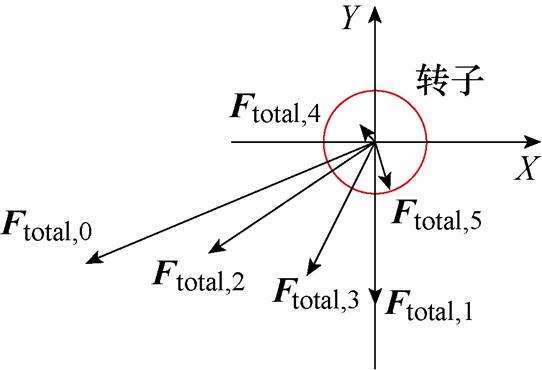
图23 优化前后不平衡电磁力矢量
Fig.23 Unbalanced electromagnetic force vector before and after optimization
将五种优化方法的优缺点总结见表7。从加工制造的角度来看，方法1、2、3、5都可以较容易地实现，方法4的实现对加工工艺水平要求较高；从对不平衡力的优化效果来看，方法4＞方法5＞方法1≈方法3＞方法2；从转矩脉动的大小来看，方法2、4的转矩脉动较大，方法5其次，方法1、方法3的转矩脉动较小。此外，方法2受转轴中心距的影响；方法4需要考虑定子铁心的振动噪声问题；方法5更适用于多极、多槽结构的电机，同时会增加电机的额定电流，本文方法5中采用的方案二使电机的额定电流从68 A增加到75 A。
表7 不同优化方法的优缺点
Tab.7 Advantages and disadvantages of different optimization methods
方法优点缺点 1能够降低转矩脉动对电磁力的削弱效果有限，但当占空角过小时，对工艺要求较高 2最容易实现加工对电磁力的削弱效果最差、优化范围可能会受到转轴中心距的影响，增加转矩脉动 3易实现加工，能够有效降低转矩脉动对电磁力的削弱效果有限 4对电磁力削弱效果最好，基本能完全消除对工艺要求最高，需要考虑定子的振动问题，增加转矩脉动 5对电磁力的削弱效果较好，非常适用于模块电机的加工制造切除的单元电机受耦合角、极数和槽数的影响，不能够完全消除电磁力，额定电流增加
综上所述，对于本文所研究的DR-PMDM，采用切除部分单元电机的方法是最合适的，此种方法不仅能够较好地削弱转子所受的不平衡电磁力，同时对电机的转矩脉动也有一定的削弱作用。此外，此种方法十分契合低速大转矩电机的模块化制作。
本文对双并列转子永磁直驱电机转子所受的电磁力进行了分析和优化。平衡了电机的电感参数后，研究了转子所受不平衡电磁力的组成，分析了各个力的分量产生的原因及影响因素，采用了优化占空角、优化耦合间距、采用定子端部不对称结构、采用转子偏心结构和切除部分单元电机的方法对转子所受的电磁力进行了削弱。得到的主要结论如下：
1）对于采用定子模块化结构的双并列转子永磁直驱电机，通过合理选择绕组跨距及A相绕组的首端可以有效地平衡电感参数，平衡后的各相总电感参数分别为0.627、0.626、0.626 mH。
2）转子所受的不平衡电磁力Ftotal共有五部分力组成。当定子端部结构对称时，Ftotal的X方向力与五个力都有关，而Ftotal的Y方向力仅与F1有关，且F1、Fmag、Fend是Ftotal的最主要成分。
3）提出的五种优化方法都能够削弱转子所受的不平衡电磁力。其中，采用转子偏心结构的方法优化效果最好；切除部分单元电机的方法最适合工程应用，优化后的Ftotal的大小为19.74 kN。实际应用中，可以考虑多种优化方法的结合使用。
参考文献
[1] 孙立国. 二辊带钢轧机机座刚度计算[J]. 机械设计, 2021, 38(增刊1): 225-227.
Sun Liguo. Calculation of stand stiffness of 2H strip mill[J]. Journal of Machine Design, 2021, 38(S1): 225-227.
[2] 周兴杰, 李峰. 热轧板带立辊轧机主传动型式分析比较[J]. 轧钢, 2021, 38(4): 75-79.
Zhou Xingjie, Li Feng. Analysis and comparison of main drive types of the edge mill for the hot rolled plate and strip[J]. Steel Rolling, 2021, 38(4): 75-79.
[3] Valavi M, Le Besnerais J, Nysveen A. An investi- gation of zeroth-order radial magnetic forces in low- speed surface-mounted permanent magnet machines[J]. IEEE Transactions on Magnetics, 2016, 52(8): 1-6.
[4] Crider J M, Sudhoff S D. An inner rotor flux- modulated permanent magnet synchronous machine for low-speed high-torque applications[J]. IEEE Transactions on Energy Conversion, 2015, 30(3): 1247-1254.
[5] 张炳义, 贾宇琪, 冯桂宏. 新型模块组合式定子永磁电机[J]. 电工技术学报, 2015, 30(12): 243-252.
Zhang Bingyi, Jia Yuqi, Feng Guihong. Novel permanent magnet synchronous machines with modules combination stator[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 243-252.
[6] Tan Qiang, Huang Xuzhen, Li Liyi, et al. Research on inductance unbalance and thrust ripple suppression of slot-less tubular permanent magnet synchronous linear motor[J]. IEEE Access, 2018, 6: 51011-51020.
[7] Chang Jiujian, Ma Wenli, Fan Yongkun, et al. New methods for arc permanent magnet linear synchronous motor to decrease torque ripple[J]. IEEE Transactions on Magnetics, 2012, 48(10): 2659-2663.
[8] Liu Fei, Hu Jianhui, Li Yong. Torque and radial force optimization of arc flux switching permanent magnet linear motor used for large scanning equipment[J]. IEEE Transactions on Energy Conversion, 2022, 37(1): 304-315.
[9] 蒋钱, 卢琴芬, 李焱鑫. 双三相永磁直线同步电机的推力波动及抑制[J]. 电工技术学报, 2021, 36(5): 883-892.
Jiang Qian, Lu Qinfen, Li Yanxin. Thrust ripple and depression method of dual three-phase permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 883-892.
[10] 郭科宇, 李耀华, 史黎明. 分段供电双三相永磁同步直线电机电流解耦与扰动抑制[J]. 电工技术学报, 2022, 37(24): 6332-6344.
Guo Keyu, Li Yaohua, Shi Liming. Current decoupling and force disturbance suppression of dual three-phase permanent magnet linear synchronous motors with section power supply[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6332- 6344.
[11] Zhang Jiaxu, Zhang Bingyi, Feng Guihong. Influence of pole and slot combination on torque characteristics and radial force of fractional slot permanent magnet machines[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2021, 16(8): 1055-1066.
[12] Yang Haodong, Chen Yangsheng. Influence of radial force harmonics with low mode number on elec- tromagnetic vibration of PMSM[J]. IEEE Transa- ctions on Energy Conversion, 2014, 29(1): 38-45.
[13] 刘蓉晖, 刘锦坤, 章君达, 等. 基于双曲余切变换的Halbach阵列表贴式永磁电机转子偏心气隙磁场解析模型[J]. 电工技术学报, 2023, 38(6): 1433- 1446.
Liu Ronghui, Liu Jinkun, Zhang Junda, et al. Analytical model for air-gap magnetic field in Halbach arrays surface-mounted permanent magnet motor with rotor eccentricity based on hyperbolic cotangent transformation[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1433-1446.
[14] 李泽星, 夏加宽, 刘铁法, 等. 基于分段交错梯形磁极的分数槽集中绕组永磁电机局部切向力的削弱[J]. 电工技术学报, 2023, 38(6): 1447-1459, 1485.
Li Zexing, Xia Jiakuan, Liu Tiefa, et al. Reduction of local tangential force of fractional-slot concentrated winding permanent magnet synchronous machines with piecewise stagger trapezoidal poles[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(6): 1447-1459, 1485.
[15] 黄守道, 成双银, 罗德荣, 等. 盘式对转双转子永磁同步电机的设计和特性分析[J]. 电工技术学报, 2017, 32(23): 72-80.
Huang Shoudao, Cheng Shuangyin, Luo Derong, et al. Design and characteristic analysis of an axial-flux permanent magnet synchronous motor with contra- rotating rotors[J]. Transactions of China Electro- technical Society, 2017, 32(23): 72-80.
[16] 巫川, 李冠醇, 王东. 永磁电动悬浮系统三维解析建模与电磁力优化分析[J]. 电工技术学报, 2021, 36(5): 924-934.
Wu Chuan, Li Guanchun, Wang Dong. 3-D analytical modeling and electromagnetic force optimization of permanent magnet electrodynamic suspension system[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 924-934.
[17] Zhu Sa, Lu Jianbo, Zeng Feng. Fast calculation of electromagnetic forces in IPMSMs under PWM VSI supply based on small-signal time-harmonic finite element method[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 67-76.
[18] 历建刚. 永磁体间的磁力和磁力矩研究[D]. 长春: 吉林大学, 2015.
Li Jiangang. Research on the force and torque between permanent magnets[D]. Changchun: Jilin University, 2015.
[19] 瞿川. 钕铁硼永磁体磁力和磁刚度理论及应用研究[D]. 长春: 吉林大学, 2022.
Qu Chuan. Study on the theory and application of magnetic force and magnetic stiffness of NdFeB permanent magnets[D]. Changchun: Jilin University, 2022.
Abstract Most parallel synchronous drive equipment, such as the two-roll mill and twin-screw pump, are driven by an induction motor with synchronous mechanical gear. Such drive systems have large volumes, poor synchronization of master and slave shafts, requiring regular maintenance. A dual-parallel rotor permanent magnet direct-driven motor has gradually come into view.
Due to the distance limitation between rotating shafts, part of the stator core and windings are cut off in the design of a dual-parallel rotor permanent magnet direct-driven motor, resulting in unbalanced rotor electromagnetic force. Therefore, this paper analyzes the inductance parameter asymmetry of the motor windings. Inductance parameters of the motor with windings pitch of 4 and 3 are calculated. On this basis, a mathematical model for the total electromagnetic force on the rotor is constructed, and the influence of each component force on the rotor’s total electromagnetic force is studied. Five optimization methods are proposed to optimize the electromagnetic force on the rotor: optimizing the duty angle, optimizing the coupling distance, adopting the asymmetric stator end structure, adopting the eccentric rotor structure, and eliminating part of the unit motors. Finally, the optimization effects of different methods on torque ripple are discussed. The advantages and disadvantages of different optimization methods are summarized, laying a foundation for studying dual-parallel rotor permanent magnet direct-driven motors.
The following conclusions can be drawn: (1) The long-pitch coil of the modular structure may cause asymmetric three-phase inductance parameters. Three-phase inductance can be effectively balanced by reasonably selecting the winding pitch and the head end of the A-phase winding. (2) The electromagnetic force Ftotal on the rotor includes the electromagnetic force F1 between the stator with windings and the corresponding rotor, the magnetic force Fmag between two permanent magnet rotors in the coupling area, the force Fend between the core end and the rotor outside the duty area in the coupling area, and the magnetic resistance force Fend,cog of the rotor against the core end in the coupling area and additional electromagnetic force Fad. The X direction force of Ftotal is related to the above forces, while the Y direction force of Ftotal is only relevant to F1. F1, Fmag, and Fend are the most important components of Ftotal. (3) According to the analysis of the Ftotal, five methods are proposed to weaken the Ftotal. The influence of the five optimization methods on the electromagnetic force is given, and the advantages and disadvantages of the five optimization methods are discussed. The method with a rotor eccentric structure has the best optimization effect but requires higher processing technology. The method of eliminating partial unit motors is the most practical. (4) The motor can output rated electromagnetic torque using five optimization methods. In practical application, the combination of various optimization methods can be considered.
keywords：Dual-parallel rotor, permanent magnet direct-driven motor, electromagnetic force, optimization method
DOI: 10.19595/j.cnki.1000-6753.tces.230427
中图分类号：TM351
国家自然科学基金资助项目（51777048）。
收稿日期 2023-04-06
改稿日期 2023-04-17
陶大军 男，1982年生，教授，博士生导师，研究方向为大电机和特种电机的基础理论、设计与分析。E-mail: tao.dj@163.com（通信作者）
陈 阳 男，1995年生，博士研究生，研究方向为永磁及特种电机的设计与分析。E-mail: chenyang2022@foxmail.com
（编辑 崔文静）