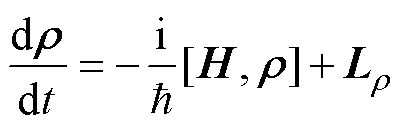 (1)
(1)
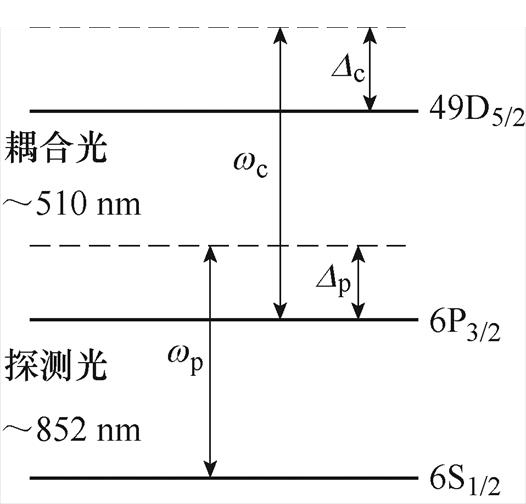
图1 阶梯型三能级结构
Fig.1 Ladder-type three-level system structural drawing
摘要 基于里德堡原子电磁诱导透明(EIT)效应的电场量子测量方法,能够突破传统基于电学原理、光学原理测量法在测量精度和灵敏度上的极限,并且具有自校准性。采用热里德堡原子进行测量具有工程应用的便捷性,但是原子热运动形成的多普勒效应会导致EIT谱峰发生频移和形变,混淆电场对原子的相干效应,从而影响电场测量精度。基于激光、电场与原子的作用机理,以及原子热力学,该文提出通过调整探测光和耦合光频率,修正原子热运动对电场量子测量影响的方法。首先,假设里德堡原子静止不动,建立和求解密度矩阵方程,描述双光子阶梯型三能级系统的EIT光谱;然后,引入温度与原子运动数学关系,将温度造成的原子热运动多普勒影响量化为探测光和耦合光频率失谐量,通过修正探测光和耦合光的频率来抵消该影响。仿真实验表明,该文提出的修正方法效果良好,该研究有利于推进基于里德堡原子电场量子测量的实用化进程。
关键词:电场测量 里德堡原子 电磁诱导透明 原子热运动 多普勒效应 修正
在电力系统中,电场测量被广泛应用于电气设备的状态监测与评估、故障诊断、结构和材料优化设计、电磁兼容等场合[1-6]。可以说,电场测量对于确保电气设备安全稳定运行、实现电力系统信息化管理具有重要意义。目前电场测量主要有电学法[7]和光学法[8-9],但基于电学原理的金属传感器会造成待测电场畸变,测量准确性有限;光学测量受环境影响大且不确定性高。要突破传统电场测量方法在测量精度和灵敏度方面的局限,且实现短链条溯源,有必要探索场与物质作用的物理机制,采用全新的电场传感和测量方式。近年来发展起来的量子测量具有高精度、自校准等显著优势,有望成为电工技术发展的一个新方向。
电场量子测量的基本原理是具有一定量子态的微观粒子在外场作用下产生相干效应,表现出具有固定特征的光谱,提取光谱特征参数换算电场强度。里德堡(Ryberg)原子是指最外层电子具有较高主量子数n的高激发态原子,具有极化率大、偶极矩强、相干时间长等特点[10],对外场作用极为敏感[11-12],适用于电场量子测量。
目前普遍采用双激光(探测光、耦合光)共振激发制备碱金属原子的里德堡态并且形成电磁诱导透明(Electromagnetic Induced Transparency, EIT)[13-16]光谱。当电场频率小于1 GHz且为非共振频率时,EIT谱峰会因外电场的作用发生Stark频移,EIT光峰频移大小与电场强度的二次方成正比[17-19]。电力系统中工频电场量子测量的原理即为里德堡原子的EIT效应和Stark效应[20-22]。
理想情况下,应采用静止的冷原子进行电场量子测量,但是所需设备结构复杂、价格高昂、操控繁琐,不具实用性。若采用处于室温下的热原子进行测量,原子的热运动影响其与激光之间的相对运动速度,从而产生多普勒效应。K. Boller的研究团队[23]研究了EIT效应,发现原子的热运动会使EIT光谱展宽。Y. Li的研究团队[24]将探测光和耦合光设置为相向传输的配置,以此来减弱由原子热运动引起的多普勒效应。D. X. Khoa等[25]研究了多普勒展宽对EIT窗深度和宽度的影响,并发现结果与低温实验的验证非常一致。R. Hazra等[26]通过实验发现,随着介质温度的升高,EIT吸收曲线和色散曲线的振幅均逐渐减少,同时还伴随着频率的移动。Zhang Guiyin等[27]分析了当频率高于1 GHz的电场作用于系统时原子热运动对EIT效应的影响,发现多普勒展宽大于透明窗口的宽度时,会导致EIT光峰的消失。上述实验结果表明,原子热运动所产生的多普勒效应会导致EIT光谱的频移和形变,这些现象会混淆电场对原子的相干效应。要提高基于热里德堡原子的电场量子测量准确性,有必要消除多普勒效应的影响。
本文提出通过计算激光和原子相对运动速率,转化为激光器的频率失谐量,对激光器频率设置进行修正的方法,以此削弱原子热运动产生的多普勒效应对EIT光谱的影响。首先基于多光子与原子的作用机理,建立密度矩阵方程,求解方程并推导出原子系统对探测光的吸收率、色散率与耦合光频率失谐量之间的数学关系式,从而描述EIT效应;研究和阐释原子热运动所产生的多普勒效应对EIT光谱的影响原理。然后通过热原子速率分布函数计算里德堡原子系综的等效运动速率,将其转化为激光器端的频率失谐量。最后根据计算量对激光器频率输入参数进行反向调整,从而修正EIT光谱。
需要指出的是,低频非共振电场与原子作用使里德堡态原子精细能级分裂,导致EIT谱线发生频移;温度引起的原子热运动会使原子吸收的频率与激光器设定频率不匹配,产生光谱频移。两者对EIT谱线的影响机理是相互独立的,故本文提出的修正方法只能修正温度对EIT谱线的影响,对电场作用效果不会造成影响。因此,本研究有利于提高室温下基于里德堡原子电场测量的精度。
本文研究以铯原子为对象,里德堡态制备及EIT形成采用图1所示的阶梯型三能级结构。图中三个能级分别为基态(6S1/2)、第一激发态(6P3/2)、里德堡态(49D5/2)。探测光的波长为852 nm,将基态原子激发到第一激发态;耦合光的波长为510 nm,其加入导致铯原子从第一激发态跃迁至里德堡态。探测光和耦合光相向传播通过铯原子气室,有利于减小多普勒效应[28]。
针对图1所示阶梯型三能级结构,采用半经典理论的密度矩阵方法来描述系统动力学的演化 过程:
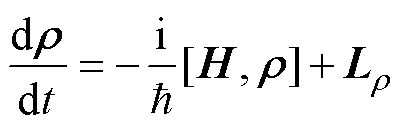 (1)
(1)

图1 阶梯型三能级结构
Fig.1 Ladder-type three-level system structural drawing
式中,r 为系统能级跃迁的分布率;H为系统的哈密顿量;Lr为系统中能级的衰减及退相干项;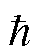 为约化普朗克常数。
为约化普朗克常数。
三能级结构的密度矩阵方程可表示为
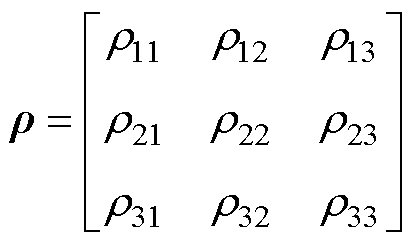 (2)
(2)
式中,当x≠y时rxy表示从能级x跃迁到y的粒子分布率,当x=y时rxy表示x能级上的粒子布局率。Lr可表示为
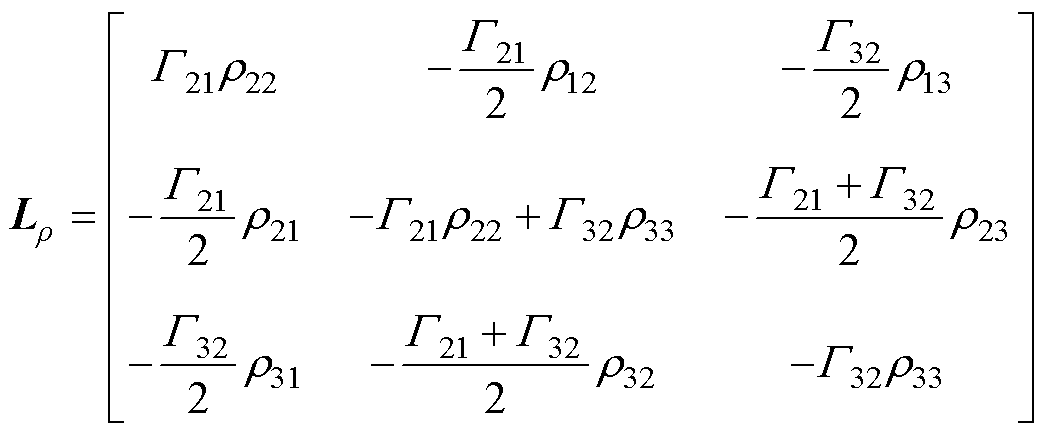 (3)
(3)
式中,Gab 为从能级a 跃迁到能级b 的辐射率。
考虑旋转波近似,在光场和原子互相作用绘景下的哈密顿量可表示为
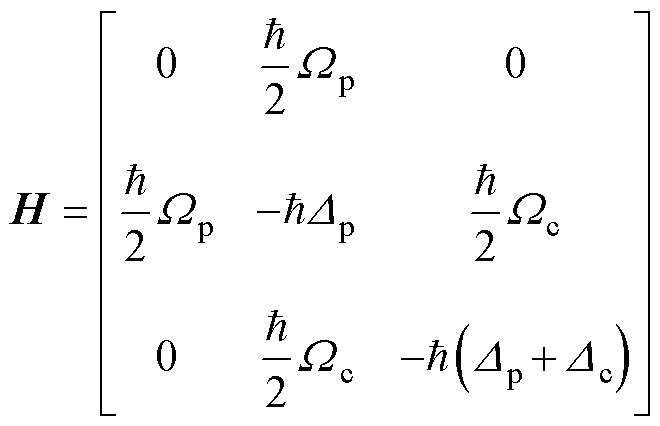 (4)
(4)
式中,Wp和Wc分别为探测光和耦合光的拉比频率;Dp和Dc分别为探测光和耦合光的频率失谐量。
设初始条件[29]:①r11=1,r22=r33=r32=0;②Wc Wp,Dp=0。将式(3)、式(4)代入式(1)可得
Wp,Dp=0。将式(3)、式(4)代入式(1)可得
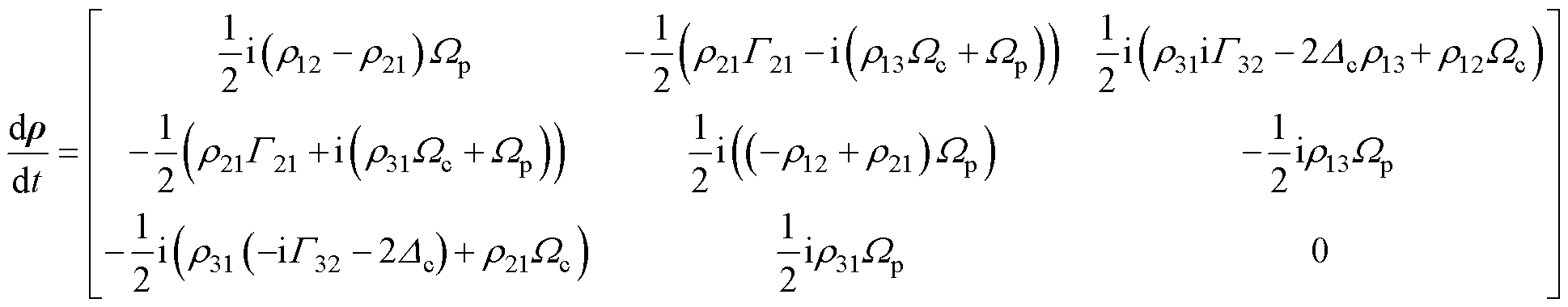 (5)
(5)
当系统趋于稳定时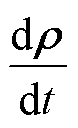 =0,可求得密度矩阵中探测光跃迁项r21的稳态解为
=0,可求得密度矩阵中探测光跃迁项r21的稳态解为
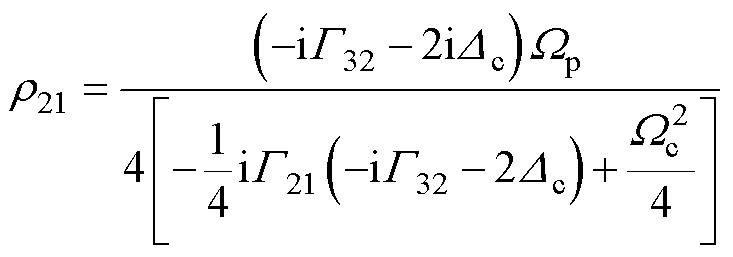 (6)
(6)
根据系统复极化率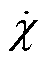 与r21的关系[25]可得
与r21的关系[25]可得
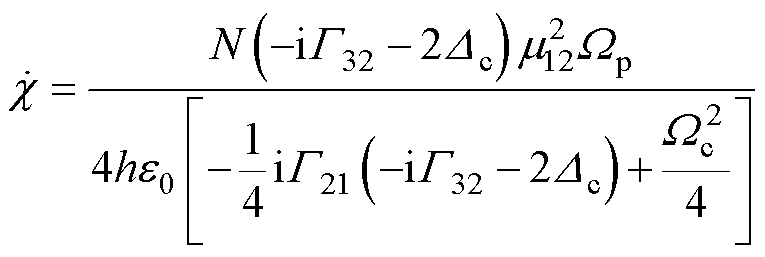 (7)
(7)
式中,N为原子密度。
复极化率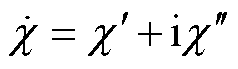 的实部和虚部分别反映原子在探测光和耦合光作用下的色散和吸收特征,其中
的实部和虚部分别反映原子在探测光和耦合光作用下的色散和吸收特征,其中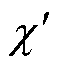 计算式为
计算式为
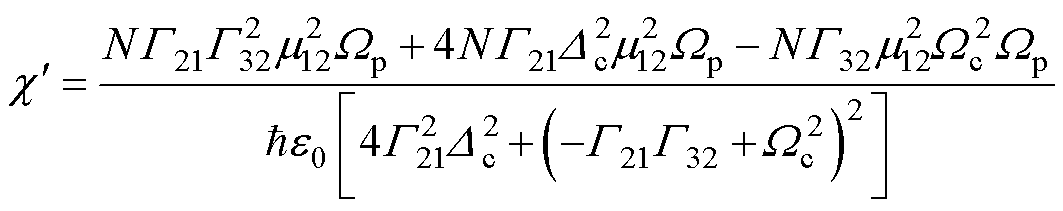 (8)
(8)
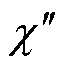 计算式为
计算式为
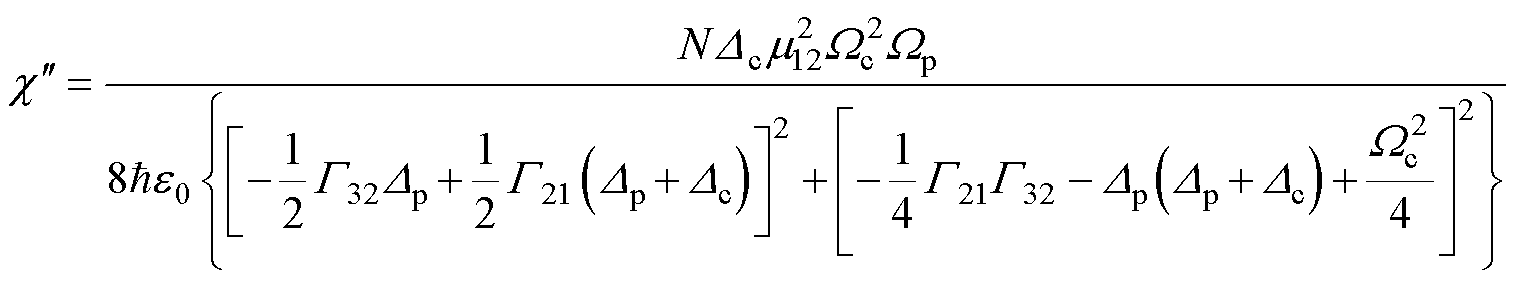 (9)
(9)
图2所示为理论计算得到的图1阶梯型三能级系统原子的色散光谱和吸收光谱。
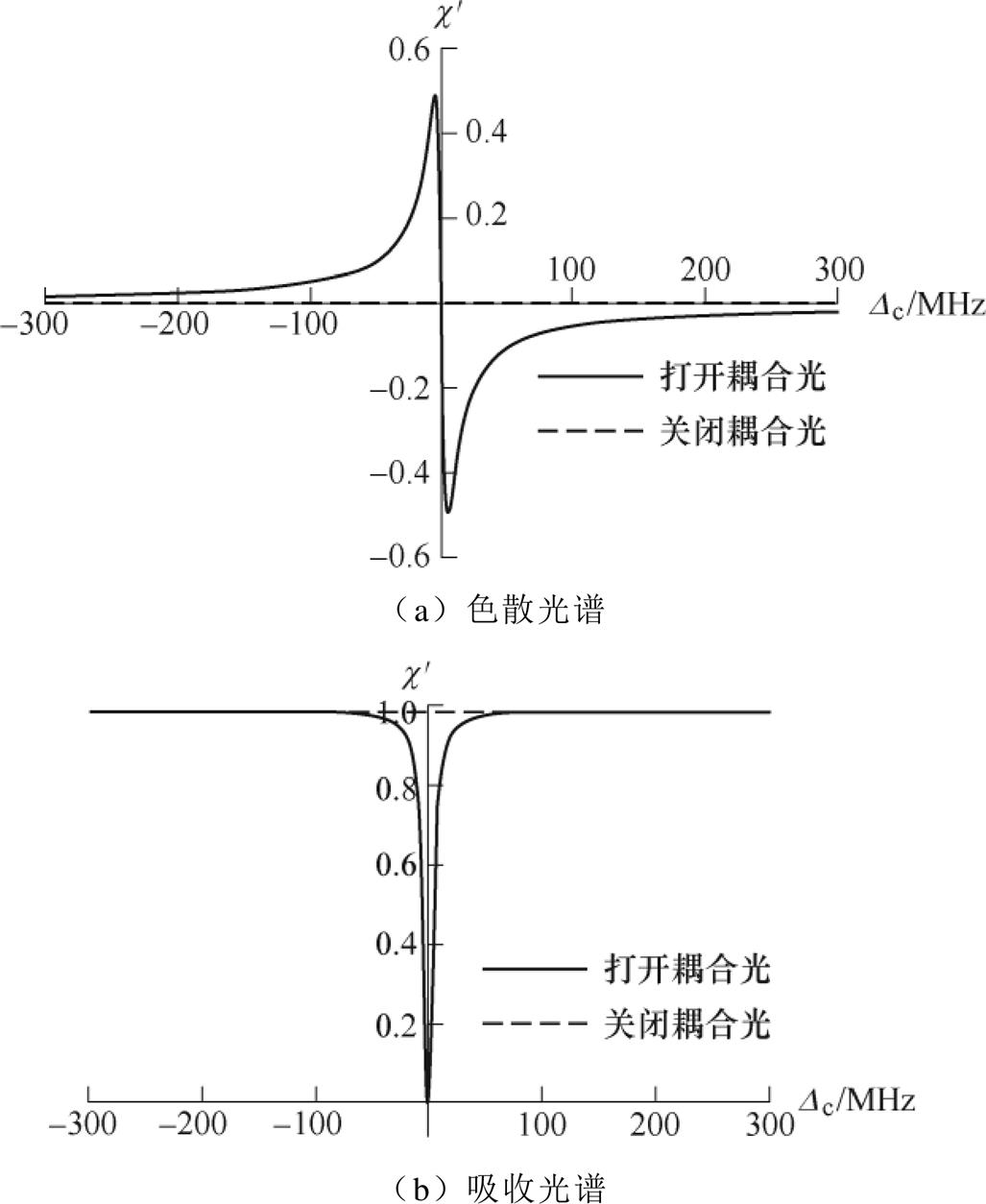
图2 阶梯型三能级系统EIT光谱
Fig.2 Ladder-type three-level system EIT spectrum
从图2可以看出,系统未加入耦合光时,若探测光频率正好是原子从基态跃迁到第一激发态的共振频率,则原子系统对探测光的色散始终为0、吸收为1(归一化量)。若系统加入匹配共振频率的耦合光时,原子吸收耦合光的能量跃迁至里德堡态,原子系统对探测光的色散骤增而吸收骤减,形成“透明窗口”;随着耦合光失谐量|Dc|的增加,耦合光对原子系统的作用减少,原子系统对探测光的吸收逐渐增加。
第1节是在假设原子静止不动的理想情况下所进行的EIT模型描述,但很难确保原子处于绝对零度而“冻结”,实际应用时甚至希望相关操作在室温下进行。原子热运动会使原子与激光之间存在相对运动,影响原子所接收的激光能量,从而产生多普勒效应,具体表现为EIT光谱发生频移、展宽和扭曲的现象,影响基于EIT光谱的电场强度测定。因此有必要就原子热运动对EIT的影响进行量化分析和修正。
当里德堡原子处于热力学平衡态时,其运动速率沿激光传输方向符合一维麦克斯韦速率分布[25],运动速率分布函数为
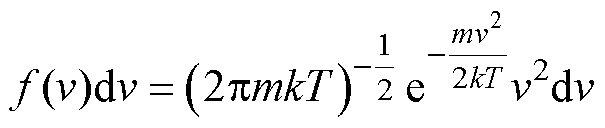 (10)
(10)
式中,v为原子运动速率;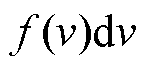 为在速率v下原子所占比例;k为玻耳兹曼常量;T为环境热力学温度;m为原子质量。
为在速率v下原子所占比例;k为玻耳兹曼常量;T为环境热力学温度;m为原子质量。
进而可以推导出里德堡原子系综的等效热运动速度ve为
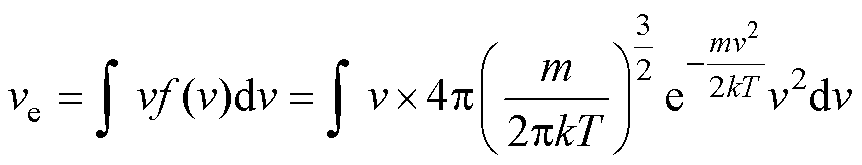 (11)
(11)
设激光沿z轴传播,原子在z方向的运动速率范围为-20~20 m/s,取T为50、100、300、500、1 000 K分别计算里德堡原子的等效热运动速度,计算结果见表1。
原子热运动影响原子与激光之间的相对运动,在原理模型中体现为对探测光和耦合光频率失谐量的影响。设探测光的传输方向为正,则探测光和耦合光频率失谐量应做如下调整:
表1 不同环境温度下里德堡原子等效热运动速率
Tab.1 Equivalent thermalrate of Rydberg atoms at different ambient temperatures

温度/K等效热运动速率/(m/s) 502.822 1003.991 3006.912 5008.923 1 00012.619
 (12)
(12)
式中,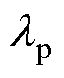 为探测光波长;
为探测光波长;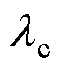 为耦合光波长。
为耦合光波长。
进一步可以解出考虑原子热运动的系统复极化率,以及对应的色散率和吸收率分别为
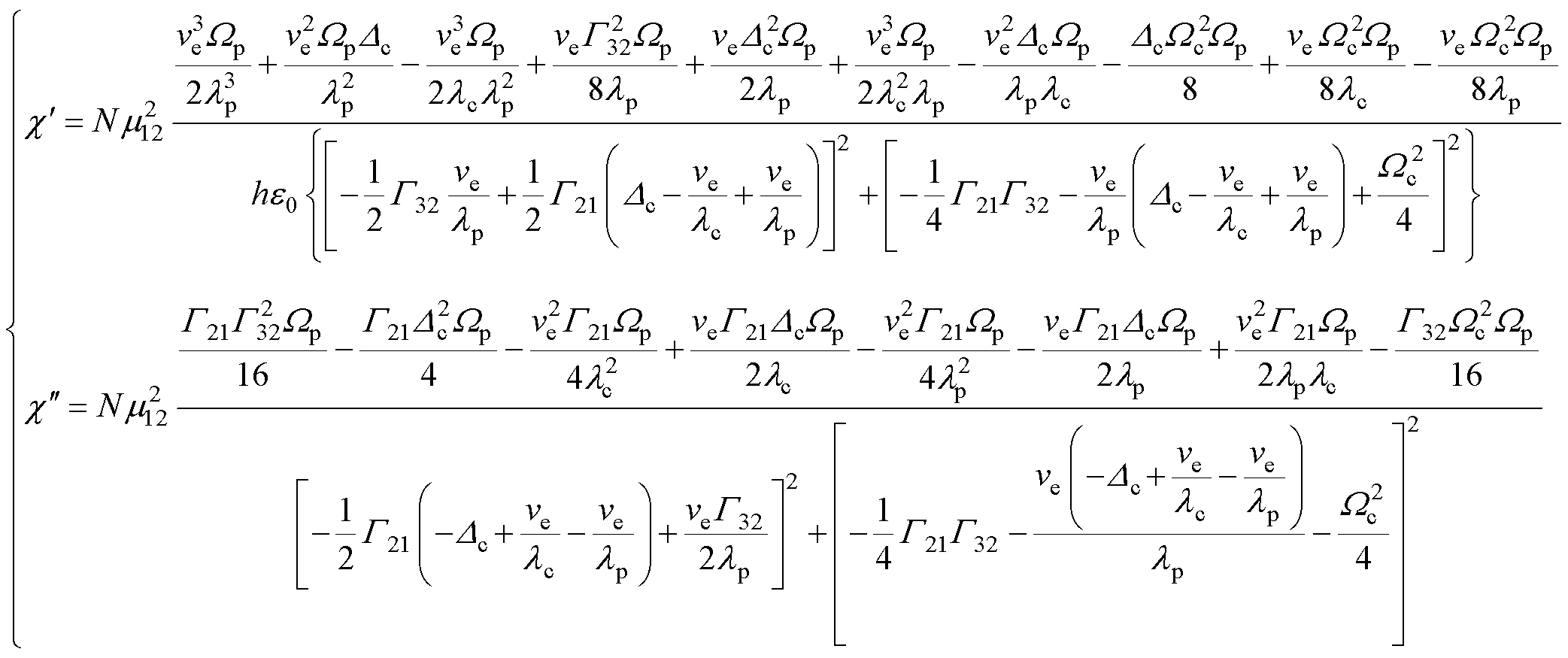 (13)
(13)
根据式(13),绘制不同温度下的EIT光谱曲线如图3所示。
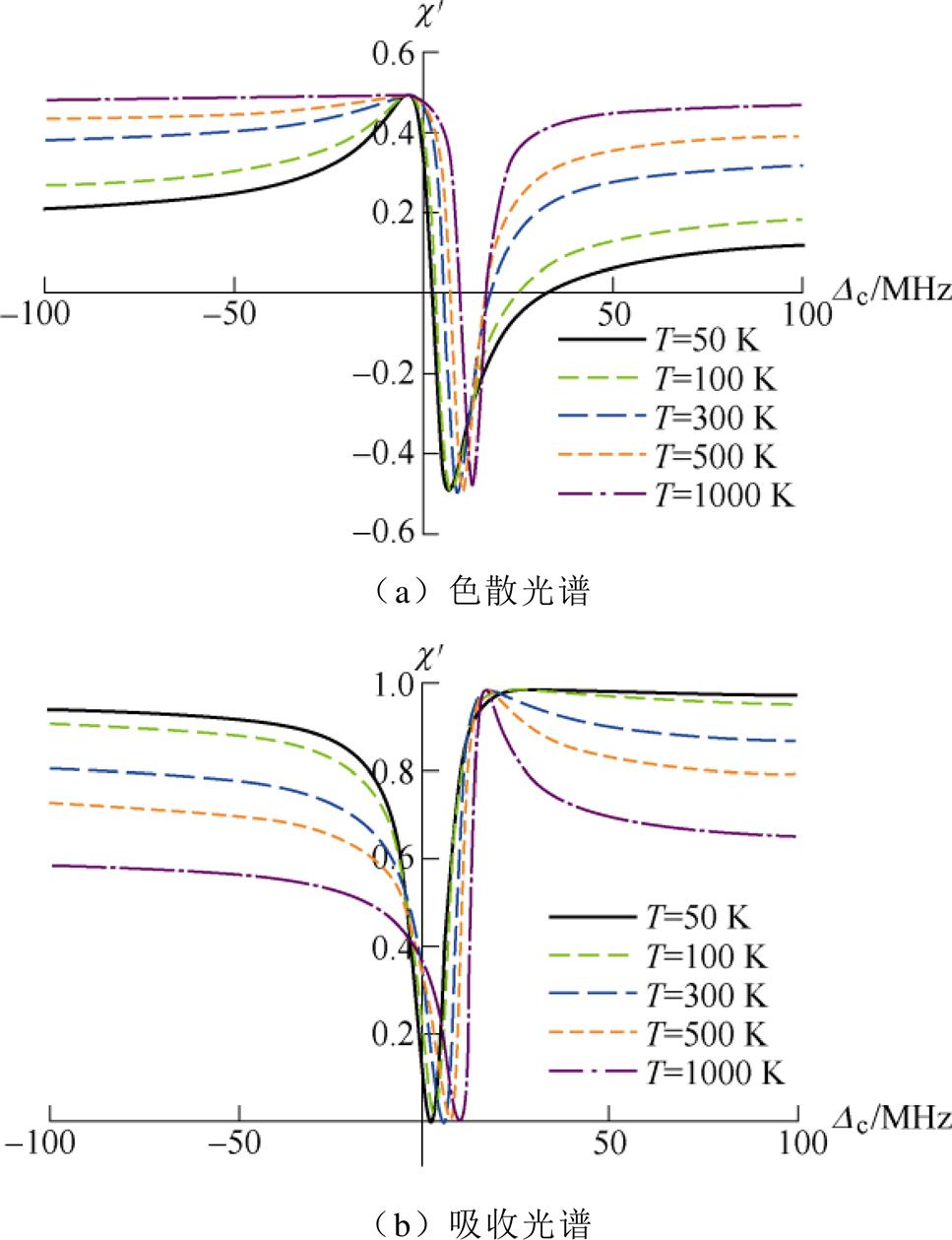
图3 考虑多普勒效应的EIT光谱曲线
Fig.3 EIT spectrum considering Doppler effect
根据图3a、图3b可知,随着温度升高,EIT吸收和色散曲线线形的对称性丧失。同时,吸收曲线左侧整体下移,导致吸收窗口深度降低并发生不均匀展宽,这种不均匀展宽导致吸收光谱出现蓝移。
文献[27]求解与探测光吸收和色散相关的密度矩阵元r21,通过扫描其探测光失谐量的方式来研究温度对探测场的吸收特性的影响,如图4所示。研究发现,随着温度升高,原子吸收曲线的EIT窗口的凹陷深度逐渐降低,直至消失,并且谱线也随之发生展宽。与本文提出的理论模型所得结果规律保持一致,可验证本文理论方法的准确性。
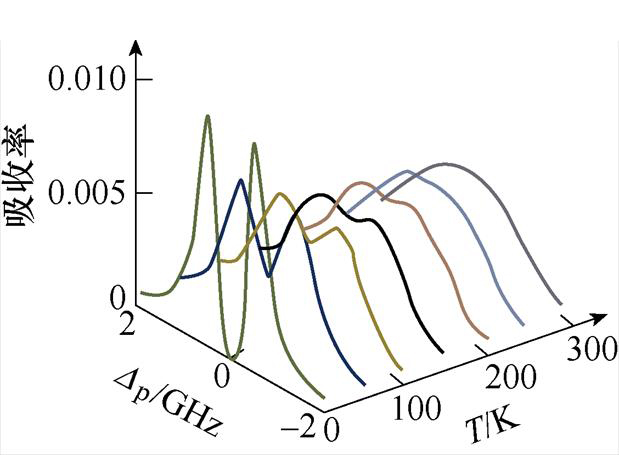
图4 不同温度下的原子吸收光谱[27]
Fig.4 Atomic absorption spectraat different temperatures[27]
原子热运动导致EIT数学模型中探测光和耦合光频率失谐量变化,调整探测光和耦合光的激光器频率进行反向补偿,便可修正原子热运动多普勒效应造成的影响。修正方法流程如图5所示。
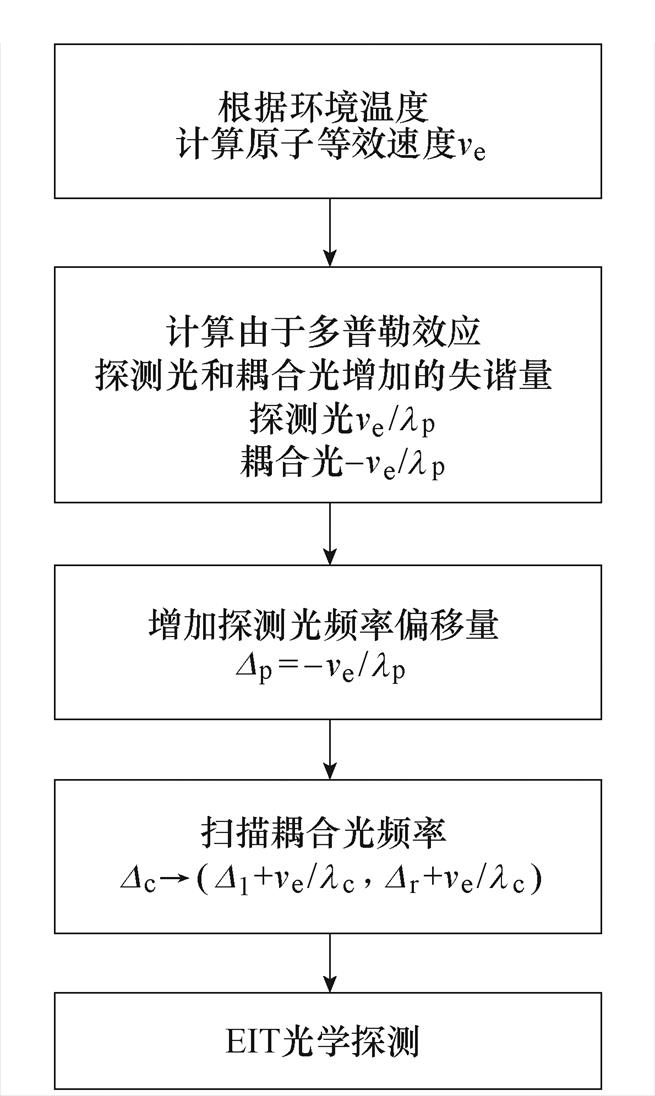
图5 消除原子热运动多普勒效应方法
Fig.5 Method of eliminating the Doppler effect caused by the thermal motion of atoms
图5中,Dl和Dr分别为激光器不加修正参数时扫描的负极限值和正极限值。
根据表2设定参数,得到结果如图6中的虚线部分所示。随后,使用本文提出的修正方法对其进行修正,修正效果如图6中的实线部分所示。
表2 参数对照
Tab.2 Parameter comparison
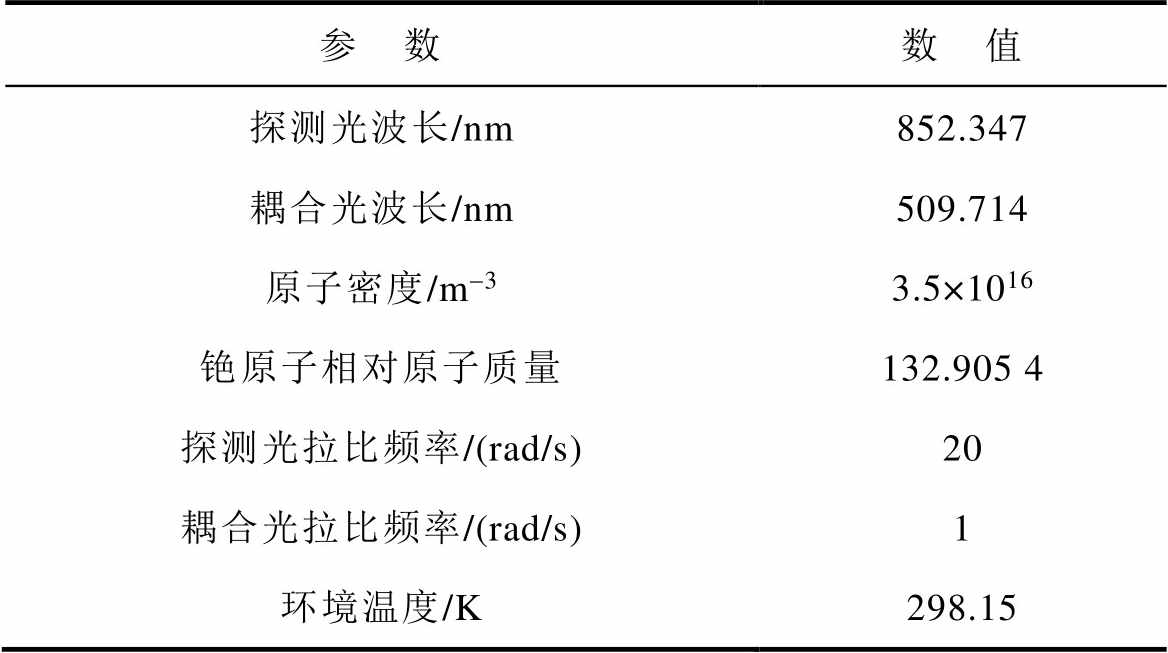
参 数数 值 探测光波长/nm852.347 耦合光波长/nm509.714 原子密度/m-33.5×1016 铯原子相对原子质量132.905 4 探测光拉比频率/(rad/s)20 耦合光拉比频率/(rad/s)1 环境温度/K298.15
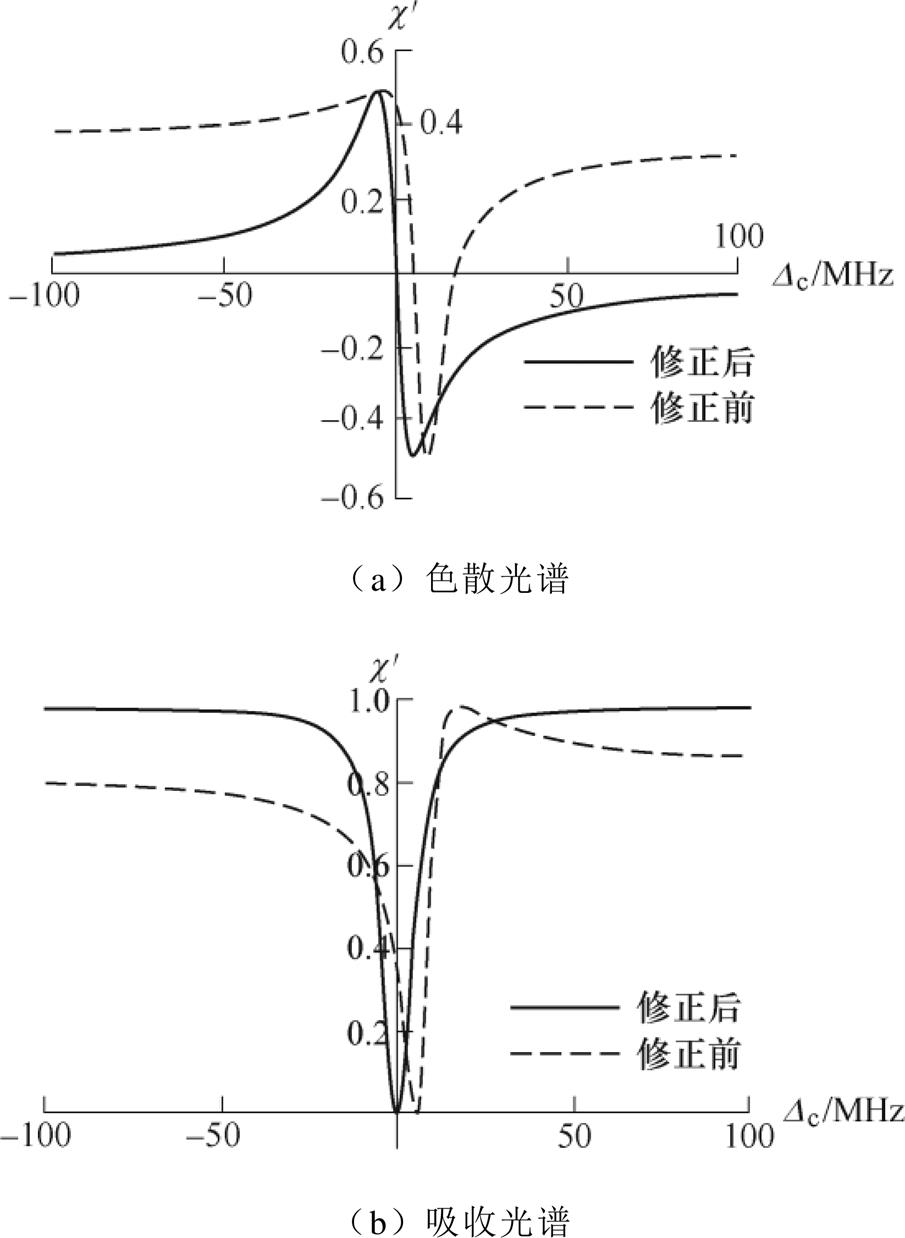
图6 修正多普勒效应的EIT光谱(T=298.15 K)
Fig.6 Correcting the Doppler effect in the EIT spectrum (T=298.15 K)
由图6可见,采取修正方法后,色散光谱和吸收光谱的反常趋势被矫正,有效消除了由于原子热运动所导致的多普勒效应影响。
本文建立描述多光子与原子作用的密度矩阵方程,结合热原子运动速率分布函数,得到了理论模型,量化分析了原子热运动对原子系统复极化率以及EIT光谱的影响;通过反向补偿探测光和耦合光的频率失谐量,可修正温度导致的多普勒效应对EIT光谱所造成的影响。仿真结果表明本文提出方法的有效性。本文研究可提高基于里德堡原子的电场测量系统的测量精度,为激光器频率设置提供理论依据。
本文是以阶梯型三能级系统为例建立数学模型、对仿真结果进行分析来说明通过对激光器频率进行反向补偿来修正原子热运动多普勒效应的原理。实际上还有研究者提出三能级Λ结构、V结构,四能级阶梯结构、Y结构等,针对不同的能级结构,该修正原理和方法是通用的,只不过三能级系统对两束激光进行修正,而四能级系统要对三束激光进行修正。
此外,本文重点考虑温度所引起的原子热运动对基于里德堡原子电场量子测量的影响,实际测量应用场景中还会存在其他影响因素,若一并考虑进行有效控制,将能够达到更精确的测量目的。
参考文献
[1] 吴桂芳, 崔勇, 刘宏, 等. 基于差分进化算法的三维电场传感器解耦标定方法[J]. 电工技术学报, 2021, 36(19): 3993-4001.
Wu Guifang, Cui Yong, Liu Hong, et al. Decoupling calibration method of 3D electric field sensor based on differential evolution algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 3993- 4001.
[2] 杨圆, 高克利, 袁帅, 等. 典型电场下C4F7N/CO2/O2混合气体工频击穿特性研究[J]. 电工技术学报, 2022, 37(15): 3913-3922.
Yang Yuan, Gao Keli, Yuan Shuai, et al. Research on the power frequency breakdown characteristics of C4F7N/CO2/O2 gas mixture under typical electric fields[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3913-3922.
[3] 李国倡, 梁箫剑, 魏艳慧, 等. 配电电缆附件复合绝缘界面缺陷类型和位置对电场分布的影响研究[J]. 电工技术学报, 2022, 37(11): 2707-2715.
Li Guochang, Liang Xiaojian, Wei Yanhui, et al. Influence of composite insulation interface defect types and position on electric field distribution of distribution cable accessories[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2707- 2715.
[4] 米彦, 葛欣, 刘露露, 等. 微秒脉冲电场强度对BNNSs取向程度和环氧树脂复合材料热导率的影响[J]. 电工技术学报, 2022, 37(6): 1533-1541.
Mi Yan, Ge Xin, Liu Lulu, et al. Effect of microsecond pulsed electric field strength on the BNNSs orientation degree and the thermal con- ductivity of epoxy resin composites[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1533- 1541.
[5] 陈蔚, 黎卫国, 欣振宇, 等. GIL三支柱绝缘子电场仿真与表面电荷测量[J]. 高压电器, 2021, 57(11): 42-50.
Chen Wei, Li Weiguo, Xin Zhenyu, et al. Electric field simulation and surface charge measurement of tri-post insulator in GIL[J]. High Voltage Apparatus, 2021, 57(11): 42-50.
[6] 刘鹏, 吴泽华, 朱思佳, 等. 缺陷对交流1100kV GIL三支柱绝缘子电场分布影响的仿真[J]. 电工技术学报, 2022, 37(2): 469-478.
Liu Peng, Wu Zehua, Zhu Sijia, et al. Simulation on electric field distribution of 1100kV AC tri-post insulator influenced by defects[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 469- 478.
[7] Xue Fen, Hu Jun, Guo Yue, et al. Piezoelectric- piezoresistive coupling MEMS sensors for measure- ment of electric fields of broad bandwidth and large dynamic range[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 551-559.
[8] 吴昊, 齐波, 李成榕, 等. 基于Kerr效应法的油纸复合绝缘交直流复合电场测量[J]. 电工技术学报, 2013, 28(4): 28-34.
Wu Hao, Qi Bo, Li Chengrong, et al. The measurement of AC-DC composite field for oil-paper insulation system based on the Kerr electro-optic effect[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 28-34.
[9] 林飞宏, 周吉, 张建培, 等. 反射式小型光学电场传感器[J]. 浙江大学学报(工学版), 2021, 55(11): 2207-2214.
Lin Feihong, Zhou Ji, Zhang Jianpei, et al. Reflective miniature optical electric field sensor[J]. Journal of Zhejiang University(Engineering Science), 2021, 55(11): 2207-2214.
[10] Bussey L W, Burton F A, Bongs K, et al. Quantum shot noise limit in a Rydberg RF receiver compared to thermal noise limit in a conventional receiver[J]. IEEE Sensors Letters, 2022, 6(9): 1-4.
[11] Simons M T, Haddab A H, Gordon J A, et al. Embedding a Rydberg atom-based sensor into an antenna for phase and amplitude detection of radio-frequency fields and modulated signals[J]. IEEE Access, 2019, 7: 164975-164985.
[12] Robinson A K, Prajapati N, Senic D, et al. Determining the angle-of-arrival of a radio-frequency source with a Rydberg atom-based sensor[J]. Applied Physics Letters, 2021, 118(11): 114001.
[13] Rajasree K S, Karlsson K, Ray T, et al. 1.6 GHz frequency scanning of a 482 nm laser stabilized using electromagnetically induced transparency[J]. IEEE Photonics Technology Letters, 2021, 33(15): 780-783.
[14] Huang Chutian, Huang Bei, Zhang Bingsheng, et al. An electromagnetically induced transparency inspired antenna sensor for crack monitoring[J]. IEEE Sensors Journal, 2021, 21(1): 651-658.
[15] Song Zhengyong, Chu Qiongqiong, Zhu C, et al. Polarization-independentterahertz tunable analog of electromagnetically induced transparency[J]. IEEE Photonics Technology Letters, 2019, 31(15): 1297- 1299.
[16] Ashkarin I N, Beterov I I, Yakshina E A, et al. Toffoli gate based on a three-body fine-structure-state- changing Förster resonance in Rydberg atoms[J]. Physical Review A, 2022, 106(3): 032601.
[17] 焦月春, 赵建明, 贾锁堂. 基于Rydberg原子的超宽频带射频传感器[J]. 物理学报, 2018, 67(7): 137-145.
Jiao Yuecun, Zhao Jianming, Jia Suotang. Broadband Rydberg atom-based radio-frequency field sensor[J]. Acta Physica Sinica, 2018, 67(7): 137-145.
[18] Veit C, Epple G, Kübler H, et al. RF-dressed Rydberg atoms in hollow-core fibres[J]. Journal of Physics B: Atomic, Molecular and Optical Physics, 2016, 49(13): 134005.
[19] Hao Liping, Xue Yongmei, Fan Jiabei, et al. Precise measurement of a weak radio frequency electric field using a resonant atomic probe[J]. Chinese Physics B, 2020, 29(3): 033201.
[20] 张淳刚, 李伟, 张好, 等. 基于调制射频场电磁诱导透明光谱的工频电场测量[J]. 光子学报, 2021, 50(6): 162-168.
Zhang Chungang, Li Wei, Zhang Hao, et al. Power frequency electric field measurement based on electromagnetic induced transparent spectrum under radio frequency field[J]. Acta Photonica Sinica, 2021, 50(6): 162-168.
[21] 李伟, 张淳刚, 张好, 等. 基于里德伯原子AC- Stark效应的工频电场测量[J]. 激光与光电子学进展, 2021, 58(17): 144-148.
Li Wei, Zhang Chungang, Zhang Hao, et al. Power-frequency electric field measurement based on AC-stark effect of Rydberg atoms[J]. Laser & Optoelectronics Progress, 2021, 58(17): 144-148.
[22] 崔帅威, 彭文鑫, 李松浓, 等. 基于里德堡原子的工频电场测量[J]. 高电压技术, 2023, 49(2): 644-650.
Cui Shuaiwei, Peng Wenxin, Li Songnong, et al. Power frequency electric field measurement based on Rydberg atoms[J]. High Voltage Engineering, 2023, 49(2): 644-650.
[23] Boller K, Imamolu A, Harris S E. Observation of electromagnetically induced transparency[J]. Physical Review Letters, 1991, 66(20): 2593-2596.
[24] Li Y, Jin S, Xiao M. Observation of an electro- magnetically induced change of absorption in multilevel rubidium atoms[J]. Physical Review A, 1995, 51(3): 1754-1757.
[25] Khoa D X, Trong P V, Doai L V, et al. Elec- tromagnetically induced transparency in a five-level cascade system under Doppler broadening: an analytical approach[J]. Physica Scripta, 2016, 91(3): 035401.
[26] Hazra R, Hossain M M. Study of multi-window electromagnetically induced transparency (EIT) and related dispersive signals in V-type systems in the Zeeman sublevels of hyperfine states of 87 Rb-D2 line[J]. Journal of Physics B: Atomic, Molecular and Optical Physics, 2020, 53(23): 235401.
[27] Zhang Guiyin, Tao Qiyong, Zhao Zhanlong, et al. Effect of thermal motion on the phenomenon of electromagnetically induced transparency[J]. Optik, 2017, 138: 153-159.
[28] Gea-banacloche J, Li Yongqing, Jin Shaozheng, et al. Electromagnetically induced transparency in ladder- type inhomogeneously broadened media: theory and experiment[J]. Physical Review A, 1995, 51(1): 576- 584.
[29] 赵嘉栋, 张好, 杨文广, 等. 基于里德伯原子电磁诱导透明效应的光脉冲减速[J]. 物理学报, 2021, 70(10): 99-107.
Zhao Jiadong, Zhang Hao, Yang Wenguang, et al. Deceleration of optical pulses based on electro- magnetically induced transparency of Rydberg atoms[J]. Acta Physica Sinica, 2021, 70(10): 99-107.
Abstract The quantum measurement of the electric field based on the electromagnetically induced transparency (EIT) effect of the Rydberg atom surpasses the limitations of traditional measuring methods in accuracy and sensitivity, offering self-calibration capability. Ideally, the electric fieldismeasured by stationary cold atoms. However, preparing cold atoms requires multi-lasersynergy and gradient magnetic field coils to reduce the atomtemperature, which needs complex experimental setups, precise operational techniques, and expensive equipment. Using hot atoms at room temperature is convenient in engineering applications. However, the atom’s thermal motion affects the relative velocity between atoms and lasers, resulting in the Doppler effect. Accordingly, frequency shifts and deformations in the EIT spectruminterfere with the coherent effect of the electric field. Mitigating the Doppler effectis essential to enhance the quantum measurement accuracy of theelectric field using hot Rydberg atoms.
This paper proposes a method to correct the Doppler effect by adjusting the probe and coupling laserfrequencies. The density matrix equation is established based on the multiphot on interaction with atoms. By solving the equation and deriving the mathematical relationship among the absorption rate of the probe laser, the dispersion rate of the probe laser, and the frequency detuning of the coupled laser in the atomic system, an accurate description of the EIT effect is obtained. Then, the relationship between temperature and atomic motion is introduced to quantify the Doppler effect of atomic thermal motion, which convertsatomic thermal motion into the quantity of probe laser and coupled laser frequency detuning. The Doppler effect on the absorbance and dispersion of the atomic system is analyzed. Finally, the EIT spectrum is corrected by reverselyadjusting the input frequency parameters of lasers based on the calculated quantities. Simulations verify the effectiveness of the proposed method.
The results show that the EIT absorption and dispersion curve line is asymmetric with the increase in temperature. Simultaneously, the deformation of the absorption curve reduces the depth of the absorption window and inhomogeneous broadening, leading to a frequency shift in the absorption spectrum. The proposed method corrects the anomalous trend of the dispersion and absorption spectra, eliminating the Doppler effect due to the atom’s thermal motion. The quantum measurement accuracy of the electric field is enhanced based on Rydberg atoms at room temperature, which promotes the engineering application process of quantum measurement.
keywords:Electric field measurement, Rydberg atoms, electromagnetically induced transparency (EIT), thermal motion of atoms, Doppler effect, correction
DOI: 10.19595/j.cnki.1000-6753.tces.230395
中图分类号:TM930.12
国家自然科学基金项目(U22B2095)和民用航天技术预先研究项目(D010103)资助。
收稿日期 2023-03-29
改稿日期 2023-04-25
阎 晟 男,1998年生,博士研究生,研究方向为量子测量。E-mail: 18843150725@163.com
肖冬萍 女,1977年生,副教授,博士生导师,研究方向为电磁测量、量子测量、电磁环境建模与数值计算、电气设备状态监测与故障诊断等。E-mail: xiaodongping@cqu.edu.cn(通信作者)
(编辑 郭丽军)