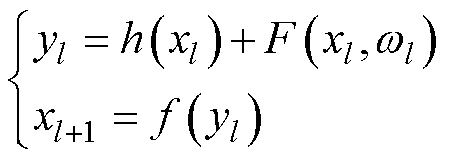（1）
式中，xl和xl+1分别为第l个残差块的输入与输出；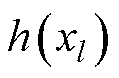
为单位映射函数；
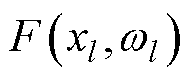为残差函数；
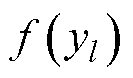为激活函数。当残差函数为0时，相当于引入恒等映射，至少网络的性能不会下降。短残差的连接方式将多个不同尺度卷积核提取的特征信息进行融合，解决对图像细节特征提取不够充分和图像纹理区域不够清晰等问题。
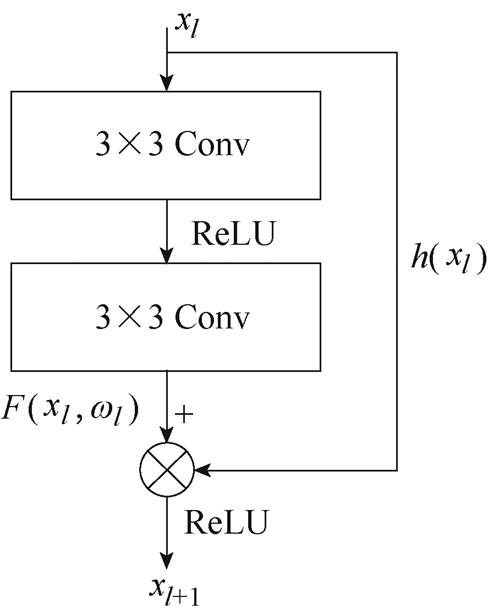
图1 ResNet残差块
Fig.1 ResNet-block
摘要 利用有限元方法对几何结构复杂的电机和变压器进行磁场分析，存在仿真时间长且无法复用的问题。因此，该文提出一种基于残差U-Net和自注意力Transformer编码器的磁场预测方法。首先建立永磁同步电机（PMSM）和非晶合金变压器（AMT）有限元模型，得到深度学习训练所需的数据集；然后将Transformer模块与U-Net模型结合，并引入短残差机制建立ResUnet-Transformer模型，通过预测图像的像素实现磁场预测；最后通过Targeted Dropout算法和动态学习率调整策略对模型进行优化，解决拟合问题并提高预测精度。计算实例证明，ResUnet-Transformer模型在PMSM和AMT数据集上测试集的平均绝对百分比误差（MAPE）均小于1%，且仅需500组样本。该文提出的磁场预测方法能减少实际工况和多工况下精细模拟和拓扑优化的时间和资源消耗，亦是虚拟传感器乃至数字孪生的关键实现方法之一。
关键词：有限元方法 电磁场 深度学习 U-Net Transformer
电工装备磁场的精确数值模拟有助于其性能分析、内部场的实时演算，亦是实现产品设计与多物理场数字孪生的基础[1-2]。以有限元方法为代表的电磁性能分析方法存在计算量大、计算耗时长且无法复用的问题[3]，难以满足实际需求。当仿真模型结构稍加复杂，有限元方法仿真时间可能需要数十到上百小时，严重时导致计算机系统崩溃。若几何结构尺寸或材料特性上稍有变化，需重新进行仿真求解。
AlphaGo击败职业围棋选手[4-5]、自动驾驶的无人汽车、ChatGPT的横空出世，标志着人工智能，特别是深度学习技术，具有强大的函数拟合能力，可以从大量的数据中挖掘有用的信息，无需特征提取且适用性强[6-7]。随着深度学习技术的快速发展，电机和变压器等电工装备的电磁特性分析正在向着智能化、数字化方向前进。
卷积神经网络（Convolutional Neural Network, CNN）[8]是深度学习的经典算法之一，具有强大的空间特征提取能力[9]，被广泛应用于图像处理[10]、语音识别[11]等领域。CNN多用于分类任务中，一系列卷积和池化操作可以提取图像的空间特征，但是末端的全连接层会使得部分图像空间特征丢失。全卷积神经网络（Fully Convolutional Network, FCN）[12]使用卷积-上采样的结构替换掉CNN的卷积-全连接结构，上采样层可以提高图像特征的空间分辨率，以实现像素级别的预测。FCN使用长跳跃连接将最终的预测层与浅层低级特征以逐元素相加的方式融合，提高了网络的性能和预测准确性。U-Net[13]可以看作是FCN的扩展，编码器和解码器对称分布的特性使其在结构上更为“优雅”。与FCN不同，U-Net解码器部分在分级进行上采样的同时衰减特征通道数量，解码器进行分级上采样时均通过长跳跃连接与编码器对应的图像特征以矩阵拼接的方式融合，具有更强的细节捕获能力和少样本学习能力，这种融合不同尺度特征的编码器和解码器结构使其广泛应用于医学图像分割任务中。此后，越来越多的改进的U型网络架构出现在医学分割领域。残差网络（Residual Network, ResNet）[14]的核心思想是引入残差连接（短残差）来解决深层网络训练过程中的梯度消失和网络性能退化问题，残差网络的思想在很多网络中均有应用。文献[15]在U-Net编码器与解码器中引入残差连接（短残差）构建深度ResUnet，其性能优于U-Net模型。文献[16]依据U-Net架构，设计了一种带残差连接（短残差）的双注意力模块，其分割定量指标优于其他相似的经典深度模型。尽管如此，卷积运算自身存在局限性，只能捕获局部特征，无法很好地学习全局特征[17]，一定程度上限制了U型网络架构的发展。2017年，Transformer首次被提出，它是一种基于自注意力机制的模型[18]。自注意力机制旨在学习特征之间的潜在关系，并赋予高价值的信息以较高的权重。凭借强大的长距离建模能力和并行计算能力，Transformer从自然语言处理领域取得巨大成功并逐步扩展至计算机视觉等领域。文献[19]将基于自注意力机制的纯Transformer结构应用到图像分类任务中。文献[20]将Transformer与U-Net相结合，提出了TransUNet，将其应用在医学分割领域并取得了不错的效果。TransUNet是首个将Transformer应用到医学图像分割领域的U型网络，此后各种Transformer和U型网络相结合的架构相继被提出。
凭借深度学习强大的学习能力，国内外学者将其应用于磁场、温度场和流场的预测问题中。针对这一问题的基本思路是：使用数值模拟方法得到少量计算结果并形成数据集，然后对深度学习模型进行训练和测试，使得该网络模型能够有效地模拟某一特定场的数值模拟计算过程。在电气工程领域，文献[21]在CNN中引入长跳跃连接，构建基于编解码结构的CNN，预测不同几何形状、材料和激励信息下变压器的磁场分布，提高了计算效率。文献[22]利用具有长跳跃连接且不含池化层的U-Net实现对变压器不同拓扑结构下磁场的端对端预测。文献[23]在U-Net中引入短残差和门控结构，预测具有复杂纳米结构的孤立散射体的磁场分布，具有较高的计算效率。文献[24]使用基于卷积神经单元的长短期记忆神经网络（ConvLSTM）和基于卷积神经单元的门控循环单元（ConvGRU）预测变压器电工钢片磁化过程中的磁畴动态演变图像，提高了电工钢磁特性的准确表征效率。在流场领域，文献[25]建立含有池化层和没有池化层两种路径融合的CNN网络，预测不同雷诺数下圆柱体周围的速度场。文献[26]提出基于深度CNN和深度多层感知机相结合的数据驱动方法，可在几秒内获得翼型周围的流场。文献[27]建立静态CNN和具有特征提取模块和重建模块的多时间路径CNN两种网络，预测高分辨率的流场。文献[28]提出一种基于共享编码和解码层的CNN流场近似模型，预测不可见流动条件下的速度和压力场。
本文提出一种基于残差U-Net和自注意力Trans- former编码器的磁场预测方法。受残差网络和Transformer启发，在U-Net模型的编码和解码过程引入短残差机制，并在长跳跃连接中添加Trans- former模块，建立ResUnet-Transformer模型，利用短残差机制防止网络性能退化同时加快收敛，依据自注意力机制掌控全局信息。模型训练过程中引入Targeted Dropout算法和动态学习率调整策略，防止训练过程中出现过拟合问题，并提高磁场的预测精度。以一台永磁同步电机（Permanent Magnet Syn- chronous Motor, PMSM）和小型单项非晶合金变压器（Amorphous Metal Transformer, AMT）为预测实例，验证了该方法的可行性。
1.1.1 ResNet
为解决网络层数过深而出现性能退化现象，提出了卷积网络ResNet[14]。卷积神经网络[8]通过一系列卷积和池化操作实现图像空间特征的逐层提取，卷积层的局部感受野机制和权值共享的特点，使得网络的参数量大幅度降低，池化层使得卷积层提取的特征具有缩放不变性，提高了网络的泛化能力。而作为一种残差网络，ResNet通过在每个网络层之间引入跳跃连接，允许前一层的特征直接跳过当前层并与后续层的特征相加，提高了网络的表达能力。ResNet通过堆叠多个残差块（ResNet-block）组成，本文采用两层卷积基本残差单元结构，如图1所示。在残差块中，输入特征可通过层间连接的方式更快地向前传播，本文将这种连接方式描述为短残差机制。
每个残差块可以描述为
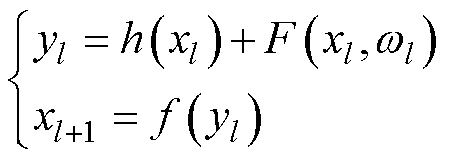（1）
式中，xl和xl+1分别为第l个残差块的输入与输出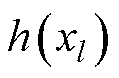；为单位映射函数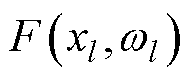；为残差函数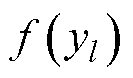；为激活函数。当残差函数为0时，相当于引入恒等映射，至少网络的性能不会下降。短残差的连接方式将多个不同尺度卷积核提取的特征信息进行融合，解决对图像细节特征提取不够充分和图像纹理区域不够清晰等问题。
图1 ResNet残差块
Fig.1 ResNet-block
1.1.2 U-Net
U-Net[13]是一种编解码结构的U型卷积神经网络，包括编码器、瓶颈（Bottleneck）模块[29]、解码器几部分组成。编码器通过卷积、池化等方法从图像中提取空间特征，解码器根据编码器提供的信息通过多尺度特征融合、上采样等方法修复细节特 征[30]，瓶颈模块负责连接编码器与解码器，其网络架构如图2所示。
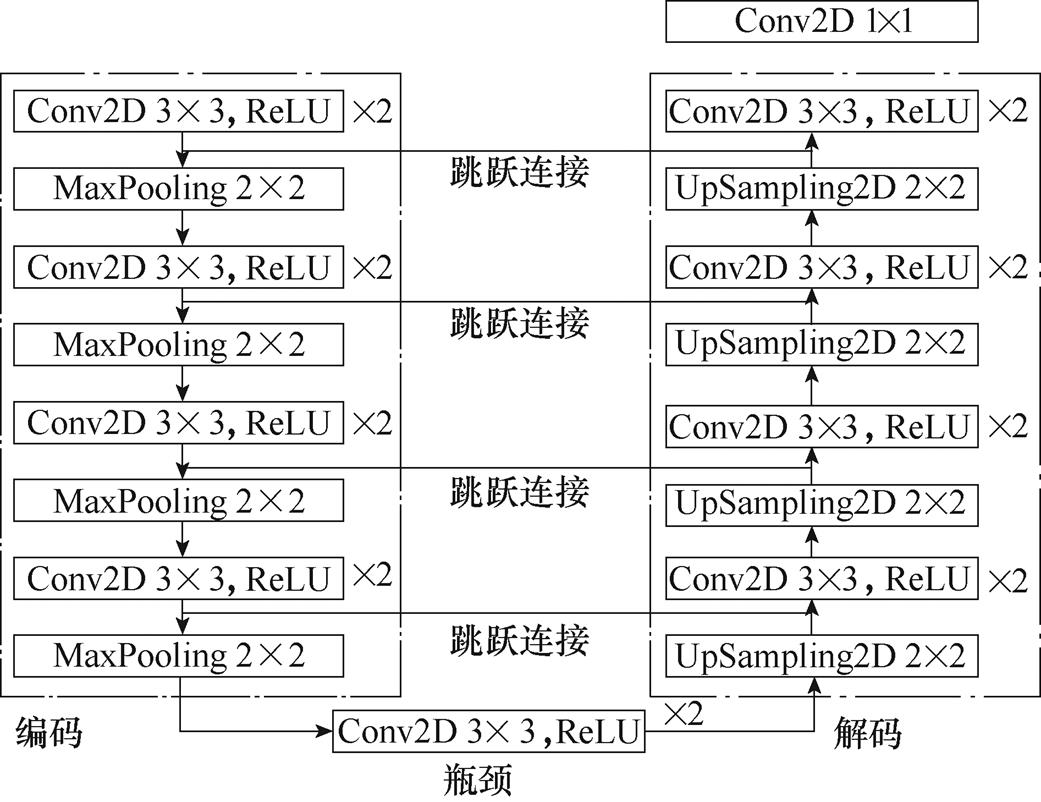
图2 U-Net模型结构
Fig.2 U-Net model structure
U-Net最巧妙之处在于使用跳跃连接结构将编码器与解码器级联，与ResNet网络中的连接方式不同，本文将这种连接方式称为长跳跃连接。在编码器的池化操作之前，卷积层的输出均被传输到解码器[31]，长跳跃连接的结构可以将上采样得到的图像特征与下采样得到的图像特征进行拼接融合，使融合后的图像同时具备低级细节特征与高级抽象特征，提高了对于低阶特征的利用率。长跳跃连接的结构实际上为信息的传播创建了一条路径，不仅有助于训练过程中的反向传播，而且可以修复编码器阶段因池化操作而丢失的图像细节特征。
1.1.3 Transformer
Transformer[18]兴起于自然语言处理领域，由编码器和解器组成。长短期记忆（Long Short-Term Memory, LSTM）网络[32]对循环神经网络（Recurrent Neural Network, RNN）训练时可能出现的长距离梯度消失问题进行了改进，而Transformer的提出解决了RNN、LSTM等无法并行训练以及需要大量存储资源记忆整个序列信息的问题。相比于RNN，LSTM具有更强的长距离特征捕获能力、并行计算能力及运行效率。注意力机制起源于人类视觉认知科学。为合理利用有限的视觉信息处理资源，人类认知系统会选择将注意力集中在收集信息的重要部分，而忽略其他无关信息[33]。Transformer的核心正是多头自注意力机制，多头自注意力机制通过并行h次注意力计算，将单一的注意力模块映射到多个不同的子空间，允许模型共同关注来自不同位置的子空间信息，扩展了模型专注于不同特征的能力[34]。Transformer网络完全基于注意力机制，而注意力机制缺乏捕获输入特征相对位置信息的能力。为解决上述问题，Transformer采用位置编码为输入特征向量提供位置信息。位置编码的计算公式为
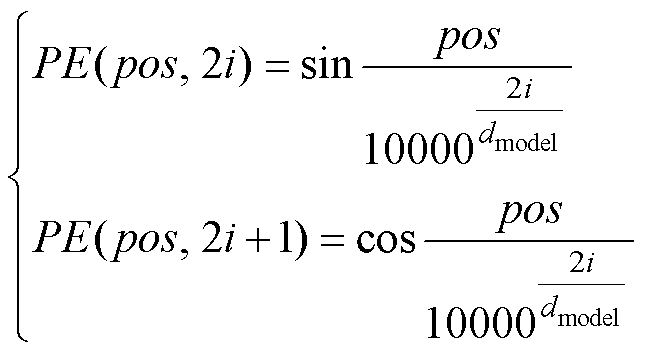（2）
式中，pos为序列长度；i为特征向量的维度下标；dmodel为特征长度。由于正弦和余弦函数具有周期性，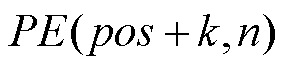
表示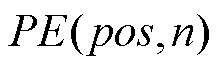
的线性变化，位置编码的每个维度对应于不同周期的正余弦函数，从而产生独一无二的纹理位置信息，最终识别特征间的相对位置关系。
Transformer通过位置编码标记特征的相对位置，通过多头自注意力机制实现全局特征的快速交互。本文利用Transformer编码器提取图像的空间特征，Transformer编码器由多个相同的子模块（Trans- former Block）堆叠而成，如图3所示。每个子模块包含两个子层，分别是多头自注意力层和前馈神经网络。每个子层都添加了残差连接以防止梯度消失，增强信息之间的流动，在残差连接之后进行层归一化操作以加速算法收敛。
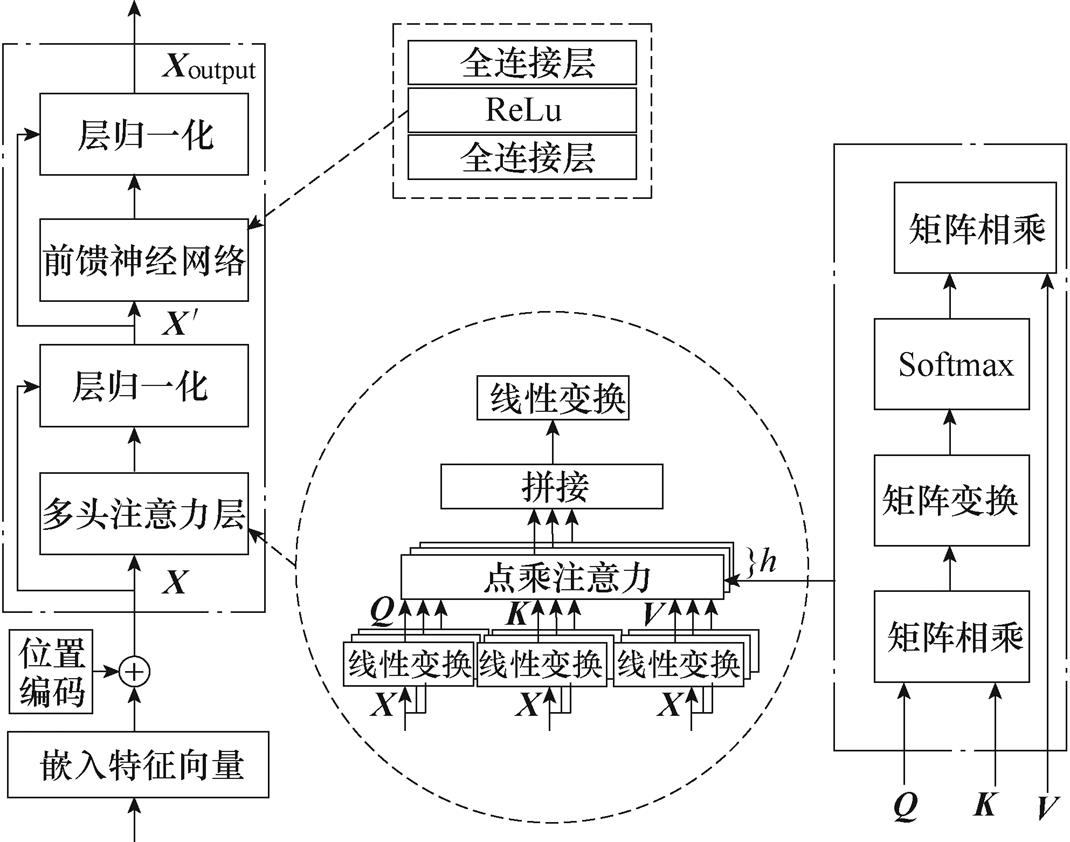
图3 Transformer子模型基本架构
Fig.3 The basic structure of Transformer encoder block
ResUnet-Transformer模型主要由编码器、解码器、瓶颈模块、长跳跃连接和Transformer模块五部分组成，如图4所示。编码器、解码器和瓶颈模块均含有ResNet残差块，每个残差块由两个3×3卷积块和短残差机制组成。每个卷积块包括3×3卷积层、批标准化（Batch Normalization）层ReLU激活层。批标准化层可以将输入激活层中分散的数据标准化，起到优化网络的效果，引入ReLU激活函数可以增强网络的非线性。
ResUnet-Transformer模型编码器由3个ResNet残差块和3个池化层组成，经过两次卷积运算后特征通道数加倍，以完成图像特征信息更高层次的抽象表达。每个残差块后使用池化核大小为4×4的最大池化层对卷积块输出的图像特征进行下采样，将其尺寸减少。下采样可以增加对输入图像的干扰（如图像平移、旋转等）的鲁棒性，从而可以减少过拟合的风险和计算量，并增加感受野的大小。在最后一个ResNet残差块的两个卷积层之后引入Dropout层，使用Targeted Dropout算法对模型进行正则化，减少训练过程中网络参数的数量，防止模型发生过拟合，提高泛化能力。
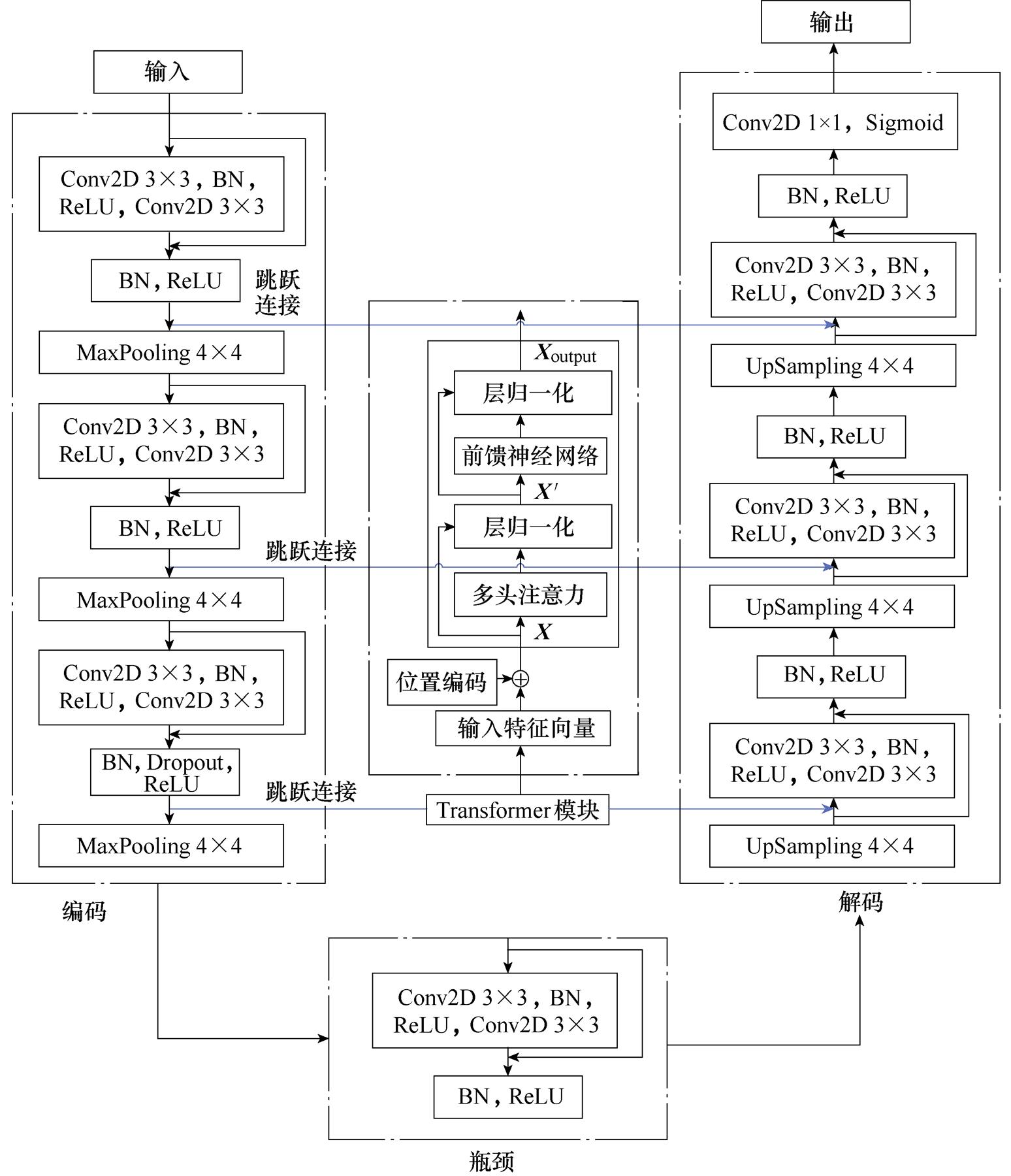
图4 ResUnet-Transformer模型结构
Fig.4 ResUnet-Transformer model structure
ResUnet-Transformer模型的瓶颈模块由1个ResNet残差块组成，经过编码器三次下采样后的图像特征经过瓶颈模块连接到解码器。
ResUnet-Transformer模型解码器首先使用4×4转置卷积运算对图像进行上采样，将特征通道数减少，上采样可以恢复图像抽象的特征信息，并将其解码为原始图像的大小。上采样后的图像再次经过ResNet残差块，特征通道数量减半。与编码器类似，这一系列的上采样和两次卷积操作重复3次。在解码器的末端是1×1的卷积层，仅改变特征图的通道数量，而不改变特征图的尺寸。
ResUnet-Transformer模型编码器的每次池化操作之间通过长跳跃连接与解码器级联，长跳跃连接可以使解码器直接学习编码器部分提取到的特征，从而防止多次池化下采样造成的部分图像特征丢失而影响最终的预测精度。在编码器第三次池化操作之前的长跳跃连接中引入Transformer模块，首先利用前馈神经网络学习位置信息，对经过下采样和短残差机制得到的图像各个像素点进行位置编码。其次，编码后的图像特征通过多头自注意力机制有效处理图像中各个像素点之间的相互作用关系，重点关注提取的图像空间特征中最有价值的部分，提高全局感知能力，防止特征的丢失，提升图像预测的细致度。最后，通过两个前馈神经网络对图像维度进行变换并与上采样后的图像特征进行融合，使融合后的图像同时具备高级特征和低级特征。
综上所述，ResUnet-Transformer模型使用ResNet中的残差块代替原始U-Net模型中两个3×3的卷积序列，同时在编码器的第三次池化操作之前的长跳跃连接中引入Transformer模块，卷积层的输出通过Transformer模块传输到解码器。ResUnet- Transformer模型具有以下优点：
（1）使用残差块代替原始模型编码器、解码器和瓶颈模块中的两个3×3的卷积序列，短残差机制的存在使得梯度在反向传播的过程中直接传回到上一层，加快了信息的传递。
（2）编码器和解码器仅含三个残差块，与原始U-Net模型的23层结构相比，ResUnet-Transformer模型仅包含15个卷积层，模型参数减少，大大简化了网络的训练。
（3）编码器的第三次池化操作之前的长跳跃连接中引入一个Transformer模块，利用短残差机制提取图像的空间特征，将提取到的高级图像特征借助Transformer模块挖掘图像中各个像素点之间的相互作用关系，借助位置编码和多头自注意力机制弥补U-Net在捕获全局特征方面的局限性，实现全局特征的有效交互。
磁场预测模型（ResUnet-Transformer）的建立与测试过程如图5所示，具体包括以下步骤：
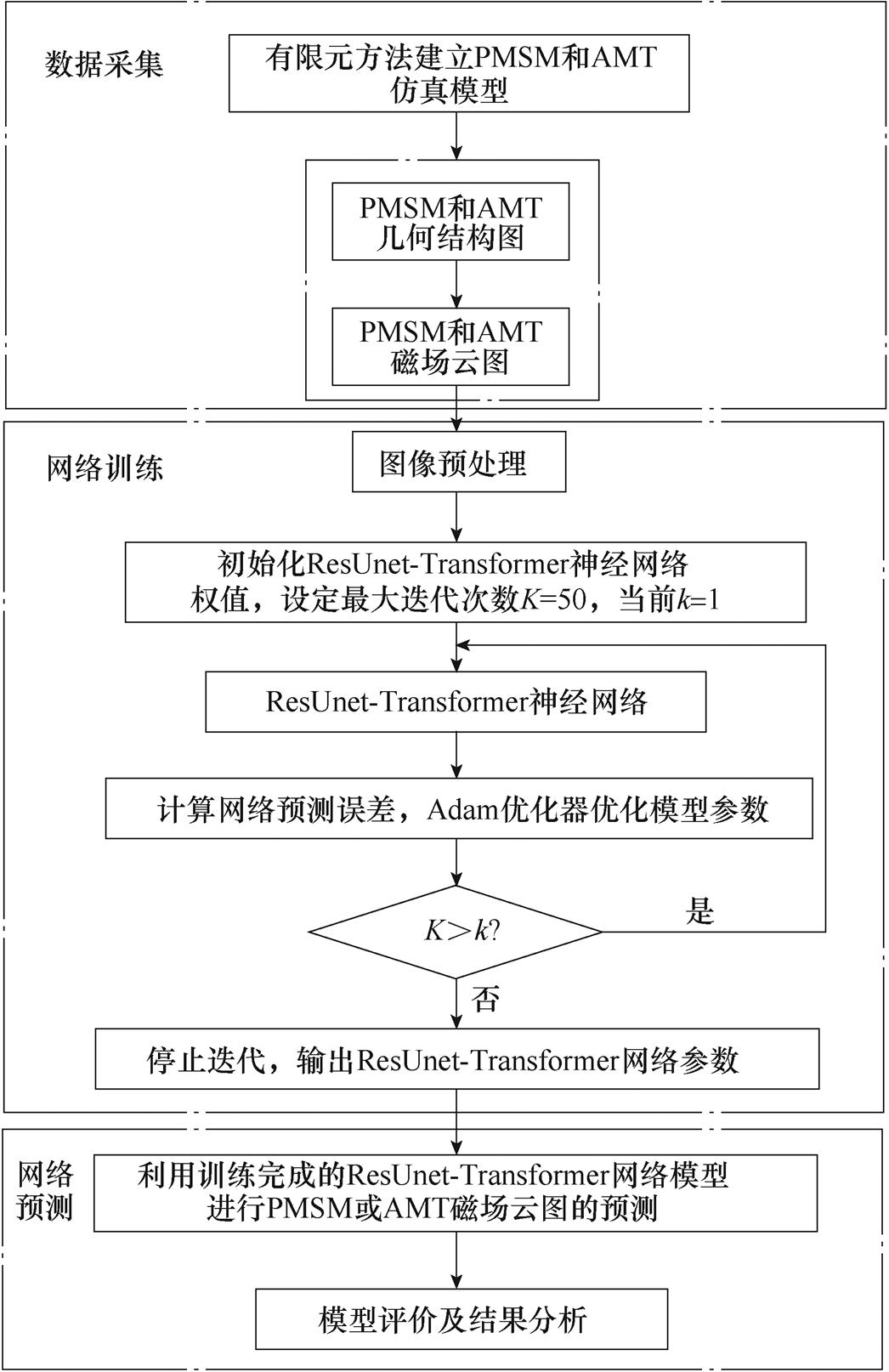
图5 磁场预测模型的建立与测试过程
Fig.5 Establishment and test of magnetic field prediction model
（1）利用有限元仿真软件建立PMSM和AMT仿真模型，改变PMSM和AMT几何结构参数计算不同参数设置下的磁场云图，得到PMSM和AMT的“几何结构图像-磁场云图”数据集，并将数据集随机划分为训练集和测试集。
（2）对PMSM和AMT的几何结构图进行图像预处理，包括对图像的裁剪、矩阵化及归一化等前处理操作。
（3）建立ResUnet-Transformer模型，利用训练集对其进行训练。将PMSM或AMT的几何结构图作为ResUnet-Transformer模型的输入，将几何结构图对应的磁场云图作为ResUnet-Transformer模型的输出，把场值分布（彩图）转化为图像，通过预测图像像素实现磁场的预测。
（4）将训练好的ResUnet-Transformer模型预测PMSM或AMT的磁场分布，比较PMSM或AMT磁场云图像素值的实际值与预测值，对所建立模型进行评价。
3.1.1 PMSM模型
普锐斯（Prius）混动汽车的驱动电机均有公开研究报告[35-36]，本文选择第Ⅱ代Prius混合动力汽车的PMSM作为预测案例，建立其二维有限元仿真模型，如图6所示。该电机为8极48槽内置式V型永磁同步电机，其结构参数，见表1。
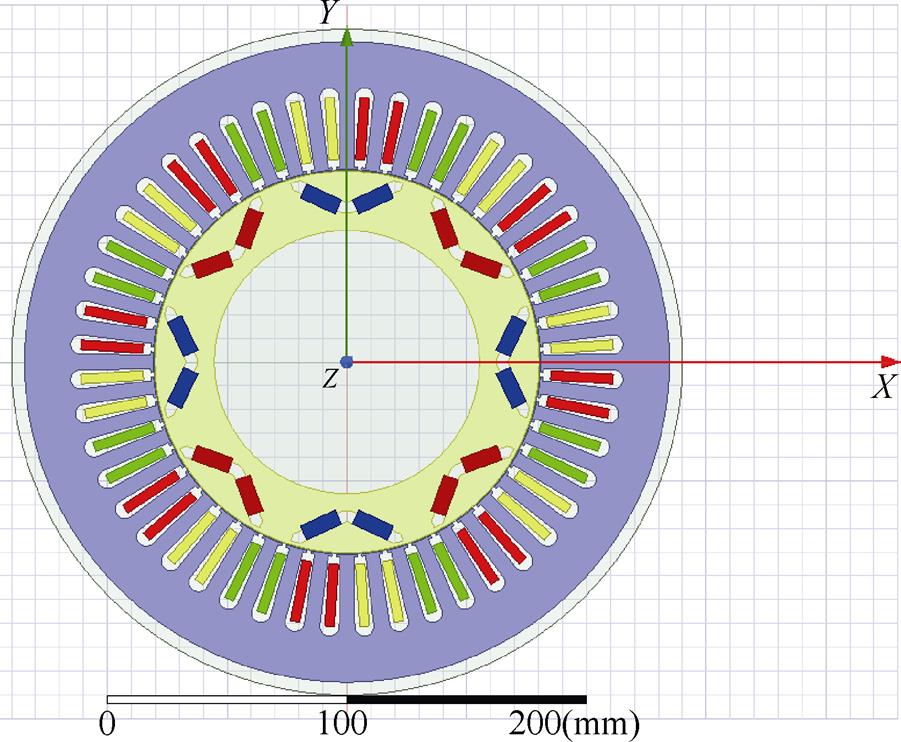
图6 PMSM二维仿真模型
Fig.6 Two-dimensional simulation model of PMSM
3.1.2 AMT模型
通过在铁心上缠绕初级和次级绕组的方式，制作了一台小型单项AMT样机，其铁心模型结构如图7所示。图中的字母对应变压器的设计参数，铁心的主要设计参数见表2。
通过有限元仿真软件建立AMT的有限元仿真模型，如图8所示。根据计算需求和实际情况对其进行了部分简化，如非晶合金变压器铁心由极薄的非晶带材压制而成，在仿真建模中，建模为整块铁心，简化建模复杂度；线圈绕组也由线圈体所代替。在实际工程应用中，当作为铁心材料时，额定工作磁通密度约在1.2～1.3 T。
表1 PMSM结构参数
Tab.1 PMSM structural parameters
参 数数 值 定子铁心外径/mm195 定子铁心内径/mm150 永磁体宽度/mm32 永磁体厚度/mm6.48 永磁体极弧系数0.8 转子内径/mm35 转子铁心长度/mm102 气隙长度/mm0.8
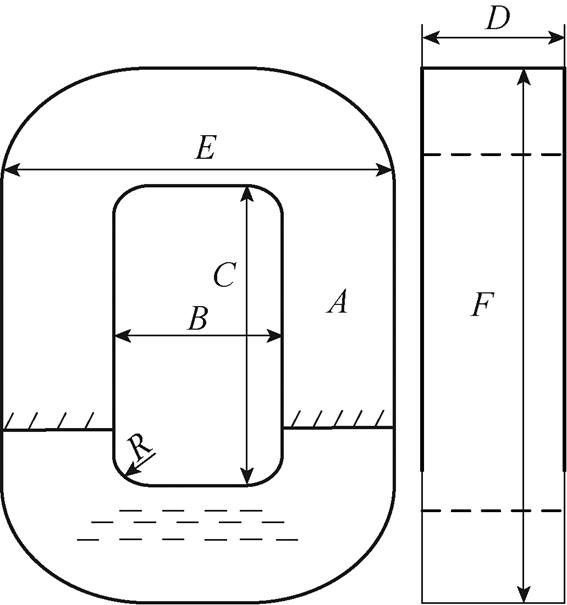
图7 铁心模型结构
Fig.7 Structure drawing of core model
表2 设计参数
Tab.2 Design parameters
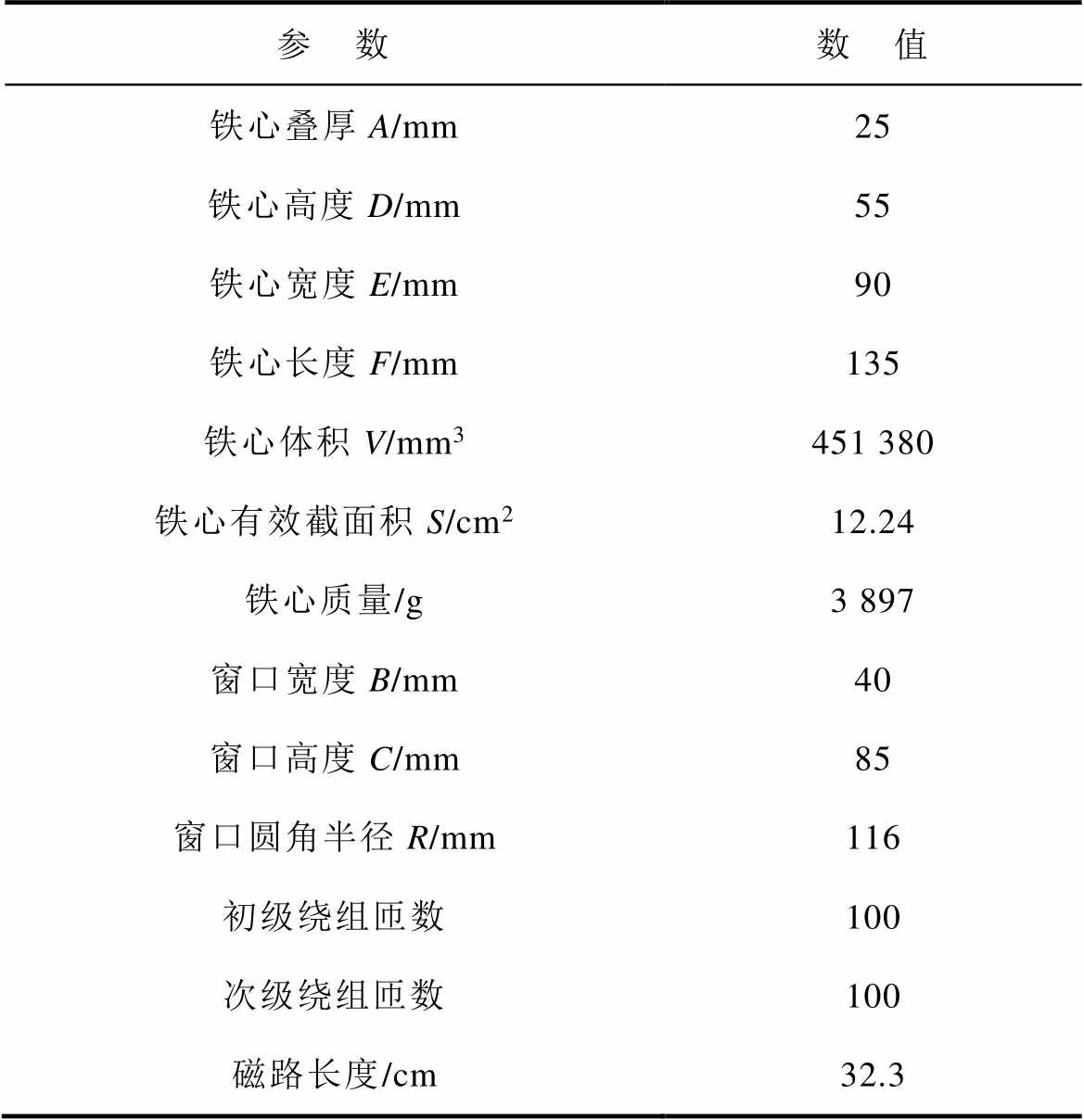
参 数数 值 铁心叠厚A/mm25 铁心高度D/mm55 铁心宽度E/mm90 铁心长度F/mm135 铁心体积V/mm3451 380 铁心有效截面积S/cm212.24 铁心质量/g3 897 窗口宽度B/mm40 窗口高度C/mm85 窗口圆角半径R/mm116 初级绕组匝数100 次级绕组匝数100 磁路长度/cm32.3
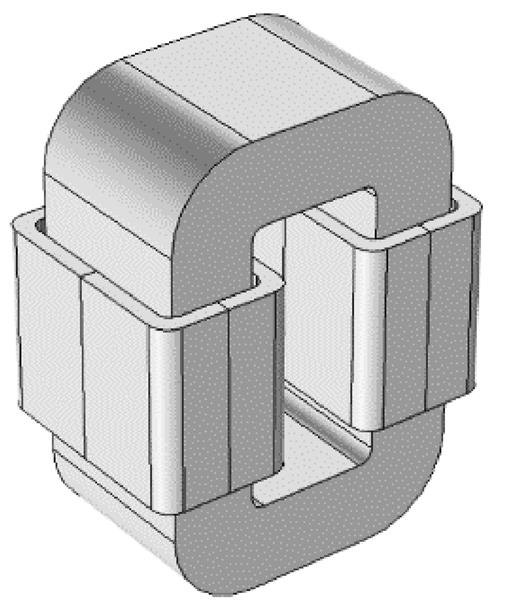
图8 AMT有限元仿真模型
Fig.8 Finite element simulation model of AMT
3.2.1 PMSM数据集建立
选择PMSM的几何结构参数作为变量，见表3。由于硅钢片存在非线性，三相定子绕组电流选择220 A和330 A，永磁体材料选择钕铁硼（NdFe35）。为了减小计算规模，选择PMSM的1/8模型作为仿真模型。为验证ResUnet-Transformer模型的性能，通过有限元方法分别获得PMSM不同参数设置下的几何结构和其对应的磁场云图，并通过翻转、旋转等数据增强方式将数据扩充至600组，其中500组用来训练，100组用来测试模型的泛化能力。一组PMSM的样本数据如图9所示。
表3 PMSM结构变量取值
Tab.3 PMSM structure variable value （单位: mm）
参 数取值范围步长 永磁体宽度28～341 永磁体厚度6～101 定子齿高28～32.51.5 定子齿宽7～11.51.5
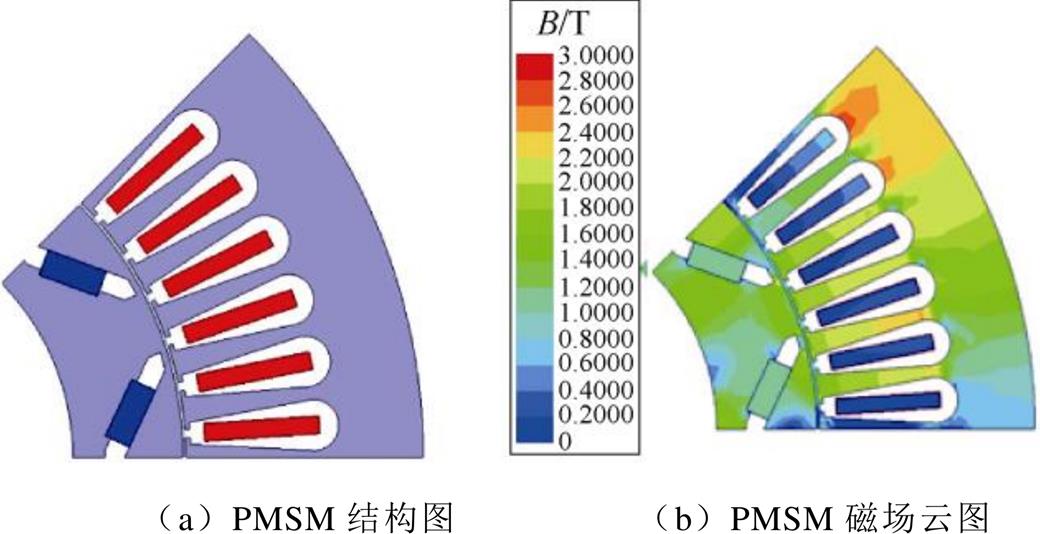
图9 PMSM样本数据示例
Fig.9 Example of PMSM sample data
3.2.2 AMT数据集建立
同样以AMT的几何结构参数作为变量，变量取值见表4。借助有限元分析进行参数化扫描，在XZ平面上获得AMT不同参数设置下的几何结构和磁场云图共600组。将600组样本数据划分为500组训练数据集和100组测试数据集。一组AMT样本数据如图10所示。
表4 变压器结构变量取值
Tab.4 Transformer structure variable value （单位: mm）
参 数取值范围步长 铁心宽度86～901 窗口宽度37～401 窗口高度79.5～83.51 铁心高度52～571
图10 AMT样本数据示例
Fig.10 Example of AMT sample data
为了保证网络训练时收敛加快，提高模型性能，需对ResUnet-Transformer模型训练前进行图像预处理工作，从而消除无关信息，改善图像效果，突出图像特征，便于计算机进行识别和分析。将几何结构进行矩阵化，用不同的数字标记不同的结构，以完成区域划分。由于PMSM磁场是RGB三通道彩色图像，R为红色通道，G为绿色通道，B为蓝色通道，需转换为单通道图像，并将像素值简单缩放归一化到[0, 1]区间，公式为
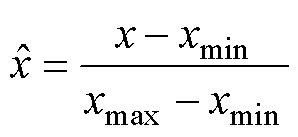（3）
式中，x为图像像素点值；xmax、xmin分别为图像像素的最大与最小值。
由于采用翻转、旋转等数据增强方式进行扩充时翻转、旋转的角度是随机的，因此使用该数据增强方式得到的每张图像的分布位置与倾斜角度可能会不统一。但此种信息差异与图像本身的其他信息与模型无直接关联，但都会被网络作为特征进行提取并训练，最终会影响模型的性能。针对此问题，以中心对称的方式将图像裁剪为608×608像素大小，使得网络能够在较小的固定区域内提取出有效特征，以提高ResUnet-Transformer模型的性能表现。
在预测实验进行对比分析的过程中，采用方均误差（Mean Square Error, MSE）和平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）作为ResUnet-Transformer模型的性能指标来评估预测磁场分布的准确性，其公式为
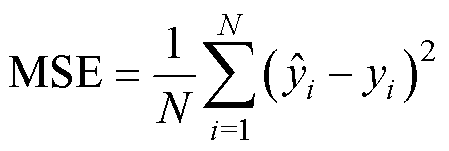（4）
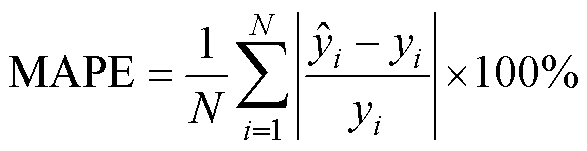（5）
式中，yi和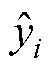
分别为第i个样本的真实值和预测值；N为样本个数。
4.1.1 抑制过拟合方法
为抑制网络训练过程中出现的过拟合现象，引入Targeted Dropout算法[37]。Targeted Dropout算法的核心思想是对神经元和权重的重要性进行排序，随机丢弃重要性较低的元素。其具体实现方法为：
（1）剪枝操作：对参数化的神经网络Wa按照权重剪枝与单元剪枝的方法进行剪枝操作，寻找最优参数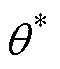
，在保留神经网络最高数量级的k个权重的同时使得损失函数
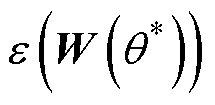尽可能少。权重剪枝和单元剪枝运算如下
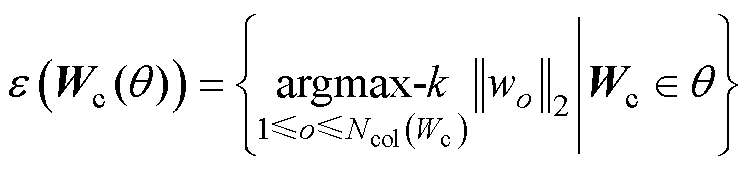（6）
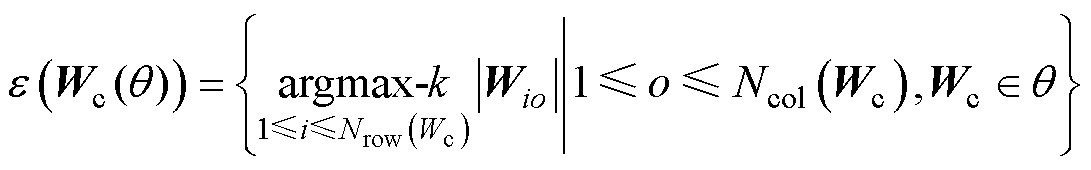（7）
式中，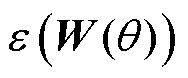
为网络损失函数；Wc为网络权重矩阵；argmax-k为返回所有元素中最大的k个元素的函数；wo为权重矩阵W第o列列向量；Wio为权重矩阵第i行、第o列元素；Ncol、Nrow分别表示参数矩阵列数与行数。
（2）引入随机性：为将随机性引入这个过程，使用靶向比例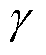
和删除概率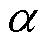
。其中靶向比例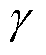表示Dropout候选权值为最小的
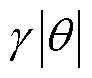个权重，并以删除概率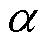独立地去除候选集合中的权值。
Targeted Dropout算法将事后剪枝策略结合到神经网络的训练过程中，可有效抑制模型的过拟合现象，提升模型的泛化水平。
4.1.2 ResUnet-Transformer模型训练与调优
网络训练一般采用梯度下降算法，根据批量大小（Batch-size）的不同可分为批量梯度下降（Batch Gradient Descent, BGD）、随机梯度下降（Stochastic Gradient Descent, SGD）和小批量梯度下降（Mini- batch Gradient Descent, MBGD）三种[38]。当Batch- size为1时，该算法为SGD。SGD算法所需的计算资源较小，但在训练过程中梯度的更新具有随机性，可能会带来噪声。当Batch-size为训练数据的样本数时，该算法为BGD。BGD算法在计算同样数目样本的情况下所需的时间较少，但是每个小批量梯度中可能含有更多的冗余信息。当Batch-size小于总样本数目的样本时，该算法为MBGD。一般选用MBGD算法计算网络的梯度和更新权重参数，这样可以降低网络反向传播过程中的计算量和提高算法的稳定性。
合适的超参数可以加快模型训练速度、减少训练时间和防止模型过拟合，使预测精度提高。常用的超参数变量取值见表5。
表5 超参数变量取值
Tab.5 Values of hyperparameter variables
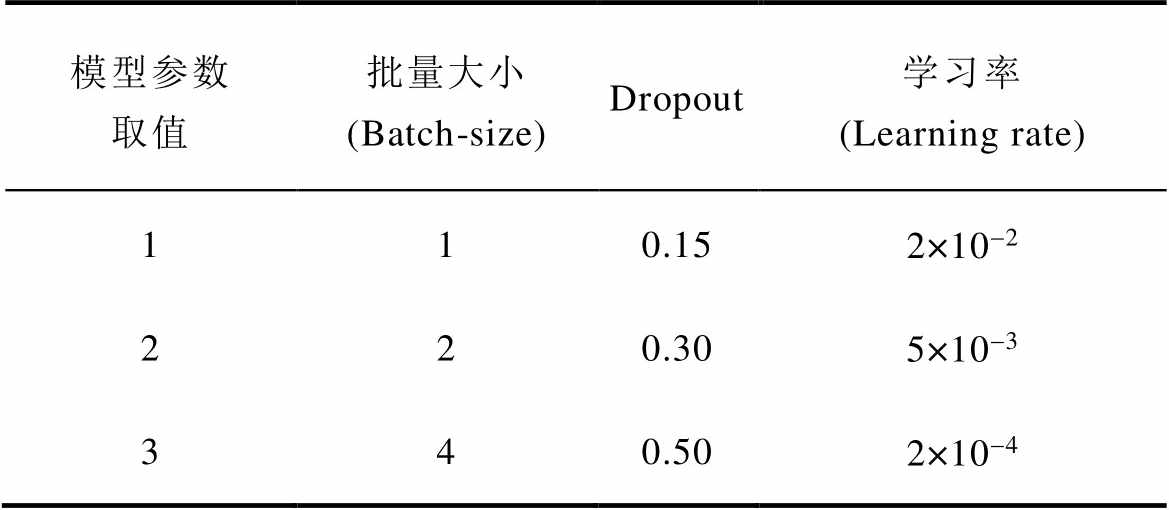
模型参数取值批量大小(Batch-size)Dropout学习率(Learning rate) 110.152×10-2 220.305×10-3 340.502×10-4
使用田口正交实验法对ResUnet-Transformer模型的Batch-size、Dropout、Learning rate进行超参数调优。为简化模型训练时间，选择100组PMSM数据集对ResUnet-Transformer模型进行训练，三相定子电流选择220 A。选定L9(33)正交表并建立实验矩阵，其中L代表正交矩阵，下标9为试验编号，3为每个参数变量取值次数，上标3为优化参数数量正交表及模型预测评估值，正交表及模型预测结果见表6。
表6 正交表及模型预测结果
Tab.6 Orthogonal table and model prediction results
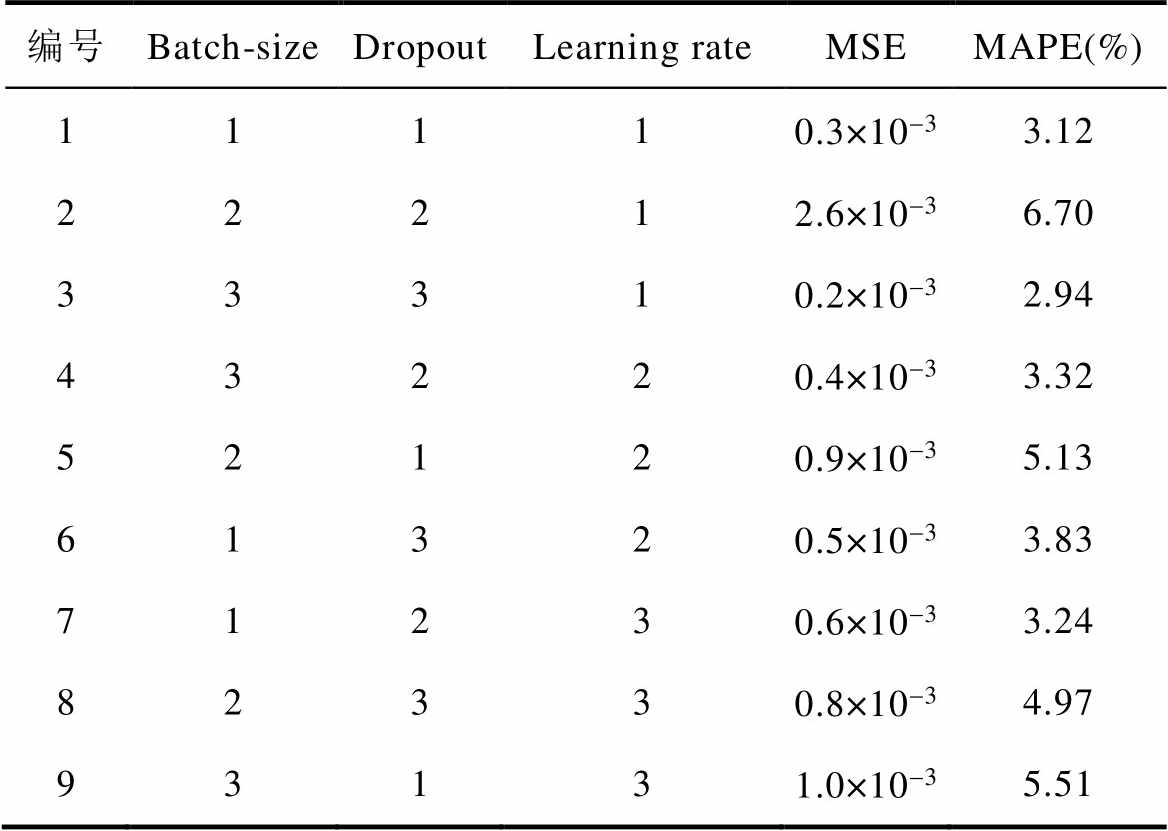
编号Batch-sizeDropoutLearning rateMSEMAPE(%) 11110.3×10-33.12 22212.6×10-36.70 33310.2×10-32.94 43220.4×10-33.32 52120.9×10-35.13 61320.5×10-33.83 71230.6×10-33.24 82330.8×10-34.97 93131.0×10-35.51
由表6可知，编号为3时，Batch-size为4、Dropout为0.50、Learning rate为2×10-2，ResUnet- Transformer模型的预测性能最好。选择方均误差（MSE）作为损失函数来调整所有层的权重，采用自适应矩估计（Adaptive Moment Estimation, Adam）优化器作为最小化目标函数，在收敛速度和计算效率方面具有很好的优势。Adam优化算法的迭代过程如下
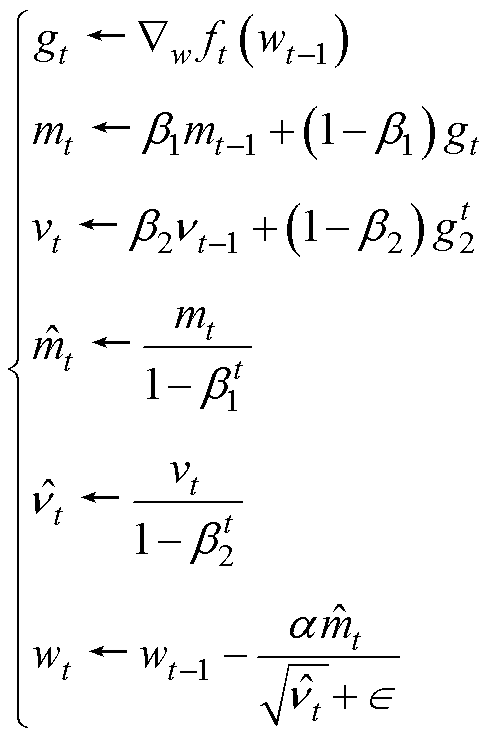（8）
式中，t为迭代次数，初始值为0；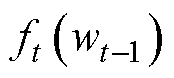
为损失函数；
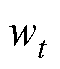为权重参数；gt为损失函数的梯度；mt为一阶矩估计，m0=0；vt为二阶矩估计，v0=0；
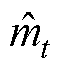为修正后的一阶矩估计；
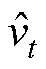为修正后的二阶矩估计。
4.1.3 动态学习率调整策略
学习率（Learning rate）是模型训练过程中的重要超参数，学习率过小或过大都不利于模型的训练，合适的学习率有助于加快模型的收敛。理想的学习率在训练初始阶段不可过小，以确保模型的收敛速度；当目标函数在最优值附近收敛时，学习率应逐渐递减，以避免振荡或不收敛[39]。本文在Adam优化算法的基础上采用余弦退火算法自适应地调整学习率，使得学习率随着训练步数逐渐减少，动态变化学习率公式为
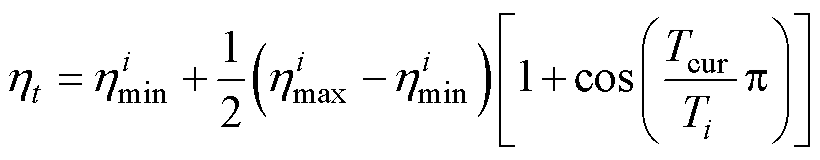（9）
式中，
和
为学习率变化的范围最小值和最大值；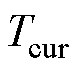
为最近一次重启后经历的epoch数；
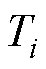为每个调整周期内epoch总数。
4.2.1 小样本数据集条件下模型的性能比较
任何深度学习模型的训练都需要大量的样本数据，考虑到实际工程中样本的获取成本高昂，为减少磁场计算的成本，在降低训练集样本数的情况下，验证ResUnet-Transformer模型的极限性能。保持模型参数不变，三相定子绕组电流选择220 A，改变训练集样本数，使用测试集测试模型每次训练的结果。不同样本数下训练集的MSE如图11所示。
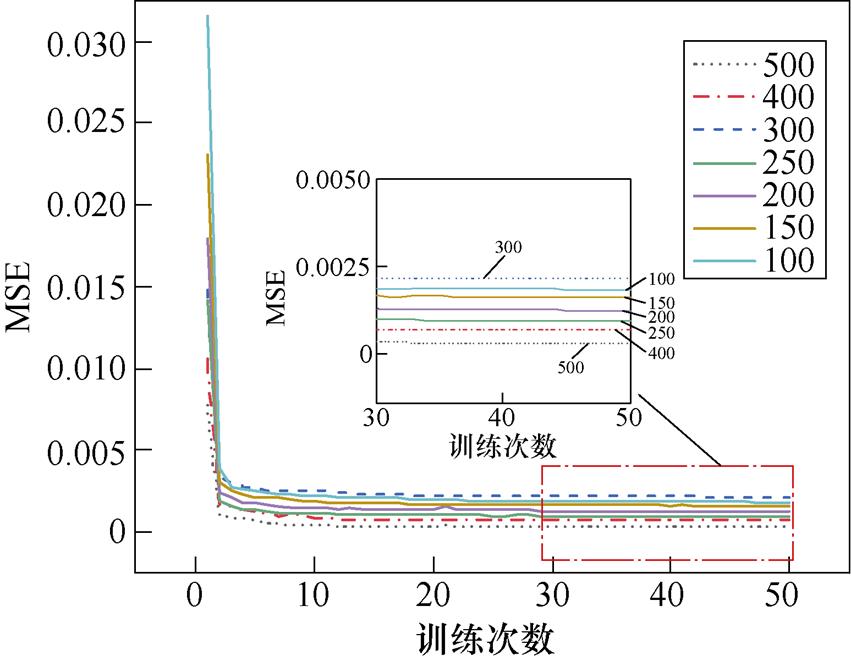
图11 不同样本数下的训练集MSE对比
Fig.11 MSE comparison chart of training sets with different sample numbers
经过50次训练，训练集误差已基本稳定。不同训练集样本数下的模型训练时间和测试集误差见表7。当训练集样本数为100和150时，磁场预测效果较差，不能满足精度要求。当训练集样本数为200和250时，误差显著减小。当训练集样本数为300时，预测误差非但没有减少，反而有所回升。当训练集样本数为400时，误差显著减少，且比训练集样本数为250时的预测效果更加理想，但是会显著增加模型的训练时间。当训练集样本数为500时，测试集的误差较样本数为400时误差进一步降低，PMSM磁场云图的MAPE值可以达到0.7%，但训练时间更长。因此，为保证训练速度和预测精度，后续实验均在训练样本数为250的情况下进行。
表7 不同训练集样本数下模型的预测误差和训练时间
Tab.7 Prediction error and training time of the model with different training set samples
训练集样本数MSEMAPE(%)训练时间/h 1000.22×10-32.90.75 1500.15×10-32.51.19 2000.12×10-31.91.57 2500.07×10-31.41.97 3000.31×10-33.52.31 4000.04×10-31.02.98 5000.02×10-30.73.96
4.2.2 模型结构影响分析
为分析ResUnet-Transformer模型的网络结构对本文提出的磁场预测方法的影响。本节从卷积层数、短残差机制、Dropout结构、余弦退火算法等方面开展相关实验，实验结果见表8。
表8 不同ResUnet-Transformer结构下磁场预测结果
Tab.8 Magnetic field prediction results under different ResUnet Transformer structures
结构变量变化情况MSEMAPE(%)训练时间/h 卷积层数190.17×10-32.42.41 150.07×10-31.41.97 110.13×10-32.12.31 短残差机制有0.07×10-31.41.97 无0.08×10-31.52.01 余弦退火算法有0.07×10-31.41.97 无0.11×10-31.91.93 Dropout结构有0.07×10-31.41.97 无0.09×10-32.21.83
从表8的实验结果可以看出：
（1）对于卷积层数而言，并非网络越深，模型的预测效果越好。当ResUnet-Transformer模型的卷积层数为19层时，磁场预测效果差且训练时间长。当模型的卷积层数降为15层时，磁场预测效果显著提升，训练时间也明显缩短。当模型的卷积层数降为11层时，磁场预测效果没有显著提升。
（2）对于短残差机制而言，其能够促进梯度的反向传播，节省网络的训练时间。但是由于网络层数较浅，引入短残差机制并不会明显提高磁场的预测精度。
（3）对于余弦退算法而言，余弦退火算法可以使模型训练过程中自适应地调整学习率。在余弦退火算法的调整下，PMSM磁场云图的MAPE值为1.4%，未使用余弦退火算法时磁场云图的MAPE值为1.9%，提高了约26.3%的预测准确度。
（4）对于Dropout结构而言，Dropout结构可以提高模型的泛化能力，提高磁场预测效果。但是，在模型引入Dropout会增加计算量与算法耗时。
4.2.3 不同深度学习模型的性能比较
为验证本文提出的ResUnet-Transformer模型的先进性，对比模型选择CNN、U-Net和传统的Linknet三种模型。使用250组样本对每个模型进行训练，三相定子绕组电流选择220 A，每个模型的超参数和数据预处理部分的设置均相同，共迭代50次，利用测试集的100组样本验证模型的泛化能力，各个模型的预测误差和训练时间见表9。
表9 不同算法模型的预测误差和训练时间
Tab.9 Prediction error and training time of different algorithm models
算法模型MSEMAPE(%)训练时间/h CNN5.32×10-39.41.62 U-Net1.42×10-35.22.24 Linknet1.03×10-34.72.39 ResUnet-Transformer0.07×10-31.41.97
通过对比可以发现，CNN模型的结构比较简单，相同样本数下的训练时间最短，但是预测误差相对较高。U-Net模型中的长跳跃连接可以融合不同抽象层次的图像特征，预测效果显著提升。Linknet模型不仅存在长跳跃连接，同时编码器中的短残差机制促进了信息的传递，预测效果较U-Net模型有所提升。ResUnet-Transformer模型相比于U-Net，增加了短残差机制和Transformer模块，预测效果更加理想，同时其模型参数量相对较少，因此训练时间也明显减少。
由于PMSM中存在磁材料，具有非线性特性，因此分别选择不同工作电流下的结果，证明ResUnet- Transformer模型的泛化能力。将数据集分别输入到四种网络进行训练，每种网络训练50批次，然后进行测试，测试时间在40～50 s范围内，如图12所示。
为更直观地展示预测结果，在激励电流为220 A和330 A时分别选择同一种几何参数设置条件下的PMSM有限元仿真结果和不同网络模型的预测结果进行对比，如图13所示。
从图12、图13可以看出，CNN模型单纯通过一系列卷积池化操作提取特征，预测效果相对较差，在转子内部永磁体靠近气隙部位和定子齿槽气隙处，磁场分布明显区别于有限元仿真图。U-Net和Linknet模型相比于CNN单纯的卷积池化操作，通过长跳跃连接将不同抽象层次的特征融合，编码器和解码器的结构更利于特征的有效提取，磁场预测效果有所提升。但是两者在提取复杂结构的PMSM磁场特征信息时，没有考虑磁场云图各个像素点之间的关联关系，尤其对磁场云图中重要特征的信息关注度较低，在永磁体和定子槽附近的误差较大。ResUnet-Transformer模型利用Transformer编码器中的多头自注意力机制重点关注磁场云图中的重要特征，从而忽略其他无关信息，Transformer模块输出的图像特征与对应的解码器的特征有效融合，防止细节特征的丢失，预测效果最好，高精度地重现了磁场在局部的分布特性。
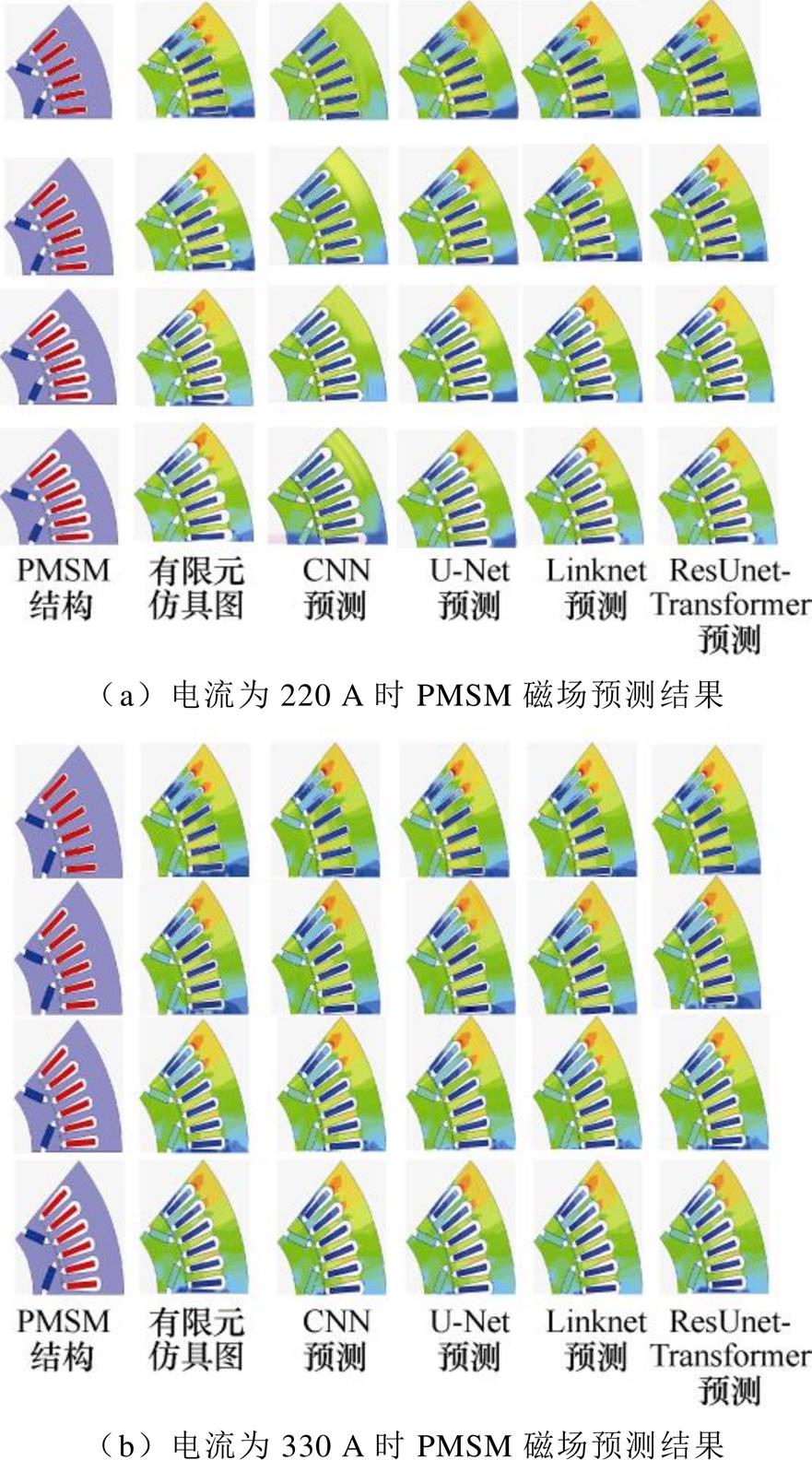
图12 不同网络模型预测结果
Fig.12 Different network model prediction results
图13 同一参数设置下不同网络模型的预测结果
Fig.13 Prediction results of different network models under the same parameter setting
4.2.4 ResUnet-Transformer模型与有限元性能比较
为验证ResUnet-Transformer模型的性能，从测试数据集中随机选择一组预测结果，通过ResUnet- Transformer模型预测磁场与有限元计算的结果进行对比，如图14所示。从图中可以观察到ResUnet- Transformer模型预测PMSM磁场时，在转子内部永磁体靠近气隙和定子齿槽气隙等磁场变化率较高处预测精细度也很高，磁通密度的百分比误差最高约为1.75%。预测结果表明，ResUnet-Transformer模型能够很好地学习到PMSM结构参数与磁场之间的映射关系，生成高分辨率和高质量的图像。
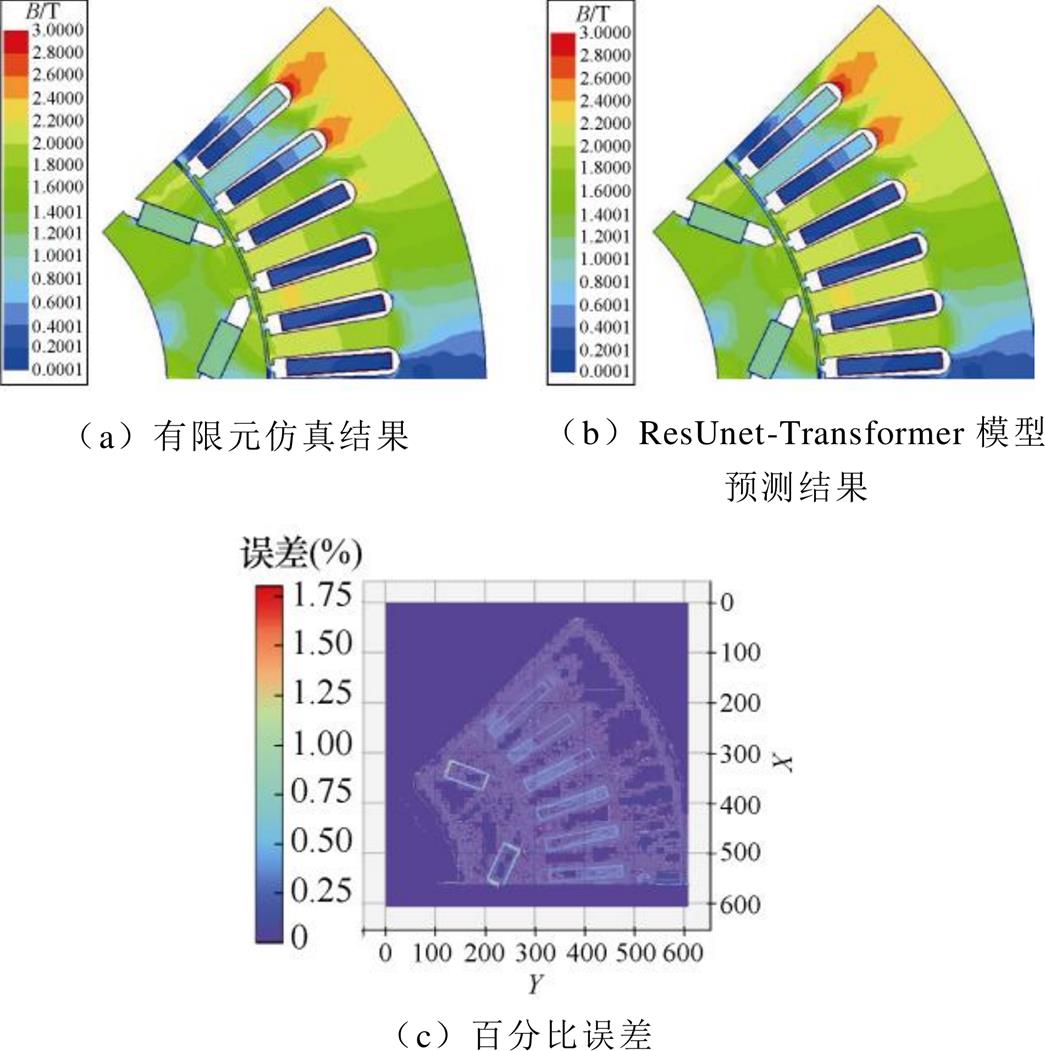
图14 PMSM磁场预测结果对比
Fig.14 Comparison of PMSM magnetic field prediction results
ResUnet-Transformer模型仅需250组样本和50次训练即可训练成功，ResUnet-Transformer模型训练成功后使用100组样本进行测试，前期进行数据采样制作样本集及训练和计算的总时间需6.78 h。使用有限元方法进行磁场求解时，若PMSM的几何结构参数发生改变，需重新计算。特别在小步长的参数化扫描过程中，有限元方法磁场分析时所需时间成倍增加。ResUnet-Transformer模型训练成功后使用100组样本进行测试，若采样有限元方法对这100个样本进行磁场计算需要近20 h，本文方法相比于有限元法计算效率提高了66.1%。深度学习具有“一次训练，多次调用”的优势，尽管前期制作样本集及模型训练需要一定的时间，但模型一旦训练成功可以多次调用，直接用于磁场的预测，解决有限元方法磁场分析时无法复用的问题，计算次数越多或计算规模越大，本文磁场预测方法优势就越明显，具有实时演算的优势。
为进一步验证提出基于残差U-Net和自注意力机制Transformer编码器的磁场预测方法的适用性，本节在AMT数据集上对该方法进行应用。所采用的ResUnet-Transformer模型结构与参数设置及数据预处理部分均与4.1节和3.3节的设置相同，且该结构与参数设置已经通过4.2节的实验验证了其有效性。通过有限元仿真软件共得到不同参数设置下的几何结构和磁场云图共600组。改变训练集样本数，共迭代50次，使用100组样本测试模型的泛化能力。不同训练集样本数下的模型训练时间和测试集误差见表10。
表10 不同训练集样本数下模型的预测误差和训练
Tab.10 Prediction error and training time of the model with different training set samples
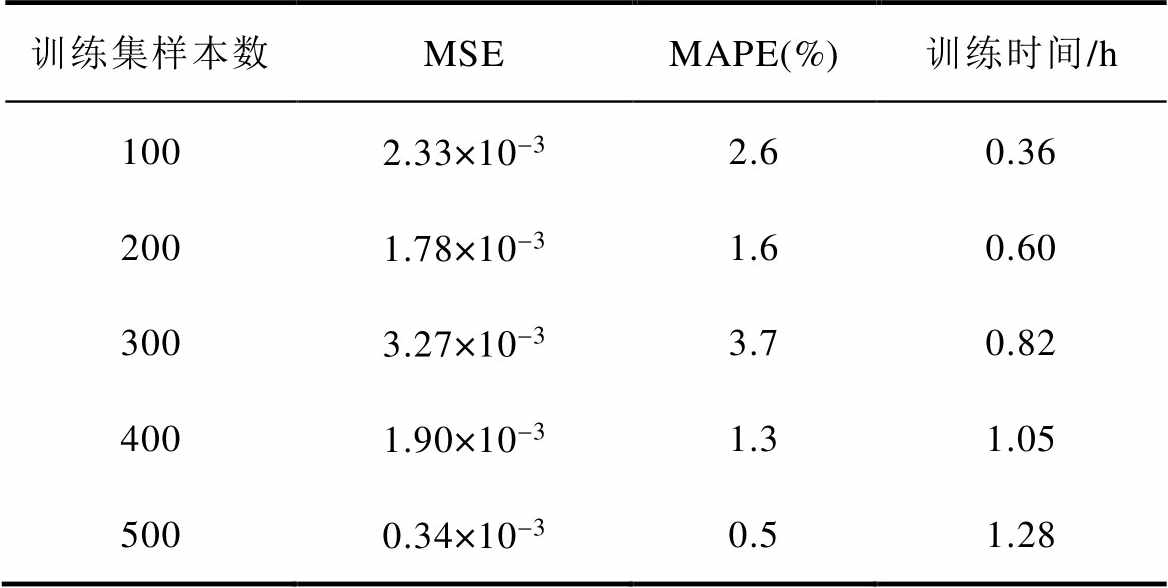
训练集样本数MSEMAPE(%)训练时间/h 1002.33×10-32.60.36 2001.78×10-31.60.60 3003.27×10-33.70.82 4001.90×10-31.31.05 5000.34×10-30.51.28
从表10可以看出，当训练样本数为100时，AMT的磁场预测精度较差。当训练样本数为200时，AMT的磁场预测精度显著提高，相应的训练时间也增长。当训练样本数为300时，AMT的磁场预测精度非但没有提高反而有所下降。当训练样本数为400时，误差显著降低，且比训练样本数为200时预测效果更好。当训练样本数为500时，测试集的误差进一步降低，AMT磁场云图的MAPE值可以达到0.5%，但是相比于训练样本数为400时，训练时间明显增加。同样本着“用较少数量的样本进行训练便可以达到较高的磁场预测精度”这一原则，后续进行实验分析时的训练样本数为200组。
从测试数据集中选择一组预测结果，通过ResUnet-Transformer模型预测磁场与有限元计算的结果进行对比，如图15所示。
从图15可以观察到，ResUnet-Transformer模型在预测AMT磁场时，误差主要集中于变压器铁心的圆角位置，磁通密度的最大误差百分比约为1.5%。结果表明，本文提出的ResUnet-Transformer模型同样能够在AMT数据集上实现快速精确的磁场预测。当非晶合金变压器结构参数发生变化时，可以直接从训练过的模型中得到预测结果，不需要对模型进行重新训练。
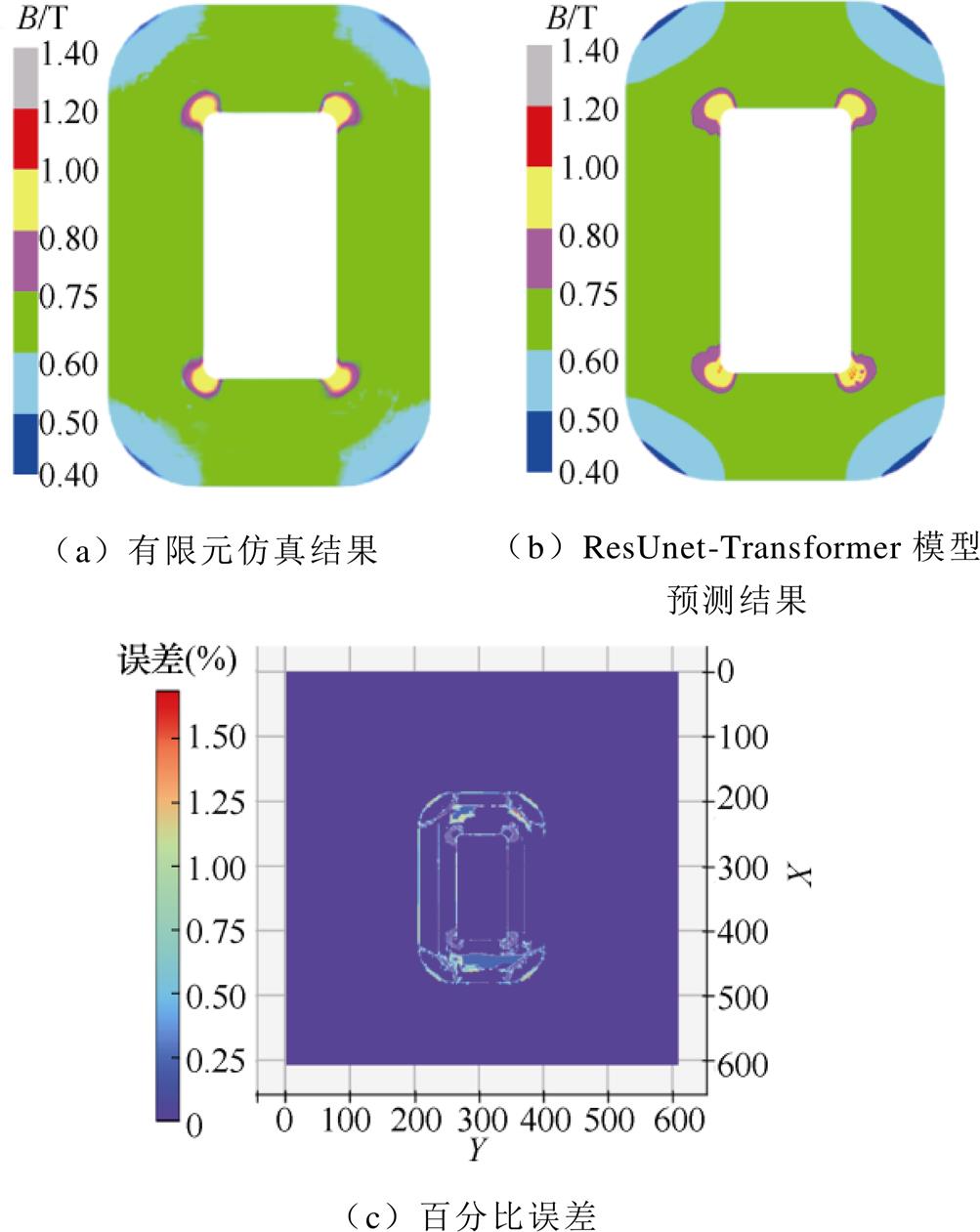
图15 AMT磁场预测结果对比
Fig.15 Comparison of AMT magnetic field prediction results
利用有限元方法对几何结构复杂的电机和变压器进行磁场分析是一个成本高昂的过程，且亟须减少计算时间和计算资源。本文提出一种基于残差U-Net和自注意力Transformer编码器的磁场预测方法，为电机或变压器等电工装备多物理场的实时演算问题提供了思路，具体结论如下：
1）在U-Net模型的基础上引入短残差机制和Transformer模块，建立了ResUnet-Transformer模型，其性能优于其他算法。同等条件下，相比于有限元方法其计算效率提升了66.1%。
2）模型训练过程中引入Targeted Dropout算法可有效防止模型的过拟合问题，并在Adam优化算法的基础上采用余弦退火算法自适应地调整学习率，提高了约26.3%的预测准确度。
3）本文建立的ResUnet-Transformer模型小样本数据集下可以快速准确地实现PMSM和AMT磁场的准确预测。在测试集的验证中，PMSM和AMT数据集上的MAPE分别可以达到0.7%和0.5%。
下一步将对工程中较为通用的超参数调优方法和三维磁场问题开展进一步研究。
参考文献
[1] 金亮, 王飞, 杨庆新, 等. 永磁同步电机性能分析的典型深度学习模型与训练方法[J]. 电工技术学报, 2018, 33(增刊1): 41-48.
Jin Liang, Wang Fei, Yang Qingxin, et al. Typical deep learning model and training method for per- formance analysis of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 41-48.
[2] 杨帆, 吴涛, 廖瑞金, 等. 数字孪生在电力装备领域中的应用与实现方法[J]. 高电压技术, 2021, 47(5): 1505-1521.
Yang Fan, Wu Tao, Liao Ruijin, et al. Application and implementation of digital twins in the field of electric equipment[J]. High Voltage Engineering, 2021, 47(5): 1505-1521.
[3] Zheng Weiying, Cheng Zhiguang. An inner-constrained separation technique for 3-D finite-element modeling of grain-oriented silicon steel laminations[J]. IEEE Transactions on Magnetics, 2012, 48(8): 2277-2283.
[4] Silver D, Huang A, Maddison C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489.
[5] Silver D, Schrittwieser J, Simonyan K, et al. Mastering the game of Go without human knowledge[J]. Nature, 2017, 550(7676): 354-359.
[6] 赵洋, 王瀚墨, 康丽, 等. 基于时间卷积网络的短期电力负荷预测[J]. 电工技术学报, 2022, 37(5): 1242-1251.
Zhao Yang, Wang Hanmo, Kang Li, et al. Temporal convolution network-based short-term electrical load forecasting[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1242-1251.
[7] 张翼, 朱永利. 结合知识蒸馏和图神经网络的局部放电增量识别方法[J]. 电工技术学报, 2023, 38(5): 1390-1400.
Zhang Yi, Zhu Yongli. Partial discharge incremental recognition method combining knowledge distillation and graph neural network[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1390-1400.
[8] LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436-444.
[9] 王艳新, 闫静, 王建华, 等. 基于域对抗迁移卷积神经网络的小样本GIS绝缘缺陷智能诊断方法[J]. 电工技术学报, 2022, 37(9): 2150-2160.
Wang Yanxin, Yan Jing, Wang Jianhua, et al. Intelligent diagnosis for GIS with small samples using a novel adversarial transfer learning in convolutional neural network[J]. Transactions of China Electro- technical Society, 2022, 37(9): 2150-2160.
[10] Krizhevsky A, Sutskever I, Hinton G. Imagenet classification with deep convolutional neural net- works[J]. Communications of the ACM, 2017, 60(6): 84-90.
[11] Hinton G, Deng Li, Yu Dong, et al. Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups[J]. IEEE Signal Processing Magazine, 2012, 29(6): 82-97.
[12] Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation[J]. IEEE Transa- ctions on Pattern Analysis and Machine Intelligence, 2015, 39(4): 640-651.
[13] Ronneberger O, Fischer P, Brox T. U-Net: convolu- tional networks for biomedical image segmentation[C]// 18th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), 2015: 234-241.
[14] He Kaiming, Zhang Xianyu, Ren Shaoqing, et al. Deep residual learning for image recognition[C]// IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016: 770-778.
[15] Zhang Zhengxin, Liu Qingjie, Wang Yunhong. Road extraction by deep residual U-net[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(5): 749-753.
[16] 徐宏伟, 闫培新, 吴敏, 等. 基于残差双注意力U-Net模型的CT图像囊肿肾脏自动分割[J]. 计算机应用研究, 2020, 37(7): 2237-2240.
Xu Hongwei, Yan Peixin, Wu Min, et al. Automated segmentation of cystic kidney in CT images using residual double attention motivated U-Net model[J]. Application Research of Computers, 2020, 37(7): 2237-2240.
[17] 李耀仟, 李才子, 刘瑞强, 等. 面向手术器械语义分割的半监督时空Transformer网络[J]. 软件学报, 2022, 33(4): 1501-1515.
Li Yaoqian, Li Caizi, Liu Ruiqiang, et al. Semi- supervised spatiotemporal transformer network for semantic segmentation of surgical instruments[J]. Journal of Software, 2022, 33(4): 1501-1515.
[18] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//Advances in Neural Information Processing Systems, 2017: 5998-6008.
[19] Dosovitskiy A, Beyer L, Kolesnikov A, et al. An image is worth 16x16 words: transformers for image recognition at scale[J]. arXiv: 2010.11929, 2020.
[20] Chen Jieneng, Lu Yongyi, Yu Qihang, et al. TransUNet: transformers make strong encoders for medical image segmentation[J]. arXiv: 2102.04306, 2021.
[21] Saakaar B, Yaser A, Shaowu P, et al. Deep learning for magnetic field estimation[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-4.
[22] Gong Ruohai, Tang Zuqi. Investigation of convolu- tional neural network U-net under small datasets in transformer magneto-thermal coupled analysis[J]. COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2020, 39(4): 959-970.
[23] Li Y, Wang Y, Qi S, et al. Predicting scattering from complex nano-structures via deep learning[J]. IEEE Access, 2020, 8: 139983-139993.
[24] 吴鑫, 张艳丽, 王振, 等. 基于深度学习的电工钢片磁畴磁化过程预测与特征量提取[J]. 电工技术学报, 2023, 38(9): 2289-2298.
Wu Xin, Zhang Yanli, Wang Zhen, et al. Prediction of domain magnetization process and feature extraction of electrical steel sheet based on deep learning[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2289-2298.
[25] Xiaowei J, Cheng Peng, Chen Wenli, et al. Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder[J]. Physics of Fluids, 2018, 30(4): 1-16.
[26] Vinothkumar S, Qinghua J, Chang S, et al. Fast flow field prediction over airfoils using deep learning approach[J]. Physics of Fluids, 2019, 31(5): 1-69.
[27] Liu Bo, Tang Jiupeng, Huang Haibo, et al. Deep learning methods for super-resolution reconstruction of turbulent flows[J]. Physics of Fluids, 2020, 32(2): 1-13.
[28] Bhatnagar, Saakaar, Afshar, et al. Prediction of aerodynamic flow fields using convolutional neural networks[J]. Computational Mechanics, 2019, 64(2): 525-545.
[29] 殷晓航, 王永才, 李德英. 基于U-Net结构改进的医学影像分割技术综述[J]. 软件学报, 2021, 32(2): 519-550.
Yin Xiaohang, Wang Yongcai, Li Deying. Summary of medical image segmentation technology based on U-Net structure improvement[J]. Journal of Software, 2021, 32(2): 519-550.
[30] Liu Zhenqing, Cao Yiwen, Wang Yize, et al. Com- puter vision-based concrete crack detection using U-net fully convolutional networks[J]. Automation in Construction, 2019, 104: 129-139.
[31] Ibtehaz N, Rahman M S. MultiResUNet: rethinking the U-Net architecture for multimodal biomedical image segmentation[J]. Neural Networks, 2020, 121: 74-87.
[32] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735- 1780.
[33] 王琛, 王颖, 郑涛, 等. 基于ResNet-LSTM网络和注意力机制的综合能源系统多元负荷预测[J]. 电工技术学报, 2022, 37(7): 1789-1799.
Wang Chen, Wang Ying, Zheng Tao, et al. Multi- energy load forecasting in integrated energy system based on ResNet-LSTM network and attention mechanism[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1789-1799.
[34] 房佳姝, 刘崇茹, 苏晨博, 等. 基于自注意力Trans- former编码器的多阶段电力系统暂态稳定评估方法[J]. 中国电机工程学报, 2022: 1-13.
Fang Jiashu, Liu Chongru, Su Chenbo, et al. Multi- stage power system transient stability assessment method based on self-attention transformer encoder[J]. Proceedings of the CSEE, 2022: 1-13.
[35] Ayers C W, Hsu J S, Marlino L D, et al. Evaluation of 2004 Toyota prius hybrid electic drive system interim report[R]. Oak Ridge National Laboratory, 2004.
[36] Burress T A, Campbell S L, Coomer C, et al. Evaluation of the 2010 Toyota prius hybrid synergy drive system[R]. Oak Ridge National Laboratory, 2011.
[37] 余光正, 陆柳, 汤波, 等. 基于云图特征提取的改进混合神经网络超短期光伏功率预测方法[J]. 中国电机工程学报, 2021, 41(20): 6989-7003.
Yu Guangzheng, Lu Liu, Tang Bo, et al. Improved hybrid neural network ultra-short term photovoltaic power prediction method based on cloud image feature extraction[J]. Proceedings of the CSEE, 2021, 41(20): 6989-7003.
[38] 余印振, 韩哲哲, 许传龙. 基于深度卷积神经网络和支持向量机的NOx浓度预测[J]. 中国电机工程学报, 2022, 42(1): 238-248.
Yu Yinzhen, Han Zhezhe, Xu Chuanlong. The concentration prediction of Nox based on deep convolution neural network and support vector machine[J]. Proceedings of the CSEE, 2022, 42(1): 238-248.
[39] 朱煜峰, 许永鹏, 陈孝信, 等. 基于卷积神经网络的直流XLPE电缆局部放电模式识别技术[J]. 电工技术学报, 2020, 35(3): 659-668.
Zhu Yufeng, Xu Yongpeng, Chen Xiaoxin, et al. Partial discharge pattern recognition technology of DC XLPE cable based on convolution neural net- work[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 659-668.
Abstract Accurate simulation of electromagnetic characteristics in electrical equipment relies on the finite element method. However, the increasing complexity of large electrical machines and transformers poses challenges, leading to prolonged simulation time and significant computational resource consumption. At the same time, the finite element method cannot establish a priori model. When design parameters, structures, or operating conditions change, it is necessary to reestablish the model. Considering the powerful feature extraction ability of deep learning, this paper proposes a magnetic field prediction method based on a residual U-Net and a self-attention Transformer encoder. The finite element method is used to obtain the dataset for deep learning training. The deep learning model can be trained once and used for multiple predictions, addressing the limitations of the finite element method and reducing computational time and resource consumption.
Firstly, this paper leverages the inherent advantages of the convolutional neural network (CNN) in image processing, particularly the U-shaped CNN, known as U-Net, based on the encoder and decoder structure. This architecture exhibits a stronger ability to capture fine details and learn from limited samples than the traditional CNN. To mitigate network degradation and address convolutional operation limitations, short residual connections and Transformer modules are introduced to the U-Net architecture, creating the ResUnet- Transformer model. The short residual connections accelerate network training, while the self-attention mechanism from the Transformer network facilitates the effective interaction of global features. Secondly, this paper introduces the Targeted Dropout algorithm and adaptive learning rate to suppress overfitting and enhance the accuracy of magnetic field predictions. The Targeted Dropout algorithm incorporates post-pruning strategies into the training process of neural networks, effectively mitigating overfitting and improving the model’s generalization. Additionally, an adaptive learning rate is implemented using the cosine annealing algorithm based on the Adam optimization algorithm, gradually reducing the learning rate as the objective function converges to the optimal value and avoiding oscillations or non-convergence. Finally, the ResUnet-Transformer model is validated through engineering cases involving permanent magnet synchronous motors (PMSM) and amorphous metal transformers (AMT).
On the PMSM dataset, training the ResUnet-Transformer model with 250 samples and testing it with 100 samples, the mean square error (MSE) and mean absolute percentage error (MAPE) are used as performance evaluation metrics. Compared to CNN, U-Net, and Linknet models, the ResUnet-Transformer model achieves the highest prediction accuracy, with an MSE of 0.07×10-3 and a MAPE of 1.4%. The prediction efficiency of the 100 test samples using the ResUnet-Transformer model surpasses the finite element method by 66.1%. Maintaining consistency in structural and parameter settings, introducing the Targeted Dropout algorithm and cosine annealing algorithm improves the prediction accuracy by 36.4% and 26.3%, respectively. To evaluate the model's generalization capability, the number of training samples for PMSM and AMT datasets is varied, and the model is tested using 100 samples. Inadequate training samples result in poor magnetic field prediction performance. When the training dataset size increases to 300, the prediction error does not decrease but shows a slight rise. However, with further increases in the training dataset size, the error significantly decreases, and the MAPE for the PMSM and AMT datasets reaches 0.7% and 0.5%, respectively, with just 500 training samples.
keywords：Finite element method, electromagnetic field, deep learning, U-net, Transformer
DOI: 10.19595/j.cnki.1000-6753.tces.230265
中图分类号：TM153
国家自然科学基金面上项目（51977148），国家自然科学基金重大研究计划项目（92066206）和中央引导地方科技发展专项自由探索项目（226Z4503G）资助。
收稿日期 2023-03-08
改稿日期 2023-06-27
金 亮 男，1982年生，博士，教授，研究方向为工程电磁场与磁技术、电磁场云计算和电磁无损检测等。E-mail: jinliang_email@163.com（通信作者）
尹振豪 男，2000年生，硕士研究生，研究方向为深度学习在电工装备中的应用。E-mail: 1691150589@qq.com
（编辑 郭丽军）