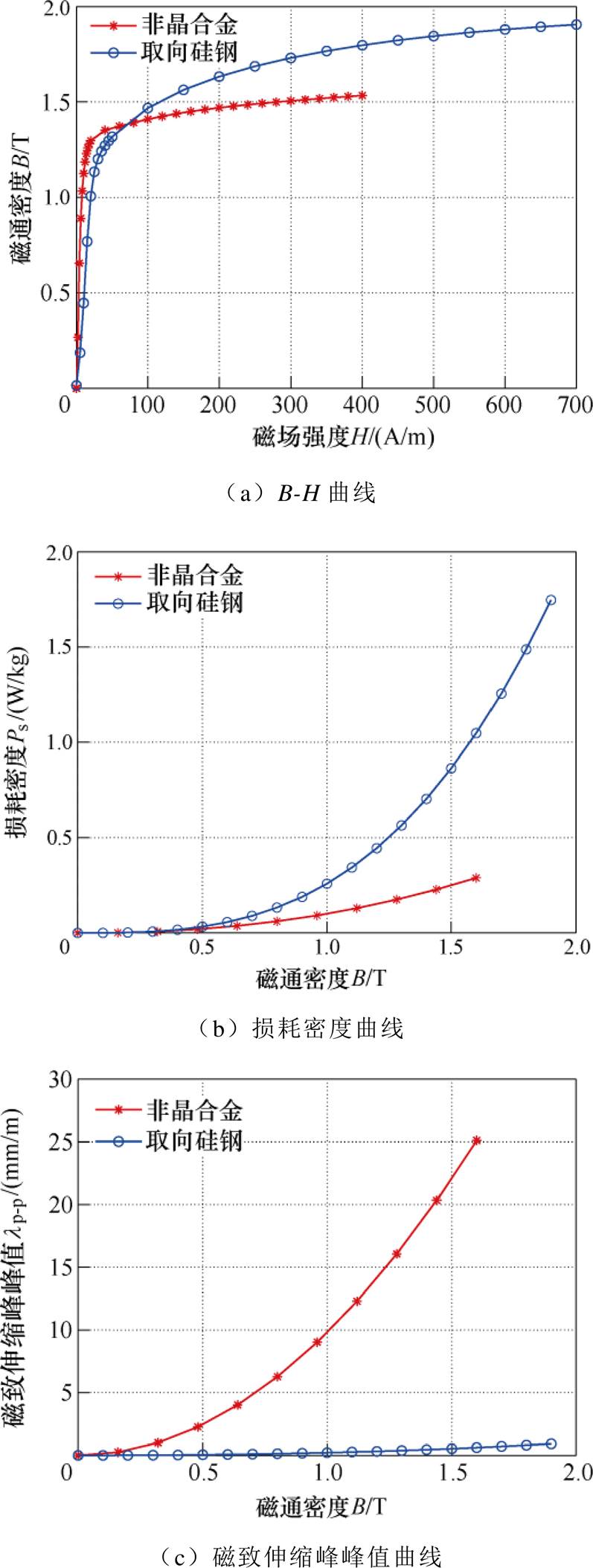
图1 非晶合金和取向硅钢的磁化特性
Fig.1 The magnetization characteristics of amorphous alloy and oriented silicon steel
摘要 非晶合金和取向硅钢是制作配电变压器铁心常用的两种软磁材料，各有优劣。采用非晶合金-取向硅钢组合铁心结构可以综合两者的优势。该文以非晶合金和取向硅钢铁心并排的组合结构为基础，选取组合铁心的取向硅钢占比和尺寸参数为自由变量，提出一种基于自由参数扫描法的组合铁心结构设计方法。首先，根据非晶合金-取向硅钢组合铁心结构特点，建立组合铁心的等效双非线性磁路模型；其次，采用磁路法迭代求解组合铁心的磁通密度分布，并制定组合铁心的结构设计流程；最后，根据结构设计结果制作了组合铁心的实验模型，采用实验和有限元仿真结合的方法分析了其磁-振动特性，验证了所提设计方法的准确性，并与传统纯非晶合金和纯取向硅钢铁心进行对比分析，阐述了组合铁心的优势。
关键词：非晶合金-取向硅钢组合 铁心自由参数 扫描法 结构设计 双非线性磁路模型磁-振动特性
非晶合金和取向硅钢是制作配电变压器铁心常用的两种软磁材料[1-3]。其中，非晶合金材料具有损耗密度小的优点，但也存在饱和磁通密度低、磁致伸缩系数大的问题[4]；而取向硅钢材料具有饱和磁通密度高、磁致伸缩系数小的优点，但损耗密度较大。两种软磁材料不同的磁化特性导致当前配电变压器铁心不能兼顾低损耗和低振动。将非晶合金和取向硅钢铁心进行装配组合形成非晶合金-取向硅钢组合铁心可以综合两种材料的优点[5-6]。合理地分配非晶合金和取向硅钢占比对降低配电变压器铁心损耗以及减小配电变压器铁心振动具有重要意义。因此，有必要研究组合铁心的结构设计方法和磁-机械振动特性。
当前，配电变压器组合铁心结构主要是采用硅钢与硅钢组合的方案，具体又可以分为两类：取向硅钢-无取向硅钢组合铁心[7-9]及不同型号取向硅钢装配形成的组合铁心[10-15]。其中，文献[8]针对取向硅钢磁化偏离轧制方向时会引起磁性能下降，从而导致在铁轭和心柱交接位置损耗增大的问题，提出了在交接位置采用无取向硅钢替代的结构方案，即取向硅钢-无取向硅钢组合铁心结构。从有限元仿真结果来看，该组合铁心结构相比传统取向硅钢铁心损耗降低了2%，但缺乏相应的实验验证。不同型号取向硅钢装配形成的组合铁心是根据卷铁心磁通密度分布不均匀特性，在铁心不同位置使用不同等级的取向硅钢。如文献[11]提出多层组合卷铁心结构，在卷铁心磁通密度较小的内层和外层使用常规取向硅钢，在磁通密度较大的中间层使用高磁导率取向硅钢，并以铁心损耗和成本为目标，采用遗传算法和模拟退火算法对组合铁心进行优化设计。又如文献[14]针对三相五柱卷铁心，基于各框峰值磁通密度分布不均匀特性（边框小，内框大），由此提出了复合铁心的结构，其中两只边框采用常规取向硅钢卷铁心，两只内框采用高磁导率取向硅钢卷铁心。不同型号取向硅钢装配形成的组合铁心虽然在一定程度上实现了成本和损耗的折中，但是该组合铁心结构仍然没有摆脱取向硅钢损耗密度过大的缺点。
针对硅钢与硅钢组合方案存在的问题，文献[16]提出了非晶合金-取向硅钢并排的组合铁心结构，采用有限元方法分析了组合铁心的磁特性，并搭建了组合铁心磁特性测量平台进行实验验证。从结果来看，该组合铁心结构综合了非晶合金损耗低和取向硅钢饱和磁通密度高的优点，具有广阔的应用前景。然而，文中缺少对组合铁心中非晶合金和取向硅钢的配比以及结构尺寸参数设计，并且未进行组合铁心振动特性仿真分析及实验验证。
为此，本文以非晶合金-取向硅钢组合铁心结构为基础，以组合铁心中取向硅钢占比和结构尺寸参数为自由变量，通过建立等效双非线性磁路模型求解组合铁心的磁通密度分布，从而提出一种基于自由参数扫描法的非晶合金-取向硅钢组合铁心结构设计方法。根据结构设计结果，搭建组合铁心实验测试平台，基于实验测量和有限元仿真，分析了组合铁心的磁-机械振动特性。
由于非晶合金和取向硅钢内部成分和生产工艺不同，两种软磁材料表现出的磁化特性也不同[17-18]。非晶合金（AN101）和取向硅钢（B30P120）在工频正弦激励下的磁化特性如图1所示。其中，图1a是单值B-H曲线，图1b是损耗密度曲线，图1c是单值磁致伸缩峰峰值曲线。从图1中可以看出，非晶合金的饱和磁通密度（约为1.56 T）低于取向硅钢（约为1.98 T）、非晶合金的损耗密度高于取向硅钢，非晶合金的磁致伸缩系数远远大于取向硅钢。以上非晶合金和取向硅钢材料所表现出的磁化特性差异将导致非晶合金铁心的工作磁通密度低于取向硅钢铁心，取向硅钢铁心的空载损耗高于非晶合金铁心，非晶合金铁心的振动噪声强于取向硅钢铁心。即传统非晶铁心和取向硅钢铁心不能兼顾低损耗和低振动的要求。
图1 非晶合金和取向硅钢的磁化特性
Fig.1 The magnetization characteristics of amorphous alloy and oriented silicon steel
将非晶合金铁心和取向硅钢铁心进行装配形成组合铁心可以综合两者的优势。具体来说，组合铁心利用取向硅钢饱和磁通密度大的优势，可以提高工作磁通密度，以减小铁心体积，并且取向硅钢的存在可以防止非晶合金过饱和；利用非晶合金损耗密度小的优势可以减小铁心损耗；利用硅钢磁致伸缩系数小的优势减小铁心振动。因此，对非晶合金-取向硅钢组合铁心的结构参数进行设计，明确组合铁心的磁-机械特性，对充分发挥组合铁心的优势具有重要意义。
非晶合金和取向硅钢铁心并排的组合结构如图2所示。其中，图2a是组合铁心的三维结构，根据实际配电变压器铁心生产工艺，在该结构中非晶合金部分采用平面卷铁心结构，取向硅钢部分采用平面叠铁心结构，励磁线圈同时绕过两只铁心；图2b是组合铁心的三视图，其中l为组合铁心的长度，h为组合铁心的高度，d为铁轭的厚度，wA为非晶合金铁心的宽度，wS为取向硅钢铁心的宽度。wS和wA满足关系
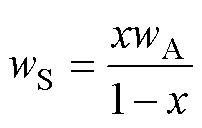（1）
式中，x为取向硅钢铁心与组合铁心的宽度之比。
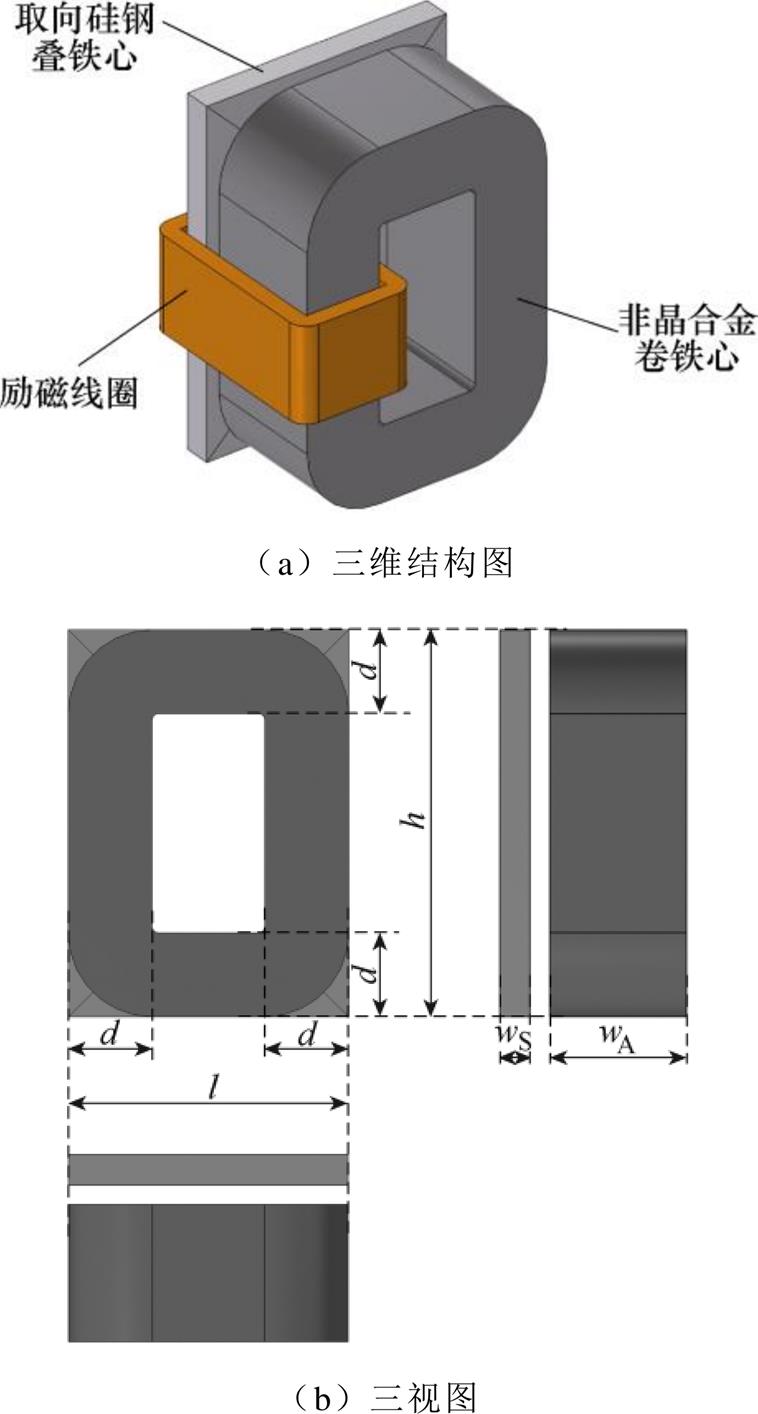
图2 非晶合金-取向硅钢组合铁心结构
Fig.2 The structure diagram of amorphous alloy-oriented silicon steel composite iron core
非晶合金-取向硅钢组合铁心由于两种非线性软磁材料同时存在，传统根据励磁线圈端电压、匝数和截面积仅能获取组合铁心的平均磁通密度，而难以获取磁通密度在非晶合金和取向硅钢铁心中的分布结果。为此，本文通过考虑非晶合金和取向硅钢的磁化饱和特性建立组合铁心的等效双非线性磁路模型，采用磁路法迭代求解组合铁心的磁通密度分布。
在图2所示的组合铁心结构中，由于励磁线圈同时绕过非晶合金和取向硅钢铁心，因此非晶合金铁心和取向硅钢铁心相当于磁路并联，两者的磁动势相等。基于此，建立如图3所示的组合铁心等效双非线性磁路模型。图3中，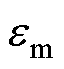
和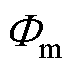
分别为组合铁心励磁线圈产生的磁动势和磁通量，RA和RS分别为非晶合金和取向硅钢铁心的非线性磁阻，
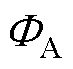和
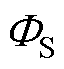分别为非晶合金和取向硅钢铁心的磁通量。
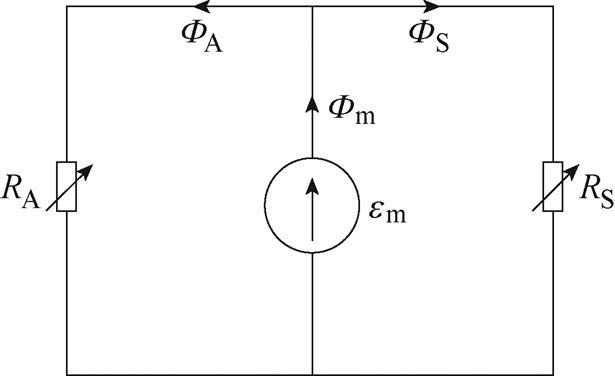
图3 组合铁心的等效双非线性磁路模型
Fig.3 The equivalent dual nonlinear magnetic circuit model of composite iron core
根据图2所示的组合铁心结构，得到组合铁心的磁通量和磁通密度分别为
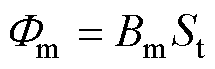（2）
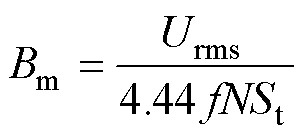（3）
式中，Bm为组合铁心的磁通密度；St为组合铁心的总有效截面积，St=SA+SS，其中，SA和SS分别为非晶合金铁心和取向硅钢铁心的有效截面积，SA= dKAwA，SS=dKSwS，KA和KS分别为非晶合金铁心和取向硅钢铁心的叠片系数；Urms为励磁线圈端口电压的有效值；f为励磁电压的频率；N为励磁线圈的匝数。
图3所示的在组合铁心等效双非线性磁路模型中，非晶合金铁心和取向硅钢铁心的非线性磁阻计算公式分别为
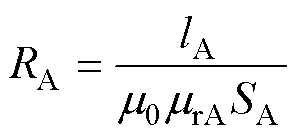（4）
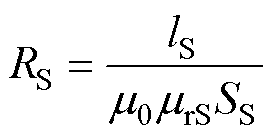（5）
式中，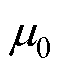
为真空中的磁导率；
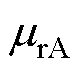和
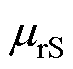分别为非晶合金和取向硅钢的相对微分磁导率，与非晶合金铁心和取向硅钢铁心的磁通密度分布有关；lA和lS分别为非晶合金铁心和取向硅钢铁心的平均磁路长度，其计算公式分别为
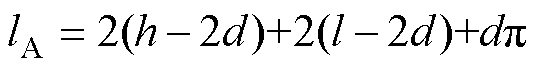（6）
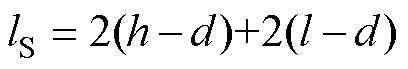（7）
类比磁路和电路理论，即磁动势对应电压，磁通量对应电流，磁阻对应电阻，得到非晶合金铁心和取向硅钢铁心的磁通量分别为
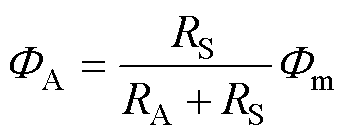（8）
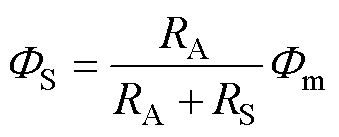（9）
进而根据磁通量与磁通密度的关系，得到组合铁心中非晶合金铁心和取向硅钢铁心的磁通密度分布结果。值得注意的是，在求解时需要根据计算得到的磁通密度分布结果和图1a所示的B-H值，更新非晶合金和取向硅钢的相对微分磁导率，直至非晶合金铁心和取向硅钢铁心的磁通密度达到预设的精度要求。然而，图1a所示的B-H值通常是离散的实验数据，因此在进行组合铁心设计之前，需要对离散的B-H值进行插值以得到连续的B-H曲线。则非晶合金和取向硅钢的相对微分磁导率可分别表示为
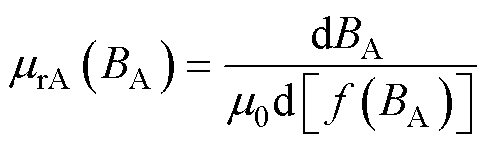（10）
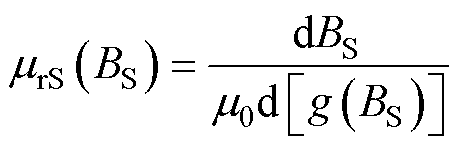（11）
式中，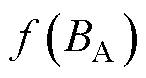
为非晶合金以磁通密度为自变量的B-H曲线插值函数；
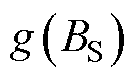为取向硅钢以磁通密度为自变量的B-H曲线插值函数。B-H曲线的插值函数可以根据软磁材料的B-H测量值经过线性插值得到。
从2.2节组合铁心磁通密度分布的求解过程来看，励磁线圈端口电压有效值Urms、频率f、匝数N、非晶合金和取向硅钢的相对磁导率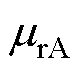和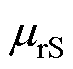以及叠片系数KA和KS均是由系统和材料决定的已知参数，而组合铁心的长度l、高度h、铁轭的厚度d、非晶合金铁心的宽度wA以及取向硅钢铁心与组合铁心的宽度之比x为未知参数。
为此，本文选取组合铁心的5个未知参数作为自由参数，采用自由参数扫描法[19-20]，对组合铁心的5个结构参数进行设计。自由参数扫描法的基本原理是对全部候选方案进行逐一枚举和检验，从而确定所有满足收敛和约束条件的解集。该方法可以避免遗漏可行的方案、实现简单，成为当前变压器设计的常用方法。基于自由参数扫描法的组合铁心结构设计流程如图4所示。该方法首先设置5个自由参数的取值范围；其次，通过排列组合的方式确定所有候选自由参数集，其中每组自由参数代表一种组合铁心结构方案；再次，迭代计算每种方案非晶合金和取向硅钢铁心的磁通密度分布，根据预设收敛误差e判断解是否稳定，当达到预设最大迭代次数qmax还未收敛时，则自动剔除该候选方法，进行下一组候选方案的磁通密度分布迭代计算；最后，根据取向硅钢铁心磁通密度是否高于非晶合金铁心磁通密度这一约束条件，确定可行的结构设计方案集。
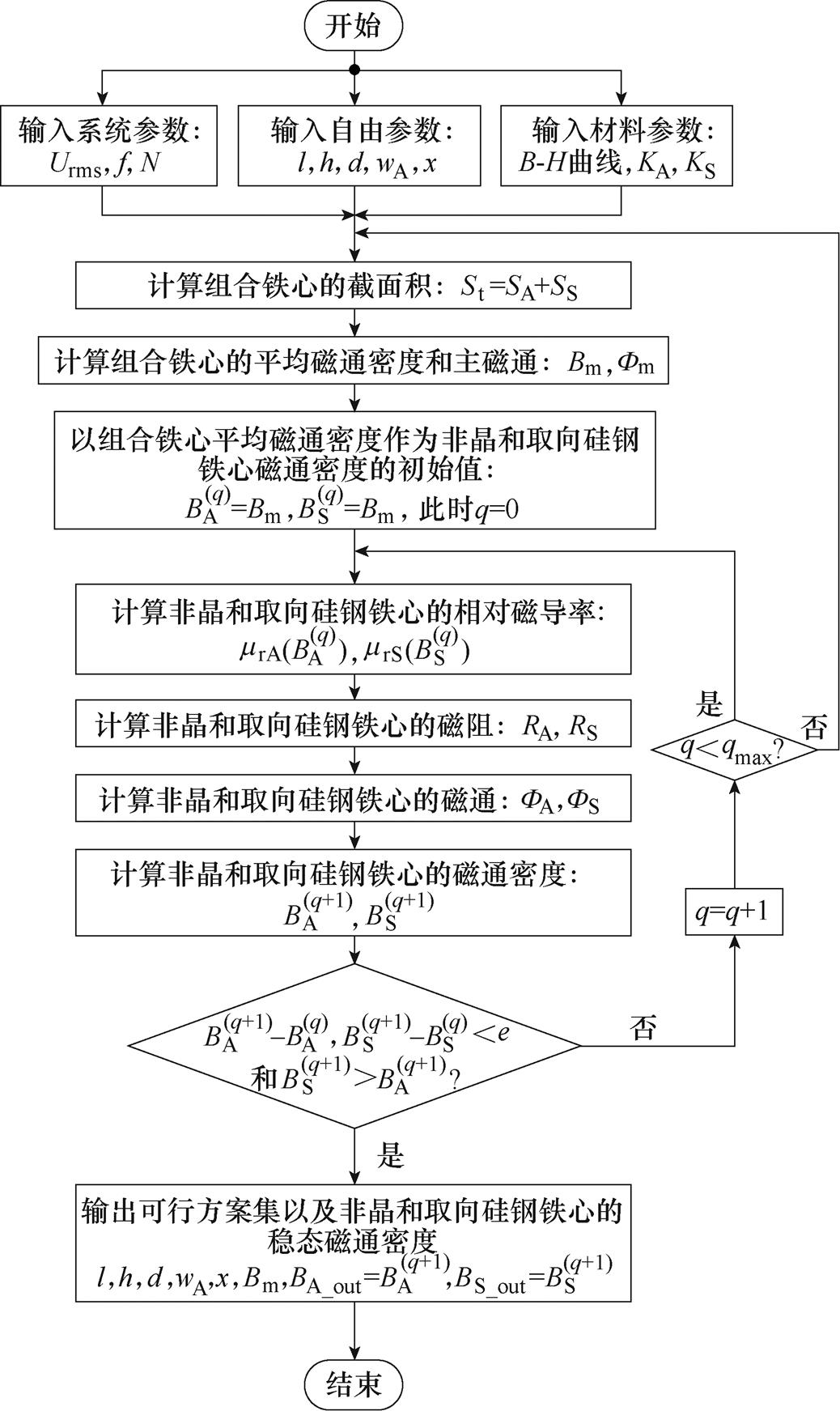
图4 基于自由参数扫描法的组合铁心结构设计流程
Fig.4 The structure design flow of composite iron core based on free parameter scanning method
根据上述的组合铁心结构设计方法，设计一套单相组合铁心。组合铁心的系统参数、材料参数以及自由参数取值范围见表1。进行组合铁心磁通密度分布迭代计算时，预设收敛误差e的取值设置为0.01 T，预设最大迭代次数qmax的取值设置为1 000。需要指出的是，为了后续实验方便可行，将组合铁心的励磁电压有效值和励磁线圈匝数设置为45 V和10匝。
表1 组合铁心各参数取值
Tab.1 The value of each parameter of composite iron core
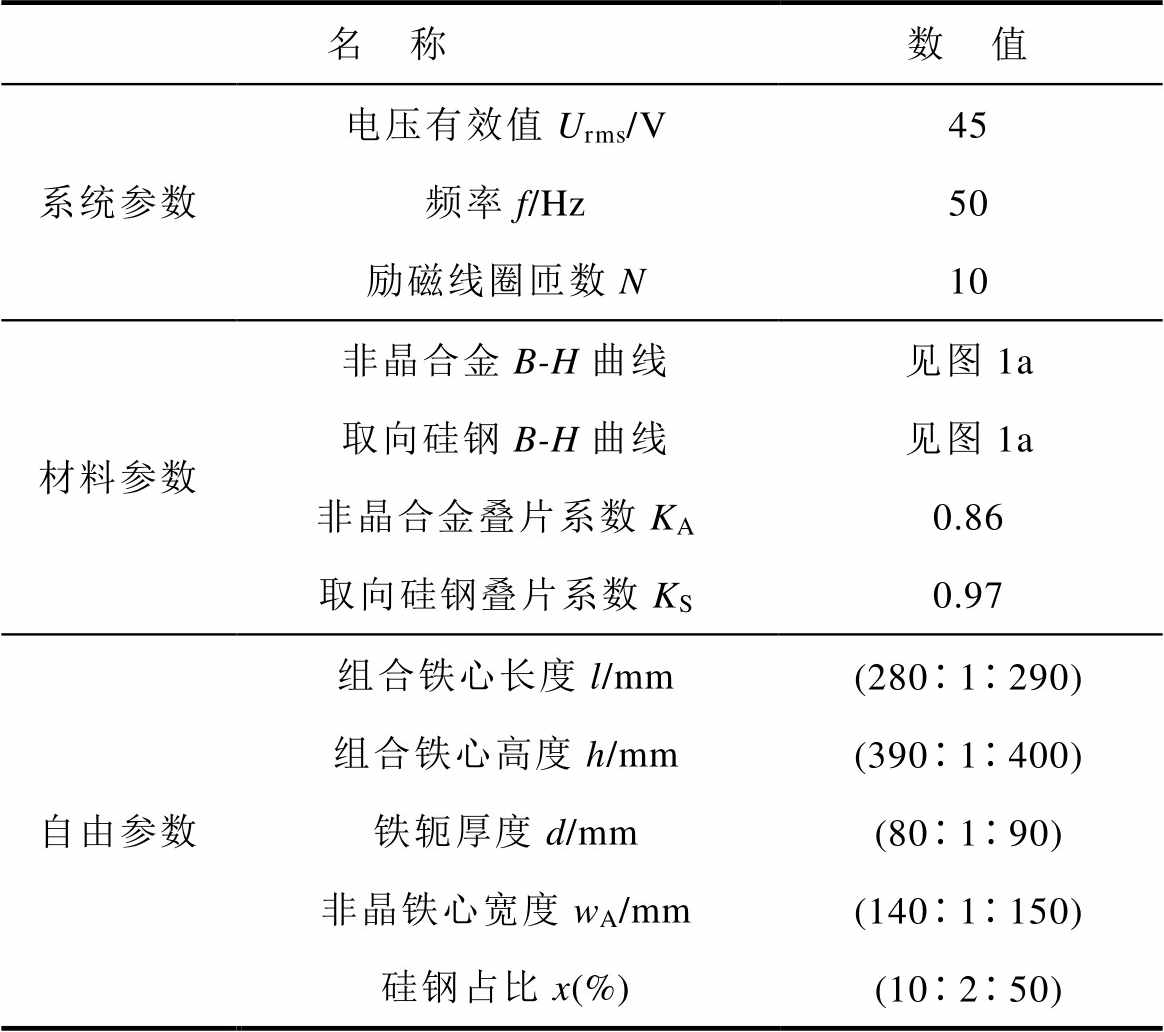
名 称数 值 系统参数电压有效值Urms/V45 频率f/Hz50 励磁线圈匝数N10 材料参数非晶合金B-H曲线见图1a 取向硅钢B-H曲线见图1a 非晶合金叠片系数KA0.86 取向硅钢叠片系数KS0.97 自由参数组合铁心长度l/mm(2801290) 组合铁心高度h/mm(3901400) 铁轭厚度d/mm(80190) 非晶铁心宽度wA/mm(1401150) 硅钢占比x(%)(10250)
根据图4所示组合铁心设计流程和表1所示的各参数取值，编写组合铁心结构设计程序，运行程序得到组合铁心的结构设计方案集如图5所示，图中每一点表示一组方案，共80 705组方案。其中，图5中红色点表示满足取向硅钢磁通密度大于非晶合金的所有可行方案，共8 946组方案。从图5中可以看出，随着组合铁心磁通密度升高，红色点越来越稀疏，其原因在于，在高磁通密度下非晶合金和取向硅钢接近各自的饱和区，磁路法的收敛性变差。理论上，图5中红色点均可以作为组合铁心的结构设计方案，但考虑到铁心因加工工艺引起的性能误差会导致非晶合金铁心磁通密度大于取向硅钢铁心磁通密度的问题，且越靠近红色区域和蓝色区域分界面的方案越容易出现该问题。为了保留设计裕度，选择设计方案时应尽可能远离该分界面。因此，选取图5中右上角的红色点对应的方案作为组合铁心的最终设计方案，该方案的具体参数取值见表2。
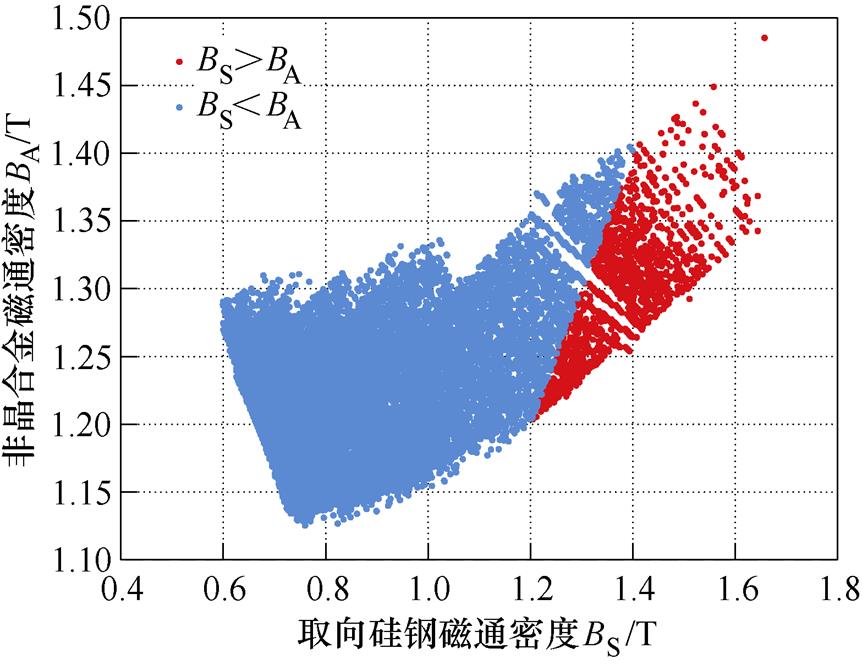
图5 组合铁心结构设计方案集
Fig.5 The structure design scheme set of composite iron core
表2 组合铁心结构设计结果
Tab.2 The structure design result of composite iron core
参 数设计数值 组合铁心长度l/mm290 组合铁心高度h/mm400 铁轭的厚度d/mm87 非晶合金铁心宽度wA/mm142 取向硅钢占比x(%)18
根据表2所示的非晶合金-取向硅钢组合铁心结构设计结果，制作了组合铁心实验模型。其中，非晶合金平面卷铁心由AN101型带材卷制而成，为多层搭接结构，搭接长度为18 mm，可以有效减少气隙对铁心磁性能的影响。取向硅钢叠铁心由B30P120型单片叠制而成，为斜接缝结构，并装配环氧树脂夹件进行夹紧处理，可有效减小接缝处气隙的影响。搭配可编程电源及其上位机、示波器、电压和电流探头、振动传感器、振动数据采集器以及PC形成了如图6所示的组合铁心磁-振动特性测量平台。
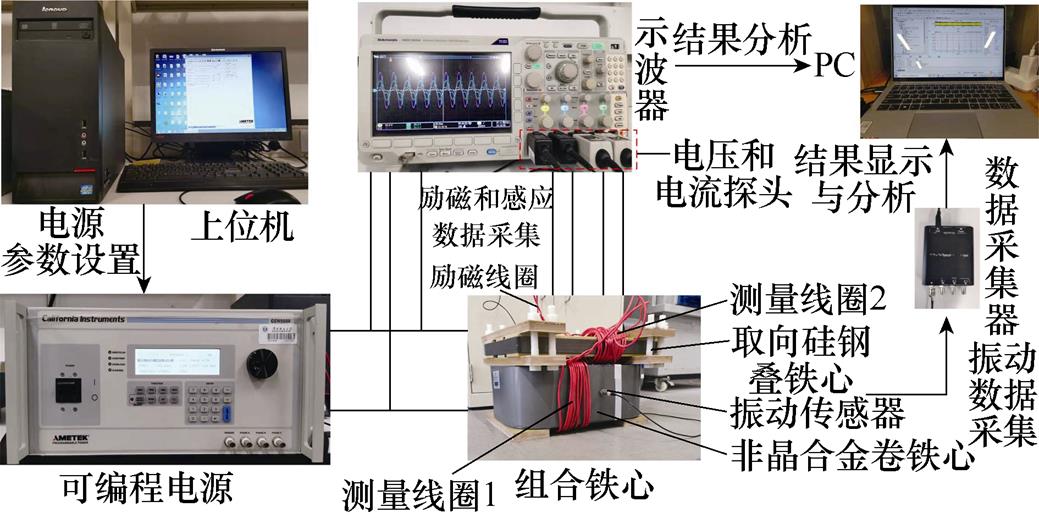
图6 组合铁心磁-振动特性测量平台
Fig.6 The magnetic-vibration characteristics measurement platform of combined iron core
该测量平台中，组合铁心绕制有1个励磁线圈和2个测量线圈。其中，励磁线圈同时绕过非晶合金和取向硅钢铁心，实现两只铁心同时励磁；测量线圈1绕制在非晶合金铁心上，匝数为10，测量线圈2绕制在取向硅钢铁心上，匝数为15。实验时，采用差分电压探头分别测量组合铁心的励磁电压、非晶合金铁心和取向硅钢铁心的感应电压，采用电流探头测量组合铁心的励磁电流，采用振动传感器测量组合铁心的振动位移，采用示波器进行测量数据采集。励磁电压、感应电压、励磁电流以及振动位移的采样频率均设置为100 kHz。
3.2.1 磁通密度分布特性
图7为励磁电压有效值为21 V和45 V时，非晶合金铁心和取向硅钢铁心的感应电压测量结果。从图中可以看出，当励磁电压有效值为21 V时，测量线圈1的感应电压与励磁电压十分接近，近似为正弦波，而测量线圈2的感应电压较小。随着组合铁心的励磁电压有效值增大，虽然励磁电压仍是正弦波形，但测量线圈1和2的感应电压呈现出明显的非正弦波形，并且测量线圈1和2的感应电压此消彼长。出现图7所示结果的原因在于，当励磁电压有效值较小时，此时组合铁心的工作磁通密度较小，而根据图1a所示的非晶合金和取向硅钢B-H曲线可知，在低磁通密度下非晶合金的微分磁导率大于取向硅钢，此时磁通量主要分布在非晶合金铁心中，而取向硅钢铁心中仅分布有较少的磁通量，即低磁通密度下组合铁心优先磁化非晶合金铁心；随着励磁电压有效值逐渐上升，非晶合金和取向硅钢的微分磁导率逐渐上升后又逐渐下降，当励磁电压超过某一临界值时，非晶合金的磁导率会小于取向硅钢，此时取向硅钢铁心中的磁通量占比会增大，导致非晶合金铁心中的磁通量占比会减小，因此非晶合金和取向硅钢铁心中出现此消彼长且非正弦变化的感应电压。
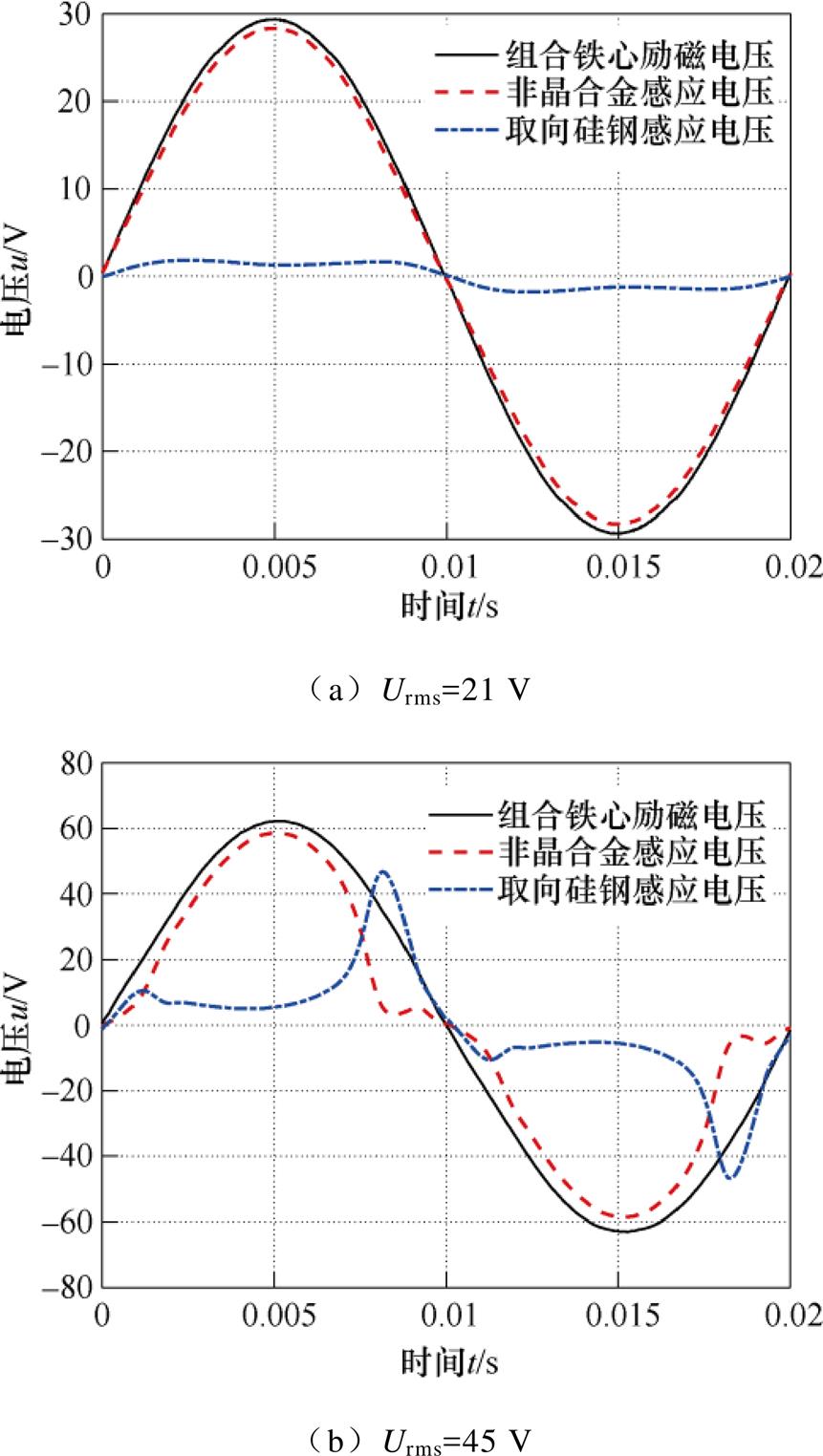
图7 不同励磁下组合铁心的感应电压测量结果
Fig.7 The measured results of induced voltage of composite core under different excitations
为了验证本文所提组合铁心结构设计方法的准确性，将本文方法计算得到的组合铁心磁通密度分布结果与实验测量结果进行对比分析。表3为额定励磁条件下（励磁电压有效值为45 V）组合铁心的磁通密度分布对比结果。从表3中的结果可以看出，本文方法的计算结果准确度较高，相对误差分别是0.858%、3.484%和5.073%。造成误差的主要原因是，非晶合金铁心多层搭接和取向硅钢夹紧措施可以减小但不能完全消除气隙漏磁的影响，导致实验测量结果偏小，而本文所建的组合铁心等效双非线性磁路模型未考虑漏磁的影响。此外，在本文所设计的组合铁心方案中，无论是理论计算还是实验测量结果，非晶合金铁心的磁通密度均低于组合铁心，而取向硅钢铁心的磁通密度高于组合铁心，并且取向硅钢铁心的磁通密度距离完全饱和还有一定裕度，实现了取向硅钢铁心防止非晶合金铁心过饱和的目的。
表3 额定励磁下组合铁心的磁通密度分布对比结果
Tab.3 The comparison of flux density distribution of composite core under rated excitation
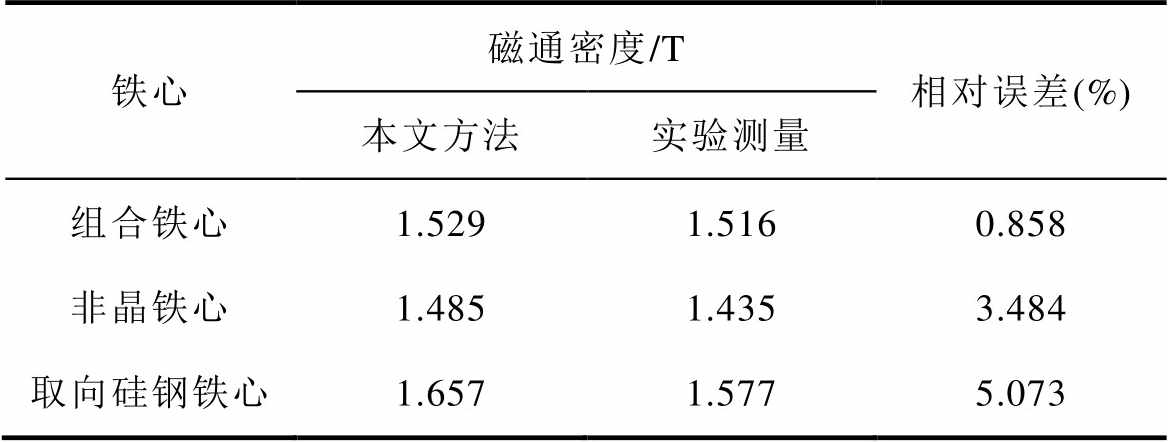
铁心磁通密度/T相对误差(%) 本文方法实验测量 组合铁心1.5291.5160.858 非晶铁心1.4851.4353.484 取向硅钢铁心1.6571.5775.073
图8为不同励磁条件下组合铁心磁通密度分布对比结果。从图8结果看出，当组合铁心处于低励磁磁通密度下时，由于非晶合金铁心的微分磁导率大于取向硅钢铁心，取向硅钢铁心中的磁通量占比较小，导致非晶合金铁心磁通密度高于取向硅钢铁心；随着组合铁心励磁磁通密度逐渐上升，达到某一临界点时，取向硅钢铁心的微分磁导率会大于非晶合金铁心，取向硅钢铁心中的磁通量占比会逐渐增加，也就出现了取向硅钢铁心磁通密度高于非晶合金铁心的结果。该临界点即为图8中非晶合金和取向硅钢铁心磁通密度曲线的交点。为了实现取向硅钢铁心防止非晶合金铁心过饱和的目的，组合铁心的工作点应该选择在临界点的右侧，本文所设计的方案满足这一要求。
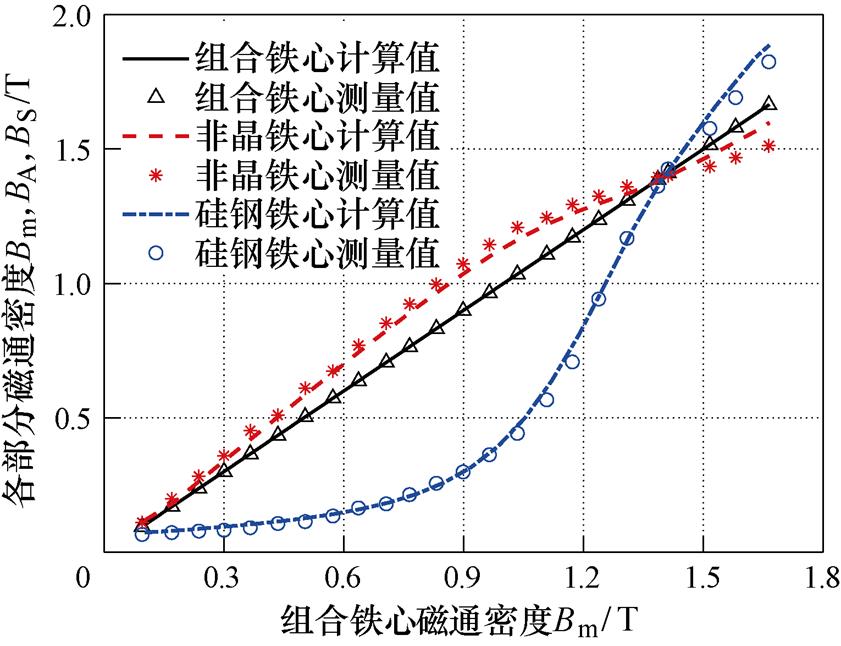
图8 不同励磁下组合铁心的磁通密度分布对比结果
Fig.8 The comparison results of magnetic density distribution of composite core under different excitations
以平均相对误差（Mean Relative Error, MRE）为评价指标，说明本文所提方法的求解精度，平均相对误差的定义如式（12）所示。根据式（12）计算得到本文所提方法的平均相对误差整体较小，其中组合铁心磁通密度的平均相对误差为1.747%，非晶合金铁心为3.129%，取向硅钢铁心为7.663%，进一步验证了本文所提组合铁心设计方法的有效性。造成误差的原因同前。
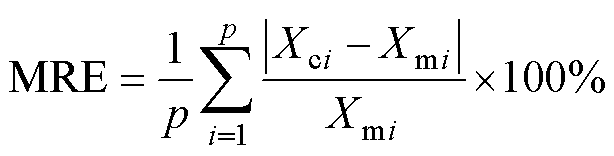（12）
式中，Xmi为第i个测点的磁通密度测量值；Xci为对应Xmi的磁通密度计算值；p为测点个数。
以额定励磁为例，对组合铁心的磁通密度分布进行时域和频域分析。根据图7b所示的励磁和感应电压测量结果，由电压与磁通密度的数学积分关系，可得到组合铁心以及组合铁心中非晶铁心和硅钢铁心的磁通密度时域分布结果如图9a、图9c和图9e所示。采用傅里叶分析得到组合铁心以及组合铁心中非晶铁心和硅钢铁心的磁通密度频域结果如图9b、图9d和图9f所示。从图9所示的结果可以看出，组合铁心整体的磁通密度呈正弦分布，但组合铁心中的非晶合金铁心和取向硅钢铁心成非正弦分布。其中，非晶合金铁心的磁通密度以3次谐波为主，取向硅钢铁心的磁通密度以3次和5次谐波为主。
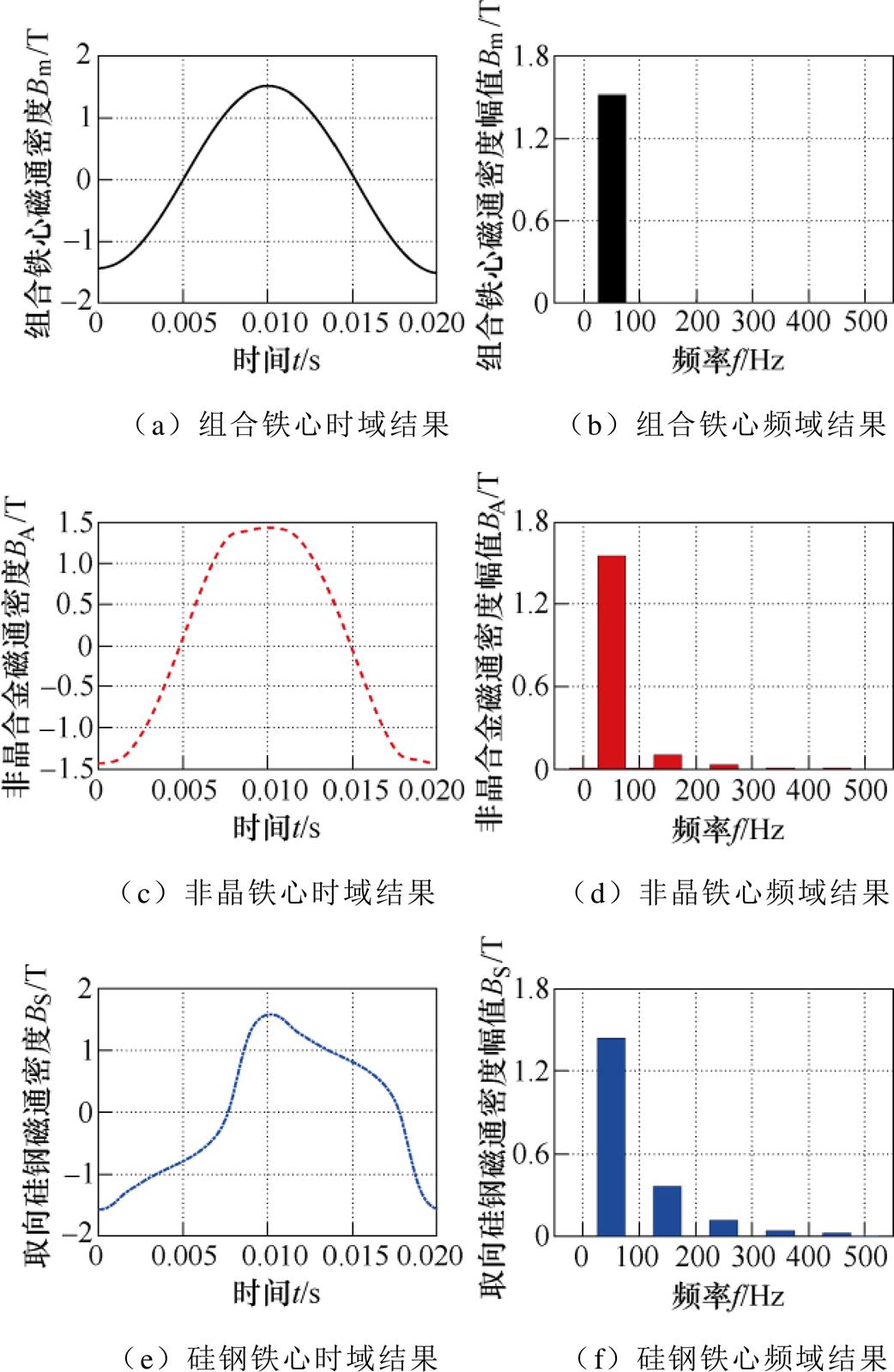
图9 额定励磁下组合铁心磁通密度的时域和频域结果
Fig.9 The time-domain and frequency-domain results of flux density of combined iron core at rated excitation
3.2.2 空载损耗特性
基于实验测量和有限元仿真，分析非晶合金-取向硅钢组合铁心的空载损耗大小。组合铁心的空载损耗测量结果可以根据励磁和感应电压与励磁电流计算得到，表达式为
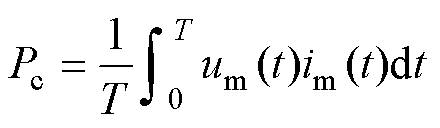（13）
式中，Pc为组合铁心损耗；um为组合铁心励磁电压；im为组合铁心励磁电流，其测量结果如图10所示。
根据组合铁心励磁电压和励磁电流实验测量数据，采用式（13）计算得到组合铁心的空载损耗为39.095 W。组合铁心空载损耗密度仿真结果如图11所示，经体积分后得到空载损耗为35.327 W。相比实验测量结果，有限元仿真结果的相对误差为9.638%，验证了仿真方法的有效性。
为了说明组合铁心在空载损耗方面的优势，进行组合铁心与纯非晶合金铁心以及纯取向硅钢铁心的空载损耗仿真对比分析。为了保证三种铁心在同一额定工作磁通密度（Bm=1.529 T）条件下进行对比，建立仿真模型时令铁心的长度l、高度h以及铁轭厚度d保持不变，由式（14）计算纯非晶合金铁心和纯取向硅钢铁心的宽度，计算结果分别是177.2 mm和157.1 mm。三种铁心空载损耗仿真对比结果如图12所示。其中，纯非晶合金铁心的空载损耗为29.064 W，纯硅钢铁心的空载损耗为109.810 W，组合铁心的损耗介于纯非晶铁心和纯取向硅钢铁心之间。相比纯取向硅钢铁心，组合铁心的空载损耗减小67.829%。因此，相比纯取向硅钢铁心，组合铁心在降低空载损耗方面具有明显优势。
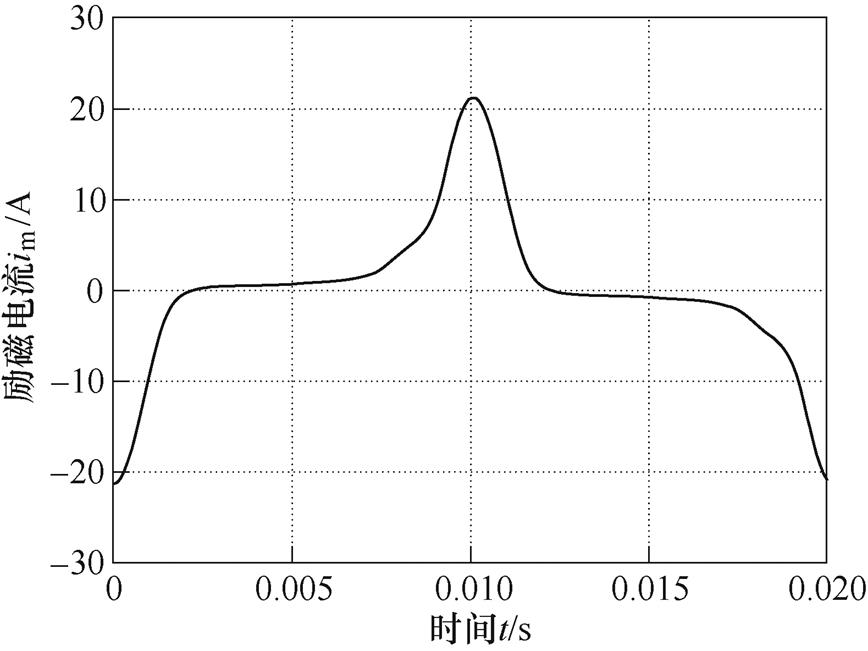
图10 额定励磁下组合铁心励磁电流测量结果
Fig.10 The measured results of exciting current of combined iron core at rated excitation
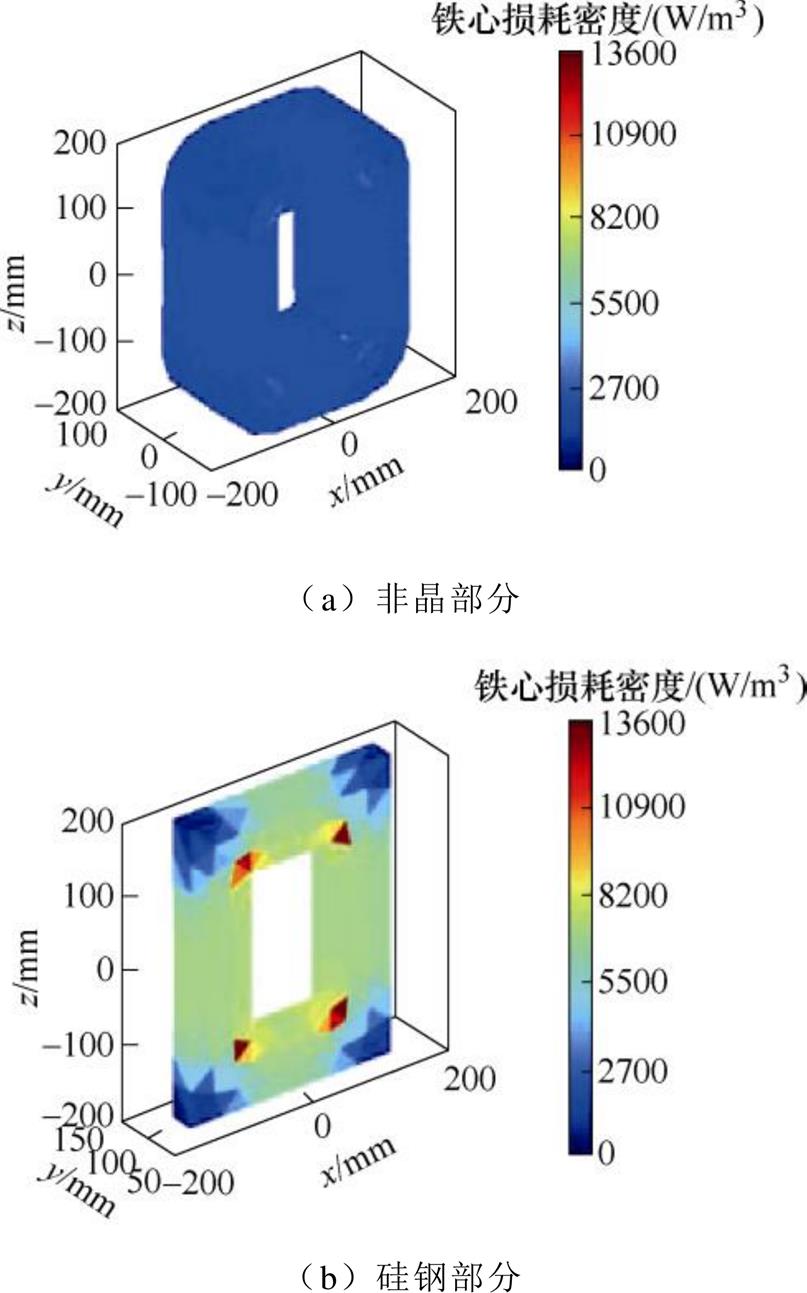
图11 额定励磁下组合铁心损耗密度仿真结果
Fig.11 The simulated results of loss density of combined iron core at rated excitation
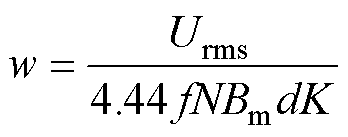（14）
式中，w为纯非晶合金铁心或者纯取向硅钢铁心的宽度；K为铁心叠片系数，对于纯非晶合金铁心取值为KA，对于纯取向硅钢铁心取值为KS。
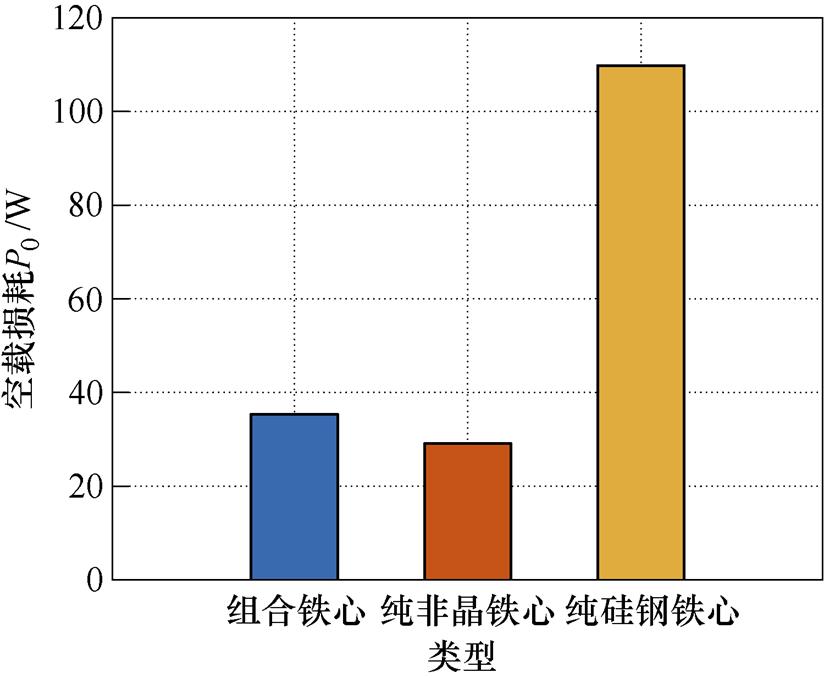
图12 不同类型铁心的空载损耗对比结果
Fig.12 The comparison results of no-load loss of different types of iron core
铁心振动强弱是评价变压器综合性能的重要指标，因此有必要进行组合铁心振动特性分析。由图1c可知，非晶合金的磁致伸缩系数峰-峰值远大于取向硅钢，因此在进行组合铁心振动特性分析时，以组合铁心中非晶合金铁心的振动位移作为指标评估组合铁心的振动强弱。图13为额定励磁条件下组合铁心在非晶合金铁心心柱外表面正中心处的振动位移有限元仿真和实验测量对比结果，其中图13a为时域结果，图13b为频域结果。从图13a所示的时域结果可以看出，有限元仿真结果与实验测量结果的吻合情况较好，其中振动位移峰值的相对误差为4.088%。从图13b所示的频域结果可以看出，组合铁心振动位移以直流和100 Hz分量为主，此外还含有少量的200 Hz和300 Hz分量。工频正弦激励下，振动位移以100 Hz分量为主的原因在于，软磁材料的磁致伸缩在磁通密度的一个周期内变化两 次[21-23]，从而导致铁心振动出现倍频现象。在较高磁通密度下软磁材料的磁畴旋转是引起铁心振动出现200 Hz分量的原因[24]。出现300 Hz分量的原因在于，组合铁心中非晶合金铁心部分的磁通密度分布出现3次谐波分量，经倍频后即为300 Hz，具体可见图9d所示的结果。
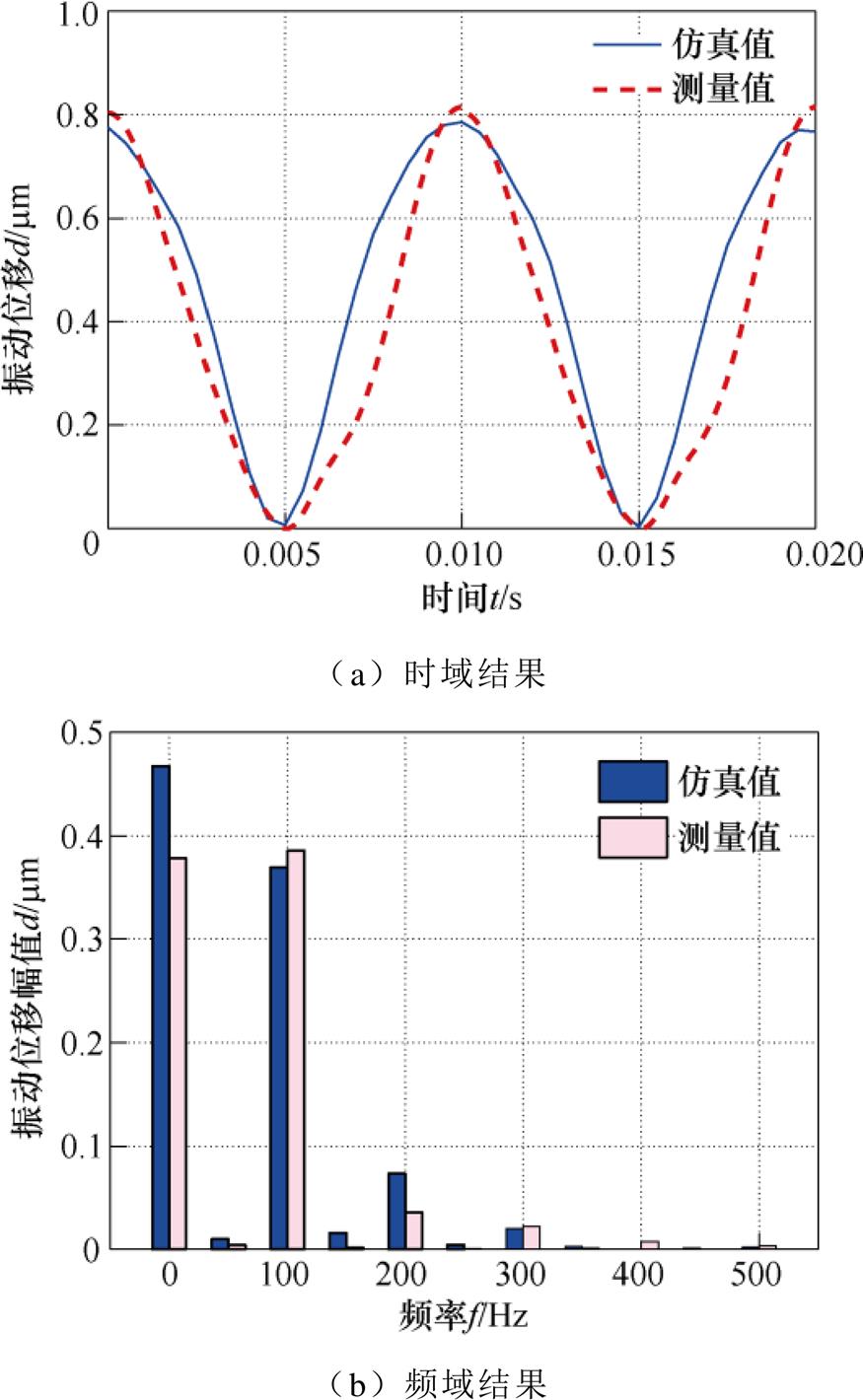
图13 额定励磁下组合铁心振动位移的时域和频域结果
Fig.13 The time-domain and frequency-domain results of vibration displacement of combined iron core at rated excitation
为了说明组合铁心在机械振动方面的优势，进行组合铁心与纯非晶合金铁心以及纯取向硅钢铁心的振动位移仿真对比分析。三种铁心振动位移仿真对比结果如图14所示。从图14所示的结果可以看出，纯非晶合金铁心的振动位移最大，峰值为1.085 mm；组合铁心的振动位移次之，峰值为0.785 mm；纯取向硅钢铁心的振动位移最小，峰值仅为0.019 mm。相比纯非晶合金铁心，组合铁心的振动位峰值降低38.20%，表明在相同条件下组合铁心的振动特性优于纯非晶合金铁心。
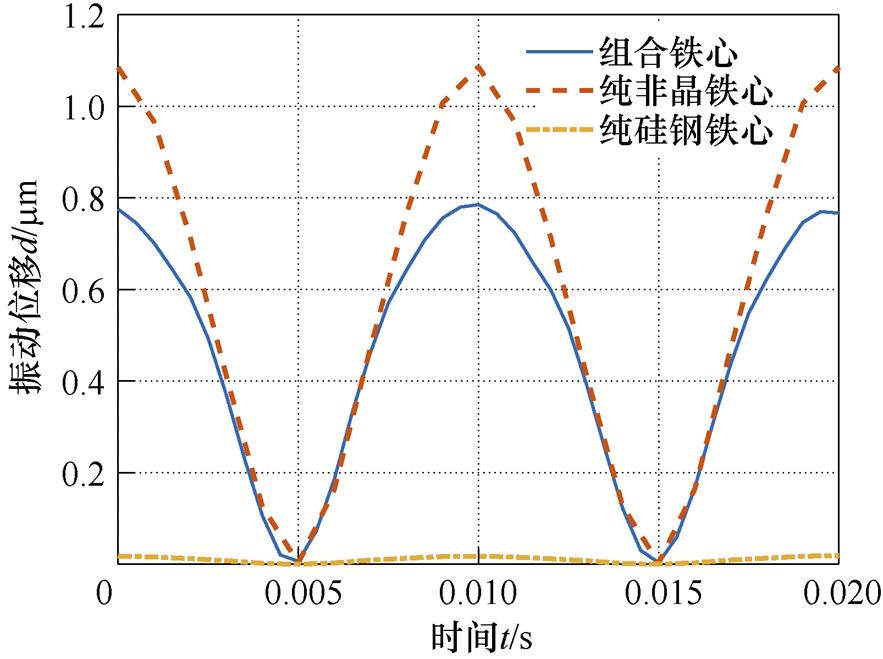
图14 不同类型铁心的振动位移对比结果
Fig.14 The comparison results of vibration displacement of different types of iron core
1）非晶合金-取向硅钢组合铁心可以综合非晶合金损耗密度低和取向硅钢磁致伸缩系数小、饱和磁通密度高的优势。本文以组合铁心中取向硅钢占比和结构尺寸参数为自由变量，提出一种基于自由参数扫描法的组合铁心结构设计方法，并根据设计结果制作了组合铁心实验模型，对比分析了组合铁心磁通密度分布的计算值和测量值，相对误差分别为0.858%、3.484%和5.073%，验证了所提设计方法的有效性。
2）对比分析了组合铁心与传统纯非晶合金铁心和纯取向硅钢铁心的空载损耗大小和振动位移大小，结果表明，相比传统纯取向硅钢铁心，组合铁心的空载损耗降低了67.829%；相比传统纯非晶合金铁心，组合铁心的振动位移峰值降低了38.20%。
3）本文考虑非晶合金和取向硅钢的磁化饱和特性建立了组合铁心的双非线性磁路模型，实现了组合铁心的磁通密度分布计算，暂未考虑软磁材料的磁滞特性。建立考虑磁滞效应的组合铁心双非线性磁路-电路耦合模型以及研究考虑磁滞效应的组合铁心双非线性有限元数值计算方法是下一步工作。
参考文献
[1] 杨北超, 范学鑫, 王瑞田, 等. 考虑铁心非线性的三相立体卷铁心变压器建模及空载特性分析[J]. 电工技术学报, 2022, 37(9): 2263-2274.
Yang Beichao, Fan Xuexin, Wang Ruitian, et al. Modeling and no-load characteristics analysis of 3D wound coretransformer considering core non- linearity[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2263-2274.
[2] Liu Gang, Liu Cong, Xiong Xiaofu, et al. Simulation of the magnetic field distribution and voltage error- characteristics of the three-phase three-component combinedtransformer with new three-cylinder core structure[J]. IEEE Transactions on Magnetics, 2020, 56(4): 1-4.
[3] Romaric K N, Liu Daosheng, Du Boxue. Investigation on vibration characteristics of amorphous metal alloy core dry-type distribution transformer[J]. CES Transa- ctions on Electrical Machines and Systems, 2022, 6(3): 324-331.
[4] 冯月磊, 刘洋, 李琳, 等. 考虑磁致伸缩效应的非晶合金立体卷铁心振动仿真与实验研究[J]. 电工电能新技术, 2022, 41(3): 15-22.
Feng Yuelei, Liu Yang, Li Lin, et al. Vibration simulation and experiment of amorphous alloy three- dimensional wound core considering magnetostrictive effect[J]. Advanced Technology of Electrical Engin- eering and Energy, 2022, 41(3): 15-22.
[5] Kurita N, Nishimizu A, Morooka H, et al. Demon- stration of loss-reduction effect of the amorphous coresfor larger-capacity transformers by trial manufa- cture[J]. Electrical Engineering in Japan, 2018, 204(1): 12-21.
[6] Kobayashi C, Kurita N, Nishimizu A, et al. Demon- stration of loss reduction effect of 66 kV-classed 30 MVA three phase hybrid-core transformer by trialmanufacture[J]. Electrical Engineering in Japan, 2021, 214(1): 26-34.
[7] Pytlech R. Mixed D-core with a distributed air gap as an alternative formedium voltage instrument trans- formers[J]. IEEE Transactions on Magnetics, 2010, 46(10): 3816-3825.
[8] Guan Weimin, Zhang Di, Yang Mu, et al. Flux and loss distribution in iron coreswith hybrid T-joint[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(2): 1-4.
[9] Gao Yanhui, Ichimaru S, Miyabe T, et al. Proposal of core structures for iron loss and noise reduction of three-phase reactor with anisotropic iron core[J]. IEEE Transactions on Magnetics, 2021, 57(2): 1-5.
[10] Kefalas T D, Kladas A G. FEM package for iron loss evaluation and minimization of two grade lamination- wound cores[J]. Journal of Optoelectronics and Advanced Materials, 2008, 10(5): 1197-1202.
[11] Kefalas T D, Georgilakis P S, Kladas A G, et al. Multiple grade lamination wound core: a novel technique for transformer iron loss minimization using simulated annealing with restarts and an anisotropy model[J]. IEEE Transactions on Magnetics, 2008, 44(6): 1082-1085.
[12] Hernández I, Olivares-Galván J C, Georgilakis P S, et al. A novel octagonal wound core for distribution transformer svalidated by electromagnetic field analysis and comparison with conventional wound core[J]. IEEE Transactions on Magnetics, 2010, 46(5): 1251-1258.
[13] Kefalas T D, Kladas A G. Development of distri- bution transformers assembled of composite wound cores[J]. IEEE Transactions on Magnetics, 2012, 48(2): 775-778.
[14] Kefalas T D, Kladas A G. Mixed Si-Fe wound cores five legged transformer: losses and flux distribution analysis[J]. IEEE Transactions on Magnetics, 2012, 48(4): 1609-1612.
[15] Kefalas T D, Magdaleno-Adame S. Techno-economic comparative evaluation of mixed and conventional magnetic wound cores for three-phase distribution transformers[J]. Electric Power Systems Research, 2018, 155: 331-339.
[16] Kurita N, Nishimizu A, Kobayashi C, et al. Magnetic properties of simultaneously excited amorphousand silicon steel hybrid cores for higherefficiency distribution transformers[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-4.
[17] 张希蔚. 软磁材料高频磁特性测量与模拟方法研究[D]. 北京: 华北电力大学, 2022.
[18] 贲彤, 方敏, 陈龙, 等. 非晶合金铁心电抗器减振结构的电磁-机械耦合拓扑优化[J]. 电工技术学报, 2023, 38(24): 6553-6564.
Ben Tong, Fang Min, Chen Long, et al. Optimization of magnetic-mechanical coupling topology for vibration damping structures of amorphous alloy core reactor[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6553-6564.
[19] 陈彬, 李琳, 赵志斌, 等. 电感集成式大容量高频变压器精细化设计方法[J]. 中国电机工程学报, 2018, 38(5): 1356-1368.
Chen Bin, Li Lin, Zhao Zhibin, et al. Design method of inductor-integrated high-power high-frequency transformer[J]. Proceedings of the CSEE, 2018, 38(5): 1356-1368.
[20] 王佳宁, 邹强, 胡嘉汶, 等. 一种中压绝缘大功率中频变压器的优化设计方法[J]. 电工技术学报, 2022, 37(12): 3048-3060.
Wang Jianing, Zou Qiang, Hu Jiawen, et al. An optimal design method for medium-voltage insulated high-powermedium-frequency transformer[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(12): 3048-3060.
[21] 迟青光, 张艳丽, 陈吉超, 等. 非晶合金铁心损耗与磁致伸缩特性测量与模拟[J]. 电工技术学报, 2021, 36(18): 3876-3883.
Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of loss and magneto- strictive propertiesfor the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.
[22] Li Yang, Zhu Jianguo, Li Yongjian, et al. Modeling dynamic magnetostriction of amorphous core mate- rials based on Jiles-Atherton theory for finite element simulations[J]. Journal of Magnetism and Magnetic Materials,2021,529:1-11.
[23] 王振, 张艳丽, 龚圆, 等. 机械应力下无取向电工钢片磁致伸缩特性研究[J]. 电工技术学报, 2023, 38(21): 5682-5690.
Wang Zhen, Zhang Yanli, Gong Yuan, et al. Study on magnetostrictive properties of non-oriented electrical steel sheet under mechanical stress[J].Transactions of China Electrotechnical Society, 2023, 38(21): 5682- 5690.
[24] 张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报, 2018, 33(22): 5273-5281.
Zhang Pengning, Li Lin, Cheng Zhiguang, et al. Vibration simulation and experiment comparison of shunt reactor and transformer model core[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(22): 5273-5281.
Abstract Amorphous alloy and oriented silicon steel are common soft magnetic materials used in manufacturing distribution transformer iron cores. Amorphous alloy with the advantage of low loss density faces challenges like low saturation flux density and large magnetostriction. Oriented silicon steel has the advantages of high saturation flux density and small magnetostriction, but its loss density is high. The opposite magnetization characteristics of the sematerials make the distribution transformer iron core difficult to simultaneously achieve low loss and low vibration. The combination of amorphous alloy and oriented silicon steel can synthesize the advantages of both materials. Specifically, the composite iron core can take advantage of the high saturation flux density of oriented silicon steel to prevent the supersaturation of amorphous alloy. The core loss is reduced by the low loss density of amorphous alloy, and the vibration of iron cores is reduced by the small magnetostriction of oriented silicon steel. Therefore, it is essential to design the structural parameters of the composite iron core and rationally allocate the proportion of amorphous alloy and oriented silicon steel to reduce the core loss and vibration indistribution transformer iron cores.
In the composite iron core, the amorphous alloy part adopts a planar wound iron core structure, and the oriented silicon steel part adopts aplanar stack iron core structure. The exciting coil bypasses both iron cores to realize simultaneous excitation. According to the structure of the composite iron core and the magnetization saturation characteristics of amorphous alloy and oriented silicon steel, an equivalent dual nonlinear magnetic circuit model is established, and the iterative calculation method of flux density distribution is proposed. On this basis, the free parameter scanning method is used to design the structural parameters of the composite iron core. Firstly, the value range of free parameters is set. Secondly, all candidate-free parameter sets are determined by arrangement and combination. Each group of free parameters represents a composite iron core structure scheme. Finally, the flux density distribution of the composite iron core in each scheme is iteratively calculated. Based on the constraint that the flux density of the oriented silicon steel iron core is higher than that of the amorphous alloy iron core, feasible structural design scheme sets are determined.
A composite iron core is designed, and an experimental prototype is manufactured according to the design results. The calculated and measured results of the flux density distribution of the composite iron core are compared. The mean relative error of the flux density for the composite iron core is 1.747%, for the amorphous alloy iron core is 3.129%, and for the oriented silicon steel iron core is 7.663%, which verifies the proposed method. The no-load loss of the pure amorphous alloy core is 29.064 W, the pure silicon steel core is 109.810 W, and the composite core is 35.327 W. Compared with the pure oriented silicon steel iron core, the no-load loss of the composite iron core is reduced by 67.829%. The vibration displacement of the pure-amorphous alloy iron core is the largest, with a peak value of 1.085 mm. The composite iron core is the second, with a peak value of0.785 mm. The pure oriented silicon steel iron core is the smallest, with a peak value of0.019 mm. Compared with the pure amorphous alloy iron core, the vibration displacement peak of the composite iron core is reduced by 38.200%.
keywords：Amorphous alloy and oriented silicon steel composite iron, core free parameter, scanning method, structure design, dual nonlinear magnetic circuit model, magnetic-vibration characteristics
DOI: 10.19595/j.cnki.1000-6753.tces.230255
中图分类号：TM201.4
国家重点研发计划课题（2021YFB2401700）和国家自然科学基金（52177005）资助项目。
收稿日期 2023-03-06
改稿日期 2023-04-10
陈 昊 男，1994年生，博士研究生，研究方向为软磁材料磁弹性耦合模拟与电工装备结构优化设计。E-mail: chenhao_xmzdls@126.com（通信作者）
李 琳 男，1962年生，教授，博士生导师，研究方向为电磁场原理及应用与先进输电技术。E-mail: lilin@ncepu.edu.cn
（编辑 郭丽军）