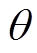的扇形区域，R和r分别为电缆外导体内半径和内导体外半径，rt为水树顶端到轴心的距离。等效电路如图1b所示。图中，C1和G1分别为水树区域的电容与电导；C2和G2分别为正常绝缘的电容与电导。摘要 配电网中中压电缆的敷设条件相对较差，在环境水分和工作电压等因素的共同作用下容易在绝缘中生成水树缺陷，影响电缆绝缘的性能。时域反射法（TDR）可用于检测电缆故障，近来也有研究将其用于检测电缆绝缘局部缺陷，但检测结果与绝缘缺陷情况的关联尚不明晰。针对此问题，该文基于等效电路原理推导了同轴绝缘含水树缺陷时的等效介电常数，在此基础上结合传输线理论建立计及双界面反射的时域解析模型，可用于分析与预测电缆绝缘局部存在水树缺陷时TDR实验的反射波形。通过制作含模拟水树的电缆试样并进行TDR实验，考察了模拟水树缺陷的含水量、缺陷段长度和电导率等因素对TDR实验结果的影响。结果显示，模拟水树的TDR实验结果与解析模型的计算结果具有较好的对应性，初步验证了该模型用于分析与预测电缆绝缘局部缺陷反射特性的有效性。预期该解析模型有助于为TDR在电缆绝缘水树检测中的应用提供参考。
关键词：电力电缆 绝缘老化 水树 有限元 时域反射 双界面
交联聚乙烯（Cross-Linked Polyethylene, XLPE）电缆绝缘的水树老化是诱发电缆故障的主要原因之一[1]。我国老旧电缆主要集中于10 kV与35 kV线路上[2]，这些中压电缆的运行环境较差，容易被水分侵入。水树老化是电缆绝缘在电场、水分共同作用下于绝缘微小缺陷处引发并生长的一种树状降解现象[3]。虽然水树通常不会直接造成短路故障[4]，但电缆运行中电场会促使水树缓慢生长，并可能发展为电树[5]，电树出现后电缆绝缘可能会迅速发生击穿[1,4]。因此，对电缆绝缘水树老化情况进行监测，及时了解绝缘水树老化的程度和位置，为检修维护提供参考，对于提升电缆寿命、降低故障率、提高电网安全稳定运行有着重要意义。
目前应用于电缆绝缘水树老化诊断的方法有介电谱法[6-7]、空间电荷法[8]及极化去极化电流法[9]等。但是上述方法都属于离线的测量方法，仍然缺少在线且能实现定位的水树诊断方法。反射法是一种基于介质波阻抗变化的测量技术，主要包括时域反射法（Time Domain Reflectometry, TDR）与频域反射法（Frequency Domain Reflectometry, FDR）。反射法在原理上具有可实现在线测量和缺陷定位的优点，因此在水树老化诊断上具有较大的应用潜力。
FDR通过扫频信号的反射波对电缆绝缘状态进行分析，目前国内外学者利用FDR原理在电缆绝缘缺陷与水树老化的诊断和定位上已取得了一定的成果[10-12]。TDR则利用脉冲信号的时域反射特征对缺陷进行诊断和定位，目前多用于电缆测距、低阻故障定位[13-15]等场合。由于高频信号衰减、反射信号偏弱等问题的限制，TDR用于诊断电缆线路上某点存在绝缘缺陷的有效性尚不确定。针对水树老化缺陷的诊断，文献[16]验证了对于一段500 m的电缆，通过TDR能够有效检测出其水树老化段；文献[17]基于TDR建立了一个配电电缆的在线监测系统，可以定期观察跟踪电缆绝缘的状态。然而，针对TDR反射波与绝缘水树老化状况之间关系的研究和报道还比较少。
本文基于等效电路原理确定了同轴电缆绝缘含水树缺陷时的等效介电常数，在此基础上根据传输线理论建立了可用于预测水树缺陷时域反射特征的双界面反射解析模型，有助于为TDR测试在电缆绝缘水树缺陷检测中的应用提供参考。本文首先介绍了水树老化绝缘等效介电常数的确定方法，并通过有限元仿真验证了该参数能够可靠反映正常绝缘和水树老化绝缘交界面的波反射特性；其次，基于等效介电常数和行波折反射理论建立了计及双界面的时域反射解析模型；最后，在含模拟水树的电缆样本上对该解析模型的有效性进行了验证。
为了便于研究电缆绝缘局部缺陷的波反射特性，引入等效介电常数的概念，即将水树老化绝缘的不均匀材料性质用一个平均介电常数来等效表示。
设同轴电缆绝缘局部（如图1a所示的扇形区域）含有由外导体侧生长的水树缺陷，并假设水树未贯穿绝缘，所以可进一步将该扇形区域划分为含水树区域和无水树区域。如图1a所示角度为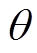的扇形区域，R和r分别为电缆外导体内半径和内导体外半径，rt为水树顶端到轴心的距离。等效电路如图1b所示。图中，C1和G1分别为水树区域的电容与电导；C2和G2分别为正常绝缘的电容与电导。
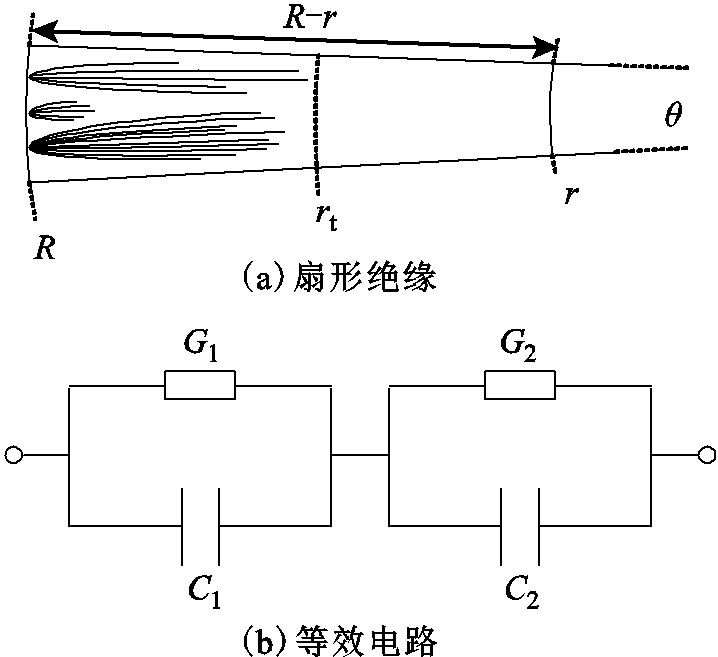
图1 含水树缺陷的扇形绝缘及其等效电路
Fig.1 Sector insulation containing the water tree area and its equivalent circuit
根据电路原理，图1b所示等效电路满足关系
（1）
式中，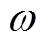
为角频率；C12和G12分别为整体的电容与电导；下标12代表扇形绝缘整体部分，下标1和2分别代表水树区域和正常绝缘，后文均采用此表示方法。电容和电导分别取决于绝缘的介电常数和电导率。令p=θ/360°，由于电缆绝缘的电容与电导在θ的旋转方向上均为并联关系，则θ范围内单位长度扇形绝缘的电容和电导分别为
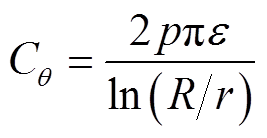（2）
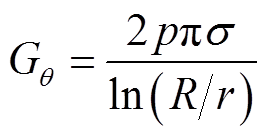（3）
式中，ε为绝缘的介电常数；σ为电导率。将式（2）与式（3）代入式（1），经整理后可得
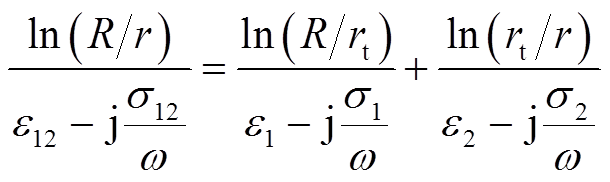（4）
式（4）中各项分母即为复介电常数ε*，因此可以写为
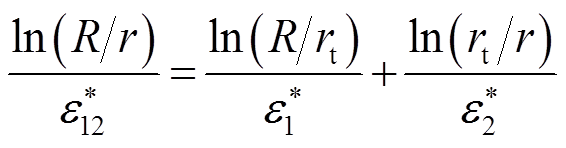（5）
由式（5）可得到整体的复介电常数为
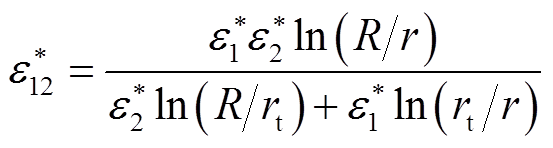（6）
对于由内导体侧生长的水树，其整体的复介电常数为
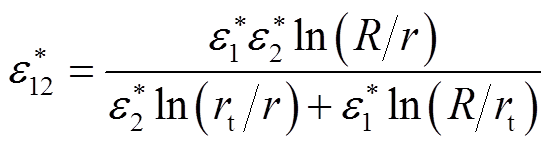（7）
令k为水树长度占绝缘厚度的比例，对于从外导体侧生长的水树，有k=(R-rt)/(R-r)，所以rt=R-k(R-r)；对于从内导体侧生长的水树，有k=(rt-r)/(R-r)，所以rt=k(R-r)+r。
同轴电缆绝缘可由多个扇形绝缘并联而成，其结构如图2a所示。以复介电常数的实部为例，根据同轴电容的计算式，其绝缘的介电常数可以表示为
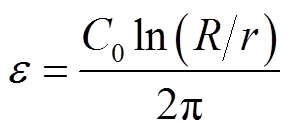（8）
式中，C0为电缆单位长度电容。对于同一电缆而言，ln(R/r)为定值，C0会因为绝缘老化而产生变化。如图2a所示，将同轴结构的绝缘视为许多并联起来的扇形绝缘电容，则其单位长度电容可以表示为
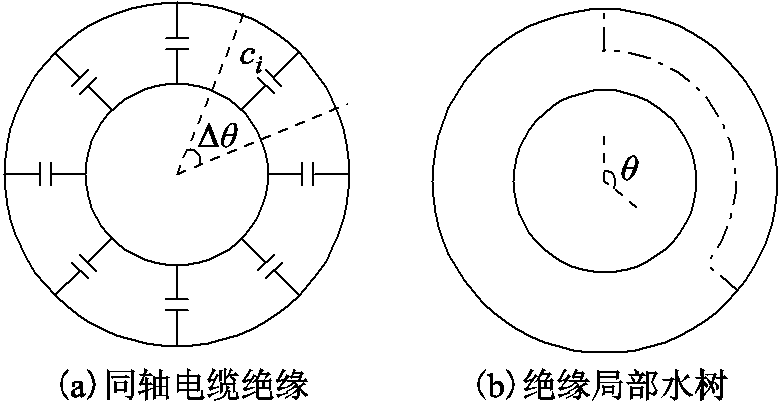
图2 用扇形绝缘表征同轴电缆绝缘及其局部水树
Fig.2 Parallel capacitance model for cable insulation and water tree area
（9）
式中，ci为第i个小电容，每一个小电容对应角度为∆θ区域内的电容值；n为小电容数量，n=360°/∆θ。由于绝缘均匀，令ci=cut，式（9）可以写为
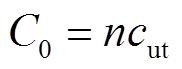（10）
设绝缘中有一范围为θ的水树区域如图2b点画线范围内所示，同样假设水树绝缘区域也是均匀的，则此时电缆单位长度电容可表示为
（11）
式中，ct-ut为含水树时ci的值，与cut相对应。根据式（2），它们有如下关系
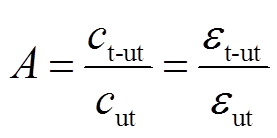（12）
式中，εt-ut为扇形绝缘含水树时的等效介电常数；εut为正常绝缘的介电常数。根据式（6）和式（7），A可以表示为
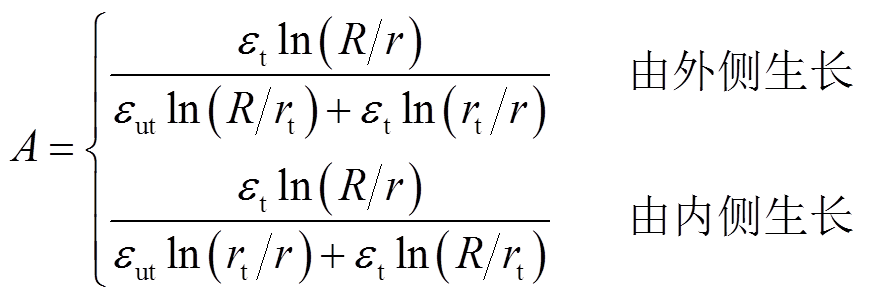（13）
式中，εt为水树区域（图2b点画线区域）的介电常数。将ct-ut=Acut与式（10）代入式（11），再将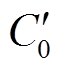
作为C0代入式（8），可得包含水树电缆段的等效介电常数为
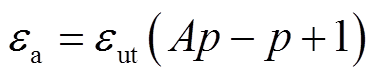（14）
使用相对介电常数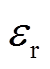
进行计算，
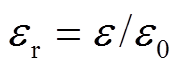，其中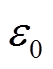
为真空介电常数，下标r代表介电常数相对值。设εrut=2.3、εrt=6、R=8.5 mm、r=3.5 mm，等效相对介电常数
随p与k的变化规律如图3所示。
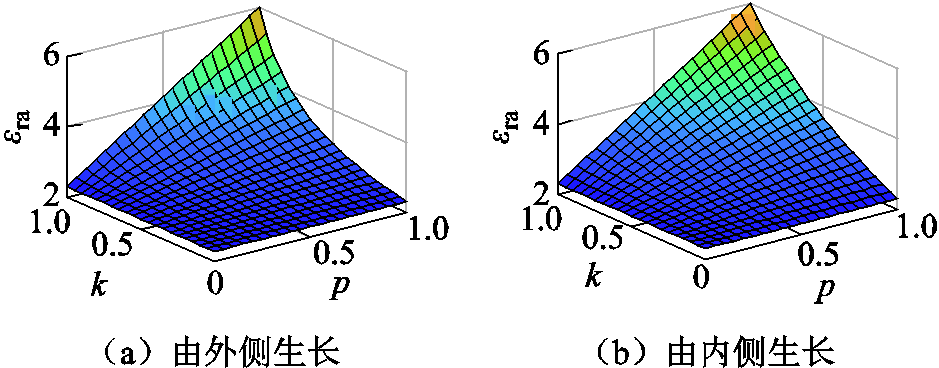
图3 同轴绝缘等效相对介电常数随p、k的变化规律
Fig.3 The change of equivalent relative permittivity of coaxial insulation with p and k
根据相同的方法可知，若同轴电缆截面上存在N个不同的水树老化区域，其等效介电常数可以表示为
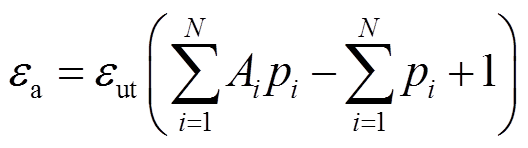（15）
复介电常数的虚部，即电导率，可使用同样方法进行解析。
为验证上述等效介电常数用于预测缺陷反射特性的有效性，使用COMSOL软件进行有限元仿真研究。电缆绝缘局部区域存在缺陷的模型如图4a所示，模型中电缆内径为3.5 mm，外径为8.5 mm，电缆正常绝缘（灰色）部分的相对介电常数设置为2.3，含有水树的绝缘（蓝色）部分的相对介电常数设置为6，含水树的电缆段长度为40 mm。
图4 等效介电常数的有限元仿真验证
Fig.4 Simulation model of the equivalent permittivity
通过式（15）可以计算出图4a中缺陷段电缆绝缘的等效相对介电常数=2.76，在模型中使用等效相对介电常数来表示同样长度缺陷段的电缆绝缘如图4b所示。TDR仿真采用上升时间约为1 ns、幅值约为13 V的高斯脉冲信号分别从图4中两个电缆模型的端部输入，信号输入端口与缺陷段的距离为0.4 m，得到TDR仿真结果如图5所示。
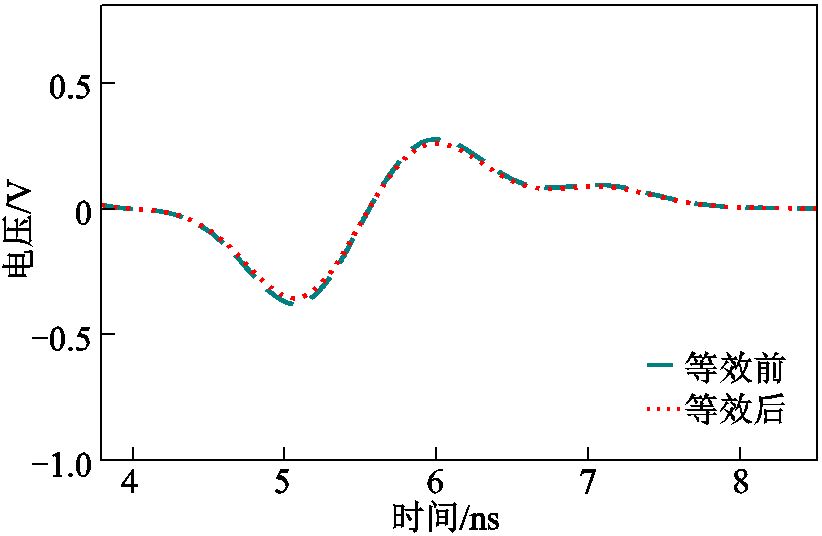
图5 等效前后缺陷段的TDR仿真结果对比
Fig.5 Comparison of experimental results of equivalent permittivity
从图5中可以看出，在模型中用等效介电常数表征缺陷段电缆绝缘前后反射波的幅值和波形几乎完全相同。该结果说明可以通过将含缺陷的电缆段绝缘整体设置为一等效介电常数εa来表征电缆绝缘局部缺陷的反射特性。通过有限元仿真还考虑了不同局部缺陷的情况，获取了等效前后的TDR反射波形，结果均显示采用等效介电常数能准确地表征电缆绝缘局部缺陷的反射特性，限于篇幅，这里不再赘述。
利用等效介电常数能够分析电缆绝缘中介质属性不连续界面上的反射特性，但缺陷段两端界面上的反射叠加对缺陷反射特性的影响尚需要进一步探讨。
采用TDR进行电缆缺陷诊断时通常将缺陷视作一个阻抗不匹配界面，考虑入射波在该界面上的反射，而不考虑缺陷的缺陷段长度d可能对反射波形造成的影响。为了研究缺陷段长度，即缺陷两端的界面对TDR反射波形的影响，本文基于传输线理论[18]建立了一个“时域双界面”解析模型，模型的基本原理如图6所示。
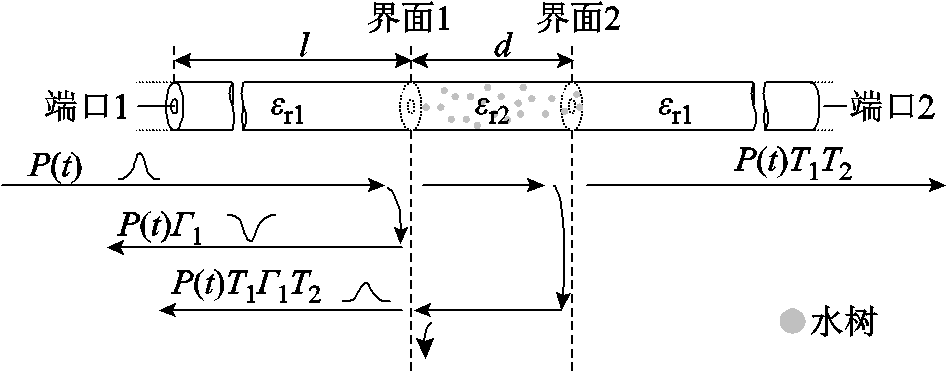
图6 “时域双界面”解析模型基本原理
Fig.6 Basic principle of ‘time-domain dual interface’ analytical model
假设电缆线路上长度为d的一段绝缘中含有许多水树，将该段电缆绝缘的特性用上文方法计算得到的等效相对介电常数er2来表示，两侧正常电缆绝缘的相对介电常数为er1，界面1与界面2表示该水树老化电缆段和两侧正常电缆的分界面，并且假设两侧的电缆足够长，可以不考虑来自电缆末端的反射。由于界面1和2两侧的波阻抗不连续，TDR的输入信号在两个界面处均会发生折反射。假设入射波来自端口1，则从端口1到端口2的方向上，界面1与界面2的反射系数分别为G1和G2，相对介电常数er1到er2方向与相对介电常数er2到er1方向的折射系数分别为T1和T2。如图6所示，由含水树的电缆段d引起的第一次反射仅与界面1相关，其反射系数为
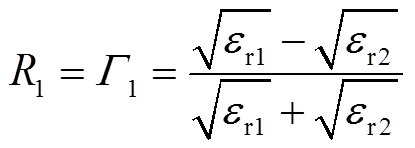（16）
后续的第m次反射与两个界面都有关，它们的系数可以表示为
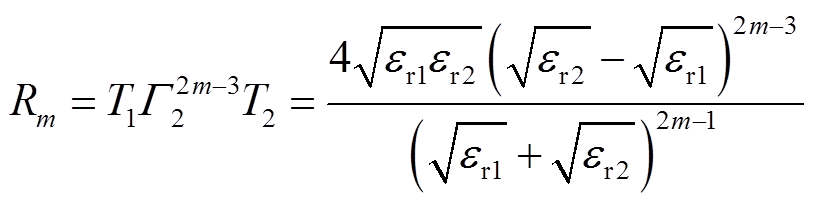（17）
在式（17）中，由于0＜Γ2＜1，因此Rm随着m的增大呈指数递减。把通过系数Rm计算的各次反射波称为独立反射波，在端口1处观察到的反射波为各个独立反射波的叠加，称为叠加波。两个相邻独立波在时域上存在一个时间差，可以表示为
（18）
式中，v2为电磁波在水树老化段的传播速度。
结合式（16）～式（18），叠加波可以表示为
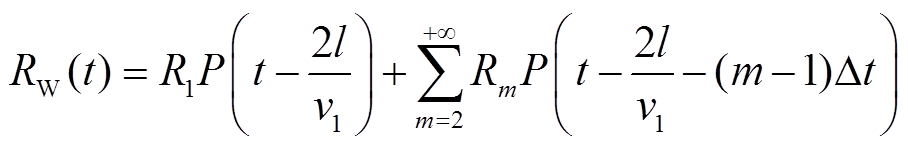（19）
式中，P(t)为入射信号的时域表达式；l为端口1到界面1的距离；v1为电磁波在正常绝缘中的传播速度。er1=2.3、er2=8、d=5 cm时使用高频脉冲作为检测信号的模型计算结果如图7所示，包括1～4次独立反射波的时域波形和它们叠加后的波形。
长满水树的XLPE绝缘的平均相对介电常数通常认为在2.3～9.2之间[19]，图8展示了当er2在1～15之间变化时，反射系数R1～R4的数值变化情况。可以看出，当er2＞2.3时，R1始终为负值，并且其绝对值与R2较为接近；由于Rm呈指数衰减，R3与R4的数值相对于R1与R2来说很小，因此在后续的讨论中只考虑R1与R2计算的独立反射波的作用。
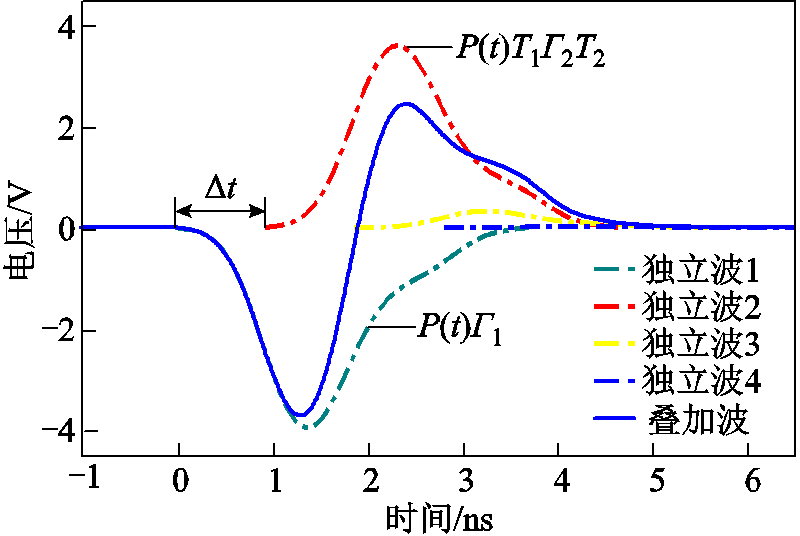
图7 解析模型的时域叠加结果
Fig.7 Time-domain superposition results of analytic model
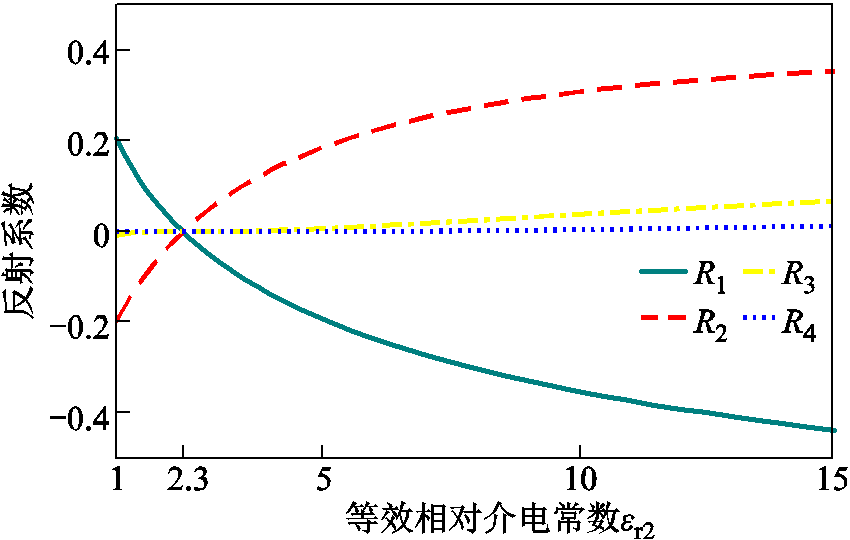
图8 1～4次独立反射的反射系数与等效相对介电常数的关系
Fig.8 
R1～R4 against the equivalent relative permittivity of the water treeing insulation
上述分析表明，Δt是影响反射波形的一个重要因素，这也是本文计及双界面的解析模型能够更准确地预测波形的原因。设tr为脉冲信号的上升时间（从0～100%），tf为脉冲信号的下降时间（从100%～0），ti为信号持续时间，则有
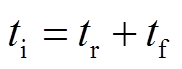（20）
当d较大使得ti≤Δt时，独立反射波之间不存在重叠的部分，因此叠加后反射波的波形不受影响；而当d较小使得ti＞Δt时，极性相反的独立反射波叠加会相互抵消一部分，导致叠加波波形发生畸变。根据以上讨论，独立反射波相互没有重叠的条件为
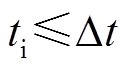（21）
进一步可知叠加波的正负峰值不被影响的条件分别为
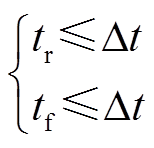（22）
当输入脉冲波形不满足式（22）时，可能会使反射信号幅值较小。例如，图9展示了解析模型计算的同一水树缺陷情况（er2=3、d=35 mm）下，不同输入脉冲波形（幅值相同）产生的反射波形，可见tr较小的输入脉冲产生的反射幅值更大。图9中的点画线和虚线分别表示三种输入波形情况下的第1次反射波与第2次反射波。
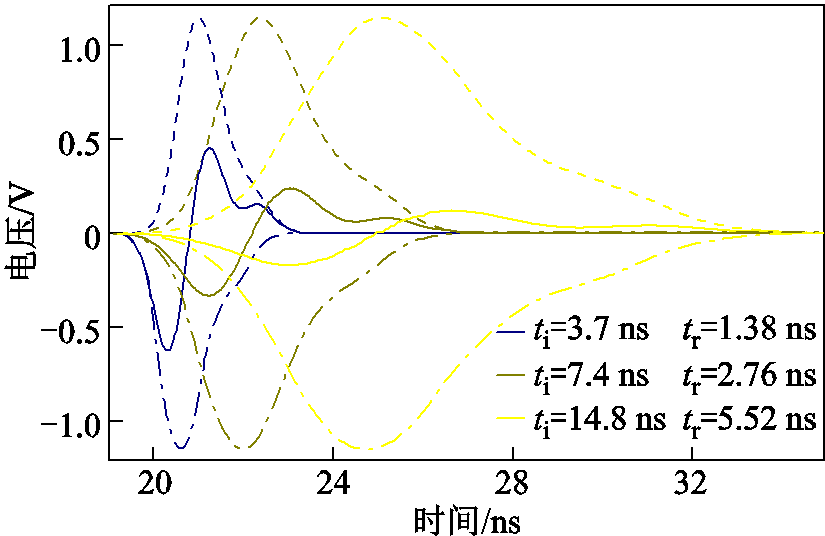
图9 不同输入脉冲波形下相同水树缺陷的反射波形
Fig.9 Detection of different input pulses on the same insulation aging
XLPE绝缘属于低损耗介质，相比之下，绝缘层内外的半导电层电导率较高（通常为0.1～10 S/m），是电缆中高频衰减的主要原因。TDR实验输入信号的带宽较高，频率上限可达到10 MHz～1 GHz，这些高频信号在电缆中传播衰减较快，影响TDR实验的检测范围。
电缆中的高频衰减可以用衰减常数表征，高于1 MHz时电缆衰减常数与频率近似呈正比关系[20]。以文献[21]中某中压电缆的数据为例，图10计算了某11 kV电缆（导体半径为13.15 mm，XLPE绝缘厚度为3.4 mm，内外半导电层厚度均为0.5 mm）在不同频率下的衰减特性。从图10可以看出，频率越高的信号衰减越严重。若以衰减至原信号大小的20%为依据估算可检测范围，并考虑到从电缆端部输入的TDR信号在缺陷处反射再回到输入端实际传播了双倍的缺陷距离，则输入信号的1 MHz频率分量对应的检测范围约为2 300 m；10 MHz频率分量的检测范围约为270 m；100 MHz和1 GHz频率分量的检测范围分别约为15 m和10 m。虽然更高的频率分量对应的检测范围迅速减小，但由2.2节的讨论可知，包含较高频率分量（tr和tf较小）的输入信号对于同一缺陷的检测灵敏度更高。因此，实际检测中如果能综合考虑检测灵敏度和检测范围的要求来确定TDR实验的输入信号，可能有助于获得更好的检测效果。
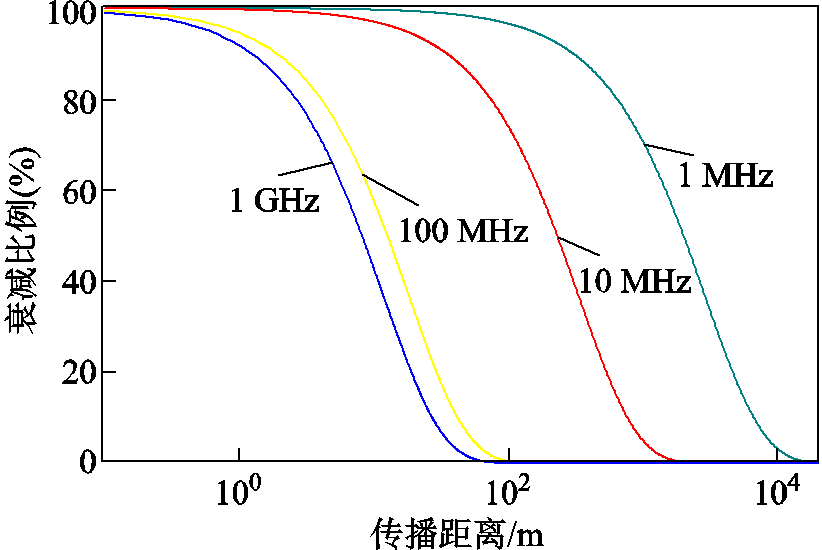
图10 某中压电缆中不同频率信号的衰减特性
Fig.10 Attenuation characteristics of signals of different frequencies in a medium voltage cable
为验证所提解析模型预测电缆局部绝缘缺陷时域反射的有效性，对含模拟水树的10 kV电缆进行TDR实验并与解析模型进行对比。
3.1.1 模拟水树的方法
实验室中通常用“水针电极”法使绝缘中产生水树[22]，这种方法能真实还原水树的生长过程，对于研究水树的生长机理和影响其生长的因素等有重要的意义，但这种方法不易控制水树的形态和特性，例如，水树长度、含水量等。在本实验中，采用在绝缘中钻孔并注水的方法模拟水树。这种方法的优点在于放大了水树的介电特性以便于研究，同时能够保留水树含水通道的基本特征[23]，并控制模拟水树的宽度和含水量等特性。
含有模拟水树的10 kV XLPE电缆模型如图11所示。将一段10 m长的10 kV电缆的护套、外导体剥开，露出外半导电层，用直径为2 mm的钻头向着轴心钻出细孔，钻孔深度hhole=4.5 mm（90%绝缘厚度），然后用针筒在细孔中注入纯净水。以电缆横截面圆周上均匀分布的8个孔为1列，沿电缆轴向交错排列6列，每列之间距离7 mm，钻孔的电缆段宽度d=35 mm，总注入纯净水约0.4 mL。
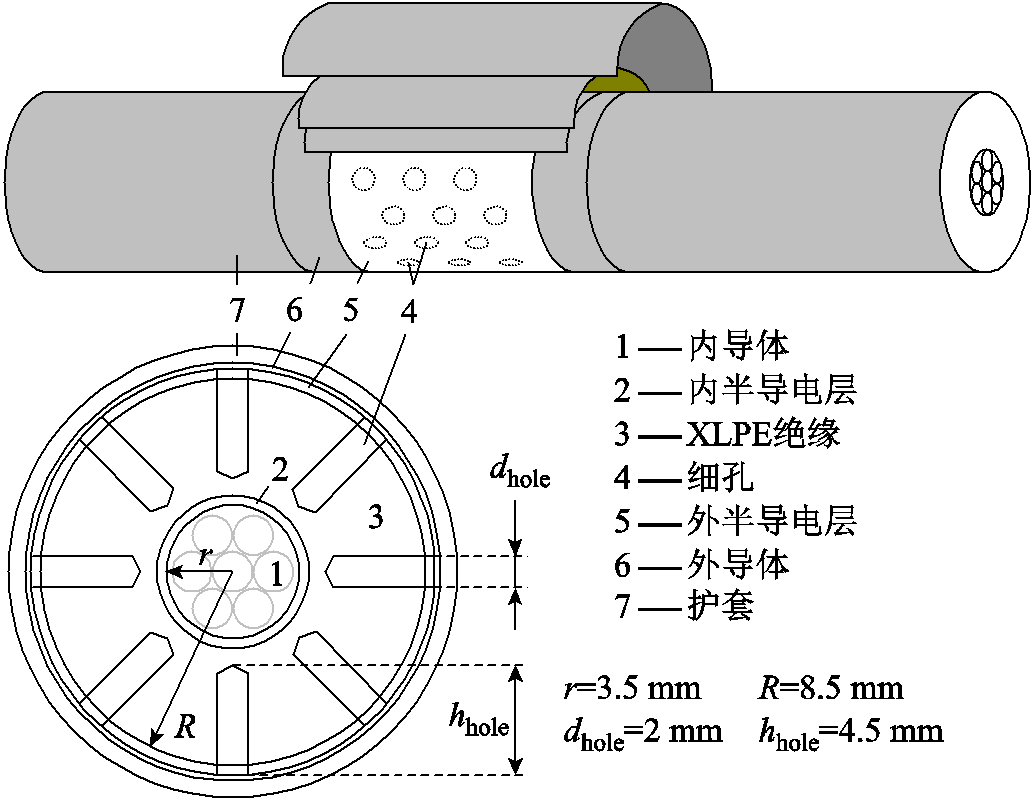
图11 含有模拟水树的10kV XLPE电缆
Fig.11 10 kV XLPE cable sample with mimic water trees
3.1.2 时域反射实验装置
使用的TDR实验装置如图12所示，其中信号发生器能产生上升时间为1 ns、半峰宽为1.2 ns的脉冲信号；示波器采样频率为5 GS/s，带宽为500 MHz。信号发生器、示波器和10 m电缆通过三通接头连接，连接线尽量短以减少传播路径上折反射的干扰。
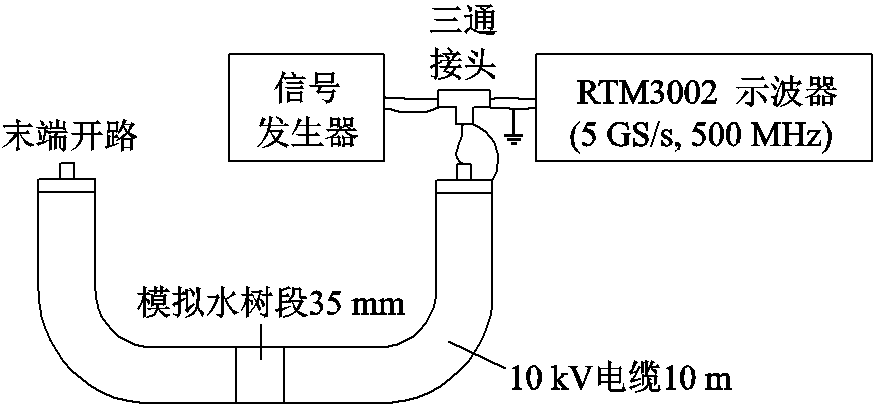
图12 TDR实验装置
Fig.12 TDR measurement setup
为便于比较实验和模型的反射波形，避免电缆中信号衰减所带来的影响，本节的波形图都进行了归一化处理，基准值为各反射幅值绝对值的最大值；实验波形的脉宽相对于解析模型的会更宽，主要是因为解析模型没有考虑电缆中的色散现象。还需要说明的是，模拟水树放大了真实水树的介电特征，其反射比实际水树更加明显。
3.2.1 不同模拟水树数量的实验结果
为研究模拟水树的数量对反射波的影响，在原模拟水树段范围内再增加5个细孔，变化前后的TDR实验结果如图13a所示，可见细孔的增加使反射波形的正负幅值变大，其中负极性幅值变为原来的2.6倍。以样品参数d=35 mm、er1=2.3设置解析模型，调整等效相对介电常数er2的值以匹配实验结果，当er2分别等于3.3、5时能较好地与实验结果对应，解析模型所得的波形如图13b所示，其中点画线与虚线分别代表解析模型所计算的第1次反射波与第2次反射波。
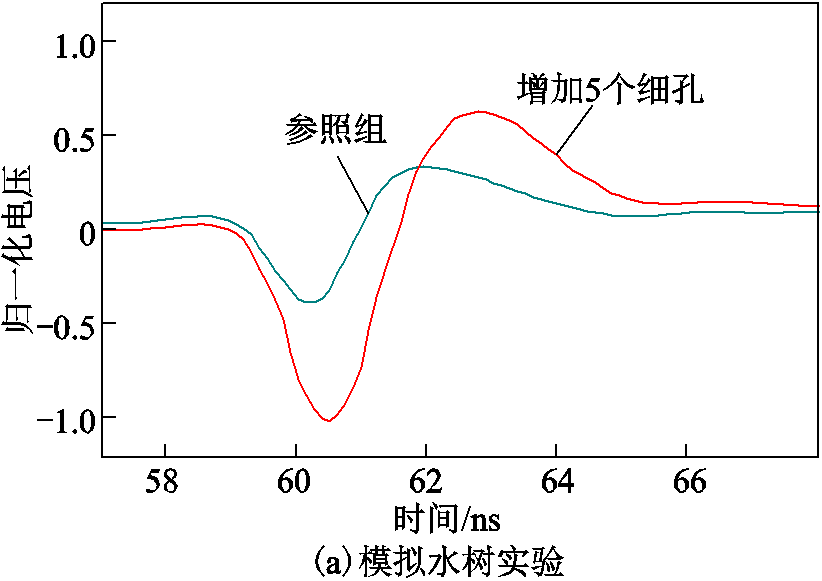
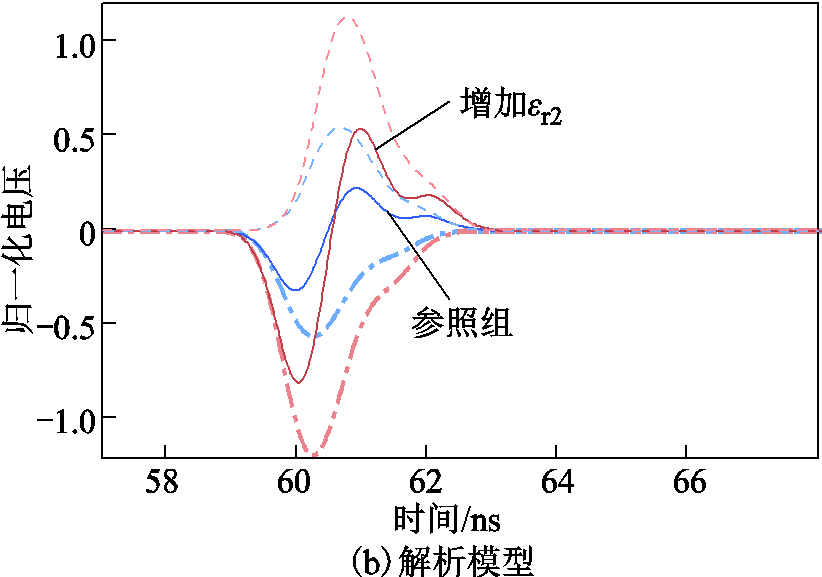
图13 模拟水树的数量对反射时域波形的影响
Fig.13 Waveforms comparison of different simulated water tree quantities
3.2.2 不同模拟水树段长度的实验结果
为研究模拟水树段的长度对反射波的影响，在原模拟水树段远离入射端的一侧再增加5列细孔，此时d由35 mm变为70 mm。变化前后TDR结果如图14a所示，可见d的变化使反射波的正负幅值发生了变化，其中负极性幅值变为原来的1.6倍。以er1=2.3、er2=3.3，d分别为35 mm、70 mm设置解析模型，计算结果如图14b所示，其中点画线和虚线的含义同图13b。可见，模型计算的波形及其变化规律可以与实验结果较好地匹配。另外解析模型的结果还显示，独立反射波之间时延的变化导致了叠加反射波波形的变化。
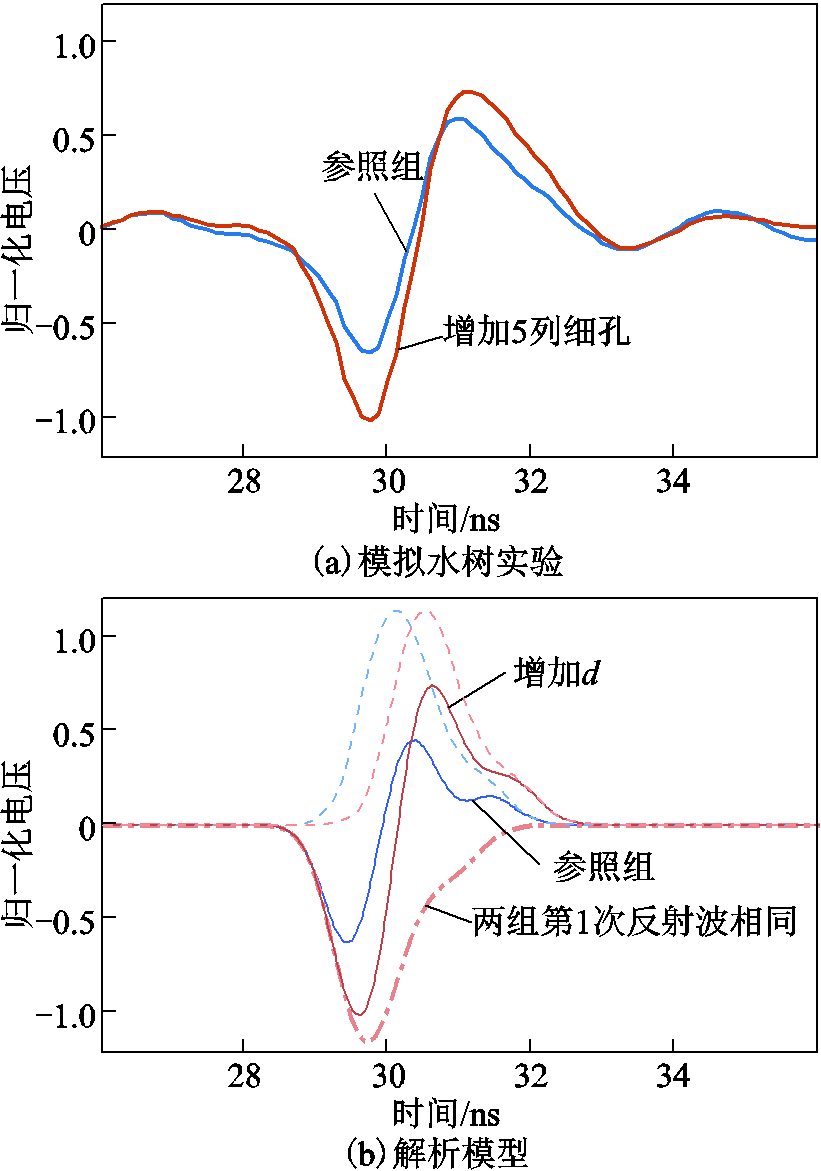
图14 模拟水树段的长度对反射时域波形的影响
Fig.14 Waveforms comparision of different simulated water tree segment widths
本文基于水树老化绝缘等效介电常数和行波理论，建立了可用于预测电缆绝缘水树缺陷TDR反射波形的时域双界面解析模型，得到了以下结论：
1）使用等效介电常数能够表征电缆绝缘局部缺陷的波反射特性，据此建立的计及双界面的时域反射模型通过考虑信号在缺陷段两端的多次反射，能够更准确地预测绝缘缺陷产生的反射波形。对比模拟水树实验和解析模型的结果显示，实验与模型获取的反射在幅值和波形上具有较好的对应性，验证了该解析模型用于预测电缆绝缘局部缺陷时域反射特征的效果。
2）模拟水树缺陷的TDR实验表明反射波的幅值和波形与缺陷段的含水量（模拟水树的数量）及长度密切相关，例如，本次实验在缺陷段中增加5个细孔使反射波幅值增加到原来的2.6倍，将缺陷段长度增加一倍使得反射波幅值增加到原来的1.6倍，初步表明TDR测量结果可以为判断类似绝缘缺陷（局部受潮、水树）的发展程度和范围提供依据。
本文建立的时域双界面解析模型有助于将电缆绝缘水树缺陷状况与TDR测试结果联系起来，例如，本文后续工作拟利用2.1节给出的反射波公式，对TDR实验测量的反射波进行拟合，确定反射波公式中的参数，如水树段的等效介电常数和水树段长度等，为缺陷状况的判断提供依据。另外，后续工作还将进一步研究利用该模型分析其他类型局部绝缘缺陷和电缆接头的时域反射。
参考文献
[1] Shu Wen, Guo Jun, Boggs S A. Water treeing in low voltage cables[J]. IEEE Electrical Insulation Magazine, 2013, 29(2): 63-68.
[2] 吴明祥, 欧阳本红, 李文杰. 交联电缆常见故障及原因分析[J]. 中国电力, 2013, 46(5): 66-70. Wu Mingxiang, Ouyang Benhong, Li Wenjie. Common faults and cause analysis of XLPE cables[J]. Electric Power, 2013, 46(5): 66-70.
[3] Ross R, Smit J J. Composition and growth of water trees in XLPE[J]. IEEE Transactions on Electrical Insulation, 1992, 27(3): 519-531.
[4] Burkes K M. Water tree analysis and on-line detection algorithm using time domain relectometry[D]. Clemson: Clemson University, 2014.
[5] 周凯, 陈泽龙, 尹游, 等. XLPE电缆水树老化及其诊断技术的研究进展[J]. 绝缘材料, 2019, 52(2): 7-14. Zhou Kai, Chen Zelong, Yin You, et al. Research progress in water tree ageing of XLPE cables and its diagnosis technologies[J]. Insulating Materials, 2019, 52(2): 7-14.
[6] 王昊月, 李成榕, 王伟, 等. 高压频域介电谱诊断XLPE电缆局部绝缘老化缺陷的研究[J]. 电工技术学报, 2022, 37(6): 1542-1553. Wang Haoyue, Li Chengrong, Wang Wei, et al. Local aging diagnosis of XLPE cables using high voltage frequency domain dielectric spectroscopy[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1542-1553.
[7] 王昊月, 王晓威, 孙茂伦, 等. XLPE电缆绝缘热老化的高压频域介电谱诊断方法[J]. 电工技术学报, 2022, 37(17): 4497-4507. Wang Haoyue, Wang Xiaowei, Sun Maolun, et al. High voltage frequency domain dielectric spectroscopy diagnosis method for thermal aging of XPLE cables[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4497-4507.
[8] Suzuki K, Tanaka Y, Takada T, et al. Correlation between space charge distribution and water-tree location in aged XLPE cable[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2001, 8(1): 78-81.
[9] 李陈, 雷勇, 周凯, 等. 极化去极化电流技术用于诊断XLPE电缆绝缘老化状态[J]. 电工电能新技术, 2014, 33(4): 32-35, 66. Li Chen, Lei Yong, Zhou Kai, et al. Diagnosis of XLPE cable insulation using polarization and depolarization current measurements[J]. Advanced Technology of Electrical Engineering and Energy, 2014, 33(4): 32-35, 66.
[10] 周湶, 王鑫源, 欧阳希, 等. 基于反射系数谱的XLPE电缆水树缺陷定位方法[J]. 电工电能新技术, 2021, 40(7): 28-39. Zhou Quan, Wang Xinyuan, Ouyang Xi, et al. Location of water tree in XLPE cable based on reflection coefficient spectrum[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(7): 28-39.
[11] 饶显杰, 徐忠林, 陈勃, 等. 基于频域反射的电缆缺陷定位优化方法[J]. 电网技术, 2022, 46(9): 3681-3689. Rao Xianjie, Xu Zhonglin, Chen Bo, et al. Cable defect location optimization based on frequency domain reflection[J]. Power System Technology, 2022, 46(9): 3681-3689.
[12] 赵洪山, 孙京杰, 许向东. 基于反射系数谱积分的电缆缺陷诊断方法[J]. 电网技术, 2022, 46(11): 4548-4556. Zhao Hongshan, Sun Jingjie, Xu Xiangdong. Diagnosis of local defects in cables based on integral reflection coefficient spectrum[J]. Power System Technology, 2022, 46(11): 4548-4556.
[13] 范伟松, 厉冰. 基于行波信号的配网成盘电缆长度快速检测方法研究[J]. 高压电器, 2022, 58(9): 190-196. Fan Weisong, Li Bing. Study on fast detection method for drum cable length of distribution network based on traveling wave signal[J]. High Voltage Apparatus, 2022, 58(9): 190-196.
[14] 陶宇航, 张熹, 宫祥龙. 10kV电缆故障测距及定位典型案例分析[J]. 电气技术, 2022, 23(2): 88-93. Tao Yuhang, Zhang Xi, Gong Xianglong. Typical cases analysis of 10kV cable fault location[J]. Electrical Engineering, 2022, 23(2): 88-93.
[15] 操雅婷, 周凯, 孟鹏飞, 等. 基于正交匹配-伪魏格纳分布的电缆缺陷定位[J]. 电工技术学报, 2023, 38(16): 4489-4498. Cao Yating, Zhou Kai, Meng Pengfei, et al. Cable defect location based on orthogonal matching pursuit and pseudo Wigner-Ville distribution[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4489-4498.
[16] Reyes V, Celeita D, Ramos G. A simulation study on locating water trees on single core XLPE underground cables using reflectometry diagnosis techniques [C]//2021 IEEE/IAS 57th Industrial and Commercial Power Systems Technical Conference (I&CPS), Las Vegas, NV, USA, 2021: 1-7.
[17] Burkes K W, Makram E B, Hadidi R. Water tree detection in underground cables using time domain reflectometry[J]. IEEE Power and Energy Technology Systems Journal, 2015, 2(2): 53-62.
[18] Balanis C A. Advanced engineering electromagnetics [M]. 2nd ed. Hoboken: John Wiley & Sons, 2012.
[19] Ross R. Inception and propagation mechanisms of water treeing[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1998, 5(5): 660-680.
[20] Tozzi M, Cavallini A, Montanari G C, et al. PD detection in extruded power cables: an approximate propagation model[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2008, 15(3): 832-840.
[21] Md Thayoob Y H, Ariffin A M, Sulaiman S. Analysis of high frequency wave propagation characteristics in medium voltage XLPE cable model[C]//2010 International Conference on Computer Applications and Industrial Electronics, Kuala Lumpur, Malaysia, 2011: 665-670.
[22] 周凯, 黄科荣, 黄明, 等. 交联聚乙烯电缆绝缘中的水树生长特性[J]. 高电压技术, 2019, 45(10): 3207-3213. Zhou Kai, Huang Kerong, Huang Ming, et al. Water tree growth characteristics in XLPE power cable insulation[J]. High Voltage Engineering, 2019, 45(10): 3207-3213.
[23] Hvidsten S, Ildstad E, Sletbak J, et al. Understanding water treeing mechanisms in the development of diagnostic test methods[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1998, 5(5): 754-760.
Abstract Due to the poor operating environment, medium voltage cables in distribution networks are prone to water tree aging under the combined effect of moisture and voltage, which can degrade the insulation performance. The time-domain reflectometry (TDR) method can be used to detect cable faults, and some recent studies have used it to detect the aging of the local insulation of cables. However, the relationship between the detection results and the aging condition of the insulation is not clear. To address this problem, an equivalent permittivity for the coaxial insulation with water tree defects is derived. Moreover, a time-domain analytical model considering the reflection of dual interfaces is developed to analyze and predict the results of TDR experiments on cables with local water tree defects.
First, the equivalent permittivity of the coaxial insulation with water trees was derived based on circuit theory, and the effectiveness of using the equivalent permittivity to characterize the reflection characteristics of water tree defects in cable insulation was verified through finite element simulation. Then, a time-domain dual-interface reflection model considering the interfaces at both ends of the defect was established based on transmission line theory and the equivalent permittivity. This model was used to analyze the relationship between the reflection of water tree defects and the condition of water treeing as well as the characteristics of the input signal (such as amplitude and waveform). Finally, by making cable samples with mimic water tree defects and conducting TDR tests, the effects of factors such as water content, length, and conductivity of the defects on TDR test results were investigated. The results showed that the TDR test results of the mimic water tree defects agreed well with the calculated results of the proposed analytical model, preliminarily validating the effectiveness of the proposed model for analyzing and predicting the reflection characteristics of local water tree defects in cable insulation.
The following conclusions can be drawn from this study: (1) The equivalent permittivity can characterize the wave reflection characteristics of local defects in cable insulation. The proposed analytical model considering multiple reflections at both ends of the defect can more accurately predict the reflected waveform generated by local insulation defects. (2) The TDR experiments on the mimic water tree defects showed that the reflection magnitude and waveform were closely related to the water content (quantity of the mimic water trees) and length of the defective section. For example, in this experiment, adding 5 small holes to the defective section increased the amplitude of the reflected wave to 2.6 times the original value, while doubling the length of the defective section increased the amplitude of the reflected wave to 1.6 times the original value. This preliminary result indicates that TDR measurements can provide a basis for assessing the extent and range of similar insulation defects (such as localized moisture and water treeing). The analytical model established in this study helps to link the water treeing condition of cable insulation with TDR test results, and it is expected to provide a reference for the application of TDR testing in detecting water treeing in cable insulation.
keywords：Power cable, insulation aging, water tree, finite element (FEM), time domain reflectometry (TDR), dual interfaces
DOI:10.19595/j.cnki.1000-6753.tces.230994
中图分类号：TM247
浙江天际互感器股份有限公司企业博士后科研项目资助（243930）。
收稿日期 2023-06-27
改稿日期 2023-08-05
叶 源 男，1997年生，硕士研究生，研究方向为电缆绝缘缺陷检测。E-mail：yu.ye97@foxmail.com
胡 晓 男，1985年生，讲师，博士，研究方向为电力设备绝缘高频测试与诊断。E-mail：xhu3@gzu.edu.cn（通信作者）
（编辑 李 冰）