
图1 电池容量衰减曲线
Fig.1 Decay curves of battery capacity
摘要 针对锂离子电池退化数据噪声大、数据量少以及不同生命时期的退化趋势不同而导致的模型预测精度低、泛化能力差等问题,从数据预处理、预测模型的构建与训练三方面展开研究:首先结合变分自编码器(VAE)和生成对抗网络模型(GAN)构建VAE-GAN模型生成多组数据,实现电池的退化数据增强;然后结合降噪自编码器(DAE)和长短时记忆(LSTM)神经网络构建DAE-LSTM模型进行数据降噪和容量预测,为了降低模型参数,此过程中的数据降噪和预测共享同一个损失函数;最后先利用生成数据对DAE-LSTM模型进行预训练,再利用真实数据对其进行迁移训练。在CACLE和NASA公开数据集进行性能测试,实验结果表明该文所提方法精度高、鲁棒性强,能够有效提高锂离子电池剩余寿命的预测效果。
关键词:锂离子电池 剩余寿命预测 降噪 自编码器 长短时记忆神经网络 迁移学习
锂离子电池凭借其能量密度高、使用寿命长且绿色环保等特点,被广泛应用于消费电子、新能源汽车及航空航天领域[1]。在面对不同的工作环境时,频繁充放电及环境温度变化等因素都可能会导致锂离子电池的使用寿命受到影响[2]。电池的老化主要表现在容量的减少及等效内阻的增加上[3]。当电池达到其规定的寿命阈值时,便要进行及时更换,以保证电池及其运行系统的安全性[4]。因此,锂离子电池剩余使用寿命(Remaining Useful Life, RUL)的精准预测十分必要。
近年来,随着机器学习和深度学习的蓬勃发展,基于数据驱动的锂离子电池剩余使用寿命预测被人们广泛关注。相比于基于等效电路[5]和物理模型[6]的传统研究方法而言,基于数据驱动的预测方法更加灵活,可以免去繁杂的物理建模过程,只利用电池工作过程中的历史数据便可进行建模,实现电池剩余使用寿命的有效预测[7]。循环神经网络凭借其独特的记忆结构在处理时序数据上具有显著的优势,因此常适用于各种寿命预测任务中[8]。Zhang Yongzhi等[9]采用长短时记忆(Long Short Term Memory, LSTM)神经网络学习锂离子电池退化容量之间的长期相关性,利用滑动窗口对容量数据进行分割,通过不断迭代预测的方法获取未来多个时间步的容量退化数据,这种滑动窗口分割数据以及迭代预测的方法也是锂离子电池剩余使用寿命预测中最常用的方法。P. Khumprom等[10]提出以LSTM网络层为主体的预测模型进行电池寿命预测,分别采用寿命周期50%和70%的容量数据进行模型训练,并进行剩余寿命预测,实验结果表明采用70%的寿命数据训练的模型具有更高的精度。这不仅与训练模型的数据量有关,也与锂离子电池的退化特性有关,电池的寿命退化曲线是非线性的,其寿命前中期的退化速度远低于寿命后期的退化速度[11],所以只对电池早期退化速度缓慢的数据建模,然后通过自回归的方式进行寿命预测,往往会导致预测结果偏差较大。
由于锂离子电池在退化过程中常出现容量回升现象[12],并且实验过程中的电磁干扰、充放电倍率差异等因素都会导致电池容量数据中包含噪声,这对于数据预测模型的建立具有极大的干扰,所以电池容量数据的降噪处理是有必要的。Qiao Jianshu等[13]通过自适应双指数模型(Adaptive Bi-exponential Model Smooth, ABMS)和完全自适应噪声集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)算法对电池容量数据进行了降噪处理,并利用LSTM网络进行容量预测,对比未降噪数据的预测结果,进行数据预处理的预测模型展现出更高精度的预测能力。Wang Zhuqing等[14]通过局部切线空间对齐(Local Tangent Dpace Alignment, LTSA)的方法进行电池容量数据的特征提取,降低退化数据中的波动数据,并利用自适应滑动窗口LSTM模型进行寿命预测,实验结果表明,进行数据降噪的预测模型在预测RUL时更加准确。尽管现有的大多数预测模型都展示出了不俗的预测能力,但是他们普遍存在以下三个问题:
1)预测模型局限性:由于锂离子电池不同寿命阶段的退化速度不同,只采用局部退化数据进行寿命建模具有一定的局限性。
2)降噪预测关联性:大多数的预测方法中,数据降噪和容量预测常常分开处理,被视为两个独立的任务,这忽略了二者之间的关联性。
3)退化数据稀少性:基于深度学习的训练方法需要有一定的数据量作为支撑,但现实的电池退化数据有限,这对于预测模型的建立具有一定的影响。
为了降低上述问题对结果的影响,本文提出基于迁移学习的DAE-LSTM锂离子电池RUL预测模型。首先,结合变分自编码器(Variational Autoencoder,VAE)和生成对抗网络(Generative Adversarial Nets, GAN)构建VAE-GAN数据生成模型:将小样本全周期电池退化数据输入模型中,VAE的编码器会先提取输入数据的分布状况,然后利用解码器和判别网络实现容量数据的再生,既弥补了VAE模型生成数据的单一性,又解决了GAN模型难以收敛的问题,最终生成多组电池全周期退化数据;其次,利用降噪自编码器(Denoising Autoencoder, DAE)和LSTM网络构建容量预测模型DAE-LSTM:降噪自编码器对利用滑动窗口分割后的输入数据进行降噪处理,数据输入编码器前会被添加高斯白噪声,以使得整体模型的鲁棒性更强,然后压缩成隐藏向量传输到LSTM网络当中。多层的LSTM网络学习隐藏向量之间的时序特征,通过全连接层映射为容量预测值。为了使模型具有更好的泛化能力,本文提出一个全新的目标函数用来连接数据降噪和寿命预测两个任务,使其能够在学习过程中同时得到优化。
本文通过消融试验,找到最优的训练方式。首先利用VAE-GAN模型生成的退化数据对DAE-LSTM预测模型进行预训练,然后将除被测电池外的真实退化数据对预测模型的全部网络层进行微调,使模型更加适应真实数据的分布状况,更具针对性。此外,本文增设基础模型的对照试验,通过对比未降噪处理和未数据增强的模型预测结果,验证了DAE-LSTM模型的优越性。
本文采用两种电极材料在室温环境下的锂离子电池数据集进行模型性能验证。
第一组数据由马里兰大学CALCE研究中心的CS2_35、CS2_36、CS2_37和CS2_38四组电池的容量退化数据组成[15]。CS2系列电池属于钴酸锂电池,以碳作为导电添加剂混合的LiCoO2为阳极,以与聚丙烯氟化物结合在一起的层状石墨作为阴极,额定容量为1.1 A×h。试验过程为:首先以0.55 A的电流恒流充电,直至截止电压4.2 V;然后恒压保持,直到充电电流降至0.05 A;最后以0.55 A的电流进行恒流放电,将电压降至2.7 V。锂离子电池寿命循环试验的结束条件为电池容量降为额定容量的70%。对于此数据集,阈值容量设置为其额定容量的80%[16]。
第二组数据由NASA PcoE研究中心的B5、B6、B7、B18四组电池的容量退化数据组成[17]。NASA电池组属于三元锂电池,其阳极材料为镍钴铝酸锂,阴极材料为石墨,额定容量为2 A·h。试验过程为:首先以1.5 A恒定电流充电,直至截止电压4.2 V;然后恒压保持,直到充电电流降至0.02 mA;最后以2 A恒定电流进行放电,直到B5、B6、B7、B18电池电压分别降至2.7 V、2.5 V、2.2 V和2.5 V时停止。对于此数据集,阈值容量设置为其额定容量的70%,即1.38 A·h。由于B7号电池容量始终大于1.38 A·h,所以其阈值容量设置为其额定容量的74.5%,即1.47 A·h[18]。图1为两组数据的容量衰减曲线。
深度学习网络需要有足够多分布均衡的数据作为支撑才能够发挥较好的效果,但这两组数据集的数据量均较小,特别是NASA数据集,每个电池的退化数据不足200个,仅使用这些数据进行深度学习建模是远远不能满足建模要求的,因此需要提出一种数据增强的方法来解决数据量少的问题。

图1 电池容量衰减曲线
Fig.1 Decay curves of battery capacity
深度学习领域常使用的生成模型包括VAE[19]和GAN[20],虽然二者都可进行数据再生,但是各自应用起来都有一定的缺陷。VAE模型可以通过重采样得到原始数据的分布状况,但生成数据的多样性较低;GAN模型生成数据更具多样性,但是训练过程异常困难,生成器和判别器难以同时收敛。因此,本文结合VAE模型的数据生成和GAN模型的对抗学习机制,提出VAE-GAN模型。
VAE-GAN模型总共分为三部分,分别为编码网络、解码网络(生成网络)和判断网络,对应VAE模型的Encoder、Decoder和GAN模型的Discriminator部分。可以理解为在GAN网络的基础上增添了真实数据的编码过程,利用具有先验信息的隐式z代替原本输入生成器的随机向量,使模型的表达能力大大提升,VAE-GAN模型结构如图2所示。
编码网络由三个全连接层构成,第一个全连接层对输入的高维数据进行下采样操作,激活函数采用Relu;其余两个全连接层分别将下采样后的样本映射成两个低维的参数特征,即正态分布的均值和方差。编码网络的损失函数为KL散度,用来衡量隐式向量分布和标准正态分布之间的差异,KL损失函数为
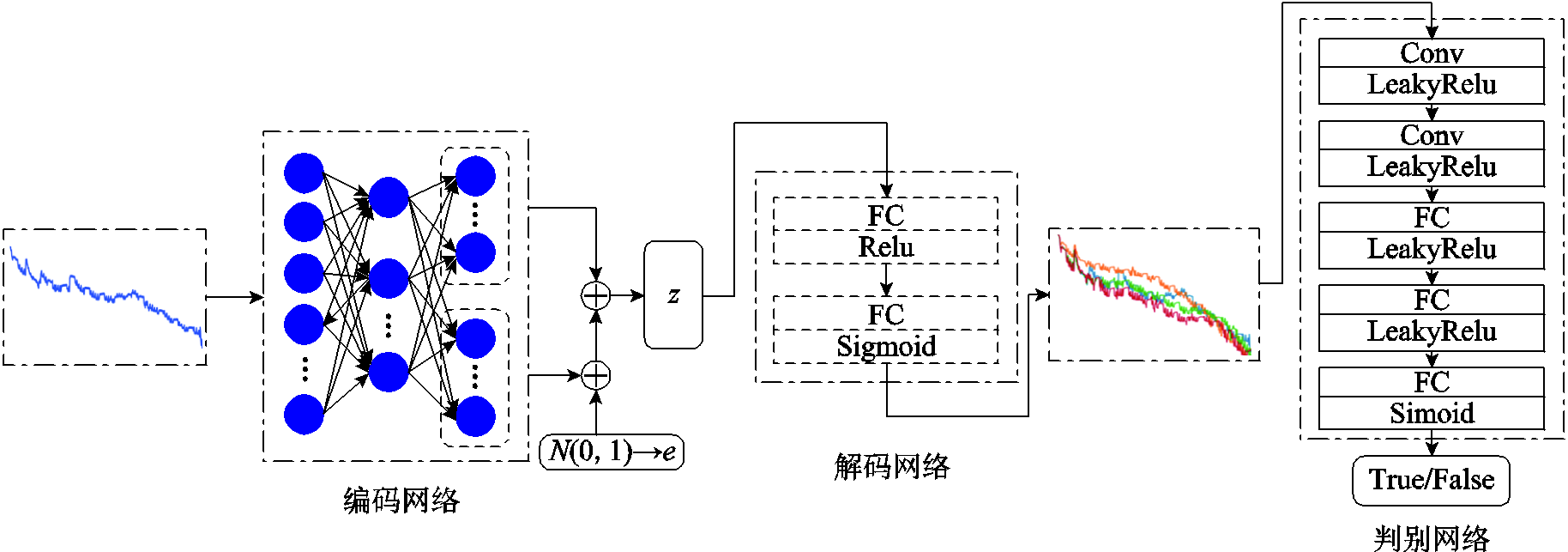
图2 VAE-GAN结构
Fig.2 Structure diagram of VAE-GAN
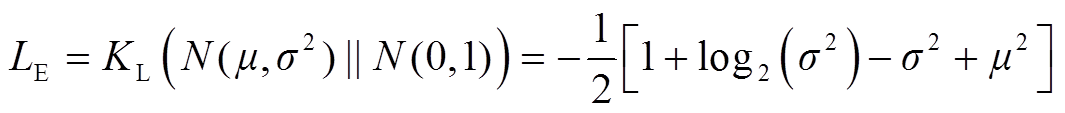 (1)
(1)
式中,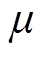 和
和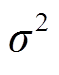 分别为编码网络输出的均值和方差。式(1)表示计算两个近似分布的KL散度,这里用来表示本文所求的数据分布与标准正态分布N(0,1)之间的KL散度。
分别为编码网络输出的均值和方差。式(1)表示计算两个近似分布的KL散度,这里用来表示本文所求的数据分布与标准正态分布N(0,1)之间的KL散度。
解码网络(生成网络)由两层全连接网络构成,这两层网络的参数设置和编码网络的参数设置相反,将输入的低维隐藏变量进行特征放大,最终生成和输入数据相同尺寸的生成数据,两个网络层间采用Relu激活函数,最终的输出层采用Sigmoid激活函数。生成网络的优化目标既要保证最小化生成样本与真实样本之间的特征损失,还要保证生成数据能够欺骗判别网络,其损失函数为
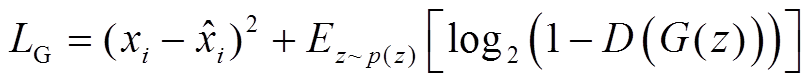 (2)
(2)
式中,右侧第一项表示编码器的损失重构,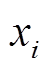 和
和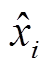 为真实样本和预测值;z为参数重构生成的隐藏变量,服从p(z)分布;E表示期望;G(z)为生成样本;D(×)为判别网络对于生成数据的真伪判断。
为真实样本和预测值;z为参数重构生成的隐藏变量,服从p(z)分布;E表示期望;G(z)为生成样本;D(×)为判别网络对于生成数据的真伪判断。
判别网络由2个卷积层和3个全连接层组成,每个网络层之间的激活函数采用LeakyRelu,输出层通过Sigmoid激活函数输出真伪标签,判别网络的损失函数采用更加稳定的最小二乘损失函数为
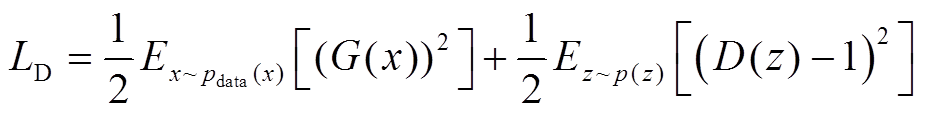 (3)
(3)
式中,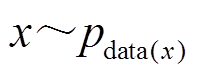 表示真实样本服从
表示真实样本服从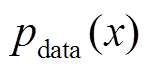 分布。
分布。
VAE-GAN模型利用VAE的编码优势,将蕴含先验信息的隐藏向量代替随机向量输入给GAN模型进行数据生成,缓解模型训练不收敛的问题。GAN网络通过对抗学习,改善生成数据的质量,完成对VAE模型的改善,二者相辅相成。
VAE-GAN模型训练时的迭代次数设置为500次,由于总共只有四组数据,所以Batchsize设置为2,采用Adam优化器进行参数优化,学习率设置为1×10-4,训练前需要对输入数据进行归一化,否则生成网络的输出层所连接的Sigmoid激活函数无法对数据进行完整的映射,输出数据可进行反归一化还原到原来的值域。具体参数设置见表1,其中神经元个数括号中的数值分别代表当前网络的输入节点数和输出节点数。
表1 VAE-GAN模型参数设置
Tab.1 Parameter setup of VAE-GAN

网络名称结构组成主要参数输出尺寸 编码网络输入层神经元个数630630 全连接层(隐层)神经元个数(630,300)300 全连接层(输出)神经元个数(300,150)150 全连接层(输出)神经元个数(300,150)150 生成网络输入层150 全连接层+Relu神经元个数(150,300)300 全连接层+Sigmoid神经元个数(300,630)630 判别网络输入层630 一维卷积+LeakyRelu卷积参数(1,32,12)32×619 一维卷积+LeakyRelu卷积参数(32,1,12)1×608 全连接层+Relu神经元个数(630,256)256 全连接层+Relu神经元个数(256,256)256 全连接层+Sigmoid神经元个数(256,1)1
本文利用VAE-GAN模型分别对两组数据集各生成十组完整的退化数据,如图3所示。为了衡量生成数据与真实数据之间的相似性,采用文献[21]中的相似度计算法,求解真实数据与生成数据的方均根误差并对其进行归一化,结果越接近1表示二者的相似程度越高,相似度计算式为
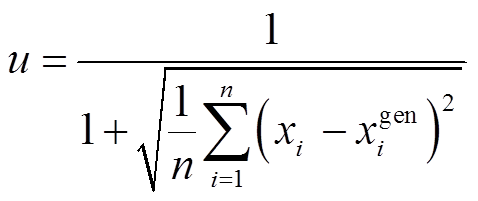 (4)
(4)
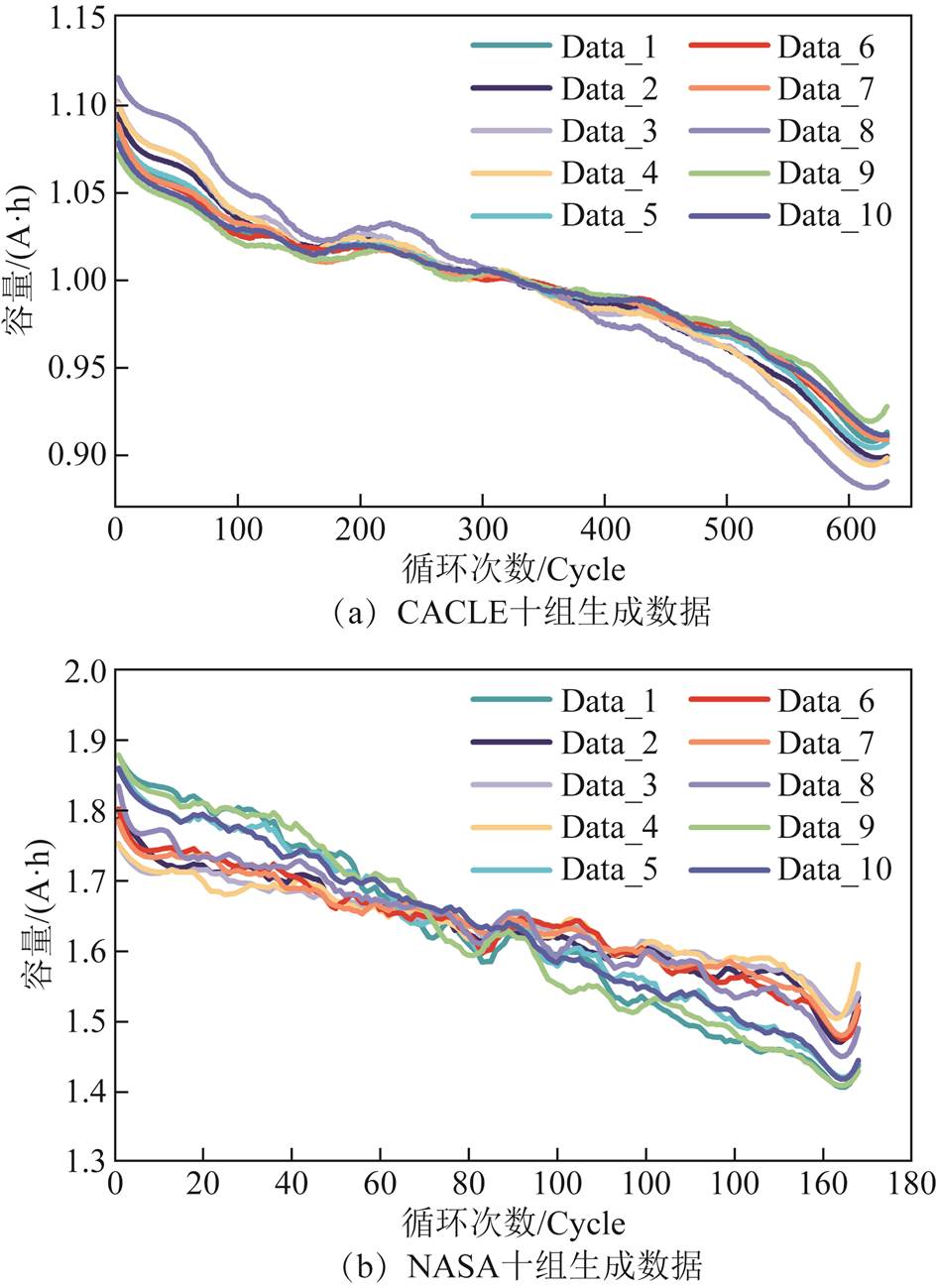
图3 VAE-GAN扩充数据
Fig.3 VAE-GAN expanded data
式中,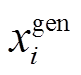 为生成样本。
为生成样本。
对比每组电池和所有生成数据之间的平均相似度,结果见表2。可以看出,十组生成样本与每组真实样本的平均相似度都达到了0.95以上,可以有效表示出锂离子电池真实的退化趋势,并且相较原始数据而言,生成数据更加符合产品退化的浴盆曲线[22],适合用来进行后续锂离子电池RUL预测的模型训练。
表2 生成数据相似度计算
Tab.2 Similarity calculation of generated data

序号平均相似度序号平均相似度 CS2_350.966 8B50.965 6 CS2_360.953 0B60.935 9 CS2_370.971 2B70.967 2 CS2_380.975 5B180.924 8
容量大小可以直接反映锂离子电池的老化情况,但电池的老化过程中容易出现容量回升现象,并且试验过程中的电磁干扰、充放电倍率差异等因素会导致测得的电池容量数据波动较大,这为电池RUL的精准预测增加了许多难度。因此,本文基于数据降噪和容量预测任务设计DAE-LSTM预测模型,模型包括两部分:DAE数据降噪和LSTM容量预测,两个任务在一个模型框架中实现。DAE-LSTM网格架构如图4所示。
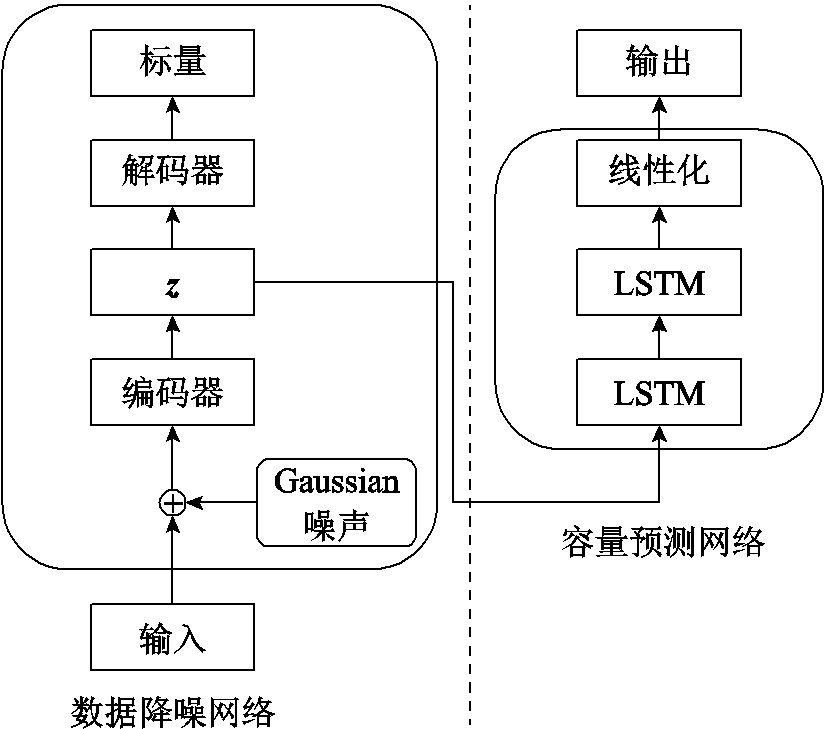
图4 DAE-LSTM网络架构
Fig.4 DAE-LSTM network architecture
降噪自编码器(DAE)是一种具有数据降噪功能的特征提取算法[23],DAE的编码器将充满噪声的输入数据压缩成低维向量,尽量保留数据的原始特征,然后解码器将低维向量还原成退化趋势明显的原始数据,本文采用该算法作为容量数据的降噪算法。
DAE的编码器在对原始数据进行压缩前,会向输入数据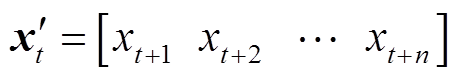 中加入高斯白噪声使其变成输入向量
中加入高斯白噪声使其变成输入向量 ,目的是为了增加模型的鲁棒性和非线性表达能力。编码器会将输入数据压缩成低维的中间向量,过程表示为
,目的是为了增加模型的鲁棒性和非线性表达能力。编码器会将输入数据压缩成低维的中间向量,过程表示为
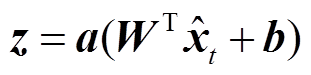 (5)
(5)
式中,W为编码器权重矩阵;b为偏置项;a(×)为激活函数;z为压缩而成的隐藏向量。
解码器进行信息重构,将携带原始数据信息的中间向量映射成与输入数据尺寸相同的输出向量,过程可表示为
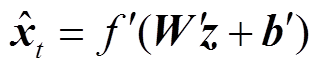 (6)
(6)
式中,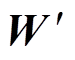 为解码器的权重矩阵;
为解码器的权重矩阵;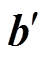 为偏置项;
为偏置项;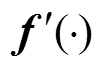 为激活函数;
为激活函数;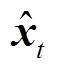 为解码得到的输出向量。
为解码得到的输出向量。
为了增加网络的稀疏性,缓解过拟合现象的出现,选择Relu函数作为编码器和解码器中隐藏层的激活函数。为了有效地将输出数据映射到有效的值域内,输出层的激活函数选择Sigmoid函数。故此,DAE部分的损失函数定义为
式中,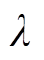 为权重值;
为权重值;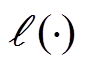 为损失的激活函数。由于DAE模型结构的对称性,编码矩阵W和解码矩阵
为损失的激活函数。由于DAE模型结构的对称性,编码矩阵W和解码矩阵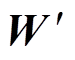 的权重可以进行绑定,减少模型的训练时间。
的权重可以进行绑定,减少模型的训练时间。
锂离子电池的容量退化过程是一个具有时序特性的动态过程,当前时刻的容量与之前多个历史时刻的退化容量均存在依赖关系。LSTM网络的隐藏层具有记忆功能,能够分析不同时刻容量的时序关系,因此本文将LSTM网络用于单个锂离子电池容量的预测任务。
相较于循环神经网络,LSTM网络给原始的隐藏层ht添加了一个单元状态ct,单元状态ct内部设置了三个类似于开关的门机制,能够控制状态单元内信息流的更新与遗忘[24],具体公式为
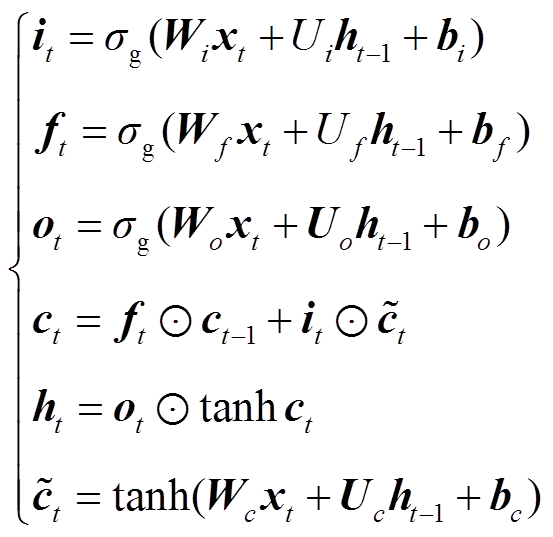 (8)
(8)
式中,it、ft和ot分别代表输入门、遗忘门和输出门的激活向量;xt和ht分别表示当前时刻的输入和隐藏状态;W和b分别代表网络中需要学习的权重矩阵和偏置向量;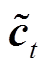 、
、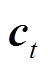 为单元的中间状态和输出状态;sg为Sigmoid激活函数。LSTM的神经元内部结构框图如图5所示。
为单元的中间状态和输出状态;sg为Sigmoid激活函数。LSTM的神经元内部结构框图如图5所示。
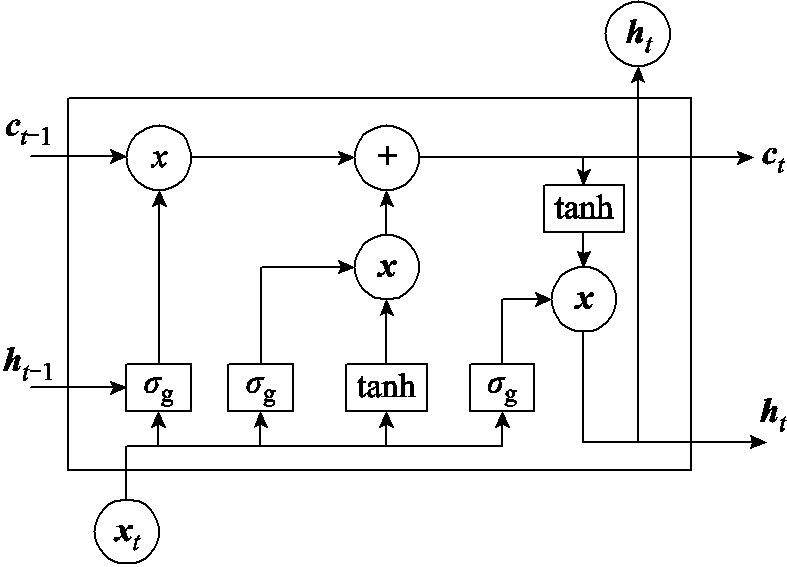
图5 经典LSTM框图
Fig.5 The diagram of LSTM
容量预测阶段将DAE的Encoder生成的隐藏向量z作为输入数据,通过LSTM层和全连接层建立预测数据与隐藏向量z之间的映射关系,通过反向传播优化模型参数,完成容量预测任务。
本文提出的DAE-LSTM模型没有将数据降噪和预测任务分割开来,而是提出一个新的损失函数,在训练过程中对两项任务同时进行优化,最大程度地保证数据降噪和容量预测之间的关联性。方均根误差(Root Mean Square Error, RMSE)作为统一的损失重构函数,进行降噪和预测部分的损失评估,DAE-LSTM模型完整的损失函数为
式中,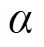 为用来平衡两个任务之间的优化力度;W(×)为正则化项;l为正则化参数;q为模型参数。DAE-LSTM模型的参数设置见表3。参数均为网格搜索优化结果,详见后文。
为用来平衡两个任务之间的优化力度;W(×)为正则化项;l为正则化参数;q为模型参数。DAE-LSTM模型的参数设置见表3。参数均为网格搜索优化结果,详见后文。
表3 DAE-LSTM模型参数
Tab.3 Parameter setup of DAE-LSTM
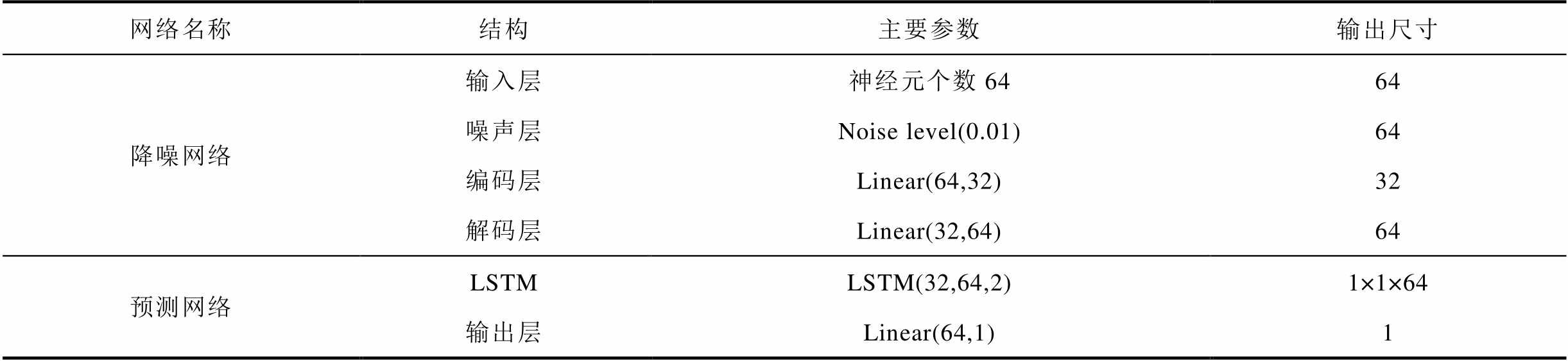
网络名称结构主要参数输出尺寸 降噪网络输入层神经元个数6464 噪声层Noise level(0.01)64 编码层Linear(64,32)32 解码层Linear(32,64)64 预测网络LSTMLSTM(32,64,2)1×1×64 输出层Linear(64,1)1
锂离子电池RUL预测方法,是将容量数据利用滑动窗口进行数据分割,保留相邻容量间的关联性,并将数据变为有监督学习的形式供模型训练。设置适当的迭代步长,将预测数据替换到训练数据中并不断迭代,最终可以获得长序列的预测结果。样本生成过程如图6所示。
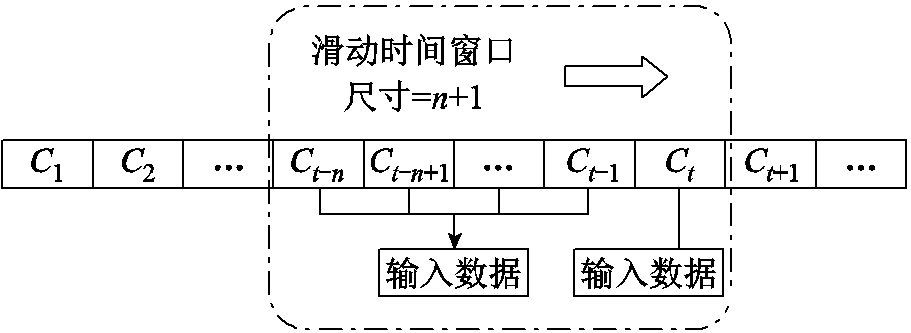
图6 滑动窗口结构
Fig.6 Architecture of the sliding window
锂离子电池的寿命退化曲线是非线性的,其寿命前中期的退化速度低于寿命后期的退化速度,单凭某一阶段的退化数据训练模型具有局限性。因此,本文为提高预测精度采用多组全周期退化数据训练模型。首先通过VAE-GAN生成十组电池退化数据进行数据增强,然后利用迁移学习降低生成数据与实际数据的差异。
在迁移学习中,首先会用大量数据训练一个基础模型,面对新任务时,基础模型的网络参数会作出针对性的修改。常见的迁移策略有两种:一种是训练基础模型的输出层;另一种是训练基础模型的全部层。但不论哪种迁移方式,都要用较小的学习率进行训练,充分利用模型预训练时学习到的知识。
3.2.1 基础模型
迁移学习的难点在于迁移策略的选择上,考虑锂离子电池RUL预测的特殊性,本文采取的迁移策略如下:首先利用生成的十组数据对模型进行预训练;然后利用真实退化数据对模型进行微调,使得模型能够适应真实电池退化数据的噪声分布状况和退化趋势。这样的训练方法能够保证模型从大量的先验数据中学习大概的退化趋势,然后通过针对性的训练保证模型能够适应真实的退化情况。
以CACLE数据为例,训练数据可分为两部分:一个是由VAE-GAN模型生成的十组退化数据,称为生成数据集,用于基础模型的训练;另一个是由四组电池退化数据组成的数据集,称为真实数据集,用于模型的迁移。针对基础模型DAE-LSTM的训练,需要确定的超参数如下:①时间步长Input size;②学习率Lr;③隐藏层数量Num layers;④神经元个数Hidden dim;⑤高斯白噪声值域Noise level;⑥正则化系数alpha。值得注意的是,关键参数Batch size并不在需优化的超参数中,原因是每组电池数据都会被滑动窗口分割成566组特征和标签对应的数组,为了保证数据的时序性,Batchsize设置为566,这样可以让模型在每个epoch中学习一组电池的全部数据。在生成数据集上确定模型的最优结构,以最小化交叉验证误差为优化目标,对模型的超参数进行优化。生成数据集需进行五折交叉验证以防止出现过拟合现象,优化器采用Adam,迭代次数为1500次,由于基础模型的训练任务是对陌生数据进行拟合,不需要进行迭代预测,因此评价指标为RMSE和平均绝对误差(Mean Absolute Error, MAE)。超参数空间及最优值见表4。
表4 超参数空间和最优值
Tab.4 Hyperparameter’ range in hyperparameter space and opitimal values
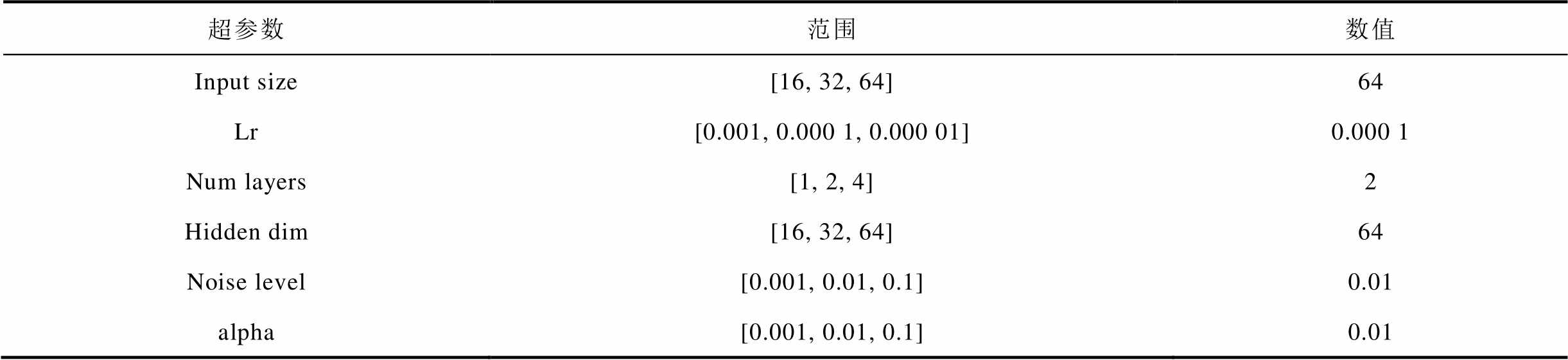
超参数范围数值 Input size[16, 32, 64]64 Lr[0.001, 0.000 1, 0.000 01]0.000 1 Num layers[1, 2, 4]2 Hidden dim[16, 32, 64]64 Noise level[0.001, 0.01, 0.1]0.01 alpha[0.001, 0.01, 0.1]0.01
3.2.2 迁移策略
基础模型训练完毕后,需要确定合适的迁移策略,保证迁移学习的效果最佳。本文采用留一法训练全部网络层的迁移方式,完整的电池RUL预测流程如图7所示。
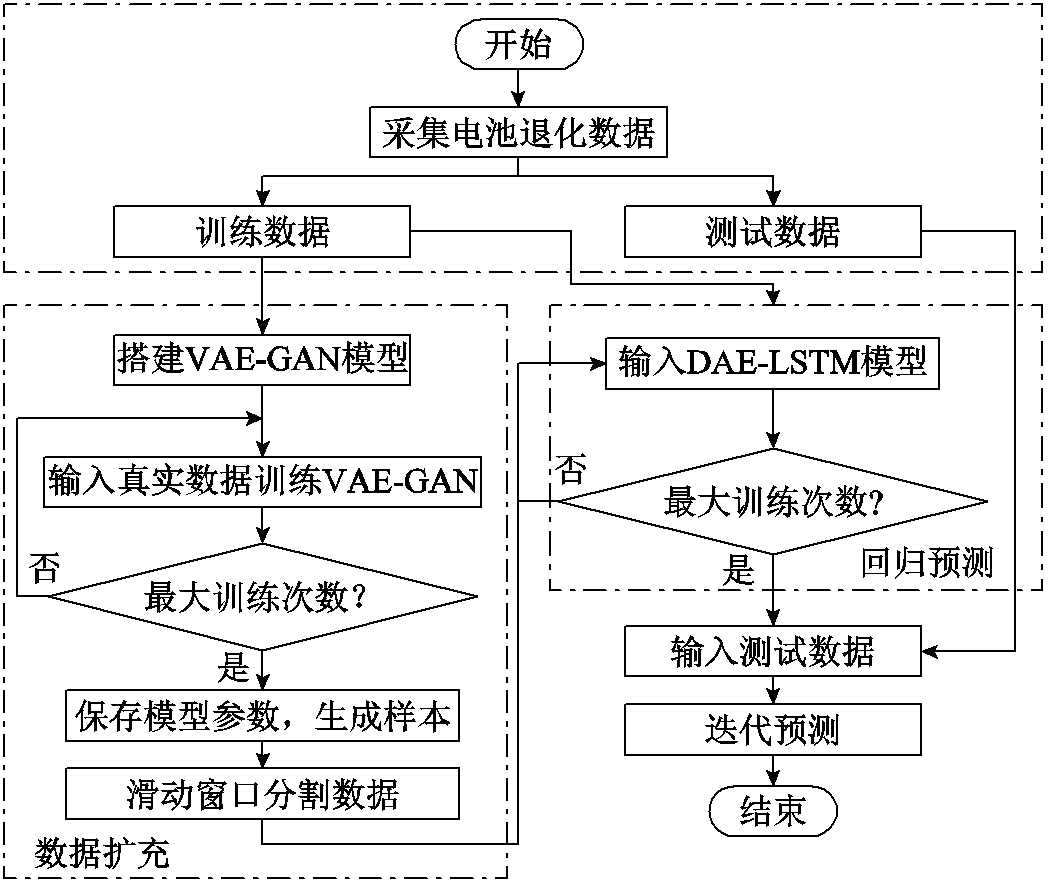
图7 电池RUL预测流程
Fig.7 Prediction flow chart of battery RUL
实际中尝试过多种迁移策略,包括:①只训练输出层,冻结其他网络层;②训练VAE部分和输出层,冻结LSTM网络层;③训练全部网络层。实验结果表示训练全部网络层的迁移方式最优,同时修改数据降噪和预测部分的网络权重,既能够使模型适应真实数据的噪声分布,又能学习真实数据的退化趋势,并且训练方式较为简单,不需要再进行额外的超参数优化,只需要降低迁移训练时的学习率即可。因此,本文将迁移学习率设置为1×10-5,迭代次数为1 500次。
本文的模型评价指标采用回归问题中常用的平均绝对误差(MAE)、方均根误差(RMSE),另外引入针对锂离子电池容量预测任务的RUL误差RE(relative error)和相对精度Pre,分别为
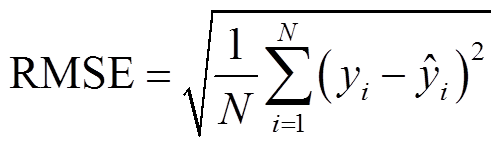 (11)
(11)
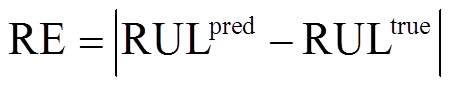 (12)
(12)
 (13)
(13)
式中,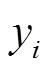 和
和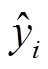 分别为第i次循环时锂离子电池的真实容量和预测容量;
分别为第i次循环时锂离子电池的真实容量和预测容量;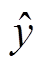 表示真实容量的平均值; RULpred和RULtrue分别为电池容量达到失效阈值时,剩余寿命的预测值和实际值。在进行容量预测任务时,Pre为主要的评价指标。
表示真实容量的平均值; RULpred和RULtrue分别为电池容量达到失效阈值时,剩余寿命的预测值和实际值。在进行容量预测任务时,Pre为主要的评价指标。
为了验证本文提出的基于迁移学习和DAE-LSTM方法(M3)的可靠性,从训练数据和网络结构上设计了两组对照试验。M1为未经迁移学习的LSTM方法;M2为未经迁移学习的DAE-LSTM方法。通过M1和M2验证DAE-LSTM模型的优越性;通过M2和M3验证数据增强的优越性。评价指标为MAE、RMSE、RE和Pre,其中RE和Pre作为主要的参考目标。
4.2.1 CALCE数据验证
首先在CALCE电池数据集上进行实验,每个测试电池设置两个不同的预测起点,分别为第364次和第464次循环。表5和表6为不同起点实验结果。
表5 CACLE数据集在364次循环的实验结果
Tab.5 Experimental results of CACLE batteries at 364 cycles
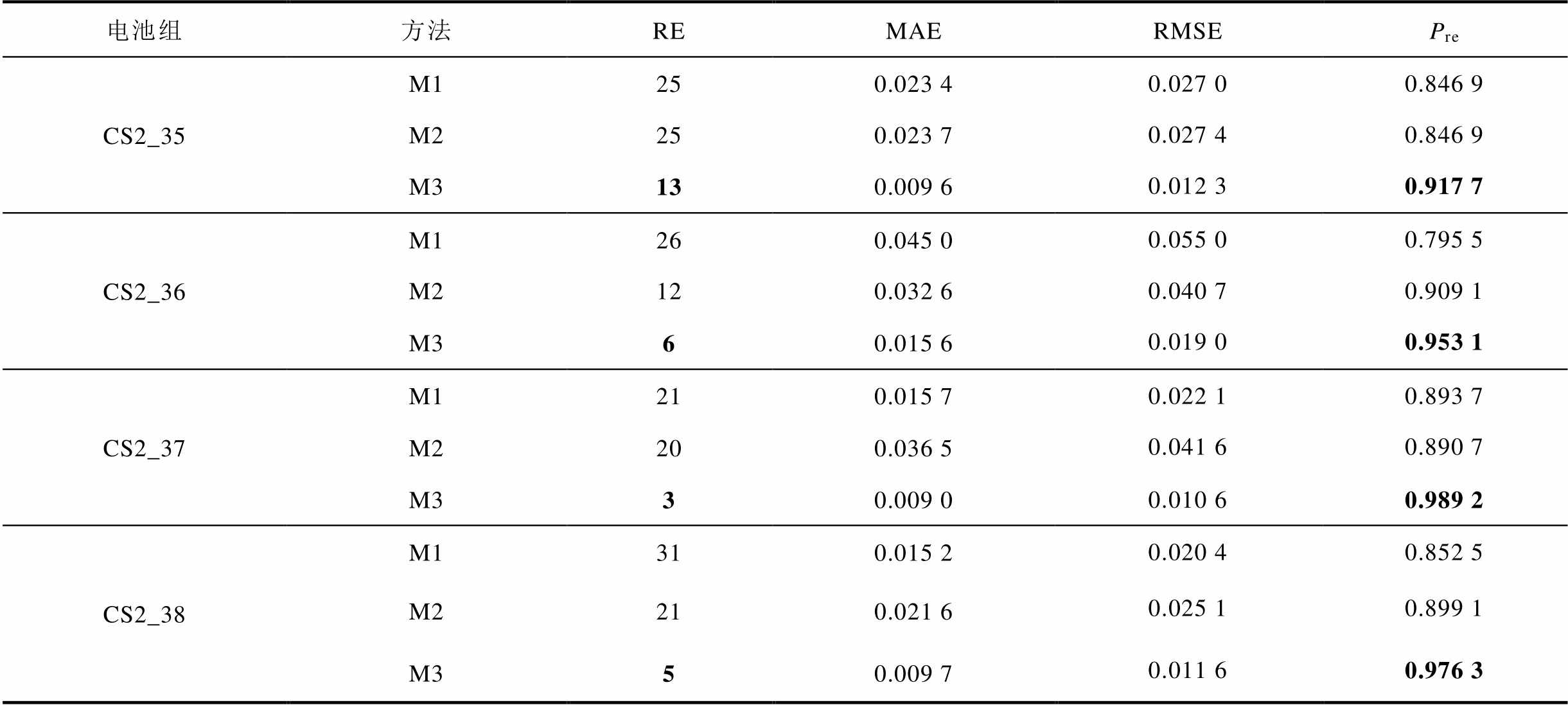
电池组方法REMAERMSEPre CS2_35M1250.023 40.027 00.846 9 M2250.023 70.027 40.846 9 M3130.009 60.012 30.917 7 CS2_36M1260.045 00.055 00.795 5 M2120.032 60.040 70.909 1 M360.015 60.019 00.953 1 CS2_37M1210.015 70.022 10.893 7 M2200.036 50.041 60.890 7 M330.009 00.010 60.989 2 CS2_38M1310.015 20.020 40.852 5 M2210.021 60.025 10.899 1 M350.009 70.011 60.976 3
观察评价指标可以看出,M3方法的所有评价指标在绝大部分任务中均为最优值,RE和Pre值表明其预测精度高;MAE和RMSE表明退化曲线拟合情况好。CS2_35号电池在364预测起点前有一个幅度较大容量波动状况,对预测结果产生较大影响,但是M3方法仍然取得了较好的预测效果。CS2_36号电池的退化曲线的单调性更强,不符合产品退化时中期退化慢、前期和后期退化快的特点,与其他数据相差较大,所以三种方法在464起点均有较大误差。图8~图11为三种方法在不同预测起点的迭代曲线。
表6 CACLE数据集在464次循环的实验结果
Tab.6 Experimental results of CACLE batteries at 464 cycles

电池组方法REMAERMSEPre CS2_35M1100.009 30.012 20.827 5 M2140.006 80.008 30.758 6 M360.009 50.012 60.896 6 CS2_36M1330.033 30.037 1— M2750.056 90.061 7— M3410.039 20.035 8— CS2_37M1130.012 30.01570.857 1 M230.009 80.011 50.967 0 M310.009 50.010 90.989 0 CS2_38M160.011 10.012 40.943 9 M210.013 40.015 70.990 6 M320.015 60.017 90.981 3
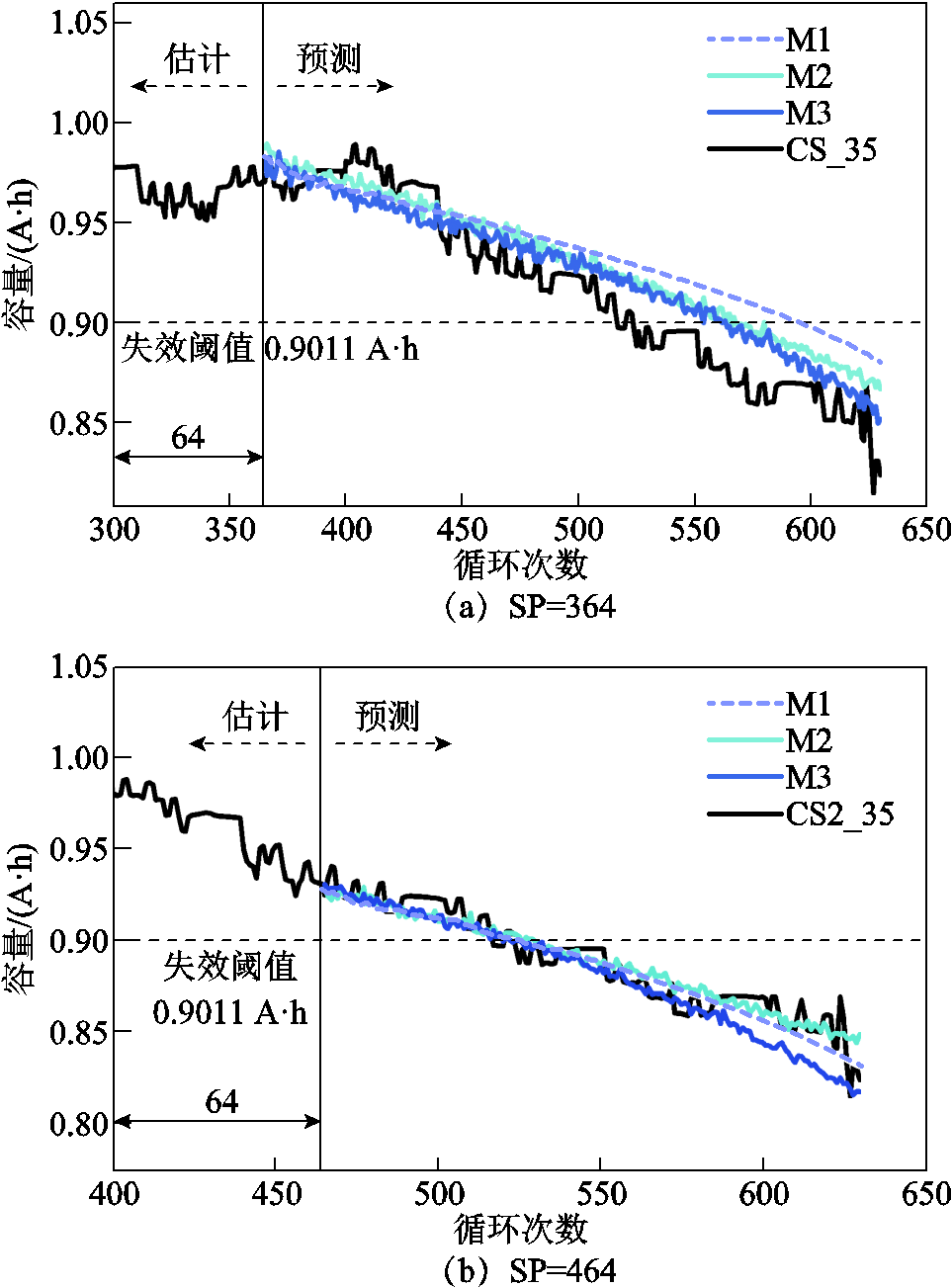
图8 CS2_35号电池RUL预测结果
Fig.8 RUL prediction results of CS2_35
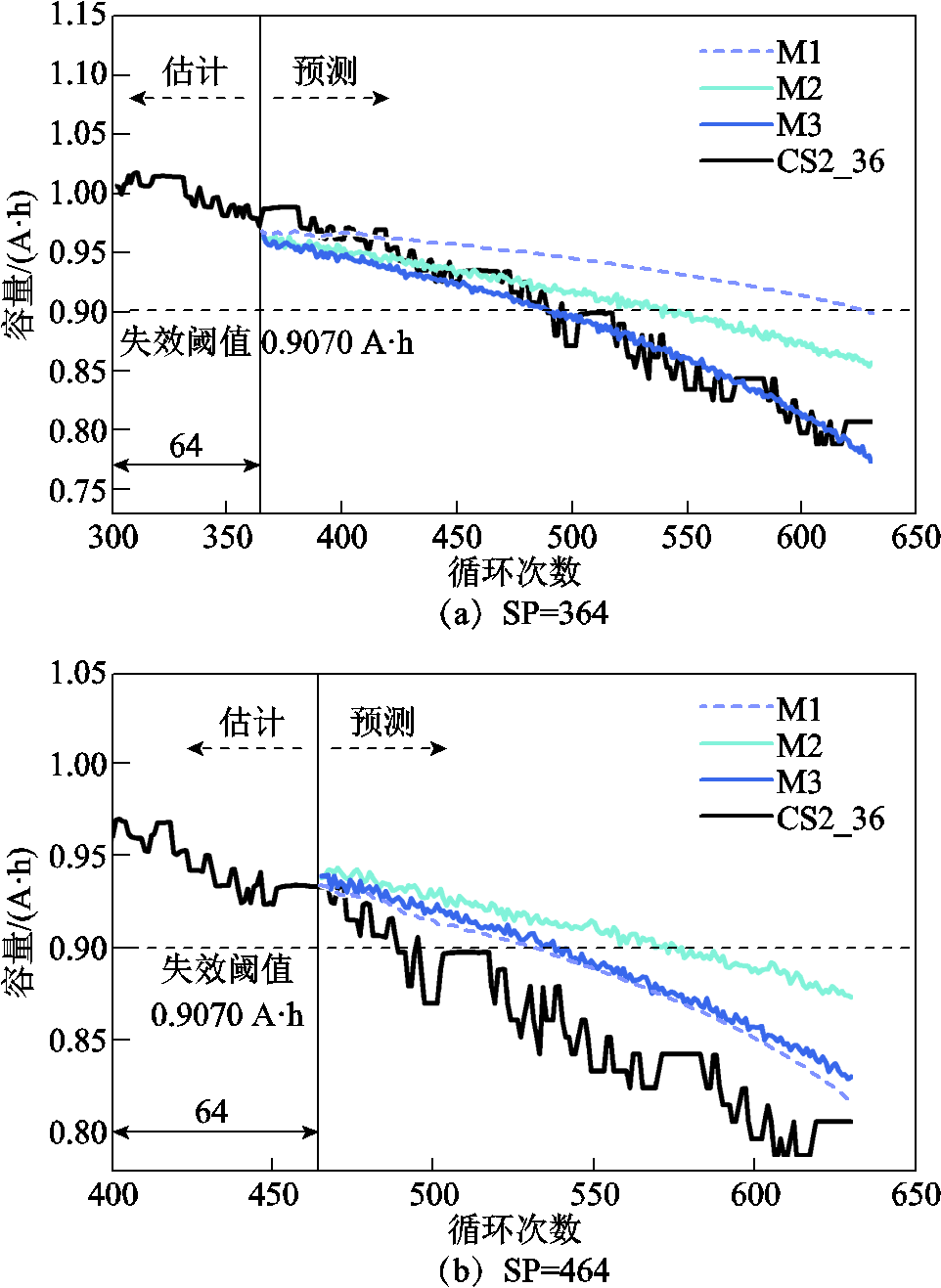
图9 CS2_36号电池RUL预测结果
Fig.9 RUL prediction results of CS2_36
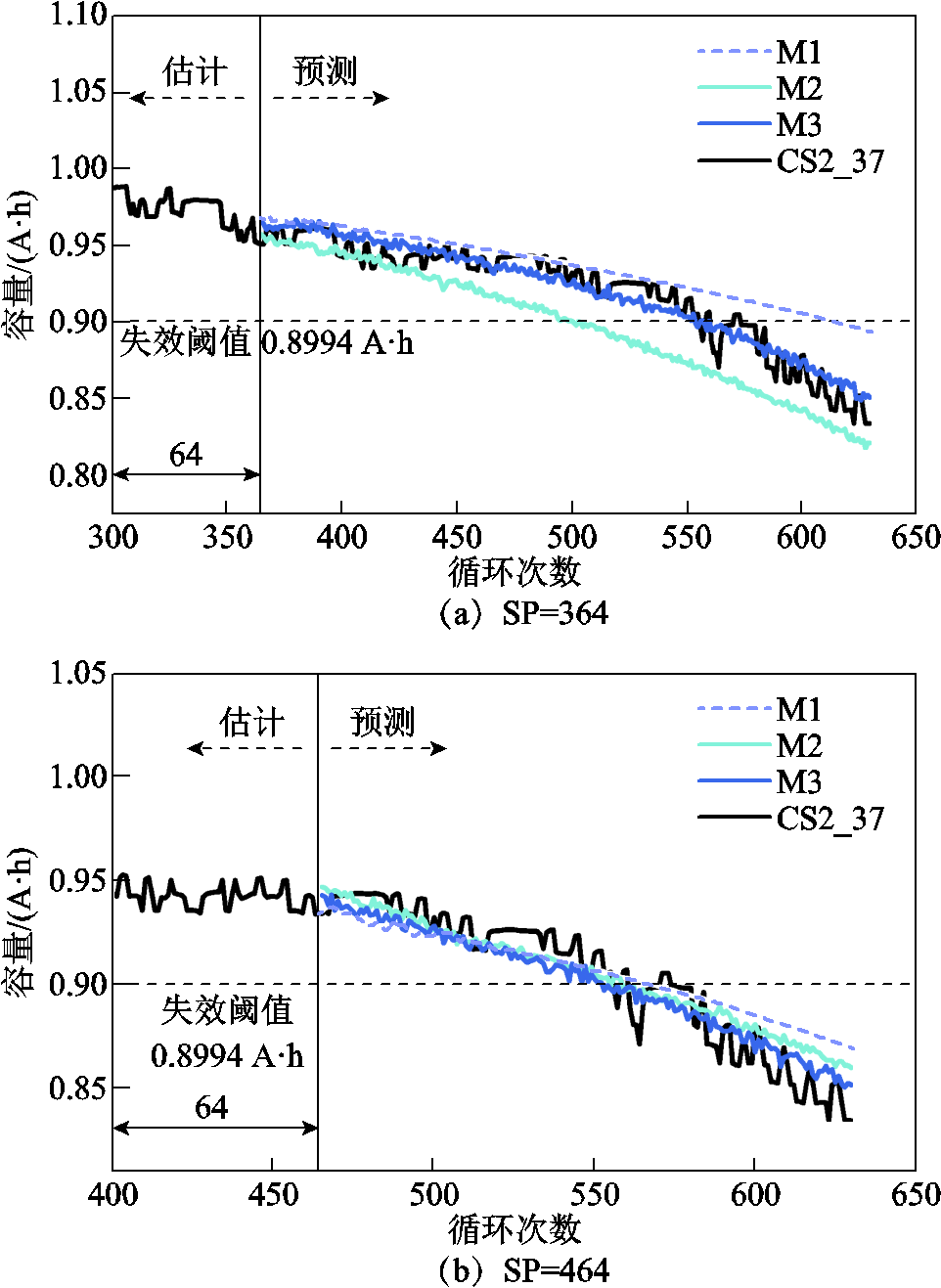
图10 CS2_37号电池RUL预测结果
Fig.10 RUL prediction results of CS2_37
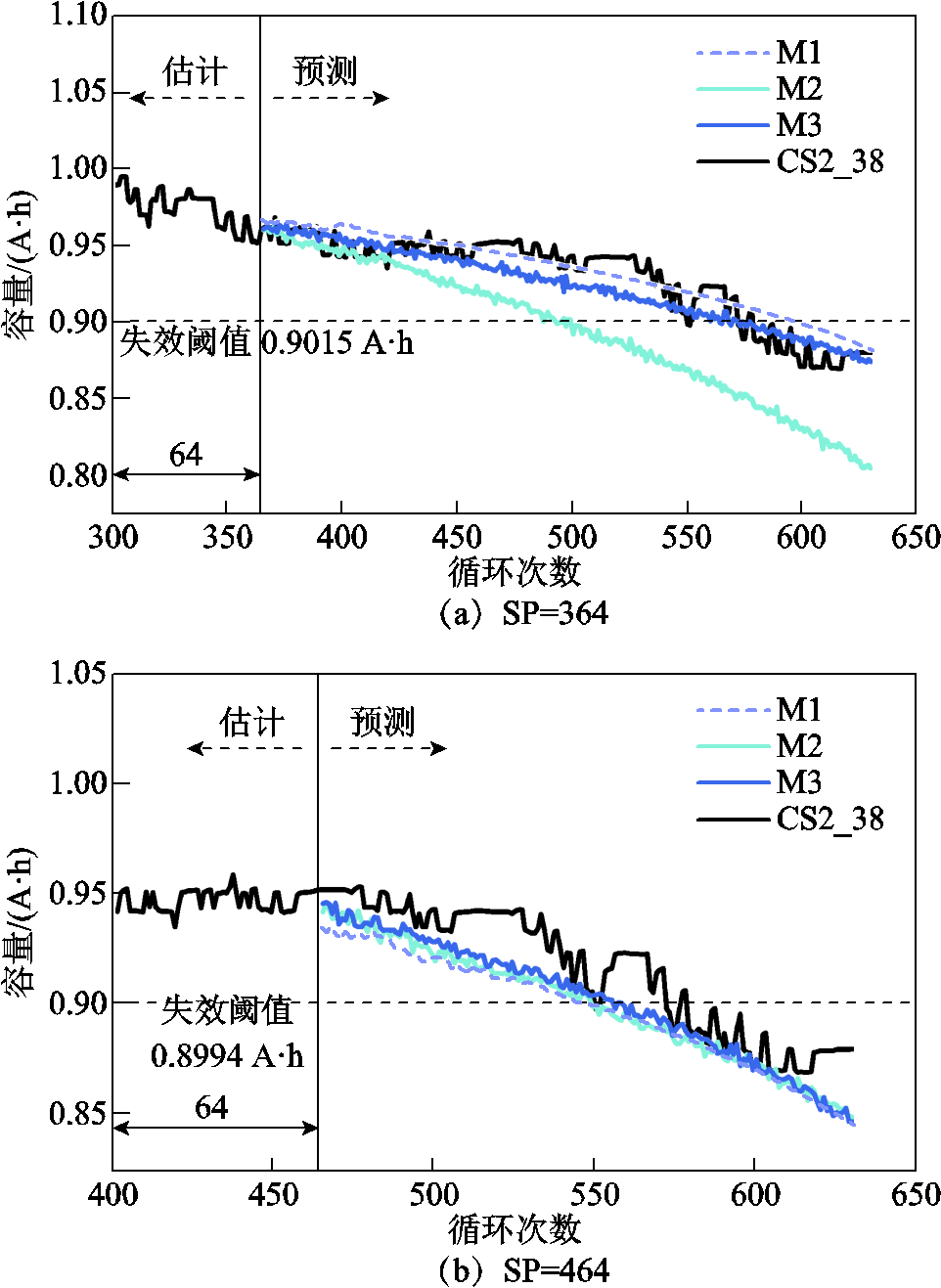
图11 CS2_38号电池RUL预测结果
Fig.11 RUL prediction results of CS2_38
观察容量退化曲线可以看出,M3方法可以准确地捕捉电池容量的退化趋势。不同预测起点的预测结果表明,起始预测位置越靠近失效阈值,其预测精度越高,表明模型对于寿命后期退化趋势明显的数据,具有更加敏锐的识别能力。M1和M2方法的实验结果表明,加入降噪部分的DAE-LSTM方法可以有效地减少噪声干扰,对退化数据进行准确的退化分析;M2和M3方法的实验结果表明,进行数据增强是有必要的,通过生成数据预训练模型能够有效地缓和模型的过拟合现象,并且对电池的整体退化趋势有更精准的把控。
CALCE的电池退化趋势都有较大的起伏,难以用简单的线性关系表示,这对模型的鲁棒性要求极高。因此从预测结果中可以看出,本文的预测方法具有较高的鲁棒性和预测精度。
4.2.2 NASA数据验证
为了全面展示M3方法的适应性,本文在数据量更少的NASA数据集上进行验证。数据增强实验见1.3节,由于NASA数据的波动情况较大且数据长度较小,所以Noise level设为0.008;Input size设为48;Batch size设为168,其他参数不变。预测起点设为60,评价指标选择MAE、RMSE、R2和Pre。为了提高说服力,增设100次运行结果的RUL概率密度函数和90%置信区间。图12为三种方法在NASA四块电池上的迭代曲线,表7为所有的实验结果。
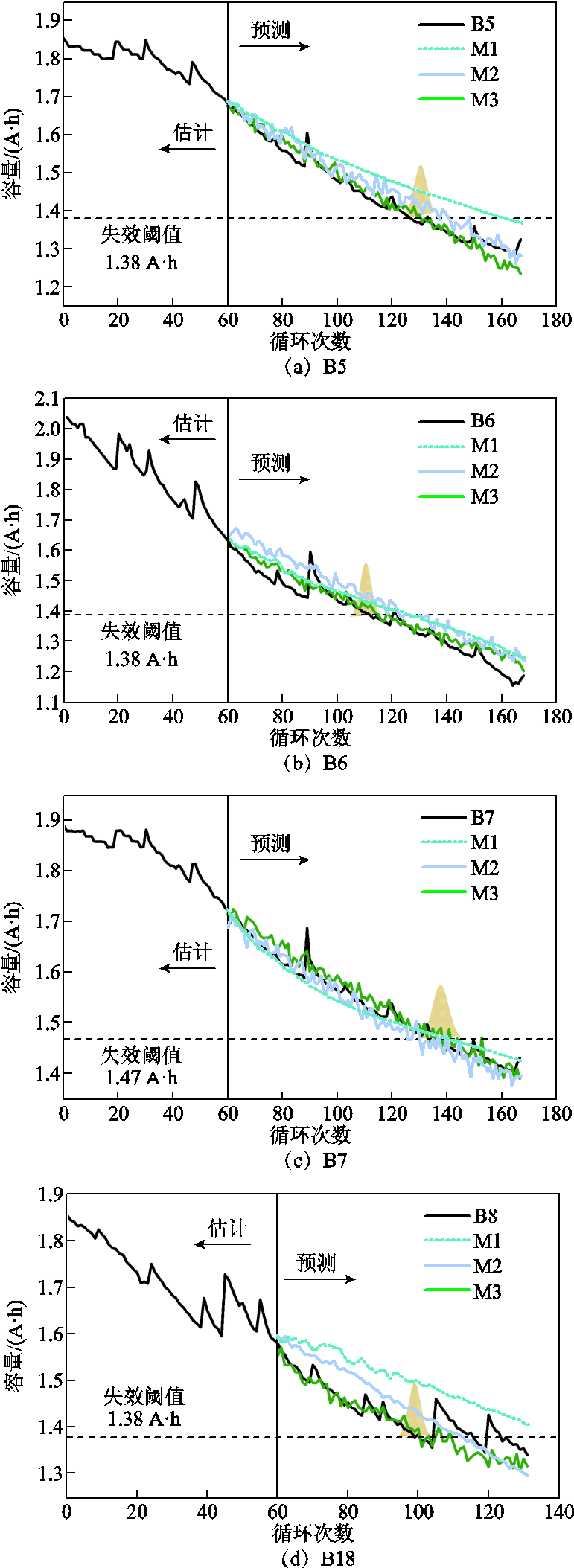
图12 NASA电池RUL预测结果
Fig.12 Prediction results for NASA batteries
表7 NASA数据集实验结果(起点为60)
Tab.7 Experimental results of NASA batteries(the starting point is 60)

电池M1M2M3 REMAERMSEPreREMAERMSEPreREMAERMSEPre B5350.059 40.684 10.437 590.028 70.034 10.887 520.022 40.028 60.970 5 B6170.049 00.053 60.734 4100.064 40.070 90.812 530.024 80.030 90.944 4 B790.014 70.020 10.892 960.016 90.021 70.928 620.016 80.020 20.976 2 B18330.075 00.080 60.352 9140.044 70.0490.725 530.024 60.037 60.960 8
观察评价指标和退化曲线可以看出,M3方法在NASA数据上同样具有优秀的预测精度和稳定性,其MAE、RMSE、R2和Pre四个评价指标均为对比方法中的最优值。表明本文所提方法具有良好的适应性,在不同的数据集上展现出较强的泛化能力。
另外,由于B18电池在预测起点前的波动严重,未加降噪的M1方法预测效果格外糟糕,但M3方法仍然可以精准地捕捉到电池的退化趋势,这表明DAE部分具有极强的抗干扰能力,展现出降噪和预测阶段同处一个框架的统一性和关联性。表8为所有NASA数据集100次RUL预测结果90%置信区间。
表8 NASA数据集的RUL90%置信区间(100次运行结果)
Tab.8 The 90% confidence interval (100 run results) of NASA batteries

电池置信区间 B5[133,139] B6[103,109] B7[107,113] B18[133,143]
通过两组数据的仿真结果和评价指标对比可概括规律如下:
1)本文提出的基于迁移学习的DAE-LSTM模型的预测精度明显高于其他对照方法,预测效果更加稳定,除了CACLE数据中CS2_36号电池的退化趋势较为异常,大部分电池的退化趋势都能被很好地捕捉,MAE和RMSE两个指标分别控制在2.46%和3.76%以内,最低为0.95%和1.06%。
2)通过观察不同预测起点的结果可以发现,预测位置越靠近失效阈值预测精度越高,表明模型对于寿命后期退化趋势明显的数据具有敏锐的识别能力。
3)更换不同的实验数据集,表明M3方法具有极强的适应能力和泛化能力,能够有效地完成小数据样本下的锂离子电池RUL预测任务,NASA预测任务中RUL90%置信区间范围较窄,表明模型具有较强的鲁棒性。
为了进一步验证本文方法的性能,在NASA数据集上与四种现有预测方法进行比较,分别为基于优化组合策略的无痕卡尔曼滤波的方法(Unscented Kalman Filter and Optimal Combination Strategy, UPF-OCS)[25]、基于自适应莱维飞行优化的粒子滤波及长短时记忆神经网络的方法(Adaptive Levy Flight optimized Particle Filter and Long Short-Term Memory network, ALF-PF-LSTM)[26]、基于无痕卡尔曼滤波和遗传算法优化支持向量回归的方法(Adaptive Unscented Kalman Filter and Genetic Algorithm optimized Support Vector Regression, AUKF-GASVR)[27]和基于容量增量分析和高斯回归过程的方法(Incremental Capacity Analysis and Gaussian Process Regression, ICA-GPR)[28]。预测起点设为60,评价指标选用RMSE和Pre。对比结果见表9,可以看出本文所提方法具有最小的Pre值,能够提供精度较高且稳定的预测效果。
表9 其他方法的预测结果比较
Tab.9 Comparison of prediction results of other methods
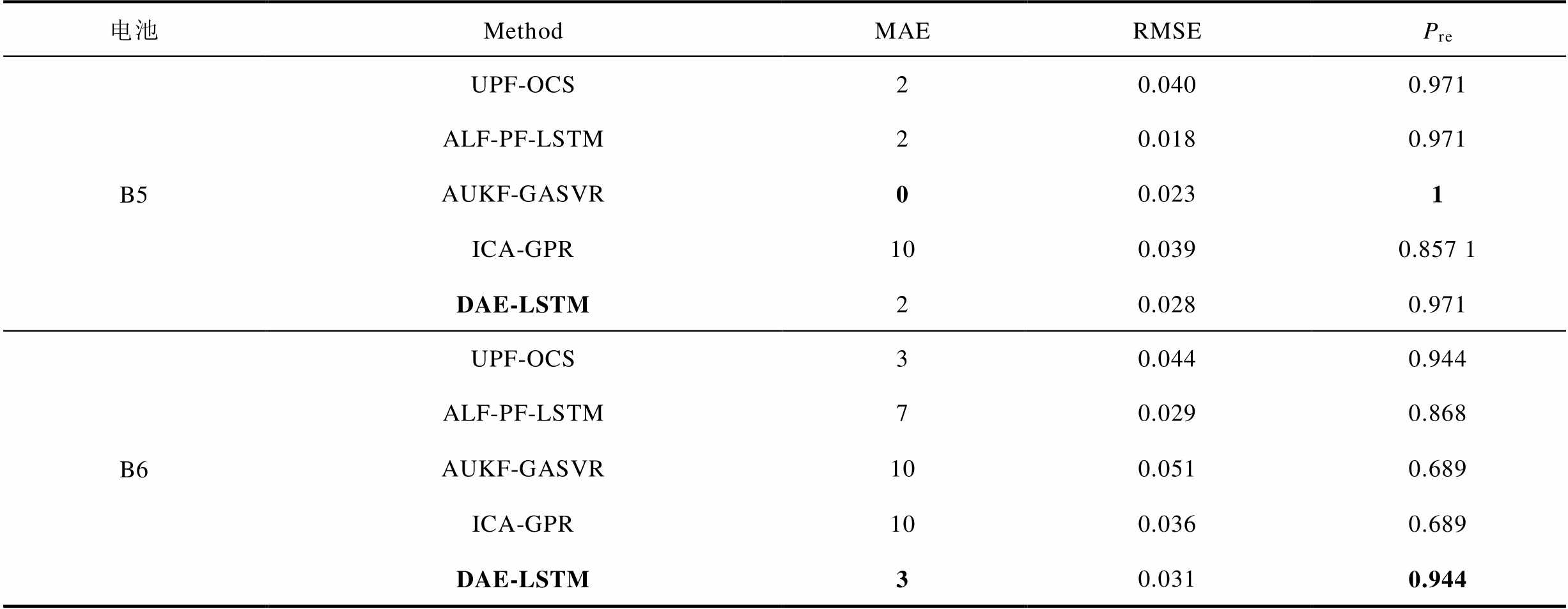
电池MethodMAERMSEPre B5UPF-OCS20.0400.971 ALF-PF-LSTM20.0180.971 AUKF-GASVR00.0231 ICA-GPR100.0390.857 1 DAE-LSTM20.0280.971 B6UPF-OCS30.0440.944 ALF-PF-LSTM70.0290.868 AUKF-GASVR100.0510.689 ICA-GPR100.0360.689 DAE-LSTM30.0310.944
(续)
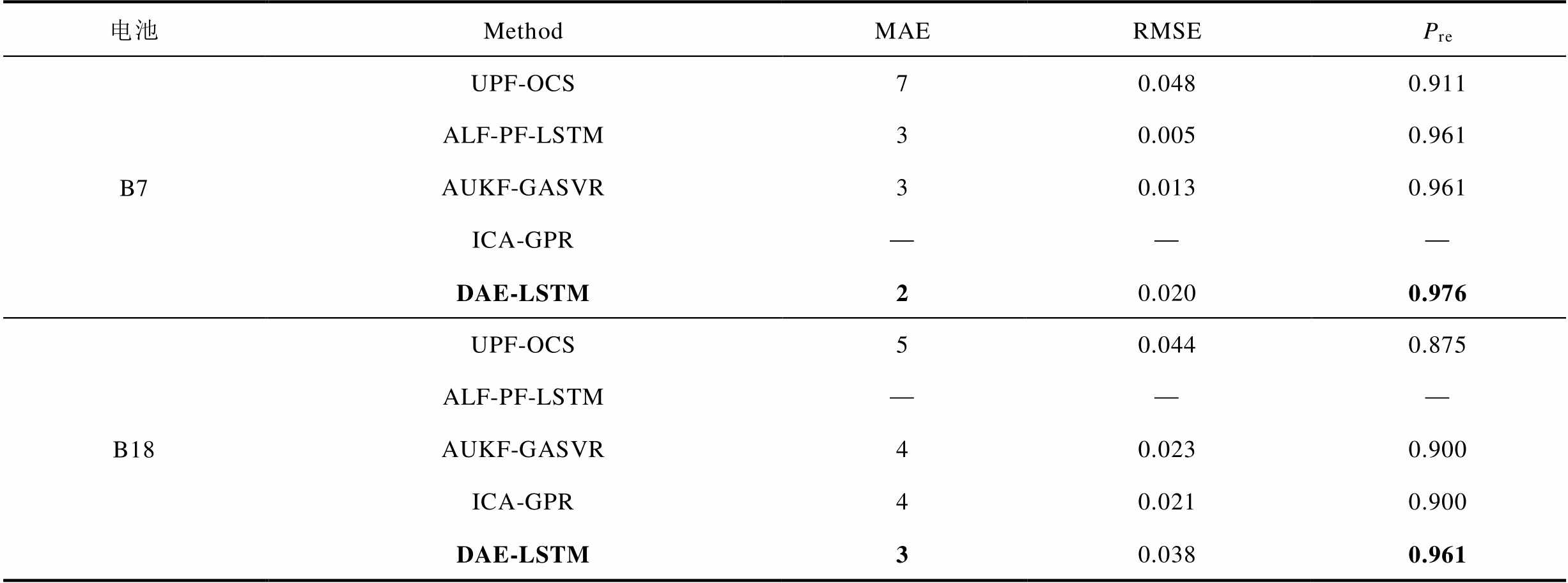
电池MethodMAERMSEPre B7UPF-OCS70.0480.911 ALF-PF-LSTM30.0050.961 AUKF-GASVR30.0130.961 ICA-GPR——— DAE-LSTM20.0200.976 B18UPF-OCS50.0440.875 ALF-PF-LSTM——— AUKF-GASVR40.0230.900 ICA-GPR40.0210.900 DAE-LSTM30.0380.961
此外,本文统计了不同数据集完成RUL预测的耗时情况,详见表10。以CACLE数据的364次循环为起点的预测任务总耗时190.64 s,以NASA数据的60次循环为起点的预测任务总耗时69.95 s。由于电池的剩余寿命预测是离线预测,实时性要求较低,模型的训练与测试时间符合离线预测要求。
表10 耗时情况统计
Tab.10 Time consumption of the method(单位:s)

数据集数据再生预训练迁移训练预测总耗时 CACLE22.08152.1315.460.97190.64 NASA15.6650.164.090.0469.95
本文针对锂离子电池退化数据噪声大、数据量少以及不同生命时期的退化趋势不同而导致的模型预测精度低、泛化能力差等问题,本文从数据预处理、预测模型的构建与训练三方面展开了研究:
1)结合变分自编码器(VAE)和生成对抗网络(GAN)构建VAE-GAN模型,少量电池全周期退化数据输入VAE-GAN网络模型中,利用编码层、生成网络以及判别网络映射出原始数据的分布状态并生成新的退化数据。在两组数据集上的所有生成数据与真实数据之间的平均相关度均高于0.92,说明生成数据质量较好。
2)利用降噪自编码器(DAE)和长短时记忆(LSTM)神经网络构建DAE-LSTM模型进行容量预测,数据降噪阶段和预测阶段共享同一个损失函数,使得降噪和预测过程得以同时优化。
3)通过多组模型的不同训练方法,确定出最优预测方案,即先利用VAE-GAN模型的生成数据对DAE-LSTM网络进行模型预训练,再利用真实数据迁移训练全部网络层。实验结果表明,在相同的预测条件下,基于迁移学习和DAE-LSTM方法总能取得最好的预测结果,预测RUL的90%置信区间较窄反映了本文方法具有强鲁棒性。
通过对比不同方法在不同起点的预测结果,并且横向对比现有文献的预测结果,证明本文提出的基于迁移学习的DAE-LSTM模型在保证鲁棒性的同时,能够有效地提高锂离子电池剩余寿命的预测效果,为锂离子电池的RUL预测提供参考。此外,本文所提模型的结构待继续优化,降低模型耗时,以满足实时性要求较高的任务需求。
参考文献
[1] 黄凯, 丁恒, 郭永芳, 等. 基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测[J]. 电工技术学报, 2022, 37(15): 3753-3766. Huang Kai, Ding Heng, Guo Yongfang, et al. Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3753-3766.
[2] 肖迁, 焦志鹏, 穆云飞, 等. 基于LightGBM的电动汽车行驶工况下电池剩余使用寿命预测[J]. 电工技术学报, 2021, 36(24): 5176-5185. Xiao Qian, Jiao Zhipeng, Mu Yunfei, et al. LightGBM based remaining useful life prediction of electric vehicle lithium-ion battery under driving conditions[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5176-5185.
[3] 徐佳宁, 倪裕隆, 朱春波. 基于改进支持向量回归的锂电池剩余寿命预测[J]. 电工技术学报, 2021, 36(17): 3693-3704. Xu Jianing, Ni Yulong, Zhu Chunbo. Remaining useful life prediction for lithium-ion batteries based on improved support vector regression[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3693-3704.
[4] 牛志远, 姜欣, 谢镔, 等. 电动汽车过充燃爆事故模拟及安全防护研究[J]. 电工技术学报, 2022, 37(1): 36-47, 57. Niu Zhiyuan, Jiang Xin, Xie Bin, et al. Study on simulation and safety protection of electric vehicle overcharge and explosion accident[J]. Transactions of China Electrotechnical Society, 2022, 37(1):36-47, 57.
[5] Ahmad Rahmoun,Helmuth Biechl. Modelling of li-ion batteries usingequivalent circuit diagrams[J]. Przeglad Elektrotechniczny, 2012, 88(7): 152-156.
[6] Quentin Badey, Guillaume Cherouvrier,Yvan Reynier, et al. Ageing forecast of li-ion batteries for electric and hybridvehicles[J]. Curr. Top. Electrochem, 2011, 16: 65-79.
[7] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207. Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.
[8] Shahid F, Zameer A, Muneeb M. A novel genetic LSTM model for wind power forecast[J]. Energy, 2021, 223: 120069.
[9] Zhang Yongzhi, Xiong Rui, He Hongwen, et al. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries[J]. IEEE Transactions on Vehicular Technology, 2018, 67(7): 5695-5705.
[10] Khumprom P, Yodo N. A data-driven predictive prognostic model for lithium-ion batteries based on a deep learning algorithm[J]. Energies, 2019, 12(4): 660.
[11] 李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J]. 电工技术学报, 2020, 35(19): 4106-4119. Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106-4119.
[12] Yu Yong, Hu Changhua, Si Xiaosheng, et al. Averaged Bi-LSTM networks for RUL prognostics with non-life-cycle labeled dataset[J]. Neurocomputing, 2020, 402: 134-147.
[13] Qiao Jianshu, Liu Xiaofeng, Chen Zehua. Prediction of the remaining useful life of lithium-ion batteries based on empirical mode decomposition and deep neural networks[J]. IEEE Access, 2020, 8: 42760-42767.
[14] Wang Zhuqing, Liu Ning, Guo Yangming. Adaptive sliding window LSTM NN based RUL prediction for lithium-ion batteries integrating LTSA feature reconstruction[J]. Neurocomputing, 2021, 466: 178-189.
[15] He Wei, Williard N, Osterman M, et al. Prognostics of lithium-ion batteries based on Dempster–Shafer theory and the Bayesian Monte Carlo method[J]. Journal of Power Sources, 2011, 196(23): 10314-10321.
[16] Wang Haiyang, Song Wanqing, Zio E, et al. Remaining useful life prediction for Lithium-ion batteries using fractional Brownian motion and Fruit-fly Optimization Algorithm[J]. Measurement, 2020, 161: 107904.
[17] Saha B, Goebel K. Battery Data Set, NASA Ames Prognostics Data Repository[OL]. NASA Ames Research Center, Moffett Field, CA. 2007. Available: http://ti.arc.nasa.gov/project/prognostic-data-repository.
[18] Dong Hancheng, Jin Xiaoning, Lou Yangbing, et al. Lithium-ion battery state of health monitoring and remaining useful life prediction based on support vector regression-particle filter[J]. Journal of Power Sources, 2014, 271: 114-123.
[19] Kingma D P, Welling M. Auto-encoding variational Bayes[C]//International Conference in Learning Representations, Banff, Canada, 2014, 10.48550/ arXiv.1312.6144.
[20] Goodfellow I J, Pouget-Abadie Jran, Mirza M, et al. Generative adversarial nets[C]// Neural Information Processing Systems, 2014: 2672-2680.
[21] 郑华林, 王超, 潘盛湖, 等. 基于EEMD和分层阈值的磁记忆信号降噪方法研究[J]. 工程设计学报, 2020, 27(4): 433-440. Zheng Hualin, Wang Chao, Pan Shenghu, et al. Research on noise reduction method of magnetic memory signal based on EEMD and layered threshold[J]. Chinese Journal of Engineering Design, 2020, 27(4): 433-440.
[22] Frangopol D M, Lin K Y, Estes A C. Life-cycle cost design of deteriorating structures[J]. Journal of Structural Engineering, 1997, 123(10): 1390-1401.
[23] Vincent P, Larochelle H, Bengio Y, et al. Extracting and composing robust features with denoising autoencoders[C]//Proceedings of the 25th international conference on Machine learning, Helsinki, Finland, 2008: 1096-1103.
[24] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780.
[25] Yang Jinsong, Fang Weiguang, Chen Jiayu, et al. A lithium-ion battery remaining useful life prediction method based on unscented particle filter and optimal combination strategy[J]. Journal of Energy Storage, 2022, 55: 105648.
[26] Zhang Yong, Chen L, Li Yi, et al. A hybrid approach for remaining useful life prediction of lithium-ion battery with adaptive levy flight optimized particle filter and long short-term memory network[J]. Journal of Energy Storage, 2021, 44: 103245.
[27] Xue Zhiwei, Zhang Yong, Cheng Cheng, et al. Remaining useful life prediction of lithium-ion batteries with adaptive unscented Kalman filter and optimized support vector regression[J]. Neurocomputing, 2020, 376: 95-102.
[28] Pang Xiaoqiong, Liu Xiaoyan, Jia Jianfang, et al. A lithium-ion battery remaining useful life prediction method based on the incremental capacity analysis and Gaussian process regression[J]. Microelectronics Reliability, 2021, 127: 114405.
Abstract Degradation data of battery capacity can be used to predict the battery remaining using life(RUL), but there exist numerous noise data in the battery degradation process caused by factors such as ambient temperature, charge/discharge process and capacity recovery phenomenon. It makes prediction of data-driven life lithium-ion battery challenging. To improve the prediction accuracy and generalization ability of batteries RUL, we proposed a method based on transfer learning and denoising autoencoder-long short term memory (DAE-LSTM).
Firstly, the variational autoencoder - generative adversarial network (VAE-GAN) method was constructed designed. Encoding network was used to estimate the distribution of input data, and generating network and discriminant network were used for data regeneration. It improved the reliability of generated data by VAE method, and solved the problem that GAN method had been difficult to train. Secondly, the DAE-LSTM method was constructed for data denoising and capacity prediction. The DAE can reconstruct the input data and its encoder improved the robustness of the method by adding Gaussian noise. LSTM layer can analyze the temporal characteristics of data for capacity prediction. Due to the small amount of data, the network layer of the overall method was less to avoid overfitting. To reduce the parameters, the same loss function was used in both data denoising and capacity prediction. Finally, the optimal training scheme was determined through the different experiment: The data generated by VAE-GAN was used for method pre-training, then all network layers of the basic method were fine-tuned by actual data. This would effectively improve the prediction accuracy of the method, and ensure the reliability of the prediction results.
Experimental results showed that the proposed method has better predictive performance, and degradation trend of most batteries can be well predicted. MAE and RMSE were controlled within 2.46% and 3.76% respectively, and the lowest was 0.95% and 1.06%. Experimental results with different prediction starting points showed that the prediction were more accurate when the prediction starting point was closer to the failure threshold. This indicates that the method can accurately predict the degradation trend in later stages of battery life. Experimental results with other datasets showed that the proposed method has strong adaptability and generalization ability. It can effectively predict the lithium-ion battery RUL in small data samples. The 90% confidence interval of the prediction results with NASA dataset is narrow, indicating that the method has strong robustness. In addition, we counted the time taken to complete the RUL prediction for different datasets. As the RUL prediction of batteries is offline prediction with low real-time requirement, the training and testing time of the method meets the offline prediction requirement.
The following conclusions can be drawn from the simulation results: (1) The DAE-LSTM method can effectively denoising the degradation data of lithium-ion batteries, and making the prediction result more accurate. (2) VAE-GAN method can generate multiple groups of degradation data conforming to the real degradation to achieve the purpose of data enhancement. (3) Transfer Learning can ensure that the effective information of generated data and real data is fully utilized, so that the prediction model has higher accuracy and better generalization ability. By comparing the prediction results of other literatures, it is proved the proposed method has higher Pre and can be used to predict the RUL of lithium-ion batteries.
keywords:Li-ion battery, remaining useful life, denoising autoencoder, long short term memory, transfer learning
DOI: 10.19595/j.cnki.1000-6753.tces.221890
中图分类号:TM912; TP206+.3
收稿日期 2022-10-05
改稿日期 2023-01-09
尹 杰 男,1999年生,硕士研究生,研究方向为复杂系统可靠性与机器学习。E-mail:yin_jie1212@163.com
刘 博 男,1979年生,副教授,硕士生导师,研究方向为复杂系统可靠性与机器学习。E-mail:liubo1900@hrbust.edu.cn(通信作者)
(编辑 郭丽军)